- Health Impacts and Exposure Science, Pacific Northwest National Laboratory, Richland, WA, USA
Quantitative exposure data is important for evaluating toxicity risk and biomonitoring is a critical tool for evaluating human exposure. Direct personal monitoring provides the most accurate estimation of a subject’s true dose, and non-invasive methods are advocated for quantifying exposure to xenobiotics. In this regard, there is a need to identify chemicals that are cleared in saliva at concentrations that can be quantified to support the implementation of this approach. This manuscript reviews the computational modeling approaches that are coupled to in vivo and in vitro experiments to predict salivary uptake and clearance of xenobiotics and provides additional insight on species-dependent differences in partitioning that are of key importance for extrapolation. The primary mechanism by which xenobiotics leave the blood and enter saliva involves paracellular transport, passive transcellular diffusion, or transcellular active transport with the majority of xenobiotics transferred by passive diffusion. The transcellular or paracellular diffusion of unbound chemicals in plasma to saliva has been computationally modeled using compartmental and physiologically based approaches. Of key importance for determining the plasma:saliva partitioning was the utilization of the Schmitt algorithm that calculates partitioning based upon the tissue composition, pH, chemical pKa, and plasma protein-binding. Sensitivity analysis identified that both protein-binding and pKa (for weak acids and bases) have significant impact on determining partitioning and species dependent differences based upon physiological variance. Future strategies are focused on an in vitro salivary acinar cell based system to experimentally determine and computationally predict salivary gland uptake and clearance for xenobiotics. It is envisioned that a combination of salivary biomonitoring and computational modeling will enable the non-invasive measurement of chemical exposures in human populations.
Introduction
The National Research Council of the National Academies report, Toxicity Testing in the 21st Century: A Vision and Strategy, highlighted the importance of quantitative exposure data for evaluating human toxicity risk (Hubal, 2009). The report supports the use of chemical exposure data to provide critical information on the magnitude, timing, and duration of a biologically relevant dose delivered to target tissues (Sheldon and Cohen Hubal, 2009; Cohen Hubal et al., 2010). Direct measurement of chemical exposures using personal monitoring provides the most accurate estimation of a subject’s true exposure (Nieuwenhuijsen et al., 2006). In this context, biomonitoring is a critical tool for quantitatively evaluating exposure from both environmental and occupational settings to a wide range of pollutants, including pesticides (Borzelleca and Skalsky, 1980; Nigg and Wade, 1992; Friberg and Elinder, 1993; Christensen, 1995; Angerer et al., 2006, 2007; Barr et al., 2006). Non-invasive methods have also been advocated for quantifying the pharmacokinetics and bioavailability of drugs and xenobiotics, and the use of saliva has been suggested as an ideal body fluid that can be substituted for blood in biomonitoring (Pichini et al., 1996; Timchalk et al., 2004; Timchalk et al., 2007b). In this regard, a broad range of drugs, organic chemicals, metals, and pesticides are readily secreted in saliva (Borzelleca and Skalsky, 1980; Drobitch and Svensson, 1992; Nigg and Wade, 1992; Lu et al., 1997, 1998; Silva et al., 2005). For many of these xenobiotics, saliva concentration readily correlates with blood concentration; hence, it is feasible to utilize pharmacokinetic models to accurately estimate systemic dose based upon a saliva measurement.
The mechanism of acinar cell activation, electrolyte transport and saliva formation illustrated in Figure 1 is derived from an extensive literature that has characterized these processes in detail (Nauntofte, 1992). Salivary glands are comprised of a number of major (parotid, submandibular, and sublingual) and minor glands that primarily consist of acinar cells that collectively produce saliva (for review, see Hold et al., 1995b). Salivary glands are highly perfused and blood flow is in a countercurrent direction to salivary flow (Figure 1B; Davenport, 1977). The primary mechanism by which xenobiotics leave the blood and enter saliva is thought to involve paracellular transport, passive transcellular diffusion, or transcellular active transport (Figure 1A; Landon and Mahmod, 1982). Paracellular transport (i.e., ultrafiltration) favors small (MW ∼300 Da) polar lipid insoluble molecules that generally have a low (i.e., <1.0) saliva/plasma (S/P) ratio. Whereas, transcellular diffusion or active transport are favored by lipid soluble materials that can readily cross cell membranes (Hold et al., 1995a). The majority of drugs and xenobiotics are cleared from plasma into saliva by a passive diffusion process that is a function of concentration gradient, surface area, membrane thickness, and diffusion constants (Hold et al., 1995b). This focused review will describe how the modeling of this passive diffusion process in both rats and humans was accomplished utilizing a pharmacokinetic model that were initially developed for the organophosphorus insecticide chlorpyrifos (CPF) and its major metabolite trichloropyridinol (TCPy; Smith et al., 2010, 2012).
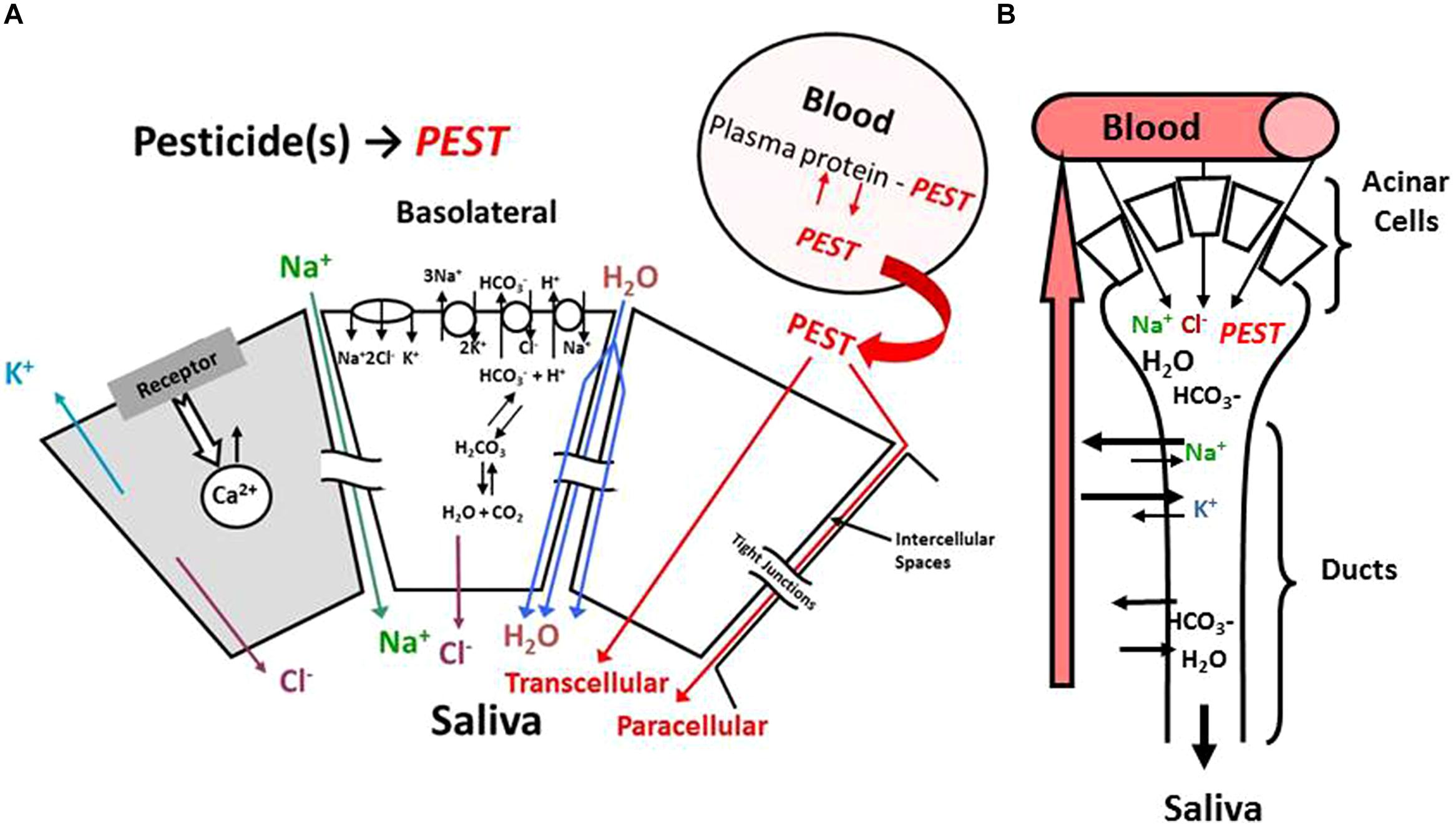
FIGURE 1. Schematic model illustrating (A) acinar cell and (B) salivary duct function associated with saliva formation. PEST is used as a general notation for pesticides.
It is well recognized that biomonitoring offers one of the best strategies for quantifying human dosimetry and assessing risk associated with both occupational and environmental chemical exposures (Friberg and Elinder, 1993; Christensen, 1995). As noted above, saliva has been suggested as an ideal non-invasive body fluid, yet there are a number of limitations which have hampered saliva’s use in biomonitoring. First, to utilize saliva for biomonitoring the relationship between blood and saliva concentrations for target biomonitoring, analytes needs to be well established (Timchalk et al., 2004). Second, to more broadly exploit saliva as a matrix it is critical to a priori identify which chemicals are readily cleared in saliva at levels that can be quantified analytically. The current manuscript reviews the initial saliva model development focused on in vivo uptake and clearance studies in the rat as well as computational prediction in humans (Smith et al., 2010, 2012). In addition, a partitioning coefficient algorithm that readily accommodates species-dependent differences in plasma protein-binding and pH is presented. This is of particular importance since changes in binding and/or pH appear to have a significant impact on plasma:saliva partitioning thereby contributing to variable saliva analyte concentrations. Finally, a brief perspective on the utility of cell based in vitro assay systems and computational modeling are presented as a potential strategy for broad based screening of chemicals for their salivary clearance potential (Weber et al., 2015).
Computational Methods
Pharmacokinetic Modeling Strategy
The overarching computational modeling approach utilizes a physiologically based pharmacokinetic (PBPK) model as illustrated in Figure 2. Within this PBPK model both the CPF and TCPy blood to saliva pharmacokinetics in the rat was handled as a simple one-compartment pharmacokinetic model as previously described (Smith et al., 2012). The model was further modified to enable the prediction of CPF and TCPy concentrations in human saliva after simulated exposures, by accommodating differential partitioning based upon species dependent differences in pH (see below for details). In this model, CPF and it neurotoxic metabolite chlorpyrifos-oxon (CPF-oxon) were distributed among internal compartments mediated by blood circulation described as a flow-limited process. The fraction of CPF or TCPy that was not bound to plasma-protein is described simply as a fraction bound, where FBCPF or FBTCPy are the fractions of CPF or TCPy bound to plasma-proteins, CCPFb and CTCPyb are the concentration of CPF or TCPy bound to plasma proteins, and CCPFbl and CTCPybl are the total concentration of CPF or TCPy in blood, respectively (Eqs 1 and 2). The free CPF and TCPy concentrations (i.e., CCPFf and CTCPyf) are available to partition to various tissue compartments based upon their tissue specific partition coefficients (Timchalk et al., 2002). Fractional plasma protein-binding of CPF and TCPy were measured previously and both determined to be ∼98–99% bound (Lowe et al., 2009; Smith et al., 2010). As CPF-oxon undergoes rapid hydrolysis in the presence of albumin, it was assumed that CPF and CPF-oxon have equivalent fraction binding in plasma. Human metabolic parameters, including CPF dearylation, CPF desulfuration, and CPF-oxon hydrolysis, were updated (Smith et al., 2011). Other human parameters were also updated from a variety of literature sources, including cholinesterase activities, enzyme aging, degradation, reactivation, and turnover rates (Sidell and Kaminskis, 1975; Hojring and Svensmark, 1976; Maxwell et al., 1987; Mortensen et al., 1998; Li et al., 2005; Albers et al., 2010; Smith et al., 2011). To accommodate the effects of isoflurane anesthesia (required during in vivo experiments) on rat physiology, the cardiac output was reduced 15% from standard values based upon observed in vivo effects [15 × body weight (kg)0.75; Conzen et al., 1992; Vollmar et al., 1992; Brown et al., 1997].
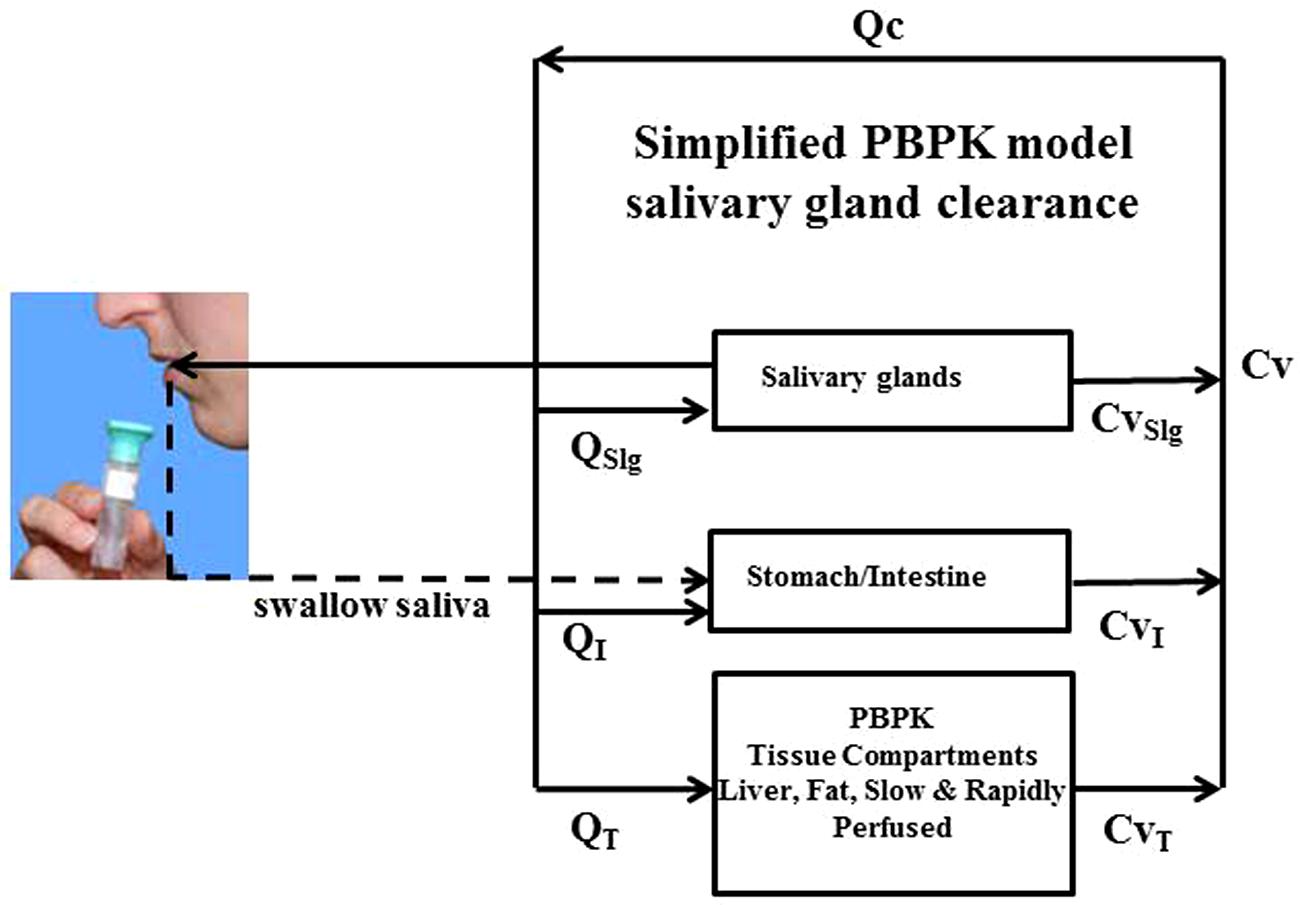
FIGURE 2. Schematic model illustrating physiologically based pharmacokinetic (PBPK) model structure for simulating in vivo salivary gland clearance of pesticides.
Saliva Partitioning
In the current PBPK model structure, transport of CPF or TCPy from blood to saliva is modeled as a passive diffusion process based upon their respective partitioning. Briefly, for both analytes the saliva concentration (Csal) was defined as their blood concentration (Cbl) multiplied by the saliva/blood partitioning coefficient (Psal/bl) [Eq. 3], which was determined experimentally (in rats) using the mean saliva/blood concentration ratio.
However, due to experimentally observed saliva pH changes in rats (8.5–9.5; Smith et al., 2010), and the reported variability in saliva pH between humans (6.2–7.4), species differences may exist for ionizable compounds with pKa/pKb values near physiologically relevant pH ranges. Thus in the absence of human-specific experimental data, algorithms can be useful for estimating partitioning and/or extrapolating partitioning measured in animal models. Numerous partitioning algorithms exist (Poulin and Krishnan, 1995; Rodgers et al., 2005; Schmitt, 2008; Peyret et al., 2010). Here, the Schmitt algorithm was utilized, because it is the only algorithm that has been previously validated for predicting salivary partitioning measured in rats (Schmitt, 2008; Smith et al., 2010). The approach calculates partition coefficients based upon the tissue composition in terms of water, lipid and phospholipid contents, proteins, pH differences using chemical compound-specific lipophilicity, pKa, as well as plasma protein-binding. As noted in Smith et al. (2010), this algorithm assumes that ionized compounds are capable of traversing membranes, although at a much lower rate (∼3-orders of magnitude) than non-ionized forms and estimates the difference in rates based upon the ratio of distribution coefficients for the ionized and unionized forms (Schmitt, 2008).
The Schmitt algorithm was adapted for use in saliva (Schmitt, 2008; Smith et al., 2010). This original approach did not consider salivary partitioning, thus “tissue-specific” parameters were used to make these predictions with saliva (Table 1). Otherwise the Schmitt algorithm was used as described (Schmitt, 2008). Briefly, for each of the model compartments, the unbound fraction (fu; Eq. 4) is the ratio of analyte unbound concentration (Cu) over total concentration (Ctotal). Generally, it is thought that neutral compounds cross biological membranes much more easily than charged compounds. Thus pH gradients that exist across membranes can have a profound influence on the ability of ionizable compounds to cross that barrier, where the ratio of ionized to neutral compounds can vary by pH and the pKa of the compound. For example, a week acid can accumulate of the side of the barrier that has the higher pH, since the ionized form cannot cross the membrane as easily as the uncharged compound. The equilibrium salivary gland:blood (Psal:bl) partitioning coefficient is based upon the relationships expressed in Eq. 5; where Ct, Cp, Cint, and Ccell are the total concentrations in saliva tissue, plasma, interstitial, and cellular spaces, respectively. The volume fractions of interstitial and cellular space are Fint and Fcell while the unbound fractions in interstitial, cellular and plasma are fuint,fucell, and fup, respectively. The unbound fraction in the interstitial space is estimated relative to the unbound fraction in plasma, based on the fact that the interstitial fluid is quite similar to plasma but with lower concentrations of proteins and lipids (Schmitt, 2008); whereas the unbound fraction in the cellular space is determined by chemical affinity for cellular macromolecules such as protein and lipids (both neutral and charged phospholipids). Finally, the tissue pH gradients are critical since they will influence the unbound concentrations for weak acids and bases which are charged under physiological conditions. This is of particular importance when considering salivary gland clearance where saliva formation results in acinar cell acidification (see Figure 1) as a result of carbonic anhydrase conversion of CO2 and H2O to HCO3- and H+ (Nauntofte, 1992).
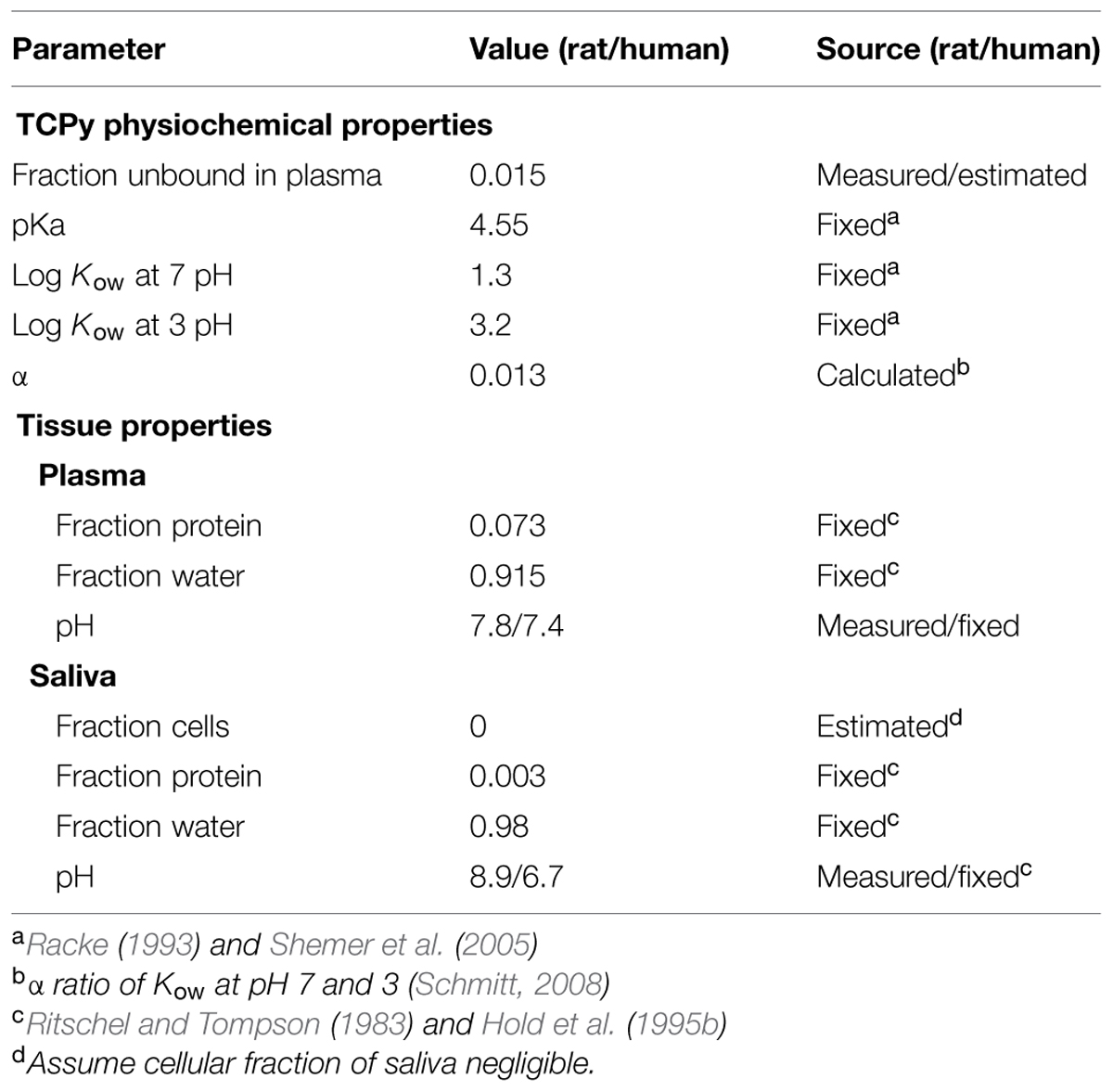
TABLE 1. Input parameters for a modified algorithm for calculating the saliva:blood trichloropyridinol (TCPy) partitioning coefficient (based upon Schmitt, 2008).
Parameter inputs (Table 1) for this algorithm include: physical/chemical properties of CPF and TCPy, physiological properties of rat and human plasma and mixed saliva; additional assumptions included pH dependent partitioning to the interstitial space fraction and negligible cellular fraction of saliva (Ritschel and Tompson, 1983; Racke, 1993; Hold et al., 1995b; Shemer et al., 2005).
Salivary Flow Rate
To experimentally obtain adequate saliva from rats, animals were administered a cholinergic agonist, pilocarpine to induce significant salivation (Timchalk et al., 2006; Smith et al., 2010). To facilitate a more accurate model simulation of this physiological response, the salivary flow rate (Qsal) was defined as a non-linear dynamic equation where A, B, and C are constants used to fit salivary flow rate data (Smith et al., 2010) from rats infused (3 ml/h) with pilocarpine (1 mg/ml; Eq. 6).
The CPF or TCPy elimination rates in saliva were defined as their respective concentrations in saliva (Csal) multiplied by the saliva flow rate (Eq. 7). However, PBPK model simulations of humans did not accommodate differences in saliva flow rates.
Sensitivity Analysis
To provide additional insight into the relative importance of model parameters, as part of this review, a local sensitivity analysis was conducted to identify the most important parameters for estimating the plasma:saliva partitioning coefficient for a generic compound with 50% plasma-protein binding, pKa = 7.0, log Kow (non-ionized) = 2 and log Kow (ionized) = -1. The analysis focused on the impact of changes in these parameters on the partitioning coefficient at steady-state. The normalized sensitivity coefficients were calculated for a 1% change in a given model parameter when all other parameters were held fixed. Sensitivity analysis was performed using the forward difference method coded in acslX version 3.0.2.1 (AEgis Technologies, Inc., Huntsville, AL, USA).
Saliva Model Development Review
Initial in vivo studies in rats focused on the comparison of blood and saliva TCPy concentration time-course following intravenous (IV) administration of the CPF over a broad dose range (0.5–5 mg/kg). These in vivo experiments focused on exposing rats to CPF by IV administration and quantifying the time-course of CPF and TCPy in both blood and saliva over a range of CPF doses. Previous studies have characterized route-dependent pharmacokinetic differences in rats, and IV administration was chosen for these studies to minimize first-pass hepatic metabolism thereby maximizing the concentration of CPF in blood available for salivary clearance (Busby-Hjerpe et al., 2010). These previous studies demonstrated that the blood:saliva ratios were not impacted by a range of factors including: CPF or TCPy dose, pilocarpine dose, or the timing of saliva collection (Smith et al., 2010, 2012). In Figures 3A–C where the time-course of CPF (blood) and it major metabolite TCPy (blood and saliva) are illustrated following a 5 mg/kg IV dose. These results are very consistent with previous observations that CPF undergoes rapid metabolism to TCPy (Poet et al., 2003; Timchalk et al., 2007a; Busby-Hjerpe et al., 2010), although CPF was detectable in three saliva samples (data not shown). Results (Figure 3D) were also consistent with previous TCPy dosing experiments where the ratio of TCPy in saliva/blood (ratios ∼0.04–0.06) demonstrated AUC linearity consistent with parallel pharmacokinetics of TCPy in blood and saliva. These initial in vivo studies in rats clearly demonstrate that saliva analyte concentrations are highly proportional to blood concentrations and PBPK model simulations accurately predict saliva/blood concentrations over a range of doses, consistent with a diffusion based transport mechanism.
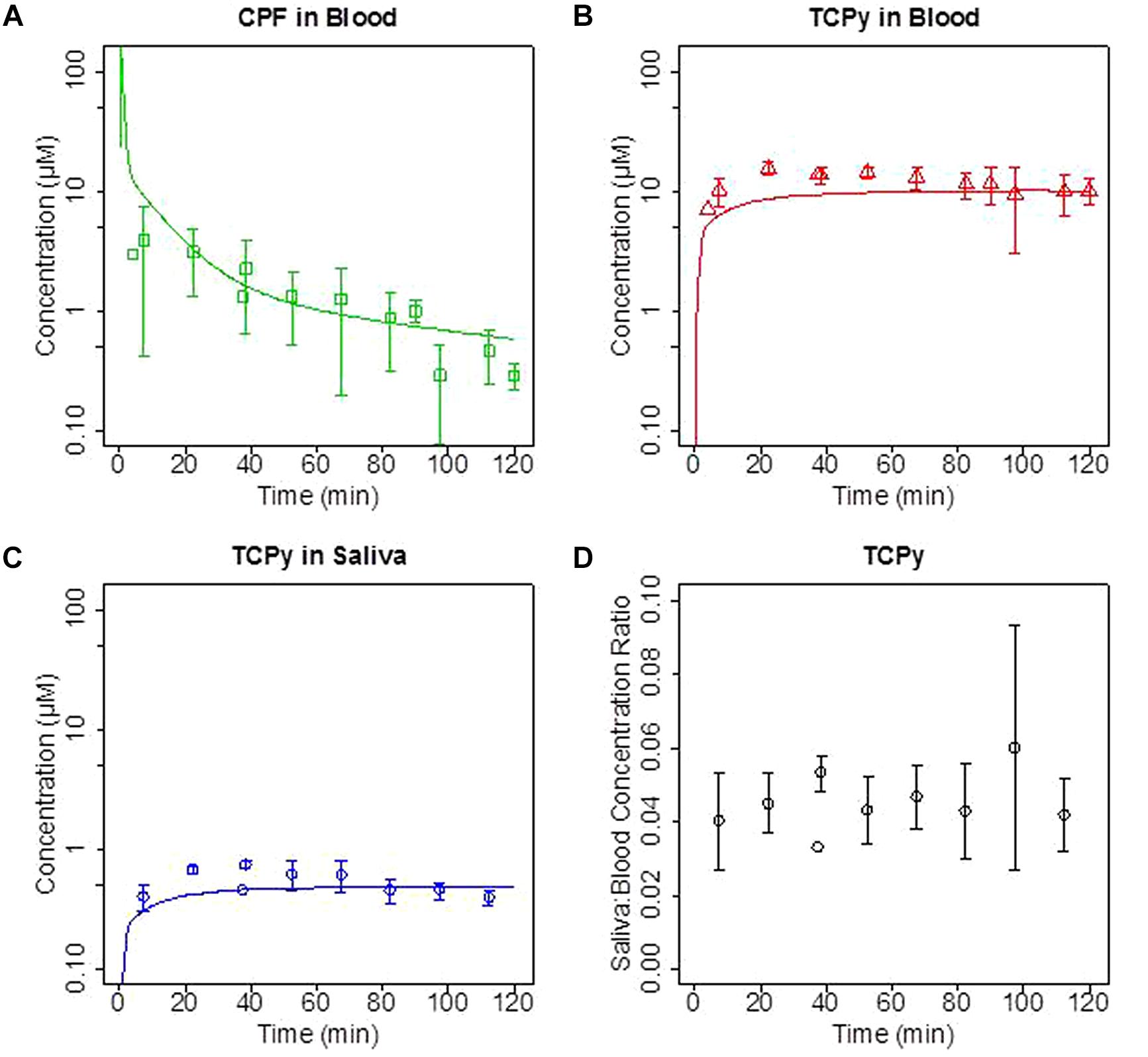
FIGURE 3. Groups of rats were administered a single intravenous (IV) dose of 5 mg/kg chlorpyrifos (CPF). (A) Concentration (μM) of CPF in blood; (B,C) trichloropyridinol (TCPy) in blood and saliva, respectively; and (D) saliva:blood TCPy concentration ratios from 10–120 min post-dosing. Lines are PBPK model fit to data.
Although in the rat in vivo model system saliva/blood TCPy concentration ratios did not change over varying experimental conditions (Figure 3D), as previously mentioned normal differences in saliva pH values for humans (range 5.6–7.9) have been noted in the literature (Hold et al., 1995b). Hence, to adequately accommodate differences in partitioning due to variable pH, and to enable accurate rat to human extrapolation it was critical to simulate changes in analyte ionization states particularly when the pKa was bracketed by the pH range of saliva. In this regard, the Schmitt algorithm provided a good model prediction of the saliva/blood partitioning (Smith et al., 2010). These initial finding do suggest that inter- and intra-species differences in blood:saliva partitioning may be of importance. To further evaluate the potential impact of these differences a model sensitivity analysis was conducted.
Sensitivity Analysis
Model simulations and a sensitivity analysis was conducted to further evaluate the impact of variable pKa (4→10) or protein-binding fractions (0.1→0.9) on the saliva:blood partitioning coefficient. A summary of model parameters for both rat and human are presented in Table 2. For the model sensitivity analysis, it was assumed that generic compounds were 50% bound to plasma proteins, the log Kow was 2 for non-ionized compounds, and the log Kow was -1 for ionized compounds. The sensitivity analysis (Table 3) specifically focused on four model parameters that modulate the plasma:saliva partitioning coefficient, these included: plasma protein-binding, Kow (non-ionized and ionized) and pKa. For this analysis, the model is highly sensitive [normalized sensitivity coefficient (SC) >0.5] to changes in plasma protein-binding (SC- 2.0) and pKa (-0.6 and 0.9) for both humans and rats. Hence, these parameters are of critical importance and can substantially impact partitioning.
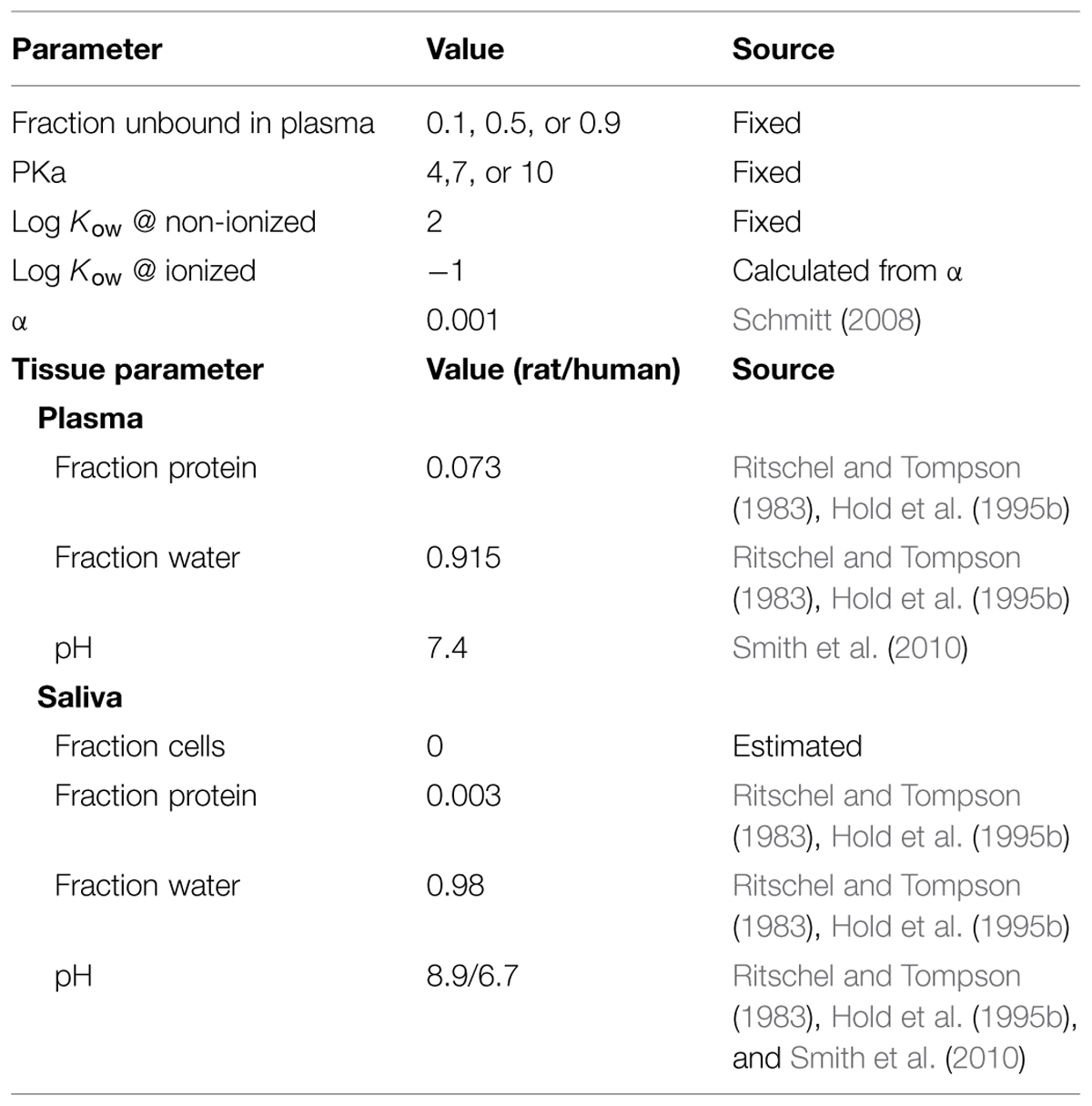
TABLE 2. Input chemical and tissue parameters used to simulate the saliva:blood partitioning for generic over a range of pKa and protein-binding values.

TABLE 3. Sensitivity analysis for selected parameters for generalized compound plasma:saliva partitioning coefficent.
To illustrate the impact of plasma protein-binding on the saliva:plasma partitioning coefficient, model simulations were conducted for three generic compounds with 0.1, 0.5, and 0.9 unbound fraction in plasma of rats and humans. It was assumed that generic compounds had a pKa of 7, the log Kow was 2 for non-ionized compounds, the log Kow was -1 for ionized compounds, and salivary pH was 6.7 and 8.9 for humans and rats, respectively (Table 2). Model simulations are presented in Figure 4. For both rats and humans the plasma:saliva partitioning coefficient increases as a function of the unbound chemical fraction in plasma; however, it is also of interest to note that the partitioning is substantially greater in humans (2.7–3.3x) than in rats.
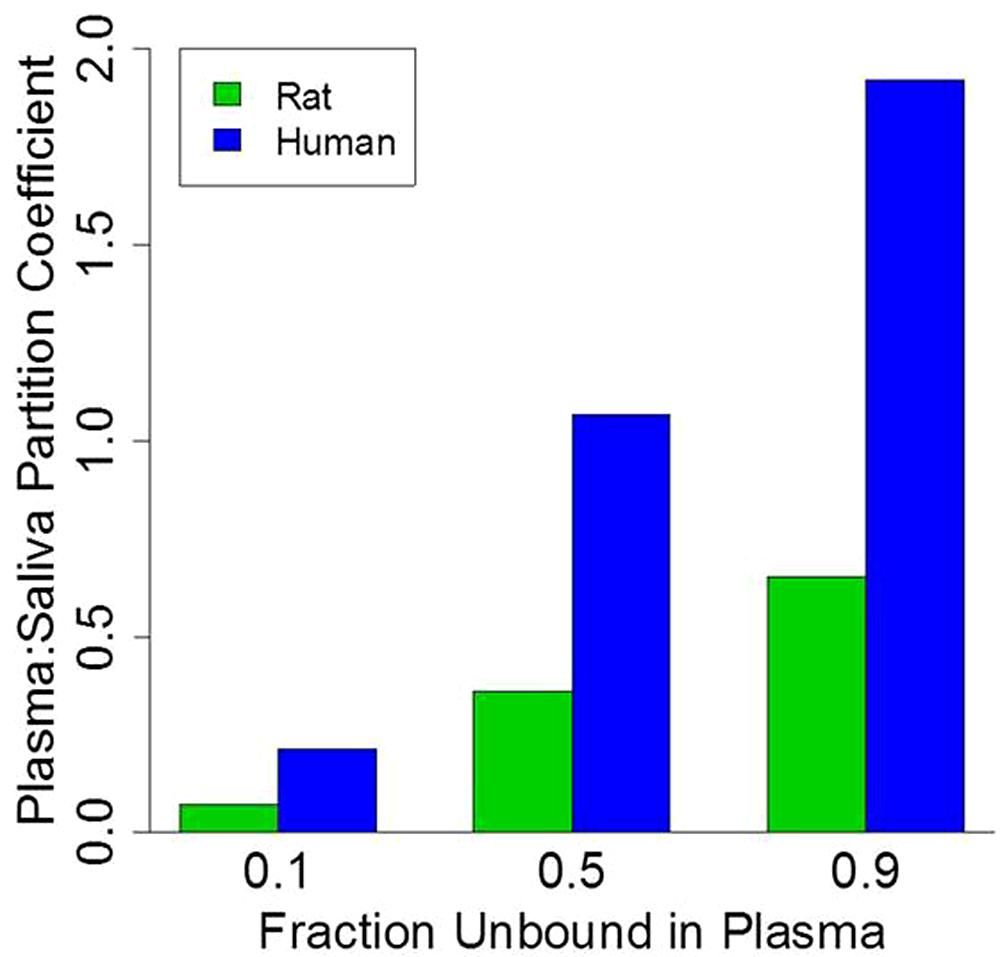
FIGURE 4. Physiologically based pharmacokinetic model simulation of plasma:saliva partitioning coefficients for three generic compounds with varying plasma protein-binding.
To further explore the impact of pH on the salivary:plasma partition coefficients a similar simulation was run but in this case the protein-binding was assumed to be 50% while the pKa values were 4, 7, and 10. As illustrated in Figure 5, generic model simulations indicate that for those chemicals with pKa of ∼7 the partitioning coefficient will vary by a factor of 3 between rats and humans with substantially greater partitioning in humans. However, for chemicals with low or high pKa values (relative to pH) the rat and human plasma:saliva partitioning are comparable. It is also important to note that inter-individual differences is the extent of plasma protein-binding and saliva pH within a population would also contribute to variations in the saliva:plasma partitioning (data not shown); which could result in variable salivary clearance.
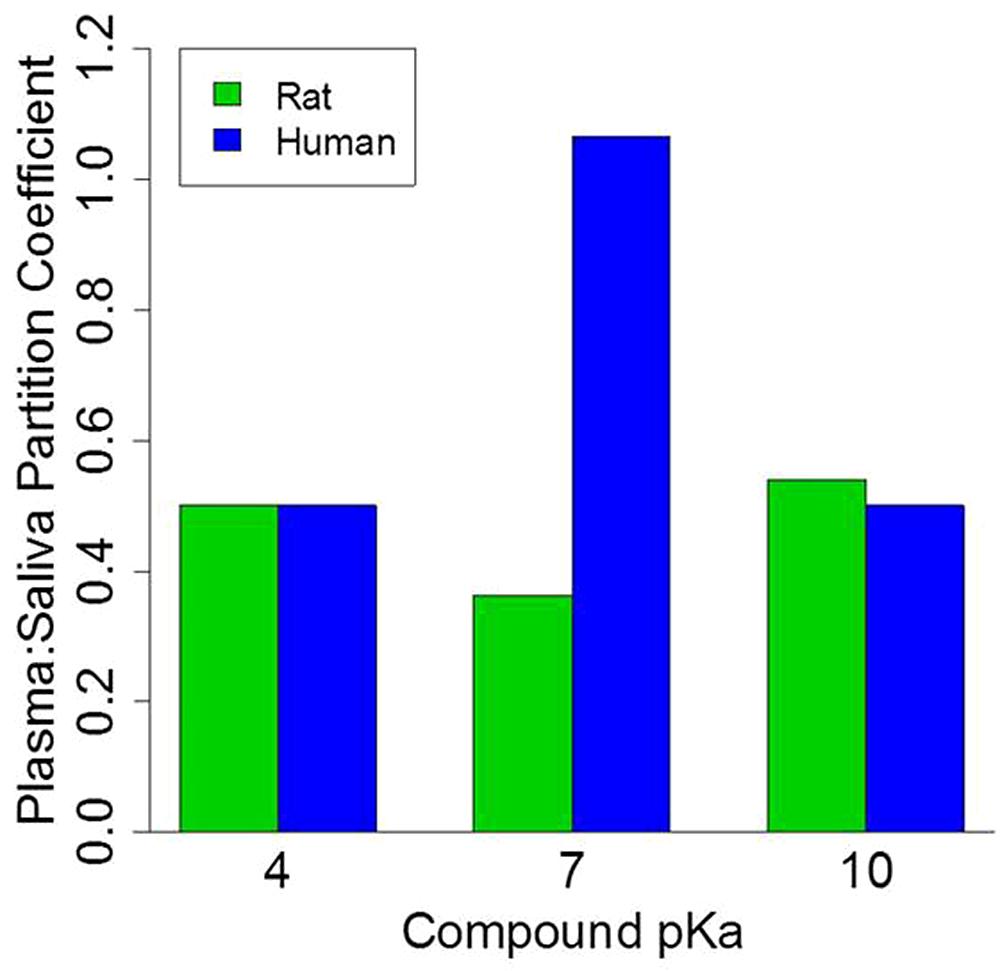
FIGURE 5. Physiologically based pharmacokinetic model simulation of plasma:saliva partitioning coefficients for three generic compounds with varying pKa values. Protein binding set at 50%.
Discussion
Physiologically based pharmacokinetic models have been developed that incorporated saliva clearance as a computational tool to quantify non-invasive biomonitoring of heavy metals and pesticides (Timchalk et al., 2001, 2007b; Barry et al., 2009; Smith et al., 2010, 2012). As previously noted, transcellular diffusion (Figure 1) is thought to be the primary method by which many drugs, chemicals, and pesticides, including the CPF metabolite TCPy transfer from blood to saliva (Haeckel, 1993; Jusko and Milsap, 1993; Lu et al., 1997, 1998, 2003; Smith et al., 2010, 2012). As noted in Figure 3D, in vivo partitioning of TCPy from blood to saliva in rats is very constant over a range of varying conditions which is entirely consistent with a partitioning mechanism associated with transcellular diffusion as proposed by Smith et al. (2010, 2012).
When considering transcellular or paracellular diffusion, it is of interest to note that a number of physiochemical properties including molecular size, lipid solubility, the dissociation constant of ionized compounds, and the extent of plasma-protein binding all contribute to modifying the diffusion across a concentration gradient from blood to saliva. In the current model simulation (Figure 3) the analyte concentration in saliva (based upon partitioning) is directly reflective of the concentration that is not bound to plasma proteins in blood, since protein-analyte complexes are too large for transcellular/paracellular diffusion (Haeckel, 1993; Jusko and Milsap, 1993; Lu et al., 1998; Smith et al., 2012).
Likewise, as shown in Figure 5, the pH of blood and saliva are important parameters modulating salivary clearance of compounds particularly where the chemical pKa is comparable to the pH of biological fluids (Haeckel, 1993; Jusko and Milsap, 1993). Although blood pH is reasonably consistent (pH 7.4), saliva pH can vary and is primarily controlled by the amount of bicarbonate present in saliva (Haeckel, 1993). Hence, due to variation in rat and human pH values (Smith et al., 2010), the Schmitt algorithm (Schmitt, 2008) has been utilized successfully to calculate plasma:saliva partitioning. This modification enables the extrapolation of the blood to saliva analyte partitioning coefficient to humans over a range of reported human salivary pH levels.
Although transcellular or paracellular diffusion across tight junctions has been noted as a key transport mechanism for many drugs and environmental contaminants (Haeckel, 1993; Jusko and Milsap, 1993), both active and carrier-assisted cellular transport may be of importance for some xenobiotics. In this regard, transport is dependent upon specific rate-limiting transport mechanisms. In salivary glands, unidirectional and saturable influx of amino acids, neurotransmitters, and drugs have been shown to follow classic Michaelis–Menten kinetics where affinity and velocity constants can be experimentally derived and computationally solved (Eq. 8). In this scenario, Tr is the transport rate, Tmax the maximum rate of transport, Cu the unbound analyte concentration and Km is the transport affinity constant. Hence, the current model structure can be readily modified to accommodate these active transport processes; thereby, enabling the models to simulate salivary clearance for a broad range of chemicals and drugs.
For saliva biomonitoring to be more broadly utilized there is a need to rapidly identify a comprehensive range of chemical and drugs that can readily be quantified in saliva and utilized to predict systemic dose based upon these saliva measurements. A major limitation of the current experimental and modeling strategy is the dependence upon in vivo animal model systems as a means of identifying and screening chemical/drug candidates for salivary clearance. In this regard, the current in vivo models are limited by relatively low throughput and experimental complexity. To address these limitations we are developing an in vitro salivary gland epithelial cell based Transwell® assay to enable broad based screening of uptake and clearance mechanisms associated with both diffusional and active transport mechanisms (Figure 6; Weber et al., 2015). Initial characterization of the cell system has demonstrated that tight junctions are well formed and cells maintain functional characteristics (Figure 6C) associated with salivary acinar cells. The computational approach is based on a simplified four-compartment model (Figure 6D) exploiting the Schmitt algorithm (Schmitt, 2008) to describe diffusional based processes along with active transport (Eq. 8). It is anticipated that this novel experimental and computational strategy will enable the prediction of chemical uptake and clearance in saliva for a broad range of chemicals based upon limited in vitro experiments which are integrated into the pharmacokinetic modeling framework.
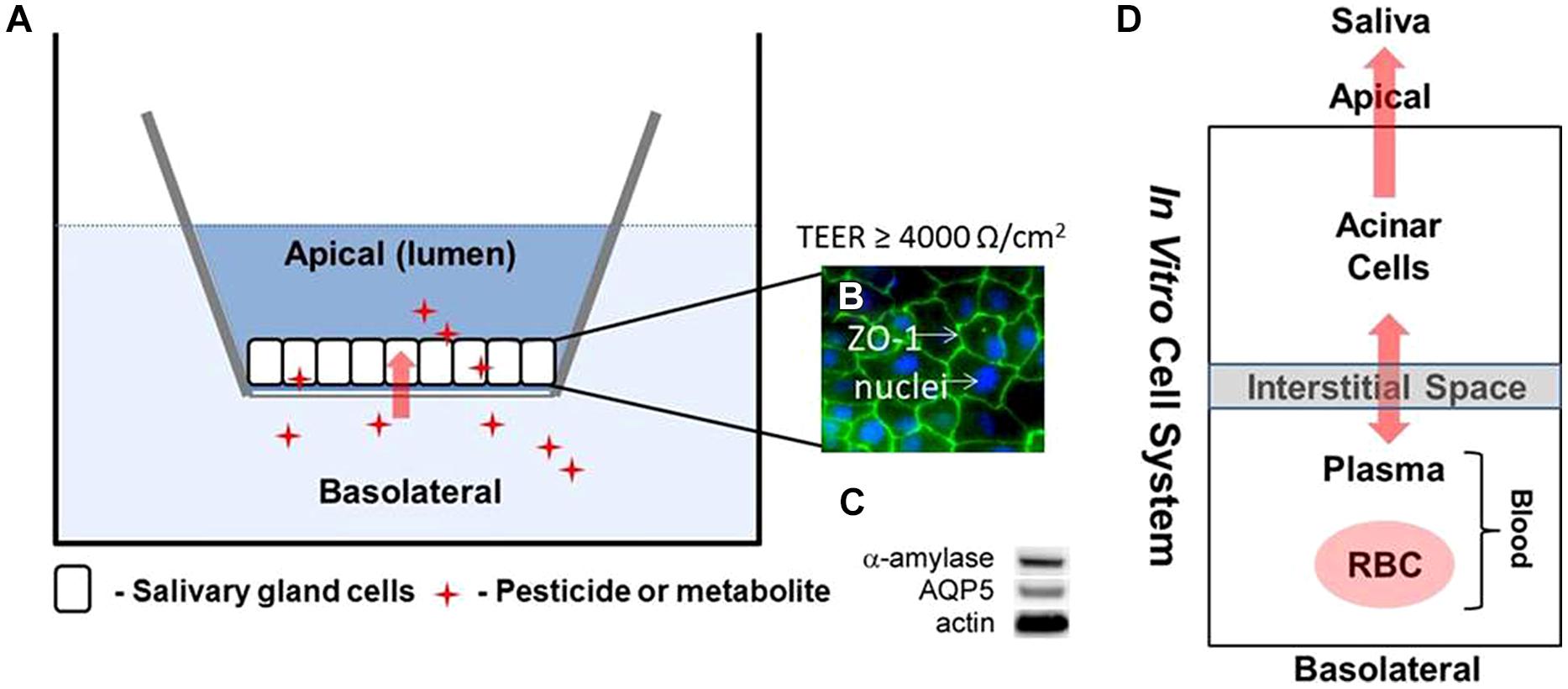
FIGURE 6. Schematic model illustrating (A,B) Transwell® with salivary gland epithelial cell (SGEC) system. The tight junction marker zona occludins-1 (ZO-1) localizes to points of cell–cell contact in association with excellent tight junction formation as indicated by measurements of transepithelial electrical resistance (TEER). (C) Western blot analysis showing expression of α-amylase and AQ5 proteins in SGEC lysates indicative of acinar cells; and (D) four-compartment (blood: RBC/plasma and salivary gland: interstitial and cellular space) model structure for calculating steady-state transport.
Conclusion
Biomonitoring is a critical tool for quantitatively evaluating exposure from both environmental and occupational settings and saliva has been advocated as a potentially important non-invasive method that could be substituted for blood or urine. However, there are a number of limitations that have hampered saliva’s use in biomonitoring, including the need to initially identify which chemicals are readily cleared in saliva at concentrations that can be quantified. This review describes recent advances in the use of a computational modeling approach that is closely coupled to in vivo and in vitro experiments to predict salivary uptake and clearance of xenobiotics. The approach simulates transcellular or paracellular diffusion of unbound chemicals in plasma to saliva using a combination of compartmental and physiologically based computational models. Of key importance for determining the plasma:saliva partitioning is the utilization of a modified Schmitt algorithm (Schmitt, 2008) that calculates partitioning based upon the tissue composition, pH, chemical pKa, and plasma protein-binding. Sensitivity analysis of key model parameters specifically identified that both protein-binding and pH/pKa had the most significant impact on the determination of partitioning and that there were clear species dependent differences based upon physiological variance between rats and humans. Future research needs to focus on extending this modeling strategy to an in vitro salivary acinar cell based system that can be utilized to experimentally determine and computationally predict salivary gland update and clearance for a broad range of xenobiotics. Hence, it is envisioned that a combination of salivary biomonitoring and computational modeling will enable the non-invasive measurement of both environmental and occupational exposure in human populations.
Funding
Centers for Disease Control and Prevention/National Institute of Occupational Safety and Health (CDC/NIOSH; R01 OH008173-07). Findings in this study were those of the authors and do not necessarily reflect the opinion of CDC/NIOSH.
Conflict of Interest Statement
Dr. Charles Timchalk and Dr. Jordan N. Smith have previously received funding from The Dow Chemical Company, the manufacturer of chlorpyrifos (CPF), to conduct research. However, the Dow Chemical Company had no input on the current research.
References
Albers, J. W., Garabrant, D. H., Berent, S., and Richardson, R. J. (2010). Paraoxonase status and plasma butyrylcholinesterase activity in chlorpyrifos manufacturing workers. J. Expo. Sci. Environ. Epidemiol. 20, 79–89. doi: 10.1038/jes.2009.9
Angerer, J., Bird, M. G., Burke, T. A., Doerrer, N. G., Needham, L., Robison, S. H., et al. (2006). Strategic biomonitoring initiatives: moving the science forward. Toxicol. Sci. 93, 3–10. doi: 10.1093/toxsci/kfl042
Angerer, J., Ewers, U., and Wilhelm, M. (2007). Human biomonitoring: state of the art. Int. J. Hyg. Environ. Health 210, 201–228. doi: 10.1016/j.ijheh.2007.01.024
Barr, D. B., Thomas, K., Curwin, B., Landsittel, D., Raymer, J., Lu, C. S., et al. (2006). Biomonitoring of exposure in farmworker studies. Environ. Health Perspect. 114, 936–942. doi: 10.1289/ehp.8527
Barry, R. C., Lin, Y., Wang, J., Liu, G., and Timchalk, C. A. (2009). Nanotechnology-based electrochemical sensors for biomonitoring chemical exposures. J. Expo. Sci. Environ. Epidemiol. 19, 1–18. doi: 10.1038/jes.2008.71
Borzelleca, J. F., and Skalsky, H. L. (1980). The excretion of pesticides in saliva and its value in assessing exposure. J. Environ. Sci. Health B 15, 843–866. doi: 10.1080/03601238009372220
Brown, R. P., Delp, M. D., Lindstedt, S. L., Rhomberg, L. R., and Beliles, R. P. (1997). Physiologicaly parameter values for physiologically based pharmacokinetic models. Toxicol. Ind. Health 13, 407–484. doi: 10.1177/074823379701300401
Busby-Hjerpe, A. L., Campbell, J. A., Smith, J. N., Lee, S., Poet, T. S., Barr, D. B., et al. (2010). Comparative pharmacokinetics of chlorpyrifos versus its major metabolites following oral administration in the rat. Toxicology 268, 55–63. doi: 10.1016/j.tox.2009.11.022S0300-483X(09)00602-7
Christensen, J. M. (1995). Human exposure to toxic metals: factors influencing interpretation of biomonitoring results. Sci. Total Environ. 166, 89–135. doi: 10.1016/0048-9697(95)04478-J
Cohen Hubal, E. A., Richard, A. M., Shah, I., Gallagher, J., Kavlock, R., Blancato, J., et al. (2010). Exposure science and the U. S. EPA National Center for Computational Toxicology. J. Expo. Sci. Environ. Epidemiol. 20, 231–236. doi: 10.1038/jes.2008.70
Conzen, P. F., Vollmar, B., Habazettl, H., Frink, E. J., Peter, K., and Messmer, K. (1992). Systemic and regional hemodynamics of isoflurane and sevoflurane in rats. Anesth. Analg. 74, 79–88. doi: 10.1213/00000539-199201000-00014
Drobitch, R. K., and Svensson, C. K. (1992). Therapeutic drug monitoring in saliva. An update. Clin. Pharmacokinet. 23, 365–379. doi: 10.2165/00003088-199223050-00003
Friberg, L., and Elinder, C. G. (1993). Biological monitoring of toxic metals. Scand. J. Work Environ. Health 19(Suppl. 1), 7–13.
Haeckel, R. (1993). Factors influencing the saliva/plasma ratio of drugs. Ann. N. Y. Acad. Sci. 694, 128–142. doi: 10.1111/j.1749-6632.1993.tb18347.x
Hojring, N., and Svensmark, O. (1976). Carboxylesterases with defferent substrate specificity in human brain extracts. J. Neurochem. 27, 525–528. doi: 10.1111/j.1471-4159.1976.tb12277.x
Hold, K. M., de Boer, D., Soedirman, J. R., Zuidema, J., and Maes, R. A. (1995a). The secretion of propranolol enantiomers in human saliva: evidence for active transport? J. Pharm. Biomed. Anal. 13, 1401–1407. doi: 10.1016/0731-7085(95)01569-7
Hold, K. M., de Boer, D., Zuidema, J., and Maes, R. A. A. (1995b). Saliva as an analytical tool in toxicology. Int. J. Drug Test. 1, 1–36.
Hubal, E. A. (2009). Biologically relevant exposure science for 21st century toxicity testing. Toxicol. Sci. 111, 226–232. doi: 10.1093/toxsci/kfp159
Jusko, W. J., and Milsap, R. L. (1993). Pharmacokinetic principles of drug distribution in saliva. Ann. N. Y. Acad. Sci. 694, 36–47. doi: 10.1111/j.1749-6632.1993.tb18340.x
Landon, J., and Mahmod, S. (eds). (1982). Distribution of Drugs between Blood and Saliva. Cardiff: Alpha Omega Publishing Limited.
Li, B., Sedlacek, M., Manoharan, I., Boopathy, R., Duysen, E. G., Masson, P., et al. (2005). Butyrylcholinesterase, paraoxonase, and albumin esterase, but not carboxylesterase, are present in human plasma. Biochem. Pharmacol. 70, 1673–1684. doi: 10.1016/j.bcp.2005.09.002
Lowe, E. R., Poet, T. S., Rick, D. L., Marty, M. S., Mattsson, J. L., Timchalk, C., et al. (2009). The effect of plasma lipids on the pharmacokinetics of chlorpyrifos and the impact on interpretation of blood biomonitoring data. Toxicol. Sci. 108, 258–272. doi: 10.1093/toxsci/kfp034
Lu, C., Anderson, L. C., and Fenske, R. A. (1997). Determination of atrazine levels in whole saliva and plasma in rats: potential of salivary monitoring for occupational exposure. J. Toxicol. Environ. Health 50, 101–111. doi: 10.1080/009841097160519
Lu, C., Anderson, L. C., Morgan, M. S., and Fenske, R. A. (1998). Salivary concentrations of atrazine reflect free atrazine plasma levels in rats. J. Toxicol. Environ. Health A 53, 283–292. doi: 10.1080/009841098159286
Lu, C., Irish, R. M., and Fenske, R. (2003). Biological monitoring of diazinon exposure using saliva in an animal model. J. Toxicol. Environ. Health A 66, 2315–2325. doi: 10.1080/716100640
Maxwell, D. M., Lenz, D. E., Groff, W. A., Kaminskis, A., and Froehlich, H. L. (1987). The effects of blood flow and detoxification on in vivo cholinesterase inhibition by soman in rats. Toxicol. Appl. Pharmacol. 88, 66–76. doi: 10.1016/0041-008X(87)90270-5
Mortensen, S. R., Hooper, M. J., and Padilla, S. (1998). Rat brain acetylcholinesterase activity: developmental profile and maturational sensitivity to carbamate and organophosphorus inhibitors. Toxicology 125, 13–19. doi: 10.1016/S0300-483X(97)00157-1
Nauntofte, B. (1992). Regulation of electrolyte and fluid secretion in salivary acinar cells. Am. J. Physiol. 263, G823–G837.
Nieuwenhuijsen, M., Paustenbach, D., and Duarte-Davidson, R. (2006). New developments in exposure assessment: the impact on the practice of health risk assessment and epidemiological studies. Environ. Int. 32, 996–1009. doi: 10.1016/j.envint.2006.06.015
Nigg, H. N., and Wade, S. E. (1992). Saliva as a monitoring medium for chemicals. Rev. Environ. Contam. Toxicol. 129, 95–119. doi: 10.1007/978-1-4684-7106-9_7
Peyret, T., Poulin, P., and Krishnan, K. (2010). A unified algorithm for predicting partition coefficients for PBPK modeling of drugs and environmental chemicals. Toxicol. Appl. Pharmacol. 249, 197–207. doi: 10.1016/j.taap.2010.09.010
Pichini, S., Altieri, I., Zuccaro, P., and Pacifici, R. (1996). Drug monitoring in nonconventional biological fluids and matrices. Clin. Pharmacokinet. 30, 211–228. doi: 10.2165/00003088-199630030-00003
Poet, T. S., Wu, H., Kousba, A. A., and Timchalk, C. (2003). In vitro rat hepatic and intestinal metabolism of the organophosphate pesticides chlorpyrifos and diazinon. Toxicol. Sci. 72, 193–200. doi: 10.1093/toxsci/kfg035
Poulin, P., and Krishnan, K. (1995). An algorithm for predicting tissue: blood partition coefficients of organic chemicals from n-octanol: water partition coefficient data. J. Toxicol. Environ. Health 46, 117–129. doi: 10.1080/15287399509532021
Racke, K. D. (1993). Environmental fate of chlorpyrifos. Rev. Environ. Contam. Toxicol. 131, 1–150. doi: 10.1007/978-1-4612-4362-5_1
Ritschel, W. A., and Tompson, G. A. (1983). Monitoring of drug concentrations in saliva: a non-invasive pharmacokinetic procedure. Methods Find. Exp. Clin. Pharmacol. 5, 511–525.
Rodgers, T., Leahy, D., and Rowland, M. (2005). Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J. Pharm. Sci. 94, 1259–1276. doi: 10.1002/jps.20322
Schmitt, W. (2008). General approach for the calculation of tissue to plasma partition coefficients. Toxicol. In Vitro 22, 457–467. doi: 10.1016/j.tiv.2007.09.010
Sheldon, L. S., and Cohen Hubal, E. A. (2009). Exposure as part of a systems approach for assessing risk. Environ. Health Perspect. 117, 119–1194. doi: 10.1289/ehp.0800407
Shemer, H., Sharpless, C. M., and Linden, K. G. (2005). Photodepradation of 3,5,6-trichloro-2-pyridinol in aqueous solution. Water Air Soil Poll. 168, 145–155. doi: 10.1007/s11270-005-0960-z
Sidell, F. R., and Kaminskis, A. (1975). Influence of age, sex, and oral contraceptives on human blood cholinesterase activity. Clin. Chem. 21, 1393–1395.
Silva, M. J., Reidy, J. A., Samandar, E., Herbert, A. R., Needham, L. L., and Calafat, A. M. (2005). Detection of phthalate metabolites in human saliva. Arch. Toxicol. 79, 647–652. doi: 10.1007/s00204-005-0674-4
Smith, J. N., Timchalk, C., Bartels, M. J., and Poet, T. S. (2011). In vitro age-dependent enzymatic metabolism of chlorpyrifos and chlorpyrifos-oxon in human hepatic microsomes and chlorpyrifos-oxon in plasma. Drug Metab. Dispos. 39, 1353–1362. doi: 10.1124/dmd.111.038745
Smith, J. N., Wang, J., Lin, Y., Klohe, E. M., and Timchalk, C. (2012). Pharmacokinetics and Pharmacodynamics of chlorpyrifos and 3,5,6-trichloro-2-pyridinol in rat saliva after chlorpyrifos administration. Toxicol. Sci. 130, 245–256. doi: 10.1093/toxsci/kfs251kfs251
Smith, J. N., Wang, J., Lin, Y., and Timchalk, C. (2010). Pharmacokinetics of the chlorpyrifos metabolite 3,5,6-trichloro-2-pyridinol (TCPy) in rat saliva. Toxicol. Sci. 113, 315–325. doi: 10.1093/toxsci/kfp283
Timchalk, C., Busby, A., Campbell, J. A., Needham, L. L., and Barr, D. B. (2007a). Comparative pharmacokinetics of the organophosphorus insecticide chlorpyrifos and its major metabolites diethylphosphate, diethylthiophosphate and 3,5,6-trichloro-2-pyridinol in the rat. Toxicology 237, 145–157. doi: 10.1016/j.tox.2007.05.007
Timchalk, C., Campbell, J. A., Liu, G., Lin, Y., and Kousba, A. A. (2007b). Development of a non-invasive biomonitoring approach to determine exposure to the organophosphorus insecticide chlorpyrifos in rat saliva. Toxicol. Appl. Pharmacol. 219, 217–225. doi: 10.1016/j.taap.2006.10.002
Timchalk, C., Lin, Y., Weitz, K. K., Wu, H., Gies, R. A., Moore, D. A., et al. (2006). Disposition of lead (Pb) in saliva and blood of Sprague-Dawley rats following a single or repeated oral exposure to Pb-acetate. Toxicology 222, 86–94. doi: 10.1016/j.tox.2006.01.030
Timchalk, C., Nolan, R. J., Mendrala, A. L., Dittenber, D. A., Brzak, K. A., and Mattsson, J. L. (2002). A Physiologically based pharmacokinetic and pharmacodynamic (PBPK/PD) model for the organophosphate insecticide chlorpyrifos in rats and humans. Toxicol. Sci. 66, 34–53. doi: 10.1093/toxsci/66.1.34
Timchalk, C., Poet, T. S., Kousba, A. A., Campbell, J. A., and Lin, Y. (2004). Noninvasive biomonitoring approaches to determine dosimetry and risk following acute chemical exposure: analysis of lead or organophosphate insecticide in saliva. J. Toxicol. Environ. Health A 67, 635–650. doi: 10.1080/15287390490428035
Timchalk, C., Poet, T. S., Lin, Y., Weitz, K. K., Zhao, R., and Thrall, K. D. (2001). Development of an integrated microanalytical system for analysis of lead in saliva and linkage to a physiologically based pharmacokinetic model describing lead saliva secretion. AIHAJ 62, 295–302. doi: 10.1202/0002-8894(2001)062<0295:DOAIMS>2.0.CO;2
Vollmar, B., Conzen, P. F., Kerner, T., Habazettl, H., Vierl, M., Waldner, H., et al. (1992). Blood flow and tissue oxygen pressures of liver and pancreas in rats: effects of volatile anesthetics and of hemorrhage. Anesth. Analg. 75, 421–430. doi: 10.1213/00000539-199209000-00019
Keywords: saliva, biomonitoring, salivary gland, uptake, clearance, pesticides
Citation: Timchalk C, Weber TJ and Smith JN (2015) Computational strategy for quantifying human pesticide exposure based upon a saliva measurement. Front. Pharmacol. 6:115. doi: 10.3389/fphar.2015.00115
Received: 05 February 2015; Accepted: 14 May 2015;
Published online: 27 May 2015.
Edited by:
George D. Loizou, Health and Safety Laboratory, UKReviewed by:
Marina Evans, United States Environmental Protection Agency, USAJoseph Paul Bressler, Kennedy Krieger Institute, USA
Cory L. Strope, The Hamner Institutes for Health Sciences, USA
Copyright © 2015 Timchalk, Weber and Smith. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Charles Timchalk, Health Impacts and Exposure Science, Pacific Northwest National Laboratory, 902 Battelle Boulevard, P.O. Box 999, Richland, WA 99352, USA,Y2hhcmxlcy50aW1jaGFsa0Bwbm5sLmdvdg==
 Charles Timchalk
Charles Timchalk Thomas J. Weber
Thomas J. Weber Jordan N. Smith
Jordan N. Smith