- 1Beijing Academy of Quantum Information Sciences, Beijing, China
- 2Frontier Science Center for Quantum Information, School of Integrated Circuits, Tsinghua University, Beijing, China
Cavity optomechanical systems are demonstrating diverse applications in sensing and transduction, profiting from advances in related theories and experiments, which also promotes quantum research based on them. Here, we first briefly introduce typical applications of cavity optomechanical systems and some of our recent progress in this field and then discuss the potential of cavity optomechanical systems for exploring fundamental questions in quantum theory and the challenges encountered in current developments. Cavity optomechanical systems will play a vital role in quantum computing and quantum information and will enrich the quantum toolbox, particularly in quantum interfaces and quantum memory.
1 Introduction
Cavity optomechanical systems explore the interaction between the light and the motion of a mechanical resonator, where the radiation pressure forces mediate the movement of the mechanical resonator and vice versa. Conventional effects, such as bistability and optical spring effects, were observed in the 1980s (Dorsel et al., 1983; Gozzini et al., 1985). Thanks to the progress in cryogenic technology and micro/nanofabrication technology, cavity optomechanical systems display various advanced applications ranging from quantum interfaces and quantum memories to quantum metrology and quantum computing. It not only expands the toolbox of quantum information and quantum computing but also has the potential to explore the foundations of quantum mechanics because of the macroscopic properties of the quantum states.
2 Structure of cavity optomechanics
From the frequency range of the optical mode, we generally describe the cavity as an optical (THz) or a microwave (GHz) cavity. The optical cavity usually consists of mirrors or tapered fibers, and the microwave cavity behaves as a 3D metal structure or planar superconducting microwave circuit. Representatives of cavity optomechanical systems at optical frequency (Fabry-Pérot cavity) and microwave frequency (LC circuit) are illustrated in Figures 1A, B, respectively. The typical shapes of cavity optomechanical systems include moveable mirrors on a cantilever or beams, microtoroid/microsphere/microdisk close to tapered fibers, membranes/nanowires/micropillars inside or next to a cavity, atomic clouds in an optical cavity, nanobeams or vibrating plate capacitors in a superconducting microwave resonator, photonic crystals patterned into free-standing nanobeams, etc. (Aspelmeyer et al., 2014). Considering that the current quantum network scheme is to calculate at microwave frequencies and transmit at optical frequencies, the optomechanical system is seen as the optimal candidate for quantum interfaces in quantum communication and quantum computing due to its ability to interact with optical and microwave light.
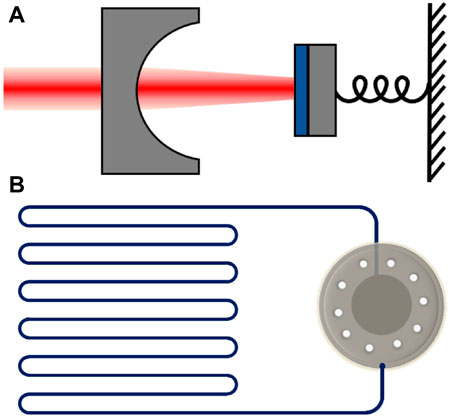
FIGURE 1. Representatives of cavity optomechanical systems with optical frequency and microwave frequency. (A) Photons in the Fabry-Pérot cavity interact with the motion of a mechanical resonator. (B) The mechanical resonator acts as a part of a capacitor to make the microwave field interact with the mechanical motion.
3 Progress in cavity optomechanics
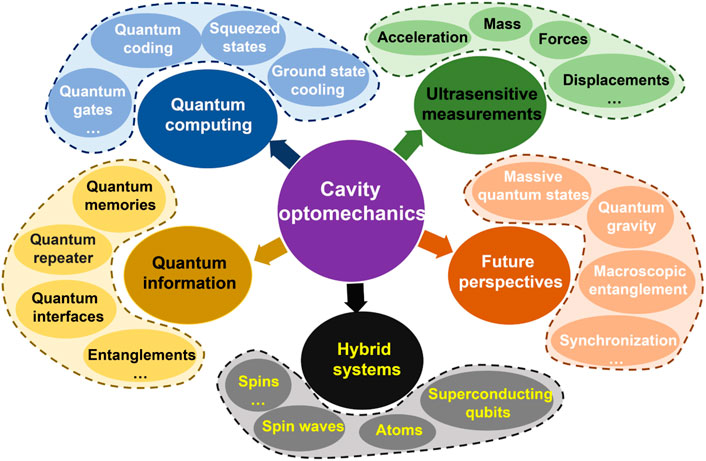
Cavity optomechanical systems have potential applications in sensitive measurement, quantum computing, quantum information, hybrid systems, and the foundation tests of quantum theory (Kippenberg and Vahala, 2007; Aspelmeyer et al., 2014). Examples of typical applications are shown in Figure 2. The high detection accuracy of optomechanical systems is a result of interferometry, which is restricted by the so-called standard quantum limit because of the quantum fluctuation of the radiation pressure force. Furthermore, the observables could be measured with arbitrary precision by the method of quantum non-demolition measurement.
Quantum manipulation requires the object to be in a quantum state. The quantum ground state of the mechanical resonator in optomechanical systems can be prepared through optical feedback cooling and radiation pressure cooling. The main idea of the former is that the oscillator will be imposed a negative feedback depending on the position of the oscillator achieved by the phase-sensitive detection (Genes et al., 2008). The latter is the conventional method for ground state preparation, where the cavity is driven by a red detuned frequency compared to the cavity resonance frequency and the detuning is equal to the mechanical phonon frequency. The driven beam will be upconverted to the cavity frequency by absorbing phonon energy, and then the mechanical resonator can be cooled down, accompanied by the extra energy being released into the environment (Teufel et al., 2011). Optomechanically induced transparency and optomechanically induced amplification were observed during detuned pumping (Weis et al., 2010; Massel et al., 2011; Lai et al., 2020). In addition to the above methods, we propose theoretically that the mechanical resonator ground state could be cooled without a cryogenic setup precooling process through an auxiliary gain cavity (Liu and Liu, 2017). In contrast, the quantum ground state of cavity photons can also be prepared by mediating the mechanical mode in the cavity optomechanism system. The achievement of the quantum state is the basis of a series of quantum computing and quantum metrology, such as the quantum gates, superposition state and squeezed state.
The mechanical resonator is the optimal candidate for quantum memories because of its low dissipation rate, which could be decreased to several mHz due to dissipation dilution. The quantum state to be transmitted and processed can be stored in the phonon states for the next processing. The ability to store quantum states in the low-loss mechanical oscillators provides an attractive tool, e.g., mechanical quantum memory (Palomaki et al., 2013; Wallucks et al., 2020), in the growing field of quantum information technology. For the system consisting of a passive optical cavity and an active mechanical resonator, it is shown that the optical amplification and absorption, optomechanically induced transparency and ultralong group delay can be controlled by tuning the gain and loss (Liu et al., 2017). The optomechanically induced anti-laser and phase singular transition has been observed experimentally in a compound system composed of a three-dimensional superconducting cavity and a silicon nitride membrane resonator (Liu et al., 2021a). The phenomenon of infinite group delay paves the way for quantum memories.
Hybrid systems composed of components with various strengths have become a main means of scientific research and application development. Hybrid systems coupling the cavity optomechanical system to spins, magnons, atoms, and superconducting qubits are one of the leading platforms for quantum applications because of their flexibility and more controllable degrees of freedom. In hybrid quantum systems based on micro- and nanomechanical oscillators, mechanical resonators can be prepared for the quantum ground state or as a way to modulate the cavity, such as ground state cooling of the cavity. However, mechanical strain also provides a way for us to handle quantum states. The squeezed state of the nitrogen vacancy (NV) center ensemble could be prepared in a diamond nanostructure mediated in resonance with drive power (Bennett et al., 2013), in which the dephasing relaxation could be largely suppressed. Experiments have demonstrated that the coupling of the NV ground-state spin to the mechanical mode is enhanced in a nanoscale diamond cantilever, and its temporal dynamics are measured via spin echo (Meesala et al., 2016). Generally, qubits based on defects in solid structures can be mediated via strain engineering. The scalability and compatibility of hybrid systems make them significant in quantum information processing.
The wealth of non-linearities in cavity optomechanical systems is receiving much attention. Phonon lasing, frequency comb and chaos have been predicted and observed (Jing et al., 2014; Lü et al., 2015). For the configuration of a linear cavity coupled with an optomechanical system, we demonstrated that the quantum non-linearity of the optomechanical component can be transformed to the cavity by the coherent feedback loop; hence, tunable bistability and strong photon blockade of the cavity modes can be achieved (Liu et al., 2015). Formation for single mechanical mode-mediated frequency combs and the hybridized frequency combs between cavity mode and mechanical mode were experimentally observed in a multimode cavity electromechanical system. The application of non-linearity in cavity optomechanical systems will benefit timing, metrology and synchronization.
The multimode cavity optomechanical system provides a promising platform for studying new physics and technologies. It is of great significance in the fields of dark state dynamics, non-reciprocity, entanglement among mechanical oscillators or between oscillators and cavity photons and so on. It offers new means to control and measure both the mechanical motion and electromagnetic fields, such as squeezed state preparation and the coherent conversion between microwave and optical light. Mechanical modes designed with a phononic bandgap and buckling properties will benefit the development of multimode cavity optomechanics (Reyes et al., 2020). In addition, the array of the cavity optomechanical system will contribute to the foundation study of quantum theory and application, such as gravity decoherence, the Casimir effect, macroscopic non-local entanglement, synchronization of mechanical frequencies, and many-body quantum simulation. In the cavity-optomechanical system consisting of two membranes loaded by two microspheres, we studied the gravitational force and the non-local quantum correlations between the oscillators (Liu et al., 2021b). The synchronization for two mechanical modes is investigated in two coupled optomechanical resonators with parity-time (PT) symmetry, which shows that the degree of synchronization between the two far-off-resonant mechanical modes can be increased by the sensitivity near the exceptional point (Zhu et al., 2021). The utility of multimode cavity optomechanical systems shows great potential as quantum transducers and optomechanical interface devices for future hybrid quantum networks.
4 Future perspectives and encountered difficulties
With advances in experience and theory, cavity optomechanical systems have potential perspectives in the development of advanced applications and the fundamental investigations of quantum mechanics. The accuracy of displacement on the order of the Planck scale was achieved in the gravitational wave detection experiment. The detection accuracy will be further improved with the achievement of quantum states, e.g., the squeezed state. The scale of the quantum network will be expanded with the help of cavity optomechanical systems due to its advantages in terms of quantum interfaces and quantum memories.
Cavity optomechanical systems show substantial potential for studying the fundamental issues of quantum theory because of the macroscopic quantum properties of mechanical resonators. The ability to achieve coherent quantum control over massive objects will answer why it is difficult to prepare superposition states for macroscopic objects, how gravity affects the decoherence of quantum states and the boundary between the classical world and quantum world. The study of the non-local quantum entanglement of the many-body systems will provide an opportunity to make new breakthroughs in mathematics and to explain the origin of elementary particles.
At present, the encountered difficulties for the development of cavity optomechanical systems are mainly the resonator quality and the noise effect, which hinders the mechanical resonator or the cavity from entering the quantum region and limits the decoherence time. Improvements in the resonance frequency and quality factor of the resonator will be an ongoing pursuit. Meanwhile, the effect of the noise, such as the phase noise (i.e., frequency stability), thermal noise, amplifier noise, etc., should be carefully controlled in the experiment. Another goal is the stronger intrinsic coupling between cavity photons and phonons. Fortunately, these obstacles are being overcome via structure design and stress engineering with advances in micro/nanofabrication technology.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
YL and TL initiated and guided the project. HS organized the main ideas of the manuscript and prepared figures. All authors contributed to the writing of the manuscript.
Funding
This work is supported by the National Key Research and Development Program of China (Grant No. 2022YFA1405200), the National Natural Science Foundation of China (Grant Nos. 12004044, 62074091, and U1930402) and Tsinghua University Initiative Scientific Research Program.
Acknowledgments
The authors thank to Qichun Liu for fruitful comments and suggestions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aspelmeyer, M., Kippenberg, T. J., and Marquardt, F. (2014). Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452. doi:10.1103/RevModPhys.86.1391
Bennett, S. D., Yao, N. Y., Otterbach, J., Zoller, P., Rabl, P., and Lukin, M. D. (2013). Phonon-induced spin-spin interactions in diamond nanostructures: Application to spin squeezing. Phys. Rev. Lett. 110, 156402. doi:10.1103/PhysRevLett.110.156402
Dorsel, A., McCullen, J. D., Meystre, P., Vignes, E., and Walther, H. (1983). Optical bistability and mirror confinement induced by radiation pressure. Phys. Rev. Lett. 51, 1550–1553. doi:10.1103/PhysRevLett.51.1550
Genes, C., Vitali, D., Tombesi, P., Gigan, S., and Aspelmeyer, M. (2008). Ground-state cooling of a micromechanical oscillator: Comparing cold damping and cavity-assisted cooling schemes. Phys. Rev. A 77, 033804. doi:10.1103/PhysRevA.77.033804
Gozzini, A., Maccarrone, F., Mango, F., Longo, I., and Barbarino, S. (1985). Light-pressure bistability at microwave frequencies. J. Opt. Soc. Am. B 2, 1841–1845. doi:10.1364/JOSAB.2.001841
Jing, H., Özdemir, S. K., Lü, X.-Y., Zhang, J., Yang, L., and Nori, F. (2014). PT-symmetric phonon laser inline>{\mathcal{PT}}. Phys. Rev. Lett. 113, 053604. doi:10.1103/PhysRevLett.113.053604
Kippenberg, T., and Vahala, K. (2007). Cavity opto-mechanics. Opt. Express 15, 17172–17205. doi:10.1364/OE.15.017172
Lai, D.-G., Wang, X., Qin, W., Hou, B.-P., Nori, F., and Liao, J.-Q. (2020). Tunable optomechanically induced transparency by controlling the dark-mode effect. Phys. Rev. A 102, 023707. doi:10.1103/PhysRevA.102.023707
Liu, Y.-L., and Liu, Y.-x. (2017). Energy-localization-enhanced ground-state cooling of a mechanical resonator from room temperature in optomechanics using a gain cavity. Phys. Rev. A 96, 023812. doi:10.1103/PhysRevA.96.023812
Liu, Y.-L., Liu, Z.-P., and Zhang, J. (2015). Coherent-feedback-induced controllable optical bistability and photon blockade. J. Phys. B Atomic, Mol. Opt. Phys. 48, 105501. doi:10.1088/0953-4075/48/10/105501
Liu, Y.-L., Wu, R., Zhang, J., Özdemir, i. m. c. K., Yang, L., Nori, F., et al. (2017). Controllable optical response by modifying the gain and loss of a mechanical resonator and cavity mode in an optomechanical system. Phys. Rev. A 95, 013843. doi:10.1103/PhysRevA.95.013843
Liu, Y., Liu, Q., Wang, S., Chen, Z., Sillanpää, M. A., and Li, T. (2021a). Optomechanical anti-lasing with infinite group delay at a phase singularity. Phys. Rev. Lett. 127, 273603. doi:10.1103/PhysRevLett.127.273603
Liu, Y., Mummery, J., Zhou, J., and Sillanpää, M. A. (2021b). Gravitational forces between nonclassical mechanical oscillators. Phys. Rev. Appl. 15, 034004. doi:10.1103/PhysRevApplied.15.034004
Lü, X.-Y., Jing, H., Ma, J.-Y., and Wu, Y. (2015). PT-Symmetry-Breaking chaos in optomechanics inline>{\mathcal{P}}\mathcal{T}. Phys. Rev. Lett. 114, 253601. doi:10.1103/PhysRevLett.114.253601
Massel, F., Heikkilä, T. T., Pirkkalainen, J.-M., Cho, S. U., Saloniemi, H., Hakonen, P. J., et al. (2011). Microwave amplification with nanomechanical resonators. Nature 480, 351–354. doi:10.1038/nature10628
Meesala, S., Sohn, Y.-I., Atikian, H. A., Kim, S., Burek, M. J., Choy, J. T., et al. (2016). Enhanced strain coupling of nitrogen-vacancy spins to nanoscale diamond cantilevers. Phys. Rev. Appl. 5, 034010. doi:10.1103/PhysRevApplied.5.034010
Palomaki, T. A., Harlow, J. W., Teufel, J. D., Simmonds, R. W., and Lehnert, K. W. (2013). Coherent state transfer between itinerant microwave fields and a mechanical oscillator. Nature 495, 210–214. doi:10.1038/nature11915
Reyes, D., Martínez, D., Mayorga, M., Heo, H., Walker, E., and Neogi, A. (2020). Optimization of the spatial configuration of local defects in phononic crystals for high q cavity. Front. Mech. Eng. 6. doi:10.3389/fmech.2020.592787
Teufel, J. D., Donner, T., Li, D., Harlow, J. W., Allman, M. S., Cicak, K., et al. (2011). Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363. doi:10.1038/nature10261
Wallucks, A., Marinković, I., Hensen, B., Stockill, R., and Gröblacher, S. (2020). A quantum memory at telecom wavelengths. Nat. Phys. 16, 772–777. doi:10.1038/s41567-020-0891-z
Weis, S., Rivière, R., Deléglise, S., Gavartin, E., Arcizet, O., Schliesser, A., et al. (2010). Optomechanically induced transparency. Science 330, 1520–1523. doi:10.1126/science.1195596
Keywords: cavity optomechanics, quantum memory, quantum interface, squeezed state, gravitational quantum effect, entanglement
Citation: Sun H, Liu Y and Li T (2023) Application perspective of cavity optomechanical system. Front. Quantum Sci. Technol. 1:1091691. doi: 10.3389/frqst.2022.1091691
Received: 07 November 2022; Accepted: 28 December 2022;
Published: 09 January 2023.
Edited by:
Juan José García-Ripoll, Spanish National Research Council (CSIC), SpainReviewed by:
Chuan Wang, Beijing Normal University, ChinaCopyright © 2023 Sun, Liu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yulong Liu, bGl1eWxAYmFxaXMuYWMuY24=; Tiefu Li, bGl0ZkB0c2luZ2h1YS5lZHUuY24=
 Huanying Sun
Huanying Sun Yulong Liu
Yulong Liu Tiefu Li1,2*
Tiefu Li1,2*