Quantum non-Markovianity: Overview and recent developments

In the current era of noisy intermediate-scale quantum (NISQ) devices, research on the theory of open system dynamics has a crucial role to play. In particular, understanding and quantifying memory effects in quantum systems is critical to gain a better handle on the effects of noise in quantum devices. The main focus of this review is to address the fundamental question of defining and characterizing such memory effects—broadly referred to as quantum non-Markovianity—utilizing various approaches. We first discuss the two-time-parameter maps approach to open system dynamics and review the various notions of quantum non-Markovianity that arise in this paradigm. We then discuss an alternate approach to quantum stochastic processes based on the quantum combs framework, which accounts for multi-time correlations. We discuss the interconnections and differences between these two paradigms and conclude with a discussion on the necessary and sufficient conditions for quantum non-Markovianity.

1 Introduction

A quantum system is said to be open when it interacts with its environment (Breuer and Petruccione, 2002). As such a system evolves, it builds up correlations, such as entanglement, with the environment (de Vega and Alonso, 2017). This in turn results in decoherence and dissipation (Breuer et al., 2016a), which are known to be generally detrimental to quantum information tasks. The study of open system dynamics has thus become more important than ever in today’s era of noisy intermediate-scale quantum (NISQ) devices (Preskill, 2018). Of particular interest is the characterization of memory effects, or quantum non-Markovianity, that arises due to strong system–environment (S-E) coupling. A precise and universal definition of non-Markovianity has remained elusive, and understanding its origins and characteristics is pertinent for emerging quantum technologies.

The study of open quantum system dynamics has been formalized in a number of approaches, from traditional approaches (Breuer and Petruccione, 2002; Banerjee, 2018) to operational characterizations (Pollock et al., 2018a) and, more recently, approaches based on quantum collision models (Campbell and Vacchini, 2021; Ciccarello et al., 2022). From the quantum information theory point of view, system dynamics are represented by quantum dynamical maps, which are linear, completely positive (CP), and trace-preserving (TP) maps. Such maps, referred to as quantum channels, can be described using an operator-sum representation (the so-called Kraus representation) (Nielsen and Chuang, 2010), which can be derived by tracing out the environment degrees of freedom from the full S-E unitary dynamics.

Open system dynamics may be broadly classified as Markovian and non-Markovian. In the natural sciences, a process is said to be Markovian if the future outcomes of the measurement of the system are independent of the past ones, conditioned on the present. When such past–future independence fails, or when the environment retains the history of the system, then the process is said to be non-Markovian. Over the past decade, there have been significant efforts to characterize, witness, and quantify non-Markovianity in the quantum domain. A number of witnesses and measures have been proposed, based on divisibility (Rivas et al., 2010), distinguishability (or trace distance) (Breuer et al., 2009), fidelity (Rajagopal et al., 2010), quantum channel capacity (Bylicka et al., 2014; Pineda et al., 2016), accessible information (Fanchini et al., 2014), mutual information (Luo et al., 2012), quantum discord (Alipour et al., 2012), interferometric power (Dhar et al., 2015), and deviation from semigroup structure (Wolf et al., 2008; Utagi et al., 2020b), to name a few.

However, a precise and universal definition of quantum (non-) Markovianity continues to remain one of the unsolved problems in open systems theory (Li et al., 2018). The traditional approach to quantum non-Markovianity does not have a well-defined classical limit and lacks a clear operational interpretation (Pollock et al., 2018b). In fact, the traditional approach characterizes dynamical processes either via one-parameter semigroups of dynamical maps or two-parameter families of maps that are divisible and indivisible, thus incorporating only two-time correlation functions of the environment. The results emerging from such approaches cannot necessarily be generalized to situations where multi-time correlations become prominent. A new approach, known as the process tensor formalism, promises a solution to this problem through complete tomographic characterization of a quantum stochastic process by taking into account multi-time correlations as well as the (possibly unknown) initial S-E correlations (Modi, 2012), offering an operationally motivated characterization of open systems that the previous approaches need not provide.

The present review attempts to survey this active area of defining and characterizing quantum non-Markovian dynamics. While there have been a few good reviews on this topic in the literature in the past (see, for example, Rivas et al., 2014; Breuer et al., 2016a; Breuer et al., 2016b; de Vega and Alonso, 2017; Li et al., 2018), our article focuses on the more notable recent developments aimed at detecting and quantifying non-Markovianity via temporal quantum correlations. After briefly reviewing the well-known definitions based on CP-divisibility (Rivas et al., 2010) and distinguishability (Breuer et al., 2009), which are only necessary but not sufficient indicators of non-Markovianity, we discuss a measure proposed by Chen et al. (2016) based on temporal steerable correlations and one subsequently proposed by Utagi (2021) based on the causality measure arising out of the pseudo-density matrix (PDM). However, as we note in this review, the definitions based on quantum temporal correlations are only sufficient but not necessary indicators of non-Markovianity. Later, we discuss the recent approaches in which multi-time correlations are taken into account, specifically the process tensor framework proposed by Pollock et al. (2018a) and Pollock et al. (2018b) and a definition of non-Markovianity based on conditional past–future (CPF) correlations proposed by Budini (2018b), Budini (2019), and Budini (2022). Specifically, we address the issue of necessary and sufficient criteria for quantum non-Markovianity in this review.

Regarding the terminology used in this article: i) we use system to refer to an open quantum system; ii) environment refers to a quantum environment having quantum degrees of freedom, unless otherwise stated; iii) the master equation is an equation that describes the reduced dynamics of the system alone, after tracing out the environment degrees of freedom; and iv) correlations implies quantum correlations, unless otherwise stated.

The remainder of this review is structured as follows: in sections 2.1 and 2.2, we briefly review the well-known master equation and dynamical map approaches to open system dynamics. In Section 2.3, we discuss some of the famous measures of non-Markovianity, including those based on the distinguishability of states and CP-divisibility. We also briefly note some of the measures that are based on quantum correlations. In Section 2.4, we review some recent measures that are based on correlations in time, namely, temporal steering and temporal non-separability, and note an important relationship between the two. Interestingly, these measures are known not to be strictly equivalent, as we discuss in Section 2.5, leaving open the question of equivalence between the measures based on the temporal steerable weight (TSW) and the causality measure.

Sections 3.1 and 3.2 form an interlude where we discuss some curious features of open systems and S-E correlations, as well as mentioning some recent developments. We then move on to Part II in Section 4, where we mainly focus on the frameworks that overcome the limitations of the existing two-time maps. Given that a notion of Markovianity exists, namely, the independence of future outcomes on past measurement results, non-Markovianity is commensurate with the notion of causality and the causal influence of past history on future evolution. In Section 4, we present the notion of non-Markovianity based on an operational framework, called the process tensor, and discuss various features, as well as mentioning recent progress. In Section 4.3, we review the notion of non-Markovianity based on CPF independence, which is operationally motivated and yet does overcome the limitations of previous approaches. In Section 5, we briefly review some of the aspects of non-Markovian dynamics in experimental settings. We conclude in Section 6 with a brief discussion of the necessary and sufficient criteria for a witness and measure of non-Markovianity for any arbitrary quantum stochastic dynamics and provide a note on future prospects.

2 Part I: Two-time quantum dynamical maps and non-Markovianity

2.1 The master equation

Traditionally, the reduced dynamics of a system coupled to an environment is described by a Nakajima–Zwanzig master equation, also called the time-non-local equation, which takes the form:

$\dot{\rho }\left(t\right)=-\frac{i}{\hslash }\left[H_S,\rho \left(t\right)\right]+{\int }_{t_0}^t{\mathcal{K}}_{t,\tau }\left[\rho \left(\tau \right)\right]d\tau ,(1)$

where ∀t ≥ τ ≥ 0, $\dot{\rho }=\frac{d\rho }{dt}$, and H_S is the system Hamiltonian. The linear map ${\mathcal{K}}_{t,\tau }$ incorporates the non-Markovian memory effects that may be present in the system’s evolution. One may go from the time-non-local equation to a time-local one by assuming that there exists a linear map Φ which is invertible at all times, i.e., ΦΦ⁻¹ = I, such that (Andersson et al., 2007):

$\begin{array}{ll}\hfill \dot{\rho }\left(t\right)& ={\int }_{t_0}^{t}d\tau \left({\mathcal{K}}_{\tau ,t}◦{\mathrm{\Phi }}_{\tau }\right)\left[\rho \left(0\right)\right]\hfill \\ \hfill & ={\int }_{t_0}^{t}d\tau \left({\mathcal{K}}_{\tau ,t}◦{\mathrm{\Phi }}_{\tau }◦{\mathrm{\Phi }}_t^{-1}\right){\mathrm{\Phi }}_t\left[\rho \left(0\right)\right]={\mathcal{L}}_t\left[\rho \left(t\right)\right],\hfill \end{array}(2)$

where ${\mathcal{L}}_t$ is the time-local generator or the Lindbladian, which is a linear super-operator on the space of density operators. When the corresponding dynamical map is non-invertible, it is not necessary that a time-local master equation should exist (Andersson et al., 2007), although one may make use of the Moore–Penrose pseudo-inverse (Rivas et al., 2014) or generalized inverse and still be able to construct a generator, at least for divisible dynamics (Chakraborty and Chruściński, 2021). In other words, the existence of a master equation is sufficient to imply the existence of a corresponding dynamical map; however, the converse is not true (Li et al., 2018).

In order to arrive at an exact Lindbladian $\mathcal{L}$, one uses the famous Born–Markov (BM) approximation (see Section 2.2), under which the time-local evolution of the open system is described by the famous Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) equation (Sudarshan et al., 1961a; Lindblad, 1976), which in its canonical form reads:

$\dot{\rho }=\mathcal{L}\left[\rho \right]=\sum _j{\gamma }_j\left(L_j\rho L_j^{†}-\frac{1}{2}\left\{L_j^{†}{L}_j,\rho \right\}\right).(3)$

Here, $\dot{A}=\frac{dA}{dt}$ for any time-continuous operator A and the linear operators L_j are called the Lindblad operators or simply the jump operators. The dynamics described by Eq. 3 are referred to as time-homogeneous Markovian. Generally, the decay rates γ_j may be time-dependent. In this case, the BM approximation does not hold, but the rotating approximation is retained, so that the master equation modifies to the time-dependent GKSL-like equation (in the canonical form):

$\dot{\rho }=\mathcal{L}\left(t\right)\left[\rho \right]=\sum _j{\gamma }_j\left(t\right)\left(L_j\left(t\right)\rho L_j^{†}\left(t\right)-\frac{1}{2}\left\{L_j^{†}\left(t\right)L_j\left(t\right),\rho \right\}\right).(4)$

Now the jump operators themselves are time-dependent along with the decay rates γ_j(t). The process in Eq. 4 is termed time-inhomogeneous Markovian when all the decay rates γ_j(t) are positive for all times. When at least one of the decay rates is negative for a certain interval of time-evolution, then the process is termed non-Markovian (Garraway, 1997; Breuer and Petruccione, 2002).

The price one pays for going from a non-local to a local description is that the generator may become highly singular (Chruściński and Kossakowski, 2010), which makes the solution to dynamics analytically hard. Indeed, the non-local equation might be more natural and easier to handle in certain physical situations (see Megier et al., 2020a; Megier et al., 2020b). The distinction between the notions of Markovianity in Eqs 3, 4 becomes clearer when one looks at the properties of the corresponding dynamical maps, which we discuss next.

2.2 Quantum dynamical maps

From a quantum information theoretic perspective, the general time evolution of a quantum system is described by a quantum dynamical map, which takes density operators to density operators. Since the environment is generally a many-body system with many degrees of freedom, it becomes difficult for an experimenter to fully control it. Therefore, studying the reduced dynamics of the system in a consistent manner becomes useful.

Figure 1 depicts a simple example of an open quantum system, namely, qubit interacting with an environment. Let us denote the system Hamiltonian (also called the free Hamiltonian) as H_S and the environment Hamiltonian as H_E. The interaction Hamiltonian H_int determines the nature of S-E interaction and the coupling with the environment. The total S-E evolution may be represented by a global unitary $U=\exp \{-\frac{i}{\hslash }(H_S+H_E+H_{\mathit{int}})t\}$. The effect of the environment on the system is often called quantum noise in the context of quantum information processing and the open-system evolution is termed noisy evolution, in contrast to closed-system evolution, which is unitary.

FIGURE 1

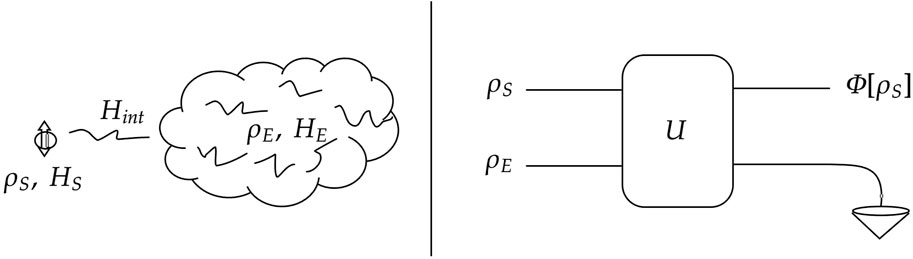
FIGURE 1. Left: A simple representation of a qubit interacting with environment degrees of freedom. Right: A simple model of quantum operation after tracing out the environment from the global unitary U. Here, ρ_S and ρ_E are system and environment states and H_S, H_E, and H_int are system, environment, and S-E interaction Hamiltonians, respectively.

Tracing out the environment degrees of freedom gives rise to the operator-sum representation of the effect of noise on the system, which falls under the broad formalism of quantum operations. Mathematically, the effect of the environment of the system is represented by a set of linear operators on the system, called the Kraus operators, and the reduced dynamics of the system is obtained as follows:

$\rho \left(t\right)={\text{Tr}}_E\left[U\left({\rho }_S\left(0\right)\otimes {\rho }_E\right)U^{†}\right]=\sum _j\left.⟨e_j\right|U\left({\rho }_S\left(0\right)\otimes \left|e_0\right.⟩\left.⟨e_0\right|\right)U^{†}\left|e_j\right.⟩,(5)$

where the states $\{\left|e_j\right.⟩\}$ represent environment degrees of freedom. Equivalently, Eq. 5 can be written for any input system state ρ in the so-called Kraus form (Sudarshan et al., 1961b; Kraus, 1971; Choi, 1975; Kraus et al., 1983):

$\rho \left(t\right)=\mathrm{\Phi }\left(t\right)\left[\rho \right]=\sum _j{K}_j\left(t\right)\rho K_j^{†}\left(t\right).(6)$

Here, $K_j\equiv \left.⟨e_j\right|U\left|e_0\right.⟩$ are called the Kraus operators, which obey ${\sum }_j{K}_j^{†}{K}_j\le I$. This operator-sum representation is an important and powerful tool today in the context of quantum information and computation (Nielsen and Chuang, 2010). The map Φ in Eq. 6 obeys the time-homogeneous (or time-independent) master Eq. 3, i.e., $\dot{\mathrm{\Phi }}=\mathcal{L}[\mathrm{\Phi }]$, whose solution is given by $\mathrm{\Phi }=\exp \{t\mathcal{L}\}$, which is a one-parameter quantum dynamical semigroup. Similarly, a two-parameter map Φ(t, t₀) [or Φ(t) for simplicity, setting t₀ = 0] obeys a master Eq. 4 of the form $\dot{\mathrm{\Phi }}(t)=\mathcal{L}(t)[\mathrm{\Phi }(t)]$, whose solution is given by:

$\mathrm{\Phi }\left(t,t_0\right)=\mathcal{T}\exp \left\{{\int }_{t_0}^t\mathcal{L}\left(\tau \right)d\tau \right\},(7)$

where $\mathcal{T}$ is the time-ordering operator. In a sense, a map that is derivable from a given generator depends on the nature of $\mathcal{L}$.

One must note that Eqs 3, 4, 6 are derived after assuming that the S-E state factors out at t = 0, which need not be the case generally. Furthermore, the environment state ρ_e is assumed to be fixed for all times, in which case the BM approximation holds. Under the time-coarse-grained weak coupling limit, the evolution quickly “forgets” initial S-E correlations and tends to the Lindblad form (Royer, 1996). The existence of the time-independent Lindblad form in Eq. 3 implies the following equivalent statements. First, the environment auto-correlation function is a delta function and corresponds to the white noise approximation. There is no back-action on the system due to the static environment state, which also means that τ_E ≪ τ_S, where τ_E is the environmental correlation time and τ_S is the system relaxation time. In other words, the environment cannot store any information about the system’s past evolution; this is the famous BM approximation. Second, the system uniformly couples to all the degrees of freedom of the environment. Third, the Lindbladian $\mathcal{L}$ is time-independent and the corresponding solution to the equation $\dot{\mathrm{\Phi }}(t)=\mathcal{L}[\mathrm{\Phi }(t)]$ is $\mathrm{\Phi }(t)=\exp \{t\mathcal{L}\}$, which is a semigroup satisfying the property Φ(t + τ) = Φ(t)Φ(τ) for all 0 ≤ τ ≤ t.

Historically, any process that deviates from semigroup structure has been termed non-Markovian (Breuer et al., 2016a). Later developments in the quantum information community have indicated that this is not the complete story, as we will elaborate in the following sections.

2.3 Measures of non-Markovianity: Spatial domain

2.3.1 CP-indivisibility

Divisibility is a property of dynamical maps that allows us to write a map as a concatenation of intermediate maps (Wolf and Cirac, 2008; Wolf et al., 2008; Rivas et al., 2010; Chruściński et al., 2011; Chruściński and Maniscalco, 2014; Chruściński et al., 2018; Davalos et al., 2019). In the classical case, a divisible (hence Markovian) stochastic process is given by concatenation of transition matrices. As far as the traditional approach is concerned, there is no known way of carrying the classical definition of non-Markovianity over to the quantum case. However, an approach based on divisibility states that a map Φ(t, 0) = Φ(t, s)Φ(s, 0) is CP-indivisible if the intermediate map Φ(t, s) is not completely positive (NCP) in the sense that at least one of the eigenvalues of the matrix:

$\chi =\left(\mathrm{\Phi }\left(t,s\right)\times I\right)\left[\left|\psi \right.⟩\left.⟨\psi \right|\right](8)$

is negative, where χ is called the Choi state (Choi, 1975) or Sudarshan B matrix (Sudarshan et al., 1961a), which is dual to the intermediate map Φ(t, s), and $\left|\psi \right.⟩=\frac{1}{\sqrt{2}}(\left|00\right.⟩+\left|11\right.⟩)$ is a maximally entangled state. Based on the aforementioned considerations, the Rivas–Huelga–Plenio (RHP) measure of non-Markovianity was introduced by Rivas et al. (2010):

${\mathcal{N}}_{\text{RHP}}={\int }_{0;\chi \left(t,\tau \right)<0}^{t_{\text{max}}}g\left(t\right)dt;g\left(t\right)=\underset{\tau \to 0^{+}}{\lim }\frac{\Vert \chi \left(t,\tau \right){\Vert }_1-1}{\tau },(9)$

where χ is the Choi matrix such that whenever g(t) > 0, the divisibility condition is broken, and the time integral over the positive regions of g(t) quantifies the quantum memory in the dynamics. Note that ${\mathcal{N}}_{\text{RHP}}$ goes up to infinity, hence requiring a suitable normalization so that it falls in the interval {0, 1}, implying that for Markov processes ${\mathcal{N}}_{\text{RHP}}=0$.

In fact, for any finite d-dimensional open system, the RHP measure in Eq. 9 is equivalent to the Hall–Cressor–Li–Anderson (HCLA) measure given by Hall et al. (2014)and Shrikant et al. (2018):

${\mathcal{N}}_{\text{RHP}}=\frac{d}{2}{\mathcal{N}}_{\text{HCLA}};{\mathcal{N}}_{\text{HCLA}}=-{\int }_{0;\gamma \left(t\right)<0}^{t_{\text{max}}}\gamma \left(t\right)dt,(10)$

where the integration is carried over only to the negative regions of the time-dependent decay rate γ(t). Historically, it has been understood that, when maps generating the dynamics deviate from having a semigroup structure, one speaks of non-Markovianity (Breuer et al., 2016a). The condition γ_j(t) ≥ 0 pertains to the Markovian approximation for the time-dependent noisy dynamics, and the corresponding dynamical maps do not belong to a semigroup; such processes are termed time-dependent Markovian. Note that the dynamics represented by the Lindblad form in Eq. 3 is strictly Markovian (Hall et al., 2014). When the decay rates in Eq. 4 are temporarily negative, the corresponding dynamical maps are no longer CP-divisible.

2.3.2 Information back-flow

As an open system evolves, it generally sets up correlations with the environment and loses its information content irreversibly. However, this is true only when the system couples weakly to the environment. Under the strong coupling limit, the information might periodically return to the state from the environment, leading to information back-flow. This also means that the environment remembers the history of the evolution of the system. We briefly review here the Breuer–Laine–Piilo (BLP) approach (Breuer et al., 2009) to quantify this information back-flow based on the trace distance.

One may find a distance measure on the space of density operators that is contractive under the given CPTP map. Since the matrix trace norm is known to be CP-contractive under a CPTP map (Nielsen and Chuang, 2010), the trace distance is one such natural candidate¹. Mathematically, the trace distance is defined as:

$\mathcal{D}\left({\rho }_1,{\rho }_2\right)=\frac{1}{2}\Vert {\rho }_1-{\rho }_2{\Vert }_1,(11)$

where $\Vert A{\Vert }_1=\text{Tr}[\sqrt{A{A}^{†}}]$ is the trace norm of an operator A. A map Φ(t₂, t₀), that takes a density operator from t₀ to t₂, is said to be Markovian if it satisfies the following data processing inequality:

$\mathcal{D}\left(\mathrm{\Phi }\left[{\rho }_1\right],\mathrm{\Phi }\left[{\rho }_2\right]\right)\le \mathcal{D}\left({\rho }_1,{\rho }_2\right),(12)$

for all times, where Φ[ρ] is given by Eq. 6.

The breakdown of the monotonicity of trace distance shown in Eq. 12 between any two orthogonal initial states under a CPTP map has been used as a witness of non-Markovianity. The decrease in the non-orthogonality of the states is interpreted as the back-flow of information from the environment to the system. Note that, when there is information back-flow, the intermediate map Φ(t₂, t₁) is not even positive, which in turn implies that the dynamical map Φ(t₂, t₀) = Φ(t₂, t₁)Φ(t₁, t₀) is positive (P-) indivisible (Chruściński et al., 2011; Chruściński and Maniscalco, 2014). This is equivalent to saying that $\frac{d}{dt}\Vert \mathrm{\Phi }[({\rho }_1-{\rho }_2)]{\Vert }_1\ge 0$. Note that complete positivity of the map Φ(t₂, t₀) requires that the trace distance only decreases at t = 0, but it can increase and decrease for t > 0 due to P-indivisibility.

Quantum non-Markovianity in the sense of P-indivisibility can be quantified as follows (Breuer et al., 2009):

${\mathcal{N}}_{\text{BLP}}≔\underset{{\rho }_1,{\rho }_2}{\mathrm{m}\mathrm{a}\mathrm{x}}{\int }_{\frac{d\mathcal{D}}{dt}>0}dt\frac{d\mathcal{D}}{dt},(13)$

where integration is carried out over the positive slope of $\mathcal{D}$. Note that this criterion is only sufficient but not necessary, since it might fail as a witness of memory for some non-unital channels (Liu et al., 2013b; Chruściński et al., 2017), as well as for certain unital channels (Hall et al., 2014). In other words, P-indivisibility implies CP-indivisibility, but the converse may not be true.

Finally, we may note that, as far as the revival of quantum information and correlations is concerned, this is also possible when the environment is classical and therefore cannot store information about the system. In other words, for the revival of information to take place, the environment need not be quantum. This observation calls for attention on re-evaluating the notion of S-E back-action (Xu et al., 2013).

2.3.3 Correlation-based measures

We know that quantum mechanics allows for various forms of correlations, namely, non-local correlations (Brunner et al., 2014) that violate Bell inequalities, steering (Uola et al., 2020), entanglement (Horodecki et al., 2009), entropic accord (Szasz, 2019), and quantum discord (Modi et al., 2012). While the RHP measure discussed in Eq. 9 is based on entanglement, there exist various proposals based on different measures of correlation, such as quantum discord (Alipour et al., 2012), mutual information (Luo et al., 2012), and accessible information (Fanchini et al., 2014; Haseli et al., 2014; De Santis et al., 2019). Interestingly, some works have shown a peculiar relationship between non-Markovianity and certain forms of correlations, for example, quantum discord and non-Markovianity (Mazzola et al., 2011; Alipour et al., 2012). It has been shown that a measure based on mutual information between the reduced system and an ancilla detects the range of non-Markovianity similar to the BLP approach (Luo et al., 2012). Similar assertions may be made for any measure based on the correlation between the system and an ancilla, for example, the one proposed by Rivas et al. (2010), in which entanglement is used to quantify non-Markovianity. However, it must be noted that some of these may be easier to calculate than others. For instance, correlations between the system and an ancilla might be simpler compared to quantum discord between system and environment states, which requires full knowledge of the S-E dynamics (Alipour et al., 2012).

As we have seen, a number of measures and witnesses have been proposed based on correlations in space. However, recently, a few works have made use of correlations in time to witness and measure non-Markovianity, which we discuss up in the next sub-section.

2.4 Measures of non-Markovianity: Temporal domain

As previously noted, the (spatial) correlations form a hierarchy. Quantum temporal correlations also do this, as shown recently by Ku et al. (2018), with the temporal non-locality (Leggett and Garg, 1985), temporal steering (Chen et al., 2014), and temporal non-separability (Fitzsimons et al., 2015) of the PDM framework forming the hierarchy. In the same paper, these authors also showed that temporal steering is a form of weak direct cause, while temporal non-separability forms a stronger form of direct cause in quantum mechanics. Interestingly, temporal steering has been quantified by the TSW, which has been proven to be contractive under a divisible CPTP map and has been used to quantify quantum non-Markovianity by Chen et al. (2016). Here, we briefly review the measure based on the TSW and the causality measure based on the PDM.

2.4.1 Temporal steering

Quantum steering is a way to prepare a part of an entangled bipartite state by making measurements on the other. In spatial steering, Alice performs a positive operator-valued measure (POVM) on her system. Bob does not trust Alice or her apparatus and wishes to distinguish between the correlations established due to the true manipulation of his local state and that due to underlying classical local hidden variables.

Similar to the steering in space with a given spatially entangled state, one may steer a state in time by making a measurement on the input state and sending it via a quantum channel followed by a complete quantum state tomography of the output state at the end of the channel. Now, we shall introduce the notion of the TSW. Alice performs a POVM measurement on an input state ρ at t = 0, transforming it into:

${\rho }_{a|x}=\frac{{\mathrm{\Pi }}_{a|x}\rho {\mathrm{\Pi }}_{a|x}^{†}}{p\left(a|x\right)},(14)$

where $p(a|x)=\text{Tr}[{\mathrm{\Pi }}_{a|x}\rho {\mathrm{\Pi }}_{a|x}^{†}]$ is the probability that an outcome a occurs given that Alice preforms a measurement in the basis x. Now, the state ρ_a|x is sent to Bob down a noisy quantum channel Φ for a time t. When Bob receives the state at t, he performs a quantum state tomography to get the state ${\sigma }_{a|x}(t)=\mathrm{\Phi }\left[{\sigma }_{a|x}\right.(0)$. We may call the set of states σ_a|x(t) temporal assemblages, and let the unnormalized assemblage be σ_a|x(t) ≡ p (a|x)σ_a|x. Now, by assumption, Bob does not trust Alice or her devices, and he wants to distinguish the correlations due to Alice’s measurements from the correlations that might have originated from a hidden variable λ, making the correlations to satisfy locality in time and realism. Therefore, we may represent the correlations that might be produced by such classical origins as:

${\sigma }_{a|x}^{US}\left(t\right)=\sum _{\lambda }P\left(\lambda \right)P\left(a|x,\lambda \right){\sigma }_{\lambda },(15)$

where ${\sigma }_{a|x}^{US}(t)$ is the unsteerable assemblage and P (a|x, λ) is the probability that an outcome a occurs given that Alice makes a measurement x, and λ is the hidden variable that might have influenced the outcome, in which case Bob will be able to write down his assemblage in the form of Eq. 15, and when he cannot, then he is sure that the state is prepared by Alice’s measurement. In this context, a measure of temporal steering was introduced by Chen et al. (2016) called the TSW. In order to define the TSW, consider a convex mixture:

${\sigma }_{a|x}\left(t\right)=w{\sigma }_{a|x}^{US}\left(t\right)+\left(1-w\right){\sigma }_{a|x}^S\left(t\right)\forall a,x.(16)$

Clearly, σ_a|x(t) is an assemblage that might contain both unsteerable and steerable correlations, with the constraint 0 ≤ w ≤ 1. The TSW for a given assemblage σ_a|x(t) is defined by:

$W^{\text{TS}}=1-w^{\prime },(17)$

where w′ is the maximum value of w. The TSW may be interpreted as the minimal steerable resources required to reproduce temporal steerable assemblage, i.e., W^TS = 0 and 1 for minimal and maximal steerability, respectively. w′ may be obtained by semi-definite programming:

$\begin{array}{ll}\hfill \text{Find}{w}^{\prime }& =\text{max}\text{Tr}\sum _{\lambda }w{\sigma }_{\lambda },\hfill \\ \hfill \text{subject\hspace{0.17em}\hspace{0.17em}to}& \left({\sigma }_{a|x}\left(t\right)-\sum _{\lambda }{q}_{\lambda }\left(a|x\right)w{\sigma }_{\lambda }\right)\ge 0\forall a,x\hfill \\ \hfill & w{\sigma }_{\lambda }\ge 0\forall \lambda ,\hfill \end{array}(18)$

where q_λ(a|x) are the extremal values of P_λ(a|x).

Now, under the noisy quantum channel, these correlations deteriorate, and Chen et al.(2016) showed that W^TS is non-increasing under local operations. Therefore, we have the monotonicity condition:

$W_{\rho }^{\text{TS}}\ge W_{\mathrm{\Phi }\left[\rho \right]}^{\text{TS}}.(19)$

A Markov process satisfies the aforementioned condition, and a non-Markovian process violates it. Given this fact, a measure of non-Markovianity is nothing but the area under the positive slope of $W_{\mathrm{\Phi }[\rho ]}^{\text{TS}}$:

${\mathcal{N}}_{\text{TSW}}={\int }_{t=0;\frac{d{W}^{\text{TS}}}{dt}>0}^t\frac{d{W}^{\text{TS}}}{dt}dt,(20)$

which, by the factor of $\frac{1}{2}$ is equivalent, to:

$N≔{\int }_{t_0}^{t_{\text{max}}}\left|\frac{d{W}^{\text{TS}}}{dt}\right|dt+\left(W_{t_{\text{max}}}^{\text{TS}}{W}_{t_0}^{\text{TS}}\right).(21)$

It is important to mention that ${\mathcal{N}}_{\text{TSW}}$ is only a sufficient and not a necessary condition for the non-Markovianity of Φ. There may be channels that will be detected as Markovian by this measure, while other measures may detect them as non-Markovian. The breakdown of the monotonicity of the TSW may be interpreted as information back-flow from the environment to the system; hence, this measure captures the range of memory effects similar to the BLP approach.

2.4.2 Pseudo-density matrix

Recently, attempts have been made to define states across time, similar to the states defined in space (Cotler et al., 2018; Zhang et al., 2020; Zhang, 2021). It has been shown that both these states have different structures, and a construction by Fitzsimons et al. (2015) and Pisarczyk et al. (2019) called the PDM was developed, which is a state correlated in spacetime, allowing for a treatment of correlations in space and time on an equal footing. However, one should note that the framework is ambiguous for systems of dimensions other than prime power (Horsman et al., 2017).

Recently, Utagi (2021) defined a measure for non-Markovianity based on temporal correlation in the PDM. Utilizing the fact that the most general PDM is constructed by making measurements before and after a system passes through a quantum channel, one could quantify quantum non-Markovianity in the quantum channel in a straightforward way. Here, for simplicity, we consider a qubit across time evolved through a quantum channel. Let ρ be the input state and Φ(t_B, t_A) a quantum channel that takes a density operator ρ_A on $\mathcal{L}({\mathcal{H}}_A)$ at time t_A to an operator ρ_B on $\mathcal{L}({\mathcal{H}}_B)$ at time t_B. Then, the two-point PDM is given by:

$R_{AB}=\left(I\otimes \mathrm{\Phi }\right)\left[\left\{\rho \otimes \frac{I}{2},\mathsf{s}\mathsf{w}\mathsf{a}\mathsf{p}\right\}\right](22)$

where $\mathsf{s}\mathsf{w}\mathsf{a}\mathsf{p}≔\frac{1}{2}{\sum }_{i=0}^3{\sigma }_i\otimes {\sigma }_i$, $\{\widehat{a},\widehat{b}\}=\widehat{a}\widehat{b}+\widehat{b}\widehat{a}$ is the anti-commutator of operators $\widehat{a}$ and $\widehat{b}$, and σ_i are Pauli-X, -Y, and -Z operators with σ₀ = I. In fact, it can be shown (Horsman et al., 2017) that the two-point PDM can be written as:

$R_{AB}=\frac{1}{2}\left({\rho }_A\otimes \frac{I_B}{2}{\chi }_{AB}+{\chi }_{AB}{\rho }_A\otimes \frac{I_B}{2}\right),(23)$

where χ_AB is the Choi state of the channel Φ, which derives from the so-called start product. One must note that the PDM is Hermitian and has unit trace but is not positive semi-definite when it is constructed out of measurements made in time. The reason is that this framework considers the tensor product over the same Hilbert space of the input and output density operators in order to define a state across time. However, under partial trace, it describes a positive semi-definite operator at each instant of time, which is consistent with the current formulation of quantum mechanics.

A measure of temporal correlations in the PDM has been defined by Pisarczyk et al. (2019):

$F={\log }_2\Vert R_{\text{AB}}{\Vert }_1,(24)$

which implies that, when F > 0, the state R_AB is temporally correlated. Since F is non-increasing under local quantum operations, for a Markovian channel Φ, the following condition holds:

$F_{\mathrm{\Phi }\left[\rho \right]}\left(t\right)\ge F_{\mathrm{\Phi }\left[\rho \right]}\left(t+\tau \right),(25)$

with t + τ ≥ t. A non-Markovian (or CP-indivisible) channel breaks the monotonicity condition (Eq. 25). Following Rivas et al.(2010) and Chen et al.(2016), a measure has been proposed by Utagi (2021) as the area under the positive slope of F_Φ[ρ]t):

${\mathcal{N}}_{\text{causality}}≔\underset{\rho }{\mathrm{m}\mathrm{a}\mathrm{x}}{\int }_{{\sigma }_{\left(\rho ,\mathcal{E},t\right)}>0}dt{\sigma }_{\left(\rho ,\mathcal{E},t\right)},(26)$

where

${\sigma }_{\left(\rho ,\mathcal{E},t\right)}=\frac{dF}{dt}.$

The aforementioned definition, by a factor of $\frac{1}{2}$, is equivalent to:

${\mathcal{N}}_{\text{causality}}≔\underset{\rho }{\mathrm{m}\mathrm{a}\mathrm{x}}{\int }_{t_0}^{t_{\text{max}}}\left|\frac{dF}{dt}\right|dt+\left(F_{t_{\text{max}}}-F_{t_0}\right).(27)$

The integral (Eq. 27) is such that, for a non-Markovian process, the derivative of F is positive and ${\mathcal{N}}_{\text{causality}}>0$. For a time-dependent Markovian (or CP-divisible) process, the derivative of F is negative and hence ${\mathcal{N}}_{\text{causality}}=0$. It has been shown, using a phenomenological process, that ${\mathcal{N}}_{\text{causality}}>0$ corresponds to the negativity of the decay rate in the master equation, which is equivalent to the RHP definition. It has also been shown that, for a pair of states optimal for the process under consideration, ${\mathcal{N}}_{\text{causality}}>0$ also corresponds to information back-flow, and hence is understood to be equivalent to the BLP definition. This equivalence is due to the fact that the process considered in Utagi (2021) has a single jump operator in the Lindbladian. Interestingly, however, Utagi (2021) showed that this equivalence between the PDM-based measure and the BLP measure breaks down when non-Markovianity solely originates from the non-unital part of the channel.

Here again, we mention that the PDM-based non-Markovianity measure is a sufficient but not a necessary criterion for non-Markovianity. However, Ku et al. (2018) showed that PDM correlations contain a stronger form of quantum direct cause, while temporal steerable correlations contain a weaker form. There are certain advantages to using the PDM-based measure over the TSW. The PDM-based measure (Eq. 27) does not require any optimization procedure, and it is easy to compute. However, both measures do not require optimization over the input states as the BLP measure requires, making these measures relatively easy to compute. A limitation of the PDM is that, in its current form, it is ambiguously defined for a system with a dimension other than prime power (Horsman et al., 2017). The full validity of these two measures requires further study.

2.5 Equivalence of the measures and regimes of failure

In fact, there exists a hierarchy among divisible maps (Chruściński et al., 2011; Chruściński and Maniscalco, 2014), in which if a process is non-Markovian according to the BLP measure, then the corresponding map Φ(t, 0) is termed positive (P-) indivisible even when the intermediate map Φ(t, s) is not positive, in the sense that it takes a positive state to a negative state. In contrast, a CP-indivisible map can be P-divisible. This suggests that these definitions need not be equivalent, which is the case for an “eternally” non-Markovian Pauli channel (Hall et al., 2014), for example, which is CP-indivisible but P-divisible. However, for certain non-unital channels, the BLP measure fails and may require some modification (Liu et al., 2013b). The BLP indicator essentially fails when the environment evolves independent of the system (Budini, 2018a). It is interesting to note that, when there is only a single decoherence channel, which corresponds to single jump operator in the Lindbladian, both CP- and P-indivisibility definitions coincide (Breuer et al., 2016a) for any non-Markovian process. P- and CP-divisibility-based witnesses, in general, coincide for bijective maps (Bylicka et al., 2017). Interestingly, Chakraborty and Chruściński (2019) showed that information back-flow and CP-indivisibility are equivalent notions for any open qubit evolution. Recently, it has been noted that the negativity of the decay rate is not sufficient to capture CP-indivisibility for non-invertible maps (Chruściński et al., 2018), particularly when there are multiple time-dependent decay rates in the master equation. Interestingly, P- and CP-divisibility as notions of Markovianity coincide for multi-level amplitude damping processes (Chruściński et al., 2022).

It must be noted that the PDM contains correlations that characterize a form of strong direct quantum cause, while temporal steerable correlations contain a weaker form. Chen et al. (2016) noted that the measure based on the TWS is necessary but sufficient to detect non-Markovianity. Therefore, it remains an open question as to whether these measures for non-Markovianity vary in their ability to detect weaker and stronger forms of non-Markovianity, as the RHP and BLP measures, respectively, do. So far, it is clear that the causality-based measure of Utagi (2021) is sufficient, but it is not yet known whether it is also necessary as a non-Markovianity indicator.

However, these definition and measures, respectively, detect and quantify the non-Markovianity of only CP- and P-indivisible processes. However, it is known that there exist non-Markovian processes with a colored environmental memory spectrum, hence being non-Markovian (Yu and Eberly, 2010; Kumar et al., 2018) but CP-divisible. These processes, even though CP-divisible, can delay entanglement sudden death because of the quantum memory effect. It has also been noted that, when the generator of the dynamics depends on the initial time, this leads to a kind of memory effect in the dynamics on the level of the master equation even when the dynamics are CP-divisible (Chruściński and Kossakowski, 2010; Benatti et al., 2012; Utagi et al., 2020b).

An interesting notion of memorylessness (or Markovianity) was proposed by Utagi et al. (2020b), in which a dynamical map is said to be Markovian (more precisely a semigroup) if the dynamical map is independent of the initial time. This notion was termed “temporal self-similarity” in the sense that the form of the map remains the same throughout the dynamics. This notion is, in fact, commensurate with the time-homogeneity of semigroup evolution. The motivation behind this notion was to find a witness and measure of non-Markovianity for certain kinds of noise, such as Ornstein–Uhlenbeck and power-law noise, that have a colored memory spectrum (Kumar et al., 2018) but are CP-divisible, and hence undetectable by the RHP measure. The measure based on the deviation from semigroup structure proposed by Utagi et al. (2020b) is as follows.

From Eq. 7, one may obtain the infinitesimal map:

$\left(\delta \mathrm{\Phi }\right)\rho \left(t\right)=\mathcal{T}\exp \left({\int }_t^{t+dt}\mathcal{L}\left(\tau \right)d\tau \right)\rho \left(t\right)=\left(1+\mathcal{L}\left(t\right)dt\right)\rho \left(t\right).(28)$

From Choi–Jamiołkowski (CJ) isomorphism, the Choi state χ_Φ(t) of the infinitesimal map (Eq. 28) is found to be $(d\left|{\psi }^{+}\right.⟩\left.⟨{\psi }^{+}\right|+{\chi }_{\mathcal{L}(t)}dt)$, where χ_A denotes the Choi state of the operator A in question and $\left|{\psi }^{+}\right.⟩\equiv d^{-1/2}{\sum }_i\left|i,i\right.⟩$ is the maximally entangled d-dimensional state. Some simple algebra gives one the Choi state of the generator. The authors use the time-averaged distance between the Choi states of the time-independent $(\mathcal{L})$ and time-dependent $(\mathcal{L}(t))$ generators to quantify non-Markovianity, given as:

${\mathcal{N}}_{\text{SSS}}=\underset{\gamma }{\min }\frac{1}{T}{\int }_0^T\Vert \mathrm{\Delta }L{\Vert }_{1}dt,(29)$

where T represents some time interval. Here, $\mathrm{\Delta }L\equiv \delta {\chi }_{\mathrm{\Phi }(t)}-\delta {\chi }_{\mathrm{\Phi }}=({\chi }_{\mathcal{L}(t)}-{\chi }_{\mathcal{L}})dt$. The minimization over time-independent $\mathcal{L}$ leads to the minimization over all possible time-independent decay rates γ. Positive ${\mathcal{N}}_{\text{SSS}}$ means that a process is non-Markovian even when it is CP-divisible. This feature makes this measure a sufficient and necessary criterion for non-Markovianity.

Recently, Budini (2018b) and Budini (2019) proposed a definition of non-Markovianity that can detect memory present even in CP-divisible processes (de Lima Silva et al., 2020). Here, the memory effect is associated with the breakdown of CPF independence (or to the existence of CPF correlations), which is calculated using only three (sufficient) consecutive measurements on the system and post-selection on the outcomes. Although past–future independence, shown by Li et al. (2018) to be equivalent to “composability,” and thence to the semigroup structure of the dynamical maps, one may expect that semigroup dynamics generate statistics that obey CPF independence as proposed by Budini (2018b) and Yu et al.(2019).

From this section, one understands that any witness that detects the non-Markovianity of a CP-divisible process is necessary and sufficient. We discuss this in detail in sections 4 and 6.

3 Interlude: The problem of (initial) system-environment correlations

As previously noted, a master equation, under BM approximation, need not exist if the initial S-E correlations are taken into account. Before going into these details, it is pertinent to ask when decoherence actually begins, given that the underlying system evolution is described by a CP map (i.e., assuming no initial S-E correlations). We briefly highlight the relevant literature in the next sub-section and then move on to the issues surrounding the physically viable description of quantum stochastic processes without needing the initial S-E state to be separable.

3.1 S-E correlations, decoherence, and non-Markovianity

It is generally understood that decoherence takes place when the system degrees of freedom “entangle” with that of the environment; hence, entanglement must be necessary for decoherence (Schlosshauer, 2007). However, this common wisdom might be mistaken, as Pernice and Strunz (2011) showed that this holds only when the system state starts out as a pure state. If the system’s initial state is a mixed state, then decoherence may begin well before the system and environment get entangled. This also suggests that classical correlations might suffice for decoherence to take place.

Given that correlations, whether classical or quantum, are responsible for the onset of decoherence, it is interesting to explore the relationship between S-E correlations and non-Markovianity. The earliest notion of quantum non-Markovianity actually goes back to the deviation from semigroup structure, which arises out of the so-called BM approximation (Breuer et al., 2016a), which basically means that the system and environment are weakly coupled for all times.

The connection of S-E correlations with non-Markovianity has attracted the attention of the quantum information community (Devi and Rajagopal, 2011; Breuer et al., 2016a; de Vega and Alonso, 2017; Li et al., 2018). The S-E joint state may start out as a product state, and later, due to strong coupling between the system and environment, there may be certain points in time when the S-E correlations either weaken or even break momentarily, causing the open system dynamics to transition from being Markovian to non-Markovian. It has been noted that the S-E correlations decrease when there is information back-flow from the environment to the system (Mazzola et al., 2012). However, it has also been shown by Pernice et al. (2012) that there need not be any relationship between the decrease in S-E quantum correlations (specifically S-E entanglement) and non-Markovianity. Interestingly, if the environment is classical, there may be maximally non-Markovian evolution without S-E back-action or information flow (Budini, 2018a). When two qubits are independently interacting with a classical random field, there may be revivals of classical correlations, quantum discord, and entanglement between them even when there is no back-action from the environment to qubits (Franco et al., 2012).

3.2 Initial S-E quantum correlations, CP evolution, and non-Markovianity

As previously noted, S-E correlations play a central role in open systems. To describe the reduced dynamics of the system via Lindblad Eq. 3, the joint S-E state is assumed to be factorized, i.e., ρ_s (0) ⊗ ρ_e, at the initial time, and the environment state ρ_E is assumed to be fixed for all times. Now, given that the initial S-E state in not a product, it has been argued that the reduced dynamics of the system are not-CP (Pechukas, 1994; Alicki, 1995; Pechukas, 1995; Shaji and Sudarshan, 2005; Rodríguez-Rosario et al., 2008; Schmid et al., 2019) for some early results. However, it is possible to have physically meaningful not-CP maps, given that the domain of validity is known where such a map would still output a positive state (Jordan et al., 2004). Moreover, Pechukas’s assignment map can be made linear by sacrificing either positivity or reasonable consistency (Rodríguez-Rosario et al., 2010). There have also been arguments for and against vanishing quantum discord as being a necessary and sufficient condition for complete positivity (Shabani and Lidar, 2009; Brodutch et al., 2013; Sabapathy et al., 2013). However, it has been clearly established that, when initial S-E correlations are classical, the reduced dynamics can always be described by a CP map (Rodríguez-Rosario et al., 2008).

Buscemi (2014) argued that, if there are no anomalous information back-flows from the environment to system, it is necessary and sufficient to describe the reduced dynamics of the system by a CPTP map. Interestingly, it has been shown previously that a witness for initial S-E correlations upper bounds the witness of non-Markovianity based on the BLP (or information back-flow) criterion (Rodríguez-Rosario et al., 2012). This prompts further investigations into the problem of initial S-E correlations and non-Markovianity. Recently, Strasberg and Esposito (2018) introduced a measure that quantifies non-Markovianity even when the initial S-E state is entangled. Schmid et al. (2019) argued that initial S-E correlations do not imply the failure of complete positivity, from the point of view of quantum causality. Ringbauer et al. (2015) proposed a method to characterize a superchannel by making measurements on the system alone, even when it is correlated with the environment. A more general result by Paz-Silva et al. (2019) asserts that it is still possible to have a d² (or less) number (i.e., a family) of CP maps describing d-dimensional system evolution with initial S-E (quantum) correlations, i.e., by doing local operations on the system, one could derive a set of CP maps that describe the S-E evolution with the initially correlated state.

This is still an active area of research in which there is no clear consensus concerning the role of initial S-E (quantum) correlations in open system dynamics where complete positivity is paramount. Alipour et al. (2020) proposed a technique that makes use of the correlation parent operator that allows one to write a master equation with the initial correlation within a weak coupling regime. A technique based on adapted projection operators was introduced by Trevisan et al. (2021), in which they applied a perturbative method to model a global S-E evolution that incorporates fully general initial correlations. For other recent attempts that have been made to accommodate initial S-E correlations into a valid theory of open systems, without sacrificing linearity and complete positivity, see Paz-Silva et al. (2019), Pollock et al. (2018b), and Pollock et al. (2018a), who specifically aimed to characterize open system evolution operationally and allow a quantum stochastic process to have an appropriate classical limit. We discuss this further in Section 4.

4 Part II: Multi-time correlations and non-Markovian processes

So far, we have been considering only the two-time parameter dynamical maps that are related to two-time correlation functions of the environment. In fact, the quantum regression hypothesis (QRH) or quantum regression formula (QRF) can be obtained through two-time maps, which helps us relate its satisfaction to the semigroup evolution of the open system under the initial factorized state assumption (Li et al., 2018). However, recent interest has grown in reconsidering quantum multi-time processes (Lindblad, 1979) generalizing the so-called quantum stochastic process (Sudarshan et al., 1961a) in light of operational quantum theory.

4.1 Quantum regression

The QRH or QRF must be invoked for the calculation of multi-time correlation functions, without the knowledge of environmental degrees of freedom, i.e., only with the mean values of the operator on the system Hilbert space alone. However, while non-Markovian evolution must violate the QRH, Markovian evolution (in the sense of CP-divisibility) can also violate the QRH (Guarnieri et al., 2014). Under the weak coupling and singular coupling limit, semigroup dynamics obey the QRH (Davies, 1974; Davies, 1976; Swain, 1981; Dümcke, 1983). It has been shown that the BM approximation implies no-back-action (Swain, 1981), which means that the environment does not evolve due to the interaction with the system, and the S-E state remains factorized for all times. It has been shown that CP-divisible dynamics violate the QRH (Guarnieri et al., 2014). This suggests that even the RHP- or CP-divisibility-based criteria for non-Markovianity, such as the BLP criterion, are also not necessary but sufficient. Therefore, one is tempted to conjecture that violation of the QRH is a necessary and sufficient condition for a quantum stochastic process to be non-Markovian.

4.2 Process tensor

A classical stochastic process (X, t) is a collection of the joint probability distribution of a system’s state:

$P\left(X_j,t_j;X_{j-1},t_{j-1};\cdots ;X_1,t_1;X_0,t_0\right)\forall j\in N,(30)$

which must satisfy Kolmogorov consistency conditions, where X is the random variable defining the process and t_j are the time instances at which X_j outcomes occur with probabilities P (X_j, t_j). Then, a Markov process or chain satisfies the following condition:

$P\left(X_j,t_j|X_{j-1},t_{j-1};\cdots ;X_1,t_1;X_0,t_0\right)=P\left(X_j,t_j|X_{j-1},t_{j-1}\right)\forall j\in N,(31)$

where P (A|B) denotes the probability of obtaining A given B.

It is not straightforward to define similar joint probability distribution in the quantum domain. There is uncertainty regarding the most general way in which one may represent a physical process that also has an operational meaning. Quantum combs formalism is one such method (Chiribella et al., 2009; Pollock et al., 2018b). As opposed to the traditional approach discussed in Section 2, where only two-time correlations are considered to define quantum non-Markovianity, process tensor formalism defines non-Markovianity based on the presence of temporal correlations in a multi-time quantum stochastic process (Pollock et al., 2018a; Pollock et al., 2018b). Such descriptions of open systems might have specific implications for designing information processing tasks in the laboratory, where two-time correlations might not capture the full characteristics of an underlying process.

A quantum process is characterized by j steps, with 0 ≤ j ≤ N, when the system’s state can be predicted at any instant j. The system is subjected to intermediary operations A which may be interrogations, manipulations, unitaries, or CP maps in general, and let {A_j} and {M_j} be the set of local operations and measurements, respectively, on the system. The “process tensor” T_j:0 is a mapping from the sequence of operations (see Figure 2):

${\mathbf{A}}_{j-1:0}≔\left\{A_{j-1};A_{j-1};\cdots A_1;A_0\right\}(32)$

to the state ρ_j:

${\rho }_j=T_{j:0}\left[{\mathbf{A}}_{j-1:0}\right].(33)$

In general, T_j:0 satisfies: i) linearity: $T\left[a\right.\mathbf{A}+b\mathbf{B}=aT[\mathbf{A}]+bT[\mathbf{B}]$; ii) complete positivity, that it is a positive map on an extended space: (T ⊗ I)[A_SA] = ρ_SA ≥ 0; and iii) containment: if j ≥ j′ ≥ k′ ≥ k, then T_j′:k′ is contained in T_j:k, in the sense that the process tensor based on fewer times is not obtained by summing over excessive times, but rather by appending the identity maps for the excessive times.

FIGURE 2

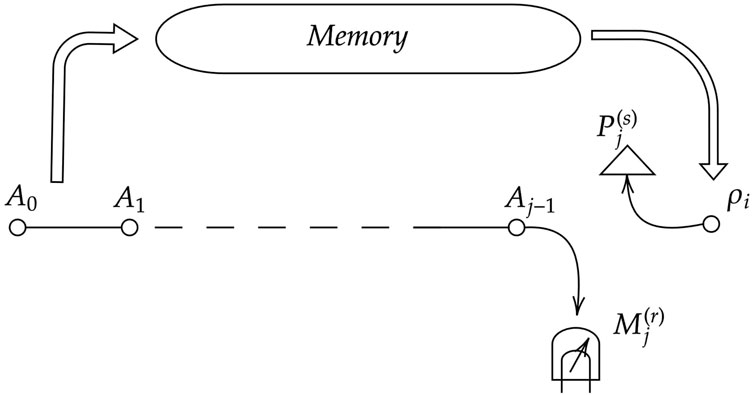
FIGURE 2. Schematic representation of the process tensor framework with memory. A_j are the control operations and $M_j^{(r)}$ and $P_j^{(s)}$ are the measurements and re-prepared states, respectively.

The process tensor can be used to describe open quantum system dynamics. Let ${\mathcal{U}}_{j:j-1}$ be the S-E unitary that acts on S-E space as ${\mathcal{U}}_{k:l}[{\rho }_l^{\mathit{SE}}]=U_{k:l}{\rho }_l^{\mathit{SE}}{U}_{k:l}^{†}={\rho }_k^{\mathit{SE}}$, with $U_{k:l}{U}_{k:l}^{†}=I$, and the system state be given by tracing over the environment ${\rho }_j={\mathrm{Tr}}_E[{\rho }_j^{\mathit{SE}}]$; then, the total dynamics are as follows:

${\rho }_j^{\mathit{SE}}={\mathcal{U}}_{j:j-1}{A}_{j-1}{\mathcal{U}}_{j-1:j-2}\cdots A_1{\mathcal{U}}_{1:0}{A}_0\left[{\rho }_0^{\mathit{SE}}\right],(34)$

where ${\rho }_0^{\mathrm{SE}}$ is the initial S-E state. Note that T_j:0 itself can be given a Kraus decomposition (Pollock et al., 2018a). In an appropriate limit, the process tensor reduces to the conventional two-time maps picture of open system evolution:

${\rho }_j={\mathrm{Tr}}_E\left(U_{j:0}{\rho }_0^S\otimes {\rho }_0^E{U}_{j:0}^{†}\right)={\mathrm{\Phi }}_{j:0}\left[{\rho }_0\right],(35)$

where Φ_j:0 is a CPTP map. Therefore, ρ_j can be obtained from the process tensor by applying the identity as intermediate control operations on the system:

${\rho }_j=T_{j:0}\left[I;I;\cdots I;A_0\right].(36)$

The advantage of using the process tensor framework is that one may map temporal correlations in the process to a many-body entangled state. A j-step process can be mapped to a many-body state via generalized CJ isomorphism:

$T_{j:0}\left[{\mathbf{A}}_{j-1:0}\right]={\mathrm{Tr}}_S\left[{\xi }_{j:0}\left(I_S\otimes A_{j-1}\otimes I\otimes \cdots \otimes A_0\otimes I\left[{\left({\mathrm{\Psi }}^{+}\right)}^{\otimes j-1}\right]\right)\right],(37)$

where the partial trace is over all subsystems except the one corresponding to the output of the T_j:0 and Ψ⁺ is a maximally entangled bipartite density operator. In other words, the action of the process tensor T_j:0 on the sequence of operations A_j−1:0 is equivalent to projecting the Choi state ξ_j:0 onto the Choi state of A_j−1:0. Here, ξ_j:0 is called the generalized Choi state of the j-step process that is mapped to a (2j + 1)-body state that has a matrix-product-operator representation (Perez-Garcia et al., 2007), and the Choi state ξ_j:0 has the bond dimension that is bounded by the effective dimension of the environment (Pollock et al., 2018a).

Given the aforementioned framework, we are in a position to discuss a definition of quantum (non-) Markovianity from an operational point of view. Let us denote the system at time step i as a function of control operations: ρ_i = ρ_i (A_i−1:0). After the measurement, the system is re-prepared in a state $P_j^{(s)}$, selected randomly out of a set $\{P_j^{(s)}\}$. The procedure for measuring and re-preparing the system introduces a “causal break” between the past k ≤ j and future i > j (see Figure 2). Similar to the classical definition, the Markov condition in the quantum regime reads:

${\rho }_i\left(P_j^{\left(s\right)}|M_j^{\left(r\right)};{\mathbf{A}}_{j-1:0}\right)={\rho }_i\left(P_j^{\left(s\right)}\right)\forall \left\{P_j^{\left(s\right)},M_j^{\left(r\right)},{\mathbf{A}}_{j-1:0}\right\}\text{and}\forall i,j\in \left\{0,N\right\}.(38)$

On the contrary, a quantum process is non-Markovian if there exist at least two distinct, independent operation sets $\{M_j^{(r)};{\mathbf{A}}_{j-1:0}\}$ and $\{M_j^{\prime (r^{\prime })};{\mathbf{A}}_{j-1:0}^{\prime }\}$, such that the resulting two conditional states are different:

${\rho }_i\left(P_j^{\left(s\right)}|M_j^{\left(r\right)};{\mathbf{A}}_{j-1:0}\right)\ne {\rho }_i\left(P_j^{\left(s\right)}|M_j^{\prime \left(r^{\prime }\right)};{\mathbf{A}}_{j-1:0}^{\prime }\right).(39)$

The system itself cannot carry the information into the future across the causal breaks. An environment and the S-E correlations carry the information about the initial state of the system across causal breaks (see Figure 2), and this is what is called quantum non-Markovian memory in the process tensor. In order to quantify the memory in the process, one makes use of the mapping from the temporal correlated process tensor to a many-body state via generalized CJ isomorphism. Given the intermediate maps Φ_j:j−1 that take a state from time step j − 1 to j, a Markov process is fully characterized by its Choi state on the tensor product of the initial system state and the Choi states of independent CPTP two-time maps:

$\begin{array}{ll}\hfill {\xi }_{j:0}^{\text{Markov}}& ={\chi }_{j:j-1}\otimes {\chi }_{j-1:j-2}\otimes \cdots \otimes {\chi }_{1:0}\otimes {\rho }_0\hfill \\ \hfill & =\underset{j=1}{\overset{N}{\otimes }}{\chi }_{j:j-1}\otimes {\rho }_0,\hfill \end{array}(40)$

where ρ₀ is the average initial state of the process. In other words, the process is said to be a Markov chain if and only if the process tensor is a product state across time. This allows one to make use of a quasi-distance based measure of non-Markovianity:

$\mathcal{N}=\underset{{\xi }_{j:0}^{\text{Markov}}}{\min }D\left({\xi }_{j:0}\Vert {\xi }_{j:0}^{\text{Markov}}\right),(41)$

which can be interpreted as the minimum distance from the closest Markov process, where D could be any CP-contractive² quasi-distance, such as quantum relative entropy D (ρ‖σ) = Tr [ρ log  ρ − ρ log  σ] (White et al., 2021).

Here, some important remarks are in order. The definition in Eq. 41 is a necessary and sufficient condition for a process to be called non-Markovian; however, the converse may not be true. For example, Milz et al. (2019) recently proposed a notion of “operational divisibility,” which captures the memory effect present in a CP-divisible process. The process tensor is generally sufficient to capture all the notions of non-Markovianity under certain limits; for example, it incorporates BLP- and RHP-based witnesses assuming that all intermediary control operations are identities. It circumvents the problems of the conventional two-time map approach when initial S-E correlations are present; it allows CP, linear dynamics to be reconstructed from measurement data via quantum process tomography (for proofs and further details, see Pollock et al., 2018a). The process tensor also tends to a definition of classical memory when the choice of instruments, as well as the causal breaks, is fixed. It provides a clear operational meaning in addressing the questions of open system evolution by separating the experimenter from the underlying process that is inaccessible, making it a suitable framework to handle information processing tasks in the laboratory. One such situation where one wants to remove certain unwanted memory effects arising from cross-talk was recently studied in detail by White et al. (2022) using the process tensor framework.

Quantum combs, in fact, provide a unified framework to describe quantum channels with classical and quantum memory. Therefore, it is pertinent to ask how one can distinguish such memory effects. Interestingly, Giarmatzi and Costa (2021) used the process matrix framework, proposed by Oreshkov et al. (2012), to “witness” genuinely quantum memory. It is interesting to note that the process tensor can be used to identify genuinely quantum memory effects in an arbitrary process. Considering that a non-Markovian process deviates from a product of marginals, given in Eq. 40, the positive value of entanglement negativity, given by $\underset{{\tau }_B}{\mathrm{m}\mathrm{a}\mathrm{x}}\frac{1}{2}[\Vert {\xi }_{j:0}^{{\tau }_B}{\Vert }_1-1]$, of the Choi state ξ_j:0 gives a measure of the “quantumness” of non-Markovian memory, where τ_B is the partial transpose over some bi-partition, which could be an interval between any two time-steps (White et al., 2021).

4.3 Conditional past–future correlations

The notion of past–future independence as a definition of Markovianity was used by Li et al. (2018) to analyze a hierarchy in the definition of quantum Markovianity. Recently, Budini (2018b) proposed a definition of non-Markovianity based on the violation of CPF independence. Similar to process tensor formalism, CPF independence is generated by the “causal break” in the process via intermediate measurements. Hence, it is claimed that the definition via CPF independence has operational meaning in the traditional approach (Budini, 2022).

In a classical stochastic process, measuring a system at three successive instances t_a < t_b < t_c yields outcomes a → b → c. A Markov process gives rise to factorized joint probability conditioned on immediate past outcomes:

$P\left(a,b,c\right)=P\left(c|b\right)P\left(b|a\right)P\left(a\right),(42)$

where P(a) is the probability that the outcome a occurs and P (b|a) is the probability of b occurring given that a has been learned. Bayes’ rule allows us to formulate the criterion for Markovianity: that given a fixed intermediate state, the future outcomes become statistically independent from the past ones. So, the conditional probability of future event c and past event a given the present b is given by:

$P\left(c,a|b\right)=P\left(c|b\right)P\left(a|b\right).(43)$

This, in fact, can be quantified via the correlation function (Budini, 2018b):

$C_{pf}\equiv {⟨O_c{O}_a⟩}_b-{⟨O_c⟩}_b{⟨O_a⟩}_b,(44)$

where the operator O is specific system property one would want to measure for each system state. Given this, we can write C_pf as:

$C_{pf}=\sum _{ca}\left[P\left(c,a|b\right)-P\left(c|b\right)P\left(a|b\right)\right]O_c{O}_a.(45)$

Here, the sum is over all possible outcomes c ∈ {c₁, c₂, … } and a ∈ {a₁, a₂, … } that occur at $t_c\in \{t_{c_1},t_{c_1}\dots \}$ and $t_a\in \{t_{a_1},t_{a_1}\dots \}$, respectively, with a given, fixed value of b ∈ {b₁, b₂, … }. Generally, a quantum Markov process condition satisfies Eq. 43 in the quantum setting as well, yielding C_pf = 0, which provides a straightforward generalization of the classical definition to the quantum domain.

Calculating the CPF correlation measure for the quantum non-Markovian process boils down to finding the predictive and retrodictive probabilities for given system operators and substituting them in Eq. 45, which we discuss in the following paragraphs.

Let M_a, M_b, and M_c be the measurement operators successively performed on the system at t_a, t_b, and t_c, respectively, with the condition that ${\sum }_j{M}_j^{†}{M}_j=I$, where j = a or b or c. Given that a is in the past of b, the conditional probability P (a|b) is a retrodicted quantum probability. In terms of the measurement operators M_a and the past quantum state ρ ≡ (ρ₀, E_b), this can be written as $P(a|b)=\mathrm{Tr}[E_b{M}_a{\rho }_0{M}_a^{†}{E}_b^{†}]$, where ρ₀ is the initial density matrix and $E_b=M_a^{†}{M}_a$ is the “effect” operator. On the other hand, P (c|b, a) is the standard predictive probability. Therefore, substituting these conditional probabilities in the LHS of Eq. 43, we have:

$P\left(c,a|b\right)=\mathrm{Tr}\left(E_c{\rho }_b\right)\cdot \frac{\mathrm{Tr}\left(E_b{M}_a{\rho }_0{M}_a^{†}\right)}{{\sum }_{a^{\prime }}\mathrm{Tr}\left(E_b{M}_{a^{\prime }}{\rho }_0{M}_{a^{\prime }}^{†}\right)}.(46)$

Assuming that the system evolves under the action of the environment, one may adopt the two-time dynamical (CPTP) map between two successive instances. Then, the conditional probabilities will vary according to the intermediate evolution between measurements as:

$P\left(c,a|b\right)=\mathrm{Tr}\left(E_c{\mathrm{\Phi }}^{\prime }\left[{\rho }_b\right]\right)\cdot \frac{\mathrm{Tr}\left(E_b\mathrm{\Phi }\left[M_a{\rho }_0{M}_a^{†}\right]\right)}{{\sum }_a^{\prime }\mathrm{Tr}\left(E_b\mathrm{\Phi }\left[M_{a^{\prime }}\rho M_{a^{\prime }}^{†}\right)\right]},(47)$

where Φ = Φ(t_b, t_a) and Φ′ = Φ′(t_c, t_b), with ${\mathrm{\Phi }}_t=\exp \{t\mathcal{L}\}$, where $\mathcal{L}$ is the generator of the semigroup dynamics. In general, environment interaction may generate dynamics that are not semigroup and may even be non-Markovian. In this case, the dynamical map Φ(t, t₀) between two successive instances will follow Eq. 7.

The CPF correlation measure has some interesting properties. For a non-Markovian process, either C_pf < 0 or C_pf > 0. Since this criterion witnesses memory in CP-divisible processes, it may be termed a necessary and sufficient condition for non-Markovianity. Furthermore, the process is Markovian if C_pf = 0. The reader is referred to Budini (2018b) for other properties.

5 Quantum non-Markovianity in experiments

It is now well-acknowledged that simulating open quantum systems is important for many technological applications. Memory effects could prove advantageous or disadvantageous for quantum information processing, depending on the task at hand. Therefore, it is imperative to discuss and understand aspects of simulating quantum non-Markovianity in experimental setups. In this section, we present a brief review of experimental realizations of open system dynamics, with a particular focus on experiments also studying signatures of non-Markovianity.

One of the robust methods for simulating open system dynamics is via optical setups (Salles et al., 2008; Cialdi et al., 2017; Rossi et al., 2017; Cuevas et al., 2019). These setups mimic the effect of an environment on a quantum system and have proven effective in experimentally realizing a quantum channel. In Chiuri et al. (2012), the non-Markovian dynamics of a qubit attached to an ancilla and in a simulated environment (an Ising chain, for instance) were experimentally implemented, and the importance of strong S-E correlations in the emergence of non-Markovianity was highlighted. A similar setup was also used in Liu et al. (2018), where a simulated Ising chain in a transverse field was used as the environment to study the arbitrary dephasing dynamics of a photonic qubit. Similar setups to simulate quantum channels have been used to understand the transition from Markovian to non-Markovian dynamics by controlling the S-E coupling (Liu et al., 2011; Chiuri et al., 2012; Fisher et al., 2012; Tang et al., 2012; Lyyra et al., 2022).

We noted previously that an open system (S) coupled to an ancilla (A), while undergoing non-Markovian evolution, establishes quantum correlations with A that vary non-monotonously in time. In Wu et al. (2020), by coupling the polarization degree (system) with the frequency degree (environment), it was experimentally demonstrated that quantum-incoherent relative entropy of coherence (QI-REC) is commensurate with the S-A entanglement, thus establishing a relationship between QI-REC and information back-flow from the environment to the system.

Interestingly, it has been shown via experiments (Farías et al., 2012) that, when a part of a Bell pair interacts with an environment, the dynamics might lead to genuine multipartite entanglement between all the environment degrees of freedom and the initial Bell pair. When there are initial correlations in a composite environment, an open bipartite system interacting with it might have locally Markovian evolution, while globally, it may show strong non-local memory effects (Laine et al., 2012), and this counter-intuitive effect has been realized experimentally in Liu et al. (2013a). Quantum non-Markovianity may also arise when two Markovian channels are convex combined, and Uriri et al.(2020) experimentally confirmed how a convex mixture of two Pauli semigroups may result in a CP-indivisible quantum channel. In Fanchini et al. (2014), the polarization degree of freedom was taken to be the two-level open system, and a Sagnac interferometer was used to realize the non-Markovian amplitude damping of photon polarization.

All of the aforementioned works in the optical domain used an interferometric setup to simulate the decoherence of quantum systems. In Figure 3, we provide a schematic example of such a setup. The photonic simulation of quantum channels may find certain unique applications in quantum information tasks. For example, Utagi et al. (2020a) showed that, by deliberately adding amplitude damping quantum noise on the polarization degree of freedom (via optical simulation) in the ping-pong protocol proposed by Boström and Felbinger (2002), one could improve security against an attack (Wójcik, 2003; Boström and Felbinger, 2008). It is known that squeezing is a resource for continuous variable quantum information processing. Xiong et al. (2018) showed that a cavity-optomechanical system interacting with a non-Markovian environment can lead to the enhanced squeezing of the mechanical mode. Therefore, exploring the optical implementation of non-Markovian quantum channels may find similar counter-intuitive benefits in quantum information tasks.

FIGURE 3

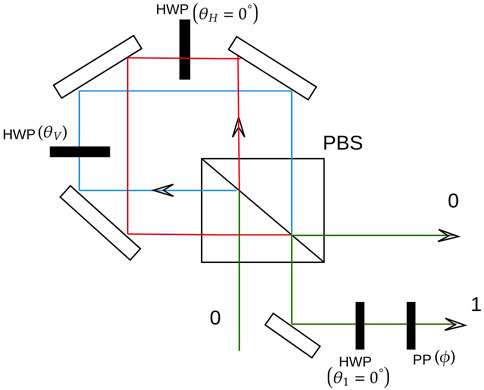
FIGURE 3. Optical simulation of the amplitude damping channel using a Sagnac interferometer (Salles et al., 2008). Here, PBS is the polarization beam splitter and HWP(θ_V) (the black rectangular slabs) is a half-wave plate that rotates the vertical polarization by an angle θ, as well as the horizontal polarization. PP(ϕ) is a phase plate. The white rectangular slabs are perfectly reflecting mirrors. In the aforementioned setup, setting ϕ = 0, one realizes an amplitude damping channel for arbitrary θ_V. Note that the symbols 0 and 1 are labels for optical modes. For different values of θ_H, θ_V, θ₁, and ϕ, other prototypical quantum channels can be realized (see Table II in Salles et al., 2008).

Although we have focused mainly on optical setups in this section, other platforms, such as NMR (Bernardes et al., 2015), trapped ions (Wittemer et al., 2018), and multi-qubit superconducting devices (White et al., 2020), have also been used to implement non-Markovian open system dynamics. The importance of such experimental characterizations of non-Markovianity has been further highlighted by recent works showing how unwanted memory effects that creep in due to cross-talk between superconducting qubits in quantum computer can be removed (Gambetta et al., 2012; White et al., 2022); however, mitigating errors due to non-Markovian memory effects arising from an uncontrollable environment can prove to be significantly harder.

6 Afterword: Summary and future outlook

Traditionally, the dynamics of an open system is described by either the master equation or a two-time dynamical map (Breuer and Petruccione, 2002; Banerjee, 2018). Open system evolution may be categorized mainly as Markovian or non-Markovian (Rivas et al., 2014). However, a precise and universal definition of non-Markovianity has remained elusive (Li et al., 2018), with no known way of translating the classical definitions to the quantum domain until recently (Pollock et al., 2018a; Pollock et al., 2018b; Budini, 2018b). We have reviewed some recent developments in the field, followed by brief accounts of traditional approaches to characterizing and quantifying quantum non-Markovianity.

Quantum causality has been a long-standing puzzle within quantum theory (Brukner, 2014; Costa, 2022; Vilasini and Renner, 2022). It is interesting to note that quantum causality and non-Markovianity have been shown to be intimately connected via quantum temporal correlations. Notably, Milz et al. (2018) showed that a causally non-separable process with a tripartite initial entangled state can simulate a multi-time non-Markovian process. In this review, we have studied how one can quantify non-Markovianity using temporal quantum correlations, such as temporal steering (Chen et al., 2016) and causal correlations in the PDM (Utagi, 2021). Note, however, that these correlations are between the states across time. In the future, it will be interesting to understand whether the PDM can offer a multi-time characterization of correlations in the process, at least for the case of qubits. In fact, Zhang et al. (2020) showed that there are three different mappings from the PDM to a process matrix, and since the process matrix (Oreshkov et al., 2012; Costa and Shrapnel, 2016) and the process tensor Pollock et al. (2018a) essentially arise from quantum combs (Chiribella et al., 2009), it would be interesting to find mappings from the multi-time PDM to the process tensor, if any exist.

If one studies open systems within the paradigm of two-time dynamical maps, one runs into the problem of defining a physically valid dynamical map that is both CP and linear when initial S-E quantum correlations are present. Pechukas’s theorem states that, in order to create such a map, one has to give up either complete positivity or linearity (Pechukas, 1994; Alicki, 1995; Pechukas, 1995). Later, the debate continued with regards to the nature of initial S-E correlations, for example, that of quantum discord, and whether vanishing discord provides a necessary and sufficient condition. However, recently, some approaches have been proposed to describe the dynamics of an open system with initial S-E correlations in a consistent manner, some of which we have mentioned in Section 3.

The quantum comb (Chiribella et al., 2009) framework talks about the temporal correlations between observables corresponding to the dynamical process by mapping a process to a state via CJ isomorphism. Particularly in the process tensor framework (Pollock et al., 2018a), temporal correlations in the multi-time description of a process corresponds to memory (or non-Markovianity), and the framework offers the incorporation of (unknown) initial S-E correlation without sacrificing the linearity and complete positivity of the map. Moreover, it offers an operational definition of (non-) Markovianity via quantum process tomography, which has an appropriate classical limit. It also offers a solution to the problem of necessary and sufficient conditions for non-Markovianity.

Figure 4 depicts the containment of non-Markovian processes according to various criteria, particularly with regards to necessary and/or sufficient conditions for these criteria to witness non-Markovianity. The processes that are non-Markovian according to the BLP approach are non-Markovian according to all other criteria; hence, such processes are strongly non-Markovian. However, if the BLP approach identifies a process as Markovian, it may still be non-Markovian according to the RHP criterion, and hence also according to the CPF correlation measure and process tensor measure. However, there may be processes that are non-Markovian according CPF correlations and the process tensor measure, but that are Markovian according to the RHP measure. Therefore, one may conclude that Box 1 criteria are sufficient and not necessary relative to boxes 2 and 3. Recent developments (Budini, 2018b; Pollock et al., 2018b; Milz et al., 2019; Utagi et al., 2020b) have shown that the RHP criterion is also only sufficient but not necessary for detecting non-Markovianity relative to Box 3. Thus, one may conclude that Box 3 represents necessary and sufficient criteria for quantum non-Markovianity. Interestingly, it is known that the measure based on the TSW detects the range of non-Markovianity similar to the BLP approach; however, it is yet to be found where the TSW measure (Eq. 21) and the causality based measure (Eq. 27) fit in the aforementioned containment boxes.

FIGURE 4

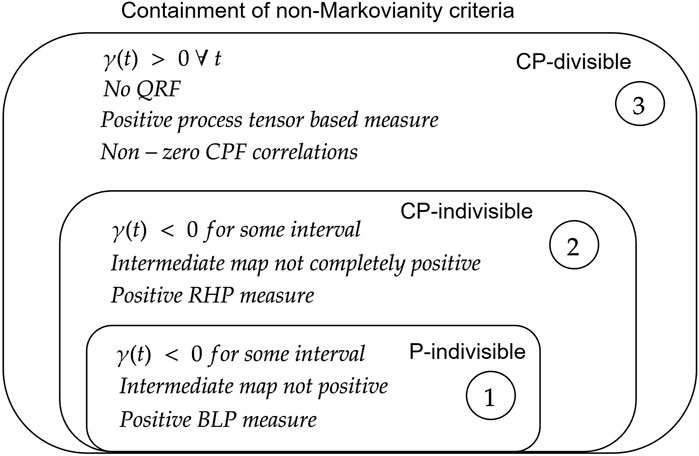
FIGURE 4. Containment of non-Markovianity criteria. Here, Box 1 sufficiently implies boxes 2 and 3, and Box 2 sufficiently implies Box 3, but Box 3 does not necessarily imply boxes 2 and 1, and Box 2 does not necessarily imply Box 1. Here, we have depicted the containment for the processes that can be fully characterized by two-time correlations of the environment. Note that the process tensor here is for a two-time step process, and quantum regression is for two-time correlation functions. The function γ(t) represents the decay rate in the time-local master equation.

From the perspective of quantum information theory, it is possible that quantum non-Markovianity may be useful in certain specific situations. In particular, since quantum non-Markovianity brings information that is “lost” to the environment back to the system for certain time-intervals of the evolution, it might prove advantageous in certain quantum information processing tasks (Bylicka et al., 2014; Laine et al., 2014; Utagi et al., 2020a).

On the otherhand, witnessing and characterizing the extent of non-Markovianity is essential in obtaining a complete understanding of noise in quantum systems. Indeed, one of the biggest challenges in scaling up quantum technologies today is to protect quantum information from environment-induced decoherence. The theory of quantum error correction (QEC) (Nielsen and Chuang, 2010) provides the means to protect information from noise by appending a large number of physical qubits to create a single, protected logical qubit. Standard works on QEC have heavily focused on Markovian noise and, barring a couple of works (Oreshkov and Brun, 2007; Taranto et al., 2021), the role of QEC in mitigating noise in the non-Markovian regime remains largely unexplored. Going beyond error correction, the question of achieving quantum fault tolerance in the presence of non-Markovian quantum noise has also been explored in the past (Terhal and Burkard, 2005; Aharonov et al., 2006). Recently, there have been attempts to extend the theory of noise-adapted QEC (Ng and Mandayam, 2010; Mandayam and Ng, 2012) to non-Markovian noise models (Len and Ng, 2018; Kwon et al., 2022; Lautenbacher et al., 2022). Going forward, characterizing non-Markovianity in near-term quantum devices and developing QEC protocols adapted to non-Markovian noise promises to be an important and fruitful research avenue.

In this contribution, we have attempted to put in perspective some of the recent developments in defining and measuring quantum non-Markovianity. It will be interesting to see how various frameworks of open system dynamics and definitions of quantum non-Markovianity allow for their uses in highly specific cases of quantum information processing.

Author contributions

US was the primary resource person for this article and the primary contributor. PM contributed to the writing and structural organization of this review.

Funding

US thanks IIT Madras for the support through the Institute Postdoctoral Fellowship. This work was partially funded under Grant No. DST/ICPS/QuST/Theme-3/2019/Q59 from the Department of Science and Technology, Government of India and a grant from the Mphasis Foundation to the Centre for Quantum Information, Communication, and Computing (MCQuICC), IIT Madras.

Acknowledgments

US thanks Simon Milz for insightful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In fact, Bures distance and quantum relative entropy are other measures that are contractive under CPTP maps and can witness non-Markovianity (Liu et al., 2013b; Megier et al., 2021).

²Here, contractivity means that a CP-contractive distance must satisfy the data processing inequality under a Markov CPTP map Φ: D(Φ[ρ]‖Φ[σ]) ≤ D(ρ‖σ).

References

Aharonov, D., Kitaev, A., and Preskill, J. (2006). Fault-tolerant quantum computation with long-range correlated noise. Phys. Rev. Lett. 96, 050504. doi:10.1103/physrevlett.96.050504

PubMed Abstract | CrossRef Full Text | Google Scholar

Alicki, R. (1995). Comment on “Reduced dynamics need not be completely positive”. Phys. Rev. Lett. 75, 3020. doi:10.1103/physrevlett.75.3020

PubMed Abstract | CrossRef Full Text | Google Scholar

Alipour, S., Mani, A., and Rezakhani, A. T. (2012). Quantum discord and non-Markovianity of quantum dynamics. Phys. Rev. A 85, 052108. doi:10.1103/PhysRevA.85.052108

CrossRef Full Text | Google Scholar

Alipour, S., Rezakhani, A. T., Babu, A. P., Mølmer, K., Möttönen, M., and Ala-Nissila, T. (2020). Correlation-picture approach to open-quantum-system dynamics. Phys. Rev. X 10, 041024. doi:10.1103/PhysRevX.10.041024

CrossRef Full Text | Google Scholar

Andersson, E., Cresser, J. D., and Hall, M. J. W. (2007). Finding the Kraus decomposition from a master equation and vice versa. J. Mod. Opt. 54, 1695–1716. doi:10.1080/09500340701352581

CrossRef Full Text | Google Scholar

Banerjee, S. (2018). Open quantum systems. Springer Nature Singapore Pte Ltd.

Google Scholar

Benatti, F., Floreanini, R., and Olivares, S. (2012). Non-divisibility and non-Markovianity in a Gaussian dissipative dynamics. Phys. Lett. A 376, 2951–2954. doi:10.1016/j.physleta.2012.08.044

CrossRef Full Text | Google Scholar

Bernardes, N. K., Cuevas, A., Orieux, A., Monken, C. H., Mataloni, P., Sciarrino, F., et al. (2015). Experimental observation of transition between strong and weak non-Markovianity. Quantum Opt. Quantum Inf. Transf. Process. 9505, 125–131. doi:10.1038/srep17520

PubMed Abstract | CrossRef Full Text | Google Scholar

Boström, K., and Felbinger, T. (2002). Deterministic secure direct communication using entanglement. Phys. Rev. Lett. 89, 187902. doi:10.1103/physrevlett.89.187902

PubMed Abstract | CrossRef Full Text | Google Scholar

Boström, K., and Felbinger, T. (2008). On the security of the ping-pong protocol. Phys. Lett. A 372, 3953–3956. doi:10.1016/j.physleta.2008.03.048

CrossRef Full Text | Google Scholar

Breuer, H.-P., Laine, E.-M., and Piilo, J. (2009). Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 103, 210401. doi:10.1103/physrevlett.103.210401

PubMed Abstract | CrossRef Full Text | Google Scholar

Breuer, H.-P., Laine, E.-M., Piilo, J., and Vacchini, B. (2016a). Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 88, 021002. doi:10.1103/revmodphys.88.021002

CrossRef Full Text | Google Scholar

Breuer, H.-P., Laine, E.-M., Piilo, J., and Vacchini, B. (2016b). Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 88, 021002. doi:10.1103/RevModPhys.88.021002

CrossRef Full Text | Google Scholar

Breuer, H.-P., and Petruccione, F. (2002). The theory of open quantum systems. Oxford University Press.

Google Scholar

Brodutch, A., Datta, A., Modi, K., Rivas, A., and Rodriguez-Rosario, C. A. (2013). Vanishing quantum discord is not necessary for completely positive maps. Phys. Rev. A 87, 042301. doi:10.1103/physreva.87.042301

CrossRef Full Text | Google Scholar

Brukner, Č. (2014). Quantum causality. Nat. Phys. 10, 259–263. doi:10.1038/nphys2930

CrossRef Full Text | Google Scholar

Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V., and Wehner, S. (2014). Bell nonlocality. Rev. Mod. Phys. 86, 419–478. doi:10.1103/revmodphys.86.419

CrossRef Full Text | Google Scholar

Budini, A. A. (2019). Conditional past-future correlation induced by non-Markovian dephasing reservoirs. Phys. Rev. A 99, 052125. doi:10.1103/PhysRevA.99.052125

CrossRef Full Text | Google Scholar

Budini, A. A. (2018a). Maximally non-Markovian quantum dynamics without environment-to-system backflow of information. Phys. Rev. A 97, 052133. doi:10.1103/physreva.97.052133

CrossRef Full Text | Google Scholar

Budini, A. A. (2022). Quantum non-Markovian environment-to-system backflows of information: Nonoperational vs. operational approaches. Entropy 24, 649. doi:10.3390/e24050649

PubMed Abstract | CrossRef Full Text | Google Scholar

Budini, A. A. (2018b). Quantum non-Markovian processes break conditional past-future independence. Phys. Rev. Lett. 121, 240401. doi:10.1103/PhysRevLett.121.240401

PubMed Abstract | CrossRef Full Text | Google Scholar

Buscemi, F. (2014). Complete positivity, Markovianity, and the quantum data-processing inequality, in the presence of initial system-environment correlations. Phys. Rev. Lett. 113, 140502. doi:10.1103/PhysRevLett.113.140502

PubMed Abstract | CrossRef Full Text | Google Scholar

Bylicka, B., Chruściński, D., and Maniscalco, S. (2014). Non-Markovianity and reservoir memory of quantum channels: A quantum information theory perspective. Sci. Rep. 4, 5720. doi:10.1038/srep05720

PubMed Abstract | CrossRef Full Text | Google Scholar

Bylicka, B., Johansson, M., and Acín, A. (2017). Constructive method for detecting the information backflow of non-Markovian dynamics. Phys. Rev. Lett. 118, 120501. doi:10.1103/PhysRevLett.118.120501

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, S., and Vacchini, B. (2021). Collision models in open system dynamics: A versatile tool for deeper insights? Europhys. Lett. 133, 60001. doi:10.1209/0295-5075/133/60001

CrossRef Full Text | Google Scholar

Chakraborty, S., and Chruściński, D. (2019). Information flow versus divisibility for qubit evolution. Phys. Rev. A 99, 042105. doi:10.1103/physreva.99.042105

CrossRef Full Text | Google Scholar

Chakraborty, U., and Chruściński, D. (2021). Construction of propagators for divisible dynamical maps. New J. Phys. 23, 013009. doi:10.1088/1367-2630/abd43b

CrossRef Full Text | Google Scholar

Chen, S.-L., Lambert, N., Li, C.-M., Miranowicz, A., Chen, Y.-N., and Nori, F. (2016). Quantifying non-Markovianity with temporal steering. Phys. Rev. Lett. 116, 020503. doi:10.1103/physrevlett.116.020503

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y.-N., Li, C.-M., Lambert, N., Chen, S.-L., Ota, Y., Chen, G.-Y., et al. (2014). Temporal steering inequality. Phys. Rev. A 89, 032112. doi:10.1103/physreva.89.032112

CrossRef Full Text | Google Scholar

Chiribella, G., D’Ariano, G. M., and Perinotti, P. (2009). Theoretical framework for quantum networks. Phys. Rev. A 80, 022339. doi:10.1103/physreva.80.022339

CrossRef Full Text | Google Scholar

Chiuri, A., Greganti, C., Mazzola, L., Paternostro, M., and Mataloni, P. (2012). Linear optics simulation of quantum non-Markovian dynamics. Sci. Rep. 2, 968–975. doi:10.1038/srep00968

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, M.-D. (1975). Completely positive linear maps on complex matrices. Linear algebra its Appl. 10, 285–290. doi:10.1016/0024-3795(75)90075-0

CrossRef Full Text | Google Scholar

Chruściński, D., Hesabi, S., and Lonigro, D. (2022). On Markovianity and classicality in multilevel spin-boson models. arXiv preprint arXiv:2210.06199

Google Scholar

Chruściński, D., and Kossakowski, A. (2010). Non-Markovian quantum dynamics: Local versus nonlocal. Phys. Rev. Lett. 104, 070406. doi:10.1103/physrevlett.104.070406

PubMed Abstract | CrossRef Full Text | Google Scholar

Chruściński, D., Kossakowski, A., and Rivas, Á. (2011). Measures of non-Markovianity: Divisibility versus backflow of information. Phys. Rev. A 83, 052128. doi:10.1103/physreva.83.052128

CrossRef Full Text | Google Scholar

Chruściński, D., Macchiavello, C., and Maniscalco, S. (2017). Detecting non-Markovianity of quantum evolution via spectra of dynamical maps. Phys. Rev. Lett. 118, 080404. doi:10.1103/physrevlett.118.080404

PubMed Abstract | CrossRef Full Text | Google Scholar

Chruściński, D., and Maniscalco, S. (2014). Degree of non-Markovianity of quantum evolution. Phys. Rev. Lett. 112, 120404. doi:10.1103/physrevlett.112.120404

PubMed Abstract | CrossRef Full Text | Google Scholar

Chruściński, D., Rivas, Á., and Størmer, E. (2018). Divisibility and information flow notions of quantum Markovianity for noninvertible dynamical maps. Phys. Rev. Lett. 121, 080407. doi:10.1103/physrevlett.121.080407

PubMed Abstract | CrossRef Full Text | Google Scholar

Cialdi, S., Rossi, M. A., Benedetti, C., Vacchini, B., Tamascelli, D., Olivares, S., et al. (2017). All-optical quantum simulator of qubit noisy channels. Appl. Phys. Lett. 110, 081107. doi:10.1063/1.4977023

CrossRef Full Text | Google Scholar

Ciccarello, F., Lorenzo, S., Giovannetti, V., and Palma, G. M. (2022). Quantum collision models: Open system dynamics from repeated interactions. Phys. Rep. 954, 1–70. doi:10.1016/j.physrep.2022.01.001

CrossRef Full Text | Google Scholar

Costa, F. (2022). A no-go theorem for superpositions of causal orders. Quantum 6, 663. doi:10.22331/q-2022-03-01-663

CrossRef Full Text | Google Scholar

Costa, F., and Shrapnel, S. (2016). Quantum causal modelling. New J. Phys. 18, 063032. doi:10.1088/1367-2630/18/6/063032

CrossRef Full Text | Google Scholar

Cotler, J., Jian, C.-M., Qi, X.-L., and Wilczek, F. (2018). Superdensity operators for spacetime quantum mechanics. J. High Energy Phys. 2018, 93–57. doi:10.1007/jhep09(2018)093

CrossRef Full Text | Google Scholar

Cuevas, Á., Geraldi, A., Liorni, C., Bonavena, L. D., De Pasquale, A., Sciarrino, F., et al. (2019). All-optical implementation of collision-based evolutions of open quantum systems. Sci. Rep. 9, 3205. doi:10.1038/s41598-019-39832-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Davalos, D., Ziman, M., and Pineda, C. (2019). Divisibility of qubit channels and dynamical maps. Quantum 3, 144. doi:10.22331/q-2019-05-20-144

CrossRef Full Text | Google Scholar

Davies, E. B. (1974). Markovian master equations. Commun. Math. Phys. 39, 91–110. doi:10.1007/bf01608389

CrossRef Full Text | Google Scholar

Davies, E. B. (1976). Markovian master equations. ii. Math. Ann. 219, 147–158. doi:10.1007/bf01351898

CrossRef Full Text | Google Scholar

de Lima Silva, T., Walborn, S. P., Santos, M. F., Aguilar, G. H., and Budini, A. A. (2020). Detection of quantum non-Markovianity close to the Born-Markov approximation. Phys. Rev. A 101, 042120. doi:10.1103/physreva.101.042120

CrossRef Full Text | Google Scholar

De Santis, D., Johansson, M., Bylicka, B., Bernardes, N. K., and Acín, A. (2019). Correlation measure detecting almost all non-Markovian evolutions. Phys. Rev. A 99, 012303. doi:10.1103/physreva.99.012303

CrossRef Full Text | Google Scholar

de Vega, I., and Alonso, D. (2017). Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 89, 015001. doi:10.1103/RevModPhys.89.015001

CrossRef Full Text | Google Scholar

Devi, A. U., and Rajagopal, A., (2011). Open-system quantum dynamics with correlated initial states, not completely positive maps, and non-Markovianity. Phys. Rev. A 83, 022109. doi:10.1103/physreva.83.022109

CrossRef Full Text | Google Scholar

Dhar, H. S., Bera, M. N., and Adesso, G. (2015). Characterizing non-Markovianity via quantum interferometric power. Phys. Rev. A 91, 032115. doi:10.1103/physreva.91.032115

CrossRef Full Text | Google Scholar

Dümcke, R. (1983). Convergence of multitime correlation functions in the weak and singular coupling limits. J. Math. Phys. 24, 311–315. doi:10.1063/1.525681

CrossRef Full Text | Google Scholar

Fanchini, F. F., Karpat, G., Çakmak, B., Castelano, L., Aguilar, G., Farías, O. J., et al. (2014). Non-Markovianity through accessible information. Phys. Rev. Lett. 112, 210402. doi:10.1103/physrevlett.112.210402

CrossRef Full Text | Google Scholar

Farías, O. J., Aguilar, G., Valdés-Hernández, A., Ribeiro, P. S., Davidovich, L., and Walborn, S. P. (2012). Observation of the emergence of multipartite entanglement between a bipartite system and its environment. Phys. Rev. Lett. 109, 150403. doi:10.1103/physrevlett.109.150403

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisher, K. A., Prevedel, R., Kaltenbaek, R., and Resch, K. J. (2012). Optimal linear optical implementation of a single-qubit damping channel. New J. Phys. 14, 033016. doi:10.1088/1367-2630/14/3/033016

CrossRef Full Text | Google Scholar

Fitzsimons, J. F., Jones, J. A., and Vedral, V. (2015). Quantum correlations which imply causation. Sci. Rep. 5, 18281. doi:10.1038/srep18281

PubMed Abstract | CrossRef Full Text | Google Scholar

Franco, R. L., Bellomo, B., Andersson, E., and Compagno, G. (2012). Revival of quantum correlations without system-environment back-action. Phys. Rev. A 85, 032318. doi:10.1103/physreva.85.032318

CrossRef Full Text | Google Scholar

Gambetta, J. M., Córcoles, A. D., Merkel, S. T., Johnson, B. R., Smolin, J. A., Chow, J. M., et al. (2012). Characterization of addressability by simultaneous randomized benchmarking. Phys. Rev. Lett. 109, 240504. doi:10.1103/physrevlett.109.240504

PubMed Abstract | CrossRef Full Text | Google Scholar

Garraway, B. (1997). Nonperturbative decay of an atomic system in a cavity. Phys. Rev. A 55, 2290–2303. doi:10.1103/physreva.55.2290

CrossRef Full Text | Google Scholar

Giarmatzi, C., and Costa, F. (2021). Witnessing quantum memory in non-Markovian processes. Quantum 5, 440. doi:10.22331/q-2021-04-26-440

CrossRef Full Text | Google Scholar

Guarnieri, G., Smirne, A., and Vacchini, B. (2014). Quantum regression theorem and non-Markovianity of quantum dynamics. Phys. Rev. A 90, 022110. doi:10.1103/physreva.90.022110

CrossRef Full Text | Google Scholar

Hall, M. J. W., Cresser, J. D., Li, L., and Andersson, E. (2014). Canonical form of master equations and characterization of non-Markovianity. Phys. Rev. A 89, 042120. doi:10.1103/PhysRevA.89.042120

CrossRef Full Text | Google Scholar

Haseli, S., Karpat, G., Salimi, S., Khorashad, A. S., Fanchini, F. F., Çakmak, B., et al. (2014). Non-markovianity through flow of information between a system and an environment. Phys. Rev. A 90, 052118. doi:10.1103/PhysRevA.90.052118

CrossRef Full Text | Google Scholar

Horodecki, R., Horodecki, P., Horodecki, M., and Horodecki, K. (2009). Quantum entanglement. Rev. Mod. Phys. 81, 865–942. doi:10.1103/revmodphys.81.865

CrossRef Full Text | Google Scholar

Horsman, D., Heunen, C., Pusey, M. F., Barrett, J., and Spekkens, R. W. (2017). Can a quantum state over time resemble a quantum state at a single time? Proc. R. Soc. A Math. Phys. Eng. Sci. 473, 20170395. doi:10.1098/rspa.2017.0395

PubMed Abstract | CrossRef Full Text | Google Scholar

Jordan, T. F., Shaji, A., and Sudarshan, E. C. G. (2004). Dynamics of initially entangled open quantum systems. Phys. Rev. A 70, 052110. doi:10.1103/PhysRevA.70.052110

CrossRef Full Text | Google Scholar

Kraus, K., Böhm, A., Dollard, J. D., and Wootters, W. (1983). States, effects, and operations fundamental notions of quantum theory: Lectures in mathematical physics at the university of Texas at Austin. Springer.

Google Scholar

Kraus, K. (1971). General state changes in quantum theory. Ann. Phys. 64, 311–335. doi:10.1016/0003-4916(71)90108-4

CrossRef Full Text | Google Scholar

Ku, H.-Y., Chen, S.-L., Lambert, N., Chen, Y.-N., and Nori, F. (2018). Hierarchy in temporal quantum correlations. Phys. Rev. A 98, 022104. doi:10.1103/physreva.98.022104

CrossRef Full Text | Google Scholar

Kumar, N. P., Banerjee, S., Srikanth, R., Jagadish, V., and Petruccione, F. (2018). Non-Markovian evolution: A quantum walk perspective. Open Syst. Inf. Dynam. 25, 1850014. doi:10.1142/S1230161218500142

CrossRef Full Text | Google Scholar

Kwon, H., Mukherjee, R., and Kim, M. (2022). Reversing Lindblad dynamics via continuous Petz recovery map. Phys. Rev. Lett. 128, 020403. doi:10.1103/physrevlett.128.020403

PubMed Abstract | CrossRef Full Text | Google Scholar

Laine, E.-M., Breuer, H.-P., Piilo, J., Li, C.-F., and Guo, G.-C. (2012). Nonlocal memory effects in the dynamics of open quantum systems. Phys. Rev. Lett. 108, 210402. doi:10.1103/physrevlett.108.210402

PubMed Abstract | CrossRef Full Text | Google Scholar

Laine, E.-M., Breuer, H.-P., and Piilo, J. (2014). Nonlocal memory effects allow perfect teleportation with mixed states. Sci. Rep. 4, 4620–4625. doi:10.1038/srep04620

PubMed Abstract | CrossRef Full Text | Google Scholar

Lautenbacher, L., de Melo, F., and Bernardes, N. K. (2022). Approximating invertible maps by recovery channels: Optimality and an application to non-Markovian dynamics. Phys. Rev. A 105, 042421. doi:10.1103/physreva.105.042421

CrossRef Full Text | Google Scholar

Leggett, A. J., and Garg, A. (1985). Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 54, 857–860. doi:10.1103/PhysRevLett.54.857

PubMed Abstract | CrossRef Full Text | Google Scholar

Len, Y. L., and Ng, H. K. (2018). Open-system quantum error correction. Phys. Rev. A 98, 022307. doi:10.1103/PhysRevA.98.022307

CrossRef Full Text | Google Scholar

Li, L., Hall, M. J., and Wiseman, H. M. (2018). Concepts of quantum non-Markovianity: A hierarchy. Phys. Rep. 759, 1–51. doi:10.1016/j.physrep.2018.07.001

CrossRef Full Text | Google Scholar

Lindblad, G. (1979). Non-Markovian quantum stochastic processes and their entropy. Commun. Math. Phys. 65, 281–294. doi:10.1007/bf01197883

CrossRef Full Text | Google Scholar

Lindblad, G. (1976). On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119–130. doi:10.1007/bf01608499

CrossRef Full Text | Google Scholar

Liu, B.-H., Cao, D.-Y., Huang, Y.-F., Li, C.-F., Guo, G.-C., Laine, E.-M., et al. (2013a). Photonic realization of nonlocal memory effects and non-Markovian quantum probes. Sci. Rep. 3, 1781. doi:10.1038/srep01781

CrossRef Full Text | Google Scholar

Liu, B.-H., Li, L., Huang, Y.-F., Li, C.-F., Guo, G.-C., Laine, E.-M., et al. (2011). Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 7, 931–934. doi:10.1038/nphys2085

CrossRef Full Text | Google Scholar

Liu, J., Lu, X.-M., and Wang, X. (2013b). Nonunital non-markovianity of quantum dynamics. Phys. Rev. A 87, 042103. doi:10.1103/PhysRevA.87.042103

CrossRef Full Text | Google Scholar

Liu, Z.-D., Lyyra, H., Sun, Y.-N., Liu, B.-H., Li, C.-F., Guo, G.-C., et al. (2018). Experimental implementation of fully controlled dephasing dynamics and synthetic spectral densities. Nat. Commun. 9, 3453. doi:10.1038/s41467-018-05817-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, S., Fu, S., and Song, H. (2012). Quantifying non-markovianity via correlations. Phys. Rev. A 86, 044101. doi:10.1103/physreva.86.044101

CrossRef Full Text | Google Scholar

Lyyra, H., Siltanen, O., Piilo, J., Banerjee, S., and Kuusela, T. (2022). Experimental snapshot verification of non-markovianity by quantum probing of convex coefficients. Phys. Rev. A 106, 032603. doi:10.1103/physreva.106.032603

CrossRef Full Text | Google Scholar

Mandayam, P., and Ng, H. K. (2012). Towards a unified framework for approximate quantum error correction. Phys. Rev. A 86, 012335. doi:10.1103/physreva.86.012335

CrossRef Full Text | Google Scholar

Mazzola, L., Piilo, J., and Maniscalco, S. (2011). Frozen discord in non-Markovian dephasing channels. Int. J. Quantum. Inf. 9, 981–991. doi:10.1142/s021974991100754x

CrossRef Full Text | Google Scholar

Mazzola, L., Rodríguez-Rosario, C. A., Modi, K., and Paternostro, M. (2012). Dynamical role of system-environment correlations in non-Markovian dynamics. Phys. Rev. A 86, 010102. doi:10.1103/PhysRevA.86.010102

CrossRef Full Text | Google Scholar

Megier, N., Smirne, A., and Vacchini, B. (2021). Entropic bounds on information backflow. Phys. Rev. Lett. 127, 030401. doi:10.1103/physrevlett.127.030401

PubMed Abstract | CrossRef Full Text | Google Scholar

Megier, N., Smirne, A., and Vacchini, B. (2020a). Evolution equations for quantum semi-Markov dynamics. Entropy 22, 796. doi:10.3390/e22070796

PubMed Abstract | CrossRef Full Text | Google Scholar

Megier, N., Smirne, A., and Vacchini, B. (2020b). The interplay between local and non-local master equations: Exact and approximated dynamics. New J. Phys. 22, 083011. doi:10.1088/1367-2630/ab9f6b

CrossRef Full Text | Google Scholar

Milz, S., Kim, M., Pollock, F. A., and Modi, K. (2019). Completely positive divisibility does not mean Markovianity. Phys. Rev. Lett. 123, 040401. doi:10.1103/physrevlett.123.040401

PubMed Abstract | CrossRef Full Text | Google Scholar

Milz, S., Pollock, F. A., Le, T. P., Chiribella, G., and Modi, K. (2018). Entanglement, non-markovianity, and causal non-separability. New J. Phys. 20, 033033. doi:10.1088/1367-2630/aaafee

CrossRef Full Text | Google Scholar

Modi, K., Brodutch, A., Cable, H., Paterek, T., and Vedral, V. (2012). The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655–1707. doi:10.1103/revmodphys.84.1655

CrossRef Full Text | Google Scholar

Modi, K. (2012). Operational approach to open dynamics and quantifying initial correlations. Sci. Rep. 2, 581–585. doi:10.1038/srep00581

PubMed Abstract | CrossRef Full Text | Google Scholar

Ng, H. K., and Mandayam, P. (2010). Simple approach to approximate quantum error correction based on the transpose channel. Phys. Rev. A 81, 062342. doi:10.1103/physreva.81.062342

CrossRef Full Text | Google Scholar

Nielsen, M. A., and Chuang, I. L. (2010). Quantum computation and quantum information: 10th anniversary edition. Cambridge University Press. doi:10.1017/CBO9780511976667

CrossRef Full Text | Google Scholar

Oreshkov, O., and Brun, T. A. (2007). Continuous quantum error correction for non-Markovian decoherence. Phys. Rev. A 76, 022318. doi:10.1103/physreva.76.022318

CrossRef Full Text | Google Scholar

Oreshkov, O., Costa, F., and Brukner, Č. (2012). Quantum correlations with no causal order. Nat. Commun. 3, 1092–1098. doi:10.1038/ncomms2076

PubMed Abstract | CrossRef Full Text | Google Scholar

Paz-Silva, G. A., Hall, M. J. W., and Wiseman, H. M. (2019). Dynamics of initially correlated open quantum systems: Theory and applications. Phys. Rev. A 100, 042120. doi:10.1103/PhysRevA.100.042120

CrossRef Full Text | Google Scholar

Pechukas, P. (1995). Pechukas replies. Phys. Rev. Lett. 75, 3021. doi:10.1103/physrevlett.75.3021

PubMed Abstract | CrossRef Full Text | Google Scholar

Pechukas, P. (1994). Reduced dynamics need not be completely positive. Phys. Rev. Lett. 73, 1060–1062. doi:10.1103/physrevlett.73.1060

PubMed Abstract | CrossRef Full Text | Google Scholar

Perez-Garcia, D., Verstraete, F., Wolf, M. M., and Cirac, J. I. (2007). Matrix product state representations. Quantum Info. Comput. 7, 401–430. doi:10.26421/qic7.5-6-1

CrossRef Full Text | Google Scholar

Pernice, A., Helm, J., and Strunz, W. T. (2012). System–environment correlations and non-Markovian dynamics. J. Phys. B Atomic, Mol. Opt. Phys. 45, 154005. doi:10.1088/0953-4075/45/15/154005

CrossRef Full Text | Google Scholar

Pernice, A., and Strunz, W. T. (2011). Decoherence and the nature of system-environment correlations. Phys. Rev. A 84, 062121. doi:10.1103/PhysRevA.84.062121

CrossRef Full Text | Google Scholar

Pineda, C., Gorin, T., Davalos, D., Wisniacki, D. A., and García-Mata, I. (2016). Measuring and using non-markovianity. Phys. Rev. A 93, 022117. doi:10.1103/physreva.93.022117

CrossRef Full Text | Google Scholar

Pisarczyk, R., Zhao, Z., Ouyang, Y., Vedral, V., and Fitzsimons, J. F. (2019). Causal limit on quantum communication. Phys. Rev. Lett. 123, 150502. doi:10.1103/physrevlett.123.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

Pollock, F. A., Rodríguez-Rosario, C., Frauenheim, T., Paternostro, M., and Modi, K. (2018a). Non-Markovian quantum processes: Complete framework and efficient characterization. Phys. Rev. A 97, 012127. doi:10.1103/physreva.97.012127

CrossRef Full Text | Google Scholar

Pollock, F. A., Rodríguez-Rosario, C., Frauenheim, T., Paternostro, M., and Modi, K. (2018b). Operational Markov condition for quantum processes. Phys. Rev. Lett. 120, 040405. doi:10.1103/PhysRevLett.120.040405

PubMed Abstract | CrossRef Full Text | Google Scholar

Preskill, J. (2018). Quantum computing in the NISQ era and beyond. Quantum 2, 79. doi:10.22331/q-2018-08-06-79

CrossRef Full Text | Google Scholar

Rajagopal, A., Devi, A. U., and Rendell, R. (2010). Kraus representation of quantum evolution and fidelity as manifestations of Markovian and non-Markovian forms. Phys. Rev. A 82, 042107. doi:10.1103/physreva.82.042107

CrossRef Full Text | Google Scholar

Ringbauer, M., Wood, C. J., Modi, K., Gilchrist, A., White, A. G., and Fedrizzi, A. (2015). Characterizing quantum dynamics with initial system-environment correlations. Phys. Rev. Lett. 114, 090402. doi:10.1103/physrevlett.114.090402

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivas, A., Huelga, S. F., and Plenio, M. B. (2014). Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 77, 094001. doi:10.1088/0034-4885/77/9/094001

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivas, Á., Huelga, S. F., and Plenio, M. B. (2010). Entanglement and non-markovianity of quantum evolutions. Phys. Rev. Lett. 105, 050403. doi:10.1103/physrevlett.105.050403

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodríguez-Rosario, C. A., Modi, K., and Aspuru-Guzik, A. (2010). Linear assignment maps for correlated system-environment states. Phys. Rev. A 81, 012313. doi:10.1103/physreva.81.012313

CrossRef Full Text | Google Scholar

Rodríguez-Rosario, C. A., Modi, K., Kuah, A.-m., Shaji, A., and Sudarshan, E. C. G. (2008). Completely positive maps and classical correlations. J. Phys. A Math. Theor. 41, 205301. doi:10.1088/1751-8113/41/20/205301

CrossRef Full Text | Google Scholar

Rodríguez-Rosario, C. A., Modi, K., Mazzola, L., and Aspuru-Guzik, A. (2012). Unification of witnessing initial system-environment correlations and witnessing non-markovianity. EPL Europhys. Lett. 99, 20010. doi:10.1209/0295-5075/99/20010

CrossRef Full Text | Google Scholar

Rossi, M. A., Benedetti, C., Tamascelli, D., Cialdi, S., Olivares, S., Vacchini, B., et al. (2017). Non-markovianity by undersampling in quantum optical simulators. Int. J. Quantum Inf. 15, 1740009. doi:10.1142/s0219749917400093

CrossRef Full Text | Google Scholar

Royer, A. (1996). Reduced dynamics with initial correlations, and time-dependent environment and Hamiltonians. Phys. Rev. Lett. 77, 3272–3275. doi:10.1103/PhysRevLett.77.3272

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabapathy, K. K., Ivan, J. S., Ghosh, S., and Simon, R. (2013). Quantum discord plays no distinguished role in characterization of complete positivity: Robustness of the traditional scheme. arXiv preprint arXiv:1304.4857

Google Scholar

Salles, A., de Melo, F., Almeida, M., Hor-Meyll, M., Walborn, S., Ribeiro, P. S., et al. (2008). Experimental investigation of the dynamics of entanglement: Sudden death, complementarity, and continuous monitoring of the environment. Phys. Rev. A 78, 022322. doi:10.1103/physreva.78.022322

CrossRef Full Text | Google Scholar

Schlosshauer, M. A. (2007). Decoherence: And the quantum-to-classical transition. Springer Science and Business Media.

Google Scholar

Schmid, D., Ried, K., and Spekkens, R. W. (2019). Why initial system-environment correlations do not imply the failure of complete positivity: A causal perspective. Phys. Rev. A 100, 022112. doi:10.1103/physreva.100.022112

CrossRef Full Text | Google Scholar

Shabani, A., and Lidar, D. A. (2009). Vanishing quantum discord is necessary and sufficient for completely positive maps. Phys. Rev. Lett. 102, 100402. doi:10.1103/physrevlett.102.100402

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaji, A., and Sudarshan, E. C. G. (2005). Who’s afraid of not completely positive maps? Phys. Lett. A 341, 48–54. doi:10.1016/j.physleta.2005.04.029

CrossRef Full Text | Google Scholar

Shrikant, U., Srikanth, R., and Banerjee, S. (2018). Non-Markovian dephasing and depolarizing channels. Phys. Rev. A 98, 032328. doi:10.1103/PhysRevA.98.032328

CrossRef Full Text | Google Scholar

Strasberg, P., and Esposito, M. (2018). Response functions as quantifiers of non-markovianity. Phys. Rev. Lett. 121, 040601. doi:10.1103/PhysRevLett.121.040601

PubMed Abstract | CrossRef Full Text | Google Scholar

Sudarshan, E. C. G., Mathews, P. M., and Rau, J. (1961a). Stochastic dynamics of quantum-mechanical systems. Phys. Rev. 121, 920–924. doi:10.1103/PhysRev.121.920

CrossRef Full Text | Google Scholar

Sudarshan, E. C. G., Mathews, P. M., and Rau, J. (1961b). Stochastic dynamics of quantum-mechanical systems. Phys. Rev. 121, 920–924. doi:10.1103/PhysRev.121.920

CrossRef Full Text | Google Scholar

Swain, S. (1981). Master equation derivation of quantum regression theorem. J. Phys. A Math. General 14, 2577–2580. doi:10.1088/0305-4470/14/10/013

CrossRef Full Text | Google Scholar

Szasz, A. (2019). Measure of quantum correlations that lies approximately between entanglement and discord. Phys. Rev. A 99, 062313. doi:10.1103/physreva.99.062313

CrossRef Full Text | Google Scholar

Tang, J.-S., Li, C.-F., Li, Y.-L., Zou, X.-B., Guo, G.-C., Breuer, H.-P., et al. (2012). Measuring non-markovianity of processes with controllable system-environment interaction. Europhys. Lett. 97, 10002. doi:10.1209/0295-5075/97/10002

CrossRef Full Text | Google Scholar

Taranto, P., Pollock, F. A., and Modi, K. (2021). Non-Markovian memory strength bounds quantum process recoverability. npj Quantum Inf. 7, 149–158. doi:10.1038/s41534-021-00481-4

CrossRef Full Text | Google Scholar

Terhal, B. M., and Burkard, G. (2005). Fault-tolerant quantum computation for local non-Markovian noise. Phys. Rev. A 71, 012336. doi:10.1103/physreva.71.012336

CrossRef Full Text | Google Scholar

Trevisan, A., Smirne, A., Megier, N., and Vacchini, B. (2021). Adapted projection operator technique for the treatment of initial correlations. Phys. Rev. A 104, 052215. doi:10.1103/physreva.104.052215

CrossRef Full Text | Google Scholar

Uola, R., Costa, A. C., Nguyen, H. C., and Gühne, O. (2020). Quantum steering. Rev. Mod. Phys. 92, 015001. doi:10.1103/revmodphys.92.015001

CrossRef Full Text | Google Scholar

Uriri, S., Wudarski, F., Sinayskiy, I., Petruccione, F., and Tame, M. (2020). Experimental investigation of Markovian and non-Markovian channel addition. Phys. Rev. A 101, 052107. doi:10.1103/physreva.101.052107

CrossRef Full Text | Google Scholar

Utagi, S. (2021). Quantum causal correlations and non-markovianity of quantum evolution. Phys. Lett. A 386, 126983. doi:10.1016/j.physleta.2020.126983

CrossRef Full Text | Google Scholar

Utagi, S., Srikanth, R., and Banerjee, S. (2020a). Ping-pong quantum key distribution with trusted noise: Non-Markovian advantage. Quantum Inf. Process. 19, 366–412. doi:10.1007/s11128-020-02874-4

CrossRef Full Text | Google Scholar

Utagi, S., Srikanth, R., and Banerjee, S. (2020b). Temporal self-similarity of quantum dynamical maps as a concept of memorylessness. Sci. Rep. 10, 15049–15110. doi:10.1038/s41598-020-72211-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Vilasini, V., and Renner, R. (2022). Embedding cyclic causal structures in acyclic spacetimes: No-go results for process matrices. arXiv preprint arXiv:2203.11245

Google Scholar

White, G. A., Hill, C. D., Pollock, F. A., Hollenberg, L. C., and Modi, K. (2020). Demonstration of non-Markovian process characterisation and control on a quantum processor. Nat. Commun. 11, 6301. doi:10.1038/s41467-020-20113-3

PubMed Abstract | CrossRef Full Text | Google Scholar

White, G. A., Modi, K., and Hill, C. D. (2022). Filtering crosstalk from bath non-markovianity via spacetime classical shadows. arXiv preprint arXiv:2210.15333

Google Scholar

White, G. A., Pollock, F. A., Hollenberg, L. C., Hill, C. D., and Modi, K. (2021). From many-body to many-time physics. arXiv preprint arXiv:2107.13934

Google Scholar

Wittemer, M., Clos, G., Breuer, H.-P., Warring, U., and Schaetz, T. (2018). Measurement of quantum memory effects and its fundamental limitations. Phys. Rev. A 97, 020102. doi:10.1103/physreva.97.020102

CrossRef Full Text | Google Scholar

Wójcik, A. (2003). Eavesdropping on the “ping-pong” quantum communication protocol. Phys. Rev. Lett. 90, 157901. doi:10.1103/physrevlett.90.157901

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolf, M. M., and Cirac, J. I. (2008). Dividing quantum channels. Commun. Math. Phys. 279, 147–168. doi:10.1007/s00220-008-0411-y

CrossRef Full Text | Google Scholar

Wolf, M. M., Eisert, J., Cubitt, T., and Cirac, J. I. (2008). Assessing non-Markovian quantum dynamics. Phys. Rev. Lett. 101, 150402. doi:10.1103/physrevlett.101.150402

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, K.-D., Hou, Z., Xiang, G.-Y., Li, C.-F., Guo, G.-C., Dong, D., et al. (2020). Detecting non-markovianity via quantified coherence: Theory and experiments. npj Quantum Inf. 6, 55. doi:10.1038/s41534-020-0283-3

CrossRef Full Text | Google Scholar

Xiong, B., Li, X., Chao, S.-L., and Zhou, L. (2018). Optomechanical quadrature squeezing in the non-Markovian regime. Opt. Lett. 43, 6053–6056. doi:10.1364/ol.43.006053

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, J.-S., Sun, K., Li, C.-F., Xu, X.-Y., Guo, G.-C., Andersson, E., et al. (2013). Experimental recovery of quantum correlations in absence of system-environment back-action. Nat. Commun. 4, 2851–2857. doi:10.1038/ncomms3851

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, S., Budini, A. A., Wang, Y.-T., Ke, Z.-J., Meng, Y., Liu, W., et al. (2019). Experimental observation of conditional past-future correlations. Phys. Rev. A 100, 050301. doi:10.1103/physreva.100.050301

CrossRef Full Text | Google Scholar

Yu, T., and Eberly, J. (2010). Entanglement evolution in a non-Markovian environment. Opt. Commun. 283, 676–680. doi:10.1016/j.optcom.2009.10.042

CrossRef Full Text | Google Scholar

Zhang, T., Dahlsten, O., and Vedral, V. (2020). Quantum correlations in time. arXiv preprint arXiv:2002.10448

Google Scholar

Zhang, T. (2021). Quantum correlations in space-time: Foundations and applications. arXiv preprint arXiv:2101.08693

Google Scholar