Robust atomic states for quantum information with continuous variables

Using a set of Zeeman sublevels of an alkali atom such as rubidium or sodium, we propose to construct a pair of coherentc population trap (CPT) states, which can be individually addressed and populated at will. The system can be arranged such that there exists a dressed state that is a linear combination of these two CPT states. We have earlier shown the capability of forming discrete quantum gates using this configuration [J.Phys. B, (2006), 39, 3919]. In the present communication, we will show how the same configuration can be used to prepare and operate continuously varying states. The state can be mapped to a 2D parametric space in such a way that any desired vector within it can be prepared, and a continuous, adiabatic evolution from one vector to another is also possible. A method to exploit a continuous interaction potential, which can be used in quantum computation, is also suggested. We discuss how a continuous variable quantum computation can be performed using such states.

1 Introduction

Quantum information deals with representing bits “0” and “1” by objects that obey the rules of quantum mechanics. The fact that quantum objects can be prepared in a superposition of |0⟩ and |1⟩ opens a new facet wherein operations hitherto not possible in the realm of classical mechanics can be performed. Although quantum mechanics deals with discrete states, it is possible to use “continuous functions” for quantum information in three different methods. In the first method, we use parameters that take up continuous values, such as voltage pulse, etc., as given by Lloyd and Braunstein (Lloyd and Braunstein, 1999). The second method involves using measurement-based quantum mechanics, where values of continuous measurements are used to map the states (Menicucci et al., 2006; Zhang and Braunstein, 2006). The third option is to use a discrete spectrum of a quantum object but create a linear superposition of those states such that every point on the Hilbert space can be spanned continuously, as given by (Gottesman et al., 2001). We will use a variation of the third method that involves CPT states as the basis instead.

CPT states are a special form of dressed states, which are eigenstates of the total atom + field Hamiltonian (Cohen-Tannoudji and Reynaud, 1977; Arimondo and Wolf, 1996). Once the atom is prepared in such a state, it ceases to interact with the laser that prepares it, and hence, there is no further evolution of the state. In addition, the states we propose to use are formed out of ground states of alkali atoms and therefore do not decay by spontaneous emission. Hence, the CPT states are robust and reliable. The unique combination of selection rules we exploit here will allow a superposition of a pair of such trap states, which allows continuously spanning an entire 2D space. We also discuss how these states can be used for quantum operations.

2 The configuration

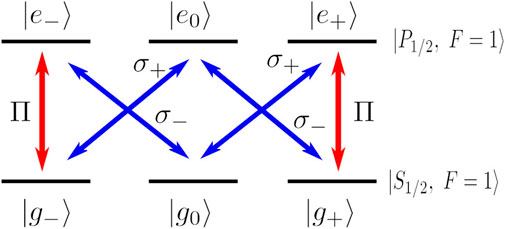
The configuration considered here consists of two hyperfine levels S_1/2|F = 1⟩ and P_1/2|F = 1⟩ of an alkali atom such as rubidium, sodium, or potassium. Both these levels have three Zeeman sublevels each. The sublevels of ground state |S_1/2, F = 1⟩ with magnetic quantum numbers −1, 0 and +1 are labeled |g₋⟩, |g₀⟩, and |g₊⟩, respectively. Similarly, sublevels of the excited state P_1/2 are labeled |e₋⟩, |e₀⟩, and |e₊⟩. The transitions |g₋⟩↔|e₋⟩ and |g₊⟩ ↔|e₊⟩ are coupled by light polarized in the “z” direction with respect to the axis of quantization (labeled as Π polarization in the figure). Due to the symmetry of the corresponding wavefunctions, the transition |g₀⟩ ↔|e₀⟩ turns out to be forbidden. Transitions |g₋⟩↔|e₀⟩ and |g₀⟩ ↔|e₊⟩ are coupled by circularly polarized light that is σ₊ helicity, and similarly, σ₋ polarized light couples transitions |g₊⟩ ↔|e₀⟩ and |g₀⟩ ↔|e₋⟩, as shown in Figure 1.

FIGURE 1

FIGURE 1. Energy levels of an alkali atom with relevant couplings.

2.1 Case I: optical pumping leading to a trap

If only the Π polarized light is present, then the atoms in states |g_±⟩ are excited to states |e_±⟩, respectively, and subsequently decay to any one of the three ground states with equal probability, as shown in Figure 2. Atoms that reach states |g₊⟩ and |g₋⟩ are again excited by the light, whereas atoms that reach |g₀⟩ are left behind. This results in all atoms being emptied from |g_±⟩ and “pumped” into state |g₀⟩ in a finite time.

FIGURE 2

FIGURE 2. Pathways of spontaneous emission decay, leading to optical pumping.

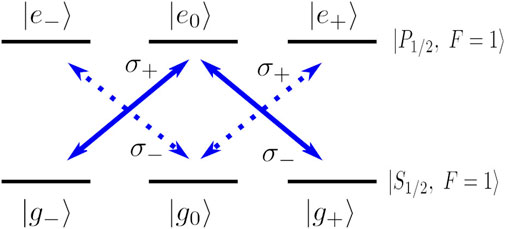
2.2 Case II: Λ scheme and CPT

When only the circularly polarized light is present, the pair of σ₊ and σ₋ forms a Λ configuration as shown in Figure 3. This configuration has been extensively studied (Cohen-Tannoudji and Reynaud, 1977; Arimondo and Wolf, 1996; Ruostekoski and Walls, 1999). Under the interaction with the light fields, the Λ configuration always ends up in a CPT state $|{\psi }_{-}\rangle =(1/\sqrt{2})[|g_{+}\rangle -|g_{-}\rangle ]$.

FIGURE 3

FIGURE 3. Λ configuration, leading to CPT. See text for description.

This gives us two independent trap states to work with, which are orthogonal to each other—the application of π polarized laser will create the atoms in |ψ₀⟩ = |g₀⟩, and the pair of σ_± beams will prepare the atoms in the $|{\psi }_{-}\rangle =(1/\sqrt{2})[|g_{+}\rangle -|g_{-}\rangle ]$ state. i) The trap states are endpoints of the atom–laser interaction, and, therefore, the atoms will reach the relevant state irrespective of values of intensity, detuning, and pulse widths. The relevant values affect only the time taken to reach the endpoint and not the state itself (Cohen-Tannoudji and Reynaud, 1977; Arimondo and Wolf, 1996). ii) Once the atoms reach the trap state, they cease to interact with the laser and, therefore, are stable in this state. iii) Both trap states are formed of the ground states of bare atoms and hence are free from spontaneous emission decay to any other state. iv) The atoms can be transferred from one trap state to the other by simply switching off one laser and switching on the other. However, this transfer involves incoherent processes of spontaneous emission. In the next section, we show a coherent transfer of atoms between the states and also the preparation of a continuous variable state.

Therefore, the states can be mapped to qubits such that |g₀⟩ → |0⟩ and |ψ₋⟩ → |1⟩. Such state preparation is robust and reliable.

2.3 Robustness of a generic CPT state

The robustness of any CPT configurations can be understood by looking at the effect of decoherence on a generic CPT system. A typical system is shown in Figure 4. It consists of two ground states labeled |g⟩ and |f⟩ and an excited state labeled |e⟩. Two optical fields with Rabi frequencies Ω_eg and Ω_ef couple the states as shown in the figure.

FIGURE 4

FIGURE 4. Three-level schematic to explore CPT.

The corresponding Hamiltonian, in units of ℏ is as

$\mathcal{H}=\left[\begin{array}{ccc}\hfill {\omega }_g\hfill & \hfill -{\mathrm{\Omega }}_{eg}\hfill & \hfill 0\hfill \\ \hfill -{\mathrm{\Omega }}_{eg}^{*}\hfill & \hfill {\omega }_e\hfill & \hfill -{\mathrm{\Omega }}_{ef}^{*}\hfill \\ \hfill 0\hfill & \hfill -{\mathrm{\Omega }}_{ef}\hfill & \hfill {\omega }_f\hfill \end{array}\right],(1)$

where ω_e,g,f‘ are the eigen energies of the levels, scaled to ℏ. The eigenstates of the above Hamiltonian are as follows. They are called ‘dressed states’ by Cohen-Tannoudji and Reynaud (Cohen-Tannoudji and Reynaud, 1977), under resonance condition, are

$\begin{array}{ccc}\hfill |{\mathrm{\Psi }}_{+}\rangle & =\hfill & {\mathrm{\Omega }}_{eg}|g\rangle +{\mathrm{\Omega }}_{ef}|f\rangle +G|e\rangle \hfill \\ \hfill |{\mathrm{\Psi }}_0\rangle & =\hfill & {\mathrm{\Omega }}_{ef}|g\rangle -{\mathrm{\Omega }}_{eg}|f\rangle \hfill \\ \hfill |{\mathrm{\Psi }}_{-}\rangle & =\hfill & {\mathrm{\Omega }}_{eg}|g\rangle +{\mathrm{\Omega }}_{ef}|f\rangle -G|e\rangle ,\hfill \end{array}(2)$

where $G=\sqrt{|{\mathrm{\Omega }}_{eg}{|}^2+|{\mathrm{\Omega }}_{ef}{|}^2}$. The state |Ψ₀⟩ is a CPT state (also called a “dark state”) because any atoms prepared in this state will remain there due to coherent cancellation of absorption probability. The population in state |e⟩ will always be zero.

However, collisions will cause a decoherence effect, due to which the cancellation of absorption will be incomplete (Arimondo and Wolf, 1996). To understand the effect of collisions, we must look at the time evolution of the system in the presence of collisions. The time evolution of the system can be obtained by solving the Liouville equation in density matrix formalism, scaled to ℏ, as

$\frac{\partial \rho }{\partial t}=-i\left[\mathcal{H},\rho \right]-\mathcal{L}\rho .(3)$

ρ is the density matrix,

$\rho =\left[\begin{array}{ccc}\hfill {\rho }_{gg}\hfill & \hfill {\rho }_{ge}\hfill & \hfill {\rho }_{gf}\hfill \\ \hfill {\rho }_{eg}\hfill & \hfill {\rho }_{ee}\hfill & \hfill {\rho }_{ef}\hfill \\ \hfill {\rho }_{fg}\hfill & \hfill {\rho }_{fe}\hfill & \hfill {\rho }_{ff}\hfill \end{array}\right],$

$[\mathcal{H},\rho ]$ is the commutator. $\mathcal{L}\rho$ is the Liouville operator containing decay terms. From Eq. 3, the specific equation for the coherence term ρ_gf will take the following form (7):

$\frac{\partial {\rho }_{gf}}{\partial t}=\left[i\left({\mathrm{\Delta }}_{ge}-{\mathrm{\Delta }}_{ef}\right)-\left({\gamma }_{eg}+{\gamma }_{ef}+{\gamma }_c\right)\right]{\rho }_{eg}-i{\mathrm{\Omega }}_{ef}{\rho }_{ge}+i{\mathrm{\Omega }}_{eg}{\rho }_{ef},$

indicating the role of collision decay γ_c.

The Liouville Eq. 3 is solved for time evolution using the Runge–Kutta method with Python code. Decoherence manifests as collisional damping rate γ_c that affects only the ground state coherence term ρ_gf. A few typical values of γ_c were chosen for the simulation to study its effect on coherence. Figure 5 shows the evolution of three population terms, ρ_gg, ρ_ee, and ρ_ff, for two different collision rates (a) γ_c = 0.1 and (b)γ_c = 0.4. Under ideal conditions, the dark state should have ρ_gg = ρ_ff = 0.5 and coherence term ρ_gf = −0.5.

FIGURE 5

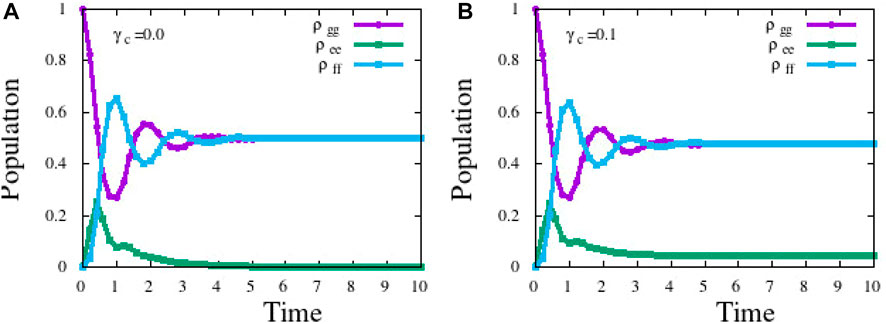
FIGURE 5. Populations of all three levels as a function of time for (A) γ_c = 0.0 and (B) γ_c =0.1, respectively. ρ_ee becomes zero after some time in case (A), whereas it acquires a finite population when γ_c is a finite value.

It is evident that at a long time limit, the populations of ground states ρ_gg and ρ_ff reach 0.5 at a long time limit, in the absence of any collisions (Figure 6A). In the presence of collision, the values are no longer 0.5, and the excited state ρ_ee acquires a finite population, indicating that the dressed state Ψ₀ is a leaky, rather than perfect, dark state (Cohen-Tannoudji and Reynaud, 1977; Arimondo and Wolf, 1996).

FIGURE 6

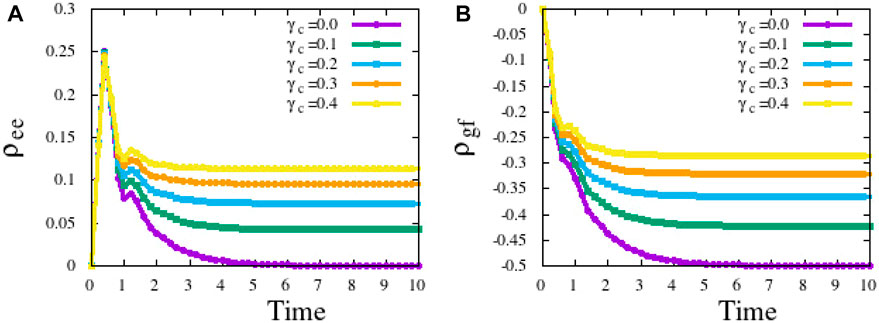
FIGURE 6. (A) The population of the excited state increases as γ_c increases. (B) Coherence ρ_gf between two ground states decreases and deviates from the ideal value of −0.5 as collisional damping increases.

Figure 6A shows the population of excited states for different collision-damping values, ranging from 0.0 to 0.4. The steady-state value of ρ_ee increases with γ_c. The ground state coherence, as shown in Figure 6B, deviates from the ideal value of 0.5. Due to this, the coherent cancellation of absorption is incomplete, and atoms absorb light to reach level |e⟩.

However, increasing the intensity of lasers results in an increase of the Rabi frequency, which can overcome the effect of collisional damping, as shown in Figure 7. The inset of the figure shows an expanded part of a long time limit. This shows how a coherent trap state can be made robust against collisional damping by increasing the laser intensity. This property is applicable to all coherent states.

FIGURE 7

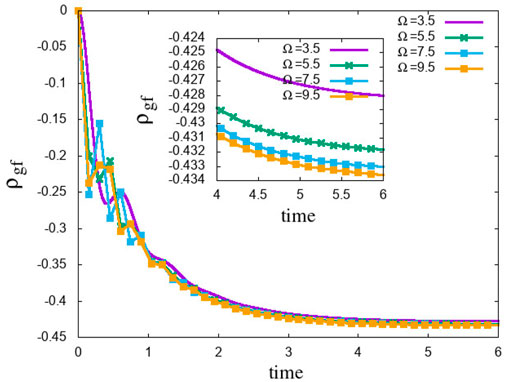
FIGURE 7. ρ_gf for γ_c = 0.4 shifts towards the ideal value when the Rabi frequency Ω_eg = Ω_ef = Ω is increased, indicating that higher intensity can overcome the loss of coherence due to collisions. The inset shows an expanded part of a long time limit.

2.4 Case III: both π and σ combined

When both the π and σ lasers are simultaneously present in Figure 1, the system goes into a unique eigenstate involving all three states, which is of interest to the rest of the communication (Vudayagiri and Tewari, 2006; Vudayagiri, 2011). This unique state is the dressed state of the six-state Hamiltonian,

$\mathcal{H}=\left(\begin{array}{cccccc}\hfill {\omega }_{g_{-}}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_{\pi }\hfill & \hfill {\mathrm{\Omega }}_{\sigma +}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_{g_0}\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_{\sigma -}\hfill & \hfill {\mathrm{\Omega }}_{\pi }\hfill & \hfill {\mathrm{\Omega }}_{\sigma +}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{g_{+}}\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_{\sigma -}\hfill & \hfill {\mathrm{\Omega }}_{\pi }\hfill \\ \hfill {\mathrm{\Omega }}_{\pi }\hfill & \hfill {\mathrm{\Omega }}_{{\sigma }_{-}}\hfill & \hfill 0\hfill & \hfill {\omega }_{e_{-}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathrm{\Omega }}_{\sigma -}\hfill & \hfill {\mathrm{\Omega }}_{\pi }\hfill & \hfill {\mathrm{\Omega }}_{\sigma +}\hfill & \hfill 0\hfill & \hfill {\omega }_{e_0}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Omega }}_{{\sigma }_{-}}\hfill & \hfill {\mathrm{\Omega }}_{\pi }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_{e_{+}}\hfill \end{array}\right),(4)$

and obtains the dressed state under the condition Ω_σ+ = Ω_σ− = Ω_σ

$|\psi \rangle =\frac{\left({\mathrm{\Omega }}_{\sigma }/{\mathrm{\Omega }}_{\pi }\right)|g_0\rangle -\left[|g_{-}\rangle -|g_{+}\rangle \right]}{\sqrt{2+|\left({\mathrm{\Omega }}_{\sigma }/{\mathrm{\Omega }}_{\pi }\right){|}^2}}$

Here, Ω_σ and Ω_π are the Rabi frequencies associated with the σ and π transitions, respectively, as shown in Figure 1. The above equation can be rewritten as

$|\psi \rangle =\frac{\left({\mathrm{\Omega }}_{\sigma }/{\mathrm{\Omega }}_{\pi }\right)|{\psi }_0\rangle -\sqrt{2}|{\psi }_{-}\rangle }{\sqrt{2+|\left({\mathrm{\Omega }}_{\sigma }/{\mathrm{\Omega }}_{\pi }\right){|}^2}},(5)$

or, with a few rearrangements, as

$|\psi \rangle =\frac{{\mathrm{\Omega }}_{\sigma }|{\psi }_0\rangle -\sqrt{2}{\mathrm{\Omega }}_{\pi }|{\psi }_{-}\rangle }{\sqrt{{\mathrm{\Omega }}_{\sigma }^2+2{\mathrm{\Omega }}_{\pi }^2}},(6)$

$|\psi \rangle =\sin \left(\theta /2\right)|0\rangle +\exp \left(i\varphi \right)\cos \left(\theta /2\right)|1\rangle ,(7)$

where

$\sin \left(\theta /2\right)=\frac{|{\mathrm{\Omega }}_{\sigma }|}{\sqrt{|{\mathrm{\Omega }}_{\sigma }{|}^2+2|{\mathrm{\Omega }}_{\pi }{|}^2}}\mathrm{a}\mathrm{n}\mathrm{d}\cos \left(\theta /2\right)=\frac{\sqrt{2}|{\mathrm{\Omega }}_{\pi }|}{\sqrt{|{\mathrm{\Omega }}_{\sigma }{|}^2+2|{\mathrm{\Omega }}_{\pi }{|}^2}}$

and states |ψ₀⟩ = |0⟩ and |ψ₋⟩ = |1⟩ as defined earlier. Exp(iϕ) is the relative phase between |0⟩ and |1⟩, which can be controlled by the phase between Ω_π and Ω_σ.

The dressed state shown in Eq. 6 is a combination of two trap states |ψ₀⟩ and |ψ₋⟩. This combined state is also a trap state and will not evolve further (Vudayagiri and Tewari, 2006). In the form given in Eq. 7, this state is a combination of bits |0⟩ and |1⟩, which has four distinct advantages. i) This is a stationary state of the atom + field Hamiltonian described in Eq. 4 and, therefore, will not evolve, even in the presence of fields. ii) Being made of all ground states, the state will not be affected by decay, unlike those that involve excited states. iii) The value of θ/2 of Eq. 7 can be continuously varied by changing the intensities of the two lasers, which, in turn, varies Ω_π and Ω_σ. When this change is brought about adiabatically and slowly, then the state is continuously and adiabatically varied. This transition does not populate the excited states and hence is a coherent transformation. iv) Varying angle θ/2 will allow the state to span the entire 2D space made up of basis vectors |0⟩ and |1⟩, as explained in the next section.

At first look, Eq. 6 appears to be counterintuitive because setting Ω_π = 0 gives |ψ₀⟩ and setting Ω_σ = 0 gives |ψ₋⟩, which is the opposite of the effect created by individual lasers. However, this must be seen in the context of properties of coherent superpositions of states that lead to the coherence-induced phenomena. For instance, for the dark state |Ψ₀⟩ in Eq. 2 in Section 2.2, the coefficient corresponding to each bare state is the Rabi frequency of the alternative transition. The coefficient of state |g⟩ is Ω_ef, and for state |e⟩, the coefficient is Ω_eg (Cohen-Tannoudji and Reynaud, 1977). The relevance of this will be seen when transition probabilities are computed, as we have shown in Eq. 9.

In the case of the stimulated Raman adiabatic passage (STIRAP) (Gaubatz et al., 1990; Bergmann et al., 2015), a superposition state is first created and later manipulated to achieve a 99% population transfer. This is why the two relevant pulses are required to appear in counterintuitive order, as explained in the references. These indicate that a superposition state that forms contains alternative Rabi frequencies as coefficients.

3 State preparation with continuous variable

An experimental setup is proposed to achieve states that continuously span the vector space. A pair of magnetic coils (labeled Mg) will help define the “z” axis of quantization for the rubidium atoms (labeled Rb). A combination of a half-wave plate (HWP1) and a polarizing beamsplitter (PBS) will divide the laser light into vertical and horizontally polarized lights, whose ratio can be very precisely controlled. The vertically polarized light forms the π light, and the horizontally polarized light is seen by atoms as a sum of σ₊ and σ₋ lights. The second half-wave plate (HWP2) helps align the second beam in a proper polarization, overcoming any changes that arise due to reflections.

Precise positioning of the HWP1 will enable varying Rabi frequencies Ω_π and Ω_σ, such that sin²(θ/2) + cos²(θ/2) = 1 for all values of Ω_π,σ when used in Eq. 7. The parametric angle θ/2 would be related to the angular position of the half-wave plate, and this allows preparing a state with any value of θ as desired. Phase plate “P” allows control of the relative phase ϕ.

Figure 8B depicts a vectorial representation of state given in Eq. 7.

FIGURE 8

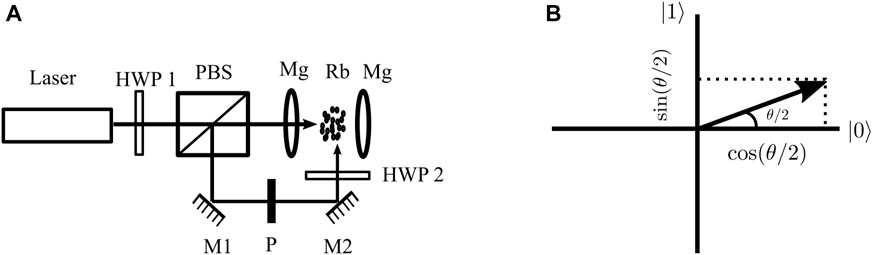
FIGURE 8. (A) Proposed experimental setup to achieve various states—Rb: rubidium atoms; Mg: magnetic coils; M: mirrors; P: phase plate; PBS: polarizing beamsplitter; and HWP1 and 2: half-wave plates. (B) Vector representation of the prepared state.

3.1 Continuous state preparation

By rotating HWP1, the laser light can be precisely divided into the π and σ lasers, whose intensities are precisely controlled to form any θ in state given in Eq. 7. This allows continuously varying the value of θ from zero to 2π, by simply rotating HWP1. Preparing the vector with a given parametric angle θ/2 can be mathematically represented as a rotational operation:

$H\left(\theta \right)=\left(\begin{array}{cc}\hfill \sin \left(\theta /2\right)\hfill & \hfill e^{i\varphi }\cos \left(\theta /2\right)\hfill \\ \hfill -e^{-i\varphi }\cos \left(\theta /2\right)\hfill & \hfill \sin \left(\theta /2\right)\hfill \end{array}\right)(8)$

that acts on column vectors

$|0\rangle \equiv \left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \end{array}\right)\mathrm{a}\mathrm{n}\mathrm{d}|1\rangle \equiv \left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right).$

4 A continuous spatial arrangement of states

We propose a setup as follows. A pair of beams with σ₊ and σ₋ polarizations in the yz plane, coming from opposite directions, +x and −x, is on a sample of atoms. The two beams are

$\begin{array}{ccc}\hfill E_{+}\left(x,t\right)& =\hfill & {\mathcal{E}}_0\left[{ϵ}_y+i{ϵ}_z\right]\exp \left(i{k}_{x}x\right)\exp \left(i\omega t\right)\hfill \\ \hfill E_{-}\left(x,t\right)& =\hfill & {\mathcal{E}}_0\left[{ϵ}_y-i{ϵ}_z\right]\exp \left(-i{k}_{x}x\right)\exp \left(i\omega t\right)\hfill \end{array}$

The two beams will add up to give (Metcalf and Peter van der Straaten, 1999)

$E\left(x,t\right)={\mathcal{E}}_0\left[{ϵ}_y.\cos \left(k_x.x\right)-{ϵ}_z.\sin \left(k_x.x\right)\right]\exp \left(i\omega t\right).(9)$

This results in a light beam propagating in the x-direction, with a continuously varying polarization from y-polarized to z-polarized and back to y-polarized, with a periodicity of k_x = 2π/λ, as shown in Figure 9.

FIGURE 9

FIGURE 9. Polarization of light as a function of distance “x.”

Wherever the light beam is z-polarized, it is equivalent to the π beam and the atoms at that position will reach |g₀⟩ = |ψ₀⟩, equivalent to θ/2 = (n + 1)π/2. Wherever the beam is y-polarized, the electric field is equivalent to the sum of the σ₊ and σ₋ fields, and hence, the atoms will get into the CPT state of |ψ₋⟩. In the region between, the light is in different polarizations, and hence, the atoms will be in state |ψ⟩ with different θ/2 values.

4.1 Continuous transformation of the state of the atom

There are now two methods of obtaining continuous variable states—in the first option, consider a slow atom moving along the “z” direction. This atom encounters light with a continuously varying polarization, which results in the atom adiabatically changing its state as per Eq. 7 in a continuous fashion. As a result, the state vector of the atom traverses a closed trajectory on a corresponding Bloch sphere, acquiring a Berry phase in the process (Tewari, 1989). Atoms traveling in +z and −z acquire opposite and equal phases, which would be very useful in atom interferometry and also in quantum computation.

4.2 Spin–spin interaction

The second option is to take a collection of cold atoms and have the σ_± beams incident on them as described earlier. Atoms at different spatial points experience different polarizations and therefore are prepared in different states, in a continuous distribution of states, the state vector depending upon its “z” position.

In the presence of an external magnetic field, each of these atoms aligns at an angle with respect to the magnetic field direction, depending upon its position. The |g₀⟩ component of the state aligns perpendicular to the field, and the |g₋⟩ component aligns parallel to the field due to their spin values. For the combination of these two states in the form given in Eq. 7, the angle of alignment will be a vector sum of these parallel and perpendicular components, with a weightage of sin(θ/2) and cos(θ/2), the value of θ/2 depending upon the position of the given atom. Two nearby atoms will now have their respective spins aligned, depending upon the net polarization at their respective positions as given by Eq. 9, and subsequently, the spin–spin interaction between the two is given by Cohen-Tannodji et al. (1977):

$W=\frac{{\mu }_0}{4\pi }{\gamma }_1{\gamma }_2\frac{1}{r^3}\left[S_1.S_2-2\left(S_1.n\right)\left(S_2.n\right)\right],$

where M₁ = γ₁S₁ and M₂ = γ₂S₂ are, respectively, the magnetic moments of the two atoms. S₁ and S₂ are the net spins of the two atoms, and r is the perpendicular distance between the two. This would cause continuous spin interactions between atoms, with the interaction potential depending upon the relative positions of the atoms. The interaction would lead to a steady state and redistribution of the atoms. Following the formation of a controlled-phase gate, as described in Vudayagiri (2011), this phenomenon could be used in a “continuous” phase-gate, in a fashion similar to analog computation.

5 Conclusion

We have considered a system consisting of the two ground states of an alkali atom and their Zeeman sublevels. This makes a total of six levels, coupled by two lasers that differ in their polarizations. The interaction leads to a dressed state that is a combination of all three ground states in such a way that it can be mapped to a state of the form |ψ⟩ = sin(θ/2)|0⟩ + exp(iϕ) cos(θ/2)|1⟩. We have earlier shown that a discrete gate operation can be performed using this system (Vudayagiri, 2011). Here, we show that the same system can be used to perform continuous state preparation and, therefore, continuous operations as well.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

AV developed most calculations; BS created the numerical simulations. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arimondo, E. (1996). “Coherent population trapping in laser spectroscopy,” in Progress in optics Editor E. Wolf (Amsterdam, Netherlands: Elsevier).

Google Scholar

Bergmann, K., Nikolay, V., and Shore, B. W. (2015). Perspective: Stimulated Raman adiabatic passage: The status after 25 years. J. Chem. Phys. 142, 170901. doi:10.1063/1.4916903

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen-Tannodji, C., Bernard, D., and Laloë, F. (1977). Quantum mechanics. Wiley – VCH, 1120.

Google Scholar

Cohen-Tannoudji, C., and Reynaud, S. (1977). Dressed-atom description of resonance fluorescence and absorption spectra of a multi-level atom in an intense laser beam. J. Phys. B 10, 2311.

CrossRef Full Text | Google Scholar

Gaubatz, U., Rudecki, P., Schiemann, S., and Bergmann, K. (1990). Population transfer between molecular vibrational levels by stimulated Raman scattering with partially overlapping laser fields. A new concept and experimental results. J. Chem. Phys. 92, 5363–5376. doi:10.1063/1.458514

CrossRef Full Text | Google Scholar

Gottesman, D., Kitaev, A., and Preskill, J. (2001). Encoding a qubit in an oscillator. Phys. Rev. A 64, 012310. doi:10.1103/physreva.64.012310

CrossRef Full Text | Google Scholar

Lloyd, S., and Braunstein, S. (1999). Quantum computation over continuous variables. Phys. Rev. Let. 82, 1784–1787. doi:10.1103/physrevlett.82.1784

CrossRef Full Text | Google Scholar

Menicucci, N., Peter van Loock, , Gu, M., Weedbrook, C., Ralph, T. C., and Nielsen, M. (2006). Universal quantum computation with continuous-variable cluster states. Phys. Rev. Let. 97, 110501. doi:10.1103/physrevlett.97.110501

PubMed Abstract | CrossRef Full Text | Google Scholar

Metcalf and Peter van der Straaten, H. (1999). Laser cooling and trapping. Berlin, Germany: Springer, 47.

Google Scholar

Ruostekoski, J., and Walls, D. F. (1999). Coherent population trapping of Bose-Einstein condensates: Detection of phase diffusion. Eur. Phys. J. D. 5, 335–339. doi:10.1007/s100530050263

CrossRef Full Text | Google Scholar

Tewari, S. P. (1989). Berry’s phase in a two-level atom. Phys. Rev. A 39, 6082–6085. doi:10.1103/physreva.39.6082

PubMed Abstract | CrossRef Full Text | Google Scholar

Vudayagiri, A. (2011). Quantum logic gates using coherent population trapping states. Pramana J. Sci. 77, 1127–1133. doi:10.1007/s12043-011-0148-6

CrossRef Full Text | Google Scholar

Vudayagiri, A., and Tewari, S. P. (2006). Tuneable nonlinearity in atomic response to a bichromatic field. J. Phys. B At. Mol. Opt. Phys. 39, 3919–3933. doi:10.1088/0953-4075/39/18/021

CrossRef Full Text | Google Scholar

Zhang, J., and Braunstein, S. L. (2006). Continuous-variable Gaussian analog of cluster states. Phys. Rev. A 73, 032318. doi:10.1103/physreva.73.032318

CrossRef Full Text | Google Scholar