Postponing the decay of entanglement and quantum coherence for maximally entangled mixed states under the action of correlated noise channels

We investigate the dynamics of a maximally entangled mixed state (MEMS) under the action of correlated noise channels. The channel acts in a way that its successive uses are correlated. We have studied the MEMS properties, including quantum coherence and entanglement. For partially correlated channels, both the entanglement and coherence of MEMS are found to decay much slower than those of the memoryless channels. Moreover, we observe a freezing effect of coherence for phase damping as well as depolarizing channels and freezing of entanglement for phase-damping channels with perfect memory. For amplitude damping and depolarizing channels, memory helps in either delaying the sudden death of entanglement or slowing the decay rate of coherence. These observations suggest that memory channels perform better than memoryless channels in maintaining the integrity of quantum states and have utility in quantum information processing protocols.

1 Introduction

Coherence is a fundamental concept in physics that plays a pivotal role in the occurrence of interference phenomena observed in nature (Mandel and Wolf, 1995). The concept of quantum coherence lies at the heart of quantum theory, which plays a crucial role in describing certain quantum physical phenomena, such as the single-particle interference pattern observed in a double-slit experiment. In fact, quantum coherence arises as a manifestation of the superposition principle that can occur either among a set of quantum mechanical systems or between different energy levels of a single quantum system. The former is known as inter-particle or global coherence, and the latter is called intra-particle or local coherence. The early studies in quantum optics established that quantum entanglement, a characteristic quantum correlation (Paulson et al., 2021), is closely connected to inter-particle quantum coherence. Therefore, quantum coherence (Mohanty et al., 2022) is considered more fundamental than quantum correlations such as entanglement (Streltsov et al., 2015) and discord, as it is one of the important resources for creating them.

In classical physics, the visibility of the interference pattern is used to quantify coherence using correlation functions that depend on the product of field amplitudes. The investigation of quantum coherence has been a focal point in various fields, including quantum optics, where researchers have examined the fundamental nature of coherence using techniques such as phase-space distributions and higher-order correlation functions. For a considerable time, a comprehensive theory of quantum coherence, which holds profound importance as a physical resource, remained elusive. Only recently was a rigorous mathematical framework introduced by Baumgratz, Cramer, and Plenio to quantify coherence (Baumgratz et al., 2014) and provide computable measures of coherence. Such coherence measures include relative entropy, l₁-norm, and skew information. Following this, a resource theory of quantum coherence (Winter and Yang, 2016; Streltsov et al., 2017) was developed and enabled the study of operational applications, dynamical evolution, interconversion, and manipulation of quantum coherence (Wu et al., 2020).

Quantum entanglement, on the other hand, is a purely quantum mechanical correlation that is considered to be a defining characteristic of quantum mechanics. It is one of the most important properties that differentiate the quantum world from the classical one (Horodecki et al., 2009). The origin of entanglement dates back to 1935 when Einstein, Podolsky, and Rosen questioned the completeness of quantum mechanics through a Gedanken experiment (Einstein et al., 1935) involving entangled particles. Owing to the significance of entanglement in the foundations of quantum mechanics and advanced quantum technologies, it continues to be at the forefront of current research. Harnessing the power of entanglement has enormous potential to revolutionize fields from quantum computing to secure communications, metrology, sensing, imaging, and precision measurements. Entanglement is, in fact, an indispensable resource in quantum information processing tasks (Horodecki et al., 2009) and has applications ranging from the quantum key distribution (Ursin et al., 2007), teleportation, remote state preparation (Bennett et al., 2001), and dense coding (Jing et al., 2003) to quantum computation (Nielsen and Chuang, 2010).

A recent advancement in the field of quantum information is the study of the dynamics of quantum correlations and coherence in the presence of environmental influences. Entanglement and coherence are both invaluable yet delicate resources that degrade as a result of the unavoidable interaction between the quantum system and its environment. Several theoretical and experimental investigations have revealed that entanglement can undergo a finite time decay known as entanglement sudden death (ESD) (Yu and Eberly, 2004; Almeida et al., 2007; Yu and Eberly, 2009), even in the presence of noise that results in single-particle decoherence only asymptotically. Decay of coherence and entanglement thus pose a serious threat to quantum information processing tasks that require these physical resources. Numerous studies have examined the measures of entanglement and coherence to acquire deep knowledge of the decoherence mechanism in an open quantum system. Several methods have been proposed and experimentally demonstrated to protect entanglement from decoherence, such as quantum measurement reversal (Korotkov10 and Keane, 2010), using local unitary operations (Singh et al., 2017; Singh, 2022; Singh and Sinha, 2022), feedback control (Doherty et al., 2000), and quantum Zeno effect (Itano et al., 1990). It is always interesting to find new methods (Merkli et al., 2012) to protect entanglement and coherence from the detrimental effects of the environment.

The assumption of an uncorrelated noise channel in real-world quantum systems cannot be justified. Hence, the effect of memory needs to be taken into account, and the development of a framework encompassing uncorrelated and correlated noise channels is desirable (Kretschmann and Werner, 2005). The concept of memory was introduced by C. Macchiavello and G.M. Palma (Macchiavello and Palma, 2002). The study of memory channels has gained much attention while studying information transmission over successive uses of quantum channels. Information backflow due to memory plays a significant role in suppressing decoherence. The objective of this work is to study the effect of quantum channels with memory, such as an amplitude-damping channel (ADC), a phase-damping channel (PDC), and a depolarizing channel (DC), on the entanglement and quantum coherence of MEMS. In this work, we have used two coherence measures, namely, the l₁ norm and the relative entropy of coherence, to quantify the quantum coherence of MEMS. We used concurrence as a computable measure of entanglement to study entanglement dynamics.

This paper is organized as follows: In Section 1, we provide a general introduction to concepts of quantum coherence, entanglement, and how these properties of an open quantum system get impacted by the environment. In Section 2, we discuss the preliminaries and present an introduction to entanglement and quantum coherence measures, followed by an overview of the initial state and the memory channels. In Section 3, we focus on the examination of entanglement in different correlated noise channels, highlighting the distinction between Kraus operators for the correlated and uncorrelated noise channels and corresponding results. In Section 4, we provide the results related to quantum coherence measures for different channels with memory effect. Finally, in Section 5, we conclude the discussion with a future outlook.

2 Preliminaries

In this section, we start by reviewing the measures of entanglement and coherence for quantifying them. We provide a basic description of the initial state and the noise model. The initial state considered here is the maximally entangled mixed state (MEMS), which has a mixedness parameter. This state was investigated by Munro et al. (2001) and Munro and Nemoto (2001), and it has been shown that MEMS’s entanglement is higher than that of the Werner state. For the noise model, we consider an ADC, a PDC, and a DC with and without memory in the successive uses of the channels.

2.1 Entanglement measure

Entanglement of two-qubit pure or mixed states can be quantified by several entangled measures (Plenio and Virmani, 2007), and they are shown to be monotonic (Singh et al., 2020) with respect to each other. Here, we use concurrence as a computable measure of entanglement that is also shown to be an entanglement monotone for pure and mixed states for low-dimensional systems. Concurrence was introduced by Hill and Wootters (1997) for two-qubit pure states. Subsequently, Wootters (1998) developed a closed-form expression for its convex roof extension and provided a computable formula for the entanglement of formation in the two-qubit case (Wootters, 2001). For a general two-qubit state represented by a density matrix ρ, concurrence is given as follows:

$C\left(\rho \right)=\mathit{max}\left\{0,{\lambda }_1-{\lambda }_2-{\lambda }_3-{\lambda }_4\right\},(1)$

where ${\lambda }_i^{\prime }s$ are the square roots of the eigenvalues of the matrix $\rho \tilde{\rho }$ in decreasing order. Here, $\tilde{\rho }$ is obtained by applying the spin-flip matrix to ρ as follows:

$\tilde{\rho }=\left({\sigma }^y\otimes {\sigma }^y\right){\rho }^{*}\left({\sigma }^y\otimes {\sigma }^y\right),(2)$

where the complex conjugation (ρ*) is determined in the computational basis {|00⟩, |01⟩, |10⟩, |11⟩}.

2.2 Quantum coherence measure

Quantum coherence (Streltsov et al., 2017), one of the basic features of quantum physics and a key resource in the field of quantum information processing, requires a quantitative measure for studying its dynamical evolution under different quantum maps. A broad range of coherence measures is utilized, often relying on the off-diagonal terms of the density matrix. The primary justification for employing these measures is typically based on physical intuition. Recently, the characterization and quantification of coherence have gained much attention, and a quantitative theory of coherence as a resource was developed (Baumgratz et al., 2014) using entanglement-based approaches (Vedral and Plenio, 1998; Brandão and Plenio, 2008; Brandão and Plenio, 2010). These articles suggested that any proper measure of coherence must satisfy several criteria, some of which focused on the properties of specific coherence measures based on entanglement (Napoli et al., 2016), operation (Yuan et al., 2015), or convex roof construction (D’Arrigo et al., 2013). In this work, we adopt two proper measures of coherence that are computable and monotonic to study the evolution of coherence in the presence of correlated noise channels. The first measure is the l₁-norm, and the second is the relative entropy of coherence.

The l₁-norm of coherence is based on the absolute sum of the off-diagonal elements of the density matrix and is defined as

$C_{l_1}\left(\rho \right)=\mathit{min}D\left(\rho ,\delta \right)={\displaystyle \sum _{i\ne j}}|{\rho }_{i,j}|,(3)$

where D(ρ, δ) = ‖ρ − δ‖ denotes the distance of ρ to a set of incoherent states I(δ ∈ I), and ρ_i,j are the off-diagonal elements of ρ (Baumgratz et al., 2014). Note that the l₁-norm of coherence depends on the basis in which the density matrix is expressed. In general, for a d-dimensional system, $0\le C_{l_1}(\rho )\le d-1$, and the maximum value is achieved for a maximally coherent state that is in a uniform superposition of the basis states: $|{\psi }_d\rangle ≔\frac{1}{\sqrt{d}}{\sum }_{i=1}^d|i\rangle$. The relative entropy of coherence (C_R) is defined as

$C_R\left(\rho \right)=\mathit{min}S\left(\rho \Vert \delta \right)=S\left({\rho }_{diag}\right)-S\left(\rho \right),(4)$

where ρ_diag is the diagonal density matrix of ρ and S(ρ) indicates the Von Neumann entropy (Breuer and Petruccione, 2002; Baumgratz et al., 2014). For a given state ρ, the relative entropy is bounded as C_R ≤ S(ρ_diag) ≤ log₂(d) and, again, the maximum value is achieved for the maximally coherent state.

2.3 Initial state and memory channel

Let us begin with a brief introduction of the initial state and the noise channels in terms of memory and memoryless channels (D’Arrigo et al., 2013; Paulson et al., 2022). We chose MEMS as the initial state for our study as this is the class of mixed states that are maximally entangled for a given purity. This state was introduced by Munro et al. (2001) and Munro and Nemoto (2001); its density matrix is given by

${\rho }_M=\left(\begin{array}{cccc}\hfill g\left(\gamma \right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\gamma }{2}\hfill \\ \hfill 0\hfill & \hfill 1-2g\left(\gamma \right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{\gamma }{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill g\left(\gamma \right)\hfill \end{array}\right),(5)$

where

$g\left(\gamma \right)=\left\{\begin{array}{cc}\frac{1}{3},\hfill & 0\le \gamma <\frac{2}{3},\hfill \\ \frac{\gamma }{2},\hfill & \frac{2}{3}\le \gamma \le 1.\hfill \end{array}\right.$

From here onward, we will denote g(γ) simply as g, and its dependence on γ is considered implied. The state (5) is entangled for all values of γ > 0. Here, we discuss two different cases of MEMS, that is., $0\le \gamma <\frac{2}{3}$ and with $\frac{2}{3}\le \gamma <1$. For comparison, the Werner state (or W-state) (Werner, 1989) is another class of mixed entangled states that are a mixture of a maximally entangled state and the maximally mixed state: $|W\rangle =(\frac{1-\gamma }{4})I_2\otimes I_2+\gamma |{\varphi }_{+}\rangle \langle {\varphi }_{+}|$. It is entangled for γ > 1/3 and maximally entangled for γ = 1. When considering a specific level of mixture, the maximally entangled mixed state is typically much more entangled than the Werner state with an equivalent degree of mixture.

A quantum channel can be broadly classified into two categories: a memoryless channel and a memory channel. In the case of a memoryless channel, the environmental correlation time is smaller than the time between successive uses of the channel over two qubits. Conversely, in the case of a memory channel, the environmental correlation time is greater than the time between two consecutive uses of the channel. Mathematically, a quantum channel can be defined as a completely positive trace-preserving (CPTP) map between input and output states (density matrices), and the action of the channel (ϵ) on a quantum state ρ can be expressed as follows:

$ϵ\left(\rho \right)={\displaystyle \sum _i}{E}_i\rho E_i^{†},(6)$

where E_i are the Kraus operators of the channel satisfying the completeness condition ${\sum }_i{E}_i{E}_i^{†}=1$, and $E_i=\sqrt{P_{i_1\dots i_N}}{A}_i$. Here, $P_{i_1\dots i_N}$ is the joint probability distribution for a random sequence of operations applied to N qubits passing through quantum channels. Kraus operators are obtained by tracing the environmental degrees of freedom from the global unitary operation between the system and the environment. When $P_{i_1\dots .i_N}=P_{i_1}{P}_{i_2}\dots P_{i_N}$, these operations are said to be independent, and the corresponding channel is called memoryless. However, for memory channels, $P_{i_1\dots i_N}=P_{i_1}{P}_{i_2|i_1}\dots P_{i_N|i_{N-1}}$ are correlated, and $P_{i_N|i_{N-1}}=(1-\mu )P_{i_N}+\mu {\delta }_{i_N,i_{N-1}}$ is the conditional probability with the memory parameter of the channel 0 ≤ μ ≤ 1 (Guo et al., 2017; Awasthi et al., 2022). The evolution of an initial state ρ under two successive uses of a memory channel can be written as follows (Yeo and Skeen, 2003; Sharma and Gerdt, 2020):

$ϵ\left(\rho \right)=\left(1-\mu \right){\displaystyle \sum _{i,j}}{E}_{i,j}^u\rho E_{i,j}^{u†}+\mu {\displaystyle \sum _k}{E}_{k,k}^c\rho E_{k,k}^{c†}.(7)$

It can be seen from the aforementioned expression that the action of the correlated noise is specified by the Kraus operator $E_{k,k}^c$ with probability μ, and the action of the uncorrelated noise is specified by the Kraus operator $E_{i,j}^u$ with probability (1 − μ).

3 Action of correlated channels with memory on the entanglement of MEMS

In this section, we analyze the effect of amplitude damping, phase damping, depolarizing channel, and bit-flip channel with memory on the entanglement and quantum coherence of the MEMS.

3.1 Amplitude-damping channel with memory

ADC can be conceptualized as a simplified representation of the decay of the energy of an excited state in a two-level atom over time due to the emission of a photon through spontaneous decay. The ADC Kraus operators (Preskill, 1998) for a single qubit are given as

$E_0^u=\left(\begin{array}{cc}\hfill \sqrt{1-p}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right),E_1^u=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill \sqrt{p}\hfill & \hfill 0\hfill \end{array}\right),(8)$

where p = 1 − exp(−λt) is the probability of decay (0 ≤ p ≤ 1) of the qubit from the excited state to the ground state, which we call the noise parameter for ADC, and λ is the decay rate of the excited state. The Kraus operators governing the evolution of a two-qubit quantum system are given as

$E_{ij}^u=E_i^u\otimes E_j^u,\left(i,j=\mathrm{0,1}\right).(9)$

In contrast, the Kraus operators for the correlated part of the ADC are given as

$E_{00}^c=\left(\begin{array}{cccc}\hfill \sqrt{1-p}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),E_{11}^c=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill \\ \hfill \sqrt{p}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(10)$

where the value of p ranges between 0 and 1 (Yeo and Skeen, 2003). Substituting Eqs 5, 8–10 into Eq. 7, the density matrix of MEMS after evolution through correlated ADC is given as

${\rho }_{MA}=\left(\begin{array}{cccc}\hfill g\left(1-\mu \right){\left(1-p\right)}^2+g\mu \left(1-p\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{2}\gamma \left(1-\mu \right)\left(1-p\right)+\frac{1}{2}\gamma \mu \sqrt{1-p}\hfill \\ \hfill 0\hfill & \hfill \left(1-2g\right)\mu +\left(1-\mu \right)\left(\left(1-2g\right)\left(1-p\right)+gp\left(1-p\right)\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill g\left(1-\mu \right)\left(1-p\right)p\hfill & \hfill 0\hfill \\ \hfill \frac{1}{2}\gamma \left(1-\mu \right)\left(1-p\right)+\frac{1}{2}\gamma \mu \sqrt{1-p}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left(1-\mu \right)\left(g{p}^2+\left(1-2g\right)p+g\right)+\mu \left(gp+g\right)\hfill \end{array}\right).(11)$

3D plots of concurrence (C) vs. ADC parameter (p) and memory parameter (μ) for MEMS with γ = 0.5 and 0.9 are shown in Figures 1, 3, respectively. Two-dimensional projections of these plots in the (C − p) plane for different memory parameters are shown in Figures 2, 4.

FIGURE 1

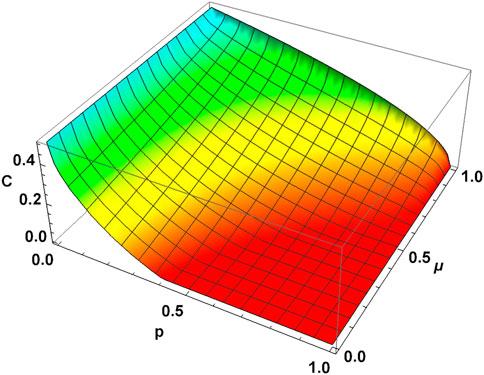
FIGURE 1. Concurrence vs. ADC parameter p and memory parameter μ for MEMS with γ = 0.5. For μ = 0, MEMS undergoes ESD, and μ > 0.63 leads to ADE. MEMS retains more entanglement for the same p-value as the memory parameter increases.

FIGURE 2

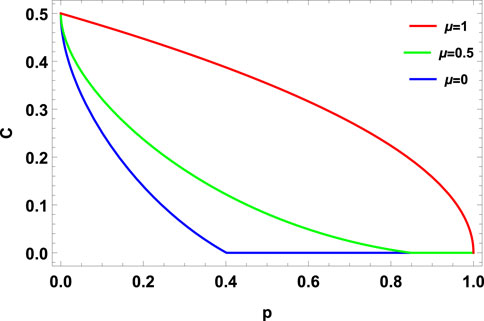
FIGURE 2. Concurrence vs. noise parameter p for ADC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

According to Eq. 5, we have bifurcated the study of MEMS into two ranges of the g(γ) parameter: (i) when $0\le \gamma <\frac{2}{3}$ and (ii) $\frac{2}{3}\le \gamma <1$. It is evident from Figures 1, 3 that MEMS undergoes ESD for both choices of γ parameter (γ = 0.5 & 0.9) in the presence of pure memoryless ADC (μ = 0). It can be easily verified from Eq. 5 that the higher the value of γ, the higher the entanglement in MEMS. Figures 1–4 show that as the value of the memory parameter (μ) increases from zero, MEMS contains a higher amount of entanglement for the same value of ADC parameter (p). As the value of μ increases, there is a delay in the sudden death of entanglement (Ficek and Tanaś, 2008). Moreover, ESD can be completely avoided for sufficiently high memory parameters for a given γ as MEMS undergoes asymptotic decay of entanglement (ADE). Further increase in μ increases the amount of entanglement for a given p.

FIGURE 3

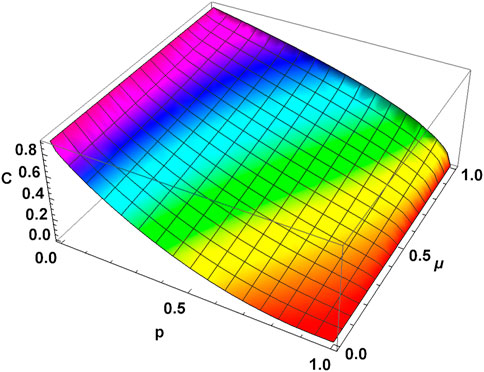
FIGURE 3. Concurrence vs. ADC parameter p and memory parameter μ for MEMS with γ = 0.9. MEMS retains more entanglement for the same p-value as the memory parameter increases.

FIGURE 4

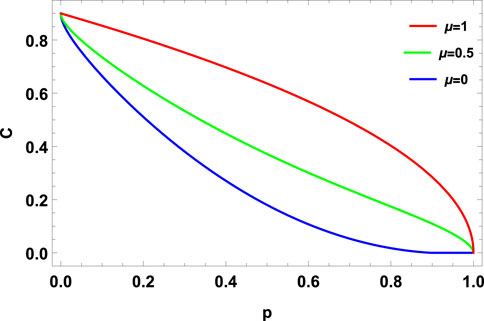
FIGURE 4. Concurrence vs. noise parameter p for ADC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.9.

3.2 Phase-damping channel with memory

PDC is a unital channel that describes the loss of quantum information without the loss of energy. The single-qubit Kraus operators for a memoryless PDC are given as $\sqrt{P_i}{\sigma }_i$, where i = {0, 3}, P₀ = 1 − p/2, P₃ = p/2, and 0 ≤ p ≤ 1. For two successive uses of channels, no correlation is generated for memoryless channels. The uncorrelated or memoryless Kraus operators for two qubits (Datta et al., 2018; D’Arrigo et al., 2007) are given as

$E_{i,j}^u=\sqrt{P_i{P}_j}{\sigma }_i\otimes {\sigma }_j,i,j=\left\{\mathrm{1,3}\right\}.(12)$

In the presence of memory, two uses of channels generate some correlation, and the correlated Kraus operators (Datta et al., 2018; D’Arrigo et al., 2007) for two qubits are given as

$E_{k,k}^c=\sqrt{P_K}{\sigma }_k\otimes {\sigma }_k,k=\left\{\mathrm{0,3}\right\},(13)$

where P₀ = 1 − p/2, P₃ = p/2. Substituting Eqs 5, 12, 13 into Eq. 7, the final density matrix of the MEMS can be expressed as

${\rho }_{MP}=\left(\begin{array}{cccc}\hfill g\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{2}\left(\gamma -\gamma \left(\mu -1\right)\left(p-2\right)p\right)\hfill \\ \hfill 0\hfill & \hfill 1-2g\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{1}{2}\left(\gamma -\gamma \left(\mu -1\right)\left(p-2\right)p\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill g\hfill \end{array}\right).(14)$

3D plots of concurrence (C) vs. PDC parameter (p) and memory parameter (μ) for γ = 0.5 and 0.9 are shown in Figures 5, 7. Two-dimensional projections of these plots in the (C − p) plane for different memory parameters are shown in Figures 6, 8.

FIGURE 5

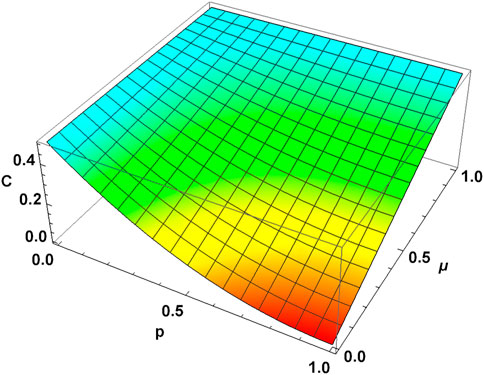
FIGURE 5. Concurrence vs. PDC parameter p and memory parameter μ for MEMS with γ = 0.5. MEMS retains more entanglement for the same p-value as the memory parameter increases.

FIGURE 6

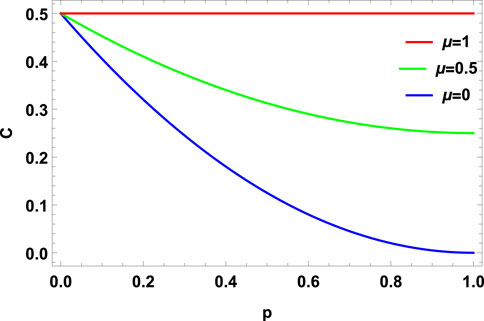
FIGURE 6. Concurrence vs. noise parameter p for PDC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

It is evident from Figures 5, 7 that MEMS undergoes ADE for both choices of γ parameter (γ = 0.5 & 0.9) in the presence of a pure memoryless ADC (μ = 0). As soon as the value of μ becomes non-zero, MEMS retains a non-zero entanglement even at p → 1. Figures 5–8 show that as the value of the memory parameter (μ) increases from zero, MEMS contains a higher amount of entanglement for a non-zero p-value. For a perfectly correlated channel (μ = 1), the entanglement of MEMS (for arbitrary γ values) freezes at the same value as the initial state for all values of p.

FIGURE 7

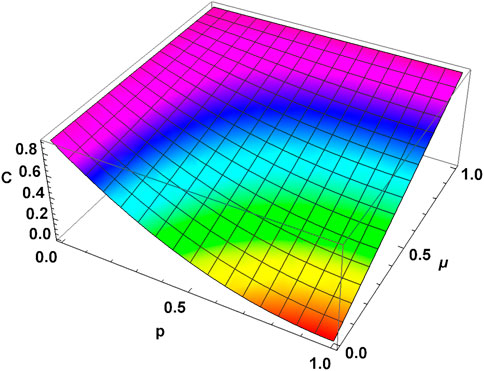
FIGURE 7. Concurrence vs. noise parameter p for PDC with memory (μ) for MEMS with γ = 0.9. MEMS retains more entanglement for the same p-value as the memory parameter increases.

FIGURE 8

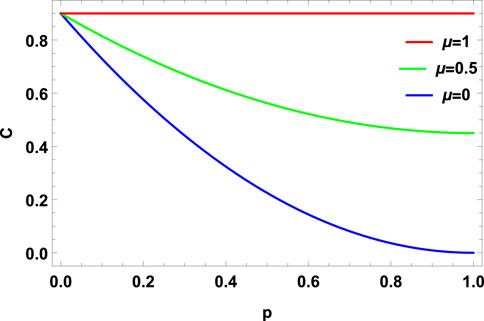
FIGURE 8. Concurrence vs. noise parameter p for PDC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.9.

In Awasthi and Joshi (2023), we studied the effect of memory and memoryless channels on entanglement for different values of noise and MEMS parameters in the context of ADCs and PDCs. In previous work, a delay in the sudden death of entanglement in two different cases was observed. Motivated by our previous work, we explored our results for other channels on entanglement and quantum coherence. We again bifurcated our calculations into two cases based on the γ parameter of MEMS. Here, our main focus is on two noise channels, that is, depolarizing and bit-flip channels, and how they compare with the ADC and PDC channels with memory.

3.3 Depolarizing channel with memory

A depolarizing channel describes how the density matrix is dynamically replaced by the state I₂/2, where I₂ denotes the identity matrix. The Kraus operators for a single qubit (Macchiavello et al., 2004) are given as

$A_i=\sqrt{P_i}{\sigma }_i,(15)$

where P₀ = 1 − p, P₁ = P₂ = P₃ = p/3, and p = 1 − e^−λt. The Kraus operators of the depolarizing channel without memory, where no correlation is generated by successive uses of channels, can be written as

$E_{i,j}^u=\sqrt{P_i{P}_j}{\sigma }_i\otimes {\sigma }_j.(16)$

The case of two successive uses of a channel with partial memory that generates some correlation is given as

$E_{k,k}^c=\sqrt{P_k}{\sigma }_k\otimes {\sigma }_k,(17)$

where i, j, k = {0, 1, 2, 3}.

Substituting Eqs 5, 16, 17 into Eq. 7, the final density matrix of MEMS can be expressed as

${\rho }_{MD}=\left(\begin{array}{cccc}\hfill g\mu -\frac{1}{9}\left(\mu -1\right)\left(g{\left(3-4p\right)}^2+2p\left(3-2p\right)\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{18}\gamma \left(9-8\left(\mu -1\right)p\left(2p-3\right)\right)\hfill \\ \hfill 0\hfill & \hfill \frac{1}{9}\left(2p-3\right)\left(g\left(8\left(\mu -1\right)p+6\right)-2\left(\mu -1\right)p-3\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{2}{9}p\left(\left(3-6g\right)\mu -2\left(\mu -1\right)\left(g\left(3-4p\right)+p\right)\right)\hfill & \hfill 0\hfill \\ \hfill \frac{1}{18}\gamma \left(9-8\left(\mu -1\right)p\left(2p-3\right)\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill g\mu -\frac{1}{9}\left(\mu -1\right)\left(g{\left(3-4p\right)}^2+2p\left(3-2p\right)\right)\hfill \end{array}\right).(18)$

3D plots of concurrence (C) vs. depolarizing channel parameter (p) and memory parameter (μ) for γ = 0.5 & 0.9 are shown in Figures 9, 11. Two-dimensional projections of these plots in the (C − p) plane for different memory parameters are shown in Figures 10, 12.

FIGURE 9

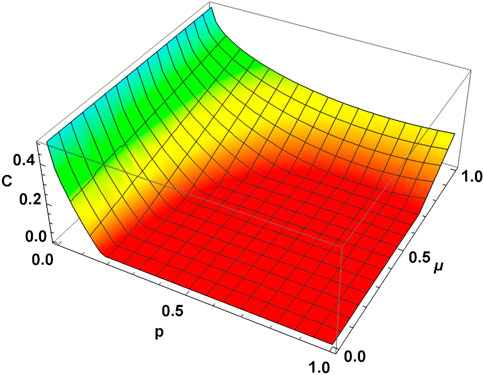
FIGURE 9. Concurrence vs. depolarizing parameter p and memory parameter μ for MEMS with γ = 0.5. MEMS retains more entanglement for the same p-value as the memory parameter increases. In particular, MEMS undergoes ESD for μ = 0, whereas μ = 1 leads to ADE.

FIGURE 10

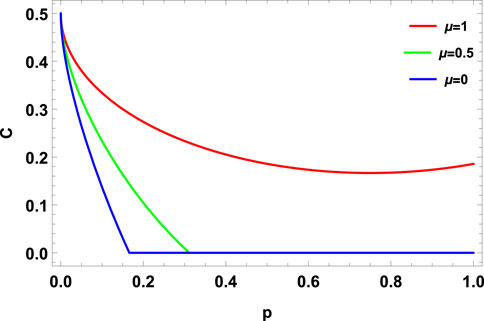
FIGURE 10. Concurrence vs. noise parameter p for DC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

It is evident from Figures 9, 11 that MEMS undergoes ESD for both choices of γ parameter (γ = 0.5 & 0.9) in the presence of a pure memoryless depolarizing channel (μ = 0). In Figures 9–12, one can see that as μ increases from zero, MEMS contains a higher amount of entanglement for the same value of p. Furthermore, as the value of μ increases, there is a delay in the sudden death of entanglement. Moreover, ESD can be completely avoided for sufficiently high memory parameters for a given γ as MEMS undergoes ADE. Further increase in μ increases the amount of entanglement for a given p.

FIGURE 11

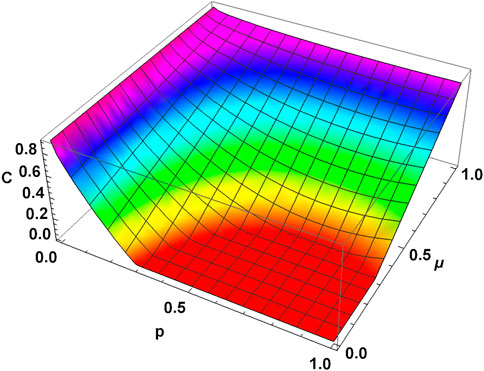
FIGURE 11. Concurrence vs. depolarizing parameter p and memory parameter μ for MEMS with γ = 0.9. MEMS retains more entanglement for the same p-value as the memory parameter increases. In particular, for μ = 0, MEMS undergoes ESD, whereas μ = 1 leads to ADE.

FIGURE 12

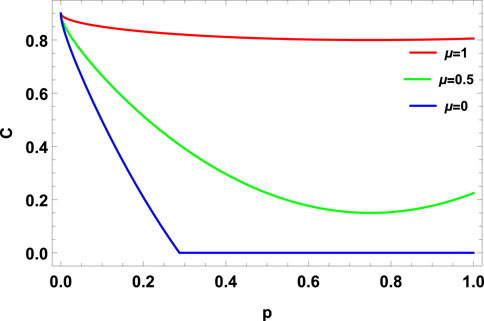
FIGURE 12. Concurrence vs. noise parameter p for DC with memory μ = 0, 0.5, 1 for MEMS with γ = 0.9.

4 Quantum coherence in correlated noise channels

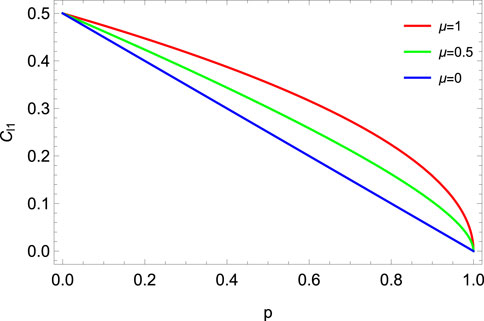
In this section, we provide the results of the quantum coherence dynamics of MEMS under the action of correlated noise channels with memory. We use the density matrices for ADC, PDC, and DC with memory, as given in Eqs 11, 14, 18, respectively, and coherence measures defined in Eqs 3, 4 to study the dynamics of quantum coherence in these channels. Here, we have chosen γ = 0.5 for MEMS. A 3D plot of the l₁-norm of coherence (C_l1) vs. the damping channel parameter (p) and the memory parameter (μ) for ADC is given in Figure 13. The plot of C_l1 vs. p for different μ values is given in Figure 14. The plot of relative entropy of coherence (C_R) vs. p is shown in Figure 15. The analytical expression of the l₁-norm of coherence for ADC with memory is given as

$l_1=\left|\gamma \left(\left(\mu -1\right)p+\mu \left(\sqrt{1-p}-1\right)+1\right)\right|,(19)$

where |X| indicates the absolute value or modulus of X. Eq. 19 and these plots indicate that MEMS asymptotically loses coherence, and as the memory parameter increases, MEMS retains a higher amount of coherence for the same value of p.

FIGURE 13

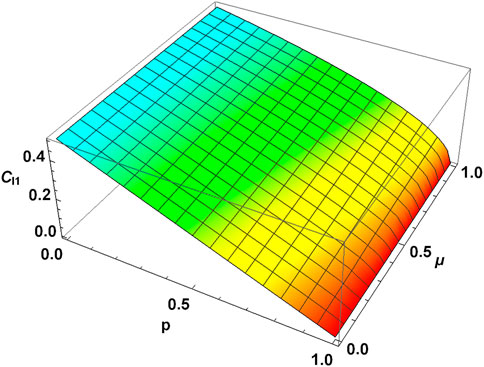
FIGURE 13. l₁-norm vs. ADC parameter p and memory parameter μ for MEMS with γ = 0.5. MEMS has a higher amount of quantum coherence for p ∈ (0, 1) as the memory parameter increases.

FIGURE 14

FIGURE 14. l₁-norm vs. noise parameter p for ADC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

FIGURE 15

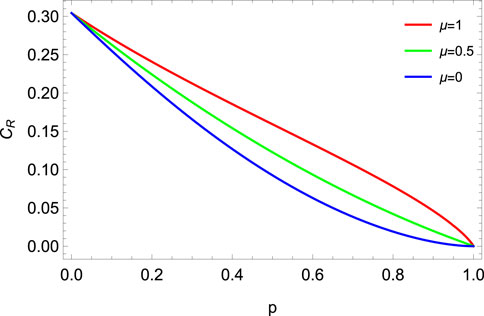
FIGURE 15. Relative entropy of coherence (C_R) vs. noise parameter p for ADC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

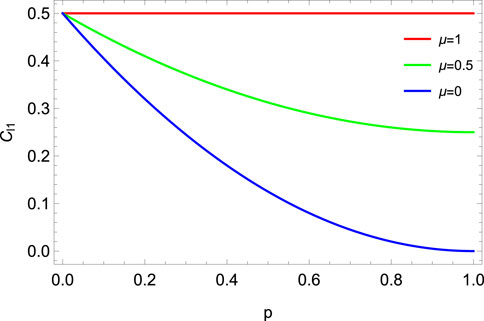
Figure 16 shows the plot of the l₁-norm of coherence (C_l1) vs. p and μ for PDC. The plot of C_l1 vs. p for different μ values is given in Figure 17 whereas Figure 18 shows a plot of relative entropy of coherence (C_R) vs. p for different μ. Both plots indicate that MEMS asymptotically loses coherence for μ = 0. The analytic expression of the l₁-norm of coherence for PDC with memory is given as

$l_1=|\gamma -\gamma \left(\mu -1\right)\left(p-2\right)p|.(20)$

It is clear from Eq. 20 that for μ > 0, MEMS ends with a non-zero coherence as p →, 1, and coherence completely freezes for μ = 1.

FIGURE 16

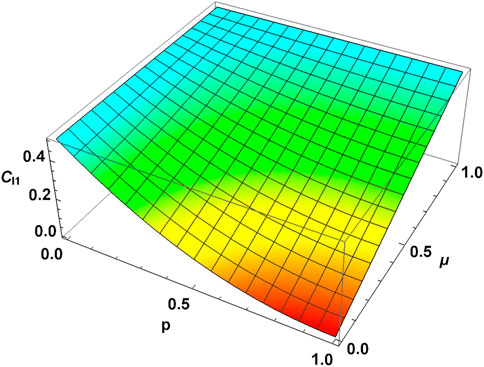
FIGURE 16. l₁-norm vs. PDC parameter p and memory parameter μ for MEMS with γ = 0.5. MEMS has a higher amount of quantum coherence for the higher values of the memory parameter for the noise parameter p ∈ (0, 1). In particular, for μ = 1, the quantum coherence freezes at the initial value for p ∈ [0, 1].

FIGURE 17

FIGURE 17. l₁-norm vs. noise parameter p for PDC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

FIGURE 18

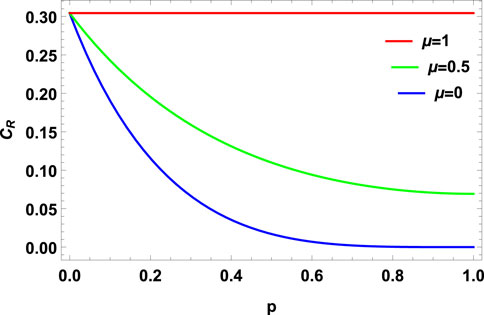
FIGURE 18. Relative entropy of coherence (C_R) vs. the noise parameter p for PDC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5.

Figure 19 shows the plot of the l₁-norm of coherence (C_l1) vs. p and μ for the depolarizing channel. The plot of C_l1 vs. p for different μ values is given in Figure 20, whereas Figure 21 shows a plot of relative entropy of coherence (C_R) vs. p for different μ. The analytical expression for the l₁-norm of coherence for a DC with memory is given as

$l_1=\frac{1}{9}|\gamma ||9-8p\left(2p-3\right)\left(\mu -1\right)|.(21)$

FIGURE 19

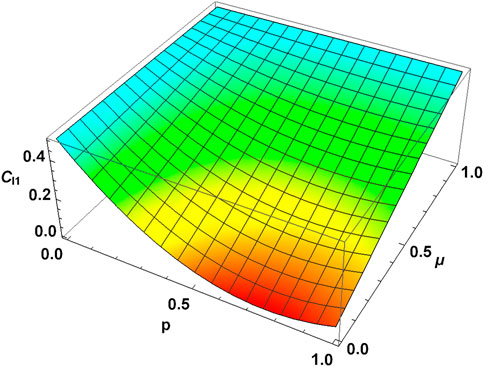
FIGURE 19. l₁-norm of coherence vs. depolarizing channel parameter p and memory parameter μ for MEMS with γ = 0.5. MEMS retains more coherence for the same p-value as the memory parameter increases. It is further observed that the l₁ norm of coherence freezes for μ = 1.

FIGURE 20

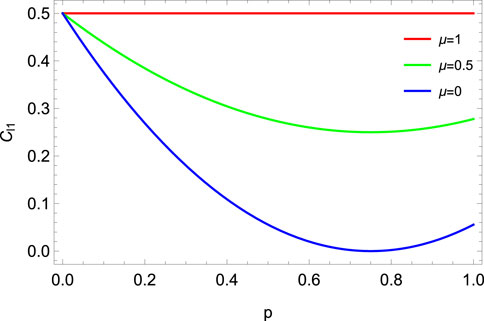
FIGURE 20. l₁-norm of coherence vs. noise parameter p for DC with memory (μ = 0, 0.5, 1) for MEMS with γ = 0.5. The l₁-norm of coherence freezes for μ = 1.

FIGURE 21

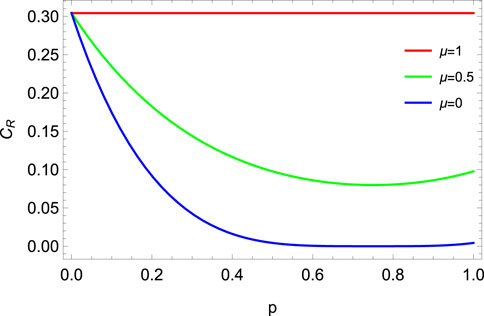
FIGURE 21. Relative entropy of coherence (C_R) vs. the noise parameter p for DC with memory (μ) for MEMS with γ = 0.5.

Eq. 21 and these plots indicate that in the presence of a DC with memory, the MEMS loses coherence slowly, reaches a minimum value for a given μ, and regains coherence, ending with a non-zero coherence at p → 1. Similar to PDC, for μ = 1, coherence also completely freezes for DC. Furthermore, while the l₁-norm and the relative entropy of coherence offer distinct measures of coherence, they exhibit a monotonic relationship with one another.

5 Conclusion and future outlook

In the present study, we have investigated two features of MEMS: the quantum entanglement and quantum coherence in the presence of decoherence channels, such as amplitude damping, phase damping, and depolarizing channels with memory. The fundamentals of quantum channels with memory and the evolution of the state have been discussed in detail. Quantum coherence is quantified using the l₁-norm and relative entropy of coherence, whereas entanglement is quantified using concurrence. A generic observation for all these channels is that as the memory parameter increases, MEMS contains a higher amount of coherence and entanglement. For μ = 1, MEMS undergoes ADE in the presence of ADC, whereas for PDC, entanglement freezes. On the other hand, for DC, while the entanglement of MEMS degrades a little, it ends with a non-zero entanglement at p → 1. Likewise, for quantum coherence, the higher the value of μ, the higher the coherence of MEMS for the same values of γ and p. Specifically, for perfectly correlated channels (μ = 1), MEMS shows asymptotic decay of coherence in the presence of ADC. In contrast, for PDC and DC, the coherence completely freezes at the same value contained in the initial state. These results establish that the non-zero memory parameter of the channel makes MEMS robust against the detrimental effects of the noise channels. In a more general setting, memory channels perform better than memoryless channels in maintaining the integrity of quantum states and their utility in quantum information processing protocols. The future scope of this work could involve an investigation of the efficacy of entanglement protection schemes in the presence of memory channels on MEMS.

Like entanglement and coherence, the Markovian noise channels also degrade the utility of quantum states in quantum information processing protocols (Nielsen and Chuang, 2010), such as dense coding and teleportation. Once again, channels with memory are found to improve the capacity of dense coding and the fidelity of teleportation (Tian and Zhang, 2018; Wang et al., 2023) of MEMS. To illustrate this further, plots of the capacity of dense coding vs. ADC parameter (p) for different memory parameters (μ) for MEMS with γ = 0.5 & 0.9 are shown in Figures 22, 23, respectively. The horizontal line at 1 shows the classical bound of dense coding. Even though the memory parameter improves the capacity of dense coding at intermediate values of the decoherence parameter, it does not exceed the classical bound for γ = 0.5. From Figure 23, it is clear that the non-zero memory parameter increases the range of decoherence parameters, for which MEMS offers the quantum advantage.

FIGURE 22

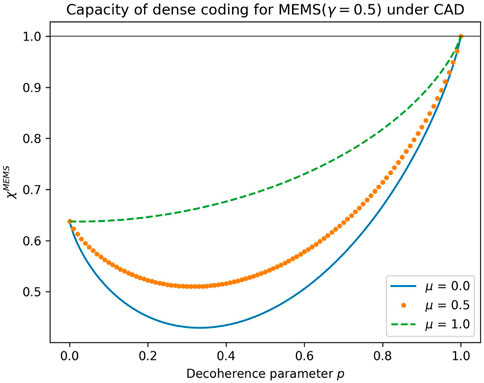
FIGURE 22. Capacity of dense coding of MEMS with γ = 0.5 under a correlated ADC for μ = 0, 0.5, and 1.

FIGURE 23

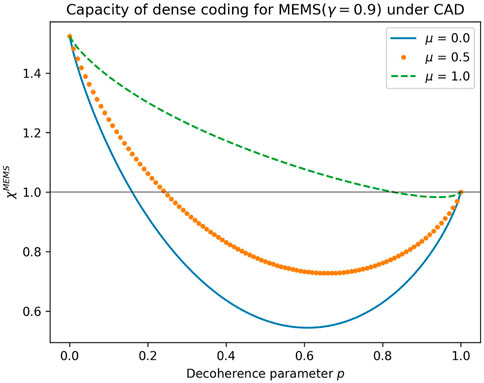
FIGURE 23. Capacity of dense coding of MEMS with γ = 0.9 under correlated ADC for μ = 0, 0.5, and 1.

Plots of the fidelity of quantum teleportation vs. the ADC parameter (p) for different memory parameters (μ) for MEMSs with γ = 0.5 & 0.9 are shown in Figures 24, 25, respectively. The horizontal line at 2/3 shows the classical bound for teleportation fidelity. It is evident from these plots that a non-zero memory parameter not only increases the fidelity of quantum teleportation for a given p but also increases the range for which MEMS offers a quantum advantage in teleportation.

FIGURE 24

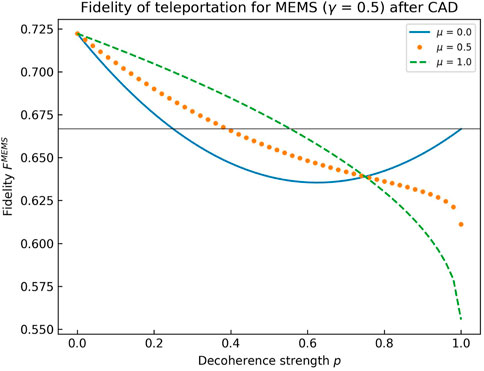
FIGURE 24. Fidelity of quantum teleportation of MEMS with γ = 0.5 under correlated ADC for μ = 0, 0.5, and 1.

FIGURE 25

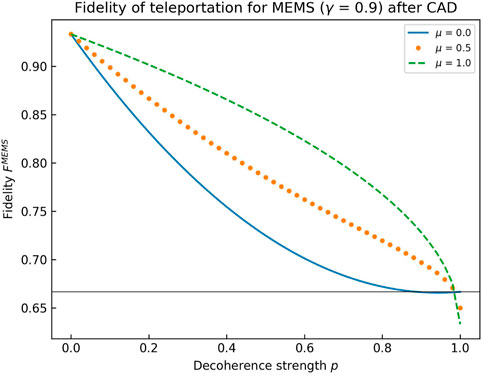
FIGURE 25. Fidelity of quantum teleportation of MEMS with γ = 0.9 under correlated ADC for μ = 0, 0.5, and 1.

A future direction of this line of study could involve the investigation of single and two-qubit weak measurement reversal protocols (Kim et al., 2012) on the protection of coherence, entanglement, and capacity of quantum information protocols such as dense coding and teleportation for MEMS in the presence of ADC with memory. We are exploring this line of study and plan to present these results in a future article.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

NA made a substantial contribution to the concept and design of the article; AS drafted the article and revised it critically for important intellectual content; DK contributed to drafting and content writing. All authors contributed to the article and approved the submitted version.

Acknowledgments

AS would like to thank Bidyut Bikash Boruah for the useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Almeida, M. P., De Melo, F., Hor-Meyll, M., Salles, A., Walborn, S. P., Ribeiro, P. Q., et al. (2007). Environment-induced sudden death of entanglement. Science 316, 579–582. doi:10.1126/science.1139892

PubMed Abstract | CrossRef Full Text | Google Scholar

Awasthi, N., and Joshi, D. K. (2023). Sustainability of entanglement sudden death under the action of memory channel. Laser Phys. Lett. 20, 025202. doi:10.1088/1612-202x/acaece

CrossRef Full Text | Google Scholar

Awasthi, N., Kumar, J. D., and Sachdev, S. (2022). Variation of quantum speed limit under Markovian and non-Markovian noisy environment. Laser Phys. Lett. 19, 035201. doi:10.1088/1612-202x/ac4be5

CrossRef Full Text | Google Scholar

Baumgratz, T., Cramer, M., and Plenio, M. B. (2014). Quantifying coherence. Phys. Rev. Lett. 113, 140401. doi:10.1103/physrevlett.113.140401

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, C. H., DiVincenzo, D. P., Shor, P. W., Smolin, J. A., Terhal, B. M., and Wootters, W. K. (2001). Remote state preparation. Phys. Rev. Lett. 87, 077902. doi:10.1103/physrevlett.87.077902

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandão, F. G. S. L., and Plenio, M. B. (2010). A reversible theory of entanglement and its relation to the second law. Commun. Math. Phys. 295, 829–851. doi:10.1007/s00220-010-1003-1

CrossRef Full Text | Google Scholar

Brandão, F. G. S. L., and Plenio, M. B. (2008). Entanglement theory and the second law of thermodynamics. Nat. Phys. 4, 873–877. doi:10.1038/nphys1100

CrossRef Full Text | Google Scholar

Breuer, H.-P., and Petruccione, F. (2002). The theory of open quantum systems. United States: Oxford University Press.

Google Scholar

D’Arrigo, A., Benenti, G., Falci, G., and Macchiavello, C. (2013). Classical and quantum capacities of a fully correlated amplitude damping channel. Phys. Rev. A 88, 042337. doi:10.1103/physreva.88.042337

CrossRef Full Text | Google Scholar

D’Arrigo, A., Benenti, G., and Falci, G. (2007). Quantum capacity of dephasing channels with memory. New J. Phys. 9, 310. doi:10.1088/1367-2630/9/9/310

CrossRef Full Text | Google Scholar

Datta, S., Mal, S., and Majumdar, A. S. (2018). Protecting temporal correlations of two-qubit states using quantum channels with memory. Available at: https://arxiv.org/abs/1808.10345.

Google Scholar

Doherty, A. C., Habib, S., Jacobs, K., Mabuchi, H., and Tan, S. M. (2000). Quantum feedback control and classical control theory. Phys. Rev. A 62, 012105. doi:10.1103/physreva.62.012105

CrossRef Full Text | Google Scholar

Einstein, A., Podolsky, B., and Rosen, N. (1935). Phys. Rev. 47, 777–780. doi:10.1103/physrev.47.777

CrossRef Full Text

Ficek, Z., and Tanaś, R. (2008). Delayed sudden birth of entanglement. Phys. Rev. A 77, 054301. doi:10.1103/physreva.77.054301

CrossRef Full Text | Google Scholar

Guo, Y.-n., Tian, Q.-l., Zeng, K., and Li, Z.-d. (2017). Quantum Inf. Process. 16, 1. doi:10.1007/s11128-017-1749-x

CrossRef Full Text

Hill, S. A., and Wootters, W. K. (1997). Entanglement of a pair of quantum bits. Phys. Rev. Lett. 78, 5022–5025. doi:10.1103/physrevlett.78.5022

CrossRef Full Text | Google Scholar

Horodecki, R., Horodecki, P., Horodecki, M., and Horodecki, K. (2009). Quantum entanglement. Rev. Mod. Phys. 81, 865–942. doi:10.1103/revmodphys.81.865

CrossRef Full Text | Google Scholar

Itano, W. M., Heinzen, D. J., Bollinger, J. J., and Wineland, D. J. (1990). Quantum Zeno effect. Phys. Rev. A 41, 2295–2300. doi:10.1103/physreva.41.2295

PubMed Abstract | CrossRef Full Text | Google Scholar

Jing, J., Zhang, J., Yan, Y., Zhao, F., Xie, C., and Peng, K. (2003). Experimental demonstration of tripartite entanglement and controlled dense coding for continuous variables. Phys. Rev. Lett. 90, 167903. doi:10.1103/physrevlett.90.167903

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y.-S., Lee, J.-C., Kwon, O., and Kim, Y.-H. (2012). Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat. Phys. 8, 117–120. doi:10.1038/nphys2178

CrossRef Full Text | Google Scholar

Korotkov10, A. N., and Keane, K. (2010). Decoherence suppression by quantum measurement reversal. Phys. Rev. A 81, 040103. doi:10.1103/physreva.81.040103

CrossRef Full Text | Google Scholar

Kretschmann, D., and Werner, R. F. (2005). Quantum channels with memory. Phys. Rev. A 72, 062323. doi:10.1103/physreva.72.062323

CrossRef Full Text | Google Scholar

Macchiavello, C., and Palma, G. M. (2002). Entanglement-enhanced information transmission over a quantum channel with correlated noise. Phys. Rev. A 65, 050301. doi:10.1103/physreva.65.050301

CrossRef Full Text | Google Scholar

Macchiavello, C., Palma, G. M., and Virmani, S. (2004). Transition behavior in the channel capacity of two-quibit channels with memory. Phys. Rev. A 69, 010303. doi:10.1103/physreva.69.010303

CrossRef Full Text | Google Scholar

Mandel, L., and Wolf, E. (1995). Optical coherence and quantum optics. Cambridge: Cambridge University Press.

Google Scholar

Merkli, M., Berman, G., Borgonovi, F., and Tsifrinovich, V. (2012). Adv. Math. Phys., 2012.

Mohanty, S. D., Sharma, G., Sazim, S., Pradhan, B., and Pati, A. K. (2022). Creation of quantum coherence with general measurement processes. Quantum Inf. Process. 21, 48. doi:10.1007/s11128-021-03394-5

CrossRef Full Text | Google Scholar

Munro, W. J., James, D. F., White, A. G., and Kwiat, P. G. (2001). Maximizing the entanglement of two mixed qubits. Phys. Rev. A 64, 030302. doi:10.1103/physreva.64.030302

CrossRef Full Text | Google Scholar

Munro, W. J., and Nemoto, K. (2001). Maximally entangled mixed states and the bell inequality. Z. für Naturforsch. A 56, 152–154. doi:10.1515/zna-2001-0123

CrossRef Full Text | Google Scholar

Napoli, C., Bromley, T. R., Cianciaruso, M., Piani, M., Johnston, N., and Adesso, G. (2016). Robustness of coherence: an operational and observable measure of quantum coherence. Phys. Rev. Lett. 116, 150502. doi:10.1103/physrevlett.116.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, M. A., and Chuang, I. L. (2010). Quantum computation and quantum information: 10th anniversary edition. Cambridge: Cambridge University Press.

Google Scholar

Paulson, K., Banerjee, S., and Srikanth, R. (2022). The effect of quantum memory on quantum speed limit time for CP-(in)divisible channels. Quantum Inf. Process. 21, 335. doi:10.1007/s11128-022-03675-7

CrossRef Full Text | Google Scholar

Paulson, K., Panwar, E., Banerjee, S., and Srikanth, R. (2021). Quantum information processing Berlin, Germany: Springer.

Google Scholar

Plenio, M. B., and Virmani, S. (2007). An introduction to entanglement measures. Quantum Inf. comput. 7, 1–51. doi:10.26421/qic7.1-2-1

CrossRef Full Text | Google Scholar

Preskill, J. (1998)., 16. California Institute of Technology, 1.

Sharma, K. K., and Gerdt, V. P. (2020). Entanglement sudden death and birth effects in two qubits maximally entangled mixed states under quantum channels. Int. J. Theor. Phys. 59, 403–414. doi:10.1007/s10773-019-04332-z

CrossRef Full Text | Google Scholar

Singh, A., Ahamed, I., Home, D., and Sinha, U. (2020). Revisiting comparison between entanglement measures for two-qubit pure states. J. Opt. Soc. Am. B 37, 157. doi:10.1364/josab.37.000157

CrossRef Full Text | Google Scholar

Singh, A. (2022). Creation, characterization, and manipulation of quantum entanglement in a photonic system. Available at: https://arxiv.org/abs/2212.10658.

Google Scholar

Singh, A., Pradyumna, S., Rau, A. R. P., and Sinha, U. (2017). Manipulation of entanglement sudden death in an all-optical setup. J. Opt. Soc. Am. B 34, 681. doi:10.1364/josab.34.000681

CrossRef Full Text | Google Scholar

Singh, A., and Sinha, U. (2022). Entanglement protection in higher-dimensional systems. Phys. Scr. 97, 085104. doi:10.1088/1402-4896/ac8200

CrossRef Full Text | Google Scholar

Streltsov, A., Adesso, G., and Plenio, M. B. (2017). Colloquium: quantum coherence as a resource. Rev. Mod. Phys. 89, 041003. doi:10.1103/revmodphys.89.041003

CrossRef Full Text | Google Scholar

Streltsov, A., Singh, U., Dhar, H. S., Bera, M. N., and Adesso, G. (2015). Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403. doi:10.1103/physrevlett.115.020403

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, M.-B., and Zhang, G.-F. (2018). Quantum Inf. Process. 17, 1. doi:10.1007/s11128-017-1786-5

CrossRef Full Text

Ursin, R., Tiefenbacher, F., Schmitt-Manderbach, T., Weier, H., Scheidl, T., Lindenthal, M., et al. (2007). Entanglement-based quantum communication over 144 km. Nat. Phys. 3, 481–486. doi:10.1038/nphys629

CrossRef Full Text | Google Scholar

Vedral, V., and Plenio, M. B. (1998). Entanglement measures and purification procedures. Phys. Rev. A 57, 1619–1633. doi:10.1103/physreva.57.1619

CrossRef Full Text | Google Scholar

Wang, M., Sun, B., Cao, L., Yang, Y., Liu, X., Wang, X., et al. (2023). Improving the capacity of quantum dense coding and the fidelity of quantum teleportation by weak measurement and measurement reversal. Entropy 25, 736. doi:10.3390/e25050736

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, R. F. (1989). Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277–4281. doi:10.1103/physreva.40.4277

PubMed Abstract | CrossRef Full Text | Google Scholar

Winter, A., and Yang, D. (2016). Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404. doi:10.1103/physrevlett.116.120404

PubMed Abstract | CrossRef Full Text | Google Scholar

Wootters, W. K. (2001). Entanglement of formation and concurrence. Quantum Inf. comput. 1, 27–44. doi:10.26421/qic1.1-3

CrossRef Full Text | Google Scholar

Wootters, W. K. (1998). Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248. doi:10.1103/physrevlett.80.2245

CrossRef Full Text | Google Scholar

Wu, K. H., Theurer, T., Xiang, G.-Y., Li, C.-F., Guo, G.-C., Plenio, M. B., et al. (2020). Quantum coherence and state conversion: theory and experiment. npj Quantum Inf. 6, 22. doi:10.1038/s41534-020-0250-z

CrossRef Full Text | Google Scholar

Yeo, Y., and Skeen, A. (2003). Time-correlated quantum amplitude-damping channel. Phys. Rev. A 67, 064301. doi:10.1103/physreva.67.064301

CrossRef Full Text | Google Scholar

Yu, T., and Eberly, J. H. (2004). Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93, 140404. doi:10.1103/physrevlett.93.140404

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, T., and Eberly, J. H. (2009). Sudden death of entanglement. Science 323, 598–601. doi:10.1126/science.1167343

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, X., Zhou, H., Cao, Z., and Ma, X. (2015). Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124. doi:10.1103/physreva.92.022124

CrossRef Full Text | Google Scholar