Indirect interaction of 13C nuclear spins in diamond with NV centers: simulation of the full J-coupling tensors

1 Introduction

In the past years, there has been rapid progress in the development of quantum magnetic sensing technologies based on nitrogen-vacancy (NV) color centers in diamonds (e.g., see (Schwartz, 2019; Barry et al., 2020; Pezzagna and Meijer, 2021) for reviews). The use of single NV centers makes it possible to implement a magnetometer that provides nanometer-scale spatial resolution and extraordinary sensitivity, allowing the detection and imaging of multiple individual ¹³C nuclear spins (see, e.g., Zhao et al., 2012; Kolkowitz et al., 2012; Taminiau et al., 2012; Dréau et al., 2012; Mȕller et al., 2014; Zopes et al., 2018; Sasaki et al., 2018; Abobeih et al., 2019; Cujia et al., 2022; Vorobyov et al., 2022; van de Stolpe et al., 2023) inside the diamond. Due to their large coherence times, resulting from high isolation from the environment, these ¹³C nuclear spins are widely used as a quantum memory in emerging quantum technologies (see, e.g., Awschalom et al., 2018). In addition to single ¹³C nuclear spins, it has also been proposed (Reiserer et al., 2016; Chen et al., 2017) to use for the purpose pairs of coupled ¹³C nuclear spins or ¹³C–¹³C dimers (Zhao et al., 2012), since, in singlet state, such spin systems demonstrate exceptionally long coherence times (Stevanato et al., 2015; Levitt, 2019). Experimentally, individual dimers were observed and analyzed earlier in diamond with NV centers (Zhao et al., 2011; Shi et al., 2014; Ma and Liu, 2016). Recently, they have been studied in detail in (Abobeih et al., 2018; Bradley et l., 2019; Yang et al., 2020; Bartling et al., 2022; van de Stolpe et al., 2023) where a single NV center was used not only to detect and to characterize multiple ¹³C nuclear spins and few individual ¹³C–¹³C dimers in the specific spin environment of the studied NV center with sub-Hertz spectral resolution but also to initialize, control and readout the states of these dimers (Abobeih et al., 2018; Yang et al., 2020). In particular, in (Bradley et al., 2019), it was shown that the inhomogeneous dephasing time for the studied ¹³C–¹³C dimers was about 1 min at room temperature, the longest reported for individually controlled qubits. It should be noted also, that the parameters of the ¹⁴NV center itself can now be measured at Hz-level precision (Xie et al., 2021).

In the works (Zhao et al., 2011; Shi et al., 2014; Ma and Liu, 2016; Abobeih et al., 2018; Bradley et al., 2019; Yang et al., 2020; Bartling et al., 2022; van de Stolpe et al., 2023), the experimental results have been interpreted on the basis of theoretical analysis of a quantum system NV-¹³C–¹³C with the account of the Zeeman interaction of its spins with an external magnetic field, the hyperfine interaction of the electron spin of the NV center with the ¹³C nuclear spins forming the dimer, and of the direct dipole-dipole interaction of ¹³C nuclear spins. The magnetic field lifts the degeneracy of the NV center states with projections m_S = ±1 and initiates the precession of the ¹³C nuclear spins of the dimer, the frequencies of which depend on the projection m_S of the electronic spin S of the NV center. When the NV center is in the m_S = 0 state, both spins of the dimer do not hyperfine-coupled to the NV center and have the same Larmor frequencies (the case of equivalent nuclear spins in the Nuclear Magnetic Resonance (NMR) terminology (Wasylishen, 2007). Taking into account the interaction of nuclear spins with each other, the dimer can be considered (Wasylishen, 2007) as four-state system involving three triplet states $\left|\uparrow \uparrow \right.〉,$ $\left(\left|\uparrow \downarrow \right.〉+\left|\downarrow \uparrow \right.〉\right)/\sqrt{2},$ $\left|\downarrow \downarrow \right.〉$ and one singlet state $\left(\left|\uparrow \downarrow \right.〉-\left|\downarrow \uparrow \right.〉\right)/\sqrt{2},$ where the arrows mean the projections of ¹³C nuclear spins. In this case only two transitions $\left|\downarrow \downarrow \right.〉\leftrightarrow \left(\left|\uparrow \downarrow \right.〉+\left|\downarrow \uparrow \right.〉\right)/\sqrt{2},$ $\left(\left|\uparrow \downarrow \right.〉+\left|\downarrow \uparrow \right.〉\right)/\sqrt{2}\leftrightarrow \left|\uparrow \uparrow \right.〉$ between triplet states are possible, giving two lines in the NMR spectrum, known as the Pake doublet (Pake, 1948). The two lines separation is determined mainly by the direct dipolar coupling of nuclear spins, the magnitude of which depends on the distance between them and on the orientation of the dimer relative to the external magnetic field. Typical values of the direct dipolar coupling for neighbor spin pairs range from a few hundred Hz to several kHz (Wasylishen, 2007). In the case of ¹³C nuclear spins in diamond this coupling is ∼2 kHz (Shi et al., 2014; Bartling et al., 2022) when the dimer is oriented parallel to the magnetic field, and approximately 3 times less (∼690 Hz) if it is oriented at a tetrahedral angle of 109.5° relative to the external magnetic field (Shi et al., 2014). For the dimer consisting of non-nearest neighbors, the magnitude of the interaction drops to ∼200 Hz (Bartling et al., 2022).

Different situation takes place, when the NV center is transferred to the m_S = ±1 states, for example, by microwaves having resonant frequency for respective transition. In these cases both nuclear spins of the dimer experience a hyperfine interaction with the electron spin of the center, which can either differ significantly (Shi et al., 2014) or be quite similar (Bartling et al., 2022) in characteristics depending on the position of the dimer with respect to the NV center. As a result, the ¹³C nuclear spins belonging to the dimer cease to be equivalent and four-level nuclear-spin subsystems of a dimer with the NV center in m_S = ±1 states are not purely triplet and singlet. In such cases, NMR transitions between all nuclear-spin states of a NV-¹³C–¹³C spin system become possible, giving the corresponding four lines in the NMR spectra of the NV center in each of states m_S = ±1. In addition, in a NV-¹³C–¹³C system, microwaves can initiate transitions between different nuclear-spin sublevels of the states of the NV center with projections, for example, m_S = 0 and m_S = −1. The frequencies and amplitudes of all these transitions are determined by the strength and direction of the magnetic field acting on the system, the hyperfine interactions of the NV center with the nuclear spins of the dimer and the interaction of these nuclear spins with each other. The accuracy of characterization of dimers achieved in the above works, in particular, the measurement of their resonant frequencies, requires a detailed analysis and consideration of all interactions actually presenting in such spin systems.

The most obvious additional spin-spin interaction, which was not taken into account earlier, is indirect nuclear spin–spin interaction (J-coupling) that arise due to second-order hyperfine interactions with electrons from chemical bonds connecting the studied nuclei (see, e.g., (Ramsey, 1953; Vandersypen and Chuang, 2004; Wasylishen, 2009)). Usually this interaction is expected to be weaker in comparison with the above mentioned ones, but it still can have a significant impact on the evolution of spin systems. As far as the J-coupling is mediated by electrons, it is sensitive to subtle changes in geometry, conformation and electronic structure of molecules and solids, thus being a valuable source of important structural and dynamical information usually revealed by NMR spectroscopy. Typically, the strength of J-couplings is about tens or hundreds Hz for proton and carbon nuclei separated by a single covalent bond, and quickly decreases as the number of inter-mediate bonds grows.

Generally, a second-rank tensor ⁿJ_KL(K, L = X, Y, Z) is required to fully describe J-coupling between two nuclei (Harris et al., 2009). However, until recently, most conventional high-resolution NMR experiments were focused on measuring only isotropic scalar constant ⁿJ_iso = Sp(ⁿJ_KL)/3 because the anisotropic parts of the J-tensor were averaged out to zero by fast molecular motion in solution-state NMR or fast magic-angle spinning (MAS) in solid-state experiments (Frydman, 2001; Vaara et al., 2002; Harris et al., 2009; Reif et al., 2021). In the case of crystalline solids, the constituent atoms are located in a certain order determined by the crystal structure so that many important NMR interactions are orientation-dependent, and the information about anisotropic NMR interaction tensors becomes essential (Vaara et al., 2002; Harris et al., 2009). In particular, both the symmetric ¹J_iso=(¹J_ZZ+¹J_XX+¹J_YY)/3 (=70 Hz) and the asymmetric Δ¹J = ¹J_ZZ-(¹J_XX+¹J_YY)/2 (=90 Hz) parts of the J-coupling tensor ¹J_KL for the nearest-neighbor (N–N) ²⁹Si nuclear spins have been determined in single-crystal silicon (Christensen and Price, 2017). This was achieved by measuring the NMR lineshapes, which are sensitive to the value of Δ¹J, at four different crystallographic orientations relative to the applied magnetic field.

In diamond with ¹³C nuclear spins, a similar experiment was performed many years ago (Lemann et al., 1994), however, at that time, any effects associated with the presence of indirect interactions of ¹³C spins could not be studied due to the low detection sensitivity. Currently, owing to the development of new highly sensitive NV-based methods of NMR spectroscopy (Boss et al., 2017; Schmitt et al., 2017; Bucher et al., 2020) used in the above-mentioned papers (Abobeih et al., 2018; Bradley et l., 2019; Yang et al., 2020; Bartling et al., 2022; van de Stolpe et al., 2023), direct observation and study of J-coupling effects have become possible. In this respect, predicting their characteristics for studied spin systems is essential. Up to the recent time, there were no theoretical works on the quantum-chemical simulation of J-coupling of ¹³C nuclear spins in diamond. The first such attempt was made in our article (Nizovtsev et al., 2022), where we used a rather simple density functional theory (DFT) level to simulate full tensors J_KL describing the J-couplings of nuclear spins ¹³C in small H-terminated diamond clusters, as well as in a cluster hosting the NV-color center. Here, we extended findings using an additionally more advanced DFT level and presented our results in conjunction with those obtained in (Nizovtsev et al., 2022).

2 Methods

Basically, the theoretical foundations of J-coupling are well established (Ramsey, 1953; Wray, 1979; Helgaker et al., 1999; Krivdin, 2004; Helgaker et al., 2008; Krivdin, 2021), and there has been considerable progress in calculating the J-coupling characteristics for many simple molecules (e.g., see (Wray, 1979; Kamienska-Trela, 1995; Helgaker et al., 1999; Krivdin, 2004; Krivdin and Contreras, 2007; Antušek et al., 2008; Krivdin, 2018), including ¹³C–¹³C pairs (Wray, 1979; Kamienska-Trela, 1995; Jaszunsi et al., 2003; Krivdin, 2004; Peralta et al., 2004; Krivdin, 2018). However, previously, most software packages were aimed specifically at the calculation of the scalar J-coupling constants. Only recently has it become possible to get information about full J-coupling tensors. Here, we have used for the purpose version 5.0.3 of the ORCA package (Neese, 2012; Neese, 2022). The diamond crystal was modeled by H-terminated carbon clusters. We optimized the cluster geometry with the package at the B3LYP/UKS/def2/J/RIJCOSX level of theory and then simulated the n-bond J-coupling tensors ⁿJ_KL(Ci, Cj) for all possible ¹³Ci–¹³Cj pairs in the clusters using two levels of theory. The first one is the B3LYP/UKS/TZVPP level of theory which was used in (Nizovtsev et al., 2022) according to (Makhyoun et al., 2019) where it was shown that the functional B3LYP in combination with TZVPP doubly polarized triple-zeta basis set is quite successful in comparative calculations of J-coupling parameters performed using different levels of theory. Additionally, here we have also used the PBE0/UKS/pcJ-2 level of theory with standard DFT hybrid level PBE0 employing a special pcJ-2 segmented contracted basis set (Jensen, 2008), which was specially developed for spin–spin coupling constants calculation. The successful application of the ORCA software with the second level of theory was demonstrated in (Grimme et al., 2017).

In order to test the ORCA opportunities, we first calculated the J-tensors for all possible pairs ¹³C–¹³C in the diamond-like adamantane molecule C₁₀H₁₆ (see Figure 1A), for which the isotropic J-coupling constants ¹J_iso for N-N nuclear spins ¹³C was experimentally measured to be 31.4 ± 0.5 Hz (Gay et al., 1991). Having obtained for them the values of ∼29.9 Hz and ∼30.1 Hz (illustrated in Figure 2A) when using basis sets 1 and 2, respectively, which both were quite close to the experimental value, we performed similar calculations for the H-terminated carbon cluster C₃₅H₃₆ (Figure 1B), as well as for the cluster C₃₃[NV⁻]H₃₆ hosting the NV color center (Figure 1C). It should be noted that the choice of these small clusters was due to the fact that, as is known (Krivdin, 2004; Helgaker et al., 2008; Krivdin, 2021), the calculations of the J-coupling characteristics are very computationally demanding for even modest-sized molecules.

FIGURE 1

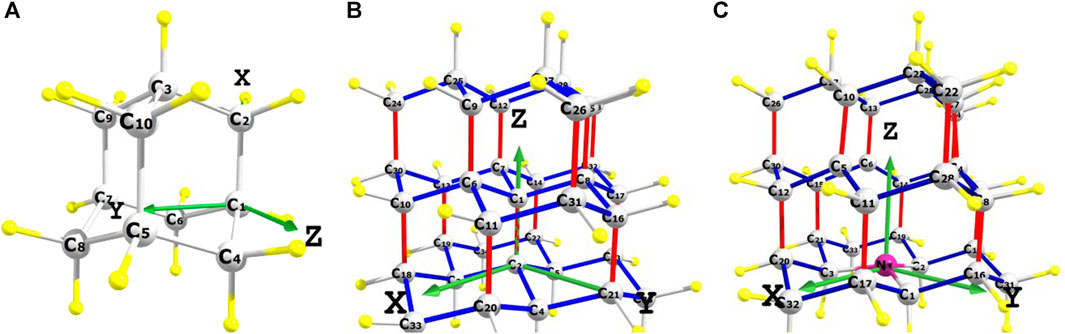
FIGURE 1. Simulated clusters with the carbon atoms numerated and the coordinate systems indicated. (A) Adamantane molecule C₁₀H₁₆, (B) cluster C₃₅H₃₆, (C) cluster C₃₃[NV⁻]H₃₆. Carbon atoms Ci are shown in grey, passivating H-atoms in yellow, and nitrogen atom N in (C) in purple.

FIGURE 2

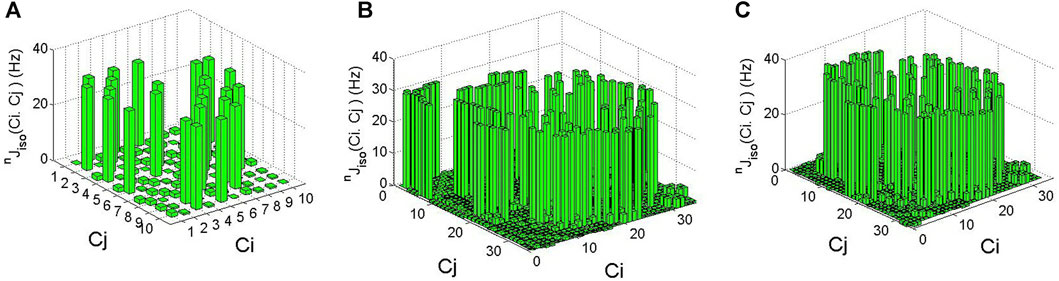
FIGURE 2. Illustrations of calculated isotropic scalar constants ⁿJ_iso(Ci,Cj) for all possible ¹³Ci–¹³Cj pairs in (A) adamantane molecule, (B) Cluster C₃₅H₃₆, (C) Cluster C₃₃[NV⁻]H₃₆.

The package returns matrices describing the diamagnetic, paramagnetic, Fermi-contact, spin-dipolar, and spin-dipolar/Fermi contact cross-term contributions to the total ⁿJ_KL tensor in the coordinate systems indicated in Figure 1. Using them and taking into account the known coordinates of carbon atoms belonging to some definite ¹³Ci–¹³Cj pair in the cluster, one can find respective J-coupling matrices in the other coordinate system. In particular, for neighboring nuclear spins ¹³C, separated by a single bond in diamond (∼1.54 Å), the total ¹J_KL matrix becomes diagonal with J_XX ≈ J_YY in the coordinate system in which the Z-axis is directed along this bond (Christensen and Price, 2017). In this case, it is conventional to describe an axial J-coupling tensor in terms of two parameters: the scalar constant ¹J_iso and the asymmetric part Δ¹J. Since the magnitude of the J-coupling decreases rapidly with bond order, we will mainly consider here such N–N nuclear spins.

3 Results and discussion

3.1 Adamantane cluster C₁₀H₁₆

In the case of adamantane, we first calculated the isotropic J-coupling constants ⁿJ_iso for all possible pairs Ci–Cj with the numbers i and j shown in Figure 1A, using two different theory levels, indicated in the previous paragraph. All simulations were performed in the chosen coordinate system, in which the origin was on the C1 atom, the X axis was directed from the C1 atom to the C2 atom, and the Y and Z axes were directed as it is shown in Figure 1A. The calculation results in both cases were close to each other and are illustrated graphically in Figure 2A, which shows, in the form of a bar graph, the calculated values of the isotropic constants ⁿJ_iso(Ci,Cj) for all pairs of ¹³C nuclear spins. In the molecule, there are 12 pairs (C1–C2, C1–C4, C1–C6, C2–C3, C3–C9, C3–C10, C4–C5, C5–C8, C5–C10, C6–C7, C7–C8, C7–C9) wherein carbon atoms are nearest neighbors separated by single C–C bond. Note that in all these pairs, the one carbon atom is in the bridgehead (bh) position while the other one–is in the bridge (b) position (see, e.g. (Grillaud and Bianco, 2015)). For these one-bond pairs, the calculated values of the ¹J_iso(bh-b) constants were in the ranges of 29.799–29.923 Hz, and 30.018–30.168 Hz using the basis sets 1 and 2, respectively. Оne can see that all these calculated values were close to the experimentally measured (Gay et al., 1991) value of 31.4 ± 0.5 Hz, with the better result obtained in the case of the more complicated basis set 2. For all these pairs, the calculated total matrices ¹J_KL(Ci, Cj) were close to diagonal since the isotropic Fermi-contact interaction made the main contribution to them. Moreover, taking into account the symmetry of the N–N Ci–Cj pairs about their midpoint in the transformed coordinate system, in which the Z axis is directed along some Ci–Cj bond, it is possible to transform the J-coupling matrices to their simplest diagonal form (Christensen and Price, 2017). As an example, we considered here the C1–C2 pair, in which both nuclear spins are located on the X axis (see Figure 1A) so that the transformation of the calculated matrices to the new coordinate system, where the Z axis is directed along the C1–C2 bond, is carried out simply by rotation counterclockwise by 90° around the Y axis. For the C1–C2 pair, the partial matrices in the thus transformed coordinate system are presented in Table 1. One can see from these data the relative contributions of various interactions. They also show that the total matrix ¹J(C1, C2) is, as expected (Christensen and Price, 2017), near-diagonal with ¹J_XX(C1, C2) ≈ ¹J_YY(C1, C2) so that for this pair the asymmetric part of the J-coupling tensor is Δ¹J = −12.1623 Hz (for basis 2). Similar data can be obtained for other pairs of N–N nuclear spins in the adamantane molecule. Figure 2A also shows that the isotropic constants ²J_iso and ³J_iso for more distant nuclear spins are only a couple of Hertz or less (in particular, we got ²J_iso(bh-bh) ≈ −2 Hz, ²J_iso(b-b) ≈ −1 Hz, and ³J_iso(bh-b) ≈ 1.6 Hz using the basis 2).

TABLE 1

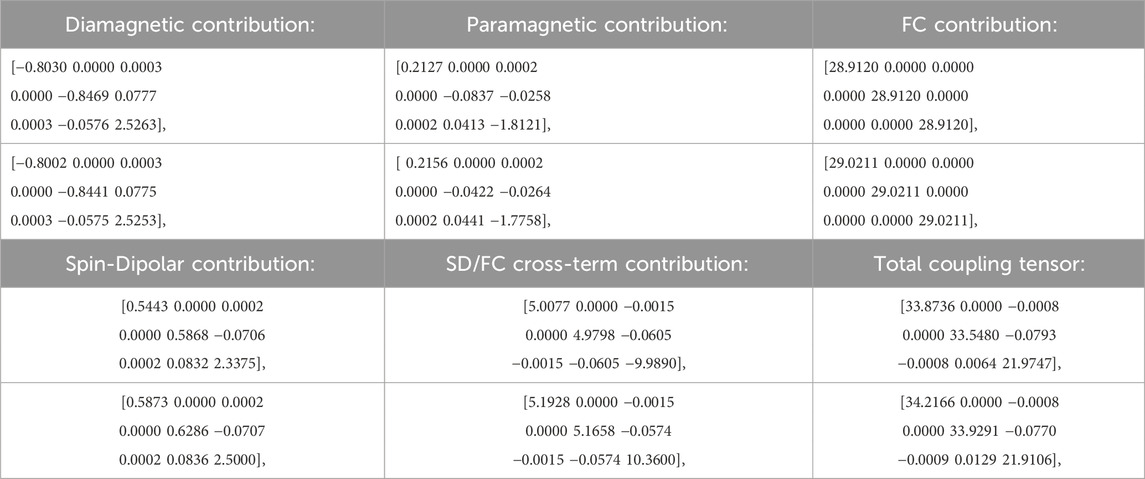
TABLE 1. The total J-coupling matrix ¹J_KL(C1, C2) and partial contributions to it (in Hz) for the ¹³C1–¹³C2 pair in the adamantane molecule in the transformed coordinate system, having the Z axis along the C1–C2 bond, calculated using two above-indicated levels of theory with the first and the second rows in Table 1 showing respective data obtained with TZVPP (see also (Nizovtsev et al., 2022) and pcJ-2 basis sets, respectively.

3.2 Clusters C₃₅H₃₆ and C₃₃[NV⁻]H₃₆

The results of similar calculations of isotropic constants ⁿJ_iso, performed for all possible pairs ¹³C–¹³C in the clusters C₃₅H₃₆ and C₃₃[NV⁻]H₃₆, are illustrated by bar graphs shown in Figures 2B, C, respectively. As one can see from Figure 1B, in the case of the cluster C₃₅H_36, we chose the coordinate systems in which the origin was taken at the C2 carbon atom and the Z axis was directed from the C2 to the C1 atom. In this cluster, there are 595 different ¹³C–¹³C pairs, with 52 of them being N–N carbons. Among these N–N pairs, 13 have their bonds near-parallel to the chosen Z axis. These bonds are shown in red in Figure 1B. For the remaining 39 N–N pairs, shown in blue in Figure 1B, the angles between their bonds and the Z axis were approximately equal to the tetrahedral angle 109.47° (or 180°–109.47°). Respectively, in the case of the cluster C₃₃[NV⁻]H₃₆, the origin of the coordinate system was taken on the N atom, and the Z axis coincided with the NV center axis. In this cluster, there are 45 N–N ¹³C–¹³C pairs, 12 of them having bonds directed near-parallel to the Z axis. Again, these 12 pairs are shown in red in Figure 1C, and the other ones are shown in blue.

As one can see from Figure 2B, for the cluster C₃₅H₃₆, simulated one-bond isotropic constants ¹J_iso were in the range of 28.55–29.98 Hz (basis set 1, see also (Nizovtsev et al., 2022) and 28.76–30.86 Hz (basis set 2) (for specific values see Table 2), i.e., very close to those obtained for the adamantane molecule. Conversely, in the case of the cluster C₃₃[NV⁻]H₃₆ containing the NV center, there were several pairs of N–N ¹³C atoms located near the vacancy of the NV center, for which the values of the ¹J_iso constants were slightly higher (∼37.1 Hz) than for the other pairs (∼31.5–31.8 Hz, see Table 3).

TABLE 2

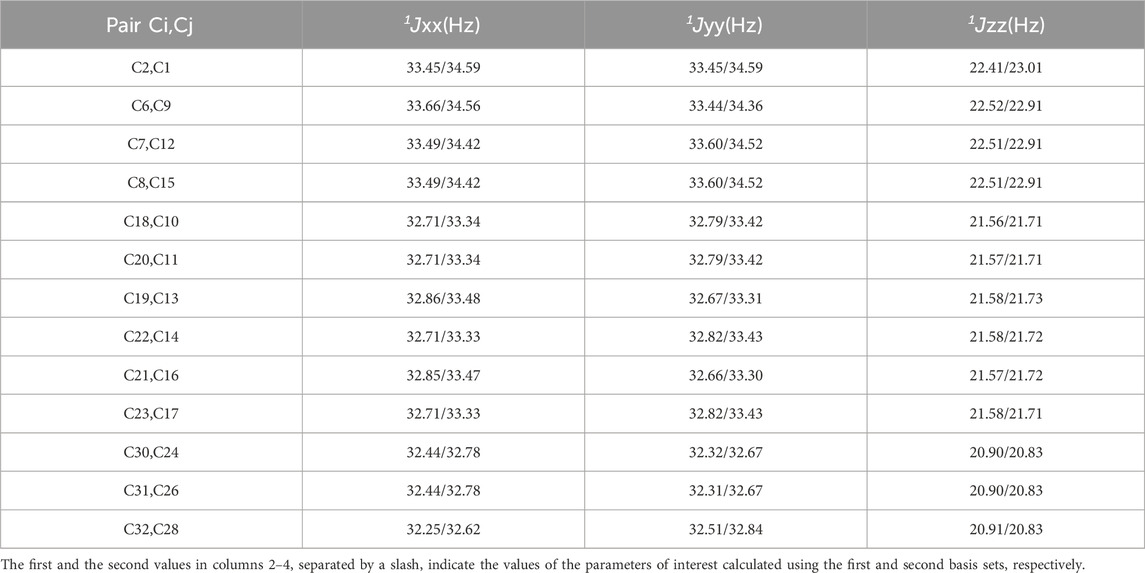
TABLE 2. Diagonal elements ¹J_KK(Ci, Cj) of the total J-coupling tensors calculated for the N–N ¹³Ci–¹³Cj pairs in the cluster C₃₅H₃₆ having their bonds near-parallel to the Z-axis of the coordinate system shown in Figure 1B.

TABLE 3

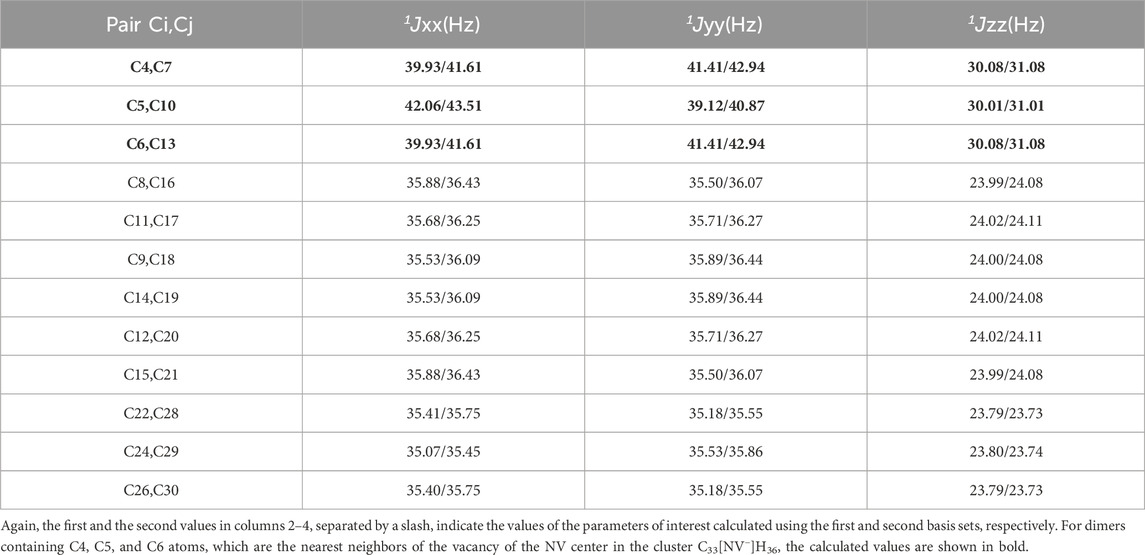
TABLE 3. Diagonal elements ¹J_KK(Ci, Cj) of total J-coupling tensors calculated for the N–N ¹³Ci–¹³Cj pairs in the cluster C₃₃[NV⁻]H₃₆having their bonds near-parallel to the Z-axis of the coordinate systems shown in Figure 1C.

The above data on the isotropic constants ¹J_iso for the clusters C₃₅H₃₆ and C₃₃[NV⁻]H₃₆ have been obtained from total J-coupling matrices ¹J_KL calculated for these clusters. Generally, as in the case of adamantane, the matrices have diagonal elements which are much larger than the non-diagonal ones. These diagonal elements are illustrated by Figures 3A–F. In these figures, the red bars display the values of the corresponding diagonal elements for those adjacent carbon pairs for which the C–C bond is directed almost parallel to the Z axis of the coordinate system used, whereas the blue bars are for pairs in which the C–C bond makes a tetrahedral angle with the Z axis. More specifically, the values of the diagonal elements ¹J_KK (K = X, Y, Z) of the J-coupling matrices of N–N ¹³C–¹³C pairs shown in red in Figure 3 are given below in Tables 2, 3.

FIGURE 3

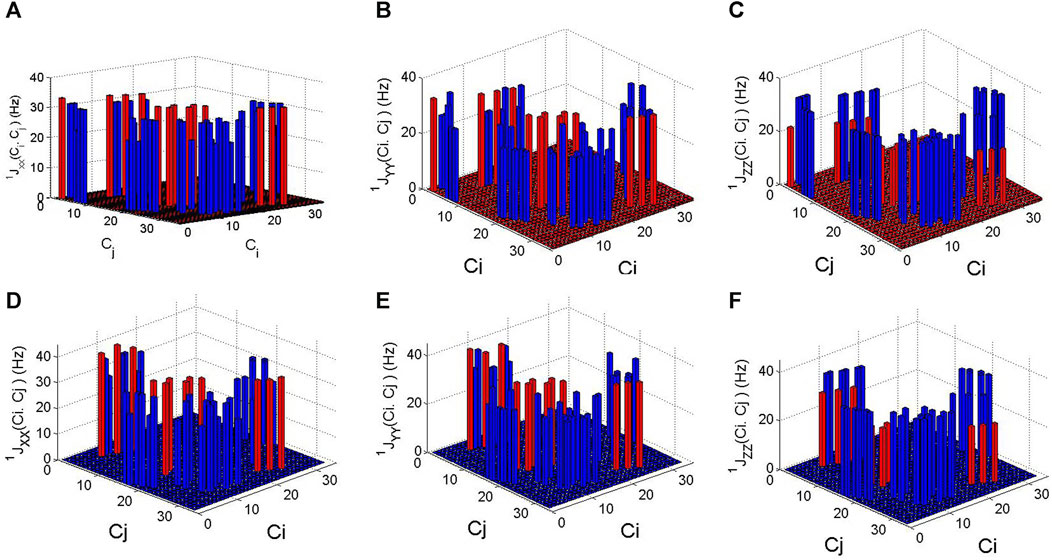
FIGURE 3. Diagonal elements ¹J_XX(Ci, Cj) (A, D), ¹J_YY(Ci, Cj) (B, E), and ¹J_ZZ(Ci, Cj) (C, F) of the ¹J-coupling matrices, calculated for nearest-neighbor ¹³C–¹³C pairs in the C₃₅H₃₆ cluster (A–C) and in the C₃₃[NV⁻]H₃₆ cluster (D–F).

One can see from Figure 3 and from Table 2 that for the Ci–Cj pairs, which are near-parallel to the Z axis, the values ¹J_XX(Ci,Cj) ≈ ¹J_YY(Ci, Cj) are about one and a half times larger than ¹J_ZZ(Ci, Cj). Moreover, the presence of the negatively charged NV⁻ center in the cluster C₃₃[NV⁻]H₃₆, which introduces additional electron density, leads to some increase in the diagonal elements ¹J_KK of the J-coupling matrices for all Ci–Cj pairs compared with the cluster C₃₅H₃₆. As follows from Table 3, such an increase in the ¹J_KK values is especially pronounced (∼9%) for the (C4, C7), (C5, C10), and (C6, C13) pairs, in which the atoms C4, C5, and C6 are the nearest neighbors of the vacancy of the NV center on which the electron density of the center is mainly localized (Nizovtsev et al., 2022). A similar increase in J-coupling takes place for other pairs C4/5/6-Cj, for which the corresponding bonds make an angle of ∼109.47° with the axis Z of the chosen coordinate system.

4 Conclusion

Using quantum chemistry software ORCA at two theory levels we simulated full tensors describing the indirect interaction (J-coupling) of ¹³C nuclear spins in H-terminated diamond cluster C₃₅H₃₆ and in the cluster C₃₃[NV⁻]H₃₆ hosting the NV center. We found that the PBE0/UKS/pcJ-2 level of theory provides, in the case of adamantine molecule, better agreement with the only available experimental data on the isotropic constant ¹J_iso in comparison with previously used (Nizovtsev et al., 2022) more simple and less time-consuming B3LYP/UKS/TZVPP level of theory. At the same time, it is shown that the calculations of full J-coupling tensors J_KL performed using these two different levels of theory give fairly close results, which, in particular, is important in itself for developing methods for calculating the total J-coupling tensors.

Here, we have focused mainly on the calculation of the full tensors J_KL for nuclear spins ¹³C in diamond separated by one bond for which the J-coupling is strongest. For such ¹³C–¹³C dimers, the calculated J-coupling tensors are almost diagonal in the coordinate system in which the Z-axis is directed along the bond connecting the nuclei. We found that in addition to the usually considered isotropic scalar ⁿJ-coupling constant, the anisotropic contributions to the ⁿJ-coupling tensor are essential. It is also shown that the NV center affects the characteristics of the J-coupling of ¹³C nuclear spins, especially if they are located near the vacancy of the NV center.

The obtained data on the J-coupling of ¹³C nuclear spins, being supplemented by the previously simulated data (Nizovtsev et al., 2018) on the hyperfine interaction of the NV center with the ¹³C nuclear spins forming some specific dimer, as well as on the spatial locations of these nuclear ¹³C spins relative to the NV center, forms a complete set of data allowing to simulate numerically energy levels and eigenstates of studied spin systems by analyzing their spin-Hamiltonians and to predict frequencies and strengths of transitions between states of the system. Such analysis of multi-spin systems NV–¹³C–¹³C with the account of both direct dipole–dipole interactions of ¹³C nuclear spins and of their J-coupling has been done recently in (Nizovtsev et al., 2023). Simulating numerically the specific spin system we demonstrated that for accurate determination of the Pake doublet splitting in a state with the spin projection of the NV center m_S = 0, along with the main dipole-dipole interaction of ¹³C nuclear spins in the dimer, it is necessary to take into account their anisotropic J-coupling. The account of the J-coupling can also be important in cases where the gradient of hyperfine interactions for the nuclear spins of the studied dimer is small. In addition, we also performed simulations of their EPR and NMR spectra and discuss effective ways to convert the studied dimer to the desired long-lived singlet state using microwave and radiofrequency pulses having predicted characteristics.

Theoretical simulation of J-coupling tensors is also important in conjunction with studies aimed at the creation of nanoscale NV-based quantum sensors for the detection of molecules/radicals adsorbed on the surface of nanostructured diamond (see, e.g., Glenn et al., 2018) and the determination of their chemical structure. The data obtained can also be useful for studies of NMR in the zero-to ultralow-field (ZULF) regime (Theis et al., 2013; Blanchard and Budker, 2016; Jiang et al., 2018; DeVience et al., 2021), where the internal spin interactions are dominated in their natural environment.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

AN: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Validation, Visualization, Writing–original draft, Writing–review and editing. AP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–review and editing. SKu: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–review and editing. DM: Investigation, Resources, Software, Writing–review and editing. DL: Resources, Software, Writing–review and editing. NK: Funding acquisition, Resources, Supervision, Validation, Visualization, Writing–review and editing. SKi: Methodology, Resources, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by RSF, project No. 21-42-04416, and, in the part of calculations for adamantane, by the Belarus State Scientific Program Convergence-2025. DL and DM were partially supported by KAUST baseline funding.

Acknowledgments

The content of this manuscript has been presented in part at the 3rd International Online-Conference on Nanomaterials, 25 April–10 May 2022 and available online: https://iocn2022.sciforum.net. After the Conference, these data partially have been published in the MDPI ”Materials Proceedings” as the paper: AN, AP, SKu, DM, DL, NK, SKi. Simulation of Indirect ¹³C–¹³C J-Coupling Tensors in Diamond Clusters Hosting the NV Center. Mater. Proc. 2022, 9, 4. https://doi.org/10.3390/materproc2022009004. All Orca 5.0.3 package computations were performed on KAUST’s Ibex HPC. The authors thank the KAUST Supercomputing Core Lab team for assistance with execution tasks on Skylake nodes. We are grateful to F. Jelezko for the long-time fruitful cooperation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abobeih, M. H., Cramer, J., Bakker, M. A., Kalb, N., Markham, M., Twitchen, D. J., et al. (2018). One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Communs. 9, 2552. doi:10.1038/s41467-018-04916-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Abobeih, M. H., Randall, J., Bradley, C. E., Bartling, H. P., Bakker, M. A., Degen, M. J., et al. (2019). Atomic-scale imaging of a 27-nuclear-spin cluster using a quantum sensor. Nature 576, 411–415. doi:10.1038/s41586-019-1834-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Antušek, A., Kędziera, D., Jackowski, K., Jaszuński, M., and Makulski, W. (2008). Indirect spin–spin coupling constants in CH₄, SiH₄ and GeH₄–Gas-phase NMR experiment and ab initio calculations. Chem. Phys. 352, 320–326. doi:10.1016/j.chemphys.2008.07.002

CrossRef Full Text | Google Scholar

Awschalom, D. D., Hanson, R., Wrachtrup, J., and Zhou, B. B. (2018). Quantum technologies with optically interfaced solid-state spins. Nat. Photonics 12, 516–527. doi:10.1038/s41566-018-0232-2

CrossRef Full Text | Google Scholar

Barry, J. F., Schloss, J. M., Bauch, E., Turner, M. J., Hart, C. A., Pham, L. M., et al. (2020). Sensitivity optimization for NV-diamond magnetometry. Rev. Mod. Phys. 92, 015004. doi:10.1103/RevModPhys.92.015004

CrossRef Full Text | Google Scholar

Bartling, H. P., Abobeih, M. H., Pingault, B., Degen, M. J., Loenen, S. J. H., Bradley, C. E., et al. (2022). Entanglement of spin-pair qubits with intrinsic dephasing times exceeding a minute. Phys. Rev. X 12, 011048. doi:10.1103/PhysRevX.12.011048

CrossRef Full Text | Google Scholar

Blanchard, J. W., and Budker, D. (2016). Zero-to ultralow-field NMR. eMagRes 5, 1395–1410. doi:10.1002/9780470034590.emrstm1369

CrossRef Full Text | Google Scholar

Boss, J. M., Cujia, K. S., Zopes, J., and Degen, C. L. (2017). Quantum sensing with arbitrary frequency resolution. Science 356, 837–840. doi:10.1126/science.aam7009

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradley, C. E., Randall, J., Abobeih, M. H., Berrevoets, R. C., Degen, M. J., Bakker, H., et al. (2019). A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045. doi:10.1103/PhysRevX.9.031045

CrossRef Full Text | Google Scholar

Bucher, D. B., Glenn, D. R., Park, H., Lukin, M. D., and Walsworth, R. L. (2020). Hyperpolarization-enhanced NMR spectroscopy with femtomole sensitivity using quantum defects in diamond. Phys. Rev. X. 10, 021053. doi:10.1103/PhysRevX.10.021053

CrossRef Full Text | Google Scholar

Chen, Q., Schwarz, I., and Plenio, M. B. (2017). Steady-state preparation of long-lived nuclear spin singlet pairs at room temperature. Phys. Rev. B 95, 224105. doi:10.1103/PhysRevB.95.224105

CrossRef Full Text | Google Scholar

Christensen, B., and Price, J. C. (2017). NMR lineshape of ²⁹Si in single-crystal silicon. Phys. Rev. B 95, 134417. doi:10.1103/PhysRevB.95.134417

CrossRef Full Text | Google Scholar

Cujia, K. S., Herb, K., Zopes, J., Abendroth, J. M., and Degen, C. L. (2022). Parallel detection and spatial mapping of large nuclear spin clusters. Nat. Commun. 13, 1260–1310. doi:10.1038/s41467-022-28935-z

PubMed Abstract | CrossRef Full Text | Google Scholar

DeVience, S. J., Greer, M., Mandal, S., and Rosen, M. S. (2021). Homonuclear J-coupling spectroscopy at low magnetic fields using spin-lock induced crossing. ChemPhysChem 22, 2128–2137. doi:10.1002/cphc.202100162

PubMed Abstract | CrossRef Full Text | Google Scholar

Dréau, A., Maze, J. R., Lesik, M., Roch, J. F., and Jacques, V. (2012). High-resolution spectroscopy of single NV defects coupled with nearby C-13 nuclear spins in diamond. Phys. Rev. B 85, 134107. doi:10.1103/PhysRevB.85.134107

CrossRef Full Text | Google Scholar

Frydman, L. (2001). Spin-1/2 and beyond: a perspective in solid state NMR spectroscopy. Annu. Rev. Phys. Chem. 52, 463–498. doi:10.1146/annurev.physchem.52.1.463

PubMed Abstract | CrossRef Full Text | Google Scholar

Gay, I. D., Jones, C. H. W., and Sharma, R. D. (1991). INADEQUATE in the solid state. Homonuclear couplings in [(CH₃)₂SnE]₃. J. Magn. Reson. 91, 186–189. doi:10.1016/0022-2364(91)90424-R

CrossRef Full Text | Google Scholar

Glenn, D. R., Bucher, D. B., Lee, J., Lukin, M. D., Park, H., and Walsworth, R. L. (2018). High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 555, 351–354. doi:10.1038/nature25781

PubMed Abstract | CrossRef Full Text | Google Scholar

Grillaud, M., and Bianco, A. (2015). Multifunctional adamantane derivatives as new scaffolds for the multipresentation of bioactive peptides. J. Pept. Sci. 21, 330–345. doi:10.1002/psc.2719

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimme, S., Bannwarth, Ch., Dohm, S., Hansen, A., Pisarek, J., Pracht, Ph., et al. (2017). Fully automated quantum-chemistry-based computation of spin–spin-coupled nuclear magnetic resonance spectra. Spectra angew.chem. Int. Ed. 56, 14763–14769. doi:10.1002/anie.201708266

CrossRef Full Text | Google Scholar

Harris, K. J., Bryce, D. L., and Wasylishen, R. E. (2009). NMR line shapes from AB spin systems in solids—the role of antisymmetric spin-spin coupling. Can. J. Chem. 87, 1338–1351. doi:10.1139/V09-089

CrossRef Full Text | Google Scholar

Helgaker, T., Jaszinski, M., and Ruud, K. (1999). Ab initio methods for the calculation of NMR shielding and indirect Spin−Spin coupling constants. Chem. Rev. 99, 293–352. doi:10.1021/cr960017t

PubMed Abstract | CrossRef Full Text | Google Scholar

Helgaker, T., Jaszuński, M., and Pecul, M. (2008). The quantum-chemical calculation of NMR indirect spin–spin coupling constants. Prog. Nucl. Magn. Reson. Spectrosc. 53, 249–268. doi:10.1016/j.pnmrs.2008.02.002

CrossRef Full Text | Google Scholar

Jaszunsi, M., Ruud, R., and Helgaker, T. (2003). Density-functional theory calculation of the nuclear magnetic resonance indirect nuclear spin—spin coupling constants in C₆₀. Mol. Phys. 101, 1997–2002. doi:10.1080/0026897031000109301

CrossRef Full Text | Google Scholar

Jensen, F. (2008). The optimum contraction of basis sets for calculating spin–spin coupling constants. Theor. Chem. Acc. 126, 371–382. doi:10.1007/s00214-009-0699-5

CrossRef Full Text | Google Scholar

Jiang, M., Wu, T., Blanchard, J. W., Feng, G., Peng, X., and Budker, D. (2018). Experimental benchmarking of quantum control in zero-field nuclear magnetic resonance. Sci. Adv. 4, eaar6327. doi:10.1126/sciadv.aar6327

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamienska-Trela, K. (1995). One-bond ¹³C-¹³C spin-spin coupling constants. Annu. Rep. NMR Spectrosc. 30, 131–230. doi:10.1016/S0066-4103(08)60026-5

CrossRef Full Text | Google Scholar

Kolkowitz, S., Unterreithmeier, Q. P., Bennett, S. D., and Lukin, M. D. (2012). Sensing distant nuclear spins with a single electron spin. Phys. Rev. Lett. 109, 137601. doi:10.1103/PhysRevLett.109.137601

PubMed Abstract | CrossRef Full Text | Google Scholar

Krivdin, L. B. (2004). Non-empirical calculations of NMR indirect carbon–carbon coupling constants. Part 10—carbocages. Part 10†—Carbocages. magn.reson. Chem. 42, 919–930. doi:10.1002/mrc.1483

PubMed Abstract | CrossRef Full Text | Google Scholar

Krivdin, L. B. (2018). Carbon-carbon spin-spin coupling constants: practical applications of theoretical calculations. Prog. NMR Spectrosc. 105, 54–99. doi:10.1016/j.pnmrs.2018.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Krivdin, L. B. (2021). Computational NMR of carbohydrates: theoretical background, applications, and perspectives. Molecules 26, 2450–2465. doi:10.3390/molecules26092450

PubMed Abstract | CrossRef Full Text | Google Scholar

Krivdin, L. B., and Contreras, R. H. (2007). Recent advances in theoretical calculations of indirect spin–spin coupling constants. Annu. Rep. Nucl. Magn.Reson.Spectrosc. 61, 133–245. doi:10.1016/S0066-4103(07)61103-X

CrossRef Full Text | Google Scholar

Lefmann, K., Buras, B., Pedersen, E. J., Shabanova, E. S., Thorsen, P. A., Rasmussen, F. B., et al. (1994). NMR spectra of pure ¹³C diamond. Phys. Rev. B 50, 15623–15627. doi:10.1103/PhysRevB.50.15623

PubMed Abstract | CrossRef Full Text | Google Scholar

Levitt, M. H. (2019). Long live the singlet state. J. Magn. Res. 306, 69–74. doi:10.1016/j.jmr.2019.07.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, W.-L., and Liu, R.-B. (2016). Angstrom-resolution magnetic resonance imaging of single molecules via wave-function fingerprints of nuclear spins. Phys. Rev. Appl. 6, 024019. doi:10.1103/PhysRevApplied.6.024019

CrossRef Full Text | Google Scholar

Makhyoun, M. A., Lees-Gayed, N., and Massoud, R. A. (2019). Effect of DFT exchange correlation functionals and basis set quality on the calculations of the magnetic coupling parameter J. Glob. J. Sci. Front. Res. B Chem. 19, 1–6. Available at: https://journalofscience.org/index.php/GJSFR/article/view/2482/2343.

Google Scholar

Mȕller, C., Kong, X., Cai, J.-M., Melentijević, K., Stacey, A., Markham, M., et al. (2014). Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 5, 4703–4706. doi:10.1038/ncomms5703

PubMed Abstract | CrossRef Full Text | Google Scholar

Neese, F. (2012). The ORCA program system. Wiley Interdiscip. Rev. -Computational Mol. Sci. 2, 73–78. doi:10.1002/wcms.81

CrossRef Full Text | Google Scholar

Neese, F. (2022). Software update: the ORCA program system—version 5.0. WIREs Comput. Mol. Sci. 12, e1606. doi:10.1002/wcms.1606

CrossRef Full Text | Google Scholar

Nizovtsev, A., Pushkarchuk, A., Kuten, S., Michels, D., Lyakhov, D., Kargin, N., et al. (2022). Simulation of indirect ¹³C–¹³C J-coupling tensors in diamond clusters hosting the NV center. Mater. Proc. 9, 4. doi:10.3390/materproc2022009004

CrossRef Full Text | Google Scholar

Nizovtsev, A. P., Kilin, S.Ya., Pushkarchuk, A. L., Pushkarchuk, V. A., Kuten, S. A., Zhikol, H., et al. (2018). Non-flipping ¹³C spins near an NV center in diamond: hyperfine and spatial characteristics by density functional theory simulation of the C₅₁₀[NV]H₂₅₂ cluster. New J. Phys. 20, 023022. doi:10.1088/1367-2630/aaa910

CrossRef Full Text | Google Scholar

Nizovtsev, A. P., Pushkarchuk, A. L., Kuten, S. A., Michels, D. L., Lyakhov, D., Gusev, A. S., et al. (2023). Quantum memory on ¹³C-¹³C dimers in diamond with NV centers: simulation by quantum chemistry methods. J. Appl. Spectrosc. 90, 1000–1011. doi:10.1007/s10812-023-01625-4

CrossRef Full Text | Google Scholar

Pake, G. E. (1948). Nuclear resonance absorption in hydrated crystals: fine structure of the proton line. J. Chem. Phys. 16, 327–336. doi:10.1063/1.1746878

CrossRef Full Text | Google Scholar

Peralta, J. E., Barone, V., Scuseria, G. E., and Contrera, R. H. (2004). Density functional theory calculation of indirect nuclear magnetic resonance spin-spin coupling constants in C₇₀. J. Am. Chem. Soc. 126, 7428–7429. doi:10.1021/ja048141e

PubMed Abstract | CrossRef Full Text | Google Scholar

Pezzagna, S., and Meijer, J. (2021). Quantum computer based on color centers in diamond. Appl. Phys. Rev. 8, 011308. doi:10.1063/5.0007444

CrossRef Full Text | Google Scholar

Ramsey, F. (1953). Electron coupled interactions between nuclear spins in molecules. Phys. Rev. 91, 303–307. doi:10.1103/PhysRev.91.303

CrossRef Full Text | Google Scholar

Reif, B., Ashbrook, S. E., Emsley, L., and Hong, M. (2021). Solid-state NMR spectroscopy. Nat. Rev. Methods Prim. 1, 2. doi:10.1038/s43586-020-00002-1

CrossRef Full Text | Google Scholar

Reiserer, A., Kalb, N., Blok, M. S., van Bemmelen, K. J. M., Taminiau, T. H., Hanson, R., et al. (2016). Robust quantum-network memory using decoherence-protected subspaces of nuclear spins. Phys. Rev. X 6, 021040. doi:10.1103/PhysRevX.6.021040

CrossRef Full Text | Google Scholar

Sasaki, K., Itoh, K. M., and Abe, E. (2018). Determination of the position of a single nuclear spin from free nuclear precessions detected by a solid-state quantum sensor. Phys. Rev. B 98, 121405. doi:10.1103/PhysRevB.98.121405

CrossRef Full Text | Google Scholar

Schmitt, S., Gefen, T., Stürner, F. M., Unden, T., Wolff, G., Müller, Ch., et al. (2017). Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. Science 356, 832–837. doi:10.1126/science.aam5532

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwartz, I., Rosskopf, J., Schmitt, S., Tratzmiller, B., Chen, Q., McGuinness, H., et al. (2019). Blueprint for nanoscale NMR. Sci. Rep. 9, 6938. doi:10.1038/s41598-019-43404-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, F., Kong, X., Wang, P., Kong, F., Zhao, N., Liu, R.-B., et al. (2014). Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21–25. doi:10.1038/nphys2814

CrossRef Full Text | Google Scholar

Stevanato, G., Hill-Cousin, s J. T., Håkansson, P., Roy, S. S., Brown, L. J., Brown, R. C., et al. (2015). A nuclear singlet lifetime of more than one hour in room-temperature solution. Angew. Chem. Int. Ed. 54, 3740–3743. doi:10.1002/anie.201411978

PubMed Abstract | CrossRef Full Text | Google Scholar

Taminiau, T. H., Wagenaar, J. J. T., Van der Sar, T., Jelezko, F., Dobrovitski, V. V., and Hanson, R. (2012). Detection and control of individual nuclear spins using a weakly coupled electron spin. Phys. Rev. Lett. 109, 137602. doi:10.1103/PhysRevLett.109.137602

PubMed Abstract | CrossRef Full Text | Google Scholar

Theis, T., Blanchard, J. W., Butler, M. C., Ledbetter, M. P., Budker, D., and Pines, A. (2013). Chemical analysis using J-coupling multiplets in zero-field NMR. Chem. Phys. Lett. 580, 160–165. doi:10.1016/j.cplett.2013.06.042

CrossRef Full Text | Google Scholar

Vaara, J., Jokisaari, J., Wasylishen, R. E., and Bryce, D. L. (2002). Spin-spin coupling tensors as determined by experiment and computational chemistry. Prog. Nucl. Magn. Reson. Spectrosc. 41, 233–304. doi:10.1016/S0079-6565(02)00050-X

CrossRef Full Text | Google Scholar

Vandersypen, L. M. K., and Chuang, I. L. (2004). NMR techniques for quantum control and computation. Rev. Mod. Phys. 76, 1037–1069. doi:10.1103/revmodphys.76.1037

CrossRef Full Text | Google Scholar

Van de Stolpe, G. L., Kwiatkowski, D. P., Bradley, C. E., Randall, J., Breitweiser, S. A., Bradley, C. E., et al. (2023). Mapping a 50-spin-qubit network through correlated sensing. Available at: https://arxiv.org/abs/2307.06939.

Google Scholar

Vorobyov, V., Javadzade, J., Joliffe, M., Kaiser, F., and Wrachtrup, J. (2022). Addressing single nuclear spins quantum memories by a central electron spin. Appl. Mag. Res. 53, 1317–1330. doi:10.1007/s00723-022-01462-2

CrossRef Full Text | Google Scholar

Wasylishen, R. E. (2007). Dipolar and indirect coupling tensors in solids. eMagRes. doi:10.1002/9780470034590.emrstm0125

CrossRef Full Text | Google Scholar

Wasylishen, R. E. (2009). Dipolar and indirect coupling: basics. eMagRes. doi:10.1002/9780470034590.emrstm1023

CrossRef Full Text | Google Scholar

Wray, V. (1979). Carbon-carbon coupling constants: a compilation of data and a practical guide. Prog. NMR Spectrosc. 13, 177–256. doi:10.1016/0079-6565(79)80006-0

CrossRef Full Text | Google Scholar

Xie, T., Zhao, Z., Guo, M., Wang, M., Fazhan Shi, F., and Du, J. (2021). Identity test of single NV⁻ centers in diamond at hz-precision level. Phys. Rev. Lett. 127, 053601. doi:10.1103/PhysRevLett.127.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Kong, X., Li, Z., Yang, K., Yu, P., Wang, P., et al. (2020). Structural analysis of nuclear spin clusters via 2D nanoscale nuclear magnetic resonance spectroscopy. Adv. Quant. Technol. 3, 1900136. doi:10.1002/qute.201900136

CrossRef Full Text | Google Scholar

Zhao, N., Honert, J., Schmid, B., Klas, M., Isoya, J., Markham, M., et al. (2012). Sensing single remote nuclear spins. Nat. Nanotechnol. 7, 657–662. doi:10.1038/nnano.2012.152

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, N., Hu, J.-L., Ho, S.-W., Wan, J. T. K., and Liu, R.-B. (2011). Atomic-scale magnetometry of distant nuclear spin clusters via nitrogen-vacancy spin in diamond. Nat. Nanotech. 6, 242–246. doi:10.1038/nnano.2011.22

PubMed Abstract | CrossRef Full Text | Google Scholar

Zopes, J., Cujia, K. S., Sasaki, K., Boss, J. M., Itoh, K. M., and Degen, C. L. (2018). Three-dimensional localization spectroscopy of individual nuclear spins with sub-Angstrom resolution. Nat. Commun. 9, 4678. doi:10.1038/s41467-018-07121-0

PubMed Abstract | CrossRef Full Text | Google Scholar