Quantum machine learning early opportunities for the energy industry: a scoping review

Quantum computing innovations have garnered significant attention for their potential to revolutionize industries, with the energy sector being one of the most promising areas for application. As global energy demand increases and sustainability becomes more critical, computational technologies offer groundbreaking solutions for energy production, storage, and distribution. In this landscape, quantum computing plays a crucial role in unlocking the full potential of artificial intelligence and machine learning as research and development in the quantum machine learning field grows constantly. We here present a scoping review of early quantum machine learning applications within the energy industry value chain. Starting from 34 sources, we analyze and discuss 22 use cases in the energy sector, thoroughly examining each to understand its potential applications and impact. We then evaluate these early-stage quantum applications to determine their feasibility and benefits, offering insights into their relevance and effectiveness in the context of the industry’s evolving landscape. This is done by introducing a novel framework: the Assessment Model for Innovation Management (AMIM). Our research highlights the opportunities that quantum innovations present for the energy sector and offers actionable insights into which applications are the best investments and why. Overall, the feasibility and technological maturity of quantum machine learning use cases are still in the early stages, though their market compatibility and potential benefits are mostly relatively high. This indicates that while quantum machine learning holds immense potential, further development is necessary to fully realize its benefits in the energy sector.

1 Introduction

The energy industry is undergoing a profound transformation, driven by the increasing complexity of power systems, the integration of decentralized renewable energy sources, growing global demand, and the imperative of decarbonization. These global challenges have become particularly central to strategic European Union (EU) initiatives such as the Green Deal (European Commission, 2019), which are then reinforced by the dynamics of liberalized energy markets and the need for resilient and sustainable operations (European Commission, 2023). In this context, data-driven technologies, particularly machine learning (ML) and artificial intelligence (AI), have become indispensable tools for functions such as demand forecasting, fault detection, and grid stability assessment.

As the reliance on ML grows, so does the demand for computational power. This is where quantum computing (QC) emerges as a potentially transformative technology. With its theoretical ability to outperform classical computing in complex workloads such as optimization and simulation (Grover, 1996; Shor, 1997; Farhi et al., 2001), QC offers a promising path forward. The field of quantum machine learning (QML) specifically addresses challenging mathematical problems to enhance ML tasks (Biamonte et al., 2017).

Although commercially available quantum workloads remain an open challenge, the rapid evolution of quantum hardware has enabled exploratory studies for near-term applications. With this in mind, this review adopts a scoping approach to investigate the emerging intersection of QML and the energy sector. We therefore formulated the following research questions.

1. How can the energy and utilities sector benefit from QC, and which specific ML applications or challenges will QC address in the near-to-medium-term future?

2. Which use cases of QML have the most significant impact on the energy and utilities sector related to their level of readiness?

To answer these questions, this review identifies, categorizes, and assesses early-stage QML applications that address real-world energy challenges. To provide a structured evaluation, we introduce a novel framework, the Assessment Model for Innovation Management (AMIM), which is designed to assess use cases based on their market readiness and potential benefits.

This study is structured to be accessible to a diverse audience. We begin with a condensed overview of the fundamental concepts of quantum computing (Section 2), classical machine learning (Section 3), and quantum machine learning (Section 4), with deeper technical details moved to an Appendix. The core of the paper follows, presenting the scoping review methodology and findings (Section 5). Finally, Section 6 introduces the AMIM framework and discusses the evaluation of the identified use cases, providing insights for innovation strategy in the energy sector.

2 Quantum computing fundamentals

A quantum computer uses quantum bits, or qubits, to store information and perform computations by harnessing principles of quantum mechanics like superposition and entanglement (National Academies of Sciences, Engineering, and Medicine, 2019). Unlike a classical bit (0 or 1), a qubit can exist in a superposition of both states simultaneously, represented as $|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$, where $|\alpha {|}^2+|\beta {|}^2=1$. This allows a system of $n$ qubits to explore a computational space of $2^n$ dimensions. Entanglement creates strong correlations between qubits, where measuring one instantaneously influences the others, regardless of distance. These properties give quantum computers their potential for immense computational power.

2.1 Technology outlook

Quantum technology holds great promise but faces challenges in scalability and error correction. Research is ongoing across various physical implementations, including superconducting, photonic, and trapped-ion qubits, with no single standard yet dominant. The journey toward practical application is often described in stages of quantum advantage.

1. Quantum Utility: the current stage, where NISQ devices begin to provide valuable results for specific problems, even without a proven theoretical speed-up over classical methods (Kim et al., 2023).

2. Quantum Advantage: expected around 2029–2030, where error-corrected quantum computers will consistently outperform the best classical computers on a range of commercially relevant problems (IBM, 2025; Google Quantum AI, 2025).

3. Quantum Supremacy: the highest level, expected after 2030, where quantum computers can solve problems that are practically impossible for any classical computer.

Investing in QC R&D today is crucial for companies to build expertise and secure a competitive advantage in a future where computational resources may be scarce (Figure 1).

Figure 1

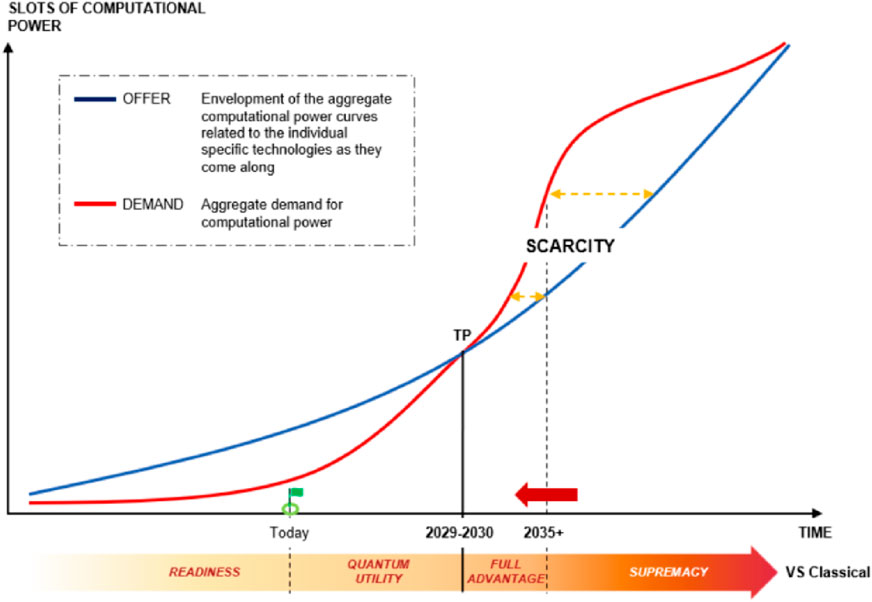
Figure 1. Impact of quantum computing technology on the predicted temporal evolution of offer-demand computational power curves. Today, quantum hardware demand is limited to experimental studies while we are entering the Quantum Utility era. Once full Quantum Advantage is virtually reached, there will be a severe turning point (TP), and demand is expected to grow much faster than offer. Even more so once quantum computers are fully mature, demand will just grow further. The time in which companies must wait for computational resources will likely increase, creating a significant competitive disadvantage for those unprepared. At the end of this lag, the market will settle, and demand and offer will match.

2.2 Types of hardware

Quantum computing hardware is broadly categorized into two models.

Analog quantum computing. This approach is a model of quantum computation in which a quantum system evolves continuously under a precisely controlled Hamiltonian, using the natural dynamics of quantum mechanics to directly simulate or solve problems. A prime example is quantum annealing, which involves smoothly evolving a quantum system towards a final state that encodes the solution to optimization problems. It takes advantage of the natural tendency of a quantum system to settle in its lowest energy state, which is designed to correspond to the optimal solution (Albash and Lidar, 2018). Machines designed thus, called “quantum annealers”, implement this adiabatic quantum process to find the ground state of a specific Hamiltonian, making them well-suited for specific optimization tasks that seek to maximize or minimize an objective function.

Digital gate-based quantum computing. This model is analogous to classical computing, manipulating qubits through a sequence of discrete and controllable quantum gates, also called “quantum processing units” (QPUs). This approach offers greater flexibility and universality, with the capability to address a wider range of problems, including those in machine learning (Ding et al., 2020). The current generation of these devices operates in the noisy intermediate-scale quantum (NISQ) era, meaning that they have a limited number of qubits (tens to a few hundreds) and are susceptible to errors from environmental noise and imperfect controls (Preskill, 2018).

2.3 Quantum error handling

A major challenge in the NISQ era is managing quantum errors, or decoherence. Three primary strategies are used.

$•$ Error suppression: hardware-level techniques that proactively alter control signals to make quantum operations more robust against known sources of noise (Baum et al., 2021).

$•$ Error mitigation: software-based methods that run an algorithm multiple times with slight variations and use statistical post-processing to estimate a noise-free result from noisy outputs (Giurgica-Tiron et al., 2020).

$•$ Quantum error correction (QEC): creating fault-tolerant quantum computers by encoding information from a single “logical qubit” across many physical qubits. This redundancy allows for the detection and correction of errors without disturbing the computation (Shor, 1995). QEC is a great challenge in terms of advanced quantum engineering and remains a key area of research.

3 Machine learning fundamentals

Machine learning (ML) is a subfield of AI where algorithms learn patterns from data to make predictions or decisions. We will focus on techniques relevant to this review.

Supervised learning involves training a model on labeled data. One of the most popular tasks is regression, which is to predict continuous numerical values learning from past data. Another key task is classification, or learning how to assign inputs to predefined categories. An important classification model is the support vector machine (SVM), which finds an optimal hyperplane to separate classes. For nonlinearly separable data, SVMs use the kernel trick to map data into a higher-dimensional space where separation is possible.

Unsupervised learning works with unlabeled data to find hidden structures. A key model is the restricted Boltzmann machine (RBM), a generative neural network used for tasks like feature learning.

Reinforcement learning is a type of machine learning in which an agent learns to make decisions by interacting with an environment whose past data are in principle not available at all, receiving feedback in the form of rewards or penalties, and optimizing its actions to maximize cumulative reward over time.

Used broadly in each category of machine learning, artificial neural networks (ANNs) are brain-inspired models consisting of layers of interconnected nodes. Deep learning uses ANNs with many layers (deep architectures) to learn complex hierarchical features from data, excelling at tasks involving unstructured data such as images or time series. ANNs are trained using optimization algorithms like gradient descent to minimize the difference between predicted and true outputs.

4 Quantum machine learning

Quantum machine learning (QML) aims to leverage quantum computing to enhance ML tasks, either by processing classical data on a quantum computer or by analyzing quantum data. The primary advantage lies in using the vast Hilbert space of qubits for more powerful data representation and harnessing quantum algorithms for computational speedups (Biamonte et al., 2017).

Current QML research for NISQ devices is dominated by variational quantum algorithms (VQAs). These are hybrid quantum–classical algorithms in which a quantum computer executes a parameterized quantum circuit (an ansatz) and a classical computer optimizes these parameters to minimize a cost function. This process is analogous to training a classical neural network.

4.1 Quantum variational models

VQAs can be broadly categorized on the basis of how they use the quantum circuit.

$•$ Explicit models (quantum neural networks), in which the output is a direct measurement of the quantum state produced by the circuit. This includes quantum neural networks (QNNs), which often use a layered structure with data re-uploading to increase their expressive power (Pérez-Salinas et al., 2020). The model parameters are tuned via a hybrid optimization loop. A key challenge in training these models is the “barren plateau” phenomenon where gradients can vanish, making optimization difficult. A technical discussion of this and mitigation strategies is provided in Appendix A.1.

$•$ Implicit models (quantum kernels), which exclusively use the quantum computer to calculate a quantum kernel, which measures the similarity between data points in a quantum feature space (Schuld and Killoran, 2019). The kernel matrix is then fed into a classical algorithm, such as an SVM, for the final classification or regression task. This avoids the direct optimization of the parameters of a quantum circuit but can be computationally expensive as it requires comparing every pair of data points.

$•$ Hybrid models simply combine the models from the previous two categories with other quantum-inspired or purely classical methods to form a hybrid architecture. One prominent example is hybrid neural networks, which mix classical neural layers with quantum data re-uploading.

Data are encoded into a quantum state using a feature map. Common methods include angle embedding and amplitude embedding. The mathematical details of these encoding strategies are available in Appendix A.2.

4.2 Quantum annealing for machine learning

Beyond gate-based models, quantum annealing is used to solve optimization problems inherent in some ML tasks. For example, it has been applied to feature selection, which can be framed as an optimization problem to find the most informative subset of features from a large dataset (Ferrari Dacrema et al., 2022). It is also used to train models such as RBMs by finding the optimal network weights that correspond to the minimum energy of an equivalent physical system (Dixit et al., 2021).

5 Case-based research in the energy sector

5.1 Rationale

Electricity is arguably the most important energy resource in modern society. Today, electricity operators face dual challenges: rising global demand and the urgent need to shift toward more sustainable and decarbonized processes. The adoption of new technologies such as AI and HPC is a key solution. QC is particularly interesting for its disruptive potential in the energy and utilities (E&U) industry, which is full of computational complexity, especially in forecasting and optimization problems. The focus of this review is on QML applications that can be practically assessed with today’s technology maturity, aiming to shed light on early opportunities for quantum technology adoption.

5.2 Methods and overview

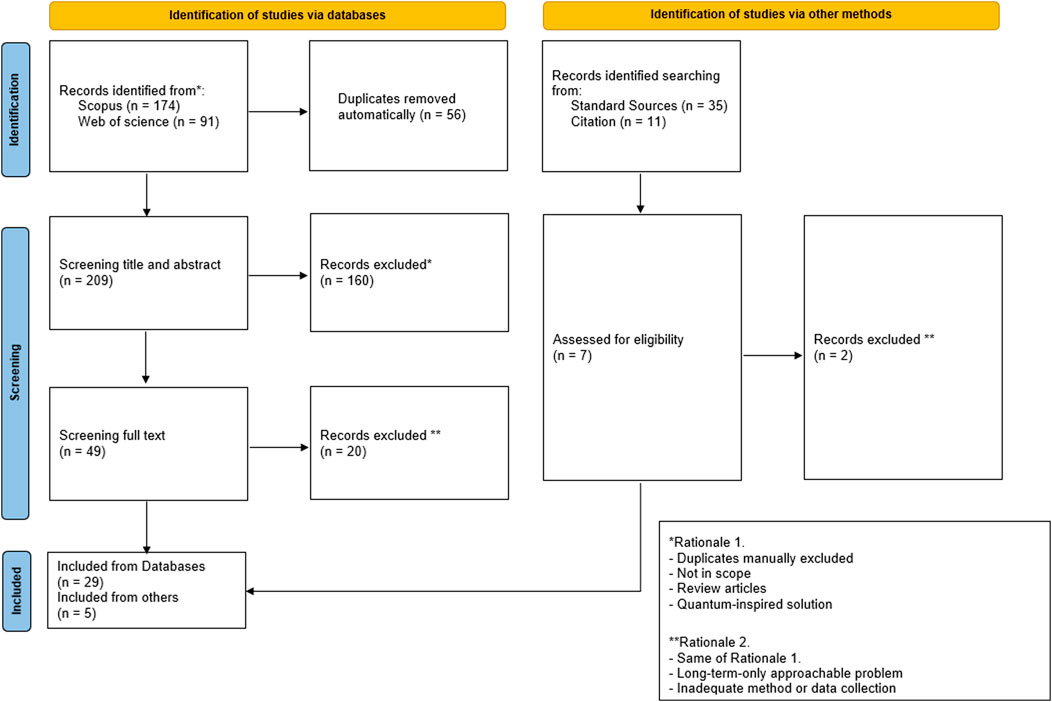
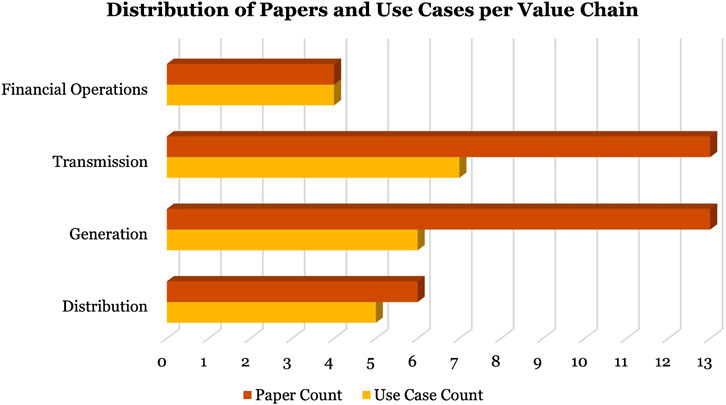
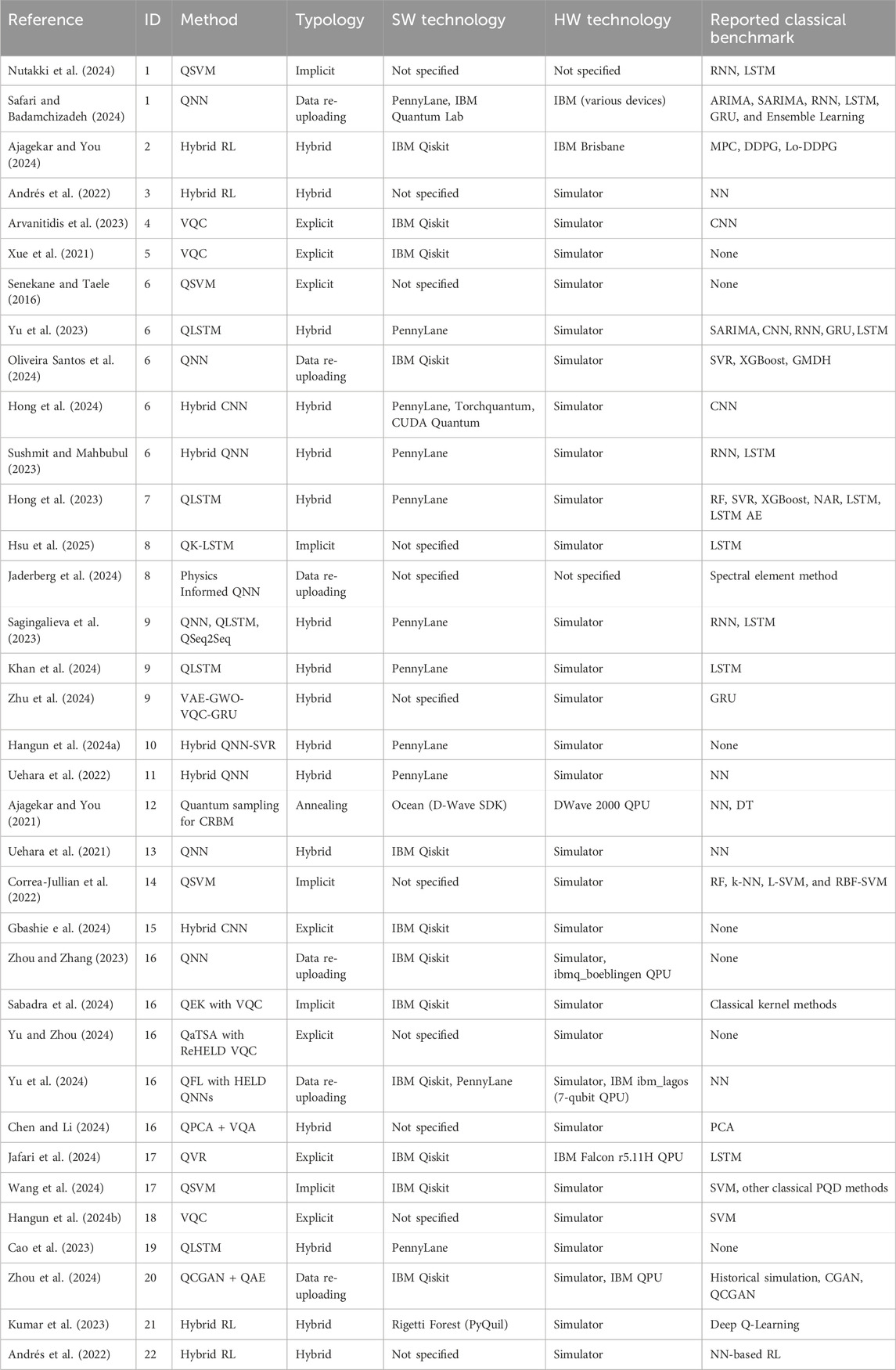
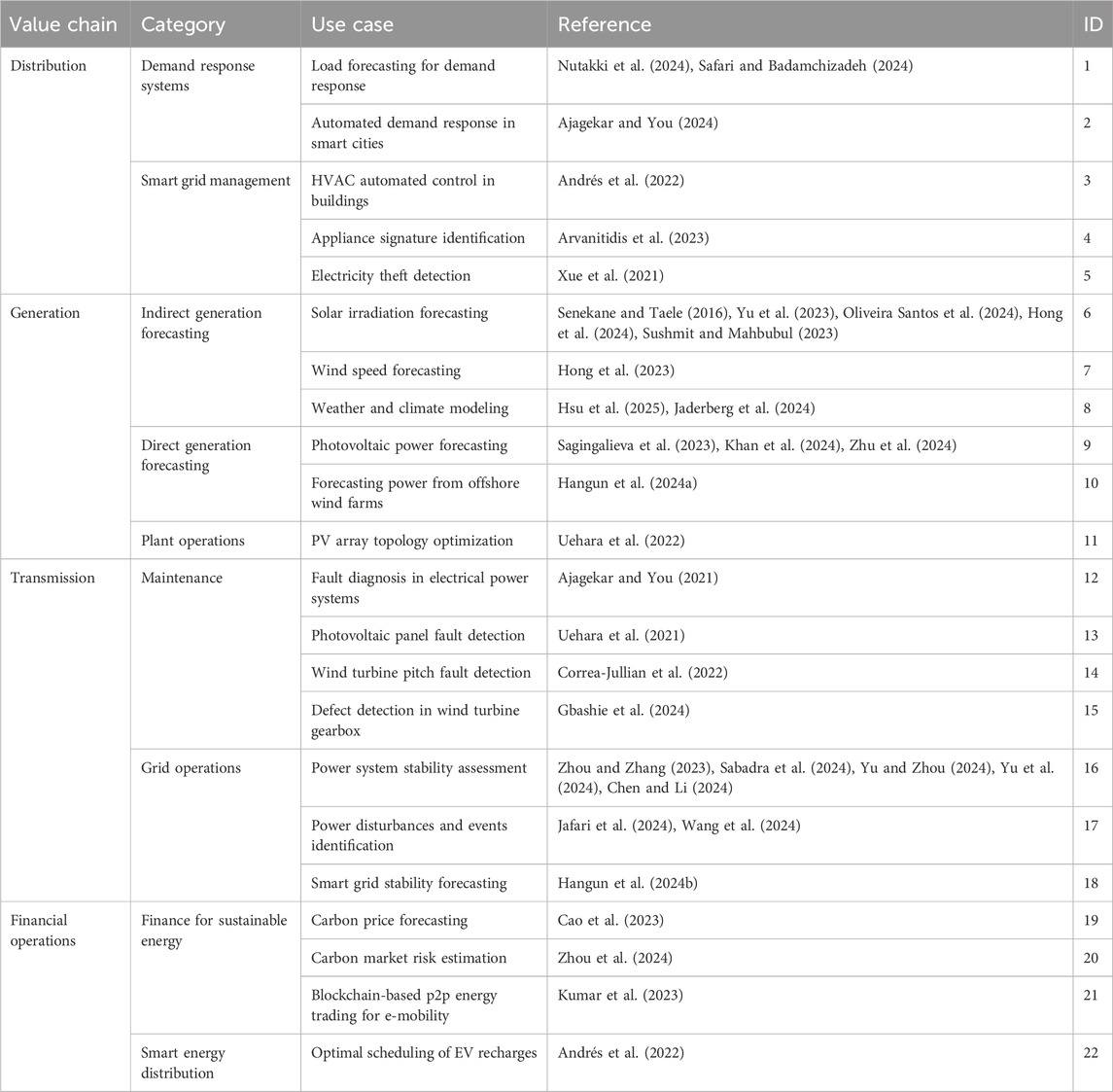
To answer the research questions given in the introduction, we follow the PRISMA-ScR guidelines for scoping reviews (Tricco et al., 2018) (Figure 2). We searched Scopus, Web of Science, and Google Scholar using a comprehensive query combining energy-sector terms (e.g., “smart grid” and “fault detection”) and QML terms (e.g., “quantum neural network” and “quantum kernel”). We applied inclusion criteria to select studies focused on near-term viable QML applications (variational, hybrid, or annealing-based) tested on real-world energy datasets. We excluded studies which relied only on purely theoretical fault-tolerant quantum computers (e.g., using Grover’s or Shor’s algorithm) or classical quantum-inspired approaches. This process yielded 34 key studies, from which we identified and analyzed 22 distinct use cases across the energy value chain: distribution, generation, transmission, and financial operations (Figure 3). A set of descriptive characteristics was extracted for each, including the QML method, typology, and the hardware/software technologies used (Table 1). As shown in Figures 4 and 5, “generation” and “transmission” are the value chain segments with the highest number of studies, suggesting that these are areas of high interest and data availability. The “transmission” segment, in particular, features the most diverse set of use cases, reflecting its operational complexity and high business impact. Finally, the most significant merit figure from each study is collected and compared with the best classical counterpart in terms of method when present (Table 2). As evidenced by this comparison, the quantum method is often comparable to and sometimes even better than the classical in performance.

Figure 2

Figure 2. PRISMA flow diagram of the source selection process.

Figure 3

Figure 3. Distribution of papers and use cases per value chain.

Table 1

Table 1. Use case Method’s overview.

Figure 4

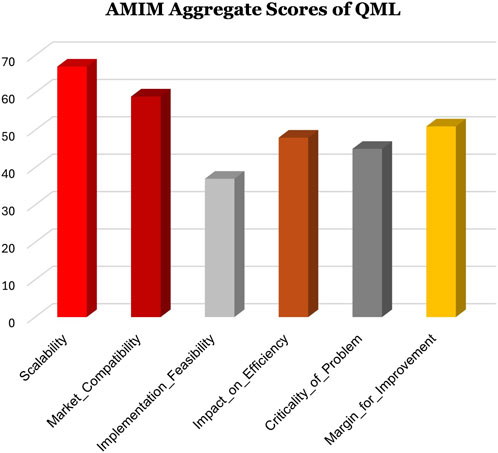
Figure 4. Aggregate scores of AMIM features for quantum machine learning applied to the energy industry. Scalability is the most rated characteristic, highlighting the strategic potential of this technology to this sector. On the other hand, feasibility concerns may arise, especially in the near-mid-term horizon, as expressed by the lowest score of the implementation feasibility feature.

Figure 5

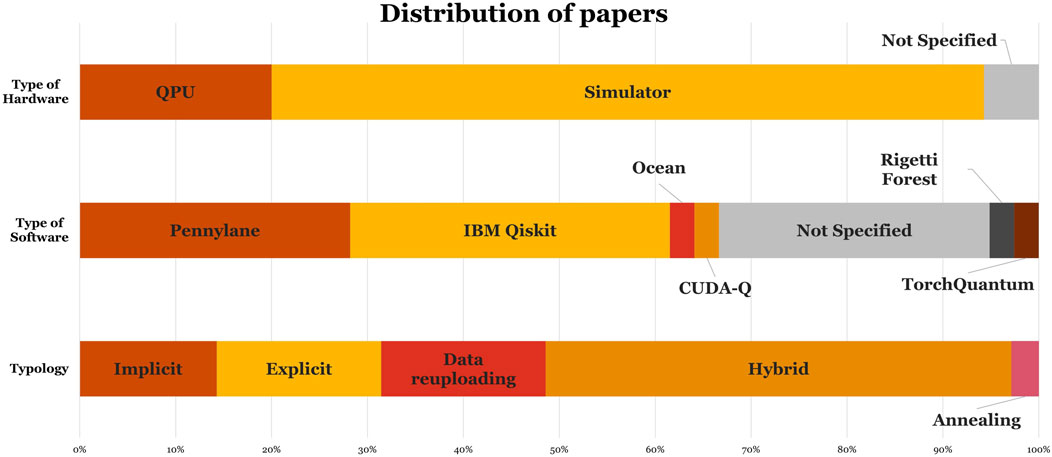
Figure 5. Distribution of papers by QML model typology (top), software framework used (middle), and hardware type (bottom; QPU vs. simulator). Hybrid model typologies are the most prevalent in the literature reviewed.

Table 2

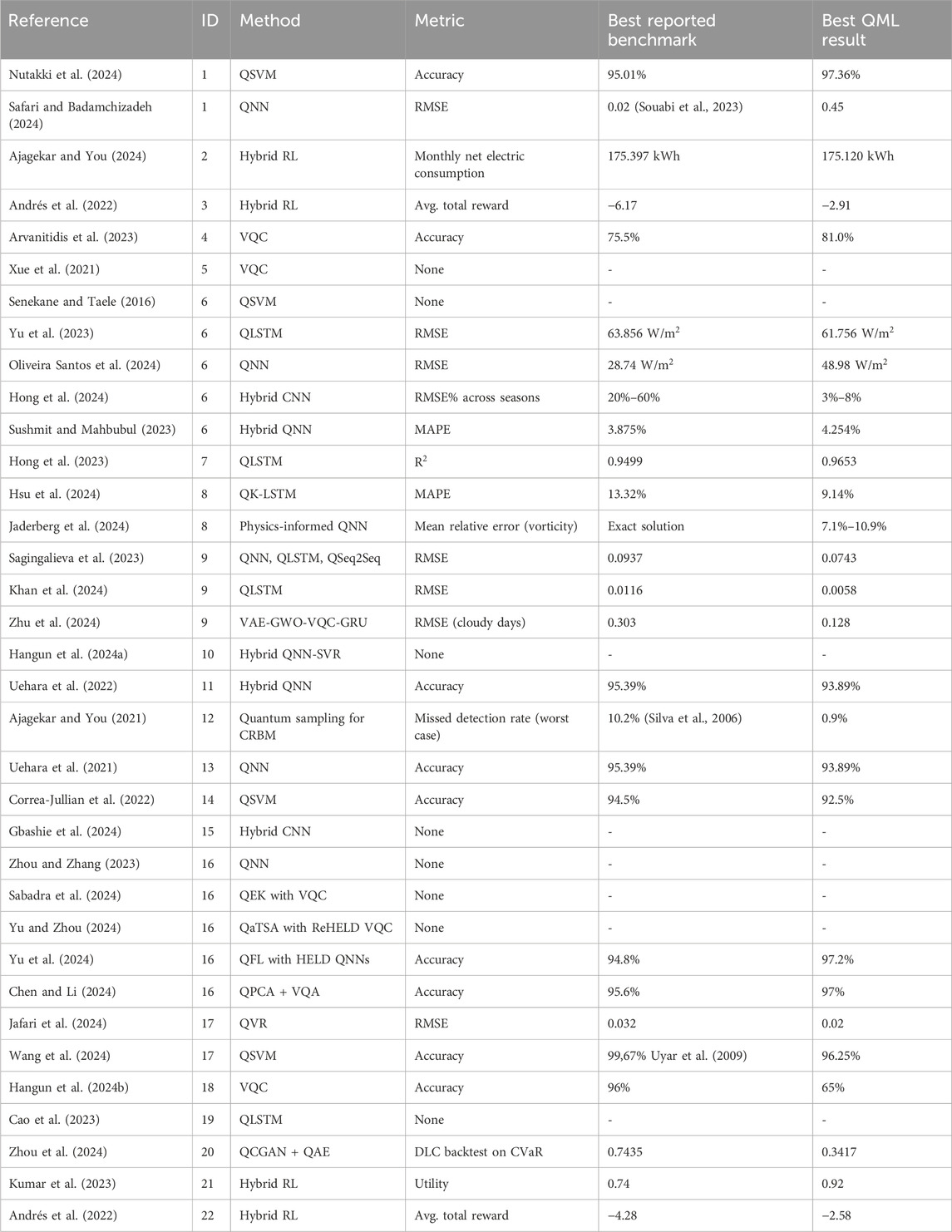
Table 2. Use case overview of results. The most representative metric of each study has been extracted and compared. When no metric is reported, the study has no classical benchmark. When no unit of measure is present for metrics like MSE or RMSE, values have been scaled.

5.3 Distribution

5.3.1 Overview

Predicting energy demand is a critical challenge for power systems. Forecasting methods vary in spatial and temporal resolution, from single appliances to national grids and from sub-hourly to yearly predictions (Debnath and Mourshed, 2018). Classical methods include statistical time-series models (e.g., ARIMA) and regression, while modern approaches heavily rely on machine learning models like NNs and SVMs to capture complex, nonlinear relationships in consumption data (Wei et al., 2019).

5.3.2 Key studies

QML offers new avenues for improving forecasting accuracy. Nutakki et al. (2024) applied a quantum support vector machine (QSVM) to forecast household energy consumption. This addresses the challenge classical SVMs face with highly complex, nonlinear consumption patterns by leveraging quantum feature spaces to potentially find more effective separating hyperplanes. Their results showed that the QSVM achieved higher accuracy (97.36%) than classical deep learning models like RNN and LSTM.

Safari and Badamchizadeh (2024) introduced “NeuroQuMan,” a QNN-based system to predict energy demand based on user reaction times, which demonstrated superior accuracy over classical benchmarks in simulations. Similarly, hybrid quantum-classical frameworks for demand response in buildings have shown promise. Ajagekar and You (2024) used a VQC within a reinforcement learning (RL) framework to optimize energy use, reporting a 13.6% reduction in energy consumption compared to classical control methods. Another QRL approach by Andrés et al. (2022) demonstrated that a hybrid quantum agent could learn an optimal energy-saving policy for an HVAC system more effectively than a classical neural network agent.

For smart grid management, Arvanitidis et al. (2023) used a variational quantum classifier (VQC) for appliance identification from power consumption data, achieving a 5% accuracy improvement over a classical CNN. The VQC’s ability to map data into a high-dimensional Hilbert space allows it to distinguish subtle signatures that are challenging for classical feature extraction methods.

5.4 Generation

5.4.1 Overview

Energy generation forecasting (EGF) plays a crucial role in managing the variability of renewable sources such as solar and wind, whose intermittent and volatile nature requires accurate forecasting to maintain grid stability and optimize resource use. Direct approaches often rely on time-series analysis or meteorological data from numerical weather prediction (NWP) models, while indirect approaches first predict site-specific weather profiles and then convert these into power output via weather-to-power performance models. Modern forecasting increasingly employs ML techniques—particularly NNs, SVMs, and LSTMs—whose performance can be enhanced by hyperparameter optimization methods such as ACO, genetic algorithms, and PSO (Jallal et al., 2020). Deep architectures, hybrid ML–physical approaches, and physics-informed methods have further improved accuracy and robustness in renewable generation forecasting (Sharadga et al., 2020; Mayer, 2022).

5.4.2 Key studies

Early QML applications to EGF include Senekane and Taele (2016), who used a QSVM to forecast solar irradiance from Cambridge University weather station data, and Li et al. (2015), who demonstrated a full quantum pipeline involving state preparation, matrix inversion, and variational classification. Building on this, Oliveira Santos et al. (2024) compared QNNs using angle encoding and a two-local ansatz against classical models on the Folsom, California dataset, finding that while XGBoost excelled in short-term horizons, QNNs were more effective for longer-term predictions. Extending to recurrent architectures, Yu et al. (2023) embedded VQCs into LSTM gates to create a QLSTM that outperformed SARIMA, CNN, RNN, GRU, and classical LSTM across five Chinese solar observatories.

Hybrid convolutional designs have also been explored, with Hong et al. (2024) developing an HQCNN optimized via Bayesian methods on Taiwanese irradiance data, demonstrating improved loss metrics, robustness to sensor faults, and superior speed using CUDA Quantum. Similarly, Sushmit and Mahbubul (2023) integrated PQC-based quantum layers into deep FFNs trained on NASA POWER data, showing that a two-quantum-layer hybrid achieved the best balance of accuracy and efficiency, while pure PQC models lagged behind. Sagingalieva et al. (2023) extended the hybrid concept to temporal models, proposing HQNN, HQLSTM, and HQSeq2Seq architectures for PV power forecasting, achieving 16%–41% accuracy gains over MLP and LSTM with fewer parameters and stronger performance on limited datasets. In another comparative study, Khan et al. (2024) found that QLSTM models trained on Indian and NREL datasets converged faster, exhibited more stable learning, and achieved higher accuracy than classical LSTM, although at the cost of longer evaluation times.

More complex hybrid pipelines have been proposed, such as the VAE-GWO-VQC-GRU framework of Zhu et al. (2024), which augmented and clustered Alice Springs PV data by weather condition before prediction, significantly outperforming GRU and VQC-GRU baselines. Beyond forecasting, Uehara et al. (2022) applied a hybrid QNN to optimize PV array topology under partial shading, achieving 85.12% classification accuracy for optimal configurations. In wind forecasting, Hong et al. (2023) combined LSTM with QNN and used the Taguchi method for systematic hyperparameter tuning, enhancing robustness across seasonal variations, while Hangun et al. (2024a) employed amplitude-encoded QNNs as feature extractors feeding into SVR for offshore wind farms, improving MAE and $R^2$ over classical baselines. Expanding to broader climate series, Hsu et al. (2025) embedded quantum kernels into LSTM transformations to create QK-LSTM, achieving higher accuracy with fewer parameters. Finally, Karniadakis et al. (2021) and Kashinath et al. (2021) reviewed physics-informed ML for climate and weather modeling, with Jaderberg et al. (2024) demonstrated that a quantum PINN could solve the barotropic vorticity equation, thus illustrating the potential for physically grounded quantum models in EGF.

5.5 Transmission

5.5.1 Overview

Transmission systems face new challenges from renewable integration, the rise of prosumers, and the reduced inertia of non-synchronous generation, making fault detection, diagnosis, and stability assessment increasingly critical. Traditional FDD approaches, rule-based, model-based, and more recently, ML- and DL-based, struggle with the growing data volume and complexity, opening opportunities for QML to improve detection accuracy, computational speed, robustness, and predictive maintenance (Correa-Jullian et al., 2022).

5.5.2 Key studies

For fault diagnosis, Ajagekar and You (2021) proposed a hybrid QC-trained CRBM on the IEEE 30-bus system, combining quantum generative training with discriminative fine-tuning to match or exceed ANN and DT performance while halving classification latency. In PV fault detection, Uehara et al. (2021) compared QNNs with different feature maps and ansatz choices on NREL datasets, showing competitive accuracy and reduced training epochs. Extending to wind turbine pitch systems, Correa-Jullian et al. (2022) benchmarked Q-SVMs against classical SVM, RF, and k-NN, finding that angular encoding Q-SVMs outperform RF and k-NN in certain feature settings when combined with PCA or AE-based reduction.

In transient stability assessment, Zhou and Zhang (2023) introduced qTSA with VQCs to separate stable and unstable states in SMIB, two-area, and NPCC systems, maintaining >95% accuracy on IBM hardware despite noise. Similarly, Sabadra et al. (2024) employed quantum-embedded kernels optimized by aligning the target kernel, achieving up to 98. 4% precision in SMIB. Hangun et al. (2024b) found that classical SVM outperformed VQC on a small smart grid, highlighting the need for careful feature map and ansatz tuning. Chen and Li (2024) demonstrated that combining QPCA, quantum inner products, and VQA could yield 98.7% accuracy in microgrid TSA with fewer measurements.

Distributed approaches have been explored by Yu et al. (2024), whose Q-dTSA used HELD-based federated QNNs to preserve local data privacy while matching DNN accuracy with 75% fewer parameters and faster convergence. The robustness to adversarial manipulation was addressed by Yu and Zhou (2024), who developed ReHELD circuits that improved classification under data poisoning and deletion by up to 18%. Optimization-based methods also feature, with Fei et al. (2024) formulating combinatorial fault diagnosis as a QAOA problem, introducing symmetric equivalent decomposition for efficient multi-z-rotation gates. For time anomaly detection in PMU streams, Jafari et al. (2024) proposed the QVR algorithm, optimized for shallow NISQ circuits and integrated with high-speed classical computing.

In power quality analysis, Wang et al. (2024) applied QSVMs with quantum feature mapping and kernel computation, achieving perfect disturbance detection in some datasets and maintaining over 87% accuracy under noise. Finally, Gbashie et al. (2024) integrated VQCs into CNN architectures for wind turbine gearbox fault detection, surpassing 99.2% accuracy with faster convergence when using the Adam optimizer.

5.6 Financial Operations

5.6.1 Overview

Carbon markets are a key instrument for mitigating climate change; this makes accurate carbon price forecasting and risk estimation essential for investors and policymakers. Other financial-related operations, such as energy trading and scheduling, could also benefit from advanced ML.

5.6.2 Key studies

Cao et al. (2023) developed an improved quantum long-term memory model (L-QLSTM) to predict carbon prices. By replacing classical gates in an LSTM with VQCs, the model leverages quantum expressivity to capture complex temporal dependencies that may be difficult for classical LSTMs to model efficiently. The L-QLSTM showed performance comparable to that of a classical LSTM but with improved learning stability.

For estimating carbon market risk, Zhou et al. (2024) proposed a framework using a quantum conditional generative adversarial network (QCGAN) to model return distributions and quantum amplitude estimation (QAE) to measure risk. This quantum approach offers a potential quadratic speedup over classical Monte Carlo methods for risk estimation, which are notoriously computationally intensive. The framework demonstrated a significant reduction in computational time and improved accuracy over classical models.

In energy trading, Kumar et al. (2023) designed a system combining blockchain with quantum reinforcement learning (QRL) to optimize P2P energy trading for EVs. The QRL agent learned an optimal pricing policy faster and more effectively than its classical counterparts.

6 Analysis and discussion

6.1 Assessment Model for Innovation Management

To evaluate the use cases identified, we introduce the Assessment Model for Innovation Management (AMIM). In an era of technological uncertainty, a structured framework is essential to allocate resources effectively. AMIM assesses use cases along two dimensions: readiness to market (scalability, market compatibility, and implementation feasibility) and potential benefit (impact on efficiency, problem criticality, and room for improvement). It is designed to be impartial with respect to the sector and technology, drawing inspiration from frameworks such as TRL (Héder, 2017) and SMART (Kumari et al., 2022) but focusing on the use case as a whole rather than just the technology.

6.1.1 Readiness to market

This dimension reflects how prepared a use case is for real-world deployment, looking at its ability to scale, fit market conditions, and be implemented with minimal friction. Scalability concerns whether the use case can handle growing demand, larger user bases, and evolving needs, paying attention to its capacity for user growth and flexibility to integrate with new technologies or adapt to changing business contexts. Market compatibility examines how well the current environment, society, stakeholders, technology, business structures, and ecosystems can support adoption, considering both customer readiness and the availability of the necessary technological infrastructure. Implementation feasibility captures the ease of integrating the use case into existing systems and processes, focusing on the complexity of the required integrations and the ability to meet regulatory requirements without excessive effort.

6.1.2 Potential benefit

This dimension measures the value a use case provides to the industry in terms of efficiency and long-term advantage. Impact on efficiency addresses the potential for cost reduction, return on investment, and productivity gains, showing whether the benefits justify the investment and improve operations. Criticality of the problem assesses the urgency and importance of the issue to be addressed, taking into account its severity, the level of market demand for a solution, and the sustainability of the impact—environmental, social and economic. Margin for further improvement looks at how much room remains for both vertical and horizontal development, taking into account the current stage of maturity and any performance gaps that signal opportunities for improvement.

6.1.3 Results

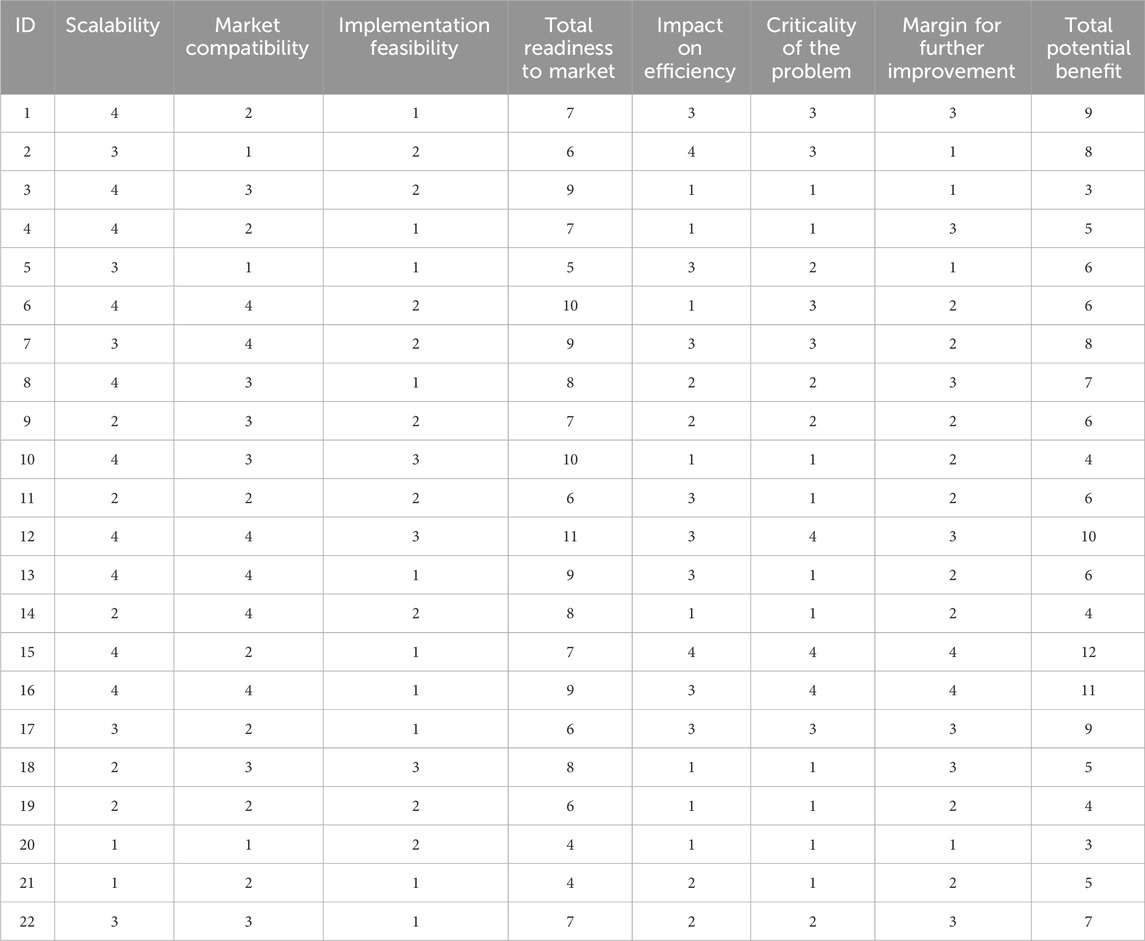
Each use case was scored from 1 (weak) to 4 (high) according to the AMIM criteria (Table 3). The aggregated scores position each use case in one of four quadrants (Figure 6): transformative leaders, research-heavy innovators, emerging niches, and experimental niches. Our analysis identifies power stability assessment (ID 16), fault diagnosis (ID 12), and wind speed forecasting (ID 7) as transformative leaders. These use cases are critical for the energy transmission and generation sectors, especially with growing grid complexity, and show both high market readiness and significant potential benefit from QML solutions. The transmission value chain stands out for hosting the most valuable use cases. In contrast, financial applications currently fall more into the experimental category. A key finding is that, while the technological feasibility of QML is still low, the overall market readiness is often decent due to the strong demand of the energy industry for innovative and scalable solutions (Figure 4).

Table 3

Table 3. Assessment model for innovation management.

Figure 6

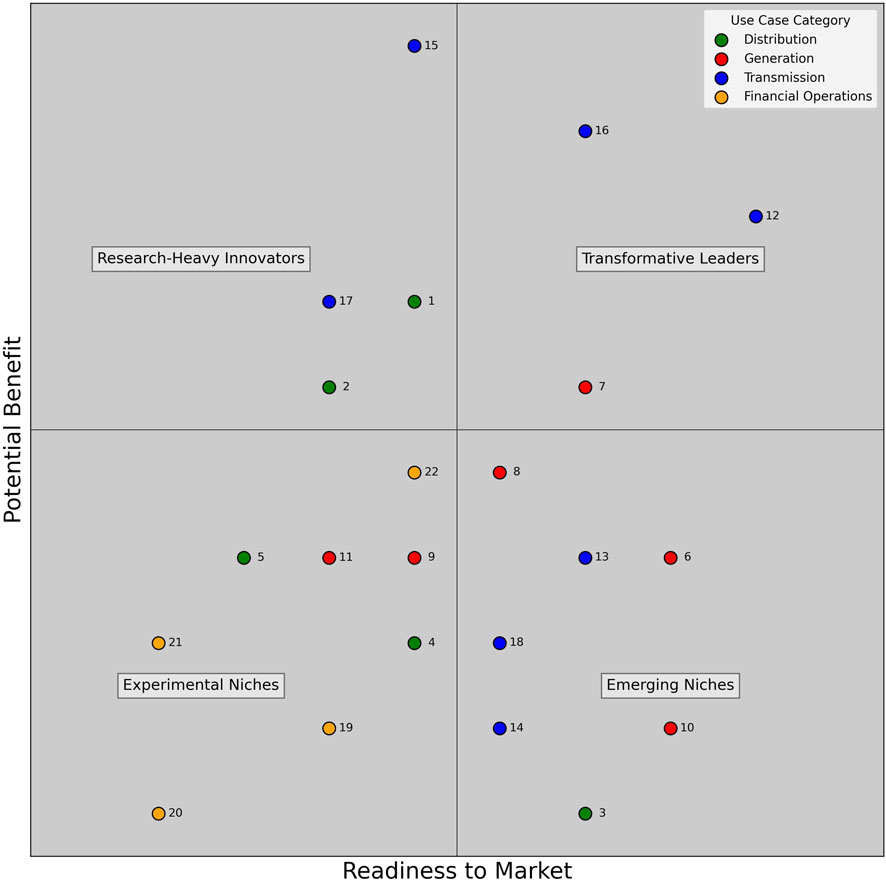
Figure 6. Graphical representation of AMIM quadrants. The two axes represent the potential benefit that each use case could give industrial workloads and its respective readiness to market—the state of maturity of that application. The mid-values separate the four quadrants, which classify the innovative figure of each use case (for use case ID mapping, see Table 4).

Table 4

Table 4. Look-up table for use cases.

6.1.4 Limitations and future validation of AMIM

It is important to acknowledge that AMIM is a novel framework proposed in this study. As such, it has not yet undergone external validation. Its current application relies on our assessment based on the literature reviewed. To strengthen its credibility and promote broader adoption, future research should focus on validating the framework. Potential validation methods include the following.

$•$ Expert review: engaging a panel of industry and academic experts from both the energy and quantum computing sectors to review and refine the AMIM dimensions and KPIs.

$•$ Pilot testing: applying the framework in a real-world corporate innovation setting to assess its utility as a practical decision-support tool for prioritizing R&D investments.

$•$ Comparative analysis: benchmarking the outcomes of an AMIM assessment against those produced by other established technology or innovation readiness frameworks.

This validation process would enhance the robustness of AMIM and solidify its value as a tool for strategic innovation management.

7 Conclusion

This scoping review maps the early applications of quantum machine learning (QML) in the energy industry. We provide a condensed overview of the relevant concepts of QC and ML and focus on near-term viable QML techniques, such as VQAs, hybrid architectures, and quantum annealing. Key studies show promising results, particularly for hybrid models that integrate quantum and classical computing, suggesting that they are a practical first step for applying QML to real-world workloads.

Although a scoping review does not permit a quantitative synthesis of results, our novel assessment framework, AMIM, provides a structured way to evaluate the 22 identified use cases based on their technological maturity and potential benefits. A key strength of AMIM is its versatility, which makes it applicable to other exploratory research fields. The analysis revealed that while quantum hardware limitations remain the main bottleneck, as evidenced by the prevalent use of simulators, the market readiness for these innovations is surprisingly high. This study highlights a clear path for future QML applications in the critically important energy sector and provides a framework for navigating innovation in this pioneering field.

Author contributions

FS: Formal Analysis, Supervision, Project administration, Validation, Methodology, Writing – review and editing, Funding acquisition, Software, Writing – original draft, Investigation, Resources, Conceptualization, Data curation, Visualization. LM: Investigation, Writing – review and editing, Writing – original draft, Validation, Data curation, Visualization, Formal Analysis. NG: Writing – original draft, Writing – review and editing, Visualization, Investigation. NG: Data curation, Formal Analysis, Writing – review & editing, Investigation, Writing – original draft. GC: Writing – original draft, Methodology, Conceptualization, Writing – review and editing, Data curation. SP: Writing – original draft, Writing – review and editing, Project administration. EL: Writing – review and editing, Supervision, Project administration, Writing – original draft, Conceptualization.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by Spoke 10 - ICSC - “National Research Centre in High Performance Computing, Big Data and Quantum Computing” grant number N. 2 - prot. 117080, 15/05/2024. This work is also framed within the strategic context of the European Union’s NextGenerationEU program, which supports research in key enabling technologies for a sustainable and resilient future.

Acknowledgments

First and foremost, we are thankful to PwC Italy, particularly to our Data & AI leader Massimo Iengo for being the first to believe in our innovative journey into quantum computing, not to forget all the people from the Data & AI team who have helped in making all of this work possible. We also wish to acknowledge the valuable financial support from Spoke 10 - ICSC - “National Research Centre in High Performance Computing, Big Data and Quantum Computing”, funded by the European Union–NextGenerationEU. Notably, we express our sincere gratitude to Professor Paolo Cremonesi and Beatrice Goretti from Politecnico di Milano for their essential support and encouragement since the very beginning of this entire quantum computing exploration initiative.

Conflict of interest

Authors FS, LM, NG, GC, SP, and EL were employed by PwC.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajagekar, A., and You, F. (2021). Quantum computing based hybrid deep learning for fault diagnosis in electrical power systems. Appl. Energy 303, 117628. doi:10.1016/j.apenergy.2021.117628

CrossRef Full Text | Google Scholar

Ajagekar, A., and You, F. (2024). Variational quantum circuit based demand response in buildings leveraging a hybrid quantum-classical strategy. Appl. Energy 364, 123244. doi:10.1016/j.apenergy.2024.123244

CrossRef Full Text | Google Scholar

Albash, T., and Lidar, D. A. (2018). Demonstration of a scaling advantage for a quantum annealer over simulated annealing. Phys. Rev. X 8, 031016. doi:10.1103/physrevx.8.031016

CrossRef Full Text | Google Scholar

Andrés, E., Cuéllar, M. P., and Navarro, G. (2022). On the use of quantum reinforcement learning in energy-efficiency scenarios. Energies 15, 6034. doi:10.3390/en15166034

CrossRef Full Text | Google Scholar

Arvanitidis, A. I., Valdez, L. A., and Alamaniotis, M. (2023). “A quantum machine learning methodology for precise appliance identification in smart grids,” in 2023 14th International Conference on Information, Intelligence, Systems & Applications (IISA), 1–6. doi:10.1109/IISA59645.2023.10345929

CrossRef Full Text | Google Scholar

Baum, Y., Amico, M., Howell, S., Hush, M., Liuzzi, M., Mundada, P., et al. (2021). Experimental deep reinforcement learning for error-robust gate-set design on a superconducting quantum computer. PRX Quantum 2, 040324. doi:10.1103/PRXQuantum.2.040324

CrossRef Full Text | Google Scholar

Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., and Lloyd, S. (2017). Quantum machine learning. Nature, 549 (7671), 195–202. doi:10.1038/nature23474

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Y., Zhou, X., Fei, X., Zhao, H., Liu, W., and Zhao, J. (2023). Linear-layer-enhanced quantum long short-term memory for carbon price forecasting. Quantum Mach. Intell. 5, 26. doi:10.1007/s42484-023-00115-2

CrossRef Full Text | Google Scholar

Cerezo, M., Sone, A., Volkoff, T., Cincio, L., and Coles, P. J. (2021). Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nat. Comm, 12 (1), 1791. doi:10.1038/s41467-021-21728-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., and Li, Y. (2024). “Extended abstract: quantum-accelerated transient stability assessment for power systems,” in 2024 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), 593–594. doi:10.1109/ISVLSI61997.2024.00112

CrossRef Full Text | Google Scholar

Correa-Jullian, C., Cofre-Martel, S., Martin, G. S., Droguett, E. L., de Novaes Pires Leite, G., and Costa, A. (2022). Exploring quantum machine learning and feature reduction techniques for wind turbine pitch fault detection. Energies 15, 2792. doi:10.3390/en15082792

CrossRef Full Text | Google Scholar

Debnath, K. B., and Mourshed, M. (2018). Forecasting methods in energy planning models. Renew. Sustain. Energy Rev. 88, 297–325. doi:10.1016/j.rser.2018.02.002

CrossRef Full Text | Google Scholar

Ding, C., Dong, F., and Tang, Z. (2020). Research progress on catalysts for the electrocatalytic oxidation of methanol. ChemistrySelect 5, 13318–13340. doi:10.1002/slct.202003365

CrossRef Full Text | Google Scholar

Dixit, V., Selvarajan, R., Aldwairi, T., Koshka, Y., Novotny, M. A., Humble, T. S., et al. (2021). Training a quantum annealing based restricted Boltzmann machine on cybersecurity data. IEEE Trans. Emerg. Top. Comput. Intell. 6, 417–428. doi:10.1109/tetci.2021.3074916

CrossRef Full Text | Google Scholar

European Commission (2019). The european green deal. Available online at: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en?prefLang=it (Accessed October 05, 2019).

Google Scholar

European Commission (2023). Next generation eu. Available online at: https://next-generation-eu.europa.eu/index_en (Accessed October 05, 2023).305–322. doi:10.2307/jj.7583926.19

CrossRef Full Text | Google Scholar

Farhi, J., Edward, G., Gutmann, S., Lapan, J., Lundgren, A., and Preda, D. (2001). A quantum adiabatic evolution algorithm applied to random instances of an np-complete problem. Science 292, 472–475. doi:10.1126/science.1057726

PubMed Abstract | CrossRef Full Text | Google Scholar

Fei, X., Zhao, H., Zhou, X., Zhao, J., Shu, T., and Wen, F. (2024). Power system fault diagnosis with quantum computing and efficient gate decomposition. Sci. Rep. 14, 16991. doi:10.1038/s41598-024-67922-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferrari Dacrema, M., Moroni, F., Nembrini, R., Ferro, N., Faggioli, G., and Cremonesi, P. (2022). “Towards feature selection for ranking and classification exploiting quantum annealers,” in Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, 2814–2824. doi:10.1145/3477495.3531755

CrossRef Full Text | Google Scholar

Gbashie, S. M., Olatunji, O. O., Adedeji, P. A., and Madushele, N. (2024). “Hybrid quantum convolutional neural network for defect detection in a wind turbine gearbox,” in 2024 IEEE PES/IAS PowerAfrica, 01–06. doi:10.1109/PowerAfrica61624.2024.10759407

CrossRef Full Text | Google Scholar

Giurgica-Tiron, T., Hindy, Y., LaRose, R., Mari, A., and Zeng, W. J. (2020). “Digital zero noise extrapolation for quantum error mitigation,” in 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), 306–316. doi:10.1109/QCE49297.2020.00045

CrossRef Full Text | Google Scholar

Google Quantum AI (2025). Quantum ai roadmap.

Google Scholar

Grover, L. K. (1996). “A fast quantum mechanical algorithm for database search,” in Proceedings of the 28th Annual ACM Symposium on Theory of Computing, 212–219. doi:10.1145/237814.237866

CrossRef Full Text | Google Scholar

Hangun, B., Akpinar, E., Oduncuoglu, M., Altun, O., and Eyecioglu, O. (2024a). “A hybrid quantum-classical machine learning approach to offshore wind farm power forecasting,” in 2024 13th international Conference on renewable energy research and applications (ICRERA) (IEEE), 1105–1110.

CrossRef Full Text | Google Scholar

Hangun, B., Eyecioglu, O., and Altun, O. (2024b). “Quantum computing approach to smart grid stability forecasting,” in 2024 12th International Conference on Smart Grid (icSmartGrid), 840–843. doi:10.1109/icSmartGrid61824.2024.10578114

CrossRef Full Text | Google Scholar

Héder, M. (2017). From nasa to eu: the evolution of the trl scale in public sector innovation. Innovation J. 22, 1–23.

Google Scholar

Holmes, Z., Sharma, K., Cerezo, M., and Coles, P. J. (2022). Connecting ansatz expressibility to gradient magnitudes and barren plateaus. PRX quantum, 3 (1), 010313. doi:10.1103/PRXQuantum.3.010313

CrossRef Full Text | Google Scholar

Hong, Y.-Y., Arce, C. J. E., and Huang, T.-W. (2023). A robust hybrid classical and quantum model for short-term wind speed forecasting. IEEE Access 11, 90811–90824. doi:10.1109/access.2023.3308053

CrossRef Full Text | Google Scholar

Hsu, Y.-C., Chen, N.-Y., Li, T.-Y., Lee, P. H. H., and Chen, K. C. (2025).“Quantum kernel-based long short-term memory for climate time-series forecasting,” in 2025 International Conference on Quantum Communications, Networking, and Computing (QCNC) (IEEE), 421–426. doi:10.1109/QCNC64685.2025.00072

CrossRef Full Text | Google Scholar

Hsu, Y.-C., Chen, N.-Y., Li, T.-Y., and Chen, K.-C. (2024). Quantum kernel-based long short-term memory for climate time-series forecasting. arXiv preprint arXiv:2412.08851.

Google Scholar

IBM (2025). Superconducting quantum roadmap.

Google Scholar

Jaderberg, B., Gentile, A. A., Ghosh, A., Elfving, V. E., Jones, C., Vodola, D., et al. (2024). Potential of quantum scientific machine learning applied to weather modelling. arXiv.

Google Scholar

Jafari, H., Aghababa, H., and Barati, M. (2024). “Quantum leaps: dynamic event identification using phasor measurement units in power systems,” in 2024 international conference on smart grid synchronized measurements and analytics (SGSMA) (IEEE), 1–6.

CrossRef Full Text | Google Scholar

Jallal, M., Chabaa, S., and Zeroual, A. (2020). A novel deep neural network based on randomly occurring distributed delayed pso algorithm for monitoring the energy produced by four dual-axis solar trackers. Renew. Energy 149, 1182–1196. doi:10.1016/j.renene.2019.10.117

CrossRef Full Text | Google Scholar

Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., and Yang, L. (2021). Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440. doi:10.1038/s42254-021-00314-5

CrossRef Full Text | Google Scholar

Kashif, M., Rashid, M., Al-Kuwari, S., and Shafique, M. (2024). “Alleviating barren plateaus in parameterized quantum machine learning circuits: investigating advanced parameter initialization strategies,” in 2024 Design, Automation & Test in Europe Conference & Exhibition (DATE) (IEEE), 1–6. doi:10.23919/date58400.2024.10546644

CrossRef Full Text | Google Scholar

Kashinath, K., Mustafa, M., Albert, A., Wu, J.-L., Jiang, C., Esmaeilzadeh, S., et al. (2021). Physics-informed machine learning: case studies for weather and climate modelling. Philosophical Trans. R. Soc. A 379, 20200093. doi:10.1098/rsta.2020.0093

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, S. Z., Muzammil, N., Ghafoor, S., Khan, H., Zaidi, S. M. H., Aljohani, A. J., et al. (2024). Quantum long short-term memory (qlstm) vs. classical lstm in time series forecasting: a comparative study in solar power forecasting. Front. Phys. 12, 1439180. doi:10.3389/fphy.2024.1439180

CrossRef Full Text | Google Scholar

Kim, Y., Eddins, A., Anand, S., Wei, K. X., Van Den Berg, E., Rosenblatt, S., et al. (2023). Evidence for the utility of quantum computing before fault tolerance. Nature 618, 500–505. doi:10.1038/s41586-023-06096-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, M., Dohare, U., Kumar, S., and Kumar, N. (2023). Blockchain based optimized energy trading for e-mobility using quantum reinforcement learning. IEEE Trans. Veh. Technol. 72, 5167–5180. doi:10.1109/TVT.2022.3225524

CrossRef Full Text | Google Scholar

Kumari, A., Schiffner, S., and Schmitz, S. (2022). Smart: a technology readiness methodology in the frame of the nis directive. arXiv Prepr. arXiv:2201.00546. doi:10.48550/arXiv.2201.00546

CrossRef Full Text | Google Scholar

Li, Z., Liu, X., Xu, N., and Du, J. (2015). Experimental realization of a quantum support vector machine. Phys. Rev. Lett. 114, 140504. doi:10.1103/physrevlett.114.140504

PubMed Abstract | CrossRef Full Text | Google Scholar

Lloyd, S., Schuld, M., Ijaz, A., Izaac, J., and Killoran, N. (2020). Quantum embeddings for machine learning. arXiv preprint arXiv:2001.03622.

Google Scholar

Mayer, M. (2022). Benefits of physical and machine learning hybridization for photovoltaic power forecasting. Renew. Sustain. Energy Rev. 168, 112772. doi:10.1016/j.rser.2022.112772

CrossRef Full Text | Google Scholar

National Academies of Sciences, Engineering, and Medicine. (2019). Quantum Computing: Progress and Prospects. Washington, DC: The National Academies Press. doi:10.17226/25196

CrossRef Full Text | Google Scholar

Nutakki, M., Koduru, S., and Mandava, S. (2024). Quantum support vector machine for forecasting house energy consumption: a comparative study with deep learning models. J. Cloud Comput. 13, 105–112. doi:10.1186/s13677-024-00669-x

CrossRef Full Text | Google Scholar

Oliveira Santos, V., Marinho, F. P., Costa Rocha, P. A., Thé, J. V. G., and Gharabaghi, B. (2024). Application of quantum neural network for solar irradiance forecasting: a case study using the folsom dataset, California. Energies 17, 3580. doi:10.3390/en17143580

CrossRef Full Text | Google Scholar

Patti, T. L., Najafi, K., Gao, X., and Yelin, S. F. (2021). Entanglement devised barren plateau mitigation. Phys. Rev. Res. 3, 033090. doi:10.1103/physrevresearch.3.033090

CrossRef Full Text | Google Scholar

Pérez-Salinas, A., Cervera-Lierta, A., Gil-Fuster, E., and Latorre, J. I. (2020). Data re-uploading for a universal quantum classifier. Quantum 4, 226. doi:10.22331/q-2020-02-06-226

CrossRef Full Text | Google Scholar

Preskill, J. (2018). Quantum computing in the nisq era and beyond. Quantum 2, 79. doi:10.22331/q-2018-08-06-79

CrossRef Full Text | Google Scholar

Rudolph, M. S., Miller, J., Motlagh, D., Chen, J., Acharya, A., and Perdomo-Ortiz, A. (2022). Synergy between quantum circuits and tensor networks: short-cutting the race to practical quantum advantage. arXiv preprint arXiv:2208.13673.

Google Scholar

Sabadra, T., Yu, S., and Zhou, Y. (2024). “Quantum kernel based transient stability assessment of power systems and its implementation in nisq environment,” in 2024 IEEE International Conference on Big Data (BigData), 7402–7406. doi:10.1109/BigData62323.2024.10825774

CrossRef Full Text | Google Scholar

Safari, A., and Badamchizadeh, M. A. (2024). Neuroquman: quantum neural network-based consumer reaction time demand response predictive management. Neural Comput. Appl. 36, 19121–19138. doi:10.1007/s00521-024-10201-6

CrossRef Full Text | Google Scholar

Sagingalieva, A., Komornyik, S., Senokosov, A., Joshi, A., Sedykh, A., Mansell, C., et al. (2023). Photovoltaic power forecasting using quantum machine learning. arXiv preprint arXiv:2312.16379.

Google Scholar

Schuld, M., and Killoran, N. (2019). Quantum machine learning in feature hilbert spaces. Phys. Rev. Lett. 122, 040504. doi:10.1103/physrevlett.122.040504

PubMed Abstract | CrossRef Full Text | Google Scholar

Senekane, M., and Taele, B. M. (2016). Prediction of solar irradiation using quantum support vector machine learning algorithm. Smart Grid Renew. Energy 7, 293–301. doi:10.4236/sgre.2016.712022

CrossRef Full Text | Google Scholar

Sharadga, H., Hajimirza, S., and Balog, R. (2020). Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 150, 797–807. doi:10.1016/j.renene.2019.12.131

CrossRef Full Text | Google Scholar

Shor, P. W. (1995). Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496. doi:10.1103/PhysRevA.52.R2493

PubMed Abstract | CrossRef Full Text | Google Scholar

Shor, P. W. (1997). “Algorithms for quantum computation: discrete logarithms and factoring,” in Proceedings of the 35th Annual ACM Symposium on Theory of Computing, 124–134. doi:10.1109/sfcs.1994.365700

CrossRef Full Text | Google Scholar

Silva, K., Souza, B. A., and Brito, N. S. (2006). Fault detection and classification in transmission lines based on wavelet transform and ann. IEEE Trans. power Deliv. 21, 2058–2063. doi:10.1109/tpwrd.2006.876659

CrossRef Full Text | Google Scholar

Skolik, A., McClean, J. R., Mohseni, M., Van Der Smagt, P., and Leib, M. (2021). Layerwise learning for quantum neural networks. Quantum Mach. Intell. 3, 5–11. doi:10.1007/s42484-020-00036-4

CrossRef Full Text | Google Scholar

Souabi, S., Chakir, A., and Tabaa, M. (2023). Data-driven prediction models of photovoltaic energy for smart grid applications. Energy Rep. 9, 90–105. doi:10.1016/j.egyr.2023.05.237

CrossRef Full Text | Google Scholar

Sushmit, M. M., and Mahbubul, I. M. (2023). Forecasting solar irradiance with hybrid classical–quantum models: a comprehensive evaluation of deep learning and quantum-enhanced techniques. Energy Convers. Manag. 294, 117555. doi:10.1016/j.enconman.2023.117555

CrossRef Full Text | Google Scholar

Tricco, A. C., Lillie, E., Zarin, W., O’Brien, K. K., Colquhoun, H., Levac, D., et al. (2018). Prisma extension for scoping reviews (prisma-scr): checklist and explanation. Ann. Intern. Med. 169, 467–473. doi:10.7326/m18-0850

PubMed Abstract | CrossRef Full Text | Google Scholar

Uehara, G., Rao, S., Dobson, M., Tepedelenlioglu, C., and Spanias, A. (2021). “Quantum neural network parameter estimation for photovoltaic fault detection,” in 2021 12th International Conference on Information, Intelligence, Systems & Applications (IISA), 1–7. doi:10.1109/IISA52424.2021.9555558

CrossRef Full Text | Google Scholar

Uehara, G. S., Narayanaswamy, V., Tepedelenlioglu, C., and Spanias, A. (2022). “Quantum machine learning for photovoltaic topology optimization,” in 2022 13th International Conference on Information, Intelligence, Systems & Applications (IISA), 1–5. doi:10.1109/IISA56318.2022.9904368

CrossRef Full Text | Google Scholar

Uyar, M., Yildirim, S., and Gencoglu, M. T. (2009). An expert system based on s-transform and neural network for automatic classification of power quality disturbances. Expert Syst. Appl. 36, 5962–5975. doi:10.1016/j.eswa.2008.07.030

CrossRef Full Text | Google Scholar

Wang, Q.-L., Jin, Y., Li, X.-H., Li, Y., Li, Y.-C., Zhang, K.-J., et al. (2024). An advanced quantum support vector machine for power quality disturbance detection and identification. EPJ Quantum Technol. 11, 70. doi:10.1140/epjqt/s40507-024-00283-5

CrossRef Full Text | Google Scholar

Wei, N., Li, C., Peng, X., Zeng, F., and Lu, X. (2019). Conventional models and artificial intelligence-based models for energy consumption forecasting: a review. J. Petroleum Sci. Eng. 181, 106187–187. doi:10.1016/j.petrol.2019.106187

CrossRef Full Text | Google Scholar

Xue, L., Cheng, L., Li, Y., and Mao, Y. (2021). “Quantum machine learning for electricity theft detection: an initial investigation,” in 2021 IEEE international conferences on Internet of things (iThings) and IEEE green computing & communications (GreenCom) and IEEE Cyber, physical & social computing (CPSCom) and IEEE smart data (SmartData) and IEEE congress on cybermatics (cybermatics) (IEEE), 204–208.

CrossRef Full Text | Google Scholar

Yu, S., and Zhou, Y. (2024). “Quantum adversarial machine learning for robust power system stability assessment,” in 2024 IEEE Power & Energy Society General Meeting (PESGM), 1–5. doi:10.1109/PESGM51994.2024.10688912

CrossRef Full Text | Google Scholar

Yu, Y., Hu, G., Liu, C., Xiong, J., and Wu, Z. (2023). Prediction of solar irradiance one hour ahead based on quantum long short-term memory network. IEEE Trans. Quantum Eng. 4, 1–15. doi:10.1109/tqe.2023.3271362

CrossRef Full Text | Google Scholar

Yu, S., Zhou, Y., and Wang, L. (2024). “Quantum-enabled distributed transient stability assessment of power systems,” in 2024 IEEE International Conference on Quantum Computing and Engineering (QCE). 593–599. doi:10.1109/QCE60285.2024.00075

CrossRef Full Text | Google Scholar

Zhou, Y., and Zhang, P. (2023). Noise-resilient quantum machine learning for stability assessment of power systems. IEEE Trans. Power Syst. 38, 475–487. doi:10.1109/TPWRS.2022.3160384

CrossRef Full Text | Google Scholar

Zhou, X., Zhao, H., Cao, Y., Fei, X., Liang, G., and Zhao, J. (2024). Carbon market risk estimation using quantum conditional generative adversarial network and amplitude estimation. Energy Convers. Econ. 5, 193–210. doi:10.1049/enc2.12122

CrossRef Full Text | Google Scholar

Zhu, W., He, Y., and Li, H. (2024). “Deep learning model for short-term photovoltaic power prediction based on data augmentation and quantum computing,” in 2024 China Automation Congress (CAC), 4097–4102. doi:10.1109/CAC63892.2024.10864724

CrossRef Full Text | Google Scholar

Appendix A Technical foundations of quantum machine learning

Appendix A.1 The barren plateau problem

A significant challenge in training variational quantum algorithms (VQAs) is the “barren plateau” phenomenon. It has been shown that for many parameterized quantum circuits (PQCs), the variance of the cost function’s gradient decreases exponentially with the number of qubits (Cerezo et al., 2021; Holmes et al., 2022). This ‘vanishing gradient” means that for larger quantum systems, the optimization landscape becomes extremely flat, making it nearly impossible for gradient-based optimizers to find a path towards the minimum.

This issue is particularly pronounced for PQCs that are highly expressive or ‘random-like,” as they tend to explore the entire Hilbert space uniformly. Several mitigation strategies have been proposed:

$•$ Problem-inspired ansätze: designing circuits with structures that reflect the problem’s symmetries or constraints, thus reducing the search space and avoiding overly random structures (Patti et al., 2021).

$•$ Parameter initialization strategies: techniques like “warm-starting” parameters from a classically presolved smaller problem or initializing parameters in a way that avoids the plateau region (Rudolph et al., 2022; Kashif et al., 2024).

$•$ Layer-wise learning: training the PQC one layer at a time and freezing the parameters of trained layers before adding new ones. This breaks down the global optimization into a series of smaller, more manageable problems (Skolik et al., 2021).

Appendix A.2 Quantum feature maps

A crucial step in QML is encoding classical data $x\in {\mathbb{R}}^d$ into a quantum state $|\varphi (x)\rangle$. This is done by a feature map, implemented as a parameterized unitary transformation $U(x)$. The choice of feature map determines how data is represented in the quantum feature space and significantly impacts the model’s performance. The most common strategies include (Lloyd et al., 2020):

$•$ Amplitude embedding, which encodes a normalized N-dimensional feature vector $x$ into the amplitudes of an $n$-qubit state, where $N=2^n$.

$|{\psi }_x\rangle ={\displaystyle \underset{i=1}{{\displaystyle \sum ^N}}}{x}_i|i\rangle (1)$

This is very efficient in terms of qubit count but can be challenging to implement physically.

$•$ Angle embedding, which encodes a d-dimensional vector $x=[x_1,\dots ,x_d]$ into the rotation angles of single-qubit gates. For $n=d$ qubits:

$U\left(x\right)=\underset{i=1}{\stackrel{n}{⨂}}{R}_P\left(x_i\right),P\in \left\{X,Y,Z\right\}(2)$

This is one of the most common and physically realizable encoding methods for near-term hardware.

$•$ Basis embedding encodes a binary string $x=(b_1,\dots ,b_n)$ directly into a computational basis state $|b_1{b}_2\dots b_n\rangle$. This is straightforward but requires a qubit for each bit of input.