Optimally Temperature Compensated FBG-Based Sensor Dedicated to Non-Intrusive Pipe Internal Pressure Monitoring

1 Introduction

Non-intrusive measurements first aim at keeping structures integrity safe while providing relevant information from their external surface. In the oil & gas industry, the monitoring of internal pressure and temperature of pipelines is necessary to prevent hydrate-plugs formation (Barker and Gomez (1989)) since it can interrupt the extraction process, with potentially significant economical and environmental consequences.

Non-intrusive measurements also make it possible to consider local inspections without any downtime, with external sensors installed and then removed on-demand from the structures to monitor, which is a key parameter for a widespread use in subsea environment.

Water distribution networks and Nuclear Power Plants (NPP) are two other examples where pipe structural integrity is equally important, with wider temperature ranges and additional ionizing radiations in the latter case, this is why non-intrusive measurement techniques must be proven reliable and safe by design.

However, none of the previous attempts to develop such non-intrusive pressure sensors has been satisfactory so far, because some of the underlying measurement principles, mainly based on ultrasonics or strain measurements, still suffer from shortcomings in their implementation.

Ultrasonic measurements already depend on many parameters, at least stresses and temperature (Salama and Ling (1980)), but the pipe dimensional changes must also be taken into account if the measurement principle relies on the analysis of the acoustic path length variations.

Diodati (1986) showed a linear dependence between the amplitude of an acoustic pulse propagating in a cylindrical vessel wall and its internal pressure, but also experienced a dependence on the compressibility of the fluid to monitor, making this measurement method unsuitable for general purpose on field.

Zhou et al. (2016) improved this technique thanks to propagation time measurements of multiple longitudinal waves propagating in the vessel wall, between several transducers located at precise positions along the pipe. But this technique also requires calibration in order to mitigate the temperature influence on pressure measurement.

From the mechanical point of view, the underlying principle usually relies on surface strains measurement, the pipe playing the role of the membrane of the traditional sensor, with strains proportional to the applied pressure in the elastic range. It has the advantage over ultrasonics not to depend on the fluid properties, but on its sole mechanical action on the pipe internal surface. But any uncontrolled mechanical effect other than hydrostatic pressure is also liable to introduce a significant pressure measurement bias.

Meiring et al. (2016) proposed to use FBG (Fiber Bragg Grating) transducers placed helically around the pipe, with a first transducer attached to it, sensitive to both strains and temperature, and a second one, loose, for temperature compensation. However, this solution only overcomes the thermal dependence of the optical fiber refractive index, on which the Bragg wavelengths depend; the pipe thermal expansion also must be compensated, as long as there is differential thermal expansion with regards to the optical fiber.

Roussel et al. (2019) adapted the original thermal compensation principle from Magne et al. (2005)¹, mainly due to installation (lack of space) issues, with a loose temperature compensation FBG transducer located in a micro-tube (thus introducing the same measurement bias vs. temperature as Meiring et al. (2016)), and two additional FBGs in rosette configuration (Ferdinand et al. (1994); Magne et al. (1997)) dedicated to strains measurement once attached to the pipe surface.

But the thermal inertia discrepancy between the strains and the temperature compensation sensors also inherently introduces a bias, notably in case of rapid pressure changes (this is the same for Meiring et al. (2016)—see Table 4 for some orders of magnitude).

Last, Ekechukwu and Sharma (2021) demonstrated a well-scale distributed pressure measurement based on fiber optic DAS (Dynamic Acoustic Sensing) and DTS (Distributed Temperature Sensing), and the analysis of the DAS low-frequency components which are sensitive to both strains and temperature perturbations. Then, a machine learning process is used to predict the pressure along the optical fiber. This method produces incredibly nice results, but is not fully adapted to rapid temperature changes, and may be questionable if the fluid does not flow.

Some of these solutions (Magne et al. (2005); Zhou et al. (2016)) also suffer from the approximation of the thin-shell theory, which is not accurate enough to describe the gradients inside the pipe wall (radial stress σ_rr can typically range from 300 bar down to the atmospheric pressure over only a few centimeters in metallic pipes), nor the right strains values on pipe surface (recipes from materials’ strength rules are very often the results of averaged calculations over pipe sections for the relevant parameters).

The solution proposed by Adams et al. (2018), based on two FBG transducers attached in hoop & longitudinal directions, falls into this trap: even if the temperature cross-sensitivity compensation principle is correct (however similar to Maurin et al. (2007)), the thin-shell theory is also not applied correctly either, with a confusion between the concepts of “absolute pressure” and “pressure variation between two states” (the FBG transducers are used for measurements relative to a known reference state), these shortcomings being hidden by a compulsory calibration process.

This is why to overcome the drawbacks of the previous attemps to develop a non-intrusive pressure sensor, the temperature dependence of the pressure measurement must first be solved, while relying on a better description of the pressurized pipe behavior between two thermomechanical states.

2 Preliminaries Specific to Purely Mechanical Measurements

Transducers usually exhibit a cross-sensitivity with temperature; this is the case for the traditional electrical strain gauges, but also for the Fiber Bragg Gratings in the field of strain measurements.

One solution to circumvent the temperature influence on the desired mechanical measurement is simply to make the difference between the raw measurements provided by two transducers attached to the structure: as long as they exhibit the same sensitivity to temperature and are subject to its same influence, there is indeed a chance to take advantage of at least the transverse Poisson effect to get a non-zero difference value, thus only sensitive to the mechanical deformation of the structure.

One key parameter is the strains distribution in the structure at the location of each transducer, which may be complex since it depends on many parameters such as its geometry and the stresses applied onto it. But if for instance, the structure is a cylinder with circular cross-section $\mathcal{S}$, only submitted to elongation or compression along its axis due to an external force $\vec{F}$, the difference between the mechanical longitudinal strain ${\epsilon }_{{zz}_{mec}}$ and the mechanical hoop strain ${\epsilon }_{{\theta \theta }_{mec}}$ is non-zero if F ≠ 0:

$\begin{array}{cccccc}\hfill \mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:\hfill & \hfill {\epsilon }_{{\theta \theta }_{mec}}=-\nu {\epsilon }_{{zz}_{mec}}\hfill & \hfill \Rightarrow \hfill & \hfill {\epsilon }_{{zz}_{mec}}-{\epsilon }_{{\theta \theta }_{mec}}=\left(1+\nu \right){\epsilon }_{{zz}_{mec}}\hfill & \hfill \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\hfill & \hfill {\epsilon }_{{zz}_{mec}}=\frac{F}{\mathcal{S}E}\hfill \end{array}(1)$

where E is the Young’s modulus and ν the Poisson’s ratio of the cylinder, with a positive difference in case of elongation:

$\begin{array}{cccc}\hfill \mathrm{i}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{o}\mathrm{f}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:\hfill & \hfill F>0\hfill & \hfill \Rightarrow \hfill & \hfill {\epsilon }_{{zz}_{mec}}-{\epsilon }_{{\theta \theta }_{mec}}>0\hfill \end{array}(2)$

FBG transducers are mainly sensitive to strains in the direction of the optical waveguide of the optical fiber, and are therefore good candidates for such selective measurements.

This principle to get rid of the temperature influence on the strains measurement, already described by Maurin et al. (2007) in case of bending, is however not fully adapted to pressure measurements for pipes, mainly because:

• the longitudinal and the hoop strains of a closed pipe behave the same with its internal pressure P_int (which results in inflating the pipe):

$\begin{array}{cccc}\hfill \mathrm{for\; a\; closed\; pipe}:\hfill & \hfill \frac{\partial {\epsilon }_{{zz}_{mec}}}{\partial P_{int}}>0\hfill & \hfill \mathrm{a}\mathrm{n}\mathrm{d}\hfill & \hfill \frac{\partial {\epsilon }_{{\theta \theta }_{mec}}}{\partial P_{int}}>0\hfill \end{array}(3)$

and make Eq. 1, by itself, inadequate for pressure measurement:

$\begin{array}{cccc}\hfill \mathrm{for\; a\; closed\; pipe}:\hfill & \hfill {\epsilon }_{{\theta \theta }_{mec}}>{\epsilon }_{{zz}_{mec}}>0\hfill & \hfill \Rightarrow \hfill & \hfill {\epsilon }_{{zz}_{mec}}-{\epsilon }_{{\theta \theta }_{mec}}<0\hfill \end{array}(4)$

• the strains sensitivity depends on pipe thickness and diameter, which are two other parameters to be taken into account to explain the relationship with the internal pressure.

The dedicated model developed hereafter (Sections 3 and 4) takes advantage of the same temperature compensation principle (by subtraction of two raw measurements), but with transducers located at different locations on the pipe surface (unlike the solution for bending described by Maurin et al. (2007)), and also facilitates the establishment of rules to compensate for other additional mechanical effects, such as pure bending (Section 4.2), thanks to a better understanding of the pipe behavior under hydrostatic pressure.

This type of measurement is also more suitable for rapid pressure and temperature changes as long as the transducers are similarly attached to the structure, e.g.: glued: then, they behave in the same way with temperature, their inertia being mainly controlled by the thermal properties of the structure (Section 4.1.3.2.3).

Last, thermal sensitivities, for both transducers and pipe, no longer interfere significantly with the pressure measurement, which is also an improvement over previous methods involving FBG transducers (Magne et al. (2005); Meiring et al. (2016)), and therefore leads to better results (Section 5).

3 The Simplified Thermomechanical Model

The principle is to develop a thermomechanical model of a straight pipe section submitted to simple mechanical stresses and forces, leading to the expressions of the strains and stresses tensors components on its external surface, then to establish the relationship for their measurement with transducers like e.g.: FBGs between two thermomechanical states, to finally get the variation ΔP_int of its internal pressure (Section 4.1.3.2).

The generalization of this model to additional mechanical sollicitations like pure bending, based on the principle that in the elastic domain, all contributions are cumulative, follows (Section 4.2.2.2).

3.1 Mathematical Description of the Thermoelastic Behavior of the Infinitely Long Pipe

The description of the pipe behavior is obtained by means of the formulation of the mechanical problem in terms of displacements. This method is different from Timoshenko and Goodier (1970) with the Airy’s function, but leads to quite the same results. The underlying hypotheses are also fully described and let the door open for a better or easier consideration of the temperature distribution in the pipe wall (Section 6).

This method first permits to calculate the components of the mechanical strains tensor, then the components of the stresses tensor (according to the Hooke’s law as long as the pipe behavior remains elastic).

The fundamental equation of dynamics for deformable bodies then leads to a set of partial differential equations, with integration coefficients expressed as functions of boundary conditions (internal and external hydrostatic pressures P_int and P_ext, the longitudinal force $\vec{F}$, but also the temperature T–Figure 1).

FIGURE 1

FIGURE 1. Mechanical sollicitations of the pipe in the cylindrical $\left(O,r,\theta ,z\right)$ coordinate system (no torsion).

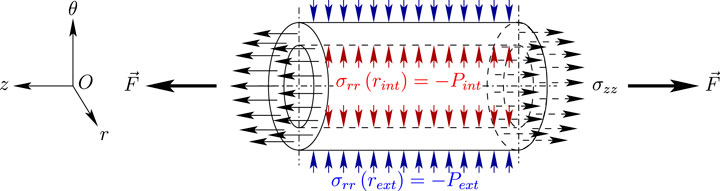
3.1.1 Schematic Description of the Pipe Under Hydrostatic Pressure

The mechanical sollicitations of the pipe, supposed to be infinitely long, can be modelled as described in Figure 1:

• a radial stress σ_rr resulting at least from the hydrostatic pressures P_int and P_ext applied respectively on the inner (at r_int) and the outer (at r_ext) pipe surfaces:

${\sigma }_{rr}\left(r_{int}\right)=-P_{int}\mathrm{a}\mathrm{n}\mathrm{d}{\sigma }_{rr}\left(r_{ext}\right)=-P_{ext}(5)$

• a longitudinal stress σ_zz representative of the external longitudinal force $\vec{F}$ applied on the pipe, which may also result from the inner pressure P_int if the pipe is closed at its ends:

$\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{e}:\vec{F}={\iint }_{\mathcal{S}}{\sigma }_{zz}\left(r\right)d\vec{\mathcal{S}}(6)$

For the sake of simplicity, but also because it is a few orders of magnitude lower than the hydrostatic pressure, the shear stress σ_rz (which may result from friction of the fluid flow on the inner pipe surface) is neglected.

This description will also help to correctly define the boundary conditions applied to the pipe, in order to solve the set of partial differential equations resulting from the mechanical balance.

The principle is first to establish the mathematical form of the displacement vector $\vec{u}$ of a point $M\left(r,\theta ,z\right)$ located inside the pipe wall at initial reference temperature T₀, taking into account the pipe axicylindrical symmetry, but also its isotropic thermomechanical properties.

3.1.2 Simplifications in Axicylindrical Symmetry, Displacements and Strains Tensor

The displacement vector $\vec{u}\left(u,v,w,T\right)$ can be written as the sum of a first displacement vector depending only on the mechanical effects ${\vec{u}}_{\sigma }\left(u_{\sigma },v_{\sigma },w_{\sigma }\right)$, and a second displacement vector depending only on the thermal effects ${\vec{u}}_T\left(u_T,v_T,w_T,T\right)$:

$\vec{u}={\vec{u}}_{\sigma }\left(\begin{array}{c}\hfill u_{\sigma }\left(r,\theta ,z\right)\hfill \\ \hfill v_{\sigma }\left(r,\theta ,z\right)\hfill \\ \hfill w_{\sigma }\left(r,\theta ,z\right)\hfill \end{array}\right)+{\vec{u}}_T\left(\begin{array}{c}\hfill u_T\left(r,\theta ,z,T\right)\hfill \\ \hfill v_T\left(r,\theta ,z,T\right)\hfill \\ \hfill w_T\left(r,\theta ,z,T\right)\hfill \end{array}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\left\{\begin{array}{cc}{T}_0\hfill & \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\hfill \\ T\hfill & \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\hfill \end{array}\right.(7)$

The usual assumptions in terms of axicylindrical symmetry, infinite pipe length, absence of torsion, isotropic material properties and temperature homogeneity, then lead to the simplified expressions of the displacement vectors ${\vec{u}}_{\sigma }$ and ${\vec{u}}_T$ after a first integration:

$\begin{array}{ccc}\hfill {\vec{u}}_{\sigma }\left(\begin{array}{c}\hfill u_{\sigma }\left(r\right)\hfill \\ \hfill 0\hfill \\ \hfill w_{\sigma }\left(r,z\right)\hfill \end{array}\right)\hfill & \hfill \mathrm{a}\mathrm{n}\mathrm{d}\hfill & \hfill {{\vec{u}}_{}}_T\left(\begin{array}{c}\hfill \alpha r\left(T-T_0\right)\hfill \\ \hfill 0\hfill \\ \hfill K_0+\alpha z\left(T-T_0\right)\hfill \end{array}\right)\hfill \end{array}(8)$

α is the thermal expansion coefficient of the pipe, and K₀ a first integration coefficient.

The linearized Green-Lagrange mechanical strains tensor ${\left[\mathit{\epsilon }\right]}_{mec}$ (Forest et al., 2009–2010) is calculated from the mechanical displacement ${\vec{u}}_{\sigma }$, taking into account the simplified expressions of the displacements detailed by Eq. 8, with the addition of the diagonal thermal strains tensor ${\left[\mathit{\epsilon }\right]}_{th}$, which gives the total (mechanical + thermal) strains tensor $\left[\mathit{\epsilon }\right]$:

$\left[\mathit{\epsilon }\right]={\left[\mathit{\epsilon }\right]}_{mec}+{\left[\mathit{\epsilon }\right]}_{th}\Rightarrow \left[\mathit{\epsilon }\right]=\left[\begin{array}{ccc}\hfill \frac{d{u}_{\sigma }\left(r\right)}{dr}\hfill & \hfill 0\hfill & \hfill \frac{1}{2}\frac{\partial w_{\sigma }\left(r,z\right)}{\partial r}\hfill \\ \hfill 0\hfill & \hfill \frac{u_{\sigma }\left(r\right)}{r}\hfill & \hfill 0\hfill \\ \hfill \frac{1}{2}\frac{\partial w_{\sigma }\left(r,z\right)}{\partial r}\hfill & \hfill 0\hfill & \hfill \frac{\partial w_{\sigma }\left(r,z\right)}{\partial z}\hfill \end{array}\right]+\alpha \left(T-T_0\right)\left[\mathit{I}\right](9)$

3.1.3 The Stresses Tensor and the Mechanical Equilibrium of Forces

The pipe is supposed to be used in its nominal range of deformation, typically one order of magnitude below its yield strength, so the Hooke’s law for elastic bodies applies:

$\left[\mathit{\sigma }\right]=2\mu {\left[\mathit{\epsilon }\right]}_{mec}+\mathrm{\lambda }\mathrm{Tr}\left({\left[\mathit{\epsilon }\right]}_{mec}\right)\left[\mathit{I}\right](10)$

$\left[\mathit{\sigma }\right]$ and $\left[\mathit{I}\right]$ are respectively the stress and the identity tensors, λ and μ are the Lamé’s coefficients.

The fundamental equation of dynamics for deformable bodies:

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\mathit{\sigma }\right]+\rho \left(\vec{f}-\vec{\gamma }\right)=\vec{0}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\left\{\begin{array}{cc}\rho \hfill & \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}\hfill \\ \vec{f}\hfill & \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{s}(\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{l}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}e.g.:\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y})\hfill \\ \vec{\gamma }\hfill & \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\hfill \end{array}\right.(11)$

applies with the assumptions of negligible volume forces and static conditions, and then leads to the set of two partial differential equations:

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\mathit{\sigma }\right]=\vec{0}\Rightarrow \left\{\begin{array}{cc}\frac{d^2{u}_{\sigma }\left(r\right)}{{dr}^2}+\frac{1}{r}\left(\frac{d{u}_{\sigma }\left(r\right)}{dr}-\frac{u_{\sigma }\left(r\right)}{r}\right)+\frac{\mathrm{\lambda }+\mu }{\mathrm{\lambda }+2\mu }\frac{{\partial }^2{w}_{\sigma }\left(r,z\right)}{\partial r\partial z}\hfill & =0\hfill \\ \frac{{\partial }^2{w}_{\sigma }\left(r,z\right)}{{\partial r}^2}+\frac{1}{r}\frac{\partial w_{\sigma }\left(r,z\right)}{\partial r}\hfill & =0\hfill \end{array}\right.(12)$

3.1.4 Formal Expressions of the Displacements, Strains and Stresses in the Pipe Wall

Set of partial differential Eq. 12 is solved by separation of variables r and z for the mechanical displacement $w_{\sigma }\left(r,z\right)$ if the pipe is infinitely long. After integration, it first leads to the formal expression of the mechanical displacement vector components ${\vec{u}}_{\sigma }$ (L₁, L₂, K₁, K₂, K₃ and K₄ are integration coefficients):

$\left\{\begin{array}{cc}{u}_{\sigma }\left(r\right)\hfill & =\frac{\left(L_1+L_2\right)r}{2}+\frac{L_1-L_2}{2r}+\frac{\left(\mathrm{\lambda }+\mu \right)K_4\left[1-2\ln \left(r\right)\right]r}{4\left(\mathrm{\lambda }+2\mu \right)}\hfill \\ w_{\sigma }\left(r,z\right)\hfill & =\left(K_2+K_{4}z\right)\ln \left(r\right)+K_{1}z+K_3\hfill \end{array}\right.(13)$

then to the formal expressions of the mechanical strains tensor ${\left[\mathit{\epsilon }\right]}_{mec}$ components (ɛ_rθ = ɛ_θz = 0):

$\left\{\begin{array}{cc}{\epsilon }_{{rr}_{mec}}\left(r\right)\hfill & =\frac{L_1+L_2}{2}-\frac{L_1-L_2}{2r^2}-\frac{\left(\mathrm{\lambda }+\mu \right)K_4\left[1+2\ln \left(r\right)\right]}{4\left(\mathrm{\lambda }+2\mu \right)}\hfill \\ {\epsilon }_{{\theta \theta }_{mec}}\left(r\right)\hfill & =\frac{L_1+L_2}{2}+\frac{L_1-L_2}{2r^2}+\frac{\left(\mathrm{\lambda }+\mu \right)K_4\left[1-2\ln \left(r\right)\right]}{4\left(\mathrm{\lambda }+2\mu \right)}\hfill \\ {\epsilon }_{{zz}_{mec}}\left(r\right)\hfill & =K_1+K_4\ln \left(r\right)\hfill \\ {\epsilon }_{{rz}_{mec}}\left(r,z\right)\hfill & =\frac{K_2+K_{4}z}{2r}\hfill \end{array}\right.(14)$

and last to the formal expressions of the stresses tensor $\left[\mathit{\sigma }\right]$ components (σ_rθ = σ_θz = 0):

$\left\{\begin{array}{cc}{\sigma }_{rr}\left(r\right)\hfill & =\left(\mathrm{\lambda }+\mu \right)\left(L_1+L_2\right)+\mathrm{\lambda }{K}_1-\frac{\mu \left(L_1-L_2\right)}{r^2}-\frac{\mu K_4}{2\left(\mathrm{\lambda }+2\mu \right)}\left[\mathrm{\lambda }+\mu \left(1+2\ln \left(r\right)\right)\right]\hfill \\ {\sigma }_{\theta \theta }\left(r\right)\hfill & =\left(\mathrm{\lambda }+\mu \right)\left(L_1+L_2\right)+\mathrm{\lambda }{K}_1+\frac{\mu \left(L_1-L_2\right)}{r^2}+\frac{\mu K_4}{2\left(\mathrm{\lambda }+2\mu \right)}\left[\mathrm{\lambda }+\mu \left(1-2\ln \left(r\right)\right)\right]\hfill \\ {\sigma }_{zz}\left(r\right)\hfill & =\mathrm{\lambda }\left(L_1+L_2\right)+\left(\mathrm{\lambda }+2\mu \right)K_1+\frac{\mu \left(3\mathrm{\lambda }+4\mu \right)K_4\ln \left(r\right)}{\mathrm{\lambda }+2\mu }\hfill \\ {\sigma }_{rz}\left(r,z\right)\hfill & =\frac{\mu \left(K_2+K_{4}z\right)}{r}\hfill \end{array}\right.(15)$

3.1.5 Boundary Conditions–First Order Linearized Solution

Boundary conditions are as follows:

1. no shear stress is applied on the outer pipe surface:

$\forall z\in \mathbb{R}:{\sigma }_{rz}\left(r_{ext}\left(T\right),z\right)=0(16)$

2. both mechanical w_σ and thermal w_T longitudinal displacements are arbitrary equal to zero at z = 0 on the pipe outer surface:

$\begin{array}{cc}\hfill \forall T\ge 0:\hfill & \hfill \left\{\begin{array}{c}{w}_{\sigma }\left(r_{ext}\left(T\right),0\right)=0\hfill \\ w_T\left(r_{ext}\left(T\right),0,T\right)=0\hfill \end{array}\right.\hfill \end{array}(17)$

3. the hydrostatic pressure P_int is applied on the pipe inner surface:

${\sigma }_{rr}\left(r_{int}\left(T\right)\right)=-P_{int}(18)$

4. the hydrostatic pressure P_ext is applied on the pipe outer surface:

${\sigma }_{rr}\left(r_{ext}\left(T\right)\right)=-P_{ext}(19)$

5. the longitudinal stress σ_zz acting on the pipe cross-section results in the longitudinal force $\vec{F}$ (see Figure 1):

$\frac{1}{r_{ext}\left(T\right)-r_{int}\left(T\right)}{\int }_{r_{int}\left(T\right)}^{r_{ext}\left(T\right)}{\sigma }_{zz}\left(r\right)dr=\frac{F}{\pi \left(r_{ext}^2\left(T\right)-r_{int}^2\left(T\right)\right)}(20)$

6. the initial inner radius $r_{0_{int}}$ is subject to a radial displacement $u\left({r_0}_{int},T\right)$:

$r_{int}\left(T\right)=r_{0_{int}}+u\left(r_{0_{int}},T\right)\left({\mathit{r}}_{int}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}\right)(21)$

7. the initial outer radius $r_{0_{ext}}$ is subject to a radial displacement $u\left(r_{0_{ext}},T\right)$:

$r_{ext}\left(T\right)=r_{0_{ext}}+u\left(r_{0_{ext}},T\right)\left({\mathit{r}}_{\mathit{ext}}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}\right)(22)$

3.1.5.1 First Four Integration Coefficients

The resolution of boundary conditions Eqs. 16, 17 first leads to:

$\mathrm{fi}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{e}\mathrm{ffi}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}:K_0=K_2=K_3=K_4=0(23)$

and to the expression of the mechanical ${\vec{u}}_{\sigma }$ and thermal ${\vec{u}}_T$ displacements:

$\left\{\begin{array}{cc}{u}_{\sigma }\left(r\right)\hfill & =\frac{L_1+L_2}{2}r+\frac{L_1-L_2}{2r}\hfill \\ v_{\sigma }\hfill & =0\hfill \\ w_{\sigma }\left(z\right)\hfill & =K_{1}z\hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}\left\{\begin{array}{cc}{u}_T\left(r,T\right)\hfill & =\alpha r\left(T-T_0\right)\hfill \\ v_T\hfill & =0\hfill \\ w_T\left(z,T\right)\hfill & =\alpha z\left(T-T_0\right)\hfill \end{array}\right.(24)$

for the mechanical ${\left[\mathit{\epsilon }\right]}_{mec}$ and thermal ${\left[\mathit{\epsilon }\right]}_{th}$ diagonal strains tensors (no shear strain):

$\left\{\begin{array}{cc}{\epsilon }_{{rr}_{mec}}\left(r\right)\hfill & =\frac{L_1+L_2}{2}-\frac{L_1-L_2}{2r^2}\hfill \\ {\epsilon }_{{\theta \theta }_{mec}}\left(r\right)\hfill & =\frac{L_1+L_2}{2}+\frac{L_1-L_2}{2r^2}\hfill \\ {\epsilon }_{{zz}_{mec}}\hfill & =K_1\hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}\left\{\begin{array}{cc}{\epsilon }_{{rr}_{th}}\hfill & =\alpha \hfill \\ {\epsilon }_{{\theta \theta }_{th}}\hfill & =\alpha \hfill \\ {\epsilon }_{{zz}_{th}}\hfill & =\alpha \hfill \end{array}\right.(25)$

and for the diagonal stresses tensor $\left[\mathit{\sigma }\right]$ (no shear stress):

$\left\{\begin{array}{cc}{\sigma }_{rr}\left(r\right)\hfill & =\left(\mathrm{\lambda }+\mu \right)\left(L_1+L_2\right)+\mathrm{\lambda }{K}_1-\mu \frac{L_1-L_2}{r^2}\hfill \\ {\sigma }_{\theta \theta }\left(r\right)\hfill & =\left(\mathrm{\lambda }+\mu \right)\left(L_1+L_2\right)+\mathrm{\lambda }{K}_1+\mu \frac{L_1-L_2}{r^2}\hfill \\ {\sigma }_{zz}\hfill & =\mathrm{\lambda }\left(L_1+L_2\right)+\left(\mathrm{\lambda }+2\mu \right)K_1\hfill \end{array}\right.(26)$

In particular, these first intermediate integration coefficients do not depend on the pressure states, nor the longitudinal force applied on the pipe, and the expressions given by equations sets Eqs. 24–26 are exact (with respect to the assumptions from the previous paragraphs, at thermomechanical equilibrium).

But the last three integration coefficients K₁, L₁ and L₂ do depend on the pressure states and the longitudinal force, and at a lesser extent on temperature. It is necessary to take it into account later on for transducers measurements, which are always relative to an initial reference state.

3.1.5.2 Last Three Integration Coefficients–First Order Approximation

Unfortunately, the last boundary conditions do not admit any formal solution for $\left\{K_1,L_1,L_2\right\}$, thus linearization of boundary conditions Eqs. 21, 22 is mandatory. There are several degrees of freedom, but one of the most accurate is to take into account the thermal expansion phenomenon at this early stage:

$\mathrm{fi}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}:\left\{\begin{array}{c}{r}_{int}\left(T\right)\leftarrow {r_0}_{int}\left[1+\alpha \left(T-T_0\right)\right]\hfill \\ r_{ext}\left(T\right)\leftarrow {r_0}_{ext}\left[1+\alpha \left(T-T_0\right)\right]\hfill \end{array}\right.(27)$

Boundary conditions Eqs. 18–20, combined with first order approximations Eq. 27 of r_int and r_ext, then lead to the set of first order linearized solutions for the last three integration coefficients (E is the Young’s modulus, and ν the Poisson’s ratio):

$\left\{\begin{array}{cc}{K}_1\hfill & \simeq \frac{2\nu }{E}\frac{P_{ext}{r}_{0ext}^2-P_{int}{r}_{0int}^2}{r_{0ext}^2-r_{0int}^2}+\frac{1}{E}\frac{F}{\pi \left(r_{0ext}^2-r_{0int}^2\right)}\hfill \\ \frac{L_1+L_2}{2}\hfill & \simeq -\frac{\left(1-\nu \right)}{E}\frac{P_{ext}{r}_{0ext}^2-P_{int}{r}_{0int}^2}{r_{0ext}^2-r_{0int}^2}-\frac{\nu }{E}\frac{F}{\pi \left(r_{0ext}^2-r_{0int}^2\right)}\hfill \\ \frac{L_1-L_2}{2}\hfill & \simeq -\frac{\left(1+\nu \right)}{E}\frac{\left(P_{ext}-P_{int}\right)r_{0int}^2{r}_{0ext}^2{\left[1+\alpha \left(T-T_0\right)\right]}^2}{r_{0ext}^2-r_{0int}^2}\hfill \end{array}\right.(28)$

The set of solutions Eq. 28 can be used with equations sets Eqs. 24–26 to get a first valid approximation of displacements, strains and stresses tensors components anywhere in the pipe wall.

This model is valid for all dimensions of pipes and not limited to thin-shells, and brings essentially the additional information of temperature dependency (Timoshenko and Goodier (1970)), and later on, for the closed pipe with the longitudinal force $\vec{F}$ parameter, the formal solution for the temperature self-compensated pressure variation measurement (Section 4.1.3.2).

Also, the model accuracy improvement, based on a step by step correction of the current radiuses r_int and r_ext, is more easily taken into account, with better results with temperature (Section 3.2).

3.2 Formal Model Accuracy Improvement–Iterative Algorithm

The model accuracy for the desired parameter is evaluated by comparison of its exact solution computed numerically by solving (Marquardt (1963)) the non linear set of boundary equations (Section 3.1.5) leading to the exact values for the set of integration coefficients $\left\{K_1,L_1,L_2\right\}$, and their formal approximation starting with their first order, linearized solution (Section 3.1.5.2).

Then, the improvement of this first order formal model is based on an iterative algorithm, leading to more and more accurate formal approximations for the exact values of the coefficients $\left\{K_1,L_1,L_2\right\}$, which can be then applied to any of the solutions in terms of displacements Eq. 24, strains Eq. 25 or stresses Eq. 26.

This algorithm simply relies on a step by step improvement of the current inner r_int and current outer r_ext radiuses approximation Eq. 27.

3.2.1 Iterative Improvement of the Formal Model Applied to the Internal Pressure P_int

The iterative procedure to correct the bias of the first order formal solution is described as follows:

1. initialization of radiuses ${\left(r_{0_{int}}\right)}_{\left(0\right)}$ and ${\left(r_{0_{ext}}\right)}_{\left(0\right)}$ with their known values $r_{0_{int}}$ and $r_{0_{ext}}$ corresponding to the pipe reference state:

$\left\{\begin{array}{c}{\left(r_{0_{int}}\right)}_{\left(0\right)}\leftarrow r_{0_{int}}\hfill \\ {\left(r_{0_{ext}}\right)}_{\left(0\right)}\leftarrow r_{0_{ext}}\hfill \end{array}\right.(29)$

2.compute the integration coefficients ${\left\{K_1,L_1,L_2\right\}}_{\left(0\right)}$ according to Eq. 28,

3.compute the internal pressure ${\left(P_{int}\right)}_{\left(0\right)}$ according to Eqs. 18, 26 or even Eqs. 35, 57 in case of surface strains measurements,

4.for each step i ≥ 0:

  a. correct the radiuses approximations ${\left(r_{0_{int}}\right)}_{\left(i\right)}$ and ${\left(r_{0_{ext}}\right)}_{\left(i\right)}$ for the next iteration i + 1 with the improvement of their radial displacement u provided by Eq. 24:

$\left\{\begin{array}{c}{\left(r_{0_{int}}\right)}_{\left(i+1\right)}\leftarrow r_{0_{int}}+u_{{\left\{K_1,L_1,L_2\right\}}_{\left(i\right)}}\left(r_{0_{int}},{\left(\mathrm{\Delta }T\right)}_{\left(i\right)}\right)\hfill \\ {\left(r_{0_{ext}}\right)}_{\left(i+1\right)}\leftarrow r_{0_{ext}}+u_{{\left\{K_1,L_1,L_2\right\}}_{\left(i\right)}}\left(r_{0_{ext}},{\left(\mathrm{\Delta }T\right)}_{\left(i\right)}\right)\hfill \end{array}\right.(30)$

value for ${\left(\mathrm{\Delta }T\right)}_{\left(i\right)}$ can be provided by an additional temperature sensor², or by the transducers themselves³,b. compute the integration coefficients {K₁, L₁, L₂}_(i+1) according to Eq. 28,c. compute the internal pressure (P_int)_(i+1) according to Eqs. 18, 26, or even Eqs. 35, 57 in case of surface strains measurements,d. repeat every step from item 4a until the convergence criterion Eq. 31 is satisfied:

$\sqrt{{\left[{\left(r_{0_{int}}\right)}_{\left(i+1\right)}-{\left(r_{0_{int}}\right)}_{\left(i\right)}\right]}^2+{\left[{\left(r_{0_{ext}}\right)}_{\left(i+1\right)}-{\left(r_{0_{ext}}\right)}_{\left(i\right)}\right]}^2}\le ϵ(31)$

where ϵ is an arbitrary small positive number, for instance: $ϵ=\frac{r_{0_{ext}}-r_{0_{int}}}{k}$, and k an arbitrary strictly positive number, for instance: k = 10⁶,

5. the desired internal pressure P_int value is the last computed iterative ${\left(P_{int}\right)}_{\left(i+1\right)}$ value.

This algorithm can be applied similarly for the computation of any other parameter like the strains or stresses tensors components in the pipe wall, but also for the variations of such components between two thermomechanical states of the pipe (Section 4).

However in this latter case, the procedure has to be adapted to take into account the variations of each component between the two thermomechanical states.

3.2.2 Accuracy of the Formal Model for Internal Pressure P_int Measurement

The accuracy of the formal model is illustrated hereafter for the internal pressure measurement P_int between 0 bar and 150 bar and between 0°C and 320°C, according to boundary condition Eq. 18.

The relative errors of the iterative model are presented for Ø 2″ NPS Sch. 80 and Ø 4” NPS Sch. 160 steel pipes, and are computed as follows:

$\text{formal\hspace{0.17em}model\hspace{0.17em}error}=\frac{\text{value\hspace{0.17em}from\hspace{0.17em}formal\hspace{0.17em}iterative\hspace{0.17em}model}-\text{exact\hspace{0.17em}numerical\hspace{0.17em}value}}{\text{exact\hspace{0.17em}numerical\hspace{0.17em}value}}(32)$

The results, illustrated in Figure 2 for these two steel pipes with transducers in hoop & longitudinal configurations, show that the maximum relative error is observed for the first order linearized solution (computed with integration coefficients Eq. 28), at the maximum pressure (150 bar) and temperature (320°C):

• for the Ø 2″ NPS Sch. 80 steel pipe, the model accuracy is better than 0.147%,

• for the Ø 4” NPS Sch. 160 steel pipe, the model accuracy is better than 0.109%.

FIGURE 2

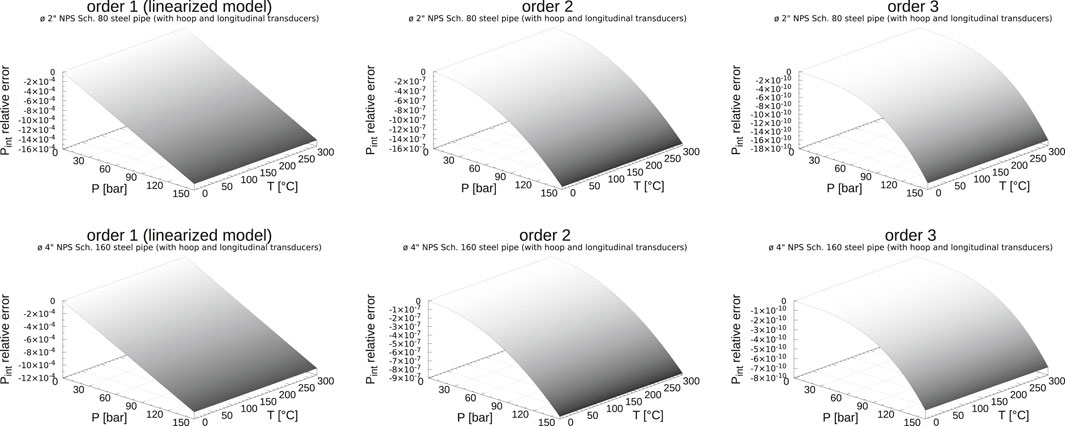
FIGURE 2. Iterative model relative error for P_int, from initialization (linear approximation–order 1) to iteration 2 (order 3) (P_ref = 0 bar and T_ref = 0°C)—First row: Ø 2″ NPS Sch. 80 steel pipe–Second row: Ø 4” NPS Sch. 160 steel pipe.

The accuracy of this algorithm, which corrects at each iteration the current pipe inner and outer radiuses approximations (Eq. 27), and therefore the radial forces resulting from the inner and outer hydrostatic pressures, is typically improved by three orders of magnitude from one iteration to another (Figure 2).

However, the first order linearized solution, with integration coefficients (Eq. 28), is accurate enough for most applications (i.e.: metallic pipes), but this iterative algorithm will be particularly useful for highly deformable structures (e.g.: Composite Overwrapped Pressure Vessels (Maurin et al. (2014))).

The other main advantages of the iterative algorithm is its simplicity (well suited to lightweight implementations) and its very fast convergence (a few iterations are enough).

4 Application to Non-intrusive Pressure Variation Measurements

The first step is to establish the relationships between two different thermomechanical states of the pipe, and their respective boundary conditions.

The second step is to connect these relationships to the raw measurements performed by the transducers.

4.1 Recipe for Pressure Variation Measurement

The recipe for pressure variation measurement is to make use of the set of linearized solutions (Section 3.1.5.2) between two thermomechanical states, considering that:

1. the reference measurement is performed at known temperature T₀, hydrostatic pressures P_int and P_ext, and longitudinal force $\vec{F}$:

• this measurement is associated to the first set of coefficients $\left\{K_{1_{ref}},L_{1_{ref}},L_{2_{ref}}\right\}$,

2. the current measurement is performed at unknown temperature T₀ + ΔT, hydrostatic pressures P_int + ΔP_int and P_ext + ΔP_ext, and longitudinal force $\vec{F}+\mathrm{\Delta }\vec{F}$:

• this measurement is associated to the second set of coefficients $\left\{K_{1_{\mathrm{\Delta }}},L_{1_{\mathrm{\Delta }}},L_{2_{\mathrm{\Delta }}}\right\}$.

These two sets of coefficients, $\left\{K_{1_{ref}},L_{1_{ref}},L_{2_{ref}}\right\}$ and $\left\{K_{1_{\mathrm{\Delta }}},L_{1_{\mathrm{\Delta }}},L_{2_{\mathrm{\Delta }}}\right\}$, are in direct relationship with the variations of the boundary conditions ΔT, ΔP_int, ΔP_ext and $\mathrm{\Delta }\vec{F}$, and must be used with the correct formulae describing the physical parameter measured by each transducer.

For FBG transducers, this physical parameter is the mechanical strain, therefore these constants must be used with the expression of the strains tensor described by equations set Eq. 25.

4.1.1 Pressure Variation Measurement Expressed in Terms of Strains

The resolution of the two sets of boundary conditions is a three steps process:

1. the relationship between the absolute strains measurement ɛ (formulae established so far) and the relative strains measurement Δɛ (performed by the transducers between two different thermomechanical states) is first described:

$\begin{array}{cc}\hfill {\left.\mathrm{\Delta }\epsilon \right|}_{\begin{array}{c}{P}_{int}\to P_{int}+{\mathrm{\Delta }P}_{int}\\ T_0\to T_0+\mathrm{\Delta }T\end{array}}\hfill & \hfill ={\left.\mathrm{\Delta }\epsilon \right|}_{\begin{array}{c}0\to P_{int}+{\mathrm{\Delta }P}_{int}\\ T\to T_0+\mathrm{\Delta }T\end{array}}-{\left.\mathrm{\Delta }\epsilon \right|}_{\begin{array}{c}0\to P_{int}\\ T\to T_0\end{array}}\hfill \\ \hfill \hfill & \hfill ={\left.\epsilon \right|}_{\begin{array}{c}{P}_{int}+{\mathrm{\Delta }P}_{int}\\ T_0+\mathrm{\Delta }T\end{array}}-{\left.\epsilon \right|}_{\begin{array}{c}{P}_{int}\\ T_0\end{array}}\hfill \end{array}(33)$

2. then, the difference (Eq. 33) is expressed according to the relative hoop Δɛ_θθ and longitudinal Δɛ_zz strains measurements given by the transducers attached to the pipe external surface (at radius r_ext):

$\left\{\begin{array}{c}{\left.\mathrm{\Delta }{\epsilon }_{\theta \theta }\left(r_{ext}\right)\right|}_{\begin{array}{c}{P}_{int}\to P_{int}+{\mathrm{\Delta }P}_{int}\\ T_0\to T_0+\mathrm{\Delta }T\end{array}}={\left.{\epsilon }_{\theta \theta }\left(r_{ext}\right)\right|}_{\begin{array}{c}{P}_{int}+{\mathrm{\Delta }P}_{int}\\ T_0+\mathrm{\Delta }T\end{array}}-{\left.{\epsilon }_{\theta \theta }\left(r_{ext}\right)\right|}_{\begin{array}{c}{P}_{int}\\ T_0\end{array}}\hfill \\ {\left.\mathrm{\Delta }{\epsilon }_{zz}\left(r_{ext}\right)\right|}_{\begin{array}{c}{P}_{int}\to P_{int}+{\mathrm{\Delta }P}_{int}\\ T_0\to T_0+\mathrm{\Delta }T\end{array}}={\left.{\epsilon }_{zz}\left(r_{ext}\right)\right|}_{\begin{array}{c}{P}_{int}+{\mathrm{\Delta }P}_{int}\\ T_0+\mathrm{\Delta }T\end{array}}-{\left.{\epsilon }_{zz}\left(r_{ext}\right)\right|}_{\begin{array}{c}{P}_{int}\\ T_0\end{array}}\hfill \end{array}\right.(34)$

3. last, the set of Eq. 34 is solved in terms of ΔP_int and ΔF:

$\left\{\begin{array}{cc}{\mathrm{\Delta }P}_{int}\hfill & =\frac{E\left(r_{0_{ext}}^2-r_{0_{int}}^2\right)\left({\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}+\nu {\mathrm{\Delta }\epsilon }_{{zz}_{mec}}\right)}{2\left(1-{\nu }^2\right)r_{0_{int}}^2}+\frac{\left[\left(1-2\nu \right)r_{0_{ext}}^2+r_{0_{int}}^2\right]{\mathrm{\Delta }P}_{ext}}{2\left(1-\nu \right)r_{0_{int}}^2}\hfill \\ \mathrm{\Delta }F\hfill & =\frac{E\pi \left(r_{0_{ext}}^2-r_{0_{int}}^2\right)\left(\nu {\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}+{\mathrm{\Delta }\epsilon }_{{zz}_{mec}}\right)}{1-{\nu }^2}-\frac{\nu \pi \left(r_{0_{ext}}^2-r_{0_{int}}^2\right){\mathrm{\Delta }P}_{ext}}{1-\nu }\hfill \end{array}\right.(35)$

It has to be underlined that solution Eq. 35 is valid whether the pipe is closed or not.

4.1.2 Link With the Raw Measurements–The Fiber Bragg Grating Transducer

The raw measurement performed by a transducer usually exhibits a cross-sensitivity with temperature; this is the case for the FBG which acts as a narrowband mirror filter in wavelength, with characteristic reflected first order wavelength λ_B (Martinez (1999)):

${\mathrm{\lambda }}_{\text{B}}=2n_{\text{eff}}\mathrm{\Lambda }\left\{\begin{array}{cc}{n}_{\text{eff}}\hfill & \text{the\hspace{0.17em}effective\hspace{0.17em}refractive\hspace{0.17em}index\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}optical\hspace{0.17em}waveguide}\hfill \\ \mathrm{\Lambda }\hfill & \text{the\hspace{0.17em}grating\hspace{0.17em}pitch}\hfill \end{array}\right.(36)$

which differentiates as follows:

$\frac{d{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}=\left(\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial T}+\frac{1}{\mathrm{\Lambda }}\frac{\partial \mathrm{\Lambda }}{\partial T}\right)dT+\left(\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{mec}}+\frac{1}{\mathrm{\Lambda }}\frac{\partial \mathrm{\Lambda }}{\partial {\epsilon }_{mec}}\right)d{\epsilon }_{mec}(37)$

where:

•dT is the infinitesimal temperature variation at the exact FBG location,

•dɛ_mec is the infinitesimal longitudinal mechanical strain variation at the exact FBG location,

•$\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial T}$ is the thermo-optic coefficient of the optical fiber,

•$\frac{1}{\mathrm{\Lambda }}\frac{\partial \mathrm{\Lambda }}{\partial T}$ is the thermal expansion coefficient α of the optical fiber,

•$\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{mec}}$ is the photo-elastic coefficient of the optical fiber in elongation⁴,

•$\frac{1}{\mathrm{\Lambda }}\frac{\partial \mathrm{\Lambda }}{\partial {\epsilon }_{mec}}$ is equal to 1.

It leads to Eq. 37, with coefficients values valid for a germanosilicate optical fiber⁵:

$\frac{d{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}=\underset{\begin{array}{c}\text{depends\hspace{0.17em}on}\\ \text{temperature}\end{array}}{\underbrace{\stackrel{{\kappa }_{T_{\text{fiber}}}}{\overbrace{\left(\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial T}+\alpha \right)}}dT}}+\underset{\begin{array}{c}\text{depends\hspace{0.17em}on\hspace{0.17em}the}\\ \text{longitudinal\hspace{0.17em}mechanical}\\ \text{strain\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}optical\hspace{0.17em}fiber}\end{array}}{\underbrace{\stackrel{{\kappa }_{\epsilon }}{\overbrace{\left(\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{mec}}+1\right)}}d{\epsilon }_{mec}}}\left\{\begin{array}{cc}\alpha \hfill & \mathrm{the\; thermal\; expansion}\hfill \\ \hfill & \mathrm{coefficient\; of\; the\; optical\; fiber}\hfill \\ {\epsilon }_{mec}\hfill & \mathrm{the\; longitudinal\; mechanical}\hfill \\ \hfill & \mathrm{strain\; of\; the\; optical\; fiber}\hfill \\ \frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial T}\hfill & \simeq 6.45\times {10}^{-6}{\text{K}}^{-1}\hfill \\ \frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{mec}}\hfill & \simeq -0.22\hfill \end{array}\right.(38)$

Provided that the optical fiber is correctly attached to the structure⁶, the total (mechanical + thermal) strains variations, for both the optical fiber and the structure, are equal:

$\underset{\text{optical\hspace{0.17em}fiber}}{\underbrace{{\alpha }_{\text{fiber}}dT+d{\epsilon }_{{mec}_{\text{fiber}}}}}=\underset{\text{structure}}{\underbrace{{\alpha }_{\text{struct}}dT+d{\epsilon }_{{mec}_{\text{struct}}}}}\Rightarrow d{\epsilon }_{{mec}_{\text{fiber}}}=d{\epsilon }_{{mec}_{\text{struct}}}+\underset{\mathrm{\Delta }\alpha }{\underbrace{\left({\alpha }_{\text{struct}}-{\alpha }_{\text{fiber}}\right)}}dT(39)$

then, it is correct to rewrite Eq. 38 from the point of view of the mechanical strains of the structure:

$\frac{d{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}=\underset{\begin{array}{c}\text{depends\hspace{0.17em}on}\\ \text{temperature}\end{array}}{\underbrace{\stackrel{{\kappa }_{T_{\text{struct}}}}{\overbrace{\left({\kappa }_{T_{\text{fiber}}}+{\kappa }_{\epsilon }\mathrm{\Delta }\alpha \right)}}dT}}+\underset{\begin{array}{c}\text{depends\hspace{0.17em}on\hspace{0.17em}the}\\ \text{mechanical\hspace{0.17em}strain\hspace{0.17em}of\hspace{0.17em}the}\\ \text{structure\hspace{0.17em}according\hspace{0.17em}to\hspace{0.17em}the}\\ \text{orientation\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}optical\hspace{0.17em}fiber}\end{array}}{\underbrace{\stackrel{{\kappa }_{\epsilon }}{\overbrace{\left(\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{mec}}+1\right)}}d{\epsilon }_{mec}}}\left\{\begin{array}{cc}\hfill \mathrm{\Delta }\alpha \hfill & \hfill \mathrm{the\; difference\; between\; the}\hfill \\ \hfill \hfill & \hfill \mathrm{structure\; and\; the\; optical\; fiber}\hfill \\ \hfill \hfill & \hfill \mathrm{thermal\; expansion\; coefficients}\hfill \\ \hfill {\epsilon }_{mec}\hfill & \hfill \mathrm{the\; mechanical\; strain\; component}\hfill \\ \hfill \hfill & \hfill \mathrm{of\; the\; structure\; in\; the\; orientation}\hfill \\ \hfill \hfill & \hfill \mathrm{of\; the\; FBG\; transducer}\hfill \end{array}\right.(40)$

with an apparent FBG temperature sensitivity ${\kappa }_{T_{\text{struct}}}$, once attached to the structure, such as:

${\kappa }_{T_{\text{struct}}}={\kappa }_{T_{\text{fiber}}}+{\kappa }_{\epsilon }\mathrm{\Delta }\alpha \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{\Delta }\alpha ={\alpha }_{\text{struct}}-{\alpha }_{\text{fiber}}(41)$

According to these expressions (depending on whether it has to deal with the mechanical strain of the optical fiber or the structure), the Bragg relationship dedicated to temperature and strain measurements can be written, after integration and with the hypothesis of κ_ɛ and κ_T constant sensitivities:

$\ln \left(1+\frac{\mathrm{\Delta }{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}\right)={\kappa }_T\mathrm{\Delta }T+{\kappa }_{\epsilon }{\mathrm{\Delta }\epsilon }_{mec}\iff {\mathrm{\Delta }\epsilon }_{mec}=\frac{1}{{\kappa }_{\epsilon }}\left[\ln \left(1+\frac{\mathrm{\Delta }{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}\right)-{\kappa }_T\mathrm{\Delta }T\right](42)$

which is rewritten as follows:

$\begin{array}{cc}\hfill {\mathrm{\Delta }\epsilon }_{mec}=\frac{1}{{\kappa }_{\epsilon }}\left(\underline{\mathrm{\Delta }}\mathrm{\Psi }-{\kappa }_T\mathrm{\Delta }T\right)\hfill & \hfill \left\{\begin{array}{cc}\hfill {\kappa }_T\mathrm{a}\mathrm{n}\mathrm{d}{\kappa }_{\epsilon }\hfill & \hfill \mathrm{sensitivity\; coefficients}\hfill \\ \hfill {\mathrm{\Delta }\epsilon }_{mec}\hfill & \hfill \mathrm{the\; variation\; of\; longitudinal\; mechanical\; strain}\hfill \\ \hfill \underline{\mathrm{\Delta }}\mathrm{\Psi }\hfill & \hfill \mathrm{the\; transducer\; true\; relative\; variation\; measurement}\hfill \end{array}\right.\hfill \end{array}(43)$

with a true relative variation measurement $\underline{\mathrm{\Delta }}\mathrm{\Psi }$ for the FBG transducer, expressed in terms of its raw measurement λ_B:

$\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{F}\mathrm{B}\mathrm{G}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{e}\mathrm{r}:\underline{\mathrm{\Delta }}\mathrm{\Psi }=\ln \left(1+\frac{\mathrm{\Delta }{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}\right)˜0\frac{\mathrm{\Delta }{\mathrm{\lambda }}_{\text{B}}}{{\mathrm{\lambda }}_{\text{B}}}(44)$

and a mechanical strain Δɛ_mec such as:

${\mathrm{\Delta }\epsilon }_{\text{mec}}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{f}\left\{\begin{array}{cc}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{fi}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\hfill & {\kappa }_T={\kappa }_{T_{\text{fiber}}}\hfill \\ \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{f}\hfill & {\kappa }_T={\kappa }_{T_{\text{struct}}}\hfill \end{array}\right.(45)$

The notation $\underline{\mathrm{\Delta }}\mathrm{\Psi }$ allows to get rid of the type of transducer, considering that whatever the measurement technique in use, it is usually sensitive to both the temperature and the mechanical strain.

From now on, the mechanical strain variation Δɛ_mec measured by the transducer is assumed to be the mechanical strain variation of the structure to which it is attached to, as described by Eq. 40, with sensitivities κ_T and κ_ɛ such as:

$\mathrm{once\; attached\; to\; the\; structure}:\left\{\begin{array}{ccc}\hfill {\kappa }_T\hfill & \hfill ={\kappa }_{T_{\text{fiber}}}+{\kappa }_{\epsilon }\mathrm{\Delta }\alpha \hfill & \hfill \left(\mathrm{thermal\; strain\; sensitivity}\right)\hfill \\ \hfill {\kappa }_{\epsilon }\hfill & \hfill =\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{{mec}_{\text{fiber}}}}+1\hfill & \hfill \left(\mathrm{mechanical\; strain\; sensitivity}\right)\hfill \end{array}\right.(46)$

If all transducers are similarly attached to the structure (from the thermal and mechanical points of view), it can be assumed that there is almost no dispersion between each sensitivity coefficient ${{\kappa }_T}_i$ associated to each transducer i; we can therefore legitimately consider that they are all identical:

$\forall i:{\kappa }_{T_i}={\kappa }_T\mathrm{if\; all\; transducers\; are\; attached\; the\; same\; way\; to\; the\; structure}(47)$

and it is possible to make the same assumption for all the products ${\kappa }_{{\epsilon }_i}\mathrm{\Delta }{\alpha }_i$:

$\forall i:{\kappa }_{{\epsilon }_i}\mathrm{\Delta }{\alpha }_i={\kappa }_{\epsilon }\mathrm{\Delta }\alpha \mathrm{if\; all\; transducers\; are\; attached\; the\; same\; way\; to\; the\; structure}(48)$

Thus, if two FBG transducers are respectively oriented with angles φ₁ (defining ${\vec{u}}_1$) and φ₂ (defining ${\vec{u}}_2$) (Figure 3), the longitudinal mechanical strains variations ${\mathrm{\Delta }\epsilon }_{{\vec{u}}_{1_{mec}}}$ and ${\mathrm{\Delta }\epsilon }_{{\vec{u}}_{2_{mec}}}$ are equal to⁷:

$\left\{\begin{array}{c}{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{1_{mec}}}={\cos }^2\left({\phi }_1\right){\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}+{\sin }^2\left({\phi }_1\right){\mathrm{\Delta }\epsilon }_{{zz}_{mec}}\hfill \\ {\mathrm{\Delta }\epsilon }_{{\vec{u}}_{2_{mec}}}={\cos }^2\left({\phi }_2\right){\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}+{\sin }^2\left({\phi }_2\right){\mathrm{\Delta }\epsilon }_{{zz}_{mec}}\hfill \end{array}\right.(49)$

FIGURE 3

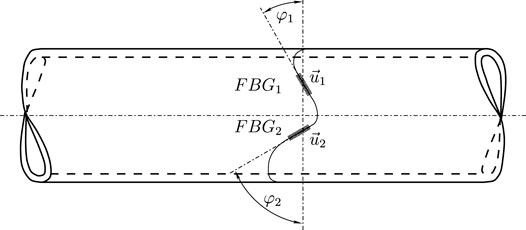
FIGURE 3. Definition of the FBG transducers angles φ₁ and φ₂ associated to vectors ${\vec{u}}_1$ and ${\vec{u}}_2$ once attached to the pipe external surface.

which leads to ${\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}$ and ${\mathrm{\Delta }\epsilon }_{{zz}_{mec}}$ expressed in terms of mechanical strain variation measurements ${\mathrm{\Delta }\epsilon }_{{\vec{u}}_{1_{mec}}}$ and ${\mathrm{\Delta }\epsilon }_{{\vec{u}}_{2_{mec}}}$:

$\left\{\begin{array}{c}{\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}=\frac{\left[1-\cos \left(2{\phi }_2\right)\right]{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{1_{mec}}}-\left[1-\cos \left(2{\phi }_1\right)\right]{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{2_{mec}}}}{\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)}\hfill \\ {\mathrm{\Delta }\epsilon }_{{zz}_{mec}}=\frac{\left[1+\cos \left(2{\phi }_1\right)\right]{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{2_{mec}}}-\left[1+\cos \left(2{\phi }_2\right)\right]{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{1_{mec}}}}{\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)}\hfill \end{array}\right.(50)$

and to their expression in terms of true relative raw transducer $\underline{\mathrm{\Delta }}\mathrm{\Psi }$ and temperature ΔT variations measurements:

$\left\{\begin{array}{c}{\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}=\frac{2}{{\kappa }_{\epsilon }}\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1{\sin }^2\left({\phi }_2\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2{\sin }^2\left({\phi }_1\right)+{\kappa }_T\mathrm{\Delta }T\left[{\sin }^2\left({\phi }_1\right)-{\sin }^2\left({\phi }_2\right)\right]}{\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)}\hfill \\ {\mathrm{\Delta }\epsilon }_{{zz}_{mec}}=\frac{2}{{\kappa }_{\epsilon }}\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2{\cos }^2\left({\phi }_1\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1{\cos }^2\left({\phi }_2\right)+{\kappa }_T\mathrm{\Delta }T\left[{\cos }^2\left({\phi }_2\right)-{\cos }^2\left({\phi }_1\right)\right]}{\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)}\hfill \end{array}\right.(51)$

and therefore to:

$\left\{\begin{array}{cc}{\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}+\nu {\mathrm{\Delta }\epsilon }_{{zz}_{mec}}=\hfill & \frac{\left(1+\nu \right)\left[\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2\cos \left(2{\phi }_1\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1\cos \left(2{\phi }_2\right)\right]-\left(1-\nu \right)\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1\right)}{{\kappa }_{\epsilon }\left[\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)\right]}\hfill \\ \hfill & -\frac{\left(1+\nu \right){\kappa }_T\mathrm{\Delta }T}{{\kappa }_{\epsilon }}\hfill \\ \nu {\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}+{\mathrm{\Delta }\epsilon }_{{zz}_{mec}}=\hfill & \frac{\left(1+\nu \right)\left[\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2\cos \left(2{\phi }_1\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1\cos \left(2{\phi }_2\right)\right]+\left(1-\nu \right)\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1\right)}{{\kappa }_{\epsilon }\left[\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)\right]}\hfill \\ \hfill & -\frac{\left(1+\nu \right){\kappa }_T\mathrm{\Delta }T}{{\kappa }_{\epsilon }}\hfill \end{array}\right.(52)$

4.1.3 Temperature Self-Compensated Pressure Variation Measurements

The temperature variation ΔT is seamlessly introduced in the previous sets of equations with the temperature transducer cross-sensitivity κ_T, thus making the use of an additional sensor unnecessary.

According to the set of Eq. 35, the only way to solve the temperature dependency is through the expression of the longitudinal force. Two cases can be distinguished:

1. if the longitudinal force variation $\mathrm{\Delta }\vec{F}$ is known (Section 4.1.3.1),

2. if the pipe is closed (Section 4.1.3.2).

In both cases, the hypotheses of identical temperature sensitivities⁸ and temperature ΔT variation must be verified.

4.1.3.1 Solution in Case of Known Longitudinal Force Variation

The second equation of set (Eq. 52) combined with the second equation of set (Eq. 35) lead to the expression of temperature ΔT variation in terms of longitudinal force ΔF and external pressure ΔP_ext variations:

$\begin{array}{cc}\hfill \mathrm{\Delta }T=\hfill & \hfill \frac{\left(1-\nu \right)\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1\right)}{{\kappa }_T\left(1+\nu \right)\left[\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)\right]}+\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2\cos \left(2{\phi }_1\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1\cos \left(2{\phi }_2\right)}{{\kappa }_T\left[\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)\right]}\hfill \\ \hfill \hfill & \hfill -\frac{{\kappa }_{\epsilon }\nu {\mathrm{\Delta }P}_{ext}}{{\kappa }_{T}E}-\frac{{\kappa }_{\epsilon }\left(1-\nu \right)\mathrm{\Delta }F}{{\kappa }_{T}E\pi \left(r_{0_{ext}}^2-r_{0_{int}}^2\right)}\hfill \end{array}(53)$

which used in combination with the first equation of set (Eq. 52) and the first equation of set Eq. 35, leads to the internal pressure variation ΔP_int:

${\mathrm{\Delta }P}_{int}=\frac{\left(r_{0_{int}}^2+r_{0_{ext}}^2\right){\mathrm{\Delta }P}_{ext}}{2r_{0_{int}}^2}+\frac{\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2\right)E\left(r_{0_{ext}}^2-r_{0_{int}}^2\right)}{{\kappa }_{\epsilon }\left(1+\nu \right)r_{0_{int}}^2\left[\cos \left(2{\phi }_1\right)-\cos \left(2{\phi }_2\right)\right]}+\frac{\mathrm{\Delta }F}{2\pi r_{0_{int}}^2}(54)$

Thus, assuming known longitudinal force ΔF and external pressure ΔP_ext variations, internal pressure ΔP_int (Eq. 54) and surface temperature ΔT (Eq. 53) variations can be obtained by means of non-intrusive measurements, without any additional extrinsic sensor to compensate for transducers temperature cross-sensitivity.

Eqs. 53 and 54 are valid whether the pipe is closed or not. However, the value of the longitudinal force variation ΔF is very often not known. Moreover, if the pipe is closed, its internal pressure also acts as a longitudinal force (Section 4.1.3.2).

4.1.3.2 Solution for the Closed Pipe

If the pipe is closed, which is the majority of field cases⁹, the longitudinal force variation ΔF is expressed as follows¹⁰:

$\mathrm{\Delta }F=\underset{\begin{array}{c}\text{variation\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}longitudinal\hspace{0.17em}force\hspace{0.17em}due\hspace{0.17em}to}\\ \mathrm{hydrostatic\; pressures}\mathrm{\Delta }{P}_{int}and\mathrm{\Delta }{P}_{ext}\mathrm{variations}\end{array}}{\underbrace{\pi \left(r_{int}^2\mathrm{\Delta }{P}_{int}-r_{ext}^2\mathrm{\Delta }{P}_{ext}\right)}}+\delta F\delta F\mathrm{is\; the\; unexplained\; residual\; longitudinal\; force}(55)$

approximated by:

$\mathrm{\Delta }F\simeq \pi \left(r_{0_{int}}^2\mathrm{\Delta }{P}_{int}-r_{0_{ext}}^2\mathrm{\Delta }{P}_{ext}\right)+\delta F(56)$

and used in combination with Eqs. 53, 54, gives the first order linearized expression of the internal pressure ΔP_int and surface temperature ΔT variations for the closed pipe:

$\left\{\begin{array}{cc}\mathrm{\Delta }{P}_{int}=\hfill & \mathrm{\Delta }{P}_{ext}+\frac{r_{0_{ext}}^{2}E\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2\right)}{{\kappa }_{\epsilon }\left(1+\nu \right)\left[{\cos }^2\left({\phi }_1\right)-{\cos }^2\left({\phi }_2\right)\right]}\left(\frac{1}{r_{0_{int}}^2}-\frac{1}{r_{0_{ext}}^2}\right)+\frac{\delta F}{\pi r_{0_{int}}^2}\hfill \\ \mathrm{\Delta }T=\hfill & \frac{1}{{\kappa }_T}\left[\frac{1-2\nu }{1+\nu }\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2}{{\cos }^2\left({\phi }_2\right)-{\cos }^2\left({\phi }_1\right)}+\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_1{\cos }^2\left({\phi }_2\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_2{\cos }^2\left({\phi }_1\right)}{{\cos }^2\left({\phi }_2\right)-{\cos }^2\left({\phi }_1\right)}\right.\hfill \\ \hfill & \left.+\frac{{\kappa }_{\epsilon }\left(1-2\nu \right)}{E}\mathrm{\Delta }{P}_{ext}-\frac{1}{\pi E}\frac{2{\kappa }_{\epsilon }\left(1-\nu \right)}{r_{0_{ext}}^2-r_{0_{int}}^2}\delta F\right]\hfill \end{array}\right.(57)$

4.1.3.2.1 Properties of This Non-intrusive Pressure ΔP_int Variation Measurement

Equations set (Eq. 57) first demonstrates, as already suggested in Section 2, that only one pair of transducers is necessary for the non-intrusive pressure ΔP_int and surface temperature ΔT variations measurement¹¹, with orientation angles φ₁ and φ₂ such as:

$\left|{\phi }_1\right|\ne \left|{\phi }_2\right|\mathrm{mod}\pi (58)$

with the maximum sensitivity for pressure measurement obtained for:

$\left\{\begin{array}{cc}{\phi }_1=0\hfill & \mathrm{mod}\pi \hfill \\ {\phi }_2=\pi /2\hfill & \mathrm{mod}\pi \hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}\left\{\begin{array}{cc}{\phi }_1=\pi /2\hfill & \mathrm{mod}\pi \hfill \\ {\phi }_2=0\hfill & \mathrm{mod}\pi \hfill \end{array}\right.(59)$

The temperature compensation process for purely mechanical measurement is straightforward, by simple subtraction of two true relative variation of raw transducers measurements.

This also implies that any additional physical phenomenon which has the same effect on the raw measurement performed by each transducer can be expected to be optimally mitigated (e.g.: nuclear radiations on Bragg wavelengths) by the same compensation process.

In this case, the effects of additional physical phenomena are combined to those of temperature. Then, the second equation of set Eq. 56 has to be interpreted in terms of “combined additional effects other than purely mechanical”, with a specific global sensitivity (a priori different from κ_T used until now for temperature only) depending on the instantaneous relative ratios and intensities of any of these additional phenomena.

4.1.3.2.2 Comments on a Possible Thermal Dependency of the Non-intrusive Pressure ΔP_int Variation Measurement

First equation of set Eq. 57 also demonstrates that this pressure measurement does not depend on the pipe, nor the transducer thermal properties anymore: it is therefore independent from any external temperature variation influence (provided that all the underlying hypotheses are fulfilled, especially in terms of identical thermal sensitivities ${\kappa }_{T_i}$ and products of sensitivities ${\kappa }_{{\epsilon }_i}\mathrm{\Delta }{\alpha }_i$ for all transducers–Eqs. 47 and 48).

This is all the more true since the surface temperature (where the transducers are located), in applications with metallic pipes, is mainly weighted by the thermal effusivity a of the structure, defined as follows:

$\mathrm{thermal\; effusivity}:a=\sqrt{k\rho C_p}\left\{\begin{array}{cc}k\hfill & \mathrm{the\; thermal\; conductivity}\hfill \\ \rho \hfill & \mathrm{the\; volume\; mass}\hfill \\ C_p\hfill & \mathrm{the\; mass\; heat\; capacity}\hfill \end{array}\right.(60)$

As a reminder, at thermal equilibrium, two semi-infinite media in flat contact have the temperature $T_{\left(1|2\right)}$ of their interface equal to the arithmetic mean of their respective temperatures T₁ and T₂, weighted by their thermal effusivities a₁ and a₂:

$\mathrm{contact\; temperature\; at\; thermal\; equilibrium}:T_{\left(1|2\right)}=\frac{a_1{T}_1+a_2{T}_2}{a_1+a_2}(61)$

In other words, and according to Table 1, if the transducers are attached to the external surface of a stainless steel 310 pipe surrounded by air or water, its contact temperature $T_{\left(1|2\right)}$ with the surrounding medium is mainly controlled by the pipe temperature, since its thermal effusivity is three orders of magnitude greater than the surrounding medium effusivity in case of air, and four times greater in case of water. Thus, whatever the evolution of the temperature (in any case, limited in range) of the medium surrounding the pipe, it has a little influence on this non-intrusive measurement since temperature discrepancies between two transducers are kept very small, even if the cylindrical symmetry hypothesis for temperature is broken.

TABLE 1

TABLE 1. Thermal effusivities at 25 °C and 1 bar calculated from physical properties (for air, water and stainless steel 310—from Rumble (2021)).

4.1.3.2.3 Comments on the Associated Surface Temperature ΔT Variation Measurement

The associated pipe surface temperature ΔT variation measurement described by Eq. 57 corresponds in fact to the contact temperature $\mathrm{\Delta }{T}_{\left(1|2\right)}$ between the pipe and its surrounding medium, defined at thermal equilibrium by Eq. 61.

In order to get a more accurate pipe wall temperature ΔT_wall variation (especially if the surrounding medium is water), Eq. 61 has to be solved, which leads to:

$\mathrm{\Delta }{T}_{\text{wall}}=\mathrm{\Delta }T+\underset{\begin{array}{c}\mathrm{temperature\; correction}\\ \mathrm{for\; pipe\; wall}\end{array}}{\underbrace{\frac{a_{\text{ext}}}{a_{\text{wall}}}\left(\mathrm{\Delta }T-\mathrm{\Delta }{T}_{\text{ext}}\right)}}\left\{\begin{array}{cc}\mathrm{\Delta }T\hfill & \mathrm{the\; contact\; temperature\; change}\mathbf{(Eq.\; 57)}\hfill \\ \mathrm{\Delta }{T}_{\text{wall}}\hfill & \mathrm{the\; pipe\; wall\; temperature\; change\; on\; the\; outer\; surface}\hfill \\ \mathrm{\Delta }{T}_{\text{ext}}\hfill & \mathrm{the\; external\; medium\; temperature\; change}\hfill \\ a_{\text{wall}}\hfill & \mathrm{the\; pipe\; thermal\; effusivity}\hfill \\ a_{\text{ext}}\hfill & \mathrm{the\; external\; medium\; thermal\; effusivity}\hfill \end{array}\right.(62)$

but this requires the additional temperature ΔT_ext variation measurement of the surrounding medium.

Thermal effusivities ratios given in Table 2 confirm that the temperature correction introduced by Eq. 62 will actually remain small in most cases.

TABLE 2

TABLE 2. Thermal effusivities ratios relative to stainless steel 310 (for air and water).

4.2 Pressure Variation Measurements Free From Pipe Bending

The model established so far relies on the hypothesis of an infinitely long and straight pipe (Section 3.1). However on field, the pipe is submitted to many different external forces which may lead to bending, thus potentially introducing significant measurement biases.

But it is still possible to cope such biases while using the same formal model dedicated to straight pipes if some hypotheses are fulfilled.

4.2.1 Mechanical Strains due to Bending

The mechanical strains in the bended pipe can be described by Figure 4. The associated coordinate system is the Cartesian coordinate system $\left(O,x,y,z\right)$; the osculating plane is defined by $\left(O,x,z\right)$, with x axis oriented towards the curvature center ${\mathcal{C}}_R$ corresponding to the current local curvature radius R (Figure 4).

FIGURE 4

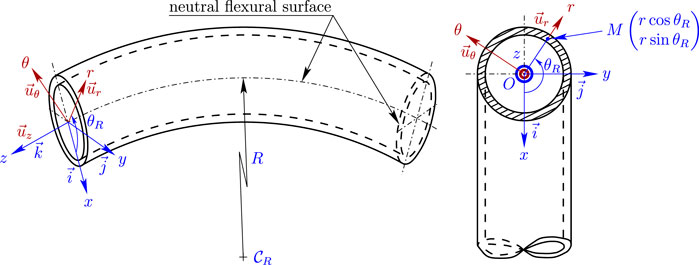
FIGURE 4. Bended pipe–Relationship between the local Cartesian coordinate system $\left(O,x,y,z\right)$ used to describe the bending model, and the cylindrical coordinate system $\left(O,r,\theta ,z\right)$ used so far to establish the formal model for the infinitely long and straight pipe under hydrostatic pressure.

Without any other longitudinal force than those applied by the internal and external hydrostatic pressures (Eq. 55 for the closed pipe), the neutral flexural surface is located exactly at half height of the pipe. When the longitudinal force variation is not null $(\mathrm{\Delta }\vec{F}\ne \vec{0})$, the mechanical balance leads to:

$\mathrm{\Delta }\vec{F}={\iint }_{\mathcal{S}}\mathrm{\Delta }{\sigma }_{{zz}_{\text{bending}}}d\vec{\mathcal{S}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\left\{\begin{array}{cc}\hfill \mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{\text{bending}}}}\hfill & \hfill =\frac{x_0-x}{R}-\frac{x_{0_{ref}}-x}{R_{ref}}\hfill \\ \hfill x_0\hfill & \hfill \mathrm{the\; current\; position\; of\; the\; neutral\; flexural\; surface}\hfill \\ \hfill x_{0_{ref}}\hfill & \hfill \mathrm{the\; initial\; position\; of\; the\; neutral\; flexural\; surface}\hfill \\ \hfill \mathcal{S}\hfill & \hfill \mathrm{the\; pipe\; cross-section}\hfill \\ \hfill R_{ref}\hfill & \hfill \mathrm{the\; initial\; curvature\; radius}\hfill \end{array}\right.(63)$

with a longitudinal stress component variation $\mathrm{\Delta }{\sigma }_{{zz}_{\text{bending}}}$ due to bending, which can be written according to Hooke’s law (Eq. 10):

$\mathrm{\Delta }{\sigma }_{{zz}_{\text{bending}}}=E\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{\text{bending}}}}\Rightarrow \mathrm{\Delta }{\sigma }_{{zz}_{\text{bending}}}=E\left(\frac{x_0-x}{R}-\frac{x_{0_{ref}}-x}{R_{ref}}\right)(64)$

which leads to the equilibrium equation expressed in terms of ΔF and the two curvature radiuses R and R_ref:

$\mathrm{\Delta }F={\iint }_{x\in \mathcal{S}}E\left(\frac{x_0-x}{R}-\frac{x_{0_{ref}}-x}{R_{ref}}\right)d\mathcal{S}(65)$

In the local cylindrical coordinate system $\left(O,r,\theta ,z\right)$, the three mechanical strains variations are described as follows:

in the cylindrical coordinate system(O, r, θ, z)

$\left\{\begin{array}{c}\mathrm{\Delta }{\epsilon }_{{rr}_{{mec}_{\text{bending}}}}=-\nu \mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{\text{bending}}}}\hfill \\ \mathrm{\Delta }{\epsilon }_{{\theta \theta }_{{mec}_{\text{bending}}}}=-\nu \mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{\text{bending}}}}\hfill \\ \mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{\text{bending}}}}=\frac{x_0-r\cos \left(\theta \right)}{R}-\frac{x_{0_{ref}}-r\cos \left(\theta \right)}{R_{ref}}\hfill \end{array}\right.(66)$

The set of mechanical strain components (Eq. 66) can be added to the components of the previous model developped in Section 3.1 for the infinitely long and straight pipe, to give, at radius r in the pipe wall, the resulting mechanical strain $\mathrm{\Delta }{\epsilon }_{{\vec{u}}_{mec}}\left(r\right)$ variation measured at location of point M (Figure 4) by the FBG transducer oriented in direction of vector $\vec{u}$ with angle φ (Figure 3):

$\begin{array}{cc}\hfill \mathrm{\Delta }{\epsilon }_{{\vec{u}}_{mec}}\left(r\right)=\hfill & \hfill {\cos }^2\left(\phi \right)\left[{\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}\left(r\right)+\mathrm{\Delta }{\epsilon }_{{\theta \theta }_{{mec}_{\text{bending}}}}\left(r,R,R_{ref},{\theta }_R,x_0,x_{0_{ref}}\right)\right]\hfill \\ \hfill \hfill & \hfill +{\sin }^2\left(\phi \right)\left[{\mathrm{\Delta }\epsilon }_{{zz}_{mec}}+\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{\text{bending}}}}\left(r,R,R_{ref},{\theta }_R,x_0,x_{0_{ref}}\right)\right]\hfill \end{array}(67)$

Equation 67 introduces at least three additional parameters (R, x₀ and θ_R), which complicates the formal resolution of the problem in terms of pressure, and the first temptation is to solve it numerically (with the appropriate number of independent strain measurements corresponding to at least the same number of independent equations of type Eq. 67).

4.2.2 Specific Solutions if the Neutral Flexural Surface Passes Through the Pipe Axis

The idea is to get rid of the influence of bending by noticing that it generates both compressive and tensile stresses over all its cross-section. The summation of each of these contributions, when the transducers are properly positioned, should therefore lead to the cancellation of their global contribution.

And one way to distribute the transducers around the pipe is evenly.

4.2.2.1 Benefits of Uniformly Distributed Measurements Around the Pipe

If the neutral flexural surface passes through the pipe axis (i.e.: $x_{0_{ref}}=x_0=0$), it is possible to get rid of the additional effects of bending by summation of N mechanical strains variation measurements ${\left(\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}\right)}_{1\le k\le N}$ associated to N pairs of transducers uniformly arranged around the pipe.

This method has the major advantage to be free from the relative angular position θ_R of the osculating plane for each point M (Figure 4) which no longer needs to be known. In the general case, Eq. 66 leads by averaging to:

$\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}=\frac{x_0-r\cos \left(\frac{2k\pi }{N}\right)}{R}-\frac{x_{0_{ref}}-r\cos \left(\frac{2k\pi }{N}\right)}{R_{ref}}\Rightarrow \frac{1}{N}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}=\frac{x_0}{R}-\frac{x_{0_{ref}}}{R_{ref}}(68)$

Thus, as long as the neutral flexural surface passes through the pipe axis, the average of the mechanical strains in bending is equal to zero if the pairs of transducers are evenly located around the pipe (Figure 5), which implies, taking into account equations set Eq. 66:

$\left\{\begin{array}{c}{x}_{0_{ref}}=0\hfill \\ x_0=0\hfill \end{array}\right.\Rightarrow \forall N\ge 2\left\{\begin{array}{c}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}=0\hfill \\ \sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{\theta \theta }_{{mec}_{{\text{bending}}_k}}}=0\hfill \end{array}\right.(69)$

FIGURE 5

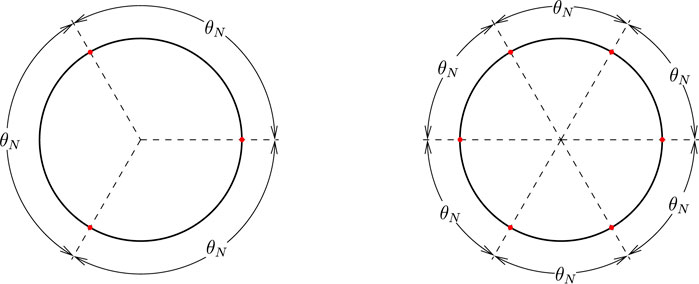
FIGURE 5. N pairs of transducers evenly arranged around the pipe, every θ_N = 2π/N (N ≥ 2), to get rid of the bending effects by summation of their mechanical strains variation measurement – Examples for N = 3 (left) and N = 6 (right).

Then, Eq. 67 can be used for the mechanical strains variation measurement corresponding to the N pairs of FBG transducers evenly located, every θ_N = 2π/N around the pipe:

$\begin{array}{cc}\hfill \underset{\begin{array}{c}\text{average\hspace{0.17em}of\hspace{0.17em}mechanical strains}\\ \text{variation around\hspace{0.17em}the\hspace{0.17em}pipe}\end{array}}{\underbrace{\frac{1}{N}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{mec}\left(r,{\phi }_k\right)}}\hfill & \hfill =\frac{1}{N}\sum _{k=1}^{k=N}\left({\cos }^2\left({\phi }_k\right)\left[{\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}\left(r\right)+\mathrm{\Delta }{\epsilon }_{{\theta \theta }_{{mec}_{{\text{bending}}_k}}}\right]\right.\hfill \\ \hfill \hfill & \hfill \left.+{\sin }^2\left({\phi }_k\right)\left[{\mathrm{\Delta }\epsilon }_{{zz}_{mec}}+\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}\right]\right)\hfill \\ \hfill \hfill & \hfill =\underset{\text{average\hspace{0.17em}of\hspace{0.17em}mechanical strains variation\hspace{0.17em}}\left(\text{excluding\hspace{0.17em}bending}\right)}{\underbrace{\frac{1}{N}\sum _{k=1}^{k=N}\left({\cos }^2\left({\phi }_k\right){\mathrm{\Delta }\epsilon }_{{\theta \theta }_{mec}}\left(r\right)+{\sin }^2\left({\phi }_k\right){\mathrm{\Delta }\epsilon }_{{zz}_{mec}}\right)}}\hfill \\ \hfill +\underset{\text{average\hspace{0.17em}of\hspace{0.17em}mechanical strains variation\hspace{0.17em}}\left(\text{pure\hspace{0.17em}bending}\right)}{\underbrace{\frac{1}{N}\sum _{k=1}^{k=N}\left({\sin }^2\left({\phi }_k\right)-\nu {\cos }^2\left({\phi }_k\right)\right)\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}}}\hfill \end{array}(70)$

According to this last expression, the mechanical strain variation corresponding to pure bending is equal to zero as long as each transducer is oriented with the same angle φ₀ or − φ₀; thus:

$\begin{array}{cc}\hfill \sum _{k=1}^{k=N}\left({\sin }^2\left({\phi }_k\right)-\nu {\cos }^2\left({\phi }_k\right)\right)\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}=\hfill & \hfill \left({\sin }^2\left({\phi }_0\right)-\nu {\cos }^2\left({\phi }_0\right)\right)\underset{=0\left(\text{Eq.}\left(\text{69}\right)\right)}{\underbrace{\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_{{\text{bending}}_k}}}}}\hfill \\ \hfill \hfill & \hfill =0\hfill \end{array}(71)$

The additional condition on φ₀ leading to ${\sin }^2\left({\phi }_0\right)-\nu {\cos }^2\left({\phi }_0\right)=0$ is however not a good idea for at least two reasons:

1. this non-intrusive measurement requires at least one pair of transducers, thus if the first transducer angle φ₁ already satisfies the equation ${\sin }^2\left({\phi }_1\right)-\nu {\cos }^2\left({\phi }_1\right)=0$, the second transducer angle φ₂ has to be compliant with condition Eq. 58, which leads to ${\sin }^2\left({\phi }_2\right)-\nu {\cos }^2\left({\phi }_2\right)\ne 0$,

2. Poisson’s ratio ν must be known with precision, which is rarely the case for a pipe already on field.

However, this additional condition on angle φ would have been probably a good idea to mitigate the bending effect on the pressure measurement if the transducer was already natively temperature insensitive (thus, only one transducer providing a purely mechanical measurement would have been necessary).

But this is another topic, out of the scope of this paper.

4.2.2.2 Recipe for Pressure Variation Measurement in Case of Additional Bending

As long as the N pairs of transducers are evenly distributed around the pipe (every θ_N = 2π/N), and according to Eq. 71, the mechanical strains variations due to pure bending are eliminated if the average mechanical strain variation $⟨\mathrm{\Delta }{\epsilon }_{mec}⟩$ is taken into account, which leads to:

$\left\{\begin{array}{cc}⟨\mathrm{\Delta }{\epsilon }_{{\vec{u}}_{1_{mec}}}\left(r_{0_{ext}}\right)⟩=\hfill & {\cos }^2\left({\phi }_1\right)\left(\frac{1}{N}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{\theta \theta }_{{mec}_k}}\left(r_{0_{ext}}\right)\right)+{\sin }^2\left({\phi }_1\right)\left(\frac{1}{N}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_k}}\right)\hfill \\ ⟨\mathrm{\Delta }{\epsilon }_{{\vec{u}}_{2_{mec}}}\left(r_{0_{ext}}\right)⟩=\hfill & {\cos }^2\left({\phi }_2\right)\left(\frac{1}{N}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{\theta \theta }_{{mec}_k}}\left(r_{0_{ext}}\right)\right)+{\sin }^2\left({\phi }_2\right)\left(\frac{1}{N}\sum _{k=1}^{k=N}\mathrm{\Delta }{\epsilon }_{{zz}_{{mec}_k}}\right)\hfill \end{array}\right.(72)$

with:

$\left\{\begin{array}{c}⟨{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{1_{mec}}}\left(r_{0_{ext}}\right)⟩=\left(\frac{1}{N}\sum _{k=1}^{k=N}\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{1_k}}{{\kappa }_{\epsilon }}\right)-\frac{{\kappa }_T}{{\kappa }_{\epsilon }}\mathrm{\Delta }T\hfill \\ ⟨{\mathrm{\Delta }\epsilon }_{{\vec{u}}_{2_{mec}}}\left(r_{0_{ext}}\right)⟩=\left(\frac{1}{N}\sum _{k=1}^{k=N}\frac{\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{2_k}}{{\kappa }_{\epsilon }}\right)-\frac{{\kappa }_T}{{\kappa }_{\epsilon }}\mathrm{\Delta }T\hfill \end{array}\right.(73)$

Solutions of equations sets Eqs. 72, 73 are essentially the same than without bending, with a single pair of transducers measurement, the average measurements replacing the single measurement as long as the N pairs of transducers are all oriented with the same couples of angles $\left\{\pm {\phi }_1,\pm {\phi }_2\right\}$ $(\left|{\phi }_1\right|\ne \left|{\phi }_2\right|\mathrm{mod}\pi )$.

Thus, equations set Eq. 57 is adapted for N ≥ 2 pairs of transducers evenly arranged around the pipe:

$\left\{\begin{array}{cc}\mathrm{\Delta }{P}_{int}\hfill & =\mathrm{\Delta }{P}_{ext}+\frac{r_{0_{ext}}^{2}E\frac{1}{N}{\sum }_{k=1}^{k=N}\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{1_k}-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{2_k}\right)}{{\kappa }_{\epsilon }\left(1+\nu \right)\left[{\cos }^2\left({\phi }_1\right)-{\cos }^2\left({\phi }_2\right)\right]}\left(\frac{1}{r_{0_{int}}^2}-\frac{1}{r_{0_{ext}}^2}\right)+\frac{\delta F}{\pi r_{0_{int}}^2}\hfill \\ \mathrm{\Delta }T\hfill & =\frac{1}{{\kappa }_T}\left[\frac{1-2\nu }{1+\nu }\frac{\frac{1}{N}{\sum }_{k=1}^{k=N}\left(\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{1_k}-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{2_k}\right)}{{\cos }^2\left({\phi }_2\right)-{\cos }^2\left({\phi }_1\right)}+\frac{\frac{1}{N}{\sum }_{k=1}^{k=N}\left[\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{1_k}{\cos }^2\left({\phi }_2\right)-\underline{\mathrm{\Delta }}{\mathrm{\Psi }}_{2_k}{\cos }^2\left({\phi }_1\right)\right]}{{\cos }^2\left({\phi }_2\right)-{\cos }^2\left({\phi }_1\right)}\right.\hfill \\ \hfill & \left.+\frac{{\kappa }_{\epsilon }\left(1-2\nu \right)}{E}\mathrm{\Delta }{P}_{ext}-\frac{1}{\pi E}\frac{2{\kappa }_{\epsilon }\left(1-\nu \right)}{r_{0_{ext}}^2-r_{0_{int}}^2}\delta F\right]\hfill \end{array}\right.(74)$

However, this set (Eq. 74) of solutions is valid only if the neutral flexural surface passes through the pipe axis, which implies the additional hypothesis of pure bending, hence δF = 0.

If δF ≠ 0, several additional parameters must be known with precision as long as the transducers are temperature sensitive: the curvature radiuses, the orientations of the osculating planes and the positions of the neutral flexural surfaces in both the reference and the current thermomechanical states (Section 4.2.1).

5 Experimental Validations

The measurement method disclosed in this paper has been validated experimentally. Three lab-tests are presented hereafter:

1. the first test involves a closed pipe with no external force applied on it: it enables to have a first look to its bare performances in terms of pressure measurement accuracy, once calibrated (Section 5.1),

2. the second test involves an air pressure loop controlled by flow rate, very similar to an industrial installation: it demonstrates the ability of this measurement principle to get a realistic pressure variation measurement (interpretable in terms of pressure drop) directly correlated to an air flow rate (Section 5.2),

3. the last tests involve a water pressure loop dedicated to reproduce a Nuclear Power Plant (NPP) primary coolant circuit, with wide temperature and pressure changes, in order to push to its limits this non-intrusive measurement principle (Section 5.3).

For all these tests, one FBG is oriented with φ = π/2, thus sensitive to the longitudinal mechanical strain ${\epsilon }_{{zz}_{mec}}$, whereas the other FBG is oriented with φ = 0, thus sensitive to the hoop mechanical strain ${\epsilon }_{{\theta \theta }_{mec}}$.

All transducers were attached to the pipe surface with a thin film of glue, and except for the last test (Section 5.3.3), FBGs were in direct contact with the surrounding air, at room temperature.

Bragg wavelengths were recorded with a commercial measurement system from Micron-Optics™, model Si255 (and all FBGs are quite standard FBGs, from mass-market production).

5.1 Bare Performances of the Non-intrusive Pressure Variation Measurement Evaluated on a Mechanically Isolated Pipe

This test involves an experimental setup including a closed pipe with the following characteristics:

$\left\{\begin{array}{cc}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}:\hfill & r_{0_{ext}}\simeq 151\text{mm}\hfill \\ \mathrm{i}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}:\hfill & r_{0_{int}}\simeq 127.5\text{mm}\hfill \\ \mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}:\hfill & L\ge 10r_{0_{ext}}\hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}\left\{\begin{array}{cc}\mathrm{Y}\mathrm{o}\mathrm{u}\mathrm{n}{\mathrm{g}}^{\prime }\mathrm{s}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}:\hfill & E\simeq 203\text{GPa}\hfill \\ \mathrm{P}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{n}\prime \mathrm{s}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}:\hfill & \nu \simeq 0.3\hfill \end{array}\right.(75)$

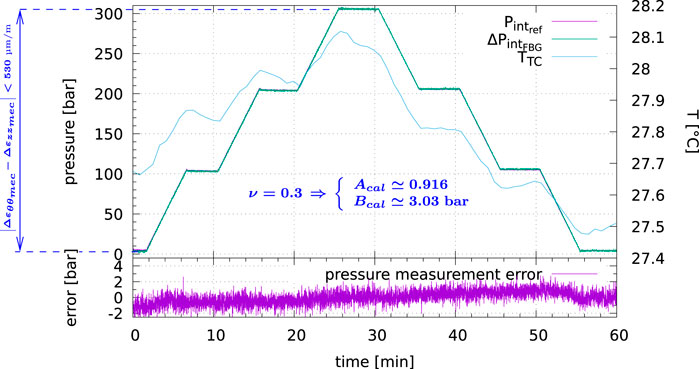
This pipe is equipped with a reference pressure sensor in direct contact with the fluid (some water), and a dedicated external hydraulic circuit is in charge of its pressurization (Figure 6). This pressure testing facility is located at Technip Energies in Marseille (France) and enables to inflate the pipe up to 300 bar.

FIGURE 6

FIGURE 6. Detailed view of the water pressure testing facility at Technip Energies in Marseille, with two FBG transducers glued on the pipe external surface.

The FBG raw measurements, leading to internal pressure variation $\mathrm{\Delta }{P}_{{int}_{FBG}}$ measurements (Eq. 57), and the internal pressure reference measurements $P_{{int}_{ref}}$ were post-synchronized by least-squares minimization of the error function $\mathcal{E}$ described as follows (see also Eq. 78):

${\mathcal{E}}_{\left(A,B\right)}\left(\mathrm{\Delta }t\right)=‖\left(A\times \mathrm{\Delta }{P}_{{int}_{FBG}}\left(t+\mathrm{\Delta }t\right)+B\right)-P_{{int}_{ref}}\left(t\right)‖\left\{\begin{array}{cc}A\hfill & \mathrm{a}\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\hfill \\ B\hfill & \mathrm{a}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{o}\mathrm{ff}\mathrm{s}\mathrm{e}\mathrm{t}\hfill \end{array}\right.(76)$

The two pressure data sets are post-synchronized once the error function $\mathcal{E}$ reaches its minimum value at Δt_sync, thus the optical measurements are also calibrated with calibration coefficients A_cal and B_cal:

$\frac{d{\mathcal{E}}_{\left(A_{cal},B_{cal}\right)}\left({\mathrm{\Delta }t}_{sync}\right)}{d\mathrm{\Delta }t}=0\Rightarrow \left\{\begin{array}{cc}{A}_{cal}\hfill & \mathrm{the\; calibration\; scale\; factor}\hfill \\ B_{cal}\hfill & \mathrm{the\; calibration\; pressure\; offset}\hfill \end{array}\right.(77)$

The pressure test held in Marseille in July 2019 consisted in several pressure steps up to 300 bar (Figure 7). The sampling rate of the reference pressure measurements $P_{{int}_{ref}}$ was set to 2 Hz, whereas the optical fiber measurements rate was set to 5 Hz.

FIGURE 7

FIGURE 7. Results of the pressure test held at Technip Energies facility in Marseille in July 2019.

The average quadratic FBG measurement error ${\sigma }_{{\text{error}}_P}$ is calculated as follows (w_i is the weight–the time period–associated to each measurement i):

${\sigma }_{{\text{error}}_P}=\sqrt{\frac{1}{{\sum }_{i=1}^{i=N}{w}_i}\sum _{i=1}^{i=N}{w}_i{\left[\left(A_{cal}\times \mathrm{\Delta }{P}_{{int}_{{FBG}_i}}+B_{cal}\right)-P_{{int}_{{ref}_i}}\right]}^2}(78)$

Between the minimum pressure $P_{{int}_{\min }}$ (a few bars) and the maximum pressure $P_{{int}_{\max }}\simeq 306\text{bar}$, this error is equal to 0.84 bar, i.e.: better than 0.54% Full Scale $(2{\sigma }_{{\text{error}}_P})$, with a calibration scale factor (i.e.: the gauge factor) equal to 0.916, the pipe thickness uncertainty explaining its difference from 1.

It has to be noticed that the FBG surface temperature variation ΔT_FBG (computed with the standard Poisson’s ratio (Eq. 75)) varies in opposite to the reference thermocouple temperature ΔT_TC (Figure 8, left). This may be due to at least two reasons; formula for temperature variation ΔT in equations set (Eq. 57):

• depends on the Poisson’s ratio ν, which is often not known with the adequate accuracy for all structures,

• is valid at thermomechanical equilibrium with the underlying hypothesis of an homogeneous temperature in the pipe wall.

FIGURE 8

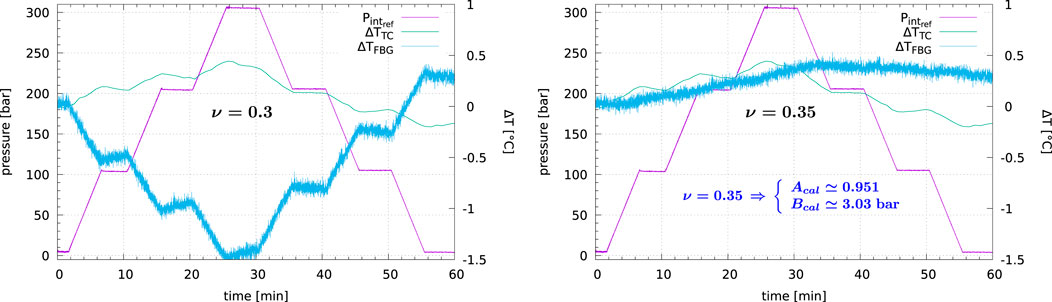
FIGURE 8. Results of the pressure test held at Technip Energies facility in Marseille in July 2019—With additional surface temperature variation computed from FBG measurements (ν = 0.3 (left) and ν = 0.35 (right)).

After manual adjustment of the Poisson’s ratio, set to ν = 0.35 (which is an over-estimated value for steel) in the second equation of set (Eq. 57), this discrepancy was reduced by a factor of four (Figure 8 right), with no impact on pressure measurement average error ${\sigma }_{{\text{error}}_P}$. At thermal equilibrium, if ν_cal is the Poisson’s ratio which best fits for surface temperature measurements, the first relationship given by least-squares minimization of the error function $\mathcal{E}$ for pressure calibration (Eq. 76) then leads to a corrected value E_cal for the Young’s modulus:

$A_{cal}\frac{E}{1+\nu }=\frac{E_{cal}}{1+{\nu }_{cal}}\hspace{0.17em}\Rightarrow \hspace{0.17em}{E}_{cal}=\underset{\begin{array}{c}\text{correction\hspace{0.17em}factor}\end{array}}{\underbrace{A_{cal}\frac{1+{\nu }_{cal}}{1+\nu }}}E(79)$

and for this specific pressure test:

$\left\{\begin{array}{cc}{A}_{cal}\hfill & =0.951\hfill \\ {\nu }_{cal}\hfill & =0.35\hfill \end{array}\right.\Rightarrow E_{cal}=0.951\times \frac{1+0.35}{1+0.3}\times 203\text{GPa}\simeq 200.5\text{GPa}(80)$

which is a valid value for steel.

Anyway, such temperature measurement should be considered with limited confidence out of thermal balance, at best as indicative only, especially since it depends on the mechanical properties of the structure (but other kinds of FBG transducers–on their side, totally decorrelated from the strains of the structure to which they are attached to–may provide this measurement in a better way (Roussel et al. (2018))).

5.2 Non-intrusive Pressure Variation Measurement on an Air Pressure Loop

The second type of validation occured in October 2019 on an air pressure loop controlled by flow rate (Mercure facility located at CEA in Cadarache, France). The main advantage of such test facility, for the qualification of the non-intrusive measurement, is its complexity in terms of pipe layout, including several bends (Figure 9), then potentially leading to additional external forces acting on the pipe, such as:

• longitudinal forces due to differential thermal expansion between the pipe and its attachments,

• bending forces due to the changes in air flow rate or/and direction when crossing each bend.

FIGURE 9

FIGURE 9. Mercure air pressure loop facility (DES, CEA/Cadarache)—Overview of the pipe layout (left) and detailed view of FBG transducers installation on pipe surface (right).

The FBG transducers are located in the middle of a 5 m long pipe section. The pipe characteristics are described hereafter:

$\left\{\begin{array}{cc}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}:\hfill & r_{0_{ext}}\simeq 79.2\text{mm}\hfill \\ \mathrm{i}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}:\hfill & r_{0_{int}}\simeq 76.2\text{mm}\hfill \end{array}\right.\mathrm{a}\mathrm{n}\mathrm{d}\left\{\begin{array}{cc}\mathrm{Y}\mathrm{o}\mathrm{u}\mathrm{n}{\mathrm{g}}^{\prime }\mathrm{s}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}:\hfill & E\simeq 200\text{GPa}\hfill \\ \mathrm{P}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{n}\prime \mathrm{s}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\hfill & \nu \simeq 0.3\hfill \end{array}\right.(81)$

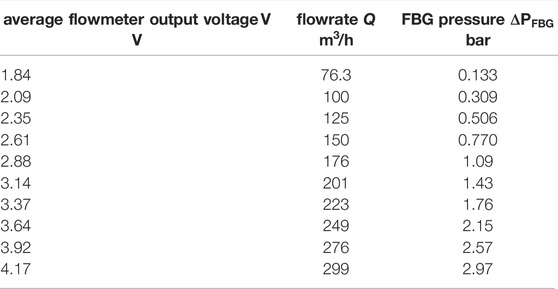
The optical measurements were performed at 5 kHz, then averaged to 2.5 Hz to improve the signal to noise ratio (Figure 10 left). The flow rate Q is measured with a Rosemount™ flowmeter device:

$Q_{\left[{\text{m}}^3/\text{h}\right]}=3600\times \left(0.02661V_{\left[\text{V}\right]}-0.02778\right)\left(V,\mathrm{is\; the\; flowmeter\; output\; voltage}\right)(82)$

FIGURE 10

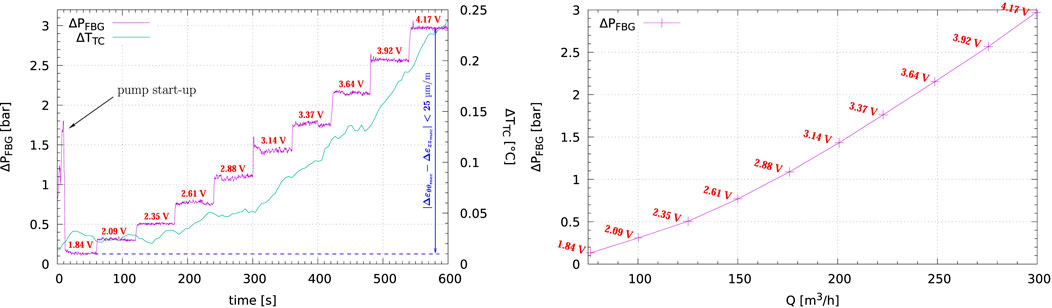
FIGURE 10. Air flow rate steps and corresponding FBG non-intrusive pressure variation measurement vs. time (left) and non-intrusive pressure variation vs. air flow rate measurements (right) on Mercure facility.

Measurements are reported in Table 3 (Reynolds number is greater than 9,600—the flow is turbulent).

TABLE 3

TABLE 3. Air flow rate and corresponding FBG non-intrusive pressure variation measurements.

FBG pressure variation ΔP_FBG vs. air flow rate Q (Figure 10 right) is very similar to pressure drops which can be calculated from recipes for natural gas pipelines (e.g.: Coelho and Pinho (2007)), with a clearly univocal relationship of pressure drop vs. air flow rate, which confirms the relevance of this non-intrusive measurement method in such situation.

5.3 Non-intrusive Pressure Variation Measurement on a Water Pressure Loop

The last experimental tests were performed at BEARN 2 facility in Saclay (France). This water pressure loop enables flow rates up to 14 m³/h with temperatures up to 320 °C, and pressures up to 150 bar. The pipe layout includes several bends and attachments (Figure 11).

FIGURE 11

FIGURE 11. CEA BEARN 2 pressure loop facility (left) and detailed view of a typical attachment (right).

All non-intrusive FBG pressure measurements were performed with standard thermomechanical values for steel (E = 195 GPa, ν = 0.3 and α = 16.4 × 10^–6 K⁻¹).

In order to put the next results into perspective, some orders of magnitude have been estimated from Eqs. 41, 57: if δλ_B = 1 pm is the Bragg wavelength resolution, and δP_int = 1 bar the pressure measurement resolution target, they highlight that the most critical parameter is the FBG temperature cross-sensitivity compensation process (Table 4), which has to be as efficient as possible.

TABLE 4

TABLE 4. Orders of magnitude for standard FBG transducers attached on pipe surface, operating at λ_B = 1550 nm (with E = 195 GPa, ν = 0.3 and α = 16.4 × 10⁻⁶ K⁻¹ for steel).

5.3.1 Pressure Variation Measurements at Constant Temperature, No Flow

The first test was performed on a Ø 4” NPS Sch. 160 pipe section.

$\varnothing 4\text{“NPS\hspace{0.17em}Sch.}160\text{:}\left\{\begin{array}{c}{r}_{0_{ext}}\simeq 57.15\text{mm}\hfill \\ r_{0_{int}}\simeq 43.66\text{mm}\hfill \end{array}\right.(83)$

Without any flow, the water temperature remained constant, so the thermal differential expansion between the pipe and its attachments (responsible for δF in equations set Eq. 57) remained under control as long as the room temperature did not change too much.

The single sensor¹² pressure measurement (Figure 12 left) was calibrated during the first two and a half hours with a typical average model error equal to 1.36 bar $(2{\sigma }_{{\text{error}}_P})$. The pressure measurement average error until the end of the test is equal to −0.18 bar.

FIGURE 12

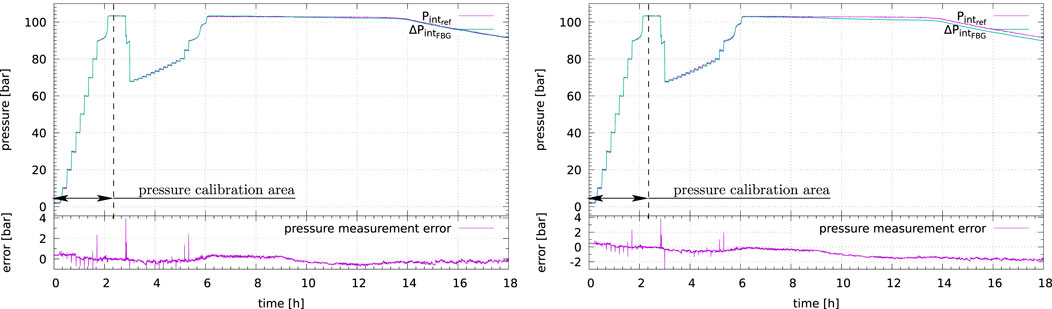
FIGURE 12. First pressure test with no fluid flow and fluid constant temperature (Ø 4” NPS Sch. 160)—Single sensor (left) vs. three sensors average measurements to mitigate potential bending effects (right).

The average of three sensors measurements to mitigate the potential bending effects on pressure measurement (Figure 12 right) does not improve the measurement with an absolute pressure measurement error drift close to 2 bar after 18 h of test. Additional effects other than pure bending might be suspected.

The maximum errors correspond to the rapid pressure changes between two steps, mainly due to the sampling rates difference between optical (10 Hz) and reference (every 17 s) pressure measurements.

5.3.2 Pressure Variation Measurements With Temperature Changes, No Flow

The second test involves the same section, but isolated from the other part of the pressure circuit with fluid flow. Temperature variations are due to heat conduction between the two isolated pipe sections.

The pressure measurement was calibrated at constant temperature during the first 2 hours, with a typical average model error equal to 2.12 bar $(2{\sigma }_{{\text{error}}_P})$, and the pressure measurement average error until the end of the test is equal to −1.5 bar, with fluid temperature increase greater than 19 °C (Figure 13 left).

FIGURE 13

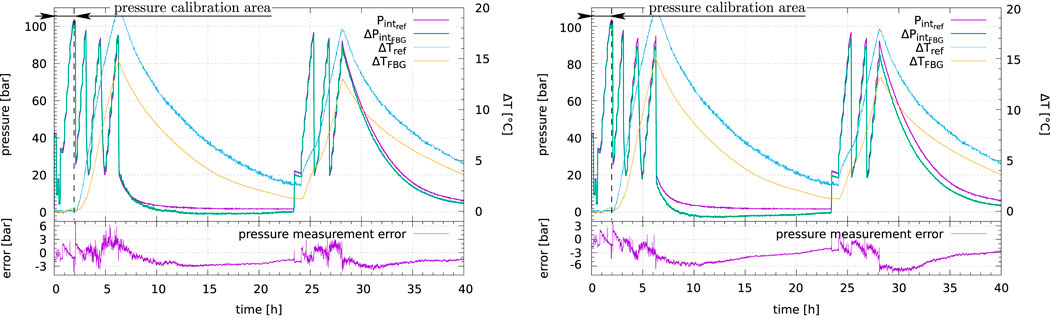
FIGURE 13. Second pressure test with no fluid flow and temperature changes (Ø 4” NPS Sch. 160)—Single sensor (left) vs. three sensors average measurements to mitigate potential bending effects (right).

Both temperature measurements behave the same way, with a limited discrepancy (a few °C) which also may be due to the temperature gradient along the pipe section since these two measurements were not performed at the same location.

The average of three pairs of sensors measurement to mitigate the potential bending effects on pressure measurement (Section 4.2.2.2) does not lead to significant better results (Figure 13 right): this might be due to additional longitudinal forces, e.g.: due to differential thermal expansion and pipe attachments.

5.3.3 Pressure Variation Measurements With Flow Rate and Temperature Changes

Transducers are now attached to a Ø 2” NPS Sch. 80 pipe section, with pressure measurements three times more sensitive to any unexplained longitudinal force variation δF (Table 4).

$⌀2\text{”NPS\hspace{0.17em}Sch.}80\text{:}\left\{\begin{array}{c}{r}_{0_{ext}}\simeq 30.15\text{mm}\hfill \\ r_{0_{int}}\simeq 24.61\text{mm}\hfill \end{array}\right.(84)$

The other main difference is the fluid which flows up to 14 m³/h with significant friction effect, and the thermal isolation of the instrumented section.

Also, the mechanical effect of a rapid and massive fluid flow change (from 14 m³/h to zero–Figure 14) has been experienced in a more significant way than previously on the air pressure loop (Section 5.2), mainly due to the mass volume difference between air and water, therefore resulting in more important external bending forces acting directly on the pipe.

FIGURE 14

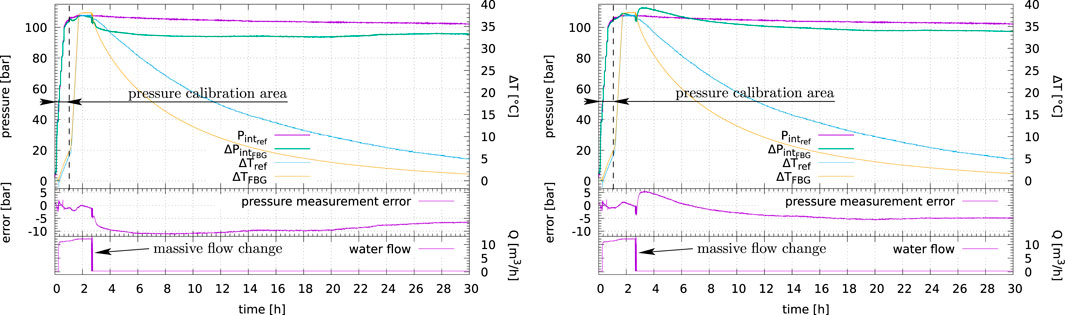
FIGURE 14. Last pressure test with fluid flow and temperature changes (Ø 2″ NPS Sch. 80)—Single sensor (left) vs. two sensors average measurements to mitigate potential bending effects resulting from massive flow change (right).

This last pressure measurement was calibrated during the first 42 min while both temperature and flow changed, with a typical average model error equal to 2 bar $(2{\sigma }_{{\text{error}}_P})$.

The pressure measurement average error until the end of the test is equal to −8.6 bar with one pair of transducers (Figure 14 left), with fluid temperature increase up to 38 °C; the average of two measurements to mitigate potential bending effects led this time to at best twice better results (Figure 14 right).

Both temperature measurements behave the same way, with a limited discrepancy as long as the fluid flows, during the first two and a half hours.

As soon as the flow is stopped, the temperature discrepancy increases, which may be explained by the difference in heat exchange along the pipe section, these measurements being not performed at the same place. Pressure discrepancy also increases, which may be the result of a change in the mechanical efforts exerted on the pipe, since the flow change also modifies the external efforts balance.

The pumps vibrations may also have modified the mechanical balance, since the pipe is in reality partially locked in its attachments (Figure 11 right).

6 Conclusion, Discussion and Perspectives

The non-intrusive pressure variation measurement disclosed in this paper is an improvement over previous methods in terms of temperature compensation, considering that 1 bar pressure resolution typically requires a temperature compensation error better than 0.054 °C for a Ø 2” NPS Sch. 80 steel pipe (Table 4).

It is based on a formal model, which demonstrates that the pressure change in a pipe can be measured by simple subtraction of two direction-sensitive surface measurements, the temperature influence being intrinsically cancelled.

This is the result of the application of a spherical stress (the hydrostatic pressure) on a closed cylindrical structure (the pipe). This asymmetry intrinsically generates significant different mechanical strains variations in two directions (hoop vs. longitudinal), allowing the exploitation of this remarkable property for the purpose of purely mechanical measurements with only two direction-sensitive transducers, and therefore hydrostatic pressure variation measurements as long as the pipe keeps its axicylindrical geometry with a circular cross-section, and remains in its elastic domain¹³.

Its experimental validation in harsh conditions led to at maximum 8.6 bar pressure error, with temperature changes up to 38 °C, but also flow change from 14 m³/h to zero, thus significantly modifying the mechanical balance of the pipe layout including several bends (Section 5.3.3).

This sensor used on a straight (without any bend) pipe with constant inner section (e.g.: vertical onshore drilling), should therefore lead to more accurate non-intrusive hydrostatic pressure measurements, since in such conditions, the pipe is no longer subject to external forces that can be generated by any change in fluid flow or/and direction.

By extension, this method should also enable the mitigation of any other physical effect as long as it has the same influence on all raw measurements (Section 4.1.3.2.1): this is a key advantage for measurements in a Nuclear Power Plant, in order to mitigate the effects of ionizing radiations on transducers (even some additional work is required to validate the reliability of this non-intrusive pressure measurement in such harsh environment).

Its bare performances, better than 0.54% Full Scale $(2{\sigma }_{{\text{error}}_P})$, already enable to consider the development of new kinds of pressure sensors based on a closed cylindrical pipe structure, submitted to the sole mechanical effect of the hydrostatic pressure (Section 5.1) for internal, but also external pressure variations measurement, since formulae from sets Eq. 57, 74 can be used for either ΔP_int or ΔP_ext.

Such measurement principle could also probably benefit to other kinds of cylindrical structures, like type IV Composite Overwrapped Pressure Vessels (COPV) dedicated to high pressure dihydrogen H₂ storage, since the non-intrusive hydrostatic pressure measurement, when combined with the fluid reference pressure measurement, is a crucial information to establish a Damage Assessment Parameter, with the advantages over the previous method (Maurin et al. (2014)) based on the OFDR Rayleigh backscattering technique (Froggatt and Moore (1998)), to be intrinsically temperature-compensated and compatible with real-time requirements (for instance to evaluate the vessel damage assessment status during the H₂ filling process).

Anyway, the measurement bias introduced by some unexplained residual longitudinal force δF (e.g.: due to differential thermal expansions) is one limitation for an application on pipe structures, which therefore must be taken into account before any deployment. Also the additional measurement provided by other means of such longitudinal efforts, combined with the recipe to mitigate the bending effects (Section 4.2), should help to improve the accuracy for pressure measurements on field.

On their side, surface temperature measurements should be considered with limited confidence, since they also depend on the mechanical characteristics of the structure, even if the discrepancy with the reference measurements remained under control during the BEARN 2 pressure tests (Section 5.3). But this surface temperature measurement could still be used as an additional information, for instance to prevent hydrate-plugs formation during subsea oil & gas extraction (Barker and Gomez (1989)).

The formal model developped in Sections 3 and 4 can also probably be improved, first by introducing a radial temperature gradient in the pipe wall (but this would require to have a temperature measurement on the pipe inner surface … ).

The temperature κ_T and strain κ_ɛ sensitivities dependency on strains and temperature, supposed to be constant in this paper, can also be introduced in Eq. 40, which should lead, after integration, to a more precise relationship than Eq. 42, thus to more accurate measurements in case of wider temperature changes.

On another level, as soon as the transducers measurement principle is orientation-sensitive, the recipes disclosed in this paper should apply.

Thus, measurement techniques like ultrasonics should be able to benefit from this work, provided that the acoustic wave propagation time Δt variation, between two thermomechanical states and two transducers, is interpreted in terms of total (mechanical + thermal) true strain variation Δɛ (Eq. 25):

$\mathrm{\Delta }\epsilon =\ln \left(1+\frac{\mathrm{\Delta }L}{L}\right){˜}^0\frac{\mathrm{\Delta }L}{L}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\left\{\begin{array}{cc}\hfill L\hfill & \hfill \mathrm{the\; length\; of\; the\; acoustic\; path}\mathcal{P}\hfill \\ \hfill \mathrm{\Delta }L=⟨v⟩\mathrm{\Delta }t\hfill & \hfill \mathrm{the\; acoustic\; path\; length\; variation}\hfill \\ \hfill ⟨v⟩=\frac{1}{L}{\int }_{\mathcal{P}}vdL\hfill & \hfill \mathrm{the\; average\; acoustic\; wave\; velocity\; along}\mathcal{P}\hfill \end{array}\right.(85)$

The stresses tensor components described by equations set Eq. 26 should also help for better ultrasonics velocity v prediction in the pipe wall (Salama and Ling (1980)).

Last, since non-contact image correlation techniques can be applied to measure surface strains (Sutton et al. (2009)), their application to pipe structures should also enable non-contact hydrostatic pressure variation measurements relying on the recipes disclosed in this paper.

This could be a major advantage in order to perform such measurements in restricted areas where it is no more possible to enter (for example in case of a nuclear accident, after a release of fission products), and therefore install or repair sensors.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation in the CEA HAL open archive, as an attached compressed file to this paper, and available online at: https://hal-cea.archives-ouvertes.fr/cea-03541365.

Author Contributions

LM is the main contributor to this article, from the development of the formal model for non-intrusive pressure and surface temperature measurements with only two direction-sensitive transducers, with the elaboration of the recipe to mitigate the bending effects on pressure measurement, to the participation to all the pressure tests reported in this paper, the measurements data post-processing, their analysis, the conclusion and the discussion.

Funding

This research topic was first co-funded by the FSH¹⁴ public fund (CEP&M¹⁵ project n° 9512/01), then by TotalEnergies (contracts ref. TEPRD: FR00008107, and ref. CEA: C23466-1).

Conflict of Interest

This research topic was first co-funded by the FSH public fund (CEP&M project n° 9512/01), then by TotalEnergies (contracts ref. TEPRD: FR00008107, and ref. CEA: C23466-1, on the basis of non-standard FBG transducers) for the sole co-funding of the last pressure test on BEARN 2 facility. TotalEnergies was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, nor the decision to submit it for publication. All authors declare no other competing interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge TotalEnergies and M. Marc Baqué for their support, which permitted the rehabilitation of the BEARN 2 pressure loop, and thus to carry out the pressure tests in harsh, close to field conditions. Authors also acknowledge Technip Energies and M. Daniel Mabily for their kind permission to publish the results of the pressure test held in Marseille (Section 5.1), M. Kévin Cruz from CEA DES IRESNE for the pressure test held on Mercure facility in Cadarache (Section 5.2), M. Franck Ruffet from CEA DES DM2S for its availability during the pressure tests held on BEARN 2 facility in Saclay (Section 5.3), and the FSH public fund, which permitted to initiate the research work on the formal pressure and temperature model.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsens.2022.835140/full#supplementary-material

Footnotes

¹Based on an additional FBG attached to a separate and unstressed piece of the same pipe material, supposed to be maintained at pipe temperature, for FBG thermo-optic and pipe thermal expansion compensations in such configuration.

²Strictly speaking, this is the product α ΔT which has to be taken into account. Also, the thermal expansion coefficient α must be known, but a rough approximation is acceptable since it has a minor impact on pressure measurement.

³See Sections 4.1.3.1 and 4.1.3.2 in case of temperature self-compensated pressure variation measurements.

⁴The type of mechanical sollicitation plays a role: $\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial {\epsilon }_{mec}}=-\frac{{n^2}_{\text{eff}}}{2}$ [(1−ν)p₁₂ − νp₁₁]• ε_mec is the longitudinal mechanical strain (in the direction of the optical waveguide), without any other mechanical influence,• p₁₁ ≃ 0.113 and p₁₂ ≃ 0.252 are the elasto-optic coefficients (see for instance Lawrence et al. (1997)).

⁵Published thermo-optic coefficient $\frac{1}{n_{\text{eff}}}\frac{\partial n_{\text{eff}}}{\partial T}$ values vary from 6.1 × 10^–6 K⁻¹ to 8 × 10^–6 K⁻¹, and can be explained by the diversity of germanocilicate optical fibers on the market (Ferdinand (2018)). Strictly speaking, the mechanical polymer coating of the optical fibers also has an influence on κ_T, because its thermal expansion coefficient is at least one order of magnitude greater than the thermal expansion coefficient of the bare optical fiber.

⁶To the extent that the mechanical strength of the optical fiber is negligible compared to the mechanical strength of the structure.

⁷There is no surface shear strain: Δɛ_rθ = Δɛ_θz = 0.

⁸It is supposed to be true if all the transducers are, for instance, glued the same way to the structure, see Eqs. 47, 48.

⁹For instance, in subsea oil & gas extraction, the pipe is connected on one side to the well (which is a closed volume), and on the other side to the storage station (which is also a closed volume).

¹⁰The theoretical justification can be found, for instance, in Forest et al. (2009–2010), Section 12.1.5, pp. 277–279.

¹¹Whereas previous solution from Magne et al. (2005) and Roussel et al. (2019) requires at least one additional transducer for FBG temperature compensation.

¹²One sensor is defined as one pair of transducers attached to the pipe surface, compliant with Eq. 58.

¹³So the Hooke’s law Eq. 10 still applies, otherwise, the triaxiality of the stresses in the plastic domain, at least for metallic structures according to the von Mises’ criterion, with the additional property of iso-volume deformations (Forest et al. (2009–2010)), will then impose to develop a different thermomechanical model.

¹⁴FSH: Fonds de Soutien aux Hydrocarbures (French public fund for oil & gas research works).

¹⁵CEP&M: Comité d’Études Pétrolières et Marines (committee for oil & gas and marine studies).

References

Adams, C., Engle, D. T., Ryan, R. S., and Wilson, J. W. (2018). Fiber Optic Pressure Apparatus, Methods, and Applications. (US: US 2018/0172536 A1).

Google Scholar

Barker, J. W., and Gomez, R. K. (1989). Formation of Hydrates During Deepwater Drilling Operations. J. Pet. Technol. 41, 297–301. doi:10.2118/16130-PA

CrossRef Full Text | Google Scholar

Coelho, P. M., and Pinho, C. (2007). Considerations About Equations for Steady State Flow in Natural Gas Pipelines. J. Braz. Soc. Mech. Sci. Eng. 29, 262–273. doi:10.1590/S1678-58782007000300005

CrossRef Full Text | Google Scholar

Diodati, P. (1986). Ultrasonic Method for Static Pressure Measurement. Rev. Scientific Instr. 57, 293–295. doi:10.1063/1.1138932

CrossRef Full Text | Google Scholar

Ekechukwu, G. K., and Sharma, J. (2021). Well-Scale Demonstration of Distributed Pressure Sensing Using Fiber-Optic DAS and DTS. Sci. Rep. 11, 12505. doi:10.1038/s41598-021-91916-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferdinand, P. (2018). “Capteurs à fibres optiques à réseaux de Bragg – Fabrication et caractéristiques,” in Mesures et contrôle (Paris, France: Techniques de l’Ingénieur), Vol. R 6 735v2, 1–37.

Google Scholar

Ferdinand, P., Magne, S., and Rougeault, S. (1994). Micro-système optique de type rosette de jauges de contraintes à guides diélectriques pour la mesure d’une contrainte longitudinale en structure plane. Paris, France: FR 2 727 203 B1.

Google Scholar

Forest, S., Amestoy, M., Damamme, G., Kruch, S., Maurel, V., and Mazière, M. (2009–2010). Mécanique des milieux continus. Paris, France: Mines ParisTech.

Google Scholar

Froggatt, M., and Moore, J. (1998). High-Spatial-Resolution Distributed Strain Measurement in Optical Fiber with Rayleigh Scatter. Appl. Opt. 37, 1735–1740. doi:10.1364/ao.37.001735

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawrence, C. M., Nelson, D. V., and Udd, E. (1997). “Measurement of Transverse Strains with Fiber Bragg Gratings,” in Smart Structures and Materials 1997: Smart Sensing, Processing, and Instrumentation. Editor R. O. Claus (Bellingham, Washington, USA: International Society for Optics and Photonics), Vol. 3042, 218–228. doi:10.1117/12.275739

CrossRef Full Text | Google Scholar

Magne, S., Ferdinand, P., and Daniel, P.-J. (2005). Instrumented Tubular Device for the Transport of a Pressurized Fluid Using Bragg Grating Rosettes. Paris, France: WO 2005/064300.

Google Scholar

Magne, S., Rougeault, S., Vilela, M., and Ferdinand, P. (1997). State-of-Strain Evaluation with Fiber Bragg Grating Rosettes: Application to Discrimination Between Strain and Temperature Effects in Fiber Sensors. Appl. Opt. 36, 9437–9447. doi:10.1364/AO.36.009437

PubMed Abstract | CrossRef Full Text | Google Scholar

Marquardt, D. W. (1963). An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Maths. 11, 431–441. doi:10.1137/0111030

CrossRef Full Text | Google Scholar

Martinez, C. (1999). Étude et réalisation de composants à réseaux de Bragg dans les fibres optiques. Ph.D. thesis (Paris, France: Université de Paris-Sud, Centre d’Orsay).

Google Scholar

Maurin, L., Ferdinand, P., Nony, F., and Villalonga, S. (2014). “OFDR Distributed Strain Measurements for SHM of Hydrostatic Stressed Structures: An Application to High Pressure Hydrogen Storage Type IV Composite Vessels - H2E Project,” in EWSHM - 7th European Workshop on Structural Health Monitoring. Editors V. Le Cam, L. Mevel, F. Schoefs, and I. Inria (Nantes, France: INRIA: Université de Nantes), 930–937.

Google Scholar

Maurin, L., Laffont, G., Ferdinand, P., and Rougeault, S. (2007). Device and Method for Measuring the Mechanical Deformation of a Section. Paris, France: EP 2 102 585 B1.

Google Scholar

Meiring, C., Allwood, G., Hinckley, S., and Wild, G. (2016). “Monitoring of Pressure in Pipelines Using Externally-Mounted Fiber Bragg Gratings,” in Photonics and Fiber Technology 2016 (ACOFT, BGPP, NP). BM5B.2 (Washington, D.C., USA: Optical Society of America). doi:10.1364/BGPP.2016.BM5B.2

CrossRef Full Text | Google Scholar

Roussel, N., Cotillard, R., Laffont, G., and Baqué, M. (2019). “Non-Intrusive Pipeline Pressure Monitoring with a Fiber Bragg Gratings-Based Sensing Patch,” in Optical Sensors and Sensing Congress (ES, FTS, HISE, Sensors). STu4D.3 (Washington, D.C., USA: Optical Society of America). doi:10.1364/SENSORS.2019.STu4D.3

CrossRef Full Text | Google Scholar

Roussel, N., Cotillard, R., and Laffont, G. (2018). Capteur de température à réseau de Bragg insensible aux déformations. Paris, France: FR 3 087 008 B1.

Google Scholar

J. Rumble (Editor) (2021). CRC Handbook of Chemistry and Physics: 2020–2021. 102 edn. (Boca Raton, FL: CRC Press/Taylor & Francis).

Google Scholar

Salama, K., and Ling, C. K. (1980). The Effect of Stress on the Temperature Dependence of Ultrasonic Velocity. J. Appl. Phys. 51, 1505–1509. doi:10.1063/1.327800

CrossRef Full Text | Google Scholar

Schreier, H., Orteu, J.-J., and Sutton, M. A. (2009). Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications. Berlin, Germany: Springer. doi:10.1007/978-0-387-78747-3

CrossRef Full Text | Google Scholar

Timoshenko, S. P., and Goodier, J. N. (1970). Theory of Elasticity. third edn. New York, NY, USA: McGraw-Hill, Chap. 4. 68–71.

Google Scholar

Zhou, H., Lin, W., Ge, X., and Zhou, J. (2016). A Non-Intrusive Pressure Sensor by Detecting Multiple Longitudinal Waves. Sensors 16, 1237. doi:10.3390/s16081237

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

BEARN Boucle en Eau à l’Ambiance des Réacteurs Nucléaires (water pressure loop in nuclear reactors ambience)

FBG Fiber Bragg Grating

NPP Nuclear Power Plant

NPS Nominal Pipe Size

Sch. Schedule

Thermomechanical parameters

λ, μ Lamé’s coefficients

E Young’s modulus

ν Poisson’s ratio

α thermal expansion coefficient

a thermal effusivity

k thermal conductivity

ρ volume mass

C_p mass heat capacity

Geometrical parameters

$r_{0_{int}}$ initial inner radius

r_int current inner radius

$r_{0_{ext}}$ initial outer radius

r_ext current outer radius

R_ref initial curvature radius

R current curvature radius

Displacement, strain and stress

$\vec{u}\left(u,v,w\right)$ displacement vector $\vec{u}$ expressed in the cylindrical $\left(O,r,\theta ,z\right)$ coordinate system (Figure 1)

${\vec{u}}_{\sigma }$ mechanical displacement vector

${\vec{u}}_T$ thermal displacement vector

ɛ_mec mechanical strain

ɛ_th thermal strain

σ stress

Boundary conditions and integration coefficients

$P_{0_{int}}$ initial inner hydrostatic pressure

P_int current inner hydrostatic pressure

$P_{0_{ext}}$ initial outer hydrostatic pressure

P_ext current outer hydrostatic pressure

T₀ initial temperature

T current temperature

$\vec{F}$ longitudinal force

$\delta \vec{F}$ unexplained longitudinal force variation

$\vec{f}$ volume forces (including e.g.: gravity)

$\vec{\gamma }$ volume forces of acceleration

$\begin{array}{c}{K}_0\text{,\hspace{0.17em}}{K}_1\text{,\hspace{0.17em}}{K}_2\text{,\hspace{0.17em}}{K}_3\text{,}\\ K_4\text{,\hspace{0.17em}}{L}_1\text{\hspace{0.17em}\&\hspace{0.17em}}{L}_2\end{array}$ integration coefficients relative to the set of partial differential Eq. 12

Measurements

Ψ transducer raw measurement (e.g.: λ_B for the FBG transducer)

$\underline{\mathrm{\Delta }}\mathrm{\Psi }$ true relative variation of parameter Ψ between reference Ψ₀ and current Ψ₁ = Ψ₀ + Δ Ψ values $\underline{\mathrm{\Delta }}\mathrm{\Psi }=\ln \left(1+\frac{\mathrm{\Delta }\mathrm{\Psi }}{{\mathrm{\Psi }}_0}\right)$

ΔΨ variation of parameter Ψ between reference Ψ₀ and current Ψ₁ values ΔΨ = Ψ₁ − Ψ₀

FBG transducer

κ_T transducer sensitivity to temperature

κ_ɛ transducer sensitivity to longitudinal mechanical strain

n_eff optical fiber waveguide effective refractive index

Λ grating pitch

λ_B Bragg wavelength