Orbital motions as gradiometers for post-Newtonian tidal effects

1. Introduction

Gravitation is one of the known fundamental interactions of physics, and the General Theory of Relativity (GTR) is, at present, its best theoretical description (Will, 2009). As such, GTR is one of the pillars of our knowledge of Nature; intense experimental and observational scrutiny is required not only to gain an ever-increasing confidence about it, but also to explore the borders of the realm of its validity at different scales. To this aim, a variety of different theoretical, experimental and observational approaches are required to extend the frontiers of our knowledge of the gravitational phenomena. Are there some founded hopes to testing newly predicted gravitational effects in the near future in some suitable astronomical and astrophysical laboratories? What are the possibilities opened up by forthcoming space-based missions? The present paper will try to address these questions by looking at certain effects that the components of the Riemann spacetime curvature tensor are expected to induce on local systems according to GTR.

The internal dynamics of a gravitationally bound binary system immersed in the external gravitational field of a massive rotating body is tidally affected at both the Newtonian and the post-Newtonian level (Mashhoon, 1977; Chicone and Mashhoon, 2002, 2006; Kopeikin et al., 2011). In this paper, we will look in detail at some of the post-Newtonian orbital effects of tidal origin arising in the relative motion of a restricted two-body system, and at the possibility of detecting them in either natural or artificial space-based scenarios. Special cases widely treated in the literature are the post-Newtonian tidal effects of the rotating Sun's field in the Earth-Moon system (Braginsky and Polnarev, 1980; Mashhoon and Theiss, 1982, 1986; Gill et al., 1989; Mashhoon and Theiss, 1991, 2001) and of the spinning Earth itself in arrays of spaceborne artificial gradiometers (Mashhoon and Theiss, 1982; Theiss, 1985; Mashhoon et al., 1989; Paik, 1989; Theiss, 1992; Paik, 2008; Li et al., 2014). Our calculation will have a broad range of validity. Indeed, while, on the one hand, certain assumptions on the characteristic orbital frequencies of the three-body system considered will be necessarily made, on the other hand, we will remove the limitations existing in the literature (Chicone and Mashhoon, 2006) on either the orientation of the spin axes of the external objects and on the orbital configurations of the moving bodies.

The paper is organized as follows. In Section 2, the long-term rates of change of the orbital parameters of the test particle of the restricted two-body system are calculated by keeping the elements of a generic tidal matrix constant over the orbital period of the particle around its primary. In Section 3, the direct orbital effects due to both the gravitoelectric and the gravitomagnetic tidal matrices are obtained by averaging their elements over the orbital period of the motion around the distant body. Section 4 is devoted to exploring some experimental possibilities offered by forthcoming spacecraft-based missions to astronomical bodies. Section 5 summarizes our findings.

2. The Long-Term Orbital Rates of Change Averaged Over P_b

Let us consider an isolated rotating body of mass M′, equatorial radius R′ and proper angular momentum J′ at rest in some parameterized post-Newtonian coordinate system 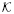′ whose spatial axes point to distant stars; as such, 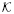′ is kinematically and dynamically non-rotating (Brumberg and Kopeikin, 1989). Let a local gravitationally bound system S move geodesically around M′; S is assumed to be made of a body of mass M, equatorial radius R and proper angular momentum J, and of a test particle of mass m revolving about M itself. For the sake of simplicity, we will assume m « M « M′; examples of such scenarios are spacecraft like MESSENGER (Solomon et al., 2007) and the forthcoming BepiColombo (Benkhoff et al., 2010) to orbit Mercury in the field of the Sun as well as the future JUICE mission (Grasset et al., 2013) to orbit Ganymede and to study the Jovian system. To the Newtonian level, the spatial trajectory of S about M′ can be parameterized in terms of the usual Keplerian orbital elements. They are the semimajor axis a′, the eccentricity e′, the inclination I′ to the reference $\left\{x^{\pr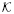ime },y^{\prime }\right\}$ plane of ′, the longitude of the ascending node Ω′, and the argument of pericenter ω′; $n_{\text{b}}{}^{\prime }=\sqrt{G{M}^{\prime }{a^{\prime }}^{-3}}$ is the Keplerian orbital frequency, where G is the Newtonian constant of gravitation. In general, such orbital parameters do not stay constant because of the well known Newtonian and post-Newtonian departures from spherical symmetry of the field of M′. They induce the post-Newtonian Einstein (gravitoelectric) (Einstein, 1915; Nobili and Will, 1986) and Lense-Thirring (gravitomagnetic) (Lense and Thirring, 1918) orbital precessions as well as the classical ones due to the oblateness J₂′ of M′ and, possibly, to its other multipoles of higher order (Bertotti et al., 2003).

Let a local inertial frame 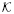, attached to M, be parallel transported along the geodesic worldline of M through the spacetime of M′ (Fermi, 1922; Levi-Civita, 1926; Synge, 1927). As such, the spatial axes of 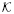change naturally their orientation with respect to the fixed “Copernican” spatial axes of 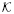′ because of the geodesic motion of 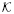itself through the external spacetime deformed by M′ and J′. As such, 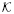is also said to be kinematically rotating because of the resulting de Sitter-Fokker (gravitoelectric) (de Sitter, 1916; Fokker, 1921) and Pugh-Schiff (gravitomagnetic) precessions¹ of its axes with respect to those of 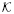′, but it is dynamically nonrotating because of the absence of Coriolis and centrifugal inertial forces (Brumberg and Kopeikin, 1989). To the Newtonian level, also the motion of m about M will be parameterized in terms of a set of Keplerian orbital elements a, e, I, Ω, ω in such a way that $n_{\text{b}}=\sqrt{GM{a}^{-3}}$ denotes its Keplerian orbital frequency. Usually, the frequencies of the de Sitter-Fokker and Pugh-Schiff precessions are quite smaller than both n_b′ and n_b; for a critical discussion tidal phenomena occurring in the Sun-Earth-Moon system over timescales comparable to or larger than the de Sitter-Fokker and Pugh-Schiff ones, see (Gill et al., 1989; Mashhoon and Theiss, 1991). Thus, we can safely assume 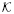as kinematically nonrotating over timescales comparable to the orbital periods P_b = 2πn⁻¹_b and P′_b = 2πn_b′⁻¹ of the three-body system considered. As a further assumption, we will consider the local motion of m about M much faster than the one of S itself around M′, i.e., n_b′ « n_b. In general, the internal dynamics of S is not purely Keplerian because of possible departures from sphericity of M and of the post-Newtonian components of the field of M. As such, the orbit of m with respect to M undergoes the well-known Newtonian and post-Newtonian orbital precessions. As it occurs in the systems considered here, the timescales of such changes are quite longer than the orbital periods P_b, P′_b, i.e., $\dot{\Psi }$ « n_b′, where Ψ denotes a generic precessing osculating Keplerian orbital element of m.

At both the Newtonian and the post-Newtonian level, the internal dynamics of S is locally affected also by tidal effects due to its motion through the external deformed spacetime of M′. The tidal acceleration experienced by m is of the form (Mashhoon et al., 1989)

$\begin{array}{cc}{A}_{\text{tid}}=-Kr,& \left(1\right)\end{array}$

where the elements of the tidal matrix K

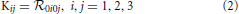
are the tetrad components of the curvature Riemann tensor evaluated onto the geodesic of the observer in 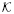, and have dimensions of T⁻². It is

$\begin{array}{cc}K=K^{\left(\text{N}\right)}+K^{\left(\text{GE}\right)}+K^{\left(\text{GM}\right)},& \left(3\right)\end{array}$

with the Newtonian (N), gravitoelectric (GE) and gravitomagnetic (GM) tidal matrices given by (Mashhoon et al., 1989)

$\begin{array}{cc}{\text{K}}_{ij}^{\left(\text{N}\right)}=\frac{G{M}^{\prime }}{{r^{\prime }}^3}\left({\delta }_{ij}-3{\widehat{r^{\prime }}}_i{\widehat{r^{\prime }}}_j\right),& \left(4\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\text{K}}_{ij}^{\left(\text{GE}\right)}=-\frac{G^2{M^{\prime }}^2}{c^2{r^{\prime }}^4}(3{\delta }_{ij}-9{\widehat{r^{\prime }}}_i{\widehat{r^{\prime }}}_j)\\ +\frac{G{M}^{\prime }}{c^2{r^{\prime }}^3}\{3[{v^{\prime }}^2{\delta }_{ij}-{v^{\prime }}_i{v^{\prime }}_j+3(v^{\prime }·\widehat{r^{\prime }}\left){\widehat{r^{\prime }}}_{(i}{v^{\prime }}_{j)}\right]\\ -3{(v^{\prime }·\widehat{r^{\prime }})}^2{\delta }_{ij}-6{\widehat{r^{\prime }}}_i{\widehat{r^{\prime }}}_j{v^{\prime }}^2\},\end{array}& \left(5\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\text{K}}_{ij}^{\left(\text{GM}\right)}=-\frac{6G{J}^{\prime }}{c^2{r^{\prime }}^4}\{3{(v^{\prime }\times \widehat{k^{\prime }})}_{(i}{\widehat{r^{\prime }}}_{j)}+{(\widehat{r^{\prime }}\times \widehat{k^{\prime }})}_{(i}{v^{\prime }}_{j)}\\ +\widehat{r^{\prime }}·(v^{\prime }\times \widehat{k^{\prime }})({\delta }_{ij}-5{\widehat{r^{\prime }}}_i{\widehat{r^{\prime }}}_j)\\ -5(\widehat{r^{\prime }}·v^{\prime }){(\widehat{r^{\prime }}\times \widehat{k^{\prime }})}_{(i}{\widehat{r^{\prime }}}_{j)}\}.\end{array}& \left(6\right)\end{array}$

In Equations (4–6), which are symmetric and traceless, c is the speed of light in vacuum, $\widehat{r^{\prime }}$ = r′/r′ is the versor of the position vector r′ from M′ to M, v′ is the velocity vector of M with respect to M′, δ_ij is the Kronecker symbol, $\widehat{k^{\prime }}$ is the unit vector of the spin axis of M′, the symbols · and × denote the usual scalar and cross products among vectors, and parentheses around indices denote symmetrization.

The tidal acceleration of Equation (1) can be considered as a small perturbation A_pert of the Newtonian monopole of M. As such, its impact on the orbital dynamics of m can be treated perturbatively with standard techniques. By recalling the condition n_b′ « n_b, the elements of the tidal matrix K can be considered as constant over an orbital period P_b. Thus, by evaluating the right-hand-sides of the Gauss equations (Burns, 1976)

$\begin{array}{cc}\frac{da}{dt}=\frac{2}{n_{\text{b}}\sqrt{1-e^2}}(e{A}_R\sin f+\frac{p}{r}{A}_T),& \left(7\right)\end{array}$

$\begin{array}{cc}\frac{de}{dt}=\frac{\sqrt{1-e^2}}{n_{\text{b}}a}\left\{A_R\sin f+A_T\text{}\left[\cos f+\frac{1}{e}(1-\frac{r}{a})\right]\right\}\text{},& \left(8\right)\end{array}$

$\begin{array}{cc}\frac{dI}{dt}=\frac{\cos \text{(}\omega +f)}{n_{\text{b}}a\sqrt{1-e^2}}\left(\frac{r}{a}\right)A_N,& \left(9\right)\end{array}$

$\begin{array}{cc}\frac{d\Omega }{dt}=\frac{\sin (\omega +f)}{n_{\text{b}}a\sin \text{I}\sqrt{1-e^2}}\left(\frac{r}{a}\right)A_N,& \left(10\right)\end{array}$

$\begin{array}{cc}\frac{d\omega }{dt}+\cos I\frac{d\Omega }{dt}=\frac{\sqrt{1-e^2}}{n_{\text{b}}ae}\left[-A_R\cos f+A_T(1+\frac{r}{p})\sin f\right]\text{}.& \left(11\right)\end{array}$

onto the unperturbed Keplerian ellipse

$\begin{array}{cc}r=\frac{p}{1+e\cos f},& \left(12\right)\end{array}$

where p = a (1 − e²) is the semilatus rectum and A_R, A_T, A_N are the radial, transverse and out-of-plane components of Equation (1), the orbital variations of m averaged over P_b can be calculated. To this aim, let us note that, in principle, the average should be made by means of (Brumberg, 1991; Will, 2014)

$\begin{array}{cc}\frac{df}{dt}=n_{\text{b}}(\frac{a}{r}{)}^2\sqrt{1-e^2}-(\frac{d\omega }{dt}+\cos I\frac{d\Omega }{dt}),& \left(13\right)\end{array}$

where t is the proper time along the observer's geodesic, f is the true anomaly, and $\stackrel{.}{\Omega }$,$\dot{\omega }$ are to be intended as the instantaneous, non-averaged precessions of the node and the pericenter (Brumberg, 1991). Indeed, f is reckoned from the pericenter position, which, in general, changes because of possible variations of Ω and ω due to the non-Keplerian Newtonian and post-Newtonian effects within S. As such, the instantaneous expressions for $\stackrel{.}{\Omega }$ and $\dot{\omega }$ in Equation (13) should be taken from Equations (10,11) themselves evaluated for the specific Newtonian and post-Newtonian perturbations (Brumberg, 1991). However, by limiting ourselves just to the order 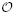(c⁻²), and by neglecting small mixed terms of order 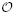(J₂c⁻²) arising from the interplay between the external tidal and the local Newtonian perturbations due to J₂, the approximate expression

$\begin{array}{cc}\frac{df}{dt}=n_{\text{b}}(\frac{a}{r}{)}^2\sqrt{1-e^2}& \left(14\right)\end{array}$

can be used by integrating over f between 0 and 2π. By using the following Keplerian expressions for the position r

$\begin{array}{cc}x=r\text{[}\cos \Omega \cos \left(f+\omega \right)-\cos I\sin \Omega \sin \left(f+\omega \right)],& \left(15\right)\end{array}$

$\begin{array}{cc}y=r[\sin \Omega \cos \left(f+\omega \right)+\cos I\cos \Omega \sin \left(f+\omega \right)],& \left(16\right)\end{array}$

$\begin{array}{cc}z=r[\sin I\sin \left(f+\omega \right)],& \left(17\right)\end{array}$

and the velocity v

$\begin{array}{cc}{v}_x=-\frac{\begin{array}{l}a{n}_{\text{b}}\{\cos I\sin \Omega \text{[}e\cos \omega +\cos \left(f+\omega \right)]\hfill \\ +\cos \Omega \text{[}e\sin \omega +\sin \left(f+\omega \right)]\}\hfill \end{array}}{\sqrt{1-e^2}},& \left(18\right)\end{array}$

$\begin{array}{cc}{v}_y=\frac{\begin{array}{l}\begin{array}{l}a{n}_{\text{b}}\{\cos I\cos \Omega \text{[}e\cos \omega +\cos \left(f+\omega \right)]\\ -\sin \Omega \text{[}e\sin \omega +\sin \left(f+\omega \right)]\}\end{array}\hfill \end{array}}{\sqrt{1-e^2}},& \left(19\right)\end{array}$

$\begin{array}{cc}{v}_z=\frac{a{n}_{\text{b}}\sin I\text{[}e\cos \omega +\cos \left(f+\omega \right)]}{\sqrt{1-e^2}},& \left(20\right)\end{array}$

it is possible to compute from Equations (15–20) the unit vector $\widehat{L}$ along the orbital angular momentum as

$\begin{array}{cc}\widehat{L}=\frac{r\times v}{\left|r\times v\right|}.& \left(21\right)\end{array}$

Then, the radial, transverse and normal components of Equation (1) turn out to be

$\begin{array}{cc}\begin{array}{l}{A}_R=A_{\text{tid}}·\widehat{r}=\frac{\text{K}a(1-e^2)}{1+e\cos f}\\ ·\{\left[\cos I\sin \left(f+\omega \right)\sin \Omega -\cos \left(f+\omega \right)\cos \Omega \right]\\ ·[\sin f(K_{21}\cos I\cos \omega \cos \Omega +\left(K_{22}+K_{33}\right)\sin \omega \cos \Omega \\ +K_{31}\cos \omega \sin I)+\cos f(K_{11}\cos \omega \cos \Omega \\ +\left(K_{21}\cos I\cos \Omega +K_{31}\sin I\right)\sin \omega )+(K_{21}\cos \left(f+\omega \right)\\ +\left(K_{22}+K_{33}\right)\cos I\sin \left(f+\omega \right))\sin \Omega ]\\ +\left(\cos I\cos \Omega \sin \left(f+\omega \right)+\cos \left(f+\omega \right)\sin \Omega \right)\\ ·(\cos \left(f+\omega \right)\left(K_{21}\cos \Omega +K_{22}\sin \Omega \right)\\ +\sin \left(f+\omega \right)\left(K_{32}\sin I+\cos I\left(K_{22}\cos \Omega -K_{21}\sin \Omega \right)\right))\\ +\sin I\sin \left(f+\omega \right)(\cos \left(f+\omega \right)\left(K_{31}\cos \Omega +K_{32}\sin \Omega \right)\\ +\sin \left(f+\omega \right)\left(K_{33}\sin I+\cos I\left(K_{32}\cos \Omega -K_{31}\sin \Omega \right)\right))\},\end{array}& \left(22\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{A}_T=A_{\text{tid}}·(\widehat{L}\times \widehat{r})=-\frac{\text{K}a(1-e^2)}{4(1+e\cos f)}\{\left(f+\omega \right)(-K_{33}+\left(2K_{22}+K_{33}\right)\\ ·\cos 2\Omega -2K_{21}\sin 2\Omega ){\cos }^{2}I\sin \left(2f+2\omega \right)\\ +2(2\sin I\left(K_{32}\cos \Omega -K_{31}\sin \Omega \right)\sin \left(2f+2\omega \right)\\ +\left[2K_{21}\cos 2\Omega +\left(2K_{22}+K_{33}\right)\sin 2\Omega \right])\cos I\cos \left(2f+2\omega \right)\\ +4\sin I\left(K_{31}\cos \Omega +K_{32}\sin \Omega \right)\cos \left(2f+2\omega \right)\\ +[\left(2-\cos 2I\right)K_{33}+\left(2K_{22}+K_{33}\right)\cos 2\Omega \\ -2K_{21}\sin 2\Omega ]\sin \left(2f+2\omega \right)\},\end{array}& \left(23\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{A}_N=A_{\text{tid}}·\widehat{L}=-\frac{\text{K}a(1-e^2)}{4(1+e\cos f)}\{4\cos I\left(K_{31}\cos \Omega +K_{32}\sin \Omega \right)\\ ·\cos \left(f+\omega \right)+2\sin I\left[-2K_{21}\cos 2\Omega -\left(2K_{22}+K_{33}\right)\sin 2\Omega \right]\\ ·\cos \left(f+\omega \right)+4\cos 2I\left(K_{32}\cos \Omega -K_{31}\sin \Omega \right)\sin \left(f+\omega \right)\\ +\sin 2I\left[3K_{33}-\left(2K_{22}+K_{33}\right)\cos 2\Omega +2K_{21}\sin 2\Omega \right]\\ ·\sin \left(f+\omega \right)\},\end{array}& \left(24\right)\end{array}$

where K is the dimensional scaling factor of the tidal matrix considered having dimensions of T⁻², while the dimensionless coefficients K_ij, i, j = 1, 2, 3 depend only on the orbital parameters of M and on the orientation of $\widehat{k^{\prime }}$. Thus, by inserting Equations (22–24) in the right-hand-sides of Equations (7–11) and averaging them over P_b with Equation (14), one finally has

$\begin{array}{cc}{\langle \frac{da}{dt}\rangle }_{P_{\text{b}}}=0,& \left(25\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\langle \frac{de}{dt}\rangle }_{P_{\text{b}}}=\frac{5\text{K}e\sqrt{1-e^2}}{8n_{\text{b}}}\{-2\sin 2\omega \sin \Omega (2K_{21}\text{}\cos \Omega +K_{33}\sin \Omega \text{)}\\ +{\cos }^{2}I+2[2\sin I\sin 2\omega \left(K_{32}\cos \Omega -K_{31}\sin \Omega \right)\\ +\cos 2\omega \left(2K_{21}\cos 2\Omega +\left(2K_{22}+K_{33}\right)\sin 2\Omega \right)]\cos I\\ +4\cos 2\omega \sin I\left(K_{31}\cos \Omega +K_{32}\sin \Omega \right)\\ +\sin 2\omega [K_{22}\left(\cos 2I+3\right)\cos 2\Omega \\ +K_{33}\left(-\cos 2I+\cos 2\Omega +2\right)-2K_{21}\sin 2\Omega ]\},\end{array}& \left(26\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle \frac{dI}{dt}\rangle P_b=-\frac{K}{8n_b\sqrt{1-e^2}}\{10e^2\cos 2I\sin 2\omega (K_{32}\text{}\cos \Omega -K_{31}\text{}\sin \Omega )\text{}\hfill \\ -\frac{5}{2}{e}^2\sin 2I\sin 2\omega [-3K_{33}+(2K_{22}+K_{33})\cos 2\Omega \hfill \\ -2K_{21}\sin 2\Omega ]+2\cos I(5e^2\cos 2\omega +3e^2+2)\hfill \\ ·(K_{31}\cos \Omega +K_{32}\sin \Omega )-(5e^2\cos 2\omega +3e^2+2)\sin I\hfill \\ ·[2K_{21}\cos 2\Omega +(2K_{22}+K_{33})\sin 2\Omega ]\},\hfill \end{array}& \left(27\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle \frac{d\Omega }{dt}\rangle P_b=-\frac{K\csc I}{16n_b\sqrt{1-e^2}}\{20e^2\sin 2\omega \text{}(\cos I(K_{31}\cos \Omega +K_{32}\sin \Omega )\text{}\hfill \\ -\sin I(K_{21}\cos 2\Omega +(2K_{22}+K_{33}\left)\cos \Omega \sin \Omega \right))\hfill \\ +4\cos 2I(5e^2\cos 2\omega -3e^2-2)(K_{31}\sin \Omega -K_{32}\cos \Omega )\hfill \\ +(5e^2\cos 2\omega -3e^2-2)\sin 2I[-3K_{33}+(2K_{22}+K_{33})\hfill \\ ·\cos 2\Omega -2K_{21}\sin 2\Omega ]\},\hfill \end{array}& \left(28\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\langle \frac{d\omega }{dt}\rangle }_{P_{\text{b}}}+\cos I{\langle \frac{d\Omega }{dt}\rangle }_{P_{\text{b}}}\\ =\frac{\text{K}\sqrt{1-e^2}}{16n_{\text{b}}}\{-40\sin I\sin 2\omega \left(K_{31}\cos \Omega +K_{32}\sin \Omega \right)\\ +4\left(5\cos 2\omega -3\right)\sin 2I\left(K_{32}\cos \Omega -K_{31}\sin \Omega \right)\\ -20\cos I\sin 2\omega \left[2K_{21}\cos 2\Omega +\left(2K_{22}+K_{33}\right)\sin 2\Omega \right]\\ +\cos 2I\left(5\cos 2\omega -3\right)[-3K_{33}+\left(2K_{22}+K_{33}\right)\cos 2\Omega \\ -2K_{21}\sin 2\Omega ]+3\left(5\cos 2\omega +1\right)[K_{33}+\left(2K_{22}+K_{33}\right)\\ ·\cos 2\Omega -2K_{21}\sin 2\Omega ]\}.\end{array}& \left(29\right)\end{array}$

The long-term rates of Equations (25–29) are valid for any symmetric and traceless tidal-type perturbation of the form of Equation (1) whose coefficients can be considered as constant over the characteristic orbital frequency n_b of the local binary system considered. As such, Equations (25–29) are not limited just to Equations (5,6). Moreover, Equations (25–29) hold for a general orbital configuration of the test particle m since no a priori simplifying assumptions concerning its eccentricity and inclination were made. As shown by Equation (26), the eccentricity of a circular orbit is not affected by a tidal-type perturbation.

3. The Long-Term Orbital Rates of Change Averaged Over P′_b

In general, Equations (25–29) may not be regarded as truly secular rates over timescales arbitrarily long because of the slow time dependence encoded in both the tidal matrix elements themselves and in the orbital elements of m, collectively denoted as {Ψ}, due to possible non-Keplerian local effects taking place in the non-spherically symmetric field of M.

Let us, now, assume that the characteristic timescales P_Ψ of all the non-Keplerian orbital effects within S are much longer than the orbital period P′_b of S itself about M′. It is a reasonable tenet, satisfied in several astronomical scenarios of potential experimental interest. Thus, it is possible to perform a further average of Equations (25–29) over P′_b by keeping a, e, I, Ω, ω constant over the integration with respect to some fast variable² of the motion of M around M′.

The direct effects of order 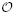(c⁻²) can be obtained by evaluating the post-Newtonian tidal matrices Equations (5,6) onto an unchanging Keplerian ellipse as reference unperturbed trajectory.

Below, the averaged tidal matrix elements of Equations (4–6), computed to order 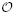(c⁻²) and to zero order in J₂′, are listed. They are to be inserted in Equations (25–29) to have the direct long-term rates of change of m averaged over P′_b.

As far as the Newtonian tidal matrix of Equation (4) is concerned, its average, to the zero order in J₂′, is

$\begin{array}{cc}{\langle {\text{K}}_{11}^{\left(\text{N}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=-\frac{G{M}^{\prime }(1+3\cos 2I^{\prime }+6{\sin }^2{I}^{\prime }\cos 2{\Omega }^{\prime })}{8{a^{\prime }}^3{(1-{e^{\prime }}^2)}^{3/2}},& \left(30\right)\end{array}$

$\begin{array}{cc}{\langle {\text{K}}_{22}^{\left(\text{N}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=-\frac{G{M}^{\prime }(1+3\cos 2I^{\prime }+6{\sin }^2{I}^{\prime }\cos 2{\Omega }^{\prime })}{8{a^{\prime }}^3{(1-{e^{\prime }}^2)}^{3/2}},& \left(31\right)\end{array}$

$\begin{array}{cc}{\langle {\text{K}}_{33}^{\left(\text{N}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=\frac{G{M}^{\prime }(1+3\cos 2I^{\prime })}{4{a^{\prime }}^3{(1-{e^{\prime }}^2)}^{3/2}},& \left(32\right)\end{array}$

$\begin{array}{cc}{\langle {\text{K}}_{12}^{\left(\text{N}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=-\frac{3G{M}^{\prime }{\sin }^2{I}^{\prime }\sin 2{\Omega }^{\prime }}{4{a^{\prime }}^3(1-{e^{\prime }}^2{}^{3/2})},& \left(33\right)\end{array}$

$\begin{array}{cc}{\langle {\text{K}}_{13}^{\left(\text{N}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=\frac{3G{M}^{\prime }\sin 2I^{\prime }\sin {\Omega }^{\prime }}{4{a^{\prime }}^3(1-{e^{\prime }}^2{}^{3/2}\text{)}},& \left(34\right)\end{array}$

$\begin{array}{cc}{\langle {\text{K}}_{23}^{\left(\text{N}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=-\frac{3G{M}^{\prime }\sin 2I^{\prime }\cos {\Omega }^{\prime }}{4{a^{\prime }}^3(1-{e^{\prime }}^2{}^{3/2}\text{)}}.& \left(35\right)\end{array}$

For the post-Newtonian gravitoelectric tidal field of M′, Equation (5) yields

$\begin{array}{cc}\begin{array}{l}{\langle {\text{K}}_{11}^{\left(\text{GE}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=-\frac{3G^2{M^{\prime }}^2{e^{\prime }}^2}{32c^2{a^{\prime }}^4(1-{e^{\prime }}^2{}^{5/2}\text{)}}\\ ·\{12\cos 2I^{\prime }+2\cos 2{\omega }^{\prime }-2\cos 2I^{\prime }\cos 2{\omega }^{\prime }\\ +\cos 2{\Omega }^{\prime }\left[24{\sin }^2{I}^{\prime }+2\left(\cos 2I^{\prime }+3\right)\cos 2{\omega }^{\prime }\right]\\ -8\cos I^{\prime }\sin 2{\Omega }^{\prime }\sin 2{\omega }^{\prime }+4\},\end{array}& \left(36\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\langle {\text{K}}_{22}^{\left(\text{GE}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=\frac{3G^2{M^{\prime }}^2{e^{\prime }}^2}{32c^2{a^{\prime }}^4{(1-{e^{\prime }}^2)}^{5/2}}\\ ·\{-12\cos 2I^{\prime }-2\cos 2{\omega }^{\prime }+2\cos 2I^{\prime }\cos 2{\omega }^{\prime }\\ +\cos 2{\Omega }^{\prime }[24{\sin }^2{I}^{\prime }+2\left(\cos 2I^{\prime }+3\right)\cos 2{\omega }^{\prime }]\\ -8\cos I^{\prime }\sin 2{\Omega }^{\prime }\sin 2{\omega }^{\prime }-4\},\end{array}& \left(37\right)\end{array}$

$\begin{array}{cc}{\langle {\text{K}}_{33}^{\left(\text{GE}\right)}\rangle }_{{P^{\prime }}_{\text{b}}}=\frac{3G^2{M^{\prime }}^2{e^{\prime }}^2}{4c^2{a^{\prime }}^4{(1-{e^{\prime }}^2)}^{5/2}}({\sin }^2{I}^{\prime }\cos 2{\omega }^{\prime }+3\cos 2I^{\prime }+1),& \left(38\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{12}^{\left(\text{GE}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =-\frac{3G^2{M^{\prime }}^2{e^{\prime }}^2}{16c^2{a^{\prime }}^4{(1-{e^{\prime }}^2)}^{5/2}}\{4\cos I^{\prime }\cos 2{\Omega }^{\prime }\sin 2{\omega }^{\prime }\\ +\left[12{\sin }^2{I}^{\prime }+\left(\cos 2I^{\prime }+3\right)\cos 2{\omega }^{\prime }\right]\sin 2{\Omega }^{\prime }\},\end{array}& \left(39\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{13}^{\left(\text{GE}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =-\frac{3G^2{M^{\prime }}^2{e^{\prime }}^2}{4c^2{a^{\prime }}^4{(1-{e^{\prime }}^2)}^{5/2}}\\ ·\left\{\sin I^{\prime }\left[\cos {\Omega }^{\prime }\sin 2{\omega }^{\prime }+\cos I^{\prime }\left(\cos 2{\omega }^{\prime }-6\right)\sin {\Omega }^{\prime }\right]\right\},\end{array}& \left(40\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{23}^{\left(\text{GE}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =\frac{3G^2{M^{\prime }}^2{e^{\prime }}^2}{4c^2{a^{\prime }}^4{(1-{e^{\prime }}^2)}^{5/2}}\\ ·\left\{\sin I^{\prime }\left[\cos I^{\prime }\left(\cos 2{\omega }^{\prime }-6\right)\cos {\Omega }^{\prime }-\sin 2{\omega }^{\prime }\sin {\Omega }^{\prime }\right]\right\}.\end{array}& \left(41\right)\end{array}$

In the limit of e′ → 0, Equations (36–41) vanish.

For the post-Newtonian gravitomagnetic tidal field of M′ due to J′, from Equation (6) one obtains

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{11}^{\left(\text{GM}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =-\frac{3G{J}^{\prime }{n}_{{\text{b}}^{\prime }}}{64c^2{a^{\prime }}^3{(1-{e^{\prime }}^2)}^3}\\ ·\{40{e^{\prime }}^2\sin 2{\omega }^{\prime }\left(2{\widehat{k}}_{z^{\prime }}\cos 2I^{\prime }+3{\widehat{k}}_{x^{\prime }}\sin 2I^{\prime }\sin {\Omega }^{\prime }\right)\sin 2{\Omega }^{\prime }\\ +5\cos 2{\omega }^{\prime }(12\sin 3I^{\prime }\left({\widehat{k}}_{x^{\prime }}\sin {\Omega }^{\prime }-{\widehat{k}}_{y^{\prime }}\cos {\Omega }^{\prime }\right){\sin }^2{\Omega }^{\prime }\\ +\sin I^{\prime }({\widehat{k}}_{y^{\prime }}\left(\cos {\Omega }^{\prime }+15\cos 3{\Omega }^{\prime }\right)\\ -3{\widehat{k}}_{x^{\prime }}\left(\sin {\Omega }^{\prime }+5\sin 3{\Omega }^{\prime }\right))){e^{\prime }}^2\\ -20\left(3{e^{\prime }}^2+2\right){\widehat{k}}_{z^{\prime }}\cos 3I^{\prime }-4\cos I^{\prime }(5{\widehat{k}}_{z^{\prime }}\cos 2{\omega }^{\prime }(6{\sin }^2{I}^{\prime }\\ +\left(3\cos 2I^{\prime }+1\right)\cos 2{\Omega }^{\prime }){e^{\prime }}^2-10{\widehat{k}}_{y^{\prime }}\sin I^{\prime }\sin 2{\omega }^{\prime }\\ ·\left(\sin {\Omega }^{\prime }-3\sin 3{\Omega }^{\prime }\right){e^{\prime }}^2+\left(3{e^{\prime }}^2+2\right){\widehat{k}}_{z^{\prime }}\\ ·\left(20\cos 2{\Omega }^{\prime }{\sin }^2{I}^{\prime }+3\right))\\ +2\left(3{e^{\prime }}^2+2\right)(20\sin 3I^{\prime }\left({\widehat{k}}_y^{\prime }\cos {\Omega }^{\prime }-{\widehat{k}}_x^{\prime }\sin {\Omega }^{\prime }\right){\sin }^2{\Omega }^{\prime }\\ +\sin I^{\prime }\left({\widehat{k}}_{y^{\prime }}\left(\cos {\Omega }^{\prime }+15\cos 3{\Omega }^{\prime }\right)-3{\widehat{k}}_{x^{\prime }}\left(\sin {\Omega }^{\prime }+5\sin 3{\Omega }^{\prime }\right)\right))\},\end{array}& \left(42\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{22}^{\left(\text{GM}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =-\frac{3G{J}^{\prime }{n}_{\text{b}}^{\prime }}{64c^2{a^{\prime }}^3{(1-{e^{\prime }}^2)}^3}\\ ·\{20{e^{\prime }}^2{\widehat{k}}_x^{\prime }\left(\cos {\Omega }^{\prime }+3\cos 3{\Omega }^{\prime }\right)\sin 2I^{\prime }\sin 2{\omega }^{\prime }\\ -80{e^{\prime }}^2{\widehat{k}}_z^{\prime }\cos 2I^{\prime }\sin 2{\omega }^{\prime }\sin 2{\Omega }^{\prime }-20\left(3{e^{\prime }}^2+2\right){\widehat{k}}_z^{\prime }\cos 3I^{\prime }\\ +20\left(3{e^{\prime }}^2\cos 2{\omega }^{\prime }-6{e^{\prime }}^2-4\right){\cos }^2{\Omega }^{\prime }\sin 3I^{\prime }\\ ·\left({\widehat{k}}_x^{\prime }\sin {\Omega }^{\prime }-{\widehat{k}}_y^{\prime }\cos {\Omega }^{\prime }\right)\\ +4{e^{\prime }}^2\cos I^{\prime }(5{\widehat{k}}_z^{\prime }\cos 2{\omega }^{\prime }\left(\left(3\cos 2I^{\prime }+1\right)\cos 2{\Omega }^{\prime }-6{\sin }^2{I}^{\prime }\right)\\ +120{e^{\prime }}^2{\widehat{k}}_y^{\prime }{\cos }^2{\Omega }^{\prime }\sin I^{\prime }\sin 2{\omega }^{\prime }\sin {\Omega }^{\prime }\\ +\left(3{e^{\prime }}^2+2\right){\widehat{k}}_z^{\prime }\left(20\cos 2{\Omega }^{\prime }{\sin }^2{I}^{\prime }-3\right))\\ +\left(5{e^{\prime }}^2\cos 2{\omega }^{\prime }+6{e^{\prime }}^2+4\right)\sin I^{\prime }(3{\widehat{k}}_{y^{\prime }}\cos {\Omega }^{\prime }\\ -15{\widehat{k}}_y^{\prime }\cos 3{\Omega }^{\prime }-{\widehat{k}}_x^{\prime }\sin {\Omega }^{\prime }+15{\widehat{k}}_x^{\prime }\sin 3{\Omega }^{\prime })\},\end{array}& \left(43\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{33}^{\left(\text{GM}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =-\frac{3G{J}^{\prime }{n}_{{\text{b}}^{\prime }}}{16c^2{a^{\prime }}^3{(1-{e^{\prime }}^2\text{)}}^3}\\ ·\{-20{e^{\prime }}^2\sin 2I^{\prime }\sin 2{\Omega }^{\prime }\left({\widehat{k}}_x^{\prime }\cos {\Omega }^{\prime }+{\widehat{k}}_y^{\prime }\sin {\Omega }^{\prime }\right)\\ +5{e^{\prime }}^2\cos 2{\Omega }^{\prime }(12{\widehat{k}}_z^{\prime }\cos I^{\prime }{\sin }^2{I}^{\prime }+{\widehat{k}}_y^{\prime }\cos {\Omega }^{\prime }\left(3\sin 3I^{\prime }-\sin I^{\prime }\right)\\ +{\widehat{k}}_x^{\prime }\left(\sin I^{\prime }-3\sin 3I^{\prime }\right)\sin {\Omega }^{\prime })\\ +2\left(3{e^{\prime }}^2+2\right)(3{\widehat{k}}_z^{\prime }\cos I^{\prime }+5{\widehat{k}}_z^{\prime }\cos 3I^{\prime }\\ -\left(\sin I^{\prime }+5\sin 3I^{\prime }\right)\left({\widehat{k}}_y^{\prime }\cos {\Omega }^{\prime }-{\widehat{k}}_x^{\prime }\sin {\Omega }^{\prime }\right))\},\end{array}& \left(44\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{12}^{\left(\text{GM}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =-\frac{3G{J}^{\prime }{n}_{{\text{b}}^{\prime }}}{64c^2{a^{\prime }}^3{(1-{e^{\prime }}^2)}^3}\\ ·\{-80{e^{\prime }}^2{\widehat{k}}_z^{\prime }\cos 2I^{\prime }\cos 2{\Omega }^{\prime }\sin 2{\omega }^{\prime }\\ +20{e^{\prime }}^2\sin 2I^{\prime }\sin 2{\omega }^{\prime }({\widehat{k}}_y^{\prime }\cos {\Omega }^{\prime }+3{\widehat{k}}_y^{\prime }\cos 3{\Omega }^{\prime }\\ +{\widehat{k}}_x^{\prime }\left(\sin {\Omega }^{\prime }-3\sin 3{\Omega }^{\prime }\right))\\ -10{\widehat{k}}_z^{\prime }\cos 3I^{\prime }\left(3{e^{\prime }}^2\cos 2{\omega }^{\prime }-6{e^{\prime }}^2-4\right)\sin 2{\Omega }^{\prime }\\ -10{\widehat{k}}_z^{\prime }\cos I^{\prime }\left(5{e^{\prime }}^2\cos 2{\omega }^{\prime }+6{e^{\prime }}^2+4\right)\sin 2{\Omega }^{\prime }\\ +10\left(3{e^{\prime }}^2\cos 2{\omega }^{\prime }-6{e^{\prime }}^2-4\right)\sin 3I^{\prime }\\ ·\left({\widehat{k}}_y^{\prime }\cos {\Omega }^{\prime }-{\widehat{k}}_x^{\prime }\sin {\Omega }^{\prime }\right)\sin 2{\Omega }^{\prime }\\ +\left(5{e^{\prime }}^2\cos 2{\omega }^{\prime }+6{e^{\prime }}^2+4\right)\sin I^{\prime }({\widehat{k}}_x^{\prime }\cos {\Omega }^{\prime }+15{\widehat{k}}_x^{\prime }\cos 3{\Omega }^{\prime }\\ -{\widehat{k}}_y^{\prime }\sin {\Omega }^{\prime }+15{\widehat{k}}_y^{\prime }\sin 3{\Omega }^{\prime })\},\end{array}& \left(45\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{13}^{\left(\text{GM}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =\frac{3G{J}^{\prime }{n}_{{\text{b}}^{\prime }}}{32c^2{a^{\prime }}^3{(1-{e^{\prime }}^2\text{)}}^3}\\ ·\{-10{e^{\prime }}^2{\widehat{k}}_z^{\prime }\cos 2{\omega }^{\prime }\left(\sin I^{\prime }-3\sin 3I^{\prime }\right)\sin {\Omega }^{\prime }\\ +40{e^{\prime }}^2\sin 2{\omega }^{\prime }({\widehat{k}}_z^{\prime }\cos {\Omega }^{\prime }\sin 2I^{\prime }\\ +\cos 2I^{\prime }\left({\widehat{k}}_y^{\prime }\cos 2{\Omega }^{\prime }-{\widehat{k}}_y^{\prime }\sin 2{\Omega }^{\prime }\right))\\ -4\left(3{e^{\prime }}^2+2\right){\widehat{k}}_z^{\prime }\left(\sin I^{\prime }+5\sin 3I^{\prime }\right)\sin {\Omega }^{\prime }\\ +5{e^{\prime }}^2\cos 3I^{\prime }(3\cos 2{\omega }^{\prime }\left({\widehat{k}}_x^{\prime }\cos 2{\Omega }^{\prime }+{\widehat{k}}_y^{\prime }\sin 2{\Omega }^{\prime }\right)\\ +2\left(3{e^{\prime }}^2+2\right){\widehat{k}}_x^{\prime })\\ +{e^{\prime }}^2\cos I^{\prime }(5\cos 2{\omega }^{\prime }(12{\widehat{k}}_x^{\prime }{\sin }^2{I}^{\prime }\\ +5{\widehat{k}}_x^{\prime }\cos 2{\Omega }^{\prime }+5{\widehat{k}}_y^{\prime }\sin 2{\Omega }^{\prime })\\ +2\left(3{e^{\prime }}^2+2\right)(20({\widehat{k}}_x^{\prime }\cos 2{\Omega }^{\prime }\\ +{\widehat{k}}_y^{\prime }\sin 2{\Omega }^{\prime }){\sin }^2{I}^{\prime }+3{\widehat{k}}_x^{\prime }))\},\end{array}& \left(46\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}\langle {\text{K}}_{23}^{\left(\text{GM}\right)}{}_{{P^{\prime }}_{\text{b}}}\rangle =\frac{-3G{J}^{\prime }{n}_{\text{b}}^{\prime }}{64c^2{a^{\prime }}^3{(1-{e^{\prime }}^2)}^3}\\ ·\{10{e^{\prime }}^2\cos 2{\omega }^{\prime }(-12{\widehat{k}}_y^{\prime }\cos I^{\prime }{\sin }^2{I}^{\prime }\\ +{\widehat{k}}_y^{\prime }\left(5\cos I^{\prime }+3\cos 3I^{\prime }\right)\cos 2{\Omega }^{\prime }\\ -2{\widehat{k}}_z^{\prime }\cos {\Omega }^{\prime }\left(\sin I^{\prime }-3\sin 3I^{\prime }\right)\\ -{\widehat{k}}_x^{\prime }\left(5\cos I^{\prime }+3\cos 3I^{\prime }\right)\sin 2{\Omega }^{\prime })\\ -80{e^{\prime }}^2\sin 2{\omega }^{\prime }({\widehat{k}}_z^{\prime }\sin 2I^{\prime }\sin {\Omega }^{\prime }\\ +\cos 2I^{\prime }\left({\widehat{k}}_x^{\prime }\cos 2{\Omega }^{\prime }+{\widehat{k}}_y^{\prime }\sin 2{\Omega }^{\prime }\right))\\ +4\left(3{e^{\prime }}^2+2\right)(-5{\widehat{k}}_y^{\prime }\cos 3I^{\prime }\\ -2{\widehat{k}}_z^{\prime }\cos {\Omega }^{\prime }\left(\sin I^{\prime }+5\sin 3I^{\prime }\right)\\ +\cos I^{\prime }\left(20{\sin }^2{I}^{\prime }\left({\widehat{k}}_y^{\prime }\cos 2{\Omega }^{\prime }-{\widehat{k}}_x^{\prime }\sin 2{\Omega }^{\prime }\right)-3{\widehat{k}}_y^{\prime }\right))\},\end{array}& \left(47\right)\end{array}$

Note that Equations (42–47) have a general validity since they are restricted neither to any specific spatial orientation of the spin axis of M′ nor to circular and/or equatorial orbits of M about M′.

It should be remarked that indirect, mixed effects of order (c⁻²) arise, in principle, also from the Newtonian tidal matrix of Equation (4) when the post-Newtonian effects of the field of M′ onto the orbital motion of M are taken into account (Mashhoon et al., 1989). The same holds also with J₂′, accounting for possible deviations of M′ from spherical symmetry at the Newtonian level itself. The calculation of such further effects, whose size may be comparable with that of the direct ones, is beyond the scope of this paper.

4. Possible Scenarios of Interest for Empirical Tests

Forthcoming space-based missions to astronomical bodies orbiting large primaries such as the Sun and Jupiter, in conjunction with expected progresses in interplanetary tracking techniques (Iess and Asmar, 2007; Iess et al., 2009, 2014), may, in principle, represent an opportunity to put on the test the post-Newtonian tidal effects calculated in the previous sections.

Let us consider the forthcoming BepiColombo³ (Benkhoff et al., 2010) and JUICE⁴ (Grasset et al., 2013) missions targeted to Mercury and the Jovian natural satellite Ganymede, respectively; in the following, the symbol ι will be adopted for the inclinations of the orbital planes of such spacecrafts to the equators of the orbited bodies. A probe named Mercury Planetary Orbiter⁵ (MPO) (Ashby et al., 2007) is planned to be released in a polar (ι_MPO = 90°), elliptical orbit (e_MPO = 0.16) around Mercury with an orbital period of approximately 2.3 h (a_MPO = 3,394 km). The nominal science duration is one year, with a possible extension of another year. Importantly, orbital maneuvers to change the attitude of the spacecraft are scheduled every about 44 d, so that long smooth orbital arcs should be available. The JUICE mission (Grasset et al., 2013) to the Jovian system will culminate in a dedicated orbital tour around Ganymede which should encompass a 30 d science phase during which JUICE will orbit⁶ the satellite in a polar, circular low path with an altitude as little as h = 200 km. Table 1 summarizes the characteristic frequencies of both the scenarios considered, showing that our results of the previous sections are applicable to them. In Table 2, we maximize the values of the post-Newtonian tidal perturbations for both MPO and JGO with respect to their unknown node Ω and pericenter ω. We do the same also for some of the most important competing Newtonian and post-Newtonian orbital perturbations. It can be noticed that, while for MPO the gravitoelectric tidal effects are larger than the gravitomagnetic ones, the situation is reversed for JGO because of its scheduled zero eccentricity. As far as the magnitudes of the tidal effects are concerned, they are larger for JGO; its gravitomagnetic tidal precessions reach the ≈ 10⁻¹ − 10⁻² mas yr⁻¹ level. In principle, a rate of ≈ 0.5 mas yr⁻¹, which naively corresponds to a range-rate as little as ≈ 0.05 mm s⁻¹ at the distance of Jupiter from us, might be detectable with the expected improvement down to 0.01 mm s⁻¹ at 60 s integration time in the Doppler range-rate techniques from the ASTRA study (Iess et al., 2014). Unfortunately, such figures are too small if compared with those of the competing orbital effects. Suffice it to say that the oblateness of Ganymede is presently known with a relative uncertainty of the order of just σ_J2/J₂ = 2× 10⁻² (Anderson et al., 1996). An improvement of 6−7 orders of magnitude is beyond the goals of the JUICE mission itself (Grasset et al., 2013). Strictly speaking, such considerations hold only for the direct post-Newtonian tidal effects calculated in the previous sections; the total sensitivity budget should account for the indirect, mixed effects of order (c⁻²) as well.

TABLE 1

Table 1. Some characteristic orbital frequencies, in s⁻¹, of the Sun-Mercury-Mercury Planetary Orbiter (MPO) and of the Jupiter-Ganymede-Jupiter Ganymede Orbiter (JGO) (Grasset et al., 2013) systems.

TABLE 2

Table 2. Maximum nominal values of the direct orbital rates of change $\dot{\Psi }$ of MPO and JGO, averaged over both P_b and P′_b, induced by the post-Newtonian gravitoelectric and gravitomagnetic tidal field of M′, by its Newtonian tidal field, and by some competing Newtonian and post-Newtonian perturbations due to the deviation from spherical symmetry of the field of M.

In principle, a rather unconventional possibility could be the realization of an artificial mini-planetary system to be carried onboard a drag-free spacecraft orbiting, say, the Earth; such an idea was already proposed in the past to accurately measure the Newtonian constant of gravitation G (Nobili et al., 1987, 1988, 1990; Keyser, 1992; Sanders and Deeds, 1992; Sanders et al., 1999, 2000), and more recently, to put on the test the MOND theory (Sahni and Shtanov, 2008). The conditions of validity of the present analysis could be fulfilled, e.g., by placing a non-rotating sphere made of tungsten with density ρ_W = 19.6 g cm⁻³ and M = 28 kg, R = 7 cm inside a drag-free spacecraft orbiting the Earth in some suitably chosen High Earth Orbit (HEO). By assuming, say, a = 10 cm for the test particle orbiting the tungsten sphere and a geostationary orbit with a′ = 42,164 km for the spacecraft, it would be possible to obtain

$\begin{array}{cc}\frac{n_{\text{b}}^{\prime }}{n_{\text{b}}}=5\times {10}^{-2}.& \left(48\right)\end{array}$

Moreover, the local dynamics of such a spaceborne artificial planetary system would be practically free from systematic non-Keplerian gravitational perturbations due to M. Indeed, careful manufacturing of the sphere would allow to make its oblateness negligible; the post-Newtonian gravitoelectric pericenter precession would be completely irrelevant being as little as $\dot{\omega }$≈ 10⁻¹² mas yr⁻¹. Table 3 summarizes the nominal maximum values of the precessions of a “planet” orbiting the aforementioned tungsten sphere along a circular path perpendicular to the Earth's equator in a spacecraft following a highly eccentric polar orbit around the Earth. In fact, the size of the post-Newtonian tidal effects are not negligible. Nonetheless, the tidal precessions of Newtonian origin would overwhelm them since the gravitational parameter GM′ of the Earth is currently known with a 2 × 10⁻⁹ relative accuracy (Petit and Luzum, 2010), insufficient by 1 −2 orders of magnitude for our purposes.

TABLE 3

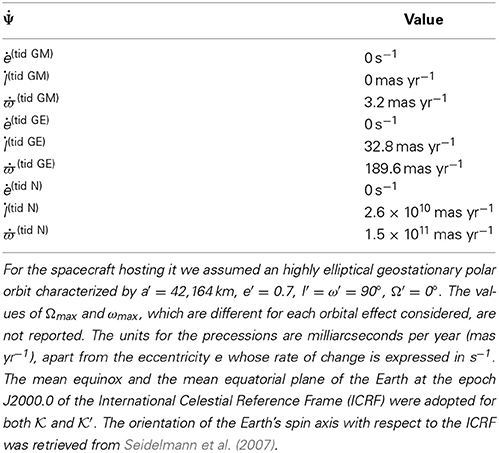
Table 3. Maximum nominal values of the direct orbital rates of change $\dot{\Psi }$ (here, ϖ ≐ Ω + ω is the longitude of the pericenter) of a member of a spaceborne artificial mini-planetary system orbiting a tungsten sphere of mass M = 28 kg and radius R = 7 cm in a circular orbit with a = 10 cm, e = 0, I = 90° averaged over both P_b and P′_b, induced by the post-Newtonian gravitoelectric and gravitomagnetic tidal field of the Earth and by its Newtonian tidal field.

5. Overview and Conclusions

We looked at the direct long-term orbital rates of change occurring within a local gravitationally bound two-body system as gradiometers to potentially detect post-Newtonian tidal effects due to its slow motion in the external field of a distant third body. We also assumed that the characteristic orbital frequencies of the internal dynamics of the local binary are quite smaller than the frequency of its orbital motion around the external source. We obtained general analytical expressions valid for arbitrary orbital configurations and for a generic orientation of the spin axis of the external body. Future work should be devoted to the calculation of the indirect, mixed post-Newtonian effects arising from the interplay between the Newtonian tidal matrix and the post-Newtonian orbital motion of the binary in the external field.

We applied our results to the future BepiColombo and JUICE man-made missions to Mercury and Ganymede, respectively. It turned out that that, although the expected improvements in interplanetary tracking may, perhaps, allow for a detection of the tidal effects we are interested in, especially for JUICE, the impact of several competing orbital effects of Newtonian and post-Newtonian origin, acting as sources of potential systematic errors, should be carefully considered.

Another possibility which, in principle, may be further pursued is the realization of an artificial mini-planetary system to be carried onboard an Earth-orbiting drag-free spacecraft. If, on the one hand, the post-Newtonian tidal precessions occurring in such a system may be relatively large, amounting to about 1 −10² mas yr⁻¹, on the other hand, the product of the Earth's mass times the Newtonian gravitational constant is currently known with insufficient accuracy to allow for an effective subtraction of the competing Newtonian tidal precessions.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^A comoving coordinate system is said to be kinematically nonrotating if it is corrected for the post-Newtonian precessions of its axes.

2. ^It turned out computationally more convenient to adopt the true anomaly f′

3. ^See also http://sci.esa.int/bepicolombo/ on the Internet.

4. ^See also http://sci.esa.int/juice/ on the Internet.

5. ^See http://sci.esa.int/bepicolombo/48872-spacecraft/ on the Internet.

6. ^See http://sci.esa.int/juice/50074-scenario-operations/ on the Internet.

References

Anderson, J. D., Lau, E. L., Sjogren, W. L., Schubert, G., and Moore, W. B. (1996). Gravitational constraints on the internal structure of Ganymede. Nature 384, 541–543. doi: 10.1038/384541a0

CrossRef Full Text

Ashby, N., Bender, P. L., and Wahr, J. M. (2007). Future gravitational physics tests from ranging to the BepiColombo Mercury planetary orbiter. Phys. Rev. D 75:022001. doi: 10.1103/PhysRevD.75.022001

CrossRef Full Text

Benkhoff, J., van Casteren, J., Hayakawa, H., Fujimoto, M., Laakso, H., Novara, M., et al. (2010). BepiColombo–Comprehensive exploration of Mercury: mission overview and science goals. Planet. Space Sci. 58, 2–20. doi: 10.1016/j.pss.2009.09.020

CrossRef Full Text

Bertotti, B., Farinella, P., and Vokrouhlický, D. (2003). Physics of the Solar System. Dordrecht: Kluwer Academic Press. doi: 10.1007/978-94-010-0233-2

CrossRef Full Text

Braginsky, V. B., and Polnarev, A. G. (1980). Relativistic spin-quadrupole gravitational effect. J. Exp. Theor. Phys. Lett. 31, 415–418.

Brumberg, V. A. (1991). Essential Relativistic Celestial Mechanics. Bristol: Adam Hilger.

Brumberg, V. A., and Kopeikin, S. M. (1989). Relativistic reference systems and motion of test bodies in the vicinity of the Earth. Nuovo Cimento B 103, 63–98. doi: 10.1007/BF02888894

CrossRef Full Text

Burns, J. A. (1976). Elementary derivation of the perturbation equations of celestial mechanics. Am. J. Phys. 44, 944–949. doi: 10.1119/1.10237

CrossRef Full Text

Byrne, P. K., Klimczak, C., Celâl şengör, A. M., Solomon, S. C., Watters, T. R., and Hauck, S. A. II (2014). Mercury's global contraction much greater than earlier estimates. Nat. Geosci. 7, 301–307. doi: 10.1038/ngeo2097

CrossRef Full Text

Chicone, C., and Mashhoon, B. (2002). The generalized Jacobi equation. Class. Quant. Grav. 19, 4231–4248. doi: 10.1088/0264-9381/19/16/301

CrossRef Full Text

Chicone, C., and Mashhoon, B. (2006). Tidal dynamics in Kerr spacetime. Class. Quant. Grav. 23, 4021–4033. doi: 10.1088/0264-9381/23/12/002

CrossRef Full Text

de Sitter, W. (1916). On Einstein's theory of gravitation and its astronomical consequences. Second paper. Monthly notices of the royal astronomical society. 77, 155–184. doi: 10.1093/mnras/77.2.155

CrossRef Full Text

Einstein, A. (1915). Erklärung der perihelbewegung des merkur aus der allgemeinen relativitätstheorie. Sitzungsberichte der Preußischen Akademie der Wissenschaften 47, 831–839.

Fermi, E. (1922). Sopra i fenomeni che avvengono in vicinanza di una linea oraria. Rendiconti dei Lincei 31, 21–23; 51–52.

Fokker, A. D. (1921). The geodesic precession: a consequence of Einsteinss theory of graviation. Koninklijke Nederlandsche Akademie van Wetenschappen 23, 729–738.

Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., and Kuchynka, P. (2014). The Planetary and Lunar Ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep 196:C1.

Gill, E., Schastok, J., Soffel, M. H., and Ruder, H. (1989). On the Mashhoon-Theiss “anomaly”. Phys. Rev. D 39, 2441–2443. doi: 10.1103/PhysRevD.39.2441

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grasset, O., Dougherty, M. K., Coustenis, A., Bunce, E. J., Erd, C., Titov, D., et al. (2013). JUpiter ICy moons Explorer (JUICE): an ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 78, 1–21. doi: 10.1016/j.pss.2012.12.002

CrossRef Full Text

Iess, L., and Asmar, S. (2007). Probing space-time in the solar system:. from cassini to bepicolombo. Int. J. Modern Phys. D 16, 2117–2126. doi: 10.1142/S0218271807011449

CrossRef Full Text

Iess, L., Asmar, S., and Tortora, P. (2009). MORE: An advanced tracking experiment for the exploration of Mercury with the mission BepiColombo. Acta Astronautica 65, 666–675. doi: 10.1016/j.actaastro.2009.01.049

CrossRef Full Text

Iess, L., Di Benedetto, M., James, N., Mercolino, M., Simone, L., and Tortora, P. (2014). Astra: interdisciplinary study on enhancement of the end-to-end accuracy for spacecraft tracking techniques. Acta Astronautica 94, 699–707. doi: 10.1016/j.actaastro.2013.06.011

CrossRef Full Text

Iorio, L. (2011). Perturbed stellar motions around the rotating black hole in Sgr A* for a generic orientation of its spin axis. Phys. Rev. D 84:124001. doi: 10.1103/PhysRevD.84.124001

CrossRef Full Text

Jacobson, R. A. (2003). JUP230 orbit solution. NASA Tech. Memorandum.

Keyser, P. T. (1992). Perturbative forces on an artificial binary for measuring G. Phys. Lett. A 167, 29–31. doi: 10.1016/0375-9601(92)90621-R

CrossRef Full Text

Kopeikin, S., Efroimsky, M., and Kaplan, G. (2011). Relativistic Celestial Mechanics of the Solar System. New York, NY: Wiley. doi: 10.1002/9783527634569

CrossRef Full Text

Lense, J., and Thirring, H. (1918). Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Physikalische Zeitschrift 19, 156–163.

Levi-Civita, T. (1926). Sur l' écart géodésique. Matematische Annalen 97, 291–320. doi: 10.1007/BF01447869

CrossRef Full Text

Li, X.-Q., Shao, M.-X., Paik, H. J., Huang, Y.-C., Song, T.-X., and Bian, X. (2014). Effects of satellite positioning errors and earths multipole moments in the detection of the gravitomagnetic field with an orbiting gravity gradiometer. Gen. Relat. Gravit. 46, 1–14. doi: 10.1007/s10714-014-1737-8

CrossRef Full Text

Margot, J.-L., Peale, S. J., Solomon, S. C., Hauck, II, S. A. Ghigo, F. D., Jurgens, R. F., et al. (2012). Mercury's moment of inertia from spin and gravity data. J. Geophys. Res. 117. doi: 10.1029/2012JE004161

CrossRef Full Text

Mashhoon, B. (1977). Tidal radiation. Astrophys. J. 216, 591–609.

Mashhoon, B., Paik, H. J., and Will, C. M. (1989). Detection of the gravitomagnetic field using an orbiting superconducting gravity gradiometer. Theoretical principles. Phys. Rev. D 39, 2825–2838. doi: 10.1103/PhysRevD.39.2825

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mashhoon, B., and Theiss, D. S. (1982). Relativistic tidal forces and the possibility of measuring them. Phys. Rev. Lett. 49, 1542–1545. doi: 10.1103/PhysRevLett.49.1542

CrossRef Full Text

Mashhoon, B., and Theiss, D. S. (1986). Gravitational influence of the rotation of the sun on the earth-moon system. Phys. Lett. A 115, 333–337. doi: 10.1016/0375-9601(86)90625-0

CrossRef Full Text

Mashhoon, B., and Theiss, D. S. (1991). Relativistic lunar theory. Nuovo Cimento B 106, 545–571. doi: 10.1007/BF02726789

CrossRef Full Text

Mashhoon, B., and Theiss, D. S. (2001). “Relativistic effects in the motion of the moon,” in Gyros, Clocks, Interferometers…: Testing Relativistic Gravity in Space, eds C. Lämmerzahl, C. W. F.Everitt and F. W. Hehl, Vol. 562 of Lecture Notes in Physics (Berlin: Springer Verlag), 310.

Nobili, A. M., Milani, A., and Farinella, P. (1987). Testing Newtonian gravity in space. Phys. Lett. A 120, 437–441. doi: 10.1016/0375-9601(87)90105-8

CrossRef Full Text

Nobili, A. M., Milani, A., and Farinella, P. (1988). The orbit of a space laboratory for the measurement of G. Astronom. J. 95, 576–578. doi: 10.1086/114657

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nobili, A. M., Milani, A., Polacco, E., Roxburgh, I. W., Barlier, F., Aksnes, K., et al. (1990). The Newton mission - a proposed manmade planetary system in space to measure the gravitational constant. ESA J. 14, 389–408.

Nobili, A. M., and Will, C. M. (1986). The real value of Mercury's perihelion advance. Nature 320, 39–41. doi: 10.1038/320039a0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Paik, H. J. (1989). Tests of general relativity in earth orbit using a superconducting gravity gradiometer. Adv. Space Res. 9, 41–50. doi: 10.1016/0273-1177(89)90006-9

CrossRef Full Text

Paik, H. J. (2008). Detection of the gravitomagnetic field using an orbiting superconducting gravity gradiometer: principle and experimental considerations. Gen. Relat. Gravit. 40, 907–919. doi: 10.1007/s10714-007-0582-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Petit, G., and Luzum, B. (2010). IERS Conventions (2010). IERS Tech. Note 36:1. Available online at: http://www.iers.org/nn_11216/sid_FC7D9322CF807240D40C53641833295B/nsc_true/IERS/EN/Publications/TechnicalNotes/tn36.html

Pijpers, F. P. (1998). Helioseismic determination of the solar gravitational quadrupole moment. Month. Notic. R. Astronom. Soc. 297, L76–L80. doi: 10.1046/j.1365-8711.1998.01801.x

CrossRef Full Text

Sahni, V., and Shtanov, Y. (2008). Apsis:. an artificial planetary system in space to probe extra-dimensional gravity and MOND. Int. J. Modern Phys. D 17, 453–466. doi: 10.1142/S0218271808012127

CrossRef Full Text

Sanders, A. J., Alexeev, A. D., Allison, S. W., Antonov, V., Bronnikov, K. A., Campbell, J. W., et al. (2000). Project SEE (Satellite Energy Exchange): an international effort to develop a space-based mission for precise measurements of gravitation. Class. Q. Grav. 17, 2331–2346. doi: 10.1088/0264-9381/17/12/305

CrossRef Full Text

Sanders, A. J., Alexeev, A. D., Allison, S. W., Bronnikov, K. A., Campbell, J. W., Cates, M. R., et al. (1999). Project SEE (Satellite Energy Exchange): proposal for space-based gravitational measurements. Measure. Sci. Technol. 10, 514–524. doi: 10.1088/0957-0233/10/6/317

CrossRef Full Text

Sanders, A. J., and Deeds, W. E. (1992). Proposed new determination of the gravitational constant G and tests of Newtonian gravitation. Phys. Rev. D 46, 489–504. doi: 10.1103/PhysRevD.46.489

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Seidelmann, P. K., Archinal, B. A., A'Hearn, M. F., Conrad, A., Consolmagno, G. J., Hestroffer, D., et al. (2007). Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006. Celest. Mech. Dyn. Astron. 98, 155–180. doi: 10.1007/s10569-007-9072-y

CrossRef Full Text

Smith, D. E., Zuber, M. T., Phillips, R. J., Solomon, S. C., Neumann, G. A., Lemoine, F. G., et al. (2010). The equatorial shape and gravity field of Mercury from MESSENGER flybys 1 and 2. Icarus 209, 88–100. doi: 10.1016/j.icarus.2010.04.007

CrossRef Full Text

Soffel, M., Klioner, S. A., Petit, G., Wolf, P., Kopeikin, S. M., Bretagnon, P., et al. (2003). The IAU 2000 resolutions for astrometry, celestial mechanics, and metrology in the relativistic framework: explanatory supplement. Astron. J. 126, 2687–2706. doi: 10.1086/378162

CrossRef Full Text

Solomon, S. C., McNutt, R. L., Gold, R. E., and Domingue, D. L. (2007). MESSENGER Mission Overview. Space Sci. Rev. 131, 3–39. doi: 10.1007/s11214-007-9247-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Synge, J. L. (1927). On the Geometry of Dynamics. R. Soc. Lond. Philos. Trans. A 226, 31–106. doi: 10.1098/rsta.1927.0002

CrossRef Full Text

Theiss, D. S. (1985). A general relativistic effect of a rotating spherical mass and the possibility of measuring it in a space experiment. Phys. Lett. A 109, 19–22. doi: 10.1016/0375-9601(85)90382-2

CrossRef Full Text

Theiss, D. S. (1992). “A gradiometer experiment to detect the gravitomagnetic field of the earth,” in Relativistic Gravity Research, Vol. 410 of Lecture Notes in Physics, eds J. Ehlers and G. Schäfer, (Berlin Springer Verlag), 131. doi: 10.1007/3-540-56180-3_6

CrossRef Full Text

Will, C. M. (2009). The confrontation between general relativity and experiment. Space Sci. Rev. 148, 3–13. doi: 10.1007/s11214-009-9541-6

CrossRef Full Text

Will, C. M. (2014). Incorporating post-Newtonian effects in N-body dynamics. Phys. Rev. D 89:044043. doi: 10.1103/PhysRevD.89.044043

CrossRef Full Text