- 1Center for Theoretical Physics, Polish Academy of Sciences, Warsaw, Poland
- 2Key Laboratory for Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
- 3Copernicus Astronomical Center, Polish Academy of Sciences, Warsaw, Poland
- 4Astronomical Institute, Czech Academy of Sciences, Prague, Czechia
We develop a self-consistent description of the Broad Line Region based on the concept of a failed wind powered by radiation pressure acting on a dusty accretion disk atmosphere in Keplerian motion. The material raised high above the disk is illuminated, dust evaporates, and the matter falls back toward the disk. This material is the source of emission lines. The model predicts the inner and outer radius of the region, the cloud dynamics under the dust radiation pressure and, subsequently, the gravitational field of the central black hole, which results in asymmetry between the rise and fall. Knowledge of the dynamics allows us to predict the shapes of the emission lines as functions of the basic parameters of an active nucleus: black hole mass, accretion rate, black hole spin (or accretion efficiency) and the viewing angle with respect to the symmetry axis. Here we show preliminary results based on analytical approximations to the cloud motion.
1. Introduction
The Broad Emission Line Region (BLR) is the key ingredient of most active nuclei, and its true nature remains illusive. Huge observational progress allowed the accumulation of a lot of constraints/requirements for the material which is the source of emission lines. This (clumpy ?) wind emission is mostly powered by the emission from the most central parts, with (possibly) some contribution from mechanical heating. The distribution of the emitting material is rather flat since BLR clouds are rarely seen in absorption despite covering a relatively large fraction of the sky as seen from the nucleus, which is required by the total line luminosity. The study of emission line variability allows measurement of the distance to the BLR, and shows that in general the region is extended, with High Ionization Lines (HIL) forming closer in, and Low Ionization Lines (LIL) forming further down (Collin-Souffrin et al., 1986; Gaskell, 2009). The motion is predominantly Keplerian, which opened a way to use the BLR for black hole mass measurements (Wandel et al., 1999). The wavelength-resolved reverberation mapping now allows for a few well-studied sources to provide an insight into the velocity field, confirming predominantly Keplerian motion but with traces of inflow as well as outflow (Grier et al., 2013).
The outflow suggests that the emitting material is connected with the cold accretion disk present in the nucleus, and a disk wind. There are also observational arguments for the co-existence of the cold disk and BLR.
Several mechanisms are known to drive winds (radiation pressure driven winds; e.g., Elvis, 2012; magnetically driven winds, e.g., Fukumura et al., 2015; pressure driven winds, e.g., Fukue, 2004, and the references therein), and a combination of all effects is likely to contribute although various mechanisms could dominate at various distances from the black hole, as the local densities and ionizing flux changes with the disk radius. Inflow might seem less expected, but the winds in some parameter space are actually failed winds, not escaping to infinity, and reversing to inflow. Also the thermal instability in the circumnuclear material may lead to selective inflow of the denser phase (e.g., Elvis, 2017).
This tremendously complicated region, however, produces a strikingly good correlation between the BLR size and the source monochromatic luminosity. More specifically, this is the relation between the delay of the β line with respect to the 5,100 Å continuum, which in addition is not the continuum driving this line. This relation is now observationally studied in a broad luminosity range as well as in redshift (Peterson et al., 2004; Bentz et al., 2013; Shen et al., 2016).
Failed Radiatively Accelerated Dusty Outflow (FRADO) model (Czerny and Hryniewicz, 2011; Czerny et al., 2015) offers a natural way to understand this relation. Other BLR models, like the one developed by Netzer and Marziani (2010) are parametric, they do not uniquely predict the radial extension of the BLR without referring to an observational scaling while FRADO gives the location of the LIL part, at the basis of the dust microscopic properties. Below we briefly outline the model itself, the dynamics of the clouds and the exemplary line profiles. The model parameters are just the global parameters of the stationary accretion flow in the nucleus: the black hole mass, the accretion rate, the spin (or accretion efficiency) and the viewing angle toward the nucleus.
2. FRADO Model
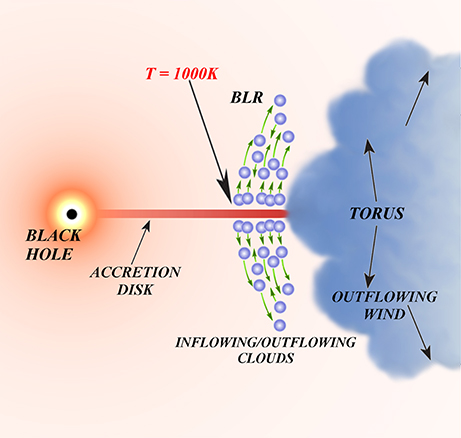
The model is based on the known observational fact that stellar winds are much more prominent in cooler stars with dusty atmospheres than in the hotter stars. Since the accretion disk in a given source has a broad temperature range, there exists a distance from the black hole where the effective temperature of the disk drops below the dust sublimation temperature. There the material is risen efficiently above the disk by the local radiation pressure. However, with increasing disk height the dusty material is exposed to the irradiation by the central regions, the plasma temperature rises above the sublimation temperature, the dust evaporates, and the radiation pressure vanishes, so the clouds move by following ballistic motion, first up and then down toward the disk surface. We neglect here the other sources of the radiation pressure, like line-driven outflow. In the present work we aim at catching the most characteristic properties of the model in a broad parameter range, so we introduce some simplifications which allow us to describe the cloud dynamics analytically. The basic model parameters are simply the global parameters of an active nucleus, i.e., the black hole mass, accretion rate, black hole spin (or accretion efficiency) and the viewing angle with respect to the symmetry axis. Other parameters, like the dust sublimation temperature and the dust opacity should result, at least in principle, from the basic physics. The scenario is outlined in Figure 1.
3. Cloud Dynamics
We assume that the dust opacity can be described in gray approximation as a wavelength-independent value, and we neglect its dependence on the temperature as well, as long as the temperature is lower than the dust sublimation temperature. In the presence of the dust within the cloud, the cloud motion can be approximated as
where ζ = z − Hdisk is the distance measured from the disk surface. Here Hdisk is the disk thickness, MBH is the black hole mass, and r is the current disk radius. If the disk is dominated by the radiation pressure, Hdisk is constant and its value is given by accretion rate Ṁ as . The clouds also perform circular motion with the local Keplerian velocity. If both the Planck mean κP and the Rosseland mean κR are constant and the dust does not evaporate, this equation can be easily integrated analytically to get
where ΩK is the local Keplerian angular velocity. The cloud does perform an oscillatory motion from ζ = 0 to ζmax = 2Hdisk(κP/κR − 1). The maximum cloud velocity in the vertical direction is a constant fraction of the local Keplerian velocity so it depends on the radius. The cloud maximum height in this approximation is independent of the radius, so the nearest clouds intercept most of the central radiation. Both the velocity and the height scale with the accretion rate, Ṁ, in physical units, i.e., scales both with the black hole mass and accretion rate in Eddington units. Such a description is only valid when the dust within the cloud survives. However, close to the inner radius of the BLR evaporation is important, and the condition for dust evaporation can be formulated as
where is the gravitational radius and η is the accretion efficiency which connects the accretion rate to the bolometric luminosity. If ζ > ζevap the pressure term in the equation of motion disappears. The further motion of the cloud up and down can still be calculated analytically but the formulae become more complicated due to asymmetry between part of the rise supported by the dust and the second part of the rise and subsequent fall of the cloud. The schematic structure of the BLR parts is shown in Figure 2, left panel, and the asymmetry in motion is illustrated in Figure 2, right panel.
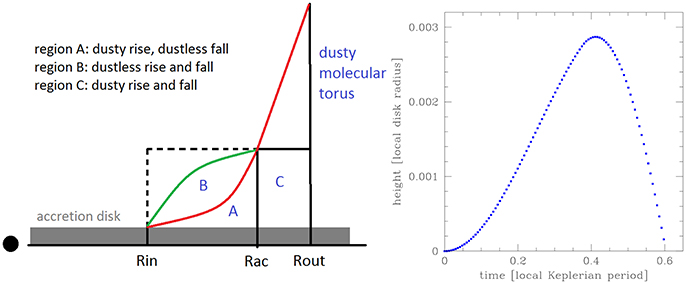
Figure 2. Schematic drawing of the BLR region (left) and an example of a single cloud motion in the A/B region showing clear asymmetry in the rise and fall motion due to the dust evaporation (right).
The inner radius of the BLR is set by the condition of ζmax = 0, and the outer radius of the BLR is given by ζevap = r, i.e., by the condition that the dust survives the irradiation even high above the disk mid-plane. This region in general consists of two parts: the inner part where both dusty and dustless clouds are present and the outer region where ζmax is smaller than ζevap and only dusty clouds exist. The transition between the A/B and C zones is set by the condition ζmax = ζevap. This structure is shown schematically in Figure 2. The extension of the zones depend on the mass, accretion rate and the accretion efficiency.
The position of the transition radius, rAC, can be used to evaluate the basic expected trends of the model. The ratio of rAC to the inner radius increases with Ṁ1/3/M1/3, i.e., the dimensionless accretion rate, thus the emission comes from a broader range of radii and the double-peak character of the line profile is less expected with the rise of the Eddington ratio.
4. Line Profiles
We now assume that the line is emitted as a monochromatic line, later broadened by the vertical and rotational motion. The line emissivity is assumed to be directly proportional to the incident flux, i.e., the efficiency of radiation reprocessing characteristic for a specific emission line is neglected in the current model. Thus, the local emissivity at a given radius is simply assumed to be proportional to the local disk surface element, drdϕ/r2, where dr and dϕ are the elements of the radial and azimuthal grid. The cloud distribution is sampled in all three dimensions, the distribution in the z direction is consistent with the cloud motion, and the Moon-type effect in the cloud emission is taken into account. The computations of the line profile neglect the Doppler boosting and gravitational reddening but the profiles are computed for an arbitrary viewing angle of an observer. The final line shape is then calculated numerically.
In the final computations we adopted at present the following values of the constants: Tdust = 1,500 K, κP = 8.0 cm−2g−1, κR = 4.0 cm−2g−1, and the accretion efficiency η = 0.1, corresponding to a moderate black hole spin.
Figure 3 (left) shows the dependence of the predicted line profiles on the accretion rate, for a fixed black hole mass and accretion efficiency of 0.1 but for three values of the accretion rate corresponding to the Eddington ratio of 0.01, 0.1, and 1, for a viewing angle of 30°. The line always shows a two peak structure but this disk-like component is much stronger in the case of a low Eddington ratio than in the case of a high Eddington ratio. This change reflects two trends: (i) with the rise of the accretion rate the BLR moves outwards so the line in general becomes narrower (ii) the ratio of the maximum vertical to the local azimuthal velocity also rises with the accretion rate so that the contribution of the vertical motion to the line profile is more important. This trend well reproduces the fact that the lines in Narrow Line Seyfert galaxies do not show the double peak structure, while this double peak structure is clearly visible in low Eddington ratio sources, particularly in the variable part of the spectrum. In Figure 3 (right) we show a sequence of the solutions for a different black hole mass and the Eddington ratio 1.0. We see that the line shape still shows some double-peak structure, but it is much smaller in high Eddington ratio sources than in the low Eddington ratio sources. The trend depends also on the black hole mass itself (see Figure 3, right panel), with larger black hole mass showing more double-peak behavior. It is consistent with the division of the Seyfert 1 galaxies into two classes at FWHM of 2,000 km s−1 (Seyfert 1 and Narrow Line Seyfert 1 objects) and similar division into class A and B in quasars at much higher FWHM of 4,000 km s−1 (type A and type B quasars).
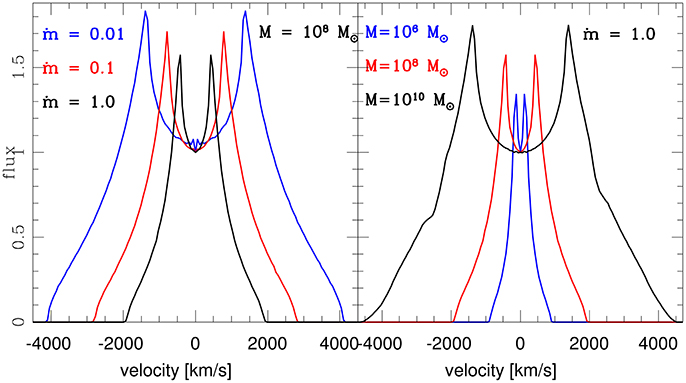
Figure 3. An example of the dependence of the line profile on the accretion rate, for a black hole mass of (left), and on the black hole mass for the Eddington accretion rate (right). The viewing angle is fixed at 30 deg. The inner and outer BLR radii calculated for the model are: 1.98 × 1016 cm and 1.87 × 1017 cm, 4.26 × 1016 cm and 5.91 × 1017 cm, 9.18 × 1016 cm and 1.87 × 1018 cm in the left panel, and 4.26 × 1015 cm and 1.87 × 1017 cm, 9.18 × 1016 cm and 1.87 × 1018 cm, 1.98 × 1018 cm and 1.87 × 1019 cm in the right panel. Line flux is normalized to 1 at zero velocity.
5. Discussion
The results above show the first very simplified attempt to use the FRADO model for explaining the structure of the BLR. It has a number of properties consistent with the observed trends, like narrower lines for higher Eddington rate sources and smaller black hole mass. However, the model is not yet ready for a detailed comparison with the AGN spectra, as the Baldwin effect is not expected from the current version of the model. First of all, the exact values of the physical constants describing the dust properites should be included in the model. The mean time delay suggesting dust values ~900K is most likely incorrect since the measured delay does not simply translate to the BLR inner radius. Spectroscopic studies indicate larger hot dust temperatures, which will give broader line profiles. At a later step cloud shielding should be included, combined with a better description of the radial weight of the line contribution due to geometrical setup. The disk thickness should include the transition from the radiation-pressure supported inner part to the gas-supported outer part which makes the disk shape more complex than the constant disk thickness used in the current work. Finally, the real cloud emissivity should be included, and the radiation pressure should be described much more carefully, taking into account the wavelength-dependence of the radiation pressure acting on dust, dust composition and the radiation pressure due to the absorption in lines. Those last aspects are particularly complicated, although some progress have been already done in this direction (Gallagher et al., 2015; Chan and Krolik, 2016; Hönig and Kishimoto, 2017; Waters et al., 2017).
The picture outlined in this paper is basically stationary. In order to include the time-dependent behavior we would have to introduce the time-dependent emission from the inner disk. Thermal and/or magnetic field fluctuations are required to model the usual red noise variability of an AGN continuum, and they would lead to delayed line response but most likely without strong change in the line shape. Observed longer systematic trends in the line shapes (e.g., Bon et al., 2016; Li et al., 2016; Średzińska et al., 2017) require additional factors perturbing the disk symmetry like a secondary black hole, accretion disk precession or spiral waves present in the disk due to self-gravity effects.
Author Contributions
BC was responsible for the idea that resulted in the paper and most of the text. KH contributed to the concept and the text. JS derived the basic formulae for dusty clouds, later modified by VK, SP, and CW for the dust evaporation effect. YL contributed to the line profile computations.
Funding
Part of this work was supported by Polish grant Nr. 2015/17/B/ST9/03436/.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Jian-Min Wang for many helpful discussions of the project during the stay of BC in Beijing.
References
Bentz, M. C., Denney, K. D., Grier, C. J., Barth, A. J., Peterson, B. M., Vestergaard, M., et al. (2013). The Low-luminosity End of the Radius-Luminosity Relationship for Active Galactic Nuclei. Astrophys. J. 767:149. doi: 10.1088/0004-637X/767/2/149
Bon, E., Zucker, S., Netzer, H., Marziani, P., Bon, N., Jovanović, P., et al. (2016). Evidence for Periodicity in 43 year-long Monitoring of NGC 5548. Astrophys. J. Suppl. 225:29. doi: 10.3847/0067-0049/225/2/29
Chan, C.-H., and Krolik, J. H. (2016). Radiation-driven Outflows from and Radiative Support in Dusty Tori of Active Galactic Nuclei. Astrophys. J. 825:67. doi: 10.3847/0004-637X/825/1/67
Collin-Souffrin, S., Joly, M., Pequignot, D., and Dumont, S. (1986). The emission spectrum of active galactic nuclei. II - High column density photoionization models and low ionization lines. Astron. Astrophys. 166, 27–35.
Czerny, B., and Hryniewicz, K. (2011). The origin of the broad line region in active galactic nuclei. Astron. Astrophys. 525:L8. doi: 10.1051/0004-6361/201016025
Czerny, B., Modzelewska, J., Petrogalli, F., Pych, W., Adhikari, T. P., Życki, P. T., et al. (2015). The dust origin of the Broad Line Region and the model consequences for AGN unification scheme. Adv. Space Res. 55, 1806–1815. doi: 10.1016/j.asr.2015.01.004
Elvis, M. (2012). “Quasar structure emerges from the three forms of radiation pressure,” in AGN Winds in Charleston, Vol. 460 of Astronomical Society of the Pacific Conference Series, (Charleston, SC).
Elvis, M. (2017). Quasar Rain: The Broad Emission Line Region as Condensations in the Warm Accretion Disk Wind. ArXiv e-prints. arXiv:1703.02956
Fukue, J. (2004). Radiato-magneto-thermal winds from an accretion disk. Publ. Astronom. Soc. Japan 56, 181–192. doi: 10.1093/pasj/56.1.181
Fukumura, K., Tombesi, F., Kazanas, D., Shrader, C., Behar, E., and Contopoulos, I. (2015). Magnetically driven accretion disk winds and ultra-fast outflows in PG 1211+143. Astrophys. J. 805:17. doi: 10.1088/0004-637X/805/1/17
Gallagher, S. C., Everett, J. E., Abado, M. M., and Keating, S. K. (2015). Investigating the structure of the windy torus in quasars. Monthly Notices R. Astron. Soc. 451, 2991–3000. doi: 10.1093/mnras/stv1126
Gaskell, C. M. (2009). What broad emission lines tell us about how active galactic nuclei work. New Astronom. Rev. 53, 140–148. doi: 10.1016/j.newar.2009.09.006
Grier, C. J., Peterson, B. M., Horne, K., Bentz, M. C., Pogge, R. W., Denney, K. D., et al. (2013). The Structure of the Broad-line Region in Active Galactic Nuclei. I. Reconstructed Velocity-delay Maps. Astrophys. J. 764:47. doi: 10.1088/0004-637X/764/1/47
Hönig, S. F., and Kishimoto, M. (2017). Dusty winds in active galactic nuclei: reconciling observations with models. Astrophys. J. Lett. 838:L20. doi: 10.3847/2041-8213/aa6838
Li, Y.-R., Wang, J.-M., Ho, L. C., Lu, K.-X., Qiu, J., Du, P., et al. (2016). Spectroscopic indication of a centi-parsec supermassive black hole binary in the galactic center of NGC 5548. arXiv 822:4. doi: 10.3847/0004-637X/822/1/4
Netzer, H., and Marziani, P. (2010). The effect of radiation pressure on emission-line profiles and black hole mass determination in active galactic nuclei. Astrophys. J. 724, 318–328. doi: 10.1088/0004-637X/724/1/318
Peterson, B. M., Ferrarese, L., Gilbert, K. M., Kaspi, S., Malkan, M. A., Maoz, D., et al. (2004). Central masses and broad-line region sizes of active galactic nuclei. II. A homogeneous analysis of a large reverberation-mapping database. Astrophys. J. 613, 682–699. doi: 10.1086/423269
Shen, Y., Horne, K., Grier, C. J., Peterson, B. M., Denney, K. D., Trump, J. R., et al. (2016). The Sloan Digital Sky Survey Reverberation Mapping Project: First Broad-line Hβ and Mg ii Lags at z > 0.3 from Six-month Spectroscopy. Astrophys. J. 818:30. doi: 10.3847/0004-637X/818/1/30
Średzińska, J., Czerny, B., Hryniewicz, K., Krupa, M., Kurcz, A., Marziani, P., et al. (2017). SALT long-slit spectroscopy of quasar HE 0435-4312: fast displacement of the Mg II emission line. Astron. Astrophys. 601:A32. doi: 10.1051/0004-6361/201628257
Wandel, A., Peterson, B. M., and Malkan, M. A. (1999). Central masses and broad-line region sizes of active galactic Nuclei. I. Comparing the photoionization and reverberation techniques. Astrophys. J. 526, 579–591. doi: 10.1086/308017
Keywords: emission lines, active galactic nuclei, Broad Line Region, accretion disk, black hole
Citation: Czerny B, Li Y-R, Sredzinska J, Hryniewicz K, Panda S, Wildy C and Karas V (2017) Self-Consistent Dynamical Model of the Broad Line Region. Front. Astron. Space Sci. 4:5. doi: 10.3389/fspas.2017.00005
Received: 26 April 2017; Accepted: 08 June 2017;
Published: 22 June 2017.
Edited by:
Paola Marziani, National Institute for Astrophysics (INAF), ItalyReviewed by:
Giovanna Maria Stirpe, Osservatorio Astronomico di Bologna (INAF), ItalyEdi Bon, Belgrade Astronomical Observatory, Serbia
Copyright © 2017 Czerny, Li, Sredzinska, Hryniewicz, Panda, Wildy and Karas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bozena Czerny, YmN6QGNmdC5lZHUucGw=
 Bozena Czerny
Bozena Czerny Yan-Rong Li2
Yan-Rong Li2