Theoretical Re-evaluations of Scaling Relations between SMBHs and Their Host Galaxies–2. Importance of AGN Feedback Suggested by Stellar Age–Velocity Dispersion Relation

1. Introduction

There is a lot of work aimed at understanding star formation histories by comparing theoretical models with observational results. Recent theoretical work has revealed that in order to explain observational properties of galaxies, some feedback effects are important, which suppress star formation activities by heating or ejecting cold gas (e.g., Springel et al., 2005; Okamoto et al., 2010; Vogelsberger et al., 2014). Supernovae (SN) feedback is important for less massive (less luminous) galaxies (Benson et al., 2003) with M_K ≳ −22, where M_K is K-band absolute magnitude of galaxies. On the other hand, SN feedback cannot quench the cooling flow of massive and luminous galaxies because such massive galaxies have deep potential wells and cold gas cannot escape from the galaxies. Some theoretical studies (e.g., Bower et al., 2006; Croton et al., 2006; Okamoto et al., 2014) reveals that feedback processes related to active galactic nuclei (AGNs) are important for such massive galaxies. Observational studies have explored whether AGN feedback really exists. Their results are controversial (see, e.g., McNamara et al., 2016; Nesvadba et al., 2017; Smolčić et al., 2017).

It is necessary to compare theoretical models with “statistical” observational properties of galaxies in order to investigate the existence of AGN feedback because individual AGN has different stages of AGN and star formation activities. Martín-Navarro et al. (2016) present evidence of existing AGN feedback by re-analyzing observational data. They divide galaxy sample obtained from van den Bosch (2016) between “over-/under- massive black hole galaxies” following the M_BH − σ relation. They then estimate stacked, luminosity weighted age of galaxies with these two populations and find that over massive BH galaxies are older than under massive galaxies. Over-massive BH galaxies have potential to have experienced energetic AGN phases and to have stronger AGN feedback effects since over massive BHs might have grown in earlier universe in which the amount of the cold gas is larger.

Here we investigate, by using a semi-analytic model of galaxy formation (hereafter SA model), whether the relation proposed by Martín-Navarro et al. (2016) can really be explained with AGN feedback effect. In Section 2 we briefly review the SA model we used. Section 3 includes the main results.

2. Methods

We employ a revised version of an SA model, “New Numerical Galaxy Catalog” (ν²GC; Makiya et al., 2016). We consider star formation in galactic disk and bulge, mergers of galaxies, atomic gas cooling, gas heating by UV feedback and feedbacks via supernovae and AGNs, and the growth of super massive black holes (SMBHs) by coalescence and gas fueling. We here skipped the detailed model description about SMBH growth via galaxy mergers and disk instability because of the limited numbers of characters for this paper. In our model, we assume the timescale of gas accretion onto a SMBH is proportional to the dynamical timescale of the bulge in the host galaxy. We neglect the mass which might be in the dusty torus surrounding a SMBH since it is uncertain that how the dusty tori form and grow with their host galaxies. In addition, it is not clear whether the tori really exist for all types of AGNs including violent quasars, Seyfert galaxies, and low luminosity AGNs. We leave the treatment of the torus for future work. We have confirmed that the model can explain SMBH mass function at z ~ 0 and bright ends of quasar luminosity functions in 0.0 < z < 6.0. More detailed descriptions are available in Shirakata et al. (2016) and Shirakata et al. in preparation.

We create merging histories of dark matter haloes from N-body simulations. In this paper, we employ ν²GC-SS simulation, which has 70h⁻¹Mpc (comoving) in box size, 512³ simulated particles, $2.20\times 10^8{M}_{\odot }$ in particle mass resolution. Minimum halo mass of this simulation is $8.79\times 10^9{M}_{\odot }$. We employ ν²GC-S simulation which has 280h⁻¹Mpc in box size in order to obtain K-band luminosity functions of galaxies (Figure 1). The mass resolution of ν²GC-S simulation is the same as ν²GC-SS. The details of the merger trees are given in Ishiyama et al. (2015).

FIGURE 1

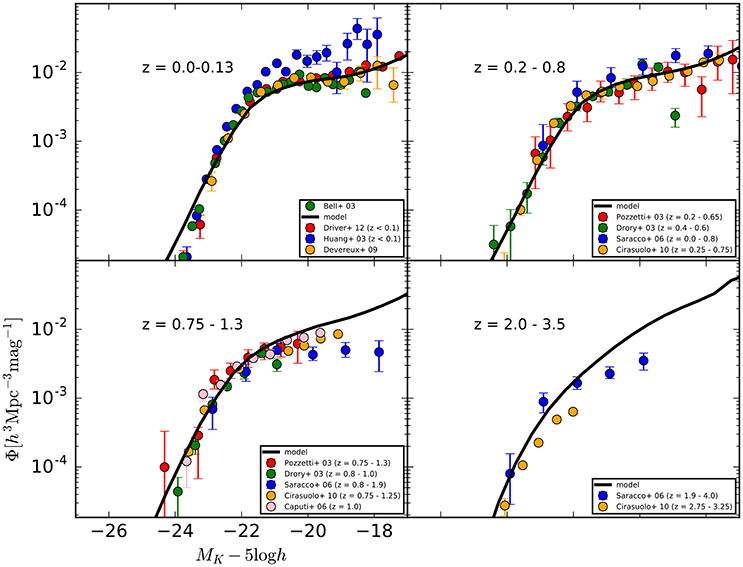
Figure 1. K-band luminosity functions of galaxies from z = 3.5 to 0. The model results are shown in black lines. Dots describe observational results obtained from Bell et al. (2003); Driver et al. (2012); Huang et al. (2003); Devereux et al. (2009); Pozzetti et al. (2003); Drory et al. (2003); Saracco et al. (2006); Cirasuolo et al. (2010); Caputi et al. (2006) (see labels in this figure).

We assume a ΛCDM universe with the following parameters: Ω₀ = 0.31, λ₀ = 0.69, Ω_b = 0.048, σ₈ = 0.83, n_s = 0.96, and a Hubble constant of $H_0=100\text{ h }km{s}^{-1}$ Mpc⁻¹, where h = 0.68 (Planck Collaboration et al., 2014).

2.1. Gas Cooling

Here we describe how we calculate the amount of the cold gas, which gets accreted to a central galaxy. We note that we define a central galaxy as a central galaxy of the most massive progenitor halo.

We firstly calculate cooling radius r_cool(t). Same as Makiya et al. (2016), we assume Navarro-Frenk-White (NFW) density profile (Navarro et al., 1997) for dark matter (DM) haloes and isothermal density profile with a finite core radius, r_c for hot gas haloes;

$\begin{array}{cc}{\rho }_{\text{NFW}}(r)=\frac{{\rho }_{\text{DM},\text{0}}}{(r/r_s){(1+r/r_s)}^2},& (1)\end{array}$

$\begin{array}{cc}{\rho }_{\text{hot}}(r)=\frac{{\rho }_{\text{hot},\text{0}}}{1+{(r/r_c)}^2},& (2)\end{array}$

where r_s is the specific radius of the DM halo, which is described by using concentration parameter, c, and virial radius, R_vir, as R_vir/r_s ≡ c. We assume r_c = 0.22r_s (Makino et al., 1998). We use the analytical formulae of c obtained from fitting of cosmological N-body simulations (Prada et al., 2012). After the collapse of a DM halo, the hot gas gradually cools via radiative cooling. Then, the cooling time is described with r_cool as

$\begin{array}{cc}{t}_{\text{cool}}(r_{\text{cool}})=\frac{3}{2}\frac{{\rho }_{\text{hot}}(r_{\text{cool}})}{\mu m_p}\frac{k_B{T}_{\text{vir}}}{n_e^2(r)\Lambda (T_{\text{vir}},Z_{\text{hot}})},& (3)\end{array}$

where μ, m_p, k_B, and n_e are the mean molecular weight, proton mass, Boltzmann constant, and electron number density, respectively. We employ a cooling function, Λ, provided by Sutherland and Dopita (1993), which is a function of hot gas metallicity, Z_hot, and virial temperature, T_vir. Virial temperature is calculated from circular velocity of the host DM halo, V_circ, as

$\begin{array}{cc}{T}_{\text{vir}}=\frac{1}{2}\frac{\mu m_p}{k_B}{V}_{\text{circ}}^2.& (4)\end{array}$

r_cool(t) is defined at which t_cool of Equation (3) is equal to the time elapsed since the halo formation epoch.

We next calculate free fall radius, r_ff(t) with ρ_NFW(r);

$\begin{array}{cc}{t}_{\text{ff}}(r_{\text{ff}})=\frac{\pi }{2}\sqrt{\frac{r_{\text{ff}}^3}{2GM(r<r_{\text{ff}})}},& (5)\end{array}$

where G is the gravitational constant. Now t_ff = t_cool, in order to compare the size of r_cool with r_ff at the same time.

We then evaluate the accretion radius, r_acc(t), in which gas can actually cool and get accreted to the central galaxy. We set r_acc as the minimum value among r_cool, r_ff, and R_vir, where R_vir is the virial radius of the halo. The case with r_acc = r_cool means the gas cooling is not so efficient and gas can free-fall rapidly. This case occurs only for the massive (>10¹³ M_⊙) haloes. Since Makiya et al. (2016) assume r_acc = MIN{r_cool, R_vir}, they would overestimate the amount of cold gas especially at z < 1.0 if they employ the same parameter set as that of in this paper. We note that we assume that the existence of a “cooling hole” same as Makiya et al. (2016); the radial profile of hot gas remains unchanged until the DM halo mass doubles.

2.2. Radio Mode AGN Feedback

We introduce the so-called radio-mode AGN feedback process in order to prevent gas in massive haloes from cooling and forming stars. Following Bower et al. (2006), gas cooling in a halo is quenched when the following two conditions are satisfied:

$\begin{array}{cc}{t}_{\text{ff}}(r_{\text{cool}})<{\alpha }_{\text{cool}}{t}_{\text{cool}},& (6)\end{array}$

$\begin{array}{cc}{ϵ}_{\text{SMBH}}{L}_{\text{Edd}}>L_{\text{cool}},& (7)\end{array}$

where L_Edd is the Eddington luminosity, L_cool is the cooling luminosity of the gas, α_cool and ϵ_SMBH are free parameters which are determined in order to reproduce the luminous end of the luminosity function of galaxies at z ~ 0. In this paper, we fiducially set (α_cool, ϵ_SMBH) = (1.00, 0.012).

From Equation (6), we can see that the radio-mode AGN feedback is more efficient for more massive galaxies at lower redshifts since t_ff and t_cool are roughly proportional to (1 + z)^−3/2 and (1 + z)⁻³, respectively. Galaxies with radio-mode AGN feedback might correspond to FR-I radio galaxies (Fanaroff and Riley, 1974). It is however uncertain how the FR-I radio galaxies have triggered their activity. We thus cannot define galaxies with radio-mode AGN feedback in our model as mock FR-I radio galaxies. We have not included the model of FR-II radio galaxies, which would have intense cold gas accretion. We leave it for future work.

3. Results and Future Prospects

3.1. Basic Statistical Properties of Galaxies

The model which employed for this study includes some revisions from Makiya et al. (2016). We skipped the details of the revisions because of the limitation of the numbers of characters for this paper. For more details appear in Shirakata et al. (2016) and Shirakata et al. in preparation. We find that the fiducial model can explain observational galaxy properties well. In Figure 1, we compare K-band luminosity functions obtained from the model with observations (see the figure caption). The bright end slope of K-band luminosity function of galaxies at z ~ 0 is sensitive to the strength of the radio-mode AGN feedback. If the AGN feedback is weak, we overproduce bright galaxies with M_K < −22.0 and the luminosity function has a single-power law. We also find that the fiducial model can explain SMBH mass function, Faber-Jackson relation, Tully-Fisher relation at z ~ 0.

3.2. M_BH, σ, and Luminosity Weighted Age Relations

Figure 2 shows the M_BH − σ relation at z ~ 0 with the fiducial model. We select the galaxies with M_V < −20, where M_V is the absolute AB magnitude in V-band. We derive the best fit function with the least square method (black line):

$\begin{array}{cc}\log \left(\frac{M_{\text{BH}}}{M_{\odot }}\right)=2.35\log \left(\frac{\sigma }{200\text{km/s}}\right)+\mathrm{8.24.}& (8)\end{array}$

For comparison, we also depict the best fit function obtained from van den Bosch (2016) (gray line):

$\begin{array}{cc}\log \left(\frac{M_{\text{BH}}}{M_{\odot }}\right)=5.27\log \left(\frac{\sigma }{200\text{km/s}}\right)+\mathrm{8.33.}& (9)\end{array}$

We classify galaxies between over-massive BH galaxies and under-massive BH galaxies following our best fit function of M_BH − σ relation with 1σ errors. We then depict M_BH−age relation in Figure 3. We find that galaxies with larger σ have older stellar ages and over-massive BH galaxies have older stellar ages. These results are roughly consistent with the result obtained from Martín-Navarro et al. (2016). On the other hand, when we employ the model with weak AGN feedback, in which α_cool set 0.1 times smaller than the fiducial value, the model cannot explain the result of Martín-Navarro et al. (2016) (Figure 4); all galaxies have younger stellar age than those obtained from Martín-Navarro et al. (2016) and galaxies with under-massive BHs become older. This result would be explained as follows. From Equation (6), more massive (i.e., more luminous) galaxies tend to be quenched their star formation by the AGN feedback. We thus get the steeper slope for the fiducial model compared to the model with the weak AGN feedback (α_cool is smaller). In addition, from Equation (7), galaxies with more massive SMBHs should have so much heating luminosity with the AGN activity that compensates the cooling luminosity. Therefore, we can get the same trend as Martín-Navarro et al. (2016), over-massive black hole galaxies have older stellar ages. From these results, we have concluded that radio mode AGN feedback model might play a role for quenching the star formation of massive galaxies.

FIGURE 2

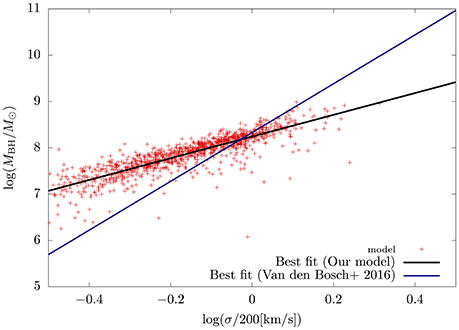
Figure 2. M_BH − σ relation at z ~ 0. Red points are model result, and black thick line describes the fitting function of the model result. Blue line is the fitting function of the data obtained from van den Bosch (2016).

FIGURE 3

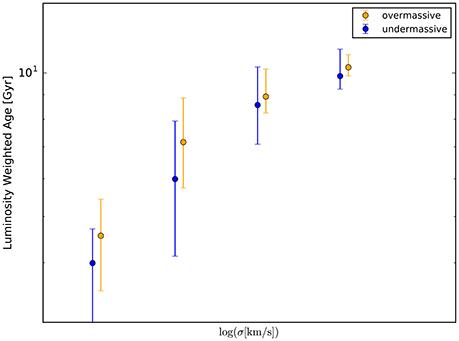
Figure 3. σ− age relation with the fiducial model. The age is luminosity weighted. Orange and blue points with errorbars show the median values of over-/under- massive BH galaxies with 1 − σ error.

FIGURE 4

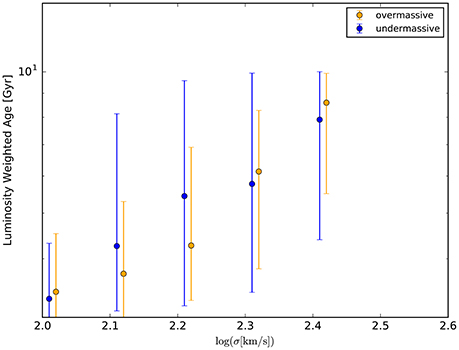
Figure 4. The same figure as Figure 3 with weak AGN feedback model: the parameter, α_cool, is 0.1 times smaller than the fiducial value.

We find that the difference between galaxies with over-massive BHs and under-massive BHs is smaller than those obtained from the observation (Martín-Navarro et al., 2016). For observations, as noted in Martín-Navarro et al. (2016), their estimation of the galactic ages have large observational errors especially for the galaxies with smaller velocity dispersion. It would thus be important to use a larger amount of observational data.

For the theoretical model, the smaller difference between galaxies with over- and under- massive BHs would be partly because of the radio-mode AGN feedback modeling. Since more massive haloes tend to have more massive SMBHs, under-massive galaxies with larger velocity dispersion (and with larger bulge mass) could be quenched their star formation because of the AGN feedback. The ages of over- and under- massive galaxies with large velocity dispersion in the model thus overlap. We then test the effect of the galaxy selection and find the relation between M_BH, σ, and stellar age is sensitive to the sample selection; when we select only brighter galaxies with M_V < −22.0, the difference between galaxies with over- and under- massive BHs becomes clear. It might suggest that the efficiency of the radio-mode AGN feedback should more strongly depend on the BH mass.

Another possible way to explain the results of Martín-Navarro et al. (2016) would be to introduce quasar-mode AGN feedback. Since the number density of bright quasars peaks at higher redshift (e.g., Ueda et al., 2014), quasar-mode AGN feedback could be effective at higher redshift while the radio-mode becomes efficient at lower redshift. We will leave it for future work.

Author Contributions

HS has developed ν²GC. In addition, HS analyze the output data obtained from ν²GC. TK and TO gave comments for the analysis. TI provides merger trees obtained from cosmological N-body simulations for ν²GC.

Funding

TK was supported in part by a University Research Support Grant from the NAOJ and JSPS KAKENHI (17K05389). TO was financially supported by JSPS Grant-in-Aid for Young Scientists (16H01085). TI has been supported by MEXT HPCI STRATEGIC PROGRAM and MEXT/JSPS KAKENHI (15K12031) and by Yamada Science Foundation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We deeply appreciate the detailed review and useful suggestions by the referees, which have drastically improved our paper. We also appreciate the comments about English grammar by A. Pettitt.

References

Bell, E. F., McIntosh, D. H., Katz, N., and Weinberg, M. D. (2003). The optical and near-infrared properties of galaxies. I. luminosity and stellar mass functions. Astrophys. J. Suppl. 149, 289–312. doi: 10.1086/378847

CrossRef Full Text | Google Scholar

Benson, A. J., Bower, R. G., Frenk, C. S., Lacey, C. G., Baugh, C. M., and Cole, S. (2003). What shapes the luminosity function of galaxies? Astrophys. J. 599, 38–49. doi: 10.1086/379160

CrossRef Full Text | Google Scholar

Bower, R. G., Benson, A. J., Malbon, R., Helly, J. C., Frenk, C. S., Baugh, C. M., et al. (2006). Breaking the hierarchy of galaxy formation. Month. Notices R. Astron. Soc. 370, 645–655. doi: 10.1111/j.1365-2966.2006.10519.x

CrossRef Full Text | Google Scholar

Caputi, K. I., McLure, R. J., Dunlop, J. S., Cirasuolo, M., and Schael, A. M. (2006). Further constraints on the evolution of K_s-selected galaxies in the GOODS/CDFS field. Month. Notices R. Astron. Soc. 366, 609–623. doi: 10.1111/j.1365-2966.2005.09887.x

CrossRef Full Text | Google Scholar

Cirasuolo, M., McLure, R. J., Dunlop, J. S., Almaini, O., Foucaud, S., and Simpson, C. (2010). A new measurement of the evolving near-infrared galaxy luminosity function out to z~4: a continuing challenge to theoretical models of galaxy formation. Month. Notices R. Astron. Soc. 401, 1166–1176. doi: 10.1111/j.1365-2966.2009.15710.x

CrossRef Full Text | Google Scholar

Croton, D. J., Springel, V., White, S. D. M., De Lucia, G., Frenk, C. S., Gao, L., et al. (2006). The many lives of active galactic nuclei: cooling flows, black holes and the luminosities and colours of galaxies. Month. Notices R. Astron. Soc. 365, 11–28. doi: 10.1111/j.1365-2966.2005.09675.x

CrossRef Full Text | Google Scholar

Devereux, N., Hriljac, P., Willner, S. P., Ashby, M. L. N., and Willmer, C. N. A. (2009). “The morphological type dependence of K-band luminosity functions,” in Galaxy Evolution: Emerging Insights and Future Challenges, Vol. 419 of Astronomical Society of the Pacific Conference Series, eds S. Jogee, I. Marinova, L. Hao, and G. A. Blanc (San Fransisco, CA), 171.

Google Scholar

Driver, S. P., Robotham, A. S. G., Kelvin, L., Alpaslan, M., Baldry, I. K., Bamford, S. P., et al. (2012). Galaxy And Mass Assembly (GAMA): the 0.013 < z < 0.1 cosmic spectral energy distribution from 0.1 μm to 1 mm. Month. Notices R. Astron. Soc. 427, 3244–3264. doi: 10.1111/j.1365-2966.2012.22036.x

CrossRef Full Text | Google Scholar

Drory, N., Bender, R., Feulner, G., Hopp, U., Maraston, C., Snigula, J., et al. (2003). The munich near-infrared cluster survey. II. The K-Band luminosity function of field galaxies to z~1.2. Astrophys. J. 595, 698–711. doi: 10.1086/377497

CrossRef Full Text | Google Scholar

Fanaroff, B. L. and Riley, J. M. (1974). The morphology of extragalactic radio sources of high and low 179 luminosity. MNRAS 167, 31P–36P. doi: 10.1093/mnras/167.1.31P

CrossRef Full Text | Google Scholar

Huang, J.-S., Glazebrook, K., Cowie, L. L., and Tinney, C. (2003). The Hawaii+Anglo-Australian Observatory K-Band Galaxy Redshift Survey. I. The Local K-Band Luminosity Function. Astrophys. J. 584, 203–209. doi: 10.1086/345619

CrossRef Full Text | Google Scholar

Ishiyama, T., Enoki, M., Kobayashi, M. A. R., Makiya, R., Nagashima, M., and Oogi, T. (2015). The ν²GC simulations: quantifying the dark side of the universe in the Planck cosmology. Publ. Astron. Soc. Jap. 67:61. doi: 10.1093/pasj/psv021

CrossRef Full Text | Google Scholar

Makino, N., Sasaki, S., and Suto, Y. (1998). X-Ray Gas Density Profile of Clusters of Galaxies from the Universal Dark Matter Halo. Astrophys. J. 497, 555–558. doi: 10.1086/305507

CrossRef Full Text | Google Scholar

Makiya, R., Enoki, M., Ishiyama, T., Kobayashi, M. A. R., Nagashima, M., Okamoto, T., et al. (2016). The New Numerical Galaxy Catalog (ν²GC): an updated semi-analytic model of galaxy and active galactic nucleus formation with large cosmological N-body simulations. Publ. Astron. Soc. Jap. 68:25. doi: 10.1093/pasj/psw005

CrossRef Full Text | Google Scholar

McNamara, B. R., Russell, H. R., Nulsen, P. E. J., Hogan, M. T., Fabian, A. C., Pulido, F., et al. (2016). A Mechanism for stimulating AGN feedback by lifting gas in massive galaxies. Astrophys. J. Lett. 832:L11. doi: 10.3847/2041-8205/832/1/L11

CrossRef Full Text

McNamara, B. R., Russell, H. R., Nulsen, P. E. J., Hogan, M. T., Fabian, A. C., Pulido, F., et al. (2016). A Mechanism for stimulating AGN feedback by lifting gas in massive galaxies. Astrophys. J. 830:79. doi: 10.3847/0004-637X/830/2/79

CrossRef Full Text | Google Scholar

Navarro, J. F., Frenk, C. S., and White, S. D. M. (1997). A Universal density profile from hierarchical clustering. Astrophys. J. 490:493. doi: 10.1086/304888

CrossRef Full Text | Google Scholar

Nesvadba, N. P. H., De Breuck, C., Lehnert, M. D., Best, P. N. and Collet, C. (2017). The SINFONI survey of powerful radio galaxies at z~2: Jet-driven AGN feedback during the Quasar Era. Astron. Astrophys. 599:A123. doi: 10.1051/0004-6361/201528040

CrossRef Full Text | Google Scholar

Okamoto, T., Frenk, C. S., Jenkins, A., and Theuns, T. (2010). The properties of satellite galaxies in simulations of galaxy formation. Month. Notices R. Astron. Soc. 406, 208–222. doi: 10.1111/j.1365-2966.2010.16690.x

CrossRef Full Text | Google Scholar

Okamoto, T., Shimizu, I., and Yoshida, N. (2014). Reproducing cosmic evolution of galaxy population from z = 4 to 0. Publ. Astron. Soc. Jap. 66:70. doi: 10.1093/pasj/psu046

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Alves, M. I. R., Armitage-Caplan, C., Arnaud, M., et al. (2014). Planck 2013 results. I. Overview of products and scientific results. Astron. Astrophys. 571:A1. doi: 10.1051/0004-6361/201321529

CrossRef Full Text | Google Scholar

Pozzetti, L., Cimatti, A., Zamorani, G., Daddi, E., Menci, N., Fontana, A., et al. (2003). The K20 survey. V. The evolution of the near-IR Luminosity Function. Astron. Astrophys. 402, 837–848. doi: 10.1051/0004-6361:20030292

CrossRef Full Text

Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., and Primack, J. (2012). Halo concentrations in the standard Λ cold dark matter cosmology. Month. Notices R. Astron. Soc. 423, 3018–3030. doi: 10.1111/j.1365-2966.2012.21007.x

CrossRef Full Text | Google Scholar

Saracco, P., Fiano, A., Chincarini, G., Vanzella, E., Longhetti, M., Cristiani, S., et al. (2006). Probing the evolution of the near-infrared luminosity function of galaxies to z~3 in the Hubble Deep Field-South. Month. Notices R. Astron. Soc. 367, 349–365. doi: 10.1111/j.1365-2966.2006.09967.x

CrossRef Full Text | Google Scholar

Shirakata, H., Kawaguchi, T., Okamoto, T., Makiya, R., Ishiyama, T., Matsuoka, Y., et al. (2016). Theoretical re-evaluations of the black hole mass-bulge mass relation - I. Effect of seed black hole mass. Month. Notices R. Astron. Soc. 461, 4389–4394. doi: 10.1093/mnras/stw1798

CrossRef Full Text | Google Scholar

Smolčić, V., Novak, M., Delvecchio, I., Ceraj, L., Bondi, M., Delhaize, J. (2017). The VLA-COSMOS 3 GHz Large Project: cosmic evolution of radio AGN and implications for radio-mode feedback since z~5. Astron. Astrophys. 602:A6. doi: 10.1051/0004-6361/201730685

CrossRef Full Text | Google Scholar

Springel, V., White, S. D. M., Jenkins, A., Frenk, C. S., Yoshida, N., Gao, L., et al. (2005). Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 435, 629–636. doi: 10.1038/nature03597

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutherland, R. S., and Dopita, M. A. (1993). Cooling functions for low-density astrophysical plasmas. Astrophys. J. Suppl. 88, 253–327. doi: 10.1086/191823

CrossRef Full Text | Google Scholar

Ueda, Y., Akiyama, M., Hasinger, G., Miyaji, T., and Watson, M. G. (2014). Toward the Standard Population Synthesis Model of the X-Ray Background: Evolution of X-Ray Luminosity and Absorption Functions of Active Galactic Nuclei Including Compton-thick Populations. Astrophys. J. 786:104. doi: 10.1088/0004-637X/786/2/104

CrossRef Full Text | Google Scholar

van den Bosch, R. C. E. (2016). Unification of the fundamental plane and Super Massive Black Hole Masses. Astrophys. J. 831:134. doi: 10.3847/0004-637X/831/2/134

CrossRef Full Text | Google Scholar

Vogelsberger, M., Genel, S., Springel, V., Torrey, P., Sijacki, D., Xu, D., et al. (2014). Introducing the Illustris Project: simulating the coevolution of dark and visible matter in the Universe. Month. Notices R. Astron. Soc. 444, 1518–1547. doi: 10.1093/mnras/stu1536

CrossRef Full Text | Google Scholar