- Relativistic Astrophysics Laboratory: Basic and Applied Studies of Space Objects, School of Fundamental and Applied Physics, Moscow Institute of Physics and Technology, Dolgoprudny, Russia
Magnetic field threading a black hole ergosphere is believed to play the key role in both driving the powerful relativistic jets observed in active galactic nuclei and extracting the rotational energy from a black hole via Blandford-Znajek process. The magnitude of magnetic field and the magnetic flux in the vicinity of a central black hole is predicted by theoretical models. On the other hand, the magnetic field in a jet can be estimated through measurements of either the core shift effect or the brightness temperature. In both cases the obtained magnetic field is in the radiating domain, so its direct application to the calculation of the magnetic flux needs some theoretical assumptions. In this paper we address the issue of estimating the magnetic flux contained in a jet using the measurements of a core shift effect and of a brightness temperature for the jets, directed almost at the observer. The accurate account for the jet transversal structure allow us to express the magnetic flux through the observed values and an unknown rotation rate of magnetic surfaces. If we assume the sources are in a magnetically arrested disk state, the lower limit for the rotation rate can be obtained. On the other hand, the flux estimate may be tested against the total jet power predicted by the electromagnetic energy extraction model. The resultant expression for power depends logarithmically weakly on an unknown rotation rate. We show that the total jet power estimated through the magnetic flux is in good agreement with the observed power. We also obtain the extremely slow rotation rates, which may be an indication that the majority of the sources considered are not in the magnetically arrested disk state.
1. Introduction
One of the key issues of theoretical modeling of relativistic jets is determining the magnetic field magnitude. There are several theoretical ways to estimate the latter. The Eddington magnetic field (Beskin, 2010) sets up an upper limit on the magnetic field magnitude in the vicinity of a black hole, since it is set by equipartition of magnetic field density and the total energy density in the accreting plasma that is needed to support the Eddington luminosity. The state of magnetically arrested disk (MAD) (Narayan et al., 2003; Tchekhovskoy et al., 2011; McKinney et al., 2012) sets up the limiting magnetic field that can be accreted onto a black hole basing on an assumption that in such a state the pressure of previously accreted magnetic field can affect the dynamical process of accretion itself.
There are observational means to evaluate the magnetic field in a jet. Blazar spectrum is successfully modeled by the synchrotron self-Compton model. The lower part of the spectrum is dominated by synchrotron radiation of relativistic plasma in a jet magnetic field. Thus, the high-resolution radio interferometry observations provide us with data for unveiling the physical conditions at the very jet origin—in so called radio core. The way to estimate the magnetic field amplitude through the observations is measurements of core shift effect together with several theoretical assumptions on the radiating volume properties (Lobanov, 1998). However, the measurement of radio flux itself, or, equally, the brightness temperature, can provide us with the instrument to probe the magnetic field magnitude (Zdziarski et al., 2015; Nokhrina, 2017).
The magnetic field estimates is an important parameter that allows to test the theoretical models against observations. Zamaninasab et al. (2014) used the magnetic field measurements to calculate the flux and to show that the total flux is in accordance with the magnetically arrested state of the sources. In this paper we make use of the brightness temperature and core shift measurements coupled with the transversal jet model to express the magnetic field magnitude and the magnetic flux contained in a blazar jet through the rotation rate of magnetic surfaces. Our aim is to compare the magnetic flux in a jet against theoretically limited flux by MAD state and to estimate the rotation rate. We also test the obtained magnetic flux against the observed jet power. If the jet power PΨ is fully determined by the electromagnetic energy extraction mechanism, so we denote it with the subscript Ψ, than it can be expressed as Beskin (2010)
where Ψ is the total magnetic flux, rg is a gravitational radius, c is a speed of light, and the rotation rate a = rg/RL is a ratio of a gravitational radius to the light cylinder radius RL.
Although there are estimates for magnetic field amplitude (Lobanov, 1998; Hirotani, 2005; OŚullivan and Gabuzda, 2009; Nokhrina et al., 2015; Zdziarski et al., 2015; Nokhrina, 2017), it cannot be explicitly used for flux calculation. Indeed, the magneto hydrodynamical theoretical and numerical modeling (see e.g., Lyubarsky, 2009; Nokhrina et al., 2015; Bromberg and Tchekhovskoy, 2016) show that the toroidal magnetic field is greater than the poloidal one outside the light cylinder radius. Thus, measurements provide us with the magnitude of the toroidal magnetic field, while the poloidal one is needed to estimate the total magnetic flux (Zamaninasab et al., 2014).
2. Magnetic Flux in a Jet
The observed flux, or observed brightness temperature, can be used to estimate the magnetic field in the radiating domain, and, thus, the magnetic flux. The blazar spectrum in radio band is accurately modeled within the self-absorbed synchrotron model (see e.g., Abdo et al., 2011). The simplest model for the source is a uniform sphere with chaotic magnetic field B and relativistic electrons with the power-law energy distribution described by the amplitude particle number density ke and spectral index p:
γ ∈ [γmin, γmax] (Gould, 1979), where γ is a Lorentz factor of relativistic plasma. The observed spectral flux Sν at the frequency ν for the optically thick uniform self-absorbed source of radius R at the distance d can be written using the spectral photon emission rate ρν and effective absorption coefficient æν as:
and the function of the optical depth u(2Ræν) is defined by Gould (1979). The emission and absorption coefficients for the self-absorbed synchrotron model ρν and æν are the functions of the magnetic field B and of particle number density amplitude ke. These coefficients, written in a jet frame, i.e., in a frame where the electric field vanishes, are:
Here νB = eB/mc is a gyrofrequency in the jet frame, ℏ is the Planck constant, α = e2/ℏc is the fine structure constant, and the functions a(p) and c(p) of the electron distribution spectral index p are defined in Gould (1979). The spectral flux depends on the magnetic field amplitude, while the particle number density amplitude defines the maximum of a function u and, thus, the position of the observed radio core—the domain where the optical depth τ is equal to unity. So, the spectral flux measurement provide us with an instrument to evaluate the magnetic field in a source. The spectral flux may be expressed through the brightness temperature Tb as
where θ is the angular size of a radiating domain. Thus one can express the magnetic field amplitude in a source having measured brightness temperature. The method was first applied by Zdziarski et al. (2015) to check the magnetic field amplitude in AGN radio cores independently of the equipartition assumption. Equating the right-hand sides of Equations (3) and (6), and expressing the jet frame values through the nucleus frame values, we obtain for p = 2 the magnetic field (Zdziarski et al., 2015, see also details in Nokhrina, 2017)
Here Γ is a flow bulk Lorentz factor, z is a source redshift, and δ is a Doppler factor.
On the other hand, the measurements of core shift effect (Lobanov, 1998; Hirotani, 2005; OŚullivan and Gabuzda, 2009; Zamaninasab et al., 2014) provides the following expression for the magnetic field amplitude Bcs at 1 pc distance from the central source:
here ηcs is a coefficient determining the slope of the apparent core position dependence on the inverse observation frequency:
χ is the jet opening angle that may obtained having the measured in Pushkarev et al. (2009) apparent opening angle χapp as χ = χappsinφ/2, DL is a luminosity distance, the bulk plasma motion Lorentz factor is Γ, δ is the Doppler factor, and the observation angle φ = Γ−1 (Cohen et al., 2007). The Expression (Equation 8) has been obtained under the same assumption of synchrotron self-absorbed source, but the method utilizes the core shift effect—the shift of the observed radio core on different frequencies. This shift is due to the fact that the surface of optical depth τ = 1 is situated at different distance from the central source for each frequency. We must stress that the relation (Equation 7) uses only the synchrotron self-absorbed source model, but the position of the radio core in the model is not known. If we use the core shift effect, we may also obtain the core position (Nokhrina, 2017):
The relation for Bcs (Equation 8) has been obtained with more assumptions: equipartition between magnetic field energy and plasma energy assumption, and the Blanford-Königl model (Blanford and Königl, 1979) B(r) = B1(r1/r), , where n1 and B1 are particle number density and magnetic field magnitude at distance r along the jet equal to r1 = 1 pc. Relation (Equation 8) provides the magnetic field amplitude together with its position along the jet.
Both Expressions (Equation 7) and (Equation 8) are based on the model of uniform radiating sphere (Gould, 1979). In particular, such a model does not allow us to estimate the total magnetic flux, contained in a jet—one of the important values, defining the total jet power, and the value that could be restricted by the magnetically arrested disk model. Indeed, as the toroidal magnetic field Bφ dominates the major part of a jet, it is the toroidal component of a field we imply by the spectral flux measurement. However, it is the poloidal component BP that carries the magnetic flux. However, the transversal modeling of field profiles allow us in a simple case of blazar jets, i.e., jets pointing almost directly at us, to calculate the flux from non-homogeneous cylindrical self-absorbed synchrotron source, and to correlate the measured magnetic field amplitude with the poloidal field in a jet that defines the total flux. Indeed, it has been shown by Lyubarsky (2009), that the relation
holds outside the light cylinder RL = c/ΩF. Further we model the transversal magnetic field and particle number density profiles as follows. Inside the light cylinder the poloidal magnetic field remains almost constant (Beskin and Nokhrina, 2009), while Bφ = B0r⊥/RL. Both numerical and semi-analytical modeling (Nokhrina et al., 2015; Bromberg and Tchekhovskoy, 2016) show, that outside the light cylinder the power-law is a good approximation for magnetic field and particle number density profiles across the jet for small opening angles. We set
where B0 and n0 are the magnetic field and particle number density amplitudes, i.e., magnitudes at the light cylinder RL.
For the simplest case of a jet pointing almost at us, when the radiation domain may be treated as a stratified cylinder with the profiles (Equations 12–14), we calculate the spectral flux Sν (see details in Nokhrina, 2017). Equating the obtained Sν to the expression (Equation 6), we obtain the following relation for the amplitude magnetic field B0:
Here the fast rotation ΓRL ≪ Rj is assumed. While Rj can be estimated through observations, the light cylinder radius is usually unknown. However, its value can be somewhat restricted by theoretical models predicting that Blandford-Znajek process works effectively for RL of the order of 2rg (Blanford and Znajek, 1977; Tchekhovskoy et al., 2012). Still, the value B0 cannot be readily extracted from the observations.
The total flux Ψ in a jet with given cross-section magnetic filed profile is defined as
Using the magnetic field profile (Equation 12) we obtain
Substituting explicitly B0RL into Equation (17) and using the correlation B0RL = 0.86BuniRj following from Equations (7) and (15), we obtain the relation for the magnetic flux:
Here one may use Bcs or Buni, since both values are obtained under the same assumptions on the geometry and structure of radiating domain. The amplitude magnetic flux Ψa = aΨ. The Equation (18) coincides with the expression for the magnetic flux in Zamaninasab et al. (2014). The expression (Equation 18) for the flux depends inversely on a rotation rate a, because the dependence on the physical values in square brackets is logarithmically weak and can be neglected. Taking the fiducial value for , we take the expression in square brackets being of the order of a few to ten.
3. The Jet Power and the Rotation Rate
We apply the obtained expression for the flux (Equation 18) to test it against the following theoretical predictions. If we assume that most of the sources are in MAD state, we can compare the amplitude flux Ψa and ΨMAD and obtain the rotation parameter a = Ψa/ΨMAD. However, we must bear in mind that the energy losses mechanism Blanford and Znajek (1977) works effectively for relatively high rotation rates a > 0.5. Thus, with the difference in ΨMAD and Ψa is greater, we might think that the source is not in the MAD state.
We also use the obtained flux (Equation 18) to calculate the total jet power given by the Equation (1). As the Expression (Equation 1) depends on the product Ψa = Ψa (Equation 18) that depends on a logarithmically weakly only through the term 1 + 2 ln(Rja/rg), so does the total power. So this result is independent on the assumption of the particular value for a. That is why such a test may be important for the flux determination. We do it for the magnetic field estimated by two methods: the brightness temperature measurements and the core shift measurements in order to compare the two methods.
We have found 48 sources meeting the following conditions: (i) the observational angle of a jet must be small enough for the model of head-on jet for Buni can be applied; (ii) the source has a measured core shift, central black hole mass, and the apparent opening angle. We use the following samples: we take the brightness temperature measured by Kovalev et al. (2005) and the core shifts by Pushkarev et al. (2012). The apparent velocity βapp we take from Lister et al. (2009). We also use the black hole masses MBH and the accretion luminosities Lacc collected by Zamaninasab et al. (2014). For the unknown Lorentz factor we use Γ = σM, and the Michel's magnetization parameter σM has been evaluated by Nokhrina et al. (2015), We use for the observed opening angle the results from Pushkarev et al. (2009). This is in contrast with Zamaninasab et al. (2014), where the causal connectivity across the jet Γ χ ~ 1 is assumed. We obtain the magnetic field magnitudes using the above values and Equations (7) and (8). On average, the values of Buni is less and more scattered than values of Bcs, which is in agreement with results obtained in Zdziarski et al. (2015). To calculate the flux using Bcs we employ Rj = χ × 1 pc. For Buni we use Equation (10), so we define Rj = rcoreχ.
One of the possible upper limits on the magnetic field amplitude in relativistic jets may be imposed by MAD model. Magnetically arrested disk is a disk in a state of equilibrium of the accretion rate and the pressure of magnetic field frozen in previously accreted matter (Narayan et al., 2003; Tchekhovskoy et al., 2011; McKinney et al., 2012). There is observational support of AGNs staying in MAD state (Zamaninasab et al., 2014). Equation (18) relate the total magnetic flux in a jet with the observable jet radius, magnetic field, gravitational radius (through the black hole mass estimates), and unknown rotation rate a. Setting ΨMAD as the upper limit on a magnetic flux, one can obtain the lower limit for the rotational rate of a central black hole. Here we compare the magnetic flux Ψ calculated with expression (Equation 18) for Buni, obtained by the brightness temperature measurements, or Bcs obtained by core shift measurements, and the magnetic flux ΨMAD set by MAD model. In order to obtain the magnetic flux predicted by MAD ΨMAD, we use the equation (Zamaninasab et al., 2014)
where we use relation between disk luminosity .
The results for Ψ calculated for a = 0.5 and ΨMAD are presented in Table 1. We present in the table the values for ΨMAD (Zamaninasab et al., 2014), the total magnetic flux obtained using brightness temperature measurements Ψbr and core shift measurements Ψcs. We see the reasonable agreement between Ψbr and Ψcs, although the former is more scattered. We see that aΨ ≪ ΨMAD for almost all the sources for magnetic filed estimates by both methods. If we assume that all the sources are in MAD state, the rotational rate of a black hole must be in a range (0.0001;0.1) for 36 sources. Only 12 have the rotational rate between 0.1 and 1. Thus, assumption of the sources being in the MAD state leads us to a conclusion that the rotation must be much less than the critical one.
Otherwise, we may assume that 36 sources have rotation parameters close to critical a ∈ [0.5; 1], but not in a MAD state. We must stress that the expressions for the magnetic field estimate through the core shift measurement are different here from the one used in Zamaninasab et al. (2014). In this paper the Equation (8) uses the assumtions from Nokhrina et al. (2015) of the total outflow magnetization equal to the unity. This condition means that the total Poynting flux in a core region is equal to the total bulk particle kinetic energy flux, with about 1% (Sironi et al., 2013) of radiating particles having the relativistic energy distribution (Equation 2). This assumption has been used to estimate maximal possible Lorentz factor of the flow (Nokhrina et al., 2015), which correlates very good with the Lorentz factor estimates basing the observed super-luminal velocities (Lister et al., 2009). In this point our approach differs from the one used by Zamaninasab et al. (2014).
In order to check our flux estimates, we test it against the total jet power (Equation 1). This result is robust under the model assumptions, since it the total power depends on a very weakly. The calculation of the total jet power for the obtained flux is in Table 1. We compare the total power PΨ, calculated substituting Equation (18) into Equation (1), with the jet power, estimated basing on the correlation of Pjet with the luminosities of jet radio band Cavagnolo et al. (2010):
We plot PΨ against the obtained with Equation (20) power Pjet in Figure 1. We observe the reasonable correlation of PΨ and Pjet. The histogram of the ratio of PΨ/Pjet is presented in Figure 2. We see that the ratio has a well determined peak around a few. Although it gives the systematic excess of PΨ over Pjet, we state that PΨ is in accordance with Pjet bearing in mind uncertainties in the determination of all the values including Ptot. The systematic excess may be attributed to the probable overestimating the magnetic field Bcs, the hints of which we see in discrepancy between Bcs and Bbr, the latter being lower.
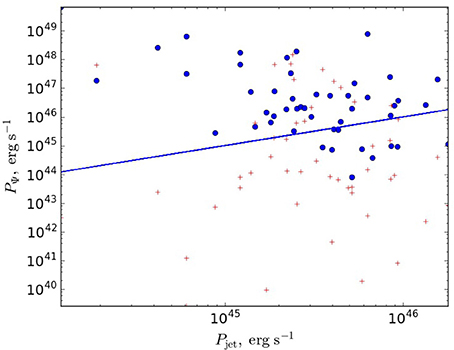
Figure 1. The jet power PΨ, calculated using magnetic flux, against the total kinetic jet power. The straight line is a theoretical prediction. The blue circle stand for the total flux obtained using the core shift effect, the red crosses are for the total flux obtained using the brightness temperature. The sources with the flux approximately equal to the MAD flux are in the upper left corner.
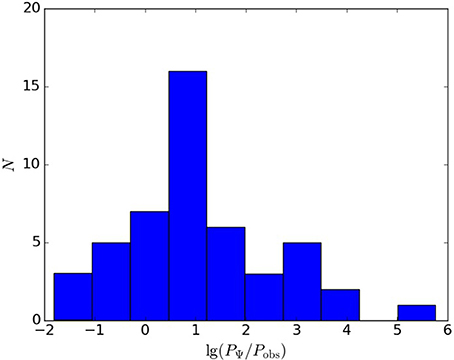
Figure 2. The histogram showing the number of sources with the ration of calculated power PΨ to the total jet power Pjet, the ratio is in the log-scale. We see the systematic excess of power estimated through the flux against the jet power by a factor of few.
We have also tested the jet power obtained with the flux determined by Buni (see Figure 1). The second method provides systematically lower powers and more scattering. This is in agreement with the result by Zdziarski et al. (2015) who have found the scattering in magnetic field amplitude calculated with no equipartition assumption while still have the majority of sources having the equipartition magnetic field.
4. Summary
We have discussed estimates for the magnetic flux using the jet core magnetic field obtained through the brightness temperature measurements and by the core shift effect. Usually, any estimates of the magnetic field in a radiating domain of relativistic jet cannot be readily put into the expression for the magnetic flux. This is because theoretical modeling show, that the toroidal magnetic field dominates the poloidal magnetic field outside the light cylinder. Thus, the field we measure using synchrotron self-Compton model of radiation, must be toroidal, while the magnetic flux is determined by the poloidal one. Consideration of transversal field configuration is needed to estimate accurately the magnetic flux in a jet using the available evaluation of magnetic field magnitude through observations—either using the core-shift effect, or spectral flux measurements. In this work has been considered the simplest case—the transversal structure of jets observed with very small viewing angle.
We test the method of estimating the flux against the limiting flux determined by the magnetically arrested disk model. For 36 of 48 sources the obtained flux is much less than the MAD flux. This suggest either the extremely slow rotation rate a ∈ (0.0001; 0.1) or that the sources are not in MAD state. For 12 sources both fluxes coincide for a ∈ (0.1; 1)—the fast rotation that is needed for the efficient energy extraction from a black hole.
We also test the flux estimate against the total jet power determined by the electromagnetic mechanism of energy extraction. This result does not depend on the particular value for a, as the Expression (Equation 1) depends on the product of Ψ and a Ψa that can be estimated directly. In this case we see a good agreement between the total power determined by the flux and the total power obtained from the observations, with the distribution of powers ration being well peaked around a few.
Author Contributions
The results presented in the paper has been obtained by EN.
Funding
This work was supported by Russian Science Foundation, grant 16-12-10051.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author thanks the referees for the suggestions which helped to improve the paper. This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al., 2009).
References
Abdo, A., Ackermann, M., Ajello, M., Baldini, L., Ballet, J., Barbiellini, G., et al. (2011). Fermi large area telescope observations of markarian 421: the missing piece of its spectral energy distribution. Astrophys. J. 736:131. doi: 10.1088/0004-637X/736/2/131
Beskin, V. (2010). Magnetohydrodynamic models of astrophysical jets. Phys. Uspekhi 53, 1199–1233. doi: 10.3367/UFNe.0180.201012b.1241
Beskin, V., and Nokhrina, E. (2009). On the central core in MHD winds and jets. Month. Notices R. Astron. Soc. 397, 1486–1497. doi: 10.1111/j.1365-2966.2009.14964.x
Blanford, R., and Königl, A. (1979). Relativistic jets as compact radio sources. Astrophys. J. 232, 34–48. doi: 10.1086/157262
Blanford, R., and Znajek, R. (1977). Electromagnetic extraction of energy from kerr black holes. Month. Notices R. Astron. Soc. 179, 433–456. doi: 10.1093/mnras/179.3.433
Bromberg, O., and Tchekhovskoy, A. (2016). Relativistic mhd simulations of core-collapse GRB jets: 3d instabilities and magnetic dissipation. Month. Notices R. Astron. Soc. 456, 1739–1760. doi: 10.1093/mnras/stv2591
Cavagnolo, K., McNamara, B., Nulsen, P., Carilli, C., Jones, C., and Brzan, L. (2010). A relationship between agn jet power and radio power. Astrophys. J. 720, 1066–1072. doi: 10.1088/0004-637X/720/2/1066
Cohen, M., Lister, M., Homan, D., Kadler, M., Kellermann, K., Kovalev, Y., et al. (2007). Relativistic beaming and the intrinsic properties of extragalactic radio jets. Astrophys. J. 658, 232–244. doi: 10.1086/511063
Gould, R. (1979). Compton and synchrotron processes in spherically-symmetric non-thermal sources. Astron. Astrophys. 76, 306–311.
Hirotani, K. (2005). Kinetic luminosity and composition of active galactic nuclei jets. Astrophys. J. 619, 73–85. doi: 10.1086/426497
Kovalev, Y., Kellermann, K., Lister, M., Homan, D., Vermeulen, R., Cohen, M., et al. (2005). Sub-milliarcsecond imaging of quasars and active galactic nuclei. IV. Fine-scale structure. Astron. J. 130, 2473–2505. doi: 10.1086/497430
Lister, M., Aller, H., Aller, M., Cohen, M., Homan, D., Kadler, M., et al. (2009). MOJAVE: monitoring of jets in active galactic nuclei with VLBA experiments. V. Multi-epoch VLBA images. Astron. J. 137, 3718–3729. doi: 10.1088/0004-6256/137/3/3718
Lister, M., Aller, M., Aller, H., Homan, D., Kellermann, K., Kovalev, Y., et al. (2013). MOJAVE. X. Parsec-scale jet orientation variations and superluminal motion in active galactic nuclei. Astron. J. 146, 120–142. doi: 10.1088/0004-6256/146/5/120
Lyubarsky, Y. (2009). Asymptotic structure of poynting-dominated jets. Astrophys. J. 698, 1570–1589. doi: 10.1088/0004-637X/698/2/1570
McKinney, J., Tchekhovskoy, A., and Blandford, R. (2012). General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Month. Notices R. Astron. Soc. 423, 3083–3117. doi: 10.1111/j.1365-2966.2012.21074.x
Narayan, R., Igumenshchev, I., and Abramowicz, M. (2003). Magnetically arrested disk: an energetically efficient accretion flow. Publ. Astron. Soc. Jpn. 55, L69–L72. doi: 10.1093/pasj/55.6.L69
Nokhrina, E. (2017). Brightness temperature - obtaining the physical properties of a non-equipartition plasma. Month. Notices R. Astron. Soc. 468, 2372–2381. doi: 10.1093/mnras/stx521
Nokhrina, E., Beskin, V., Kovalev, Y., and Zheltoukhov, A. (2015). Intrinsic physical conditions and structure of relativistic jets in active galactic nuclei. Month. Notices R. Astron. Soc. 447, 2726–2737. doi: 10.1093/mnras/stu2587
OŚullivan, S., and Gabuzda, D. (2009). Magnetic field strength and spectral distribution of six parsec-scale active galactic nuclei jets. Month. Notices R. Astron. Soc. 400, 26–42. doi: 10.1111/j.1365-2966.2009.15428.x
Pushkarev, A., Hovatta, T., Kovalev, Y., Lister, M., Lobanov, A., Savolainen, T., et al. (2012). MOJAVE: monitoring of jets in active galactic nuclei with VLBA experiments. IX. Nuclear opacity. Astron. Astrophys. 545:A113. doi: 10.1051/0004-6361/201219173
Pushkarev, A., Kovalev, Y., Lister, M., and Savolainen, T. (2009). Jet opening angles and gamma-ray brightness of AGN. Astron. Astrophys. 507, L33–L36. doi: 10.1051/0004-6361/200913422
Sironi, L., Spitkovsky, A., and Arons, J. (2013). The maximum energy of accelerated particles in relativistic collisionless shocks. Astrophys. J. 771:54. doi: 10.1088/0004-637X/771/1/54
Tchekhovskoy, A., McKinney, J. C., and Narayan, R. (2012). General relativistic modeling of magnetized jets from accreting black holes. J. Phys. 372:012040. doi: 10.1088/1742-6596/372/1/012040
Tchekhovskoy, A., Narayan, R., and McKinney, J. (2011). Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Month. Notices R. Astron. Soc. 418, L79–L83. doi: 10.1111/j.1745-3933.2011.01147.x
Zamaninasab, M., Clausen-Brown, E., Savolainen, T., and Tchekhovskoy, A. (2014). Dynamically important magnetic fields near accreting supermassive black holes. Nature 510, 126–128. doi: 10.1038/nature13399
Keywords: active galaxies, jets, BL Lacertae objects, non-thermal radiation, magnetic flux
Citation: Nokhrina EE (2017) The Correlation between the Total Magnetic Flux and the Total Jet Power. Front. Astron. Space Sci. 4:63. doi: 10.3389/fspas.2017.00063
Received: 31 August 2017; Accepted: 06 December 2017;
Published: 22 December 2017.
Edited by:
Mauro D'Onofrio, Università degli Studi di Padova, ItalyReviewed by:
Maria Dainotti, Jagiellonian University, PolandAlberto Martin Gago, Pontifical Catholic University of Peru, Peru
Copyright © 2017 Nokhrina. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elena E. Nokhrina, bm9raHJpbmFAcGh5c3RlY2guZWR1
 Elena E. Nokhrina
Elena E. Nokhrina