Perspectives for Cosmological Reionization From Future CMB and Radio Projects

1. Introduction

In the past decades, the present Λ cold dark matter (ΛCDM) cosmological model describing our Universe has been established as the standard model. While a wide set of cosmological parameters has been measured to high precision, many fundamental questions are still open in cosmology, as, for example, the physics of the very early Universe, the origin of the recent cosmic acceleration and the nature of dark matter (DM). Although the Cosmic Microwave Background (CMB) has greatly contributed in the past decades to our understanding of the most important cosmological problems, the next step toward a precision cosmology requires extra information (Yamauchi et al., 2016). The forthcoming radio telescope, the Square Kilometer Array (SKA), in its complete operational mode will be the world's largest observational facility able to open a new frontier in cosmology. The SKA, with its unprecedented sensitivity and resolution, will perform cosmological surveys potentially able to answer to many fundamental questions in cosmology, so representing a step forward in the so called precision cosmology. The SKA, a new technology radio-telescope based on large arrays, will allow us to investigate these and other different cosmological and astrophysical topics and, in combination with future CMB experiments, among others, will contribute to probe various types of dissipation processes relevant at different cosmic epochs.

Together with the cosmic expansion and the primordial nucleosynthesis, the CMB is one of the fundamental observational evidence of the hot big bang theory (Danese and de Zotti, 1977), representing a powerful tool of investigation in a cosmological context. Since the discovery of the CMB in 1964, and in particular in the past two decades, the improved measurements in temperature fluctuations achieved an unprecedented accuracy in constraining the majority of the cosmological parameters values. The presence of small CMB temperature anisotropies would have been, as realized, the seeds for galaxy formation, hence, a direct probe of the formation and evolution of the structures we observe today.

In early 1990's the NASA COsmic Background Explorer (COBE) satellite¹ inaugurated the “precision cosmology” era, determining the CMB spectrum temperature of T₀ = 2.72548±0.00057K (Mather et al., 1990; Fixsen et al., 1996; Fixsen, 2009) and then discovering the CMB temperature fluctuations of few tens of μK on angular scales larger than 7° (Smoot et al., 1991), the so called anisotropies. Remarkably, already in 1990, Efstathiou et al. (1990) argued that a positive cosmological constant is necessary to jointly explain large scale structures observations and CMB anisotropy upper limits at small angular scales in a spatially flat cosmology, anticipating the paradigm transition from a cold dark matter (CDM) to a cosmological constant plus CDM (ΛCDM) model of the Universe accounting for the evidence of the recent cosmic acceleration derived through Type Ia Supernovae (SNIa) observations (Perlmutter et al., 1999) and the flatness of the Universe determined by the Balloon Observations Of Millimetric Extragalactic Radiation and Geophysics (BOOMERanG) CMB anisotropy experiment (de Bernardis et al., 2002).

The great amount of more recent available data coming from ground-based and balloon-borne experiments to space borne experiments, as the Wilkinson Microwave Anisotropy Probe² (WMAP) and Planck³ missions, allows to explore cosmological and astrophysical key aspects. High precision measurements from the Planck satellite confirmed that only 5% of Universe energy budget is apparently made of ordinary baryonic matter and the remaining 95% of possibly exotic components as DM and dark energy (DE) (Planck Collaboration, 2014). Indeed, the wealth of information encoded in the CMB has contributed significantly to bring cosmology to a precision science, and allowed us to access the very first stages of cosmic evolution.

The linear polarization pattern of CMB anisotropies (Hu and White, 1997) has been generated in two distinct cosmological epochs: the recombination era (z≃1100) during which, because of the Universe expansion and cooling, the photon diffusion length in a medium with decreasingly ionization fraction became large enough to reveal the quadrupole moment of the local anisotropy pattern at the last scattering surface and the Universe then became almost neutral and transparent to radiation, as Thomson scattering, the most efficient fundamental process involved, was no longer able to tightly couple matter and radiation; much later, during the primeval stages of bound structures formation, when photoionizing photons were able to escape from them, permeating the intergalactic medium (IGM) that became again significantly ionized (reionization epoch). During this period, free electrons interacted, through Thomson scattering, with CMB photons once more. Since the size of the Hubble horizon at reionization was much larger than at recombination, this new contribution generated a characteristic bump in the CMB anisotropy pattern at large angular scales (i.e., at low multipoles, ℓ ≲ 10) in the pure polarization angular power spectra, as well as in the temperature to polarization correlation.

It is well known that the temperature increase of the cosmic gas in ionized regions leads to a dramatic suppression of the formation of low-mass galaxies (see Ciardi and Ferrara, 2005 for a review). The impact of this effect during cosmic reionization depends on radiative feedback mechanisms, that can be modeled according to different prescriptions. Among them, we remember the suppression (S) model, where galaxies can efficiently form stars provided that their circular velocity is larger than a critical threshold evolving according to gas temperature (Choudhury and Ferrara, 2006), and the filtering (F) model, where, according to the mass of the galaxy, the fraction of gas that feeds star formation, reduced with respect of the universal value, is defined by the redshift dependent filtering mass (Gnedin, 2000). With proper choices of few parameters, these models can reproduce “a wide range of observational data, such as the redshift evolution of Lyman-limit absorption systems, the Gunn-Peterson and electron scattering optical depths, the cosmic star formation history, and number counts in high-z sources” (Schneider et al., 2008). These prescriptions have been implemented into a physically-motivated model of reionization consistent with observations (Choudhury and Ferrara, 2005, 2006). Their quite different reionization and thermal histories are shown in Figure 1. Their optical depths, τ_S = 0.1017 and τ_F = 0.0631, are in agreement with the WMAP and Planck 2013 results (based on WMAP polarization data) and with Planck 2015 results, respectively.

FIGURE 1

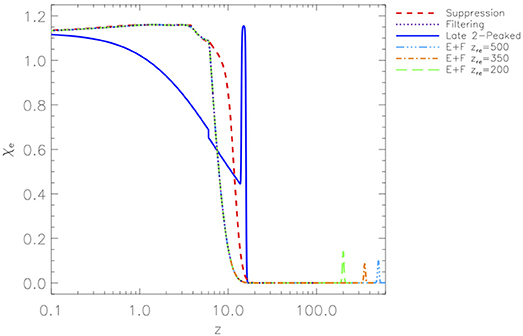
Figure 1. Redshift dependence of the electron ionization fraction for a set of astrophysical and phenomenological reionization histories. For the considered phenomenological models the lower contribution to the global value of τ at z < 10 is compensated by a peaked ionization phase at higher redshift. See also the text. Reprinted from Trombetti and Burigana (2012).

Various models have been proposed including also earlier phases of reionization possibly produced by ionizing photons by both astrophysical and fundamental physics processes (briefly discussed in section 5). When combined with the observationally motivated reionization process associated to galaxy and star formation as in the models mentioned above, they imply a long duration of complete or partial ionization, or, remarkably, a double peaked reionization history. In principle, earlier processes could affect the CMB spectra also at intermediate and high multipoles. Late double peaked (L) and early reionization phenomenological models have been proposed (Naselsky and Chiang, 2004) to mimic with suitable choices of few parameters a variety of electron ionization fraction histories. In Figure 1 we report also for comparison a L scenario and three high redshift phases of reionization peaked at a redshift z = z_re followed by the filtering model (E+F) described above and defined by main parameters set to have τ = τ_S (see Trombetti and Burigana (2012) and references therein for further information and parameters of these models and the electron temperature history characterization).

Recently, cosmic reionization has been widely studied combining the Planck data in temperature with the low-multipole polarization data including also HFI channels. Various parameterizations of the reionization history in ΛCDM models have been fitted (Planck Collaboration, 2016e). For the commonly adopted instantaneous reionization model, a Thomson optical depth τ = 0.058±0.012 was derived, in good agreement with Planck 2015 results combined with other data sets, but with smaller uncertainties. The history of the ionization fraction in the transition between the neutral and ionized phases was reconstructed using either a symmetric or an asymmetric model (see Figure 2). To determine better constraints on the duration of the reionization process, the amplitude of the kinetic Sunyaev-Zel'dovich (SZ) effect (kSZE) was taken into account including the additional information based on the observations with the high-resolution Atacama Cosmology Telescope (ACT) and South Pole Telescope (SPT) experiments. The derived average redshift at which reionization occurs lies between z = 7.8 and 8.8, depending on the model. Using kSZE constraints and a redshift-symmetric reionization model, the upper limit to the width of the reionization period turned to be Δz < 2.8. The Universe is found to be “ionized at less than the 10% level at z ≳ 10, strongly constraining an early onset of reionization. This result also reduces the tension between CMB-based analyses and constraints from other astrophysical sources” (Planck Collaboration, 2016e).

FIGURE 2

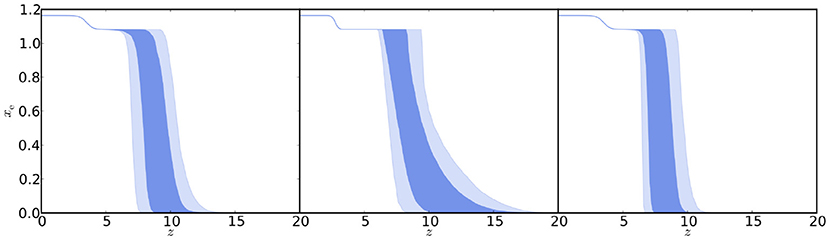
Figure 2. “Constraints on ionization fraction during reionization. The allowed models, in terms of z_re and Δz, translate into an allowed region in x_e(z) (68 and 95% in dark blue and light blue, respectively), including the z_end > 6 prior here.” Left: “Constraints from CMB data using a redshift-symmetric function [x_e(z) as a hyperbolic tangent with δz = 0.5].” Middle: “Constraints from CMB data using a redshift-asymmetric parameterization (x_e(z) as a power law).” Right: “Constraints from CMB data using a redshift-symmetric parameterization with additional constraints from the kSZE effect.” Reprinted from Planck Collaboration (2016e) [Credit: Planck Collaboration, A&A 596, A108, 2016, reproduced with permission ©ESO].

Given the relevance of cosmological reionization for the comprehension of early phases of structure formation and evolution and its connection with a large variety of astrophysical and cosmological questions, it is important to discriminate among the various models compatible with current data. Future CMB and radio surveys will offer unique and particular ways to jointly study the evolution and energetics of reionization process providing both global and tomographic information. In this work, we review the information carried out by CMB polarization anisotropies and how the combined analysis of low and high multipoles beyond the simple τ approximation could in principle shed light on the ionization history in a wide range of redshifts. CMB spectral distortions, namely Comptonization distortions, are instead particularly sensitive to the global energy released in the IGM. The perspectives of absolute temperature measurements and of differential approaches, based on the analysis of the dipole spectrum in anisotropy experiments, are critically discussed. The evolution of neutral hydrogen is well mapped by the redshifted 21-cm line emission, whose fluctuations provide a tomographic view of the complex evolution of the astrophysical sources since the dawn age to the fully ionized phase. The recent results on the global signal and the perspectives opened by forthcoming interferometers are reviewed. The analysis of the free-free diffuse radio emission represents a complementary tool to globally constrain the reionization process and its link with the matter power spectrum at small scales related to the nature of dark matter particles, an aspect discussed here considering the limitation by astrophysical foregrounds.

In sections 2, 3 we present respectively a brief overview of the proposals of future CMB missions and a (certainly not complete) description of on-going and future (namely SKA and its precursors/pathfinders) radio projects (see also sections 4–6, we discuss the scientific outcome of future CMB missions, focussing respectively on the information carried out by polarization anisotropies, spectral (absolute temperature) distortions and dipole (anisotropy) distortions. In sections 7, 8 we discuss the promising perspectives opened by forthcoming and future radio surveys, focussing respectively on the information carried out by the redshifted 21-cm line and by the free-free diffuse emission. Finally, in section 9, we describe the contribution of future radio surveys to reionization studies with CMB polarization projects.

2. Toward Future CMB Missions

The angular power spectrum (APS) of the CMB anisotropies in polarization can be decomposed into E-modes, mainly produced by scalar perturbations in the early Universe, and B-modes, to be mainly ascribed at large scales (i.e., low multipoles, ℓ) to tensor metric perturbations⁴. Discovering primordial B-modes is considered the most important goal of present and future CMB polarization experiments. The energy scale tested by extremely accurate observations of the CMB B-mode polarization is ~10¹⁶ GeV, more than 12 orders of magnitude beyond the energy scales accessible to the Large Hadron Collider at CERN. Since cosmic inflation does not provide a unique prediction for the amplitude of the primordial tensor mode, parameterized by r, a precise measurement of, or upper bound on r is essential for constraining inflationary physics. More in general, the comprehensive study of the CMB polarization is a crucial scientific theme that requires observations with exquisite sensitivity, control of systematic errors, and broad frequency coverage. Particularly for studying reionization imprints, mainly relevant at large angular scales, or low multipoles, space observations are crucial because of the necessity to cover very wide sky areas (and possibly the full sky) and to accurately remove foreground contamination to achieve a precise characterization.

The observation of the sky looking for the reionization bump at ℓ = 2 − 10 (and not only at the recombination epoch imprinted at ℓ = 20 − 100) is important to firmly reveal the primordial inflationary B-modes. On the other side, since tensor perturbations generate both B- and E-modes, a direct measure of the B-modes would allow a better characterization of tensor contribution to E-modes and then of the reionization process.

The main requirements for a B-modes detection mission, to reveal a tensor to scalar ratio r ~ 10⁻³, are an improvement in sensitivity of a factor ~100 with respect to Planck and a suppression of systematic effects at a level of few tens of nK, together with a very accurate (at the level of 1% or better) understanding of polarized foregrounds.

While the good agreement between the CMB spectral shape and the blackbody spectrum assessed by the COBE/Far Infrared Absolute Spectrophotometer (FIRAS) instrument is a crucial confirmation of big bang cosmology, theory predicts that at higher sensitivity this agreement breaks down. Energy injection at any redshift z ≲(few) × 10⁶ superimposes spectral distortions relative to a perfect CMB blackbody spectrum. Detecting and characterizing them will represent a powerful way to study dissipation processes at various cosmic times. Remarkably, Thomson scattering of CMB photons from free electrons at the epoch of reionization responsible for E-mode polarization on large angular scales also distorts the CMB spectrum away from a blackbody.

Different classes of missions have been proposed to space agencies in order to achieve the above scientific objectives. In the following subsections we present an updated overview of the various proposals presented in the last 10 years to significantly improve our comprehension of CMB polarization, possibly detecting B-modes, and to discover the tiny spectral distortions predicted from the theory but still undetected.

2.1. CMB Mission Proposals Dedicated to Temperature and Polarization Anisotropies

In 2009, in response to the ESA Cosmic Vision 2015–2025 call for Proposals, a medium class space mission has been presented, B-Pol (De Bernardis et al., 2009), aimed at detecting the primordial gravitational waves on cosmological scales expected from the inflationary epoch through the detection of the primordial B-mode polarization, thus confirming the quantum origin of the CMB fluctuations. It was designed to host six broad frequency bands detectors, from 45 to 353 GHz, coupled to a set of lens to perform degree resolution observations.

In February 2015, a Lite (Light) Satellite for the studies of B-mode polarization and Inflation from cosmic background Radiation Detection (LiteBIRD) at the extremely early Universe, has been formally proposed as a strategic mission to the ISAS, JAXA, and 1 year later it has started the conceptual design phase-A1 (Matsumura et al., 2014; Ishino et al., 2016). LiteBird is a focussed, low-cost Japanese B-mode mission concept, in several scientific aims analogous to the B-Pol mission. It is designed to detect B-modes at the level of r ~ 10⁻³, providing that the foregrounds are not too complicated. The instrument on board the satellite, coupled with the sky through a reflective optical system in order to achieve a resolution of about one degree, is equipped with a relatively small telescope design to achieve a resolution of about one degree and with a superconducting detector array cooled to 4 K in order to allow the achievement of a sensitivity of 2 μK·arcmin over 15 frequency bands from 40 to 400 GHz (Matsumura et al., 2014) with relative bandwidth Δν/ν~ 30%.

While the specific B-modes pattern from the primordial gravitational waves is imprinted at angular scales larger than about one degree, gravitational lensing of the CMB by intervening massive structures also generates B-modes, peaking on 10 arcmin angular scales. Their accurate subtraction represents the major limitation of CMB space missions at degree resolution, alleviated through a combination with data from ground based super telescopes, as foreseen for CMB-S4 (Abazajian et al., 2016). On the other hand, the atmosphere (with the possible exception of some selected narrow frequency ranges) prevents accurate observations at frequencies above ~250 GHz, thus significantly limiting the understanding of Galactic and extragalactic foreground emissions. At small angular scales, this could be a serious problem affecting the ultra-precise characterization of CMB polarization needed for very low values of r and to disentangle subtle high multipoles effects possible introduced by early ionizing sources. A precise measurement of the lensing effect provides also the opportunity to derive a high fidelity map of DM distribution at times and scales inaccessible otherwise (Planck Collaboration, 2016d; Challinor et al., 2018). CMB lensing will also provide crucial inputs concerning the early stages of galaxy formation, a key ingredient for a precise modeling of cosmological reionization, as well as their arrangement into large-scale structures.

In December 2010, a new proposal has been submitted to ESA to trace the polarization in the microwaves (The COrE Collaboration, 2011), the Cosmic Origin Explorer (COrE). The spacecraft, designed to host 15 frequency bands from 45 to 795 GHz with angular resolution comparable to Planck and a sensitivity from 10 to 30 times better than Planck is addressed to look for primordial gravitational waves generated during inflation up to r ~ 10⁻³ at more than 3 σ level. In 2015, a medium-class space mission, Cosmic Origins Explorer + (COrE+), was proposed to ESA to perform full sky observations of the polarized microwave and sub-millimeter sky between 60 and 600 GHz in order to explore the origin of stars and cosmic structures on large scales. The primary science goal of COrE+ is to investigate the physics of the very early Universe, which is the source of the entire cosmic web we observe today.

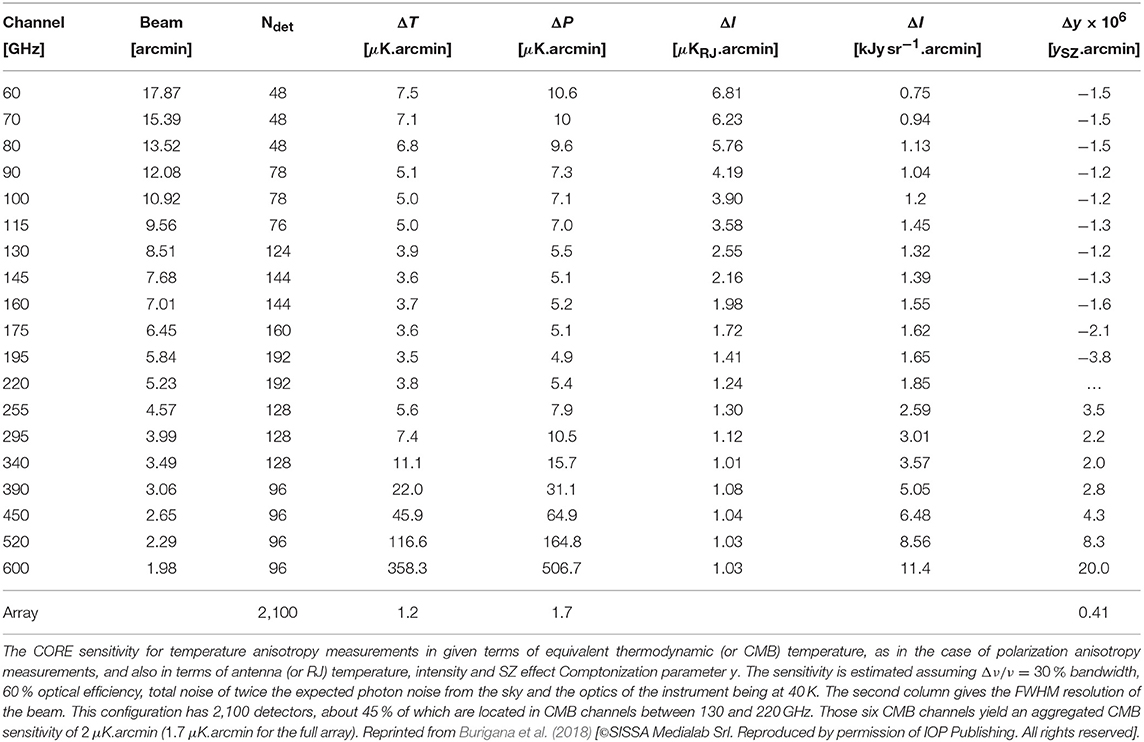
Starting from the COrE and COrE+ studies, in October 2016 the Cosmic ORigins Explorer (CORE) was submitted (Delabrouille et al., 2016) in response to a call for future medium-sized space mission proposals for the M5 launch opportunity of ESA's Cosmic Vision programme, with the aim of providing the definitive full-sky maps of the CMB polarization anisotropies at low and intermediate multipoles.⁵ The CORE specifications are summarized in Table 1. CORE (Delabrouille et al., 2018) is designed to achieve a mean noise level of approximately 2 μK · arcmin (25 times better than the Planck mission) with an angular resolution of order 5 arcmin at around 200 GHz, able to allow a significant improvement in cosmological parameter estimation including a variety of model extensions (Di Valentino et al., 2018) and, in case of a detection of primordial gravitational waves, a determination of the shape of their spectrum over the largest possible range of cosmological scales (Finelli et al., 2018). The instrument (de Bernardis et al., 2018) will host about 19 frequency channels, distributed over a broad frequency range spanning the 60-600 GHz interval, to control astrophysical foreground emission (Remazeilles et al., 2018). The entire sky will be observed repeatedly during 4 years of continuous scanning, with a combination of three rotations of the spacecraft over different time scales so that each sky pixel is observed repeatedly with many different beam orientations, providing polarization measurements at many different angles. Another key requirement is the measurement accuracy: all systematic effects, further corrected also (Natoli et al., 2018) in combination with data processing, will be controlled so that no more than approximately 10⁻⁴ of the intensity leaks into polarization maps, and that no more than about 1% of E-type polarization leaks into B-type modes.

TABLE 1

Table 1. Proposed CORE-M5 frequency channels and performance.

2.2. CMB Mission Proposals Dedicated Also to Spectral Distortions

High accuracy CMB spectrum space missions, such as the Diffuse Microwave Emission Survey (DIMES) (Kogut, 1996) (0.5 ≲ λ~15 cm) and FIRAS II (Fixsen and Mather, 2002) (λ ≲ 1 cm), were proposed since time in order to constrain spectral distortions up to 100 times better than FIRAS. Energy exchanges in the plasma at early epochs (z ≳ 10⁵) result in Bose-Einstein (BE)-like distortions (Sunyaev and Zeldovich, 1970), while late time processes (z ≲ 10⁴, before or after the recombination era) produce Comptonization and FF distortions (Bartlett and Stebbins, 1991).

New space missions were proposed to study the origin and evolution of the Universe combining high accuracy maps of CMB temperature and polarization anisotropies and high precision absolute measurements of the CMB frequency spectrum.

PIXIE (Kogut et al., 2011) is an Explorer-class mission submitted to NASA with the aim to map the CMB and the diffuse astrophysical foregrounds in absolute intensity and linear polarization over the whole sky, from 30 GHz to 6 THz (1 cm to 50 μm wavelength) at degree resolution. PIXIE uses a polarizing Michelson interferometer to measure the difference spectrum between two orthogonal linear polarizations from two co-aligned beams (Kogut et al., 2010) to detect CMB B-modes from the inflationary epoch with r < 10⁻³. The PIXIE concept is an improved version of the FIRAS spectrometer by adding large area detectors. PIXIE is designed to simultaneously perform absolute spectroscopy and large-scale polarization measurements. It is designed to be perfectly symmetric in order to reduce its sensitivity to potential systematics since the rotation of a non circular beam around a non polarized sky induces a spurious polarization signal. Hence, PIXIE distinctive scheme can gather breakthrough sensitivity both in polarization and spectral distortions (Kogut et al., 2014). PIXIE will provide crucial constraints on Universe ionization history and on cosmic infrared (IR) background (CIB) spectrum and anisotropies, tracing its monopole, dipole and higher order power spectrum. Moreover, more stringent constraints on the optical depth parameter, the gas temperature and the Universe reionization at z ~ 10 will be performed owing to the cross correlation analysis of the temperature polarization anisotropies.

In May 2013, a large class mission has been proposed to ESA, the Polarized Radiation Imaging and Spectroscopy Mission (PRISM) (André et al., 2014), a full sky, high sensitivity and resolution observer, in total intensity and polarization, from the microwaves to the IR. PRISM was conceived as the almost definitive CMB/far-IR space mission, able to cover almost all the topics affordable with a single satellite. PRISM consists of two instruments: (i) a polarimetric imager with a 3.5 m usable diameter telescope, cooled to below 10 K to maximally reduce the photon noise due to the thermal emission of the mirrors, dedicated to map the intensity and polarization anisotropies on the whole sky in 32 broad frequency bands between 30 GHz (1 cm) and 6 THz (50 microns) with unprecedented sensitivity and with an angular resolution ranging from about 17 arcminutes to about 6 arcseconds, in order to detect B-modes at 5σ for r = 5 × 10⁻⁴ even for complex astrophysical foreground emissions; (ii) a lower angular resolution (1.4°) spectrometer that will compare the sky frequency spectrum to a nearly perfect reference blackbody to measure the absolute sky emission over the same frequency range more than three orders of magnitude better than FIRAS. While BE-like distortions and more general spectral distortions have the potential to discover decaying DM and to constrain the primordial power spectrum on very small scales, not measurable by other means, the characterization of Comptonization distortions from the re-ionized gas as well as from hot clusters represents a firm outcome of a mission like PRISM.

2.2.1. Differential Approach to CMB Spectral Distortions

The peculiar motion of an observer with respect to an ideal reference frame set in rest with respect to the CMB produces boosting effects in several observable quantities, the largest of which is the CMB dipole, i.e., the multipole ℓ = 1 anisotropy in the Solar System barycentre _. These effects can be explored by future CMB anisotropy missions. CMB anisotropy missions will not perform absolute measurements of the CMB spectrum, but can in principle reveal the frequency spectral behavior of the CMB dipole (Danese and de Zotti, 1981; Balashev et al., 2015). Precise inter-frequency calibration foreseen for e.g., a mission like CORE will therefore offer the possibility to constrain or even detect CMB spectral distortions, in particular those produced by the cosmological reionization process, exploiting the dipole spectrum frequency dependence (Burigana et al., 2018) without resorting to delicate CMB absolute spectrum measurements.

In general, combining results from experiments with absolute calibration although with a relatively poor resolution, like e.g., PIXIE, with high resolution anisotropy experiments, like e.g., CORE, will offer a chance to have maps with substantially improved calibration, sensitivity and resolution.

When this paper was finalized, the PICO and LiteBIRD proposals were already approved for further studies. The European and US CMB teams are working to repropose to ESA and NASA projects based on the studies carried out for CORE and PIXIE, possibly involving international partnerships.

3. The Square Kilometer Array and Its Precursors and Pathfinders

The SKA will be a giant radio telescope with an effective collecting area of one-million square meters observing in the radio band with different antenna concepts and a continuous frequency coverage from 50 MHz to 14 GHz, allowing all-sky surveys and redshift depth observations (Maartens et al., 2015), or possibly at higher frequencies up to 25 GHz, a range typically accessible from the ground (Barbosa et al., 2012).

In 2008, the SKA Science and Engineering Committee, SSEC, recognized in the “Precursors” designation the telescopes built on one of the two SKA candidate sites, Australia or South Africa, while in the “Pathfinders” classification all SKA-related technology, science and operations activity telescopes.

3.1. The Square Kilometer Array

Following the preparatory phase in the years 2008–2012 and the pre-construction phase in the years 2013–2015, the SKA is planned to be built in two phases, with a first science expected in 2019 and it is foreseen to be fully operational by 2024. The low-frequency part of the observatory will be located in Western Australia, while the mid- and high-frequency part will be developed in Southern Africa where it can be assembled with its precursor MeerKAT and linked with the large European and German radio telescopes. The array will be 10–100 times more sensitive than the current facilities and 50 times more sensitive than Jansky Very Large Array (JVLA). The SKA 2, to be constructed in the years 2018–2023, is planned to achieve a factor 10 in sensitivity improvement over SKA 1, whose construction phase in the years 2016-2019 provides for a full operation phase from 2020. Another fundamental gain of the SKA is the extremely wide FOV, from 200 square degrees at the lowest frequencies to, at least, 1 square degree at 1.4 GHz. The main configuration is designed to achieve high sensitivity and resolution images and can be divided into two main parts: a core that will be densely populated and a central region with logarithmically positioned antennas set in groups along five spiral arms.

Each antenna group will be equipped with single dipoles, small dipoles arrays, or single small telescopes, all allowing a continuous frequency coverage. The high frequency dishes will be either made up by single pixel feeds or, likely, with Phased Array Feeds (PAF). Currently, both phases should consist of three elements: SKA-LOW operating at low frequency, SKA-MID covering the intermediate/high frequency, and SKA-SUR optimized for surveys (Jarvis et al., 2015). The SKA 1 will host most of the low frequency aperture arrays (SKA1-LOW), a small part of the middle frequency (SKA1-MID) dishes, and the survey aperture arrays (SKA1-SUR) that should be deferred. During the Phase 2 the total array will be completed. A third SKA 3 phase is envisaged and is designed to extend SKA operations to high radio frequencies (>20 GHz and possibly up to 30 GHz).

The project, consisting of two consecutive phases, will be able to perform HI intensity mapping surveys (SKA 1) and will allow to carry out a wide HI galaxy redshift survey (SKA 2), the biggest spectroscopic survey of ~1 billion of galaxies. The SKA is likely to become one of the leading DE measuring machines, bringing breakthroughs in cosmology by combining CMB (Planck outcomes), optical (from LSST, SNAP), optical and near-IR (from the ESA Euclid mission) and other early 21st century datasets (Rawlings et al., 2004).

Since radio-continuum surveys play an important role in many relevant research fields, various reference surveys have been taken into account as the top priority SKA continuum science cases (Prandoni and Seymour, 2015). The Ultra Deep Survey devoted to trace the Star Formation History of the Universe (SFHU) and the SKA 1 extremely high sensitivity at the μJy level and resolution over wide areas (0.5″ or lower at ~ 1 GHz) will allow the disentangling of the single radio source populations and their number counts down to very faint fluxes. Assuming 1 GHz as a reference frequency, the flux limit will be 0.05, 0.2, 1, μJy/beam for the Ultra Deep (1 deg² sky coverage), Deep (10–30 deg²) and Wide (1–5 × 10³ deg²) survey, respectively. Furthermore, source number counts below the survey sensitivity can be characterized through P(D) methods (Condon et al., 2012), especially in low frequency continuum surveys, dedicated to non-thermal emission in clusters and filaments.

In Table 2, we report the main technical specifications of the SKA1-SUR, SKA1-LOW, and SKA-MID.

TABLE 2

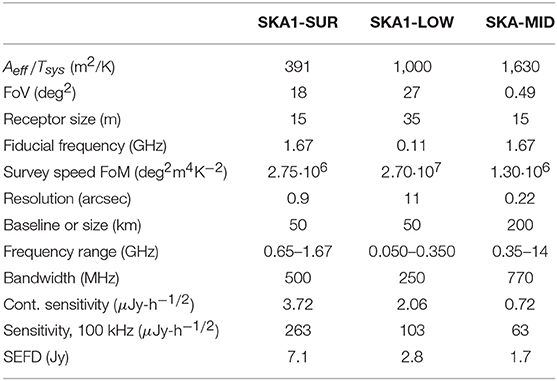
Table 2. Parameters for SKA, according to Dewdney et al. (2013); see https://www.skatelescope.org/wp-content/uploads/2012/07/SKA-TEL-SKO-DD-001-1_BaselineDesign1.pdf.

3.2. SKA Precursors

Among many different next generations radio telescopes built around the world, two are the official SKA precursors, MeerKAT and ASKAP (Australian SKA Pathfinder).

MeerKAT is the South African SKA pathfinder telescope which, in Phase 1, consists of 64 dishes, each of 13.5-m diameter and equipped with single-pixel receivers, distributed over two components. The 70% of the dishes are located in a dense inner component with a Gaussian uv-distribution and a dispersion of 300 m. The remaining 30% of the dishes constitutes the outer component, with a Gaussian uv-distribution with a dispersion of 2,500 m and a longest baseline of 8 km. A set of 7 additional dishes is foreseen for the potential future extension (Meerkat Phase 2) designed to broaden the longest baselines to about 16 km. A wide range of observing modes (among which deep continuum, polarization and spectral line imaging, as well as pulsar timing and source transient searches), will be supported by MeerKAT. The goal is to release standard data products, including an imaging pipeline (Aharonian et al., 2013).

The Australian SKA Pathfinder (ASKAP) is a new radio telescope in realization on the Australian SKA site in Western Australia, at the Murchison Radio-astronomy Observatory. Its 36, 12-m antennas are distributed over an area with a maximum baseline of 6 km diameter that requires a high speed survey instrument, a high dynamic range and an extremely wide field-of-view interferometer with Phased Array Feeds (PAFs). The PAF has a total of 188 elements dual-polarization pixels, 94 in each of two polarizations operating in a frequency band from 700 MHz to 1.8 GHz and a field of view up to 30 deg². ASKAP total collecting area is approximately 4,000 square meters and its system temperature is less than 50 K. There are 36 independent beams, each of about 1 square degree, yielded overlapping a 30 square degree field-of-view at 1.4 GHz (Govoni et al., 2013). To guarantee good calibration, the feed and reflector rotate to mimic the effect of an equatorial mount, ensuring a constant position angle of the PAF and sidelobes on the sky. Some of the technical components of ASKAP will be shared by the SKA, as the sky mount telescopes configuration, the PAF and, in particular, their array set up, the large amount of data transported, digital hardware studies (also in terms of costs and capabilities), instrument calibration, power and communication solutions, system engineering, logistics and, finally, the science case.

3.3. SKA Pathfinders

Among the numerous SKA pathfinders, we briefly illustrate here the main characteristics of two specific projects, e-MERLIN⁶ and LOw Frequency radio ARray (LOFAR)⁷.

MERLIN is a cm-wavelength array of 7 radio telescopes distributed in the UK and linked with the Jodrell Bank Observatory (JBO) central unit by a new dark fiber network. It operates as a high resolution interferometer with a maximum baseline length of 220 km and a unique capability of detecting radio images with a resolution from 0.01 to 0.15 arcsec at 1.5, 5 and 22 GHz (corresponding to L, C and K band).

Telescope main activity is to produce, manage, maintain and extend this new low cost fiber network. The instrument has been largely involved in the e-MERGE Survey programme to exploit the formation and evolution of star forming galaxies and AGN at z > 5 in two well studied extragalactic fields with a resolution of 50–200 mas (less than 0.5–1.5 kpc at z > 5) and providing a truly view of star formation distribution within typical galaxies. e-MERLIN will be able to disentangle the contribution coming from AGNs and young forming stars.

The LOFAR (Best and LOFAR-UK Consortium, 2008) is a pan European radio phased-array telescope equipped with two types of antenna, one optimized for observations between 30 MHz and 80 MHz and the other between 110 and 240 MHz. The antennas are grouped together in stations a few hundreds meter wide, with 40 stations in The Netherlands distributed over an area of 100 km diameter, and a further eight stations located in Germany, UK, Sweden, and France. The received signals are digitized to form many beams on the sky, significantly enhancing the LOFAR survey capability.

LOFAR supplies continuum surveys of the radio sky covering the northern half of the sky at high sensitivity and resolution. The design of the LOFAR planned surveys is driven by three scientific open questions: (i) formation of massive galaxies at the epoch of reionization, (ii) magnetic fields and shocked hot gas associated with the first bound clusters of galaxies, (iii) star formation processes in distant galaxies. Other fundamental astrophysical key aspects are understanding the origin of the cosmic magnetism and of the cosmological distribution of magnetic fields by studying the low frequency linear polarization of the Milky Way, pulsars, nearby galaxies, giant radio galaxies, galaxy groups and filaments. The intensity of many synchrotron radio sources is much larger at low frequencies, where they are therefore better studied, because of their steep spectra. Furthermore, Faraday rotation is another important tool for studying cosmic magnetism, being proportional to the wavelength square. Therefore, low frequency observations can provide much more precise measurements of the weak fields and low plasma densities expected in galaxy halos and filaments. Mostly important in this context, LOFAR should measure the 21-cm power spectrum (see Patil et al., 2017 for preliminary results) allowing a tomographic view of the reionization process in a redshift range 7 ≲ z ≲ 12. Table 3 summarizes the main technical specifications of the SKA pathfinders and precursors described above.

TABLE 3

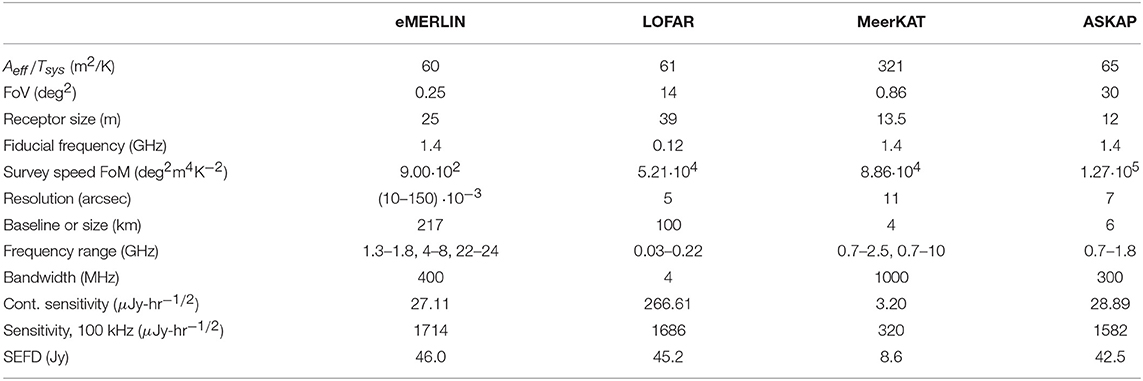
Table 3. Parameters for the SKA precursors and pathfinders described in the text, according to Dewdney et al. (2013); see https://www.skatelescope.org/wp-content/uploads/2012/07/SKA-TEL-SKO-DD-001-1_BaselineDesign1.pdf.

4. Information From CMB Anisotropies

To first approximation, the initial stage of the reionization era is defined by the Thomson optical depth, τ = ∫χ_en_eσ_Tcdt, that can be directly computed for each ionization history, given the cosmological model and parameters. According to the convention, the integral is calculated over the relevant epochs, and it is mainly contributed by the epochs from the redshift at which χ_e starts to increase, after its decreasing following the recombination era. This simple “τ-parametrization” represents a sufficiently good modeling for computing the reionization imprints on the CMB anisotropy in the joint analysis a set of cosmological parameters, as for example in the base ΛCDM described by only six parameters and in various model extensions. Beyond this parametrization, great efforts have been devoted to accurately compute the reionization imprints in the CMB for a wide set of models and considering different physical mechanisms (see e.g., Peebles et al., 2000; Doroshkevich and Naselsky, 2002; Cen, 2003; Ciardi et al., 2003; Doroshkevich et al., 2003; Hansen and Haiman, 2004; Kasuya et al., 2004; Popa et al., 2005; Wyithe and Cen, 2007).

The evolution of ionization fraction can be evaluated from the balance between the recombination and ionization processes:

$\begin{array}{rc}\frac{d{x}_e}{dt}=-{\alpha }_{rec}(T)n_b{x}_e^2+{\epsilon }_i(z)(1-x_e)H(z)& (1)\end{array}$

where ${\alpha }_{rec}~4·10^{-13}{(T/10^{4}K)}^{-0.6}$ s⁻¹cm⁻³ is the recombination coefficient.

Assuming for simplicity a curvature term Ω_k = 0, implying Ω_Λ = 1−Ω_m, the Hubble parameter, H(z), is given by:

$\begin{array}{rc}H(z)=H_0\sqrt{{\Omega }_m{(1+z)}^3+{\Omega }_{\Lambda }},& (2)\end{array}$

where H₀ is the Hubble constant.

In Equation (1) the ionization fraction, x_e, and the matter (electron, baryon) temperature, T, are linked by the dependence on the temperature of the recombination coefficient α_rec. Since the relatively weak dependence, ${\alpha }_{rec}\propto T^{-0.6}$, the details of the matter temperature history are not particularly critical, although, in particular during the active phases, they could be relevant.

Cosmological Boltzmann codes for computing the APS of the anisotropies of the CMB, as for instance the widely used CAMB code⁸ (Lewis et al., 2000) [see also Seljak and Zaldarriaga (1996)], can be modified to introduce the ionization fraction evaluated according to considered reionization model, alternative to the reionization treatment originally implemented. A detailed discussion of such an extension with a particular attention to all polarization modes, and specially on the B-mode, has been presented in Trombetti and Burigana (2012). A certain care is needed to properly define the normalization of the quantities entering in the ionization evolution treatment. As widely used in literature, in the CAMB code the ionization fraction is referred to the hydrogen. Thus, when including helium reionization, in the simple case of hydrogen plus helium gas, the global ionization fraction in the case of full ionization is larger than unit and is given by ${\chi }_e^{full}=1+n_{He}/n_H$. Of course, each model will present its specific final (at z = 0) value of χ_e. Furthermore, there are the alternatives to specify in CAMB the Thomson optical depth parameter, and let the code to compute the reionization redshift, or to provide the selected reionization redshift, and deriving τ with a dedicated function. While for the established astrophysical models τ is known, we wrote a modified version of this function to calculate τ bf for to the considered model.

In Figure 3, we show some examples of predictions for the CMB E- and B-mode APS computed for the mentioned models. As mentioned in section 1, the constraints on τ set by Planck points toward models with χ_e evolution close to the filtering one, while significantly different models are clearly no longer compatible with current data. Anyway, the figure allows to appreciate the main dependence of the low-ℓ reionization bump on the value of τ and the type of features induced at intermediate and high multipoles by possible early reionization phases as well as to note the relevance of high sensitivity and foreground mitigation necessary to detect B-modes and to distinguish fine details of reionization in the E-modes, given also the unknown value of r (see also section 9).

FIGURE 3

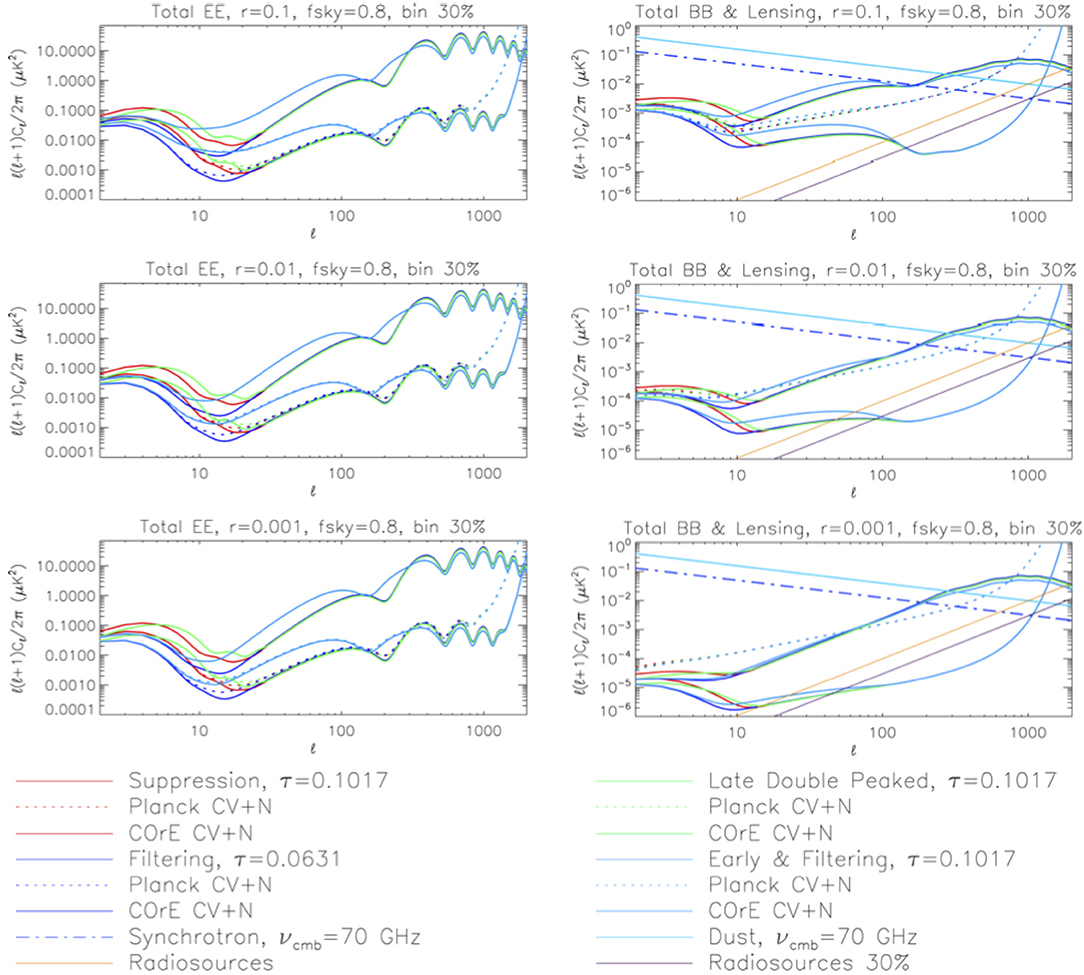
Figure 3. EE and BB “APS for the reionization histories: suppression, filtering, late double peaked, early plus filtering (E+F for z_re = 500) for different values of tensor to scalar ratio r.” For the case of BB APS we display also pre-Planck estimates of astrophysical foregrounds: “Galactic synchrotron (dash-dotted blue line) and thermal dust (dash-triple-dotted cyan line) polarized emission, and extragalactic point source fluctuations (solid orange line) and their potential residual (solid violet line).” See plot legend and text for details. Estimates of the overall sensitivity for Planck and COrE missions, including cosmic, sampling variance and noise limitations (CV+N) are also displayed. Reprinted from Trombetti and Burigana (2012).

5. Information From CMB Spectrum

Immediately after the thermalization epoch, at z ~ 10⁶−10⁷, the CMB spectrum was well characterized by a blackbody (BB) shape because of the high efficiency of interaction processes in the cosmic plasma able to re-establish the matter-radiation thermal equilibrium even in the presence of a significant departure. After this phase and passing through the recombination epoch, the thermodynamical equilibrium is no longer ensured since the reduced interaction of CMB photons with the plasma, because of the Universe expansion and the decrease of electron and photon number densities and temperatures.

The distorted spectra (see Figure 4 for typical shapes) mainly depends on the fractional amount of energy exchanged during the interaction, the epoch and type of the heating or cooling process, and the baryon density. The photon occupation number and its evolution at different frequencies and times is described by the complete kinetic Boltzmann equation, very well approximated in terms of the Kompaneets equation. Theoretically, the departure from a perfect BB is predicted by three main unavoidable mechanisms (Sunyaev and Khatri, 2013).

FIGURE 4

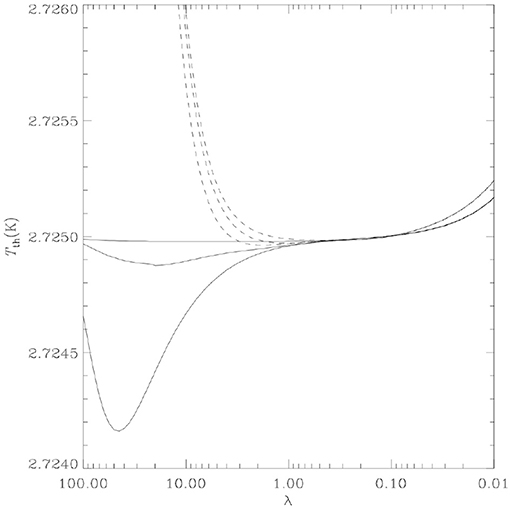
Figure 4. “Distorted spectra in equivalent thermodynamic temperature vs. λ (in cm) with late energy injection $\Delta \epsilon /{\epsilon }_i\simeq 4y=5\times 10^{-6}$ plus an early/intermediate energy injection $\Delta \epsilon /{\epsilon }_i=5\times 10^{-6}$ (~ 20 times smaller than current upper limits) at the “time” Comptonization parameter y_h = 5, 1, 0.01 (bottom to top; the cases at y_h = 5 and 1 are very similar at short λ; solid lines) plus a FF distortion with $y_B=10^{-6}$ (dashes).” y_h = y, but assuming electron temperature equal to the radiation one and computing the integral “from the energy injection time to the current time.” For a negative value of distortion parameter the shape of the distorted spectrum is almost specular with respect to a horizontal line with T = T₀ to that derived assuming the same absolute, but positive, parameter value. Reprinted from Burigana et al. (2004), Copyright (2004), with permission from Elsevier.

(i) Cosmological reionization and related electron heating, which produce physically correlated Comptonization distortion characterized by an (energy) Comptonization parameter, u ≈ 10 ^{− 7} − 10⁻⁶, proportional to the fractional energy exchanged in the interaction, Δε/ε_i ≃ 4y, and free-free (FF) distortion.

(ii) Dissipation of primordial perturbations at small scales that are damped by photon diffusion and then disappeared in CMB anisotropies. It generates mainly BE-like distortions characterized by a positive chemical potential ${\mu }_0\simeq 1.4\Delta \epsilon /{\epsilon }_i\approx 10^{-9}-10^{-7}$ (and in particular ≃2.52 × 10⁻⁸ for a primordial scalar perturbation spectral index n_s = 0.96, without running) (Hu et al., 1994; Chluba and Sunyaev, 2012). Very small scales, not observed by current CMB anisotropy data, are important in this context. Thus, a wider set of primordial spectral indices has to be considered. Allowing also for modifications in the primordial perturbation amplitude at very small scales, according to some inflation models, a more extended range of chemical potentials is found by Chluba et al. (2012).

(iii) In the expanding Universe the matter temperature decreases faster than the radiation temperature, and electrons are then colder than radiation. This generates Bose-Einstein condensation of CMB photons with a negative chemical potential ${\mu }_0\approx -3\times 10^{-9}$ (Chluba and Sunyaev, 2012; Sunyaev and Khatri, 2013).

Recent constraints on CMB spectral distortions and limits on energy exchanges in the plasma (Salvaterra and Burigana, 2002) ($|\Delta \epsilon /{\epsilon }_i|\lesssim 10^{-4}$ at 95% C.L., the exact value depending on the dissipation epoch and on considering a single process or two different processes jointly) mainly rely on the COBE/FIRAS data (Mather et al., 1990) in the wavelength range between 1 cm and 0.5 mm. The measured monopole of the background radiation resulted compatible with a BB spectrum (Fixsen, 2009) at the current temperature of T₀ = (2.72548±0.00057) K, because of the Universe expansion, a value that well accounts also for the main (Doppler effect) dipole induced by the solar system velocity (v≃369 km/s) relative to the CMB restframe.

The photon distribution function of the BE spectrum is given by Sunyaev and Zeldovich (1970)

$\begin{array}{rc}{\eta }_{\text{BE}}=\frac{1}{e^{x_{\text{e}}+\mu }-1},& (3)\end{array}$

where μ is the chemical potential that quantifies the fractional energy, Δϵ/ε_i, exchanged in the plasma during the interaction,⁹ x_e = x/ϕ(z), ϕ(z) = T_e(z)/T_CMB(z), where x = hν/(kT_CMB), T_CMB = T₀(1+z) and T_e(z) are the redshift invariant dimensionless frequency, the redshift dependent CMB effective temperature and the electron temperature.¹⁰ For a BE spectrum, ϕ = ϕ_BE(μ).

For small distortions, μ≃1.4Δϵ/ε_i and ${\varphi }_{\text{BE}}\simeq {(1-1.11\mu )}^{-1/4}$. The current FIRAS 95 % CL upper limit is $\left|{\mu }_0\right|<9\times 10^{-5}$ (Fixsen et al., 1996), where μ₀ is the value of μ at the redshift z₁ corresponding to the end of the kinetic equilibrium era. At earlier times μ can be significantly higher, and the ultimate limits on Δϵ/ε_i before the thermalization redshift (when any distortion can be erased) comes from cosmological nucleosynthesis.

The cosmological reionization process associated with the primeval formation phases of bound structures, sources of photon, and energy production, generates electron heating that is responsible for Comptonization distortions (Zel'dovich et al., 1972). The key parameter for characterizing this effect is

$\begin{array}{rc}u(t)={\displaystyle {\int }_{t_{\text{i}}}^t}\left[(\varphi -{\varphi }_{\text{i}})/\varphi \right](k_{\text{B}}{T}_{\text{e}}/m_{\text{e}}{c}^2)n_{\text{e}}{\sigma }_{\text{T}}cdt.& (4)\end{array}$

In the limit of small energy injections and performing the integral over the relevant cosmic times then u≃(1/4)Δε/ε_i. In Equation (5), ${\varphi }_{\text{i}}=\varphi (z_{\text{i}})={(1+\Delta ϵ/{\epsilon }_{\text{i}})}^{-1/4}\simeq 1-u$ is the ratio between the equilibrium matter temperature and the radiation temperature at the beginning of the heating process (i.e., at z_i). The distorted photon occupation number is then

$\begin{array}{rc}{\eta }_{\text{C}}\simeq {\eta }_{\text{i}}+u\frac{x/{\varphi }_{\text{i}}\text{exp}(x/{\varphi }_{\text{i}})}{{\left[\text{exp}(x/{\varphi }_{\text{i}})-1\right]}^2}\left(\frac{x/{\varphi }_{\text{i}}}{\text{tanh}(x/2{\varphi }_{\text{i}})-4}\right),& (5)\end{array}$

where η_i is the initial photon occupation number (i.e., before the beginning of the dissipation process)¹¹.

Reionization necessarily implies Comptonization distortions with, at least, minimal values of u≃10⁻⁷ (Burigana et al., 2008). In addition to this, a wide set of energy injection processes “are expected in astrophysical reionization models, including energy produced by nuclear reactions in stars and/or by nuclear activity that mechanically heats the IGM, super-winds from supernova explosions and active galactic nuclei, IGM heating by quasar radiative energy, and shocks associated with structure formation” (Burigana et al., 2018). Together these produce much higher values of u (≃several×10⁻⁶) (Refregier et al., 2000; Hill et al., 2015), i.e., not much smaller than the current FIRAS 95 % CL upper limit of |u| < 1.5 × 10⁻⁵ (Fixsen et al., 1996).

The FF signal generated by cosmological reionization is expected to be the most remarkable kind of global spectral distortion at low frequency, below 10GHz (see Figure 4). Its amplitude is characterized by the free-free parameter y_B(t):

$\begin{array}{l}{y}_B={\displaystyle {\int }_{t_h}^t}(\varphi -{\varphi }_i){\varphi }^{-3/2}{g}_B(x,\varphi )K_{0B}dt\\ ={\displaystyle {\int }_z^{z_h}}(\varphi -{\varphi }_i){\varphi }^{-3/2}{g}_B(x,\varphi )K_{0B}{t}_{exp}\frac{dz}{1+z};& (6)\end{array}$

here $K_{0B}\simeq 2.6·10^{-25}{(T_0/2.7\text{K})}^{-7/2}{(1+z)}^{5/2}{\widehat{\Omega }}_b^2$ sec⁻¹, t_exp is the cosmic expansion time, g_B(x, ϕ) the Gaunt factor, and ${\widehat{\Omega }}_b={\Omega }_b{\left[H_0/\left(50\text{Km }{\text{s}}^{-1}{\text{Mpc}}^{-1}\right)\right]}^2$, being Ω_b the baryon density parameter. In the above equation a uniform medium is assumed. Recent low frequency spectrum measurements with TRIS (Gervasi et al., 2008) improve constraints on FF distortion based on FIRAS and previous low frequency measurements (Salvaterra and Burigana, 2002) and set $-6.3\times 10^{-6}<y_B<12.6\times 10^{-6}$ at 95% CL, while ARCADE 2 (Singal et al., 2011) relax the previous 2σ upper limits to $\left|y_B\right|<10^{-4}$ mainly because of the excess found at ≃3.3 GHz (Seiffert et al., 2011) (if not interpreted in terms of a population of faint radio sources; see also section 7.1). Given its relevance in the frequency range of future radio surveys, FF distortion will be discussed in section 8.

Furthermore, the possible contribution of non-standard heating sources should be considered. During the pre-recombination epoch, decaying and annihilating particles may distort the CMB spectrum with process timescale dependent shapes that, depending on the relevant parameters, could differ from the classical one produced by energy dissipation. This is of particular interest for decaying particles with lifetimes t_X≃ few × 10⁸–10¹¹ s (Hu and Silk, 1993; Danese and Burigana, 1994; Chluba, 2013). A large amount of electromagnetic radiation would also be produced by superconducting cosmic strings, causing forms of CMB spectral distortion (Ostriker and Thompson, 1987) that could be revealed in principle with high precision measurements. Another possible source of energy injection is represented by evaporating primordial black holes that could generate a distortion shape depending on the black hole mass function (Carr et al., 2010). The spin of non-evaporating black holes (Pani and Loeb, 2013) could also be constrained with high accuracy measurements of the CMB spectral distortion. Furthermore, the CMB spectrum could be used to provide limits on the power spectrum of magnetic fields at small scales (Jedamzik et al., 2000), the decay of vacuum energy density (Bartlett and Silk, 1990), axions (Ejlli and Dolgov, 2014), and other physical mechanisms beyond standard models.

6. Reionization Distortions With Anisotropy Measures

The effect of peculiar velocity on the frequency spectrum at each desired observational frequency can be evaluated on the whole sky using the complete description of the Compton-Getting effect (Forman, 1970). To this aim, we can simulate the corresponding maps on the basis of the Lorentz-invariance of the distribution function, including all orders of the effect and their link with the geometrical properties induced at each multipole. We review here the fundamental concepts and the observational perspectives opened by the next generation of CMB anisotropy missions including realistic simulations of foreground and calibration limitations.

We first discuss the dipole spectrum frequency dependence (Danese and de Zotti, 1981; Balashev et al., 2015). The “dipole amplitude is directly proportional to the first derivative of the photon occupation number, η(ν), which is related to the thermodynamic temperature, T_therm(ν), i.e., to the temperature of the blackbody having the same η(ν) at the frequency ν, by ” Burigana et al. (2018)

$\begin{array}{ll}{T}_{\text{therm}}=\frac{h\nu }{k_{\text{B}}ln(1+1/\eta (\nu ))}.& (7)\end{array}$

The difference in T_therm measured in the direction of motion and in the perpendicular direction is given by Danese and de Zotti (1981):

$\begin{array}{ll}\Delta T_{\text{therm}}=\frac{h\nu }{k}\left\{\frac{1}{ln\left[1+1/\eta (\nu )\right]}-\frac{1}{ln\left[1+1/\eta (\nu (1+\beta ))\right]}\right\},& (8)\end{array}$

which, to first order, can be approximated by:

$\begin{array}{ll}\Delta T_{\text{therm}}\simeq -\frac{x\beta T_0}{(1+\eta ){ln}^2(1+1/\eta )}\frac{dln\eta }{dlnx},& (9)\end{array}$

where x≡hν/kT₀ is the dimensionless frequency.

In Figure 5 (left panel) we show the dipole spectrum derived for the Comptonization distortion.

FIGURE 5

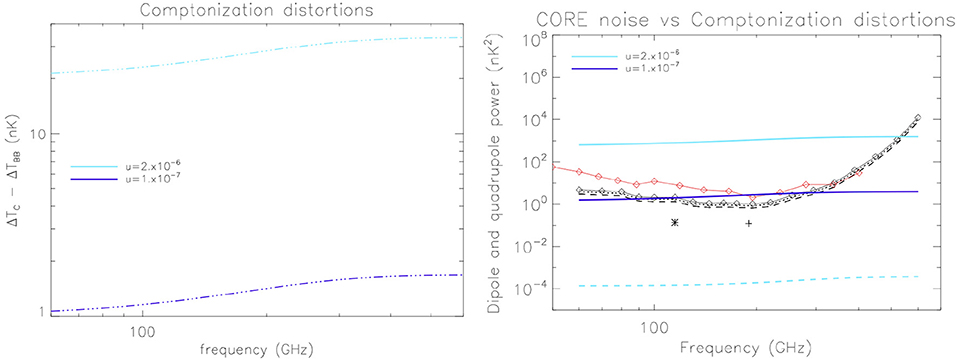
Figure 5. Left: “spectrum of dipole (in equivalent thermodynamic, or CMB, temperature) expressed as the difference between that produced by a distorted spectrum and that corresponding to the blackbody at the current temperature T₀. Thick solid lines (or thin three dots-dashes) correspond to positive (or negative) values.” Comptonization “distortions for u = 2 × 10⁻⁶ (upper curves) and u = 10⁻⁷ (lower curves), representative of imprints by astrophysical or minimal reionization models, respectively”, are shown. Right: APS of the dipole map, derived from the difference between distorted spectra and the current blackbody spectrum vs. CORE sensitivity. The CORE white noise APS (independent of multipole, shown as the black upper solid curve and with diamonds for different frequency channels) and its rms uncertainty (for ℓ = 1, using dots, and for ℓ = 2, using dashes) are plotted in black. The cross (asterisk) displays aggregated CORE noise from all channels (up to 220 GHz). We shown also for comparison the LiteBIRD white noise APS (red solid curve and diamonds for different frequency channels). Again, Comptonization distortions for u = 2 × 10⁻⁶ (upper solid curve for the dipole map and bottom dashed curve for the quadrupole map) and u = 10⁻⁷ (lower solid curve for the dipole map) are displayed. Reprinted from Burigana et al. (2018) [SISSA Medialab Srl. Reproduced by permission of IOP Publishing. All rights reserved].

To extend the analysis beyond the dipole and compute the effect at each multipole we can produce the maps “at a given observational frequency ν by computing the photon distribution function, η^BB/dist, for the considered type of spectrum at a frequency given by the observational frequency ν but multiplied by the product $(1-\widehat{n}·\overrightarrow{\beta })/{(1-{\overrightarrow{\beta }}^2)}^{1/2}$ to account for all the possible sky directions with respect to the observer peculiar velocity” (Burigana et al., 2018). Here the notation ‘BB/dist’ stands for a BB spectrum or for any type of non pure BB signal, namely, in the case of reionization, the Comptonization (C) spectrum. Finally, a simple generalization of Equation (8) allows to write the observed signal map in terms of thermodynamic temperature as:

$\begin{array}{ll}{T}_{\text{therm}}^{\text{BB}/\text{dist}}(\nu ,\widehat{n},\overrightarrow{\beta })=\frac{x{T}_0}{\mathrm{\text{log}}(1/{(\eta (\nu ,\widehat{n},\overrightarrow{\beta }))}^{\text{BB}/\text{dist}}+1)};& (10)\end{array}$

here $\eta (\nu ,\widehat{n},\overrightarrow{\beta })=\eta ({\nu }^{\prime })$ with ${\nu }^{\prime }=\nu (1-\widehat{n}·\overrightarrow{\beta })/{(1-{\overrightarrow{\beta }}^2)}^{1/2}$.

6.1. Detectability

In order to understand the detectability of the dipolar and quadrupolar signals, we compare them with the dipole of the noise at each frequency of interest, in terms of APS. Since in this case each multipole pattern has its specific angular dependence, there is no cosmic-variance related component in the noise. For each frequency we consider the specifications given in Table 1, assuming full-sky coverage for simplicity.

Figure 5 (right panel) shows the results derived from Equation (11) for the dipole signal in the case of Comptonization distortions after the subtraction of the dipole signal in the case of a blackbody at the current temperature T₀. “In black we show the CORE noise as a function of frequency. The signal is clearly above the noise up to around 500 GHz for u ≳ 2 × 10⁻⁶ and comparable to or above the noise between approximately 100 and 300 GHz for u ≳ 10⁻⁷. The analogous analysis for the quadrupole (shown for simplicity only for the largest value of u) shows that, for CORE sensitivity, noise dominates at any frequency for CMB spectral distortion parameters compatible with FIRAS limits, thus experiments beyond CORE are needed to use the quadrupole pattern to infer constraints on CMB spectral distortions. We report for comparison the APS sensitivity of LiteBIRD: it is similar to that of CORE around 300 GHz and significantly worse at ν ≲ 150 GHz” (Burigana et al., 2018).

Numerical Monte Carlo simulations allow to quantify the overall information contained in the adopted wide frequency range, as well as the impact of imperfect relative (and cross-frequency) calibration and of residual foregrounds, including also the use of suitable masks to avoid highly contaminated sky regions, the corresponding limitation from sampling variance and the sky sampling resolution, an aspect found to be crucial for ultra-accurate dipole analyses (Burigana et al., 2018). The sky sampling is typically tightly related to the experiment resolution, thus passing from some arcmin to degree resolution could be an issue. Also, the availability of a large number of frequency channels is clearly important, particularly for taking advantage from the exploitation of the dipole spectral shape based on comparison between the combination of different pairs of frequencies, the number of which scales approximately as the square of the number of frequency channels. In addition, a large number of frequency channels and especially the joint analysis of frequencies around 300 GHz and above 400 GHz greatly helps the extraction of the different kinds of signals, and, especially, the precise treatment of the Galactic dust emission.

Table 4 reports a summary of the most important forecast results. The improvement with respect to FIRAS in constraining Comptonization distortions is given for different values of the parameters defining the overall levels of residual contamination from imperfect foreground subtraction and calibration, E_for and E_cal, at different resolution and for different sky region coverages.

TABLE 4

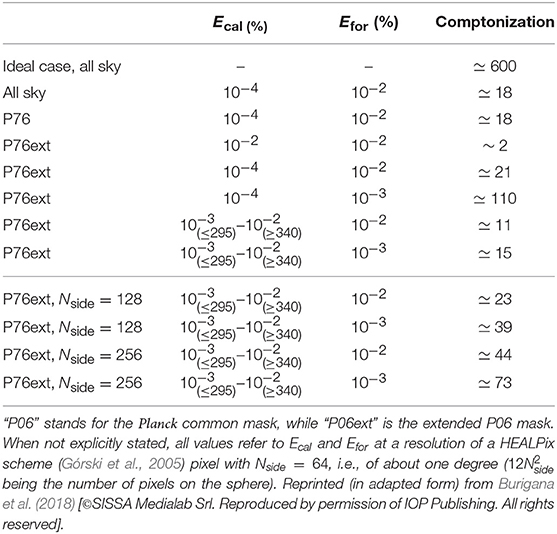
Table 4. Predicted improvement in the recovery of the distortion parameters discussed in the text with respect to FIRAS for different calibration and foreground residual assumptions.

“Assuming perfect relative calibration and absence of foreground contamination, the CORE sensitivity and frequency coverage, combined with its resolution (to cope with sampling uncertainty), could allow us to achieve an improvement with respect to FIRAS by a factor of around 600 in the recovery of u. In the case of 1% accuracy (at a reference scale of about 1°) in both foreground removal and relative calibration (i.e., $E_{\text{for}}=E_{\text{cal}}=10^{-2}$), CORE will be able to achieve a marginal detection of the energy release associated with astrophysical reionization models. On the other hand, an improvement of a factor of 10 for u is found by improving the relative calibration error to ≃0.1%. Any further improvement in foreground mitigation and calibration will enable still more precise results to be achieved.” (Burigana et al., 2018).

Achieving a very precise treatment of foreground emissions suitable for fine CMB spectral distortions analyses is difficult in both absolute and differential approaches. Performing accurate relative calibration is crucial and challenging in CMB anisotropy experiments as well as for dipole analyses. Data analysis pipelines often use the dipole itself to calibrate time ordered data or maps, thus exploiting dipole amplitude to extract information on spectral distortions may raise a circular argument issue. However, modern high-precision all-sky missions ultimately use the orbital dipole from the Earth and satellite motion for calibration, rather than the CMB dipole itself. Various approaches can be improved and integrated into the data reduction design, ranging from a better instrumental characterization to cross-correlation between different CMB surveys and substantial refinements in astronomical calibration sources.

7. Information From the Redshifted 21-cm Line

A precise measure and mapping of the redshifted 21-cm line signal with current and next-generation of radio telescopes is likely the best way to investigate on the evolution and distribution of neutral Hydrogen (HI) in the Universe and on the reionization history (Epoch of Reionization, EoR), happened soon after the Dark Ages and following the dawn of galaxies. After a brief introduction to the fundamental concepts, we provide a description of the recent claim of the first view of the dawn age with the global redshifted 21-cm line signal and of the theoretical information carried out by the 21-cm line signal fluctuations, to be likely revealed with the forthcoming generation of interferometers.

7.1. Information From the Monopole

The radiation from the first galaxies and their descendants, permeating the Universe, drove the last global phase change in the cosmic history, which is the era of second ionization. The high relevance of this process in astrophysics relies on its connection with the study the first galaxies as well as on spread out of the baryonic matter in the IGM. These early phases, corresponding to the bulk of our light cone, contain orders of magnitude more linear modes than the well-studied CMB fluctuations. This 21-cm line corresponds to the spin-flip transition in the ground state of neutral hydrogen. In cosmology, the 21-cm signal is usually described in terms of the offset of the 21-cm brightness temperature from the CMB temperature, T_CMB, along the observed line of sight at frequency ν (Furlanetto et al., 2006):

$\begin{array}{l}\delta T_b(\nu )=\frac{T_S-T_{\text{CMB}}}{1+z}(1-e^{-{\tau }_{{\nu }_0}})\\ \simeq 27x_{HI}\left(1-\frac{T_{\text{CMB}}}{T_S}\right)(1+{\delta }_{nl})\left(\frac{H(z)}{d{\nu }_r/dr+H(z)}\right)\\ \sqrt{\frac{1+z}{10}\frac{0.15}{{\Omega }_M{h}^2}}\left(\frac{{\Omega }_b{h}^2}{0.023}\right)\text{ mk},& (11)\end{array}$

where T_S is the gas spin temperature, which represents the excitation temperature of the 21-cm transition, τ_ν0 is the optical depth at the 21-cm frequency ν₀, ${\delta }_{nl}(\overrightarrow{x},z)\equiv \rho /\bar{\rho }-1$ is the evolved (Eulerian) density contrast, dν_r/dr is the comoving gradient of the line of sight component of the comoving velocity, and all the terms are computed at redshift z = ν₀/ν−1. The CMB is assumed as a backlight, thus if T_S < T_CMB the gas is seen in absorption, while if T_S > T_CMB it appears in emission.

Since the 21-cm signal is a line transition, its frequency redshifts from each specific cosmic time during the EoR up to the current time into a well defined frequency. The signal detected at a given frequency then refers to a particular redshift, implying that the 21-cm analysis constitutes a unique tomographic observation of cosmic evolution. Actually, Equation (12) shows a dependence on both the IGM temperature (T_S) and ionization (x_HI) evolution, as well as fundamental cosmological parameters (H, Ω_M, Ω_b and h²).

To deeply understand the 21-cm physical signal there are three main issues to overcome: an extremely large parameter space, due to our limited comprehension of the high-redshift Universe, a huge dynamic range of the relevant physical scales, and the treatment of foreground emissions together with their coupling with the instrument.

Indeed, different models predict different gas ionization fraction and spin temperature evolutions and, correspondingly, different predictions for the global 21-cm background signal, T_b(ν), related to the underlying astrophysical emission sources and feedback mechanisms. A wide set of models have been considered in Cohen et al. (2017), resulting into a wide envelope of possible predictions for T_b(ν), with negative signals up to ~−250mK and positive signals up to ~50 mK, peaking at frequencies located a wide range, between ~50 and 150 MHz, corresponding to a redshifts from about 30 to 10, according to the model.

For example, for the two feedback models (suppression and filtering) mentioned in section 1 the predicted global 21-cm background signals fall at observational frequencies between ≃75MHz and ≃200 MHz. The most remarkable differences between the two models (see Figure 4 in Schneider et al., 2008) are a ~15 mK absorption feature occurring at frequencies between ≃75 and 100 MHz in filtering model (and nearly absent in suppression one) and a global shift of the emission feature preceding reionization toward higher frequencies in the same model (see Figure 5 in Schneider et al., 2008).

In general, the global 21-cm background signals and foregrounds exhibit different frequency dependences. Thus, the gradient of the brightness fluctuation with frequency might help to distinguish the cosmological signal from the relatively smooth foreground emission and to discriminate between different reionization models (see e.g., Figures 6, 7 in Schneider et al., 2008).

Recent limits on the global 21-cm background signals have been set by Bernardi et al. (2016) applying a fully Bayesian method for extracting the faint signal from the much brighter foreground emission to a 19-min-long observation from the Large aperture Experiment to detect the Dark Ages (LEDA). They found a signal amplitude between −890 and 0 mK (with a width >6.5 MHz corresponding to a spread in redshift z > 1.9 at z ~ 20) at 95% C.l. in the frequency range 100>ν>50 MHz corresponding to a redshift range 13.2 < z < 27.4. These data set limits on the 21-cm signal from the cosmic dawn before or at the beginning of the increasing of electron ionization fraction, constraining structures and IGM thermal history in connection with heating sources.

Surprisingly, a pronounced absorption profile, with an almost symmetric U-shape, centred at 78MHz±1 has been recently found by Bowman et al. (2018) analysing a set of observational campaigns, started in August 2015, carried out with low-band instruments of the Experiment to Detect the Global Epoch of Reionization Signature (EDGES). The amplitude of the absorption feature is found to be of $0.5_{-0.2}^{+0.5}$ K, more than a factor of two greater than those predicted by the most extreme astrophysical models (Cohen et al., 2017) that unlikely account for a such deep signature. The spread of the profile has a full-width at half-maximum of $19_{-2}^{+4}$ MHz, the low- frequency edge supporting the existence of a ionizing background by 180 million years after the Big Bang, the high-frequency edge indicating that the gas was heated to “above the radiation temperature less than 100 million years later” (Bowman et al., 2018).

The explanation of the profile amplitude is very intriguing (see Equation 11): either the primeval gas was much colder than in the standard model, as in the case of gas cooling caused by interactions between DM and baryons (Barkana, 2018; Muñoz and Loeb, 2018), and/or the background radiation temperature was hotter than expected, owing to a substantial contribution by a high-z, faint population of radio sources as proposed by Feng and Holder (2018), in line with the interpretation of the signal excess found by ARCADE 2 (Seiffert et al., 2011), or in the model by Ewall-Wice et al. (2018), involving a radio background, overwhelming that of the CMB, generated by black hole remnants of Pop-III stars at z≈17 from black holes formed at higher z, and heavily obscured or with a radio loud fraction larger than that in the local Universe in order to avoid high τ values ruled out by Planck, with strong emission and growth declining at z < 16.

The limits on the monopole by LEDA and the results by EDGES, calling for further investigations and possible confirmations from other experiments, indicate that their improvement as well as observations with existing or forthcoming low-frequency radio projects, including the Sonda Cosmológica de las Islas para la Detección de Hidrógeno Neutro (SCI-HI) (Voytek et al., 2014), the Probing Radio Intensity at high z from Marion (PRIZM) and the Shaped Antenna measurement of the background Radio Spectrum 2 (SARAS 2) (Singh et al., 2017), can provide a clear view of the global signal expected by the cosmic dawn and the EoR.

7.2. Information From the Fluctuations

Theoretically, the evolution of structures responsible for cosmological reionization since cosmic dawn ages can be modeled via numerical simulations (see Mesinger, 2018 for a recent review) but it requires enormous simulating boxes in order to statistically model ionized regions, distribution of absorption systems and highly biased quasars.

Different cosmological simulation tools have been developed to model the source/sink fields (e.g., galaxies and recombining clumps) and the radiative transfer, respectively through coupled N-body and hydrodynamic codes and ray-tracing approaches, working typically on ~1 – 10 Mpc scales, able to resolve the first (typically molecular-cooled) galaxy population [e.g., Xu et al. (2016)] in halos of ~10⁶−10⁸ solar masses, including radiative feedback, metal pollution, stochastic star formation and recombining clumps in the IGM. With approximate treatments, these approaches can be extended to larger scales (~100 Mpc) (e.g., Trac and Cen, 2007; Kakiichi et al., 2017) to statistically sample the distribution of ionized regions. On the other hand, these methods miss the description of stellar environment sub-structures, turbulence, early phases of SNe explosions, ISM of galaxies, presenting limitations in hydrodynamics treatment.

Semi-numerical schemes (e.g., Mesinger and Furlanetto, 2007; Choudhury et al., 2009), replacing ray-tracing of ionizing photons with an excursion-set approach (Furlanetto et al., 2004) comparing the produced cumulative number of ionizing photons with the number of neutral atoms in decreasing scale regions, allow to treat X-rays and soft UV photons having longer mean free paths (Santos et al., 2010). A large astrophysical parameter space can be explored thanks to their speed and wide dynamic range, at the price of inaccuracies on sub-Mpc scales relevant for galactic star-formation. Semi-numerical algorithms with ≥ 100 realizations of the EoR (Zahn et al., 2007) indicate that either: (i) the early phases of reionization occurred much more homogeneously than in the fiducial, stellar-driven scenarios and/or (ii) that there is a relevant correlation between the CIB and the thermal SZ effect.

Hybrid techniques combine pros and cons of the two above sets of approaches to match wider scale ranges. The reionization patchiness at large scales derived from semi-numerical codes can be statistically combined with the IGM structure at small scales obtained from hydrodynamic simulations (Choudhury et al., 2015; Mesinger et al., 2015) to study the effect of IGM damping wing absorption to Lyman α emitting galaxies, while combining semi-analytic star-formation model and reionization semi-numeric treatment allows for a more physical parametrization of source properties (Mutch et al., 2016).

Results of an extensive simulation work on the evolution of the 21-cm structure during cosmic dawn age and EoR using the code 21CMFAST¹² (Mesinger et al., 2011) have been presented by Mesinger et al. (2016). Adopting the Planck 2015 measurement of τ, the authors included calibrated, sub-grid prescriptions for inhomogeneous recombinations and photo-heating suppression of star formation in small mass galaxies, setting the efficiency of SNe feedback as a free parameter to produce sets of simulations accounting for a suitable range of faint unseen galaxies. The duration of reionization is predicted to be in the range 2.7 ≲ Δz_re ≲ 5.7, while the 21-cm power at large scales during the advanced EoR phases can be very different (by a factor up to ~ ten, according to the model), the main difference to be ascribed to the typical bias of involved sources and the negative feedback, more efficient in models with a faint galaxies driven extended EoR. For example, the simulation performed for the Faint Galaxies model (see Figure 4 in Mesinger et al., 2016) characterizes a case of inefficient or halo-mass independent SNe feedback, with star forming galaxies hosted mainly by fairly small halos close to the atomic cooling threshold of virial temperature ${\text{T}}_{\text{vir}}~10^4$ K, implying that the dominant galaxies are relatively numerous, with a small bias, an early formation and a slow evolution. So far, these simulations show how the 21-cm power spectrum evolution reflects the midpoints of the sequence of the three main astrophysical epochs corresponding to Lyman-α pumping, X-ray heating and EoR. “The throughs in the large-scale power evolution roughly correspond to the boundaries between three main phases following Dark Ages, while the EoR peak occurs somewhat after the midpoint, due to the overlap between X-ray heating and EoR” (Mesinger et al., 2016).

In general, the richness of the information contained in the 21-cm power spectrum evolution strongly calls for deeper investigations aimed at mapping ionization history since Dark Ages through 21-cm tomography.

The preliminary results and the great development of interferometric facilities, including LOFAR, 21 CentiMeter Array (21CMA) (Huang et al., 2016), Murchison Widefield Array (MWA) (Beardsley et al., 2016; Jacobs et al., 2016), the Hydrogen Epoch of Reionization Array (HERA) (DeBoer et al., 2017), the Donald C. Backer Precision Array for Probing the Epoch of Reionization (PAPER) (Cheng et al., 2016), expansion of existing Long Wavelength Array station (Dowell et al., 2017) and, obviously, SKA, are very promising about a next identification of redshifted 21-cm fluctuations. The wide frequency coverage of SKA-LOW (~ 70–200 MHz) would allow to trace the entire EoR, but, likely, also the epoch of IGM heating.

Great expectations will likely come also from the combination of data coming from monopole and fluctuations observations, regarding for example cross-calibration, sky mapping and, ultimately, scientific interpretation. In general, the accurate subtraction of foreground emissions, which amplitudes are expected to be larger than the reionization signal by some orders of magnitude, will be crucial for the achievement of these scientific goals.

8. Information From the Diffuse Free-Free Radio Emission

The SKA, with its extreme sensitivity and resolution, can significantly help to further constrain CMB spectral distortions and dissipation processes beyond current limits.

Before discussing the information carried out by the diffuse FF emission, we remember that SKA could map the evolution of ionized medium by directly observing the FF emission from ionized halos (Oh, 1999; Ponente et al., 2011). Remarkably, the model by Oh (1999) predicts a very large global (i.e., integrated over the ensemble of halos) FF signal, corresponding to $y_B~1.5\times 10^{-6}$. Dedicated high resolution sky areas observations with the excellent imaging capabilities of SKA will allow to distinguish FF distortion by ionized halos. SKA 2 should allow to discover up to ~10⁴ individual FF emission halos with z > 5 in 1 deg², discerning their relevance for reionization in comparison with that of diffuse ionized IGM FF distortions.

8.1. Dependence on Dark Matter

Diffuse FF emission from ionized medium can generate a relevant distortion in the CMB spectrum, particularly remarkable at long wavelengths. The baryonic matter variance can be computed from the corresponding power spectrum with an integral over the suitable interval:

$\begin{array}{rc}{\sigma }^2(z)=\frac{1}{2{\pi }^2}\int P(k,z)k^{2}dk.& (12)\end{array}$

The considered cosmological model and its parameters determine the matter density contrast. The DM particles nature influences especially the density perturbations power spectrum at small scales, with consequences for the clumping factor. Warm Dark Matter (WDM) particles, having sterile neutrinos or gravitinos as possible candidates with typical masses in the range of the keV scale (m_warm~1÷10 keV) (Boyanovsky et al., 2008) larger than those of hot DM particles (~ few eV), have intrinsic thermal velocities, resulting into velocity dispersions larger than those of CDM particles (with typical masses of ~10÷10² GeV) and characteristic free streaming scales relevant to determine clustering properties, as the suppression of small scale structures formation. This fluctuations suppression, efficient on scales smaller than their free-streaming scale, implies a cut-off of the total matter power at large k, delaying the growth of structures (Viel et al., 2005). It can be represented in terms of different cut-off values in the transfer function, describing, for a given cosmological model, the effect induced by the free-streaming length on the matter distribution such $T(k)={\left[P{(k)}_{WDM}/P{(k)}_{CDM}\right]}^{1/2}$. Differently from the formation of the first generation of stars, depending on the considered cosmological model, large scale structure distributions are almost independent of the model (Gao and Theuns, 2007). The loss of small scale power in WDM models with different particle properties can be approximated by a CDM model with a suitable cut-off, k_max, in the typical range ≃(20÷10³). Thus, σ²(z) mainly depends on two crucial parameters, the perturbations amplitude and small scale cut-off. Defining the density as the sum of a mean term and a small perturbation ρ = 〈ρ〉(1+δρ/〈ρ〉) and averaging over a volume representative of the Universe, we introduce the time dependent clumping factor as:

$\begin{array}{rc}\frac{\langle {\rho }^2\rangle }{{\langle \rho \rangle }^2}=1+\frac{\langle {(\delta \rho )}^2\rangle }{{\langle \rho \rangle }^2}=1+{\sigma }^2>1.& (13)\end{array}$

In this context, the clumping factor is a multiplicative term accounting for the modification of the bremsstrahlung rate from a homogeneous to an inhomogeneous medium. The complete FF term is then obtained in a separation approach by introducing ${\Omega }_b^2(z)={\Omega }_{b,homog}^2(1+{\sigma }^2(z))$, where ${\Omega }_{b,homog}^2$ corresponds to the (standard) homogeneous case¹³. In this way the main effect from IGM matter density contrast and its coupling with all the other relevant aspects in the thermal and ionization history can be introduced with versatility regarding the underlying cosmological model (Trombetti and Burigana, 2014), in order to characterize the reionization process effects on diffuse FF emission. As examples, we consider specific reionization models (S, F, L) described in section 1. Various underlying cosmological models can be explored, evaluating the variance first assuming a fixed cut-off value of the matter power spectrum (k_max = 100). To this aim, the CAMB code can be used to calculate the matter power spectrum in a suitable range of redshifts, 0 < z < 30, for different combinations of cosmological parameters and according to the considered reionization histories. The differences between models are typically larger at small scales and tend to be smaller at intermediate scales. The shape of the power spectrum depends on the cosmological model and the full set of parameters. Given the other parameters, the perturbation amplitude mainly sets the P(k) overall level. Thus, both the power spectrum and the variance scale quite linearly with the perturbation amplitude. The results can be simply extended to different cut-off parameters. Figure 6(left panel) shows the clumping factor evolution for a set of cosmological parameter of the ΛCDM model consistent with CMB data and for three values of k_max (200, 500 and 1,000) among those exploited for numerical estimates.

FIGURE 6

Figure 6. Left: Evolution of clumping factor for three values of k_max. Middle: Brightness temperature relative excess predicted at current time “as function of the wavelength assuming the y_B(x) value properly evaluated at each frequency in the entire range.” The upper panel refers to the suppression model for k_max = 200 and 1000 and “without the correction due to the IGM density contrast.” The bottom panel shows a comparison between the three considered reionization histories for k_max = 500. Right: “FF distortion in SKA 2 frequency range by two astrophysical reionization histories and a late phenomenological model, displayed for comparison.” The inset shows the absolute differences between these models. The vertical lines illustrate the ranges of SKA 1 configurations. Left and middle panels reprinted from Trombetti (2018), right panel reprinted from Burigana et al. (2015).

8.2. Expected Signal

At low frequencies, the CMB spectrum can be described in terms of brightness temperature by the relation:

$\begin{array}{rc}{T}_{br}(x)\simeq \left(\frac{y_B(x)}{x^2}-2u{\varphi }_i+{\varphi }_i\right)T_{\text{CMB}}.& (14)\end{array}$

Equation (15) holds at any redshift, provided that the coupled free-free and Comptonization distortion parameters, y_B and u, are integrated over the corresponding redshift interval. As found by Trombetti and Burigana (2014), the largest fractional contributions to y_B come from two epochs, the first one at higher redshifts, when ionization fraction starts to increase and the rate of bremsstrahlung process [see Equation (7)] is still very efficient, the second one at redshifts less than few units, when the clumping factor becomes significantly larger than unity. Figure 6 (right panel) shows the signals expected in the three above (almost minimal) models together with the frequency ranges of different SKA configurations. The frequency dependence of the temperature excess produced by FF mechanism can be expressed rewriting Equation (15) as $\Delta T_{ff}(x)/T_{\text{CMB}}\simeq y_B(x)/x^2$, being ΔT_ff = (T_br−T_CMBϕ_i). This is displayed in middle panel of Figure 6 for the three considered reionization models and different cut-off parameters.

At wavelengths λ = c/ν ≳ 1.5 cm, y_B(λ) can be well approximated with a simple power law dependence on k_max: $y_B(\lambda )\simeq A{k}_{max}^m(log\lambda +B)$ with B = 0.6288 and (A, m) = (1.337 × 10⁻⁹, 0.2275) for the S model (resp. (1.078 × 10⁻⁹, 0.2424) or (2.096 × 10⁻¹⁰, 0.2482) for the F and L models). The (weak) dependence of the exponent, m, on the model characterizing the dependence of y_B(λ) on the cut-off wavenumber, k_max, has a physical explanation: m increases with the fractional contribution Δy_B(z)/y_B to y_B at low redshifts, because of the relative larger importance of clumping. Remarkably, the value of m≃0.24 implies a significant dependence of the FF signal amplification on k_max.

The FF signal monotonically increases at decreasing frequencies and the same holds for the extragalactic radio sources confusion noise. Their comparison is then observationally very important.

8.2.1. Astrophysical Confusion Noise

The models of Galactic emissions and extragalactic foregrounds can be significantly improved on the basis of SKA high sensitivity and resolution observations, substantially helping their mitigation necessary to accurately identify reionization imprints. Extragalactic source contribution is smaller than Galactic radio emission, the major astrophysical limitation in CMB spectrum determination. The subtraction of the Galactic emission from the CMB takes advantage from the exploitation of their different angular correlation properties. The limited resolution typically adopted in CMB monopole temperature experiments, particularly at low frequencies, makes this approach difficult for the extragalactic sources. Measuring the absolute temperature monopole at many frequencies in a wide frequency range permits to jointly fit the parameters of the CMB distorted spectra and of the astrophysical signals (Salvaterra and Burigana, 2002), but the precise determination of source number counts allows to estimate the radio background, resulting into a proper definition of suitable priors for this type of analyses.

Even though the radio source background at extremely low brightness temperature is still not well described, recent observations at GHz frequencies (Prandoni et al., 2001; Condon et al., 2012) have tens of μJy sensitivity levels. The differential number counts of extragalactic sources in various flux densities ranges at 0.153 GHz (Williams et al., 2013), 0.325 GHz (Mauch et al., 2013), 1.4 and 1.75 GHz, can be used to compute their contribution to the radio background. These signals are negligible in comparison with the current precision of CMB absolute temperature measurements, particularly at wavelengths ≳1 cm, but they can significantly affect the interpretation of future high accuracy experiments.

Whether the sources brighter than several tens of nJy have been subtracted from the radio background, the brightness temperature from unresolved sources turns be less than ~1 mK at frequencies above ~1 GHz, but larger than ~10 mK below ~0.3 GHz. An estimate of the minimum threshold for source detection is related to the source confusion noise, σ_conf. At ν≃1.4 GHz, Condon et al. (2012) quoted:

$\begin{array}{rc}5{\sigma }_{conf}\simeq 5\times 1.2{(\nu /3\text{GHz})}^{-0.7}{(\theta /8^{″})}^{10/3}\mu \text{Jy},& (15)\end{array}$

where θ defines the relevant resolution. Thus, a “natural confusion limit” of about 10 nJy at ν~1.4 GHz is derived for a finite angular extension of faint galaxies, θ~1″, implying that source confusion will not represent an important limiting factor for deep surveys.

At 1GHz ≲ ν ≲ someGHz (corresponding to λ≈1 dm), well above the ones where the redshifted 21-cm line shows up, the signal amplitudes derived for CMB distorted spectra sufficiently below FIRAS limits, and FF distortions in particular (even for the minimal models considered in right panel of Figure 6), are remarkably “larger than the estimates of the background from extragalactic sources fainter than some tens of nJy” (Burigana et al., 2015). Unfortunately, at decreasing frequencies the source confusion noise increases steeper than the FF distortion amplitude. Therefore, the range around few GHz is likely the most advantageous to use the FF distortion to jointly constrain reionization astrophysical scenarios and DM thermal properties influencing the small scale matter power spectrum.

As said, with the SKA excellent imaging capabilities it would be possible to study the fluctuations of the FF signal, and, for instance, their APS, expected in principle to have amplitude and shape related to the statistical distribution and astrophysical properties of ionized IGM.

9. Radio Surveys and Foreground Analyses in CMB Polarization Experiments

As discussed in previous sections, the intrinsically interesting understanding of astrophysical foreground emissions is crucial for the mitigation of their effects in CMB and radio background analyses. After a discussion of the contribution of radio surveys to the understanding of the low frequency foregrounds, we present updated estimates of the potential contamination from Galactic and extragalactic polarized emissions and discuss their impact for the analysis of the fine cosmological reionization imprints.

Future radio surveys will allow a better study of the low frequency tail of Galactic diffuse foregrounds, largely dominated by polarized synchrotron emission. This is a key point for B-mode detection and characterization as well as for investigations based on ultra-precise E-mode analyses, also because CMB mission projects are more focused on higher frequencies. Radio surveys are of particular relevance to probe models, relying on dedicated numerical codes (Strong and Moskalenko, 1998; Waelkens et al., 2009), of the Galactic synchrotron emission, of the 3D structure of the Galaxy and of the coherent, large scale component of the Galactic magnetic field (Sun et al., 2008; Sun and Reich, 2009, 2010; Fauvet et al., 2011, 2012), along with turbulence phenomena (Cho and Lazarian, 2002). Furthermore, it is important to achieve a better understanding of the anomalous microwave emission (AME), which relevance in total intensity has been re-assessed by Planck, and that seems to exhibit a significant correlation with far-IR dust emission. The spectrum of the AME, ascribed to rapidly spinning small dust grains having an electric dipole moment, is predicted to peak at frequencies between ≃15 and ≃50 GHz. Its fractional polarization degree is currently essentially unknown, although values at the per cent level are typically expected. Although likely subdominant in polarization, this component may affect the accurate treatment of foregrounds in fine analyses aimed at B-mode detection for small values of r. The AME low frequency tail could be precisely mapped by SKA 2.

Figure 7 compares the CMB B-mode APS for different values of r (top-left panel) and the tiny differences of the imprints generated by different reionization models (bottom-left panel) in the CMB E-mode APS (right panel) with examples of potential residuals from Galactic emission (where a mask excluding about 27% of the sky around to the Galactic plane has been applied, because of the high contamination by Galactic emission) based on Planck 2015 results (Planck Collaboration, 2016a,c). Polarized dust emission is the most critical foreground (see BICEP2/Keck Collaboration and Planck Collaboration (2015); Planck Collaboration (2016f) for its impact in CMB B-mode polarization analyses), but, in order to detect and characterize B-modes if r≲ some × 10⁻² and for analyzing fine details in the E-modes, a detailed knowledge of low frequency polarized foregrounds, synchrotron and (for very low values of r) AME, it is also crucial.

FIGURE 7

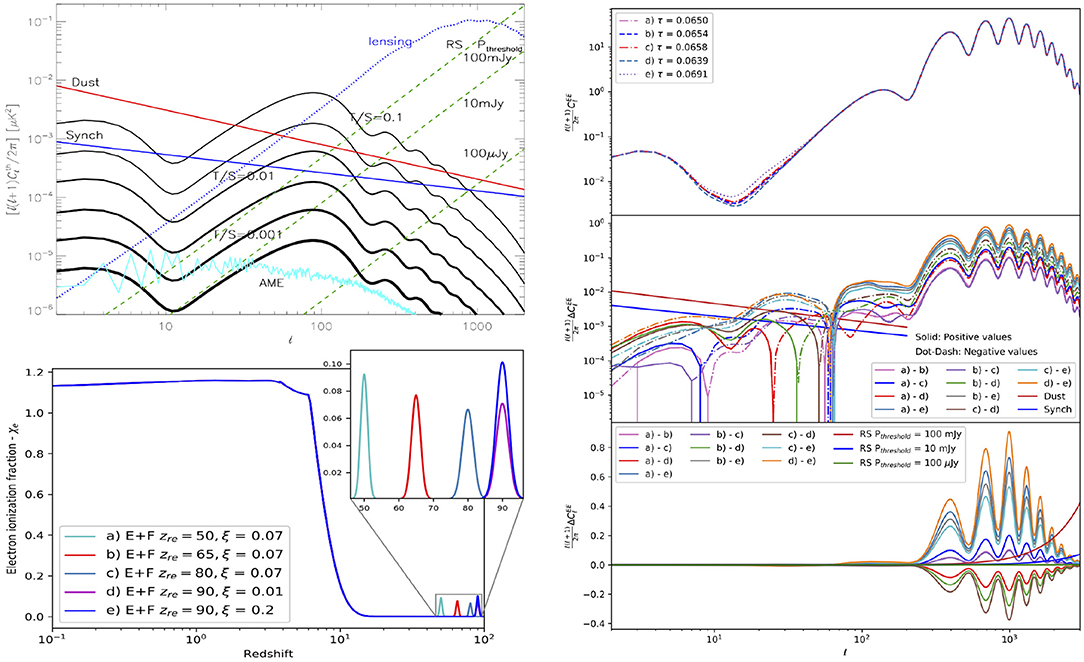
Figure 7. Top-Left: CMB primordial B-mode polarization APS for different tensor-to-scalar perturbation ratios (from 1 to 3 × 10⁻⁴; solid black lines), lensing B-mode APS (blue dots), estimates of potential residuals of Galactic foregrounds (at 70 GHz) in B-mode polarization APS, and APS from polarized radio sources (at 100 GHz) below different detection thresholds in polarized flux density (green dashes; from top to bottom, 100 mJy and 10 mJy, representative of thresholds achievable, respectively, in current and future CMB experiments, and 100 μJy representative of potential improvement achievable with SKA). Red curve shows typical potential residuals from Galactic polarized dust emission APS extrapolated from 353 GHz assuming an error of 0.01 in the dust grain spectral index. Blue curve shows typical potential residuals from Galactic polarized synchrotron emission APS extrapolated from 30 GHz assuming an error of 0.02 in the synchrotron emission spectral index. Cyan curve shows an estimate of AME APS scaled from total intensity to polarization with a polarization degree of 2% and assuming equal power in E- and B-modes. Bottom-Left: Evolution of the electron ionization fraction for five models assuming a phenomenological early phase of reionization peaked at a redshift z = z_re and for various values of the parameter ξ (defining the amplitude of the ionizing photons production coefficient ε_i) followed by the filtering model (E+F) resulting into slightly different values of τ (see right panel). Right: CMB E-mode polarization APS (in μK² units) computed for the reionization models shown in the bottom-left panel (Top), their differences compared to potential residual of Galactic dust and synchrotron polarized emissions as in top-left panel but for the E-mode (Middle), and their differences (Bottom) compared to APS from polarized radio sources as in top-left panel but in linear scale to make high multipoles more evident. All data and methods used for producing this figure have been published. The CMB B-mode polarization APS have been computed using the CAMB code (Lewis et al., 2000). The methods described in Trombetti and Burigana (2012) have been used to compute the CMB E-mode polarization APS. The CMB lensing B-mode polarization APS is based on Planck Collaboration (2016b). Potential residuals of Galactic foreground emissions are based on Planck Collaboration (2016a,c) and on the ESA Planck Legacy Archive. The E- and B-mode APS of radio sources are modeled according to Trombetti et al. (in press). See also the legends and the text.

A large sky coverage mapping of the above Galactic radio emissions is very important for these cosmological applications. Among the SKA continuum surveys (Prandoni and Seymour, 2015), it is interesting to compare the sensitivity (on the same resolution element) of the surveys at 1.4 GHz and at 120 MHz designed to cover about 75% of the sky in 1–2 years of integration and dedicated, respectively, to strong gravitational lensing and legacy/rare serendipity and to non-thermal emission in clusters and filaments, with that of radio surveys (La Porta et al., 2008) currently employed for foreground mitigation in CMB experiments. At 1.4 GHz, the SKA survey is expected to achieve a sensitivity ≃20 times better than the available all-sky radio survey, while the SKA survey at 120 MHz will improve in sensitivity by a factor of ≃4 with respect to the Haslam map at 408 MHz (Haslam et al., 1982). Therefore, SKA will provide a substantial improvement with respect to currently available ancillary radio maps.

Extragalactic radio sources (see e.g., De Zotti et al., 2018 and references therein) are the most important source of fluctuations of the microwave sky in temperature and in polarization at angular scales smaller than 30 arcmin up to frequencies ~100 GHz. Understanding radio source emission and contribution to the APS at high multipoles is crucial for an accurate and reliable CMB polarization analysis and for the precise treatment of the lensing B-mode signal, resulting into a significant improvement of our understanding of polarization at intermediate and large scales. Correcting the CMB APS requires precise measurements of radio sources contribution to within several factors below the detection threshold of the considered experiment, which is related to the noise, background and foreground signal levels depending on the direction in the sky. Indeed, source polarization fluctuations are due to the sources below the detection limit of CMB observations, i.e., from those not observed directly and then subtracted in CMB experiments, having relatively shallow resolution (~ arcmin) and sensitivity (of the order of tens to few hundreds of mJy), but are accessible, for instance, to interferometric observations, that have better sensitivity and resolution, being then more suitable for point-like sources. SKA will allow a deep understanding of polarized sources up to about 20 GHz (and hopefully, with SKA 3, up to 30 GHz), but at the most extreme faint flux densities. The error on the estimate of the source polarization fluctuations based on extrapolation from lower to higher frequencies, more suitable for CMB anisotropy experiments, obviously decreases going down into source flux density detection threshold. Thus, combining ultra-sensitive SKA with observations at millimeter wavelengths will be very important to quantify source contribution to CMB polarization fluctuations at large multipoles.

Figure 7 shows a comparison between CMB polarization modes and residual foregrounds. The E- and B-mode APS (from the dominant Poissonian term) of radio sources are shown for different detection thresholds in polarized flux density, considering the number counts model and the median polarization degree, averaged over frequencies, Π_{IDA, median}≃2.8 %, according to Trombetti et al. (in press). While on-going or planned CMB polarization experiments with performance better than Planck, and, in particular, missions like CORE, could significantly improve over Planck in extragalactic source mitigation going down to ~100 mJy or ~10 mJy detection thresholds, we expect that SKA characterization of polarization properties of radio sources, in spite of unavoidable frequency extrapolation errors (generously accounted in the figure by the very conservative assumed threshold of 100μJy), will make their residual polarization fluctuations almost negligible.

Author Contributions

TT and CB wrote the paper, preparing all the material included (assembling, re-editing, and generation of figures, tables, equations, checking of references) when not differently specified and properly quoted.

Funding

We gratefully acknowledge financial support from the INAF PRIN SKA/CTA project FORmation and Evolution of Cosmic STructures (FORECaST) with Future Radio Surveys, from ASI/INAF agreement n. 2014-024-R.1 for the Planck LFI Activity of Phase E2 and from the ASI/Physics Department of the university of Roma–Tor Vergata agreement n. 2016-24-H.0 for study activities of the Italian cosmology community.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

It is a pleasure to thank the many colleagues of the Planck, Cosmic ORigins Explorer (CORE) and SKA collaborations for constructive discussions and collaborations. We also thank two referees for comments that helped improve the paper. Some of the results in this paper have been derived using the HEALPix (Górski et al., 2005) package. We acknowledge the use of the ESA Planck Legacy Archive (PLA) and of the Legacy Archive for Microwave Background Data Analysis (LAMBDA, supported by the NASA Office of Space Science).

Footnotes

1. ^http://lambda.gsfc.nasa.gov/product/cobe/

2. ^lambda.gsfc.nasa.gov/product/map/

3. ^www.cosmos.esa.int/web/planck

4. ^Both E- and B-modes are also generated by vector perturbations, but, except for particular scenarios, they are expected to be typically subdominant.

5. ^Almost in the same period, the Probe of Inflation and Cosmic Origin (PICO) was proposed to NASA (see https://zzz.physics.umn.edu/ipsig/_media/missionstudyproposal_science.pdf). It is currently one of the 8 Probe-Scale – $ 400M – $ 1000 M – space missions whose study is being funded by NASA. The concept and performance of PICO is similar to that of CORE regarding CMB polarization anisotropies, but also the possibility of CMB absolute measurements to carry out spectrum studies with a sensitivity similar or slightly better that that proposed for PIXIE is under investigation.

6. ^http://www.e-merlin.ac.uk/

7. ^http://www.lofar.org/

8. ^http://camb.info/

9. ^Here, the subscript i denotes the beginning of the dissipation process.

10. ^In an expanding Universe, the dimensionless frequency x is redshift invariant, scaling both T_CMB and the physical frequency ν as (1+z).

11. ^Here and in Equation (4), but not in Figure 4, we do not include photon emission/absorption processes, which are instead very important at long wavelengths (see Danese and de Zotti, 1980; Burigana et al., 1995)

12. ^http://homepage.sns.it/mesinger/Sim.html

13. ^Note that the density contrasts of free electrons and atoms in different ionization states could be in principle different. Also, inhomogeneities in the medium temperature could be in principle taken into account. On the other hand, being weak the dependence on electron temperature, T_e, of the bremsstrahlung rate $K_B/x_e^3\propto {\varphi }^{-1/2}$, x_e = hν/(kT_e) being a dimensionless photon frequency, and of the term $e^{-x_e}\simeq 1-x_e$ at low frequencies, where free-free process is particularly relevant, we can neglect to first order this further correction. Higher order corrections could be evaluated from the variances of the various terms. On the basis of the currently available studies on IGM temperature, these corrections are expected to be very small (see Trombetti and Burigana, 2014 and references therein for further details).

References

Abazajian, K. N., Adshead, P., Ahmed, Z., et al. (2016). CMB-S4 Science Book, First Edition. arXiv:1610.02743.

Google Scholar

Aharonian, F., Arshakian, T. G., Allen, B., Banerjee, R., Beck, R., Becker, W., et al. (2013). Pathway to the square kilometre array-The German White Paper-. arXiv:1301.4124.

Google Scholar

André, P., Baccigalupi, C., Banday, A., Barbosa, D., Barreiro, B., Bartlett, J., et al. (2014). PRISM (Polarized Radiation Imaging and Spectroscopy Mission): an extended white paper. J. Cosmol. Astroparticle Phys. 2:6. doi: 10.1088/1475-7516/2014/02/006

CrossRef Full Text | Google Scholar

Balashev, S. A., Kholupenko, E. E., Chluba, J., Ivanchik, A. V., and Varshalovich, D. A. (2015). Spectral distortions of the CMB dipole. Astrophys. J., 810:131. doi: 10.1088/0004-637X/810/2/131

CrossRef Full Text | Google Scholar

Barbosa, D., Anton, S., Gurvits, L., and Maia, D. (eds.). (2012). “The square kilometre array: paving the way for the new 21st century radio astronomy paradigm,” in Astrophysics and Space Science Proceedings, Proceedings of Symposium 7 of JENAM 2010 (Lisbon: Springer). doi: 10.1007/978-3-642-22795-0

CrossRef Full Text | Google Scholar

Barkana, R. (2018). Possible interaction between baryons and dark-matter particles revealed by the first stars. Nature 555, 71–74. doi: 10.1038/nature25791

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartlett, J. G., and Silk, J. (1990). A comptonization model for the submillimeter background. Astrophys. J. 353, 399–405.

Google Scholar

Bartlett, J. G., and Stebbins, A. (1991). Did the universe recombine? Astrophys. J. 371, 8–13.

Google Scholar

Beardsley, A. P., Hazelton, B. J., Sullivan, I. S., Carroll, P., Barry, N., Rahimi, M., et al. (2016). First season MWA EoR power spectrum results at redshift 7. Astrophys. J. 833:102. doi: 10.3847/1538-4357/833/1/102

CrossRef Full Text | Google Scholar

Bernardi, G., Zwart, J. T. L., Price, D., Greenhill, L. J., Mesinger, A., Dowell, J., et al. (2016). Bayesian constraints on the global 21-cm signal from the cosmic Dawn. Mthly Notices RAS 461, 2847–2855. doi: 10.1093/mnras/stw1499

CrossRef Full Text | Google Scholar

Best, P. N., and The LOFAR-UK Consortium (2008). LOFAR-UK White Paper: a science case for UK involvement in LOFAR. arXiv:0802.1186.

Google Scholar

BICEP2/Keck Collaboration and Planck Collaboration (2015). Joint analysis of BICEP2/Keck array and Planck data. Phys. Rev. Lett. 114:101301. doi: 10.1103/PhysRevLett.114.101301

CrossRef Full Text

Bowman, J. D., Rogers, A. E. E., Monsalve, R. A., Mozdzen, T. J., and Mahesh, N. (2018). An absorption profile centred at 78 megahertz in the sky-averaged spectrum. Nature 555, 67–70. doi: 10.1038/nature25792

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyanovsky, D., de Vega, H. J., and Sanchez, N. G. (2008). Constraints on dark matter particles from theory, galaxy observations, and N-body simulations. Phys. Rev. D 77:043518. doi: 10.1103/PhysRevD.77.043518

CrossRef Full Text | Google Scholar

Burigana, C., Alexander, P., Baccigalupi, C., Barbosa, D. S., Blanchard, A., De Rosa, A., et al. (2015). “SKA synergy with microwave background studies,” Proceedings of Science, Advancing Astrophysics with the Square Kilometre Array (AASKA14) (Giardini Naxos), 149.

Google Scholar

Burigana, C., Carvalho, C. S., Trombetti, T., Notari, A., Quartin, G., De Gasperis, G., Buzzelli, A., et al. (2018). Exploring cosmic origins with CORE: effects of observer peculiar motion. J. Cosmol. Astroparticle Phys. 4:21. doi: 10.1088/1475-7516/2018/04/021

CrossRef Full Text | Google Scholar

Burigana, C., de Zotti, G., and Danese, L. (1995). Analytical description of spectral distortions of the cosmic microwave background. Astron. Astrophys. 303, 323–330.

Google Scholar

Burigana, C., De Zotti, G., and Feretti, L. (2004). Sunyaev Zeldovich effects, free free emission, and imprints on the cosmic microwave background. N. Astron. Rev. 48, 1107–1117. doi: 10.1016/j.newar.2004.09.044

CrossRef Full Text | Google Scholar

Burigana, C., Popa, L. A., Salvaterra, R., Schneider, R., Choudhury, T. R., and Ferrara, A. (2008). Cosmic microwave background polarization constraints on radiative feedback. Mthly Notices RAS 385, 404–410. doi: 10.1111/j.1365-2966.2008.12845.x

CrossRef Full Text | Google Scholar

Carr, B. J., Kohri, K., Sendouda, Y., and Yokoyama, J. (2010). New cosmological constraints on primordial black holes. Phys. Rev. D 81:104019. doi: 10.1103/PhysRevD.81.104019

CrossRef Full Text | Google Scholar

Cen, R. (2003). The universe was reionized twice. Astrophys. J. 591, 12–37. doi: 10.1086/375217

CrossRef Full Text | Google Scholar

Challinor, A., Allison, R., Carron, J., Errard, J., Feeney, S., Kitching, T., et al. (2018). Exploring cosmic origins with CORE: gravitational lensing of the CMB. J. Cosmol. Astroparticle Phys. 4:18. doi: 10.1088/1475-7516/2018/04/018

CrossRef Full Text | Google Scholar

Cheng, C., Jacobs, D., Aryeh Kohn, S., and Parsons, A., and PAPER Collaboration (2016). “PAPER-128 status update: towards a 21cm power spectrum detection,” in American Astronomical Society Meeting Abstracts #227 Vol. 227 (Kissimmee, FL), 307.

Chluba, J. (2013). Distinguishing different scenarios of early energy release with spectral distortions of the cosmic microwave background. Mthly Notices RAS 436, 2232–2243. doi: 10.1093/mnras/stt1733

CrossRef Full Text | Google Scholar

Chluba, J., Erickcek, A. L., and Ben-Dayan, I. (2012). Probing the inflaton: small-scale power spectrum constraints from measurements of the cosmic microwave background energy spectrum. Astrophys. J. 758:76. doi: 10.1088/0004-637X/758/2/76

CrossRef Full Text | Google Scholar

Chluba, J., and Sunyaev, R. A. (2012). The evolution of CMB spectral distortions in the early Universe. Mthly Notices RAS 419, 1294–1314. doi: 10.1111/j.1365-2966.2011.19786.x

CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2002). Magnetohydrodynamic turbulence as a foreground for cosmic microwave background studies. Astrophys. J. 575, L63–L66. doi: 10.1086/342722

CrossRef Full Text | Google Scholar

Choudhury, T. R., and Ferrara, A. (2005). Experimental constraints on self-consistent reionization models. Mthly Notices RAS 361, 577–594. doi: 10.1111/j.1365-2966.2005.09196.x

CrossRef Full Text | Google Scholar

Choudhury, T. R., and Ferrara, A. (2006). Updating reionization scenarios after recent data. Mthly Notices RAS 371, L55–L59. doi: 10.1111/j.1745-3933.2006.00207.x

CrossRef Full Text | Google Scholar

Choudhury, T. R., Haehnelt, M. G., and Regan, J. (2009). Inside-out or outside-in: the topology of reionization in the photon-starved regime suggested by Lyα forest data. Mthly Notices RAS 394, 960–977. doi: 10.1111/j.1365-2966.2008.14383.x

CrossRef Full Text | Google Scholar

Choudhury, T. R., Puchwein, E., Haehnelt, M. G., and Bolton, J. S. (2015). Lyman α emitters gone missing: evidence for late reionization? Mthly Notices RAS 452, 261–277. doi: 10.1093/mnras/stv1250

CrossRef Full Text | Google Scholar

Ciardi, B., and Ferrara, A. (2005). The first cosmic structures and their effects. Space Sci. Rev. 116, 625–705. doi: 10.1007/s11214-005-3592-0

CrossRef Full Text | Google Scholar

Ciardi, B., Ferrara, A., and White, S. D. M. (2003). Early reionization by the first galaxies. Mthly Notices RAS 344, L7–L11. doi: 10.1046/j.1365-8711.2003.06976.x

CrossRef Full Text | Google Scholar

Cohen, A., Fialkov, A., Barkana, R., and Lotem, M. (2017). Charting the parameter space of the global 21-cm signal. Mthly Notices RAS 472, 1915–1931. doi: 10.1093/mnras/stx2065

CrossRef Full Text | Google Scholar

Condon, J. J., Cotton, W. D., Fomalont, E. B., Kellermann, K. I., Miller, N., Perley, R. A., et al. (2012). Resolving the radio source background: deeper understanding through confusion. Astrophys. J. 758:23. doi: 10.1088/0004-637X/758/1/23

CrossRef Full Text | Google Scholar

Danese, L., and Burigana, C. (1994). “Theoretical aspects of the CMB spectrum,” in Present and Future of the Cosmic Microwave Background, Vol. 429, Lecture Notes in Physics, eds J. L. Sanz, E. Martinez-Gonzalez, and L. Cayon (Berlin: Springer Verlag), 28.

Google Scholar

Danese, L., and de Zotti, G. (1977). The relic radiation spectrum and the thermal history of the Universe. Nuovo Cimento Rivista Serie 7, 277–362.

Google Scholar

Danese, L., and de Zotti, G. (1980). On distortions in the Rayleigh-Jeans region of the cosmic background radiation spectrum. Astron. Astrophys. 84:364.

Google Scholar

Danese, L., and de Zotti, G. (1981). Dipole anisotropy and distortions of the spectrum of the cosmic microwave background. Astron. Astrophys. 94:L33.

Google Scholar

de Bernardis, P., Ade, P. A. R., Baselmans, J. J. A., Benoit, E. S., Bersanelli, M., Bideaud, A., et al. (2018). Exploring cosmic origins with CORE: the instrument. J. Cosmol. Astroparticle Phys. 4:15. doi: 10.1088/1475-7516/2018/04/015

CrossRef Full Text | Google Scholar

de Bernardis, P., Ade, P. A. R., Bock, J. J., Bond, J. R., Borrill, J., Boscaleri, A., et al. (2002). Multiple peaks in the angular power spectrum of the cosmic microwave background: significance and consequences for cosmology. Astrophys. J. 564, 559–566. doi: 10.1086/324298

CrossRef Full Text | Google Scholar

De Bernardis, P., Bucher, M., Burigana, C., and Piccirillo, L. (2009). B-Pol: detecting primordial gravitational waves generated during inflation. Exp. Astron. 23, 5–16. doi: 10.1007/s10686-008-9120-y

CrossRef Full Text | Google Scholar

De Zotti, G., González-Nuevo, J., Lopez-Caniego, M., Negrello, M., Greenslade, J., Hernandez-Monteagudo, C., et al. (2018). Exploring cosmic origins with CORE: Extragalactic sources in cosmic microwave background maps. J. Cosmol. Astroparticle Phys. 4:20. doi: 10.1088/1475-7516/2018/04/020

CrossRef Full Text | Google Scholar

DeBoer, D. R., Parsons, A. R., Aguirre, J. E., Alexander, P., Ali, Z. S., Beardsley, A. P., et al. (2017). Hydrogen epoch of reionization array (HERA). Publ. ASP 129:045001. doi: 10.1088/1538-3873/129/974/045001

CrossRef Full Text | Google Scholar

Delabrouille, J., de Bernardis, P., Bouchet, F. R., et al. (2018). Exploring cosmic origins with CORE: survey requirements and mission design. J. Cosmol. Astroparticle Phys. 4:14. doi: 10.1088/1475-7516/2018/04/014

CrossRef Full Text | Google Scholar

Delabrouille, J., de Bernardis, P., and Bouchet, F. R., and the CORE Collaboration (2016). “CORE – the cosmic origins explorer,” in A proposal in response to the ESA call for a Medium Size space mission for launch in 2029-2030.

Dewdney, P. E., Turner, W., Millenaar, R., McCool, R., Lazio, J., and Cornwell, T. J. (2013). SKA1 System Baseline Design. SKA Program Development Office, SKA-TEL-SKO-DD-001, Revision: 1.

Di Valentino, E., Brinckmann, T., Gerbino, M., et al. (2018). Exploring cosmic origins with CORE: cosmological parameters. J. Cosmol. Astroparticle Phys. 4:17. doi: 10.1088/1475-7516/2018/04/017

CrossRef Full Text | Google Scholar

Doroshkevich, A. G., Naselsky, I. P., Naselsky, P. D., and Novikov, I. D. (2003). Ionization history of the cosmic plasma in the light of the recent cosmic background imager and future Planck data. Astrophys. J. 586, 709–717. doi: 10.1086/367819

CrossRef Full Text | Google Scholar

Doroshkevich, A. G., and Naselsky, P. D. (2002). Ionization history of the universe as a test for superheavy dark matter particles. Phys. Rev. D 65:123517. doi: 10.1103/PhysRevD.65.123517

CrossRef Full Text | Google Scholar

Dowell, J., Taylor, G. B., Schinzel, F. K., Kassim, N. E., and Stovall, K. (2017). The LWA1 low frequency sky survey. Mthly Notices RAS 469, 4537–4550. doi: 10.1093/mnras/stx1136

CrossRef Full Text | Google Scholar

Efstathiou, G., Sutherland, W. J., and Maddox, S. J. (1990). The cosmological constant and cold dark matter. Nature 348, 705–707.

Google Scholar

Ejlli, D., and Dolgov, A. D. (2014). CMB constraints on mass and coupling constant of light pseudoscalar particles. Phys. Rev. D 90:063514. doi: 10.1103/PhysRevD.90.063514

CrossRef Full Text | Google Scholar

Ewall-Wice, A., Chang, T.-C., Lazio, J., Doré, O., Seiffert, M., and Monsalve, R. A. (2018). Modeling the radio background from the first black holes at cosmic dawn: implications for the 21 cm absorption amplitude. arXiv:1803.01815.

Google Scholar

Fauvet, L., Macías-Pérez, J. F., Aumont, J., Désert, F. X., Jaffe, T. R., Banday, A. J., et al. (2011). Joint 3D modelling of the polarized Galactic synchrotron and thermal dust foreground diffuse emission. Astron. Astrophys. 526:A145. doi: 10.1051/0004-6361/201014492

CrossRef Full Text | Google Scholar

Fauvet, L., Macías-Pérez, J. F., and Désert, F. X. (2012). Model of the polarized foreground diffuse Galactic emissions from 33 to 353 GHz. Astropart. Phys. 36, 57–63. doi: 10.1016/j.astropartphys.2012.04.013

CrossRef Full Text | Google Scholar

Feng, C., and Holder, G. (2018). Enhanced global signal of neutral hydrogen due to excess radiation at cosmic dawn. arXiv:1802.07432.

Google Scholar

Finelli, F., Bucher, M., Achúcarro, A., Ballardini, M., Bartolo, N., Baumann, D., et al. (2018). Exploring cosmic origins with CORE: inflation. J. Cosmol. Astroparticle Phys. 4:16. doi: 10.1088/1475-7516/2018/04/016

CrossRef Full Text | Google Scholar

Fixsen, D. J. (2009). The temperature of the cosmic microwave background. Astrophys. J. 707, 916–920. doi: 10.1088/0004-637X/707/2/916

CrossRef Full Text | Google Scholar

Fixsen, D. J., Cheng, E. S., Gales, J. M., Mather, J. C., Shafer, R. A., and Wright, E. L. (1996). The cosmic microwave background spectrum from the full COBE FIRAS data set. Astrophys. J. 473:576.

Google Scholar

Fixsen, D. J., and Mather, J. C. (2002). The spectral results of the far-infrared absolute spectrophotometer instrument on COBE. Astrophys. J. 581, 817–822. doi: 10.1086/344402

CrossRef Full Text | Google Scholar

Forman, M. A. (1970). The Compton-Getting effect for cosmic-ray particles and photons and the Lorentz-invariance of distribution functions. Planet. Space Sci. 18, 25–31. doi: 10.1016/0032-0633(70)90064-4

CrossRef Full Text | Google Scholar

Furlanetto, S. R., Hernquist, L., and Zaldarriaga, M. (2004). Constraining the topology of reionization through Lyα absorption. Mthly Notices RAS 354, 695–707. doi: 10.1111/j.1365-2966.2004.08225.x

CrossRef Full Text | Google Scholar

Furlanetto, S. R., Oh, S. P., and Briggs, F. H. (2006). Cosmology at low frequencies: the 21 cm transition and the high-redshift Universe. Phys. Rep. 433, 181–301. doi: 10.1016/j.physrep.2006.08.002

CrossRef Full Text | Google Scholar

Gao, L., and Theuns, T. (2007). Lighting the universe with filaments. Science 317:1527. doi: 10.1126/science.1146676

PubMed Abstract | CrossRef Full Text | Google Scholar

Gervasi, M., Zannoni, M., Tartari, A., Boella, G., and Sironi, G. (2008). TRIS. II. Search for CMB spectral distortions at 0.60, 0.82, and 2.5 GHz. Astrophys. J. 688, 24–31. doi: 10.1086/592134

CrossRef Full Text | Google Scholar

Gnedin, N. Y. (2000). Effect of reionization on structure formation in the universe. Astrophys. J. 542, 535–541. doi: 10.1086/317042

CrossRef Full Text | Google Scholar

Górski, K. M., Hivon, E., Banday, A. J., Wandelt, B. D., Hansen, F. K., Reinecke, M., and Bartelmann, M. (2005). HEALPix: a framework for high-resolution discretization and fast analysis of data distributed on the sphere. Astrophys. J. 622, 759–771. doi: 10.1086/427976

CrossRef Full Text | Google Scholar

Govoni, F., Murgia, M., Xu, H., Li, H., Norman, M. L., Feretti, L., Giovannini, G., and Vacca, V. (2013). Polarization of cluster radio halos with upcoming radio interferometers. Astron. Astrophys. 554:A102. doi: 10.1051/0004-6361/201321403

CrossRef Full Text | Google Scholar

Hansen, S. H., and Haiman, Z. (2004). Do we need stars to reionize the universe at high redshifts? Early reionization by decaying heavy sterile neutrinos. Astrophys. J., 600, 26–31. doi: 10.1086/379636

CrossRef Full Text | Google Scholar

Haslam, C. G. T., Salter, C. J., Stoffel, H., and Wilson, W. E. (1982). A 408 MHz all-sky continuum survey. II-The atlas of contour maps. Astron. Astrophys. Suppl. 47:1.

Google Scholar

Hill, J. C., Battaglia, N., Chluba, J., Ferraro, S., Schaan, E., and Spergel, D. N. (2015). Taking the universe's temperature with spectral distortions of the cosmic microwave background. Phys. Rev. Lett. 115:261301. doi: 10.1103/PhysRevLett.115.261301

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, W., Scott, D., and Silk, J. (1994). Power spectrum constraints from spectral distortions in the cosmic microwave background. Astrophys. J. 430, L5–L8.

Google Scholar

Hu, W., and Silk, J. (1993). Thermalization constraints and spectral distortions for massive unstable relic particles. Phys. Rev. Lett. 70, 2661–2664.

PubMed Abstract | Google Scholar

Hu, W., and White, M. (1997). A CMB polarization primer. N. Astron. 2, 323–344.

Google Scholar

Huang, Y., Wu, X.-P., Zheng, Q., Gu, J.-H., and Xu, H. (2016). The radio environment of the 21 centimeter array: RFI detection and mitigation. Res. Astron. Astrophys. 16:36. doi: 10.1088/1674-4527/16/2/036

CrossRef Full Text | Google Scholar

Ishino, H., Akiba, Y., Arnold, K., et al. (2016). “LiteBIRD: lite satellite for the study of B-mode polarization and inflation from cosmic microwave background radiation detection,” in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 9904, Proceedings of the SPIE (Edinburgh), 99040X.

Google Scholar

Jacobs, D. C., Hazelton, B. J., Trott, C. M., Dillon, J. S., Pindor, B., Sullivan, I. S., et al. (2016). The Murchison widefield array 21 cm power spectrum analysis methodology. Astrophys. J. 825:114. doi: 10.3847/0004-637X/825/2/114

CrossRef Full Text | Google Scholar

Jarvis, M., Bacon, D., Blake, C., Brown, M., Lindsay, S., Raccanelli, A., Santos, M., and Schwarz, D. J. (2015). “Cosmology with SKA radio continuum surveys,” in Proceedings of Science, Advancing Astrophysics with the Square Kilometre Array (AASKA14) (Giardini Naxos), 18.

Google Scholar

Jedamzik, K., Katalinić, V., and Olinto, A. V. (2000). Limit on primordial small-scale magnetic fields from cosmic microwave background distortions. Phys. Rev. Lett. 85, 700–703. doi: 10.1103/PhysRevLett.85.700

PubMed Abstract | CrossRef Full Text | Google Scholar

Kakiichi, K., Graziani, L., Ciardi, B., Meiksin, A., Compostella, M., Eide, M. B., and Zaroubi, S. (2017). The concerted impact of galaxies and QSOs on the ionization and thermal state of the intergalactic medium. Mthly Notices RAS 468, 3718–3736. doi: 10.1093/mnras/stx603

CrossRef Full Text | Google Scholar

Kasuya, S., Kawasaki, M., and Sugiyama, N. (2004). Partially ionizing the universe by decaying particles. Phys. Rev. D 69:023512. doi: 10.1103/PhysRevD.69.023512

CrossRef Full Text | Google Scholar

Kogut, A. (1996). Diffuse microwave emission survey. arXiv:astro-ph/9607100.

Google Scholar

Kogut, A., Fixsen, D. J., Chuss, D. T., Dotson, T., Dwek, E., Halpern, M., et al. (2011). The Primordial Inflation Explorer (PIXIE): a nulling polarimeter for cosmic microwave background observations. J. Cosmol. Astroparticle Phys. 7:25. doi: 10.1088/1475-7516/2011/07/025

CrossRef Full Text | Google Scholar

Kogut, A. J., Chuss, D. T., Dotson, J. L., Fixsen, D. J., Halpern, M., Hinshaw, G. F., et al. (2010). “The primordial inflation explorer (PIXIE) mission,” in Space Telescopes and Instrumentation 2010: Optical, Infrared, and Millimeter Wave, Vol. 7731, Proceedings of the SPIE (San Diego, CA), 77311S.

Google Scholar

Kogut, A. J., Chuss, D. T., Dotson, J. L., et al. (2014). “The primordial inflation explorer (PIXIE),” in American Astronomical Society Meeting Abstracts #223, Vol. 223 American Astronomical Society Meeting Abstracts (Washington, DC), id.439.01.

Google Scholar

La Porta, L., Burigana, C., Reich, W., and Reich, P. (2008). The impact of Galactic synchrotron emission on CMB anisotropy measurements. I. Angular power spectrum analysis of total intensity all-sky surveys. Astron. Astrophys. 479, 641–654. doi: 10.1051/0004-6361:20078435

CrossRef Full Text | Google Scholar

Lewis, A., Challinor, A., and Lasenby, A. (2000). Efficient computation of cosmic microwave background anisotropies in closed Friedmann-Robertson-Walker models. Astrophys. J., 538, 473–476. doi: 10.1086/309179

CrossRef Full Text | Google Scholar

Maartens, R., Abdalla, F. B., Jarvis, M., and Santos, M. G. (2015). “Overview of cosmology with the SKA,” Proceedings of Science, Advancing Astrophysics with the Square Kilometre Array (AASKA14) (Giardini Naxos), 16.

Google Scholar

Mather, J. C., Cheng, E. S., Eplee, R. E. Jr., Isaacman, R. B., Meyer, S. S., Shafer, R. A., et al. (1990). A preliminary measurement of the cosmic microwave background spectrum by the Cosmic Background Explorer (COBE) satellite. Astrophys. J. 354, L37–L40.

Google Scholar

Matsumura, T., Akiba, Y., Borrill, J., Chinone, Y., Dobbs, M., Fuke, H., Ghribi, A., et al. (2014). Mission design of LiteBIRD. J. Low Temp. Phys. 176, 733–740. doi: 10.1007/s10909-013-0996-1

CrossRef Full Text | Google Scholar

Mauch, T., Klöckner, H.-R., Rawlings, S., Jarvis, M., Hardcastle, M. J., Obreschkow, D., et al. (2013). A 325-MHz GMRT survey of the Herschel-ATLAS/GAMA fields. Mthly Notices RAS 435, 650–662. doi: 10.1093/mnras/stt1323

CrossRef Full Text | Google Scholar

Mesinger, A. (2018). “Reionization and Cosmic Dawn: theory and simulations,” in Proceedings of IAU Symposium 333, Peering Towards Cosmic Dawn (Dubrovnik).

Google Scholar

Mesinger, A., Aykutalp, A., Vanzella, E., Pentericci, L., Ferrara, A., and Dijkstra, M. (2015). Can the intergalactic medium cause a rapid drop in Lyα emission at z > 6? Mthly Notices RAS 446, 566–577. doi: 10.1093/mnras/stu2089

CrossRef Full Text | Google Scholar

Mesinger, A., and Furlanetto, S. (2007). Efficient simulations of early structure formation and reionization. Astrophys. J. 669, 663–675. doi: 10.1086/521806

CrossRef Full Text | Google Scholar

Mesinger, A., Furlanetto, S., and Cen, R. (2011). 21CMFAST: a fast, seminumerical simulation of the high-redshift 21-cm signal. Mthly Notices RAS 411, 955–972. doi: 10.1111/j.1365-2966.2010.17731.x

CrossRef Full Text | Google Scholar

Mesinger, A., Greig, B., and Sobacchi, E. (2016). The evolution Of 21 cm Structure (EOS): public, large-scale simulations of Cosmic Dawn and reionization. Mthly Notices RAS 459, 2342–2353. doi: 10.1093/mnras/stw831

CrossRef Full Text | Google Scholar

Muñoz, J. B., and Loeb, A. (2018). Insights on dark matter from hydrogen during Cosmic Dawn. Nature 557, 684–686. doi: 10.1038/s41586-018-0151-x

CrossRef Full Text | Google Scholar

Mutch, S. J., Geil, P. M., Poole, G. B., Angel, P. W., Duffy, A. R., Mesinger, A., and Wyithe, J. S. B. (2016). Dark-ages reionization and galaxy formation simulation - III. Modelling galaxy formation and the epoch of reionization. Mthly Notices RAS 462, 250–276. doi: 10.1093/mnras/stw1506

CrossRef Full Text | Google Scholar

Naselsky, P., and Chiang, L.-Y. (2004). Late reionizations of the Universe and their manifestation in the WMAP and future Planck data. Mthly Notices RAS 347, 795–801. doi: 10.1111/j.1365-2966.2004.07250.x

CrossRef Full Text | Google Scholar

Natoli, P., Ashdown, M., Banerji, R., Borrill, J., Buzzelli, A., de Gasperis, J., et al. (2018). Exploring cosmic origins with CORE: Mitigation of systematic effects. J. Cosmol. Astroparticle Phys. 4:22. doi: 10.1088/1475-7516/2018/04/022

CrossRef Full Text | Google Scholar

Oh, S. P. (1999). Observational signatures of the first luminous objects. Astrophys. J. 527, 16–30.

Google Scholar

Ostriker, J. P., and Thompson, C. (1987). Distortion of the cosmic background radiation by superconducting strings. Astrophys. J. 323, L97–L101.

Google Scholar

Pani, P., and Loeb, A. (2013). Constraining primordial black-hole bombs through spectral distortions of the cosmic microwave background. Phys. Rev. D 88:041301. doi: 10.1103/PhysRevD.88.041301

CrossRef Full Text | Google Scholar

Patil, A. H., Yatawatta, S., Koopmans, L. V. E., de Bruyn, A. G., Brentjens, M. A., Zaroubi, S., et al. (2017). Upper limits on the 21 cm epoch of reionization power spectrum from one night with LOFAR. Astrophys. J. 838:65. doi: 10.3847/1538-4357/aa63e7

CrossRef Full Text | Google Scholar

Peebles, P. J. E., Seager, S., and Hu, W. (2000). Delayed Recombination. Astrophys. J. 539, L1–L4. doi: 10.1086/312831

CrossRef Full Text | Google Scholar

Perlmutter, S., Aldering, G., Goldhaber, G., et al. (1999). Measurements of Ω and Λ from 42 high-Redshift supernovae. Astrophys. J. 517, 565–586.

Google Scholar

Planck Collaboration (2014). Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 571:A16.

Planck Collaboration (2016a). Planck 2015 results. X. Diffuse component separation: foreground maps. Astron. Astrophys. 594:A10. doi: 10.1051/0004-6361/201525967

CrossRef Full Text

Planck Collaboration (2016b). Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text

Planck Collaboration (2016c). Planck 2015 results. XXV. Diffuse low-frequency Galactic foregrounds. Astron. Astrophys. 594:A25. doi: 10.1051/0004-6361/201526803

CrossRef Full Text

Planck Collaboration (2016d). Planck intermediate results. XLI. A map of lensing-induced B-modes. Astron. Astrophys. 596:A102. doi: 10.1051/0004-6361/201527932

CrossRef Full Text

Planck Collaboration (2016e). Planck intermediate results. XLVII. Planck constraints on reionization history. Astron. Astrophys. 596:A108. doi: 10.1051/0004-6361/201628897

CrossRef Full Text

Planck Collaboration (2016f). Planck intermediate results. XXX. The angular power spectrum of polarized dust emission at intermediate and high Galactic latitudes. Astron. Astrophys. 586:A133. doi: 10.1051/0004-6361/201425034

CrossRef Full Text

Ponente, P. P., Diego, J. M., Sheth, R. K., Burigana, C., Knollmann, S. R., and Ascasibar, Y. (2011). The cosmological free-free signal from galaxy groups and clusters. Mthly Notices RAS 410, 2353–2362. doi: 10.1111/j.1365-2966.2010.17611.x

CrossRef Full Text | Google Scholar

Popa, L. A., Burigana, C., and Mandolesi, N. (2005). Radiative effects by high- z UV radiation background: implications for the future CMB polarization measurements. N. Astron. 11, 173–184. doi: 10.1016/j.newast.2005.07.003

CrossRef Full Text | Google Scholar

Prandoni, I., Gregorini, L., Parma, P., de Ruiter, H. R., Vettolani, G., Wieringa, M. H., and Ekers, R. D. (2001). The ATESP radio survey. III. Source counts. Astron. Astrophys. 365, 392–399. doi: 10.1051/0004-6361:20000142

CrossRef Full Text | Google Scholar

Prandoni, I., and Seymour, N. (2015). “Revealing the physics and evolution of galaxies and galaxy clusters with SKA Continuum surveys,” in Proceedings of Science, Advancing Astrophysics with the Square Kilometre Array (AASKA14) (Giardini Naxos), 67.

Rawlings, S., Abdalla, F. B., Bridle, S. L., Blake, C. A., Baugh, C. M., Greenhill, L. J., and van der Hulst, J. M. (2004). Galaxy evolution, cosmology and dark energy with the Square Kilometer Array. N. Astron. Rev. 48, 1013–1027. doi: 10.1016/j.newar.2004.09.024

CrossRef Full Text | Google Scholar

Refregier, A., Komatsu, E., Spergel, D. N., and Pen, U.-L. (2000). Power spectrum of the Sunyaev-Zel'dovich effect. Phys. Rev. D 61:123001. doi: 10.1103/PhysRevD.61.123001

CrossRef Full Text | Google Scholar

Remazeilles, M., Banday, A. J., Baccigalupi, C., Basak, S., Bonaldi, A., De Zotti, J., et al. (2018). Exploring cosmic origins with CORE: B-mode component separation. J. Cosmol. Astroparticle Phys. 4:23. doi: 10.1088/1475-7516/2018/04/023

CrossRef Full Text | Google Scholar

Salvaterra, R., and Burigana, C. (2002). A joint study of early and late spectral distortions of the cosmic microwave background and of the millimetric foreground. Mthly Notices RAS 336, 592–610. doi: 10.1046/j.1365-8711.2002.05784.x

CrossRef Full Text | Google Scholar

Santos, M. G., Ferramacho, L., Silva, M. B., Amblard, A., and Cooray, A. (2010). Fast large volume simulations of the 21-cm signal from the reionization and pre-reionization epochs. Mthly Notices RAS 406, 2421–2432. doi: 10.1111/j.1365-2966.2010.16898.x

CrossRef Full Text | Google Scholar

Schneider, R., Salvaterra, R., Choudhury, T. R., Ferrara, A., Burigana, C., and Popa, L. A. (2008). Detectable signatures of cosmic radiative feedback. Mthly Notices RAS 384, 1525–1532. doi: 10.1111/j.1365-2966.2007.12801.x

CrossRef Full Text | Google Scholar

Seiffert, M., Fixsen, D. J., Kogut, A., Levin, S. M., Limon, M., Lubin, P. M., et al. (2011). Interpretation of the ARCADE 2 Absolute Sky Brightness Measurement. Astrophys. J. 734:6. doi: 10.1088/0004-637X/734/1/6

CrossRef Full Text | Google Scholar

Seljak, U., and Zaldarriaga, M. (1996). A line-of-sight integration approach to cosmic microwave background anisotropies. Astrophys. J. 469:437.

Google Scholar

Singal, J., Fixsen, D. J., Kogut, A., Levin, S., Limon, M., Lubin, P., et al. (2011). The ARCADE 2 instrument. Astrophys. J. 730:138. doi: 10.1088/0004-637X/730/2/138

CrossRef Full Text | Google Scholar

Singh, S., Subrahmanyan, R., Udaya Shankar, N., Sathyanarayana Rao, M., Fialkov, A., Cohen, A., et al. (2017). First Results on the Epoch of Reionization from First Light with SARAS 2. Astrophys. J. 845:L12. doi: 10.3847/2041-8213/aa831b

CrossRef Full Text | Google Scholar

Smoot, G. F., Bennett, C. L., Kogut, A., Aymon, J., Backus, C., de Amici, G., et al. (1991). Preliminary results from the COBE differential microwave radiometers-Large angular scale isotropy of the cosmic microwave background. Astrophys. J. 371, L1–L5.

Google Scholar

Strong, A. W., and Moskalenko, I. V. (1998). Propagation of cosmic-ray nucleons in the galaxy. Astrophys. J. 509, 212–228.

Google Scholar

Sun, X.-H., and Reich, W. (2010). The Galactic halo magnetic field revisited. Res. Astron. Astrophys. 10, 1287–1297. doi: 10.1088/1674-4527/10/12/009

CrossRef Full Text | Google Scholar

Sun, X. H., and Reich, W. (2009). Simulated square kilometre array maps from Galactic 3D-emission models. Astron. Astrophys. 507, 1087–1105. doi: 10.1051/0004-6361/200912539

CrossRef Full Text | Google Scholar

Sun, X. H., Reich, W., Waelkens, A., and Enßlin, T. A. (2008). Radio observational constraints on Galactic 3D-emission models. Astron. Astrophys. 477, 573–592. doi: 10.1051/0004-6361:20078671

CrossRef Full Text | Google Scholar

Sunyaev, R. A., and Khatri, R. (2013). Unavoidable CMB spectral features and blackbody photosphere of our universe. Int. J. Modern Phys. D 22:1330014. doi: 10.1142/S0218271813300140

CrossRef Full Text | Google Scholar

Sunyaev, R. A., and Zeldovich, Y. B. (1970). The interaction of matter and radiation in the hot model of the Universe, II. Astrophys. Space Sci. 7, 20–30.

Google Scholar

The COrE Collaboration (2011). COrE (Cosmic Origins Explorer) A White Paper. arXiv:1102.2181.

Trac, H., and Cen, R. (2007). Radiative transfer simulations of cosmic reionization. I. Methodology and initial results. Astrophys. J. 671, 1–13. doi: 10.1086/522566

CrossRef Full Text | Google Scholar

Trombetti, T. (2018). Astrophysical and Cosmological Background Signals from the Radio to the Microwaves. Ph.D. thesis in Physics, Department of Physics and Earth Science, University of Ferrara.

Trombetti, T., and Burigana, C. (2012). Imprints on CMB angular power spectrum modes from cosmological reionization. J. Modern Phys. 3, 1918–1944. doi: 10.4236/jmp.2012.312242

CrossRef Full Text | Google Scholar

Trombetti, T., and Burigana, C. (2014). Semi-analytical description of clumping factor and cosmic microwave background free-free distortions from reionization. Mthly Notices RAS 437, 2507–2520. doi: 10.1093/mnras/stt2063

CrossRef Full Text | Google Scholar

Trombetti, T., Burigana, C., De Zotti, G., Galluzzi, V., and Massardi, M. (in press). Average fractional polarization of extragalactic sources at Planck frequencies. Astron. Astrophys. doi: 10.1051/0004-6361/201732342

CrossRef Full Text | Google Scholar

Viel, M., Lesgourgues, J., Haehnelt, M. G., Matarrese, S., and Riotto, A. (2005). Constraining warm dark matter candidates including sterile neutrinos and light gravitinos with WMAP and the Lyman-α forest. Phys. Rev. D 71:063534. doi: 10.1103/PhysRevD.71.063534

CrossRef Full Text | Google Scholar

Voytek, T. C., Natarajan, A., Jáuregui García, J. M., Peterson, J. B., and López-Cruz, O. (2014). Probing the dark ages at z ˜ 20: The SCI-HI 21 cm all-sky spectrum experiment. Astrophys. J. 782:L9. doi: 10.1088/2041-8205/782/1/L9

CrossRef Full Text | Google Scholar

Waelkens, A., Jaffe, T., Reinecke, M., Kitaura, F. S., and Enßlin, T. A. (2009). Simulating polarized Galactic synchrotron emission at all frequencies. The Hammurabi code. Astron. Astrophys. 495, 697–706. doi: 10.1051/0004-6361:200810564

CrossRef Full Text | Google Scholar

Williams, W. L., Intema, H. T., and Röttgering, H. J. A. (2013). T-RaMiSu: the two-meter radio mini survey. I. The Boötes field. Astron. Astrophys. 549:A55. doi: 10.1051/0004-6361/201220235

CrossRef Full Text | Google Scholar

Wyithe, J. S. B., and Cen, R. (2007). The extended star formation history of the first generation of stars and the reionization of cosmic hydrogen. Astrophys. J. 659, 890–907. doi: 10.1086/511948

CrossRef Full Text | Google Scholar

Xu, H., Wise, J. H., Norman, M. L., Ahn, K., and O'Shea, B. W. (2016). Galaxy properties and UV escape fractions during the epoch of reionization: results from the renaissance simulations. Astrophys. J. 833:84. doi: 10.3847/1538-4357/833/1/84

CrossRef Full Text | Google Scholar

Yamauchi, D., Ichiki, K., Kohri, K., Namikawa, T., Oyama, Y., Sekiguchi, T., et al. (2016). Cosmology with the Square Kilometre Array by SKA-Japan. Publ. ASJ 68:R2. doi: 10.1093/pasj/psw098

CrossRef Full Text | Google Scholar

Zahn, O., Lidz, A., McQuinn, M., Dutta, S., Hernquist, L., Zaldarriaga, M., et al. (2007). Simulations and analytic calculations of bubble growth during hydrogen reionization. Astrophys. J. 654, 12–26. doi: 10.1086/509597

CrossRef Full Text | Google Scholar

Zel'dovich, Y. B., Illarionov, A. F., and Sunyaev, R. A. (1972). The effect of energy release on the emission spectrum in a hot universe. Soviet J. Exp. Theor. Phys. 35:643.

Google Scholar