Pulsation in Intermediate-Mass Stars

A new perspective of pulsation in stars within the δ Scuti instability strip has recently emerged as a result of Kepler observations. The majority of stars within the instability strip do not pulsate and practically all δ Scuti stars contain low frequencies. Because γ Doradus stars co-exist with δ Sct stars in the same region of the instability strip, it follows that γ Dor stars are driven by the same mechanism as δ Sct stars. The difference must be due to different mode selection processes. The search for an unknown damping factor which is missing from the models will be essential for further progress. Maia variables and hot γ Dor stars are briefly discussed. Luminosities of roAp stars obtained from Gaia DR2 parallaxes and spectroscopic effective temperatures show that the roAp stars are slightly evolved with temperatures in the range 6,300–8,300 K, considerably cooler than predicted by the models. The roAp stars and stars with solar-like oscillations share the same mass—temperature—luminosity relation, but with frequencies which are about 50 percent higher. This suggests that roAp frequencies are determined by the critical acoustic frequency, but this frequency is larger than in standard models, perhaps as a result of a temperature inversion in the atmosphere.

1. Introduction

The main types of pulsating variables of intermediate mass on the main sequence are the γ Doradus, δ Scuti, and roAp stars. At the low-mass end (≈1.3 M/M_⊙), solar-like oscillations are present in stars right up to the red edge of the δ Sct/γ Dor instability strip. The red edge of the slowly pulsating B star (SPB star) instability strip defines the high-mass end at about 2.8 M/M_⊙. Besides these well-established variables, two possibly new types of pulsating star have recently been proposed. One is the extension of the γ Dor type to hotter temperatures (hot γ Dor variables, Balona et al., 2016). The other is the presence of δ Sct-type pulsation in stars lying between the cool end of the β Cep instability strip and the hot end of the δ Sct instability strip (Mowlavi et al., 2013; Balona et al., 2016). These have been historically been called Maia variables (Struve, 1955; Struve et al., 1957; Percy and Wilson, 2000), though the star of the same name in the Pleiades cluster is not of this type.

Our perspective on pulsation in these stars have changed quite radically over the last decade. Before the advent of photometric space observations, a complete picture seemed to have been formulated. For stars with radiative envelopes the models predict multiple p-mode pulsations driven by the opacity κ mechanism. All unstable pulsation frequencies exceed 5 d⁻¹, corresponding to the δ Sct stars. In cooler models where convection becomes important, instability is thought to be driven by the convection blocking mechanism (Guzik et al., 2000). Frequencies driven by this mechanism are less than about 5 d⁻¹, corresponding to the γ Dor stars. The few δ Sct/γ Dor hybrids then known were satisfactorily accommodated by more sophisticated time-dependent convection treatments (Dupret et al., 2005a).

For the roAp stars, which are pulsating Ap stars with strong global magnetic fields, Balmforth et al. (2001) proposed that the high-frequency pulsations are driven by the κ mechanism in the H/HeI partial ionization zone. In the models these pulsations are stable, but suppression of convection at the magnetic poles will cause instability. Pulsational driving confined to the magnetic poles also explains why the pulsation axis and the magnetic axis appear to be aligned.

Photometry from space, first with the MOST, then CoRoT and especially with the Kepler missions have shown that some of these ideas need to be revised. As early as the first Kepler data release, it became clear that hybrid δ Sct/γ Dor pulsation is not confined to just a few stars spanning the the two instability regions, but occurs across the whole δ Sct instability strip (Grigahcène et al., 2010). Then there was the realization that most stars in the instability strip did not seem to pulsate at all (Balona and Dziembowski, 2011). The third surprise was the finding that rotational modulation is common among the A stars (Balona, 2011). It even seems that a small fraction of A stars flare like the Sun (Balona, 2012). Most recently, it was found that non-pulsating stars, γ Dor stars and δ Sct stars all co-exist within the same region of the H-R diagram (Balona, 2018). That is, the pulsations in δ Sct and γ Dor stars are not a result of two separate mechanisms as previously thought, but probably a result of different mode selection processes.

There were surprises in Kepler observations of roAp stars as well. The first roAp star discovered in the Kepler field, KIC 8677585 (Balona et al., 2011a), exhibits an unexpected γ Dor-like pulsation with a frequency of 3.14 d⁻¹ which is still unexplained.

This paper highlights the main problems associated with pulsation among main sequence stars of intermediate mass. Evidence is presented of an, as yet unknown, physical factor which seems to control mode selection and to damp pulsations. This factor clearly varies from star to star and even between stars with the same effective temperatures and luminosities. The search for this factor will be essential for further progress. Much of the work reported here is based on visual inspection of Kepler light curves and periodograms of over 22,000 stars classified according to variability type and complete to magnitude 12.5.

2. Non-pulsating Stars in the δ Scuti Instability Strip

A mechanism which drives pulsations in one star is naturally expected to drive pulsations in another star with the same mass, effective temperature, age, and composition. An effect peculiar to the star, such as rotation, might however modify the pulsation frequencies and amplitudes. If one of the stars is not observed to pulsate, it is natural to conclude that pulsation is probably present but at a level too low to be detected. Of course, it would be important to understand the cause of the difference in pulsational amplitude, but unfortunately this is beyond our present capabilities.

A study of the Kepler data shows that less than half the stars in the δ Sct instability strip appear to pulsate (Balona and Dziembowski, 2011). While the above argument might still be applicable, the superb photometric precision of Kepler and the shear number of apparently non-pulsating stars is reason for a deeper examination of the problem. One might expect that the number of stars with a given maximum amplitude will increase as the amplitude tends to zero. There is, of course, an amplitude below which any pulsation will be hidden in the noise. If pulsation is present in all stars, then the “non-pulsating” stars are those with amplitudes below the detection limit and should be included in the bin containing the lowest amplitude.

The resulting amplitude distribution should appear to be smooth and physically reasonable. In other words, if the trend in the amplitude distribution is extrapolated to zero amplitude, it should approximately agree with the actual number of stars in the lowest amplitude bin. On the other hand, if the predicted number is far below the observed number of “non-pulsating” stars, then there is good reason to suspect that the “non-pulsating” stars actually belong to a different population altogether and should not be included in the distribution for pulsating stars. In other words, that they actually do not pulsate at all.

From the first year of Kepler observations, Balona and Dziembowski (2011) performed this exercise. As a measure of amplitude, the mode of highest amplitude with a frequency ν>5 d⁻¹ in each star was used. This choice eliminates variability due to rotational or binary effects which have lower frequencies. They concluded that the number of non-pulsating stars was at least ten times larger than predicted from the extrapolated amplitude distribution.

In the above analysis, only the first year of Kepler data was used. The calculation was recently repeated using the complete 4 year Kepler data set (Balona, 2018), giving the amplitude distribution shown in the left panel of Figure 1. It can be seen that the number of δ Sct stars increases as the amplitude decreases, as expected. There are 190 δ Sct stars with maximum amplitudes in the range 0–10 ppm. Extrapolation to zero amplitude suggests that not more than about 300 δ Sct stars might be expected to have undetectable amplitudes. However, the actual number of apparently non-pulsating stars in the instability strip is 1781, much larger than the expected number. If these are, indeed, δ Sct stars pulsating at an undetectable level, they should be added to the lowest-amplitude bin of the distribution as shown in the right panel of Figure 1. This amplitude distribution clearly suggests that these apparently non-pulsating stars do not belong to the same population as the δ Sct stars. The conclusion is that these stars are indeed non-pulsating.

FIGURE 1

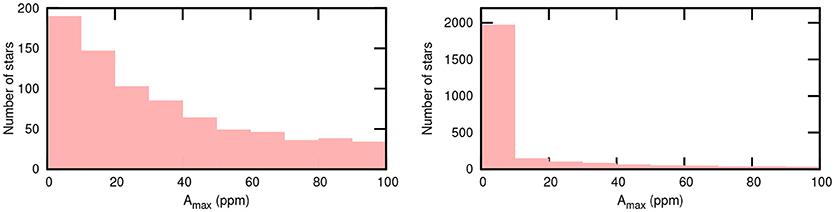
Figure 1. (Left) The distribution of the maximum amplitude (ppm) in Kepler δ Sct stars with K_p < 12.5 mag in the instability box. (Right) The same distribution, but including all non-pulsating stars in the δ Sct instability box on the assumption that these “constant” stars actually pulsate with amplitude below the detection limit.

The implication is that there is a missing factor in current pulsation models which adds to the damping. Further evidence for the existence of an unknown damping factor is presented below.

3. Low Frequencies in δ Sct Stars

It was already evident from the early days of the CoRoT and Kepler missions that low frequencies are very common among δ Sct stars. Recently, Balona (2018) has provided a list of all Kepler δ Sct and γ Dor stars complete to magnitude 12.5. It is concluded that at least 98 percent of δ Sct stars have significant low-frequency peaks in their periodograms. Under the circumstances, it is clear that the term “δ Sct/γ Dor hybrid” has lost its meaning.

The simplest explanation for low frequencies is rotational frequency splitting. The Coriolis force induced by rotation breaks the degeneracy of a spherical harmonic of degree l into 2l + 1 components. For slow rotation the frequencies of each component are more-or-less equally spaced. As rotation increases, the frequency spacing between multiplets increases and are no longer equally spaced. One may therefore expect to see peaks below the minimum frequency predicted by non-rotating models.

To test the idea that rotation might be responsible for the low frequencies, Balona et al. (2015b) used non-rotating stellar models to calculate unstable frequencies predicted by the κ mechanism. From the known distribution of rotational periods of these stars, and using a fairly simple model of rotational splitting which takes the second-order effect described above into account, it is possible to calculate the likely frequency distribution. While there is an increase in the relative numbers of stars showing low frequencies, it is still well below the numbers in the observed distribution. Thus, rotation can safely be ruled out as an explanation for the low frequencies.

Pulsational instability in the models can be induced by artificially increasing the opacities in the stellar envelope. This exercise was performed by Balona et al. (2015b) who showed that modes of spherical degree l = 1 could be driven by an opacity increase by a factor of at least two in certain region in the stellar envelope. However, the effect is weak, few modes are excited and the required opacity enhancement is unreasonably large. It is highly unlikely that opacity changes will resolve the problem.

Another idea is that the low frequencies might be mixed gravity-Rossby modes of the type discussed by Papaloizou and Pringle (1978). These modes have been recently proposed as an explanation of the broad hump that appears just below the rotation frequency in many A stars and also to explain the period spacings in some γ Dor stars (Saio et al., 2018). If this explanation is correct, inertial modes should be observed in all rotating stars within the instability strip with similar amplitudes. The fact that these are not observed in the majority of A stars immediately rules out this idea.

The convective blocking mechanism (Guzik et al., 2000) uses the simplest description of “frozen-in” convection which does not take into account the interaction between pulsation and convection. More recent treatments use a time-dependent perturbation theory (Dupret et al., 2005a,b). In any calculation involving convection there are free parameters which are chosen to give agreement with the observations. In contrast, no free parameters exist in the opacity κ mechanism.

Even for the hottest δ Sct stars, convection may be an important factor in pulsational driving. Kallinger and Matthews (2010) show that in all A-star models there is a very thin outer convection zone with a thickness of less than one percent of the stellar radius while on the main sequence. The thickness of the convection zone expands with subsequent evolution. They conclude that all stars located in the δ Scuti regime are expected to have thin, but non-negligible, sub-surface convection. These thin convective zones do not contribute significantly to energy transport, but may be important for mixing.

The recent work by Xiong et al. (2015, 2016) looks to be promising in resolving the issue of the low frequencies. Using a non-local and time-dependent convection theory, they find that unstable g and p modes are located in two partially overlapping instability strips with the g-mode instability strip systematically cooler than the p-mode instability strip. There is no distinct difference in the excitation and damping between p and g modes. Both are due to the combination of the κ mechanism and coupling between convection and the oscillations. The κ mechanism plays a major role in driving pulsations in hot δ Sct and γ Dor stars, while the coupling between convection and the oscillations is responsible for excitation and damping of pulsations in cool stars. Xiong et al. (2016) conclude that there is no essential difference between δ Sct and γ Dor stars. They are just two subgroups of one broader type, with δ Sct stars belonging to the p-mode subgroup and γ Dor stars to the g-mode subgroup.

Figure 2 shown the location of the Kepler δ Sct and γ Dor stars in the H–R diagram. This is based on visual classification of the the full 4-year Kepler data complete to magnitude 12.5 but extending to fainter magnitudes (Balona, 2018). The latest effective temperatures and luminosities derived from Gaia DR2 parallaxes (Gaia Collaboration et al., 2016, 2018) are used. Theoretical considerations predict that F stars should have strong surface differential rotation, a result supported by observations (Balona and Abedigamba, 2016). Great care was taken to distinguish between F stars which are multiperiodic due to differential rotation and the γ Dor stars.

FIGURE 2

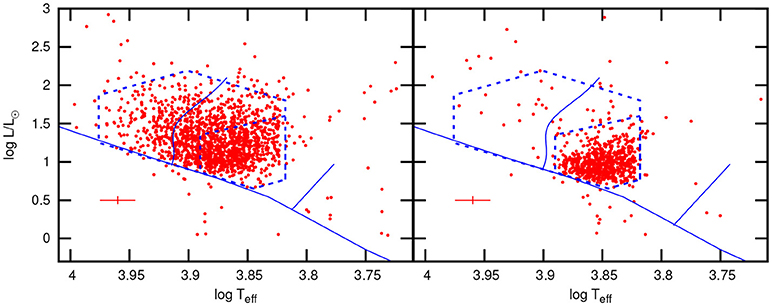
Figure 2. Kepler δ Sct stars (Left) and γ Dor stars (Right) in the H-R diagram (dots). Gaia D2 luminosities are used. The solid lines are the zero-age main sequence (solar abundance from Bertelli et al., 2008) and the non-radial red and blue edges from Xiong et al. (2016). The dashed polygon defines the region which includes the majority of δ Sct (larger box) and γ Dor (smaller box) stars. The cross at bottom left shows the 1-σ error bars.

It can be seen from Figure 2 that the red and blue edges predicted by Xiong et al. (2016) do not agree with observations. The figures also show that both δ Sct and γ Dor (as well as non-pulsating stars) co-exist within the confines of the γ Dor instability region. In fact, there are more δ Sct stars in the γ Dor region than γ Dor stars themselves.

It is clear that the difference between the two types of variable cannot be ascribed to differences in the driving mechanism or even the p- and g-mode subgroups advocated by Xiong et al. (2016). Instead, it seems that an unknown mode-selection factor is suppressing high frequencies in some stars (giving rise to γ Dor stars), but not in others (giving rise to the δ Sct stars). One presumes that if this factor is sufficiently strong, all pulsations are suppressed, giving rise to the non-pulsating stars.

Further evidence that mode selection varies strongly from star to star within the δ Sct instability strip is that stars occupying the same region in the H-R diagram can have very different frequency spectra (Balona et al., 2015b; Balona, 2018). In fact, the frequency spectrum acts as a unique identifier or fingerprint of a particular star.

4. Non-linearity in γ Dor Stars

Even a brief inspection of the Kepler photometry curves will reveal one of the strangest light curves among variable stars. The light curve consists of a periodic variation with typical time scale 0.3–3 d and strong, asymmetrical beats. The light maxima are very sharp and high. In fact, they can be mistaken for flares and are sometimes flagged as bad points in the Kepler data. Examples are shown in Figure 3. These γ Dor stars were first described by Balona et al. (2011b) who named them the ASYM (asymmetric) type of γ Dor variable. They comprise about 16 percent of the γ Dor type. Another two types, SYM (symmetric with beats) and MULT (multiperiodic, no beats) also exist, comprising respectively about 54 and 26 percent of these stars. In Balona (2018) they have been renamed GDORA, GDORS and GDORM respectively. These stars are all evenly distributed in the γ Dor instability region.

FIGURE 3

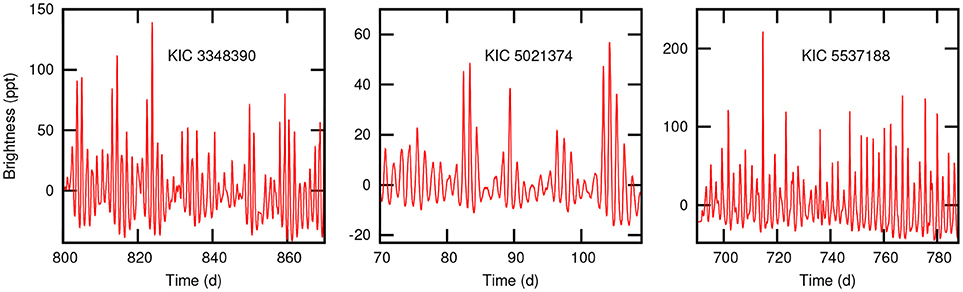
Figure 3. A selection of ASYM (GDORA) γ Dor light curves. The fractional brightness variation is in parts per thousand.

This raises the question as to whether some fraction the δ Sct stars within the γ Dor instability box show the same light curve asymmetry seen in the GDORA stars. To test this idea, 883 δ Sct stars lying entirely within the γ Dor instability box in the H-R diagram, were examined. For each star, all significant frequencies higher than 5 d⁻¹ were removed from the light curve. Inspection of the modified light curves showed no sign of asymmetry as seen in GDORA stars. Evidently, the strong non-linearity seen in GDORA stars does not occur in δ Sct stars.

What the different types of γ Dor stars seem to be telling us is that the factor driving the mode selection also incorporates a high degree of non-linearity. Nonlinearities are important in convection zones and lead, for example, to combination frequencies in pulsating white dwarfs (Brickhill, 1992). The possibility exists that the non-linearities seen in γ Dor stars originate in a similar way.

5. Maia Variables and Hot γ Dor Stars

Struve (1955) suggested that the late B star Maia, a member of the Pleiades, might be pulsating with a period of just a few hours. Later, Struve et al. (1957) disclaimed such variability except for the strengths of the helium lines. Main sequence stars pulsating with high frequencies cooler than the β Cep stars and hotter than the δ Sct stars are not predicted by standard pulsation models. Over the years persistent reports of such stars have been made, but none have been confirmed. For example, the A0 III star α Dra seems to have a period of around 53 min (Kallinger et al., 2004), while Degroote et al. (2009) found several Maia-like stars among the B-type variables observed by CoRoT. Balona et al. (2015a) found several examples of possible Maia variables in the Kepler field, though these could be binaries or stars with erroneous effective temperatures. However, spectroscopic observations have confirmed that these stars are indeed anomalous (Balona et al., 2016).

Mowlavi et al. (2013) found 36 anomalous pulsating variables from photometric observations of the young open cluster NGC 3766. Most of these stars have frequencies in the range 1–10 d⁻¹ and amplitudes 1–4 mmag. The cluster is known to have a particularly high population of rapidly-rotating stars and Mowlavi et al. (2013) suggested that rapid rotation may be a requirement for the presence of these high-frequency modes. This idea was investigated by Salmon et al. (2014) who proposed that they might be rapidly-rotating SPB stars. In a further study, Mowlavi et al. (2016) obtained spectra of the 36 stars and found that most are indeed fast rotators. They also found a relationship between the period of the pulsation of highest amplitude and the stellar magnitude. Saio et al. (2017) found that such a relationship is consistent with similar period-luminosity relations predicted for excited sectoral prograde g modes of azimuthal orders m = 1 and 2 in fast-rotating stars along an isochrone.

The relationship between these stars and the other Maia stars discussed here is not at all clear and must await further work. For example, Balona et al. (2016) found that the mean projected rotational velocity of seven Maia stars in the general field is less than 100 km s⁻¹, which is not consistent with rapid rotation. At this stage it is very difficult to be certain that the pulsations in these stars cannot be explained by conventional means. Daszyńska-Daszkiewicz et al. (2017) considered three possible explanations for the Maia stars. It seems that it is possible to obtain instability at high frequencies without rapid rotation only if there is a significant enhancement of opacities and only for modes of high degree (l > 6). Clearly, there is much uncertainty and no definite conclusions can be drawn at this stage.

The hot γ Dor variables are stars with multiple low frequencies characteristic of γ Dor or SPB variables, but located between the red edge of the SPB instability strip and the blue edge of the γ Dor instability strip. These can be thought of as normal γ Dor stars much hotter than the blue edge of the γ Dor instability strip. Balona et al. (2016) obtained spectra of some of these stars and verified that the photometric temperature estimates are correct. As mentioned above, rapid rotation may explain the Maia variables discovered by Mowlavi et al. (2013). However, it is not possible to explain the hot γ Dor stars as SPB stars which are moved to the A star region by the effects of gravity darkening induced by rapid rotation because the required shift in apparent temperature is much too large.

Further progress in understanding the Maia and hot γ Dor stars must await photometric space observations together with spectroscopic estimates of effective temperature. In this regard, the TESS space mission promises to be a valuable resource in discovering a larger sample of these anomalous pulsating variables.

6. The roAp Stars

The Ap stars are slowly rotating A and F stars with non-uniform distributions of chemical elements having over abundances of rare earth elements in the range 10³–10⁶ and strong magnetic fields of several kG. The magnetic poles are tilted with respect to the rotational axis, which leads to periodic light variations. The magnetic field is thought to be of fossil origin, i.e., a relic of the initial field in the interstellar medium. The patches of overabundant elements on the surfaces of these stars are thought to be a result of variable diffusion caused by differences in gravitational settling and radiative acceleration from place to place as a result of the magnetic field geometry.

The coolest subgroup of Ap stars are the SrCrEu group with 6400 < T_eff < 10000 K. Kurtz (1982) discovered that while most of the Ap stars do not show any oscillations, some exhibit single or multiperiodic pulsations with periods in the range 4–21 min. These pulsating stars are called the “rapidly oscillating Ap stars” (roAp stars). There are currently 61 known roAp stars. There have been a number of photometric surveys yielding negative results (e.g., Joshi et al., 2016; Paunzen et al., 2018) and it is unlikely that ground-based observations will lead to a significant increase in the number of roAp stars.

Due to line blanketing caused by the peculiar surface abundances, it is very difficult to obtain the effective temperatures of Ap stars. Modeling of the Hα or Hβ line profiles probably give the best estimates of T_eff. Fortunately, spectroscopic estimates of T_eff from Hα or Hβ are available for 48 stars. There is a strong linear correlation between the Strömgren β index, which measures the strength of the Hβ line, and the spectroscopic T_eff for the roAp stars when both measurements are available. This calibration can be used to obtain T_eff for a further 11 stars. Figure 4 shows the location of the roAp stars in the H-R diagram using luminosities estimated from the Gaia DR2 parallaxes (Gaia Collaboration et al., 2016, 2018). The roAp stars span the temperature range 6,300–8,300 K and seem to lie between the ZAMS and the end of core hydrogen burning.

FIGURE 4

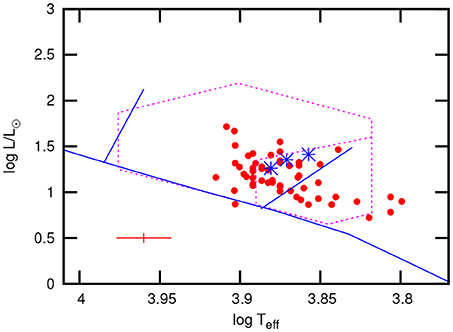
Figure 4. Location of the roAp stars in the H-R diagram (filled circles) showing the δ Sct region of instability (large dotted polygon) and the γ Dor instability region (small dotted polygon within the δ Sct region). The three asterisks are roAp stars with low frequencies. The two slanted lines are the red and blue edges of the instability region calculated by Cunha (2002). The ZAMS for solar abundances from Bertelli et al. (2008) is shown. The cross at bottom left shows the estimated 1-σ error bars.

It is interesting to note that more than half of the roAp stars lie within the γ Dor instability region where low-frequency pulsation is most common. Yet it is only in KIC 8677585 where a high-amplitude low frequency pulsation is seen (Balona et al., 2011a). Two other roAp stars, KIC 10483436 and KIC 10195926, appear to have pulsations close to half the rotation frequency (Balona, 2013). All three stars lie at the hot edge of the γ Dor instability region (Figure 4). It is difficult to understand the low frequencies in these stars as typical γ Dor pulsations.

As mentioned in the introduction, Balmforth et al. (2001) proposed that the high-frequency pulsations in roAp stars are driven by the κ mechanism in the H/HeI partial ionization zone at the magnetic poles where convection is suppressed. Calculations by Cunha (2002) show that pulsation instability is present in main sequence models with 7000 < T_eff < 9300 K. Comparison with Figure 4 suggests that the actual region of instability is considerably cooler.

All Ap stars with sufficiently strong magnetic fields should pulsate. Ground-based searches have clearly shown that pulsations are detectable in only a small fraction of Ap stars. It is quite possible, therefore, that the distribution of roAp stars in the H-R diagram shown in Figure 4 only represents stars with the highest amplitudes. The true distribution could be entirely different. Of course, the possibility that most Ap stars do not pulsate must also be considered. The situation is clearly similar to the δ Sct stars discussed above. Unfortunately, the amplitude distribution of roAp stars cannot be determined because there are too few stars. However, the fact that only 4 roAp stars out of 15 known Ap stars have been found in the Kepler field indicates that the relative number of roAp to Ap stars must be quite low. The TESS mission affords an ideal opportunity to map out the instability region.

The pulsation frequencies of many roAp stars appear to exceed the critical acoustic cut-off frequency, ν_c (Saio, 2014). This is the frequency above which the outer boundary is no longer able to reflect roAp-type modes, so that much of the wave energy is dissipated in the outer atmosphere as a running wave. This means that pulsational driving must be sufficiently strong to overcome the damping effect of running waves. It is not clear if current models can lead to sufficiently strong driving, even if the destabilizing effect of turbulent pressure (Cunha et al., 2013) is taken into account.

The acoustic cut-off frequency for an isothermal atmosphere is roughly dependent on the surface gravity, g, and the effective temperature: ${\nu }_c\propto g/\sqrt{T_{\text{eff}}}$. In stars with solar-like oscillations this leads to the well-known relationship between the frequency of maximum amplitude, ν_max, and the basic stellar parameters (Chaplin et al., 2011):

$\begin{array}{l}\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max}\odot }}=\left(\frac{M}{M_{\odot }}\right){\left(\frac{R}{R_{\odot }}\right)}^{-2}{\left(\frac{T_{\text{eff}}}{T_{\text{eff}\odot }}\right)}^{-\frac{1}{2}}\\ =\left(\frac{M}{M_{\odot }}\right){\left(\frac{L}{L_{\odot }}\right)}^{-1}{\left(\frac{T_{\text{eff}}}{T_{\text{eff}\odot }}\right)}^{\frac{7}{2}}.\end{array}$

Given the effective temperature and luminosity, the stellar mass, M/M_⊙, may be estimated by interpolating evolutionary tracks and thus ν_max may be calculated. Using the evolutionary tracks for solar abundances by Bertelli et al. (2008) and luminosities derived from Gaia DR2 parallaxes, the following relationship is found to reproduce the observed ν_max (in μHz) of solar-like stars hotter than 6,000 K in the catalog by Huber et al. (2017):

$\begin{array}{l}log({\nu }_{\text{max}})=log(M/M_{\odot })-log(L/L_{\odot })+\frac{7}{2}log(T_{\text{eff}})-9.6108.\end{array}$

This equation may be used to derive ν_max for roAp stars. Figure 5 shows an interesting linear correlation between ν_obs and ν_max. The implication is that frequencies of roAp stars are related to the critical acoustic frequency. However, the roAp frequencies are roughly 50 percent higher than the estimate based on solar-like oscillations. It appears that most, if not all roAp stars are pulsating at frequencies in excess of ν_c. Note that this empirical approach to the problem differs from that by Saio (2014) and others. Gautschy et al. (1998) found that by introducing a temperature inversion in the atmosphere, wave reflection can occur and ν_c increased. The required temperature inversion is fairly modest: about 1,000–3,000 K. This might be a way of resolving the problem.

FIGURE 5

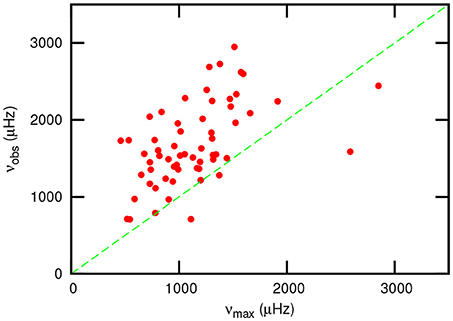
Figure 5. The observed roAp pulsation frequency, ν_obs, as a function of ν_max, the frequency of maximum amplitude extrapolated from hot stars with solar-like oscillations. The straight line has unit slope and zero intercept.

7. Conclusions

Most of the stars in the δ Sct instability strip do not seem to pulsate. Practically all δ Sct stars contain low frequencies. The difference between δ Sct and γ Dor stars has nothing to do with two different driving mechanisms, but is a mode selection effect. In some γ Dor stars the pulsation is highly non-linear. δ Sct or γ Dor stars with the same physical parameters may have very different frequencies which cannot be explained by differences in rotation. These findings, together with the fact that A stars have spots and possibly even flares, make a radical departure from what was accepted before Kepler.

It is clear that there is at least one damping factor missing from the models. When damping is large the star does not pulsate. When it is smaller, it preferentially damps the high frequencies in cool stars (γ Dor stars). When it is smaller still it allows the full frequency range (δ Sct stars). Of course, this may be an over-simplification but perhaps a good starting point in seeking for an understanding of these stars. Mode selection in δ Sct stars has been studied by Nowakowski (2005). It is found that in all evolved δ Sct stars non-resonant saturation of the driving effect is most likely the dominant damping mechanism. Resonant mode coupling does not seem to play an important role.

The standard description of pulsational driving: the κ mechanism in δ Sct stars and the convective blocking mechanism in γ Dor stars, has also fallen aside. The approach taken by Xiong et al. (2016) which includes the κ mechanism, but also a time-dependent convection treatment of turbulent pressure, turbulent thermal convection and other factors seems the most promising approach.

The existence of pulsating stars outside the known instability strips such as the Maia variables or hot γ Dor stars cannot yet be conclusively demonstrated. For now, these stars must simply be considered anomalous until a sufficient sample with verified physical parameters can be obtained. The TESS mission provides an opportunity for detecting many more such stars.

The roAp stars are also poorly understood. The first priority must be to determine the extent of the roAp instability strip. It is quite possible that the 61 known roAp stars simply represent stars with the highest amplitudes. What is required is an unbiased survey of Ap stars right across the H-R diagram to detect roAp pulsations of low amplitude. It is very important to select targets evenly spread over the full temperature range of Ap stars. Hopefully, this will be accomplished by the TESS mission.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

LB wishes to thank the National Research Foundation of South Africa for financial support. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission directorate. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia).

References

Balmforth, N. J., Cunha, M. S., Dolez, N., Gough, D. O., and Vauclair, S. (2001). On the excitation mechanism in roAp stars. Mon. Notices R. Astron. Soc. 323, 362–372. doi: 10.1046/j.1365-8711.2001.04182.x

CrossRef Full Text | Google Scholar

Balona, L. A. (2011). Rotational light variations in Kepler observations of A-type stars. Mon. Notices R. Astron. Soc. 415, 1691–1702. doi: 10.1111/j.1365-2966.2011.18813.x

CrossRef Full Text | Google Scholar

Balona, L. A. (2012). Kepler observations of flaring in A-F type stars. Mon. Notices R. Astron. Soc. 423, 3420–3429. doi: 10.1111/j.1365-2966.2012.21135.x

CrossRef Full Text | Google Scholar

Balona, L. A. (2013). Long periods in two Kepler roAp stars. Mon. Notices R. Astron. Soc. 436, 1415–1421. doi: 10.1093/mnras/stt1660

CrossRef Full Text | Google Scholar

Balona, L. A. (2018). Gaia luminosities of pulsating A-F stars in the Kepler field. Mon. Notices R. Astron. Soc. 479, 183–191. doi: 10.1093/mnras/sty1511

CrossRef Full Text | Google Scholar

Balona, L. A., and Abedigamba, O. P. (2016). Differential rotation in K, G, F and A stars. Mon. Notices R. Astron. Soc. 461, 497–506. doi: 10.1093/mnras/stw1443

CrossRef Full Text | Google Scholar

Balona, L. A., Baran, A. S., Daszyńska-Daszkiewicz, J., and De Cat, P. (2015a). Analysis of Kepler B stars: rotational modulation and Maia variables. Mon. Notices R. Astron. Soc., 451:1445–1459. doi: 10.1093/mnras/stv1513

CrossRef Full Text | Google Scholar

Balona, L. A., Cunha, M. S., Kurtz, D. W., Brandão, I. M., Gruberbauer, M., Saio, H., et al. (2011a). Kepler observations of rapidly oscillating Ap, δ Scuti and γ Doradus pulsations in Ap stars. Mon. Notices R. Astron. Soc., 410:517–524. doi: 10.1111/j.1365-2966.2010.17461.x

CrossRef Full Text | Google Scholar

Balona, L. A., Daszyńska-Daszkiewicz, J., and Pamyatnykh, A. A. (2015b). Pulsation frequency distribution in δ Scuti stars. Mon. Notices R. Astron. Soc. 452, 3073–3084. doi: 10.1093/mnras/stv1017

CrossRef Full Text | Google Scholar

Balona, L. A., and Dziembowski, W. A. (2011). Kepler observations of δ Scuti stars. Mon. Notices R. Astron. Soc. 417, 591–601. doi: 10.1111/j.1365-2966.2011.19301.x

CrossRef Full Text | Google Scholar

Balona, L. A., Engelbrecht, C. A., Joshi, Y. C., Joshi, S., Sharma, K., Semenko, E., et al. (2016). The hot γ Doradus and Maia stars. Mon. Notices R. Astron. Soc. 460, 1318–1327. doi: 10.1093/mnras/stw1038

CrossRef Full Text | Google Scholar

Balona, L. A., Guzik, J. A., Uytterhoeven, K., Smith, J. C., Tenenbaum, P., and Twicken, J. D. (2011b). The Kepler view of γ Doradus stars. Mon. Notices R. Astron. Soc. 415, 3531–3538. doi: 10.1111/j.1365-2966.2011.18973.x

CrossRef Full Text | Google Scholar

Bertelli, G., Girardi, L., Marigo, P., and Nasi, E. (2008). Scaled solar tracks and isochrones in a large region of the Z-Y plane. I. From the ZAMS to the TP-AGB end for 0.15-2.5 {M} _sun; stars. Astron. Astrophys. 484, 815–830. doi: 10.1051/0004-6361:20079165

CrossRef Full Text | Google Scholar

Brickhill, A. J. (1992). The pulsations of ZZ Ceti stars. V - The light curves. VI - The amplitude spectra. Mon. Notices R. Astron. Soc. 259, 519–535.

Google Scholar

Chaplin, W. J., Kjeldsen, H., Bedding, T. R., Christensen-Dalsgaard, J., Gilliland, R. L., Kawaler, S. D., et al. (2011). Predicting the detectability of oscillations in solar-type stars observed by kepler. Astrophys. J. 732:54. doi: 10.1088/0004-637X/732/1/54

CrossRef Full Text | Google Scholar

Cunha, M. S. (2002). A theoretical instability strip for rapidly oscillating Ap stars. Mon. Notices R. Astron. Soc. 333, 47–54. doi: 10.1046/j.1365-8711.2002.05377.x

CrossRef Full Text | Google Scholar

Cunha, M. S., Alentiev, D., Brandão, I. M., and Perraut, K. (2013). Testing excitation models of rapidly oscillating Ap stars with interferometry. Mon. Notices R. Astron. Soc. 436, 1639–1647. doi: 10.1093/mnras/stt1679

CrossRef Full Text | Google Scholar

Daszyńska-Daszkiewicz, J., Walczak, P., and Pamyatnykh, A. (2017). “On possible explanations of pulsations in Maia stars,” in TASC2 & KASC9 Workshop-SPACEINN & HELAS8 Conference, Vol. 160, eds M. J. P. F. G. Monteiro, M. S. Cunha, and J. M. T. S. Ferreira (EPJ Web of Conferences).

Google Scholar

Degroote, P., Aerts, C., Ollivier, M., Miglio, A., Debosscher, J., Cuypers, J., et al. (2009). CoRoT's view of newly discovered B-star pulsators: results for 358 candidate B pulsators from the initial run's exoplanet field data. Astron. Astrophys. 506, 471–489. doi: 10.1051/0004-6361/200911884

CrossRef Full Text | Google Scholar

Dupret, M., Grigahcène, A., Garrido, R., Gabriel, M., and Scuflaire, R. (2005a). Convection-pulsation coupling. II. Excitation and stabilization mechanisms in δ Sct and γ Dor stars. Astron. Astrophys. 435, 927–939. doi: 10.1051/0004-6361:20041817

CrossRef Full Text | Google Scholar

Dupret, M.-A., Grigahcène, A., Garrido, R., De Ridder, J., Scuflaire, R., and Gabriel, M. (2005b). Time-dependent convection seismic study of δ Sct stars. Mon. Notices R. Astron. Soc. 361, 476–486. doi: 10.1111/j.1365-2966.2005.09187.x

CrossRef Full Text | Google Scholar

Gaia Collaboration, Brown, A. G. A., Vallenari, A., Prusti, T., de Bruijne, J. H. J., Babusiaux, C., et al. (2018). Gaia Data Release 2. Summary of the contents and survey properties. ArXiv e-prints.

Google Scholar

Gaia Collaboration, Prusti, T., de Bruijne, J. H. J., Brown, A. G. A., Vallenari, A., Babusiaux, C., et al. (2016). The Gaia mission. Astron. Astrophys. 595:A1. doi: 10.1051/0004-6361/201629272

CrossRef Full Text | Google Scholar

Gautschy, A., Saio, H., and Harzenmoser, H. (1998). How to drive roAp stars. Mon. Notices R. Astron. Soc. 301, 31–41.

Google Scholar

Grigahcène, A., Antoci, V., Balona, L., Catanzaro, G., Daszyńska-Daszkiewicz, J., Guzik, J. A., et al. (2010). Hybrid γ Doradus-δ scuti pulsators: new insights into the physics of the oscillations from kepler observations. Astrophys. J. Lett. 713, L192–L197. doi: 10.1088/2041-8205/713/2/L192

CrossRef Full Text | Google Scholar

Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., and Neuforge, C. (2000). Driving the gravity-mode pulsations in γ doradus variables. Astrophys. J. Lett. 542, L57–L60. doi: 10.1086/312908

CrossRef Full Text | Google Scholar

Huber, D., Zinn, J., Bojsen-Hansen, M., Pinsonneault, M., Sahlholdt, C., Serenelli, A., et al. (2017). Asteroseismology and gaia: testing scaling relations using 2200 kepler stars with TGAS parallaxes. Astrophys. J. 844:102. doi: 10.3847/1538-4357/aa75ca

CrossRef Full Text | Google Scholar

Joshi, S., Martinez, P., Chowdhury, S., Chakradhari, N. K., Joshi, Y. C., van Heerden, et al. (2016). The Nainital-Cape Survey. IV. A search for pulsational variability in 108 chemically peculiar stars. Astron. Astrophys. 590:A116. doi: 10.1051/0004-6361/201527242

CrossRef Full Text | Google Scholar

Kallinger, T., Iliev, I., Lehmann, H., and Weiss, W. W. (2004). “The puzzling Maia candidate star α Draconis,” in The A-Star Puzzle, volume 224 of IAU Symposium, eds J. Zverko, J. Ziznovsky, S. J. Adelman, and W. W. Weiss (Poprad), 848–852.

Google Scholar

Kallinger, T., and Matthews, J. M. (2010). Evidence for granulation in early A-type stars. Astrophys. J. Lett., 711:L35–L39. doi: 10.1088/2041-8205/711/1/L35

CrossRef Full Text | Google Scholar

Kurtz, D. W. (1982). Rapidly oscillating AP stars. Mon. Notices R. Astron. Soc. 200, 807–859.

Google Scholar

Mowlavi, N., Barblan, F., Saesen, S., and Eyer, L. (2013). Stellar variability in open clusters. I. A new class of variable stars in NGC 3766. Astron.Astrophys. 554:A108. doi: 10.1051/0004-6361/201321065

CrossRef Full Text | Google Scholar

Mowlavi, N., Saesen, S., Semaan, T., Eggenberger, P., Barblan, F., Eyer, L., et al. (2016). Stellar variability in open clusters. II. Discovery of a new period-luminosity relation in a class of fast-rotating pulsating stars in NGC 3766. Astron.Astrophys. 595:L1. doi: 10.1051/0004-6361/201629175

CrossRef Full Text | Google Scholar

Nowakowski, R. M. (2005). Multimode resonant coupling in pulsating stars. Acta Astron. 55, 1–41.

Google Scholar

Papaloizou, J., and Pringle, J. E. (1978). Non-radial oscillations of rotating stars and their relevance to the short-period oscillations of cataclysmic variables. Mon. Notices R. Astron. Soc. 182, 423–442.

Google Scholar

Paunzen, E., Handler, G., Honkova, K., Jurysek, J., Masek, M., Drozdz, M., et al. (2018). The search for roAp stars: null results and new candidates from Stroemgren-Crawford photometry. ArXiv e-prints.

Google Scholar

Percy, J. R., and Wilson, J. B. (2000). Another Search for Maia Variable Stars. Publ. Astrono. Soc. Pac. 112, 846–851. doi: 10.1086/316577

CrossRef Full Text | Google Scholar

Saio, H. (2014). “Pulsation of magnetic stars,” in Precision Asteroseismology, volume 301 of IAU Symposium, eds J. A.Guzik, W. J. Chaplin, G. Handler, and A. Pigulski (Wroclaw), 197–204.

Google Scholar

Saio, H., Ekström, S., Mowlavi, N., Georgy, C., Saesen, S., Eggenberger, P., et al. (2017). Period-luminosity relations of fast-rotating B-type stars in the young open cluster NGC 3766. Mon. Notices R. Astron. Soc. 467, 3864–3873. doi: 10.1093/mnras/stx346

CrossRef Full Text | Google Scholar

Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., and Lee, U. (2018). Theory and evidence of global Rossby waves in upper main-sequence stars: r-mode oscillations in many Kepler stars. Mon. Notices R. Astron. Soc. 474, 2774–2786. doi: 10.1093/mnras/stx2962

CrossRef Full Text | Google Scholar

Salmon, S. J. A. J., Montalbán, J., Reese, D. R., Dupret, M.-A., and Eggenberger, P. (2014). The puzzling new class of variable stars in NGC 3766: old friend pulsators? Astron. Astrophys. 569:A18. doi: 10.1051/0004-6361/201323259

CrossRef Full Text | Google Scholar

Struve, O. (1955). Some unusual short-period variables. S&T 14:461.

Google Scholar

Struve, O., Sahade, J., Lynds, C. R., and Huang, S. S. (1957). On the spectrum and brightness of maia (20 C Tauri). Astrophys. J. 125:115.

Google Scholar

Xiong, D. R., Deng, L., and Zhang, C. (2015). Turbulent convection and pulsation stability of stars - I. Basic equations for calculations of stellar structure and oscillations. Mon. Notices R. Astron. Soc. 451, 3354–3365. doi: 10.1093/mnras/stv1170

CrossRef Full Text | Google Scholar

Xiong, D. R., Deng, L., Zhang, C., and Wang, K. (2016). Turbulent convection and pulsation stability of stars - II. Theoretical instability strip for δ Scuti and γ Doradus stars. Mon. Notices R. Astron. Soc. 457, 3163–3177. doi: 10.1093/mnras/stw047

CrossRef Full Text | Google Scholar