- 1ISAE-SUPAERO, Toulouse, France
- 2Dipartimento di Scienze e Tecnologie Aerospaziali (DAER), Politecnico di Milano, Milan, Italy
In the context of Human Spaceflight exploration mission scenario, with the Lunar Orbital Platform- Gateway (LOP-G) orbiting about Earth-Moon Lagrangian Point (EML), Rendezvous and Docking (RVD) operational activities are mandatory and critical for the deployment and utilization of the LOP-G (station assembly, crew rotations, cargo delivery, lunar sample return). There is extensive experience with RVD in the two-body problem: in Low Earth Orbit (LEO) to various space stations, or around quasi-circular Low Lunar Orbits (LLO), the latter by Apollo by means of manual RVD. However, the RVD problem in non-Keplerian environments has rarely been addressed and no RVD has been performed to this date in the vicinity of Lagrangian points (LP) where Keplerian dynamics are no longer applicable. Dynamics in such regions are more complex, but multi-body dynamics also come with strong advantages that need to be further researched by the work proposed here. The aim of this paper is to present methods and results of investigations conducted to first set up strategies for far and close rendezvous between a target (the LOP-G, for example) and a chaser (cargo, crew vehicle, ascent and descent vehicle, station modules, etc.) depending on target and chaser orbit. Semi-analytical tools have been developed to compute and model families of orbits about the Lagrangian points in the Circular Restricted Three Body Problem (CR3BP) like NRHO, DRO, Lyapunov, Halo and Lissajous orbits. As far as close rendezvous is concerned, implementation of different linear and non-linear models used to describe cis-lunar relative motion will be discussed and compared, in particular for NRHO and DRO.
Introduction
On the road to a solar system human exploration, the International Space Exploration Coordination Group (ISEGC) (ISECG, 2018) has identified several mission scenarios beyond Low Earth Orbit (LEO) as significant landmarks. In particular, it envisions to develop and operate with the collaboration of all main international space agencies a Lunar Orbital Platform—Gateway (LOP-G) as an outpost, located about one of the Earth-Moon Lagrangian points. This station will be used as a strategic platform and a logistic hub for human missions in cis-lunar space, including lunar surface and even beyond (Mars or asteroids destinations). Moreover, innovative technologies could be tested onboard, taking benefit from a unique environment. At this time, such an option is likely to rely on the NASA/ESA Orion MPCV (Multi-Purpose Crew Vehicle) and a heavy launcher, like the Space Launch System (SLS). Thus, Rendezvous and Docking (RVD) operational activities become mandatory and critical for the deployment and utilization of the LOP-G (like station assembly, crew rotations, cargo delivery, or lunar sample return). As the next space station will be a gateway for future exploration missions, various rendezvous missions may be performed, including logistics flight and crew transportation missions from the Low Earth Orbit (LEO), Geostationary (GEO) or LLO (Lunar Low Orbit), so as to reach NRHO (Near Rectilinear Halo Orbit), DRO (Distant Retrograde Orbit) or Halo Orbits. As the capacity to rendezvous in the vicinity of Earth-Moon Lagrangian Points is by nature necessary, its analysis becomes fundamental.
Despite a very extensive experience with RVD in the two-body problem (in Low Earth Orbit to various space stations, or around quasi circular Low Lunar Orbits, the latter by Apollo by means of manual RVD), the RVD problem in non-Keplerian environment has rarely been addressed and no RVD has yet been performed to this date in the vicinity of Lagrangian points where Keplerian dynamics are no longer applicable. As a consequence, researches presented in this paper contribute to a better understanding of potential mission scenarios to rendezvous in the vicinity of Earth-Moon Lagrangian Points.
This paper aims to study the rendezvous trajectories in the vicinity of the Earth-Moon Lagrangian points, EML1 or EML2. The Circular Restricted Three–Body Problem (CR3BP) has been highlighted among more complex models so as to describe the non-linear dynamics in this area. In the selected scenario, the target's orbit is assumed to belong to Halo orbits, NRHO or DRO families, with a fixed attitude. The chaser is supposed to be equipped with chemical propulsion. Considering only impulsive maneuvers, their effect is instantaneous and chaser's motion is ballistic between maneuvers. This paper addresses the feasibility of a rendezvous based on trajectories benefiting from natural dynamics and limiting fuel consumption. Once the feasibility has been demonstrated, an optimization process will be carried out in order to minimize rendezvous operations' duration and the consumption. This optimal scenario can be then used as a first guess to develop refined trajectories with intermediate maneuvers so as to correct the effects of orbit estimation's errors, of maneuvers inaccuracies and perturbations (gravitational influence of the other celestial bodies like the Sun, the Sun radiation pressure, etc.). In this paper, those effects are neglected.
After transfer from LEO, lunar surface or other distant locations (Mars, asteroids, etc.) and before docking activities, the rendezvous is decomposed in two main stages. On the one hand, far rendezvous and close rendezvous are analyzed independently from the theoretical point of view. On the other hand, for application purposes, a unique scenario will be presented for NRHO, with proposed extensions to other families of orbits, and in particular when the chaser and the target's orbit are of a different type. Moreover, when close rendezvous is concerned, the objective is to extend classical methods proven in the two-body problem to the three-body problem. The first contribution of this paper is to propose a far rendezvous strategy with the use of invariant structures extended by Lambert arcs to minimize the cost of the mission. A second contribution lies in the use of a non-linear model to describe the relative motion during close rendezvous stage. The third contribution corresponds to a preliminary safety analysis in case of a failure of the propulsion sub-system (either in direction or in magnitude).
After a summary of the bibliographical context and a description of the theoretical background, this paper will propose strategies for far and close rendezvous between a target and a chaser depending on both vehicles' initial orbits. In the case of the far rendezvous, a strategy in three maneuvers is presented, with the main objective of using the invariant structures derived from the natural dynamics in the vicinity of the Lagrange point. In the case of the close rendezvous, the algorithm used to compute the trajectory of the chaser to the target is detailed in two steps: a first guess, where the relative motion between the chaser and the target is linearized, then a more precise computation of the trajectory arcs with a non-linearized relative motion. The last paragraph depicts two specific scenarios where the chaser and the target are in orbits (from the same family) around the EML2. The selected examples mainly concern the Halo and NRHO orbits. They are chaining the far rendezvous and the close rendezvous, before analyzing the safety aspects.
Historical Overview of the Bibliographical Context
A growing interest of the space scientific community for trajectories toward, around and from Lagrangian points has been registered in recent years. In particular, the three-body problem (Szebehely, 1967) is one of the most studied models not only in celestial mechanics, but also in mathematics. For the early first solar system exploration missions (like Voyager), a patched conics model was satisfactory to compute the trajectory. As interplanetary missions became more demanding (as far as fuel consumption or accuracy are concerned), this strategy connecting several two body-problems was applied as a first design approximation. Thus, other strategies (like three body-problem and more) can be preferred. Moreover, some science space missions take advantage of particular properties of the Lagrangian points. In recent decades, many theoretical studies have demonstrated the benefits of highly non-linear dynamics to space exploration missions.
When looking at the set of studies performed in the field of Lunar Libration Points, one stumbles upon the fathers and main advocates of utilization concepts for these points repeatedly. Lagrangian points are defined as equilibrium points in the rotating referential of the studied system. R. Farquhar published the first papers on the utilization of co-linear EMLs in the late sixties and early seventies, including the application for communication relay satellites (Farquhar, 1967), inhabited space stations in a Halo orbit around EML2 (Farquhar, 1972) and moreover, on the utility of Lagrangian Points (LPs) for human solar system exploration (Farquhar et al., 2004)
Beyond the study of utilization of the Lagrangian Points location, the interest in these models focuses on the emergence of invariant structures, such as periodic or quasi-periodic orbits (Farquhar, 1973; Richardson, 1980; Howell, 1984) and their related stable and unstable manifolds (Gómez et al., 2001, 2004; Koon et al., 2001). These invariant structures make it possible first to design staging orbits in the vicinity of the Lagrangian points, then to establish low-energy trajectories for transfer between the Earth, the Moon and the Lagrangian points. This paved the way for mission's concepts taking benefit of these invariant structures so as to minimize fuel consumption through various strategies like Indirect transfer (Alessi et al., 2010), Weak Stability Boundary (Belbruno and Carrico, 2000; Belbruno, 2002) or Lunar flyby (Mingtao and Zheng, 2010), for Earth-to-EML2 (Parker and Anderson, 2013) or Earth-to-Moon tranfers (Mingotti et al., 2012).
Despite this vast literature on orbits about the Lagrangian points and transfers in the cis-lunar realm, the scientific community has, at the moment, very few relevant researches on rendezvous trajectories in non-keplerian dynamics. Actually, a large amount of publications from 1950s to today dealing with rendezvous can be found. But the typical rendezvous problem considers that both vehicles are in orbit about a massive celestial body (Earth, Moon, Mars…) and lies only in the two-body problem. Even though rendezvous is a critical phase, it has rarely been studied in the context of the non-keplerian dynamics except by Gerding (1971) in 1971, Jones and Bishop (1994) in 1993 and 1994 and by Canalias (Canalias and Masdemont, 2006) in 2006. Nevertheless, a recent emergence of some sparse publications can be observed since 1993, with a growing interest after 2015 that can be explained by the studies related to LOP-G and Orion missions (Davis et al., 2017; Williams et al., 2017). Two main periods can be noticed: first scenario with the target on Halo orbit around EML2, second scenario with the target on NRHO or a DRO around EML1/2. During the first period, Mand (2014) expressed linearized relative motion of the chaser compared to the target on a Halo orbit around the EML2 within an ephemeris model. Afterwards Ueda and Murakami (Murakami et al., 2015; Ueda and Murakami, 2015) presented a global scenario with a departure from LEO, a transfer in cis-lunar realm, a lunar flyby, an insertion on the target's Halo orbit around EML2, close rendezvous and proximity operations, within ephemeris model for transfer and CR3BP in the vicinity of EML2. This scenario is limited to a unique case with a given Halo orbit of the target, with a fixed attitude and only one insertion point for the chaser (best compromise between fuel consumption and time of flight). Meanwhile, Lizy-Destrez (2015) proposed a different strategy with three burns, relying on invariant structures in the CR3BP to transfer the chaser from a Halo parking orbit to the target's parking orbit. This approach is detailed in section Far Rendezvous Strategy. A parametric analysis was conducted to evaluate the impact of the chaser's departure location, of the position of the intermediate maneuver and of the insertion location on the target's Halo orbit on the rendezvous performances (duration, time of flight). Colagrossi (Colagrossi et al., 2016) extended the theme to rendezvous with very large infrastructures, including coupling effects between orbital and attitude motion. A second period took place after recent publications from NASA (Whitley and Martinez, 2016; Davis et al., 2017; Williams et al., 2017), that confirmed the attractiveness of less classical families of orbits, like DRO and NRHO. In 2015, Murakami (Murakami and Yamanaka, 2015) introduced transfer trajectories from LEO to DRO with three-impulsive maneuvers, one of which is a lunar flyby. In 2017, Ueda (Ueda et al., 2017) evaluates the guidance performance of a linearized relative motion on Halo orbits, a NRHO or a DRO. In 2017, Campolo (Campolo et al., 2017) presented a general close approach rendezvous strategy designed to ensure safety throughout during all rendezvous stages in the NRHO about EML2 case.
Thanks to this analysis of the bibliographic context, it can be observed that the theme of the transfer trajectories in the Earth-Moon system has been largely covered, that the theme of the rendezvous strategies is booming and that the theme of the safety begins slowly.
Theoretical Problem Overview
The mathematical model selected here to represent the dynamical environment is the Circular Restricted Three-Body Problem, as it produces quick and efficiently quantitative results for transfers between primaries and libration orbits. As this model has been deeply detailed in many publications, this paper mainly refers to Parker and Chua (2012), which proposes a complete synthesis.
Circular Restricted Three-Body Problem
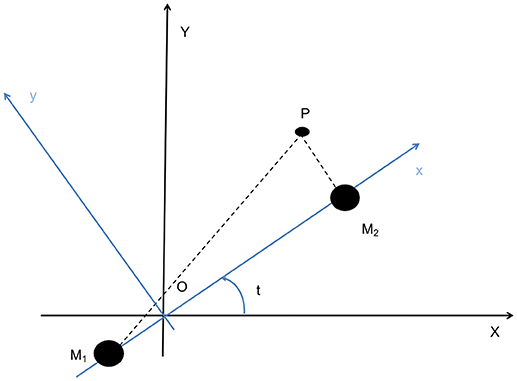
The 3-body problem consists in the prediction of the motion of a particle of mass m under the gravitational influence of two massive bodies with respective masses (m1 and m2), with m << m2 < m1. The three bodies are assumed to be isolated, that is to say that no other effect has to be taken into account. Considering that the particle is massless, the problem is said to be “Restricted.” The model becomes the Circular Restricted Three-Body Problem (CR3BP) when the primaries are supposed to be on circular orbits about their common center of mass. The equations of motion of the particle are described in the rotating reference synodic frame, centered on O, the center of mass of the system M1-M2 and with the x-axis directed from M1 (the larger primary) to M2 (the smaller primary) and the y-axis in the plane of the primaries' motion (see Figure 1), the z-axis completes the right hand system.
Masses, distances and time are normalized respectively with the sum of the primaries' masses, the distance between them and their angular velocity around their barycenter. The unit of time is taken such that the period of the orbits of the primaries is 2π. The universal constant of gravitation, G, becomes then G = 1. The only remaining parameter in the system of equations is the mass parameter, μ, defined as where .
When the position vector of the particle is given by r = (x, y, z), its equations of motion in the CR3BP (Koon et al., 2001), using Newton's law are:
where the effective potential, is given by:
where and are the distances from the particle to M1 and M2 primaries.
The dot (.) denotes the time first derivative (velocity) and the double dot (..) denotes the time second derivative (acceleration). The state of the particle is given by: X = (x, y, z, ẋ, ẏ, ż). The equations of motion (1) can be written as:
From the equation of motion (3), let's denote, Φ, the flow map of the system, mapping the position of the particle from its initial location at time, t0 to its location at time, t, with under initial conditions X0: Φ(t, t0, X0) : X(t0) → X(t) ∀ t ≥ t0 with Φ(t0, t0, X(t0)) = X0.
Lagrangian Points and Families of Orbits in the CR3BP
The system (1) has five equilibrium points, referred to as Libration or Lagrangian points, Li, i = 1…5 or EMLi in the Earth-Moon system. The collinear points L1, L2, and L3 are on the line connecting the two primaries, while L4 and L5 are equilateral points. In this paper, the distance from Li, to the smallest primary, is named γi (Szebehely, 1967). According to the literature (Szebehely, 1967; Farquhar, 1972, 1973; Whitley and Martinez, 2016), several families of orbits around them exist, usually designated as: Lissajous orbits, Horizontal Lyapunov orbits, Vertical Lyapunov orbits, Halo orbits (including Near Rectilinear Halo Orbits) or Distant Retrograde Orbits. This paper mainly focuses on Halo orbits, which are three-dimensional and periodic with the same in- and out-of-plane oscillation and NRHO, which are particular case of Halo orbits, with a close passage over a lunar pole. Moving inside the family toward the Moon, the Halo orbits become more and more rectilinear as the lunar gravitational influence becomes highly predominant. Some studied cases refer to Horizontal Lyapunov orbits, which lays in the orbital plane of the primaries (xy-plane), to Vertical Lyapunov (or eight-shaped) orbits, which are three-dimensional, almost vertical and periodic orbits. Some scenarios are also applied on DRO, which are very stable solutions, encircling the Moon in a clockwise way in the Earth-Moon rotating frame.
Figure 2 depicts some examples of periodic orbits about EML2, obtained from an expansion of the linearized equations of motions in the CR3BP with Legendre polynomials, as a first guess for the Lindstedt-Poincaré method (Parker and Chua, 2012). Plots on Figure 2 correspond to (A) Lissajous trajectory with Ay = Az = 3,500 km, (B) Halo trajectory Az = 5,000 km, (C) Eight shape Lissajous trajectory with Ay = Az = 3,500 km and (D) Horizontal Lyapunov trajectory with Ay = 3,500 km.
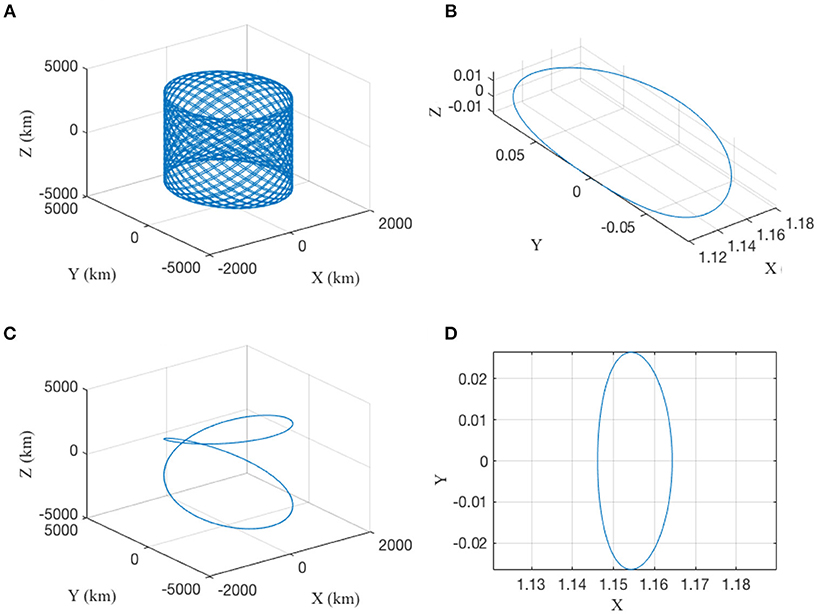
Figure 2. Examples of periodic orbits around EML2. (A) Lissajous trajectory with Ay = Az = 3,500 km, (B) Halo trajectory Az = 5,000 km, (C) Eight shape Lissajous trajectory with Ay = Az = 3,500 km and (D) Horizontal Lyapunov trajectory with Ay = 3,500 km.
From (Canalias, 2007), the system (1) of equations of motion of the particle can be linearized in the vicinity of the studied Lagrangian point with the Legendre polynomial. Under those conditions, the solutions of the linearized system can be expressed as:
where A1, A2, Ax, Az, ϕ, and ψ depend on the initial condition (±λ, ±iωp, ±iωv,) are the eigenvalues of the characteristic equation of the system (1) and c, κ depend exclusively on the mass parameter μ and the Libration point that is studied (in our case EML2). Solutions with A1 and A2 equal to zero correspond to periodic orbits, with an amplitude Ax and a phase φ in xy-plane and an amplitude Az and a phase ψ in z direction.
A differential correction scheme is deployed to compute the orbits, with a high order analytical approximation as first guess (Howell, 1984). The method used for the first guess depends on the orbit family studied.
Invariant Manifolds
The concept of unstable and stable manifold is exploited to determine transfers from the orbits about the primaries to the vicinity of the Lagrangian points as well as periodic solutions.
For a given orbit, the stable (resp. unstable) invariant manifold is defined as the sub-space of the 6-dimensional phase space consisting of all vectors whose future (resp. past) positions converge to the periodic orbit. The corresponding trajectories in the vicinity of the orbit are often called asymptotic orbits since they slowly converge to or diverge from the orbit. As the equations of motion are Hamiltonian, the system has an energy integral of motion. Its expression is given by
From the expression of the solutions of the linearized system of Equations (4), it can be concluded that a small variation of the trajectory can put the spacecraft on the unstable manifold A1 and correspond to the hyperbolic amplitudes of the solution, with A1 for the unstable component and A2 for the stable one. This concept is then used to compute trajectories that converge toward the orbit around the Lagrangian point (stable manifold) and departs from the orbit (unstable manifold). Actually, the stable manifold will converge to the desired orbit, while the unstable manifold will exit the region of the Lagrangian point.
The invariant manifolds are often referred as “tubes“ since they exhibit tube-like shapes when projected onto the 3-dimensional position space.
For any given state X = (x, y, z, ẋ, ẏ, ż), on the aforementioned given periodic orbit, the invariant stable (resp. unstable) manifold can be computed thank to a linear approximation, while considering a small perturbation ε applied to X which becomes Xs (resp. Xu) and propagating the equations of motion backward (resp. forward) from Xs (resp. Xu), with:
- For the stable manifold Ws: Xs =X ± εvs
- For the unstable manifold Wu: Xu =X ± εvu
where vs and vu are eigenvectors associated to the real eigenvalues of the monodromy matrix of the closed trajectory. vu corresponds to the eigenvalue > 1 and vs to the eigenvalue smaller than one.
As the small perturbation, ε, can be positive or negative, two stable (resp. unstable) manifolds can be obtained, which are denominated, respectively interior and exterior. The manifold is generated from a starting point, selected at a distance dM in the stable or unstable direction provided by the eigenvector. For this study, dM is set to 50 km (Gómez et al., 2001).
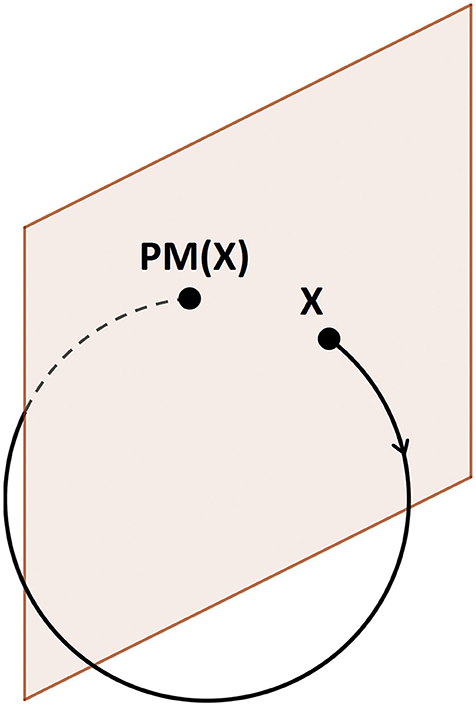
In order to decide when to stop the propagation of the manifold branches, a Poincaré map (recorded as PΣp) is used. Considering Φ(t, t0, X(t0)), the trajectory representing one solution of the system with X0 as initial conditions and Σp, a hypersurface, the Poincaré map, PΣp, is defined as the set of points of the trajectory, Φ(t, t0, X(t0)) when it intersects the hypersurface, Σp with:
Figure 3 provides a schematic representation of the use of a Poincaré Map.
Manifolds Connection
Given an initial orbit and a final orbit, denoted by ψi and ψf, respectively. Intersections between the unstable manifold of the initial orbit and the stable manifold of the final orbit is defined as the set
Intersections in 6-D space of the manifolds are called free intersections and provide an asymptotic path from one periodic solution to another one (Parker and Chua, 2012). However, such connections require stringent conditions on the initial and final orbits, for example, they must be of the same energy level (5). For the purpose of this study, only physical intersections (x,y,z) between the manifolds will be sought for. While intersections can happen at any point of space, the search space will be restricted on a Poincaré map to reduce the computational burden.
Rendezvous
This paper focuses on rendezvous problematic in the vicinity of EML2, as it constitutes one of the most critical sets of operations during a Human spaceflight mission scenario.
Rendezvous Concepts Definition
Houbolt (1960) defines the rendezvous as:
”The problem of rendezvous in space, involving, for example, the ascent of a satellite or space ferry as to make a soft contact with another satellite or space station already in orbit.“
The space vehicle that is already in orbit is commonly called the target, while the one that is arriving, is named the chaser. Rendezvous then consists in all maneuvers and trajectories performed by both vehicles to get nearer and nearer before contact. The different phases and maneuvers of a typical rendezvous mission from launch to docking have been extensively studied from the Apollo missions to the International Space Station (ISS) resupply missions. They are mostly named: launch, transfer, orbital injection, phasing, and proximity maneuvers (including homing, closing and final approach). Rendezvous can be followed by either docking or berthing, depending on the nature of the chaser. Rendezvous operations considered in this study will start from the departure of the chaser from its parking orbit to the injection maneuver onto the target orbit in the vicinity of the Lagrangian point. As an extension of successful rendezvous operations performed in Low Earth Orbit, it is possible to identify three successive phases in a rendezvous scenario: transfer phase, far rendezvous and close rendezvous.
Far Rendezvous Strategy
Two different scenarios can be identified depending on the chaser injection. The chaser can either travel on its transfer trajectory from the Earth to the target orbit or can be injected on a parking orbit about the Lagrangian point. It is not necessary that the chaser's parking orbit belong to the same families as target's orbit. In the second case, the chaser will wait there until far approach operational activities start. Considering the launch and transfer uncertainties inherent to the first scenario, the paper focuses on scenarios including the use of a parking orbit. Four phases are considered: parking orbit, far approach, insertion on the target's orbit and close rendezvous operations. Both chaser and target are assumed to be traveling on two different closed orbits about the L2 libration point, which admit stable and unstable manifolds.
The far approach strategy proposed in this paper takes advantage of the natural dynamics of the system and follows two steps. A 3-maneuver scenario is considered first. The chaser performs a first maneuver (Δv1) to leave its parking orbit and to travel on the unstable manifold. It will then perform a second maneuver (Δv2) to leave the unstable manifold so as to reach the stable manifold of the target orbit. Finally, arriving near the target, it will perform a third maneuver (Δv3) to leave the manifold and enter the target parking orbit. As mentioned previously, finding exact intersections between manifolds is difficult and resource-consuming, a distance gap between the stable and unstable manifold at the intersection exists in this scenario. The second and final step is to use the 3-burns trajectory as a first guess for a 4-burns trajectory design with a lambert arc connecting the extremities of both manifolds. Figure 4 presents an example of the methodology used in this work for a Halo-to-Halo rendezvous about EML2 (target and chaser amplitudes km and km, respectively). On the upper hand (A), the 3-maneuvers strategy is presented, while on the lower hand (B), the connection between the manifolds is depicted for the 4-maneuvers refinement: the two burns (Δv21) and (Δv22) replace the single burn (Δv2) of the 3-maneuvers scenario.
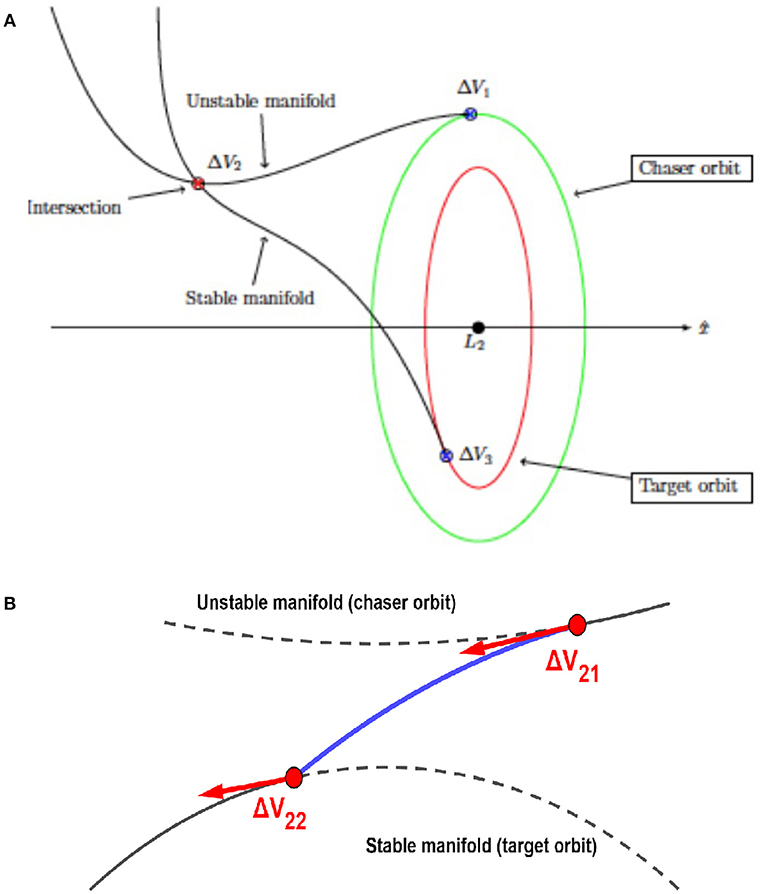
Figure 4. Example of a 3-maneuvers scenario for Halo-to-Halo far rendezvous. (A) 3-maneuvers, manifold-to-manifold far rendezvous scenario, (B) 4-maneuvers trajectory refinement: Lambert's arc.
3-Maneuvers Scenario
The total Δv for the 3-maneuvers scenario is, as defined previously:
The main challenge of this study case is to find the right location and best moment to perform the intermediate maneuver (Δv2), to compute a trajectory that resembles a free connection. This leads to finding a compromise between the time of flight (duration of the transfer) and the cost (quantified by the total Δv).
Assuming that the chaser leaves its parking orbit at time, t1, reaches the intersection between both manifolds at time, t2, and is inserted in the target parking orbit at time, t3, the rendezvous trajectory of the chaser is split into three arcs:
• From t1 to t2, the chaser travels on the unstable manifold of the chaser parking orbit, after the first maneuver (Δv1)
• At t2 the second burn (Δv2), the chaser leaves and gets into the stable manifold of the target parking orbit, .
• From t2 to t3, the chaser travels on before the last maneuver (Δv3).
As mentioned previously, only physical intersections between manifolds in the (x,y,z) subspace are sought. The resulting gap in the velocity subspace will provide the intermediate required burn, (Δv2). Writing the position vector on the unstable manifold issued from the chaser parking orbit and the position vector on the stable manifold issued from the target parking orbit, the rendezvous problem can be stated as:
- t ∈ [t1; t2[, with
- at t = t2,
- ∀t ∈ [t2; t3], with
Solving the problem is equivalent to finding the three unknown variables, (t1, t2, t3) that satisfy system (9). This is equivalent to finding three others variables , where defines the angular parameter of the chaser on its parking orbit at time t1 (defined as an angular fraction of the period of the orbit), defines as well the angular parameter of the chaser on the target orbit at time t3. With this parameterization, the NRHO aposelene corresponds to θ = π, while the periselene corresponds to θ = 0. φPM is the angle defining the Poincaré map, used to determine the location of spatial intersections of the two manifolds. The manifold propagation stops at its spatial intersection with the plane defined, by the angle φPM.
Figure 5 depicts examples of possible connections between stable (blue) and unstable (purple) manifolds for part (A) with EML2 Southern Halo orbit (with for the chaser, in purple = 8,000 km and = 10,000 km) and for part (B), with EML2 northern NRHO (with for the chaser, in purple = 70,000 km and = 74,960 km). φPM is set equal to 2° for Halo orbits and 3° for NRHO.
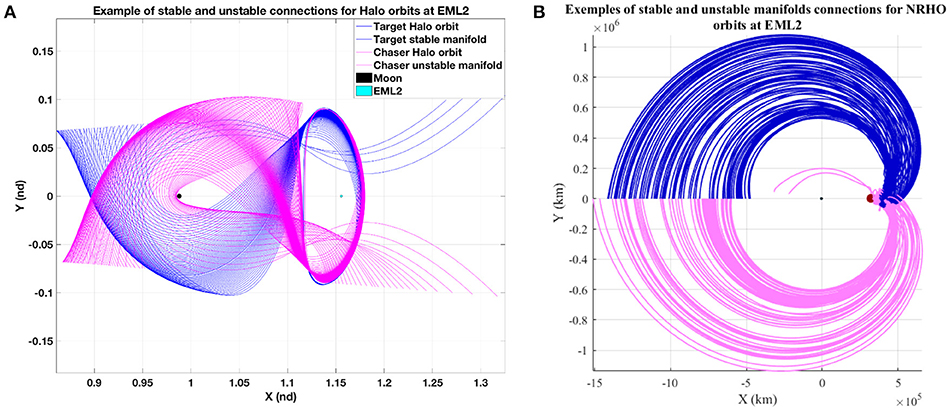
Figure 5. Example of stable and unstable manifolds connections for EML2 Halo orbits and NRHO. (A) stable and unstable manifolds originated from Halo Southern orbits (with 8,000 km in purple and = 10,000 km in blue) (B) stable and unstable manifolds originated from Northern NRHO (with = 70,000 km and = 74,960 km).
The selected Poincaré map is a plane perpendicular to the xy-plane, forming an angle φPM with the x-axis from EMLi, where i = 1 or 2 depending on the considered Lagrangian point. As a summary:
- is determined by at t = t1,
- is determined by at t = t3,
-
As the problem cannot be solved analytically, the following numerical methodology is applied:
- Generating the target orbit and the chaser parking orbit.
- Propagating the stable manifold, issued from each angular location θTon the target orbit until the Poincaré map, PM .
- Propagating the unstable manifold, , from each angular location θC on the chaser parking orbit until the Poincaré map, PM.
- Computing for each pair , the distance gap, ΔX, and the velocity gap, Δv2.
The integration of the equations of motion must be performed using a numerical solver. This work relies on Runge-Kutta propagators, ODE45 (or even ODE113), implemented in Matlab. The solver implies that all components (time and state) have been discretized. As a consequence, the concept of exact intersection in the spatial sub-space is replaced by the minimization of the distance between the positions on both manifolds at the Poincaré map location.
To select the best candidate, the following optimization process has been applied, so as to:
- Find a compromise between cost (total ΔV) and duration (time of flight, ΔT).
- Ensure feasibility (distance gap, ΔX), that is to say, to define numerically the acceptable distance between the two manifolds at the intersection.
The problem to be optimized is:
||.|| denotes the quadratic norm: ||ΔX|| refers to the gap in position between the position of the chaser on the unstable manifold and the position of the chaser on the stable manifold, at the intersection, ||ΔV2|| refers to the gap in velocity between the position of the chaser on the unstable manifold and the velocity of the chaser on the stable manifold, at the intersection and d = 50 km is the maximum distance allowed between the two spacecrafts at the Poincaré section.
4-Maneuvers Trajectory Refinement
Results from the 3-maneuvers strategy are used as an initial guess, feeding a local optimization process based on the variation the time of flight in both the unstable and stable manifold. The connection between the manifolds is not considered as a simple discontinuity in the state space anymore but is “patched” by means of a Lambert's arc computed in the CR3BP. In this scenario, the PM intersection constraint at the manifold end points is relaxed.
The cost function of the new optimization problem, using the terminology presented in the introduction of section Far Rendezvous Strategy, is:
The outputs of this process are the new positions of the end points of both manifolds, the total ||ΔV|| and the time of flight required to perform the transfer between both manifolds. An entire continuous trajectory can then be built, for the chaser to rendezvous the target, starting from its parking orbit, passing by an unstable manifold, Lambert arc and stable manifold and finishing on the target parking orbit. The far rendezvous strategy now includes an additional trajectory arc that connects properly the unstable and stable manifolds.
Figure 6 provides an example of the procedure detailed in this section. The study case is between two Halo orbits of the Southern family about EML2, with an elongation of 8,000 km for the target orbit and 7,800 km for the chaser parking orbit The chaser transfer trajectory from its parking orbit to the chaser orbit is plotted in bold dark blue solid line. The chaser initial angular location is and the target final location is Performances are obtained for φPM = 4.46. Figure 6A shows the result of the 3-burn strategy as an initial guess, and Figure 6B showcases the continuation of the solution and relaxation of the ToF constraint. The total velocity increment in that particular case is 0.374 .s−1 km with a Lambert's time of flight of ~ 1.39 h.
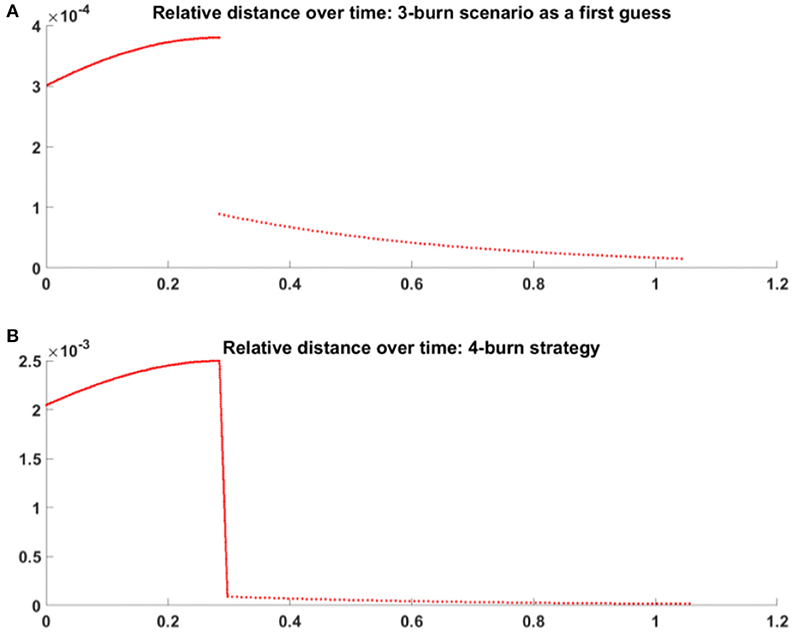
Figure 6. Example of Halo-to-Halo far rendezvous, 7,800 km, 8,000 km, , , φPM=4.46. (A) Relative distance between chaser and target over time, 3-burn strategy as a first guess, adimensional units, (B) Relative distance between chaser and target over time, 4-burn continuation, adimensional units.
Close Rendezvous Strategy
The main goal of the close rendezvous phase is to conduct gradually the chaser from its insertion location closer to the target so as to allow berthing or docking operations. This time, unlike for the far rendezvous phase, chaser and target are traveling on the same trajectory, but with a gap in position. For safety considerations, the close rendezvous trajectory is split into several legs, delimited by hold points (HP), as security checkpoints. In this phase, maneuvers are considered impulsive, performed instantaneously at the HPs and the motion on the arcs is ballistic. The proposed strategy is based firstly on the selection of breakpoints, then on the calculation of the arc-by-arc trajectory from the equations of motion. Finally, safety aspects are discussed. Actually, trajectory design must take into account an assortment of random errors acquired while in orbit, such as the initial condition dispersions or inaccurate thrust velocities. Free drift motion may occur if the thrusters of the chaser cease to operate. This phenomenon has been simulated while assuming dispersion on maneuver. Safety analyses must verify that the selected trajectory of the chaser will not enter the safety region, in case of a missed maneuver, so as to avoid collision with the target in case of failure.
Hold-on Points Determination
In close rendezvous scenarii, the HP are significant locations on chaser's trajectories where to perform maneuvers after security checks (missions parameters, chaser health status), as the chaser is not permitted to approach freely the target. In case of failure, braking may become impossible and the failure could jeopardize the mission. The chaser must thus follow a precise path, meeting all the hold points. Similarly to Mand (2014), two geometrical strategies are proposed to define their positions: line-of-sight corridor (LoS-C) and line-of-sight glide (LoS-G). With them, the chaser is always approaching the target along its docking port direction within the field of view of its rendezvous sensors modeled by a cone. The target attitude is not taken into account, as its attitude is assumed to be perfect. The implemented strategies are:
- LoS-C, characterized by three angles: two trigger angles (α, β) and an offset angle, φ as ϕ < α and ϕ < β. Each time the chaser's trajectory (assumed to be locally rectilinear) intersects one side of the cone, a maneuver is performed to reorient the chaser inside the field of view. Hold points are then located at this intersection.
- LoS-G, characterized by two angles: one trigger angle α and one offset angle ϕ as ϕ < α. Within LoS-G, the chaser does not cross the line of sight as in LoS-C, but remains on the same side of the cone.
Figure 7 represents both strategies, with a definition of the angles, in the LVLH (Local-Vertical/Local-Horizontal) reference frame, defined in section Clohessy-Wiltshire Equations.
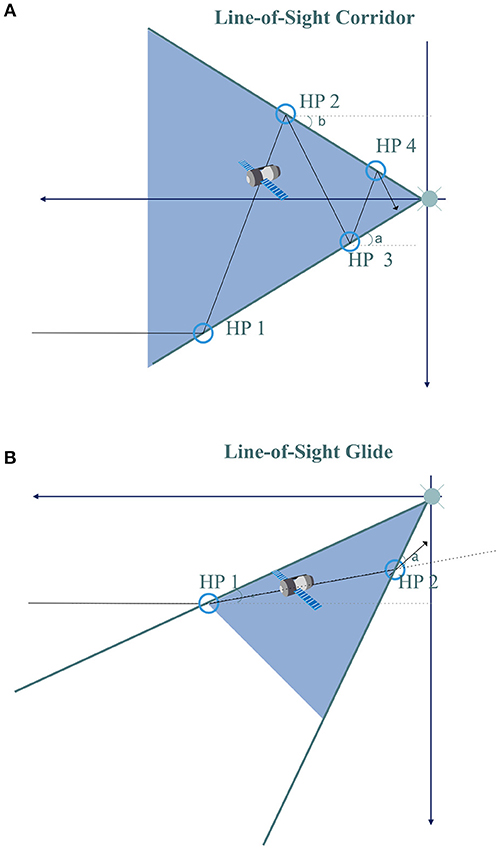
Figure 7. Line of Sight Corridor and Line of sight Glide scenario strategies in the LVLH. (A) Line of Sight Corridor, (B) Line of sight Glide.
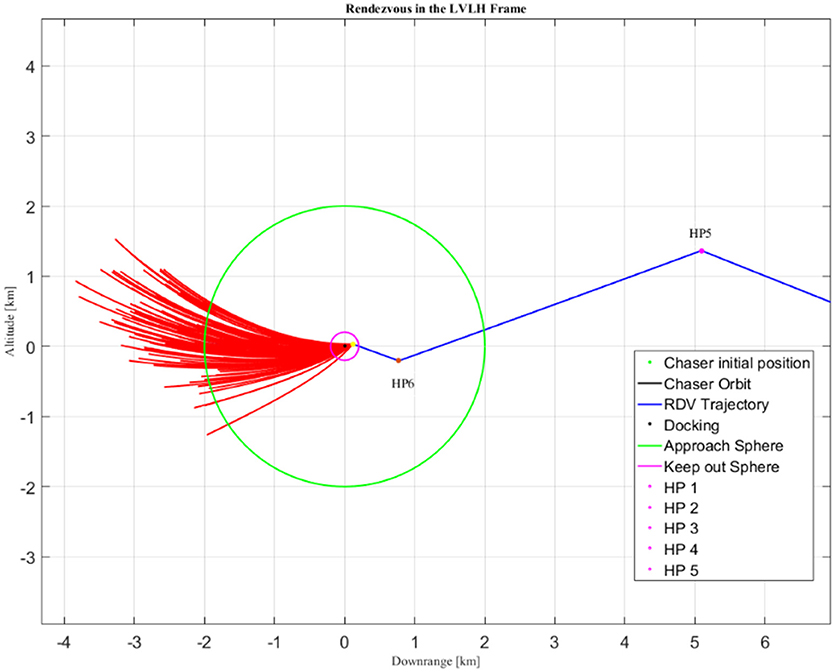
The process outputs the number of required hold points. In addition to HP, two safety regions are defined around the target, as an extension of concepts developed in Keplerian dynamic (mainly in LEO). They are identified as two spheres: the Approach Sphere (AS) and the Keep Out Sphere (KOS), both centered on the target.
Trajectory Arcs Computation
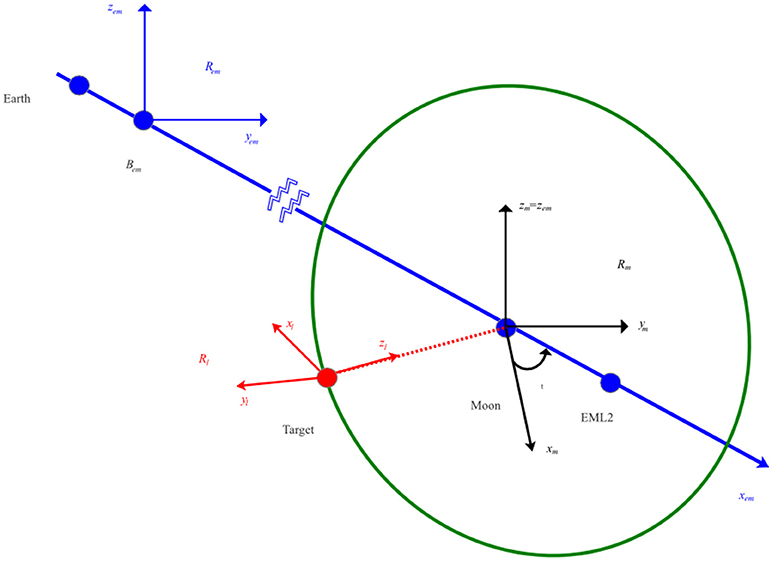
Dealing with close rendezvous means an analytic description of the relative motion of the chaser according to the target, referring to two relative reference frames and one inertial frame, presented on Figure 8.
In blue, the Earth-Moon synodic reference frame is a rotating frame centered on the center of gravity of Earth-Moon system, with Moon and Earth fixed on the x-axis. The z-axis is orthogonal to the plane of motion of the celestial bodies. The y-axis completes the right-hand rule. In black, the Moon-Centered inertial (MCI) frame is defined such that the origin is at the center of the Moon. An Earth-Centered inertial (ECI) reference frame could also have been selected. x-axis and y-axis are selected so as to overlap at initial conditions. In red, the LVLH reference frame is presented.
The equations of motion of both vehicles and their relative motions are described in the CR3BP in (Mand, 2014) and (Campolo et al., 2017). Their expression leads to a complete set of non-dimensional non-linear relative equations. As the distance between chaser and target is very low compared to the dimensions of the system (for example, distance between the two primaries), the expression of the relative motion can be linearized to simplify the problem, as a first approximation.
The expression of the simplified equations of the relative motion will all be presented in a state-space form as where i denominates the selected simplified method. Three models are compared: Linearized Relative (LR), Clohessy—Wiltshire (C–W), and Straight-Line (SL).
Since the matrix A is time-dependent, the trick consists in dividing each transfer in smaller arcs, where A can be considered as constant. The approach to compute the trajectory arc between two HP corresponds to solving arc-by-arc small Lambert problems. It lies in finding a trajectory between an initial and final position given a specific time of flight, (ΔT). For each arc, the time of flight is fixed and the HP provide initial and final points.
The algorithm is divided into two steps:
- Linear targeting: computation of the maneuver ΔvHPi_linear first guess
- Shooting method: computation of final ΔvHPi to be performed by the chaser with ΔvHPi_linear as a first guess. The shooting algorithm cycles with a full non-linear relative model in CR3BP until the final position error is considered acceptable.
For certain families of orbits (above all for NRHO), the accuracy of linear models depends on the orbital regions where the computation is performed. As a consequence, the first section compares the three methods to estimate the error introduced by the three relative linear models with respect to the non-linear model and consequently, to assess their ability to accurately model the dynamics during close rendezvous operations. For each arc of the trajectory, an approximation of the solution of the system is computed numerically with the three previously linearized methods. The linear method that presents the lowest error in terms of final position (distance from the target) is then selected to perform the second step. This two-steps algorithm is an iterative process to compute the entire close rendezvous trajectory of the chaser.
Non-linear relative equations
The non-dimensional non-linear relative equations of motion written in the synodic reference frame can be obtained by the difference of the absolute equations of motion (2) of the chaser and the target, respectively, in the CR3BP:
where the relative state is , the absolute state of the target is given by , the absolute state of the chaser is given by . The position vector of the target to M1 is , the position of the target to M2 is and the relative position is ρ=(xr, yr, zr).
The absolute distances of the target from M1 and M2 are respectively:
Linearized relative equations
The Linearized Relative equations can be adapted from formation flight studies (Luquette, 2006), while linearizing the dynamics about the target as a reference vehicle, taking into account a canonical CR3BP synodic frame. From (12), assuming that „ and applying a second order Taylor expansion (1 + ε)−3 ≈ 1 − 3ε + o(ε) to linearize relative equations of motion in the synodical frame:
where
with the transpose vector of and the transpose vector of , ,
Clohessy—wiltshire equations
The Clohessy-Wiltshire equations (Clohessy and Wiltshire, 1960) describe relative motion in a 2-Body environment. This model assumes only one primary mass, the target's orbit is circular and that the relative distance between target and chaser is small with respect to target-attractor distance. These assumptions are not usually valid in the CR3BP, and can only be applied locally to generate a first guess. The model is given in the local-vertical/local-horizontal (LVLH) reference frame of the primary M2, centered on the center of gravity of the target. The x-axis points along the direction of the velocity of the target. The z-axis points the direction from the target to M2. The y-axis is mutually perpendicular to the x- and z-axes so as to form a right-handed coordinate frame. An example of LVLH is given in red on Figure 8 for motion description of an NRHO in cis-lunar space. The Earth-Moon synodical reference frame Rem is represented in blue, while, the Moon-Centered Inertial (MCI) frame Rm is in black.
The C-W equations, written in the LVLH reference frame are:
Where n represents the mean angular motion of the M2-centered keplerian circular orbit with a radius of and is given by .
The C-W equations can also be written in state-space representation:
where and
Straight line equations
In the Straight-Line approach, the velocity vector of the chaser points to the target at time, ti, after a maneuver Δvi, disregarding any gravitational effect. The expression of Δvi in the LVLH reference frame is, during the period of time Δti = ti+1 − ti
Where ri and vi indicate the initial position and velocity at time, ti, and ri+1 the final position at time, ti+1. The state-space representation of the system is:
Studied Cases
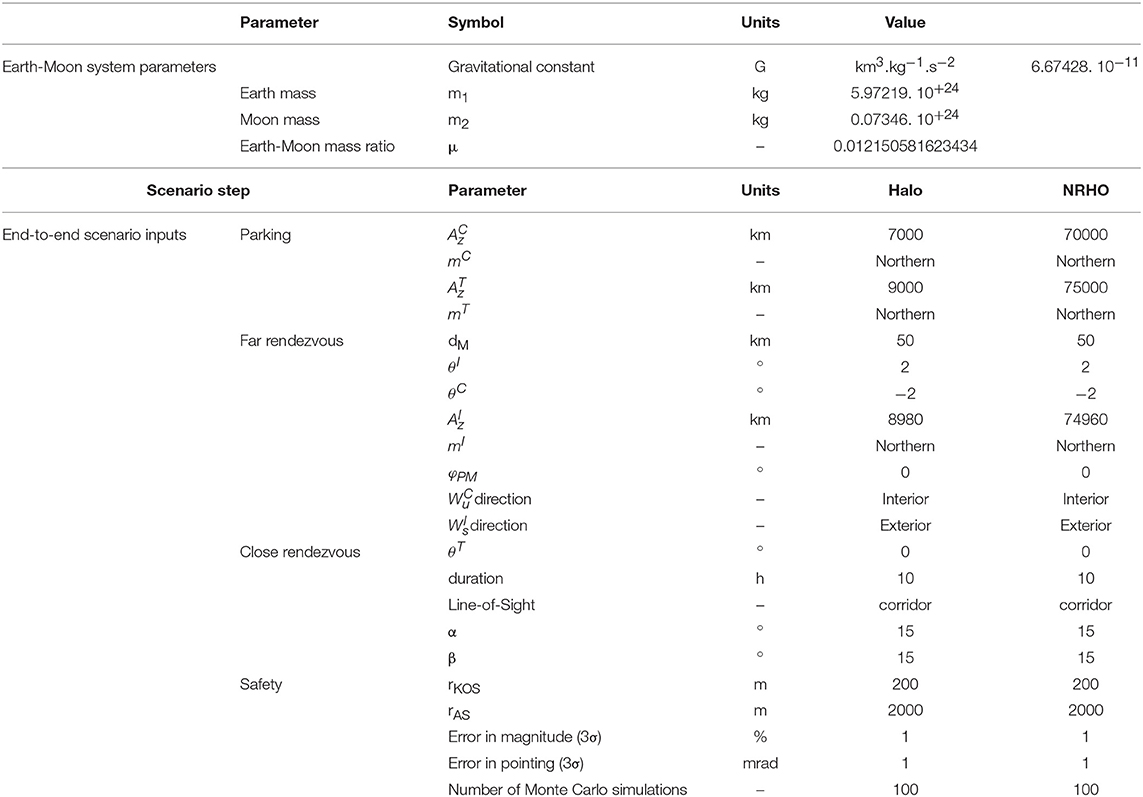
The objective of this paragraph is to assess the feasibility of the proposed strategies for far and close rendezvous, then to study the safety aspects of an end-to-end scenario. The output is the entire trajectory of the chaser from its parking orbit to the target orbit, in a three-steps process (far and close rendezvous and safety analysis). Guaranteeing the safety aspects requires going through an intermediate orbit, which is the final objective of the far rendezvous and the starting point of close rendezvous. Two study cases have been selected to illustrate the proposed strategies, in order to be consistent with the results of the historical study of the bibliography. They both lie in the Earth-Moon system, modeled by the CR3BP. Chaser parking orbit and target parking orbit belong to the same family. The first part of Table 1 summarizes the parameters of the Earth-Moon system. The name of a study case is composed by:
“NAME_of_chaser_parking_orbit-to-NAME_of_target_orbit.”
For example, HALO-to-HALO means that the chaser parking orbit is a Halo orbit and the target orbit is a Halo orbit. The considered study cases are: Halo-to-Halo and NRHO-to-NRHO.
At the end of this chapter, further conducted analyses are presented: a systematic analysis for far rendezvous (paragraph 5.4) within different orbit families and a close rendezvous on a DRO (paragraph 5.4 and section 5.5).
Scenario Algorithm
The final angular location, θT, of the chaser on the target orbit being fixed, the corresponding scenario is divided into four steps:
- Parking orbit: the chaser parking orbit at the beginning of the scenario is defined by its maximal elongation and its family mC ∈ {1;3}. The target orbit is also defined by its maximal elongation and its family mT ∈ {1;3}.
- Far rendezvous strategy: at this stage, the chaser leaves its parking orbit and targets an angular location θI, on the intermediate orbit, defined by its maximal elongation and its family mI ∈ {1;3}. θI is forced to be equal to θT. An optimization process is run to identify the best θC to minimize criterion (10). The outputs are: θC, TOF and v, where TOF is the time of flight, necessary for the chaser to travel from θC to θI.
- Close rendezvous strategy: the chaser then approaches the target situated at θT on the target orbit defined by from its intermediate angular location θI on the intermediate orbit defined by . The outputs are the number of HP (nHP), the position of the HP and the total velocity vclose.
- Safety analysis: A failure is injected at the selected HP with dispersion of velocity in magnitude and in direction. A Monte Carlo process models the influence of random dispersion on the trajectory. Chaser trajectory is propagated for a time of 24h starting with new conditions of velocity. The output is a label that indicates if there is a risk of collision. Lessons learnt from ISS resupply cargo missions lead to defining two spheres centered on the target identified as the safety regions: the Approach Sphere (AS) with radius rAS and the Keep out Sphere (KOS) with radius rKOS. The values of rAS and rKOS are selected from operational missions like the European cargo ATV (Automated Transfer Vehicle) and the Japanese HTV (H-1 Transfer Vehicle).
Scenario Input Parameters and Results
The second part of Table 1 presents input parameters for the two study cases. Selected values for (α, β) correspond to actual navigation sensor field-of-view equal to 30°, which imposes a relative distance of 20 km (resp. 40 km) between the intermediate Halo (resp. NRHO) orbit and the target Halo (resp. NRHO) orbit. direction” represents the chosen direction to propagate the unstable manifold issued from chaser parking orbit, while direction” corresponds to the propagation direction for the stable manifold that converges to the intermediate orbit. Direction can take two values: “interior” or “exterior” for interior realm or exterior realm. Proposed variation ranges for θC and φM come from preliminary exploratory analyses. Chaser and target angular locations are computed with respect to EML2 (resp. the center of the Moon) for Halo case (resp. for NRHO case). The angle reference is set on the Earth-Moon axis in the synodic frame. The angle value grows clockwise: 0° is on the side of the Earth. The angle φM is also measured from the same reference axis and origin, but anti-clockwise.
For the studied scenario, the selected angular location for rendezvous is (θT = 0). In the case of the close rendezvous on a NRHO, it corresponds to the periselene. Consequentially, it is an interesting location for ISRU (In-Situ Resource Utilization) or Moon sample return missions. Preliminary analyses conducted in this orbital zone have shown that the LR method appears less reliable than C-W or SL. Performances were thus obtained, by computing the difference in position, at the HP, between the arc generated by the linearized model and the Lambert's arc. Result can mainly be explained by the particularity of the observed zone. On the one hand, as LR equations are designed in the CR3BP problem, their validity is quite limited when the Moon influence is very predominant . On the other hand, the CW model evaluated under a Two-Body problem is the most suitable method in the periselene zone. As a consequence, it is recommended to select the LR model only for very large Halo orbits or in aposelenic zones. The selected initial angular location of the chaser on its parking orbit is (θC = −2), since the chaser and target must be in a same proximity area. The location of the PM, φPM, is set equal to 0° to minimize the transfer distance.
For close rendezvous, the chaser starts its trajectory on the intermediate orbit defined by , at angular location θI. The algorithm computes the number of HPs, their location, the maneuver to be performed at each HP and the arc of trajectory between two of them, so as to comply with a maximal duration of 10 h and following the LoS-C strategy. Results highly depend on the location on orbit where the rendezvous will take place.
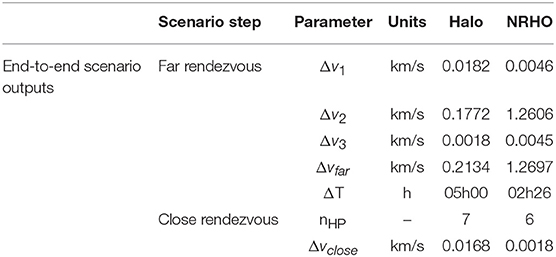
Table 2 provides syntheses of main results computed for the entire RDV scenario in both study cases, for far and close rendezvous. Results obtained for far rendezvous in the Halo study case are very encouraging, with a total duration about 5 h and a total cost about 0.21 km/s. In the NRHO case, the duration is even more affordable with about 2h26, but with the cost > 1.27 km/s. The selection of the rendezvous location at periselene can explain these performances. Actually, in this zone, the gravitational influence of the Moon cannot be neglected. The out-of-plane component of the maneuver between both trajectories is thus very expensive. Those results are coherent with the ones presented in (Campolo et al. (2017), recommending to perform close rendezvous at the aposelene.
Those far rendezvous simulations support the use of invariant structures for low-cost transfer from the chaser parking orbit to the target, extended with a Lambert arc at the connection. Parametric analysis on the angular location of both vehicles could then be conducted to propose best scenarios compliant with operational constraints of ground segments.
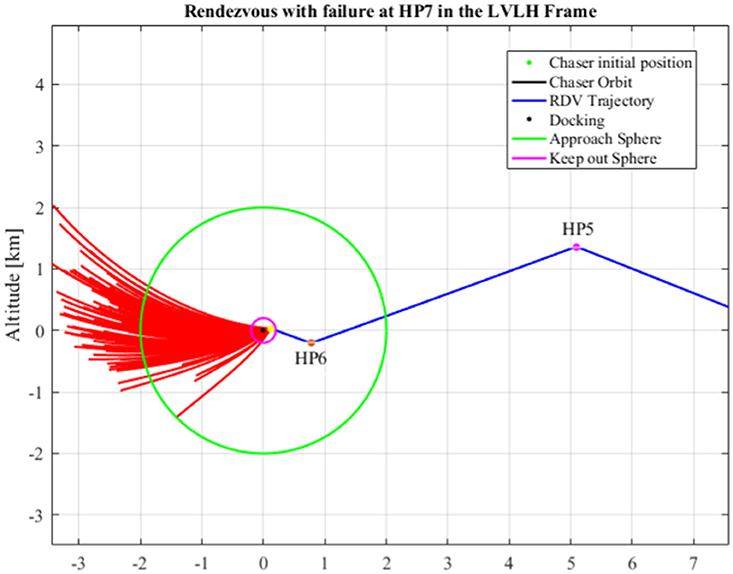
For close rendezvous, with a fixed duration of 10 h, computed cost is affordable, for both scenarios. At this stage, the most important criteria are the safety performances, because of the highly non-linear dynamics. Actually, the proposed far rendezvous strategy tries to take advantage to reduce fuel consumption. On the contrary, safety analysis seeks to prevent collision when the chaser motion becomes ballistic, after a failure. For both study cases, one injects a failure at each HP. The chaser trajectory is then propagated during 24 h, taking into account the dispersion (1% in magnitude (3σ) and an error of 1 mrad in pointing direction (3σ). In the particular Halo-to-Halo case, it results that when the failure takes place between HP n°1 and HP n°4, there is no risk of collision between the chaser and the target, as the chaser doesn't not get into the AS. When the failure occurs at HP n°5 or HP n°6, the chaser trajectory with dispersion may enter the AS but not the KOS. Finally, when the failure happens beyond the 6th HP, the chaser enters the KOS and thus, there is a risk of collision. Figure 9 presents the dispersion (in red) of the chaser trajectory when a failure is injected at HP n°7 in the Halo-to-Halo study case. The green circle represents the AS, while the purple one is the KOS. In the NRHO-to-NRHO study case, there is no risk of collision from the first HP to the third one. When there is a failure at HP n°4, the chaser enters the AS, but not the KOS. If the failure occurs at HP n°5 or HP n°6, the collision is certain. Figure 10 presents the dispersion of the chaser trajectory when a failure is injected at HP n°7 (in red) in the NRHO-to-NRHO study case. This safety analysis emphasizes the necessity for an accurate definition of safety areas as AS or KOS. Inside these zones, the HP should not only be maneuver locations, but also safety check-points, where decision are made with Go/No-Go to continue close rendezvous approach, depending on the vehicle heath status.
Two additional studies were conducted to analyze the impact of orbits from different families and close rendezvous on a DRO orbit and are presented in the two next sections.
Exploration n°1: Far Rendezvous Systematic Analysis
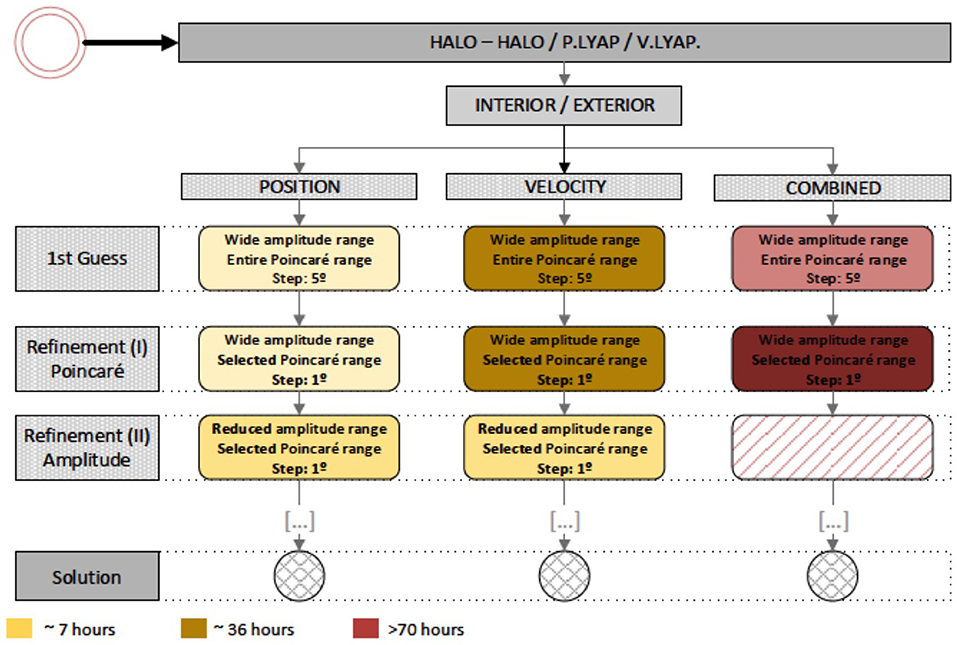
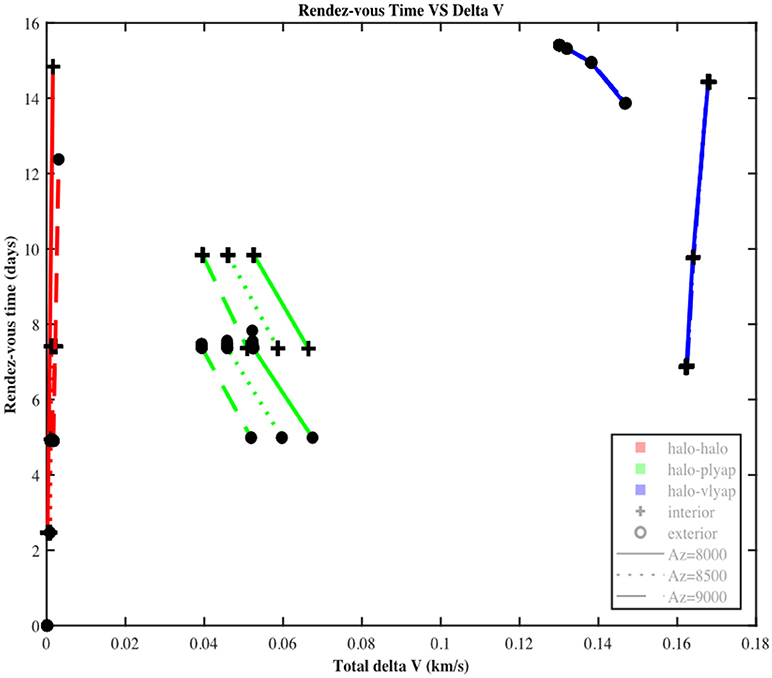
Actually, some exploration missions (vehicle coming back from Mars, Asteroids, or the Moon) can include parking orbit issued from other periodic families so as to take into account the inclination. The far rendezvous proposed strategy has been applied extensively to three rendezvous scenarios, so as to compare their performance cost (Δvfar), duration (ΔT), and feasibility (ΔX), in the Earth-Moon system, to extend the preceding studies cases to others libration periodic orbits families. It is assumed that the target is on a Halo orbit with a maximal elongation, . The chaser parking orbit can be a Halo orbit, a Horizontal Lyapunov orbit or Vertical Lyapunov orbit. For each type of chaser parking orbit, performances are computed with interior or exterior manifolds. A wide simulation campaign was run based on an inclusive Matlab-based tool whose algorithm is presented on Figure 11. For each category of simulation, a first set was run so as to refine the range of variation of the parameters: amplitude of the chaser parking orbit and angular location of the intermediate maneuver (φPM) at the Poincaré map. This first step was followed by two successive sets so as to further refine the results. The preliminary scenarios present a 5° step in φPMwhile the refined ones present a 1° step.
Figure 12 presents the best results obtained for three scenarios (Halo-to-Halo, Halo-to-Planar Lyapunov and Halo-to-Vertical Lyapunov) with interior and exterior directions, φPM ϵ [0:1:5] in deg., fixed equal to 8,000 km, in km, (θC, θT) ϵ [0:1:5] × [0:1:5] in deg. On this figure, the plot depicts the duration “Rendezvous time” in days and the cost “Total delta v” in km/s for three scenarios (Halo-to-Halo in red, Halo-to-Planar Lyapunov in blue and Halo-to-Vertical Lyapunov in green), for interior (+) and exterior (o) manifolds at three different value of ( km in solid line, in km in dot line and km in dashed line). The plot makes it easy to infer the variation of cost and duration required as the parking orbit changes. Best results are obtained for Halo-to-Halo rendezvous with a km on interior manifold with a Δvfar = 0.83 m / s and a ΔT = 2,47 days. Being only initial guesses, these results do not take into account the Lambert arc to connect the manifolds. The doubly iterative process, proposed in this paper, can improve them. From this graph, it can be observed that obtained performances belong to four distinct groups, depending on the type of chaser parking orbit and type of manifold. It can obviously be deduced that cost increases largely from Halo to Planar Lyapunov and Vertical Lyapunov, for both interior and exterior manifolds. This confirms initial intuition that the best option is a Halo-to-Halo rendezvous, which can help for decision-making during mission design phase.
However, this study remained within the context of periodic orbits. It could be interesting to further investigate Lissajous and other quasi-periodic orbits, but it would require a different approach in term of procedures, that could be part of future research work.
Exploration n°2: Close Rendezvous on a DRO
First planed mission for Orion will take place on a DRO (Whitley and Martinez, 2016). Figure 13 presents on the left the 14 first orbits computed from Henon (1969) data and on the right the enlarged family obtained by the continuation process.
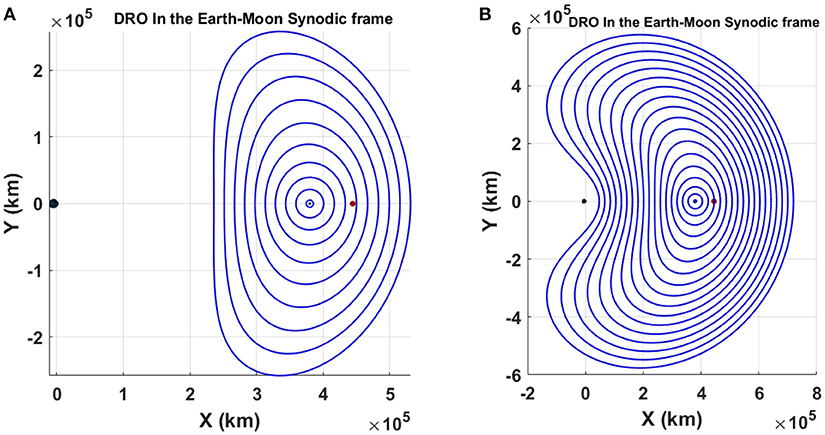
Figure 13. DRO family in the Earth-Moon synodic frame. (A) 14 first DRO in the Earth-Moon synodic frame, (B) Enlarged DRO family obtained with the continuation process.
As a consequence, it seems relevant to envisage rendezvous on this kind of orbit. Lunar DRO cannot be related to invariant structure such as stable or unstable manifolds (Ueda et al., 2017). The proposed strategy for far rendezvous cannot be applied. This exploratory analysis therefore focuses on the close rendezvous, applying a simplified algorithm compared to the one presented in 5.1. with only three steps: parking orbit (the chaser parking orbit defined by its maximal elongation and target orbit defined by its maximal elongation ), close rendezvous strategy (the chaser approaches the target situated at θT on the target orbit from its initial location θC on its parking orbit defined by ) and safety analysis (with Monte Carlo simulations to model failure occurrence).
In this analysis, the rendezvous is assumed to take place on DRO at θT = 180, on the target orbit defined by km. The chaser initial conditions are: km and θC = 178. The reference angle is the x-axis (i.e., the Earth-Moon axis in the synodic reference frame), and the origin is the center of the Moon. Angles are measured clockwise. The Line-of-Sight corridor strategy is applied with a cone with a half top angle of ±15. The same parameters as Halo and NRHO study cases are taken into account for safety analysis. The AS is a sphere with a radius, rAS, equal to 2km, and the KOS with a radius, rKOS, equal to 200 m. Both spheres are centered on the target position. 100 simulations are run to model an error of 1% in magnitude (3σ) and an error of 1 mrad in pointing direction (3σ).
As far as the accuracy obtained along the chaser trajectory arcs is concerned, the differences in position, at the HP obtained by the three linearized model and the Lambert's arc are compared. From this simulation campaign, it appears that, in the particular case of close rendezvous on a DRO, the LR algorithm is far more precise, than C-W and SL, with even a wider validity domain. In fact only C-W can lead to better performance when the rendezvous occurs on a DRO with an elongation km. However, the length of the elongation is not the only influencing parameter. The angular location of the final point for the rendezvous on the DRO plays a major role.
Coupled analyses for close rendezvous and safety aspects are then conducted. As a result, seven HP are obtained, with a vclose = 8, 92 m/s, within 10 h and LOS-C strategy. When a failure occurs at HP n°1 to HP n°4, there is no risk of collision as the chaser trajectory does not intersect neither AS, nor KOS. For a failure injected at HP n°5, the rendezvous is still safe as the chaser enters the AS, but not the KOS. From HP n°6 and HP n°7, the chaser trajectory becomes dangerous for the target as the chaser enters the KOS after the failure injection.
It can be concluded that the proposed strategy for close rendezvous on a DRO is applicable. Close rendezvous and safety analyses performed at DRO lead to results similar to the ones obtained for Halo orbits and NRHO. Further research will be necessary to propose a generic strategy, including an innovative far rendezvous strategy.
Perspectives and Conclusion
In a context of growing interest of the international space community to design Human spaceflight missions to Earth-Moon Lagrangian point, the strategy for rendezvous in the vicinity of the Moon becomes an actual challenge. This paper studies a scarcely explored field of astrodynamics, dealing with relative motion in highly non-linear dynamics. The intrinsic complexity of the three-body problem demands a departure from the standards of relative motion in the two-body problem, while still ensuring a smooth transition between far rendezvous and close proximity operations. This paper has first summarized the bibliographical context and a description of the theoretical background for rendezvous strategy in the vicinity of Lagrangian point in the CR3BP. Then, it has discussed strategies for far and close rendezvous. As far as far rendezvous was concerned, a three-maneuvers strategy based on natural connection between manifolds of the target orbit and the chaser orbit was presented. Then a close rendezvous strategy was described, composed of two main steps to obtain the chaser's approach trajectory arcs: a first guess computed from the best-adapted linearized model, then a second iteration with a non-linear model as a solution of the Lambert's problem. Afterwards, safety aspects were discussed, adapted from lessons learned from cargo missions to resupply the ISS. Finally, two studies cases were introduced to illustrate the end-to-end scenario from parking orbit to close rendezvous, with safety criteria. Complementary analyses were presented to explore different rendezvous scenario when the chaser and target orbits belong to different periodic solution family and to study close rendezvous on a DRO.
Studies cases and exploratory analyses have shown that, for a given mission stating target and chaser initial conditions, an end-to-end scenario can be established, based on two-steps scenario, chaining sequentially far rendezvous and close rendezvous. The scenario will be unique for each given mission. The methodology will recommend locations for maneuvers (angular location for far rendezvous and HP number and position for close rendezvous). This study also highlighted the sensitivity of the close rendezvous performance to the performance of navigation sensors. Finally, it also emphasized the definition of safety zones such as the Approach Sphere and the Keep-Out Sphere, which should be standardized for better collaboration in international programs such as the future Lunar Orbital Platform-Gateway.
Complementary studies could be conducted so as to compare this methodology to other ones. A first option could be to elaborate a systematic process to find spatial intersections between the manifolds, without using Poincaré map. A second option could be based on a direct Lambert arc between chaser and target parking orbits, without the utilization of stable and unstable manifolds. To go even further the exploratory systematic analysis should be completed with planar (like DRO) and quasi-periodic solutions. The close rendezvous strategy is almost mature. It would now be interesting to see the possibilities of embedding it in flight software, taking into account the actual characteristics of flight equipment.
Author Contributions
SL-D proposed strategies for far rendezvous, perform the corresponding analyses, supervised the research over several years. AC performed close rendezvous strategies analyses. VQ performed safety analyses for close rendezvous. LB and EB contributed to far rendezvous strategies, in particular to 4-maneuvers strategy. SM performed analyses for close rendezvous on NRO.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer FT declared a past supervisory role with one of the authors AC and a shared affiliation, with no collaboration, with the author SM to the handling editor at the time of review.
Acknowledgments
The authors would like to thank all the students involved in the different research projects that permitted to write this paper as a synthesis: Jean-Baptiste Bouvier, Adrien Brunel, Loic Cousin Raul Delgado Cuevas, Mani Vinayak Gopalan-Singamani, Rashika Jain, Bastien Le Bihan, Marc Morales, Nathanael Tepakbong-Tematio, Alejandro José Valverde, William Zanga. This research was entirely funded by ISAE-SUPAERO.
References
Alessi, E. M., Gomez, G., and Masdemont, J. (2010). Two-manoeuvres transfers between LEOs and Lissajous orbits in the Earth-Moon system. Adv. Space Res. 45, 1276–1291. doi: 10.1016/j.asr.2009.12.010
Belbruno, E. A. (2002). Analytic estimation of weak stability boundaries and low energy transfers. Contem. Math. 292, 17–45. doi: 10.1007/s10569-006-9053-6
Belbruno, E. A., and Carrico, J. P. (2000). “Calculation of weak stability boundary ballistic lunar transfer trajectories,” in AIAA/AAS Astrodynamics Specialist Conference Denver, CO.
Campolo, A, Manglaviti, S., Le Bihan, B., and Lizy-Destrez, S. (2017). “Safety analysis for near rectilinear orbit close approach rendezvous in the circular restricted three-body problem,” in IAC-17-F1.2.3, IP,20,x37564 (Adelaide, SA), 25–29.
Canalias, E. (2007). Contributions to Libration Mission Design Using Hyperbolic Invariant Manifolds. Valencia: Universitat Politecnica de Catalunya.
Canalias, E., and Masdemont, J. J. (2006). Rendezvous in Lissajous Orbits using the Effective Phases Plane. Available online at: arc.aiaa.org
Clohessy, W., and Wiltshire, R. (1960). Terminal guidance system for satellite Rendezvous. J. Aerospace Sci. 27, 653–658.
Colagrossi, A., Lavagna, M., and Rafano Carna, S. F. (2016). “Dynamical analysis of rendezvous and docking with very large infrastructures in non-keplerian orbits,” in 6th International Conference on Astrodynamics Tools and Techniques (Darmstadt).
Davis, D. C., Bhatt, S., Howell, K., Jang, J.-W., Whitley, R., Clark, F., et al. (2017). “Orbit maintenance and navigation of human spacecraft at cislunar near rectilinear halo orbits,” in 27th AAS/AIAA Space Flight Mechanics Meeting (San Antonio, TX; United States), 5–9.
Farquhar, R. (1967). Lunar communications with libration-point satellites. J. Spacecraft Rockets. 4, 1383–1384.
Farquhar, R. (1973). Quasi-periodic orbits about the translunar libration point. Celestial Mech. 7, 458–473.
Farquhar, R. W., Dunham, D. W., Guo, Y., and McAdams, J. V. (2004). Utilization of libration points for human exploration in the Sun–Earth–Moon system and beyond. Acta Astron. 55, 687–700. doi: 10.1016/j.actaastro.2004.05.021
Gerding, R. B. (1971). Rendezvous equations in the vicinity of the second libration point. J. Spacecraft Rockets 8, 292–294. doi: 10.2514/3.30263
Gómez, G. W. S, Koon, M., Lo, J. E., Marsden Masdemont, J., and Ross, S. D (2004). Connecting orbits and invariant manifolds in the spatial three-body proble. Nonlinearity 17, 1571–1606. doi: 10.1088/0951-7715/17/5/002
Gómez, G. W. S, Koon, M., Lo, J. E., Marsden Masdemont, J., and Ross, S. D. (2001). “Invariant Manifolds, The Spatial Three-body Problem and Space Mission Design,” in Advances in Astronautical Science (San Diego, CA: American Astronautical Society), 3–22.
Houbolt, J. C. (1960). Considerations of the Rendezvous Problems for Space Vehicles. New York, NY: SAE international. doi: 10.4271/600268
Jones, B. L., and Bishop, R. H. (1994). Rendezvous targeting and navigation for a translunar Halo orbit. J. Guidance Control Dynam. 17, 1109–1114.
Koon, W. S., Lo, M. W., Marsden, J. E., and Ross, S. D. (2001). Low energy transfer to the Moon. Celestial Mech. Dynam. Astron. 81, 63–73. doi: 10.1023/A:1013359120468
Lizy-Destrez, S (2015). “Rendezvous optimization with an inhabited space station at EML2,” in Proceedings of 25th International Symposium on Space Flight Dynamics ISSFD 2015 (Munich).
Luquette, R. J. (2006). Nonlinear Control Design Techniques for Precision Formation Flying at Lagrange Points, Ph.D. thesis, University of Maryland.
Mand, K. (2014). Rendezvous and Proximity Operations at the Earth-Moon L2 Lagrange Point: Navigation Analysis for Preliminary Trajectory Design. MSc Thesis, Rice University, Houston, TX.
Mingotti, G., Topputo, F., and Bernelli-Zazzera, F. (2012). Efficient invariant manifold,low-thrust planar trajectories to the Moon. Commun. Nonlinear Sci. Numer. Simul. 17, 817–831. doi: 10.1016/j.cnsns.2011.06.033
Mingtao, L., and Zheng, J. (2010). Impulsive lunar halo transfers using the stable manifolds and lunar flybys. Acta Astron.66, 1481–1492. doi: 10.1016/j.actaastro.2009.11.014
Murakami, N., and Yamanaka, K. (2015). “Trajectory design for rendezvous in lunar distant retrograde orbit,” in Japan Aerospace Exploration Agency. Big Sky, MT
Murakami, N., Ueda, S., Ikenaga, T., Maeda, M., Yamamoto, T., Ikeda, H., et al. (2015). “Practical rendezvous scenario for transportation missions to cis-lunar station in earth-moon L2 Halo orbit,” in Proceedings of 25th International Symposium on Space Flight Dynamics ISSFD 2015 (Munich).
Parker, J. S., and Anderson, R. L. (2013). Low Energy Lunar Trajectory Design. New York, NY: Jet Propulsion Laboratory
Parker, T. S., and Chua, L. (2012). Practical Numerical Algorithms for Chaotic Systems, Berlin: Springer-Verlag
Richardson, D. L. (1980). Analytic construction of periodic orbits about the collinear points. Celestial Mech. 22, 241–253.
Szebehely, V. (1967). Theory of Orbits: The Restricted Problem of Three Bodies. New York, NY: Academic Press Inc.
Ueda, S., and Murakami, N. (2015). “Optimim guidance strategy for rendezvous mission in Earth-Moon L2 Halo orbit,” in Proceedings of 25th International Symposium on Space Flight Dynamics ISSFD 2015 (Munich).
Ueda, S., Murakami, N., and Ikenaga, T. (2017). “A study on rendezvous trajectory design utilizing invariant manifolds of cislunar periodic orbits,” in AIAA 2017-1729, AIAA SciTech (Grapevine, TX), 9–13.
Keywords: rendezvous, trajectory, CR3BP, Earth-Moon system, Lagrangian points, relative motion
Citation: Lizy-Destrez S, Beauregard L, Blazquez E, Campolo A, Manglativi S and Quet V (2019) Rendezvous Strategies in the Vicinity of Earth-Moon Lagrangian Points. Front. Astron. Space Sci. 5:45. doi: 10.3389/fspas.2018.00045
Received: 26 February 2018; Accepted: 05 December 2018;
Published: 22 January 2019.
Edited by:
Elisa Maria Alessi, Italian National Research Council, ItalyReviewed by:
Francesco Topputo, Politecnico di Milano, ItalyFabio Ferrari, NASA Jet Propulsion Laboratory (JPL), United States
Maksim Shirobokov, Keldysh Institute of Applied Mathematics (RAS), Russia
Copyright © 2019 Lizy-Destrez, Beauregard, Blazquez, Campolo, Manglativi and Quet. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stephanie Lizy-Destrez, c3RlcGhhbmllLmxpenktZGVzdHJlekBpc2FlLXN1cGFlcm8uZnI=
 Stephanie Lizy-Destrez
Stephanie Lizy-Destrez Laurent Beauregard1
Laurent Beauregard1 Antonino Campolo
Antonino Campolo Sara Manglativi
Sara Manglativi