Interferometric Observations of Magnetic Fields in Forming Stars

The magnetic field is a key ingredient in the recipe of star formation. However, the importance of the magnetic field in the early stages of the formation of low- and high-mass stars is still far from certain. Over the past two decades, the millimeter and submillimeter interferometers BIMA, OVRO, CARMA, SMA, and most recently ALMA have made major strides in unveiling the role of the magnetic field in star formation at progressively smaller spatial scales; ALMA observations have recently achieved spatial resolutions of up to ~ 100 and ~ 1,000 au in nearby low- and high-mass star-forming regions, respectively. From the kiloparsec scale of molecular clouds down to the inner few hundred au immediately surrounding forming stars, the polarization at millimeter and submillimeter wavelengths is dominated by polarized thermal dust emission, where the dust grains are aligned relative to the magnetic field. Interferometric studies have focused on this dust polarization and occasionally on the polarization of spectral-line emission. We review the current state of the field of magnetized star formation, from the first BIMA results through the latest ALMA observations, in the context of several questions that continue to motivate the studies of high- and low-mass star formation. By aggregating and analyzing the results from individual studies, we come to several conclusions: (1) Magnetic fields and outflows from low-mass protostellar cores are randomly aligned, suggesting that the magnetic field at ~ 1,000 au scales is not the dominant factor in setting the angular momentum of embedded disks and outflows. (2) Recent measurements of the thermal and dynamic properties in high-mass star-forming regions reveal small virial parameters, challenging the assumption of equilibrium star formation. However, we estimate that a magnetic field strength of a fraction of a mG to several mG in these objects could bring the dense gas close to a state of equilibrium. Finally, (3) We find that the small number of sources with hourglass-shaped magnetic field morphologies at 0.01–0.1 pc scales cannot be explained purely by projection effects, suggesting that while it does occur occasionally, magnetically dominated core collapse is not the predominant mode of low- or high-mass star formation.

1. Introduction

Magnetic fields are known to play a critical role in many aspects of both low- and high-mass star formation. Even weakly ionized star-forming material is coupled to the ambient magnetic field, and thus the field can regulate (or prevent) the collapse and fragmentation of star-forming clouds (Hennebelle and Inutsuka, 2019; Krumholz and Federrath, 2019; Teyssier and Commerçon, 2019¹, in this volume), can influence the formation of protoplanetary disks (Wurster and Li, 2018, in this volume), and can launch bipolar outflows and jets from young protostars (Pudritz and Ray, 2019², in this volume). Mapping the morphology of magnetic fields in low- and high-mass star-forming regions is therefore critical to better understand how magnetic fields affect the star-formation process at early times, and how the role of the field changes relative to other dynamical effects (e.g., turbulence, rotation, thermal and radiation pressure, and gravitational collapse) as a function of spatial scale, source environment, and source mass. Over more than 50 years, studies of magnetic fields in low- and high-mass star-forming regions have been performed across a wide range of spatial scales, from the >100 pc scale of molecular clouds, to the 1 pc scale of clumps, to the 0.1 pc scale of dense cores, and finally to the 1,000–100 au scale of protostellar envelopes surrounding forming protostellar systems³.

In this review we introduce the typical tracers of the magnetic field in star-forming regions, as well as the methods used to analyze the observations. We then discuss the state of the field of magnetized star formation, focusing primarily on the last three decades of high-resolution polarization studies by millimeter and submillimeter [hereafter combined into “(sub)millimeter”] interferometers including the Berkeley-Illinois-Maryland Association (BIMA) millimeter array, the Combined Array for Research in Millimeter-wave Astronomy (CARMA), the Submillimeter Array (SMA), and the Atacama Large Millimeter/submillimeter Array (ALMA)⁴.

1.1. Magnetic Field Tracers (Plane-of-Sky Component)

1.1.1. Polarized Dust Emission

Polarized thermal emission from dust grains is the main tracer of the magnetic field in star-forming regions observed at high resolution and at (sub)millimeter wavelengths. Under most circumstances, oblong interstellar medium (ISM) dust grains with sizes ≪ 100 μm are aligned with their long axes perpendicular to magnetic field lines (e.g., Hildebrand, 1988). The currently accepted way to achieve this alignment is via the “radiative torque” (RAT) mechanism, where an anisotropic radiation field (e.g., the external UV field in the ISM, or the radiation from a deeply embedded protostar) causes grains to become aligned relative to the magnetic field (Lazarian, 2007; Hoang and Lazarian, 2009; Andersson et al., 2015)⁵. Thus, at the physical scales of star-forming clouds, cores, and envelopes (i.e., scales ≳ 100 au), magnetically aligned dust grains emit thermal radiation that is polarized perpendicular to the magnetic field. Observations of dust polarization, which comprise the vast majority of the single-dish and interferometric polarization observations to date, are discussed at length throughout this article.

1.1.2. Polarized Molecular-Line Emission

Polarization of molecular-line emission is another tracer of the magnetic field in star-forming regions. Molecular and atomic lines are sensitive to magnetic fields, which cause their spectral levels to split into magnetic sub-levels. For some molecules, linear polarization can arise when an anisotropy in the radiation and/or velocity field yields a population of magnetic sub-levels that are not in local thermodynamic equilibrium (LTE); this is known as the Goldreich-Kylafis (G-K) effect. Polarization from the G-K effect is most easily detected where the spectral line emission has an optical depth τ≈1, when the ratio of the collision rate to the radiative transition rate (i.e., the spontaneous emission rate) is ~ 1, and where the gradient in the radiation and/or velocity field is large. The effect is strongest in the lowest rotational transitions of simple molecules such as CO, CS, HCN, SiO, or HCO⁺. Spectral-line polarization from the G-K effect can be parallel or perpendicular to the magnetic field. Due to the different optical depths of the parallel and perpendicularly polarized components in different locations on the sky, polarization from the G-K effect ultimately traces the plane-of-sky magnetic field orientation with an ambiguity of 90° (Goldreich and Kylafis, 1981, 1982; Kylafis, 1983; Deguchi and Watson, 1984; Lis et al., 1988).

The first detections of the G-K effect were by Glenn et al. (1997), who presented National Radio Astronomy Observatory (NRAO) 12 m telescope observations of the evolved star IRC +10216, and by Greaves et al. (1999), who observed the galactic center and the high-mass star-forming clouds S140 and DR 21 using the James Clerk Maxwell Telescope (JCMT). In addition to these first observations, others have detected the G-K effect in molecular outflows from low-mass protostellar sources (e.g., Girart et al., 1999; Lai et al., 2002; Cortes et al., 2006; Lee et al., 2014, 2018a; Ching et al., 2016) as well as in high-mass protostellar sources (e.g., Lai et al., 2003; Cortes et al., 2005, 2008; Cortes and Crutcher, 2006). The G-K effect is a powerful way to trace the magnetic field in regions where the brightness of the thermal dust emission is too low to detect polarization at the few-percent level, either because the source is too distant or because the column density of dust is too low (e.g., in an outflow cavity where the gas and dust have been driven away).

One way to resolve the 90° ambiguity in G-K observations is via radiative transfer modeling. This was done in Cortes et al. (2005), who expanded on the original G-K models (which assumed that gradients in the CO optical depth were responsible for the necessary anisotropy in the radiation field) by including bright, central sources as additional causes of anisotropy. They used these models to successfully reproduce the 90° difference in polarization angles seen toward the high-mass star-forming region DR 21(OH) in their 3 mm BIMA observations of CO (J = 1 → 0) versus earlier 1.3 mm observations of CO (J = 2 → 1) by Lai et al. (2003). While the modeling in Cortes et al. (2005) was successful, in general it is difficult to know the structure of the radiation field, especially in high-mass star-forming regions. Other methods exist to resolve the ambiguity, such as comparing polarization from both dust and spectral lines in the same region. This was done in DR 21(OH) by Lai et al. (2003) and Ching et al. (2016); however, it is not clear how strong the correlation should be between the polarization angles from the two types of emission, as the dust emission traces much denser material than the CO.

Looking to the future, in low-mass sources with well behaved outflows, or in protoplanetary disks, the radiation and velocity fields may be simple enough to allow us to more confidently break the ambiguity in polarization orientation. Given the high quality of ALMA data toward these types of sources and the fact that ALMA's sensitivity will allow us to probe polarization in multiple transitions of many different molecules, spectral-line polarization studies have a bright future.

Finally, one must exercise caution when interpreting polarized spectral-line observations, as linearly polarized spectral-line emission can be converted into circularly polarized emission via anisotropic resonant scattering. Several studies have detected non-Zeeman circularly polarized emission, including Houde et al. (2013) in Orion KL and Hezareh et al. (2013) in the supernova remnant SNR IC 443. These observations were from the polarimeters at the Caltech Submillimeter Observatory (CSO) and the Institut de Radioastronomie Millimétrique (IRAM) 30 m telescope, respectively (see Chamma et al., 2018 for more results from the SMA). The model described in those publications shows that resonant scattering can cause a rotation in the polarization position angle in maps of linear spectral-line polarization. Hezareh et al. (2013) used the detected Stokes V signal toward SNR IC 443 to correct the map of linear spectral-line polarization. After doing so, the polarization was well aligned with dust polarization observations using the PolKA polarimeter at the Atacama Pathfinder Experiment (APEX) telescope. The authors note that this effect is proportional to the square of the magnitude of the plane-of-sky magnetic field, which opens up the possibility of detecting the magnetic field via circular polarization observations of Zeeman-insensitive spectral lines.

1.1.3. The Velocity-Gradient Technique

Another method for probing the plane-of-sky magnetic field in star-forming regions is the “velocity-gradient technique” (VGT), which estimates the magnetic field orientation using the velocity gradients present in spectral-line observations. In turbulent regions that are not gravitationally bound, González-Casanova and Lazarian (2017) and Yuen and Lazarian (2017) showed that the magnetic field is expected to be oriented perpendicular to velocity gradients. The authors also extended their study to shocked and gravitationally bound regions (Yuen and Lazarian, under review), and argued that the VGT provides an even better view of the plane-of-sky magnetic field morphology in the interstellar medium (particularly in diffuse regions with a low column density of dust) than both the Planck polarization data (e.g., Planck Collaboration et al., 2015b) and observations of neutral HI “fibers,” which also trace the interstellar magnetic field (Clark et al., 2014, 2015).

1.2. Magnetic Field Tracers (Line-of-Sight Component): The Zeeman Effect

The Zeeman effect is another important tracer of the magnetic field that has been observed primarily with single-dish radio telescopes to infer the line-of-sight magnetic field strength⁶ in molecular clouds (Troland and Heiles, 1986; Crutcher et al., 1993; Crutcher, 1999). When threaded by a magnetic field, atomic hydrogen and molecules with a strong magnetic dipole moment will have the degeneracy in magnetic sub-levels lifted for states with non-zero angular momentum. This will split the radio frequency transitions into a number of linearly and elliptically polarized components separated slightly in frequency. Measuring this Zeeman splitting is the only way to directly measure a component of the magnetic field strength. However, we will not focus more on the thermal Zeeman effect in this review, as there are no reported observations with a (sub)millimeter-wavelength interferometer. For reviews of single-dish observations of magnetic fields in molecular clouds via the Zeeman effect, see Crutcher (2012) and Crutcher and Kemball (2019⁷, in this volume).

1.3. Analysis Methods

1.3.1. Indirect Estimates of Magnetic Field Strength

The polarization arising from magnetically aligned dust grains and from the G-K effect yields the plane-of-sky magnetic field morphology. However, these observations do not contain information about the magnetic field strength. Since knowing the field strength is critical to our understanding of the importance of magnetic fields, a variety of indirect methods have thus been developed to estimate the field strength from these types of observations.

The most longstanding of these methods is the Davis-Chandrasekhar-Fermi (DCF) method (Davis, 1951; Chandrasekhar and Fermi, 1953), which uses the fact that turbulent motions should cause an observable scatter in what would otherwise be a well ordered mean magnetic field. The original, simplest form of the DCF formula yields an estimate of the plane-of-sky magnetic field strength

$\begin{array}{ll}{B}_{\mathrm{\text{POS}}}=\frac{\sqrt{4\pi \rho }}{\delta \varphi }\delta V,& (1)\end{array}$

where ρ is the gas density, δV is the one-dimensional velocity dispersion, and δϕ is the dispersion in polarization position angles. δV and δϕ are both assumed to be caused by turbulent motions in the region being studied. The derivation of this expression also assumes that there is a mean magnetic field in the region, that the turbulence is incompressible and isotropic, and that the turbulent components of the kinetic and magnetic energies are in equipartition. Note that the DCF method also assumes that the dispersion is “small,” i.e., that the turbulent magnetic energy is small compared with the mean-field magnetic energy in the system.

The DCF method was originally developed to estimate magnetic field strengths in the diffuse ISM, where perturbations in the magnetic field can be assumed to be caused by turbulent motions in the magnetized medium. Comparisons with MHD simulations of giant molecular clouds (GMCs) by Ostriker et al. (2001) found that at these scales, the original DCF method typically overestimates the magnetic field strength by a factor of ~ 2 because line-of-sight field tangling is not taken into account. Further simulations by Heitsch et al. (2001) also found that the true field strength is overestimated unless finite telescope resolution and self-gravity within the GMC are accounted for.

At the smaller scales of the individual star-forming clumps and cores that are probed by interferometers, gravity is almost always the dominant dynamical factor, and thus the structure of the background field must be removed before calculating the dispersion in polarization position angles. In two ideal cases with very clean examples of hourglass-shaped magnetic fields, Girart et al. (2006) and Qiu et al. (2014) removed the background hourglass field by subtracting a set of parabolic field lines from the data, after which they calculated the magnetic field dispersion relative to the background structure. In complicated cases, however, a more general method is necessary to remove arbitrary background field structure. This has been achieved by employing a second-order structure function of the polarization angle that allows the separation of the turbulent and mean magnetic-field components, with the underlying assumption that the mean-field component has an intrinsically larger spatial scale than the turbulent component (Falceta-Gonçalves et al., 2008; Hildebrand et al., 2009; Houde et al., 2009, 2011; Chitsazzadeh et al., 2012). Further refinements of these studies have also taken into account interferometric filtering effects (Houde et al., 2016).

Falceta-Gonçalves et al. (2008) used the structure-function approach to test the validity of the DCF technique using their MHD simulations. In addition to analyzing the effect of different telescope resolutions (their conclusion: lower-resolution observations tend to overestimate the field strength), they also derived a generalized form of the DCF equation, which allows for the separation of the turbulent and mean magnetic field components, and yielded magnetic-field estimates that were accurate to within ~ 20%. More recently, Juárez et al. (2017) performed SMA observations of a magnetized high-mass star-forming region and used the structure-function method to compare the data with synthetic observations of gravity-dominated MHD simulations. They found the magnetic field strength estimates from both the observations and simulations to be in good agreement.

Koch et al. (2012) proposed another method of indirectly measuring the magnetic field strength that is also based on an ideal MHD framework. They argue that a position-dependent magnetic field strength in a polarization map can be calculated using the angle between the magnetic field and the gradient of the total-intensity emission, and a second angle between the local gravity direction and the gradient of the total-intensity emission. This is based on the assumption that the intensity gradient is a proxy for the direction of motion in the MHD force equation. For example, in a centrally concentrated, gravitationally bound core, the infalling motion will be along the intensity gradient (across the iso-intensity contours). This method requires observations of the magnetic-field morphology (i.e., via observations of thermal dust polarization or the G–K effect) in order to produce a spatial distribution of the magnetic field strength. However, unlike the DCF method, this method does not require spectral-line observations in the analysis. Estimations of magnetic field strengths using this method have been found to be consistent with previous estimations from the DCF method (see e.g., section 3.1).

1.3.2. The Mass-to-Flux Ratio

Merely measuring the magnetic field strength does not allow us to determine immediately the importance of the magnetic field in a given star-forming region. Therefore, in magnetic field studies it is common to compare the magnetic energy density with that of other dynamical quantities such as gravity, turbulence, and outflow feedback (see, e.g., Hull et al. 2017b for a comparison of magnetic energy with gravitational and outflow energy densities in the intermediate-mass Class 0 protostellar core Serpens SMM1).

Historically, there has been a strong focus on the comparison of gravity (which causes inward motion) and the magnetic field (whose tension provides resistance against infall across the field lines). The common quantity quoted as a metric for the importance of the magnetic field with respect to gravity is the “mass-to-flux ratio” M/Φ, where M is the mass of the object of interest and Φ is the flux of the magnetic field threading the object. As discussed in Crutcher (2004, and references therein), the maximum mass that can be supported by a given magnetic flux is given by $M_{\mathrm{\text{crit}}}=\Phi /2\pi \sqrt{G}$. However, it is more useful to discuss the dynamical status of an object by measuring the ratio λ of the observed mass-to-flux ratio to the critical mass-to-flux ratio:

$\begin{array}{ll}\lambda =\frac{{(M/\Phi )}_{\mathrm{\text{obs}}}}{{(M/\Phi )}_{\mathrm{\text{crit}}}}.& (2)\end{array}$

Clouds that are supported by the magnetic field and are not collapsing are deemed “subcritical” (λ < 1), whereas those where gravity has overcome the resistance of the magnetic field are referred to as “supercritical” (λ > 1). Crutcher (2012) analyzed data across a wide range of spatial scales that trace more than five orders of magnitude in densities, and found that when the hydrogen column density $N_H>10^{21}$ cm⁻², all star-forming objects are supercritical (i.e., are collapsing). This value is less than the typical column densities of low-mass ($N_H~10^{22}-10^{23}$ cm⁻²; e.g., Girart et al. 2006; Hull et al. 2017b) and high-mass ($N_H~10^{23}-10^{24}$ cm⁻²; e.g., Girart et al. 2009) protostellar cores, and thus the types of objects we review in this article are all supercritical. This is reasonable, as most of them have already formed stars, as revealed by the presence of bipolar outflows. Furthermore, due to the sensitivity limits of CARMA and the SMA, most of the sources in previous interferometric surveys of polarization (Hull et al., 2014; Zhang et al., 2014) were chosen based on their strong millimeter flux, which correlates with the presence of embedded star formation.

1.4. Core-Mass Estimates From Dust Emission

In order to convert the observed millimeter-wave flux density S_ν contained within a given spatial area into a corresponding gas mass M_gas, we can use the following relation:

$\begin{array}{ll}{M}_{\text{gas}}=\frac{S_{\nu }{d}^2}{{\kappa }_{\nu }{B}_{\nu }(T_d)},& (3)\end{array}$

where d is the distance to the source, κ_ν is the opacity of the dust (Ossenkopf and Henning, 1994), and B_ν(T_d) is the Planck function at the frequency of the observations. T_d is the temperature of the dust, which is usually ~ 20–50 K in a low-mass protostellar core (Girart et al., 2006), and as high as (or greater than) 100 K in a high-mass core (Girart et al., 2009). Once the dust mass is calculated, a gas-to-dust mass ratio of 100 is usually assumed in order to calculate the total (gas + dust) mass of the protostellar core. Note that such an estimate does not include the mass of the central star(s), which must be obtained by other means, e.g., via direct detection of a Keplerian disk around the source (e.g., Tobin et al., 2012; Ohashi et al., 2014) or via determination of the source's bolometric luminosity.

1.5. Motivating Questions in Low- and High-Mass Star Formation

The primary goal of observing the magnetic field at any spatial scale is to determine the importance (or lack thereof) of the magnetic field in the star-formation process. The steady progress toward this goal over the last two decades began with single-dish submillimeter polarization surveys probing ≳ 20″ scales using the Viper 2 m telescope at the South Pole (SPARO polarimeter, e.g., Dotson et al., 1998; Renbarger et al., 2004; Li et al., 2006), the JCMT (850 μm SCUBA polarimeter, e.g., Matthews et al. 2009), and the CSO (350 μm SHARP Li et al. 2008 and Hertz Dotson et al. 2010 polarimeters). A resurgence of single-dish studies has been brought about by results from the PolKa polarimeter at the APEX telescope (Siringo et al., 2004, 2012; Hezareh et al., 2013; Alves et al., 2014; Wiesemeyer et al., 2014), the BISTRO survey with the upgraded POL-2 polarimeter at the JCMT (e.g., Pattle et al., 2017, 2018; Ward-Thompson et al., 2017; Kwon J. et al., 2018; Soam et al., 2018), results from the polarimeter on the Balloon-borne Large Aperture Submillimeter Telescope (BLAST; Roy et al., 2011; Fissel et al., 2016; Gandilo et al., 2016), observations from the HAWC+ polarimeter (Vaillancourt et al., 2007) on the Stratospheric Observatory for Infrared Astronomy (SOFIA; e.g., Chuss et al., 2018; Gordon et al., 2018; Lopez-Rodriguez et al., 2018), and the galactic polarization maps from the Planck satellite (e.g., Planck Collaboration et al., 2015a,b,c, 2016a,b,c). These new studies will pave the way for future work with even more sensitive instruments such at the next-generation BLAST instrument (BLAST-TNG; Galitzki et al. 2014), the NIKA2 polarimeter at the IRAM 30 m telescope (Ritacco et al., 2017), and the TolTEC polarimeter at the Large Millimeter Telescope (LMT). For reviews on multi-scale/multi-wavelength studies and single-dish observations of magnetic fields, respectively, see Li and Law (2019)⁸ and Pattle and Fissel (2019)⁹, both in this volume.

There are a number of questions applicable to both low- and high-mass star formation that have been investigated using (sub)millimeter polarimetric observations. These include the (direct or indirect) measurements of the absolute magnetic field strength in star-forming material at different spatial scales, as well as the estimation of the dynamical importance of the magnetic field with respect to gravity (i.e., the mass-to-flux ratio; see section 1.3.2). Observations of magnetic fields across multiple spatial scales toward both low-mass (Li et al., 2009; Hull et al., 2014) and high-mass (Zhang et al., 2014; Li et al., 2015) protostellar sources have also been used to constrain the dynamical importance of the magnetic field based on the morphological consistency (or lack thereof) of the field as a function of scale. Generally, however, these observations have only compared two or three of the relevant spatial scales (i.e., 100 pc cloud scales, 1 pc clump scales, 0.1 pc dense-core scales, 1,000 au protostellar envelope scales, and 100 au disk scales). A full characterization of the magnetic field from galactic (Planck) scales down to scales approaching the 100 au size of protoplanetary disks has yet to be accomplished, but will be possible in the near future when upcoming polarization surveys of the full populations of protostars in entire molecular clouds are completed.

In the low-mass regime, single-dish observations probe the magnetic field in star-forming clouds at large scales, revealing the magnetic field from the scale of entire molecular clouds (Planck, BLAST) to the canonical, ~ 0.1 pc dense core, where one or a few protostars will form (JCMT, CSO). One of the main benefits of single-dish studies is their ability to recover a larger range of spatial scales than interferometers, thus enabling an accurate characterization of the magnetic field in ambient cloud material. However, higher resolution is needed in order to probe the environments of individual stars; this is where results from the BIMA, CARMA, SMA, and ALMA interferometers dominate the discussion, allowing us to characterize the magnetic field from scales of several × 1,000 au down to the scales of a few × 10 au accessible to ALMA¹⁰. The main questions that have been tackled over the last two decades using data from these interferometers include: (1) What is the importance of the magnetic field in regulating the collapse of star-forming cores? (section 2.1); (2) What is the relationship of bipolar outflows with the magnetic field? (section 2.2); and (3) What is the role of the magnetic field in the launching and collimation of bipolar outflows in low-mass protostars? (section 2.3).

Moving to the high-mass regime: high-mass stars (M_* > 8 M_⊙) form predominantly in clustered environments where a population of stars are born with a range of stellar masses (Lada and Lada, 2003). These high-mass stellar populations form in dense cores that are embedded in parsec-scale, massive molecular clumps. This review will focus on several questions raised in recent studies of these high-mass sources, including (4) What is the dynamical role of magnetic fields in dense cores? (section 3.1); (5) What is the role of the magnetic field in the formation of disks and the launching of protostellar outflows in high-mass protostars? (section 3.2); (6) Do magnetic fields play a significant role in the fragmentation of molecular clumps and the formation of dense cores? (section 3.3); and (7) Does high-mass star formation proceed in virial equilibrium? (section 3.4).

The dense clustering nature of high-mass star formation implies considerable fragmentation within these massive molecular clumps, which distinguishes high-mass star formation from the more isolated process of low-mass star formation. High-mass regions also tend to have much more intense radiation environments, hosting HII regions whose radiative feedback and ionization can impact the ambient magnetic field. Another clear difference arises from the fact that the best-studied low-mass stars are forming at distances ~ 10 × closer than typical high-mass star forming regions, allowing us to study the formation of individual low-mass protostellar systems and their associated outflows, jets, and disks in much greater detail than is possible in high-mass systems. Ultimately, however, studies of both low- and high-mass star formation use the same observing techniques and confront many of the same questions. In this review we focus on those questions that have been of the most interest to both communities in recent years.

2. Magnetic Fields in Low-Mass Star Formation

The revolution of high-resolution, interferometric observations of polarization began with BIMA and the Owens Valley Radio Observatory (OVRO). These two sets of antennas were later combined into CARMA (Bock et al., 2006). Early observations with BIMA and OVRO¹¹ covered a wide range of topics, including polarization observations of dust, SiO, CO, and SiO masers toward iconic regions in Orion (Rao et al., 1998; Plambeck et al., 2003; Girart et al., 2004; Matthews et al., 2005) as well as observations of individual protostars (Girart et al., 1999; Cortes et al., 2006; Kwon et al., 2006). These first observations, combined with the extensive follow-up from CARMA, the SMA, ALMA form the body of work motivating this review. Below we put this work in the context of a narrative addressing several of the major open questions in the field of magnetized low-mass¹² star formation.

2.1. The Role of the Magnetic Field in Protostellar Collapse

In models of magnetically regulated protostellar collapse (e.g., Mouschovias, 1976a,b, 1991; Mouschovias and Ciolek, 1999), a strong, well ordered magnetic field provides outward pressure support of the infalling material. This is because the field is coupled (or “frozen”) to the small fraction of charged particles in the weakly ionized gas. However, in non-turbulent models, the non-ideal MHD effect of ambipolar diffusion (Mestel and Spitzer, 1956) enables the neutral material (which comprises the bulk of the star-forming core) to slip slowly past the magnetic field lines, thus removing magnetic flux and eventually allowing collapse to proceed once the mass-to-flux ratio exceeds the critical value.

One of the predicted signposts of highly magnetized star formation is that at high enough densities (≳10⁴ cm⁻³), the collapse of strongly magnetized gas should pinch the magnetic field into an “hourglass” shape with a symmetry axis perpendicular to the major axis of a flattened, ~ 1000 au “pseudodisk” (Galli and Shu, 1993a,b). The hourglass is expected to persist down to scales < 1,000 au (Fiedler and Mouschovias, 1993; Galli and Shu, 1993b; Allen et al., 2003; Gonçalves et al., 2008; Frau et al., 2011; Kataoka et al., 2012; Mocz et al., 2017); see Figure 1. And indeed, the predicted hourglass has now been seen in a number of interferometric observations of low-mass protostellar cores (Girart et al., 1999, 2006, 2008; Rao et al., 2009; Stephens et al., 2013; Hull et al., 2014; Maury et al., 2018; Sadavoy et al., 2018a; Kwon W. et al., under review, see Figure 2), suggesting that some protostellar cores do form in strongly magnetized regions. For a discussion of constraining strong-field star formation via observations of hourglass-shaped magnetic fields, see section 4.

FIGURE 1

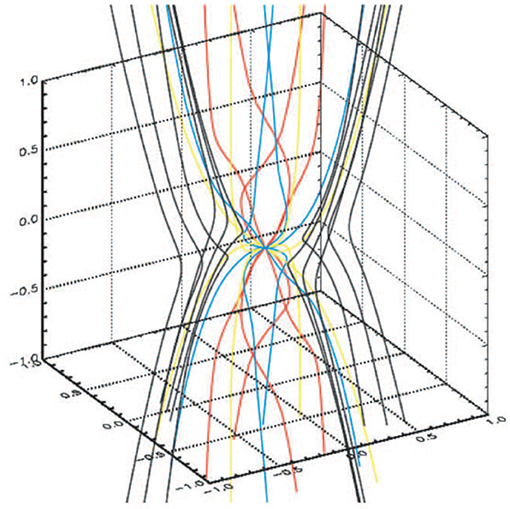
Figure 1. A model from Allen et al. (2003) showing an hourglass-shaped magnetic field configuration in a collapsing, magnetized star-forming core. Reproduced with permission from the American Astronomical Society (AAS).

FIGURE 2

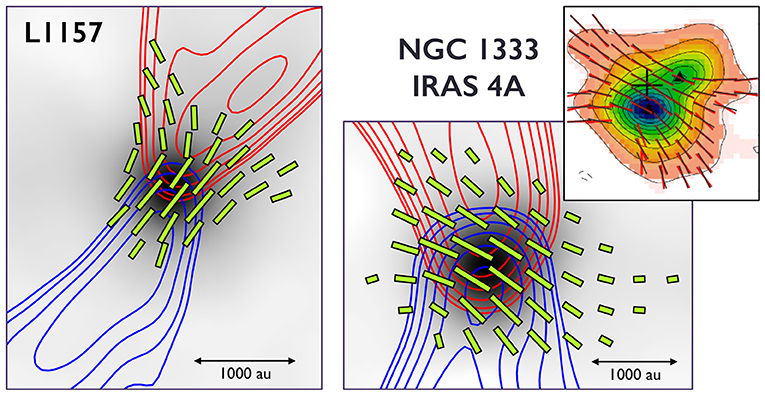
Figure 2. Observations of hourglass-shaped magnetic field configurations (line segments). The rightmost, overlapping panels are NGC 1333-IRAS 4A, observed by the SMA in Girart et al. (2006, top), and again by CARMA in Hull et al. (2014, bottom/background). The SMA and CARMA observations are zoomed to the same spatial scale. The left-hand panel is the isolated Class 0 protostar L1157 (adapted from Hull et al., 2014; see also Stephens et al., 2013). Figures reproduced with permission from Science magazine and the AAS.

A second signpost of strong-field star formation is the consistency of the magnetic field orientation across multiple spatial scales. If the field is strong relative to other dynamical effects, observations at small scales should reveal a magnetic field whose original orientation is preserved from the parsec scale of the cloud in which the source is embedded. To date, multi-scale studies of the magnetic field in low- and high-mass star-forming regions have compared two or three scales: i.e., ~ kpc galactic scales to ~ 0.1 pc dense-core scales in Stephens et al. (2011); 100 pc cloud scales to 0.1 pc dense-core scales in Li et al. (2009, 2015); 1 pc clump scales to 0.1 pc dense-core scales in Zhang et al. (2014), continuing down to ~ 0.01 pc scales in Girart et al. (2013) and Ching et al. (2017); 0.1 pc dense core scales to 1,000 au protostellar envelope scales in Hull et al. (2014) and Davidson et al. (2014); and 0.1 pc to 1,000 au to 100 au scales in Hull et al. (2017a,b).

In the low-mass regime, Li et al. (2009) found striking consistency between the magnetic field orientation in the Orion molecular cloud derived from background starlight polarization at ~ 100 pc scales versus polarized thermal dust emission at ~ 0.1 pc scales. Hull et al. (2014) took this one step further, finding consistency in the field orientation in just a few of the low-mass protostars in their sample from scales of ~ 0.1 pc to ~ 1,000 au. The sample of sources from Hull et al. (2014) that maintained consistency in the magnetic field orientation down to scales of ~ 1,000 au tended to be those sources with a higher polarization fraction, which implies that the magnetic fields in those sources are more ordered, and thus may be more dynamically important.

Among those sources with consistent large-to-small scales magnetic fields are several with known hourglass morphologies, including OMC3 MMS6 (Hull et al., 2014), NGC 1333-IRAS 4A (Girart et al., 2006), L1157 (Stephens et al., 2013), and L1448 IRS 2 (Kwon W. et al., under review). The magnetic field strengths have been estimated toward the latter three objects, an are all relatively high, on the order of ≳1 mG, which is similar to values obtained in high-mass regions (see section 3.1). However, while the values are high [5 mG in IRAS 4A (Girart et al., 2006); 1.3–3.5 mG in L1157 (Stephens et al., 2013); and 750 μG in L1448 IRS 2 (Kwon W. et al., under review)], the mass-to-flux ratios calculated for the two most magnetized sources (IRAS 4A and L1157) are both slightly greater than the critical value (1.7 and 1.1 for IRAS 4A and L1157, respectively), which is reasonable, considering that the objects have already collapsed to form protostars.

Follow-up studies with ALMA of individual sources from previous surveys (e.g., Hull et al., 2014) have suggested that consistency in the magnetic field orientation across spatial scales may be the exception rather than the rule at scales smaller than ~ 0.1 pc. Indeed, detailed multi-scale follow-up studies by Hull et al. (2017a,b) of Ser-emb 8 and Serpens SMM1, two Class 0 protostellar sources in the Serpens Main molecular cloud, found significant deviations in the magnetic field morphology across spatial scales ranging from ~ 0.1 pc down to ~ 100 au.

In the case of Serpens SMM1, it appears that the deviations at the ~ 100 au scales probed by ALMA are due to shaping of the magnetic field by the bipolar outflow. This is in spite of the fact that the magnetic field strength is estimated to be quite high, ~ 5.7 mG (Hull et al., 2017b). The fact that dynamics are shaping the magnetic field morphology in this source is not surprising, however, as the magnetic is comparable to the kinetic energy in the outflow. This is in contrast to sources like NGC 1333-IRAS 4A, where estimates by Girart et al. (2006) show that the magnetic energy is clearly dominant over turbulent motions in the source.

In the case of Ser-emb 8, the outflow does not have a clear effect on the magnetic field, and yet the field morphology is still not consistent across scales. A comparison of the Ser-emb 8 data with moving-mesh AREPO gravoturbulent MHD simulations (Mocz et al., 2017) suggests that Ser-emb 8 may have formed in an environment where dynamical effects such as turbulence and infall dominate the magnetic field, in contrast to the strong-field examples described above; see Figure 3. These results are qualitatively consistent with other simulations studying star formation in weakly magnetized turbulent environments (e.g., Seifried et al., 2015; Offner and Chaban, 2017), suggesting that the importance of the magnetic field at the smallest scales of star formation lies along a continuum, from the bright, highly polarized examples of strong-field star formation to the more complex examples of star formation in regions dominated by dynamical processes. Large, high-resolution polarization surveys by ALMA will reveal the distribution of low-mass protostars across this continuum of magnetic importance, and will allow us to compare with results from high-mass regions such as those by Zhang et al. (2014), who found that the magnetic field is dynamically important at the larger spatial scales probed by their observations (see section 3.3).

FIGURE 3

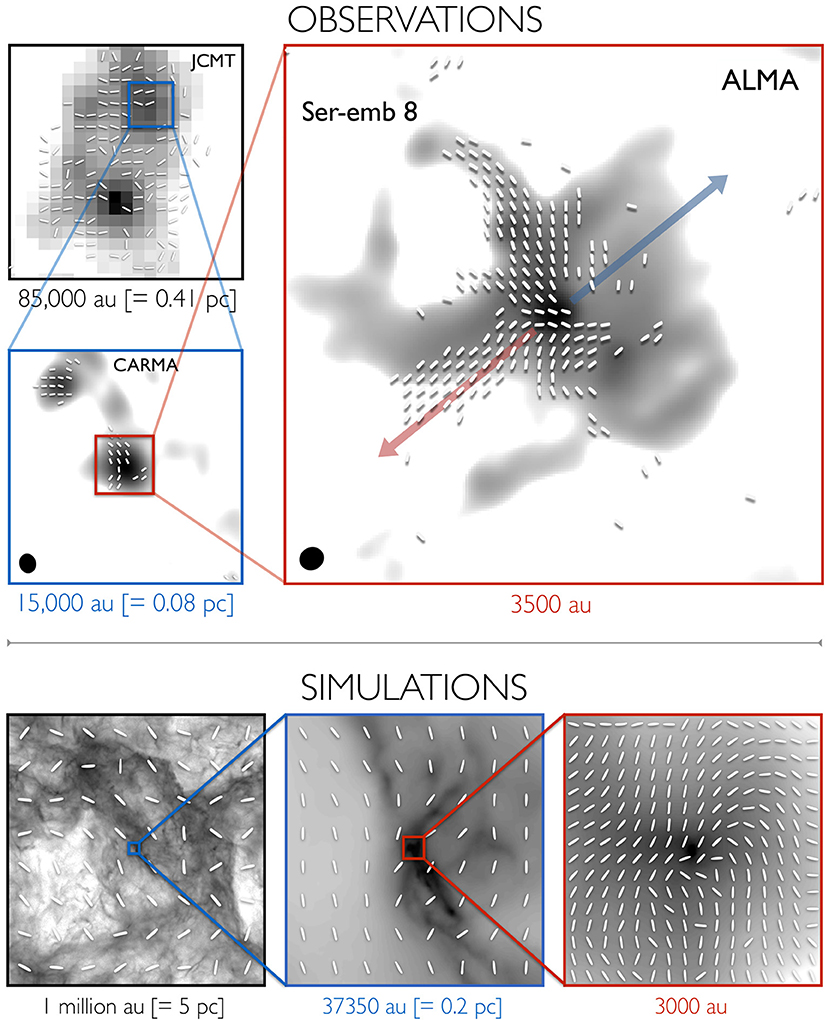
Figure 3. (Top) Multi-scale observations of the magnetic field (line segments) toward the low-mass Class 0 protostar Ser-emb 8. Grayscale is total-intensity (Stokes I) thermal dust emission. Observations are from the JCMT at 850 μm (top-left; Matthews et al., 2009), CARMA at 1.3 mm (bottom-left; Hull et al., 2014), and ALMA at 870 μm (right). The red and blue arrows indicate the red- and blueshifted lobes of the bipolar outflow from Ser-emb 8 traced in CO (J = 2 → 1). The data show the inconsistency of the magnetic field across spatial scales, and are consistent with moving-mesh AREPO MHD simulations (Bottom) whose initial conditions include a magnetic field that is weak compared with turbulence at large (5 pc) scales. Adapted from Hull et al. (2017a). Reproduced with permission from the AAS.

2.2. Misalignment of Outflows and Magnetic Fields

For more than a decade, one of the primary ways that astronomers have tested the importance of the magnetic field in star-forming regions has been via comparisons of the orientations of bipolar outflows/jets and the ambient magnetic field. This is because if a protostellar core is very strongly magnetized, the magnetic field has the ability to align all of the relevant axes: the axis of the (well ordered and poloidal) magnetic field, the symmetry axis of the pseudodisk, the rotational axis of the protostellar disk, and the axis of the outflow and/or jet emanating from the central source. This happens because of the “magnetic braking” phenomenon (Allen et al., 2003), where a strong magnetic field removes angular momentum from the central source and causes the angular momentum (and thus disk/outflow) and magnetic axes to align (e.g., Machida et al., 2006).

This same magnetic braking phenomenon can potentially lead to what has come to be known as the “magnetic braking catastrophe,” where a strong magnetic field aligned with the core rotation axis can suppress the formation of a Keplerian disk in MHD simulations (e.g., Galli et al., 2006; Mellon and Li, 2008; Li et al., 2011). This may lead to the formation of sources like L1157 (Stephens et al., 2013) and B335 (Maury et al., 2018), which have outflows aligned with the magnetic field, and which have as-of-yet undetectably small disks (≲10 au). However, since it is known that large Keplerian disks form around many protostellar sources, a variety of methods have been proposed to overcome this problem, including the introduction of an initial misalignment between the rotation axis and the magnetic field, which enhances disk formation (e.g., Hennebelle and Ciardi, 2009; Joos et al., 2012; Krumholz et al., 2013; Li et al., 2013), and the consideration of non-ideal MHD effects such as ambipolar diffusion (Dapp et al., 2012; Masson et al., 2016; Tsukamoto et al., 2018), Ohmic dissipation (Dapp et al., 2012; Tomida et al., 2015; Tsukamoto et al., 2018), the Hall effect (Tsukamoto et al., 2015, 2017; Wurster et al., 2018), and magnetic reconnection (Santos-Lima et al., 2012; Li et al., 2014).

Observationally, if very strong magnetic fields were the norm, then the rotational axes of protostellar disks, and the jets and outflows that emanate from them, should all be parallel with the ambient magnetic field. A study of seven low-mass protostellar cores by Chapman et al. (2013) found a correlation between outflows and magnetic fields at ~ 0.1 pc scales. However, the majority of the studies of this type have come to the opposite conclusion. For example, Ménard and Duchêne (2004) found that the optical jets from classical T Tauri stars in the Taurus-Auriga molecular cloud are randomly oriented with respect to the parsec-scale magnetic field observed via background-starlight polarization observations. Targon et al. (2011) obtained a similar result for 28 regions spread over the Galaxy, finding no strong correlations between protostellar jets and the ambient magnetic field. On the ~ 0.1 pc scales of high-mass star-forming cores, Curran and Chrysostomou (2007) and Zhang et al. (2014) used thermal dust polarization observations by the JCMT and the SMA, respectively, to determine that outflows and inferred magnetic fields are randomly aligned. Finally, Hull et al. (2013, 2014) used the 1.3 mm polarization system at CARMA (Hull and Plambeck, 2015) to observe dust polarization toward a sample of low- and high-mass sources, and found that the outflows and ~ 1,000 au-scale magnetic fields in the low-mass sources were randomly aligned. In Figure 4, we compile all of the outflow-versus-magnetic-field angles derivable to date from interferometric observations of low-mass protostellar cores (Girart et al., 1999, 2006, 2008; Rao et al., 2009; Hull et al., 2013, 2014, 2017a,b; Stephens et al., 2013; Cox et al., 2018; Galametz et al., 2018; Harris et al., 2018; Maury et al., 2018; Sadavoy et al., 2018a; Kwon W. et al., under review), and come to the same conclusion: while a few sources have well-aligned outflows and magnetic fields (e.g., those on the very bottom-left of the plot in Figure 4 that are climbing the 0–20° curve, several of which have hourglass-shaped field morphologies; see section 4), overall protostellar outflows and magnetic fields measured at 1,000 au-scales are randomly aligned.

FIGURE 4

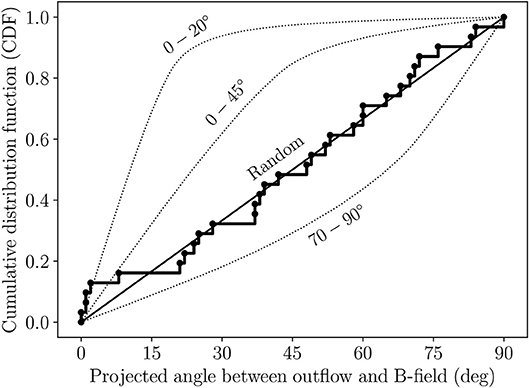
Figure 4. The thick, stepped curve shows the cumulative distribution function (CDF) of the (projected) angles between the bipolar outflows and the mean magnetic-field orientations in the full sample of low-mass protostellar cores observed to date in full polarization with BIMA, the SMA, CARMA, and ALMA. The dotted curves are the CDFs from Monte Carlo simulations where the magnetic fields and outflows are oriented within 20, 45, and 70–90° of one another, respectively. The straight line is the CDF for random orientation. The plot shows that outflows appear to be randomly aligned with magnetic fields in the sample of low-mass sources whose magnetic fields have been observed with ~ 500–1,000 au resolution.

The finding from several studies that magnetic fields and outflows are randomly oriented suggests that most protostars form out of material with a magnetic field that is too weak to maintain a consistent orientation all the way down to the 0.1–10 au scales where outflows are launched. Rather, it seems likely that dynamical effects such as turbulence and infall are more important than the magnetic field when it comes to dictating the ultimate angular-momentum direction at the small (< 1,000 au) scales relevant for the formation of protostellar disks and outflows/jets. This claim is corroborated by the analysis by Lee J. W. Y. et al. (2017) of the synthetic observations (produced using the Dustpol radiative transfer software; Padovani et al., 2012) of two MHD simulations with different initial mass-to-flux ratios (Offner and Chaban, 2017). They concluded that while the protostar that formed in the strong-field case exhibited a correlation between the outflow and the magnetic field, the weaker-field case showed a random orientation. This is most likely because asymmetric accretion from the turbulent envelope stochastically reoriented the disk/outflow during the earliest (Class 0) formation stage, ultimately decoupling the source from the natal magnetic field (see, e.g., simulations by Chen and Ostriker, 2018).

Two non-magnetic studies focused on the alignment of protostellar outflows with respect to the natal filamentary structure in which the sources formed, and on the relative alignment of the outflows from wide (~ 1,000 au) and tight (< 250 au) binary/multiple systems. Both studies used data from the MASSES survey at the SMA (Lee et al., 2015; Stephens et al., 2018). Regarding outflows versus filaments, Stephens et al. (2017a) studied the relative orientation of 57 protostellar outflows in the Perseus molecular cloud (derived from the SMA MASSES data) with the local filamentary structure (derived from Herschel observations), and found that the orientations are consistent with a random distribution. Their results held regardless of protostellar age, multiplicity, or the opacity of the dense core, suggesting that the angular momentum of the protostellar cores and outflow-launching disks are independent of the large-scale structure out of which the protostars are forming. Regarding the orientation of outflows from multiple systems, Lee et al. (2016) used SMA MASSES observations to determine that the outflows from proto-multiple systems in the Perseus molecular cloud are randomly aligned. Offner et al. (2016) followed up with MHD simulations that are consistent with the SMA observations, arguing that multiple systems with randomly oriented angular momenta are likely to have formed from turbulent fragmentation.

The turbulent fragmentation scenario is consistent with recent ALMA observations of multiple systems with misaligned protoplanetary disks (Jensen and Akeson, 2014; Lee J.-E. et al., 2017). However, observations by Tobin et al. (2016a) have found evidence for an alternative theory of multiple formation: disk fragmentation (Kratter et al., 2010). The VLA Nascent Disk and Multiplicity Survey of Perseus Protostars (VANDAM) by Tobin et al. (2016b) found a bimodality in the multiplicity of systems; they argued that the wide multiples are the result of turbulent fragmentation, whereas the tight multiples are the result of disk fragmentation. This latter conclusion was strengthened in a follow-up study by Tobin et al. (2018), who observed a sample of tight binaries from the VANDAM survey with ALMA in both continuum and spectral lines.

Recent work by Galametz et al. (2018) focused on the role of the magnetic field in the formation of multiple systems using an SMA survey of magnetic fields in protostellar cores. They found tantalizing evidence that a large misalignment between the outflow and the magnetic field is found preferentially in protostars with higher rotational energies. This ~ 90° misalignment observed in some objects could thus be due to the winding of the magnetic field lines in the equatorial plane by strong rotation. Furthermore, they found hints that many of those same sources (i.e., those with approximately perpendicular outflows and magnetic fields) are wide multiple sources and/or have large disks, whereas the sources with well aligned magnetic fields and outflows tend to be single objects with small (or undetected) disks at the ~ 500–1,500 au resolution of their observations. The trend of large disks being associated with sources that have misaligned magnetic fields and outflows was also tentatively seen in an analysis of Karl G. Jansky Very Large Array (VLA) observations of Class 0 and I protostars by Segura-Cox et al. (2018). These results suggest that the morphology and dynamical importance of magnetic fields at the scale of the protostellar envelope may significantly impact the outcome of protostellar collapse as well as the formation of disks and multiple systems. Large ALMA surveys in polarization toward binary/multiple systems will shed light on the impact of the magnetic field on multiple formation via both turbulent and disk fragmentation.

2.3. The Importance of the Magnetic Field in Launching Jets and Outflows

Magnetic fields play a critical role in launching and collimating both bipolar outflows and jets from young forming stars (Frank et al., 2014). Several theories exist to explain how outflows and jets are generated, including the “disk wind” theory where an outflow is launched from the magnetized, rotating surface of a disk (Konigl and Pudritz, 2000), and the “X-wind” theory where jets are launched close to the central protostar itself (Shu et al., 2000). Both of these theories require a magnetic field to function, and that magnetic field is expected to have both poloidal (i.e., along the outflow) and toroidal (perpendicular to the outflow) components due to the combination of infall, outflow, and rotational motions present near a forming star. Characterizing the magnetic field in outflows and jets can thus allow us to investigate the origin of outflows in the context of these different theories.

Historically, observations of dust polarization have been used mainly to study the magnetic field morphology in the optically thin dense cores of dust and gas surrounding embedded protostars. With the sensitivity and resolution of ALMA, it is now possible to detect polarized dust emission along the edges of outflow cavities (Hull et al., 2017b; Maury et al., 2018). However, there is not enough dust in the cavity itself (where the outflow has evacuated most of the material) to allow for a detection of the polarized emission. Therefore, in order to probe the magnetic field in the outflowing material, one must turn to observations of spectral-line polarization (see section 1.1.2).

While several studies have focused on SiO maser polarization (e.g., Plambeck et al., 2003), the majority of spectral-line polarization studies toward low-mass forming stars have targeted thermal CO and SiO emission polarized due to the G-K effect. Pioneering CO (J = 2 → 1) polarization observations were performed with BIMA by Girart et al. (1999, 2004), Cortes et al. (2006), and Kwon et al. (2006). So far there has been one detection of SiO (J = 8 → 7) polarization toward the low-mass protostar HH 211, tentatively detected by Lee et al. (2014) using the SMA, and recently confirmed by ALMA observations reported in Lee et al. (2018a): see the bottom panel of Figure 5.

FIGURE 5

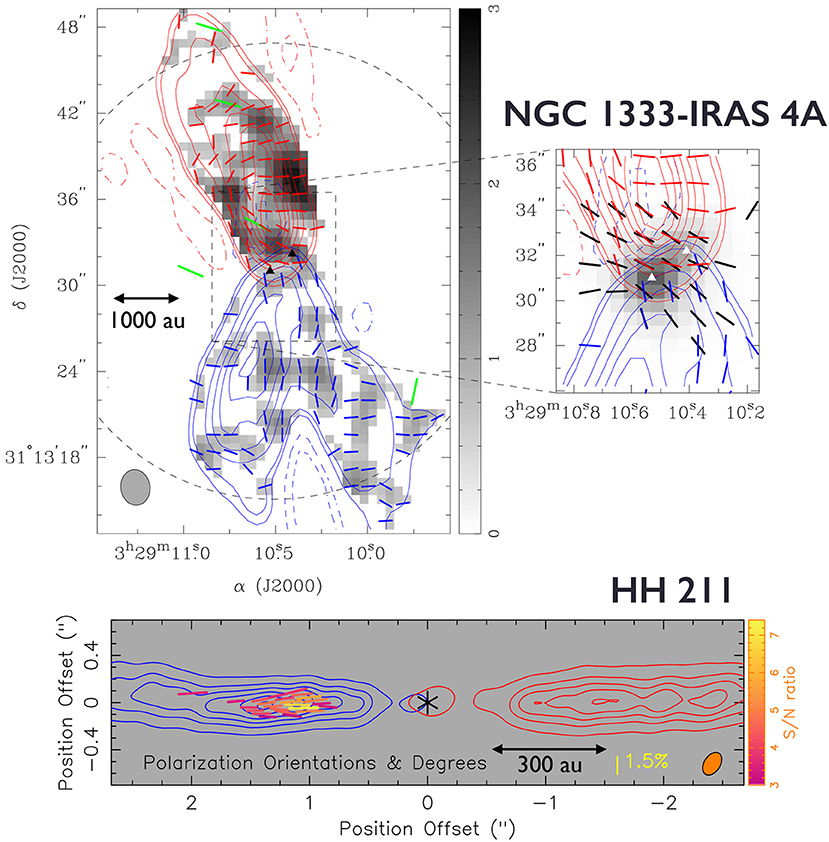
Figure 5. Observations of spectral-line polarization from the G-K effect toward bipolar outflows from low-mass protostellar sources. (Top left) SMA observations of polarization of the CO (J = 3 → 2) line (red and blue line segments) toward NGC 1333-IRAS 4A, adapted from Ching et al. (2016). The grayscale shows the CO (J = 3 → 2) polarized intensity in units of Jy beam⁻¹ km s⁻¹. The authors also compare with CO (J = 2 → 1) BIMA polarization results from Girart et al. (1999), plotted in green. (Top right) Comparison of the SMA CO polarization data with the 870 μm dust polarization map (the black line segments have been rotated by 90° to reflect the inferred magnetic field direction). (Bottom) SMA observations of polarization in the SiO (J = 8 → 7) line, adapted from Lee et al. (2018a). The colors of the line segments indicate different levels of significance in the polarized intensity; the lengths of the segments are scaled to the polarization fraction. The top panel was reproduced with permission from the AAS. The bottom panel was reproduced, with modifications, in accordance with the Creative Commons Attribution 4.0 International License (creativecommons.org/licenses/by/4.0).

The BIMA observations of CO (J = 2 → 1) polarization toward the iconic Class 0 protostar NGC 1333-IRAS 4A by Girart et al. (1999) were the first interferometric detection of the G-K effect. Toward the central core, these observations are consistent with the magnetic field inferred from polarized dust emission. The observations by Girart et al. were followed up with the SMA by Ching et al. (2016) in the higher-energy transition CO (J = 3 → 2). Ching et al. found good consistency between their observations and those by Girart et al. in the inner regions of the outflow where the polarization detections overlap. These SMA observations, shown in Figure 5 (top panel), allowed the authors to come to a number of conclusions. First was the fact that the data are consistent with a magnetic field in IRAS 4A that is poloidal at the base of the outflows (there are two outflows, each launched by a member of the embedded binary) and toroidally wrapped up further out in the outflow cavity. This observation, combined with the coexistence of a low-velocity outflow and a high-velocity jet in the source, led the authors to conclude that the outflows in IRAS 4A are most likely driven by MHD winds from the surface of a rotating disk.

3. Magnetic Fields in High-Mass Star Formation

3.1. Magnetic Field Measurements at Core Scales

The first pioneering high-resolution observations of linearly polarized continuum and spectral-line emission toward high-mass star-forming regions were made with the BIMA interferometer. Rao et al. (1998) reported the first interferometric polarization observations of a high-mass star-forming region, toward Orion KL. They detected linear polarization at both 3.3 and 1.3 mm in the BIMA data at a resolution of 1,000–3,000 au, revealing abrupt changes in the magnetic field orientations among the continuum emission peaks. This chaotic distribution is in contrast to the uniform magnetic field topology in the lower resolution polarization maps revealed by single dish telescopes (e.g., Schleuning, 1998; Houde et al., 2004; Pattle et al., 2017; Ward-Thompson et al., 2017).

Shortly after the Orion KL study, Lai et al. (2001) reported polarization observations of W51 e1 and e2 in the 1.3 mm continuum emission using BIMA. Later, Tang et al. (2009b) and Koch et al. (2018) published results toward the same source using the SMA and ALMA, respectively. W51 is a cloud complex that harbors massive star formation at various evolutionary stages (Ginsburg et al., 2015; Saral et al., 2017). W51 east hosts an active star-forming molecular clump with as many as 10 compact radio continuum sources over the 0.2 pc projected area of sources e1 and e2 (Ginsburg et al., 2016). Zhang and Ho (1997) reported inverse P-Cygni profile in the e2 core in the NH₃ (J,K) = (1,1), (2,2), and (3,3) spectral lines, consistent with infall motions of the dense gas. Lai et al. (2001) detected linear polarization in the continuum emission in the e2 and e8 cores at a resolution of 14,000 au using BIMA and found that the inferred plane-of-sky components of the magnetic fields are mostly uniform, with an average position angle of 113° in the e2 and 105° in the e8 core. Using the DCF method, the authors estimated a magnetic field strength of 0.8 and 1.3 mG in the e2 and e8 cores, respectively.

More sensitive observations of continuum emission at 870 μm toward W51 using the SMA revealed a non-uniform magnetic field morphology at a higher resolution of 3,300 au (Tang et al., 2009b). Tang et al. explored the possible reasons for the different distributions between the BIMA and the SMA images, finding that interferometric spatial filtering is the most likely cause. This spatial filtering by interferometers can be an advantage, as it allows us to probe magnetic fields at different spatial scales, thus revealing the dynamical role of the magnetic field across the many spatial scales relevant to the star-formation process.

Figure 6 shows the magnetic field maps obtained by the SMA and later by ALMA at various spatial resolutions toward W51 e2 and e8. The figure shows a pinched, hourglass morphology in the e2 core at a resolution of 3,300 au (the top-middle panel), and significantly more substructures at a resolution of 1,500 au (top-right panel). Koch et al. (2018) speculate that the additional substructure in the magnetic field is the result of gravitational collapse at high densities that pulls and/or bends the field lines.

FIGURE 6

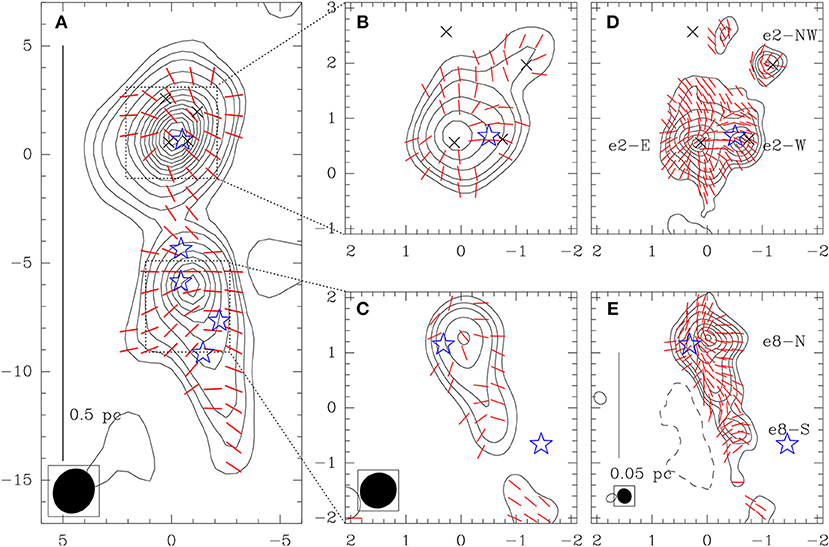
Figure 6. Magnetic fields (red line segments) in W51 e2 and e8 obtained from the SMA and ALMA that exhibit more substructure at higher angular resolution. (A) SMA observations at 870 μm probing large scales at a resolution of 2″ (~ 10,000 au). (B,C) SMA observations with a resolution of 0.^′′7 (~ 3,500 au) at 870 μm. (D,E) ALMA observations at 1.3 mm with a resolution of 0.^′′26 (~ 1,330 au). Contours are Stokes I dust continuum intensity at levels of 3, 6, 10, 20, 35, 50, 65, 80, 95…times 75 mJy beam⁻¹ in (A), 60 mJy beam⁻¹ in (B,C), and 6 mJy beam⁻¹ in (D,E). × symbols in (A,B,D) mark the known continuum sources W51 e2-E, e2-W, e2-NW, and e2-N. Star symbols indicate known ultra-compact HII (UCHII) regions. Synthesized beams are shown as ellipses at the lower-left corner of (A,C,E). Adapted from Koch et al. (2018). Reproduced with permission from the AAS.

One of the key questions in the fields of magnetized low- and high-mass star formation is whether the magnetic field is dynamically important relative to turbulence and gravity. Koch et al. (2010) applied the two-point correlation function technique (Hildebrand et al., 2009) and found a ratio of turbulent to magnetic energy ranging from 0.7 to 1.27 at scales ranging from ~ 15,000 au down to ~ 500 au. Koch et al. (2012) proposed a polarization-intensity-gradient technique that can be used to derive a distribution of magnetic field strength in a given source (see section 1.3.1). Applying the technique to the polarization map of W51 e2, Koch et al. (2012) found a field strength of 7.7 mG. This value is in agreement with the estimate by Tang et al. (2009b), who derived the field strength from the SMA polarization observations. However, it is higher than that found by Lai et al. (2001), who used lower-resolution BIMA polarization observations probing larger spatial scales. The different values reported by Lai et al. (2001) and Koch et al. (2012) can be explained by the fact that the magnetic field strength increases toward smaller spatial scales where the gas density is higher.

Besides W51, another region of massive star formation whose magnetic field has been well studied is DR 21(OH) and its neighboring regions along the DR 21 filament (Lai et al., 2003; Cortes et al., 2005; Girart et al., 2013; Hull et al., 2014; Houde et al., 2016; Ching et al., 2017, 2018). DR 21(OH) was first imaged in linear polarization using BIMA in the CO (J = 2 → 1) transition and 1.3 mm continuum emission (Lai et al., 2003). These results were followed up in the CO (J = 1 → 0) transition and 3.4 mm continuum emission using BIMA (Cortes et al., 2005); in the CO (J = 3 → 2) transition and 870 μm continuum emission using the SMA (Girart et al., 2013; Zhang et al., 2014); and in the CO (J = 2 → 1) transition and 1.3 mm continuum emission with CARMA (Hull et al., 2014; Houde et al., 2016). Strong polarization was detected in both 1.3 mm and 870 μm continuum emission. The field strength derived using the two-point correlation function is 2.1 mG, yielding a mass-to-flux ratio of 6 × the critical value (Girart et al., 2013). The field strength is consistent with the value reported by Lai et al. (2003) using the DCF method. Ching et al. (2017) imaged five additional regions along the DR 21 filament using the SMA. The magnetic fields in all six cores display large dispersions, in contrast to the ordered magnetic field obtained with the JCMT at lower angular resolution (Vallée and Fiege, 2006; Matthews et al., 2009). The field strength derived from the DCF method ranges from 0.4 to 1.7 mG among the five cores, with mass-to-flux ratios from 1 to 4.3 × the critical value.

As was the case in many low-mass star formation studies (see section 2.1), significant effort has been devoted to the search for pinched, hourglass-shaped magnetic field morphologies in massive dense cores. So far, the best examples of hourglass-shaped magnetic fields in massive dense cores are G31.41+0.31 and G240.31+0.07 (Girart et al., 2009; Qiu et al., 2014). G31.41+0.31 is a 500 M_⊙ hot molecular core with a luminosity of 3 × 10⁵ L_⊙. Observed at resolutions as high as 2,400 au, the dense core does not appear to fragment in the dust continuum emission. However, sensitive observations with the VLA at 1.3 and 0.7 cm wavelength revealed two compact continuum objects with a projected separation of 1,300 au (Cesaroni et al., 2010). The dense core exhibits infall motions as well as rotation over a scale of 14,000 au. Magnetic fields inferred from the 870 μm continuum emission reveal a distribution that is pinched along the major axis of the flattened core (Girart et al., 2009). No molecular outflows have been definitively identified in this region. Observations in the CO (J = 2 → 1) transition found a velocity gradient along the major axis of the flattened core (Cesaroni et al., 2011); however, it is not clear if the gradient represents an outflow, or if it is due to core rotation. The strength of the plane-of-sky component of the magnetic field is 9.7 mG, implying a turbulence-to-magnetic-energy ratio of 0.35. The rotational velocity within the core inferred from spectral-line observations of high-density tracers indicates significant magnetic braking. G31.41+0.31 is a case where the magnetic field dominates the turbulence and the dynamics in the system.

Similar to G31.41+0.31, G240.31+0.07 is a massive star-forming region with an hourglass magnetic field morphology (Qiu et al., 2014). As shown in Figure 7, the dust continuum emission reveals a flattened structure extended along the northeast–southwest direction that has fragmented into three cores, each harboring at least one massive young star. A wide-angle, bipolar outflow is seen in the CO emission (Qiu et al., 2009), with the outflow axis parallel to the minor axis of the flattened dense core. Polarization observations at 870 μm reveal a magnetic field topology pinched along the major axis of the core. The magnetic field strength estimated from the DCF method is 1.2 mG, with a mass-to-flux ratio of 1.2 × the critical value, and a turbulent-to-magnetic-energy ratio of 0.4. G240.31+0.07 is another clear example of a massive star-forming core in which the magnetic field dominates the turbulence and the dynamics in the system.

FIGURE 7

Figure 7. Magnetic field (red line segments in the right panel) in the high-mass star formation region G240.31+0.07 inferred from dust continuum polarization at 870 μm with the SMA (Qiu et al., 2014; Zhang et al., 2014). The left panel presents an overview of the region in a three-color composite of Spitzer IRAC images in the 3.6 μm (green), 4.5 μm (blue), and 8.0 μm (red) bands; the middle panel shows a wide-angle bipolar molecular outflow in the CO (J = 2 → 1) line (Qiu et al., 2009). The star symbols indicate the known continuum peaks. Reproduced with permission from the AAS.

So far, the overwhelming majority of publications on interferometric observations of magnetic fields are studies of individual objects. The improvement in sensitivity with the advent of the CARMA and SMA polarimeters led to surveys of small—but significantly larger—samples of objects. See section 2.1 for a discussion of the TADPOL survey of predominantly low-mass sources by Hull et al. (2014). On the high-mass end, Zhang et al. (2014) reported polarization detections in 14 massive star-forming clumps from a survey of 21 star forming regions. This effort significantly increased the number of clumps with magnetic fields detections and consequently enabled statistical analyses of the ensemble behavior of magnetic fields in massive star-forming regions. To date, there are approximately 24 unique high-mass star forming clumps that have been observed in polarization with interferometers. They are Orion KL, NGC 2071, W3, W3(OH), DR 21(OH), DR 21 filament, G192, G30.79, NGC 6334 I/In/IV/V, W51 e and N, IRAS 18306, IRAS 18089, W43, NGC 7538, G5.89, NGC 2264C1, G34.4, G35.2N, G31.41+0.31, and G240.31+0.07 (Rao et al., 1998; Lai et al., 2001, 2003; Cortes and Crutcher, 2006; Cortes et al., 2006, 2008, 2016; Girart et al., 2009, 2013; Tang et al., 2009a,b, 2010; Beuther et al., 2010; Chen et al., 2012; Liu et al., 2013; Qiu et al., 2013, 2014; Frau et al., 2014; Hull et al., 2014; Sridharan et al., 2014; Wright et al., 2014; Zhang et al., 2014; Li et al., 2015; Houde et al., 2016; Ching et al., 2017; Juárez et al., 2017; Koch et al., 2018) Magnetic fields toward these sources display diverse topologies. In sections 3.2, 3.3, 3.4, and 4 we discuss findings and interesting trends from the statistical analysis of this sample. While the analysis represents a significant advance in the study of the role of the magnetic field in high-mass star formation, the limitations and biases in the sample used in the analysis cannot be overlooked. One of the most significant limitations is that non-detections are not included in the statistics. The advent of ALMA will increase the size of the sample drastically, enabling significantly more robust analysis within the next decade.

3.2. Outflow—Core Magnetic Field Connection

Linear polarization from CO rotational transitions (i.e., from the G-K effect) probes magnetic fields in molecular gas with densities from 10² to 10³ cm⁻³. This can be an effective tool for tracing magnetic fields in protostellar outflows. In the context of high-mass star formation, Lai et al. (2003) reported the first detection of linear polarization in the CO (J = 2 → 1) transition in DR 21(OH). The inferred magnetic field orientation is in the east–west direction, aligned with the major axis of the CO outflows. Subsequent polarimetric observations in the CO (J = 1 → 0) transition by Cortes et al. (2005) found linear polarization perpendicular to that of the CO (J = 2 → 1) transition. While this disagreement may be reconciled by anisotropy in the CO optical depth and external radiation field (see section 1.1.2), it highlights the difficulty of interpreting spectral-line polarization from the G-K effect. Finally, Beuther et al. (2010) reported detections of spectral-line polarization in the CO (J = 3 → 2) transition in IRAS 18089-1732. Using the DCF method, they derived a magnetic field strength of 28 μG. A similar field strength of 10 μG is reported in DR 21(OH) by Cortes et al. (2005).

Despite the early success in detecting spectral-line polarization primarily in DR 21(OH), very few protostellar sources have shown detectable spectral-line linear polarization since those early results. In the survey of 14 high-mass protostellar clumps by Zhang et al. (2014), only DR 21(OH) had detectable polarization in the CO (J = 3 → 2) transition (Girart et al., 2013). The limited sensitivity of the SMA may be a contributing factor to these non-detections. Furthermore, the CO emission is typically spatially extended, which presents an additional challenge when imaging linear polarization, since Stokes Q and U can be either positive or negative, and a lack of short-spacing information in sparsely sampled interferometric data can produce negative emission that may be confused with the polarization signal in Stokes Q and U. Both factors are mitigated by ALMA, which provides significant improvements in sensitivity and imaging fidelity over BIMA, CARMA, and the SMA.

Probing magnetic fields in accretion disks around high-mass protostars is challenging in two regards. First, extremely high angular resolution observations are required to achieve the ~ 100 au linear scales of a disk at a typical source distance of several kpc. Second, at the typical high densities and optical depths in these disks, the polarized emission may be contaminated (and sometimes dominated) by self-scattering of large dust grains (see section 5). For example, Girart et al. (2018) observed polarized emission from the disk associated with the radio jet HH 80-81. These deep ALMA observations in the 1.14 mm continuum emission spatially resolved a flattened disk with a radius of 291 au. The disk is partially optically thick and its polarized emission appears to be dominated by self-scattering of large dust grains.

In the absence of magnetic field information in protostellar outflows and disks, the comparison of magnetic fields in cores with outflow axes offers an alternative to assess the importance of magnetic fields in the formation of disks and outflows in high-mass systems. As discussed in section 2.1, when collapsing to form stars, strongly magnetized cores are expected to form a disk and outflow system with the major axis of the outflow parallel to the magnetic field. Zhang et al. (2014) compared outflow axes with the plane-of-the-sky component of magnetic fields in cores from which the outflows originate. They found a slight preference around 0° and 90° in angles between the magnetic field and the outflow axis. However, due to the small sample size, the data are consistent with a random orientation of magnetic fields and outflows. This lack of correlation, if confirmed by more statistically significant samples, suggests that angular momentum in accretion disks is not dictated by the orientation of the magnetic field in the cores. The dynamical importance of the magnetic field thus appears to weaken relative to gravity and angular momentum from the core to the disk scales.

3.3. Fragmentation and Cluster Formation

The clustering nature of massive stars implies that there must be considerable fragmentation in parsec-scale molecular clumps in order to produce a cluster of stars. Gravity, turbulence, magnetic fields, and stellar feedback all influence fragmentation and the outcome of cluster formation. The dynamical role of the magnetic field during the fragmentation of molecular clumps can be assessed if the magnetic field strength is measured directly. As mentioned in section 1.2, this can be achieved by observing circular polarization from the Zeeman effect. While observations of the Zeeman effect have been carried in HI and OH line emission using the VLA (Crutcher, 2012; Crutcher and Kemball, 2019⁷), these observations probe a low-density medium that may not be directly involved in gravitational collapse. There are no reported interferometric observations of the Zeeman effect in dense molecular gas, although ALMA is likely to reshape this field once precise measurements of circular polarization become available to the user community. Future interferometric observations of the Zeeman effect (measuring the line-of-sight magnetic field), when combined with linear dust and spectral-line polarization observations (measuring the plane-of-sky field), will allow much more robust estimates of the total magnetic field strengths in star-forming regions.

A powerful indirect method that can be used to assess the dynamical role of magnetic fields in protocluster formation is the analysis of the distribution of magnetic fields within cluster-forming molecular clumps. Numerical simulations of turbulent, magnetized molecular clouds offer clues about magnetic field topologies in strong and weak field regimes. When the magnetic field is strong relative to turbulence, the field is less disturbed and appears to be ordered (e.g., Ostriker et al., 2001).

Observationally, such a study becomes meaningful only when a statistically significant sample is involved. Zhang et al. (2014) compared dust polarization in dense cores probed by the SMA with the polarization in the parental molecular clumps observed by single-dish telescopes in a sample of 14 high-mass star forming regions; the results show a bimodal distribution in polarization angles. As shown in Figure 8, magnetic fields on dense-core scales are not randomly distributed, but are either parallel or perpendicular to the field orientations in their parental clumps. A later study of a larger sample of 50 primarily high-mass sources by Koch et al. (2014) compared the magnetic field orientation with the gradient of the total dust emission and came to the same conclusion. These findings indicate that the magnetic fields are dynamically important in cluster-forming clumps, and that the field is strong enough on the clump scale to channel the material along the field lines into dense cores during the gravitational collapse. While Hull et al. (2014) found hints of consistency in the magnetic field orientation from ~ 0.1 pc to ~ 1,000 au scales in a few low-mass sources (see section 2.1), the results at the ~ 1–0.1 pc scales from Koch et al. (2014) and Zhang et al. (2014) are much more significant, suggesting that the magnetic field may be more dynamically important at parsec scales.

FIGURE 8

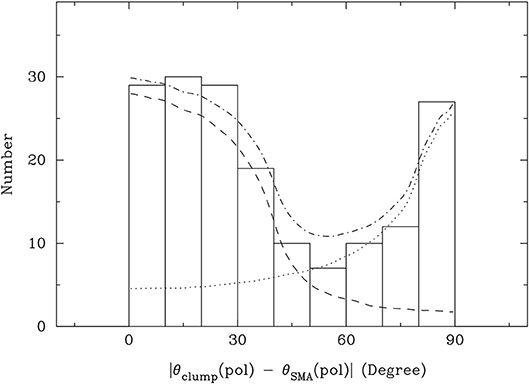
Figure 8. The distribution of polarization angles in dense cores with respect to polarization angles of their parental clumps. The dashed line represents the probability distribution of the plane-of-the-sky-projected orientations of pairs of vectors with 0−40° opening angles randomly oriented in space. The dotted line represents the probability distribution where the vectors are preferentially perpendicular, with 80−90° opening angles. The dashed-dotted line represents the contributions from the two distributions. Adapted from Zhang et al. (2014). Figures reproduced with permission from the AAS.

3.4. Virial Equilibrium in Massive Cores and Cluster Formation

An essential component of the classical view of star formation is that dense cores should be in a state of an approximate virial equilibrium (Larson, 1981; Shu et al., 1987; McKee and Tan, 2003). However, there is increasing evidence from recent observations that cores forming high-mass protostars may not be in virial equilibrium. Pillai et al. (2011) carried out a stability analysis in two infrared dark clouds (IRDCs) and found that the virial parameter α_vir, defined as the ratio between the virial mass M_Virial and the gas mass M_gas, is typically between 0.1 to 0.3. These results are corroborated by Kauffmann et al. (2013), who compiled a large sample of massive clumps from surveys and found that a significant fraction of them have virial parameters ≪ 2, where 2 is the value expected from a pressure confined, self-gravitating Bonnor-Ebert sphere. More recently, Traficante et al. (2018) pointed out that the virial mass can be underestimated because the spectral line emission of a tracer molecule preferentially probes sections of a cloud with gas densities above the critical density of the line transition. This effect may result in an underestimate of the observed line width, and hence lead to a small virial parameter. However, since the effective excitation density of a line transition is typically lower than the critical density due to radiative trapping of photons when the optical depth is non-negligible, this effect may not be as significant. For example, many of the virial analyses in the literature use the NH₃ and N₂H⁺ lines, which often exhibit consistent line widths despite having critical densities that differ by more than a factor of 5.

These small virial parameters appear to challenge the picture of star formation in which gas evolves in a state of equilibrium. However, the virial analyses discussed above do not include contributions from magnetic fields, which may provide significant support in dense cores. Frau et al. (2014) carried out continuum polarization measurements of NGC 7538 with the SMA and found a magnetic field strength of 2.3–2.6 mG in the region. Frau et al. also performed a detailed energetics comparison of the gravitational potential energy, turbulent support, thermal pressure, and magnetic support. Among the 13 dense cores analyzed, the magnetic support amounts to 0.2 to 2.4 × the combined effect from turbulent and thermal pressure. More than half (eight out of 14) of the cores have magnetic support comparable to the turbulent and thermal support. In addition, the virial parameters including the magnetic support vary from 0.1 in the central region where star formation takes place to 8 in cores that are influenced significantly by molecular outflows.

The studies of NGC 7538 by Frau et al. (2014) and Wright et al. (2014) demonstrate that magnetic fields can indeed be a significant contributor to the support of dense cores. Such an analysis should be extended to high-mass star-forming regions at earlier evolutionary stages when stellar feedback has not significantly altered the initial physical conditions. To that end, Pillai et al. (2011) Zhang et al. (2015) Ohashi et al. (2016), Sanhueza et al. (2017), and Lu et al. (2018) performed virial analyses in high-mass star forming regions prior to the development of strong HII regions. The interferometric observations allowed the identification of structures < 0.1 pc in size within massive clumps. Figure 9 presents a comparison of the virial mass and the gas mass for structures identified in 12 high-mass star forming regions (Pillai et al., 2011; Zhang et al., 2015; Ohashi et al., 2016; Lu et al., 2018). The virial mass is computed as

$\begin{array}{ll}{M}_{\mathrm{\text{Virial}}}=\frac{3kR{\sigma }_v^2}{G},& (4)\end{array}$

where σ_v is the line-of-sight velocity dispersion due to both non-thermal and thermal broadening, R is the radius, and G the gravitational constant. $k=\frac{5-2a}{3-a}$ is a correction factor related to the density profile ρ∝r^−a. We assume a constant density in the structure, i.e., a = 0, which leads to the maximum value in the correction factor (k = 5/3) and thus the maximum virial mass. The gas mass is derived from the dust continuum emission (see section 1.4). Figure 9 reveals that the dense gas structures in these high-mass star forming regions have virial parameters < 2. Furthermore, a large fraction of the dense gas structures have virial parameters ≪ 2. Since there are no direct measurements of magnetic fields for this sample, we compute the magnetic field required to increase the virial parameter from 0.5 to 1.0. The magnetic virial mass (Hennebelle and Chabrier, 2008) is computed as

$\begin{array}{ll}{M}_{\mathrm{\text{Mag}}}=\frac{5R{\sigma }_A^2}{6G},& (5)\end{array}$

where ${\sigma }_A=\frac{B}{\sqrt{4\pi \rho }}$ is the Alfvénic velocity corresponding to a magnetic field strength B and density ρ. We compute the magnetic field strengths when M_Mag = M_Virial = 0.5M_gas. Assuming a representative gas mass M_gas and radius R for the clumps (M_gas = 1,000 M_⊙, R = 0.5 pc), cores (M_gas = 50 M_⊙, R = 0.05 pc), and condensations (M_gas = 5 M_⊙, R = 0.005 pc), we find required magnetic field strengths of 0.29, 1.46, and 14.4 mG, respectively. Under these conditions, the virial parameters would be 0.5 without the contribution of magnetic fields, and would increase to 1 after the inclusion of magnetic fields. The required field strengths are in broad agreement with typical literature values of magnetic fields that were derived using the DCF method based on polarization observations of massive star-forming regions.

FIGURE 9

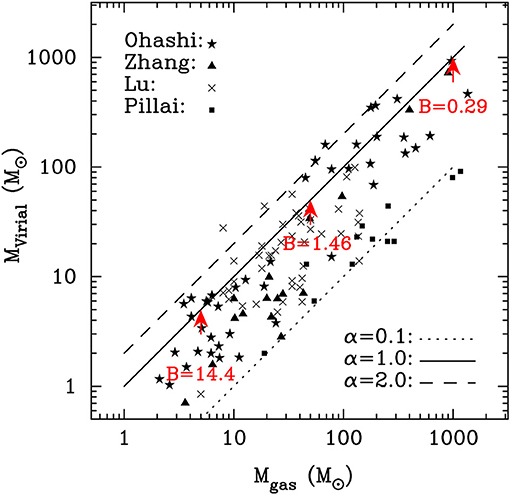
Figure 9. Virial mass M_Virial vs. gas mass M_gas for clumps and cores in 12 high-mass star forming regions. The data were taken from Pillai et al. (2011), Zhang et al. (2015), Ohashi et al. (2016) and Lu et al. (2018). The virial mass includes contributions from thermal and non-thermal line widths. The gas mass was derived from dust continuum emission. The dashed, solid, and dotted lines denote virial parameters α_vir = M_Virial/M_gas of 2, 1, and 0.1, respectively. The majority of the data points have α_vir < 1, indicating that clumps and cores are far from virial equilibrium when contributions from magnetic fields are not included. The red arrows indicate the strength of the magnetic field (in mG) that are required to increase α_vir from 0.5 to 1.0 (see section 3.4).

Recent measurements of the thermodynamic properties in high-mass star-forming regions reveal small virial parameters that appear to challenge the assumption of equilibrium star formation. However, a lack of magnetic field measurements in these same regions leaves open the possibility of virialized star formation, since the field strength of a fraction of a mG to several mG could bring the dense gas close to a state of equilibrium. With the advent of ALMA, we expect significant progress to be made on this vital question in high-mass star formation as more observations of both spectral lines and polarization are carried out over the coming years.

4. Constraining Strong-Field Star Formation With Statistics of Hourglass-Shaped Magnetic Fields

There are approximately 32 unique interferometric observations of low-mass (Class 0, 0/I, or I) star-forming cores exhibiting significant polarization detections that are not obviously dominated by dust scattering. They are L1448 IRS 2, L1448N(B), L1448C, NGC 1333-IRAS 2A, SVS 13A, SVS 13B, NGC 1333-IRAS 4A, Per-emb-21, NGC 1333-IRAS 7, NGC 1333-IRAS 4B, IRAS 03282+3035, IRAS 03292+3039, B1-c, B1-b, HH 211 mm, HH797, L1551 NE, NGC 2024 FIR 5, OMC3-MMS5, OMC3-MMS6, OMC2-FIR3, OMC2-FIR4, VLA 1623, IRAS 16293A, IRAS 16293B, Ser-emb 8, Ser-emb 8 (N), Serpens SMM1-a, Serpens SMM1-b, B335, L1157, and CB 230 (Girart et al., 1999, 2006; Lai et al., 2002; Rao et al., 2009; Alves et al., 2011; Hull et al., 2013, 2014, 2017a,b; Stephens et al., 2013; Segura-Cox et al., 2015; Cox et al., 2018; Galametz et al., 2018; Harris et al., 2018; Maury et al., 2018; Sadavoy et al., 2018a,b; Kwon W. et al., under review).

Among them, NGC 1333-IRAS 4A, IRAS 16293A, L1157, NGC 2024 FIR 5, OMC3 MMS 6, L1448 IRS 2, B335, VLA 1623, and B1-c (9/32 ≈ 28%) exhibit hourglass morphologies, consistent with magnetically dominant star formation (Girart et al., 1999, 2006; Lai et al., 2002; Rao et al., 2009; Alves et al., 2011; Stephens et al., 2013; Hull et al., 2014; Cox et al., 2018; Galametz et al., 2018; Maury et al., 2018; Sadavoy et al., 2018a; Kwon W. et al., under review).

On the high-mass side, there are 24 unique high-mass star forming clumps observed in polarization with interferometers. They are Orion KL, NGC 2071, W3, W3(OH), DR 21(OH), DR 21 filament, G192, G30.79, NGC 6334 I/In/IV/V, W51 e and N, IRAS 18306, IRAS 18089, W43, NGC 7538, G5.89, NGC 2264C1, G34.43+0.24, G35.2N, G31.41+0.31, and G240.31+0.07 (Rao et al., 1998; Lai et al., 2001, 2003; Cortes and Crutcher, 2006; Cortes et al., 2006, 2008, 2016; Girart et al., 2009, 2013; Tang et al., 2009a,b, 2010; Beuther et al., 2010; Chen et al., 2012; Liu et al., 2013; Qiu et al., 2013, 2014; Frau et al., 2014; Hull et al., 2014; Sridharan et al., 2014; Wright et al., 2014; Zhang et al., 2014; Li et al., 2015; Houde et al., 2016; Ching et al., 2017; Juárez et al., 2017; Koch et al., 2018).

Of these, G31.41+0.31, G240.31+0.07, NGC 6334 I and In, and W51 e2 (5/24 ≈ 21%) exhibit hourglass magnetic field configurations (Girart et al., 2009; Tang et al., 2009a; Qiu et al., 2014; Li et al., 2015).

A pinched/hourglass-shaped magnetic field configuration can yield a range of magnetic-field morphologies when projected in the plane of the sky (Frau et al., 2011). When the main axis of the system is aligned with the line of sight, the plane-of-sky component of the field is oriented radially outward. This scenario was proposed by Girart et al. (2013) to explain the magnetic field topology in DR 21(OH). Among the low- and high-mass objects with robust detections of polarization (and thus inferred magnetic fields), 28% of the low-mass sources and 21% of the high-mass sources exhibit hourglass configurations. Assuming that the sample is randomly oriented in three dimensions, the probability than an hourglass axis will be oriented within 30° of the line of sight is ~ 13% (Frau et al., 2011 show that an angle closer to the line of sight than ~ 30° yields a mostly radial pattern). Therefore, the majority of the objects (~ 87%) should display an hourglass shape if the variations in magnetic field morphologies were solely due to projection effects.

The fact that only a small fraction of the objects exhibit hourglass morphologies suggests that the scenario of magnetically dominant core collapse is not the predominant mode of low- or high-mass star formation. However, we should note that when taking into account the projection effect, the fraction of the detected hourglass reaches 28/87% ≈1/3 for low-mass and 21/87% ≈1/4 for high-mass sources. Such fractions are not negligible, and are even more significant considering the various environmental and dynamical differences between sources, as well as the observational limitations that may hinder the detection of an hourglass—in particular the sensitivity and dynamic range limitations of the pre-ALMA interferometers.

Of the sources observed by ALMA that clearly lack hourglass magnetic field morphologies, only one so far (Ser-emb 8 in Hull et al., 2017a; see Figure 3) shows a truly chaotic morphology, presumably having been influenced by turbulence and infall. However, the few ALMA polarization observations published to date have shown more examples of magnetic fields that seem to have been shaped by bipolar outflows. These observations are challenging to interpret, as magnetic fields aligned with the walls of an outflow cavity can look quite similar to an hourglass when observed with low resolution. Thus, future studies will need to carefully consider how to determine which “hourglasses” are preserved from the natal collapse phase, such as in NGC 1333-IRAS 4A, where at ~ 1,000 au scales the hourglass appears to be unperturbed by the two outflows emanating at different angles from the embedded binary (Girart et al., 2006); vs. which are caused by outflow/jet feedback, such as in Serpens SMM1 (Hull et al., 2017b) and B335 (Maury et al., 2018).

We further caution that the above values are lower limits that are limited by telescope resolution: i.e., in the high-mass case, we consider each source as unique, despite the fact that each clump is likely to have more than one protostellar object. This is even true in the low-mass case: for example, SMA observations were able to distinguish the magnetic fields in SVS 13A and B, whereas CARMA observations were not; and ALMA observations were able to map the magnetic fields in Serpens SMM1-a and b separately, whereas CARMA and SMA observations were not. Finally, and perhaps most important, the number of objects observed with interferometers remains small: observations by ALMA are likely to increase the sample size significantly in the near future, enabling studies that will establish far better statistical constraints.

5. Polarization From Dust Scattering

While polarized emission from dust scattering is independent of the magnetic field, we briefly mention it here because this young, quickly growing subfield emerged from studies that were attempting to make resolved maps of the magnetic field in protoplanetary disks, which is one of the longstanding goals of disk- and star-formation studies. Rao et al. (2014) reported a tentative detection of a toroidally wrapped magnetic field in the Class 0 protostar IRAS 16293B at ~ 75 au resolution using the SMA. However, on the whole, pre-ALMA full polarization observations of disks did not have the sensitivity or the resolution necessary to make well resolved maps of low-level (≲ 1%) polarized dust emission (Hughes et al., 2009, 2013).

Around the same time that ALMA started producing polarization results, several theoretical studies suggested that polarized (sub)millimeter-wave emission from protoplanetary disks could be caused by the self-scattering of emission from (sub)millimeter-sized dust grains (Kataoka et al., 2015, 2016a; Pohl et al., 2016; Yang et al., 2016a,b), consistent with previous work by Cho and Lazarian (2007). Kataoka et al. (2016a) and Yang et al. (2016b) explained the 1.3 mm CARMA polarization observations by Stephens et al. (2014) of the Class I/II source HL Tau in the context of this self-scattering mechanism. Self-scattering can also explain the polarization pattern observed in the Class II protoplanetary disk IM Lup in 870 μm ALMA observations by Hull et al. (2018b), and similar observations of HD 163296 by Dent et al. (2019).

The situation became even more complex when Tazaki et al. (2017) proposed yet another mechanism that can cause polarization in disks: dust grains whose minor axes are aligned with the gradient in the dust emission (this work is rooted in the radiative torque model by Lazarian, 2007). This mechanism, which is sometimes referred to as “k-RATs” (i.e., where k is the orientation of the gradient in the dust emission; see also Footnote 3), is different from self-scattering by dust grains. However, similar to self-scattering, it is independent of any magnetic field that might be in the disk. Polarization from k-RATs, which has a morphology that is azimuthal, is broadly consistent with 3 mm ALMA observations of polarization in the HL Tau disk (Kataoka et al., 2017), although Yang et al. (2019) found that their k-RAT model did not reproduce the data when examined in detail. The transition from possible k-RAT alignment at long (3 mm) wavelengths to scattering at short (870 μm) wavelengths was shown clearly by Stephens et al. (2017b), who reported high-resolution ALMA polarization results at 870 μm and 1.3 mm, complementing the 3 mm observations reported by Kataoka et al. (2017). The intermediate-wavelength 1.3 mm data exhibit a morphology consistent with roughly equal contributions of self-scattering and k-RATs.

Other recent results have interpretations that are not as clear. These include observations of the edge-on HH 111 and HH 212 disks (Lee et al., 2018b), the high-mass protostellar disk Cepheus A HW2 (Fernández-López et al., 2016), and the transition disk HD 142527 (Kataoka et al., 2016b; Ohashi et al., 2018); the polarized emission from these objects may be caused by either scattering or magnetically aligned grains (B-RATs). Observations of the low-mass disks CW Tau and DG Tau (Bacciotti et al., 2018) and the massive GGD27 MM1 disk (Girart et al., 2018) associated with the iconic HH 80-81 radio jet show polarization that may be caused by dust self-scattering and/or k-RATs. Polarization observations of a number of embedded Class 0 protostars by Segura-Cox et al. (2015), Cox et al. (2018), Harris et al. (2018), Sadavoy et al. (2018a,b), and Takahashi et al. (2019) sometimes show signs of scattering in the inner regions of sources and magnetic alignment in the outer regions. Finally, Alves et al. (2018) reported ~ 30 au-resolution observations of the Class I binary source BHB07-11, which exhibits consistent polarization patterns at 3 mm, 1.3 mm, and 850 μm. They argue that the polarized emission most likely arises from magnetically aligned dust grains.

We emphasize that studies of (sub)millimeter polarization from disks are in their infancy. More observations and more mature, detailed models are necessary before we will be able to determine whether there is, in fact, any contribution from magnetic fields in the polarized emission from disks around young forming stars.

6. Summary

The steady improvement in telescope sensitivity at the (sub)millimeter-wave bands where dust continuum emission is strong has led to a revolution in interferometric observations of linear polarization over the past two decades. In recent years, both CARMA and the SMA conducted surveys of magnetic fields in samples of > 10 star-forming cores/clumps. These studies have proven insightful in revealing the statistical behavior of magnetic fields in star formation. However, while individual case studies continue to be fruitful, large, less biased surveys that target statistically significant samples of sources are the only way to further constrain the dynamical role of magnetic fields in the star formation process.

Studies of low-mass star formation have found that while there are a few cases where the magnetic field seems to regulate the collapse of star-forming material across the scales from clouds/clumps to cores to envelopes, there are also many cases where the multi-scale magnetic field morphology shows no consistency. Furthermore, the resolution and sensitivity of ALMA have yielded new observations that show evidence of shaping of the magnetic field by bipolar outflows at the ~ 100 au scale in some (but not all) sources. A few recent observations of spectral-line polarization by the SMA and ALMA have shed light on the importance of magnetic fields in the launching of outflows. More observations of this type with ALMA will enhance this subfield significantly in the coming years.

Studies of high-mass star formation found that magnetic fields are not the dominant force within the parsec scale of molecular clumps. However, fields appear to be dynamically important in the fragmentation of clumps into 0.1 pc-scale cores. Furthermore, molecular gas with densities >10⁴ cm⁻³ in high-mass star formation appears to be far from virial equilibrium if magnetic fields do not contribute significantly to the dynamical process. This significant departure from the state of virialization appears to challenge the basic assumption of equilibrium star formation. Direct measurements of magnetic fields will shed more insight on this important issue.

In both the low- and high-mass regimes, comparisons of outflow vs. magnetic field orientations have yielded random alignment. The outflow is a probe of the angular momentum at the smallest scales in the source, and thus the limited data currently available point to a scenario where angular momentum is far more important than the magnetic field at the small (< 1,000 au) scales of individual forming protostars.

The role of magnetic fields in the formation of high- and low-mass disks is less clear due to a small number of observations, and the issue of scattering by dust. Near-future studies targeting the Zeeman and G-K effects may finally be able to access information about the magnetic field in disks (e.g., Brauer et al., 2017). Furthermore, high resolution studies at longer wavelengths in regions that are optically thick (and thus dominated by scattering) in the ALMA data will be made possible by future telescopes such as the Next Generation Very Large Array (ngVLA; Carilli et al., 2015). The ngVLA will be a powerful tool for studying magnetized star formation (Isella et al., 2015; Hull et al., 2018a), as it will offer dramatic improvements in the sensitivity, resolution, and image fidelity over the current VLA, which has enabled just a few studies of polarization in the very brightest low- and high-mass star-forming sources (Carrasco-González et al., 2010; Cox et al., 2015); (Liu et al., 2016, 2018).

Despite major advances in recent years, the studies presented in this review—in particular the survey studies—are biased toward objects with detectable polarization. Nearly all low- and high-mass star forming objects have embedded protostars (and sometimes HII regions, in the case of high-mass sources). A crucial, under-explored area of star formation involves studying the initial conditions of the magnetic field before feedback (e.g., infall, outflows, and radiation) has altered its morphology. However, this has rarely been achieved due to a lack of sensitivity. In the coming years, large, multi-scale, multi-telescope surveys of magnetic fields in star-forming clouds covering the full range of evolutionary stages will allow us to break new ground in our studies of magnetized star formation.

Author Contributions

CH led the writing of the sections about low-mass star formation and scattering. QZ led the section about high-mass star formation. Both authors wrote the abstract, introduction, hourglass-statistics section, and summary.

Funding

CH acknowledges the support of both the NAOJ Fellowship as well as JSPS KAKENHI grant 18K13586. QZ acknowledges the support of the the Smithsonian Institute SSA grant, Are Magnetic Fields Dynamically Important in Massive Star Formation?

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer KQ declared a past co-authorship with one of the authors QZ to the handling editor.

Acknowledgments

CH and QZ acknowledge the two referees for their careful reading of the manuscript and for the insightful comments, which led to a more clear and thorough presentation of this review. CH acknowledges Paulo Cortés, Martin Houde, and Josep Miquel Girart for the useful discussion. The BIMA array was operated by the Berkeley-Illinois-Maryland Association with support from the National Science Foundation. Support for CARMA construction was derived from the states of California, Illinois, and Maryland, the James S. McDonnell Foundation, the Gordon and Betty Moore Foundation, the Kenneth T. and Eileen L. Norris Foundation, the University of Chicago, the Associates of the California Institute of Technology, and the National Science Foundation. The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics, and is funded by the Smithsonian Institution and the Academia Sinica. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

Facilities: ALMA, APEX, BIMA, BLAST, BLAST-TNG, CARMA, CSO, IRAM 30 m, JCMT, LMT, NRAO 12 m, SMA, SOFIA, Viper, VLA.

Software: APLpy, an open-source plotting package for Python hosted at aplpy.github.com (Robitaille and Bressert, 2012). Common Astronomy Software Applications (CASA, McMullin et al., 2007). Astropy (Astropy Collaboration et al., 2018).

Footnotes

1. ^Teyssier, R., and Commerçon, B. (2019). Numerical methods for simulating star formation. Front. Astron. Space Sci. under review.

2. ^Pudritz, R. E., and Ray, T. P. (2019). The role of magnetic fields in protostellar outflows and star formation. Front. Astron. Space Sci. under review.

3. ^In this review we follow the nomenclature used in Zhang et al. (2009) and Motte et al. (2018), who refer to a cloud as a structure 10–100 pc in size; a molecular clump as a structure 1 pc in size that forms massive stars along with a population of lower mass stars; and a dense core as a structure 0.01–0.1 pc in size that forms one or a group of stars. Following the nomenclature of, e.g., Hull et al. (2014), a protostellar envelope is a ~ 1,000 au (~ 0.005 pc) structure comprising the densest part of the dense core, inside of which one or a few protostars form.

4. ^Note that while we aim to provide an exhaustive review of the literature surrounding millimeter-wave interferometric observations of low- and high-mass stars, we mention only a few theoretical and single-dish polarization studies in order to support our narrative. We do not discuss other types of millimeter-wave polarization observations, i.e., toward the galactic center, quasars, or evolved stars.

5. ^RATs that align grains with respect to the magnetic field B are sometimes known as “B-RATs,” in contrast to other radiative torque mechanisms such as the “k-RATs” mentioned in section 5, where RATs align grains with respect to the radiation direction.

6. ^Note that under certain conditions one can derive the total magnetic field strength from the Zeeman effect (Heiles et al., 1993; Heiles and Crutcher, 2005). This has been seen several times toward galactic OH masers (Hutawarakorn et al., 2002; Fish and Reid, 2006; Caswell et al., 2014). However, in typical Zeeman observations of star-forming molecular clouds, the Zeeman signal is only strong enough to yield the strength of the magnetic field along the line of sight.

7. ^Crutcher, R. M. and Kemball, A. J. (2019). Zeeman effect observations of regions of star formation. Front. Astron. Space Sci. under review.

8. ^Li, H.-B., and Law, C. Y. (2019). Observing the impacts of magnetic fields on molecular clouds. Front. Astron. Space Sci. under review.

9. ^Pattle, K., and Fissel, L. M. (2019). Submillimeter and far-infrared polarimetric observations of magnetic fields in star-forming regions. Front. Astron. Space Sci. under review.

10. ^At the high resolutions achievable by ALMA, several studies have revealed polarization in well resolved maps of protoplanetary disks; however, it appears that in many cases the polarized emission is from dust scattering and not from magnetically aligned dust grains (see section 5).

11. ^The two polarization results from OVRO are observations toward NGC 1333-IRAS 4A and IRAS 16293 (Akeson et al., 1996; Akeson and Carlstrom, 1997); however, OVRO was known to have issues with polarization calibration, which is the most likely explanation for the inconsistency of those results with later observations of the same sources (Girart et al., 1999, 2006, 2008; Rao et al., 2009).

12. ^We do not treat the topic of intermediate-mass star formation separately in this review. As many of the characteristics of the early stages of intermediate- and low-mass star formation are thought to be similar (Beltrán, 2015), we include references to several intermediate-mass objects and regions in this section. Many of these intermediate-mass sources are in Orion (e.g., Takahashi et al., 2006, 2019; Hull et al., 2014), but there are also objects in other regions, such as Serpens SMM1 in the Serpens Main molecular cloud (van Kempen et al., 2016; Hull et al., 2017b).

References

Akeson, R. L., and Carlstrom, J. E. (1997). Magnetic field structure in protostellar envelopes. Astrophys. J. 491, 254–266. doi: 10.1086/304949

CrossRef Full Text | Google Scholar

Akeson, R. L., Carlstrom, J. E., Phillips, J. A., and Woody, D. P. (1996). Millimeter interferometric polarization imaging of the young stellar object NGC 1333/IRAS 4A. Astrophys. J. 456:L45. doi: 10.1086/309856

CrossRef Full Text | Google Scholar

Allen, A., Li, Z.-Y., and Shu, F. H. (2003). Collapse of magnetized singular isothermal toroids. II. Rotation and magnetic braking. Astrophys. J. 599, 363–379. doi: 10.1086/379243

CrossRef Full Text | Google Scholar

Alves, F. O., Frau, P., Girart, J. M., Franco, G. A. P., Santos, F. P., and Wiesemeyer, H. (2014). On the radiation driven alignment of dust grains: detection of the polarization hole in a starless core. Astron. Astrophys. 569:L1. doi: 10.1051/0004-6361/201424678

CrossRef Full Text | Google Scholar

Alves, F. O., Girart, J. M., Lai, S.-P., Rao, R., and Zhang, Q. (2011). The magnetic field in the NGC 2024 FIR 5 dense core. Astrophys. J. 726:63. doi: 10.1088/0004-637X/726/2/63

CrossRef Full Text | Google Scholar

Alves, F. O., Girart, J. M., Padovani, M., Galli, D., Franco, G. A. P., Caselli, P., et al. (2018). Magnetic field in a circumbinary disk around a Class I YSO. Astron. Astrophys. 616:A56.

Google Scholar

Andersson, B.-G., Lazarian, A., and Vaillancourt, J. E. (2015). Interstellar dust grain alignment. Annu. Rev. Astron. Astrophys. 53, 501–539. doi: 10.1146/annurev-astro-082214-122414

CrossRef Full Text | Google Scholar

Astropy Collaboration, Price-Whelan, A. M., Sipőcz, B. M., Günther, H. M., Lim, P. L., Crawford, S. M., et al. (2018). The astropy project: building an open-science project and status of the v2.0 Core Package. Astron. J. 156:123. doi: 10.3847/1538-3881/aabc4f

CrossRef Full Text | Google Scholar

Bacciotti, F., Girart, J. M., Padovani, M., Podio, L., Paladino, R., Testi, L., et al. (2018). ALMA observations of polarized emission toward the CW Tau and DG Tau protoplanetary disks: constraints on dust grain growth and settling. ApJ. 865:L12. doi: 10.3847/2041-8213/aadf87

CrossRef Full Text | Google Scholar

Beltrán, M. T. (2015). Observational perspective of the youngest phases of intermediate-mass stars. Astrophys. Space Sci. 355, 283–290. doi: 10.1007/s10509-014-2151-0

CrossRef Full Text | Google Scholar

Beuther, H., Vlemmings, W. H. T., Rao, R., and van der Tak, F. F. S. (2010). Magnetic field structure in a high-mass outflow/disk system. Astrophys. J. Lett. 724, L113–L117. doi: 10.1088/2041-8205/724/1/L113

CrossRef Full Text | Google Scholar

Bock, D., Bolatto, A. D., Hawkins, D. W., Kemball, A. J., Lamb, J. W., Plambeck, R. L., et al. (2006). “First results from CARMA: the combined array for research in millimeter-wave astronomy,” in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 6267. 13.

Google Scholar

Brauer, R., Wolf, S., and Flock, M. (2017). Magnetic fields in circumstellar disks. The potential of Zeeman observations. Astron. Astrophys. 607:A104. doi: 10.1051/0004-6361/201731140

CrossRef Full Text | Google Scholar

Carilli, C. L., McKinnon, M., Ott, J., Beasley, A., Isella, A., Murphy, E., et al. (2015). Next generation very large Array Memo No. 5: science working groups – project overview. arXiv [Preprints]. arXiv: 1510.06438.

Google Scholar

Carrasco-González, C., Rodríguez, L. F., Anglada, G., Martí, J., Torrelles, J. M., and Osorio, M. (2010). A magnetized jet from a massive protostar. Science 330:1209. doi: 10.1126/science.1195589

PubMed Abstract | CrossRef Full Text | Google Scholar

Caswell, J. L., Green, J. A., and Phillips, C. J. (2014). Parkes full polarization spectra of OH masers - II. Galactic longitudes 240deg to 350deg. Month. Not. R. Astron. Soc. 439, 1680–1739. doi: 10.1093/mnras/stu046

CrossRef Full Text | Google Scholar

Cesaroni, R., Beltrán, M. T., Zhang, Q., Beuther, H., and Fallscheer, C. (2011). Dissecting a hot molecular core: the case of G31.41+0.31. Astron. Astrophys. 533:A73. doi: 10.1051/0004-6361/201117206

CrossRef Full Text | Google Scholar

Cesaroni, R., Hofner, P., Araya, E., and Kurtz, S. (2010). The structure of hot molecular cores over 1000 AU. Astron. Astrophys. 509:A50. doi: 10.1051/0004-6361/200912877

CrossRef Full Text | Google Scholar

Chamma, M. A., Houde, M., Girart, J. M., and Rao, R. (2018). Non-Zeeman circular polarization of molecular spectral lines in the ISM. Month. Not. R. Astron. Soc. 480, 3123–3131. doi: 10.1093/mnras/sty2068

CrossRef Full Text | Google Scholar

Chandrasekhar, S., and Fermi, E. (1953). Magnetic fields in spiral arms. Astrophys. J. 118:113. doi: 10.1086/145731

CrossRef Full Text | Google Scholar

Chapman, N. L., Davidson, J. A., Goldsmith, P. F., Houde, M., Kwon, W., Li, Z.-Y., et al. (2013). Alignment between flattened protostellar infall envelopes and ambient magnetic fields. Astrophys. J. 770:151. doi: 10.1088/0004-637X/770/2/151

CrossRef Full Text | Google Scholar

Chen, C.-Y., and Ostriker, E. C. (2018). Geometry, kinematics, and magnetization of simulated prestellar cores. Astrophys. J. 865:34. doi: 10.3847/1538-4357/aad905

CrossRef Full Text | Google Scholar

Chen, H.-R., Rao, R., Wilner, D. J., and Liu, S.-Y. (2012). The magnetized environment of the W3(H₂O) protostars. Astrophys. J. Lett. 751:L13. doi: 10.1088/2041-8205/751/1/L13

CrossRef Full Text | Google Scholar

Ching, T.-C., Lai, S.-P., Zhang, Q., Girart, J. M., Qiu, K., and Liu, H. B. (2017). Magnetic fields in the massive dense cores of the DR21 filament: weakly magnetized cores in a strongly magnetized filament. Astrophys. J. 838:121. doi: 10.3847/1538-4357/aa65cc

CrossRef Full Text | Google Scholar

Ching, T.-C., Lai, S.-P., Zhang, Q., Girart, J. M., Qiu, K., and Liu, H. B. (2018). Interactions between gas dynamics and magnetic fields in the massive dense cores of the DR21 filament. Astrophys. J. 865:110. doi: 10.3847/1538-4357/aad9fc

CrossRef Full Text | Google Scholar

Ching, T.-C., Lai, S.-P., Zhang, Q., Yang, L., Girart, J. M., and Rao, R. (2016). Helical magnetic fields in the NGC 1333 IRAS 4A protostellar outflows. Astrophys. J. 819:159. doi: 10.3847/0004-637X/819/2/159

CrossRef Full Text | Google Scholar

Chitsazzadeh, S., Houde, M., Hildebrand, R. H., and Vaillancourt, J. (2012). Characterization of turbulence from submillimeter dust emission. Astrophys. J. 749:45. doi: 10.1088/0004-637X/749/1/45

CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2007). Grain alignment and polarized emission from magnetized T tauri disks. Astrophys. J. 669, 1085–1097. doi: 10.1086/521805

CrossRef Full Text | Google Scholar

Chuss, D. T., Andersson, B.-G, Bally, J., Dotson, J. L., Dowell, C. D., Guerra, J. A., et al. (2018). HAWC+/SOFIA multiwavelength polarimetric observations of OMC-1. arXiv:1810.08233.

Google Scholar

Clark, S. E., Hill, J. C., Peek, J. E., Putman, M. E., and Babler, B. L. (2015). Neutral hydrogen structures trace dust polarization angle: implications for cosmic microwave background foregrounds. Phys. Rev. Lett. 115:241302. doi: 10.1103/PhysRevLett.115.241302

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, S. E., Peek, J. E. G., and Putman, M. E. (2014). Magnetically aligned H I fibers and the rolling hough transform. Astrophys. J. 789:82. doi: 10.1088/0004-637X/789/1/82

CrossRef Full Text | Google Scholar

Cortes, P., and Crutcher, R. M. (2006). Interferometric mapping of magnetic fields: G30.79 FIR 10. Astrophys. J. 639, 965–968. doi: 10.1086/498971

CrossRef Full Text | Google Scholar

Cortes, P. C., Crutcher, R. M., and Matthews, B. C. (2006). Interferometric mapping of magnetic fields: NGC 2071IR. Astrophys. J. 650, 246–251. doi: 10.1086/507460

CrossRef Full Text | Google Scholar

Cortes, P. C., Crutcher, R. M., Shepherd, D. S., and Bronfman, L. (2008). Interferometric mapping of magnetic fields: the massive star-Forming region G34.4+0.23 MM. Astrophys. J. 676, 464–471. doi: 10.1086/524355

CrossRef Full Text | Google Scholar

Cortes, P. C., Crutcher, R. M., and Watson, W. D. (2005). Line polarization of molecular lines at radio frequencies: the case of DR 21(OH). Astrophys. J. 628, 780–788. doi: 10.1086/430815

CrossRef Full Text | Google Scholar

Cortes, P. C., Girart, J. M., Hull, C. L. H., Sridharan, T. K., Louvet, F., Plambeck, R., et al. (2016). Interferometric mapping of magnetic fields: the ALMA view of the massive star-forming clump W43-MM1. Astrophys. J. Lett. 825:L15. doi: 10.3847/2041-8205/825/1/L15

CrossRef Full Text | Google Scholar

Cox, E. G., Harris, R. J., Looney, L. W., Li, Z.-Y., Yang, H., Tobin, J. J., et al. (2018). ALMA's polarized view of 10 protostars in the perseus molecular cloud. Astrophys. J. 855:92. doi: 10.3847/1538-4357/aaacd2

CrossRef Full Text | Google Scholar

Cox, E. G., Harris, R. J., Looney, L. W., Segura-Cox, D. M., Tobin, J., Li, Z.-Y., et al. (2015). High-resolution 8 mm and 1 cm polarization of IRAS 4A from the VLA Nascent Disk and Multiplicity (VANDAM) Survey. Astrophys. J. Lett. 814:L28. doi: 10.1088/2041-8205/814/2/L28

CrossRef Full Text | Google Scholar

Crutcher, R. M. (1999). Magnetic fields in molecular clouds: observations confront theory. Astrophys. J. 520, 706–713. doi: 10.1086/307483

CrossRef Full Text | Google Scholar

Crutcher, R. M. (2004). What drives star formation? Astrophys. Space Sci. 292, 225–237. doi: 10.1023/B:ASTR.0000045021.42255.95

CrossRef Full Text | Google Scholar

Crutcher, R. M. (2012). Magnetic fields in molecular clouds. Annu. Rev. Astron. Astrophys. 50, 29–63. doi: 10.1146/annurev-astro-081811-125514

CrossRef Full Text | Google Scholar

Crutcher, R. M., Troland, T. H., Goodman, A. A., Heiles, C., Kazes, I., and Myers, P. C. (1993). OH Zeeman observations of dark clouds. Astrophys. J. 407, 175–184. doi: 10.1086/172503

CrossRef Full Text | Google Scholar

Curran, R. L., and Chrysostomou, A. (2007). Magnetic fields in massive star-forming regions. Month. Not. R. Astron. Soc. 382, 699–716. doi: 10.1111/j.1365-2966.2007.12399.x

CrossRef Full Text | Google Scholar

Dapp, W. B., Basu, S., and Kunz, M. W. (2012). Bridging the gap: disk formation in the Class 0 phase with ambipolar diffusion and Ohmic dissipation. Astron. Astrophys. 541:A35. doi: 10.1051/0004-6361/201117876

CrossRef Full Text | Google Scholar

Davidson, J. A., Li, Z.-Y., Hull, C. L. H., Plambeck, R. L., Kwon, W., Crutcher, R. M., et al. (2014). Testing magnetic field models for the class 0 protostar L1527. Astrophys. J. 797:74. doi: 10.1088/0004-637X/797/2/74

CrossRef Full Text | Google Scholar

Davis, L. (1951). The strength of interstellar magnetic fields. Phys. Rev. 81, 890–891. doi: 10.1103/PhysRev.81.890.2

CrossRef Full Text | Google Scholar

Deguchi, S., and Watson, W. D. (1984). Linear polarization of molecular lines at radio frequencies. Astrophys. J. 285, 126–133. doi: 10.1086/162483

CrossRef Full Text | Google Scholar

Dent, W. R. F., Pinte, C., Cortes, P. C., Ménard, F., Hales, A., Fomalont, E., et al. (2019). Submillimetre dust polarisation and opacity in the HD163296 protoplanetary ring system. Month. Not. R. Astron. Soc. 482, L29–L33. doi: 10.1093/mnrasl/sly181

CrossRef Full Text | Google Scholar

Dotson, J. L., Novak, G., Renbarger, T., Pernic, D., and Sundwall, J. L. (1998). “SPARO: the submillimeter polarimeter for Antarctic remote observing,” in Advanced Technology MMW, Radio, and Terahertz Telescopes, Vol. 3357, ed T. G. Phillips, 543–547. doi: 10.1117/12.317388

CrossRef Full Text | Google Scholar

Dotson, J. L., Vaillancourt, J. E., Kirby, L., Dowell, C. D., Hildebrand, R. H., and Davidson, J. A. (2010). 350 μm polarimetry from the caltech submillimeter observatory. Astrophys. J. Suppl. Ser. 186, 406–426. doi: 10.1088/0067-0049/186/2/406

CrossRef Full Text | Google Scholar

Falceta-Gonçalves, D., Lazarian, A., and Kowal, G. (2008). Studies of regular and random magnetic fields in the ISM: statistics of polarization vectors and the chandrasekhar-fermi technique. Astrophys. J. 679, 537-551. doi: 10.1086/587479

CrossRef Full Text | Google Scholar

Fernández-López, M., Stephens, I. W., Girart, J. M., Looney, L., Curiel, S., Segura-Cox, D., et al. (2016). 1.3 mm polarized emission in the circumstellar disk of a massive protostar. Astrophys. J. 832:200. doi: 10.3847/0004-637X/832/2/200

CrossRef Full Text | Google Scholar

Fiedler, R. A., and Mouschovias, T. C. (1993). Ambipolar diffusion and star formation: formation and contraction of axisymmetric cloud cores. II. Results. Astrophys. J. 415:680. doi: 10.1086/173193

CrossRef Full Text | Google Scholar

Fish, V. L., and Reid, M. J. (2006). Full-polarization observations of OH masers in massive star-forming regions. II. Maser properties and the interpretation of polarization. Astrophys. J. Suppl. Ser. 164, 99–123. doi: 10.1086/502650

CrossRef Full Text | Google Scholar

Fissel, L. M., Ade, P. A. R., Angilè, F. E., Ashton, P., Benton, S. J., Devlin, M. J., et al. (2016). Balloon-borne submillimeter polarimetry of the vela C molecular cloud: systematic dependence of polarization fraction on column density and local polarization-angle dispersion. Astrophys. J. 824:134. doi: 10.3847/0004-637X/824/2/134

CrossRef Full Text | Google Scholar

Frank, A., Ray, T. P., Cabrit, S., Hartigan, P., Arce, H. G., Bacciotti, F., et al. (2014). “Jets and outflows from star to cloud: observations confront theory,” in Protostars and Planets VI, eds H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning (Tucson, AZ: University of Arizona Press), 451–474. doi: 10.2458/azu_uapress_9780816531240-ch020

CrossRef Full Text

Frau, P., Galli, D., and Girart, J. M. (2011). Comparing star formation models with interferometric observations of the protostar NGC 1333 IRAS 4A. I. Magnetohydrodynamic collapse models. Astron. Astrophys. 535:A44. doi: 10.1051/0004-6361/201117813

CrossRef Full Text | Google Scholar

Frau, P., Girart, J. M., Zhang, Q., and Rao, R. (2014). Shaping a high-mass star-forming cluster through stellar feedback. The case of the NGC 7538 IRS 1-3 complex. Astron. Astrophys. 567:A116. doi: 10.1051/0004-6361/201423917

CrossRef Full Text | Google Scholar

Galametz, M., Maury, A., Girart, J. M., Rao, R., Zhang, Q., Gaudel, M., et al. (2018). SMA observations of the polarized dust emission in solar-type Class 0 protostars: the magnetic field properties at envelope scales. Astron. Astrophys. 616:A139. doi: 10.1051/0004-6361/201833004

CrossRef Full Text | Google Scholar

Galitzki, N., Ade, P. A. R., Angilè, F. E., Ashton, P., Beall, J. A., Becker, D., et al. (2014). The next generation BLAST experiment. J. Astron. Instrum. 3:1440001. doi: 10.1142/S2251171714400017

CrossRef Full Text | Google Scholar

Galli, D., Lizano, S., Shu, F. H., and Allen, A. (2006). Gravitational collapse of magnetized clouds. I. Ideal magnetohydrodynamic accretion flow. Astrophys. J. 647, 374–381. doi: 10.1086/505257

CrossRef Full Text | Google Scholar

Galli, D., and Shu, F. H. (1993a). Collapse of magnetized molecular cloud cores. I. Semianalytical solution. Astrophys. J. 417:220. doi: 10.1086/173305

CrossRef Full Text | Google Scholar

Galli, D., and Shu, F. H. (1993b). Collapse of magnetized molecular cloud cores. II. Numerical results. Astrophys. J. 417:243. doi: 10.1086/173306

CrossRef Full Text | Google Scholar

Gandilo, N. N., Ade, P. A. R., Angilè, F. E., Ashton, P., Benton, S. J., Devlin, M. J., et al. (2016). Submillimeter polarization spectrum in the vela C molecular cloud. Astrophys. J. 824:84. doi: 10.3847/0004-637X/824/2/84

CrossRef Full Text | Google Scholar

Ginsburg, A., Bally, J., Battersby, C., Youngblood, A., Darling, J., Rosolowsky, E., et al. (2015). The dense gas mass fraction in the W51 cloud and its protoclusters. Astron. Astrophys. 573:A106. doi: 10.1051/0004-6361/201424979

CrossRef Full Text | Google Scholar

Ginsburg, A., Goss, W. M., Goddi, C., Galván-Madrid, R., Dale, J. E., Bally, J., et al. (2016). Toward gas exhaustion in the W51 high-mass protoclusters. Astron. Astrophys. 595:A27. doi: 10.1051/0004-6361/201628318

CrossRef Full Text | Google Scholar

Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., and Estalella, R. (2009). Magnetic fields in the formation of massive stars. Science 324:1408. doi: 10.1126/science.1171807

PubMed Abstract | CrossRef Full Text | Google Scholar

Girart, J. M., Crutcher, R. M., and Rao, R. (1999). Detection of polarized CO emission from the molecular outflow in NGC 1333 IRAS 4A. Astrophys. J. Lett. 525, L109–L112. doi: 10.1086/312345

PubMed Abstract | CrossRef Full Text | Google Scholar

Girart, J. M., Fernandez-Lopez, M., Li, Z.-Y., Yang, H., Estalella, R., Anglada, G., et al. (2018). Resolving the polarized dust emission of the disk around the massive star powering the HH80-81 radio jet~. Astrophys. J. Lett. 856:L27. doi: 10.3847/2041-8213/aab76b

CrossRef Full Text | Google Scholar

Girart, J. M., Frau, P., Zhang, Q., Koch, P. M., Qiu, K., Tang, Y.-W., et al. (2013). DR 21(OH): a highly fragmented, magnetized, turbulent dense core. Astrophys. J. 772:69. doi: 10.1088/0004-637X/772/1/69

CrossRef Full Text | Google Scholar

Girart, J. M., Greaves, J. S., Crutcher, R. M., and Lai, S.-P. (2004). BIMA and JCMT spectropolarimetric observations of the CO J = 2 - 1 line towards Orion KL/IRc2. Astrophys. Space Sci. 292, 119–125. doi: 10.1023/B:ASTR.0000045007.35868.17

CrossRef Full Text | Google Scholar

Girart, J. M., Rao, R., and Marrone, D. P. (2006). Magnetic fields in the formation of sun-like stars. Science 313, 812–814. doi: 10.1126/science.1129093

PubMed Abstract | CrossRef Full Text | Google Scholar

Girart, J. M., Rao, R., and Marrone, D. P. (2008). SMA observations of the magnetic fields around a low-mass protostellar system. Astrophys. Space Sci. 313, 87–90. doi: 10.1007/s10509-007-9592-7

CrossRef Full Text | Google Scholar

Glenn, J., Walker, C. K., Bieging, J. H., and Jewell, P. R. (1997). Millimeter-wave spectropolarimetry of evolved stars: evidence for polarized molecular line emission. Astrophys. J. Lett. 487, L89–L92. doi: 10.1086/310863

CrossRef Full Text | Google Scholar

Goldreich, P., and Kylafis, N. D. (1981). On mapping the magnetic field direction in molecular clouds by polarization measurements. Astrophys. J. Lett. 243, L75–L78. doi: 10.1086/183446

CrossRef Full Text | Google Scholar

Goldreich, P., and Kylafis, N. D. (1982). Linear polarization of radio frequency lines in molecular clouds and circumstellar envelopes. Astrophys. J. 253, 606–621. doi: 10.1086/159663

CrossRef Full Text | Google Scholar

Gonçalves, J., Galli, D., and Girart, J. M. (2008). Modeling the magnetic field in the protostellar source NGC 1333 IRAS 4A. Astron. Astrophys. 490, L39–L42. doi: 10.1051/0004-6361:200810861

CrossRef Full Text | Google Scholar

González-Casanova, D. F., and Lazarian, A. (2017). Velocity gradients as a tracer for magnetic fields. Astrophys. J. 835:41. doi: 10.3847/1538-4357/835/1/41

CrossRef Full Text | Google Scholar

Gordon, M. S., Lopez-Rodriguez, E., Andersson, B.-G., Clarke, M., Coude, S., Moullet, A., et al. (2018). SOFIA community science I: HAWC+ Polarimetry of 30 Doradus. eprint arXiv:1811.03100.

Google Scholar

Greaves, J. S., Holland, W. S., Friberg, P., and Dent, W. R. F. (1999). Polarized CO emission from molecular clouds. Astrophys. J. Lett. 512, L139–L142. doi: 10.1086/311888

CrossRef Full Text | Google Scholar

Harris, R. J., Cox, E. G., Looney, L. W., Li, Z.-Y., Yang, H., Fernández-López, M., et al. (2018). ALMA observations of polarized 872 μm dust emission from the protostellar systems VLA 1623 and L1527. Astrophys. J. 861:91. doi: 10.3847/1538-4357/aac6ec

CrossRef Full Text | Google Scholar

Heiles, C., and Crutcher, R. (2005). “Magnetic fields in diffuse HI and molecular clouds,” in Cosmic Magnetic Fields, Vol. 664 of Lecture Notes in Physics, eds R. Wielebinski and R. Beck (Berlin: Springer Verlag), 137. doi: 10.1007/11369875_7

CrossRef Full Text | Google Scholar

Heiles, C., Goodman, A. A., McKee, C. F., and Zweibel, E. G. (1993). “Magnetic fields in star-forming regions - Observations,” in Protostars and Planets III, eds E. H. Levy and J. I. Lunine, 279–326.

Google Scholar

Heitsch, F., Zweibel, E. G., Mac Low, M.-M., Li, P., and Norman, M. L. (2001). Magnetic field diagnostics based on far-infrared polarimetry: tests using numerical simulations. Astrophys. J. 561, 800–814. doi: 10.1086/323489

CrossRef Full Text | Google Scholar

Hennebelle, P., and Chabrier, G. (2008). Analytical theory for the initial mass function: CO clumps and prestellar cores. Astrophys. J. 684, 395–410. doi: 10.1086/589916

CrossRef Full Text | Google Scholar

Hennebelle, P., and Ciardi, A. (2009). Disk formation during collapse of magnetized protostellar cores. Astron. Astrophys. 506, L29–L32. doi: 10.1051/0004-6361/200913008

CrossRef Full Text | Google Scholar

Hennebelle, P., and Inutsuka, S.-I. (2019). The role of magnetic field in molecular cloud formation and evolution. Front. Astron. Space Sci. arXiv [Preprint]. arXiv:1902.00798.

Google Scholar

Hezareh, T., Wiesemeyer, H., Houde, M., Gusdorf, A., and Siringo, G. (2013). Non-Zeeman circular polarization of CO rotational lines in SNR IC 443. Astron. Astrophys. 558:A45. doi: 10.1051/0004-6361/201321900

CrossRef Full Text | Google Scholar

Hildebrand, R. H. (1988). Magnetic fields and stardust. Q. J. R. Astron. Soc. 29, 327–351.

Google Scholar

Hildebrand, R. H., Kirby, L., Dotson, J. L., Houde, M., and Vaillancourt, J. E. (2009). Dispersion of magnetic fields in molecular clouds. I. Astrophys. J. 696, 567–573. doi: 10.1088/0004-637X/696/1/567

CrossRef Full Text | Google Scholar

Hoang, T., and Lazarian, A. (2009). Grain alignment induced by radiative torques: effects of internal relaxation of energy and complex radiation field. Astrophys. J. 697, 1316–1333. doi: 10.1088/0004-637X/697/2/1316

CrossRef Full Text | Google Scholar

Houde, M., Dowell, C. D., Hildebrand, R. H., Dotson, J. L., Vaillancourt, J. E., Phillips, T. G., et al. (2004). Tracing the Magnetic Field in Orion A. Astrophys. J. 604, 717–740. doi: 10.1086/382067

CrossRef Full Text | Google Scholar

Houde, M., Hezareh, T., Jones, S., and Rajabi, F. (2013). Non-zeeman circular polarization of molecular rotational spectral lines. Astrophys. J. 764:24. doi: 10.1088/0004-637X/764/1/24

CrossRef Full Text | Google Scholar

Houde, M., Hull, C. L. H., Plambeck, R. L., Vaillancourt, J. E., and Hildebrand, R. H. (2016). Dispersion of magnetic fields in molecular clouds. IV. analysis of interferometry data. Astrophys. J. 820:38. doi: 10.3847/0004-637X/820/1/38

CrossRef Full Text | Google Scholar

Houde, M., Rao, R., Vaillancourt, J. E., and Hildebrand, R. H. (2011). Dispersion of magnetic fields in molecular clouds. III. Astrophys. J. 733:109. doi: 10.1088/0004-637X/733/2/109

CrossRef Full Text | Google Scholar

Houde, M., Vaillancourt, J. E., Hildebrand, R. H., Chitsazzadeh, S., and Kirby, L. (2009). Dispersion of magnetic fields in molecular clouds. II. Astrophys. J. 706, 1504–1516. doi: 10.1088/0004-637X/706/2/1504

CrossRef Full Text | Google Scholar

Hughes, A. M., Hull, C. L. H., Wilner, D. J., and Plambeck, R. L. (2013). Interferometric upper limits on millimeter polarization of the disks around DG Tau, GM Aur, and MWC 480. Astron. J. 145:115. doi: 10.1088/0004-6256/145/4/115

CrossRef Full Text | Google Scholar

Hughes, A. M., Wilner, D. J., Cho, J., Marrone, D. P., Lazarian, A., Andrews, S. M., et al. (2009). Stringent limits on the polarized submillimeter emission from protoplanetary disks. Astrophys. J. 704, 1204–1217. doi: 10.1088/0004-637X/704/2/1204

CrossRef Full Text | Google Scholar

Hull, C. L. H., Carrasco-González, C., Williams, P. K. G., Girart, J. M., Robishaw, T., Galván-Madrid, R., et al. (2018a). “Magnetic fields in forming stars with the ngVLA,” in Science with a Next Generation Very Large Array, ASP Conference Series, Vol. 517, ASP Monograph 7, ed E. Murphy. 357.

Google Scholar

Hull, C. L. H., Girart, J. M., Tychoniec, Ł., Rao, R., Cortés, P. C., Pokhrel, R., et al. (2017b). ALMA observations of dust polarization and molecular line emission from the class 0 protostellar source serpens SMM1. Astrophys. J. 847:92. doi: 10.3847/1538-4357/aa7fe9

CrossRef Full Text | Google Scholar

Hull, C. L. H., Mocz, P., Burkhart, B., Goodman, A. A., Girart, J. M., Cortés, P. C., et al. (2017a). Unveiling the role of the magnetic field at the smallest scales of star formation. Astrophys. J. Lett. 842:L9. doi: 10.3847/2041-8213/aa71b7

CrossRef Full Text | Google Scholar

Hull, C. L. H., and Plambeck, R. L. (2015). The 1.3 mm full-stokes polarization system at CARMA. J. Astron. Instrum. 4:1550005. doi: 10.1142/S2251171715500051

CrossRef Full Text | Google Scholar

Hull, C. L. H., Plambeck, R. L., Bolatto, A. D., Bower, G. C., Carpenter, J. M., Crutcher, R. M., et al. (2013). Misalignment of Magnetic Fields and Outflows in Protostellar Cores. Astrophys. J. 768:159. doi: 10.1088/0004-637X/768/2/159

CrossRef Full Text | Google Scholar

Hull, C. L. H., Plambeck, R. L., Kwon, W., Bower, G. C., Carpenter, J. M., Crutcher, R. M., et al. (2014). TADPOL: A 1.3 mm survey of dust polarization in star-forming cores and regions. Astrophys. J. Suppl. Ser. 213:13. doi: 10.1088/0067-0049/213/1/13

CrossRef Full Text | Google Scholar

Hull, C. L. H., Yang, H., Li, Z.-Y., Kataoka, A., Stephens, I. W., Andrews, S., et al. (2018b). ALMA observations of polarization from dust scattering in the IM Lup protoplanetary disk. Astrophys. J. 860:82. doi: 10.3847/1538-4357/aabfeb

CrossRef Full Text | Google Scholar

Hutawarakorn, B., Cohen, R. J., and Brebner, G. C. (2002). OH masers and magnetic fields in the bipolar outflow source W75N. Month. Not. R. Astron. Soc. 330, 349–364. doi: 10.1046/j.1365-8711.2002.05068.x

CrossRef Full Text | Google Scholar

Isella, A., Hull, C. L. H., Moullet, A., Galván-Madrid, R., Johnstone, D., Ricci, L., et al. (2015). Next generation very large Array Memo No. 6, Science Working Group 1: the cradle of life. arXiv [Preprints]. arXiv:1510.06444.

Google Scholar

Jensen, E. L. N., and Akeson, R. (2014). Misaligned protoplanetary disks in a young binary star system. Nature 511, 567–569. doi: 10.1038/nature13521

PubMed Abstract | CrossRef Full Text | Google Scholar

Joos, M., Hennebelle, P., and Ciardi, A. (2012). Protostellar disk formation and transport of angular momentum during magnetized core collapse. Astron. Astrophys. 543:A128. doi: 10.1051/0004-6361/201118730

CrossRef Full Text | Google Scholar

Juárez, C., Girart, J. M., Zamora-Avilés, M., Tang, Y.-W., Koch, P. M., Liu, H. B., et al. (2017). Magnetized converging flows toward the hot core in the intermediate/high-mass star-forming region NGC 6334 V. Astrophys. J. 844:44. doi: 10.3847/1538-4357/aa78a6

CrossRef Full Text | Google Scholar

Kataoka, A., Machida, M. N., and Tomisaka, K. (2012). Exploring magnetic field structure in star-forming cores with polarization of thermal dust emission. Astrophys. J. 761:40. doi: 10.1088/0004-637X/761/1/40

CrossRef Full Text | Google Scholar

Kataoka, A., Muto, T., Momose, M., Tsukagoshi, T., and Dullemond, C. P. (2016a). Grain size constraints on HL tau with polarization signature. Astrophys. J. 820:54. doi: 10.3847/0004-637X/820/1/54

CrossRef Full Text | Google Scholar

Kataoka, A., Muto, T., Momose, M., Tsukagoshi, T., Fukagawa, M., Shibai, H., et al. (2015). Millimeter-wave polarization of protoplanetary disks due to dust scattering. Astrophys. J. 809:78. doi: 10.1088/0004-637X/809/1/78

CrossRef Full Text | Google Scholar

Kataoka, A., Tsukagoshi, T., Momose, M., Nagai, H., Muto, T., Dullemond, C. P., et al. (2016b). Submillimeter polarization observation of the protoplanetary disk around HD 142527. Astrophys. J. Lett. 831:L12. doi: 10.3847/2041-8205/831/2/L12

CrossRef Full Text | Google Scholar

Kataoka, A., Tsukagoshi, T., Pohl, A., Muto, T., Nagai, H., Stephens, I. W., et al. (2017). The evidence of radio polarization induced by the radiative grain alignment and self-scattering of dust grains in a protoplanetary disk. Astrophys. J. Lett. 844:L5. doi: 10.3847/2041-8213/aa7e33

CrossRef Full Text | Google Scholar

Kauffmann, J., Pillai, T., and Goldsmith, P. F. (2013). Low virial parameters in molecular clouds: implications for high-mass star formation and magnetic fields. Astrophys. J. 779:185. doi: 10.1088/0004-637X/779/2/185

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y., and Ho, P. T. P. (2010). Magnetic field properties in high-mass star formation from large to small scales: a statistical analysis from polarization data. Astrophys. J. 721, 815–827. doi: 10.1088/0004-637X/721/1/815

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., and Ho, P. T. P. (2012). Magnetic field strength maps for molecular clouds: a new method based on a polarization-intensity gradient relation. Astrophys. J. 747:79. doi: 10.1088/0004-637X/747/1/79

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., Ho, P. T. P., Yen, H.-W., Su, Y.-N., and Takakuwa, S. (2018). Polarization properties and magnetic field structures in the high-mass star-forming region W51 observed with ALMA. Astrophys. J. 855:39. doi: 10.3847/1538-4357/aaa4c1

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., Ho, P. T. P., Zhang, Q., Girart, J. M., Chen, H.-R. V., et al. (2014). The importance of the magnetic field from an SMA-CSO-combined sample of star-forming regions. Astrophys. J. 797:99. doi: 10.1088/0004-637X/797/2/99

CrossRef Full Text | Google Scholar

Konigl, A., and Pudritz, R. E. (2000). “Disk winds and the accretion-outflow connection,” in Protostars Planets IV, eds V. Mannings, A. P. BOSS, and S. S. Russell (Tucson: The University of Arizona Press), 759.

Kratter, K. M., Matzner, C. D., Krumholz, M. R., and Klein, R. I. (2010). On the role of disks in the formation of stellar systems: a numerical parameter study of rapid accretion. Astrophys. J. 708, 1585–1597. doi: 10.1088/0004-637X/708/2/1585

CrossRef Full Text | Google Scholar

Krumholz, M. R., Crutcher, R. M., and Hull, C. L. H. (2013). Protostellar disk formation enabled by weak, misaligned magnetic fields. Astrophys. J. Lett. 767, L11–L15. doi: 10.1088/2041-8205/767/1/L11

CrossRef Full Text | Google Scholar

Krumholz, M. R., and Federrath, C. (2019). The role of magnetic fields in setting the star formation rate and the initial mass function. Front. Astron. Space Sci. 6:7. doi: 10.3389/fspas.2019.00007

CrossRef Full Text | Google Scholar

Kwon, J., Doi, Y., Tamura, M., Matsumura, M., Pattle, K., Berry, D., et al. (2018). A first look at BISTRO observations of the ρ Oph-A core. Astrophys. J. 859:4. doi: 10.3847/1538-4357/aabd82

CrossRef Full Text | Google Scholar

Kwon, W., Looney, L. W., Crutcher, R. M., and Kirk, J. M. (2006). Two bipolar outflows and magnetic fields in the multiple protostar system L1448 IRS 3. Astrophys. J. 653, 1358–1368. doi: 10.1086/508920

CrossRef Full Text | Google Scholar

Kylafis, N. D. (1983). Polarization of interstellar radio-frequency lines and magnetic field direction. Astrophys. J. 267, 137–150. doi: 10.1086/160851

CrossRef Full Text | Google Scholar

Lada, C. J., and Lada, E. A. (2003). Embedded clusters in molecular clouds. Annu. Rev. Astron. Astrophys. 41, 57–115. doi: 10.1146/annurev.astro.41.011802.094844

CrossRef Full Text | Google Scholar

Lai, S.-P., Crutcher, R. M., Girart, J. M., and Rao, R. (2001). Interferometric mapping of magnetic fields in star-forming regions. I. W51 e1/e2 Molecular Cores. Astrophys. J. 561, 864–870. doi: 10.1086/323372

CrossRef Full Text | Google Scholar

Lai, S.-P., Crutcher, R. M., Girart, J. M., and Rao, R. (2002). Interferometric mapping of magnetic fields in star-forming regions. II. NGC 2024 FIR 5. Astrophys. J. 566, 925–930. doi: 10.1086/338336

CrossRef Full Text | Google Scholar

Lai, S.-P., Girart, J. M., and Crutcher, R. M. (2003). Interferometric mapping of magnetic fields in star-forming regions. III. Dust and CO Polarization in DR 21(OH). Astrophys. J. 598, 392–399. doi: 10.1086/378769

CrossRef Full Text | Google Scholar

Larson, R. B. (1981). Turbulence and star formation in molecular clouds. Month. Not. R. Astron. Soc. 194, 809–826. doi: 10.1093/mnras/194.4.809

CrossRef Full Text | Google Scholar

Lazarian, A. (2007). Tracing magnetic fields with aligned grains. J. Quant. Spec. Radiat. Transf. 106, 225–256. doi: 10.1016/j.jqsrt.2007.01.038

CrossRef Full Text | Google Scholar

Lee, C.-F., Hwang, H.-C., Ching, T.-C., Hirano, N., Lai, S.-P., Rao, R., et al. (2018a). Unveiling a magnetized jet from a low-mass protostar. Nat. Commun. 9:4636. doi: 10.1038/s41467-018-07143-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C.-F., Li, Z.-Y., Ching, T.-C., Lai, S.-P., and Yang, H. (2018b). ALMA dust polarization observations of two young edge-on protostellar disks. Astrophys. J. 854:56. doi: 10.3847/1538-4357/aaa769

CrossRef Full Text | Google Scholar

Lee, C.-F., Rao, R., Ching, T.-C., Lai, S.-P., Hirano, N., Ho, P. T. P., et al. (2014). Magnetic field structure in the flattened envelope and jet in the young protostellar system HH 211. Astrophys. J. Lett. 797:L9. doi: 10.1088/2041-8205/797/1/L9

CrossRef Full Text | Google Scholar

Lee, J.-E., Lee, S., Dunham, M. M., Tatematsu, K., Choi, M., Bergin, E. A., et al. (2017). Formation of wide binaries by turbulent fragmentation. Nat. Astron. 1:0172. doi: 10.1038/s41550-017-0172

CrossRef Full Text | Google Scholar

Lee, J. W. Y., Hull, C. L. H., and Offner, S. S. R. (2017). Synthetic observations of magnetic fields in protostellar cores. Astrophys. J. 834:201. doi: 10.3847/1538-4357/834/2/201

CrossRef Full Text | Google Scholar

Lee, K. I., Dunham, M. M., Myers, P. C., Arce, H. G., Bourke, T. L., Goodman, A. A., et al. (2016). Misalignment of outflow axes in the proto-multiple systems in perseus. Astrophys. J. Lett. 820:L2. doi: 10.3847/2041-8205/820/1/L2

CrossRef Full Text | Google Scholar

Lee, K. I., Dunham, M. M., Myers, P. C., Tobin, J. J., Kristensen, L. E., Pineda, J. E., et al. (2015). Mass assembly of stellar systems and their evolution with the SMA (MASSES). Multiplicity and the physical environment in L1448N. Astrophys. J. 814:114. doi: 10.1088/0004-637X/814/2/114

CrossRef Full Text | Google Scholar

Li, H., Dowell, C. D., Kirby, L., Novak, G., and Vaillancourt, J. E. (2008). Design and initial performance of SHARP, a polarimeter for the SHARC-II camera at the Caltech Submillimeter Observatory. Appl. Opt. 47, 422–430. doi: 10.1364/AO.47.000422

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Griffin, G. S., Krejny, M., Novak, G., Loewenstein, R. F., Newcomb, M. G., et al. (2006). Results of SPARO 2003: mapping magnetic fields in giant molecular clouds. Astrophys. J. 648, 340–354. doi: 10.1086/505858

CrossRef Full Text | Google Scholar

Li, H.-b., Dowell, C. D., Goodman, A., Hildebrand, R., and Novak, G. (2009). Anchoring magnetic field in turbulent molecular clouds. Astrophys. J. 704, 891–897. doi: 10.1088/0004-637X/704/2/891

CrossRef Full Text | Google Scholar

Li, H. B., Yuen, K. H., Otto, F., Leung, P. K., Sridharan, T. K., Zhang, Q., et al. (2015). Self-similar fragmentation regulated by magnetic fields in a region forming massive stars. Nature 520, 518–521. doi: 10.1038/nature14291

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., and Shang, H. (2011). Non-ideal MHD effects and magnetic braking catastrophe in protostellar disk formation. Astrophys. J. 738:180. doi: 10.1088/0004-637X/738/2/180

CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., and Shang, H. (2013). Does magnetic-field-rotation misalignment solve the magnetic braking catastrophe in protostellar disk formation? Astrophys. J. 774:82. doi: 10.1088/0004-637X/774/1/82

CrossRef Full Text | Google Scholar

Li, Z.-Y., Krasnopolsky, R., Shang, H., and Zhao, B. (2014). On the role of pseudodisk warping and reconnection in protostellar disk formation in turbulent magnetized cores. Astrophys. J. 793:130. doi: 10.1088/0004-637X/793/2/130

CrossRef Full Text | Google Scholar

Lis, D. C., Goldsmith, P. F., Dickman, R. L., Predmore, C. R., Omont, A., and Cernicharo, J. (1988). Linear polarization of millimeter-wave emission lines in clouds without large velocity gradients. Astrophys. J. 328, 304–314. doi: 10.1086/166293

CrossRef Full Text | Google Scholar

Liu, H. B., Hasegawa, Y., Ching, T.-C., Lai, S.-P., Hirano, N., and Rao, R. (2018). Detection of 40-48 GHz dust continuum linear polarization towards the Class 0 young stellar object IRAS 16293-2422. Astron. Astrophys. 617:A3. doi: 10.1051/0004-6361/201832699

CrossRef Full Text | Google Scholar

Liu, H. B., Lai, S.-P., Hasegawa, Y., Hirano, N., Rao, R., Li, I.-H., et al. (2016). Detection of linearly polarized 6.9 mm continuum emission from the class 0 young stellar object NGC 1333 IRAS4A. Astrophys. J. 821:41. doi: 10.3847/0004-637X/821/1/41

CrossRef Full Text | Google Scholar

Liu, H. B., Qiu, K., Zhang, Q., Girart, J. M., and Ho, P. T. P. (2013). Gas kinematics and the dragged magnetic field in the high-mass molecular outflow source G192.16-3.84: an SMA View. Astrophys. J. 771:71. doi: 10.1088/0004-637X/771/1/71

CrossRef Full Text | Google Scholar

Lopez-Rodriguez, E., Antonucci, R., Chary, R.-R., and Kishimoto, M. (2018). The highly polarized dusty emission core of cygnus A. Astrophys. J. Lett. 861:L23. doi: 10.3847/2041-8213/aacff5

CrossRef Full Text | Google Scholar

Lu, X., Zhang, Q., Liu, H. B., Sanhueza, P., Tatematsu, K., Feng, S., et al. (2018). Filamentary fragmentation and accretion in high-mass star-forming molecular clouds. Astrophys. J. 855:9. doi: 10.3847/1538-4357/aaad11

CrossRef Full Text | Google Scholar

Machida, M. N., Matsumoto, T., Hanawa, T., and Tomisaka, K. (2006). Evolution of rotating molecular cloud core with oblique magnetic field. Astrophys. J. 645, 1227–1245. doi: 10.1086/504423

CrossRef Full Text | Google Scholar

Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., and Commerçon, B. (2016). Ambipolar diffusion in low-mass star formation. I. General comparison with the ideal magnetohydrodynamic case. Astron. Astrophys. 587:A32. doi: 10.1051/0004-6361/201526371

CrossRef Full Text | Google Scholar

Matthews, B. C., Lai, S.-P., Crutcher, R. M., and Wilson, C. D. (2005). Multiscale magnetic fields in star-forming regions: interferometric polarimetry of the MMS 6 core of OMC-3. Astrophys. J. 626, 959–965. doi: 10.1086/430127

CrossRef Full Text | Google Scholar

Matthews, B. C., McPhee, C. A., Fissel, L. M., and Curran, R. L. (2009). The legacy of SCUPOL: 850 μm imaging polarimetry from 1997 to 2005. Astrophys. J. Suppl. Ser. 182, 143–204. doi: 10.1088/0067-0049/182/1/143

CrossRef Full Text | Google Scholar

Maury, A. J., Girart, J. M., Zhang, Q., Hennebelle, P., Keto, E., Rao, R., et al. (2018). Magnetically regulated collapse in the B335 protostar? I. ALMA observations of the polarized dust emission. Month. Not. R. Astron. Soc. 477, 2760–2765. doi: 10.1093/mnras/sty574

CrossRef Full Text | Google Scholar

McKee, C. F., and Tan, J. C. (2003). The formation of massive stars from turbulent cores. Astrophys. J. 585, 850–871. doi: 10.1086/346149

CrossRef Full Text | Google Scholar

McMullin, J. P., Waters, B., Schiebel, D., Young, W., and Golap, K. (2007). “CASA architecture and applications,” in Astronomical Data Analysis Software and Systems XVI, Vol. 376 of Astronomical Society of the Pacific Conference Series, Vol. 376, eds R. A. Shaw, F. Hill, and D. J. Bell (Arizona), 127.

Google Scholar

Mellon, R. R., and Li, Z.-Y. (2008). Magnetic braking and protostellar disk formation: the ideal MHD limit. Astrophys. J. 681, 1356–1376. doi: 10.1086/587542

CrossRef Full Text | Google Scholar

Ménard, F., and Duchêne, G. (2004). On the alignment of Classical T Tauri stars with the magnetic field in the Taurus-Auriga molecular cloud. Astron. Astrophys. 425, 973–980. doi: 10.1051/0004-6361:20041338

CrossRef Full Text | Google Scholar

Mestel, L., and Spitzer, L. Jr. (1956). Star formation in magnetic dust clouds. Month. Not. R. Astron. Soc. 116:503. doi: 10.1093/mnras/116.5.503

CrossRef Full Text | Google Scholar

Mocz, P., Burkhart, B., Hernquist, L., McKee, C. F., and Springel, V. (2017). Moving-mesh simulations of star-forming cores in magneto-gravo-turbulence. Astrophys. J. 838:40. doi: 10.3847/1538-4357/aa6475

CrossRef Full Text | Google Scholar

Motte, F., Bontemps, S., and Louvet, F. (2018). High-mass star and massive cluster formation in the milky way. 56, 41–82. doi: 10.1146/annurev-astro-091916-055235

CrossRef Full Text

Mouschovias, T. C. (1976a). Nonhomologous contraction and equilibria of self-gravitating, magnetic interstellar clouds embedded in an intercloud medium: star formation. I Formulation of the problem and method of solution. Astrophys. J. 206, 753–767. doi: 10.1086/154436

CrossRef Full Text | Google Scholar

Mouschovias, T. C. (1976b). Nonhomologous contraction and equilibria of self-gravitating, magnetic interstellar clouds embedded in an intercloud medium: star formation. II - Results. Astrophys. J. 207, 141–158. doi: 10.1086/154478

CrossRef Full Text | Google Scholar

Mouschovias, T. C. (1991). Magnetic braking, ambipolar diffusion, cloud cores, and star formation - Natural length scales and protostellar masses. Astrophys. J. 373, 169–186. doi: 10.1086/170035

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Ciolek, G. E. (1999). “Magnetic fields and star formation: a theory reaching adulthood,” in NATO Advanced Science Institutes (ASI) Series C, eds C. J. Lada and N. D. Kylafis, 305.

Google Scholar

Offner, S. S. R. and Chaban, J. (2017). Impact of protostellar outflows on turbulence and star formation efficiency in magnetized dense cores. Astrophys. J. 847:104. doi: 10.3847/1538-4357/aa8996

CrossRef Full Text | Google Scholar

Offner, S. S. R., Dunham, M. M., Lee, K. I., Arce, H. G., and Fielding, D. B. (2016). The turbulent origin of outflow and spin misalignment in multiple star systems. Astrophys. J. Lett. 827:L11. doi: 10.3847/2041-8205/827/1/L11

CrossRef Full Text | Google Scholar

Ohashi, N., Saigo, K., Aso, Y., Aikawa, Y., Koyamatsu, S., Machida, M. N., et al. (2014). Formation of a keplerian disk in the infalling envelope around L1527 IRS: transformation from infalling motions to kepler motions. Astrophys. J. 796:131. doi: 10.1088/0004-637X/796/2/131

CrossRef Full Text | Google Scholar

Ohashi, S., Kataoka, A., Nagai, H., Momose, M., Muto, T., Hanawa, T., et al. (2018). Two different grain size distributions within the protoplanetary disk around HD 142527 revealed by ALMA polarization observation. Astrophys. J. 864:81. doi: 10.3847/1538-4357/aad632

CrossRef Full Text | Google Scholar

Ohashi, S., Sanhueza, P., Chen, H.-R. V., Zhang, Q., Busquet, G., Nakamura, F., et al. (2016). Dense core properties in the infrared dark cloud G14.225-0.506 revealed by ALMA. Astrophys. J. 833:209. doi: 10.3847/1538-4357/833/2/209

CrossRef Full Text | Google Scholar

Ossenkopf, V., and Henning, T. (1994). Dust opacities for protostellar cores. Astron. Astrophys. 291, 943–959.

Google Scholar

Ostriker, E. C., Stone, J. M., and Gammie, C. F. (2001). Density, velocity, and magnetic field structure in turbulent molecular cloud models. Astrophys. J. 546, 980–1005. doi: 10.1086/318290

CrossRef Full Text | Google Scholar

Padovani, M., Brinch, C., Girart, J. M., Jørgensen, J. K., Frau, P., Hennebelle, P., et al. (2012). Adaptable radiative transfer innovations for submillimetre telescopes (ARTIST). Dust polarisation module (DustPol). Astron. Astrophys. 543:A16. doi: 10.1051/0004-6361/201219028

CrossRef Full Text | Google Scholar

Pattle, K., Ward-Thompson, D., Berry, D., Hatchell, J., Chen, H.-R., Pon, A., et al. (2017). The JCMT BISTRO survey: the magnetic field strength in the Orion A filament. Astrophys. J. 846:122. doi: 10.3847/1538-4357/aa80e5

CrossRef Full Text | Google Scholar

Pattle, K., Ward-Thompson, D., Hasegawa, T., Bastien, P., Kwon, W., Lai, S.-P., et al. (2018). First observations of the magnetic field inside the Pillars of Creation: results from the BISTRO survey. Astrophys. J. Lett. 860:L6. doi: 10.3847/2041-8213/aac771

CrossRef Full Text | Google Scholar

Pillai, T., Kauffmann, J., Wyrowski, F., Hatchell, J., Gibb, A. G., and Thompson, M. A. (2011). Probing the initial conditions of high-mass star formation. II. Fragmentation, stability, and chemistry towards high-mass star-forming regions G29.96-0.02 and G35.20-1.74. Astron. Astrophys. 530:A118. doi: 10.1051/0004-6361/201015899

CrossRef Full Text | Google Scholar

Plambeck, R. L., Wright, M. C. H., and Rao, R. (2003). Magnetic field morphology of Orion IRc2 from 86 GHz SiO maser polarization images. Astrophys. J. 594, 911–918. doi: 10.1086/377097

CrossRef Full Text | Google Scholar

Planck Collaboration, Adam, R., Ade, P. A. R., Aghanim, N., Alves, M. I. R., et al. (2016a). Planck intermediate results. XXXII. The relative orientation between the magnetic field and structures traced by interstellar dust. Astron. Astrophys. 586:A135. doi: 10.1051/0004-6361/201425044

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Alina, D., Alves, M. I. R., et al. (2015b). Planck intermediate results. XIX. An overview of the polarized thermal emission from Galactic dust. Astron. Astrophys. 576:A104. doi: 10.1051/0004-6361/201424082

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Alina, D., Alves, M. I. R., Aniano, G., et al. (2015a). Planck intermediate results. XX. Comparison of polarized thermal emission from Galactic dust with simulations of MHD turbulence. Astron. Astrophys. 576:A105. doi: 10.1051/0004-6361/201424086

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Alina, D., Aniano, G., Armitage-Caplan, C., et al. (2015c). Planck intermediate results. XXI. Comparison of polarized thermal emission from Galactic dust at 353 GHz with interstellar polarization in the visible. Astron. Astrophys. 576:A106. doi: 10.1051/0004-6361/201424087

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., et al. (2016b). Planck intermediate results. XXXIII. Signature of the magnetic field geometry of interstellar filaments in dust polarization maps. Astron. Astrophys. 586:A136. doi: 10.1051/0004-6361/201425305

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., et al. (2016c). Planck intermediate results. XXXV. Probing the role of the magnetic field in the formation of structure in molecular clouds. Astron. Astrophys. 586:A138. doi: 10.1051/0004-6361/201525896

CrossRef Full Text | Google Scholar

Pohl, A., Kataoka, A., Pinilla, P., Dullemond, C. P., Henning, T., and Birnstiel, T. (2016). Investigating dust trapping in transition disks with millimeter-wave polarization. Astron. Astrophys. 593:A12. doi: 10.1051/0004-6361/201628637

CrossRef Full Text | Google Scholar

Qiu, K., Zhang, Q., Menten, K. M., Liu, H. B., and Tang, Y.-W. (2013). From poloidal to toroidal: detection of a well-ordered magnetic field in the high-mass protocluster G35.2-0.74 N. Astrophys. J. 779:182. doi: 10.1088/0004-637X/779/2/182

CrossRef Full Text | Google Scholar

Qiu, K., Zhang, Q., Menten, K. M., Liu, H. B., Tang, Y.-W., and Girart, J. M. (2014). Submillimeter array observations of magnetic fields in G240.31+0.07: an hourglass in a massive cluster-forming core. Astrophys. J. Lett. 794:L18. doi: 10.1088/2041-8205/794/1/L18

CrossRef Full Text | Google Scholar

Qiu, K., Zhang, Q., Wu, J., and Chen, H.-R. (2009). Submillimeter array observations of the molecular outflow in high-mass star-forming region G240.31+0.07. Astrophys. J. 696, 66–74. doi: 10.1088/0004-637X/696/1/66

CrossRef Full Text | Google Scholar

Rao, R., Crutcher, R. M., Plambeck, R. L., and Wright, M. C. H. (1998). High-resolution millimeter-wave mapping of linearly polarized dust emission: magnetic field structure in Orion. Astrophys. J. Lett. 502:L75. doi: 10.1086/311485

CrossRef Full Text | Google Scholar

Rao, R., Girart, J. M., Lai, S.-P., and Marrone, D. P. (2014). Detection of a magnetized disk around a very young protostar. Astrophys. J. Lett. 780:L6. doi: 10.1088/2041-8205/780/1/L6

CrossRef Full Text | Google Scholar

Rao, R., Girart, J. M., Marrone, D. P., Lai, S.-P., and Schnee, S. (2009). IRAS 16293: a ”Magnetic” tale of two cores. Astrophys. J. 707, 921–935. doi: 10.1088/0004-637X/707/2/921

CrossRef Full Text | Google Scholar

Renbarger, T., Chuss, D. T., Dotson, J. L., Griffin, G. S., Hanna, J. L., Loewenstein, R. F., et al. (2004). Early results from SPARO: instrument characterization and polarimetry of NGC 6334. Publ. ASP 116, 415–424. doi: 10.1086/383623

CrossRef Full Text | Google Scholar

Ritacco, A., Ponthieu, N., Catalano, A., Adam, R., Ade, P., André, P., et al. (2017). Polarimetry at millimeter wavelengths with the NIKA camera: calibration and performance. Astron. Astrophys. 599:A34. doi: 10.1051/0004-6361/201629666

CrossRef Full Text | Google Scholar

Robitaille, T., and Bressert, E. (2012). APLpy: astronomical plotting library in python. Astrophysics Source Code Library.

Google Scholar

Roy, A., Ade, P. A. R., Bock, J. J., Chapin, E. L., Devlin, M. J., Dicker, S. R., et al. (2011). The balloon-borne large aperture submillimeter telescope (BLAST) 2005: a 10 deg² survey of star formation in cygnus X. Astrophys. J. 727:114. doi: 10.1088/0004-637X/727/2/114

CrossRef Full Text | Google Scholar

Sadavoy, S. I., Myers, P. C., Stephens, I. W., Tobin, J., Commercon, B., Henning, T., et al. (2018a). Dust polarization toward embedded protostars in ophiuchus with ALMA. I. VLA 1623. Astrophys. J. 859:165. doi: 10.3847/1538-4357/aac21a

CrossRef Full Text | Google Scholar

Sadavoy, S. I., Myers, P. C., Stephens, I. W., Tobin, J., Kwon, W., Segura-Cox, D., et al. (2018b). Dust polarization toward embedded protostars in ophiuchus with ALMA. II. IRAS 16293-2422. Astrophys. J. 869:115. doi: 10.3847/1538-4357/aaef81

CrossRef Full Text | Google Scholar

Sanhueza, P., Jackson, J. M., Zhang, Q., Guzmán, A. E., Lu, X., Stephens, I. W., et al. (2017). A massive prestellar clump hosting no high-mass cores. Astrophys. J. 841:97. doi: 10.3847/1538-4357/aa6ff8

CrossRef Full Text | Google Scholar

Santos-Lima, R., de Gouveia Dal Pino, E. M., and Lazarian, A. (2012). The role of turbulent magnetic reconnection in the formation of rotationally supported protostellar disks. Astrophys. J. 747:21. doi: 10.1088/0004-637X/747/1/21

CrossRef Full Text | Google Scholar

Saral, G., Hora, J. L., Audard, M., Koenig, X. P., Martínez-Galarza, J. R., Motte, F., et al. (2017). Young stellar objects in the massive star-forming regions W51 and W43. Astrophys. J. 839:108. doi: 10.3847/1538-4357/aa6575

CrossRef Full Text | Google Scholar

Schleuning, D. A. (1998). Far-infrared and submillimeter polarization of OMC-1: evidence for magnetically regulated star formation. Astrophys. J. 493:811. doi: 10.1086/305139

CrossRef Full Text | Google Scholar

Segura-Cox, D. M., Looney, L. W., Stephens, I. W., Fernández-López, M., Kwon, W., Tobin, J. J., et al. (2015). The magnetic field in the class 0 protostellar disk of L1527. Astrophys. J. Lett. 798:L2. doi: 10.1088/2041-8205/798/1/L2

CrossRef Full Text | Google Scholar

Segura-Cox, D. M., Looney, L. W., Tobin, J. J., Li, Z.-Y., Harris, R. J., Sadavoy, S., et al. (2018). The VLA nascent disk and multiplicity survey of perseus protostars (VANDAM). V. 18 Candidate Disks around Class 0 and I Protostars in the Perseus Molecular Cloud. Astrophys. J. 866:161. doi: 10.3847/1538-4357/aaddf3

CrossRef Full Text | Google Scholar

Seifried, D., Banerjee, R., Pudritz, R. E., and Klessen, R. S. (2015). Accretion and magnetic field morphology around Class 0 stage protostellar discs. Month. Not. R. Astron. Soc. 446, 2776–2788. doi: 10.1093/mnras/stu2282

CrossRef Full Text | Google Scholar

Shu, F. H., Adams, F. C., and Lizano, S. (1987). Star formation in molecular clouds - Observation and theory. Annu. Rev. Astron. Astrophys. 25, 23–81. doi: 10.1146/annurev.aa.25.090187.000323

CrossRef Full Text | Google Scholar

Shu, F. H., Najita, J. R., Shang, H., and Li, Z.-Y. (2000). X-winds theory and observations. Protostars and Planets IV, eds V. Mannings, A. P. Boss, and S. S. Russell (Tucson: University of Arizona Pres), 789–814.

Google Scholar

Siringo, G., Kovács, A., Kreysa, E., Schuller, F., Weiss, A., Guesten, R., et al. (2012). “First results of the polarimeter for the Large APEX Bolometer Camera (LABOCA),” in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI, 845206. doi: 10.1117/12.925697

CrossRef Full Text | Google Scholar

Siringo, G., Kreysa, E., Reichertz, L. A., and Menten, K. M. (2004). A new polarimeter for (sub)millimeter bolometer arrays. Astron. Astrophys. 422, 751–760. doi: 10.1051/0004-6361:20035832

CrossRef Full Text | Google Scholar

Soam, A., Pattle, K., Ward-Thompson, D., Lee, C. W., Sadavoy, S., Koch, P. M., et al. (2018). Magnetic fields towards Ophiuchus-B derived from SCUBA-2 polarization measurements. Astrophys. J. 861:65. doi: 10.3847/1538-4357/aac4a6

CrossRef Full Text | Google Scholar

Sridharan, T. K., Rao, R., Qiu, K., Cortes, P., Li, H., Pillai, T., et al. (2014). Hot Core, outflows, and magnetic fields in W43-MM1 (G30.79 FIR 10). Astrophys. J. Lett. 783:L31. doi: 10.1088/2041-8205/783/2/L31

CrossRef Full Text | Google Scholar

Stephens, I. W., Dunham, M. M., Myers, P. C., Pokhrel, R., Bourke, T. L., Vorobyov, E. I., et al. (2018). Mass assembly of stellar systems and their evolution with the SMA - 1.3 mm subcompact data release. Astrophys. J. Suppl. 237:22. doi: 10.3847/1538-4365/aacda9

CrossRef Full Text | Google Scholar

Stephens, I. W., Dunham, M. M., Myers, P. C., Pokhrel, R., Sadavoy, S. I., Vorobyov, E. I., et al. (2017a). Alignment between protostellar outflows and filamentary structure. Astrophys. J. 846:16. doi: 10.3847/1538-4357/aa8262

CrossRef Full Text | Google Scholar

Stephens, I. W., Looney, L. W., Dowell, C. D., Vaillancourt, J. E., and Tassis, K. (2011). The galactic magnetic field's effect in star-forming regions. Astrophys. J. 728:99. doi: 10.1088/0004-637X/728/2/99

CrossRef Full Text | Google Scholar

Stephens, I. W., Looney, L. W., Kwon, W., Fernández-López, M., Hughes, A. M., Mundy, L. G., et al. (2014). Spatially resolved magnetic field structure in the disk of a T Tauri star. Nature 514, 597–599. doi: 10.1038/nature13850

PubMed Abstract | CrossRef Full Text | Google Scholar

Stephens, I. W., Looney, L. W., Kwon, W., Hull, C. L. H., Plambeck, R. L., Crutcher, R. M., et al. (2013). The magnetic field morphology of the class 0 protostar L1157-mm. Astrophys. J. Lett. 769:L15. doi: 10.1088/2041-8205/769/1/L15

CrossRef Full Text | Google Scholar

Stephens, I. W., Yang, H., Li, Z.-Y., Looney, L. W., Kataoka, A., Kwon, W., et al. (2017b). ALMA reveals transition of polarization pattern with wavelength in HL Tau's disk. Astrophys. J. 851:55. doi: 10.3847/1538-4357/aa998b

CrossRef Full Text | Google Scholar

Takahashi, S., Machida, M. N., Tomisaka, K., Ho, P. T. P., Fomalont, E. B., Nakanishi, K., et al. (2019). ALMA high angular resolution polarization study: an extremely young class 0 source, OMC-3/MMS 6. Astrophys. J. 872:70. doi: 10.3847/1538-4357/aaf6ed

CrossRef Full Text | Google Scholar

Takahashi, S., Saito, M., Takakuwa, S., and Kawabe, R. (2006). Millimeter- and submillimeter-wave observations of the OMC-2/3 region. I. Dispersing and rotating core around the intermediate-mass protostar MMS 7. Astrophys. J. 651, 933–944. doi: 10.1086/507482

CrossRef Full Text | Google Scholar

Tang, Y.-W., Ho, P. T. P., Girart, J. M., Rao, R., Koch, P., and Lai, S.-P. (2009a). Evolution of magnetic fields in high mass star formation: submillimeter array dust polarization image of the ultracompact H II region G5.89-0.39. Astrophys. J. 695, 1399–1412. doi: 10.1088/0004-637X/695/2/1399

CrossRef Full Text | Google Scholar

Tang, Y.-W., Ho, P. T. P., Koch, P. M., Girart, J. M., Lai, S.-P., and Rao, R. (2009b). Evolution of magnetic fields in high-mass star formation: linking field geometry and collapse for the W51 e2/e8 Cores. Astrophys. J. 700, 251–261. doi: 10.1088/0004-637X/700/1/251

CrossRef Full Text | Google Scholar

Tang, Y.-W., Ho, P. T. P., Koch, P. M., and Rao, R. (2010). High-angular resolution dust polarization measurements: shaped B-field lines in the massive star-forming region Orion BN/KL. Astrophys. J. 717, 1262–1273. doi: 10.1088/0004-637X/717/2/1262

CrossRef Full Text | Google Scholar

Targon, C. G., Rodrigues, C. V., Cerqueira, A. H., and Hickel, G. R. (2011). Correlating the interstellar magnetic field with protostellar jets and its sources. Astrophys. J. 743:54. doi: 10.1088/0004-637X/743/1/54

CrossRef Full Text | Google Scholar

Tazaki, R., Lazarian, A., and Nomura, H. (2017). Radiative grain alignment in protoplanetary disks: implications for polarimetric observations. Astrophys. J. 839:56. doi: 10.3847/1538-4357/839/1/56

CrossRef Full Text | Google Scholar

Tobin, J. J., Hartmann, L., Chiang, H.-F., Wilner, D. J., Looney, L. W., Loinard, L., et al. (2012). A 0.2-solar-mass protostar with a Keplerian disk in the very young L1527 IRS system~. Nature 492, 83–85. doi: 10.1038/nature11610

PubMed Abstract | CrossRef Full Text | Google Scholar

Tobin, J. J., Kratter, K. M., Persson, M. V., Looney, L. W., Dunham, M. M., Segura-Cox, D., et al. (2016a). A triple protostar system formed via fragmentation of a gravitationally unstable disk. Nature 538, 483–486. doi: 10.1038/nature20094

PubMed Abstract | CrossRef Full Text | Google Scholar

Tobin, J. J., Looney, L. W., Li, Z.-Y., Chandler, C. J., Dunham, M. M., Segura-Cox, D., et al. (2016b). The VLA nascent disk and multiplicity survey of perseus protostars (VANDAM). II. Multiplicity of protostars in the perseus molecular cloud. Astrophys. J. 818:73. doi: 10.3847/0004-637X/818/1/73

CrossRef Full Text | Google Scholar

Tobin, J. J., Looney, L. W., Li, Z.-Y., Sadavoy, S. I., Dunham, M. M., Segura-Cox, D., et al. (2018). The VLA/ALMA Nascent Disk and Multiplicity (VANDAM) survey of perseus protostars. VI. Characterizing the formation mechanism for close multiple systems. 867:43. doi: 10.3847/1538-4357/aae1f7

CrossRef Full Text

Tomida, K., Okuzumi, S., and Machida, M. N. (2015). Radiation magnetohydrodynamic simulations of protostellar collapse: nonideal magnetohydrodynamic effects and early formation of circumstellar disks. Astrophys. J. 801:117. doi: 10.1088/0004-637X/801/2/117

CrossRef Full Text | Google Scholar

Traficante, A., Lee, Y.-N., Hennebelle, P., Molinari, S., Kauffmann, J., and Pillai, T. (2018). A possible observational bias in the estimation of the virial parameter in virialized clumps. Astron. Astrophys. 619:L7. doi: 10.1051/0004-6361/201833513

CrossRef Full Text | Google Scholar

Troland, T. H., and Heiles, C. (1986). Interstellar magnetic field strengths and gas densities Observational and theoretical perspectives. Astrophys. J. 301, 339–345. doi: 10.1086/163904

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., and Inutsuka, S. (2015). Bimodality of circumstellar disk evolution induced by the hall current. Astrophys. J. Lett. 810:L26. doi: 10.1088/2041-8205/810/2/L26

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Okuzumi, S., Iwasaki, K., Machida, M. N., and Inutsuka, S. (2018). Does misalignment between magnetic field and angular momentum enhance or suppress circumstellar disk formation? Astrophys. J. 868:22. doi: 10.3847/1538-4357/aae4dc

CrossRef Full Text | Google Scholar

Tsukamoto, Y., Okuzumi, S., Iwasaki, K., Machida, M. N., and Inutsuka, S.-i. (2017). The impact of the Hall effect during cloud core collapse: Implications for circumstellar disk evolution. Publ. ASJ 69:95. doi: 10.1093/pasj/psx113

CrossRef Full Text | Google Scholar

Vaillancourt, J. E., Chuss, D. T., Crutcher, R. M., Dotson, J. L., Dowell, C. D., Harper, D. A., et al. (2007). “Far-infrared polarimetry from the Stratospheric Observatory for Infrared Astronomy,” in Infrared Spaceborne Remote Sensing and Instrumentation XV, 66780D. doi: 10.1117/12.730922

CrossRef Full Text | Google Scholar

Vallée, J. P., and Fiege, J. D. (2006). A cool filament crossing the warm protostar DR 21(OH): geometry, kinematics, magnetic vectors, and pressure balance. Astrophys. J. 636, 332–347. doi: 10.1086/497957

CrossRef Full Text | Google Scholar

van Kempen, T. A., Hogerheijde, M. R., van Dishoeck, E. F., Kristensen, L. E., Belloche, A., Klaassen, P. D., et al. (2016). Outflow forces in intermediate-mass star formation. Astron. Astrophys. 587:A17. doi: 10.1051/0004-6361/201424725

CrossRef Full Text | Google Scholar

Ward-Thompson, D., Pattle, K., Bastien, P., Furuya, R. S., Kwon, W., Lai, S.-P., et al. (2017). First results from BISTRO: a SCUBA-2 polarimeter survey of the gould belt. Astrophys. J. 842:66. doi: 10.3847/1538-4357/aa70a0

CrossRef Full Text | Google Scholar

Wiesemeyer, H., Hezareh, T., Kreysa, E., Weiss, A., Güsten, R., Menten, K. M., et al. (2014). Submillimeter polarimetry with PolKa, a reflection-type modulator for the APEX telescope. Publ. ASP 126:1027. doi: 10.1086/679002

CrossRef Full Text | Google Scholar

Wright, M. C. H., Hull, C. L. H., Pillai, T., Zhao, J.-H., and Sandell, G. (2014). NGC 7538 IRS 1: interaction of a polarized dust spiral and a molecular outflow. Astrophys. J. 796:112. doi: 10.1088/0004-637X/796/2/112

CrossRef Full Text | Google Scholar

Wurster, J., Bate, M. R., and Price, D. J. (2018). Hall effect-driven formation of gravitationally unstable discs in magnetized molecular cloud cores. Month. Not. R. Astron. Soc. 480, 4434–4442. doi: 10.1093/mnras/sty2212

CrossRef Full Text | Google Scholar

Wurster, J., and Li, Z.-Y. (2018). The role of magnetic fields in the formation of protostellar discs. Front. Astron. Space Sci. 5:39. doi: 10.3389/fspas.2018.00039

CrossRef Full Text | Google Scholar

Yang, H., Li, Z.-Y., Looney, L., and Stephens, I. (2016a). Inclination-induced polarization of scattered millimetre radiation from protoplanetary discs: the case of HL Tau. Month. Not. R. Astron. Soc. 456, 2794–2805. doi: 10.1093/mnras/stv2633

CrossRef Full Text | Google Scholar

Yang, H., Li, Z.-Y., Looney, L. W., Cox, E. G., Tobin, J., Stephens, I. W., et al. (2016b). Disc polarization from both emission and scattering of magnetically aligned grains: the case of NGC 1333 IRAS 4A1. Month. Not. R. Astron. Soc. 460, 4109–4121. doi: 10.1093/mnras/stw1253

CrossRef Full Text | Google Scholar

Yang, H., Li, Z.-Y., Stephens, I. W., Kataoka, A., and Looney, L. (2019). Does HL Tau disk polarization in ALMA band 3 come from radiatively aligned grains? 483, 2371–2381. doi: 10.1093/mnras/sty3263

CrossRef Full Text

Yuen, K. H., and Lazarian, A. (2017). Tracing interstellar magnetic field using velocity gradient technique: application to atomic hydrogen data. Astrophys. J. Lett. 837:L24. doi: 10.3847/2041-8213/aa6255

CrossRef Full Text | Google Scholar

Zhang, Q., and Ho, P. T. P. (1997). Dynamical collapse in W51 massive cores: NH₃ observations. Astrophys. J. 488, 241–257. doi: 10.1086/304667

CrossRef Full Text | Google Scholar

Zhang, Q., Qiu, K., Girart, J. M., Liu, H. B., Tang, Y.-W., Koch, P. M., et al. (2014). Magnetic fields and massive star formation. Astrophys. J. 792:116. doi: 10.1088/0004-637X/792/2/116

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, K., Lu, X., and Jiménez-Serra, I. (2015). Fragmentation of molecular clumps and formation of a protocluster. Astrophys. J. 804:141. doi: 10.1088/0004-637X/804/2/141

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, Y., Pillai, T., and Rathborne, J. (2009). Fragmentation at the earliest phase of massive star formation. Astrophys. J. 696, 268–273. doi: 10.1088/0004-637X/696/1/268

CrossRef Full Text | Google Scholar