The Role of Magnetic Field in Molecular Cloud Formation and Evolution

1. Introduction

The interstellar cycle, which takes place within galaxies, is fundamental for our universe as it controls the formation of stars and therefore the evolution of galaxies. Yet given the broad range of spatial scales and the profusion of physical processes involved, our understanding is still very incomplete. Amongst other processes, namely gravity, compressible turbulence, radiation, cosmic rays and stellar feedback, magnetic field is also contributing significantly to the evolution of the interstellar medium (ISM) and more specifically to the formation of stars. As a matter of evidence, the magnetic energy in the ISM is comparable to the other energies as for example the kinematic one. Deciphering the various roles that magnetic field is playing is however not obvious, (i) because measuring it remains a challenge, (ii) because magnetic field is not a mere pressure and is highly non-isotropic in nature, (iii) because observations do not allow us to easily vary the parameters as it is possible to do in experiments. This however can be done in numerical simulations where the influence of a specific parameter, like the magnetic intensity, can be modified and studied.

This review is dedicated to the role magnetic field is playing in the formation and evolution of molecular clouds. Given the complex multi-scale nature of these latter, this represents a challenge as several physical processes and astrophysical objects have to be discussed, in particular because as stressed above, the magnetic field is strongly interacting with other phenomena, that need to be described for self-consistency.

The plan of the paper is as follows. In section 2, we describe the equations of the magneto-hydrodynamics (MHD) that are used to compute and predict the evolution of molecular clouds. We give some ideas of how these equations are inferred first in the ideal MHD framework, that is to say when the fluid and the magnetic field are perfectly coupled. Then we briefly discuss the most important correction that must be taken into account in molecular clouds, namely the ion-neutral drift or ambipolar diffusion. In section 3, the multi-phase nature of the ISM is discussed: how the gas cools and heats, the principle of thermal instability and its non-linear regime. The role that magnetic field may have in the transition from warm atomic gas into cold and dense gas is emphasized. In section 4, the nature of the turbulence in the ISM is presented. First some elements of the magnetized incompressible turbulence are given, stressing the ideas and problems that are still debated. Second the more realistic compressible and multi-phase magnetized turbulence is addressed, reporting the various numerical studies that have been performed. The influence that the ion-neutral drift may have on turbulence is discussed. Section 5 is specifically dedicated to the correlation between density and magnetic field including the magnetic intensity and the magnetic orientation. Section 6 is specifically dedicated to puzzling astrophysical objects, namely the filaments that, in a sense, constitute sub-structures of molecular clouds. The question of their formation, the physical origin of the possible characteristic width that has been recently inferred and their fragmentation in star forming cores are discussed. In section 7, the molecular clouds themselves are eventually addressed. We start by reviewing the role that ambipolar diffusion may have in the magnetically dominated clouds, particularly regarding the fundamental question of the low efficient formation of stars in galaxies. Then the properties of the prestellar cores which form in dedicated numerical simulations of these clouds are described stressing the effect that magnetic field may have. Finally the role that magnetic field may have in stellar clusters formation is presented. In section 8, we briefly review the works in which the impact of the magnetic field on molecular cloud formation has been addressed. Section 9 concludes the paper.

2. MHD Equations

For the sake of completeness and because readers may find it useful, a short derivation and discussion of the MHD equations is given. We start with the ideal MHD, which amongst other approximations assume the non-relativistic limit, that is to say the fluid velocities are much smaller than the speed of light c. We also discuss a correction to these set of equations in the presence of neutral particles since the ionization degree in the ISM is small.

2.1. Ideal MHD

The equations of ideal MHD assume that the fluids are perfect conductors. The Lorentz force, which is the force that the electromagnetic fields E and B exert on the fluid must be taken into account. The electromagnetic fields evolution is obviously described by the Maxwell equations. Written in CGS units, these equations are

$\begin{array}{cc}\begin{array}{lll}\nabla ·B& =& 0,\end{array}& (1)\end{array}$

$\begin{array}{cc}\begin{array}{lll}\nabla ·E& =& 4\pi {\rho }_e,\end{array}& (2)\end{array}$

$\begin{array}{cc}\begin{array}{lll}c\nabla \times E& =& -\frac{\partial B}{\partial t},\end{array}& (3)\end{array}$

$\begin{array}{cc}\begin{array}{lll}c\nabla \times B& =& 4\pi j+\frac{\partial E}{\partial t},\end{array}& (4)\end{array}$

ρ_e and j are the fluid charge and current densities. The equation for charge conservation links these two quantities

$\begin{array}{cc}\begin{array}{l}\frac{\partial {\rho }_e}{\partial t}+\nabla ·j=0.\end{array}& (5)\end{array}$

While in a perfect conductor at rest, E_R vanishes, the situation is different when it moves. The rest fields E_R and B_R and the fields in the observer frame, E and B are related using the Lorentz transformation, as detailed by e.g., Landau and Lifshitz (1960), Shu (1992), and Spruit (2013). Considering the Lorentz force F and F_R, we get:

$\begin{array}{cc}\begin{array}{lll}F& =& q(E+\frac{v}{c}\times B),\end{array}& (6)\end{array}$

$\begin{array}{cc}\begin{array}{lll}{F}_R& =& q{E}_R.\end{array}& (7)\end{array}$

Since the force does not depend on the reference frame: F =F_R and therefore

$\begin{array}{cc}\begin{array}{lll}{E}_R& =& E+\frac{v}{c}\times B,\end{array}& (8)\end{array}$

$\begin{array}{cc}\begin{array}{lll}{B}_R& =& B.\end{array}& (9)\end{array}$

Since the perfect conductor assumption is made, E_R = 0, and

$\begin{array}{cc}\begin{array}{l}E=-\frac{v}{c}\times B.\end{array}& (10)\end{array}$

Combining it with Equation (3) we obtain:

$\begin{array}{cc}\begin{array}{l}\frac{\partial B}{\partial t}=\nabla \times (v\times B).\end{array}& (11)\end{array}$

The Lorentz force per unit volume, f_L, can be expressed as

$\begin{array}{cc}\begin{array}{l}{f}_L={\rho }_{e}E+\frac{1}{c}j\times B.\end{array}& (12)\end{array}$

In the non-relativistic limit, the displacement current in Equation (4) can be neglected, leading to

$\begin{array}{cc}\begin{array}{l}\nabla \times B=\frac{4\pi }{c}j.\end{array}& (13)\end{array}$

Since local electroneutrality is assumed, we have ρ_E = 0 and

$\begin{array}{cc}\begin{array}{l}{f}_L=\frac{(\nabla \times B)\times B}{4\pi }.\end{array}& (14)\end{array}$

This leads to the standard form of the ideal MHD equations

$\begin{array}{cc}\begin{array}{lll}\frac{\partial \rho }{\partial t}+\nabla ·(\rho v)& =& 0,\end{array}& (15)\end{array}$

$\begin{array}{cc}\begin{array}{lll}\rho \left[\frac{\partial v}{\partial t}+(v·\nabla )v\right]& =& -\nabla P+\frac{(\nabla \times B)\times B}{4\pi },\end{array}& (16)\end{array}$

$\begin{array}{cc}\begin{array}{lll}\rho \left[\frac{\partial e}{\partial t}+(v·\nabla )e\right]& =& -P(\nabla ·v)-\rho {L},\end{array}& (17)\end{array}$

$\begin{array}{cc}\begin{array}{lll}\frac{\partial B}{\partial t}& =& \nabla \times (v\times B).\end{array}& (18)\end{array}$

where ${L}$ is the net loss function and describes the radiative heating and cooling of the gas. This must be complemented by an equation of state to close the system of equations. A perfect gas is a good assumption for the ISM, P = (γ−1)ρϵ, where γ is the adiabatic index of the gas.

It is useful to get a better insight and physical interpretation of the MHD equations to rewrite the Lorentz force as

$\begin{array}{cc}\begin{array}{l}{f}_L=\frac{\left(\nabla \times B\right)\times B}{4\pi }=-\nabla \left(\frac{B^2}{8\pi }\right)+\frac{(B·\nabla )B}{4\pi }\end{array}& (19)\end{array}$

The first term is called the magnetic pressure. The second is the magnetic tension (see the detailed discussion page 13 in the lecture by Spruit, 2013).

2.2. Non-ideal MHD: the Ion-Neutral Drift

In many situations, ideal MHD is not a sufficiently good assumption and additional effects need to be accounted for. In the context of molecular clouds the dominant correction is the so-called ambipolar diffusion. Since the neutrals are not charged they are not subject to the Lorentz force which applies only on the ions. However through collisions the neutrals and the ions exchange momentum and therefore the Lorentz force has an influence on the neutrals through the ions. If the number of ions is large, i.e., if the ionization is high, the number of collisions is expected to be large and ideal MHD remains a good approximation. However in molecular clouds the ionization is usually of the order of 10⁻⁷ and therefore the two fluid are not perfectly coupled. The ions drag the field lines and drift with respect to the neutrals implying that the latter can cross the field lines. The field is not frozen in the gas anymore. Because of the low ionization, it is thus possible to neglect the inertia of the ions and a reasonable assumption is that of the equilibrium between the Lorentz force and the drag force exerted on the ions. This leads to:

$\begin{array}{cc}\begin{array}{l}\frac{(\nabla \times \text{B})\times \text{B}}{4\pi }={\gamma }_{ad}\rho {\rho }_i({\text{V}}_i-\text{V}),\end{array}& (20)\end{array}$

where ρ_i and V_i are the ion density and velocity, respectively, ${\gamma }_{ad}\simeq 3.5\times 10^{13}$ cm³ g⁻¹ s⁻¹ is the drag coefficient (Mouschovias and Paleologou, 1981). Equation (20), gives the ion velocity as a function of the neutral velocity and the Lorentz force. Combining it with the induction equation one gets

$\begin{array}{cc}\begin{array}{l}{\partial }_t\text{B}+\nabla \times (\text{B}\times \text{V})=\nabla \times \left(\frac{1}{4\pi {\gamma }_{ad}\rho {\rho }_i}((\nabla \times \text{B})\times \text{B})\times \text{B}\right).\end{array}& (21)\end{array}$

The left-hand side is the induction equation of ideal MHD. The right-hand side describes the ion-neutral drift. It is not rigorously speaking a diffusion term although it entails second order spatial derivatives. From this equation a typical time scale for ambipolar diffusion can easily be inferred

$\begin{array}{cc}\begin{array}{l}{\tau }_{\text{ad}}\simeq \frac{4\pi {\gamma }_{ad}\rho {\rho }_i{L}^2}{B^2},\end{array}& (22)\end{array}$

where L is the characteristic spatial scale of the problem, which could be the size of the prestellar cores or the filaments as described below. Ionization equilibrium leads to ${\rho }_i=C\sqrt{\rho }$, where C = 3 × 10⁻¹⁶ cm^−3/2 g^1/2.

As Equation (20) neglects the ion inertia, it is called the strong coupling limit (e.g., Shu, 1992; Mac Low et al., 1995; Masson et al., 2012). Ideally, it is necessary to consider two fluids the neutral and the ions coupled through the collisional term. The difficulty however with this approach is that the Alfvén speed associated to the ions is several orders of magnitude larger than the Alfvén speed associated to the neutrals. This makes numerical simulations very difficult to perform because the timesteps are then very small. For this reason an alternative approximation, called the heavy ion approximation has been developed (Li et al., 2006). It consists in artificially increasing the mass of the ions to lower their Alfvén speed while modifying the ion-neutral cross-section to maintain constant the friction coefficient.

Finally, let us mention that the ion-neutral friction leads to energy dissipation and therefore constitute a source of heating in Equation (17) which is equal to ${\gamma }_{ad}\rho {\rho }_i{({\text{V}}_i-\text{V})}^2$.

3. The Formation of Dense Gas in the ISM

Here we describe how the formation of dense gas out of diffuse atomic gas is achieved in the ISM. A brief description of the cooling and heating processes, essential to understand how the ISM becomes denser is given. We then describe the principle of thermal instability on the role magnetic field may have. Finally, a dynamical scenario for the formation of molecular clouds is sketched, stressing how magnetic field is acting.

3.1. Thermal Structure of ISM and Thermal Instability

In this section, our knowledge about thermal physics of ISM is presented. To calculate the equilibrium temperature of ISM as a function of gas density, one must equate heating and cooling function taking into account several physical processes. The detailed analysis for the thermal equilibrium state in the neutral atomic phase can be found, for example, in Wolfire et al. (2003) while Koyama and Inutsuka (2000) (see also e.g., Glover and Clark, 2012; Gong et al., 2017) extended their calculation for unshielded gas up to gas densities 10³cm⁻³< n < 10⁶cm⁻³ (see Figure 1). The main heating mechanisms are the photoelectric emission from small grains and PAHs, ionization by cosmic rays and soft X-rays, and the formation and photodissociation of H₂. The local FUV field is supposed to be on the order of Habing's value (G₀ = 1.7 and is adopted in Figure 1). The dominant cooling processes are the line emission from H, C, O, Si, and Fe, by rovibrational lines from H₂ and CO, as well as by atomic and molecular collisions with dust grains. The transition to the molecule-dominated phase depends on both gas density and column density as well as the radiation field (see Sternberg et al., 2014 for analysis and discussion of the relative importance of H₂ self-shielding and dust shielding). The chemistry and cooling in gas with a range of density, column, metallicity, and radiation fields is discussed e.g., in Glover and Clark (2012) and Gong et al. (2017). To describe these thermal processes a set of three time-dependent equations for ionization and recombination of hydrogen, and formation and dissociation of molecules should be solved. Self-shielding effects must also be taken into account to calculate the H₂ photodissociation. Figure 1 portrays the resulting temperature, pressure, and the relevant chemical species as functions of number density for unshielded gas. At high column density, inside molecular clouds, the dominant molecular cooling process is due to the CO molecules (at densities above 10⁵ cm⁻³ dust cooling becomes dominant) and the heating one comes from cosmic rays. A complete thermal balance description of the high density gas, which can be found for instance in Neufeld et al. (1995), is beyond the scope of the present review.

FIGURE 1

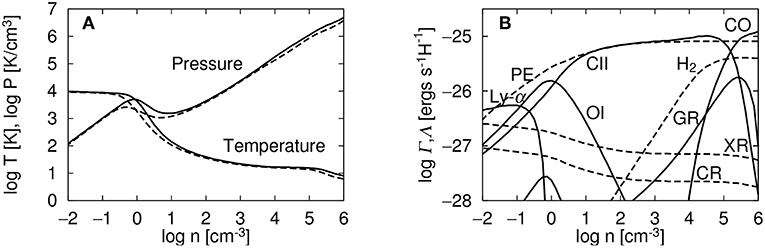
Figure 1. A phase diagram of ISM and important heating and cooling processes shown in Koyama and Inutsuka (2000). (A) Equilibrium temperature and pressure with absorbing column density of 10¹⁹cm⁻² (solid lines), 10²⁰cm⁻² (dashed lines). (B) Heating (dashed lines) and cooling rates (solid lines) for unshielded gas per hydrogen nucleus at equilibrium. Heating processes are, photoelectric effect from small grains and PAHs (PE), X-ray (XR), Cosmic-ray (CR), and H₂ formation/destruction. Cooling processes are CII fine-structure (CII), OI fine-structure (OI), Hydrogen Lyman-α (Ly-α), CO rotation/vibration line (CO), and atomic and molecular collisions with dust grains (GR). Reproduced from Koyama and Inutsuka (2000) with permission of ApJ.

The basic property of thermal stability can be related to the slope of heat-loss function, ${L}=\rho \Lambda -\text{Γ}$, where ρΛ is the cooling function per volume and Γ is the heating function. Field (1965) studied in details the stability conditions of a uniform medium subject to heating and cooling. In particular, he inferred the isobaric criterion which is given by

$\begin{array}{cc}\begin{array}{l}{\left(\frac{\partial {L}}{\partial T}\right)}_{\text{P}}<0\iff {\left(\frac{\partial P}{\partial \rho }\right)}_{{L}}<0.\end{array}& (23)\end{array}$

Mathematically, it corresponds to p < 1 in the case Λ ∝ T^p. Typically this unstable phase occurs for temperature between ~ 100 and ~ 5,000 K. Figure 2 shows the growth rate of thermal instability as a function of the wavelength of the linear perturbation. The dashed curve corresponds to the case of the unperturbed state in equilibrium. The thermal conduction tends to make the system isothermal, and hence, it stabilizes the perturbations with sufficiently small wavelengths. The critical wavelength (the largest wavelength stabilized by thermal conduction) is called “Field length” named after the pioneer of this analysis:

$\begin{array}{cc}\begin{array}{l}{\lambda }_{\text{c}}=2\pi {\left\{\frac{\rho }{K}{\left[\frac{\partial {L}}{\partial T}\right]}_{\text{P}}\right\}}^{-1/2}~\sqrt{\frac{KT}{{\rho }^2\Lambda }}\equiv {\lambda }_{\text{F}},\end{array}& (24)\end{array}$

where K denotes the coefficient of thermal conduction.

FIGURE 2

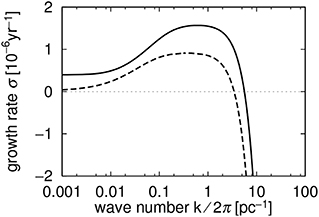
Figure 2. The dispersion relation for condensation mode of thermal instability analyzed in Koyama and Inutsuka (2000). The dashed curve denotes the classical result for the case of thermal equilibrium unperturbed state. The solid curve denotes for the case of an isobarically contracting unperturbed state. Reproduced from Koyama and Inutsuka (2000) with permission of ApJ.

In the case where the spatially uniform perturbed state is not in thermal balance, the criterion for the instability is p < 2 for Λ ∝ T^p, and hence, the range of the unstable temperature becomes wider (Schwarz et al., 1972). The dispersion relation for isobarically cooling medium is portrayed by the solid curve in Figure 2 (Koyama and Inutsuka, 2000). The growth rate presents a peak at a wavelength that is about ten times larger than the Field length implying that thermal instability tends to produce structures larger than the Field length.

3.2. The Effect of Magnetic Field on Thermal Instability

The effect of magnetic field on the linear growth of thermal instability was studied in detail by Ames (1973). Obviously a sufficiently strong magnetic field suppresses the motion perpendicular to the magnetic field lines. This is because in slab geometry, the magnetic pressure is simply proportional to the density square (as magnetic field is proportional to density), therefore the increase of the magnetic pressure can compensate for the decrease of the thermal pressure. However the perturbations in the direction along the magnetic field are not suppressed and remain unstable, if the cooling function satisfies the instability criteria. The non-linear development of the thermal instability has been studied by various authors (Hennebelle and Pérault, 2000; Piontek and Ostriker, 2004; Inoue et al., 2007; van Loo et al., 2007; Inoue and Inutsuka, 2008, 2009; Choi and Stone, 2012) while the effects of non-ideal MHD on thermal instability have been studied by various papers. Inoue et al. (2007) have done one-dimensional two-fluid simulations where neutral and charged components are self-consistently described as two fluids. They found that regardless of the initial conditions used to set up the simulation, the magnetic field strength in dense regions ends up being a few μG.

3.3. Formation of Molecular Clouds

It is believed that most of the volume in the thin (~10²pc) disk of our Milky Way Galaxy is filled by warm neutral medium (WNM) and warm or hot ionized medium (e.g., Ferrière, 2001). In contrast, a significant fraction of gaseous mass resides in the cold dense medium that occupies only a small fraction of the spatial volume. Sufficiently dense (> 10³cm⁻³) gas tends to be in large ( > a few pc ) clouds whose column density is sufficiently large to protect molecular hydrogen against external dissociating radiation. Giant molecular clouds are observed to be the sites of massive star formation. Once a massive (> 10M_⊙) star is created in a molecular cloud, it radiates intense ultraviolet radiation inside the cloud that results in the creation of an expanding ionized region, i.e., HII region. The expanding HII regions are supposed not only to quench the further star formation, but also to destroy the parental molecular clouds (Dale and Bonnell, 2011; Walch et al., 2012; Dale et al., 2013; Geen et al., 2015, 2017; Gavagnin et al., 2017; Kim et al., 2018). Since we suppose that our Milky Way Galaxy is in a steady state over a timescale of Galactic rotation (~ 10⁸yr), molecular clouds are continuously created at a rate that compensate the destruction by massive stars.

How are the cold dense clouds created? According to the phase diagram of ISM shown in section 3.1, we can identify that the formation process of cold dense HI gas (>10cm⁻³) from WNM should be a phase transition dynamics that increase the density abruptly (Hennebelle and Pérault, 1999; Koyama and Inutsuka, 2000). Several studies (Koyama and Inutsuka, 2002; Piontek and Ostriker, 2004; Audit and Hennebelle, 2005; Heitsch et al., 2006; Vázquez-Semadeni et al., 2006) have shown that this phase transition always results in the creation of long-lasting turbulent motions where cold HI clumps are embedded in WNM. The amplitude of turbulent velocities of cold HI gas tends to be a few km s⁻¹, a fraction of the sound speed of the WNM (10 km s⁻¹). Therefore, the resulting turbulence appears to be supersonic with respect to the sound speed of cold medium (~1km s⁻¹) but actually subsonic with respect to the WNM, which constitutes the inter clump medium. Therefore the turbulence of the atomic interstellar gas is a combination of subsonic and supersonic motions. Let us stress that the CNM tends to behave as a supersonic gas even so it is embedded into an environment with respect to which it is subsonic. This is because the CNM fragments collide supersonically.

Now a description of how molecular clouds are created is proposed. An important question is whether they can be created by a single compression event from WNM or whether they are more gradually created from cold dense HI clouds. Inoue and Inutsuka (2008), Inoue and Inutsuka (2009), Heitsch et al. (2009), and Körtgen and Banerjee (2015) have given a somewhat negative answer to the former question. Inoue and Inutsuka (2012) have given the positive answer to the latter question. More detailed analyses are done by Iwasaki et al. (2018). Figure 3 shows typical results of the compression of magnetized multiphase HI clouds by shock waves. The relative angle (θ) between the shock wave propagation direction and the mean magnetic field is 3° (upper panel), 11° (middle panel), 36° (lower panel), respectively. The compression with a small angle results in the creation of substantial molecular gas. But if the relative angle is larger than a certain critical value, the propagation of shock wave only result in the magnetically supported HI clouds. Note that the value of this critical angle depends on the velocity of the incoming flow of the magnetic field and of the time since for long enough time, the post-shock layer will always be at least partially molecular. In practice, there is however a distribution of angles between the magnetic field and the incoming flow. Quantifying this distribution would therefore be important to constraint the scenario of molecular cloud formation. Detailed investigations from larger scale simulations (see section 8) have shown that there is a clear trend for magnetic and velocity fields to be preferentially aligned (e.g., Iffrig and Hennebelle, 2017), which would imply that aligned configurations are more frequent than expected.

FIGURE 3

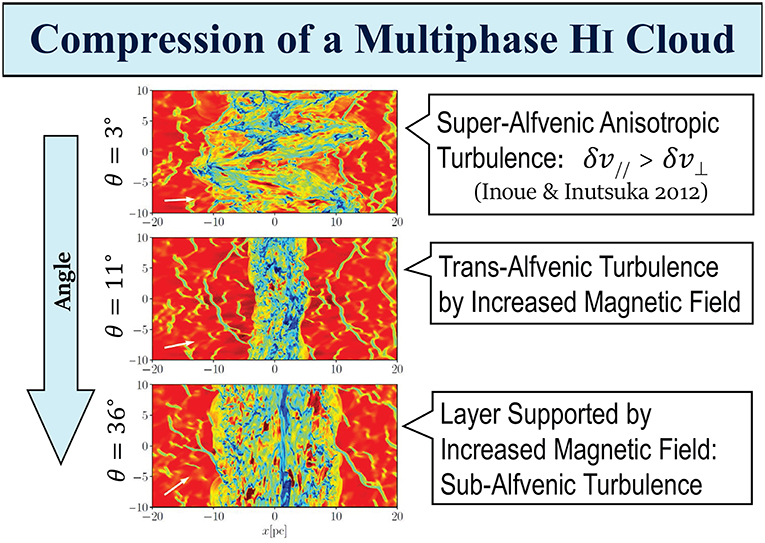
Figure 3. The result of compression of multiphase HI clouds by shock waves (Iwasaki et al., 2018). The column density is shown (red stands for WNM while Blue-green represents CNM). The relative angle (θ) between the shock wave propagation direction and the mean magnetic field is 3° (Upper panel), 11° (Middle panel), and 36° (Lower panel), respectively.

4. The Nature of MHD Turbulence in the Dense ISM

Turbulence is ubiquitous in fluid dynamics and unsurprisingly, many observations suggest that molecular clouds are turbulent (e.g., Elmegreen and Scalo, 2004; Hennebelle and Falgarone, 2012). It is likely the case that together with gravity, turbulence is playing a significant role in the evolution of molecular clouds for example by creating strong density fluctuations, owing to its supersonic nature, that may serve as seed for the mass reservoir of future stars. More generally, interstellar turbulence is an agent that imposes order in the form of coherent structures and correlations between the various fields of the flows. Turbulence is likely responsible of many, if not almost all¹, of the observed motions. How magnetic field affects turbulence in molecular clouds is the main focus of this section.

4.1. Turbulence in Ideal MHD Framework

Before starting a description of the turbulence, an important issue should be stressed. Ideal MHD implies that fluid particles are attached to their field lines, that is to say they can flow along the field lines but cannot go across them. In a turbulent fluid, given the stochastic nature of the motions, such a situation would lead to a field that would be so tangled, that quickly motions would be prohibited. This implies that Ideal MHD cannot, strictly speaking, be correct for a turbulent fluid and that some reconnection, that is to say some changes of the field lines topology must be occurring. The physical origin of this reconnection is still debated but an appealing model has been proposed by Lazarian and Vishniac (1999). In this view the reconnection is driven by turbulence and is a multi-scale process, that is unrelated to the details of the microphysical processes (Lazarian et al., 2015). It is certainly the case, at least in numerical simulations of MHD turbulence, where the numerical diffusivity is often controlling the reconnection, that the MHD is far to be ideal. This process, in particular, induces an effective diffusion of the magnetic flux, that is therefore not fully frozen as one would expect if MHD was truly ideal.

4.1.1. Incompressible Magnetized Turbulence

For pure hydrodynamics, i.e., in the absence of magnetic field, the Kolmogorov dimensional scaling relation, appears to provide a good description (Kolmogorov, 1941). However, MHD flows are more complicated and in spite of intensive efforts, even the energy powerspectrum of MHD turbulence is still debated. The first model to predict a powerspectrum has been done by Iroshnikov (1963) and Kraichnan (1965) who infer $v_l\propto l^{1/4}$ and $E(k)=k^2{P}_v(k)\propto k^{-3/2}$. The power spectrum E(k) ∝ k^−3/2 is therefore shallower than the Kolmogorov one. One of the fundamental assumptions of Iroshnikov (1963) and Kraichnan (1965) is that the eddies are isotropic. However, numerical and observational data suggest that in MHD turbulence the energy transfer occurs mainly in the field perpendicular direction (Biskamp, 2003).

An important step forward has been accomplished by Goldreich and Sridhar (1995). They proposed a theory in which anisotropy of the eddies is accounted for. As the energy cascade proceeds to smaller scales, turbulent eddies get more and more elongated in the direction of the magnetic field. They assume that the Alfvén time-scale and the non-linear cascade time-scale are comparable, k_zV_a≃vk_⊥, while the cascade time in the direction perpendicular to the field leads to $v_{\perp }\propto k_{\perp }^{-1/3}$. The wave vector along the z-axis is thus expressed as $k_z\propto k_{\perp }^{2/3}$. The energy transfer time is therefore different from the Iroshnikov-Kraichnan estimate, and identical to the one obtained by Kolmogorov. One gets $E(k_{\perp })\propto k_{\perp }^{-5/3}$. This issue has been further studied (e.g., Cho et al., 2002; Boldyrev, 2005; Lee et al., 2010; Beresnyak, 2011; Mason et al., 2012; Wan et al., 2012) and remains still debated. It is however clear from the numerous numerical simulations performed that the turbulence is very anisotropic (e.g., Grappin and Müller, 2010).

4.1.2. Compressible Magnetized Turbulence

Since molecular clouds are both magnetized and super-sonic (with typical Mach numbers on the order of 10), compressible magnetized turbulence has received considerable attention during the last two decades. Because of its simplicity many works have been assuming an isothermal equation of state. More recently 2-phase medium has also been considered.

One of the major question that has been under investigation when the importance of turbulence was established, was the origin of the turbulence in molecular clouds and more precisely how the observed turbulence could be maintained. Since turbulence is expected to decay in one crossing time, this would imply that either molecular clouds were young, either there was a source that was continuously rejuvenating the turbulent energy, either the turbulence was decaying slower than expected. Several works have been investigating the latter assumption (e.g., Mac Low et al., 1998; Ostriker et al., 2001; Birnboim et al., 2018). They conclude that while magnetic field introduces some delay compared to the hydrodynamical case, the decay still occurs too rapidly, that is to say in about one crossing time, to explain the high level of turbulence found in molecular clouds.

The second major reason to study turbulence is obviously to get a statistical description of the fluctuations arising in molecular clouds and this has been addressed in several studies (e.g., Mac Low et al., 1998; Padoan and Nordlund, 1999; Ostriker et al., 2001; Cho and Lazarian, 2003). In this respect, one of the most comprehensive set of simulations relevant for the MHD turbulence arising in the 2-phase interstellar medium has been performed by Kritsuk et al. (2017). Five runs are presented where the mean density (2 and 5 cm⁻³), magnetic field (≃ 1, 3, and 10 μG) and root mean square velocity are varied. The total box size is 200 pc and a random forcing in the Fourier space is applied to sustain the turbulent motions. A cooling function relevant for the ISM is employed and it leads to the existence of WNM and CNM. Figure 4 displays the energies as a function of time, the magnetic field PDF, the powerspectra of kinetic and magnetic energies as well as the longitudinal structure function for run A (mean density is 5 cm⁻³, magnetic intensity of 10 μG and rms velocity about 16 km s⁻¹) of Kritsuk et al. (2017). As can be seen for this particular run the magnetic and kinetic energies are comparable. The PDF is broad and magnetic intensities larger than 100 μG are sometimes found. The energies present power spectra with exponent compatible with -3/2 although the inertial range is probably not extended enough to make this value well determined. Interestingly, we note that the structure function is stiffer in the CNM than in the WNM. Clearly this is because the former is highly supersonic while the latter is nearly transsonic. Let us also stress that the anisotropic nature of the MHD turbulence, which present elongated structures along the magnetic field as inferred in the incompressible case, is still present in the compressible case as shown for example by Vestuto et al. (2003) or Beresnyak et al. (2005).

FIGURE 4

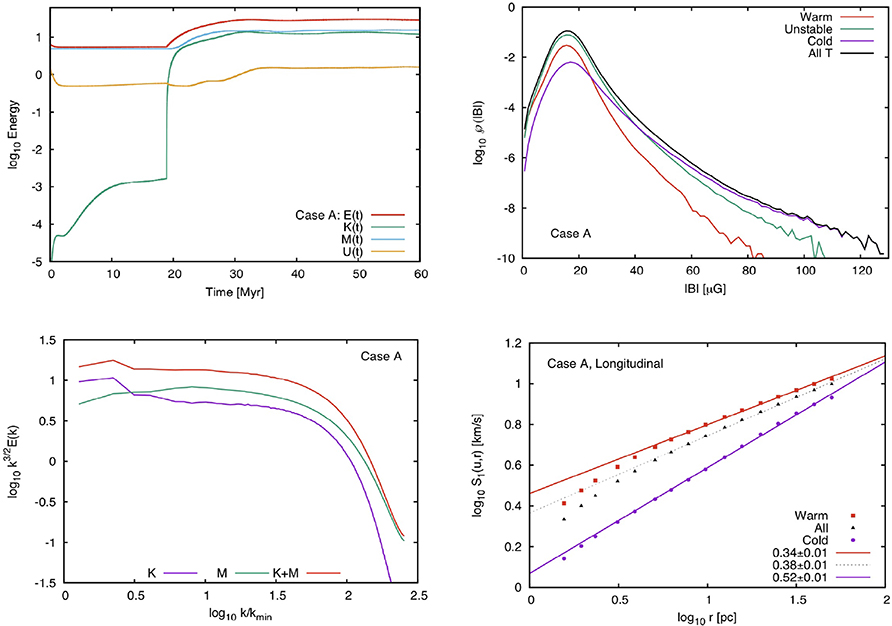
Figure 4. Results of simulations of ISM magnetized turbulence performed by Kritsuk et al. (2017). (Top-left panel) Shows the total, kinetic, magnetic and internal energies as a function of time. (Top-right panel) Displays the magnetic field PDF in the warm, unstable and cold phases. (Bottom-left panel) Portrays the powerspectra of the kinetic, magnetic and total energies while (bottom-right panel) shows the structure functions of the velocity in the various phases of the ISM.

Due to its very non-linear nature, the description presented in most works is essentially numerical however some recent theoretical progress have been accomplished for the understanding of how the cascade proceeds in a magnetized, compressible, self-gravitating and isothermal gas by Banerjee and Kritsuk (2017) and Banerjee and Kritsuk (2018) following the work of Galtier and Banerjee (2011). In this work a complete expression of the total energy transfer is obtained as mixed second-order structure functions (see Equation 33 of Banerjee and Kritsuk, 2018). The contributions of pure kinetic, magnetic, gravitational and thermodynamic terms are clearly identified and will allow future works to clarify their respective roles and importance.

4.1.3. How Magnetic Field Affects the Density PDF

The density PDF is a key quantity in the ISM, particularly for the star formation process. Several models aiming at providing explanations for the two most fundamental problems of star formation, namely the initial mass function of stars (Padoan et al., 1997; Hennebelle and Chabrier, 2008) and the star formation rate (Padoan and Nordlund, 2011; Hennebelle and Falgarone, 2012; Federrath and Banerjee, 2015) directly depend on the density PDF.

The density of cold and weakly self-gravitating molecular gas has been found to present a lognormal distribution. It is likely the result of random shocks induced by the compressible turbulence and the multiplicative nature of the density variable leading, to a Gaussian distribution of logρ. A useful calculation has been inferred by Hopkins (2013), who derived a log-Poisson distribution for the density, using intermittent models developed in the context of incompressible turbulence. The mathematical expression of the density distribution presents a free parameter that controls the degree of intermittency and the deviation from the lognormal distribution. Hopkins (2013) compared this expression with PDF from numerical simulations and obtain very good agreement. This is particularly interesting for the high Mach number runs in which important deviations from the lognormal behavior are observed. Another important aspect regarding the cold and non-self-gravitating gas is the cooling or more precisely the effective equation of state, that is to say the pressure vs. density relation. In most of the studies the isothermal assumption has been made. However powerlaws instead of lognormal have been inferred for polytropic flows. Federrath and Banerjee (2015) carried out a set of calculations for polytropic flows, i.e., following P ∝ ρ^Γ for Γ = 0.7, 1 and 5/3. They inferred modest differences between Γ = 0.7 and 1 that do not strongly deviate from lognormal distribution. On the other hand, significant deviations were obtained for Γ = 5/3 in particular the low density part of the PDF is better described by a powerlaw.

The effect of the magnetic field on the density PDF has also been studied in the isothermal case (e.g., Ostriker et al., 2001; Lemaster and Stone, 2008) and in two-phase flows (e.g., Hennebelle et al., 2008; Kritsuk et al., 2018). It has generally been found that magnetic field has a limited impact. This agrees with the conclusion that the gas which is not self-gravitating tends to flow along magnetic field lines. Molina et al. (2012) carried out isothermal simulations with various Mach numbers. They inferred that in the transsonic and subsonic flows, the density PDF of magnetized and pure hydrodynamical cases are very similar. They report however significant differences for supersonic flows. An analytic expression which is an extension of the lognormal distribution has been proposed. From their Figure 1, it appears that the difference between hydrodynamical and magnetized runs are important only for the low density gas while the PDF at high densities are almost identical.

4.2. The Influence of the Ion-Neutral Drift on MHD Turbulence

As discussed in section 2.2 the ion-neutral friction is an important source of energy dissipation in the interstellar medium and particularly within molecular clouds. Likely enough this should have an impact on the development of turbulence and presumably modifies the fluctuations at small scales. Here we describe the various efforts that have been undertaken to investigate this aspect. We first describe the effects of the ion-neutral friction on MHD waves and then discuss the numerical simulations, which have been performed and the conclusions.

4.2.1. How Ion-Neutral Drift Affects Wave Propagation

The impact of ion-neutral friction on the propagation of MHD waves has been first investigated by Kulsrud and Pearce (1969) considering a fluid of ions and a fluid of neutrals (see e.g., Lequeux, 2005, for a more recent and complete discussion). Although they restrict the discussion to Alfvén waves only, the dispersion relation obtained is of the third order making a complete discussion a little tedious. They found that there are several wavelength domains to be considered.

In the long wavelength limit, the ions and the neutrals are well coupled because the dynamical time is short with respect to the ion-neutral friction time. In this limit the strong coupling approximation can be used and the dispersion relation is

$\begin{array}{cc}\begin{array}{l}\omega =i\frac{k^2{V}_A^2}{2{\gamma }_{ad}{\rho }_i}\pm \sqrt{k^2{V}_A^2-{\left(\frac{k^2{V}_A^2}{2{\gamma }_{ad}{\rho }_i}\right)}^2},\end{array}& (25)\end{array}$

where k is the wavenumber and V_A is the Alfvén speed of the neutrals (i.e., $V_A=B/\sqrt{4\pi \rho }$). The waves propagate at the Alfvén speed of the neutrals. They dissipate in a time scale that is proportional to k² ∝ λ⁻², where λ is the wavelength. If k > 2γ_adρ_i/V_A, the waves do not propagate any more. This is because the friction is too intense.

In the short wavelength limit (which is not described by Equation 25), the waves propagate at the Alfvén speed of the ions, which for typical molecular cloud conditions, is roughly thousand times the Alfvén speed of the neutral (because typical ionization is on the order of 10⁻⁷). This is because in this limit the wave frequency is shorter than the ion-neutral friction time, thus the neutrals cannot follow the ions. The dissipation time, in this regime is independent of λ.

Balsara (1996) has been performing a complete analysis by solving for all modes and also by solving for the strong coupling approximation. He concluded that the slow MHD modes are less affected by the dissipation induced by the ion-neutral friction, particularly when the propagation of the waves is along the field lines. He also found that in the long wavelength limit, the strong coupling approximation is very accurate and can be employed.

4.2.2. Turbulence With Ion-Neutral Drift

From these analytical results, it is clear that ion-neutral friction leads to wave damping and should therefore affect the turbulent cascade. To quantify the scale at which this may happen it is usual to infer the scale at which the Reynolds number, in which the viscosity is taken to be the ion-neutral friction, is about 1 (see section 6.2.3). This scales is called l_ad or l_diss, depending on the authors.

One of the first simulations, that have been performed, are the ones by Oishi and Mac Low (2006) using the strong coupling approximation. They conclude that contrary to the simple analytical estimate, the simulations do not reveal a clear sign of a specific smoothing or dissipative scale. Other simulations like the ones performed by Li et al. (2008), Downes and O'Sullivan (2011), and Ntormousi et al. (2016) found that ion-neutral friction affects the turbulent fluctuations at a scale below the ambipolar diffusion one leading to a smoother structure. Left-panel of Figure 5 displays the velocity powerspectra of ideal MHD simulations at various resolution and of simulations that include the ion-neutral friction for the same numerical resolutions and for various minimum timesteps allowed (in these calculation an explicit scheme is employed and the smallest timesteps is enforced by raising the ionization if needed). Clearly the powerspectra with ion-neutral friction present sign of dissipation at a scale that is about l_ad although numerical convergence could not be obtained.

FIGURE 5

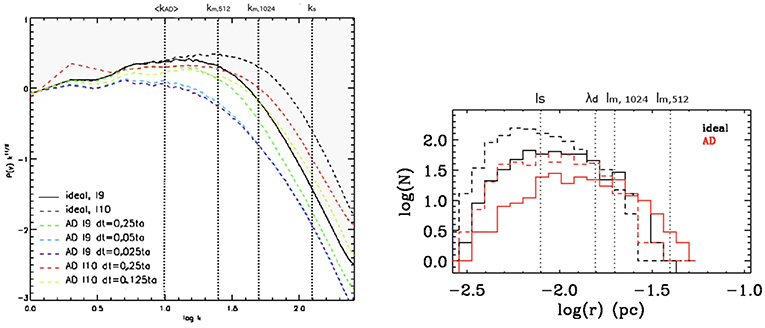
Figure 5. (Left panel) Compensated velocity powerspectra for the decaying MHD simulations with ambipolar diffusion (from Ntormousi et al., 2016). The various runs include ideal MHD with 512³ (l9) and 1024³ (l10) resolution and a series of runs with ambipolar diffusion with the same two resolutions and various values of the minimum timesteps allowed. The powerspectra present major deviation from the ideal MHD runs at scales smaller than the ambipolar diffusion one. (Right panel) Distribution of filament width in MHD simulations with and without ambipolar diffusion. The solid lines are for a resolution of 512³ while the dashed ones correspond to 1024³. Reproduced from Ntormousi et al. (2016) with permission of A&A.

Burkhart et al. (2015) presented three calculations with various Alfvénic and sonic Mach numbers using the heavy ions approximation. They computed structure functions and compare the results with the prediction made by Goldreich and Sridhar (1995). They also performed mode decomposition as described by Cho and Lazarian (2003), that is to say identifying the Alfvén, fast and slow modes. Part of their results are displayed in Figure 6. While the super-Alfvénic simulation present structure functions compatible with the prediction of Goldreich and Sridhar (1995), even below the ambipolar diffusion scale, l_ad, the Alfvén waves component of the sub-Alfvénic simulation shows clear sign of decay below l_ad.

FIGURE 6

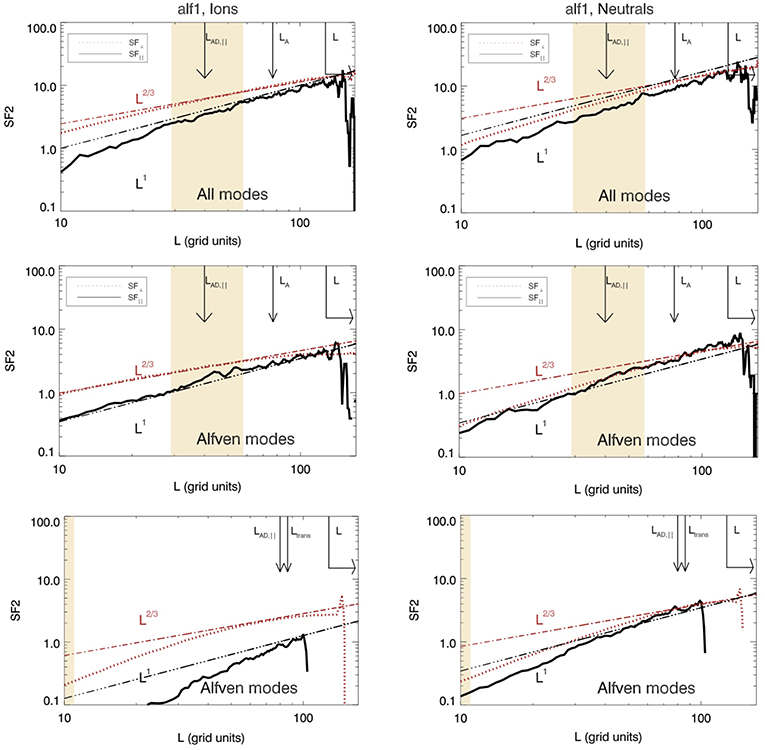
Figure 6. Structure function in MHD turbulence with ion-neutral friction from Burkhart et al. (2015). (Left panel) Show the structure function for the ions while the right panels display the structure functions for the neutrals. The first and second rows are for a supersonic and super Alfvénic simulation while the third row is for a sub-Alfvénic one. For the second and third panel mode decomposition has been performed and only the Alfvén modes are shown. As can be seen from third row, they are strongly damped in the sub-Alfvévic case why they roughly follow the expected scaling from ideal MHD theory in the super-Alfvénic one. Reproduced from Burkhart et al. (2015) with permission of ApJ.

Clearly the nature of MHD turbulence in the presence of ion-neutral friction is not well understood and requires further investigation.

5. How Magnetic Field Correlates With the Density Field

A major question to understand the role of the magnetic field in molecular cloud evolution is how it correlates with the other fields and in particular with the density. Two aspects are particularly important, first how the mean magnetic intensity varies with the density and second how the magnetic field direction correlates with structures like filaments and more generally how the magnetic field direction correlates with density gradients.

5.1. The Bvs.N Relation

Since the pioneering work of Troland and Heiles (1986), it is well established (Crutcher et al., 2010) that the mean magnetic intensity is independent of gas density, n, for values up to about 300 cm⁻³. At higher densities, that is to say at least up to 10⁶⁻⁷ cm⁻³, the mean magnetic intensity has been found to increase with n broadly like a powerlaw, that is to say B≃n^κ. The exact value of κ is still a matter of debate. Earlier works (Crutcher, 1999) obtained κ = 1/2 but more elaborated Bayesian analysis led to κ≃0.65 (Crutcher et al., 2010). Understanding the physical origin of this behavior is important to unravel the star formation process in general. In particular, the mass to magnetic flux ratio, M/ϕ, can be estimated by combining the column density of the observed component along the line of sight and the observed magnetic intensity. This leads to the conclusion that the atomic and diffuse molecular gas is subcritical, that is to say dominated by the magnetic field, while dense regions, such as dense cores, are generally supercritical.

Before describing the results inferred from numerical simulations, it is worth to recall the different behaviors that can be expected. If the contraction occurs along the field lines, then the magnetic field is not amplified and B ∝ n^κ with κ = 0. If the motion is perpendicular to the field lines, then it is easy to show that n/B stays constant (combining the continuity and induction equations in one dimension) and thus κ = 1. Note that in this configuration the magnetic pressure is proportional to n² and therefore quickly halts any contraction. Qualitatively at least, these two cases represent, respectively, a situation in which the magnetic field is strong and weak with respect to the kinetic motions, i.e., sub and super-Alfvénic situations. In the sub-Alfvénic case, the magnetic field guides the flow and forces the contraction along the field lines while in the super-Alfvénic case, it is advected by the flow and the transverse component of the field is amplified.

If the contraction is spherical, for example driven by gravity, then the mass enclosed is simply ∝ ρR³, R being the cloud radius, while the magnetic flux is ∝ BR² thus leading to B ∝ n^2/3. It is, however, likely that a contracting cloud does not remain spherical, especially if the magnetic field is not negligible. In this case, it is expected that an equilibrium along the field lines settles leading to $c_s^2\simeq \varphi$, where ϕ is the gravitational potential. The Poisson equation leads ϕ ∝ nh² where h is the thickness of the cloud along the field lines. Then, as the mass enclosed is now ∝ nR²h while the magnetic flux is still ∝ BR², we get $B\propto c_s{n}^{1/2}$. Basu (2000) has compared the data provided by Crutcher (1999) with this expression and has obtained a good agreement, which improves if the velocity dispersion σ instead of c_s is used. Another even simpler interpretation of this relation is energy equipartition between magnetic and kinetic energy, B²/(4π) ∝ nσ².

Several theoretical studies have been investigating the Bvsn relation. In particular various simulations of 3D ideal MHD turbulence tend to show that in realistic ISM conditions and without gravity (e.g., Padoan and Nordlund, 1999; Hennebelle et al., 2008; Banerjee et al., 2009), the magnetic intensity weakly depends on the density field. A weak correlation is found with typically κ≃0.1−0.2. This has been interpreted in the context of the 2-phase ISM by Hennebelle and Pérault (2000) as a consequence of the magnetic tension, which tends to unbend the magnetic field lines and to align the magnetic and the velocity fields. This eventually facilitates the gas contraction. For polytropic flows, the lack of correlation is due to the various types of MHD waves having different scalings of the field strength with the density (Ostriker et al., 2001; Passot and Vázquez-Semadeni, 2003; Burkhart et al., 2009). Indeed while for fast waves, magnetic intensity and density are correlated, they are anti-correlated for slow waves and not correlated for Alfvén waves. Thus, in a turbulent transsonic flow, as is the multi-phase HI, the field strength is a consequence of the complete history of wave propagation. Note that in supersonic and superalfvénic simulations, more vigorous dependence of B on the density is inferred (Ostriker et al., 2001; Burkhart et al., 2009). The simulations which treat both self-gravity and turbulence find that at high density the magnetic intensity is ∝ n^0.5 (Hennebelle et al., 2008; Banerjee et al., 2009), which accords well with the analytical predictions deduced above. More recently Li et al. (2015) performed high resolution adaptive mesh simulations for a weak and a strong initial magnetization and performed clump identification. They then investigated the relation between the mean magnetic field, $\bar{B}$ and the mean density, $\bar{n}$, within the clumps and inferred $\bar{B}\propto {\bar{n}}^{0.65}$ in good agreement with the Crutcher et al. (2010) result. This may seemingly suggest that at the scale of the clumps themselves, the contraction is nearly isotropic. This is in good agreement with the results reported by Mocz et al. (2017) where simulations with a broad range of Alfvénic Mach number, ${{M}}_A$, have been presented. When ${{M}}_A>1$, the clumps follow B∝n^2/3, while when ${{M}}_A<1$, B ∝ n^1/2 is inferred.

5.2. The Orientation of Magnetic Field

The orientation, or more generally the topology, of the magnetic field is expected to play a significant role in the formation of structures. For example as discussed above strong toroidal fields can induce instabilities in filaments while poloidal ones tend to stabilize them (Fiege and Pudritz, 2000). Another example comes from the work of Nagai et al. (1998), where linear stability analysis of a magnetized self-gravitating layer has been performed (see also Van Loo et al., 2014). They show that the orientation of the most unstable mode tends to be correlated with the magnetic field direction. The result depends on the external pressure that determines the scale height, z_b at which the solution is truncated. If z_b ≫ l₀, l₀ being the Jeans length, then the fastest growing mode is aligned with the magnetic field, resulting in filaments which are perpendicular to the field direction. The physical reason is that, since the width is large relative to the Jeans length, the layer is compressible and density fluctuations are easier to develop along the magnetic field. On the other hand when z_b ≪ l₀, the fastest growing mode is perpendicular to the magnetic field and the filaments are aligned with it. This is because the layer is almost incompressible (since the scale height is smaller than the Jeans length), thus the instability develops through the bending of the layer. As perturbations whose wave vectors are perpendicular to the magnetic field do not bend the field lines, these perturbations develop more easily.

Observationally significant progresses have recently been accomplished regarding the magnetic field orientation. The polarization observations by the Planck satellite reveal that in the diffuse ISM, the elongated column density structures traced tend to be predominantly aligned with the magnetic field within the structures (Planck Collaboration et al., 2016). This statistics for the low column density gas are comparable to that found between low column density fibers traced by H_I emission and the magnetic field (Clark et al., 2014). The analysis of the Planck data toward nearby molecular clouds reveals that the relative orientation between the structures and the magnetic field depends on the column density, N_H. It is mostly parallel at $log(N_{\text{H}})\simeq 21.7{\mathrm{\text{cm}}}^{-2}$ and mostly perpendicular at $log(N_{\text{H}})\ge 21.7{\mathrm{\text{cm}}}^{-2}$ (Planck Collaboration et al., 2016).

A detailed analysis of the angle, ϕ between the magnetic field and the density gradient,

$\begin{array}{cc}\cos \varphi =\frac{\nabla \rho \times B}{|\nabla \rho |\left|B\right|},& (26)\end{array}$

in numerical simulations has been carried out by Soler et al. (2013) using the simulations presented in Dib et al. (2010). In these numerical experiments the gas is isothermal and the turbulence, seeded initially with an initial Mach number of about 10, is decaying. Through shocks and self-gravity dense clumps and filaments quickly form. Three values of magnetization, characterized by the initial β, equals to the thermal over magnetic pressure have been explored namely 100 (weakly magnetized), 1 and 0.1 (strongly magnetized). A value of ξ > 0 means that the dominant configuration is cos ϕ ≃ 0, that is to say the magnetic field and the density gradient tend to be perpendicular, which in turns implies that the magnetic field and density isocontour tend to be parallel. To quantify the alignment, in each density bin, the difference between the numbers of cells having, respectively |cos ϕ | < 0.25 and |cos ϕ| > 0.75 (see Soler et al., 2013) has been computed. Figure 7 shows the dependence of ξ with the gas density for the three runs at two timesteps. For the low magnetization (β = 100), ξ remains positive for all density bins, with a clear trend for cos ϕ to increase at large densities (i.e., ϕ goes to smaller values). For the more magnetized case, ξ becomes negative at high densities and the density value at which this happens drops with β. This in particular shows that at low densities the magnetic field tends to be aligned with the filaments while at high densities it is more perpendicular to them. While the physical origin of this last trend is simply that the gas is channeled by the magnetic field, when it is strong enough, along the field lines, the mechanism by which the alignment occurs at low density is less obvious. To better understand it, Soler and Hennebelle (2017) have obtained an exact equation for the evolution of ϕ. It is simply obtained by combining the Faraday and continuity equations,

$\begin{array}{cc}\begin{array}{l}\frac{d(cos\varphi )}{dt}=\frac{{\partial }_i\left({\partial }_j{v}_j\right)}{{\left(R_k{R}_k\right)}^{1/2}}\left[-b_i+r_{i}cos\varphi \right]+{\partial }_i{v}_j\left[r_i{r}_j-b_i{b}_j\right]cos\varphi ,\end{array}& (27)\end{array}$

where

$\begin{array}{cc}\begin{array}{l}{r}_i\equiv \frac{R_i}{{\left(R_k{R}_k\right)}^{1/2}},R_i={\partial }_i\rho ,\end{array}& (28)\end{array}$

$\begin{array}{cc}\begin{array}{l}{b}_i\equiv \frac{B_i}{{\left(B_k{B}_k\right)}^{1/2}},\end{array}& (29)\end{array}$

FIGURE 7

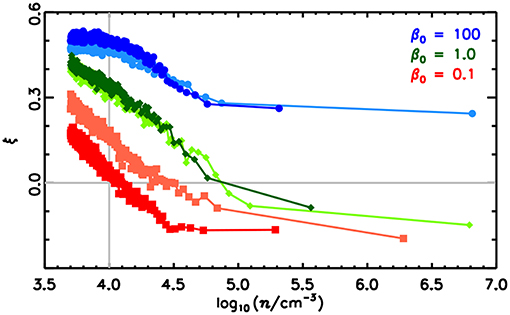
Figure 7. Relative orientation parameter, ξ vs. gas density, n≡ρ/μ from Soler et al. (2013). The values of ξ correspond to the relative orientation between ∇ρ and B in density bins with n>500 cm⁻³. The values ξ>0 correspond to ∇ρ mostly perpendicular to B and ξ < 0 correspond to ∇ρ mostly parallel to B. The gray horizontal line is ξ = 0. The darker colors represent the early snapshots and the lighter colors, the later snapshots. The gray vertical line, drawn for reference, corresponds to n = 10⁴ cm⁻³. Reproduced from Soler et al. (2013) with permission of A&A.

By numerically estimating the different terms in the right-hand side of Equation (27), Soler and Hennebelle (2017) showed that the mean value of the first term, which entails second spatial derivatives, quickly goes to zero. They therefore concluded that the second term is mainly responsible of the evolution of cos ϕ. As can be seen this second term vanishes either if B and ∇ρ are orthogonal, in which case cos θ = 0, or if they are parallel, in which case r_ir_j−b_ib_j = 0. This could suggest that cos ϕ has two attractors, 0 and ±1 although this obviously depend on the sign of the velocity derivatives. Numerical estimates using MHD simulations, show that indeed, on average, the mean value of cos ϕ follows the sign of the velocity terms.

Therefore the aligned configurations (ϕ = 0 or π) and perpendicular ones (ϕ = π/2) are favored. They are simple consequences of the fluid equations (more precisely continuity and Faraday equations).

Recently Gómez et al. (2018) have investigated the detailed structure of the magnetic field inside a self-gravitating filament, which forms in a turbulent environment. Similarly to other studies, they found that the magnetic field is primarily perpendicular to the supercritical filaments. However, they note that due to the gravitational infall along the filament, the field lines are further bent resulting in a “U”-shaped magnetic field line geometry. An equilibrium eventually settles due to the diffusion processes, that equilibrate with the transport by the infall motions. Figure 8 displays the magnetic field structure on top of the column density within the filament.

FIGURE 8

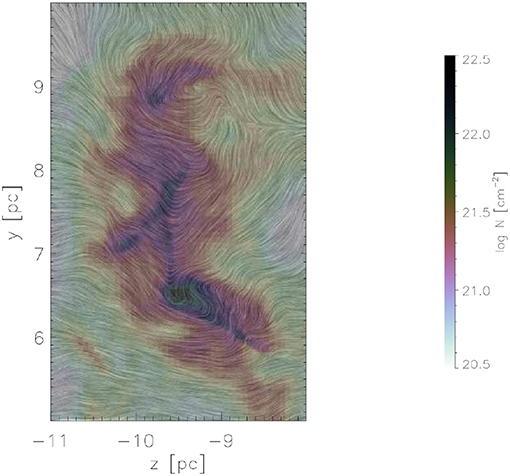
Figure 8. Structure of the magnetic field within a self-gravitating filament (Gómez et al., 2018). The structure of the mass weighted magnetic field integrated along the line of sight is shown on top of the column density. The magnetic field, that is primarily perpendicular to the direction of the filament, is then further stretched by the collapsing motions along the filament, resulting in a “U”-shaped magnetic field line geometry.

6. Filaments

While the density PDF provides very important information on the ISM, it should be kept in mind that they miss an essential piece of information, i.e., the spatial correlations or the shape of the interstellar clouds. While it has been recognized that the ISM is remarkably filamentary for many years, recent studies carried out by Herschel led to quantitative statistical estimates of their properties (André et al., 2014).

The first question that has to be addressed is what is the origin of this ubiquitous filamentary structure? Second, Herschel studies have also revealed that the filaments have a possible characteristic width of about 0.1 pc, which is surprising and needs to be explained although it is worth stressing that this result has for now been obtained only in nearby molecular clouds. Finally, it seems that most star forming cores sit inside self-gravitating filaments (Polychroni et al., 2013; Könyves et al., 2015), seemingly suggesting that filaments may be one important step of the star formation process.

6.1. Formation of Filaments

It is well known that gravity amplifies anisotropies and tends to promote the formation of filaments. In the context of molecular clouds this is particularly evident in studies like the ones performed by Nagai et al. (1998), Smith et al. (2014), Gómez and Vázquez-Semadeni (2014), Federrath (2015), Gong and Ostriker (2015), Chen and Ostriker (2015), and Camacho et al. (2016). This is simply because the gravitational force being the gradient of a scalar, it is stronger along the shortest axis of a clump. However, gravity can not explain all the observed filaments because many filaments are not self-gravitating. Indeed, the atomic gas (HI) is itself rather filamentary (Miville-Deschênes et al., 2003; McClure-Griffiths et al., 2006; Clark et al., 2014), but is far from being self-gravitating. It seems therefore that other processes could lead to filament formation. To investigate this issue Hennebelle (2013) performed MHD and hydrodynamical turbulent simulations of the ISM and computed the clump aspect ratio. These simulations include interstellar cooling and therefore present a 2-phase structure as described above. Gravity is not included. They have an initial velocity dispersion which corresponds to a Mach number of 10 and then decay. Hennebelle (2013) found that magnetic field makes the clumps more filamentary as seen from Figure 9 that portray the column density in an hydrodynamical and an MHD run. This is indeed quantified by Figure 10, which shows the aspect ratio of the clumps that have been extracted from the simulations using a friend of friend algorithm. It reveals that on average the clumps in the MHD case have a smaller μ₂/μ₃, where μ₂ and μ₃ are the inertia matrix eigenvalues of the clumps. Hennebelle (2013) also found that the filament axis tends to be aligned with the strain, i.e., the direction along which the fluid particles are stretched by the velocity field. This suggests that indeed turbulence, and even more likely, MHD turbulence naturally produces elongated structures. This is in good agreement with the anisotropic nature of MHD turbulence which, as discussed in sections 4.1.1 and 4.1.2 produces structures elongated along the magnetic field.

FIGURE 9

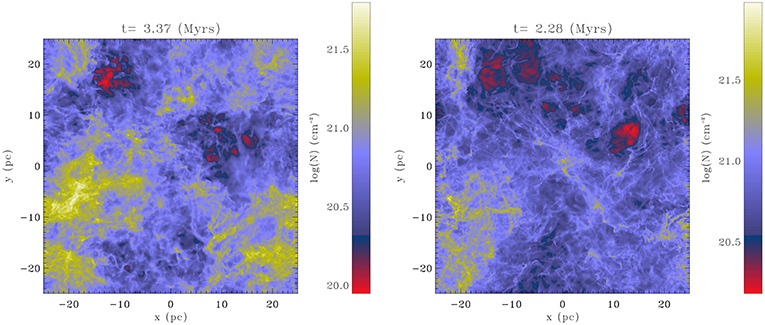
Figure 9. Column density for one snapshot of a decaying turbulence experiment. Left hydrodynamical run, right MHD run (from Hennebelle, 2013). Initially the field is uniform and has an intensity of 5μG. The magnetized run presents a more filamentary structure that the hydrodynamical run as can seen through visual inspection and confirmed by detailed analysis (see Figure 10). Reproduced from Hennebelle (2013) with permission of A&A.

FIGURE 10

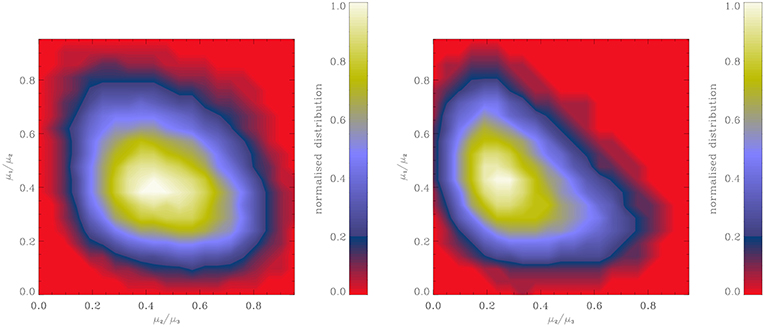
Figure 10. Normalized bidimensional histogram displaying μ₁/μ₂ as a function of μ₂/μ₃ where μ₁, μ₂, and μ₃ are the inertia matrix eigenvalues, μ₁ being the smallest (from Hennebelle, 2013). (Left panel) Hydrodynamical simulation. (Right panel) MHD simulation. Clearly the MHD run present structures that on average tends to be more elongated (i.e., have a smaller μ₂/μ₃) than the hydrodynamical ones. Reproduced from Hennebelle (2013) with permission of A&A.

Inoue and Inutsuka (2016) demonstrated that, in shock compressed layers of typical magnetized ISM, filamentary cold HI clouds are naturally created by thermal instability, and they also showed that stretched HI filaments that align with the local magnetic fields are due to the turbulent shear strain induced at the shock front. Prominent filaments are also found in magnetized shock-compressed dense layer (Inutsuka et al., 2015; Ntormousi et al., 2017), as illustrated in Figure 11, while again the unmagnetized runs produce much less elongated structures (Ntormousi et al., 2017), seemingly suggesting that the effect is generic and not sensitive to particular configurations. In the case of shock-compressed molecular layers denser than HI clouds, the massive filamentary clouds are perpendicular to the mean magnetic field lines. The mechanism to create such a prominent feature can be interpreted as the generic interaction of a shock wave and a magnetized medium with significant density inhomogeneity in pre-shock state (Inoue and Fukui, 2013; Inoue et al., 2018). This mechanism does not require self-gravity but the latter enhances the accretion of gas along the magnetic field lines onto the massive filament. Note that in some calculations (e.g., Inutsuka et al., 2015), substructures connected, and often perpendicular, to the main filaments are also observed. These structures are reminiscent of the striations that have been reported in molecular clouds (e.g., Heyer et al., 2016), where they appear as highly elongated along the magnetic field. Tritsis and Tassis (2016) have performed several numerical calculations to investigate their origin and concluded that they are most likely a consequence of non-linear MHD waves due to inhomogeneous density fields. Similar conclusion has been reached by Chen and Ostriker (2014) who presented a series of magnetized simulations and identified a network of small filaments aligned with the magnetic field in the simulations with the lowest β and estimate that this later must be < 0.2 to get prominent striations.

FIGURE 11

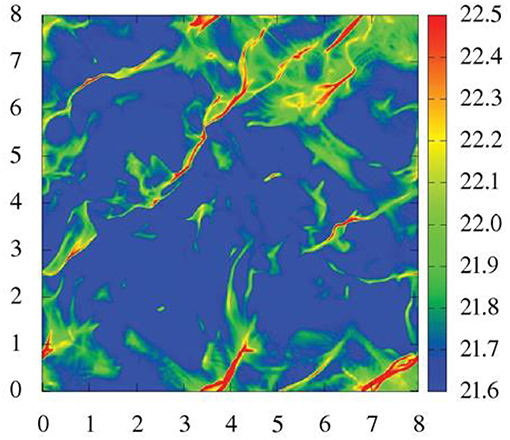
Figure 11. Formation of supercritical filaments and striations (Inutsuka et al., 2015) in a shocked layer (seen face on). In this calculation the filaments are self-gravitating (and therefore named supercritical) and the striations are mainly perpendicular to the filaments. Reproduced from Inutsuka et al. (2015) with permission of A&A.

The role of the magnetic field in the formation of filaments is likely important because it makes the flow more coherent therefore allowing the existing filaments to survive longer. In a related way, the flows tend also to be more organized when they are magnetized. For example several studies have concluded that velocity and magnetic field are preferentially aligned (see for example Matthaeus et al., 2008; Banerjee et al., 2009; Iffrig and Hennebelle, 2017). This is also consistent with the recent finding that the magnetic field direction and the density gradients are clearly correlated (Koch et al., 2013, 2014; Soler et al., 2013; Planck Collaboration et al., 2016; Soler and Hennebelle, 2017) as discussed in section 5.2.

Let us reiterate that there is not necessarily a unique mechanism that leads to the formation of filaments. In particular it is clear that both magnetic field and self-gravity tend to produce highly elongated structures. While it seems difficult to invoke the latter in the formation of diffuse filaments, it very likely plays a determinant role in the formation of the most massive ones. This is particularly obvious in series of simulations presented by Federrath (2016) where filaments can form under the influence of gravity and MHD turbulence only.

6.2. A Characteristic Width?

Perhaps the most intriguing and recent aspect of filaments is the possible existence of a characteristic width, of about 0.1 pc, and even more surprising is the fact that this remains true for filaments of column densities spanning almost 3 orders of magnitude (Arzoumanian et al., 2011; André et al., 2014; Koch and Rosolowsky, 2015). Indeed both gravity and turbulence tend to be scale free processes and usually produce powerlaws. For example the Jeans length varies by more than one order of magnitude in the above mentioned filament sample. This analysis on the width distribution in Herschel observation has triggered many subsequent papers on this issue. While Juvela et al. (2012), Alves de Oliveira et al. (2014), and Koch and Rosolowsky (2015) essentially confirmed the earlier findings, Panopoulou et al. (2017) pointed out the tension between the characteristic width and the spatial power spectra of the data that show no characteristic scale. This tension could be removed by the fact that the masses in the filaments with a characteristic width corresponds to a small fraction of the total mass in the whole molecular clouds and hence they provide small contribution in the spatial power spectra in observational emission maps. Hacar et al. (2018) showed the velocity coherent filamentary structures (so-called fibers) have a median widths that is a factor of three smaller than 0.1pc in the integral shape filament in Orion using ALMA observation of molecular emission from ${\text{N}}_2{\text{H}}^{+}$ (1-0). However, Clarke et al. (2018) cautioned about line-of-sight confusion in the analysis of velocity coherent structure according to their synthetic observations of simulated filaments. Note also that high-resolution ALMA observation has not yet been reported for dust continuum emission that has a dynamic range in emission much larger than in molecular line observation. These observations lead to the question of why we tend to observe a characteristic width of molecular filaments, at least, apparently with the spatial resolution typical in Herschel observation. Part of the answer may be the finite resolution as recently claimed by Panopoulou et al. (2017). This may account for some of the observed filaments in particular the low column density ones that are not as prominent as the very dense ones.

Various explanations (André et al., 2014) have been put forward to account for this fact, three of them are described below.

6.2.1. Jeans Length and Self-Gravitational Equilibrium

It would appear logical that the width of supercritical filaments is directly related to the mean Jeans length within the filament. However, as stressed by (Arzoumanian et al., 2011), the Jeans length drops with density which is at odds from the nearly constant width that is inferred from observations. However Fischera and Martin (2012) argued that the characteristic size of the filaments is simply the result of mechanical equilibrium in the radial direction. Assuming that the filaments are pressure bounded, they find that the equilibrium of the isothermal gas, between thermal pressure and gravity leads to a diameter of about 0.1 pc with a weak dependence on the column density. While this explanation could be valid for nearly critical filaments and is indeed observed in numerical simulations (Smith et al., 2014), it cannot account for very supercritical filaments as thermal support is unable to resist gravity. The effects of magnetic field are also studied by Tomisaka (2014) and Auddy et al. (2016) where a bidimensional equilibrium is considered, with the filaments being rather ribbons due to the anisotropic Lorentz force. Again the finite width of the massive filament cannot be explained even with magnetic field, unless the strength of the field is exceptionally large.

6.2.2. The Sonic Length Argument

If filaments are produced in shocks, then their density, ρ_f, should be linked to the background density, ρ₀ by the Rankine-Hugoniot relation: ${\rho }_f={\rho }_0{M}^2$, where M is the Mach number, M = v/c_s. The velocity on the other hand is linked to the scale as $v(L)\simeq v_0{(L/1\text{pc})}^{\eta }$ which is simply the Larson relation discussed above and $v_0\simeq 0.8\text{km}{\text{s}}^{-1}$ while η ≃ 0.4−0.5. As the size of the shocked layer is simply given by L_f = Lρ₀/ρ_f, we get $L_f={(c_s/v_0)}^2\times L{(L/1\text{pc})}^{-2\eta }$. In particular assuming that η = 0.5, the shocked layer becomes independent of the fluctuation size and with c_s ≃ 0.2 km s⁻¹, we get L_f ≃ 0.07 pc which is close to the thickness inferred by Arzoumanian et al. (2011). This explanation has been generalized to the magnetic case by Federrath (2015), who argue that it reproduces the simulations well. Note, however, that this argument only explains the thickness of the sheet-like structure that is geometrically different from the filament. In addition, this explanation neglects the effect of self-gravity, and hence, cannot explain why the massive filaments are supported against excessive self-gravitational forces that are expected to trigger the radial collapse of the filaments.

The model considered by Auddy et al. (2016) is more elaborated as they considered a 2D equilibrium with magnetic field lines perpendicular to its surface. Along the field lines the structure, which is described as a ribbon, is really narrow and typically below 0.1 pc, while perpendicularly it is confined by the ram pressure and its length, close to 0.1 pc, is essentially the sonic length.

6.2.3. The Ion-Neutral Friction

A third class of explanations has invoked the ion-neutral friction that provides a source of dissipation, the ion-neutral drift presents a characteristic time namely ρ_iγ. From Equation (21) a magnetic Reynolds number (e.g., McKee et al., 2010; Hennebelle, 2013) can be inferred

$\begin{array}{cc}\begin{array}{l}{R}_{e,m}=\frac{V(l)l}{\nu },\end{array}& (30)\end{array}$

where $\nu =B^2/(4\pi {\gamma }_{ad}\rho {\rho }_i)$. Assuming that the energy flux, ϵ = ρV(l)³/l, is constant through the scales, one gets

$\begin{array}{cc}\begin{array}{l}{R}_{e,m}=\frac{{ϵ}^{1/3}{\rho }^{-1/3}{l}^{4/3}}{\nu }.\end{array}& (31)\end{array}$

Estimating ϵ at the integral scale, L₀, we obtain

$\begin{array}{cc}\begin{array}{l}{R}_{e,m}={\left(\frac{{\rho }_0}{\rho }\right)}^{1/3}\frac{V_0}{L_0^{1/3}}\frac{4\pi {\gamma }_{ad}\rho {\rho }_i}{B^2}{l}^{4/3}.\end{array}& (32)\end{array}$

The smallest scale that can be reached in a turbulent cascade is typically obtained when the Reynolds number is equal to about 1. This leads for l_diss, the dissipation length, the following expression:

$\begin{array}{cc}\begin{array}{l}{l}_{diss}={\left(\frac{L_0^{1/3}}{{\rho }_0^{1/3}{V}_0}\right)}^{3/4}{\left(\frac{B^2}{4\pi {\gamma }_{ad}{\rho }^{2/3}{\rho }_i}\right)}^{3/4}.\end{array}& (33)\end{array}$

Typical values for the ISM are V₀ = 2.5 km s⁻¹, ρ₀ = 100 cm⁻³ and L₀ = 10 pc The magnetic intensity is about 5 μG in the diffuse gas and 10-20μG in the molecular gas for densities of a few 10³ cm⁻³. In the molecular gas the ionization is about 10⁻⁶−10⁻⁷ (Le Petit et al., 2006; Bergin and Tafalla, 2007) and the ion density ρ_i is given by $C\sqrt{\rho }$, where C = 3 × 10⁻¹⁶ cm^−3/2 g^1/2. For a density of 10³ cm⁻³, a magnetic intensity of 20μG, this leads to l_diss ≃ 0.2 pc. Obviously Equation (33) depends on physical parameters such as V₀ and B and therefore should present variations. It is worth realizing that the first term of the right-hand side is the energy flux to the power 1/4. The energy flux, at least in Kolmogorov theory, is expected to be constant through scales. The second term may also present weak variations since ${\rho }_i\propto {\rho }^{1/2}$, it is proportional to (B²ρ^−7/6)^3/4 while observations reveal that B ∝ ρ^1/2 is not a bad approximation (Crutcher, 1999).

Hennebelle and André (2013) have developed a phenomenological model of a self-gravitating and accreting filament in which turbulent support insures the filament stability. The turbulence is maintained by the kinetic energy of accreting material, while the dissipation comes from the ion-neutral friction. A key prediction of this model is that the thickness of the filament is indeed about 0.1 pc and importantly does not depend on the density and column density of the filament. The reason stems from the fact that the ion-neutral drift operates on a timescale that is proportional to the ion density and that this latter is proportional to the neutral density in this regime. This dependence cancels out with the square-root of the gas density dependence of the freefall time.

However, so far this characteristic width has not been observed in numerical simulations. Ntormousi et al. (2016) have performed a detailed analysis of the filament width distribution (in simulations that do not include self-gravity) and found that while ion-neutral friction affects the density structure and reduces the numbers of small scale filaments, it does not produce a characteristic width near 0.1 pc as can be seen in Figure 5. This may be a consequence of the non-isotropic nature of this dissipation. In particular motions along the magnetic field lines are not dissipated by this mechanism.

To conclude, let us stress that while some of these explanations succeed to explain the observed width in some specific range of column density, none of the existing simulations performed so far have reproduced the characteristic width over 3 orders of magnitude in column density. Therefore, the origin of the apparent universal widths of the filamentary molecular clouds is still unclear. The problem could possibly be less severe because of the bias due to finite resolution (Panopoulou et al., 2017) which may lead to artificial structures. Let us stress however that the massive filaments are surrounded by an extended r⁻² envelope which has not been considered in the bias analysis of Panopoulou et al. (2017), therefore these objects are clearly defined and apparently well resolved. Note that it is quite possible that the bias described by Panopoulou et al. (2017) may also be present in the analysis of some of the numerical simulations.

6.3. Fragmentation and Core Formation Within Filaments

It has since long been recognized that cores often form in dense filaments (e.g., Dutrey et al., 1991) and several studies have performed stability analysis of hydrodynamical (e.g., Inutsuka and Miyama, 1992) and magnetized filaments (e.g., Nakamura et al., 1993; Fiege and Pudritz, 2000; Hanawa and Tomisaka, 2015; Hanawa et al., 2017). As the fastest growing mode has been found to be about four times the filament diameter, Inutsuka and Miyama (1992) argued that the fragments are expected to be separated by nearly four times this value. Fiege and Pudritz (2000) investigated the stability of filament threated by an helical magnetic field and conclude that although significant toroidal field can reduce significantly the growth rate of gravitationally driven modes, they lead to the development of the sausage instability.

Recent Herschel results have rejuvenated interest in filament forming cores. In particular (Polychroni et al., 2013; Könyves et al., 2015) have established that in nearby molecular clouds about 70–80% of dense cores lie within filaments. This may indicate that filaments are playing a significant role in the star formation process although the mass distribution of cores lying inside and outside filaments may not be drastically different (see Figure 17 of Könyves et al., 2015).

In light of recent results by Herschel, several other studies aiming at understanding the fragmentation of filaments in cores have been carried out to investigate various aspects of the non-linear fragmentation of filaments into cores. Clarke et al. (2016) performed a series of numerical simulations to study the fragmentation of a filament that is accreting instead of being at equilibrium as assumed in previous studies. Due to the gravo-acoustic modes induced by accretion, the dispersion relation varies with the accretion rate. Gritschneder et al. (2017) carried out simulations to study the response of a critical filaments to bending modes. These modes, which tend to make the filament oscillates perpendicularly to its main axis, lead to fragmentation. The cores which form have a spacing that matches the wavelength of the sinusoidal perturbation of the bending modes. Therefore inferring filament properties from characteristic spacing should be considered with care. Clarke et al. (2017) performed simulations where turbulence is seeded in accreting filaments and show that this generates fibers that are similar to the ones observed in Taurus (Hacar et al., 2013). They speculate that these fibers may suppress radial collapse within super-critical filaments.

Given the importance of filaments, it seems important to clarify the outcome of the fragmentation of filamentary molecular clouds and to understand the resulting properties of star forming cores. One of the most important outcome is the mass distribution of dense core, or so-called “core mass function” (Könyves et al., 2015).

Chen and Ostriker (2014) and Chen and Ostriker (2015) proposed a model for anisotropic core formation. In this model, filaments first form by flow of material along the magnetic field in post-shock layers where the field is strong. After filaments have acquired enough material that quasi-spherical regions are supercritical, strongly self-gravitating cores condense out. The two-step process predicts a characteristic core size and mass (Equation 7 of Chen and Ostriker, 2015) and post-shock magnetic field that depends on the pre-shock density and inflow velocity but not on the pre-shock magnetic field strength. Numerical results are generally consistent with this (see Figures 10, 11 of Chen and Ostriker, 2015).

The first attempt to obtain the mass function of prestellar cores from a filament structure was done by Inutsuka (2001) in the case of the simple quasi-equilibrium filament, i.e., the filament supported by the thermal pressure and hence not radially collapsing. In particular, Inutsuka (2001) found that a line-mass spectrum δ² ∝ kⁿ with n ~ −1.5 leads to a mass function of clumps whose power law exponent is close to −2.5, i.e., dn/dM ∝ M^−2.5. Note that the mass function discussed in his paper corresponds to the mass function of the systems, i.e., groups of stars, that may include binary or multiple stars. Roy et al. (2015) have recently measured the power spectrum of density fluctuations along sub-critical filaments of the Gould Belt Survey. They infer that δ² ∝ k^−1.6. If confirmed in a larger ensemble of filaments, this could explain the origin of the core mass function and its apparent universality.

Lee et al. (2017) have recently proposed an analytical theory to predict both the core mass function (CMF) and the mass function of groups of cores of supercritical filaments. The theory, which generalizes the calculations performed by Inutsuka (2001) and Hennebelle and Chabrier (2008), considers magnetized filaments assumed to be radially supported by turbulent motions and takes into account thermal, turbulent and magnetic supports. It predicts the CMF, which is found to depend on the mass per unit lengths (MpL) and the magnetic intensity. In particular, it is found that in the absence of magnetic field, filaments with high MpL fragment in too many small cores. In the presence of magnetic field with moderate intensities and for sufficiently high MpL, CMF compatible with observed ones are inferred.

7. The Role of Magnetic Field in the Evolution of Molecular Clouds and Clusters

In this section we more specifically address the role of the magnetic field regarding the evolution of molecular clouds as a whole and their ability to form stars. We also discuss the properties of the star forming dense cores, which form in these clouds.

7.1. Subcritical Clouds

Historically, one of the important questions related to the star formation process in the universe is the rate at which a galaxy is forming stars. In particular it is known since the work of Zuckerman and Evans (1974) (see Kennicutt and Evans, 2012, for a more recent discussion) that the star formation rate, at least in the Milky Way, is about hundred times lower than one would expect if the dense gas would be entirely in freefall. The origin of this factor hundred has remained mysterious during many years and magnetic field has been invoked to solve the problem (e.g., Shu et al., 1987).

To assess the importance of the magnetic field, one can compute the ratio of the magnetic over gravitational energies. As an illustrative example one can envisage a uniform spherically symmetric cloud of mass M, volume V, radius R. It is threaded by a uniform magnetic field of intensity B. The magnetic flux, Φ, is given by πR²B. In ideal MHD, the field is frozen into the gas and Φ remains constant. In this case we have

$\begin{array}{cc}\begin{array}{l}\frac{E_{\text{mag}}}{E_{\text{grav}}}=\frac{B^{2}V}{8\pi }\times \frac{2R}{5G{M}^2}\propto \frac{B^2{R}^4}{M^2}\propto {\left(\frac{\text{Φ}}{M}\right)}^2.\end{array}& (34)\end{array}$

Interestingly, E_mag/E_grav is constant and in particular does not depend on the cloud radius.

It is clear from Equation (34), that there is a critical value of the magnetic intensity for which the gravitational collapse is impeded even if the cloud was strongly compressed. Mouschovias and Spitzer (1976) have calculated accurately the critical value of the mass-to-flux ratio using the virial theorem and numerical calculations of the cloud bidimensional equilibrium. A cloud which has a mass-to-flux ratio smaller than this critical value cannot collapse and is called subcritical. It is called supercritical when the mass-to-flux is larger than the critical value. It is usual to define μ = (M/Φ)/(M/Φ)_crit. Large values of μ correspond to small magnetic fields and thus supercritical clouds.

Considering a magnetically supported dense core, also called subcritical core, the evolution is considerably slown down being almost quasi-static for most of the time. The neutrals slowly cross the field lines and the magnetic flux is gradually reduced up to the point where the core becomes critical and dynamical collapse proceeds. Estimating the time it takes is obviously the central question. To do so, clouds in virial equilibrium are considered, leading to B²/4π ≃ MρG/R. The ratio of the ambipolar time, τ_ad given by Equation 22, and the freefall time, ${\tau }_{\text{ff}}\propto {(G\rho )}^{-1/2}$, (Shu et al., 1987) is then estimated to be

$\begin{array}{cc}\begin{array}{l}\frac{{\tau }_{\text{ad}}}{{\tau }_{\text{ff}}}\propto \frac{{\gamma }_{ad}C}{\sqrt{G}},\end{array}& (35)\end{array}$

where it has been assumed that $\rho =C\sqrt{{\rho }_i}$. It is remarkable that in this expression there is no dependence in the physical parameters, such as the density, magnetic field and size. The exact value of τ_ad/τ_ff depends on the assumed geometrical coefficients. It is typically on the order of 10 [Shu et al. (1987) estimated τ_ad/τ_dyn = 8].

Equation (35) shows that the ambipolar diffusion process can reduce the star formation rate by almost an order of magnitude if the field is strong enough to compensate gravity. This would bring the star formation rate much closer to the observed values (e.g., Shu et al., 1987). To better quantify this process, one dimensional simulations of subcritical clouds have been performed (e.g., Basu and Mouschovias, 1995). For very subcritical cores and values of μ of about 0.1, Basu and Mouschovias (1995) inferred a collapse time equal to 15 freefall times. With critical cores, μ ≃ 1, the collapse takes roughly ≃ 3 freefall times.

More recently, a series of simulations aiming at simulating subcritical and turbulent molecular clouds have been performed (Basu and Ciolek, 2004; Heitsch et al., 2004; Li and Nakamura, 2004; Nakamura and Li, 2008, 2011; van Loo et al., 2008; Vázquez-Semadeni et al., 2011; Bailey and Basu, 2014; Bailey et al., 2017). Typically it has been found that under the influence of ambipolar diffusion but also of turbulence, areas of high column densities and lower magnetization develop. These regions are typically supercritical and form gravitationally bound cores, that in turns form stars. This is portrayed in Figure 12 where the column density in the direction of the initial magnetic field is shown as well as the isocontour of critical mass-to-flux ratio.

FIGURE 12

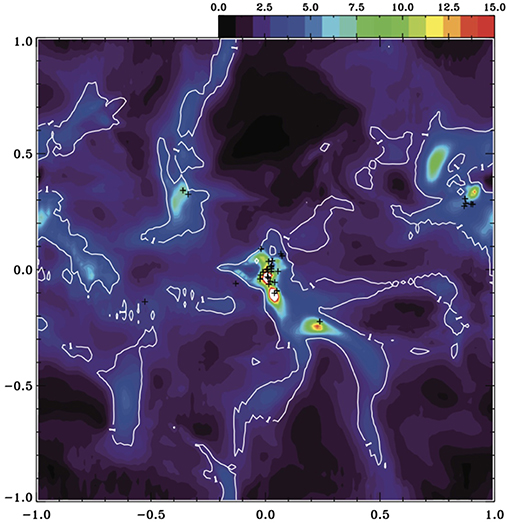
Figure 12. Spatial distribution of column density and mass-to-flux ratio in an initially subcritical and turbulent molecular cloud (Nakamura and Li, 2008). Inside the contour the gas is supercritical and has collapsed at several places. Outside the contour it is still subcritical. Reproduced from Nakamura and Li (2008) with permission of ApJ.

In all these calculations, it has been found that subcritical magnetic fields decrease very substantially, down to few percent, the star formation rate. For example Figure 13 shows the mass of the dense gas and the mass within sink particles for a series of calculations including different magnetizations and with or without ambipolar diffusion. As can be seen the mass within sink particles (i.e., “stars”) is almost 2 orders of magnitude smaller with an initial magnetic field of 4 μG than with a field of 2μG (one must keep in mind that these values correspond to the magnetization of the diffuse gas out of which the molecular cloud is assembled). It is also interesting to notice that in these calculations, the ambipolar diffusion makes only a modest difference. This indicates that a lot of magnetic flux is actually diffused through turbulence rather than ambipolar diffusion. Alternatively, this may also indicate that some gas is being accreted along the field lines, therefore reducing locally the mass-to-flux ratio.

FIGURE 13

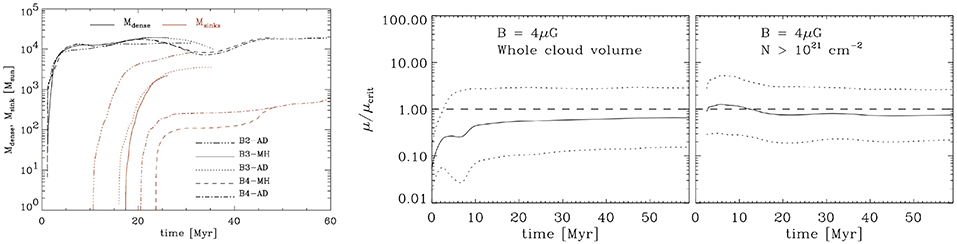
Figure 13. Mass of dense gas and distribution of mass-to-flux ratio in a molecular clouds formed from colliding flows (Vázquez-Semadeni et al., 2011). Three initial magnetizations are being shown, namely 2, 3, and 4 μG and runs with and without ambipolar diffusion have been performed.

Note that the interaction between turbulence and ambipolar diffusion can be complex. For example Li and Nakamura (2004) and Nakamura and Li (2008) found that stars may actually form more rapidly when the turbulence is higher because turbulence leads to a faster ambipolar diffusion by creating stronger shocks where the gradients of magnetic field are steep.

7.2. The Properties of Cores in Magnetized Molecular Clouds

We now turn to a discussion on the core properties that have been inferred from MHD simulations. As various rather different setups have been inferred we first start with a brief description of the numerical experiments, which have been performed. Here we restrict the discussion to studies that have explicitly discussed core statistics, i.e., self-gravitating structures formed within simulations that handle MHD and gravity. The cores are identified using a clump finding algorithm and then only the ones which are effectively self-gravitating are selected. Given that the typical size of dense cores is a fraction of 0.1 pc (e.g., Ward-Thompson et al., 2007), the spatial resolution achieved in these calculations is typically a fraction of 0.01 pc.

7.2.1. Numerical Setups of the Various Numerical Experiments

As several setups and initial conditions have been considered, we first give a quick overview of the different choices that have been made.

7.2.1.1. Prescribed molecular clouds

Many numerical experiments start with a uniform density cloud or a mildly peaked one (Basu and Ciolek, 2004; Li and Nakamura, 2004; Vázquez-Semadeni et al., 2005; Tilley and Pudritz, 2007; Nakamura and Li, 2008, 2011; Bailey and Basu, 2014; Bailey et al., 2017). The gas is assumed to be isothermal and self-gravity is treated. The initial field is usually uniform and various intensities ranging from 0 to significantly magnetized, are being assumed. Some velocity field with an amplitude corresponding to a Mach number up to 10, is usually prescribed. In these works either artificial driving of the turbulence is applied (Vázquez-Semadeni et al., 2005) either turbulence is free to decay. Nakamura and Li (2008) and Nakamura and Li (2011) include protostellar outflows, which drive turbulent motions. Ambipolar diffusion in the strong coupling limit is applied in some of these works.

7.2.1.2. Colliding flows

The colliding flow setup (e.g., Hennebelle et al., 2008; Banerjee et al., 2009; Vázquez-Semadeni et al., 2011; Clark et al., 2012; Valdivia et al., 2016) has also been used to study core formation (Chen and Ostriker, 2014, 2015). It consists in imposing two streams of gas with supersonic sound speed that create a dense shocked layer, which eventually gives rise to a layer of denser gas. The advantage of this setup is that the cloud is built and not imposed as it is the case for the previous setup. In particular, it is initially not self-gravitating. The other advantage is that the turbulence within the cloud is a consequence of the incoming flow. Chen and Ostriker (2014) and Chen and Ostriker (2015) vary the Mach number of the incoming flow and the magnetization. They treat ambipolar diffusion in the strong coupling approximation. In this scenario the transverse component of the magnetic field is amplified in the shock bounded layer as the colliding flow is super-Alfvénic.

7.2.1.3. Zooming-in from galactic box calculations

One of the restrictions of the two previous setups is that the initial conditions or boundary conditions have to be assumed. Moreover the statistics remain limited because, to unsure good resolution, the computational domain is typically few parsecs across. To circumvent these difficulties, Hennebelle (2018) has performed adaptive mesh refinement simulations of a kpc numerical domain. These simulations includes stratification, induced by the gravitational field due to stars and dark matter. They start with only WNM and have an initial magnetic field parallel to the equatorial plane of about 3μG. In a first phase, supernova driving is applied. Once a self-consistent multi-phase and turbulent ISM is obtained, nine levels of adaptive mesh are employed to refine a region of 100 × 100 pc². This provides a final resolution of about 4 × 10⁻³ pc.

7.2.2. Core Properties

In the studies presented above, many core properties have been inferred. Here we restrict the discussion to 4 of them, comparing the results obtained in the different configurations explored. In spite of the relatively broad diversity of these latter, the results are in relatively good agreement.

7.2.2.1. Core mass spectrum

The mass spectrum of dense cores is likely to be important because they constitute the eventual mass reservoirs of stars. Moreover the core mass function (CMF) has been found to have a shape similar to the stellar initial mass function (IMF) (Ward-Thompson et al., 2007; Offner et al., 2014), seemingly suggesting that the CMF may be at the origin of the IMF. Note that this possible link between the CMF and the IMF is still a matter of debate and numerous studies argue that the IMF is not linked to the CMF (see section 7.4.1 and Offner et al., 2014 for a recent review on this topic). The CMF has been computed by Tilley and Pudritz (2007), Nakamura and Li (2008), Nakamura and Li (2011), Chen and Ostriker (2014), and Hennebelle (2018). It has generally been found that the CMF resembles the observed ones (Könyves et al., 2015). In particular, it presents a peak and a powerlaw at large masses (see top-right panel of Figure 14) with a slope close to the observed one (Tilley and Pudritz, 2007; Nakamura and Li, 2011; Hennebelle, 2018). The slope is compatible with the idea that cores form under the combined influence of gravity and turbulent support (Hennebelle and Chabrier, 2008) while magnetic field does not appear to have a strong influence (e.g., Figure 11 of Nakamura and Li, 2011) in good agreement with theory (Hennebelle and Chabrier, 2013).

FIGURE 14

Figure 14. Global flow properties and dense core statistics in a zooming-in calculation that goes from 1 kpc box size to 4 × 10⁻³ pc resolution (Hennebelle, 2018). Top-left panel: magnetic intensity vs. density in the whole refined region of the AMR simulation and in 5 star-forming subregions. Top-middle panel: same as top-left panel for the density distribution. Top-right: mass spectrum of dense cores (defined as thermally supercritical objects for 2 different thresholds of their mean density). Bottom-left panel: mass-to-flux ratio vs. mass for the thermally supercritical cores. Bottom-middle: mass-size relation of the thermally supercritical cores. Bottom-right: internal velocity dispersion relation vs. mass of all cores. Reproduced from Hennebelle (2018) with permission of A&A.

The question of the peak is far less clear. Observationally a peak around 0.5–1 M_⊙ has been inferred (Könyves et al., 2015), though higher resolution observations need to confirm its robustness. In the simulations the existence of the peak must also be handled with care. First of all, simulations that have no preferred scales like isothermal simulations with ideal MHD can be freely rescaled to any units. This means that the peak is a direct function of the initial conditions. Second of all numerical convergence must be carefully verified. For example Hennebelle (2018) performed runs at different resolutions and concluded that indeed the peak of the CMF varies with numerical resolution. Note that Gong and Ostriker (2015) on the contrary concluded that numerical convergence is reached in their colliding flow calculations. The most likely reason of this discrepancy comes from the differences of the physical conditions studied and in particular the global gravitational stability of the simulated regions. Indeed gravity induces density PDF with high density powerlaw tails in which case the CMF may not present a peak at all (see discussion in Lee and Hennebelle, 2018a,b).

Once rescaled to the mean Jeans mass (e.g., Tilley and Pudritz, 2007; Chen and Ostriker, 2014, 2015), the dependence of the CMF on physical parameters has been found to be limited. In particular, Chen and Ostriker (2015) found a modest dependence of the CMF onto the magnetic intensity. This is at first surprising as magnetic field is part of the total support. To account for this weak dependence, they propose an anisotropic scenario in which contraction first start along the field lines before enough mass is accumulated to trigger contraction perpendicularly to the field lines.

A complementary information is provided by the mass-size relation (displayed in bottom-middle panel of Figure 14) which has been studied by Chen and Ostriker (2014), Chen and Ostriker (2015), and Hennebelle (2018). Typically a relation M ∝ R^α, with α ≃ 2 has been inferred.

7.2.2.2. Magnetization

The magnetization of cores is a fundamental parameter to determine. Indeed magnetic field has been found to influence significantly the collapse of cores and in particular the formation of planet-forming disks through magnetic braking (Inutsuka, 2012; Li et al., 2014; Hennebelle et al., 2016).

Chen and Ostriker (2015) provide (Figure 12) the mass-to-flux as a function of the core mass. They found that most cores are supercritical with typical values for μ of about 2. A clear trend is seen for μ to increase with the core mass. The dependence of the μ distribution on the initial large scale magnetic field and the Mach number of the colliding flow is found to be relatively weak

Hennebelle (2018) has been measuring the mass-to-flux ratio in cores identified as thermally supercritical, that is to say cores that would collapse if only thermal support was present. The result is displayed in bottom-left panel of Figure 14 where the mass-to-flux is displayed as a function of the core mass. The mass-to-flux is found to increase with the mass and is roughly proportional to it with μ ≃ 1 for M ≃ 1M_⊙. However, a relatively broad distribution is inferred and for a given mass, the mass-to-flux distribution spans almost one order of magnitude. Note that many of these cores would actually not collapse (unless they accrete more mass along the field lines) as they are subcritical and therefore magnetically supported.

7.2.2.3. Velocity dispersion

The velocity dispersion in and around cores has received a lot of attention. Nakamura and Li (2008) and Nakamura and Li (2011) found that the velocity dispersion in cores present a large spread and goes from sonic (i.e., the velocity dispersion is close to the sound speed) to a Mach number larger than 5, with values up to 2–3 km s⁻¹. They found that there is no clear dependence of the velocity dispersion with the mass or the size. This is very similar with what is reported in Hennebelle (2018) and displayed in the bottom-right panel of Figure 14.

Nakamura and Li (2011) reported that the velocity dispersion is significantly reduced when the magnetization is high. Typically the cores formed in highly magnetized clouds tend to have trans-sonic to sub-sonic motions only.

7.2.2.4. Magnetic field orientation and core shape

The relationship between core shapes and the direction of the magnetic field has been analyzed by Chen and Ostriker (2018). They found that in colliding flow simulations cores are generally triaxial, and the magnetic field tends to be parallel to the shortest axis and perpendicular to the longest axis, with internal and external magnetic field direction correlated. This is a natural consequence of the formation of cores within filaments and the fact that magnetic field tends to be perpendicular to self-gravitating filaments as explained previously (e.g., Soler et al., 2013; Gómez et al., 2018). They also found that core angular momentum vectors are not aligned with the direction of the (internal or external) magnetic field. As explained below, this may be important in the context of protoplanetary disk formation.

7.3. The Influence of Magnetic Field on Low Mass Collapsing Cores

The collapse of low mass prestellar cores leads to the formation of small groups of stars, a process known as fragmentation, and to the formation of protoplanetary centrifugally supported disks. It is presently believed that magnetic field has a drastic influence on the outcome of collapsing cores.

7.3.1. The Magnetic Braking Process

A fundamental difference between hydrodynamical and magnetized prestellar cores comes from the evolution of angular momentum. In the absence of a substantial magnetic field, the latter is essentially conserved and becomes dominant drastically affecting the evolution of the core (e.g., Matsumoto and Hanawa, 2003). In a magnetized core, the situation is different. Because of magnetic tension, angular momentum can be exchanged between fluid particles. Typically this exchange occurs between a cloud and an intercloud medium and happens through torsional Alfvén waves, which propagate in the intercloud medium (Mouschovias and Paleologou, 1981; Shu et al., 1987; Joos et al., 2012). To estimate the characteristic time scale of magnetic braking let ρ_icm be the density of the intercloud medium. For simplicity, we consider that the magnetic field is parallel to the cloud rotation axis. The torsional Alfvén waves propagate at a speed, $V_a=B/\sqrt{4\pi {\rho }_{\text{icm}}}$. The magnetic braking is important if a significant fraction of the cloud angular momentum has been delivered to the intercloud medium. This occurs when the waves have reached a distance l×ρ_icm ≃ R×ρ₀. This leads to

$\begin{array}{cc}\begin{array}{l}{\tau }_{\text{br}}\simeq \frac{R}{V_a}\frac{{\rho }_0}{{\rho }_{\text{icm}}}.\end{array}& (36)\end{array}$

Equation (36) is obtained assuming a very simple geometry. Other estimates in different geometries can be found in the references mentioned above. In particular, the braking depends on the angle between the magnetic field and the rotation axis, it also depends whether the field lines are uniform or fan out, in which case the braking time can be considerably reduced.

7.3.2. Disk Formation: A Magnetically Controlled Process?

In the aligned configuration, the braking time can become so short that the formation of the centrifugally supported disks can be even entirely prevented (e.g., Allen et al., 2003; Galli et al., 2006; Price and Bate, 2007; Hennebelle and Fromang, 2008; Li et al., 2014), a process known as catastrophic braking. More recent studies have revealed that the aligned configuration is however too simplified and that disks should form in magnetized clouds, although in general the disks are smaller and fragment less than in the hydrodynamical case. These studies fall in two categories. First, the magnetic braking is reduced because (i) the magnetic field and the rotation axis are non-aligned (Joos et al., 2012; Gray et al., 2018), (ii) the turbulent velocity field diffuses the magnetic field (Santos-Lima et al., 2012; Joos et al., 2013), (iii) the turbulent field makes the structure of the magnetic field less coherent (Seifried et al., 2013). Note that Gray et al. (2018) performed turbulent simulations in which the angular momentum is aligned with the magnetic field and show that disks do not form or are much smaller than in the same simulations for which there is no alignment. They concluded that misalignment may be the dominant effect. The second category of processes that limits catastrophic braking is non-ideal MHD. This has been studied by numerous groups (Inutsuka, 2012; Li et al., 2014; Hennebelle et al., 2016; Machida et al., 2016; Masson et al., 2016; Wurster et al., 2016; Zhao et al., 2018). These works found that small disks (i.e., disks significantly smaller than in the hydrodynamical case) form. Moreover, the turbulence and the magnetic configurations (i.e., misalignment) tend to be less important when non-ideal MHD processes are accounted for.

7.3.3. How Magnetic Field Changes the Fragmentation of Low Mass Cores

In typical conditions, that is to say with low rotation speed and relatively high thermal support, low mass cores generally fragment in several objects (Matsumoto and Hanawa, 2003). This fragmentation is due to the generation of the density fluctuations induced by turbulence or by gravity itself. Rotation considerably helps by maintaining important quantities of gas in equilibrium leading to the formation of massive, highly unstable disks. The issue of fragmentation is therefore strongly dependent of the initial conditions, namely the rotation and turbulence level as well as the presence of density perturbations initially. Several studies have been dedicated to the influence of magnetic field in this process (e.g., Machida et al., 2005, 2008; Hennebelle and Teyssier, 2008; Commerçon et al., 2010; Wurster et al., 2017). It has been found that when the density perturbations are low, typically 10% or so, the magnetic field is drastically reducing fragmentation, which happens only when the magnetic intensity is low. This is because when no strong density perturbations is initially present, the fragmentation occurs through rotation and the formation of massive, highly unstable disks. However, magnetic field gets efficiently wind up by the differential rotation which develops in the core inner part. As discussed above, angular momentum is then efficiently extracted and the disks are smaller. Another important effect, which further reduces rotationally induced fragmentation, is the magnetic pressure itself, particularly the one associated to the toroidal magnetic field. This pressure adds up to the thermal one and makes the disks more stable (Hennebelle and Teyssier, 2008). This stabilization seems to persist even when non-ideal MHD effects are accounted for (Wurster et al., 2017). On the other hand density perturbations of large amplitude, that is to say of about 50%, are sufficiently unstable to collapse individually even in the absence of rotation. In this case, magnetic field is unable to impede fragmentation (Hennebelle and Teyssier, 2008; Wurster et al., 2017).

7.4. Is Magnetic Field Playing a Role in the Formation of Clusters?

It is believed that stars do not form in isolation but rather in clusters (e.g., Longmore et al., 2014). Indeed, observationally stars do not form in the bulk of molecular clouds but instead in their denser parts. Large surveys have recently revealed ensemble of massive clumps in which stars are actively forming (Fall et al., 2010; Urquhart et al., 2014; Traficante et al., 2015). These clumps have masses up to several thousands of solar masses and are very good candidates for being stellar cluster progenitors. Given that these objects are relatively massive it is unlikely that magnetic field plays a major contribution on the formation and global equilibrium of these massive clumps. Numerical simulations are able to reproduce reasonably well the global properties of these massive clumps such as their mass-size relation, simply by invoking gravity and turbulence (Lee and Hennebelle, 2016a,b), starting with reasonable ISM magnetic intensities, magnetic energies a few times above the thermal ones but well below the kinetic and gravitational energies are obtained.

There are however several aspects that deserve particular attention and which are now examined. First of all, does magnetic field influences the small scale fragmentation, that is to say the formation of the stars themselves? Does magnetic field enhance stellar feedback? Does magnetic field increase the coupling between clusters and outflows and jets?

7.4.1. Does Magnetic Field Affect the Small Scale Fragmentation in Stellar Clusters?

One fundamental goal of cluster studies is to infer the mass function of stars that form and whether it can reproduce the IMF. Several studies have been investigating this issue using sink particles (e.g., Bate, 2012; Myers et al., 2013; Offner et al., 2014; Lee and Hennebelle, 2018a). As the present review focusses on the possible role of magnetic field, the discussion below is restricted to this aspect specifically.

7.4.1.1. MHD barotropic calculations

Before we describe the calculations that include radiative processes, we first consider the simpler barotropic case. Such simulations have been performed by Price and Bate (2008) and Hennebelle et al. (2011) (see also Peters et al., 2011, who even included photo-ionisation from the central star) who have simulated the collapse of several tens M_⊙ turbulent cores. The turbulent and gravitational energies were initially comparable and various magnetic intensities have been explored. It has been found that the fragmentation is reduced when the mass-to-flux is smaller than ≃ 5. The fragment number is reduced by roughly a factor of 2 for the strongest magnetization. It has been found that during the collapse, efficient magnetic diffusion occurs due to the turbulent velocity field, which explains why fragmentation is reduced by a factor 2 only.

Recently Lee and Hennebelle (2018c) studied the collapse of 1000 M_⊙ clumps with various magnetization. As sink particles, are being used, the initial mass function was studied. They concluded that while magnetic field reduces a bit the number of objects, it is of secondary importance to determine the shape of the IMF. This is in part due to the fact that the peak is determined at very small scale (100 AU or so) and at very high density where the magnetic intensity weakly depends on the large scale initial conditions and therefore tends to have the same value irrespectively of the initial value.

7.4.1.2. MHD radiative calculations

Collapse calculations of massive collapsing cores, in which both the magnetic field and the radiative transfer have been taken into account, have been carried out.

Price and Bate (2009), found that the magnetic field and the radiative feedback play complementary effects. Magnetic field supports the diffuse gas at large scale and radiative feedback, by heating the inner part of the core, reduces the fragmentation in many objects.

Simulations including magnetic field and radiative feedback, which follow the collapse up to AU scales, have been performed by Commerçon et al. (2011), Myers et al. (2013), Myers et al. (2014), and Cunningham et al. (2018). It has been found that in some circumstances, the combination of magnetic field and radiative feedback may be reducing fragmentation significantly. This is due to the fact that magnetic field induces efficient magnetic braking and reduces the amount of angular momentum in the cloud inner part. Consequently, the accretion is more focused in a magnetized core than in an hydrodynamical one. In this latter case strong angular momentum prevents the gas to fall in the cloud center. Thus the accretion luminosity, which is ∝ MṀ/R is much higher since M and Ṁ are larger while R is smaller. The temperature in magnetized cores is therefore higher than in hydrodynamical ones and this reduces the fragmentation within the former.

7.4.2. Does Magnetic Field Enhance Stellar Feedback?

A possibly important consequence of the magnetic field could be related to this very last point. This is because stellar feedback critically depends on the stellar masses. This is the case for the HII radiation, the winds and of course the supernova explosions, which require the stellar mass to be larger than 8 M_⊙. For example numerous authors (Dale and Bonnell, 2011; Walch et al., 2012; Geen et al., 2015, 2017) found that in Milky Way type conditions, HII regions likely destroy molecular clouds quickly after they form stars, likely limiting the star formation efficiency of these objects.

Arthur et al. (2011) (see also Mackey and Lim, 2011; Gendelev and Krumholz, 2012) performed both unmagnetized and magnetized simulations of the expansion of an HII region in a molecular clumps and studied in details the resulting structure of the field. They found that the magnetic field does not change very significantly the expansion in itself but reduces the small scale fragmentation and radiation-driven pillars. The field in the neutral expanding shell is preferentially parallel to the shell while in the ionized gas inside the shell it is more perpendicular to it.

Since magnetic field tends to reduce fragmentation, it is likely that without magnetic field the stars would be on average less massive and therefore their HII radiation which is proportional to M²⁻³ (e.g., Vacca et al., 1996), would be significantly reduced. Since numerical simulations are not able yet to self-consistently predict the mass of the stars and follow the large scale evolution of the parent clouds subject to their feedback, it is however not possible to get a firm confirmation of this effect.

7.4.3. Does Magnetic Field Improve the Coupling With Jets?

The influence that jets may have on a proto stellar clusters has been investigated at pc scales (Li and Nakamura, 2006; Carroll et al., 2009; Cunningham et al., 2009; Wang et al., 2010; Federrath, 2015) and inside massive cores (e.g., Cunningham et al., 2011).

Li and Nakamura (2006) (see also Wang et al., 2010; Federrath, 2015) carried out calculations for a 10³ M_⊙ clump. A stationary state has been obtained. Turbulence is sustained by outflows which counteract gravity, delaying the collapse significantly. Wang et al. (2010) and Federrath (2015) carried out simulations in which several physical processes are progressively included, namely initial turbulence, magnetic field and outflows. Each of them reduces the star formation rate by a factor of a few. When all of them are included the star formation rate is typically 10 times lower than when the protocluster is in freefall.

The question as to whether turbulence may be sustained by protostellar outflows has been investigated by Cunningham et al. (2009) and Carroll et al. (2009). They reached the conclusion that in a turbulent medium, even without a magnetic field, the outflows couple to the surrounding gas and trigger turbulence efficiently. They inferred an energy powerspectrum that is stiffer than the usual powerspectra found in large scale driven turbulence (e.g., Kritsuk et al., 2007; Hennebelle and Falgarone, 2012). Murray et al. (2018) have reached a somehow different conclusion as they find that the outflows have only a modest influence on the driving of turbulence.

Offner and Chaban (2017) and Offner and Liu (2018) have performed a series of low mass dense core collapse and studied the influence of outflows on the collapsing core and in particular, the efficiency of the driving of turbulence within the envelope of the core. They conclude that outflows can drive efficiently turbulence in the envelope and that the efficiency of the driving increases with magnetic intensity.

8. The Role of Magnetic Field in ISM Self-Regulated Models

Important efforts have also been undertaken to self-consistently simulate the interstellar medium within galaxies. Because modeling galaxies as a whole is very challenging in terms of scales, many models (e.g., de Avillez and Breitschwerdt, 2005; Joung and Mac Low, 2006; Gent et al., 2013; Kim et al., 2013) consider a computational box of about 1 kpc sometimes called galactic box. Since the typical supernova remnant radius is about 50 pc, this constitutes a good compromise between spatial resolution and molecular cloud statistics (though at the expense of solving the large galactic scales). The most recent models consider an external vertical gravitational field, which represents the gravity of stars and dark matter, follow the star formation (up to spatial scales of about 1–4 pc) and deliver stellar feedback (due to massive stars and essentially though not exclusively supernovae). This leads to a self-regulated ISM in which a turbulent cascade takes place. The energy is injected at the large and intermediate (around or above 100 pc) scales and decay at the small ones.

8.1. Star Formation Rate and Vertical Equilibrium

The importance of the spatial and temporal correlations between the supernova remnants and the star forming dense gas has been stressed by recent studies (Hennebelle and Iffrig, 2014; Gatto et al., 2015). When the supernovae are randomly placed, the feedback they provide is inefficient and does not reduce the star formation rate appreciably. On the other hand, when the supernova explosions correlate with the dense gas, star formation rates in better agreement with the observed values are inferred (Kim et al., 2013; Hennebelle and Iffrig, 2014). In these simulations, the thickness of the galactic disk is also compatible with the observed values while it is too thin in simulations where the supernovae are randomly placed. As recently stressed by Girichidis et al. (2016) cosmic rays may change this conclusion. Also these models produce a realistic multi-phase magnetized ISM with densities and temperature that are reminiscent of the WNM and CNM. When a magnetic field of a few μG is initially present in the simulations, the magnetic intensities stay compatible with the observed values. It has been found that magnetic field contributes to the galactic vertical equilibrium although its contribution is lower than the one of the turbulent dispersion and it has also been inferred that the star formation rate is somewhat reduced in the presence of a magnetic field by a factor that is on the order of 2 (Kim and Ostriker, 2015; Iffrig and Hennebelle, 2017; Girichidis et al., 2018). One important limit of these models is that the feedback is delivered immediately after the stars are formed, while supernovae arise 4-40 Myr after their progenitor formation. Given that the typical freefall time of a typical star forming cloud is only a few Myr. This is a significant effect that the most advanced models (Kim and Ostriker, 2017; Colling et al., 2018; Girichidis et al., 2018) are now taking into account. It should be stressed however that in order to treat the feedback injection properly star formation and evolution should be treated self-consistently. In practice, this would require to resolve spatial scales that are much smaller than what is currently possible for this type of modeling.

8.2. Turbulence and Clumps

Iffrig and Hennebelle (2017) have carried out a series of 1024³ simulations which allow to infer the statistics of turbulence and the properties of structures. In spite of the stratification, the powerspectra are broadly compatible with earlier works (see e.g., Kritsuk et al., 2007) though the velocity powerspectrum is closer to the classical Kolmogorov exponent than the stiffer, almost Burgers like, values inferred in supersonic isothermal turbulence. This likely is a consequence of the magnetized, multi-phase structure since the velocity dispersion is not much larger than the sound speed and Alfvén speed of the WNM. The ratio of the energies of the compressible modes and solenoidal ones depends on the altitude. In the mid-plane, the compressible modes dominate while above a certain altitude, which varies with the magnetic intensity, the solenoidal ones dominate. The stronger the magnetic intensity, the lower is the altitude above which solenoidal modes dominate. This conclusion is different from the one of Padoan et al. (2016) who found that the solenoidal modes always dominate. The discrepancy is most certainly due to the absence of stratification in Padoan et al. (2016). The dense clouds have been extracted from the simulations of Iffrig and Hennebelle (2017) and Padoan et al. (2016) using simple clump finders. Their statistical properties such as the mass spectra, the mass-size and the internal velocity dispersion-size relations are all reminiscent of the observed cloud properties (e.g., Miville-Deschênes et al., 2017) though Iffrig and Hennebelle (2017) mentioned that the internal velocity dispersion are possibly smaller than within observed clouds. This may indicate the need for other energy injection sources such as the one due to the large galactic scale gravitational instabilities (Krumholz and Burkhart, 2016). The distribution of the mass-to-flux ratio, μ, of the clouds has also been inferred (see also Inoue and Inutsuka, 2012). It is broadly proportional to the square-root of the cloud mass, which has been interpreted as the mass being proportional to the volume while the flux is proportional to the surface. The value of μ also depends on the density threshold used to define the clouds. The lower the density threshold, the lower μ.

8.3. A Possible Link Between Magnetic Field and Clump Mass Function

To understand the overall star formation rates in the Galaxy we have to know, not only the star formation rate in an individual cloud, but also the mass distribution of molecular clouds, which determines the total number of stars created in the Galaxy. It is actually difficult to accurately determine the mass function of molecular clouds in our Galaxy because of the line-of-sight contamination and limited knowledge on the distances to the clouds. Thanks to the development of observations, the mass function of GMC can now be determined in nearby face-on galaxies such as M51 (Colombo et al., 2014). For example Colombo et al. (2014) reported that the exponent of the power-law slope of mass function varies depending on relative location to the spiral arm structure and the galactic center. Thus theoretical studies for the cloud properties may shed light on our understanding of the formation and destruction of molecular clouds. As mentioned in the previous sections, however, it is still difficult to perform direct numerical simulations of an ensemble of molecular clouds and study in details the small scale physics such as formation and destruction of molecular clouds. Earlier attempts to propose analytical models can be found in Kwan (1979), Scoville and Hersh (1979), and Tomisaka (1986) that formulated the so-called coagulation equation for molecular clouds. In these investigation the growth of clouds are, however, supposed to be driven by the cloud-cloud collision and missed the importance of gas accretion onto molecular clouds. The recent theoretical finding of the long timescale of molecular cloud formation (Inoue and Inutsuka, 2009) and the importance of gradual growth process by accretion of dense HI gas (Inoue and Inutsuka, 2012) stress the crucial need for accretion contribution in the coagulation equation (Kobayashi et al., 2017, 2018).

In this section, we present an analytical model that suggests a link between the magnetic field and the clump mass function because of the impact of the former onto the cloud formation time. In section 3.3 we have shown that the existence of magnetic field may possibly significantly increase the formation timescale of molecular clouds. Let's propose an estimate of the actual value of the cloud formation timescale in our Galaxy. The radius of a supernova remnant (SNR) can be on the order of 100pc after the expansion over the typical age ~ 1 Myr. We may assume that the creation rate of SNRs in our Galaxy is 10⁻²yr⁻¹ Thus, the volume occupied by SNRs can be calculated as 100³×10⁻²yr⁻¹×1Myr = 10¹⁰pc³. This value is roughly the same as the volume of Galactic thin disk (10kpc²×100pc) where molecular clouds reside. This means that ISM in Galactic thin disk is swept up by SNR once per 1 Myr (McKee and Ostriker, 1977). If we ignore the magnetic field, the molecular cloud can be simply created by a single, may be a few compressions of warm neutral medium by the propagation of a shock wave. As shown in Section 3.3, however, molecular clouds could be created after several compressions (up to 10) and thus, the actual timescale of cloud formation should be several Myr.

To infer the clump mass spectrum, we can adopt coarse graining of short-timescale (~ a few Myr) events of the growth and destruction of clouds, and describe the long timescale evolution by the continuity equation of molecular clouds in mass space (Kobayashi et al., 2017)

$\begin{array}{cc}\begin{array}{l}\frac{\partial N}{\partial t}+\frac{\partial }{\partial M}\left(N\frac{dM}{dt}\right)=-\frac{N}{T_{\text{d}}}+{\left(\frac{dN}{dt}\right)}_{\text{coll}},\end{array}& (37)\end{array}$

where N(dM/dt) denotes the flux of mass function in mass space, T_d is the cloud disruption timescale, dM/dt describes the growth rate of the molecular cloud, and the last term accounts for the growth due to cloud-cloud collision. If the contribution from cloud-cloud collisions is negligible (Kobayashi et al., 2017, 2018) and the mass growth can be approximated by dM/dt = M/T_f with the growth timescale T_f, a steady state solution of the above equation is N(M) = M^−α, where α = 1+T_f/T_d (Inutsuka et al., 2015). In a gas rich environment such as a spiral arm of a disk galaxy, we expect T_* ~ T_f, and thus, T_f ≲ T_d, which corresponds to 1 < α ≲ 2. For example, T_f = 10Myr corresponds to α ≈ 1.7, which agrees nicely with observations (Solomon et al., 1987; Kramer et al., 1998; Heyer et al., 2001; Roman-Duval et al., 2010). However, in a region with very limited amount of gaseous material, T_f is expected to be large and possibly even larger than T_d = T_* + 4Myr, which produces α > 2. This may explain the observations in M33 (Gratier et al., 2012) and in M51 (Colombo et al., 2014). The more detailed description of the molecular cloud mass function can be found in Kobayashi et al. (2017, 2018) where the effect of cloud-cloud collisions is explicitly taken into account.

Note that the effects of magnetic field that slows down the cloud formation are taken into account in the above analysis as a large value of the cloud formation timescale (T_f > 1 Myr). If we ignore the effect of magnetic field and simply choose the dynamical compression rate of ISM as the value of the cloud formation timescale T_f=1Myr, the powerlaw exponent of the mass function of molecular cloud would be too small (α ~ 1), which is in stark contrast to the observed values. Therefore we may conclude that magnetic field is playing an important role in the mass distribution of molecular clouds in our Galaxy.

9. Conclusions

This review is dedicated to the role that magnetic field may have in the formation and evolution of molecular clouds. Significant progress has been accomplished in the last years in our understanding of the molecular cloud in particular and star formation process in general. We have a better, although still incomplete, knowledge of the structures, filaments, cores, clumps, clusters, formation mechanisms.

Most likely these gaseous structures are all the product of magnetized turbulence interacting with gravity. Given the values of the magnetic intensities that have been measured, numerical simulations seem to indicate that the number of objects that form at all scales, from clumps to stars, is likely reduced by a factor of a few due to the action of the magnetic field. Accordingly their masses tend to be also a few times larger than what it would be with pure hydrodynamics. The shapes of the clouds are also strongly affected by magnetic field, which tends to create filamentary structures as well as clouds that have flattened along the magnetic field lines that permeate them. More generally the whole dynamics of the ISM is significantly modified and cannot be accurately interpreted without taking magnetic fields into account.

While it is now almost certain that magnetic fields do not regulate the star formation process by reducing the star formation rate drastically, as proposed three decades ago, it is likely the case that magnetic fields contribute to reduce it by a factor of a few. Moreover since it has been found by various groups that magnetic field tends to reduce the fragmentation and to produce stars with larger mass, another possible consequence of magnetic field is to enhance stellar feedback and therefore to reduce the star formation rate and efficiency in molecular clouds. This latter aspect remains however to be confirmed as numerical simulations are not able now to cover the necessary range of scales. Finally we stress that magnetic field is likely to have drastic consequences on the formation of protoplanetary disks through magnetic braking by reducing and even possibly controlling their size.

Author Contributions

PH and SI were both responsible for writing and editing the manuscript.

Funding

This work is supported by Grant-in-aids from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan (16H02160, 18H05436, 18H05437).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the two referees for constructive remarks and critical reading of the manuscript. We thank various contributions from Philippe André, Edouard Audit, Doris Arzoumanian, Gilles Chabrier, Benoit Commerçon, Edith Falgarone, Sébastien Fromang, Samuel Geen, Olivier Iffrig, Tsuyoshi Inoue, Kazunari Iwasaki, Hiroshi Koyama, Yueh-Ning Lee, Anaelle Maury, Evangelia Ntormousi, Juan-Diego Soler, Romain Teyssier, Valeska Valdivia.

Footnotes

1. ^In principle gravity and stellar feedback are two other sources whose signature can sometimes be clearly recognized. In many circumstances however, it is likely difficult to clearly separate the different contributions as gravity and feedback trigger turbulent motions.

References

Allen, A., Li, Z.-Y., and Shu, F. H. (2003). Collapse of Magnetized Singular Isothermal Toroids. II. Rotation and Magnetic Braking. Astrophys. J. 599, 363–379. doi: 10.1086/379243

CrossRef Full Text | Google Scholar

Alves de Oliveira, C., Schneider, N., Merín, B., Prusti, T., Ribas, Á., Cox, N. L. J., et al. (2014). Herschel view of the large-scale structure in the < ASTROBJ>Chamaeleon < /ASTROBJ> dark clouds. Astron. Astrophys. 568:A98. doi: 10.1051/0004-6361/201423504

CrossRef Full Text | Google Scholar

Ames, S. (1973). Magneto-gravitational and thermal instability in the galactic disk. Astrophys. J. 182, 387–404. doi: 10.1086/152147

CrossRef Full Text | Google Scholar

André, P., Di Francesco, J., Ward-Thompson, D., Inutsuka, S.-I., Pudritz, R. E., and Pineda, J. E. (2014). “From filamentary networks to dense cores in molecular clouds: toward a new paradigm for star formation,” in Protostars Planets VI, eds H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning (Tucson, AZ: University of Arizona Press), 27–51.

Google Scholar

Arthur, S. J., Henney, W. J., Mellema, G., de Colle, F., and Vázquez-Semadeni, E. (2011). Radiation-magnetohydrodynamic simulations of H II regions and their associated PDRs in turbulent molecular clouds. Mont. Notices RAS 414, 1747–1768. doi: 10.1111/j.1365-2966.2011.18507.x

CrossRef Full Text | Google Scholar

Arzoumanian, D., André, P., Didelon, P., Könyves, V., Schneider, N., Men'shchikov, A., et al. (2011). Characterizing interstellar filaments with Herschel in IC 5146. Astron. Astrophys. 529:L6. doi: 10.1051/0004-6361/201116596

CrossRef Full Text | Google Scholar

Auddy, S., Basu, S., and Kudoh, T. (2016). A magnetic ribbon model for star-forming filaments. Astrophys. J. 831:46. doi: 10.3847/0004-637X/831/1/46

CrossRef Full Text | Google Scholar

Audit, E., and Hennebelle, P. (2005). Thermal condensation in a turbulent atomic hydrogen flow. Astron. Astrophys. 433, 1–13. doi: 10.1051/0004-6361:20041474

CrossRef Full Text | Google Scholar

Bailey, N. D., and Basu, S. (2014). Non-ideal magnetohydrodynamic simulations of the two-stage fragmentation model for cluster formation. Astrophys. J. 780:40. doi: 10.1088/0004-637X/780/1/40

CrossRef Full Text | Google Scholar

Bailey, N. D., Basu, S., and Caselli, P. (2017). Ionisation in turbulent magnetic molecular clouds. I. Effect on density and mass-to-flux ratio structures. Astron. Astrophys. 601:A18. doi: 10.1051/0004-6361/201628273

CrossRef Full Text | Google Scholar

Balsara, D. S. (1996). Wave propagation in molecular clouds. Astrophys. J. 465:775. doi: 10.1086/177462

CrossRef Full Text | Google Scholar

Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., and Klessen, R. S. (2009). Clump morphology and evolution in MHD simulations of molecular cloud formation. Mont. Notices RAS 398, 1082–1092. doi: 10.1111/j.1365-2966.2009.15115.x

CrossRef Full Text | Google Scholar

Banerjee, S., and Kritsuk, A. G. (2017). Exact relations for energy transfer in self-gravitating isothermal turbulence. Phys. Rev. E 96:053116. doi: 10.1103/PhysRevE.96.053116

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, S., and Kritsuk, A. G. (2018). Energy transfer in compressible magnetohydrodynamic turbulence for isothermal self-gravitating fluids. Phys. Rev. E 97:023107. doi: 10.1103/PhysRevE.97.023107

PubMed Abstract | CrossRef Full Text | Google Scholar

Basu, S. (2000). Magnetic fields and the triaxiality of molecular cloud cores. Astrophys. J. Lett. 540, L103–L106. doi: 10.1086/312885

CrossRef Full Text | Google Scholar

Basu, S., and Ciolek, G. E. (2004). Formation and collapse of nonaxisymmetric protostellar cores in planar magnetic molecular clouds. Astrophys. J. Lett. 607, L39–L42. doi: 10.1086/421464

CrossRef Full Text | Google Scholar

Basu, S., and Mouschovias, T. C. (1995). Magnetic braking, ambipolar diffusion, and the formation of cloud cores and protostars. III. Effect of the initial mass-to-flux ratio. Astrophys. J. 453:271. doi: 10.1086/176387

CrossRef Full Text | Google Scholar

Bate, M. R. (2012). Stellar, brown dwarf and multiple star properties from a radiation hydrodynamical simulation of star cluster formation. Mont. Notices RAS 419, 3115–3146. doi: 10.1111/j.1365-2966.2011.19955.x

CrossRef Full Text | Google Scholar

Beresnyak, A. (2011). Spectral slope and kolmogorov constant of MHD turbulence. Phys. Rev. Lett. 106:075001. doi: 10.1103/PhysRevLett.106.075001

PubMed Abstract | CrossRef Full Text | Google Scholar

Beresnyak, A., Lazarian, A., and Cho, J. (2005). Density scaling and anisotropy in supersonic magnetohydrodynamic turbulence. Astrophys. J. Lett. 624, L93–L96. doi: 10.1086/430702

CrossRef Full Text | Google Scholar

Bergin, E. A., and Tafalla, M. (2007). Cold dark clouds: the initial conditions for star formation. Annu. Rev. Astron. Astrophys. 45, 339–396. doi: 10.1146/annurev.astro.45.071206.100404

CrossRef Full Text | Google Scholar

Birnboim, Y., Federrath, C., and Krumholz, M. (2018). Compression of turbulent magnetized gas in giant molecular clouds. Mont. Notices RAS 473, 2144–2159. doi: 10.1093/mnras/stx2426

CrossRef Full Text | Google Scholar

Biskamp, D. (2003). Magnetohydrodynamic Turbulence. Cambridge, UK: Cambridge University Press.

Google Scholar

Boldyrev, S. (2005). On the spectrum of magnetohydrodynamic turbulence. Astrophys. J. Lett. 626, L37–L40. doi: 10.1086/431649

CrossRef Full Text | Google Scholar

Burkhart, B., Falceta-Gonçalves, D., Kowal, G., and Lazarian, A. (2009). Density studies of MHD interstellar turbulence: statistical moments, correlations and bispectrum. Astrophys. J. 693, 250–266. doi: 10.1088/0004-637X/693/1/250

CrossRef Full Text | Google Scholar

Burkhart, B., Lazarian, A., Balsara, D., Meyer, C., and Cho, J. (2015). Alfvénic turbulence beyond the ambipolar diffusion scale. Astrophys. J. 805:118. doi: 10.1088/0004-637X/805/2/118

CrossRef Full Text | Google Scholar

Camacho, V., Vázquez-Semadeni, E., Ballesteros-Paredes, J., Gómez, G. C., Fall, S. M., and Mata-Chávez, M. D. (2016). Energy budget of forming clumps in numerical simulations of collapsing clouds. Astrophys. J. 833:113. doi: 10.3847/1538-4357/833/1/113

CrossRef Full Text | Google Scholar

Carroll, J. J., Frank, A., Blackman, E. G., Cunningham, A. J., and Quillen, A. C. (2009). Outflow-driven turbulence in molecular clouds. Astrophys. J. 695, 1376–1381. doi: 10.1088/0004-637X/695/2/1376

CrossRef Full Text | Google Scholar

Chen, C.-Y., and Ostriker, E. C. (2014). Formation of magnetized prestellar cores with ambipolar diffusion and turbulence. Astrophys. J. 785:69. doi: 10.1088/0004-637X/785/1/69

CrossRef Full Text | Google Scholar

Chen, C.-Y., and Ostriker, E. C. (2015). Anisotropic formation of magnetized cores in turbulent clouds. Astrophys. J. 810:126. doi: 10.1088/0004-637X/810/2/126

CrossRef Full Text | Google Scholar

Chen, C.-Y., and Ostriker, E. C. (2018). Geometry, kinematics, and magnetization of simulated prestellar cores. Astrophys. J. 865:34. doi: 10.3847/1538-4357/aad905

CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2003). Compressible magnetohydrodynamic turbulence: mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. Mont. Notices RAS 345, 325–339. doi: 10.1046/j.1365-8711.2003.06941.x

CrossRef Full Text | Google Scholar

Cho, J., Lazarian, A., and Vishniac, E. T. (2002). Simulations of magnetohydrodynamic turbulence in a strongly magnetized medium. Astrophys. J. 564, 291–301. doi: 10.1086/324186

CrossRef Full Text | Google Scholar

Choi, E., and Stone, J. M. (2012). The effect of anisotropic conduction on the thermal instability in the interstellar medium. Astrophys. J. 747:86. doi: 10.1088/0004-637X/747/2/86

CrossRef Full Text | Google Scholar

Clark, P. C., Glover, S. C. O., Klessen, R. S., and Bonnell, I. A. (2012). How long does it take to form a molecular cloud? Mont. Notices RAS 424, 2599–2613. doi: 10.1111/j.1365-2966.2012.21259.x

CrossRef Full Text | Google Scholar

Clark, S. E., Peek, J. E. G., and Putman, M. E. (2014). Magnetically aligned H I fibers and the rolling hough transform. Astrophys. J. 789:82. doi: 10.1088/0004-637X/789/1/82

CrossRef Full Text | Google Scholar

Clarke, S. D., Whitworth, A. P., Duarte-Cabral, A., and Hubber, D. A. (2017). Filamentary fragmentation in a turbulent medium. Mont. Notices RAS 468, 2489–2505. doi: 10.1093/mnras/stx637

CrossRef Full Text | Google Scholar

Clarke, S. D., Whitworth, A. P., and Hubber, D. A. (2016). Perturbation growth in accreting filaments. Mont. Notices RAS 458, 319–324. doi: 10.1093/mnras/stw407

CrossRef Full Text | Google Scholar

Clarke, S. D., Whitworth, A. P., Spowage, R. L., Duarte-Cabral, A., Suri, S. T., Jaffa, S. E., et al. (2018). Synthetic C¹⁸O observations of fibrous filaments: the problems of mapping from PPV to PPP. Mont. Notices RAS 479, 1722–1746. doi: 10.1093/mnras/sty1675

CrossRef Full Text | Google Scholar

Colling, C., Hennebelle, P., Geen, S., Iffrig, O., and Bournaud, F. (2018). Impact of galactic shear and stellar feedback on star formation. Astron. Astrophys. 620:A21. doi: 10.1051/0004-6361/201833161

CrossRef Full Text | Google Scholar

Colombo, D., Hughes, A., Schinnerer, E., Meidt, S. E., Leroy, A. K., Pety, J., et al. (2014). The PdBI arcsecond whirlpool survey (PAWS): environmental dependence of giant molecular cloud properties in M51. Astrophys. J. 784:3. doi: 10.1088/0004-637X/784/1/3

CrossRef Full Text | Google Scholar

Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., and Teyssier, R. (2010). Protostellar collapse: radiative and magnetic feedbacks on small-scale fragmentation. Astron. Astrophys. 510:L3. doi: 10.1051/0004-6361/200913597

CrossRef Full Text | Google Scholar

Commerçon, B., Hennebelle, P., and Henning, T. (2011). Collapse of massive magnetized dense cores using radiation magnetohydrodynamics: early fragmentation inhibition. Astrophys. J. Lett. 742:L9. doi: 10.1088/2041-8205/742/1/L9

CrossRef Full Text | Google Scholar

Crutcher, R. M. (1999). Magnetic fields in molecular clouds: observations confront theory. Astrophys. J. 520, 706–713. doi: 10.1086/307483

CrossRef Full Text | Google Scholar

Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., and Troland, T. H. (2010). Magnetic fields in interstellar clouds from zeeman observations: inference of total field strengths by Bayesian analysis. Astrophys. J. 725, 466–479. doi: 10.1088/0004-637X/725/1/466

CrossRef Full Text | Google Scholar

Cunningham, A. J., Frank, A., Carroll, J., Blackman, E. G., and Quillen, A. C. (2009). Protostellar outflow evolution in turbulent environments. Astrophys. J. 692, 816–826. doi: 10.1088/0004-637X/692/1/816

CrossRef Full Text | Google Scholar

Cunningham, A. J., Klein, R. I., Krumholz, M. R., and McKee, C. F. (2011). Radiation-hydrodynamic simulations of massive star formation with protostellar outflows. Astrophys. J. 740:107. doi: 10.1088/0004-637X/740/2/107

CrossRef Full Text | Google Scholar

Cunningham, A. J., Krumholz, M. R., McKee, C. F., and Klein, R. I. (2018). The effects of magnetic fields and protostellar feedback on low-mass cluster formation. Mont. Notices RAS 476, 771–792. doi: 10.1093/mnras/sty154

CrossRef Full Text | Google Scholar

Dale, J. E., and Bonnell, I. (2011). Ionizing feedback from massive stars in massive clusters: fake bubbles and untriggered star formation. Mont. Notices RAS 414, 321–328. doi: 10.1111/j.1365-2966.2011.18392.x

CrossRef Full Text | Google Scholar

Dale, J. E., Ercolano, B., and Bonnell, I. A. (2013). Ionizing feedback from massive stars in massive clusters - III. Disruption of partially unbound clouds. Mont. Notices RAS 430, 234–246. doi: 10.1093/mnras/sts592

CrossRef Full Text | Google Scholar

de Avillez, M. A., and Breitschwerdt, D. (2005). Global dynamical evolution of the ISM in star forming galaxies. I. High resolution 3D simulations: effect of the magnetic field. Astron. Astrophys. 436, 585–600. doi: 10.1051/0004-6361:20042146

CrossRef Full Text | Google Scholar

Dib, S., Hennebelle, P., Pineda, J. E., Csengeri, T., Bontemps, S., Audit, E., et al. (2010). The angular momentum of magnetized molecular cloud cores: a two-dimensional-three-dimensional comparison. Astrophys. J. 723, 425–439. doi: 10.1088/0004-637X/723/1/425

CrossRef Full Text | Google Scholar

Downes, T. P., and O'Sullivan, S. (2011). Multifluid magnetohydrodynamic turbulent decay. Astrophys. J. 730:12. doi: 10.1088/0004-637X/730/1/12

CrossRef Full Text | Google Scholar

Dutrey, A., Duvert, G., Castets, A., Langer, W. D., Bally, J., and Wilson, R. W. (1991). Periodically spaced fragmentation in Orion A. Astron. Astrophys. 247, L9–L12.

Google Scholar

Elmegreen, B. G., and Scalo, J. (2004). Interstellar turbulence I: observations and processes. Annu. Rev. Astron. Astrophys. 42, 211–273. doi: 10.1146/annurev.astro.41.011802.094859

CrossRef Full Text | Google Scholar

Fall, S. M., Krumholz, M. R., and Matzner, C. D. (2010). Stellar feedback in molecular clouds and its influence on the mass function of young star clusters. Astrophys. J. Lett. 710, L142–L146. doi: 10.1088/2041-8205/710/2/L142

CrossRef Full Text | Google Scholar

Federrath, C. (2015). Inefficient star formation through turbulence, magnetic fields and feedback. Mont. Notices RAS 450, 4035–4042. doi: 10.1093/mnras/stv941

CrossRef Full Text | Google Scholar

Federrath, C. (2016). On the universality of interstellar filaments: theory meets simulations and observations. Mont. Notices RAS 457, 375–388. doi: 10.1093/mnras/stv2880

CrossRef Full Text | Google Scholar

Federrath, C., and Banerjee, S. (2015). The density structure and star formation rate of non-isothermal polytropic turbulence. Mont. Notices RAS 448, 3297–3313. doi: 10.1093/mnras/stv180

CrossRef Full Text | Google Scholar

Ferrière, K. M. (2001). The interstellar environment of our galaxy. Rev. Mod. Phys. 73, 1031–1066. doi: 10.1103/RevModPhys.73.1031

CrossRef Full Text | Google Scholar

Fiege, J. D., and Pudritz, R. E. (2000). Helical fields and filamentary molecular clouds - II. Axisymmetric stability and fragmentation. Mont. Notices RAS 311, 105–119. doi: 10.1046/j.1365-8711.2000.03067.x

CrossRef Full Text | Google Scholar

Field, G. B. (1965). Thermal instability. Astrophys. J. 142:531. doi: 10.1086/148317

CrossRef Full Text | Google Scholar

Fischera, J., and Martin, P. G. (2012). Physical properties of interstellar filaments. Astron. Astrophys. 42:A77. doi: 10.1051/0004-6361/201218961

CrossRef Full Text | Google Scholar

Galli, D., Lizano, S., Shu, F. H., and Allen, A. (2006). Gravitational collapse of magnetized clouds. I. Ideal magnetohydrodynamic accretion flow. Astrophys. J. 647, 374–381. doi: 10.1086/505257

CrossRef Full Text | Google Scholar

Galtier, S., and Banerjee, S. (2011). Exact relation for correlation functions in compressible isothermal turbulence. Phys. Rev. Lett. 107:134501. doi: 10.1103/PhysRevLett.107.134501

PubMed Abstract | CrossRef Full Text | Google Scholar

Gatto, A., Walch, S., Low, M.-M. M., Naab, T., Girichidis, P., Glover, S. C. O., et al. (2015). Modelling the supernova-driven ISM in different environments. Mont. Notices RAS 449, 1057–1075. doi: 10.1093/mnras/stv324

CrossRef Full Text | Google Scholar

Gavagnin, E., Bleuler, A., Rosdahl, J., and Teyssier, R. (2017). Star cluster formation in a turbulent molecular cloud self-regulated by photoionization feedback. Mont. Notices RAS 472, 4155–4172. doi: 10.1093/mnras/stx2222

CrossRef Full Text | Google Scholar

Geen, S., Hennebelle, P., Tremblin, P., and Rosdahl, J. (2015). Photoionization feedback in a self-gravitating, magnetized, turbulent cloud. Mont. Notices RAS 454, 4484–4502. doi: 10.1093/mnras/stv2272

CrossRef Full Text | Google Scholar

Geen, S., Soler, J. D., and Hennebelle, P. (2017). Interpreting the star formation efficiency of nearby molecular clouds with ionizing radiation. Mont. Notices RAS 471, 4844–4855. doi: 10.1093/mnras/stx1765

CrossRef Full Text | Google Scholar

Gendelev, L., and Krumholz, M. R. (2012). Evolution of blister-type H II regions in a magnetized medium. Astrophys. J. 745:158. doi: 10.1088/0004-637X/745/2/158

CrossRef Full Text | Google Scholar

Gent, F. A., Shukurov, A., Fletcher, A., Sarson, G. R., and Mantere, M. J. (2013). The supernova-regulated ISM - I. The multiphase structure. Mont. Notices RAS 432, 1396–1423. doi: 10.1093/mnras/stt560

CrossRef Full Text | Google Scholar

Girichidis, P., Naab, T., Walch, S., Hanasz, M., Mac Low, M.-M., Ostriker, J. P., et al. (2016). Launching cosmic-ray-driven outflows from the magnetized interstellar medium. Astrophys. J. Lett. 816:L19. doi: 10.3847/2041-8205/816/2/L19

CrossRef Full Text | Google Scholar

Girichidis, P., Seifried, D., Naab, T., Peters, T., Walch, S., Wünsch, R., et al. (2018). The SILCC project - V. The impact of magnetic fields on the chemistry and the formation of molecular clouds. Mont. Notices RAS 480, 3511–3540. doi: 10.1093/mnras/sty2016

CrossRef Full Text | Google Scholar

Glover, S. C. O., and Clark, P. C. (2012). Approximations for modelling CO chemistry in giant molecular clouds: a comparison of approaches. Mont. Notices RAS 421, 116–131. doi: 10.1111/j.1365-2966.2011.20260.x

CrossRef Full Text | Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. 2: strong alfvenic turbulence. Astrophys. J. 438, 763–775. doi: 10.1086/175121

CrossRef Full Text | Google Scholar

Gómez, G. C., and Vázquez-Semadeni, E. (2014). Filaments in simulations of molecular cloud formation. Astrophys. J. 791:124. doi: 10.1088/0004-637X/791/2/124

CrossRef Full Text | Google Scholar

Gómez, G. C., Vázquez-Semadeni, E., and Zamora-Avilés, M. (2018). The magnetic field structure in molecular cloud filaments. Mont. Notices RAS 480, 2939–2944. doi: 10.1093/mnras/sty2018

CrossRef Full Text | Google Scholar

Gong, M., and Ostriker, E. C. (2015). Prestellar core formation, evolution, and accretion from gravitational fragmentation in turbulent converging flows. Astrophys. J. 806:31. doi: 10.1088/0004-637X/806/1/31

CrossRef Full Text | Google Scholar

Gong, M., Ostriker, E. C., and Wolfire, M. G. (2017). A simple and accurate network for hydrogen and carbon chemistry in the interstellar medium. Astrophys. J. 843:38. doi: 10.3847/1538-4357/aa7561

CrossRef Full Text | Google Scholar

Grappin, R., and Müller, W. C. (2010). Scaling and anisotropy in magnetohydrodynamic turbulence in a strong mean magnetic field. Phys. Rev. E 82:026406. doi: 10.1103/PhysRevE.82.026406

PubMed Abstract | CrossRef Full Text | Google Scholar

Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., Schuster, K. F., Kramer, C., Corbelli, E., et al. (2012). Giant molecular clouds in the Local Group galaxy M 33. Astron. Astrophys. 542:A108. doi: 10.1051/0004-6361/201116612

CrossRef Full Text | Google Scholar

Gray, W. J., McKee, C. F., and Klein, R. I. (2018). Effect of angular momentum alignment and strong magnetic fields on the formation of protostellar discs. Mont. Notices RAS 473, 2124–2143. doi: 10.1093/mnras/stx2406

CrossRef Full Text | Google Scholar

Gritschneder, M., Heigl, S., and Burkert, A. (2017). Oscillating filaments. I. Oscillation and geometrical fragmentation. Astrophys. J. 834:202. doi: 10.3847/1538-4357/834/2/202

CrossRef Full Text | Google Scholar

Hacar, A., Tafalla, M., Forbrich, J., Alves, J., Meingast, S., Grossschedl, J., et al. (2018). An ALMA study of the Orion Integral Filament. I. Evidence for narrow fibers in a massive cloud. Astron. Astrophys. 610:A77. doi: 10.1051/0004-6361/201731894

CrossRef Full Text | Google Scholar

Hacar, A., Tafalla, M., Kauffmann, J., and Kovács, A. (2013). Cores, filaments, and bundles: hierarchical core formation in the L1495/B213 Taurus region. Astron. Astrophys. 554:A55. doi: 10.1051/0004-6361/201220090

CrossRef Full Text | Google Scholar

Hanawa, T., Kudoh, T., and Tomisaka, K. (2017). Fragmentation of a filamentary cloud permeated by a perpendicular magnetic field. Astrophys. J. 848:2. doi: 10.3847/1538-4357/aa8b6d

CrossRef Full Text | Google Scholar

Hanawa, T., and Tomisaka, K. (2015). Structure and stability of filamentary clouds supported by lateral magnetic field. Astrophys. J. 801:11. doi: 10.1088/0004-637X/801/1/11

CrossRef Full Text | Google Scholar

Heitsch, F., Slyz, A. D., Devriendt, J. E. G., Hartmann, L. W., and Burkert, A. (2006). The birth of molecular clouds: formation of atomic precursors in colliding flows. Astrophys. J. 648, 1052–1065. doi: 10.1086/505931

CrossRef Full Text | Google Scholar

Heitsch, F., Stone, J. M., and Hartmann, L. W. (2009). Effects of magnetic field strength and orientation on molecular cloud formation. Astrophys. J. 695, 248–258. doi: 10.1088/0004-637X/695/1/248

CrossRef Full Text | Google Scholar

Heitsch, F., Zweibel, E. G., Slyz, A. D., and Devriendt, J. E. G. (2004). Turbulent ambipolar diffusion: numerical studies in two dimensions. Astrophys. J. 603, 165–179. doi: 10.1086/381428

CrossRef Full Text | Google Scholar

Hennebelle, P. (2013). On the origin of non-self-gravitating filaments in the ISM. Astron. Astrophys. 556:A153. doi: 10.1051/0004-6361/201321292

CrossRef Full Text | Google Scholar

Hennebelle, P. (2018). The FRIGG project: from intermediate galactic scales to self-gravitating cores. Astron. Astrophys. 611:A24. doi: 10.1051/0004-6361/201731071

CrossRef Full Text | Google Scholar

Hennebelle, P., and André, P. (2013). Ion-neutral friction and accretion-driven turbulence in self-gravitating filaments. Astron. Astrophys. 560:A68. doi: 10.1051/0004-6361/201321761

CrossRef Full Text | Google Scholar

Hennebelle, P., Banerjee, R., Vázquez-Semadeni, E., Klessen, R. S., and Audit, E. (2008). From the warm magnetized atomic medium to molecular clouds. Astron. Astrophys. 486, L43–L46. doi: 10.1051/0004-6361:200810165

CrossRef Full Text | Google Scholar

Hennebelle, P., and Chabrier, G. (2008). Analytical theory for the initial mass function: CO clumps and prestellar cores. Astrophys. J. 684, 395–410. doi: 10.1086/589916

CrossRef Full Text | Google Scholar

Hennebelle, P., and Chabrier, G. (2013). Analytical theory for the initial mass function. III. Time dependence and star formation rate. Astrophys. J. 770:150. doi: 10.1088/0004-637X/770/2/150

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Chabrier, G., and Marchand, P. (2016). Magnetically self-regulated formation of early protoplanetary disks. Astrophys. J. Lett. 830:L8. doi: 10.3847/2041-8205/830/1/L8

CrossRef Full Text | Google Scholar

Hennebelle, P., Commerçon, B., Joos, M., Klessen, R. S., Krumholz, M., Tan, J. C., et al. (2011). Collapse, outflows and fragmentation of massive, turbulent and magnetized prestellar barotropic cores. Astron. Astrophys. 528:A72. doi: 10.1051/0004-6361/201016052

CrossRef Full Text | Google Scholar

Hennebelle, P., and Falgarone, E. (2012). Turbulent molecular clouds. Astron. Astrophys. Rev. 20:55. doi: 10.1007/s00159-012-0055-y

CrossRef Full Text | Google Scholar

Hennebelle, P., and Fromang, S. (2008). Magnetic processes in a collapsing dense core. I. Accretion and ejection. Astron. Astrophys. 477, 9–24. doi: 10.1051/0004-6361:20078309

CrossRef Full Text | Google Scholar

Hennebelle, P., and Iffrig, O. (2014). Simulations of magnetized multiphase galactic disc regulated by supernovae explosions. Astron. Astrophys. 570:A81. doi: 10.1051/0004-6361/201423392

CrossRef Full Text | Google Scholar

Hennebelle, P., and Pérault, M. (1999). Dynamical condensation in a thermally bistable flow. Application to interstellar cirrus. Astron. Astrophys. 351, 309–322.

Google Scholar

Hennebelle, P., and Pérault, M. (2000). Dynamical condensation in a magnetized and thermally bistable flow. Application to interstellar cirrus. Astron. Astrophys. 359, 1124–1138.

Google Scholar

Hennebelle, P., and Teyssier, R. (2008). Magnetic processes in a collapsing dense core. II. Fragmentation. Is there a fragmentation crisis? Astron. Astrophys. 477, 25–34. doi: 10.1051/0004-6361:20078310

CrossRef Full Text | Google Scholar

Heyer, M., Goldsmith, P. F., Yıldız, U. A., Snell, R. L., Falgarone, E., and Pineda, J. L. (2016). Striations in the Taurus molecular cloud: Kelvin-Helmholtz instability or MHD waves? Mont. Notices RAS 461, 3918–3926. doi: 10.1093/mnras/stw1567

CrossRef Full Text | Google Scholar

Heyer, M. H., Carpenter, J. M., and Snell, R. L. (2001). The equilibrium state of molecular regions in the outer galaxy. Astrophys. J. 551, 852–866. doi: 10.1086/320218

CrossRef Full Text | Google Scholar

Hopkins, P. F. (2013). A model for (non-lognormal) density distributions in isothermal turbulence. Mont. Notices RAS 430, 1880–1891. doi: 10.1093/mnras/stt010

CrossRef Full Text | Google Scholar

Iffrig, O., and Hennebelle, P. (2017). Structure distribution and turbulence in self-consistently supernova-driven ISM of multiphase magnetized galactic discs. Astron. Astrophys. 604:A70. doi: 10.1051/0004-6361/201630290

CrossRef Full Text | Google Scholar

Inoue, T., and Fukui, Y. (2013). Formation of massive molecular cloud cores by cloud-cloud collision. Astrophys. J. Lett. 774:L31. doi: 10.1088/2041-8205/774/2/L31

CrossRef Full Text | Google Scholar

Inoue, T., Hennebelle, P., Fukui, Y., Matsumoto, T., Iwasaki, K., and Inutsuka, S.-i. (2018). The formation of massive molecular filaments and massive stars triggered by a magnetohydrodynamic shock wave. Publ. ASJ 70:S53. doi: 10.1093/pasj/psx089

CrossRef Full Text | Google Scholar

Inoue, T., and Inutsuka, S.-i. (2008). Two-fluid magnetohydrodynamic simulations of converging H I flows in the interstellar medium. I. Methodology and basic results. Astrophys. J. 687, 303–310. doi: 10.1086/590528

CrossRef Full Text | Google Scholar

Inoue, T., and Inutsuka, S.-i. (2009). Two-fluid magnetohydrodynamics simulations of converging H I flows in the interstellar medium. II. Are molecular clouds generated directly from a warm neutral medium? Astrophys. J. 704, 161–169. doi: 10.1088/0004-637X/704/1/161

CrossRef Full Text | Google Scholar

Inoue, T., and Inutsuka, S.-i. (2012). Formation of turbulent and magnetized molecular clouds via accretion flows of H I clouds. Astrophys. J. 759:35. doi: 10.1088/0004-637X/759/1/35

CrossRef Full Text | Google Scholar

Inoue, T., and Inutsuka, S.-i. (2016). Formation of H I clouds in shock-compressed interstellar medium: physical origin of angular correlation Between filamentary structure and magnetic field. Astrophys. J. 833:10. doi: 10.3847/0004-637X/833/1/10

CrossRef Full Text | Google Scholar

Inoue, T., Inutsuka, S.-i., and Koyama, H. (2007). The role of ambipolar diffusion in the formation process of moderately magnetized diffuse clouds. Astrophys. J. Lett. 658, L99–L102. doi: 10.1086/514816

CrossRef Full Text | Google Scholar

Inutsuka, S.-I. (2001). The mass function of molecular cloud cores. Astrophys. J. Lett. 559, L149–L152. doi: 10.1086/323786

CrossRef Full Text | Google Scholar

Inutsuka, S.-I. (2012). Present-day star formation: from molecular cloud cores to protostars and protoplanetary disks. Prog. Theor. Exp. Phys. 2012:01A307. doi: 10.1093/ptep/pts024

CrossRef Full Text | Google Scholar

Inutsuka, S.-I., Inoue, T., Iwasaki, K., and Hosokawa, T. (2015). The formation and destruction of molecular clouds and galactic star formation. An origin for the cloud mass function and star formation efficiency. Astron. Astrophys. 580:A49. doi: 10.1051/0004-6361/201425584

CrossRef Full Text | Google Scholar

Inutsuka, S.-I., and Miyama, S. M. (1992). Self-similar solutions and the stability of collapsing isothermal filaments. Astrophys. J. 388, 392–399. doi: 10.1086/171162

CrossRef Full Text | Google Scholar

Iroshnikov, P. S. (1963). Turbulence of a conducting fluid in a strong magnetic field. Astronomicheskii Zhurnal 40:742.

Google Scholar

Iwasaki, K., Tomida, K., Inoue, T., and Inutsuka, S.-i. (2018). The early stage of molecular cloud formation by compression of two-phase atomic gases. arXiv.

Google Scholar

Joos, M., Hennebelle, P., and Ciardi, A. (2012). Protostellar disk formation and transport of angular momentum during magnetized core collapse. Astron. Astrophys. 543:A128. doi: 10.1051/0004-6361/201118730

CrossRef Full Text | Google Scholar

Joos, M., Hennebelle, P., Ciardi, A., and Fromang, S. (2013). The influence of turbulence during magnetized core collapse and its consequences on low-mass star formation. Astron. Astrophys. 554:A17. doi: 10.1051/0004-6361/201220649

CrossRef Full Text | Google Scholar

Joung, M. K. R., and Mac Low, M.-M. (2006). Turbulent structure of a stratified supernova-driven interstellar medium. Astrophys. J. 653, 1266–1279. doi: 10.1086/508795

CrossRef Full Text | Google Scholar

Juvela, M., Malinen, J., and Lunttila, T. (2012). Profiles of interstellar cloud filaments. Observational effects in synthetic sub-millimetre observations. Astron. Astrophys. 544:A141. doi: 10.1051/0004-6361/201219558

CrossRef Full Text | Google Scholar

Kennicutt, R. C., and Evans, N. J. (2012). Star formation in the milky way and nearby galaxies. Annu. Rev. Astron. Astrophys. 50, 531–608. doi: 10.1146/annurev-astro-081811-125610

CrossRef Full Text | Google Scholar

Kim, C.-G., and Ostriker, E. C. (2015). Vertical equilibrium, energetics, and star formation rates in magnetized galactic disks regulated by momentum feedback from supernovae. Astrophys. J. 815:67. doi: 10.1088/0004-637X/815/1/67

CrossRef Full Text | Google Scholar

Kim, C.-G., and Ostriker, E. C. (2017). Three-phase interstellar medium in galaxies resolving evolution with star formation and supernova feedback (TIGRESS): algorithms, fiducial model, and convergence. Astrophys. J. 846:133. doi: 10.3847/1538-4357/aa8599

CrossRef Full Text | Google Scholar

Kim, C.-G., Ostriker, E. C., and Kim, W.-T. (2013). Three-dimensional hydrodynamic simulations of multiphase galactic disks with star formation Feedback. I. Regulation of star formation rates. Astrophys. J. 776:1. doi: 10.1088/0004-637X/776/1/1

CrossRef Full Text | Google Scholar

Kim, J.-G., Kim, W.-T., and Ostriker, E. C. (2018). Modeling UV radiation feedback from massive stars. II. Dispersal of star-forming giant molecular clouds by photoionization and radiation pressure. Astrophys. J. 859:68. doi: 10.3847/1538-4357/aabe27

CrossRef Full Text | Google Scholar

Kobayashi, M. I. N., Inutsuka, S.-I., Kobayashi, H., and Hasegawa, K. (2017). Evolutionary description of giant molecular cloud mass functions on galactic disks. Astrophys. J. 836:175. doi: 10.3847/1538-4357/836/2/175

CrossRef Full Text | Google Scholar

Kobayashi, M. I. N., Kobayashi, H., Inutsuka, S.-I., and Fukui, Y. (2018). Star formation induced by cloud-cloud collisions and galactic giant molecular cloud evolution. Publ. ASJ 70:S59. doi: 10.1093/pasj/psy018

CrossRef Full Text | Google Scholar

Koch, E. W., and Rosolowsky, E. W. (2015). Filament identification through mathematical morphology. Mont. Notices RAS 452, 3435–3450. doi: 10.1093/mnras/stv1521

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., and Ho, P. T. P. (2013). Interpreting the role of the magnetic field from dust polarization maps. Astrophys. J. 775:77. doi: 10.1088/0004-637X/775/1/77

CrossRef Full Text | Google Scholar

Koch, P. M., Tang, Y.-W., Ho, P. T. P., Zhang, Q., Girart, J. M., Chen, H.-R. V., et al. (2014). The importance of the magnetic field from an SMA-CSO-combined sample of star-forming regions. Astrophys. J. 797:99. doi: 10.1088/0004-637X/797/2/99

CrossRef Full Text | Google Scholar

Kolmogorov, A. (1941). The local structure of turbulence in incompressible viscous fluid for very large reynolds' numbers. Akademiia Nauk SSSR Doklady 30, 301–305.

Google Scholar

Könyves, V., André, P., Men'shchikov, A., Palmeirim, P., Arzoumanian, D., Schneider, N., et al. (2015). A census of dense cores in the Aquila cloud complex: SPIRE/PACS observations from the Herschel Gould Belt survey. Astron. Astrophys. 584:A91. doi: 10.1051/0004-6361/201525861

CrossRef Full Text | Google Scholar

Körtgen, B., and Banerjee, R. (2015). Impact of magnetic fields on molecular cloud formation and evolution. Mont. Notices RAS 451, 3340–3353. doi: 10.1093/mnras/stv1200

CrossRef Full Text | Google Scholar

Koyama, H., and Inutsuka, S.-I. (2000). Molecular cloud formation in shock-compressed layers. Astrophys. J. 532, 980–993. doi: 10.1086/308594

CrossRef Full Text | Google Scholar

Koyama, H., and Inutsuka, S.-i. (2002). An origin of supersonic motions in interstellar clouds. Astrophys. J. Lett. 564, L97–L100. doi: 10.1086/338978

CrossRef Full Text | Google Scholar

Kraichnan, R. H. (1965). Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385–1387. doi: 10.1063/1.1761412

CrossRef Full Text | Google Scholar

Kramer, C., Stutzki, J., Rohrig, R., and Corneliussen, U. (1998). Clump mass spectra of molecular clouds. Astron. Astrophys. 329, 249–264.

Google Scholar

Kritsuk, A. G., Flauger, R., and Ustyugov, S. D. (2018). Dust-polarization maps for local interstellar turbulence. Phys. Rev. Lett. 121:021104. doi: 10.1103/PhysRevLett.121.021104

PubMed Abstract | CrossRef Full Text | Google Scholar

Kritsuk, A. G., Norman, M. L., Padoan, P., and Wagner, R. (2007). The statistics of supersonic isothermal turbulence. Astrophys. J. 665, 416–431. doi: 10.1086/519443

CrossRef Full Text | Google Scholar

Kritsuk, A. G., Ustyugov, S. D., and Norman, M. L. (2017). The structure and statistics of interstellar turbulence. N. J. Phys. 19:065003. doi: 10.1088/1367-2630/aa7156

CrossRef Full Text | Google Scholar

Krumholz, M. R., and Burkhart, B. (2016). Is turbulence in the interstellar medium driven by feedback or gravity? An observational test. Mont. Notices RAS 458, 1671–1677. doi: 10.1093/mnras/stw434

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulsrud, R., and Pearce, W. P. (1969). The effect of wave-particle interactions on the propagation of cosmic rays. Astrophys. J. 156:445. doi: 10.1086/149981

CrossRef Full Text | Google Scholar

Kwan, J. (1979). The mass spectrum of interstellar clouds. Astrophys. J. 229, 567–577. doi: 10.1086/156990

CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1960). “Electrodynamics of Continuous Media,” in Course of Theoretical Physics (Oxford: Pergamon Press).

Google Scholar

Lazarian, A., Eyink, G. L., Vishniac, E. T., and Kowal, G. (2015). “Magnetic reconnection in astrophysical environments,” in Magnetic Fields in Diffuse Media, volume 407 of Astrophysics and Space Science Library, Vol. 311, eds A. Lazarian, E. M. de Gouveia Dal Pino, and C. Melioli (Royal Society).

Google Scholar

Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a weakly stochastic field. Astrophys. J. 517, 700–718. doi: 10.1086/307233

CrossRef Full Text | Google Scholar

Le Petit, F., Nehmé, C., Le Bourlot, J., and Roueff, E. (2006). A model for atomic and molecular interstellar gas: the meudon PDR code. Astrophys. J. Suppl. 164, 506–529. doi: 10.1086/503252

CrossRef Full Text | Google Scholar

Lee, E., Brachet, M. E., Pouquet, A., Mininni, P. D., and Rosenberg, D. (2010). Lack of universality in decaying magnetohydrodynamic turbulence. Phys. Rev. E 81:016318. doi: 10.1103/PhysRevE.81.016318

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y.-N., and Hennebelle, P. (2016a). Formation of a protocluster: a virialized structure from gravoturbulent collapse. I. Simulation of cluster formation in a collapsing molecular cloud. Astron. Astrophys. 591:A30. doi: 10.1051/0004-6361/201527981

CrossRef Full Text | Google Scholar

Lee, Y.-N., and Hennebelle, P. (2016b). Formation of a protocluster: a virialized structure from gravoturbulent collapse. II. A two-dimensional analytical model for a rotating and accreting system. Astron. Astrophys. 591:A31. doi: 10.1051/0004-6361/201527982

CrossRef Full Text | Google Scholar

Lee, Y.-N., and Hennebelle, P. (2018a). Stellar mass spectrum within massive collapsing clumps. I. Influence of the initial conditions. Astron. Astrophys. 611:A88. doi: 10.1051/0004-6361/201731522

CrossRef Full Text | Google Scholar

Lee, Y.-N., and Hennebelle, P. (2018b). Stellar mass spectrum within massive collapsing clumps. II. Thermodynamics and tidal forces of the first Larson core. A robust mechanism for the peak of the IMF. Astron. Astrophys. 611:A89. doi: 10.1051/0004-6361/201731523

CrossRef Full Text | Google Scholar

Lee, Y.-N., and Hennebelle, P. (2018c). Stellar mass spectrum within massive collapsing clumps III. Effects of temperature and magnetic field. arXiv.

Google Scholar

Lee, Y.-N., Hennebelle, P., and Chabrier, G. (2017). Analytical core mass function (CMF) from filaments: under which circumstances can filament fragmentation reproduce the CMF? Astrophys. J. 847:114. doi: 10.3847/1538-4357/aa898f

CrossRef Full Text | Google Scholar

Lemaster, M. N., and Stone, J. M. (2008). Density probability distribution functions in supersonic hydrodynamic and MHD turbulence. Astrophys. J. Lett. 682:L97. doi: 10.1086/590929

CrossRef Full Text | Google Scholar

Lequeux, J. (2005). “The Interstellar Medium,” in Translation from the French language edition of: Le Milieu Interstellaire 2003, Astronomy and Astrophysics Library (Berlin: Springer; EDP Sciences).

Google Scholar

Li, P. S., McKee, C. F., and Klein, R. I. (2006). The heavy-ion approximation for ambipolar diffusion calculations for weakly ionized plasmas. Astrophys. J. 653, 1280–1291. doi: 10.1086/508977

CrossRef Full Text | Google Scholar

Li, P. S., McKee, C. F., and Klein, R. I. (2015). Magnetized interstellar molecular clouds - I. Comparison between simulations and Zeeman observations. Mont. Notices RAS 452, 2500–2527. doi: 10.1093/mnras/stv1437

CrossRef Full Text | Google Scholar

Li, P. S., McKee, C. F., Klein, R. I., and Fisher, R. T. (2008). Sub-Alfvénic nonideal MHD turbulence simulations with ambipolar diffusion. I. Turbulence statistics. Astrophys. J. 684, 380–394. doi: 10.1086/589874

CrossRef Full Text | Google Scholar

Li, Z.-Y., Banerjee, R., Pudritz, R. E., Jørgensen, J. K., Shang, H., Krasnopolsky, R., et al. (2014). “The earliest stages of star and planet formation: core collapse, and the formation of disks and outflows,” in Protostars and Planets VI, eds H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning (Tucson, AZ: University of Arizona Press), 173–194.

Google Scholar

Li, Z.-Y., and Nakamura, F. (2004). Magnetically regulated star formation in turbulent clouds. Astrophys. J. Lett. 609, L83–L86. doi: 10.1086/422839

CrossRef Full Text | Google Scholar

Li, Z.-Y., and Nakamura, F. (2006). Cluster formation in protostellar outflow-driven turbulence. Astrophys. J. Lett. 640, L187–L190. doi: 10.1086/503419

CrossRef Full Text | Google Scholar

Longmore, S. N., Kruijssen, J. M. D., Bastian, N., Bally, J., Rathborne, J., Testi, L., et al. (2014). “The formation and early evolution of young massive clusters,” in Protostars and Planets VI, eds H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning (Tucson, AZ: University of Arizona Press), 291–314.

Google Scholar

Mac Low, M.-M., Klessen, R. S., Burkert, A., and Smith, M. D. (1998). Kinetic energy decay rates of supersonic and Super-Alfvénic turbulence in star-forming clouds. Phys. Rev. Lett. 80, 2754–2757. doi: 10.1103/PhysRevLett.80.2754

CrossRef Full Text | Google Scholar

Mac Low, M.-M., Norman, M. L., Konigl, A., and Wardle, M. (1995). Incorporation of ambipolar diffusion into the ZEUS magnetohydrodynamics code. Astrophys. J. 442, 726–735. doi: 10.1086/175477

CrossRef Full Text | Google Scholar

Machida, M. N., Matsumoto, T., Hanawa, T., and Tomisaka, K. (2005). Collapse and fragmentation of rotating magnetized clouds - II. Binary formation and fragmentation of first cores. Mont. Notices RAS 362, 382–402. doi: 10.1111/j.1365-2966.2005.09327.x

CrossRef Full Text | Google Scholar

Machida, M. N., Matsumoto, T., and Inutsuka, S.-I. (2016). Conditions for circumstellar disc formation - II. Effects of initial cloud stability and mass accretion rate. Mont. Notices RAS 463, 4246–4267. doi: 10.1093/mnras/stw2256

CrossRef Full Text | Google Scholar

Machida, M. N., Tomisaka, K., Matsumoto, T., and Inutsuka, S.-I. (2008). Formation scenario for wide and close binary systems. Astrophys. J. 677, 327–347. doi: 10.1086/529133

CrossRef Full Text | Google Scholar

Mackey, J., and Lim, A. J. (2011). Effects of magnetic fields on photoionized pillars and globules. Mont. Notices RAS 412, 2079–2094. doi: 10.1111/j.1365-2966.2010.18043.x

CrossRef Full Text | Google Scholar

Mason, J., Perez, J. C., Boldyrev, S., and Cattaneo, F. (2012). Numerical simulations of strong incompressible magnetohydrodynamic turbulence. Phys. Plasmas 19:055902. doi: 10.1063/1.3694123

CrossRef Full Text | Google Scholar

Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., and Commerçon, B. (2016). Ambipolar diffusion in low-mass star formation. I. General comparison with the ideal magnetohydrodynamic case. Astron. Astrophys. 587:A32. doi: 10.1051/0004-6361/201526371

CrossRef Full Text | Google Scholar

Masson, J., Teyssier, R., Mulet-Marquis, C., Hennebelle, P., and Chabrier, G. (2012). Incorporating ambipolar and ohmic diffusion in the AMR MHD code RAMSES. Astrophys. J. Suppl. 201:24. doi: 10.1088/0067-0049/201/2/24

CrossRef Full Text | Google Scholar

Matsumoto, T., and Hanawa, T. (2003). Fragmentation of a molecular cloud core versus fragmentation of the massive protoplanetary disk in the main accretion phase. Astrophys. J. 595, 913–934. doi: 10.1086/377367

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Pouquet, A., Mininni, P. D., Dmitruk, P., and Breech, B. (2008). Rapid alignment of velocity and magnetic field in magnetohydrodynamic turbulence. Phys. Rev. Lett. 100:085003. doi: 10.1103/PhysRevLett.100.085003

PubMed Abstract | CrossRef Full Text | Google Scholar

McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., Green, A. J., and Haverkorn, M. (2006). Magnetically dominated strands of cold hydrogen in the riegel-crutcher cloud. Astrophys. J. 652, 1339–1347. doi: 10.1086/508706

CrossRef Full Text | Google Scholar

McKee, C. F., Li, P. S., and Klein, R. I. (2010). Sub-Alfvénic non-ideal MHD turbulence simulations with ambipolar diffusion. II. Comparison with observation, clump properties, and scaling to physical units. Astrophys. J. 720, 1612–1634. doi: 10.1088/0004-637X/720/2/1612

CrossRef Full Text | Google Scholar

McKee, C. F., and Ostriker, J. P. (1977). A theory of the interstellar medium - Three components regulated by supernova explosions in an inhomogeneous substrate. Astrophys. J. 218, 148–169. doi: 10.1086/155667

CrossRef Full Text | Google Scholar

Miville-Deschênes, M.-A., Joncas, G., Falgarone, E., and Boulanger, F. (2003). High resolution 21 cm mapping of the Ursa Major Galactic cirrus: power spectra of the high-latitude H I gas. Astron. Astrophys. 411, 109–121. doi: 10.1051/0004-6361:20031297

CrossRef Full Text | Google Scholar

Miville-Deschênes, M.-A., Murray, N., and Lee, E. J. (2017). Physical properties of molecular clouds for the entire milky way disk. Astrophys. J. 834:57. doi: 10.3847/1538-4357/834/1/57

CrossRef Full Text | Google Scholar

Mocz, P., Burkhart, B., Hernquist, L., McKee, C. F., and Springel, V. (2017). Moving-mesh simulations of star-forming cores in magneto-gravo-turbulence. Astrophys. J. 838:40. doi: 10.3847/1538-4357/aa6475

CrossRef Full Text | Google Scholar

Molina, F. Z., Glover, S. C. O., Federrath, C., and Klessen, R. S. (2012). The density variance-Mach number relation in supersonic turbulence - I. Isothermal, magnetized gas. Mont. Notices RAS 423, 2680–2689. doi: 10.1111/j.1365-2966.2012.21075.x

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Paleologou, E. V. (1981). Ambipolar diffusion in interstellar clouds - Time-dependent solutions in one spatial dimension. Astrophys. J. 246, 48–64. doi: 10.1086/158897

CrossRef Full Text | Google Scholar

Mouschovias, T. C., and Spitzer, L, Jr. (1976). Note on the collapse of magnetic interstellar clouds. Astrophys. J. 210:326. doi: 10.1086/154835

CrossRef Full Text | Google Scholar

Murray, D., Goyal, S., and Chang, P. (2018). The effects of protostellar jet feedback on turbulent collapse. Mont. Notices RAS 475, 1023–1035. doi: 10.1093/mnras/stx3153

CrossRef Full Text | Google Scholar

Myers, A. T., Klein, R. I., Krumholz, M. R., and McKee, C. F. (2014). Star cluster formation in turbulent, magnetized dense clumps with radiative and outflow feedback. Mont. Notices RAS 439, 3420–3438. doi: 10.1093/mnras/stu190

CrossRef Full Text | Google Scholar

Myers, A. T., McKee, C. F., Cunningham, A. J., Klein, R. I., and Krumholz, M. R. (2013). The fragmentation of magnetized, massive star-forming cores with radiative feedback. Astrophys. J. 766:97. doi: 10.1088/0004-637X/766/2/97

CrossRef Full Text | Google Scholar

Nagai, T., Inutsuka, S.-I., and Miyama, S. M. (1998). An origin of filamentary structure in molecular clouds. Astrophys. J. 506, 306–322. doi: 10.1086/306249

CrossRef Full Text | Google Scholar

Nakamura, F., Hanawa, T., and Nakano, T. (1993). Fragmentation of filamentary molecular clouds with longitudinal and helical magnetic fields. Publ. ASJ 45, 551–566.

Google Scholar

Nakamura, F., and Li, Z.-Y. (2008). Magnetically regulated star formation in three dimensions: the case of the taurus molecular cloud complex. Astrophys. J. 687, 354–375. doi: 10.1086/591641

CrossRef Full Text | Google Scholar

Nakamura, F., and Li, Z.-Y. (2011). Clustered star formation in magnetic clouds: properties of dense cores formed in outflow-driven turbulence. Astrophys. J. 740:36. doi: 10.1088/0004-637X/740/1/36

CrossRef Full Text | Google Scholar

Neufeld, D. A., Lepp, S., and Melnick, G. J. (1995). Thermal balance in dense molecular clouds: radiative cooling rates and emission-line luminosities. Astrophys. J. Suppl. 100:132. doi: 10.1086/192211

CrossRef Full Text | Google Scholar

Ntormousi, E., Dawson, J. R., Hennebelle, P., and Fierlinger, K. (2017). The role of magnetic fields in the structure and interaction of supershells. Astron. Astrophys. 599:A94. doi: 10.1051/0004-6361/201629268

CrossRef Full Text | Google Scholar

Ntormousi, E., Hennebelle, P., André, P., and Masson, J. (2016). The effect of ambipolar diffusion on low-density molecular ISM filaments. Astron. Astrophys. 589:A24. doi: 10.1051/0004-6361/201527400

CrossRef Full Text | Google Scholar

Offner, S. S. R., and Chaban, J. (2017). Impact of protostellar outflows on turbulence and star formation efficiency in magnetized dense cores. Astrophys. J. 847:104. doi: 10.3847/1538-4357/aa8996

CrossRef Full Text | Google Scholar

Offner, S. S. R., Clark, P. C., Hennebelle, P., Bastian, N., Bate, M. R., Hopkins, P. F., et al. (2014). “The origin and universality of the stellar initial mass function,” in Protostars and Planets VI, eds H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning (Tucson, AZ: University of Arizona Press), 53–75.

Google Scholar

Offner, S. S. R., and Liu, Y. (2018). Turbulent action at a distance due to stellar feedback in magnetized clouds. Nat. Astron. 2, 896–900. doi: 10.1038/s41550-018-0566-1

CrossRef Full Text | Google Scholar

Oishi, J. S., and Mac Low, M.-M. (2006). The inability of ambipolar diffusion to set a characteristic mass scale in molecular clouds. Astrophys. J. 638, 281–285. doi: 10.1086/498818

CrossRef Full Text | Google Scholar

Ostriker, E. C., Stone, J. M., and Gammie, C. F. (2001). Density, velocity, and magnetic field structure in turbulent molecular cloud models. Astrophys. J. 546, 980–1005. doi: 10.1086/318290

CrossRef Full Text | Google Scholar

Padoan, P., and Nordlund, Å. (1999). A super-Alfvénic model of dark clouds. Astrophys. J. 526, 279–294. doi: 10.1086/307956

CrossRef Full Text | Google Scholar

Padoan, P., and Nordlund, Å. (2011). The star formation rate of supersonic magnetohydrodynamic turbulence. Astrophys. J. 730:40. doi: 10.1088/0004-637X/730/1/40

CrossRef Full Text | Google Scholar

Padoan, P., Nordlund, A., and Jones, B. J. T. (1997). The universality of the stellar initial mass function. Mont. Notices RAS 288, 145–152. doi: 10.1093/mnras/288.1.145

CrossRef Full Text | Google Scholar

Padoan, P., Pan, L., Haugbølle, T., and Nordlund, Å. (2016). Supernova driving. I. The origin of molecular cloud turbulence. Astrophys. J. 822:11. doi: 10.3847/0004-637X/822/1/11

CrossRef Full Text | Google Scholar

Panopoulou, G. V., Psaradaki, I., Skalidis, R., Tassis, K., and Andrews, J. J. (2017). A closer look at the ‘characteristic’ width of molecular cloud filaments. Mont. Notices RAS 466, 2529–2541. doi: 10.1093/mnras/stw3060

CrossRef Full Text | Google Scholar

Passot, T., and Vázquez-Semadeni, E. (2003). The correlation between magnetic pressure and density in compressible MHD turbulence. Astron. Astrophys. 398, 845–855. doi: 10.1051/0004-6361:20021665

CrossRef Full Text | Google Scholar

Peters, T., Banerjee, R., Klessen, R. S., and Mac Low, M.-M. (2011). The interplay of magnetic fields, fragmentation, and ionization feedback in high-mass star formation. Astrophys. J. 729:72. doi: 10.1088/0004-637X/729/1/72

CrossRef Full Text | Google Scholar

Piontek, R. A., and Ostriker, E. C. (2004). Thermal and magnetorotational instability in the interstellar medium: two-dimensional numerical simulations. Astrophys. J. 601, 905–920. doi: 10.1086/380785

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., et al. (2016). Planck intermediate results. XXXV. Probing the role of the magnetic field in the formation of structure in molecular clouds. Astron. Astrophys. 586:A138. doi: 10.1051/0004-6361/201525896

CrossRef Full Text | Google Scholar

Polychroni, D., Schisano, E., Elia, D., Roy, A., Molinari, S., Martin, P., et al. (2013). Two mass distributions in the L 1641 molecular clouds: the herschel connection of dense cores and filaments in orion A. Astrophys. J. Lett. 777:L33. doi: 10.1088/2041-8205/777/2/L33

CrossRef Full Text | Google Scholar

Price, D. J., and Bate, M. R. (2007). The impact of magnetic fields on single and binary star formation. Mont. Notices RAS 377, 77–90. doi: 10.1111/j.1365-2966.2007.11621.x

CrossRef Full Text | Google Scholar

Price, D. J., and Bate, M. R. (2008). The effect of magnetic fields on star cluster formation. Mont. Notices RAS 385, 1820–1834. doi: 10.1111/j.1365-2966.2008.12976.x

CrossRef Full Text | Google Scholar

Price, D. J., and Bate, M. R. (2009). Inefficient star formation: the combined effects of magnetic fields and radiative feedback. Mont. Notices RAS 398, 33–46. doi: 10.1111/j.1365-2966.2009.14969.x

CrossRef Full Text | Google Scholar

Roman-Duval, J., Jackson, J. M., Heyer, M., Rathborne, J., and Simon, R. (2010). Physical properties and galactic distribution of molecular clouds identified in the galactic ring survey. Astrophys. J. 723, 492–507. doi: 10.1088/0004-637X/723/1/492

CrossRef Full Text | Google Scholar

Roy, A., André, P., Arzoumanian, D., Peretto, N., Palmeirim, P., Könyves, V., et al. (2015). Possible link between the power spectrum of interstellar filaments and the origin of the prestellar core mass function. Astron. Astrophys. 584:A111. doi: 10.1051/0004-6361/201526431

CrossRef Full Text | Google Scholar

Santos-Lima, R., de Gouveia Dal Pino, E. M., and Lazarian, A. (2012). The role of turbulent magnetic reconnection in the formation of rotationally supported protostellar disks. Astrophys. J. 747:21. doi: 10.1088/0004-637X/747/1/21

CrossRef Full Text | Google Scholar

Schwarz, J., McCray, R., and Stein, R. F. (1972). Formation of clouds in a cooling interstellar medium. Astrophys. J. 175:673. doi: 10.1086/151588

CrossRef Full Text | Google Scholar

Scoville, N. Z., and Hersh, K. (1979). Collisional growth of giant molecular clouds. Astrophys. J. 229, 578–582. doi: 10.1086/156991

CrossRef Full Text | Google Scholar

Seifried, D., Banerjee, R., Pudritz, R. E., and Klessen, R. S. (2013). Turbulence-induced disc formation in strongly magnetized cloud cores. Mont. Notices RAS 432, 3320–3331. doi: 10.1093/mnras/stt682

CrossRef Full Text | Google Scholar

Shu, F. H. (1992). The Physics of Astrophysics. Volume II: Gas Dynamics. Mill Valley, CA: University Science Books.

Google Scholar

Shu, F. H., Adams, F. C., and Lizano, S. (1987). Star formation in molecular clouds - Observation and theory. Annu. Rev. Astron. Astrophys. 25, 23–81. doi: 10.1146/annurev.aa.25.090187.000323

CrossRef Full Text | Google Scholar

Smith, R. J., Glover, S. C. O., and Klessen, R. S. (2014). On the nature of star-forming filaments - I. Filament morphologies. Mont. Notices RAS 445, 2900–2917. doi: 10.1093/mnras/stu1915

CrossRef Full Text | Google Scholar

Soler, J. D., and Hennebelle, P. (2017). What are we learning from the relative orientation between density structures and the magnetic field in molecular clouds? Astron. Astrophys. 607:A2. doi: 10.1051/0004-6361/201731049

CrossRef Full Text | Google Scholar

Soler, J. D., Hennebelle, P., Martin, P. G., Miville-Deschênes, M.-A., Netterfield, C. B., and Fissel, L. M. (2013). An imprint of molecular cloud magnetization in the morphology of the dust polarized emission. Astrophys. J. 774:128. doi: 10.1088/0004-637X/774/2/128

CrossRef Full Text | Google Scholar

Solomon, P. M., Rivolo, A. R., Barrett, J., and Yahil, A. (1987). Mass, luminosity, and line width relations of Galactic molecular clouds. Astrophys. J. 319, 730–741. doi: 10.1086/165493

CrossRef Full Text | Google Scholar

Spruit, H. C. (2013). Essential magnetohydrodynamics for astrophysics. arXiv.

Google Scholar

Sternberg, A., Le Petit, F., Roueff, E., and Le Bourlot, J. (2014). H I-to-H₂ transitions and H I column densities in galaxy star-forming regions. Astrophys. J. 790:10. doi: 10.1088/0004-637X/790/1/10

CrossRef Full Text | Google Scholar

Tilley, D. A., and Pudritz, R. E. (2007). The formation of star clusters - II. 3D simulations of magnetohydrodynamic turbulence in molecular clouds. Mont. Notices RAS 382, 73–94. doi: 10.1111/j.1365-2966.2007.12371.x

CrossRef Full Text | Google Scholar

Tomisaka, K. (1986). Formation of giant molecular clouds by coagulation of small clouds and spiral structure. Publ. ASJ 38, 95–109.

Google Scholar

Tomisaka, K. (2014). Magnetohydrostatic equilibrium structure and mass of filamentary isothermal cloud threaded by lateral magnetic field. Astrophys. J. 785:24. doi: 10.1088/0004-637X/785/1/24

CrossRef Full Text | Google Scholar

Traficante, A., Fuller, G. A., Peretto, N., Pineda, J. E., and Molinari, S. (2015). The initial conditions of stellar protocluster formation - II. A catalogue of starless and protostellar clumps embedded in IRDCs in the Galactic longitude range 15° ≤ l ≤ 55°. Mont. Notices RAS 451, 3089–3106. doi: 10.1093/mnras/stv1158

CrossRef Full Text | Google Scholar

Tritsis, A., and Tassis, K. (2016). Striations in molecular clouds: streamers or MHD waves? Mont. Notices RAS 462, 3602–3615. doi: 10.1093/mnras/stw1881

CrossRef Full Text | Google Scholar

Troland, T. H., and Heiles, C. (1986). Interstellar magnetic field strengths and gas densities Observational and theoretical perspectives. Astrophys. J. 301, 339–345. doi: 10.1086/163904

CrossRef Full Text | Google Scholar

Urquhart, J. S., Moore, T. J. T., Csengeri, T., Wyrowski, F., Schuller, F., Hoare, M. G., et al. (2014). ATLASGAL - towards a complete sample of massive star forming clumps. Mont. Notices RAS 443, 1555–1586. doi: 10.1093/mnras/stu1207

CrossRef Full Text | Google Scholar

Vacca, W. D., Garmany, C. D., and Shull, J. M. (1996). The Lyman-Continuum fluxes and stellar parameters of O and early B-type stars. Astrophys. J. 460:914. doi: 10.1086/177020

CrossRef Full Text | Google Scholar

Valdivia, V., Hennebelle, P., Gérin, M., and Lesaffre, P. (2016). H₂ distribution during the formation of multiphase molecular clouds. Astron. Astrophys. 587:A76. doi: 10.1051/0004-6361/201527325

CrossRef Full Text | Google Scholar

van Loo, S., Falle, S. A. E. G., Hartquist, T. W., and Barker, A. J. (2008). The effect of ambipolar resistivity on the formation of dense cores. Astron. Astrophys. 484, 275–280. doi: 10.1051/0004-6361:200809432

CrossRef Full Text | Google Scholar

van Loo, S., Falle, S. A. E. G., Hartquist, T. W., and Moore, T. J. T. (2007). Shock-triggered formation of magnetically-dominated clouds. Astron. Astrophys. 471, 213–218. doi: 10.1051/0004-6361:20077430

CrossRef Full Text | Google Scholar

Van Loo, S., Keto, E., and Zhang, Q. (2014). Core and filament formation in magnetized, self-gravitating isothermal layers. Astrophys. J. 789:37. doi: 10.1088/0004-637X/789/1/37

CrossRef Full Text | Google Scholar

Vázquez-Semadeni, E., Banerjee, R., Gómez, G. C., Hennebelle, P., Duffin, D., and Klessen, R. S. (2011). Molecular cloud evolution - IV. Magnetic fields, ambipolar diffusion and the star formation efficiency. Mont. Notices RAS 414, 2511–2527. doi: 10.1111/j.1365-2966.2011.18569.x

CrossRef Full Text | Google Scholar

Vázquez-Semadeni, E., Kim, J., Shadmehri, M., and Ballesteros-Paredes, J. (2005). The lifetimes and evolution of molecular cloud cores. Astrophys. J. 618, 344–359. doi: 10.1086/425951

CrossRef Full Text | Google Scholar

Vázquez-Semadeni, E., Ryu, D., Passot, T., González, R. F., and Gazol, A. (2006). Molecular cloud evolution. I. molecular cloud and thin cold neutral medium sheet formation. Astrophys. J. 643, 245–259. doi: 10.1086/502710

CrossRef Full Text | Google Scholar

Vestuto, J. G., Ostriker, E. C., and Stone, J. M. (2003). Spectral properties of compressible magnetohydrodynamic turbulence from numerical simulations. Astrophys. J. 590, 858–873. doi: 10.1086/375021

CrossRef Full Text | Google Scholar

Walch, S. K., Whitworth, A. P., Bisbas, T., Wünsch, R., and Hubber, D. (2012). Dispersal of molecular clouds by ionizing radiation. Mont. Notices RAS 427, 625–636. doi: 10.1111/j.1365-2966.2012.21767.x

CrossRef Full Text | Google Scholar

Wan, M., Osman, K. T., Matthaeus, W. H., and Oughton, S. (2012). Investigation of intermittency in magnetohydrodynamics and solar wind turbulence: scale-dependent kurtosis. Astrophys. J. 744:171. doi: 10.1088/0004-637X/744/2/171

CrossRef Full Text | Google Scholar

Wang, P., Li, Z.-Y., Abel, T., and Nakamura, F. (2010). Outflow feedback regulated massive star formation in parsec-scale cluster-forming clumps. Astrophys. J. 709, 27–41. doi: 10.1088/0004-637X/709/1/27

CrossRef Full Text | Google Scholar

Ward-Thompson, D., André, P., Crutcher, R., Johnstone, D., Onishi, T., and Wilson, C. (2007). “An observational perspective of low-mass dense cores II: evolution toward the initial mass function,” in Protostars and Planets V, eds B. Reipurth, D. Jewitt, and K. Keil (Tucson: University of Arizona Press), 33–46.

Google Scholar

Wolfire, M. G., McKee, C. F., Hollenbach, D., and Tielens, A. G. G. M. (2003). Neutral atomic phases of the interstellar medium in the galaxy. Astrophys. J. 587, 278–311. doi: 10.1086/368016

CrossRef Full Text | Google Scholar

Wurster, J., Price, D. J., and Bate, M. R. (2016). Can non-ideal magnetohydrodynamics solve the magnetic braking catastrophe? Mont. Notices RAS 457, 1037–1061. doi: 10.1093/mnras/stw013

CrossRef Full Text | Google Scholar

Wurster, J., Price, D. J., and Bate, M. R. (2017). The impact of non-ideal magnetohydrodynamics on binary star formation. Mont. Notices RAS 466, 1788–1804. doi: 10.1093/mnras/stw3181

CrossRef Full Text | Google Scholar

Zhao, B., Caselli, P., Li, Z.-Y., and Krasnopolsky, R. (2018). Decoupling of magnetic fields in collapsing protostellar envelopes and disc formation and fragmentation. Mont. Notices RAS 473, 4868–4889. doi: 10.1093/mnras/stx2617

CrossRef Full Text | Google Scholar

Zuckerman, B., and Evans, N. J. II (1974). Models of massive molecular clouds. Astrophys. J. Lett. 192, L149–L152.

Google Scholar