- 1Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, São Paulo, Brazil
- 2Institut de Physique Nucléaire d'Orsay, Université Paris-Sud, Université Paris/Saclay, CNRS-IN2P3, Orsay, France
- 3Niels Bohr International Academy & DARK, Niels Bohr Institute, Copenhagen, Denmark
- 4Ludwig-Maximilians Universität München, Universitäts-Sternwarte, München, Germany
- 5Max-Planck-Institut für Astrophysik, Garching, Germany
- 6Karlsruhe Institute of Technology, Institut für Kernphysik, Karlsruhe, Germany
- 7Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, Stanford, CA, United States
- 8Department of Physics, Bergische Universität Wuppertal, Wuppertal, Germany
- 9Deutsches Elektronen-Synchrotron, Zeuthen, Germany
- 10Department of Physics and Astronomy, Pennsylvania State University, University Park, PA, United States
- 11Yukawa Institute for Theoretical Physics, Kyoto, Japan
- 12European Southern Observatory, Garching, Germany
- 13Enrico Fermi Institute, University of Chicago, Chicago, IL, United States
- 14Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
- 15II. Institut für Theoretische Physik, Universität Hamburg, Hamburg, Germany
We review open questions and prospects for progress in ultrahigh-energy cosmic ray (UHECR) research, based on a series of discussions that took place during the “The High-Energy Universe: Gamma-Ray, Neutrino, and Cosmic-ray Astronomy” MIAPP workshop in 2018. Specifically, we overview open questions on the origin of the bulk of UHECRs, the UHECR mass composition, the origin of the end of the cosmic-ray spectrum, the transition from Galactic to extragalactic cosmic rays, the effect of magnetic fields on the trajectories of UHECRs, anisotropy expectations for specific astrophysical scenarios, hadronic interactions, and prospects for discovering neutral particles as well as new physics at ultrahigh energies. We also briefly overview upcoming and proposed UHECR experiments and discuss their projected science reach.
1. Introduction
Cosmic rays with energy exceeding 1018 eV≡ 1 EeV, are referred to as ultrahigh-energy cosmic rays (UHECRs). Extensive air showers (EAS) produced when a UHECR interacts with an air nucleus in the upper atmosphere have been measured since their discovery by Pierre Auger in the 1930s. The first observation of an EAS with an energy of ~1020 eV was made at Volcano Ranch in February 1962 (Linsley, 1963). The study of UHECRs has continued ever since, with increasingly large detector arrays. Nevertheless, many aspects of the nature of UHECRs remain an enigma: What is the origin of these particles? What is their mass composition? How do the astrophysical sources accelerate particles to such extreme energies?
This document summarizes the discussions that took place during the workshop “The High Energy Universe: Gamma-ray, Neutrino, and Cosmic-ray Astronomy” at the Munich Institute for Astro- and Particle Physics (MIAPP). We met for 1 month in March 2018 and had daily discussions and presentations about the status and future of the field of UHECR study. What have we learned about UHECRs in the last years? Which of the open questions can we expect to be able to address with forthcoming detector upgrades and proposed next-generation experiments? What are the requirements for probing remaining open questions and going forward in the study of UHECRs?
An overview of the current status of experimental measurements is given in section 2. Section 3 presents the open questions in the field of UHECRs. The theoretical models that successfully describe UHECR data are summarized. Predictions are given of the sensitivity of forthcoming and proposed experimental measurements to specific theoretical models and to the presented open questions in general. In section 4, upcoming and proposed Earth-based and space-based experiments are presented. We conclude in section 5, with our view of the outlook of the field, and a set of suggestions that we judge as beneficial for addressing open questions at ultrahigh energies in the coming years.
2. Status of Ultrahigh Energy Cosmic Ray Research
2.1. Anisotropy
The detection of an UHECR flux excess in the direction of a (few) prominent nearby source(s) would act as a pharos in the search for ultrahigh-energy accelerators. The volume of the Universe accessible at ultrahigh energies is limited by interactions with the extragalactic background light (EBL) and cosmic microwave background (CMB) to about 1 Gpc around 1019 eV, dropping down to a few hundreds of Mpc beyond 5 × 1019 eV (Greisen, 1966; Zatsepin and Kuzmin, 1966). As UHECRs are charged particles, their propagation is further affected by extragalactic and Galactic magnetic fields: the higher the rigidity (energy over charge), the smaller the deflection. Searches for UHECR anisotropies have consequently focused on large angular scales around 1019 eV, where the cumulative flux from multiple objects could possibly be seen despite magnetic deflections. At rigidities beyond ~ 20 EV, the trajectories of cosmic rays through extragalactic and Galactic magnetic fields are expected to be ballistic, with small (< 10 degree) deflections over 100 Mpc of propagation, motivating searches for small-scale anisotropies. Beyond this energy threshold, localized excesses at small (1°) to intermediate (30°) scales have been sought for (Aab et al., 2015d), possibly emerging from a few nearby objects.
Studies at large angular scales are often performed with ground-based observatories through a Rayleigh analysis (Linsley, 1975) in right ascension, α, of the UHECR arrival direction. Because of rotation of the Earth, the exposure of UHECR observatories only depends on declination, δ, when averaged over several years of observations. Using more than 8 years of full-operation data (12 years since the start of deployment), the Pierre Auger Collaboration discovered a modulation of the event rate in right ascension at EAuger > 8 EeV with a post-trial significance of 5.4σ accounting for the search in two independent energy bins (Aab et al., 2017b).
Combining the right-ascension analysis with an azimuthal one, the anisotropy signal appears to be consistent with a dipolar modulation over ~85% of the sky covered by Auger. The amplitude of the dipole, , is 10 times larger than that expected from proper motion in a cosmic-ray frame coincident with the CMB reference frame, suggesting an anisotropic distribution of UHECR sources within a few hundreds of Mpc. As shown in Figure 1, the direction of the dipole lies 125° from the Galactic center, disfavoring a Galactic origin for cosmic rays observed above eight EeV. This detection thus possibly constitutes the first observational piece of evidence for an extragalactic origin of cosmic rays beyond the ankle. Interestingly, further splitting events at EAuger > 4 EeV into four energy bins, the Pierre Auger Collaboration found an indication at the 3.7σ level of growth of the dipolar amplitude with energy, expected from the shrinking horizon with increasing energy (Aab et al., 2018a). Given the sharp drop in statistics at the highest energies, searches for large-scale features remain under-constrained beyond EAuger > 32EeV.
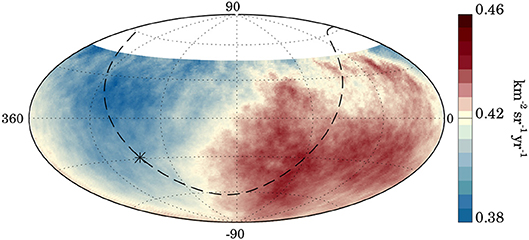
Figure 1. Smoothed cosmic-ray flux for EAuger > 8 EeV in equatorial coordinates. The dashed line and the star indicate the Galactic plane and center, respectively. Reproduced with permission from Aab et al. (2017b).
The Pierre Auger Collaboration has performed searches for intrinsic anisotropy at small angular scales at energies exceeding 40 EeV, by comparing the observed number of events within angular windows of a specified radius with that expected from an isotropic UHECR flux. The strongest excess revealed by this search is obtained at EAuger > 54 EeV in a window of radius 12° centered on (α, δ) = (198°, −25°) (Aab et al., 2015d). This is shown on the left panel of Figure 2. Although the local significance obtained from this excess reaches 4.3σ, a penalization for the scan in energy and in search radius results in a post-trial value of 0.4σ (p = 69%). The Telescope Array (TA) Collaboration has performed a search for flux excesses at energies exceeding 10 EeV, 40 EeV and 57 EeV with 5 years of data. The largest excess, with a local significance of 5.1σ, is obtained at ETA > 57 EeV in the direction (α, δ) = (147°, 43°) on a 20° angular scale (Tinyakov et al., 2016). The skymap of events with energy ETA > 57 EeV, smeared on a 20° angular scale, is shown on the right panel of Figure 2. The colormap gives the pre-trials corrected significance of the observation in each direction in the sky with respect to background expectations. Accounting for the scan in search radius results in a penalized significance of 3.4σ, hinting at a possible over-density coined the TA “hotspot.” An update of the analysis presented with 7 and 10 years of data (Abbasi et al., 2018a; Sagawa, 2018) indicates no increase in the significance of the excess.
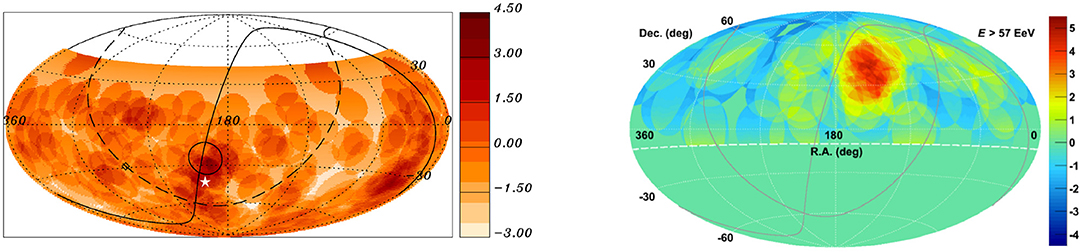
Figure 2. Local-significance maps from searches for localized UHECR excess in equatorial coordinates. Left: Southern sky observed at EAuger > 54 EeV smeared on a 12° angular scale. The solid and long-dashed lines indicate the supergalactic and Galactic plane, respectively. Reproduced with permission from Aab et al. (2015d). Right: Northern sky observed at ETA > 57 EeV smeared on a 20° angular scale. Reproduced with permission from Abbasi et al. (2014).
The directions with largest departures from UHECR isotropy have been compared with the position of nearby prominent objects. The two most significant excesses in the Northern and Southern hemispheres are located near the supergalactic plane, and multiple candidate sources have been discussed either within or outside from Collaborations. For example, in Fang et al. (2014) and Heet al. (2016), a ranking of gamma-ray emitting sources detected within 200 Mpc attempted to identify possible candidates for the TA hotspot, such as the starburst galaxy M82, blazars of BL Lac type such as Mrk 180 and Mrk 421, but also regular star-forming galaxies and galaxy clusters. Similarly, Cen A, an FR-I radio galaxy, or starburst galaxies such as NGC 4945 and M 83 have been pointed out as lying 10−20° away from the Southernmost significant UHECR excess. These sources are powerful X-ray and (or) γ-ray emitters and could potentially explain the UHECR flux from the TA hotspot region.
To reach a more complete view of the UHECR sky, cross-correlation studies against numerous astronomical catalogs have been performed within the Auger and TA collaborations, as well as by independent groups. Models often assume that the UHECR source distribution follows the distribution of luminous matter in the nearby Universe, based on radio — 3CRR catalog—or infrared—IRAS and 2MASS—or X-ray—Swift-BAT—or gamma ray— Fermi-LAT—observations. These models account for the expected energy losses and deflections of UHECRs during their extragalactic propagation (Kashti and Waxman, 2008; Oikonomou et al., 2013; Aab et al., 2015d; Tinyakov, 2018). While such studies have not yet revealed any statistically significant (> 5σ) departure from isotropy, a recent search against γ-ray bright sources, that accounted for their expected relative flux has unveiled an indication of excess UHECR flux at 4.0 σ post-trial in the direction of starburst galaxies (at EAuger > 39 EeV), and at 2.7σ post-trial in the direction of jetted active galactic nuclei (AGN) at EAuger > 60 EeV (Aab et al., 2018c). A search by the TA Collaboration with fixed parameters at ETA > 43 EeV is consistent with the Auger result for starburst galaxies, but also with isotropy, indicating that the currently limited statistics from the Northern hemisphere is not sufficient to discriminate between the two hypotheses (Abbasi et al., 2018b).
2.2. Spectrum
Measuring the energy spectrum of UHECRs at high precision is of prime importance for understanding the origin and mechanisms of CR acceleration and propagation. Data at the highest energies have been accumulated for decades by AGASA (Yoshida et al., 1995), Yakutsk (Egorova et al., 2004), HiRes (Abbasi et al., 2008b), and more recently by the Pierre Auger Observatory and Telescope Array. Given the steeply falling energy spectrum, particularly above 5 · 1019 eV, event statistics is important. The statistical power of different observatories can best be compared by their integrated exposures. For illustration, after more than 20 years of operation, AGASA has reached an exposure of 0.18 · 104 km2 sr yr. As of ICRC 2017, the Telescope Array has collected 0.8 · 104 km2 sr yr, and Auger dominates with 9 · 104 km2 sr yr. This is a factor of 50 higher relative to AGASA and about a factor of 10 higher relative to TA and demonstrates the enormous progress that has been made during the last decade.
Both TA and Auger are hybrid observatories comprising a set of fluorescence telescopes and a surface detector array (Tokuno et al., 2011; Aab et al., 2015a). Their absolute energy calibration is based on the calibration of the telescopes and on knowing the fluorescence yield of the atmosphere. The details of the energy calibrations differ between the two observatories. Auger uses the absolute light yield and its wavelength dependence as measured by the Airfly Collaboration (Ave et al., 2008). TA uses the absolute yield measured by Kakimoto et al. (1996) at 337 nm and the wavelength dependence of the fluorescence yield measured by FLASH (Abbasi et al., 2008a). The dependence on atmospheric pressure, temperature, and humidity is treated identically by both collaborations using the reference model formula reported in UHECR2012 (Keilhauer et al., 2013). The corrections for the invisible energy of air showers are based on data in the case of Auger (Aab et al., 2019) and on Monte Carlo simulations in the case of TA. Finally, Auger uses the data-driven constant intensity method to account for the zenith angle dependence of shower absorption, while TA uses again Monte Carlo simulations (Ikeda, 2011). The joint working group of Auger and TA established that the relative differences between Auger and TA solely due these effects amount to 6 %. This is well in line with the total uncertainties of the absolute energy scales of 14 % in case of Auger (Verzi, 2013) and 21 % in case of TA (Abbasi et al., 2016). The additional contributions mostly stem from the absolute calibrations of the telescopes and from reconstruction methods (Dawson et al., 2013). Despite of these differences, a remarkable agreement in the energy scale of the two observatories is found up to about 1019.4 eV. As demonstrated in Figure 3, (left) (The Pierre Auger and Telescope Array Collaborations, 2018), re-scaling the energy scale of each experiment by only 5.2 %, which is well within the aforementioned systematic uncertainties of the two experiments, provides an excellent agreement of their measured fluxes. However, above this energy, larger differences remain present, which cannot be accounted for by an independent scaling of their reconstructed energies. It will be important to understand whether this difference is caused by systematic uncertainties arising at the highest energies only, or whether it has an astrophysics origin related to seeing different parts of the sky. To study that question, the joint working group between the Auger and TA collaborations has generated energy spectra for the Southern sky, seen by Auger only, for the Northern sky, seen by TA only, and for the declination range −15° ≤ δ ≤ 24.8°, seen by both observatories. The energy spectrum for the common declination band is depicted in the right panel of Figure 3. Obviously, the agreement is much better, but some differences are still seen. It should also be noted that the energy spectrum measured by Auger does not show any significant declination dependence, but that of TA does. As it is still too early to draw definite conclusions about the source of the differences, the joint working group will continue their studies. It is also worthwhile to note that the declination dependence of the energy spectrum seen by TA should cause a significant anisotropy in the arrival directions of UHECR. This has been studied in Globus et al. (2017) and was found to be in tension with astrophysical models aimed at reproducing observational constraints on anisotropies.
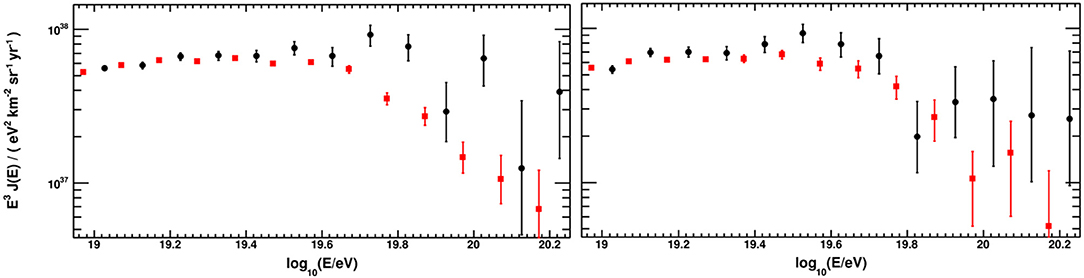
Figure 3. Left: Comparison of the UHECR energy spectrum of Auger and TA after rescaling the energies of Auger by +5.2 % (red squares) and that of TA by −5.2 % (black circles). Right: Keeping the rescaling factors of the left figure, but restricting the declination to −15° ≤ δ ≤ 24.8° so that the same part of the sky is observed. Reproduced with permission from The Pierre Auger and Telescope Array Collaborations (2018).
Another important question related to the UHECR energy spectrum is about the origin of the flux suppression observed at the highest energies. The GZK cut-off was predicted 50 years ago independently by Greisen (1966); Zatsepin and Kuzmin (1966) and was claimed to be found by the HiRes collaboration in 2008 (Abbasi et al., 2008b). At the same time, the Auger collaboration reported a flux suppression at about the same energy and with a significance of more than 6σ (Abraham et al., 2008). Above 1019.8 eV, TA has reported the observation of 26 events (Tsunesada et al., 2018) and Auger has reported 100 events (Fenu, 2017) by ICRC2017. However, these numbers cannot be compared directly due to the difference in the energy calibration of the experiments. We discuss more this problem in section 3.1.
2.3. Mass Composition
The most reliable technique to measure the mass composition of UHECRs is the simultaneous measurement of the depth, Xmax, at which the number of particles in an air shower reaches its maximum and the energy, E, of the shower. These quantities can be directly observed with non-imaging Cherenkov detectors, radio arrays, and fluorescence telescopes. As of today, only fluorescence detectors have reached enough exposure to measure Xmax at ultrahigh energies. After pioneering measurements from Fly's Eye (Baltrusaitis et al., 1985) and HiRes (Abu-Zayyad et al., 2000), the fluorescence technique is currently employed by the Pierre Auger Observatory (Abraham et al., 2010) and the Telescope Array (Tokuno et al., 2012). Traditional particle detector arrays are in principle also capable to estimate the energy and mass of cosmic rays, e.g., by measuring separately the number of muons and electrons at ground level, but usually with a worse resolution and, more importantly, larger theoretical uncertainties from hadronic interactions during the air shower development. The latter source of uncertainty can be eliminated by cross-calibrating the measurements with the Xmax and energy of a subset of so-called hybrid events (air showers observed simultaneously with both, fluorescence and surface detectors).
The current data on the average shower maximum, 〈Xmax〉, as a function of energy from fluorescence (Aab et al., 2014a; Abbasi et al., 2018d; Bellido, 2018) and surface detectors (Aab et al., 2017a) is shown in the left panel of Figure 4. The event-by-event fluctuations of the shower maximum, σ(Xmax), are displayed on the right panel of Figure 4. Only the measurements with fluorescence detectors have enough resolution to determine the intrinsic (as opposed to detector-related) standard deviation of shower fluctuations. For comparison, the predictions of 〈Xmax〉 of proton- and iron-initiated air showers simulations using hadronic interaction models (Ostapchenko, 2011; Pierog et al., 2015; Riehn et al., 2016) tuned to LHC data are shown as red and blue lines.
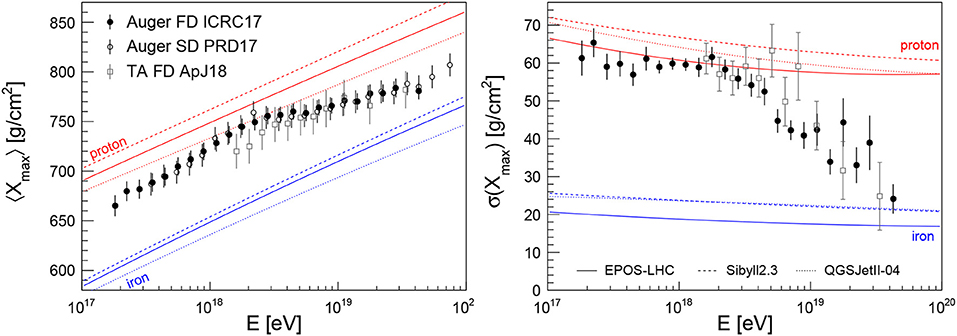
Figure 4. Measurements (Abbasi et al., 2018d; Bellido, 2018) of the mean (Left) and standard deviation (Right) of the distribution of shower maximum as a function of energy. Data points from the Pierre Auger Observatory are shown as published since they have been corrected for detector effects. Data from the Telescope Array have been approximately corrected for detector effects by shifting the mean by +5 g/cm2 (Yushkov, 2018) and by subtracting an Xmax-resolution of 15 g/cm2 (Abbasi et al., 2018d) in quadrature. Furthermore, the TA data points were shifted down by 10.4% in energy to match the energy scale of the Pierre Auger Observatory (Ivanov, 2018) (see also De Souza, 2018 for a discussion of the good overall compatibility of the Xmax measurements from the Pierre Auger Observatory and the Telescope Array). All error bars denote the quadratic sum of the quoted statistical and systematic uncertainties. The energy evolution of the mean and standard deviation of Xmax obtained from simulations (Bergmann et al., 2007) of proton- and iron-initiated air showers are shown as red and blue lines respectively. The line styles indicate the different hadronic interaction models (Ostapchenko, 2011; Pierog et al., 2015; Riehn et al., 2016) used in the simulation. M. Unger for this review.
These measurements of the first two moments (mean and standard deviation) of the Xmax distribution suggest that the composition of cosmic rays becomes lighter as the energy increases toward the ankle (until around 1018.3 eV) and then becomes heavier again when approaching ultrahigh energies. The data points from the surface detector of Auger might indicate a flattening of this trend at ultrahigh energies, but more statistics are needed to confirm this finding. Note that, whereas 〈Xmax〉 scales linearly with the average logarithmic mass of cosmic-ray primaries, a large value of σ(Xmax) can either signify a light composition or a mixture of light and heavy nuclei, whereas a small value of σ(Xmax) corresponds to intermediate or heavy composition with a small admixture of light elements (see, e.g., Linsley, 1983; Kampert and Unger, 2012).
For a more quantitive insight on the mass composition of UHECRs, the Pierre Auger Collaboration fitted templates of four mass groups (p, He, N, Fe) to the Xmax distributions (Aab et al., 2014b; Bellido, 2018). The derived mass fractions are displayed in Figure 5 and reveal an interesting pattern of alternating dominance of certain mass groups. At low energies, there are hints for a rapidly disappearing contribution of iron, which is qualitatively in accordance with the “knee” in the flux of the heavy Galactic component at 1016.9 eV reported by the KASCADE-Grande Collaboration (Apel et al., 2011). In addition to this heavy component, there seems to be a large fraction of intermediate-mass nuclei at low energy, possibly signifying a second Galactic component (Hillas, 2006; Thoudam et al., 2016). Above 1018 eV the flux of cosmic rays is dominated by light primaries. These have to be of extragalactic origin to avoid a large anisotropy toward the Galactic plane that would conflict with the level of isotropy of cosmic-ray arrival directions reported by Auger (Abreu et al., 2012a) and TA (Abbasi et al., 2017). As the energy increases, there is a trend that protons are gradually replaced by helium, helium by nitrogen, and there might be an iron contribution emerging above 1019.4 eV when the statistics of the fluorescence measurement run out.Due to the limited statistics and unknowns about hadronic interaction models, this trend is still largely uncertain.
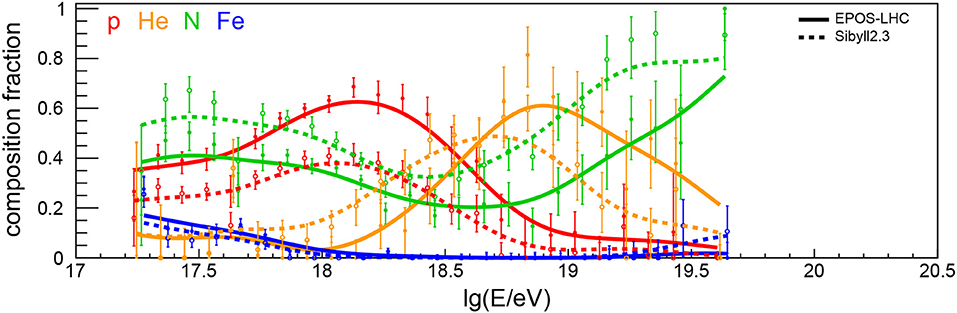
Figure 5. Composition fractions arriving at Earth derived from fitting templates of four mass groups to the Xmax distribution measured with the fluorescence detectors of the Pierre Auger Observatory (adapted from Bellido, 2018). Error bars denote statistical uncertainties and lines were added to guide the eye. The two interpretations of the data with EPOS-LHC and Sibyll2.3 are shown as closed and open symbols with solid and dashed lines styles, respectively. The QGSJetII-04 interpretation from Bellido (2018) is not shown, since it does not give a good description of the Xmax distributions over a wide range in energy (see also discussion in Aab et al., 2014b). As of today, no composition fractions are available around and above 1020 eV. M. Unger for this review.
2.4. Neutral Secondaries: Ultrahigh Energy Photons and Neutrinos
Neutral secondaries including neutrinos and photons are expected to be produced when UHECRs interact with extragalactic background photons during intergalactic propagation. These secondary particles are also referred to as cosmogenic or GZK neutrinos and photons in the literature. Their flux mainly depends on the chemical composition, maximum energy of UHECRs, and the source evolution model (e.g., Takami et al., 2009; Kotera et al., 2010; see Hooper et al., 2005; Anchordoqui et al., 2008 for secondaries from heavy nuclei). In general, photopion production is more efficient than photo-disintegration in producing secondaries. Figure 6 presents the expected cosmogenic neutrino flux from Alves Batista et al. (2019), based on UHECR models that best fit the Auger spectrum and composition measurements.
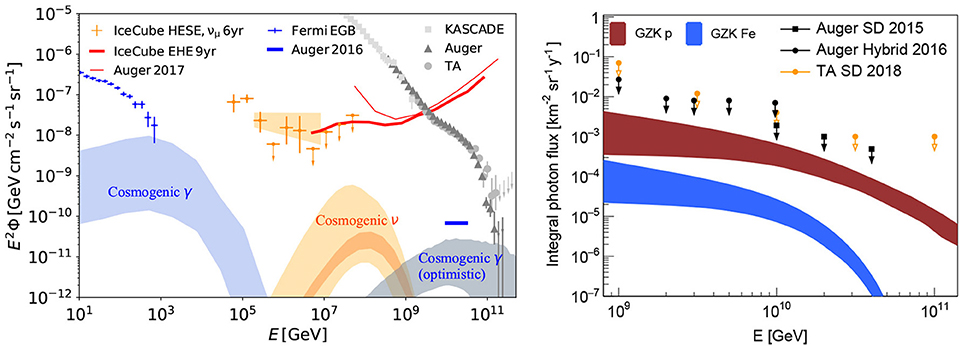
Figure 6. Left: Cosmogenic photon (blue) and neutrino (orange) fluxes for models that fit the Auger data including spectrum and composition (Alves Batista et al., 2019). Specifically, the dark orange band corresponds to a best-fit model with 99% CL, and the light orange band covers the AGN, star-formation rate (SFR), and gamma-ray burst (GRB) models for fits at 90% CL (Alves Batista et al., 2019). In more optimistic models that assume a larger maximum energy eV, a second photon bump appears at 1–10 EeV as indicated by the gray shaded area (Decerprit and Allard, 2011). In comparison, we show the fluxes of the six-year high-energy starting events (HESE, orange data points) (Kopper, 2018), six-year muon neutrino events (orange shaded region) (Aartsen et al., 2016d), nine-year extreme-high-energy (EHE) 90% upper limit (Aartsen et al., 2018) measured by IceCube (thick red curve), and the 90% upper limit provided by Auger with data from 1 Jan 04 to 31 Mar 17 (thin red curve, Bellido, 2018), as well as the extragalactic gamma-ray background observed by Fermi-LAT (Ackermann et al., 2015, 2016), and the differential limit of UHE photons in the bin of 10–30 EeV by Auger (Aab et al., 2017c). For reference, we also show the cosmic-ray spectra measured by KASCADE, Auger, and TA (Abraham et al., 2008; Apel et al., 2013; Abbasi et al., 2018e). K. Fang for this review. Right: Upper limits on the integral photon flux obtained with the Auger surface detector (Auger SD 2015) (Aab et al., 2015c), a hybrid analysis of 9 years of Auger data (Auger Hybrid 2016) Aab et al. (2017c), and the Telescope Array surface detector (TA SD 2018) (Abbasi et al., 2018c). The shaded regions give the predicted cosmogenic photon flux assuming a pure proton (GZK p) and pure iron (GZK Fe) UHECR composition of reference (Sarkar et al., 2011). F. Oikonomou for this review.
Specifically, the orange shaded area covers the expectation of the best-fit models with 90% CL and assuming a source evolution following the AGN, star-formation rate (SFR), and γ-ray burst (GRB) redshift evolution (Alves Batista et al., 2019). The dark orange shaded area shows the neutrino flux of the best-fit scenario with 99% confidence level (CL). In this scenario, the source evolution is assumed to be a power law of the cosmic scale factor (1 + z)m and the index m is left as a free parameter. Alves Batista et al. (2019) found that for energy spectral index between 1 and 2.2, their fit preferred negative source evolution, i.e., m < 0. This may be due to an actual evolution of sources, or an effect of cosmic variance and local over-density. In addition to Heinze et al. (2016), Romero-Wolf and Ave (2018), Das et al. (2018), Wittkowski and Kampert (2018), and Heinze et al. (2019) also predicted the cosmogenic neutrino flux based on fitting to the UHECR data.
Upper limits to the UHE neutrino flux have been obtained by the IceCube Observatory (Aartsen et al., 2018), the Auger Observatory (Bellido, 2018), and ANITA Gorham et al. (2018a). The blue shaded area shows the cosmogenic photons in the best-fit scenario of Alves Batista et al. (2019) and 99% CL. In more optimistic models, which assume larger maximum energy, 1–10 EeV photons may be observed. The gray shaded area presents such a flux, which covers the predictions by a range of models in Figure 7 of Decerprit and Allard (2011). For comparison, the upper limit of the differential photon flux in the bin of 10–30 EeV has been derived based in Aab et al. (2017c) and is shown as the blue solid line. For reference, we also present the high-energy neutrino flux measured by IceCube (Aartsen et al., 2016d; Kopper, 2018), cosmic rays (Abraham et al., 2008; Apel et al., 2013; Abbasi et al., 2018e), as well as the extragalactic gamma-ray background measured by Fermi-LAT (Ackermann et al., 2015).
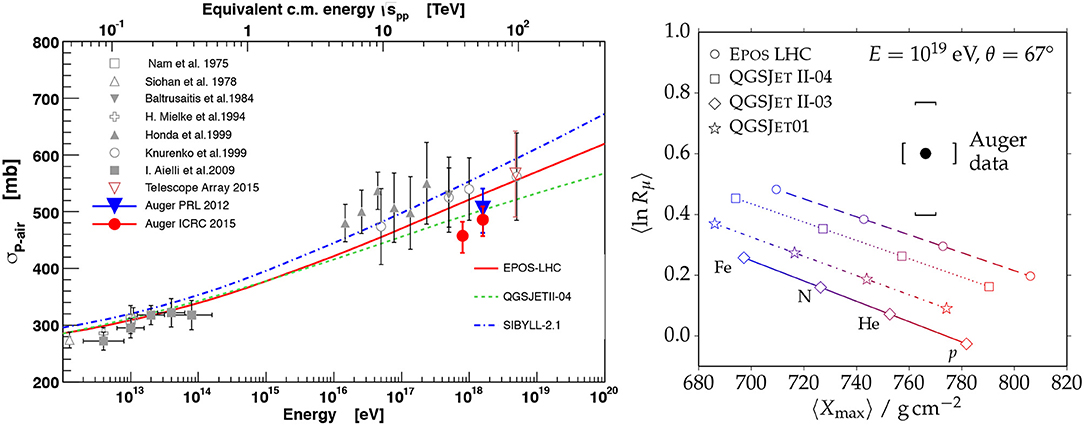
Figure 7. Left: Compilation of proton-air cross section measurements. See Ulrich et al. (2009) for references. Recent results are the Auger and TA measurements (Abreu et al., 2012; Abbasi et al., 2015; Ulrich, 2016). Reproduced with permission from Ulrich (2016). Right: Correlation between the muon density and the depth of shower maximum in inclined air showers. Here Rμ is the muon number relative to the prediction of QGSjet II.03 for proton primaries. Reproduced with permission from Aab et al. (2015b).
The Figure 6, right shows the latest upper limits in searches for UHE photons. The strictest upper limits in this energy range come from Auger. The predicted cosmogenic photon fluxes are from Sarkar et al. (2011). With its current exposure, Auger constraints the photon fraction to be ≤ 0.1% above 1018 eV (Aab et al., 2015c; Aab et al., 2017c). Measurements with the Telescope Array surface detector provide complementary limits in the same energy range in the Northern Hemisphere (Abbasi et al., 2018c).
2.5. Hadronic Interactions at Ultrahigh Energies
Good understanding of hadronic multiparticle production is needed for being able to derive composition information from air-shower data. While measuring shower profiles using fluorescence and Cherenkov light allows an almost model-independent determination of the shower energy (up to a correction of the order of 10–15% for “invisible” channels Barbosa et al., 2004), there is no model-independent means for estimating the primary mass composition. The most productive approach is the detailed simulation of a library of reference air showers with Monte Carlo models that have been designed and tuned to describe hadronic multiparticle production at man-made accelerator experiments Engel et al. (2011). Hadronic interaction models of this type include EPOS (Liu et al., 2004; Werner et al., 2006; Werner and Pierog, 2007; Pierog et al., 2015), QGSJET (Kalmykov and Ostapchenko, 1989; Kalmykov et al., 1997; Ostapchenko, 2006a,b, 2014), Sibyll (Engel et al., 1992, 2017; Fletcher et al., 1994; Ahn et al., 2009; Riehn et al., 2016; Fedynitch et al., 2018), and DPMJET (Ranft, 1995; Roesler et al., 2001) for high-energy interactions, typically with a laboratory frame momentum larger than 100 GeV, and FLUKA (Ferrari et al., 2005; Böhlen et al., 2014) and UrQMD (Bleicher et al., 1999) for low-energy interactions. In general, a very good description of inclusive air-shower observables is obtained (see Abreu et al., 2011; Abu-Zayyad et al., 2012).
An important aspect of the hadronic interaction models is the extrapolation of accelerator data to center-of-mass energies of up to TeV, well beyond energies accessible at colliders, to forward phase space regions not accessible in experiments, and to projectile and target particle combinations not measured in accelerator experiments. Given that we still cannot calculate predictions of QCD for the bulk of hadron production of importance for air showers, there is considerable ambiguity in modeling hadronic interactions. This ambiguity leads to model-dependent results for the mass composition as shown, for example, in Figure 5. Additional data from collider and fixed-target experiments and progress in the theory and phenomenology of multiparticle production are required to lower these uncertainties. For example, the LHC data at equivalent energy of eV show a moderate rise of the proton-proton cross section and secondary particle multiplicity. Updating the interaction models led to a shift of the Xmax predictions to larger depths (Engel et al., 2011; Pierog, 2018). While it was still possible to interpret the measured mean depth of shower maximum with a pure proton composition within the uncertainties using pre-LHC models, a mixed composition is clearly preferred if post-LHC models are applied. The shower-by-shower fluctuations of Xmax provide an even stronger constraint; see Figure 4. The depth of the first interaction point of an air shower is exponentially distributed, dP/dX0 ~ exp(−X/λ), with λ the interaction length. Hence, the fluctuations of X0 are σ(X0) = λ. Using the measured values of the proton-air cross section (see Figure 7, left), one gets σ(X0) ~ 50 g/cm2. Even if there were no additional fluctuations introduced by the shower evolution from the first interaction to the shower maximum, the proton-air cross section would have to be two times larger to bring these fluctuations down to 25 g/cm2. Such a drastic increase in the proton-air cross section would violate unitarity constraints in QCD and would require a new type of interaction taking over at energies beyond 2 × 1018 eV.
Air-shower measurements can also be used to derive information on hadronic interactions. Given that the primary cosmic-ray composition appears to be mixed in the energy range of relevance here, there is typically a strong correlation between the results of such measurements and the assumed primary mass composition. An exception is the measurement of the proton-air cross section. If done in an energy range in which there is a large fraction of protons in the mass composition of cosmic rays, one can select showers that develop very deep in the atmosphere to build a proton-dominated sample. Then the depth fluctuations can be related to the proton-air cross section for particle production. Recent results are shown in Figure 7, left.
There is increasing evidence for a discrepancy between the number of muons predicted by model calculations and that measured at very high energy. One of the most direct measurements demonstrating this muon discrepancy is shown in Figure 7, left. Depending on the interaction model used for reference and the measurement, there are about 30 − 60% more muons found in data than predicted. This muon puzzle is one of the most important problems in hadronic interaction physics as it is very difficult, if not impossible, to increase the number of muons by such a large fraction just by changing the physics of the first interaction. Enhanced production rates of baryon-antibaryon pairs (Pierog and Werner, 2008) and ρ0 mesons in air showers (Drescher, 2008; Ostapchenko, 2013) have been shown to have a large impact on the muon number. While NA61 measurements (Aduszkiewicz et al., 2017) have confirmed an enhanced forward production rate of ρ0 mesons, no increased proton-antiproton production rate has been found at LHC. Even though tuning these production processes increases the predicted muon number (Riehn et al., 2016), the discrepancy to air shower measurements still persists. It is likely that not only the number but also the production depth (Aab et al., 2014c; Collica, 2016), energy spectrum and, hence, the lateral distribution of muons is not well described by the models.
3. Open Questions
3.1. Precision Measurements of Spectrum and Mass-Composition
3.1.1. Relevance of the Energy Resolution
Enormous progress has been made recently from observing simple all-particle power-law distributions with just seeing the knee and ankle of the cosmic-ray spectrum, to uncovering a much more complex structure with an additional “second knee” at about 1017 eV, an ankle-like structure between the knee and this second knee, and the steep cut-off at the highest energies. Moreover, not only all-particle spectra can be derived from the air-shower data, but also energy spectra of different mass groups. All these achievements provided new insight into the astrophysics causing those structures. This became possible only by advancing both the precision of air-shower observations and reconstructions and the statistics of the data. In fact, improving simultaneously the quality and quantity will also be the key to making progress in the future.
The disentanglement of the all-particle energy spectrum into that of individual mass groups from about 1015 eV to 1017 eV, most notably by KASCADE and KASCADE-Grande, has provided new insights into the origin of the knee and ankle and will be discussed in section 3.2.2 in the context of the transition from Galactic to extragalactic cosmic rays. The origin of the flux suppression of cosmic rays at highest energies is still debated. The two competing explanations are energy-losses of UHECR in the CMB or nearby sources of UHECR with corresponding maximum acceleration energies (see section 3.2.5).
Identifying individual sources of UHECR would answer that question and remains the ultimate goal of future studies. It can be expected that the arrival directions of light primaries at the highest energies are correlated with UHECR sources located within the GZK sphere. Identifying such sources calls for a precise shower-by-shower determination of the energy and mass of the primary particle to avoid cosmic rays of lower energy diluting the event sample and to avoid heavy primaries, suffering stronger deflections, blurring the source spots in the sky. In both cases, the experimental energy and mass resolution determine the ratio of possibly source-correlated events to background events so that compromises in experimental resolution need to be paid for by larger event statistics, i.e., by larger exposures. Obviously, the steeper the spectrum in the region of interest, the stronger is the effect of spillover. This has been studied in a simplified model in Brümmel et al. (2013), depicted in Figure 8. Here, the blue line represents the energy spectrum observed with 30 % energy resolution from the true parent distribution (shown as dashed line). The red line shows the distribution of events that leak into the region of interest (above the vertical black line) despite having a true energy eV. Assuming all events below Ethresh being isotropic and those above being correlated to sources, 58 % of the events observed above the applied threshold would be isotropic background and dilute the signal. To compensate for this unwanted effect, the applied energy threshold could be increased as is illustrated in the right panel of Figure 8. Increasing the threshold of a 30 % energy resolution detector from 1019.63 eV to 1019.83 eV would yield the same “signal purity” as a 10 % energy resolution detector has reached at 1019.63 eV. However, the flux of UHECRs drops at the same time by an increase of a factor of two, so that the relaxation in energy resolution from 10 % to 30 % needs to be compensated by a factor two in exposure. We understand this to be a simplified model, but it serves the general discussion and demonstrates the importance of the effect.
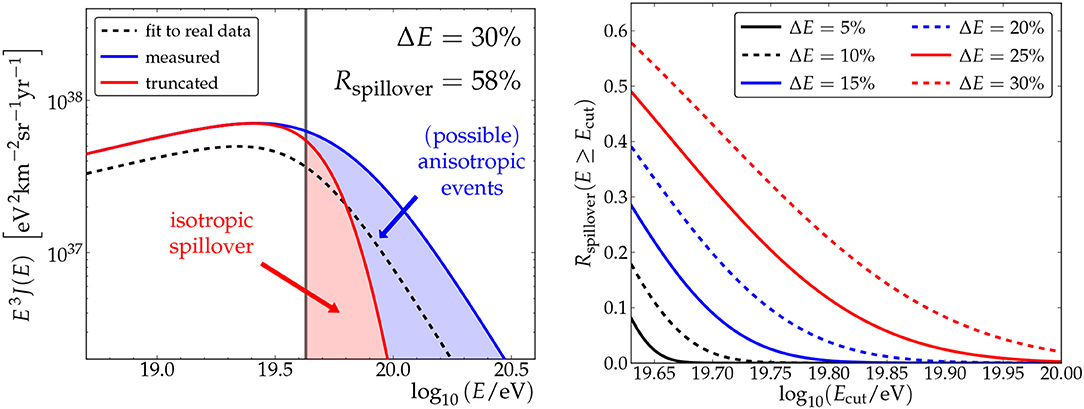
Figure 8. Effect of spillover. Left: The dashed line represents the true energy spectrum, the blue line shows the observed one measured for energy resolution of 30 %, and the red curve shows the distribution of unwanted spillover events leaking into the sample of events above an applied threshold (vertical line). Right: Evolution of the spillover ratio as a function of the cut energy. Shown are ratios for six different energy resolutions. The respective intersection with the y-axis represents the ratio calculated without applying an additional energy cut in data. Reproduced with permission from Brümmel et al. (2013).
3.1.2. Composition at Ultrahigh Energies
As mentioned in section 2.3, the inferred cosmic-ray composition at Earth shows a peculiar dependence on energy (cf. Figure 5). The sequence of alternating groups of elements and the increase of mass with energy could be caused by a Peters cycle (Peters, 1961) at the accelerators, i.e., maximum energy that depends on rigidity R = E/Z or due to photonuclear spallation processes during propagation (e.g., Allard et al., 2007, 2008; Hooper and Taylor, 2010) to Earth and in the source (Unger et al., 2015), leading to scaling with energy per nucleon E/A.
The factor between the maximum fraction of protons and helium in Figure 5 is close to 4, which would favor a spallation scenario. However, the data does not yet constrain the maximum of the N and Fe group and, moreover, a combination of Peters cycle and spallation effects is not excluded. Only the detection of several cycles (if any) will allow for an unambiguous disentanglement of the combined effect of spallation effects from the propagation to Earth and the possible existence of a Peters cycle and/or photonuclear interactions in the source. For this purpose, large-exposure observatories with a good (equivalent or better to current fluorescence detectors) mass resolution is needed.
Another important open question related to mass composition is the evolution of the rigidity R = E/Z with energy. The angular deflections are proportional to θ ∝ 1/R and for an ensemble of different charge-groups with fraction fi and charge Zi it is 〈θ〉 ~ 〈1/R〉 = ∑fiZi/E. The evolution of the average rigidity with energy is shown in Figure 9. As can be seen, the rigidity is increasing with energy and therefore the angular deflection in magnetic fields should decrease with energy, i.e., the increase in the average mass of cosmic rays with energy as shown in Figure 5 is slow enough to not outrun the increase of energy. No high-quality data currently exists at ultrahigh energies where hints for anisotropies at intermediate scales were reported. Note that the average logarithmic mass derived from 〈Xmax〉 is not enough to determine the rigidity, because the mass-to-charge ratio is 1 for protons and ~ 2 for other elements.
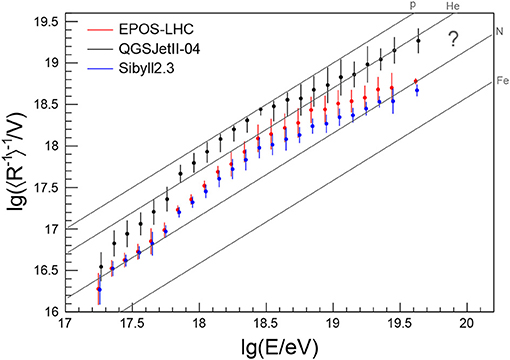
Figure 9. Evolution of the UHECR rigidity with energy using the composition fractions estimated from Auger data in Bellido (2018) and Aab et al. (2014b) using air shower simulations with different hadronic interaction models. M. Unger for this review.
3.2. Astrophysics
3.2.1. Origin of the Bulk of UHECRs
The challenge of accelerating cosmic rays to 1020 eV was succinctly presented in the form of the minimum requirement for the accelerators, in what is now commonly referred to as the “Hillas condition” (Hillas, 1984). It states that a necessary condition to accelerate particles to ultrahigh energy is that of confinement; particles can stay in the acceleration region as long as their Larmor radius is smaller than the size of the accelerator. Thus, the maximum energy achievable, Emax, in a source with characteristic size, R, and magnetic field strength, B, is, Emax = eBR. Here, R = l · Γ, with l the comoving size of the source, and Γ the Lorentz factor of the motion, which is thought to be Γ ~ 10 − 50 in AGN jets (e.g., Lister et al., 2019), and Γ ~ 10 − 1, 000 in GRBs.
For acceleration in a shock with velocity βsh (in units of the speed of light), the maximum achievable energy is,
where η parametrises the efficiency of acceleration, with η = 1 the maximum achievable efficiency when diffusion proceeds in the Bohm limit.
The confinement condition is not sufficient to guarantee cosmic-ray acceleration to 1020 eV. This depends on the details of the acceleration mechanism and the timescale for energy loss in the source environment. A summary of constraints on astrophysical sources based on the Hillas condition was presented in Ptitsyna and Troitsky (2010).
Figure 10 shows classes of objects in terms of the product of their radial size, R, magnetic field strength, B, and associated uncertainty in the ideal limit where η = 1. The solid diagonal lines show the minimum product of BR required to accelerate protons (red) or iron nuclei (blue) to 1020 eV for a fast shock where βsh = 1. Classes of objects to the left of the lines do not satisfy the Hillas criterion. As shown with the dashed diagonal lines, the required product of BR is higher for slower shocks (βsh = 0.01 is shown for illustration). The plot reveals that normal galaxies, supernovae, and stars that drive massive magnetized winds such as Wolf-Rayet stars do not satisfy the confinement condition. For the other source classes in the plot, the confinement condition is satisfied.
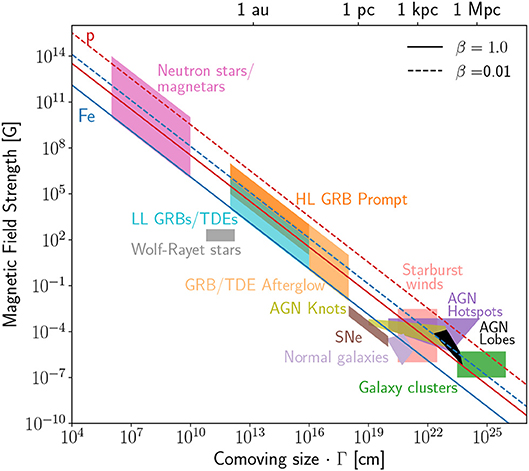
Figure 10. Hillas diagram. Source classes are shown as function of their characteristic size, R, and magnetic field strength, B, in the ideal, Bohm limit, where η = 1. Quoted values of B are in the comoving frame of the source. The abscissa gives R, the radius from the engine, which is equal to comoving size of the source times the Lorentz factor of the flow, Γ. Solid (dashed) lines indicate the BR product beyond which confinement of protons (red) and iron (blue) nuclei with energy 1020eV are possible for outflows with velocity, βsh = 1 (βsh = 0.01). Inferred values of B and R for low-luminosity gamma-ray bursts (LL GRBs) and high-luminosity GRBs (HL GRBs) are from Piran (2005) and Murase et al. (2008b). For tidal disruption events they are based on the prototypical jetted-TDE Swift J1644+57 (Burrows et al., 2011; Kumar et al., 2013; Senno et al., 2017), for starburst galaxies and normal galaxies they were estimated in Thompson et al. (2006). Inferred values of B and R for AGN lobes, hotspots, and knots, were presented in Kataoka and Stawarz (2005) and summarized in Ptitsyna and Troitsky (2010). For galaxy clusters, we used the inferred value range from Ptitsyna and Troitsky (2010). Inferred B and R values for supernovae were collected from Reynolds et al. (2012), Asvarov (2014), and Thompson et al. (2009) and for Wolf-Rayet stars from de la Chevrotière et al. (2014). For neutron stars and magnetars the quoted values of B, and R correspond to the expected UHECR acceleration sites in Arons (2003), Murase et al. (2009), and Fang et al. (2012). F. Oikonomou and K. Murase for this review.
Another condition that must be met by UHECR accelerators is that they must possess the required energy budget to produce the observed UHECR diffuse flux. The energy production rate of UHECRs has been estimated in Waxman (1995b), Berezinsky et al. (2006), Katz et al. (2009), and Murase and Takami (2009) under the assumption that UHECRs are extragalactic protons. Most recently the energy production rate of UHECRs was estimated in Aab et al. (2017d), where a combined fit to the all-particle spectrum and Xmax distributions at energy 5 × 1018 eV and beyond measured at the Pierre Auger Observatory was performed. Here, a mixed injected composition was allowed. The best-fit model corresponds to a UHECR energy-production rate, . The true value of the UHECR energy budget depends on the source-by-source injected spectrum, composition, and luminosity density evolution of the sources, and may differ from that of Aab et al. (2017d). Further, the inferred UHECR production rate depends on the chosen energy range (see e.g., Murase and Fukugita, 2018). Most estimates converge to .
Figure 11 shows the energy budget of various source classes based on infrared, radio, X-ray, and gamma-ray observations, and compares it to the UHECR production rate estimated in Aab et al. (2017d). We used characteristic luminosities for each source type and the luminosity density at z = 0, motivated by the fact that locally observed UHECRs must originate in nearby sources located at ≲ 100 Mpc. The solid diagonal line shows the required energy budget to power observed UHECRs assuming that the UHECR luminosity of the sources, Lcr, is equal to the luminosity of the sources in the wavelength studied, Lγ. Sources to the left of the line do not satisfy the energy budget condition. The UHECR luminosity of individual sources need not be equal to their radiative luminosity. In the absence of knowledge of the relation between the two, we show for illustration dashed diagonal lines for the condition LCR = 0.1 × Lγ and LCR = 10.0 × Lγ. Note that the Hillas criterion imposes an independent lower limit on the magnetic luminosity of a UHECR source as shown in Equation (4) [see relevant discussion in Lemoine and Waxman (2009); Fang and Kotera (2016)].
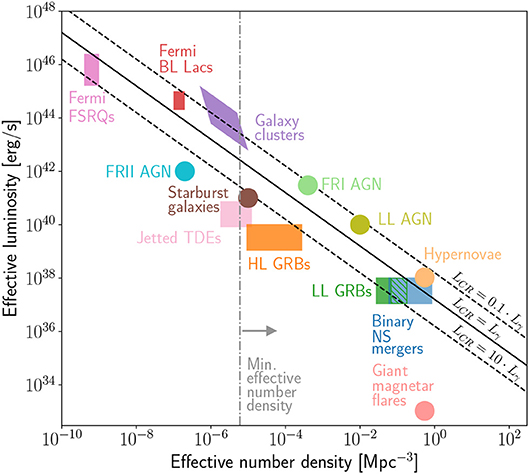
Figure 11. Characteristic source luminosity vs. source number density for steady sources, and effective luminosity vs. effective number density for transient sources assuming a characteristic time spread, τ = 3 × 105 yr. The effective number density for bursting sources is only valid for the assumed value of τ, which corresponds to mean extragalactic-magnetic-field strength of 1 nG. Stronger magnetic fields would imply larger τ and hence, larger effective number density. The black solid line gives the best-fit UHECR energy production rate derived in Aab et al. (2017d), which corresponds to 5 × 1044 erg Mpc−3 yr−1. The gray horizontal line gives the lower limit to the UHECR source number density estimated in Abreu et al. (2013). For beamed sources, the “apparent” number density and luminosity are shown meaning that no beaming corrections have been applied to the luminosity or number density. The quoted characteristic luminosity and local burst rate for HL and LL GRB rates are based on the X-ray luminosity functions of Guetta and Piran (2007) and Liang et al. (2007), respectively. In the case of LL GRBs the hatched lines show that the true rate could be larger than the quoted uncertainty of Liang et al. (2007) and should be comparable to that of binary neutron star mergers. For binary neutron star mergers we used the LIGO estimate (Abbott et al., 2017b). The rate of magnetar flares quoted follows the estimate of Murase and Takami (2009). For blazars, the quoted values are based on the gamma-ray luminosity as estimated by Ajello et al. (2014), at z = 0. For low-luminosity AGN, we used the median values derived in Ho (2008) based on Hα luminosities. For galaxy clusters, we used the estimated rate at z = 0, based on the X-ray luminosity functions of Warren et al. (2006) and Inoue (2011). For starburst galaxies, we used the infrared luminosity density derived in Gruppioni et al. (2013). For FRI and FRII AGN, we used the radio luminosity functions of Urry and Padovani (1995). For TDEs, the local burst rate was estimated in Sun et al. (2015). For hypernovae we quote 10% of the kinetic energy estimate of Murase and Fukugita (2018) and the burst rate of Guetta and Della Valle (2007). F. Oikonomou for this review.
The orange dashed line gives the minimum source number density constraint, which comes from the analysis of arrival directions of UHECRs detected in Auger of Abreu et al. (2013). The lack of significant clustering in the arrival directions of UHECRs with energy exceeding 70 EeV was used to derive a lower limit to the UHECR source number density, considering that UHECRs might have suffered deflections as large as 30°. Classes of steady sources to the left of the orange diagonal line do not satisfy the source number density constraint, unless UHECR deflections are significantly larger than investigated in Abreu et al. (2013).
In order to compare the energy budget constraint to the energy budget of transient source classes, the observed burst rate, ρ, must be converted to the effective number density for UHECRs, neff = (3/5)ρ · τ (see e.g., Murase and Takami, 2009), with τ the apparent burst duration of the UHECR burst (Waxman and Miralda-Escude, 1996),
where D is the distance traveled by the UHECR, λ the correlation length of the regular magnetic field, and Z the atomic number of the UHECR nucleus. Similarly, the effective luminosity can be estimated by modulating the burst fluence by τ. Figure 11, also shows the effective luminosity and number density for transient sources, where we have used τ = 3 × 105 yr. The effective number density shown for bursting sources is only valid for the assumed value of τ, which corresponds to mean extragalactic magnetic field strength 1 nG. Stronger magnetic fields would imply larger τ and hence, larger effective number density. In this case, the bursting sources satisfy the number density constraint more comfortably, but the effective luminosity also decreases so the comparison with the energy-budget constraint does not change. On the other hand, τ cannot be arbitrarily small. A lower limit comes from the time spread induced from the coherent component of the Galactic magnetic field, τmin ~ 300 − 3, 000 years (see Murase and Takami, 2009 for details).
Below, we discuss the most plausible UHECR-source candidates in turn.
Gamma-ray bursts and energetic supernovae. Gamma-ray bursts are during their short lives some of the most spectacularly bright objects in the sky. They have long been discussed as likely sites of UHECR acceleration (Vietri, 1995; Waxman, 1995a). In general, GRBs are thought to easily satisfy the maximum energy requirement (see however Samuelsson et al., 2018). Inspection of the energy budget diagram reveals that high-luminosity GRBs are roughly consistent with the energy budget requirement, though on the low side. As cautioned earlier, the UHECR energy budget is uncertain and consistent with being ten times lower than the model shown in Figure 11 as a benchmark.
Low-luminosity GRBs, which are a less-well-known source population, seem to occur with a much larger rate locally than high-luminosity GRBs. They are appealing as sources of UHECRs (Murase et al., 2006; Liu et al., 2011) as the relatively milder radiation fields with respect to those of high-luminosity GRBs would better allow the survival of UHECR nuclei. Several articles have addressed the conditions of acceleration and survival of nuclei in high-luminosity (Murase et al., 2008b; Wang et al., 2008; Horiuchi et al., 2012; Baerwald et al., 2015; Globus et al., 2015), and low-luminosity GRBs (Murase et al., 2008b; Horiuchi et al., 2012; Boncioli et al., 2018; Zhang et al., 2018) and find regimes in which GRBs could power all the observed UHECRs and be consistent with the UHECR composition measurements.
Though standard supernovae are not expected to be able to accelerate cosmic rays to ultrahigh energies, the ejecta of trans-relativistic and engine-driven supernovae which typically reach mildly relativistic speeds may also be able to accelerate UHECRs (Wang et al., 2007; Chakraborty et al., 2011; Liu and Wang, 2012; Fang et al., 2018; Zhang and Murase, 2018). A feature of GRB and engine-drive SN models is that the composition resulting from stellar evolution models can explain the UHECR composition data observed by Auger.
In 2017 the detection of gravitational waves from the merger of a neutron star binary, followed by a short GRB and electromagnetic emission from the remnant marked the discovery of this, long-sought-for, class of events (Abbott et al., 2017a,b). In Rodrigues et al. (2019) it was shown this class of sources could be producing the cosmic rays observed right below the ankle. On the other hand, Kimura et al. (2018a) showed that the tail of the Galactic cosmic-ray spectrum around the second knee can be explained by remnants of Galactic neutron star mergers.
A brief mention to the winds of Wolf-Rayet stars is also due here. Though inspection of Figure 10 reveals that the winds of these sources likely do not satisfy the Hillas criterion for 1020 eV UHECRs, (see however Biermann and Cassinelli (1993) for a different view) the magnetized, powerful winds they drive have been proposed as possible acceleration sites of cosmic rays up to 1018 eV and could thus be responsible for the end of the Galactic cosmic-ray spectrum (Thoudam et al., 2016; Murase and Fukugita, 2018).
Active galactic nuclei. Active galactic nuclei (AGN) with powerful jets have long been considered as promising candidate sources of UHECRs. AGN with jets pointing to the Earth, referred to as blazars, would be the natural candidates if UHECRs escape the sources beamed and do not suffer severe deflections (Dermer and Razzaque, 2010; Resconi et al., 2017; Rodrigues et al., 2018). The signature of UHECR acceleration could be detectable in the gamma-ray spectra of blazars (Gabici and Aharonian, 2005; Essey and Kusenko, 2010; Essey et al., 2010; Kotera et al., 2011; Murase et al., 2012; Prosekin et al., 2012; Aharonian et al., 2013; Takami et al., 2013; Oikonomou et al., 2014; Tavecchio, 2014). However, the present-day density of nearby blazars shown in Figure 10 suggests that blazars alone do not satisfy the number density constraint. On the other hand, radio galaxies, the parent population of blazars (BL Lacs and FSRQs) with jets pointing away from the line of sight, are also UHECR source candidates, with Cen A, the nearest radio galaxy, a long standing candidate (Rachen and Biermann, 1993; Romero et al., 1996; Atoyan and Dermer, 2008; Dermer et al., 2009; Gopal-Krishna et al., 2010; Biermann and de Souza, 2012; Wykes et al., 2018). In recent literature, several models have been proposed, which show that the observed UHECR flux and composition can be produced by radio-galaxies under different assumptions about the acceleration mechanism at the sources, namely shear (Kimura et al., 2018b) and “one-shot” re-acceleration (Caprioli, 2015). The re-acceleration models can explain the nucleus-rich composition data observed by Auger.
In jetted AGN, a lot of the power goes to energizing the lobes, which are very extended features with relatively small magnetic fields (B ~ 10−5 G) and proposed sites of UHECR acceleration (Takahara, 1990; Rachen and Biermann, 1993). It was recently shown in Matthews et al. (2019) with hydrodynamical simulations that acceleration to 1020 eV is possible in these regions, and in Eichmann et al. (2018); Matthews et al. (2018) that nearby radio galaxies are strong UHECR candidates.
In addition, radio-quiet, low-luminosity AGN and quasar outflows have been discussed as possible sources of UHECRs (Pe'er et al., 2009; Duan and Caramete, 2015; Wang and Loeb, 2017). These are less powerful individually than jetted AGN but significantly more numerous.
Tidal disruption events. Stars that pass within the tidal radius of a super-massive black hole are disrupted and a large fraction of the resulting debris gets accreted onto the black hole. If the disruption occurs outside the black hole horizon a luminous flare of thermal emission is emitted and in a fraction of these events a jet forms (Hills, 1975; Rees, 1988). Only a handful of jetted TDEs have been observed to date, whereas the total number of known and candidate TDEs is at present close to 100. It was shown in Farrar and Piran (2014), based on the analysis of the prototypical jetted-TDE Swift J144+57, that jetted-TDEs can likely produce the bulk of observed UHECRs. The expected UHECR output from TDEs was more recently studied in Zhang et al. (2017), Dai and Fang (2017), Biehl et al. (2018), and Guépin et al. (2018) in the internal shock model. The above analyses conclude that given the relatively low inferred rate of jetted TDEs based on Swift data, whether the energy-budget constraint is satisfied depends intricately on the relation between the TDE radiative luminosity and UHECR luminosity. Based on theoretical arguments Farrar and Piran (2014), Biehl et al. (2018) showed that the energy-budget constraint is likely satisfied, despite the apparent failure of TDEs to satisfy the constraint based on the Swift data as shown in Figure 11.
Intermediate-mass black holes may also tidally disrupt stars. Depending on the combination of masses of both objects, tidal squeezing may trigger nuclear burning in the core of white dwarfs, leading to a supernova and potentially accelerating cosmic rays to ultrahigh energies (Alves Batista and Silk, 2017; Zhang et al., 2017; Guépin et al., 2018).
Starburst galaxies. Starburst galaxies are galaxies that are undergoing intense star-formation activity, typically demonstrated by infrared luminosities > 10 times higher than normal galaxies. They are observed to drive powerful, magnetized “winds” (nuclear outflows), which might be sites of high-energy particle acceleration (Anchordoqui et al., 1999). The maximum UHECR energy that can be achieved in the wind driven by starburst galaxies was recently studied in Anchordoqui (2018); Romero et al. (2018) and Murase and Fukugita (2018), with conflicting conclusions as to the feasibility of UHECR acceleration in starburst winds. Another natural possibility is that UHECR acceleration can occur in the disproportionately frequent extreme explosions that take place in starburst galaxies due to the high star-formation activity. These include low-luminosity gamma-ray bursts, trans-relativistic supernovae, and hypernovae, which do not have to occur only in low-metallicity environments (Zhang and Murase, 2018; Zhang et al., 2018).
Galaxy clusters. Galaxy clusters, the largest bound objects in the Universe, have also been considered as possible sites of UHECR production (Kang et al., 1997; Ryu et al., 2003; Murase et al., 2008a; Kotera et al., 2009). Though they possess moderate magnetic fields ~ μG (see e.g., Kim et al., 1991; Carilli and Taylor, 2002) they are extremely extended ~ 2 − 3 Mpc, and should thus be able to confine particles to extremely high energies (Fang and Olinto, 2016). Galaxy clusters could otherwise act as “reservoirs” which contain sites of UHECR acceleration, for example, jetted AGN (Murase et al., 2008a; Kotera et al., 2009; Fang and Murase, 2018).
Pulsars. Pulsars, the smallest and most highly-magnetized objects shown in Figure 10, induce strong magnetic potentials that can potentially also accelerate UHECRs (Gunn and Ostriker, 1969; Blasi et al., 2000; Arons, 2003; Murase et al., 2009; Philippov and Spitkovsky, 2018). Since they are the product of the death of massive stars and shrouded by a remnant enriched in heavy elements, it has been shown that they may produce UHECRs rich in nuclei (Fang et al., 2012, 2013).
3.2.2. Galactic to Extragalactic Transition
The cosmic-ray spectrum features three distinct spectral breaks in the energy range between 1015 and 1018eV. In order of increasing energy, these are the “knee,” “second-knee” (or “iron-knee”) and “ankle,” illustrated in Figure 12. Below we discuss the origin of each of the three features and viable scenarios for the transition between Galactic and extragalactic cosmic rays.
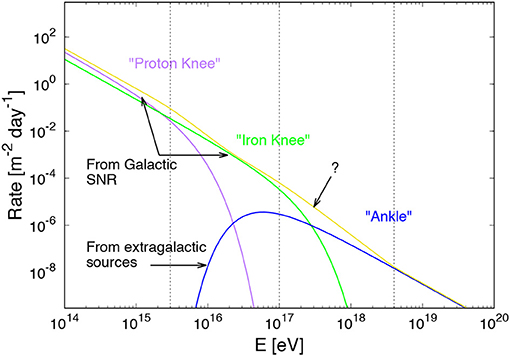
Figure 12. Schematic illustration of the rate of cosmic rays incident on Earth as a function of energy, and the three distinct spectral breaks which can be seen in the cosmic-ray spectrum in this energy range, the proton knee, second knee, and ankle. A. Taylor for this review.
The physical origin of the knee feature remains unclear. Both a propagation and sources maximum energy origin of this feature remain viable candidates. An outline of these two scenarios is given below.
Propagation origin of the knee. Galactic cosmic rays are believed to diffuse within the Galactic magnetic turbulent sea. Within the plane of the Galactic disk, the dominant drivers of this MHD turbulence are believed to be supernova remnants (SNR), which inflate bubbles tens of parsec in size, driving magnetic turbulence on this scale (λmax). Although turbulence is driven on such a scale, it subsequently cascades down to smaller wave modes, eventually terminating at the dissipation scale, λmin.
Assuming that cosmic rays of a given Larmor radius rLar predominantly scatter resonantly from magnetohydrodynamic (MHD) turbulent modes λ of the same size (i.e., rLar = λ), the multi-PeV energy scale denotes the energy range at which the abundance of such modes diminishes rapidly. PeV cosmic-ray protons in ~ μG Galactic magnetic fields possess Larmor radii of 1 pc. The PeV energy scale is therefore motivated to denote the energy range in which CR diffusion within the Galactic disk magnetic field becomes inefficient (i.e., rLar ~ λmax) (Giacinti et al., 2014). In such a scenario, the confinement of cosmic rays at higher energies becomes significantly less efficient, giving rise to a steepening of the cosmic ray spectrum capable of explaining the shape of the knee feature. More generally, any scenario in which a change in the transport regime occurs leading to inefficient confinement can also lead to this feature ( e.g., the transition from diffusive propagation to particle drift Ptuskin et al., 1993).
It is important to note, however, that such propagation origin scenarios for the knee make a considerable implicit assumption. For these scenarios it is necessary that luminous Galactic cosmic ray sources exist, capable of accelerating particles to energies well beyond the knee energy. Within the framework of our current understanding of Galactic SNR accelerators, however, such an assumption presents a considerable challenge (Bell et al., 2013). Indeed, presently, the only known Galactic source capable of achieving acceleration to the PeV scale is Galactic nucleus, Sgr A* (Abramowski et al., 2016), whose cosmic ray luminosity at these energies appears to be rather low (see e.g., Fujita et al., 2017).
Maximum-energy origin of the knee. Alternative to this propagation origin of the knee is the possibility that the PeV energy scale denotes the maximum energy of their Galactic sources, believed to be SNRs. An application of the Hillas criterion in Equation (1) to SNR gives a maximum energy of,
where the factor η describes how close to Bohm diffusion the maximum energy particles in the source achieve, βsh is the shock velocity in units of c, B is the magnetic field in the acceleration region and R is the size of the source. Equation (3) indicates the need for considerable magnetic field enhancement to occur in order for such sources to act as effective PeVatron candidates. Such an enhancement may occur by the Bell mechanism (Bell, 1978a,b) in which CR accelerated by the SNR run ahead of the shock, whose current drives an instability in the upstream medium enhancing the upstream magnetic field present. Furthermore, observationally, there is now growing evidence that such magnetic field enhancement takes place within these sources. However, whether SNRs are actually able to accelerate up to the knee energy (3 PeV) remains an open question.
In either the propagation or maximum-energy scenario which describes the origin of the knee feature at 3 PeV, a family of corresponding knee features for the other nuclear species are naturally expected. Observationally, it remains unclear whether the composition of CRs at the energy of the knee feature (3 PeV) are protons, helium, or heavier species. Assuming the composition of the knee to be dominated by protons (i.e., a proton knee at 3 PeV), a corresponding iron knee feature at 100 PeV would be expected. Observational evidence for such a second knee feature was reported from the analysis of the KASCADE-Grande data (Apel et al., 2011).
On theoretical grounds, it remains extremely challenging for known Galactic CR accelerators to accelerate protons above PeV energies. The known magnetic field amplification scenarios place a hard cap for maximum energies achievable by SNR (Bell et al., 2013).
In addition, the low level of anisotropy of cosmic rays in the energy range 1017 − 1018 eV also disfavors a Galactic origin of any light component in this range (Abreu et al., 2012; Giacinti et al., 2012).
At energies at/just above that of the second knee, observational evidence suggesting the onset of a new component in the light composition spectrum is found in the KASCADE-Grande data, referred to as the proton ankle. Evidence pointing in this direction is also supported by the low-energy Auger HEAT Xmax data, which show a lightening in the composition above 100 PeV. If the interpretation of these observational results is correct, the onset of this new light component marks the beginning of an extragalactic component in the arriving CR flux. Such an interpretation has considerable implications, which provide the possibility to shed new light on the extragalactic origins of these protons.
Extragalactic cosmic-ray protons at EeV energies undergo frequent Bethe-Heitler energy loss interactions with CMB photons, losing their energy through this process on Gyr timescales. These losses give rise to electron/positron pairs, , which subsequently feed electromagnetic cascades, with the energy flux cascading down to energies below 100 GeV, contributing to the diffuse gamma-ray background, particularly since such a source evolution allows for a Fermi type source injection spectrum (Taylor et al., 2015). Recent improvements in our understanding of the contributions to this background constrain the allowed level of these losses, which could prefer scenarios with negative evolution, i.e., that these extragalactic cosmic rays have a small filling factor in extragalactic space (Liu et al., 2016) (but see also e.g., Fang and Murase, 2018).
3.2.3. Source Identification Beyond the Ankle
The large-scale anisotropy discovered beyond the ankle by the Pierre Auger Observatory appears to be consistent with the distribution of extragalactic matter traced by near-infrared observations from 2MASS (Aab et al., 2017b). This can be seen as the first observational evidence, also supported by theoretical expectations, for UHECRs beyond the ankle originating from extragalactic sources. Most likely, not all galaxies behave as UHE accelerators, so that the question of which galaxies or galaxy types host UHE accelerators remains open.
Cross-correlation with catalogs of objects observed throughout the electromagnetic bands has proven a powerful means to address the question of possible associations. Such searches recently hinted (3–4σ) at a fraction of 10–15% of UHECR events being consistent with the directional and flux distributions expected from either extragalactic matter—traced by 2MASS or Swift-BAT X-ray observations—or specific types of extragalactic sources—starburst galaxies and jetted AGNs—traced by their radio and gamma-ray emission (Abbasi et al., 2018b). Even if such an anisotropic signal reached the 5σ discovery threshold in the near future, it probably would not be sufficient to claim identification of UHECR sources. As correlation does not imply causation, a necessary condition for an identification of some or all the sources would be to leave as little room as possible for a confounding variable, that is, a hidden variable causing a spurious correlation. Such a feat would require coverage over the entire celestial sphere—to avoid blind regions where a different source type could contribute—constraints on the redshift evolution of the UHECR production rate—to enable a tomographic probe of source populations—and completeness in the source models up to the propagation horizon and down to a sufficiently low luminosity.
Ground-based observations come with a partial view of the celestial sphere. Nonetheless, attempts at full-sky coverage by combining data from the largest Northern and Southern observatories have been performed by the Pierre Auger and Telescope Array Collaborations. Such an approach is limited by the mismatch in energy scale between the two experiments, which could cause spurious anisotropies due to an improper contrast between the flux inferred from each dataset. The collaborations have designed a method to match the flux in the declination band covered from both sites, providing a common view on the UHECR sky beyond the ankle and above the flux suppression (Aab et al., 2014d; Biteau et al., 2018; di Matteo et al., 2018). Future tests against catalogs with such a dataset could prove informative regarding correlations with extragalactic sources. Moreover, the ongoing upgrade of the Telescope Array, aimed at increasing the effective area of the observatory by a factor of 4 (Sagawa, 2016), will significantly reduce the contrast between the Northern and Southern exposures. Space-based observations with sufficient angular resolution could provide in the mid-term future a complementary approach to avoid UHECR blind spots over the celestial sphere.
Most current anisotropy studies exploit the arrival directions of UHECR events above a given (or scanned) energy threshold. This information could be supplemented by spectral and composition data to perform tomography of the UHECR production rate. Propagation of nuclei of different species affects the expected composition and spectrum as detected on Earth. Combined fits of the spectral and composition data show constraining power on the evolution of the density of sources at a fixed a luminosity (see e.g., Aab et al., 2017d). Constraints on composition are mostly inferred from fluorescence data, limited in statistics beyond few tens of EeV. With the upgrade of the Pierre Auger Observatory, the joint detection of showers with scintillators and water tanks will provide a composition-dependent observable with nearly 100% duty cycle (Aab et. al., 2016b). The selection of a “light” component, expected to be more localized than heavier nuclei, or the development and fit of models accounting for different propagation effects through diffuse photon and magnetic fields for different species could provide a clearer view on the population of sources (Alves Batista et al., 2015; Boulanger et al., 2018). Finally, interesting new approaches have emerged that aim to jointly model the UHECR spectrum and arrival directions, suggesting the possibility to associate a larger fraction of events to sources in catalog-based studies when accounting for the energy on an event-by-event basis (e.g., Farrar, 2008; Capel and Mortlock, 2019). These recent works suggest the possibility in the mid-term future to design analyses jointly accounting for the energy, composition, and arrival directions of UHECRs. This could for the first time enable a three-dimensional probe of the UHECR production rate, to be compared to the distribution of sources in the nearby Universe.
Assuming that sources of UHECRs also accelerate electrons radiating photons in a relativistic flow with speed β and bulk Lorentz factor Γ, the Hillas condition imposes a minimum photon luminosity Lγ which reads, under the assumption of equipartition between electrons and the magnetic field (Blandford, 2000; Lemoine and Waxman, 2009):
where the rigidity E/Z is currently estimated to be in the range 1018 − 1019 V beyond the ankle and where Γ2/β can range down to 10 for a mildly relativistic shock with β = 0.1 and Γ2/β = 100 either for Γ ~ 10, typical of blazar jets on pc scales, or for β ~ 10−2, typical of starburst winds. UHECRs beyond the ankle could originate from sources up to about a Gpc. Then, the condition in Equation (4) corresponds to a minimum detectable flux for a full-sky electromagnetic survey at the level of , matching the current sensitivity limits of full-sky surveys from, e.g, Fermi-LAT in the gamma-ray band or WISE in the infrared1. It thus appears that a census of potential UHECR sources beyond the ankle based on some electromagnetic full-sky surveys could be at hand. Two hurdles limit this statement. The first one is the sensitivity to extragalactic sources behind the Galactic plane, which acts as a strong foreground. The second one lies in the lack of full-sky spectroscopic surveys providing redshift information down to photometric sensitivity limits. While significant progress has been made in constraining the redshift distribution from electromagnetic surveys (see e.g., Bilicki et al., 2016; Cuoco et al., 2017 for recent contributions), further efforts may be needed to identify the best tracers of UHECR sources in a tomographic manner, accounting for incompleteness and possible contamination in every corner of the visible UHECR Universe.
3.2.4. Steady and Transient Sources
All known non-thermal sources are transient on some timescale. For UHECR sources, what defines whether a candidate object is classified as a transient or steady source is the ratio of the mean propagation timescale between sources to the source emission timescale, tprop/temiss. For steady (transient) sources this ratio is < (>) 1. Both quantities, tprop and temiss, are dependent on the UHECR energy.
The propagation timescale depends on the mode by which UHECRs propagate, which itself depends on the distance between sources and the UHECR scattering length. For a given source density, a CR energy can be found for which the distance between sources matches the cosmic-ray scattering length in the turbulent medium it is propagating through (Kotera and Lemoine, 2008b; Takami and Murase, 2012). Below this energy, cosmic rays propagate between sources on timescales significantly longer than than the ballistic propagation time.
The source emission timescale, temiss, is dictated by the collective timescale for particle acceleration, escape, and losses. On energetic grounds, only efficient Fermi acceleration (η ≲ 10) in sites associated to particular regions in AGN and GRB outflows satisfy the Hillas criterion in order to be considered as potential UHECR sources (see Equation 3). Much of what we know about these classes of astrophysical accelerators and their acceleration efficiency comes from the observation and analysis of their non-thermal emission (Murase and Takami, 2009).
For AGN, the longest timescale which may be associated to particle acceleration is the jet activity timescale, estimated to be of the order 300 Myr (Wykes et al., 2013). However, much shorter variability timescales are observed in the very-high energy gamma-ray (VHE,>100 GeV) emission of AGN. Studies of distant bright AGN sources over long epochs indicate that these objects release roughly an equal amount of power in logarithmic variability time bins over all epochs currently probed, from ~100 year down to daily timescales (Abdalla et al., 2017).
For GRBs, extensive efforts to detect VHE gamma rays have until recently failed to achieve a detection (Mirzoyan, 2019). Currently, the published record for the highest-energy emission observed is that seen at energies close to 100 GeV by Fermi-LAT, from the brightest GBM (in fluence) GRB event GRB130427A. The timescale for this emission was < 1,000 s. These results leave unclear whether GRBs operate as efficient particle accelerators (i.e., close to the Bohm limit), and on what timescale the acceleration takes place on. It therefore remains unclear whether these objects can be considered as viable UHECR sources.
Adopting a fiducial distance between sources of ~ 10 Mpc, a ballistic propagation time between sources of 30 Myr sets a lower limit to the actual propagation time. Adopting the 300 Myr AGN jet activity timescales as a fiducial value for temiss, only cosmic rays which diffusively scatter on a length scale >1 Mpc will contribute to the total flux as a steady-state contribution.
The above example demonstrates that the flux from any source class of a similar number density whose emission timescale is significantly shorter than a Myr will almost certainly be transient, and unable to achieve steady state. Furthermore, steady-state emission at low energies eventually becomes invariably unachievable for all source classes, once the diffusive sphere of cosmic rays around each source ceases to overlap with even neighboring sources—a phenomenon referred to as the magnetic horizon.
At high energies, energy losses during propagation affect whether the flux can achieve steady-state or not through a reduction of temiss. Should the reduction in this timescale lead to tprop/temiss > 1, the flux at high energies will not be in the steady-state regime. Indeed, it is possible for a source class to only achieve steady-state emission in a finite energy range, both below and above which the cosmic-ray flux is only transient.
3.2.5. Origin of the End of the Cosmic-Ray Spectrum
The cut-off at the highest energies in the cosmic-ray spectrum has been established unambiguously recently, but the origin of this most prominent and significant feature is still a matter of debate. It has been tempting to identify the flux suppression with the long-predicted GZK-effect given its close coincidence to the expected threshold energy of about 6 · 1019 eV. Several fits of the end of the cosmic-ray spectrum with a propagated cosmic-ray composition consisting of a single element (p, He, N, Si, or Fe) at the source are shown in Figure 13. Different model lines are for different distances of the closest source and the source evolution was assumed to follow either the star formation rate from Robertson et al. (2015) or the AGN density from Ahlers et al. (2005). The cosmic-ray energy losses in the background photon fields were simulated with the CRPropa package (Alves Batista et al., 2016). In all panels, the spectral index at the source was a free parameter. Introducing additionally the maximum energy at the source as a free parameter (second and fourth panel) the measured spectra at Earth can be described well, no matter what is the composition at the source. However, “pure” GZK scenarios (first and third column) for which the maximum energy was fixed to 1022 eV and the flux suppression is only due to propagation effects do not fit the flux measured by the Pierre Auger Observatory well with the exception of Fe. For the TA measurement, which has larger statistical uncertainties and a higher energy scale, the GZK scenarios fit reasonably well.
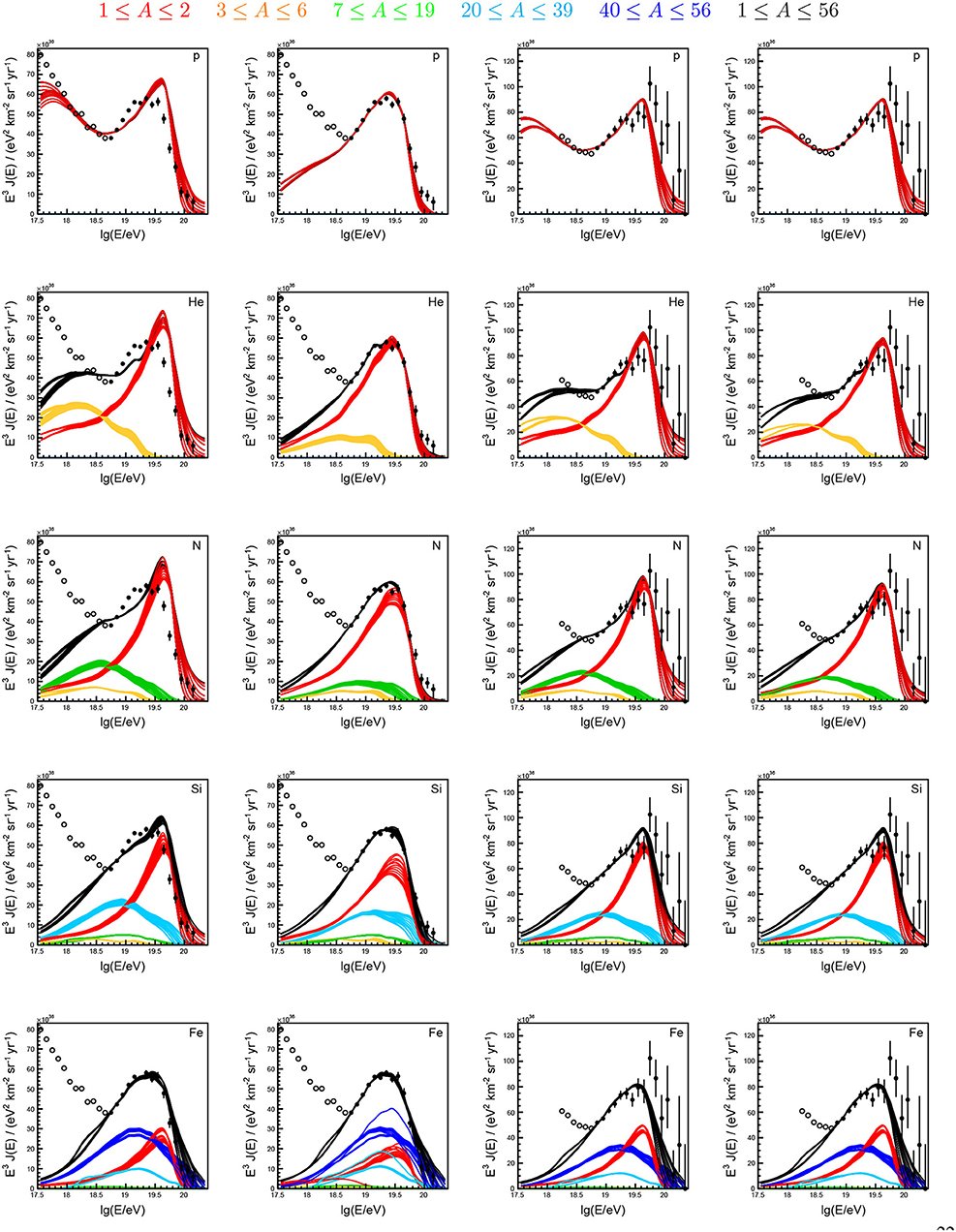
Figure 13. Illustration of pure GZK scenarios (free injection index, maximum energy fixed at 1022 eV, first and third column) and scenarios with a freely floating maximum energy (free injection index and maximum energy, second and fourth column) for different primary masses. The first and second columns are for the Auger measurements of the flux (Abraham et al., 2008) and the third and fourth column for TA (Abbasi et al., 2018e). Open symbols were not used in the fit. Different model lines are for different distances of the closest source (1 Mpc to 100 Mpc) and for two source evolutions (SFR Robertson et al., 2015 and AGN Ahlers et al., 2005). The simulations were performed with CRPropa3 (Alves Batista et al., 2016) using the EBL model from Gilmore et al. (2012). M. Unger for this review.
A closer look at GZK scenarios is given in Figure 14, where a subset of fits from Figure 13 is shown. Here the sources are homogeneously distributed in the Universe following the star formation rate and emit pure beams of either protons, nitrogen, or iron nuclei with spectral indices γ chosen to fit the shape of the observed distribution. The source spectra are truncated exponentially at energies above 1022 eV so that the observed cut-off is caused by the GZK-effect. Also shown are the reconstructed compositions from Auger in terms of the mean mass 〈ln A〉 and its variance V(ln A). The lines show the results of the CRPropa simulations for the all-particle energy spectra (left), 〈ln A〉 (middle), and V(ln A) (right) for p, N, and Fe beams emitted from the sources. None of these simulations provides an acceptable description of the Auger and TA data. This is most obvious for the expected and observed compositions but also the simulated and observed all-particle spectra differ: in the Auger data sets, the suppression is below the GZK cut-off and in the TA datesets, all data points are above the GZK cut-off. The results question the interpretation of the flux suppression as caused solely by the GZK effect. While the energy spectra of Auger and TA could be made to agree with the GZK effect if the uncertainties of the energy scales are accounted for—14% in Auger and 21% in TA—the mass compositions of data and simulations for each experiment are totally different.
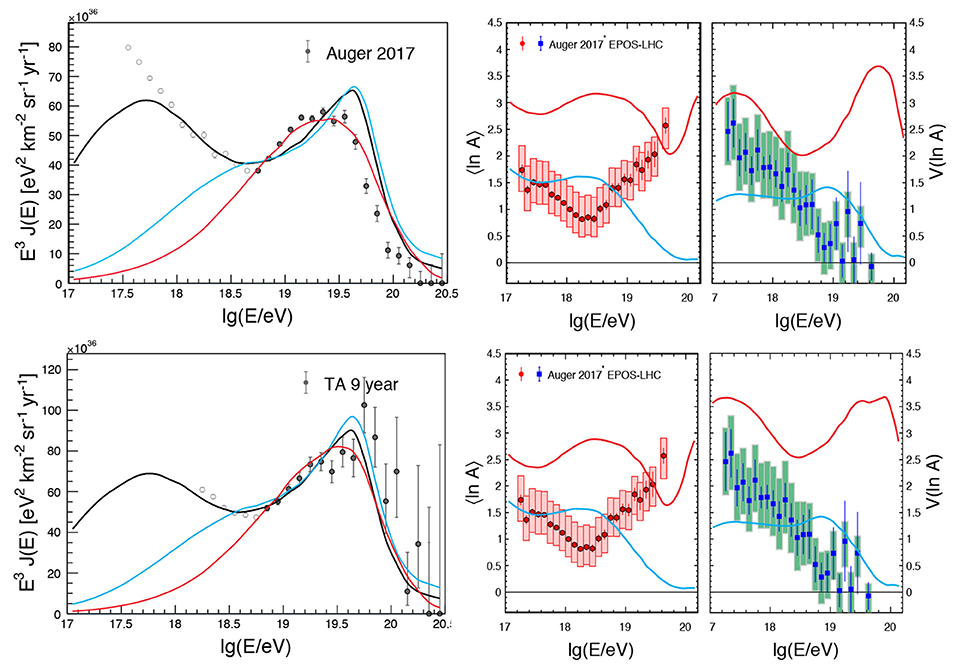
Figure 14. CRPropa simulations of the energy spectrum and composition at Earth for UHECR sources injecting pure beams of protons (black lines), nitrogen (7 ≤ A ≤ 19) (blue lines), and iron-like nuclei (40 ≤ A ≤ 56) (red lines). The sources follow an SFR evolution and their spectra are pure power-law distributions up to 1022 eV. For each of the primary beams, the index is chosen such as to provide the best fit to the data from Auger (Top) and TA (Bottom). K.-H. Kampert and M. Unger for this review.
On the other hand, a simple astrophysical model of identical UHECR sources that accelerate nuclei through a rigidity-dependent mechanism provides a perfect description of the energy spectrum and mass composition above the ankle if the maximum rigidity is at about 1018.8 V, the composition is dominated by intermediate mass nuclei, and the source spectra are harder (γ ≃ 1.6) than expected by the standard Fermi mechanism (Fang et al., 2013; Aab et al., 2017d; Wittkowski, 2018). In such a scenario, the flux suppression is a combination of propagation effects and the maximum energy at the source.
3.2.6. Magnetic Fields
Magnetic fields in scales comparable to and larger than the size of the Galaxy may affect the propagation of UHECRs. Little is known about extragalactic magnetic fields (EGMFs). The mechanisms whereby they originated are broadly divided into two classes, astrophysical and primordial. The latter postulates that fields in the present epoch result from the amplification of seed fields generated through a cosmological process in the early Universe, whereas in the former scenarios astrophysical processes such as feedback by active galaxies and stars would seed the intergalactic medium. Comprehensive reviews on cosmic magnetogenesis can be found in Durrer and Neronov (2013) and Subramanian (2016). Most of the Universe is filled with cosmic voids, whose magnetic fields are poorly constrained, ranging from 10−17G (Neronov and Vovk, 2010), estimated using gamma-ray-induced electromagnetic cascades, up to ~ 10−9G, from CMB measurements (Ade et al., 2016; Jedamzik and Saveliev, 2018). The lower bound, however, has been subject to much controversy (see e.g., Tiede et al., 2017; Broderick et al., 2018). In cosmic filaments, magnetic fields are B ~ nG, and in the center of galaxy clusters, B ~ μG; for reviews (see e.g., Vallee, 2011; Ryu et al., 2012).
The Galactic magnetic field (GMF) is understood better than EGMFs. Observationally driven models have been developed using polarized synchrotron maps, combined with Faraday rotation measurements (RMs) for the regular field and synchrotron intensity maps to derive the random field component. One of the most complete models was developed by Jansson and Farrar (2012a,b)—henceforth JF12. Yet, uncertainties are significant and improvements can be made. For instance, in Terral and Ferrière (2017) different models of the halo field were compared to the rotation measures. Different models for the disk and halo field were also studied in Unger and Farrar (2017) and in addition the uncertainties on the GMF due to the uncertainty of the synchrotron data and models for the thermal and cosmic-ray electrons were quantified. Theory-driven models of the GMF based on MHD simulations of structure formation can also provide complementary information and possibly improve the current picture (Pakmor et al., 2014; Pakmor et al., 2017; Marinacci et al., 2018) or alternatively dynamo-inspired models can be used to describe the large-scale GMF (Shukurov et al., 2018).
A detailed study of the deflection of UHECRs in the GMF model by JF12 has been performed (Farrar and Sutherland, 2017). By backtracking UHECRs at various energies to the edge of the Galaxy, the authors show that deflections for rigidities below 10 EV are large (≳ 90°). They also show that significant (de)magnification occurs for most of the rigidities studied (between 1 and 100 EV). The image patterns formed due to magnetic lensing have a considerable dependence on the ill-constrained turbulent component of the field (see also Battaner et al., 2011).
In Erdmann et al. (2016), the authors investigate UHECR deflections in the JF12 and Pshirkov et al. (2011) models. They point out that for cosmic-ray rigidities higher than 20 EV, these models lead to deflections compatible with each other, except near the Galactic disc (|b| ≤ 19.5°). A similar conclusion was reached by Unger and Farrar (2017) studying a larger ensemble of GMF models (19 variations of the JF12 model). If these different GMF models give a fair representation of the uncertainty of our knowledge of the deflections in the Galaxy, then it might be possible to correct the arrival directions of UHECRs for GMF-deflections above 20 EV.
Due to the lack of observationally derived models for the distribution of EGMFs in the local Universe, most studies of the kind have been done using cosmological simulations of structure formation. Early works by Sigl et al. (2003a,b) and Dolag et al. (2005) have reached conflicting conclusions regarding the role played by EGMFs on UHECR deflections. The latter concluded that deflections are small for E ≳ 40EeV, whereas the prospects for UHECR astronomy according to the former seem unfavorable. The origin of this discrepancy is related to the assumptions made, such as magnetogenesis mechanism (astrophysical or primordial), power spectrum of the seed magnetic field, local distribution of magnetic fields near the observer, among others. In Das et al. (2008) it has been argued that deflections would be <~ 5° in about a third of the sky. More recent works (Hackstein et al., 2016, 2018) considered both astrophysical and primordial magnetic field seeds. The authors attempt to cover the aforementioned uncertainties by studying the impact of different models of dynamo amplification and feedback by active galaxies, which may considerably change the distribution of magnetic fields. They confirm the predictions by Dolag et al., that UHECR deflections due to EGMFs are rather small. An extreme scenario with strong magnetic fields has been studied in Alves Batista et al. (2017), considering several magnetic power spectra for the seed fields. In this case, deflections of UHE protons with E ≳ 50 EeV are estimated to be <2° in about a quarter of the sky. For E ≳ 100EeV, nearly all protons would be deflected <~ 10°.
In addition to magnetic deflections, EGMFs induce energy and charge dependent time-delays as discussed in section 3.2.1. If the sources of UHECRs are transient, these time-delays are expected to produce an observable distortion of the arrival direction distribution with respect to that of steady sources (Kalli et al., 2011), a different energy dependence of the apparent UHECR source number density than steady sources (Takami and Murase, 2012), and spiky features at the highest energies of the UHECR spectrum from the brightest, most recent UHECR transients, that could help distinguish between steady and transient UHECR source populations (Miralda-Escude and Waxman, 1996).
Note, however, that magnetic power spectra which contain most of the energy at large scales would completely spoil UHECR astronomy in this case, though this is an unlikely scenario. Ultimately the deflection of UHECRs in EGMFs depends on the distribution of EGMFs in the local Universe. This can be understood in terms of volume filling factors, shown in Figure 15.
Figure 15. Cumulative volume filling factors for EGMFs according to several models. Details about each model can be found in the corresponding publications: Alves Batista et al. (2017), Das et al. (2008), Dolag et al. (2005), Hackstein et al. (2018), Kotera and Lemoine (2008a), and Sigl et al. (2003b). R. Alves Batista for this review.
The effects of EGMFs on the spectrum and composition measured at Earth depend on the characteristic lengths involved. In the limit of a continuous source distribution, the propagation theorem states that the spectrum will have a universal form regardless of the modes of propagation (Aloisio and Berezinsky, 2004); this condition may not be easily realized, though. When the propagation time of a cosmic ray from its source to Earth is comparable to the age of the Universe, magnetic horizon effects suppress the lower energy region of the spectrum. In Mollerach and Roulet (2013) it was argued that this effect may play a role at E ≳ EeV for B ~ 1 nG. However, for realistic magnetic field distributions obtained from cosmological simulations, this effect may not be relevant at these energies depending on the source distribution and the distance to the nearest sources (Alves Batista and Sigl, 2014). Ultimately, it depends on the magnetic field distribution between Earth and the nearest sources.
A combined spectrum-composition fit of the Pierre Auger Observatory data including a particular model of EGMF has been presented in Wittkowski (2018). The results indicate a softening of the best-fit spectrum compared to the case where no magnetic field is assumed. This demonstrates the importance of understanding EGMFs in detail to improve phenomenological models.
Knowledge about the intervening magnetic fields is important to understand the origins of UHECRs. Conversely, UHECRs may also be used to constrain cosmic magnetic fields. A number of methods have been proposed for this purpose (Golup et al., 2009; Erdmann and Schiffer, 2010; Sutherland et al., 2012; Zimbres et al., 2014). In particular, Golup et al. (2009); Giacinti et al. (2010); Giacinti and Semikoz (2011); Zimbres et al. (2014); Oikonomou and Mostafa (2018) have proposed different searches for magnetically-aligned energy-ordered multiplets, which could be used to constrain the GMF, although none have been observed so far (Abreu et al., 2012).
Some attempts to constrain EGMFs using UHECRs have been made. Yuksel et al. (2012) have argued that at energies of ~100 EeV, a putative correlation of events observed by Auger with Cen A (Aab et al., 2015d) would imply an EGMF with strength B ≳ 20 nG, assuming a pure proton composition and the GMF model from Pshirkov et al. (2011). It is also possible to constrain properties of EGMFs other than the magnetic field strength. For instance, in Alves Batista and Saveliev (2019) a method has been proposed to infer the helicity—a topological quantity related to the degree of twisting and linkage of magnetic field lines — of cosmic magnetic fields. Although helicity is often neglected in UHECR studies, it has been proven to leave imprints in the large-scale distribution of UHECRs.
Given the considerable uncertainties in the GMF and the inconclusive results on the effects of EGMFs on cosmic-ray propagation due to the model dependencies, the unambiguous identification of individual UHECRs will require better constraints on EGMFs and improved models of the GMF. Therefore, until we have a more accurate description of GMFs and unless EGMFs are small or better understood, charged-particle astronomy will remain challenging if cosmic rays at the highest energies are heavy nuclei until new data on the RMs of Galactic pulsars and Faraday tomography [e.g., from LOFAR and SKA (Beck, 2008)]. Large-scale surveys of starlight polarization (Magkos and Pavlidou, 2019) will soon allow for a better three-dimensional reconstruction of the GMF.
3.3. Particle Physics
3.3.1. Hadronic Interactions at Ultrahigh Energies
Even though the current generation of hadronic interaction models gives a good description of many properties of air showers, we are far from having reached a satisfactory level in the quality and reliability of modeling extensive air showers.
First of all, there is the muon discrepancy that is still not understood. An excess in the muon number of ~ 30% relative to simulation predictions is not accounted for (Aab et al., 2015b; Aab et al., 2016a). This is the most important question to be addressed in model development and forthcoming fixed-target and collider measurements. The difficulty is that so far no “smoking gun” signature has been found that might indicate in what direction to search. It will be the task of further air-shower measurements to characterize the muon discrepancy in terms of the energy spectrum, production depth, and lateral distribution. Also going beyond measuring mean values will be important, as muon fluctuations give a handle on features of the first few interactions in a shower (Cazon et al., 2018a,b). Conventional explanations of the muon discrepancy have to be developed to find out whether we indeed have to assume that the muon excess is related to physics beyond the Standard Model of particle physics.
Secondly, the accuracy of the predictions of hadronic interaction models has to be improved to reduce the systematic uncertainties of composition measurements. For example, the tension between the mean depth of shower maximum and the shower-by-shower fluctuations of Xmax imply an almost mono-elemental mass composition. The astrophysical implications of such an unexpected change of mass composition with energy, without reaching a truly mixed composition, are severe (see e.g., Aab et al., 2017d). Therefore, it is of prime interest to figure out whether this apparent tension is not an artifact of inaccurate expectations for the mean Xmax. Moreover, the comparison of the electromagnetic and muonic shower components at surface level offers an even larger composition sensitivity than that provided by the depth of shower maximum. Currently, this sensitivity cannot be fully exploited. Muon-based mass measurements systematically lead to heavier mass compositions than Xmax-based analyses (Kampert and Unger, 2012).
Over the last decades, a rich dataset on proton-proton and proton-antiproton interactions at high energy has been accumulated in various collider experiments. In an air shower, most of the interactions are initiated by pions and kaons, except the first one. There is a severe lack of pion-proton and kaon-proton data that are needed for improving our understanding of hadronic interactions and for tuning interaction models. Of prime importance are the measurement of the pion-proton, kaon-proton, pion-light-nuclei, and kaon-light-nuclei cross sections and the corresponding distributions of leading secondary particles. Taking data at LHC and selecting events in which a beam proton becomes a neutron by emitting a π+ is one possibility to study pion interactions at energies not accessible in fixed target experiments. Similar measurements have been done at HERA (Khoze et al., 2006). Such measurements could help determine the secondary particle distributions, but the interaction cross section of pions and kaons can only be measured in fixed-target experiments. Additional information could be obtained from air showers by studying the muon production depth (Ostapchenko and Bleicher, 2016).
Similarly, there is almost no data available on particle production with light nuclei in the mass range of air (〈A〉 ≈ 14.45). The current understanding of nuclear processes is too limited to be able to reliably predict the secondary particle distributions in proton-air interactions if they were known for proton-proton and proton-neutron interactions. Also, the measurements of heavy-ion interactions, such as p-Pb and Pb-Pb, cannot be transferred to light nuclei with the needed accuracy. Taking data of proton-oxygen at LHC is technically possible and would be a key measurement for improving air shower predictions.
And, last but not least, particle detectors covering the forward direction would help significantly to reduce the needed extrapolation of collider measurements to phase space regions of relevance to air showers. Understanding the scaling of the forward particle distributions at collider energies is the key to extrapolating to higher interaction energies. LHCf (Adriani et al., 2018) is a good example that such detectors can be built even though there are large technical challenges and limitations.
Although it can be expected that progress in understanding hadronic multiparticle production will be mainly driven by experimental results for the next years, efforts to develop a more consistent theoretical framework will be equally important. The transition between soft and hard processes (i.e., processes with small and large momentum transfer) is not understood at all. Applying Regge parameterizations for soft processes is common practice, while hard processes are treated within the QCD-improved parton model. Closely related to this transition between two regimes is the question of non-linear effects, or even parton density saturation, expected at very high parton densities. LHC data show that proton-proton interactions of high multiplicity exhibit features previously only seen in heavy ion collisions (see e.g., Khachatryan et al., 2010; Aad et al., 2016c; Adam et al., 2017). Effects related to high parton densities will have to also be considered in hadronic interaction models for air showers.
3.3.2. Physics Beyond the Standard Model
The center-of-mass energy of an UHECR of energy E, in the lab frame, interacting with a low-energy particle of energy ϵ is given by
Thus, UHECR propagation in the cosmic radiation backgrounds, which have energy ϵ≪ GeV, cannot probe Lorentz-invariant physics beyond the Standard Model, but it can still probe invariance violations under Lorentz boosts. In addition, the development of air showers can be influenced both by Lorentz-invariant new physics acting on primaries or secondaries with energy E ≳ 2 × 1017eV and targets of mass ϵ ≳ mN, and also by Lorentz-invariance violations involving large Lorentz boosts.
Air-shower physics. Observed air showers show an excess of muons compared to predictions of standard hadronic interaction models above ≃ 1016 eV in the KASCADE-Grande experiment, which indicates a longer-than-expected muon attenuation length (Apel et al., 2017). The Pierre Auger Observatory also sees a muon excess by a factor ≃1.5 (Aab et al., 2016a). Since a large number of muons is observed, this cannot be a statistical effect but rather points to shortcomings in the models. If this muon excess cannot be explained by improved hadronic event generators within the Standard Model, new physics could qualitatively play a role in the following way.
The muon abundance is roughly proportional to the energy fraction going into hadrons. Since over one hadronic interaction depth of about a fraction — the branching ratio of hadronic interactions into neutral pions—of the hadronic energy is converted into electromagnetic energy, after n hadronic generations the hadronic energy fraction of the shower is proportional to . Therefore, a larger muon number could be caused by decreasing the number of generations n, decreasing , or both. However, the number of generations is well constrained by detailed measurements of Xmax. Therefore, assuming neutral pions still decay quasi-instantaneously, the most likely explanation of the observed large muon number is a significant decrease in the fraction of energy going into neutral pions, . For example, it has been suggested (Farrar and Allen, 2013a,b) that if chiral symmetry is restored above a certain center-of-mass energy, pions may become much heavier and their production may be suppressed in favor of baryon-anti-baryon production. This would put more energy into the hadronic channel compared to the electromagnetic channel, thus producing more muons. A similar effect could be achieved by the production of a fireball consisting of deconfined quarks and gluons (Anchordoqui et al., 2017).
Alternatively, if high-energy neutral pions were stable or had a decay rate smaller than their interaction rate in the atmosphere, for example, due to Lorentz symmetry violation at very high Lorentz factors, then their energy could contribute to increasing the energy fraction going into the hadronic channel and thus the muon signal. Generally speaking, an increase of the fraction of air-shower energy in the hadronic channel would likely be a hint for new physics. One could imagine such effects to have energy thresholds, so one could also search for comparatively large increases of muon number over a small primary energy range.
Lorentz-invariance violation. Lorentz invariance violation (LIV) can be induced by non-renormalizable operators that conserve gauge invariance but break parts of the Poincaré group (Colladay and Kostelecky, 1998). For example, it has been shown that in quantum electrodynamics the most general non-renormalizable dimension-five CPT−odd operator that is quadratic in the fields and preserves rotation and gauge invariance, but is not invariant under Lorentz boosts, can be written as (Myers and Pospelov, 2003)
Here, ξ, χ1 and χ2 are dimensionless constants, MPl is the Planck mass, uμ is a constant time-like four-vector which corresponds to a preferred Lorentz frame such as the cosmic microwave background rest frame and is the dual electromagnetic field strength tensor.
Operators such as Equation (6) can manifest through modifications of dispersion relations for particles of energy E, momentum p, and mass m, by terms that are suppressed by a power n of the Planck mass MPl(Amelino-Camelia et al., 2005; Christian, 2005; Diaz, 2014). The dispersion relation for left- and right-handed photons or fermions can be written as
Here, n = d − 4 for a d-dimensional operator and the dimensionless numbers η± refer to positive and negative helicity states, respectively. In general, in effective field theory one has . For example, Equation (6) implies n = 1 and η± = ±ξ for right- or left-circularly polarized photons, respectively, and η± = 2(χ1 ± χ2) for positive and negative electron helicity, respectively. For renormalizable LIV terms, d ≤ 4 and n is negative in Equation (7).
Dispersion relations of the form of Equation (7) can modify both the free propagation of particles and the kinematics and thresholds of interactions (Amelino-Camelia and Piran, 2001; Dubovsky and Tinyakov, 2002; Moffat, 2003; Gagnon and Moore, 2004; Stecker and Scully, 2005; Galaverni and Sigl, 2008; Bi et al., 2009; Maccione et al., 2009; Scully and Stecker, 2009; Cowsik et al., 2012). Kinematics are typically modified when the LIV terms become comparable to the particle rest mass, i.e., when the particle energy is larger than a critical energy Ecr,
Therefore, the larger the particle mass, the higher the energy at which LIV effects become relevant.
In the relativistic limit, to first order in m2 and η±, the group velocity corresponding to Equation (7) is
For positive η this would lead to superluminal motion for E > Ecr. Particles with tend to emit vacuum Cherenkov radiation, similar to the motion of an ultra-relativistic charge in a medium with index of refraction larger than one, and would lose energy rapidly (Cohen and Glashow, 2011). Therefore, observing a particle of energy E implies Ecr ≳ E which, from Equation (8), leads to an upper bound on η. For n = 1, the observation of EeV protons places a stringent limit on LIV, of
If LIV exists and its effect is non-negligible, the corresponding parameter η should naturally be of order 1; constraining it to values much smaller than unity (Gagnon and Moore, 2004; Galaverni and Sigl, 2008) would suggest that the corresponding LIV does not exist; however, see Aloisio et al. (2014). Additionally, Equation (9) leads to energy-dependent delays in the propagation time from the sources to Earth. Thus, strong constraints on LIV may be placed by the detection of UHE photons from local sources (Murase, 2009).
New physics in UHE neutrinos. High-energy astrophysical neutrinos, with TeV–PeV energies, recently discovered, have opened up a new regime to test for new physics (Anchordoqui et al., 2005; Gonzalez-Garcia et al., 2005; Ahlers et al., 2018). They are unparalleled in two key features: they have the highest neutrino energies detected—so they can probe effects at new energy scales— and they travel over the longest baselines—so tiny new-physics effects could accumulate en route to us, and reach detectable levels. Cosmogenic neutrinos, with EeV energies, when discovered, could extend the reach of these tests.
IceCube astrophysical neutrinos have been used to measure the neutrino-nucleon cross section in the TeV–PeV range for the first time (Aartsen et al., 2017; Bustamante and Connolly, 2019). It was found to be compatible with high-precision Standard Model predictions based on collider data (Cooper-Sarkar et al., 2011), though there is still room for small deviations due to new physics. Cosmogenic neutrinos could be used to measure the cross section at the EeV scale for the first time, test strong dynamics more deeply than colliders (Anchordoqui et al., 2019; Bertone et al., 2019), and search for new physics at an even higher energy scale.
Numerous new-physics models have effects that are proportional to some power of the neutrino energy E and to the propagated distance L, i.e., they grow as , where the energy dependence n and the proportionality constant κn are model-dependent. For instance, for neutrino decay (Chikashige et al., 1980; Gelmini et al., 1982; Tomas et al., 2001), n = −1; for CPT-odd Lorentz violation (Colladay and Kostelecky, 1997; Coleman and Glashow, 1999; Barger et al., 2000) or coupling to a torsion field (De Sabbata and Gasperini, 1981), n = 0; and for CPT-even Lorentz violation (Coleman and Glashow, 1997; Glashow et al., 1997) or violation of the equivalence principle (Gasperini, 1988, 1989; Halprin et al., 1996; Adunas et al., 2001), n = 1. An experiment that sees neutrinos of energy E coming from sources located at a distance L is, in principle, able to probe new physics with sensitivities of , a significant improvement over current limits of PeV and (Abbasi et al., 2010; Abe et al., 2015).
New physics of different types can affect all neutrino observables: the energy spectrum (see e.g., Baerwald et al., 2012; Blum et al., 2014; Ibe and Kaneta, 2014; Ioka and Murase, 2014; Ng and Beacom, 2014; Kopp et al., 2015; Bustamante et al., 2017), distribution of arrival directions (see e.g., Davis and Silk, 2015; Argüelles et al., 2017), and the flavor composition, i.e., the proportion of each neutrino flavor to the total in the incoming flux (see e.g., Argüelles et al., 2015; Bustamante et al., 2015; Shoemaker and Murase, 2016; Rasmussen et al., 2017).
At high and ultra-high energies, there are a few challenges to detecting new physics in high-energy cosmic neutrinos:
• New-physics effects might be sub-dominant; in this case, their discovery is contingent on detecting a large enough number of events and on accurately reconstructing key properties of events, like energy and arrival direction;
• When extracting fundamental neutrino properties from the data, one must factor in astrophysical uncertainties (e.g., shape of the energy spectrum, redshift evolution of the number density of sources, etc.), which can be significant;
• Flavor is a difficult property to measure in neutrino telescopes (Aartsen et al., 2015a,b; Vincent et al., 2016; Bustamante and Ahlers, 2019); improved methods of flavor identification might be needed to fully exploit flavor in studying fundamental neutrino physics (e.g., Wang et al., 2013; Li et al., 2016).
These challenges are likely surmountable. High- and ultra-high-energy observatories are in a unique position to perform powerful tests of neutrino physics, complementing and expanding tests performed by experiments with lower energies and shorter propagation baselines.
4. Discussion
4.1. The Current Status and Perspectives of Earth-Based UHECR Detectors
The most promising step in the activity of ground UHECR detection is the upcoming upgrade of the Pierre Auger Observatory (Aab et. al., 2016b). It consists in the improvement of the surface detector (SD), namely water-Cherenkov tanks, by equipping each tank with solid-state scintillator plates on top. This configuration allows one to improve the sensitivity to the CR mass composition by simultaneous measurements of electrons and muons passing through both detectors. Although the total aperture of the surface detector will not increase, the fraction of events with a reliable reconstruction of the mass composition will be larger; day-time SD data as well as night-time data recorded by the fluorescence detectors (FD) will be cross-checked with new scintillators, thus improving the quality of hybrid SD+FD events.
Another upgrade of the Pierre Auger Observatory, recently confirmed, is the equipment of the SD with radio antennas. Contrary to the existing AERA detector (Aab et al., 2018b), which densely covers only a small part of the observatory, the new detector will feature a sparser layout and cover the full area of the observatory. In recent years, different antenna types for air-shower detection (Abreu et al., 2012) were investigated by a number of experiments. Based on these studies, the loop antenna, which was successfully exploited at the Tunka-Rex experiment (Bezyazeekov et al., 2015, 2018), was selected for the Pierre Auger upgrade. Joint operation of particle and radio detectors decreases the systematic uncertainty of energy and mass composition reconstruction, since radio detection allows one to reconstruct the calorimetric energy of the electromagnetic part of the air shower as well as the depth of shower maximum.
Also TA has recently started to be upgraded (Kido, 2018). Once the upgrade is complete, the array, TA × 4, will consist of three times more surface detectors than TA, similar to the original ones (two solid-state scintillators separated by a metal plate). The upgraded detector will cover an area of about 3 000 km2, with the new scintillators two times sparser than the old ones. Additional FD will be built for hybrid operation with the extended array. The aperture of TA × 4 will facilitate the study of anisotropies at ultrahigh energy in the Northern Hemisphere and aid the comparison of the spectrum in the two hemispheres at the highest energies.
The detection of ultrahigh energy cosmic rays is also included in the scientific program of GRAND, the most ambitious ground-based experiment proposed so far (Alvarez-Muniz et al., 2018). Since the detector will consist of antennas tuned for the detection of very inclined events, its exposure overlaps both with TA and Auger. Due to the unprecedented exposure of GRAND in its envisaged final configuration (200 000 km2), it will be possible to detect about 32 000 cosmic-ray events with E > 1019.5 eV in five years. Since GRAND exploits the radio technique for air-shower detection, cosmic-ray properties will be studied via measurements of the calorimetric energy of the air-shower and should achieve good Xmax resolution.
4.2. The Current Status and Perspectives of Space Experiments to Study UHECRs
J. Linsley and R. Benson were the first to propose measurements of the fluorescent radiation of EAS using a UV telescope on-board a satellite (Benson and Linsley, 1981). Y. Takahashi, later proposed the idea of using wide-angle optics and CCD readout in the MASS concept (Takahashi, 1995). A space-based detector for UHECR research has the advantage of a much larger exposure and uniform coverage of the celestial sphere. This idea has been developed in a number of projects. In the late 1990s, the Airwatch concept was developed by J. Linsley, B. Scarsi, Y. Takahashi and others based on Fresnel optics. They later collaborated with a team from Utah/GSFC who separately developed the OWL/Crystal Eye idea to propose OWL-Airwatch (Streitmatter, 1998), a concept for a 2-spacecraft mission. The OWL concept later moved to Schmidt telescopes and into the final OWL study.
The original Airwatch concept, developed into the Extreme Universe Space Observatory (EUSO) (Catalano et al., 2001). This was the start of the JEM-EUSO program which originally took its name from the Japanese Experiment Module (JEM) but currently stands for Joint Experiment Missions. In the JEM-EUSO Collaboration, a large Fresnel lens telescope was developed (Adams et al., 2015). In Russia, detectors that use concentrator mirrors for collecting fluorescence light, TUS (Klimov et al., 2017) and KLYPVE (Panasyuk et al., 2016), were proposed and developed.
The TUS experiment was the first orbital detector of UHECRs. It was launched on board the Moscow State University (MSU) satellite “Lomonosov” (Klimov et al., 2017) on 28 April 2016. TUS is a UV telescope looking downward into the atmosphere in the nadir direction. It consists of two main parts: a modular Fresnel mirror-concentrator and 256 photomultiplier tubes (PMTs) arranged in a 16 × 16 photodetector located in the focal plane of the mirror. The overall field of view (FOV) of the detector is 4.5° × 4.5°. During 1.5 years of operation in EAS mode about 200 000 events of various types were measured during the night-time part of the orbit. The events differ in the spatial dynamics and temporal structure of their waveforms. Some EAS candidates have been registered.
Another, much larger space instrument, KLYPVE, is being developed in close cooperation with the JEM-EUSO Collaboration and is known as KLYPVE-EUSO (K-EUSO) (Panasyuk et al., 2016). To fulfill the requirements of the K-EUSO experiment, a Schmidt UV telescope covering a FOV of 40° with an entrance pupil diameter of 2.5 m, and a 4 m diameter mirror was developed. The baseline variant consists of a spherical mirror, a corrector plate and a spherical focal surface concentric with the mirror, placing the aperture stop on the frontal surface of the corrector plate. Even though the expected statistics of UHECR events will not exceed those of upcoming on ground installations (see Figure 16), with the current design, the K-EUSO instrument can perform the first all-sky observation of UHECRs, in order to establish whether the particle fluxes of the two hemispheres are different.
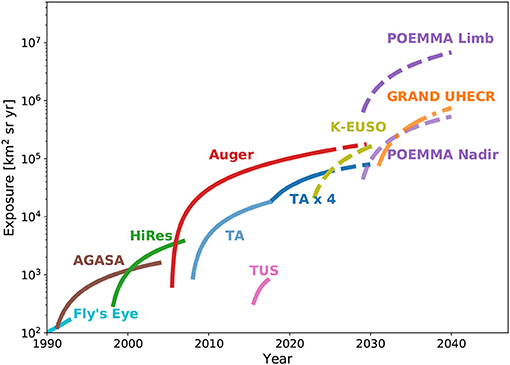
Figure 16. Evolution of the exposure of past, current, and upcoming (solid lines) UHECR experiments as a function of time for ground-based and space experiments. Proposed experiments are also shown (dashed lines). F. Oikonomou and M. Panasyuk for this review.
K-EUSO will measure about 140 UHECR events in the Northern hemisphere and 30 events in the Southern hemisphere at E > 57 EeV in one year of observations if the difference of the TA and Auger spectra is due to different fluxes. In contrast, the numbers of events from both hemispheres are expected to be nearly equal if the flux is isotropic. Also, K-EUSO data will allow for a full-sky search for UHECR anisotropy to independently confirm or rule out the presence of hotspots in the Northern and Southern hemispheres.
The project concept of OWL, based on the simultaneous detection of UHECRs by UV telescopes placed on two satellites, was recently developed in the POEMMA project (Olinto et al., 2018). This project, based on the use of Schmidt optics with 45° FOV and a large photodetector camera, can become a space instrument of record characteristics and surpass in terms of exposure the ground-based Auger and TA installations (see Figure 16).
4.3. The Current Status and Perspectives of UHE Neutrino Experiments
Currently the UHE neutrino flux is best confined by the IceCube Observatory (Aartsen et al., 2018) and the Auger Observatory (Bellido, 2018) at the level of ~ 3 × 10−8 GeVcm−2s−1sr−1 around EeV (all-flavor). Figure 17 summarizes the sensitivity of current and proposed experiments that target EeV neutrinos. The Askaryan Radio Array (ARA) (Allison et al., 2012, 2016) and ARIANNA (Barwick et al., 2017; Nelles, 2018) are in-ice radio arrays which detect UHE neutrinos via the Askaryan effect. As an alternative to the expensive ice-Cherenkov technique the three experiments equipped with radio antennas are located in Antarctica and optimized for UHE neutrino detection, namely two in-ice arrays, the Askaryan Radio Array (ARA) (Allison et al., 2012, 2016) and ARIANNA (Barwick et al., 2017; Nelles, 2018), and a balloon-borne interferometer ANITA (Gorham et al., 2018a; Gorham et al., 2018b). The propose GRAND (Alvarez-Muniz et al., 2018) will use large arrays of cost-effective radio antennas to detect particle cascades produced in media and air by UHE tau neutrinos. POEMMA (Olinto et al., 2018) will also detect tau neutrinos, by observing the Cherenkov radiation produced by upward-going tau decays (Neronov et al., 2017). Trinity (Otte, 2018), an Earth-based imaging telescope experiment, will detect air showers induced by taus or tau neutrinos by observing the Cherenkov or fluorescence light produced by the EAS.
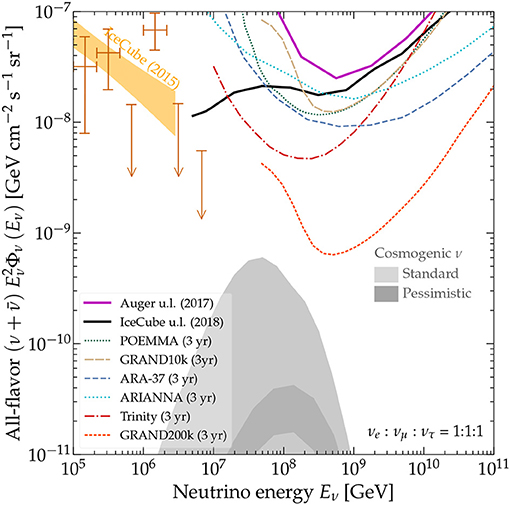
Figure 17. Predicted fluxes of cosmogenic neutrinos and expected sensitivities of current, upcoming and proposed UHECR and UHE neutrino experiments. Upper limits are from IceCube (Aartsen et al., 2018) and the Pierre Auger Observatory (Bellido, 2018). Sensitivities are for POEMMA (Olinto et al., 2018) (assuming full-sky coverage), GRAND in its 10,000-antenna (GRAND10k) and 200,000-antenna configurations (GRAND200k) Alvarez-Muniz et al. (2018), ARA-37 (Allison et al., 2016) (trigger level), ARIANNA (Persichilli, 2018) (“optimal wind” sensitivity), and Trinity (Otte, 2018) (10 m2 mirror). M. Bustamante for this review.
5. Outlook
Despite revolutionary progress, some critical, long-standing questions in the field of UHECRs remain unanswered, or only answered partially: What are the sources of UHECRs? What is the mass composition of UHECRs at the highest energies? What mechanism accelerates CRs beyond PeV energies? What is the flux of secondary messengers—neutrinos, gamma rays—associated with UHECRs, and what can we infer from them about UHECR sources?
Observations performed by current and planned ultrahigh-energy facilities have an opportunity to give definite answers to these questions. Yet, to fulfill this potential, it is necessary to undertake a number of essential steps toward experimental and theoretical progress. Below, we list what we believe are the most important of these. This list is, of course, non-exhaustive and only expresses our views.
• UHECR composition: Precise measurement of the UHECR mass composition near the end of the spectrum is hindered by uncertainties in models of hadronic interaction, uncertainties in measuring Xmax, and small statistics. The latter issue will be addressed by upgraded configurations of current facilities and larger, next-generation facilities.
Action item 1: Craft a program of accelerator measurements of cross sections and multiplicities to reduce uncertainties in models of hadronic interaction.
Action item 2: Explore experimental methods to infer the composition with precision comparable to that of fluorescence detectors and at a duty cycle of 100%.
• Identification of UHECR sources: Sources of UHECRs can be searched for either by self-correlation of arrival directions or by searching for positional correlations with sources catalogs.
Action item 3: Thorough studies of the effects Galactic and extragalactic magnetic fields.
Action item 4: When looking for correlations with source catalogs, generate catalogs providing a tomographic mapping of possible UHECR sources, for viable source populations, accounting for incompleteness and bias, up to the GZK radius at the energy of the ankle, possibly down to the minimum luminosity imposed by theoretical criteria.
• Particle acceleration: An accurate understanding of particle acceleration in astrophysical sources could help to interpret the transition from Galactic to extragalactic origin of cosmic rays and the shape of the UHECR spectrum at the highest energies, and would influence predictions of spectra of cosmogenic secondaries.
Action item 5: Perform detailed studies of particle acceleration in collisionless shocks and magnetic reconnection under conditions as close to those in real sources, either via simulations or in the lab, when possible.
• Muon excess problem: The mismatch between the number of muons with energies above 109.5 GeV predicted by shower models and the number detected points to further problems with the hadronic interaction models. Independent measurements of the electromagnetic and muon component of air showers could help solve this issue.
Action item 6: Favor the construction of air-shower facilities with separate electromagnetic and muon detectors.
• Updated prediction of cosmogenic neutrinos: Recent recalculations of the predicted flux of cosmogenic neutrinos, fitting the latest UHECR data, have resulted in fluxes significantly lower than before. Yet, the uncertainties in the prediction are large. This represents a problem in planning for the next-generation of UHE neutrino detectors.
Action item 7: Generate predictions of the cosmogenic neutrino flux by scanning across all of the available parameter space of UHECR model parameters—including uncertainties in magnetic fields and hadronic interaction models—in order to fully characterize the uncertainties.
• Updated predictions of UHE neutrinos from point sources: Because the flux of cosmogenic neutrinos might be tiny, UHE neutrinos from point sources might be detected first in next-generation neutrino telescopes. However, the literature on models of UHE neutrinos is outdated or lacking.
Action item 8: Generate updated predictions of the emission of UHE neutrinos from point sources, steady-state and transient.
• Global studies: A complete picture of the high-energy Universe needs to account for all messengers
Action item 9: Assess the validity of UHECR models by considering the full UHECR, neutrino, and photon data, from as many experiments as possible; avoid picking and choosing observables and experiments.
• Open data policies: For progress to be faster, the community should have access to detected events in UHE facilities, in a usable, non-raw form.
Action item 10: Existing and future facilities should have an open data policy, including software analysis tools when possible.
More than five decades of experimental and theoretical progress in the field of UHECRs will soon be compounded on by upgrades of Auger and TA, and by a suite of potential next-generation detectors. On one hand, thanks to these, in the next 5–10 years the increased statistics of UHECRs alone will refine the measurement of the energy spectrum, mass composition, and anisotropies to the point where several of the open questions above could already be answered. Additional improvements in analysis techniques will only enhance these prospects. On the other hand, upcoming detectors will potentially trigger a transformative change in the field: for the first time, we could reach the sensitivity needed to discover even tiny fluxes of cosmogenic neutrinos and gamma rays. Opening up the full breadth of UHE multi-messenger observables could answer most of the remaining open questions, and finally, provide a complete picture of the Universe at the highest energies.
Author Contributions
RB, JB, MB, RE, KF, K-HK, DK, GS, FO, MP, AT, and MU contributed to the original material and writing of the manuscript. FO and KF coordinated this review. All authors contributed to the discussions at MIAPP, read the manuscript and provided critical feedback.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge the support of the Munich Institute for Astro- and Particle Physics (MIAPP) of the DFG cluster of excellence Origin and Structure of the Universe, where this work was initiated. We thank the organizers of the The High-Energy Universe: Gamma-Ray, Neutrino, and cosmic-ray astronomy MIAPP Program, Francis Halzen, Angela Olinto, Elisa Resconi, and Paolo Padovani, for the very fruitful workshop.
RB is supported by grant #2017/12828-4, São Paulo Research Foundation (FAPESP). MB is supported by the Danmarks Grundforskningsfond Grant 1041811001 and Villum Fonden project no. 13164. RE, K-HK, GS, and MU are supported by the Bundesministerium für Bildung und Forschung (BMBF) and the Deutsche Forschungsgemeinschaft (DFG). KF acknowledges support from the Einstein Fellowship from the NASA Hubble Fellowship Program. The work of KM is supported by Alfred P. Sloan Foundation and NSF grant No. PHY-1620777. FO is supported by the Deutsche Forschungsgemeinschaft through grant SFB 1258 Neutrinos and Dark Matter in Astro- and Particle Physics.
Footnotes
1. ^One should note though that this sensitivity limit would go down by two orders of magnitude in the case of β~0.1 and near the ankle.
References
Aab, A., Abreu, P., Aglietta, M., Ahlers, M., Ahn, E. J., Al Samarai, I., et al. (2014c). Muons in air showers at the Pierre Auger Observatory: measurement of atmospheric production depth. Phys. Rev. D 90:012012. doi: 10.1103/PhysRevD.90.012012
Aab, A., Abreu, P., Aglietta, M., Ahn, E., Samarai, I. A., Albert, J., et al. (2015a). The Pierre Auger Cosmic Ray Observatory. Nucl. Instrum. Meth. A 798:172. doi: 10.1016/j.nima.2015.06.058
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Al Samarai, I., Albuquerque, I. F. M., et al. (2014a). Depth of maximum of air-shower profiles at the Pierre Auger Observatory. I. Measurements at energies above 1017.8 eV. Phys. Rev. D 90:122005. doi: 10.1103/PhysRevD.90.122005
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Al Samarai, I., Albuquerque, I. F. M., et al. (2014b). Depth of maximum of air-shower profiles at the Pierre Auger Observatory. II. Composition implications. Phys. Rev. D 90:122006. doi: 10.1103/PhysRevD.90.122006
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Al Samarai, I., Albuquerque, I. F. M., et al. (2015b). Muons in air showers at the Pierre Auger Observatory: mean number in highly inclined events. Phys. Rev. D 91:032003. doi: 10.1103/PhysRevD.91.032003
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Al Samarai, I., Albuquerque, I. F. M., et al. (2016a). Testing hadronic interactions at ultrahigh energies with air showers measured by the Pierre Auger Observatory. Phys. Rev. Lett. 117:192001. doi: 10.1103/PhysRevLett.117.192001
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Samarai, I. A., Albuquerque, I. F. M., et al. (2014d). Searches for large-scale anisotropy in the arrival directions of cosmic rays detected above energy of 1019 eV at the Pierre Auger Observatory and the Telescope Array. Astrophys. J. 794:172. doi: 10.1088/0004-637X/794/2/172
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Samarai, I. A., Albuquerque, I. F. M., et al. (2015c). “The Pierre Auger Observatory,” in Contributions to the 34th International Cosmic Ray Conference (ICRC 2015) (The Hague).
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Samarai, I. A., Albuquerque, I. F. M., et al. (2015d). Searches for anisotropies in the arrival directions of the highest energy cosmic rays detected by the Pierre Auger Observatory. Astrophys. J. 804:15. doi: 10.1088/0004-637X/804/1/15
Aab, A., Abreu, P., Aglietta, M., Ahn, E. J., Samarai, I. A. L., and Albuquerque, I. F. M., et al (2016b). The Pierre Auger Observatory Upgrade-Preliminary Design Report. arxiv:1604.03637
Aab, A., Abreu, P., Aglietta, M., Al Samarai, I., Albuquerque, I. F. M., Allekotte, I., et al. (2017a). Inferences on mass composition and tests of hadronic interactions from 0.3 to 100 EeV using the water-Cherenkov detectors of the Pierre Auger Observatory. Phys. Rev. D 96:122003. doi: 10.1103/PhysRevD.96.122003
Aab, A., Abreu, P., Aglietta, M., Al Samarai, I., Albuquerque, I. F. M., Allekotte, I., et al. (2017b). Observation of a large-scale anisotropy in the arrival directions of cosmic rays above 8 × 1018 eV. Science 357:1266. doi: 10.1126/science.aan4338
Aab, A., Abreu, P., Aglietta, M., Albuquerque, I. F. M., Albury, J. M., Allekotte, I., et al. (2018a). Large-scale cosmic-ray anisotropies above 4 EeV measured by the Pierre Auger Observatory. Astrophys. J. 868:4. doi: 10.3847/1538-4357/aae689
Aab, A., Abreu, P., Aglietta, M., Albuquerque, I. F. M., Albury, J. M., Allekotte, I., et al. (2018b). Observation of inclined EeV air showers with the radio detector of the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 1810:026. doi: 10.1088/1475-7516/2018/10/026
Aab, A., Abreu, P., Aglietta, M., Albuquerque, I. F. M., Albury, J. M., Allekotte, I., et al. (2019). Data-driven estimation of the invisible energy of cosmic ray showers with the Pierre Auger Observatory Phys. Rev. D arXiv:1901.08040.
Aab, A., Abreu, P., Aglietta, M., Albuquerque, I. F. M., Allekotte, I., Almela, A., et al. (2018c). An Indication of anisotropy in arrival directions of ultra-high-energy cosmic rays through comparison to the flux pattern of extragalactic gamma-ray sources. Astrophys. J. 853:L29. doi: 10.3847/2041-8213/aaa66d
Aab, A., Abreu, P., Aglietta, M., Samarai, I. A., Albuquerque, I., Allekotte, I., et al. (2017c). Search for photons with energies above 1018 eV using the hybrid detector of the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 1704:009. doi: 10.1088/1475-7516/2017/04/009
Aab, A., Abreu, P., Aglietta, M., Samarai, I. A., Albuquerque, I. F. M., Allekotte, I., et al. (2017d). Combined fit of spectrum and composition data as measured by the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 1704:038. doi: 10.1088/1475-7516/2017/04/038
Aad, G., Abbott, B., Abdallah, J., Abdinov, O., Aben, R., Abolins, M., et al. (2016c). Observation of long-range elliptic azimuthal anisotropies in 13 and 2.76 TeV pp collisions with the ATLAS detector. Phys. Rev. Lett. 116:172301. doi: 10.1103/PhysRevLett.116.172301
Aartsen, M. G., Abraham, K., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., et al. (2015a). A combined maximum-likelihood analysis of the high-energy astrophysical neutrino flux measured with IceCube. Astrophys. J. 809:98. doi: 10.1088/0004-637X/809/1/98
Aartsen, M. G., Abraham, K., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., et al. (2016d). Observation and Characterization of a Cosmic Muon Neutrino Flux from the Northern Hemisphere Using Six Years of IceCube Data. Astrophys. J. 833:3. doi: 10.3847/0004-637X/833/1/3
Aartsen, M. G., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., Ahrens, M., et al. (2015b). Flavor ratio of astrophysical neutrinos above 35 TeV in IceCube. Phys. Rev. Lett. 114:171102. doi: 10.1103/PhysRevLett.114.171102
Aartsen, M. G., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., Ahrens, M., et al. (2018). Differential limit on the extremely-high-energy cosmic neutrino flux in the presence of astrophysical background from nine years of IceCube data. Phys. Rev. D 98:062003. doi: 10.1103/PhysRevD.98.062003
Aartsen, M. G., Hill, G. C., Kyriacou, A., Robertson, S., Wallace, A., Whelan, B. J., et al. (2017). Measurement of the multi-TeV neutrino cross section with IceCube using Earth absorption. Nature 551:596. doi: 10.1038/nature24459
Abbasi, R., Abdou, Y., Abu-Zayyad, T., Adams, J., Aguilar, J. A., Ahlers, M., et al. (2010). Search for a lorentz-violating sidereal signal with atmospheric neutrinos in IceCube. Phys. Rev. D 82:112003. doi: 10.1103/PhysRevD.82.112003
Abbasi, R., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2016). The energy spectrum of cosmic rays above 1017.2 eV measured by the fluorescence detectors of the Telescope Array experiment in seven years. Astropart. Phys. 80:131. doi: 10.1016/j.astropartphys.2016.04.002
Abbasi, R., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2017). Search for EeV Protons of Galactic Origin. Astropart. Phys. 86:21. doi: 10.1016/j.astropartphys.2016.11.001
Abbasi, R., Abu-Zayyad, T., Belov, K., Belz, J., Cao, Z., Dalton, M., et al. (2008a). Air fluorescence measurements in the spectral range 300-420 nm using a 28.5-GeV electron beam. Astropart. Phys. 29:77. doi: 10.1016/j.astropartphys.2007.11.010
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Anderson, R., Azuma, R., et al. (2014). Indications of intermediate-scale anisotropy of cosmic rays with energy greater than 57 EeV in the Northern sky measured with the surface detector of the Telescope Array experiment. Astrophys. J. 790:L21. doi: 10.1088/2041-8205/790/2/L21
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2015). Measurement of the proton-air cross section with Telescope Array Middle Drum detector and surface array in hybrid mode. Phys. Rev. D 92:032007. doi: 10.1103/PhysRevD.92.032007
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2018a). Evidence of intermediate-scale energy spectrum anisotropy of cosmic rays E≥1019.2 eV with the Telescope Array surface detector. Astrophys. J. 862:91. doi: 10.3847/1538-4357/aac9c8
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2018b). Testing a reported correlation between arrival directions of ultrahigh-energy cosmic rays and a flux pattern from nearby starburst galaxies using Telescope Array data. Astrophys. J. Lett. 867:L27. doi: 10.3847/2041-8213/aaebf9
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2018c). Constraints on the diffuse photon flux with energies above 1018 eV using the surface detector of the Telescope Array experiment. Astropart. Phys. 110, 8–14. doi: 10.1016/j.astropartphys.2019.03.003
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2018d). Depth of ultra high energy cosmic ray induced air shower maxima measured by the Telescope Array black rock and long ridge FADC fluorescence detectors and surface array in hybrid mode. Astrophys. J. 858:76. doi: 10.3847/1538-4357/aabad7
Abbasi, R. U., Abe, M., Abu-Zayyad, T., Allen, M., Azuma, R., Barcikowski, E., et al. (2018e). Evidence for declination dependence of ultrahigh energy cosmic ray spectrum in the Northern Hemisphere. arXiv:1801.07820.
Abbasi, R. U., Abu-Zayyad, T., Allen, M., Amman, J. F., Archbold, G., Belov, K., et al. (2008b). First observation of the Greisen-Zatsepin-Kuzmin suppression. Phys. Rev. Lett. 100:101101. doi: 10.1103/PhysRevLett.100.101101
Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017a). Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys. J. 848:L13. doi: 10.3847/2041-8213/aa920c
Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017b). GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119:161101. doi: 10.1103/PhysRevLett.119.161101
Abdalla, H. et al. (2017). Characterizing the ray long-term variability of PKS 2155–304 with H.E.S.S. and Fermi-LAT. Astron. Astrophys. 598:A39. doi: 10.1051/0004-6361/201629419
Abe, K., Haga, Y., Hayato, Y., Ikeda, M., Iyogi, K., Kameda, J., et al. (2015). Test of lorentz invariance with atmospheric neutrinos. Phys. Rev. D 91:052003. doi: 10.1103/PhysRevD.91.052003
Abraham, J., Abreu, P., Aglietta, M., Aguirre, C., Ahn, E., Allard, D., et al. (2010). The Fluorescence detector of the Pierre Auger Observatory. Nucl. Instrum. Meth. A 620:227. doi: 10.1016/j.nima.2010.04.023
Abraham, J., Abreu, P., Aglietta, M., Aguirre, C., Allard, D., Allekotte, I., et al. (2008). Observation of the suppression of the flux of cosmic rays above 4 × 1019eV. Phys. Rev. Lett. 101:061101. doi: 10.1103/PhysRevLett.101.061101
Abramowski, A., Aharonian, F., Benkhali, F. A., Akhperjanian, A. G., Angüner, E. O., Backes, M., et al. (2016). Acceleration of petaelectronvolt protons in the Galactic Centre. Nature 531:476. doi: 10.1038/nature17147
Abreu, P., Aglietta, M., Ahlers, M., Ahn, E., Albuquerque, I., Allekotte, I., et al. (2013). Bounds on the density of sources of ultra-high energy cosmic rays from the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 1305:009. doi: 10.1088/1475-7516/2013/05/009
Abreu, P., Aglietta, M., Ahlers, M., Ahn, E. J., Albuquerque, I. F. M., Allard, D., et al. (2012). Antennas for the detection of radio emission pulses from cosmic-ray induced air showers at the Pierre Auger Observatory. JINST 7:P10011. doi: 10.1088/1748-0221/7/10/P10011
Abreu, P., Aglietta, M., Ahlers, M., Ahn, E. J., Albuquerque, I. F. M., Allard, D., Allekotte, I., et al. (2012a). Constraints on the origin of cosmic rays above 1018 eV from large scale anisotropy searches in data of the Pierre Auger Observatory. Astrophys. J. 762:L13. doi: 10.1088/2041-8205/762/1/L13
Abreu, P., Aglietta, M., Ahn, E., Allard, D., Allekotte, I., Allen, J., et al. (2011). The exposure of the hybrid detector of the Pierre Auger Observatory. Astropart. Phys. 34:368. doi: 10.1016/j.astropartphys.2010.10.001
Abreu, P., Aglietta, M., Ahn, E. J., Albuquerque, I. F. M., Allard, D., Allekotte, I., et al. (2012). Search for signatures of magnetically-induced alignment in the arrival directions measured by the Pierre Auger Observatory. Astropart. Phys. 35:354. doi: 10.1016/j.astropartphys.2011.10.004
Abreu, P., Aglietta, M., Ahn, E. J., Albuquerque, I. F. M., Allard, D., Allekotte, I., et al. (2012b). Measurement of the proton-air cross-section at TeV with the Pierre Auger Observatory. Phys. Rev. Lett. 109:062002. doi: 10.1103/PhysRevLett.109.062002
Abu-Zayyad, T., Aida, R., Allen, M., Anderson, R., Azuma, R., Barcikowski, E., et al. (2012). The energy spectrum of Telescope Array's Middle Drum detector and the direct comparison to the high resolution Fly's eye experiment. Astropart. Phys. 39:109. doi: 10.1016/j.astropartphys.2012.05.012
Abu-Zayyad, T., Al-Seady, M., Belov, K., Bird, D., Boyer, J., Chen, G., et al. (2000). The prototype high-resolution Fly's Eye cosmic ray detector. Nucl. Instrum. Meth. A 450:253. doi: 10.1016/S0168-9002(00)00307-7
Ackermann, M., Ajello, M., Albert, A., Atwood, W. B., Baldini, L., Ballet, J., et al. (2015). The spectrum of isotropic diffuse gamma-ray emission between 100 MeV and 820 GeV. Astrophys. J. 799:86. doi: 10.1088/0004-637X/799/1/86
Ackermann, M., Ajello, M., Albert, A., Atwood, W. B., Baldini, L., Ballet, J., et al. (2016). Resolving the extragalactic γ-Ray background above 50 GeV with the Fermi Large Area Telescope. Phys. Rev. Lett. 116:151105. doi: 10.1103/PhysRevLett.116.151105
Adam, J., Adamova, D., Aggarwal, M., Aglieri Rinella, G., Agnello, M., Agrawal, N., et al. (2017). Enhanced production of multi-strange hadrons in high-multiplicity proton-proton collisions. Nat. Phys. 13:535. doi: 10.1038/nphys4111
Adams, J. H., Ahmad, S., Albert, J.-N., AllardL, D., Anchordoqui, L., Andreev, V., et al. (2015). The JEM-EUSO mission: an introduction. Exper. Astron. 40:3. doi: 10.1007/s10686-015-9482-x
Ade, P. A. R., Aghanim, N., Arnaud, M., Arroja, F., Ashdown, M., Aumont, J., Baccigalupi, C., et al. (2016). Planck 2015 results. XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 594:A19. doi: 10.1051/0004-6361/201525821
Adriani, O., Berti, E., Bonechi, L., Bongi, M., D'Alessandro, R., Detti, S., et al. (2018). Measurement of inclusive forward neutron production cross section in proton-proton collisions at TeV with the LHCf Arm2 detector. J. High Energy Phys. 11:073. doi: 10.1007/JHEP11(2018)073
Adunas, G. Z., Rodriguez-Milla, E., and Ahluwalia, D. V. (2001). Probing quantum violations of the equivalence principle. Gen. Rel. Grav. 33:183. doi: 10.1023/A:1002749217269
Aduszkiewicz, A., Ali, Y., Andronov, E. V., Antićić, T., Baatar, B., Baszczyk, M., et al. (2017). Measurement of meson resonance production in π−+ C interactions at SPS energies. Eur. Phys. J. C 77:626. doi: 10.1140/epjc/s10052-017-5184-z
Aharonian, F., Essey, W., Kusenko, A., and Prosekin, A. (2013). TeV gamma rays from blazars beyond z=1? Phys. Rev. D 87:063002. doi: 10.1103/PhysRevD.87.063002
Ahlers, M., Anchordoqui, L. A., Goldberg, H., Halzen, F., Ringwald, A., and Weiler, T. J. (2005). Neutrinos as a diagnostic of cosmic ray galactic/extra-galactic transition. Phys. Rev. D 72:023001. doi: 10.1103/PhysRevD.72.023001
Ahlers, M., Helbing, K., and Pérez de los Heros, C. (2018). Probing particle physics with IceCube. Eur. Phys. J. C 78:924. doi: 10.1140/epjc/s10052-018-6369-9
Ahn, E.-J., Engel, R., Gaisser, T. K., Lipari, P., and Stanev, T. (2009). Cosmic ray interaction event generator SIBYLL 2.1. Phys. Rev. D 80:094003. doi: 10.1103/PhysRevD.80.094003
Ajello, M., Romani, R. W., Gasparrini, D., Shaw, M. S., Bolmer, J., Cotter, G., et al. (2014). The cosmic evolution of fermi BL lacertae objects. Astrophys. J. 780:73. doi: 10.1088/0004-637X/780/1/73
Allard, D., Busca, N. G., Decerprit, G., Olinto, A. V., and Parizot, E. (2008). Implications of the cosmic ray spectrum for the mass composition at the highest energies. J. Cosmol. Astropart. Phys. 0810:033. doi: 10.1088/1475-7516/2008/10/033
Allard, D., Olinto, A. V., and Parizot, E. (2007). Signatures of the extragalactic cosmic-ray source composition from spectrum and shower depth measurements. Astron. Astrophys. 473:59. doi: 10.1051/0004-6361:20077478
Allison, P., Auffenberg, J., Bard, R., Beatty, J. J., Besson, D. Z., Böser, S., et al. (2012). Design and initial performance of the Askaryan Radio Array prototype EeV neutrino detector at the South Pole. Astropart. Phys. 35:457. doi: 10.1016/j.astropartphys.2011.11.010
Allison, P., Bard, R., Beatty, J. J., Besson, D. Z., Bora, C., Chen, C. C., et al. (2016). Performance of two Askaryan Radio Array stations and first results in the search for ultrahigh energy neutrinos. Phys. Rev. D 93:082003. doi: 10.1103/PhysRevD.93.082003
Aloisio, R., and Berezinsky, V. (2004). Diffusive propagation of UHECR and the propagation theorem. Astrophys. J. 612:900. doi: 10.1086/421869
Aloisio, R., Boncioli, D., di Matteo, A., Ghia, P. L., Grillo, A. F., Petrera, S., et al. (2014). Are cosmic rays still a valuable probe of lorentz invariance violations in the Auger era? Frascati Phys. Ser. 58:274. Available online at: http://inspirehep.net/record/1311963/
Alvarez-Muniz, J., Alves Batista, R., Balagopal, V A, Bolmont, J., Bustamante, M., Carvalho, W. R., et al. (2018). The Giant Radio Array for neutrino detection (GRAND): science and design. arXiv e-prints arXiv:1810.09994.
Alves Batista, R., Boncioli, D., di Matteo, A., van Vliet, A., and Walz, D. (2015). Effects of uncertainties in simulations of extragalactic UHECR propagation, using CRPropa and SimProp. J. Cosmol. Astropart. Phys. 1510:063. doi: 10.1088/1475-7516/2015/10/063
Alves Batista, R., de Almeida, R. M., Lago, B., and Kotera, K. (2019). Cosmogenic photon and neutrino fluxes in the Auger era. J. Cosmol. Astropart. Phys. 2019:002. doi: 10.1088/1475-7516/2019/01/002
Alves Batista, R., Dundovic, A., Erdmann, M., Kampert, K.-H., Kuempel, D., Müller, G., et al. (2016). CRPropa 3-a public astrophysical simulation framework for propagating extraterrestrial ultra-high energy particles. J. Cosmol. Astropart. Phys. 1605:038. doi: 10.1088/1475-7516/2016/05/038
Alves Batista, R., and Saveliev, A. (2019). On the measurement of the helicity of intergalactic magnetic fields using ultra-high-energy cosmic rays. J. Cosmol. Astropart. Phys. 03:011. doi: 10.1088/1475-7516/2019/03/011
Alves Batista, R., Shin, M.-S., Devriendt, J., Semikoz, D., and Sigl, G. (2017). Implications of strong intergalactic magnetic fields for ultrahigh-energy cosmic-ray astronomy. Phys. Rev. D 96:023010. doi: 10.1103/PhysRevD.96.023010
Alves Batista, R., and Sigl, G. (2014). Diffusion of cosmic rays at EeV energies in inhomogeneous extragalactic magnetic fields. J. Cosmol. Astropart. Phys. 1411:031. doi: 10.1088/1475-7516/2014/11/031
Alves Batista, R., and Silk, J. (2017). Ultrahigh-energy cosmic rays from tidally-ignited white dwarfs. Phys. Rev. D 96:103003. doi: 10.1103/PhysRevD.96.103003
Amelino-Camelia, G., Kowalski-Glikman, J., Mandanici, G., and Procaccini, A. (2005). Phenomenology of doubly special relativity. Int. J. Mod. Phys. A 20:6007. doi: 10.1142/S0217751X05028569
Amelino-Camelia, G., and Piran, T. (2001). Planck scale deformation of Lorentz symmetry as a solution to the UHECR and the TeV gamma paradoxes. Phys. Rev. D 64:036005. doi: 10.1103/PhysRevD.64.036005
Anchordoqui, L. A. (2018). Acceleration of ultrahigh-energy cosmic rays in starburst superwinds. Phys. Rev. D 97:063010. doi: 10.1103/PhysRevD.97.063010
Anchordoqui, L. A., Garcia Canal, C., and Soriano, J. F. (2019). Probing strong dynamics with cosmic neutrinos. arxiv:1902.10134
Anchordoqui, L. A., Goldberg, H., Gonzalez-Garcia, M. C., Halzen, F., Hooper, D., Sarkar, S., et al. (2005). Probing Planck scale physics with IceCube. Phys. Rev. D 72:065019. doi: 10.1103/PhysRevD.72.065019
Anchordoqui, L. A., Goldberg, H., and Weiler, T. J. (2017). Strange fireball as an explanation of the muon excess in Auger data. Phys. Rev. D 95:063005. doi: 10.1103/PhysRevD.95.063005
Anchordoqui, L. A., Hooper, D., Sarkar, S., and Taylor, A. M. (2008). High-energy neutrinos from astrophysical accelerators of cosmic ray nuclei. Astropart. Phys. 29:1. doi: 10.1016/j.astropartphys.2007.10.006
Anchordoqui, L. A., Romero, G. E., and Combi, J. A. (1999). Heavy nuclei at the end of the cosmic ray spectrum? Phys. Rev. D 60:103001. doi: 10.1103/PhysRevD.60.103001
Apel, W., Arteaga-Velázquez, J., Bekk, K., Bertaina, M., Blümer, J., Bozdog, H., et al. (2013). KASCADE-Grande measurements of energy spectra for elemental groups of cosmic rays. Astropart. Phys. 47:54. doi: 10.1016/j.astropartphys.2013.06.004
Apel, W. D., Arteaga-Velázquez, J. C., Bekk, K., Bertaina, M., Blümer, J., Bozdog, H., et al. (2011). Knee-like structure in the spectrum of the heavy component of cosmic rays observed with KASCADE-Grande. Phys. Rev. Lett. 107:171104. doi: 10.1103/PhysRevLett.107.171104
Apel, W. D., Arteaga-Velázquez, J. C., Bekk, K., Bertaina, M., Blümer, J., Bozdog, H., et al. (2017). Probing the evolution of the EAS muon content in the atmosphere with KASCADE-Grande. Astropart. Phys. 95:25. doi: 10.1016/j.astropartphys.2017.07.001
Argüelles, C. A., Katori, T., and Salvado, J. (2015). New physics in astrophysical neutrino flavor. Phys. Rev. Lett. 115:161303. doi: 10.1103/PhysRevLett.115.161303
Argüelles, C. A., Kheirandish, A., and Vincent, A. C. (2017). Imaging galactic dark matter with high-energy cosmic neutrinos. Phys. Rev. Lett. 119:201801. doi: 10.1103/PhysRevLett.119.201801
Arons, J. (2003). Magnetars in the metagalaxy: an origin for ultrahigh-energy cosmic rays in the nearby universe. Astrophys. J. 589:871. doi: 10.1086/374776
Asvarov, A. I. (2014). Size distribution of supernova remnants and the interstellar medium: the case of M 33. Astron. Astrophys. 561:A70. doi: 10.1051/0004-6361/201322774
Atoyan, A., and Dermer, C. D. (2008). Gamma rays from ultra-high energy cosmic rays in Cygnus a. Astrophys. J. 687:L75. doi: 10.1086/593202
Ave, M., Bohacova, M., Buonomo, B., Busca, N., Cazon, L., Chemerisov, S., et al. (2008). Spectrally resolved pressure dependence measurements of air fluorescence emission with AIRFLY. Nucl. Instrum. Meth. A 597:41. doi: 10.1016/j.nima.2008.08.052
Baerwald, P., Bustamante, M., and Winter, W. (2012). Neutrino Decays over Cosmological Distances and the Implications for Neutrino Telescopes. J. Cosmol. Astropart. Phys. 1210:020. doi: 10.1088/1475-7516/2012/10/020
Baerwald, P., Bustamante, M., and Winter, W. (2015). Are gamma-ray bursts the sources of ultra-high energy cosmic rays? Astropart. Phys. 62:66. doi: 10.1016/j.astropartphys.2014.07.007
Baltrusaitis, R. M., Cady, R., Cassiday, G. L., Cooperv, R., Elbert, J. W., Gerhardy, P. R., et al. (1985). The utah fly's eye detector. Nucl. Instrum. Meth. A 240:410. doi: 10.1016/0168-9002(85)90658-8
Barbosa, H. M. J., Catalani, F., Chinellato, J. A., and Dobrigkeit, C. (2004). Determination of the calorimetric energy in extensive air showers. Astropart. Phys. 22:159. doi: 10.1016/j.astropartphys.2004.06.007
Barger, V. D., Pakvasa, S., Weiler, T. J., and Whisnant, K. (2000). CPT odd resonances in neutrino oscillations. Phys. Rev. Lett. 85:5055. doi: 10.1103/PhysRevLett.85.5055
Barwick, S. W., Besson, D. Z., Burgman, A., Chiem, E., Hallgren, A., Hanson, J. C., et al. (2017). Radio detection of air showers with the ARIANNA experiment on the Ross Ice Shelf. Astropart. Phys. 90:50. doi: 10.1016/j.astropartphys.2017.02.003
Battaner, E., Castellano, J., and Masip, M. (2011). Cosmic Magnetic Lenses. Astron. Astrophys. 527:5. doi: 10.1051/0004-6361/201015663
Beck, R. (2008). “Magnetic Visions: Mapping Cosmic Magnetism with LOFAR and SKA,” in Magnetic Fields in the Universe II: From Laboratory and Stars to the Primordial Universe Cozumel (Mexico). Available online at: https://inspirehep.net/record/784599/export/hx
Bell, A., Schure, K., Reville, B., and Giacinti, G. (2013). Cosmic ray acceleration and escape from supernova remnants. Mon. Not. Roy. Astron. Soc. 431:415. doi: 10.1093/mnras/stt179
Bell, A. R. (1978a). The acceleration of cosmic rays in shock fronts. II. Mon. Not. Roy. Astron. Soc. 182:443. doi: 10.1093/mnras/182.3.443
Bell, A. R. (1978b). The acceleration of cosmic rays in shock fronts. I. Mon. Not. Roy. Astron. Soc. 182:147. doi: 10.1093/mnras/182.2.147
Bellido, J. (2018). Depth of maximum of air-shower profiles at the Pierre Auger Observatory: measurements above 1017.2 eV and composition implications. PoS(ICRC2017) 301:506. doi: 10.22323/1.301.0506
Benson, R., and Linsley, J. (1981). Satellite observation of cosmic ray air showers. International Cosmic Ray Conference, 17th, Paris, France, July 13-25, 1981 Vol. 8 (Gif-sur-Yvette), 145.
Berezinsky, V., Gazizov, A. Z., and Grigorieva, S. I. (2006). On astrophysical solution to ultrahigh-energy cosmic rays. Phys. Rev. D 74:043005. doi: 10.1103/PhysRevD.74.043005
Bergmann, T., Engel, R., Heck, D., Kalmykov, N. N., Ostapchenko, S., Pierog, T., et al. (2007). One-dimensional hybrid approach to extensive air shower simulation. Astropart. Phys. 26:420. doi: 10.1016/j.astropartphys.2006.08.005
Bertone, V., Gauld, R., and Rojo, J. (2019). Neutrino Telescopes as QCD Microscopes. J. High Energy Phys. 01:217. doi: 10.1007/JHEP01(2019)217
Bezyazeekov, P. A., Budnev, N. M., Chernykh, D., Fedorov, O., Gress, O. A., Haungs, A., et al. (2018). Reconstruction of cosmic ray air showers with Tunka-Rex data using template fitting of radio pulses. Phys. Rev. D 97:122004. doi: 10.1103/PhysRevD.97.122004
Bezyazeekov, P. A., Budnev, N. M., Gress, O. A., Haungs, A., Hiller, R., Huege, T., et al. (2015). Measurement of cosmic-ray air showers with the Tunka Radio Extension (Tunka-Rex). Nucl. Instrum. Meth. A 802:89. doi: 10.1016/j.nima.2015.08.061
Bi, X.-J., Cao, Z., Li, Y., and Yuan, Q. (2009). Testing lorentz invariance with ultra high energy cosmic ray spectrum. Phys. Rev. D 79:083015. doi: 10.1103/PhysRevD.79.083015
Biehl, D., Boncioli, D., Lunardini, C., and Winter, W. (2018). Tidally disrupted stars as a possible origin of both cosmic rays and neutrinos at the highest energies. Sci. Rep. 8:10828. doi: 10.1038/s41598-018-29022-4
Biermann, P. L., and Cassinelli, J. P. (1993). Cosmic rays. 2. Evidence for a magnetic rotator Wolf Rayet star origin. Astron. Astrophys. 277:691.
Biermann, P. L., and de Souza, V. (2012). Centaurus A: the one extragalactic source of cosmic rays with energies above the knee. Astrophys. J. 746:72. doi: 10.1088/0004-637X/746/1/72
Bilicki, M., Peacock, J. A., Jarrett, T. H., Cluver, M. E., Maddox, N., Brown, M. J. I., et al. (2016). WISE × SuperCOSMOS photometric redshift catalog: 20 million galaxies over 3/pi steradians. Astrophys. J. Suppl. 225:5. doi: 10.3847/0067-0049/225/1/5
Biteau, J., Bister, T., Caccianiga, L., Deligny, O., Di Matteo, A., and Fujii, T., et al (2018). Report of the Auger-TA Working Group on UHECR Anisotropies. Presentation at UHECR. Available online at: https://indico.in2p3.fr/event/17063/contributions/64362/attachments/50395/64305/Anisotropy_report_AugerTA_v3.pdf
Blandford, R. D. (2000). Acceleration of ultrahigh-energy cosmic rays. Phys. Scripta T85:191. doi: 10.1238/Physica.Topical.085a00191
Blasi, P., Epstein, R. I., and Olinto, A. V. (2000). Ultrahigh-energy cosmic rays from young neutron star winds. Astrophys. J. 533:L123. doi: 10.1086/312626
Bleicher, M., Zabrodin, E., Spieles, C., Bass, S. A., Ernst, C., Soff, S., et al. (1999). Relativistic hadron collisions in the ultrarelativistic quantum molecular dynamics model. J. Phys. G 25:1859. doi: 10.1088/0954-3899/25/9/308
Blum, K., Hook, A., and Murase, K. (2014). High energy neutrino telescopes as a probe of the neutrino mass mechanism. arXiv:1408.3799
Böhlen, T., Cerutti, F., Chin, M., Fass, A., Ferrari, A., Ortega, P., et al. (2014). The FLUKA code: developments and challenges for high energy and medical applications. Nucl. Data Sheets 120:211. doi: 10.1016/j.nds.2014.07.049
Boncioli, D., Biehl, D., and Winter, W. (2018). On the Common Origin of Cosmic Rays Across the Ankle and Diffuse Neutrinos at the Highest Energies From Low-Luminosity Gamma-Ray Bursts. Available online at: https://inspirehep.net/record/1690906/export/hx
Boulanger, F., Enßlin, T., Fletcher, A., Girichides, P., Hackstein, S., Haverkorn, M., Hörandel, et al. (2018). IMAGINE: A comprehensive view of the interstellar medium, Galactic magnetic fields and cosmic rays. J. Cosmol. Astropart. Phys. 1808:049. doi: 10.1088/1475-7516/2018/08/049
Broderick, A. E., Tiede, P., Chang, P., Lamberts, A., Pfrommer, C., Puchwein, E., et al. (2018). Missing gamma-ray halos and the need for new physics in the gamma-ray sky. Astrophys. J. 868:87. doi: 10.3847/1538-4357/aae5f2
Brümmel, V., Engel, R., and Roth, M. (2013). “On the importance of the energy resolution for identifying sources of UHECR,” in Proceedings, 33rd International Cosmic Ray Conference (ICRC2013), 0667.
Burrows, D. N., Kennea, J. A., Ghisellini, G., Mangano, V., Zhang, B., Page, K. L., et al. (2011). Relativistic jet activity from the tidal disruption of a star by a massive black hole. Nature 476, 421–424. doi: 10.1038/nature10374
Bustamante, M., and Ahlers, M. (2019). Inferring the flavor of high energy astrophysical neutrinos at their sources. e-Print: arXiv:1901.10087
Bustamante, M., Beacom, J. F., and Murase, K. (2017). Testing decay of astrophysical neutrinos with incomplete information. Phys. Rev. D 95:063013. doi: 10.1103/PhysRevD.95.063013
Bustamante, M., Beacom, J. F., and Winter, W. (2015). Theoretically palatable flavor combinations of astrophysical neutrinos. Phys. Rev. Lett. 115:161302. doi: 10.1103/PhysRevLett.115.161302
Bustamante, M., and Connolly, A. (2019). Extracting the energy-dependent neutrino-nucleon cross section above 10 TeV using iceCube showers. Phys. Rev. Lett. 122:041101. doi: 10.1103/PhysRevLett.122.041101
Capel, F., and Mortlock, D. J. (2019). Impact of using the ultra-high-energy cosmic ray arrival energies to constrain source associations. Mon. Not. Roy. Astron. Soc. 484:2324. doi: 10.1093/mnras/stz081
Caprioli, D. (2015). “Espresso” acceleration of ultra-high-energy cosmic rays. Astrophys. J. 811:L38. doi: 10.1088/2041-8205/811/2/L38
Carilli, C. L., and Taylor, G. B. (2002). Cluster magnetic fields. Ann. Rev. Astron. Astrophys. 40:319. doi: 10.1146/annurev.astro.40.060401.093852
Catalano, O., Maccarone, M. C., Sacco, B., and Scarsi, L. (2001). “EUSO-extreme universe space observatory,” in 27th International Cosmic Ray Conference, Hamburg, Vol. 2, 835.
Cazon, L., Conceio, R., Martins, M. A., and Riehn, F. (2018a). Probing the π0 Spectrum at High-x in Proton-Air Interactions at Ultra-High Energies. Available online at: https://ui.adsabs.harvard.edu/abs/2018arXiv181209121C/abstract
Cazon, L., Conceio, R., and Riehn, F. (2018b). Probing the energy spectrum of hadrons in proton air interactions at ultrahigh energies through the fluctuations of the muon content of extensive air showers. Phys. Lett. B 784:68. doi: 10.1016/j.physletb.2018.07.026
Chakraborty, S., Ray, A., Soderberg, A. M., Loeb, A., and Chandra, P. (2011). Ultra high energy cosmic ray acceleration in engine-driven relativistic supernovae. Nat. Commun. 2:175. doi: 10.1038/ncomms1178
Chikashige, Y., Mohapatra, R. N., and Peccei, R. D. (1980). Spontaneously broken lepton number and cosmological constraints on the neutrino mass spectrum. Phys. Rev. Lett. 45:1926. doi: 10.1103/PhysRevLett.45.1926.2
Christian, J. (2005). Testing quantum gravity via cosmogenic neutrino oscillations. Phys. Rev. D 71:024012. doi: 10.1103/PhysRevD.71.024012
Cohen, A. G., and Glashow, S. L. (2011). Pair creation constrains superluminal neutrino propagation. Phys. Rev. Lett. 107:181803. doi: 10.1103/PhysRevLett.107.181803
Coleman, S. R., and Glashow, S. L. (1997). Cosmic ray and neutrino tests of special relativity. Phys. Lett. B 405:249. doi: 10.1016/S0370-2693(97)00638-2
Coleman, S. R., and Glashow, S. L. (1999). High-energy tests of Lorentz invariance. Phys. Rev. D 59:116008. doi: 10.1103/PhysRevD.59.116008
Colladay, D., and Kostelecky, V. A. (1997). CPT violation and the standard model. Phys. Rev. D 55:6760. doi: 10.1103/PhysRevD.55.6760
Colladay, D., and Kostelecky, V. A. (1998). Lorentz violating extension of the Standard Model. Phys. Rev. D 58:116002. doi: 10.1103/PhysRevD.58.116002
Collica, L. (2016). Measurement of the muon production depths at the Pierre Auger Observatory. Eur. Phys. J. Plus 131:301. doi: 10.1140/epjp/i2016-16301-6
Cooper-Sarkar, A., Mertsch, P., and Sarkar, S. (2011). The high energy neutrino cross-section in the Standard Model and its uncertainty. J. High Energy Phys. 08:042. doi: 10.1007/JHEP08(2011)042
Cowsik, R., Madziwa-Nussinov, T., Nussinov, S., and Sarkar, U. (2012). Testing violations of lorentz invariance with cosmic-rays. Phys. Rev. D 86:045024. doi: 10.1103/PhysRevD.86.045024
Cuoco, A., Bilicki, M., Xia, J.-Q., and Branchini, E. (2017). Tomographic imaging of the fermi-LAT gamma-ray sky through cross-correlations: a wider and deeper look. Astrophys. J. Suppl. 232:10. doi: 10.3847/1538-4365/aa8553
Dai, L., and Fang, K. (2017). Can tidal disruption events produce the IceCube neutrinos? Mon. Not. Roy. Astron. Soc. 469:1354. doi: 10.1093/mnras/stx863
Das, S., Kang, H., Ryu, D., and Cho, J. (2008). Propagation of UHE protons through magnetized cosmic web. Astrophys. J. 682:29. doi: 10.1086/588278
Das, S., Razzaque, S., and Gupta, N. (2018). Ultra-High Energy Cosmic Rays and Neutrinos From Light Nuclei Composition. Available online at: https://journals.aps.org/prd/abstract/10.1103/PhysRevD.99.083015
Davis, J. H., and Silk, J. (2015). Spectral and Spatial Distortions of PeV Neutrinos from Scattering with Dark Matter. arXiv:1505.01843
Dawson, B. R., Maris, I. C., Roth, M., Salamida, F., Abu-Zayyad, T., Ikeda, D., et al. (2013). The energy spectrum of cosmic rays at the highest energies. EPJ Web Conf. 53:01005. doi: 10.1051/epjconf/20135301005
de la Chevrotière, A., St-Louis, N., and Moffat, A. F. J. (2014). Searching for magnetic fields in 11 Wolf-Rayet stars: analysis of circular polarization measurements from ESPaDOnS. Astrophys. J. 781:73. doi: 10.1088/0004-637X/781/2/73
De Sabbata, V., and Gasperini, M. (1981). Neutrino oscillations in the presence of torsion. Nuovo Cim. A 65:479. doi: 10.1007/BF02902051
De Souza, V. (2018). “Testing the agreement between the Xmax distributions measured by the Pierre Auger and Telescope Array Observatories,” in The 35th International Cosmic Ray Conference-ICRC 2017, Busan, Vol. 301, 522.
Decerprit, G., and Allard, D. (2011). Constraints on the origin of ultrahigh energy cosmic rays from cosmogenic neutrinos and photons. Astron. Astrophys. 535:A66. doi: 10.1051/0004-6361/201117673
Dermer, C. D., and Razzaque, S. (2010). Acceleration of ultra-high energy cosmic rays in the colliding shells of blazars and GRBs: constraints from the Fermi Gamma ray space telescope. Astrophys. J. 724:1366. doi: 10.1088/0004-637X/724/2/1366
Dermer, C. D., Razzaque, S., Finke, J. D., and Atoyan, A. (2009). Ultrahigh energy cosmic rays from black hole jets of radio galaxies. New J. Phys. 11:065016. doi: 10.1088/1367-2630/11/6/065016
di Matteo, A., Deligny, O., Kawata, K., Menezes de Almeida, R., Mostafá, M., Moura Santos, E., et al. (2018). “Arrival Directions of Cosmic Rays at Ultra-High Energies,” in Ultra-High Energy Cosmic Rays (UHECR2016), Kyoto, 011020.
Diaz, J. S. (2014). Neutrinos as probes of Lorentz invariance. Adv. High Energy Phys. 2014:962410. doi: 10.1155/2014/962410
Dolag, K., Grasso, D., Springel, V., and Tkachev, I. (2005). Constrained simulations of the magnetic field in the local Universe and the propagation of UHECRs. J. Cosmol. Astropart. Phys. 0501:009. doi: 10.1088/1475-7516/2005/01/009
Drescher, H.-J. (2008). Remnant break-up and muon production in cosmic ray air showers. Phys. Rev. D 77:056003. doi: 10.1103/PhysRevD.77.056003
Duan, I., and Caramete, L. I. (2015). Ultra-high-energy cosmic rays From low-luminosity active galactic nuclei. Astropart. Phys. 62:206. doi: 10.1016/j.astropartphys.2014.09.007
Dubovsky, S. L., and Tinyakov, P. G. (2002). Violation of Lorentz invariance and neutral component of UHECR. Astropart. Phys. 18:89. doi: 10.1016/S0927-6505(02)00114-7
Durrer, R., and Neronov, A. (2013). Cosmological magnetic fields: their generation, evolution and observation. Astron. Astrophys. Rev. 21:62. doi: 10.1007/s00159-013-0062-7
Egorova, V. P., Glushkov, A. V., Ivanov, A. A., Knurenko, S. P., Kolosov, V. A., Krasilnikov, A. D., et al. (2004). The Spectrum features of UHECRs below and surrounding GZK. Nucl. Phys. Proc. Suppl. 136:3. doi: 10.1016/j.nuclphysbps.2004.10.060
Eichmann, B., Rachen, J. P., Merten, L., van Vliet, A., and Becker Tjus, J. (2018). Ultra-high-energy cosmic rays from radio galaxies. J. Cosmol. Astropart. Phys. 1802:036. doi: 10.1088/1475-7516/2018/02/036
Engel, J., Gaisser, T. K., Stanev, T., and Lipari, P. (1992). Nucleus-nucleus collisions and interpretation of cosmic ray cascades. Phys. Rev. D 46:5013. doi: 10.1103/PhysRevD.46.5013
Engel, R., Heck, D., and Pierog, T. (2011). Extensive air showers and hadronic interactions at high energy. Ann. Rev. Nucl. Part. Sci. 61:467. doi: 10.1146/annurev.nucl.012809.104544
Engel, R., Riehn, F., Fedynitch, A., Gaisser, T. K., and Stanev, T. (2017). The hadronic interaction model Sibyllpast, present and future. EPJ Web Conf. 145:08001. doi: 10.1051/epjconf/201714508001
Erdmann, M., Müller, G., Urban, M., and Wirtz, M. (2016). The Nuclear Window to the Extragalactic Universe. Astropart. Phys. 85:54. doi: 10.1016/j.astropartphys.2016.10.002
Erdmann, M., and Schiffer, P. (2010). A method of measuring cosmic magnetic fields with ultra high energy cosmic ray data. Astropart. Phys. 33:201. doi: 10.1016/j.astropartphys.2010.01.011
Essey, W., Kalashev, O. E., Kusenko, A., and Beacom, J. F. (2010). Secondary photons and neutrinos from cosmic rays produced by distant blazars. Phys. Rev. Lett. 104:141102. doi: 10.1103/PhysRevLett.104.141102
Essey, W., and Kusenko, A. (2010). A new interpretation of the gamma-ray observations of active galactic nuclei. Astropart. Phys. 33:81. doi: 10.1016/j.astropartphys.2009.11.007
Fang, K., Fujii, T., Linden, T., and Olinto, A. V. (2014). Is the ultra-high energy cosmic-ray excess observed by the Telescope Array correlated with IceCube neutrinos? Astrophys. J. 794:126. doi: 10.1088/0004-637X/794/2/126
Fang, K., and Kotera, K. (2016). The highest-energy cosmic rays cannot be dominantly protons from steady sources. Astrophys. J. 832:L17. doi: 10.3847/2041-8205/832/1/L17
Fang, K., Kotera, K., and Olinto, A. V. (2012). Newly-born pulsars as sources of ultrahigh energy cosmic rays. Astrophys. J. 750:118. doi: 10.1088/0004-637X/750/2/118
Fang, K., Kotera, K., and Olinto, A. V. (2013). Ultrahigh energy cosmic ray nuclei from extragalactic pulsars and the effect of their Galactic counterparts. J. Cosmol. Astropart. Phys. 1303:010. doi: 10.1088/1475-7516/2013/03/010
Fang, K., Metzger, B. D., Murase, K., Bartos, I., and Kotera, K. (2018). Multimessenger implications of AT2018cow: high-energy cosmic ray and neutrino emissions from magnetar-powered super-luminous transients. arXiv:1812.11673.
Fang, K., and Murase, K. (2018). Linking high-energy cosmic particles by black hole jets embedded in large-scale structures. Nat. Phys. 14:396. doi: 10.1038/s41567-017-0025-4
Fang, K., and Olinto, A. V. (2016). High-energy neutrinos from sources in clusters of galaxies. Astrophys. J. 828:37. doi: 10.3847/0004-637X/828/1/37
Farrar, G. R. (2008). Generalized maximum likelihood method for ultrahigh energy cosmic rays. arXiv:0810.0226
Farrar, G. R., and Allen, J. (2013a). Evidence for some new physical process in ultrahigh-energy collisions. EPJ Web Conf. 52:07005. doi: 10.1051/epjconf/20135207005
Farrar, G. R., and Allen, J. D. (2013b). A new physical phenomenon in ultra-high energy collisions. EPJ Web Conf. 53:07007. doi: 10.1051/epjconf/20135307007
Farrar, G. R., and Piran, T. (2014). Tidal disruption jets as the source of Ultra-High Energy Cosmic Rays. arXiv:1411.0704F
Farrar, G. R., and Sutherland, M. S. (2017). Deflections of UHECRs in the Galactic magnetic field. arXiv:171102730F
Fedynitch, A., Riehn, F., Engel, R., Gaisser, T. K., and Stanev, T. (2018). The hadronic interaction model Sibyll-2.3c and inclusive lepton fluxes. arXiv:180604140
Fenu, F. (2017). The cosmic ray energy spectrum measured using the Pierre Auger Observatory. [PoSICRC2017] 486, 9–16. doi: 10.22323/1.301.0486
Ferrari, A., Sala, P. R., Fasso, A., and Ranft, J. (2005). FLUKA: A Multi-Particle Transport Code (Program Version 2005).
Fletcher, R. S., Gaisser, T. K., Lipari, P., and Stanev, T. (1994). SIBYLL: an event generator for simulation of high-energy cosmic ray cascades. Phys. Rev. D 50:5710. doi: 10.1103/PhysRevD.50.5710
Fujita, Y., Murase, K., and Kimura, S. S. (2017). Sagittarius A* as an Origin of the Galactic PeV Cosmic Rays? J. Cosmol. Astropart. Phys. 1704:037. doi: 10.1088/1475-7516/2017/04/037
Gabici, S., and Aharonian, F. A. (2005). Point-like gamma ray sources as signatures of distant accelerators of ultrahigh energy cosmic rays. Phys. Rev. Lett. 95:251102. doi: 10.1103/PhysRevLett.95.251102
Gagnon, O., and Moore, G. D. (2004). Limits on Lorentz violation from the highest energy cosmic rays. Phys. Rev. D 70:065002. doi: 10.1103/PhysRevD.70.065002
Galaverni, M., and Sigl, G. (2008). Lorentz violation in the photon sector and ultra-high energy cosmic rays. Phys. Rev. Lett. 100:021102. doi: 10.1103/PhysRevLett.100.021102
Gasperini, M. (1988). Testing the principle of equivalence with neutrino oscillations. Phys. Rev. D 38:2635. doi: 10.1103/PhysRevD.38.2635
Gasperini, M. (1989). Experimental constraints on a minimal and nonminimal violation of the equivalence principle in the oscillations of massive neutrinos. Phys. Rev. D 39:3606. doi: 10.1103/PhysRevD.39.3606
Gelmini, G. B., Nussinov, S., and Roncadelli, M. (1982). Bounds and prospects for the majoron model of left-handed neutrino masses. Nucl. Phys. B 209:157. doi: 10.1016/0550-3213(82)90107-9
Giacinti, G., Derkx, X., and Semikoz, D. V. (2010). Search for single sources of ultra high energy cosmic rays on the sky. J. Cosmol. Astropart. Phys. 1003:022. doi: 10.1088/1475-7516/2010/03/022
Giacinti, G., Kachelrie, M., and Semikoz, D. V. (2014). Explaining the spectra of cosmic ray groups above the Knee by Escape from the galaxy. Phys. Rev. D 90:041302. doi: 10.1103/PhysRevD.90.041302
Giacinti, G., Kachelriess, M., Semikoz, D. V., and Sigl, G. (2012). Cosmic ray anisotropy as signature for the transition from galactic to extragalactic cosmic rays. J. Cosmol. Astropart. Phys. 1207:031. doi: 10.1088/1475-7516/2012/07/031
Giacinti, G., and Semikoz, D. V. (2011). Method to look for imprints of ultrahigh energy nuclei sources. Phys. Rev. D 83:083002. doi: 10.1103/PhysRevD.83.083002
Gilmore, R. C., Somerville, R. S., Primack, J. R., and Dominguez, A. (2012). Semi-analytic modeling of the EBL and consequences for extragalactic gamma-ray spectra. Mon. Not. Roy. Astron. Soc. 422:3189. doi: 10.1111/j.1365-2966.2012.20841.x
Glashow, S. L., Halprin, A., Krastev, P. I., Leung, C. N., and Pantaleone, J. T. (1997). Comments on neutrino tests of special relativity. Phys. Rev. D 56:2433. doi: 10.1103/PhysRevD.56.2433
Globus, N., Allard, D., Mochkovitch, R., and Parizot, E. (2015). UHECR acceleration at GRB internal shocks. Mon. Not. Roy. Astron. Soc. 451:751. doi: 10.1093/mnras/stv893
Globus, N., Allard, D., Parizot, E., Lachaud, C., and Piran, T. (2017). Can we reconcile the TA excess and hotspot with Auger observations? Astrophys. J. 836:163. doi: 10.3847/1538-4357/836/2/163
Golup, G., Harari, D., Mollerach, S., and Roulet, E. (2009). Source position reconstruction and constraints on the galactic magnetic field from ultra-high energy cosmic rays. Astropart. Phys. 32:269. doi: 10.1016/j.astropartphys.2009.09.003
Gonzalez-Garcia, M. C., Halzen, F., and Maltoni, M. (2005). Physics reach of high-energy and high-statistics icecube atmospheric neutrino data. Phys. Rev. D 71:093010. doi: 10.1103/PhysRevD.71.093010
Gopal-Krishna, Biermann, P. L., de Souza, V., and Wiita, P. J. (2010). Ultra-high energy cosmic rays from centaurus a: jet interaction with gaseous shells. Astrophys. J. 720:L155. doi: 10.1088/2041-8205/720/2/L155
Gorham, P. W., Allison, P., Banerjee, O., Batten, L., Beatty, J. J., Bechtol, K., et al. (2018a). Constraints on the diffuse high-energy neutrino flux from the third flight of ANITA. Phys. Rev. D 98:022001. doi: 10.1103/PhysRevD.98.022001
Gorham, P. W., Rotter, B., Allison, P., Banerjee, O., Batten, L., Beatty, J. J., et al. (2018b). Observation of an Unusual Upward-going Cosmic-ray-like Event in the Third Flight of ANITA. Phys. Rev. Lett. 121:161102. doi: 10.1103/PhysRevLett.121.161102
Greisen, K. (1966). End to the cosmic ray spectrum? Phys. Rev. Lett. 16:748. doi: 10.1103/PhysRevLett.16.748
Gruppioni, C., Pozzi, F., Rodighiero, G., Delvecchio, I., Berta, S., Pozzetti, L., et al. (2013). The herschel PEP/HerMES luminosity function. I: probing the evolution of PACS selected Galaxies to z 4. Mon. Not. Roy. Astron. Soc. 432:23. doi: 10.1093/mnras/stt308
Guépin, C., Kotera, K., Barausse, E., Fang, K., and Murase, K. (2018). Ultra-high-energy cosmic rays and neutrinos from tidal disrupt ions by massive black holes. Astron. Astrophys. 616:A179. doi: 10.1051/0004-6361/201732392
Guetta, D., and Della Valle, M. (2007). On the rates of gamma ray bursts and type Ib/c supernovae. Astrophys. J. 657:L73–L76. doi: 10.1086/511417
Guetta, D., and Piran, T. (2007). Do long duration gamma ray bursts follow star formation? J. Cosmol. Astropart. Phys. 2007:003. doi: 10.1088/1475-7516/2007/07/003
Gunn, J. E., and Ostriker, J. P. (1969). Acceleration of high-energy cosmic rays by pulsars. Phys. Rev. Lett. 22:728. doi: 10.1103/PhysRevLett.22.728
Hackstein, S., Vazza, F., Brüggen, M., Sigl, G., and Dundovic, A. (2016). Propagation of ultrahigh energy cosmic rays in extragalactic magnetic fields: a view from cosmological simulations. Mon. Not. Roy. Astron. Soc. 462:3660. doi: 10.1093/mnras/stw1903
Hackstein, S., Vazza, F., Brüggen, M., Sorce, J. G., and Gottlöber, S. (2018). Simulations of ultra-high energy cosmic rays in the local universe and the origin of cosmic magnetic fields. Mon. Not. Roy. Astron. Soc. 475:2519. doi: 10.1093/mnras/stx3354
Halprin, A., Leung, C. N., and Pantaleone, J. T. (1996). A Possible violation of the equivalence principle by neutrinos. Phys. Rev. D 53:5365. doi: 10.1103/PhysRevD.53.5365
He, H.-N., Kusenko, A., Nagataki, S., Zhang, B.-B., Yang, R.-Z., and Fan, Y.-Z. (2016). Monte carlo bayesian search for the plausible source of the Telescope Array hotspot. Phys. Rev. D 93:043011. doi: 10.1103/PhysRevD.93.043011
Heinze, J., Boncioli, D., Bustamante, M., and Winter, W. (2016). Cosmogenic neutrinos challenge the cosmic ray proton dip model. Astrophys. J. 825:122. doi: 10.3847/0004-637X/825/2/122
Heinze, J., Fedynitch, A., Boncioli, D., and Winter, W. (2019). A New View on Auger Data and Cosmogenic Neutrinos in Light of Different Nuclear Disintegration and Air-Shower Models. Available online at: https://inspirehep.net/record/1713425/export/hx
Hillas, A. M. (1984). The origin of ultrahigh-energy cosmic rays. Ann. Rev. Astron. Astrophys. 22:425. doi: 10.1146/annurev.aa.22.090184.002233
Hillas, A. M. (2006). “Cosmic rays: recent progress and some current questions,” in Conference on Cosmology, Galaxy Formation and Astro-Particle Physics on the Pathway to the SKA Oxford, England, April 10-12, 2006, Oxford.
Hills, J. G. (1975). Possible power source of seyfert galaxies and QSOs. Nature 254:295. doi: 10.1038/254295a0
Ho, L. C. (2008). Nuclear activity in nearby galaxies. Ann. Rev. Astron. Astrophys. 46:475. doi: 10.1146/annurev.astro.45.051806.110546
Hooper, D., Taylor, A., and Sarkar, S. (2005). The Impact of heavy nuclei on the cosmogenic neutrino flux. Astropart. Phys. 23:11. doi: 10.1016/j.astropartphys.2004.11.002
Hooper, D., and Taylor, A. M. (2010). On The Heavy Chemical Composition of the Ultra-High Energy Cosmic Rays. Astropart. Phys. 33:151. doi: 10.1016/j.astropartphys.2010.01.003
Horiuchi, S., Murase, K., Ioka, K., and Meszaros, P. (2012). The survival of nuclei in jets associated with core-collapse supernovae and gamma-ray bursts. Astrophys. J. 753:69. doi: 10.1088/0004-637X/753/1/69
Ibe, M., and Kaneta, K. (2014). Cosmic neutrino background absorption line in the neutrino spectrum at IceCube. Phys. Rev. D 90:053011. doi: 10.1103/PhysRevD.90.053011
Ikeda, D. (2011). Results from the Telescope Array Experiment. Astrophys. Space Sci. Trans. 7:257. doi: 10.5194/astra-7-257-2011
Inoue, Y. (2011). Contribution of the gamma-ray loud radio galaxies core emissions to the cosmic MeV and GeV gamma-ray background radiation. Astrophys. J. 733:66. doi: 10.1088/0004-637X/733/1/66
Ioka, K., and Murase, K. (2014). IceCube PeV EeV neutrinos and secret interactions of neutrinos. Progr. Theor. Exper. Phys. 2014:061E01. doi: 10.1093/ptep/ptu090
Ivanov, A. (2018). Report of the Auger-TA Working Group on the Spectrum of UHECRs. Presentation at UHECR . Available online at: https://indico.in2p3.fr/event/17063/contributions/64389/attachments/50301/64168/Ivanov_Uhecr2018_TA_spectrum_v04.pdf
Jansson, R., and Farrar, G. R. (2012a). A new model of the Galactic magnetic field. Astrophys. J. 757:14. doi: 10.1088/0004-637X/757/1/14
Jansson, R., and Farrar, G. R. (2012b). The galactic magnetic field. Astrophys. J. 761:L11. doi: 10.1088/2041-8205/761/1/L11
Jedamzik, K., and Saveliev, A. (2018). A stringent limit on primordial magnetic fields from the cosmic microwave backround radiation. arXiv:1804.06115
Kakimoto, F., Loh, E. C., Nagano, M., Okuno, H., Teshima, M., and Ueno, S. (1996). A measurement of the air fluorescence yield. Nucl. Instrum. Meth. A 372:527.
Kalli, S., Lemoine, M., and Kotera, K. (2011). Distortion of the ultrahigh energy cosmic ray flux from rare transient sources in inhomogeneous extragalactic magnetic fields. Astron. Astrophys. 528:A109. doi: 10.1051/0004-6361/201015688
Kalmykov, N. N., and Ostapchenko, S. S. (1989). Comparison of nucleus- nucleus interaction characteristics in the model of quark - gluon strings and in the superposition model. (In Russian). Sov. J. Nucl. Phys. 50:315.
Kalmykov, N. N., Ostapchenko, S. S., and Pavlov, A. I. (1997). Quark-gluon string model and EAS simulation problems at ultra-high energies. Nucl. Phys. Proc. Suppl. 52:17.
Kampert, K.-H., and Unger, M. (2012). Measurements of the cosmic ray composition with air shower experiments. Astropart. Phys. 35:660. doi: 10.1016/j.astropartphys.2012.02.004
Kang, H., Rachen, J. P., and Biermann, P. L. (1997). Contributions to the cosmic ray flux above the ankle: clusters of galaxies. Mon. Not. Roy. Astron. Soc. 286:257.
Kashti, T., and Waxman, E. (2008). Searching for a correlation between cosmic-ray sources above 1019 eV and large-scale structure. J. Cosmol. Astropart. Phys. 0805:006. doi: 10.1088/1475-7516/2008/05/006
Kataoka, J., and Stawarz, L. (2005). X-ray emission properties of large scale jets, hotspots and lobes in active galactic nuclei. Astrophys. J. 622:797. doi: 10.1086/428083
Katz, B., Budnik, R., and Waxman, E. (2009). The energy production rate & the generation spectrum of UHECRs. J. Cosmol. Astropart. Phys. 0903:020. doi: 10.1088/1475-7516/2009/03/020
Keilhauer, B., Bohacova, M., Fraga, M., Matthews, J., Sakaki, N., Tameda, Y., et al. (2013). Nitrogen fluorescence in air for observing extensive air showers. EPJ Web Conf. 53:01010. doi: 10.1051/epjconf/20135301010
Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., Bergauer, T., Dragicevic, M., et al. (2010). Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC. J. High Energy Phys. 09:091. doi: 10.1007/JHEP09(2010)091
Khoze, V. A., Martin, A. D., and Ryskin, M. G. (2006). Information from leading neutrons at HERA. Eur. Phys. J. C 48:797. doi: 10.1140/epjc/s10052-006-0015-7
Kim, K.-T., Kronberg, P. P., and Tribble, P. C. (1991). Detection of excess rotation measure due to intracluster magnetic fields in clusters of galaxies. Astrophys. J. 379:80. doi: 10.1086/170484
Kimura, S. S., Murase, K., and Mészáros, P. (2018a). Super-knee cosmic rays from galactic neutron star merger remnants. Astrophys. J. 866:51. doi: 10.3847/1538-4357/aadc0a
Kimura, S. S., Murase, K., and Zhang, B. T. (2018b). Ultrahigh-energy cosmic-ray nuclei from black hole jets: recycling galactic cosmic rays through shear acceleration. Phys. Rev. D 97:023026. doi: 10.1103/PhysRevD.97.023026
Klimov, P. A., Panasyuk, M. I., Khrenov, B. A., Garipov, G. K., Kalmykov, N. N., Petrov, V. L., et al. (2017). The TUS detector of extreme energy cosmic rays on board the Lomonosov satellite. Space Sci. Rev. 212:1687.
Kopp, J., Liu, J., and Wang, X.-P. (2015). Boosted dark matter in iceCube and at the galactic center. J. High Energy Phys. 04:105. doi: 10.1007/s11214-017-0403-3
Kopper, C. (2018). Observation of astrophysical neutrinos in six years of IceCube data. PoS ICRC2017:981. doi: 10.22323/1.301.0981
Kotera, K., Allard, D., and Lemoine, M. (2011). Detectability of ultrahigh energy cosmic ray signatures in gamma rays. Astron. Astrophys. 527:A54. doi: 10.1051/0004-6361/201015259
Kotera, K., Allard, D., Murase, K., Aoi, J., Dubois, Y., Pierog, T., et al. (2009). Propagation of ultrahigh energy nuclei in clusters of galaxies: resulting composition and secondary emissions. Astrophys. J. 707:370. doi: 10.1088/0004-637X/707/1/370
Kotera, K., Allard, D., and Olinto, A. V. (2010). Cosmogenic neutrinos: parameter space and detectabilty from PeV to ZeV. J. Cosmol. Astropart. Phys. 1010:013. doi: 10.1088/1475-7516/2010/10/013
Kotera, K., and Lemoine, M. (2008a). Inhomogeneous extragalactic magnetic fields and the second knee in the cosmic ray spectrum. Phys. Rev. D 77:023005. doi: 10.1103/PhysRevD.77.023005
Kotera, K., and Lemoine, M. (2008b). The optical depth of the universe for ultra-high energy cosmic ray scattering in the magnetized large scale structure. Phys. Rev. D 77:123003. doi: 10.1103/PhysRevD.77.123003
Kumar, P., Barniol Duran, R., Bošnjak, Ž., and Piran, T. (2013). A model for the multiwavelength radiation from tidal disruption event swift J1644+57. Mon. Not. Roy. Astron. Soc. 434:3078. doi: 10.1093/mnras/stt1221
Lemoine, M., and Waxman, E. (2009). Anisotropy vs chemical composition at ultra-high energies. J. Cosmol. Astropart. Phys. 0911:009. doi: 10.1088/1475-7516/2009/11/009
Li, S. W., Bustamante, M., and Beacom, J. F. (2016). Echo technique to distinguish flavors of astrophysical neutrinos. Phys. Rev. Lett. 122:151101. doi: 10.1103/PhysRevLett.122.151101
Liang, E., Zhang, B., and Dai, Z. G. (2007). Low luminosity gamma-ray bursts as a unique population: luminosity function, local rate, and beaming factor. Astrophys. J. 662:1111-1118. doi: 10.1086/517959
Linsley, J. (1963). Evidence for a primary cosmic-ray particle with energy 10**20-eV. Phys. Rev. Lett. 10:146.
Linsley, J. (1975). Fluctuation effects on directional data. Phys. Rev. Lett. 34:1530–1533. doi: 10.1103/PhysRevLett.34.1530
Linsley, J. (1983). Spectra, anisotropies and composition of cosmic rays above 1000 GeV. Proc. 18th ICRC 12:135.
Lister, M. L., Homan, D. C., Hovatta, T., Kellermann, K. I., Kiehlmann, S., Kovalev, Y. Y., et al. (2019). MOJAVE. XVII. jet kinematics and parent population properties of relativistically beamed radio-loud blazars. ApJ 874:43. doi: 10.3847/1538-4357/ab08ee
Liu, F. M., Aichelin, J., Werner, K., and Bleicher, M. (2004). Microcanonical hadron production in pp collisions. Phys. Rev. C 69:054002. doi: 10.1103/PhysRevC.69.054002
Liu, R.-Y., Taylor, A. M., Wang, X.-Y., and Aharonian, F. A. (2016). Indication of a local fog of subankle ultrahigh energy cosmic rays. Phys. Rev. D 94:043008. doi: 10.1103/PhysRevD.94.043008
Liu, R.-Y., and Wang, X.-Y. (2012). Energy spectrum and chemical composition of ultrahigh energy cosmic rays from semi-relativistic hypernovae. Astrophys. J. 746:40. doi: 10.1088/0004-637X/746/1/40
Liu, R.-Y., Wang, X.-Y., and Dai, Z.-G. (2011). Nearby low-luminosity gamma-ray bursts as the sources of ultra-high-energy cosmic rays revisited. Mon. Not. Roy. Astron. Soc. 418, 1382–1391. doi: 10.1111/j.1365-2966.2011.19590.x
Maccione, L., Taylor, A. M., Mattingly, D. M., and Liberati, S. (2009). Planck-scale lorentz violation constrained by ultra-high-energy cosmic rays. J. Cosmol. Astropart. Phys. 0904:022. doi: 10.1088/1475-7516/2009/04/022
Magkos, G., and Pavlidou, V. (2019). Deflections of ultra-high energy cosmic rays by the Milky Way magnetic field: how well can they be corrected? Mon. Not. Roy. Astron. Soc. 2019:004. doi: 10.1088/1475-7516/2019/02/004
Marinacci, F., Vogelsberger, M., Pakmor, R., Torrey, P., Springel, V., Hernquist, L., et al. (2018). First results from the illustrisTNG simulations: radio haloes and magnetic fields. Mon. Not. Roy. Astron. Soc. 480:5113. doi: 10.1093/mnras/sty2206
Matthews, J. H., Bell, A. R., Blundell, K. M., and Araudo, A. T. (2018). Fornax A, Centaurus A, and other radio galaxies as sources of ultrahigh energy cosmic rays. Mon. Not. Roy. Astron. Soc. 479:L76. doi: 10.1093/mnrasl/sly099
Matthews, J. H., Bell, A. R., Blundell, K. M., and Araudo, A. T. (2019). Ultra-high energy cosmic rays from shocks in the lobes of powerful radio galaxies. Mon. Not. Roy. Astron. Soc. 482:4303. doi: 10.1093/mnras/sty2936
Miralda-Escude, J., and Waxman, E. (1996). Signatures of the origin of high-energy cosmic rays in cosmological gamma-ray bursts. Astrophys. J. 462:L59. doi: 10.1086/310042
Mirzoyan, R. (2019). First time detection of a GRB at sub-TeV energies; MAGIC detects the GRB 190114C. Astronomer's Telegram 12390. Available online at: http://adsabs.harvard.edu/abs/2019ATel12390….1
Moffat, J. W. (2003). Spontaneous violation of lorentz invariance and ultrahigh- energy cosmic rays. Int. J. Mod. Phys. D 12, 1279–1287. doi: 10.1142/S0218271803003633
Mollerach, S., and Roulet, E. (2013). Magnetic diffusion effects on the ultra-high energy cosmic ray spectrum and composition. J. Cosmol. Astropart. Phys. 1310:013. doi: 10.1088/1475-7516/2013/10/013
Murase, K. (2009). Ultrahigh-energy photons as a probe of nearby transient ultrahigh-energy cosmic-ray sources and possible lorentz-invariance violation. Phys. Rev. Lett. 103:081102. doi: 10.1103/PhysRevLett.103.081102
Murase, K., Dermer, C. D., Takami, H., and Migliori, G. (2012). Blazars as ultra-high-energy cosmic-ray sources: implications for TeV gamma-ray observations. Astrophys. J. 749:63. doi: 10.1088/0004-637X/749/1/63
Murase, K., and Fukugita, M. (2018). Energetics of high-energy cosmic radiations. Phys. Rev. D 99:063012. doi: 10.1103/PhysRevD.99.063012
Murase, K., Inoue, S., and Nagataki, S. (2008a). Cosmic rays above the second knee from clusters of galaxies and associated high-energy neutrino emission. Astrophys. J. 689:L105. doi: 10.1086/595882
Murase, K., Ioka, K., Nagataki, S., and Nakamura, T. (2006). High energy neutrinos and cosmic-rays from low-luminosity gamma-ray bursts? Astrophys. J. 651:L5. doi: 10.1086/509323
Murase, K., Ioka, K., Nagataki, S., and Nakamura, T. (2008b). High-energy cosmic-ray nuclei from high- and low-luminosity gamma-ray bursts and implications for multi-messenger astronomy. Phys. Rev. D 78:023005. doi: 10.1103/PhysRevD.78.023005
Murase, K., Meszaros, P., and Zhang, B. (2009). Probing the birth of fast rotating magnetars through high-energy neutrinos. Phys. Rev. D 79:103001. doi: 10.1103/PhysRevD.79.103001
Murase, K., and Takami, H. (2009). Implications of ultra-high-energy cosmic rays for transient sources in the auger era. Astrophys. J. 690:L14–L17. doi: 10.1088/0004-637X/690/1/L14
Myers, R. C., and Pospelov, M. (2003). Ultraviolet modifications of dispersion relations in effective field theory. Phys. Rev. Lett. 90:211601. doi: 10.1103/PhysRevLett.90.211601
Nelles, A. (2018). ARIANNA: Current Developments and Understanding the Ice for Neutrino Detection. Available online at: https://ui.adsabs.harvard.edu/abs/2018arXiv181110660N/abstract
Neronov, A., Semikoz, D. V., Anchordoqui, L. A., Adams, J., and Olinto, A. V. (2017). Sensitivity of a proposed space-based Cherenkov astrophysical-neutrino telescope. Phys. Rev. D 95:023004. doi: 10.1103/PhysRevD.95.023004
Neronov, A., and Vovk, I. (2010). Evidence for strong extragalactic magnetic fields from Fermi observations of TeV blazars. Science, 328:73–75. doi: 10.1126/science.1184192
Ng, K. C. Y., and Beacom, J. F. (2014). Cosmic neutrino cascades from secret neutrino interactions. Phys. Rev. D 90:065035. doi: 10.1103/PhysRevD.90.065035 [Erratum: Phys. Rev. D 90, 089904 (2014)].
Oikonomou, F., Connolly, A., Abdalla, F. B., Lahav, O., Thomas, S. A., Waters, D., and Waxman, E. (2013). A Search for Correlation of Ultra-High Energy Cosmic Rays with IRAS-PSCz and 2MASS-6dF Galaxies. J. Cosmol. Astropart. Phys. 1305:015. doi: 10.1088/1475-7516/2013/05/015
Oikonomou, F., and Mostafa, M. (2018). A Magnetic spectrometer analysis of ultra high energy cosmic ray arrival directions. PoS, ICRC2017:525. doi: 10.22323/1.301.0525
Oikonomou, F., Murase, K., and Kotera, K. (2014). Synchrotron pair halo and echo emission from blazars in the cosmic web: application to extreme TeV blazars. Astron. Astrophys. 568:A110. doi: 10.1051/0004-6361/201423798
Olinto, A. V., Adams, J. H., Aloisio, R., Anchordoqui, L. A., Bergman, D. R., Bertainaet, M. E., et al. (2018). POEMMA: probe of extreme multi-messenger astrophysics. PoS, ICRC2017:542. doi: 10.22323/1.301.0542
Ostapchenko, S. (2006a). Nonlinear screening effects in high energy hadronic interactions. Phys. Rev. D 74:014026. doi: 10.1103/PhysRevD.74.014026
Ostapchenko, S. (2006b). On the re-summation of enhanced Pomeron diagrams. Phys. Lett. B 636, 40–45. doi: 10.1016/j.physletb.2006.03.026
Ostapchenko, S. (2011). Monte carlo treatment of hadronic interactions in enhanced pomeron scheme: I. QGSJET-II model. Phys. Rev. D 83:014018. doi: 10.1103/PhysRevD.83.014018
Ostapchenko, S. (2013). QGSJET-II: physics, recent improvements, and results for air showers. EPJ Web Conf. 52:02001. doi: 10.1051/epjconf/20135202001
Ostapchenko, S. (2014). LHC data on inelastic diffraction and uncertainties in the predictions for longitudinal extensive air shower development. Phys. Rev. D 89:074009. doi: 10.1103/PhysRevD.89.074009
Ostapchenko, S., and Bleicher, M. (2016). Constraining pion interactions at very high energies by cosmic ray data. Phys. Rev. D 93:051501. doi: 10.1103/PhysRevD.93.051501
Otte, A. N. (2018). Trinity: an air-shower imaging system for the detection of cosmogenic neutrinos. arXiv:1811.09287
Pakmor, R., Gómez, F. A., Grand, R. J. J., Marinacci, F., Simpson, C. M., Springel, V., et al. (2017). Magnetic field formation in the milky way like disc galaxies of the auriga project. Mon. Not. R. Astron. Soc. 469:3185. doi: 10.1093/mnras/stx1074
Pakmor, R., Marinacci, F., and Springel, V. (2014). Magnetic fields in cosmological simulations of disk galaxies. Astrophys. J. 783:L20. doi: 10.1088/2041-8205/783/1/L20
Panasyuk, M. I., Klimov, P., Khrenov, B., Sharakin, S., Zotov, M., Picozza, P., et al. (2016). Ultra high energy cosmic ray detector KLYPVE on board the Russian Segment of the ISS. PoS ICRC2015:669. doi: 10.22323/1.236.0669
Pe'er, A., Murase, K., and Meszaros, P. (2009). Radio quiet AGNs as possible sources of ultra-high energy cosmic rays. Phys. Rev. D 80:123018. doi: 10.1103/PhysRevD.80.123018
Persichilli, C. R. (2018). Performance and simulation of the ARIANNA pilot array, With implications for future ultra-high energy neutrino astronomy (Ph.D. thesis). University of California, Irvine. Available online at: http://arianna.ps.uci.edu/sites/default/files/Persichilli_Thesis.pdf
Philippov, A. A., and Spitkovsky, A. (2018). Ab-initio pulsar magnetosphere: particle acceleration in oblique rotators and high-energy emission modeling. Astrophys. J. 855:94. doi: 10.3847/1538-4357/aaabbc
Pierog, T. (2018). Air shower simulation with a new generation of post-LHC hadronic interaction models in CORSIKA. PoS ICRC2017:1100. doi: 10.22323/1.301.1100
Pierog, T., Karpenko, I. U., Katzy, J. M., Yatsenko, E., and Werner, K. (2015). EPOS LHC: test of collective hadronization with data measured at the CERN large hadron Collider. Phys. Rev. C 92:034906. doi: 10.1103/PhysRevC.92.034906
Pierog, T., and Werner, K. (2008). Muon production in extended air shower simulations. Phys. Rev. Lett. 101:171101. doi: 10.1103/PhysRevLett.101.171101
Piran, T. (2005). Magnetic fields in gamma-ray bursts: a short overview. AIP Conf. Proc. 784:164. doi: 10.1063/1.2077181
Prosekin, A., Essey, W., Kusenko, A., and Aharonian, F. (2012). Time structure of gamma-ray signals generated in line-of-sight interactions of cosmic rays from distant blazars. Astrophys. J. 757:183. doi: 10.1088/0004-637X/757/2/183
Pshirkov, M. S., Tinyakov, P. G., Kronberg, P. P., and Newton-McGee, K. J. (2011). Deriving global structure of the galactic magnetic field from faraday rotation measures of extragalactic sources. Astrophys. J. 738:192. doi: 10.1088/0004-637X/738/2/192
Ptitsyna, K. V., and Troitsky, S. V. (2010). Physical conditions in potential sources of ultra-high-energy cosmic rays. I. updated hillas plot and radiation-loss constraints. Phys. Usp. 53, 691–701. doi: 10.3367/UFNe.0180.201007c.0723
Ptuskin, V. S., Rogovaya, S. I., Zirakashvili, V. N., Chuvilgin, L. G., Khristiansen, G. B., Klepach, E. G., et al. (1993). Diffusion and drift of very high energy cosmic rays in galactic magnetic fields. Astron. Astrophys. 268, 726–735. Available online at: http://adsabs.harvard.edu/full/1993A%26A…268.726P
Rachen, J. P., and Biermann, P. L. (1993). Extragalactic ultrahigh-energy cosmic rays. 1. contribution from hot spots in FR-II radio galaxies. Astron. Astrophys. 272, 161–175.
Rasmussen, R. W., Lechner, L., Ackermann, M., Kowalski, M., and Winter, W. (2017). Astrophysical neutrinos flavored with beyond the standard model physics. Phys. Rev. D 96:083018. doi: 10.1103/PhysRevD.96.083018
Rees, M. J. (1988). Tidal disruption of stars by black holes of 10 to the 6th-10 to the 8th solar masses in nearby galaxies. Nature 333:523.
Resconi, E., Coenders, S., Padovani, P., Giommi, P., and Caccianiga, L. (2017). Connecting blazars with ultrahigh-energy cosmic rays and astrophysical neutrinos. Mon. Not. Roy. Astron. Soc. 468:597. doi: 10.1093/mnras/stx498
Reynolds, S. P., Gaensler, B. M., and Bocchino, F. (2012). Magnetic fields in supernova remnants and pulsar-wind nebulae. Space Sci. Rev. 166:231. doi: 10.1007/s11214-011-9775-y
Riehn, F., Engel, R., Fedynitch, A., Gaisser, T. K., and Stanev, T. (2016). A new version of the event generator sibyll. PoS ICRC2015:558. doi: 10.22323/1.236.0558
Robertson, B. E., Ellis, R. S., Furlanetto, S. R., and Dunlop, J. S. (2015). Cosmic reionization and early star-forming galaxies: a joint analysis of new constraints from planck and the hubble space telescope. Astrophys. J. 802:L19. doi: 10.1088/2041-8205/802/2/L19
Rodrigues, X., Biehl, D., Boncioli, D., and Taylor, A. M. (2019). Binary neutron star merger remnants as sources of cosmic rays below the Ankle. Astropart. Phys. 106:10. doi: 10.1016/j.astropartphys.2018.10.007
Rodrigues, X., Fedynitch, A., Gao, S., Boncioli, D., and Winter, W. (2018). Neutrinos and ultra-high-energy cosmic-ray nuclei from blazars. Astrophys. J. 854:54. doi: 10.3847/1538-4357/aaa7ee
Roesler, S., Engel, R., and Ranft, J. (2001). “The monte carlo event generator dpmjet-iii at cosmic ray energies,” in Proceedings of 27th International Cosmic Ray Conference, Vol. 2, (Hamburg), 439–442.
Romero, G. E., Combi, J. A., Anchordoqui, L. A., and Perez Bergliaffa, S. (1996). A possible source of extragalactic cosmic rays with arrival energies beyond the GZK cutoff. Astropart. Phys. 5:279.
Romero, G. E., Müller, A. L., and Roth, M. (2018). Particle acceleration in the superwinds of starburst galaxies. Astron. Astrophys., 616:A57. doi: 10.1051/0004-6361/201832666
Romero-Wolf, A., and Ave, M. (2018). Bayesian inference constraints on astrophysical production of ultra-high energy cosmic rays and cosmogenic neutrino flux predictions. J. Cosmol. Astropart. Phys. 1807:025. doi: 10.1088/1475-7516/2018/07/025
Ryu, D., Kang, H., Hallman, E., and Jones, T. W. (2003). Cosmological shock waves and their role in the large scale structure of the universe. Astrophys. J. 593:599. doi: 10.1086/376723
Ryu, D., Schleicher, D. R. G., Treumann, R. A., Tsagas, C. G., and Widrow, L. M. (2012). Magnetic fields in the large-scale structure of the universe. Space Sci. Rev. 166:1. doi: 10.1007/s11214-011-9839-z
Sagawa, H. (2018). TA Anisotropy Summary. Presentation at UHECR 2018. Available online at: https://indico.in2p3.fr/event/17063/contributions/64318/attachments/50389/64298/UHECR2018-kawata-v2.pdf
Samuelsson, F., Bgu, D., Ryde, F., and Pe'er, A. (2018). The limited contribution of low- and high-luminosity gamma-ray bursts to ultra-high energy cosmic rays.
Sarkar, B., Kampert, K.-H., and Kulbartz, J. (2011). “Ultra-high energy photon and neutrino fluxes in realistic astrophysical scenarios,” in Proceedings of 32nd International Cosmic Ray Conference Vol. 2, 198. doi: 10.7529/ICRC2011/V02/1087
Scully, S. T., and Stecker, F. W. (2009). Lorentz invariance violation and the observed spectrum of ultrahigh energy cosmic rays. Astropart. Phys. 31:220. doi: 10.1016/j.astropartphys.2009.01.002
Senno, N., Murase, K., and Meszaros, P. (2017). High-energy neutrino flares from X-ray bright and dark tidal disruption events. Astrophys. J. 838:3. doi: 10.3847/1538-4357/aa6344
Shoemaker, I. M., and Murase, K. (2016). Probing BSM neutrino physics with flavor and spectral distortions: prospects for future high-energy neutrino telescopes. Phys. Rev. D 93:085004. doi: 10.1103/PhysRevD.93.085004
Shukurov, A., Rodrigues, L. F. S., Bushby, P. J., Hollins, J., and Rachen, J. P. (2018). A physical approach to modelling large-scale galactic magnetic fields. Astron. Astrophys. 623:A113. doi: 10.1051/0004-6361/201834642
Sigl, G., Miniati, F., and Ensslin, T. A. (2003a). Signatures of magnetized large scale structure in ultrahigh-energy cosmic rays. D70:043007.
Sigl, G., Miniati, F., and Ensslin, T. A. (2003b). Ultrahigh-energy cosmic rays in a structured and magnetized universe. Phys. Rev. D 68:043002. doi: 10.1103/PhysRevD.68.043002
Stecker, F. W., and Scully, S. T. (2005). Lorentz invariance violation and the spectrum and source power of ultrahigh energy cosmic rays. Astropart. Phys. 23, 203–209. doi: 10.1016/j.astropartphys.2005.01.001
Streitmatter, R. E. (1998). Orbiting wide angle light-collectors (OWL): observing cosmic rays from space. AIP Conf. Proc. 433:95. doi: 10.1063/1.56149
Subramanian, K. (2016). The origin, evolution and signatures of primordial magnetic fields. Rept. Prog. Phys. 79:076901. doi: 10.1088/0034-4885/79/7/076901
Sun, H., Zhang, B., and Li, Z. (2015). Extragalactic high-energy transients: event rate densities and luminosity functions. Astrophys. J. 812:33. doi: 10.1088/0004-637X/812/1/33
Sutherland, M. S., Baughman, B. M., and Beatty, J. J. (2012). A method for constraining cosmic magnetic field models using ultra-high energy cosmic rays: the field scan method. Astropart. Phys. 37:17. doi: 10.1016/j.astropartphys.2012.07.001
Takahashi, Y. (1995). Maximum-energy auger air shower satellite (MASS) for observing cosmic rays in the energy region 1019−22 eV. Int. Cosmic Ray Conf. 3:595.
Takami, H., and Murase, K. (2012). The role of structured magnetic fields on constraining properties of transient sources of ultra-high-energy cosmic rays. Astrophys. J. 748:9. doi: 10.1088/0004-637X/748/1/9
Takami, H., Murase, K., and Dermer, C. D. (2013). Disentangling hadronic and leptonic cascade scenarios from the very-high-energy gamma-ray emission of distant hard-spectrum blazars. Astrophys. J. 771:L32. doi: 10.1088/2041-8205/771/2/L32
Takami, H., Murase, K., Nagataki, S., and Sato, K. (2009). Cosmogenic neutrinos as a probe of the transition from galactic to extragalactic cosmic rays. Astropart. Phys. 31, 201–211. doi: 10.1016/j.astropartphys.2009.01.006
Tavecchio, F. (2014). On the hadronic cascade scenario for extreme BL lacs. Mon. Not. Roy. Astron. Soc. 438:3255. doi: 10.1093/mnras/stt2437
Taylor, A. M., Ahlers, M., and Hooper, D. (2015). Indications of negative evolution for the sources of the highest energy cosmic rays. Phys. Rev. D 92:063011. doi: 10.1103/PhysRevD.92.063011
Terral, P., and Ferrière, K. (2017). Constraints from faraday rotation on the magnetic field structure in the galactic halo. Astron. Astrophys. 600:A29. doi: 10.1051/0004-6361/201629572
The Pierre Auger and Telescope Array Collaborations (2018). “Pierre Auger Observatory and Telescope Array,” in Joint Contributions to the 35th International Cosmic Ray Conference (ICRC 2017), Busan. arXiv:1801.01018
Thompson, T. A., Quataert, E., and Murray, N. (2009). Radio emission from supernova remnants: implications for post-shock magnetic field amplification and the magnetic fields of galaxies. Mon. Not. Roy. Astron. Soc. 397, 1410–1419. doi: 10.1111/j.1365-2966.2009.14889.x
Thompson, T. A., Quataert, E., Waxman, E., Murray, N., and Martin, C. L. (2006). Magnetic fields in starburst galaxies and the origin of the FIR-radio correlation. Astrophys. J. 645, 186–198. doi: 10.1086/504035
Thoudam, S., Rachen, J. P., van Vliet, A., Achterberg, A., Buitink, S., Falcke, H., et al. (2016). Cosmic-ray energy spectrum and composition up to the ankle: the case for a second galactic component. Astron. Astrophys. 595:A33. doi: 10.1051/0004-6361/201628894
Tiede, P., Broderick, A. E., Shalaby, M., Pfrommer, C., Puchwein, E., Chang, P., et al. (2017). Constraints on the intergalactic magnetic field from bow ties in the gamma-ray sky. arXiv:1702.02586
Tinyakov, P., Sagawa, H., Troitsky, S., Thomson, G., Kawata, K., and Okuda, T. (2016). TA Anisotropy Summary. PoS ICRC2015:326. Available online at: http://inspirehep.net/record/1483631/
Tokuno, H., Abu-Zayyad, T., Aida, R., Allen, M., Azuma, R., Barcikowski, E., et al. (2011). The status of the Telescope Array experiment. J. Phys. Conf. Ser. 293:012035. doi: 10.1088/1742-6596/293/1/012035
Tokuno, H., Tameda, Y., Takeda, M., Kadota, K., Ikeda, D., Chikawa, M., et al. (2012). New air fluorescence detectors employed in the Telescope Array experiment. Nucl. Instrum. Meth. A 676, 54–65. doi: 10.1016/j.nima.2012.02.044
Tomas, R., Pas, H., and Valle, J. W. F. (2001). Generalized bounds on majoron - neutrino couplings. Phys. Rev. D 64:095005. doi: 10.1103/PhysRevD.64.095005
Tsunesada, Y., Abuzayyad, T., Ivanov, D., Thomson, G., Fujii, T., and Ikeda, D. (2018). Energy spectrum of ultra-high-energy cosmic rays measured by the Telescope Array. PoS ICRC2017:535. doi: 10.22323/1.301.0535
Ulrich, R. (2016). Extension of the measurement of the proton-air cross section with the pierre auger observatory. PoS ICRC2015:401. doi: 10.22323/1.236.0401
Ulrich, R., Blumer, J., Engel, R., Schussler, F., and Unger, M. (2009). On the measurement of the proton-air cross section using air shower data. New J. Phys. 11:065018. doi: 10.1088/1367-2630/11/6/065018
Unger, M., and Farrar, G. R. (2017). Uncertainties in Themagnetic Field of Themilky Way. Available online at: http://adsabs.harvard.edu/abs/2017ICRC…35.558U
Unger, M., Farrar, G. R., and Anchordoqui, L. A. (2015). Origin of the ankle in the ultrahigh energy cosmic ray spectrum, and of the extragalactic protons below it. Phys. Rev. D 92:123001. doi: 10.1103/PhysRevD.92.123001
Urry, C. M., and Padovani, P. (1995). Unified schemes for radio-loud active galactic nuclei. Publ. Astron. Soc. Pac. 107:803.
Vallee, J. P. (2011). Magnetic fields in the galactic universe, as observed in supershells, galaxies, intergalactic and cosmic realms. New Astron. Rev. 55:91. doi: 10.1016/j.newar.2011.01.002
Verzi, V. (2013). “The energy scale of the pierre auger observatory,” in Proceedings 33rd International Cosmic Ray Conference (ICRC2013): Rio de Janeiro, Brazil, July 2-9, 2013, (Rio de Janeiro), 0928.
Vietri, M. (1995). On the acceleration of ultrahigh-energy cosmic rays in gamma-ray bursts. Astrophys. J. 453:883.
Vincent, A. C., Palomares-Ruiz, S., and Mena, O. (2016). Analysis of the 4-year IceCube high-energy starting events. Phys. Rev. D 94:023009. doi: 10.1103/PhysRevD.94.023009
Wang, S.-H., Chen, P., Huang, M., and Nam, J. (2013). Feasibility of determining diffuse ultra-high energy cosmic neutrino flavor ratio through ARA neutrino observatory. J. Cosmol. Astropart. Phys. 1311:062. doi: 10.1088/1475-7516/2013/11/062
Wang, X., and Loeb, A. (2017). Ultrahigh energy cosmic rays from nonrelativistic quasar outflows. Phys. Rev. D 95:063007. doi: 10.1103/PhysRevD.95.063007
Wang, X.-Y., Razzaque, S., and Meszaros, P. (2008). On the origin and survival of UHE cosmic-ray nuclei in GRBs and hypernovae. Astrophys. J. 677:432. doi: 10.1086/529018
Wang, X.-Y., Razzaque, S., Meszaros, P., and Dai, Z.-G. (2007). High-energy cosmic rays and neutrinos from semi-relativistic hypernovae. Phys. Rev. D 76:083009. doi: 10.1103/PhysRevD.76.083009
Warren, M. S., Abazajian, K., Holz, D. E., and Teodoro, L. (2006). Precision determination of the mass function of dark matter halos. Astrophys. J. 646, 881–885. doi: 10.1086/504962
Waxman, E. (1995a). Cosmological gamma-ray bursts and the highest energy cosmic rays. Phys. Rev. Lett. 75:386.
Waxman, E., and Miralda-Escude, J. (1996). Images of bursting sources of high-energy cosmic rays. 1. effects of magnetic fields. Astrophys. J. 472:L89.
Werner, K., Liu, F.-M., and Pierog, T. (2006). Parton ladder splitting and the rapidity dependence of transverse momentum spectra in deuteron-gold collisions at RHIC. Phys. Rev. C 74:044902. doi: 10.1103/PhysRevC.74.044902
Werner, K., and Pierog, T. (2007). Extended air shower simulations based on EPOS. AIP Conf. Proc. 928:111. doi: 10.1063/1.2775903
Wittkowski, D. (2018). Reconstructed properties of the sources of UHECR and their dependence on the extragalactic magnetic field. PoS ICRC2017:563. doi: 10.22323/1.301.0563
Wittkowski, D., and Kampert, K.-H. (2018). Predictions for the flux of highenergy cosmogenic neutrinos and the influence of the extragalactic magnetic field. arxiv:1810.03769
Wykes, S., Croston, J. H., Hardcastle, M. J., Eilek, J. A., Biermann, P. L., Achterberg, A., et al. (2013). Mass entrainment and turbulence-driven acceleration of ultra-high energy cosmic rays in centaurus A. Astron. Astrophys. 558:A19. doi: 10.1051/0004-6361/201321622
Wykes, S., Taylor, A. M., Bray, J. D., Hardcastle, M. J., and Hillas, M. (2018). UHECR propagation from centaurus A. Nucl. Part. Phys. Proc. 297, 234–241. doi: 10.1016/j.nuclphysbps.2018.07.033
Yoshida, S., Hayashida, N., Honda, K., Honda, M., Imaizumi, S., Inoue, N., et al. (1995). The cosmic ray energy spectrum above 3 1018 ev measured by the akeno giant air shower array. Astropart. Phys. 3:105.
Yuksel, H., Stanev, T., Kistler, M. D., and Kronberg, P. P. (2012). The centaurus A ultrahigh-energy cosmic ray excess and the local extragalactic magnetic field. Astrophys. J. 758, 16–23. doi: 10.1088/0004-637X/758/1/16
Yushkov, A. (2018). Report of the Auger-TA Working Group on the Composition of UHECRs. Presentation at UHECR 2018. Available online at: https://indico.in2p3.fr/event/17063/contributions/64358/attachments/50228/64070/Yushkov_MassWG_AugerTA_UHECR2018_Presented.pdf
Zatsepin, G. T., and Kuzmin, V. A. (1966). Upper limit of the spectrum of cosmic rays. JETP Lett. 4:78.
Zhang, B. T., and Murase, K. (2018). Ultrahigh-energy cosmic-ray nuclei and neutrinos from engine-driven supernovae. arXiv:1812.10289
Zhang, B. T., Murase, K., Kimura, S. S., Horiuchi, S., and Mészáros, P. (2018). Low-luminosity gamma-ray bursts as the sources of ultrahigh-energy cosmic ray nuclei. Phys. Rev. D 97:083010. doi: 10.1103/PhysRevD.97.083010
Zhang, B. T., Murase, K., Oikonomou, F., and Li, Z. (2017). High-energy cosmic ray nuclei from tidal disruption events: origin, survival, and implications. Phys. Rev. D 96:063007. doi: 10.1103/PhysRevD.96.063007
Keywords: ultrahigh energy cosmic rays, ultrahigh energy neutrinos, extensive air shower detectors, intergalactic magnetic fields, mass composition, hadronic interactions, anisotropies
Citation: Alves Batista R, Biteau J, Bustamante M, Dolag K, Engel R, Fang K, Kampert K-H, Kostunin D, Mostafa M, Murase K, Oikonomou F, Olinto AV, Panasyuk MI, Sigl G, Taylor AM and Unger M (2019) Open Questions in Cosmic-Ray Research at Ultrahigh Energies. Front. Astron. Space Sci. 6:23. doi: 10.3389/fspas.2019.00023
Received: 15 January 2019; Accepted: 21 March 2019;
Published: 04 June 2019.
Edited by:
Frank Franz Deppisch, University College London, United KingdomReviewed by:
Francis Halzen, University of Wisconsin-Madison, United StatesSoebur Razzaque, University of Johannesburg, South Africa
Copyright © 2019 Alves Batista, Biteau, Bustamante, Dolag, Engel, Fang, Kampert, Kostunin, Mostafa, Murase, Oikonomou, Olinto, Panasyuk, Sigl, Taylor and Unger. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Foteini Oikonomou, Zm9pa29ub21AZXNvLm9yZw==; Ke Fang, a2VmYW5nQHN0YW5mb3JkLmVkdQ==
 Rafael Alves Batista
Rafael Alves Batista Jonathan Biteau2
Jonathan Biteau2 Mauricio Bustamante
Mauricio Bustamante Karl-Heinz Kampert
Karl-Heinz Kampert Dmitriy Kostunin
Dmitriy Kostunin Miguel Mostafa
Miguel Mostafa Kohta Murase
Kohta Murase Foteini Oikonomou
Foteini Oikonomou Mikhail I. Panasyuk
Mikhail I. Panasyuk Andrew M. Taylor
Andrew M. Taylor