Linear Waves in Partially Ionized Plasmas in Ionization Non-equilibrium

1. Introduction

One of the most intriguing aspects that have been largely omitted so far in the field of dynamical process in solar plasmas is that the plasma in the lower atmosphere is partially ionized, with plasma made up from charged particles and neutrals that are interacting through collision. Although the exact degree of ionization is not fully known, the ratio of electron density to neutral hydrogen density covers a few orders of magnitude from the photosphere to the top of the chromosphere. The ionization state of the plasma is a very important factor, as the collision between various species will significantly enhance transport processes that control the appearance and evolution of instabilities in the presence of inhomogeneous flows. Depending on the range of frequencies we are interested in, the description of the dynamics in these regions can be described within the framework of single fluid magnetohydrodynamics (MHD) (for frequencies smaller than the ion-neutral frequency), two-fluid MHD (when frequencies of interest are larger than the ion-neutral collisional frequency), or multi-fluid description (in the high-frequency regime when waves' frequency is comparable to the electron-ion collisional frequency).

Research in the dynamical evolution of physical phenomena in the solar atmosphere is based on the assumption of ionization equilibrium and the equilibrium Maxwellian distribution of particles. However, this model is not accurate for rapidly changing phenomena (e.g., high frequency waves, shock waves), for rapid energy releases where high-energy tail of the electron distribution are observed. Non-equilibrium ionization can occur during heating or cooling events, significantly affecting line intensities and subsequently the plasma diagnostics (Bradshaw and Mason, 2003; Bradshaw et al., 2004). Departures from the equilibrium Maxwellian distribution have also been inferred from chromospheric and transition region line emission (Dzifčáková and Kulinová, 2011). In the chromosphere the ionization/recombination relaxation times scales are of the order of 10³ − 10⁵ s (Carlsson and Stein, 2002), meaning that dynamics occurring below this scales will be affected by non-equilibrium effects. Because the relaxation timescale is much longer than dynamic timescales, H ionization does not have time to reach its equilibrium value and its fluctuations are much smaller than the variation of its statistical equilibrium value appropriate for the instantaneous conditions. The problem of waves and oscillations in two fluid partially ionized plasmas is a relatively new area of solar physics, nevertheless some fundamental properties of such environments are already established (see, e.g., Soler et al., 2010, 2013; Zaqarashvili et al., 2011; Ballester et al., 2018b).

The process of non-equilibrium ionization is very much related to the process of irreversible physics via inelastic collision between particles. In the present paper we will restrict our attention to collision impact ionization and radiative recombination. In addition, we assume that the collision between particles can lead to either ionization of recombination, while the processes of collisions leading to excited states of articles will be neglected. This approximation requires that the collision involving neutrals would imply an energy exchange that is at least equal to the first ionization potential, while excited states (if they appear) will have a lifetime that is much shorter than the dynamical scales involved in our problem.

The paper is structured as follows: in section 2 we introduce the necessary equations with their implications and limitations. Given the complexity of the problem, here we are employing a simplified model. In section 3 we study the propagation characteristics of Alfvén waves and investigate the effect of non-equilibrium ionization on the propagation speed of waves and their damping with respect to the collisional parameter between particles for different ionization degrees of the plasma. Using a simple configuration the wave characteristics of decoupled slow waves are studied in section 4. Finally our results are summarized in section 5.

2. Basic Equations and Assumptions

The physical processes of ionization and recombination are far from trivial given the multitude of mechanisms that can result in one or more electrons being removed from a neutral atom and the reversed process of combination between positive ions and an energetic electrons to form neutral atoms. However, for simplicity here we are going to concentrate on collisions, as the main mechanism that can generate ions and neutrals. In order to describe the effects on non-equilibrium ionization and recombination processes let us introduce the quantities ${\Gamma }_q^r$, denoting the interaction rate of process r, affecting fluid q (Leake et al., 2012; Meier and Shumlak, 2012; Maneva et al., 2017). The radiative recombination rate of ions is proportional to the number of ions (with number density n_i) and electrons (with number density n_e) of the system, and it is given by,

$\begin{array}{ll}{\Gamma }_n^{rec}=n_i{n}_{e}R.& (1)\end{array}$

In the above equation the recombination frequency, R, is given by Cox and Tucker (1969) and Moore and Fung (1972)

$R=5.2\times 10^{-20}\sqrt{X}(0.4288+0.5lnX+0.4698X^{-1/3})(\text{m}{ }^3\text{s}{ }^{-1}),$

where X = Aϵ_i/T(eV) is a quantity that is defined as the ratio between the ionization potential and thermal energy, and the constant A takes the value of 0.6. In can be shown that at temperatures we can find in the lower part of the chromosphere the electrons in hydrogen atoms are predominantly in the ground state (corresponding to n = 1 energy level), meaning that ϵ_i is the first ionization potential, therefore ϵ_i = 13.6 eV. Indeed, the relative population at the n = 2 energy level compared to the ground level in the hydrogen atom is given by the Boltzmann equation,

$\frac{N_2}{N_1}=\frac{g_2}{g_1}{e}^{-(E_2-E_1)/k_{B}T},$

where $g_n=2n^2$ is the statistical weight of each energy level, E₁ = ϵ_i and E₂ = 3.4 eV are the energies of electrons on the two levels. In a H plasma at T = 10⁴ K we can obtain that $N_2/N_1=2.5\times 10^{-5}$, while at T = 4 × 10³ K, this ratio is of the order of 10⁻¹³. We should point out here that the radiative recombination should be treated with care. Under normal circumstances the recombination takes place as a result of the collision between a positive ion (proton in a H plasma) and an electron that has an energy, at least, equal to ϵ_i. As a result of this interaction a photon is emitted that can further ionize the neutral H atoms. With a significant amount of neutral H, the emitted photon will have a higher probability of being absorbed by a neutral atom in the neighborhood of emission, with a creation of an ion. Therefore, recombination to the ground state has virtually no effect on the ionization state of the plasma. However, in our analysis we are going to consider that the photon emitted during recombination escapes, this corresponds to the response of optically thin plasma to ionizing radiation.

Since we are dealing with spatial scales that are larger than the Debye radius in a H plasma, the plasma can be considered to be quasi-neutral, therefore, n_e = n_i. In addition, for simplicity we are going to deal with a uni-thermal plasma, where T_e = T_i = T_n = T.

The impact ionization reaction takes place as a result of the collisional interaction between neutrals (with number density n_n) and electrons with energies larger than the ionization potential. As a result, the ionization rate of neutrals is given by,

$\begin{array}{ll}{\Gamma }_i^{ion}=n_n{n}_{e}I=n_n{n}_{i}I,& (2)\end{array}$

where I is the ionization rate and is given empirically by Cox and Tucker (1969) and Moore and Fung (1972)

$I=2.34\times 10^{-14}\sqrt{X}{e}^X(\text{m}{ }^3\text{s}{ }^{-1}).$

In order to determine the variation of the ionization/recombination rates in the solar atmosphere we use the VAL III C model (Vernazza et al., 1981) to plot the height dependence of these two quantities on logarithmic scale (see Figure 1). It is obvious that the variation with height of these rates follows closely the variation of the characteristic values typical for the atmospheric model employed here. Accordingly, the height-dependance of the recombination rate (R) resembles the height-dependance of the number density, while the ionization rate (I) shows similarity with the variation of the temperature, meaning that these physical quantities are the ones that determine the shape of variation with height. Both rates show an extreme value at the height of about 500 km (bottom of chromosphere, the point corresponding to the temperature minimum in the VALIII C model). The ionization rate overcomes the recombination rate at a height of 2 Mm, a height that corresponds to a temperature of approximately 7660 K.

FIGURE 1

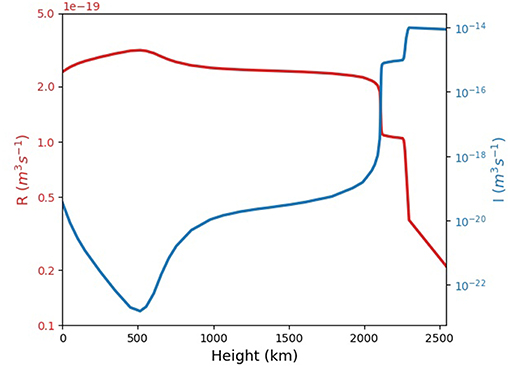
Figure 1. The variation of the real and imaginary part of the dimensionless frequency for slow magnetoacoustic waves with respect to the dimensionless collisional frequency, a₁, for two different values of the ionization degree of the plasma (color coded). Solid lines represent solutions obtained in the ionization non-equilibrium and dashed lines denote the slow waves in ionization equilibrium.

The other effect we are going to consider is the collision between particles. Assuming a uni-thermal plasma, electrons will have their velocity (thermal velocity) $\sqrt{m_i/m_e}$ times larger than the thermal velocity of ions (and neutrals), where m_e and m_i are the masses of electrons and ions, respectively. During collisions between electrons and neutrals, electrons suffer a large change in momentum, but small change in their energy (given approximately by $\sqrt{m_e/m_i}$). In contrast, ion-neutral collisions are less frequent than electron-neutral collisions, however, the momentum exchange between these particles can influence the most propagation of waves, therefore, we are going to consider this effect as the dominant collisional mechanism. Collision between ions and neutrals will also ensure that neutrals (that are not influenced by the presence of magnetic field) are kept in the system.

In order to assess the importance of all physical effects included in our model, let us define the characteristic times involved connected to ionization, recombination, and collision as

${\tau }_i=\frac{1}{n_{n}I},{\tau }_r=\frac{1}{n_{i}R},{\tau }_c=\frac{1}{{\nu }_{in}},$

where ν_in is the collisional frequency between ions and neutrals defined as,

${\nu }_{in}=4n_n{\sigma }_{in}{\left(\frac{k_{B}T}{\pi m_i}\right)}^{1/2},$

with ${\sigma }_{in}=1.16\times 10^{-18}$ m² being the ion-neutral collisional cross section (Vranjes and Krstic, 2013), and k_B is the Boltzmann constant. Obviously, the waves we are interested in must have periods that are larger than any of these times. It is clear that the smallest time scale is the collisional time scale (basically τ_c gives the time between two consecutive collisions) and for most of lower solar atmosphere this characteristic time is several orders of magnitude smaller than ionization and recombination time. For temporal scales that are near or shorter than the ion-neutral collisional time the plasma dynamics has to be described within the framework of two-fluid magnetohydrodynamics, where charged particles (here denoted by index i) and neutrals (denoted by an index n) can have separate behavior, depending on the relative strength of collision.

Before embarking on finding the characteristics of waves in non-equilibrium plasmas we need to discuss one more limitation of the problem we are going to consider. In the presence of non-equilibrium ionization and recombination, the linearized mass conservation equations for the two species are written as,

$\begin{array}{ll}\frac{\partial {\rho }_i}{\partial t}+{\rho }_{0i}\nabla ·{\text{v}}_i=m_i({\Gamma }_i^{ion}+{\Gamma }_i^{rec}),& (3)\end{array}$

$\begin{array}{ll}\frac{\partial {\rho }_n}{\partial t}+{\rho }_{0n}\nabla ·{\text{v}}_n=m_n({\Gamma }_n^{ion}+{\Gamma }_n^{rec}),& (4)\end{array}$

where ρ_{0i, 0n}andρ_i,n are the background and perturbation values of the densities for ions and neutrals, respectively and v_i and v_n are the velocity perturbations for the two species. In the above equations ${\Gamma }_i^{ion}=-{\Gamma }_n^{ion}$ and ${\Gamma }_i^{rec}=-{\Gamma }_n^{rec}$. A direct consequence of the above two equation is that the processes of ionization and recombination are not balanced, particles are created and annihilated during the temporal length of the dynamics we are interested in. In addition, these two equations also imply that under normal circumstances (and in a static equilibrium) the equilibrium density of ions and neutrals should be time dependent quantities, i.e., the background state of the plasma is changing in time. In the absence of this temporal change the ionization and recombination rates must be equal and the system will be in equilibrium. Unfortunately, the description of a physical process when the background is a time-dependent is one of the most complex tasks, as it requires cumbersome mathematics.

We have three possibilities to deal with this problem. The first possibility is to leave the background as time dependent, and determine the evolution of perturbations. This task could be easily accomplished by numerical investigations. The second possibility to deal with the temporal variation of the background that makes the problem mathematically tractable would be to impose the condition that the ionization and recombination rates are much longer than the variation rate of the equilibrium density, that could be occurring over the scales presented by Carlsson and Stein (2002). In addition, temporal variation of perturbations (for instance their frequency) are of the same order as the ionization and recombination rates, so

$\frac{1}{{\rho }_{0i}}\frac{d{\rho }_{0i}}{dt},\frac{1}{{\rho }_{0n}}\frac{d{\rho }_{0n}}{dt}\ll \omega ,n_{n}I,n_{i}R.$

Finally, as a third possibility is to deal with this problem by assuming that non-equilibrium effects appear only in the perturbed state (and this is the possibility employed in the present paper). Similar to the assumption by, e.g., Brandenburg and Zweibel (1995), we can fix the rate of ionization and the recombination rate is chosen in such a way that in the unperturbed stage the right-hand sides of Equations (3, 4) are identically zero. The problem with this approach is that only one of the rates can be realistic, the chosen value of the other rate is artificially imposed. Assuming a VAL IIIC atmospheric model this assumption agrees with realistic values in the photosphere, i.e., in a weakly ionized region of the solar atmosphere. In our study we will employ the later assumption and choose,

$R=\frac{n_{0n}}{n_{0i}}I.$

With this assumption the characteristic times for ionization and recombination defined earlier become equal. This assumption also means that the empirical formula for R given earlier becomes redundant, as its value will be always given in terms of I, as above

The dynamics of the coupled two fluids is given by a set of linearized equations that describe the conservation of mass (given earlier by Equations 3–4), together with a conservation of momentum, induction equation and energy equation (see, e.g., Zaqarashvili et al., 2011; Khomenko et al., 2014; Maneva et al., 2017; Martinez-Gomez et al., 2017),

$\begin{array}{l}{\rho }_{0i}\frac{\partial {\text{v}}_i}{\partial t}+\nabla p_i-\frac{1}{{\mu }_0}(\nabla \times \text{b})\times {\text{B}}_0=m_i{\text{v}}_n{\Gamma }_i^{ion}-m_i{\text{v}}_i{\Gamma }_n^{rec}\\ +m_{in}{n}_i{\nu }_{in}({\text{v}}_n-{\text{v}}_i)=\end{array}$

$\begin{array}{ll}={\rho }_{0i}\left(\frac{{\nu }_{in}}{2}+n_{0n}I\right)({\text{v}}_n-{\text{v}}_i)& (5)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\rho }_{0n}\frac{\partial {\text{v}}_n}{\partial t}+\nabla p_n=m_i{\text{v}}_i{\Gamma }_n^{rec}-m_i{\text{v}}_n{\Gamma }_i^{ion}-m_{in}{n}_i{\nu }_{in}({\text{v}}_n-{\text{v}}_i)=\\ =-{\rho }_{0i}\left(\frac{{\nu }_{in}}{2}+n_{0n}I\right)({\text{v}}_n-{\text{v}}_i)\hfill \end{array}& (6)\end{array}$

$\begin{array}{ll}\frac{\partial \text{b}}{\partial t}=\nabla \times ({\text{v}}_i\times {\text{B}}_0),& (7)\end{array}$

$\begin{array}{ll}\frac{\partial p_i}{\partial t}=-c_{Si}^2{\rho }_{0i}\nabla ·{\text{v}}_i+c_{Si}^2{m}_i({\Gamma }_i^{ion}+{\Gamma }_i^{rec})& (8)\end{array}$

$\begin{array}{ll}\frac{\partial p_n}{\partial t}=-c_{Sn}^2{\rho }_{0n}\nabla ·{\text{v}}_n+c_{Sn}^2{m}_n({\Gamma }_n^{ion}+{\Gamma }_n^{rec})& (9)\end{array}$

$\begin{array}{ll}\nabla ·\text{b}=0,& (10)\end{array}$

where B₀ is the background magnetic field, v_i = (v_ix, v_iy, v_iz) and v_n = (v_nx, v_ny, v_nz) are the components of the velocity perturbation of ions and neutrals, p_i and p_n are the pressure perturbations of the ion and neutral fluids, b = (b_x, b_y, b_z) is the magnetic field perturbation, and m_in = m_im_n/(m_i + m_n) ≈ m_i/2 is the reduced mass. Frictions between charged and neutral (close-range interaction) particles is ensured via collisional processes. The above equations must be supplemented by the equation of state for ions and neutrals p_i,n = n_i,nk_BT_i,n

As explained earlier, the ionization non-equilibrium is present only in the perturbed state, the perturbations we are considering to take place will drive the system out of ionization equilibrium. Equations (5, 6) are the linearized momentum equations of the ion-electron fluid and neutrals, respectively. The terms on their right-hand side express the transfer of momentum between ions and neutrals through the diffusion of one species into the other. As a result of collisions, particles can loose energy and momentum.The same equations reveal an interesting aspect of non-equilibrium plasma. When the background is in equilibrium, in the limit of vanishing collisions (ν_in = 0) the only dynamics that can be described is related to ions and the momentum equation reduces to the standard equation used in MHD. Of course, such a limit cannot exist as in that case there is nothing that can keep neutrals in the system and the two-fluid description is meaningless. However, in the ionization non-equilibrium the two-fluid description can be applied even in the vanishing collision limit, as the creation and annihilation of ions generates a force per unit volume that acts to keep neutrals in the system.

The above system of equations will be used to study the properties of magnetic and slow magnetoacoustic waves propagating in non-equilibrium plasma and compare these with the values we obtain in the ionization equilibrium.

3. Alfvén waves

The simplest wave to study are Alfvén waves, for which the only restoring force is the Lorentz force and the driving force of Alfvén waves is the magnetic tension. We assume a homogeneous equilibrium magnetic field, B₀, pointing in the z-direction. Alfvén waves will propagate plasma along the magnetic field and they will be polarized in the y-direction. Given the properties of Alfvén waves, the pressure terms in Equations (5–6) are neglected and, therefore, Equations (8, 9) are not needed. As a result, the dynamics of Alfvén waves is described by the system of Equations

$\begin{array}{ll}{\rho }_{0i}\frac{\partial v_{iy}}{\partial t}=\frac{B_0}{\mu }\frac{\partial b_y}{\partial z}+{\rho }_{0i}{\tilde{\nu }}_{in}(v_{ny}-v_{iy}),& (11)\end{array}$

$\begin{array}{ll}{\rho }_{0n}\frac{\partial v_{ny}}{\partial t}=-{\rho }_{0i}{\tilde{\nu }}_{in}(v_{ny}-v_{iy}),& (12)\end{array}$

$\begin{array}{ll}\frac{\partial b_y}{\partial t}=B_0\frac{\partial v_{iy}}{\partial z},& (13)\end{array}$

where

${\tilde{\nu }}_{in}=\frac{{\nu }_{in}}{2}+n_{0n}I,$

is the modified ion-neutral collisional frequency by the ionization non-equilibrium effects. Obviously, if I = 0, then we recover the case of Alfvén waves in ionization equilibrium, a case discussed earlier by Zaqarashvili et al. (2011).

Let us Fourier-analyse the system of Equations (11–13) considering that all perturbations are proportional to exp[i(kz − ωt)], where k is the real wavenumber along the z-axis. The neutral fluid exerts a drag force against the motion of ions around the magnetic field and, therefore, Alfvén waves will decay. As a result, the frequency of waves, ω, will be a complex quantity, with negative imaginary part of it describing the damping of waves. After simple calculations the dispersion relation of Alfvén waves is obtained to be

$\begin{array}{ll}{\omega }^3+i{\omega }^2{\tilde{\nu }}_{in}(1+\chi )-k^2{v}_A^2\omega -i{k}^2{v}_A^2\chi {\tilde{\nu }}_{in}=0,& (14)\end{array}$

where χ = n_0i/n_0n ≈ ρ_0i/ρ_0n. In the absence of any partially ionized effects (e.g., ${\tilde{\nu }}_{in}=0$) the dispersion relation would reduce to the standard dispersion relation for Alfvén waves ω = ±kv_A. The third order polynomial (14) describes the propagation of two Alfvén waves (propagating in opposite direction) and a third mode that is non-oscillatory (i.e., its frequency has a zero real part).

Let us introduce the dimensionless quantities,

$\begin{array}{ll}\Omega =\frac{\omega }{k{v}_A},a=\frac{{\nu }_{in}}{k{v}_A},{\xi }_n=\frac{{\rho }_{0n}}{{\rho }_0},\tilde{I}=\frac{n_{0}I}{k{v}_A},& (15)\end{array}$

where n₀ = n_0i + n_0n is the total number density of the plasma and ρ₀ is the total mass density. After some simple calculations the dispersion relation can be written in dimensionless form as,

$\begin{array}{ll}{\Omega }^3+i{\Omega }^{2}N(1+\chi )-\Omega -i\chi N=0,& (16)\end{array}$

where N = a/2 + ξ_nĨ. Luckily some analytical progress can be made by assuming that Alfvén waves will have a small damping. Accordingly, the dimensionless frequency of waves can be written as Ω = Ω_r + iΩ_i (with both Ω_r, Ω_i real quantities) and we write |Ω_i| ≪ |Ω_r|. Focussing only on the forward propagating modes, the real and imaginary part of the frequencies can be easily obtained as,

$\begin{array}{ll}{\Omega }_r={\left(1-\frac{{\xi }_n{(a+2{\xi }_n\tilde{I})}^2}{4{\xi }_n^2+{(a+{\xi }_n\tilde{I})}^2}\right)}^{1/2},& (17)\end{array}$

and

$\begin{array}{ll}{\Omega }_i=-{\xi }_n^2\frac{a+2{\xi }_n\tilde{I}}{4{\xi }_n^2+{(a+{\xi }_n\tilde{I})}^2}.& (18)\end{array}$

It is obvious that the imaginary part of the frequency is negative, meaning that waves will damp, regardless what is the strength of collisions between particles or degree of ionization. The corresponding values for ionization equilibrium can be found once the quantity Ĩ is set to zero. In ionization equilibrium the imaginary part of the frequency tends to zero when the collisional frequency, a, is set to zero, i.e., Alfvén waves in collisionless plasma do not damp. In this case the governing equations describe the dynamics of ions alone, while the dynamics of neutrals becomes undetermined. Since ions and neutrals do not interact through collisions, the possibility of having neutrals in such systems becomes a problem (technically speaking the plasma can be considered collisionless when the mean free path between collisions is much larger than the lengths over which the plasma quantities vary). In the limit of strong collisions (a ≫ 1) the imaginary part of the frequency becomes smaller and at a → ∞ the mixture of ions and neutrals behaves like a single fluid with no damping; this limit corresponding to the MHD limit. Before further discussion we need to clarify that the term “collisionless" used above refers to the case when the collisional frequency between ions and neutrals becomes zero. However, this does not exclude the possibility of having collisions between ions and electrons and neutrals and electrons, i.e., the collisions that affect the ionization state of the plasma.

In contrast, in the ionization non-equilibrium, when we set the collisional frequency to zero we arrive to a critical damping rate,

$\begin{array}{ll}{\Omega }_i^{cr}=-\frac{{\xi }_n\tilde{I}}{2+2{\tilde{I}}^2},& (19)\end{array}$

meaning that Alfvén waves will damp even in the absence of collisions between ions and neutrals and the ionization/recombination processes will ensure that the mixture of ions and neutrals stay coupled. The damping whose rate is given by Equation (19) constitute a new damping mechanism that roots itself in the additional drag force generated by different drift velocities of ions and neutrals during the process of ionization and recombination. For the sake of completeness, we should mention that Landau damping is also a mechanism that appears in collisionless plasmas, and this damping is not associated with an increase in entropy, and therefore is a thermodynamically reversible process. It remains to be seen whether the damping mechanism described in the present study has the same properties as Landau damping. The damping we discuss here can be due to the fact that with the number of ions changing in time, more and more ions become attached to magnetic field lines, increasing their inertia, eventually causing the attenuation of Alfvén waves.

Let us investigate the variation of the real and imaginary parts of the dimensionless frequency of forward propagating Alfvén waves in terms of the dimensionless collisional frequency, a for three different values of the relative neutral density (ξ_n = 0.2, 0.5, 0.8). Clearly ξ_n = 0 describes a fully ionized plasma, while the limit ξ_n = 1 corresponds to a completely neutral fluid. The upper panel of Figure 2 shows the variation of the real part of the dimensionless frequency (solid lines) for the three values of ξ_n and the corresponding dispersion curves corresponding to the ionization equilibrium (shown by dashed lines). Here the dimensionless quantity Ω can be understood as the propagation speed of Alfvén waves in units of Alfvén speed, v_A.

FIGURE 2

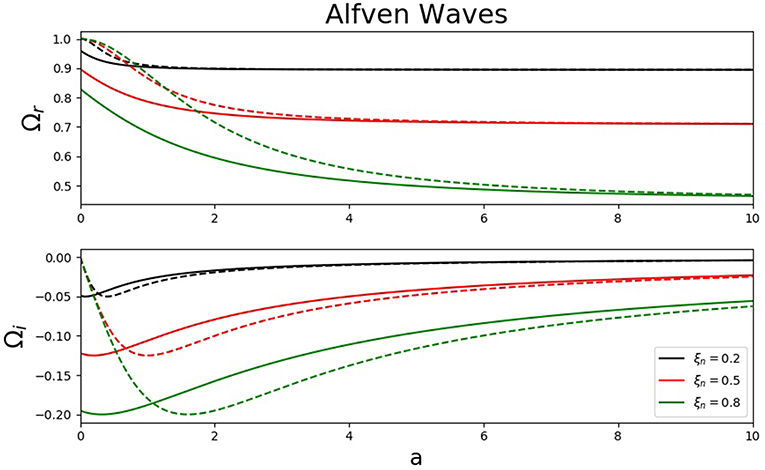
Figure 2. The variation of the recombination rate (R, shown in red line) and the ionization rate (I, blue line) with height (on logarithmic scale) in the lower solar atmosphere based on a VALIII C solar atmosphere model (Vernazza et al., 1981).

First of all it is clear that for very large collisional frequency the propagation speed of Alfvén waves and damping rate in the two regimes become identical and in a strongly collisional plasma the propagation speed of Alfvén waves and their damping rate are not influenced by collisions between ions and neutrals. Secondly, Alfvén waves in ionization non-equilibrium will propagate with a lower speed and the difference in propagation speed increases with the number of neutrals in the system. Furthermore, the more ionized the plasma is, the faster these Alfvén waves will propagate. Similarly, as long as the collisional frequency is larger than $(\sqrt{{\tilde{I}}^2+4}-\tilde{I}){\xi }_n$, Alfvén waves in ionization equilibrium will have a larger damping rate (smaller damping time) than those waves that propagate in a plasma in ionization non-equilibrium, however, these differences are not significant. For collisional frequency smaller than this threshold value, Alfvén waves damp much quicker in a non-equilibrium plasma. As pointed our earlier, the damping rate of Alfvén waves in equilibrium plasma tends to zero in the collisionless plasma. In contrast, in a non-equilibrium collisionless plasma, Alfvén waves damp with a rate given by ${\Omega }_i^{cr}$. In conclusion, in a strongly collisional plasma the propagation and attenuation of Alfvén waves is independent whether the plasma is in ionization equilibrium or not. Here the collisional time is at least one order of magnitude larger than the characteristic time for ionization and any non-uniformity that could potentially influence the characteristics of waves is smoothed out by collisions.

Finally we need to mention that Alfvén waves in the present configuration become dispersive, and dispersion is proportional to ${\tilde{\nu }}_{in}^2$. Figure 2 also shows that for a given collisional parameter, a, waves with shorter wavelength will propagate slower and the larger the amount of neutrals in the system, the more dispersive Alfvén waves are.

4. Slow Magnetoacoustic Modes

To be able to decouple magnetoacoustic modes, we assume that slow magnetoacoustic waves propagate along the background magnetic field and the dominant dynamics occurs in the z direction. Since the species of the plasma have the same temperature, we can write

$c_{Si}^2=\frac{\gamma (p_i+p_e)}{{\rho }_{i0}}=\frac{\gamma k_B(T_i+T_e)}{m_i}=\frac{2\gamma k_B{T}_n}{m_n}=\frac{2\gamma p_n}{{\rho }_{0n}}=2c_{Sn}^2.$

Since slow waves propagate along the background magnetic field we assume that all perturbations are proportional to e^{i(kz − ωt)}. This particular choice for the form of perturbations and background magnetic field can reduce the slow waves to acoustic modes. The dynamics of linear slow waves propagating along the magnetic field in a partially ionized plasma in the presence of non-equilibrium ionization is described by the system of Equations (3–10) where perturbations are considered to be proportional to the exponential factor introduced above. Accordingly the set of equations used are,

$\begin{array}{ll}{\rho }_i=k\frac{i{n}_{0i}I{\rho }_{0n}{v}_{nz}+{\rho }_{0i}(\omega +i{n}_{0i}I)v_{iz}}{\omega (\omega +i{n}_{0i}I)},& (20)\end{array}$

$\begin{array}{ll}{\rho }_n=k\frac{{\rho }_{0n}(\omega +i{n}_{0n}I)v_{nz}+i{n}_{0n}{\rho }_{0i}I{v}_{iz}}{\omega (\omega +i{n}_{0i}I)},& (21)\end{array}$

$\begin{array}{ll}(\omega +i{\tilde{\nu }}_{in})v_{iz}-\frac{k{c}_{Si}^2}{{\rho }_{0i}}{\rho }_i-i{\tilde{\nu }}_{in}{v}_{nz}=0,& (22)\end{array}$

$\begin{array}{ll}(\omega +i{\tilde{\nu }}_{in})v_{nz}-\frac{k{c}_{Sn}^2}{{\rho }_{0n}}{\rho }_i-i{\tilde{\nu }}_{in}{v}_{iz}=0.& (23)\end{array}$

These four equations can be reduced a set of coupled equations for the z-components of ion and neutral velocities. The compatibility condition of this system gives us the dispersion relation,

$\begin{array}{ll}{\omega }^4+i{\omega }^{3}A-{\omega }^{2}B-i{k}^2\omega C+D=0,& (24)\end{array}$

where the coefficients A, B, C, and D depend on the parameters of the problem. This fourth-order polynomial in ω describes the propagation of two families of waves: one associated to ions, and the other one to neutrals. Due to collisions and non-equilibrium effects, the two kinds of modes are coupled. Again, let us introduce similar dimensionless quantities as in the case of Alfvén waves, but now we use the quantity kc_Sn to write variables and constants in dimensionless form. As a result, the dispersion relation reduces to,

$\begin{array}{ll}{\Omega }^4+i{\Omega }^3{A}_1-{\Omega }^2{B}_1-i\Omega C_1+D_1=0,& (25)\end{array}$

where the constant coefficients are given by,

$A_1=2{\tilde{I}}_1+\frac{a_1}{2{\xi }_n},B_1=3+{\tilde{I}}_1^2+\frac{a_1{\tilde{I}}_1}{2{\xi }_n}+$

$C_1=(2-{\xi }_n)\left[\frac{a_1}{2}+{\tilde{I}}_1(1+{\xi }_n)\right],D_1=2+\frac{a_1{\tilde{I}}_1}{2{\xi }_n}(2-{\xi }_n)+{\tilde{I}}_1^2(2-{\xi }_n)$

where the parameters a₁ and Ĩ₁ are defined in the same way as parameters a and Ĩ given by Equation (15), but the quantity that is used to write them in dimensionless form is kc_Sn. In the absence of collisions and ionization non-equilibrium the two pairs of sound waves are propagating with the sound speed of ions and neutrals, with the wave associated to ions propagating faster.

Figure 3 shows the variation of the dimensionless frequency of slow waves (or the phase speed of slow waves in units of the neutral sound speed) with respect to the dimensionless collisional parameter, a₁, for two distinct values of the ionization factor, ξ_n (0.2 and 0.8, respectively). Due to the collision between particles and non-equilibrium effects, the quantity Ω is complex, where the imaginary part describes the temporal modification of the amplitude of waves. The upper panel of Figure 3 shows the real part of Ω, while the lower panel shows the imaginary part of this quantity. Similar to the plot obtained for Alfvén waves, the solid lines denote the dispersion curves for slow waves in ionization non-equilibrium, while dashed line correspond to the case when the plasma is in ionization equilibrium.

FIGURE 3

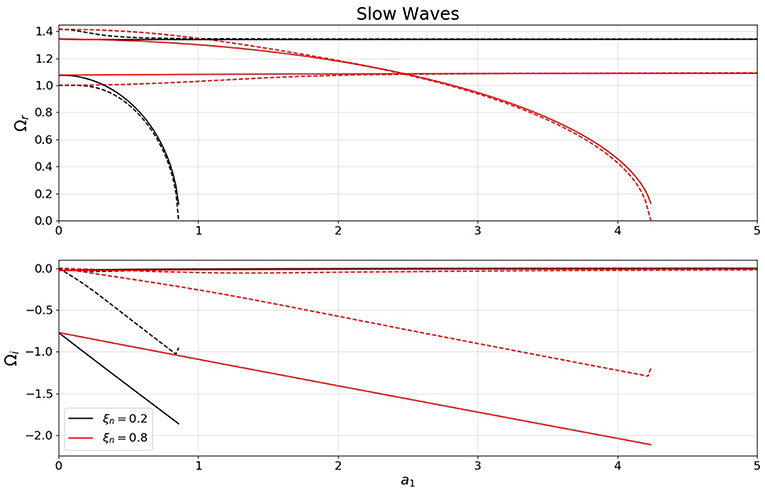
Figure 3. The variation of the real (Upper) and imaginary part (Lower) of the dimensionless frequency, Ω, for Alfvén waves with respect to the dimensionless collisional frequency, a for three different values of the ionization degree of the plasma (color coded). Solid lines represent solutions obtained in the ionization non-equilibrium while dashed line denote the Alfvén waves in ionization equilibrium.

It is clear that for the whole spectrum of parameters, the imaginary part of the frequency will be negative, meaning that slow waves will damp; this result is in agreement with the conclusions of previous studies by, e.g., Braginskii (1965) and Zaqarashvili et al. (2011). The two sets of waves shown in Figure 3 have different behavior in terms of collisional frequency. Let us concentrate first on the dispersion curves obtained for the real part of the frequency. Depending on the amount of neutrals in the system, the ion-acoustic waves can have an enhanced propagation speed in the limit of weakly collisional plasma. For ξ_n = 0.2 (black curves) the slow wave that corresponds to an ionization equilibrium travels slightly faster, however very quickly the propagation speed of these slow waves in the two regimes is equal. When the amount of neutrals is increased (red lines) we can see that the wave corresponding to the non-equilibrium state propagates faster but at the value of a₁ ≈ 2.5 the two speeds become identical. At this point the collisions between ions and neutrals become so frequent that their effect can overcome any modification due to the additional change in the ionization degree of the plasma.

On the other hand the slow waves associated to neutrals display a completely different behavior. In a plasma with ξ_n = 0.2 these slow waves have a smaller phase speed, and the speed in a non-equilibrium plasma is slightly larger than the corresponding value obtained in an equilibrium state. Once the amount of neutrals is increased (the curves corresponding to ξ_n = 0.8) the slow waves in an equilibrium plasma is larger, and this relation is maintained again, until the dimensionless collisional frequency, a, reaches the value of a₁ ≈ 2.5, after which, for a given value of a₁, the neutral slow waves in equilibrium plasma propagates faster. It is also clear that at a₁ ≈ 2.5 the propagation speed of ion-slow waves and neutral-slow wave is equal. Similar to the results obtained by Zaqarashvili et al. (2011), the neutral-slow waves can exist up to a certain level of collisional rate and the value of collision where these waves cease to exist increases with the amount of neutrals in the system. At this point the collision between neutrals and ions is so frequent that the mixture of charged and neutral particles starts behaving like a single fluid. Increasing the frequency of collisions between ions and neutrals cause a slow down of neutral-slow waves.

Now let us concentrate on the imaginary part of the frequency. It is clear that regardless what is the ionization degree of the plasma, the damping rate of ion-acoustic modes is very small, practically these waves can propagate with no attenuation for any value of collision. In contrast, the neutral-slow waves have a very different behavior. These waves show a very strong damping (with damping times of the order of the period of waves, or larger). For both ionization degrees chosen here, the damping time of neutral-slow waves is decreasing with the increase in the collisional frequency. Comparing the results we obtained in the two regimes, it is clear that the neutral-slow waves in an ionization equilibrium plasma have no damping in the absence of collision (as we would expect), however, in the presence of non-equilibrium these waves decay due to ionization/recombination processes and—in the absence of collisions—the damping time of these waves is independent on the amount of neutrals in the system. Once the collisional rate in increased, the mode that corresponds to smaller amount of neutrals will have a shorter damping time.

Similar to Alfvén waves, slow magnetoacoustic modes will also be dispersive, however the ion-acoustic modes will be practically non-dispersive (similar to the slow waves in the MHD description), while neutral-acoustic modes are strongly dispersive, again waves with larger wavelength traveling faster. Figure 3 also shows that in the case of neutral-acoustic modes there will be always a critical wavenumber above which these modes do not propagate.

It is very likely that the problem of propagation and decay of these waves will display a different behavior once the full polarization in the xz plane is considered. In that case slow waves will have a magnetic component and it remains to be seen how these waves will behave for different value of plasma-beta. However, this consideration requires numerical investigation.

5. Conclusions

Given the nature of partially ionized plasma in the lower solar plasma and prominences requires a different approach. For particular high frequencies range a two-fluid description is needed and neutrals can considerably influence the properties of waves. This framework was used to study the characteristics of Alfvén and slow waves propagation along a unidirectional homogeneous magnetic field. The novelty of our research resides in consideration of the effects of ionization non-equilibrium, i.e., the case when the rates at which neutrals are ionized through impact ionization and ions recombine with energetic electrons through radiative recombination are not equal. Our results show that this effect is more important when the collisional frequency is comparable with the frequency of waves. Any information about the existence of two fluids and the drag forces exerted by neutrals upon ions is lost in the case of strong collisions. Here the plasma behaves like a single fluid and the dynamics can be confidently described within the framework is MHD. We ought to mention that the non-equilibrium applies only to the perturbed state of the plasma; in the background state the plasma remains in ionization equilibrium. This assumption was needed to be able to make analytical progress.

Using a simple configuration we studied separately Alfvén and slow magnetoacoustic modes. The collision between heavy particles and non-equilibrium effects renders the frequency of waves to be complex, where the imaginary part of it describes damping. One of the main results of our investigation is that in a plasma that is in ionization non-equilibrium waves can damp even in the collisionless limit. In this case waves will damp due to the drag forces by neutrals that appear due to the ionization non-equilibrium. Given that waves are damped even in the collisionless limit makes us to think about the physical explanation of this effect to be similar as the theory of Landau damping. However, this statement needs to be investigated properly in the future. The processes of ionization and recombination will increase the degree of entropy in the system that could cause the additional damping.

Finally we should mention our results should treated with precaution when making far reaching conclusions valid for the whole photosphere and/or chromosphere. For simplicity the present study assumed collisional ionization and radiative recombination as the dominant mechanisms that determine the non-equilibrium, however, in reality this can change from region to region in the solar atmosphere. It is very likely that in the dense photosphere photoinduction and three-body recombination are more important effects. In addition, most of the partially ionized plasma is optically thick, in which case a similar treatment as presented by Ballester et al. (2018a) is needed. Moreover, the relatively low temperature plasma in these regions means that the gravitational scale-height is short, therefore, in the case of waves traveling over long distances in the solar lower atmosphere, the gravitational stratification could influence the propagation of waves and work against the damping of waves. It remains to be seen how a realistic variation of ionization and recombination rate together with stratification will affect the characteristics of waves.

Author Contributions

IB is the sole author of this paper and it contains original research.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

IB acknowledges the financial support by STFC UK.

References

Ballester, J. L., Alexeev, I., Collados, M., Downes, T., Pfaff, R. F., Gilbert, H., et al. (2018b). Partially ionized plasmas in astrophysics. Space Sci. Rev. 241, 58–206. doi: 10.1007/s11214-018-0485-6

CrossRef Full Text | Google Scholar

Ballester, J. L., Carbonell, M., Soler, R., and Terradas, J. (2018a). The temporal behaviour of MHD waves in partially ionised prominence-like plasma: effect of heating and cooling. Astron. Astrophys. 609, 6–22. doi: 10.1051/0004-6361/201731567

CrossRef Full Text | Google Scholar

Bradshaw, S. J., Del Zanna, G., and Mason, H. E. (2004). On the consequences of a non-equilibrium ionisation balance for compact flare emission and dynamics. Astron. Astrophys. 425, 287–299. doi: 10.1051/0004-6361:20040521

CrossRef Full Text | Google Scholar

Bradshaw, S. J., and Mason, H. E. (2003). The radiative response of solar loop plasma subject to transient heating. Astron. Astrophys. 407, 1127–1138. doi: 10.1051/0004-6361:20030986

CrossRef Full Text | Google Scholar

Braginskii, S. I. (1965). Transport Processes in a Plasma. Rev. Plasma Phys. 1, 205–283.

Google Scholar

Brandenburg, A., and Zweibel, E. G. (1995). Effects of pressure and resistivity on the ambipolar diffusion singularity: too little, too late. Astrophys. J. 448, 734–635. doi: 10.1086/176001

CrossRef Full Text | Google Scholar

Carlsson, M., and Stein, R. F. (2002). Dynamic hydrogen ionization. Astrophys. J. 572, 626–635. doi: 10.1086/340293

CrossRef Full Text | Google Scholar

Cox, D. P., and Tucker, W. H. (1969). Ionization equilibrium and radiative cooling of a low-density plasma. Astrophys. J. 157:1157. doi: 10.1086/150144

CrossRef Full Text | Google Scholar

Dzifčáková, E., and Kulinová, A. (2011). Diagnostics of the κ-distribution using Si III lines in the solar transition region. Astron. Astrophys. 531, 122–131. doi: 10.1051/0004-6361/201016287

CrossRef Full Text | Google Scholar

Khomenko, E., Collados, M., Diaz, A., and Vitas, N. (2014). Fluid description of multi-component solar partially ionised plasma. Phys. Plasmas 21:092901. doi: 10.1063/1.4894106

CrossRef Full Text | Google Scholar

Leake, J. E., Lukin, V. S., Linton, M. G., and Meier, E. T. (2012). Multi-fluid simulations of chromospheric magnetic reconnection in a weakly ionized reacting plasma. Astrophys. J. 760, 109–120. doi: 10.1088/0004-637X/760/2/109

CrossRef Full Text | Google Scholar

Maneva, Y. G., Alvarez Laguna, A., Lani, A., and Poedts, S. (2017). Multi-fluid modeling of magnetosonic wave propagation in the solar chromosphere: effects of impact ionization and radiative recombination. Astrophys. J. 836, 197–211. doi: 10.3847/1538-4357/aa5b83

CrossRef Full Text | Google Scholar

Martinez-Gomez, D., Soler, R., and Terradas, J. (2017). Multi fluid approach to high-frequency waves in plasmas. II small amplitude regime in partially ionised medium. Astrophys. J. 837, 80–97. doi: 10.3847/1538-4357/aa5eab

CrossRef Full Text | Google Scholar

Meier, E. T., and Shumlak, U. (2012). A general nonlinear fluid model for reacting plasma-neutral mixtures. Phys. Plasmas 19:072508. doi: 10.1063/1.4736975

CrossRef Full Text | Google Scholar

Moore, R. L., and Fung, P. C. W. (1972). Structure of the chromosphere-corona transition region. Sol. Phys. 23, 78–102. doi: 10.1007/BF00153893

CrossRef Full Text | Google Scholar

Soler, R., Carbonell, M., Ballester, J. L., and Terradas, J. (2013). Alfvén waves in partially ionised to-fluid plasmas. Astrophys. J. 767, 171–184. doi: 10.1088/0004-637X/767/2/171

CrossRef Full Text | Google Scholar

Soler, R., Oliver, R., and Ballester, J. L. (2010). Time damping on non-adiabatic MHD waves in partially ionised prominence plasmas: the effect of He. Astron. Astrophys. 512, 28–32. doi: 10.1051/0004-6361/200913478

CrossRef Full Text

Vernazza, J. E., Avrett, E. H., and Loeser, R. (1981). Structure of the solar chromosphere. III - Models of the EUV brightness components of the quiet-sun. Astrophys. J. Suppl. S. 45, 635–725. doi: 10.1086/190731

CrossRef Full Text | Google Scholar

Vranjes, J., and Krstic, P. S. (2013). Collisions, magnetization, and transport coefficients in the lower solar atmosphere. Astron. Astrophys. 554, 22–32. doi: 10.1051/0004-6361/201220738

CrossRef Full Text | Google Scholar

Zaqarashvili, T. V., Khodachenko, M. L., and Rucker, H. O. (2011). Magnetohydrodynamic waves in solar partially ionized plasmas: two-fluid approach. Astron. Astrophys. 529, 82–90. doi: 10.1051/0004-6361/201016326

CrossRef Full Text | Google Scholar