Tensor Non-Gaussianity Search: Current Status and Future Prospects

1. Introduction

Recent cosmic-variance-limited-level measurements of the scalar sector in primordial fluctuations using the temperature and E-mode polarization fields of the cosmic microwave background (CMB), indicate that the Universe experienced an inflationary expansion at very early stages (Aghanim et al., 2018; Akrami et al., 2018). Now, compelling evidence is expected to lie in the tensor sector; namely, the primordial gravitational wave (GW). Even without any particular source, primordial GWs arise naturally from inflationary vacuum fluctuations. Since their amplitude directly reflects the inflationary energy scale, various observational projects aim at hunting them. There, the measurements of the large-scale CMB B-mode polarization have attracted everyone's attention as it is a distinctive observable of the tensor mode (see e.g., Guzzetti et al., 2016; Kamionkowski and Kovetz, 2016 and references therein).

In order to investigate the primordial tensor sector using the CMB anisotropies, the power spectrum (2-point correlation) is primarily employed. In single-field inflation with Einstein gravity, GWs are nearly Gaussian and hence the higher-order correlations vanish (Acquaviva et al., 2003; Maldacena, 2003). In this case, only the power spectrum becomes an informative observable. This paper, however, will address the potential of the bispectrum (3-point correlation) as a probe of inflationary physics.

One possible way, making it more informative, is the addition of some extra source fields. In the presence of the gauge field, the anisotropic stress fluctuations are formed, generating GWs. Because this is a non-linear process, the resulting GWs are non-Gaussian (NG) and therefore a large tensor bispectrum can be realized. In particular, the production of NG GWs becomes more efficient when the gauge field is coupled to the axion (Namba et al., 2016; Agrawal et al., 2018a). Moreover, production due to higher-spinning particles has been studied intensively in recent years (Goon et al., 2018; Dimastrogiovanni et al., 2019). There is also the possibility of a post-inflationary generation of NG GWs due to magnetic fields (Shiraishi et al., 2011c). Another possible way to produce large tensor NGs comes from non-trivial non-linear gravitational interactions predicted in some modified theories of gravity (e.g., Gao et al., 2011, 2013; Maldacena and Pimentel, 2011; Akita and Kobayashi, 2016; Bartolo and Orlando, 2017; Domenech et al., 2017; Naskar and Pal, 2018; Anninos et al., 2019; Ozsoy et al., 2019). Then, the induced bispectra can have distinctive shapes compared with that from the usual Einstein term.

In this sense, the CMB tensor-mode bispectrum is a key indicator of the inflationary particle content and/or high energy gravity. Since a general formalism was established in Shiraishi et al. (2010, 2011b), various signatures of various theoretical models in the CMB bispectra have been studied [see (Shiraishi et al., 2011c, 2012; Shiraishi, 2012, 2013) for primordial magnetic field (PMF) models (Shiraishi et al., 2013, 2016; Namba et al., 2016), for the axion inflation ones (Shiraishi et al., 2011a,b; Domenech et al., 2017; Tahara and Yokoyama, 2018; Bartolo et al., 2019), for modified gravity ones and (Meerburg et al., 2016; Kothari and Nandi, 2019) for other motivations]. One of the most interesting phenomena discovered there (unseen in the scalar bispectrum analysis) is that the tensor bispectrum can yield the non-vanishing signal in not only even but also odd ℓ₁ + ℓ₂ + ℓ₃ multipoles. The GW bispectra generate the CMB auto and cross bispectra including the B-mode polarization. In the usual theories where the GW bispectra are parity-invariant, the odd ℓ₁ + ℓ₂ + ℓ₃ signal can arise in TTB, TEB, EEB, and BBB (Shiraishi, 2013; Meerburg et al., 2016; Domenech et al., 2017; Tahara and Yokoyama, 2018). Moreover, parity-odd GW bispectra motivated by parity-breaking theories can also induce the non-zero odd ℓ₁ + ℓ₂ + ℓ₃ signal in TTT, TTE, TEE, TBB, EEE, and EBB (Shiraishi et al., 2011a, 2013, 2016; Shiraishi, 2012, 2016;Bartolo et al., 2019).

Now, any type of theoretical bispectrum template is testable with the temperature and E/B-mode polarization data by use of a general bispectrum estimator for the even (Fergusson et al., 2010, 2012; Fergusson, 2014; Shiraishi et al., 2019) and odd ℓ₁ + ℓ₂ + ℓ₃ domain (Shiraishi et al., 2014, 2019). The magnitudes of some representative tensor NG templates have already been estimated from the temperature map of WMAP (Shiraishi and Sekiguchi, 2014; Shiraishi et al., 2015, 2018) and the temperature and E-mode polarization from Planck (Ade et al., 2016a,b; Akrami et al., 2019). Absence of NG reported there, constrains the various inflationary models mentioned above.

In this paper, besides reviewing previous studies, we discuss future prospects of the tensor NG search assuming the detection of B-mode polarization in next-generation CMB experiments. We found that, in terms of observational limits on the size of some scale-invariant templates, an improvement up to three orders of magnitude is expected assuming LiteBIRD-level sensitivities (Hazumi et al., 2012; Matsumura et al., 2013; Matsumura et al., 2016).

This paper is organized as follows. In the next section, we summarize theoretical scenarios predicting characteristic primordial tensor bispectra. In section 3, we compute the CMB bispectra and show their behavior. In section 4, we present the current observational constraints on tensor NGs and discuss future prospects assuming B-mode polarization surveys. The final section is devoted to the conclusions of this paper.

2. Theoretical Motivations

In this section, we briefly review the primordial tensor bispectra predicted in some theoretical scenarios. For convenience, let us work with the helicity basis; thus, the primordial perturbation is represented as ${\xi }_{\text{k}}^{(\lambda )}$ (Shiraishi et al., 2011b). Here, λ denotes the helicity and takes 0, ±1, and ±2 for the scalar, vector, and tensor modes, respectively. In practice, we identify ${\xi }_{\text{k}}^{(0)}$ and ${\xi }_{\text{k}}^{(\pm 2)}$ with the curvature perturbation ζ_k and the GW $h_{\text{k}}^{(\pm 2)}$, respectively.

Assuming statistical homogeneity, the primordial bispectrum takes the form:

$\begin{array}{ll}\langle {\displaystyle \prod _{n=1}^3{\xi }_{k_n}^{({\lambda }_n)}}\rangle ={(2\pi )}^3{\delta }^{(3)}\left({\displaystyle \sum _{n=1}^3{k}_n}\right){\langle {\displaystyle \prod _{n=1}^3{\xi }_{k_n}^{({\lambda }_n)}}\rangle }^{\prime }.& (1)\end{array}$

Then, let us split this in two:

$\begin{array}{ll}{\langle {\displaystyle \prod _{n=1}^3}{\xi }_{{\text{k}}_n}^{({\lambda }_n)}\rangle }^{\prime }={{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}.& (2)\end{array}$

In what follows, how the shape, represented by ${{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}$, and the angular structure, represented by $A_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}$, changes depending on the model is argued.

2.1. Extra Sources

Efficient tensor NG production is realized by adding extra source fields to the theory. In what follows, we discuss the vector field as a source.

2.1.1. Inflationary Axion-Gauge Coupling

A characteristic tensor NG is realized in inflationary models involving the coupling between the axion ϕ and a gauge field like $f(\varphi )\tilde{F}F$, with F and $\tilde{F}$ the gauge field strength tensor and its dual, respectively (Cook and Sorbo, 2013; Maleknejad, 2016; Namba et al., 2016; Dimastrogiovanni et al., 2017; Agrawal et al., 2018a,b). In this case, the chirality of the gauge field is transferred into the GW sector and hence only the plus mode of GW, h⁽⁺²⁾, survives. The resulting production is efficient at specific scales, and the tensor-tensor-tensor bispectrum peaks for equilateral configurations, k₁ ~ k₂ ~ k₃ (Cook and Sorbo, 2013).

The detailed spectral feature varies with the shape of the coupling f(ϕ) or the axion potential (Namba et al., 2016; Agrawal et al., 2018b). For example, adopting f(ϕ) ∝ ϕ and a nearly flat potential, one can obtain a scale-invariant shape as (Shiraishi et al., 2013).

$\begin{array}{llll}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}& =& \frac{16\sqrt{2}}{27}{f}_{\text{NL}}^{ttt,\text{eq}}{S}_{k_1{k}_2{k}_3}^{\text{eq}}{\delta }_{{\lambda }_1,2}{\delta }_{{\lambda }_2,2}{\delta }_{{\lambda }_3,2},& (3)\end{array}$

$\begin{array}{llll}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}& =& e_{ij}^{(-{\lambda }_1)}({\widehat{k}}_1)e_{jk}^{(-{\lambda }_2)}({\widehat{k}}_2)e_{ki}^{(-{\lambda }_3)}({\widehat{k}}_3),& (4)\end{array}$

where $e_{ij}^{(\lambda )}(\widehat{k})$ is the polarization tensor defined in the helicity basis obeying $e_{ii}^{(\lambda )}(\widehat{k})={\widehat{k}}_i{e}_{ij}^{(\lambda )}(\widehat{k})=0$, $e_{ij}^{(\lambda )*}(\widehat{k})=e_{ij}^{(-\lambda )}(\widehat{k})=e_{ij}^{(\lambda )}(-\widehat{k})$, and $e_{ij}^{(\lambda )}(\widehat{k})e_{ij}^{({\lambda }^{\prime })}(\widehat{k})=2{\delta }_{\lambda ,-{\lambda }^{\prime }}$ (Shiraishi et al., 2011b), and $S_{k_1{k}_2{k}_3}^{\text{eq}}$ is the usual scalar equilateral bispectrum template, given by:

$\begin{array}{ll}\begin{array}{l}{S}_{k_1{k}_2{k}_3}^{\text{eq}}\equiv \frac{18}{5}{\left(2{\pi }^2{{P}}_{\zeta }\right)}^2[-\left(\frac{1}{k_1^3{k}_2^3}+2\text{ perm}\right)-\frac{2}{k_1^2{k}_2^2{k}_3^2}\hfill \\ +\left(\frac{1}{k_1{k}_2^2{k}_3^3}+5\text{ perm}\right)].\hfill \end{array}& (5)\end{array}$

Here ${{P}}_{\zeta }$ is the amplitude of the curvature power spectrum. A newly introduced parameter $f_{\text{NL}}^{ttt,\text{eq}}$ quantifies the relative size of the λ = +2 bispectrum to $S_{k_1{k}_2{k}_3}^{\text{eq}}$ and satisfies¹

$\begin{array}{ll}{f}_{\text{NL}}^{ttt,\text{eq}}\equiv {\displaystyle \underset{k_i\to k}{lim}}\frac{{{B}}_{k_1{k}_2{k}_3}^{+2+2+2}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{+2+2+2}}{S_{k_1{k}_2{k}_3}^{\text{eq}}}.& (6)\end{array}$

The expected size of the GW bispectrum, of course, depends on the case. If the axion is identified with the inflaton field, the amount of scalar production exceeds the GW one (Barnaby et al., 2011). Then, the scalar bispectrum measurement gives much tighter constraints on the model (Ade et al., 2016b; Akrami et al., 2019). In contrast, in multifield models where the inflaton field and the axion coexist, more effective GW production occurs. In the model where the axion is coupled to the U(1) gauge field, a characteristic bump appears in the GW bispectrum, and, depending on its location, it is detectable by the CMB BBB bispectrum measurement (Namba et al., 2016; Shiraishi et al., 2016). However, at the same time, a similar bump in the GW power spectrum is measured with a higher signal-to-noise ratio from the CMB BB power spectrum. The strongest constraints are obtained through the GW power spectrum measurement, and the GW bispectrum provides complementary information. In the model including a SU(2)-gauge coupling, the GW bispectrum can dominate the scalar one, and more interestingly, in some regions of the parameter space, the GW bispectrum has high detectability compared to the GW power spectrum (Agrawal et al., 2018a,b). The GW bispectrum is nearly scale-invariant and therefore parameterized by $f_{\text{NL}}^{ttt,\text{eq}}$, which is related to the tensor-to-scalar ratio r and the energy density fraction of the SU(2) gauge field Ω_A according to Agrawal et al. (2018a).

$\begin{array}{ll}{f}_{\text{NL}}^{ttt,\text{eq}}~2.5\frac{r^2}{{\Omega }_A}.& (7)\end{array}$

This indicates that $f_{\text{NL}}^{ttt,\text{eq}}$ can take detectably large values, i.e., $f_{\text{NL}}^{ttt,\text{eq}}>1$, when Ω_A is smaller than r².

2.1.2. Primordial Magnetic Fields

If PMFs, B_i, are created via some non-trivial mechanism before inflation, they are stretched beyond the horizon by the inflationary expansion and there remain relic fields at large scales. Such a scenario has been widely argued to explain galactic or extragalactic magnetic fields observed at present (for reviews see Widrow, 2002; Kulsrud and Zweibel, 2008). In this case, PMFs form the anisotropic stress fluctuations, and they source the GW at super-horizon scales until neutrino decoupling. The induced GW is called a passive mode and behaves as the initial condition of the CMB fluctuations after reentering the horizon (Shaw and Lewis, 2010).

Assuming Gaussianity of PMFs, the induced GW, $h_{ij}\propto {(B_i{B}_j)}^{TT}$, becomes a chi-square random field (Brown and Crittenden, 2005). When the PMF power spectrum has a scale-invariant shape, in analogy with the usual local type NG, the tensor-tensor-tensor bispectrum has the squeezed shape (Shiraishi et al., 2011c, 2012):

$\begin{array}{ll}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}=\sqrt{2}{f}_{\text{NL}}^{ttt,\text{sq}}{S}_{k_1{k}_2{k}_3}^{\text{loc}},& (8)\end{array}$

where the usual scalar local bispectrum template reads:

$\begin{array}{ll}{S}_{k_1{k}_2{k}_3}^{\text{loc}}\equiv \frac{6}{5}{(2{\pi }^2{{P}}_{\zeta })}^2\left(\frac{1}{k_1^3{k}_2^3}+2\text{ perm}\right),& (9)\end{array}$

and $A_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}$ is given in the same form as Equation (4). A newly introduced parameter $f_{\text{NL}}^{ttt,\text{sq}}$ represents the relative size of the λ = +2 bispectrum to $S_{k_1{k}_2{k}_3}^{\text{loc}}$ and satisfies:

$\begin{array}{ll}{f}_{\text{NL}}^{ttt,\text{sq}}\equiv {\displaystyle \underset{\begin{array}{c}{k}_1\to 0\\ k_2\to k_3\end{array}}{lim}}\frac{{{B}}_{k_1{k}_2{k}_3}^{+2+2+2}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{+2+2+2}}{S_{k_1{k}_2{k}_3}^{\text{loc}}}.& (10)\end{array}$

As the GW bispectrum has a sextic dependence on PMFs, $f_{\text{NL}}^{ttt,\text{sq}}$ takes the form:

$\begin{array}{ll}{f}_{\text{NL}}^{ttt,\text{sq}}~{\left(\frac{B_{1\text{Mpc}}}{1\text{ nG}}\right)}^6,& (11)\end{array}$

where B_1Mpc is the PMF strength smoothed on 1Mpc. This means that $f_{\text{NL}}^{ttt,\text{sq}}>1$ is realized if nano-Gauss-level PMFs exist. Note that, in the same mechanism, the scalar local type bispectrum is generated, however, it is subdominant compared with the GW one (Shiraishi, 2013).

This is the result under the absence of a helical (parity-odd) term in the PMF power spectrum, however, the bispectrum shape is modified if it exists (Shiraishi, 2012).

2.2. Modified Gravity

The above scenarios rely on some extra source fields. Let us discuss another NG GW production through the modification of Einstein gravity.

2.2.1. Weyl Gravity

In the context of the Weyl gravity, there may exist the Chern-Simons term $f(\varphi )\tilde{W}W$, where W is the Weyl tensor and $\tilde{W}$ is its dual. Like the axion inflation models, this term also sources chiral GWs (Lue et al., 1999; Alexander and Martin, 2005). The tensor-tensor-scalar bispectrum, whose angular structure reads:

$\begin{array}{ll}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_{2}0}=({\widehat{k}}_1·{\widehat{k}}_2)e_{ij}^{(-{\lambda }_1)}({\widehat{k}}_1)e_{ij}^{(-{\lambda }_2)}({\widehat{k}}_2),& (12)\end{array}$

surpasses the tensor-tensor-tensor and tensor-scalar-scalar ones in amplitude (Bartolo and Orlando, 2017). Due to the parity-violating nature in the GW sector, the helical bispectrum obeys:

$\begin{array}{ll}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_{2}0}\propto \frac{{\lambda }_1}{2}{\delta }_{{\lambda }_1,{\lambda }_2}.& (13)\end{array}$

One can also construct the cubic actions f(ϕ)W³ and $f(\varphi )\tilde{W}{W}^2$ (Maldacena and Pimentel, 2011; Shiraishi et al., 2011a; Soda et al., 2011). The tensor-tensor-tensor bispectra generated from both terms have identical angular dependence as Equation (4). In contrast, the helicity dependence is completely different (Shiraishi et al., 2011a): the former gives rise to the non-helical (parity-even) contribution:

$\begin{array}{ll}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}\propto {\delta }_{{\lambda }_1,{\lambda }_2}{\delta }_{{\lambda }_2,{\lambda }_3},& (14)\end{array}$

while the latter induces the helical (parity-odd) one:

$\begin{array}{ll}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}\propto \frac{{\lambda }_1}{2}{\delta }_{{\lambda }_1,{\lambda }_2}{\delta }_{{\lambda }_2,{\lambda }_3}.& (15)\end{array}$

2.2.2. Massive Gravity

In single-field slow-roll inflation with Einstein gravity, the tensor-scalar-scalar bispectrum is affected by slow-roll suppression (Maldacena, 2003). However, in a massive gravity model (Domenech et al., 2017), the size of the bispectrum is controlled by the graviton mass. The bispectrum, taking the form:

$\begin{array}{l}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_{1}00}=-\frac{8\sqrt{2}}{5}{f}_{\text{NL}}^{tss,\text{sq}}{\left(2{\pi }^2{{P}}_{\zeta }\right)}^2\frac{1}{k_1^3{k}_2^2{k}_3^2}\\ \left[-k_t+\frac{k_1{k}_2+k_2{k}_3+k_3{k}_1}{k_t}+\frac{k_1{k}_2{k}_3}{k_t^2}\right],& (16)\end{array}$

$\begin{array}{llll}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_{1}00}& =& e_{ij}^{(-{\lambda }_1)}({\widehat{k}}_1){\widehat{k}}_{2i}{\widehat{k}}_{3j},& (17)\end{array}$

with k_t ≡ k₁ + k₂ + k₃, is amplified at long-wavelength tensor and short-wavelength scalar configurations (k₁ ≪ k₂ ~ k₃). A newly introduced parameter $f_{\text{NL}}^{tss,\text{sq}}$ denotes the relative size of the λ = +2 bispectrum to $S_{k_1{k}_2{k}_3}^{\text{loc}}$, obeying:

$\begin{array}{ll}{f}_{\text{NL}}^{tss,\text{sq}}\equiv {\displaystyle \underset{\begin{array}{c}{k}_1\to 0\\ k_2\to k_3\end{array}}{lim}}\frac{{{B}}_{k_1{k}_2{k}_3}^{+200}{A}_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{+200}}{S_{k_1{k}_2{k}_3}^{\text{loc}}}.& (18)\end{array}$

With an upper bound on the tensor-to-scalar ratio r ≲ 0.1, the prediction in Einstein gravity, $f_{\text{NL}}^{tss,\text{sq}}~0.1r$, indicates $f_{\text{NL}}^{tss,\text{sq}}\lesssim 0.01$. In contrast, massive gravity model modifies this as:

$\begin{array}{ll}{f}_{\text{NL}}^{tss,\text{sq}}~0.1r{\lambda }_{sst},& (19)\end{array}$

and $f_{\text{NL}}^{tss,\text{sq}}>1$ can then be realized depending on the strength parameter of a non-linear interaction λ_sst. Note that the spectral index of the GW power spectrum is also a possible observable of this model (Domenech et al., 2017) but has been unconstrained so far.

3. CMB Bispectra From Tensor Non-gaussianities

Next, let us discuss the CMB bispectra generated from GW NGs.

3.1. General Formalism for CMB Angular Bispectrum

We start by reviewing how to compute the CMB bispectra generated from the primordial scalar, vector, and tensor NGs based on the general formalism developed in Shiraishi et al. (2010, 2011b).

The CMB field is characterized by temperature and two linear polarizations called E and B modes. All of these are spin-0 fields, and the temperature and E-mode fields have even parity, while the B mode is parity-odd. Since temperature (X = T), E-mode (X = E), and B-mode (X = B) fields are distributed on the 2D sphere, they can be expanded using the spherical harmonic basis according to

$\begin{array}{ll}X(\widehat{n})={\displaystyle \sum _{\ell m}}{a}_{\ell m}^X{Y}_{\ell m}(\widehat{n}),& (20)\end{array}$

where we have assumed the spatial flatness of the Universe. The spherical harmonic coefficients $a_{\ell m}^X$ are given by the sum of the scalar, vector, and tensor modes as:

$\begin{array}{ll}{a}_{\ell m}^X=a_{\ell m}^{X(s)}+a_{\ell m}^{X(v)}+a_{\ell m}^{X(t)}.& (21)\end{array}$

Note that the scalar mode cannot generate a B-mode signal due to zero helicity. The coefficients of the scalar (z = s), vector (z = v), and tensor (z = t) modes have the structure:

$\begin{array}{ll}{a}_{\ell m}^{X(z)}=4\pi {(-i)}^{\ell }{\displaystyle \int \frac{d^{3}k}{{(2\pi )}^3}}{T}_{\ell ,k}^{X(z)}{\displaystyle \sum _{\lambda }{[\text{sgn}(\lambda )]}^{\lambda +x}{\xi }_k^{(\lambda )}{}_{-\lambda }{Y}_{\ell m}^{*}(\widehat{k})},& (22)\end{array}$

where x changes depending on the parity of the CMB field according to x = 0 for X = T, E and x = 1 for X = B, and recall that λ represents helicity as λ = 0 for z = s, λ = ±1 for z = v, and λ = ±2 for z = t. The linear transfer function ${{T}}_{\ell ,k}^{X(z)}$ represents the time evolution of the CMB fluctuations originating from the primordial perturbation ${\xi }_{\text{k}}^{(\lambda )}$. Using Equation (22), one can form the CMB bispectrum as:

$\begin{array}{ll}\langle {\displaystyle \prod _{n=1}^3{a}_{{\ell }_n{m}_n}^{X_n(z_n)}}\rangle =\left[{\displaystyle \prod _{n=1}^3{(-i)}^{{\ell }_n}}{\displaystyle \int \frac{d^3{k}_n}{2{\pi }^2}}{T}_{{\ell }_n,k_n}^{X_n(z_n)}{\displaystyle \sum _{{\lambda }_n}{[\text{sgn}({\lambda }_n)]}^{{\lambda }_n+x_n}{}_{-{\lambda }_n}{Y}_{{\ell }_n{m}_n}^{*}({\widehat{k}}_n)}\right]\langle {\displaystyle \prod _{n=1}^3{\xi }_{k_n}^{({\lambda }_n)}}\rangle .& (23)\end{array}$

The primordial curvature perturbation and the primordial GW act as initial conditions of the scalar and tensor CMB anisotropies, respectively; thus, ${\xi }_{\text{k}}^{(0)}={\zeta }_{\text{k}}$ and ${\xi }_{\text{k}}^{(\pm 2)}=h_{\text{k}}^{(\pm 2)}$. Employing the harmonic expansion:

$\begin{array}{ll}{\xi }_{\text{k}}^{(\lambda )}={\displaystyle \sum _{\ell m}}{\xi }_{\ell m}^{(\lambda )}{(k)}_{-\lambda }{Y}_{\ell m}(\widehat{k}),& (24)\end{array}$

the above formula is rewritten as:

$\begin{array}{ll}\langle {\displaystyle \prod _{n=1}^3}{a}_{{\ell }_n{m}_n}^{X_n(z_n)}\rangle =\left[{\displaystyle \prod _{n=1}^3}{(-i)}^{{\ell }_n}{\displaystyle {\int }_0^{\infty }}\frac{k_n^{2}d{k}_n}{2{\pi }^2}{{T}}_{{\ell }_n,k_n}^{X_n(z_n)}{\displaystyle \sum _{{\lambda }_n}}{\left[\text{sgn}({\lambda }_n)\right]}^{{\lambda }_n+x_n}\right]\langle {\displaystyle \prod _{n=1}^3}{\xi }_{{\ell }_n{m}_n}^{({\lambda }_n)}(k_n),\rangle & (25)\end{array}$

where,

$\begin{array}{ll}\langle {\displaystyle \prod _{n=1}^3}{\xi }_{{\ell }_n{m}_n}^{({\lambda }_n)}(k_n)\rangle =\left[{\displaystyle \prod _{n=1}^3}{\displaystyle \int }{d}^2{\widehat{k}{}_n}_{-{\lambda }_n}{Y}_{{\ell }_n{m}_n}^{*}({\widehat{k}}_n)\right]\langle {\displaystyle \prod _{n=1}^3}{\xi }_{{\text{k}}_n}^{({\lambda }_n)}\rangle .& (26)\end{array}$

This is further simplified once the explicit formula of $\langle {\prod }_{n=1}^3{\xi }_{{\text{k}}_n}^{({\lambda }_n)}\rangle$ is given. The computation procedure is as follows:

1. Expand $\langle {\prod }_{n=1}^3{\xi }_{{\text{k}}_n}^{({\lambda }_n)}\rangle$ using the (spin-weighted) spherical harmonics in terms of ${\widehat{k}}_1$, ${\widehat{k}}_2$, and ${\widehat{k}}_3$.

2. Perform the angular integrals, $\int d^2{\widehat{k}}_1$, $\int d^2{\widehat{k}}_2$, and $\int d^2{\widehat{k}}_3$, of the resultant spherical harmonics and convert them into products of Wigner symbols.

3. Simplify the resultant products of the Wigner symbols by adding angular momenta.

If the primordial bispectrum $\langle {\prod }_{n=1}^3{\xi }_{{\text{k}}_n}^{({\lambda }_n)}\rangle$ respects rotational invariance, via the above computation, the Wigner 3j symbol $\left(\begin{array}{lll}{\ell }_1\hfill & {\ell }_2\hfill & {\ell }_3\hfill \\ m_1\hfill & m_2\hfill & m_3\hfill \end{array}\right)$ is singled out in $\langle {\prod }_{n=1}^3{\xi }_{{\ell }_n{m}_n}^{({\lambda }_n)}(k_n)\rangle$ and hence the resulting CMB bispectrum takes the form:

$\begin{array}{ll}\langle {\displaystyle \prod _{n=1}^3}{a}_{{\ell }_n{m}_n}^{X_n(z_n)}\rangle =\left(\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ m_1& m_2& m_3\end{array}\right)B_{(z_1{z}_2{z}_3){\ell }_1{\ell }_2{\ell }_3}^{X_1{X}_2{X}_3}.& (27)\end{array}$

In this case, the non-zero signal is confined to the tetrahedral domain:

$\begin{array}{ll}|{\ell }_1-{\ell }_2|\le {\ell }_3\le {\ell }_1+{\ell }_2.& (28)\end{array}$

3.2. Practical Examples

In the following, we demonstrate the CMB bispectrum computation in the context of the practical cases discussed in section 2.

3.2.1. Three Tensors

First, we discuss the CMB bispectra sourced by primordial tensors where we examine the axion model $f_{\text{NL}}^{ttt,\text{eq}}$ template (3) (Shiraishi et al., 2013), the W³ model (14) (Shiraishi et al., 2011a), the $\tilde{W}{W}^2$ model (15) (Shiraishi et al., 2011a), and the PMF model $f_{\text{NL}}^{ttt,\text{sq}}$ (8) (Shiraishi et al., 2011c). Since $A_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}$ takes the identical form, $\langle {\prod }_{n=1}^3{h}_{{\ell }_n{m}_n}^{({\lambda }_n)}(k_n)\rangle$ can be computed in a similar way.

For the first step, in order to simplify the R.H.S. of Equation (26), we expand $A_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}$ and the Dirac delta function:

$\begin{array}{l}{e}_{ij}^{(-{\lambda }_1)}({\widehat{k}}_1)e_{jk}^{(-{\lambda }_2)}({\widehat{k}}_2)e_{ki}^{(-{\lambda }_3)}({\widehat{k}}_3)\\ =-\frac{{(8\pi )}^{3/2}}{10}\sqrt{\frac{7}{3}}\left[{\displaystyle \prod _{n=1}^3{\displaystyle \sum _{{\mu }_n}{}_{{\lambda }_n}}}{Y}_{2{\mu }_n}^{*}({\widehat{k}}_n)\right]\left(\begin{array}{ccc}2& 2& 2\\ {\mu }_1& {\mu }_2& {\mu }_3\end{array}\right),& (29)\end{array}$

$\begin{array}{l}{\delta }^{(3)}\left({\displaystyle \sum _{n=1}^3{k}_n}\right)\\ \begin{array}{l}=8{{\displaystyle \int }}_0^{\infty }{y}^{2}dy\left[{\displaystyle \prod _{n=1}^3}{\displaystyle \sum _{L_n{M}_n}}{(-1)}^{L_n/2}{j}_{L_n}(k_{n}y)Y_{L_n{M}_n}^{*}({\widehat{k}}_n)\right]\hfill \\ \begin{array}{c}\times h_{L_1{L}_2{L}_3}^{000}\left(\begin{array}{ccc}{L}_1& L_2& L_3\\ M_1& M_2& M_3\end{array}\right),\end{array}\hfill \end{array}& (30)\end{array}$

where

$\begin{array}{ll}{h}_{l_1{l}_2{l}_3}^{s_1{s}_2{s}_3}\equiv \sqrt{\frac{(2l_1+1)(2l_2+1)(2l_3+1)}{4\pi }}\left(\begin{array}{ccc}{l}_1& l_2& l_3\\ s_1& s_2& s_3\end{array}\right).& (31)\end{array}$

For the second step, the angular integrals of the resultant spherical harmonics are performed, such that:

$\begin{array}{ll}{\displaystyle \int }{d}^2{\widehat{k}{}_n}_{-{\lambda }_n}{Y}_{{\ell }_n{m}_n}^{*}({\widehat{k}}_n)Y_{L_n{M}_n}^{*}{({\widehat{k}}_n)}_{{\lambda }_n}{Y}_{2{\mu }_n}^{*}({\widehat{k}}_n)=h_{{\ell }_n{L}_{n}2}^{{\lambda }_{n}0-{\lambda }_n}\left(\begin{array}{ccc}{\ell }_n& L_n& 2\\ m_n& M_n& {\mu }_n\end{array}\right).& (32)\end{array}$

As a final step, the summation of the Wigner 3j symbols appearing above over angular momenta is computed according to:

$\begin{array}{l}{\displaystyle \sum _{\begin{array}{c}{M}_1{M}_2{M}_3\\ {\mu }_1{\mu }_2{\mu }_3\end{array}}}\left(\begin{array}{ccc}{L}_1& L_2& L_3\\ M_1& M_2& M_3\end{array}\right)\left(\begin{array}{ccc}2& 2& 2\\ {\mu }_1& {\mu }_2& {\mu }_3\end{array}\right)\left(\begin{array}{ccc}{\ell }_1& L_1& 2\\ m_1& M_1& {\mu }_1\end{array}\right)\\ \times \left(\begin{array}{ccc}{\ell }_2& L_2& 2\\ m_2& M_2& {\mu }_2\end{array}\right)\left(\begin{array}{ccc}{\ell }_3& L_3& 2\\ m_3& M_3& {\mu }_3\end{array}\right)=\left(\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ m_1& m_2& m_3\end{array}\right)\left\{\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ L_1& L_2& L_3\\ 2& 2& 2\end{array}\right\}.& (33)\end{array}$

Consequently, we obtain:

$\begin{array}{l}\langle {\displaystyle \prod _{n=1}^3}{h}_{{\ell }_n{m}_n}^{({\lambda }_n)}(k_n)\rangle =\left(\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ m_1& m_2& m_3\end{array}\right)\\ \times \frac{-{(8\pi )}^{3/2}}{10}\sqrt{\frac{7}{3}}{\displaystyle \sum _{L_1{L}_2{L}_3}}{(-1)}^{\frac{L_1+L_2+L_3}{2}}{h}_{L_1{L}_2{L}_3}^{000}\\ \times \left\{\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ L_1& L_2& L_3\\ 2& 2& 2\end{array}\right\}{\displaystyle {\int }_0^{\infty }}{y}^{2}dy\left[{\displaystyle \prod _{n=1}^3}4\pi j_{L_n}(k_{n}y)h_{{\ell }_n{L}_{n}2}^{{\lambda }_{n}0-{\lambda }_n}\right]{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}.& (34)\end{array}$

Here, the prefactor $\left(\begin{array}{lll}{\ell }_1\hfill & {\ell }_2\hfill & {\ell }_3\hfill \\ m_1\hfill & m_2\hfill & m_3\hfill \end{array}\right)$ is due to rotational invariance of the primordial bispectrum. Inserting this into Equation (25) and simplifying the resultant equation, we find that the CMB bispectra take the rotational-invariant form (27) with:

$\begin{array}{l}{B}_{(ttt){\ell }_1{\ell }_2{\ell }_3}^{X_1{X}_2{X}_3}=\frac{-{(8\pi )}^{3/2}}{10}\sqrt{\frac{7}{3}}{(-i)}^{{\ell }_1+{\ell }_2+{\ell }_3}{\displaystyle \sum _{L_1{L}_2{L}_3}}\\ \times {(-1)}^{\frac{L_1+L_2+L_3}{2}}{h}_{L_1{L}_2{L}_3}^{000}\left\{\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ L_1& L_2& L_3\\ 2& 2& 2\end{array}\right\}\\ \times {\displaystyle {\int }_0^{\infty }}{y}^{2}dy\left[{\displaystyle \prod _{n=1}^3}\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }}{k}_n^{2}d{k}_n{{T}}_{{\ell }_n,k_n}^{X_n(t)}{j}_{L_n}(k_{n}y)\right]\\ \times \left[{\displaystyle \prod _{n=1}^3}{\displaystyle \sum _{{\lambda }_n=\pm 2}}{\left[\text{sgn}({\lambda }_n)\right]}^{x_n}{h}_{{\ell }_n{L}_{n}2}^{{\lambda }_{n}0-{\lambda }_n}\right]{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_2{\lambda }_3}.& (35)\end{array}$

The ℓ-space domain containing the non-zero signal is determined by the summation over the helicities λ₁, λ₂, and λ₃. In the $\tilde{W}{W}^2$ model, performing the summation of Equation (15) leads to the non-vanishing condition: (Shiraishi et al., 2011a)

$\begin{array}{ll}{\ell }_1+{\ell }_2+{\ell }_3+x_1+x_2+x_3=\text{odd}.& (36)\end{array}$

On the other hand, in the W³ and PMF models, due to the helicity dependence in Equations (14) and (8), the non-vanishing signal is confined to Shiraishi et al. (2011a,c):

$\begin{array}{ll}{\ell }_1+{\ell }_2+{\ell }_3+x_1+x_2+x_3=\text{even}.& (37)\end{array}$

In the axion model, however, the helicity dependence in Equation (3) does not yield any restriction, allowing a non-vanishing signal in the whole tetrahedral domain (Shiraishi et al., 2013).

The left and center panels of Figure 1 show the intensity distributions of the temperature bispectra from the axion model $f_{\text{NL}}^{ttt,\text{eq}}$ template (3) and the PMF model $f_{\text{NL}}^{ttt,\text{sq}}$ template (8), respectively. As expected, it is confirmed that the signal comes mostly from the equilateral (ℓ₁ ~ ℓ₂ ~ ℓ₃) and squeezed (ℓ₁ ≪ ℓ₂ ~ ℓ₃, ℓ₂ ≪ ℓ₃ ~ ℓ₁ and ℓ₃ ≪ ℓ₁ ~ ℓ₂) configurations, respectively. The decaying nature for ℓ≳100 due to the lack of the tensor-mode integrated Sachs-Wolfe contribution (Shiraishi et al., 2011c, 2013) is also visually apparent.

FIGURE 1

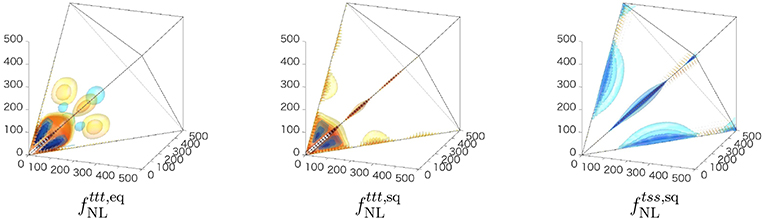
Figure 1. Intensity distributions of the CMB temperature bispectra from the axion model $f_{\text{NL}}^{ttt,\text{eq}}$ template (3), the PMF model $f_{\text{NL}}^{ttt,\text{sq}}$ one (8), and the massive gravity model $f_{\text{NL}}^{tss,\text{sq}}$ one (16) in the ℓ-space tetrahedral domain where the axes correspond to ℓ₁, ℓ₂, and ℓ₃, respectively. Here, the bispectra are rescaled using a constant Sachs-Wolfe template (Fergusson et al., 2010). Dense red (blue) color expresses a larger positive (negative) signal. The current and future observational limits on $f_{\text{NL}}^{ttt,\text{eq}}$, $f_{\text{NL}}^{ttt,\text{sq}}$, and $f_{\text{NL}}^{tss,\text{sq}}$ are discussed in sections 4.2 and 4.3, respectively.

3.2.2. Two Tensors and One Scalar

Here, we compute the CMB tensor-tensor-scalar bispectrum from the $\tilde{W}W$ model (13) (Bartolo et al., 2019). The angular dependence in $A_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_1{\lambda }_{2}0}$ (12) is decomposed according to:

$\begin{array}{ll}\begin{array}{l}({\widehat{k}}_1\cdot {\widehat{k}}_2)e_{ij}^{(-{\lambda }_1)}({\widehat{k}}_1)e_{ij}^{(-{\lambda }_2)}({\widehat{k}}_2)\hfill \\ =\frac{32{\pi }^2}{15}{\displaystyle \sum _{J\mu }{\lambda }_1}{Y}_{J\mu }^{*}{({\widehat{k}}_1)}_{{\lambda }_2}{Y}_{J-\mu }^{*}({\widehat{k}}_2){(-1)}^{\mu +1+J}\frac{h_{12J}^{0{\lambda }_1-{\lambda }_1}{h}_{12J}^{0{\lambda }_2-{\lambda }_2}}{2J+1}.\hfill \end{array}& (38)\end{array}$

By means of the above methodology, we obtain (Bartolo et al., 2019):

$\begin{array}{l}{B}_{(tts){\ell }_1{\ell }_2{\ell }_3}^{X_1{X}_2{X}_3}=\frac{32{\pi }^2}{15}{(-i)}^{{\ell }_1+{\ell }_2+{\ell }_3}{\displaystyle \sum _{L_1{L}_2}}{(-1)}^{\frac{L_1+L_2+{\ell }_3}{2}}{h}_{L_1{L}_2{\ell }_3}^{000}\\ \times {\displaystyle \sum _J}\frac{{(-1)}^{1+J+L_2+{\ell }_1}}{2J+1}\left\{\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ L_2& L_1& J\end{array}\right\}\\ \times {\displaystyle {\int }_0^{\infty }}{y}^{2}dy\left[{\displaystyle \prod _{n=1}^2}\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }}{k}_n^{2}d{k}_n{{T}}_{{\ell }_n,k_n}^{X_n(t)}{j}_{L_n}(k_{n}y)\right]\\ \times \frac{2}{\pi }{\displaystyle {\int }_0^{\infty }}{k}_3^{2}d{k}_3{{T}}_{{\ell }_3,k_3}^{X_3(s)}{j}_{{\ell }_3}(k_{3}y)\\ \times \left[{\displaystyle \prod _{n=1}^2}{\displaystyle \sum _{{\lambda }_n=\pm 2}}{\left[\text{sgn}({\lambda }_n)\right]}^{x_n}{h}_{L_n{\ell }_{n}J}^{0{\lambda }_n-{\lambda }_n}{h}_{12J}^{0{\lambda }_n-{\lambda }_n}\right]{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_1{\lambda }_{2}0}.& (39)\end{array}$

Performing the summation over λ₁ and λ₂ with Equation (13), we find that the non-vanishing signal obeys (Bartolo et al., 2019):

$\begin{array}{ll}{\ell }_1+{\ell }_2+{\ell }_3+x_1+x_2=\text{odd}.& (40)\end{array}$

3.2.3. One Tensor and Two Scalars

We here compute the CMB bispectrum from the massive gravity model $f_{\text{NL}}^{tss,\text{sq}}$ template (16) (Domenech et al., 2017). The spherical harmonic expansion of $A_{{\widehat{k}}_1{\widehat{k}}_2{\widehat{k}}_3}^{{\lambda }_{1}00}$ (17) then reads:

$\begin{array}{l}{e}_{ij}^{(-{\lambda }_1)}({\widehat{k}}_1){\widehat{k}}_{2i}{\widehat{k}}_{3j}=\frac{{(8\pi )}^{3/2}}{6}{\displaystyle \sum _{{\mu }_1{\mu }_2{\mu }_3}{}_{{\lambda }_1}}{Y}_{2{\mu }_1}^{*}({\widehat{k}}_1)Y_{1{\mu }_2}^{*}({\widehat{k}}_2)Y_{1{\mu }_3}^{*}({\widehat{k}}_3)\\ \left(\begin{array}{ccc}2& 1& 1\\ {\mu }_1& {\mu }_2& {\mu }_3\end{array}\right).& (41)\end{array}$

In the same manner, we can derive the CMB bispectrum as (Shiraishi et al., 2011b; Domenech et al., 2017):

$\begin{array}{l}{B}_{(tss){\ell }_1{\ell }_2{\ell }_3}^{X_1{X}_2{X}_3}=\frac{{(8\pi )}^{3/2}}{6}{(-i)}^{{\ell }_1+{\ell }_2+{\ell }_3}{\displaystyle \sum _{L_1{L}_2{L}_3}}{(-1)}^{\frac{L_1+L_2+L_3}{2}}\\ \times h_{L_1{L}_2{L}_3}^{000}{h}_{{\ell }_2{L}_{2}1}^{000}{h}_{{\ell }_3{L}_{3}1}^{000}\left\{\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ L_1& L_2& L_3\\ 2& 1& 1\end{array}\right\}\\ \times {\displaystyle {\int }_0^{\infty }}{y}^{2}dy\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }}{k}_1^{2}d{k}_1{{T}}_{{\ell }_1,k_1}^{X_1(t)}{j}_{L_1}(k_{1}y)\\ \times \left[{\displaystyle \prod _{n=2}^3}\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }}{k}_n^{2}d{k}_n{{T}}_{{\ell }_n,k_n}^{X_n(s)}{j}_{L_n}(k_{n}y)\right]\\ \times {\displaystyle \sum _{{\lambda }_1=\pm 2}}{\left[\text{sgn}({\lambda }_1)\right]}^{x_1}{h}_{{\ell }_1{L}_{1}2}^{{\lambda }_{1}0-{\lambda }_1}{{B}}_{k_1{k}_2{k}_3}^{{\lambda }_{1}00}.& (42)\end{array}$

By summing over λ₁, we confirm that, because of the absence of the helicity dependence in Equation (16), the non-vanishing signal is distributed on (Shiraishi et al., 2011b; Domenech et al., 2017):

$\begin{array}{ll}{\ell }_1+{\ell }_2+{\ell }_3+x_1=\text{even}.& (43)\end{array}$

The right panel of Figure 1 describes the intensity distribution of the resultant temperature bispectrum showing explicitly that it is amplified in the squeezed limit. Differently from the $f_{\text{NL}}^{ttt,\text{sq}}$ case, the squeezed signal survives even for ℓ≳100 because of the presence of the scalar-mode acoustic oscillation.

4. Measurements of CMB Tensor-Mode Bispectra

In this section, we examine the present and future constraints on GW NGs through the CMB bispectrum measurements.

4.1. Optimal Tensor-Mode Bispectrum Estimation

Let us begin by explaining how to estimate the overall magnitude of the primordial bispectrum, dubbed as f_NL, from the CMB data.

An optimal f_NL estimator takes the form (Komatsu et al., 2005):

$\begin{array}{ll}{\widehat{f}}_{\text{NL}}=\frac{1}{F}{\displaystyle \sum _{{\ell }_1{\ell }_2{\ell }_3}}{(-1)}^{{\ell }_1+{\ell }_2+{\ell }_3}\frac{B_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}}{B}_{{\ell }_1{\ell }_2{\ell }_3}^{\text{obs}}}{6C_{{\ell }_1}{C}_{{\ell }_2}{C}_{{\ell }_3}},& (44)\end{array}$

where C_ℓ is the CMB angular power spectrum, $B_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}}$ is the theoretical template of the angle-averaged CMB bispectrum one wants to measure [corresponding to $B_{(z_1{z}_2{z}_3){\ell }_1{\ell }_2{\ell }_3}^{X_1{X}_2{X}_3}$ in Equation (27) for f_NL = 1],

$\begin{array}{l}{B}_{{\ell }_1{\ell }_2{\ell }_3}^{\text{obs}}\equiv {\displaystyle \sum _{m_1{m}_2{m}_3}\left(\begin{array}{ccc}{\ell }_1& {\ell }_2& {\ell }_3\\ m_1& m_2& m_3\end{array}\right)}[a_{{\ell }_1{m}_1}{a}_{{\ell }_2{m}_2}{a}_{{\ell }_3{m}_3}\\ -\left(\langle a_{{\ell }_1{m}_1}{a}_{{\ell }_2{m}_2}\rangle a_{{\ell }_3{m}_3}+2\text{ perm}\right)]& (45)\end{array}$

is the bispectrum reconstructed from the observed a_ℓm, and

$\begin{array}{ll}F\equiv {\displaystyle \sum _{{\ell }_1{\ell }_2{\ell }_3}}{(-1)}^{{\ell }_1+{\ell }_2+{\ell }_3}\frac{{\left(B_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}}\right)}^2}{6C_{{\ell }_1}{C}_{{\ell }_2}{C}_{{\ell }_3}}& (46)\end{array}$

is the Fisher matrix. The bestfit value and the error bar on f_NL is obtained computing ${\widehat{f}}_{\text{NL}}$ from the observed data and the simulation maps, respectively. The straightforward computation of Equation (44) is not a wise manner since the ${O}({\ell }_{\text{max}}^5)$ numerical operation required here is quite time-consuming and practically unfeasible for ℓ_max≳100.

To reduce the computational cost, factorizing the summation as $\sum _{{\ell }_1{\ell }_2{\ell }_3}f({\ell }_1,{\ell }_2,{\ell }_3)=\left[\sum _{{\ell }_1}a({\ell }_1)\right]\left[\sum _{{\ell }_2}b({\ell }_2)\right]\left[\sum _{{\ell }_3}c({\ell }_3)\right]$ is a tested approach². This idea was implemented in Komatsu et al. (2005) for the first time, enabling the analysis for originally separable templates such as local, equilateral and orthogonal NGs. Later, it was generalized by developing the modal decomposition technique of any originally non-separable $B_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}}$ (Fergusson et al., 2010, 2012). The original version of the modal methodology is for the analysis of even ℓ₁ + ℓ₂ + ℓ₃ domain, while the spin-weighted version developed recently (Shiraishi et al., 2014, 2015) can also cover odd ℓ₁ + ℓ₂ + ℓ₃ domain. As seen in section 3, the tensor-mode CMB bispectrum is generally non-separable and does not always vanish in the odd ℓ₁ + ℓ₂ + ℓ₃ domain. In this sense, the modal methodology is an indispensable tool for the tensor NG search. In fact, except for the results obtained brute forcing the ℓ-space summation with ℓ_max = 100 (Shiraishi and Sekiguchi, 2014), all observational constraints reported so far have been obtained by it Shiraishi et al. (2015, 2018); Ade et al. (2016a,b); Akrami et al. (2019). In what follows, for simplicity, we explain the modal methodology for the auto bispectra (TTT, EEE, and BBB) based on Fergusson et al. (2010, 2012), Shiraishi et al. (2014, 2015), while one can deal with the cross bispectra (TTE, TTB, TEE, TEB, TBB, EEB, and EBB) in the very similar way (Fergusson, 2014; Shiraishi et al., 2019).

Let us introduce the reduced bispectrum according to:

$\begin{array}{ll}{B}_{{\ell }_1{\ell }_2{\ell }_3}\equiv h_{{\ell }_1{\ell }_2{\ell }_3}^{\left\{xyz\right\}}{b}_{{\ell }_1{\ell }_2{\ell }_3},& (47)\end{array}$

where,

$\begin{array}{ll}{h}_{{\ell }_1{\ell }_2{\ell }_3}^{\left\{xyz\right\}}\equiv \frac{1}{6}{h}_{{\ell }_1{\ell }_2{\ell }_3}^{xyz}+5\text{ perm in }x,y,z.& (48)\end{array}$

Here and hereinafter, we follow the notation for the symmetric operation $A^{\{}{}^x{A}^y{A}^z{}^{\}}\equiv \frac{1}{6}{A}^x{A}^y{A}^z+5\text{ perm in }x,y,z.$ The spined weight (x, y, z) is fixed to be, e.g., (0, 0, 0) and (1, 1, −2) for even and odd ℓ₁ + ℓ₂ + ℓ₃ analysis, respectively. The reduced bispectrum of the theoretical template is decomposed in the odd/even ℓ₁ + ℓ₂ + ℓ₃ domain separately, according to:

$\begin{array}{ll}\frac{v_{{\ell }_1}{v}_{{\ell }_2}{v}_{{\ell }_3}}{\sigma \sqrt{C_{{\ell }_1}{C}_{{\ell }_2}{C}_{{\ell }_3}}}{b}_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}(o/e)}={\displaystyle \sum _{ijk}}{\alpha }_{ijk}^{(o/e)}{Q}_{ijk}({\ell }_1,{\ell }_2,{\ell }_3),& (49)\end{array}$

where the separable modal basis Q_ijk is composed of the products of the eigenfunctions q_i(ℓ) ∈ ℝ as:

$\begin{array}{l}{Q}_{ijk}({\ell }_1,{\ell }_2,{\ell }_3)\equiv q_{\{i}({\ell }_1)q_j({\ell }_2)q_{k\}}({\ell }_3)\\ =\frac{1}{6}{q}_i({\ell }_1)q_j({\ell }_2)q_k({\ell }_3)+5\text{ perm in }i,j,k.& (50)\end{array}$

The σ factor, defined by:

$\begin{array}{ll}\sigma \equiv \{\begin{array}{cc}1& :{\ell }_1+{\ell }_2+{\ell }_3=\text{even}\\ i& :{\ell }_1+{\ell }_2+{\ell }_3=\text{odd}\end{array},& (51)\end{array}$

makes the L.H.S of Equation (49) real, so the modal coefficients ${\alpha }_{ijk}^{(o/e)}$ are always real. The convergence speed of the modal decomposition relies on the choice of the v_ℓ weighting and q_i(ℓ). Employing the Q_ijk templates, we define a matrix according to:

$\begin{array}{ll}{\gamma }_{np}^{(o/e)}\equiv {{\langle Q}_n({\ell }_1,{\ell }_2,{\ell }_3)Q_p({\ell }_1,{\ell }_2,{\ell }_3)\rangle }_{o/e},& (52)\end{array}$

where the triples ijk in Q_ijk are labeled by means of a single index n, and the bracket 〈⋯〉_o/e denotes the summation in terms of the odd/even ℓ₁ + ℓ₂ + ℓ₃ domain as:

$\begin{array}{ll}{\langle F_{{\ell }_1{\ell }_2{\ell }_3}\rangle }_{o/e}\equiv {\displaystyle \sum _{{\ell }_1+{\ell }_2+{\ell }_3=\text{odd}/\text{even}}}{\left(\frac{h_{{\ell }_1{\ell }_2{\ell }_3}^{\left\{xyz\right\}}}{v_{{\ell }_1}{v}_{{\ell }_2}{v}_{{\ell }_3}}\right)}^2{F}_{{\ell }_1{\ell }_2{\ell }_3}.& (53)\end{array}$

Then, the modal coefficients are computed according to the inverse operation:

$\begin{array}{ll}{\alpha }_n^{(o/e)}={\displaystyle \sum _p}{\left({\gamma }^{(o/e)}\right)}_{np}^{-1}{\langle \frac{v_{{\ell }_1}{v}_{{\ell }_2}{v}_{{\ell }_3}{b}_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}(o/e)}}{\sigma \sqrt{C_{{\ell }_1}{C}_{{\ell }_2}{C}_{{\ell }_3}}}{Q}_p({\ell }_1,{\ell }_2,{\ell }_3)\rangle }_{o/e}.& (54)\end{array}$

Using Equation (49) and the identity:

$\begin{array}{l}{h}_{l_1{l}_2{l}_3}^{s_1{s}_2{s}_3}\left(\begin{array}{ccc}{l}_1& l_2& l_3\\ m_1& m_2& m_3\end{array}\right)\\ ={\displaystyle \int }{d}^2{\widehat{n}}_{-s_1}{Y}_{l_1{m}_1}{(\widehat{n})}_{-s_2}{Y}_{l_2{m}_2}{(\widehat{n})}_{-s_3}{Y}_{l_3{m}_3}(\widehat{n}),& (55)\end{array}$

the sum over ℓ₁, ℓ₂, and ℓ₃ in the estimator (44) is rewritten into the sum over finite eigenmodes as:

$\begin{array}{ll}{\widehat{f}}_{\text{NL}}=\frac{{\displaystyle {\sum }_n}{\alpha }_n^{(o)}{\beta }_n^{(o)}+{\displaystyle {\sum }_n}{\alpha }_n^{(e)}{\beta }_n^{(e)}}{{\displaystyle {\sum }_{np}}{\alpha }_n^{(o)}{\gamma }_{np}^{(o)}{\alpha }_p^{(o)}+{\displaystyle {\sum }_{np}}{\alpha }_n^{(e)}{\gamma }_{np}^{(e)}{\alpha }_p^{(e)}},& (56)\end{array}$

where the ${\beta }_n^{(o/e)}$ coefficients, reading:

$\begin{array}{ll}\begin{array}{l}{\beta }_{ijk}^{(o/e)}=\frac{1}{\sigma }{{{\displaystyle \int }}^{\text{}}}^{\text{}}{d}^2\widehat{n}{\displaystyle \sum _{a+b+c=o/e}[{}_{\{-x}{M}_{\{i}^{(a)}{(\widehat{n})}_{-y}{M}_j^{(b)}{(\widehat{n})}_{-z\}}{M}_{k\}}^{(c)}(\widehat{n})}\hfill \\ -3{\langle }_{\{-x}{M}_{\{i}^{(a)}{(\widehat{n})}_{-y}{M}_j^{(b)}(\widehat{n})\rangle {}_{-z\}}{M}_{k\}}^{(c)}(\widehat{n})]\text{ },\hfill \end{array}& (57)\end{array}$

are computed from the filtered maps:

$\begin{array}{ll}\begin{array}{l}{}_x{M}_i^{(o/e)}(\widehat{n})\equiv {\displaystyle \sum _{\ell =\text{odd}/\text{even}}{\displaystyle \sum _m{q}_i(\ell ){\frac{a_{\ell m}}{v_{\ell }\sqrt{C_{\ell }}}}_x{Y}_{\ell m}(\widehat{n}).}}\hfill \end{array}& (58)\end{array}$

The most time-consuming task is the computation of 〈⋯〉_o/e in ${\alpha }_n^{(o/e)}$, however, it requires, at most, ${O}({\ell }_{\text{max}}^3)$ operations (assuming that the modal decomposition converges within a reasonable time), and hence the separable estimator (56) makes the tensor bispectrum analysis feasible.

4.2. Current Observational Limits

Table 1 summarizes the current CMB limits on $f_{\text{NL}}^{ttt,\text{eq}}$, $f_{\text{NL}}^{ttt,\text{sq}}$, and $f_{\text{NL}}^{tss,\text{sq}}$ obtained from the WMAP and Planck maps³. Regarding $f_{\text{NL}}^{ttt,\text{eq}}$ and $f_{\text{NL}}^{ttt,\text{sq}}$, the consistency between the WMAP T only results and Planck T only ones is confirmed there. Note that the unimproved constraints are expected because, as inferred from Figure 1, $B_{{\ell }_1{\ell }_2{\ell }_3}^{\text{th}}$ decays rapidly for ℓ≳100 and hence the estimator sum (44) saturates well below the WMAP resolution (ℓ_max = 500). In contrast, for $f_{\text{NL}}^{tss,\text{sq}}$ the current constraint from WMAP is expected to be much improved by Planck since the squeezed-limit signal survives even for high ℓ (Shiraishi et al., 2011b; Domenech et al., 2017). We also confirm the improvement of the constraint on $f_{\text{NL}}^{ttt,\text{eq}}$ by analyzing the temperature and E-mode polarization data jointly.

TABLE 1

Table 1. CMB constraints on three tensor non-linearity parameters: $f_{\text{NL}}^{ttt,\text{eq}}$ (6), $f_{\text{NL}}^{ttt,\text{sq}}$ (10), and $f_{\text{NL}}^{tss,\text{sq}}$ (18).

As seen in Table 1, no significant deviation from Gaussianity has been found so far.

4.3. Future Prospects

Finally, we discuss future prospects of detecting these tensor NGs by adding B-mode polarization to the data analysis. Here, we evaluate expected 1σ errors $\Delta f_{\text{NL}}^{ttt,\text{eq}}$ and $\Delta f_{\text{NL}}^{ttt,\text{sq}}$ from BBB, and $\Delta f_{\text{NL}}^{tss,\text{sq}}$ from BTT, through the computation of the Fisher matrix. The covariance matrices [corresponding to the denominator of Equation (46)] are given by $C_{{\ell }_1}^{BB}{C}_{{\ell }_2}^{BB}{C}_{{\ell }_3}^{BB}$ and $C_{{\ell }_1}^{BB}{C}_{{\ell }_2}^{TT}{C}_{{\ell }_3}^{TT}$, respectively. Note that these are estimated under the diagonal covariance matrix approximation. The B-mode power spectrum is computed by summing up the primordial contribution parameterized by the tensor-to-scalar ratio r, the lensing B-mode one and the experimental noise spectrum as $C_{\ell }^{BB}=C_{\ell }^{\text{prim}}(r)+C_{\ell }^{\text{lens}}+N_{\ell }$. Then, let us examine three cleanliness levels of the B-mode data: a perfectly-delensed and noiseless full-sky case (i.e., $C_{\ell }^{\text{lens}}=N_{\ell }=0$), a non-delensed and noiseless full-sky one (i.e., N_ℓ = 0), and a non-delensed realistic case where experimental uncertainties due to beam, noise, mask and residual foreground in LiteBIRD (Hazumi et al., 2012; Matsumura et al., 2013, 2016) are considered⁴. The first example provides the theoretical limits. In this case, the size of the covariance matrix is determined by r alone and, accordingly, the errors simply scale like:

$\begin{array}{ll}\Delta f_{\text{NL}}^{ttt,\text{eq}}\propto r^{3/2},\Delta f_{\text{NL}}^{ttt,\text{sq}}\propto r^{3/2},\Delta f_{\text{NL}}^{tss,\text{sq}}\propto r^{1/2}.& (59)\end{array}$

Comparing this with Equations (7) or (19), one can see that the error on a model parameter of the axion model, ${\Omega }_A^{-1}$, or that of the massive gravity model, λ_sst, is proportional to r^−1/2.

The left panel of Figure 2 describes the ℓ_max dependence of Δf_NL in the perfectly-delensed and non-delensed cases with r = 10⁻³ and N_ℓ = 0. From the former results (corresponding to the dot-dashed lines), the sensitivity improvement by increasing ℓ_max is confirmed. From the latter results (corresponding to the solid lines), it is visually apparent that $\Delta f_{\text{NL}}^{ttt,\text{eq}}$ and $\Delta f_{\text{NL}}^{ttt,\text{sq}}$ immediately saturate because $C_{\ell }^{\text{lens}}$ dominates over $C_{\ell }^{BB}$ for $\ell >{O}(10)$. In contrast, $\Delta f_{\text{NL}}^{ttt,\text{sq}}$ is free from such a degradation since the dominant signal in the Fisher matrix comes from large-scale B modes, more precisely, long-wavelength B and short-wavelength T squeezed configurations (${\ell }_1^B\ll {\ell }_2^T~{\ell }_3^T$) (Meerburg et al., 2016; Domenech et al., 2017). However, of course, $\Delta f_{\text{NL}}^{ttt,\text{sq}}$ would also saturate at very small scales, i.e., ℓ^T≳3000, where the scalar-mode lensing contamination dominates $C_{\ell }^{TT}$. Higher-order lensing contributions introduce non-vanishing off-diagonal components in the covariance matrix; thus, the above simple Fisher matrix computation would no longer be credible. In the left panel of Figure 2, the results of the LiteBIRD-like experiment are not shown, however, they have similar ℓ_max scalings and the slightly larger overall sizes in comparison with the no-delensed and noiseless full-sky results.

FIGURE 2

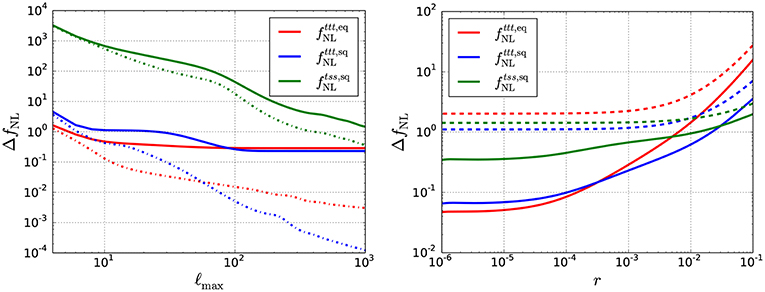
Figure 2. Expected 1σ errors: $\Delta f_{\text{NL}}^{ttt,\text{eq}}$ (red lines) and $\Delta f_{\text{NL}}^{ttt,\text{sq}}$ (blue lines) from BBB, and $\Delta f_{\text{NL}}^{tss,\text{sq}}$ (green lines) from BTT, as a function of the maximum multipole number ℓ_max (left panel) and the tensor-to-scalar ratio r (right panel). The left panel is depicted adopting r = 10⁻³, and $\Delta f_{\text{NL}}^{tss,\text{sq}}$ in the right panel is computed with ℓ_max = 2000. The linestyle discriminates the cleanliness level of the B-mode data: a perfectly-delensed and noiseless full-sky case (dot-dashed lines in left panel), a non-delensed and noiseless full-sky one (solid lines in both panels), and a LiteBIRD-like realistic one (dashed lines in right panel).

In the right panel of Figure 2, the r dependence of Δf_NL for the no-delensed and noiseless case (corresponding to the solid lines) and a LiteBIRD-like experiment (corresponding to the dashed lines) is presented. For large r, $C_{\ell }^{\text{prim}}$ dominates over $C_{\ell }^{BB}$ within a wide range of ℓ and hence the r dependence reaches the ideal case (59). On the other hand, for decreasing r, $C_{\ell }^{\text{lens}}$ or N_ℓ starts to dominate and errors converge. We find that LiteBIRD could measure an ${O}(1)$ signal of $f_{\text{NL}}^{ttt,\text{eq}}$, $f_{\text{NL}}^{ttt,\text{sq}}$, or $f_{\text{NL}}^{tss,\text{sq}}$.⁵ If detected, as discussed in section 2, we will have compelling evidence for a deviation from Einstein gravity or the existence of extra source fields, which will help establish an improved picture of the early Universe.

Finally, it is worth mentioning the impact of late-time secondary bispectra. Via gravitational lensing, primordial temperature and E-mode polarization fields induce secondary BTT signals (Hu, 2000; Lewis et al., 2011). Fortunately, this has a very weak correlation with the $f_{\text{NL}}^{tss,\text{sq}}$ bispectrum template (Domenech et al., 2017). Similarly, secondary BBB is also induced, while this is subdominant compared to primordial BBB at interesting $f_{\text{NL}}^{ttt,\text{eq}}$ or $f_{\text{NL}}^{ttt,\text{sq}}$ (Shiraishi et al., 2016). Besides of these leading-order contributions, higher-order ones exist due to post-Born lensing (Marozzi et al., 2016; Pratten and Lewis, 2016). Secondary polarized bispectra can also be generated via the Sunyaev-Zel'dovich effect (Sunyaev and Zeldovich, 1972) and extragalactic foreground (Jung et al., 2018; Coulton and Spergel, 2019). These impacts are still non-trivial and should therefore be solved for more precise discussions.

5. Conclusions

The search for tensor NG is theoretically well-motivated, and the methodology for testing with the CMB temperature and E/B-mode polarization data has already been established. Observational constraints on some templates from the WMAP temperature and the Planck temperature and E-mode polarization data do exist. Any significant signal has not yet been discovered, implying the smallness of tensor NGs. There is still a chance of approaching such a small signal by including B-mode polarization in the data analysis. As we have found, an ${O}(1)$ signal of $f_{\text{NL}}^{ttt,\text{eq}}$, $f_{\text{NL}}^{ttt,\text{sq}}$, or $f_{\text{NL}}^{tss,\text{sq}}$ would be detectable in LiteBIRD; current constraints are expected to be updated in the next decade.

Throughout this paper, we have focused mainly on scale-invariant cases, while specific scale dependences can be generated for tensor NGs depending on the shapes of the inflationary potentials and non-linear interactions. The detectability is then enhanced at specific multipoles (Shiraishi et al., 2016) or outside the CMB scales. In the latter case, the information from other probes such as an intereferometric GW survey (e.g., Bartolo et al., 2018; Tsuneto et al., 2019), the galaxy one (e.g., statistical anisotropy in the galaxy power spectrum Jeong and Kamionkowski, 2012) and the 21-cm line one also becomes indispensable. A more comprehensive analysis based on multi-wavelength observations remains an interesting and important future issue.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by the JSPS Grant-in-Aid for Research Activity Start-up Grant Number 17H07319 and the JSPS Grant-in-Aid for Early-Career Scientists Grant Number 19K14718. Numerical computations were in part carried out on Cray XC50 at the Center for Computational Astrophysics, National Astronomical Observatory of Japan.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank the editors of Status and Prospects of Cosmic Microwave Background Analysis and especially, Maurizio Tomasi and Michele Liguori for their invitation to contribute to this special issue and for all their support. I also appreciate the careful reviews of the manuscript by the referees.

Footnotes

1. ^This $f_{\text{NL}}^{ttt,\text{eq}}$ is equivalent to $f_{\text{NL}}^P$ in Shiraishi et al. (2015) and $f_{\text{NL}}^{\text{tens}}$ in Ade et al. (2016b), Akrami et al. (2019).

2. ^See Bucher et al. (2016) for another approach by binning the ℓ-space domain

3. ^See (Shiraishi et al., 2015) for the CMB limits on a few other shapes

4. ^In the third case, we compute N_ℓ by taking into account the contamination due to residual foregrounds in the same manner as Shiraishi et al. (2016); namely, we assume that foregrounds due to galactic dust emission and synchrotron radiation are subtracted using 9 channels (corresponding to 40-89 GHz and 280-402 GHz) and therefore reduce to the 2% level in CMB maps. Any higher-order contribution is not considered for simplicity

5. ^Comparable detectability is expected in the other next-generation CMB experiments such as CMB-S4 (Abazajian et al., 2016) and CORE (Delabrouille et al., 2018)

References

Abazajian, K. N., Adshead, P., Ahmed, Z., Allen, S. W., Alonso, D., Arnold, K. S., et al. (2016). CMB-S4 science book, first edition. arXiv:1610.02743.

Google Scholar

Acquaviva, V., Bartolo, N., Matarrese, S., and Riotto, A. (2003). Second order cosmological perturbations from inflation. Nucl. Phys. B667, 119–148. doi: 10.1016/S0550-3213(03)00550-9

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Arnaud, M., Arroja, F., Ashdown, M., Aumont, J., et al. (2016a). Planck 2015 results. XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 594:A19. doi: 10.1051/0004-6361/201525821

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Arnaud, M., Arroja, F., Ashdown, M., Aumont, J., et al. (2016b). Planck 2015 results. XVII. Constraints on primordial non-Gaussianity. Astron. Astrophys. 594:A17. doi: 10.1051/0004-6361/201525836

CrossRef Full Text | Google Scholar

Aghanim, N., Akrami, Y., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2018). Planck 2018 results. VI. Cosmological parameters. arXiv:1807.06209.

Google Scholar

Agrawal, A., Fujita, T., and Komatsu, E. (2018a). Large tensor non-Gaussianity from axion-gauge field dynamics. Phys. Rev. D97:103526. doi: 10.1103/PhysRevD.97.103526

CrossRef Full Text | Google Scholar

Agrawal, A., Fujita, T., and Komatsu, E. (2018b). Tensor non-Gaussianity from axion-gauge-fields dynamics : parameter search. J. Cosmol. Astropart. Phys. 1806:027. doi: 10.1088/1475-7516/2018/06/027

CrossRef Full Text | Google Scholar

Akita, Y., and Kobayashi, T. (2016). Primordial non-Gaussianities of gravitational waves beyond Horndeski theories. Phys. Rev. D93:043519. doi: 10.1103/PhysRevD.93.043519

CrossRef Full Text | Google Scholar

Akrami, Y., Arroja, F., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2018). Planck 2018 results. X. Constraints on inflation. arXiv:1807.06211.

Google Scholar

Akrami, Y., Arroja, F., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2019). Planck 2018 results. IX. Constraints on primordial non-Gaussianity. arXiv:1905.05697.

Google Scholar

Alexander, S., and Martin, J. (2005). Birefringent gravitational waves and the consistency check of inflation. Phys. Rev. D71:063526. doi: 10.1103/PhysRevD.71.063526

CrossRef Full Text | Google Scholar

Anninos, D., De Luca, V., Franciolini, G., Kehagias, A., and Riotto, A. (2019). Cosmological shapes of higher-spin gravity. J. Cosmol. Astropart. Phys. 1904:045. doi: 10.1088/1475-7516/2019/04/045

CrossRef Full Text | Google Scholar

Barnaby, N., Namba, R., and Peloso, M. (2011). Phenomenology of a pseudo-scalar inflaton: naturally large nongaussianity. J. Cosmol. Astropart. Phys. 1104:009. doi: 10.1088/1475-7516/2011/04/009

CrossRef Full Text | Google Scholar

Bartolo, N., Domcke, V., Figueroa, D. G., García-Bellido, J., Peloso, M., Pieroni, M., et al. (2018). Probing non-gaussian stochastic gravitational wave backgrounds with LISA. J. Cosmol. Astropart. Phys. 1811:034. doi: 10.1088/1475-7516/2018/11/034

CrossRef Full Text | Google Scholar

Bartolo, N., and Orlando, G. (2017). Parity breaking signatures from a Chern-Simons coupling during inflation: the case of non-Gaussian gravitational waves. J. Cosmol. Astropart. Phys. 1707:034. doi: 10.1088/1475-7516/2017/07/034

CrossRef Full Text | Google Scholar

Bartolo, N., Orlando, G., and Shiraishi, M. (2019). Measuring chiral gravitational waves in Chern-Simons gravity with CMB bispectra. J. Cosmol. Astropart. Phys. 1901:050. doi: 10.1088/1475-7516/2019/01/050

CrossRef Full Text | Google Scholar

Brown, I., and Crittenden, R. (2005). Non-Gaussianity from cosmic magnetic fields. Phys. Rev. D72:063002. doi: 10.1103/PhysRevD.72.063002

CrossRef Full Text | Google Scholar

Bucher, M., Racine, B., and van Tent, B. (2016). The binned bispectrum estimator: template-based and non-parametric CMB non-Gaussianity searches. J. Cosmol. Astropart. Phys. 1605:055. doi: 10.1088/1475-7516/2016/05/055

CrossRef Full Text | Google Scholar

Cook, J. L., and Sorbo, L. (2013). An inflationary model with small scalar and large tensor nongaussianities. J. Cosmol. Astropart. Phys. 1311:047. doi: 10.1088/1475-7516/2013/11/047

CrossRef Full Text | Google Scholar

Coulton, W. R., and Spergel, D. N. (2019). The bispectrum of polarized galactic foregrounds. arXiv:1901.04515.

Google Scholar

Delabrouille, J., de Bernardis, P., Bouchet, F. R., Achúcarro, A., Ade, P. A. R., Allison, R., et al. (2018). Exploring cosmic origins with CORE: survey requirements and mission design. J. Cosmol. Astropart. Phys. 1804:014. doi: 10.1088/1475-7516/2018/04/014

CrossRef Full Text | Google Scholar

Dimastrogiovanni, E., Fasiello, M., and Fujita, T. (2017). Primordial gravitational waves from axion-gauge fields dynamics. J. Cosmol. Astropart. Phys. 1701:019. doi: 10.1088/1475-7516/2017/01/019

CrossRef Full Text | Google Scholar

Dimastrogiovanni, E., Fasiello, M., Tasinato, G., and Wands, D. (2019). Tensor non-gaussianities from non-minimal coupling to the inflaton. J. Cosmol. Astropart. Phys. 1902:008. doi: 10.1088/1475-7516/2019/02/008

CrossRef Full Text | Google Scholar

Domenech, G., Hiramatsu, T., Lin, C., Sasaki, M., Shiraishi, M., and Wang, Y. (2017). CMB scale dependent non-Gaussianity from massive gravity during inflation. J. Cosmol. Astropart. Phys. 1705:034. doi: 10.1088/1475-7516/2017/05/034

CrossRef Full Text | Google Scholar

Fergusson, J. R. (2014). Efficient optimal non-gaussian CMB estimators with polarisation. Phys. Rev. D90:043533. doi: 10.1103/PhysRevD.90.043533

CrossRef Full Text | Google Scholar

Fergusson, J. R., Liguori, M., and Shellard, E. P. S. (2010). General CMB and primordial bispectrum estimation I: mode expansion, map-making and measures of f_NL. Phys. Rev. D82:023502. doi: 10.1103/PhysRevD.82.023502

CrossRef Full Text | Google Scholar

Fergusson, J. R., Liguori, M., and Shellard, E. P. S. (2012). The CMB bispectrum. J. Cosmol. Astropart. Phys. 1212:032. doi: 10.1088/1475-7516/2012/12/032

CrossRef Full Text | Google Scholar

Gao, X., Kobayashi, T., Shiraishi, M., Yamaguchi, M., Yokoyama, J., and Yokoyama, S. (2013). Full bispectra from primordial scalar and tensor perturbations in the most general single-field inflation model. Progress Theoret. Exp. Phys. 2013:053E03. doi: 10.1093/ptep/ptt031

CrossRef Full Text | Google Scholar

Gao, X., Kobayashi, T., Yamaguchi, M., and Yokoyama, J. (2011). Primordial non-Gaussianities of gravitational waves in the most general single-field inflation model. Phys. Rev. Lett. 107:211301. doi: 10.1103/PhysRevLett.107.211301

PubMed Abstract | CrossRef Full Text | Google Scholar

Goon, G., Hinterbichler, K., Joyce, A., and Trodden, M. (2018). Shapes of gravity: tensor non-Gaussianity and massive spin-2 fields. arXiv:1812.07571.

Google Scholar

Guzzetti, M. C., Bartolo, N., Liguori, M., and Matarrese, S. (2016). Gravitational waves from inflation. Riv. Nuovo Cim. 39, 399–495. doi: 10.1393/ncr/i2016-10127-1

CrossRef Full Text | Google Scholar

Hazumi, M., Borrill, J., Chinone, Y., Dobbs, M. A., Fuke, H., Ghribi, A., et al. (2012). LiteBIRD: a small satellite for the study of B-mode polarization and inflation from cosmic background radiation detection. Proc. SPIE Int. Soc. Opt. Eng. 8442:844219. doi: 10.1117/12.926743

CrossRef Full Text | Google Scholar

Hu, W. (2000). Weak lensing of the CMB: a harmonic approach. Phys. Rev. D62:043007. doi: 10.1103/PhysRevD.62.043007

CrossRef Full Text | Google Scholar

Jeong, D., and Kamionkowski, M. (2012). Clustering fossils from the early universe. Phys. Rev. Lett. 108:251301. doi: 10.1103/PhysRevLett.108.251301

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, G., Racine, B., and van Tent, B. (2018). The bispectra of galactic CMB foregrounds and their impact on primordial non-Gaussianity estimation. J. Cosmol. Astropart. Phys. 1811:047. doi: 10.1088/1475-7516/2018/11/047

CrossRef Full Text | Google Scholar

Kamionkowski, M., and Kovetz, E. D. (2016). The quest for B modes from inflationary gravitational waves. Ann. Rev. Astron. Astrophys. 54, 227–269. doi: 10.1146/annurev-astro-081915-023433

CrossRef Full Text | Google Scholar

Komatsu, E., Spergel, D. N., and Wandelt, B. D. (2005). Measuring primordial non-Gaussianity in the cosmic microwave background. Astrophys.J. 634, 14–19. doi: 10.1086/491724

CrossRef Full Text | Google Scholar

Kothari, R., and Nandi, D. (2019). B-Mode auto-bispectrum due to matter bounce. arXiv:1901.06538.

Google Scholar

Kulsrud, R. M., and Zweibel, E. G. (2008). The origin of astrophysical magnetic fields. Rept. Prog. Phys. 71:0046091. doi: 10.1088/0034-4885/71/4/046901

CrossRef Full Text | Google Scholar

Lewis, A., Challinor, A., and Hanson, D. (2011). The shape of the CMB lensing bispectrum. J. Cosmol. Astropart. Phys. 1103:018. doi: 10.1088/1475-7516/2011/03/018

CrossRef Full Text | Google Scholar

Lue, A., Wang, L.-M., and Kamionkowski, M. (1999). Cosmological signature of new parity violating interactions. Phys. Rev. Lett. 83, 1506–1509.

Google Scholar

Maldacena, J. M. (2003). Non-gaussian features of primordial fluctuations in single field inflationary models. J. High Energy Phys. 05:013. doi: 10.1088/1126-6708/2003/05/013

CrossRef Full Text | Google Scholar

Maldacena, J. M., and Pimentel, G. L. (2011). On graviton non-gaussianities during inflation. J. High Energy Phys. 09:045. doi: 10.1007/JHEP09(2011)045

CrossRef Full Text | Google Scholar

Maleknejad, A. (2016). Axion inflation with an SU(2) gauge field: detectable chiral gravity waves. J. High Energy Phys. 07:104. doi: 10.1007/JHEP07(2016)104

CrossRef Full Text | Google Scholar

Marozzi, G., Fanizza, G., Di Dio, E., and Durrer, R. (2016). CMB-lensing beyond the Born approximation. J. Cosmol. Astropart. Phys. 1609:028. doi: 10.1088/1475-7516/2016/09/028

CrossRef Full Text | Google Scholar

Matsumura, T. (2013). Mission design of LiteBIRD. J. Low. Temp. Phys. 176, 733–740. doi: 10.1007/s10909-013-0996-1

CrossRef Full Text | Google Scholar

Matsumura, T., Akiba, Y., Arnold, K., Borrill, J., Chendra, R., Chinone, Y., et al. (2016). LiteBIRD: mission overview and focal plane layout. J. Low Temperat. Phys. 184, 824–831. doi: 10.1007/s10909-016-1542-8

CrossRef Full Text | Google Scholar

Meerburg, P. D., Meyers, J., van Engelen, A., and Ali-Haïmoud, Y. (2016). CMB B -mode non-Gaussianity. Phys. Rev. D93:123511. doi: 10.1103/PhysRevD.93.123511

CrossRef Full Text | Google Scholar

Namba, R., Peloso, M., Shiraishi, M., Sorbo, L., and Unal, C. (2016). Scale-dependent gravitational waves from a rolling axion. J. Cosmol. Astropart. Phys. 1601:041. doi: 10.1088/1475-7516/2016/01/041

CrossRef Full Text | Google Scholar

Naskar, A., and Pal, S. (2018). Non-gaussian features of primordial gravitational waves. Phys. Rev. D98:083520. doi: 10.1103/PhysRevD.98.083520

CrossRef Full Text | Google Scholar

Ozsoy, O., Mylova, M., Parameswaran, S., Powell, C., Tasinato, G., and Zavala, I. (2019). Squeezed tensor non-Gaussianity in non-attractor inflation. arXiv:1902.04976.

Google Scholar

Pratten, G., and Lewis, A. (2016). Impact of post-Born lensing on the CMB. J. Cosmol. Astropart. Phys. 1608:047. doi: 10.1088/1475-7516/2016/08/047

CrossRef Full Text | Google Scholar

Shaw, J. R., and Lewis, A. (2010). Massive neutrinos and magnetic fields in the early universe. Phys. Rev. D81:043517. doi: 10.1103/PhysRevD.81.043517

CrossRef Full Text | Google Scholar

Shiraishi, M. (2012). Parity violation of primordial magnetic fields in the CMB bispectrum. J. Cosmol. Astropart. Phys. 1206:015. doi: 10.1088/1475-7516/2012/06/015

CrossRef Full Text | Google Scholar

Shiraishi, M. (2013). Polarization bispectrum for measuring primordial magnetic fields. J. Cosmol. Astropart. Phys. 1311:006. doi: 10.1088/1475-7516/2013/11/006

CrossRef Full Text | Google Scholar

Shiraishi, M. (2016). Search for primordial symmetry breakings in CMB. Mod. Phys. Lett. A31:1640003. doi: 10.1142/S0217732316400034

CrossRef Full Text | Google Scholar

Shiraishi, M., Hikage, C., Namba, R., Namikawa, T., and Hazumi, M. (2016). Testing statistics of the CMB B -mode polarization toward unambiguously establishing quantum fluctuation of the vacuum. Phys. Rev. D94:043506. doi: 10.1103/PhysRevD.94.043506

CrossRef Full Text | Google Scholar

Shiraishi, M., Liguori, M., and Fergusson, J. R. (2014). General parity-odd CMB bispectrum estimation. JCAP, 1405:008. doi: 10.1088/1475-7516/2014/05/008

CrossRef Full Text | Google Scholar

Shiraishi, M., Liguori, M., and Fergusson, J. R. (2015). Observed parity-odd CMB temperature bispectrum. J. Cosmol. Astropart. Phys. 1501:007. doi: 10.1088/1475-7516/2015/01/007

CrossRef Full Text | Google Scholar

Shiraishi, M., Liguori, M., and Fergusson, J. R. (2018). CMB bounds on tensor-scalar-scalar inflationary correlations. J. Cosmol. Astropart. Phys. 1801:016. doi: 10.1088/1475-7516/2018/01/016

CrossRef Full Text | Google Scholar

Shiraishi, M., Liguori, M., Fergusson, J. R., and Shellard, E. P. S. (2019). General modal estimation for cross-bispectra. J. Cosmol. Astropart. Phys. 1906:046. doi: 10.1088/1475-7516/2019/06/046

CrossRef Full Text | Google Scholar

Shiraishi, M., Nitta, D., and Yokoyama, S. (2011a). Parity violation of gravitons in the CMB bispectrum. Prog. Theor. Phys. 126, 937–959. doi: 10.1143/PTP.126.937

CrossRef Full Text | Google Scholar

Shiraishi, M., Nitta, D., Yokoyama, S., and Ichiki, K. (2012). Optimal limits on primordial magnetic fields from CMB temperature bispectrum of passive modes. J. Cosmol. Astropart. Phys. 1203:041. doi: 10.1088/1475-7516/2012/03/041

CrossRef Full Text | Google Scholar

Shiraishi, M., Nitta, D., Yokoyama, S., Ichiki, K., and Takahashi, K. (2011b). CMB bispectrum from primordial scalar, vector and tensor non-gaussianities. Prog. Theor. Phys. 125, 795–813. doi: 10.1143/PTP.125.795

CrossRef Full Text | Google Scholar

Shiraishi, M., Nitta, D., Yokoyama, S., Ichiki, K., and Takahashi, K. (2011c). Cosmic microwave background bispectrum of tensor passive modes induced from primordial magnetic fields. Phys. Rev. D83:123003. doi: 10.1103/PhysRevD.83.123003

CrossRef Full Text | Google Scholar

Shiraishi, M., Ricciardone, A., and Saga, S. (2013). Parity violation in the CMB bispectrum by a rolling pseudoscalar. J. Cosmol. Astropart. Phys. 1311:051. doi: 10.1088/1475-7516/2013/11/051

CrossRef Full Text | Google Scholar

Shiraishi, M., and Sekiguchi, T. (2014). First observational constraints on tensor non-Gaussianity sourced by primordial magnetic fields from cosmic microwave background. Phys. Rev. D90:103002. doi: 10.1103/PhysRevD.90.103002

CrossRef Full Text | Google Scholar

Shiraishi, M., Yokoyama, S., Nitta, D., Ichiki, K., and Takahashi, K. (2010). Analytic formulae of the CMB bispectra generated from non-Gaussianity in the tensor and vector perturbations. Phys. Rev. D82:103505. doi: 10.1103/PhysRevD.82.103505

CrossRef Full Text | Google Scholar

Soda, J., Kodama, H., and Nozawa, M. (2011). Parity violation in graviton non-Gaussianity. J. High Energy Phys. 08:067. doi: 10.1007/JHEP08(2011)067

CrossRef Full Text | Google Scholar

Sunyaev, R. A., and Zeldovich, Ya. B. (1972). The Observations of relic radiation as a test of the nature of X-Ray radiation from the clusters of galaxies. Comments Astrophys. Space Phys. 4, 173–178.

Google Scholar

Tahara, H. W. H., and Yokoyama, J. (2018). CMB B-mode auto-bispectrum produced by primordial gravitational waves. Progress Theor. Exp. Phys. 2018:013E03. doi: 10.1093/ptep/ptx185

CrossRef Full Text | Google Scholar

Tsuneto, M., Ito, A., Noumi, T., and Soda, J. (2019). Searching for bispectrum of stochastic gravitational waves with pulsar timing arrays. J. Cosmol. Astropart. Phys. 1903:032. doi: 10.1088/1475-7516/2019/03/032

CrossRef Full Text | Google Scholar

Widrow, L. M. (2002). Origin of galactic and extragalactic magnetic fields. Rev. Mod. Phys. 74, 775–823. doi: 10.1103/RevModPhys.74.775

CrossRef Full Text | Google Scholar