Several Problems in Particle Physics and Cosmology Solved in One SMASH

1. Introduction

The SM is arguably the most successful theory in physics. It describes the known particles and their interactions remarkably well. No significant deviations from the theoretical predictions of the SM have been found so far at precision collider experiments and the like. On the other hand, it is generally agreed that there are a number of fundamental problems in particle physics and cosmology which require new physics beyond the SM. In fact, there is compelling evidence that nearly 85% of the matter in the Universe is non-baryonic. This evidence is supported by observations on many scales, ranging from the shapes of the rotation curves of spiral galaxies to the temperature fluctuations of the cosmic microwave background (CMB). Furthermore, the SM cannot explain the exponential expansion of the very early Universe called inflation which is required to explain the isotropic, Gaussian and nearly scale-invariant temperature fluctuations of the CMB. Moreover, the CP violation within the SM is too feeble to explain the asymmetry between the fraction of the baryonic matter and anti-matter in the Universe. Furthermore, the SM does not feature masses for the active neutrinos, while the observed flavor oscillations of the active neutrinos require tiny neutrino masses. Last, but not least, there is the strong CP problem: the SM has no explanation for the smallness of the $\overline{\theta }$-angle of quantum chromodynamics (QCD) which induces CP-violation in flavor-diagonal interactions. In fact, the non-observation of an electric dipole moment of the neutron places a very strong upper limit on the angle, $\left|\overline{\theta }\right|<10^{-10}$, requiring an extreme fine-tuning which cannot even be justified on the basis of anthropic arguments.

Three of these problems can be tackled simultaneously in the Neutrino Minimal SM (νMSM) (Asaka, 2005; Asaka et al., 2005): a remarkably simple extension of the SM by three right-handed singlet neutrinos N_i (cf. Figure 1), having Dirac masses $m_D=Fv/\sqrt{2}$ arising from Yukawa couplings F with the Higgs (H) and lepton (L_i) doublets, as well as explicit Majorana masses M,

$\begin{array}{ll}{L}\supset -[F_{ij}{L}_iϵH{N}_j+\frac{1}{2}{M}_{ij}{N}_i{N}_j],& (1)\end{array}$

(in Weyl spinor notation). In the seesaw limit, M ≫ m_D, the neutrino mass spectrum splits into a light set given by the eigenvalues m₁ < m₂ < m₃ of the matrix

$\begin{array}{ll}{m}_{\nu }=-m_D{M}^{-1}{m}_D^T,& (2)\end{array}$

with the eigenstates corresponding mainly to mixings of the active left-handed neutrinos ν_α, and a heavy set given by the eigenvalues M₁ < M₂ < M₃ of the matrix M, with the eigenstates corresponding to mixings of the sterile right-handed neutrinos N_i. The neutrino mass and mixing problem is thus solved by the usual type-I seesaw mechanism (Minkowski, 1977; Gell-Mann et al., 1979; Yanagida, 1979; Mohapatra and Senjanovic, 1980). Intriguingly, the baryogenesis and dark matter problems can be solved simultaneously if M₁ ~ keV and M₂ ~ M₃ ~ GeV. In fact, in this case N_2,3 create flavored lepton asymmetries from CP-violating oscillations in the early Universe, which generate the baryon asymmetry of the Universe via ARS leptogenesis (Akhmedov et al., 1998). The lightest sterile neutrino N₁ can act as dark matter, with the correct relic abundance achieved through freeze-in production, resonantly enhanced with the MSW effect (Wolfenstein, 1978, 1979; Mikheyev and Smirnov, 1985). Moreover, it was argued in Bezrukov and Shaposhnikov (2008) that the puzzle of inflation can be solved even in the SM by allowing a non-minimal coupling of the Higgs field to the Ricci scalar,

$\begin{array}{ll}S\supset -{\displaystyle \int }{d}^{4}x\sqrt{-g}{\xi }_H{H}^{†}HR,& (3)\end{array}$

which promotes the Higgs field to an inflaton candidate.

FIGURE 1

Figure 1. Particle/field content of the νMSM.

However, the viability of the νMSM as a minimal model of particle cosmology is threatened by several facts. First of all, recent findings in astrophysics have seriously constrained the parameter space for N₁ as a dark matter candidate (Schneider, 2016; Perez et al., 2017). Secondly, the generically large value of the non-minimal coupling ${\xi }_H~10^5\sqrt{{\lambda }_H}$, where λ_H is the Higgs self-coupling, required to fit the amplitude of the scalar perturbations inferred from the cosmic microwave background (CMB) temperature fluctuations, imply that perturbative unitarity breaks down at the scale $M_P/{\xi }_H~10^{14}$ GeV, where $M_P=1/\sqrt{8\pi G}$ is the reduced Planck mass, making the inflationary predictions unreliable (Barbon and Espinosa, 2009; Burgess et al., 2009). Even more, successful inflation cannot happen in this context if the quartic coupling λ_H in the Higgs potential:

$\begin{array}{l}V(H)={\lambda }_H{\left(H^{†}H-\frac{v^2}{2}\right)}^2,\end{array}$

runs negative at large (Planckian) field values due to loop corrections involving the top quark. In fact, the central values of the strong gauge coupling and the Higgs and top quark masses imply that λ_H becomes negative at a field value corresponding to an energy scale ${\Lambda }_I~10^{11}$ GeV. This is much lower than what is required for Higgs inflation and thus inconsistent with it. However, given the current experimental uncertainties, a definite conclusion cannot yet be drawn (see e.g., Buttazzo et al., 2013; Bednyakov et al., 2015).

These obstacles of the νMSM can be neatly circumvented¹ in SMASH-type (Ballesteros et al., 2017a,b; Ernst et al., 2018) extensions of the SM which are built around the axion for the solution of the strong CP problem (Peccei and Quinn, 1977; Weinberg, 1978; Wilczek, 1978), as well as for dark matter, and allow inflation to be driven by (a mixture of the modulus of the Higgs field with) the modulus of the Peccei-Quinn field –sometimes called saxion field (Pi, 1984; Fairbairn et al., 2015).

This review is organized as follows. In section 2 we describe a number of Peccei-Quinn-type extensions of the νMSM: bottom-up constructions featuring KSVZ- and DFSZ-type axions (cf. sections 2.1, 2.2, respectively) and top-down constructions based on non-supersymmetric grand unification (cf. section 2.3). Section 3 is devoted to inflation, while stability is analyzed in section 4. Reheating is reviewed in section 5, dark matter in section 6, and baryogenesis in section 7. Conclusions are drawn in section 8.

2. SMASH and Its Variants

In this section we will describe a number of extensions of the SM which exploit the Peccei-Quinn (PQ) mechanism (Peccei and Quinn, 1977) to solve the strong CP problem and thus have the potential to solve the big five problems of particle physics and cosmology in one smash.

2.1. SMASH

The model with smallest field content—dubbed here and in the following SMASH—is based on a KSVZ-type axion model (Kim, 1979; Shifman et al., 1980): a SM-singlet complex scalar field σ, which features a (spontaneously broken) global U(1)_PQ symmetry, and a vector-like colored Dirac fermion Q, which transforms as² (3, 1,−1/3) or, alternatively, as (3, 1, 2/3) under the SM gauge group SU(3)_C × SU(2)_L × U(1)_Y and which transforms chirally under U(1)_PQ, are added to the field content of the νMSM (cf. Figure 2). The scalar potential, which relates the Higgs field H to σ, is assumed to have the general form

$\begin{array}{l}V(H,\sigma )={\lambda }_H{\left(H^{†}H-\frac{v^2}{2}\right)}^2+{\lambda }_{\sigma }{\left(|\sigma {|}^2-\frac{v_{\sigma }^2}{2}\right)}^2\\ +2{\lambda }_{H\sigma }\left(H^{†}H-\frac{v^2}{2}\right)\left(|\sigma {|}^2-\frac{v_{\sigma }^2}{2}\right),& (4)\end{array}$

with λ_H, λ _σ > 0 and ${\lambda }_{H\sigma }^2<{\lambda }_H{\lambda }_{\sigma }$, in order to ensure that both the electroweak symmetry and the PQ symmetry are broken in the vacuum; i.e., the minimum of the scalar potential is attained at the vacuum expectation values (VEVs)

$\begin{array}{ll}\langle H^{†}H\rangle =v^2/2,\langle |\sigma {|}^2\rangle =v_{\sigma }^2/2,& (5)\end{array}$

where v = 246 GeV. The PQ symmetry breaking scale v_σ is assumed to be much larger than the Higgs VEV v. Correspondingly, the particle excitation of the modulus ρ of σ, cf.

$\begin{array}{ll}\sigma (x)=\frac{1}{\sqrt{2}}[v_{\sigma }+\rho (x)]e^{iA(x)/v_{\sigma }},& (6)\end{array}$

gets a large mass

$\begin{array}{ll}{m}_{\rho }=\sqrt{2{\lambda }_{\sigma }}{v}_{\sigma }+{O}\left(\frac{v}{v_{\sigma }}\right),& (7)\end{array}$

while the particle excitation A of the angular degree of freedom of σ – which is dubbed “axion" in the context of the PQ solution of the strong CP problem (Weinberg, 1978; Wilczek, 1978)—is a massless Nambu-Goldstone (NG) boson, m_A = 0.

FIGURE 2

Figure 2. Particle/field content of SMASH.

However, due to the assumed chiral transformation of the new vector-like fermion Q, the U(1)_PQ symmetry is broken due to the gluonic triangle anomaly,

$\begin{array}{ll}{\partial }_{\mu }{J}_{U{(1)}_{\text{PQ}}}^{\mu }\supset -\frac{{\alpha }_s}{8\pi }{G}_{\mu \nu }^c{\tilde{G}}^{c,\mu \nu }.& (8)\end{array}$

Under these circumstances, the NG field

$\begin{array}{ll}\theta (x)\equiv \frac{A(x)}{f_A},\text{ with }{f}_A\equiv v_{\sigma },& (9)\end{array}$

acts as a space-time dependent θ-angle in QCD. In fact, the anomaly ensures that, at energies above the scale of QCD, Λ_QCD, but far below the scale of PQ symmetry breaking, v_σ, that is after integrating out the saxion ρ and the vector-like quark Q, which also gets a large mass from its Yukawa coupling with the PQ scalar,

$\begin{array}{ll}{m}_Q=\frac{y}{\sqrt{2}}{v}_{\sigma }+{O}\left(\frac{v}{v_{\sigma }}\right),& (10)\end{array}$

the effective Lagrangian of the axion has the form

$\begin{array}{ll}{{L}}_{\theta }=\frac{f_A^2}{2}{\partial }_{\mu }\theta {\partial }^{\mu }\theta -\frac{{\alpha }_s}{8\pi }\theta (x)G_{\mu \nu }^c{\tilde{G}}^{c,\mu \nu }.& (11)\end{array}$

Correspondingly, the $\overline{\theta }$-angle in QCD can be eliminated by a shift $\theta (x)\to \theta (x)-\overline{\theta }$. At energies below Λ_QCD, the effective potential of the shifted field, which for convenience we again denote by θ(x), will then coincide with the vacuum energy of QCD as a function of $\overline{\theta }$

$\begin{array}{l}V(\theta )\equiv {-\frac{1}{{V}}\ln \frac{Z(\overline{\theta })}{Z(0)}|}_{\overline{\theta }=\theta }\simeq {\Sigma }_0\left(m_u+m_d\right)\\ \left(1-\frac{\sqrt{m_u^2+m_d^2+2m_u{m}_d\cos \theta }}{m_u+m_d}\right) ,& (12)\end{array}$

where ${V}$ is the Euclidean space-time volume, $Z(\overline{\theta })$ is the partition function of QCD, and ${\Sigma }_0=-\langle ūu\rangle =-\langle \bar{d}d\rangle$ is the chiral condensate (Vecchia and Veneziano, 1980; Leutwyler and Smilga, 1992). Notably, CP is conserved in the vacuum, since V(θ) has an absolute minimum at θ = 0 and thus the vacuum expectation value of θ vanishes, 〈θ〉 = 0 (Vafa and Witten, 1984). Expanding the potential around zero and using

$\begin{array}{ll}{m}_{\pi }^2=\frac{{\Sigma }_0}{f_{\pi }^2}(m_u+m_d)+{O}(m^2),& (13)\end{array}$

one finds the mass of the axion as the coefficient of the quadratic term,

$\begin{array}{ll}{m}_A\equiv \frac{\sqrt{{\chi }_0}}{f_A}\simeq \frac{m_{\pi }{f}_{\pi }}{f_A}\frac{\sqrt{m_u{m}_d}}{m_u+m_d},& (14)\end{array}$

where χ₀ is the topological susceptibility in QCD, m_π = 135 MeV the neutral pion mass, f_π ≈ 92 MeV its decay constant, and m_u, m_d are the masses of the lightest quarks, with ratio z = m_u/m_d ≈ 0.56. A recent determination in next-to-leading order (NLO) chiral perturbation theory (Grilli di Cortona et al., 2016) yielded ${\chi }_0={\left[75.5(5)\text{MeV}\right]}^4$, which agrees beautifully with the result from lattice QCD, ${\chi }_0={\left[75.6(1.8)(0.9)\text{MeV}\right]}^4$ (Borsanyi et al., 2016), resulting in³

$\begin{array}{ll}{m}_A=57.0(7)\left(\frac{10^{11}\text{GeV}}{f_A}\right)\mu \text{eV}.& (15)\end{array}$

Moreover, also couplings to the photon and the nuclei are inherited from the axion's mixing with the pion. The full low energy Lagrangian of the axion with photons (F_μν), nucleons, ψ_N = p, n, electrons (e) and active neutrinos (ν_i) has the generic form

$\begin{array}{l}{{L}}_A=\frac{1}{2}{\partial }_{\mu }A{\partial }^{\mu }A-V(A)-\frac{\alpha }{8\pi }{C}_{A\gamma }\frac{A}{f_A}{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }\\ +\frac{1}{2}{C}_{AN}\frac{{\partial }_{\mu }A}{f_A}{\overline{\psi }}_N{\gamma }^{\mu }{\gamma }_5{\psi }_N\hfill \\ +\frac{1}{2}{C}_{Ae}\frac{{\partial }_{\mu }A}{f_A}{\overline{\psi }}_e{\gamma }^{\mu }{\gamma }_5{\psi }_e+\frac{1}{2}{C}_{A\nu }\frac{{\partial }_{\mu }A}{f_A}{\overline{\nu }}_i{\gamma }^{\mu }{\gamma }_5{\nu }_i,& (16)\end{array}$

where V(A) = V(θ = A/f_A). The dimensionless coupling to photons, C_Aγ, involves a model-independent part from the mixing with the pion and a model-dependent part depending of the electric charge of Q. It is given in Table 1 for the two variants of SMASH. Similarly, the proton and neutron have a model-independent part and a model dependent contribution that arises from possible axion-quark couplings of the form $(C_{Aq}/2)({\partial }_{\mu }A/f_A){\bar{\psi }}_q{\gamma }^{\mu }{\gamma }_5{\psi }_q$ in the high-energy theory

$\begin{array}{l}{C}_{Ap}=-0.47(3)+0.88(3)C_{Au}-0.39(2)C_{Ad}-0.038(5)C_{As}\\ -0.012(5)C_{Ac}-0.009(2)C_{Ab}-0.0035(4)C_{At},\\ C_{An}=-0.02(3)+0.88(3)C_{Ad}-0.39(2)C_{Au}-0.038(5)C_{As}\\ -0.012(5)C_{Ac}-0.009(2)C_{Ab}-0.0035(4)C_{At},& (17)\end{array}$

as found in the state-of-the-art calculation (Grilli di Cortona et al., 2016). In SMASH, all the axion-quark and axion-charged-lepton couplings vanish at tree level (cf. Table 1).

TABLE 1

Table 1. Axion predictions for two SMASH variants exploiting distinct vector-like quarks transforming as R_Q under the SM gauge group factors SU(3)_C × SU(2)_L × U(1)_Y: Axion decay constant f_A, coupling to the photon C_Aγ, and tree-level couplings to quarks and charged leptons C_Ai, i = u, …, t, e, .., τ.

To avoid strong bounds from laboratory experiments and stellar astrophysics, the axion decay constant f_A has to be much larger than the electroweak scale (Tanabashi et al., 2018), notably $f_A\gtrsim 10^8\text{ GeV}$ from the measured duration of the neutrino signal of supernova 1987A (Raffelt, 2008; Fischer et al., 2016; Chang et al., 2018).

Optionally, one may unify the PQ symmetry with a lepton number symmetry by assigning PQ charges also to the leptons and sterile neutrinos (Shin, 1987; Dias et al., 2014). In this case, the latter get their Majorana masses also from PQ symmetry breaking,

$\begin{array}{ll}{M}_{ij}=\frac{Y_{ij}}{\sqrt{2}}{v}_{\sigma }+{O}\left(\frac{v}{v_{\sigma }}\right),& (18)\end{array}$

where Y_ij are Yukawa couplings, and the mass scale of the active neutrinos is determined by the PQ scale,

$\begin{array}{ll}{m}_{\nu }=0.04\text{eV}\left(\frac{10^{11}\text{GeV}}{v_{\sigma }}\right)\left(\frac{-F{Y}^{-1}{F}^T}{10^{-4}}\right).& (19)\end{array}$

Moreover, the axion A is in this case at the same time the majoron J: the NG boson arising from the breaking of the global lepton number symmetry (Chikashige et al., 1981; Gelmini and Roncadelli, 1981; Schechter and Valle, 1982). This leads to a non-zero tree-level coupling of the A/J to the active neutrinos, $(-1/4)({\partial }_{\mu }A/f_A){\bar{\nu }}_i{\gamma }^{\mu }{\gamma }_5{\nu }_i$ and to possibly sizeable loop-induced couplings to SM quarks and charged leptons from the loop involving the sterile neutrinos N_i (Shin, 1987; Pilaftsis, 1994). To lowest order in the seesaw limit, m_D/M_M ≪ 1, they are given by Garcia-Cely and Heeck (2017)

$\begin{array}{ll}{C}_{aq}\simeq \frac{1}{8{\pi }^2}{T}_3^q\text{tr}\kappa ,C_{A\ell }\simeq -\frac{1}{16{\pi }^2}(\text{tr}\kappa -2{\kappa }_{\ell \ell }),& (20)\end{array}$

where $T_3^d=-\frac{1}{2}=-T_3^u$ and the dimensionless hermitian 3 × 3 matrix κ is defined as

$\begin{array}{ll}\kappa \equiv \frac{m_D{m}_D^{†}}{v^2}=\frac{F{F}^{†}}{2}.& (21)\end{array}$

Intriguingly, a KSVZ-type axion/majoron with $f_A~10^8$ GeV may explain the ~3σ hint of an anomalously large energy loss of helium burning stars, red giants and white dwarfs, if |κ − 2κ_ee| is of order unity (Giannotti et al., 2017).

2.2. 2hdSMASH

A less minimal variant of SMASH—dubbed 2hdSMASH—exploits DFSZ-type axion models (Zhitnitsky, 1980; Dine et al., 1981): in those the SM Higgs sector is extended by two Higgs doublets, H_u and H_d, whose vacuum expectation values v_u and v_d give masses to up-type and down-type quarks, respectively. There are two possibilities, named 2hdSMASH(d) or 2hdSMASH(u), according to whether leptons couple to H_d, which occurs in familiar Grand Unified Theories (GUTs), or to H_u. The n_f = 6 SM model quarks are assumed to carry PQ charges such that the gluonic triangle anomaly arises from them alone,

$\begin{array}{ll}{\partial }_{\mu }{J}_{U{(1)}_{\text{PQ}}}^{\mu }\supset -n_f\frac{{\alpha }_s}{8\pi }{G}_{\mu \nu }^c{\tilde{G}}^{c,\mu \nu }.& (22)\end{array}$

The low-energy Lagrangian of a DFSZ-type PQ extension of the SM is identical to that of a 2 Higgs Doublet Model (2HDM), augmented by seesaw-generated neutrino masses (Equation 2), and the one of a DFSZ-type axion. The DFSZ axion properties are given in Table 2. In this case, there are tree-level couplings to quarks and leptons. In fact, the anomalous stellar energy losses mentioned above can be alternatively explained by a DFSZ-type axion with $f_A\gtrsim 10^8$ GeV and tanβ ≡ v_u/v_d ~ 1 (Giannotti et al., 2017).

TABLE 2

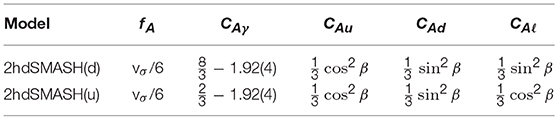
Table 2. DFSZ-type axion predictions: axion decay constant f_A, coupling to the photon C_Aγ, and tree-level couplings to quarks and charged leptons C_Ai, i = u, …, t, e, .., τ, with tanβ ≡ v_u/v_d.

Again, optionally the PQ symmetry may be unified with a lepton number symmetry (Langacker et al., 1986; Volkas et al., 1988; Clarke and Volkas, 2016), in which case the active neutrino mass scale is determined by the PQ scale and the DFSZ axion is at the same time a Majoron.

2.3. gutSMASH

As commented in the previous section, the model 2hdSMASH(d) can be embedded into a GUT. The simplest unified group is SU(5) (Georgi and Glashow, 1974; Georgi, 1975), with each generation of fermions (not including right-handed neutrinos) fitting into the representations 10_F and ${\bar{5}}_F$, with SU(5) broken into the SM group by the VEV of a scalar in the 24_H, and with the electroweak breaking carried out by two scalars in the 5_H. It was realized early on that SU(5) GUTs can accommodate an axion with a decay constant f_A tied to the unification scale (Wise et al., 1981). However, minimal non-supersymmetric SU(5) GUTs are incompatible with proton decay limits, because the SU(2) and U(1) gauge couplings meet at too low a scale. However, there are viable extensions in which particles in additional SU(5) multiplets appropriately modify the running of the gauge couplings so as to yield successful unification compatible with proton decay limits. The extension proposed in Bajc and Senjanovic (2007) and further studied in Bajc et al. (2007); Luzio and Mihaila (2013) makes use of a fermionic multiplet in the 24_F, which contains right-handed neutrinos getting a mass from the VEV of the 24_H, which breaks SU(5) into the SM. This generates masses for the light neutrinos through a combination of the type I and III seesaw mechanisms, and also allows for baryogenesis from leptogenesis. When extending this viable SU(5) model to accommodate a global PQ symmetry with its corresponding axion (Di Luzio et al., 2018), one has a SMASH-type construction with the complex scalar in the 24_H containing the axion and acting as a Majoron. The Lagrangian of this model, which we will refer to as miniSU(5)PQ, contains the following interactions (written only schematically),

$\begin{array}{l}ℒ\supset {\overline{5}}_F{10}_F{5^{\prime }}_H^{*}+{10}_F{10}_F{5}_H+{\overline{5}}_F{24}_F{5}_H+\text{Tr}{24}_F^2{24}_H^{*}\\ +{5^{\prime }}_H^{*}{24}_H^2{5}_H+{5^{\prime }}_H^{*}{5}_H\text{Tr}({24}_H^2)+\text{h}.\text{c}.,& (23)\end{array}$

which enforce the PQ charge assignments in Table 3.

TABLE 3

Table 3. Field content and PQ charge assignments in the PQ-extended SU(5) model of Di Luzio et al. (2018).

The axion decay constant is related to the unification scale v_U as f_A = v_U/11, while the axion couplings to nucleons and leptons are given in Table 4.

TABLE 4

Table 4. Axion predictions in SU(5) × U(1)_PQ (Di Luzio et al., 2018) and SO(10) × U(1)_PQ models (Ernst et al., 2018): axion decay constant f_A, coupling to the photon C_Aγ, and tree-level couplings to quarks and charged leptons C_Ai, i = u, …, t, e, .., τ.

The unification scale turns out to be highly constrained and grows with decreasing mass of the light fermion triplet contained in 24_F. This is due to the fact that increasing the unification scale requires a larger deviation in the running of the SU(2) and U(1) gauge couplings with respect to the SM case, which can only achieved if the extra particles with electroweak charges in the 24_F multiplet become lighter. The light electroweak triplets can be probed by LHC searches (Arhrib et al., 2010; Sirunyan et al., 2017), which then give upper bounds for v_U ∝ f_A. On the other hand, proton decay experiments, such as Super-Kamiokande (Abe et al., 2017) constrain the unification scale from below. Given the relation (15) between f_A and the axion mass, this results in a remarkably constrained window of allowed values of m_A:

$\begin{array}{ll}{m}_A\in \left[4.8,6.6\right]\text{neV}.& (24)\end{array}$

The upper limit can be relaxed to m_A < 330 neV when allowing for fine-tuning in the flavor structure of the model so as to close as many decay channels for the proton as possible (Dorsner and Fileviez Perez, 2005). The above axion mass window can be targeted in a complementary manner by future high-energy colliders (Ruiz, 2015; Cai et al., 2018), proton decay experiments, such as Hyper-Kamiokande (Abe et al., 2011), as well as direct axion dark matter searches with CASPER-Electric (Budker et al., 2014; Jackson Kimball et al., 2017) and ABRACADABRA (Kahn et al., 2016).

The smallness of the axion mass in this model implies that the axion can be identified with dark matter only if the Peccei-Quinn symmetry is broken before or during inflation and not restored afterwards, as reviewed in section 6. On the other hand, the large value of f_A implies that inflation can source large axionic isocurvature fluctuations which may be in conflict with observations (cf. section 6).

Compared to SU(5) GUTs, theories based on the SO(10) group (Fritzsch and Minkowski, 1975; Georgi, 1975) can yield viable unification patterns without the need to either consider supersymmetric extensions or to add additional fermion multiplets beyond those containing the SM fermions. Moreover, right-handed neutrinos are automatically incorporated, as these occur automatically with the rest of the SM quarks and leptons if one considers three spinorial representations 16_F of SO(10). The latter can have the following Yukawa couplings with scalar Higgses in the 10_H and ${\overline{126}}_H$ representations,

$\begin{array}{ll}{{L}}_Y=16_F(Y_{10}10_H+{Ỹ}_{10}10_H^{*}+Y_{126}{\overline{126}}_H)16_F+\text{h}.\text{c}.,& (25)\end{array}$

which can give rise to the seesaw mechanism (Gell-Mann et al., 1979). Moreover, a PQ symmetry, under which the fields transform as

$\begin{array}{ll}16_F\to 16_F{e}^{i\alpha };10_H\to 10_H{e}^{-2i\alpha };{\overline{126}}_H\to {\overline{126}}_H{e}^{-2i\alpha },& (26)\end{array}$

can be motivated independently from the strong CP problem: it forbids the second term in the Yukawa interactions (25), thereby crucially improving the economy and predictivity of the models (Babu and Mohapatra, 1993; Bajc et al., 2006).

Adding a further Higgs representation, say 210_H, the SO(10) symmetry can be broken at the unification scale M_U by the VEV of the 210_H to the Pati-Salam gauge group SU(4)_C × SU(2)_L × SU(2)_R, which is broken to the SM gauge group SU(3)_C × SU(2)_L × U(1)_Y at the scale of B−L breaking M_BL (which is thus the seesaw scale) by the VEV of the ${\overline{126}}_H$, which itself is broken at the weak scale M_Z by the VEV of the 10_H,

$\begin{array}{l}SO(10)\stackrel{M_{\text{U}}-210_H}{\to }{4}_C{2}_L{2}_R\stackrel{M_{\text{BL}}-{\overline{126}}_H}{\to }{3}_C{2}_L{1}_Y\stackrel{M_Z-10_H}{\to }{3}_C{1}_{\text{em}}.\end{array}$

Unfortunately, the minimal PQ symmetry (26) leads to a decay constant f_A = v/3 (Holman et al., 1983; Mohapatra and Senjanovic, 1983; Altarelli and Meloni, 2013; Ernst et al., 2018), which is clearly experimentally excluded. The simplest way to remedy this problem is to associate a PQ charge also to the 210_H,

$\begin{array}{ll}210_H\to 210_H{e}^{4i\alpha }.& (27)\end{array}$

We dub this model miniSO(10)PQ—for Minimal SO(10) × U(1)_PQ model—and summarize the field content and PQ charge assignments in the first row of Table 5. Its axion properties are given in Table 4.

TABLE 5

Table 5. Field content and PQ charge assignments in two distinct SO(10) × U(1)_PQ models (Ernst et al., 2018).

The photon and fermion couplings are the same as for 2hdSMASH(d), although the microscopic origin of the parameter β differs, as it is determined by the VEVs of four Higgses, as opposed to two in DFSZ models. Moreover, as in miniSU(5)PQ, the decay constant in miniSO(10)PQ is proportional to the scale of grand unification, f_A = v_U/3, which is determined by the requirement of gauge coupling unification. Therefore, this model is more predictive in the axion sector than SMASH or 2hdSMASH, yet less predictive than miniSU(5)PQ due to the additional freedom inherent in having a multi-step breaking of the grand unified group—as opposed to the single-step breaking in the SU(5) case—as well as due to the additional threshold corrections that can arise from the greater number of particles included in the SO(10) multiplets. Allowing for a reasonable range of scalar threshold corrections and taking into account constraints from black hole superradiance (Arvanitaki et al., 2015) and proton decay, the axion decay constant and mass is predicted to lie in the range (Ernst et al., 2018).

$\begin{array}{l}2.6\times 10^{15}\text{GeV}<f_A<3.0\times 10^{17}\text{GeV},\\ 1.9\times 10^{-11}\text{eV}<m_A<2.2\times 10^{-9}\text{eV}.& (28)\end{array}$

As in the miniSU(5)PQ model, such light axion can only be compatible with dark matter with a pre-inflationary breaking of the PQ symmetry, and isocurvature constraints can be important. In fact, a one-step breaking model analogous to miniSU(5)PQ can also be realized in SO(10) by breaking the group at a high scale not just with the 210_H, but with the added effect of a non-zero VEV in a 45_H scalar multiplet (Boucenna et al., 2019). In this model, successful unification with a proton lifetime in reach of Hyper-Kamiokande is achieved by ensuring that the octets and triplets inside the 210_H remain light, in analogy with the light triplets in miniSU(5)PQ. The PQ charge of the 210_H is now zero, while the 45_H is assigned charge 4, which still gives a GUT-scale axion with a low mass and thus affected by isocurvature constraints.

Such constraints can be definitely evaded in the SO(10) × U(1)_PQ variant dubbed gutSMASH whose field content and PQ charge assignments are specified in the second row of Table 5. In this model the 210_H has no PQ charge. Instead, it features a further complex singlet scalar σ which is charged under the PQ symmetry. Its VEV determines the PQ symmetry breaking scale (see also Babu and Khan, 2015; Boucenna and Shafi, 2018) and the axion decay constant turns out to be f_A = v_σ/3 (Ernst et al., 2018) (cf. second row of Table 4), which is a free parameter of the model.

3. Inflation

In SMASH and its variants, introduced in the last section, there are two or more scalar fields that in principle could have driven primordial inflation. Let us look into this issue in some detail.

In SMASH, the modulus of the complex PQ field, ρ² = 2|σ|², or a mixture of it with h, the neutral component of the Higgs doublet in the unitary gauge, $H^t=(0,h)/\sqrt{2}$, is a viable inflaton candidate. It was pointed out in Bezrukov and Shaposhnikov (2008) that a non-minimal coupling of the Higgs, H, to the Ricci scalar R [cf. Equation (3)], would allow h to play that role, in a model that is since dubbed Higgs inflation. Indeed, after scalar and metric field redefinitions into the so-called Einstein frame, this kind of coupling flattens any quartic potential, making it convex and asymptotically flat at large field values (Salopek et al., 1989), approaching a plateau-like form which is preferred by CMB measurements (Akrami et al., 2018). However, as mentioned in the Introduction, a large value of the non-minimal coupling ξ_H—as required to fit the amplitude of the primordial scalar fluctuations (${\xi }_H~5\times 10^4\sqrt{{\lambda }_H}$) for the central value of the top quark mass (Tanabashi et al., 2018) (see also Figure 14 of Aaboud et al., 2018)—implies that perturbative unitarity breaks down at a scale M_P/ξ_H, well below the Higgs field values during inflation $h~M_P/\sqrt{{\xi }_H}$ and comparable to the scale given by the fourth square root of the potential (Barbon and Espinosa, 2009; Burgess et al., 2009). See Bezrukov and Shaposhnikov (2014) and Hamada et al. (2014) for the statistically disfavored possibility of reducing ξ_H by considering significantly smaller top masses.

This problem can be eliminated in Hidden Scalar Inflation (HSI) (Pi, 1984; Fairbairn et al., 2015; Boucenna and Shafi, 2018) or Higgs-Hidden Scalar inflation (HHSI) (Ballesteros et al., 2017a,b), which exploit a non-minimal coupling analogous to the previous one:

$\begin{array}{ll}S\supset -{\displaystyle \int }{d}^{4}x\sqrt{-g}{\xi }_{\sigma }{\sigma }^{*}\sigma R.& (29)\end{array}$

Such couplings are not ad-hoc, since they are generated radiatively in a Friedman-Robertson-Walker background. For negligible ξ_H, slow-roll inflation with a tree-level asymptotically flat potential can thus happen along two different directions in field space: the ρ-direction for λ_Hσ > 0 (HSI) and the line $h/\rho =\sqrt{-{\lambda }_{H\sigma }/{\lambda }_H}$ for λ_Hσ < 0 (HHSI) (cf. Figure 3). In both cases, inflation can be described in the Einstein frame by a single canonically normalized field χ with potential

$\begin{array}{ll}Ṽ(\chi )=\frac{\lambda }{4}\rho {(\chi )}^4{\left(1+{\xi }_{\sigma }\frac{\rho {(\chi )}^2}{M_P^2}\right)}^{-2},& (30)\end{array}$

where

$\begin{array}{ll}\lambda \equiv \{\begin{array}{ll}{\lambda }_{\sigma },\hfill & \text{for HSI},\hfill \\ {\lambda }_{\sigma }\left(1-\frac{{\lambda }_{H\sigma }^2}{{\lambda }_{\sigma }{\lambda }_H}\right),\hfill & \text{for HHSI.}\hfill \end{array}& (31)\end{array}$

The field χ is the solution of ${\Omega }^{2}d\chi /d\rho \simeq {(b{\Omega }^2+6{\xi }_{\sigma }^2{\rho }^2/M_P^2)}^{1/2}$, with $\Omega \simeq 1+{\xi }_{\sigma }{\rho }^2/M_P^2$ being the Weyl transformation into the Einstein frame and b = 1 (for HSI) or b = 1 + |λ_Hσ/λ_H| (for HHSI). We will see in the next section that vacuum stability requires a small value of $\left|{\lambda }_{H\sigma }\right|\lesssim 10^{-6}$ and consequently b ~ 1 in HHSI, which makes practically impossible distinguishing between HSI and HHSI from the measurements of the CMB power spectra. However, even a small Higgs component in the inflaton is a key aspect for reheating, which sets apart both possibilities, as we will discuss later.

FIGURE 3

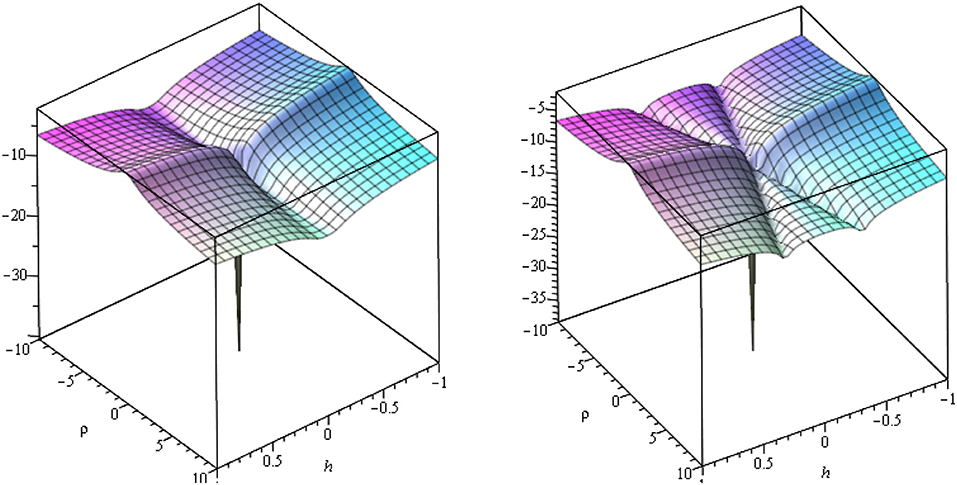
Figure 3. Decadic log of the scalar potential (4) in the Einstein frame (ξ_H ≪ ξ_σ), as a function of h and ρ, all in units of M_P, supporting, for λ_Hσ > 0, pure Hidden Scalar Inflation (HSI) (left), and, for λ_Hσ < 0, Higgs-Hidden Scalar Inflation (HHSI) (right) [taken and used with permission from Ballesteros et al. (2017b)]. Inflation proceeds along one of the valleys. The couplings have been chosen such that the amplitude of primordial scalar perturbation is properly normalized.

Figure 4 from Ballesteros et al. (2017b) shows the agreement of the non-minimally coupled potential (30) with the CMB at the pivot scale 0.05 Mpc⁻¹ (Ade et al., 2016a,b), summarized in the the amplitude of scalar perturbations A_s, the spectral index n_s, and the tensor-to-scalar ratio r,

$\begin{array}{ll}{A}_s=(2.207\pm 0.103)\times 10^{-9},& (32)\end{array}$

$\begin{array}{ll}{n}_s=0.969\pm 0.004,& (33)\end{array}$

$\begin{array}{ll}r<0.07.& (34)\end{array}$

Current constraints from the latest Planck analysis (July 2018) are very similar to the ones quoted above (Akrami et al., 2018). Importantly, the effective quartic coupling λ has to be small enough, λ≲10⁻¹⁰, so that the required non-minimal coupling to fit the amplitude of primordial scalar perturbations is at most ξ_σ ≲ 1 [cf. Figure 4 (up right)]. In this region of parameter space, the perturbative consistency of HSI and HHSI is guaranteed and superior to Higgs Inflation, which necessarily operates at large ξ_H for the measured value of the top mass, since in this latter case the value of λ_H as determined from the measured Higgs mass is sizable (Ballesteros et al., 2017b). The predictions of the potential (30) in the case λ = λ_σ (or b → 1 in HHSI) for the tensor-to-scalar ratio r vs. the scalar spectral index n_s are shown in Figure 5 for various values of ξ_σ. The requirement of predictive inflation, free of unitarity problems, demands r≳0.01, which will be probed by the next generation of CMB experiments, such as CMB-S4 (Abazajian, 2016), LiteBird (Matsumura et al., 2014), and the Simons Observatory (Aguirre et al., 2019). Since in SMASH and its extensions the particle content is known, the reheating process can be computed in detail. This allows to constrain n_s and r to a narrow band, unlike for generic inflationary potentials devoid of a connection to the SM.

FIGURE 4

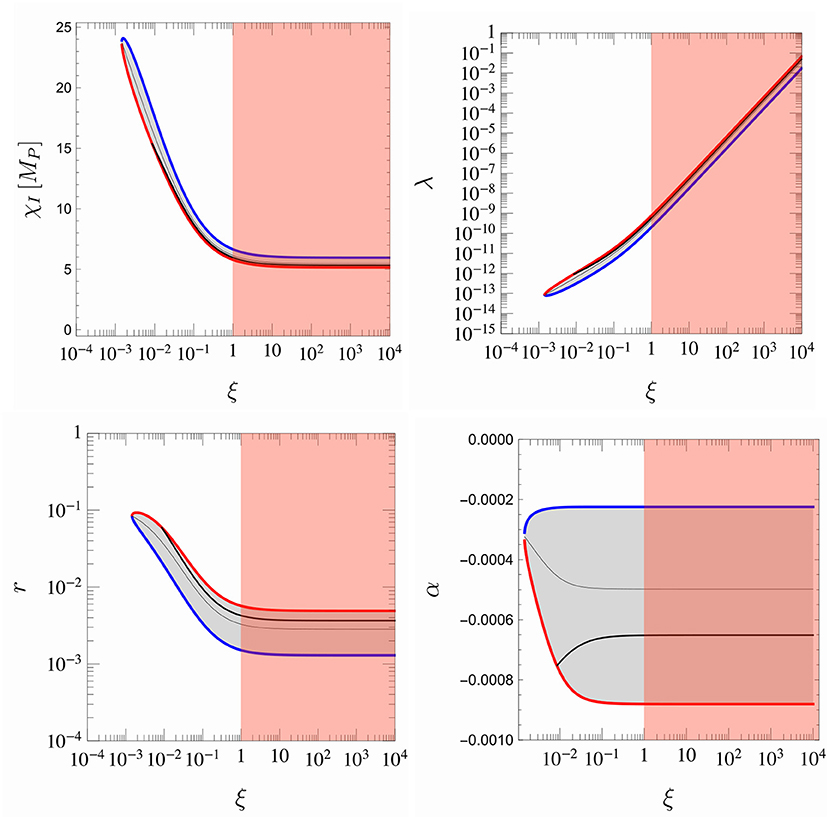
Figure 4. Confidence level (C.L.) contours (95% C. L.) of the parameters in the scalar potential (30), as a function of the non-minimal coupling parameter ξ = ξ_σ, yielding inflation constrained by Planck 2015 observations at the pivot scale 0.05 Mpc⁻¹ [taken and used with permission from Ballesteros et al. (2017b)]. (Upper left) The canonical inflaton value χ_I. (Upper right) The value of the quartic coupling. (Lower left) The predicted tensor-to-scalar ratio. (Lower right) The running of the spectral index. The best fit for a given ξ_σ is drawn as a thin black line, while the minimum and maximum values of n_s are drawn as red and blue curves, respectively, corresponding to a redder or bluer primordial spectrum of curvature perturbations. The thicker black line displays the predictions when accounting for the HHSI prediction of a universe expanding, immediately after inflation, according to the equation of state of radiation domination. The region ξ_σ > 1, where perturbative unitarity fails in SMASH, is shaded.

FIGURE 5

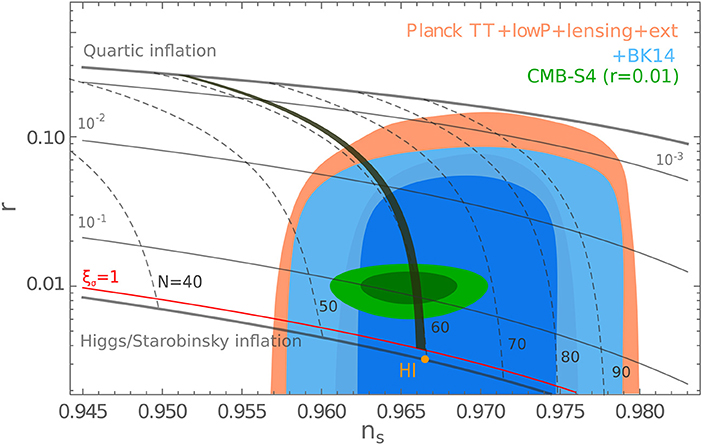
Figure 5. Predictions for the potential of Equation (30) in the r vs. n_s plane with a pivot scale of 0.002 Mpc⁻¹ [adapted and used with permission from Ballesteros et al. (2017b)]. Contours of constant ξ_σ are shown as black solid lines. The SMASH prediction accounting for a consistent reheating history is given by the thick black line, while the thin dotted lines give isocontours of the number of e-folds that ignore reheating constraints. Also shown are the 68 and 95% C.L. regions at 0.002 Mpc⁻¹ of Ade et al. (2016b) and the projected sensitivity of CMB-S4 (Abazajian, 2016) (in green). The line labeled as “Quartic inflation” shows the prediction for a quartic potential (corresponding to the limit ξ_σ → 0), while we also show a black solid line corresponding to the limit ξ_σ → ∞, in which the dynamics is analogous to that in the Starobinsky (Starobinsky, 1980) and Higgs inflation (HI) (Bezrukov and Shaposhnikov, 2008) models. The HI result of Gorbunov and Tokareva (2013) is indicated as a point on this line.

The generalization of Equation (31) to the case of a 2HDM—as relevant for the 2hdSMASH model—or to even more scalars—as relevant for gutSMASH—has not been worked out yet in full generality. For the related non-minimal Higgs Inflation in the 2HDM (see Gong et al., 2012). However, as far as HSI inflation is concerned, i.e., as long as the non-minimal couplings of all scalars apart from the saxion can be neglected, it is clear that the relevant potential for inflation is—in the Einstein frame—identical in SMASH HSI. Correspondingly, in this case, the same inflationary predictions as in SMASH HSI apply also for 2hdSMASH and gutSMASH HSI.

4. Stability

Primordial inflation of the kind described in the previous section is driven by a positive potential energy and Planckian field excursions. Therefore, a consistent realization within SMASH-type models requires a positive effective potential all the way up to the Planck scale. Although classical dynamics during inflation only requires a positive effective potential along the inflationary trajectory, instabilities in other regions of field space are dangerous because the fields can end up trapped in them as a result of the quantum fluctuations generated during inflation. To avoid this issue altogether we can demand a strictly positive potential in all field directions. Such requirement of (absolute) stability is threatened in the SM by loop corrections to the Higgs potential due to the top quark. When capturing virtual corrections by means of an RG-improved effective potential with parameters that run with the field scale (μ∝h), an instability arises for the preferred values of the Higgs and top masses as a result of negative contributions to the beta function of the Higgs quartic coupling. In SMASH(d/u) (cf. Table 1)—with a portal interaction between the Higgs and the complex scalar σ containing the axion– one can circumvent this problem thanks to the threshold stabilization mechanism pointed out in Elias-Miro et al. (2012) and Lebedev (2012). In the presence of the Higgs portal coupling, with the σ field acquiring a large VEV, the relation between the Higgs mass and the Higgs quartic coupling is altered with respect to that in the SM, such that the quartic can be larger in SMASH than in the SM. At an appropriate matching scale μ₀, the couplings in SMASH and the SM are related as

$\begin{array}{ll}{\lambda }_H({\mu }_0)={\lambda }_H^{\text{SM}}({\mu }_0)+\delta ({\mu }_0),\delta \equiv \frac{{\lambda }_{H\sigma }^2({\mu }_0)}{{\lambda }_{\sigma }({\mu }_0)}.& (35)\end{array}$

Despite the larger value of λ_H, stabilization is a bit subtle because, as expected from the decoupling of the massive σ field at low scales, the SM potential with its corresponding quartic can always be recovered in an appropriate region of field space. For λ_Hσ > 0 this region is of limited extent and can be made not to reach the SM instability scale. Then the potential in the SM-like region can stay positive, while outside of it the larger value of λ_H can ensure stability up to Planckian scales. Stabilization is then a tree-level effect and requires a small enough v_σ (which is harder to realize in GUT models), in order to ensure that the SM-like region does not go beyond the scale of the SM instability. For λ_Hσ < 0 on the other hand the SM-like region of the potential extends to arbitrary scales, and stabilization must crucially rely on loop effects that correct the running of the effective quartic coupling in the SM-like region. Stability can be achieved thanks to the positive contributions to the beta function of λ_H proportional to λ_H itself, which can counter-balance the negative corrections from the top quark: while in the SM the effect of the λ_H-dependent corrections is sub-dominant, this changes in SMASH due to the larger values of λ_H ensured by the modified matching in Equation (35).

Of course, one also needs to guarantee stability in the σ direction, which can again be endangered by fermion loops, this time coming from the RH neutrinos and the exotic quark Q. In this case stability can be achieved by demanding sufficiently small Yukawas.

After accounting for the previous effects, we have found that for the SMASH model stability in the Higgs direction can be achieved if the threshold parameter δ in Equation (35) is roughly between 10⁻³ and 10⁻² (for λ_Hσ > 0) or 10⁻³ and 10⁻¹ (for λ_Hσ > 0), depending on the top mass. On the other hand, stability in the σ direction restricts the Yukawa couplings of the RH neutrinos and Q to

$\begin{array}{ll}{\displaystyle \sum _i}{Y}_{ii}^4+6y^4\lesssim \frac{16{\pi }^2{\lambda }_{\sigma }}{log\left(\frac{30M_P}{\sqrt{2{\lambda }_{\sigma }}{v}_{\sigma }}\right)},& (36)\end{array}$

in the case that the Peccei-Quinn symmetry is extended to a lepton symmetry. Otherwise, the contribution of the Yukawas Y_ii on the left-hand side of Equation (36) is absent.

A stability analysis for 2hdSMASH and gutSMASH models is of course more involved due to the extra scalars and has not been done in full generality yet.

5. Reheating

After inflation, the background scalar fields that drove the accelerated expansion will typically oscillate around a minimum of the potential, and throughout these oscillations they will lose energy by producing SM particles that reheat into a plasma which ends up dominating the energy density of the universe. This reheating process was studied in detail in SMASH (Ballesteros et al., 2017b), and arises from the coupled dynamics of the field σ containing the axion, the Higgs and the weak gauge bosons. As long as the relevant dynamics only involves Higgses and a complex singlet, and all the other scalar fields remain heavy and decoupled, we expect that some of the features of reheating in SMASH may apply for other variants as well. Differences may arise due to choosing different parameters or from the presence of additional fields with non-trivial dynamics. For example, stability requirements end up enforcing some kinematic blockings in SMASH which could be lifted in other scenarios. And within GUT models, the presence of multiple components within the GUT multiplets containing the axion or Higgses could have non-trivial consequences.

Within the SMASH model, slow-roll inflation ends for $\rho ~{O}(M_P)$, when the inflaton field starts undergoing Hubble-damped oscillations in a quartic potential (for such field values and for ξ_σ ≲ 1, as required for predictive inflation, the effect of the non-minimal gravitational coupling can be ignored). These oscillations source a stress-energy tensor whose time-average mimics a radiation fluid. Hence, radiation domination starts right after inflation, and lasts through the phase of reheating in which the oscillating fields trigger the production of SM particles and the energy of the inflaton is transferred into the SM plasma. This post-inflationary history in a radiation-domination era (see Figure 6 for a summary of the cosmological history of SMASH) fixes the relation between the scales of the matter perturbations we observe in the Universe today and the size of the primordial fluctuations which gave rise to them, when they outgrew the Hubble horizon and became frozen until their later horizon re-entry. This relation between scales determines the number of e-folds between a perturbation's horizon crossing and the end of inflation, which fixes the thick black lines in Figures 4, 5 as the prediction for the parameters in SMASH.

FIGURE 6

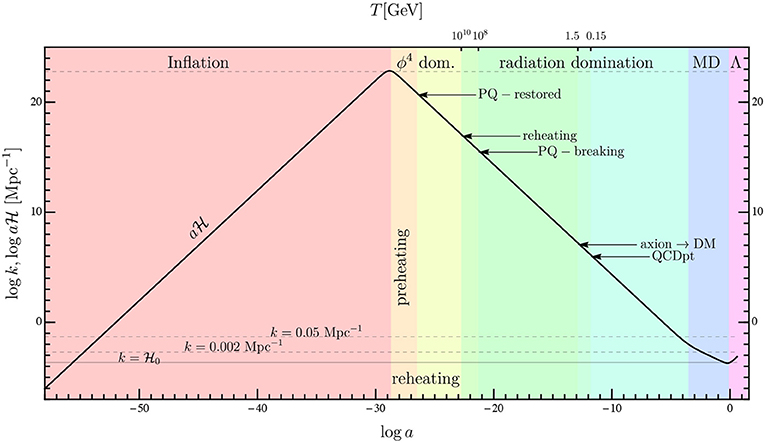
Figure 6. Expansion and thermal history of the Universe in SMASH HHSI [taken and used with permission from Ballesteros et al. (2017b)].

In order to understand the process of particle production from the oscillating background field, one has to account for non-perturbative parametric resonance effects (Kofman et al., 1997; Tkachev et al., 1998). When the background field changes slowly in time—away from successive crossings of the origin—one can describe the fields through an adiabatic approximation in which particle number is well-defined, and conserved. However, during the crossings the adiabatic approximation breaks down and the appropriately matched adiabatic solutions separated by a crossing have different particle numbers. This particle production is dominated by bosonic fields, and can be understood as a resonance effect accounting for many-body bosonic interactions. The oscillating field may be thought of as a condensate of scalar particles with energy equal to the oscillating frequency, which for a quartic potential goes as

$\begin{array}{ll}\omega =\sqrt{\lambda }{\varphi }_0,& (37)\end{array}$

with ϕ₀ the oscillating amplitude. In SMASH, the relevant effective quartic for the inflationary background is determined by λ_σ—see Equation (31)—which is fixed to ${\lambda }_{\sigma }\lesssim 10^{-10}$ by inflationary constraints. In turn, the inflaton condensate couples to Higgs particles with an effective mass dominated by background-dependent contributions, going as $\sqrt{{\lambda }_{H\sigma }}\left|\varphi \right|$. Stability constraints on the δ parameter of Equation (35) typically imply λ_Hσ ≫ λ_σ, so that the background Higgs mass is on average much larger than the energy of the particles in the condensate, and Higgs production is blocked except during crossings (ϕ = 0). Due to this, non-perturbative particle production is dominated by the growth of perturbations of the field σ itself, for both the real and imaginary part. This effect, confirmed by lattice simulations (Ballesteros et al., 2017b), breaks the coherence of the oscillating background and leads to a non-perturbative restoration of the PQ symmetry, as the phase of σ ends up taking random values across the Universe. The loss of coherence of ϕ ends up further blocking the production of Higgs particles, as |ϕ| stops having an oscillatory behavior and the Higgs mass always remains above the frequency of the condensate.

In HSI, the Higgs is the only field that couples directly to the inflaton and the production of SM particles is quenched by this effect. The energy of the inflaton gets evenly distributed between the modulus and the phase of σ, and lattice simulations show that the axion excitations generated in this preheating phase are highly relativistic (Ballesteros et al., 2017b). Reheating into SM particles only becomes possible when the σ fluctuations redshift below the scale f_A, the PQ symmetry becomes broken and the ρ field acquires a mass that finally allows the decay into Higgses. This late decay results in a low reheating temperature of around T ~ 10⁷ GeV, while the initial production of relativistic axions results in an unacceptable amount of dark radiation at late times, predicting an increase in the effective number of relativistic degrees of freedom of $\Delta N_{\nu }^{\text{eff}}={O}(1)$, which is ruled out by the Planck constraint $N_{\nu }^{\text{eff}}=3.04\pm 0.18$ at 68% CL (Ade et al., 2015).

In HHSI on the other hand the inflaton is an admixture of H and σ. This mixing endows the inflaton with a tree-level coupling to gauge bosons. Again, the gauge bosons in the Higgs background acquire oscillating masses $m_W~gH~g\sqrt{\left|{\lambda }_{H\sigma }\right|/(2{\lambda }_H)}\varphi$ whose average is typically above the frequency of the condensate, but which become zero at the inflaton's crossings of the origin. Crucially, since as argued before the growth of Higgs perturbations is thwarted by the fast production of σ excitations, the Higgs component of the background does not lose coherence and continues to oscillate, which keeps the production of electroweak gauge bosons open during crossings. The decay rate of the gauge bosons is fast enough to essentially deplete their population between crossings, so that the boson production is never resonantly enhanced. Nevertheless, a thermal feedback mechanism takes place which enhances the rate of extraction of energy from the inflaton into the SM plasma. The decay products of the gauge bosons quickly reach a thermal bath, which may in turn produce gauge bosons by inverse decays near the crossings. Away from them, the extra bosons gain energy from the condensate as their mass grows with increasing |ϕ|, and this energy is transferred into the SM plasma when the massive gauge bosons decay. Modeling this dynamics using Boltzmann equations and energy conservation constraints, one can predict a reheating temperature in HHSI near 10¹⁰ GeV. This implies a thermal restoration of the PQ symmetry, as the critical temperature T_c for the PQ transition goes as

$\begin{array}{ll}\frac{T_c}{v_{\sigma }}\simeq \frac{2\sqrt{6{\lambda }_{\sigma }}}{\sqrt{8({\lambda }_{\sigma }+{\lambda }_{H\sigma })+{\displaystyle {\sum }_i}{Y}_{ii}^2+6y^2}},& (38)\end{array}$

and T_c is below 10¹⁰ GeV for the preferred SMASH parameters. Moreover, the reheating temperature is also enough to guarantee that the axion population reaches thermal equilibrium, so that its abundance is no longer fixed by the earlier non-perturbative production. In this way the HSI problem with ΔN_eff is avoided, and one predicts a modest amount of cosmic axion background radiation (CAB) corresponding to $△N_{\nu }^{\text{eff}}\simeq 0.03$, which may be probed with future CMB and large scale structure observations (Baumann et al., 2018).

Within GUT variants, the gutSMASH model with f_A independent of the unification scale could feature similar dynamics as SMASH in appropriate regions of parameter space. On the other hand, for the miniSO(10)PQ model the large $f_A\gtrsim 2.6\times 10^{15}$ GeV can give rise to important differences.⁴ For example, if the reheating temperature is comparable to that in SMASH, the large value of f_A might mean that a thermal restoration of the PQ symmetry can be avoided, since the critical temperature is proportional to the VEV of the PQ field [see Equation (38)]. This can be a nice feature of the model, as for large f_A one should avoid a post-inflationary restoration of the PQ symmetry in order to avoid overclosure of the Universe by axion dark matter, as reviewed in the next section. However, this still leaves open the possibility of a non-thermal restoration of the PQ symmetry due to the preheating dynamics. Luckily, the large value of f_A can again come to the rescue. The large growth of perturbations in the inflaton field can be hampered for large f_A because the modulus of the field can become quickly trapped around the minimum before the fluctuations in the angular component grow large enough so as to restore the PQ symmetry. Once trapped in the minimum, the ρ fluctuations become massive and can decay quickly into SM particles, so that the growth of angular perturbations is expected to stop. With the results of the lattice simulations in SMASH (Ballesteros et al., 2017b), one can do a simple extrapolation to estimate the time at which the redshifting oscillations of the field reach a maximum of the order of a given value of f_A. If the time is below the onset of the parametric growth of the angular perturbations, one then expects that PQ restoration will be avoided. Such estimate gives that the PQ restoration might be avoided for $f_A\gtrsim 4\times 10^{16}$ GeV, which is in the allowed window of Equation (28) and raises the hope that the miniSO(10)PQ model could have a viable parameter space with a consistent cosmological history compatible with pre-inflationary axion dark matter.

6. Dark Matter

The most important prediction of SMASH is that the PQ symmetry is broken after inflation. In the post-inflationary scenario, dark matter is produced by the re-alignment mechanism (Abbott and Sikivie, 1983; Dine and Fischler, 1983; Preskill et al., 1983) and the decay of topological defects (axion strings and domain walls) (Kawasaki et al., 2015). In models, in which the axion decay constant is an integer fraction of the PQ symmetry breaking scale, f_A = v_PQ/N_DW, with N_DW > 1, and in which the PQ symmetry is exact, there are N_DW degenerate CP-preserving vacua and domain walls develop between them when the axion field becomes non-relativistic; i.e., when at some temperature T₁ the Hubble scale becomes of the order of the axion mass: ${H}(T_1)~m_A(T_1)$. Since there is no preferred vacuum, the system of strings and walls is predicted to continue a scaling regime where the energy in domain-walls soon exceeds the observations. Therefore those models have to be discarded (Sikivie, 1982) and N_DW can only be 1 in SMASH. This is the main motivation for introducing just one extra heavy quark in SMASH. The alternative models with larger values of N_DW [e.g., 2hdSMASH, with N_DW = 6 (cf. Table 2), miniSU(5)PQ, with N_DW = 11, and miniSO(10)PQ and gutSMASH, with N_DW = 3 (cf. Table 4)] can only become viable in scenarios in which the PQ symmetry is not exact—so that the degeneracy of the CP-preserving vacua can be lifted, and the domain-walls become unstable—or when the PQ symmetry is broken before or during inflation, never to be restored afterwards. In such a situation the energy density stored in the domain walls is simply diluted away by the exponential expansion of the universe during inflation.

Owing to the post-inflationary scenario, the original SMASH model becomes extremely predictive, at least in theory. In principle the axion DM abundance in this scenario is calculable by performing numerical simulations of the axion-string-wall network. The physics determining axion DM depends crucially on m_A. Uncertainties from the unknown initial conditions of the axion field are averaged away over many causal domains. Since there is no other cold DM candidate in the model, axions should provide all the observed CDM abundance and the theoretical relation ${\Omega }_A{h}^2(m_A)=0.12$ allows to obtain the required value of m_A (and thus f_A). Unfortunately, there is a long-standing controversy regarding the calculation of ${\Omega }_A{h}^2={\Omega }_A{h}^2(m_A)$. Because of the large dynamical range required ($f_A/{H}(T_1)~10^{30}$ from string cores to the horizon size) an extrapolation is mandatory and different authors have argued differently on how to perform it. Recently, a new method has been developed to endow the strings with the physically motivated effective tension, $\propto log{f}_A/{H}$, (if not the energy distribution around the string) and has lead to a very precise prediction, m_A ≃ (26.2±3.4)μeV (Klaer and Moore, 2017). The axion DM mass results so small because much of the network energy is radiated in hard axions (which count less for DM) and other hard quanta of the several extra fields that need being introduced. A recent detailed study of the string-network evolution (Gorghetto et al., 2018) has clarified substantially the results from standard numerical simulations and challenged the results of Kawasaki et al. (2015). The authors disregard the effective model of Klaer and Moore (2017) and highlight the huge uncertainty in the extrapolation to physical string-tensions.

When SMASH was proposed, the most detailed numerical simulations (Kawasaki et al., 2015) were pointing to m_A ~ 100μeV and the uncertainties where revised to 50μeV≲m_A ≲ 200μeV (Borsanyi et al., 2016; Ballesteros et al., 2017b). This corresponded to the range $3\times 10^{10}\text{GeV}\lesssim f_A\lesssim 1.2\times 10^{11}\text{GeV}$. According to the latest results, the lower limit on m_A could be a factor 2 smaller but the upper limit could be much greater. The next years might be decisive in resolving this controversy as new simulation techniques develop.

Most importantly, this axion dark matter mass window will be probed in the upcoming decade by axion dark matter direct detection experiments, such as ADMX (Boutan et al., 2018; Du et al., 2018), CAPP (Chung, 2018), HAYSTAC (Zhong et al., 2018), RADES (Melcón et al., 2018), MADMAX (Caldwell et al., 2017; Brun et al., 2019), ORPHEUS (Morris, 1984; Rybka et al., 2015), and others (cf. Figure 7). A review on axion DM experiments can be found in Irastorza and Redondo (2018).

FIGURE 7

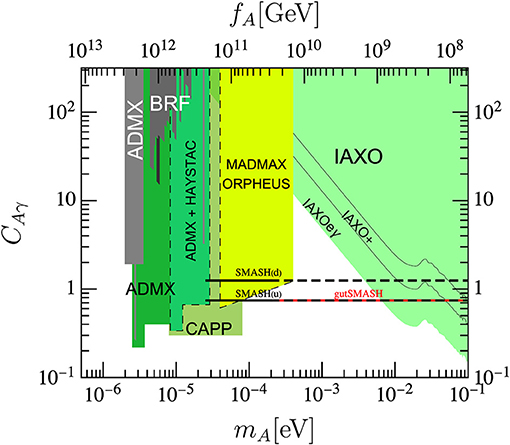
Figure 7. SMASH predictions for the axion-photon coupling [adapted and used with permission from Ballesteros et al. (2017b)]: SMASH(u,d) (thick solid horizontal lines for hypercharge assignment of −1/3 (2/3) for Q) and gutSMASH (red). The continuing dashed lines show plausible uncertainties. We also show, in gray, the current bounds on axion DM [ADMX (Boutan et al., 2018; Du et al., 2018), BRF] and, in green, prospects for next generation axion dark matter experiments, such as ADMX (Boutan et al., 2018; Du et al., 2018), CAPP (Chung, 2018), HAYSTAC (Zhong et al., 2018), MADMAX (Caldwell et al., 2017; Brun et al., 2019), ORPHEUS (Morris, 1984; Rybka et al., 2015), and the helioscope IAXO (Armengaud et al., 2014) (fiducial, extended+ sensitivities to the axion-photon channel and IAXOeγ for the electron-photon channel).

As anticipated earlier, non-minimal versions of SMASH where the degeneracy between N_DW vacua is broken are in principle possible and can be viable. Indeed, the degeneracy breaking generates a pressure between vacua that leads to the early collapse of the wall network (Sikivie, 1982). Ringwald and Saikawa (2016) studies how fundamental discrete symmetries can be invoked to protect the PQ symmetry from too large a breaking and estimates reasonable phenomenological parameters. This mechanism allows to avoid the domain wall problem for models like an extension of SMASH by further heavy quarks, 2hdSMASH and gutSMASH within a well-motivated framework. The price is however the non-minimality of the extra fields and the discrete symmetry. The best candidates tend to be Z_N symmetries with large N ~ 9, 10 and point to axion masses in the meV mass ballpark. These predictions do not include the latest results about the string-network evolution that we mentioned above.

If the axion mass is around the meV ballpark, IAXO (Armengaud et al., 2014) could find the concomitant flux of solar axions but direct DM detection will be very difficult. The solar signal can be however used to pinpoint the axion mass and couplings (Jaeckel and Thormaehlen, 2019; Dafni et al., 2019), thus constraining the SMASH scenario and ease the search for DM.

The post-inflationary scenario typically favored in SMASH has many interesting phenomenological consequences. A large part of the DM is thought to be in the form of axion miniclusters (Kolb and Tkachev, 1993, 1994), small DM halos of typical radius ~10¹² cm and mass $~10^{-12}{M}_{\odot }$ that form around matter-radiation equality with large densities ~10⁷ GeV/cm³. A recent study shows that smaller and denser objects are also unavoidable and more numerous (Vaquero et al., 2018). Axion miniclusters could be identified with pico-, femto- (Kolb and Tkachev, 1996; Zurek et al., 2007), and micro-lensing (Fairbairn et al., 2017, 2018, see also Katz et al., 2018). In many cases they will develop solitonic cores, sometimes called dilute axion stars (Visinelli et al., 2018) when considered in isolation. Most axion miniclusters survive until today and are so small that a direct encounter with the Earth is very rare. However, some others are tidally disrupted into streams whose encounters with the Earth can be more frequent and profitable for direct detection (Dokuchaev et al., 2017). The encounters of axion miniclusters/axion stars with the magnetic fields of compact objects has been speculated to be the origin of some fast-radio-bursts (Iwazaki, 2015; Tkachev, 2015).

In general, it is unfortunately impossible to predict whether SMASH variants will always realize the post-inflationary scenario. There is a strong tendency for this to be the case also in 2hdSMASH and gutSMASH if all the couplings are small and the inflaton is related to the PQ field. The addition of extra fields or non-minimal couplings could affect the isocurvature constraints from Planck and the reheating temperature. For the miniSU(5)PQ and miniSO(10)PQ models, as commented in section 5, the large values of f_A could in principle prevent the restoration of the PQ symmetry—as needed for the extremely light axion to remain compatible with dark matter—but dedicated studies are needed.

In the pre-inflationary scenario, the PQ symmetry would not be restored and the initial condition of the axion field would be an homogeneous local-Universe-wide value that could be anthropically selected for a very broad range of decay constants (Tegmark et al., 2006). For the axion to furnish all dark matter and $f_A\lesssim 3\times 10^{17}$ GeV, the initial mis-alignment angle θ_I has to satisfy (Ballesteros et al., 2017b)

$\begin{array}{ll}{\theta }_{I,c}\approx 0.0006\times {\left(\frac{f_A}{3\times 10^{17}\text{GeV}}\right)}^{-0.504}.& (39)\end{array}$

We conclude this section discussing DM isocurvature bounds. If the PQ scalar is responsible for inflation one expects that the axion, its angular degree of freedom, gets its quantum fluctuations stretched to superhorizon length scales. Since axions constitute the DM, these fluctuations would get imprinted in the temperature anisotropies of the CMB as an isocurvature component, which is severely constrained by the data (Ade et al., 2015). The isocurvature bound gets translated into an upper bound on the Hubble expansion rate ${{H}}_I$ during inflation (and in turn on the tensor-to-scalar ratio, r) as a function of f_A. Since there is an upper limit on r from the CMB (see section 3), this means a maximum possible value of f_A. Notice that this bound also depends on the initial axion mis-alignment angle, which together with f_A is the relevant parameter that determines the DM abundance in this scenario of PQ breaking during inflation. In scenarios in which the reheating temperature is such that the PQ symmetry becomes restored, the field values of the axion become processed by the thermal (or non-thermal) sub-horizon dynamics and all field perturbations end up being determined by a unique effective temperature scale and of the curvature type; thus, no isocurvature perturbations are generated.

In SMASH and its variants, the energy scale of inflation is mostly determined by the non-minimal coupling ξ, which imposes a lower bound on r (see Figure 4). The PQ symmetry is broken during inflation due to the time-dependent value of ρ—the modulus of the PQ scalar—which is not at the minimum of its potential, and thus the usual isocurvature bounds do not apply directly (see also Fairbairn et al., 2015). The reason can be understood by noticing that during inflation the effective f_A “seen” by the fluctuations in the direction orthogonal to the inflationary trajectory is actually the instantaneous value of the inflation field. Indeed, the “effective" value of f_A relevant to the isocurvature bounds is larger than the low-energy value of f_A (the one determined by the minimum of the PQ potential, entering into the axion mass equation) thanks to the non-minimal coupling and thus the ensuing constraints get weaker. A detailed calculation shows that the maximum allowed value of f_A is ~ 10¹⁴ GeV (Ballesteros et al., 2017b). This constraint, together with the fact that the PQ symmetry is always restored for $f_A\lesssim 4\times 10^{16}$ GeV, implies that the only viable SMASH realizations are those with PQ restoration after inflation, so that the DM abundance comes not only from oscillations of the axion field but also from the decay of topological defects, as discussed above.

The previous isocurvature bound in principle rules out the viability of miniSU(5)PQ or miniSO(10)PQ, with f_A tied to the unification scale. However, there is a possibility that the bound may be circumvented if one accounts for the fact that the axion field is not really massless during inflation, in contrast to what was assumed when deriving the isocurvature bound described above. During inflation the scalar fields do not sit at their minimum and Goldstone's theorem does not apply; a detailed study of the evolution of the axion mass during and after inflation is needed. Moreover, in these models additional fields exist, which opens the possibility for additional paths in field space and further suppression of the bounds.

7. Baryogenesis

In SMASH models, the presence of right-handed neutrinos with masses proportional to the axion decay constant allows to explain the baryon asymmetry of the Universe through the mechanism of thermal leptogenesis (Fukugita and Yanagida, 1986). This relies on out-of-equilibrium, CP-violating decays of heavy RH neutrinos, which generate a net lepton asymmetry which is partly converted into a baryon asymmetry by non-perturbative sphaleron processes that violate baryon plus lepton number. In SMASH-type models in which the PQ symmetry is restored thermally, such as the HHSI variant of SMASH, the RH neutrinos are massless after reheating, and are expected to acquire thermal equilibrium abundances. After the PQ phase transition they gain a mass, and as long the latter is smaller than the critical temperature of the transition, the massive RH neutrinos will typically re-enter equilibrium (Shuve and Tamarit, 2017) and decay at later times, generating the asymmetry after inverse decays become Boltzmann suppressed. This scenario is realized in SMASH, where demanding a stabilized potential in the σ direction, and assuming a hierarchy of Yukawas Y₂₂ = Y₃₃ = κY₁₁ and y = Y₁₁, one has

$\begin{array}{ll}\frac{T_c}{M_1}\gtrsim \frac{1}{\pi }\sqrt{\left(\frac{2+6{\kappa }^4}{7+2{\kappa }^2}\right)log\left(\frac{30M_P}{\sqrt{2{\lambda }_{\sigma }}{f}_A}\right)},& (40)\end{array}$

which follows from Equations (36) and (38) and is above 1 for typical SMASH parameters, including the case of near degenerate RH neutrinos with κ ≈ 1.

In SMASH realizations in which the PQ symmetry is not restored thermally, as could be the case in models with very large f_A, such as GUT variants with f_A correlated with the unification scale, notably miniSU(5)PQ and miniSO(10)PQ⁵, the RH neutrinos are massive after reheating, but a thermal initial abundance can still be achieved for a reheating temperature above the RH masses. In this case the asymmetry will again be generated during late-time decays. A thermal initial abundance might not be achieved if the Yukawas of the RH neutrinos are very small, but in these so-called “weak washout” scenarios one can still produce an asymmetry from the out-of-equilibrium production and decays of RH neutrinos.

In the vanilla realizations of thermal leptogenesis with hierarchical RH neutrinos, the requirement of a large enough source of CP-violation in RH neutrino decays gives a lower bound $M_1\gtrsim 5\times 10^8$ GeV (Casas and Ibarra, 2001; Giudice et al., 2004; Buchmuller et al., 2005). However, since the RH neutrino masses are proportional to their Yukawas with the field σ, and since these couplings tend to generate destabilizing corrections for the potential in the σ direction, having such heavy RH neutrinos can be in conflict with the requirement of stability. For example, in SMASH the stability bound in Equation (36) for a hierarchical N_i spectrum (M₃ = M₂ = 3M₁) requires $M_1\lesssim 10^8{(\lambda /10^{-10})}^{1/4}(v_{\sigma }/10^{11}\text{GeV})$ GeV, which is just borderline compatible with the leptogenesis bound. Nevertheless, leptogenesis can occur for smaller masses with a mild resonant enhancement (Pilaftsis and Underwood, 2004) for a less hierarchical RH neutrino spectrum, which relaxes the stability bound and ensures that all the RH neutrinos remain in equilibrium after the phase transition. The estimated level of degeneracy needed in order to reconcile leptogenesis with the stability bound is of the order of 4%.

Finally, even though the RH neutrino masses are typically expected to be heavy, as they are proportional to the axion decay constant, fine-tuned values of the Yukawa couplings still allow for O(GeV) masses. In such cases one recovers the νMSM at low energies, and even though lepton number violation is suppressed due to the small masses of the RH neutrinos, the baryon asymmetry can arise as a result of out-of-equilibrium oscillations of the right-handed neutrinos (Akhmedov et al., 1998). These give rise to flavored lepton asymmetries, which may even add up to zero initially, but as long as one flavor is out-of-equilibrium the washout will be incomplete and a net asymmetry will survive.

8. Conclusions

We have provided an overview of SMASHy extensions of the Standard Model which feature a new mass scale v_σ—of the order of 10¹¹ GeV in the simplest models, but which could also be tied to a Grand Unification scale around 10¹⁶ GeV—and provide a falsifiable framework that addresses the following problems in particle physics and cosmology: inflation, baryogenesis, neutrino masses, dark matter and the strong CP problem. In addition, these models stabilize the electroweak vacuum. Whenever the dynamics of the most economical model (Ballesteros et al., 2017a,b), called SMASH in this review, is also realized in other extensions (as may happen if the additional fields remain decoupled during inflation and reheating), the models reviewed here predict a tensor-to-scalar-ratio r ≳ 0.004, a running of the spectral index α ≳ −8 × 10⁻⁴ (see Figures 4, 5), and a deviation in the effective number of relativistic neutrino species ΔN_νeff ~ 0.03, values which can be probed in future CMB experiments, such as CMB-S4, LiteBIRD, and the Simons Observatory. The SMASH model predicts a lower bound on the axion mass m_A ≳ 25μeV, in the reach of future axion experiments, such as CAPP, MADMAX, ORPHEUS, and IAXO (see Figure 7). Given that the axion population in the model, constituting the totality of the DM, arises from the re-alignment mechanism and from the decay of topological defects (due to the post-inflationary breaking of the PQ symmetry), a large fraction of it may be in axion miniclusters, whose abundance may be tested via lensing studies of different astrophysical sources.

The models surveyed here revolve around the idea of exploiting the complex scalar field that implements the PQ symmetry and solves the strong CP problem. The axion –the angular part of this field– dynamically relaxes the theta parameter of QCD to a small maximum value, compatible with the upper bounds on the neutron electric dipole moment. On the other hand, the oscillations of the axion around the minimum of its potential constitute a condensate that can explain the nature of DM.

The modulus of the PQ scalar is instead the key ingredient for successful inflation. The inflationary sector of SMASH (which also contains a small Higgs component) predicts a primordial spectrum in agreement with the CMB, reheats the Universe efficiently and leads to a small relic abundance of thermal axions which may be identified through a determination of the effective number of relativistic species at early times. The coupling between the Higgs doublet and the PQ scalar is instrumental for the stabilization of the effective potential at large field values, which in the SM is threatened by the large effect on the running of the Higgs quartic coupling coming from the top Yukawa. This interplay between inflation and stability set apart SMASHy extensions of the SM from models which utilize the Higgs alone to drive inflation (an idea that has more severe consistency issues related to the breakdown of perturbative unitarity).

The small masses of the light neutrinos are explained via the see-saw mechanism, adding three extra right-handed neutrinos whose heavy masses are induced by the VEV, v_σ, of the PQ scalar, which is proportional to the axion decay constant f_A. These heavy neutrinos can also explain the matter/anti-matter asymmetry of the Universe via thermal leptogenesis. The particle content of SMASH is illustrated in Figure 2. In addition to the PQ scalar and the three right handed neutrinos, the model features a heavy vector-like quark Q which is required for the KSVZ-like implementation of the PQ symmetry. At sufficiently low energy the model reduces to the SM augmented by small neutrino masses and the axion, A.

Possible extensions of the minimal SMASH model include implementations in Two-Higgs-Doublet models featuring a DFSZ axion, as well as embeddings of the latter into SU(5) and SO(10) GUTs. As long as one of the Higgses and the extra particles in the GUT multiplets are decoupled during inflation, one can expect to recover the inflationary predictions in SMASH. A similar post-inflationary history may be also recovered for an axion decay scale as in SMASH, i.e., near 10¹¹ GeV. However, for GUTs with the axion scale f_A tied to the unification scale, as in the miniSU(5)PQ and miniSO(10)PQ models, there can be important differences. First, isocurvature axion perturbations generated during inflation might be incompatible with Planck limits; although Ballesteros et al. (2017b) discarded $f_A>1.4\times 10^{14}$ GeV on this account, the bound neglected the non-zero mass of the axion during inflation (arising from the fact that the scalar field is not at its minimum), and this needs to be accounted for. On the other hand, a large f_A is only compatible with axion dark matter in a scenario in which the PQ symmetry is not restored after inflation. Although dedicated lattice simulations are still lacking, there are indications that such behavior is possible, as very large values of f_A change the reheating dynamics and quench the generation of axion perturbations.

Given the lack of compelling new physics signals at the LHC, the idea of attempting to tackle several fundamental physics problems together in a simple (but coordinated) manner is appealing. Perhaps, one of the main take home messages from the SMASHy extensions of the SM that we have reviewed here is that the QCD axion might be a hint not only to dark matter, but also to inflation. In our opinion, it is interesting to continue exploring in the future possible connections between seemingly unrelated problems in particle physics and cosmology.

There exist other recent proposals which are also inspired by minimality and try to address simultaneously several of the SM standing issues. We will mention some of them briefly in the following. The model of Salvio (2015) has the same particle content as the one proposed in Dias et al. (2014) (and the same as in SMASH). It also attempts to address the same five problems of the SM as SMASH, but it differs from it mainly regarding the heavy neutrino masses (which are not sourced by the VEV of the PQ scalar) and, also inflation, which in this case is driven by the Higgs and thus generically suffers from the unitarity issue. It has been recently argued in Salvio (2019) that the model can be safe from this problem if the top and Higgs masses are tuned in such a way that the quartic Higgs coupling relevant at the energies of inflation is very small. The proposal of Ema et al. (2017) aims to explain—in addition to the issues that SMASHy extensions of the SM deal with—the flavor structure of masses and mixings in the SM. The model differs from SMASH at several points. For example, the origin of the SU(3) anomaly of the PQ symmetry is unspecified. A key assumption in the model is a pole in the kinetic term of the new scalar field, which leads to an asymptotically flat potential after canonical normalization (see e.g., Galante et al., 2015). It has been argued that this kind of Lagrangian also suffers from an early breakdown of perturbative unitarity, and thus of consistency (Kehagias et al., 2014). The same idea of using a single U(1) symmetry for the flavor and the strong CP problems was independently proposed in Calibbi et al. (2017), although this paper does not deal with inflation nor with the matter/anti-matter asymmetry. A very different kind of proposal has been recently put forward in Gupta et al. (2019). This model aims to solve the same problems as SMASH, except inflation, and in addition it tackles the hierarchy problem. It does so by means of the relaxion mechanism (Graham et al., 2015) (for the hierarchy problem) and the Barr-Nelson mechanism (Barr, 1984; Nelson, 1984) (for the strong CP problem). Baryogenesis is triggered in this case by oscillations of the relaxion field around its final minimum.

In summary, we are living in interesting times for particle physics and cosmology, in which simple ideas blended together are providing new theoretical insights and unveiling possible connections between different problems.

Author Contributions

AR determined the table of content and wrote mainly sections 1, 2. GB wrote section 3. JR concentrated on section 6. CT on sections 4, 5, 7. All authors contributed equally on section 8.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Many thanks to Anne Ernst and Luca Di Luzio for the great collaboration on SMASHy extensions of the SM. The work of GB is funded by a Contrato de Atracción de Talento (Modalidad 1) de la Comunidad de Madrid (Spain), with number 2017-T1/TIC-5520. It has also been supported by MINECO (Spain) under contract FPA2016-78022-P and the Spanish MINECO's Centro de Excelencia Severo Ochoa Program under the grants SEV-2012-0249 and SEV-2016-0597. GB and CT acknowledge support from the Collaborative Research Centres SFB676 and SFB1258 of the Deutsche Forschungsgemeinschaft (DFG), respectively. The work of AR is partly supported by the DFG under Germany's Excellence Strategy—EXC 2121 Quantum Universe—390833306. JR is supported by the Ramon y Cajal Fellowship 2012-10597, the grant FPA2015-65745-P (MINECO/FEDER), the EU through the ITN Elusives H2020-MSCA-ITN-2015/674896 and the Deutsche Forschungsgemeinschaft under grant SFB1258 as a Mercator Fellow.

Footnotes

1. ^Higgs inflation can also be realized in supergravity extensions of the SM (see for example Ben-Dayan and Einhorn, 2010; Choudhury et al., 2014; Pallis, 2017, 2018a,b; Pallis and Shafi, 2018).

2. ^These hypercharge assignments ensure that Q can mix with the right-handed SM down-type quarks or up-quarks, respectively, allowing its decay to the latter, thereby evading overabundance problems (Nardi and Roulet, 1990; Berezhiani et al., 1992).

3. ^Very recently, Gorghetto and Villadoro (2019) improved the theoretical prediction of χ₀ by including O(α) and NNLO corrections in the chiral expansion, resulting in ${\chi }_0^{1/4}=75.44(34)\text{ MeV}$, corresponding to $m_A=56.91(51)\mu \text{eV}(10^{11}\text{ GeV}/f_A)$, almost coinciding with the previous NLO result.

4. ^Similar considerations apply for the miniSU(5)PQ model.

5. ^Note that in order to avoid problems like monopole production, the reheating temperature in GUTs should be below the unification scale.

References

Aaboud, M., Aad, G., Abbott, B., Abdinov, O., Abeloos, B., Abhayasinghe, D. K., et al. (2018). Measurement of the top quark mass in the $t\bar{t}\to$ lepton+jets channel from $\sqrt{s}=8$ TeV ATLAS data and combination with previous results. Eur. Phys. J. 79:290. doi: 10.1140/epjc/s10052-019-6757-9

CrossRef Full Text | Google Scholar

Abazajian, K. N. (2016). CMB-S4 Science Book, 1st Edn. doi: 10.2172/1352047

CrossRef Full Text | Google Scholar

Abbott, L. F., and Sikivie, P. (1983). A cosmological bound on the invisible axion. Phys. Lett. B 120, 133–136.

Google Scholar

Abe, K., Abe, T., Aihara, H., Fukuda, Y., Hayato, Y., Huang, K., et al. (2011). Letter of intent: the hyper-kamiokande experiment—detector design and physics potential— arXiv:1109.3262.

Google Scholar

Abe, K., Haga, Y., Hayato, Y., Ikeda, M., Iyogi, K., Kameda, J., et al. (2017). Search for proton decay via p → e⁺π⁰ and p → μ⁺π⁰ in 0.31 megaton· years exposure of the Super-Kamiokande water Cherenkov detector. Phys. Rev. D 95:012004. doi: 10.1103/PhysRevD.95.012004

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Arnaud, M., Arroja, F., Ashdown, M., Aumont, J., et al. (2016a). Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 594:A20. doi: 10.1051/0004-6361/201525898

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Arnaud, M., Ashdown, M., Aumont, J., Baccigalupi, C., et al. (2015). Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

Ade, P. A. R., Ahmed, Z., Aikin, R. W., Alexander, K. D., Barkats, D., Benton, S. J., et al. (2016b). Improved constraints on cosmology and foregrounds from BICEP2 and keck array cosmic microwave background data with inclusion of 95 GHz band. Phys. Rev. Lett. 116:031302. doi: 10.1103/PhysRevLett.116.031302

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguirre, J., Aguirre, J., Ahmed, Z., Aiola, S., Ali, A., Alonso, D., et al. (2019). The Simons Observatory: science goals and forecasts. JCAP 1902:056. doi: 10.1088/1475-7516/2019/02/056

CrossRef Full Text | Google Scholar

Akhmedov, E. K., Rubakov, V. A., and Smirnov, A. Y. (1998). Baryogenesis via neutrino oscillations. Phys. Rev. Lett. 81, 1359–1362. doi: 10.1103/PhysRevLett.81.1359

CrossRef Full Text | Google Scholar

Akrami, Y., Arroja, F, Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2018). Planck 2018 results. X. Constraints on inflation. arXiv:1807.06211.

Google Scholar

Altarelli, G., and Meloni, D. (2013). A non supersymmetric SO(10) grand unified model for all the physics below M_GUT. JHEP 1308:021. doi: 10.1007/JHEP08(2013)021

CrossRef Full Text | Google Scholar

Arhrib, A., Bajc, B., Ghosh, D. K., Han, T., Huang, G. Y., Puljak, I., et al. (2010). Collider signatures for heavy lepton triplet in Type I + III seesaw. Phys. Rev. D 82:053004. doi: 10.1103/PhysRevD.82.053004

CrossRef Full Text | Google Scholar

Armengaud, E., Avignone, F. T., Betz, M., Brax, P., Brun, P., Cantatore, G., et al. (2014). Conceptual design of the International Axion Observatory (IAXO). JINST 9:T05002. doi: 10.1088/1748-0221/9/05/T05002

CrossRef Full Text | Google Scholar

Arvanitaki, A., Baryakhtar, M., and Huang, X. (2015). Discovering the QCD axion with black holes and gravitational waves. Phys. Rev. D 91:084011. doi: 10.1103/PhysRevD.91.084011

CrossRef Full Text | Google Scholar

Asaka, T., Blanchet, S., and Shaposhnikov, M. (2005). The nuMSM, dark matter and neutrino masses. Phys. Lett. B 631, 151–156. doi: 10.1016/j.physletb.2005.09.070

CrossRef Full Text | Google Scholar

Asaka, T., and Shaposhnikov, M. (2005). The nuMSM, dark matter and baryon asymmetry of the universe. Phys. Lett. B 620, 17–26. doi: 10.1016/j.physletb.2005.06.020

CrossRef Full Text | Google Scholar

Babu, K. S., and Khan, S. (2015). Minimal nonsupersymmetric SO(10) model: gauge coupling unification, proton decay, and fermion masses. Phys. Rev. D 92:075018. doi: 10.1103/PhysRevD.92.075018

CrossRef Full Text | Google Scholar

Babu, K. S., and Mohapatra, R. N. (1993). Predictive neutrino spectrum in minimal SO(10) grand unification. Phys. Rev. Lett. 70, 2845–2848. doi: 10.1103/PhysRevLett.70.2845

PubMed Abstract | CrossRef Full Text | Google Scholar

Bajc, B., Melfo, A., Senjanovic, G., and Vissani, F. (2006). Yukawa sector in non-supersymmetric renormalizable SO(10). Phys. Rev. D 73:055001. doi: 10.1103/PhysRevD.73.055001

CrossRef Full Text | Google Scholar

Bajc, B., Nemevsek, M., and Senjanovic, G. (2007). Probing seesaw at LHC. Phys. Rev. D 76:055011. doi: 10.1103/PhysRevD.76.055011

CrossRef Full Text | Google Scholar

Bajc, B., and Senjanovic, G. (2007). Seesaw at LHC. JHEP 0708:014. doi: 10.1088/1126-6708/2007/08/014

CrossRef Full Text | Google Scholar

Ballesteros, G., Redondo, J., Ringwald, A., and Tamarit, C. (2017a). Unifying inflation with the axion, dark matter, baryogenesis and the seesaw mechanism. Phys. Rev. Lett. 118:071802. doi: 10.1103/PhysRevLett.118.071802

PubMed Abstract | CrossRef Full Text | Google Scholar

Ballesteros, G., Redondo, J., Ringwald, A., and Tamarit, C. (2017b). Standard model–axion–seesaw–Higgs portal inflation. Five problems of particle physics and cosmology solved in one stroke. JCAP 1708:001. doi: 10.1088/1475-7516/2017/08/001

CrossRef Full Text | Google Scholar

Barbon, J. L. F., and Espinosa, J. R. (2009). On the naturalness of Higgs inflation. Phys. Rev. D 79:081302. doi: 10.1103/PhysRevD.79.081302

CrossRef Full Text | Google Scholar

Barr, S. M. (1984). Solving the strong CP problem without the Peccei-Quinn symmetry. Phys. Rev. Lett. 53:329. doi: 10.1103/PhysRevLett.53.329

CrossRef Full Text | Google Scholar

Baumann, D., Green, D., and Wallisch, B. (2018). Searching for light relics with large-scale structure. JCAP 1808:029. doi: 10.1088/1475-7516/2018/08/029

CrossRef Full Text | Google Scholar

Bednyakov, A. V., Kniehl, B. A., Pikelner, A. F., and Veretin, O. L. (2015). Stability of the electroweak vacuum: gauge independence and advanced precision. Phys. Rev. Lett. 115:201802. doi: 10.1103/PhysRevLett.115.201802

PubMed Abstract | CrossRef Full Text | Google Scholar

Ben-Dayan, I., and Einhorn, M. B. (2010). Supergravity Higgs inflation and shift symmetry in electroweak theory. JCAP 1012:002. doi: 10.1088/1475-7516/2010/12/002

CrossRef Full Text | Google Scholar

Berezhiani, Z. G., Sakharov, A. S., and Khlopov, M. Y. (1992). Primordial background of cosmological axions. Sov. J. Nucl. Phys. 55, 1063–1071.

Google Scholar

Bezrukov, F., and Shaposhnikov, M. (2014). Higgs inflation at the critical point. Phys. Lett. B 734, 249–254. doi: 10.1016/j.physletb.2014.05.074

CrossRef Full Text | Google Scholar

Bezrukov, F. L., and Shaposhnikov, M. (2008). The standard model Higgs boson as the inflaton. Phys. Lett. B 659, 703–706. doi: 10.1016/j.physletb.2007.11.072

CrossRef Full Text | Google Scholar

Borsanyi, S., Fodor, Z., Guenther, J., Kampert, K.-H., Katz, S. D., Kawanai, T., et al. (2016). Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 539, 69–71. doi: 10.1038/nature20115

PubMed Abstract | CrossRef Full Text | Google Scholar

Boucenna, S. M., Ohlsson, T., and Pernow, M. (2019). A minimal non-supersymmetric SO(10) model with Peccei–Quinn symmetry. Phys. Lett. B 792, 251–257. doi: 10.1016/j.physletb.2019.03.045

CrossRef Full Text | Google Scholar

Boucenna, S. M., and Shafi, Q. (2018). Axion inflation, proton decay and leptogenesis in SU(5) × U(1)_PQ. Phys. Rev. D 97:075012. doi: 10.1103/PhysRevD.97.075012

CrossRef Full Text | Google Scholar

Boutan, C., Jones, M., LaRoque, B. H., Oblath, N. S., Cervantes, R., Du, N., et al. (2018). Piezoelectrically tuned multimode cavity search for axion dark matter. Phys. Rev. Lett. 121:261302. doi: 10.1103/PhysRevLett.121.261302

PubMed Abstract | CrossRef Full Text | Google Scholar

Brun, P., Caldwell, A., Chevalier, L., Dvali, G., Freire, P., Garutti, E., et al. (2019). A new experimental approach to probe QCD axion dark matter in the mass range above 40 μeV. Eur. Phys. J. C 79:186. doi: 10.1140/epjc/s10052-019-6683-x

CrossRef Full Text | Google Scholar

Buchmuller, W., Di Bari, P., and Plumacher, M. (2005). Leptogenesis for pedestrians. Ann. Phys. 315, 305–351. doi: 10.1016/j.aop.2004.02.003

CrossRef Full Text | Google Scholar

Budker, D., Graham, P. W., Ledbetter, M., Rajendran, S., and Sushkov, A. (2014). Proposal for a cosmic axion spin precession experiment (CASPEr). Phys. Rev. X 4:021030. doi: 10.1103/PhysRevX.4.021030

CrossRef Full Text | Google Scholar

Burgess, C. P., Lee, H. M., and Trott, M. (2009). Power-counting and the validity of the classical approximation during inflation. JHEP 0909:103. doi: 10.1088/1126-6708/2009/09/103

CrossRef Full Text | Google Scholar

Buttazzo, D., Degrassi, G., Giardino, P. P., Giudice, G. F., Sala, F., Salvio, A., et al. (2013). Investigating the near-criticality of the Higgs boson. JHEP 1312:089. doi: 10.1007/JHEP12(2013)089

CrossRef Full Text | Google Scholar

Cai, Y., Han, T., Li, T., and Ruiz, R. (2018). Lepton number violation: seesaw models and their collider tests. Front. Phys. 6:40. doi: 10.3389/fphy.2018.00040

CrossRef Full Text | Google Scholar

Caldwell, A., Dvali, G., Majorovits, B., Millar, A., Raffelt, G., Redondo, J., et al. (2017). Dielectric haloscopes: a new way to detect axion dark matter. Phys. Rev. Lett. 118:091801. doi: 10.1103/PhysRevLett.118.091801

PubMed Abstract | CrossRef Full Text | Google Scholar

Calibbi, L., Goertz, F., Redigolo, D., Ziegler, R., and Zupan, J. (2017). Minimal axion model from flavor. Phys. Rev. D 95:095009. doi: 10.1103/PhysRevD.95.095009

CrossRef Full Text | Google Scholar

Casas, J. A., and Ibarra, A. (2001). Oscillating neutrinos and μ → e, γ. Nucl. Phys. B 618, 171–204. doi: 10.1016/S0550-3213(01)00475-8

CrossRef Full Text | Google Scholar

Chang, J. H., Essig, R., and McDermott, S. D. (2018). Supernova 1987A constraints on sub-GeV dark sectors, millicharged particles, the QCD axion, and an axion-like particle. J. High Energy Phys. 2018:51. doi: 10.1007/JHEP09(2018)051

CrossRef Full Text | Google Scholar

Chikashige, Y., Mohapatra, R. N., and Peccei, R. D. (1981). Are there real goldstone bosons associated with broken Lepton number? Phys. Lett. B 98, 265–268.

Google Scholar

Choudhury, S., Chakraborty, T., and Pal, S. (2014). Higgs inflation from new Kähler potential. Nucl. Phys. B 880, 155–174. doi: 10.1016/j.nuclphysb.2014.01.002

CrossRef Full Text | Google Scholar

Chung, W. (2018). CULTASK, axion experiment at CAPP in Korea. doi: 10.3204/DESY-PROC-2017-02/woohyun_chung

CrossRef Full Text | Google Scholar

Clarke, J. D., and Volkas, R. R. (2016). Technically natural nonsupersymmetric model of neutrino masses, baryogenesis, the strong CP problem, and dark matter. Phys. Rev. D 93:035001. doi: 10.1103/PhysRevD.93.035001

CrossRef Full Text | Google Scholar

Dafni, T., O'Hare, C. A. J., Lakic, B., Galán, J., Iguaz, F. J., Irastorza, I. G., et al. (2019). Weighing the solar axion. Phys. Rev. D 99:035037. doi: 10.1103/PhysRevD.99.035037

CrossRef Full Text | Google Scholar

Di Luzio, L., and Mihaila, L. (2013). Unification scale vs. electroweak-triplet mass in the SU(5)+24_F model at three loops. Phys. Rev. D 87:115025. doi: 10.1103/PhysRevD.87.115025

CrossRef Full Text | Google Scholar

Di Luzio, L., Ringwald, A., and Tamarit, C. (2018). Axion mass prediction from minimal grand unification. Phys. Rev. D 98:095011. doi: 10.1103/PhysRevD.98.095011

CrossRef Full Text | Google Scholar

Di Vecchia, P., and Veneziano, G. (1980). Chiral dynamics in the large n limit. Nucl. Phys. B 171, 253–272. doi: 10.1016/0550-3213(80)90370-3

CrossRef Full Text | Google Scholar

Dias, A. G., Machado, A. C. B., Nishi, C. C., Ringwald, A., and Vaudrevange, P. (2014). The quest for an intermediate-scale accidental axion and further ALPs. JHEP 1406:037. doi: 10.1007/JHEP06(2014)037

CrossRef Full Text | Google Scholar

Dine, M., and Fischler, W. (1983). The not so harmless axion. Phys. Lett. B 120, 137–141.

Google Scholar

Dine, M., Fischler, W., and Srednicki, M. (1981). A simple solution to the strong CP problem with a harmless axion. Phys. Lett. B 104, 199–202. doi: 10.1016/0370-2693(81)90590-6

CrossRef Full Text | Google Scholar

Dokuchaev, V. I., Eroshenko, Y. N., and Tkachev, I. I. (2017). Destruction of axion miniclusters in the galaxy. J. Exp. Theor. Phys. 125:434. doi: 10.1134/S1063776117080039

CrossRef Full Text | Google Scholar

Dorsner, I., and Fileviez Perez, P. (2005). How long could we live? Phys. Lett. B 625:88. doi: 10.1016/j.physletb.2005.08.039

CrossRef Full Text | Google Scholar

Du, N., Force, N., Khatiwada, R., Lentz, E., Ottens, R., Rosenberg, L. J., et al. (2018). A search for invisible axion dark matter with the axion dark matter experiment. Phys. Rev. Lett. 120:151301. doi: 10.1103/PhysRevLett.120.151301

PubMed Abstract | CrossRef Full Text | Google Scholar

Elias-Miro, J., Espinosa, J. R., Giudice, G. F., Lee, H. M., and Strumia, A. (2012). Stabilization of the electroweak vacuum by a scalar threshold effect. JHEP 1206:031. doi: 10.1007/JHEP06(2012)031

CrossRef Full Text | Google Scholar

Ema, Y., Hamaguchi, K., Moroi, T., and Nakayama, K. (2017). Flaxion: a minimal extension to solve puzzles in the standard model. JHEP 1701:096. doi: 10.1007/JHEP01(2017)096

CrossRef Full Text | Google Scholar

Ernst, A., Ringwald, A., and Tamarit, C. (2018). Axion predictions in SO(10) × U(1)_PQ models. JHEP 1802:103. doi: 10.1007/JHEP02(2018)103

CrossRef Full Text | Google Scholar

Fairbairn, M., Hogan, R., and Marsh, D. J. E. (2015). Unifying inflation and dark matter with the Peccei-Quinn field: observable axions and observable tensors. Phys. Rev. D 91:023509. doi: 10.1103/PhysRevD.91.023509

CrossRef Full Text | Google Scholar

Fairbairn, M., Marsh, D. J. E., and Quevillon, J. (2017). Searching for the QCD axion with gravitational microlensing. Phys. Rev. Lett. 119:021101. doi: 10.1103/PhysRevLett.119.021101

PubMed Abstract | CrossRef Full Text | Google Scholar

Fairbairn, M., Marsh, D. J. E., Quevillon, J., and Rozier, S. (2018). Structure formation and microlensing with axion miniclusters. Phys. Rev. D 97:083502. doi: 10.1103/PhysRevD.97.083502

CrossRef Full Text | Google Scholar

Fischer, T., Chakraborty, S., Giannotti, M., Mirizzi, A., Payez, A., and Ringwald, A. (2016). Probing axions with the neutrino signal from the next galactic supernova. Phys. Rev. D 94:085012. doi: 10.1103/PhysRevD.94.085012

CrossRef Full Text | Google Scholar

Fritzsch, H., and Minkowski, P. (1975). Unified interactions of leptons and hadrons. Ann. Phys. 93, 193–266. doi: 10.1016/0003-4916(75)90211-0

CrossRef Full Text | Google Scholar

Fukugita, M., and Yanagida, T. (1986). Baryogenesis without grand unification. Phys. Lett. B 174, 45–47.

Google Scholar

Galante, M., Kallosh, R., Linde, A., and Roest, D. (2015). Unity of cosmological inflation attractors. Phys. Rev. Lett. 114:141302. doi: 10.1103/PhysRevLett.114.141302

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia-Cely, C., and Heeck, J. (2017). Neutrino lines from Majoron dark matter. JHEP 1705:102. doi: 10.1007/JHEP05(2017)102

CrossRef Full Text | Google Scholar

Gell-Mann, M., Ramond, P., and Slansky, R. (1979). Complex spinors and unified theories. Conf. Proc. C 790927, 315–321.

Google Scholar

Gelmini, G. B., and Roncadelli, M. (1981). Left-handed neutrino mass scale and spontaneously broken Lepton number. Phys. Lett. B 99, 411–415.

Google Scholar

Georgi, H. (1975). The state of the art–gauge theories. AIP Conf. Proc. 23, 575–582. doi: 10.1063/1.2947450

CrossRef Full Text | Google Scholar

Georgi, H., and Glashow, S. L. (1974). Unity of all elementary particle forces. Phys. Rev. Lett. 32, 438–441. doi: 10.1103/PhysRevLett.32.438

CrossRef Full Text | Google Scholar

Giannotti, M., Irastorza, I. G., Redondo, J., Ringwald, A., and Saikawa, K. (2017). Stellar recipes for axion hunters. JCAP 1710:010. doi: 10.1088/1475-7516/2017/10/010

CrossRef Full Text | Google Scholar

Giudice, G. F., Notari, A., Raidal, M., Riotto, A., and Strumia, A. (2004). Towards a complete theory of thermal Leptogenesis in the SM and MSSM. Nucl. Phys. B 685, 89–149. doi: 10.1016/j.nuclphysb.2004.02.019

CrossRef Full Text | Google Scholar

Gong, J. O., Lee, H. M., and Kang, S. K. (2012). Inflation and dark matter in two Higgs doublet models. JHEP 1204:128. doi: 10.1007/JHEP04(2012)128

CrossRef Full Text | Google Scholar

Gorbunov, D., and Tokareva, A. (2013). R²-inflation with conformal SM Higgs field. JCAP 1312:021. doi: 10.1088/1475-7516/2013/12/021

CrossRef Full Text | Google Scholar

Gorghetto, M., Hardy, E., and Villadoro, G. (2018). Axions from strings: the attractive solution. JHEP 1807:151. doi: 10.1007/JHEP07(2018)151

CrossRef Full Text | Google Scholar

Gorghetto, M., and Villadoro, G. (2019). Topological susceptibility and QCD axion mass: QED and NNLO corrections. JHEP 1903:033. doi: 10.1007/JHEP03(2019)033

CrossRef Full Text | Google Scholar

Graham, P. W., Kaplan, D. E., and Rajendran, S. (2015). Cosmological relaxation of the electroweak scale. Phys. Rev. Lett. 115:221801. doi: 10.1103/PhysRevLett.115.221801

PubMed Abstract | CrossRef Full Text | Google Scholar

Grilli di Cortona, G., Hardy, E., Pardo Vega, J., and Villadoro, G. (2016). The QCD axion, precisely. JHEP 1601:034. doi: 10.1007/JHEP01(2016)034

CrossRef Full Text | Google Scholar

Gupta, R. S., Reiness, J. Y., and Spannowsky, M. (2019). All-in-one Relaxion, a unified solution to five BSM puzzles. arXiv:1902.08633.

Google Scholar

Hamada, Y., Kawai, H., Oda, K. Y., and Park, S. C. (2014). Higgs Inflation is Still Alive after the Results from BICEP2. Phys. Rev. Lett. 112:241301. doi: 10.1103/PhysRevLett.112.241301

PubMed Abstract | CrossRef Full Text | Google Scholar

Holman, R., Lazarides, G., and Shafi, Q. (1983). Axions and the dark matter of the universe. Phys. Rev. D 27:995. doi: 10.1103/PhysRevD.27.995

CrossRef Full Text | Google Scholar

Irastorza, I. G., and Redondo, J. (2018). New experimental approaches in the search for axion-like particles. Prog. Part. Nucl. Phys. 102, 89–159. doi: 10.1016/j.ppnp.2018.05.003

CrossRef Full Text | Google Scholar

Iwazaki, A. (2015). Axion stars and fast radio bursts. Phys. Rev. D 91:023008. doi: 10.1103/PhysRevD.91.023008

CrossRef Full Text | Google Scholar

Jackson Kimball, D. F., Afach, S., Aybas, D., Blanchard, J. W., Budker, D., Centers, G., et al. (2017). Overview of the cosmic axion spin precession experiment (CASPEr). arXiv:1711.08999.

Google Scholar

Jaeckel, J., and Thormaehlen, L. J. (2019). Distinguishing axion models with IAXO. J. Cosmol. Astropart. Phys. 2019:39. doi: 10.1088/1475-7516/2019/03/039

CrossRef Full Text | Google Scholar

Kahn, Y., Safdi, B. R., and Thaler, J. (2016). Broadband and resonant approaches to axion dark matter detection. Phys. Rev. Lett. 117:141801. doi: 10.1103/PhysRevLett.117.141801

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz, A., Kopp, J., Sibiryakov, S., and Xue, W. (2018). Femtolensing by dark matter revisited. JCAP 1812:005. doi: 10.1088/1475-7516/2018/12/005

CrossRef Full Text | Google Scholar

Kawasaki, M., Saikawa, K., and Sekiguchi, T. (2015). Axion dark matter from topological defects. Phys. Rev. D 91:065014. doi: 10.1103/PhysRevD.91.065014

CrossRef Full Text | Google Scholar

Kehagias, A., Moradinezhad Dizgah, A., and Riotto, A. (2014). Remarks on the Starobinsky model of inflation and its descendants. Phys. Rev. D 89:043527. doi: 10.1103/PhysRevD.89.043527

CrossRef Full Text | Google Scholar

Kim, J. E. (1979). Weak interaction singlet and strong CP invariance. Phys. Rev. Lett. 43:103.

Google Scholar

Klaer, V. B., and Moore, G. D. (2017). The dark-matter axion mass. JCAP 1711:049. doi: 10.1088/1475-7516/2017/11/049

CrossRef Full Text | Google Scholar

Klaer, V. B., and Moore, G. D. (2017). How to simulate global cosmic strings with large string tension. JCAP 1710:043. doi: 10.1088/1475-7516/2017/10/043

CrossRef Full Text | Google Scholar

Kofman, L., Linde, A. D., and Starobinsky, A. A. (1997). Towards the theory of reheating after inflation. Phys. Rev. D 56, 3258–3295. doi: 10.1103/PhysRevD.56.3258

CrossRef Full Text | Google Scholar

Kolb, E. W., and Tkachev, I. I. (1993). Axion miniclusters and Bose stars. Phys. Rev. Lett. 71, 3051–3054. doi: 10.1103/PhysRevLett.71.3051

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolb, E. W., and Tkachev, I. I. (1994). Large amplitude isothermal fluctuations and high density dark matter clumps. Phys. Rev. D 50, 769–773. doi: 10.1103/PhysRevD.50.769

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolb, E. W., and Tkachev, I. I. (1996). Femtolensing and picolensing by axion miniclusters. Astrophys. J. 460:L25. doi: 10.1086/309962

CrossRef Full Text | Google Scholar

Langacker, P., Peccei, R. D., and Yanagida, T. (1986). Invisible axions and light neutrinos: are they connected? Mod. Phys. Lett. A 1:541. doi: 10.1142/S0217732386000683

CrossRef Full Text | Google Scholar

Lebedev, O. (2012). On stability of the electroweak vacuum and the Higgs portal. Eur. Phys. J. C 72:2058. doi: 10.1140/epjc/s10052-012-2058-2

CrossRef Full Text | Google Scholar

Leutwyler, H., and Smilga, A. V. (1992). Spectrum of Dirac operator and role of winding number in QCD. Phys. Rev. D 46, 5607–5632. doi: 10.1103/PhysRevD.46.5607

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsumura, T., Akiba, Y., Borrill, J., Chinone, Y., Dobbs, M., Fuke, H., et al. (2014). Mission design of LiteBIRD. J. Low. Temp. Phys. 176, 733–740. doi: 10.1007/s10909-013-0996-1

CrossRef Full Text | Google Scholar

Melcón, A. Á., Cuendisb, S. A., Cogollosc, C., Díaz-Morcilloa, A., Döbrichb, B., Gallego, J. D., et al. (2018). Axion searches with microwave filters: the RADES project. JCAP 1805:040. doi: 10.1088/1475-7516/2018/05/040

CrossRef Full Text | Google Scholar

Mikheyev, S. P., and Smirnov, A. Y. (1985). Resonance amplification of oscillations in matter and spectroscopy of solar neutrinos. Sov. J. Nucl. Phys. 42, 913–917.

Google Scholar

Minkowski, P. (1977). μ → eγ at a rate of one out of 10⁹ muon decays? Phys. Lett. B 67, 421–428.

Google Scholar

Mohapatra, R. N., and Senjanovic, G.. (1980) Neutrino mass spontaneous parity violation. Phys. Rev. Lett. 44:912.

Google Scholar

Mohapatra, R. N., and Senjanovic, G. (1983). The superlight axion and neutrino masses. Z. Phys. C 17, 53–56. doi: 10.1007/BF01577819

CrossRef Full Text | Google Scholar

Morris, D. E. (1984). An Electromagnetic Detector For Relic Axions. doi: 10.2172/6446664

CrossRef Full Text | Google Scholar

Nardi, E., and Roulet, E. (1990). Are exotic stable quarks cosmologically allowed? Phys. Lett. B 245, 105–110. doi: 10.1016/0370-2693(90)90172-3

CrossRef Full Text | Google Scholar

Nelson, A. E. (1984). Naturally weak CP violation. Phys. Lett. B 136, 387–391. doi: 10.1016/0370-2693(84)92025-2

CrossRef Full Text | Google Scholar

Pallis, C. (2017). Linking Starobinsky-type inflation in no-scale supergravity to MSSM. JCAP 1404:024. doi: 10.1088/1475-7516/2014/04/024

CrossRef Full Text | Google Scholar

Pallis, C. (2018a). Gravitational waves, μ term and leptogenesis from B−L Higgs inflation in supergravity. Universe 4:13. doi: 10.3390/universe4010013

CrossRef Full Text | Google Scholar

Pallis, C. (2018b). B−L Higgs inflation in supergravity with several consequences. PoS CORFU 2017:086. doi: 10.22323/1.318.0086

CrossRef Full Text | Google Scholar

Pallis, C., and Shafi, Q. (2018). Induced-gravity GUT-scale Higgs inflation in supergravity. Eur. Phys. J. C 78:523. doi: 10.1140/epjc/s10052-018-5980-0

CrossRef Full Text | Google Scholar

Peccei, R. D., and Quinn, H. R. (1977). CP conservation in the presence of instantons. Phys. Rev. Lett. 38, 1440–1443.

Google Scholar

Perez, K., Ng, K. C. Y., Beacom, J. F., Hersh, C., Horiuchi, S., and Krivonos, R. (2017). Almost closing the νMSM sterile neutrino dark matter window with NuSTAR. Phys. Rev. D 95:123002. doi: 10.1103/PhysRevD.95.123002

CrossRef Full Text | Google Scholar

Pi, S. Y. (1984). Inflation without tears. Phys. Rev. Lett. 52, 1725–1728. doi: 10.1103/PhysRevLett.52.1725

CrossRef Full Text | Google Scholar

Pilaftsis, A. (1994). Astrophysical and terrestrial constraints on singlet Majoron models. Phys. Rev. D 49, 2398–2404. doi: 10.1103/PhysRevD.49.2398

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilaftsis, A., and Underwood, T. E. J. (2004). Resonant leptogenesis. Nucl. Phys. B 692, 303–345. doi: 10.1016/j.nuclphysb.2004.05.029

CrossRef Full Text | Google Scholar

Preskill, J., Wise, M. B., and Wilczek, F. (1983). Cosmology of the invisible axion. Phys. Lett. B 120, 127–132.

Google Scholar

Raffelt, G. G. (2008). Astrophysical axion bounds. Lect. Notes Phys. 741, 51–71. doi: 10.1007/978-3-540-73518-2_3

CrossRef Full Text | Google Scholar

Ringwald, A., and Saikawa, K. (2016). Axion dark matter in the post-inflationary Peccei-Quinn symmetry breaking scenario. Phys. Rev. D 93:085031. doi: 10.1103/PhysRevD.93.085031

CrossRef Full Text | Google Scholar

Ruiz, R. (2015). QCD corrections to pair production of type III seesaw leptons at Hadron colliders. JHEP 1512:165. doi: 10.1007/JHEP12(2015)165

CrossRef Full Text | Google Scholar

Rybka, G., Wagner, A., Brill, A., Ramos, K., Percival, R., and Patel, K. (2015). Search for dark matter axions with the Orpheus experiment. Phys. Rev. D 91:011701. doi: 10.1103/PhysRevD.91.011701

CrossRef Full Text | Google Scholar

Salopek, D. S., Bond, J. R., and Bardeen, J. M. (1989). Designing density fluctuation spectra in inflation. Phys. Rev. D 40, 1753–1788. doi: 10.1103/PhysRevD.40.1753

PubMed Abstract | CrossRef Full Text | Google Scholar

Salvio, A. (2015). A simple motivated completion of the standard model below the Planck scale: axions and right-handed neutrinos. Phys. Lett. B 743, 428–434. doi: 10.1016/j.physletb.2015.03.015

CrossRef Full Text | Google Scholar

Salvio, A. (2019). Critical Higgs inflation in a viable motivated model. Phys. Rev. D 99:015037. doi: 10.1103/PhysRevD.99.015037

CrossRef Full Text | Google Scholar

Schechter, J., and Valle, J. W. F. (1982). Neutrino decay and spontaneous violation of Lepton number. Phys. Rev. D 25:774.

Google Scholar

Schneider, A. (2016). Astrophysical constraints on resonantly produced sterile neutrino dark matter. JCAP 1604:059. doi: 10.1088/1475-7516/2016/04/059

CrossRef Full Text | Google Scholar

Shifman, M. A., Vainshtein, A. I., and Zakharov, V. I. (1980). Can confinement ensure natural CP invariance of strong interactions? Nucl. Phys. B 166, 493–506.

Google Scholar

Shin, M. (1987). Light neutrino masses and strong CP problem. Phys. Rev. Lett. 59, 2515–2518. 10.1103/PhysRevLett.59.2515

PubMed Abstract | Google Scholar

Shuve, B., and Tamarit, C. (2017). Phase transitions and Baryogenesis from decays. JHEP 1710:122. doi: 10.1007/JHEP10(2017)122

CrossRef Full Text | Google Scholar

Sikivie, P. (1982). Of axions, domain walls and the early universe. Phys. Rev. Lett. 48, 1156–1159. doi: 10.1103/PhysRevLett.48.1156

CrossRef Full Text | Google Scholar

Sirunyan, A. M., Tumasyan, A., Adam, W., Ambrogi, F., Asilar, E., Bergauer, T., et al. (2017). Search for evidence of the type-III seesaw mechanism in multilepton final states in proton-proton collisions at $\sqrt{s}=13\text{ TeV}$. Phys. Rev. Lett. 119:221802. doi: 10.1103/PhysRevLett.119.221802

CrossRef Full Text | Google Scholar

Starobinsky, A. A. (1980). A new type of isotropic cosmological models without singularity. Phys. Lett. B 91, 99–102. doi: 10.1016/0370-2693(80)90670-X

CrossRef Full Text | Google Scholar

Tanabashi, M., Hagiwara, K., Hikasa, K., Nakamura, K., Sumino, Y., Takahashi, F., et al. (2018). Review of particle physics. Phys. Rev. D 98:030001. doi: 10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

Tegmark, M., Aguirre, A., Rees, M., and Wilczek, F. (2006). Dimensionless constants, cosmology and other dark matters. Phys. Rev. D 73:023505. doi: 10.1103/PhysRevD.73.023505

CrossRef Full Text | Google Scholar

Tkachev, I., Khlebnikov, S., Kofman, L., and Linde, A. D. (1998). Cosmic strings from preheating. Phys. Lett. B 440, 262–268. doi: 10.1016/S0370-2693(98)01094-6

CrossRef Full Text | Google Scholar

Tkachev, I. I. (2015). Fast radio bursts and axion miniclusters. JETP Lett. 101:1. doi: 10.1134/S0021364015010154

CrossRef Full Text | Google Scholar

Vafa, C., and Witten, E. (1984). Parity conservation in QCD. Phys. Rev. Lett. 53:535. doi: 10.1103/PhysRevLett.53.535

CrossRef Full Text | Google Scholar

Vaquero, A., Redondo, J., and Stadler, J. (2018). Early seeds of axion miniclusters. JCAP 4:012. doi: 10.1088/1475-7516/2019/04/012

CrossRef Full Text | Google Scholar

Visinelli, L., Baum, S., Redondo, J., Freese, K., and Wilczek, F. (2018). Dilute and dense axion stars. Phys. Lett. B 777, 64–72. doi: 10.1016/j.physletb.2017.12.010

CrossRef Full Text | Google Scholar

Volkas, R. R., Davies, A. J., and Joshi, G. C. (1988). Naturalness of the invisible axion model. Phys. Lett. B 215, 133–138. doi: 10.1016/0370-2693(88)91084-2

CrossRef Full Text | Google Scholar

Weinberg, S. (1978). A new light boson? Phys. Rev. Lett. 40:223.

Google Scholar

Wilczek, F. (1978). Problem of strong p and t invariance in the presence of instantons. Phys. Rev. Lett. 40, 279–282.

Google Scholar

Wise, M. B., Georgi, H., and Glashow, S. L. (1981). SU(5) and the invisible axion. Phys. Rev. Lett. 47, 402–404. doi: 10.1103/PhysRevLett.47.402

CrossRef Full Text | Google Scholar

Wolfenstein, L. (1978). Neutrino oscillations in matter. Phys. Rev. D 17:2369. doi: 10.1103/PhysRevD.17.2369

CrossRef Full Text | Google Scholar

Wolfenstein, L. (1979). Neutrino oscillations and stellar collapse. Phys. Rev. D 20, 2634–2635. doi: 10.1103/PhysRevD.20.2634

CrossRef Full Text | Google Scholar

Yanagida, T. (1979). Horizontal symmetry and masses of neutrinos. Conf. Proc. C 7902131:95.

Google Scholar

Zhitnitsky, A. R. (1980). On possible suppression of the axion hadron interactions. Sov. J. Nucl. Phys. 31:260.

Google Scholar

Zhong, L., Al Kenany, S., Backes, K. M., Brubaker, B. M., Cahn, S. B., Carosi, G., et al. (2018). Results from phase 1 of the HAYSTAC microwave cavity axion experiment. Phys. Rev. D 97:092001. doi: 10.1103/PhysRevD.97.092001

CrossRef Full Text | Google Scholar

Zurek, K. M., Hogan, C. J., and Quinn, T. R. (2007). Astrophysical effects of scalar dark matter miniclusters. Phys. Rev. D 75:043511. doi: 10.1103/PhysRevD.75.043511

CrossRef Full Text | Google Scholar