Challenges in 2D Stellar Modeling

1. Introduction

The standard technique for modeling stars takes a 1-dimensional approach, and assumes the stars are relatively close to spherical. However, a large number of stars, especially high mass stars, are known to be rapid rotators (Huang and Gies, 2006; Huang et al., 2010), which breaks the spherical symmetry. In addition, a large fraction of stars are members of binary or multiple star systems, which can introduce tidal distortion. This distortion in surface shape and resulting variation in effective temperature has now been measured interferometrically for a number of stars (van Belle et al., 2001, 2006; Domiciano de Souza et al., 2003; Aufdenberg et al., 2006; Peterson et al., 2006; Monnier et al., 2007; Zhao et al., 2009; Che et al., 2011). To reproduce the observations requires 2D models of stars.

The effects of distortion are also becoming important as recent space missions like Kepler, CoRoT, MOST, BRITE, and TESS allow us to measure pulsation frequencies with very high precision over long times. These more precise frequencies make it easier to measure the effects of rotation and other distorting effects on the pulsation frequencies of the stars. Advances in spectropolarimetry have also given us a wealth of information on the magnetic fields of stars other than the Sun (Grunhut et al., 2017), which has triggered a number of new studies on the effects of magnetic fields on stellar evolution (Keszthelyi et al., 2018). As a result of these advances, it is becoming ever more important to improve our stellar models to be able to account for these multi-dimensional effects.

In the most general case, a static stellar structure model must obey four basic equations: Poisson's equation:

$\begin{array}{ll}{\nabla }^2\varphi =4\pi G\rho & (1)\end{array}$

where ϕ is the gravitational potential and ρ is the density; mass conservation:

$\begin{array}{ll}\nabla ·(\rho \text{v})=0& (2)\end{array}$

where v is the fluid velocity; the momentum equation:

$\begin{array}{ll}\rho \text{v}·\nabla \text{v}=-\nabla P-\rho \nabla \varphi +{\text{F}}_{\text{v}}& (3)\end{array}$

where P is the pressure and F_v is the viscous force; and an entropy (or energy) equation:

$\begin{array}{ll}\rho T\text{v}·\nabla S=-\nabla \text{F}+{ϵ}_{*}& (4)\end{array}$

where S is the entropy, T is the temperature, F is the heat flux, and ϵ_* is the energy generation rate. This set of equations, combined with an equation of state and prescriptions for F and F_v fully define the behavior of the gas in the stellar interior, and are applicable for any rotation law.

Rather than use the full equations of fluid dynamics above, another approach uses the Roche approximation to get the pressure gradient:

$\begin{array}{ll}\frac{1}{\rho }\nabla P=-\nabla \varphi +\frac{1}{2}{\Omega }^2{(rsin\theta )}^2& (5)\end{array}$

where ϕ is the gravitational potential, unmodified by rotation. This gives a purely radial gravitational acceleration g = ∇ϕ. Very little is known about the internal rotation profiles of stars, but arguments are often in favor of either cylindrical or shellular rotation laws. For conservative rotation laws like these, where Ω depends only on the distance from the rotation axis (cylinderical) or center of the star (shellular), the centrifugal acceleration can be derived from an effective potential V. Indeed, if the rotation is not conservative, it is impossible to define an effective potential, and it is not clear how the total potential should be determined. For conservative rotation laws, the centrifugal acceleration, potential, and rotation rate are all functions of the distance from the rotation axis, ϖ = r sin θ and the total potential is given by Φ = ϕ + V. This potential still follows Poisson's equation, so ∇²Φ = ∇²ϕ + ∇²V. For conservative rotation laws, ∇²V = −2Ω², so the total potential is given by ∇²Φ = 4πGρ − 2Ω², and the equation of hydrostatic equilibrium becomes:

$\begin{array}{ll}\frac{1}{\rho }\nabla P=-\nabla \Phi ={\text{g}}_{\text{eff}}.& (6)\end{array}$

The other equations of stellar structure must be written in 2D in the presence of rotation or other distortion, but the equations themselves take the same form as in the 1D case.

In 1D models, the equations can easily be written in terms of mass instead of radius. In 2D models, this is not generally possible. In the case of shellular rotation (Zahn, 1992), the radius is associated with isobars, and since most quantities are constant on isobars, the problem becomes a pseudo-1D calculation, and the equations can be written in terms of the mass as for the non-rotating case. For a fully 2D calculation, the mass inside a spherical shell of radius r is difficult to define, and is less useful as a coordinate. In general, 2D calculations either use the radius r and colatitude θ as coordinates, or map these coordinates to spheroidal coordinates r(ζ, θ).

As in the 1D problem, 2D models of stellar structure must apply boundary conditions at the surface, but in 2D, it is more difficult to determine what the appropriate conditions are. In 1D, the mass is used as the coordinate, and the surface is given by the radius where the enclosed mass is equal to the total mass of the star. As discussed above, in 2D the radius and colatitude (or some mapping of these variables) is used, and it is difficult to define the mass inside a radius r since the density is a function of colatitude θ as well. Some other method must be used to determine the radius at the surface of the star. Generally it is assumed that the surface of the star is an equipotential (Deupree, 1990; Maeder and Meynet, 2012; Espinosa Lara and Rieutord, 2013), but this still leaves the problem of how the location of the equipotential is determined.

When stars are not spherically symmetric the surface becomes distorted, the temperature varies with colatitude (discussed below) and this introduces large-scale meridional currents. The best-known of these is the meridional circulation introduced by rotation, but tidal or magnetic distortions can also introduce flows (Tassoul, 1978). These currents are expected to be slow, with theoretical velocities on the order of 3 × 10⁻¹⁰ cm s⁻¹ (Sweet, 1950). Despite the slow velocities, they are a significant source of mixing within the star. For shellular rotation laws, the effective chemical diffusion depends on the square of the velocity of the meridional circulation, so the contribution to chemical mixing is expected to be small in most cases (Zahn, 1992). The angular momentum transport is governed by an advection diffusion equation which can be horizontally averaged in the case of shellular rotation to give:

$\begin{array}{ll}\rho \frac{d}{dt}\left(\rho r^2\bar{\Omega }\right)=\frac{1}{5r^2}\frac{\partial }{\partial r}\left(\rho r^{4}U\left(r\right)\frac{\partial \bar{\Omega }}{\partial r}\right)+\frac{1}{r^2}\frac{\partial }{\partial r}\left(\rho D{r}^4\frac{\partial \bar{\Omega }}{\partial r}\right)& (7)\end{array}$

where $\bar{\Omega }$ is the horizontally averaged angular rotation rate, U(r) is the radial velocity of the meridional circulation, and D is the total vertical diffusion due to all transport mechanisms (Zahn, 1992; Ekström et al., 2012). However, because the velocity of the meridional circulation is so slow, it is very difficult to model these flows self-consistently on an evolutionary time scale.

Indeed, one of the biggest challenges to 2D modeling is the variety of timescales involved. To model the meridional flows or the details of internal convection requires high resolution simulations with short time steps, but these requirements are not possible with the computational power currently available. Modeling of multidimensional stars has so far taken two approaches: either to model the detailed structure and ignore the longer evolution timescales; or to neglect many of the internal processes and model the evolutionary timescales. However, unless we can find good models for the internal processes, the evolution problem is not completely separable from the short timescale simulations. To fully understand the evolution of distorted stars, we will need to understand how both angular momentum and internal composition gradients are transported through convection and turbulence, how the distortion affects radiatively driven winds and subsequent angular momentum loss, and the influence of magnetic fields.

In this review, I discuss some of the recent progress in modeling the structure, evolution, and pulsation frequencies of stars in 2D in section 2. In section 3 I summarize the effects of rotation on stellar evolution, highlighting the importance of 2D modeling. In section 4 I briefly discuss 2D modeling of binary stars, and in section 5 I discuss the challenges that 2D modeling still faces. A brief summary is presented in section 6.

2. A Brief History of 2D Modeling

2.1. Stellar Modeling

The first attempts to model stellar structure in 2D were performed by Sweet and Roy (1953), using first order perturbations to Cowling models. They assume that the stars were uniformly rotating, so that the total effective potential is given by ∇²Φ = −4πGρ + 2Ω². They then introduce the dimensionless variable $\lambda ={\Omega }^2/2\pi G{\rho }_c(0)$, where ρ_c(0) is the central density of the non-rotating star. All of the structure equations can then be expanded as a power series in λ. This method only worked for slowly rotating stars, or the perturbations become too large for the method to apply.

More realistic models were developed by Roxburgh et al. (1965), which divided the star into two regions. The innermost region, which contained most of the mass, was treated as spherical, while the outer, low density region is allowed to deform. This works since the innermost region is relatively unaffected by rotation, while the gravitational potential in the low density region depends primarily on the potential due to the inner region, which is approximately a Roche potential. Once the potential is known, the other structure equations can be integrated as for 1D stars. This method was found to work best for uniformly rotating stars.

Two dimensional static models have also been produced using the self-consistent field (SCF) method (Ostriker and Mark, 1968), later extended by Jackson (1970). This method uses an iterative approach to solve the equations of hydrostatic equilibrium and the gravitational potential to determine the stellar structure. Early implementations encountered convergence problems for stars below 9 M_⊙, limiting the applicability. Later implementations reformulated the method, and were able to avoid this problem (Jackson et al., 2005; MacGregor et al., 2007).

Eriguchi (1978) calculated the structure of rotating polytropes by transforming the equations of stellar structure to a complex plane. This work was expanded to include relativistic polytropes (Eriguchi, 1980), non-axisymmetric polytropes (Hachisu et al., 1982) and binary systems (Hachisu and Eriguchi, 1984a,b). However, this method still faced many limitations. In particular, the method breaks down if there are any discontinuities in the physical properties inside the star. Such discontinuities can be caused by a change in the composition or ionization state, which means this method cannot be used to study evolution.

However, Eriguchi and Sugimoto (1981) came up with another method, this time mapping the equation of hydrostatic equilibrium and Poisson's equation onto a 2D grid such that r_ij = r_i(θ_j). This allows the radial grid to adjust to the shape of the star at each angle. Using this method, it is possible to calculate the structure for a number of rapidly rotating, axisymmetric polytropes (Eriguchi and Sugimoto, 1981; Eriguchi and Mueller, 1985). The method can also be extended to piece-wise polytropes, which can then be used to approximate the structure of real stars.

A different approach to solving the equations of stellar structure used a 2D finite difference technique (Clement, 1974, 1978, 1979, 1994) on a 2D grid in colatitude θ and total potential. Rather than radius, the equations are rewritten to relate the mass and volume of the star, with the constraint that in the outermost zone, the enclosed mass must equal the total mass of the star. This technique was still limited to relatively slowly rotating stars, and is restricted to equilibrium models.

In recent years, 2D hydrostatic models have been calculated for use in asteroseismology (Roxburgh, 2004, 2006). These models use spectral methods to model the angular dependence of the physical quantities, and depend on knowing the density along one particular angle as a reference point. In this way, the density profile produced by 1D models that assumes shellular rotation can be expanded to provide a 2D hydrostatic model as input to stellar pulsation codes. This technique is important since several 2D codes have been developed in recent years to calculate stellar pulsation frequencies (Lignières et al., 2006; Reese et al., 2006; Ouazzani et al., 2012).

The first 2D evolution calculations with no theoretical rotation limit were performed by Deupree using ROTORC (Deupree, 1990, 1995, 1998). This code uses the fractional radius and the colatitude θ as the independent variables. One colatitude (typically the equator) is chosen to be a reference colatitude, and the surface location there has a fractional radius of 1. This defines the potential at the surface, and at each angle, the surface is defined to be the radial zone with the total potential closest to the value of the reference potential. Once the structure of the star is determined, the radius at the equator is determined by integrating over the density and requiring the total to equal the total mass of the star. In this way, the surface deformation caused by rotation can be modeled without including assumptions like von Zeipel's law (von Zeipel, 1924).

The ESTER code (Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016) has been developed to model the internal processes of a rapidly rotating star in two dimensions. They use a modified coordinate system which can adapt to the shape of the star. These spheroidal coordinates (ζ, θ) are scaled such that ζ = 1 at the stellar surface, and then divide the star into several discrete radial domains. The transformation from spherical to spheroidal coordinates is given by:

$\begin{array}{lll}r& =& a_i\zeta +A_i(\zeta )\left[R_{i+1}(\theta )-a_i{\eta }_{i+1}\right]+B_i(\zeta )\left[R_i(\theta )-a_i{\eta }_i\right]\\ & & {\eta }_i\le \zeta \le {\eta }_{i+1}& (8)\end{array}$

where B_i(ζ) = 1 − A_i(ζ), and R_i+1 and R_i are the inner and outer boundaries of the domain. The functions A_i(ζ) and a_i are chosen to satisfy properties at the boundaries between the domains. Each of the radial domains is discretized into a spectral grid, so the horizontal dependence is expanded in terms of spherical harmonics. However, this code focuses on the shorter time-scale processes like meridonial circulation, rather than attempting to model the long-term evolution of a star.

A new code under development, 2DStars (Halabi et al., 2017) is intended to solve the stellar structure equations in 2D, assuming an axisymmetric geometry. Development of this code is still in the very preliminary stages, but if successful, it will be able to model the evolution of stars in a variety of axisymmetric environments, including the effects of binarity, disks, and rotation.

2.2. Pulsation Modeling

Fewer attempts have been made at modeling pulsation frequencies in 2 dimensions and these attempts have focused on the effects of rotation. Normally, eigenfrequencies of rotating stars are calculated using perturbation theory (Dziembowski and Goode, 1992; Soufi et al., 1998), but this is generally limited to slow rotation rates (see, for example Soufi et al., 1998, and references therein). Exactly how slow rotation is defined depends on the application, but it has been found that rotation rates as small as 50–75 km/s require more realistic calculations (Reese et al., 2006). Few people would argue that perturbation theory remains valid above rotation rates of 200–300 km/s.

The earliest attempts at 2D calculations were done by Clement (1981, 1989, 1998), and involved solving the linear pulsation equations on a 2D grid. This program, Non-Radial Oscillations (NRO) uses the degree ℓ to determine the parity of the mode, and odd modes are scaled by a factor of cos θ to make them symmetric. This allows the same method of solution to be used for both even and odd modes. The pressure perturbation is then described as expansion of k spherical harmonics, where k is the number of angular points in the grid. All other components of the eigenfunction can be expressed the same way, and the final solution is scaled to some fixed value at the surface, typically δr/r = 1 at the equator. While the initial attempts were limited to slow rotation, NRO (Clement, 1998) was able to solve the pulsation equations for very rapidly rotating stars. As initially developed, this method was restricted to uniform rotation but was later extended to include the effects of differential rotation (Lovekin et al., 2009).

Another approach uses spectral methods to calculate the eigenfunctions in 2D, including the effects of the Coriolis force and centrifugal distortion (Lignières et al., 2006; Reese et al., 2006). Using acoustic ray tracing of the frequencies calculated using this method, the resulting modes can be classified into chaotic modes, island modes, and whispering gallery modes based on their behavior in phase space (Lignières and Georgeot, 2009). Initially, this code was only applicable to polytropic models, but has since been expanded to more realistic stellar models (Reese et al., 2009). ACOR (Adiabatic Code of Oscillation including Rotation) (Ouazzani et al., 2012) has been developed using similar techniques, but has been designed to work with realistic stellar models.

For post-main sequence models, a number of attempts have been made to use full hydrodynamics to model the convection-pulsation interactions. This interaction is particularly important for classical pulsators, as the red edge of the instability strip is determined by the interaction between convection and pulsation (Tuggle and Iben, 1973). Early attempts focused on the interaction in one dimension, as was done in DYNSTAR (Ostlie, 1990). DYNSTAR has been used to model outbursts in Luminous Blue Variables (Guzik and Lovekin, 2014; Lovekin and Guzik, 2014). However, convection is inherently a multi-dimensional process, and the applicability of 1D models is limited. For this reason, a number of groups have developed 2 and 3D codes to model convective processes in pulsating stars. Cepheids have been modeled in 2D using the ANTARES (A Numerical Tool for Astrophysical RESearch) code (Mundprecht et al., 2013, 2015), focusing on the energetics of the convective zone and the possibility of developing descriptions that can be implemented in 1D models. Similarly, RR Lyrae have been modeled using SPHERLS (Stellar Pulsation with a Horizontal Eulerian Radial Lagrangian Scheme) (Geroux and Deupree, 2011, 2013, 2014, 2015). SPHERLS is able to model stars in either 2 or 3 dimensions, and has been used to calculate full pulsation amplitude models. The results agree well with observed RR Lyrae light curves. Although both ANTARES and SPHERLS are promising, calculations are time consuming, and neither has been widely used for modeling stellar pulsation.

3. Effects of Rotation

3.1. Effects on Evolution

The most pronounced effect of rapid rotation is the deformation of the stellar surface. The centrifugal force causes the star to become oblate in shape, and both temperature and emitted flux vary from pole to equator as a result. The first calculations of this effect found that the effective temperature is related to the effective gravity by:

$\begin{array}{ll}{T}_{\text{eff}}\propto g_{\text{eff}}^{\beta }& (9)\end{array}$

where β is theoretically predicted to be 0.25 for purely radiative stars (von Zeipel, 1924). As a result of the rapid rotation, this gravity darkening will cause the equatorial regions to be cooler, and hence appear dimmer than the polar regions of the star. This effect has been directly measured using interferometry in several stars, including Achernar, Alderamin, Altair, Vega, Regulus, Rasselhague, α Cephei, α Leonis, α Ophiuchi, and β Cassiopeia (van Belle et al., 2001, 2006; Domiciano de Souza et al., 2003; Aufdenberg et al., 2006; Peterson et al., 2006; Monnier et al., 2007; Zhao et al., 2009; Che et al., 2011). All of these studies have found that gravity darkening does occur, but the observed temperature variation is inconsistent with β = 0.25. For example, a best fit value of β = 0.22 was found for α Cephei (Zhao et al., 2009). Values derived for other stars are similarly lower than the traditional β = 0.25 value given in von Zeipel's law (von Zeipel, 1924). One explanation for this difference is that these stars have thin surface convection zones, where the value of β is expected to be much lower, β ≈ 0.08 (Lucy, 1967).

The original gravity darkening model required the assumption of barotropicity, and is actually incompatible with solid body rotation in a radiative zone. To address these problems, a more realistic model for gravity darkening was derived (Espinosa Lara and Rieutord, 2011). This model relaxes von Zeipel's assumption of barotopicity, and is thought to be more applicable to real stars, particularly in cases of extremely rapid rotation. This new model was compared to calculations using 2D models constructed with ESTER (Espinosa Lara and Rieutord, 2011) which calculates the gravity darkening naturally as a result of the stellar structure equations, and the results were in good agreement with the new theoretical model. These results were later extended to include differential rotation (Zorec et al., 2017).

As a consequence of the flux variation, the flux seen by an observer varies with the inclination angle i, between the rotation axis and the line of sight to the observer. Inclination is very difficult to measure directly. Spectroscopic measurements give the Doppler broadening of spectral lines, which gives the component of the rotational velocity along the line of sight, v sin i. It is possible to decouple v and i (Stoeckley, 1968; Stoeckley and Buscombe, 1987; Reiners and Schmitt, 2003), but these methods depend on high-precision spectroscopy and very accurate synthetic line profiles. However, these techniques do not work well for slowly rotating stars (v_eq ≤ 200 km/s). As a result of the large quantity of high resolution photometric data from space missions including Kepler, CoRoT, and TESS, techniques have been developed to measure stellar rotation periods using asteroseismology, as discussed in more detail below.

The variation in observed flux as a function of inclination makes it difficult to assign an exact effective temperature and luminosity to a rapidly rotating star. The observed magnitude is a function of inclination, and the star is observed as a single point on a curve in the HR diagram, parameterized by the inclination. This effect is well known (Collins, 1963, 1966; Hardorp and Strittmatter, 1968; Maeder and Peytremann, 1970), but has recently been improved using more realistic stellar structure and atmosphere models (Lovekin et al., 2006; Gillich et al., 2008).

Rotation increases mixing through shear-layer instabilities, likely driven by differential rotation (e.g., Mathis et al., 2004). This mixing is likely to be latitude dependent, an effect that is not modeled by 1D parameterizations. The extra mixing introduced by these instabilities results in changes in the evolutionary tracks. Close to the Zero Age Main Sequence (ZAMS), rotation makes a star appear cooler and less luminous than a non-rotating star of the same mass. On the later main sequence, the behavior depends on how angular momentum transport is treated in the star, with some models finding that the rotating star remains cooler and dimmer (Deupree, 1995) while others find the rotating models become brighter (Ekström et al., 2012). In stars with M > 2M_⊙, rotation has also been found to extend the main sequence lifetime by about 25%, which in turn increases the observed width of the main sequence. This effect is illustrated in Figure 1 for 2.0 M_⊙ 1D-models calculated with MESA. Models with moderate amounts of rotation show good agreement with the observed width of the main sequence (Ekström et al., 2012). The rotation provides a source of extra mixing inside the star, increasing the amount of hydrogen available, and also potentially changing the surface abundances of other elements. In extreme cases, models suggest that high levels of rotation can produce so much mixing that the star evolves in a chemically homogeneous fashion (Szécsi et al., 2015; Song et al., 2016).

FIGURE 1

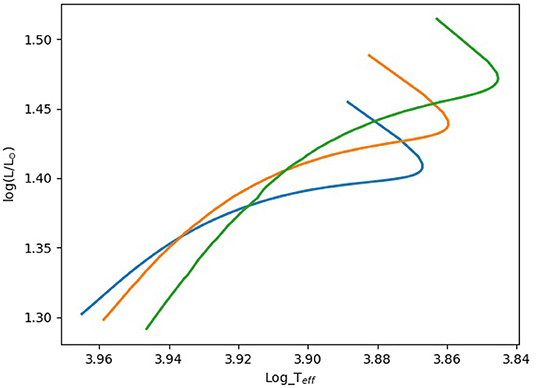
Figure 1. Evolution tracks along the main sequence for 2.0 M_⊙ models calculated with MESA. Shown are non-rotating models (blue) and models rotating at 0.3 v_crit (orange) and 0.5 v_crit (green). Initially, rotating models appear cooler and dimmer than non-rotating counterparts. As the star evolves, the rotating models become brighter, and spend a longer time on the main sequence.

Although stars generally spin down as they evolve, the effects of rotation can persist into later phases of evolution (Anderson et al., 2014). This is particularly evident for Cepheids, which have main sequence progenitors that typically rotate at v/v_crit = 0.3 − 0.4 (Huang et al., 2010). During the post main sequence evolution, the effects of rotation give these stars a luminosity that corresponds to that of a non-rotating model of higher mass. As a result, rotating stellar models have been used to resolve the Cepheid mass discrepancy (Anderson et al., 2014, 2016). Models indicate that rotating Cepheids are also older than non-rotating Cepheids, as rotation increases the main sequence lifetime of a star. This affects the period-age relationship, which in turn has implications for the use of Cepheids in Galactic archaeology. Finally, rotation extends the blue loop, and so rotating Cepheids traverse the instability strip more slowly than their non-rotating counterparts (Anderson et al., 2014).

The effects of rotation can be detected observationally via surface abundances. Models predict that the surface abundances of certain isotopes of nitrogen (¹⁴N) and helium (⁴He) should be enhanced, while light elements like lithium and boron should be depleted (Heger and Langer, 2000). Rotationally-induced mixing brings the lighter elements down to layers that are hot enough for these elements to be destroyed. These layers are also hot enough for the first steps in the CNO cycle to occur, converting the ¹²C and ¹⁶O to be converted into ¹⁴N, which is then brought to the surface. The theoretical predictions are generally in good agreement with the observations. For example, in this model, stars that have enhanced nitrogen abundances should also show depleted boron abundances, as was found by Venn et al. (1996). This model was also tested by comparing the surface abundance of ¹⁴N to the projected rotational velocity (v sin i) of stars observed as part of the VLT-FLAMES survey (Hunter et al., 2008). These results (see Figure 2) show that the nitrogen enhancement does correspond well with rotation velocity for most stars. Two populations, one with low rotation velocity and high nitrogen enhancement, and one with high rotation velocity and low nitrogen enhancement are thought to be the result of binary evolution, or possibly the presence of magnetic fields (Hunter et al., 2008).

FIGURE 2

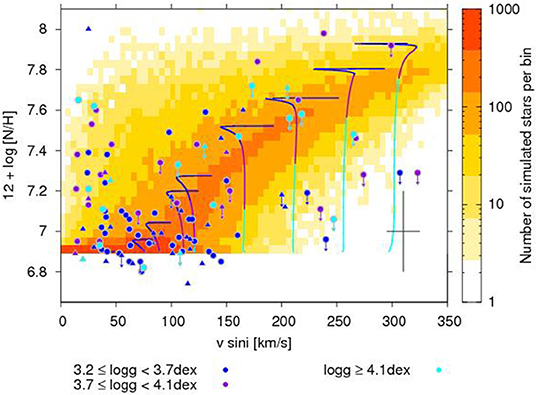
Figure 2. The observed nitrogen enhancement plotted as a function of v sin i. The background density contours are predicted enhancements from population synthesis models, with individual stars plotted as either circles or triangles. The evolution tracks are for 13 M_⊙ stars at various initial velocities. Taken from Brott et al. (2011). Reproduced with permission.

The nucleosynthetic yields of a rotating star are also expected to differ from that of a non-rotating star, increasing the amount of metals produced. This effect is especially pronounced for carbon and oxygen, which increase by a factor of 1.5–2.5 for models with M ≲ 60M_⊙ (Maeder and Meynet, 2012). As discussed above, rotation provides a source of extra mixing, which increases the size of the convective core, so a rapidly rotating model will have yields similar to a more massive star. Above 60M_⊙, the total mass lost is the same in both rotating and non-rotating models, and this effect disappears (Maeder and Meynet, 2012).

3.2. Effects on Mass Loss

Stars with initial masses above ~ 10M_⊙ lose significant amounts of mass through radiatively driven winds. However, mass loss rates are highly uncertain, even when rotation is not considered. Mass loss rates can be derived from spectroscopic observations of wind speeds, can as high as $10^{-5}{M}_{\odot }/yr$ in hot OB stars. These derivations often assume the winds are smooth, and detailed observations and simulations now suggest that the mass loss may be clumpy, which lowers the mass loss rates significantly. Mass loss rates calculated using Monte Carlo simulations (Vink et al., 2001) have been found to be in good agreement with observations (Mokiem et al., 2006). However, there are many indications that radiatively driven winds are clumpy rather than smooth, and this can reduce mass loss rates by a factor of 2 or 3 (Maeder and Meynet, 2012).

Many massive stars are rapid rotators, and so rotation is expected to have a significant impact on the way mass and angular momentum are lost from a star. Theoretical mass loss rates are sensitive functions of luminosity and effective temperature (Castor et al., 1975; Vink et al., 2001; Kudritzki, 2002), and so the variation in surface effective temperature and flux discussed above can be expected to cause variations in mass loss rates as a function of colatitude. Investigations into rotating winds have shown that there are two solutions: a classic Castor, Abbott & Klein (CAK) model (Castor et al., 1975) or fast wind solution (FWS) and a slow wind solution (SWS) which exist when the rotation speed is a significant fraction of the critical velocity (Curé et al., 2011). However, these models still assume that the mass loss from the star can be effectively described in 1D. Much work has been done on the 2D hydrodynamics of rotating stellar winds (e. g., Müller and Vink, 2014), but here I will discuss the effects on the star rather than the circumstellar environment.

The effect of gravity darkening on wind-driven mass loss has been investigated using stellar evolution codes in both 1D (Maeder, 2002; Georgy et al., 2011) and 2D (Lovekin, 2011). Initial investigations showed that rotating stars could be expected to produce a bipolar nebula, as the increased temperature near the poles enhances the mass loss rate in this region (Maeder, 2002). These models use a mass loss prescription that is based on the standard radiatively driven wind model of Castor et al. (1975) and Kudritzki (2002). An updated version of this model found an increase in the global mass loss rate as the rotation rate increased, and as expected, more mass was lost from the polar regions than the equatorial regions. This effect increased with the rotation rate (Georgy et al., 2011). Lovekin (2011) used fully 2D stellar structure models and mass loss rates calculated using Castor et al. (1975); Vink et al. (2001); Kudritzki (2002). In these 2D models, the surface is assumed to be an equipotential surface rather than relying on the Roche approximation, as is done in the Geneva models (Georgy et al., 2011). In the 2D models, the global mass loss rate actually decreased slightly as the rotation rate increased, as the increase in mass loss at the pole was offset by the decrease in mass loss from the equator. This ran counter to the conventional scaling relations for mass loss as a function of rotation rate (Bjorkman and Cassinelli, 1993). However these scaling relations are for stars at constant temperature and luminosity, while Lovekin (2011) used a fixed mass and allowed the temperature and luminosity to vary.

The differential mass loss can also affect the evolution of the angular momentum of the star. Georgy et al. (2011) and Lovekin (2011) found that the majority of the mass is lost from the polar regions of the star, however, the majority of the angular momentum is in the equatorial regions. The mass loss rates at the equator will have a significant effect on the angular momentum evolution. According to the 1D models, the majority of the angular momentum is lost from regions close to the equator, ranging from θ = 0 in the non-rotating models to θ ~ 70° at critical rotation (Georgy et al., 2011). As a result, they find that rotating models with anisotropic mass loss lose less angular momentum than those with uniform mass loss. They were able to evolve their models until the surface reached critical rotation, and found small differences in the evolution, with rotating models generally slightly cooler than their non-rotating counterparts. Lovekin (2011) also found that the angular momentum loss peaks near ~ 70° in the most rapidly rotating models, and that the rate of angular momentum loss increases overall as the rotation rate increases. In general, the 2D models lose less angular momentum than those with isotropic mass loss, as was found by Georgy et al. (2011).

3.3. Effects on Pulsation Frequencies

In non-rotating models, pulsation frequencies are described by two quantum numbers, n and ℓ. The first identifies the number of radial nodes in a particular eigenfunction, and ℓ determines the number of horizontal nodes in the latitudinal direction. The modes can be modeled as spherical harmonics, which have a third (azimuthal) quantum number, m, where m ≤ ℓ. For non-rotating models, the pulsation frequencies are independent of m for a given (ℓ, n) combination. In rotating stars, the degeneracy between modes of different m is lifted, and the modes are visible as multiplets in the pulsation spectrum. In the simplest case, the splitting is expected to follow:

$\begin{array}{ll}{\nu }_{n\ell m}={\nu }_{n\ell }+m\Delta \nu & (10)\end{array}$

where Δν is given by:

$\begin{array}{ll}\Delta \nu =\frac{1}{2\pi }{\displaystyle {\int }_0^R}{K}_{n\ell }(r)\Omega (r)dr& (11)\end{array}$

where Ω is the angular rotation velocity of the star and K_nℓ(r) is a rotation kernel, which depends on the real and imaginary components of the eigenfunction. Since the azimuthal number m can range from ℓ to −ℓ, the splitting should be uniformly spaced to first order. However, rapid rotation can complicate the spectrum by introducing non-uniform mode splitting (Reese et al., 2006). In extreme cases, the difference in frequency between members of a rotational multiplet can become larger than the difference in frequency between successive degrees ℓ, further complicating the interpretation of the spectrum. In cases where a rotational multiplet can be identified, the rotation frequency of the star can be determined, independent of the inclination. This type of analysis has been done for stars across the HR diagram (Charpinet et al., 2018; Paparó et al., 2018). If multiple triplets are detected, they can be expected to probe different radii inside the star, and it may be possible to probe the rotation profile (Aerts et al., 2003; Suárez et al., 2010).

Rotation is also known to decrease pulsation frequencies overall (Lignières et al., 2006; Reese et al., 2006; Lovekin and Deupree, 2008; Lovekin et al., 2009). As this difference depends on the order and harmonic degree (ℓ) of the mode, the rotation also changes the large and small frequency separation. However, one of the biggest challenges lies in identifying the correspondence between observed and theoretical modes for use in asteroseismology (Deupree, 2011).

A further challenge to interpretation of observed frequencies in rotating stars is the destruction of the regular frequency patterns expected for both p-mode and g-mode pulsators. For p modes, the frequencies are predicted to be regularly spaced, with a large separation that is approximately constant (Tassoul, 1980):

$\begin{array}{ll}\Delta \nu ={\nu }_{n+1,\ell ,m}-{\nu }_{n,\ell ,m}.& (12)\end{array}$

According to the ray-tracing 2D models developed by Lignières et al. (2006), the regular patterns seen in the p-modes of non-rotating stars disappear, and modes are instead divided into three categories: island modes, chaotic modes, and whispering gallery modes. Regular patterns do seem to exist for the island modes (Lignières et al., 2006), and these patterns have been successfully tested for more realistic models (Ouazzani et al., 2015).

Similarly, for g−modes, it is predicted that the periods will show regular spacings (Miglio et al., 2008). The g-mode patterns are less affected by rotation, but some new patterns do appear (Ballot et al., 2012). The regular period spacings in the g-modes do show the effects of rotation quite clearly, as shown in Figure 3. While the m = 0 modes are expected to have completely regular period spacings, the slope of the pattern is affected by the rotation rate. Retrograde modes (m = −1) show an upward slope, as shown in Figure 3, while prograde modes (m = +1) show a downward slope. In both cases, the effects are increased by rotation (Van Reeth et al., 2016; Lovekin and Guzik, 2017; Ouazzani et al., 2017). These patterns can be matched to observed g-mode spacings to determine stellar rotation rates, as has been done for many of the Kepler γ Doradus stars (Li et al., 2019).

FIGURE 3

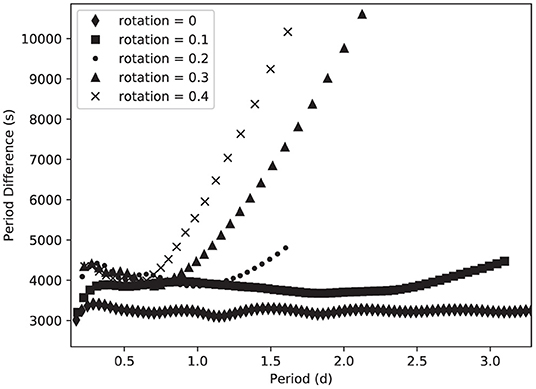
Figure 3. Period difference as a function of period for ℓ = 1, m = −1 g−modes in a 1.6 M_⊙ model. As the rotation rate increases, the upward slope in the period spacing becomes more pronounced. Taken from Lovekin and Guzik (2017) ©AAS. Reproduced with permission.

4. Binary Systems

In close binary systems, the stars are distorted as a result of the gravitational pull of the companion, and this is not currently accounted for in most work on the evolution of binary stars. For example, de Vries et al. (2014) use 1D stellar models up to the point of Roche Lobe Overflow, and then convert to a 3D hydrodynamics simulation. Using a 2D stellar structure code, Deupree and Karakas (2005) have shown that the shape of both the surface and the convective core are distorted in a binary system, although the total mass of the convective core is essentially unchanged. For the closest binaries, they found that the shape of the surface differs slightly from the Roche potential usually used in 1D models. However, this assumes that the binary star system is coplanar and tidally locked. To fully simulate the distortion in a binary star system is a 3D problem.

Indeed, observations of heartbeat stars with the Kepler telescope have shown that even in close eccentric binaries, the rotation period can be different from the orbital period (Hambleton et al., 2018). In close systems like this, the gravitational field can even produce tidally excited oscillations, and pulsations have also recently been detected in η Carinae, which have been proposed to be tidally excited (Richardson et al., 2018). Tidally excited oscillations were first suggested in binary stars where the rotation period of the components is different from the orbital period of the system (Cowling, 1941), so these systems will necessarily be at least spheroidal, and are highly likely to be triaxial.

5. The Future: Challenges and Needs

Multi-dimensional models are common in simulations of short-timescale events inside stars. Several groups have modeled the internal convection of stars (Woodward et al., 2018; Arnett et al., 2019), but even these simulations often don't include rotation. Typically, convection simulations model a part of a star, either a wedge or a shell. In either case, these simulations are much shorter in timescale than evolution calculations, and the base structure is effectively static. Rotation also breaks the symmetry between the latitudinal an azimuthal (θ and ϕ) directions, so the simulations must be 3D to capture all the details (Viallet et al., 2013). The rotation also changes the way the composition of the star changes, introducing non-local effects (Arnett and Meakin, 2010). Although great progress is being made in these 3D convection simulations, the computational power required to model both short and long timescales in a single simulation does not exist. Much work is being done on determining algorithms that can be used to replace the standard Mixing Length Theory (MLT) (Böhm-Vitense, 1958), in 1D stellar models, but this will still only approximate some of the effects.

In most 1D stellar evolution codes, rotation is included using a shellular approximation, which essentially reduces the problem to 1D (Zahn, 1992). This type of rotation law is thought to arise from strong horizontal turbulence, which forces the rotation rate to be constant along isobars. Transport of material and angular momentum via the meridional circulation can be modeled as an effective diffusion in this model. Models suggest that shellular rotation is probably a good approximation at low rotation rates, while at higher rotation rates, models produce rotation profiles that do depend on latitude (Kitchatinov and Rüdiger, 1999; Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016). Nevertheless, this is the approximation made by the vast majority of stellar evolution codes in use today. The exceptions are ESTER (Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016), which fixes a surface velocity V_eq and allows the angular momentum to evolve, and ROTORC (Deupree, 1990, 1995, 1998), which accepts an initial rotation profile, and then evolves the star with local conservation of angular momentum.

It is reasonable to expect that stars are uniformly rotating, at least initially, but as they evolve, angular momentum will be transported inside the star. Models that are created with a uniform rotation profile on the ZAMS will quickly evolve to a differential rotation profile with the core rotating more rapidly than the surface (Denissenkov et al., 1999). This profile is in good agreement with the few stars that have had core to surface rotation rates measured using asteroseismology (Aerts et al., 2003; Lovekin and Goupil, 2010). Internal transport mechanisms like meridional circulation tend to bring angular momentum from the core to the surface, where it can be carried away with the stellar winds (Ekström et al., 2012). Since the mass loss is so much more efficient in more massive stars, these models spin down more rapidly, which in turn affects the size of the core, effective temperature, and luminosity of the star. In order to accurately model these properties, the details of internal transport must be correctly included.

In massive stars, many observed magnetic fields are approximately dipolar, the magnetic axis is frequently offset from the rotation axis of the star, making this a 3D problem (Grunhut et al., 2017). In lower mass stars, magnetic fields are produced by a dynamo, which is also a 3D problem, and needs to be parameterized to include the effects in 1 or 2D models. This remains challenging to implement, and at present can only be done for simplified systems (Jennings et al., 1990). Nevertheless, magnetic fields have been included in a few 1D codes (see, for example Feiden, 2016; Keszthelyi et al., 2018).

The effects of magnetic fields on stellar evolution can be significant. Magnetic fields couple with the rotation of a star, and so affect the internal transport and mass loss of a star. The effects on internal energy transport are particularly pronounced in the convective regions, and this has been suggested to be the origin of the radius inflation problem in M dwarfs (Jackson et al., 2018). One promising line of inquiry uses post-common-envelope binaries as probes of the magnetic field (Navarrete et al., 2019). In this case, it appears that the magnetic field can have a measurable effect on the stellar structure. Clearly, magnetic fields are an important part of stellar evolution and need to be accounted for in the models. This remains a challenging problem though, as magnetic fields are intrinsically 3D and act and evolve on timescales much shorter than typical stellar evolution.

Magnetic fields are also responsible for the roAp stars, where the oscillations arise from magneto-acoustic waves (Elkin et al., 2008) which will require both 2D structure and pulsation calculations to understand fully. In addition, a number of chemically peculiar stars show horizontal inhomogeneities in the surface abundance patterns (Khokhlova, 1976). Some work has been done on the effect of magnetic fields on the pulsation frequencies in roAp stars (Saio, 2014), but the 2D effects of magnetic fields on rotation have not been investigated in detail.

Of course, many groups are working on the 2D and 3D properties of stellar convection and turbulence (Davis et al., 2018; Arnett et al., 2019), but these simulations usually cover only a small fraction of the star, and cover a timescale that is short compared to the evolutionary timescale. The ESTER code described above (Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016) models the stellar structure in 2D, and includes the effects of meridional circulation and rotation, but is not capable of modeling the longer timescales required to describe the evolution in 2D.

To date, there is no code capable of modeling the evolution of a star in 2D, while also taking into account the effects of short term processes like meridional circulation and convection. This is a serious gap in our abilities, and limits our ability to model stars with strong magnetic fields, in tidally distorted systems, or with rapid rotation. In order to progress, models for the short term processes that can be included in the evolutionary calculations need to be developed. Since 2D calculations will intrinsically take longer than their 1D counterparts, it would be appropriate to develop scaling laws that can be used in 1D, as has been done for pulsations in rotating stars (Castañeda and Deupree, 2016).

6. Conclusions

The equations of stellar structure in 1D have been well understood for nearly 100 years, but almost immediately, it was realized that the effects of rotation, binarity, and magnetic fields would introduce 2D or 3D effects that needed to be taken into account. The first attempts were made in the 1950s (Sweet and Roy, 1953), yet 70 years later, we still do not have a way of realistically modeling the evolution of a star in 2D. This remains a challenging problem, and trade-offs must be made between the ability to model detailed internal processes and the long-term evolution of the star. This multi-dimensional structure becomes ever more important as improved observations give us more details about the surface properties, binary interactions, magnetic field strengths, and pulsation frequencies. In order to accurately reproduce these observations, our models must be able to take into account the multi-D effects in a self-consistent fashion.

From a variety of box-in-star simulations, as well as structure simulations with ESTER (Espinosa Lara and Rieutord, 2013; Rieutord et al., 2016) we know that convection and rotation produce 2D effects, and that these will in turn change the evolution of the rotating stars when compared to non-rotating stars. From the nucleosynthesis in the core to the mass loss from the surface, these multidimensional processes influence the evolution of the star. A good understanding the process of stellar nucleosynthesis and the nature of supernova progenitors are the building blocks for Galactic archaeology, as well as the history of the universe. Previous studies have shown that the details of stellar evolution can influence stellar population synthesis and the derived masses of galaxies, affecting the way we understand the history of our universe (Conroy, 2013).

The evolution of a star in 2D is a very challenging problem, and requires improvements in both theoretical underpinnings and computational resources. At the same time, the disparity in size and time scales required to calculate the internal processes and the evolution suggests that no improvement in computational resources is going to make it possible to include all aspects of the multi-D structure in a single calculation. Further complicating the problem, convection, rotation, and magnetic fields are all coupled, and will interact in ways that are likely non-linear. Rather than hoping to create an ideal multi-D calculation, we must focus on finding better models for these internal processes that can be incorporated into models that include their 2D effects on evolutionary timescales. In particular, a better model for convection is needed to replace the current MLT theory, as well as a better understanding of angular momentum transport inside stars. This is an active area of research, and several groups are working on an updated convection model to replace MLT in 1D models (Garaud et al., 2010; Canuto, 2011; Arnett et al., 2019). Magnetic fields have been included in 1D models, but the details of their 2D influence on chemical mixing and angular momentum transport cannot be ignored. Many groups are working on large-scale simulations of these processes, with a goal of better understanding how they work, and how they can be modeled in evolution simulations. We are starting to progress in all of these areas, and computational resources are becoming faster, and more widely available (more cores), which will make it feasible to run 2D or 3D evolution simulations in the near future.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was supported in part by the National Science Foundation under Grant No. NSF PHY-1125915. This work was supported in part by NASA ATP grant 12-ATP12-0130 and in part by the Natural Sciences and Engineering Research Council of Canada (NSERC).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author gratefully acknowledges support from the Natural Sciences and Engineering Research Council of Canada (NSERC). This research has made use of NASA's Astrophysics Data System.

References

Aerts, C., Thoul, A., Daszyńska, J., Scuflaire, R., Waelkens, C., Dupret, M. A., et al. (2003). Asteroseismology of HD 129929: core overshooting and nonrigid rotation. Science 300, 1926–1928. doi: 10.1126/science.1084993

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, R. I., Ekström, S., Georgy, C., Meynet, G., Mowlavi, N., and Eyer, L. (2014). On the effect of rotation on populations of classical Cepheids. I. Predictions at solar metallicity. Astron. Astrophys. 564:A100. doi: 10.1051/0004-6361/201322988

CrossRef Full Text | Google Scholar

Anderson, R. I., Saio, H., Ekström, S., Georgy, C., and Meynet, G. (2016). On the effect of rotation on populations of classical Cepheids. II. Pulsation analysis for metallicities 0.014, 0.006, and 0.002. Astron. Astrophys. 591:A8. doi: 10.1051/0004-6361/201528031

CrossRef Full Text | Google Scholar

Arnett, W. D., and Meakin, C. (2010). “Turbulent mixing in stars: theoretical hurdles,” in Proceedings of the International Astronomical Union, Chemical Abundances in the Universe: Connecting First Stars to Planets, Vol. 265, eds K. Cunha, M. Spite, and B. Barbuy, 106–110.

Google Scholar

Arnett, W. D., Meakin, C., Hirschi, R., Cristini, A., Georgy, C., Campbell, S., et al. (2019). 3D Simulations and MLT. I. Renzini's critique. Astrophys. J. 882:18. doi: 10.3847/1538-4357/ab21d9

CrossRef Full Text | Google Scholar

Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., Absil, O., Di Folco, E., Kervella, P., et al. (2006). First results from the CHARA Array. VII. Long-baseline interferometric measurements of vega consistent with a Pole-On, rapidly rotating star. Astrophys. J. 645, 664–675. doi: 10.1086/504149

CrossRef Full Text | Google Scholar

Ballot, J., Lignières, F., Prat, V., Reese, D. R., and Rieutord, M. (2012). “2D computations of g-modes in fast rotating stars,” in Progress in Solar/Stellar Physics with Helio- and Asteroseismology, Vol. 462, eds H. Shibahashi, M. Takata, and A. E. Lynas-Gray (Astronomical Society of the Pacific Conference Series), 389.

Google Scholar

Bjorkman, J. E., and Cassinelli, J. P. (1993). Equatorial disk formation around rotating stars due to ram pressure confinement by the stellar wind. Astrophys. J. 409:429.

Google Scholar

Böhm-Vitense, E. (1958). Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Zeitschrift fur Astrophysik 46:108.

Google Scholar

Brott, I., Evans, C. J., Hunter, I., de Koter, A., Langer, N., Dufton, P. L., et al. (2011). Rotating massive main-sequence stars. II. Simulating a population of LMC early B-type stars as a test of rotational mixing. Astron. Astrophys. 530:A116. doi: 10.1051/0004-6361/201016114

CrossRef Full Text | Google Scholar

Canuto, V. M. (2011). Stellar mixing. I. Formalism. Astron. Astrophys. 528:A76. doi: 10.1051/0004-6361/201014447

CrossRef Full Text | Google Scholar

Castañeda, D., and Deupree, R. G. (2016). Scaling of oscillation frequencies in rotating stars. Month. Notice. Roy. Astronom. Soc. 458, 4422–4430. doi: 10.1093/mnras/stw620

CrossRef Full Text | Google Scholar

Castor, J. I., Abbott, D. C., and Klein, R. I. (1975). Radiation-driven winds in Of stars. Astrophys. J. 195, 157–174.

Google Scholar

Charpinet, S., Giammichele, N., Zong, W., Van Grootel, V., Brassard, P., and Fontaine, G. (2018). Rotation in sdB stars as revealed by stellar oscillations. Open Astronomy 27, 112–119. doi: 10.1515/astro-2018-0012

CrossRef Full Text | Google Scholar

Che, X., Monnier, J. D., Zhao, M., Pedretti, E., Thureau, N., Mérand, A., et al. (2011). Colder and hotter: interferometric imaging of β cassiopeiae and α leonis. Astrophys. J. 732:68. doi: 10.1088/0004-637X/732/2/68

CrossRef Full Text | Google Scholar

Clement, M. J. (1974). On the solution of Poisson's equation for rapidly rotating stars. Astrophys. J. 194, 709–714.

Google Scholar

Clement, M. J. (1978). On the solution of the equilibrium equations for rapidly rotating stars. Astrophys. J. 222, 967–975.

Google Scholar

Clement, M. J. (1979). On the equilibrium and secular instability of rapidly rotating stars. Astrophys. J. 230, 230–242.

Google Scholar

Clement, M. J. (1981). Normal modes of oscillation for rotating stars. I - The effect of rigid rotation on four low-order pulsations. Astrophys. J. 249, 746–760.

Google Scholar

Clement, M. J. (1989). Normal modes of oscillation for rotating stars. IV. Nonaxisymmetric variational solutions for 15 M_sun models. Astrophys. J. 339:1022.

Google Scholar

Clement, M. J. (1994). Differential rotation and the convective core mass of upper main- sequence stars. Astrophys. J. 420:797.

Google Scholar

Clement, M. J. (1998). Normal modes of oscillation for rotating stars. V. A new numerical method for computing nonradial eigenfunctions. Astrophys. J. Suppl. Ser. 116, 57–74.

Google Scholar

Collins, G. W. I. (1963). Continuum emission from a rapidly rotating stellar atmosphere. Astrophys. J. 138:1134.

Google Scholar

Collins, G. W. I. (1966). Continuum emission from rotating non-gray stellar atmospheres. II. Astrophys. J. 146:914.

Google Scholar

Conroy, C. (2013). Modeling the panchromatic spectral energy distributions of galaxies. Ann. Rev. Astron. Astrophys. 51, 393–455. doi: 10.1146/annurev-astro-082812-141017

CrossRef Full Text | Google Scholar

Cowling, T. G. (1941). The non-radial oscillations of polytropic stars. Month. Notice. Roy. Astronom. Soc. 101:367.

Google Scholar

Curé, M., Cidale, L., and Granada, A. (2011). Slow radiation-driven wind solutions of A-type supergiants. Astrophys. J. 737:18. doi: 10.1088/0004-637X/737/1/18

CrossRef Full Text | Google Scholar

Davis, A., Jones, S., and Herwig, F. (2018). Convective boundary mixing in a post-He core burning massive star model. Month. Notice. Roy. Astronom. Soc. 484, 3921–3934. doi: 10.1093/mnras/sty3415

CrossRef Full Text | Google Scholar

de Vries, N., Portegies Zwart, S., and Figueira, J. (2014). The evolution of triples with a Roche lobe filling outer star. Month. Notice. Roy. Astronom. Soc. 438, 1909–1921. doi: 10.1093/mnras/stt1688

CrossRef Full Text | Google Scholar

Denissenkov, P. A., Ivanova, N. S., and Weiss, A. (1999). Main-sequence stars of 10 and 30 M_sun: approaching the steady-state rotation. Astron. Astrophys. 341, 181–189.

Google Scholar

Deupree, R. G. (1990). Stellar evolution with arbitrary rotation laws. I. Mathematical techniques and test cases. Astrophys. J. 357:175.

Google Scholar

Deupree, R. G. (1995). Stellar evolution with arbitrary rotation laws. II. Massive star evolution to core hydrogen exhaustion. Astrophys. J. 439:357. doi: 10.1086/175179

CrossRef Full Text | Google Scholar

Deupree, R. G. (1998). Stellar evolution with arbitrary rotation laws. III. Convective core overshoot and angular momentum distribution. Astrophys. J. 499, 340–347.

Google Scholar

Deupree, R. G. (2011). Theoretical p-Mode oscillation frequencies for the rapidly rotating δ scuti star α ophiuchi. Astrophys. J. 742:9. doi: 10.1088/0004-637X/742/1/9

CrossRef Full Text | Google Scholar

Deupree, R. G., and Karakas, A. I. (2005). The structure of close binaries in two dimensions. Astrophys. J. 633, 418–423. doi: 10.1086/444611

CrossRef Full Text | Google Scholar

Domiciano de Souza, A., Kervella, P., Jankov, S., Abe, L., Vakili, F., di Folco, E., et al. (2003). The spinning-top Be star Achernar from VLTI-VINCI. Astron. Astrophys. 407, L47–L50. doi: 10.1051/0004-6361:20030786

CrossRef Full Text | Google Scholar

Dziembowski, W. A., and Goode, P. R. (1992). Effects of differential rotation on stellar oscillations: a second-order theory. Astrophys. J. 394:670.

Google Scholar

Ekström, S., Georgy, C., Eggenberger, P., Meynet, G., Mowlavi, N., Wyttenbach, A., et al. (2012). Grids of stellar models with rotation. I. Models from 0.8 to 120 M_⊙ at solar metallicity (Z = 0.014). Astron. Astrophys. 537:A146. doi: 10.1051/0004-6361/201117751

CrossRef Full Text | Google Scholar

Elkin, V. G., Kurtz, D. W., and Mathys, G. (2008). Pulsation properties of the rapidly oscillating Ap star 10Aquilae (HD176232). Month. Notice. Roy. Astronom. Soc. 386, 481–491. doi: 10.1111/j.1365-2966.2008.13049.x

CrossRef Full Text | Google Scholar

Eriguchi, Y. (1978). Hydrostatic Equilibria of Rotating Polytropes. Public. Astronom. Soc. Jpn. 30, 507–518.

Google Scholar

Eriguchi, Y. (1980). Rapidly rotating and fully general relativistic polytropes. Progress Theor. Phys. 64, 2009–2020.

Google Scholar

Eriguchi, Y., and Mueller, E. (1985). A general computational method for obtaining equilibria of self- gravitating and rotating gases. Astron. Astrophys. 146, 260–268.

Google Scholar

Eriguchi, Y., and Sugimoto, D. (1981). Another equilibrium sequence of self-gravitating and rotating incompressible fluid. Progress Theor. Phys. 65, 1870–1875.

Google Scholar

Espinosa Lara, F., and Rieutord, M. (2011). Gravity darkening in rotating stars. Astron. Astrophys. 533:A43. doi: 10.1051/0004-6361/201117252

CrossRef Full Text | Google Scholar

Espinosa Lara, F., and Rieutord, M. (2013). Self-consistent 2D models of fast-rotating early-type stars. Astron. Astrophys. 552:A35. doi: 10.1051/0004-6361/201220844

CrossRef Full Text | Google Scholar

Feiden, G. A. (2016). Magnetic inhibition of convection and the fundamental properties of low-mass stars. III. A consistent 10 Myr age for the Upper Scorpius OB association. Astron. Astrophys. 593:A99. doi: 10.1051/0004-6361/201527613

CrossRef Full Text | Google Scholar

Garaud, P., Ogilvie, G. I., Miller, N., and Stellmach, S. (2010). A model of the entropy flux and Reynolds stress in turbulent convection. Month. Notice. Roy. Astronom. Soc. 407, 2451–2467. doi: 10.1111/j.1365-2966.2010.17066.x

CrossRef Full Text | Google Scholar

Georgy, C., Meynet, G., and Maeder, A. (2011). Effects of anisotropic winds on massive star evolution. Astron. Astrophys. 527:A52. doi: 10.1051/0004-6361/200913797

CrossRef Full Text | Google Scholar

Geroux, C. M., and Deupree, R. G. (2011). Radial stellar pulsation and three-dimensional convection. I. Numerical methods and adiabatic test cases. Astrophys. J. 731:18. doi: 10.1088/0004-637X/731/1/18

CrossRef Full Text | Google Scholar

Geroux, C. M., and Deupree, R. G. (2013). Radial stellar pulsation and three-dimensional convection. II. two-dimensional convection in full amplitude radial pulsation. Astrophys. J. 771:113. doi: 10.1088/0004-637X/771/2/113

CrossRef Full Text | Google Scholar

Geroux, C. M., and Deupree, R. G. (2014). Radial stellar pulsation and three-dimensional convection. III. Comparison of two-dimensional and three-dimensional convection effects on radial pulsation. Astrophys. J. 783:107. doi: 10.1088/0004-637X/783/2/107

CrossRef Full Text | Google Scholar

Geroux, C. M., and Deupree, R. G. (2015). Radial stellar pulsation and three-dimensional convection. IV. Full amplitude three-dimensional solutions. Astrophys. J. 800:35. doi: 10.1088/0004-637X/800/1/35

CrossRef Full Text | Google Scholar

Gillich, A., Deupree, R. G., Lovekin, C. C., Short, C. I., and Toqué, N. (2008). Determination of effective temperatures and luminosities for rotating stars. Astrophys. J. 683, 441–448. doi: 10.1086/589323

CrossRef Full Text | Google Scholar

Grunhut, J. H., Wade, G. A., Neiner, C., Oksala, M. E., Petit, V., Alecian, E., et al. (2017). The MiMeS survey of magnetism in massive stars: magnetic analysis of the O-type stars. Month. Notice. Roy. Astronom. Soc. 465, 2432–2470. doi: 10.1093/mnras/stw2743

CrossRef Full Text | Google Scholar

Guzik, J. A., and Lovekin, C. C. (2014). Pulsations and hydrodynamics of luminous blue variable stars. arXiv e-prints arXiv:1402.0257.

Google Scholar

Hachisu, I., and Eriguchi, Y. (1984a). Binary fluid star. Public. Astronom. Soc. Jpn. 36, 259–276.

Google Scholar

Hachisu, I., and Eriguchi, Y. (1984b). Fission of dumbbell equilibrium and binary state of rapidly rotating polytropes. Public. Astronom. Soc. Jpn. 36, 239–257.

Google Scholar

Hachisu, I., Eriguchi, Y., and Sugimoto, D. (1982). Rapidly rotating polytropes and concave hamburger equilibrium. Progress Theor. Phys. 68, 191–205.

Google Scholar

Halabi, G. M., Izzard, R. G., Tout, C. A., Jermyn, A. S., and Cannon, R. (2017). 2DStars: a two-dimensional stellar evolution code. Mem. Soc. Astronom. Ital. 88:319.

Google Scholar

Hambleton, K., Fuller, J., Thompson, S., Prša, A., Kurtz, D. W., Shporer, A., et al. (2018). KIC 8164262: a heartbeat star showing tidally induced pulsations with resonant locking. Month. Notice. Roy. Astronom. Soc. 473, 5165–5176. doi: 10.1093/mnras/stx2673

CrossRef Full Text | Google Scholar

Hardorp, J., and Strittmatter, P. A. (1968). The effect of rotation on radiation from stars. I. Properties of the continuum. Astrophys. J. 151:1057.

Google Scholar

Heger, A., and Langer, N. (2000). Presupernova evolution of rotating massive stars. II. Evolution of the surface properties. Astrophys. J. 544, 1016–1035. doi: 10.1086/317239

CrossRef Full Text | Google Scholar

Huang, W., and Gies, D. R. (2006). Stellar rotation in young clusters. I. Evolution of projected rotational velocity distributions. Astrophys. J. 648, 580–590. doi: 10.1086/505782

CrossRef Full Text | Google Scholar

Huang, W., Gies, D. R., and McSwain, M. V. (2010). A stellar rotation census of B stars: From ZAMS to TAMS. Astrophys. J. 722, 605–619. doi: 10.1088/0004-637X/722/1/605

CrossRef Full Text | Google Scholar

Hunter, I., Brott, I., Lennon, D. J., Langer, N., Dufton, P. L., Trundle, C., et al. (2008). The VLT FLAMES survey of massive stars: rotation and nitrogen enrichment as the key to understanding massive star evolution. Astrophys. J. 676:L29. doi: 10.1086/587436

CrossRef Full Text | Google Scholar

Jackson, R. J., Deliyannis, C. P., and Jeffries, R. D. (2018). The inflated radii of M dwarfs in the Pleiades. Month. Notice. Roy. Astronom. Soc. 476, 3245–3262. doi: 10.1093/mnras/sty374

CrossRef Full Text | Google Scholar

Jackson, S. (1970). Rapidly rotating stars. V. The coupling of the henyey and the self- consistent methods. Astrophys. J. 161:579.

Google Scholar

Jackson, S., MacGregor, K. B., and Skumanich, A. (2005). On the use of the self-consistent-field method in the construction of models for rapidly rotating main-sequence stars. Astrophys. J. Suppl. Ser. 156, 245–264. doi: 10.1086/426587

CrossRef Full Text | Google Scholar

Jennings, R., Brandenburg, A., Tuominen, I., and Moss, D. (1990). Can stellar dynamos be modelled in less than three dimensions? Astron. Astrophys. 230, 463–473.

Google Scholar

Keszthelyi, Z., Wade, G. A., Petit, V., Meynet, G., and Georgy, C. (2018). The impact and evolution of magnetic confinement in hot stars. Contrib. Astronom. Observat. Skalnate Pleso 48, 124–128.

Google Scholar

Khokhlova, V. L. (1976). Mapping of “spots” on the surface of Ap stars by means of line profiles. Soviet Astron. 19:576.

Google Scholar

Kitchatinov, L. L., and Rüdiger, G. (1999). Differential rotation models for late-type dwarfs and giants. Astron. Astrophys. 344, 911–917.

Google Scholar

Kudritzki, R. P. (2002). Line-driven winds, ionizing fluxes, and ultraviolet spectra of hot stars at extremely low metallicity. I. Very massive O stars. Astrophys. J. 577:389–408. doi: 10.1086/342178

CrossRef Full Text | Google Scholar

Li, G., Bedding, T. R., Murphy, S. J., Van Reeth, T., Antoci, V., and Ouazzani, R.-M. (2019). Period spacings of γ Doradus pulsators in the Kepler field: detection methods and application to 22 slow rotators. Month. Notice. Roy. Astronom. Soc. 482, 1757–1785. doi: 10.1093/mnras/sty2743

CrossRef Full Text | Google Scholar

Lignières, F., and Georgeot, B. (2009). Asymptotic analysis of high-frequency acoustic modes in rapidly rotating stars. Astron. Astrophys. 500, 1173–1192. doi: 10.1051/0004-6361/200811165

CrossRef Full Text | Google Scholar

Lignières, F., Rieutord, M., and Reese, D. (2006). Acoustic oscillations of rapidly rotating polytropic stars. I. Effects of the centrifugal distortion. Astron. Astrophys. 455, 607–620. doi: 10.1051/0004-6361:20065015

CrossRef Full Text | Google Scholar

Lovekin, C. C. (2011). Mass-loss in 2D zero-age main-sequence stellar models. Month. Notice. Roy. Astronom. Soc. 415, 3887–3894. doi: 10.1111/j.1365-2966.2011.19004.x

CrossRef Full Text | Google Scholar

Lovekin, C. C., and Deupree, R. G. (2008). Radial and nonradial oscillation modes in rapidly rotating stars. Astrophys. J. 679, 1499–1508. doi: 10.1086/587615

CrossRef Full Text | Google Scholar

Lovekin, C. C., Deupree, R. G., and Clement, M. J. (2009). Effects of uniform and differential rotation on stellar pulsations. Astrophys. J. 693, 677–690. doi: 10.1088/0004-637X/693/1/677

CrossRef Full Text | Google Scholar

Lovekin, C. C., Deupree, R. G., and Short, C. I. (2006). Surface temperature and synthetic spectral energy distributions for rotationally deformed stars. Astrophys. J. 643, 460–470.

Google Scholar

Lovekin, C. C., and Goupil, M. J. (2010). Rotation and convective core overshoot in θ Ophiuchi. Astron. Astrophys. 515:A58. doi: 10.1051/0004-6361/200913855

CrossRef Full Text | Google Scholar

Lovekin, C. C., and Guzik, J. A. (2014). Pulsations as a driver for LBV variability. Month. Notice. Roy. Astronom. Soc. 445, 1766–1773. doi: 10.1093/mnras/stu1899

CrossRef Full Text | Google Scholar

Lovekin, C. C., and Guzik, J. A. (2017). Convection and Overshoot in Models of γ Doradus and δ Scuti Stars. Astrophys. J. 849:38. doi: 10.3847/1538-4357/aa8e0

CrossRef Full Text | Google Scholar

Lucy, L. B. (1967). Gravity-darkening for stars with convective envelopes. Zeitschrift fur Astrophysik 65:89.

Google Scholar

MacGregor, K. B., Jackson, S., Skumanich, A., and Metcalfe, T. S. (2007). On the structure and properties of differentially rotating, main- sequence stars in the 1-2 M_solar range. Astrophys. J. 663, 560–572.

Google Scholar

Maeder, A. (2002). Stellar evolution with rotation. IX. The effects of the production of asymmetric nebulae on the internal evolution. Astron. Astrophys. 392, 575–584.

Google Scholar

Maeder, A., and Meynet, G. (2012). Rotating massive stars: from first stars to gamma ray bursts. Rev. Modern Phys. 84, 25–63. doi: 10.1103/RevModPhys.84.25

CrossRef Full Text | Google Scholar

Maeder, A., and Peytremann, E. (1970). Stellar Rotation. Astron. Astrophys. 7:120.

Google Scholar

Mathis, S., Palacios, A., and Zahn, J. P. (2004). On shear-induced turbulence in rotating stars. Astron. Astrophys. 425, 243–247. doi: 10.1051/0004-6361:20040279

CrossRef Full Text | Google Scholar

Miglio, A., Montalbán, J., Noels, A., and Eggenberger, P. (2008). Probing the properties of convective cores through g modes: high-order g modes in SPB and γ Doradus stars. Month. Notice. Roy. Astronom. Soc. 386, 1487–1502. doi: 10.1111/j.1365-2966.2008.13112.x

CrossRef Full Text | Google Scholar

Mokiem, M. R., de Koter, A., Evans, C. J., Puls, J., Smartt, S. J., Crowther, P. A., et al. (2006). The VLT-FLAMES survey of massive stars: mass loss and rotation of early-type stars in the SMC. Astron. Astrophys. 456, 1131–1151. doi: 10.1051/0004-6361:20064995

CrossRef Full Text | Google Scholar

Monnier, J. D., Zhao, M., Pedretti, E., Thureau, N., Ireland, M., Muirhead, P., et al. (2007). Imaging the surface of altair. Science 317:342. doi: 10.1126/science.1143205

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, P. E., and Vink, J. S. (2014). Rotating massive O stars with non-spherical 2D winds. Astron. Astrophys. 564:A57. doi: 10.1051/0004-6361/201323031

CrossRef Full Text | Google Scholar

Mundprecht, E., Muthsam, H. J., and Kupka, F. (2013). Multidimensional realistic modelling of Cepheid-like variables - I. Extensions of the ANTARES code. Month. Notice. Roy. Astronom. Soc. 435, 3191–3205. doi: 10.1093/mnras/stt1511

CrossRef Full Text | Google Scholar

Mundprecht, E., Muthsam, H. J., and Kupka, F. (2015). Multidimensional realistic modelling of Cepheid-like variables - II. Analysis of a Cepheid model. Month. Notice. Roy. Astronom. Soc. 449, 2539–2552. doi: 10.1093/mnras/stv434

CrossRef Full Text | Google Scholar

Navarrete, F. H., Schleicher, D. R. G., Käpylä, P. J., Schober, J., Völschow, M., and Mennickent, R. E. (2019). Magneto-hydrodynamical origin of eclipsing time variations in post-common-envelope binaries for solar mass secondaries. Month. Notice. Roy. Astronom. Soc. 491, 1043–1056. doi: 10.1093/mnras/stz3065

CrossRef Full Text | Google Scholar

Ostlie, D. A. (1990). “Time dependent convection in stellar pulsation,” in Numerical Modelling of Nonlinear Stellar Pulsations Problems and Prospects, ed J. R. Buchler (Boston, MA: Kluwer Academic Publishers), 89.

Google Scholar

Ostriker, J. P., and Mark, J. W. K. (1968). Rapidly rotating stars. I. The self-consistent-field method. Astrophys. J. 151, 1075–1088.

Google Scholar

Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., Bedding, T. R., Murphy, S. J., and Roxburgh, I. W. (2017). A new asteroseismic diagnostic for internal rotation in γ Doradus stars. Month. Notice. Roy. Astronom. Soc. 465, 2294–2309. doi: 10.1093/mnras/stw2717

CrossRef Full Text | Google Scholar

Ouazzani, R. M., Dupret, M. A., and Reese, D. R. (2012). Pulsations of rapidly rotating stars. I. The ACOR numerical code. Astron. Astrophys. 547:A75. doi: 10.1051/0004-6361/201219548

CrossRef Full Text | Google Scholar

Ouazzani, R. M., Roxburgh, I. W., and Dupret, M. A. (2015). Pulsations of rapidly rotating stars. II. Realistic modelling for intermediate-mass stars. Astron. Astrophys. 579:A116. doi: 10.1051/0004-6361/201525734

CrossRef Full Text | Google Scholar

Paparó, M., Kolláth, Z., Shobbrook, R. R., Matthews, J. M., Antoci, V., Benkó, J. M., et al. (2018). The Delta Scuti star 38 Eri from the ground and from space. Month. Notice. Roy. Astronom. Soc. 477, 4362–4379. doi: 10.1093/mnras/sty885

CrossRef Full Text | Google Scholar

Peterson, D. M., Hummel, C. A., Pauls, T. A., Armstrong, J. T., Benson, J. A., Gilbreath, G. C., et al. (2006). Vega is a rapidly rotating star. Nature 440, 896–899. doi: 10.1038/nature04661

PubMed Abstract | CrossRef Full Text | Google Scholar

Reese, D., Lignières, F., and Rieutord, M. (2006). Acoustic oscillations of rapidly rotating polytropic stars. II. Effects of the Coriolis and centrifugal accelerations. Astron. Astrophys. 455, 621–637. doi: 10.1051/0004-6361:20065269

CrossRef Full Text | Google Scholar

Reese, D. R., MacGregor, K. B., Jackson, S., Skumanich, A., Metcalfe, T. S., Dikpati, M., et al. (2009). “Pulsation modes with high azimuthal orders in stellar models based on the self-consistent field method,” in Solar-Stellar Dynamos as Revealed by Helio- and Asteroseismology: GONG 2008/SOHO 21, ASP Conference Series, Vol. 416, 395.

Google Scholar

Reiners, A., and Schmitt, J. H. M. M. (2003). Differential rotation in rapidly rotating F-stars. Astron. Astrophys. 412, 813–819. doi: 10.1051/0004-6361:20034255

CrossRef Full Text | Google Scholar

Richardson, N. D., Pablo, H., Sterken, C., Pigulski, A., Koenigsberger, G., Moffat, A. F. J., et al. (2018). BRITE-Constellation reveals evidence for pulsations in the enigmatic binary η Carinae. Month. Notice. Roy. Astronom. Soc. 475, 5417–5423. doi: 10.1093/mnras/sty157

CrossRef Full Text | Google Scholar

Rieutord, M., Espinosa Lara, F., and Putigny, B. (2016). An algorithm for computing the 2D structure of fast rotating stars. J. Comput. Phys. 318, 277–304. doi: 10.1016/j.jcp.2016.05.011

CrossRef Full Text | Google Scholar

Roxburgh, I. W. (2004). 2-dimensional models of rapidly rotating stars I. Uniformly rotating zero age main sequence stars. Astron. Astrophys. 428, 171–179. doi: 10.1051/0004-6361:20041202

CrossRef Full Text | Google Scholar

Roxburgh, I. W. (2006). 2-dimensional models of rapidly rotating stars. II. Hydrostatic and acoustic models with Ω=Ω (r,θ). Astron. Astrophys. 454, 883–888. doi: 10.1051/0004-6361:20065109

CrossRef Full Text | Google Scholar

Roxburgh, I. W., Griffith, J. S., and Sweet, P. A. (1965). On models of non spherical stars I. The theory of rapildy rotating main sequence stars. With 3 figures in the text. Zeitschrift fur Astrophysik 61:203.

Google Scholar

Saio, H. (2014). “Pulsation of magnetic stars,” in Precision Asteroseismology Proceedings of the International Astronomical Union, IAU Symposium, Vol. 301, eds J. A. Guzik, W. J. Chaplin, G. Handler, and A. Pigulski, 197–204.

Google Scholar

Song, H. F., Meynet, G., Maeder, A., Ekström, S., and Eggenberger, P. (2016). Massive star evolution in close binaries. Conditions for homogeneous chemical evolution. Astron. Astrophys. 585:A120. doi: 10.1051/0004-6361/201526074

CrossRef Full Text | Google Scholar

Soufi, F., Goupil, M. J., and Dziembowski, W. A. (1998). Effects of moderate rotation on stellar pulsation. I. Third order perturbation formalism. Astron. Astrophys. 334, 911–924.

Google Scholar

Stoeckley, T. R. (1968). Absorption line strengths in rotating stars. Month. Notice. Roy. Astronom. Soc. 140:149.

Google Scholar

Stoeckley, T. R., and Buscombe, W. (1987). Axial inclination and differential rotation for 19 rapidly rotating stars. Month. Notice. Roy. Astronom. Soc. 227, 801–813.

Google Scholar

Suárez, J. C., Andrade, L., Goupil, M. J., and Janot- Pacheco, E. (2010). On the use of rotational splitting asymmetries to probe the internal rotation profile of stars: Application to β Cephei stars. Astronomische Nachrichten 331:1073. doi: 10.1002/asna.201011460

CrossRef Full Text | Google Scholar

Sweet, I. P. A., and Roy, A. E. (1953). The structure of rotating stars. Month. Notice. Roy. Astronom. Soc. 113:701. doi: 10.1093/mnras/113.6.701

CrossRef Full Text | Google Scholar

Sweet, P. A. (1950). The importance of rotation in stellar evolution. Month. Notice. Roy. Astronom. Soc. 110:548.

Google Scholar

Szécsi, D., Langer, N., Yoon, S.-C., Sanyal, D., de Mink, S., Evans, C. J., et al. (2015). Low-metallicity massive single stars with rotation. Evolutionary models applicable to I Zwicky 18. Astron. Astrophys. 581:A15. doi: 10.1051/0004-6361/201526617

CrossRef Full Text | Google Scholar

Tassoul, J. -L. (1978). Theory of Rotating Stars. Princeton, NJ: Princeton University Press.

Google Scholar

Tassoul, M. (1980). Asymptotic approximations for stellar nonradial pulsations. Astrophys. J. Suppl. Ser. 43, 469–490.

Google Scholar

Tuggle, R. S., and Iben Icko, J. (1973). Comments on nodal quenching and on convective quenching in RR lyrae stars. Astrophys. J. 186, 593–600.

Google Scholar

van Belle, G. T., Ciardi, D. R., ten Brummelaar, T., McAlister, H. A., Ridgway, S. T., Berger, D. H., et al. (2006). First results from the CHARA Array. III. Oblateness, rotational velocity, and gravity darkening of alderamin. Astrophys. J. 637, 494–505. doi: 10.1086/498334

CrossRef Full Text | Google Scholar

van Belle, G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., and Lada, E. A. (2001). Altair's Oblateness and Rotation Velocity from Long-Baseline Interferometry. Astrophys. J. 559, 1155–1164. doi: 10.1086/322340

CrossRef Full Text | Google Scholar

Van Reeth, T., Tkachenko, A., and Aerts, C. (2016). Interior rotation of a sample of γ Doradus stars from ensemble modelling of their gravity-mode period spacings. Astron. Astrophys. 593:A120. doi: 10.1051/0004-6361/201628616

CrossRef Full Text | Google Scholar

Venn, K. A., Lambert, D. L., and Lemke, M. (1996). The abundance of boron in evolved A- and B-type stars. Astron. Astrophys. 307, 849–859.

Google Scholar

Viallet, M., Meakin, C., Arnett, D., and Mocák, M. (2013). Turbulent convection in stellar interiors. III. Mean-field analysis and stratification effects. Astrophys. J. 769:1. doi: 10.1088/0004-637X/769/1/1

CrossRef Full Text | Google Scholar

Vink, J. S., de Koter, A., and Lamers, H. J. G. L. M. (2001). Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 369, 574–588. doi: 10.1051/0004-6361:20010127

CrossRef Full Text | Google Scholar

von Zeipel, H. (1924). The radiative equilibrium of a rotating system of gaseous masses. Month. Notice. Roy. Astronom. Soc. 84, 665–683.

Google Scholar

Woodward, P. R., Lin, P.-H., Mao, H., Andrassy, R., and Herwig, F. (2018). Simulating 3-D stellar hydrodynamics using PPM and PPB multifluid gas dynamics on CPU and CPU+GPU nodes. arXiv e-prints arXiv:1810.13416.

Google Scholar

Zahn, J. P. (1992). Circulation and turbulence in rotating stars. Astron. Astrophys. 265, 115–132.

Google Scholar

Zhao, M., Monnier, J. D., Pedretti, E., Thureau, N., Mérand, A., ten Brummelaar, T., et al. (2009). Imaging and modeling rapidly rotating stars: α cephei and α ophiuchi. Astrophys. J. 701, 209–224.

Google Scholar

Zorec, J., Rieutord, M., Espinosa Lara, F., Frémat, Y., Domiciano de Souza, A., and Royer, F. (2017). Gravity darkening in stars with surface differential rotation. Astron. Astrophys. 606:A32. doi: 10.1051/0004-6361/201730818

CrossRef Full Text | Google Scholar