Scaling Relations for Solar-Like Oscillations: A Review

1. Introduction

With the advent of high resolution spectrographs [e.g., UCLES (Diego et al., 1990), CORALIE (Queloz et al., 1999), HARPS (Pepe et al., 2000), UVES (Dekker et al., 2000), and SONG (Grundahl et al., 2007)] and dedicated space-based photometric missions [CoRoT (Michel et al., 1998), Kepler (Borucki et al., 2009), TESS (Ricker et al., 2014)] the number of stars for which solar-like oscillations have been observed has increased by several orders of magnitude from the single case of the Sun (Leighton et al., 1962) to several hundreds to thousands (e.g., Hekker et al., 2009; Chaplin et al., 2011; Yu et al., 2018) over the last few decades. Solar-like oscillations are stochastically excited by the turbulent convection in stars (e.g., Goldreich and Keeley, 1977; Goldreich and Kumar, 1988) with convective envelopes, i.e., in stars with effective temperatures below ~6, 700 K. Effectively, some of the convective energy is transferred into energy of global oscillations, which reveal themselves as small amplitude oscillations at the stellar surface. As essentially all modes are excited the oscillation spectrum generally shows a clear pattern of overtones, with as a dominant feature the large frequency separation between modes of the same degree and consecutive radial order Δν. The oscillations are centered around a specific frequency (also called frequency of maximum oscillation power ν_max) with the (small) amplitudes of the oscillations decreasing away from this specific frequency.

In the 1980's and early 1990's, several groups attempted to observe solar-like oscillations in our brightest neighboring stars such as Procyon, α Cen A, β Hyi, and ϵ Eri (Noyes et al., 1984; Gelly et al., 1986; Frandsen, 1987; Brown and Gilliland, 1990; Brown et al., 1991; Innis et al., 1991; Pottasch et al., 1992; Bedford et al., 1993) to name a few. It was also at these times that the scaling relations (or asteroseismic scaling relations) for solar-like oscillations were first introduced. The main purpose of these relations was to predict the frequencies and amplitudes of the solar-like oscillations based on the known mass, radius, surface gravity, and effective temperature of the target. This allowed for investigations as to whether the (null-)detections were genuine or due to limitations of the observations in terms of for instance signal-to-noise ratio and/or frequency resolution.

An early suggestion for a scaling relation was presented by Brown et al. (1991). This scaling relation was based on the acoustic cut-off frequency (ν_ac), which is expected to scale as:

$\begin{array}{ll}{\nu }_{\text{ac}}\propto g{T}_{\text{eff}}^{-\frac{1}{2}}& (1)\end{array}$

with g the surface gravity and T_eff the effective temperature. The predictions by Brown et al. (1991) were based on the fact that the acoustic cut-off frequency is about 1.8 times the frequency at which the oscillation amplitudes in the Sun are largest. From this Brown et al. (1991) predicted the location of the frequency of maximum oscillation power for Procyon to be around 1.0 mHz.

Kjeldsen and Bedding (1995) presented a dedicated study in which they predicted the amplitude [both velocity amplitude v_osc and luminosity amplitude (δL/L)_λ at wavelength λ], frequency of maximum oscillation power (ν_max) and large frequency separation (Δν) of other stars from scaling to the Sun, based on a linear adiabatic derivation. Kjeldsen and Bedding (1995) formulated the scaling relations as follows:

$\begin{array}{ll}{v}_{\text{osc}}=\frac{L/L_{\odot }}{M/M_{\odot }}(23.4\pm 1.4){\text{cm s}}^{-1}& (2)\end{array}$

$\begin{array}{ll}{(\delta L/L)}_{\lambda }=\frac{L/L_{\odot }(4.7\pm 0.3)\text{ ppm}}{(\lambda /550\text{ nm}){(T_{\text{eff}}/5777\text{ K})}^2(M/M_{\odot })}& (3)\end{array}$

$\begin{array}{ll}\Delta {\nu }_0={(M/M_{\odot })}^{\frac{1}{2}}{(R/R_{\odot })}^{-\frac{3}{2}}\Delta {\nu }_{\odot }& (4)\end{array}$

$\begin{array}{ll}{\nu }_{\text{max}}=\frac{M/M_{\odot }}{{(R/R_{\odot })}^2\sqrt{T_{\text{eff}}/5777\text{K}}}{\nu }_{\text{max},\odot }& (5)\end{array}$

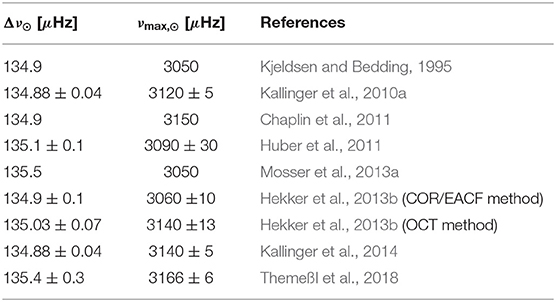
with Δν₀ the value of Δν for radial (degree = 0) modes, L luminosity, M mass, and R radius. The _⊙ symbol indicates solar values, with Δν_⊙ = 134.9 μHz and ν_max,⊙ = 3.05 mHz. Over the years, several authors have adopted different solar values based on internal calibrations from the analysis of a solar oscillation spectrum with the same method as applied to asteroseismic oscillation spectra. An overview of these values with references is provided in Table 1.

TABLE 1

Table 1. Overview of observed Δν_⊙ and ν_max,⊙ values as adopted in the literature.

The scaling relations provide decent estimates of the observed oscillations for a large range of stars. However, with the increase in the accuracy with which solar-like oscillations have been detected for a range of stars with different masses, metallicities, and effective temperatures, the inherent shortcomings of such relations, i.e., they rely on a homologous stellar structure between the target star and the reference, have been apparent. Additionally, the use of the scaling relations has reversed from predicting oscillation features from known stellar parameters (e.g., Brown et al., 1991; Kjeldsen and Bedding, 1995) to estimating stellar parameters from the observed oscillations as per Equations (6) and (7) (Stello et al., 2009b; Kallinger et al., 2010b, were the first to apply this, to solar-type stars and red-giant stars, respectively). This changed use of the scaling relations and our desire to obtain always more precise and accurate stellar parameters changed the accuracy and precision that we aim to reach with the scaling relations.

$\begin{array}{ll}\frac{M}{{\text{M}}_{\odot }}\simeq {\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right)}^3{\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^{-4}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{3/2}& (6)\end{array}$

$\begin{array}{ll}\frac{R}{{\text{R}}_{\odot }}\simeq \left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right){\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^{-2}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{1/2}& (7)\end{array}$

The amplitudes of the oscillations are related to the excitation and damping processes of the oscillations, which are still debated in the literature. Hence, the amplitude scaling relations (Equations 2, 3) are not yet widely used to derive stellar parameters. On the other hand, the Δν and ν_max scaling relations (Equations 4, 5) are now frequently used to determine stellar masses and radii (Equations 6, 7) and from these derive stellar ages. For this reason I focus here on the Δν and ν_max scaling relations.

2. The Δν and ν_max Scaling Relations

Here I first discuss the physical relation between stellar parameters and Δν and ν_max, respectively. I subsequently present an overview of many of the validity tests and suggestions to adapt the scaling relations and/or the reference values which aim to improve the accuracy of the derived stellar parameters in chronological order.

2.1. Relation of Δν and ν_max With Stellar Parameters

The Δν scaling relation is physically justified as Δν is in an asymptotic approximation equal to the inverse of the sound travel time through the star:

$\begin{array}{ll}\Delta \nu ={\left(2{\displaystyle {\int }_0^R}\frac{dr}{c_s}\right)}^{-1},& (8)\end{array}$

with c_s the adiabatic sound speed. Kjeldsen and Bedding (1995) showed that with estimates for internal values of the pressure and the temperature this results in $\Delta \nu \propto \sqrt{M/R^3}$, i.e., that the large frequency separation is directly proportional to the square root of the mean density of the star.

The ν_max scaling relation has been defined empirically based on homology arguments with another typical dynamical timescale of the atmosphere, i.e., the acoustic cut-off frequency (ν_ac, see Equation 1). Belkacem et al. (2011) aimed to provide a theoretical basis for the scaling between ν_max and ν_ac. These authors indeed confirmed for stars other than the Sun that ν_max corresponds to the plateau (depression) of the damping rates, as was already pointed out for the solar case by Chaplin et al. (2008). This combined with the suggestion by Balmforth (1992) that the plateau of the damping rate occurs when there is a resonance between the thermal time scale (τ) and the modal frequency, Belkacem et al. (2011) derived the resonance condition to be:

$\begin{array}{ll}{\nu }_{\text{max}}\simeq \frac{1}{2\pi \tau }.& (9)\end{array}$

For a grid of models Belkacem et al. (2011) found a close to linear relation between the thermal frequency τ⁻¹ and ν_ac with some dispersion related to the dispersion in mass. Hence, they concluded that the observed relation between ν_max and ν_ac is indeed the result of the resonance between ν_max and τ⁻¹, as well as the relation between τ⁻¹ and ν_ac. Belkacem et al. (2011) took this one step further to express this in thermodynamic quantities and found:

$\begin{array}{ll}{\nu }_{\text{max}}\propto \frac{1}{\tau }\propto \left(\frac{{\Gamma }_1^2}{{\chi }_{\rho }\Sigma }\right)\left(\frac{{{M}}_a^3}{{\alpha }_{\text{MLT}}}\right){\nu }_{\text{ac}},& (10)\end{array}$

with ${{M}}_a$ the Mach number, i.e., the ratio of the convective rms velocity v_conv to sound speed c_s, α_MLT the mixing-length parameter, χ_ρ = (∂ln P/∂ln ρ)_T, Σ = (∂ln ρ/∂ln T)_{μ, P}, and Γ₁ = (∂ln P/∂ln ρ)_ad with P, T, ρ, and μ the pressure, temperature, density, and mean molecular weight, respectively. Finally, Belkacem et al. (2011) stated that although the observed scaling between ν_max and ν_ac may not be obvious at first glance as ν_max depends on the dynamical properties of the convective region while ν_ac is a statistical property of the surface layers, the additional dependence on the Mach number resolves this paradox.

Together the Δν and ν_max scaling relations (Equations 4, 5) can be rewritten to provide stellar masses and radii (Equations 6, 7). This path way of deriving stellar masses and radii is now widely in use. Hence, the Δν and ν_max scaling relations are discussed here together.

2.2. Validity Tests and Suggested Improvements

After some initial general investigations in the validity of the Δν scaling relation by Stello et al. (2009a), Bruntt et al. (2010), Basu et al. (2010), and White et al. (2011) were the first to carry out an in depth study on how accurately the relation in Equation (11) is followed by models:

$\begin{array}{ll}\rho \approx {\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^2{\rho }_{\odot },& (11)\end{array}$

with ρ and ρ_⊙ the mean density of the star and the Sun, respectively. In their work, White et al. (2011) computed Δν from a linear (Gaussian-weighted) least squares fit to the frequencies of radial modes. Throughout the paper, I will refer to Δν derived in a similar way as Δν_freq. Using the same approach White et al. (2011) computed Δν_⊙ = 135.99 μHz derived from a fit to frequencies of the standard solar model, model S of Christensen-Dalsgaard et al. (1996).

White et al. (2011) showed that deviations from the scaling relation exist in models and that these are predominantly a function of effective temperature. For stars with temperatures in the range 4,700–6,700 K and masses larger than ~ 1.2 M_⊙, these authors suggested a variation of the scaling relation of the form:

$\begin{array}{ll}\frac{\rho }{{\rho }_{\odot }}={\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^2{\left(f\left(T_{\text{eff}}\right)\right)}^{-2},& (12)\end{array}$

where

$\begin{array}{ll}f\left(T_{\text{eff}}\right)=-4.29{\left(\frac{T_{\text{eff}}}{10^4\text{K}}\right)}^2+4.84\left(\frac{T_{\text{eff}}}{10^4\text{K}}\right)-0.35.& (13)\end{array}$

According to White et al. (2011), metallicity has little effect except for red giants, for which there is a slight dependence. Furthermore, they noted that their function (Equations 12, 13) is based on models and the so-called surface effect (a frequency-dependent offset between observed and modeled frequencies that affects Δν) is not accounted for. Nevertheless, they recommended (Equation 12 or Equation 11) to be used with the observed value of Δν_⊙ = 135.0 μHz.

Subsequently, Huber et al. (2012) compared the radii of stars measured from asteroseismic scaling relations with radii measured from interferometry. They obtained excellent agreement within the observational uncertainties. They furthermore showed that asteroseismic radii of main-sequence stars are accurate to ≤4 per cent. At about the same time (Silva Aguirre et al., 2012) used the oscillation data and multi-band photometry to derive stellar parameters in a self-consistent manner coupling asteroseismic analysis with the Infra Red Flux Method (IRFM). They showed an overall agreement of 4 per cent with Hipparcos parallaxes, a mean difference in T_eff of less than 1 per cent and agreement within 5 per cent for the angular diameters. Despite these encouraging results, Silva Aguirre et al. (2012) warned for systematics either due to reddening or metallicity, or due to observational uncertainties.

Following Stello et al. (2009a) and Kallinger et al. (2010b), there have been many attempts to use the scaling relations to determine stellar masses and radii, either directly or from grid-based modeling (e.g., Gai et al., 2011). In one of these works Miglio et al. (2012) explicitly addressed the fact that stars on the red-giant branch (RGB) have an internal temperature (hence sound speed) distribution different from that of stars in the core helium burning phase (CHeB). They found that an CHeB model has a mean Δν that is about 3.3 per cent larger than an RGB model, despite having the same mean density. This difference is due to the fact that the sound speed in the CHeB model is on average higher (at a given fractional radius) than that of the RGB model, mostly due to the different temperature profiles. This effect is largest in the region below the boundary of the helium core in the RGB model, though the near-surface regions (r/R ≥ 0.9) also contribute about 0.8 per cent. Based on this finding Miglio et al. (2012) suggested that a relative correction has to be considered when dealing with CHeB stars and RGB stars. This relative correction is expected to be mass-dependent and to be larger for low-mass stars, which have significantly different internal structures when ascending the RGB compared to when they are in the CHeB.

Mosser et al. (2013a, see also Mosser, 2013, Mosser et al., 2013b) made an explicit link between the asymptotic spacing (Δν_as, the value of Δν as defined in Equation 8) and the observed spacing (Δν_obs), where Δν_obs is defined as the difference in observed frequencies of radial modes. Mosser et al. (2013a) linked Δν_as with Δν_obs in the following way:

$\begin{array}{ll}\Delta {\nu }_{\text{as}}=\Delta {\nu }_{\text{obs}}\left(1+\frac{n_{\text{max}}{\alpha }_{\text{obs}}}{2}\right),& (14)\end{array}$

with α_obs the curvature and n_max a dimensionless value of ν_max defined as n_max = ν_max/Δν_obs. By taking into account the curvature, it is possible to correct the observed value of Δν and derive its asymptotic counter part, which leads to more accurate asteroseismic estimates of the stellar mass and radius (see also Belkacem et al., 2013). Mosser et al. (2013a) stated that in case the asymptotic values are used (together with the solar values as listed in Table 1) no correction has to be applied. If the observed values are used, then corrections up to 7.5 and 2.5 per cent in mass and radius should be applied. Alternatively, Mosser et al. (2013a) suggested to use in combination with the observed Δν and ν_max more general reference values, i.e., Δν_ref, instead of the solar reference values. So for stars other than the Sun, they suggested these new calibrated references to be Δν_ref = 138.8 μHz and ν_{max, ref} = 3, 104 μHz.

In response to the work by Mosser et al. (2013a), Hekker et al. (2013a) investigated whether the differences between observable oscillation parameters and their asymptotic estimates are indeed significant. Based on stellar models they found that the extent to which the atmosphere is included in the model is a key parameter. Considering a larger extension of the atmosphere beyond the photosphere reduces the difference between the asymptotic and observable values of the large frequency separation. Hence, Hekker et al. (2013a) cautioned that the corrections proposed by Mosser et al. (2013a) may be overestimated.

Epstein et al. (2014) tested masses obtained from asteroseismic scaling relations against masses of metal-poor ([Fe/H] < −1) stars. Based on the fact that the nine stars (6 halo stars and 3 thick disc stars) in their study can not be younger than 8 Gyr combined with models with a normal (near-primordial) helium abundance provided a range of theoretically allowed masses of between roughly 0.8 and 0.9 M_⊙. The masses obtained by (uncorrected) scaling relations are overestimated by about 16 per cent. This overestimate reduced by including corrections to the reference values of the scaling relations from Kallinger et al. (2010b), White et al. (2011), and Mosser et al. (2013a), though they did not mitigate the problem fully. This prompted Epstein et al. (2014) to call for further investigations into the metallicity dependence of the Δν scaling relation and the impact of the ν_max scaling relation on mass estimates.

Coelho et al. (2015) performed tests on how well the oscillations of cool main-sequence and subgiant stars adhere to the relation between ν_max and the cut-off frequency for acoustic waves in an isothermal atmosphere. The results by Coelho et al. (2015) based on a grid-based modeling approach ruled out departures from the classic ν_max scaling relation at the level of ~1.5 per cent over the full range in T_eff (5,600 K < T_eff < 6, 900 K) that they tested for. Coelho et al. (2015) stated that there is some uncertainty concerning the absolute calibration of the scaling relation, though any variation with T_eff is small, resulting in a limit similar to the ~1.5 per cent level.

Brogaard et al. (2016) concluded in their ongoing investigations of the asteroseismic scaling relations in open cluster stars and binaries that they are accurate to within their uncertainties for giant stars. They stated that this is the case as long as corrections to the reference values of the Δν scaling relation are calculated and applied along the lines of Miglio et al. (2013) whom considered a 5 per cent systematic uncertainty on the radius determination to account for inaccuracies in the scaling relations. Brogaard et al. (2016) noted that asteroseismic logg values are extremely consistent with their independent measurements which implies that the scaling for ν_max is reliable.

Sharma et al. (2016) proposed a correction factor f_Δν defined as:

$\begin{array}{ll}{f}_{\Delta \nu }=\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right){\left(\frac{\rho }{{\rho }_{\odot }}\right)}^{-0.5},& (15)\end{array}$

with Δν_⊙ = 135.1 μHz. The value of f_Δν was determined for a grid of models with −3.0 dex < [Fe/H] < 0.4 dex and 0.8 M_⊙ < M < 4.0 M_⊙ following the same approach as White et al. (2011) to derive Δν_freq for each model in a way to mimic the way Δν is measured from data. The value of f_Δν was obtained by Sharma et al. (2016) along each stellar track ranging from the zero-age main sequence until the end of helium-core burning. These results were combined in a grid, for which they computed the correction factor for each synthetic star through an interpolation and they corrected Δν based on this factor. Additionally, Sharma et al. (2016) also applied a correction to the ν_max scaling relation of f_νmax = 1.02 to improve the agreement between the models and observations.

Guggenberger et al. (2016) tackled the issue of the dependence of the Δν reference on both effective temperature and [Fe/H] by fitting a T_eff - [Fe/H] dependent reference function through a set of models spanning −1.0 dex < [Fe/H] < 0.5 dex and 0.8 M_⊙ < M < 2.0 M_⊙. Based on the variations in the ratio of the value of Δν from scaling relations with solar values to values of Δν_freq obtained from the differences between radial oscillation modes as a function of T_eff in stellar models, this reference function has the following shape:

$\begin{array}{ll}\Delta {\nu }_{\text{ref}}=A{e}^{\lambda T_{\text{eff}}/10^4\text{K}}\left(cos\left(\omega T_{\text{eff}}/10^4\text{K}+\varphi \right)\right)+B,& (16)\end{array}$

with

$\begin{array}{ll}A=0.64\text{[Fe/H]}+1.78\mu \text{Hz},& (17)\end{array}$

$\begin{array}{ll}\lambda =-0.55\text{[Fe/H]}+1.23,& (18)\end{array}$

$\begin{array}{ll}\omega =22.12{\text{ rad K}}^{-1},& (19)\end{array}$

$\begin{array}{ll}\varphi =0.48\text{[Fe/H]}+0.12,& (20)\end{array}$

$\begin{array}{ll}B=0.66\text{[Fe/H]}+134.92\mu \text{Hz},& (21)\end{array}$

and was calibrated for stars in different evolutionary states including (end of) main-sequence stars, subgiants and cool red giants down to ν_max = 6 μHz. Similar to White et al. (2011) this reference function was developed on models and does not include the surface correction. Nevertheless, Guggenberger et al. (2016) showed that this reference function allows masses and radii to be recovered through asteroseismic scaling relations with an accuracy of 5 and 2 per cent, respectively. For this they used ν_{max, ref} = ν_max,⊙ = 3, 050 μHz.

Gaulme et al. (2016) subsequently tested for 10 red-giant stars the masses and radii obtained from the asteroseismic scaling relations against masses and radii obtained from the orbital solutions of spectroscopic eclipsing binaries. These authors found that the asteroseismic scaling relations overestimate the radii by about 5 per cent on average and the masses by about 15 per cent on average, while using the Δν scaling relation where the curvature was included as proposed by Mosser et al. (2013a). Gaulme et al. (2016) also tested both the original scaling relations (Kjeldsen and Bedding, 1995) as well as other reference values (Kallinger et al., 2010a; Chaplin et al., 2011; Guggenberger et al., 2016) and corrections to the scaling relations (Sharma et al., 2016), with similar or worse results. Gaulme et al. (2016) noted that another culprit in the scaling relations is the effective temperature, i.e., overestimated temperatures can lead to overestimated values for the scaling law masses and radii. Indeed, when Gaulme et al. (2016) decreased their effective temperatures by 100 K the asteroseismic masses and radii decreased by 3.1 and 1.0 per cent, respectively.

Yıldız et al. (2016) investigated the impact of the assumption that the first adiabatic exponent (Γ₁) and mean molecular weight (μ) are assumed to be constant at the stellar surface for the purpose of deriving the scaling relations. Yıldız et al. (2016) found that depending on the effective temperature, Γ₁ changes significantly in the near surface layers of solar-like stars. Henceforth, they found that the ratio of the mean large frequency separation to square root of mean density is a linear function of Γ₁. Additionally, they also included the Γ₁ dependence into the ν_max scaling relation. The relations to determine stellar mass and radius as proposed by Yıldız et al. (2016) are as follows:

$\begin{array}{ll}\frac{M}{M_{\odot }}=\frac{{\left({\nu }_{\text{max}}/{\nu }_{\text{max}\odot }\right)}^3}{{\left(\Delta \nu /\Delta {\nu }_{\odot }\right)}^4}{\left(\frac{T_{\text{eff}}}{T_{\text{eff}\odot }}\frac{{\Gamma }_{1\odot }}{{\Gamma }_1}\right)}^{\frac{3}{2}}\frac{f_{\Delta \nu }^4}{f_{\nu }^3},& (22)\end{array}$

$\begin{array}{ll}\frac{R}{R_{\odot }}=\frac{\left({\nu }_{\text{max}}/{\nu }_{\text{max}\odot }\right)}{{\left(\Delta \nu /\Delta {\nu }_{\odot }\right)}^2}{\left(\frac{T_{\text{eff}}}{T_{\text{eff}\odot }}\frac{{\Gamma }_{1\odot }}{{\Gamma }_1}\right)}^{\frac{1}{2}}\frac{f_{\Delta \nu }^2}{f_{\nu }},& (23)\end{array}$

with

$\begin{array}{ll}{f}_{\Delta \nu }=0.430\frac{{\Gamma }_1}{{\Gamma }_{1\odot }}+0.570,& (24)\end{array}$

$\begin{array}{ll}{f}_{\nu }=0.470\frac{{\Gamma }_{1\odot }}{{\Gamma }_1}+0.530.& (25)\end{array}$

Following Yıldız et al. (2016) and Viani et al. (2017) examined the ν_max scaling relation taking into account that the first adiabatic exponent (Γ₁) and mean molecular weight (μ) are not constant at the stellar surface. Based on models they found that the largest source of the deviation in the ν_max scaling relation is the neglect of the mean molecular weight (μ) and Γ₁ terms when approximating the acoustic cut-off frequency. Viani et al. (2017) proposed the following relation to be used:

$\begin{array}{ll}\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}=\left(\frac{M}{M_{\odot }}\right){\left(\frac{R}{R_{\odot }}\right)}^{-2}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{-\frac{1}{2}}{\left(\frac{\mu }{{\mu }_{\odot }}\right)}^{\frac{1}{2}}{\left(\frac{{\Gamma }_1}{{\Gamma }_{1,\odot }}\right)}^{\frac{1}{2}}.& (26)\end{array}$

Viani et al. (2017) noted that the deviations in the scaling relations cause systematic errors in estimates of logg, mass and radius. The errors in logg are however well within errors caused by data uncertainties and are therefore not a big cause for concern, except at extreme metallicities.

Following on from the T_eff - [Fe/H] dependent reference function, Guggenberger et al. (2017) performed symbolic regression, i.e., they let both the functional form as well as the parameters vary to obtain a best fit, to mitigate the mass dependence of Δν_ref for stars with 5 μHz < ν_max < 170 μHz. Essentially, two functions were presented: one based directly on the Δν derived from the models in a way to mimic the observations and one after applying the reference function of Guggenberger et al. (2016) (see Equation 16). These functions take the following from:

$\begin{array}{ll}\Delta {\nu }_{\text{ref}}=A_1+A_2\times M+\frac{A_3}{{\nu }_{\text{max}}}+A_4\times \sqrt{{\nu }_{\text{max}}}-A_5\times {\nu }_{\text{max}}-A_6\times \text{[Fe/H]},& (27)\end{array}$

and for the residuals of Equation (16):

$\begin{array}{l}\Delta {\nu }_{\text{ref},\text{residuals}}=B_1\times M+B_2\times {\nu }_{\text{max}}+\frac{B_3\times M-B_4\times \text{[Fe/H]}}{{\nu }_{\text{max}}}\\ -B_5-B_6\times M\times {\nu }_{\text{max}},& (28)\end{array}$

where the values of the parameters and units are listed in Table 2. As the mass M is included in these functions, they have to be applied in an iterative manner. In the range 5 μHz < ν_max < 170 μHz the reference functions Equations (27) and (28) improve mass and radius determinations by 10 per cent and 5 per cent respectively (compared to using a solar reference). This is true in the limit of ideal data obtained from canonical stellar models and without including a surface effect. Guggenberger et al. (2017) noted that Equations (27, 28) as well as (16) do not have a physical meaning. However, they do represent an empirical fit optimized to the data obtained from stellar models that include canonical stellar physics.

TABLE 2

Table 2. Parameters with their units of the functions in Equations (27) and (28).

Serenelli et al. (2017) formulated a calibration factor to account for the surface effects in cases where Δν in stellar models is computed from theoretical frequencies (e.g., Sharma et al., 2016; Rodrigues et al., 2017). The advantage of relying on Δν_freq computed from theoretical frequencies is that it captures deviations from the pure scaling relation due to the detailed structure of stellar models (e.g., Belkacem et al., 2013). However, the underlying theoretical frequencies are affected by poor modeling of stellar atmospheres and the neglect of non-adiabatic effects in the outer most layers (Rosenthal et al., 1999), i.e., the surface effect. Therefore, the Δν_freq from solar models is about 1 per cent larger than the observed Δν_⊙. This difference implies that stellar model grids that rely on Δν_freq computed from theoretical frequencies will not be able to reproduce a solar model unless it is rescaled to match Δν_⊙. The calibration factor f_cal to rescale Δν_freq to Δν_⊙ suggested by Serenelli et al. (2017) is as follows:

$\begin{array}{ll}{f}_{\text{cal}}=\frac{\Delta {\nu }_{\odot }}{\Delta {\nu }_{\text{freq,SM}}},& (29)\end{array}$

where SM means solar model. Such a rescale has been applied by Serenelli et al. (2017) to the full grid of stellar models used to compute stellar parameters.

In a similar approach as Gaulme et al. (2016), Brogaard et al. (2018), and Themeßl et al. (2018) tested the asteroseismic masses and radii against masses and radii obtained from binary orbits for three eclipsing binary systems each (one system in overlap). Both studies found that asteroseismic scaling relations without corrections to the Δν scaling relations would overestimate the masses and radii. However, by including the theoretical correction factors (f_Δν) according to Rodrigues et al. (2017)¹, Brogaard et al. (2018) reached general agreement between dynamical and asteroseismic mass estimates, and no indications of systemic differences at the level of precision of the asteroseismic measurements. In the same vein, Themeßl et al. (2018) proposed an empirical reference value for Δν (Δν_ref,emp) that is consistent with the corrections by Guggenberger et al. (2016) while also including surface effects as computed for the same set of stars by Ball et al. (2018). Themeßl et al. (2018) presented the following value:

$\begin{array}{ll}\Delta {\nu }_{\text{ref,emp}}=130.8\pm 0.9\mu \text{Hz},& (30)\end{array}$

with a consistent solar reference for ν_max of 3137 ± 45 μHz. Both the studies by Brogaard et al. (2018) and Themeßl et al. (2018) indicated that this is just a start and that there is a need for a large high-precision sample of eclipsing spectroscopic binaries (eSB2) covering a range in mass, metallicity and stellar evolution to further test the masses and radii of solar-like oscillators determined through scaling relations.

Kallinger et al. (2018) devised non-linear seismic scaling relations based on six known eSB2 systems selected from Gaulme et al. (2016), Themeßl et al. (2018), and Brogaard et al. (2018). By comparing ν_max to $g_{\text{dyn}}/\sqrt{T_{\text{eff}}}$, where g_dyn is the surface gravity derived from the dynamical solution of the red-giant components in the eSB2 systems, they obtained a reference value for ν_max for RGB stars with 20 μHz < ν_max < 80 μHz of ν_max,ref,RGB = 3245 ± 50 μHz. For a more general approach Kallinger et al. (2018) fitted

$\begin{array}{ll}\frac{g_{\text{dyn}}}{\sqrt{T_{\text{eff}}}}={\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right)}^{\kappa },& (31)\end{array}$

in which ν_max,⊙ = 3140 ± 5 μHz (Kallinger et al., 2014). Kallinger et al. (2018) found κ = 1.0080 ± 0.0024. For the large frequency separation, Kallinger et al. (2018) found a similar situation. The average of the six stars provides a reference value Δν_ref,RGB of 133.1 ± 1.3 μHz. However, they found more statistical evidence for the function:

$\begin{array}{ll}\Delta \nu =\Delta {\nu }_{\text{ref}}·\sqrt{{\overline{\rho }}_{\text{dyn}}}=\Delta {\nu }_{\odot }\left[1-\gamma {log}^2\left(\Delta \nu /\Delta {\nu }_{\odot }\right)\right]·\sqrt{{\overline{\rho }}_{\text{dyn}}},& (32)\end{array}$

with γ = 0.0043 ± 0.0025 when using the average frequency spacing of the three central radial orders (local Δν or Δν_c) and a local solar value Δν_c,⊙ = 134.89 ± 0.04 μHz, or γ = 0.0085 ± 0.0025 when including a curvature and glitch correction (indicated with Δν_cor) and a corrected solar value Δν_cor,⊙ = 135.08 ± 0.04 μHz. Kallinger et al. (2018) noted that the latter solution should be preferred over the local or average value of Δν.

Ong and Basu (2019) derived an asymptotic estimator for the large frequency separation that captures most of the variations in the scaling relation with a single expression and thereby return estimates of Δν that are considerably closer to the observed value than the traditional estimator, without any ambiguity as to the outer turning point of the relevant integral (see Hekker et al., 2013a). They derived a new expression for Δν by using a more accurate description of the WKB² expression of the first-order asymptotic theory of p modes in which a more detailed asymptotic analysis (i.e., not setting terms to zero prematurely before performing the WKB analysis) was used (Deubner and Gough, 1984). Following a Taylor expansion Ong and Basu (2019) derived:

$\begin{array}{ll}\Delta \nu ~{\left(2{\displaystyle {\int }_{r_1}^{r_2}}\frac{dr}{c_s}\frac{1}{\sqrt{1-\frac{{\omega }_{\text{ac}}^2}{{\omega }^2}}}\right)}^{-1},& (33)\end{array}$

in which ω = 2πν is the angular frequency and ω_ac the angular acoustic cut-off frequency:

$\begin{array}{ll}{\omega }_{\text{ac}}^2=\frac{c_s^2}{4H^2}\left(1-2\frac{dH}{dr}\right),& (34)\end{array}$

with H the density scale height. Ong and Basu (2019) showed that in this prescription the turning points of the integral emerge naturally from the theoretical formulation and do not suffer any ambiguity independent of the choice of model atmosphere or modifications to the model metallicity. The only precaution is that the integral expression (Equation 33) becomes singular at some point during the main-sequence turn-off, which is ultimately a consequence of the failure of the WKB regime. Ong and Basu (2019) showed that these singular points occur during a transition between two extreme regimes of asymptotic behavior providing theoretical justification for separately calibrated scaling relations for stars at different evolutionary stages.

Finally, Bellinger (2019) used the Kepler Ages (Silva Aguirre et al., 2015; Davies et al., 2016) and LEGACY samples (Lund et al., 2017; Silva Aguirre et al., 2017) to investigate the scaling relations for main-sequence stars. Bellinger (2019) used the masses and radii from the Stellar Parameters in an Instant (SPI) method (Bellinger et al., 2016) as provided by Bellinger et al. (2019) to provide the following functions:

$\begin{array}{ll}\frac{M}{M_{\odot }}={\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right)}^{0.975}{\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^{-1.435}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{1.216}exp{\left(\text{[Fe/H]}\right)}^{0.270},& (35)\end{array}$

$\begin{array}{ll}\frac{R}{R_{\odot }}={\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right)}^{0.305}{\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^{-1.129}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{0.312}exp{\left(\text{[Fe/H]}\right)}^{0.100},& (36)\end{array}$

$\begin{array}{ll}\frac{\tau }{{\tau }_{\odot }}={\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right)}^{-6.556}{\left(\frac{\Delta \nu }{\Delta {\nu }_{\odot }}\right)}^{9.059}{\left(\frac{\delta \nu }{\delta {\nu }_{\odot }}\right)}^{-1.292}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{-4.245}exp{\left(\text{[Fe/H]}\right)}^{-0.426},& (37)\end{array}$

with ν_max,⊙ = 3090 ± 30 μHz, Δν_⊙ = 135.1 ± 0.1 μHz (Huber et al., 2011), T_eff,⊙ = 5772.0 ± 0.8 K (Prša et al., 2016); δν is the small frequency separation between modes of degree 0 and 2 with δν_⊙ = 8.957 ± 0.059 μHz (based on data from Davies et al., 2014) and τ is age with τ_⊙ = 4.569 ± 0.006 Gyr (Bonanno and Fröhlich, 2015). Bellinger (2019) stated that Equations (36, 38, 39) yield uncertainties of 0.032 M_⊙ (3.3 per cent), 0.011 R_⊙ (1.1 per cent), and 0.56 Gyr (12 per cent) for mass, radius, and age, respectively.

3. Discussion

The suggestions to improve the accuracy of the stellar parameters derived from the Δν and ν_max scaling relations as presented above focus on different aspects and follow different approaches, which all have pros and cons. The determination of alternative reference values (Mosser et al., 2013a; Themeßl et al., 2018) or reference functions (White et al., 2011; Guggenberger et al., 2016, 2017) have the advantage of direct applicability to observed data without any use of models. The drawback is that the values or functions may not capture all dispersions in, for instance, mass, metallicity, or temperature. Furthermore, the reference values and functions are derived for a certain parameter space or on stars in a certain parameter space, and hence, they will be most reliable in that parameter space.

When using models, a correction factor implemented throughout a grid (Sharma et al., 2016; Rodrigues et al., 2017; Serenelli et al., 2017) or the inclusion of Γ₁ and μ (Yıldız et al., 2016; Viani et al., 2017) will allow to mitigate such dispersions. However, one has to rely on stellar models, and the physics included in the models. Additionally, the surface effect has to be accounted for in any comparison between models and observed data (Serenelli et al., 2017).

The approach of altering the shape of the scaling relations by including alternative exponents or non-linear terms (Kallinger et al., 2018; Bellinger, 2019) provides accurate stellar parameters in the parameter ranges they are calibrated for. However, the direct relation to the mean density and surface gravity of the Δν and ν_max scaling relations are lost in this approach (see section 2).

Depending on the star(s) and observations of these star(s) at hand and the purpose of the stellar parameters derived using the scaling relations, the exact relation or reference function should be chosen. Table 3 provides an overview of the parameter space that reference functions are tested for. Certainly, one also has to be aware that both Δν and ν_max can be measured in different ways, which results in different values (see e.g., Hekker et al., 2011; Verner et al., 2011; Stello et al., 2017, and references therein), and that this should be taken into consideration when choosing a specific version of reference values or scaling relations. Further corrections and calibration of the scaling relations are expected based on forthcoming large datasets, such as the next APOKASC catalog, which contains stars spanning a larger parameter space in terms of surface gravity; TESS results, which span a wider range in metallicity, and are more accessible to interferometric measurements; and Gaia data (Gaia Collaboration et al., 2018), which can be used for comparisons of the stellar radii (e.g., Huber et al., 2017; Zinn et al., 2019).

TABLE 3

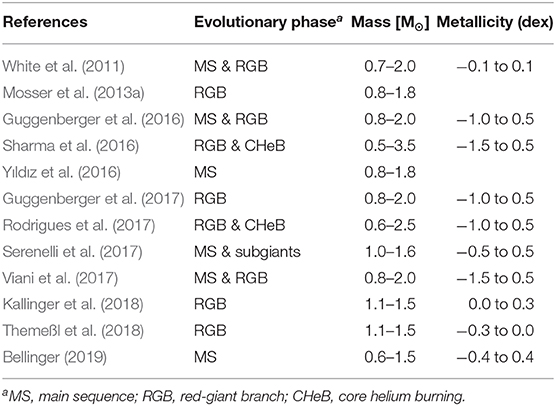
Table 3. Overview of the parameter space of different corrections to the asteroseismic scaling relations as presented in the literature.

The fact that so much effort has gone into calibrating the scaling relations is testimony to the power of the Δν and ν_max scaling relations as both a simple and precise method to determine stellar parameters. With the many stars with solar-like oscillations now detected with CoROT, Kepler, K2 and TESS, and PLATO (PLanetary Transits and Oscillations, Rauer et al., 2014) in the future, the scaling relations will provide stellar parameters for thousands of stars used in both Galactic archaeology as well as exoplanet studies, which makes the efforts discussed above worthwhile and necessary.

Author Contributions

SH has collected all the literature and wrote the manuscript.

Funding

SH has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP72007-2013) ERC grant agreement no 338251 (StellarAges).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to thank Tim Bedding and Nathalie Themeßl for useful comments on earlier versions of this manuscript.

Footnotes

1. ^Rodrigues et al. (2017) implemented a similar interpolation scheme in their models as Sharma et al. (2016). They also experimented with the impact of the period spacing ΔP on the mass and radius determination, though that is beyond the scope of this review.

2. ^One of the most useful techniques for studying wave-like solutions of ordinary linear differential equations of second order: namely the so-called Liouville-Green expansion combined with the method of Jeffreys for connecting solutions across turning points. See Gough (2007) for more details.

References

Ball, W. H., Themeßl, N., and Hekker, S. (2018). Surface effects on the red giant branch. Mon. Notices R. Astron. Soc. 478, 4697–4709. doi: 10.1093/mnras/sty1141

CrossRef Full Text | Google Scholar

Balmforth, N. J. (1992). Solar pulsational stability - I. Pulsation-mode thermodynamics. Mon. Notices R. Astron. Soc. 255, 603–649. doi: 10.1093/mnras/255.4.603

CrossRef Full Text | Google Scholar

Basu, S., Chaplin, W. J., and Elsworth, Y. (2010). Determination of stellar radii from asteroseismic data. Astrophys. J. 710, 1596–1609. doi: 10.1088/0004-637X/710/2/1596

CrossRef Full Text | Google Scholar

Bedford, D. K., Chaplin, W. J., Davies, A. R., Innis, J. L., Isaak, G. R., and Speake, C. C. (1993). “High precision velocity measurements of the star procyon - A possible stellar signal,” in GONG 1992. Seismic Investigation of the Sun and Stars, Vol. 42 of Astronomical Society of the Pacific Conference Series, ed T. M. Brown, 383.

Google Scholar

Belkacem, K., Goupil, M. J., Dupret, M. A., Samadi, R., Baudin, F., Noels, A., et al. (2011). The underlying physical meaning of the ν_max - ν_c relation. Astron. Astrophys. 530:A142. doi: 10.1051/0004-6361/201116490

CrossRef Full Text | Google Scholar

Belkacem, K., Samadi, R., Mosser, B., Goupil, M.-J., and Ludwig, H.-G. (2013). “On the Seismic Scaling Relations Δν - ρ and ν_max - ν_c,” in Progress in Physics of the Sun and Stars: A New Era in Helio- and Asteroseismology, Vol. 479 of Astronomical Society of the Pacific Conference Series, eds H. Shibahashi and A. E. Lynas-Gray, 61.

Google Scholar

Bellinger, E. P. (2019). A seismic scaling relation for stellar age. arXiv e-prints arXiv:1903.03110.

Google Scholar

Bellinger, E. P., Angelou, G. C., Hekker, S., Basu, S., Ball, W. H., and Guggenberger, E. (2016). Fundamental parameters of main-sequence stars in an instant with machine learning. Astrophys. J. 830:31. doi: 10.3847/0004-637X/830/1/31

CrossRef Full Text | Google Scholar

Bellinger, E. P., Hekker, S., Angelou, G. C., Stokholm, A., and Basu, S. (2019). Stellar ages, masses, and radii from asteroseismic modeling are robust to systematic errors in spectroscopy. Astron. Astrophys. 622:A130. doi: 10.1051/0004-6361/201834461

CrossRef Full Text | Google Scholar

Bonanno, A., and Fröhlich, H.-E. (2015). A Bayesian estimation of the helioseismic solar age. Astron. Astrophys. 580:A130. doi: 10.1051/0004-6361/201526419

CrossRef Full Text | Google Scholar

Borucki, W., Koch, D., Batalha, N., Caldwell, D., Christensen-Dalsgaard, J., Cochran, W. D., et al. (2009). “KEPLER: search for earth-size planets in the habitable zone,” in Transiting Planets, Vol. 253 of IAU Symposium, eds F. Pont, D. Sasselov, and M. J. Holman, 289–299.

Google Scholar

Brogaard, K., Hansen, C. J., Miglio, A., Slumstrup, D., Frandsen, S., Jessen-Hansen, J., et al. (2018). Establishing the accuracy of asteroseismic mass and radius estimates of giant stars - I. Three eclipsing systems at [Fe/H] ≈ -0.3 and the need for a large high-precision sample. Mon. Notices R. Astron. Soc. 476, 3729–3743. doi: 10.1093/mnras/sty268

CrossRef Full Text | Google Scholar

Brogaard, K., Jessen-Hansen, J., Handberg, R., Arentoft, T., Frandsen, S., Grundahl, F., et al. (2016). Testing asteroseismic scaling relations using eclipsing binaries in star clusters and the field. Astron. Nachrichten 337:793. doi: 10.1002/asna.201612374

CrossRef Full Text | Google Scholar

Brown, T. M., and Gilliland, R. L. (1990). A search for solar-like oscillations in Alpha Centauri A. Astrophys. J. 350, 839–845. doi: 10.1086/168435

CrossRef Full Text | Google Scholar

Brown, T. M., Gilliland, R. L., Noyes, R. W., and Ramsey, L. W. (1991). Detection of possible p-mode oscillations on Procyon. Astrophys. J. 368, 599–609. doi: 10.1086/169725

CrossRef Full Text | Google Scholar

Bruntt, H., Bedding, T. R., Quirion, P.-O., Lo Curto, G., Carrier, F., Smalley, B., et al. (2010). Accurate fundamental parameters for 23 bright solar-type stars. Mon. Notices R. Astron. Soc. 405, 1907–1923. doi: 10.1111/j.1365-2966.2010.16575.x

CrossRef Full Text | Google Scholar

Chaplin, W. J., Houdek, G., Appourchaux, T., Elsworth, Y., New, R., and Toutain, T. (2008). Challenges for asteroseismic analysis of Sun-like stars. Astron. Astrophys. 485, 813–822. doi: 10.1051/0004-6361:200809695

CrossRef Full Text | Google Scholar

Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., Basu, S., Miglio, A., Appourchaux, T., et al. (2011). Ensemble asteroseismology of solar-type stars with the NASA Kepler Mission. Science 332:213. doi: 10.1126/science.1201827

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., et al. (1996). The current state of solar modeling. Science 272, 1286–1292. doi: 10.1126/science.272.5266.1286

PubMed Abstract | CrossRef Full Text | Google Scholar

Coelho, H. R., Chaplin, W. J., Basu, S., Serenelli, A., Miglio, A., and Reese, D. R. (2015). A test of the asteroseismic ν_max scaling relation for solar-like oscillations in main-sequence and subgiant stars. Mon. Notices R. Astron. Soc. 451, 3011–3020. doi: 10.1093/mnras/stv1175

CrossRef Full Text | Google Scholar

Davies, G. R., Broomhall, A. M., Chaplin, W. J., Elsworth, Y., and Hale, S. J. (2014). Low-frequency, low-degree solar p-mode properties from 22 years of Birmingham Solar Oscillations Network data. Mon. Notices R. Astron. Soc. 439, 2025–2032. doi: 10.1093/mnras/stu080

CrossRef Full Text | Google Scholar

Davies, G. R., Silva Aguirre, V., Bedding, T. R., Handberg, R., Lund, M. N., Chaplin, W. J., et al. (2016). Oscillation frequencies for 35 Kepler solar-type planet-hosting stars using Bayesian techniques and machine learning. Mon. Notices R. Astron. Soc. 456, 2183–2195. doi: 10.1093/mnras/stv2593

CrossRef Full Text | Google Scholar

Dekker, H., D'Odorico, S., Kaufer, A., Delabre, B., and Kotzlowski, H. (2000). “Design, construction, and performance of UVES, the echelle spectrograph for the UT2 Kueyen Telescope at the ESO Paranal Observatory,” in Optical and IR Telescope Instrumentation and Detectors, Vol. 4008 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, eds M. Iye and A. F. Moorwood, 534–545.

Google Scholar

Deubner, F.-L., and Gough, D. (1984). Helioseismology: oscillations as a diagnostic of the solar interior. Annu. Rev. Astron. Astrophys. 22, 593–619. doi: 10.1146/annurev.aa.22.090184.003113

CrossRef Full Text | Google Scholar

Diego, F., Charalambous, A., Fish, A. C., and Walker, D. D. (1990). “Final tests and commissioning of the UCL echelle spectrograph,” in Instrumentation in Astronomy VII, Vol. 1235 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, ed D. L. Crawford, 562–576.

Google Scholar

Epstein, C. R., Elsworth, Y. P., Johnson, J. A., Shetrone, M., Mosser, B., Hekker, S., et al. (2014). Testing the asteroseismic mass scale using metal-poor stars characterized with APOGEE and Kepler. Astrophys. J. Lett. 785:L28. doi: 10.1088/2041-8205/785/2/L28

CrossRef Full Text | Google Scholar

Frandsen, S. (1987). An upper limit on p-mode amplitudes in Beta HYI. Astron. Astrophys. 181, 289–292.

Google Scholar

Gai, N., Basu, S., Chaplin, W. J., and Elsworth, Y. (2011). An in-depth study of grid-based asteroseismic analysis. Astrophys. J. 730:63. doi: 10.1088/0004-637X/730/2/63

CrossRef Full Text | Google Scholar

Gaia Collaboration, Brown, A. G. A., Vallenari, A., Prusti, T., de Bruijne, J. H. J., Babusiaux, C., et al. (2018). Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 616:A1. doi: 10.1051/0004-6361/201833051

CrossRef Full Text | Google Scholar

Gaulme, P., McKeever, J., Jackiewicz, J., Rawls, M. L., Corsaro, E., Mosser, B., et al. (2016). Testing the asteroseismic scaling relations for red giants with eclipsing binaries observed by Kepler. Astrophys. J. 832:121. doi: 10.3847/0004-637X/832/2/121

CrossRef Full Text | Google Scholar

Gelly, B., Grec, G., and Fossat, E. (1986). Evidence for global pressure oscillations in Procyon and Alpha Centauri. Astron. Astrophys. 164, 383–394.

Google Scholar

Goldreich, P., and Keeley, D. A. (1977). Solar seismology. II. The stochastic excitation of the solar p-modes by turbulent convection. Astrophys. J. 212, 243–251. doi: 10.1086/155043

CrossRef Full Text | Google Scholar

Goldreich, P., and Kumar, P. (1988). The interaction of acoustic radiation with turbulence. Astrophys. J. 326:462. doi: 10.1086/166108

CrossRef Full Text | Google Scholar

Gough, D. O. (2007). An elementary introduction to the JWKB approximation. Astron. Nachrichten 328:273. doi: 10.1002/asna.200610730

CrossRef Full Text | Google Scholar

Grundahl, F., Kjeldsen, H., Christensen-Dalsgaard, J., Arentoft, T., and Frandsen, S. (2007). Stellar oscillations network group. Commun. Asteroseismol. 150:300. doi: 10.1553/cia150s300

CrossRef Full Text | Google Scholar

Guggenberger, E., Hekker, S., Angelou, G. C., Basu, S., and Bellinger, E. P. (2017). Mitigating the mass dependence in the Δν scaling relation of red giant stars. Mon. Notices R. Astron. Soc. 470, 2069–2078. doi: 10.1093/mnras/stx1253

CrossRef Full Text | Google Scholar

Guggenberger, E., Hekker, S., Basu, S., and Bellinger, E. (2016). Significantly improving stellar mass and radius estimates: a new reference function for the Δν scaling relation. Mon. Notices R. Astron. Soc. 460, 4277–4281. doi: 10.1093/mnras/stw1326

CrossRef Full Text | Google Scholar

Hekker, S., Elsworth, Y., Basu, S., Mazumdar, A., Silva Aguirre, V., and Chaplin, W. J. (2013a). Tests of the asymptotic large frequency separation of acoustic oscillations in solar-type and red-giant stars. Mon. Notices R. Astron. Soc. 434, 1668–1673. doi: 10.1093/mnras/stt1238

CrossRef Full Text | Google Scholar

Hekker, S., Elsworth, Y., De Ridder, J., Mosser, B., García, R. A., Kallinger, T., et al. (2011). Solar-like oscillations in red giants observed with Kepler: comparison of global oscillation parameters from different methods. Astron. Astrophys. 525:A131. doi: 10.1051/0004-6361/201015185

CrossRef Full Text | Google Scholar

Hekker, S., Elsworth, Y., Mosser, B., Kallinger, T., Basu, S., Chaplin, W. J., et al. (2013b). Asteroseismic surface gravity for evolved stars. Astron. Astrophys. 556:A59. doi: 10.1051/0004-6361/201321630

CrossRef Full Text | Google Scholar

Hekker, S., Kallinger, T., Baudin, F., De Ridder, J., Barban, C., Carrier, F., et al. (2009). Characteristics of solar-like oscillations in red giants observed in the CoRoT exoplanet field. Astron. Astrophys. 506, 465–469. doi: 10.1051/0004-6361/200911858

CrossRef Full Text | Google Scholar

Huber, D., Bedding, T. R., Stello, D., Hekker, S., Mathur, S., Mosser, B., et al. (2011). Testing scaling relations for solar-like oscillations from the main sequence to red giants using Kepler data. Astrophys. J. 743:143. doi: 10.1088/0004-637X/743/2/143

CrossRef Full Text | Google Scholar

Huber, D., Ireland, M. J., Bedding, T. R., Brandão, I. M., Piau, L., Maestro, V., et al. (2012). Fundamental properties of stars using asteroseismology from Kepler and CoRoT and interferometry from the CHARA array. Astrophys. J. 760:32. doi: 10.1088/0004-637X/760/1/32

CrossRef Full Text | Google Scholar

Huber, D., Zinn, J., Bojsen-Hansen, M., Pinsonneault, M., Sahlholdt, C., Serenelli, A., et al. (2017). Asteroseismology and gaia: testing scaling relations using 2200 Kepler stars with TGAS parallaxes. Astrophys. J. 844:102. doi: 10.3847/1538-4357/aa75ca

CrossRef Full Text | Google Scholar

Innis, J. L., Isaak, G. R., Speake, C. C., Brazier, R. I., and Williams, H. K. (1991). High-precision velocity observations of Procyon A. I - Search for p-mode oscillations from 1988, 1989 and 1990 observations. Mon. Notices R. Astron. Soc. 249, 643–653. doi: 10.1093/mnras/249.4.643

CrossRef Full Text | Google Scholar

Kallinger, T., Beck, P. G., Stello, D., and Garcia, R. A. (2018). Non-linear seismic scaling relations. Astron. Astrophys. 616:A104. doi: 10.1051/0004-6361/201832831

CrossRef Full Text | Google Scholar

Kallinger, T., De Ridder, J., Hekker, S., Mathur, S., Mosser, B., Gruberbauer, M., et al. (2014). The connection between stellar granulation and oscillation as seen by the Kepler mission. Astron. Astrophys. 570:A41. doi: 10.1051/0004-6361/201424313

CrossRef Full Text | Google Scholar

Kallinger, T., Mosser, B., Hekker, S., Huber, D., Stello, D., Mathur, S., et al. (2010a). Asteroseismology of red giants from the first four months of Kepler data: Fundamental stellar parameters. Astron. Astrophys. 522:A1. doi: 10.1051/0004-6361/201015263

CrossRef Full Text | Google Scholar

Kallinger, T., Weiss, W. W., Barban, C., Baudin, F., Cameron, C., Carrier, F., et al. (2010b). Oscillating red giants in the CoRoT exofield: asteroseismic mass and radius determination. Astron. Astrophys. 509:A77. doi: 10.1051/0004-6361/200811437

CrossRef Full Text | Google Scholar

Kjeldsen, H., and Bedding, T. R. (1995). Amplitudes of stellar oscillations: the implications for asteroseismology. Astron. Astrophys. 293, 87–106.

Google Scholar

Leighton, R. B., Noyes, R. W., and Simon, G. W. (1962). Velocity Fields in the Solar Atmosphere. I. Preliminary Report. Astrophys. J. 135:474.

Google Scholar

Lund, M. N., Silva Aguirre, V., Davies, G. R., Chaplin, W. J., Christensen-Dalsgaard, J., Houdek, G., et al. (2017). Standing on the shoulders of dwarfs: the Kepler asteroseismic LEGACY Sample. I. Oscillation mode parameters. Astrophys. J. 835:172. doi: 10.3847/1538-4357/835/2/172

CrossRef Full Text | Google Scholar

Michel, E., Baglin, A., and COROT Team (1998). “COROT - Stellar Seismology from Space,” in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Vol. 418 of ESA Special Publication, ed S. Korzennik, 399.

Google Scholar

Miglio, A., Brogaard, K., Stello, D., Chaplin, W. J., D'Antona, F., Montalbán, J., et al. (2012). Asteroseismology of old open clusters with Kepler: direct estimate of the integrated red giant branch mass-loss in NGC 6791 and 6819. Mon. Notices R. Astron. Soc. 419, 2077–2088. doi: 10.1111/j.1365-2966.2011.19859.x

CrossRef Full Text | Google Scholar

Miglio, A., Chiappini, C., Morel, T., Barbieri, M., Chaplin, W. J., Girardi, L., et al. (2013). “Differential population studies using asteroseismology: solar-like oscillating giants in CoRoT fields LRc01 and LRa01,” in European Physical Journal Web of Conferences, Vol. 43 of European Physical Journal Web of Conferences, 03004.

Google Scholar

Mosser, B. (2013). “Red giant seismology: observations,” in European Physical Journal Web of Conferences, Vol. 43 of European Physical Journal Web of Conferences, 03003.

Google Scholar

Mosser, B., Michel, E., Belkacem, K., Goupil, M. J., Baglin, A., Barban, C., et al. (2013a). Asymptotic and measured large frequency separations. Astron. Astrophys. 550:A126. doi: 10.1051/0004-6361/201220435

CrossRef Full Text | Google Scholar

Mosser, B., Samadi, R., and Belkacem, K. (2013b). “Red giants seismology,” in SF2A-2013: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds L.Cambresy, F. Martins, E. Nuss, and A. Palacios, 25–36.

Google Scholar

Noyes, R. W., Baliunas, S. L., Belserene, E., Duncan, D. K., Horne, J., and Widrow, L. (1984). Evidence for global oscillations in the K2 dwarf Epsilon Eridani. Astrophys. J. Lett. 285, L23–L26. doi: 10.1086/184357

CrossRef Full Text | Google Scholar

Ong, J. M. J., and Basu, S. (2019). Explaining Deviations from the Scaling Relationship of the Large Frequency Separation. Astrophys. J. 870:41. doi: 10.3847/1538-4357/aaf1b5

CrossRef Full Text | Google Scholar

Pepe, F., Mayor, M., Benz, W., Bertaux, J. L., Sivan, J. P., Queloz, D., et al. (2000). “The HARPS Project,” in From Extrasolar Planets to Cosmology: The VLT Opening Symposium, eds J. Bergeron and A. Renzini, 572.

Google Scholar

Pottasch, E. M., Butcher, H. R., and van Hoesel, F. H. J. (1992). Solar-like oscillations on Alpha Centauri A. Astron. Astrophys. 264, 138–146.

Google Scholar

Prša, A., Harmanec, P., Torres, G., Mamajek, E., Asplund, M., Capitaine, N., et al. (2016). Nominal values for selected solar and planetary quantities: IAU 2015 resolution B3. Astron J. 152:41. doi: 10.3847/0004-6256/152/2/41

CrossRef Full Text | Google Scholar

Queloz, D., Casse, M., and Mayor, M. (1999). “The fiber-fed spectrograph, a tool to detect planets,” in IAU Colloq. 170: Precise Stellar Radial Velocities, Vol. 185 of Astronomical Society of the Pacific Conference Series, eds J. B. Hearnshaw and C. D. Scarfe, 13.

Google Scholar

Rauer, H., Catala, C., Aerts, C., Appourchaux, T., Benz, W., Brandeker, A., et al. (2014). The PLATO 2.0 mission. Exp. Astron. 38, 249–330. doi: 10.1007/s10686-014-9383-4

CrossRef Full Text | Google Scholar

Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2014). Transiting Exoplanet Survey Satellite (TESS), Vol. 9143 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 914320.

Google Scholar

Rodrigues, T. S., Bossini, D., Miglio, A., Girardi, L., Montalbán, J., Noels, A., et al. (2017). Determining stellar parameters of asteroseismic targets: going beyond the use of scaling relations. Mon. Notices R. Astron. Soc. 467, 1433–1448. doi: 10.1093/mnras/stx120

CrossRef Full Text | Google Scholar

Rosenthal, C. S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R. F., and Trampedach, R. (1999). Convective contributions to the frequencies of solar oscillations. Astron. Astrophys. 351, 689–700.

Google Scholar

Serenelli, A., Johnson, J., Huber, D., Pinsonneault, M., Ball, W. H., Tayar, J., et al. (2017). The first APOKASC catalog of Kepler Dwarf and subgiant stars. Astrophys. J. Suppl. Ser. 233:23. doi: 10.3847/1538-4365/aa97df

CrossRef Full Text | Google Scholar

Sharma, S., Stello, D., Bland-Hawthorn, J., Huber, D., and Bedding, T. R. (2016). Stellar population synthesis based modeling of the milky way using asteroseismology of 13,000 Kepler Red Giants. Astrophys. J. 822:15. doi: 10.3847/0004-637X/822/1/15

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Casagrande, L., Basu, S., Campante, T. L., Chaplin, W. J., Huber, D., et al. (2012). Verifying asteroseismically determined parameters of Kepler stars using hipparcos parallaxes: self-consistent stellar properties and distances. Astrophys. J. 757:99. doi: 10.1088/0004-637X/757/1/99

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Davies, G. R., Basu, S., Christensen-Dalsgaard, J., Creevey, O., Metcalfe, T. S., et al. (2015). Ages and fundamental properties of Kepler exoplanet host stars from asteroseismology. Mon. Notices R. Astron. Soc. 452, 2127–2148. doi: 10.1093/mnras/stv1388

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Lund, M. N., Antia, H. M., Ball, W. H., Basu, S., Christensen-Dalsgaard, J., et al. (2017). Standing on the shoulders of dwarfs: the Kepler asteroseismic LEGACY sample. II.Radii, masses, and ages. Astrophys. J. 835:173. doi: 10.3847/1538-4357/835/2/173

CrossRef Full Text | Google Scholar

Stello, D., Chaplin, W. J., Basu, S., Elsworth, Y., and Bedding, T. R. (2009a). The relation between Δν and ν_max for solar-like oscillations. Mon. Notices R. Astron. Soc. 400, L80–L84. doi: 10.1111/j.1745-3933.2009.00767.x

CrossRef Full Text | Google Scholar

Stello, D., Chaplin, W. J., Bruntt, H., Creevey, O. L., García-Hernández, A., Monteiro, M. J. P. F. G., et al. (2009b). Radius determination of solar-type stars using asteroseismology: what to expect from the Kepler mission. Astrophys. J. 700, 1589–1602. doi: 10.1088/0004-637X/700/2/1589

CrossRef Full Text | Google Scholar

Stello, D., Zinn, J., Elsworth, Y., Garcia, R. A., Kallinger, T., Mathur, S., et al. (2017). The K2 galactic archaeology program data release. I. Asteroseismic results from campaign 1. Astrophys. J. 835:83. doi: 10.3847/1538-4357/835/1/83

CrossRef Full Text | Google Scholar

Themeßl, N., Hekker, S., Southworth, J., Beck, P. G., Pavlovski, K., Tkachenko, A., et al. (2018). Oscillating red giants in eclipsing binary systems: empirical reference value for asteroseismic scaling relation. Mon. Notices R. Astron. Soc. 478, 4669–4696. doi: 10.1093/mnras/sty1113

CrossRef Full Text | Google Scholar

Verner, G. A., Elsworth, Y., Chaplin, W. J., Campante, T. L., Corsaro, E., Gaulme, P., et al. (2011). Global asteroseismic properties of solar-like oscillations observed by Kepler: a comparison of complementary analysis methods. Mon. Notices R. Astron. Soc. 415, 3539–3551. doi: 10.1111/j.1365-2966.2011.18968.x

CrossRef Full Text | Google Scholar

Viani, L. S., Basu, S., Chaplin, W. J., Davies, G. R., and Elsworth, Y. (2017). Changing the ν _max scaling relation: the need for a mean molecular weight term. Astrophys. J. 843:11. doi: 10.3847/1538-4357/aa729c

CrossRef Full Text | Google Scholar

White, T. R., Bedding, T. R., Stello, D., Christensen-Dalsgaard, J., Huber, D., and Kjeldsen, H. (2011). Calculating asteroseismic diagrams for solar-like oscillations. Astrophys. J. 743:161. doi: 10.1088/0004-637X/743/2/161

CrossRef Full Text | Google Scholar

Yıldız, M., Çelik Orhan, Z., and Kayhan, C. (2016). Fundamental properties of Kepler and CoRoT targets - III. Tuning scaling relations using the first adiabatic exponent. Mon. Notices R. Astron. Soc. 462, 1577–1590. doi: 10.1093/mnras/stw1709

CrossRef Full Text | Google Scholar

Yu, J., Huber, D., Bedding, T. R., Stello, D., Hon, M., Murphy, S. J., and Khanna, S. (2018). Asteroseismology of 16,000 Kepler Red Giants: global oscillation parameters, masses, and radii. Astrophys. J. Suppl. Ser. 236:42. doi: 10.3847/1538-4365/aaaf74

CrossRef Full Text | Google Scholar

Zinn, J. C., Pinsonneault, M. H., Huber, D., Stello, D., Stassun, K., and Serenelli, A. (2019). Testing the radius scaling relation with Gaia DR2 in the Kepler field. Astrophys. J. 885:166. doi: 10.3847/1538-4357/ab44a9

CrossRef Full Text | Google Scholar