- Center for Space Plasma Physics, Space Science Institute, Boulder, CO, United States
This paper reviews the properties of the magnetic and plasma structure of the solar wind in the inertial range of spatial scales (500–5 × 106 km), corresponding to spacecraft timescales from 1 s to a few hr. Spacecraft data sets at 1 AU have been statistically analyzed to determine the structure properties. The magnetic structure of the solar wind often has a flux-tube texture, with the magnetic flux tube walls being strong current sheets and the field orientation varying strongly from tube to tube. The magnetic tubes also exhibit distinct plasma properties (e.g., number density, specific entropy), with variations in those properties from tube to tube. The ion composition also varies from tube to tube, as does the value of the electron heat flux. When the solar wind is Alfvénic, the magnetic structure of the solar wind moves outward from the Sun faster than the proton plasma does. In the reference frame moving outward with the structure, there are distinct field-aligned plasma flows within each flux tube. In the frame moving with the magnetic structure the velocity component perpendicular to the field is approximately zero; this indicates that there is little or no evolution of the magnetic structure as it moves outward from the Sun. Large sudden velocity shears are seen across the boundaries between the magnetic flux tubes as the magnetic field rotates and the field-aligned flow rotates. The effect of the solar-wind current sheets on the magnetic power spectral density of the solar wind is examined: the current sheets are found to dominate the spectral properties of the solar wind.
Introduction
This review examines the plasma and magnetic-field structure of the inner heliosphere in the “inertial range” of scale sizes, corresponding to timescales in the solar wind data from about 1 s to about 3 h, equivalent to advected spatial scales of about 500 km to 5 × 106 km. These are MHD scales sizes, larger than ion gyroradii rgi ~ 20–100 km and larger than ion-inertial lengths c/ωpi ~ 50–150 km in the solar-wind plasma at 1 AU.
In this range of timescales, the magnetic-field time series is dominated by strong current sheets (directional discontinuities) and calmer regions between the current sheets. The plasma time series is dominated by sudden jumps in the plasma parameters (e.g., number density, specific entropy, proton temperature, plasma beta, magnetic-field strength, etc.) at the locations of strong current sheets. The proton flow time series is dominated by sudden jumps of the flow vector (abrupt flow shears) at the location of the current sheets, especially for the more-Alfvénic types of solar-wind plasma.
This review explores the properties of the structure of the solar wind in the inner heliosphere as gleaned from spacecraft time-series measurements. This paper is organized as follows. In Section The Flux-Tube Texture of the Heliospheric Magnetic Field the magnetic flux-tube texture of the solar wind is discussed. Section The Motion of the Magnetic Structure through the Solar-Wind Plasma examines the outward motion of the magnetic structure through the solar-wind proton plasma. Section The Alpha-to-Proton Ionic Composition and Magnetic Flux Tubes discusses how the alpha-to-proton ionic composition varies from tube to tube and Section The Electron Heat Flux (Strahl) and Magnetic Flux Tubes discusses how the electron strahl (heat flux) changes from tube to tube. Section Squashing and Stretching of Magnetic Flux Tubes describes the squashing and stretching of magnetic flux tubes in compression and rarefaction regions. Section Mixing discusses the lack of evidence of mixing in the solar wind as it moves outward through the inner heliosphere. Section Current Sheets and the Fourier Power Spectrum explains the impact of solar-wind current sheets on the magnetic power spectrum of the solar wind. Section Current Sheet Thicknesses discusses the thicknesses of the current sheets in the magnetic structure. Abrupt velocity shears in the solar wind are discussed in Section Intense Velocity Shears. Section Alfvénic Domains in Coronal-Hole-Origin Plasma discusses spatial domains of Alfvénicity that are found in the solar wind from coronal holes. Magnetic switchbacks in the solar wind are discussed in Section Magnetic Switchbacks. Section Types of Solar-Wind Plasma and the Inertial-Range Structure reviews the systematic differences in the inertial-range structure of the solar wind in four different types of solar-wind plasma originating from four different types of regions on the Sun. The review is summarized in Section Summary and Discussion, which also contains some suggestions about changes in nomenclature.
The Flux-Tube Texture of the Heliospheric Magnetic Field
Figure 1 contains a binning of the temporal angular change in the direction of the solar-wind magnetic field in 64-s time-resolution time-series measurements at 1 AU during the years 1998–2008. Two distinct populations can be seen in the occurrence distribution, both fit by exponential functions: a population of large angular changes and a population of smaller angular changes. The large-angular change population is consistent with the spacecraft crossing strong current sheets in the solar-wind plasma, and the small-angular-change population is consistent with magnetic field directional wiggles in the spatial regions between the current sheets. The two distributions are consistent with a picture of magnetic-flux tubes separated by current sheets, with the direction of the magnetic field changing from tube to tube. For a plot similar to Figure 1 closer to the Sun see the 1-s curve in Figue 3 of Chhiber et al. (2020) and for a plot further from the Sun see Figure 6 of Miao et al. (2011), indicative of a flux-tube texture throughout the inner heliosphere.
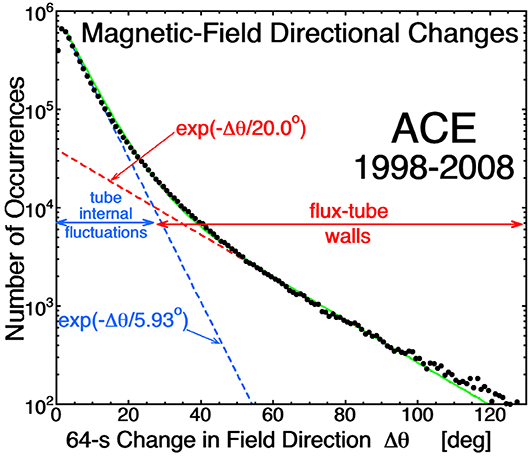
Figure 1. The 64-s change in the solar-wind magnetic-field direction is binned for 11 years of measurements at 1 AU by the ACE Magnetic Fields Experiment (Smith et al., 1998). The sum of the two exponential fit functions appears in green.
A flux-tube texture of the solar wind has been realized since early in situ measurements of the solar wind were available (Bartley et al., 1966; McCracken and Ness, 1966; Ness et al., 1966; Michel, 1967). The flux tubes were evident from the sudden changes in the anisotropy directions of energetic particles (Bartley et al., 1966; McCracken and Ness, 1966), from the sudden changes of direction of the magnetic field (Ness et al., 1966; Michel, 1967; Siscoe et al., 1968), and from sudden changes in the plasma flow vector (Thieme et al., 1989).
Depictions of this spaghetti of magnetic flux tubes can be found throughout the literature [cf. Figure 3 of McCracken and Ness (1966); Figure 6 or Bartley et al. (1966); Figures 1, Figure 5, 9 of Michel (1967); Figure 30H of Schatten (1971); Figure 5 of (Bruno et al., 2001); Figure 1A of Borovsky (2008); Figure 22 of Borovsky (2010a); Figures 7, 8 of Bruno and Carbone (2016); Figure 7 of Bruno (2019)]. In the flux-tube structure the walls of the flux tubes are current sheets wherein the magnetic-field direction changes suddenly. At 1 AU the current sheet thicknesses are on the order of 103 km (Siscoe et al., 1968; Vasquez et al., 2007) and the flux-tube diameters are on the order of 5 × 105 km (Borovsky, 2008; Zheng et al., 2017). In streamer-belt-origin plasma and coronal-hole-origin plasma the flux tubes meander along the Parker-spiral direction, with a spread in flux-tube orientations of about 40° about the Parker-spiral direction (Borovsky, 2010a). At 1 AU Tong et al. (2016) statistically measured the characteristic spatial scale L|| of flux-tube meandering to be L|| ~ 2 × 106 km = 370 RE = 0.016 AU along the Parker-spiral direction.
The origin of the flux-tube magnetic structure of the inner heliosphere is not known (Neugebauer and Giacalone, 2010, 2015; Li and Qin, 2011; Owens et al., 2011; Telloni et al., 2016; Tu et al., 2016; Viall and Borovsky, 2020). Among the possibilities are (a) active MHD turbulence (Dmitruk et al., 2004; Greco et al., 2009), (b) turbulence that has exhausted its energy and left behind a structured magnetic field (Dobrowolny et al., 1980; Telloni et al., 2016), (c) fossil magnetic structure from the corona (Huang et al., 2014; Burkholder et al., 2019; Eselevich, 2019), and (d) steepened Alfvén waves (Malara et al., 1996; Vasquez and Hollweg, 1999).
The flux-tube texture of the heliospheric magnetic field impacts energetic-particle transport in the heliosphere and the physics of particle scattering (Michel, 1967; Qin and Li, 2008), with ducting and weak scattering in the interiors of flux tubes where there are low levels of magnetic fluctuations (Trenchi et al., 2013a,b) and with energetic particles with non-zero gyroradii passing close to the flux-tube walls suffering large-angle scattering. Energetic particles with gyroradii comparable to or larger than flux-tube diameters [cf. Table 4 of Viall and Borovsky (2020)] will suffer scattering associated with the distribution of flux-tube orientations. The L|| ~ 0.16 AU wiggle of the flux-tube orientations about the Parker spiral will also produce a scattering of energetic particles [e.g., (Webb et al., 2006)].
The driving of the Earth's magnetosphere by the solar wind is very sensitive to the direction of the solar-wind magnetic field (Sonnerup, 1974; Komar et al., 2015). From one flux tube to the neighboring flux tube the magnetic-field direction of the solar wind changes (Bruno et al., 2001; Borovsky, 2008; Bruno and Carbone, 2016), with sudden strong jumps in the magnetic-field direction as a flux-tube wall is crossed. The advection of the flux-tube structure past the Earth produces a magnetic direction that is quasi-steady for 15 min or so, followed by a strong change in the field direction. Depending chiefly on the orientation of each flux tube, some flux tubes are geoeffective and some are not, with the flux-tube structure of the solar wind resulting in an intermittent driving of convection and geomagnetic activity in the Earth's magnetosphere (Borovsky, 2020a).
Statistical analysis of the orientations of the flux tubes at 1 AU finds two populations [cf. Figure 18 of Borovsky (2010a)]: a population that is on average aligned in the Parker-spiral direction with a spread of flux-tube orientations of about 40° about the Parker-spiral direction and a second, smaller, population of flux tubes that are quasi-isotropically oriented (cf. Section Types of Solar-Wind Plasma and the Inertial-Range Structure).
The magnetic-flux-tube structure of the solar wind also corresponds with a plasma-tube structure of the solar wind. When the occurrence distributions of changes of plasma properties are examined [e.g., Figure 3 of Borovsky (2008)], a dual population is seen: a population of large changes and a population of small changes, as in Figure 1. This holds for changes in the plasma number density, changes in the specific entropy, changes in the magnetic-field strength, changes in the plasma-β, etc. The locations of the large changes correspond to the locations of current sheets [(Borovsky, 2008; Owens et al., 2011)], i.e., the plasma properties change from flux tube to flux tube. In the slower types of solar wind these plasma changes across the magnetic-tube walls are robust; in the faster coronal-hole-origin wind the plasma changes are more subtle [(Borovsky, 2016)]. As will be discussed in later sections, the magnetic-flux-tube structure also corresponds to a structure in the ion composition of the solar-wind plasma and to a structure in the electron heat flux (strahl intensity) of the solar wind.
Plasma boundaries and magnetic-flux-tube boundaries are, in the MHD nomenclature, discussed as “tangential discontinuities.” In Section The Motion of the Magnetic Structure through the Solar-Wind Plasma it will be pointed out that the magnetic structure of the solar wind moves en mass away from the Sun faster than the proton plasma moves outward. It is often stated to be the case that tangential discontinuities do not propagate relative to the plasma [e.g., (Burlaga and Ness, 1969; Tsurutani and Ho, 1999)], but in the case of flux tubes a perturbation transverse to the axis of the tube will propagate axially along the tube relative to the plasma in the tube at a speed related to the Alfvén speed (Edwin and Roberts, 1983; Ruderman and Roberts, 2006; Goossens et al., 2009). Perturbations of interest for the solar wind are the shuffling of flux tubes (= plasma tubes) at the Sun, with this shuffling pattern propagating outward faster than the plasma outflow.
The Motion of the Magnetic Structure through the Solar-Wind Plasma
In Alfvénic solar wind [i.e., in coronal-hole-origin plasma and in streamer-belt-origin plasma (Xu and Borovsky, 2015; D'Amicis et al., 2019)] the flux-tube structure of the magnetic field moves outward from the Sun at a higher speed than the proton plasma does (Borovsky, 2020b; Nemecek et al., 2020). For an interval of solar-wind data, a single reference frame can be found wherein v × B ≈ 0 where v(t) is the measured solar-wind proton flow vector and B(t) is the measured magnetic-field vector. That single reference frame moves with the magnetic structure and it is found to move typically at about 0.7vA in the Parker-spiral direction relative to the proton flow vector of the solar wind, where vA = B/(4πnpmp)1/2 is the proton Alfvén speed of the solar-wind plasma with number density np (Borovsky, 2020b). Nemecek et al. (2020) refer to this frame as the DeHoffman-Teller frame of the solar wind and they find that the alpha-particle beam of the solar wind is at rest in this magnetic-structure reference frame.
In this reference frame of the magnetic structure, there is a Sunward flow of proton plasma within the flux tubes that is everywhere parallel to the local magnetic field, with the flow vector changing across the walls of the flux tubes as the orientation of one flux tube changes relative to its neighboring flux tube. In Alfvénic intervals of solar wind, the perpendicular-to-B plasma velocity v⊥ within the structure is found to be in the noise of the measurements. The fact that v⊥ ≈ 0 in the reference frame of the magnetic structure indicates that there is little or no evolution of the magnetic structure as it moves outward from the Sun through the inner heliosphere.
The heliospheric magnetic structure with its spaghetti of flux tubes moves en mass through the plasma in the Parker-spiral direction. This outward-moving magnetic structure could be the outward propagation of flux-tube dynamics happening in the corona: the shuffling of flux tubes as they become rearranged by reconnection in the dynamic corona.
When the solar wind at 1 AU is not Alfvénic, a reference frame where v × B ≈ 0 cannot be found. When the solar wind is not Alfvénic, the solar-wind plasma is found to be inhomogeneous (lumpy) with variations in the proton number density np(t). In this inhomogeneous plasma there are strong variations in the local Alfvén speed from flux tube to flux tube. It could be the case that owing to spatial variations in the Alfvén speed the spaghetti of magnetic flux tubes cannot coherently propagate relative to the proton plasma in the Parker-spiral direction; Alfvénic fluctuations from the Sun are not expected to survive into the inner heliosphere when the flux tubes have substantially different internal Alfvén speeds [cf. (Heyvaerts and Priest, 1983; Magyar et al., 2017)]. In these non-Alfvénic-wind cases, the pattern of shuffling of flux tubes at the Sun appears to be advected out into the heliosphere at the solar wind (proton) speed.
The Alpha-to-Proton Ionic Composition and Magnetic Flux Tubes
The alpha-to-proton number-density ratio α/p varies with time in the solar wind, characterized by sudden jumps in the ratio [e.g., (Safrankova et al., 2013; Zastenker et al., 2014)]. [See also Figure 3 of Borovsky (2008)] The jumps in the α/p ratio at 1 AU are statistically co-located with the magnetic walls of flux tubes (Borovsky, 2020c). This is demonstrated in Figure 2. Here strong jumps in the alpha-to-proton number-density ratio α/p are collected with the ACE spacecraft and with the WIND spacecraft, these jumps representing boundaries of the ion composition of the solar-wind plasma. For each spacecraft the angular change Δθ of the magnetic-field vector (every 64-s on ACE and every 97-s on WIND) is measured and the superposed-epoch average of Δθ is plotted (in green for ACE and in red for WIND), with the zero epoch being the crossing of each α/p boundary. Figure 2 shows that the magnetic field tends to undergo a strong change in direction at the α/p boundaries, with a storng change in direction being indicative of the crossing of a strong current sheet (a magnetic-flux-tube wall). Jumps in α/p represent ion-composition boundaries in the solar-wind plasma and ion-composition boundaries can only be created at the Sun; they can be stretched and folded in the solar wind, but they cannot be formed in the solar wind. Hence, the α/p boundaries are fossils from the Sun. This implies that the magnetic boundaries at 1 AU that are co-located with the α/p boundaries (the flux-tube walls) are also fossils from the Sun not created in the solar wind.
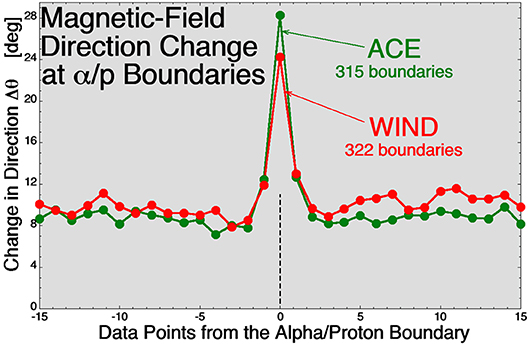
Figure 2. For 315 α/p boundaries located with the ACE spacecraft (green) and for 322 α/p boundaries located with the WIND spacecraft, the superposed-epoch average of the magnetic-field vector direction change (over 64-s for ACE and over 97-s for WIND) is plotted with the zero epoch being the α/p boundary crossing time.
Note that Owens et al. (2011) analyzed fractional changes in the alpha-to-proton number-density ratio α/p in the 64-s ACE data set in comparison with angular changes in the magnetic-field direction and found that about 25% of strong current sheets were associated with strong changes in α/p. Two comments are relevant to this finding. First, there are solar-wind types that exhibit strong plasma inhomogeneity (i.e., sector-reversal-region plasma and streamer-belt-origin plasma) and solar wind that exhibits weak inhomogeneity (coronal-hole-origin plasma), with all exhibiting strong current sheets; the more-homogeneous types of plasma will only rarely show strong fractional jumps in the plasma properties such at α/p. Secondly, the measurements of α/p at 1 AU are notoriously noisy and the measurements from different instruments do not agree [cf. Figure 7E of Borovsky (2016) and discussion therein]; this means that the jumps in the measured values of α/p at current sheets are not that different from the jumps in the measured values of α/p away from the current sheets. The study of Borovsky (2020c) only focused on distinct α/p changes that were above the noise level; those α/p changes are overwhelmingly occurring at strong current sheets.
The Electron Heat Flux (Strahl) and Magnetic Flux Tubes
The electron strahl is a magnetic-field-aligned distribution of energetic electrons moving outward from the Sun (Feldman et al., 1976), representing the electron heat flux from the Sun. At 1 AU the measured intensity of the energetic-electron strahl of the solar wind is not steady, rather it undergoes sudden temporal jumps in intensity. Those sudden intensity changes are statistically co-located with the walls of the magnetic flux tubes (Borovsky, 2020c): a superposed-epoch average of the magnetic-field direction change associated with events where the strahl-intensity jump (strahl-intensity boundaries) looks very much like Figure 2 for α/p boundaries does. I.e., different magnetic flux tubes have different strahl intensities (different values of the heat flux).
The co-location of strahl-intensity boundaries and flux-tube walls implies that there is a long-distance coherence of the flux tubes seen at 1 AU going back toward the Sun. The confinement of solar energetic particles by flux tubes (Trenchi et al., 2013a,b) also implies a long-distance coherence of the magnetic tubes.
The electron strahl is associated with an electron-mobility-driven (electron-pressure-gradient driven) ambipolar interplanetary electric field E|| that points outward from the Sun to retard electrons (Lin, 1998; Pierrard et al., 2001; Maksimovic et al., 2005). This E|| acts to accelerate solar-wind ions outward to increase the solar wind speed in the inner heliosphere (Jockers, 1972; Lemaire and Pierrard, 2001; Pierrard and Peters, 2014). Between 0.3 AU and 1 AU this interplanetary electric field produces an observed statistical increase in the speed of the slow solar wind (Schwenn et al., 1981; Arya and Freeman, 1991; Lemaire, 2010). The fact that the strahl intensity varies from flux tube to flux tube implies that the interplanetary electric field may act independently in each tube. The acceleration of the solar wind in the heliosphere might vary from tube to tube.
Squashing and Stretching of Magnetic Flux Tubes
When a spacecraft crosses the wall between two flux tubes in the solar wind, the orientation of the current sheet separating the two flux tubes can be obtained using the cross-product method (Burlaga and Ness, 1969; Knetter et al., 2004), taking the normal to the current sheet being in the B1 × B2 direction where B1 and B2 are the magnetic-field vectors on either side of the current sheet. At 1 AU, the statistical orientations of the current sheets indicate that the magnetic flux tubes are on average round (cylindrical) (Borovsky, 2008). However, in compression and rarefaction regions of the solar wind at 1 AU the magnetic-flux tubes are no longer statistically round, rather they are squashed and stretched into flattened shapes (Borovsky and Denton, 2016). This effect is outlined in Figure 3. The top panel depicts the cross section of a round flux tube with red arrows showing a sampling of the orientations of the normals to the current-sheet walls. In the middle and bottom panels a round flux tube that was compressed (middle) and rarefacted (bottom) are depicted along with a sampling of the orientations of the normals. Comparing in Figure 3 these orientations to the orientations for the round flux tube, the normals of the compressed tube are more-concentrated toward the equatorial plane and the normals of the rarefacted tube are more-concentrated normal to the ecliptic plane. In corotating interaction regions (CIRs) of the solar wind the compression factor of the solar-wind plasma can be measured by the increase in the magnetic-field strength and in the trailing edges of high-speed streams the rarefaction factor of the solar-wind plasma can be measured by the decrease of the magnetic-field strength. The squashing factor for an initially round flux tube in a compression region and the stretching factor for an initially round flux tube in a rarefaction region can both be predicted knowing the compression or rarefaction factor. Hence, the shape changes of the flux tubes can be predicted, and the systematic variation in the statistical orientations of the current sheets can be predicted. For CIRs and for trailing edges, those flux-tube shape predictions agree with the measured statistics of the current-sheet orientations [cf. Figures 3, 14, and A1 of Borovsky and Denton (2016)]. In compression regions the normals of the walls of the flux tubes tend to be concentrated toward the ecliptic plane and in rarefaction regions the normals of the walls of the flux tubes tend to be concentrated perpendicular to the ecliptic plane. In reality, because the flux tubes are pressed against each other an unperturbed flux tube will not be round, rather it will have a cross section more like the shape of a cell in a Voronoi pattern [cf. Figure 8 of Borovsky (2018a)]. Nevertheless, the statistics of the current-sheet orientations will follow the statistics for round flux tubes and compressed or rarefactive round flux tubes.
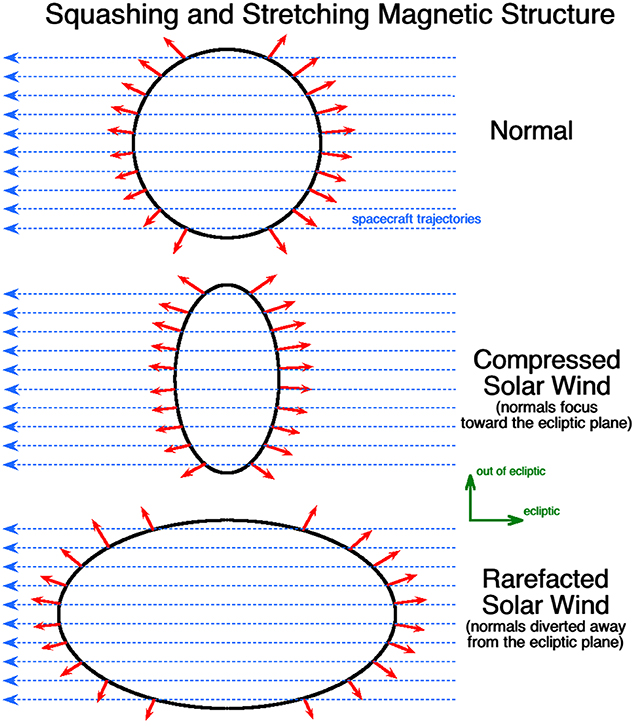
Figure 3. The cross sections of three flux tubes are sketched: a round flux tube (Top), a round flux tube that was compressed (Middle), and a round flux tube that was rafefacted (Bottom). The blue dashed curves are sample spacecraft trajectories through the flux tubes and the red arrows are normals to the flux-tube walls at the point where the spacecraft crosses the wall. The ecliptic plane and normal to the ecliptic plane are noted in green.
If current sheets were being newly created in the solar wind (e.g., by an active MHD turbulence), then the current sheets would be created isotropically giving the statistical impression of round-shaped flux tubes. At 1 AU, CIR compressions and trailing-edge rarefactions have been ongoing for about 100 h. In that 100 h the current sheets were not newly created; rather their orientations reflect the ~100-h evolution of the compression or rarefaction.
Mixing
A universal process occurring in active turbulence is mixing (Liepmann, 1979; Ottino, 1990; Dimotakis, 2005), involving (1) the stretching and folding of structure and (2) the eventual homogenization of the medium. These two stages of mixing are denoted as mesomixing and micromixing (Paul et al., 2003). In the inhomogeneous slow solar wind, Borovsky (2012a) attempted to quantify these two processes using solar-wind plasma measurements from 0.3 to 1 AU.
The stretching and folding processes produce a temporal evolution of the distribution of structure sizes, with structure sizes decreasing as time increases (cf. Figure 7 of Corrsin (1959)]. Between 0.3 and 1 AU Borovsky (2012a) found no evolution of the distribution of plasma “chunk” sizes, i.e., no evidence for ongoing stretching and folding in the solar-wind plasma.
The homogenization process produces a temporal evolution in the distribution of passive-scalar values in the medium, with the occurrence distribution narrowing with time toward a single value. Between 0.3 and 1 AU Borovsky (2012a) found no evolution in either the occurrence distribution of solar-wind proton number density or the occurrence distribution of solar-wind proton specific entropy, i.e., no evidence for ongoing homogenization of the solar-wind plasma. (A passive scalar is a scalar quantity that is convected by the fluid without perturbing the fluid behavior; density, strictly speaking is not a passive scalar but is still expected to homogenize under the action of stretching and folding followed by diffusion).
The absence of measured mixing seen in the statistics of plasma structure sizes agrees with the observation of the survival of periodic density structures in the solar wind from the corona to the Earth (Kepko and Viall, 2019). Periodic density structures emitted by the corona are imaged by white-light cameras (Viall and Vourlidas, 2015) and seen advecting into the inner heliosphere. Upstream solar-wind monitors at L1 pick up these periodic density structures at Earth, where they excite periodic ULF disturbances in the Earth's magnetosphere (Kepko et al., 2002; Kepko and Spence, 2003). The frequencies of these periodic solar-wind structures are typically 1 × 10−3-5 × 10−3 Hz (4–17 min periods), in the inertial range of the solar wind. In the inertial range of an MHD turbulence one expects modes to be destroyed and the energy of the modes to be cascaded to higher frequencies (higher wavenumbers), but the action of MHD turbulence in the solar wind does not destroy these periodic perturbations in the ~100-h travel time from the Sun to the Earth.
Current Sheets and the Fourier Power Spectrum
The solar wind's magnetic power spectral density in the inertial range of frequencies comes dominantly from the strong current sheets (directional discontinuities) in the solar wind's magnetic structure (Siscoe et al., 1968; Sari and Ness, 1969; Borovsky, 2010b); since the solar wind's magnetic correlation function is the Fourier transform of the magnetic power spectral density, magnetic correlation functions of the solar wind are also dominated by the current sheets. By creating an artificial time series that only contained the occurrence statistics (waiting times) and the amplitudes of the current sheets seen in solar-wind measurements, Borovsky (2010b) was able to reproduce the amplitude and spectral slope of the inertial range of frequencies of the solar wind's trace-B power spectral density with the artificial time series. An implication of this finding is that understanding the origin of the strong current sheets in the solar wind is key to understanding the inertial range of the solar-wind magnetic-field spectra.
At the high-frequency end of the inertial range (at about 1 Hz), the magnetic power spectral density of the solar wind exhibits a breakpoint to a steeper magnetic spectrum above the breakpoint. Using artificial time series wherein the current-sheet thicknesses of the solar wind were stretched in time, Borovsky and Podesta (2015) demonstrated that the frequency at which the magnetic spectral breakpoint occurs is governed by the thicknesses of the strong current sheets in the solar wind. When the strong current sheets in the solar-wind magnetic time series are thickened by a multiplicative factor X, the magnetic power spectral breakpoint terminating the inertial-range spectrum shifts to lower frequencies by a factor of 1/X (Borovsky and Podesta, 2015; Podesta and Borovsky, 2016). An implication of this finding is that the physics of what governs the breakpoint frequency of the solar-wind spectrum is the physics of what governs current-sheet thicknesses in the solar wind.
With the strong current sheets of the solar wind dominating the Fourier power, and with the thicknesses of the current sheets determining the breakpoint frequency, it follows that the temporal shapes (profiles) of the current sheets should determine the Fourier spectrum at frequencies above the breakpoint. By statistically examining the Fourier transforms of Gaussian-windowed current sheets in the solar-wind magnetic-field measurements, Borovsky and Burkholder (2020) demonstrated the consistency (amplitude and shape) of the high-frequency spectrum of the solar wind with the Fourier spectrum of solar-wind current sheets. An implication of this demonstration is that physical mechanisms acting within solar-wind current sheets should be investigated to understand the high-frequency spectra of the solar wind.
Current Sheet Thicknesses
At 1 AU the current-sheet (directional-discontinuity) thicknesses are on the order of 103 km (Siscoe et al., 1968; Vasquez et al., 2007), about 1–3 s in the time series. [The solar-wind current sheets appear to be thicker further from the Sun [cf. Figure 7 of Miao et al. (2011)], and since the high-frequency magnetic Fourier breakpoint appears at higher frequencies closer to the Sun (Bruno and Trenchi, 2014; Duan et al., 2020), the current sheets are probably thinner closer to the Sun]. At 1 AU the current sheets are many times thicker than typical proton gyroradii rgp and typical ion-inertial lengths c/ωpi [cf. Figures 3A,B of Borovsky et al. (2019)]. The thicknesses of solar-wind current sheets may be more consistent with Bohm diffusion DB = ckBTp/16eB (Borovsky, 2006) or gyro-Bohm diffusion DgB = (ckBTp/16eB) (rgp/L) acting over the age of the solar-wind plasma. When the scalesizes of gradients in a plasma are much larger than ion gyroradii, it has been argued that Bohm diffusion transitions over to gyro-Bohm diffusion (Perkins et al., 1993; Hannum et al., 2001), which is weakened by a term proportional to the ratio of the gyroradius to the gradient scalelength: rgp/L.
It is well-known that the solar-wind plasma contains weak double layers (time domain structures) [e.g., (Mangeney et al., 1999; Lacombe et al., 2002; Salem et al., 2003a,b; Mozer et al., 2020a)]. Malaspina et al. (2013) point out that the solar-wind time domain structures are localized in the strong current sheets of the solar wind.
Intense Velocity Shears
Figure 4 plots the occurrence distribution (black points) of the 64-s change in the solar-wind flow vector for 11 years of measurements by the ACE spacecraft at 1 AU. As was the case for the magnetic-field direction change distribution in Figure 1, the velocity-change distribution shows two distinct populations, both fit by exponential functions: a population of large velocity changes and a population of smaller velocity changes. The population of large velocity changes are abrupt wind shears in the solar-wind plasma that are co-located with the strong current sheets that form the walls of the flux-tube structure [cf. top panels of Figure 3 of Owens et al. (2011)]. As was pointed out in Section The Motion of the Magnetic Structure through the Solar-Wind Plasma, the abrupt wind shears are field-aligned flows in the flux tubes that spatially change direction at the boundaries between flux tubes owing to the change in the magnetic-field direction. The vorticity ω = ∇ × v of these velocity shears is perpendicular to the local magnetic field direction.
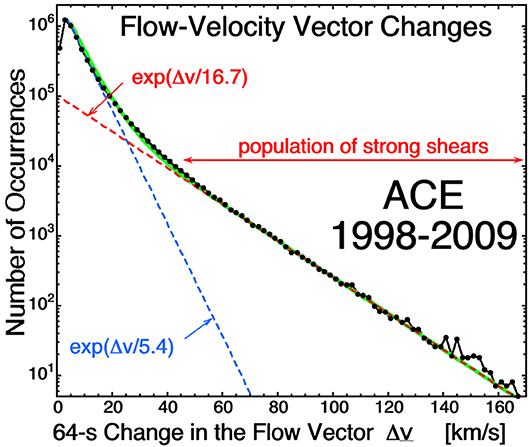
Figure 4. The 64-s change in the solar-wind velocity vector is binned for 11 years of measurements at 1 AU by the ACE SWEPAM instrument (McComas et al., 1998). The sum of the two exponential fit functions appears in green.
The thicknesses of the velocity shear layers in the solar wind are the same as the thicknesses of the current sheets, about 103 km (Borovsky and Steinberg, 2014). Note the intense velocity shear in Figure 3A of Borovsky (2020b) at time 9.8 UT where the flow vector of the solar wind is observed to change by 98 km/s in 3 s.
Very strong wind shears, which occur on average about once per day at Earth, can lead to comet-like disconnections of the Earth's magnetotail (Borovsky, 2012b, 2018b).
Alfvénic Domains in Coronal-Hole-Origin Plasma
In the Alfvénic solar wind from coronal holes, there are patches of solar wind that are highly Alfvénic separated by abrupt non-Alfvénic transitions. Within each patch, the Alfvénicity is very high as measured by a high correlation between the vector v and the vector vA = B/(4πnpmp)1/2. A set of these Alfvénic domains in coronal-hole-origin plasma appears in Figure 14 of Borovsky (2016) with the Alfvénic correlation in each domain shown in Figure 14A. Each domain lasts a few hours (corresponding to the lower-frequency end of the inertial range). The Alfvénic domains may represent some larger-than-flux-tube structure of the solar wind at the low-frequency (large-spatial-scale) edge of the inertial range: the Alfvénic-domain spatial scales magnetically map to the expected sizes of supergranules in the coronal-hole photosphere.
Magnetic Switchbacks
Localized magnetic-field foldings (magnetic switchbacks, field reversals) are well-known in the coronal-hole plasma at 1 AU [e.g., (Kahler et al., 1996)], further out in the polar coronal-hole plasma of the Ulysses data set [e.g., (Balogh et al., 1999; Yamauchi et al., 2004; Neugebauer and Goldstein, 2013)], at 0.3 AU in the Helios data set (Borovsky, 2016; Horbury et al., 2018), and at 0.17 AU in the Parker Solar Probe data set (Bale et al., 2019). These magnetic-field deviations from the Parker spiral are associated with localized increases in the solar-wind radial velocity: a “velocity excess” [cf. Figure 5 of Michel (1967)], “one-sided Alfvénic fluctuations” (Gosling et al., 2009), or “pulsed Alfvénic fluctuations” (Gosling et al., 2011). An example with three switchbacks appears in Figure 5, where 0.1 day = 2.4 h of measurements from the Helios 1 spacecraft at 0.31 AU are plotted. The switchbacks are labeled in red. Figure 5 (bottom panel) plots the direction of the magnetic field with respect to the local Parker-spiral direction: the switchbacks are noted by the reversal of the field from the Parker-spiral direction. Figure 5 (bottom panel) plots the radial proton flow velocity, which is locally increased within each switchback. A sketch of a magnetic switchback appears in Figure 6, where the flow within a folded flux tube is examined. With the magnetic structure of the solar wind moving en mass outward from the Sun faster than the average proton plasma flow (cf Section The Motion of the Magnetic Structure through the Solar-Wind Plasma), in the reference frame of the magnetic structure there is a Sunward flow of plasma within the magnetic structure that is locally field aligned (red arrows in Figure 6). Where there is a fold in the magnetic structure, the flow within the structure is locally anti-Sunward. A spacecraft sees this flow within the field folding as a local increase in the solar-wind speed. These magnetic and velocity structures can often be quite small (10's of RE), since the switchback structure seen by the WIND and ACE spacecraft, both upstream of the Earth near L1, can be very different [cf. Figure 10 of Borovsky (2016)]. Magnetic switchbacks close to the Sun are presently of great interest for Parker Solar Probe observations [e.g., (Bale et al., 2019; Kasper et al., 2019; de Wit et al., 2020; Horbury et al., 2020; Mozer et al., 2020b; Rouillard et al., 2020; Tenerani et al., 2020)].
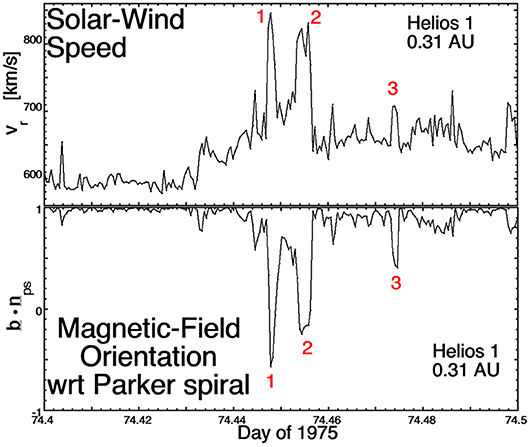
Figure 5. Magnetic switchbacks (labeled 1, 2, and 3) and the associated solar-wind-velocity pulses at 0.31 AU. The curves are 40-s resolution measurements by Helios 1 [cf. Fig. 11 of Borovsky (2016)].
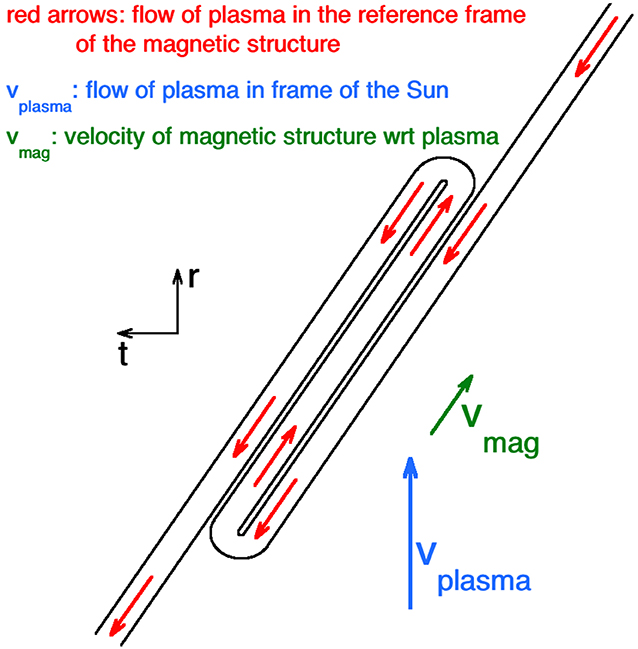
Figure 6. A sketch in the ecliptic plane of a magnetic switchback (folded flux tube) and the associated velocity perturations. The Sun is at the bottom of the sketch. The sketched structure is approximately Parker-spiral aligned (see r-t coordinates in black). The red arrows are the flow of plasma in the reference frame of the magnetic structure, with the structure moving at a velocity vmag (green arrow) with respect to the average plasma flow vplama = vsw (blue arrow). A spacecraft crossing the folded flux tube sees a localized increase in the radial flow velocity where the magnetic field is reversed from the Parker spiral.
Near the Sun (0.3 AU) the magnetic field in coronal-hole-origin plasma tends to be aligned with the Parker spiral direction, but with increasing distance from 0.3 to 2.3 AU the coronal-hole-origin solar-wind magnetic field evolves into a less-aligned state [cf. Figure 13D of Borovsky (2016)].
Types of Solar-Wind Plasma and the Inertial-Range Structure
Based on unambiguous collections of solar wind from different origins on the Sun, Xu and Borovsky (2015) developed a solar-wind categorization scheme applicable to solar-wind data at 1 AU [see also (Camporeale et al., 2017)]. The scheme categorizes solar wind into four types: (1) coronal-hole-origin plasma, (2) streamer-belt-origin plasma, (3) sector-reversal-region plasma, and (4) ejecta.
In Table 1 some of the statistical properties of the four types of plasma at 1 AU are collected. The first 3 rows are the wind speed, the number density, and the Alfvén speed, with mean values ± standard deviations as taken from the OMNI2 data set (King and Papitashvili, 2005) from the years 1995–2018. Note the low average Alfvén speed in sector-reversal-region plasma and the high average Alfvén speed in ejecta. For the inertial range of timescales the homogeneity (lumpiness) of the plasma, the magnetic-field orientation, and the Alfvénicity are noted in rows 4–6 of Table 1. Coronal-hole-origin plasma and streamer-belt-origin plasma are quasi-homogeneous, they have magnetic fields that tend to be Parker-spiral oriented (plus variations about the Parker-spiral direction), and they tend to be Alfvénic. [Streamer-belt-origin plasma is the “Alfvénic slow wind” (D'Amicis and Bruno, 2015; Bale et al., 2019; D'Amicis et al., 2019; Perrone et al., 2020)]. On the contrary, sector-reversal-region plasma and ejecta tend to be inhomogeneous, with non-Parker-spiral-oriented magnetic fields, and tend to be non-Alfvénic. A Parker-spiral magnetic-field orientation is consistent with a plasma that is continuously emitted from a spot on the Sun; non-Parker-spiral fields are characteristic of impulsive emission of plasma from the Sun. Consistent with this is the strahl (row 7 of Table 1): coronal-hole-origin plasma and streamer-belt-origin plasma have unidirectional strahls indicative of one magnetic footpoint on the Sun, sector-reversal-region plasma tends to have no strahl indicative of no magnetic connection to the Sun, and ejecta often has a bidirectional strahl indicative of both magnetic footpoints on the Sun. Row 8 of Table 1 indicates the age of the plasma at 1 AU (approximated using the velocity of the plasma at 1 AU). Row 9 is the fraction of time each type of plasma was seen at Earth in the years 1995–2018. These fractions vary strongly through the 11-year solar cycle (Xu and Borovsky, 2015).

Table 1. Some systematic differences in the properties of the four types of solar-wind plasma; the values are from the OMNI2 1-AU data set in the years 1995–2018.
Summary and Discussion
A coherent picture of the structure of the magnetic field and plasma of the solar wind in the inner heliosphere is being uncovered. Many of the properties of that structure are as yet underappreciated. The multiple properties of the structure that were discussed in this review are summarized in the final paragraph of Section Introduction.
Examination specifically of the solar-wind spatial structure leads to a description that differs from the description of physics common in the solar wind in the literature, that common description dominated by a Fourier analysis in frequency or a structure-function analysis of time differences (Viall and Borovsky, 2020). Some common terminology in the literature may be biased and not as accurate as another terminology. Five terminology examples are commented upon.
(1) The term “pressure balanced structure” [e.g., (Riazantseva et al., 2005)] might be more-accurately replaced by “plasma boundary”; the term plasma boundary better reflects the inhomogeneity of the solar wind and the fact that the ion composition, the specific entropy, the strahl, etc. can change across the boundary between two flux tubes, whereas a pressure balanced structure could be created by a localized heating of the plasma accompanied by expansion. There will, of course, be pressure balance across a plasma boundary.
(2) The interpretation of plasma number density variations or magnetic-field-strength variations as a signature of “compressibility” [e.g., (D'Amicis and Bruno, 2015)] might be better described as “inhomogeneity” of the solar-wind plasma, or lumpiness of the plasma.
(3) The high-frequency spectral breakpoint of the solar-wind representing an “onset of dissipation” in an eddy-cascade picture of the Fourier fluctuations [e.g., (Gary, 1999)] might be better described as the “physics of current-sheet thicknesses” in collisionless plasmas.
(4) Some of the concern with wave-vector anisotropy in the solar wind [e.g., (Oughton et al., 2015)] might be refocused on the question of current-sheet orientations.
(5) The focus on high-frequency plasma-wave dispersion relations to explain the shape of the high-frequency magnetic spectrum of the solar wind [e.g., (Podesta et al., 2010)] might be refocused on the shapes (profiles) of current sheets in the solar wind.
Author Contributions
The author planned, outlined, researched, and wrote the manuscript.
Funding
Work at the Space Science Institute was supported by the NSF SHINE program via award AGS-1723416, by the NASA Heliophysics Guest Investigator Program via Grant No. NNX17AB71G, and by NASA Heliophysics LWS TRT program via Grant No. NNX14AN90G.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author thanks Brandon Burkholder, Mick Denton, Zdenek Nemecek, John Podesta, Chuck Smith, and Nicki Viall for helpful conversations.
References
Arya, S., and Freeman, J. W. (1991). Estimates of solar wind velocity gradients between 0.3 and 1 AU based on velocity probability distributions from Helios 1 at perihelion and aphelion. J. Geophys. Res. 96, 14183–14187. doi: 10.1029/91JA01135
Bale, S. D., Badman, S. T., Bonnell, J. W., Bowen, T. A., Burgess, D., Case, A. W., et al. (2019). Highly structured slow solar wind emerging from an equatorial coronal hole. Nature 576, 237–242. doi: 10.1038/s41586-019-1818-7
Balogh, A., Forsyth, R. J., Lucek, A., Horbury, T. S., and Smith, E. J. (1999). Heliophysics magnetic field polarity inversions at high heliographic latitudes. Geophys. Res. Lett. 26, 631–634. doi: 10.1029/1999GL900061
Bartley, W. C., Bakata, R. P., McCracken, K. G., and Rao, U. R. (1966). Anisotropic cosmic radiation fluxes of solar origin. J. Geophys. Res. 71, 3297–3304. doi: 10.1029/JZ071i013p03297
Borovsky, J. E. (2006). The eddy viscosity and flow properties of the solar wind: CIRs, CME sheaths, and solar-wind/magnetosphere coupling. Phys. Plasmas 13, 056505–056526. doi: 10.1063/1.2200308
Borovsky, J. E. (2008). The flux-tube texture of the solar wind: strands of the magnetic carpet at 1 AU? J. Geophys. Res. 113:A08110. doi: 10.1029/2007JA012684
Borovsky, J. E. (2010a). On the variations of the solar-wind magnetic field about the Parker-spiral direction. J. Geophys. Res. 115:A09101. doi: 10.1029/2009JA015040
Borovsky, J. E. (2010b). On the contribution of strong discontinuities to the power spectrum of the solar wind. Phys. Rev. Lett. 105:111102. doi: 10.1103/PhysRevLett.105.111102
Borovsky, J. E. (2012a). Looking for evidence of mixing in the solar wind from 0.31 to 0.98 AU. J. Geophys. Res. 117:A06107. doi: 10.1029/2012JA017525
Borovsky, J. E. (2012b). The effect of sudden wind shear on the Earth's magnetosphere: statistics of wind-shear events and CCMC simulations of magnetotail disconnections. J. Geophys. Res. 117:6224. doi: 10.1029/2012JA017623
Borovsky, J. E. (2016). Plasma structure of the coronal-hole solar wind: origins and evolution. J. Geophys. Res. 121, 5055–5087. doi: 10.1002/2016JA022686
Borovsky, J. E. (2018a). The spatial structure of the oncoming solar wind at Earth and the shortcomings of a solar-wind monitor at L1. J. Atmos. Solar-Terr. Phys. 177, 2–11. doi: 10.1016/j.jastp.2017.03.014
Borovsky, J. E. (2018b). Looking for evidence of wind-shear disconnections of the Earth's magnetotail: GEOTAIL measurements and LFM MHD simulations, J. Geophys. Res. 123, 5538–5560. doi: 10.1029/2018JA025456
Borovsky, J. E. (2020a). What magnetospheric and ionospheric researchers should know about the solar wind. J. Atmos. Solar-Terr. Phys. 204:105271. doi: 10.1016/j.jastp.2020.105271
Borovsky, J. E. (2020b). On the motion of the heliospheric magnetic structure through the solar wind plasma. J. Geophys. Res. 125:e2019JA027377. doi: 10.1029/2019JA027377
Borovsky, J. E. (2020c) The magnetic structure of the solar wind: Ionic composition and the electron strahl. Geophys. Res. Lett. 47:e2019GL084586. doi: 10.1029/2019GL084586.
Borovsky, J. E., and Burkholder, B. L. (2020). On the fourier contribution of strong current sheets to the high-frequency magnetic power spectral density of the solar wind. J. Geophys. Res. 125:e2019JA027307. doi: 10.1029/2019JA027307
Borovsky, J. E., and Denton, M. H. (2016). The trailing edges of high-speed streams at 1 AU. J. Geophys. Res. 121, 6107–6140. doi: 10.1002/2016JA022863
Borovsky, J. E., Denton, M. H., and Smith, C. W. (2019). Some properties of the solar-wind turbulence at 1 AU statistically examined in the different types of solar-wind plasma. J. Geophys. Res. 124, 2406–2424. doi: 10.1029/2019JA026580
Borovsky, J. E., and Podesta, J. J. (2015). Exploring the effect of current-sheet thickness on the high-frequency fourier spectrum of the solar wind, J. Geophys. Res. 120, 9256–9268. doi: 10.1002/2015JA021622
Borovsky, J. E., and Steinberg, J. T. (2014). No evidence for the localized heating of solar-wind protons at intense velocity shear zones. J. Geophys. Res. 119, 1455–1462. doi: 10.1002/2013JA019746
Bruno, R. (2019). Intermittency in solar wind turbulence from fluid to kinetic scales. Earth Space Sci. 6, 656–672. doi: 10.1029/2018EA000535
Bruno, R., and Carbone, V. (2016). Turbulence in the solar wind. Lecture. Notes Phys. 928:1. doi: 10.1007/978-3-319-43440-7
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying intermittency events in the solar wind. Planet. Space Sci. 49, 1201–1210. doi: 10.1016/S0032-0633(01)00061-7
Bruno, R., and Trenchi, L. (2014). Radial dependence of the frequency break between fluid and kinetic scales in the solar wind fluctuations. Astrophys. J. Lett. 787:L24. doi: 10.1088/2041-8205/787/2/L24
Burkholder, B. L., Otto, A., Delamere, P. A., and Borovsky, J. E. (2019). Magnetic connectivity in the corona as a source of structure in the solar wind. J. Geophys. Res. 124, 32–49. doi: 10.1029/2018JA026132
Burlaga, L. F., and Ness, N. F. (1969). Tangential discontinuities in the solar wind. Solar Phys. 9, 467–477. doi: 10.1007/BF02391672
Camporeale, E., Care, A., and Borovsky, J. E. (2017). Classification of solar wind with machine learning. J. Geophys. Res. 122, 10,910–10,920. doi: 10.1002/2017JA024383
Chhiber, R., Goldstein, M. L., Maruca, B. A., Chasapis, A., Matthaeus, W. H., et al. (2020). Clustering of intermittent magnetic and flow structures near parker solar probe's first perihelion – a partial-variance-of-increments analysis. Astrophys. J. Suppl. Ser. 246:31. doi: 10.3847/1538-4365/ab53d2
Corrsin, S. (1959). Outline of some topics in homogeneous turbulent flow. J. Geophys. Res. 64:2134. doi: 10.1029/JZ064i012p02134
D'Amicis, R., and Bruno, R. (2015). On the origin of highly alfvénic slow solar wind. Astrophys. J. 805:84. doi: 10.1088/0004-637X/805/1/84
D'Amicis, R., Matteini, L., and Bruno, R. (2019). On the slow solar wind with high alfvénicity: from composition and microphysics to spectral properties. Mon. Not. Roy. Astron. Soc. 483, 4665–4677. doi: 10.1093/mnras/sty3329
de Wit, T. D., Krasnoselskikh, V., Bale, S. D., Bonnell, J. W., Bowen, T. A., et al. (2020). Switchbacks in the near-sun magnetic field: long memory and impact on the turbulent cascade. Astrophys. J. Suppl. Ser. 246:39. doi: 10.3847/1538-4365/ab5853
Dimotakis, P. E. (2005). Turbulent mixing. Ann. Rev. Fluid. Mech. 37, 329–56. doi: 10.1146/annurev.fluid.36.050802.122015
Dmitruk, P., Matthaeus, W. H., and Seenu, N. (2004). Test particle energization by current sheets and nonuniform fields in magnetohydrodynamic turbulence. Astrophys. J. 617:667. doi: 10.1086/425301
Dobrowolny, M., Mangeney, A., and Veltri, P. (1980). Fully developed anisotropic turbulence in interplanetary space. Phys. Rev. Lett. 45:144. doi: 10.1103/PhysRevLett.45.144
Duan, D., Bowen, T. A., Chen, C. H. K., Mallet, A., He, J., et al. (2020). The radial dependence of proton-scale magnetic spectral break in slow solar wind during PSP encounter 2. Astrophys. J. Suppl. Ser. 246:55. doi: 10.3847/1538-4365/ab672d
Edwin, P. M., and Roberts, B. (1983). Wave propagation in a magnetic cylinder. Solar Phys. 88, 179. doi: 10.1007/BF00196186
Eselevich, V. G. (2019). Diamagnetic structures as a basis of quasi-stationary slow solar wind. Solar Terr. Phys. 5, 29–41. doi: 10.12737/stp-53201904
Feldman, W. C., Asbridge, J. R., Bame, S. J., Gary, S. P., Montgomery, M. D., and Zink, S. M. (1976). Evidence for the regulation of solar wind heat flux at 1 AU. J. Geophys. Res. 81:5207. doi: 10.1029/JA081i028p05207
Gary, S. P. (1999). Collisionless dissipation wavenumber: linear theory. J. Geophys. Res. 104, 6759–6762. doi: 10.1029/1998JA900161
Goossens, M., Trradas, J., Andries, J., Arregui, I., and Ballester, J. L. (2009). On the nature of kink MHD waves in magnetic flux tubes. Astron. Astrophys. 503, 213–223. doi: 10.1051/0004-6361/200912399
Gosling, J. T., McComas, D. J., Roberts, D. A., and Skoug, R. M. (2009). A one-sided aspect of alfvénic fluctuations in the solar wind. Astrophys. J. 695:L213. doi: 10.1088/0004-637X/695/2/L213
Gosling, J. T., Tian, H., and Phan, T. D. (2011). Pulsed Alfvén waves in the solar wind. Astrophys. J. 737:L35. doi: 10.1088/2041-8205/737/2/L35
Greco, A., Matthaeus, W. H., Servidio, S., Chuychai, P., and Dmitruk, P. (2009). Statistical analysis of discontinuities in solar wind ACE data and comparison with intermittent MHD turbulence. Astrophys. J. 691:L111. doi: 10.1088/0004-637X/691/2/L111
Hannum, D., Bateman, G., Kinsey, J., Kritz, A. H., Onjun, T., and Pankin, A. (2001). Comparison of high-mode predictive simulations using mixed Bohm/gyro-bohm and multi-mode (MMM95) transport models. Phys. Plasmas 8, 964–974. doi: 10.1063/1.1338534
Heyvaerts, J., and Priest, E. R. (1983). Coronal heating by phase-mixed shear alfvén waves. Astron. Astrophys. 117, 220–234.
Horbury, T. S., Woolley, T., Laker, R., Matteini, L., Eastwood, J., et al. (2020). Sharp Alfvénic impulses in the near-Sun solar wind. Astrophys. J. Suppl. Ser. 246:45. doi: 10.3847/1538-4365/ab5b15
Horbury, T. S., Woolley, T., and Stansby, D. (2018). Short, large-amplitude speed enhancemnts in the near-sun fast solar wind. Mon. Not. R. Astron. Soc. 478, 1980–1986. doi: 10.1093/mnras/sty953
Huang, C., Yan, Y., Li, G., Deng, Y., and Tan, B. (2014). Tracking back the solar wind to its photospheric footpoints from wind observations – a statistical study. Solar Phys. 289, 3109–3119. doi: 10.1007/s11207-014-0508-8
Kahler, S. W., Crooker, N. U., and Gosling, J. T. (1996). The topology of intrasector reversals of the interplanetary magnetic field. J. Geophys. Res. 101, 24,373–24,382. doi: 10.1029/96JA02232
Kasper, J. C., Bale, S. D., Belcher, J. W., Berthomier, M., Case, A. W., et al. (2019). Alfvénic velocity spikes and rotational flows in the near-Sun solar wind. Nature 576, 228–231. doi: 10.1038/s41586-019-1813-z
Kepko, L., and Spence, H. E. (2003). Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. 108:1257. doi: 10.1029/2002JA009676
Kepko, L., Spence, H. E., and Singer, H. J. (2002). ULF waves in the solar wind as direct drivers of magnetospheric pulsations. Geophys. Res. Lett. (2002) 29:39-1–39-4. doi: 10.1029/2001GL014405
Kepko, L., and Viall, N. M. (2019). The source, significance, and magnetospheric impact of periodic density structures within stream interaction regions. J. Geophys. Res. (2019) 124, 1–22. doi: 10.1029/2019JA026962
King, J. H., and Papitashvili, N. E. (2005). Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. 110:2104. doi: 10.1029/2004JA010649
Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2004). Four-point discontinuity observations using cluster magnetic field data: a statistical survey. J. Geophys. Res. 109:A06102. doi: 10.1029/2003JA010099
Komar, C. M., Fermo, R. L., and Cassak, P. A. (2015). Comparative analysis of dayside magnetic reconnection models in global magnetosphere simulations. J. Geophys. Res. 120, 276–294. doi: 10.1002/2014JA020587
Lacombe, C., Salem, C., Mangeney, A., Hubert, D., Perche, C., Bougeret, J. L., et al. (2002). Evidence for the interplanetary electric potential? WIND observations of electrostatic fluctuations. Ann. Geophys. 20, 609–618. doi: 10.5194/angeo-20-609-2002
Lemaire, J. (2010). Half a century of kinetic solar wind models. AIP Conf. Proc. 1216:8. doi: 10.1063/1.3395971
Lemaire, J., and Pierrard, V. (2001). Kinetic models of solar and polar winds. Astrophys. Space Sci. 277, 169–180. doi: 10.1007/978-94-010-0904-1_22
Li, G., and Qin, G. (2011). “A solar wind model with current sheets,” in Proceedings of a 5th International Conference Held at San Diego, California, USA 13-18 June 2010. ed. N.V. Pogorelov (San Francisco: Astronomical Society of the Pacific), 117.
Lin, R. P. (1998). WIND observations of suprathermal electrons in the interplanetary medium. Space Sci. Rev. 86, 61–78. doi: 10.1007/978-94-011-4762-0_4
Magyar, N., Van Doorsselaere, T., and Goosens, M. (2017). Generalized phase mixing: turbulence-like behaviour from unidirectional propagating MHD waves. Sci. Rep. 7:14820. doi: 10.1038/s41598-017-13660-1
Maksimovic, M., Zouganelis, I., Chaufray, J. Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial evolution of the electron distribution functions in the fast solar wind between 0.3 and 1.5 AU. J. Geophys. Res. 110:A09104. doi: 10.1029/2005JA011119
Malara, F., Primavera, L., and Veltri, P. (1996). Compressive fluctuations generated by time evolution of Alfvénic perturbations in the solar wind current sheet. J. Geophys. Res. 101:21597–21617. doi: 10.1029/96JA01637
Malaspina, D. M., Newman, D. L., Wilson, L. B., Goetz, K., Kellogg, P. J., and Kerstin, K. (2013). Electrostatic solitary waves in the solar wind: evidence for instability at solar wind current sheets. J. Geophys. Res. 118, 591–599. doi: 10.1002/jgra.50102
Mangeney, A., Salem, C., Lacombe, C., Bougeret, J. L., Perche, C., Manning, R., et al. (1999). WIND observations of coherent electrostatic waves in the solar wind. Ann. Geophys. 17, 307–320. doi: 10.1007/s00585-999-0307-y
McComas, D. J., Blame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Riley, P., et al. (1998). Solar wind electron proton alpha monitor (SWEPAM) for the advanced composition explorer. Space Sci. Rev. 86, 563–612. doi: 10.1007/978-94-011-4762-0_20
McCracken, K. G., and Ness, N. F. (1966). The collimation of cosmic rays by the interplanetary magnetic field. J. Geophys. Res. 71, 3315–3318. doi: 10.1029/JZ071i013p03315
Miao, B., Peng, B., and Li, G. (2011). Current sheets from Ulysses observation. Ann. Geophys. 29, 237–249. doi: 10.5194/angeo-29-237-2011
Michel, F. C. (1967). Model of solar wind structure. J. Geophys. Res. 72:1917. doi: 10.1029/JZ072i007p01917
Mozer, F. S., Agapiov, O. V., Bale, S. D., Bonnell, J. W., and Case, T. (2020b) Switchbacks in the solar magnetic field: their evolution, their content, their effects on the plasma. Astrophys. J. Suppl. Ser. 246:68. doi: 10.3847/1538-4365/ab7196.
Mozer, F. S., Agapitov, O. V., Bale, S. D., Bonnell, J. W., Goetz, K., and Goodrich, R. (2020a) Time domain structures dust in the solar vicinity: parker solar probe observations. Astrophys. J. Suppl. Ser. 246:50. doi: 10.3847/1538-4365/ab5e4b.
Nemecek, Z., Durovcova, T., Safrankova, J., Nemec, F., Matteini, L., Stansvy, D., et al. (2020). What is the solar wind frame of reference? Astrophys. J. 889:163. doi: 10.3847/1538-4357/ab65f7
Ness, N. F., Scearce, C. S., and Cantarano, S. (1966). Preliminary results fro the pioneer 6 magnetic field experiment. J. Geophys. Res. 71:3305. doi: 10.1029/JZ071i013p03305
Neugebauer, M., and Giacalone, J. (2010). Progress in the study of interplanetary discontinuities. AIP Conf. Proc. 1216:194. doi: 10.1063/1.3395834
Neugebauer, M., and Giacalone, J. (2015). Energetic particles, tangential discontinuities, and solar flux tubes. J. Geophys. Res. 120, 8281–8287. doi: 10.1002/2015JA021632
Neugebauer, M., and Goldstein, B. (2013). E. Double-proton beams and magnetic switchbacks in the solar wind. AIP Conf. Proc. 1539:46. doi: 10.1063/1.4810986
Ottino, J. (1990). M. Mixing, chaotic advection, and turbulence. Ann. Rev. Fluid Mech. 22, 207–254. doi: 10.1146/annurev.fl.22.010190.001231
Oughton, S., Matthaeus, W. H., Wan, M., and Osman, K. T. (2015). Anisotropy in solar wind plasma turbulence. Phil. Trans. Roy. Soc. A 373, 1–23. doi: 10.1098/rsta.2014.0152
Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic discontinuities in the near-Earth solar wind: evidence of in-transit turbulence or remnants of coronal structure? Solar Phys. 269, 411–420. doi: 10.1007/s11207-010-9695-0
Paul, E. L., Atiemo-Obeng, V. A., and Kresta, S. M. (2003). Handbook of Industrial Mixing Wiley-Interscience. (Hoboken, NJ: Wiley-Interscience; John Wiley & Sons). doi: 10.1002/0471451452
Perkins, F. W., Barnes, C. W., Hohnson, D. W., Scott, S. D., et al. (1993). Nondimensional transport scaling in the tokamak fusion test reactor: is tokamak transport bohm or gyro-bohm? Phys. Fluids B 5, 477–498. doi: 10.1063/1.860534
Perrone, D., D'Amicis, R., De Marco, R., Matteini, L., Stansby, D., Bruno, R., and Horbury, T. S. (2020). Highly alfvénic slow solar wind at 0.3 AU during a solar minimum: helios insights for parker solar probe and solar orbiter. Astron. Astrophys. 633:A166. doi: 10.1051/0004-6361/201937064
Pierrard, V, Issautier, K, Meyer-Vernet, N, and Lemaire, J. Collisionless model of the solar wind in a spiral magnetic field. Geophys. Res. Lett (2001) 28:223.
Pierrard, V., and Peters, M. (2014). Coronal heating and solar wind acceleration for electrons, protons, and minor ions obtained from kinetic models based on kappa distributions. J. Geophys. Res. 119, 9441–9455. doi: 10.1002/2014JA020678
Podesta, J. J., and Borovsky, J. E. (2016). Relationship between the durations of jumps in solar wind time series and the frequency of the spectral break. J. Geophys. Res. 121, 1817–1838. doi: 10.1002/2015JA021987
Podesta, J. J., Borovsky, J. E., and Gary, S. P. (2010). A kinetic Alfvén wave cascade subject to collisionless damping cannot reach electron scales in the solar wind at 1 AU. Astrophys. J. 712:685. doi: 10.1088/0004-637X/712/1/685
Qin, G., and Li, G. (2008). Effect of flux tubes in the solar wind on the diffusion of energetic particles. Astrophys. J. 682:L129 doi: 10.1063/1.2982464
Riazantseva, M. O., Khabarova, O. V., Zastenker, G. N., and Richardson, J. D. (2005). Sharp boundaries of solar wind plasma structures and an analysis of their pressure balance. Cosmic. Res. 43, 157–164. doi: 10.1007/s10604-005-0030-8
Rouillard, A. P., Kouloumvakos, A., Vourlidas, A., Kasper, J., Bale, S., et al. (2020). Related streamer flows to density and magnetic structures at the parker solar probe. Astrophys. J. Suppl. Ser. 246:37. doi: 10.3847/1538-4365/ab579a
Ruderman, M. S., and Roberts, B. Leaky non-leaky kink oscillations of magnetic flux tubes. J. Plasma Phys. (2006) 72, 285–308. doi: 10.1017/S0022377805004101
Safrankova, J., Memecek, Z., Cagas, P., Pavlu, J., Zastenker, G. N., Riazantseva, M. O., et al. (2013). Short-scale variations of the solar wind helium abundance. Astrophys. J. 778:25. doi: 10.1088/0004-637X/778/1/25
Salem, C., Hubert, D., Lacombe, C., Bale, S. D., Mangeney, A., Larson, D. E., et al. (2003a). Electron properties and Coulomb collisions in the solar wind at 1 AU: WIND observations. Astrophys. J. 585:1147. doi: 10.1086/346185
Salem, C., Lacombe, C., Mangeney, A., Kellogg, P. J., and Bougeret, J. L. (2003b). Weak double layers in the solar wind and their relation to the interplanetary electric field. AIP Conf. Proc. 679:513. doi: 10.1063/1.1618647
Sari, J. W., and Ness, N. F. (1969). Power spectra of the interplanetary magnetic field. Solar Phys. 8, 155–165. doi: 10.1007/BF00150667
Schatten, K. H. (1971). Large-scale properties of the interplanetary magnetic field. Rev. Geophys. Space Phys. 9:773. doi: 10.1029/RG009i003p00773
Schwenn, R., Muhlhauser, K. H., Marsch, E., and Rosenbauer, H. (1981). “Two states of the solar wind at the time of solar activity minimum II. Radial gradients of plasma parameters in fast and slow streams,” in Solar Wind Four MPAE-W-100-81-31, (Lindau: Max Planck Institut fur eronomie), 126.
Siscoe, G. L., Davis, L., Coleman, P. J., Smith, E. J., and Jones, D. E. (1968). Power spectra and discontinuities of the interplanetary magnetic field: mariner 4. J. Geophys. Res. 73:61. doi: 10.1029/JA073i001p00061
Smith, C. W., Acuna, M. H., Burlaga, L. F., L'Heureux, J., Ness, N. F., and Scheifele, J. (1998). The ACE magnetic fields experiment. Space Sci. Rev. 86, 611–632. doi: 10.1023/A:1005092216668
Sonnerup, B. U. O. (1974). Magnetopause reconnection rate. J. Geophys. Res. 79:1546. doi: 10.1029/JA079i010p01546
Telloni, D., Perri, S., Carbone, V., and Bruno, R. (2016). Selective decay and dynamic alignment in the MHD turbulence: the role of the rugged invariants. AIP Conf. Proc. 1720:040015. doi: 10.1063/1.4943826
Tenerani, A., Velli, M., Matteini, L., Reville, V., Shi, C., et al. (2020). Magnetic field kinks and folds in the solar wind. Astrophys. J. Suppl. Ser. 246:32. doi: 10.3847/1538-4365/ab53e1
Thieme, K. M., Schwenn, R., and Marsch, E. (1989). Are structures in high-speed streams signatures of coronal fine structures? Adv. Space Res. 9, 127–130. doi: 10.1016/0273-1177(89)90105-1
Tong, Y., Borovsky, J. E., and Steinberg, J. T. (2016). “Using ACE-Earth magnetic connection events to measure wandering length scale of interplanetary magnetic field in the solar wind,” in 2016 Los Alamos Space Weather Summer School Research Reports, Report LA-UR-16-29471, (Los Alamos: NM: Los Alamos National Laboratory), 55.
Trenchi, L., Bruno, R., D'Amicis, R., Marcucci, M. F., and Telloni, E. (2013b). Observation of IMF coherent structures and their relationship to SEP dropout events. Ann. Geophys. 31, 1333–1341. doi: 10.5194/angeo-31-1333-2013
Trenchi, L., Bruno, R., Telloni, D., D'Amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013a). Solar energetic particle modulation associated with coherent magnetic structures. Astrophys. J. 770:11. doi: 10.1088/0004-637X/770/1/11
Tsurutani, B. T., and Ho, C. M. (1999). A review of discontinuities and Alfvén waves in interplanetary space: ulysses results. Rev. Geophys. 37, 517–541. doi: 10.1029/1999RG900010
Tu, C. Y., Wang, X., He, J., Marsch, E., and Wang, L. (2016). Two cases of convecting structure in the slow solar wind turbulence. AIP Conf. Proc. 1720:040017 doi: 10.1063/1.4943828
Vasquez, B. J., Abramenko, V. I., Haggerty, D. K., and Smith, C. W. (2007). Numerous small magnetic field discontinuities of Bartels rotation 2286 and the potential role of Alfvénic turbulence. J. Geophys. Res. 112:A11102. doi: 10.1029/2007JA012504
Vasquez, B. J., and Hollweg, J. V. (1999). Formation of pressure-balanced structures and fast waves from nonlinear Alfvén waves. J. Geophys. Res. 104, 4681–4696. doi: 10.1029/1998JA900090
Viall, N. M., and Borovsky, J. E. (2020). Nine outstanding questions of solar wind physics. J. Geophys. Res. 125. doi: 10.1002/essoar.10502606.1
Viall, N. M., and Vourlidas, A. (2015). Periodic density structures and the origin of the slow solar wind. Astrophys. J. 807:176. doi: 10.1088/0004-637X/807/2/176
Webb, G. M., Zank, G. P., Kaghashvili, E. K., and le Roux, J. A. (2006). Compound and perpendicular diffusion of cosmic rays and random walk of the field lines. I. Parallel particle transport models. Astrophys. J. 651:211. doi: 10.1086/507415
Xu, F., and Borovsky, J. E. (2015). A new 4-plasma categorization scheme for the solar wind. J. Geophys. Res. 120, 70–100. doi: 10.1002/2014JA020412
Yamauchi, Y., Suess, S. T., Steinberg, J. T., and Sakurai, T. (2004). Differential velocity between solar wind protons and alpha particles in pressure balanced structures. J. Geophys. Res. 109:A03104. doi: 10.1029/2003JA010274
Zastenker, G. N., Koloskova, I. V., Riazantseva, M. O., Yurasov, A. S., Safrankova, J., Nemecek, Z., et al. (2014). Observation of fast variations of the helium-ion abundance in the solar wind. Cosmic. Res. 52, 25–36. doi: 10.1134/S0010952514010109
Keywords: solar wind, heliospheric structure, turbulence, Alfvén waves, current sheets
Citation: Borovsky JE (2020) Plasma and Magnetic-Field Structure of the Solar Wind at Inertial-Range Scale Sizes Discerned From Statistical Examinations of the Time-Series Measurements. Front. Astron. Space Sci. 7:20. doi: 10.3389/fspas.2020.00020
Received: 03 March 2020; Accepted: 21 April 2020;
Published: 20 May 2020.
Edited by:
Luca Sorriso-Valvo, National Research Council, ItalyReviewed by:
Bernard Vasquez, University of New Hampshire, United StatesYasuhito Narita, Austrian Academy of Sciences (OAW), Austria
Julia E. Stawarz, Imperial College London, United Kingdom
Copyright © 2020 Borovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
 Joseph E. Borovsky
Joseph E. Borovsky