Understanding the Fundamental Plane and the Tully Fisher Relation

1. Introduction

The fundamental plane (FP) of early type galaxies is fairly aptly named, because in the 3-space of velocity dispersion (σ), surface brightness and effective radius is expressed the dynamical equilibrium that a galaxy has reached, but not (the interesting part) how it got there. It has long been understood that the virial theorem¹ will place quiescent galaxies with a well-defined mass to light ratio in a plane in this space. The observed tilt of the plane differs from the expectation, however, and the deviation can be patched using the halo occupation distribution formalism (e.g., Moster et al., 2010; Mould, 2014, 2017). But that formalism is not physics: it is a mapping between the dark matter universe and the observed one. The reason for the copout, of course, is the difficulty of modeling baryonic processes, such as star formation with their challenging demands for spatial resolution.

2. Building the FP

If mergers are the manner in which early type galaxies are formed, a schematic understanding can be based on the serial accretion by a galaxy with mass, kinetic and potential energies (m, T, V) of dwarfs (δm, δT, δV). Each is in virial equilibrium², so that 2T = –V and 2δT = −δV. If energy D is dissipated in the interaction, the energy equation is

$\begin{array}{ll}\frac{1}{2}\delta m{\sigma }_0^2+\frac{1}{2}\delta m{\sigma }^2+D=\frac{1}{2}\delta (m+g\delta m){(\sigma +\delta \sigma )}^2& (1)\end{array}$

where $\delta T=\frac{1}{2}\delta m{\sigma }_0^2$ and T = $\frac{1}{2}m{\sigma }^2$ and g is unity if mass is conserved.

If D = fGmδm/r_e, where f is a free parameter and r_e is the effective radius, then

$\begin{array}{ll}\sigma \delta \sigma (m+g\delta m)=\frac{1}{2}\delta m({\sigma }_0^2-g{\sigma }^2)+fGm\delta m/r_e& (2)\end{array}$

which yields the differential equation

$\begin{array}{ll}\frac{d\text{ log }\sigma }{d\text{ log }m}=\frac{1}{2}(\frac{{\sigma }_0^2}{{\sigma }^2}-g)+\frac{r_0}{r_e}& (3)\end{array}$

where r₀ has replaced f to keep a dimensionless equation simple.

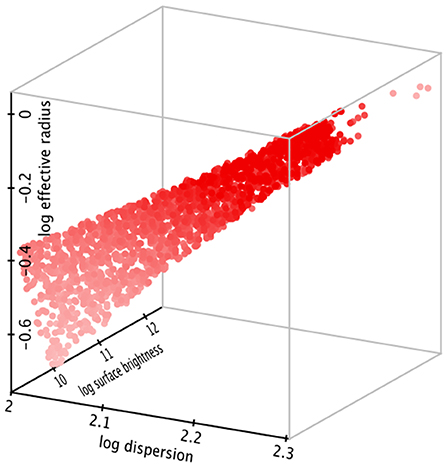
We integrate Equation (3) numerically and adopt M/L ∝ σ^ϵ, following Mould (2014), and $r_e=r_0{\sigma }^{1.75}$ plus a dispersion, to obtain the fundamental plane shown in Figure 1. In our adopted M/L ϵ is not a free parameter³ The proportionality constant will contain stellar population dependences, such as metallicity. The fit to Figure 1 is $r_e\propto {\sigma }^{1.6}S{B}^{-0.4}$, where SB is surface brightness, which is not too dissimilar to that found for 6dF by Magoulas et al. (2012): $r_e\propto {\sigma }^{1.53}S{B}^{-0.89}$.

FIGURE 1

Figure 1. A simulated FP obtained by integrating Equation (3).

The foregoing is just a schematic insight into the FP, illustrating how a tilt from the virial plane may arise from dissipation, parameterized by f and feedback/mass loss parameterized by g, both of which could be functions of scale⁴. With two free parameters it is not surprising that the observed FP can be approximated. But the point is, they stand for two processes which must be fully physically modeled if the FP is to be understood.

2.1. Bulges and Nuclei

The 6dFGS (Jones et al., 2009) selected early type galaxies from 2MASS (Skrutskie et al., 2006). The sample therefore contains ellipticals, S0s and spiral galaxies with large bulges. Bulges are believed to form in a hybrid manner, some more like ellipticals, others as a result of the secular evolution of disks (Kormendy and Kennicutt, 2004). In either case the formalism of this section applies and it is not surprising that all of these galaxies fall on a common FP. Pseudobulges, as secular evolution dominated bulges are called, distinguish themselves by the low bulge fraction of the total light, flatter shapes, high ratio of rotation to velocity dispersion, bars, small Sersic index and tendency toward exponential surface brightness profiles. We examine shape (or ellipticity) and Sersic index, n, in section 4.

We note that, within bulges, nuclei form by a similar accretion process and are said to co-evolve with bulges (e.g., Kormendy and Ho, 2013). So it is not surprising to see a power law relation between nuclear black hole mass and velocity dispersion (Magorrian et al., 1998; Ferrarese and Merritt, 2000; Graham, 2012), again following the formalism of the preceding section, leading to a power law relation. Spectra of active galactic nuclei arising from 6dFGS were discussed by Masci et al. (2010).

3. Stellar Mass

The 6dFGS sample (Campbell et al., 2014) at z ≈ 0 has the merit of considerable volume and southern complementarity to SDSS.

To describe the deviation from the virial plane, following D'Onofrio et al. (2013), we take

$\begin{array}{ll}{\Delta }_{FP}=(a-2)\text{ log }\sigma +(b-1)\text{ log }SB& (4)\end{array}$

where a and b are FP coefficients given in that reference.

$\begin{array}{ll}{r}_e\propto {\sigma }^{a}S{B}^b& (5)\end{array}$

Proctor et al. (2008) and Springob et al. (2012) measured Lick indices for the galaxies, giving estimates of metallicity, Z, and age, t, for their stellar populations. Here and in Magoulas et al. (2012) we use those spectra for which the quality factor is 10 or less and S/N > 9. Maraston (2005) models⁵ for the 2MASS J band adopted in the Campbell et al. (2014) dataset predict M_model/L = M/L(Z, t) for Salpeter IMF and an assumed horizontal branch distribution.

Based on these mass-to-light ratios, Figure 2 is the deviation from the virial plane as a function of stellar mass. The primary tilt of the FP is large and dependent on the mass of the galaxy. Its origin is a hybrid of M/L dependence on mass and structural variation with mass. In this context M/L refers to both the dark and baryonic matter components.

FIGURE 2

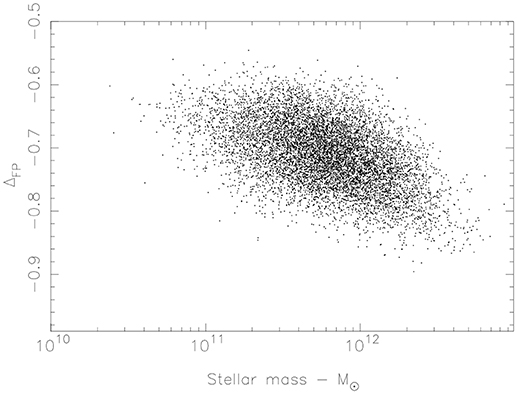
Figure 2. Deviation from the virial plane. 8,971 6dF galaxies. The values of a and b defining the virial plane are those of Magoulas et al. (2012). An IMF dependence on stellar mass could be a key influence here (Conroy and van Dokkum, 2012; Conroy et al., 2013), but the real situation could be more complex (see text).

3.1. Galaxy Structure

Pursuing structural variation with mass, Ciotti et al. (1996) considered spherical, non-rotating, two-component models to find trends along the FP in orbital radial anisotropy, dark matter and luminous matter profiles. Mould (2014) compared the mass profile M(r) and luminosity profile L(r) with reference to the Jeans equation, whose three terms, the density derivative, the velocity dispersion derivative and β, relate to concentration, dispersion profile and anisotropy.

A new chapter on scaling relations is being opened by the Ultra Diffuse Galaxies. The difficulty of measuring their velocity dispersions means that few have been placed in the FP. Their formation may be environment dependent (Forbes et al., 2020). Their dark matter content may be different from the standard halo mass/stellar mass relation.

3.1.1. Concentration

Sersic indices have been measured from 2MASS data for the Campbell et al. (2014) 6dFGS sample. Figure 3 is the deviation from the virial plane as a function of Sersic index. A list of 129 galaxies was excluded, usually the result of missing parts of the image in the original 2MASS processing or close contamination by another galaxy or a star.

FIGURE 3

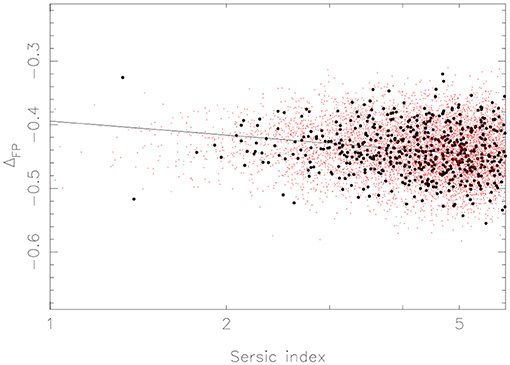
Figure 3. Deviation from the virial plane. To separate resolution effects, the apparently largest 541 galaxies are filled black symbols and the line is a least squares fit.

The strong dependence of tilt on stellar mass is not repeated with Sersic index. The trend is weaker than that seen by D'Onofrio et al. in their WINGS-Sample II.

3.1.2. Dispersion Profile

Single fibers were allocated to galaxies in 6dFGS, and central velocity dispersions for the galaxies are all that is available. The SAMI survey, however, Croom et al. (2012) offers fiber bundle resolution on a 6dFGS sized sample of galaxies. As this technology takes over from slit or single fiber spectroscopy, it will allow us to pursue the influence of the remaining terms in the Jeans equation on deviation from the virial plane, an exciting development.

3.1.3. Anisotropy

Anisotropic kinematics have been explored in many papers on triaxiality (e.g., Binney, 1987). Anisotropy manifests itself in crudely ellipticity and one can look for dependences. D'Onofrio et al. in their WINGS-Sample II also see a trend with ellipticity. The majority of our 6dFGS galaxies have axial ratios given by NED. We see this trend too in Figure 4, but the slope is 0.03, rather than 0.24.

FIGURE 4

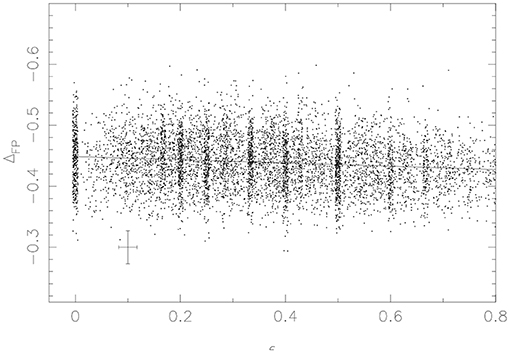
Figure 4. Deviation from the virial plane vs. ellipticity (1-r), where 1/r is the ratio of the major and minor axes. The horizontal error is the mean rounding error in these quantities, and a lower limit on the observational uncertainty. Popular values of ellipticity have been slightly blurred for improved visibility.

3.2. Halo Mass

Behroozi et al. (2010) developed a relation between stellar mass and halo mass based on mass assignment of dark matter halos in simulations to stellar masses in standard luminosity functions. We have used their Equation (21) with their standard parameters⁶ for zero redshift to plot Figure 5. The tilt is reduced by an order of magnitude from Figure 2, indicating that the stellar mass/halo mass relation is crucial to setting the tilt of the FP.

FIGURE 5

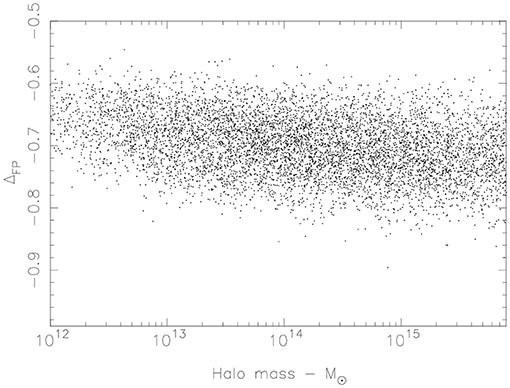
Figure 5. Deviation from the virial plane vs. halo mass. The tilt is reduced by an order of magnitude from Figure 2.

4. Star Formation History and Chemical Enrichment

It is known that there are strong stellar population trends with velocity dispersion for red sequence galaxies (e.g., Nelan et al., 2005). Higher velocity dispersion red-sequence galaxies are, on average, older, more metal-rich, and more alpha-enhanced than lower velocity dispersion galaxies. Allanson et al. (2009) examined how these trends and different star formation histories could give the tilt of the FP. They found that the FP tilt and scatter are driven primarily by stellar age effects and also concluded that “the contribution of stellar populations to the tilt of the fundamental plane is highly dependent on the assumed star formation history (SFH).” Fitzpatrick and Graves (2014), on the other hand, find that to zeroth-order the SFH of their early-type galaxy (ETG) sample is fully captured by the structural parameters σ and I_e, and any differences in the SFH with environment at fixed structure are only slight. The SFH-structure correlation they observe constrains the degree to which late-time evolutionary processes can alter the SFHs/structures of early-type galaxies in their sample.

Following the analysis of SDSS spectra by Graves and Faber (2010), we have calculated SB residuals from the FP, Δ log SB_e = log SB_e − (log r_e − a log σ)/b, by comparing the observed SB of each galaxy with the Magoulas et al. (2012) expectation (Equation 5). High SB can come about from high stellar density or relatively recent star formation or both. Figures 6, 7 show that 6dFGS spectra lead us to concur with Graves and Faber (2010) on that point. Graves and Faber go on to correlate stellar mass/halo mass ratio with population characteristics. Population correlations in 6dFGS lead in a somewhat different direction.

FIGURE 6

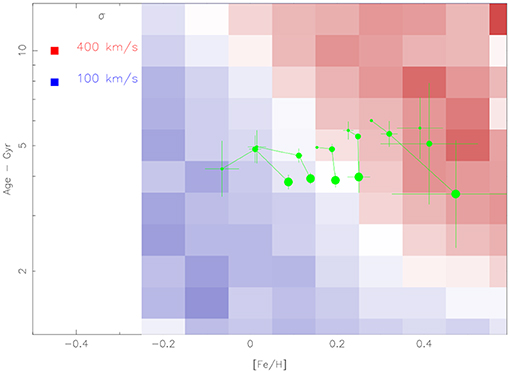
Figure 6. Location of 6dFGS galaxies in the metallicity, age plane. Properties are color coded by velocity dispersion with giant (red) galaxies old and metal rich and lesser (blue) galaxies younger and metal poorer. Galaxies which are low surface brightness relative to the mean for their σ and r_e on the FP are small green symbols; high SB galaxies are large green symbols. Green lines connect bins characterized by their range in σ. An upward vertical green line would be a stellar population fading at constant metallicity.

FIGURE 7

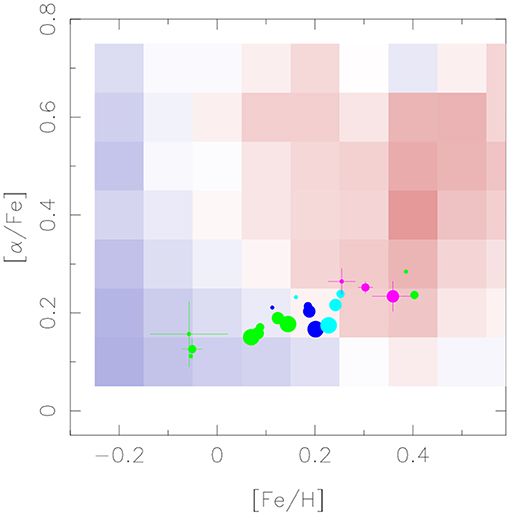
Figure 7. Location of 6dFGS galaxies in the metallicity, α-richness plane. The giant/dwarf red/blue σ color coding is that of the previous figure. Symbols are also sized by surface brightness as in the previous figure, but the intermediate σ bins are color coordinated, rather than connected. Green <150 km/s; blue is 150–250 km/s; aqua is 250–350 km/s; pink > 350 km/s. At a given σ α-richness tends to anti-correlate with metallicity. More colors are needed to distinguish the four green constant σ bins, which show the same effect, but this is not apparent, as they are all green.

The stellar populations of early-type galaxies form a two dimensional family in σ and SB. [Fe/H] and [α/Fe] increase⁷ with σ. In the other dimension age and [α/Fe] decrease with SB, while [Fe/H] increases. At fixed σ, galaxies with younger ages, lower [α/Fe], and greater total metal enrichment also have larger SB and formed more stars. Enhanced [α/Fe] ratios imply that enrichment proceeded by mostly core-collapse supernovae. and that this star formation was of short duration.

Figure 8 shows the correlation between SB excess and age at every value of σ. SB excess can arise through star formation modifying M/L or a mass density excess. For a Salpeter IMF fading of a billion years old burst of star formation occurs at the rate of Δ log SB ≈ Δ log t. The vertical pillars in Figure 8 correspond to $\Delta \text{ log }SB\stackrel{>}{~}2\Delta \text{ log }t$. Either the fading is fast due to a steeper than Salpeter IMF in the 1–2 M_⊙ regime or there is also present a mass density excess in the SB excess galaxies. Following our model in section 2, galaxies with more than average dissipation (small r_e) could achieve the observed SB excess in this way without an abnormal IMF.

FIGURE 8

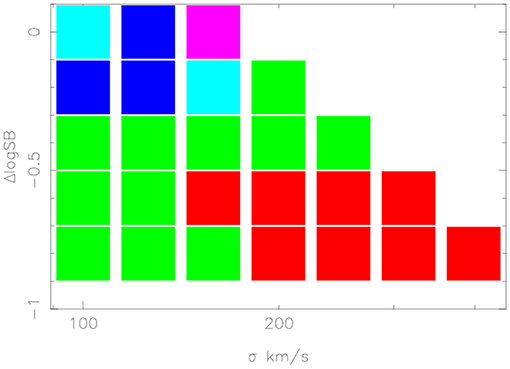
Figure 8. SB excess over the FP as a function of age and σ. Color increments from red through blue are each 0.11 dex in age. Vertical pillars, blue toward the top, are a stellar population fading at constant velocity dispersion.

It is also important to note that the age of a stellar population measured here really refers to the date of the most recent burst of star formation. Graves and Faber present a “staged star formation” model in which there are systematic variations in the duration of star formation at fixed σ. At fixed σ, galaxies with longer duration star formation have higher SB, and higher total stellar mass at fixed effective radius. They also are more enhanced in both Fe and α-elements, with lower [α/Fe] than their counterparts that experienced a shorter run of star formation. This could be due to higher “conversion efficiencies” of turning gas into stars. Galaxies with low metallicity may have truncated their SFH due to feedback.

A new aspect is the realization that the stellar initial mass function (IMF) probably depends on velocity dispersion (e.g., Spiniello et al., 2014). Tortora et al. (2013) see “a clear trend of steepening IMF with σ” and this is also seen (apart from one anomalous galaxy) in Figure 8 of Smith and Lucey (2013). This trend changes the stellar population contribution to the FP tilt (e.g., Grillo and Gobat, 2010). Smith (2014) worries that one (or both) of the dynamical and spectroscopic constraints on the IMF has not accounted fully for the main confounding factors, element abundance ratios and dark matter contributions. Clearly more work needs to be done on this aspect of the FP, with due recognition of degeneracy between dark matter fraction and IMF.

Dutton and Treu (2014) and Lagattuta et al. (2017) find that a “bottom heavy” Salpeter-like IMF is preferred for massive galaxies over the light Chabrier-like IMFs usually preferred for Milky Way-type galaxies⁸. The line indices measured by Campbell et al. (2014) in 6dFGS are not IMF sensitive, and we cannot comment from this perspective on its influence on the FP (cf. Mould, 2014).

The FP can also be studied as a function of redshift and the evolution of early type galaxy radius is seen in Naab et al. (2009) (models) and Papovich et al. (2012) (deep survey data), for example. In due course this approach will be immensely helpful in understanding the FP, but a large sample of z ~ 1 velocity dispersions is not yet available (cf. Cerulo et al., 2014).

5. The Tully Fisher Relation

Studies of the relation between rotation velocity or 21 cm profile width and disk galaxy luminosity have been carried out both in clusters of galaxies and in the field (Tully and Fisher, 1977; Masters et al., 2008). In clusters loaded with x-ray emitting hot gas the disks can be depleted of gas, spoiling the rotation velocity measurement (Teerikorpi et al., 1992). In the field there is a requirement for accurate distances, as found locally in galaxies with Cepheids (Sakai et al., 2000; Mould and Sakai, 2008).

Aaronson et al. (1979) pointed out that some of the complexity in a halo mass, spiral galaxy luminosity relation can be avoided in the infrared. Aaronson and Mould (1983) did not find a morphological type dependence of the infrared Tully Fisher relation, but when bulge velocity dispersion is substituted for type, a second parameter in the scaling relation does become apparent (Cortese et al., 2014; Tonini et al., 2014).

Ultra diffuse galaxies (van Dokkum et al., 2015) have now arrived at an opportune time. There are clearly different processes involved in forming them from those that make normal galaxies and shape the well-populated plane. Discover those processes and we shall be adding physically to the understanding of galaxy formation, rather than just achieving a good mapping to plausible semi-analytic models of what is happening “sub-grid.”

The dynamical understanding of UDGs is at a very early stage, however. There are perhaps a dozen, but more properly half a dozen UDGs, fully investigated kinematically (e.g., Forbes et al., 2019; van Dokkum et al., 2019). It is apparent that in the projection of the FP (Faber-Jackson or Tully-Fisher⁹) UDGs are overluminous (Pina et al., 2019) for their dynamical parameter (σ or rotation) and that this can arise simply from their deviation in surface brightness, the virial theorem referenced to the surface brightness law of normal galaxies, Equation (5) of Aaronson et al. (1979) is

$\begin{array}{l}{V}_{max}^4\propto {\mu }_{0}M\end{array}$

where the LHS (velocity) is the maximum rotation velocity of the disk, μ₀ is its central surface brightness and M is the mass of the galaxy. Clearly, for a given rotation velocity, low surface brightness is compensated by high mass and elevated luminosity for constant M/L.

However, choosing between different theories of how UDGs came to be where they are in the FP will require both accurate placement of a significant sample in the FP, and development of theories, such as Silk (2019) mini-bullet cluster notion (for removal of dark matter), formation in clusters (Sales et al., 2019), formation in groups (Jiang et al., 2019) and tidal heating (Burkert, 2017; Carleton et al., 2019) to locate them in the FP.

5.1. Eagle Simulations of the TF Relation

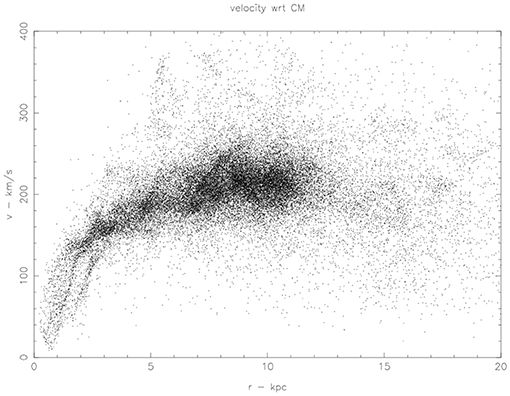
A development that is full of promise for understanding scaling relations is the advent of galaxy evolution simulations with baryons (Lagos et al., 2016; Brooks et al., 2017). Figure 9 shows the gas distribution in a galaxy with stellar mass ${10}^{10}{M}_{\odot }$.

FIGURE 9

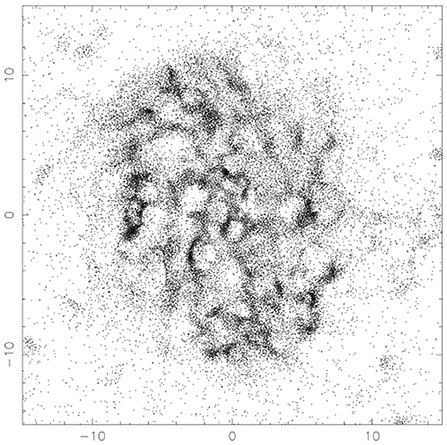
Figure 9. Neutral hydrogen particles in a disk galaxy in the Eagle simulations. Observed HI images can be compared, such as the LMC (Kim and Park, 2007), which shows such structure, and M31 (Braun, 1990).

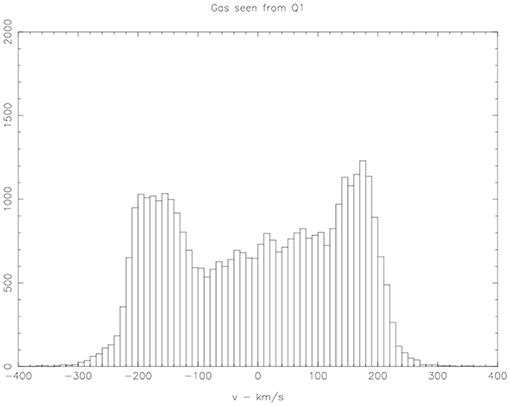
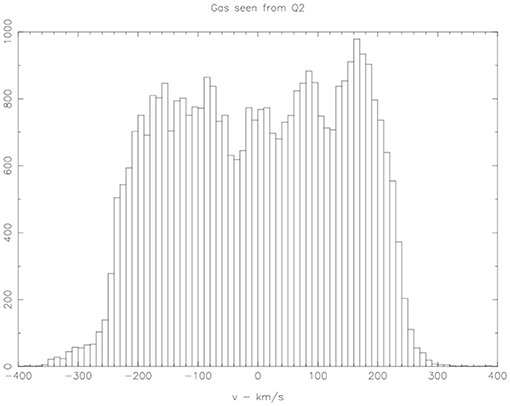
To plot the rotation curve of the gas particles in Figure 10, it is necessary to find the rotation axis, and this was done by rotating the disk to edge on. This can be done by operating on the Eagle datacube phase space using rotation matrices or quaternions. The location of the observer in an Eagle datacube is arbitrary. Therefore, we can obtain a 21 cm profile of the gas particles from infinity in any radial direction of the disk. Two views are shown in Figures 11, 12.

FIGURE 10

Figure 10. The rotation curve of the gas particles in the previous figure.

FIGURE 11

Figure 11. Neutral hydrogen profile viewed from one of the disk axes.

FIGURE 12

Figure 12. Neutral hydrogen profile viewed from the orthogonal axis.

A Tully-Fisher relation can be predicted from these simulations at a variety of rotation velocities. Residuals from the Tully Fisher relation can be studied for second parameters, such as the velocity dispersion of the bulge stars.

Lu et al. (2020) have studied the evolution of the FP in the Illustris simulations (Springel et al., 2018). They find that the proportionality constant in Equation (5) evolves, but not the power law coefficients (a, b).

6. Promising Pathways

The most rapidly advancing insights into scaling relations are coming from simulations. As the resolution of simulations improve, and as their subgrid physics assumptions become more realistic and more fundamental, some of the clues that appear from the observations will receive support, and other will be seen to be less relevant.

A partial list of physical influences on the FP is

• dissipation resulting from the merger process fundamental to the formation of early type galaxies

• feedback resulting from merger induced star formation and other processes

• mass to light ratio systematics including the IMF, metallicity and age of stellar populations and the dark matter fraction.

We have shown that the primary tilt of the FP is large and dependent on the mass of the galaxy. Its origin is a hybrid of M/L dependence on mass and structural variation with mass. Our principal new insight is Figure 8 where we have also shown that galaxies with more recent star formation stand out from the FP in SB. This can be understood in terms of efficient star formation and the additional light emitted by billion years old main sequence stars. Separation of the effects of SFH and IMF here requires further work.

If hydrodynamic simulations of the formation of ellipticals were available right down to the star formation scale, then theory could make a statement not only about dissipation and feedback but also about the 0.5M_⊙/0.1M_⊙ stellar mass ratio expectations for massive and intermediate mass ellipticals. However, at present that may be a bridge too far, and IMF issues should be pursued observationally in the near term.

Dissipation, feedback and chemical enrichment are active development areas of the current generation of galaxy formation simulations. Comparison of their predictions with large integral field surveys of early type galaxies, such as ATLAS^3D (Cappellari et al., 2013a,b) and SAMI, which measure the density profile and dispersion profile terms in the Jeans equation, promise further progress in understanding the FP, especially as regards the relationship we see in 6dFGS between structure and FP tilt.

With the advent of new surveys DESI, Taipan (da Cunha et al., 2017), Wallaby (Koribalski et al., 2020), and Dragonfly (Abraham, 2020) we can expect a deeper and more general understanding of the dynamical equilibrium of galaxies to emerge, and also of galaxy scaling relations that stem from them. Combining this with galaxy simulations of the Eagle type, an exciting new era of understanding galaxy scaling relations is beginning.

Data Availability Statement

Data from 6dFGS are archived at the Widefield Astronomy Unit of the Royal Observatory Edinburgh and Data Central at Macquarie University. This study has also used 2MASS data provided by NASA-JPL.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

I am grateful for ARC grants DP1092666 and LP130100286 in partial support of this work. Work on dark matter at Swinburne University is supported by the ARC Centre of Excellence for Dark Matter Particle Physics.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank MIAPP, the Munich Institute for Astro and Particle Physics for inviting me to their workshop Galaxy Evolution in a New Era of HI Surveys. MIAPP was funded by the DFG under Germany's Excellence Strategy—EXC-2094-390783311. I am grateful to Edoardo Tescari for assistance with Eagle datacubes, and referees for recommending improvements.

Footnotes

1. ^An anonymous referee has pointed out that the Virial Theorem does not hold at any arbitrary radius in a system in dynamical equilibrium. It holds for a particular radius. This is shown in work on mass estimators, for example by Walker et al. (2009) and Wolf (2010).

2. ^Or in a tilted virial plane.

3. ^Cappellari et al. (2013a), find ϵ = 0.72.

4. ^A particular choice of f(σ) and g, for example, yields the Faber and Jackson (1976) power law relation.

5. ^http://www.icg.port.ac.uk/maraston/Claudia%27s_Stellar_Population_Model.html

6. ^With a 1σ reduction in M_*0.

7. ^α refers to α elements, such as Mg, Ca, and Ti. The bracket notation is the conventional element number density relative to that of the Sun.

8. ^Chabrier (2003).

9. ^Faber and Jackson (1976) and Tully and Fisher (1977).

References

Aaronson, M., Huchra, J., and Mould, J. (1979). The infrared luminosity/H I velocity-width relation and its application to the distance scale. Astrophys. J. 229, 1–13. doi: 10.1086/156923

CrossRef Full Text | Google Scholar

Aaronson, M., and Mould, J. (1983). A distance scale from the infrared magnitude/H I velocity-width relation. IV. The morphological type dependence and scatter in the relation; the distances to nearby groups. Astrophys. J. 265, 1–17. doi: 10.1086/160648

CrossRef Full Text | Google Scholar

Abraham, R. (2020). “The dragonfly telephoto array: how it works and where it is going.” in American Astronomical Society meeting #235, Vol. 52 (Bulletin of the American Astronomical Society), 2354401.

Google Scholar

Allanson, S., Hudson, M., Smith, R. J., and Lucey, J. R. (2009). The star formation histories of red-sequence galaxies, mass-to-light ratios and the fundamental plane. Astrophys. J. 702, 1275–1296. doi: 10.1088/0004-637X/702/2/1275

CrossRef Full Text | Google Scholar

Behroozi, P. S., Conroy, C., and Wechsler, R. (2010). A comprehensive analysis of uncertainties affecting the stellar mass-halo mass relation for 0 < z <4. Astrophys. J. 717, 379–403. doi: 10.1088/0004-637X/717/1/379

CrossRef Full Text | Google Scholar

Binney, J. (1987). Observable consequences of triaxial halos. Proc. IAU Symp. 117:303. doi: 10.1017/S0074180900150405

CrossRef Full Text | Google Scholar

Braun, R. (1990). The interstellar medium of M31. I. A survey of neutral hydrogen emission. Astrophys. J. Suppl. 72:755. doi: 10.1086/191431

CrossRef Full Text | Google Scholar

Brooks, A., Papastergis, E., Christensen, C. R., Governato, F., Stilp, A., Quinn, T. R., et al. (2017). How to reconcile the observed velocity function of galaxies with theory. Astrophys. J. 850:97. doi: 10.3847/1538-4357/aa9576

CrossRef Full Text | Google Scholar

Burkert, A. (2017). The geometry and origin of ultra-diffuse ghost galaxies. Astrophys. J. 838:93. doi: 10.3847/1538-4357/aa671c

CrossRef Full Text | Google Scholar

Campbell, L., Lucey, J., Colless, M., Jones, D. H., Springob, C., Magoulas, C., et al. (2014). The 6dF galaxy survey: fundamental plane data. Mon. Not. R. Astron. Soc. 443:1231. doi: 10.1093/mnras/stu1198

CrossRef Full Text | Google Scholar

Cappellari, M., McDermid, R. M., Alatalo, K., Blitz, L., Bois, M., Bournaud, F., et al. (2013b). The ATLAS 3D project–XX. Mass-size and mass- distributions of early-type galaxies: bulge fraction drives kinematics, mass-to-light ratio, molecular gas fraction and stellar initial mass function. Mon. Not. R. Astron. Soc. 432, 1862–1893. doi: 10.1093/mnras/stt644

CrossRef Full Text | Google Scholar

Cappellari, M., Scott, N., Alatalo, K., Blitz, L., Bois, M., Bournaud, F., et al. (2013a). The ATLAS 3D project–XV. Benchmark for early-type galaxies scaling relations from 260 dynamical models: mass-to-light ratio, dark matter, fundamental plane and mass plane. Mon. Not. R. Astron. Soc. 432, 1709–1741. doi: 10.1093/mnras/stt562

CrossRef Full Text | Google Scholar

Carleton, T., Errani, R., Cooper, M., Kaplinghat, M., Penarrubia, J., Guo, Y., et al. (2019). The formation of ultra-diffuse galaxies in cored dark matter haloes through tidal stripping and heating. Mon. Not. R. Astron. Soc. 485, 382–395. doi: 10.1093/mnras/stz383

CrossRef Full Text | Google Scholar

Cerulo, P., Couch, W. J., Lidman, C., Delaye, L., Demarco, R., Huertas-Company, M., et al. (2014). The morphological transformation of red sequence galaxies in the distant cluster XMMU J1229+0151. Mon. Not. R. Astron. Soc. 439, 2790–2812. doi: 10.1093/mnras/stu135

CrossRef Full Text | Google Scholar

Chabrier, G. (2003). Galactic stellar and substellar initial mass function. Publ. Astron. Soc. Pac. 115, 763–795. doi: 10.1086/376392

CrossRef Full Text | Google Scholar

Ciotti, L., Lanzoni, B., and Renzini, A. (1996). The tilt of the fundamental plane of elliptical galaxies–I. Exploring dynamical and structural effects. Mon. Not. R. Astron. Soc. 282, 1–12. doi: 10.1093/mnras/282.1.1

CrossRef Full Text | Google Scholar

Conroy, C., Dutton, A. A., Graves, G. J., Mendel, J. T., and van Dokkum, P. G. (2013). Dynamical versus stellar masses in compact early-type galaxies: further evidence for systematic variation in the stellar initial mass function. Astrophys. J. Lett., 776, L26. doi: 10.1088/2041-8205/776/2/L26

CrossRef Full Text | Google Scholar

Conroy, C., and van Dokkum, P. G. (2012). The stellar initial mass function in early-type galaxies from absorption line spectroscopy. ii. results. Astrophys. J. 760, 71. doi: 10.1088/0004-637X/760/1/71

CrossRef Full Text | Google Scholar

Cortese, L., Fogarty, L. M. R., Ho, I.-T., Bekki, K., Bland-Hawthorn, J., Colless, M., et al. (2014). The SAMI galaxy survey: toward a unified dynamical scaling relation for galaxies of all types. Astrophys. J. Lett. 795:L37. doi: 10.1088/2041-8205/795/2/L37

CrossRef Full Text | Google Scholar

Croom, S. M., Dawe, J., Bland-Hawthorn, J., Bryant, J. J., Fogarty, L., Richards, S., et al. (2012). The Sydney-AAO multi-object integral field spectrograph. Mon. Not. R. Astron. Soc. 421, 872–893. doi: 10.1111/j.1365-2966.2011.20365.x

CrossRef Full Text | Google Scholar

da Cunha, E., Hopkins, A., Colless, M., Taylor, E. N., Blake, C., Howlett, C., et al. (2017). The Taipan galaxy survey: scientific goals and observing strategy. Publ. Astron. Soc. Aust. 34:47. doi: 10.1017/pasa.2017.41

CrossRef Full Text | Google Scholar

D'Onofrio, M., Fasano, G., Moretti, A., Marziani, P., Bindoni, D., Fritz, J., et al. (2013). The hybrid solution for the fundamental plane. Mon. Not. R. Astron. Soc. 435, 45–63. doi: 10.1093/mnras/stt1278

CrossRef Full Text | Google Scholar

Dutton, A., and Treu, T. (2014). The bulge-halo conspiracy in massive elliptical galaxies: implications for the stellar initial mass function and halo response to baryonic processes. Mon. Not. R. Astron. Soc. 438, 3594–3602. doi: 10.1093/mnras/stt2489

CrossRef Full Text | Google Scholar

Faber, S., and Jackson, R. (1976). Velocity dispersions and mass-to-light ratios for elliptical galaxies. Astrophys. J. 204, 668–683. doi: 10.1086/154215

CrossRef Full Text | Google Scholar

Ferrarese, L., and Merritt, D. (2000). A fundamental relation between supermassive black holes and their host galaxies. Astrophys. J. 539, L9–L12. doi: 10.1086/312838

CrossRef Full Text | Google Scholar

Fitzpatrick, P., and Graves, G. (2014). Early-type galaxy star formation histories in different environments. Mon. Not. R. Astron. Soc. 447, 1383–1397. doi: 10.1093/mnras/stu2509

CrossRef Full Text | Google Scholar

Forbes, D., Alabi, A., Romanowsky, A. J., Brodie, J., and Arimoto, N. (2019). An ultra diffuse galaxy in the NGC 5846 group from the VEGAS survey. Astron. Astrophys. 626:66.

Google Scholar

Forbes, D., Martin, C., Matuszewski, M., Romanowsky, A. J., and Villaume, A. (2020). The formation of ultradiffuse galaxies in clusters. Mon. Not. R. Astron. Soc. 492, 4874–4883. doi: 10.1093/mnras/staa180

CrossRef Full Text | Google Scholar

Graham, A. (2012). Extending the MBH, diagram with dense nuclear clusters. Mon. Not. R. Astron. Soc. 422, 1586. doi: 10.1111/j.1365-2966.2012.20734.x

CrossRef Full Text | Google Scholar

Graves, G., and Faber, S. (2010). Dissecting the red sequence. III. Mass-to-light variations in three dimensional fundamental plane space. Astrophys. J. 717, 803–824. doi: 10.1088/0004-637X/717/2/803

CrossRef Full Text | Google Scholar

Grillo, C., and Gobat, R. (2010). On the initial mass function and tilt of the fundamental plane of massive early-type galaxies. Mon. Not. R. Astron. Soc. 402, L67–L71. doi: 10.1111/j.1745-3933.2009.00803.x

CrossRef Full Text | Google Scholar

Jiang, F., Dekel, A., Freundlich, J., and Romanowsky, A. (2019). Formation of ultra-diffuse galaxies in the field and in galaxy groups. Mon. Not. R. Astron. Soc. 487, 5272–5290. doi: 10.1093/mnras/stz1499

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, D. H., Read, M., Saunders, W., Colless, M., Jarrett, T., Parker, Q., et al. (2009). The 6dF galaxy survey: final redshift release (DR3) and southern large-scale structures. Mon. Not. R. Astron. Soc. 399, 683–698. doi: 10.1111/j.1365-2966.2009.15338.x

CrossRef Full Text | Google Scholar

Kim, S., and Park, C. (2007). Topology of H I gas distribution in the large magellanic cloud. Astrophys. J. 663:244. doi: 10.1086/518470

CrossRef Full Text | Google Scholar

Koribalski, B., Staveley-Smith, L., Westmeier, T., Serra, P., Spekkens, K., Wong, O. I., et al. (2020). WALLABY–an SKA pathfinder HI survey. arXiv[Preprint].arXiv:2002.07311.

Google Scholar

Kormendy, J., and Ho, L. (2013). Coevolution (or not) of supermassive black holes and host galaxies. Annu. Rev. Astron. Astrophys. 51, 511–653. doi: 10.1146/annurev-astro-082708-101811

CrossRef Full Text | Google Scholar

Kormendy, J., and Kennicutt, R. (2004). Secular evolution and the formation of pseudobulges in disk galaxies. Annu. Rev. Astron. Astrophys. 42, 603–683. doi: 10.1146/annurev.astro.42.053102.134024

CrossRef Full Text | Google Scholar

Lagattuta, D., Mould, J., Forbes, D., Monson, P.astorello, and Persson, S. E. (2017). Evidence of a bottom-heavy initial mass function in massive early-type galaxies from near-infrared metal lines. Astrophys. J. 846:166. doi: 10.3847/1538-4357/aa8563

CrossRef Full Text | Google Scholar

Lagos, C., Obreschkow, D., Ryan-Weber, E., Zwaan, M., Kilborn, V., Bekiaris, G., et al. (2016). The fundamental plane of star formation in galaxies revealed by the EAGLE hydrodynamical simulations. Mon. Not. R. Astron. Soc. 459, 2632–2650. doi: 10.1093/mnras/stw717

CrossRef Full Text | Google Scholar

Lu, S., Xu, D., Wang, Y., Mao, S., and Ge, J. (2020). SDSS-IV MaNGA: Stellar population correlates with stellar root-mean-square velocity gradients or total-density-profile slopes at fixed effective velocity dispersion σe. Mon. Not. R. Astron. Soc. 492, 5930–5939.

PubMed Abstract | Google Scholar

Magorrian, J., Tremaine, S., Richstone, D., Bender, R., Bower, G., Dressler, A., et al. (1998). The demography of massive dark objects in galaxy centers. Astron. J. 115, 2285–2305. doi: 10.1086/300353

CrossRef Full Text | Google Scholar

Magoulas, L. J., Lagos, C., Kuehn, K. G., Barat, D., and Bian, F. (2012). The 6dF galaxy survey: the near infrared fundamental plane of early type galaxies. Mon. Not. R. Astron. Soc. 427:245. doi: 10.1111/j.1365-2966.2012.21421.x

CrossRef Full Text | Google Scholar

Maraston, C. (2005). Evolutionary population synthesis: models, analysis of the ingredients and application to high-z galaxies. Mon. Not. R. Astron. Soc. 362, 799–825. doi: 10.1111/j.1365-2966.2005.09270.x

CrossRef Full Text | Google Scholar

Masci, F., Cutri, R., Francis, P., Nelson, B., and Huchra, J. (2010). The southern 2MASS active galactic nuclei survey: spectroscopic follow-up with six degree field. Publ. Astron. Soc. Aust. 27, 302–320. doi: 10.1071/AS10001

CrossRef Full Text | Google Scholar

Masters, K., Springob, C., and Huchra, J. (2008) 2MTF. I. The Tully-Fisher relation in the two micron all sky survey J, H, K Bands. Astron. J. 135, 1738–1748. doi: 10.1088/0004-6256/135/5/1738

CrossRef Full Text | Google Scholar

Moster, B., Somerville, R., Maulbetsch, C., van den Bosch, F., Maccio, A., Thorsten, N., et al. (2010). Constraints on the relationship between stellar mass and halo mass at low and high redshift. Astrophys. J. 710:903. doi: 10.1088/0004-637X/710/2/903

CrossRef Full Text | Google Scholar

Mould, J. (2014). What are we missing in elliptical galaxies? arXiv[Preprint].arXiv:1403.1623.

Google Scholar

Mould, J. (2017). Modified gravity and large scale flows, a review. Astrophys. Space Sci. 362:25. doi: 10.1007/s10509-017-3005-3

CrossRef Full Text | Google Scholar

Mould, J., and Sakai, S. (2008). The extragalactic distance scale without cepheids. Astrophys. J. Lett. 686:L75. doi: 10.1086/592964

CrossRef Full Text | Google Scholar

Naab, T., Oosterloo, T., Sarzi, M., Serra, P., Weijmans, A., and Young, L. (2009). Minor mergers and the size evolution of elliptical galaxies. Astrophys. J. 699, L178–L182. doi: 10.1088/0004-637X/699/2/L178

CrossRef Full Text | Google Scholar

Nelan, J., Smith, R., Hudson, M., and Wegner, G. (2005). NOAO fundamental plane survey. II. Age and metallicity along the red sequence from line-strength data. Astrophys. J. 632, 137–156. doi: 10.1086/431962

CrossRef Full Text | Google Scholar

Papovich, C., Bassett, R., Lotz, J., van der Wel, A., Tran, K. V., Finkelstein, S., et al. (2012). CANDELS observations of the structural properties of cluster galaxies at z = 1.62. Astrophys. J. 750:93. doi: 10.1088/0004-637X/750/2/93

CrossRef Full Text | Google Scholar

Pina, M., Fraternali, F., Adams, E., Marasco, A., Oosterloo, T., Oman, K., et al. (2019). Off the Baryonic Tully-Fisher relation: a population of Baryon-dominated ultra-diffuse galaxies. Astrophys. J. 883:L33. doi: 10.3847/2041-8213/ab40c7

CrossRef Full Text | Google Scholar

Proctor, R., Colless, M., Jones, D. H., Kobayashi, C., Campbell, L., Lucey, J., et al. (2008). The effects of stellar populations on galaxy scaling relations in the 6dF galaxy survey. Mon. Not. R. Astron. Soc. 386, 1781–1796. doi: 10.1111/j.1365-2966.2008.13208.x

CrossRef Full Text | Google Scholar

Sakai, S., Mould, J., Hughes, S., Huchra, J., Macri, L., Kennicutt, R., et al. (2000). The Hubble space telescope key project on the extragalactic distance scale. XXIV. The calibration of Tully-Fisher relations and the value of the Hubble constant. Astrophys. J. 529, 698–722. doi: 10.1086/308305

CrossRef Full Text | Google Scholar

Sales, L., Navarro, J., Penaafiel, L., Peng, E., Lim, S., and Hernquist, L. (2019). The formation of ultradiffuse galaxies in clusters. Mon. Not. R. Astron. Soc. 494, 1848–1858. doi: 10.1093/mnras/staa854

CrossRef Full Text | Google Scholar

Silk, J. (2019). Ultra-diffuse galaxies without dark matter. Mon. Not. R. Astron. Soc. 488, L24–L28. doi: 10.1093/mnrasl/slz090

CrossRef Full Text | Google Scholar

Skrutskie, M., Cutri, R., Stiening, R., Weinberg, M., Schneider, S., Carpenter, J., et al. (2006). The two micron all sky survey (2MASS). Astron. J. 131, 1163–1183. doi: 10.1086/498708

CrossRef Full Text | Google Scholar

Smith, R. (2014). Variations in the initial mass function in early-type galaxies: a critical comparison between dynamical and spectroscopic results. Mon. Not. R. Astron. Soc. 443, L69–L73. doi: 10.1093/mnrasl/slu082

CrossRef Full Text | Google Scholar

Smith, R., and Lucey, J. (2013). A giant elliptical galaxy with a lightweight initial mass function. Mon. Not. R. Astron. Soc. 434, 1964–1977. doi: 10.1093/mnras/stt1141

CrossRef Full Text | Google Scholar

Spiniello, C., Trager, S., Koopmans, L., and Conroy, C. (2014). The stellar IMF in early-type galaxies from a non-degenerate set of optical line indices. Mon. Not. R. Astron. Soc. 438, 1483–1499. doi: 10.1093/mnras/stt2282

CrossRef Full Text | Google Scholar

Springel, V., Wang, Y., Vogelsberger, M., Naiman, J., and Hernquist, S. L. (2018). Redshift evolution of the fundamental plane relation in the IllustrisTNG simulation. Mon. Not. R. Astron. Soc. 475, 676–698. doi: 10.1093/mnras/stx3304

CrossRef Full Text | Google Scholar

Springob, C., Magoulas, C., Mould, J., Proctor, R., Colless, M., Heath Jones, D., et al. (2012). The 6dF galaxy survey: stellar 351 population trends across and through the fundamental plane. Mon. Not. R. Astron. Soc. 420, 2773–2784. doi: 10.1111/j.1365-2966.2011.19900.x

CrossRef Full Text | Google Scholar

Teerikorpi, P., Bottinelli, L., Gouguenheim, L., and Paturel, G. (1992). Investigations ofthe local supercluster velocity field. I. Observations close to Virgo, using Tully-Fisher distances and the Tolman-Bondi expanding sphere. Astron. Astrophys. 260, 17–32.

Google Scholar

Tonini, C., Jones, D. H., Mould, J., Webster, R., Danilovich, T., and Ozbilgen, S. (2014). The fundamental manifold of spiral galaxies: ordered versus random motions and the morphology dependence of the Tully-Fisher relation. Mon. Not. R. Astron. Soc. 438, 3332–3339. doi: 10.1093/mnras/stt2442

CrossRef Full Text | Google Scholar

Tortora, C., La Barbera, F., Napolitano, N. R., de Carvalho, R. R., and Romanowsky, A. J. (2013). SPIDER–VI. The central dark matter content of luminous early-type galaxies: benchmark correlations with mass, structural parameters and environment. Mon. Not. R. Astron. Soc. 425, 577–594. doi: 10.1111/j.1365-2966.2012.21506.x

CrossRef Full Text | Google Scholar

Tully, R. B., and Fisher, R. (1977). A new method of determining distance to galaxies. Astron. Astrophys. 54:661.

Google Scholar

van Dokkum, P., Romanowsky, A., Abraham, R., Brodie, J., Conroy, C., Geha, M., et al. (2015). Spectroscopic confirmation of the existence of large, diffuse galaxies in the Coma cluster. Astrophys. J. 804:26. doi: 10.1088/2041-8205/804/1/L26

CrossRef Full Text | Google Scholar

van Dokkum, P., Wasserman, A., Danieli, S., Abraham, R., and Brodie, J. (2019). Spatially resolved stellar kinematics of the ultra-diffuse galaxy dragonfly 44. I. Observations, kinematics, and cold dark matter halo fits. Astrophys. J. 880:91. doi: 10.3847/1538-4357/ab2914

CrossRef Full Text | Google Scholar

Walker, M., Mateo, M., Olszewski, E., Penarrubia, J., Evans, N., Gilmore, G., et al. (2009). A universal mass profile for dwarf spheroidal galaxies? Astrophys. J. 704, 1274–1287. doi: 10.1088/0004-637X/704/2/1274

CrossRef Full Text | Google Scholar

Wolf, J. (2010). Modeling mass independent of anisotropy: a comparison between Andromeda and Milky Way satellites. Highlights Astron. 15:79. doi: 10.1017/S174392131000832X

CrossRef Full Text | Google Scholar