- 1Physics and Astronomy Department Galileo Galilei, University of Padova, Padova, Italy
- 2INFN–Padova, Padova, Italy
- 3INAF–Osservatorio Astronomico di Padova, Padova, Italy
We review the main physical processes that lead to the formation of stellar binary black holes (BBHs) and to their merger. BBHs can form from the isolated evolution of massive binary stars. The physics of core-collapse supernovae and the process of common envelope are two of the main sources of uncertainty about this formation channel. Alternatively, two black holes can form a binary by dynamical encounters in a dense star cluster. The dynamical formation channel leaves several imprints on the mass, spin and orbital properties of BBHs.
1. Black Hole Formation From Single Stars: Where We Stand Now
About 4 years ago, the LIGO detectors obtained the first direct detection of gravitational waves, GW150914 (Abbott et al., 2016; Abbott et al., 2016a,b), associated with the merger of two black holes (BHs). This event marks the dawn of gravitational wave astronomy: we now know that binary black holes (BBHs) exist, can reach coalescence by gravitational wave emission, and are composed of BHs with mass ranging from few solar masses to ~ 50 M⊙. Here, we review the main physical processes that lead to the formation of BBHs and to their merger. We restrict our attention to stellar-born BHs. As to primordial BHs, which might form from gravitational instabilities in the early Universe, we refer the reader to Carr et al. (2016) and Belotsky et al. (2019), and references therein. Before we start discussing binaries, we must briefly summarize the state-of-the-art knowledge about stellar-origin BHs: this is a necessary step to understand their pairing mechanisms.
Stellar-mass BHs are thought to be the final outcome of the evolution of a massive star (zero-age main sequence mass mZAMS ≳ 20 M⊙). Hence the mass of the BH should be affected by the two main processes that influence the evolution of a single star: (i) mass loss by stellar winds and (ii) the final collapse.
1.1. Stellar Winds
Hot (>104 K) massive stars (mZAMS ≳ 30 M⊙) lose a non-negligible fraction of their mass by line-driven winds. This process depends on metallicity (Z): the mass-loss rate by stellar winds can be described as ṁ ∝ Zβ, where Z is the absolute metallicity (see e.g., Vink et al., 2001 and references therein). The most recent models suggest that β is not constant, but depends at least on the luminosity of the star (Gräfener and Hamann, 2008; Vink et al., 2011; Chen et al., 2015): the closer the luminosity L∗ is to the Eddington value LEdd, the higher the mass loss, basically canceling the dependence on metallicity when L∗ ≳ LEdd.
In single stars, stellar winds uniquely determine the final mass of the star at the onset of collapse. If we consider a star with mZAMS = 90 M⊙ and metallicity Z = 0.02 (i.e., approximately solar), its final mass will be only mfin ~ 30 M⊙; while the same star with Z < 0.0002 has mfin ≳ 0.8 mZAMS. The final mass of a star mfin is the strongest upper limit to the mass of the BH.
1.2. Core-Collapse Supernovae
For example, Fryer (1999) and Fryer and Kalogera (2001) suggest that if the final mass of the star is mfin ≳ 40 M⊙, the fate of the star is to collapse to a BH directly, without supernova, because the binding energy of the outer stellar layers is too big to be overcome by the explosion. Fryer et al. (2012) elaborate on these early results proposing that the mass of the compact object depends not only on mfin but also on the final mass of the carbon-oxygen core. Alternatively, O'Connor and Ott (2011) proposed the role of the compactness parameter : if the compactness is small (e.g., ξ2.5 ≤ 0.2 − 0.4), the SN explosion is successful, otherwise we expect the star to collapse directly. All of these simplified models as well as more sophisticated ones (e.g., Ertl et al., 2016) point toward a similar direction: if the star ends its life with a large final mass, its carbon-oxygen core grows larger, its compactness is generally higher, and so on. Hence, we expect that metal-poor stars, which retain a larger fraction of their mass to the very end and develop larger cores, are more likely to collapse to BHs directly, producing larger BHs (e.g., Mapelli et al., 2009, 2010; Zampieri and Roberts, 2009; Belczynski et al., 2010). This simplified picture seems to agree with observations, but must be taken with several grains of salt: we need a vigorous step forward in core-collapse SN simulations and theoretical models, before we can draw robust conclusions (e.g., Burrows et al., 2018).
1.3. Pair Instability
Core-collapse SNe are not the only mechanism that can end the life of a massive star. When the helium core of a star grows to ≥ 60 M⊙ and the central temperature reaches ~ 109 K, electron and positron pairs are produced at an efficient rate, leading to a softening of the equation of state. The star undergoes pair instability (PI, Ober et al., 1983; Bond et al., 1984; Heger et al., 2003; Woosley et al., 2007): oxygen, neon, and silicon are burned explosively and the entire star is disrupted leaving no remnant, unless its helium core is ≥ 130 M⊙. In the latter case, the gravity of the outer layers is so big that the star collapses to a massive BH directly as an effect of PI (Heger et al., 2003). Smaller helium cores (~ 30−60 M⊙) are associated with a less dramatic manifestation of PI: the softened equation of state drives oscillations of the core (pulsational PI, Barkat et al., 1967; Woosley et al., 2007; Chen et al., 2014; Yoshida et al., 2016); during each oscillation the star sheds some mass till it finds a new equilibrium to a lower core mass, but leaves a BH smaller than expected without pulsational PI (Belczynski et al., 2016a; Spera and Mapelli, 2017; Woosley, 2017, 2019; Marchant et al., 2019; Stevenson et al., 2019; Renzo et al., 2020).
From the combination of PI, core-collapse SNe and stellar-wind mass loss prescriptions, we expect the mass spectrum of BHs to behave roughly as shown in Figure 1. In particular, PI is expected to carve a gap in the mass spectrum of BHs between ~ 50(−10, +20) M⊙ and ≈ 120 − 130 M⊙. The uncertainty on this mass gap is mainly connected with uncertainties nuclear reaction rates (Farmer et al., 2019), on the collapse of the residual hydrogen envelope and on the role of stellar rotation (Mapelli et al., 2020). Within this framework, we predict a reasonable mass range for stellar-origin BHs to be ~ 3 − 65 M⊙ (assuming the most conservative value for the lower edge of pair-instability mass gap). If exotic metal-poor stars exist with mass mZAMS > 250 M⊙, these might directly collapse to intermediate-mass BHs (IMBHs) with mass > 100 M⊙.
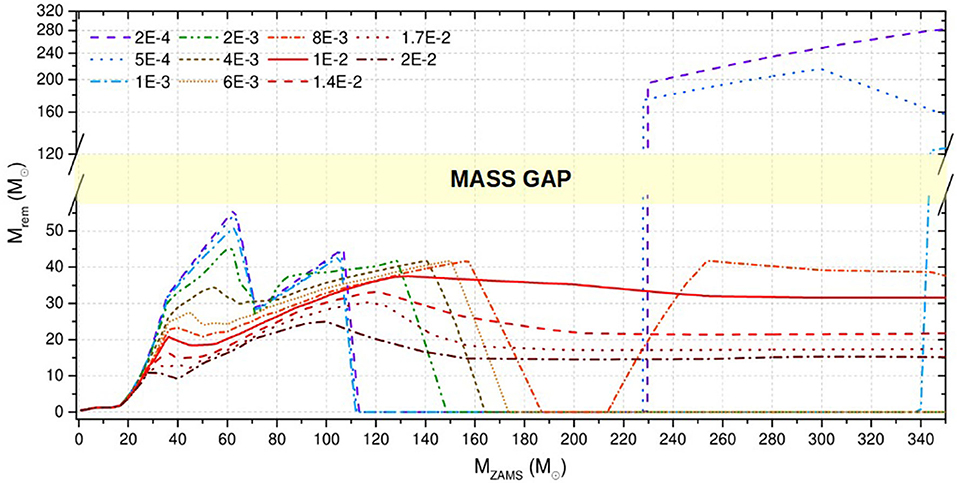
Figure 1. Predicted compact object mass (Mrem) as a function of the zero-age main-sequence (ZAMS) mass of the progenitor star (MZAMS) for 11 different metallicities, ranging from Z = 2 × 10−4 to Z = 2 × 10−2, as shown in the legend. The yellow area highlights the pair-instability mass gap. These models are obtained with the SEVN population synthesis code (Spera et al., 2019), using PARSEC evolutionary tracks (Bressan et al., 2012) and the delayed model from Fryer et al. (2012). See Spera and Mapelli (2017) for details.
2. Binary BH Formation in Isolation
The scenario highlighted in the previous section assumes that the progenitor star is single. But gravitational waves have shown the existence of BBHs with a very short orbital separation: the initial separation of a BBH must be of the order of few ten solar radii for the BBH to merge within a Hubble time by gravitational-wave emission. This challenges our understanding of binary star evolution. A close binary star undergoes several physical processes during its life, which can completely change its final fate (see e.g., Eggleton, 2006). The most important processes include mass transfer and common envelope, tides and natal kicks (Hurley et al., 2002).
Mass transfer and common envelope are crucial in this regard. After main sequence, a massive star can develop a stellar radius as large as several thousand solar radii. Hence, if this star is member of a binary system and its orbital separation is of few hundred to few thousand solar radii, the binary system undergoes Roche lobe overflow and possibly common envelope (Ivanova et al., 2013). If common envelope occurs between a BH and a giant companion star, the BH and the core of the giant star orbit about each other surrounded by the giant's envelope: they feel a strong gas drag from the envelope and lose kinetic energy, inspiralling about each other. This transfers thermal energy to the envelope, which might trigger the ejection of the envelope. If the envelope is not ejected, the binary system merges prematurely giving birth to a single BH. In contrast, if the envelope is ejected, the final binary system is composed of the BH and the core of the giant. Because of the spiral-in, the final semi-major axis of the binary is just few solar radii, much smaller than the initial one. If the naked core collapses to a BH without receiving a strong natal kick, the system becomes a BBH with a short orbital period, able to merge within a Hubble time. Unfortunately, our understanding of common envelope is still poor (see Fragos et al., 2019 for a recent simulation) and this uncertainty heavily affects our knowledge of BBH demography. The left-hand panel of Figure 2 is a schematic view of the isolated binary evolution channel through common envelope.
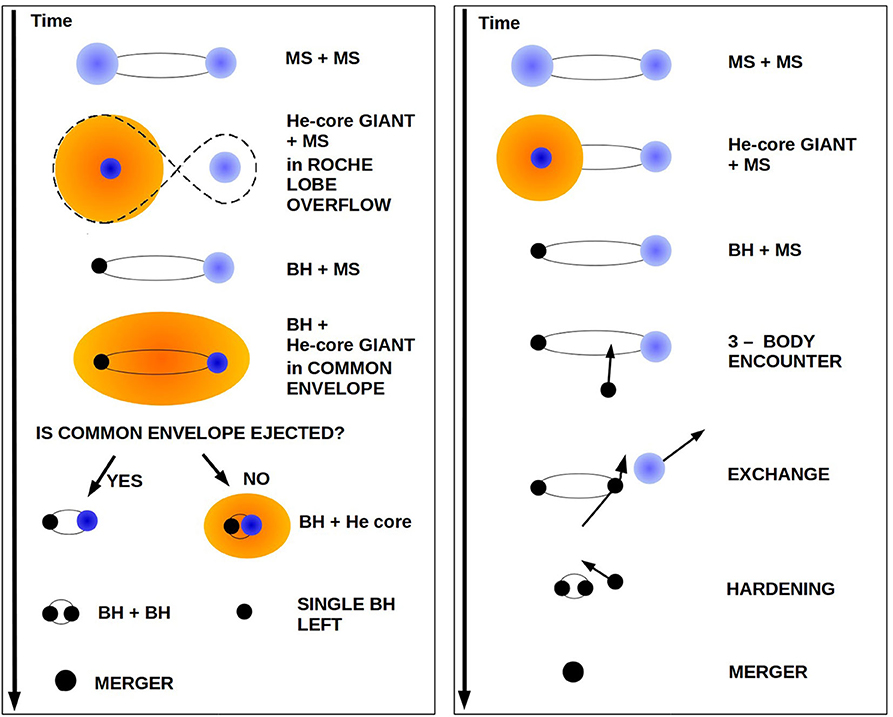
Figure 2. Left: cartoon of isolated BBH formation through common envelope; Right: cartoon of dynamical BBH formation in star clusters.
Several alternative scenarios to common envelope have been proposed (de Mink and Mandel, 2016; Mandel and de Mink, 2016; Marchant et al., 2016). For example, in the over-contact binary evolution, Marchant et al. (2016) show that, when two massive stars in a tight binary are fast rotators, they remain fully mixed as a result of their tidally induced high spin; in this case, the binary avoids premature merger even if it is overfilling its Roche lobe and might evolve into a tight BBH.
The isolated binary evolution scenario has several characteristic signatures. In the common envelope isolated binary evolution scenario, the masses of the two BHs span from ~ 3 M⊙ up to ~ 45 M⊙ (see e.g., Giacobbo and Mapelli, 2018) and the mass ratios are preferentially close to 1 (although all mass ratios q = m2/m1 ≳ 0.1 are possible, see e.g., Giacobbo and Mapelli, 2018). Most processes in binary evolution tend to produce aligned spins (e.g., Rodriguez et al., 2016), while the magnitude of the spin is basically unconstrained (but see Qin et al., 2018, 2019; Fuller and Ma, 2019 for some recent attempts to quantify spins). Mass transfer episodes and gravitational-wave decay are expected to efficiently damp eccentricity, so that almost all isolated binaries have near zero eccentricity in the LIGO-Virgo band. Finally, local merger rate densities span from a few to few thousand events Gpc−3 yr−1, depending on the details of common envelope and natal kicks (e.g., Dominik et al., 2013; Belczynski et al., 2016b; Mapelli et al., 2017; Giacobbo and Mapelli, 2018, 2020; Mapelli and Giacobbo, 2018; Neijssel et al., 2019; Santoliquido et al., 2020; Tang et al., 2020). The scenarios which include alternatives to common envelope predict an even stronger prevalence of systems with q ~ 1, a preferred mass range ~ 25 − 60 M⊙ (Marchant et al., 2016), high and aligned spins, zero eccentricity in the LIGO-Virgo band, and long delay times (≳ 3 Gyr, de Mink and Mandel, 2016). Local merger rate densities are expected to be ~ 10 Gpc−3 yr−1 (Mandel and de Mink, 2016), with large uncertainties.
3. Binary BH Formation in Star Clusters
Star clusters are among the densest places in the Universe. There is a plethora of star clusters, with their distinguishing features: (i) globular clusters (Gratton et al., 2019) are old (~ 12 Gyr) and massive systems (~ 104−6 M⊙), (ii) nuclear star clusters can be even more massive (~ 107 M⊙) and lie at the center of many galaxies, in some cases coexisting with the supersessive BH (Neumayer et al., 2020), (iii) open clusters and young star clusters (Portegies Zwart et al., 2010) are generally less massive (up to ~ 105 M⊙) and short lived (less than a few Gyr), but are the main birthplace of massive stars in the local Universe (Lada and Lada, 2003).
The central density of star clusters is sufficiently high (≳ 103 stars pc−3) and their typical velocity dispersion sufficiently low (from a few to a few tens of km s−1, possibly with the exception of nuclear star clusters) that their central two-body relaxation time (Spitzer, 1987) is shorter than their lifetime. This has one fascinating implication: the orbits of stars and binary stars in a star cluster are constantly perturbed by dynamical encounters with other cluster members. This process affects the formation and the evolution of binary BHs in multiple ways (e.g., Portegies Zwart and McMillan, 2000).
Dynamical Exchanges
Dynamical exchanges occur when a binary system interacts with a single stellar object and the latter replaces one of the members of the binary. We have known for a long time that massive objects are more likely to acquire companions by dynamical exchanges (Hills and Fullerton, 1980). Since BHs are among the most massive objects in a star cluster, they are very efficient in forming new binaries through exchanges (e.g., Ziosi et al., 2014).
During a three-body encounter, a binary star exchanges a fraction of its internal energy with the third body. If the binary is particularly tight (hard binary), such encounters tend to harden the binary star, i.e., to increase its binding energy by reducing its semi-major axis (dynamical hardening). In the case of a BBH, this hardening might speed up the merger, because it drives the semi-major axis of the BBH in the regime where orbital decay by gravitational waves becomes efficient (see e.g., Figure 10 of Mapelli, 2018). On the other hand, the least massive BBHs can even be ionized, i.e., split by strong dynamical encounters with massive intruders.
Mergers of Massive Stars
Mergers of massive stars are common in dense young star clusters, because of the short dynamical friction timescale (Portegies Zwart et al., 2010). Under some assumptions, these mergers can lead to the formation of massive BHs (mBH > 60 M⊙), with mass in the pair-instability gap (Di Carlo et al., 2019a). In star clusters, such massive BHs can acquire a companion by dynamical exchanges, leading to the formation of BBHs in the mass gap. A fast sequence of stellar mergers in the dense core of a young star cluster (also known as runaway collision, Portegies Zwart et al., 2004; Giersz et al., 2015) might even lead to the formation of intermediate-mass BHs (IMBHs), i.e., BHs with mass mBH > 100 M⊙, especially at low metallicity (Mapelli, 2016).
The dynamical processes we briefly summarized above (and in the right-hand panel of Figure 2) leave a clear imprint on BBHs. First, dynamically formed BBHs extend to higher masses than isolated BBHs: they might even be in the pair-instability mass gap or in the IMBH regime (Di Carlo et al., 2019b; Rodriguez et al., 2019). Secondly, dynamical exchanges randomize the spin direction, leading to an isotropic distribution of BH spins. In contrast, isolated BBHs have a preference for aligned spins (Rodriguez et al., 2016; Gerosa et al., 2018). Third, dynamics can trigger the merger of BBHs with non-zero eccentricity even in the LIGO-Virgo band (Samsing et al., 2014; Rodriguez et al., 2018; Samsing, 2018; Zevin et al., 2019). These signatures provide an unique opportunity to differentiate among the isolated and the dynamical formation channel when the number of gravitational-wave detections will be of the order of a few hundreds (e.g., Zevin et al., 2017; Bouffanais et al., 2019).
Author Contributions
MM collected the material and wrote the review.
Funding
MM acknowledges financial support from the European Research Council for the ERC Consolidator grant DEMOBLACK, under contract no. 770017.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016). Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116:061102. doi: 10.1103/PhysRevLett.116.061102
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016a). Astrophysical implications of the binary black-hole merger GW150914. Astrophys. J. Lett. 818:L22. doi: 10.3847/2041-8205/818/2/l22
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016b). Binary black hole mergers in the first advanced LIGO observing run. Phys. Rev. X 6:041015. doi: 10.1103/PhysRevX.6.041015
Barkat, Z., Rakavy, G., and Sack, N. (1967). Dynamics of supernova explosion resulting from pair formation. Phys. Rev. Lett. 18, 379–381. doi: 10.1103/PhysRevLett.18.379
Belczynski, K., Bulik, T., Fryer, C. L., Ruiter, A., Valsecchi, F., Vink, J. S., et al. (2010). On the maximum mass of stellar black holes. Astrophys. J. 714, 1217–1226. doi: 10.1088/0004-637X/714/2/1217
Belczynski, K., Heger, A., Gladysz, W., Ruiter, A. J., Woosley, S., Wiktorowicz, G., et al. (2016a). The effect of pair-instability mass loss on black-hole mergers. Astron. Astrophys. 594:A97. doi: 10.1051/0004-6361/201628980
Belczynski, K., Holz, D. E., Bulik, T., and O'Shaughnessy, R. (2016b). The first gravitational-wave source from the isolated evolution of two stars in the 40-100 solar mass range. Nature 534, 512–515. doi: 10.1038/nature18322
Belotsky, K. M., Dokuchaev, V. I., Eroshenko, Y. N., Esipova, E. A., Khlopov, M. Y., Khromykh, L. A., et al. (2019). Clusters of primordial black holes. Eur. Phys. J. C 79:246. doi: 10.1140/epjc/s10052-019-6741-4
Bond, J. R., Arnett, W. D., and Carr, B. J. (1984). The evolution and fate of very massive objects. Astrophys. J. 280, 825–847. doi: 10.1086/162057
Bouffanais, Y., Mapelli, M., Gerosa, D., Di Carlo, U. N., Giacobbo, N., Berti, E., et al. (2019). Constraining the fraction of binary black holes formed in isolation and young star clusters with gravitational-wave data. Astrophys. J. 886:25. doi: 10.3847/1538-4357/ab4a79
Bressan, A., Marigo, P., Girardi, L., Salasnich, B., Dal Cero, C., Rubele, S., et al. (2012). PARSEC: stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mnthly. Notices R Astron. Soc. 427, 127–145. doi: 10.1111/j.1365-2966.2012.21948.x
Burrows, A., Vartanyan, D., Dolence, J. C., Skinner, M. A., and Radice, D. (2018). Crucial physical dependencies of the core-collapse supernova mechanism. Space Sci. Rev. 214:33. doi: 10.1007/s11214-017-0450-9
Carr, B., Kühnel, F., and Sandstad, M. (2016). Primordial black holes as dark matter. Phys. Rev. D 94:083504. doi: 10.1103/PhysRevD.94.083504
Chen, K.-J., Woosley, S., Heger, A., Almgren, A., and Whalen, D. J. (2014). Two-dimensional simulations of pulsational pair-instability supernovae. Astrophys. J. 792:28. doi: 10.1088/0004-637X/792/1/28
Chen, Y., Bressan, A., Girardi, L., Marigo, P., Kong, X., and Lanza, A. (2015). PARSEC evolutionary tracks of massive stars up to 350 M⊙ at metallicities 0.0001 ≤ Z ≤ 0.04. Mnthly. Notices R Astron. Soc. 452, 1068–1080. doi: 10.1093/mnras/stv1281
de Mink, S. E., and Mandel, I. (2016). The chemically homogeneous evolutionary channel for binary black hole mergers: rates and properties of gravitational-wave events detectable by advanced LIGO. Mnthly. Notices R Astron. Soc. 460, 3545–3553. doi: 10.1093/mnras/stw1219
Di Carlo, U. N., Giacobbo, N., Mapelli, M., Pasquato, M., Spera, M., Wang, L., et al. (2019a). Merging black holes in young star clusters. Mnthly. Notices R Astron. Soc. 487, 2947–2960. doi: 10.1093/mnras/stz1453
Di Carlo, U. N., Mapelli, M., Bouffanais, Y., Giacobbo, N., Bressan, S., Spera, M., et al. (2019b). Binary black holes in the pair-instability mass gap. arXiv [Preprint] arXiv:1911.01434.
Dominik, M., Belczynski, K., Fryer, C., Holz, D. E., Berti, E., Bulik, T., et al. (2013). Double compact objects. II. Cosmological merger rates. Astrophys. J. 779:72. doi: 10.1088/0004-637X/779/1/72
Eggleton, P. (2006). Evolutionary processes in binary and multiple stars. doi: 10.1017/CBO9780511536205
Ertl, T., Janka, H. T., Woosley, S. E., Sukhbold, T., and Ugliano, M. (2016). A two-parameter criterion for classifying the explodability of massive stars by the neutrino-driven mechanism. Astrophys. J. 818:124. doi: 10.3847/0004-637X/818/2/124
Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., and Justham, S. (2019). Mind the gap: the location of the lower edge of the pair-instability supernova black hole mass gap. Astrophys. J. 887:53. doi: 10.3847/1538-4357/ab518b
Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., Meynet, G., Kalogera, V., Taam, R. E., et al. (2019). The complete evolution of a neutron-star binary through a common envelope phase using 1D hydrodynamic simulations. Astrophys. J. Lett. 883:L45. doi: 10.3847/2041-8213/ab40d1
Fryer, C. L. (1999). Mass limits for black hole formation. Astrophys. J. 522, 413–418. doi: 10.1086/307647
Fryer, C. L., Belczynski, K., Wiktorowicz, G., Dominik, M., Kalogera, V., and Holz, D. E. (2012). Compact remnant mass function: dependence on the explosion mechanism and metallicity. Astrophys. J. 749:91. doi: 10.1088/0004-637X/749/1/91
Fryer, C. L., and Kalogera, V. (2001). Theoretical Black Hole Mass Distributions. Astrophys. J. 554, 548–560. doi: 10.1086/321359
Fuller, J., and Ma, L. (2019). Most black holes are born very slowly rotating. Astrophys. J. Lett. 881:L1. doi: 10.3847/2041-8213/ab339b
Gerosa, D., Berti, E., O'Shaughnessy, R., Belczynski, K., Kesden, M., Wysocki, D., et al. (2018). Spin orientations of merging black holes formed from the evolution of stellar binaries. Phys. Rev. D 98:084036. doi: 10.1103/PhysRevD.98.084036
Giacobbo, N., and Mapelli, M. (2018). The progenitors of compact-object binaries: impact of metallicity, common envelope and natal kicks. Mnthly. Notices R Astron. Soc. 480, 2011–2030. doi: 10.1093/mnras/sty1999
Giacobbo, N., and Mapelli, M. (2020). Revising natal kick prescriptions in population synthesis simulations. Astrophys. J. 891:141. doi: 10.3847/1538-4357/ab7335
Giersz, M., Leigh, N., Hypki, A., Lützgendorf, N., and Askar, A. (2015). MOCCA code for star cluster simulations - IV. A new scenario for intermediate mass black hole formation in globular clusters. Mnthly. Notices R Astron. Soc. 454, 3150–3165. doi: 10.1093/mnras/stv2162
Gräfener, G., and Hamann, W.-R. (2008). Mass loss from late-type WN stars and its Z-dependence. Very massive stars approaching the Eddington limit. Astron. Astrophys. 482, 945–960. doi: 10.1051/0004-6361:20066176
Gratton, R., Bragaglia, A., Carretta, E., D'Orazi, V., Lucatello, S., and Sollima, A. (2019). What is a globular cluster? An observational perspective. Astron. Astrophys. Rev. 27:8. doi: 10.1007/s00159-019-0119-3
Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., and Hartmann, D. H. (2003). How massive single stars end their life. Astrophys. J. 591, 288–300. doi: 10.1086/375341
Hills, J. G., and Fullerton, L. W. (1980). Computer simulations of close encounters between single stars and hard binaries. Astrophys. J. 85, 1281–1291. doi: 10.1086/112798
Hurley, J. R., Tout, C. A., and Pols, O. R. (2002). Evolution of binary stars and the effect of tides on binary populations. Mnthly. Notices R Astron. Soc. 329, 897–928. doi: 10.1046/j.1365-8711.2002.05038.x
Ivanova, N., Justham, S., Chen, X., De Marco, O., Fryer, C. L., Gaburov, E., et al. (2013). Common envelope evolution: where we stand and how we can move forward. Astron. Astrophys. Rev. 21:59. doi: 10.1007/s00159-013-0059-2
Lada, C. J., and Lada, E. A. (2003). Embedded clusters in molecular clouds. Annu. Rev. Astron. Astrophys. 41, 57–115. doi: 10.1146/annurev.astro.41.011802.094844
Mandel, I., and de Mink, S. E. (2016). Merging binary black holes formed through chemically homogeneous evolution in short-period stellar binaries. Mnthly. Notices R Astron. Soc. 458, 2634–2647. doi: 10.1093/mnras/stw379
Mapelli, M. (2016). Massive black hole binaries from runaway collisions: the impact of metallicity. Mnthly. Notices R Astron. Soc. 459, 3432–3446. doi: 10.1093/mnras/stw869
Mapelli, M., Colpi, M., and Zampieri, L. (2009). Low metallicity and ultra-luminous X-ray sources in the Cartwheel galaxy. Mnthly. Notices R Astron. Soc. 395, L71–L75. doi: 10.1111/j.1745-3933.2009.00645.x
Mapelli, M., and Giacobbo, N. (2018). The cosmic merger rate of neutron stars and black holes. Mnthly. Notices R Astron. Soc. 479, 4391–4398. doi: 10.1093/mnras/sty1613
Mapelli, M., Giacobbo, N., Ripamonti, E., and Spera, M. (2017). The cosmic merger rate of stellar black hole binaries from the Illustris simulation. Mnthly. Notices R Astron. Soc. 472, 2422–2435. doi: 10.1093/mnras/stx2123
Mapelli, M., Ripamonti, E., Zampieri, L., Colpi, M., and Bressan, A. (2010). Ultra-luminous X-ray sources and remnants of massive metal-poor stars. Mnthly. Notices R Astron. Soc. 408, 234–253. doi: 10.1111/j.1365-2966.2010.17048.x
Mapelli, M., Spera, M., Montanari, E., Limongi, M., Chieffi, A., Giacobbo, N., et al. (2020). Impact of the rotation and compactness of progenitors on the mass of black holes. Astrophys. J. 888:76. doi: 10.3847/1538-4357/ab584d
Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., and Moriya, T. J. (2016). A new route towards merging massive black holes. Astron. Astrophys. 588:A50. doi: 10.1051/0004-6361/201628133
Marchant, P., Renzo, M., Farmer, R., Pappas, K. M. W., Taam, R. E., de Mink, S. E., et al. (2019). Pulsational pair-instability supernovae in very close binaries. Astrophys. J. 882:36. doi: 10.3847/1538-4357/ab3426
Neijssel, C. J., Vigna-Gómez, A., Stevenson, S., Barrett, J. W., Gaebel, S. M., Broekgaarden, F. S., et al. (2019). The effect of the metallicity-specific star formation history on double compact object mergers. Mnthly. Notices R Astron. Soc. 490, 3740–3759. doi: 10.1093/mnras/stz2840
Neumayer, N., Seth, A., and Boeker, T. (2020). Nuclear star clusters. arXiv [Preprint] arXiv:2001.03626.
Ober, W. W., El Eid, M. F., and Fricke, K. J. (1983). Evolution of massive pregalactic stars - part two - nucleosynthesis in pair creation supernovae and pregalactic enrichment. Astron. Astrophys. 119:61.
O'Connor, E., and Ott, C. D. (2011). Black hole formation in failing core-collapse supernovae. Astrophys. J. 730:70. doi: 10.1088/0004-637X/730/2/70
Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., and McMillan, S. L. W. (2004). Formation of massive black holes through runaway collisions in dense young star clusters. Nature 428, 724–726. doi: 10.1038/nature02448
Portegies Zwart, S. F., and McMillan, S. L. W. (2000). Black hole mergers in the universe. Astrophys. J. Lett. 528:L17–L20. doi: 10.1086/312422
Portegies Zwart, S. F., McMillan, S. L. W., and Gieles, M. (2010). Young massive star clusters. Annu. Rev. Astron. Astrophys. 48, 431–493. doi: 10.1146/annurev-astro-081309-130834
Qin, Y., Fragos, T., Meynet, G., Andrews, J., Sørensen, M., and Song, H. F. (2018). The spin of the second-born black hole in coalescing binary black holes. Astron. Astrophys. 616:A28. doi: 10.1051/0004-6361/201832839
Qin, Y., Marchant, P., Fragos, T., Meynet, G., and Kalogera, V. (2019). On the Origin of Black Hole Spin in High-mass X-Ray Binaries. Astrophys. J. Lett. 870:L18. doi: 10.3847/2041-8213/aaf97b
Renzo, M., Farmer, R. J., Justham, S., de Mink, S. E., Götberg, Y., and Marchant, P. (2020). Sensitivity of the lower edge of the pair-instability black hole mass gap to the treatment of time-dependent convection. Mnthly. Notices R Astron. Soc. 493, 4333–4341. doi: 10.1093/mnras/staa549
Rodriguez, C. L., Amaro-Seoane, P., Chatterjee, S., and Rasio, F. A. (2018). Post-newtonian dynamics in dense star clusters: highly eccentric, highly spinning, and repeated binary black hole mergers. Phys. Rev. Lett. 120:151101. doi: 10.1103/PhysRevLett.120.151101
Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., Chatterjee, S., Kremer, K., Rasio, F. A., and Ye, C. S. (2019). Black holes: The next generation-repeated mergers in dense star clusters and their gravitational-wave properties. Phys. Rev. D 100:043027. doi: 10.1103/PhysRevD.100.043027
Rodriguez, C. L., Zevin, M., Pankow, C., Kalogera, V., and Rasio, F. A. (2016). Illuminating black hole binary formation channels with spins in advanced LIGO. Astrophys. J. Lett. 832:L2. doi: 10.3847/2041-8205/832/1/L2
Samsing, J. (2018). Eccentric black hole mergers forming in globular clusters. Phys. Rev. D 97:103014. doi: 10.1103/PhysRevD.97.103014
Samsing, J., MacLeod, M., and Ramirez-Ruiz, E. (2014). The formation of eccentric compact binary inspirals and the role of gravitational wave emission in binary-single stellar encounters. Astrophys. J. 784:71. doi: 10.1088/0004-637X/784/1/71
Santoliquido, F., Mapelli, M., Bouffanais, Y., Giacobbo, N., Di Carlo, U. N., Rastello, S., et al. (2020). The cosmic merger rate density evolution of compact binaries formed in young star clusters and in isolated binaries. arXiv [Preprint] arXiv:2004.09533.
Spera, M., and Mapelli, M. (2017). Very massive stars, pair-instability supernovae and intermediate-mass black holes with the sevn code. Mnthly. Notices R Astron. Soc. 470, 4739–4749. doi: 10.1093/mnras/stx1576
Spera, M., Mapelli, M., Giacobbo, N., Trani, A. A., Bressan, A., and Costa, G. (2019). Merging black hole binaries with the SEVN code. Mnthly. Notices R Astron. Soc. 485, 889–907. doi: 10.1093/mnras/stz359
Stevenson, S., Sampson, M., Powell, J., Vigna-Gómez, A., Neijssel, C. J., Szécsi, D., et al. (2019). The impact of pair-instability mass loss on the binary black hole mass distribution. Astrophys. J. 882:121. doi: 10.3847/1538-4357/ab3981
Tang, P. N., Eldridge, J. J., Stanway, E. R., and Bray, J. C. (2020). Dependence of gravitational wave transient rates on cosmic star formation and metallicity evolution history. Mnthly. Notices R Astron. Soc. 493, L6–L10. doi: 10.1093/mnrasl/slz183
Vink, J. S., de Koter, A., and Lamers, H. J. G. L. M. (2001). Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 369, 574–588. doi: 10.1051/0004-6361:20010127
Vink, J. S., Muijres, L. E., Anthonisse, B., de Koter, A., Gräfener, G., and Langer, N. (2011). Wind modelling of very massive stars up to 300 solar masses. Astron. Astrophys. 531:A132. doi: 10.1051/0004-6361/201116614
Woosley, S. E. (2017). Pulsational Pair-instability Supernovae. Astrophys. J. 836:244. doi: 10.3847/1538-4357/836/2/244
Woosley, S. E. (2019). The evolution of massive helium stars, including mass loss. Astrophys. J. 878:49. doi: 10.3847/1538-4357/ab1b41
Woosley, S. E., Blinnikov, S., and Heger, A. (2007). Pulsational pair instability as an explanation for the most luminous supernovae. Nature 450, 390–392. doi: 10.1038/nature06333
Yoshida, T., Umeda, H., Maeda, K., and Ishii, T. (2016). Mass ejection by pulsational pair instability in very massive stars and implications for luminous supernovae. Mnthly. Notices R Astron. Soc. 457, 351–361. doi: 10.1093/mnras/stv3002
Zampieri, L., and Roberts, T. P. (2009). Low-metallicity natal environments and black hole masses in ultraluminous X-ray sources. Mnthly. Notices R Astron. Soc. 400, 677–686. doi: 10.1111/j.1365-2966.2009.15509.x
Zevin, M., Pankow, C., Rodriguez, C. L., Sampson, L., Chase, E., Kalogera, V., et al. (2017). Constraining formation models of binary black holes with gravitational-wave observations. Astrophys. J. 846:82. doi: 10.3847/1538-4357/aa8408
Zevin, M., Samsing, J., Rodriguez, C., Haster, C.-J., and Ramirez-Ruiz, E. (2019). Eccentric black hole mergers in dense star clusters: the role of binary-binary encounters. Astrophys. J. 871:91. doi: 10.3847/1538-4357/aaf6ec
Keywords: stars: black holes, black hole physics, Galaxy: open clusters and associations: general, stars: kinematics and dynamics, gravitational waves
Citation: Mapelli M (2020) Binary Black Hole Mergers: Formation and Populations. Front. Astron. Space Sci. 7:38. doi: 10.3389/fspas.2020.00038
Received: 25 February 2020; Accepted: 03 June 2020;
Published: 09 July 2020.
Edited by:
Rosalba Perna, Stony Brook University, United StatesReviewed by:
Maxim Yurievich Khlopov, UMR7164 Astroparticule et Cosmologie (APC), FranceAtaru Tanikawa, The University of Tokyo, Japan
Copyright © 2020 Mapelli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michela Mapelli, bWljaGVsYS5tYXBlbGxpQHVuaXBkLml0
 Michela Mapelli
Michela Mapelli