Measuring Magnetic Field With Atacama Large Millimeter/Submillimeter Array

Introduction

Magnetic field can affect radio emission in two ways: via the Lorentz force, which causes the emitting electrons to spiral in the magnetic field providing a direct source of opacity for gyroemission, and via modification of the plasma response to electromagnetic fields, leading to different refractive index and polarization for the ordinary (o) and extraordinary (x) magnetoionic wave modes. Their polarization becomes dependent on the properties of the plasma through which they propagate, in particular on the local values of the plasma parameters $u={\left(\frac{{\nu }_B}{\nu }\right)}^2$ (dimensionless magnetic field parameter) and $v={\left(\frac{{\nu }_p}{\nu }\right)}^2$ (dimensionless electron density); where ν is the frequency, ν_B and ν_p are the gyrofrequency and the plasma frequency, respectively (see, e.g., Alissandrakis, 2020). By observing polarized radio emission, we can generally get access to the information it contains on magnetic field (but also on density and temperature).

While gyroresonance emission from non-relativistic plasma at low harmonics of the gyrofrequency, which is an example of the direct effect of magnetic field on opacity, is responsible for the coronal emission of non-flaring solar active regions observed at centimeter (cm) wavelengths, the thermal bremsstrahlung is dominant in the corona of the quiet Sun (QS), as well as in more dense chromospheric layers. Bremsstrahlung emission (also known as free–free emission, as free electrons remain unbound after being deflected by ions), is an example of the plasma response to the presence of magnetic field. Bremsstrahlung becomes weakly polarized in a magnetized plasma like the solar outer atmosphere.

The radio regime has the advantage over the other wavelengths as radio emission gets optically thick in the solar atmosphere. Measuring radio emission at different frequencies, we in fact get access to different layers of the solar atmosphere. Free–free emission provides sufficient opacity at long radio wavelengths for the solar corona to become optically thick, while at short wavelengths (millimeter and submillimeter) it gets optically thick in the chromospheric layers. Submillimeter (submm) emission gets optically thick already at the heights near the temperature minimum and in the lower chromosphere, while the emission at longest millimeter (mm) wavelengths originates from the upper chromosphere and the transition region. This makes observations of free–free emission at mm and submm wavelengths a vital source of information about the enigmatic layers of the solar atmosphere, which play a significant role in defining the dynamics and energy budget of not only the solar corona, but also of the solar wind.

The Solar Chromosphere

Without any exaggeration, understanding the physics of chromosphere is the key to understanding the whole solar atmosphere, as the major transitions, e.g., from fully ionized to partially ionized plasma, from local thermodynamic equilibrium (LTE) to non-local thermodynamic equilibrium (non-LTE) radiative transfer, from strong to weak collisional coupling, and from plasma-dominated to magnetic field–dominated media, take place at chromospheric heights (Carlsson et al., 2019).

In the solar atmosphere, plasma motions dominate the magnetic field in the photosphere and low chromosphere, but as the density decreases exponentially with height, the magnetic field starts to govern the dynamics of the plasma in the upper chromosphere. Due to exponentially decreasing gas pressure, the magnetic field also starts to spread rapidly horizontally, and already in the lower chromosphere, essentially all the space, including regions of weak photospheric field, is filled with the magnetic field. Thus, the chromospheric structure is largely set by the magnetic field. Images in traditional optical and UV lines clearly show that the chromospheric plasma is organized along the magnetic field lines and concentrations (e.g., De Pontieu et al., 2007; Rutten, 2007). At the same time, numerous chromospheric simulations confirm that the magnetic field plays a critical role in chromospheric heating and dynamics (e.g., see Wiegelmann et al., 2014, for a review).

However, due to its highly structured, dynamic, and physically complex nature, the chromosphere is difficult to observe and those observations are not easy to interpret quantitatively. The traditional chromospheric diagnostic using the UV and IR lines suffers from the fact that it can only sample the hotter component of the gas, as at these wavelengths the Planck function depends on the temperature exponentially, implying that any average is weighted toward the maximum temperature (Carlsson and Stein, 1995). Additionally, as the source function is decoupled from the Planck function, a careful treatment of non-LTE effects is required for these lines.

Mainly due to the shortcomings of the traditional diagnostics, our knowledge about the chromospheric field and its role in creating and maintaining the chromosphere outside active regions remains quite poor. While measuring of Zeeman splitting of the spectral lines has been successfully employed in the optical polarimeters for diagnosing the photospheric field, in the chromosphere, the situation is less prosperous. Spectral lines that are sensitive to the chromospheric heights are usually very broad and only their cores reflect chromospheric features. The few chromospheric lines in the optical and near infrared that are sensitive to the Zeeman and Hanle effects, like the lines of singly ionized calcium, neutral hydrogen, and neutral helium, might be useful for chromospheric magnetometry, but are, in fact, extremely difficult to exploit in the regions of weak field because their polarization signal from the latter is commonly weak and requires high signal-to-noise ratio (SNR). In addition, the use of these lines in the quiet Sun is restricted due to a wide range of formation heights and the necessity for non-LTE treatment in the inversions. Successful examples of measuring chromospheric magnetic field outside of sunspots with these spectral lines typically refer to the observational structures with a relatively strong magnetic field [e.g., fibrils observed in the CaII 854.2 nm line by de la Cruz Rodríguez et al. (2010) and de la Cruz Rodríguez and Socas-Navarro (2011), or erupting filament prior to and during the eruption observed in the He I 1,083 nm line by Wang et al. (2020)] or to observations off-disk [e.g., He D3 line observations of prominences by Casini et al. (2003) and of spicules by López Ariste and Casini (2005)]. Recent unique observations of the active region flaring loops at the limb in the CaII 854.2 nm line with unprecedented spatial and temporal resolution by Kuridze et al. (2019) allowed the use of the chromospheric diagnostics at the coronal heights and to obtain measurements of the coronal magnetic field up to 25 Mm height. Commonly in the corona, measurements of magnetic fields in the spectral lines are obtained by means of the coronal emission line spectropolarimetry [e.g., observation in the Fe XIII 1,075 nm coronal emission line in active regions above the solar limb reported in Lin et al. (2004)]. The most recent reviews on the current and future instrumentation for solar spectropolarimetry and on the results of the solar polarimetric measurements can be found in Iglesias and Feller (2019) and Suárez (2019).

Chromospheric observations at long wavelengths like the mm wavelengths have the advantage that in the Rayleigh-Jeans regime, the Planck function varies linearly with temperature and LTE is a good approximation for the free–free processes dominant in the formation of the radiation at these wavelengths. As a result, at a given wavelength, the temperature of the emitting material is linearly proportional to the observed intensity. This unique capability makes mm wavelengths a primary candidate for diagnostics of the thermal structure of the chromospheric plasma. Furthermore, mm wavelength observations of the free–free polarization contain information on the magnetic field and provide a method of measuring the longitudinal component of magnetic fields in the solar chromosphere.

While previous available radio data were used to address general properties of large-scale solar chromospheric structures, the spatial resolution of those observations was insufficient to diagnose the small-scale processes that define the solar outer atmosphere. The situation has changed drastically after commissioning of the Atacama Large Millimeter/Submillimeter Array (ALMA) for the solar observations.

ALMA

The ALMA is located in Chile at an altitude of 5,000 m and is operated in cooperation between the National Radio Astronomy Observatory, the European Organization for Astronomical Research in the Southern Hemisphere, and the National Astronomical Observatory of Japan. ALMA interferometer is composed of 66 high-precision antennas, including the 12 m Array of 50 antennas for high-resolution imaging, and the Atacama Compact Array of twelve 7 m antennas together with four total power (TP) antennas 12 m in diameter, to enhance wide-field imaging (Wootten and Thompson, 2009; Hills et al., 2010). Currently, ALMA antennas are equipped with eight receivers, covering the range of wavelengths from 0.3 mm (Band 10, 950 GHz) to 3.6 mm (Band 3, 84 GHz). Two receivers for longer wavelengths are planned to be added, with one receiver up to 8.6 mm (Band 1, 35 GHz, Huang et al., 2016, 2018) being in construction, and the second one, for the wavelengths up to 4.6 mm (Band 2, 67–116 GHz, Yagoubov et al., 2020), being under development. The array is reconfigurable in multiple patterns (configurations) ranging in size from 150 m (compact) up to 16 km (extended), depending on the required sensitivity and spatial resolution. At the shortest ALMA wavelengths and in the most extended configurations, the array can achieve the spatial resolution of a few milliarcseconds. The instantaneous field of view (FOV) of the interferometer is a function of wavelength and the primary beam size of the array antennas: when observing at Bands 3 and 6, the 12 m antenna FOV size is ~60″ and ~25″, respectively. When observational targets require larger size of FOV, as in the case of mapping of the structures in the solar chromosphere, regime of mosaicing is offered.

Regular ALMA solar observing started in 2016, preceded by commissioning and science verification activities (Shimojo et al., 2017; White et al., 2017). Current solar ALMA capabilities include interferometric observations in the three frequency bands: Band 3 (3 mm), Band 6 (1 mm), and Band 7 (0.85 mm) in compact array configurations, with a maximum spatial resolution of 0.9″, 0.6″, and 0.6″, respectively, with 1 s time integration (Remijan et al., 2019). In principle, ALMA is able to provide about two orders of magnitude improvement in resolution, sensitivity, and frequency coverage, over the previously existing instruments operated at short radio wavelengths. As the emission at ALMA wavelengths is optically thick at different heights in the solar chromosphere and the sampled intensity linearly translates into the local gas temperature, ALMA provides a nearly perfect thermometer for the chromospheric heights. For instance, its ability to probe a wide range of chromospheric temperatures from cool to hot gas and to detect chromospheric features missed by the SDO and IRIS has been recently demonstrated by Loukitcheva et al. (2019). At present ALMA is able to acquire height and time-dependent diagnostics of thermal plasma properties at high spatial, spectral, and temporal resolution. Future ALMA observations of circular polarization (see section ALMA Polarization Measurements) will offer a diagnostic tool for the chromospheric magnetic fields. The use of ALMA observations for solar studies is not limited to diagnostics of the thermal and magnetic structures of the chromosphere and is thoroughly discussed by Wedemeyer et al. (2016).

Measuring Magnetic Field from Free–Free Emission

Magnetic Bremsstrahlung

The physics of bremsstrahlung emission in the solar context has been reviewed by many authors (e.g., Zlotnik, 1968; Dulk, 1985; Zheleznyakov, 1996; Gelfreikh, 2004) and can also be found in the previous chapters of this volume. Among the two oppositely polarized natural (or normal) modes of electromagnetic wave that propagate in a magnetized plasma, the extraordinary mode interacts stronger with the magnetic field than the ordinary mode. Consequently, in the presence of magnetic fields, the absorption coefficients for the two modes are different.

The generalized formulas for the free–free absorption coefficients for x- and o-modes include the full anisotropic term, and can be written as follows (e.g., Zlotnik, 1968; Fleishman and Toptygin, 2013; Loukitcheva et al., 2017):

$\begin{array}{ll}{k}_{\sigma }\simeq k_{\sigma }^0\frac{F_{\sigma }}{n_{\sigma }}& (1)\end{array}$

where subscript σ denotes one of the modes (σ = −1, 1 for the x- and the o-modes, respectively), $k_{\sigma }^0$ is the absorption coefficient for the isotropic plasma, and n_σ is the refraction index, as defined by, e.g., Alissandrakis (2020).

The magnetic field factor F_σ has the following form:

$\begin{array}{ll}{F}_{\sigma }=2\frac{\sigma \sqrt{D}\left(usi{n}^2\theta +2{(1-\text{v})}^2\right)-u^{2}si{n}^4\theta }{\sigma \sqrt{D}{\left(2(1-\text{v})-usi{n}^2\theta +\sigma \sqrt{D}\right)}^2}& (2)\end{array}$

where $u={\left(\frac{{\nu }_B}{\nu }\right)}^2$, $v={\left(\frac{{\nu }_p}{\nu }\right)}^2$, ν_p is the plasma frequency, and θ is the angle between magnetic field and the line of sight.

Commonly, the absorption coefficients for x- and o-modes are calculated using the quasilongitudinal approximation (QL), which remains valid for most of the angles of the magnetic field to the line of sight except transverse propagation (Zlotnik, 1968; Zheleznyakov, 1996):

$\begin{array}{ll}{k}_{\sigma }\bumpeq \frac{k_{\sigma }^0}{{\left(1+\sigma \frac{{\nu }_B}{\nu }|cos\theta |\right)}^2}& (3)\end{array}$

where ν_B is the gyrofrequency.

As can be seen from Equation (3), the absorption coefficient and thus the opacity for the x-mode are higher, leading to separation of the optically thick layers of the two modes. In isothermal plasma, both modes will have the same brightness temperature that is equal to the temperature of the medium. However, in plasma with a vertical temperature gradient, like in the solar atmosphere with temperature increasing outwards, at a given frequency, the corresponding brightness temperature of the modes will be different, as the x-mode will be observed from higher and thus hotter layers than the o-mode. In other words, the presence of magnetic field shifts the optically thick layers (and consequently the formation heights) of the two modes in opposite directions along the temperature gradient. The observed temperature difference between two layers is interpreted as net circular polarization. The difference between the formation heights of the two modes is proportional to the magnetic field strength, resulting in a proportionally stronger net polarization. Thus, polarization measurements contain information about the magnetic field strength, but indirectly, via the temperature gradient.

Method for Magnetic Field Estimate

The basic concepts of the method of estimation of magnetic field from thermal free–free were introduced by Bogod and Gelfreikh (1980), while the diagnostic potential as well as the examples of the application of the free–free polarization observations for coronal/chromospheric magnetic field measurements were thoroughly discussed by Gelfreikh (2004). As was noted above, measured polarized signal carries information on the magnetic field indirectly via the temperature gradient. This implies that to isolate the effect of magnetic field in the measured polarization, it is required to deduce the temperature gradient independently. Bogod and Gelfreikh (1980) demonstrated a method to derive the temperature gradient from the variation of brightness temperature with frequency, using the scaling law, which relates the brightness temperatures of the natural modes in a magnetic field $T_b^{\sigma }$ to the total unpolarized brightness temperature T_b,

$\begin{array}{ll}{T}_b^{\sigma }(\nu )=T_b(\nu +\sigma {\nu }_B|cos\theta |)& (4)\end{array}$

Bogod and Gelfreikh (1980) introduced the logarithmic spectral index n, which corresponds to the slope of the brightness spectrum, as:

$\begin{array}{ll}n=\frac{\partial \left(ln{T}_b\right)}{\partial \left(ln\nu \right)}& (5)\end{array}$

where the frequency serves as a proxy for height, and derived circular polarization degree P using the scaling law from Equation (4) as:

$\begin{array}{ll}P=\frac{T_b^x-T_b^o}{T_b^x+T_b^o}=n\frac{{\nu }_B}{\nu }cos\theta & (6)\end{array}$

Taking into account that the longitudinal component of the magnetic field is B_l = B cosθ, and the electron gyrofrequency is ${\nu }_B=2.8·10^{6}B$, an estimate for the longitudinal component of the magnetic field can be written as follows:

$\begin{array}{ll}{B}_l=\frac{P\nu }{2.8·10^{6}n}& (7)\end{array}$

Thereby, this technique requires measurements of polarization at a given frequency as well as of the brightness spectrum around the frequency to measure the slope. The method uses the assumption of a homogeneous magnetic field within the layer where the normal modes are formed. According to the simulations (e.g., section Magnetic Fields in the Quiet Sun) in the quiescent regions, the width of this layer does not exceed a few kilometers. The obtained estimation of the magnetic field refers to the height where the emission at a given frequency is generated (further discussed in section Simulating Magnetic Field Measurements With ALMA), implying that, tuning the frequency, we can measure the magnetic field at different heights in the chromosphere. Finally, multi-frequency measurements of polarization degrees and of spectral indexes make chromospheric magnetography (of longitudinal component) possible.

Equation (7) provides a general form for estimation of the longitudinal component of the magnetic field that is applicable for the optically thick at mm wavelengths chromosphere as well as for the optically thin free–free emission from the corona. As bremsstrahlung is sensitive to the regions of the enhanced density, solar images at mm and short cm can reflect not only the optically thick chromospheric part but also plasma structures from the transition region and solar corona. These coronal condensations, characterized by the local density enhancements, are commonly seen in the radio maps at short cm wavelengths as brightness sources and are typically optically thin. Using the fact that for the optically thin isothermal emission we expect the spectral index n = 2 and thus spectral observations are not required, we can obtain the following simplified version of Equation (7) in case of optically thin coronal contribution:

$\begin{array}{ll}{B}_l=\frac{P\nu }{5.6·10^6}& (8)\end{array}$

The magnetic field in coronal condensations both on the limb and on the disk can be studied using thermal bremsstrahlung. However, when observing a bright polarized source on the disk, which implies the presence of inhomogeneous magnetic field over the line of sight, it needs to be found out which of the layers (chromosphere or corona) are responsible for its polarization at a given wavelength and further it is typically required to separate the contributions from the two layers into the recorded polarized emission. In a more general case of inhomogeneous thermal structures (composed of multi-thermal components, such as filaments, chromospheric and coronal jets, flare loops) present on the disk, employment of additional observations from other spectral domains and advanced modeling will be required to separate the contributions from the different structures.

The method to study the magnetic field from the thermal bremsstrahlung was modified by Grebinskij et al. (1998, 2000) to be used for single-frequency observations [at the Nobeyama Radioheliograph (NoRH) at 17 GHz] and for multiple frequencies (for RATAN at 1–18 GHz). A comprehensive review of the applicability of the technique for different combinations of optical thickness in homogeneous and inhomogeneous sources, as well as discussion on how to discriminate between contributions from the chromosphere and corona in the measured polarization, and how to account for the combined effect of bremsstrahlung and gyroresonance emission at cm wavelength, is beyond the scope of the present paper and can be found in Gelfreikh (2004); see also the previous chapter by Kostas Allissandrakis.

At mm wavelengths, the method can be applied effectively in the regions with weak fields, like quiescent and plage areas, coronal holes, prominences, as well as in sunspots where the magnetic field is strong, provided that the measured polarization is of the free–free nature. Thus, using Equation (7), we can get an estimate of the longitudinal component of the magnetic field in the plasma structures of the chromosphere and transition region up to the solar corona, both on the disk and above the solar limb.

Measurements of free–free polarization require high precision and low noise level, as free–free polarization effects are known to be quite weak at these frequencies, with the circular polarization degree not exceeding 10% for the strongest magnetic fields (Grebinskij et al., 2000). This makes observational noise level one of the major concerns for the application of this method. One of the approaches that help to reduce the noise level of the data consists of averaging of the data over time. Thus, as was shown by Gelfreikh (2004), the sensitivity of the NoRH data at 17 GHz can be substantially improved by averaging the images over 10 min intervals. It was demonstrated by Bogod and Gelfreikh (1980) that for the NoRH data, the restored longitudinal magnetic field component can be approximated by the value of the measured polarization signal ($B_l\approx T_b^x-T_b^o=T_b^V$). This implies that for the default image integration of 10 s, the sensitivity of the NoRH maps of about 1% (of the quiet-Sun brightness level of 10,000 K) translates into the accuracy of the restored field of about 100 G, while averaging over 10 min instead of 10 s brings the statistical polarization noise in the synthesized images down to a few Kelvin and thus the sensitivity of the method to a few Gauss.

Selected Observational Examples

The polarization of free–free emissions from the active regions, including sunspots, plages, prominences, coronal holes, loops, and arches has been previously observed with the RATAN-600 (Bogod and Gelfreikh, 1980; Grebinskij et al., 1998, 2000), the VLA (e.g., Shevgaonkar and Kundu, 1984; Schmelz et al., 1994), and the NoRH (e.g., Gelfreikh and Shibasaki, 1999). Longitudinal magnetic fields measured from the circular polarization at short cm were found to be in the range from 60 to 150 G in the chromosphere and corona of active regions. Recently, Kallunki et al. (2020) reported the first successful solar polarization observations at 3 and 13 mm carried out with the Aalto University Metsähovi Radio Telescope. Figures 1–3 provide the examples of the most recent observations, obtained with the NoRH (Iwai and Shibasaki, 2013; Miyawaki et al., 2016) and with the RATAN-600 (Kaltman, 2019). Iwai and Shibasaki (2013) derived the coronal and chromospheric magnetic fields in the active region NOAA 11455 from the circular polarization observations at 17 GHz and spectral observations at 17 and 34 GHz obtained by NoRH on April 13, 2012 (Figure 1). Time averaging of the images over 20 min allowed to reach the minimum detectable polarization level of 0.5%. The observed circular polarization degrees were 0.5 and 1.7% for the two polarities, and the restored magnetic fields were found to be about 20–50% of the their photospheric value. However, for the central part of the active region, the authors were not able to discriminate between the coronal and chromospheric components of the derived magnetic field, and the reported values were considered to be emission-measure-weighted.

FIGURE 1

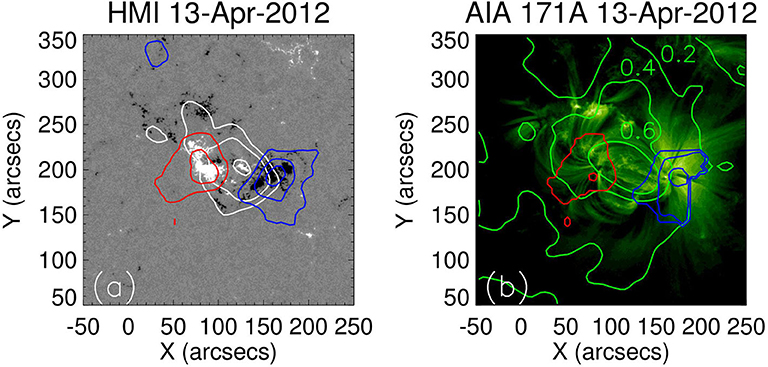
Figure 1. (a) The photospheric magnetogram observed by SDO/HMI on April 13, 2012, with the overlaid contours of radio intensity at 17 GHz plotted in white and circular polarization at 17 GHz with positive components at 0.5 and 1.0% plotted in red, and negative components at 0.5, 1.0, and 1.5% plotted in blue. (b) The corresponding EUV image at 171A observed by SDO/AIA with the overlaid contours of the magnetic field (with positive components at 50 and 150 G shown in red, negative components at 50, 150, and 250 G plotted in blue) derived from the measured polarization at 17 GHz and the spectral index, and with the contours of the local spectral index at the levels of 0.2, 0.4, and 0.6 depicted in green.

FIGURE 2

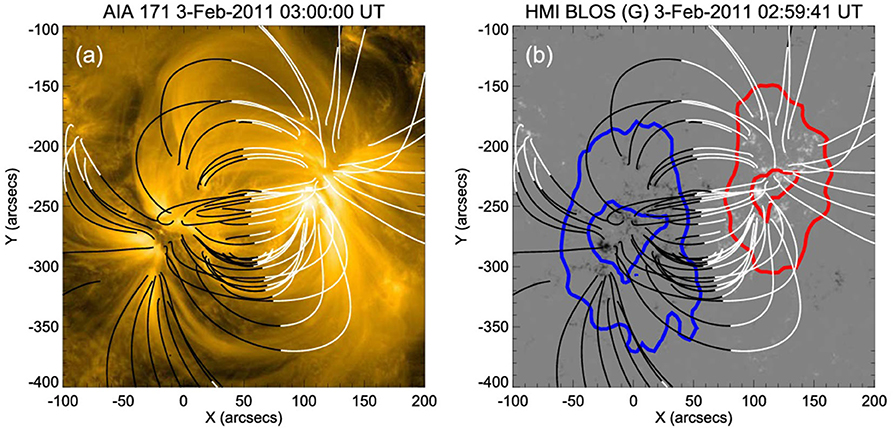
Figure 2. (a) 171A image of AR NOAO 11150 observed with SDO/AIA on February 2, 2011 with the overlaid outward (white) and inward (black) magnetic field lines from the potential field extrapolation. (b) The same for the photospheric longitudinal magnetic field observed with SDO/HMI with the contours of the degree of positive circular polarization at 0.4 and 0.8% at 17 GHz, shown in red, and the contours of the degree of negative circular polarization at −0.4 and −0.8% at 17 GHz, shown in blue. From Miyawaki et al. (2016). Reproduced by permission of the AAS.

FIGURE 3

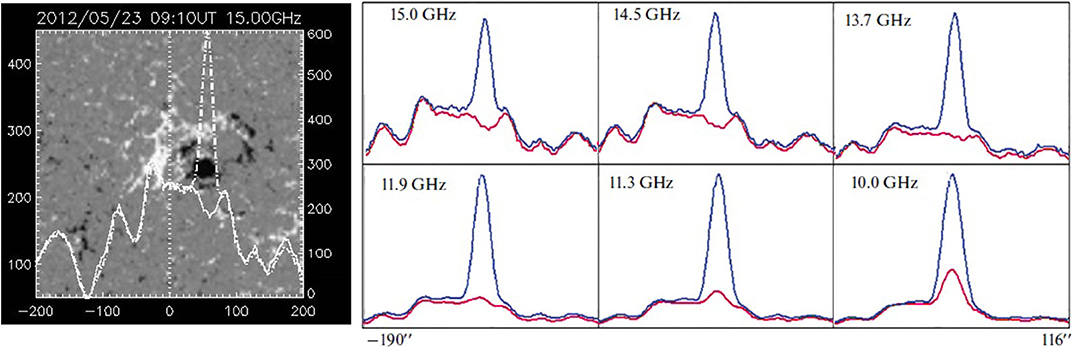
Figure 3. (Left) One-dimensional scans of the active region NOAO 11486 in the ordinary (solid line) and extraordinary (dotted) wave modes observed at 15 GHz with the RATAN-600 on May 23, 2012, superimposed on the SDO/HMI magnetogram. (Right) The evolution of the sunspot-associated sources in the range of 10–15 GHz, with the ordinary mode shown in red and the extraordinary mode depicted in blue.

An example of the successful separation of the two components is presented in Miyawaki et al. (2016). For analysis of the active region NOAO 11150, the authors selected a part of the active region consisting of coronal loops and only weak chromospheric magnetic field, and combined the circular polarization measurements at 17 GHz with the coronal emission measure estimations from the EUV observations. The derived coronal magnetic fields in the range of 100–210 G were compared with the results of the potential field extrapolation using the photospheric magnetograms from the SDO/HMI (Figure 2) and were interpreted as the upper limits of the coronal longitudinal magnetic fields.

A recent study of the free–free sources above sunspots observed with the RATAN-600 is presented in Kaltman (2019), with the accurate analysis of the contributions from thermal bremsstrahlung and gyroresonance radiation into the observed polarized emission in the high-frequency part of the RATAN-600 spectrum of 12–20 GHz (1.5–2.5 cm). The observations and the simulations confirmed that at high frequencies (15 and 14.5 GHz), for which the magnetic field is not enough to generate significant gyroresonance emission in both modes, magnetic bremsstrahlung is strong enough to clearly separate the intensities of the two modes (Figure 3). At these frequencies, a bright sunspot cyclotron source is observed in the extraordinary mode, while the ordinary mode is due to bremsstrahlung and shows a pronounced dip in the intensity. The wide frequency coverage and fine frequency resolution of the RATAN-600 made it possible to follow the transition from the pure bremsstrahlung to a growing cyclotron source in the ordinary mode, when moving to lower frequencies.

Simulating Magnetic Field Measurements With ALMA

As was reviewed in the previous section, the technique to estimate magnetic fields from the observed free–free emission was employed solely to the measurements at cm wavelengths, primarily because of the absence of the instruments in the mm range, capable to measure the relatively low degree of free–free polarization and brightness temperature spectra with sufficient accuracy. The advent of the ALMA interferometer operating at these wavelengths has changed the scene as the instrument's potential capabilities fully satisfy the requirements for the successful application of the method.

Magnetic Fields in the Quiet Sun

As was noted above, the described method is in general suitable for determination of the chromospheric magnetic fields in the QS regions. Loukitcheva et al. (2017) used advanced three-dimensional (3D) radiative magnetohydrodynamic (R-MHD) simulations of the enhanced network (ENW) made with the Bifrost code (Gudiksen et al., 2011) to predict the polarization that can be observed in the QS with ALMA. The authors calculated the free–free emission in the ALMA frequency bands (including Bands 1 and 2, which have not yet been delivered) from the 3D model and analyzed the simulated brightness temperatures as if they were observational data to derive the longitudinal magnetic field. The latter were then compared with the magnetic field in the model to study the precision of the method.

The Model Atmosphere

The model snapshot that was used by Loukitcheva et al. (2017) is described in detail by Carlsson et al. (2016). The simulation box includes the upper convection zone, photosphere, chromosphere, and the lower corona with the horizontal grid spacing of 48 km (0.06″), and with the non-uniform vertical grid spacing of 19–98 km. The model includes the non-equilibrium ionization of hydrogen. The average unsigned magnetic field strength is 48 G at the photospheric level. It is concentrated in the two clusters of opposite polarity, which represent the QS enhanced network (ENW) with the maximum field strength of 2,000 G, lying about 8 Mm apart. The magnetic field expands with height and fills all space above heights of around 1 Mm with higher temperatures seen in the regions of strong field than in neighboring regions and with pronounced loop-like structures connecting the two ENW patches.

Simulated Polarization and Magnetic Field

The time-dependent simulations show evolving chromospheric patterns with a time scale of a few 10 s due to the waves passing through the simulation box in three dimensions. The brightness structure seen in the synthesized mm images is found to be similar: it shows a complex pattern of intermittent bright (hot) and dark (cool) regions, with prominent bright fibrils aligned along the chromospheric magnetic field lines, seen at wavelengths around 3 mm (Band 3) and longer (Figure 4).

FIGURE 4

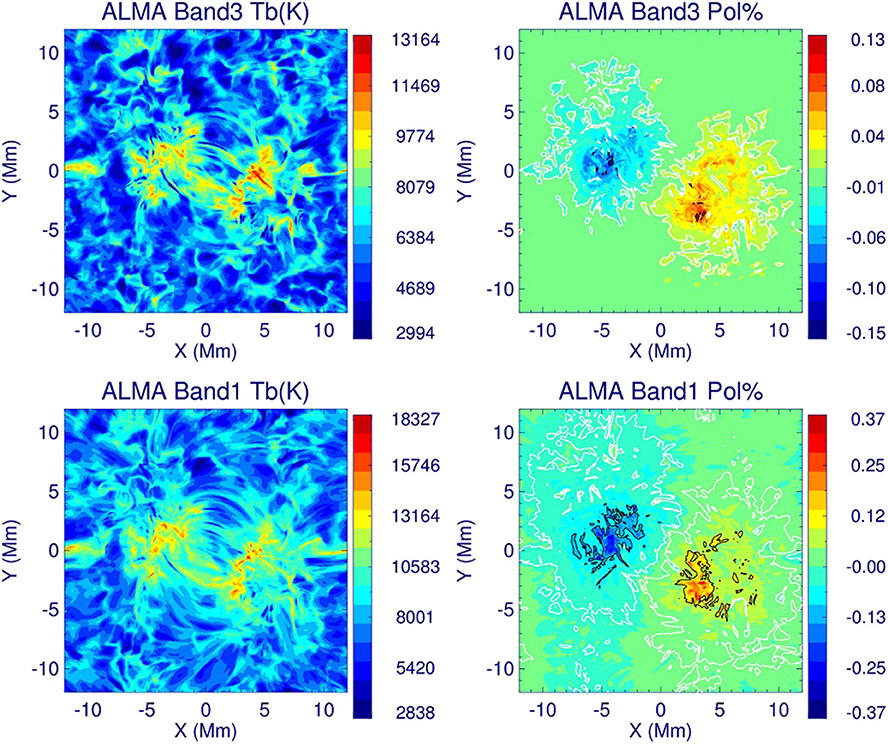
Figure 4. Maps of simulated total brightness (left) and circular polarization degree (right) at the resolution of the ENW dynamic model (0.06″) for ALMA Bands 3 (3 mm) and 1 (8.6 mm). White and black contours indicate the polarization degrees |P| = 0.01% and |P| = 0.1%, respectively.

In Band 3, the simulated brightness temperatures are found in the range from 3,000 to 13,000 K with an average of 6,200 K and a standard deviation of 1,400 K. The values for Band 6 are, respectively, from 2,600 to 12,000 K with an average of 5,000 K and a standard deviation of 1,000 K. In Band 1, the brightness varies from 2,800 to 18,300 K with an average of around 8,200 K. The heights corresponding to the ALMA frequency bands range from about 750 km (Band 9) to 2,000 km (Band 1, see below for the details). Interestingly, in the ALMA commissioning data, the average temperatures at ALMA Bands 3 and 6 were found to be at 7,300 and 5,900 K, respectively (White et al., 2017), which is significantly higher than the values obtained from the ENW simulations.

As can be seen from the maps of simulated circular polarization degree for ALMA Bands 3 and 1, shown in Figure 4, the simulated polarization on an absolute scale is quite low, not reaching 0.5% for the longest Band 1, and being only 0.15% in Band 3. Higher polarization degree is found in the regions of enhanced brightness due to steeper temperature gradients at these locations, as well as at the locations of strong magnetic field, which causes stronger separation of the formation heights of the two modes. However, these degrees of polarization are obtained on the absolute temperature scale, while the interferometer measures only brightness temperature contrast (the absolute brightness difference between the two polarizations in K) across the solar atmosphere, which means that measured interferometer polarization will be actually about 10 times larger than the degrees of polarization on the absolute temperature scale, leading to about 1.5% at Band 3 and 5% at Band 1. More details of the measuring the solar polarization with ALMA are given in the next section, but for a detailed discussion, please refer to Loukitcheva et al. (2017). The authors stated that although the estimated polarization is quite low, it is higher than the technical requirement for ALMA circular polarization measurements, which is defined as 0.1%, implying that the ALMA interferometer can be employed to measure solar polarization.

Examples of the reconstruction of the magnetic field from the estimated circular polarization degree and the local brightness spectrum are shown in Figure 5 for individual spatial locations, and the results of the reconstruction for Band 3 and Band 1 in the form of the 2D maps together with the comparison with the model field are given in Figure 6. The restored chromospheric magnetic field lies in the range from −100 to 100 G, and there is a good general correlation between the restored values of the magnetic field and the model field taken at the heights where emission at corresponding frequency is formed. Thus, within the regions where unsigned polarization degree exceeds 0.01%, the relative error does not exceed 10%, and the model and restored fields agree reasonably well, although the restored field is on average systematically underestimated (Figure 6). The latter might be due to the fact that the restored field corresponds to the average over the heights contributing to the radiation.

FIGURE 5

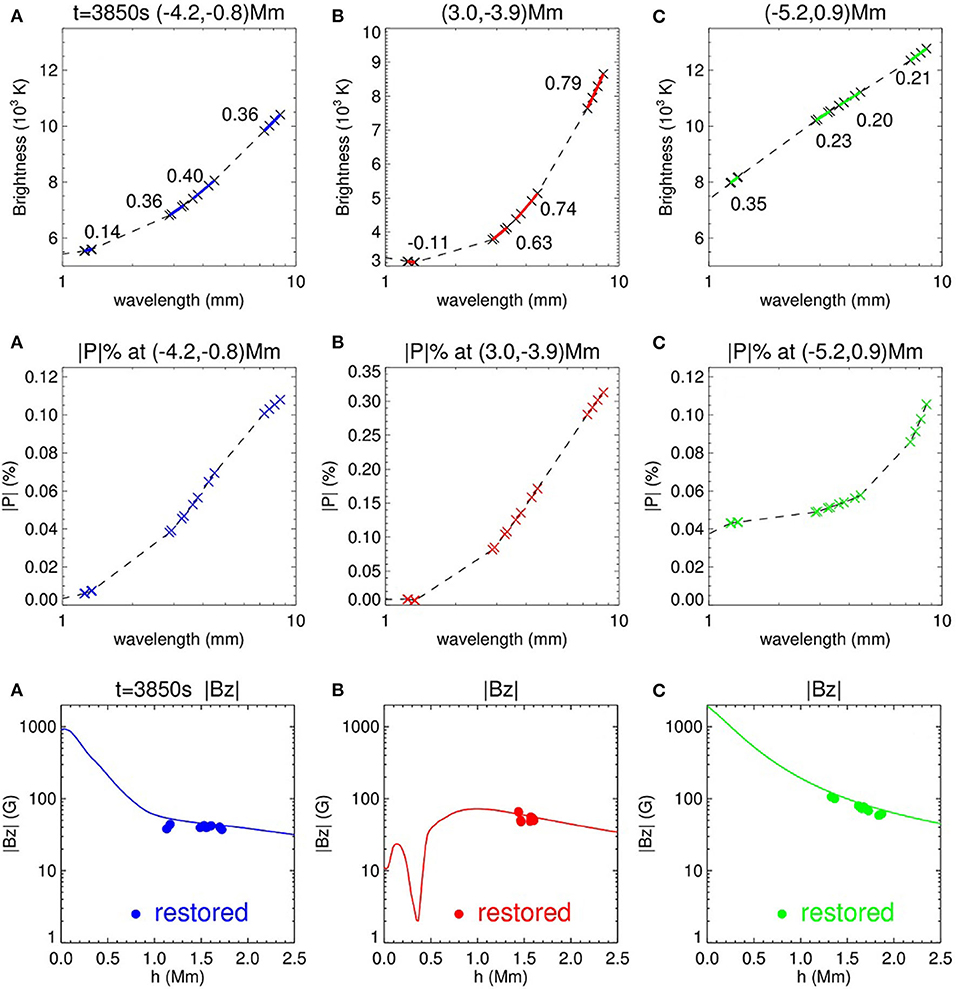
Figure 5. The demonstration of the method for three individual spatial locations within the ENW snapshot. (Top) Simulated total brightness spectrum at mm wavelengths for spatial locations (A) (−4.2, 0.8) Mm, (B) (3.0, −3.9) Mm, and (C) (−5.2, 0.9) Mm, with colored crosses showing the wavelengths of the four ALMA Bands analyzed in detail. The values of the local slope n are given for each band. (Middle) Absolute value of simulated circular polarization degree as a function of wavelength for the same spatial locations and bands. (Bottom) Absolute value of the model longitudinal magnetic field as a function of height plotted together with the values of the magnetic field (circles) derived from the mm brightness spectrum and polarization degree plotted at the effective formation heights of the mm radiation.

FIGURE 6

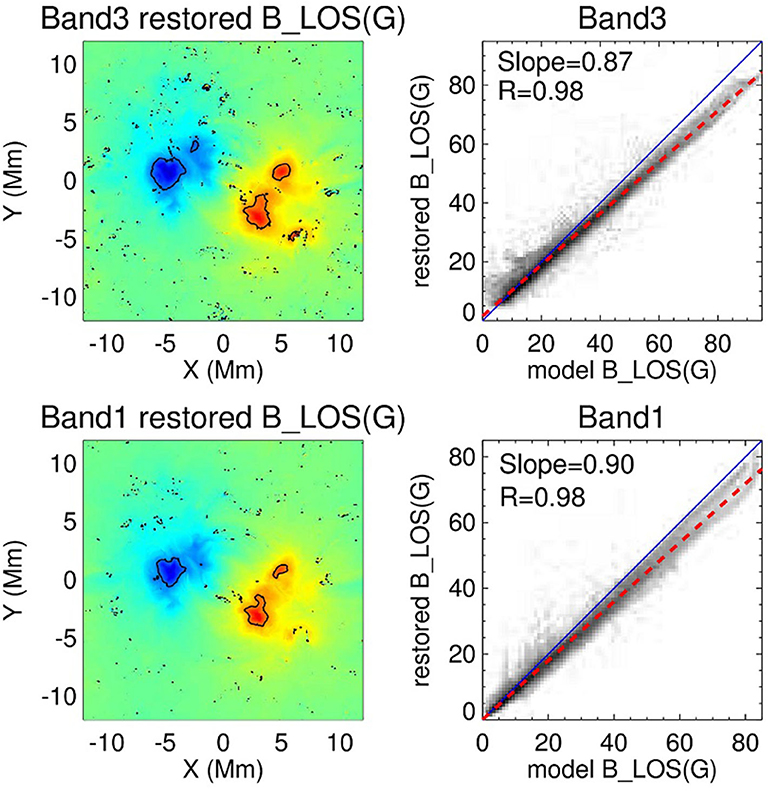
Figure 6. (Left) Maps of the restored longitudinal component of the magnetic field at ALMA Bands 3 and 1, plotted in the range from −100 to 100 G. Black contours depict |B_l| = 50 G. (Right) Restored longitudinal magnetic field vs. model field taken at the effective formation heights plotted in the form of the density plots (2D histograms). Darker shading indicates a higher density of pixels in the bin. Solid lines denote the expectation value, when restored field is equal to the model field. Dashed lines depict the linear regressions with the slopes and the Pearson correlation coefficients given in the upper left corner of each frame.

Loukitcheva et al. (2017) concluded that the method is applicable to measurements of weak chromospheric magnetic field in the QS (and stronger fields in active regions), providing the estimate of the longitudinal component of the field at the effective height of formation. From the simulations, it follows that robust application of this technique might require sensitivity in circular polarization better than 0.1%. The simulated degrees of polarization are further reduced, when the effect of instrumental smearing is taken into account, yielding for Band 3 interferometer observations at a resolution of 1″ polarization smaller than 1% and even lower values at higher frequency bands, implying the importance of the observations in the lower frequency Bands 1 and 2 for reliable polarization measurements in the QS. All in all, the method was found to reproduce the longitudinal magnetic field quite well with the model data. However, realistic ALMA polarization measurements are required for practical estimations of the potential measurements of the magnetic field with ALMA.

Heights of Formation of mm Emission in the Quiet Chromosphere

The individual heights of formation of the ALMA Bands can vary significantly as the local values of electron density and temperature, as well as the steepness of their gradients, which mainly define the location of the optically thick layer, vary in space and time. But in general, the effective formation heights of the mm continuum increase with height and are located around the height of the temperature minimum at the highest frequencies and in the upper chromosphere and transition region at the lowest ALMA frequencies. For instance, average (effective) formation heights for both natural modes, derived from the forms of the contribution functions, which describe how much of the emergent radiation is contributed over height, for Bands 3 and 1 are around 1,600 and 2,000 km above the photosphere, respectively. An overview of the heights of the radiation at different ALMA Bands can be seen in Figure 7 in the form of the histograms of the effective formation heights for the extraordinary mode at Bands 9, 6, 3, 2, and 1, taken for all spatial locations within the ENW model snapshot. The formation heights of the ordinary mode are similar, with the maximum difference between the effective formation heights of the two individual modes not exceeding 4 km for the longest Band 1 (Loukitcheva et al., 2017). Note that this height difference refers to the width of the layer where the magnetic field is measured. The distributions are seen to be quite wide, with a significant overlap between the frequency bands. There also seems to be a tendency for the effective height range to get wider with wavelength, which implies that the diversity of individual height distributions of electron temperature and density gets more pronounced with height. All in all, the increase of the effective heights with wavelength allows ALMA to observe different chromospheric layers and get access to the magnetic fields at different heights by tuning the wavelength. As was discussed in section Method for Magnetic Field Estimate, ALMA can extend its coverage to coronal heights, when observing bremsstrahlung emission from the coronal condensations.

FIGURE 7

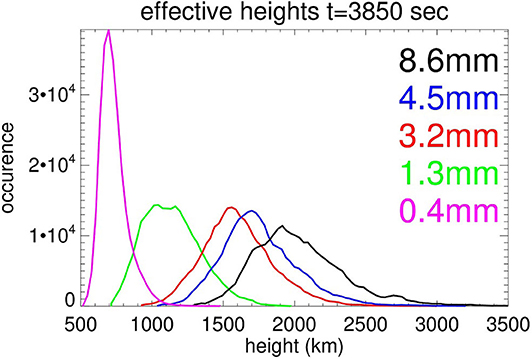
Figure 7. Histograms of the effective heights of formation of the radiation in the ALMA Bands 1 (8.6 mm, plotted in black), 2 (4.5 mm, blue), 3 (3.2 mm, red), 6 (1.3 mm, green), and 9 (0.4 mm, magenta) for all spatial locations within the ENW model snapshot.

Polarization and Magnetic Field in AR

In active regions, the observed values of circular polarization are typically higher than the values reported in the previous section for the QS. Thus, degrees of circular polarization in the range from about 1 to 4% were detected in an active region by Kundu and McCullough (1971) at a wavelength of 9 mm. Similar polarization degrees in active regions, ranging from 1–3% at Band 3 to 5–6% at Band 1 were obtained in Loukitcheva et al. (2017), where the authors studied simulated circular polarization at ALMA frequencies using two sets of umbral models with the magnetic field simulated by a vertical dipole located under the photosphere (e.g., Zlotnik, 1968). Fleishman et al. (2015) simulated the radio emission from AR 12158 at the ALMA frequencies using the 3D modeling tool GX Simulator (Nita et al., 2018), which take into account not only free–free emission but also gyroresonance emission. Their findings are also in line with the results reported in Loukitcheva et al. (2017). Higher values of polarization degree in AR can be explained by stronger magnetic field in sunspots than in the QS and also by steeper gradients of temperature in umbral atmosphere, resulting in higher values of brightness spectrum slopes. For active regions, the magnetic fields restored using the discussed above method are found to be in a general agreement with the model fields (Loukitcheva et al., 2017). Another example of successful restoration of magnetic fields in active regions from polarized radio emission using the model atmosphere by Mok et al. (2005) is given in Gary and Hurford (2004) in the context of the future FASR polarization measurements.

ALMA Polarization Measurements

The ALMA receivers are sensitive to linear polarization. Consequently, observations are carried in two orthogonal linear polarizations (X and Y) by using a wave-splitting device and then the data are correlated using the 64-input correlator to obtain the four cross-correlation visibilities XX, YY, XY, and YX. The relation between these cross-correlations and the Stokes parameters are given by Remijan et al. (2019):

$\begin{array}{l}I=\frac{XX+YY}{2},Q=\frac{XX-YY}{2},U=\frac{XY+YX}{2},V=\frac{XY-YX}{2i},\\ \text{and circular polarization }P=\frac{V}{I}.\end{array}$

The wave-splitting operation produces a residual projection from one polarization into the other, which is called the instrumental polarization or D-terms. Additionally, there exist a relative delay between the X and Y polarizations (the cross-polarization delay), and a phase bandpass between the XY and YX cross-correlations (the XY-phase). The latter is especially crucial for circular polarization measurements, as XY-phase error can cause spurious Stokes V. To account for all these effects, ALMA needs to observe an unresolved strongly polarized source for a certain time (for about 3 h) to cover a sufficient set of parallactic angles (Cortes et al., 2016).

The use of linearly polarized feeds in ALMA receivers is, in fact, an advantage for the precise measurement of circular polarization. As can be seen from above, amplitude gain differences between linear polarizations X and Y do not affect circular polarization, as the latter is determined only from the cross-correlations XY and YX. For the Sun, there is also an additional advantage that Faraday rotation sweeps out linear polarization, resulting in XX = YY. For high-precision circular polarimetry, it is required to measure the instrumental polarization leakage (of linear into circular) terms, which are typically stable in time. In practice, degrees of circular polarization as low as 0.01% can be measured with linearly polarized feeds (Rayner et al., 2000).

The first full-polarization ALMA observations within Science Verification campaign were performed in July 2014 of a bright compact radio quasar 3C 286 (Nagai et al., 2016). Since the last ALMA cycle (Cycle 6), full-polarization mode is available at ALMA (Warmels et al., 2018). Commissioning and science verification of measuring circular polarization with ALMA was based on the observations of the two objects, the SiO maser emission at 86 GHz toward VY-CMA and Band 3 mapping of the highly circularly polarized star HR5907 (V1040 Sco) (Cortes et al., 2019). It was demonstrated that ALMA can detect circular polarization with an estimated error of 0.6% for on-axis observations within 1/10 of the primary beam FWHM, for both narrow-band spectroscopy and wide-band continuum modes. The minimum detectable degree of circular polarization was 1.8% of the peak flux. As the reported level of accuracy is for on-axis measurements, the circular polarization imaging is currently restricted to within 1/10 of the FWHM to avoid beam squint effects (Remijan et al., 2019). However, improving accuracy for circular polarization is one of the capabilities prioritized for Cycle 9. The reported restrictions complicate the use of ALMA for solar polarization measurements, as for the observational targets like the solar chromosphere, we need to measure polarization across the entire FOV. In this case, careful measurement of the beam patterns of the two polarizations independently is required to account for the variations in the circular polarization measurement fidelity within the primary beam. While the absence of the solar disk component from the interferometer data provides larger degrees of polarization and therefore better measurements of circular polarization, The interpretation of polarization measurements, including their conversion into degrees of polarization on the absolute scale, will not be trivial and will additionally require measurements of the disk component, as for obtaining accurate brightness temperature spectrum, the brightness temperatures at each frequency need to be on the same relative scale. First ALMA solar polarization tests were run at the end of 2019 and the obtained data are currently being analyzed. This will be followed by commissioning and science verification phases. In case the solar cycle will grant a suitable observational target during 2020 for completing the commissioning efforts, ALMA might offer a new truly exciting capability of solar polarization measurements already for ALMA Cycle 9 starting in 2021.

Concluding Remarks

This chapter presented a particular case of measuring the magnetic field at the chromospheric heights from the thermal free–free observed at the mm wavelengths in the light of the future circular polarization measurements with ALMA. Radio observations offer a powerful and diversified diagnostic of chromospheric and coronal magnetic fields. In particular, being applied to multi-wavelength mm data, or being combined with magnetic field measurements from atomic lines, high-precision observations of the polarized emission with ALMA should be able to provide a 3D picture of the longitudinal component of the chromospheric magnetic field. Based on the results presented here, magnetic field measurements in active regions will clearly be feasible. Regarding such measurements for the quiet Sun regions, given ALMA's high sensitivity, they will be possible once ALMA achieves the planned 0.1% polarization accuracy for extended sources.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Part of the work was supported by Russian RFBR Grant No. 18-29-21016.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research on the potential use of ALMA for the solar polarization measurements was done in collaboration with Stephen White and Sami K. Solanki. The author acknowledges Dr. Tatyana Kaltman and Dr. Kazumasa Iwai for sharing the results of their work. The work was performed within the SAO RAS state assignment in the part Conducting Fundamental Science Research.

References

Alissandrakis, C. (2020). Structure of the solar atmosphere: a radio perspective. Front. Astron. Space Sci. 7.

Bogod, V. M., and Gelfreikh, G. B. (1980). Measurements of the magnetic field and the gradient of temperature in the solar atmosphere above a flocculus using radio observations. Sol. Phys. 67, 29–46. doi: 10.1007/BF00146680

CrossRef Full Text | Google Scholar

Carlsson, M., De Pontieu, B., and Hansteen, V. (2019). New view of the solar chromosphere. Annu. Rev. Astron. Astrophys. 57, 189–226. doi: 10.1146/annurev-astro-081817-052044

CrossRef Full Text | Google Scholar

Carlsson, M., Hansteen, V., Gudiksen, B. V., Leenaarts, J., and De Pontieu, B. (2016). A publicly available simulation of an enhanced network region of the sun. Astron. Astrophys. 585:A4. doi: 10.1051/0004-6361/201527226

CrossRef Full Text | Google Scholar

Carlsson, M., and Stein, R. F. (1995). Does a nonmagnetic solar chromosphere exist? Astrophys. J. 440:L29. doi: 10.1086/187753

CrossRef Full Text

Casini, R., López Ariste, A., Tomczyk, S., and Lites, B. W. (2003). Magnetic maps of prominences from full stokes analysis of the He I D3 line. Astrophys. J. 598:L67. doi: 10.1086/380496

CrossRef Full Text | Google Scholar

Cortes, P., Hull, C. L. H., Kameno, S., Fomalont, E. B., Le Gouellec, V., Etoh, Yu., et al. (2019). “Current status of ALMA EOC polarization commissioning, past, present, and future,” in ALMA2019: Science Results and Cross-Facility Synergies (Cagliari). doi: 10.5281/zenodo.3585356

CrossRef Full Text | Google Scholar

Cortes, P. C., Girart, J. M., Hull, Ch. L. H., Sridharan, T. K., Louvet, F., Plambeck, R., et al. (2016). Interferometric mapping of magnetic fields: the alma view of the massive star-forming clump W43-MM1. Astrophys. J. Lett. 825:L15.

Google Scholar

de la Cruz Rodríguez, J., and Socas-Navarro, H. (2011). Are solar chromospheric fibrils tracing the magnetic field? Astron. Astrophys. 527:L8. doi: 10.1051/0004-6361/201016018

CrossRef Full Text | Google Scholar

de la Cruz Rodríguez, J., Socas-Navarro, H., van Noort, M., and Rouppe van der Voort, L. (2010). Observation and analysis of chromospheric magnetic fields. Memorie della Societa Astronomica Italiana 81:716.

Google Scholar

De Pontieu, B., Hansteen, V. H., Rouppe van der Voort, L., van Noort, M., and Carlsson, M. (2007). High-resolution observations and modeling of dynamic fibrils. Astrophys. J. 655, 624–641. doi: 10.1086/509070

CrossRef Full Text | Google Scholar

Dulk, G. A. (1985). Radio emission from the sun and stars. Annual Rev. Astron. Astrophys. 23, 169–224. doi: 10.1146/annurev.aa.23.090185.001125

CrossRef Full Text | Google Scholar

Fleishman, G., Loukitcheva, M., and Nita, G. (2015). “Solar ALMA: observation-based simulations of the mm and sub-mm emissions from active regions,” in Revolution in Astronomy with ALMA: The Third Year, Vol. 499, ASP Conference Series, eds D. Iono, K. Tatematsu, A. Wootten, and L. Testi (San Francisco, CA: Astronomical Soc Pacific), 351–352.

Google Scholar

Fleishman, G. D., and Toptygin, I. N. (2013). Cosmic Electrodynamics. New York, NY: Springer. doi: 10.1007/978-1-4614-5782-4

CrossRef Full Text | Google Scholar

Gary, D. E., and Hurford, G. J. (2004). “Radio spectral diagnostics,” in Solar and Space Weather Radio Physics. Current Status and Future Development, Vol. 314, eds D. E. Gary, and C. U. Keller (Dordrecht: Kluwer), 71–87. doi: 10.1007/1-4020-2814-8

CrossRef Full Text | Google Scholar

Gelfreikh, G. B. (2004). “Coronal magnetic field measurements through bremsstrahlung emission,” in Solar and Space Weather Radio Physics. Current Status and Future Development, Vol. 314, eds D. E. Gary, and C. U. Keller (Dordrecht: Kluwer), 115–133.

Google Scholar

Gelfreikh, G. B., and Shibasaki, K. (1999). “Radio magnetography of solar active regions using radio observations,” in Magnetic Fields and Solar Processes. The 9th European Meeting on Solar Physics, ed A. Wilson (Noordwijk: European Space Agency, ESA SP-448), 1339–1343.

Google Scholar

Grebinskij, A., Bogod, V., Gelfreikh, G., Urpo, S., Pohjolainen, S., and Shibasaki, K. (2000). Microwave tomography of solar magnetic fields. Astron. Astrophy. Suppl. 144, 169–180. doi: 10.1051/aas:2000202

CrossRef Full Text | Google Scholar

Grebinskij, A., Bogod, V., Gelfrejkh, G., Shibasaki, K., Fu, Q., and Zhang, H. (1998). Microwave measurements of solar magnetic fields at chromosphere – corona. Astroph. Rep. 4, 101–106.

Google Scholar

Gudiksen, B. V., Carlsson, M., Hansteen, V. H., Hayek, W., Leenaarts, J., and Martínez-Sykora, J. (2011). The stellar atmosphere simulation code Bifrost. Code description and validation. Astron. Astrophys. 531:A154. doi: 10.1051/0004-6361/201116520

CrossRef Full Text | Google Scholar

Hills, R. E., Kurz, R. J., and Peck, A. B. (2010). “ALMA: status report on construction and early results from commissioning, Ground-based and Airborne Telescopes III,” in: Proceedings of the SPIE, Vol. 7733, eds L. M. Stepp, R. Gilmozzi, H. J. Hall, 773317. doi: 10.1117/12.857017

CrossRef Full Text | Google Scholar

Huang, Y. D., Morata, O., Koch, P. M., Kemper, C., Hwang, Y.-J., and Chiong, Ch.-Ch. (2016). “The Atacama Large Millimeter/sub-millimeter Array band-1 receiver,” in Modeling, Systems Engineering, and Project Management for Astronomy VII [99111V] (Proceedings of SPIE - The International Society for Optical Engineering), Vol. 9911, eds P. Dierickx, and G. Z. Angeli (Edinburgh: SPIE).

PubMed Abstract | Google Scholar

Huang, Y. D., Morata, O., Koch, P. M., Kemper, C., Hwang, Y.-J., and Chiong, Ch.-Ch. (2018). “Performance of pre-production band 1 receiver for the Atacama Large Millimeter/submillimeter Array (ALMA),” in SPIE Conf. Ser., Proc. SPIE 10708, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy IX (Austin, TX), 1070833.

Google Scholar

Iglesias, F. A., and Feller, A. (2019). Instrumentation for solar spectropolarimetry: state of the art and prospects. Opt. Eng. 58:082417. doi: 10.1117/1.OE.58.8.082417

CrossRef Full Text | Google Scholar

Iwai, K., and Shibasaki, K. (2013). Measurements of coronal and chromospheric magnetic fields using polarization observations by the Nobeyama radioheliograph. Publ. Astron. Society Jpn. 65:S14. doi: 10.1093/pasj/65.sp1.S14

CrossRef Full Text | Google Scholar

Kallunki, J., Tornikoski, M., Kirves, P., Oinaskallio, E., Aatrokoski, J., Mujunen, A., et al. (2020). Solar polarization observations at 3 and 13 mm. Astronomische Nachrichten 341, 118–124. doi: 10.1002/asna.202013684

CrossRef Full Text | Google Scholar

Kaltman, T. I. (2019). Thermal bremsstrahlung of local sources over solar spots based on microwave observations. Geomagn. Aeronomy 59, 1088–1095. doi: 10.1134/S0016793219080097

CrossRef Full Text | Google Scholar

Kundu, M. R., and McCullough, T. P. (1971). Polarization of solar active regions at 9 millimeter wavelength. Bull. American Astron. Soc. Conf. Proc. 3:449.

Google Scholar

Kuridze, D., Mathioudakis, M., Morgan, H., Oliver, R., Kleint, L., Zaqarashvili, T. V., et al. (2019). Mapping the magnetic field of flare coronal loops. Astroph. J. 874:126. doi: 10.3847/1538-4357/ab08e9

CrossRef Full Text | Google Scholar

Lin, H., Kuhn, J. R., and Coulter, R. (2004). Coronal magnetic field measurements. Astrophys. J. 613, L177–L180. doi: 10.1086/425217

CrossRef Full Text | Google Scholar

López Ariste, A., and Casini, R. (2005). Inference of the magnetic field in spicules from spectropolarimetry of He I D3. Astron. Astrophys. 436, 325–331. doi: 10.1051/0004-6361:20042214

CrossRef Full Text | Google Scholar

Loukitcheva, M., White, S. M., Solanki, S. K., Fleishman, G. D., and Carlsson, M. (2017). Millimeter radiation from a 3D model of the solar atmosphere. II. Chromospheric magnetic field. Astron. Astrophys. 601:A43. doi: 10.1051/0004-6361/201629099

CrossRef Full Text | Google Scholar

Loukitcheva, M. A., White, S. M., and Solanki, S. K. (2019). ALMA detection of dark chromospheric holes in the quiet Sun. Astrophys. J. Lett. 877:L26. doi: 10.3847/2041-8213/ab2191

CrossRef Full Text | Google Scholar

Miyawaki, S.h., Iwai, K., Shibasaki, K., Shiota, D., and Nozawa, S. (2016). Coronal magnetic fields derived from simultaneous microwave and EUV observations and comparison with the potential field model. Astrophys. J. 818:8. doi: 10.3847/0004-637X/818/1/8

CrossRef Full Text | Google Scholar

Mok, Y., Mikić, Z., Lionello, R., and Linker, J. A. (2005). Calculating the thermal structure of solar active regions in three dimensions. Astrophys. J. 621, 1098–1108. doi: 10.1086/427739

CrossRef Full Text | Google Scholar

Nagai, H., Nakanishi, K., Paladino, R., Hull, C. L. H., Cortes, P., Moellenbrock, G., et al. (2016). ALMA science verification data: millimeter continuum polarimetry of the bright radio quasar 3C 286. Astrophys. J. 824:132. doi: 10.3847/0004-637X/824/2/132

CrossRef Full Text | Google Scholar

Nita, G. M., Viall, N. M., Klimchuk, J. A., Loukitcheva, M. A., Gary, D. E., Kuznetsov, A. A., et al. (2018). Dressing the coronal magnetic extrapolations of active regions with a parameterized thermal structure. Astrophys. J. 853:66. doi: 10.3847/1538-4357/aaa4bf

CrossRef Full Text | Google Scholar

Rayner, D. P., Norris, R. P., and Sault, R. J. (2000). Radio circular polarization of active galaxies. MNRAS 319, 484–496. doi: 10.1046/j.1365-8711.2000.03854.x

CrossRef Full Text | Google Scholar

Remijan, A., Biggs, A., Cortes, P. A., Dent, B., Di Francesco, J., Fomalont, E., et al. (2019). ALMA Technical Handbook. ALMA Doc. 7.3, ver. 1.1.

Google Scholar

Rutten, R. J. (2007). “Observing the solar chromosphere,” in The Physics of Chromospheric Plasmas: Proc. of the Coimbra conference, Vol. 368, ASP Conference Series, eds. P. Heinzel, I. Dorotovic, and R. J. Rutten (San Francisco, CA: Astronomical Society of the Pacific), 27–48.

PubMed Abstract | Google Scholar

Schmelz, J. T., Holman, G. D., Brosius, J. W., and Willson, R. F. (1994). Coronal magnetic structures observing campaign. III. Coronal plasma and magnetic field diagnostics derived from multiwaveband active region observations. Astrophys. J. 434:786. doi: 10.1086/174781

CrossRef Full Text | Google Scholar

Shevgaonkar, R. K., and Kundu, M. R. (1984). Three-dimensional structures of two solar active regions from VLA observations at 2, 6, and 20 centimeter wavelengths. Astrophys. J. 283, 413–420. doi: 10.1086/162320

CrossRef Full Text | Google Scholar

Shimojo, M., Bastian, T. S., Hales, A., White, S. M., Iwai, K., Hills, R. E., et al. (2017). Observing the Sun with ALMA: high resolution interferometric imaging. Solar Phys. 292, 87–115. doi: 10.1007/s11207-017-1095-2

CrossRef Full Text

Suárez, D. O. (2019). “Polarimetric observations of the Sun,” in Astronomical Polarisation from the Infrared to Gamma Rays, Vol. 460, Astrophysics and Space Science Library, eds R. Mignani, A. Shearer, A. Słowikowska, and S. Zane (Cham: Springer Nature Switzerland AG), 147–172. doi: 10.1007/978-3-030-19715-5_6

CrossRef Full Text | Google Scholar

Wang, S., Jenkins, J. M., Martinez Pillet, V., Beck, C., Long, D. M., Prasad Choudhary, D., et al. (2020). Magnetic structure of an erupting filament. Astrophys. J. 892:75. doi: 10.3847/1538-4357/ab7380

CrossRef Full Text | Google Scholar

Warmels, R., Biggs, A., Cortes, P. A., Dent, B., Di Francesco, J., Fomalont, E., et al. (2018). ALMA Technical Handbook, ALMA Doc. 6.3, ver. 1.0.

Wedemeyer, S., Bastian, T., Brajša, R., Hudson, H., Fleishman, G., Loukitcheva, M., et al. (2016). Solar science with the Atacama Large Millimeter/Submillimeter Array - a new view of our Sun. Space Sci. Rev. 200, 1–73. doi: 10.1007/s11214-015-0229-9

CrossRef Full Text | Google Scholar

White, S. M., Iwai, K., Phillps, N. M., Hills, R. E., Hirota, A., Yagoubov, P., et al. (2017). Observing the Sun with ALMA: fast-scan single-dish mapping. Solar Phys. 292, 88–115. doi: 10.1007/s11207-017-1123-2

CrossRef Full Text

Wiegelmann, T., Thalmann, J., and Solanki, S. K. (2014). The magnetic field in the solar atmosphere. Astron. Astroph. Rev. 22:78. doi: 10.1007/s00159-014-0078-7

CrossRef Full Text | Google Scholar

Wootten, A., and Thompson, A. R. (2009). The atacama large millimeter/submillimeter array. Proc. IEEE 97, 1463–1471. doi: 10.1109/JPROC.2009.2020572

CrossRef Full Text | Google Scholar

Yagoubov, P., Mroczkowski, T., Belitsky, V., Cuadrado-Calle, D., Cuttaia, F., Fuller, G., et al. (2020). Wideband 67-116 GHz receiver development for ALMA band 2. Astron. Astroph. 634:A46. doi: 10.1051/0004-6361/201936777

CrossRef Full Text | Google Scholar

Zheleznyakov, V. V. (1996). Radiation in Astrophysical Plasmas. Dordrecht: Kluwer Academic Publisher. doi: 10.1007/978-94-009-0201-5

CrossRef Full Text | Google Scholar

Zlotnik, E. Y. (1968). Theory of the slowly changing component of solar radio emission. I. Soviet Astron. 12:245.

Google Scholar