Indirect Measurements of n- and p-Induced Reactions of Astrophysical Interest on Oxygen Isotopes

Observations of abundances and isotopic ratio determinations in stars yield powerful constraints on stellar models. In particular, the oxygen isotopic ratios are of particular interest because they are affected not only by nucleosynthesis but also by mixing processes, which are not very well-understood yet. This review is focused on the measurements via the Trojan Horse Method (THM) that have been carried out to investigate the low-energy cross sections of proton and neutron-induced reactions on ¹⁷O as well as the proton-induced reaction on ¹⁸O, overcoming extrapolation procedures and enhancement effects due to electron screening. The (p,α) reactions induced on these oxygen isotopes are of paramount importance for the nucleosynthesis in a number of stellar sites, including red giants (RGs), asymptotic giant branch (AGB) stars, massive stars, and classical novae. In detail, the indirect measurement of the low-energy region of ¹⁷O(p,α)¹⁴N was performed. The strength of the narrow resonance at 65 keV was evaluated, and it was used to renormalize the corresponding resonance strength in the ¹⁷O+p radiative capture channel. The reaction rate was then evaluated for both the ¹⁷O(p,α)¹⁴N and the ¹⁷O(p,γ)¹⁸F reactions, and significant differences of 30 and 20% with respect the literature data were found, respectively, in the temperature range relevant for RG, AGB, and massive stars nucleosynthesis. Regarding the ¹⁸O(p,α)¹⁵N reaction, the strength of the 20 keV resonance was extracted, which is the main contribution to the reaction rate for astrophysical applications. This approach has allowed us to improve the data accuracy of a factor 8.5, as it is based on the measured strength instead of educated guesses or spectroscopic measurements. Finally, the ¹⁷O(n,α)¹⁴C reaction was studied because of its role during the s-process nucleosynthesis as a possible neutron poison reaction. This study represents the extension of THM to resonant neutron-induced reactions. In this measurement, the subthreshold level centered at −7 keV in the center-of-mass system, corresponding to the 8.039 MeV ¹⁸O excited level, was observed. Moreover, the THM measurements showed a clear agreement with the available direct measurements and the additional contribution of the 8.121 MeV ¹⁸O level, strongly suppressed in direct measurements because of its l = 3 angular momentum. The contributions of those levels to the total reaction rate were than evaluated for future astrophysical applications.

1. Introduction

In recent years, the Trojan Horse Method (THM) has been used to investigate the low-energy cross sections of proton-induced reactions on A = 17 and A = 18 oxygen isotopes, overcoming extrapolation procedures and enhancement effects due to electron screening. The (p,α) reactions induced on these oxygen isotopes are, indeed, related to various open questions in astrophysics: the relative abundances of the oxygen isotopes have been observed at the surface of some Red Giant (RG) stars (Dearborn, 1992) and hundreds of presolar grains found in meteorites are composed of oxides with laboratory measured isotopic compositions (Zinner, 2014).

In particular, the ¹⁷O+p reactions are of paramount importance for the nucleosynthesis in a number of stellar sites, including RGs, asymptotic giant branch (AGB) stars, massive stars, and classical novae. The ¹⁷O(p,α)¹⁴N and ¹⁷O(p,γ)¹⁸F reactions govern the destruction of ¹⁷O and the formation of the short-lived radio-isotope ¹⁸F, which is of special interest for gamma ray astronomy (Hernanz et al., 1999; José and Hernanz, 2007). At temperatures typical of the above-mentioned astrophysical scenario, T = 0.01–0.1 GK for RGs, AGB, and massive stars and T = 0.1–0.4 GK for classical nova explosions, the ¹⁷O(p,α)¹⁴N cross section is expected to be dominated by a resonance at E_c.m. = 65 keV, corresponding to the E_X(J^π) = 5.673 MeV (1⁻) level in ¹⁸F. A sub-threshold level at E_X(J^π) = 5.605 MeV (1⁻) could also play a significant role in the reaction rate both through its high-energy tail and because of possible interference effects with the 5.673 MeV level. Other states that could be involved in the stellar reaction rates are the E_X(J^π) = 5.603 MeV (1⁺) level, bound only by 3 keV against proton decay, and the E_X(J^π) = 5.786 MeV (2⁻) level for high-temperature processes, corresponding to the E_c.m. = 183 keV resonance in the ¹⁷O(p,α)¹⁴N and ¹⁷O(p,γ)¹⁴N reactions (Hernanz et al., 1999; José and Hernanz, 2007).

Regarding the ¹⁸O(p,α)¹⁵N reaction, it is of primary importance to pin down the uncertainties affecting present-day models of AGB stars that are the observationally confirmed astrophysical scenarios for fluorine nucleosynthesis. The ¹⁸O(p, α)¹⁵N is the main ¹⁵N production channel, which is then burnt to ¹⁹F by means of the ¹⁵N(α,γ)¹⁹F radiative capture during thermal pulses that arise in the ⁴He-rich intershell region of AGB stars at temperatures of the order of 10⁸ K. However, the observed abundances of ¹⁹F (Jorissen et al., 1992) are in clear discrepancy with the theoretical predictions because the largest ¹⁹F abundances cannot be justified for the typical ¹²C/¹⁶O values (Lugaro et al., 2004). Nine resonances are present, at least, in the ¹⁸O(p,α)¹⁵N cross section in the 0–1 MeV energy range, which is the most relevant to astrophysics. However, only a few of them, those at 20, 144, and at 656 keV strongly influences the reaction rate (Angulo et al., 1999). Though these resonances have been directly studied by many authors (Mak et al., 1978; Lorenz-Wirzba et al., 1979) and have been subject of spectroscopic investigations (Yagi et al., 1962; Schmidt and Duhm, 1970; Wiescher et al., 1980; Champagne and Pitt, 1986), the reaction rate for the ¹⁸O(p, α)¹⁵N reaction is still affected a sizeable uncertainty (Angulo et al., 1999) at astrophysical energies. This is especially true for the 20 keV resonance, whose strength is known from spectroscopic studies carried out using the transfer reaction ¹⁸O(³He, d)¹⁹F (Champagne and Pitt, 1986) and the radiative capture reaction ¹⁸O(p, γ)¹⁹F (Wiescher et al., 1980). Because of the experimental and optical potentials uncertainties, the deduced reaction rate is affected by unpredictable uncertainties, owing to the model dependence affecting the spectroscopic factors. Also, the error on the resonance energy is exponentially contributing to the uncertainty on the reaction rate, making the investigation of the 20 keV resonance of high importance (Champagne and Pitt, 1986). Regarding the other influential resonances, the one at 143.5 keV is fairly well-established (Lorenz-Wirzba et al., 1979). The broad resonance at 656 keV, which strongly contributes both at low and high temperatures, has, however, a total width that is not as well known (La Cognata et al., 2008b), and, consequently, a poorly known corresponding contribution to the reaction rate.

Finally, in the case of the ¹⁷O(n,α)¹⁴C reaction, its importance is two-fold, first in nuclear reactors and second in many astrophysical scenarios. With regards to the nuclear reactor, the neutron-induced reactions on ¹⁴N or ¹⁷O are the dominant sources of the radioactive isotope ¹⁴C (T_1/2 = 5730 yr), thus constituting a dangerous possible contaminant for life, because it is carcinogenic (Yim and Caron, 2006). In massive stars (M>8M_⊙), it is considered as a neutron poison for the weak component of the s-process since it may reduce the total neutron flux (Käppeler et al., 2011). On the other hand, ¹⁷O can experience also the (α,n) reaction, thus re-injecting the captured neutrons into the nucleosynthesis path. Therefore, it is of key importance to fix the (α,n) to (n,α) cross section ratios to determine the net neutron flux for the s-process. Direct measurements of ¹⁷O(n,α)¹⁴C reaction cross section have shown the population of the two excited states at energies 8,213 and 8,282 keV and the influence of the sub-threshold level at 8,038 keV, while no evidence for the 8,125 keV level is present. Indeed, as this resonance is populated in the f-wave, its contribution is suppressed by the centrifugal barrier penetrability (Ajzenberg-Selove, 1987).

In this paper we report on the indirect studies of the ¹⁷O(p,α)¹⁴N, ¹⁸O(p,α)¹⁵N, and ¹⁷O(n,α)¹⁴C reactions via the Trojan Horse method by applying the approach developed for extracting the strength of narrow resonances at ultra-low energies. Moreover, the strength of the 65 keV resonance in the ¹⁷O(p,α)¹⁴N reaction, measured by means of the THM, is used to renormalize the corresponding resonance strength in the ¹⁷O+p radiative capture channel and in the ¹⁷O(p,γ)¹⁸F reaction-rate evaluation.

2. The Trojan Horse Method

The THM is an indirect technique for determining bare nucleus cross sections of astrophysical interest. It allows the measurement of a binary reaction a + x → c + d of astrophysical interest for which direct measurements require the use of the extrapolation procedure to reach the relevant Gamow peak energy region (Spitaleri et al., 2011, 2016, 2019; Tribble et al., 2014) and references therein. In the last decades, the THM gave a relevant contribution to solve several problems, varying from pure nuclear physics to nuclear astrophysics. In recent past, an extension of the THM pointed out the ability of the method to overcome also the centrifugal barrier, measuring the bare nuclear cross section in neutron induced reactions (Gulino et al., 2010, 2013; Guardo et al., 2017, 2019). In addition, a brand new application of the method demonstrated the possibility to measure astrophysical relevant reaction cross section involving radioactive ion beams (Cherubini et al., 2015; Pizzone et al., 2016; La Cognata et al., 2017), with clear consequences in shedding light on research of neutron-induced reaction with unstable beams, usually tricky to perform with direct experiments (Lamia et al., 2019).

The direct reaction mechanism approach is the basic theory of the THM, having its background in the research of the Quasi Free (QF) reaction mechanism (Baur, 1986; Zadro et al., 1989; Calvi et al., 1990). Essentially, in this kind of direct reactions, an impinging nucleus may cause during the interaction a break-up of the target (or likewise of the projectile). A schematic description of the THM is reported in Figure 1, where choosing an opportune reaction a + A → c + d + s (with the target A characterized by a strong x ⊕ s cluster configuration) induced at energies well above the Coulomb barrier the selection of the QF contribution grants to measure the relevant a(x, c)d two-body reaction cross section (Shapiro, 1967). The appropriate adopted energy allows to avoid Coulomb barrier, centrifugal barrier, and electron screening effects in the TH yield of the a + x → c + d reaction. A precise selection of peculiar kinematical conditions ensures that the QF process represents the dominant process, while other ones, such as re-scattering among the emerging products, can be neglected (Shapiro, 1967). In this framework (called pole approximation), the s-cluster of the nucleus A does not take part on the a + x → c + d virtual reaction, where the projectile a interacts only with the x-cluster (participant).

FIGURE 1

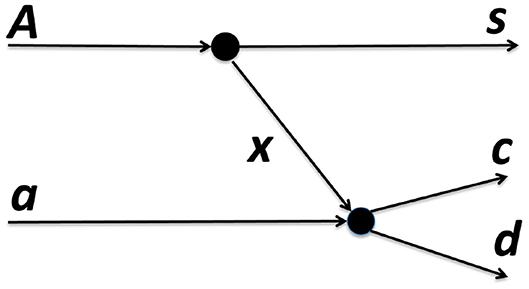
Figure 1. The quasi-free (QF) a + A → c + d + s reaction described by a pole diagram (see text for details). The upper pole represents the breakup of the nucleus A into its cluster x and s. In this description, the x nucleus is called participant of the binary reaction a(x, c)d (lower pole), while the s particle flies away without taking part to the reaction (spectator).

The prescriptions of the impulse approximation (IA) establish that the a+A → c+d+s reaction cross section is related to the a+x → c+d two-body one (Chew, 1952) and in particular, applying the simple Plane Wave Impulse Approximation (PWIA), it can be written as (Spitaleri et al., 2011):

$\begin{array}{ll}\frac{d^3\sigma }{d{\Omega }_{c}d{\Omega }_{d}d{E}_c}\propto KF·\mid \varphi (\overrightarrow{p_s}){\mid }^2·{\left(\frac{d\sigma }{d\Omega }\right)}^{HOES}& (1)\end{array}$

where:

• KF is a kinematical factor containing the final state phase-space factor, and it is a function of the masses, momenta, and emission angles of the two detected particles c and d;

• $\varphi (\overrightarrow{p_s})$ is the Fourier transform of the radial wave function $\chi ({\overrightarrow{r}}_{xs})$ of the x − s inter-cluster motion;

• ${\left(\frac{d\sigma }{d\Omega }\right)}^{HOES}$ represents the half-off-energy-shell (HOES) differential cross section for the a(x,c)d reaction, referred to energy in the center-of-mass system E_cm. The latter can be expressed following the post-collision prescription by the relation

$\begin{array}{ll}{E}_{cm}=E_{cd}-Q_{2b}& (2)\end{array}$

where Q_2b is the two-body reaction Q-value and E_cd indicates the c and d nuclei relative energy.

When the lower vertex of Figure 1 proceeds via the a + x → F_i → c + d process showing the population of the i^th resonant state of the F compound nucleus, the a + A reaction can be described using a two steps approach: the stripping a + A → s + F to a resonant state in the compound system F_i, which later decays to the c + d channel (La Cognata et al., 2008a, 2010a; Mukhamedzhanov et al., 2008).

In this case, the TH double differential cross section is composed as reported in Dolinsky et al. (1973), Mukhamedzhanov et al. (2008), and La Cognata et al. (2008a) following the PWIA approach (Dolinsky et al., 1973) for stripping reactions to a resonant state (Dolinsky et al., 1973):

$\begin{array}{ll}\frac{d^2{\sigma }^{TH}}{d{\Omega }_{{\text{k}}_{sF}}d{E}_{cd}}=\frac{1}{2\pi }\frac{{\Gamma }_{cd}(E_{cd})}{{(E_{cd}-E_{R_{cd}})}^2+\frac{1}{4}{\Gamma }^2(E_{cd})}\times \frac{d{\sigma }_{(a+A\to s+F)}}{d{\Omega }_{{\text{k}}_{sF}}},& (3)\end{array}$

where the differential cross section can be written as:

$\begin{array}{l}\frac{\text{d}{\sigma }_{(a+A\to s+F)}}{\text{d}{\Omega }_{{\text{Ok}}_{sF}}}=\frac{{\mu }_{sF}{\mu }_{aA}}{4{\pi }^2}\frac{k_{sF}}{k_{aA}}\frac{1}{{\widehat{J}}_A{\widehat{J}}_a}\\ \begin{array}{l}\times {\displaystyle \sum _{M_F{M}_s{M}_A{M}_a}}|M_{M_F{M}_s;M_A{M}_a}({\text{k}}_{sF},{\text{k}}_{aA}){|}^2\end{array}& (4)\end{array}$

where J_j is the spin of the particle j and M_j its projection. Finally, the transfer reaction amplitude M results as

$\begin{array}{ll}{M}_i\approx \varphi (p_{xs})W_{xA}^{{\text{F}}_i}({\text{p}}_{xA}),& (5)\end{array}$

where ϕ(p_xs) is the Fourier transform of the radial x − s bound-state wave function, p_xs is the x − s relative momentum, while

$\begin{array}{ll}{W}_{xA}^{{\text{F}}_i}({\text{p}}_{xA})=<I_{xA}^{F_i}|V_{xA}|{\text{p}}_{xA}>& (6)\end{array}$

is the form factor for the A + x → F_i process.

The main advantage in the use of the THM is the presence of the transfer reaction amplitude M_i(E) instead of the entrance channel partial resonance width Γ_(ax)i(E_ax). As a consequence, the cross section of the three-body process can be connected to the one for the two-body reaction of interest by evaluating the transfer amplitude M_i(E).

3. The ¹⁷O(p, α)¹⁴N Reaction

The cross section of the ¹⁷O(p,α)¹⁴N reaction has been the subject of several experimental investigations (Brown, 1962; Rolfs and Rodney, 1975; Berka et al., 1977; Kieser et al., 1979; Mak et al., 1980; Landre et al., 1989; Berheide et al., 1992; Blackmon et al., 1995; Angulo et al., 1999; Hannam and Thompson, 1999; Fox et al., 2004, 2005; Chafa et al., 2007; Moazen et al., 2007; Newton et al., 2007; Iliadis et al., 2010; Scott et al., 2012; Di Leva et al., 2014) in the last 50 years, mainly focusing on the 65 and 183 keV resonances showing up in the ¹⁷O-p interaction at astrophysical energies. Although the resonance energy and strength of the 183 keV resonance have been extensively studied by direct measurements, several issues concern the 65 keV and the subthreshold resonances parameters. The direct measurements of low-lying resonance strengths such as of the 65 keV peak are, in fact, very difficult because of the Coulomb barrier. Therefore, large uncertainties are present in the available direct data (see Sergi et al., 2015 for more details). In 2006, we therefore started a campaign of measurements to investigate the contribution of the 65 keV resonance to the reaction rate of the ¹⁷O(p,α)¹⁴N by using the indirect THM. Recently, a new direct measurement (Bruno et al., 2016) of the 65 keV resonance strength performed at the Laboratory for Underground Nuclear Astrophysics (LUNA) accelerator has led to an value ωγ = 10.0 ± 1.4_stat ± 0.7_syst neV, a factor of three larger with respect to value obtained by using THM (Sergi et al., 2015). In the following sections we discuss the results of the indirect study of the ¹⁷O(p,α)¹⁴N reaction via the THM by applying the approach recently developed for extracting the strength of narrow resonances at ultra-low energies.

3.1. The Experiment and the Reaction Channel Selection

The experiment was performed at INFN-LNS in Catania (Italy) by using a 41 MeV ¹⁷O beam that hit a 150 μg/cm² CD₂ target fixed orthogonally with respect to the beam axis. In addition, a detailed data analysis was also made on the ¹⁷O+²H experimental data belonging to the NSL experiment (University of Notre Dame, South Bend, Indiana, USA) for studying the ¹⁷O(p,α)¹⁴N reaction, although the NSL experiment was initially devoted to the ¹⁷O(n,α)¹⁴C study (described in detail in section five of the present paper). This approach allowed us to improve the statistics of the experimental data. The angles and the energies of the ejected α and ¹⁴N were detected in coincidence by using an experimental setup, symmetric with respect to the beam axis, which consists of six single-area, resistive-readout position-sensitive silicon detectors (PSDs) with spatial resolution of 0.5 mm. Since the neutron was not detected in these experiments, and its energy and emission angle were reconstructed from the momenta of the detected particles. The PSDs covered the angular ranges (in the laboratory reference system) 5.1° − 10.1° (PSD_1,4), 13.8° − 21.2° (PSD_2,5) and 21.3° − 28.7° (PSD_3,6) in the LNS experiment, and 5.0° − 10.0° (PSD_1,4), 13.1° − 18.1° (PSD_2,5), and 23.8° − 28.8° (PSD_3,6), in the NSL experiment (Figure 2). The forward one (PSD 1) was optimized for ¹⁴N detection, PSDs 2 and 3 were optimized instead for α-particles detection. The other three PSDs (4, 5, and 6) were placed on the opposite side with respect to the beam axis, at symmetrical angles. Two ionization chambers were used as ΔE detectors to discriminate nitrogen from carbon ions, thus allowing for the distinction between the ²H(¹⁷O,α¹⁴N)n and ²H(¹⁷O,α¹⁴C)p channels. After detectors calibration, the first step of the analysis was the identification of the events corresponding to the ²H(¹⁷O,α¹⁴N)n TH reaction. In order to identify the channel of interest and to choose the kinematical conditions where the QF process is dominant, ¹⁴N particles were selected using the standard ΔE-E technique. For these selected events, the experimental Q-value spectrum was reconstructed (Figure 3) and it results in good agreement with the theoretical one (Q_th = −1.033 MeV). The agreement, within the experimental uncertainties, is a signature of a good detector calibration. Events inside the experimental Q-value peak were selected for further analysis.

FIGURE 2

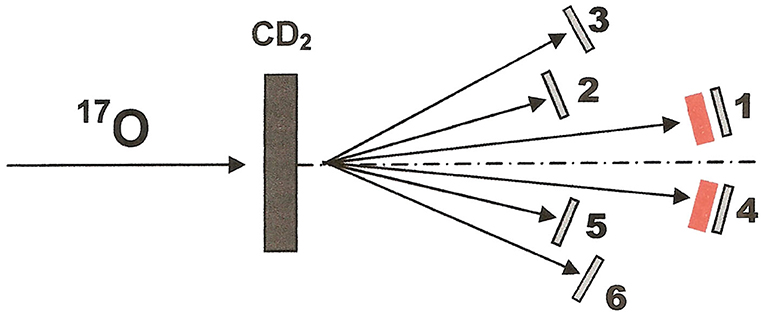
Figure 2. Experimental set-up adopted for the study of the ²H(¹⁷O,α¹⁴N)n reaction. The position of the detectors assures the covering of the QF angular region.

FIGURE 3

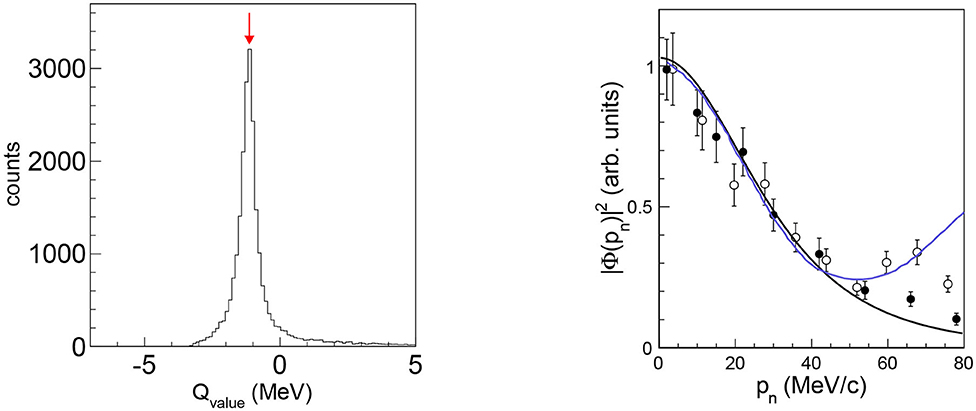
Figure 3. (Left) Experimental Q-value spectrum for LNS experiment. A single peak shows up, centered at about −1.0 MeV, corresponding to the ²H(¹⁷O,α¹⁴N)n channel. The red arrow corresponds to the theoretical Q-value, Q_th = −1.033 MeV. Similar spectrum was obtained for the ND experimental data. (Right) Experimental momentum distribution (full dots for LNS experiment and empty dots for NSL experiments) compared with the theoretical one given by the squared Hulthén wave function in momentum space (black line) and the one given in terms of a DWBA calculation performed via the FRESCO code (blue line). The error bars include only statistical errors.

3.2. Reaction Mechanism Selection

After the three-body reaction selection, the identification of the different reaction mechanisms is a crucial step in the data analysis. In fact, the application of THM are possible only under the assumption that particle s, namely the neutron, acts as a spectator to the A − x interaction (QF-condition). A standard way to investigate the reaction mechanisms is the study of the experimental momentum distribution, this quantity being very sensitive to the reaction mechanism. By selecting a narrow E_c.m. relative energy window, ΔE = 100 keV, at the top of the 183 keV resonant peak where the differential two-body cross section of the ¹⁷O-p reaction can be considered to be almost constant (Spitaleri et al., 2004), the experimental neutron momentum distribution is obtained in arbitrary units by inverting Equation (1):

$\begin{array}{ll}|\varphi ({\overrightarrow{p}}_n){|}^2\propto \left[\frac{d^3\sigma }{d{\Omega }_{\alpha }d{\Omega }_{{\text{}}^{14}\text{N}}d{E}_{c.m.}}\right]·{\left[KF\right]}^{-1},& (7)\end{array}$

Figure 3 shows the experimental momentum distributions $|\varphi ({\overrightarrow{p}}_n){|}^2$ for the LNS data (solid black line) and for the NSL data (empty circle). The black line corresponds to the square of the Hulthén function in momentum space, representing the shape of the n-p momentum distribution inside the deuteron in the PWIA, while the blue line represents the DWBA distribution evaluated by means of the FRESCO code (Thompson, 1988). In DWBA calculation the optical potential parameters adjusted from the Perey and Perey compilation (Perey and Perey, 1976) were adopted. The good agreement, within $|{\overrightarrow{p}}_n|\le$ 30 MeV/c, between the two theoretical approaches and the experimental data, means that the QF mechanism is present and dominant in the considered ${\overrightarrow{p}}_n$ range. For this reason the narrower 0–30 MeV/c momentum range was chosen for the next analysis.

3.3. Results: Cross Section and Reaction Rate Evaluation

The resulting ²H(¹⁷O,α ¹⁴N)n reaction cross section is shown in Figure 4 as full dots for both the LNS (Figure 4A) and the NSL experiments (Figure 4B). The vertical error bars include only the statistical error (about 20%) while the horizontal ones the data bin width. The solid line represents the incoherent sum of the three Gaussian functions (dashed lines) used to fit the resonant behavior and of the first-order polynomial (dot-dashed straight line) used to fit the combinatorial background. The fits were performed to extract the parameters describing the resonance top values, the peak values N_i of the two resonances (N₁ for the 65 keV resonance and N₂ for the 183 keV resonance) with their statistical errors. In case of narrow resonance, the N_i peak values are connected to the resonance strengths (ωγ)_i (Rolfs and Rodney, 1988) of the ¹⁸F levels, which are the key parameters to evaluate the reaction rate for astrophysical applications.

$\begin{array}{ll}{(\omega \gamma )}_i=\frac{1}{2\pi }{\omega }_i{N}_i\frac{{\Gamma }_{{(p^{17}\text{O})}_i}(E_{R_i})}{{\sigma }_{R_i}(\theta )},& (8)\end{array}$

where ω_i = $(2J_{{\text{}}^{18}{\text{F}}_i}+1)/[(2J_{{\text{}}^{17}\text{O}}+1)(2J_p+1)]$ (i = 1, 2) is the statistical factor, ${\Gamma }_{{(p^{17}O)}_i}(E_{R_i})$ is the partial widths for the p + ¹⁷O → ¹⁸F_i channel leading to the population of the ith excited state in ¹⁸F and σ_Ri(θ) the direct transfer reaction cross section for the binary reaction ¹⁷O + d → ¹⁸F_i + n populating the ith resonant state in ¹⁸F with the resonance energyE_Ri. Since we did not measure the absolute value of the cross section, the absolute strength of the resonance at 65 keV (ωγ)₁ was obtained from the ratio between the N₁ and N₂ peak values through the relation (La Cognata et al., 2010a; Sergi et al., 2010)

$\begin{array}{ll}{(\omega \gamma )}_1=\frac{{\omega }_1}{{\omega }_2}\frac{{\Gamma }_{{(p^{17}\text{O})}_1}}{{\sigma }_{R_1}(\theta )}\frac{{\sigma }_{R_2}(\theta )}{{\Gamma }_{{(p^{17}\text{O})}_2}}\frac{N_1}{N_2}{(\omega \gamma )}_2.& (9)\end{array}$

where (ωγ)₂ is the strength of 183 keV resonance, which is well-known from the literature. In particular, the adopted value for (ωγ)₂ is (1.67 ± 0.07) × 10⁻³ eV, obtained by the weighted average of the four strength values reported in literature (Chafa et al., 2007; Moazen et al., 2007; Newton et al., 2007; Iliadis et al., 2010). The resulting weighted average for the two measurements ${(\overline{\omega \gamma })}_1^{THM}$=(3.42 ± 0.60) × 10⁻⁹ eV is in good agreement with the strength given by NACRE, ${(\omega \gamma )}_N=(5.5_{-1.5}^{+1.8})\times 10^{-9}$ eV (Angulo et al., 1999) and with the direct value, (ωγ)_D = (4.7 ± 0.8) × 10⁻⁹ eV calculated by using the same Γ_p and Γ_α reported in Chafa et al. (2007) and Iliadis et al. (2010), namely, Γ_α = 130 eV (Mak et al., 1980), and Γ_p = 19 ± 3 neV (Hannam and Thompson, 1999; Fox et al., 2005). The results of the THM measurement and the strengths of the low-energy resonances are summarized in Table 1.

FIGURE 4

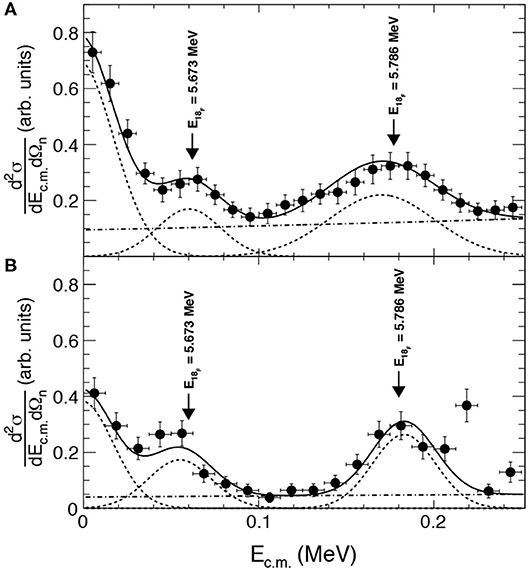
Figure 4. Cross section of the ²H(¹⁷O, α¹⁴N)n TH reaction (full circles) for the LNS (A) and NSL (B) experiments. See text for more details.

TABLE 1

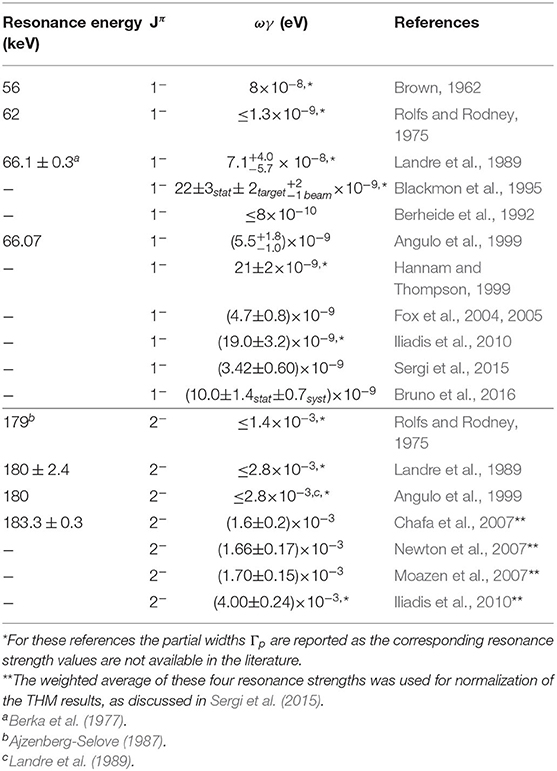
Table 1. Summary table of the strengths of the low-energy resonances in the ¹⁷O(p, α)¹⁴N astrophysical factor.

In the application of Equation (9), it is worth noting that the presence of the Γ/σ double ratio makes it possible to strongly reduce the model dependence of the THM resonance strength. This is due to a number of reasons: (i) since the same spectroscopic factor would appear in both the partial width and the transfer cross section, it cancels out so the corresponding single particle quantities can be used; (ii) the same p+¹⁷O single particle wave function enters the calculation of both Γ and σ, so their ratio reduces the sensitivity on the potential well; (iii) the dependence on the other potentials used in the evaluation of the transfer cross sections is also reduced thanks to the normalization procedure, leading to the appearance of the ratio of the transfer cross sections for two nearby resonances. A more detailed discussion can be found in La Cognata et al. (2010a).

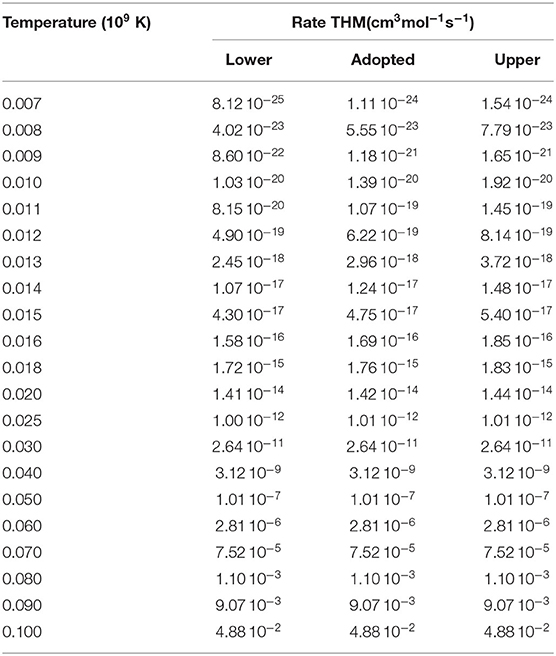
In the calculation of the ¹⁷O(p,α)¹⁴N reaction rate, we followed the method based on Monte Carlo technique adopted in Iliadis et al. (2010). The interference effects between the 65 and the −1.64 keV and between the 183 and 1,202 keV were also evaluated, resulting smaller than 1% in the temperature range between 0.02 and 0.07 GK, where the ¹⁷O(p,α)¹⁴N reaction rate is dominated by the 65 keV resonance. Thus, the total reaction rate $N_A{\langle \sigma v\rangle }_{tot}^{THM}$ was calculated using the following equation:

$\begin{array}{l}{N}_A{\langle \sigma v\rangle }_{tot}^{THM}=N_A{\langle \sigma v\rangle }_{tot}^{Iliadis}-N_A{\langle \sigma v\rangle }_{65}^{Iliadis}\\ \begin{array}{l}+N_A{\langle \sigma v\rangle }_{65}^{THM},\end{array}& (10)\end{array}$

where $N_A{\langle \sigma v\rangle }_{tot}^{Iliadis}$ is the total reaction rate calculated in Iliadis et al. (2010).

Figure 5 (left panel) shows the ratio (red middle line) between the reaction rate R extracted here by Equation (10) and the reaction rate R_Iliadis (Iliadis et al., 2010). The red area of Figure 5, instead, marks the reaction-rate interval allowed by the experimental uncertainties on the 65 keV resonance strength only. The blue area is used to display the uncertainty range characterizing direct data (Iliadis et al., 2010). A significant variation (~30%) can be seen in the range T₉ = 0.02−0.07, while no significant differences are present at higher temperatures.

FIGURE 5

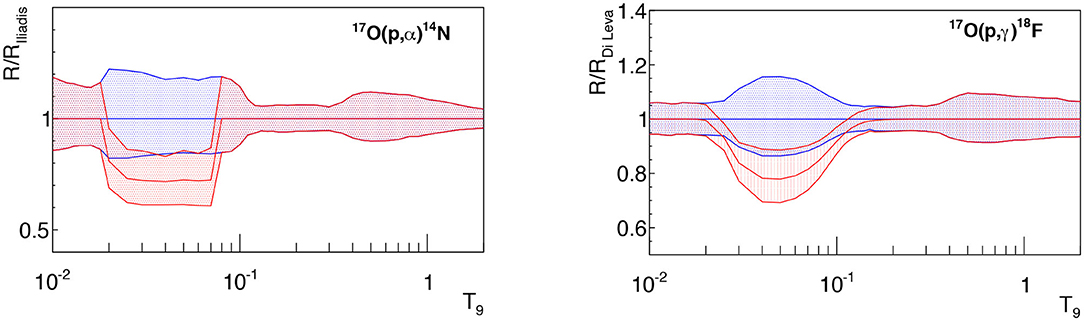
Figure 5. (Left) Comparison of the THM reaction rate of the ¹⁷O(p,α)¹⁴N reaction with the direct one (Iliadis et al., 2010). See text for more details. (Right) Comparison of the THM reaction rate of the ¹⁷O(p,γ)¹⁸F reaction with the direct one (Di Leva et al., 2014). See text for more details.

The definition of the resonance strength (Equation 9) allows us to calculate a new value for the strength of the E_R = 65 keV resonance also in the ¹⁷O(p,γ)¹⁸F channel. By using the following formula

$\begin{array}{ll}{(\omega \gamma )}_{p\gamma }^{THM}={(\omega \gamma )}_{p\alpha }^{THM}\frac{{\Gamma }_{\gamma }}{{\Gamma }_{\alpha }},& (11)\end{array}$

the 65 keV resonance strength in the (p,γ) channel has been evaluated equal to ${\left(\omega \gamma \right)}_{p\gamma }^{THM}$ = (1.18 ± 0.21) × 10⁻¹¹ eV. This obtained value is 39% smaller than the value of (1.6±0.3) × 10⁻¹¹ eV given in literature (Fox et al., 2005; Chafa et al., 2007) and in the most recent reviews (Iliadis et al., 2010; Adelberger et al., 2011). The Γ_γ and Γ_α values used in Equation (11) are those reported in Iliadis et al. (2010). The right panel of Figure 5 shows the ratio (red middle line) of the THM reaction rate to reaction rate evaluation R_DiLeva of Di Leva et al. (2014) (blue line) for the ¹⁷O(p,γ)¹⁸F reaction. The red area marks the reaction-rate interval allowed by the experimental uncertainties on the 65 keV resonance strength only, while the blue area is used to display the uncertainty range characterizing direct data (Di Leva et al., 2014). Also in this case, a significant reduction (~20%) of the reaction rate in the T₉=0.03−0.09 temperature range was obtained due to the THM measurement of the 65 keV resonance strength.

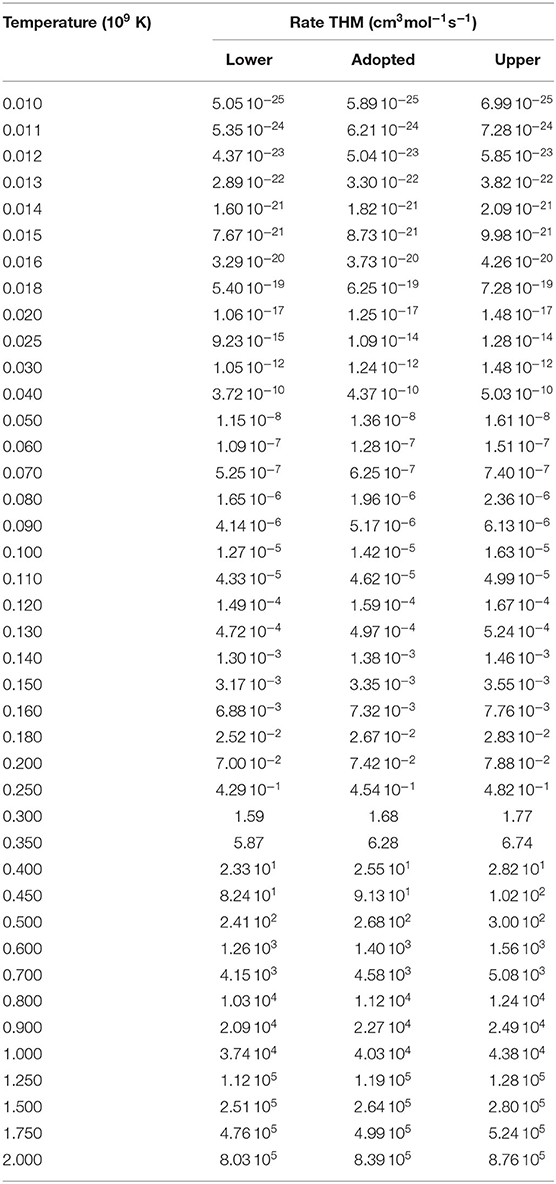
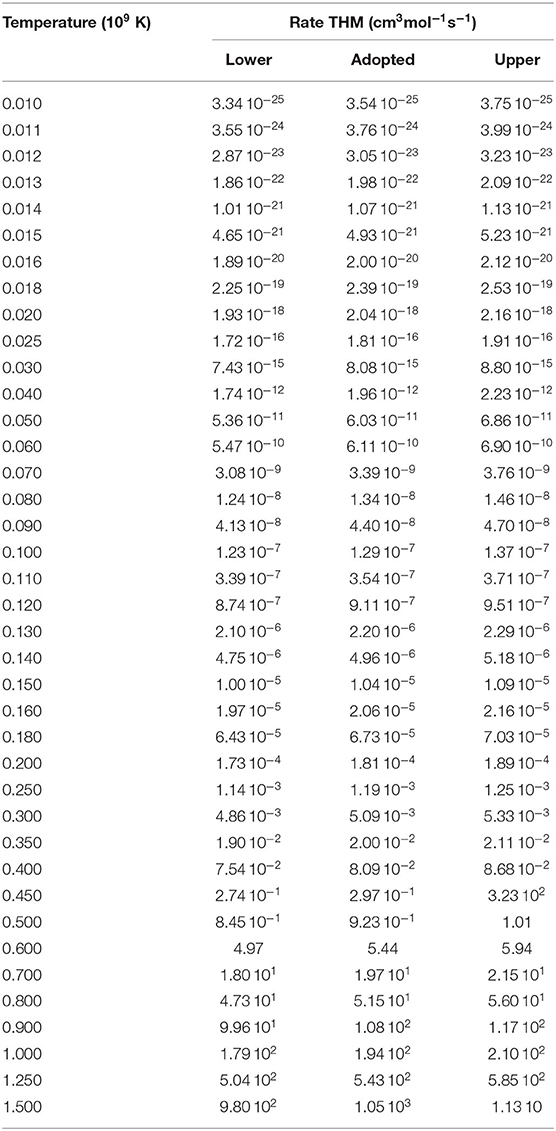
Finally, Tables 2, 3 contains the THM reaction rate together with the upper and lower limits allowed by experimental uncertainties of (p,α) and (p,γ) channels, respectively.

TABLE 2

Table 2. Rate of the ¹⁷O(p, α)¹⁴N reaction.

TABLE 3

Table 3. Rate of the ¹⁷O(p, γ)¹⁸F reaction.

The discrepancy between THM results and the direct data is still under study, especially after the results published by LUNA (Bruno et al., 2016). However, as discussed in Sergi et al. (2015) a possible explanation for the discrepancies between direct and THM results in both (p,α) and (p,γ) channels could be attributable to the electron screening effect that affects direct measurements.

4. The ¹⁸O(p, α)¹⁵N Reaction

As already widely discussed in section 1, even if the cross section of the ¹⁸O(p, α)¹⁵N reaction has been the subject of several experimental investigations in the past, several issues concern the 20 keV resonance. Recently, the work of Bruno et al. (2019) supplied a new direct measurement of the ¹⁸O(p, α)¹⁵N cross section. The authors used the thick target technique to come close to the energy region of astrophysical interest and perform the spectroscopy of ¹⁹F. Though the 20 keV state could not be observed, the authors reported a factor of 10 larger strength for the 90 keV resonance reaching about 1.6 μeV, with respect to existing measurements (Lorenz-Wirzba et al., 1979; La Cognata et al., 2008a, 2010a). Their R-matrix analysis also seems to suggest the occurrence of a previously unaccounted, very broad resonance at about 106 keV (Γ ~ 86 keV). As a result, the reaction rate is enhanced up to a factor of about 2 at about 50 MK, with respect to the one in Iliadis et al. (2010). This makes astrophysical predictions far from conclusive and calls for alternative investigations aiming at reducing uncertainties on nuclear physics inputs. With this in mind, the THM offers the opportunity of an independent investigation right at astrophysical energies, devoid of the need of extrapolation. In detail, the cross section of the ¹⁸O(p, α)¹⁵N reaction is deduced from the ²H(¹⁸O, α¹⁵N)n three-body process, performed in QF kinematics. The beam energy is chosen larger than the Coulomb barrier for the d + ¹⁸O system, so the break-up of the Trojan-horse nucleus, d, takes place inside the ¹⁸O nuclear field. So the ¹⁸O(p, α)¹⁵N HOES process is not suppressed by the Coulomb interaction, and no electron screening is enhancing the astrophysical factor.

4.1. Experimental Investigation

The experiment was performed at Laboratori Nazionali del Sud, Catania (Italy), where the 15 MV Tandem Van de Graaff accelerator delivered a ϕ = 1 mm, 54 MeV ¹⁸O beam, with an average intensity of 5 enA. The experiment target was a 100-μg/cm²-thick self-supported deuterated polyethylene foil (CD₂). The detection setup consisted of a telescope (A), to single out nitrogen isotopes, made up of an ionization chamber and a silicon position sensitive detector (PSD A). On the opposite side with respect to the beam direction, we placed three additional silicon PSD's (B, C, and D) optimized to detect α particles from the ²H(¹⁸O, α¹⁵N)n reaction. The experimental setup is described in La Cognata et al. (2008a); here we underscore that the detector angles were chosen to span the whole QF angular region. After detector calibration, we carried out the reaction channel selection, to pick up the three-body reaction of interest among the several reactions which can take place in the target. Since no particle identification was performed in PSD's B, C, and D and no isotope discrimination was possible in telescope A, the reaction channel selection was performed from the kinematics of the events. Indeed, in a reaction with three particles in the exit channel the events pile up in a well-defined kinematical regions, fixed by the Q-value of the ²H(¹⁸O, α¹⁵N)n reaction. A clear event selection was performed by means of the procedure described in Costanzo et al. (1990), after gating on the ΔE − E 2D spectra to select the nitrogen locus. The deduced kinematic locus of the ²H(¹⁸O,α¹⁵N)n reaction was extracted and compared with the one simulated using a Monte Carlo simulation, showing no additional contribution besides the one of the ²H(¹⁸O, α¹⁵N)n.

Next step was the selection of the QF process. Indeed, direct break-up (DBU) or sequential decay (SD) may populate the reaction channel, besides the QF break up. This was accomplished by studying the $E_{{\text{}}^{15}\text{N}-n}$ and the E_α−n relative energy spectra, to deduce whether excited states from ¹⁶N^* and ⁵He^* contribute to the reaction yield. However, states in ¹⁹F^* could be fed through QF and SD reaction mechanisms, and the experimental neutron momentum distribution was therefore also evaluated. Indeed, a necessary condition for the occurrence of QF break-up is that the ejected neutron keeps the same momentum distribution as inside d, given by the squared Hulthén wave function in momentum space (Lamia et al., 2012). The inspection of the relative energy spectra and of the experimental momentum distribution, as extensively discussed in La Cognata et al. (2010a,c), shows that the QF reaction mechanism is present and dominant in the 0–50 MeV/c neutron momentum range and that the SD of ⁵He, ¹⁶N, and ¹⁹F excited states is negligible in the energy range of astrophysical interest. Additionally, distortions due to the Coulomb interaction in the entrance channel, for instance, turned out to be negligible as in La Cognata et al. (2010b).

Gating on the 0–50 MeV/c neutron momentum range, we extracted the three-body cross section and integrated it over the whole ¹⁸O(p, α)¹⁵N c.m. angular range (see La Cognata et al., 2010a,c for details). In this way, we deduced the ²H(¹⁸O, α¹⁵N)n reaction cross section given in Figure 6. Horizontal error bars in the figure represent the integration bin while the vertical ones stand for statistical uncertainty. The dashed, dotted, and dot-dashed lines in the figure are Gaussian fitting of the resonances at E_R1 = 19.5 ± 1.1 keV, E_R2 = 96.6 ± 2.2 keV, and E_R3 = 145.5 ± 0.6 keV, in good agreement with the values reported in the literature (Angulo et al., 1999). The solid line is the sum of three Gaussian functions while the straight line is used to fit the non-resonant behavior. The fitting also allowed us to deduce the peak value of each resonance: N₁ = 138 ± 8, N₂ = 82 ± 9, and N₃ = 347 ± 8 (arbitrary units), which were used to derive the resonance strengths using the formula:

$\begin{array}{ll}{(\omega \gamma )}_i=\frac{2J_{{\text{}}^{19}{\text{F}}_i}+1}{(2J_{{\text{}}^{18}\text{O}}+1)(2J_p+1)}\frac{{\Gamma }_{{(p^{18}\text{O})}_i}{\Gamma }_{{({\alpha }^{15}\text{N})}_i}}{{\Gamma }_i},& (12)\end{array}$

through the equation (La Cognata et al., 2010a):

$\begin{array}{ll}{N}_i=4\frac{{\Gamma }_{{\alpha }_i}(E_{R_i})M_i^2(E_{R_i})}{{\Gamma }_i^2(E_{R_i})},& (13)\end{array}$

where ${\Gamma }_{{({\alpha }^{15}\text{N})}_i}(E)\equiv {\Gamma }_{{\alpha }_i}(E)$. In fact, the transfer amplitude is proportional to the entrance channel reduced width ${\gamma }_{{(p^{18}\text{O})}_i}$, and the N_i factors thus represent the THM resonance strengths in arbitrary units and devoid of Coulomb suppression, the penetration factor P_l(kr) does not appearing in Equation (13). Normalization is then achieved by scaling the THM resonance strengths, corrected to include the Coulomb effects, to the strength of a well-known resonance. Indeed, since the proton and alpha partial widths for the ~ 144 keV resonance are well-known (Angulo et al., 1999), we can determine the absolute values of the strengths of the 20 and 90 keV resonances from normalization to the strength of the ~ 144 keV peak, as discussed by La Cognata et al. (2008a). The normalization is accurate also because electron screening gives a negligible contribution close to 144 keV (4% maximum; Assenbaum et al., 1987). Taking (ωγ)₃ from Becker et al. (1995), we got (ωγ)₁ =$8.3_{-2.6}^{+3.8}\times 10^{-19}$ eV, which is well within the confidence range established by NACRE, $6_{-5}^{+17}\times 10^{-19}$ eV (Angulo et al., 1999), with a much reduced uncertainty, because Angulo et al. (1999) value is based on spectroscopic data while the present result is obtained from experimental ones. The largest contribution to the error is due to the uncertainty on the resonance energy, while statistical and normalization errors sum up to about 9.5%. To cross check the method, we extracted the resonance strength of the 90 keV resonance, which turned out to be (ωγ)₂ = (1.76 ± 0.33) × 10⁻⁷ eV, in good agreement with the Angulo et al. (1999) strength, (1.6 ± 0.5) × 10⁻⁷ eV. The results of the THM measurement and the strengths of the low-energy resonances are summarized in Table 4.

FIGURE 6

Figure 6. Cross section of the ²H(¹⁸O, α¹⁵N)n TH reaction. See text for details.

TABLE 4

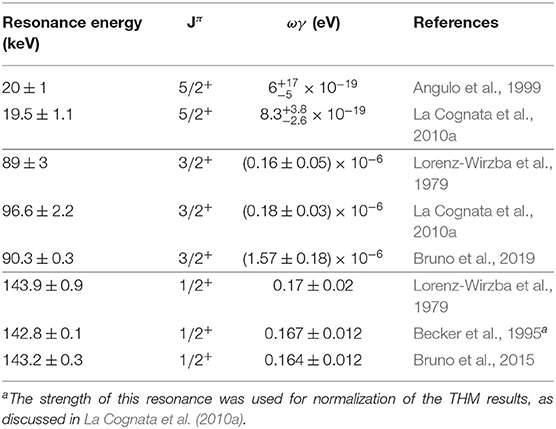
Table 4. Summary table of the strengths of the low-energy resonances in the ¹⁸O(p, α)¹⁵N astrophysical factor.

4.2. Extraction of the Reaction Rate

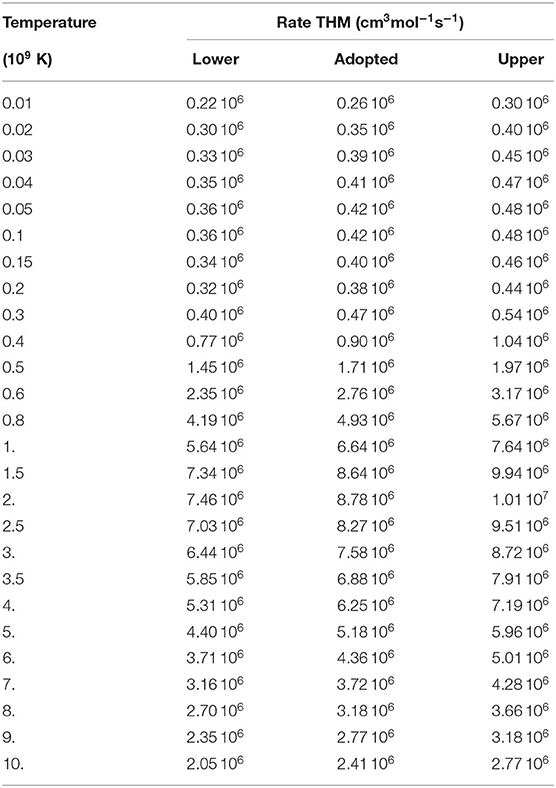
By using the narrow resonance approximation (Angulo et al., 1999), which is satisfied for these resonances at ~ 20, ~ 90, and ~ 144 keV, we calculated the reaction rate for the ¹⁸O(p, α)¹⁵N reaction using the equation:

$\begin{array}{l}{N}_A\langle \sigma v{\rangle }_{R_i}=N_A{\left(\frac{2\pi }{\mu k_B}\right)}^{3/2}\\ \begin{array}{l}{\hslash }^2{\displaystyle \sum _i}{(\omega \gamma )}_i{T}^{-3/2}\text{exp}\left(-E_{R_i}/k_{B}T\right)\end{array}& (14)\end{array}$

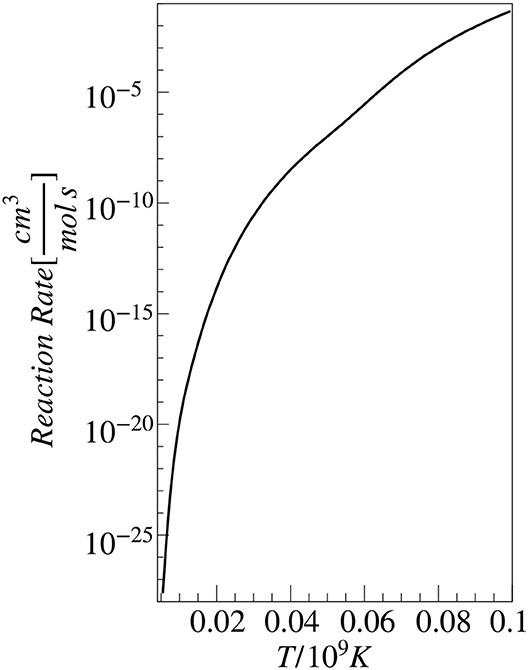
where μ is the reduced mass for the projectile-target system, T is the temperature of the astrophysical site, and the index i runs over the relevant resonances. The resulting rate $R_{{\text{}}^{18}\text{O}{(p,\alpha )}^{15}\text{N}}$ is displayed in Figure 7 as a function of the temperature given in units of T₉ = T/10⁹ K. We also obtained the analytic expression of the reaction rate, with an accuracy of about 10%:

$\begin{array}{l}{R}_{{\text{}}^{18}\text{O}{(p,\alpha )}^{15}N}=\frac{5.58{10}^{11}}{T_9^{2/3}}\\ \text{ exp}\left(-\frac{16.732}{T_9^{1/3}}-{\left(\frac{T_9}{0.51}\right)}^2\right)(1+3.2T_9+21.8T_9^2)\\ +\frac{1.375{10}^{-13}}{T_9^{3/2}}\exp \left(-\frac{0.232}{T_9}\right)\\ +\frac{2.58{10}^4}{T_9^{3/2}}\exp \left(-\frac{1.665}{T_9}\right)\\ +\frac{3.24{10}^8}{T_9^{0.378}}\exp \left(-\frac{6.395}{T_9}\right)& (15)\end{array}$

where the reaction rate $R_{{\text{}}^{18}\text{O}{(p,\alpha )}^{15}\text{N}}$ is expressed in cm³mol⁻¹sec⁻¹.

FIGURE 7

Figure 7. Reaction rate of the ¹⁸O(p, α)¹⁵N reaction.

The next Figure 8 shows the comparison of the present results with the one in the literature, reported in NACRE compilation (Angulo et al., 1999). Owing to the steep slope of the reaction rate, for sake of comparison the ratio of the THM rate to the NACRE one for the ¹⁸O(p, α)¹⁵N is shown. In detail, the full black line is used to show the ratio of the recommended THM reaction rate to the NACRE one, while the dot-dashed and dotted black lines represent the upper and lower limits, respectively, in the same representation. Red lines are instead used, with the same meaning, for the Angulo et al. (1999) reaction rate.

FIGURE 8

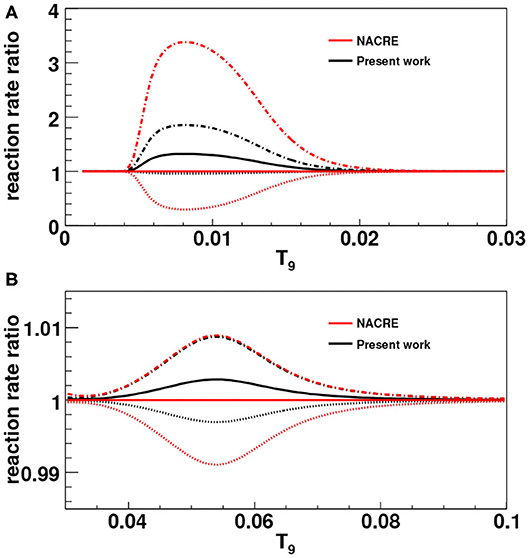
Figure 8. Comparison of the reaction rate of the ¹⁸O(p, α)¹⁵N reaction with the NACRE one (Angulo et al., 1999). In (A), the contribution of the 20 keV resonance is shown; in (B), the one of the 90 keV resonance (the upper limits for the NACRE and present-work rates overlap).

In the low temperature region (below T₉ = 0.03, see Figure 8A) the reaction rate was found to be about 35% larger than the one in NACRE, while the uncertainty is considerably reduced by a factor ≈ 8.5, taking into account the contribution of the 20 keV resonance only. The corresponding temperatures match with those typical of the bottom of the convective envelope, thus an increase of the reaction rate might influence the surface abundances resulting from the cool bottom process (Nollett et al., 2003) in AGB stars. Regarding the 90 keV resonance in the ¹⁸O(p, α)¹⁵N reaction, we confirmed that its contribution is negligible since an increase of <1% was obtained due to the THM measurement, taking as reference the NACRE rate (Figure 8B). Finally, Table 5 contains the THM reaction rate together with the upper and lower limits allowed by experimental uncertainties. In particular, in the inclusion of the uncertainties on the Angulo et al. (1999) reaction rate, it is assumed that the only source of error is coming from the 20 keV resonance.

TABLE 5

Table 5. Rate of the ¹⁸O(p, α)¹⁵N reaction.

5. The ¹⁷O(n, α)¹⁴C Reaction

The ¹⁷O(n, α)¹⁴C reaction has been studied as an extension of the THM to the neutron-induced reactions. This investigation pointed out the ability of the THM to overcome the centrifugal barrier suppression effects in the entrance channel. This study demonstrates the effectiveness of the THM to emphasize the mere nuclear interaction, which avoids the centrifugal suppression or the electron screening effect, thus opening new perspectives in the use of the method for nuclear structure studies. Moreover, as regards the ¹⁷O(n, α)¹⁴C, only few direct measurements are reported in literature, showing discordance at neutron thermal energy range (Sanders, 1956; Koehler and Graff, 1991; Schatz et al., 1993; Wagemans et al., 2002).

In the following section, we discuss the main results of the ¹⁷O(n, α)¹⁴C cross section measurement in the energy range from 0 up to a few hundred keV.

5.1. The Experiment

The ¹⁷O(n,α)¹⁴C reaction has been studied via the three-body ²H(¹⁷O, α¹⁴C)p reaction. The experiment has been performed at NSL of the University of Notre Dame (South Bend, Indiana, USA) using the JN Tandem Van der Graaff. The ¹⁷O beam impinged on a deuterated polyethylene target (CD₂) with an energy of 43.5 MeV. The target thickness was about 150 μg/cm², and the target itself has been placed at 90° with respect to the beam direction. A sketch of the used experimental setup is shown in Figure 9, chosen accordingly with a preliminary study that pointed out the phase-space region where a strong contribution of the QF reaction mechanism is expected.

FIGURE 9

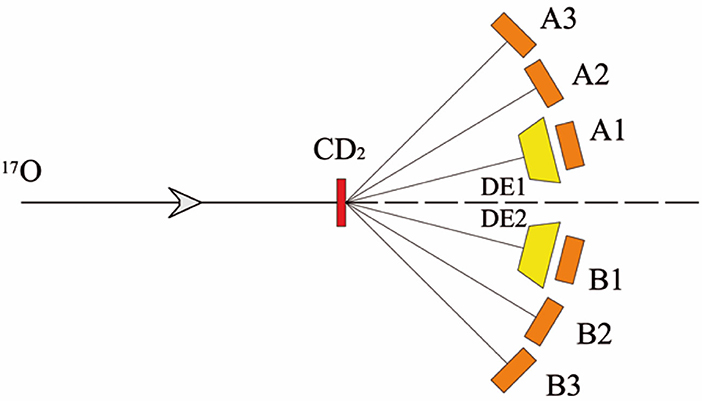
Figure 9. Sketch of the experimental setup. The ¹⁷O beam was impinging on a CD₂ target. The emitted particles were detected by four PSDs (A2, A3, B2, and B3) and by two ΔE-E telescopes (DE1-A1 and DE2-B1).

The detection setup consists of two telescopes, made up of a ionization chamber (IC) as ΔE and a 1,000μm PSD (A1 and B1 in Figure 9) as E stage. The telescopes have been placed at d_A1 = 46.4 cm and d_B1 = 49.5 cm from the target covering and angular range 7.5±2.5°. The ICs have been filled with about 50 mbar isobutane gas allowing to an energy resolution of ~10%, which was enough to discriminate particles by their charge but not their mass. Entrance and exit windows of ICs consist of two thin mylar foils, respectively of 0.9 and 1.5 μm in order to minimize the angular straggling. In addition, four 500μm thick PSDs referred to as A2, A3, B2, and B3 have been employed, placed at a distance d_A2 = 47.6 cm, d_A3 = 38.1 cm, d_B2 = 49.4 cm, and d_B3 = 40.5 cm from the target, covering the angular ranges 17.5° ± 2.5° for A2 and B2 while 27.3° ± 3.5° for A3 and B3. The telescopes have been optimized for C detection while the other PSDs for alpha particles.

Moreover, since the required kinematical conditions are very similar, the presence of the ¹⁷O(n,α)¹⁴C reaction channel was also checked in the LNS experiment optimized for the measurement of the ¹⁷O(p,α)¹⁴N reaction (described in section three of the present paper) (Gulino et al., 2013; Guardo et al., 2017). The good agreement between the two THM measurements, within the experimental uncertainties, allow us to average the two data sets, weighting the respective errors, in order to improve the statistics and data quality.

5.2. Reaction Channel Selection

After detector calibration, the three-body ²H(¹⁷O,α¹⁴C)p reaction channel of interest has been selected. This separation has been accomplished by studying the coincidence events corresponding to a carbon particle detected in one of the two ΔE − E telescopes with any particles on opposite PSDs. The kinematic of the undetected emerging proton has been deduced by means of momentum and energy conservation laws. In left panel of Figure 10, the experimental Q-value spectrum for the selected events is plotted showing a prominent peak, centered at about −0.4 MeV, in good agreement with the expected value of −0.407 MeV, marked by the black vertical arrow. The very low background (≤7% with respect the total statistics) clearly demonstrates that no other reaction channels influence the one of interest. This result represents a signature of a good calibration and a precise selection of the ²H(¹⁷O,α¹⁴C)p reaction channel.

FIGURE 10

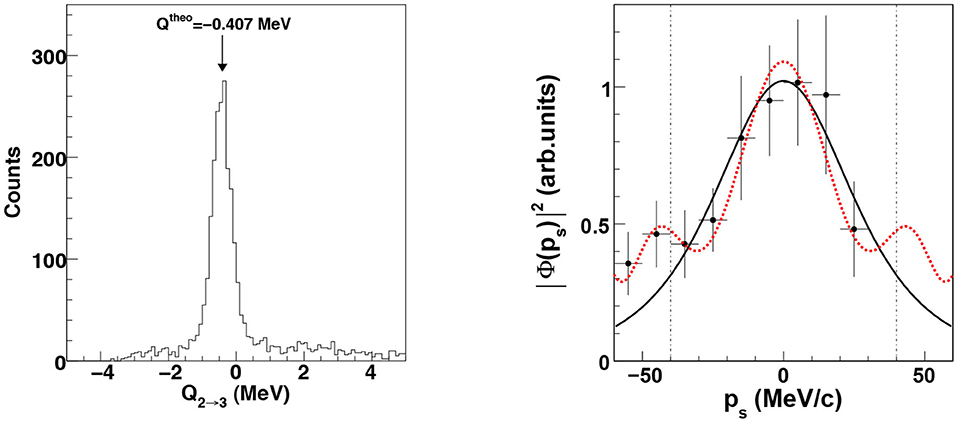
Figure 10. (Left) Reconstructed Q-value spectrum. The theoretical value of −0.407 MeV for the ²H(¹⁷O,α¹⁴C)¹H reaction is reported with the black arrow and it is in good agreement with the experimental peak. (Right) Experimental momentum distribution (full dots) compared with theoretical ones, given by the square of the Hulthén wave function in momentum space (black solid line) and by the DWBA momentum distribution evaluated by means of the FRESCO code (red dotter lines). The agreement is a necessary condition for the presence of the QF-mechanism in the data.

5.3. Selection of the QF Reaction Mechanism

The next essential step for a precise selection of the TH data is a detailed study of the momentum distribution for the p − n intercluster motion in the deuteron. By using the same procedure already described in section 3.2, the experimental proton momentum distribution has been obtained. The comparison between the experimental momentum distribution (black dots) and the theoretical one (black solid line) is shown in the right panel of Figure 10. The present distribution returns an FWHM value of 58±11 MeV/c, in good agreement with the theoretical one of ~60 MeV/c.

Moreover, the experimental data are also compared with the DWBA distribution (red dashed line in Figure 10) evaluated via the FRESCO code (Thompson, 1988) in order to check if the simple PWIA approach gives an accurate description of the p − n momentum distribution. For this calculation, optical potential parameters adjusted from the Perey and Perey (1976) compilation have been adopted. The good agreement, within $|{\overrightarrow{p}}_s|\le$ 40 MeV/c, between DWBA, PWIA, and the experimental data makes us confident that the QF mechanism gives the main contribution to the reaction in the considered p_s range. Finally, the vertical dot-dashed lines mark the position of the selected events for which the TH has been applied.

5.4. Extraction of the Reaction Rate

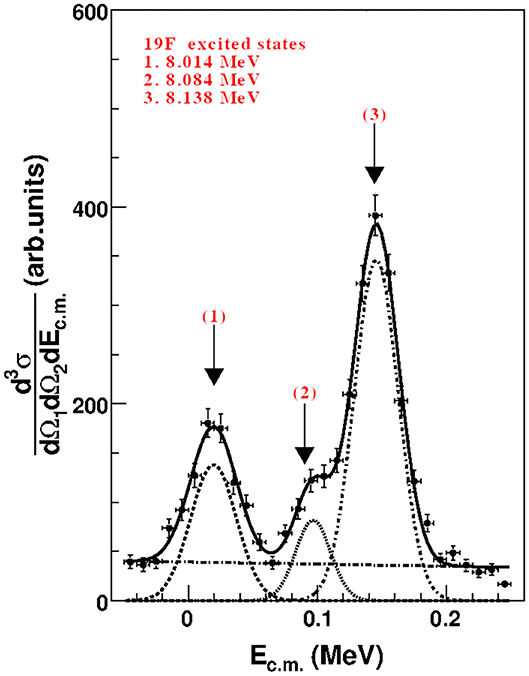
Now that the presence of the QF process is completely ascertained and following the prescription of Equation (1), the two-body cross section can be extracted by dividing the experimental three-body one by the product of the momentum distribution of the spectator inside the Trojan Horse nucleus and the kinematic factor. The result has been corrected for the penetration factor (described in this case in terms of the spherical Bessel and Neumann functions) in order to be compared with direct data and to perform the normalization at high energies, namely, to the well-known resonances at 8,213 and 8,282 keV reported in Wagemans et al. (2002) (see Table 6). This extracted (dσ/dΩ)^HOES as a function of E_cm integrated over the whole θ_cm range (for further information see Gulino et al., 2013) is reported in Figure 11 with black points. The error bars take into account the statistical and angular distribution integration uncertainties. The arrows in Figure 11 indicate four resonances corresponding to ¹⁸O states at 8.039, 8.125, 8.213, and 8.282 MeV (Ajzenberg-Selove, 1987) clearly present in the THM cross section. It is important to underline the presence of the 8,125 keV level (J^π = 5⁻) since its population occurs via f-wave ¹⁷O-n relative motion and consequently is strongly suppressed in the available direct measurements (Wagemans et al., 2002). Hence, this experimental result shows the power of THM for n-induced reactions to extrapolate information about resonant levels that are suppressed in direct measurements due to the presence of the centrifugal barrier. Finally, the experimental data have been fitted following the modified R-matrix approach. The result, for which a reduced χ² of $\tilde{\chi }$ = 0.8 has been found, is displayed in Figure 11 with the solid red line, while the red band accounts for the error introduced by the normalization procedure, evaluated here at about 15% [for a detailed procedure see Guardo et al. (2017) and references therein].

TABLE 6

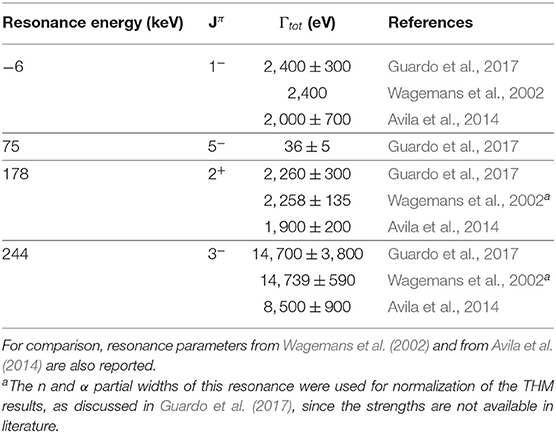
Table 6. Summary table of the ¹⁸O resonance parameters observed in Guardo et al. (2017).

FIGURE 11

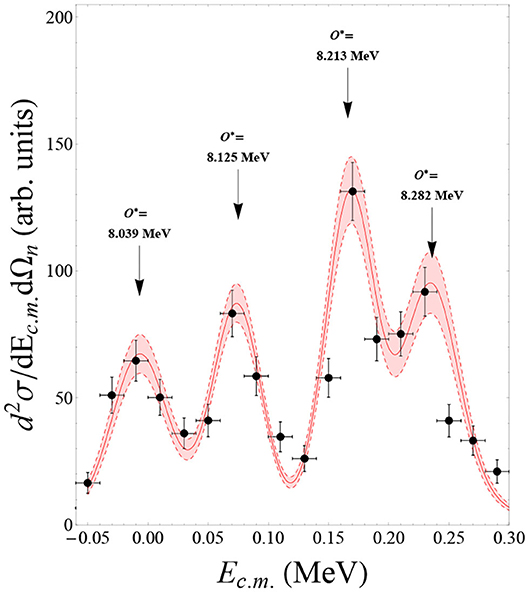
Figure 11. Integrated QF two-body cross section for the ¹⁷O(n,α)¹⁴C reaction in arbitrary units. Experimental data are displayed with black points. The n-¹⁷O relative energy binning are reported with the horizontal error bars, while the vertical ones represent the statistical and integration uncertainties. The red line is the best fit to the data calculated with the modified R-matrix approach.

Figure 12 (left panel) shows the astrophysical rate, calculated from the cross section according to the usual definition (Iliadis et al., 2010). The red band highlights the region allowed by uncertainties (statistical and normalization). The values of the astrophysical rate calculated here is reported in Table 7. In addition, the application of the THM allowed for the first time to excite and disentangle the contribution of the subthreshold level centered at −7 keV in the center-of-mass system. This result is fundamental to determine the total reaction rate at low energies and may change significantly the abundance ratios of the elements involved in the nucleosynthesis network of the weak component of the s-process (Wagemans et al., 2002; Guardo et al., 2017). Indeed, in the right panel of Figure 12, the contribution of the −7 keV resonance state to the total reaction rate is disentangled showing its pivotal importance at astrophysical relevant temperatures (Guardo et al., 2017).

FIGURE 12

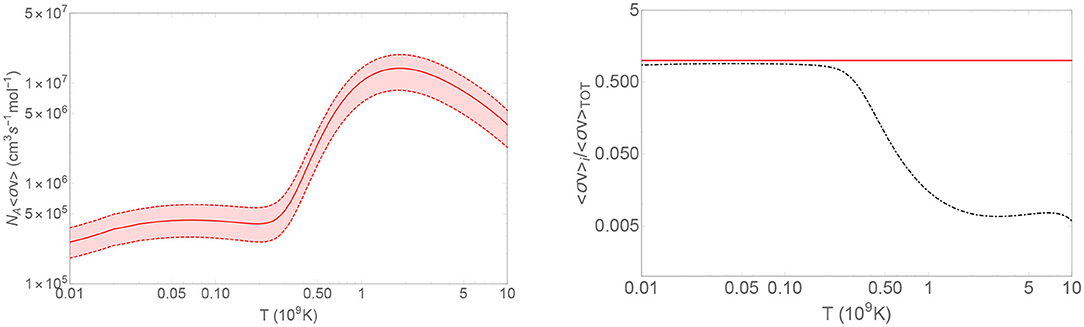
Figure 12. (Left) The experimental TH reaction rate (red line). The red band represents the statistical and normalization errors. (Right) Contribution of the subthreshold resonant state to the total reaction rate.

TABLE 7

Table 7. Rate of the ¹⁷O(n, α)¹⁴C reaction.

6. Final Remarks

In this paper we have discussed the influence of the neutron and proton induced reactions on the stable, neutron-rich oxygen isotopes, ¹⁷O and ¹⁸O.

In detail, we reported on the application of the THM to the QF ²H(¹⁷O, α¹⁴N)n reaction for extracting the ¹⁷O(p, α)¹⁴N cross section and reaction rate, by using the approach for the resonant case discussed in La Cognata et al. (2010a). Two measurements were carried out, at LNS and at NSL, with the main aim of extracting the strength of the 65 keV resonance, laying right at astrophysical energies. By normalizing to the strength of the well-known 183 keV resonance, the THM measurements led to a recommended value of ωγ = 3.42 ± 0.60 × 10⁻⁹ eV, from the weighted average of the results of the two experiments. Such strength was then used to calculate the ¹⁷O(p, α)¹⁴N reaction rate, resulting in an increase of ~ 30% with respect the data in the literature at the temperatures typical of RGs, AGB stars and massive stars (Iliadis et al., 2010). From such result we could also provide a revised value for the strength of the 65 keV resonance in the ¹⁷O(p, γ)¹⁸F reaction, leading to an increase of about 20% with respect to the literature (Di Leva et al., 2014).

In the case of the ¹⁸O(p, α)¹⁵N reaction, we underscore that, for the first time, the strength of the low-lying 20 keV resonance was experimentally determined thanks to the use of the THM. Thanks to this result, the reaction rate was calculated, which turned out to be about 35% larger than the NACRE rate (Angulo et al., 1999) in the temperature region where the effect of the 20 keV resonance is dominant. Since no spectroscopic factor was needed to fix the strength of this state, the reaction rate was determined with high accuracy, reducing the uncertainty due to the modest knowledge of the resonance parameters by a factor ~ 8.5. Moreover, the THM result is not affected by the electron screening, which can enhance the astrophysical factor by a factor larger than about 2.4 at 20 keV (Assenbaum et al., 1987), making any direct measurement of the nuclear cross section presently impossible.

Finally, the same QF reaction, under slightly different kinematic conditions, made also possible to measure the ¹⁷O(n, α)¹⁴C with no need of neutron beams. In detail, it was possible to observe the subthreshold level centered at −7 keV in the center-of-mass system corresponding to the ¹⁸O level at 8.039 MeV, that strongly affects the total reaction rate. Also, since the THM approach allows us to bypass the Coulomb and centrifugal barriers, we could observe the 8.121 MeV ¹⁸O level that, having a spin parity J^π=5⁻ is suppressed in direct measurements because of it is populated in f-wave. Therefore, we could obtain an accurate experimental trend of the ¹⁷O(n, α)¹⁴C cross section over the whole range of astrophysical interest, up to about 250 keV, in good agreement with the results available in the literature (where present). Then the recommended reaction rate was calculated, combining the results of the THM measurement and the direct data of Wagemans et al. (2002) above ~ 100 keV, leading to an increase of the rate over the whole temperature range of interest, with potential consequences for the weak component of the s-process.

Author Contributions

Nuclear data of ¹⁷O(p, α)¹⁴N and ¹⁸O(p, α)¹⁵N were analyzed by MS and ML, respectively, and GG and MG took care of the ¹⁷O(n, α)¹⁴C data analysis. All the listed authors contributed to the writing of the paper.

Funding

This work has been partially supported by the Italian Ministry of University MIUR under Grants No. RFBR082838 (FIRB2008), LNS-Astrofisica Nucleare (fondi premiali). It has been partially supported also by Grants No. LC 07050 of the Czech MSMT, No. M10480902 of the Czech Academy of Science, No. LH1101 of the AMVIS project, and of the GAČR Project under Grant No. P203/10/0310. The Notre Dame collaborators were supported by Grant No. PHY-1713857 and JINA-CEE Grant No. PHY-1430152.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge Alain Coc for his suggestions about the topics discussed in the present article and also Programma ricerca di ateneo UNICT 2020-22 linea2 by University of Catania.

References

Adelberger, E. G., García, A., Robertson, R. G. H., Snover, K. A., Balantekin, A. B., Heeger, K., et al. (2011). Solar fusion cross sections. II. The pp chain and CNO cycles. Rev. Modern Phys. 83, 195–246. doi: 10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Ajzenberg-Selove, F. (1987). Energy levels of light nuclei A = 18-20. Nucl. Phys. A 475, 1–198. doi: 10.1016/0375-9474(87)90205-3

CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 656, 3–183. doi: 10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

Assenbaum, H. J., Langanke, K., and Rolfs, C. (1987). Effects of electron screening on low-energy fusion cross sections. Z. Phys. A Hadron. Nuclei 327, 461–468. doi: 10.1007/BF01289572

CrossRef Full Text | Google Scholar

Avila, M. L., Rogachev, G. V., Goldberg, V. Z., Johnson, E. D., Kemper, K. W., Tchuvil'sky, Y. M., et al. (2014). α-cluster structure of O18. Phys. Rev. C 90:024327. doi: 10.1103/PhysRevC.90.024327

CrossRef Full Text | Google Scholar

Baur, G. (1986). Breakup reactions as an indirect method to investigate low-energy charged-particle reactions relevant for nuclear astrophysics. Phys. Lett. B 178, 135–138. doi: 10.1016/0370-2693(86)91483-8

CrossRef Full Text | Google Scholar

Becker, H. W., Bahr, M., Berheide, M., Borucki, L., Buschmann, M., Rolfs, C., et al. (1995). Hydrogen depth profiling using¹⁸O ions. Z. Phys. A Hadron. Nuclei 351, 453–465. doi: 10.1007/BF01291151

CrossRef Full Text | Google Scholar

Berheide, M., Rolfs, C., Schröder, U., and Trautvetter, H. P. (1992). Search for the 70 keV resonance in¹⁷O(p, α)¹⁴N. Z. Phys. A Hadron. Nuclei 343, 483–487. doi: 10.1007/BF01289827

CrossRef Full Text | Google Scholar

Berka, I., Jackson, K. P., Rolfs, C., Charlesworth, A. M., and Azuma, R. E. (1977). Isospin mixing of the 5605 and 5668 keV states in ¹⁸F in the light of a new state at 5603 keV. Nucl. Phys. A 288, 317–333. doi: 10.1016/0375-9474(77)90138-5

CrossRef Full Text | Google Scholar

Blackmon, J. C., Champagne, A. E., Hofstee, M. A., Smith, M. S., Downing, R. G., and Lamaze, G. P. (1995). Measurement of the ¹⁷O(p,α)¹⁴N cross section at stellar energies. Phys. Rev. Lett. 74, 2642–2645. doi: 10.1103/PhysRevLett.74.2642

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, R. E. (1962). Experimental study of the ¹⁷O(p, α)¹⁴N reaction and a calculation of the rate of this reaction in the CNO cycle in stars. Phys. Rev. 125, 347–358. doi: 10.1103/PhysRev.125.347

CrossRef Full Text | Google Scholar

Bruno, C. G., Aliotta, M., Descouvemont, P., Best, A., Davinson, T., Bemmerer, D., et al. (2019). Improved astrophysical rate for the ¹⁸O(p,α)¹⁵N reaction by underground measurements. Phys. Lett. B 790, 237–242. doi: 10.1016/j.physletb.2019.01.017

CrossRef Full Text | Google Scholar

Bruno, C. G., Scott, D. A., Aliotta, M., Formicola, A., Best, A., Boeltzig, A., et al. (2016). Improved direct measurement of the 64.5 kev resonance strength in the ¹⁷O(p, α)¹⁴N reaction at luna. Phys. Rev. Lett. 117:142502. doi: 10.1103/PhysRevLett.117.142502

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruno, C. G., Scott, D. A., Formicola, A., Aliotta, M., Davinson, T., Anders, M., et al. (2015). Resonance strengths in the ^17,18O(p, α)^14,15N reactions and background suppression underground. Commissioning of a new setup for charged-particle detection at LUNA. Eur. Phys. J. A 51:94. doi: 10.1140/epja/i2015-15094-y

CrossRef Full Text | Google Scholar

Calvi, G., Lattuada, M., Miljanić, D., Riggi, F., Spitaleri, C., and Zadro, M. (1990). Quasi-free reaction mechanism in ²H(⁶Li,³He α)n at E₀ = 21.6-33.6 MeV. Phys. Rev. C 41, 1848–1850. doi: 10.1103/PhysRevC.41.1848

PubMed Abstract | CrossRef Full Text | Google Scholar

Chafa, A., Tatischeff, V., Aguer, P., Barhoumi, S., Coc, A., Garrido, F., et al. (2007). Experimental determination of the ¹⁷O(p, α)¹⁴N and ¹⁷O(p, γ)¹⁸F reaction rates. Phys. Rev. C 75:035810. doi: 10.1103/PhysRevC.75.035810

PubMed Abstract | CrossRef Full Text | Google Scholar

Champagne, A. E., and Pitt, M. L. (1986). The destruction of ¹⁸O in red giants. A search for a sub-threshold resonance in the ¹⁸O + p system. Nucl. Phys. A 457, 367–374. doi: 10.1016/0375-9474(86)90384-2

CrossRef Full Text | Google Scholar

Cherubini, S., Gulino, M., Spitaleri, C., Rapisarda, G. G., La Cognata, M., Lamia, L., et al. (2015). First application of the Trojan horse method with a radioactive ion beam: study of the ¹⁸F(p,α)¹⁵O reaction at astrophysical energies. Phys. Rev. C 92:015805. doi: 10.1103/PhysRevC.92.015805

CrossRef Full Text | Google Scholar

Chew, G. F. (1952). The impulse approximation. Phys. Rev 85:636. doi: 10.1103/PhysRev.85.636

CrossRef Full Text | Google Scholar

Costanzo, E., Lattuada, M., Romano, S., Vinciguerra, D., and Zadro, M. (1990). A procedure for the analysis of the data of a three body nuclear reaction. Nucl. Instrum. Methods Phys. Res. A 295, 373–376. doi: 10.1016/0168-9002(90)90715-I

CrossRef Full Text | Google Scholar

Dearborn, D. S. P. (1992). Diagnostics of stellar evolution: the oxygen isotopes. Phys. Rep. 210, 367–382. doi: 10.1016/0370-1573(92)90080-J

CrossRef Full Text | Google Scholar

Di Leva, A., Scott, D. A., Caciolli, A., Formicola, A., Strieder, F., Aliotta, M., et al. (2014). Underground study of the ¹⁷O(p,γ)¹⁸F reaction relevant for explosive hydrogen burning. Phys. Rev. C 89:015803. doi: 10.1103/PhysRevC.90.019902

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolinsky, E. I., Dzhamalov, P. O., and Mukhamedzhanov, A. M. (1973). Peripheral-model approach to stripping into resonant states. Nucl. Phys. A 202, 97–122. doi: 10.1016/0375-9474(73)90244-3

CrossRef Full Text | Google Scholar

Fox, C., Iliadis, C., Champagne, A. E., Coc, A., José, J., Longland, R., et al. (2004). Explosive hydrogen burning of ¹⁷O in classical novae. Phys. Rev. Lett. 93:081102. doi: 10.1103/PhysRevLett.93.081102

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, C., Iliadis, C., Champagne, A. E., Fitzgerald, R. P., Longland, R., Newton, J., et al. (2005). Thermonuclear reaction rate of ¹⁷O(p, γ)¹⁸F. Phys. Rev. C 71:055801. doi: 10.1103/PhysRevC.71.055801

CrossRef Full Text | Google Scholar

Guardo, G. L., Spitaleri, C., Lamia, L., Gulino, M., La Cognata, M., Tang, X., et al. (2017). Assessing the near threshold cross section of the ¹⁷O(n, α)¹⁴C reaction by means of the Trojan horse method. Phys. Rev. C 95:025807. doi: 10.1103/PhysRevC.95.025807

CrossRef Full Text | Google Scholar

Guardo, G. L., Spitaleri, C., Lamia, L., Spartá, R., Carlin, N., Cherubini, S., et al. (2019). The ¹⁰B(n,α)⁷Li cross sections at ultra-low energy through the Trojan Horse Method applied to the ²H(¹⁰B,α⁷Li)¹H. Eur. Phys. J. A 55:211. doi: 10.1140/epja/i2019-12914-0

CrossRef Full Text | Google Scholar

Gulino, M., Spitaleri, C., Cherubini, S., Crucillá, V., La Cognata, M., Lamia, L., et al. (2010). Study of the ⁶Li(n, α)³H reaction via the ²H quasi-free break-up. J. Phys. G Nucl. Phys. 37:125105. doi: 10.1088/0954-3899/37/12/125105

CrossRef Full Text | Google Scholar

Gulino, M., Spitaleri, C., Tang, X. D., Guardo, G. L., Lamia, L., Cherubini, S., et al. (2013). Suppression of the centrifugal barrier effects in the off-energy-shell neutron +¹⁷O interaction. Phys. Rev. C 87:012801. doi: 10.1103/PhysRevC.87.012801

CrossRef Full Text | Google Scholar

Hannam, M. D., and Thompson, W. J. (1999). Estimating small signals by using maximum likelihood and Poisson statistics. Nucl. Instrum. Methods Phys. Res. A 431, 239–251. doi: 10.1016/S0168-9002(99)00269-7

CrossRef Full Text | Google Scholar

Hernanz, M., José, J., Coc, A., Gómez-Gomar, J., and Isern, J. (1999). Gamma-ray emission from novae related to positron annihilation: constraints on its observability posed by new experimental nuclear data. Astrophys. J. 526, L97–L100. doi: 10.1086/312372

PubMed Abstract | CrossRef Full Text | Google Scholar

Iliadis, C., Longland, R., Champagne, A. E., Coc, A., and Fitzgerald, R. (2010). Charged-particle thermonuclear reaction rates: II. Tables and graphs of reaction rates and probability density functions. Nucl. Phys. A 841, 31–250. doi: 10.1016/j.nuclphysa.2010.04.009

CrossRef Full Text | Google Scholar

Jorissen, A., Smith, V. V., and Lambert, D. L. (1992). Fluorine in red giant stars: evidence for nucleosynthesis. Astron. Astrophys. 261, 164–187.

Google Scholar

José, J., and Hernanz, M. (2007). Nucleosynthesis in classical nova explosions. J. Phys. G 34, R431–R458. doi: 10.1088/0954-3899/34/12/R01

CrossRef Full Text | Google Scholar

Käppeler, F., Gallino, R., Bisterzo, S., and Aoki, W. (2011). The s process: nuclear physics, stellar models, and observations. Rev. Modern Phys. 83, 157–194. doi: 10.1103/RevModPhys.83.157

CrossRef Full Text | Google Scholar

Kieser, W. E., Azuma, R. E., and Jackson, K. P. (1979). The ¹⁷O(p,α)¹⁴N reaction: physics and astrophysics. Nucl. Phys. A, 331, 155–179. doi: 10.1016/0375-9474(79)90307-5

CrossRef Full Text | Google Scholar

Koehler, P. E., and Graff, S. M. (1991). ¹⁷O(n,α)¹⁴C cross section from 25 meV to approximately 1 MeV. Phys. Rev. C 44, 2788–2793. doi: 10.1103/PhysRevC.44.2788

PubMed Abstract | CrossRef Full Text | Google Scholar

La Cognata, M., Pizzone, R. G., José, J., Hernanz, M., Cherubini, S., Gulino, M., et al. (2017). A Trojan horse approach to the production of ¹⁸F in novae. AstroPhys. J. 846:65. doi: 10.3847/1538-4357/aa845f

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Mukhamedzhanov, A., Banu, A., Cherubini, S., Coc, A., et al. (2010a). A novel approach to measure the cross section of the ¹⁸O(p, α)¹⁵N resonant reaction in the 0-200 keV energy range. Astrophys. J. 708, 796–811. doi: 10.1088/0004-637X/708/1/796

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Mukhamedzhanov, A., Goldberg, V., Irgaziev, B., Lamia, L., et al. (2010b). DWBA momentum distribution and its effect on THM. Nucl. Phys. A 834, 658–660. doi: 10.1016/j.nuclphysa.2010.01.116

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., and Mukhamedzhanov, A. M. (2010c). Effect of high-energy resonances on the ¹⁸O(p, α)¹⁵N reaction rate at AGB and post-AGB relevant temperatures. Astrophys. J. 723, 1512–1522. doi: 10.1088/0004-637X/723/2/1512

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Mukhamedzhanov, A. M., Irgaziev, B., Tribble, R. E., Banu, A., et al. (2008a). Measurement of the 20 and 90keV resonances in the ¹⁸O(p,α)¹⁵N reaction via the Trojan horse method. Phys. Rev. Lett. 101:152501. doi: 10.1103/PhysRevLett.101.152501

PubMed Abstract | CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Tribble, R. E., Al-Abdullah, T., Banu, A., Cherubini, S., et al. (2008b). Indirect measurement of the ¹⁸O(p, α)¹⁵N reaction rate through the THM. J. Phys. G Nucl. Phys. 35:014014. doi: 10.1088/0954-3899/35/1/014014

CrossRef Full Text | Google Scholar

Lamia, L., La Cognata, M., Spitaleri, C., Irgaziev, B., and Pizzone, R. G. (2012). Influence of the d-state component of the deuteron wave function on the application of the Trojan horse method. Phys. Rev. C 85:025805. doi: 10.1103/PhysRevC.85.025805

CrossRef Full Text | Google Scholar

Lamia, L., Mazzocco, M., Pizzone, R. G., Hayakawa, S., La Cognata, M., Spitaleri, C., et al. (2019). Cross-section measurement of the cosmologically relevant ⁷Be(n, α)⁴He reaction over a broad energy range in a single experiment. Astrophys. J. 879:23. doi: 10.3847/1538-4357/ab2234

CrossRef Full Text | Google Scholar

Landre, V., Aguer, P., Bogaert, G., Lefebvre, A., Thibaud, J. P., Fortier, S., et al. (1989). ¹⁷O(³He,d)¹⁸F reaction and its implication in the ¹⁷O destruction in the CNO cycle in stars. Phys. Rev. C 40, 1972–1984. doi: 10.1103/PhysRevC.40.1972

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorenz-Wirzba, H., Schmalbrock, P., Trautvetter, H. P., Wiescher, M., Rolfs, C., and Rodney, W. S. (1979). The ¹⁸O(p, α)¹⁵N reaction at stellar energies. Nucl. Phys. A 313, 346–362. doi: 10.1016/0375-9474(79)90505-0

CrossRef Full Text | Google Scholar

Lugaro, M., Ugalde, C., Karakas, A. I., Görres, J., Wiescher, M., Lattanzio, J. C., et al. (2004). Reaction rate uncertainties and the production of ¹⁹F in asymptotic giant branch stars. Astrophys. J. 615, 934–946. doi: 10.1086/424559

CrossRef Full Text | Google Scholar

Mak, H. B., Evans, H. C., Ewan, G. T., and Macarthur, J. D. (1978). The ¹⁸O(p,α)¹⁵N cross section at low energies. Nucl. Phys. A 304, 210–220. doi: 10.1016/0375-9474(78)90104-5

CrossRef Full Text | Google Scholar

Mak, H. B., Ewan, G. T., Evans, H. C., MacArthur, J. D., McLatchie, W., and Azuma, R. E. (1980). The alpha widths of the 5603, 5605 and 5668 keV states in ¹⁸F. Nucl. Phys. A 343, 79–90. doi: 10.1016/0375-9474(80)90641-7

CrossRef Full Text | Google Scholar

Moazen, B. H., Bardayan, D. W., Blackmon, J. C., Chae, K. Y., Chipps, K., Domizioli, C. P., et al. (2007). Measurement of the 183 keV resonance in ¹⁷O(p,α)¹⁴N using a novel technique. Phys. Rev. C 75:065801. doi: 10.1103/PhysRevC.75.065801

CrossRef Full Text | Google Scholar

Mukhamedzhanov, A. M., Blokhintsev, L. D., Irgaziev, B. F., Kadyrov, A. S., La Cognata, M., Spitaleri, C., et al. (2008). Trojan Horse as an indirect technique in nuclear astrophysics. J. Phys. G Nucl. Phys. 35:014016. doi: 10.1088/0954-3899/35/1/014016

CrossRef Full Text | Google Scholar

Newton, J. R., Iliadis, C., Champagne, A. E., Longland, R., and Ugalde, C. (2007). Remeasurement of the 193 keV resonance in ¹⁷O(p,α)¹⁴N. Phys. Rev. C 75:055808. doi: 10.1103/PhysRevC.75.055808

CrossRef Full Text | Google Scholar

Nollett, K. M., Busso, M., and Wasserburg, G. J. (2003). Cool bottom processes on the thermally pulsing asymptotic giant branch and the isotopic composition of circumstellar dust grains. Astrophys. J. 582, 1036–1058. doi: 10.1086/344817

CrossRef Full Text | Google Scholar

Perey, C. M., and Perey, F. G. (1976). Compilation of phenomenological optical-model parameters 1954-1975. Atom. Data Nucl. Data Tables 17:1. doi: 10.1016/0092-640X(76)90007-3

CrossRef Full Text | Google Scholar

Pizzone, R. G., Roeder, B. T., McCleskey, M., Trache, L., Tribble, R. E., Spitaleri, C., et al. (2016). Trojan Horse measurement of the ¹⁸F(p,α)¹⁵O astrophysical S(E)-factor. Eur. Phys. J. A 52:24. doi: 10.1140/epja/i2016-16024-3

CrossRef Full Text | Google Scholar

Rolfs, C., and Rodney, W. (1988). Cauldrons in the Cosmos. Chicago, IL: The University of Chicago Press.

Google Scholar

Rolfs, C., and Rodney, W. S. (1975). Hydrogen burning of ¹⁷O in the CNO cycle. Nucl. Phys. A 250, 295–308. doi: 10.1016/0375-9474(75)90260-2

CrossRef Full Text | Google Scholar

Sanders, R. M. (1956). Study of the ¹⁴C(p, n)¹⁴N and ¹⁴C(α, n)¹⁷O reactions. Phys. Rev. C 104, 1434–1440. doi: 10.1103/PhysRev.104.1434

CrossRef Full Text | Google Scholar

Schatz, H., Kaeppeler, F., Koehler, P. E., Wiescher, M., and Trautvetter, H. P. (1993). ¹⁷O(n, α)¹⁴C: closure of a primordial CNO Bi-Cycle? AstroPhys. J. 413:750. doi: 10.1086/173042

CrossRef Full Text | Google Scholar

Schmidt, C., and Duhm, H. H. (1970). The ¹⁸O(³He,d)¹⁹F reaction at E₃He = 16 MeV. Nucl. Phys. A 155, 644–658. doi: 10.1016/0375-9474(70)90918-8

CrossRef Full Text | Google Scholar

Scott, D. A., Caciolli, A., Di Leva, A., Formicola, A., Aliotta, M., Anders, M., et al. (2012). First direct measurement of the ¹⁷O(p,γ)¹⁸F reaction cross section at gamow energies for classical novae. Phys. Rev. Lett. 109:202501. doi: 10.1103/PhysRevLett.109.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

Sergi, M. L., Spitaleri, C., La Cognata, M., Coc, A., Mukhamedzhanov, A., Burjan, S. V., et al. (2010). New high accuracy measurement of the ¹⁷O(p,α)¹⁴N reaction rate at astrophysical temperatures. Phys. Rev. C 82:032801. doi: 10.1103/PhysRevC.82.032801

PubMed Abstract | CrossRef Full Text | Google Scholar

Sergi, M. L., Spitaleri, C., La Cognata, M., Lamia, L., Pizzone, R. G., Rapisarda, G. G., et al. (2015). Improvement of the high-accuracy ¹⁷O(p, α)¹⁴N reaction-rate measurement via the Trojan horse method for application to ¹⁷O nucleosynthesis. Phys. Rev. C 91:065803. doi: 10.1103/PhysRevC.91.065803

CrossRef Full Text | Google Scholar

Shapiro, I. S. (1967). Interaction of High-Energy Particles with Nuclei. New York, NY: Academic Press.

PubMed Abstract

Spitaleri, C., La Cognata, M., Lamia, L., Mukhamedzhanov, A. M., and Pizzone, R. G. (2016). Nuclear astrophysics and the Trojan horse method. Eur. Phys. J. A 52:77. doi: 10.1140/epja/i2016-16077-2

CrossRef Full Text | Google Scholar

Spitaleri, C., La Cognata, M., Lamia, L., Pizzone, R. G., and Tumino, A. (2019). Astrophysics studies with the Trojan Horse method. Eur. Phys. J. A 55:161. doi: 10.1140/epja/i2019-12833-0

CrossRef Full Text | Google Scholar

Spitaleri, C., Lamia, L., Tumino, A., Pizzone, R. G., Cherubini, S., del Zoppo, A., et al. (2004). The ¹¹B(p,α₀)⁸Be reaction at sub-Coulomb energies via the Trojan-horse method. Phys. Rev. C 69:055806. doi: 10.1103/PhysRevC.69.055806

CrossRef Full Text | Google Scholar

Spitaleri, C., Mukhamedzhanov, A. M., Blokhintsev, L. D., La Cognata, M., Pizzone, R. G., and Tumino, A. (2011). The Trojan horse method in nuclear astrophysics. Phys. Atom. Nucl. 74, 1725–1739. doi: 10.1134/S1063778811110184

CrossRef Full Text | Google Scholar

Thompson, I. J. (1988). Coupled reaction channels calculations in nuclear physics. Comput. Phys. Rep. 7, 167–212. doi: 10.1016/0167-7977(88)90005-6

CrossRef Full Text | Google Scholar

Tribble, R. E., Bertulani, C. A., La Cognata, M., Mukhamedzhanov, A. M., and Spitaleri, C. (2014). Indirect techniques in nuclear astrophysics: a review. Rep. Prog. Phys. 77:106901. doi: 10.1088/0034-4885/77/10/106901

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagemans, J., Wagemans, C., Goeminne, G., Serot, O., Loiselet, M., and Gaelens, M. (2002). The ¹⁷O(n,α)¹⁴C reaction from subthermal up to approximately 350 keV neutron energy. Phys. Rev. C 65:034614. doi: 10.1103/PhysRevC.65.034614

CrossRef Full Text | Google Scholar

Wiescher, M., Becker, H. W., Görres, J., Kettner, K. U., Trautvetter, H. P., Kieser, W. E., et al. (1980). Nuclear and astrophysical aspects of ¹⁸O(p,γ)¹⁹F. Nucl. Phys. A 349, 165–216. doi: 10.1016/0375-9474(80)90451-0

CrossRef Full Text | Google Scholar

Yagi, K., Katori, K., Ohnuma, H., Hashimoto, Y., and Nogami, Y. (1962). Experiment on elastic scattering of protons by ¹⁸O. J. Phys. Soc. Jpn. 17, 595–603. doi: 10.1143/JPSJ.17.595

CrossRef Full Text | Google Scholar

Yim, M.-S., and Caron, F. (2006). Life cycle and management of carbon-14 from nuclear power generation. Prog. Nucl. Energy 48, 2–36. doi: 10.1016/j.pnucene.2005.04.002

CrossRef Full Text | Google Scholar

Zadro, M., Miljanić, D., Spitaleri, C., Calvi, G., Lattuada, M., and Riggi, F. (1989). Excitation function of the quasifree contribution in the ²H(⁷Li,αα)n reaction at E₀ = 28-48 MeV. Phys. Rev. C 40, 181–185. doi: 10.1103/PhysRevC.40.181

CrossRef Full Text | Google Scholar

Zinner, E. (2014). Presolar grains. 1, 181–213. doi: 10.1016/B978-0-08-095975-7.00101-7

CrossRef Full Text | Google Scholar