Convection Theory and Relevant Problems in Stellar Structure, Evolution, and Pulsational Stability I Convection Theory and Structure of Convection Zone and Stellar Evolution

Introduction

Convection occurs within most stars. Convection causes the transfer of energy and momentum, and the mixing of matter in stellar interiors. Therefore, it strongly influences the internal structure, evolution, and pulsational stability of stars. Stellar convection is always turbulent due to its large scale. It is impossible to expect to have a perfect convection theory until a better understanding of turbulence has been achieved. Up to now the most popularly applied convection theory is still the MLT developed by Bohm-Vitense (1958), and its many versions. The most obvious advantages of the MLT are its straightforwardness in physical picture and simplicity of use. However, the MLT is not a dynamic theory following the hydrodynamic equations and turbulence theory, but is a phenomenological theory based on a simple analogy of turbulence with the kinetic theory of gas molecules. In fact, turbulence is more complex than the kinetic theory of gas molecules. The fundamental shortcoming of the MLT is that it cannot give a correct description for the dynamic behaviors of turbulent convection. When dealing with the dynamic problems of turbulent convection, such as time-dependent and non-local convection, this shortcoming becomes prominent. A possible approach to turbulent convection is direct hydrodynamic numerical simulation. Taking into account the fact that both the time and space scales of turbulence are more than ten orders of magnitude less than the stellar ones, a direct hydrodynamic numerical simulation of stellar convection would be impossible for the calculation of stellar structure and evolution in the foreseeable future. Therefore, it is a reasonable choice to develop a theoretical approach exact enough and simple enough for treating turbulent convection in the calculation of stellar evolution and oscillations. Helio- and astero-seismology have made significant progress in the past two decades thanks to the GONG, SOHO, OGLE, MACHO, 2MASS, CoRoT, and Kepler ground-based and space projects. They offer the best opportunity to test stellar evolution and convection theories. In the present paper we pay close attention to convection theory and the relevant problems in stellar structure, evolution, and pulsational stability. Based on the reflections above, we decided to abandon the phenomenological MLT, and to develop a non-local and time-dependent theory of convection based on hydrodynamic equations and turbulence theory (Xiong, 1978; Xiong, 1980; Xiong, 1981; Xiong, 1989; Xiong et al., 1997; Deng et al., 2006). In contrast to the MLT, it is a dynamic theory of correlation functions of turbulent velocity and temperature (and, in addition, of the element abundance for chemically inhomogeneous stars) following the hydrodynamic equations and turbulence theory. So, it can be expected that our theory has a more solid hydrodynamic foundation and can give a more exact description of the hydrodynamic behavior of turbulent convection than the MLT does. Our purpose is to improve the treatment of overshooting mixing in calculations of stellar evolution and the treatment of dynamic and thermodynamic coupling between convection and oscillations in calculations of stellar oscillations. Canuto (1993, 1997, 1999) and Li of the Yunnan group of China (Zhang, 2012a; Zhang and Li, 2012a; Zhang, 2012b; Zhang and Li, 2012b; Zhang, 2013) proposed a similar theory. In the present paper, we do not attempt to make a comprehensive review and comparison for convection theories and relevant problems, which would be a large and difficult amount of work. In A Non-Local and Time-Dependent Theory of Convection section, a brief description of our non-local and time-dependent convection theory is given. The following sections review the progress of its applications in theoretical calculations of the structure of the solar convection zone (Structure of the Solar Convection Zone section), of stellar evolution and lithium depletion in the atmosphere of the Sun and late-type dwarfs (Overshooting Mixing and Stellar Evolution section), and of stellar oscillations (in PartⅡ). These applications are not only the primary motivations of our research on the theory of stellar convection, but also an important means for testing convection theory. A summary and discussion follow in section 7 of PartⅡ, where we try to evaluate the successes and failures of our theory, analyze their reasons and identify direction for improvement. It is known that this paper will contain strong personal bias. Our viewpoint on the excitation mechanism for red giants may not gain widespread approval. Nowadays, our understanding of many problems is still inconclusive, and will need more time to verify. Disputes over different academic viewpoints will contribute to the development of science. Our theory is far from perfect, however it has shown obvious improvements in comparison with MLT.

This article is divided into two parts. Convection theory and its applications in theoretical calculations of the structure of the solar convection zone and for stellar evolution are contained in PartⅠ; the applications of the theory in calculations of stellar oscillations, and summary and discussions are contained in PartⅡ.

A Non-Local and Time-Dependent Theory of Convection

In order to overcome the defects of the MLT, we developed a non-local and time-dependent theory of convection based on the hydrodynamic equations and turbulence theory (Xiong, 1978; Xiong, 1980; Xiong, 1981; Xiong, 1989; Xiong et al., 1997; Deng et al., 2006). In our theory, the classical Reynolds decomposition is used. Each of the physical variables X is expressed as the sum of its average value $\overline{X}$ and (Eulerian) turbulent fluctuation $X^{\mathit{\prime }}$,

$X=\overline{X}+X^{\mathit{\prime }},(1)$

substituting Eq. 1 into the hydrodynamic equations and the radiation transfer equation, and making a Taylor expansion for $X^{\mathit{\prime }}$, retaining only its first-order terms, ignoring all the second and higher-order terms, then averaging for each of the equations, we can obtain the following average hydrodynamic equations and the radiation transfer equation,

$\frac{ D\overline{\rho }}{Dt}+\overline{\rho }{\nabla }_k{\overline{u}}^k=0, (2)$

$\frac{ D{\overline{u}}^i}{Dt}+\frac{1}{\overline{\rho }}{\nabla }_k\left(g^{ik}\overline{P}+\overline{\rho }\overline{u{\mathit{\prime }}^{i}u{\mathit{\prime }}^k}\right)+g^{ik}{\nabla }_k\overline{\Phi }=\frac{1}{\overline{\rho }}{\nabla }_k{\sigma }_{\left(\overline{u}\right)}^{ik}, (3)$

$\overline{\rho }\overline{C_p}\frac{D\overline{T}}{Dt}-\alpha \frac{D\overline{P}}{Dt}+{\nabla }_k\left(\overline{C_p}\overline{\rho u{\mathit{\prime }}^{k}T\mathit{\prime }}\right)+{\nabla }_k\overline{F_r^k}=\overline{\rho {\epsilon }_N}+\overline{{\sigma }_{\left(u\mathit{\prime }\right)}^{ik}{\nabla }_{k}u{\mathit{\prime }}_{\mathit{i}}} ,(4)$

$F_r^i=-\frac{4ac{\overline{T}}^3}{3\overline{\rho }\overline{\kappa }}{g}^{ik}{\nabla }_k\overline{T}, (5)$

where

$\frac{ D}{Dt}=\frac{\partial }{\partial t}+{\overline{u}}^k{\nabla }_k .(6)$

is the comoving differential, and T, P, $\rho$ are, respectively, the temperature, pressure, and density of gas, $C_P$ is the specific heat at constant pressure, $\alpha = -{\left(\partial \ln \rho /\partial \ln T\right)}_P$ the expansion coefficient, ${\epsilon }_N$ the effective nuclear energy-generation rate per gram, ${\sigma }^{ik}$ the viscosity tensor, $\Phi$the gravitational potential, $\kappa$ the radiative opacity, and $F_r^i$ the radiation flux vector. It can be seen that, when convection sets in, an extra term $\overline{\rho u^{\mathit{\prime i}}{u}^{\mathit{\prime k}} }$ in the average equation of momentum conservation and another extra term $\overline{C_p}$$\overline{\rho u^{\mathit{\prime i}}{T}^{\mathit{\prime }} }$ in the average equation of energy conservation will emerge. They are, respectively, the well-known Reynolds stress and convective enthalpy flux. In the present paper, all the equations are expressed in the tensor format. $g^{ik}$ is the metric tensor for the current framework. The implicit summation rule of tensors is used, i.e., a summation should be performed for an index k running from 1 to 3 if both the subscript and superscript k appear in a term. Subtracting the average equations, Eqs. 3, 4, from the corresponding original equations of momentum and energy conservation, after a long derivation, it is not difficult to obtain the following dynamic equations of turbulent velocity and temperature:

$\frac{ Dw{\mathit{\prime }}^i}{Dt}+w^{\mathit{\prime k}}{\nabla }_k\overline{u^i }-\frac{1}{\overline{\rho }}{\nabla }_k\left(g^{ik}P\mathit{\prime }+\rho u{\mathit{\prime }}^{i}u{\mathit{\prime }}^k-\overline{\rho u{\mathit{\prime }}^{i}u{\mathit{\prime }}^k }\right)-\alpha \frac{T\mathit{\prime }}{\overline{T}}\left(g^{ik}{\nabla }_k\overline{\Phi }+\frac{ D\overline{u^i }}{Dt}\right)=\frac{1}{\overline{\rho }}{\nabla }_k{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{ik}, (7)$

$\frac{ D}{Dt}\left(\frac{T\mathit{\prime }}{\overline{T}}\right)+\frac{T\mathit{\prime }}{\overline{T}}\left\{\left[1-\alpha +C_{P,T}\right]\frac{D\ln \overline{T}}{Dt}+\left[C_{P,P}+\left(1-\alpha \right){\nabla }_{ad}\right]\frac{D\ln \overline{P}}{Dt}\right\}+w^{\mathit{\prime k}}\left({\nabla }_k\ln \overline{T}-{\nabla }_{ad}{\nabla }_k\ln \overline{P}\right)+ \frac{1}{\overline{\rho }{C}_P\overline{T}}{\nabla }_k\left[\overline{\rho }{C}_P\overline{T}\left(w{\mathit{\prime }}^k\frac{T\mathit{\prime }}{\overline{T}}-\overline{w{\mathit{\prime }}^k\frac{T\mathit{\prime }}{\overline{T}}}\right)\right]=\frac{1}{\overline{\rho }{C}_P\overline{T}}\left[\left(\rho {\epsilon }_N\right)\mathit{\prime }+{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{ik}{\nabla }_{k}u{\mathit{\prime }}_i-\overline{{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{ik}{\nabla }_{k}u{\mathit{\prime }}_i}-{\nabla }_{k}F{\mathit{\prime }}_r^k\right], (8)$

where $w^{\mathit{\prime i}}=\rho u^{\mathit{\prime i}}/\overline{\rho }$ is the density-weighted turbulent velocity, ${\nabla }_{ad}=\alpha P/\rho C_{p}T= \left({\Gamma }_2-1\right)/{\Gamma }_2$ is the adiabatic temperature gradient, $C_{P,T}={\left(\partial \ln C_p/\partial \ln T\right)}_p$ and $C_{P,P}={\left(\partial \ln C_p/\partial \ln P\right)}_T$ are, respectively, the partial derivative of Cp with respect to T and P, and ${\Gamma }_2 \left(\mathrm{along}\mathrm{with} {\Gamma }_1 and {\Gamma }_{3 }\mathrm{below}\right)$ are the adiabatic exponents introduced by Chandrasekhar (1939). Starting from Eqs. 7, 8, it is not difficult to constitute the dynamic equations of auto- and cross-correlations for turbulent velocity and temperature. For example, we have the equation of velocity correlations as,

$\begin{array}{l}\frac{ D}{Dt}\overline{w{\mathit{\prime }}^{i}w{\mathit{\prime }}^j}+\overline{w{\mathit{\prime }}^{i}w{\mathit{\prime }}^k}{\nabla }_k\overline{u^j }+\overline{w{\mathit{\prime }}^{j}w{\mathit{\prime }}^k}{\nabla }_k\overline{u^i }\\ +\frac{1}{\overline{\rho }}{\nabla }_k\left(\overline{\rho }\overline{u{\mathit{\prime }}^k{u}^{\mathit{\prime i}}{u}^{\mathit{\prime j}}}\right)-\overline{w{\mathit{\prime }}^i\frac{T^{\mathit{\prime }}}{\overline{T}}}\left(\frac{D\overline{u^j }}{Dt}+g^{jk}{\nabla }_k\overline{\Phi }\right)-\overline{w{\mathit{\prime }}^j\frac{T^{\mathit{\prime }}}{\overline{T}}}\left(\frac{D\overline{u^i }}{Dt}+g^{ik}{\nabla }_k\overline{\Phi }\right)+\frac{1}{\overline{\rho }}{\nabla }_k\left[g^{ik}\overline{w^{\mathit{\prime j}}P\mathit{\prime }}+g^{jk}\overline{{\mathit{\prime }}^i{P}^{\mathit{\prime }}}+\overline{w{\mathit{\prime }}^j{\sigma }_{\left(u\mathit{\text{'}}\right)}^{ik}}+\overline{w{\mathit{\prime }}^i{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{jk}}\right]-\frac{1}{\overline{\rho }}\left(g^{ik}\overline{P^{\mathit{\prime }}{\nabla }_{k}w{\mathit{\prime }}^j}+g^{jk}\overline{P^{\mathit{\prime }}{\nabla }_{k}w{\mathit{\prime }}^i}\right)= -\frac{1}{\overline{\rho }}\left[{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{ik}{\nabla }_{k}w{\mathit{\prime }}^j+{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{jk}{\nabla }_k{w}^{\mathit{\prime i}}\right].\end{array}(9)$

The terms in square brackets on the left-hand side of Eq. 9 are the energy fluxes of pressure and viscous stress. They are negligible in comparison with the next two terms when it is assumed that the size scale of turbulent elements is far smaller than the characteristic length of the mean fluid fields. This implies that the turbulence is near quasi-isotropic. The terms on the right-hand side of Eq. 9 are the turbulent dissipation due to molecular viscosity. Based on isotropic turbulence theory, this dissipation can be expressed as (Hinze, 1975)

$\frac{ 1}{\overline{\rho }}\left[\overline{{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{ik}{\nabla }_{k}w{\mathit{\prime }}^j}+\overline{{\sigma }_{\left(u^{\mathit{\prime }}\right)}^{jk}{\nabla }_{k}w{\mathit{\prime }}^i}\right]=\frac{2\sqrt{3}{\eta }_{e}x\overline{w{\mathit{\prime }}^{i}w{\mathit{\prime }}^j}}{l_e} , (10)$

where η_e is the Heisenberg eddy coupling constant, $l_e$ is the characteristic length of energy-containing eddies of turbulence, and x is the rms turbulent velocity,

$x=\sqrt{\frac{g_{ij}\overline{w{\mathit{\prime }}^{i}w{\mathit{\prime }}^j}}{3}} .(11)$

In the dynamic equations for second-order correlations, the third-order correlations must appear due to nonlinearity of the hydrodynamic equations. The fourth-order correlations will appear if we constitute the dynamic equation for the third-order correlations. The equations of the correlation functions are never closed, as is well-known in turbulence theory (Hinze, 1975). In order to close the equation of second-order correlations, we use the gradient-type diffusion approximation for treatment of the third-order correlations (Xiong, 1980; Xiong, 1981; Xiong, 1989)

$\overline{u{\mathit{\prime }}^{k}w{\mathit{\prime }}^{i}w{\mathit{\prime }}^j}=-w{\mathit{\prime }}^{k}w{\mathit{\prime }}^d{\tau }_c{\nabla }_{\alpha }\overline{w{\mathit{\prime }}^{i}w{\mathit{\prime }}^j} , (12)$

where

${\tau }_c=\frac{ \wedge }{x} .(13)$

is the lifetime of turbulence and $\wedge$ is the diffusion length of turbulence. We then further assume that both $l_e$ and $\wedge$ are proportional to the local pressure scale height $H_p$,

$le =C_1{H}_p=C_1\frac{r^2\overline{P}}{G{M}_r\overline{\rho }} , (14)$

$\wedge = \frac{\sqrt{3}}{4}{C}_2{H}_p=C_2\frac{\sqrt{3}{r}^2\overline{P}}{4G{M}_r\overline{\rho }} .(15)$

The third-order correlations represent the non-local transport of turbulent convection. $\overline{\rho }\overline{u^{\mathit{\prime k}}{w}^{\mathit{\prime i}}{w}^{\mathit{\prime j}}}$ is the energy flux of turbulent stress. The gradient-type diffusion approximation means that turbulence diffuses from one location where it is strong to another location where it is weak. This is a very simple but reasonable physical assumption. Another closure scheme is to construct dynamic equations of third-order correlations (Canuto, 1993; Xiong et al., 1997). The fourth-order correlations will appear; they are expressed as three products of two second-order correlations of turbulent fluctuations in terms of the fourth-order correlation (Orszag, 1977; Lesieur, 1987). This standard normal approximation seems to have a more solid basis in stochastic theory. However, the physically positive quantities, such as the auto-correlations of turbulent velocity and temperature (namely $x^2$ and Z in the present paper), sometimes become negative. The numerical calculations will eventually fail to converge. Grossman (1996) compares in detail these two closure schemes (namely, our gradient-type diffusion approximation for third-order correlations and the quasi-normal approximations for fourth-order correlations). He concluded “. . . the Xiong solution predicts second moments better, with third-moment agreement not as good. The Full solution [namely with the quasi-normal approximation] predicts third moments better, but the second moments [namely $x^2$, Z, and V in present paper] show inferior agreement. . . . Since the second moments are most important for constructing stellar models, we conclude that the Xiong closures perform impressively well.” Therefore, we abandoned the closure schemes of the quasi-normal approximations, and adopted the gradient-type diffusion approximation for the closure of the dynamic equations of turbulent correlations, because it is a simpler and more practical scheme than the quasi-normal approximation for calculations of stellar evolution and oscillations (Xiong et al., 1997).

Convection results from the thermal instability of a fluid medium. In a gravitationally stratified fluid medium, a perturbed fluid element will be accelerated by buoyant forces along the direction of gravity, when the local temperature gradient exceeds the adiabatic one. The original direction of convective motion is along with gravity, i.e., along the radial direction of the star. Therefore, convection is highly anisotropic in the low wave number range of the turbulent spectrum. Due to the continuity and nonlinearity of hydrodynamics, a part of the kinetic energy of convective elements will be converted into horizontal motion. Turbulence becomes more and more isotropic in the high wave-number range. Rotta (1951) pointed out that the correlation of the pressure and velocity gradients tends to make turbulence isotropic. Therefore, we assume (Deng et al., 2006)

$\overline{\frac{1}{\rho }{P}^{\mathit{\prime }}\left(g^{ik}{\nabla }_k{w}^{\mathit{\prime i}}+g^{jk}{\nabla }_k{w}^{\mathit{\prime i}}-\frac{2}{3}{g}^{ij}{\nabla }_k{\mathit{\prime }}^k\right)} =-C_3\frac{4\sqrt{3}{\eta }_{e}G{M}_r\overline{\rho }x}{3C_1{r}^2\overline{P}}{\chi }^{ij}, (16)$

where x² and ${\chi }^{ij}$ are, respectively, the isotropic and anisotropic component of the velocity correlation.

$\overline{w{\mathit{\prime }}^{i}w{\mathit{\prime }}^j} =g^{ij}{x}^2+{\chi }^{ij}.(17)$

Substituting Eq. 17 into Eq. 9 and contracting with respect to indices i and j and noting Eqs. 10–16, we have

$\frac{3}{2}\frac{D{x}^2}{Dt}-x^2\frac{D\ln \overline{\rho }}{Dt}+{\chi }^{ij}{\nabla }_i\overline{u_j }-\frac{3}{2\overline{\rho }}{\nabla }_k\left(Q^{\alpha k}{\nabla }_{\alpha }{x}^2\right)-\alpha {\mathrm{V}}^k\left(\frac{D\overline{u_k}}{Dt}+{\nabla }_k\overline{\Phi }\right)=-\frac{2\sqrt{3}{\eta }_{e}G{M}_r}{C_1{r}^2\overline{P}}{x}^3.(18)$

Subtracting the product of $g^{ik}$ and Eq. 18 from Eq. 9 and noting Eq. 16, we can obtain the dynamic equation of the anisotropic component of the velocity correlation ${\chi }^{ij}$,

$\frac{D{\chi }^{ij}}{Dt}+x^2\left(g^{ik}{\nabla }_k\overline{u^j }+g^{jk}{\nabla }_k\overline{u^i }-\frac{2}{3}{g}^{ij}{\nabla }_k\overline{u^k}\right)+{\chi }^{ik}{\nabla }_k\overline{u^j }+{\chi }^{jk}{\nabla }_k\overline{u^i }-\frac{2}{3}{g}^{ij}{x}^{\alpha \beta }{\nabla }_{\alpha }\overline{u_{\beta }}-\alpha \left(g^{ik}{\mathrm{V}}^j+g^{jk}{\mathrm{V}}^i-\frac{2}{3}{g}^{ij}{\mathrm{V}}^k\right)\left(\frac{D\overline{u_k}}{Dt}+{\nabla }_k\overline{\Phi }\right)-\frac{1}{\overline{\rho }}{\nabla }_k\left(Q^{k\alpha }{\nabla }_{\alpha }{\chi }^{ij}\right)=-\frac{4\sqrt{3}{\eta }_e\left(1+C_3\right)G{M}_r}{3C_1{r}^2\overline{P}}{\chi }^{ij}.(19)$

In the same way, we can derive the dynamic equations of the temperature auto-correlation and cross-correlation of velocity and temperature from Eqs. 7, 8:

$\frac{DZ}{Dt}+Z\left\{\left[1-\alpha +C_{P,T}\right]\frac{D\ln \overline{T}}{Dt}+\left[C_{P,P}+\left(1-\alpha \right){\nabla }_{ad}\right]\frac{D\ln \overline{P}}{Dt}\right\}+2{\vee }^k\left({\nabla }_k\ln \overline{T}-{\nabla }_{ad}{\nabla }_k\ln \overline{P}\right)-\frac{1}{{\overline{\rho }}^2{C}_p^2}{\nabla }_k\left(\overline{\rho }{C}_p^2{Q}^{\alpha k}{\nabla }_{\alpha }Z\right)=-\frac{2\sqrt{3}{\eta }_{e}G{M}_r\overline{\rho }}{C_1{r}^2\overline{P}}\left(x+x_c\right)Z ,(20)$

$\frac{D{\mathrm{V}}^i}{Dt}+{\mathrm{V}}^k+{\mathrm{V}}^i\left\{\left[1-\alpha +C_{P,T}\right]\frac{D\ln \overline{T}}{Dt}+\left[C_{P,P}+\left(1-\alpha \right){\nabla }_{ad}\right]\frac{D\ln \overline{P}}{Dt}\right\}-\alpha Z\left(\frac{D\overline{u^i}}{Dt}+g^{ik}{\nabla }_k\overline{\Phi }\right)+\left(g^{ik}{x}^2+{\chi }^{ik}\right)\left({\nabla }_k\ln \overline{T}-{\nabla }_{ad}{\nabla }_k\ln \overline{P}\right)-\frac{1}{\overline{\rho }{C}_p}{\nabla }_k\left(C_p{Q}^{\alpha k}{\nabla }_{\alpha }{\mathrm{V}}^i\right)=-\frac{\sqrt{3}{\eta }_{e}G{M}_r\overline{\rho }}{C_1{r}^2\overline{P}}\left(3x+x_c\right){\mathrm{V}}^i, (21)$

where

$Z=\overline{{\left(\frac{T^{\mathit{\prime }}}{\overline{T}}\right)}^2} , (22)$

$V^i=\overline{u\mathit{\prime }i\frac{T^{\mathit{\prime }}}{\overline{T}} } , (23)$

$Q^{ij}=\frac{\sqrt{3}{C}_2{r}^2\overline{P}}{4G{M}_r\overline{\rho }}\left(g^{ij}x+\frac{{\chi }^{ij}}{x}\right), (24)$

$x_c=\frac{3acG{M}_r{\overline{T}}^3}{C_1\overline{\rho }\overline{C_P}\overline{\kappa }{r}^2\overline{P}}. (25)$

$P_e=x/x_c$ is the effective Peclet number of turbulent convection. Eqs. 3, 4 can be rewritten as

$\frac{D\overline{u^i }}{Dt}+\frac{1}{\overline{\rho }}{\nabla }_k\left[g^{ik}\left(\overline{P}+\overline{\rho }{x}^2\right)+\overline{\rho }{\chi }^{ik}\right]+g^{ik}{\nabla }_k\overline{\Phi }=0,\left(3\prime \right)$

$\frac{D\ln \overline{T}}{Dt}+{\nabla }_{ad}\frac{D\ln \overline{P}}{Dt}+\frac{1}{\overline{\rho }\overline{C_p}\overline{T}}\left[\overline{\rho }{x}^2\left(3\frac{D\ln x}{Dt}-\frac{D\ln \overline{\rho }}{Dt}\right)+\overline{\rho }{\chi }^{ik}{\nabla }_k\overline{u^i}+{\nabla }_k\left(\overline{F_r^k}+F_c^k+F_t^k\right)\right]=0, \left(4\prime \right)$

where $\overline{F_r^k}$, $F_c^k$, $F_t^k$ are, respectively, the radiative, convective enthalpy, and turbulent kinetic energy fluxes,

$F_c^k= \overline{\rho }{C}_P\overline{T}{V}^k, (26)$

$F_t^k= -3\overline{\rho }x{Q}^{k\alpha }{\nabla }_{\alpha }x. (27)$

The contribution of pressure fluctuations to the enthalpy flux Eq. 26 has been neglected, because it is much less than the contribution of the temperature fluctuation. The combination of the average hydrodynamic equations Eqs. 2, 3′, 4′, 5, and the dynamic equations of auto- and cross-correlations for turbulent velocity and temperature Eqs. 18–21 form a complete and closed system of radiation-hydrodynamic equations for the calculation of stellar structure and oscillations.

The details of the derivation and main simplifications can be found in our original works (Xiong, 1978; Xiong, 1980; Xiong, 1981; Xiong, 1989; Xiong et al., 1997; Deng et al., 2006). The main simplifications and assumptions can be summarized as follows:

1) Turbulence is near quasi-isotropic; the characteristic linear size of turbulent elements is far less than the characteristic length of the average fields.

2) The relative fluctuations of temperature $T\mathit{\prime }/\overline{T}$ and density ${\rho }^{\mathit{\prime }}/\overline{\rho }$ are much less than 1, so our theory is applicable only for subsonic convection.

3) The anelastic approximation (Gough, 1969; Xiong et al., 1997) is adopted. We assume that the only effect of pressure fluctuations is to make turbulence more isotropic (Eq. 16), and all of the other dynamic effects of pressure fluctuations were neglected. These assumptions are slightly weaker than the Boussinesq approximation. In our theory, the density-weighted turbulent velocity is used, so the compressibility is partially taken into account. However, noise sound waves are filtered due to the assumption that $\mathrm{D}({\rho }^{\mathit{\prime }}/\overline{\rho })/\mathrm{Dt}=0$

4) The turbulent fluctuations of the gravitational potential $\Phi \mathit{\prime }$ have been neglected because they cancel out between each other, so gravity waves are also filtered.

5) The gradient-type diffusion approximation for the treatment of the third-order correlations is adopted (Xiong, 1980; Xiong, 1981; Xiong, 1989).

The turbulent dissipation, diffusion, and anisotropy are carefully taken into account. Based on the turbulence theory, they are expressed, respectively, by Eqs. 10, 12, 16, 19. There are three convective parameters (C₁, C₂, C₃) in our convection theory. They are associated, respectively, with turbulent dissipation, diffusion, and anisotropy. They can be calibrated by using the comparison between the observed and theoretical depth and T-P structure of the solar convection zone, the turbulence velocity-temperature fields in the solar atmosphere, the lithium depletion in the atmosphere of the Sun and late-type dwarfs, and 3D simulations (Deng et al., 2006). The calibration of the convective parameters (C₁, C₂, C₃) is somewhat complex. First, the convective parameters (C₁, C₂, C₃) are not a set of constants, but they vary slowly as a function of stellar parameters such as mass M, luminosity L, effective temperature ${\mathrm{T}}_e$ (Ludwig et al., 1999); even in the interior of the same star they vary with radius r. Fortunately, in the deep interior of stars, apart from the surface layer, convective transport of energy is very effective $\left(P_e= x/x_c\gg 1\right)$. Therefore, the temperature gradient is very close to the adiabatic one, independent of the choice of convective parameters. The depth of the convection zone is almost defined by the structure of the surface super-adiabatic convection zone, where convective energy transport is inefficient $\left(P_e=x/x_c\le 1\right)$. Our research shows that, if only the pulsational stability is of concern, by using a fixed set of (C₁, C₂, C₃) calibrated to the Sun, all of the pulsational instability strips in the H-R diagram, such as the RR Lyrae (Xiong et al., 1998b), $\delta Scuti-\gamma Doradus$(Xiong et al., 2016), Mira (Xiong et al., 1998a), and LPV (Xiong et al., 2018) instability strips, can be defined. The effects of (C₁, C₂, C₃) on convection are not completely independent and the available observations for calibration are too rare, so it is difficult to calibrate (C₁, C₂, C₃) independently. After theoretical considerations, these entanglements for calibration of (C₁, C₂, C₃) can be removed, at least partially. C₃, unlike C₁ and C₂, is a rather independent convective parameter. It is related to the anisotropy of turbulent convection. In the deep interior of a convectively unstable zone, the ratio of the squared radial component of turbulent velocity to the horizontal one $\overline{w_r^2}/ \overline{ w_h^2} \approx \left(3+C_3\right)/ 2 C_3$. Anisotropy increases and convective overshooting decreases with decreasing C_3. C₃ = 3 is a reasonable value, which agrees well with the observations of turbulent velocity in the solar atmosphere, the lithium depletion of the Sun and late-type main-sequence stars, and hydrodynamic simulations (Deng et al., 2006; Deng and Xiong, 2008). C₁ and C₂ are two convective parameters related to turbulent dissipation and diffusion. It can be seen from Eqs. 14, 15 that $l_e$ and ∧ are, respectively, the dissipation and diffusion length of turbulence. So, one can expect that C₂/C₁ is approximately a constant independent of the stellar parameters M, L, and ${\mathrm{T}}_e$. C₂/C₁ = 1/2 is a good choice. Once C₂/C₁ and C₃ are identified, C₁ becomes the only adjustable convective parameter. Our research shows that a non-local and anisotropic convective model of the Sun with (C₁, C₂, C₃) = (0.64, 0.50, 3.0) can reproduce almost all of the observed characteristics of the solar convection zone very well (Deng et al., 2006; Xiong and Deng, 2001).

Structure of the Solar Convection Zone

Astronomy is a science based on the observations of astronomical objects. Stellar convection theory originated from the requirement for a treatment of convective transport of energy and momentum, and of convective mixing of materials in the stellar interior. In the previous section, we described a non-local and time-dependent theory of convection. In this section we will present its application in studies of the solar convection zone.

The Sun is the closest star to us, and is the only star that can provide high spatial resolution observations. Therefore, the Sun is an ideal natural laboratory for testing convection theory. By using our non-local and anisotropic convection theory described in the previous section, we calculated a model of the solar convective envelope (Unno, et al., 1985; Xiong and Cheng, 1992; Xiong and Deng, 2001). The MHD equation of state (Däppen et al., 1988; Hummer and Mihalas, 1988; Mihalas et al., 1988) and OPAL opacity (Rogers and lglesias, 1992) supplemented by low-temperature opacities (Alexander and Ferguson, 1994) were used. The chemical abundance is X = 0.70 and Z = 0.02. The surface boundary was located at optical depth τ = 10⁻³. By choosing a first trial set of T and r at the surface boundary T = T₀, r = R₀, and $P= a{T}_0^4$, by using a relaxation procedure, it is not difficult to obtain that $\mathrm{T}={\mathrm{T}}_e$, $\mathrm{r}={\mathrm{R}}_{\odot }$, and $L= 4\pi R_{\odot }^2{T}_e^4$, at τ = 2/3. The original fundamental equations are our radiation-hydrodynamic equations for the calculation of stellar structure and oscillations, Eqs. 2, 3′, 4′, 5, 18–21. The Henyey method (Henyey et al., 1964) for the integration of differential equations was used. The details of the working equations and boundary conditions can be found by referring to the original works of the author cited above.

Structure of Turbulent Velocity and Temperature Fields

Convection stops suddenly at the boundary of the convection zone in the local convection theory; however, convection penetrates deeply into the convectively stable zone in the non-local convection model. Figure 1 shows the variation of x, Z, $\left|V\right|, and \left|{\chi }_1^1\right|$ vs. $\log P$ in our non-local convection model. $V and {\chi }_1^1$ change their sign passing through the boundary of the convection zone. In the convectively unstable zone, $V and {\chi }_1^1$ are greater than zero. Convective flux $F_C >0$ and the ratio of the squared radial component of turbulent velocity to the horizontal one $\overline{w_r^2}/\overline{ w_h^2}= \left(x^2+{\chi }_1^1\right)/\left(x^2-{\chi }_1^1\right) \approx \left(3+C_3\right)/2C_3 >1/2$, when C₃ < 3. Turbulent motions dominate in the radial direction. In the overshooting zones, $V and {\chi }_1^1$ become negative, $\left(V<0, {\chi }_1^1<0\right)$, convective flux Fc < 0 and $\overline{w_r^2}/\overline{ w_h^2}= \left(x^2+{\chi }_1^1\right)/\left(x^2-{\chi }_1^1\right) <1/2$, and turbulent motions become dominant in the horizontal direction. In the surface overshooting zone, the correlation coefficient of turbulent velocity with temperature $R_{VT}=V/x{Z}^{\frac{1}{2}}\approx -1$. Passing through the boundary of the convection zone, $R_{VT}$ changes abruptly from -1 to +1. In most of the convection zone, far from the boundary, $R_{VT}$ is very near to 1, and decreases rapidly to zero toward the bottom boundary of the convection zone. This asymmetry of $R_{VT}$ at the surface and bottom boundaries of the convection zone results from the fact that, in the surface zone, the effective Peclet number $P_e=x_e/x_{C }\ll 1$, and convective energy transport is very inefficient; however, in the deep interior of stars, $P_e\gg 1$, and convective energy transport is very efficient.

FIGURE 1

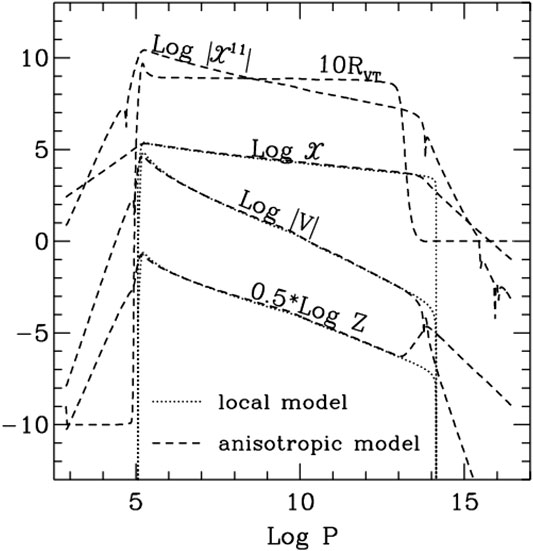
FIGURE 1. Auto- and cross-correlations of turbulent velocity and temperature,$x, {\chi }^{ij}$(Eq. 17), Z (Eq. 22), and V (Eq. 23) versus $\log P$ for the local (dotted-lines) and non-local (dashed-lines) convective models of the Sun having the same convection zone depth.

Convective overshooting is different for the different physical variables. It can be seen that turbulent velocity and temperature penetrate deeply into the convectively stable zone. x, Z, and V decrease exponentially with $\ln P$ in the overshooting zone, and the e-folding length of turbulent velocity is about $1.4\sqrt{C_1{C}_2}$ times the pressure scale height. However, overshooting of the convective flux is negligible because the convective energy transport is inefficient $\left(x/ x_{C } \ll 1\right)$ in the surface overshooting zone and the correlation coefficient of turbulent velocity and temperature is far less than 1 ($R_{\mathrm{VT}}=V/{x_{Z }}^{(1/2)}$ in the bottom overshooting zone). The overshooting distance decreases with decreasing $C_3$ and $x/ x_{C }$. It can be seen that x, Z, and V decline more rapidly in the surface overshooting zone, where $x/x_{C }\le 1$, than that in the bottom overshooting zone, where $x/x_{C }\gg 1$.

Remarks About MLT

The local MLT is still a good first approximation for the treatment of convection in the calculation of the thermal structure of stars, when the non-locality and time dependence of convection are not important for the problem concerned. Figure 3 illustrates $\log T$ vs. $\log P$ for the local and non-local models of the solar convective envelope, with the same convection zone depth. It can be seen that they agree with each other very well. Figure 4 illustrates the relative differences in the squared sound speed and density between the non-local and local convection models. Except for the regions closest to the surface, the relative differences are within approximately one percent.

Figure 2 illustrates the fractional convective enthalpy and turbulent kinetic fluxes $L_C/L$, $L_t/L \left(L_C=4\pi r^2{F}_c ,L_t=4\pi r^2{F}_t\mathrm{and}L=L_r+L_C+L_t\right)$, the ratio of turbulent pressure to gas pressure $P_t/ P$, and the super-adiabatic temperature gradient $\nabla - {\nabla }_{ad}$ versus depth $\left(\log P\right)$. It can be seen that in the convectively unstable zone, away from the convection zone boundaries, these quantities are very nearly the same for the local and the non-local models, and the turbulent pressure and turbulent kinetic energy flux are negligible in comparison with the gas pressure and convective enthalpy flux. It is not difficult to prove that, neglecting turbulent pressure and the third-order correlation (i.e., turbulent kinetic energy flux), the dynamic equations of correlation functions Eqs. 18, 20, 21 will return to a form analogous to the local MLT formulae (Xiong, 1978; Xiong, 1989). It is not difficult to prove that $\nabla \approx {\nabla }_{ad}+\left({\nabla }_{rad}-{\nabla }_{ad}\right)4x_c/9x$ when $x/x_C\gg 1$, and $\nabla \approx {\nabla }_{rad}- \left({\nabla }_{rad}-{\nabla }_{ad}\right){\left(x/x_c\right)}^{2}9/4$ when $x/x_C\ll 1$. In the deep convection zone, where $P_e=x/x_{C }\gg 1$, convective energy transport is effective, and the temperature gradient is near the adiabatic one independent of the convection theory used. So, it is not difficult to understand why the T-P structures are so close to each other for the local and non-local convective envelope models in Figures 3, 4.

FIGURE 2

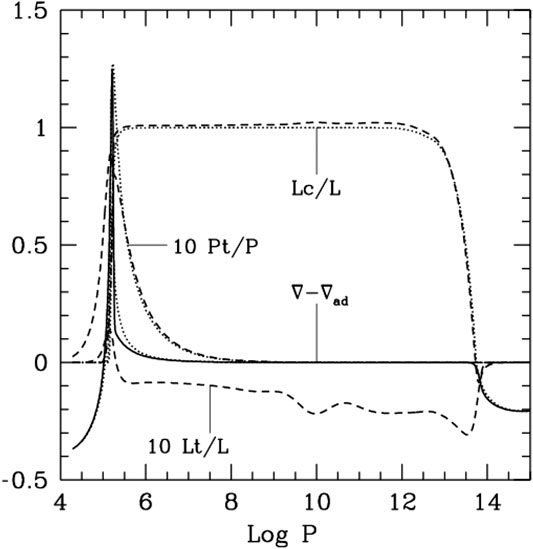
FIGURE 2. Fractional convective flux $L_c/L$, turbulent kinetic energy flux $L_t/L$, super-adiabatic temperature gradient $\nabla - {\nabla }_{ad}$, and the ratio of turbulent pressure to gas pressure $P_t/P$ vs. $\log P$ for the local (dotted-line) and non-local (solid-line) convective models.

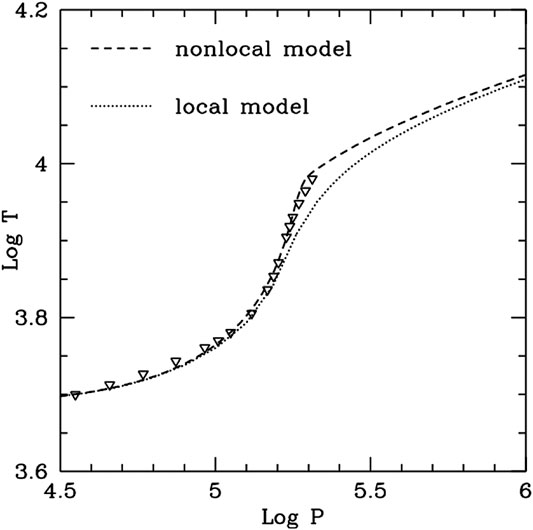
FIGURE 3

FIGURE 3. $\log T$ as a function of $\log P$ in the solar atmosphere for the non-local (dashed-line) and local convection models of the Sun (dotted-line). The inverse triangles are the Harvard-Smithsonian reference atmosphere (Gingerich et al., 1971).

FIGURE 4

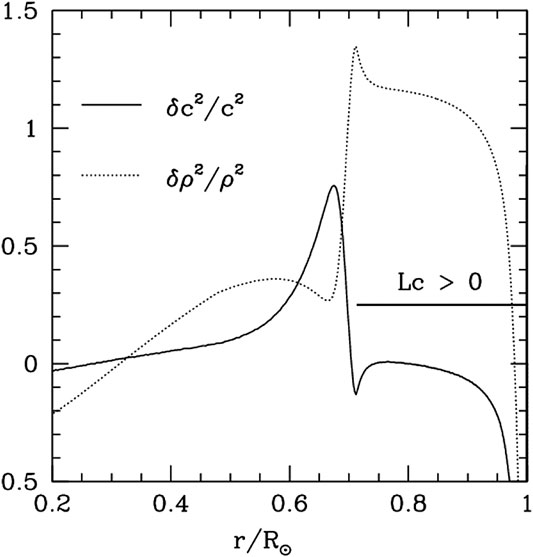
FIGURE 4. Relative difference in the squared sound speed $\delta C^2/ C^2$ (solid-line) and density $\delta \rho /\rho$ (dotted-line) between the non-local and local convection models of the Sun versus fractional radius $r/R_{\odot }$.

Structure of the Convective Overshooting Zone

Overshooting is a very natural phenomenon from the viewpoint of hydrodynamics. However, it was an outstanding problem for a long time in the astronomical community. Up to now, the community still cannot cast off the influence of the MLT. The first non-local MLT is the generalized mixing-length theory by Spiegel (Spiegel, 1963). Ulrich (1970) proposed an analogous non-local MLT. Their theories were used to construct a model of the Sun (Ulrich, 1970; Travis and Matsushima, 1973). Observations show that the temperature gradient of their theoretical models were too gentle in the atmosphere of the Sun, because the efficiency of convective energy transport was overestimated by their theory. Figure 3 shows $\log T$ as a function of $\log P$ for our non-local and local convection models of the Sun. The inverse triangles mark the Harvard-Smithsonian reference atmosphere (Gingerich et al., 1971). The obvious feature of our non-local model is a larger temperature gradient at the top of the convection zone, which agrees with the Harvard-Smithsonian reference atmosphere very well. Helioseismology provides a direct method for probing solar interior structure. Figure 5 shows the results of the sound-speed inversion (Zhang et al., 2012). The open circles are relative differences in squared sound speed between the Sun and the standard solar model S (Christensen-Dalsgaard et al., 1996), which is a local MLT model. It can be seen that the relative difference of squared sound speed between the Sun and the reference model has a bump below the bottom boundary of the convection zone. This bump was understood as an indication of gravitational diffusion (Richard et al., 1996; Brun et al., 1999; Christensen-Dalsgaard, et al., 2007) for a long time. However, we already indicated long ago that this bump was not a result of gravitational diffusion, but was an indication of non-local convective overshooting (Xiong and Deng, 2001). We can see from Figure 2 that, in our non-local convection theory, the convective flux $L_{C }/ L$ becomes negative and the fractional radiative flux $L_{r }/ L$ = $\nabla /{\nabla }_{rad}$ becomes slightly larger than 1, and the temperature gradient $(\nabla )$ will be greater than the radiative one $\left({\nabla }_{rad}\right)$ in the bottom overshooting zone. Therefore, the temperature in the overshooting zone will be higher than that predicted by the local theory of convection as shown in Figure 4. So, we predicted that this bump will be removed, or at least reduced to a great extent, if the reference model of inversion is replaced by our non-local model for the Sun (Xiong and Deng, 2001). This theoretical prediction has been confirmed by sound-speed inversion. In Figure 5 the filled circles are for our non-local model for the Sun as the reference model for inversion. The relative difference in squared sound speed is indeed reduced greatly in comparison with the standard solar model S (open circles).

FIGURE 5

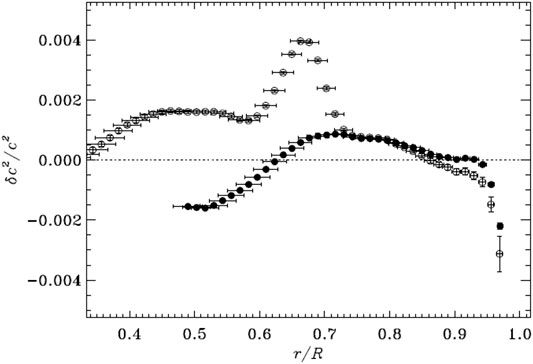
FIGURE 5. Relative differences in squared sound speed between the Sun and the reference model from the sound-speed inversion (Zhang et al., 2012). The open and filled circles are, respectively, for the standard model S (Christensen-Dalsgaard et al., 1996) and our non-local model of the Sun (Xiong and Deng, 2001) as the reference model.

Up to now the MLT is still a dominant idea in the astronomical community. All of the non-local MLT (Spiegel, 1963; Ulrich, 1970; Shaviv and Salpeter, 1973; Maeder, 1975; Bressan et al., 1981; Zahn, 1991) models still use a ballistic-type phenomenological theory. Figure 6A illustrates a sketch of the structure for the bottom overshooting zone of the Sun in the non-local MLT (Monteiro et al., 2000). In the convection zone, the temperature gradient is close to and slightly higher than the adiabatic gradient $\left(\nabla - {\nabla }_{ad}\ge 0\right)$. There is an overshooting zone under the convection zone, where the temperature gradient is near to and slightly lower than the adiabatic gradient. Passing through a very thin transition layer, the temperature gradient jumps from the adiabatic value to the radiative one. So, there is a near discontinuity of the second derivative of sound speed at the bottom boundary of the solar convection zone. This discontinuity will reflect incident acoustic waves and induce an oscillation component in the frequencies of p-modes as a function of radial order n (Gough, 1990). However, helioseismology observations show that the Sun has a mostly smooth stratification (Gough and Sekii, 1993), or the discontinuity is very small (Basu and Antia, 1994; Monteiro et al., 1994; Roxburgh and Vorontsov, 1994). Figure 6B shows the temperature gradient as a function of fractional radius around the bottom boundary of the convection zone predicted by our non-local convection theory (Xiong and Deng, 2001). There is not any discontinuity in the temperature gradient, and it transforms smoothly from the adiabatic one in the convectively unstable zone into the radiative one in the convectively stable zone. In our non-local convection theory, the temperature gradient has already become sub-adiabatic $\left(\nabla <{\nabla }_{ad}\right)$ in the convectively unstable zone before reaching the bottom boundary of the convection zone. It becomes sub-adiabatic and super-radiative $\left({\nabla }_{rad}<\nabla <{\nabla }_{ad}\right)$ in the overshooting zone below, until it approaches the radiative value $\left(\nabla ={\nabla }_{rad}\right)$ in the deep radiative zone. It can be seen from Figures 6A,B that the structure of the transition zone around the boundary of the convection zone is very different between our non-local convection theory and MLT, which reflects the profound difference between two convection theories in the understanding and treatment of convection. Recently, Christensen-Dalsgaard et al. (2011) revisited this problem. They support our viewpoint of a smoothly stratified bridge from the region of the lower convection zone to the radiative interior, such as shown in Figure 6B, and believe that it will be in better agreement with helioseismic data than that of the standard solar model.

FIGURE 6

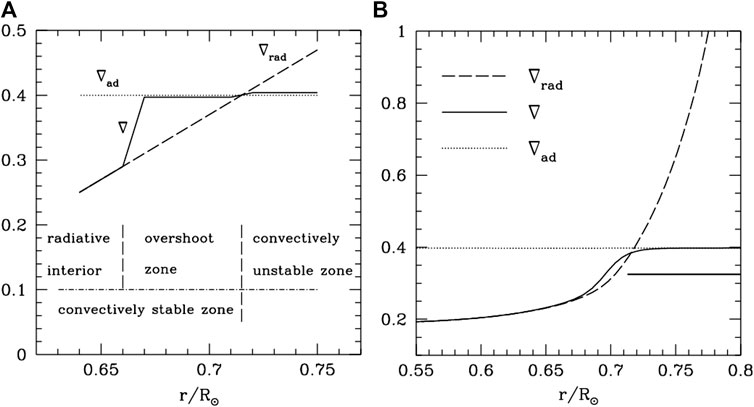
FIGURE 6. The temperature gradient $(\nabla )$, the radiative gradient $\left({\nabla }_{rad}\right)$, and the adiabatic gradient $\left({\nabla }_{ad}\right)$ versus the fractional radius $r/R_{\odot }$ near the bottom boundary of the solar convection zone. Panel (A): a sketch for the non-local MLT model; Panel (B): the same as for panel (A), but for our non-local convection model. The horizontal black line shows the range of the convectively unstable zone.

Eq. 18 is the dynamic equation for the isotropic component of the auto-correlation of turbulent velocity; it can be also understood as the conservation equation of turbulent kinetic energy. The first term is the growth rate of turbulent kinetic energy, which could be set equal to (taking into account minus signs) the sum of the rest of the terms in the equation. The second and third terms are the transformation rate between the average motion and the turbulent kinetic energy. The fourth term is the net gain from the non-local transport of turbulent kinetic energy, which is the key term distinguishing our non-local convection theory from the local theory. The fifth term is the boundary work W_b, which is directly proportional to the convective flux $F_{C }\left(=\overline{\rho }\overline{C_P}\overline{T}V\right)$ and represents the transformation rate between turbulent kinetic energy and thermal energy. The convectively unstable zone, where $F_{C }$and $W_{b }>0$, is the driving region for turbulent convection, where the thermal energy is transformed into turbulent kinetic energy by buoyancy work. On the other hand, the convectively stable (including overshooting) zone is the damping zone for turbulent convection, where the turbulent kinetic energy is transformed into thermal energy due to buoyancy work. Therefore, it is reasonable to define $F_{C }=0$ as the boundary of the convection zone (Xiong and Deng, 2001; Deng and Xiong, 2008).

During the past 20 years, rapid progress has been made in numerical simulations, and these have become an important means to study stellar convection. We have tried to use 2D or 3D simulations to test some basic assumptions of our non-local and time-dependent theory of convection and to calibrate the convection parameters (Kupka, 2002; Deng et al., 2006; Kupka and Muthsam, 2007; Kupka, 2007a; Kupka, 2007b; Kupka, 2007c; Cai, 2008; Tian et al., 2009; Chan et al., 2008; Chan et al., 2011; Cai and Chan, 2012; Cai, 2014; Kupka, 2017; Cai, 2018; Cai, 2020a; Cai, 2020b; Cai, 2020c). Some meaningful results were obtained. Because of limitations on the number of figures, these results cannot be described in detail. Interested readers can refer to the original texts, as well as to extensive reviews by Asplund et al. (2009) and Nordlund et al. (2009).

Overshooting Mixing and Stellar Evolution

We know from the theory of stellar structure and evolution that the stellar structure should be defined once the mass and element abundances of a star are assigned. Therefore, stellar evolution in the H-R diagram is, in fact, a reflection of nuclear evolution in the stellar interior. Convection (including overshooting) is the most important means of element mixing in the stellar interior. Our non-local convection theory has been successfully used to treat non-local convective mixing of elements in the evolution of massive stars (Xiong, 1986) and to calculate lithium depletion in the atmosphere of the Sun (Xiong and Deng, 2002) and late-type main sequence stars (Xiong and Deng, 2009).

Evolution of Massive Stars

Schwarzschild and Härm (1958) have shown that the hydrogen-rich radiative envelope adjacent to the helium-rich convective core cannot be stable against convection for massive stars $\left(M\ge 9 {\mathrm{M}}_{\odot }\right)$. This is the familiar so-called semi-convection contradiction. Schwarzchild and Härm continued the local treatment of convection and introduced a so-called semi-convective zone in order to overcome this contradiction. However, there is not a self-consistent method for the construction of this semi-convection zone. Various researchers constructed their respective models of the semi-convection zone using their own methods. A review of these methods was given by Stothers (1970). He shows that at least ten schemes are available in the literature to treat this unstable intermediate zone. The different treatments of semi-convection resulted in some discrepancies in the evolution of massive stars. The semi-convection contradiction, in our opinion, results from the local treatment of convection; it will be removed automatically if a non-local treatment of convection is applied. In order to treat non-local mixing of nuclear fuels in stellar evolution, we need to develop a non-local theory of convection for chemically inhomogeneous stars (Xiong, 1981). An advantage of our dynamic theory of correlation functions is its convenience for generalization. For a chemically inhomogeneous star, apart from the conservation of total mass, Eq. 2, the conservation equation for each type of nuclear fuel should be added,

$\frac{\partial \left(\rho C_n\right)}{\partial t}+{\nabla }_k\left(\rho C_n{u}^k+J^k\right)=-\rho q_n, (28)$

where $C_n$ is the content per gram of the nth nuclear fuel, $q_n$ and $\overline{J_n^k}$ are, respectively, its destruction rate and the molecular diffusion flux for the nth nuclear fuel. By using the same method of Reynolds decomposition and after an averaging procedure, mentioned in A Non-Local and Time-Dependent Theory of Convection section, it is not difficult to obtain the average conservation equation of fractional mass,

$\frac{D\overline{C_n}}{Dt}+\frac{1}{\rho }{\nabla }_k\left(\overline{\rho u^{\mathit{\prime k}}C{\mathit{\prime }}_{\mathit{n}}}+\overline{J_n^k}\right)=-{\overline{q}}_n,(29)$

and the corresponding dynamic equations of auto- and cross-correlations $\overline{C{\mathit{\prime }}_n^2}$,$\overline{u^{\mathit{\prime k}}C{\mathit{\prime }}_n}$and $\overline{C{\mathit{\prime }}_{n}T\mathit{\prime }}/\overline{T}$. Eqs. 2, 3′, 4′, 18, 19, 20, 21, 29, and the dynamic equations for $\overline{C{\mathit{\prime }}_n^2}$,$\overline{u{\mathit{\prime }}^{k}C{\mathit{\prime }}_n}$and $\overline{C{\mathit{\prime }}_{n}T\mathit{\prime }}/\overline{T}$ form a set of equations for the calculation of stellar evolution (Xiong, 1981; Xiong, 1986).

By using our non-local theory of convection for chemically inhomogeneous stars mentioned above (Xiong, 1981), we calculated the evolution of massive stars in the hydrogen-burning stages (Xiong, 1986). The semi-convection contradiction was indeed removed automatically, as predicted by us. Figure 7 shows the outline of the hydrogen content at various evolution ages for a $60{\mathrm{M}}_{\odot }$star. It can be seen that non-local mixing of helium penetrates deeply into the convectively stable zone beyond the boundary of the convectively unstable core marked by the dashed line. A molecular-weight gradient region adjacent to the convective core formed automatically. The convective core size increases due to non-local overshooting mixing, so the evolutionary track runs at a higher luminosity for a star with fixed mass, and the main sequence band becomes noticeably wider and main sequence lifetimes become longer in comparison with those calculated using the local MLT (the dotted lines, Maeder, 1981). It can be seen from Figure 8 that these influences of non-local convective mixing on the structure and evolution of stars increase toward lower mass, because the relative increase of convective core size increases with the decreasing mass of the star. These theoretical predictions have been confirmed by subsequent research (Stothers, 1991; Chiosi, et al., 1992; Schootemeijer, et al., 2019; Higgins and Vink, 2020). This means that the evolution masses for a given luminosity were overestimated and the width of the main sequence band was underestimated when convective overshooting mixing was neglected. This might be one of the important causes for the Cepheid mass discrepancy (Christy, 1968; Stobie, 1969; Cogan, 1970; Rodgers, 1970) and the contradiction between the theoretical and observed distribution of luminous stars in the H-R diagram (Humphreys, 1979; Humphreys and Davidson, 1979). The MLT models can be made to agree with observations by adjusting core overshooting and semi-convection parameters, which makes such models less predictive, in contrast to our models.

FIGURE 7

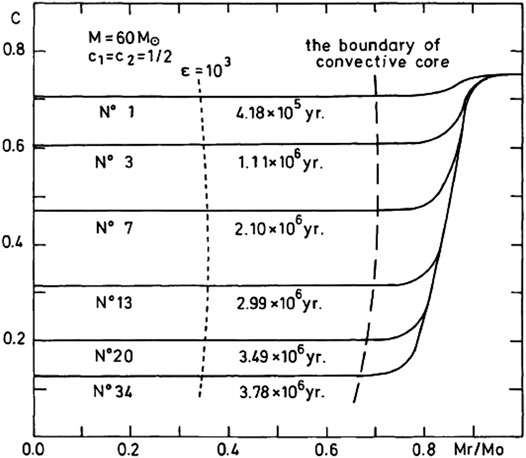
FIGURE 7. Outlines of hydrogen content at various evolution ages for a $60{\mathrm{M}}_{\odot }$ star. The dashed line is the boundary of the convectively unstable core, and the dotted line indicates the location of the nuclear energy generation rate $\epsilon =1000 \mathrm{erg}/\mathrm{s}$(Xiong, 1986).

FIGURE 8

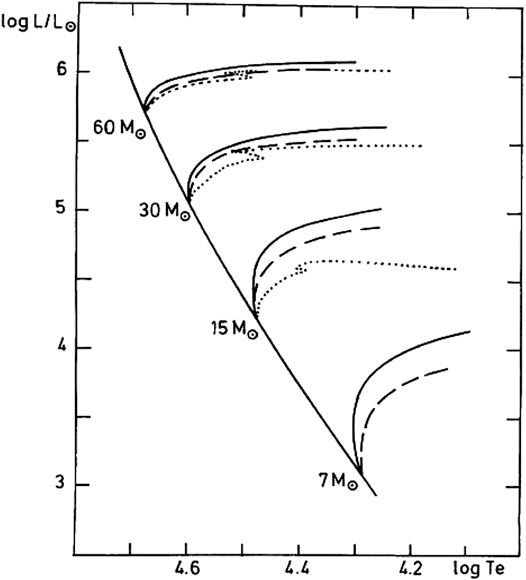
FIGURE 8. Theoretical evolutionary tracks in the H-R diagram for 7–$60{\mathrm{M}}_{\odot }$ stars (Xiong, 1986). The solid and dashed lines are for our non-local convection theory with two different convective parameters, and the dotted lines are for the local MLT theory (Maeder, 1981).

How one defines the boundary of convective zone is another contributor to the uncertainty in the treatment of non-local convection overshooting, and therefore to the uncertainty in the evolution. For a long time, a disputed question has been whether the criterion for convective instability should follow the Schwarzschild criteria or the Ledoux criteria. Our research shows that the Schwarzschild and Ledoux criteria are only applicable for local convective instability. In our non-local convection theory, the convective instability criterion follows neither Schwarzschild nor Ledoux. $F_{C }=0$ is a more convenient and reasonable definition for the boundary of the convection zone, as described in Structure of the Convective Overshooting Zone section, and the details can be found in our earlier works (Xiong, 1986; Xiong and Deng, 2001; Deng and Xiong, 2008). The difficulty in determining the boundary of the convective core results from the local treatment of convection. This difficulty is also removed automatically. There is no longer any ambiguity in defining the convective core and constructing the overshooting zone in our non-local convection theory. Therefore, the uncertainties in massive star evolution due to ambiguous semi-convection and overshooting do not arise.

Chiosi et al. studied the mass discrepancy of the Cepheids. They found that “the mass discrepancy problem likely originates from the adoption of semi-convective models and insufficient accuracy in the determination of the mass by one of the two methods. When this is feasible, as in the ideal laboratory given by the young LMC clusters with Cepheids, the discrepancy no longer exists” (Chiosi, et al., 1992). By using the new and improved equation of state (Däppen, et al., 1988; Hummer and Mihalas, 1988; Mihalas et al., 1988) and opacity (Roger and Iglesias, 1992), not only were the excitation mechanism of β Cephei and SPB stars explained (Cox et al., 1992; Moskalik and Dziembowski, 1992; Dziembowski and Pamyatnykh, 1993), but also the mass discrepancy between the evolutionary mass and the “bump” and “beat” masses of the Cepheids was reduced further (Carson and Stothers, 1988; Moskalik and Dziembowski, 1992; Petersen, 1992; Simon, 1995; Guzik et al., 2020).

Lithium Depletion in Late-Type Main Sequence Stars

Lithium abundance was a very important problem for nucleosynthesis during the Big Bang. In addition, lithium and beryllium are both very fragile elements, which are destroyed quickly due to nuclear reaction at T∼2.5 and 4.0 million K in the stellar interior, which makes them ideal trace elements for measuring the depth of the surface convection zone during stellar evolution. Since the original observational detection of the lithium abundance in solar-type stars by Herbig (1965), rich observational data have been accumulated. Observations of the lithium abundance of Galactic open clusters of various ages and metallicities provide very conclusive constraints on the depletion mechanism of lithium. Up to now, the depletion mechanism of lithium in the Sun and stars is still not fully understood. Various depletion mechanisms have been proposed, including mass loss (Weymann and Sears, 1965; Hobbs, et al., 1989; Schramm et al., 1990) and wave-driven mixing (Garcia Lopez and Spruit, 1991; Montalban and Schatzman, 1996), among which rotationally induced mixing (Pinsonneault et al., 1989; Charbonnel et al., 1992; Chaboyer et al., 1995) has been a dominant viewpoint. In our view, convective overshooting mixing and gravitational settling seems to be the most reasonable mechanism for lithium depletion.

By using our non-local theory of convection in chemically inhomogeneous stars described in A Non-Local and Time-Dependent Theory of Convection section and the previous subsection, we calculated the lithium depletion in the atmosphere of the Sun (Xiong and Deng, 2002) and late-type dwarfs (Xiong and Deng, 2009). Apart from convective overshooting, the gravitational settling has been taken into account, because the timescale for gravitational settling in the atmosphere of warm stars becomes comparable to and even shorter than the evolutionary timescale. Referring to Chapman and Cowling (1970), the micro-diffusion flux J of lithium can be expressed as (Xiong and Deng, 2009)

$J= -\overline{C}D\left[\frac{\partial \ln \overline{C}}{\partial r}+\left(7-\frac{4{\mu }_o}{1+\phi }\right)\frac{G{M}_r}{RT{r}^2}+K_T\frac{\partial \ln \overline{T}}{\partial r}\right], (30)$

where D and $K_T$ are, respectively, the diffusion and thermal diffusion coefficients, ${\mu }_o$ the mean molecular weight and $\phi$ the mean ionization degree per ion. The first, second, and third terms in Eq. 30 are, respectively, pressure, gravitational, and thermal diffusion.

Figure 9A shows the evolution of surface lithium abundance with age for stars of different masses. We can see that lithium abundance tends to decrease exponentially with time. Figure 9B shows the e-folding time of lithium depletion as a function of stellar mass. The dotted lines are for the models in which only convective overshooting mixing is taken into account and the gravitational settling is neglected; the solid lines are for models with both convective overshooting mixing and gravitational settling. It can be seen that, for larger stars $\left(M\ge 1.1{\mathrm{M}}_{\odot }\right)$, lithium depletion mainly results from gravitational settling, because their surface convection zones are too shallow for the overshooting mixing to be efficient. The mass of surface convection zone and the timescale of gravitational settling increases with decreasing stellar mass. The effect of convective overshooting mixing on lithium depletion increases rapidly with decreasing stellar mass (Figure 9B), and convective overshooting mixing becomes the main mechanism of lithium depletion for low-mass stars $\left(M<1.1{\mathrm{M}}_{\odot }\right)$

FIGURE 9

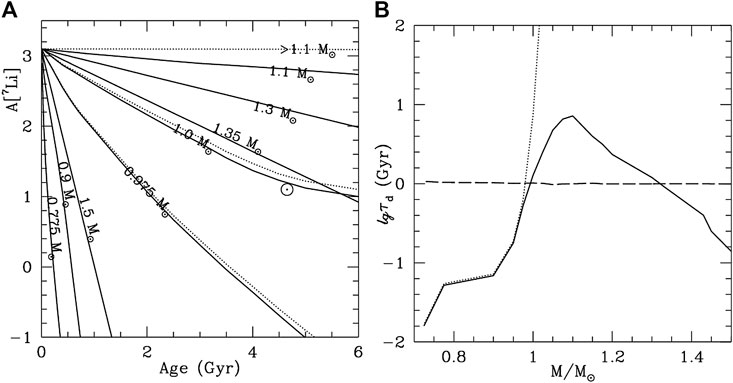
FIGURE 9. (A) Evolution of the surface lithium abundance with age for stars of different masses. The dotted and solid lines, respectively, are for models with only convective overshooting mixing, and for which both gravitational settling and convective overshooting mixing are taken into account. (B) The e-folding time of lithium depletion as a function of stellar mass. The dotted lines are the models for which only the overshooting mixing are taken into account; the solid lines are models in which both overshooting mixing and gravitational setting are taken into account.

Figure 10 shows the lithium abundance versus depth $\left(\log \Delta M_r/M_{\odot }\right)$ at different ages (indicated on the curves) for $1.5 {\mathrm{M}}_{\odot }$ and $1.0{\mathrm{M}}_{\odot }$ stars, clearly showing the physical picture for lithium depletion induced by overshooting mixing and gravitational settling. For moderately high-mass warm $\left(T_e\ge 6200\mathrm{K}\right)$ stars, which have a shallow surface convection zone, surface lithium is drawn into the deeper radiative interior by gravitational settling and stays there, and the surface lithium abundance decreases with time (Figure 10A). For low-mass stars $\left(M\le 1.0{\mathrm{M}}_{\odot } \right)$, which have an extensive convective envelope, the surface lithium is brought into high-temperature interior regions by convective overshooting and destroyed by nuclear reactions there, and the surface lithium abundance decreases with time (Figure 10B). Therefore, the mechanism of lithium depletion is very different for warm $\left(M\ge 1.1{\mathrm{M}}_{\odot }\right)$ and cool $\left(M\le 1.0{\mathrm{M}}_{\odot } \right)$ main sequence stars. Lithium depletion is very sensitive to the treatment of convection, because lithium depletion increases exponentially with time. A small error will be enlarged exponentially with time. Therefore, observations of lithium depletion provide the most rigorous constraint for stellar convection theory. Figures 11A–D show the distribution of lithium abundance with effective temperatures for the member stars of several Galactic open clusters with different ages; the theoretical isochrones are also drawn on the figures. It can be seen that the theoretical predictions, in general, agree well with the observations for Galactic open clusters over a very wide range of ages. This means that our convection theory and the assumption of the convective overshooting mechanism for lithium depletion seem to be true.

FIGURE 10

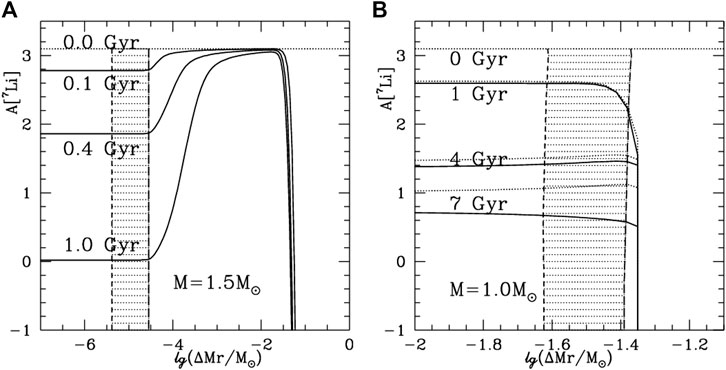
FIGURE 10. Lithium abundances as a function of depth $\log \left(\Delta M_r/M\right)$ at the ages indicated on the curves for $1.5{\mathrm{M}}_{\odot }$(A), and $1.0{\mathrm{M}}_{\odot }$(B) stars, where $\Delta M_r=M-M_r$, and $M$ and $M_r$ are, respectively, the total mass and mass within radius r. $M_{\odot }$ is the solar mass. The shaded areas mark the overshooting zone in each panel, bounded by the dashed line (left) and long dashed line (right). The dotted lines are for the theoretical model with only overshooting mixing, and the solid lines are for the theoretical model with both overshooting mixing and gravitational settling.

FIGURE 11

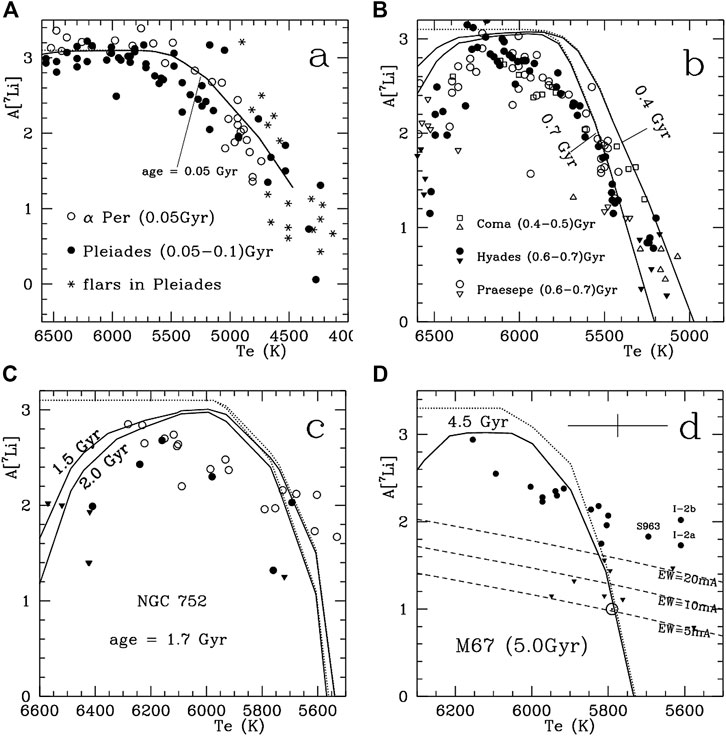
FIGURE 11. Lithium abundance as a function of $\log T_e$ for the member stars in Galactic open clusters: (A) Pleiades (filled circles and stars) and $\alpha$ Per (open circles), (B) Hyades (filled circles and inverse triangles), Praesepe (open circles and inverse triangles) and Coma Berenices (open squares and triangles), (C) NGC752, and (D) M67, where $\odot$ is the position of the Sun. The solid and dotted lines are, respectively, the theoretical isochrones with and without gravitational settling for the ages marked.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by National Natual Science Foundation of China (NSFC) through grants 11373069.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank L. Deng and C. Zhang for their valuable discussions. We would also like to thank Guzik for her great help in reviewing and revising this article. I dedicate this article to my mentor, Prof. Wasaburo Unno, with gratitude for his attention and support for our work over the years.

References

Alexander, D. R., and Ferguson, J. W. (1994). Low-temperature Rosseland opacities. Astrophys. J. 437, 879. doi:10.1086/175039

CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., Sauval, A. J., and Scott, P. (2009). The chemical composition of the Sun. Annu. Rev. Astron. Astrophys. 47, 481–522. doi:10.1146/annurev.astro.46.060407.145222

CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (1994). Helioseismic constraints on solar abundances. Mon. Not. R. Astron. Soc. 269, 1437.

Google Scholar

Bohm-Vitense, E. (1958). Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Zeitschrift für Astrophysik 46, 108.

Google Scholar

Bressan, A., Bertelli, G., and Chiosi, C. (1981). Mass loss and overshooting in massive stars. Astron. Astrophys. 102, 23.

Google Scholar

Brun, A. S., Turck‐Chieze, S., and Zahn, J. P. (1999). Standard solar models in the light of new helioseismic constraints. II. mixing below the convective zone. Astrophys. J. 525, 1032. doi:10.1086/307932

CrossRef Full Text | Google Scholar

Cai, T., and Chan, K. L. (2012). Three-dimensional numerical simulation of convection in giant planets: effects of solid core size. Planet. Space Sci. 71, 125–130. doi:10.1016/j.pss.2012.07.023

CrossRef Full Text | Google Scholar

Cai, T. (2014). Numerical analysis of non-local convection. Mon. Not. R. Astron. Soc. 443, 3703–3711. doi:10.1093/mnras/stu1357

CrossRef Full Text | Google Scholar

Cai, T. (2018). Numerical analysis of nonlocal convection-comparison with three-dimensional numerical simulations of efficient turbulent convection. Astrophys. J. 868, 12. doi:10.3847/1538-4357/aae1b3

CrossRef Full Text | Google Scholar

Cai, T. (2008). Some discussion of the nonlocal treatment of the dissipation in the Reynolds stress models. Proc. Int. Astron. Union 4, 45–46. doi:10.1017/s1743921308022412

CrossRef Full Text | Google Scholar

Cai, T. (2020a). Upward overshooting in turbulent compressible convection. I. effects of the relative stability parameter, the Prandtl number, and the Péclet number. Astrophys. J. 888, 46. doi:10.3847/1538-4357/ab58c5

CrossRef Full Text | Google Scholar

Cai, T. (2020c). Upward overshooting in turbulent compressible convection. III. calibrate parameters for one-dimensional Reynolds stress model. Astrophys. J. 891, 77. doi:10.3847/1538-4357/ab7203

CrossRef Full Text | Google Scholar

Cai, T. (2020b). Upward overshooting in turbulent compressible convection. II. simulations at large relative stability parameters. Astrophys. J. 891, 49. doi:10.3847/1538-4357/ab711c

CrossRef Full Text | Google Scholar

Canuto, V. M. (1997). Compressible turbulence. Astrophys. J. 482, 827. doi:10.1086/304175

CrossRef Full Text | Google Scholar

Canuto, V. M. (1999). Turbulence in stars. III. unified treatment of diffusion, convection, semiconvection, salt fingers, and differential rotation. Astrophys. J. 524, 311. doi:10.1086/307783

CrossRef Full Text | Google Scholar

Canuto, V. M. (1993). Turbulent convection with overshooting: Reynolds stress approach. II. Astrophys. J. 416, 331. doi:10.1086/173238

CrossRef Full Text | Google Scholar

Carson, T. R., and Stothers, R. B. (1988). Classical bump Cepheids—reconciliation of theory with observations. Astrophys. J. 328, 196. doi:10.1086/166281

CrossRef Full Text | Google Scholar

Chaboyer, B., Demarque, P., and Pinsonneault, M. H. (1995). Stellar models with microscopic diffusion and rotational mixing. I: application to the Sun. Astrophys. J. 441, 865. doi:10.1086/175408

CrossRef Full Text | Google Scholar

Chan, K. L., Cai, T., and Singh, H. P. (2011). Overshooting above a convection zone. Proc. Int. Astron. Union 6, 317–325. doi:10.1017/s1743921311017741

CrossRef Full Text | Google Scholar

Chan, K. L., and Singh, H. P. (2008). Proxies for overshooting above a convection zone. Proc. Int. Astron. Union 4, 43–44. doi:10.1017/S1743921308022400

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1939). An Introduction to the Study of Stellar Structure. Chicago, IL: University of Chicago Press.

Chapman, S., and Cowling, G. (1970). Mathematical theory of non-uniform gases. 3rd Edn. Cambridge, United Kingdom: Cambridge Univ. Press.

Charbonnel, C., Vauclair, S., and Zhan, J. P. (1992). Rotation-induced mixing and lithium depletion in galactic clusters. Astron. Astrophys. 255, 191.

Google Scholar

Chiosi, C., Bressan, A., Wood, P. R., Bertelli, G., and Mateo, M. (1992). On the mass discrepancy of the cepheid stars. Astrophys. J. 385, 205–216. doi:10.1086/170928

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Däppen, W., Ayukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., et al. (1996). The current state of solar modeling. Science 272, 1286–1292. doi:10.1126/science.272.5266.1286

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Di Mauro, M. P., Straka, C., Lebreton, Y., and Monteiro, M. (2007). “Diffusion and Helioseismology,” in EAS Publ. Ser. 26 stellar evolution and seismic tools for asteroseismology--diffusive processes in stars and seismic analysis. Editors C. W. Straka, Y. Lebreton, M. J. P. G. Monteiro, and L. E. S. Ulis (Cambridge, United Kingdom: Cambridge University Press), 3–26.

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Monteiro, M. J. P. F. G., Rempel, M., and Thompson, M. J. (2011). A more realistic representation of overshoot at the base of the solar convective envelope as seen by helioseismology. Mon. Not. R. Astron. Soc. 414, 1158–1174. doi:10.1111/j.1365-2966.2011.18460.x

CrossRef Full Text | Google Scholar

Christy, R. F. (1968). The theory of cepheid variability. Q. J. R. Astron. Soc. 9, 13.

Google Scholar

Cogan, B. C. (1970). Pulsation constants for models of cepheids. Astrophys. J. 162, 139. doi:10.1086/150639

CrossRef Full Text | Google Scholar

Cox, A. N., Morgan, S. M., Rogers, F. J., and Iglesias, C. A. (1992). An opacity mechanism for the pulsations of OB stars. Astrophys. J. 393, 272–277. doi:10.1086/171504

CrossRef Full Text | Google Scholar

Däppen, W., Mihalas, D., Hummer, D. G., and Mihalas, B. W. (1988). The equation of state for stellar envelopes. III. thermodynamic quantities. Astrophys. J. 332, 261. doi:10.1086/166650

CrossRef Full Text | Google Scholar

Deng, L., Xiong, D. R., and Chan, K. L. (2006). An anisotropic nonlocal convection theory. Astrophys. J. 643, 426. doi:10.1086/502707

CrossRef Full Text | Google Scholar

Deng, L., and Xiong, D. R. (2008). How to define the boundaries of a convective zone, and how extended is overshooting? Mon. Not. R. Astron. Soc. 386, 1270. doi:10.1111/j.1365-2966.2008.12969.x

CrossRef Full Text | Google Scholar

Dziembowski, W. A., and Pamyatnykh, A. A. (1993). The opacity mechanism in B-type stars - II. excitation of high-order g-modes in main-sequence stars. Mon. Not. R. Astron. Soc. 262, 588–600. doi:10.1093/mnras/262.1.204

CrossRef Full Text | Google Scholar

Garcia Lopez, R. J., and Spruit, H. C. (1991). Li Depletion in F stars by internal gravity waves. Astrophys. J. 377, 268. doi:10.1086/170356

CrossRef Full Text | Google Scholar

Gingerich, O., Noyes, R. W., Kalkofen, W., and Cuny, Y. (1971). The Harvard-Smithsonian reference atmosphere. Solar Phys. 18, 347–365. doi:10.1007/bf00149057

CrossRef Full Text | Google Scholar

Gough, D. O., and Sekii, T. (1993). “On the Detection of Convective Overshoot,” in Seismic investigation of the Sun and Stars ASP Conf. Ser. 42. Editor T. Brown (San Francisco, CA: Astron. Soc. Pac.), 177.

Google Scholar

Gough, D. O. (1990). “Comments on Helioseismic Inference,” in Lecture Notes in Physics. Editors Y. Osaki, and H. Shibahashi (Berlin, Germany: Springer-Verlag), Vol. 363, 283.

Google Scholar

Gough, D. O. (1969). The Anelastic Approximation for Thermal Convection. J. Atmos. Sci. 26, 448–456. doi:10.1175/1520-0469(1969)026<0448:taaftc>2.0.co;2

CrossRef Full Text | Google Scholar

Grossman, S. A. (1996). A theory of non-local mixing-length convection - III. comparing theory and numerical experiment. Mon. Not. R. Astron. Soc. 279, 305–336. doi:10.1093/mnras/279.2.305

CrossRef Full Text | Google Scholar

Guzik, J. A., Farag, E., Ostrowski, J., Evans, N. R., Neilson, H., Moschou, S., et al. (2020). Investigating opacity modifications and reaction rate uncertainties to resolve the cepheid mass discrepancy. arXiv2002. 04073.

Google Scholar

Henyey, L. G., Forbes, J. E., and Gould, N. L. (1964). A new method of automatic computation of stellar evolution. Astrophys. J. 139, 306. doi:10.1086/147754

CrossRef Full Text | Google Scholar

Herbig, G. H. (1965). Lithium abundances in F5-G8 dwarfs. Astrophys. J. 141, 588. doi:10.1086/148147

CrossRef Full Text | Google Scholar

Higgins, E. R., and Vink, J. S. (2020). Theoretical investigation of the Humphreys-Davidson limit at high and low metallicity. Astron. Astrophys. 635, 175. doi:10.1051/0004-6361/201937374

CrossRef Full Text | Google Scholar

Hinze, J. O. (1975). Turbulence. New York, NY: McGraw-Hill.

Hobbs, L. M., Iben, I. J., and Pilachowski, C. (1989). On Lithium removal from G dwarfs. Astrophys. J. 347, 817–880. doi:10.1086/168171

CrossRef Full Text | Google Scholar

Hummer, D. G., and Mihalas, D. (1988). The equation of state for stellar envelopes. I - an occupation probability formalism for the truncation of internal partition functions. Astrophys. J. 331, 794. doi:10.1086/166600

CrossRef Full Text | Google Scholar

Humphreys, R. M., and Davidson, K. (1979). Studies of luminous stars in nearby galaxies. III - comments on the evolution of the most massive stars in the Milky Way and the Large Magellanic Cloud. Astrophys. J. 232, 409–420. doi:10.1086/157301

CrossRef Full Text | Google Scholar

Humphreys, R. (1979). Studies of luminous stars in nearby galaxies. II. M supergiants in the large magellanic cloud. Astrophys. J. Suppl. Ser. 38, 309. doi:10.1086/190578

CrossRef Full Text | Google Scholar

Kupka, F. (2002). A Star Envelopes: a test of local and non-local models of convection. MNRAS 330, 6.

CrossRef Full Text | Google Scholar

Kupka, F. (2017). Modelling of stellar convection. Living Rev. Comput. Astrophys. 3, 1. doi:10.1007/s41115-017-0001-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kupka, F., and Muthsam, H. J. (2007). Probing Reynolds stress models of convection with numerical simulations: III. compressibility modelling and dissipation. Proc. Int. Astron. Union 239, 86. doi:10.1017/S1743921307000191

CrossRef Full Text | Google Scholar

Kupka, F. (2007b). Probing Reynolds stress models of convection with numerical simulations: II. non-locality and third order moments. Proc. Int. Astron. Union 239, 83. doi:10.1017/S174392130700018X

CrossRef Full Text | Google Scholar

Kupka, F. (2007a). Probing Reynolds stress models of convection with numerical simulations: I. overall properties: fluxes, mean profiles. Proc. Int. Astron. Union 239, 80. doi:10.1017/S1743921307000178

CrossRef Full Text | Google Scholar

Kupka, F. (2007c). Some open questions concerning the modelling of non-locality in Reynolds stress type models of stellar convection. Proc. Int. Astron. Union 239, 92. doi:10.1017/S174392130700021X

CrossRef Full Text | Google Scholar

Lesieur, M. (1987). Turbulence in fluids. Boston, MA: Martinus Nijhoff.

Ludwig, H. G., Freytag, B., and Steffen, M. (1999). A calibration of the mixing-length for solar-type stars based on hydrodynamical simulations. I. methodical aspects and results for solar metallicity. Astron. Astrophys. 346, 111.

Google Scholar

Maeder, A. (1975). Stellar evolution III: the overshooting from convective cores. Astron. Astrophys. 40, 303.

Google Scholar

Maeder, A. (1981). The most massive stars evolving to red supergiants - Evolution with mass loss, WR stars as post-red supergiants and pre-supernovae. Astron. Astrophys. 99, 97.

Google Scholar

Mihalas, D., Däppen, W., and Hummer, D. G. (1988). The equation of state for stellar envelopes. II - algorithm and selected results. Astrophys. J. 331, 815. doi:10.1086/166601

CrossRef Full Text | Google Scholar

Montalban, J., and Schatzman, E. (1996). Mixing by internal waves. II. Li and Be depletion rate in low mass main sequence. Astron. Astrophys. 305, 513.

Google Scholar

Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., and Thompson, M. J. (1994). Seismic study of overshoot at the base of the solar convective envelope. Astron. Astrophys. 283, 247.

Google Scholar

Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., and Thompson, M. J. (2000). Seismic study of stellar convective regions: the base of the convective envelope in low-mass stars. Mon. Not. R. Astron. Soc. 316, 165–172. doi:10.1046/j.1365-8711.2000.03471.x

CrossRef Full Text | Google Scholar

Moskalik, P., and Dziembowski, W. A. (1992). New opacities and the origin of the β Cephei pulsation. Astron. Astrophys. 256, L5.

Google Scholar

Nordlund, A., Stein, R. F., and Asplund, M. (2009). Solar Surface Convection. Living Rev. Sol. Phys. 6, 2. doi:10.12942/lrsp-2009-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Orszag, S. A. (1977). “Fluid Dynamics,”. Editors R. Balian, and J-L. Peube, (London, United Kingdom: Gordon & Breach), 235.

Google Scholar

Petersen, J. O. (1992). Studies of cepheid-type variability. X. k-effect-functions for period ratios. Astron. Astrophys. 265, 555.

Google Scholar

Pinsonneault, M. H., Kawaler, S. D., Sofia, S., and Demarque, P. (1989). Evolutionary models of the rotating Sun. Astrophys. J. 338, 424. doi:10.1086/167210

CrossRef Full Text | Google Scholar

Richard, O., Vauclair, S., Charbonnel, C., and Dziembowski, W. (1996). New solar models including helioseismological constraints and light-element depletion. Astrophys. J. 525, 1032.

Google Scholar

Rodgers, A. W. (1970). The masses of pulsating stars. Mon. Not. R. Astron. Soc. 151, 133–140. doi:10.1093/mnras/151.1.133

CrossRef Full Text | Google Scholar

Rogers, F. J., and Iglesias, C. A. (1992). Radiative atomic Rosseland mean opacity tables. Astrophys. J. Suppl. Ser. 79, 507. doi:10.1086/191659

CrossRef Full Text | Google Scholar

Rotta, J. (1951). Statistische Theorie nichthomogener Turbulenz. Zeitschrift für Physik 129, 547–572. doi:10.1007/bf01330059

CrossRef Full Text | Google Scholar

Roxburgh, I. W., and Vorontsov, S. V. (1994). Seismology of the solar envelope: the base of the convective zone as seen in the phase shift of acoustic waves. Mon. Not. R. Astron. Soc. 268, 880–888. doi:10.1093/mnras/268.4.880

CrossRef Full Text | Google Scholar

Schootemeijer, A., Nanger, N., Grin, N. J., and Wang, C. (2019). Constraining mixing in massive stars in the small magellanic cloud. Astron. Astrophys. 625, 132. doi:10.1051/0004-6361/201935046

CrossRef Full Text | Google Scholar

Schramm, D. N., Steigman, G., and Dearborn, D. S. P. (1990). Main-sequence mass loss and the lithium dip. Astrophys. J. 359, L55. doi:10.1086/185794

CrossRef Full Text | Google Scholar

Schwarzschild, M., and Härm, R. (1958). Evolution of Very Massive Stars. Astrophys. J. 128, 348. doi:10.1086/146548

CrossRef Full Text | Google Scholar

Shaviv, G., and Salpeter, E. E. (1973). Convective overshooting in stellar interior models. Astrophys. J. 184, 191. doi:10.1086/152318

CrossRef Full Text | Google Scholar

Simon, N. R. (1995). “Cepheids: pulsation, evolution, opacity, ASPC series,” in Astrophysical applications of powerful new databases. joint discussion no. 16 of the 22nd. general assembly of the I.A.U. ASP conference series, The Hague, Netherlands, August 22–23, 1994. Editors S. J. Adelman, and W. L. Weise (San Francisco, CA: Astron. Soc. Pac.), Vol. 78, 211.

Google Scholar

Spiegel, E. A. (1963). A generalization of the mixing-length theory of turbulent convection. Astrophys. J. 138, 216. doi:10.1086/147628

CrossRef Full Text | Google Scholar

Stobie, R. S. (1969). Cepheid pulsation--I: numerical technique and test calculations. Mon. Not. R. Astron. Soc. 144, 461–484. doi:10.1093/mnras/144.4.461

CrossRef Full Text | Google Scholar

Stothers, R. B. (1991). Observational tests of convective core overshooting in stars of intermediate to high mass in the galaxy. Astrophys. J. 383, 820. doi:10.1086/170840

CrossRef Full Text | Google Scholar

Stothers, R. (1970). Internal structure of upper main-sequence stars. Mon. Not. R. Astron. Soc. 151, 65–80. doi:10.1093/mnras/151.1.65

CrossRef Full Text | Google Scholar

Tian, C.-L., Deng, L.-C., Chan, K.-L., and Xiong, D.-R. (2009). Efficient turbulent compressible convection in the deep stellar atmosphere. Res. Astron. Astrophys. 9, 102. doi:10.1088/1674-4527/9/1/009

CrossRef Full Text | Google Scholar

Travis, L. D., and Matsushima, S. (1973). The role of convection in stellar atmospheres. observable effects of convection in the solar atmosphere. Astrophys. J. 180, 975. doi:10.1086/152020

CrossRef Full Text | Google Scholar

Ulrich, R. K. (1970). The five-minute oscillations on the solar surface. Astrophys. J. 162, 993. doi:10.1086/150731

CrossRef Full Text | Google Scholar

Unno, W., Xiong, D. R., and Kondo, M.-A. (1985). Preliminary report on the solar convection zone model. PASJ 37, 235.

Google Scholar

Weymann, R., and Sears, R. L. (1965). The depth of the convective envelope on the lower main sequence and the depletion of lithium. Astrophys. J. 142, 174. doi:10.1086/148274

CrossRef Full Text | Google Scholar

Xiong, D. R. (1980). A statistical theory of non-local convection. Chin. Astron. 4, 234. doi:10.1016/0146-6364(80)90004-3

CrossRef Full Text | Google Scholar

Xiong, D. R., and Cheng, Q. L. (1992). A nonlocal convection model of the solar convection zone. Astron. Astrophys. 254, 362.

Google Scholar

Xiong, D. R., Deng, L., and Zhang, C. (2016). Turbulent convection and pulsation stability of stars - II. theoretical instability strip for δ Scuti and γ Doradus stars. Mon. Not. R. Astron. Soc. 457, 3183. doi:10.1093/mnras/stw047

CrossRef Full Text | Google Scholar

Xiong, D. R. (1989). Radiation-hydrodynamic equations for stellar oscillations. Astron. Astrophys. 209, 126.

Google Scholar

Xiong, D. R. (1981). Statistical theory of non-local convection in chemically inhomogeneous stars. Sci. Sin. 24, 234.

Google Scholar

Xiong, D. R. (1978). Stochastic theory of turbulent convection in pulsating variables. Chin. Astron. 2, 118. doi:10.1016/0146-6364(78)90009-9

CrossRef Full Text | Google Scholar

Xiong, D. R. (1986). The evolution of massive stars using a non-local theory of convection. Astron. Astrophys. 167, 239.

Google Scholar

Xiong, D. R., Cheng, Q. L., and Deng, L. (1997). Nonlocal time‐dependent convection theory. Astrophys. J. Suppl. Ser. 108, 529. doi:10.1086/312959

CrossRef Full Text | Google Scholar

Xiong, D. R., Cheng, Q. L., and Deng, L. (1998b). Turbulent convection and pulsational stability of variable stars. II. oscillations of RR lyrae and horizontal branch red variable stars. Astrophys. J. 500, 449. doi:10.1086/305695

CrossRef Full Text | Google Scholar

Xiong, D. R., Deng, L., and Cheng, Q. L. (1998a). Turbulent convection and pulsational stability of variable stars. I. oscillations of long‐period variables. Astrophys. J. 499, 355. doi:10.1086/305601

CrossRef Full Text | Google Scholar

Xiong, D. R., and Deng, L. (2009). Lithium depletion in late-type dwarfs. Mon. Not. R. Astron. Soc. 395, 2013–2028. doi:10.1111/j.1365-2966.2009.14581.x

CrossRef Full Text | Google Scholar

Xiong, D. R., and Deng, L. (2002). The extent of the solar overshooting zone deduced from Li abundance. Mon. Not. R. Astron. Soc. 336, 511–519. doi:10.1046/j.1365-8711.2002.05767.x

CrossRef Full Text | Google Scholar

Xiong, D. R., and Deng, L. (2001). The structure of the solar convective overshooting zone. Mon. Not. R. Astron. Soc. 327, 1137–1144. doi:10.1046/j.1365-8711.2001.04820.x

CrossRef Full Text | Google Scholar

Xiong, D. R., Deng, L., and Zhang, C. (2018). Turbulent convection and pulsation stability of stars - III. non-adiabatic oscillations of red giants. Mon. Not. R. Astron. Soc. 480, 2698–2703. doi:10.1093/mnras/sty2014

CrossRef Full Text | Google Scholar

Zahn, J. P. (1991). Convective penetration in stellar Interiors. Astron. Astrophys. 252, 179.

Google Scholar

Zhang, C., Deng, L., Xiong, D., and Christensen-Dalsgaard, J. (2012). Sound-speed inversion of the Sun using a nonlocal statistical convection theory. Astrophys. J. 759, L14. doi:10.1088/2041-8205/759/1/l14

CrossRef Full Text | Google Scholar

Zhang, Q. S. (2013). Convective overshoot mixing in models of the stellar interior. Astrophys. J. Suppl. Ser. 205, 18. doi:10.1088/0067-0049/205/2/18

CrossRef Full Text | Google Scholar

Zhang, Q. S., and Li, Y. (2012a). Turbulent convection model in the overshooting region. I. effects of the convective mixing in the solar overshooting region. Astrophys. J. 746, 50. doi:10.1088/0004-637x/746/1/50

CrossRef Full Text | Google Scholar

Zhang, Q. S., and Li, Y. (2012b). Turbulent convection model in the overshooting region. II. theoretical analysis. Astrophys. J. 750, 11. doi:10.1088/0004-637x/750/1/11

CrossRef Full Text | Google Scholar

Zhang, Q. S. (2012a). Testing the core overshoot mixing described by a turbulent convection model on the eclipsing binary star HY VIR. Astrophys. J. 761, 153. doi:10.1088/0004-637x/761/2/153

CrossRef Full Text | Google Scholar

Zhang, Q. S. (2012b). The diffusive overshooting approach to Li abundance in clusters. Mon. Not. R. Astron. Soc. 427, 1441–1448. doi:10.1111/j.1365-2966.2012.22065.x

CrossRef Full Text | Google Scholar