- Nuclear Physics Institute of the Czech Academy of Sciences, Prague, Czechia
In this article, we review the activities of the application of the Asymptotic Normalization Coefficients (ANC) method for the determination of the cross-sections and astrophysical S-factors of the radiative (p, γ) captures, on stable and radioactive nuclei. A number of experiments were conducted at the Nuclear Physics Institute of the Czech Academy of Sciences, in cooperation with Texas A&M University and the Istituto Nazionale di Fisica Nucleare - Laboratori Nazionali del Sud (Catania, Italy). These measurements were performed using solid state detectors and a magnetic spectrometer. This method was introduced in the last decade of the twentieth century and was, at first, used to contribute to the intensively studied topic of solar neutrinos. Later its use was extended from the Li, Be, and B element region to the CNO cycle and above. The obtained results were found (where other measurements were available) to be compatible with other indirect methods and even with direct measurements. While the capacities of direct measurements constantly improve, the advantage of the ANC and other indirect methods in general is still crucial in determining the astrophysical S-factors where short living isotopes participate, e.g., in 11C(p, γ)12N, 12N(p, γ)13O, and 13N(p, γ)14O. The ANC method can also provide predictions for reactions with mirror nuclei. Other uses of ANCs are also discussed.
1. Introduction
One of the important tasks of nuclear astrophysics is the precise determination of cross-sections of nuclear reactions. This knowledge enables determining reaction rates, which influence or determine the evolution of complex systems in astrophysical scenarios. When we consider quiescent (non-explosive) processes—their typical location is a star interior and the temperatures correspond to energies only about tens of keV. Radiative captures—such as (p, γ), (n, γ), (α, γ)—typically appear in such environments.
Direct measurements in laboratory conditions at such low energies pose a great technical challenge and the analyses may still require the use of extrapolations to lower energies. The cross-sections are strongly reduced due to the presence of the Coulomb barrier (units of MeV) in case of charged particles. Neutron radiative capture measurements depend on the availability of the neutron beams at suitable energies and targets. Measurements with radioactive nuclei create another technological challenge. Indirect methods present useful tools, which do not completely replace the direct measurements, but they can add important pieces of independent information to deduce the desired cross-sections at energy regions of interest.
Nowadays, two indirect methods are used for radiative captures. (1) The Coulomb dissociation method (Baur et al., 1986) uses the reverse process of the radiative capture—the photodissociation reaction. The radiative capture process cross-section is then deduced from the detailed balance principle. The experimental feasibility of this method depends on a combination of several factors (see more in Baur and Rebel, 1996). (2) The other method is based on Asymptotic Normalization Coefficients.
1.1. ANC
The physics foundation of the method stems from the consideration that the direct radiative captures at low energies, proceed at large distances. Their cross-sections thus depend mostly on wave function tails, which have a known behavior and their amplitudes are given by a normalization coefficient. The Asymptotic normalization coefficients (ANC) method was developed in the last decade of the twentieth century (Xu et al., 1994). This method was used, in particular, to study the nuclear processes in stars (the p-p chain, CNO cycles, and cycles with heavier elements) and to investigate the Big Bang Nucleosynthesis (BBN). The interactions in these processes predominantly have a surface character. The peripheral character is also typical for direct nuclear reactions (DR), that are thus, predetermined as a tool to study the radiative captures. It appears that cross-sections of direct transfer reactions contain the same elements—vertex constants—that determine the direct radiative capture. These elements are closely related to the amplitudes of asymptotic tails of the (radial overlap) wave functions of the participating nuclei. These amplitudes are called asymptotic normalization coefficients (ANC).
The ANC method provides an accurate tool to determine the direct capture cross-section using experimental information from peripheral nucleon transfers.
1.2. Strengths and Weaknesses of ANC
Transfer reactions can be studied at larger energies than those typical for nucleosynthesis and even with radioactive beams. Their cross-sections are usually orders of a magnitude larger than direct radiative captures at astrophysically low energies.
Uncertainties of the ANC method are related to the well-known model dependence of Distorted Wave Born Approximation (DWBA) calculations: on the choice of the optical model potential (OMP) and the transferred single particle wave function. By choosing appropriate reactions and beam energies, the peripheral mechanism can be selected and thus the uncertainty associated with the choice of optical model potentials can be minimized.
The application of the ANC method in nuclear astrophysics is based on these assumptions:
• The final state is weakly bound
• The absence of resonances
Under these conditions, the direct radiative capture cross section is crucial [e.g., 7Be(p,γ)8B]. States present around the threshold (at higher masses, larger binding energies) render the resonant capture more dominant. The contribution of the direct capture may fall orders of a magnitude below the total capture.
Nevertheless, the ANCs can
• Play an important role, where resonances are narrow and distant from the energy region of interest,
• Influence the interference of resonant contributions (15N(p,γ)16O),
• Still play a significant role in the cross-section at low energies in case of a sub-threshold resonance (20Ne(p,γ)21Na),
• Be used to deduce the width of the resonance in the mirror nucleus (26Mg(n,γ)27Mg).
After each reaction, we assess the applicability of the ANC method.
1.3. Paper Organization
The paper is organized into five sections:
• Section 1 - is the introduction,
• In section 2, we describe principles of the ANC method,
• In section 3, selected reactions with ANC application are presented,
• In section 4, ANC applications for mirror nuclei and nuclear radii are briefly described,
• Section 5 - we provide a summary.
1.4. Aim of the Paper
Several reviews concerning ANC were recently published:
Huang et al. (2010) presented calculated ANC values within the simplified two-body model and consideration of single-particle states. Comparison to available experimental values works well for many cases.
Timofeyuk (2013) used a source term approach (STA) with shell model wave functions to calculate ANCs within a 0 − p shell. It is an update of the previous review of Timofeyuk (2010).
The aim of the paper is to review the experimental cases, where the authors have a deeper experimental insight, as they were part of the experimental team. The selection of reactions follows a chronological order, to show connections (where present) between experiments.
2. The Method of Asymptotic Normalization Coefficients
In case of low energy reactions of astrophysical interest, we usually express the cross-section for charged particles by the astrophysical S-factor to eliminate the Coulomb dependence of the cross-section at low energies. Without loss of generality we can consider a proton radiative capture
Then the astrophysical S-factor is expressed as
where E is the center of mass energy of the relative motion of the nucleus A and proton, η is the Sommerfeld parameter (ZA being the charge of the nucleus A, Zp=1 and v the relative velocity) and σ(E) is proportional to the square of the transition matrix element for the direct capture (see e.g., Xu et al., 1994):
where ψA and ψp are the wave functions of the nucleus A and proton, is the distorted wave function in the entrance channel, ψB is the wave function of the nucleus B, and Ô(XL) the electromagnetic operator, where (XL) refers to the electric or magnetic multipole, frequently E1. The overlap integral between the initial and final state can be written as:
The radial part of the overlap function can be approximated by a model wave function ϕnlj(r) of the proton bound state B = (Ap)
where S is the spectroscopic factor.
The tail of the nuclear overlap function contributes to the matrix element, especially at low energies. The shape of this tail has a well-known asymptotic behavior and its amplitude alone gives the rate of the direct part of the capture reaction. The asymptotic behavior of the radial overlap function is expressed by the Whittaker function W (see Mukhamedzhanov et al., 1997)
Here, the asymptotic normalization coefficient for the system A + p → B specifies the amplitude of the proton tail of the wave function for nucleus B, for distances larger than the nuclear radius RB and k is the wave number. This normalization coefficient determines the corresponding direct capture cross-section.
The asymptotic behavior of the model wave function ϕnBlBjB(r) of the proton bound state can be written as
The quantity bAp represents the single-particle ANC (SPANC) and defines the amplitude of the tail of the radial single-particle bound-state wave function.
For peripheral reactions, the differential cross-section calculated in DWBA approximation can be replaced by an integral over the external region, where the bound state is replaced by the Whittaker function, multiplied by the ANC. The cross-section of the direct (p, γ) can be finally expressed using ANC and SPANC from Equations (3) and (4) as in (Bertulani, 2003):
where is the cross-section for the electromagnetic transition to the final state lBjB.
The same asymptotic normalization coefficient as that in the radiative capture can be obtained from the direct transfer reactions. In the DWBA theory for the A(a, b)B reaction, where a = p + b, B = A + p, and p being the transferred proton, the transition amplitude is
where are distorted wave functions in input and output channels, ψA, ψB are wave functions describing inner states of A, B nuclei, φa, φb are wave functions of particles a, and b. The transition operator ΔV has a shape Vbp + UbA − Uβ for post form, where Uβ is the optical potential in final channel. The transition amplitude M can be expressed as
where is the above mentioned overlap integral and is the overlap integral of a and b particles, in analogy with . The experimental cross-section for the transfer proton reaction can be expressed at the asymptotic region larger than the nuclear radius RB in this way (Mukhamedzhanov et al., 1997)
Here, and are ANCs of the systems A + p and p + b, ji and li are the total and orbital angular momenta of the transferred proton, respectively. Coefficients b are the single-particle ANCs, defining the amplitude of the tail of the radial proton bound-state wave function. is the deduced DWBA cross-section. Using the above expression, it is possible to express the cross-section of the direct proton capture at very low energies by the relation (5) where the normalization factor is known from the transfer reaction (a, b).
For peripheral reaction, where only the outer region of the nuclear radial integrals contributes to the cross-section, the ratio
should not depend on the single particle ANCs bAp and bbp. The σDW(max)(θ) is the DWBA differential cross-section at the main maximum of the angular distribution.
The stability of this ratio represents an important peripherality check of the transfer reaction.
3. Selected Experimental Cases
In the following section, we introduce several experimental cases, where the ANCs were determined.
At first, we illustrate in detail the experimental investigation of the direct capture of 7Be(p, γ)8B. This reaction is in the center of the so-called solar neutrino problem. There was a discrepancy between the prediction of the high energy solar neutrino flux and the measured values (Bahcall, 1985). The measured values of the neutrino flux represented one third of the predicted flux. These neutrinos are mainly products of the decaying 8B from the radiative capture 7Be(p, γ)8B. The determination of astrophysical S-factor S17(0) for this capture seems to be the key to the problem.
Nowadays, the discrepancy between measured and produced flux of solar neutrinos is explained by neutrino oscillations (Ahmad et al., 2001; Bellerive et al., 2016—SNO collaboration) however, the independently and indirectly measured S-factor remains important for stellar models.
The suitable proton transfer reaction to study the direct capture 7Be(p, γ)8B by ANC method would be 8B(7Be,8B)7Be. This reaction, due to the symmetry, contains the same ANC value twice and thus, the determination would not be affected by other ANCs. However, both reaction participants are radioactive nuclei, so, the other transfer reactions were selected: 10B(7Be, 8B)9Be and 14N(7Be,8B)13C. These reactions both contain two different ANC values. The ANCs for the virtual decay 10B → 9Be + p and 14N → 13C + p had to be deduced. The techniques are described in more detail for the first reaction, and the details will not be repeated in the following experiments.
3.1. 9Be(p, γ)10B
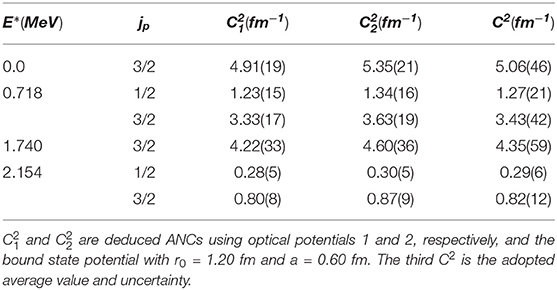
The determination of ANC for the 9Be(p, γ)10B radiative capture was one of the problems when the method of ANCs was first applied by Mukhamedzhanov et al. (1997). A suitable transfer reaction is 9Be(10B,9Be)10B, as it is symmetric in ANCs. At first, we measured the elastic scattering 10B + 9Be → 10B + 9Be to find the corresponding optical model parameters. Then, these parameters were used for the analysis of the proton transfer reaction 9Be(10B,9Be)10B. The measurement was performed at the Cyclotron Institute of the Texas A&M University using 100 MeV beam of 10B. 9Be targets with thicknesses between 200 and 300 μg/cm2 were prepared by evaporation. The targets were located in the focal plane of the Multipole magnetic spectrometer (MDM). The magnetic spectrometer was tuned to measure either elastically scattered 10B ions or 9Be ions from the proton transfer reaction. The measurement of specific energy loss in the ionization chamber was used for particle identification and the residual energy was measured by a NE102A plastic scintillator located behind the exit window of the detector. The entrance and exit windows of the detector was made of 1.8 and 7.2 mg/cm2 thick Kapton foils, respectively. The ionization chamber was filled with pure isobutane at a pressure of 30 mbar. Outgoing 9Be nuclei at forward angles are kinematically equivalent to 10B elastically scattered in the backward hemisphere. The experimental elastic scattering was fitted with three optical model potentials, that differed mainly in depths of the real part of the OM potential (Mukhamedzhanov et al., 1997, see in Figure 1). Resulting fits are plotted in Figure 1. The potential 3 gave substantially worse χ2 and therefore, it was rejected for further analysis. With these optical model parameters, the angular distribution for the proton transfers to different final states of the 10B were calculated by means of the PTOLEMY (Rhoades-Brown et al., 1983) code. The example of the fitted experimental angular distribution of the proton transfer to the ground state of 10B is given in Figure 2. ANCs for the proton transfer reaction from the calculation with parameters of the optical models 1 and 2 are given in the Table 1. Several tests were made to prove the applicability of the ANC method. The peripheral character of the 9Be(10B,9Be)10B reaction was verified. The ANC method is applicable, when the transfer process is peripheral. The peripherality can be demonstrated by showing that the cross-section does not depend on the inner part of the reaction region. Calculation of DWBA angular distribution with different cut-off radii did not reveal significant variations, when using values lower that 5 fm. This allows replacing the bound state function with the Whittaker asymptotic form. A next check was performed for the R function (Equation 9). This function should be constant in a region (1.1 ≤ r0 ≤ 1.3 fm and 0.5 ≤ a ≤ 0.7 fm), where r0 and a are bound state potential well parameters. Then the dependence on the selection of a potential is weak. In the presented case, these differences are small (see Table 1, where they are included in uncertainties of ANCs). By changing parameters r0 and a it is possible to demonstrate that the dependence of the spectroscopic factor on the single particle ANC blj is strong, it varies by factor 3 (Figure 3), while C2 changes in the considered region by only about 10%.
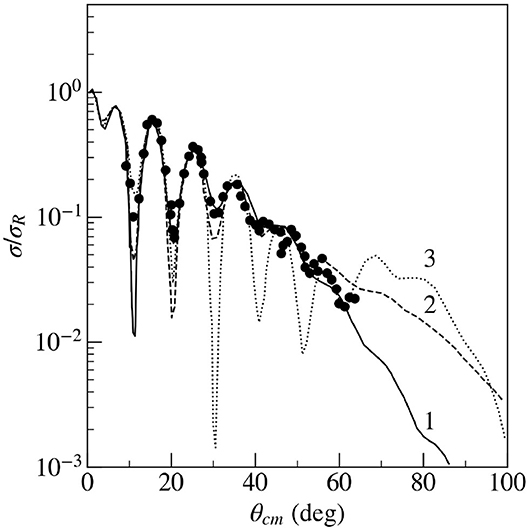
Figure 1. The elastic scattering cross-section of the 10B ions on the 9Be target, fitted by optical model calculations with potentials 1—solid line, potential 2—dashed line, and potential 3—dotted line, the depths of the real part of these three optical model potentials were 64.2, 131.2, and 203.2 MeV, respectively, see details in Mukhamedzhanov et al. (1997). Ratio to Rutherford scattering is on the y-axis.
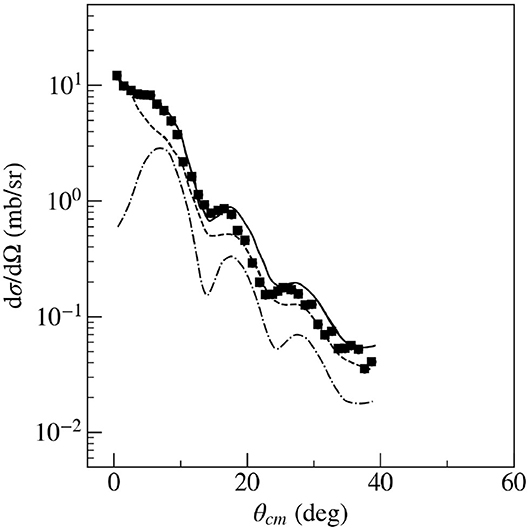
Figure 2. The calculated angular distributions of the reaction 9Be(10B,9Be)10B (g.s.) compared with the experimental data (black points). The DWBA fits for individual contributions of l = 0, 1, and 2 are represented by dashed, dotted, and dash-dotted lines, respectively. Calculations are performed with the optical potential 1 and the optical potential 2 gives the same fit.
Figure 3. The dependence of the spectroscopic factor (upper) and ANC (C2) (lower) on the geometry of the bound state potential of the state ) in 10B(g.s.). The geometry is expressed by the different single particle ANCs (value b, see Equation 4), i.e., achieved by changing the parameters r0 and a of the bound state potential in some intervals.
The extracted ANCs from Table 1 were then used for the analysis of the proton transfer reaction 10B(7Be, 8B)9Be which is suitable in determining the normalization of the cross-section for the direct proton capture 7Be(p, γ)8B at low astrophysical energies.
The ANC of 9Be(p, γ)10B reaction, due to the applicability conditions, was only used for the analysis of 7Be(p, γ)8B capture.
3.2. 16O(p, γ)17F
Prior to the application of ANC method on 7Be(p, γ)8B, the ANC method was tested on the 16O(p, γ)17F capture. The direct measurement data at low energies (Chow et al., 1975; Morlock et al., 1997) were available for comparison. Two separate measurements were performed for the transfer reaction 16O(3He, d)17F (Gagliardi et al., 1999).
One measurement was performed at the Nuclear Physics Institute of the Czech Academy of Sciences, Řež, (NPI CAS), using a 27.7 MeV 3He beam. The absolute differential cross-section for the process was measured between 6.5° and 25° in the laboratory system. Products of the reaction on the mylar target (C10H8O4) with a thickness of 134 μg/cm2 were detected by solid state dE-E telescopes with thicknesses 150 and 2,000 μm.
The second measurement was realized at the Texas A&M University K500 superconducting cyclotron with a 29.71 MeV 3He beam, with the mylar target (thickness 540 μg/cm2) at small angles between 1° and 11°. A Multipole Dipole Multipole magnetic spectrometer (MDM) was used for the detection of reaction products. A gas ionization chamber (50 cm long) was placed at the MDM focal plane and was followed by NE102A plastic scintillator, where the residual energy was measured.
Theoretical analysis was performed using the code PTOLEMY with seven different parameter sets for the entrance channel and five parameter sets for the exit channel. The experimental angular distributions corresponding to the ground and first excited state of 17F together with the best fits of OMP parameters are given in Figure 4. The conditions of peripherality were verified by changing the radius rcutoff. Angular distributions were changing very slightly within limits from 0 to 3 fm (inner part of 16O). Similarly, the change of the shape of the potential well of the captured proton did not change the corresponding angular distribution too much and consequently also C2 (see Figure 4). The value of = 3.90 ± 0.06 fm−1 was used from Mukhamedzhanov et al. (1995), where it was determined by a careful analysis based on hundreds of experimental measurements. Final derived results of ANCs gave the value = 1.08 ± 0.10 fm−1 for the ground state, and the value = 6,490 ± 680 fm−1 for the first excited state. With these ANC values, the astrophysical S-factors for the ground and first excited state of 17F were calculated and theoretical curves with the experimental values of S-factors are given in Figure 5. The agreement between experimental values of S-factors and direct measurements are very good for the interval below 1 MeV. For higher energies the agreement for the first excited state is worse because of the increasing role of the nuclear interior.
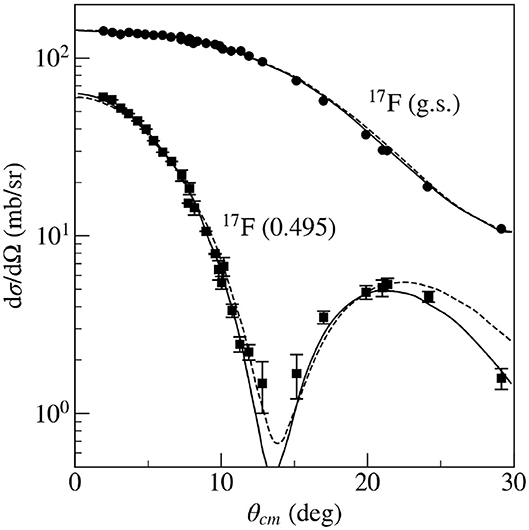
Figure 4. Angular distributions for the ground and first excited states of 17F from the 16O(3He, d)17F reaction. The dashed and solid curves are DWBA fits using two optical model potential parameter sets (Gagliardi et al., 1999).
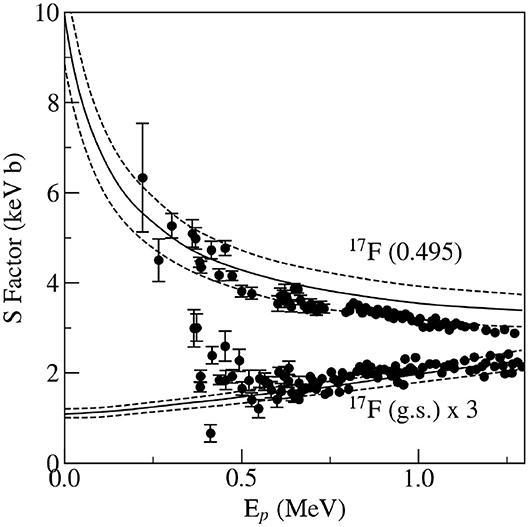
Figure 5. The experimental S-factors and S-factors determined from the ANCs of the 16O(3He, d)17F reaction (Gagliardi et al., 1999). The solid data points are from Morlock et al. (1997), and the open boxes are from Chow et al. (1975). The solid lines indicate the calculated S-factors, and the dashed lines correspond to the ±1σ error bands.
The assumptions of applicability of the ANC method are satisfied for the 16O(p, γ)17F reaction and the method was shown to work in real cases.
3.3. 7Be(p, γ)8B, 13C(p, γ)14N
The importance of the proton radiative capture p + 7Be was discussed in the previous section. Two suitable reactions for the indirect determination of 7Be were chosen: the reaction 10B(7Be, 8B)9Be which was discussed above and also the transfer reaction 14N(7Be,8B)13C. Measurements of angular distributions of elastic scattering of 7Be ions and also, of transfer reactions with these ions on the 10B and 14N targets were carried out on the K500 superconducting cyclotron at Texas A&M University (Azhari et al., 1999, 2001).
The beam of radioactive 7Be ions was produced in the 1H(7Li, 7Be)n reaction using 7Li primary beam of 135 MeV energy. The 7Li beam was striking on the liquid nitrogen cooled gas cell containing hydrogen with pressure about 1 atm. Windows of the gas cell were made from Havar foil with a 42 mg/cm2 thickness. 7Be ions from the gas cell were separated by the Momentum Achromat Recoil Spectrometer (MARS) and hit the target with a rate below 105 pps. The self-supported 10B target was prepared from a mixture of pulverized 10B and varnish deposited on a Ta backing from which the target layer was removed in distilled water. As the 14N target the evaporated melamine (C3N6H6) on a 20 μg/cm2 layer of C and a 20 μg/cm2 layer of collodion was used. The average thicknesses of the targets were 1.96 mg/cm2 and 1.50 mg/cm2 for the 10B and 14N targets. Reaction products were measured and identified by the telescope configuration consisting of a 100 μm silicon strip detector, backed by a 1,000 μm 5 × 5 cm2 Si detector. Data from the telescope were then analyzed to deduce angular distributions of the elastic scattering of 7Be and the studied transfer reactions. The angular distribution of elastic scattering was used for determination of optical model parameters. The parameters were obtained from double folding model calculations according to JLM effective interaction (Jeukenne et al., 1977).
Having the optical model parameters for the input channel and exit channels 10B + 7Be and 8B + 9Be, it was possible to calculate the differential cross-section for the transfer reaction. Similarly for the transfer reaction 14N(7Be,8B)13C, where model parameters for the input channel 7Be + 14N and the exit channel 8B + 13C were needed. The experimental angular distribution for the outgoing 8B of the 10B(7Be, 8B)9Be reaction (Q ≤ 28 MeV) is shown in Figure 6. The calculations of theoretical angular distributions were performed by the code PTOLEMY. The peripheral character of both transfer reactions 10B(7Be, 8B)9Be and 14N(7Be,8B)13C was tested using variations of radius and diffuseness values of the single-particle Woods-Saxon potential. The changes in deduced ANCs were only ±3.5%. The deduced value = 19.5 ± 2.5 fm−1, values for other states are shown in Trache et al. (1998), Table 2. The ANC value for 7Be + p reaction is = 0.388 ± 0.039 fm−1. Using the ANCs from both transfer reactions 10B(7Be, 8B)9Be and 14N(7Be,8B)13C, astrophysical S-factors S17(0) = 18.4 ± 2.5 eV b and S17(0) = 16.9 ± 1.9 eV b was obtained. The weighted average value S17(0) = 17.3 ± 1.8 eV b is included in the Figure 7 (Azhari et al., 2001). This is in good agreement with the current accepted value S17(0) = eV b.
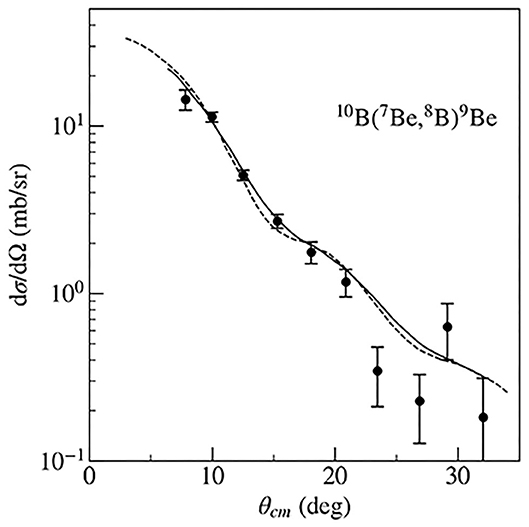
Figure 6. Experimental angular distribution from the 10B(7Be, 8B)9Be reaction for the outgoing ions 7Be. The dashed line corresponds to the predicted angular distribution and the solid line is corrected to finite angular distribution (Azhari et al., 1999).
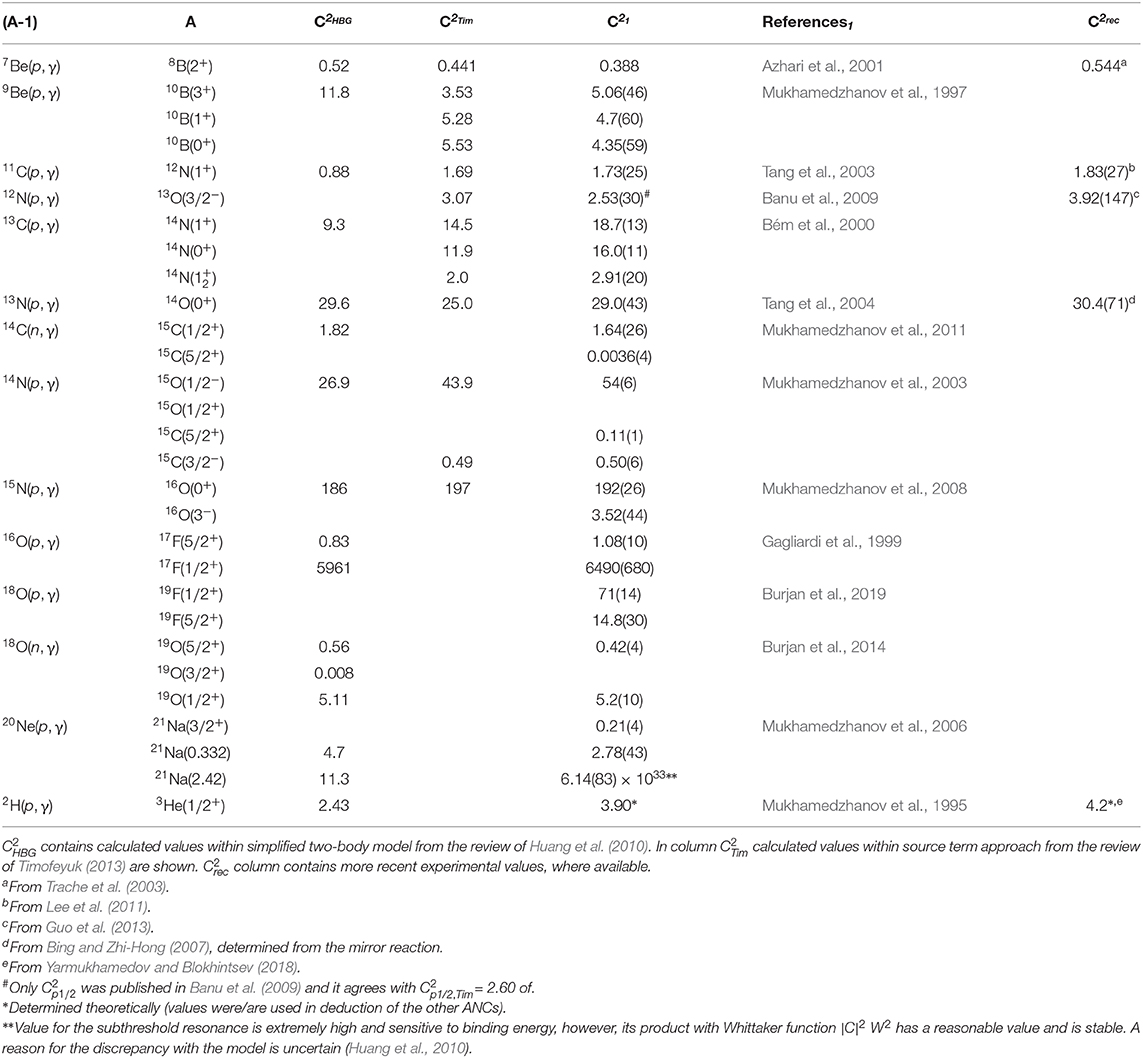
Table 2. Squared ANC values (in units of [fm−1]) for selected reactions discussed in this paper (column ).
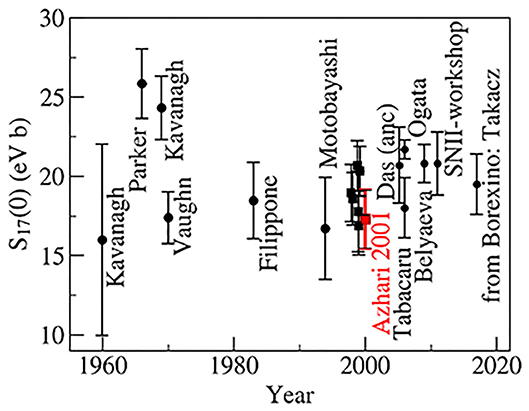
Figure 7. History of the determination of astrophysical S17(0). The value measured in the experiment, discussed in the text, is in red and labeled “Azhari 2001.” For details see (Azhari et al., 2001).
Solid targets, such as 14N in the previous section, are available in the form of compounds and/or with other element backings. This may substantially complicate an analysis, due to peak overlap in spectra and different kinematical shifts for isotopes with different mass numbers. One of the experimental challenges was ANC measurement with pure isotopic gas targets.
The assumptions of applicability of the ANC method are satisfied for the 7Be(p, γ)8B reaction. The ANC of 13C(p, γ)14N reaction, due to the applicability conditions, was only used for the analysis of 7Be(p, γ)8B and other captures (see below).
3.4. 20Ne(p, γ)21Na
The 20Ne(p, γ)21Na capture reaction is a part of the so-called NeNa-cycle, which takes place in stars larger than the Sun. This cycle produces 21Na, 21Ne, 22Na, and 22Ne nuclei, while consuming hydrogen. The 20Ne(3He, d)21Na reaction leads to four bound states of 21Na. The highest lying state with excitation energy of 2.425 MeV is only a few keV below threshold The capture to this subthreshold state dominates the value of astrophysical S-factor.
The measurement was realized on the beam of the isochronous cyclotron U120M of NPI CAS. The 3He beam with energy 25.83 MeV impinged the target gas cell filled with high purity 20Ne. The input and output windows were made of 3.05 μm Havar foils. The working pressure was kept at 195 mbar and was continuously monitored together with the gas temperature. The detection system consisted of a pair of dE-E Si(Li) surface barrier detectors of thicknesses 220 μm and 4 mm, respectively. The effective thickness of the gas target seen by the telescopes was obtained from a simulation. One telescope at a fixed angle served as a monitor and the second telescope was movable in the angular interval from 6.5° to 70°. The obtained energy resolution ranged from 100 to 120 keV, depending on the measured angle.
The experimental angular distributions of emitted deuterons from the 20Ne(3He, d)21Na reaction were analyzed within the DWBA theory. At first the angular distribution of elastic scattering of 3He was fitted by means of the code ECIS79 (Raynal, 1981) to obtain optical model parameters for the input channel. The optical model parameters for the exit channel were adopted from global formulas in works by Daehnick et al. (1980) and Vernotte et al. (1994). In Figure 8 we present, as an example, the experimental angular distribution fits for the state 2.425 MeV calculated by the code DWUCK5. The peripheral character of the reaction was verified using different cut-off radii of the integration over the radial part of interaction. The stability check of the function R(b) (9) was checked and its behavior was almost flat. To deduce ANCs for the direct capture 20Ne(p, γ)21Na from the transfer reaction 20Ne(3He, d)21Na, knowledge of ANC for the decay 3He → d + p is necessary. For further analysis we used the value = 3.90 ± 0.06 fm−1 (Mukhamedzhanov et al., 1995).
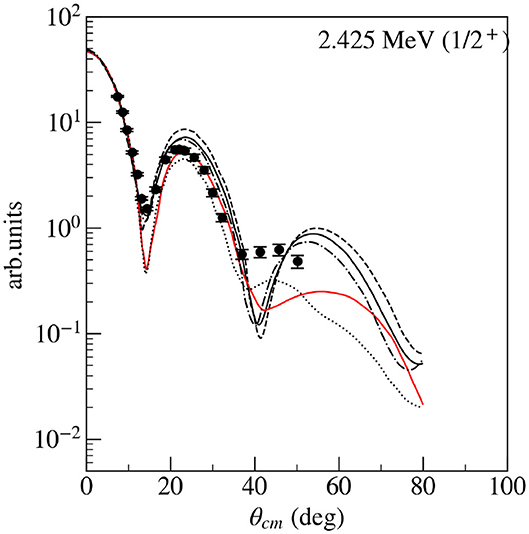
Figure 8. The angular distribution of the 20Ne(3He, d)21Na reaction corresponding to the transition to the subthreshold state of 21Na fitted by combinations of different optical model parameters for input and output channels. OM parameters for input and output channels taken from earlier works produce the black solid curve. The black dashed and dash-dotted curves use the same output channel OM parameters, but the input channel OM parameters were obtained from a fit of the elastic scattering data with two different seeds. Black dotted and red curves are produced as the two previous curves, but with a different OM parameter set for the output channel. For details see (Mukhamedzhanov et al., 2006).
Total uncertainties of ANC for the direct capture 20Ne(p, γ)21Na were estimated from 14% for the 2.425 MeV state to 28% for the 1.716 MeV state. The sources were mainly (1) the ambiguity of optical model parameters and (2) the uncertainty of absolute values of the cross-sections. R-matrix theory was used to determine S-factor, where the normalization of the direct capture amplitude was given by the ANC of the final bound state according the procedure used by Tang et al. (2003). The S-factor for direct capture to the subthreshold state was found to be S(0) = 68.30 ± 9.30 keV b. The direct capture to the ground state is very weak. The capture to the ground state is dominated by the resonant capture through the subthreshold state. It was determined as S(0)= 5,870.0 ± 1,200 keV b. The R-matrix calculations were performed with the channel radius r = 5 fm. The calculated total S(E) consists of the sum of the direct capture to the subthreshold state and the capture by the subthreshold resonance to the ground state. We have thus S(0) = 5,900 ± 1,200 keV b (Figure 9). Contributions to the total S-factor from captures to other remaining states are negligible. The newly obtained S(0) factor is higher than the value given in Rolfs and Rodney (1988).
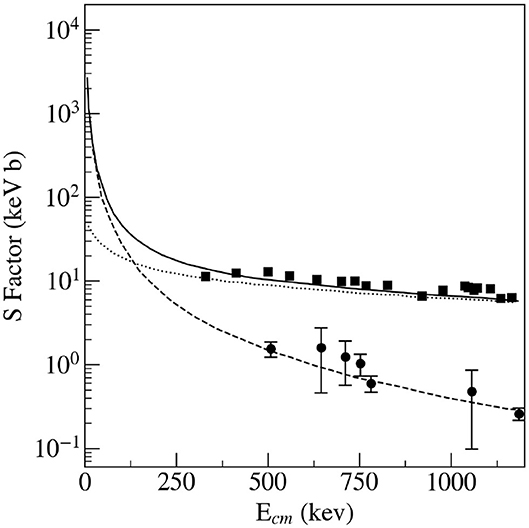
Figure 9. The astrophysical S-factor for the direct 20Ne(p, γ)21Na capture. The solid squares and dotted curve are experimental data points from Rolfs et al. (1975) and results of Mukhamedzhanov et al. (2006) for direct capture to the subthreshold state, respectively. Similarly, for the capture to the ground state the open squares and dashed curve correspond to the experimental data points and to results for the direct capture. The determined total astrophysical S-factor is given by the solid curve.
The proton partial width of the resonance, dominating the radiative capture of the 20Ne(p, γ)21Na reaction was deduced from the measured ANC.
3.5. 18O(n, γ)19O
The ANC method can be used not only for charged particle direct captures, but also, for a direct radiative neutron captures (Imai et al., 2001). However, the peripherality of the process must be ensured by a presence of a centrifugal barrier. The 18O(n, γ)19O capture is given as an example.
The inhomogeneous Big Bang models (IBBN) seemed to contain a solution for the problems of BBN. Nuclei with A > 12, in neutron-rich environments, could be formed in the reaction sequence (Wiescher et al., 1990) 14C(n, γ)15C(β−) 15N(n, γ) 16N(β−) 16O(n, γ) 17O(n, γ) 18O(n, γ) 19O, where the reaction 18O(n, γ) 19O opens the path to elements with higher mass numbers (Wiescher et al., 1990). The neutron radiative capture 18O(n, γ)19O also has a significance for the estimation of reaction rates of stellar helium burning in massive red stars and AGB stars. To determine the direct (n, γ) cross-section, a precise measurement of (d, p) differential cross-section on 18O target at forward angles (where the stripping mechanism is more pronounced) was required. Although, the transfer to higher excited states was also of interest (Herndl et al., 1999), not all were possible to resolve. The experiment was performed on the isochronous cyclotron U-120M of the NPI CAS (Burjan et al., 2013). A momentum analyzed 16.3 MeV deuteron beam impinged on an oxygen gas target. The gas chamber target was filled with a high purity 18O isotope (99.9%). The working pressure was maintained at 150 mbar. Eight dE-E telescopes [250 μm and 5 mm thick Si(Li) surface barrier detectors] were used to register the reaction products. DWBA analysis of experimental angular distributions of the transfer reaction 18O(d, p)19O was performed to extract ANCs. The phenomenological optical potential of Kunz (1990) has been used for the analysis of the angular distributions. Input channel parameters were obtained by the fit of the experimental angular distribution of elastically scattered deuterons. For this purpose, the code ECIS79 of Raynal (1979) was used. Optical model parameter sets of Perey and Perey (1976) and others (Duke, 1963; Watson et al., 1969) were used for the proton exit channel. The experimental angular distributions 18O(d, p)19O were fitted within the DWBA theory using the DWUCK5 code (by Kunz, 1990). As in the above cases, two overlap integrals and two ANCs are contained in the DWBA description of this reaction. The ANC value for the virtual decay d → p + n is = 0.77 fm−1, based on considerations about spectroscopic factor S = 1 and SPANC values at an asymptotic distance (Mukhamedzhanov et al., 2011).
For transferred neutral particle, instead of the Whittaker function, the Hankel function is used in the overlap integral in the asymptotic region. For the application of the ANC method, the condition of the weak cross-section dependence on the cut-off radius should be fulfilled. The difference of the cross-section at the maximum of the angular distribution was 13% between the case with 3 fm cut-off and no cut-off for the transfer to the ground state. Changes were negligible (2%) for other transitions. The obtained values for the transitions to five states of 19O (g. s., 1.471, 3.153, 3.231, and 3.944 MeV) were used to estimate the direct neutron capture contribution by 18O (see in Burjan et al., 2013). The FRESCO code (Thompson, 1988) was used for these (n,γ) calculations. In the calculations, the channel radius 3.3 fm was used and the E1 multipolarity was assumed in all cases. The largest contribution (black solid line in Figure 10) is from transition to the 1.471 MeV state (2s1/2). The results were compared with available experimental data (Figure 10). Data points from Meissner et al. (1996) and Ohsaki et al. (2008) for the transitions to the ground state and 1.471 MeV state are shown. The larger energy interval was measured by Vaughn et al. (1965) (transitions to the g. s. and 1.471 MeV state). The direct part of the experimental data is quite consistent with the ANC method results for this neutron capture by 18O.
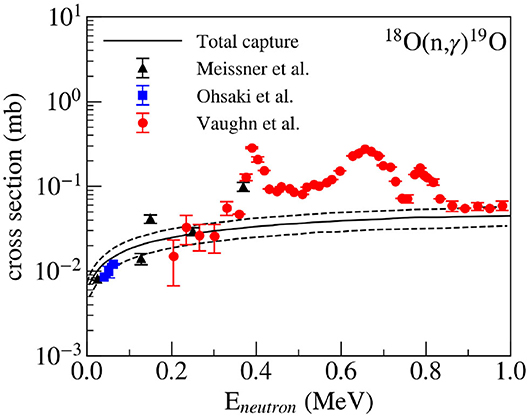
Figure 10. Comparison of the cross-section of the direct radiative neutron capture 18O(n, γ)19O determined by the ANC method from the 18O(d, p)19O reaction with experimental data of Vaughn et al. (1965), Meissner et al. (1996), and Ohsaki et al. (2008). Dashed lines show the uncertainty band 22%.
The necessity of the centrifugal barrier allowed studying the p-wave direct capture contribution with the ANC method. Direct measurements show that it dominates in the energies bellow 100 keV.
3.6. 18O(p, γ)19F
A study of the radiative capture reaction 18O(p, γ)19F helps in better understanding the processes in AGB stars (i. e. stars several times heavier than our Sun). The hydrogen burning of 18O via the (p, γ) in these stars is competing with the 18O(p, α)19F reaction (Lorenz-Wirzba et al., 1979). The (p, γ) capture causes the escape of 19F from CNO cycles, while the (p, α) reaction (with a rate of about 3 orders higher at solar energies) returns the 19F back. The ratio 18O/16O represents an important parameter that is characteristic for different nucleosynthesis locations and that can help to determine the origin of e.g., presolar grains (Abia et al., 2017; Palmerini et al., 2017). While the direct part of the 18O(p, γ) process is not the major contribution to radiative capture, it may play a role in the total S-factor, via interferences with resonant states. A measurement of the 18O(p, γ)19F in the energy range Ep = 0.08–2.2 MeV was performed by Wiescher et al. (1980), where the direct part of the (p, γ) capture was determined experimentally and also calculated theoretically. Later, Buckner et al. (2012) investigated reaction rates of 18O(p, γ)19F and determined the direct part of this capture using different capture models. However, there is a substantial difference between the astrophysical S-factor of Wiescher et al. and of Buckner et al. at low energies. The energy dependence of values of Wiescher et al. decreases while that of Buckner et al. is increases. Also, their absolute values differ considerably. We therefore, decided to determine the astrophysical S-factor of the direct capture 18O(p, γ)19F by the ANC method. The differential cross-section of the 18O(3He, d)19F transfer reaction was measured (Burjan et al., 2019). 24.6 MeV 3He beam from the isochronous cyclotron U-120M at NPI CAS was used. High purity 18O oxygen (99.9%) gas target was used as in the above experiment. Eight dE-E telescopes [250 μm and 5 mm thick Si(Li) surface barrier detectors] were used for detection of the reaction products. The geometry of detectors was very similar to the geometry used in the (d, p) experiment. Twelve deuteron peaks corresponding to the bound states of the 19F were observed and analyzed. Other 19F levels were populated weakly and were not considered further. The phenomenological optical potential was used for the analysis of the measured angular distributions. The input channel OM parameter sets were deduced from the fit of the angular distribution of elastic scattering 3He + 18O. The output channel OM parameters for deuterons were adopted from the global formula of Perey and Perey (1976). The FRESCO code (Thompson, 1988) was used to calculate the theoretical angular distributions of the 18O(3He, d)19F transfer reaction. The transitions with the largest ANCs are to the ground state and to the 0.197 and 1.554 MeV levels of 19F, = 71.1 ± 14 fm−1, = 14.8 ± 3 fm−1. The derived ANCs were used to deduce the direct capture cross-section σ(E)cap by the FRESCO code The dependence of the differential cross-section on the cut-off radius was tested to verify the surface character of the transfer reaction. E1 multipole electromagnetic operator was considered in the calculations. Woods-Saxon potential was used for calculation of the bound state wave functions (Wiescher et al., 1980). Three kinds of potentials for scattered wave functions of incoming protons were: (1) the complex optical potential of Perey and Perey (1976), (2) the Coulomb potential only (which plays a major role at low proton energies) and (3) the hard sphere potential (V = −300 MeV) simulating a repulsive potential. The total direct S-factors for all three potentials are shown in Figure 11. The capture to the ground and 0.197 MeV states dominates the total direct S-factor (60% contribution). These S-factors were compared with calculations of 18O(p, γ)19F by Buckner et al. (2012) and with the direct measurement by Wiescher et al. (1980) at the low-energy region. It appears that the direct hard sphere potential S(E)-factor is almost constant (2 keV b), while the others have the tendency to rise slowly in the interval between 0 and 2 MeV, in agreement with Buckner et al. ((S(E) = 7.06 + 2.98 × 10−3E − 2.6 × 10−7E2 [keV b]) and in disagreement with Wiescher et al. ((S(E) = 15.7 − 0.34 × 10−3E − 1.21 × 10−6E2 [keV b]) The calculation of the direct S-factor with the Coulomb potential when normalized to the measured direct capture cross-section at Ec.m. = 1751.9 keV by Wiescher et al. (1980) is in a good agreement with the result of Buckner et al. The total direct astrophysical S-factor calculated with three different interaction potentials show a tendency similar to that of Buckner et al. For the Coulomb interaction potential, the calculations reproduce these data very well, after normalization. Without normalization, they are lower than the values of Buckner et al. at least about 35%.
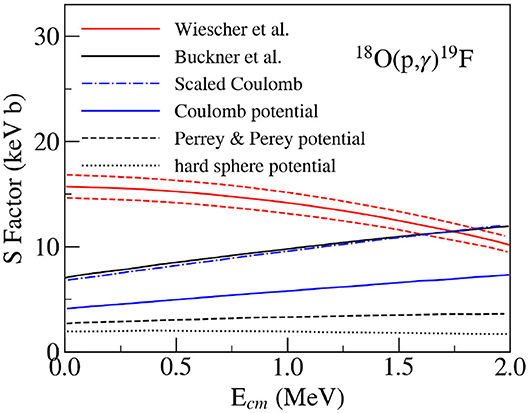
Figure 11. S-factor of the total direct proton capture 18O(p, γ)19F determined from the transfer reaction. The red solid decreasing curve is based on the measurement of the direct contribution (p, γ) by Wiescher et al. (1980) with uncertainty about 7% (dashed red curves).
Due to the large number of resonances, the applicability conditions are not satisfied. The ANC value of 18O(p, γ)19F reaction can be compared with the different calculations used for determination of the direct S-factor.
3.7. 11C(p, γ)12N
The reaction 14N(11C,12N)13C can provide ANC for the 12N → 11C + γ decay and the direct capture rate for 11C(p, γ)12N at astrophysical energies. This reaction is a part of the hot pp-chain (7Be(α, γ)11C). It may open a possibility for super-massive, low-metallicity stars to produce CNO nuclei (avoiding the three-alpha process) (Wiescher et al., 1989). The 11C radioactive beam, at an intensity of 4.2 × 105 particles/s and energy 10 MeV/u, bombarded a 1.5 mg/cm2 melamine target (C3N6H6) (Gagliardi et al., 2002). This radioactive beam was produced in the reaction 1H(11B,11C)n and purified by the Momentum Achromat Recoil Spectrometer (MARS). S-factor for direct 11C(p, γ)12N was deduced (Gagliardi et al., 2001) using the R-matrix calculation that includes effects of two low-lying resonances and the determined ANC factor (=1.73 ± 0.25 fm−1) (Tang et al., 2003). Results are shown in Figure 12. The values of S-factor are more than 10 times larger than previously given (Lefebvre et al., 1995).
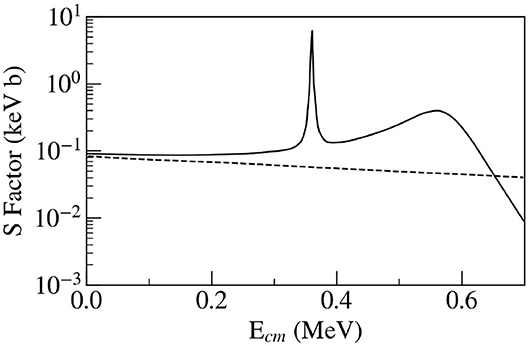
Figure 12. The astrophysical S-factor for 11C(p, γ)12N, the total S-factor (solid line) and the direct contribution alone (dotted line).
Non-resonant capture is thought to dominate the 11C(p, γ)12N reaction at low energies (Lefebvre et al., 1995; Huang et al., 2010), ANC is an important component for the R-matrix analysis.
3.8. 12N(p, γ)13O
The new experimental information on the 12N(p, γ)13O capture is important for Population II stars with lower masses, modeling a nucleosynthesis and their evolution. This capture reaction was studied by the ANCs indirect method using the peripheral proton-transfer reaction 14N(12N,13O)13C (Banu et al., 2009). The radioactive beam 12N was produced from a primary beam of 12C at 23 A MeV with an intensity of 150 pnA (particle nA) striking on a LN2-cooled H2 gas cell. To reduce the 12C energy to 12 A MeV where the reaction is peripheral a 250-μm-thick Al foil was put behind the gas cell. For the DWBA analysis of the transfer reaction 14N(12N,13O)13C, the parameters of the optical model potential for both the entrance channel (12N − 14N) and exit channel (13O − 13C) were needed to calculate the distorted scattering wave functions. Analysis of the elastic scattering data was done with the help of semi-microscopic double-folding optical potentials. The calculated angular distribution of the transfer reaction 14N(12N,13O)13C by the finite-range DWBA code PTOLEMY was used for the fit of the experimental angular distribution. From the comparison of theoretical and experimental angular distributions, the ANC was determined to be (13O) = 2.53 ± 0.30 fm−1. This value of (13O) then leads to S(0) = 0.33(4) keV b for the direct capture component. However, the resonant capture via the first excited state and the direct capture to the ground state interfere, which leads to a further increase of S-factor giving Stot(0) = 0.42(6) keV b (see Figure 13). This value is 2 orders lower than the theoretical value used by Wiescher et al. (1989). It is compatible with the analysis by Zhi-Hong (2006), who deduced the ANC from the shell-model. Later, Timofeyuk (2013) used the source term approach using shell model wave functions and it agreed with the measured value of ANC.
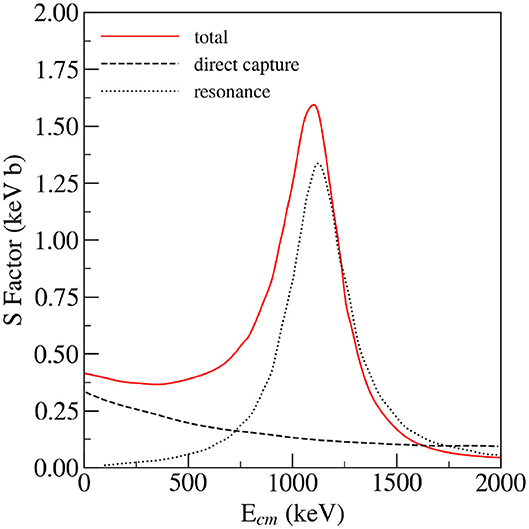
Figure 13. The astrophysical S-factor for the 12N(p, γ)13O capture as a function of the energy. The solid red line shows results for the total S-factor, dashed line is the direct component of the S-factor and the dotted line is the resonant component.
Non-resonant capture dominates the 12N(p, γ)13O reaction at low energies, where the ANC brings important information for the R-matrix analysis.
3.9. 13N(p, γ)14O
The 13N(p, γ)14O capture is one of the important reactions in the hot CNO cycle. The rate of this reaction is dominated by the resonant capture through the first excited state of 14O (Er=0.528 MeV). The transfer reaction used in this case was 14N(13N,14O)13C (Tang et al., 2004). The 13N radioactive beam needed for the determination of the S-factor of this capture was produced by the 1H(13C,13N)n reaction (Tang et al., 2004). The 13C beam of ~600 enA (electrical nA) at 15 A MeV from the K500 superconducting cyclotron bombarded a 10-cm-long, LN2-cooled, cryogenic H2 gas cell with havar windows. Recoiled 13N nuclei were then separated by the magnetic spectrometer MARS at 0° and focused on a target consisting of 1.5 mg/cm2 melamine C3N6H6 with 20 μg/cm2 carbon backing. The reaction products from the 13N secondary beam bombarding the target were recorded by two detector telescopes, each consisted of a 5 × 5 cm 16-strip position-sensitive Si detector, with a thickness of 60 μm, backed by a 500 μm Si detector. Three sets of elastic scattering data on 14N, 12C, and 1H were obtained.
The optical-model parameters were obtained from double-folding-model calculations for 13N ions scattered on the melamine target (Trache et al., 2000).
After fitting the experimental angular distribution of the transfer reaction 14N(13N,14O)13C by theoretical calculations, the value of the ANC for 14O → 13N + p was found to be = 29.0 ± 4.3 fm−1.
The S-factor was deduced from the R-matrix approach (Tang et al., 2003), where the measured ANC and the experimental resonance parameters of the (broad) first excited state was used. Parameters of Magnus et al. (1994) ( = 527.9 ± 1.7 keV, γtotal = 37.3 ± 0.9 keV, and γγ = 3.36 ± 0.72 eV) were used for the first resonance. The total astrophysical S-factor including the constructive interference with the direct part is shown in Figure 14. This result is about 38% higher than the previous value of Decrock et al. (1993), obtained from the calculation.
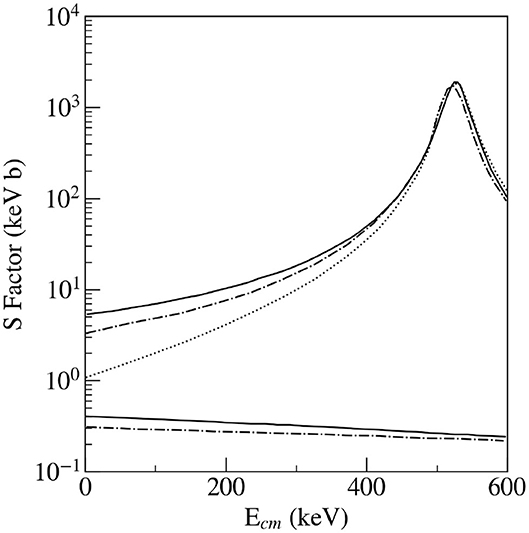
Figure 14. The astrophysical S-factor for the 13N(p, γ)14O capture. The relatively flat solid line is the direct capture contribution determined from the ANC. This result is higher than that obtained by Decrock et al. (1993) (lowest dash-dotted line). Based on constructive interference, this updated result for the total S-factor, the top solid line, is about 38% higher than the previous result (upper dash-dotted line). For the sake of completeness, the result with destructive interference is shown (the dotted line).
Although the applicability conditions for ANC method are not fulfilled in 13N(p, γ)14O reaction, the direct capture part influences the total S-factor via the interference.
4. Further Usage of ANCs
The properties of ANCs have a broader potential in nuclear physics. In the next section, we briefly outline a few examples.
4.1. Mirror Nuclei
From theoretical calculations performed over several 0p nuclei (Timofeyuk et al., 2003) it was found that the proton and neutron ANCs for mirror pairs and vary by a factor of two for different potentials used, while the ratio depends weakly on the used potential (less than 4%) (Timofeyuk et al., 2003 and references therein). This effect is connected to the fact that the Coulomb potential does not vary much inside the nucleus over the nuclear volume and thus, can be replaced by a constant equal to the energy difference between the separation energies for a proton and neutron. Hence, (see Timofeyuk et al., 2003) the bound-state wave function can be written in terms of the regular Coulomb and the Bessel functions of lth − order:
where Fl is the regular Coulomb function at momentum kp, jl are the Bessel functions at momentum kn and RN is the nuclear radius. kp and kn are defined by the proton and neutron separation energies. Assuming that the difference between the wave functions for mirror pairs can be neglected, the ratio will be equal to:
Considering the relation , where bn(p) is the single-particle ANC (SPANC), the equation 11 will become equal to . Assuming that – for p and n – both the nuclear single-particle potentials and the single-particle wave functions in the interior are the same, the ratio will be weakly dependent from the chosen potentials.
Approaching the limits of (proton) stability, the separation energy for a neutron decreases and excited states may correspond to resonances for the proton-plus-core mirror system. In such a case, the connection between the width γp for the resonance and the mirror ANC Cn can be expressed (see Timofeyuk et al., 2003) as
This ratio can be approximated by the single-particle ratio if the single-particle potentials and spectroscopic factors for mirror pairs are considered equal. These relations were presented in Timofeyuk et al. (2003), where a number of mirror cases were theoretically tested, and the results were compared with the available experimental values of ANCs.
Reactions with mirror nuclei can be a solution to study reactions that involve a radioactive participant. This method was applied e.g., for 7Be(p, γ)8B (Trache et al., 2003), deduced from 8Li → 7Li + n using 13C(7Li,8Li)12C reaction. Other cases in which the mirror nuclei procedure have been used are 20Mg(p, γ)21Al (Timofeyuk et al., 2012) from 20O(n, γ)21O using reaction 20O(d,p) 21O, 22Mg(n, γ)23Mg (Al-Abdullah et al., 2010) capture from 22Ne(p, γ)23Na using 13C(22Ne,23Ne)12C.
Using mirror reactions to study the direct (p,γ) captures proved to be an important tool, especially for radioactive nuclei. However, this technique has some potential constraints:
• Demand on peripherality of (n,γ) capture. Without the presence of Coulomb barrier the peripherality must arise from the centrifugal barrier.
• Proper treatment of (d,p) reactions, see more in a recent discussion on the role of high internal momentum of d and proper application of DWBA, FR-DWBA, and CDCC (Timofeyuk et al., 2008; Gómez-Ramos and Timofeyuk, 2018).
• Mirror symmetry breaking may play a role (effect of 18% was determined for 27Mg-27P in Timofeyuk et al., 2008) and it should be treated on a case by case basis.
4.2. Ab-initio Methods
Recently, with the developments in ab initio methods, several techniques appeared feasible to perform ANC calculations. Despite the difficulties—convergence to long-asymptotics, sampling the tails (in Monte-Carlo methods)—the calculations can nowadays offer predictions consistent with experimental measurements for light (LiBeB) elements (Nollett and Wiringa, 2011).
4.3. Nuclear Radii
ANC being the normalization of the asymptotic wave function, it can naturally contain the information on nuclear halo/skin composed of the last peripheral nucleon. The possibility to access a nuclear radius, from a knowledge of overlap integrals between states with A and (A-1), was used by Timofeyuk (1998). The simple way to correlate the halo radius to ANC was used by Carstoiu et al. (2001) for the case of 8B, where it was shown that the rms radius of the last proton can be determined and the proton is localized (in average) at the distance two times the core radius.
The ANC deduced from peripheral transfer reactions was used to determine the rms radii for 12B, 13C by Liu et al. (2001), for 13C and 11Be by Belyaeva et al. (2014), for 12B by Belyaeva et al. (2018). Rms radii of valence neutron was studied in 16N by Li et al. (2016) for several excited states. 9, 11Be, 13C and alpha cluster states were studied by Ogloblin et al. (2016).
As remarked by the above authors, the determination of the rms radius by ANC brings an independent approach, that increases reliability and is a test of other methods.
4.4. References to Computer Codes
Different computer codes were used in the above. They are listed here with the references and web sites:
- ECIS79 - Raynal, 1979, 1981,
- DWUCK5 - Kunz, 1990,
- FRESCO - Thompson, 1988,
- PTOLEMY - Rhoades-Brown et al., 1983,
- RADCAP - Bertulani, 2003
5. Summary
The ANC method is used for determination of the astrophysical S-factor at low astrophysical energies of participating particles, where the cross-section is very low, and it is extremely difficult to measure it directly. Where the experimental effort is challenging and the case is favorable, mirror symmetry is/can be used to deduce the ANCs of bound states or properties of resonances.
We have illustrated the usefulness, but also limitations of the indirect ANC method in several examples with an astrophysical interest. They include experiments with solid or isotopic gas targets with stable beams and also experiments in inverse kinematics with radioactive beams.
The ANC method was successfully tested in number of reactions, found compatible with theory predictions as shown in the summarizing (Table 2). ANCs are also frequently deduced from R-matrix fits. These values are also generally in agreement with independently found ANCs.
An important region of ANC method application are measurements with radioactive beams. The reactions with the short-lived isotopes are still not accessible to direct measurements. Nuclei distant from the valley of stability have lower separation energies and thus the level density around threshold may be smaller. This is favorable to the direct radiative capture contribution to the total astrophysical S-factor. Reactions with radioactive beams, however, always need more development both in the experimental techniques (quality of elastic scattering data, resolutions) and in theoretical analysis (reliable OMP, reaction codes). This is discussed in more detail in the remarks to ECT* workshop by Trache and Carstoiu (2019).
Author Contributions
All the listed authors contributed to the writing of the paper. VB worked on all experiments in section 3, JM has worked on 14C(n,γ)15C, 15N(p,γ)16O, and 18O(p, γ)19F.
Funding
We would like to thank for the support to the MEYS project SPIRAL2-CZ, EF16-013/0001679.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Authors want to thank to all our colleagues from the Cyclotron Institute, Texas A&M University, College Station, Texas, colleagues from Istituto Nazionale di Fisica Nucleare, Laboratori Nazionali del Sud, Italia, Sicilia, Catania, and colleagues from the Nuclear Physics Institute of the Czech Academy of Sciences with whom we were happy to collaborate on topics included in this review. Authors are also indebted to referees, whose insightful suggestions and comments importantly improved the original text. The figures are adapted from the papers referred in each reaction.
References
Abia, C., Hedrosa, R. P., Domínguez, I., and Straniero, O. (2017). The puzzle of the CNO isotope ratios in asymptotic giant branch carbon stars. Astron. Astrophys. 599:A39. doi: 10.1051/0004-6361/201629969
Ahmad, Q. R., Allen, R. C., Andersen, T. C., Anglin, J. D., Bühler, G., Barton, J. C., et al. (2001). Measurement of the rate of interactions produced by 8B solar neutrinos at the sudbury neutrino observatory. Phys. Rev. Lett. 87:071301. doi: 10.1103/PhysRevLett.87.071301
Al-Abdullah, T., Carstoiu, F., Chen, X., Clark, H. L., Fu, C., Gagliardi, C. A., et al. (2010). Stellar reaction rate for 22Mg + p → 23Al from the asymptotic normalization coefficient in the mirror nuclear system 22Ne + n → 23Ne. Phys. Rev. C 81:035802. doi: 10.1103/PhysRevC.81.035802
Azhari, A., Burjan, V., Carstoiu, F., Dejbakhsh, H., Gagliardi, C. A., Kroha, V., et al. (1999). The 10B(7Be, 8B)9Be reaction and the 7Be(p, γ)8B S factor. Phys. Rev. Lett. 82, 3960–3963.
Azhari, A., Burjan, V., Carstoiu, F., Gagliardi, C. A., Kroha, V., Mukhamedzhanov, A. M., et al. (2001). Asymptotic normalization coefficients and the 7Be(p, γ)8B astrophysical S factor. Phys. Rev. C 63:055803. doi: 10.1103/PhysRevC.63.055803
Banu, A., Al-Abdullah, T., Fu, C., Gagliardi, C. A., McCleskey, M., Mukhamedzhanov, A. M., et al. (2009). Astrophysical S factor for the radiative capture 12N(p, γ)13O determined from the 14N(12N, 13O)13C proton transfer reaction. Phys. Rev. C 79:025805. doi: 10.1103/PhysRevC.79.025805
Baur, G., Bertulani, C. A., and Rebel, H. (1986). Coulomb dissociation as a source of information on radiative capture processes of astrophysical interest. Nuclear Phys. A 458, 188–204.
Baur, G., and Rebel, H. (1996). Coulomb breakup of nuclei—applications to Astrophysics. Annu. Rev. Nuclear Part. Sci. 46, 321–350.
Bellerive, A., Klein, J. R., McDonald, A. B., Noble, A. J., and Poon, A. W. P. (2016). The Sudbury Neutrino observatory. Nuclear Phys. B 908, 30–51. doi: 10.1016/j.nuclphysb.2016.04.035
Belyaeva, T. L., Goncharov, S. A., Demyanova, A. S., Ogloblin, A. A., Danilov, A. N., Maslov, V. A., et al. (2018). Neutron halos in the excited states of 12B. Phys. Rev. C 98:034602. doi: 10.1103/PhysRevC.98.034602
Belyaeva, T. L., Perez-Torres, R., Ogloblin, A. A., Demyanova, A. S., Ershov, S. N., and Goncharov, S. A. (2014). Determination of neutron halo radii in the first excited states of 13C and 11Be with the asymptotic normalization coefficients method. Phys. Rev. C 90:064610. doi: 10.1103/PhysRevC.90.064610
Bém, P., Burjan, V., Kroha, V., Novák, J., Piskor, S., Šimečková, E., et al. (2000). Asymptotic normalization coefficients for 14N↔13C + p from 13C(3He, d)14N. Phys. Rev. C 62:024320. doi: 10.1103/PhysRevC.62.024320
Bertulani, C. A. (2003). RADCAP: A potential model tool for direct capture reactions. Comput. Phys. Commun. 156, 123–141. doi: 10.1016/S0010-4655(03)00441-7
Bing, G., and Zhi-Hong, L. (2007). Determination of astrophysical 13N(p, γ) 14O S-factors from the asymptotic normalization coefficient of 14C → 13C + n. Chin. Phys. Lett. 24, 65–68. doi: 10.1088/0256-307X/24/1/018
Buckner, M. Q., Iliadis, C., Cesaratto, J. M., Howard, C., Clegg, T. B., Champagne, A. E., et al. (2012). Thermonuclear reaction rate of 18O(p, γ)19F. Phys. Rev. C 86:065804. doi: 10.1103/PhysRevC.86.065804
Burjan, V., Hons, Z., Kroha, V., Mrázek, J., Piskor, S., Mukhamedzhanov, A. M., et al. (2013). Experimental study of the 18O(d, p)19O reaction and the ANC method. J. Phys. Conf. Ser. 420:012142. doi: 10.1088/1742-6596/420/1/012142
Burjan, V., Hons, Z., Kroha, V., Mrázek, J., Piskor, S., Mukhamedzhanov, A. M., et al. (2014). The 18O(d, p)19O reaction and the ANC method. AIP Conf. Proc. 1595, 163–167. doi: 10.1063/1.4875304
Burjan, V., Hons, Z., Kroha, V., Mrazek, J., Piskor, S., Mukhamedzhanov, A. M., et al. (2019). The determination of the astrophysical S-factor of the direct 18O(p, γ)19F capture by the ANC method. Eur. Phys. J. A 55:114. doi: 10.1140/epja/i2019-12801-8
Carstoiu, F., Trache, L., Gagliardi, C. A., Tribble, R. E., and Mukhamedzhanov, A. M. (2001). Radius of 8B halo from the asymptotic normalization coefficient. Phys. Rev. C 63:054310. doi: 10.1103/PhysRevC.63.054310
Chow, H. C., Griffiths, G. M., and Hall, T. H. (1975). The 16O(p, γ)17F direct capture cross section with an extrapolation to astrophysical energies. Can. J. Phys. 53, 1672–1686. doi: 10.1139/p75-213
Daehnick, W. W., Childs, J. D., and Vrcelj, Z. (1980). Global optical model potential for elastic deuteron scattering from 12 to 90 MeV. Phys. Rev. C 21, 2253–2274. doi: 10.1103/PhysRevC.21.2253
Decrock, P., Gaelens, M., Huyse, M., Reusen, G., Vancraeynest, G., Van Duppen, P., et al. (1993). Study of the 13N(d, n)14O reaction cross section and its astrophysical implications for the 13N proton capture reaction. Phys. Rev. C 48, 2057–2067. doi: 10.1103/PhysRevC.48.2057
Duke, C. B. (1963). Optical-model analysis of elastic scattering of protons on oxygen at intermediate energies. Phys. Rev. 129, 681–691. doi: 10.1103/PhysRev.129.681
Gagliardi, C., Azhari, A., Burjan, V., Carstoiu, F., Kroha, V., Mukhamedzhanov, A., et al. (2002). Asymptotic normalization coefficients and astrophysical direct capture rates. Eur. Phys. J. A 13, 227–232. doi: 10.1140/epja1339-38
Gagliardi, C. A., Azhari, A., Bem, P., Burjan, V., Carstoiu, F., Cejpek, J., et al. (2001). Asymptotic normalization coefficients from direct transfer reactions and astrophysical S factors. Nuclear Phys. A 682, 369–374. doi: 10.1016/S0375-9474(00)00662-X
Gagliardi, C. A., Tribble, R. E., Azhari, A., Clark, H. L., Lui, Y.-W., Mukhamedzhanov, A. M., et al. (1999). Tests of transfer reaction determinations of astrophysical S factors. Phys. Rev. C 59, 1149–1153. doi: 10.1103/PhysRevC.59.1149
Gómez-Ramos, M., and Timofeyuk, N. K. (2018). Reduced sensitivity of the (d, p) cross sections to the deuteron model beyond the adiabatic approximation. Phys. Rev. C 98:011601. doi: 10.1103/PhysRevC.98.011601
Guo, B., Su, J., Li, Z. H., Wang, Y. B., Yan, S. Q., Li, Y. J., et al. (2013). Determination of the astrophysical 12N(p, γ)13O reaction rate from the 2H(12N, 13O)n reaction and its astrophysical implications. Phys. Rev. C 87:015803. doi: 10.1103/PhysRevC.87.015803
Herndl, H., Hofinger, R., Jank, J., Oberhummer, H., Görres, J., Wiescher, M., et al. (1999). Reaction rates for neutron capture reactions to C, N, and O isotopes to the neutron rich side of stability. Phys. Rev. C 60:064614. doi: 10.1103/PhysRevC.60.064614
Huang, J. T., Bertulani, C. A., and Guimarães, V. (2010). Radiative capture of nucleons at astrophysical energies with single-particle states. Atom Data Nuclear Data Tables 96, 824–847. doi: 10.1016/j.adt.2010.06.004
Imai, N., Aoi, N., Kubono, S., Beaumel, D., Abe, K., Kato, S., et al. (2001). Test of the ANC method via (d,p) reaction. Nuclear Phys. A 688, 281–284. doi: 10.1016/S0375-9474(01)00715-1
Jeukenne, J.-P., Lejeune, A., and Mahaux, C. (1977). Optical-model potential in finite nuclei from Reid's hard core interaction. Phys. Rev. C 16, 80–96. doi: 10.1103/PhysRevC.16.80
Kunz, P. (1990). DWUCK5: computer code DWUCK5: distorted wave Born approximation. Available online at: http://www.oecd-nea.org/tools/abstract/detail/nesc9872/
Lee, D. W., Powell, J., Perajarvi, K., Guo, F. Q., Moltz, D. M., and Cerny, J. (2011). Study of the 11C(p, γ) reaction via the indirect d(11C, 12N)n transfer reaction. J. Phys. G Nuclear Part. Phys. 38:075201. doi: 10.1088/0954-3899/38/7/075201
Lefebvre, A., Aguer, P., Kiener, J., Bogaert, G., Coc, A., de Oliveira, F., et al. (1995). Astrophysical rate of the 11C + p reaction from the coulomb break-up of a 12N radioactive beam. Nuclear Phys. A 592, 69–88. doi: 10.1016/0375-9474(95)00291-8
Li, E. T., Guo, B., Li, Z. H., Wang, Y. B., Li, Y. J., Wu, Z. D., et al. (2016). Radii of the bound states in 16N from the asymptotic normalization coefficients. Chin. Phys. C 40:114104. doi: 10.1088/1674-1137/40/11/114104
Liu, Z. H., Lin, C. J., Zhang, H. Q., Li, Z. C., Zhang, J. S., Wu, Y. W., et al. (2001). Asymptotic normalization coefficients and neutron halo of the excited states in 12B and 13C. Phys. Rev. C 64:034312. doi: 10.1103/PhysRevC.64.034312
Lorenz-Wirzba, H., Schmalbrock, P., Trautvetter, H. P., Wiescher, M., Rolfs, C., and Rodney, W. S. (1979). The 18O(p, α)15N reaction at stellar energies. Nuclear Phys. A 313, 346–362. doi: 10.1016/0375-9474(79)90505-0
Magnus, P. V., Adelberger, E. G., and Garcia, A. (1994). The “hot CNO cycle” 13N(p, γ) resonance energy and the 18Ne mass. Phys. Rev. C 49, R1755–R1758. doi: 10.1103/PhysRevC.49.R1755
Meissner, J., Schatz, H., Görres, J., Herndl, H., Wiescher, M., Beer, H., et al. (1996). Neutron capture cross section of 18O and its astrophysical implications. Phys. Rev. C 53, 459–468. doi: 10.1103/PhysRevC.53.459
Morlock, R., Kunz, R., Mayer, A., Jaeger, M., Müller, A., Hammer, J. W., et al. (1997). Halo properties of the first 1/2+ state in 17F from the 16O(p, γ)17F reaction. Phys. Rev. Lett. 79, 3837–3840. doi: 10.1103/PhysRevLett.79.3837
Mukhamedzhanov, A., Burjan, V., Gulino, M., Hons, Z., Kroha, V., McCleskey, M., et al. (2011). Asymptotic normalization coefficients from the 14C(d, p)15C reaction. Phys. Rev. C 84:024616. doi: 10.1103/PhysRevC.84.024616
Mukhamedzhanov, A. M., Bém, P., Brown, B. A., Burjan, V., Gagliardi, C. A., Kroha, V., et al. (2003). Asymptotic normalization coefficients for 14N + p → 15O and the astrophysical S factor for 14N(p, γ)15O. Phys. Rev. C 67:065804. doi: 10.1103/PhysRevC.68.019901
Mukhamedzhanov, A. M., Bém, P., Burjan, V., Gagliardi, C. A., Goldberg, V. Z., Hons, Z., et al. (2008). New astrophysical S factor for the 15N(p, γ)16O reaction via the asymptotic normalization coefficient (ANC) method. Phys. Rev. C 78:015804. doi: 10.1103/PhysRevC.78.015804
Mukhamedzhanov, A. M., Bém, P., Burjan, V., Gagliardi, C. A., Irgaziev, B. F., Kroha, V., et al. (2006). Asymptotic normalization coefficients from the 20Ne(3He, d)21Na reaction and astrophysical factor for 20Ne(p, γ)21Na. Phys. Rev. C 73:035806. doi: 10.1103/PhysRevC.73.035806
Mukhamedzhanov, A. M., Clark, H. L., Gagliardi, C. A., Lui, Y.-W., Trache, L., Tribble, R. E., et al. (1997). Asymptotic normalization coefficients for 10B → 9Be + p. Phys. Rev. C 56, 1302–1312. doi: 10.1103/PhysRevC.56.1302
Mukhamedzhanov, A. M., Tribble, R. E., and Timofeyuk, N. K. (1995). Possibility to determine the astrophysical S factor for the 7Be(p, γ)8B radiative capture from analysis of the 7Be(3He, d)8B reaction. Phys. Rev. C 51, 3472–3478. doi: 10.1103/PhysRevC.51.3472
Nollett, K. M., and Wiringa, R. B. (2011). Asymptotic normalization coefficients from ab initio calculations. Phys. Rev. C 83:041001. doi: 10.1103/PhysRevC.83.041001
Ogloblin, A. A., Demyanova, A. S., Danilov, A. N., Belyaeva, T. L., Goncharov, S. A., and Trzaska, W. (2016). Nuclear states with anomalously large radius (size isomers). Phys. Atom. Nuclei 79, 514–524. doi: 10.1134/S1063778816040177
Ohsaki, T., Igashira, M., Nagai, Y., Segawa, M., and Muto, K. (2008). Role of multiparticle-multihole states of 18, 19O in 18O(n, γ)19O reactions at keV energy. Phys. Rev. C 77:051303. doi: 10.1103/PhysRevC.77.051303
Palmerini, S., Trippella, O., and Busso, M. (2017). A deep mixing solution to the aluminum and oxygen isotope puzzles in pre-solar grains. Monthly Notice R Astron. Soc. 467, 1193–1201. doi: 10.1093/mnras/stx137
Perey, C. M., and Perey, F. G. (1976). Compilation of phenomenological optical-model parameters 1954–1975. Atomic Data Nuclear Data Tables 17, 1–101. doi: 10.1016/0092-640X(76)90007-3
Raynal, J. (1979). Code ECIS79. Available online at: https://www.oecd-nea.org/tools/abstract/detail/nea-0850; https://people.nscl.msu.edu/~brown/reaction-codes/
Raynal, J. (1981). Recurrence relations for distorted-wave Born approximation Coulomb excitation integrals and their use in coupled channel calculations. Phys. Rev. C 23, 2571–2585. doi: 10.1103/PhysRevC.23.2571
Rhoades-Brown, M, Steven, P., and McFarlane, M. (1983). Ptolemy: a program for heavy-ion direct-reaction calculations. Available online at: https://inis.iaea.org/search/searchsinglerecord.aspx?recordsFor=SingleRecord&RN=9416330
Rolfs, C., Rodney, W. S., Shapiro, M. H., and Winkler, H. (1975). Hydrogen burning of 20Ne and 22Ne in stars. Nuclear Phys. A 241, 460–486. doi: 10.1016/0375-9474(75)90398-X
Rolfs, C. E., and Rodney, W. S. (1988). Cauldrons in the Cosmos: Nuclear Astrophysics. Chicago, IL: University of Chicago Press.
Tang, X., Azhari, A., Fu, C., Gagliardi, C. A., Mukhamedzhanov, A. M., Pirlepesov, F., et al. (2004). Determination of the direct capture contribution for 13N(p,γ)14O from the 14O → 13N + p asymptotic normalization coefficient. Phys. Rev. C 69:055807. doi: 10.1103/PhysRevC.69.055807
Tang, X., Azhari, A., Gagliardi, C. A., Mukhamedzhanov, A. M., Pirlepesov, F., Trache, L., et al. (2003). Determination of the astrophysical S factor for 11C(p,γ)12N from the 12N → 11C + p asymptotic normalization coefficient. Phys. Rev. C 67:015804. doi: 10.1103/PhysRevC.67.015804
Thompson, I. J. (1988). Coupled reaction channels calculations in nuclear physics. Comp. Phys. Rep. 7, 167–212. doi: 10.1016/0167-7977(88)90005-6
Timofeyuk, N. K. (1998). One nucleon overlap integrals for light nuclei. Nuclear Phys. A 632, 19–38. doi: 10.1016/S0375-9474(98)00810-0
Timofeyuk, N. K. (2010). Overlap functions, spectroscopic factors, and asymptotic normalization coefficients generated by a shell-model source term. Phys. Rev. C 81:064306. doi: 10.1103/PhysRevC.81.064306
Timofeyuk, N. K. (2013). Spectroscopic factors and asymptotic normalization coefficients for 0p-shell nuclei: recent updates. Phys. Rev. C 88:044315. doi: 10.1103/PhysRevC.88.044315
Timofeyuk, N. K., Descouvemont, P., and Thompson, I. J. (2008). Threshold effects in the and mirror decays and the stellar reaction 26Si(p, γ)27P. Phys. Rev. C 78:044323. doi: 10.1103/PhysRevC.78.044323
Timofeyuk, N. K., Fernández-Domínguez, B., Descouvemont, P., Catford, W. N., Delaunay, F., and Thomas, J. S. (2012). Core excitations and narrow states beyond the proton dripline: the exotic nucleus 21Al. Phys. Rev. C 86:034305. doi: 10.1103/PhysRevC.86.034305
Timofeyuk, N. K., Johnson, R. C., and Mukhamedzhanov, A. M. (2003). Relation between proton and neutron asymptotic normalization coefficients for light mirror nuclei and its relevance to nuclear astrophysics. Phys. Rev. Lett. 91:232501. doi: 10.1103/PhysRevLett.91.232501
Trache, L., Azhari, A., Carstoiu, F., Clark, H. L., Gagliardi, C. A., Lui, Y.-W., et al. (2003). Asymptotic normalization coefficients for 8B → 7Be + p from a study of 8Li → 7Li + n. Phys. Rev. C 67:062801. doi: 10.1103/PhysRevC.67.062801
Trache, L., Azhari, A., Clark, H. L., Gagliardi, C. A., Lui, Y.-W., Mukhamedzhanov, A. M., et al. (1998). Asymptotic normalization coefficients for 13C + p → 14N. Phys. Rev. C 58, 2715–2719. doi: 10.1103/PhysRevC.58.2715
Trache, L., Azhari, A., Clark, H. L., Gagliardi, C. A., Lui, Y.-W., Mukhamedzhanov, A. M., et al. (2000). Optical model potentials involving loosely bound p-shell nuclei around 10 MeV/nucleon. Phys. Rev. C 61:024612. doi: 10.1103/PhysRevC.61.024612
Trache, L., and Carstoiu, F. (2019). Indirect methods in nuclear astrophysics. arXiv preprint arXiv:1911.06077. Available online at: http://arxiv.org/abs/1911.06077
Vaughn, F. J., Grench, H. A., Imhof, W. L., Rowland, J. H., and Walt, M. (1965). The total neutron cross section of O18 from 0.14 to 2.47 MeV. Nuclear Phys. 64, 336–342. doi: 10.1016/0029-5582(65)90361-5
Vernotte, J., Berrier-Ronsin, G., Kalifa, J., Tamisier, R., and Wildenthal, B. H. (1994). Spectroscopic factors from one-proton stripping reactions on sd-shell nuclei: Experimental measurements and shell-model calculations. Nuclear Phys. A 571, 1–42. doi: 10.1016/0375-9474(94)90339-5
Watson, B. A., Singh, P. P., and Segel, R. E. (1969). Optical-model analysis of nucleon scattering from 1p-shell nuclei between 10 and 50 meV. Phys. Rev. 182, 977–989. doi: 10.1103/PhysRev.182.977
Wiescher, M., Becker, H. W., Görres, J., Kettner, K. U., Trautvetter, H. P., Kieser, W. E., et al. (1980). Nuclear and astrophysical aspects of 18O(p, γ)19F. Nuclear Phys. A 349, 165–216. doi: 10.1016/0375-9474(80)90451-0
Wiescher, M., Gorres, J., Graff, S., Buchmann, L., and Thielemann, F.-K. (1989). The hot proton-proton chains in low-metallicity objects. Astrophys. J. 343, 352–364. doi: 10.1086/167709
Wiescher, M., Gorres, J., and Thielemann, F.-K. (1990). Capture reactions on C-14 in nonstandard big bang nucleosynthesis. Astrophys. J. 363, 340–343. doi: 10.1086/169348
Xu, H. M., Gagliardi, C. A., Tribble, R. E., Mukhamedzhanov, A. M., and Timofeyuk, N. K. (1994). Overall normalization of the astrophysical S factor and the nuclear vertex constant for 7Be(p, γ)8B reactions. Phys. Rev. Lett. 73, 2027–2030. doi: 10.1103/PhysRevLett.73.2027
Yarmukhamedov, R., and Blokhintsev, L. D. (2018). Asymptotic normalization coefficients (nuclear vertex constants), three-body asymptotic normalization functions (on-shell vertex functions) and nuclear astrophysics. Phys. Atom. Nuclei 81, 616–629. doi: 10.1134/S1063778818050198
Keywords: nuclear physics, direct reactions, asymptotic normalization coefficient, astrophysical S-factor, CNO-cycle
Citation: Burjan V, Mrazek J and D'Agata G (2020) ANC From Experimental Perspective. Front. Astron. Space Sci. 7:562466. doi: 10.3389/fspas.2020.562466
Received: 15 May 2020; Accepted: 25 August 2020;
Published: 10 November 2020.
Edited by:
Scilla Degl'Innocenti, University of Pisa, ItalyReviewed by:
Pierre Descouvemont, Université libre de Bruxelles, BelgiumAndrea Celentano, Universities and Research, Italy
Juan Pablo Fernández García, Universidad de Sevilla, Spain
Copyright © 2020 Burjan, Mrazek and D'Agata. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jaromir Mrazek, bXJhemVrQHVqZi5jYXMuY3o=
 Vaclav Burjan
Vaclav Burjan Jaromir Mrazek
Jaromir Mrazek Giuseppe D'Agata
Giuseppe D'Agata