Solar-Like Oscillators in the Kepler Era: A Review

1 Introduction

The NASA Kepler spacecraft was launched in 2009 and spent the next four years staring at a fixed region of the sky toward the Cygnus and Lyra constellations (Borucki et al., 2010; Koch et al., 2010). After the loss of a couple of reactions wheels, the mission was revamped to carry out a series of observing campaigns in fields along the ecliptic plane, where pointing accuracy could be more easily controlled (Howell et al., 2014). The K2 mission successfully lasted for another five years. The most significant scientific objective for Kepler and K2 was the detection and characterization of terrestrial extrasolar planets by transit photometry. To accomplish this, approximately a half-million stars were monitored.

Apart from discovering new planets, a tremendous value-added benefit to these types of observations is the potential for stellar astrophysics. Almost continuous monitoring of starlight at high temporal cadence (1 or 30 min) and high precision (several tens of parts-per-million) has been a goldmine for the study of variable stars. In particular, a vast research effort has been focused on stars that are variable due to pulsations, which are present for stars across the H-R diagram, and revolutionizing the field of asteroseismology.

This review will focus on stars that pulsate in ways similar to our Sun, commonly known as “solar-like” oscillators. Such stars may not necessarily be “solar-type” main-sequence objects like the Sun; for example, red giants display solar-like oscillations. These oscillations are due to acoustic (pressure) standing waves. In most cases, they are excited to small, yet observable amplitudes, which are stochastically driven and damped by near-surface turbulent convection (Goldreich and Keeley, 1977). Classical pulsators, such as Cepheids, RR Lyrae, δ Scuti, γ Doradus, white dwarfs, etc., typically have opacity-driven oscillations and will not be discussed here, nor will systems with oscillations driven by tidal forcings in multi-star configurations.

For any star to potentially exhibit solar-like oscillations, it must be cool enough to have an outer convection zone. Therefore, the effective (surface) temperature is important, and needs to be below about 7000 K, corresponding to an upper mass of approximately $1.5M_{\odot }$ on the main sequence, and to spectral types later than mid-F, to G and K dwarf stars. For evolved stars, this temperature limit is above much of the subgiant branch and red-giant (G, K, and M) stars, whose mass can be greater than $1.5M_{\odot }$.

Kepler and K2 observed thousands of stars with detectable solar-like oscillations, and the main question this review hopes to address, is what new stellar astrophysics have we learned from stars that pulsate like the Sun? To that end, exciting asteroseismic results in the Kepler era include progress on interior rotation, mixing processes, precise mass and radius measurements, ages and evolutionary state determinations, stellar populations, binarity, granulation, magnetic fields, and interior discontinuities of structure or composition. It is difficult to overemphasize the revolution that Kepler has had on the field of asteroseismology of solar-type stars, particularly in terms of the precision with which stellar parameters can now be computed. To keep the review focused on important results, topics such as new analysis and data-reduction techniques (of which many have been developed in the past decade of Kepler science), complementary ground-based observations, new theoretical modeling tools, etc., will not be covered. Other excellent reviews have a much broader focus (Chaplin and Miglio, 2013; Hekker, 2013; García and Ballot, 2019).

In Section 2, the properties and diagnostic potential of solar-like oscillations are briefly discussed, followed by Section 3 on the most exciting asteroseismic results on different classes of stars. Section 4 present conclusions and future prospects in the field.

2 Solar-Like Oscillations in a Nutshell

First, we look at what observations of solar-type stars look like, using the best prototype - the Sun.

2.1 Observations of Solar-like Oscillators

Pulsations excited by near-surface turbulent convection can set up standing, global modes in a star. The pulsations distort the stellar surface with a spatial pattern that can usually be described by spherical harmonics. These distortions result in small luminosity fluctuations, as well as radial-velocity variations. For distant stars, only the large-scale spatial variations can be observed in integrated light due to cancellation effects, corresponding to only the lowest spherical harmonic degrees $\left(\ell =0-3\right)$. A very detailed discussion of all aspects of asteroseismology can be found in Aerts et al. (Aerts et al., 2010).

Synoptic observations of the Sun for seismic studies have been ongoing for decades from the ground using networks of dedicated telescopes, such as the Birmingham Solar Oscillation Network [BISON, (Chaplin et al., 1996)], and the Global Oscillations Network Group [GONG, (Harvey et al., 1996)]. From space, the ESA/NASA SOHO satellite, launched in 1995, had instrumentation to observe the Sun as a star both photometrically and spectroscopically, namely VIRGO (Fröhlich et al., 1995; Frohlich et al., 1997; Jiménez et al., 2002) and GOLF (Gabriel et al., 1995), respectively. Time series of luminosity or velocity fluctuations are best analyzed in the Fourier domain to search for various mode properties. The typical quantity is an amplitude or power spectrum. Power spectra of an approximately 20-years time series from VIRGO and GOLF data are shown in Figure 1. The figure shows a representative comb-like structure near $3000\mu \text{Hz}$ where the acoustic $p-$ mode envelope has the largest amplitude, whose frequency is known as ${\nu }_{\text{max}}$. At low frequencies, there are contributions in the spectrum from rotational signals (spots and other activity) and convection (granulation and supergranulation). At high frequencies, one finds the contribution from photon noise. One of the important differences between photometric and Doppler velocity measurements is the signal-to-noize ratio (SNR), which is about an order of magnitude larger in velocity near ${\nu }_{\text{max}}$. The photometric SNR is lower because background convection has a larger signal in temperature fluctuations than in the velocity fluctuations measured with spectroscopy [e.g., 8]. The higher SNR allows for better measurements of lower-frequency modes using velocity, as Figure 1 demonstrates.

FIGURE 1

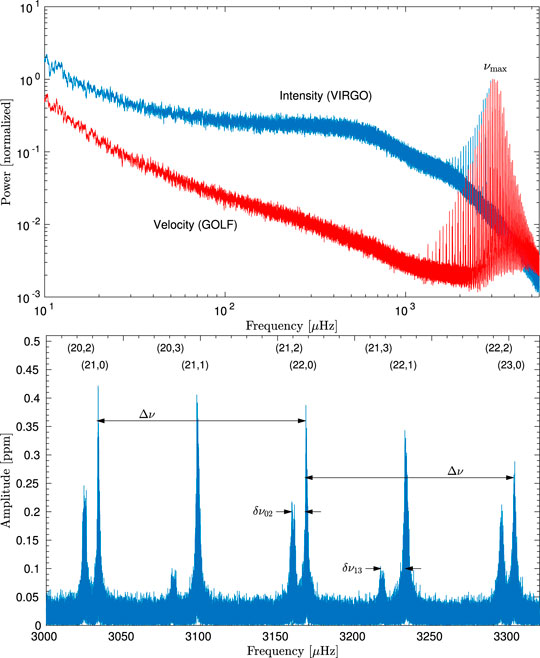
FIGURE 1. Top panel: Solar power spectra computed from almost 20 years of data from the VIRGO and GOLF instruments on board the SOHO satellite. The VIRGO observations are from the green channel at 500 nm. The power spectra have been smoothed by a boxcar function of $0.17\mu \text{Hz}$ width, and are normalized such that the amplitudes are equal near the frequency of maximum amplitude of the acoustic modes ${\nu }_{\text{max}}\approx 3100\mu$Hz. Bottom panel: Amplitude spectrum computed from the VIRGO photometric data near ${\nu }_{\text{max}}$ (note the non-logarithmic scale). The peaks are labeled by their radial order n and angular degree $\ell$ as $\left(n,\ell \right)$. A few characteristic large and small frequency spacing examples are labeled with $\text{Δ}\nu$ and $\delta \nu$, respectively.

Noting that Kepler is a photometric instrument, the bottom panel of Figure 1 shows an amplitude spectrum of the photometric VIRGO data near ${\nu }_{\text{max}}$. The comb-like pattern is evidently the result of modes very evenly spaced in frequency, at least for large radial orders n. As is the case for distant stars, this type of solar observation is only sensitive to radial $\left(\ell =0\right)$ and the first few nonradial $\left(\ell =\mathrm{1,2,3}\right)$ modes. The frequency difference between modes of consecutive radial order and the same spherical degree is known as the large frequency spacing $\text{Δ}\nu$. The frequency difference between modes of consecutive radial order and degrees different by two is the small frequency spacing $\delta \nu$. Their diagnostic potential is described in the next section. It’s worth pointing out the small amplitude of solar-like oscillations, particularly for main-sequence stars, which lies in the parts-per-million range. Kepler’s unprecedented sensitivity was necessary for similar quality observations of distant stars.

Kepler observed the photometric variations of many pulsating stars at cadences of 1 min or 30 min. Main-sequence solar-like stars show a ${\nu }_{\text{max}}$ of a few thousand μHz, corresponding to periods of about 5 min. Therefore, a faster sampling such as 1 min is required. Evolved red-giant stars, on the other hand, who also show solar-like oscillations, have frequencies as low as $\sim 20\mu$ Hz, or periods of about half a day, so 30-min sampling is sufficient. Power spectra of several pulsating Kepler stars in different evolutionary states are shown in Figure 2. Each star is approximately one solar mass. Note the different amplitude and frequency range of the p-modes. While not completely evident from this figure, the Kepler data are of extremely high quality, and in some cases comparable to what exists for the Sun, which is shown as the rightmost spectrum.

FIGURE 2

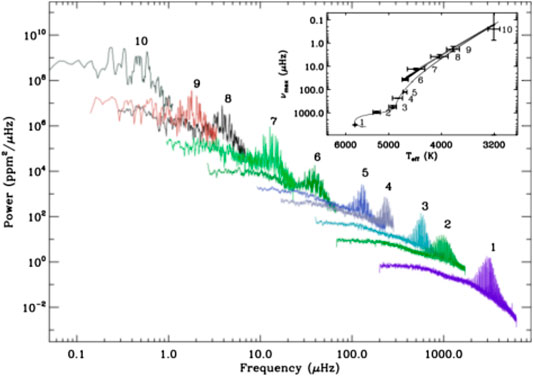
FIGURE 2. Samples of power spectral density for Kepler solar-like oscillators at different evolutionary stages. The Sun’s spectrum is labeled #1 (purple). The inset shows model tracks of a $1M_{\odot }$ star and the corresponding power spectra labels approximately related to each evolutionary state. Figure from Garcia and Stello (Garcia and Stello, 2018).

2.2 Properties and Diagnostic Potential of the Oscillations

A detailed review of the physics of solar-like oscillations can be found in many places [e.g., 16]. Here, we only provide a quick overview and focus on the major properties discernable from stellar oscillations.

The sequence of spectra in Figure 2 already provides hints of the utility of solar-like oscillations for probing stellar interiors. At a given mass, as stars evolve their intrinsic frequencies shift, resulting in a decreasing value of ${\nu }_{\text{max}}$. As discussed below, this quantity is related most closely to a star’s surface gravity. Since radii increase with time, this is the expected and observed behavior. So at zeroth order, for stars of similar masses and composition, ${\nu }_{\text{max}}$ acts as a relative clock.

Zooming in on a solar-like spectrum, as in the lower panel of Figure 1, the dominant features are peaks that are arranged according to the large and small frequency spacings. The oscillation peaks are typically high-order (large n), radial and non-radial oscillations. In this case, asymptotic theory of stellar oscillations (Tassoul, 1980) shows that the expected frequencies of such modes are well described to second order by

${\nu }_{n\ell }\simeq \text{Δ}\nu \left(n+\frac{\ell }{2}+\mathit{ϵ}\right)-\ell \left(\ell +1\right)D_0,(1)$

where $\varepsilon$ is a frequency-dependent offset term that is mostly dependent on near-surface effects (Christensen-Dalsgaard and Perez Hernandez, 1992; Kjeldsen et al., 2008; Mosser et al., 2013b), and $D_0$ is described below. The large-frequency separation $\text{Δ}\nu$ is precisely the quantity depicted in Figure 1, and is related to the sound crossing time of an acoustic wave across the star

$\text{Δ}\nu ={\nu }_{n\ell }-{\nu }_{n-1\ell }={\left(2{{{\displaystyle \int }}^{\text{}}}_0^R\frac{\text{d}r}{c}\right)}^{-1},(2)$

where c is the adiabatic sound speed. Since the sound speed scales as $c^2\propto M{R}^{-1}$, Eq. 2 implies that $\text{Δ}\nu \propto \sqrt{M{R}^{-3}}\propto \sqrt{\overline{\rho }}$, or the root of the mean stellar density, a quantity that also decreases as stars evolve (at least up until the tip of the red-giant branch).

Given this physically-motivated relationship for the large frequency spacing, and an empirically-motivated one for the frequency at maximum amplitude [but see (Belkacem et al., 2011)], ${\nu }_{\text{max}}\propto {\nu }_{\text{ac}}\propto g{T}_{\text{eff}}^{-1/2}$, where ${\nu }_{\text{ac}}$ is the atmospheric acoustic cut-off frequency, one can identify the asteroseismic scaling relations (Brown et al., 1991; Kjeldsen and Bedding, 1995; Kallinger et al., 2010) as

$\begin{array}{c}\frac{M}{M_{\odot }}={\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right)}^3{\left(\frac{\text{Δ}\nu }{\text{Δ}{\nu }_{\odot }}\right)}^{-4}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{3/2},\\ \frac{R}{R_{\odot }}=\left(\frac{{\nu }_{\text{max}}}{{\nu }_{\text{max},\odot }}\right){\left(\frac{\text{Δ}\nu }{\text{Δ}{\nu }_{\odot }}\right)}^{-2}{\left(\frac{T_{\text{eff}}}{T_{\text{eff},\odot }}\right)}^{1/2}\end{array}(3)$

These relations assume homology with the Sun and thus are scaled to solar reference values ($\odot$ symbols), and comprise the most common tool for obtaining stellar parameters from two rather straightforward asteroseismic measurements, as well as an estimate of the effective temperature, usually easily available. Note, however, in this form the lack of dependence on stellar composition, for example. Much recent effort has gone into calibrating these relations for a broad range of evolutionary states and other stellar properties [see 25, for an extensive review]. Even new data-driven scaling relations for stellar age on the main sequence and red-giant branch are now available (Bellinger, 2019; Bellinger, 2020).

The small frequency separation that appears as the other obvious feature in power spectra can be obtained from Eq. 1:

$\delta {\nu }_{n\ell }={\nu }_{n\ell }-{\nu }_{n-1\ell +2}=\left(4\ell +6\right)D_0\simeq -\frac{\text{Δ}\nu }{4{\pi }^2{\nu }_{n\ell }}{{{\displaystyle \int }}^{\text{}}}_0^R\frac{\text{d}c}{\text{d}r}\frac{\text{d}r}{r}.(4)$

The small frequency separation is a useful quantity since its weighting by the sound-speed gradient makes it sensitive to the core and its composition. Thus, it can be used to measure stellar ages in some cases, notably on the main sequence, particularly when used in an asteroseismic “C-D” diagram (Christensen-Dalsgaard, 1988; White et al., 2011). All of the above is the theoretical framework in the asymptotic limit, which describes high-frequency modes of large radial orders. In some cases, particularly for evolved stars where the observed low-degree modes do not correspond to large radial orders, the asymptotic limit is not strictly satisfied. In such instances, however, the departure from this limit is small enough that higher-order corrections and empirical calibrations are commonly adopted to retain the accuracy of this formalism. A detailed discussion can be found in Mosser et al. (Mosser et al., 2013b).

Apart from the large and small separations and the location of the mode power envelope, higher-order effects are additionally seen. One such effect is due to gravity modes in a star, which are excited in convectively stable regions where buoyancy is the restoring force. For solar-like stars, these modes are not visible at the surface like pressure modes, as their propagation cavity is in the deep radiative interior. However, if their frequencies become commensurate to those of the p-modes, they can “mix” and interact with non-radial p-modes and impart new information in the p-mode frequency spectrum. This can be interpreted as a mode having the character of acoustic modes in the outer layers, and having the character of gravity modes in the deeper layers. Asymptotic theory applied to (gravity) g-modes predicts that they will be evenly spaced, not in frequency as for the p-modes, but in wave period. The period spacing is given by

$\text{ΔΠ}=2{\pi }^2{\left({{{\displaystyle \int }}^{\text{}}}_{r_1}^{r_2}N\frac{\text{d}r}{r}\right)}^{-1},(5)$

where N is the Brunt-Väisälä buoyancy frequency, and the integration is over the internal g-mode cavity. The buoyancy frequency is approximately related to the local gravitational acceleration, which increases in radiative cores as stars evolve, allowing for this mixing to occur. Gravity-mode period spacings can be measured in the spectrum of p-modes, providing a very powerful diagnostic of the core regions of evolved stars, as discussed in Section 3.1.

Another feature in power spectra is the splitting of mode frequencies into multiplets due to rotation. Such an effect has been exploited in the Sun to determine its latitudinal and radial differential rotation profile to a very high precision (Thompson et al., 1996). In stars, p-mode frequencies can be split by somewhat rapid rotation, but even more interesting, is that the mixed modes themselves can be split by core rotation. In the evolved stars where this situation most often arises, the effects due to rotation are smaller than those due to mode mixing since such stars are typically slow rotators. There are exceptions, however, which can make the interpretation of such effects challenging. The measurement of these frequency shifts, and their amplitudes, is further affected by the inclination of the rotation axis with respect to the observer (Gizon and Solanki, 2003).

Beyond all of the observables mentioned to this point, powerful inferences can be made by measuring the frequencies of many individual modes and then using numerical models to match the expected frequencies to the observed ones. If successful, and the modes can be correctly identified, the interior model then gives all relevant stellar properties and the evolutionary state. These studies can be computationally intensive when large grids in parameter space of stellar models are required. Furthermore, to make the most robust inferences and assess theoretical uncertainties, multiple evolutionary codes are often employed for the same problem, each one with various differences in the physical prescriptions and numerical solvers [e.g., (Silva Aguirre et al., 2017; Nsamba et al., 2018)]. Powerful statistical methods are also becoming common to constrain models from observations (Rendle et al., 2019). Some examples of these efforts are provided in the following sections.

Finally, it is known from theory that interior radial discontinuities or boundaries lead to sharp variations in the local sound speed (Gough, 1990) known as “glitches.” The mode eigenfrequences then show an oscillatory behavior that departs from the regular pattern seen above, whose period is related to the depth location of the glitch. Possible sources of the glitch are the base of the stellar convection zone, where structure varies quickly, and the second helium ionization zone. These quantities are indirectly related to other interesting properties such as abundances of helium and metals. Only the best seismic data are amenable to these inferences, however.

3 What Have We Learned From Kepler?

These are the main tools in the hands of the asteroseismologist to gain better understanding of stellar interiors, evolution, and populations. The Kepler mission has been able to exploit these asteroseismic tools more successfully than any other experiment so far for stellar astrophysics.

Since solar-like oscillations are only found in late-type stars, the discussion will be limited to stars on the main sequence (MS), subgiant (SG) branch, red-giant branch (RGB), the red clump (RC), sometimes referred to as the cool horizontal branch, and the secondary red clump (RC2), the population of higher-mass clump stars that do not experience a helium flash on the RGB. A sample of about 16,500 oscillators are shown in Figure 3. These are the main phases of evolution that Kepler data has addressed. The results presented are by no means exhaustive or final, as new analysis techniques and modeling improvements will help exploit Kepler data well into the future. This should only be considered a taste of the success so far.

FIGURE 3

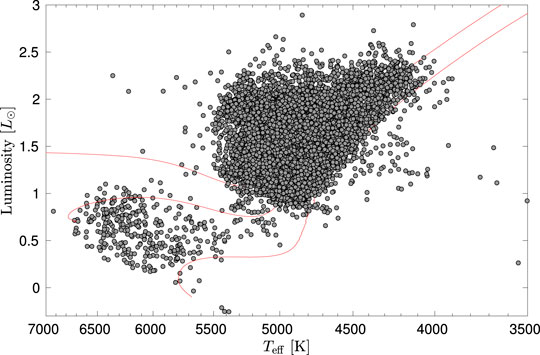
FIGURE 3. H-R diagram showing a representative sample of Kepler stars with detected solar-like oscillations. These stars comprise the main sequence, subgiant branch, red-giant branch, and red clump. Also shown in red are nominal evolution tracks for 1, 1.5, and $2M_{\odot }$ stellar models. Parameters obtained from Serenelli et al. (Serenelli et al., 2017) and Yu et al. (Yu et al., 2018).

3.1 Mass, Radius, Age, and Evolutionary State

As already remarked, one of the most straightforward, yet powerful applications of asteroseismology is to use the scaling relations (Eq. 3) to estimate a star’s mass and radius. This has led to the idea of ensemble asteroseismology.

Ensemble asteroseismology seeks to analyze a large, statistical sample of stars in one homogeneous fashion to obtain these general stellar parameters, and does not require these stars to be in clusters. One of the first attempts with Kepler main-sequence and subgiant stars was described in Chaplin et al. (Chaplin et al., 2011), where 500 stars that are mostly hotter and more massive than the Sun were observed to have detectable solar-like oscillations from only one month of short-cadence Kepler data. With reasonably good estimates of mass and radius available from the scaling relations for the first time for a large sample, it was possible to compare this cohort to predictions of galactic population synthesis models. The Kepler sample was distributed more broadly in mass, as well as peaked at a lower mass, than predictions from models (Chaplin et al., 2011). Even at this early stage of Kepler analysis, implications for models regarding the initial mass function, star-formation rate, and interior mixing processes were brought into the spotlight from the precise seismic inferences.

A subset of 87 of these stars that had spectroscopic temperatures and metallicities were studied in Chaplin et al. (Chaplin et al., 2014) in a grid-based modeling approach. This comprises computing a large number of numerical stellar models from a dense grid of initial parameters (mass, composition, etc.,). The global seismic and spectroscopic parameters of each star are then matched to a model to yield, among other things, a stellar age. The models including the spectroscopic constraints resulted in surprising precision, at the levels of $\sim 5.4\text{\%}$ in mass, $\sim 2.2\text{\%}$ in radius, $\sim 0.01$ dex in $\text{log}\left(g\right)$, $\sim 2.8\text{\%}$ in density, and $\sim 25\text{\%}$ in age. Over the subsequent lifetime of Kepler, and using some of the best-observed main-sequence stars (Bellinger, 2019; Bellinger et al., 2019), the mean precision is approximately 11%, 3.5%, and 1.5% on stellar ages, masses, and radii, respectively. The level of precision on age is about at the level of isochrone fitting in clusters.

All of these studies used global seismic parameters, such as frequency spacings or frequency differences and ratios. To do better, a powerful inference tool is to accurately measure and model individual eigenfrequencies, in addition to any other global seismic properties and any spectroscopic and photometric constraints. Metcalfe et al. (Metcalfe et al., 2014) did just that with 42 stars collected from earlier asteroseismic measurements by Appourchaux et al. (Appourchaux et al., 2012). A stellar model pipeline was used with a large amount of automatization, yielding median uncertainties of $7.9\text{\%}$ on the age, $2.8\text{\%}$ on the mass, and $1.2\text{\%}$ on the radius–improving on the other approach, but more computationally expensive.

Solar-like oscillations have been found at later evolution stages of cool stars in much greater numbers, since long-cadence Kepler data, the primary mode of operation, are sufficient for sampling the longer periods. It had been thought that non-radial modes would be strongly damped in red-giant stars (Dziembowski et al., 2001; Christensen-Dalsgaard, 2004), however De Ridder et al. (De Ridder et al., 2009) convincingly reported the first detected non-radial oscillations in several hundred giants. Over a decade later, the sample has now grown to a few tens of thousands (Yu et al., 2018).

Red giants have a “universal pattern” of modes in the frequency spectrum (Mosser et al., 2011), allowing for fast and reliable measurements of the large frequency spacing and ${\nu }_{\text{max}}$, and therefore, mass and radius measurements. Perhaps the most exciting discovery in this area from Kepler is signatures of gravity-modes (Beck et al., 2011) and their associated period spacings that almost unambiguously reveal if red-giant stars are burning hydrogen in a shell around the core only (on the RGB) or have transitioned onto the RC by igniting helium burning in the core (Bedding et al., 2011; Mosser et al., 2012b).

An example of classification of the evolutionary state of hundreds of stars is shown in Figure 4, where the period spacings of mixed modes $\left(\text{ΔΠ}\right)$ is plotted against the large frequency separation. The stars above $\sim 40\mu$Hz are subgiants, while main-sequence stars are beyond that and do not show mixed modes. As stars evolve onto and up the giant branch, the large frequency separation continues to decrease along with the period spacing of mixed modes. Once He is ignited, the period spacing increases to over 200 s. This happens because along the RGB the inert He core increases in density due to the overlying H-burning shell dropping its ashes onto it, which results in smaller period spacings (increasing N in Eq. 5). Once helium is ignited, the core becomes convective and expands, density decreases locally, N does too, and the period spacing increases. Stars on the red clump are therefore of larger period spacings. Massive stars around $2M_{\odot }$ ignite He without a flash, and occupy a slightly different region in the diagram as the lower panel highlights, offering a way to distinguish these two regions of the cool horizontal branch.

FIGURE 4

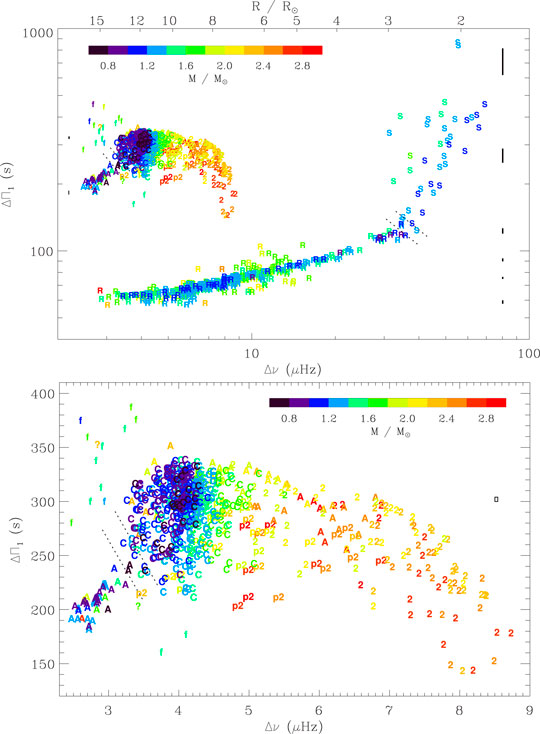
FIGURE 4. Mixed-mode period spacing ($\text{ΔΠ}$) vs. the large frequency spacing ($\text{Δ}\nu$) for a large sample of Kepler solar-like pulsators. Top: the seismic proxy for the stellar mass is indicated by the color code. The evolutionary states are indicated by S (subgiants), R (RGB), f (helium subflash stage), C (red clump), p2 (pre-secondary clump), 2 (secondary clump), and A (stars leaving the red clump moving toward the AGB). The error boxes on the right side indicate the mean uncertainties, as a function of, for stars on the RGB; for clump stars, uncertainties are indicated on the left side. Dotted lines indicate the boundaries between evolutionary stages. Bottom: zoom in the red-clump region. From Mosser et al. (Mosser et al., 2014).

These measurements are now ubiquitous tools for determining evolutionary states. Thousands of evolved stars can be analyzed using consistent pipeline methods (Stello et al., 2013; Yu et al., 2018). For giants, the scaling relations yield typical median uncertainties of approximately $7-10\text{\%}$ in mass, $2-4\text{\%}$ in radius, and about 0.01 dex in seismic $\text{log}\left(g\right)$. A thorough review of asteroseismology of evolved giant stars is given in Hekker and Christensen-Dalsgaard (Hekker and Christensen-Dalsgaard, 2017) and Basu and Hekker (Basu and Hekker, 2020).

Given the large size of the Kepler data set, a rapid area of growth in asteroseismic analysis is data-driven methods with machine learning. For example, intelligent regression algorithms can reveal subtle relationships among model quantities of stars to connect them to traditional observables very quickly (Bellinger et al., 2016). The results are similar to the grid-based approach, but with significant computational efficiency. Neural networks are being applied to well-studied power spectra of solar-like oscillators to predict stellar properties and evolutionary states of stars with less distinct spectra (Hon et al., 2017; Hon et al., 2018; Hon et al., 2020), or even from the fundamental light curves themselves (Blancato et al., 2020). The coming decade will likely see such approaches applied more frequently as the amount of available data continues to increase and the community pushes forward with open-source software initiatives (Tollerud, 2020).

As a final note, while the precision of the scalings for mass and radius estimates for large numbers of stars is greater than any other methods, what about the accuracy? While it is difficult to find “ground truth” values of these quantities to compare to, there are a few avenues beyond using models (Huber et al., 2011). One direction is with eclipsing-binary star systems. Binaries with (at least) one oscillating component and photometrically measured eclipses are extremely useful for stellar astrophysics, since stellar parameters, such as mass, can be measured in two independent ways once radial-velocity measurements are obtained. The first such system detected by Kepler was a red-giant oscillator in orbit with a main-sequence F star (Hekker et al., 2010). Since then, a catalog of a dozen or so oscillating red giants have been found in eclipsing binaries with mass and radius derived seismically and dynamically (Frandsen et al., 2013; Gaulme et al., 2013; Gaulme et al., 2016; Benbakoura et al., 2017). While different studies use various small corrections to the scaling relations, in general the masses and radii of the giants are systematically overestimated compared to the dynamical solutions, by about $10\text{\%}$ and $5\text{\%}$, respectively. On the other hand, a few other analyses using more detailed corrections to the scaling relations and different reference values, find much better agreement (Brogaard et al., 2018; Kallinger et al., 2018; Themeßl et al., 2018).

Another absolute measurement of stellar radii comes from interferometric observations of bright targets. Huber et al. (Huber et al., 2012) used the CHARA array to measure angular radii of 10 solar-like pulsators. They found agreement between seismic and interferometric radii, with an accuracy better than about 4% for main-sequence stars and no obvious systematic offset. Similarly, a comparison of radii estimated from Gaia parallax measurements with seismic radii was carried out in Huber et al. (Huber et al., 2017). Overall, for a wide range of stars of 0.8–8 R$\odot$, seismology and Gaia agree to within 5%. On the subgiant branch only (1.5–3 R$\odot$), the seismic radii are underestimated by about 5%. Zinn et al. (Zinn et al., 2019) found better radii agreement with Gaia for a few thousand stars, mostly on the giant branch. On the other hand, for almost 100 dwarf pulsators, Sahlholdt and Silva Aguirre (Sahlholdt & Silva Aguirre, 2018) found seismic radii overestimated by about 5% compared to Gaia using the basic scaling relations. These studies give a good overall picture of the level of departure from the simple scalings, which is surprisingly low given all the potential sources of uncertainty: $T_{\text{eff}}$, metallicity, reddening, parallax, and the homology assumption itself. Clearly, while some improvements are needed, the scaling relations are powerful and rather simple tools. A review of how the scaling relations have been “tuned” to provide more consistent results is found in Hekker (Hekker, 2020).

3.2 Galactic Archaeology

Galactic Archaeology is a term used to describe efforts to trace the structure and past chemical and physical evolution of the Milky Way by interpreting its current stellar populations. Key stellar parameters are age, evolutionary state, composition, kinematics, and distance. During Kepler’s early operations, the Apache Point Observatory Galactic Evolution Experiment (APOGEE) came online as part of the Sloan Digital Sky Survey (SDSS-III and IV) (Majewski et al., 2010). The APOGEE instrument is an IR (H-band) multi-fiber spectrograph, optimized to survey tens of thousands of red giants across the galaxy for “archaeological” purposes.

Traditional stellar population studies have used photometric and/or limited spectroscopic observations (Zhao et al., 2006; Gilmore et al., 2012), which can provide some of the required parameters, but with large uncertainties on masses and age. Kepler seismology adds new and more precise observables to the mix, particularly masses and evolutionary state, and is particularly powerful when considering red-giant stars, which are bright, ubiquitous, and almost always pulsating. However, on the red-giant branch, a precise mass alone is not sufficient to determine an age without composition information (Salaris et al., 2015; Martig et al., 2016; Ness et al., 2016). APOGEE provides effective temperature, surface gravity, metallicity, and a dozen individual abundances to high precision (García Pérez et al., 2016). Recognizing the tremendous synergy between APOGEE and Kepler, the APOGEE Kepler Asteroseismic Consortium (APOKASC) was spearheaded to coordinate APOGEE observations of the Kepler fields. Complementary large asteroseismic and spectroscopic surveys can yield precious new information on galactic stellar populations (clusters and field stars), stellar atmospheres, and stellar interiors.

The main product of the APOKASC effort has been a catalog containing a number of internally calibrated stellar parameters, including mass, radius, evolutionary state, surface gravity, and age, for almost 7,000 giants and about 500 main-sequence and subgiants stars (Pinsonneault et al., 2014; Serenelli et al., 2017; Pinsonneault et al., 2018). An example of how seismology and spectroscopy can work in tandem is shown in Figure 5. The H-R diagram of giants on the left is from purely photometric observables from the Kepler Input Catalog (KIC). Since surface gravity is a much more natural spectroscopic observable, the middle panel shows the APOGEE observations of the same stars, which presents a tighter red-giant branch as well as a red clump. Surface gravity is an even more precise asteroseismic observable, and is substituted in for the right panel, which now shows a secondary red clump of more massive giants, and evidence of the RGB bump. Remarkably, it is important to note that these stars are not in a cluster.

FIGURE 5

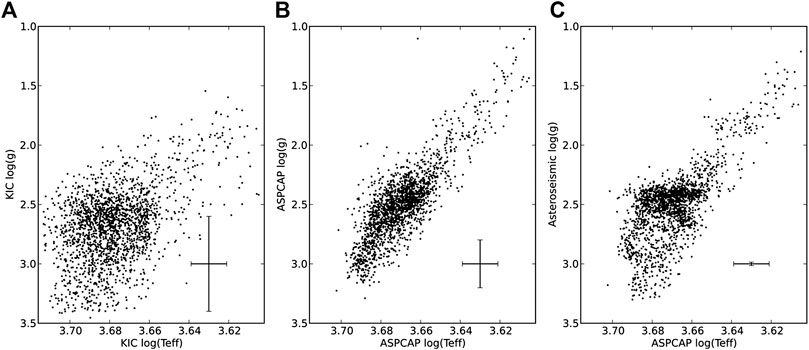
FIGURE 5. Evolved APOKASC catalog stars plotted from different sources. The left panel are parameters from the photometric Kepler Input Catalog. The middle panel uses APOGEE’s pipeline-derived spectroscopic values. The right panel uses the more precise asteroseismic surface gravity. The red clump is significantly enhanced, as is the RGB bump. Median uncertainties are given by the crosses in the lower part of each panel. From Pinsonneault et al. (Pinsonneault et al., 2014).

The APOKASC catalog has been the foundation for a number of important studies, and likely will be well into the future. One interesting example is in Silva Aguirre et al. (Silva Aguirre et al., 2018), who use a subset of the APOKASC catalog, combining precise ages and chemical information to dissect the Milky Way disk. It has been known from spectroscopic surveys and isochrone fitting that the disk contains stars with enhanced α abundances and low metallicity that are old, and young ones with lower-α abundances and high metallicity. But Silva Aguirre et al. (Silva Aguirre et al., 2018) find many older stars in the disk with low-α and high metallicity, not observed before, and which are more consistent with chemical evolution models. Without the level of precision of asteroseismic ages for large numbers of stars, this result would not have been possible.

Solar-like oscillators are improving our picture of the galaxy. Distances are also a key observable, and one can compute precise radii for far-away red giants to get distances to place stars throughout the Milky Way (Miglio et al., 2013) in 3D. Period-luminosity relations for pulsating M giants have been studied, which could be a new way to give access to distances to other galaxies (Mosser et al., 2013a; Stello et al., 2014). Seismology has even been of use to the Gaia mission to help correct parallax biases and offsets (Davies et al., 2017).

Other notable photometric and spectroscopic surveys that target the Kepler fields to exploit solar-like pulsators and study the structure of the Milky Way are the Strömgren Survey for Asteroseismology and Galactic Archaeology [SAGA, (Casagrande et al., 2014; Casagrande et al., 2016)], the Large Sky Area Multi-Object Fiber Spectroscopic Telescope [LAMOST, (Ren et al., 2016; Wang et al., 2016)], and the Galactic Archaeology with HERMES [GALAH, (De Silva et al., 2015; Martell et al., 2020)] survey, as well as some fortuitous projects such as the Asteroid Terrestrial-impact Last Alert System (ATLAS) and the All-Sky Automated Survey for Supernovae [ASAS-SN, (Auge et al., 2020)].

3.3 Stellar Clusters

A similar focus is the application of asteroseismology to clusters, which are critical astrophysical objects. The Kepler field contained four open clusters bright enough to be well observed, while K2 observed almost 20 globular and open clusters. Trusting the simple assumptions that one can ignore variations in cluster members’ age, (initial) composition, and distance, potentially stringent constraints can be placed on cluster properties. This, in turn, allows for improvements in theoretical modeling regarding isochrones, as well as for interpreting disparate observational data sets.

NGC 6791 and NGC 6819 are two well-studied open clusters observed by Kepler. Basu et al. (Basu et al., 2011) used solar-like pulsators to estimate masses, seismic distances, and ages of the clusters’ members. Adding in a third Kepler cluster, NGC 6811, Stello et al. (Stello et al., 2011) used seismology to assess membership. Consider the seismic scaling relations when $T_{\text{eff}}$ and L are substituted in for the radius. This allows the global seismic parameters to then be expressed as the dependent variables in the form $\text{Δ}\nu \left(M,T_{\text{eff}},L\right)$ and ${\nu }_{\text{max}}\left(M,T_{\text{eff}},L\right)$. On the red-giant branch of a cluster, L is expected to vary more strongly than either M or $T_{\text{eff}}$. In other words, two stars of similar luminosity should have similar values of $\text{Δ}\nu$ and ${\nu }_{\text{max}}$. If they don’t, it likely means the star is a foreground or background object. In a cluster with minimal distance variations, therefore, one should expect a strong correlation between either $\text{Δ}\nu$ or ${\nu }_{\text{max}}$ and a good proxy for the luminosity–the apparent magnitude–a quantity readily available. Indeed, this is what was found, and the membership of the clusters was improved by the simple removal of outliers to this tight relationship.

Seismology also gives a way to constrain mass loss on the RGB, a historically difficult quantity to predict theoretically, as well to observe quantitatively. Imagine a cluster with a populated RGB and RC. If one could measure the average mass of giants in the RC, and compare to the average mass of giants on the RGB at or below the luminosity of the RC, then any difference could potentially be explained by mass loss as stars climbed the RGB above that luminosity level before arriving on the clump. This is the clever strategy employed by Miglio et al. (Miglio et al., 2012) for NGC 6791 and NGC 6819. As an older high-metallicity cluster, NGC 6791 is a strong candidate to exhibit strong mass loss on the RGB. However, using several dozen stars, the authors find that the difference in average mass between the clump and branch stars is $\text{Δ}M=0.09\pm 0.03$ (random)$\pm 0.04$ (systematic), which is statistically significant, but not extreme, as other works had suggested. NGC 6819, on the other hand, did not show evidence of mass loss, which was subsequently reconfirmed (Handberg et al., 2017).

The effects of compositional variations among stars on seismic observables is not precisely known, and clusters offer great laboratories. Using shell-burning giants, McKeever et al. (McKeever et al., 2019) modeled individual p-mode frequencies to determine that NGC 6791 is rich in helium, which consequently helps constrain the age to within 300 million years. The old globular cluster M4 allows for metal-poor asteroseismology to be attempted, and (Miglio et al., 2016) found preliminary evidence that the scaling relations still give reasonable masses in this regime. The future is bright for cluster seismology as new oscillators are being discovered. Lund et al. (Lund et al., 2016) found main-sequence pulsators for the first time in an open cluster–the young Hyades cluster. Pulsating giants have also been observed in the solar metallicity cluster M67 (Stello et al., 2016).

3.4 Precision Stellar Interior Physics

Kepler pulsators with the highest-quality light curves allow for very precise experiments, particularly bright targets with long-baseline observations and/or short-cadence data. These are excellent candidates for constraining physics that are not standardized across stellar models, such as mixing length properties, convective overshooting, and microscopic diffusion of helium and metals. Many of the best candidates have also been targeted for ground-based follow up.

Perhaps the best studied and modeled stars (apart from the Sun) so far have been those in the solar analog binary system, 16 Cyg A and B (Metcalfe et al., 2012; Metcalfe et al., 2003), whose age of $\sim 7$ Gyr is now precise to less than 6% (Bazot, 2020). Over 50 global modes have been observed and identified in each star at sub-microhertz precision. Using the oscillatory “glitch” signature of the eigenfrequencies (Section 2.2), Verma et al. (Verma et al., 2014) measured the current He abundance in the outer envelope of both stars, which of course is less than the BBN value due to gravitational settling.

A sample of 66 main-sequence pulsating stars has been collated and called the Kepler seismic LEGACY project [(Lund et al., 2017; Silva Aguirre et al., 2017), which includes (Christensen-Dalsgaard, 2004) Cyg A and B]. Their global properties have been well characterized, as has the locations of the He II ionization zones (Verma et al., 2017). The signature of the bottom of the convective zones is less constrained, however. A few dozen LEGACY stars have surface helium abundance measurements (Verma et al., 2019), again showing that atomic diffusion does occur in solar-type stars.

Main-sequence stars slightly more massive than the Sun have convective cores rather than radiative ones. Silva Aguirre et al. (Silva Aguirre et al., 2013) found strong evidence in a main-sequence pulsator, very near the transition mass value, for convective core overshooting. Such processes mix extra material in the fusion region and asteroseismic constraints helped select the best models. Montalbán et al. (Montalbán et al., 2013) found evidence of extra mixing from core convective overshooting for red clump stars, while Deheuvels et al. (Deheuvels et al., 2016) were able to do the same for eight main-sequence stars. These studies crucially show that models without an extended core from overshooting cannot match the seismic data, and that new model calibrations of this effect for low-mass stars are now available, which will lead to improvements in modeling other stellar properties.

The mixing-length parameter in the outer convection zone of stars is also an important model ingredient, and most studies have used the calibrated solar value, regardless of the type of star. Bonaca et al. (Bonaca et al., 2012), using Kepler seismic constraints, calibrated this parameters for a range of stars and found that its value is generally lower than solar, with a clear metallicity dependence. Similar findings for a larger number of main-sequence stars (Creevey et al., 2017), and APOKASC stars along the red-giant branch were measured by Tayar et al. (Tayar et al., 2017), where the mixing length parameter takes on super-solar values. That work emphasized that this effect needs to be taken into account if Gaia is indeed to be used to give isochrone ages for giants. Confirmation of the need for larger model values of this parameter from a sample of red giants in eclipsing binaries is discussed in Li et al. (Li et al., 2018). Until we develop a more complete theoretical understanding of near-surface convection in the context of 1D models, or until fully 3D models are routinely employed, these mixing-length calibrations need to be taken into account.

As mentioned in Section 3.1, binary systems where one or both stars are oscillating have been crucial for independent assessment of the accuracy of the scaling relations. A host of other experiments can be carried out with such valuable objects to learn very detailed evolutionary physics. One obvious example is testing tidal interaction theories [e.g., (Remus et al., 2012)]. Beck et al. (Beck et al., 2018a) used a sample of binaries with at least one red-giant star to show that the equilibrium tide is sufficient to explain the distribution of the measured orbital eccentricities and periods. As another important example, a prediction of stellar evolution theory is that stars climbing the red-giant branch will “dredge-up” nuclear-processed material as the surface convection zone deepens, potentially altering the surface composition. Beck et al. (2018b) studied a double-lined spectroscopic binary system of two oscillating giants observed by Kepler. The mass ratio of the stars was found to be about 1%. This relatively small difference, however, translated into a drastic disparity in surface lithium abundance between the stars, indicating that each star was in a different stage of the dredge-up event. Since the interior rotation was also estimated from the oscillation frequencies, these observations place tight contraints on interior mixing processes in this dynamic evolutionary phase.

3.5 Rotation

As mentioned earlier, rotation shifts the stellar eigenfrequencies, which can be used to estimate surface and interior rotation depending on which modes are available. A consistency check is sometimes available if photometic modulations due to surface magnetic activity, presumably with the same average periodicity as the rotation, can be measured and compared to the value obtained from asteroseismology. The bright stars 16 Cyg A and B again have shown to be good candidates in this regard. From seismology, their inclination angles and surface rotation rates were measured using evidence that the internal differential rotation is weak (weaker than the Sun’s), due to their evolved state (Davies et al., 2015).

Differential rotation across latitudes is another important quantity of solar-like stars, as it can provide information about stellar activity cycles. Selecting promising targets from the Kepler LEGACY sample, Benomar et al. (Benomar et al., 2018) found strong evidence for latitudinal differential rotation in 13 stars. Motivated by this, Bazot et al. (Bazot et al., 2019) did a detailed analysis of 16 Cyg A and B, including inversions of the frequencies, and found solar-like latitudinal differential profiles, i.e., the equators rotate more rapidly than the polar regions.

Interior rotation is a powerful measure of how angular momentum evolves in a star (Pinsonneault et al., 1990). After the main sequence to the tip of the red-giant branch, in principle the stellar core is shrinking and should spin up, decoupling from the envelope. Some of the first evidence from Kepler of radial differential rotation in red-giants stars was shown in Beck et al. (2012), where the core rotation in a few stars was found to be about 10 times faster than the surface value by exploiting rotationally-split mixed modes. This was achieved because some of the mixed modes have more g-mode character and confined to the core, and some have more p-mode character confined to the outer envelope. The faster core rotation was then deduced by comparing the relative frequency shifts of such modes.

As a confirmation of this result, some of the first formal seismic inversions were carried out on frequency shifts from a low luminosity red-giant star to show a rapidly rotation core (Deheuvels et al., 2012). These results are in tension with models of angular momentum transfer (Ceillier et al., 2012), which predict cores should be rotating even more rapidly than what was found, suggesting that there may be mechanisms that transport angular momentum away from the deep interior that current models do not taking into account. Nonetheless, from large samples of evolved stars, it is generally found that core rotation decreases up the RGB Gehan et al. (Gehan et al., 2018), and continues to slow down on the red clump (Mosser et al., 2012a; Deheuvels et al., 2015).

On the subgiant branch, Deheuvels et al. (Deheuvels et al., 2014) and Eggenberger et al. (Eggenberger et al., 2019) measure rather slow core rotation. When they employed standard stellar models with rotation calibrated to match the measured surface values, the models’ core region still spins an order of magntidue faster. By introducing an artificial viscosity to the models, they were able to better reproduce the core rotation found in the seismic measurements. They also found that the efficiency of the unknown transport process actually decreases along the subgiant branch, but must then increase again on the giant branch to explain the observations there. Finally, for main-sequence solar-like stars, even those 50% more massive than the Sun, minimal internal differential rotation was measured (Benomar et al., 2015), again suggesting some efficient angular momentum transport process.

All in all, angular momentum transport on the main sequence, subgiant phase, and red-giant branch is complicated and a very active area of research. Suggested mechanisms for transferring angular momentum across the stars are mixed modes and internal gravity waves [(Belkacem et al., 2015), particularly for more evolved giants], meridional circulation, dynamos, and, most convincingly, magnetic instabilities (Fuller et al., 2019).

In terms of global rotation, solar-type, main-sequence F, G, and K stars with outer convection zones are born with relatively rapid rotation, but then should spin down as they evolve due to angular momentum loss from stellar winds entrained in magnetic fields. This torquing effect is called magnetic braking. Since ages of field stars are difficult to obtain, the rotation-age-mass relation is potentially a powerful inference tool, known as gyrochronology (Barnes, 2003). Indeed, before Kepler, the Sun was the oldest star that had a reliable age. The goal of gyrochronology in general is to provide a means of predicting the age of a star given observations of its color (or proxies like mass, or temperature) and rotation period. Empirical relationships have been calibrated successfully, but only constrained by the Sun and young clusters where ages are obtainable.

In the Kepler era, such theories can be extended outside of clusters, since age can be measured in a reasonably accurate way from seismology, and stellar rotation can be measured from seismology, or the modulation from spots of the light curves themselves, or from spectroscopy. Indeed, tight rotation-age relationships were found in early Kepler analysis (do Nascimento et al., 2014; García et al., 2014). In addition, Ceillier et al. (Ceillier et al., 2016) studied 11 planet-hosting stars with asteroseismic ages and photometric rotation periods, compared to a sample without planets, and found similar age-rotation-mass relationships.

However, using a larger sample of a few hundred field stars with asteroseismic ages, Angus et al. (Angus et al., 2015) found that many of the older stars did not obey the relation, in the sense that the older stars were rotating faster than expected. Since gyrochronology is intimately tied to magnetic fields generated through a dynamo mechanism in solar-type stars, the mismatch with current theory explored in Angus et al. (Angus et al., 2015) suggests a new complication. van Saders et al. (van Saders et al., 2016) studied a subset of 21 Kepler stars with high-precision asteroseismic measurements that are near or beyond the age of the Sun and found shorter rotation periods than gyrochronology predicts. The authors speculate that angular momentum loss from magnetic breaking depends sensitively on the global magnetic field configuration, suggesting a possible change in the dynamo mechanism as stars evolve. One common way of describing this from a modeling point of view is through the Rossby number, which describes the ratio of the rotational period to the convective turnover time. Efficient dynamo regimes are characterized by small Rossby number, typically below unity. By including a new prescription in models that has a Rossby number threshold, van Saders et al. (van Saders et al., 2016) were able to show that angular momentum loss stops abruptly in stars when their rotation slows down and Rossby numbers reach a value of about 2. The magnetic activity and rotation essentially decouple at some age, roughly corresponding to the middle age on the main sequence.

This was validated in Metcalfe et al. (Metcalfe et al., 2016) by comparing stellar activity cycles with rotation periods. An illustration is given in Figure 6 (Metcalfe & van Saders, 2017; Metcalfe et al., 2019), showing the empirical relationship between stellar magnetic activity cycles and rotation periods. The lower, flatter solid line represents a sequence whereby stars’ rotation slows down and cycles lengthen, and had been thought to continue on throughout a star’s lifetime. The new picture is that when the critical Rossby number $\sim 2$ is approached, the star’s rotation does not decrease rapidly anymore, due to an altered magnetic field configuration and less braking. The star stays at the same rotation period and moves upward on the plot. The changing global magnetic field is weakening, thus causing a lengthening of the stellar cycle. The slowest rotators with measured cycles are K-type stars, since magnetic braking stops in more massive stars before they reach such slow rotation rates. Most K stars have not had time to reach this transition yet.

FIGURE 6

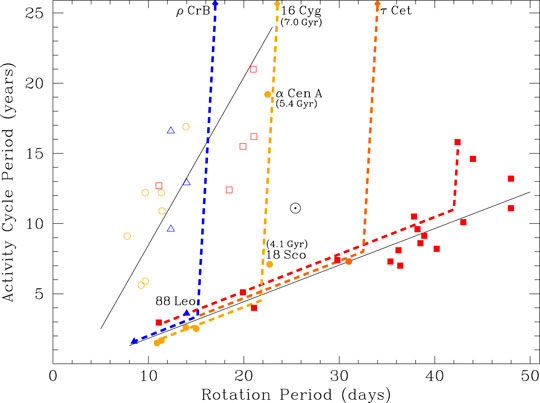
FIGURE 6. Stellar activity cycle length vs. rotation period for stars with measured cycles. The solid lines denote two different sequences that had been studied before Kepler, with the Sun ($\odot$) being a perplexing outlier (or midlier). Symbols are colored by spectral type, F (blue triangles), early G (yellow circles), late G (orange circles), and K (red squares). The dashed lines are schematic evolutionary tracks, which advance in time to the right and upwards. Some well known stars are labeled. Adapted from Metcalfe et al. (Metcalfe et al., 2019).

A star like the Sun, therefore, may be in a transition phase that occurs in all middle-aged stars whereby the rotation and magnetic-field topology are changing (likely becoming smaller scale), the solar cycle is lengthening, and will some day disappear altogether. Therefore, after their middle-age on the main sequence, stellar ages cannot reliably be predicted from their rotation. Without precise asteroseismic ages from Kepler, this discovery would not have been possible.

3.6 Magnetic Fields

Magnetic fields in other stars are very difficult to measure unless the stars are bright and the fields are strong enough to allow Zeeman observations. Perhaps the easiest seismological measurement of magnetism is based on lessons from the Sun, which have shown that the solar cycle and the variable surface magnetic fields affect the p-mode eigenfrequencies. Two potential effects are observable: the amplitude of modes can be suppressed, and the frequencies can be shifted (Howe et al., 2002). The Sun has provided an excellent test star for these behaviors, showing us that as the magnetic cycle progresses, frequencies become larger, and mode amplitudes decrease due to the absorption of acoustic energy. Importantly, the frequency shifts are smooth functions of frequency only, as larger frequencies show larger shifts (Basu, 2016). This suggests that the structural changes induced by the activity cycle are mostly confined to the near-surface region where the modes are excited.

It was noticed early on that some Kepler solar-like oscillators had heavily damped modes, likely due to some kind of magnetic activity (Chaplin et al., 2011; Campante et al., 2014; García et al., 2014; Gaulme et al., 2014). Frequency shifts with time have also been measured [e.g. (Kiefer et al., 2017)], suggesting magnetic variability. Using the entire 4-years Kepler data, however, is necessary to have any hope to detect periodicities resulting from a possible stellar cycle. With an 87-star sample, Santos et al. (Santos et al., 2018) find that 60 to 70 percent show indications of magnetic activity over time from frequency shifts, mode heights, and even a varying stellar granulation timescale. Salabert et al. (Salabert et al., 2018), using a similar sample of main-sequence solar-like oscillators, find cycle-related frequency shifts that are not smooth like Sun. They conclude that there may be other sources of frequency perturbations associated with magnetic variability that are not present in the Sun. Using oscillations to estimate differential rotation, Bazot et al. (Bazot et al., 2018) find the first evidence for a butterfly-type diagram in a distant star.

These are all likely near-surface manifestations of the magnetic fields. Evidence of potential core magnetic fields of evolved stars became possible with the connection of suppressed dipole ($\ell =1$) modes to a leaking of mode energy in the core due to interaction of the internal gravity waves with magnetic fields (Fuller et al., 2015; Stello et al., 2016). This became known as the magnetic “greenhouse effect.” The predicted core fields are on the order of a million gauss and above. One may wonder how a star with a radiative core could harbor such strong fields. The key observation is that the suppression only occurs for giants with a mass above about $1.2M_{\odot }$ (measured with seismology). This is the approximate lower limit for stars that have convective cores on the main sequence, suggesting that a dynamo mechanism generated the fields at that time and which survive into the giant phase. However, if the observed suppressed modes are mixed dipole modes rather than pure acoustic modes, this theoretical interpretation will need to be modified, as discussed in Mosser et al. (Mosser et al., 2017).

3.7 Exoplanet Host Stars

Knowing the planet requires knowing the star, as is often pointed out. If a planet host is oscillating and seismic observables can be determined, planetary properties with unmatched precision can be obtained. Asteroseismic and exoplanetary research communities have a natural synergy (Campante et al., 2018; Lundkvist et al., 2018). For example, transit observations give estimates of the ratio of the planetary and stellar radius, but there are degeneracies that are often difficult to disentangle due to other orbital parameters. However, under common conditions, the ratio of the orbital semi-major axis to the stellar radius ($a/R_{\text{*}}$) can be shown to be (Seager & Mallén-Ornelas, 2003; Huber, 2018)

${\rho }_{\text{*}}=\frac{3\pi }{G{P}^2}{\left(\frac{a}{R_{\text{*}}}\right)}^3,(6)$

where ${\rho }_{\text{*}}$ is the stellar density. A similar expression relating the mean stellar density to the orbital eccentricity can also be derived (Kipping, 2010). Eccentricity is a difficult measurement for small planets, yet a crucial one for understanding formation and habitability. Since asteroseismic observations can provide the stellar density to high precision, these expressions allow for a complementary way of measuring and constraining these important transit parameters (and without requiring radial-velocity data). This is sometimes known as asterodensity profiling (Kipping, 2014).

Using seismically-determined stellar parameters for 66 host stars, Huber et al. (Huber et al., 2013) rederived planet and orbital properties and found significant differences with previous studies that relied on transit and spectroscopic observations only. Remarkably, Kepler-93b’s radius was measured to an uncertainty of 120 km using Kepler and Spitzer Space Telescope observations by Ballard et al. (Ballard et al., 2014). Using 4 years of Kepler observations of 33 solar-like host stars and a wide array of seismic and evolutionary modeling tools, Silva Aguirre et al. (Silva Aguirre et al., 2015) were able to add the critical age dimension to planetary studies at a precision of better than 15%. No large trends were found in the distributions of planet radius or period with age. As for age, Campante et al. (Campante et al., 2015) estimated the seismic age of metal-poor Kepler-444 to be about 11.2 Gyr, making its five terrestrial planets the oldest known system of its type so far discovered.

The asterodensity profiling method to determine eccentricities was used by Sliski and Kipping (Sliski and Kipping, 2014). Interestingly, a very high false-positive rate was determined for Kepler planet candidates with red-giant host stars, nearing 70%. Van Eylen and Albrecht (Van Eylen and Albrecht, 2015) also employed seismic asterodensity profiling to measure eccentricities of 28 stars with multiple planets (mostly below about 10 Earth masses), and, like in our Solar System, found low eccentricities. The distribution of eccentricities was distinctly different from those obtained from radial-velocity measurements (of mostly higher-mass planets). Van Eylen et al. (Van Eylen et al., 2019) subsequently constrained the eccentricity of 51 small, single-transiting Kepler planets. They find a very different distribution, peaking at moderate eccentricities $\sim 0.3$. These reults, based almost solely on eccentricity estimations, suggest different formation and evolutionary pathways for single- and multi-planet sytems that models will need to reconcile.

In another interesting planetary population study, Lundkvist et al. (Lundkvist et al., 2016) used precise seismic stellar radii to show there is a “desert” of hot super Earths with radii between 2.2 and 3.8 Earth radii in ultra short period orbits, shown in Figure 7. Such exoplanets are ubiquitous at longer periods in Kepler data. These observations confirmed models that such planets’ volatile-rich atmospheres are photo-evaporated due to the intense incident flux they receive from their host star.

FIGURE 7

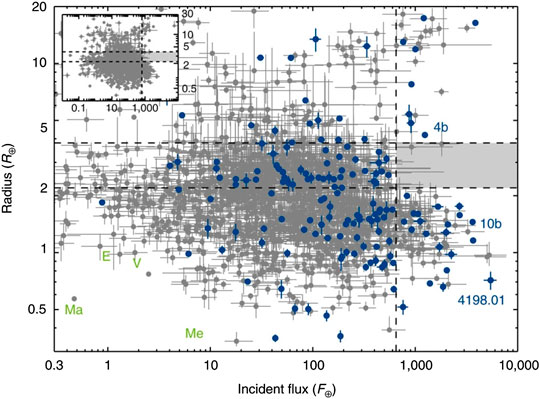
FIGURE 7. Exoplanet radius as a function of incident flux for a large sample of Kepler Objects of Interest (gray filled circles). The blue filled circles are 157 of those planets whose hosts have seismic measurements. The key point is the high level of precision on both the radius and incident flux of the seismic sample ($<10\text{\%}$). The gray shaded region is the hot super Earth desert, which receives at least 650 times the amount of incident flux as Earth and gets clearly delineated due to the seismic measurements. The inset shows a larger non-seismic sample. The four terrestrial planets are shown for reference. Figure from Lundkvist et al. (Lundkvist et al., 2016).

Stellar rotation can split solar-like oscillation modes into multiplets (Section 2.2), and the relative amplitude of the split modes depends on the viewing angle relative to the stellar rotation axis (Gizon and Solanki, 2003). Transit and radial-velocity observations (Rossiter-McLaughlin effect) provide the planet orbital axis inclination and the sky-project spin-orbit angle. A measurement of all three angles gives the absolute spin-orbit angle, or obliquity, of the system. This property is crucial for understanding the formation history and dynamical evolution of planetary systems.

Kepler transit and seismic data have allowed for the determination of the obliquity of dozens of exoplanetary systems. In cases where there is evidence for multiple exoplanets, most systems are highly aligned (low obliquity) [e.g., (Chaplin et al., 2013; Van Eylen et al., 2014; Quinn et al., 2015; Campante et al., 2016)]. Note that our Solar System has an obliquity of about 7%.

However, a large obliquity was found in Kepler-56, which is a red giant pulsator with two transiting planets (Huber et al., 2013). The misalignment (>37°) is likely caused by a third, non-transiting planet that tidally torques the system (Li et al., 2014). In general, the hot Jupiters have been found to be consistently misaligned (Albrecht et al., 2013; Winn and Fabrycky, 2015), begging the question as to why? Possible scenarios include the channels through which hot Jupiters migrated or the formation history as the star and protoplanetary disk evolved (Albrecht et al., 2013). Larger statistical samples will hopefully lead to a clearer picture (Winn et al., 2017).

Clearly, the use of pulsating stars to study their exoplanets adds a promising new avenue for understanding these distant worlds.

4 Conclusion

Asteroseismology of stars that oscillate like the Sun has experienced a paradigm shift as a result of the Kepler mission, yielding data of unprecedented quality. To fully exploit these data, one of the key developments that is needed is the improvement of 1D stellar models as discussed above. Subtle effects due to rotation, angular momentum evolution, mixing processes, meridional circulation, magnetic fields, and convection at boundaries are still not understood fully enough for the robust interpretation of Kepler data. However, tremendous progress is being made in this area, and the MESA 1D stellar evolution open-source software instrument is helping a large number of scientists to delve into theoretical modeling [see (Paxton et al., 2019), for the most recent instrument paper]. In the near future, we can expect increased implementation of 3D simulations that capture more of the physics, particularly in the outer layers of stars (Mosumgaard et al., 2020).

Solar-like oscillations are not only powerful probes of stellar interiors, but by providing precise stellar parameters, become an indispensible tool for galactic studies, particularly as large ground-based surveys scan the skies. Kepler, as well as NASA’s current Transiting Exoplanet Survey Satellite [(TESS) (Ricker et al., 2015)], have even shown that these oscillations may exist in intermediate-mass main-sequence stars that had never been considered before (Antoci et al., 2011; Bedding et al., 2020).

The legacy of revolutionary missions with dual goals of exoplanetary and stellar astrophysics, such as CoRoT (Convection Rotation and Planetary Transits), Kepler, and TESS, will be carried forward with the European Space Agency’s PLATO (PLanetary Transits and Oscillations of stars) mission, set to launch in 2026. Just as importantly, asteroseismic efforts on solar-like pulsators will be enhanced from ground-based telescopes, the most promising of which is the Stellar Oscillations Network Group [SONG, (Grundahl et al., 2007)]. This initiative follows the lead that GONG has shown for the Sun, whereby a network of small telescopes will target bright stars with high-resolution spectroscopy. The goal is for telescopes that are spread around the Earth in longitude to allow for nearly-continuous observations that permit detailed seismic investigations. As of this article, there are SONG nodes in the Canary Islands (the Hertzsprung SONG telescope), Australia, and China. Even with this initial distribution, there has tremendous success [e.g., (Grundahl et al., 2017; Arentoft et al., 2019; Fredslund Andersen et al., 2019; Li et al., 2019)], showing that dedicated asteroseismic observations from the ground can lead to an understanding of a sample of stars at the level near to that of our Sun.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

National Science Foundation under Grant Number 1351311.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author gratefully acknowledges support from the National Science Foundation under Grant Number 1351311. The VIRGO instrument onboard SoHO is a cooperative effort of scientists, engineers, and technicians, to whom we are indebted. SoHO is a project of international collaboration between ESA and NASA. Funding for the Kepler mission is provided by the NASA Science Mission Directorate. The author benefitted greatly from the Kepler Guest Observer publication database https://keplerscience.arc.nasa.gov/kpub-astrophysics.html. Three anonymous referees are also acknowledged for their very astute recommendations that have substantially improved the manuscript.

References

Aerts, C., Christensen-Dalsgaard, J., and Kurtz, DW. (2010). Asteroseismology. Cham, Switzerland: Springer.

CrossRef Full Text | Google Scholar

Albrecht, S., Winn, J. N., Marcy, G. W., Howard, A. W., Isaacson, H., and Johnson, J. A. (2013). Low stellar obliquities in compact multiplanet systems. Astrophys. J 771, 11. doi:10.1088/0004-637X/771/1/11

CrossRef Full Text | Google Scholar

Angus, R., Aigrain, S., Foreman-Mackey, D., and McQuillan, A. (2015). Calibrating gyrochronology using Kepler asteroseismic targets. Mon. Not. Roy. Astron. Soc. 450, 1787–1798. doi:10.1093/mnras/stv423

CrossRef Full Text | Google Scholar

Antoci, V., Handler, G., Campante, T. L., Thygesen, A. O., Moya, A., Kallinger, T., et al. (2011). The excitation of solar-like oscillations in a δSct star by efficient envelope convection. Nature 477, 570–573. doi:10.1038/nature10389

PubMed Abstract | CrossRef Full Text | Google Scholar

Appourchaux, T., Chaplin, W. J., García, R. A., Gruberbauer, M., Verner, G. A., Antia, H. M., et al. (2012). Oscillation mode frequencies of 61 main-sequence and subgiant stars observed by Kepler. Astron. Astrophys. 543, A54. doi:10.1051/0004-6361/201218948

CrossRef Full Text | Google Scholar

Arentoft, T., Grundahl, F., White, T. R., Slumstrup, D., Handberg, R., Lund, M. N., et al. (2019). Asteroseismology of the Hyades red giant and planet host Tauri. Astron. Astrophys. 622, A190. doi:10.1051/0004-6361/201834690

CrossRef Full Text | Google Scholar

Auge, C., Huber, D., Heinze, A., Shappee, B. J., Tonry, J., Chakrabarti, S., et al. (2020). Beyond Gaia: asteroseismic distances of M giants using ground-based transient surveys. Astron. J. 160, 18. doi:10.3847/1538-3881/ab91bf

CrossRef Full Text | Google Scholar

Ballard, S., Chaplin, W. J., Charbonneau, D., Désert, J. M., Fressin, F., Zeng, L., et al. (2014). Kepler-93b: a terrestrial world measured to within 120 km, and a test case for a new spitzer observing mode. Astrophys. J. 790, 12. doi:10.1088/0004-637X/790/1/12

CrossRef Full Text | Google Scholar

Barnes, S. A. (2003). On the rotational evolution of solar- and late-type stars, its magnetic origins, and the possibility of stellar gyrochronology. Astrophys. J 586, 464–479. doi:10.1086/367639

CrossRef Full Text | Google Scholar

Basu, S. (2016). Global seismology of the Sun. Living Rev. Sol. Phys. 13, 2. doi:10.1007/s41116-016-0003-4

CrossRef Full Text | Google Scholar

Basu, S., Grundahl, F., Stello, D., Kallinger, T., Hekker, S., Mosser, B., et al. (2011). Sounding open clusters: asteroseismic constraints from kepler on the properties of NGC 6791 and NGC 6819. Astrophys. J. Lett. 729, L10. doi:10.1088/2041-8205/729/1/L10

CrossRef Full Text | Google Scholar

Basu, S., and Hekker, S. (2020). Unveiling the structure and dynamics of red giants with asteroseismology. Frontiers in Astronomy and Space Sciences 7, 44. doi:10.3389/fspas.2020.00044

CrossRef Full Text | Google Scholar

Bazot, M., Benomar, O., Christensen-Dalsgaard, J., Gizon, L., Hanasoge, S., Nielsen, M., et al. (2019). Latitudinal differential rotation in the solar analogues 16 Cygni A and B. Astron. Astrophys. 623, A125. doi:10.1051/0004-6361/201834594

CrossRef Full Text | Google Scholar

Bazot, M., Nielsen, M. B., Mary, D., Christensen-Dalsgaard, J., Benomar, O., Petit, P., et al. (2018). Butterfly diagram of a Sun-like star observed using asteroseismology. Astron. Astrophys. 619, L9. doi:10.1051/0004-6361/201834251

CrossRef Full Text | Google Scholar

Bazot, M. (2020). Uncertainties and biases in modelling 16 Cygni A and B. Astron. Astrophys. 635, A26. doi:10.1051/0004-6361/201935565

CrossRef Full Text | Google Scholar

Beck, P. G., Bedding, T. R., Mosser, B., Stello, D., Garcia, R. A., Kallinger, T., et al. (2011). Kepler detected gravity-mode period spacings in a red giant star. Science 332, 205. doi:10.1126/science.1201939

PubMed Abstract | CrossRef Full Text | Google Scholar

Beck, P. G., Kallinger, T., Pavlovski, K., Palacios, A., Tkachenko, A., Mathis, S., et al. (2018a). Seismic probing of the first dredge-up event through the eccentric red-giant and red-giant spectroscopic binary KIC 9163796. How different are red-giant stars with a mass ratio of 1.015?. Astron. Astrophys. 612, A22. doi:10.1051/0004-6361/201731269

CrossRef Full Text | Google Scholar

Beck, P. G., Mathis, S., Gallet, F., Charbonnel, C., Benbakoura, M., García, R. A., et al. (2018b). Testing tidal theory for evolved stars by using red giant binaries observed by Kepler. Mon. Not. Roy. Astron. Soc. 479, L123–L128. doi:10.1093/mnrasl/sly114

CrossRef Full Text | Google Scholar

Beck, P. G., Montalban, J., Kallinger, T., De Ridder, J., Aerts, C., García, R. A., et al. (2012). Fast core rotation in red-giant stars as revealed by gravity-dominated mixed modes. Nature. 481, 55–57. doi:10.1038/nature10612

CrossRef Full Text | Google Scholar

Bedding, T. R., Mosser, B., Huber, D., Montalbán, J., Beck, P., Christensen-Dalsgaard, J., et al. (2011). Gravity modes as a way to distinguish between hydrogen- and helium-burning red giant stars. Nature. 471, 608–611. doi:10.1038/nature09935

PubMed Abstract | CrossRef Full Text | Google Scholar

Bedding, T. R., Murphy, S. J., Hey, D. R., Huber, D., Li, T., Smalley, B., et al. (2020). Very regular high-frequency pulsation modes in young intermediate-mass stars. Nature. 581, 147–151. doi:10.1038/s41586-020-2226-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Belkacem, K., Goupil, M. J., Dupret, M. A., Samadi, R., Baudin, F., Noels, A., et al. (2011). The underlying physical meaning of the ν - ν_c relation. Astron. Astrophys. 530, A142. doi:10.1051/0004-6361/201116490

CrossRef Full Text | Google Scholar

Belkacem, K., Marques, J. P., Goupil, M. J., Mosser, B., Sonoi, T., Ouazzani, R. M., et al. (2015). Angular momentum redistribution by mixed modes in evolved low-mass stars. II. Spin-down of the core of red giants induced by mixed modes. Astron. Astrophys. 579, A31. doi:10.1051/0004-6361/201526043

CrossRef Full Text | Google Scholar

Bellinger, E. P. (2019). A seismic scaling relation for stellar age. Mon. Not. Roy. Astron. Soc. 486, 4612–4621. doi:10.1093/mnras/stz714

CrossRef Full Text | Google Scholar

Bellinger, E. P. (2020). A seismic scaling relation for stellar age II: the red giant branch. Mon. Not. Roy. Astron. Soc. 492, L50–L55. doi:10.1093/mnrasl/slz178

CrossRef Full Text | Google Scholar

Bellinger, E. P., Angelou, G. C., Hekker, S., Basu, S., Ball, W. H., and Guggenberger, E. (2016). Fundamental parameters of main-sequence stars in an instant with machine learning. Astrophys. J. 830, 31. doi:10.3847/0004-637X/830/1/31

CrossRef Full Text | Google Scholar

Bellinger, E. P., Hekker, S., Angelou, G. C., Stokholm, A., and Basu, S. (2019). Stellar ages, masses, and radii from asteroseismic modeling are robust to systematic errors in spectroscopy. Astron. Astrophys. 622, A130. doi:10.1051/0004-6361/201834461

CrossRef Full Text | Google Scholar

Benbakoura, M., Gaulme, P., McKeever, J., Beck, P. G., Jackiewicz, J., and García, R. A. (2017). Modeling radial velocities and eclipse photometry of the kepler target KIC 4054905: an oscillating red giant in an eclipsing binary. Available at: https://arxiv.org/pdf/1712.01082.pdf.

CrossRef Full Text | Google Scholar

Benomar, O., Bazot, M., Nielsen, M. B., Gizon, L., Sekii, T., Takata, M., et al. (2018). Asteroseismic detection of latitudinal differential rotation in 13 Sun-like stars. Science. 361, 1231–1234. doi:10.1126/science.aao6571

PubMed Abstract | CrossRef Full Text | Google Scholar

Benomar, O., Takata, M., Shibahashi, H., Ceillier, T., and García, R. A. (2015). Nearly uniform internal rotation of solar-like main-sequence stars revealed by space-based asteroseismology and spectroscopic measurements. Mon. Not. Roy. Astron. Soc. 452, 2654–2674. doi:10.1093/mnras/stv1493

CrossRef Full Text | Google Scholar

Blancato, K., Ness, M., Huber, D., Lu, Y., and Angus, R. (2020). Data-driven derivation of stellar properties from photometric time series data using convolutional neural networks. Available at: https://arxiv.org/abs/2005.09682.

CrossRef Full Text | Google Scholar

Bonaca, A., Tanner, J. D., Basu, S., Chaplin, W. J., Metcalfe, T. S., Monteiro, M. J. P. F. G., et al. (2012). Calibrating convective properties of solar-like stars in the kepler field of view. Astrophys. J. Lett. 755, L12. doi:10.1088/2041-8205/755/1/L12

CrossRef Full Text | Google Scholar

Borucki, W. J., Koch, D., Basri, G., Batalha, N., Brown, T., Caldwell, D., et al. (2010). Kepler planet-detection mission: introduction and first results. Science. 327, 977. doi:10.1126/science.1185402

PubMed Abstract | CrossRef Full Text | Google Scholar

Brogaard, K., Hansen, C. J., Miglio, A., Slumstrup, D., Frandsen, S., Jessen-Hansen, J., et al. (2018). Establishing the accuracy of asteroseismic mass and radius estimates of giant stars - I. Three eclipsing systems at [Fe/H] -0.3 and the need for a large high-precision sample. Mon. Not. Roy. Astron. Soc. 476, 3729–3743. doi:10.1093/mnras/sty268

CrossRef Full Text | Google Scholar

Brown, T. M., Gilliland, R. L., Noyes, R. W., and Ramsey, L. W. (1991). Detection of possible p-mode oscillations on Procyon. Astrophys. J. 368, 599. doi:10.1086/169725

CrossRef Full Text | Google Scholar

Campante, T. L., Barclay, T., Swift, J. J., Huber, D., Adibekyan, V. Z., Cochran, W., et al. (2015). An ancient extrasolar system with five sub-earth-size planets. Astrophys. J. 799, 170. doi:10.1088/0004-637X/799/2/170

CrossRef Full Text | Google Scholar

Campante, T. L., Chaplin, W. J., Lund, M. N., Huber, D., Hekker, S., García, R. A., et al. (2014). Limits on surface gravities of kepler planet-candidate host stars from non-detection of solar-like oscillations. Astrophys. J. 783, 123. doi:10.1088/0004-637X/783/2/123

CrossRef Full Text | Google Scholar

Campante, T. L., Lund, M. N., Kuszlewicz, J. S., Davies, G. R., Chaplin, W. J., Albrecht, S., et al. (2016). Spin-orbit alignment of exoplanet systems: ensemble analysis using asteroseismology. Astrophys. J. 819, 85. doi:10.3847/0004-637X/819/1/85

CrossRef Full Text | Google Scholar

Campante, T. L., Santos, N. C., and Monteiro, M. J. P. F. G. (2018). Asteroseismology and exoplanets: listening to the stars and searching for new worlds. Cham, Switzerland: Springer.

CrossRef Full Text | Google Scholar

Casagrande, L., Silva Aguirre, V., Schlesinger, K. J., Stello, D., Huber, D., Serenelli, A. M., et al. (2016). Measuring the vertical age structure of the Galactic disc using asteroseismology and SAGA. Mon. Not. Roy. Astron. Soc. 455, 987–1007. doi:10.1093/mnras/stv2320

CrossRef Full Text | Google Scholar

Casagrande, L., Silva Aguirre, V., Stello, D., Huber, D., Serenelli, A. M., Cassisi, S., et al. (2014). Strömgren survey for asteroseismology and galactic archaeology: let the SAGA begin. Astrophys. J. 787, 110. doi:10.1088/0004-637X/787/2/110

CrossRef Full Text | Google Scholar

Ceillier, T., Eggenberger, P., García, R. A., and Mathis, S. (2012). Attempts to reproduce the rotation profile of the red giant KIC 7341231 observed by Kepler. Astron. Nachr. 333, 971. doi:10.1002/asna.201211806

CrossRef Full Text | Google Scholar

Ceillier, T., van Saders, J., García, R. A., Metcalfe, T. S., Creevey, O., Mathis, S., et al. (2016). Rotation periods and seismic ages of KOIs - comparison with stars without detected planets from Kepler observations. Mon. Not. Roy. Astron. Soc. 456, 119–125. doi:10.1093/mnras/stv2622

CrossRef Full Text | Google Scholar

Chaplin, W. J., Basu, S., Huber, D., Serenelli, A., Casagrande, L., Silva Aguirre, V., et al. (2014). Asteroseismic fundamental properties of solar-type stars observed by the NASA kepler mission. Astrophys. J. Supp. 210, 1. doi:10.1088/0067-0049/210/1/1

CrossRef Full Text | Google Scholar

Chaplin, W. J., Bedding, T. R., Bonanno, A., Broomhall, A. M., García, R. A., Hekker, S., et al. (2011). Evidence for the impact of stellar activity on the detectability of solar-like oscillations observed by kepler. Astrophys. J. Lett. 732, L5. doi:10.1088/2041-8205/732/1/L5

CrossRef Full Text | Google Scholar

Chaplin, W. J., Elsworth, Y., Howe, R., Isaak, G. R., McLeod, C. P., Miller, B. A., et al. (1996). BiSON performance. Sol. Phys. 168, 1–18. doi:10.1007/BF00145821

CrossRef Full Text | Google Scholar

Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., Basu, S., Miglio, A., Appourchaux, T., et al. (2011). Ensemble asteroseismology of solar-type stars with the NASA kepler mission. Science. 332, 213. doi:10.1126/science.1201827

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaplin, W. J., and Miglio, A. (2013). Asteroseismology of solar-type and red-giant stars. Annu. Rev. Astron. Astrophys. 51, 353–392. doi:10.1146/annurev-astro-082812-140938

CrossRef Full Text | Google Scholar

Chaplin, W. J., Sanchis-Ojeda, R., Campante, T. L., Hand berg, R., Stello, D., Winn, J. N., et al. (2013). Asteroseismic determination of obliquities of the exoplanet systems kepler-50 and kepler-65. Astrophys. J. 766, 101. doi:10.1088/0004-637X/766/2/101

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J. (1988). “A hertzsprung-russell diagram for stellar oscillations,” in Advances in helio- and asteroseismology, Aarhus, Denmark, July 11–17, 1986. Editors J. Christensen-Dalsgaard, and S. Frandsen (Dordrecht, Netherlands: D. Reidel Publishing Co.), 295.

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., and Perez Hernandez, F. (1992). The phase function for stellar acoustic oscillations. I - Theory. Mon. Not. Roy. Astron. Soc. 257, 62–88. doi:10.1093/mnras/257.1.62

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J. (2004). Physics of solar-like oscillations. Sol. Phys. 220, 137–168. doi:10.1023/B:SOLA.0000031392.43227.7d

CrossRef Full Text | Google Scholar

Creevey, O. L., Metcalfe, T. S., Schultheis, M., Salabert, D., Bazot, M., Thévenin, F., et al. (2017). Characterizing solar-type stars from full-length Kepler data sets using the Asteroseismic Modeling Portal. Astron. Astrophys. 601, A67. doi:10.1051/0004-6361/201629496

CrossRef Full Text | Google Scholar

Davies, G. R., Chaplin, W. J., Farr, W. M., García, R. A., Lund, M. N., Mathis, S., et al. (2015). Asteroseismic inference on rotation, gyrochronology and planetary system dynamics of 16 Cygni. Mon. Not. Roy. Astron. Soc. 446, 2959–2966. doi:10.1093/mnras/stu2331

CrossRef Full Text | Google Scholar

Davies, G. R., Lund, M. N., Miglio, A., Elsworth, Y., Kuszlewicz, J. S., North, T. S. H., et al. (2017). Using red clump stars to correct the Gaia DR1 parallaxes. Astron. Astrophys. 598, L4. doi:10.1051/0004-6361/201630066

CrossRef Full Text | Google Scholar

De Ridder, J., Barban, C., Baudin, F., Carrier, F., Hatzes, A. P., Hekker, S., et al. (2009). Non-radial oscillation modes with long lifetimes in giant stars. Nature. 459, 398–400. doi:10.1038/nature08022

PubMed Abstract | CrossRef Full Text | Google Scholar

De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., Martell, S., de Boer, E. W., Asplund, M., et al. (2015). The GALAH survey: scientific motivation. Mon. Not. Roy. Astron. Soc. 449, 2604–2617. doi:10.1093/mnras/stv327

CrossRef Full Text | Google Scholar

Deheuvels, S., Ballot, J., Beck, P. G., Mosser, B., Østensen, R., García, R. A., et al. (2015). Seismic evidence for a weak radial differential rotation in intermediate-mass core helium burning stars. Astron. Astrophys. 580, A96. doi:10.1051/0004-6361/201526449

CrossRef Full Text | Google Scholar

Deheuvels, S., Brandão, I., Silva Aguirre, V., Ballot, J., Michel, E., Cunha, M. S., et al. (2016). Measuring the extent of convective cores in low-mass stars using Kepler data: toward a calibration of core overshooting. Astron. Astrophys. 589, A93. doi:10.1051/0004-6361/201527967

CrossRef Full Text | Google Scholar

Deheuvels, S., Doğan, G., Goupil, M. J., Appourchaux, T., Benomar, O., Bruntt, H., et al. (2014). Seismic constraints on the radial dependence of the internal rotation profiles of six Kepler subgiants and young red giants. Astron. Astrophys. 564, A27. doi:10.1051/0004-6361/201322779

CrossRef Full Text | Google Scholar

Deheuvels, S., García, R. A., Chaplin, W. J., Basu, S., Antia, H. M., Appourchaux, T., et al. (2012). Seismic evidence for a rapidly rotating core in a lower-giant-branch star observed with kepler. Astrophys. J. 756, 19. doi:10.1088/0004-637X/756/1/19

CrossRef Full Text | Google Scholar

do Nascimento, J. J. D., García, R. A., Mathur, S., Anthony, F., Barnes, S. A., Meibom, S., et al. (2014). Rotation periods and ages of solar analogs and solar twins revealed by the kepler mission. Astrophys. J. Lett. 790, L23. doi:10.1088/2041-8205/790/2/L23

CrossRef Full Text | Google Scholar

Dziembowski, W. A., Gough, D. O., Houdek, G., and Sienkiewicz, R. (2001). Oscillations of α UMa and other red giants. Mon. Not. Roy. Astron. Soc. 328, 601–610. doi:10.1046/j.1365-8711.2001.04894.x

CrossRef Full Text | Google Scholar

Eggenberger, P., Deheuvels, S., Miglio, A., Ekström, S., Georgy, C., Meynet, G., et al. (2019). Asteroseismology of evolved stars to constrain the internal transport of angular momentum. I. Efficiency of transport during the subgiant phase. Astron. Astrophys. 621, A66. doi:10.1051/0004-6361/201833447

CrossRef Full Text | Google Scholar

Frandsen, S., Lehmann, H., Hekker, S., Southworth, J., Debosscher, J., Beck, P., et al. (2013). KIC 8410637: a 408-day period eclipsing binary containing a pulsating giant star. Astron. Astrophys. 556, A138. doi:10.1051/0004-6361/201321817

CrossRef Full Text | Google Scholar

Fredslund Andersen, M., Pallé, P., Jessen-Hansen, J., Wang, K., Grundahl, F., Bedding, T. R., et al. (2019). Oscillations in the Sun with SONG: setting the scale for asteroseismic investigations. Astron. Astrophys. 623, L9. doi:10.1051/0004-6361/201935175

CrossRef Full Text | Google Scholar

Frohlich, C., Andersen, B. N., Appourchaux, T., Berthomieu, G., Crommelynck, D. A., Domingo, V., et al. (1997). First results from VIRGO, the experiment for helioseismology and solar irradiance monitoring on SOHO. Sol. Phys. 170, 1–25. doi:10.1023/A:1004969622753

CrossRef Full Text | Google Scholar

Fröhlich, C., Romero, J., Roth, H., Wehrli, C., Andersen, B. N., Appourchaux, T., et al. (1995). VIRGO: experiment for helioseismology and solar irradiance monitoring. Sol. Phys. 162, 101–128. doi:10.1007/BF00733428

CrossRef Full Text | Google Scholar

Fuller, J., Cantiello, M., Stello, D., Garcia, R. A., and Bildsten, L. (2015). Asteroseismology can reveal strong internal magnetic fields in red giant stars. Science. 350, 423–426. doi:10.1126/science.aac6933

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuller, J., Piro, A. L., and Jermyn, A. S. (2019). Slowing the spins of stellar cores. Mon. Not. Roy. Astron. Soc. 485, 3661–3680. doi:10.1093/mnras/stz514

CrossRef Full Text | Google Scholar

Gabriel, A. H., Grec, G., Charra, J., Robillot, J. M., Roca Cortés, T., Turck-Chièze, S., et al. (1995). Global oscillations at low frequency from the SOHO mission (GOLF). Sol. Phys. 162, 61–99. doi:10.1007/BF00733427

CrossRef Full Text | Google Scholar

García Pérez, A. E., Allende Prieto, C., Holtzman, J. A., Shetrone, M., Mészáros, S., Bizyaev, D., et al. (2016). ASPCAP: the APOGEE stellar parameter and chemical abundances pipeline. Astron. J. 151, 144. doi:10.3847/0004-6256/151/6/144

CrossRef Full Text | Google Scholar

García, R. A., and Ballot, J. (2019). Asteroseismology of solar-type stars. Living Rev. Sol. Phys. 16, 4. doi:10.1007/s41116-019-0020-1

CrossRef Full Text | Google Scholar

García, R. A., Ceillier, T., Salabert, D., Mathur, S., van Saders, J. L., Pinsonneault, M., et al. (2014). Rotation and magnetism of Kepler pulsating solar-like stars. Towards asteroseismically calibrated age-rotation relations. Astron. Astrophys. 572, A34. doi:10.1051/0004-6361/201423888

CrossRef Full Text | Google Scholar

García, R. A., Pérez Hernández, F., Benomar, O., Silva Aguirre, V., Ballot, J., Davies, G. R., et al. (2014). Study of KIC 8561221 observed by Kepler: an early red giant showing depressed dipolar modes. Astron. Astrophys. 563, A84. doi:10.1051/0004-6361/201322823

CrossRef Full Text | Google Scholar

Garcia, R. A., and Stello, D. (2018). Asteroseismology of red giant stars. Available at: https://arxiv.org/abs/1801.08377.

CrossRef Full Text | Google Scholar

Gaulme, P., Jackiewicz, J., Appourchaux, T., and Mosser, B. (2014). Surface activity and oscillation amplitudes of red giants in eclipsing binaries. Astrophys. J. 785, 5. doi:10.1088/0004-637X/785/1/5

CrossRef Full Text | Google Scholar

Gaulme, P., McKeever, J., Jackiewicz, J., Rawls, M. L., Corsaro, E., Mosser, B., et al. (2016). Testing the asteroseismic scaling relations for red giants with eclipsing binaries observed by kepler. Astrophys. J. 832, 121. doi:10.3847/0004-637X/832/2/121

CrossRef Full Text | Google Scholar

Gaulme, P., McKeever, J., Rawls, M. L., Jackiewicz, J., Mosser, B., and Guzik, J. A. (2013). Red giants in eclipsing binary and multiple-star systems: modeling and asteroseismic analysis of 70 candidates from kepler data. Astrophys. J. 767, 82. doi:10.1088/0004-637X/767/1/82

CrossRef Full Text | Google Scholar

Gehan, C., Mosser, B., Michel, E., Samadi, R., and Kallinger, T. (2018). Core rotation braking on the red giant branch for various mass ranges. Astron. Astrophys. 616, A24. doi:10.1051/0004-6361/201832822

CrossRef Full Text | Google Scholar

Gilmore, G., Randich, S., Asplund, M., Binney, J., Bonifacio, P., Drew, J., et al. (2012). The gaia-ESO public spectroscopic survey. Messenger. 147, 25–31.

CrossRef Full Text | Google Scholar

Gizon, L., and Solanki, S. K. (2003). Determining the inclination of the rotation Axis of a sun-like star. Astrophys. J. 589, 1009–1019. doi:10.1086/374715

CrossRef Full Text | Google Scholar

Goldreich, P., and Keeley, D. A. (1977). Solar seismology. II. The stochastic excitation of the solar p-modes by turbulent convection. Astrophys. J. 212, 243–251. doi:10.1086/155043

CrossRef Full Text | Google Scholar

Gough, D. O. (1990). “Comments on helioseismic inference,”in Progress of seismology of the sun and stars. Editors Y. Osaki, and H. Shibahashi (Berlin, Germany: Springer), 283.

CrossRef Full Text | Google Scholar

Grundahl, F., Fredslund Andersen, M., Christensen-Dalsgaard, J., Antoci, V., Kjeldsen, H., Hand berg, R., et al. (2017). First results from the Hertzsprung SONG telescope: asteroseismology of the G5 subgiant star μ herculis. Astrophys. J. 836, 142. doi:10.3847/1538-4357/836/1/142

CrossRef Full Text | Google Scholar

Grundahl, F., Kjeldsen, H., Christensen-Dalsgaard, J., Arentoft, T., and Frandsen, S. (2007). Stellar oscillations network Group. Commun. Asteroseismol. 150, 300. doi:10.1553/cia150s300

CrossRef Full Text | Google Scholar

Handberg, R., Brogaard, K., Miglio, A., Bossini, D., Elsworth, Y., Slumstrup, D., et al. (2017). NGC 6819: testing the asteroseismic mass scale, mass loss and evidence for products of non-standard evolution. Mon. Not. Roy. Astron. Soc. 472, 979–997. doi:10.1093/mnras/stx1929

CrossRef Full Text | Google Scholar

Harvey, J. W., Hill, F., Hubbard, R. P., Kennedy, J. R., Leibacher, J. W., Pintar, J. A., et al. (1996). The global oscillation network Group (GONG) project. Science. 272, 1284–1286. doi:10.1126/science.272.5266.1284

PubMed Abstract | CrossRef Full Text | Google Scholar

Hekker, S., and Christensen-Dalsgaard, J. (2017). Giant star seismology. Astron. AstroPhys. Rev. 25, 1. doi:10.1007/s00159-017-0101-x

CrossRef Full Text | Google Scholar

Hekker, S. (2013). CoRoT and kepler results: solar-like oscillators. Adv. Space Res. 52, 1581–1592. doi:10.1016/j.asr.2013.08.005

CrossRef Full Text | Google Scholar

Hekker, S., Debosscher, J., Huber, D., Hidas, M. G., De Ridder, J., Aerts, C., et al. (2010). Discovery of a red giant with solar-like oscillations in an eclipsing binary system from kepler space-based photometry. Astrophys. J. Lett. 713, L187–L191. doi:10.1088/2041-8205/713/2/L187

CrossRef Full Text | Google Scholar

Hekker, S. (2020). Scaling relations for solar-like oscillations: a review. Frontiers in Astron. Space Sci. 7, 3. doi:10.3389/fspas.2020.00003

CrossRef Full Text | Google Scholar

Hon, M., Bellinger, E. P., Hekker, S., Stello, D., and Kuszlewicz, J. S. (2020). Asteroseismic inference of subgiant evolutionary parameters with deep learning. Mon. Not. Roy. Astron. Soc. 499, 2445–2461. doi:10.1093/mnras/staa2853

CrossRef Full Text | Google Scholar

Hon, M., Stello, D., and Yu, J. (2017). Deep learning classification in asteroseismology. Mon. Not. Roy. Astron. Soc. 469, 4578–4583. doi:10.1093/mnras/stx1174

CrossRef Full Text | Google Scholar

Hon, M., Stello, D., and Zinn, J. C. (2018). Detecting solar-like oscillations in red giants with deep learning. Astrophys. J. 859, 64. doi:10.3847/1538-4357/aabfdb

CrossRef Full Text | Google Scholar

Howe, R., Komm, R. W., and Hill, F. (2002). Localizing the solar cycle frequency shifts in global p-modes. Astrophys. J. 580, 1172–1187. doi:10.1086/343892

CrossRef Full Text | Google Scholar

Howell, S. B., Sobeck, C., Haas, M., Still, M., Barclay, T., Mullally, F., et al. (2014). The K2 mission: characterization and early results. Publ. Astron. Soc. Pac. 126, 398. doi:10.1086/676406

CrossRef Full Text | Google Scholar

Huber, D., Bedding, T. R., Stello, D., Hekker, S., Mathur, S., Mosser, B., et al. (2011). Testing scaling relations for solar-like oscillations from the main sequence to red giants using kepler data. Astrophys. J. 743, 143. doi:10.1088/0004-637X/743/2/143

CrossRef Full Text | Google Scholar

Huber, D., Carter, J. A., Barbieri, M., Miglio, A., Deck, K. M., Fabrycky, D. C., et al. (2013). Stellar spin-orbit misalignment in a multiplanet system. Science. 342, 331–334. doi:10.1126/science.1242066

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, D., Chaplin, W. J., Christensen-Dalsgaard, J., Gilliland, R. L., Kjeldsen, H., Buchhave, L. A., et al. (2013). Fundamental properties of kepler planet-candidate host stars using asteroseismology. Astrophys. J. 767, 127. doi:10.1088/0004-637X/767/2/127

CrossRef Full Text | Google Scholar

Huber, D., Ireland, M. J., Bedding, T. R., Brand ão, I. M., Piau, L., Maestro, V., et al. (2012). Fundamental properties of stars using asteroseismology from kepler and CoRoT and interferometry from the CHARA array. Astrophys. J. 760, 32. doi:10.1088/0004-637X/760/1/32

CrossRef Full Text | Google Scholar

Huber, D., Zinn, J., Bojsen-Hansen, M., Pinsonneault, M., Sahlholdt, C., Serenelli, A., et al. (2017). Asteroseismology and Gaia: testing scaling relations using 2200 kepler stars with TGAS parallaxes. Astrophys. J. 844, 102. doi:10.3847/1538-4357/aa75ca

CrossRef Full Text | Google Scholar

Huber, D. (2018). “Synergies between asteroseismology and exoplanetary science,” in Asteroseismology and exoplanets: listening to the stars and searching for new worlds. Editors T. L. Campante, N. C. Santos, and M. J. P. F. G. Monteiro (Cham, Switzerland: Springer International Publishing), 119–135.

CrossRef Full Text | Google Scholar

Jiménez, A., Roca Cortés, T., and Jiménez-Reyes, S. J. (2002). Variation of the low-degree solar acoustic mode parameters over the solar cycle. Sol. Phys. 209, 247–263. doi:10.1023/A:1021226503589

CrossRef Full Text | Google Scholar

Kallinger, T., Beck, P. G., Stello, D., and Garcia, R. A. (2018). Non-linear seismic scaling relations. Astron. Astrophys. 616, A104. doi:10.1051/0004-6361/201832831

CrossRef Full Text | Google Scholar

Kallinger, T., Weiss, W. W., Barban, C., Baudin, F., Cameron, C., Carrier, F., et al. (2010). Oscillating red giants in the CoRoT exofield: asteroseismic mass and radius determination. Astron. Astrophys. 509, A77. doi:10.1051/0004-6361/200811437

CrossRef Full Text | Google Scholar

Kiefer, R., Schad, A., Davies, G., and Roth, M. (2017). Stellar magnetic activity and variability of oscillation parameters: an investigation of 24 solar-like stars observed by Kepler. Astron. Astrophys. 598, A77. doi:10.1051/0004-6361/201628469

CrossRef Full Text | Google Scholar

Kipping, D. M. (2014). Characterizing distant worlds with asterodensity profiling. Mon. Not. Roy. Astron. Soc. 440, 2164–2184. doi:10.1093/mnras/stu318

CrossRef Full Text | Google Scholar

Kipping, D. M. (2010). Investigations of approximate expressions for the transit duration. Mon. Not. Roy. Astron. Soc. 407, 301–313. doi:10.1111/j.1365-2966.2010.16894.x

CrossRef Full Text | Google Scholar

Kjeldsen, H., and Bedding, T. R. (1995). Amplitudes of stellar oscillations: the implications for asteroseismology. Astron. Astrophys. 293, 87–106.

CrossRef Full Text | Google Scholar

Kjeldsen, H., Bedding, T. R., and Christensen-Dalsgaard, J. (2008). Correcting stellar oscillation frequencies for near-surface effects. Astrophys. J. Lett. 683, L175. doi:10.1086/591667

CrossRef Full Text | Google Scholar

Koch, D. G., Borucki, W. J., Basri, G., Batalha, N. M., Brown, T. M., Caldwell, D., et al. (2010). Kepler mission design, realized photometric performance, and early science. Astrophys. J. Lett. 713, L79–L86. doi:10.1088/2041-8205/713/2/L79

CrossRef Full Text | Google Scholar

Li, G., Naoz, S., Valsecchi, F., Johnson, J. A., and Rasio, F. A. (2014). The dynamics of the multi-planet system orbiting kepler-56. Astrophys. J. 794, 131. doi:10.1088/0004-637X/794/2/13

CrossRef Full Text | Google Scholar

Li, T., Bedding, T. R., Huber, D., Ball, W. H., Stello, D., Murphy, S. J., et al. (2018). Modelling Kepler red giants in eclipsing binaries: calibrating the mixing-length parameter with asteroseismology. Mon. Not. Roy. Astron. Soc. 475, 981–998. doi:10.1093/mnras/stx3079

CrossRef Full Text | Google Scholar

Li, T., Bedding, T. R., Kjeldsen, H., Stello, D., Christensen-Dalsgaard, J., and Deng, L. (2019). Asteroseismic modelling of the subgiant μ Herculis using SONG data: lifting the degeneracy between age and model input parameters. Mon. Not. Roy. Astron. Soc. 483, 780–789. doi:10.1093/mnras/sty3000

CrossRef Full Text | Google Scholar

Lund, M. N., Basu, S., Silva Aguirre, V., Chaplin, W. J., Serenelli, A. M., García, R. A., et al. (2016). Asteroseismology of the Hyades with K2: first detection of main-sequence solar-like oscillations in an open cluster. Mon. Not. Roy. Astron. Soc. 463, 2600–2611. doi:10.1093/mnras/stw2160

CrossRef Full Text | Google Scholar

Lund, M. N., Silva Aguirre, V., Davies, G. R., Chaplin, W. J., Christensen-Dalsgaard, J., Houdek, G., et al. (2017). Standing on the shoulders of dwarfs: the kepler asteroseismic LEGACY sample. I. Oscillation mode parameters. Astrophys. J. 835, 172. doi:10.3847/1538-4357/835/2/172

CrossRef Full Text | Google Scholar

Lundkvist, M. S., Huber, D., Aguirre, V. S., and Chaplin, W. J. (2018). “Characterizing host stars using asteroseismology,” in Handbook of Exoplanets. Editors H. Deeg, and J. Belmonte (Cham, Switzerland: Springer International Publishing), 117. doi:10.1007/978-3-319-55333-7_177

CrossRef Full Text | Google Scholar

Lundkvist, M. S., Kjeldsen, H., Albrecht, S., Davies, G. R., Basu, S., Huber, D., et al. (2016). Hot super-Earths stripped by their host stars. Nat. Commun. 7, 11201. doi:10.1038/ncomms11201

PubMed Abstract | CrossRef Full Text | Google Scholar

Majewski, S. R., Wilson, J. C., Hearty, F., Schiavon, R. R., and Skrutskie, M. F. (2010). “The Apache point observatory galactic evolution experiment (APOGEE) in sloan digital sky survey III (SDSS-III),” in Chemical abundances in the universe: connecting first stars to planets, Paris, France, August 2009. Editors K. Cunha, M. Spite, and B. Barbuy (Paris, France: International Astronomical Union), 480–481.

CrossRef Full Text | Google Scholar

Martell, S., Simpson, J., Balasubramaniam, A., Buder, S., Sharma, S., Hon, M., et al. (2020). The GALAH survey: lithium-rich giant stars require multiple formation channels. Available at: https://arxiver.moonhats.com/2020/06/04/the-galah-survey-lithium-rich-giant-stars-require-multiple-formation-channels-ssa/.

CrossRef Full Text | Google Scholar

Martig, M., Fouesneau, M., Rix, H. W., Ness, M., Mészáros, S., García-Hernández, D. A., et al. (2016). Red giant masses and ages derived from carbon and nitrogen abundances. Mon. Not. Roy. Astron. Soc. 456, 3655–3670. doi:10.1093/mnras/stv2830

CrossRef Full Text | Google Scholar

McKeever, J. M., Basu, S., and Corsaro, E. (2019). The helium abundance of NGC 6791 from modeling of stellar oscillations. Astrophys. J. 874, 180. doi:10.3847/1538-4357/ab0c04

CrossRef Full Text | Google Scholar

Metcalfe, T. S., Chaplin, W. J., Appourchaux, T., García, R. A., Basu, S., Brandão, I., et al. (2012). Asteroseismology of the solar analogs 16 Cyg A and B from kepler observations. Astrophys. J. Lett. 748, L10. doi:10.1088/2041-8205/748/1/L10

CrossRef Full Text | Google Scholar

Metcalfe, T. S., Creevey, O. L., and Davies, G. R. (2015). Asteroseismic modeling of 16 Cyg A & B using the complete kepler data set. Astrophys. J. Lett. 811, L37. doi:10.1088/2041-8205/811/2/L37

CrossRef Full Text | Google Scholar

Metcalfe, T. S., Creevey, O. L., Doğan, G., Mathur, S., Xu, H., Bedding, T. R., et al. (2014). Properties of 42 solar-type kepler targets from the asteroseismic modeling portal. Astrophys. J. Supp. 214, 27. doi:10.1088/0067-0049/214/2/27

CrossRef Full Text | Google Scholar

Metcalfe, T. S., Egeland, R., and van Saders, J. (2016). Stellar evidence that the solar dynamo may Be in transition. Astrophys. J. Lett. 826, L2. doi:10.3847/2041-8205/826/1/L2

CrossRef Full Text | Google Scholar

Metcalfe, T. S., Kochukhov, O., Ilyin, I. V., Strassmeier, K. G., Godoy-Rivera, D., and Pinsonneault, M. H. (2019). LBT/PEPSI spectropolarimetry of a magnetic morphology shift in old solar-type stars. Astrophys. J. Lett. 887, L38. doi:10.3847/2041-8213/ab5e48

CrossRef Full Text | Google Scholar

Metcalfe, T. S., and van Saders, J. (2017). Magnetic evolution and the disappearance of sun-like activity cycles. Sol. Phys. 292, 126. doi:10.1007/s11207-017-1157-5

CrossRef Full Text | Google Scholar

Miglio, A., Brogaard, K., Stello, D., Chaplin, W. J., D’Antona, F., Montalbán, J., et al. (2012). Asteroseismology of old open clusters with Kepler: direct estimate of the integrated red giant branch mass-loss in NGC 6791 and 6819. Mon. Not. Roy. Astron. Soc. 419, 2077–2088. doi:10.1111/j.1365-2966.2011.19859.x

CrossRef Full Text | Google Scholar

Miglio, A., Chaplin, W. J., Brogaard, K., Lund, M. N., Mosser, B., Davies, G. R., et al. (2016). Detection of solar-like oscillations in relics of the Milky Way: asteroseismology of K giants in M4 using data from the NASA K2 mission. Mon. Not. Roy. Astron. Soc. 461, 760–765. doi:10.1093/mnras/stw1555

CrossRef Full Text | Google Scholar

Miglio, A., Chiappini, C., Morel, T., Barbieri, M., Chaplin, W. J., Girardi, L., et al. (2013). Galactic archaeology: mapping and dating stellar populations with asteroseismology of red-giant stars. Mon. Not. Roy. Astron. Soc. 429, 423–428. doi:10.1093/mnras/sts345

CrossRef Full Text | Google Scholar

Montalbán, J., Miglio, A., Noels, A., Dupret, M. A., Scuflaire, R., and Ventura, P. (2013). Testing convective-core overshooting using period spacings of dipole modes in red giants. Astrophys. J. 766, 118. doi:10.1088/0004-637X/766/2/118

CrossRef Full Text | Google Scholar

Mosser, B., Belkacem, K., Goupil, M. J., Michel, E., Elsworth, Y., Barban, C., et al. (2011). The universal red-giant oscillation pattern. An automated determination with CoRoT data. Astron. Astrophys. 525, L9. doi:10.1051/0004-6361/201015440

CrossRef Full Text | Google Scholar

Mosser, B., Belkacem, K., Pinçon, C., Takata, M., Vrard, M., Barban, C., et al. (2017). Dipole modes with depressed amplitudes in red giants are mixed modes. Astron. Astrophys. 598, A62. doi:10.1051/0004-6361/201629494

CrossRef Full Text | Google Scholar

Mosser, B., Benomar, O., Belkacem, K., Goupil, M. J., Lagarde, N., Michel, E., et al. (2014). Mixed modes in red giants: a window on stellar evolution. Astron. Astrophys. 572, L5. doi:10.1051/0004-6361/201425039

CrossRef Full Text | Google Scholar

Mosser, B., Dziembowski, W. A., Belkacem, K., Goupil, M. J., Michel, E., Samadi, R., et al. (2013a). Period-luminosity relations in evolved red giants explained by solar-like oscillations. Astron. Astrophys. 559, A137. doi:10.1051/0004-6361/201322243

CrossRef Full Text | Google Scholar

Mosser, B., Goupil, M. J., Belkacem, K., Marques, J. P., Beck, P. G., Bloemen, S., et al. (2012a). Spin down of the core rotation in red giants. Astron. Astrophys. 548, A10. doi:10.1051/0004-6361/201220106

CrossRef Full Text | Google Scholar

Mosser, B., Goupil, M. J., Belkacem, K., Michel, E., Stello, D., Marques, J. P., et al. (2012b). Probing the core structure and evolution of red giants using gravity-dominated mixed modes observed with Kepler. Astron. Astrophys. 540, A143. doi:10.1051/0004-6361/201118519

CrossRef Full Text | Google Scholar

Mosser, B., Michel, E., Belkacem, K., Goupil, M. J., Baglin, A., Barban, C., et al. (2013b). Asymptotic and measured large frequency separations. Astron. Astrophys. 550, A126. doi:10.1051/0004-6361/201220435

CrossRef Full Text | Google Scholar

Mosumgaard, J. R., Jørgensen, A. C. S., Weiss, A., Silva Aguirre, V., and Christensen-Dalsgaard, J. (2020). Coupling 1D stellar evolution with 3D-hydrodynamical simulations on-the-fly II: stellar evolution and asteroseismic applications. Mon. Not. Roy. Astron. Soc. 491, 1160–1173. doi:10.1093/mnras/stz2979

CrossRef Full Text | Google Scholar

Ness, M., Hogg, D. W., Rix, H. W., Martig, M., Pinsonneault, M. H., and Ho, A. Y. Q. (2016). Spectroscopic determination of masses (and implied ages) for red giants. Astrophys. J. 823, 114. doi:10.3847/0004-637X/823/2/114

CrossRef Full Text | Google Scholar

Nsamba, B., Campante, T. L., Monteiro, M. J. P. F. G., Cunha, M. S., Rendle, B. M., Reese, D. R., et al. (2018). Asteroseismic modelling of solar-type stars: internal systematics from input physics and surface correction methods. Mon. Not. Roy. Astron. Soc. 477, 5052–5063. doi:10.1093/mnras/sty948

CrossRef Full Text | Google Scholar

Paxton, B., Smolec, R., Schwab, J., Gautschy, A., Bildsten, L., Cantiello, M., et al. (2019). Modules for experiments in stellar astrophysics (MESA): pulsating variable stars, rotation, convective boundaries, and energy conservation. Astrophys. J. Supp. 243, 10. doi:10.3847/1538-4365/ab2241

CrossRef Full Text | Google Scholar

Pinsonneault, M. H., Elsworth, Y., Epstein, C., Hekker, S., Mészáros, S., Chaplin, W. J., et al. (2014). The APOKASC catalog: an asteroseismic and spectroscopic joint survey of targets in the kepler fields. Astrophys. J. Supp. 215, 19. doi:10.1088/0067-0049/215/2/19

CrossRef Full Text | Google Scholar

Pinsonneault, M. H., Elsworth, Y. P., Tayar, J., Serenelli, A., Stello, D., Zinn, J., et al. (2018). The second APOKASC catalog: the empirical approach. Astrophys. J. Supp. 239, 32. doi:10.3847/1538-4365/aaebfd

CrossRef Full Text | Google Scholar

Pinsonneault, M. H., Kawaler, S. D., and Demarque, P. (1990). Rotation of low-mass stars: a new probe of stellar evolution. Astrophys. J. Supp. 74, 501. doi:10.1086/191507

CrossRef Full Text | Google Scholar

Quinn, S. N., White, T. R., Latham, D. W., Chaplin, W. J., Handberg, R., Huber, D., et al. (2015). Kepler-432: a red giant interacting with one of its two long-period giant planets. Astrophys. J. 803, 49. doi:10.1088/0004-637X/803/2/49

CrossRef Full Text | Google Scholar

Remus, F., Mathis, S., and Zahn, J. P. (2012). The equilibrium tide in stars and giant planets. I. The coplanar case. Astron. Astrophys. 544, A132. doi:10.1051/0004-6361/201118160

CrossRef Full Text | Google Scholar

Ren, A., Fu, J., De Cat, P., Wu, Y., Yang, X., Shi, J., et al. (2016). LAMOST observations in the kepler field. Analysis of the stellar parameters measured with LASP based on low-resolution spectra. Astrophys. J. Supp. 225, 28. doi:10.3847/0067-0049/225/2/28

CrossRef Full Text | Google Scholar

Rendle, B. M., Buldgen, G., Miglio, A., Reese, D., Noels, A., Davies, G. R., et al. (2019). AIMS - a new tool for stellar parameter determinations using asteroseismic constraints. Mon. Not. Roy. Astron. Soc. 484, 771–786. doi:10.1093/mnras/stz031

CrossRef Full Text | Google Scholar

Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2015). Transiting exoplanet survey satellite (TESS). J. Astronomical Telesc. Instrum. Syst. 1, 014003. doi:10.1117/1.JATIS.1.1.01400

CrossRef Full Text | Google Scholar

Sahlholdt, C. L., and Silva Aguirre, V. (2018). Asteroseismic radii of dwarfs: new accuracy constraints from Gaia DR2 parallaxes. Mon. Not. Roy. Astron. Soc. 481, L125–L129. doi:10.1093/mnrasl/sly173

CrossRef Full Text | Google Scholar

Salabert, D., Régulo, C., Pérez Hernández, F., and García, R. A. (2018). Frequency dependence of p-mode frequency shifts induced by magnetic activity in Kepler solar-like stars. Astron. Astrophys. 611, A84. doi:10.1051/0004-6361/201731714

CrossRef Full Text | Google Scholar

Salaris, M., Pietrinferni, A., Piersimoni, A. M., and Cassisi, S. (2015). Post first dredge-up [C/N] ratio as age indicator. Theoretical calibration. Astron. Astrophys. 583, A87. doi:10.1051/0004-6361/201526951

CrossRef Full Text | Google Scholar

Santos, A. R. G., Campante, T. L., Chaplin, W. J., Cunha, M. S., Lund, M. N., Kiefer, R., et al. (2018). Signatures of magnetic activity in the seismic data of solar-type stars observed by kepler. Astrophys. J. Supp. 237, 17. doi:10.3847/1538-4365/aac9b6

CrossRef Full Text | Google Scholar

Seager, S., and Mallén-Ornelas, G. (2003). A unique solution of planet and star parameters from an extrasolar planet transit light curve. Astrophys. J. 585, 1038–1055. doi:10.1086/346105

CrossRef Full Text | Google Scholar

Serenelli, A., Johnson, J., Huber, D., Pinsonneault, M., Ball, W. H., Tayar, J., et al. (2017). The first APOKASC catalog of kepler dwarf and subgiant stars. Astrophys. J. Supp. 233, 23. doi:10.3847/1538-4365/aa97df

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Basu, S., Brandão, I. M., Christensen-Dalsgaard, J., Deheuvels, S., Doğan, G., et al. (2013). Stellar ages and convective cores in field main-sequence stars: first asteroseismic application to two kepler targets. Astrophys. J. 769, 141. doi:10.1088/0004-637X/769/2/141

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., Casagrande, L., Kawata, D., Ciucǎ, I., et al. (2018). Confirming chemical clocks: asteroseismic age dissection of the Milky Way disc(s). Mon. Not. Roy. Astron. Soc. 475, 5487–5500. doi:10.1093/mnras/sty150

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Davies, G. R., Basu, S., Christensen-Dalsgaard, J., Creevey, O., Metcalfe, T. S., et al. (2015). Ages and fundamental properties of Kepler exoplanet host stars from asteroseismology. Mon. Not. Roy. Astron. Soc. 452, 2127–2148. doi:10.1093/mnras/stv1388

CrossRef Full Text | Google Scholar

Silva Aguirre, V., Lund, M. N., Antia, H. M., Ball, W. H., Basu, S., Christensen-Dalsgaard, J., et al. (2017). Standing on the shoulders of dwarfs: the kepler asteroseismic LEGACY sample. II.Radii, masses, and ages. Astrophys. J. 835, 173. doi:10.3847/1538-4357/835/2/173

CrossRef Full Text | Google Scholar

Sliski, D. H., and Kipping, D. M. (2014). A high false positive rate for kepler planetary candidates of giant stars using asterodensity profiling. Astrophys. J. 788, 148. doi:10.1088/0004-637X/788/2/148

CrossRef Full Text | Google Scholar

Stello, D., Cantiello, M., Fuller, J., Huber, D., García, R. A., Bedding, T. R., et al. (2016). A prevalence of dynamo-generated magnetic fields in the cores of intermediate-mass stars. Nature. 529, 364–367. doi:10.1038/nature16171

PubMed Abstract | CrossRef Full Text | Google Scholar

Stello, D., Compton, D. L., Bedding, T. R., Christensen-Dalsgaard, J., Kiss, L. L., Kjeldsen, H., et al. (2014). Non-radial oscillations in M-giant semi-regular variables: stellar models and kepler observations. Astrophys. J. Lett. 788, L10. doi:10.1088/2041-8205/788/1/L10

CrossRef Full Text | Google Scholar

Stello, D., Huber, D., Bedding, T. R., Benomar, O., Bildsten, L., Elsworth, Y. P., et al. (2013). Asteroseismic classification of stellar populations among 13,000 red giants observed by kepler. Astrophys. J. Lett. 765, L41. doi:10.1088/2041-8205/765/2/L41

CrossRef Full Text | Google Scholar

Stello, D., Huber, D., Kallinger, T., Basu, S., Mosser, B., Hekker, S., et al. (2011). Amplitudes of solar-like oscillations: constraints from red giants in open clusters observed by kepler. Astrophys. J. Lett. 737, L10. doi:10.1088/2041-8205/737/1/L10

CrossRef Full Text | Google Scholar

Stello, D., Vanderburg, A., Casagrande, L., Gilliland, R., Silva Aguirre, V., Sandquist, E., et al. (2016). The K2 M67 study: revisiting old friends with K2 reveals oscillating red giants in the open cluster M67. Astrophys. J. 832, 133. doi:10.3847/0004-637X/832/2/133

CrossRef Full Text | Google Scholar

Tassoul, M. (1980). Asymptotic approximations for stellar nonradial pulsations. Astrophys. J. Supp. 43, 469–490. doi:10.1086/190678

CrossRef Full Text | Google Scholar

Tayar, J., Somers, G., Pinsonneault, M. H., Stello, D., Mints, A., Johnson, J. A., et al. (2017). The correlation between mixing length and metallicity on the giant branch: implications for ages in the Gaia era. Astrophys. J. 840, 17. doi:10.3847/1538-4357/aa6a1e

CrossRef Full Text | Google Scholar

Themeßl, N., Hekker, S., Southworth, J., Beck, P. G., Pavlovski, K., Tkachenko, A., et al. (2018). Oscillating red giants in eclipsing binary systems: empirical reference value for asteroseismic scaling relation. Mon. Not. Roy. Astron. Soc. 478, 4669–4696. doi:10.1093/mnras/sty1113

CrossRef Full Text | Google Scholar

Thompson, M. J., Toomre, J., Anderson, E. R., Antia, H. M., Berthomieu, G., Burtonclay, D., et al. (1996). Differential rotation and dynamics of the solar interior. Science. 272, 1300–1305. doi:10.1126/science.272.5266.1300

PubMed Abstract | CrossRef Full Text | Google Scholar

Tollerud, E. J. (2020). “Community-oriented programming in Astronomy: astropy as a case study,” in Astronomical data analysis software and systems XXVII, Santiago de Chile, Chile, October 22–26, 2017. Editors P. Ballester, J. Ibsen, M. Solar, and K. Shortridge (San Francisco, CA: Astronomical Society of the Pacific Conference Series), 491.

CrossRef Full Text | Google Scholar

Van Eylen, V., and Albrecht, S. (2015). Eccentricity from transit photometry: small planets in kepler multi-planet systems have low eccentricities. Astrophys. J. 808, 126. doi:10.1088/0004-637X/808/2/126

CrossRef Full Text | Google Scholar

Van Eylen, V., Albrecht, S., Huang, X., MacDonald, M. G., Dawson, R. I., Cai, M. X., et al. (2019). The orbital eccentricity of small planet systems. Astron. J. 157, 61. doi:10.3847/1538-3881/aaf22f

CrossRef Full Text | Google Scholar

Van Eylen, V., Lund, M. N., Silva Aguirre, V., Arentoft, T., Kjeldsen, H., Albrecht, S., et al. (2014). What asteroseismology can do for exoplanets: kepler-410a b is a small neptune around a bright star, in an eccentric orbit consistent with low obliquity. Astrophys. J. 782, 14. doi:10.1088/0004-637X/782/1/14

CrossRef Full Text | Google Scholar

van Saders, J. L., Ceillier, T., Metcalfe, T. S., Aguirre, V. S., Pinsonneault, M. H., García, R. A., et al. (2016). Weakened magnetic braking as the origin of anomalously rapid rotation in old field stars. Nature. 529, 181–184. doi:10.1038/nature16168

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, K., Faria, J. P., Antia, H. M., Basu, S., Mazumdar, A., Monteiro, M. J. P. F. G., et al. (2014). Asteroseismic estimate of helium abundance of a solar analog binary system. Astrophys. J. 790, 138. doi:10.1088/0004-637X/790/2/138

CrossRef Full Text | Google Scholar

Verma, K., Raodeo, K., Antia, H. M., Mazumdar, A., Basu, S., Lund, M. N., et al. (2017). Seismic measurement of the locations of the base of convection zone and helium ionization zone for stars in the kepler seismic LEGACY sample. Astrophys. J. 837, 47. doi:10.3847/1538-4357/aa5da7

CrossRef Full Text | Google Scholar

Verma, K., Raodeo, K., Basu, S., Silva Aguirre, V., Mazumdar, A., Mosumgaard, J. R., et al. (2019). Helium abundance in a sample of cool stars: measurements from asteroseismology. Mon. Not. Roy. Astron. Soc. 483, 4678–4694. doi:10.1093/mnras/sty3374

CrossRef Full Text | Google Scholar

Wang, L., Wang, W., Wu, Y., Zhao, G., Li, Y., Luo, A., et al. (2016). Calibration of LAMOST stellar surface gravities using the kepler asteroseismic data. Astron. J. 152, 6. doi:10.3847/0004-6256/152/1/6

CrossRef Full Text | Google Scholar

White, T. R., Bedding, T. R., Stello, D., Appourchaux, T., Ballot, J., Benomar, O., et al. (2011). Asteroseismic diagrams from a survey of solar-like oscillations with kepler. Astrophys. J. Lett. 742, L3. doi:10.1088/2041-8205/742/1/L3

CrossRef Full Text | Google Scholar

Winn, J. N., and Fabrycky, D. C. (2015). The occurrence and architecture of exoplanetary systems. Annu. Rev. Astron. Astrophys. 53, 409–447. doi:10.1146/annurev-astro-082214-122246

CrossRef Full Text | Google Scholar

Winn, J. N., Petigura, E. A., Morton, T. D., Weiss, L. M., Dai, F., Schlaufman, K. C., et al. (2017). Constraints on the obliquities of kepler planet-hosting stars. Astron. J. 154, 270. doi:10.3847/1538-3881/aa93e3

CrossRef Full Text | Google Scholar

Yu, J., Huber, D., Bedding, T. R., Stello, D., Hon, M., Murphy, S. J., et al. (2018). Asteroseismology of 16,000 kepler red giants: global oscillation parameters, masses, and radii. Astrophys. J. Supp. 236, 42. doi:10.3847/1538-4365/aaaf74

CrossRef Full Text | Google Scholar

Zhao, G., Chen, Y. Q., Shi, J. R., Liang, Y. C., Hou, J. L., Chen, L., et al. (2006). Stellar abundance and galactic chemical evolution through LAMOST spectroscopic survey. Chin. J. Astron. Astrophys. 6, 265–280. doi:10.1088/1009-9271/6/3/01

CrossRef Full Text | Google Scholar

Zinn, J. C., Pinsonneault, M. H., Huber, D., Stello, D., Stassun, K., and Serenelli, A. (2019). Testing the radius scaling relation with Gaia DR2 in the kepler field. Astrophys. J. 885, 166. doi:10.3847/1538-4357/ab44a9

CrossRef Full Text | Google Scholar