Driving and Dissipation of Solar-Wind Turbulence: What is the Evidence?

Smith, Charles W.; Vasquez, Bernard J.

doi:10.3389/fspas.2020.611909

REVIEW article

Front. Astron. Space Sci., 25 January 2021
Sec. Space Physics
Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.611909

Driving and Dissipation of Solar-Wind Turbulence: What is the Evidence?

Charles W. Smith* www.frontiersin.org

Bernard J. Vasquez

Physics Department and Space Science Center, Morse Hall, University of New Hampshire, Durham, NH, United States

Fifty years of solar wind observations have provided extensive data that drives an evolving view of the fundamental nature and dynamics of the magnetic, velocity, and density fluctuations that are ubiquitous throughout the heliosphere. Despite the ongoing examination of ever improving data, fundamental questions remain unanswered because there are very few multi-point measurements from a sufficient number of spacecraft in close proximity to fully resolve the three-dimensional dynamics that are at the heart of the problem. Simulations provide new insights and new questions, but most simulations sacrifice one aspect of plasma physics in order to address another. Computers and computational methods remain insufficient to simulate fully compressive, fully nonlinear, collisionless plasma dynamics with sufficient spatial range and dimension to be considered a complete description of solar wind turbulence. For these reasons, there remain multiple divergent opinions as to the underlying dynamics of solar wind turbulence, dissipation, and the observed heating of the thermal plasma. We review observations of solar wind turbulence in so far as they contribute to an understanding of solar wind heating through the existence of energy reservoirs, the dynamics that move energy from the reservoirs to the dissipation scales, and the conversion into heat of energy associated with coherent fluctuations.

1 Introduction

For decades the fundamental nature of fluctuations in the solar wind has been the object of debate. Two schools of thought have structured that debate. In the first, fluctuations are described as waves, most often solutions to the linearized dynamical equation, and the leading wave form has been Alfvén waves (Coleman, 1966; Völk and Alpers, 1973; Denskat and Burlaga, 1977; Heinemann and Olbert, 1980). In the second, fluctuations are described as being the result of diverse nonlinear dynamics that are the magnetized plasma equivalent of traditional hydrodynamic turbulence (Coleman, 1968; Bavassano et al., 1982; Matthaeus and Goldstein, 1982; Goldstein et al., 1995).

Early formulations of these ideas were based primarily on the observed power spectrum, fluctuation anisotropy, and cross-field correlation (Belcher and Davis, 1971). The view evolved and became dominant that the fluctuations originated with noncompressive waves in the sub-Alfvénic region of the solar atmosphere. These waves then propagate outward and across the point where the flow becomes super-Alfvénic. This transition acts as a filter for waves propagating at the Alfvén speed resulting solar wind oscillations that are dominated by outward-propagating Alfvén waves. This explains the fact that fluctuations (both magnetic and kinetic) tend to be noncompressive and transverse to the local mean magnetic field with a reproducible power spectrum that reflects the turbulence in the collision-dominated corona.

Attempts to build on this idea led to difficulties where predictions disagreed with observations. Notably, WKB theory that was used to predict the evolution of nonevolving waves with heliocentric distance was unable to account for the apparent ability of the magnetic fluctuations to remain transverse to the local mean magnetic field that rotates according to the Parker spiral (Hollweg, 1990). The local destruction and reformation of the waves would permit the newly formed waves to reorient if the dynamics were anisotropic with regard to the mean magnetic field and simulations indicate that they are (Shebalin et al., 1983; Matthaeus et al., 1990; Matthaeus et al., 1996a, Matthaeus et al., 1998; Ghosh and Goldstein, 1997; Ghosh et al., 1998a; Ghosh et al., 1998b; Cho and Vishniac, 2000; Vasquez et al., 2014). However, that means that processes normally associated with turbulence would be active and wave propagation alone could not explain the observations. At this same time, there was a growing recognition that thermal ions in the solar wind were experiencing in situ heating and the source was not recognized. It is a basic attribute of hydrodynamics (HD) that the turbulent fluctuation energy is moved to fluctuations at smaller scales where dissipation results in heating.

In this paper we review the evidence for turbulent in situ dynamics that results in the heating of the solar wind. We examine studies of solar wind fluctuations at all scales in an effort to better understand the generation, transport, and dissipation of fluctuation energy that results in the heating of the solar wind.

2 Solar Wind Heating

It has become entirely evident that some in situ process heats the ambient thermal proton population of the solar wind. Figure 1 shows the temperature of solar wind thermal ions as measured by the Voyager 2 spacecraft (Smith et al., 2006c). The departure from adiabatic expansion from 1 AU onward clearly shows the need for some form of heating in the solar wind (Gazis et al., 1994; Richardson et al., 1995). The radial variation of the solar wind proton temperature inside 1 AU as seen by the Helios spacecraft likewise shows the need for a heating source (Marsch et al., 1983; Schwenn, 1983; Lopez and Freeman, 1986; Arya and Freeman, 1991; Freeman et al., 1992; Totten et al., 1995; Verma et al., 1995; Vasquez et al., 2007; Hellinger et al., 2013; Lamarche et al., 2014).

FIGURE 1

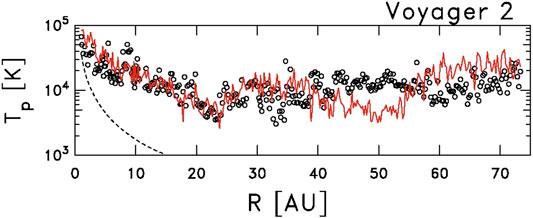
FIGURE 1. Average solar wind proton temperature as seen by Voyager 2 (circles) and prediction of transport theory (red curve). Dashed line represents predicted proton temperature derived assuming adiabatic expansion from 1 AU (Taken from Smith et al. (2006c).

Early attempts to explain the apparent heating often resembled the theories of heating that result in the acceleration of the wind from the solar corona. One notable theory, known as the cyclotron sweep mechanism, asked if it were possible to dissipate a static spectrum of magnetic fluctuations such that as the plasma moved away from the Sun and the spatial scale associated with various dissipation processes increased? Could dissipation of the observed spectrum in this manner provide the necessary energy to account for solar wind heating (Hollweg and Turner, 1978; Tu and Marsch, 1997)? It cannot (Schwartz et al., 1981). It is necessary to replace the energy that is consumed by dissipation processes or some other heating mechanism and associated source must be found to account for the observed energy budget.

Without attempting to identify the source, Vasquez et al. (2007) examined published results of the thermal proton temperature as a function of wind speed and heliocentric distance to obtain the rate of proton heating at 1 AU. They get the following expression:

ε_{V a s q u e z} = 3.6 \times 10^{- 5} T_{P} V_{S W} (1)

where $ϵ_{V a s q u e z}$ is given in J/(kg s), $T_{P}$ is given in Kelvin, and $V_{S W}$ is given in km s⁻¹. For typical solar wind conditions, $ϵ_{V a s q u e z}$ varies from 10² to 10⁴ J/(kg s).

3 THE Turbulent Spectrum

The overriding limitation of turbulence studies in space is that there is rarely more than one spacecraft in a region of interest. It is not possible to directly measure the nonlinear dynamics, or even the multi-dimensional spectrum, of fluctuations with a single spacecraft. There are techniques that attempt to overcome this limitation with interesting results, but in the end what is needed to make real progress in understanding any turbulent system is the ability to make measurements separated at multiple points in close proximity where the spacing of the measurements reflects the scale being studied. HelioSwarm is a proposed NASA MIDEX mission currently in a Phase-A study that will perform the multipoint measurement required to understand solar wind turbulence (Spence, 2019; Hautaluoma and Fox, 2020).

The cadence of magnetic measurements in the solar wind is generally more rapid than it is for thermal ion measurements. Therefore, there are more studies of solar wind turbulence using magnetic field measurements. The magnetic spectrum is generally divided into three ranges. There is the energy-containing range that is seen at 1 AU at spacecraft-frame frequencies $f_{s c} < 10^{- 4}$ Hz. These are spatial scales greater than the nominal correlation scale for the fluctuations where dynamics that are thought to originate at the Sun and persisted to the point of observation. In other words, they are direct measure of solar dynamics. The power spectrum of the energy-containing range is typically $P \sim f_{s c}^{- 1} .$ At lower frequencies the measured spectrum includes signals from large-scale transient solar activity, solar rotation, and the solar cycle. Between the correlation scale (30 min–1 h at 1 AU) and the dissipation scale (typically ∼2–5 s at 1 AU) is the inertial range. This is thought to represent the nondissipative nonlinear dynamics that transport energy through the spatial scales in a conservative manner. The power spectrum of the inertial range is often characterized at $f_{s c}^{- 5 / 3},$ but finite intervals of data can display a wide range of spectral indices and different theories for the dominant nonlinear dynamics predict varying spectral indices (Iroshnikov, 1964; Kraichnan, 1965; Matthaeus and Zhou, 1989; Goldreich and Sridhar, 1995; Goldreich and Sridhar, 1997; Leamon et al., 1999; Oughton and Matthaeus, 2020). At still smaller scales, the spectrum steepens and often demonstrates polarization signatures in association with the onset of dissipation.

Figure 2 shows a typical spectrum of the interplanetary magnetic field to illustrate the above description. It is a composite of two analyses using the Blackman–Tukey spectral technique (Blackman and Tukey, 1958). In the first analysis, nine days of data from days 117 through 125 of 2002 from the Advanced Composition Explorer (ACE) spacecraft with 16 s resolution is used to produce a measured spectrum from $2 \times 10^{- 5}$ to $3 \times 10^{- 2}$ Hz. This is a series of short-lived compression and rarefaction flows, each spanning $\sim 1$ day. The frequency range from $2 \times 10^{- 5}$ to $3 \times 10^{- 4}$ Hz is fit with a power law to obtain $f_{s c}^{- 1.21 \pm 0.02}$ . This is an example of the energy-containing range. In this spectrum, there is a subtle break in the spectral index to a steeper form that occurs at $f_{s c} \sim 5 \times 10^{- 4}$ Hz. In the second analysis, overlayed on the same figure, 24 h of high resolution data from day 123 of the same mission is used to produce a measured spectrum from $5 \times 10^{- 4}$ to 1.5 Hz. This is a rarefaction interval of expanding solar wind flow. Two frequency ranges are fit to this spectrum. The first extends from $5 \times 10^{- 4}$ to 0.1 Hz and is fit to a power law $\sim f_{s c}^{- 1.61 \pm 0.01}$ . This represents the inertial range. The last frequency range extends from 0.3 to 0.7 Hz and is fit to $f_{s c}^{- 3.38 \pm 0.01}$ . This represents the dissipation range. The spectral break at $\sim 0.2$ Hz marks the onset of dissipation.

FIGURE 2

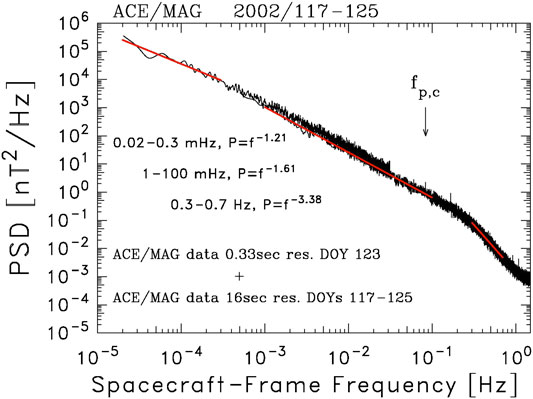
FIGURE 2. Composite spectrum using a nine-day interval of low-resolution magnetic field data from the ACE spacecraft and a single day of high-resolution data. Frequencies >1 Hz show aliasing from unresolved higher frequencies. The analysis is described in the text.

3.1 The Inertial Range

The inertial range is the most studied portion of the spectrum and the original source of the debate between waves or turbulence? Fluctuations are largely transverse to the local mean magnetic field, which suggests they are noncompressive (Belcher and Davis, 1971). This fluctuation anisotropy has now been shown to be equally correlated to two plasma parameters: the thermal proton $β_{p} = 8 π N_{P} k_{B} T_{P} B_{0}^{- 2}$ where $N_{P}$ is the proton number density, $k_{B}$ is Boltzman’s constant, and $T_{P}$ is the proton temperature and the ratio of the magnetic fluctuation amplitude to the mean field strength $δ B / B_{0}$ (Smith et al., 2006b; Pine et al., 2020b). This implies that the relative strength of the compressive fluctuations depends on one of these two parameters.

Belcher and Davis (1971) demonstrated not only the above fluctuation anisotropy, but also that the two components perpendicular to the mean field had slightly different power levels at 5:4. While this fact was widely ignored and thought to be insignificant, Bieber et al. (1996) demonstrated that the ratio of the two perpendicular components is an indication of the anisotropy of the underlying wave vectors. Using their formalism, it is easy to show that the ratio 5:4 with a nominal mean field winding angle of $45^{\circ}$ is indicative of a dominant 2D component meaning that the wave vectors as well as the fluctuations are largely confined to the plane perpendicular to the mean magnetic field. Subsequent analyses of many data intervals have supported the assertion that the 2D component is dominant in most solar wind samples (Matthaeus et al., 1990; Leamon et al., 1998a; Dasso et al., 2005; Hamilton et al., 2008; MacBride et al., 2010).

Observations combined with numerous simulations (Matthaeus et al., 1998; Cho and Vishniac, 2000; Müller and Grappin, 2005; Boldyrev et al., 2009; Beresnyak, 2011) have led to the view that the inertial range is composed largely of 2D turbulence with an undetermined underlying dynamic. Wave theories have resurfaced to assert that both the inertial and dissipation range is primarily composed of interacting kinetic Alfvén waves that form a turbulent plasma system (Leamon et al., 1999; Bale et al., 2005; Howes et al., 2008; Howes and Quataert, 2010; Sahraoui et al., 2010; TenBarge et al., 2013; Narita et al., 2020), and while there are problems with this interpretation (Smith et al., 2012; Roberts and Li, 2015; Vasquez et al., 2018a) it remains a popular view.

In HD, Kolmogorov (1941a) argued that the spectral transport of energy through the fluctuation spectrum was isotropic, energy-conserving, and based on dynamics that are local within the spectrum. Using a structure function formalism, this lead to the famous prediction for the omnidirectional inertial-range spectrum

P_{k} = C_{K} ϵ^{2 / 3} k^{- 5 / 3} (2)

where $C_{K} = 1.6$ (Batchelor, 1953), ϵ is the rate of energy transport through the inertial-range spectrum, and k is the wavenumber.

These ideas can be extended to magnetohydrodynamics (MHD) by employing the total energy (magnetic plus kinetic) and adopting a new coefficient which has been shown to apply to average solar wind conditions at 1 AU (Matthaeus and Zhou, 1989; Vasquez et al., 2007). Integrating the omnidirectional spectrum and allowing for a ratio of magnetic to kinetic energy , the extension of Eq. (2) that describes the average rate of energy transport through the spectrum at 1 AU under changing solar wind conditions is

ϵ_{M H D} = f_{s c}^{5 / 2} P_{B}^{3 / 2} {21.8}^{3} V_{S W}^{- 1} N_{P}^{- 3 / 2} (3)

where $P_{B}$ is the trace of the magnetic power spectral matrix in units of nT² Hz⁻¹, $V_{S W}$ is the solar wind speed in units of km s⁻¹, $N_{P}$ is the thermal proton density in units of cm⁻³, and 21.8 is a conversion factor. The factor $V_{S W}^{- 1}$ converts spacecraft-frame frequency to wave number and $N_{P}^{- 3 / 2}$ converts the magnetic field to units of velocity. This yields $ϵ_{M H D}$ in units of km² s⁻³. If we apply Eq. (3) to Figure 2 at $f_{s c} = 10^{- 2}$ Hz, using average plasma parameters V_SW = 400 km s⁻¹ and N_p = 5 cm⁻³, we obtain $ϵ_{M H D} = 7.3 \times 10^{- 4}$ km² s⁻³ cws If we apply Eq. (1) to the same data where the average thermal proton temperature is $9.3 \times 10^{4}$ K, we get an estimate for the average heating rate for a sample of this kind to be $ϵ_{V a s q u e z}$ = 1.3 × 10⁻³ km² s⁻³ which is twice the value obtained from the power spectrum and Eq. (3).

3.2 The Dissipation Range

In traditional HD, dissipation occurs at the smallest scales within the spectrum that are still described by fluid theory. The scale marking the spectral break and the onset of dissipation and the steepening of the spectrum depends on the rate of energy transfer through the inertial range (Smith et al., 2006a). When dissipation becomes competitive with the energy-conserving spectral transport of the inertial range, the spectrum steepens as energy is converted from fluid processes to heat.

In space, this is not the case (Leamon et al., 1999; Smith et al., 2001b; Smith et al., 2006a; Woodham et al., 2018; Pine et al., 2020a). There, the scale where dissipation sets in is determined by the ambient plasma parameters and the spectral slope associated with dissipation changes according to the rate of energy transport through the inertial range (Smith et al., 2006a; Pine et al., 2020a). Dissipation is marked by the breakdown of the fluid approximation and the necessary recovery of kinetic plasma theory. There are varying viewpoints of what dynamical processes are responsible for dissipation including cyclotron damping, Landau and transit time damping, and magnetic reconnection and those processes depend to a large degree on what form the inertial-range fluctuations take as they deliver energy to the dissipation scales (Isenberg, 1984; Isenberg, 1990; Goldstein et al., 1994; Hollweg and Isenberg, 2002; Gary et al., 2005; Isenberg and Vasquez, 2009; Parashar et al., 2009; Svidzinski et al., 2009; Markovskii et al., 2010a; Markovskii and Vasquez, 2010b; Chandran et al., 2010; Chang et al., 2011; Markovskii and Vasquez, 2011; Servidio et al., 2012; Vasquez and Markovskii, 2012; Markovskii and Vasquez, 2013a; Markovskii and Vasquez, 2013b; Bourouaine and Chandran, 2013; Chandran et al., 2013; Karimabadi et al., 2013; Kasper et al., 2013; Wu et al., 2013; Xia et al., 2013; Dalena et al., 2014; Hughes et al., 2014; Saito and Nariyuki, 2014; Servidio et al., 2014; Goldstein et al., 2015; Isenberg and Vasquez, 2015; Servidio et al., 2015; Vásconez et al., 2015; Vasquez, 2015; Wan et al., 2015; Franci et al., 2016; Gary, Hughes and Wang, 2016; Matthaeus et al., 2016; Parashar and Matthaeus, 2016; Pucci et al., 2016; Hughes et al., 2017a; Hughes et al., 2017b; Valentini et al., 2017; Yang et al., 2017; Woodham et al., 2018). Whatever the process, dissipation in space plasmas appears to become important at scales associated with the proton inertial scale or proton cyclotron scale which are strongly correlated in the solar wind at or beyond 1 AU (Pine et al., 2020a).

At the same frequency where the spectrum steepens due to dissipation (or does not if dissipation is weak), the spectrum often becomes polarized. The polarization of the dissipation range is consistent with the removal of outward propagating Alfvén waves via cyclotron damping, but analysis shows that this is only one of several active processes (Leamon et al., 1998b; Hamilton et al., 2008). Alternatively, the polarization sense could be due to the compressive nature of 2D turbulent fluctuations (Markovskii and Vasquez, 2016).

4 Transport Theory

There are three basic questions to the turbulent heating the solar wind: (1) what is the energy reservoir, (2) how does the energy get to the dissipation scales, and (3) what is the heating dynamic? Current theory holds that there are two energy reservoirs. The first is the remnant solar wind fluctuations of the energy-containing range. This includes the large-scale flow gradients of the solar wind and it is primarily responsible for the heating of the solar wind inside 10 AU. The second is the various populations of interstellar neutral atoms, primarily hydrogen, that transit the heliosphere. When ionized, they form a pickup population of suprathermal ions that excite magnetic waves at inertial-range scales close to the dissipation range. This is the dominant energy source beyond 10 AU (Zank et al., 1996; Smith et al., 2006c; Pine et al., 2020c).

It is possible to derive a transport theory describing solar wind heating without knowing the actual dissipation processes in a manner analogous to the Taylor-von Kármán approach (Taylor, 1935; von Kármán and Howarth, 1938). Under the assumption that the energy-containing range can be described to predict a rate of energy delivery to inertial-range scales, and with a description of the rate at which interstellar pickup ions excite wave energy, and assuming that all energy that is injected into the inertial range will be transported to the spectrum dissipation scales, it is possible to write equations describing the rate of solar wind heating

\frac{d Z^{2}}{d r} = - \frac{A'}{r} Z^{2} - \frac{α}{U} \frac{Z^{3}}{λ} + \frac{{\dot{E}}_{P I}}{U}, (4)

\frac{d λ}{d r} = - \frac{C'}{r} λ + \frac{β}{U} Z - \frac{β}{U} \frac{λ}{Z^{2}} {\dot{E}}_{P I}, (5)

\frac{d T}{d r} = - \frac{4}{3} \frac{T}{r} + \frac{2}{3} \frac{m_{p}}{k_{B}} \frac{α}{U} \frac{Z^{3}}{λ} . (6)

Application of these equations has focused on the energy-containing scales where $Z^{2}$ is the total fluctuation energy (magnetic plus kinetic) that is typically computed using hourly averages of the measured variables, λ is the similarity scale that is typically taken to be the correlation length, and T is the average temperature of the thermal protons. A′, C′, α and β, are heavily constrained by rotational symmetry, Taylor–Kármán local phenomenology, and solar wind conditions (Matthaeus et al., 1996b; Matthaeus et al., 1999). Figure 1 uses A′ = −1.1, C′ = 1.8, α = 1, and β = 1. The remaining parameters are the rate of energy injection into the turbulent spectrum by newborn interstellar PUIs ${\dot{E}}_{P I}$ which is obtained from other theories, the proton mass m_p, and Boltzmann’s constant k_B.

The solution of these equations using parameters from 1 AU are represented by the red curve in Figure 1. Other, sometimes more involved, versions of transport theory that follow the same general approach exist that predict a greater range of measurements and a few attempt to build specific dissipation processes into the theory (Zhou and Matthaeus, 1990a, b; Matthaeus et al., 1994; Matthaeus et al., 1996b; Matthaeus et al., 1999; Williams and Zank, 1994; Williams et al., 1995; Richardson et al., 1995; Richardson et al., 1996; Zank et al., 1996; Zank et al., 2012; Zank et al., 2017; Smith et al., 2001a; Smith et al., 2006c; Richardson and Smith, 2003; Isenberg et al., 2003; Isenberg et al., 2010; Isenberg, 2005; Breech et al., 2005; Breech et al., 2008; Breech et al., 2009; Breech et al., 2010; Oughton et al., 2006; Oughton et al., 2011; Ng et al., 2010; Usmanov et al., 2012; Usmanov et al., 2014; Usmanov et al., 2016; Usmanov et al., 2018; Adhikari et al., 2015a; Adhikari et al., b, Adhikari et al., 2017).

The intent of transport theory is that by using reasonable parameterization of the spectrum that is tightly constrained by observation, it is possible to account for the decay of the turbulent spectrum, the evolution of the break between the energy-containing and inertial range, the rate of heating, and the observed plasma temperature. While this alone may not prove that solar wind turbulence is an active heliospheric process that is responsible for the heating, it does set the bar for other theories to match.

5 Third-Moment Theory

Where Kolmogorov (1941a) argued a rate of energy transport through the HD inertial range based on local dynamics and dimensional analysis, it is possible to compute a rigorous expression for the rate of energy transport in the HD inertial-range spectrum (Kolmogorov, 1941b). By assuming isotropy, homogeneity, and stationarity, the rate of energy transport through the inertial range is given by

- (4 / 5) ϵ^{H D} | L | = 〈 {[V_{L} (x + L) - V_{L} (x)]}^{3} 〉 (7)

where $V_{L}$ is the component of the velocity fluctuation along the separation vector L, $V_{L} \equiv V \cdot L / L$ where $L = | L |,$ $ϵ^{H D}$ is the rate of energy cascade, and $〈 \dots 〉$ denote ensemble average. In single-spacecraft studies using the Taylor frozen-in-flx assumtion, $V_{L}$ is the radial component of the flow.

Politano and Pouquet (1998a, b) extend the Kolmogorov (1941b) analysis to include incompressible MHD turbulence using the Elsässer variables (Elsässer, 1950)

Z^{\pm} \equiv V \pm B / \sqrt{4 π ρ} (8)

where ρ is the mass density. Their expression for the spectral transport of energy in an isotropic MHD system is

(4 / 3) ϵ_{I S O}^{\pm} V τ = 〈 Δ Z_{R}^{\mp} (τ) \sum_{i} {[Δ Z_{i}^{\pm} (τ)]}^{2} 〉 (9)

where τ is the positive time lag and $\sum_{i}$ is the sum over all three vector components. The subscript “R” denotes the Radial component directed from the Sun’s center to the point of measurement. The total spectral transport of energy is given by

ϵ^{T} = (ϵ^{+} + ϵ^{-}) / 2. (10)

It is straightforward to extend this analysis to include other geometries including 2D. When we apply this formalism to the data represented in Figure 2, we get an average $ϵ_{T}$ = 3 × 10⁻⁴ km² s⁻³. This is half the value we obtained from Eq. (3) and a fourth the value we obtained from Eq. (1), but Stawarz et al. (2009) and Coburn et al. (2012) found better agreement between the third-moment expression and $ϵ_{v a s q u e z}$ when averaging a larger sample of observations.

Figure 3 compares the spectral transport of energy as computed using Eq. (9) for several different assumptions of geometry along with the scaling shown to be accurate by Vasquez et al. (2007) and the comparison is favorable. Since the results of (Vasquez et al., 2007) were obtained by examining Helios results, it represents a ground truth for the local heating rate at 1 AU. This comparison offers strong evidence that the solar wind fluctuation spectrum is not a static collection of non-interacting fluctuations and can be described by extensions of the HD concepts to embrace the added dynamics of MHD.

FIGURE 3

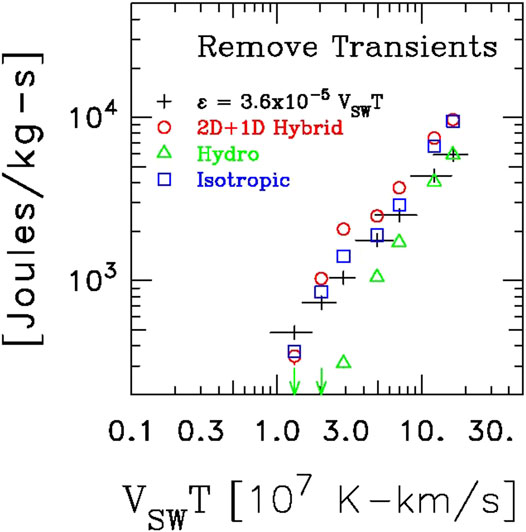
FIGURE 3. Application of Eqs (9) and (10) years of data from the Advanced Composition Explorer (ACE) spacecraft [Reproduced from Stawarz et al. (2009)].

Third-moment analyses have been developed and applied to varying solar wind conditions using single- and multi-spacecraft techniques and with efforts to extend the analysis to compressive fluctuations (MacBride et al., 2005, 2008; Sorriso-Valvo et al., 2007; Marino et al., 2008; Carbone et al., 2009; Smith et al., 2009; Stawarz et al., 2009, 2010, 2011; Wan et al., 2009; Forman et al., 2010; Osman et al., 2011; Coburn et al., 2012, 2014, 2015; Banerjee et al., 2016; Hadid et al., 2017; Vasquez et al., 2018b; Smith et al., 2018; Sorriso-Valvo et al., 2018). The compressive formalisms show agreement with the incompressible formalism under most applications as would be expected since density fluctuations in the solar wind are small.

6 Intermittent Heating

Intermittency is generally described as the result of nonlocal dynamics contributing to the spectral transport of energy (Kolmogorov, 1962). The leading diagnostic is obtained by comparing the relative value of high-order structure functions. However, if we generalize the concept of intermittency to represent the non-steady transfer of energy, we can make a direct measure of this using the third-moment techniques described above.

Third moments computed at lags corresponding to inertial-range scales are expected to be a linear function of lag with the slope proportional to the rate of energy transport through the spectrum. Using data samples comparable in duration to the measured correlation length of the magnetic fluctuations, it is possible to show that estimates of the third-moment expressions describing spectral transfer vary significantly (Coburn et al., 2014; Coburn et al., 2015). The mean of the distribution of ϵ values agrees well with the average local heating rate of the solar wind under diverse conditions as described above, but the standard deviation is $\sim 10 \times$ the mean. Despite this variation, estimates are generally linear functions as expected and yield seemingly convergent functions. However, the correlation length for primitive variables (magnetic field, velocity, density) may not correspond to the correlation length for the third-order functions and it is this length that must be used when combining statistically independent estimates of the spectral transport rate.

Smith et al. (2018) measured the correlation length for third-moment expressions using the same data that produced Figure 2 and found that the correlation length was $20 %$ of the lag value. This means that the third moment expressions decorrelate in a fraction of the scale of interest, indicating that the nonlinear dynamics of the inertial range changes significantly over any scale of interest. For instance, fluctuations seen at 0.01 Hz in the spacecraft frame have a spatial scale L = 400/0.01 = 4 × 10⁴ km assuming a wind speed of 400 km s⁻¹. The nonlinear dynamics associated with this scale can be expected to change significantly over ∼L/5 = 8 × 10³ km. This is significantly less than the 30 min to 1 h scale over which the primitive variables decorrelate.

The conclusion from this is that the spectral transfer rate is highly variable in both time and scale with energy being transfered to both smaller and larger scales at a mean-square rate that is $10 \times$ what is needed to account for the average heating rate. This ongoing redistribution of energy maintains the spectral form despite the fact that newborn interstellar pickup ions (PUIs) are responsible for driving the spectrum beyond 10 AU by depositing energy at scales close to the dissipation scale (Smith et al., 2001a; Smith et al., 2006c; Pine et al., 2020c). Therefore, the nonlinear dynamics that support solar wind turbulence are much stronger than is normally inferred from the average heating rate needed to account for the observed heating.

7 Summary

We began by discussing the multiple views that attempt to describe solar wind turbulence. To date, there is no definitive resolution to that controversy. The general morphology that describes the various ranges of the turbulent spectrum, dividing it into energy-containing, inertial, and dissipation range spans the various views, but those views offer different interpretations of the underlying dynamics. Those various dynamics each lead to predictions for the inertial-range power spectrum analogous to Eq. (2). Different forms of the transport equations, as represented here by Eqs (4)–(6), can be derived based on those same assumptions of the underlying dynamics. However, Eq. (9) embraces all underlying dynamics subject to an assumption of the underlying geometry of the wave vectors. In this way, it does provide one example of rigorous universality against which various theories of solar wind turbulence can be tested.

Author Contributions

CS lead the effort in this review. BV provided material on solar wind heating and energy cascade rate estimation especially at 1 AU. Both authors contributed to the overall presentation of the review and revised the manuscript before submission.

Funding

CS is supported by NASA Grant NNX17AB86G and by the Advanced Composition Explorer mission. BV is supported by NASA Grant 80NSSC19K0832. CS and BV are partially supported by NASA Grant 80NSSC17K0009 and NSF SHINE AGS1622413.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The data used in this analysis are available from the National Space Science Data Center and ACE Science Center.

References

Adhikari, L., Zank, G. P., Bruno, R., Telloni, D., Hunana, P., Dosch, A., et al. (2015b). The transport of low-frequency turbulence in the super-Alfvénic solar wind. J. Phys. Conf. Series 642, 012001. doi:10.1088/1742-6596/642/1/012001

REVIEW article

Driving and Dissipation of Solar-Wind Turbulence: What is the Evidence?

1 Introduction

2 Solar Wind Heating

3 THE Turbulent Spectrum

3.1 The Inertial Range

3.2 The Dissipation Range

4 Transport Theory

5 Third-Moment Theory

6 Intermittent Heating

7 Summary

Author Contributions

Funding

Conflict of Interest

Acknowledgments

References

This article is part of the Research Topic

People also looked at