- Space Research Institute, Russian Academy of Sciences, Moscow, Russia
Crossing the Earth’s bow shock is known to crucially affect solar wind plasma including changes in turbulent cascade. The present review summarizes results of more than 15 years of experimental exploration into magnetosheath turbulence. Great contributions to understanding turbulence development inside the magnetosheath was made by means of recent multi-spacecraft missions. We introduce the main results provided by them together with first observations of the turbulent cascade based on direct plasma measurements by the Spektr-R spacecraft in the magnetosheath. Recent results on solar wind effects on turbulence in the magnetosheath are also discussed.
Introduction
Coupling between solar wind (SW) and the Earth’s magnetosphere is one of the challenging problems of modern geophysics. The presence of a transition layer in front of the magnetopause has been known since the launching of the first spacecraft to the near-Earth space (e.g., Ness et al., 1964; Spreiter et al., 1966). Its presence results from an interaction between the supersonic and superalfvenic SW and the magnetosphere which leads to the formation of the outstanding bow shock (BS) wave.
The role of the magnetosheath (MSH) in Sun-Earth coupling has been focused on for several decades. At the BS plasma decelerates and diverts, it becomes denser and hotter. In general, the MSH plasma flow behind the BS can be described satisfactorily by magnetohydrodynamic (MHD) models (e.g., Spreiter and Stahara, 1980; Kartalev et al., 1996; Tóth et al., 2005; Samsonov et al., 2007; Samsonov et al., 2012). An MHD approach helps to obtain mean values of plasma and magnetic field parameters inside the MSH at large enough scales. However, small-scale variations of the parameters cannot be obtained by these models (e.g., Zastenker et al., 2002; Hayosh et al., 2006). Large amount of small-scale fluctuations, arising inside the MSH do not obey the MHD description of the plasma and may lead to discrepancies between the parameters predicted by the MHD models and the parameters, measured locally during short time intervals. In particular, the magnetic and electric field as well as density profiles which directly affect the magnetopause, were shown to be different from those measured in the SW (e.g., Šafránková et al., 2009; Pulinets et al., 2014; Pulkkinen et al., 2016). These differences are not usually taken into account by models of solar wind-magnetosphere coupling, which may be the reason for their inaccuracies.
Similar to the regions downstream of interplanetary shocks, behind the BS the fluctuations of the plasma and magnetic field parameters have higher amplitude, i.e., higher power spectral density (PSD), than those in the upstream undisturbed SW and fill a wide range of frequencies (or scales). The power of the fluctuations is strongly controlled by the geometry of the BS in the point where plasma enters the MSH (Greenstadt, 1972; Shevyrev et al., 2003; Shevyrev and Zastenker, 2005). This geometry is usually characterized by the θBN angle between the local BS normal and interplanetary magnetic field (IMF) vector. Behind the quasi-parallel BS (θBN < 45°), fluctuations are as much as 2–3 times more powerful than behind the quasi-perpendicular BS (θBN > 45°). In some cases, the fluctuations penetrate to the MSH from the SW, but in most of the cases the BS itself and processes inside the MSH are the sources of variations (Zastenker et al., 2002). Fluctuations inside the MSH have various sources. At the bow shock, temperature anisotropy increases resulting in a relaxation of energy via waves and instabilities (Anderson et al., 1994; Lacombe and Belmont, 1995; Schwartz et al., 1996). Upstream foreshock processes contribute to the fluctuations behind the quasi-parallel bow shock (Shevyrev and Zastenker, 2005; Shevyrev et al., 2006; Kozak et al., 2011; Gutynska et al., 2012). Moreover, behind the BS, the fluctuations are superimposed by the MSH dynamics in response to the changes in the upstream SW parameters (e.g., Sibeck and Gosling, 1996). The multifactor dynamics of the MSH fluctuations lead to difficulties in its analysis.
MSH fluctuations have been analyzed via experimental data for a long time in different ways: in statistical descriptions (Němeček et al., 2000; Němeček et al., 2001; Němeček et al., 2002; Shevyrev and Zastenker, 2005; Gutynska et al., 2008; Gutynska et al., 2009; Gutynska et al., 2012; Dimmock et al., 2014), in sets of case studies (Zastenker et al., 2002; Shevyrev et al., 2003; Kozak et al., 2011; Kozak et al., 2012), or as a set of wave modes (Song et al., 1992a; Song et al., 1992b; Hubert, 1994; Lacombe and Belmont, 1995; Lucek et al., 2001; Sahraoui et al., 2003; Alexandrova, 2004; Sahraoui et al., 2004). Recent achievements in hybrid simulations (Blanco-Cano et al., 2006a; Blanco-Cano et al., 2006b; Omidi et al., 2010; Ofman and Gedalin, 2013; Karimabadi et al., 2014; Omidi et al., 2014) also made a great contribution to the understanding of the dynamics of MSH variations and waves. However, MSH fluctuations usually present a set of mixed components such as different wave modes, coherent structures, and external fluctuations of the SW origin, which also present highly complex mixed structures as well (see e.g., Roberts et al., 2013; Perschke et al., 2014; Perrone et al., 2020). One of the ways to deal with the whole ensemble of fluctuations is to consider it in a framework of turbulent cascade.
Turbulence in plasma is usually regarded as the cascade of energy through scales via non-linear interacting eddies (Frisch, 1995). Moreover, in plasmas, a variety of wave modes can exist and the non-linear interaction of these waves also contributes to the formation of the turbulent cascade (e.g., Goldreich and Sridhar, 1995). Turbulence can be found in many of astrophysical and space plasmas like stellar winds, accretion discs, galaxy clusters [see review by Schekochihin et al., (2009)], planetary magnetosheaths, and in laboratory plasma as well (Budaev et al., 2015). Near-Earth space is usually referred to as a natural laboratory to study turbulence in collisionless plasma, as a large set of spacecraft data help to analyze it for different backgrounds and in a wide range of scales–from electron gyroradii up to the scales of large space phenomena (e.g., coronal mass ejections, planetary magnetospheres, etc.).
The largest eddies which form the turbulent cascade determines the scales at which energy is supposed to be injected into the system. At small scales where kinetic processes make a significant contribution to the cascade, the energy is supposed to be partially transferred to the particles (i.e., dissipated) which leads to plasma heating. A feature of systems characterized by very high Reynolds numbers is that the scales at which energy is injected and dissipated differ by many orders of scales. This difference leads to the existence of several ranges of scales in the turbulent cascade. In the energy containing scales (more than ∼106 km for the SW plasma), spectra usually follows the ∼k−1 power law. Then the spectrum steepens and follows the k−5/3 power law, predicted for the velocity fields by Kolmogorov (1941) and described more commonly for plasma flow by Frisch (1995). In the scales of dissipation, the Kolmogorov phenomenology ceases to operate and the turbulent cascade breaks and steepens. This range has been shown to start close to the scales of proton inertial length, or proton gyroradius. Since the beginning of the spacecraft era, a large dataset of in situ measurements in the SW has provided a great opportunity to study turbulence in collisionless plasma. Detailed phenomenology of turbulent cascade formation in SW plasma can be found in reviews by Tu and Marsch (1995); Alexandrova et al. (2013); Bruno and Carbone (2013); Chen (2016).
MSH turbulence is studied much less compared to those in the SW, though it has been actively explored during the last few decades. The present review focuses on the experimental study of MSH turbulence around ion scales. It does not claim to present a full unbiased review of turbulence in the MSH, but aims to give an overview of the kinds of experimental studies on turbulence spectra which have been performed during last two decades with the help of different spacecraft and different kinds of measurements. Some of them have already been reviewed by Zimbardo et al. (2010), who provided a comparison between turbulence features in different regions of the near-Earth space. Also, some of the results were included in a recent review by Sahraoui et al. (2020), which summarized several years of the authors’ explorations of turbulence in space plasma. A substantial part of the present review is devoted to the exploration of MSH turbulence with the help of high-resolution plasma measurements available on board the Spektr-R spacecraft, which have not been presented in other reviews. The main purpose of the paper is to provide a comparison between statistical studies of turbulence spectra and to point out the importance of plasma fluctuations.
Turbulent Features of the Magnetosheath Fluctuations
Spectral Indices and Shapes: Some Features and Case Studies
In the theoretical frameworks, turbulent cascade is usually described in wave vector k space, where the energy spectrum follows the ∼kα law, with α varying for different range of scales. Transition from experimentally obtained frequency spectra to those in wave vector space is one of the difficulties in comparison between a theory and an experiment. Usually, a Taylor hypothesis is applied for such a comparison (Taylor, 1938). This method assumes that waves, which form the cascade, are much slower than the plasma flow, or in other terms, that the waves have low frequency in a plasma rest frame. Klein et al. (2014) and Howes et al. (2014) checked the validity of the Taylor hypothesis for linear kinetic wave modes in SW plasma. The authors showed that the hypothesis could only be significantly violated in cases of low bulk speed of plasma V∼VA [with VA = B/(4πρm)−1/2 being the Alfven speed, B being the magnetic field magnitude, and ρm being the plasma mass density] and in case of fast or whistler turbulence. The applicability of the Taylor hypothesis was studied via compressive Hall-MHD numerical simulations by Perri et al. (2017). The authors suggested that deviations of real spectra from those measured by a single spacecraft to be significant for the flow speed close to VA and at sub ion scales in the case of a k-vector parallel to the mean magnetic field. Recently, the validity of the Taylor hypothesis at sub-ion scales was checked via direct comparison between the single-spacecraft time measurements converted to the spatial ones with the help of the hypothesis and the direct spatial measurements between pairs of the MMS spacecraft. The reported results showed that the Taylor hypothesis works well in most of the cases (e.g., Chasapis et al., 2017; Chen and Boldyrev, 2017; Chhiber et al., 2018; Stawarz et al., 2019). However, some of the cases showed a clear violation of the hypothesis (Stawarz et al., 2019). Typically, in the SW the hypothesis is satisfied as well as in the flank MSH as bulk velocity is significantly higher than the Alfven or magnetosonic speeds and whistlers are rarely observed (Rodriguez, 1985). However, a probable mismatch of spatial and temporal variation spectra should be kept in mind when considering subsolar MSH. Huang and Sahraoui (2019) presented a simple check of the validity of the Taylor hypothesis using the ratio between frequencies of ion and electron spectral breaks.
Processing in situ measurements is commonly prepared in frequency space. Usually, with the help of Fourier or wavelet analysis, one can distinguish the frequency range of at least 1 decade of scales at which spectra can be approximated with ∼fα with a constant value of α. Another method to obtain features of the turbulent fluctuations is analysis of the probability distribution function (PDF) or analysis of structure functions which represent high order moments of the field and its scaling (Frisch 1995; Bruno and Carbone 2013). Though this method provides a deeper view on the parameters of plasma turbulence, it is rather sensitive to data quality and is difficult to apply for statistical studies. Fourier and wavelet analyses are more commonly used for turbulence exploration (Dudok de Wit et al., 2013).
In theoretical frameworks, different predictions of spectral indices are usually given depending on the processes responsible for turbulence development and dissipation (e.g., Leamon et al., 1998; Smith et al., 2006; Schekochihin et al., 2009; Boldyrev and Perez, 2012). Thus, a comparison of the value of the spectral exponent, obtained by means of experimental data, with theoretical predictions was supposed to give the information of processes governing the space plasma turbulence and was a goal of a number of studies.
Since the first experimental studies of the MSH turbulence, a variety of spectral indices values have been reported. Below a set of distinct results are listed and the causes of differences are discussed in the next sections. In an early review of the magnetic field fluctuations inside the MSH, Fairfield (1976) presented a composed spectrum, obtained by the onboard measurements of different spacecraft—OGO−1,−3,−5, Mariner 4, Explorer 12—in the range of frequencies 10–2–102 Hz. This spectrum followed a two-power-law structure with a break at ∼0.2 Hz. The power exponents were close to −1 and −3 at frequencies lower and higher than the ion spectral break, respectively. Rezeau et al. (1986) analyzed 14 spectra at frequencies 0.5–11 Hz, i.e., above proton gyrofrequency, obtained by the GOES-2 spacecraft in the MSH. The spectral exponent was estimated to be close to the −3 value with the 0.3 standard deviation of the distribution of the exponent’s value. Later, a somewhat steeper spectrum was presented for the wider range of scales—0.1–100 Hz (Rezeau et al., 1999). The two-power-law spectrum of magnetic field fluctuation was observed by Dudok de Wit and Krasnosel’Skikh (1996) with the help of AMPTE-UKS measurements downstream from the subsolar quasi-parallel BS. Statistical exploration of the features of magnetic field fluctuations behind the bow shock was provided by Czaykowska et al. (2001). The authors analyzed 132 cases of bow shock crossings by the AMPTE/IRM spacecraft and presented a typical view of the magnetic field fluctuation spectrum behind the bow shock. The spectra exhibited a clear break at ion scales and followed the ∼f−1 power law at frequencies below the break while the power exponent ranged from −3 to −2 at sub-ion scales.
Note that in the case of analyzing the fluctuation spectra at scales of transition from MHD to kinetic scales, the uncertainties of the MHD-part slope calculation is higher than those of the kinetic-scale slope. Usually for measurements with high enough time resolution the slope at the kinetic scales can be calculated quite precisely. The scatter of the kinetic-scale slope values reported in various experimental studies is likely to arise from wide statistical distribution rather than errors of estimation.
One of the important factors influencing turbulence development in plasma is intermittency indicated by deviation of the PDF of fluctuations from Gaussian becoming more pronounced toward smaller scales (Tu and Marsch, 1995; Sorriso-Valvo et al., 1999; Macek, 2007; Riazantseva et al., 2015). This was usually interpreted as the concentration of turbulent energy in structures at sub-ion scales, with geometry of the structures affecting the turbulent cascade. In experimental studies, the intermittency can be easily detected by means of the flatness (or kurtosis) value which is the fourth moment of the PDF. An increase of flatness to values above three (analytically determined value for Gaussian PDF) with decreasing scales indicates the presence of intermittency. Note that commonly used theories of turbulence do not involve the intermittent nature of plasma that in some cases may result in discrepancies in the modeled predictions and observations (see reviews by Bruno and Carbone 2013; Budaev et al., 2011). In the MSH, intermittency has been rarely addressed. Dudok de Wit and Krasnosel’Skikh (1996) used high-order statistics and presented the non-Gaussian distribution of magnetic field fluctuations both upstream and downstream of the BS. Kozak et al. (2012) provided a comparison between the intermittent features of the magnetic field in the SW, MSH, and foreshock and presented an absence of intermittency in the MSH. A recent case study by Chhiber et al. (2018) demonstrated the intermittent nature of turbulence both at the electron and ion scales in front of the magnetopause. Moreover, the authors compared features of PDF in the SW and in the MSH based on two cases of MMS measurements and suggested a more intermittent character of MSH turbulence. The flatness/kurtosis value was shown to constantly increase toward the electron scales in the MSH while in the SW, the kurtosis stopped increasing around the ion scales and then decreased up to three at the electron scales. However, the authors noted that intermittency features can change significantly and rapidly in such a dynamically bounded region as the MSH. Statistical comparison between the intermittency in the SW and in the flank MSH (Riazantseva et al., 2016) showed dependencies of kurtosis on the considered scale for a variety of analyzed cases which included the kurtosis value close to three at all scales, i.e., the absence of intermittency. Thus, the character of intermittency in the MSH and its difference from the intermittency of SW turbulence is still a challenging question.
Active exploration of turbulence in the near-Earth space started in 2001 with the launch of the Cluster satellites (Escoubet et al., 1997). The Cluster measurements were prepared by four spacecraft grouped in a tetrahedron with the sides of the order of ion gyroradius. This advantage in the mission allowed for dividing temporal fluctuations from the spatial and for direct exploration of the turbulence anisotropy at the ion scales. Combined with high-quality magnetic field measurements of high cadence, Cluster data have provided a powerful instrument for the exploration of turbulence at the ion and sub-ion scales. One of the first observations of the magnetic field fluctuation spectrum in the MSH (Rezeau et al., 2001) revealed ∼f−2.31 spectrum at frequencies 1–10 Hz when the spacecraft were in the vicinity of the magnetopause at the MSH flank.
The technique of decomposition of fluctuations into frequency and wave vector domains was applied to the Cluster data by Sahraoui et al. (2003). The authors analyzed a period of magnetosheath observation close to the magnetopause. The suggested method called the k-filtering technique helped the authors to determine that the turbulent cascade was dominated by mirror mode fluctuations. Further, the authors performed a comprehensive analysis of Cluster measurements when the spacecraft were separated by ∼100 km and presented evidence of anisotropy of the cascade formation in the MSH (Sahraoui et al., 2006). The magnetopause normal was shown to serve as a constraint for the development of the turbulent cascade along with the mean magnetic field vector. Moreover, the authors presented a view of the turbulent cascade in the wave vector space along the flow direction. The spectrum exhibited a clear power law of ∼k−8/3 within the range kρ = (0.3 5), where ρ was the proton gyroradius. Note, that the power exponent was shown to differ from ∼f−7/3, measured in the frequency space, pointing out the significance of the Doppler shift effect.
Based on Cluster high resolution measurements of the magnetic and electric fields, Alexandrova et al. (2006) managed to detect an Alfven vortex-localized coherent structure in the MSH. Observations were performed in the vicinity of the quasi-perpendicular BS. The authors performed a spectrum of magnetic field fluctuations characterized by a clear bump (or spectral knee) at the scales of transition from MHD to kinetic regimes. At frequencies above the bump, the spectrum followed the f−0.5 power law, at smaller scales, the spectrum steepened and followed the ∼f−3 power law. Further, the authors presented a similar case with the spectrum following the f−4 power law at the kinetic scales and significantly decreased level of compressibility at the scales of the bump (Alexandrova, 2008). The authors concluded that the presence of incompressible Alfven vortices in compressive MSH turbulence is one of the differences between the SW and the MSH.
Based on Cluster data, Sundkvist et al. (2007) explored thin current sheets, identified as ion reconnection regions (Retinò et al., 2007), which were typically found behind the quasi-parallel BS. The magnetic field fluctuations associated with the current sheets were shown to follow two typical power law structures with a break at the range of transition from MHD to kinetic regimes. Kolmogorov scaling was identified at the frequencies below the break while at higher frequencies, the spectrum was characterized with a −3.1 power exponent. The intermittent nature of the fluctuations was also pointed out, which became significant at scales of ∼10 ρ.
Breuillard et al. (2016) performed a case study on the turbulence spectrum in the MSH for intervals associated with different instabilities: Alfven ion cyclotron (AIC) and/or mirror instability and their absence. The absence of instabilities as well as presence of both kinds of them was characterized by a nearly isotropic spectra of magnetic field fluctuations. Spectra of fluctuations of every magnetic field component as well as their sum were shown to be close to the f−2.8 power law. In the case of dominating mirror instability, the parallel component was more powerful than two perpendicular ones, with the spectrum having a slope of −2.00 ± 0.07 at the sub-ion scales; the perpendicular components had similar a spectra with a −2.65 ± 0.06 slope, and the total magnetic field spectrum followed the f−2.30±0.05 power law, that was flatter than typically observed inside the MSH. On the opposite side, in the case of AIC wave domination, the perpendicular components were more powerful than the parallel one, with the former having slopes of −2.4 ± 0.06 and −2.38 ± 0.05 while the latter had a slope of −2.65 ± 0.07. The total spectrum of the magnetic field fluctuations in that case were characterized by the power exponent of −2.45 ± 0.05, which is somewhat flatter than typically observed. Thus, spectral slopes were shown to be affected by the presence of instabilities, assuming differences in dissipation processes.
Early performed observations and case studies of the turbulence spectra showed that MSH plasma could also be used to figure out the properties of ion scale processes in plasma. Though generally similar, distinct results provided somewhat different features of turbulence from case to case. Thus, statistical studies covering various background conditions were required to obtain the typical parameters of the turbulence behind the BS.
Spectral Indices: Statistical Studies of Magnetic Field Fluctuations
Based on Cluster measurements, Mangeney et al. (2006), and Lacombe et al. (2006) performed the first comprehensive statistical analysis of the turbulent fluctuations inside the MSH at sub-ion and up to electron scales. The authors addressed magnetic and electric field fluctuations in frequency ranges of (8, 4000) Hz. Although this range of scales is out of the scope of the current review, these studies and the considered data intervals of the Cluster measurements have inspired a number of works focused on ion-scale turbulence. Moreover, these studies demonstrated the importance of Doppler-shift in the measurements’ interpretation.
For the same dataset, Alexandrova et al. (2008) presented the first results on the shape and features of magnetic field fluctuation spectra in the MSH around ion scales for various background conditions. Their study was based on more than 20 h of Cluster measurements in the MSH, mostly behind the quasi-perpendicular BS (one of the cases referred to oblique BS, with θBN = 50°). The advantage of the study was the consideration of fluctuation spectra both below and above the ion spectral break. The authors showed the differences of spectra of compressive fluctuations (namely, fluctuations of the component, which is parallel to the mean magnetic field, B||) and those of in-compressive Alfvenic fluctuations (of the component, which is normal to the mean magnetic field, B⊥). The compressive fluctuations were shown to be less powerful at the whole range of frequencies–from 10−3–10 Hz. Also, the spectra obtained for different directions had different features. The transverse Alfvenic fluctuations were shown to follow Kolmogorov scaling with ∼f−5/3 at the frequencies below ion break and the power-law scaling with the slope ranged from −3 to −2.3 at the frequencies above the break, with no clear dependence of the spectral slope on the background conditions. The compressive component was shown to follow the Alfvenic one at sub-ion scales. Both components were shown to have wave vectors k⊥ >> k||. The authors showed the evidence of 2-D turbulence domination at sub-ion scales for both components of the fluctuations. This dominance of 2-D turbulence was shown to exist for various values of plasma parameter β = pT/PB, where PT was plasma thermal pressure and PB referred to magnetic pressure.
Analyzing the same set of intervals, Matteini et al. (2017) compared the spectra of magnetic and electric field fluctuations in a wide range of scales, covering MHD, ion, and electron scales. The authors showed that for various values of plasma parameter β mutual scaling of electric and magnetic field fluctuations stayed the same: δE/δB ∼1 at MHD scales and δE/δB∼f at sub-ion scales up to electron scales. Similar results were obtained based on MMS data (Stawarz et al., 2016; Breuillard et al., 2018). Matteini et al. (2017) concluded that mutual scaling of electric and magnetic field fluctuations implied a domination of fluctuations with k⊥ >> k|| at sub-ion scales, consistent with theoretical predictions. The same study presented the ion velocity spectrum at MHD scales following ∼f−3/2 scaling while the magnetic field fluctuations followed a spectrum with a −5/3 power exponent. This result was consistent with the findings made for the SW turbulence spectra (Podesta et al., 2006; Borovsky, 2012; Šafránková et al., 2016).
Using the advantages of the multi-spacecraft Cluster mission, He et al. (2011) analyzed the spatial correlation function of the density and both transverse and parallel magnetic field fluctuations for the wide range of angles between the velocity and magnetic field vectors. Although 2-D correlation functions could not be simply recalculated to the 2-D PSDs of the fluctuations, the method was shown to be useful in analyzing anisotropy of both magnetic field and plasma fluctuations. The authors showed the existence of two dominant populations of fluctuations, with the majority of them being extended parallel to the mean magnetic field. The authors suggested this to be a signature of the same two-population view of the PSDs, with the major fluctuations having wave vectors normal to the mean magnetic field and the minor population having a wave vector along the mean field, e.g., k⊥ >> k||. A surprising similarity was pointed out between the correlation functions for density and transverse magnetic field component. Unlike previous results of a 1-D study by Alexandrova et al. (2008), this study was performed in 2-D space, and the obtained results were consistent. Also, this work presented the flattening of density PSDs at MHD scales with the increasing angle between velocity and magnetic field vectors. The spectral slope changed from −1.6 to −1.2 on average while the angle increased from 20 to 90°. Standard deviations of the slope’s values were ∼0.25, so the presented result was statistically reliable. At the same time, for the kinetic scales, the slope changed from −2.8 to −2.3, with standard deviations of ∼0.2. For the spectra of transverse magnetic field fluctuations at the kinetic scales, a similar trend was observed (the errors represent standard deviations): at the MHD scales, the slope increased from −3.5 ± 0.4 to −2.90 ± 0.15. For MHD scales, the slope changed from −1.5 ± 0.3 to −1.3 ± 0.2, thus the dependency was insignificant due to large standard deviations.
Huang et al. (2014) presented statistical analysis of the scaling of magnetic field fluctuation spectra at sub-ion scales basing on Cluster measurements. The authors used two-power-law approximation of the spectra with a break around electron scales. The considered dataset included a wide range of background conditions. This paper showed for the first time the wide distribution of power exponents at sub-ion scales (shown in Figure 1) which lay between −3.5 and −2.4 with a peak at −2.9. The results were shown to be similar to those in the undisturbed SW.
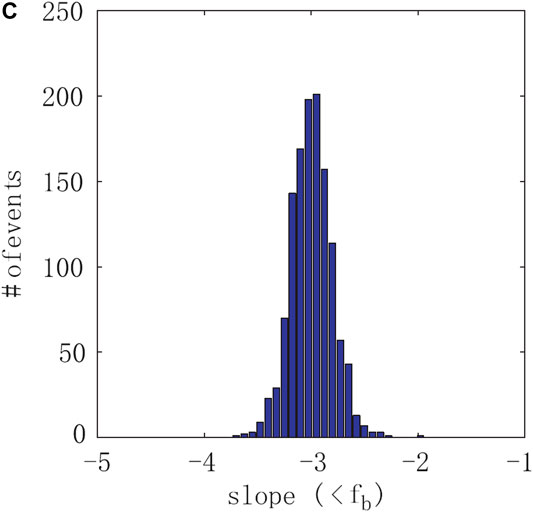
FIGURE 1. Distribution of the power exponent of magnetic field fluctuations inside the MSH at sub-ion scales [adapted from (Huang et al., 2014), Figure 5].
In situ data of the Cluster and Themis spacecraft in the MSH allowed Hadid et al. (2018) to perform the first quantitative estimate of the energy cascade rate for compressible MHD turbulence behind the BS. The authors examined two sets of the most common types of events – Alfvenic‐like and magnetosonic-like which were attributed to the developed turbulence, e.g., with Kolmogorov scaling at MHD scales. The compressible cascade rate was shown to be increased for compressible magnetosonic-like events. Interestingly, density fluctuations, which were known to be powerful inside the MSH were shown to enhance the anisotropy of the cascade rate, suggesting the dominant contribution of slow (or mirror) mode to the cascade formation. Further, Andrés et al. (2019) succeeded in obtaining quantitative estimations of the cascade rate for sub-ion scales as well, based on MMS data and analytical relations (Andrés and Sahraoui, 2017; Andrés et al., 2018; Sahraoui et al., 2020).
Fluctuations of Plasma Parameters Inside the Magnetosheath at Ion and Sub-Ion Scales: Advantages of Spektr-R Measurements
Direct spacecraft measurements revealed the importance of the compressible component in the formation of turbulent cascade in the MSH. Typically the turbulent fluctuations are considered as a mixture of linear MHD wave modes (or their kinetic counterparts) superimposed by pressure balanced structures (Tu and Marsch 1995; Howes et al., 2012; Bruno and Carbone 2013), coherent structures, or waves (e.g., Lion et al., 2016). While the incompressible Alfvenic mode is characterized by zero variations of density and parallel components of the magnetic field, for the compressible magnetosonic and mirror modes these parameters fluctuate. Thus, variations of parallel components of the magnetic field and/or density fluctuations are usually referred to as a representation of compressive fluctuations. Note that recently Borovsky (2020) suggested considering density fluctuations as a signature of plasma inhomogeneity rather than compressibility. As this review aims to summarize the results of experimental studies rather than give their theoretical interpretation, below we refer to the density fluctuations as the compressive component of the cascade consistent with most commonly used terminology. At the scales around the ion spectral break, the compressive component was only usually represented by the parallel component or magnitude of magnetic field fluctuations as measurements of plasma parameters were rare in the MSH at a high enough cadence to observe the spectral break and range of scales around it (e.g., propagation experiment on board ISEE-1 and -2 (Lacombe et al., 1995). In 2011, the Spektr-R spacecraft was launched with a BMSW instrument (Zastenker et al., 2013; Šafránková et al., 2013) on board. The spacecraft was in operation until 2019 and for the first time provided continuous measurements of ion flux value and direction with 0.031 s time resolution. Also, proton density, bulk and thermal velocity measurements with similar time resolution were available, but inside the MSH measurements of this kind were rare, though were often performed in the SW (Šafránková et al., 2015; Šafránková et al., 2016). The BMSW instrument observed both SW and MSH plasmas and for the first time allowed researchers to obtain statistically turbulent properties of directly measured plasma fluctuations at scales around the ion spectral break. As it was shown by Neugebauer et al. (1978), fluctuations of ion flux value mostly represent the fluctuations of proton density. Later, a direct comparison of density and ion flux value fluctuation spectra measured by the BMSW (Pitňa et al., 2016) confirmed their similarity. These arguments allowed for the usage of an ion flux fluctuation spectrum as a proxy of density spectrum. Also, the BMSW instrument provided measurements of the ion flux direction which were more affected by the velocity fluctuations.
The first statistical results of the BMSW measurements in the MSH were presented in Rakhmanova et al. (2016) and Riazantseva et al. (2016). Rakhmanova et al. (2016) dealt with more than 100 h of ion flux value and direction measurements. Most of the cases referred to the MSH flanks. The shape of the spectra, typical for the interplanetary magnetic field fluctuations with two power laws divided by the break only occurred for nearly half of the statistics. The authors obtained distributions of the slopes S1 and S2 which characterized the power laws at MHD and kinetic scales, respectively for 290 spectra. Figure 2 presents the obtained distributions for ion flux value (black columns) and polar angle (gray columns). The polar angle characterized the deviation of the ion flux vector from the Sun-Earth line and its fluctuations were used to analyze differences in density and velocity fluctuation spectra. This study showed that at the MHD scales, the spectra of both ion flux and polar angle fluctuation exhibited, on average, Kolmogorov-like scaling with an ∼f−5/3 power law (see Figure 2A). On the ion kinetic scales, the mean slope of the ion flux value fluctuations was −2.9 with a standard deviation of 0.3 (see Figure 2B), consistent with the statistical results of Huang et al. (2014) for the magnetic field (see Figure 1). Thus, ion flux and magnetic field fluctuation spectra were shown statistically to have similar slopes. In the MSH, this consistency was shown for the first time for kinetic scales. The spectra of polar angle fluctuations were shown to be steeper at these scales, with a mean value of the slope at −3.4 with a standard deviation of 0.6. This difference was suggested to be a signature of differences in the shapes of density and bulk velocity fluctuations at sub-ion scales in the MSH. Later, a similar result was obtained separately for density and ion velocity fluctuations in Chen and Boldyrev (2017). Also, a general similarity was pointed out between the scaling of ion flux spectra in the MSH and in the upstream SW (Riazantseva et al., 2016).
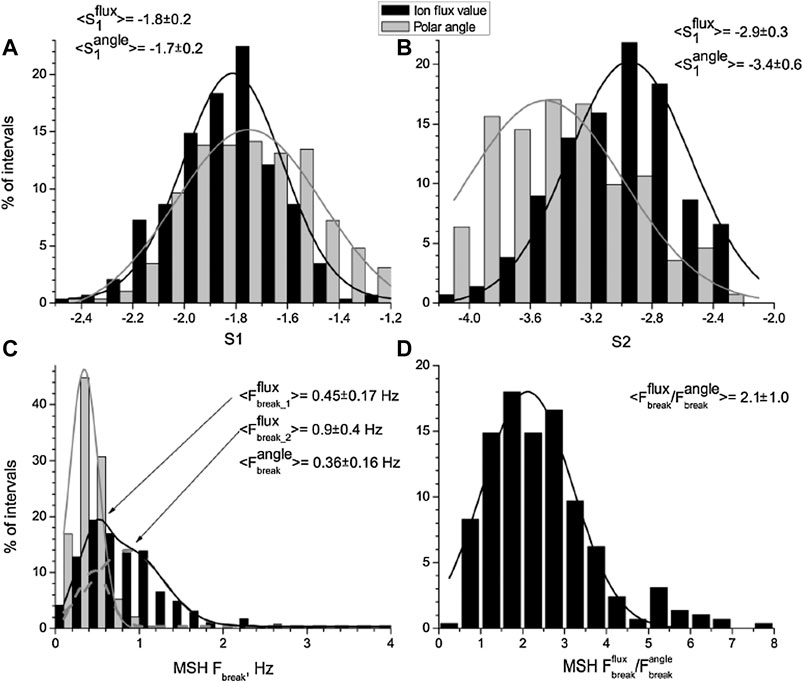
FIGURE 2. Distribution of spectral slope at MHD (A) and kinetic (B) scales and the break frequency (C) for ion flux value (black) and polar angle (gray) fluctuation spectra in the MSH; distribution of ratio between the break frequencies for the two parameters (D) [Adapted from (Rakhmanova et al., 2016)].
A significant difference was found between the break frequencies of ion flux value and polar angle fluctuation spectra. The distribution of the break frequency for ion flux value exhibited two maxima (see Figure 2C). Note that the two-peak distribution of the break frequency for ion flux fluctuations was also shown by the authors for large statistics in the SW (not shown here). The presence of two peaks may be a signature of two distinct dissipation mechanisms both in SW and MSH plasma. However, the nature of this difference is still not clear. Also, on average, spectra of the ion flux value had a break at scales two times as large as those of the polar angle (see Figure 2D). This result also uncovered differences in the spectra of density and velocity fluctuations.
As the measurements of the magnetic field were unavailable at Spektr-R, ion characteristic scales could not be determined directly except for proton inertial length. The results of Rakhmanova et al. (2016) suggested that there was no direct correspondence between the spectral break of ion flux fluctuations and proton inertial length. Also, for a single case study where magnetic field measurements were traced from the Themis-B spacecraft in the MSH, the authors demonstrated the absence of the direct correspondence between the break frequency and the Doppler-shifted proton gyroradius. Chen et al. (2014) and Šafránková et al., (2016) suggested that ion break takes place at different ion scales depending on plasma beta for the SW plasma, i.e., different leading processes are responsible for the dissipation of various background conditions.
As mentioned above, the typical two-power-law spectra were observed only in half of the cases in the MSH. For the other cases, the transition between the MHD and kinetic scales was modified in different ways. Rakhmanova et al. (2018a) demonstrated that the spectra of ion flux fluctuations inside the MSH formed three major groups of spectral shapes, presented in Figure 3: with two power laws divided by the break (52% of cases, panel a), with a bump around the break (19% of cases, panel b) and with a plateau around the break (21% of cases, panel c). A similar difference in spectral shape was also demonstrated for the SW though the proportion between the groups of cases was different (Riazantseva et al., 2017). Also, there was a small portion of events (∼8%) with non-linear steepening of the spectra at the kinetic scales, not shown here (in the SW this type is observed more frequently).
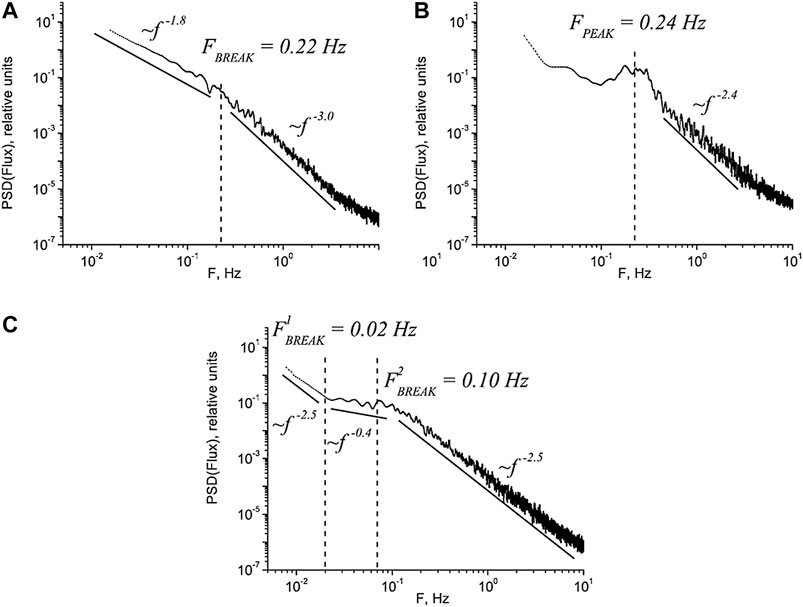
FIGURE 3. Different shapes of ion flux fluctuations observed inside the magnetosheath: (A) with two power laws and break, (B) with bump around the spectral break, and (C) with plateau around the spectral break [Adapted from (Rakhmanova et al., 2018a), Figure 3].
Note that a plateau in spectra of density (or ion flux) fluctuations was observed more often in the SW (Šafránková et al., 2015; Šafránková et al., 2016; Riazantseva et al., 2017) compared to the MSH. According to theoretical suggestions (Chandran et al., 2009), spectra with a plateau can be formed as the superposition of the typical two-power-law spectrum, including density fluctuations passively convected by Alfvenic turbulence, and kinetic Alfven wave fluctuations, which arise at ion scales and are compressive in nature. The occurrence of the plateau was suggested to be influenced by the power of the cascade at large scales and by plasma parameter β. Figure 4 shows the distribution of PSD value, measured for a frequency range of 0.018–0.022 Hz for the mentioned three groups of spectra in the MSH. Here the statistics of Rakhmanova et al. (2018a) were used which included ∼1,100 spectra of ion flux fluctuations. The frequency band was chosen to consider MHD scales according to statistical results (Rakhmanova et al., 2016). The panels in Figure 4 correspond to spectral shapes, presented in Figure 3. The results correspond well to the predictions of Chandran et al. (2009): spectra with plateau are usually less powerful at large scales (here, at the MHD scales) than those with two power laws. However, spectra with a bump are characterized by even smaller power at MHD scales. This may be due to the dominance of instabilities during quiet background conditions. The reasons for this difference are worth analyzing in the future.
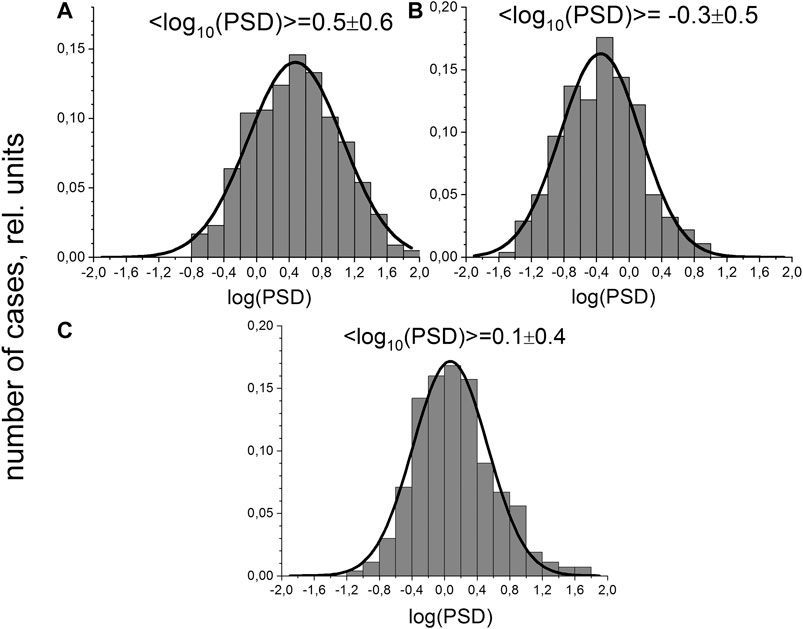
FIGURE 4. Distribution of MHD-scale PSDs for spectra of ion flux fluctuations, characterized by different shapes: (A) two power laws with break, (B) with bump, (C) with plateau; the corresponding types of spectra are presented in Figure 3. (Adapted from PHD work by L. Rakhmanova, 2019).
Recent Results on Turbulence Exploration by MMS
All the studies mentioned above pointed out the necessity of simultaneous measurements of both plasma and magnetic field parameters to clearly understand the nature of turbulence. In 2015, the MMS mission (Burch et al., 2016) was launched. The mission consisted of four identical satellites, each including a similar set of instruments. Merged data from the magnetometers FGM (Russell et al., 2016) and SCM (Le Contel et al., 2014) allow for the consideration of magnetic field fluctuations at frequencies up to 1 kHz (Fischer et al., 2016). A fast plasma instrument (FPI, Pollock et al., 2016) provides moments of ion distribution function, e.g., density, velocity, and temperature, with a 0.15 s time resolution in the burst mode while the same parameters for electrons are measured with a 0.031 s time resolution. Thus, simultaneous direct measurements of plasma and magnetic field parameters became available for the first time at boundary layers of the near-Earth’s space as well as in the SW, with time resolution being sufficient for exploring plasma turbulence at kinetic scales. In this section some of the recent results of turbulence exploration in the MSH by MMS are discussed, while a number of them are described in subsequent sections, where more specific points are focused on.
Chen and Boldyrev (2017) performed a comprehensive case study into MMS data during the 70s in the vicinity of the dusk-side magnetopause. The authors demonstrated both electron density and magnetic field fluctuation spectra to follow the f−2.8 power law between ion and electron scales which was close to the previous observations for the magnetic field by Cluster (Huang et al., 2014) and for ion flux by Spektr-R (Rakhmanova et al., 2016). The ion velocity fluctuations formed a spectrum with a −3.5 power exponent which confirmed the conjectures of Rakhmanova et al. (2016) concerning differences in density and velocity spectra at sub-ion scales. Based on normalized electron density spectra and the coherence analysis, Chen and Boldyrev (2017) suggested the low frequency KAW nature of turbulence. The authors also suggested an inertial kinetic Alfven wave mode to form a turbulent cascade at electron scales.
The nature of turbulent fluctuations was also addressed by Roberts et al. (2018). Based on MMS measurements in the inner MSH, the authors managed to calculate the Alfven ratio and suggested that for the single considered interval the ratio corresponded to KAW turbulence rather than to kinetic slow waves. Kolmogorov scaling was shown to exist at frequencies below the ion spectral break for both the magnetic field and density fluctuations.
Stawarz et al. (2016) performed turbulence exploration in regions, usually dominated by Kelvin-Helmholtz instability, i.e., in the vicinity of the equatorial flanks of the magnetopause. A magnetic field magnitude spectrum was shown to follow Kolmogorov scaling at frequencies below ion break, while above the break, the spectrum followed the f−3.2 power law. At the MHD scales, the normal components of ion as well as electron velocity fluctuations followed fluctuations of the normal component of the magnetic field. On the opposite side, at sub-ion scales, the velocity spectra diverged: the normal component of the electron velocity fluctuations flattened and followed the electric field fluctuation spectrum, while the normal component of the ion velocity fluctuations became steeper than for normal magnetic field fluctuations. The authors suggested that this was due to the decoupling of ions at sub-ion scales, while the electron remained frozen in the magnetic field.
MMS measurements allowed for careful studies of turbulence anisotropy inside the MSH. Roberts et al. (2019) presented a case study of anisotropy of turbulent fluctuations both for fields and scalars, i.e., magnetic field, density, velocity, and thermal speed. Consistent with the results of Roberts et al. (2018) and Stawarz et al. (2016), the ion velocity fluctuations were shown to form steeper spectra at ion kinetic scales compared to the spectra of magnetic field fluctuations. Also, the strong anisotropy of spectral indices was pointed out: the spectra of all the considered parameters were steeper in the direction parallel to the magnetic field. The authors suggested that the compressive component of the fluctuations inside the MSH was different from those of the SW and was likely to be formed by compressive coherent structures.
MMS data helped to reveal the importance of the compressive fluctuations in the MSH and their differences from those in the SW. Breuillard et al. (2018) showed highly compressive fluctuations inside the MSH, with the compressibility level higher behind the quasi-parallel BS vs. quasi-perpendicular. The authors concluded that the MSH turbulence was formed by coherent structures superimposed on the Alfvenic fluctuations.
The MMS data allowed for comprehensive studies of reconnection processes, both at ion and electron scales, and their effects on turbulence and dissipation. Previously in situ evidence of the reconnection have been rare (e.g., Retinò et al., 2007). Vörös et al. (2017) managed to test a reconnection event downstream of the quasi-parallel BS, when the MMS spacecraft crossed both ion and electron diffusion regions. Vörös et al. (2019) managed to compare different measures of energy exchange or dissipation based on direct measurements by MMS in the reconnecting current sheets behind the quasi-parallel BS. The authors showed the presence of net irreversible work done in the current sheets by the electric field. Also, for the analyzed case, the dissipation occurred preferentially in a direction parallel to the magnetic field. Stawarz et al. (2019) presented an analysis of two intervals in the MSH close to the BS, probed by MMS. The intervals had a different number of reconnecting current sheets with electron-scale size. The magnetic field fluctuation spectra for the two considered cases exhibited similar features at frequencies up to 10 Hz, i.e., as small as electron scales. The spectra followed the f−1.4 power law at MHD scales and the f−2.7 and f−2.8 power law at sub-ion scales. The differences occurred at electron scales and were attributed to the affection of the electron-scale reconnection on the electrons’ dissipation. These results were consistent with the earlier findings of Phan et al. (2018) revealing the reconnection events at electron scales which did not generate ion jets.
Multi-spacecraft MMS data allowed for direct calculations of the energy cascade rate in the MSH. As mentioned above, Andrés et al. (2019) performed quantitative estimations of the energy cascade rate at sub-ion scales. Bandyopadhyay et al. (2018) succeeded to compare energy cascade rates at an energy containing scale, at the inertial range, and at the dissipation range. The authors focused on the interval containing nearly incompressive fluctuations and suggested a higher energy cascade rate in the MSH turbulence than in the SW turbulence. Thus, the authors pointed out significant differences between turbulence upstream and downstream of the BS. Further, the MMS advantages were employed to explore the energy conversion at kinetic scales. Bandyopadhyay et al. (2020) considered the statistical distribution of pressure-strain interactions and compared it to the results of the kinetic simulations. The authors suggested that analyzing the statistics of such interactions gave direct information on internal energy production without employing any conjectures of mechanisms. The conversion of energy was shown to occur near intense current sheets rather than within them.
All the studies based on MMS measurements, available to date, show the great potential of these data in the analysis of MSH turbulence below ion scales. Considering simultaneous measurements of the MMS and Cluster and probable Themis and Spektr-R spacecraft could give a substantial contribution to our understanding of the compressible turbulence in the MSH. Presented case studies as well as statistics provide a basic view of the features of turbulence inside the MSH and its similarity and differences from the turbulence in the undisturbed SW. However, MSH plasma always evolves in the confined space. Also, fluctuations of plasma and magnetic field parameters in the MSH not only include the fluctuations borne at the BS, but also those originating from the upstream SW. Further sections focus on the contribution of these two factors to the development of the MSH turbulence.
Magnetosheath Turbulence Influenced by the Boundaries
Turbulence Development Between the Bow Shock and Magnetopause
The above-mentioned case studies showed similarities in spectral shapes for magnetic field and density fluctuations inside the MSH. However, different indices of the fluctuation spectra were demonstrated when considering magnetosheath plasma at regions adjacent to the bow shock and farther from it (Alexandrova et al., 2008; Czaykowska et al., 2001 etc.). Thus, one can suspect that the distance to the BS can contribute to the formation of the cascade.
BS contribution to MSH turbulence recently became a topic of interest. Yordanova et al. (2008) presented a case study of the evolution of structure functions of magnetic field fluctuations with distance from the BS with the help of Cluster data. The study was performed behind the quasi-parallel BS where variations of the field components were of the order of the mean field, i.e., the prevalent direction of the field could not influence the anisotropy of the turbulence. The intermittency level was shown to increase with the distance from the BS together with the anisotropy of magnetic field fluctuations. Also, the authors presented slightly steeper spectra of the magnetic field fluctuations at the kinetic scales at the spacecraft which was located closer to the BS then others (with distance of about 1 RE). In a study by Gutynska et al. (2009), the slope of the magnetic field magnitude fluctuation spectrum obtained by Cluster at MHD scales was shown to increase gradually from −1.6 to −1 with the distance from the magnetopause.
Rakhmanova et al. (2017) presented a case study of the evolution of turbulence features across the MSH behind the quasi-perpendicular BS. The study considered a single crossing of the MSH by the Spektr-R spacecraft and examined spectra of ion flux fluctuations at ion and sub ion scales. Fourier spectra of ion flux fluctuations were calculated over 8 min intervals shifted in time by 1 min for the whole crossing of the MSH. Though magnetic field measurements were not available at Spektr-R, the MHD modeled predictions were adapted to obtain parameters of the magnetic field for given dynamics of upstream SW parameters. Note that in that case the model did not include ion-scale fluctuations, though it fits for the determination of mean parameters through the analyzed intervals. Results of this study are illustrated in Figure 5, adapted from the mentioned paper. The figure presents the evolution of the following parameters during the crossing: (A) the ion flux value, (C) the mean PSD obtained for each spectrum at frequency band 2 ± 0.1 Hz, i.e., at the kinetic scales, (D) the spectral slope S2 at the kinetic scales, (E) break frequency of the spectra (in the case of a bump in the spectrum instead of the break, the triangles denote the bump frequency), (F) the modeled values of the magnetic field magnitude and proton parameter β, (G) plasma characteristic frequencies: ion cyclotron frequency (black line), gyrostructure frequency (blue line), and inertial length frequency (gray line) together with the break frequency (red line), and (H) kurtosis/flatness value calculated at the set of time scales: 0.1, 1, 10, and 100 s (shown in different colors). Kurtosis values were calculated over intervals of 15 min duration (∼3×104 data points) to enable the reliable determination of the parameter. For the parameters calculated over the interval, each point refers to the center of the interval. The figure shows that the break frequency of the ion flux fluctuation spectra followed different characteristic scales across the MSH (see panel g) for steady upstream SW conditions. This change in the break frequency was suggested to be due to differences in dominating processes which governed the dissipation of energy at ion scales at different distances from the BS and magnetopause. Also, signatures of highly intermittent plasma were performed in the regions close to the boundaries, while in the middle MSH, far from the BS and the magnetopause, plasma did not exhibit intermittent features. This can be seen in Figure 5H by the increasing of the flatness value with the decreasing scales (or time increments) in regions close to the boundaries. Note that this result was obtained behind the quasi-perpendicular BS, while Yordanova et al. (2008) and Kozak et al. (2012) presented a low intermittency level behind the quasi-parallel BS. On the other hand, an increased level of intermittency was shown in laboratory plasma in the vicinity of edges (Budaev et al., 2011), that show a similarity of the processes developing in turbulence close to the boundaries.
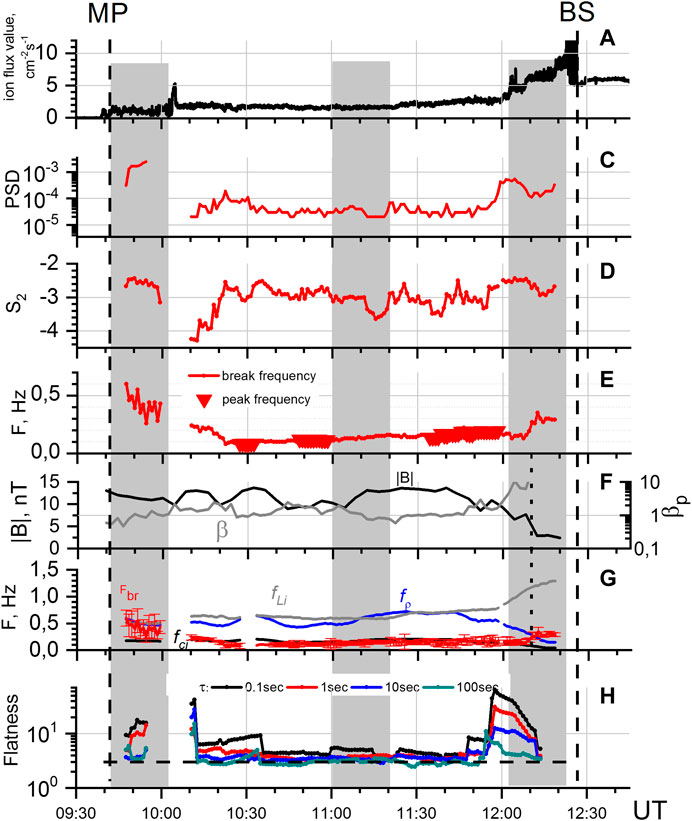
FIGURE 5. Evolution of the MSH turbulence at ion scales according to Spektr-R observations during single MSH crossing on February 9, 2012: (A) ion flux value, (C) PSD of ion flux fluctuation spectrum, (D) spectral slope at the kinetic scales, (E) frequency of spectra break (line) or peak (triangles), (F) modeled magnetic field (black) and plasma parameter β (gray), (G) plasma characteristic frequencies and the break frequency (red), (H) flatness (kurtosis) of ion flux fluctuations, calculated at different scales. (Adapted from Rakhmanova et al., 2017), panel (B) and polar angle data were eliminated.
Challenging results in boundaries’ influence on MSH turbulence were obtained with statistical studies. Huang et al. (2017) analyzed the modification of spectra throughout the MSH with the help of large statistics of the Cluster magnetic field data. The authors considered whole dayside MSH during three years of Cluster operation. In the region close to the subsolar BS, the magnetic field spectra usually follows f−1 scaling at the scales above the ion break while farther from the BS and toward the flanks spectra became more like the Kolmogorov spectrum with f−5/3 scaling. The authors suggested that crossing the BS resulted in the redistribution of energy in the cascade and the disappearance of the Kolmogorov inertial range, i.e., the energy, injected into the system was dissipated immediately.
Rakhmanova et al. (2018b) also analyzed the dependence of the spectral slopes of ion flux fluctuations at the scales above the break on the distance to the BS and the magnetopause based on statistics of Spektr-R measurements in the MSH. The analysis revealed a wide distribution of spectral slopes peaking at −1.2 in the regions adjacent to the BS. Thus, spectra were significantly flatter than predicted by the theories of developed turbulence and observed in the undisturbed SW. However, spectra with f−1 scaling were not always observed in the vicinity of the BS like those shown by Huang et al. (2017). Note that the results of Huang et al. (2017) were obtained in the dayside MSH while the results of Rakhmanova et al. (2018a) mostly referred to the nightside flank MSH. This is the most probable reason for the more pronounced results of Huang et al. (2017). Farther from the BS, the distribution of the spectral slopes had a peak at −5/3, so typically the spectra followed Kolmogorov scaling. Note, that though the values of the slope were scattered, the distributions exhibited a clear difference in the vicinity of the BS and in other parts of the MSH. Figure 6 demonstrates the comparison between the results of Huang et al. (2017) for magnetic fields fluctuations and Rakhmanova et al. (2018b) for ion flux fluctuations obtained at the MHD scales.
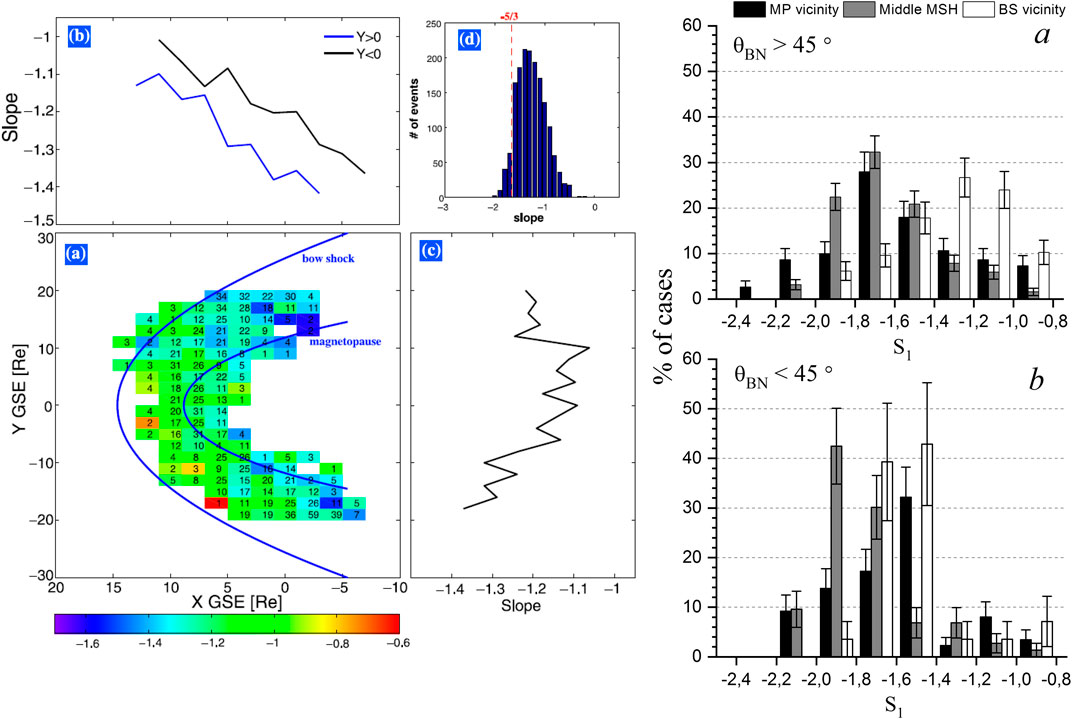
FIGURE 6. Left columns–mean values of the spectral slope of magnetic field fluctuations at MHD scales at various locations inside the MSH [adapted from (Huang et al., 2017)]; right column–distribution of values of spectral slope of ion flux fluctuations at MHD scales at different distances from the MSH [adapted from (Rakhmanova et al., 2018b)].
The influence of the BS on the spectra of magnetic field fluctuations at the kinetic scale was suggested to be insignificant (Huang et al., 2017). Rakhmanova et al. (2018a) suggested that there was a slight steepening of the ion flux fluctuation spectra closer to the BS. A comparison between the two studies is presented in Figure 7 (in the same format as Figure 6). Just behind the quasi-perpendicular BS, the spectra had a slope of −3.2 on average while farther from it, the slope was usually closer to −2.8. The standard deviations for the distributions were ∼0.4. The evolution of the slope was shown to be even more pronounced behind the quasi-parallel BS (the errors represent standard deviations): spectra of the ion flux fluctuations followed the f −3.4±0.3 power law in this region while in the middle MSH and close to the magnetopause the slopes were −2.7 ± 0.4 and −3.0 ± 0.5, respectively. Thus, significant dumping of the compressive fluctuations occurred behind the quasi-parallel bow shock.
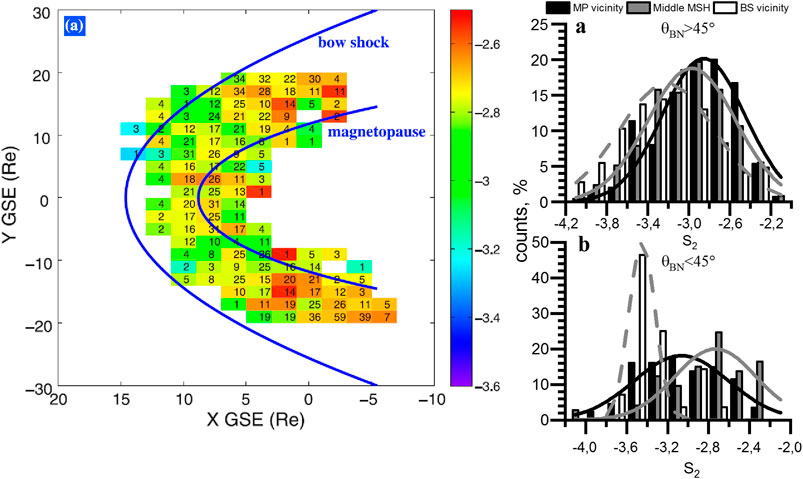
FIGURE 7. left columns–mean value of the spectral slope of magnetic field fluctuations at kinetic scales at various locations inside the MSH (adapted from Huang et al., 2017); right column–distribution of values of spectral slope of ion flux fluctuations at kinetic scales at different distances from the MSH boundaries [adapted from (Rakhmanova et al., 2018a)].
Rakhmanova et al. (2018a) also considered differences in the shapes of ion flux fluctuation spectra at various regions of the MSH. The classification of spectral shapes was used which was performed in the Section Fluctuations of Plasma Parameters Inside the Magnetosheath at Ion and Sub-Ion Scales: Advantages of Spektr-R Measurements, and the statistics showed that 1) spectra with two power laws were dominant at all distances from the BS, 2) spectra with a bump were most likely to occur in the vicinity of the BS, while 3) spectra with a plateau were usually found in the regions adjacent to the magnetopause. The authors suggested a different scenario of turbulence development in the vicinity of the bow shock and the magnetopause. Spectra were similar to the analytical predictions of Chandran et al. (2009) in the region close to the magnetopause, like it was shown in Section Fluctuations of Plasma Parameters Inside the Magnetosheath at Ion and Sub-Ion Scales: Advantages of Spektr-R Measurements. On the other hand, turbulence was strongly dominated by instabilities (most probably, mirror instability) closer to BS which led to the formation of the bump and the damping of compressive fluctuations in the turbulent cascade.
Macek et al. (2018) presented three cases of MMS measurements of magnetic field magnitude and ion velocity value at different distances from the MSH. The cases were observed behind quasi-parallel or oblique BS in nearly subsolar MSH. For the regions close to the boundaries, the authors showed a −2.60 ± 0.06 and −2.68 ± 0.05 power exponent at kinetic scales for fluctuations of magnetic field and velocity, respectively, in accordance with some of the theoretical −8/3 scaling (e.g., Boldyrev and Perez, 2012), which accounted for the geometry of structures. In the middle MSH, spectra of magnetic field fluctuations demonstrated a −2.24 ± 0.09 power exponent at the kinetic scales, which is somewhat flatter than the typical value observed in the statistical studies mentioned above, however, close to −7/3 which was predicted in the framework of KAW turbulence without considering the geometry of structures (e.g., Schekochihin et al., 2009). For this case, no high-resolution plasma measurements were available. However, at MHD scales, the velocity spectrum demonstrated clear Kolmogorov-like scaling with the slope close to −5/3 at frequencies below the break while the spectrum of magnetic field fluctuations was strongly different from the theoretical predictions of the developed turbulence and exhibited f−0.77±0.06 power law.
Recently, Li et al. (2020) performed large statistics of burst-mode MMS data which covered both flank and subsolar MSH regions at different distances from the boundaries. Magnetic field, density, and velocity fluctuations were analyzed. The authors demonstrated the steepening of the MHD part of magnetic field fluctuation spectra across the MSH, with slopes of on average −1.46 near the BS and −1.91 near the magnetopause. The standard deviations for the reported distributions were ∼0.25, thus the observed dependence was statistically significant. For the kinetic scales, only slight flattening of the spectra were presented, with slopes changing from −2.9 to −2.7 from the BS toward the magnetopause. However, the values of the slopes were highly scattered for the region in the vicinity of the BS, so the standard deviation was of about 0.6, making the change of the slope across the MSH negligible. The evolution of magnetic field spectra was shown to be similar behind the quasi-parallel and quasi-perpendicular BS. In the case of density, spectra had a −1.87 slope at MHD scales in the vicinity of the BS of both types. Behind the quasi-parallel BS, the slope decreased up to −2.44 close to the magnetopause while for the quasi-perpendicular BS, it decreased up to −2.17. However, standard deviations of ∼0.6 were performed for the observed averages, which implied no significant dependencies in that case. No differences of velocity fluctuations spectra at MHD scales were shown across the MSH. No dependence was found for kinetic-scale plasma fluctuations on the distance from the BS. Also, the authors demonstrated that at MHD scales, the magnetic field fluctuation spectra were flatter at the flank compared to the subsolar region, which was consistent with Huang et al. (2017), while features of density spectra showed no changes. The presented spectral slopes at the MHD scales were somewhat different to those obtained previously by Huang et al. (2017); Rakhmanova et al. (2018a); Rakhmanova et al. (2018b). Most probably, this difference was due to considering quite short data intervals (∼several minutes), which could result in errors in slope determination at MHD scales. However, the obtained dependencies on the position inside the MSH qualitatively corresponded to the previous studies.
Examining the dynamics of the turbulence inside the MSH has several difficult points. First, the turbulent cascade is strongly affected by the set of waves and instabilities arising at the bow shock and in the vicinity of the magnetopause (mirror instabilities, Kelvin-Helmholtz instabilities, etc.) and the presence of local structures like Alfven vortices (Alexandrova et al., 2006). Second, dynamics due to the movement between the boundaries is superimposed by the dynamics of the MSH itself as a response to the changes of the upstream SW conditions. Difficulties of the experimental analysis also come from the limited number of measurements, provided simultaneously from different points inside the MSH at various distances. Recent missions (Cluster, MMS) were focused on sub-ion plasma physics and could consider the evolution of turbulence at distances of the spacecraft separations, i.e., 10–1,000 km. To analyze the evolution of the fluctuation spectra while plasma moves through the MSH, a larger separation (of the order of the MSH thickness and larger) between the spacecraft is required. Such analysis can be prepared with the help of simultaneous data from different spacecraft missions like Themis, Cluster, Spektr-R, and MMS. However, combining data from different sets of instruments is quite difficult due to differences in the organization of spacecraft orbits and the absence of intercalibration for the instruments.
Recently, Rakhmanova et al. (2020b) performed a case study of evolution of compressive turbulence inside the MSH with the help of Spektr-R plasma and Themis magnetic field measurements. For quiet background conditions, the spectra of compressive fluctuations were compared 1) at two points, placed at closely located streamlines at the flank MSH at distances ∼30 RE, and also 2) at two points in the vicinity of the BS, but at different distances from the BS nose. The sketch of the spacecraft positions and comparison of spectra of ion flux fluctuations from the Spektr-R and magnetic field magnitude fluctuations from the Themis-B/-D are presented in Figure 8 for the two considered cases. The results demonstrated that 1) at the MHD scales, the spectra of compressive fluctuations could have Kolmogorov scaling in the vicinity of the flank BS and stay unchanged at distances up to 30 RE; and 2) when plasma crossed the dayside BS, the modification of the spectrum strongly depended on the distance to the BS nose. Note that in that study the cases referred to different types of the BS, which also might contribute to the differences in the results. However, these results first provided direct confirmation of the suggestions which came from statistical studies of Huang et al. (2017); Rakhmanova et al. (2018a); Rakhmanova et al. (2018b) on the evolution of turbulent features across the MSH and differences in BS influence on the downstream turbulence at the dayside and flank MSH.
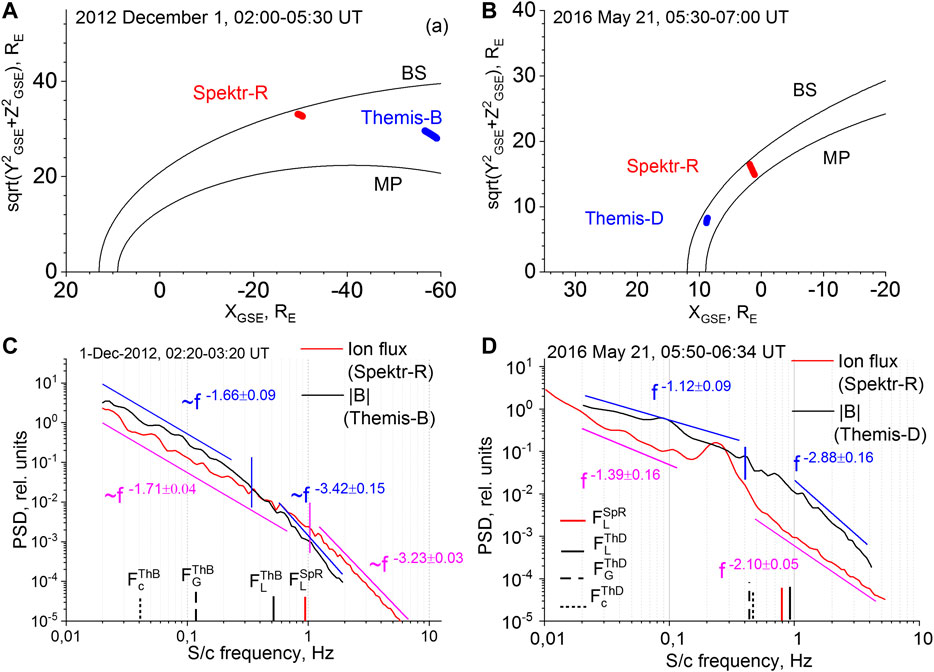
FIGURE 8. Comparison of the compressive fluctuation spectra (A,C) close to the BS (red line) and in the middle MSH (blue line) and (B,D) in the vicinity of the BS close to the BS nose (blue line) and at the flank (red line). [Adapted from Figures 1A, 3, 4, 6 of (Rakhmanova et al., 2020b)].
Differences of turbulent features behind the quasi-parallel and quasi-perpendicular Bow Shock
As mentioned in the introduction, the dynamics of fluctuations inside the MSH strongly depends on the mutual direction of the IMF and the local BS normal. A comparison of different case studies also implies the dependence of turbulence features on an θBN angle. The current section summarizes the results of the direct comparison of turbulence affected by the BS of different geometry.
Macek et al. (2015) used Themis data to compare the behavior of the Elsässer variables behind the BS with different geometry. The authors showed signatures of the most populated portion of anti-sunward propagating waves compared to those propagating toward the Sun behind the quasi-perpendicular BS. On the opposite side, the populations of waves of different directions are equal behind the quasi-parallel BS. Turbulence behind the quasi-perpendicular BS was shown to be more intermittent compared to the one behind the quasi-parallel BS.
Based on the whole set of MMS data, Breuillard et al. (2018) presented a comparison of spectral indices, anisotropy, and compressibility level behind quasi-parallel and quasi-perpendicular BS. At the MHD scales, density and magnetic field fluctuations (both parallel and transverse component) exhibited similar scaling. Interestingly, behind the quasi-perpendicular BS the spectra were characterized by a −1 power exponent while behind the quasi-parallel bow shock, typical Kolmogorov-like scaling was observed. This difference was similar to the results of the statistical and case studies (Rakhmanova et al., 2018b; Rakhmanova et al., 2020b). Note that results of Breuillard et al. (2018) were obtained in the dayside MSH. At the kinetic scales, four considered spectra showed the same f−2.8 power laws both for magnetic field and density fluctuations. Thus, upstream BS geometry does not affect kinetic-scale fluctuations in the MSH.
Yordanova et al. (2020) examined MMS data behind quasi-parallel and quasi-perpendicular BS based on single intervals. The authors analyzed properties of thin current sheets and showed their preferential population behind the quasi-parallel BS and a small amount behind the quasi-perpendicular BS. The study considered turbulent spectra associated with thin current sheets downstream of the quasi-parallel BS and without signatures of current sheets downstream of the quasi-perpendicular BS. The authors presented similar ∼f−2.8 scaling of the magnetic field magnitude fluctuation spectra at the kinetic scales behind the BS of both kinds. However, the spectrum behind the quasi-perpendicular BS was dominated by a large bump at the scales of transition from MHD to kinetic scales, and the spectrum was significantly flatter than the Kolmogorov-like spectrum at the MHD scales. On the opposite side, behind the quasi-parallel BS, the spectrum of the magnetic field magnitude fluctuations exhibited clear Kolmogorov scaling and two power laws. The results of the study are presented in Figure 9. The results are consistent with the results obtained with the help of Cluster data (Sundkvist et al., 2007) and also with the statistical results by Rakhmanova et al. (2018b) obtained by plasma measurements on board Spektr-R.
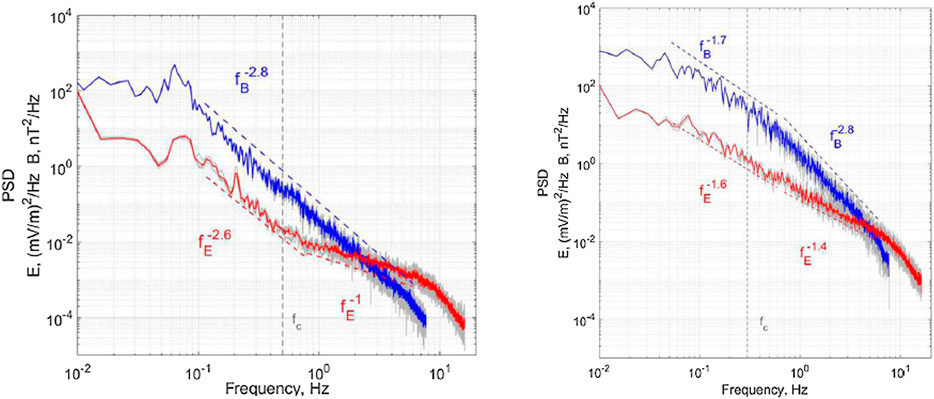
FIGURE 9. Spectra of magnetic (blue line) and electric (red line) field magnitude fluctuations behind the quasi-perpendicular (left panel) and quasi-parallel (right panel) BS [Adapted from (Yordanova et al., 2020)].
Rakhmanova et al. (2020b) statistically analyzed the influence of θBN angle on the power exponents of ion flux fluctuation spectra at MHD and kinetic scales. Crossing of the quasi-perpendicular BS was shown to result in flattening of the spectra at MHD scales and their deviation from the Kolmogorov scaling (Figure 10, top). On the contrary, spectra with a −5/3 power exponent can more often be found behind the quasi-parallel BS. Upstream foreshock processes and an altogether higher level of fluctuations were suggested to result in the formation of the turbulent cascade upstream of the shock, which led to insignificance of the BS effect during the crossing. On the other hand, steady conditions upstream of the quasi-perpendicular BS result in a greater impact on the cascade and disbalance of the energy in it, leading to a deviation of the spectral shape from those predicted by the developed turbulence theories. At the kinetic scales (Figure 10, bottom), steeper spectra were usually observed behind the quasi-parallel bow shock which is consistent with Li et al. (2020), and imply damping of plasma fluctuations in this region. On the other hand, the results of Li et al. (2020) demonstrated no differences in magnetic field spectra behind the quasi-parallel and quasi-perpendicular BS.
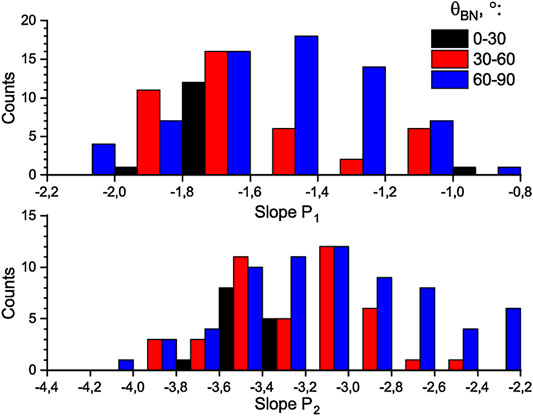
FIGURE 10. Distribution of the slopes S1 (top panel) and S2 (bottom panel) for ion flux fluctuation spectra measured behind the quasi-perpendicular (blue), oblique (red), and quasi-parallel (black) BS [adapted from (Rakhmanova et al., 2020a)].
Rakhmanova et al. (2020a) presented three examples of spectra of ion flux fluctuations just behind the quasi-perpendicular BS (θBN > 70°) and all three of them were characterized by different spectral slopes at MHD scales - from −5/3 to −1 (see detailed description of the work in the next section). Interestingly, all the analyzed cases occurred in the flank MSH, so the difference in slope was unlikely to be due to distance from the BS nose. Moreover, statistical studies of Huang et al. (2017); Rakhmanova et al. (2018a); Rakhmanova et al. (2018b) did not reveal significant differences of the turbulence features at different MSH flanks. The difference in slopes may be due to a set of factors, which are hard to distinguish, and mainly, differences in the modification of spectra at the BS for various upstream conditions like SW parameters. The next section is dedicated to our first results in analyzing those factors.
Upstream Parameters Influencing the Modification of Turbulent Cascade at the Bow Shock
In the SW, the variability of spectral properties has been known for a long time to be controlled by background conditions in plasma, like the angle between the velocity and magnetic field vectors or plasma parameter β (e.g., Chen et al., 2014). For the MSH plasma, distance to the boundaries (BS and magnetopause) was shown to contribute significantly to turbulence development. However, statistical studies (e.g., Rakhmanova et al., 2018a; Rakhmanova et al., 2018b; Li et al., 2020) as well as a large set of case studies revealed wide distributions of spectral indices in the regions close to the BS, including the conservation of Kolmogorov scaling across the BS for some cases as well as its absence for others. Therefore the challenging question is which factors could control the modification of turbulent cascade at the BS.
Rakhmanova et al. (2020a) considered the influence of the characteristics of fluctuation spectrum in the upstream SW on the properties of downstream turbulence. The authors considered three cases of the quasi-perpendicular BS crossing at the flank MSH by the Spektr-R spacecraft and analyzed ion flux fluctuation spectra upstream and downstream from the BS for stable background conditions. Comparisons of the upstream and downstream spectra, adapted from the paper, are presented in Figure 11. All three cases referred to typical spectral shapes in the upstream SW: nearly Kolmogorov scaling at frequencies below the break and with the plateau existed at the scales of transitions from MHD to kinetic regimes. However, the spectra were characterized by quite different power law exponents at the kinetic scales, which was attributed to different local background conditions. Direct comparison of the spectra obtained at both sides from the BS demonstrated that at the MHD scales, crossing of the BS could result either in significant flattening of the spectrum with the power exponent ∼ −1 (panel a), or in moderate flattening of the spectrum to the power exponent of −1.3 (panel b), or in no changes in the power exponent at all (panel c). At the kinetic scales, on the contrary, crossing of the BS seemed to result only in a slight steepening of the spectrum. Interestingly, slopes of the spectra at kinetic scales seemed to be dependent on the same slope of the upstream spectra. All three analyzed cases referred to similar BS geometry, however, they were observed during periods corresponding to different large-scale SW flows according to the classification by Yermolaev et al. (2009); Yermolaev et al. (2015). The case with the most crucial changes in the MHD part of the spectrum was observed during SW of type “Sheath,” e.g., the compressed region in front of the interplanetary manifestation of the coronal mass ejection (CME) or in front of the magnetic cloud (MC). The case which was characterized by no changes in the MHD part of spectrum was observed during periods of steady slow SW flow. Another case corresponding to the turbulent cascade developing in the MC was characterized by moderate changes in spectrum during the crossing. A recent study (Rakhmanova et al., 2020a) also demonstrated the Kolmogorov scaling of the MHD part of ion flux fluctuation spectrum in the vicinity of the BS (see Figure 8, on the left). The considered spectrum was observed behind the quasi-parallel BS during upstream slow steady SW.
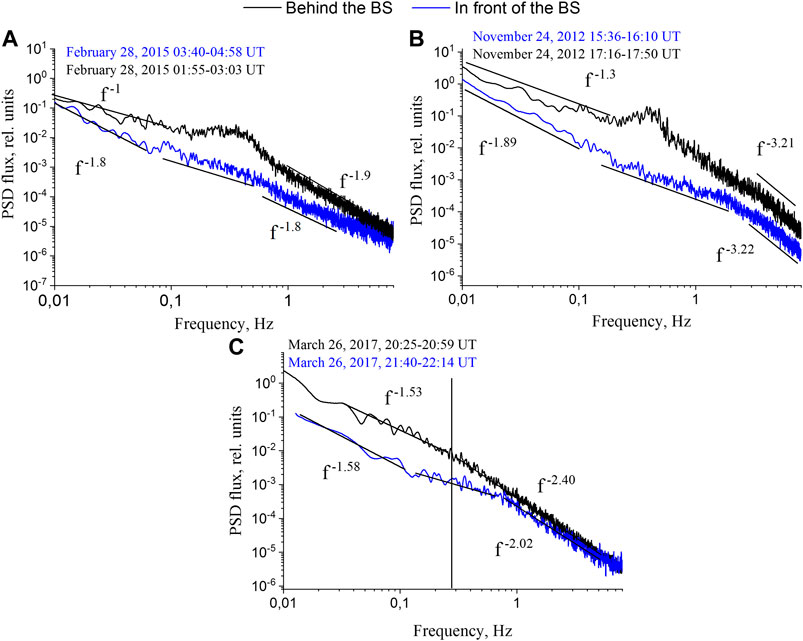
FIGURE 11. Three case studies of influence of the upstream SW turbulence on the characteristics of turbulence spectrum of compressive fluctuations downstream of the BS. (Adapted from Figures 1E, 2 of (Rakhmanova et al., 2020a), colored).
Statistical data by Spektr-R measurements in the MSH adjacent to the BS (Rakhmanova et al., 2020b) demonstrated the influence of the large-scale SW type on the modification of the turbulent cascade at MHD scales at the BS. Significant changes at the BS were shown to be most probable during compressed SW flow of type “Sheath,” while steady SW flow was typically accompanied by the nearly Kolmogorov scaling of ion flux fluctuation spectra downstream of the BS similar to the results shown in the previous section. Figure 12 presents the mean values of spectral slope at the MHD scales behind the BS for different upstream SW types. The interaction of the SW flow of different types with the BS was shown to be accompanied by an occurrence of different spectral shapes of ion flux fluctuations in the MSH. While typically (Rakhmanova et al., 2018a) in the MSH adjacent to the BS, the spectra exhibited two power laws with a break or broad peak instead of the break (see Figure 3A,B of the current paper, adapted from (Rakhmanova et al., 2018a)). During the periods of SW of type “Sheath” behind the BS, the spectra were usually characterized by the plateau (see Figure 3C). Differences in the effect of the various SW types on the MSH turbulence may result from differences in turbulence properties in the SW. Riazantseva et al. (2020) demonstrated alterations in sub-ion properties of turbulent spectra when considering SW flow of compressed and non-compressed types. Recent results by Borovsky et al. (2019), Borovsky (2020) also demonstrated distinct properties of MHD-scale fluctuations in large-scale flows of various types and different levels of Alfvenicity. The presented results therefore suggest a strong relationship between upstream SW processes and downstream MSH turbulence.
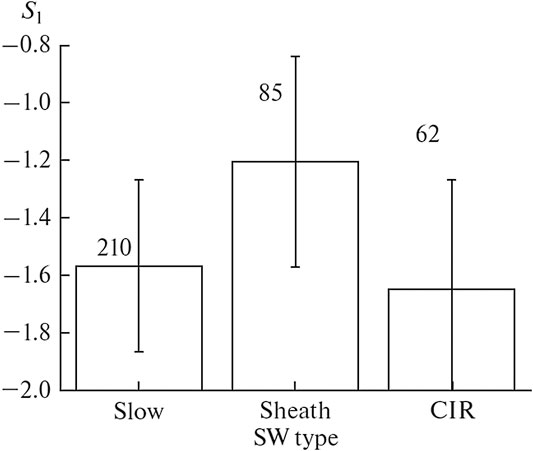
FIGURE 12. Mean values of the MHD-scale spectral slope S1 for the ion flux fluctuations in the vicinity of the BS for different upstream large-scale SW types, numbers refer to the number of analyzed data intervals, vertical lines denote standard deviations of the values (Adapted from (Rakhmanova et al., 2020b)).
Note that according to Yermolaev et al. (2009); Yermolaev et al. (2012); Yermolaev et al. (2015), the large-scale SW flows of various types affect the magnetosphere in a different way, with compressed regions like “Sheath” being highly geoeffective. That is, the obtained results may be interesting in the scopes of space weather.
Discussion
The present paper summarizes the experimental achievements in the exploration of highly turbulent plasma in front of the magnetosphere. To date, a number of distinct case studies have been reported together with a few statistical explorations of turbulence features at different parts of the MSH for various background and upstream conditions.
The whole set of studies demonstrates changes in dynamics of the turbulent cascade behind the BS. Unlike the SW, inside the MSH:Turbulence is usually characterized by a high level of compressive fluctuations.
Turbulent cascade is usually modified behind the BS: at the MHD scales spectra are usually shallower than the predicted Kolmogorov spectra for developed turbulence and observed in the SW; at the kinetic scales spectra of compressive fluctuations tend to be steeper than typically observed in the SW and MSH.
Turbulence at MHD scales develops in a different way for different BS geometry: behind the quasi-perpendicular BS, spectra often exhibit non-Kolmogorov scaling and bump around ion scales, while behind the quasi-parallel BS spectra tend to be more like those observed in the SW, with typical two-power-law shape and Kolmogorov scaling; BS geometry does not affect the kinetic-scale turbulence.
Dynamics of turbulent cascade seem to be different for various large-scale SW flow types: for slow steady SW, no significant changes in spectra may happen while during compressed SW flow the spectra are usually highly modified at the BS.
Though generally the picture of turbulence development in the MSH can be seen qualitatively from the presented works, there are still a lot of questions worth answering. How does turbulence develop in the confined space? Which conditions in the upstream SW are favorable for the most crucial changes in the turbulent cascade at the BS? What path is required for plasma to recover “developed” turbulent cascade behind the BS? Answering these questions would provide essential knowledge for laboratory plasma as well as for space weather forecasts.
Today, a large set of high quality in situ measurements of magnetic and electric fields as well as plasma parameters are available. However, basically the presented data and studies are still scattered. We would like to emphasize the importance of using the whole database of spacecraft measurements in different regions of the MSH that can lead to better understanding of turbulence dynamics in front of the magnetopause. We also hope that this review will be helpful for those who aim to present a reliable theoretical description of turbulence and its evolution inside the MSH and to those who develop models of solar wind-magnetosphere coupling, which include kinetic-scale processes and turbulence.
Author Contributions
All authors have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alexandrova, O. (2004). Cluster observations of finite amplitude Alfvén waves and small-scale magnetic filaments downstream of a quasi-perpendicular shock. J. Geophys. Res. 109, A05207. doi:10.1029/2003JA010056
Alexandrova, O. (2008). Solar wind vs. magnetosheath turbulence and Alfvén vortices. Nonlinear Process Geophys. 15, 95–108. doi:10.5194/npg-15-95-2008
Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar wind turbulence and the role of ion instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8
Alexandrova, O., Lacombe, C., and Mangeney, A. (2008). Spectra and anisotropy of magnetic fluctuations in the Earth’s magnetosheath: cluster observations. Ann. Geophys. 26, 3585–3596. doi:10.5194/angeo-26-3585-2008
Alexandrova, O., Mangeney, A., Maksimovic, M., Cornilleau-Wehrlin, N., Bosqued, J.-M., and André, M. (2006). Alfvén vortex filaments observed in magnetosheath downstream of a quasi-perpendicular bow shock. J. Geophys. Res. 111, A12208. doi:10.1029/2006JA011934
Anderson, B. J., Fuselier, S. A., Gary, S. P., and Denton, R. E. (1994). Magnetic spectral signatures in the Earth’s magnetosheath and plasma depletion layer. J. Geophys. Res. 99, 5877. doi:10.1029/93JA02827
Andrés, N., and Sahraoui, F. (2017). Alternative derivation of exact law for compressible and isothermal magnetohydrodynamics turbulence. Phys. Rev. E. 96, 053205. doi:10.1103/PhysRevE.96.053205
Andrés, N., Sahraoui, F., Galtier, S., Hadid, L. Z., Ferrand, R., and Huang, S. Y. (2019). Energy cascade rate measured in a collisionless space plasma with MMS data and compressible hall magnetohydrodynamic turbulence theory. Phys. Rev. Lett. 123, 245101. doi:10.1103/PhysRevLett.123.245101
Andrés, N., Sahraoui, F., Galtier, S., Hadid, L. Z., Dmitruk, P., and Mininni, P. D. (2018). Energy cascade rate in isothermal compressible magnetohydrodynamic turbulence. J. Plasma Phys. 84, 21. doi:10.1017/S0022377818000788
Bandyopadhyay, R., Chasapis, A., Chhiber, V., Parashar, T. N., Matthaeus, W. H., Shay, M. A., et al. (2018). Incompressive energy transfer in the Earth’s magnetosheath: magnetospheric multiscale observations. Astrophys. J. 866, 106. doi:10.3847/1538-4357/aade04
Bandyopadhyay, R., Matthaeus, W. H., Parashar, T. N., Yang, Y., Chasapis, A., Giles, B. L., et al. (2020). Statistics of kinetic dissipation in the Earth’s magnetosheath: MMS observations. Phys. Rev. Lett. 124, 255101. doi:10.1103/PhysRevLett.124.255101
Blanco-Cano, X., Omidi, N., and Russell, C. T. (2006a). Macrostructure of collisionless bow shocks: 2. ULF waves in the foreshock and magnetosheath. J. Geophys. Res. 111, A10205. doi:10.1029/2005JA011421
Blanco-Cano, X., Omidi, N., and Russell, C. T. (2006b). ULF waves and their influence on bow shock and magnetosheath structures. Adv. Space Res. 37, 1522–1531. doi:10.1016/j.asr.2005.10.043
Boldyrev, S., and Perez, J. C. (2012). Spectrum of kinetic alfven turbulence. Astrophys. J. Lett. 758 (2), 5. doi:10.1088/2041-8205/758/2/L44
Borovsky, J. E. (2012). The velocity and magnetic field fluctuations of the solar wind at 1 AU: statistical analysis of Fourier spectra and correlations with plasma properties. J. Geophys. Res. Sp. Phys. 117, 5104. doi:10.1029/2011JA017499
Borovsky, J. E. (2020). Plasma and magnetic-field structure of the solar wind at inertial-range scale sizes discerned from statistical examinations of the time-series measurements. Front. Astron. Sp. Sci. 7, 20. doi:10.3389/fspas.2020.00020
Borovsky, J. E., Denton, M. H., and Smith, C. W. (2019). Some properties of the solar wind turbulence at 1 AU statistically examined in the different types of solar wind plasma. J. Geophys. Res. Space Phys. 124, 2406–2424. doi:10.1029/2019JA026580
Breuillard, H., Matteini, L., Argall, M. R., Sahraoui, F., Andriopoulou, M., ContelLe, O., et al. (2018). New insights into the nature of turbulence in the Earth’s magnetosheath using magnetospheric multiscale mission data. Astrophys. J. 859, 127. doi:10.3847/1538-4357/aabae8
Breuillard, H., Yordanova, E., Vaivads, A., and Alexandrova, O. (2016). The effects of kinetic instabilities on small-scale turbulence in Earth’s magnetosheath. Astrophys. J. 829, 54. doi:10.3847/0004-637X/829/1/54
Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living rev. Sol. Phys. 10, 7. doi:10.12942/lrsp-2013-2
Budaev, V. P., Savin, S. P., and Zelenyi, L. M. (2011). Investigation of intermittency and generalized self-similarity of turbulent boundary layers in laboratory and magnetospheric plasmas: towards a quantitative definition of plasma transport features. Phys. Usp. 54, 875–918. doi:10.3367/ufne.0181.201109a.0905
Budaev, V. P., Zelenyi, L. M., and Savin, S. P. (2015). Generalized self-similarity of intermittent plasma turbulence in space and laboratory plasmas. J. Plasma Phys. 81, 395810602. doi:10.1017/S0022377815001099
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Chandran, B. D. G., Quataert, E., Howes, G. G., Xia, Q., and Pongkitiwanichakul, P. (2009). Constraining low-frequency alfvénic turbulence in the solar wind using density-fluctuation measurements. Astrophys. J. 707, 1668–1675. doi:10.1088/0004-637X/707/2/1668
Chasapis, A., Matthaeus, W. H., Parashar, T. N., Fuselier, S. A., Maruca, B. A., Phan, T. D., et al. (2017). High-resolution statistics of solar wind turbulence at kinetic scales using the magnetospheric multiscale mission. Astrophys. J. Lett. 844, L9. doi:10.3847/2041-8213/aa7ddd
Chen, C. H., Leung, L., Boldyrev, S., Maruca, B. A., and Bale, S. D. (2014). Ion-scale spectral break of solar wind turbulence at high and low beta. Geophys. Res. Lett. 41, 8081–8088. doi:10.1002/2014GL062009
Chen, C. H. K. (2016). Recent progress in astrophysical plasma turbulence from solar wind observations. J. Plasma Phys. 82, 535820602. doi:10.1017/S0022377816001124
Chen, C. H. K., and Boldyrev, S. (2017). Nature of kinetic scale turbulence in the Earth’s magnetosheath. Astrophys. J. 842, 122. doi:10.3847/1538-4357/aa74e0
Chhiber, R., Chasapis, A., Bandyopadhyay, R., Parashar, T. N., Matthaeus, W. H., Maruca, B. A., et al. (2018). Higher-order turbulence statistics in the Earth’s magnetosheath and the solar wind using magnetospheric multiscale observations. J. Geophys. Res. Space Phys. 123, 9941–9954. doi:10.1029/2018JA025768
Czaykowska, A., Bauer, T. M., Treumann, R. A., and Baumjohann, W. (2001). Magnetic field fluctuations across the Earth’s bow shock. Ann. Geophys. 19, 275–287. doi:10.5194/angeo-19-275-2001
Dimmock, A. P., Nykyri, K., and Pulkkinen, T. I. (2014). A statistical study of magnetic field fluctuations in the dayside magnetosheath and their dependence on upstream solar wind conditions. J. Geophys. Res. Space Phys. 119, 6231–6248. doi:10.1002/2014JA020009
Dudok de Wit, T., Alexandrova, O., Furno, I., Sorriso-Valvo, L., and Zimbardo, G. (2013). Methods for characterising microphysical processes in plasmas. Space Sci. Rev. 178, 665–693. doi:10.1007/s11214-013-9974-9
Dudok de Wit, T., and Krasnosel’Skikh, V. V. (1996). Non-Gaussian statistics in space plasma turbulence: fractal properties and pitfalls. Nonlinear Process Geophys. 3, 262–273. doi:10.5194/npg-3-262-1996
Escoubet, C. P., Schmidt, R., and Goldstein, M. L. (1997). Cluster—science and mission overview. Space Sci. Rev. 79, 11–32. doi:10.1023/A:1004923124586
Fairfield, D. H. (1976). Magnetic fields of the magnetosheath. Rev. Geophys. 14, 117. doi:10.1029/RG014i001p00117
Frisch, U. (1995). Turbulence : the legacy of A.N. Kolmogorov. Cambridge, United Kingdom: Cambridge University Press, doi:10.1017/S0022112096210791
Fischer, D., Magnes, W., Hagen, C., Dors, I., Chutter, M. W., Needell, J., et al. (2016). Optimized merging of search coil and fluxgate data for MMS. Geosci. Instrum. Method. Data Syst. 5, 521. doi:10.5194/gi-5-521-2016
Fujimoto, A., Šafránková, J., Němeček, Z., Goncharov, O., Němec, F., Přech, L., et al. (2016). Density fluctuations upstream and downstream of interplanetary shocks. Astrophys. J. 819, 41. doi:10.3847/0004-637X/819/1/41
Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. II. Strong alfvenic turbulence. Astrophys. J. 438, 763. doi:10.1086/175121
Greenstadt, E. W. (1972). Binary index for assessing local bow shock obliquity. J. Geophys. Res. 77, 5467–5479. doi:10.1029/JA077i028p05467
Gutynska, O., Šafránková, J., and Němeček, Z. (2008). Correlation length of magnetosheath fluctuations: cluster statistics. Ann. Geophys. 26, 2503–2513. doi:10.5194/angeo-26-2503-2008
Gutynska, O., Šafránková, J., and Němeček, Z. (2009). Correlation properties of magnetosheath magnetic field fluctuations. J. Geophys. Res. Sp. Phys. 114, A8. doi:10.1029/2009JA014173
Gutynska, O., Šimůnek, J., Šafránková, J., Němeček, Z., and Přech, L. (2012). Multipoint study of magnetosheath magnetic field fluctuations and their relation to the foreshock. J. Geophys. Res. Space Phys. 117, A04214. doi:10.1029/2011JA017240
Hadid, L. Z., Sahraoui, F., Galtier, S., and Huang, S. Y. (2018). Compressible magnetohydrodynamic turbulence in the Earth’s magnetosheath: estimation of the energy cascade rate using in situ spacecraft data. Phys. Rev. Lett. 120, 055102. doi:10.1103/PhysRevLett.120.055102
Hayosh, M., Šafránková, J., and Němeček, Z. (2006). MHD-modelling of the magnetosheath ion plasma flow and magnetic field and their comparison with experiments. Adv. Space Res. 37, 507–514. doi:10.1016/j.asr.2005.07.059
He, J.-S., Marsch, E., Tu, C.-Y., Zong, Q.-G., Yao, S., and Tian, H. (2011). Two-dimensional correlation functions for density and magnetic field fluctuations in magnetosheath turbulence measured by the cluster spacecraft. J. Geophys. Res. Space Phys. 116, A6. doi:10.1029/2010JA015974
Howes, G. G., Bale, S. D., Klein, K. G., Chen, C. H. K., Salem, C. S., and Tenbarge, J. M. (2012). The slow-mode nature of compressible wave power in solar wind turbulence. Astrophys. J. Lett. 753, 19. doi:10.1088/2041-8205/753/1/L19
Howes, G. G., Klein, K. G., and TenBarge, J. M. (2014). Validity of the taylor hypothesis for linear kinetic waves in the weakly collisional solar wind. Astrophys. J. 789, 106. doi:10.1088/0004-637X/789/2/106
Huang, S. Y., Hadid, L. Z., Sahraoui, F., Yuan, Z. G., and Deng, X. H. (2017). On the existence of the Kolmogorov inertial range in the terrestrial magnetosheath turbulence. Astrophys. J. Lett. 836, L10. doi:10.3847/2041-8213/836/1/L10
Huang, S. Y., and Sahraoui, F. (2019). Testing of the taylor frozen-in-flow hypothesis at electron scales in the solar wind turbulence. Astrophys. J. 876, 138. doi:10.3847/1538-4357/ab17d3
Huang, S. Y., Sahraoui, F., Deng, X. H., He, J. S., Yuan, Z. G., Zhou, M., et al. (2014). Kinetic turbulence in the terrestrial magnetosheath: cluster observations. Astrophys. J. 789, L28. doi:10.1088/2041-8205/789/2/L28
Hubert, D. (1994). Nature and origin of wave modes in the dayside earth magnetosheath. Adv. Space Res. 14, 55–64. doi:10.1016/0273-1177(94)90048-5
Karimabadi, H., Roytershteyn, V., Vu, H. X., Omelchenko, Y. A., Scudder, J., Daughton, W., et al. (2014). The link between shocks, turbulence, and magnetic reconnection in collisionless plasmas. Phys. Plasmas. 21, 062308. doi:10.1063/1.4882875
Kartalev, M. D., Nikolova, V. I., Kamenetsky, V. F., and Mastikov, I. P. (1996). On the self-consistent determination of dayside magnetopause shape and position. Planet. Space Sci. 44, 1195–1208. doi:10.1016/S0032-0633(96)00040-2
Klein, K. G., Howes, G. G., and Tenbarge, J. M. (2014). The violation of the taylor hypothesis in measurements of solar wind turbulence. Astrophys. J. Lett. 790, 20. doi:10.1088/2041-8205/790/2/L20
Kolmogorov, A. N. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc.R.Soc. A. 434, 9. doi:10.1098/rspa.1991.0075
Kozak, L. V., Pilipenko, V. A., Chugunova, O. M., and Kozak, P. N. (2011). Statistical analysis of turbulence in the foreshock region and in the Earth’s magnetosheath. Cosmic Res. 49, 194–204. doi:10.1134/S0010952511030063
Kozak, L. V., Savin, S. P., Budaev, V. P., Pilipenko, V. A., and Lezhen, L. A. (2012). Character of turbulence in the boundary regions of the Earth’s magnetosphere. Geomagn. Aeron. 52, 445–455. doi:10.1134/S0016793212040093
Lacombe, C., and Belmont, G. (1995). Waves in the Earth’s magnetosheath: observations and interpretations. Adv. Space Res. 15, 329–340. doi:10.1016/0273-1177(94)00113-F
Lacombe, C., Belmont, G., Hubert, D., Harvey, C. C., Mangeney, A., Russell, C. T., et al. (1995). Density and magnetic field fluctuations observed by ISEE 1-2 in the quiet magnetosheath. Ann. Geophys. 13, 343–357. doi:10.1007/s00585-995-0343-1
Lacombe, C., Samsonov, A. A., Mangeney, A., Maksimovic, M., Cornilleau-Wehrlin, N., Harvey, C. C., et al. (2006). Cluster observations in the magnetosheath. Part 2: intensity of the turbulence at electron scales. Ann. Geophys. 24, 3523–3531. doi:10.5194/angeo-24-3523-2006
Le Contel, O., Leroy, P., Roux, A., Coillot, C., Alison, D., Bouabdellah, A., et al. (2014). The search coil magnetometer for MMS. Space Sci. Rev. 199, 257–282. doi:10.1007/s11214-014-0096-9
Leamon, R. J., Smith, C. W., and Ness, N. F. (1998). Characteristics of magnetic fluctuations within coronal mass ejections: the January 1997 event. Geophys. Res. Lett. 25, 2505–2508. doi:10.1029/98GL00305
Li, H., Jiang, W., Wang, C., Verscharen, D., Zeng, C., Russell, C. T., et al. (2020). Evolution of the Earth’s magnetosheath turbulence: a statistical study based on MMS observations. Astrophys. J. 898, L43. doi:10.3847/2041-8213/aba531
Lion, S., Alexandrova, O., and Zaslavsky, A. (2016). Coherent events and spectral shape at ion kinetic scales in the fast solar wind turbulence. Astrophys. J. 824, 47. doi:10.3847/0004-637X/824/1/47
Lucek, E. A., Dunlop, M. W., Horbury, T. S., Balogh, A., Brown, P., Cargill, P., et al. (2001). Cluster magnetic field observations in the magnetosheath: four-point measurements of mirror structures. Ann. Geophys. 19, 1421–1428. doi:10.5194/angeo-19-1421-2001
Macek, W. M. (2007). Multifractality and intermittency in the solar wind. Nonlinear Process Geophys. 14, 695–700. doi:10.5194/npg-14-695-2007
Macek, W. M., Krasińska, A., Silveira, M. V. D., Sibeck, D. G., Wawrzaszek, A., Burch, J. L., et al. (2018). Magnetospheric multiscale observations of turbulence in the magnetosheath on kinetic scales. Astrophys. J. 864, L29. doi:10.3847/2041-8213/aad9a8
Macek, W. M., Wawrzaszek, A., and Sibeck, D. G. (2015). THEMIS observation of intermittent turbulence behind the quasi-parallel and quasi-perpendicular shocks. J. Geophys. Res. Space Phys. 120, 7466–7476. doi:10.1002/2015JA021656
Mangeney, A., Lacombe, C., Maksimovic, M., Samsonov, A. A., Cornilleau-Wehrlin, N., Harvey, C. C., et al. (2006). Cluster observations in the magnetosheath. Part 1: anisotropies of the wave vector distribution of the turbulence at electron scales. Ann. Geophys. 24, 3507–3521. doi:10.5194/angeo-24-3507-2006
Matteini, L., Alexandrova, O., Chen, C. H. K., and Lacombe, C. (2017). Electric and magnetic spectra from MHD to electron scales in the magnetosheath. Mon. Not. R. Astron. Soc. 466, 945–951. doi:10.1093/mnras/stw3163
Ness, N. F., Scearce, C. S., and Seek, J. B. (1964). Initial results of the imp 1 magnetic field experiment. J. Geophys. Res. 69, 3531–3569. doi:10.1029/JZ069i017p03531
Neugebauer, M., Wu, C. S., and Huba, J. D. (1978). Plasma fluctuations in the solar wind. J. Geophys. Res. 83, 1027. doi:10.1029/JA083iA03p01027
Němeček, Z., Šafránková, J., Pišoft, P., and Zastenker, G. N. (2001). Statistical study of ion flux fluctuations in the magnetosheath. Czech. J. Phys. 51, 853–862. doi:10.1023/A:1011630618180
Němeček, Z., Šafránková, J., Zastenker, G. N., Pišoft, P., and Jelı́nek, K. (2002). Low-frequency variations of the ion flux in the magnetosheath. Planet. Space Sci. 50, 567–575. doi:10.1016/S0032-0633(02)00036-3
Němeček, Z., Šafránková, J., Zastenker, G. N., Pišoft, P., Paularena, K. I., and Richardson, J. D. (2000). Observations of the radial magnetosheath profile and a comparison with gasdynamic model predictions. Geophys. Res. Lett. 27, 2801–2804. doi:10.1029/2000GL000063
Ofman, L., and Gedalin, M. (2013). Two-dimensional hybrid simulations of quasi-perpendicular collisionless shock dynamics: gyrating downstream ion distributions. J. Geophys. Res. Space Phys. 118, 1828–1836. doi:10.1029/2012JA018188
Omidi, N., Eastwood, J. P., and Sibeck, D. G. (2010). Foreshock bubbles and their global magnetospheric impacts. J. Geophys. Res. Sp. Phys. 115, A06204. doi:10.1029/2009JA014828
Omidi, N., Sibeck, D., Gutynska, O., and Trattner, K. J. (2014). Magnetosheath filamentary structures formed by ion acceleration at the quasi-parallel bow shock. J. Geophys. Res. Space Phys. 119, 2593–2604. doi:10.1002/2013JA019587
Perri, S., Servidio, S., Vaivads, A., and Valentini, F. (2017). Numerical study on the validity of the Taylor hypothesis in space plasmas. Astrophys. J. Suppl. 231, 4. doi:10.3847/1538-4365/aa755a
Perrone, D., Bruno, R., D’Amicis, R., Telloni, D., De Marco, R., Stangalini, M., et al. (2020). Coherent events at ion scales in the inner heliosphere: parker solar probe observations during the first encounter. Astrophys. J. 905 (2), 12. doi:10.3847/1538-4357/abc480
Perschke, C., Narita, Y., Motschmann, U., and Glassmeier, K.-H. (2014). Multi-spacecraft observations of linear modes and sideband waves in ion-scale solar wind turbulence. Astrophys. J. Lett. 793, L25. doi:10.1088/2041-8205/793/2/L25
Phan, T. D., Eastwood, J. P., Shay, M. A., Drake, J. F., Sonnerup, B. U. Ö., Fujimoto, M., et al. (2018). Electron magnetic reconnection without ion coupling in Earth’s turbulent magnetosheath. Nature. 557, 202. doi:10.1038/s41586-018-0091-5
Podesta, J. J., Roberts, D. A., and Goldstein, M. L. (2006). Power spectrum of small-scale turbulent velocity fluctuations in the solar wind. J. Geophys. Res. 111, A10109. doi:10.1029/2006JA011834
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4
Pulinets, M. S., Antonova, E. E., Riazantseva, M. O., Znatkova, S. S., and Kirpichev, I. P. (2014). Comparison of the magnetic field before the subsolar magnetopause with the magnetic field in the solar wind before the bow shock. Adv. Space Res. 54, 604–616. doi:10.1016/j.asr.2014.04.023
Pulkkinen, T. I., Dimmock, A. P., Lakka, A., Osmane, A., Kilpua, E., Myllys, M., et al. (2016). Magnetosheath control of solar wind-magnetosphere coupling efficiency. J. Geophys. Res. Space Phys. 121, 8728–8739. doi:10.1002/2016JA023011
Rakhmanova, L., Riazantseva, M., and Zastenker, G. (2016). Plasma fluctuations at the flanks of the Earth’s magnetosheath at ion kinetic scales. Ann. Geophys. 34, 1011–1018. doi:10.5194/angeo-34-1011-2016
Rakhmanova, L. S., Riazantseva, M. O., Zastenker, G. N., and Yermolaev, Y. I. (2017). High-frequency plasma fluctuations in the middle magnetosheath and near its boundaries: Spektr-R observations. J. Plasma Phys. 83, 705830204. doi:10.1017/S002237781700023X
Rakhmanova, L., Riazantseva, M., Zastenker, G., and Verigin, M. (2018a). Kinetic-scale ion flux fluctuations behind the quasi-parallel and quasi-perpendicular bow shock. J. Geophys. Res. Space Phys. 123, 5300–5314. doi:10.1029/2018JA025179
Rakhmanova, L. S., Riazantseva, M. O., Zastenker, G. N., and Verigin, M. I. (2018b). Effect of the magnetopause and bow shock on characteristics of plasma turbulence in the Earth’s magnetosheath. Geomagn. Aeron. 58, 718–727. doi:10.1134/S0016793218060129
Rakhmanova, L. S. (2019). Dynamisc of fast plasma variations in the magnetosheath. PhD work. Moscow, Russia: Russian Academy of Sciences.
Rakhmanova, L. S., Riazantseva, M. O., Zastenker, G. N., Yermolaev, Y. I., Lodkina, I. G., and Chesalin, L. S. (2020a). Turbulent cascade in the magnetosheath affected by the solar wind’s plasma turbulence. Cosmic Res. 57, 443–450. doi:10.1134/S0010952519060066
Rakhmanova, L., Riazantseva, M., Zastenker, G., Yermolaev, Y., and Lodkina, I. (2020b). Dynamics of plasma turbulence at Earth’s bow shock and through the magnetosheath. Astrophys. J. 901, 30. doi:10.3847/1538-4357/abae00
Retinò, A., Sundkvist, D., Vaivads, A., Mozer, F., André, M., and Owen, C. J. (2007). In situ evidence of magnetic reconnection in turbulent plasma. Nat. Phys. 3, 235–238. doi:10.1038/nphys574
Rezeau, L., Belmont, G., Cornilleau-Wehrlin, N., Reberac, F., and Briand, C. (1999). Spectral law and polarization properties of the low-frequency waves at the magnetopause. Geophys. Res. Lett. 26, 651–654. doi:10.1029/1999GL900060
Rezeau, L., Perraut, S., and Roux, A. (1986). Electromagnetic fluctuations in the vicinity of the magnetopause. Geophys. Res. Lett. 13, 1093–1096. doi:10.1029/GL013i011p01093
Rezeau, L., Sahraoui, F., d’Humières, E., Belmont, G., Chust, T., Cornilleau-Wehrlin, N., et al. (2001). A case study of low-frequency waves at the magnetopause. Ann. Geophys. 19, 1463–1470. doi:10.5194/angeo-19-1463-2001
Riazantseva, M., Budaev, V., Rakhmanova, L., Zastenker, G., Yermolaev, Y., Lodkina, I., et al. (2017). Variety of shapes of solar wind ion flux spectra: Spektr-R measurements. J. Plasma Phys. 83, 705830401. doi:10.1017/S0022377817000502
Riazantseva, M. O., Budaev, V. P., Zelenyi, L. M., Zastenker, G. N., Pavlos, G. P., Safrankova, J., et al. (2015). Dynamic properties of small-scale solar wind plasma fluctuations. Philos. Trans. R. Soc. A. 373, 20140146. doi:10.1098/rsta.2014.0146
Riazantseva, M. O., Budaev, V. P., Rakhmanova, L. S., Zastenker, G. N., Šafránková, J., Němeček, Z., et al. (2016). Comparison of properties of small-scale ion flux fluctuations in the flank magnetosheath and in the solar wind. Adv. Space Res. 58, 166–174. doi:10.1016/J.ASR.2015.12.022
Riazantseva, M. O., Rakhmanova, L. S., Yermolaev, Yu. I, Lodkina, I. G., Zastenker, G. N., and Chesalin, L. S. (2019). Characteristics of turbulent solar wind flow in plasma compression regions. Cosmic Res. 58 (6), 468–477. doi:10.1134/S001095252006009X
Roberts, O. W., Li, X., and Li, B. (2013). Kinetic plasma turbulence in the fast solar wind measured by cluster. Astrophys. J. 769, 58. doi:10.1088/0004-637X/769/1/58
Roberts, O. W., Narita, Y., Nakamura, R., Vörös, Z., and Gershman, D. (2019). Anisotropy of the spectral index in ion scale compressible turbulence: MMS observations in the magnetosheath. Front. Physiol. 7, 184. doi:10.3389/fphy.2019.00184
Roberts, O. W., Toledo-Redondo, S., Perrone, D., Zhao, J., Narita, Y., Gershman, D., et al. (2018). Ion-scale kinetic Alfvén turbulence: Mms measurements of the Alfvén ratio in the magnetosheath. Geophys. Res. Lett. 45, 7974–7984. doi:10.1029/2018GL078498
Rodriguez, P. (1985). Magnetosheath whistler turbulence. J. Geophys. Res. 90, 6337. doi:10.1029/JA090iA07p06337
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3
Šafránková, J., Hayosh, M., Gutynska, O., Němeček, Z., and Přech, L. (2009). Reliability of prediction of the magnetosheath BZ component from interplanetary magnetic field observations. J. Geophys. Res. Space Phys. 114. doi:10.1029/2009JA014552
Šafránková, J., Němeček, Z., Němec, F., Přech, L., Chen, C. H. K., and Zastenker, G. N. (2016). Power spectral density of fluctuations of bulk and thermal speeds in the solar wind. Astrophys. J. 825, 121. doi:10.3847/0004-637X/825/2/121
Šafránková, J., Němeček, Z., Němec, F., Přech, L., Pitňa, A., Chen, C. H. K., et al. (2015). Solar wind density spectra around the ion spectral break. Astrophys. J. 803, 107. doi:10.1088/0004-637X/803/2/107
Šafránková, J., Němeček, Z., Přech, L., Zastenker, G., Čermák, I., Chesalin, L., et al. (2013). Fast solar wind monitor (BMSW): description and first results. Space Sci. Rev. 175, 165–182. doi:10.1007/s11214-013-9979-4
Sahraoui, F., Belmont, G., Rezeau, L., Cornilleau-Wehrlin, N., Pinçon, J. L., and Balogh, A. (2006). Anisotropic turbulent spectra in the terrestrial magnetosheath as seen by the cluster spacecraft. Phys. Rev. Lett. 96, 075002. doi:10.1103/PhysRevLett.96.075002
Sahraoui, F., Belmont, G., Pinçon, J. L., Rezeau, L., Balogh, A., Robert, P., et al. (2004). Magnetic turbulent spectra in the magnetosheath: new insights. Ann. Geophys. 22 (6), 2283–2288. doi:10.5194/angeo-22-2283-2004
Sahraoui, F., Hadid, L., and Huang, S. (2020). Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: a (short) biased review. Rev. Mod. Phys. 4, 4. doi:10.1007/s41614-020-0040-2
Sahraoui, F., PinçOn, J. L., Belmont, G., Rezeau, L., Cornilleau-Wehrlin, N., Robert, P., et al. (2003). ULF wave identification in the magnetosheath: the k-filtering technique applied to Cluster II data. J. Geophys. Res. 108, 1335. doi:10.1029/2002JA009587
Samsonov, A. A., Alexandrova, O., Lacombe, C., Maksimovic, M., and Gary, S. P. (2007). Proton temperature anisotropy in the magnetosheath: comparison of 3-D MHD modelling with cluster data. Ann. Geophys. 25, 1157–1173. doi:10.5194/angeo-25-1157-2007
Samsonov, A. A., Němeček, Z., Šafránková, J., and Jelínek, K. (2012). Why does the subsolar magnetopause move sunward for radial interplanetary magnetic field? J. Geophys. Res. Space Phys. 117, A05221. doi:10.1029/2011JA017429
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E., et al. (2009). Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310–377. doi:10.1088/0067-0049/182/1/310
Schwartz, S. J., Burgess, D., and Moses, J. J. (1996). Low-frequency waves in the Earth’s magnetosheath: present status. Ann. Geophys. 14, 1134–1150. doi:10.1007/s00585-996-1134-z
Shevyrev, N. N., and Zastenker, G. N. (2005). Some features of the plasma flow in the magnetosheath behind quasi-parallel and quasi-perpendicular bow shocks. Planet. Space Sci. 53, 95–102. doi:10.1016/j.pss.2004.09.033
Shevyrev, N. N., Zastenker, G. N., Eiges, P. E., and Richardson, J. D. (2006). Low frequency waves observed by Interball-1 in foreshock and magnetosheath. Adv. Space Res. 37, 1516–1521. doi:10.1016/j.asr.2005.07.072
Shevyrev, N. N., Zastenker, G. N., Nozdrachev, M. N., Němeček, Z., Šafránková, J., and Richardson, J. D. (2003). High and low frequency large amplitude variations of plasma and magnetic field in the magnetosheath: radial profile and some features. Adv. Space Res. 31, 1389–1394. doi:10.1016/S0273-1177(03)00008-5
Sibeck, D. G., and Gosling, J. T. (1996). Magnetosheath density fluctuations and magnetopause motion. J. Geophys. Res. Space Phys. 101, 31–40. doi:10.1029/95JA03141
Smith, C. W., Hamilton, K., Vasquez, B. J., and Leamon, R. J. (2006). Dependence of the dissipation range spectrum of interplanetary magnetic fluctuations on the rate of energy cascade. Astrophys. J. 645, L85–L88. doi:10.1086/506151
Song, P., Russell, C. T., and Thomsen, M. F. (1992a). Slow mode transition in the frontside magnetosheath. J. Geophys. Res. 97, 8295. doi:10.1029/92JA00381
Song, P., Russell, C. T., and Thomsen, M. F. (1992b). Waves in the inner magnetosheath: a case study. Geophys. Res. Lett. 19, 2191–2194. doi:10.1029/92GL02499
Sorriso-Valvo, L., Carbone, V., Veltri, P., Consolini, G., and Bruno, R. (1999). Intermittency in the solar wind turbulence through probability distribution functions of fluctuations. Geophys. Res. Lett. 26, 1801–1804. doi:10.1029/1999GL900270
Spreiter, J. R., and Stahara, S. S. (1980). A new predictive model for determining solar wind-terrestrial planet interactions. J. Geophys. Res. 85, 6769–6777. doi:10.1029/JA085iA12p06769
Spreiter, J. R., Summers, A. L., and Alksne, A. Y. (1966). Hydromagnetic flow around the magnetosphere. Planet. Space Sci. 14, 223–253. doi:10.1016/0032-0633(66)90124-3
Stawarz, J. E., Eastwood, J. P., Phan, T. D., Gingell, I. L., Shay, M. A., Burch, J. L., et al. (2019). Properties of the turbulence associated with electron-only magnetic reconnection in Earth’s magnetosheath. Astrophys. J. 877, L37. doi:10.3847/2041-8213/ab21c8
Stawarz, J. E., Eriksson, S., Wilder, F. D., Ergun, R. E., Schwartz, S. J., Pouquet, A., et al. (2016). Observations of turbulence in a kelvin-helmholtz event on 8 september 2015 by the magnetospheric multiscale mission. J. Geophys. Res. Space Phys. 121, 11021–11034. doi:10.1002/2016JA023458
Sundkvist, D., Retinò, A., Vaivads, A., and Bale, S. D. (2007). Dissipation in turbulent plasma due to reconnection in thin current sheets. Phys. Rev. Lett. 99, 025004. doi:10.1103/PhysRevLett.99.025004
Taylor, G. I. (1938). The spectrum of turbulence. Proc. R. Soc. A Math. Phys. Eng. Sci. 164, 476–490. doi:10.1098/rspa.1938.0032
Tóth, G., Sokolov, I. V., Gombosi, T. I., Chesney, D. R., Clauer, C. R., De Zeeuw, D. L., et al. (2005). Space Weather Modeling Framework: a new tool for the space science community. J. Geophys. Res. Space Phys. 110. doi:10.1029/2005JA011126
Tu, C.-Y., and Marsch, E. (1995). MHD structures, waves and turbulence in the solar wind. Available at: https://ui.adsabs.harvard.edu/abs/1995mswt.book.T/abstract (Accessesd September 11, 2020)
Vörös, Z., Yordanova, E., Khotyaintsev, Y. V., Varsani, A., and Narita, Y. (2019). Energy conversion at kinetic scales in the turbulent magnetosheath. Front. Astron. Sp. Sci. 6, 60. doi:10.3389/fspas.2019.00060
Vörös, Z., Yordanova, E., Varsani, A., Genestreti, K. J., Khotyaintsev, Y. V., Li, W., et al. (2017). MMS observation of magnetic reconnection in the turbulent magnetosheath. J. Geophys. Res. Space Phys. 122, 11442–11467. doi:10.1002/2017JA024535
Yermolaev, Y. I., Nikolaeva, N. S., Lodkina, I. G., and Yermolaev, M. Y. (2009). Catalog of large-scale solar wind phenomena during 1976–2000. Cosmic Res. 47, 81–94. doi:10.1134/S0010952509020014
Yermolaev, Y. I., Nikolaeva, N. S., Lodkina, I. G., and Yermolaev, M. Y. (2012). Geoeffectiveness and efficiency of CIR, Sheath and ICME in generation of magnetic storms. J. Geophys. Res. 117. doi:10.1029/2011JA017139
Yermolaev, Y. I., Lodkina, I. G., Nikolaeva, N. S., and Yermolaev, M. Y. (2015). Dynamics of large-scale solar-wind streams obtained by the double superposed epoch analysis. J. Geophys. Res. Space Phys. 120, 7094–7106. doi:10.1002/2015JA021274
Yordanova, E., Vaivads, A., André, M., Buchert, S. C., and Vörös, Z. (2008). Magnetosheath plasma turbulence and its spatiotemporal evolution as observed by the cluster spacecraft. Phys. Rev. Lett. 100, 205003. doi:10.1103/PhysRevLett.100.205003
Yordanova, E., Vörös, Z., Raptis, S., and Karlsson, T. (2020). Current sheet statistics in the magnetosheath. Front. Astron. Sp. Sci. 7, 2. doi:10.3389/fspas.2020.00002
Zastenker, G. N., Nozdrachev, M. N., Němeček, Z., Šafránková, J., Paularena, K. I., Richardson, J. D., et al. (2002). Multispacecraft measurements of plasma and magnetic field variations in the magnetosheath: comparison with Spreiter models and motion of the structures. Planet. Space Sci. 50, 601–612. doi:10.1016/S0032-0633(02)00039-9
Zastenker, G. N., Safrankova, J., Nemecek, Z., Prech, L., Cermak, I., Vaverka, I., et al. (2013). Fast measurements of parameters of the Solar Wind using the BMSW instrument. Cosmic Res. 51, 78–89. doi:10.1134/S0010952513020081
Zimbardo, G., Greco, A., Sorriso-Valvo, L., Perri, S., Vörös, Z., Aburjania, G., et al. (2010). Magnetic turbulence in the geospace environment. Space Sci. Rev. 156, 89–134. doi:10.1007/s11214-010-9692-5
Keywords: plasma turbulence, solar wind, bow shock, magnetosheath, Sun-Earth’s coupling
Citation: Rakhmanova L, Riazantseva M and Zastenker G (2021) Plasma and Magnetic Field Turbulence in the Earth’s Magnetosheath at Ion Scales. Front. Astron. Space Sci. 7:616635. doi: 10.3389/fspas.2020.616635
Received: 12 October 2020; Accepted: 18 December 2020;
Published: 28 January 2021.
Edited by:
Alessandro Retino, UMR7648 Laboratoire de physique des plasmas (LPP), FranceReviewed by:
Silvia Perri, University of Calabria, ItalyJulia E. Stawarz, Imperial College London, United Kingdom
Copyright © 2021 Rakhmanova, Riazantseva and Zastenker. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liudmila Rakhmanova, cmFraGx1ZEBnbWFpbC5jb20=
 Liudmila Rakhmanova
Liudmila Rakhmanova Maria Riazantseva
Maria Riazantseva Georgy Zastenker
Georgy Zastenker