Primordial Fluctuations From Quantum Gravity

We study the fluctuations and the correlations between spatial regions generated in the primordial quantum gravitational era of the universe. We point out that these can be computed using the Lorentzian dynamics defined by the Loop Quantum Gravity amplitudes. We evaluate these amplitudes numerically in the deep quantum regime. Surprisingly, we find large fluctuations and strong correlations, although not maximal. This suggests the possibility that early quantum gravity effects might be sufficient to account for structure formation and solve the cosmological horizon problem.

1 Introduction

Standard cosmology–with or without inflation–requires an initial state that exhibits fluctuations and correlations between distinct regions of space. These play a key role, in particular as seeds for structure formation. Here we investigate how these fluctuations and correlations can emerge from a primordial quantum gravitational cosmological phase, using Loop Quantum Gravity (LQG) and a simple model of the early universe.

We consider the quantum transition from an empty state to a 3-geometry. The amplitude of this transition may be relevant in a Big Bang cosmology (Hartle and Hawking, 1983; Halliwell, 1987; Halliwell et al., 2019), as well as in a bouncing cosmology, where it dominates the transition through the bounce (Bianchi et al., 2010; Vidotto, 2011; Bahr et al., 2017). We treat the dynamics of gravity non-perturbatively, using covariant LQG. This calculation does not require a Wick rotation and it is well defined in the Lorentzian theory. The transition generates a quantum state that defines the probability distribution over 3-geometries. This includes correlations between spatially separated regions.

We truncate the degrees of freedom of the gravitational field to a small finite number in addition to the scale factor [cfr (Rovelli and Vidotto, 2008; Borja et al., 2012; Vidotto, 2017)]. Using numerical methods, we obtain four results: 1) The expectation value of the geometric variables at a given value of the scale factor yields precisely (the truncation of) a metric 3-sphere. 2) Contrary to our initial expectation, the variance of these variables is very large: the amplitude of the fluctuations is significant. 3) Correlations between variables in distinct regions–and entanglement entropy between regions–do not vanish with the increase of the scale factor. 4) Entanglement entropy appears to converge to a stable value asymptotically.

All this indicates that the universe emerging from an early quantum era includes fluctuations, homogeneity properties, and large scale correlations, due to the common quantum origin of spatially separated regions. These can be studied theoretically and appear to be compatible with the observed universe. In particular, inflation or a bounce might not be strictly necessary to circumvent the horizon problem. If the initial quantum phase is taken into account, our result suggests that distant regions may have not been causally disconnected in the past, as in classical cosmology.

2 Quantum Theory

We discretize a closed cosmological 3-geometry into five tetrahedra glued to one another, giving an S₃ topology. This is a regular triangulation of a topological 3-sphere, and it corresponds to the boundary of a 4-simplex. The geometry of a flat 4-simplex has twenty degrees of freedom, which capture the gravitational field in this truncation. The result of the transition from nothing to a 3-geometry is described by its covariant LQG Lorentzian amplitude (Vidotto, 2011). The truncation we consider corresponds to the single vertex amplitude, to the first order in the spinfoam expansion (Rovelli and Smerlak, 2012). We take the areas of the faces of the tetrahedra to be equal and use this common value as a proxy for the physical scale factor. The remaining degrees of freedom characterize the shapes of the five tetrahedra. We are interested in the fluctuations of these variables and the correlations between variables in distinct tetrahedra, at different values of the scale factor.

The LQG Hilbert space for this truncation is $\mathrm{\mathscr{H}}=L^2{\left[SU{\left(2\right)}^{10}/SU{\left(2\right)}^5\right]}_{{\Gamma }_5}$, where ${\Gamma }_5$ is the complete graph with five nodes. See (Rovelli and Vidotto, 2015) for the notation and an introduction to the formalism. We label the (oriented) links as $l=1,\dots ,10$, or alternatively in terms of the two nodes they link: $l=n{n}^{\prime }$. The spin network basis in $\mathrm{\mathscr{H}}$ is given by the states $|j_l,i_n\rangle$ where the j_l’s are spins (half-integer values labeling $SU\left(2\right)$ irreps) and the i_n’s are a basis in the corresponding intertwiner space ${\mathrm{ℐ}}_n=\left({\otimes }_{n^{\prime }\ne n}{V}_{j_{n{n}^{\prime }}}\right)/SU\left(2\right)$, where V_j is the spin-j representation space of $SU\left(2\right)$. We focus on the subspaces ${\mathrm{\mathscr{H}}}_j$ of $\mathrm{\mathscr{H}}$ defined by $j_l=j$. These have the tensorial structure ${\mathrm{\mathscr{H}}}_j={\otimes }_n{\mathrm{ℐ}}_n$, where each ${\mathrm{ℐ}}_n$ is isomorphic to $\left(V_j\otimes V_j\otimes V_j\otimes V_j\right)/SU\left(2\right)$. The basis states are tensor states, which we denote as $|j,i_n\rangle ={\otimes }_n|i_n\rangle$ (by this we mean $|j,i_1,\dots ,i_5\rangle =|i_1\rangle \otimes \cdots \otimes |i_5\rangle$). We choose a basis in ${\mathrm{ℐ}}_n$ fixing a pairing of the links at each node and the basis that diagonalizes the modulus square of the sum of the $SU\left(2\right)$ generators in the pair.

The transition amplitude from an empty state to a state $|j,i_n\rangle$ in ${\mathrm{\mathscr{H}}}_j$ is given by the spinfoam amplitude of the boundary state $|j,i_n\rangle$ alone. This is because this transition corresponds to the amplitude of a boundary state that has only one connected component, here interpreted as the future one. To first order in the spinfoam expansion, the amplitude of a boundary state is given by a single vertex. Hence the nothing-to- $|j,i_n\rangle$ amplitude is the vertex amplitude for the boundary state

$\langle j,i_n|\varnothing \rangle =W\left(j,i_n\right)\equiv \langle j,i_n|{\psi }_o\rangle (1)$

where $W\left(j,i_n\right)$ is the Lorentzian EPRL vertex amplitude (Engle et al., 2008). This implies that we can view the ket $|{\psi }_o\rangle$ with components $W\left(j,i_n\right)$, as the quantum state emerging from the Big Bang. This is the analogue, in (Lorentzian) LQG, of the Hartle-Hawking “no-boundary” initial state in (Euclidean) path-integral quantum gravity (Hartle and Hawking, 1983). This is the state we are interested in. We study the mean geometry it defines and the quantum fluctuations and correlations it incorporates. Specifically, we study the expectation value $\langle A\rangle =\langle {\psi }_o\left|A\right|{\psi }_o\rangle$, the spread $\Delta A=\sqrt{\langle {\psi }_o\left|A^2\right|{\psi }_o\rangle -{\langle A\rangle }^2}$ and the (normalized) correlations

$C\left(A_1,A_2\right)=\frac{\langle {\psi }_o\left|A_1{A}_2\right|{\psi }_o\rangle -\langle A_1\rangle \langle A_2\rangle }{\left(\Delta A_1\right)\left(\Delta A_2\right)}(2)$

of local geometry operators $A,A_1,A_2,\dots$ defined on $\mathrm{\mathscr{H}}$. We compute also the entanglement entropy $S=-tr\left({\rho }_n\log {\rho }_n\right)$ of a node with respect to the rest of the graph, where ${\rho }_n$ is the reduced density matrix of the state $|{\psi }_o\rangle$ at any node, all nodes being equivalent by symmetry.

3 Quantum Geometry

The spin-network basis states can be viewed as a collection of quantum tetrahedra (Bianchi et al., 2011) glued together by identifying faces. Shared faces have the same area but not necessarily matching shapes, giving rise to a twisted geometry (Freidel and Speziale, 2010). The areas of the faces are eigenvalues of the area operator

$A_{nl}|i_n\rangle =\sqrt{{\overrightarrow{E}}_{nl}\cdot {\overrightarrow{E}}_{nl}}|i_n\rangle =\left(8\pi \gamma \hslash G\right)\sqrt{j_l\left(j_l+1\right)}|i_n\rangle ,(3)$

written in terms of the flux operators

${\overrightarrow{E}}_{nl}=\left(8\pi \gamma \hslash G\right){\overrightarrow{J}}_l(4)$

entering the node n on link l, where γ is the Barbero-Immirzi constant and ${\overrightarrow{J}}_l$ is the vector of $SU\left(2\right)$ generators on link l. The shape of the tetrahedron is measured by the angle operator

$A_{ab}|i_n\rangle =\cos \left({\theta }_{ab}\right)|i_n\rangle (5)$

that gives the cosine of the external dihedral angle between faces a and b, where

$2\left|{\overrightarrow{J}}_a\right|\left|{\overrightarrow{J}}_b\right|A_{ab}=2{\overrightarrow{J}}_a\cdot {\overrightarrow{J}}_b={\left({\overrightarrow{J}}_a+{\overrightarrow{J}}_b\right)}^2-{\overrightarrow{J}}_a^2-{\overrightarrow{J}}_b^2\cdot$

Say we use the recoupling basis that pairs links $j_a$ and $j_b$ at node n, and let $|k_n\rangle$ be the intertwiner state at node n. The operator ${\left({\overrightarrow{J}}_a+{\overrightarrow{J}}_b\right)}^2$ is diagonal on $|k_n\rangle$ with eigenvalue

${\left({\overrightarrow{J}}_a+{\overrightarrow{J}}_b\right)}^2|k_n\rangle =k_n\left(k_n+1\right)|k_n\rangle (6)$

where $k_n$ is the intertwiner spin. Putting together Eqs 3, 5, and 6 we obtain

$\cos \left({\theta }_{ab}\right)=\frac{k_n\left(k_n+1\right)-j_a\left(j_a+1\right)-j_b\left(j_b+1\right)}{2\sqrt{j_a\left(j_a+1\right)j_b\left(j_b+1\right)}}(7)$

for measuring the dihedral angle $\cos \left({\theta }_{ab}\right)$ of $|k_n\rangle$ in terms of intertwiner spin $k_n$.

4 Numerical Methods

The Lorentzian EPRL vertex amplitude $W\left(j_l,i_n\right)$ can be written as Speziale (2017)

$W\left(j_l,i_n\right)={\displaystyle \sum _{l_f,k_e}\left({\displaystyle \prod _e\left(2k_e+1\right)B\left(j_l,l_f;i_n,k_e\right)}\right)}\left\{15j\right\}\left(l_f,k_e\right)(8)$

where f and e label the faces and the half-edges touching the vertex. The symbol $\left\{15j\right\}$ is the invariant $SU\left(2\right)$ symbol built from contracting the five 4-valent intertwiners at the nodes, and can be expressed as the contraction of five $SU\left(2\right)$$6j$ symbols as

$\left\{15j\right\}\left(l_f,k_e\right)={\displaystyle \sum }_x\left(2x+1\right){\left(-1\right)}^{{\displaystyle {\sum }_a{l}_a}+{\displaystyle {\sum }_a{k}_a}}$

$\times \left\{\begin{array}{ccc}{k}_1& l_{25}& x\\ k_5& l_{14}& l_{15}\end{array}\right\}\left\{\begin{array}{ccc}{l}_{14}& k_5& x\\ l_{35}& k_4& l_{45}\end{array}\right\}\left\{\begin{array}{ccc}{k}_4& l_{35}& x\\ k_3& l_{24}& l_{34}\end{array}\right\}$

$\times \left\{\begin{array}{ccc}{l}_{24}& k_3& x\\ l_{13}& k_2& l_{23}\end{array}\right\}\left\{\begin{array}{ccc}{k}_2& l_{13}& x\\ k_1& l_{25}& l_{12}\end{array}\right\}.(9)$

The functions $B\left(j_l,l_f;i_n,k_e\right)$ are defined as

$B\left(j_l,l_f;i_n,k_e\right)={\displaystyle {\sum }_{p_i}{\left(\begin{array}{c}{j}_l\\ p_i\end{array}\right)}^{\left(i_n\right)}{\left(\begin{array}{c}{l}_f\\ p_i\end{array}\right)}^{\left(k_e\right)}}(10)$

$\times {\displaystyle {\int }_0^{\infty }dr}\frac{{\sinh }^{2}r}{4\pi }{\displaystyle \prod _{i=1}^4{d}_{j_i{l}_i{p}_i}^{\left(\gamma j_i,j_i\right)}\left(r\right)}.$

where the factors in front of the integral are $SU\left(2\right)$$4jm$ symbols and the functions $d_{j_i{l}_i{p}_i}^{\left(\gamma j_i,j_i\right)}\left(r\right)$ are boost matrix elements of the Lorentz group. The product in Eq. 8 is over four of the five half-edges because one redundant factor must be eliminated by gauge-fixing. The sum is over a set of auxiliary spins $l_f$ and auxiliary intertwiners $k_e$. See Speziale (2017) for more details about this formulation of the EPRL amplitude and the full definition and analysis of all the quantities involved in the previous formulae.

Analytical results show that in the large spin limit this amplitude is generally exponentially suppressed except in two cases (Barrett et al., 2009; Donà et al., 2019). The first case is when the boundary geometry is the geometry of the boundary of a Lorentzian 4-simplex. This case can be naturally related to the semiclassical limit, where spacetime is flat and Lorentzian at scales smaller than the curvature radius. The second case is when the boundary geometry is a vector geometry, which includes the case when the boundary geometry is the geometry of the boundary of a Euclidean 4-simplex. As we shall see below, the mean geometry defined by $|{\psi }_o\rangle$ is that of a discretized metric 3-sphere i.e., the boundary of a regular Euclidean 4-simplex. Therefore this is a vector geometry. Vector geometries have been considered as a puzzling feature of the theory (Donà et al., 2018): here we can interpret them as a necessary contribution to the primordial quantum cosmological state in order to allow the tunneling from the empty state to the semiclassical 3-sphere geometry.

The form of the amplitude Eq. 8 is suited for numerical evaluation. The computational steps, in order of increasing complexity and cost, are: 1) evaluation of the $\left\{15j\right\}$ symbol; 2) evaluation of the B functions and 3) contraction over all internal and boundary spin labels. We limited our computation to spins (i.e., scale factor) $j\le 16$ given the time and memory constraints imposed by our computing facility. We used a standard laptop computer for lower spins and a 32-cores server with 196 GBs of RAM for higher spins.

The sum over spins $l_f$ in Eq. 8 is unconstrained, as $l_f\ge j_l$, where link l corresponds to face f. Hence it is necessary to introduce a cutoff $\Delta s$ so that $l_f=j_l,j_l+1,\dots ,j_l+\Delta s$ and the exact value is in the limit $\text{Δ}s\to \infty$. The case with $\Delta s=0$ has been called the simplified model (Speziale, 2017). Since the computation time is proportional to ${\left(\Delta s+1\right)}^6$, we are limited to very low values of the cutoff. It can be shown that in the simplified model the Lorentzian part of the amplitude is partially suppressed (Puchta, 2013; Speziale, 2017), and the effect of increasing the cutoff $\Delta s$ is to gradually enhance the amplitude for Lorentzian configurations. It may seem necessary to reach higher cutoffs in order to match the expected behavior in semiclassical asymptotics of Lorentzian simplices (Donà et al., 2019). However, we found that in our calculation, which spans the space of vector geometries due to the chosen (Euclidean) boundary conditions, the corrections due to higher cutoff values are minor or even negligible, so that the simplified computations effectively suffice to study the model numerically.

All the computations of the present work were carried out using the sl2cfoam library (Donà and Sarno, 2018), which is a C library for computing the spinfoam amplitude Eq. 8 using various optimization strategies. For a complete treatize of all the technical and numerical details that are relevant to this work we refer also to (Gozzetti, 2021¹), which studies extensions of the model considered here using a recently released version of the library (Gozzetti, 2021²).

5 Numerical Results

The results below are given for increasing values of the scale parameter j. In this section we fix the cutoff parameter to$\Delta s$. Therefore from now on we fix the convenient values $\Delta s=0$ and the Barbero-Immirzi constant to $\gamma =1.2$.

1.The expectation value of the angle operator $A_{ab}|i_n\rangle =\text{cos}\left({\theta }_{ab}\right)|i_n\rangle$ that measures the external dihedral angles between faces punctured by links a and b in any of the boundary tetrahedra (by symmetry all of them are equivalent) results to be

$\langle A_{ab}\rangle =-0.333(11)$

which is precisely the cosine of the external dihedral angle of an equilateral tetrahedron, for any links $a,b$ chosen. This shows that the spatial metric of $|{\psi }_o\rangle$ averages to that of the 3-boundary of a regular 4-simplex i.e., to that of a 3-sphere in our approximation. The variation of the average with the scale parameter is minor and due entirely to numerical fluctuations (Figure 1). The independence of the result from the choice of the links was tested by switching to a different recoupling basis, and also by directly performing the change of basis.

1.The spread $\Delta A_{ab}$ is large and increasing with the scale factor, see Figure 2. This suggest that quantum fluctuations in the metric are wide and are not suppressed in the large-scale regime.

2.The correlations between angle operators on different nodes depend on the pairing. We write $A_{n{n}^{\prime },n{n}^{″}}$ for the angle operator $A_{ab}$ at node n, where link a connects n with $n^{\prime }$ and link b connects n with $n^{″}$. The correlations are shown in Figure 3. For each source node n there are two pairs of correlated—anti-correlated nodes (for $n=4$ these are $\left(\mathrm{2,3}\right)$ and $\left(\mathrm{1,5}\right)$). The correlations appear to reach an asymptotic value, hence are not suppressed in the large-scale regime. The 3-metric that comes out from the quantum state $|{\psi }_o\rangle$ can correlate different spatial patches of the primordial universe, as required for solving the horizon problem of standard cosmology. It would be interesting to verify that in finer triangulations the correlations decay with the distance between non-adjacent faces, as required by local effective field theory.

3.To quantify the degree of correlation between operators we computed the entanglement entropy between different tetrahedra, viewed as quantum subsystems. A result by Page (Page, 1993) states that, given a splitting $\mathrm{\mathscr{H}}={\mathrm{\mathscr{H}}}_R\otimes {\mathrm{\mathscr{H}}}_{\overline{R}}$ of a Hilbert space $\mathrm{\mathscr{H}}$ into subspaces corresponding to a small subsystem R and its complement $\overline{R}$, the typical state in ${\mathrm{\mathscr{H}}}_R$ is found to have an entanglement entropy equal to $S_R\approx \log \left(\dim {\mathrm{\mathscr{H}}}_R\right)$ corresponding to a maximally-mixed state. In other words, the vast majority of quantum states of a small subsystem are close to being, in a broad sense, thermal see Popescu et al. (2006).

FIGURE 1

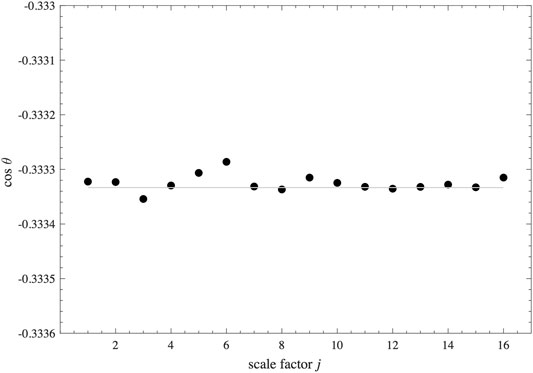
FIGURE 1. The computed average external dihedral angle of boundary tetrahedra as function of the scale factor. The gray line shows the dihedral angle of a regular tetrahedron.

FIGURE 2

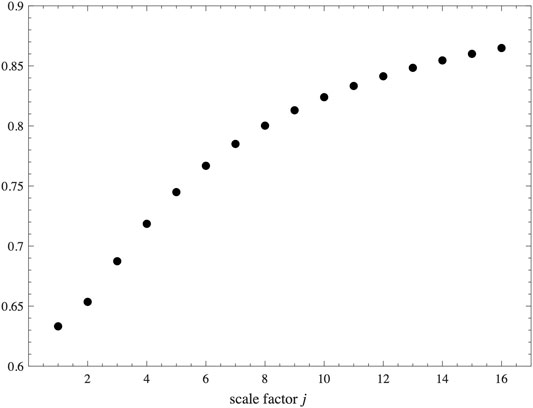
FIGURE 2. Quantum spread of the cosine of the external dihedral angle of boundary tetrahedra as function of the scale factor.

FIGURE 3

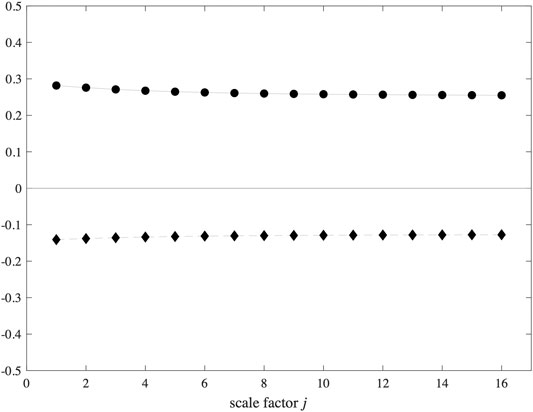
FIGURE 3. Left: correlations of angle operator $A_{\mathrm{42,43}}$ with $A_{\mathrm{23,24}}$ (top, positive) and $A_{\mathrm{34,35}}$ (bottom, negative). The same plot represents the correlations of $A_{\mathrm{41,45}}$ with $A_{\mathrm{14,15}}$ (top, positive) and $A_{\mathrm{54,53}}$ (bottom, negative).

We studied the degree of non-typicality of the primordial state $|{\psi }_o\rangle$ by looking at the entanglement entropy of any tetrahedron as function of the scale factor. The result is shown in Figure 4. It indicates that the entropy deviates significantly from the maximally-mixed case, and it appears to get close to an asymptotic value in the limit of large scale factor. We could not push the computations to spins higher than $j=16$, but the qualitative behavior is clear. For comparison, we show also the maximum entropy $S_{\max }\left(j\right)=\log \left(2j+1\right)$ and the result of (Bianchi et al., 2018) on the so-called Bell-network states (Baytaş et al., 2018), which are constructed in the same way as our primordial state $|{\psi }_o\rangle$ but using the dynamics of the simpler BF theory. See also (Bianchi et al., 2015; Bahr, 2020).

FIGURE 4

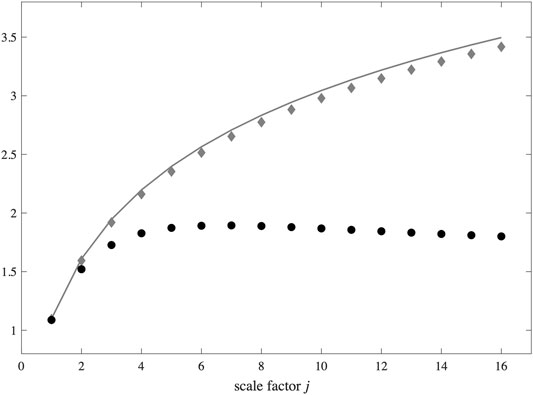
FIGURE 4. The entanglement entropy of a boundary node with respect to the rest of the graph. Gray continuous line shows the maximum entropy attainable as function of the scale factor parameter. Gray diamonds show the result of Bianchi et al. (2018). Black circles show our result for $|{\psi }_o\rangle$.

6 Conclusion

Summarizing, the quantum state for the primordial universe predicted by the dynamics of Loop Quantum Gravity can be computed in a kinematical truncation and at first order in the vertex expansion. It describes the fluctuating metric of a topologically closed universe in its early quantum regime. Its degrees of freedom encode the shapes of neighboring spatial regions. Their size (area), taken to be equal, is related to the scale factor. We have found that the mean geometry of this state is that of a (truncated) 3-sphere, as we expected by symmetry, but the fluctuations are large. Neighboring regions are correlated and correlations do not vanish as the scale factor increases. This opens the possibility that an inflationary phase may not be needed in order to circumvent the horizon problem, as the primordial quantum phase may introduce stochastic correlations in otherwise causally-independent spatial regions. We also computed the entanglement entropy of a single region viewed as a quantum subsystem of the whole universe. We found that the cosmological state is highly non-typical, showing an entanglement entropy that is apparently reaching an asymptotic value as the scale factor increases. Our work is one of the first explorations of the purely quantum regime of LQG—without resorting to the high-spin semiclassical limit of the theory—and one of the first applications to a concrete physical model of the numerical tools that are recently being developed for covariant Loop Quantum Gravity (Bianchi et al., 2018; Donà and Sarno, 2018; Donà et al., 2019; Dona et al., 2020). Our results indicate that an early quantum phase of the universe may provide an explanation for known puzzling features of the standard cosmological model, such as the horizon problem, possibly even without introducing additional inflationary and/or bouncing phases.

We thank for discussions Pietro Doná, Carlo Rovelli, Giorgio Sarno and Simone Speziale. We thank the Department of Theoretical Physics at UPV/EHU where part of this research was carried, supported by the grant IT956-16 of the Basque Government and by the grant FIS2017-85076-P (MINECO/AEI/FEDER, UE). We acknowledge the Anishinaabek, Haudenosaunee, Lūnaapéewak, and Attawandaron peoples, on whose traditional lands Western University is located.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available upon request by the authors, without undue reservation.

Author Contributions

FG contributed to this work writing an original code, performing all the numerical computations, and contributing to the analytical aspects of the computation. FV contributed with the original idea of this paper, devising the computations, supervising their completions, and analysing the results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

¹Gozzini (2021). High performance lorentzian spin foam numerics. In preparation.

²Gozzini (2021). Numerical simulation of the quantum cosmological vacuum with many spin foam vertices. In preparation.

References

Bahr, B. (2020). Entanglement entropy of physical states in hypercuboidally truncated spin foam quantum gravity. Class. Quantum Grav. 37, 094001. doi:10.1088/1361-6382/ab77ea

CrossRef Full Text | Google Scholar

Bahr, B., Klöser, S., and Rabuffo, G. (2017). Towards a cosmological subsector of spin foam quantum gravity. Phys. Rev. D. 96, 086009. doi:10.1103/PhysRevD.96.086009

CrossRef Full Text | Google Scholar

Barrett, J. W., Dowdall, R. J., Fairbairn, W. J., Gomes, H., and Hellmann, F. (2009). Asymptotic analysis of the engle-pereira-rovelli-livine four-simplex amplitude. J. Math. Phys. 50, 112504. doi:10.1063/1.3244218

CrossRef Full Text | Google Scholar

Baytaş, B., Bianchi, E., and Yokomizo, N. (2018). Gluing polyhedra with entanglement in loop quantum gravity. Phys. Rev. D. 98, 026001. doi:10.1103/PhysRevD.98.026001

CrossRef Full Text | Google Scholar

Bianchi, E., Donà, P., and Speziale, S. (2011). Polyhedra in loop quantum gravity. Phys. Rev. 83. doi:10.1103/PhysRevD.83.044035

CrossRef Full Text | Google Scholar

Bianchi, E., Donà, P., and Vilensky, I. (2018). Entanglement entropy of bell-network states in lqg: analytical and numerical results.

Google Scholar

Bianchi, E., Hackl, L., and Yokomizo, N. (2015). Entanglement time in the primordial universe. Int. J. Mod. Phys. 24, 1544006. doi:10.1142/S021827181544006X

CrossRef Full Text | Google Scholar

Bianchi, E., Rovelli, C., and Vidotto, F. (2010). Towards spinfoam cosmology. Phys. Rev. D. 82, 084035. doi:10.1103/PhysRevD.82.084035

CrossRef Full Text | Google Scholar

Borja, E. F., Garay, I., and Vidotto, F. (2012). Learning about quantum gravity with a couple of nodes. SIGMA 8. doi:10.3842/SIGMA.2012.015

CrossRef Full Text | Google Scholar

Donà, P., Fanizza, M., Sarno, G., and Speziale, S. (2019). Numerical study of the Lorentzian Engle-Pereira-Rovelli-Livine spin foam amplitude. Phys. Rev. D. 100, 106003. doi:10.1103/PhysRevD.100.106003

CrossRef Full Text | Google Scholar

Donà, P., Fanizza, M., Sarno, G., and Speziale, S. (2018). Su(2) graph invariants, regge actions and polytopes. Class. Quantum Grav. 35, 045011. doi:10.1088/1361-6382/aaa53a

CrossRef Full Text | Google Scholar

Dona, P., Gozzini, F., and Sarno, G. (2020). Searching for classical geometries in spin foam amplitudes: a numerical method. Class. Quantum Grav. 37, 094002. doi:10.1088/1361-6382/ab7ee1

CrossRef Full Text | Google Scholar

Donà, P., and Sarno, G. (2018). Numerical methods for EPRL spin foam transition amplitudes and lorentzian recoupling theory. Gen. Relat. Gravit. 50, 127. doi:10.1007/s10714-018-2452-7

CrossRef Full Text | Google Scholar

Engle, J., Livine, E. R., Pereira, R., and Rovelli, C. (2008). Lqg vertex with finite immirzi parameter. Nucl. Phys. B 799, 136–149. doi:10.1016/j.nuclphysb.2008.02.018

CrossRef Full Text | Google Scholar

Freidel, L., and Speziale, S. (2010). Twisted geometries: a geometric parametrization of su(2) phase space. Phys. Rev. 82, 084040. doi:10.1103/PhysRevD.82.084040

CrossRef Full Text | Google Scholar

Halliwell, J. J. (1987). Correlations in the wave function of the Universe. Phys. Rev. D. 36, 3626–3640. doi:10.1103/PhysRevD.36.3626

CrossRef Full Text | Google Scholar

Halliwell, J. J., Hartle, J. B., and Hertog, T. (2019). What is the no-boundary wave function of the Universe? Phys. Rev. D 99. doi:10.1103/PhysRevD.99.043526

CrossRef Full Text | Google Scholar

Hartle, J. B., and Hawking, S. W. (1983). Wave function of the universe. Phys. Rev. D. 28, 2960–2975. doi:10.1103/PhysRevD.28.2960

CrossRef Full Text | Google Scholar

Page, D. N. (1993). Average entropy of a subsystem. Phys. Rev. Lett. 71, 1291–1294. doi:10.1103/PhysRevLett.71.1291

PubMed Abstract | CrossRef Full Text | Google Scholar

Popescu, S., Short, A. J., and Winter, A. (2006). Entanglement and the foundations of statistical mechanics. Nat. Phys. 2, 754–758. doi:10.1038/nphys444

CrossRef Full Text | Google Scholar

Puchta, J. (2013). Asymptotic of lorentzian polyhedra propagator.

Google Scholar

Rovelli, C., and Smerlak, M. (2012). In quantum gravity, summing is refining. Class. Quantum Grav. 29, 055004. doi:10.1088/0264-9381/29/5/055004

CrossRef Full Text | Google Scholar

Rovelli, C., and Vidotto, F. (2015). Covariant loop quantum gravity: an elementary introduction to quantum gravity and spinfoam theory. Cambridge, United Kingdom: Cambridge University Press.

Rovelli, C., and Vidotto, F. (2008). Stepping out of homogeneity in loop quantum cosmology. Class. Quantum Grav. 25, 225024. doi:10.1088/0264-9381/25/22/225024

CrossRef Full Text | Google Scholar

Speziale, S. (2017). Boosting Wigner’s nj-symbols. J. Math. Phys. 58, 032501. doi:10.1063/1.4977752

CrossRef Full Text | Google Scholar

Vidotto, F. (2011). Many-node/many-link spinfoam: the homogeneous and isotropic case. Class. Quantum Grav. 28, 245005. doi:10.1088/0264-9381/28/24/245005

CrossRef Full Text | Google Scholar

Vidotto, F. (2017). Relational quantum cosmology. Cambridge University Press, 297–316.