Prelude to Simulations of Loop Quantum Gravity on Adiabatic Quantum Computers

1 Introduction

One can distinguish two main applications of quantum computers. The first is data processing associated with the implementation of quantum algorithms, e.g., quantum machine learning protocols (Biamonte et al., 2017). The second concerns simulations of quantum systems.

Simulating quantum systems using quantum computers is fundamentally different from what simulations performed at classical computers are. While classical simulations rely on either discretization of a given physical system or an adequate algebraic analysis, the simulations performed on quantum computers allow to imitate a given quantum system. This kind of exact simulation of a quantum system has been a subject of discussion in the seminal Feynman’s article (Feynman, 1982).

In order to understand better what we mean by exact simulations, let us consider the case of Planck scale physics. Here, the relevant degrees of freedom are defined at length scales of the order of the Planck length $l_{\text{Pl}}\sim {10}^{-35}\text{m}$. Despite significant advances made in theoretical understanding and experimental techniques, the Planck scale physics remains empirically directly inaccessible.

On the other hand, concrete examples of theories describing elementary quantum gravitational degrees of freedom exist. One such approach is loop quantum gravity (LQG) (Rovelli, 1998; Ashtekar and Lewandowski, 2004; Rovelli and Vidotto, 2014). In LQG, background-independent degrees of freedom can be defined, and predictions can be made (Agullo et al., 2012; Barrau et al., 2014). Even if the degrees of freedom under consideration are experimentally not directly accessible, one can consider their projection onto another physical realization, which will imitate its quantum behavior (see Figure 1). Under the assumption that quantum mechanics is valid at the Planck scale, the projected realization is quantum-mechanically equivalent to the original system. The only difference is appropriately rescaled couplings adjusted to the physical nature of the simulator (built, e.g., with the use of superconducting qubits). Such projection of one quantum system onto its equivalent imitation allows performing what we previously called exact simulations. As it has already been mentioned, the quantum simulations are very different from what we usually consider as physical simulations, where for instance, a given differential equation is discretized and then implemented on a computer with the use of appropriate algorithms. In contrast, in the case of exact simulations, one actually performs experiments on a quantum system which is defined as being equivalent (quantum mechanically) to a part (or a whole) of the original quantum system.

FIGURE 1

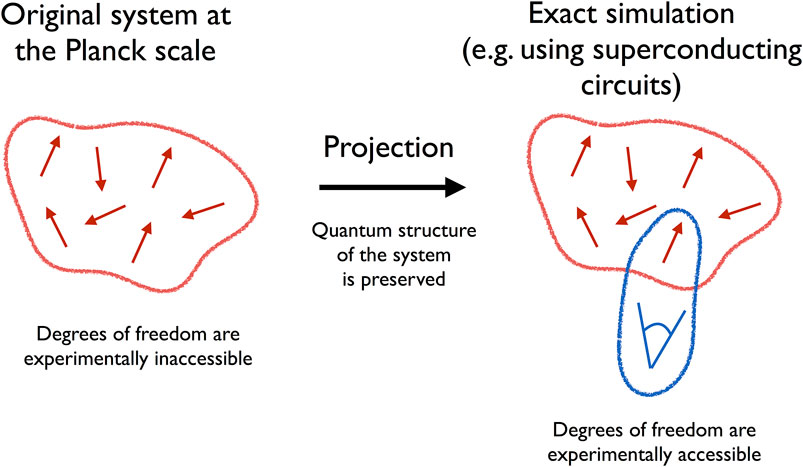
FIGURE 1. Pictorial presentation of the relation between the original quantum system defined at the Planck scales and its exact simulation. The exact simulation is performed with the use of projection of the original quantum system onto the architecture of a quantum computer. In contrast to the Planck scale system, measurements of the quantum degrees of freedom can be performed at the level of the quantum simulation.

The aim of this article is to investigate the possibility of performing exact quantum simulations of the spin network states, which are used to construct the Hilbert space in the LQG approach to quantum gravity. Our interest is focused on applying existing adiabatic quantum computers, a commercial example of which is one provided by the D-Wave Systems company.

We consider conceptual issues related to the possibility of simulating Loop Quantum Gravity based on the considered fixed graph case. Specifically, the implementation of the scalar constraint is analyzed, and a toy model of such a procedure is presented. We conclude with an outlook of the following steps to be done in the research direction initiated in this article.

The idea of employing the spin network states in quantum computations already appeared in the literature [see Refs Marzuoli and Rasetti (2005), Kauffman and Lomonaco (2008), Jordan (2010)]. However, the potential of applying spin networks for universal quantum data processing was considered only. Up to the best of our knowledge, the issue of relating spin networks with adiabatic quantum computations was not considered before. While this article was in the final stage of preparing a study in which an LQG spin network is implemented on a molecular quantum simulator appeared. A simulation of quantum fluctuations of a 5-node spin network in the kinematical regime was performed (Li et al., 2019). Here, we will consider the same type of spin network in Section 4 in the context of solving a prototype scalar constraint with the use of adiabatic quantum computations.

2 Adiabatic Quantum Computing

The last years have brought significant progress in the development of quantum computing technologies (Campbell et al., 2017). First, quantum computers have been commercialized and made available in a cloud or as independent hardware units. In both cases, the currently most advanced commercial technologies were possible to achieve thanks to the development of superconducting quantum circuits (You and Nori, 2005). In particular, the IBM Q universal quantum computers built using 5 and 20 superconducting qubits have been developed. However, from the point of view of exact simulations discussed in the Introduction, another type of quantum computer seems to be more suitable to use currently—namely the adiabatic quantum computers (Kadowaki and Nishimori, 1998).

Adiabatic quantum computers, in contrast to the universal ones, are designed to solve a specific problem of finding the minimum of a Hamiltonian $H_I$ of a coupled system of qubits (spins). In the process of finding the minimum of $H_I$ one employs a time-dependent Hamiltonian in the form

$H\left(\lambda \right)=\left(1-\lambda \right)H_B+\lambda H_I,(1)$

where $H_B$ is the so-called base Hamiltonian, which is characterized by a simple and easy to prepare ground state. In practice, the base Hamiltonian is often equal to $H_B={\displaystyle \sum }_i{\sigma }_i^x$, so that the ground state corresponds to the alignment of spins in the x direction. Then, the value of λ is changed adiabatically from $\lambda =0$ to $\lambda =1$, so that while the system that is initially in a non-degenerate ground state will remain in this state. Therefore, if the process is done correctly, the system ends up in the minimum of the Hamiltonian $H_I$. The process of transition from $\lambda =0$ to $\lambda =1$ involves quantum tunneling and is called quantum annealing. The characteristic time scales which allow keeping the system close to the adiabatic state are dependent on what kind of $H_I$ Hamiltonian is considered. This issue is closely related to the efficiency of the quantum annealing-based algorithms to the classical ones [see Ref Biamonte et al. (2017)] for discussion of this subject).

In practical implementations, the most considered form of $H_I$ corresponds to the Ising problem:

$H_I={\displaystyle \sum }_{\langle i,j\rangle }{b}_{ij}{\sigma }_i^z{\sigma }_j^z+{\displaystyle \sum }_i{h}_i{\sigma }_i^z,(2)$

where $b_{ij}$ are coupling between spins and $h_i$ quantify interactions of spins with external magnetic field. The summation $\langle i,j\rangle$ is defined such that it does not repeat over pairs. The values of couplings specify the problem to be solved while readouts of z components of the spins in the final state provide an outcome of the quantum computation (simulation).

From the mathematical viewpoint, the class of problems which can be solved in that way is the so-called Quadratic Unconstrained Binary Optimization (QUBO), which typically is of the NP-hard type. This is because, when we look a the problem from the classical perspective by measuring the orientations of spins along the z-axis, the two values of ${\sigma }_i^z\to s_i\in \left\{-\mathrm{1,1}\right\}$ are allowed. In consequence, for the system of N classical spins, there are $2^N$ configurations to be explored. Therefore, in general, finding a ground state requires exponential growth of time with the number of spins (N), which is the case for NP-hard problems.

The physical implementation of the QUBO problem using the quantum annealing procedure is provided by the D-Wave machine. In this realization, the spins (qubits) are created with the use of superconducting circuits in the form of CC JJ RF-SQUIDs (Harris et al., 2010) built with the use of Josephson junctions composed of Niobium in the superconducting state. The qubit basis states are defined employing two different orientations of quantum of magnetic flux across the superconducting circuit. SQUID (superconducting quantum interference device) introduces interactions between the qubits based circuits called couplers, which introduce the $b_{ij}{\sigma }_i^z{\sigma }_i^z$ factors in the Hamiltonian (2). The values of parameters $h_i$ can be controlled with the use of external magnetic fluxes. However, not all values of $b_{ij}$ and $h_i$ are allowed but only some fractional values from the range $[-\mathrm{1,1}]$. The readout of the final quantum states of qubits is performed with the use of sensitive magnetometers built with the use of SQUIDs.

In the D-Wave quantum annealer, the superconducting qubits $q_i$ are arranged into 8-qubit blocks forming the so-called Chimera architecture. Each block consists of 16 couplings between 8 spins. As a consequence, not all qubits are coupled. The topology of couplings between qubits in a single block is presented in Figure 2. In the so far most advanced version of the D-Wave machine (the D-Wave 2000) the 8-qubit blocks form a 16 × 16 matrix (256 blocks in total), leading to 2048 qubits.

FIGURE 2

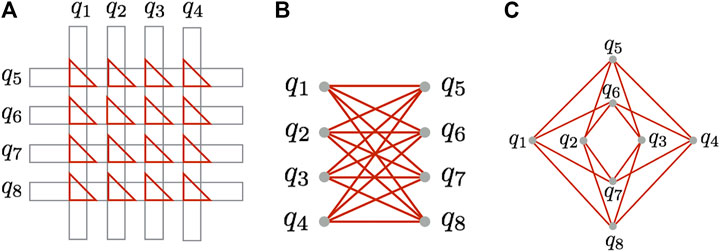
FIGURE 2. Three different representations of the structure of couplings between eight $q_i$ qubits forming an elementary block of the D-Wave processor: (A) The physical representation of quibits as closed superconducting loops. The couplers between the qubits are represented by triangles. (B) The Chimera graph structure of couplings between the eight qubits. (C) Representation of a single block which is useful when interconnections in the array of blocks are considered.

3 Spin Networks

Let us now proceed to discuss spin networks. We begin with a brief overview of how spin networks appear in the loop quantum gravity approach to quantum gravity. Then we introduce a class of spin networks that is possible to implement on the Chimera architecture of D-Wave quantum processors.

The fundamental elements of the LQG approach to quantum gravity are holonomies of Ashtekar connection $A\in \mathfrak{su}\left(2\right)$ along a curve $e\left(\lambda \right)$, with $\lambda \in \left[\mathrm{0,1}\right]$:

$h[A,e]=\mathcal{P}{e}^{{\displaystyle {\int }_{e}A}},(3)$

where $\mathcal{P}$ denotes path ordering. Performing gauge transformations, generated by the so-called Gauss constraint, the Ashtekar connection transforms as $A\to A_g=g^{-1}dg+g^{-1}Ag$. The corresponding transformation of holonomy is $h[A,e]\to h[A_g,e]=g\left(e\left(0\right)\right)h[A,e]g{\left(e\left(1\right)\right)}^{-1}$. The fact that the transformations of holonomies contribute only at the boundaries of e implies that gauge invariant objects are provided by the Wilson loops $W[A,e]:=\text{tr}\left(h[A,e]\right)$.

The key idea behind LQG is to build a Hilbert space of the theory out of Wilson loops. However, such a basis is, in general, over-complete. A solution to the problem comes from the construction of spin-networks which are a certain linear combination of products of Wilson loops (Rovelli and Smolin, 1990). Such an approach guarantees that both the Gauss constraint (ensuring local gauge invariance) is satisfied by the base states, and the Hilbert space is complete. By introducing an equivalence relation between topologically equivalent spin networks, the so-called diffeomorphism constraint can be satisfied. There is eventually a scalar (Hamiltonian) constraint, which has to be satisfied by physical states. In this section, we will focus on spin network states satisfying both Gauss and diffeomorphism constraints. The issue of satisfying the scalar constraint (with the use of adiabatic quantum computing) will be discussed in the next section.

The spin network is formally a graph composed of edges E and nodes N with spin labels at the edges and the so-called intertwiners at the nodes. The spin labels correspond to irreducible representations of the $SU\left(2\right)$ group such that triangle inequalities (reflecting the Gauss constraint) are satisfied at the nodes. The intertwiners correspond to invariant subspaces at the nodes, which we will discuss in more detail below.

In Figure 3 we present an exemplary spin network composed of 3-valent and 4-valent nodes. An essential feature of the nodes is that 3-valent nodes do not carry a volume element while 4-valent nodes and higher valent nodes are associated with 3-volume (in the sense that eigenvalues of the volume operator in such a state are non-vanishing).

FIGURE 3

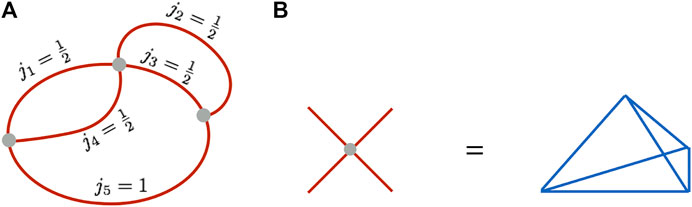
FIGURE 3. A) An exemplary spin network. (B) In the geometric picture the 4-valent node is dual to a tetrahedron (3-simplex).

The particular case is a 4-valent node that is dual to a tetrahedron (3-simplex). One can imagine that the vertex is located in the center of the tetrahedra, while each of the associated links intersects with one of the surfaces (see block b) in Figure 3).

In this article, we are considering the case of spin networks composed of 4-valent vertices only and spin labels corresponding to fundamental representations of the $SU\left(2\right)$ group i.e. $j=\frac{1}{2}$. The reason for that is that in such a case, the Hilbert space at each vertex is a tensor product of four 1/2 spins, which can be decomposed into irreducible representations in the following way:

$H_{\frac{1}{2}}\otimes H_{\frac{1}{2}}\otimes H_{\frac{1}{2}}\otimes H_{\frac{1}{2}}=H_0\oplus H_0\oplus 3H_1\oplus H_2.(4)$

There are, therefore, two possibilities in which the spins can add up to zero. In consequence, the invariant subspace for such a vertex is two dimensional:

$\text{dim}\text{Inv}\left(H_{\frac{1}{2}}\otimes H_{\frac{1}{2}}\otimes H_{\frac{1}{2}}\otimes H_{\frac{1}{2}}\right)=2.(5)$

We associate the two dimensional invariant space with the qubit space. The nature of the qubit associated with the 4-vertex under consideration is graphically presented in Figure 4.

FIGURE 4

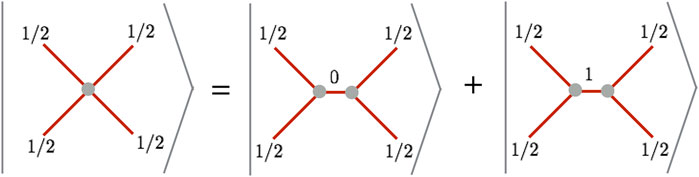
FIGURE 4. The 4-valent node with spin labels equal to $j=1/2$ corresponds to superposition of two graphs each with the different value of intertwiner. In this article, the two dimensional intertwiner space is associated with the qubit Hilbert space.

Worth mentioning here is that there is a freedom of choice of channel in which recoupling of spin labels at the vertex is performed. In particular, in the s channel the base states can be expressed in terms of the four $1/2$ spin base states ($|\uparrow \rangle$ and $|\downarrow \rangle$) as follows (Feller and Livine, 2016):

$|0_s\rangle =\frac{1}{2}\left(|\uparrow \downarrow \uparrow \downarrow \rangle +|\downarrow \uparrow \downarrow \uparrow \rangle -|\uparrow \downarrow \downarrow \uparrow \rangle -|\downarrow \uparrow \uparrow \downarrow \rangle \right)$

$|1_s\rangle =\frac{1}{\sqrt{3}}\left(|\uparrow \uparrow \downarrow \downarrow \rangle +|\downarrow \downarrow \uparrow \uparrow \rangle -\frac{|\uparrow \downarrow \uparrow \downarrow \rangle +|\downarrow \uparrow \downarrow \uparrow \rangle +|\uparrow \downarrow \downarrow \uparrow \rangle +|\downarrow \uparrow \uparrow \downarrow \rangle }{2}\right).(6)$

The above definitions of the basis states for a qubit have recently been considered in the context of universal quantum computations in Refs. Li et al. (2019), Mielczarek (2019), Czelusta and Mielczarek (2021). Alternatively, it is convenient to construct our qubit states such that they are eigenvectors of the volume operator [see e.g. Ref Feller and Livine (2016) for details]:

$\widehat{V}:=\frac{\sqrt{2}}{3}{l}_{\text{Pl}}^3{\left(8\pi \gamma \right)}^{\frac{3}{2}}\sqrt{\left|{\widehat{\overrightarrow{J}}}_1\cdot \left({\widehat{\overrightarrow{J}}}_2\times {\widehat{\overrightarrow{J}}}_3\right)\right|},(7)$

where γ is the Barbero-Immirzi parameter (Barbero G, 1995; Immirzi, 1997) and the angular momentum operators ${\widehat{\overrightarrow{J}}}_i=\left({\widehat{J}}_i^1,{\widehat{J}}_i^2,{\widehat{J}}_i^3\right)$ satisfy the $\mathfrak{su}\left(2\right)$ algebra: $\left[{\widehat{J}}_k^a,{\widehat{J}}_l^b\right]=i{\delta }_{kl}{\mathit{ϵ}}_c^{ab}{\widehat{J}}_k^c$, for $a,b,c\in \left\{\mathrm{1,2,3}\right\}$. This can be achieved by considering the following superpositions of the states Eq. 6:

$|1\rangle =\frac{1}{\sqrt{2}}\left(|0_s\rangle -i|1_s\rangle \right),(8)$

$|0\rangle =\frac{1}{\sqrt{2}}\left(|0_s\rangle +i|1_s\rangle \right),(9)$

so that $\widehat{V}|1\rangle =+V_0|1\rangle$ and $\widehat{V}|0\rangle =-V_0|0\rangle$, where $V_0:=\frac{l_{\text{Pl}}^3{\left(8\pi \gamma \right)}^{\frac{3}{2}}}{\sqrt{6\sqrt{3}}}$ is the minimal eigenvalue of the volume operator (Rovelli and Vidotto, 2014). The positive and negative signs of the eigenvalues distinguish between the two allowed orientations of a 3-simplex. Consequently, in LQG, the elementary volume can contribute with both signs: positive (for $|1\rangle$) or negative (for $|0\rangle$). However, it is expected that in the semiclassical limit, one of the contributions will dominate over the other. The eigenstates $|1\rangle$ and $|0\rangle$ are the qubit base states that we refer to in the rest of this article.

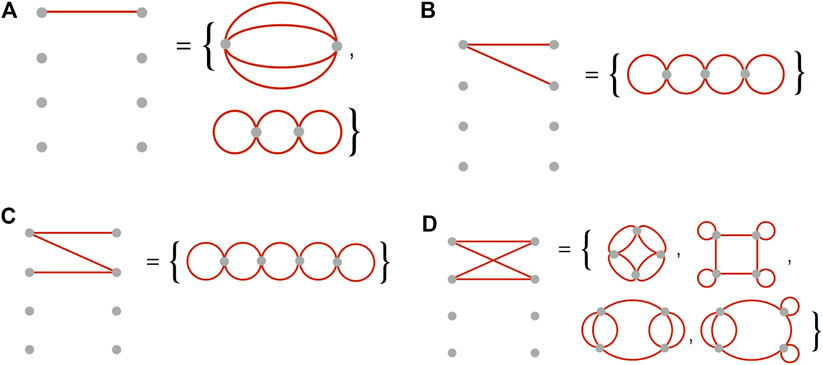
Having the definition of a qubit, one can consider different spin network topologies that are possible to implement directly with Chimera architecture. In Figure 5 we present connected spin networks with the number of nodes equal to $N=\mathrm{2,3}$ and 4, which can be directly embedded into the Chimera graph.

FIGURE 5

FIGURE 5. Connected spin networks compatible with the Chimera architecture: (A)$N=2$, (B)$N=3$, (C)$N=4$, (D)$N=4$.

A single coupling between the qubits in the quantum processor architecture can be associated with one or more links in the corresponding spin network. The difference between connections can be further encoded in the strength of the couplers. In particular, in the case a) in Figure 5 there are two possible 4-valent spin networks can be associated with two coupled qubits. Relating a single coupler with a single link in the spin network is generically not possible. In the case of 4-valent nodes and a single block of D-Wave processor, the only possibility is given by the configuration represented in blocks b) and c) in Figure 2. The situation corresponds to a spin network with $N=8$ qubits and $E=16$ edges forming the Chimera graph.

As one can notice, the structure of Chimera architecture imposes significant restrictions on the possible associated spin network topologies. In particular, it is not possible to implement a “triangular” $N=3$ spin network directly with the use of elementary qubits. In order to go beyond the limitations of the Chimera architecture, one can consider effective qubits (chain qubits) composed of two or more spins. If the coupling between the qubits is sufficiently negative, then the qubits will tend to align in the same direction, which is preferred energetically. In such a case, measurements can be performed on one of the elementary qubits contributing to the chain, while the remaining qubits can be considered ancilla qubits.

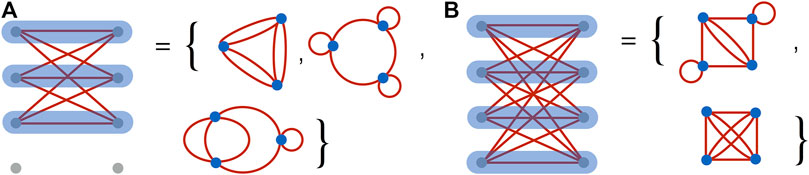
With the use of chain qubits (see Figure 6), the dictionary of spin networks can be extended further. In particular, previously inaccessible spin networks for $N=3$ and $N=4$ can now be constructed (see Figure 7).

FIGURE 6

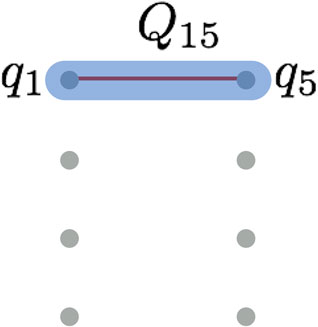
FIGURE 6. A chain qubit. If the $b_{15}$ coupling is sufficiently negative then the spins $q_1$ and $q_5$ will have tendency to align in the same direction.

FIGURE 7

FIGURE 7. Connected spin networks compatible with Chimera architecture: (A)$N=3$, (B)$N=4$.

Worth stressing is that different types of effective qubits can be considered and Figure 7 represents only a one of many possible implementations of the spin networks under consideration.

A more extended example is a regular square lattice with the nearest neighbor connections. Implementation of the regular lattice spin network on the Chimera architecture of the quantum processor is shown in Figure 8.

FIGURE 8

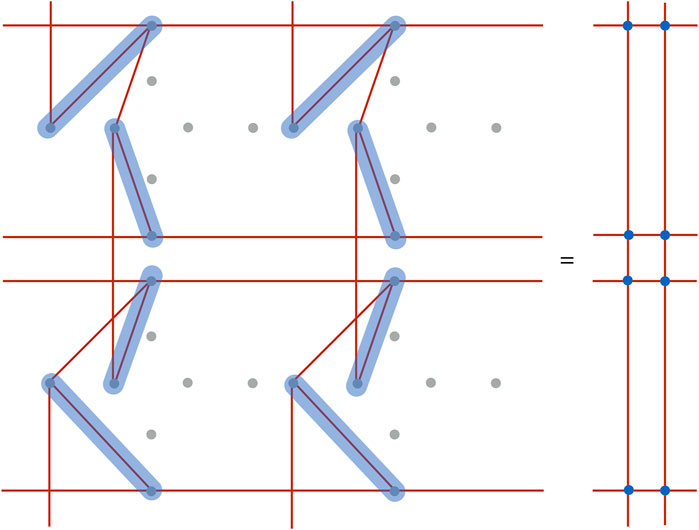
FIGURE 8. Regular lattice spin network embedded with the use of chain qubits. Here, four 8 qubit blocks of the D-Wave processor are used.

The regular lattice configuration enables simulation of a 2D Ising spin networks discussed in Ref (Feller and Livine, 2016). which provide a toy model of extended quantum spacetime. The analysis of such configurations is especially interesting in the context of phase transitions and domain formation, which may reflect the emergence of semi-classical spacetime. We will come back to this issue in the next section. Furthermore, in further studies, it would be interesting to investigate if the 3D hexagonal type Ising spin network can also be embedded into the architecture of the D-Wave processor.

4 Simulation of Loop Quantum Gravity

The spin network states discussed in the previous sections satisfy the Gauss constraint. Moreover, the diffeomorphism constraint can be imposed by considering equivalence classes under the action of spatial diffeomorphisms, which means that we equate all graphs with the same topology.

It remains the scalar (Hamiltonian) constraint, which is the most difficult one to satisfy. Finding a solution to the Hamiltonian constraint in the 3 + 1 D can be perceived as the most difficult open problem in LQG (Thiemann, 2006).

The scalar constraint reflects the fact that the total energy of the gravitational field is equal to zero. The scalar constraint is, in general, a graph-changing operator, which makes implementation of such a constraint a problematic task. However, the situation in which the action of the constraint preserves the graph structure may provide an intermediate step toward the solution of the full problem. The question is whether adiabatic quantum computation may be helpful here.

To address this question, let us observe that finding solutions to the classical constraint:

$C\approx 0,(10)$

can be mapped into a problem of minimizing some Hamiltonian. Because the quantum annealing algorithm is just searching for the minimum of the spin Hamiltonian (2), making use of adiabatic computations requires association of the minimum of the Hamiltonian with a solution of the constraint (10). The simplest way to do it is to consider the Hamiltonian H in the following form:

$H\propto C^2.(11)$

In this case, the Hamiltonian is bounded from below, and in the classical ground state, the constrain (10) is naturally satisfied.

Solution of the constraint (10) allows to extract physical states and construct a physical phase space ${\text{Γ}}_{\text{phys}}$ (or physical Hilbert space) being a subset of kinematical phase space ${\text{Γ}}_{\text{kin}}$¹. It is important to stress that the minimum energy states of the Hamiltonian (11) are just the physical states of the theory and they form ${\text{Γ}}_{\text{phys}}$. If there is no additional matter content, the states represent also a vacuum gravitational field configuration, described by the prototype scalar (Hamiltonian) constraint under considerations. The auxiliary Hamiltonian (11) is a simplified version of the Master Constraint introduced in LQG, being a square function of constraints [see Ref Thiemann (2006)].

There are, however, technical limitations in the implementation of the procedure proposed above. This is because, in the D-Wave annealer, only quadratic Hamiltonian functions are allowed. This implies that the scalar constraint cannot be higher than linear order in the spin variables. On the other hand, scalar constraints being of the higher than linear order in the spin variables is expected in the full LQG.

The most general type of the constraint that one consider in the context of D-Wave quantum computer is

$C={\displaystyle \sum }_{i=1}^N{a}_i{s}_i-c\approx 0,(12)$

with some parameters $a_i,c\in \mathrm{ℝ}$² and where $s_i\in \left\{-\mathrm{1,1}\right\}$ are classical spin variables.

Here, for the sake of simplicity we will consider the case with $a_i=1\forall i$, such that the prototype scalar constraint (12) takes the following form:

$C={\displaystyle \sum }_{i=1}^N{s}_i-c\approx 0,(13)$

with some parameter $c\in \left\{-N,-N+2,\dots ,N-2,N\right\}$. By squaring (13) we obtain:

$C^2=2\left(\stackrel{N}{{\displaystyle \sum }_{\langle i,j\rangle }}{s}_i{s}_j+\stackrel{N}{{\displaystyle \sum }_{i=1}}\left(-c\right)s_i\right)+N+c^2.(14)$

From this one can propose that the Hamiltonian to be considered is:

$H=\frac{C^2-N-c^2}{2}={\displaystyle \sum }_{\langle i,j\rangle }^N{s}_i{s}_j+h{\displaystyle \sum }_{i=1}^N{s}_i,(15)$

where $h=-c$. The obtained Hamiltonian corresponds to the QUBO problem with a complete graph and equal couplers between the qubits $\left(b_{ij}=1\right)$. In this model, the ground state (which corresponds to $C=0$) energy is:

$H_0=-\frac{N+c^2}{2}.(16)$

There is one more important aspect illustrated by the model - a degeneracy of the ground state. Namely, there are, in general, multiple spin configurations which are minimizing the Hamiltonian (15). In the model under consideration, the vacuum degeneracy depends on both c and N. Given the c and N, finding the order of degeneracy is a combinatorial problem which can be reduced to determining the number of $\left(N+c\right)/2$ subset of a set composed of N elements, which is given by the binomial coefficient:

$\left(\begin{array}{c}N\\ \frac{N+c}{2}\end{array}\right).(17)$

Then, for a fixed N the maximal degeneracy is obtained for the choices

$c=2\lfloor N/2\rfloor -N\vee c=2\lceil N/2\rceil -N,(18)$

where $\lfloor x\rfloor$ and $\lceil x\rceil$ are floor and ceiling functions respectively. Based on this, the corresponding maximal degeneracy is equal to

$\left(\begin{array}{c}N\\ \lfloor N/2\rfloor \end{array}\right)=\left(\begin{array}{c}N\\ \lceil N/2\rceil \end{array}\right).(19)$

The degeneracy is an essential quantity because it corresponds to the number of physical states satisfying the constraint (13).

One can now make relation with the spin networks. For this purpose, let us recall that the spin Hamiltonian (15) corresponding to the constraint (13) describes a complete graph. Associating a spin coupler with a single link of the spin network, one can conclude that for the 4-valent nodes under considerations, the only complete spin network must have pentagram structure with $N=5$ nodes (see block “a” in Figure 9)³.

FIGURE 9

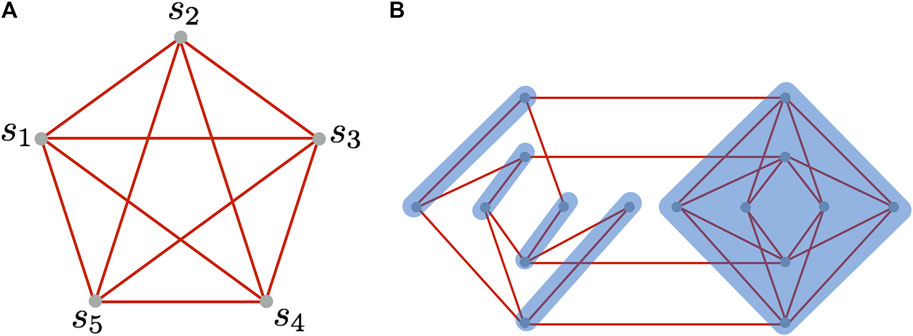
FIGURE 9. (A) Pentagram spin network with $N=5$. Each link of the graph is labeled with $j=1/2$. The qubits (here modeled by the classical bits $s_i$) are defined at the nodes. (B) An exemplary embedding of the pentagram spin network on the two neighbor blocks of the D-Wave processor. The shadowed regions represent collective (chain) qubits which correspond to the nodes of the spin network.

Such spin network corresponds to the geometry of a three-sphere. Furthermore, it turns out that introducing composite (chain) spins the pentagram spin network can be implemented using two neighbor blocks of the D-Wave processor. There are various ways to do so. One of them is presented in block “b” in Figure 9, where the shadowed regions correspond to the effective qubits composed of the elementary ones.

Finally, let us take a look at the energy landscape of the model. In Figure 10 we plot energies corresponding to all of the spin configurations for $c=-1$.

FIGURE 10

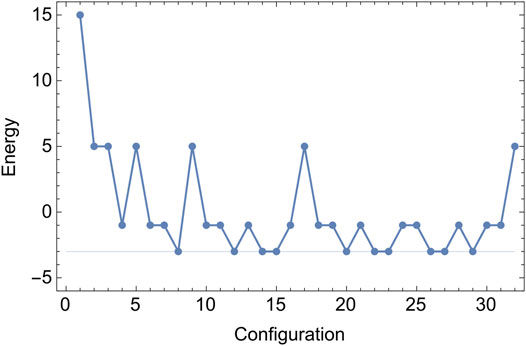
FIGURE 10. Energy landscape of the pentagram spin network with $N=5$ and $c=-1$. The ground state configurations satisfy the prototype scalar constraint (13) and span physical phase space ${\text{Γ}}_{\text{phys}}$ of the model.

The total number of spin configurations corresponds to dimensionality of the kinematical space: $\text{dim}{\text{Γ}}_{\text{kin}}=2^5=32$. On the other hand, the degeneracy of the vacuum of (15) gives us dimensionality of the physical space $\text{dim}{\text{Γ}}_{\text{phys}}=\left(\begin{array}{c}5\\ \frac{5-1}{2}\end{array}\right)=10$ (here we used Eq. 17). The physical space is a subset of kinematical space ${\text{Γ}}_{\text{phys}}\subset {\text{Γ}}_{\text{kin}}$ as expected.

In order to extract all the physical states with the use of adiabatic quantum simulations, the quantum annealing procedure has to be performed repeatedly. The outcome is a superposition of the ground states, and the procedure of measurement should select the particular ground states in the independent runs. However, as discussed in Refs (Matsuda et al., 2009; Mandrà et al., 2017) the type of quantum annealing procedure used in the D-Wave quantum computers may not be suited to identify all degenerate ground states. The studies suggest that an extension beyond the currently employed base Hamiltonians is needed to ensure that the ground state manifold is adequately sampled. Otherwise, the probability of finding some of the possible ground states may be suppressed.

Assuming that the physical states are selected, analysis of fluctuations of various observables is possible to perform. In the case under consideration, one of the interesting possibilities would be to investigate volume fluctuations. As we already mentioned, the base states corresponding to the 4-valent note qubits are eigenstates of the volume operator describing the same absolute volume but with different signs. It is, however, expected that in the classical limit, only one type of contribution would dominate such that averaged nonvanishing space volume will emerge. On the other hand, in a strongly quantum state, the positive and negative contributions can subtract one another, leading to the lack of the notion of classical geometry. Analysis of correlations of the spins in the physical states could, therefore, tell us whether domains of the same sign of volume are formed. If yes, that would be a sign of the emergence of semi-classical spacetime. Furthermore, the presence of long-range correlation would unavoidably allow associating a notion of length scale to the spin network configurations. Such observation would be a significant step toward the reconstruction of classical spacetime directly from the spin network states.

5 Summary

The purpose of this article was to investigate the possibility of the implementation of spin networks on the architecture of commercially accessible adiabatic quantum computers (quantum annealers). In the studies, we focused our attention on spin networks with fixed spin labels ($j=\frac{1}{2}$) corresponding to the fundamental representation of the $SU\left(2\right)$ group. In such a case, the 4-valent nodes give rise to two-dimensional intertwiner space associated with the qubit Hilbert space. In the geometric picture, the 4-valent nodes of a spin network are dual to the 3D simplices, and the qubit bases states represent different orientations of a 3-simplex.

We have shown that it is possible to define spin networks on the architecture of the D-Wave quantum processor in the considered case. However, due to topological restrictions of the Chimera graph, not all spin networks are possible to implement with the use of elementary qubits. However, some obstacles can be overcome by introducing effective (chain) qubits composed of two or more elementary qubits. Such effective qubits allow implementing, e.g., regular 2D square lattice topology of the nearest neighbor type of interaction Ising model.

Furthermore, we proposed a method of solving scalar (Hamiltonian) constraints using quantum annealing. In the case of D-Wave quantum annealers, we have shown that a prototype constraint being a linear function of qubit variables, is possible to solve. The solutions of the constraint (i.e., physical states) are obtained as ground states of an appropriate Ising-type Hamiltonian. The procedure has been theoretically demonstrated for the pentagram spin network, which (as we have shown) can be embedded onto the architecture of the D-Wave processor. This opens a path to simulate simplified LQG models on available quantum annealers. However, one has to keep in mind that computational complexity of the approach not been addressed yet. Consequently, it is not known whether quantum annealers may provide the quantum speed-up for solving the LQG-related scalar constraints.

Various generalizations of the investigated class of spin networks are to be considered. In particular, the situation which is motivated by the semi-classical limit is when all spin labels are equal to some $j\gg \frac{1}{2}$, instead of $j=\frac{1}{2}$. In the case of arbitrary j, the dimension of the intertwiner space of a single 4-vertex is

$\text{dim}\text{Inv}\left(H_j\otimes H_j\otimes H_j\otimes H_j\right)=2j+1.(20)$

Generalization to the case of higher than 4-valence of nodes can also be considered. In both cases, ancillary qubits have to be introduced appropriately, which is a more difficult task or, in some cases, perhaps even not possible to do. These and other issues related to quantum simulations of spin networks, especially in the context of LQG will be the subject of our further studies.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Author was supported from the Sonata Grant DEC-2014/13/D/ST2/01895 and from the Sonata Bis Grant DEC-2017/26/E/ST2/00763 of the National Science Centre Poland, and the Mobilność Plus Grant 1641/MON/V/2017/0 of the Polish Ministry of Science and Higher Education. Furthermore, this publication was made possible through the support of the ID# 61466 grant from the John Templeton Foundation, as part of the “The Quantum Information Structure of Spacetime (QISS)” Project (qiss.fr).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. Author would like to thank to Mario Flory for his careful reading of the manuscript and helpful comments.

Footnotes

¹Here, for simplicity, we define the kinematical phase space such that is obtained by solving Gauss and diffeomorphism constraints. This corresponds to all possible spin configurations at the nodes of a given 4-valent spin network. In the quantum theory, the kinematical Hilbert space $H_{\text{kin}}$ with respect to the scalar constraint $\widehat{C}|\varphi \rangle \approx 0$ is a tensor product of qubit Hilbert spaces defined at N nodes of the spin network.

²Alternatively, one can consider a complex constraint $C={\displaystyle \sum _{i=1}^N{z}_i{s}_i-c}\approx 0$ with $z_i,c\in \mathrm{ℂ}$. Then, in order to obtain a real Hamiltonian on has to consider $H\propto |C{|}^2$. This can be extended further to the case of multi-constraint model, which is not discuss here.

³The restriction is because, in the considered case, all couplers have equal value. Therefore, the couplers have to be associated with the same number of links in the spin network. The simplest example is when a single coupler is associated with a single link. However, extensions to the other cases are possible if the general form of the constraint (12) is considered.

References

Agullo, I., Ashtekar, A., and Nelson, W. (2012). Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 109, 251301. [arXiv:1209.1609 [gr-qc]]. doi:10.1103/physrevlett.109.251301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashtekar, A., and Lewandowski, J. (2004). Background Independent Quantum Gravity: A Status Report. Class. Quan. Grav. 21, R53–R152. [gr-qc/0404018]. doi:10.1088/0264-9381/21/15/r01

CrossRef Full Text | Google Scholar

Barbero G., J. F. (1995). Real Ashtekar Variables for Lorentzian Signature Space-Times. Phys. Rev. D 51, 5507–5510. [arXiv:gr-qc/9410014 [gr-qc]]. doi:10.1103/physrevd.51.5507

CrossRef Full Text | Google Scholar

Barrau, A., Cailleteau, T., Grain, J., and Mielczarek, J. (2014). Observational Issues in Loop Quantum Cosmology. Class. Quan. Grav. 31, 053001. [arXiv:1309.6896 [gr-qc]]. doi:10.1088/0264-9381/31/5/053001

CrossRef Full Text | Google Scholar

Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., and Lloyd, S. (2017). Quantum Machine Learning. Nature 549, 195–202. doi:10.1038/nature23474

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, E. T., Terhal, B. M., and Vuillot, C. (2017). Roads towards Fault-Tolerant Universal Quantum Computation. Nature 549, 172–179. doi:10.1038/nature23460

PubMed Abstract | CrossRef Full Text | Google Scholar

Czelusta, G., and Mielczarek, J. (2021). Quantum Simulations of a Qubit of Space. Phys. Rev. D 103 (4), 046001. [arXiv:2003.13124 [gr-qc]]. doi:10.1103/physrevd.103.046001

CrossRef Full Text | Google Scholar

Feller, A., and Livine, E. R. (2016). Ising Spin Network States for Loop Quantum Gravity: a Toy Model for Phase Transitions. Class. Quan. Grav. 33 (6), 065005. [arXiv:1509.05297 [gr-qc]]. doi:10.1088/0264-9381/33/6/065005

CrossRef Full Text | Google Scholar

Feynman, R. P. (1982). Simulating Physics with Computers. Int. J. Theor. Phys. 21, 467–488. doi:10.1007/bf02650179

CrossRef Full Text | Google Scholar

Harris, R., Johansson, J., Berkley, A. J., Johnson, M. W., Lanting, T., Han, S., et al. (2010). Experimental Demonstration of a Robust and Scalable Flux Qubit. Phys. Rev. B 81, 134510. doi:10.1103/physrevb.81.134510

CrossRef Full Text | Google Scholar

Immirzi, G. (1997). Quantum Gravity and Regge Calculus. Nucl. Phys. B - Proc. Supplements 57, 65–72. [arXiv:gr-qc/9701052 [gr-qc]]. doi:10.1016/s0920-5632(97)00354-x

CrossRef Full Text | Google Scholar

Jordan, S. P. (2010). Permutational Quantum Computing. Quan. Inf. Comput. 10, 470–497. doi:10.26421/qic10.5-6-7

CrossRef Full Text | Google Scholar

Kadowaki, T., and Nishimori, H. (1998). Quantum Annealing in the Transverse Ising Model. Phys. Rev. E 58, 5355–5363. doi:10.1103/physreve.58.5355

CrossRef Full Text | Google Scholar

Kauffman, L. H., and Lomonaco, S. J. (2008). Spin Networks and Quantum Computation. Bulg. J. Phys. 35, 241–256.

Google Scholar

Li, K., Li, Y., Han, M., Lu, S., Zhou, J., Ruan, D., et al. (2019). Quantum Spacetime on a Quantum Simulator. Commun. Phys. 2, 122. [arXiv:1712.08711 [quant-ph]]. doi:10.1038/s42005-019-0218-5

CrossRef Full Text | Google Scholar

Mandrà, S., Zhu, Z., and Katzgraber, H. G. (2017). Exponentially Biased Ground-State Sampling of Quantum Annealing Machines with Transverse-Field Driving Hamiltonians. Phys. Rev. Lett. 118, 070502. doi:10.1103/PhysRevLett.118.070502

PubMed Abstract | CrossRef Full Text | Google Scholar

Marzuoli, A., and Rasetti, M. (2005). Computing Spin Networks. Ann. Phys. 318, 345–407. doi:10.1016/j.aop.2005.01.005

CrossRef Full Text | Google Scholar

Matsuda, Y., Nishimori, H., and Katzgraber, H. G. (2009). Ground-state Statistics from Annealing Algorithms: Quantum versus Classical Approaches. New J. Phys. 11, 073021. doi:10.1088/1367-2630/11/7/073021

CrossRef Full Text | Google Scholar

Mielczarek, J. (2019). Spin Foam Vertex Amplitudes on Quantum Computer - Preliminary Results. Universe 5 (8), 179. [arXiv:1810.07100 [gr-qc]]. doi:10.3390/universe5080179

CrossRef Full Text | Google Scholar

Rovelli, C. (1998). Loop Quantum Gravity. Living Rev. Relativ. 1, 1. [arXiv:gr [gr-qc]]. doi:10.12942/lrr-1998-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Rovelli, C., and Smolin, L. (1990). Loop Space Representation of Quantum General Relativity. Nucl. Phys. B 331, 80–152. doi:10.1016/0550-3213(90)90019-a

CrossRef Full Text | Google Scholar

Rovelli, C., and Vidotto, F. (2014). Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory. Cambridge, United Kingdom: Cambridge Monographs on Mathematical Physics.

Thiemann, T. (2006). The Phoenix Project: Master Constraint Programme for Loop Quantum Gravity. Class. Quan. Grav. 23, 2211–2247. [gr-qc/0305080]. doi:10.1088/0264-9381/23/7/002

CrossRef Full Text | Google Scholar

You, J. Q., and Nori, F. (2005). Superconducting Circuits and Quantum Information. Phys. Today 58 (11), 42–47. doi:10.1063/1.2155757

CrossRef Full Text | Google Scholar