Shock Propagation and Associated Particle Acceleration in the Presence of Ambient Solar-Wind Turbulence

The topic of this review paper is on the influence of solar wind turbulence on shock propagation and its consequence on the acceleration and transport of energetic particles at shocks. As the interplanetary shocks sweep through the turbulent solar wind, the shock surfaces fluctuate and ripple in a range of different scales. We discuss particle acceleration at rippled shocks in the presence of ambient solar-wind turbulence. This strongly affects particle acceleration and transport of energetic particles (both ions and electrons) at shock fronts. In particular, we point out that the effects of upstream turbulence is critical for understanding the variability of energetic particles at shocks. Moreover, the presence of pre-existing upstream turbulence significantly enhances the trapping near the shock of low-energy charged particles, including those near the thermal energy of the incident plasma, even when the shock propagates normal to the average magnetic field. Pre-existing turbulence, always present in space plasmas, provides a means for the efficient acceleration of low-energy particles and overcoming the well known injection problem at shocks.

1 Introduction

Understanding shocks and its particle acceleration in the solar wind is an important topic in heliophysics, for both the effects of space weather and basic physics of shocks and particle energization. Near the Sun, the shocks emerge in front of the solar drivers and accelerate solar energetic particles (SEPs) (Reames, 1999; Desai and Giacalone, 2016). However, those shocks are farther away from most of the spacecraft, making them difficult to observe directly. At 1 astronomical unit (AU), these shocks are mostly driven by coronal mass ejections, with a smaller population driven by Stream Interaction Regions (SIRs) (Sheeley et al., 1985; Richardson and Cane, 2010; Borovsky, 2020). Strong energetic particles observed in the vicinity of interplanetary shocks are often termed as “Energetic Storm Particles” (ESP) (Bryant et al., 1962; Gosling et al., 1981), to distinguish them from the solar energetic particles (SEPs) accelerated close to the Sun, although the SEPs can be well accelerated by the coronal counterpart of the interplanetary shock driven by the same coronal mass ejection (Kallenrode, 1996; Reames, 1999). Most interplanetary shocks are weak compared to planetary bow shocks. Because of the Parker spiral magnetic field, the interplanetary shocks at 1 AU are mostly quasi-perpendicular, meaning the angle between the un-shocked, upstream magnetic field and the unit normal to the shock θ_Bn is usually larger than 45 degree. Decades of spacecraft observations by Helios, IMP, ISEE, ACE, Wind, STEREO and others have accumulated tremendous amount of shock events (as many as several dozens per year at solar maximum) for study (Neugebauer, 2013; Dresing et al., 2016), including two widely used shock lists collected by ACE¹ and Wind². Newly launched Parker Solar Probe and Solar Orbiter provide shock and energetic particle observations close to the Sun, and will further reveal the physics of interplanetary shocks and their associated energetic particles. The upcoming IMAP mission will provide high resolution measurements of suprathermal ions and provide further observation insight, especially on the variability of energetic particles in the vicinity of the shocks (McComas et al., 2018).

In addition to the mean, Parker spiral magnetic field, the solar wind is well known to be filled with numerous magnetic structures (Borovsky, 2008; Neugebauer and Giacalone, 2010) and turbulence (Tu and Marsch, 1995; Goldstein et al., 1995). In situ measurements of the solar wind have long established the existence of turbulence that has a Kolmogorov-like power spectrum with a correlation scale of about 10⁶ km at 1 AU and increases in the outer heliosphere, but could also be contributed by magnetic structures and discontinuities (Borovsky, 2010). Unlike Earth’s bow shock that is on a much smaller spatial scale and more suitable for kinetic studies, the interplanetary shocks provide a natural laboratory for physical processes involving high energy charged particles and large scale magnetic field fluctuations. Compared to other shock-turbulence systems like the solar wind termination shock and supernova remnant shocks, interplanetary shocks are frequently observed, with a wealth amount of data accumulated. The propagation and evolution of interplanetary shocks in the solar wind are influenced by fluctuations in magnetic fields, velocity, and density. The turbulent magnetic field can interact with the shock waves, distorting their surfaces, leading to shock ripples (Neugebauer and Giacalone, 2005) and enhance the downstream magnetic fluctuations (Zank et al., 2003; Lu et al., 2009). It is also important for efficient particle acceleration (Giacalone, 2005; Jokipii and Giacalone, 2007; Guo et al., 2010; Guo and Giacalone, 2010; Guo and Giacalone, 2015). These nonplanar ripples at the shock surface, coupled with turbulent upstream magnetic fields, lead to substantial variations of energetic particle flux, which has been pointed out, but never been understood in a systematic way (Giacalone and Neugebauer, 2008; Guo et al., 2010; Kóta, 2010).

The diffusive shock acceleration (DSA) theory describes the basic process of acceleration of particles at the shock front. A review of the mechanism is given by Drury (1983) [see also Desai and Giacalone (2016)], and was independently discovered by Krymskii (1977), Axford et al. (1977), Bell (1978), and Blandford and Ostriker (1978)). For the often considered one-dimensional solution, this gives the classical results:

$f_s\left(p\right)=f_0{p}^{-3r/\left(r-1\right)}H\left(p-p_0\right)\{\begin{array}{ll}\text{exp}\left(x{U}_1/\kappa \right)\hfill & x<0\hfill \\ 1\hfill & x\ge 0\hfill \end{array}(1)$

where f₀ is a normalization constant, r is the ratio of the downstream to upstream density, U₁ is the upstream flow speed in the shock frame, and H(p) is the Heaviside step function. This solution is obtained by solving the Parker transport equation (see a discussion in Section 3) for a one-dimensional time-steady shock at x = 0.

However, this result has only received limited success when applied to the interplanetary shocks. While there has been claims that an excellent agreement can be made between observations (Kennel et al., 1986) and theory (Lee, 1983) for an interplanetary shock event measured on November 12, 1978, even for that particular event, the observation over a longer time scale shows more complicated variation (Scholer et al., 1983). In fact, most of energetic particle profiles in the vicinity of interplanetary shocks are not consistent with the 1-D solution (Lario et al., 2003). While in some cases particles that interact with interplanetary shocks may have been accelerated in solar events (Li and Zank, 2005), this variation can also be induced by the fact that the 1-D solution fails due to the large-scale magnetic fluctuation, even without previous events (e.g., Neugebauer et al., 2006; Giacalone and Neugebauer, 2008). We will discuss the modification of the shock front due to the solar wind turbulence in Section 2. The pre-existing fluctuations are particularly important for the acceleration of particles at quasi-perpendicular shocks. We will discuss the effects of solar wind turbulence on the acceleration of protons and electrons at shocks in Sections 3 and 4, respectively.

Understanding shock-turbulence interaction and particle acceleration in the turbulent solar wind also has strong implication to other turbulence system, such as the magnetic field amplification when supernova shocks sweeping through the interstellar medium density and the roles of magnetic field fluctuations on particle acceleration (e.g., Giacalone and Jokipii, 2007; Inoue et al., 2009; Guo et al., 2012; Fraschetti, 2013).

Rest of this paper is organized as follows: We discuss the nonplanar shock effects led by the solar wind turbulence in Section 2. A discussion on the acceleration of protons is given in Section 3, focusing on the injection problem of protons. We discuss the issue about electron acceleration at interplanetary shock in Section 4. We emphasize the variability of energetic particles caused by turbulence in Section 5. We leave some final remarks in Section 6.

2 Nonplanar Shocks Led by Turbulence

As interplanetary shocks sweep through the turbulent solar wind, their surfaces naturally distort and fluctuate on a variety of scales. This fluctuation in the warped shock surfaces occurs not only in the large scale due to the large-scale turbulent plasma and magnetic fields (Zank et al., 2003; Giacalone, 2005; Li and Zank, 2006; Giacalone and Neugebauer, 2008; Guo and Giacalone, 2010, Guo and Giacalone, 2012b; Trotta et al., 2020), but at small scale as well, due to instabilities caused by ion reflection (Lowe and Burgess, 2003; Burgess, 2006; Yang et al., 2012; Hao et al., 2016; Trotta and Burgess, 2019). Using hybrid kinetic simulations (fluid electrons and kinetic ions) and MHD simulations, Giacalone (2005), Giacalone and Neugebauer (2008), and Guo and Giacalone (2010) have shown that the shock surface is wrapped due to the pre-existing upstream magnetic fluctuations. The angle between the shock normal and the incident magnetic field, θ_Bn, vary along the shock surface. Figure 1 shows plasma density in a 2D MHD simulations where the shock propagates through a fluctuating plasma. It clearly shows that the shock is rippled in various scales from that comparable to the system size down to very small scales. The density profiles can be quite variable as indicated by two cuts across the shock.

FIGURE 1

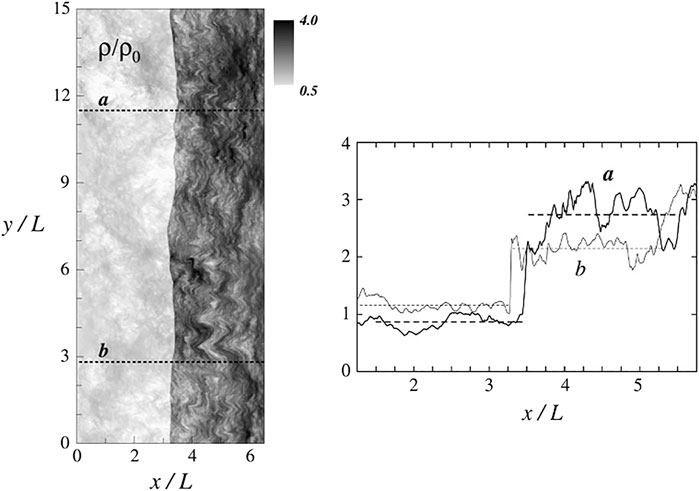
FIGURE 1. Left panel shows a gray-scale representation of simulated plasma density from a two-dimensional MHD simulation. L is the correlation scale of the turbulent fluctuations. The shock is rippled as it swept through the turbulent upstream plasma. Right panel shows two cuts for density profiles at different y positions indicated on the left panel [adapted from Giacalone and Neugebauer, 2008]. Reproduced by permission of the AAS.

The idea that interplanetary shock surface is wrapped in turbulence has been tested in the solar wind by Neugebauer and Giacalone (2005). They analysed 26 well-defined quasi-perpendicular interplanetary shocks that were observed by five spacecraft or more. They used the four spacecraft method to obtain five (five in the six spacecraft event) independent sets of normals and speeds. They also calculated normals and speeds using single-spacecraft methods. Furthermore, they estimated the shock radius of curvature with different methods. Most of the shocks were inconsistent with planar structures, or spherical structures with a radius of 1AU. In other words, the shocks were found to be rippled. They reported that the average local radius of curvature is ∼3 × 10⁶ km (∼500R_E) which is close to the observed correlation scale of the fluctuating interplanetary magnetic field. Note that the size of the ripples they could observe was limited from below by the spacecraft separations, which were of the order of 10⁵ km, corresponding to 10³ ion inertial lengths for typical solar wind conditions. Thus they were not able to discern any smaller scale (a few times of the ion inertial length) ripples existing at the same time, though such were evident in the 2D hybrid simulations presented in the same article. Later, Koval and Szabo, 2010 confirmed this basic conclusion. The scale of measured shock ripples is similar to the correlation length of the interplanetary turbulence (e.g., Coleman and Paul, 1968; Matthaeus and Goldstein, 1982; Chen et al., 2012). In a recent study, irregular surface of interplanetary shocks at ion scales has been verified by multispacecraft observations of the Cluster mission (Kajdič et al., 2019).

The shock ripples and large-scale magnetic fluctuations have also been invoked to explain the variability of interplanetary type II radio bursts (Bale et al., 1999; Pulupa and Bale, 2008; Knock et al., 2003). Bale et al. (1999) and Pulupa and Bale (2008) observed electron foreshocks and related Langmuir waves upstream of interplanetary shocks. These events appeared to be associated with irregular shock surfaces with spatial scales $\sim {10}^5$ km, in rough consistency with Neugebauer and Giacalone, 2005. They proposed that the complex upstream electron events result from large-scale irregularities in the shock surface.

3 The Physics on the Injection Problem and Its Importance to Understanding the Source of Solar Energetic Particles

Pre-existing turbulence also has an important effect on low-energy charged particles, including so-called suprathermal particles whose distribution function connects smoothly to the thermal part of the incident plasma distribution. In order to understand this, it is important to first discuss the physics of particle acceleration more generally. This is directly related to the understanding, and determination of the source of high-energy particles accelerated at shocks. It is also critical to understand the so-called ‘injection problem’ at shocks.

The mechanism for DSA has been discussed in many dedicated papers mentioned in Section 1, and it is generally accepted that this mechanism applies above some ‘injection’ energy, $E_i$. In this section we focus on the question of what happens at energies below E_i, and how it relates to the intensity and shape of the spectrum above this energy.

On the one hand, stated simply, the theory of diffusive shock acceleration does not address the injection process; thus, it might be easiest to just assume that there exists a pre-existing population of particles and that these are the particles which are further accelerated by shocks (e.g., Mewaldt et al., 2012). Moreover, the largest energetic particle events associated with coronal mass ejections often come from large active regions on the Sun which commonly also produce a number of smaller CMEs and transient shocks. It is reasonable to expect that these smaller events produce energetic particles that could be accelerated further at the later shock (c.f. Desai and Giacalone, 2016, for a review of observations). It is not clear, however, whether it is the existence of the pre-existing population of energetic particles, or the fact that the later shock moves through a more (magnetically) turbulent medium, which increases the trapping of the particles at the later shock, leading to a higher acceleration rate, which causes the higher fluxes of particles at very high energies.

On the other hand, it is important to examine the physics of particle acceleration at low energies, and to determine the conditions under which DSA theory is applicable. DSA is based on the Parker transport equation, which is given by Eq. 10, and was first derived by Parker (1965). This equation assumes the particle’s distribution is nearly isotropic.

3.1 The Proper Frame of Reference for the Energy-Change Term in the Parker Transport Equation

We start with an analysis of the term that is responsible for the acceleration, paying particular attention to the proper frame of reference since the pitch-angle distribution of low-energy particles varies considerably between the shock frame and the plasma frame.

We now show that this term follows directly from the basic physics of charged (test) particle motion in electric and magnetic fields. We follow closely the approach of Jokipii (2012), which has rarely been cited in the literature, suggesting that this important derivation has largely been forgotten. We add some more steps to this derivation which did not appear in the original manuscript, for completeness.

The motion of a charged particle, with charge q, in a plasma containing an electric field E and magnetic field B is given by:

$\frac{d\mathbf{p}}{dt}=q\mathbf{E}+\frac{q}{c}\mathbf{w}\times \mathbf{B}(2)$

where p is the momentum of the particle, w is the velocity vector, and c is the speed of light. Gravity and radiation pressure, two forces which are commonly included in macroscopic equations because these forces are negligible in most situations of interest regarding the acceleration of particles.

The rate of change of the kinetic energy K, of a charged particle is obtained by taking the vector dot product of the particle velocity with Eq. 2, given by:

$\frac{dK}{dt}=q\mathbf{w}\cdot \mathbf{E}(3)$

We consider the case in which the electric field is given by that of ideal magnetohydrodynamics: $\mathbf{E}=-\mathbf{U}\times \mathbf{B}/c$, where U is the velocity of the bulk plasma which carries with it the magnetic field B. Thus, we have

$\frac{dK}{dt}=-\frac{q}{c}\mathbf{w}\cdot \left(\mathbf{U}\times \mathbf{B}\right)(4)$

We next consider the kinetic energy in the frame moving with the bulk plasma. Using a prime to denote quantities in the plasma frame of reference, we have

$K^{\prime }=K-\mathbf{p}\cdot \mathbf{U}+\frac{1}{2}m{U}^2(5)$

Inserting this into Eq. 4, and using Eq. 2 and a vector identity, after some simple manipulation it follows that:

$\frac{d{K}^{\prime }}{dt}=-\left(\mathbf{p}-m\mathbf{U}\right)\cdot \frac{d\mathbf{U}}{dt}=-{\mathbf{p}}^{\prime }\cdot \frac{d\mathbf{U}}{dt}=-{\mathbf{p}}^{\prime }\cdot \left(\frac{\partial \mathbf{U}}{\partial t}+{\mathbf{w}}^{\prime }\cdot \nabla \mathbf{U}\right)(6)$

where the middle term on the right is from the definition of the momentum in the plasma frame, and the last term on the right follows by noting that the total time derivative is that along the particle trajectory in which the plasma velocity can change both temporally and spatially; hence, the use of the advective derivative is appropriate.

We note that the kinetic energy depends on the vector momentum and velocity, and, thus not only the magnitude of these quantities but also their direction: i.e., the particle pitch angle and phase angle. We now consider a distribution of particles and average Eq. 6 over pitch and phase angle. Denoting this average with the angle-bracket notation, we have

$\frac{d\langle K^{\prime }\rangle }{dt}=\langle -{\mathbf{p}}^{\prime }\cdot \left(\frac{\partial \mathbf{U}}{\partial t}+{\mathbf{w}}^{\prime }\cdot \nabla \mathbf{U}\right)\rangle (7)$

It is important to note that the average is taken over the plasma-frame pitch-angle distribution. We assume that the magnetic fluctuations will ‘scatter’ the particles and alter particles’ pitch angles (Jokipii, 1971) with their energy conserved upon each scattering in the plasma frame. If the time between scatterings is shorter than the time variation of the plasma velocity, then the first term inside the parenthesis on the right of Eq. 7 is small and can be neglected. Switching to index notation for the vectors, we have:

$\frac{d\langle K^{\prime }\rangle }{dt}=-\langle p{\text{′}}_{i}w{\text{′}}_j\rangle {\partial }_j{U}_i(8)$

In deriving this expression, one must also assert that the variation in space of the fluid velocity is on a scale larger than the scattering mean-free path of the particles, which is simply the magnitude of the particle velocity times the scattering time. Assuming that the distribution is isotropic, the term inside the angle brackets in this equation only gives an answer when i = j and also gives a factor of 1/3 times the magnitude of the momentum and velocity. Eq. 8 also permits contributions from fluid shear (Parker, 1965; Earl et al., 1988; Li et al., 2018; Du et al., 2018).

Noting also that the kinetic energy can be written in terms of the momentum $\left(d{K}^{\prime }/dt=w^{\prime }d{p}^{\prime }/dt\right)$, Eq. 8, in terms of the rate of change of the momentum in the plasma frame for a nearly isotropic distribution, is given by:

$\frac{d\langle p^{\prime }\rangle }{dt}=-\frac{1}{3}{p}^{\prime }\nabla \cdot \mathbf{U}(9)$

This represents the rate of change of the magnitude of the momentum, in the plasma frame of reference, in a plasma with bulk velocity U. We note that energy change only occurs when the plasma has a finite divergence, either rarefactions or compressions of the plasma. In the case of a shock wave, the plasma velocity decreases across the shock, in the shock frame of reference, so that the divergence is negative. Thus, the plasma-frame momentum of the particles increases across the shock, and the energy change occurs directly at the shock. This will be discussed further below.

In the cosmic-ray (or Parker) transport equation first derived by Parker (1965), given by Eq. 10 below, the term representing the energy change of an isotropic distribution of particles is of the same form as Eq. 9. Thus, in the Parker equation, the momentum variable is that measured in the plasma frame of reference. The Parker equation is given by:

$\frac{\partial f}{\partial t}+\mathbf{U}\cdot \nabla f=\nabla \cdot \left(\kappa \nabla f\right)+\frac{1}{3}\nabla \cdot \mathbf{U}\frac{\partial f}{\partial \text{ln}p}+S-L(10)$

where the first term on the right represents spatial diffusion, and is discussed further below. The second term on the right is energy change, as discussed above, while the last two terms of the Parker equation represent sources and losses.

The spatial diffusion tensor appearing in the Parker equation depends on the magnetic field, both its turbulent, fluctuating component, as well as its average component. It can be decomposed into components along and across the average magnetic field, and a term which represents drift motions associated with gradient and curvature drifts, according to:

$\kappa ={\kappa }_{ij}={\kappa }_{\perp }{\delta }_{ij}+\left({\kappa }_{\parallel }-{\kappa }_{\perp }\right)\frac{B_i{B}_j}{B^2}+{\mathit{ϵ}}_{ijk}{\kappa }_A\frac{B_k}{B}(11)$

where the vector $B_i$ represents the average magnetic field. ${\kappa }_{\perp }$ and ${\kappa }_{\parallel }$ are the diffusion coefficients across and along the magnetic field and these coefficients depend on rigidity of the particles as well as the turbulent component of the magnetic field (Jokipii, 1971; Giacalone and Jokipii, 1999). ${\kappa }_A$ represents particle drifts, including those associated with the curvature and gradient of the average magnetic field (Isenberg and Jokipii, 1979).

It is important to note here that the only assumption is that the distribution is isotropic, in the local plasma frame of reference. Above, when we derived the form of the energy-change term, we noted that the momentum was that in the plasma frame. Of course, for very high energy particles, the particle speed is many times greater than the bulk plasma speed, thus, the distinction between the plasma and inertial frames is not much. However, it is important in the context of understanding the acceleration at low energies, and the injection problem, since we are particularly interested in the lowest energy to which the diffusive shock acceleration theory is applicable.

3.2 The Injection Problem: The Perspective from the Diffusive Shock Acceleration Theory

In this review we are particularly interested in the injection problem of energetic particles at shock waves with different shock angles ${\theta }_{Bn}$. Without loss of generality, we can take the magnetic field to be in the $x-z$ plane, and the unit normal to the shock in the $-x$ direction, which is also common. Thus, the component of the symmetric diffusion tensor normal to the shock, for example, can be written in terms of ${\theta }_{Bn}$ as:

${\kappa }_{xx}={\kappa }_{\perp }{\text{sin}}^2{\theta }_{Bn}+{\kappa }_{\parallel }{\text{cos}}^2{\theta }_{Bn}(12)$

It is straightforward to solve the Parker equation for a shock-like discontinuity and the solution is given by Eq. 1. We note that the momentum, or energy, distribution in the shocked plasma has a power-law dependence on momentum (or energy), with an index that is only a function of the ratio of the upstream to downstream plasma velocity across the shocks. This is also the ratio of the downstream to upstream plasma density, or the shock density jump factor. This result is well known, and the physics is well studied. However, the Parker equation is a purely test-particle treatment and must assume an initial energy of the particles. It does not address where the particles at this initial energy come from, or their intensity and contribution to the overall energetics of the entire plasma. It is therefore instructive to consider the limits of applicability of the Parker equation in order to understand this particular issue better.

The Parker equation is derived by assuming the distribution is nearly isotropic in pitch and phase angle. Thus, it is averaged over these quantities, and neither appear in the equation. Thus, it is implicitly assumed that the distribution is nearly isotropic. Yet, because the equation has a diffusive term, there exists a diffusive anisotropy. In order for this equation to be internally consistent, this diffusive anisotropy must be small. At a shock, the distribution at any given energy, upstream of the shock, decays exponentially from the shock towards the upstream region (see our derivation below). The gradient in the particle intensity, in this case is purely diffusive, and leads to a diffusive streaming flux along the shock-normal direction, S_x, of the form: $S_x=-{\kappa }_{xx}\nabla f$. The normalized diffusive anisotropy is $\delta =3S_x/\left(wf\right)$, where w is the particle speed. The diffusive length scale associated with the exponential decay of particles away from the shock in the upstream region is ${\kappa }_{xx}/U_1$ (c.f. Eq. 1), where U₁ is the upstream plasma velocity, so that by using Eq. 5 in our expression for S_x, requiring $\delta \ll 1$, and after some manipulation, one obtains the following constraint on the applicability of the Parker equation applied to a shock:

$w\gg 3U_1{\left[1+\frac{{\eta }^2{\sin }^2{\theta }_{Bn}+\left(1+{\mathit{ϵ}}^2\right){\sin }^2{\theta }_{Bn}{\cos }^2{\theta }_{Bn}}{{\left(\mathit{ϵ}{\sin }^2{\theta }_{Bn}+{\cos }^2{\theta }_{Bn}\right)}^2}\right]}^{1/2}(13)$

where $\mathit{ϵ}={\kappa }_{\perp }/{\kappa }_{\parallel }$ and $\eta ={\kappa }_A/{\kappa }_{\parallel }$. This expression was first derived by Giacalone and Jokipii (1999) and Zank et al. (2006).

The smallest possible value of the second term inside the brackets (inside the radical) is zero. It cannot be negative. Thus, for any value of θ_Bn, the Parker equation is only valid for $w\gg 3U_1$. Defining the sonic Mach number, M, as the ratio of the upstream flow speed to the upstream sound speed, we have: $w\gg 3M{v}_{th,1}$. Since the most intense energetic particle events are presumably associated with shocks of fairly high Mach number, this is a particularly stringent requirement. This is true equally for both parallel $\left({\theta }_{Bn}=0^{\mathrm{o}}\right)$ and perpendicular shocks $\left({\theta }_{Bn}={90}^{\circ }\right)$.

Under certain conditions, the injection speed given by Eq. 13 has a very strong dependence on the shock-normal angle. For $\eta \ll 1$ and $\mathit{ϵ}\ll 1$, this gives $w\approx 3U_1{\text{sec}}^2{\theta }_{Bn}$ which is the (3× the) speed of a particle moving with the intersection point of a (perfectly straight) field line and the shock front. This leads to the notion of an injection threshold problem for nearly perpendicular shocks since w is very large as ${\theta }_{Bn}={90}^{\circ }$. Some hybrid simulations, which satisfy these conditions, confirm this (Giacalone and Ellison, 2000; Caprioli and Spitkovsky, 2014). These conditions are not realistic for a wide variety of heliospheric and astrophysical shocks, however. The conditions noted above unrealistically neglects particle motion normal to the average magnetic field. In the limit ${\theta }_{Bn}={90}^{\circ }$, Eq. 13 reduces to $w=3U_1{\left(1+{\eta }^2/{\mathit{ϵ}}^2\right)}^{1/2}$, whereas in the limit ${\theta }_{Bn}=0^{\circ }$, we get $w=3U_1$. These differ only by the value ${\left(\eta /\mathit{ϵ}\right)}^2={\left({\kappa }_A/{\kappa }_{\perp }\right)}^2$ which depends on the magnetic field, including its turbulent component and is not necessarily large. Field-line wandering, caused mostly by the largest scales in the fluctuating component of the magnetic field, significantly enhances the motion of particles across the mean magnetic field such that this term can be small. This is why pre-existing turbulence is fundamentally important to the injection problem. In this case, the acceleration of low-energy particles at a perpendicular shock can be nearly as efficient as that at a parallel shock.

Hybrid simulations of shocks moving through pre-existing broadband magnetic turbulence have revealed that even thermal plasma is efficiently accelerated at a perpendicular shock (Giacalone, 2005). Figure 2 shows a new hybrid simulation with parameters similar to those of strong, quasi-perpendicular interplanetary shocks. For this case, the Alfven Mach number is 5.8, the total plasma beta is 0.54, and the angle between average magnetic field and the x direction is 70^°. Other parameters are similar to those presented in Giacalone (2005) (see also Giacalone, 2017b). Similarly, in this simulation, the initial magnetic field is a combination of a mean component and a turbulent component. The turbulent component is based on a power spectrum which contains a range of scales from the size of the box down to the ion inertial length. The large scales leads to field-line meandering, which leads to a variation in the angle between the local magnetic field and the unit normal to the shock, whose surface is rippled, as discussed previously. In several places along the shock front, the local shock-normal angle is near perpendicular, as was observed for the interplanetary shock on DOY 118, 2001 by the Advanced Composition Explorer (ACE) (Lario et al., 2019), which had similar parameters to those simulated. The model also includes kinetic processes which lead to heating of the particles across the shock and the formation of a suprathermal tail which are ions accelerated directly from the thermal population. The energy spectra of protons from this particular simulation are shown in Figure 4.

FIGURE 2

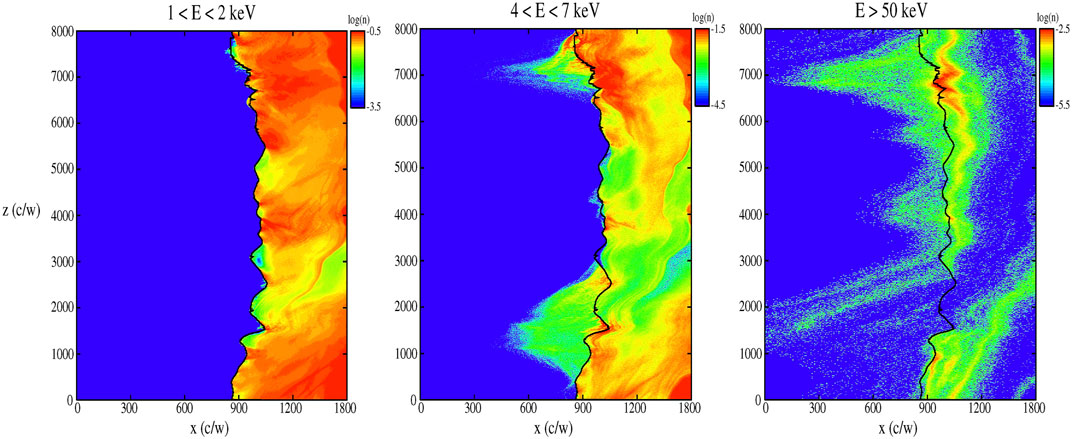
FIGURE 2. A hybrid simulation of a quasi-perpendicular shock $\left(<{\theta }_{Bn}>={70}^{\circ }\right)$, with parameters consistent with those of the DOY 118, 2001 interplanetary shock measured by ACE. Shown are suprathermal proton densities at ${\text{Ω}}_{ci}t=500$ with energies measured in local plasma frame. This result is similar to Giacalone (2005).

Observations often show significant enhancements of low-energy ions at quasi-perpendicular IP shocks (e.g., Zank et al., 2006; Giacalone, 2012; Neergaard Parker et al., 2014) suggesting the injection energy does not depend strongly on the shock-normal angle. Low-energy ions were also enhanced by over an order of magnitude at the termination shock (Decker et al., 2005; Decker et al., 2008), which is a good example of a nearly perpendicular shock. The energy of these ions is far less than the theoretical injection threshold (Eq. 13) for the nearly perpendicular termination shock, which, is readily shown to be several MeV. Moreover, as we discuss below, there are examples of nearly perpendicular interplanetary shocks which also show a very significant enhancement of very low energy ions (Lario et al., 2019). It is a common misconception that nearly perpendicular shocks are unable to accelerate low-energy ions.

3.3 The Source Population

Neergaard Parker and Zank (2012) derived the solution of diffusive shock acceleration for the case of an arbitrary distribution of pre-existing particles, either from previous events or pre-existing in the solar wind, far upstream of the shock, and also included a separate source at the shock itself (c.f. Eq. 6 in their paper). Assuming that the pre-existing population is the only source of particles, we can rewrite their solution for the distribution function downstream of the shock, as:

$f_2\left(p\right)=\alpha p^{-\alpha }{{\displaystyle \int }}^{\text{}}{p}^{\alpha -1}{f}_s\left(p\right)dp(14)$

where f is the distribution function and the subscript 2 refers to the post-shock region, and the S subscript refers to the pre-existing population of particles. p is the momentum, and $\alpha =3U_1/\left(U_1-U_2\right)$, where U₁ and U₂ are the upstream and downstream bulk plasma speeds as measured in the normal incidence frame (shock rest frame).

The pre-existing source distribution is often described in terms of a kappa distribution. As we have discussed previously, the lowest energy for which the Parker equation is valid, is much higher than $\frac{1}{2}m{U}_1^2$; thus, only the high-energy part of the kappa distribution is important. This is simply a power-law distribution. Thus, it is sufficient to assume a pre-existing source function of the form:

$f_s\left(p\right)=\{\begin{array}{ll}0\hfill & p<p_0\hfill \\ f_0{\left(\frac{p}{p_0}\right)}^{-\delta }\hfill & p\ge p_0\hfill \end{array}(15)$

where $f_0$ is a normalization constant, and $p_0$ can be regarded as the injection momentum. Later we will fit analytic solutions to observed distributions, and it turns out that $p_0$ is a free parameter. This is discussed further below.

The complete solution for the downstream distribution is obtained by inserting Eq. 15 into Eq. 14, and is given by.

$f_2\left(p\right)=\frac{\alpha }{\alpha -\delta }{f}_0\left[{\left(\frac{p}{p_0}\right)}^{-\delta }-{\left(\frac{p}{p_0}\right)}^{-\alpha }\right](16)$

It should be noted that at $p=p_0$, the downstream distribution is zero. This is because the source is upstream of the shock, and because of acceleration at the shock, there are no particles with a plasma-frame momentum $p_0$ downstream of the shock.

In the limit $\delta \to \infty$, the pre-existing source only has a value at $p_0$ and this expression reduces to $f_2\left(p\right)=C{\left(p/p_0\right)}^{-\alpha }$, valid for $p>p_0$, where C is a constant³. This is the usual result from diffusive shock acceleration. In particular, the spectral index depends only on the ratio of $U_1$ to $U_2$, which is the plasma density jump across the shock.

However, it is interesting to note that this solution implies that if the pre-existing source has a much harder spectrum than that from the acceleration at the shock (i.e., $\delta \ll \alpha$), the resulting distribution downstream of the shock retains the spectral index of the source spectrum, but that the intensity increases across the shock by the factor $\alpha /\left(\alpha -\delta \right)$. This might be the case when a very weak shock, with a density jump near unity, encounters a pre-existing population of particles with a rather flat energy spectrum. This suggests that weak shocks do not alter the spectral index of the energetic particle distributions compared to the pre-existing population, but rather, simply boost the intensity. Provided, of course, the pre-existing population has sufficiently hard energy spectrum.

In contrast, however, if the pre-existing source has a spectrum which is steeper than that from acceleration at the shock, the shock primarily accelerates particles from the lower-energy portion of the pre-existing distribution, and the shock-accelerated spectrum is consistent with that predicted by diffusive shock acceleration theory. We also note from Eq. 16 that the initial momentum, $p_0$, is an important parameter in determining the resulting intensity downstream of the shock.

It is instructive to consider the special case in which the pre-existing spectrum has a slope such that $\alpha =\delta$.

$f_2\left(p\right)=\alpha f_0{\left(\frac{p}{p_0}\right)}^{-\alpha }\text{ln}\left(\frac{p}{p_0}\right)(17)$

Thus, the ratio of the shock-accelerated to pre-existing spectrum is $\text{ln}{\left(p/p_0\right)}^{\alpha }$. At a given momentum (higher than $p_0$), the enhancement factor depends on the injection momentum, $p_0$. Thus, for this case, in which the pre-existing spectrum has a spectral exponent equal to α (the spectral index from simple DSA theory), the injection momentum plays a critical role in determining by what factor the intensity increases. Moreover, the resulting shock-accelerated spectrum is not even a simple power law. We now consider a specific application of this case.

Figure 3 is adapted from Lario et al. (2019). The data shown in this figure is from panels (b) and (f) of their Figure 10, and was provided to us by the authors. The data shows energy spectra upstream and downstream of an interplanetary shock which crossed the spacecraft ACE on DOY 118, 2001. Data from two instruments, SWICS and EPAM, are shown. The original figure, in Lario et al. (2019), also shows error bars, which are omitted here. The spectra cover a broad range of energy which includes the thermal-peak at low energies, through the suprathermal range, to high energies. Also plotted as a dashed line is the one-count level. as was also done in the original image.

FIGURE 3

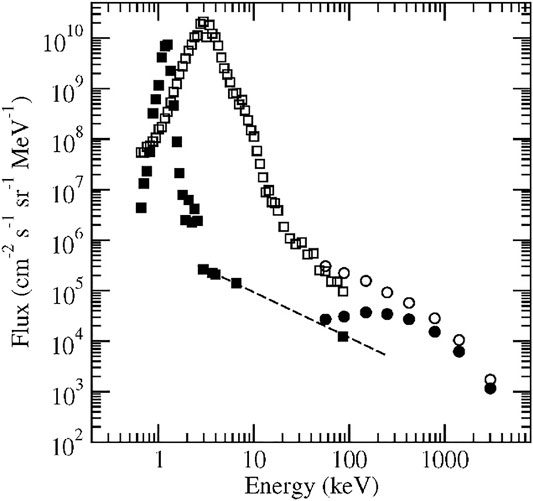
FIGURE 3. Data from Lario et al. (2019); panels (b) and (f) of their Figure 10. The filled symbols are spectra about 30 min prior to the crossing of a shock. The open symbols are about 12 min after the shock crossing. The circles are ACE/EPAM data, and the squares are ACE/SWICS data.

From Figure 3, we note that the pre-existing distribution cannot have an intensity larger than the one-count level indicated by the dashed line; thus, at an energy of 250 keV, which is approximately the energy at which the dashed line ends in this figure, the intensity cannot be larger than $5000{\text{cm}}^{-2}{\text{s}}^{-1}{\text{sr}}^{-1}{\text{MeV}}^{-1}$. The shock-accelerated particles, downstream of the shock, at this energy have an intensity of ${10}^5{\text{cm}}^{-2}{\text{s}}^{-1}{\text{sr}}^{-1}{\text{MeV}}^{-1}$ (open circle at $E=250\mathrm{kev}$). Thus, the ratio of the shock-accelerated to pre-existing intensity cannot be smaller than 20 $\left(={10}^5/5000\right)$. Moreover, since the spectral index of the one-count curve in Figure 3 is approximately the same as that of the shock-accelerated spectrum in the vicinity of 250 keV, Eq. 17 above can be used to determine the value of the injection energy $E_0$. Note also that the ratio of the distribution functions upstream and downstream are the same as the ratio of the differential intensity, in this case, because we are taking the ratio at the same energy. Thus, setting $\text{ln}{\left(p/p_0\right)}^{\alpha }$ = 20, or, in terms of energy, $\text{ln}{\left(E/E_0\right)}^{\alpha /2}=20$, we obtain $E_0=E\text{exp}\left(-40/\alpha \right)$. α is the spectral index of the distribution function vs. momentum, which can be readily shown to be $2\left(\gamma +1\right)$, where γ is the spectral exponent of the differential intensity vs. energy, as shown in Figure 3. By inspection of Figure 3, we find $\gamma \approx 1.1$, and $\alpha =4.2$, so that $E_0=\left(250\text{keV}\right)\text{exp}\left(-40/4.2\right)\approx 0.02$ keV. This is well below the so-called ram energy of the shock (the kinetic energy of the plasma as it enters the shock), and is near that of the thermal energy of the solar wind.

From the above considerations, we conclude that is not possible to explain the shock-accelerated distribution in this event simply by the ‘lifting up’ of the pre-existing distribution. The intensity of the shock-accelerated particles indicates that the particles were accelerated from a much-lower energy source; and the most-abundant source is the solar wind. We conclude that for this event, the source of the accelerated particles is the solar wind.

It is also noteworthy that the reported shock parameters for this particular event (Table 1 of Lario et al., 2019) gives a shock-normal angle of ${\theta }_{Bn}=88\pm 2$. This is a very nearly perpendicular shock. Thus, this event shows a clear example of a nearly perpendicular shock which locally accelerates particles from very low energies, forming a high-energy rail. This is consistent with analytic theory and self-consistent plasma simulations which include pre-existing large-scale magnetic fluctuations with parameters consistent with those observed in the solar wind (Figure 2; Giacalone, 2003, Giacalone, 2005).

In Figure 4 we plot the downstream energy spectra from the hybrid simulation mentioned above (c.f. Figure 2) at averaged over two different regions downstream of the shock, and compare it with the downstream spectrum seen by ACE. The regions were identified by finding regions for which the local shock normal angle (at the location of the shock for the particular value of z chosen) was very nearly perpendicular, as in the observations. Note that the simulation results, represented as either solid or dashed curves are both taken downstream of the shock, yet show differences. This means that the spectrum depends on location along the shock in these simulations which suggests this may also be the case in real interplanetary shocks. It is noteworthy that in this simulation, the initial distribution is purely Maxwellian so that the high-energy particles were accelerated (by the shock) from an initially thermal distribution. Moreover, despite the variation along the shock, the intensity of the tail particles is either consistent with, or even larger than the observations, suggesting that the efficiency of accelerating the thermal solar wind in this case is enough to account for the observations.

FIGURE 4

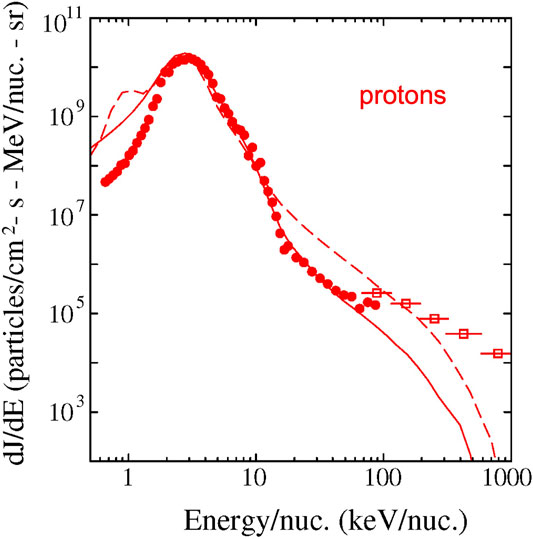
FIGURE 4. Energy spectra at two regions downstream of the shock in the hybrid simulation shown in Figure 2 (solid curve $1300<x{\omega }_{pi}/c<1500$ and $6300<z{\omega }_{pi}/c<7400$) and (dashed curve $1100<x{\omega }_{pi}/c<1300$ and $6300<z{\omega }_{pi}/c<7400$). Observed downstream spectrum on DOY 118, 2001 by Lario et al. (2019) is also plotted for comparison.

Consideration of kinetic physics is required to understand the process by which very low-energy ions, including those from the thermal solar wind, are accelerated by a shock. It is well known that supercritical collisionless shocks require a dissipation mechanism other than that afforded by anomalous resistivity (e.g., Kennel et al., 1985). It was established 40 years ago that such shocks extract a small fraction of the thermal population incident upon a shock, creating a population of ‘specularly reflected’ ions which are reflected in the shock ramp and gyrate in the upstream magnetic field, and are ultimately advected downstream with the plasma flow. This process is well studied at Earth’s bow shock (Gosling and Thomsen, 1985). The reflected particles have an energy that is about the plasma ram energy as measured in the plasma frame of reference. This is much larger than the thermal energy, thus, these particles represent a suprathermal population, albeit with the still rather low energy of the plasma ram energy. It is reasonable to expect that a fraction of these particles can undergo a further reflection at the shock, this time gaining even more energy; and some can be reflected more than once, gaining even more energy. Thus, these particles are the likely source of the high-energy tail in supercritical shocks, including those CME-driven interplanetary shocks that produce the largest SEP events observed, such as the one presented above.

4 Electron Acceleration at Collisionless Shocks Moving Through a Turbulent Magnetic Field

Collisionless shocks are efficient accelerators for a variety of energetic charged particles observed in the heliosphere. However, the acceleration of electrons at collisionless shocks is generally considered to be more difficult than that of ions. This is primarily due to the fact that the gyroradii of non-relativistic electrons are much smaller compared with that of protons at the same energy (by a factor of $\sqrt{m_p/m_e}\sim 43$), therefore low-energy electrons cannot resonantly interact with the large-scale magnetic turbulence or ion-scale waves close to the shock front. In fact, statistical results have shown that electrons are less commonly accelerated at interplanetary shocks (Lario et al., 2003).

4.1 Observations of Electron Acceleration in the Vicinity of Interplanetary Shocks

At interplanetary shocks, electrons with energy up to $\sim 100\mathrm{keV}$ have been observed close to quasi-perpendicular shocks with ${\theta }_{Bn}$ is larger than 45° (Dresing et al., 2016; Yang et al., 2018; Yang et al., 2019). Tsurutani and Lin (1985) reported the observations of energetic electrons associated with interplanetary shocks showing “spike-like” flux enhancements for energies $>2$ keV. The spike events were observed at quasi-perpendicular shocks with ${\theta }_{Bn}\ge {70}^{\circ }$. Some shock crossings had no enhancements of energetic electrons that were reported to be associated with low shock speeds and/or small ${\theta }_{Bn}$. Simnett et al., 2005 presented data which show that energetic electrons are accelerated close to shock front. They also showed some accelerated electrons can escape far upstream of quasi-perpendicular interplanetary shocks. As we will show below, this can be explained by simulations that include large scale fluctuations (Guo and Giacalone, 2010). The clear evidence of electron acceleration at interplanetary shocks by DSA is rare, but an example discussed by Shimada et al. (1999) shows evidence of the importance of whistler waves (a high frequency wave that can resonantly interact with low-energy electrons) close to a quasi-perpendicular shock (see also Wilson et al., 2012). This seems to be different from acceleration at Earth’s bow shock, where new observations have found whistler waves strongly contribute to the electron acceleration process (Oka et al., 2019; Amano et al., 2020), although more observations with high time cadences will definitely be needed to finally resolve this. The observation by Voyager 1 at the termination shock showed a spike-like enhancement of energetic electrons (Decker et al., 2005). Voyager 2 observed an exponential increase upstream of the termination shock and roughly constant downstream in the heliosheath, similar to what is predicted from DSA (Decker et al., 2008). Both of the Voyager spacecraft have observed that electrons are accelerated to at least MeV range, indicating that the termination shock can efficiently accelerate electrons.

4.2 One-Dimensional Scattering-Free Theory

In order to explain the energization of electrons within the shock layer, Wu (1984) and Leroy and Mangeney (1984) developed analytic models for electron acceleration from thermal energies by adiabatic reflection by a quasi-perpendicular shock (see also Ball and Melrose, 2001). This process is known as fast-Fermi acceleration, where electrons are reflected by the fast-moving shock along the upstream magnetic field in the de Hoffmann-Teller frame. This theory describes a scatter-free electron acceleration process in a planar, time-steady shock. It obtains a qualitative agreement with observations at Earth’s bow shock in terms of the loss-cone pitch-angle distribution and energy range of accelerated electrons, but cannot explain observed power-low-like downstream energy distribution (Gosling et al., 1989; Krauss-Varban and Wu, 1989) used the combination of electron test-particle simulation and one-dimensional (1D) hybrid simulation and verified Wu’s basic conclusions. The main energy source of fast-Fermi acceleration comes from the $-\mathbf{u}\times \mathbf{B}/c$ electric field which is the same as shock drift acceleration (SDA). It can also be demonstrated that fast-Fermi acceleration and SDA are the same process in two different frames of reference (Krauss-Varban and Wu, 1989). Thus, one would expect electrons to drift in the direction perpendicular to the flow and magnetic field. For a single reflection, the fraction and energies of accelerated particles are limited (Ball and Melrose, 2001). Holman and Pesses (1983) proposed the basic outline for type II solar radio bursts in which energetic electrons are accelerated through SDA. It is expected that multiple reflections are required in order to explain herringbone structures in type II bursts, where the electrons are accelerated to a fraction of the speed of light.

4.3 Effects of Large-Scale Magnetic Fluctuations and Shock Ripples

While the scattering provided by whistler waves (Shimada et al., 1999) is one possibility, Jokipii and Giacalone, 2007 proposed an attractive mechanism for accelerating electrons to high energy that does not require strong pitch-angle scattering, i.e., conserving the first adiabatic invariant. The idea is that the low-rigidity particles, especially electrons, can move rapidly along meandering magnetic field lines and thus travel back and forth between shock fronts. The particles gain energy from the difference between upstream and downstream flow velocities. Guo and Giacalone (2010, 2012a, 2012b) have used hybrid simulations combined with test-particle electrons to simulate effects of large-scale, preexisting magnetic fluctuations on electron acceleration at shocks. They found that efficient electron acceleration can happen after considering large-scale pre-existing upstream magnetic turbulence. The turbulent magnetic field leads to field-line meandering that allows the electrons to get accelerated at a shock front multiple times. The rippled surface of the shock front also contributes to the acceleration by mirroring electrons between the ripples. Figure 5 shows electron energy spectra at different averaged shock angles suggesting perpendicular shocks can accelerate electrons more efficiently when upstream magnetic fluctuations exist.

FIGURE 5

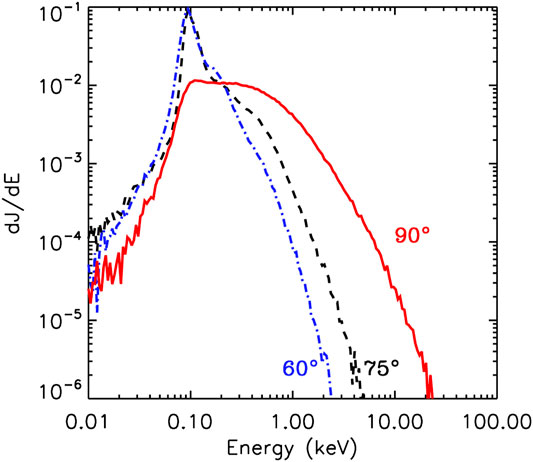
FIGURE 5. Energy flux spectra of electrons for different averaged shock normal angles. Results of hybrid simulations with test-particle electrons adapted from Guo and Giacalone (2010). Reproduced by permission of the AAS.

Energetic particles are often seen upstream of the interplanetary shocks, known as foreshocks. We note that the spatial distribution of energetic electrons is determined not only by the ripples in the shock front, but also by the global topology of the magnetic field lines. An example is shown in Figure 6, which shows the spatial distribution of energetic electrons and profiles of the number of energetic electrons as a function of x, for the case of $\left({\theta }_{Bn}\right)={90}^{\circ }$ in Guo and Giacalone (2010). The black solid line is the profile at $z=200c/{\omega }_{pi}$, and the red dash line shows the profile at $z=800c/{\omega }_{pi}$. The corresponding positions of the shock front at each of these values of z are represented using dot lines. At $z=200c/{\omega }_{pi}$, it is observed that the energetic electrons travel far upstream. However, the profile at $z=800c/{\omega }_{pi}$ shows no significant upstream energetic electron flux. The upstream energetic electron profiles show irregular features similar to in situ observations reported by Tsurutani and Lin (1985) and Simnett et al. (2005). The irregular features are controlled by the global topology of the large-scale turbulent magnetic field lines, along which the accelerated electrons could travel far upstream. Additionally, energetic electron profiles in the x-direction generally show “spike” structures close to the shock front, which is usually observed in interplanetary shocks and Earth’s bow shock. Observation by Voyager 1 at the termination shock and in the heliosheath also shows the evidence of electron spike-like enhancements at the shock front (Decker et al., 2005). The upstream spatial distribution of energetic electrons shows irregular features which depend on both the irregularity in the shock surface and the global topology of magnetic field lines. At first the electrons are accelerated and reflected at the shock front, and then they travel upstream along the magnetic field lines. The electrons could be taken far upstream due to field-line meandering. This result can possibly lead to an interpretation to the complex electron foreshock events observed to be associated with interplanetary shocks (Bale et al., 1999; Pulupa and Bale, 2008).

FIGURE 6

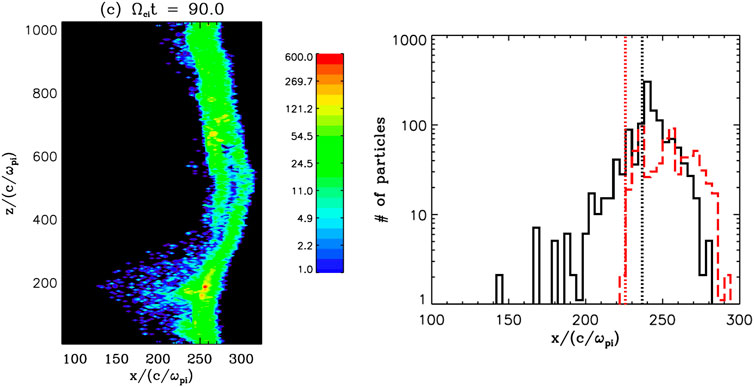
FIGURE 6. Left: Number of energetic electrons with energies $E>10E_0$ in the shock region, where the injected electron energy is $E_0=100eV$. Right: two profiles at $z=200c/{\omega }_{pi}$ (black) and at $z=800c/{\omega }_{pi}$ (red). Adapted from Guo and Giacalone (2010). Reproduced by permission of the AAS.

The relation between upstream magnetic field turbulence and energetic electrons at shocks has been further studied by Guo and Giacalone (2015) through numerical integrating test-particle electron trajectories at a shock that propagates through a prespecified, kinematically defined turbulent magnetic field. Figure 7 shows the efficiency of electron acceleration to above 10 keV (from the initial energy 1 keV). The acceleration is strongest at perpendicular shocks for all wave variance up to $\sigma =<\delta B^2/B_0^2>=10$, but quasi-parallel shocks can accelerate electrons when upstream fluctuation amplitude is sufficiently large. This trend in general agrees with observations of electron acceleration in the vicinity of interplanetary shocks (Tsurutani and Lin, 1985; Yang et al., 2019). The acceleration at parallel shock when the wave amplitude is strong enough to explain recent observation at Saturn’s bow shock (Masters et al., 2013).

FIGURE 7

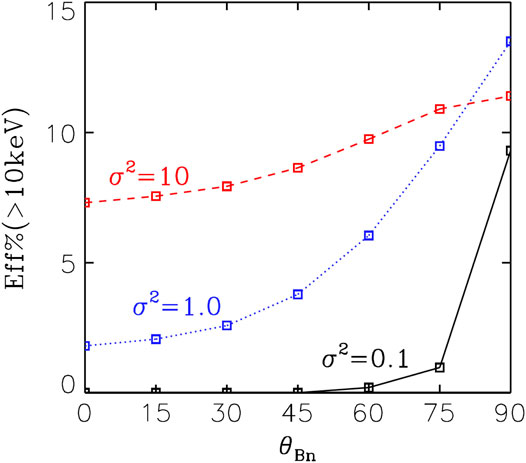
FIGURE 7. Effiency of electron acceleration for various wave variances as a function of shock angle. The efficiency is defined by the fraction of electrons that is accelerated to more than 10 keV at the end of test-particle simulations (adapted from Guo and Giacalone (2015). Reproduced by permission of the AAS.

5 Implications to Variability of Energetic Particles

Large-scale magnetic field line meandering due to magnetic turbulence is ubiquitous in the heliosphere and other astrophysical environments (Jokipii, 1966; Jokipii and Parker, 1969; Parker, 1979). Including the effects of pre-existing magnetic turbulence is necessary for a complete theory of shock acceleration. Although the 1-D steady state DSA solution gives a very elegant description for the acceleration of charged particles at the shock front, nonplanar shock and fluctuating magnetic field effects could play significant role during the acceleration and transport. These may explain many of the observed varabilities of energetic particles at shocks. Lario et al. (2003) have shown that the energetic particle profiles in the vicinity of interplanetary shocks are often not consistent with the 1-D diffusive shock acceleration and many of the profiles are ‘irregular’. A remarkable example is the in situ observation at the termination shock and in the heliosheath by Voyager 1 (Stone et al., 2005), which found that the intensity of anomalous cosmic rays (ACRs) was not saturated at the place where Voyager 1 crossed the termination shock and kept increasing after entering the heliosheath (although the low energy intensity does peak at the termination shock (Decker et al., 2005)), which strongly indicates that a simple planar shock model is inadequate to interpret the acceleration of ACRs. Numerical simulations and analytical studies suggest that possible solutions can be made by considering the temporary and/or spatial variation of magnetic field and the shock surface (Florinski and Zank, 2006; McComas and Schwadron, 2006; Guo et al., 2010; Senanayake and Florinski, 2013; Kóta, 2010). Neugebauer et al. (2006) have found that the details of energetic particle fluxes in the vicinity of interplanetary shocks are different between ACE and Wind spacecraft for the same IP shocks. The local shock parameters can significantly change, even change from quasi-parallel to quasi-perpendicular, or vice versa. The spatial scale of persistent energetic particle features is about $3\times {10}^6\mathrm{km}$, which is roughly the same as the correlation length of the interplanetary magnetic field (Neugebauer and Giacalone, 2005).

The acceleration of charged-particles in collisionless shocks has been shown to be strongly affected by magnetic-field turbulence at different scales (Giacalone, 2005; Giacalone and Neugebauer, 2008). The large-scale magnetic field variation will have important effects on the shock acceleration since the transport of charged particles is different in the direction parallel and perpendicular to the magnetic field, as shown in early work (Jokipii, 1982; Jokipii, 1987). Blunt shocks or shocks with fluctuating fronts (Li and Zank, 2006) that have a similar geometry, are also relevant to this problem. Guo et al. (2010) analyzed the effect of the large-scale spatial variation of magnetic field on DSA by considering a simple system that captures the basic physical ideas (Figure 8). They solve numerically the Parker transport equation for a shock in the presence of large-scale sinusoidal magnetic-field variations. They demonstrated that the familiar planar-shock results can be significantly altered as a consequence of large-scale, meandering magnetic lines of force. Because the perpendicular diffusion coefficient ${\kappa }_{\perp }$ is generally much smaller than the parallel diffusion coefficient ${\kappa }_{\parallel }$, energetic charged particles are trapped and preferentially accelerated along the shock front in regions where the connection points of magnetic field lines intersecting the shock surface converge, and thus create “hot spots” of accelerated particles (see also Kong et al., 2017; Kong et al., 2019a). For regions where the connection points are separated from each other, the acceleration to high energies will be suppressed. Furthermore, the particles diffuse away from the “hot spot” regions and modify the spectra of downstream particle distribution. These results are potentially important for particle acceleration at shocks propagating in turbulent magnetized plasmas as well as those that contain large-scale nonplanar structures. For example, in many interplanetary shocks, the peak of the energetic particle intensity is in the downstream rather than at the shock transition (Lario et al., 2003).

FIGURE 8

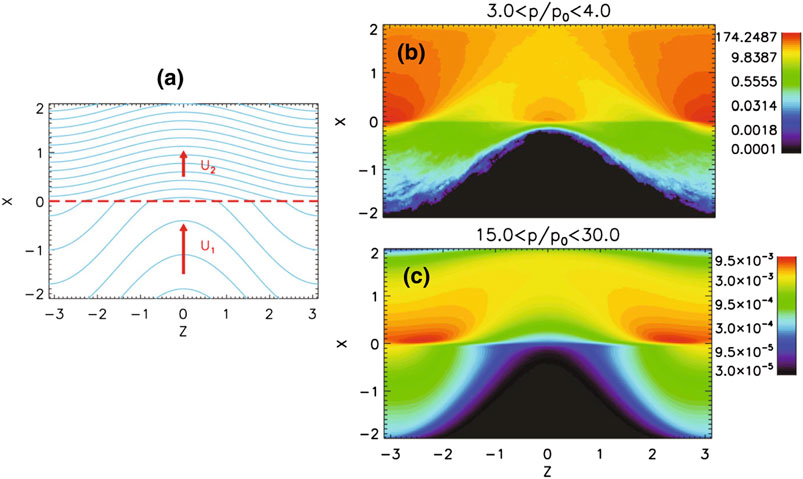
FIGURE 8. (a) Shock and magnetic field geometry for an upstream average magnetic field perpendicular to the shock normal. The blue lines represent the magnetic field lines and the red dashed line indicates the shock wave. (b) Representation of density contour of accelerated particles, for the energy range $3.0<p/p_0<4.0$, where $p_0$ is the initially injected momentum. (c) similar to (b) but for $15.0<p/p_0<30.0$ (adapted from Guo et al., 2010). Reproduced by permission of the AAS.

6 Discussion and Summary

In this review, we have discussed the effects of solar wind turbulence on the propagation of shock waves and on particle acceleration and transport in the vicinity of the shocks. The propagation of interplanetary shocks in the turbulent solar wind leads to rippling shock surfaces on various scales. These structures, along with the upstream and downstream magnetic fluctuations likely contribute to the observed energetic particles close to the interplanetary shocks. We emphasized the role of pre-existing upstream turbulence in enhancing the acceleration of low-energy particles at the shock wave, providing a promising means for solving the well known injection problem, especially at quasi-perpendicular shocks. Upstream turbulence is also important to understand the acceleration of electrons and observations at interplanetary shocks. As a remark, solar wind turbulence may be the key for interpreting the variability of energetic particles at interplanetary shocks. This, however, has not been understood in a quantitative way. Observations of interplanetary shocks provide a unique opportunity to systematically understand the system where shocks interact with large-scale turbulence and accelerate energetic particles. Understanding how these processes work is also important to many other space, solar and astrophysical systems (Giacalone, 2017a; Kong et al., 2019b).

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

FG and JG acknowledge the support in part by NASA LWS program grant 80HQTR21T0005. FG is also supported by NSF grant AST-1735414 and DOE grant DESC0018240. JG is also supported by the IS⊚IS instrument suite on NASA’s Parker Solar Probe Mission, contract NNN06AA01C, and by the Interstellar Mapping and Acceleration Probe (IMAP) under NASA contract 80GSFC19C0027. LZ is supported in part by NASA under Grants 80NSSC19K0076, 80NSSC20K1849, and 80NSSC18K0644.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

FG thanks Drs. Senbei Du and Xiaocan Li for discussion on the acceleration of particles and Dr. Mitsuo Oka for discussion on the observations of electron acceleration at interplanetary shocks.

Footnotes

¹ACE shock list http://www.ssg.sr.unh.edu/mag/ace/ACElists/obs_list.html#shocks

²Wind shock list https://www.cfa.harvard.edu/shocks/

³Note that if we take the density of the source population to be n₀, and assume the source distribution is isotropic, then we find $f_0=n_0\left(\delta -3\right)/\left(4\pi p_0^3\right)$, which leads to $C=n_0/\left(4\pi p_0^3\right)$.

References

Amano, T., Katou, T., Kitamura, N., Oka, M., Matsumoto, Y., Hoshino, M., et al. (2020). Observational evidence for stochastic shock drift acceleration of electrons at the Earth’s bow shock. Phys. Rev. Lett. 124, 065101. doi:10.1103/PhysRevLett.124.065101

PubMed Abstract | CrossRef Full Text | Google Scholar

Axford, W. I., Leer, E., and Skadron, G. (1977). The acceleration of cosmic rays by shock waves. Internatl. Cosmic Ray Conf. 11, 132.

Google Scholar

Bale, S. D., Reiner, M. J., Bougeret, J. L., Kaiser, M. L., Krucker, S., Larson, D. E., et al. (1999). The source region of an interplanetary type II radio burst. Geophys. Res. Lett. 26, 1573–1576. doi:10.1029/1999GL900293

CrossRef Full Text | Google Scholar

Ball, L., and Melrose, D. B. (2001). Shock drift acceleration of electrons. Publ.Astron. Soc. Aust. 18, 361–373. doi:10.1071/AS01047

CrossRef Full Text | Google Scholar

Bell, A. R. (1978). The acceleration of cosmic rays in shock fronts – I. Monthly Notices R. Astronom. Soc. 182, 147–156. doi:10.1093/mnras/182.2.147

CrossRef Full Text | Google Scholar

Blandford, R. D., and Ostriker, J. P. (1978). Particle acceleration by astrophysical shocks. Astrophys. J. 221, L29–L32. doi:10.1086/182658

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020). A statistical analysis of the fluctuations in the upstream and downstream plasmas of 109 strong-compression interplanetary shocks at 1 AU. J. Geophys. Res. Space Phys. 125, e27518. doi:10.1029/2019JA027518

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2010). Contribution of strong discontinuities to the power spectrum of the solar wind. Phys. Rev. Lett. 105, 111102. doi:10.1103/PhysRevLett.105.111102

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, J. E. (2008). Flux tube texture of the solar wind: strands of the magnetic carpet at 1 AU? J. Geophys. Res. 113, A08110. doi:10.1029/2007JA012684

PubMed Abstract | CrossRef Full Text | Google Scholar

Bryant, D. A., Cline, T. L., Desai, U. D., and McDonald, F. B. (1962). Explorer 12 observations of solar cosmic rays and energetic storm particles after the solar flare of September 28, 1961. J. Geophys. Res. 67, 4983–5000. doi:10.1029/JZ067i013p04983

CrossRef Full Text | Google Scholar

Burgess, D. (2006). Simulations of electron acceleration at collisionless shocks: the effects of surface fluctuations. Astrophys. J. 653, 316–324. doi:10.1086/508805

CrossRef Full Text | Google Scholar

Caprioli, D., and Spitkovsky, A. (2014). Simulations of ion acceleration at non-relativistic shocks. I. Acceleration efficiency. Astrophys. J. 783, 91. doi:10.1088/0004-637X/783/2/91

CrossRef Full Text | Google Scholar

Chen, C. H. K., Mallet, A., Schekochihin, A. A., Horbury, T. S., Wicks, R. T., and Bale, S. D. (2012). Three-dimensional structure of solar wind turbulence. Astrophys. J. 758, 120. doi:10.1088/0004-637X/758/2/120

CrossRef Full Text | Google Scholar

Coleman, J., and Paul, J. (1968). Turbulence, viscosity, and dissipation in the solar-wind plasma. Astrophys. J. 153, 371. doi:10.1086/149674

CrossRef Full Text | Google Scholar

Decker, R. B., Krimigis, S. M., Roelof, E. C., Hill, M. E., Armstrong, T. P., Gloeckler, G., et al. (2008). Mediation of the solar wind termination shock by non-thermal ions. Nature 454, 67–70. doi:10.1038/nature07030

PubMed Abstract | CrossRef Full Text | Google Scholar

Decker, R. B., Krimigis, S. M., Roelof, E. C., Hill, M. E., Armstrong, T. P., Gloeckler, G., et al. (2005). Voyager 1 in the foreshock, termination shock, and heliosheath. Science 309, 2020–2024. doi:10.1126/science.1117569

PubMed Abstract | CrossRef Full Text | Google Scholar

Desai, M., and Giacalone, J. (2016). Large gradual solar energetic particle events. Living Rev. Sol. Phys. 13, 3. doi:10.1007/s41116-016-0002-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Dresing, N., Theesen, S., Klassen, A., and Heber, B. (2016). Efficiency of particle acceleration at interplanetary shocks: statistical study of STEREO observations. Astron. Astrophys. 588, A17. doi:10.1051/0004-6361/201527853

CrossRef Full Text | Google Scholar

Drury, L. O. C. (1983). Review article: an introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 46, 973–1027. doi:10.1088/0034-4885/46/8/002

CrossRef Full Text | Google Scholar

Du, S., Guo, F., Zank, G. P., Li, X., and Stanier, A. (2018). Plasma energization in colliding magnetic flux ropes. Astrophys. J. 867, 16. doi:10.3847/1538-4357/aae30e

CrossRef Full Text | Google Scholar

Earl, J. A., Jokipii, J. R., and Morfill, G. (1988). Cosmic-ray viscosity. Astrophys. J. 331, L91. doi:10.1086/185242

CrossRef Full Text | Google Scholar

Florinski, V., and Zank, G. P. (2006). Particle acceleration at a dynamic termination shock. Geophys. Res. Lett. 33, L15110. doi:10.1029/2006GL026371

CrossRef Full Text | Google Scholar

Fraschetti, F. (2013). Turbulent amplification of a magnetic field driven by the dynamo effect at rippled shocks. Astrophys. J. 770, 84. doi:10.1088/0004-637X/770/2/84

CrossRef Full Text | Google Scholar

Giacalone, J., and Ellison, D. C. (2000). Three-dimensional numerical simulations of particle injection and acceleration at quasi-perpendicular shocks. J. Geophys. Res. 105, 12541–12556. doi:10.1029/1999JA000018

CrossRef Full Text | Google Scholar

Giacalone, J. (2012). Energetic charged particles associated with strong interplanetary shocks. Astrophys. J. 761, 28. doi:10.1088/0004-637X/761/1/28

CrossRef Full Text | Google Scholar

Giacalone, J., and Jokipii, J. R. (2007). Magnetic field amplification by shocks in turbulent fluids. Astrophys. J. 663, L41–L44. doi:10.1086/519994

CrossRef Full Text | Google Scholar

Giacalone, J., and Jokipii, J. R. (1999). The transport of cosmic rays across a turbulent magnetic field. Astrophys. J. 520, 204–214. doi:10.1086/307452

CrossRef Full Text | Google Scholar

Giacalone, J., and Neugebauer, M. (2008). The energy spectrum of energetic particles downstream of turbulent collisionless shocks. Astrophys. J. 673, 629–636. doi:10.1086/524008

CrossRef Full Text | Google Scholar

Giacalone, J. (2005). Particle acceleration at shocks moving through an irregular magnetic field. Astrophys. J. 624, 765–772. doi:10.1086/429265

CrossRef Full Text | Google Scholar

Giacalone, J. (2017a). The acceleration of charged particles at a spherical shock moving through an irregular magnetic field. Astrophys. J. 848, 123. doi:10.3847/1538-4357/aa8df1

CrossRef Full Text | Google Scholar

Giacalone, J. (2017b). The acceleration of thermal ions at a strong, quasi-parallel interplanetary shock: a hybrid simulation. J. Phys. Conf. Ser. 900, 012008. doi:10.1088/1742-6596/900/1/012008

CrossRef Full Text | Google Scholar

Giacalone, J. (2003). The physics of particle acceleration by collisionless shocks. Planet. Space Sci. 51, 659–664. doi:10.1016/S0032-0633(03)00101-6

CrossRef Full Text | Google Scholar

Goldstein, M. L., Roberts, D. A., and Matthaeus, W. H. (1995). Magnetohydrodynamic turbulence in the solar wind. Annu. Rev. Astron. Astrophys. 33, 283–325. doi:10.1146/annurev.aa.33.090195.001435

CrossRef Full Text | Google Scholar

Gosling, J. T., Asbridge, J. R., Bame, S. J., Feldman, W. C., Zwickl, R. D., Paschmann, G., et al. (1981). Interplanetary ions during an energetic storm particle event: the distribution function from solar wind thermal energies to 1.6 MeV. J. Geophys. Res. 86, 547–554. doi:10.1029/JA086iA02p00547

CrossRef Full Text | Google Scholar

Gosling, J. T., Thomsen, M. F., Bame, S. J., and Russell, C. T. (1989). Suprathermal electrons at Earth’s bow shock. J. Geophys. Res. 94, 10011–10025. doi:10.1029/JA094iA08p10011

CrossRef Full Text | Google Scholar

Gosling, J. T., and Thomsen, M. F. (1985). Specularly reflected ions, shock foot thicknesses, and shock velocity determination in space. J. Geophys. Res. 90, 9893–9896. doi:10.1029/JA090iA10p09893

CrossRef Full Text | Google Scholar

Guo, F., and Giacalone, J. (2015). The acceleration of electrons at collisionless shocks moving through a turbulent magnetic field. Astrophys. J. 802, 97. doi:10.1088/0004-637X/802/2/97

CrossRef Full Text | Google Scholar

Guo, F., and Giacalone, J. (2012a). Particle acceleration at a flare termination shock: effect of large-scale magnetic turbulence. Astrophys. J. 753, 28. doi:10.1088/0004-637X/753/1/28

CrossRef Full Text | Google Scholar

Guo, F., and Giacalone, J. (2012b). “The acceleration of electrons at perpendicular shocks and its implication for solar energetic particle events,” in American Institute of Physics Conference Series. Editors Q. Hu, G. Li, G. P. Zank, X. Ao, O. Verkhoglyadova, and J. H. Adams (Palm Springs, CA: American Institute of Physics Conference Series), 1500, 93–99.

Google Scholar

Guo, F., and Giacalone, J. (2010). The effect of large-scale magnetic turbulence on the acceleration of electrons by perpendicular collisionless shocks. Astrophys. J. 715, 406–411. doi:10.1088/0004-637X/715/1/406

CrossRef Full Text | Google Scholar

Guo, F., Jokipii, J. R., and Kota, J. (2010). Particle acceleration by collisionless shocks containing large-scale magnetic-field variations. Astrophys. J. 725, 128–133. doi:10.1088/0004-637X/725/1/128

CrossRef Full Text | Google Scholar

Guo, F., Li, S., Li, H., Giacalone, J., Jokipii, J. R., and Li, D. (2012). On the amplification of magnetic field by a supernova blast shock wave in a turbulent medium. Astrophys. J. 747, 98. doi:10.1088/0004-637X/747/2/98

CrossRef Full Text | Google Scholar

Hao, Y., Lembege, B., Lu, Q., and Guo, F. (2016). Formation of downstream high-speed jets by a rippled nonstationary quasi-parallel shock: 2-D hybrid simulations. J. Geophys. Res. Space Phys. 121, 2080–2094. doi:10.1002/2015JA021419

CrossRef Full Text | Google Scholar

Holman, G. D., and Pesses, M. E. (1983). Solar type II radio emission and the shock drift acceleration of electrons. Astrophys. J. 267, 837–843. doi:10.1086/160918

CrossRef Full Text | Google Scholar

Inoue, T., Yamazaki, R., and Inutsuka, S. I. (2009). Turbulence and magnetic field amplification in supernova remnants: interactions between a strong shock wave and multiphase interstellar medium. Astrophys. J. 695, 825–833. doi:10.1088/0004-637X/695/2/825

CrossRef Full Text | Google Scholar

Isenberg, P. A., and Jokipii, J. R. (1979). Gradient and curvature drifts in magnetic fields with arbitrary spatial variation. Astrophys. J. 234, 746–752. doi:10.1086/157551

CrossRef Full Text | Google Scholar

Jokipii, J. R. (2012). “Acceleration of energetic charged particles: shocks, reconnection or turbulence?,” in Physics of the Heliosphere: A 10 Year Retrospective. Editors J. Heerikhuisen, G. Li, N. Pogorelov, and G. Zank (Maui, HI: American Institute of Physics Conference Series), 144–156.

Google Scholar

Jokipii, J. R. (1966). Cosmic-ray propagation. I. Charged particles in a random magnetic field. Astrophys. J. 146, 480. doi:10.1086/148912

CrossRef Full Text | Google Scholar

Jokipii, J. R., and Giacalone, J. (2007). Adiabatic compression acceleration of fast charged particles. Astrophys. J. 660, 336–340. doi:10.1086/513064

CrossRef Full Text | Google Scholar

Jokipii, J. R., and Parker, E. N. (1969). Stochastic aspects of magnetic lines of force with application to cosmic-ray propagation. Astrophys. J. 155, 777. doi:10.1086/149909

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1982). Particle drift, diffusion, and acceleration at shocks. Astrophys. J. 255, 716–720. doi:10.1086/159870

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1971). Propagation of cosmic rays in the solar wind. Rev. Geophys. 9, 27–87. doi:10.1029/RG009i001p00027

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1987). Rate of energy gain and maximum energy in diffusive shock acceleration. Astrophys. J. 313, 842. doi:10.1086/165022

CrossRef Full Text | Google Scholar

Kajdič, P., Preisser, L., Blanco-Cano, X., Burgess, D., and Trotta, D. (2019). First observations of irregular surface of interplanetary shocks at ion scales by cluster. Astrophys. J. Lett. 874, L13. doi:10.3847/2041-8213/ab0e84

CrossRef Full Text | Google Scholar

Kallenrode, M. B. (1996). A statistical survey of 5-MeV proton events at transient interplanetary shocks. J. Geophys. Res. 101, 24393–24410. doi:10.1029/96JA01897

CrossRef Full Text | Google Scholar

Kennel, C. F., Coroniti, F. V., Scarf, F. L., Livesey, W. A., Russell, C. T., Smith, E. J., et al. (1986). A test of Lee’s quasi-linear theory of ion acceleration by interplanetary traveling shocks. J. Geophys. Res. 91, 11917–11928. doi:10.1029/JA091iA11p11917

CrossRef Full Text | Google Scholar

Kennel, C. F., Edmiston, J. P., and Hada, T. (1985). A quarter century of collisionless shock research. Geophys. Mono. Series 34, 1–36. doi:10.1029/GM034p0001

CrossRef Full Text | Google Scholar

Knock, S. A., Cairns, I. H., and Robinson, P. A. (2003). Type II radio emission predictions: multiple shock ripples and dynamic spectra. J. Geophys. Res. 108, 1361. doi:10.1029/2003JA009960

CrossRef Full Text | Google Scholar

Kong, X., Guo, F., Chen, Y., and Giacalone, J. (2019a). The acceleration of energetic particles at coronal shocks and emergence of a double power-law feature in particle energy spectra. Astrophys. J. 883, 49. doi:10.3847/1538-4357/ab3848

CrossRef Full Text | Google Scholar

Kong, X., Guo, F., Giacalone, J., Li, H., and Chen, Y. (2017). The acceleration of high-energy protons at coronal shocks: the effect of large-scale streamer-like magnetic field structures. Astrophys. J. 851, 38. doi:10.3847/1538-4357/aa97d7

CrossRef Full Text | Google Scholar

Kong, X., Guo, F., Shen, C., Chen, B., Chen, Y., Musset, S., et al. (2019b). The acceleration and confinement of energetic electrons by a termination shock in a magnetic trap: an explanation for nonthermal loop-top sources during solar flares. Astrohys. J. 887, L37. doi:10.3847/2041-8213/ab5f67

CrossRef Full Text | Google Scholar

Kóta, J. (2010). Particle acceleration at near-perpendicular shocks: the role of field-line topology. Astrophys. J. 723, 393–397. doi:10.1088/0004-637X/723/1/393

CrossRef Full Text | Google Scholar

Koval, A., and Szabo, A. (2010). Multispacecraft observations of interplanetary shock shapes on the scales of the Earth’s magnetosphere. J. Geophys. Res. 115, A12105. doi:10.1029/2010JA015373

CrossRef Full Text | Google Scholar

Krauss-Varban, D., and Wu, C. S. (1989). Fast Fermi and gradient drift acceleration of electrons at nearly perpendicular collisionless shocks. J. Geophys. Res. 94, 15367–15372. doi:10.1029/JA094iA11p15367

CrossRef Full Text | Google Scholar

Krymskii, G. F. (1977). A regular mechanism for the acceleration of charged particles on the front of a shock wave. Akademiia Nauk SSSR Doklady 234, 1306–1308.

Google Scholar

Lario, D., Berger, L., Decker, R. B., Wimmer-Schweingruber, R. F., Wilson, L. B., et al. (2019). Evolution of the suprathermal proton population at interplanetary shocks. Astrophys. J. 158, 12. doi:10.3847/1538-3881/ab1e49

CrossRef Full Text | Google Scholar

Lario, D., Ho, G. C., Decker, R. B., Roelof, E. C., Desai, M. I., and Smith, C. W. (2003). “ACE observations of energetic particles associated with transient interplanetary shocks,” in Solar Wind Ten, Pisa, Italy. Editors M. Velli, R. Bruno, F. Malara, and B. Bucci (American Institute of Physics Conference Series), 640–643.

Google Scholar

Lee, M. A. (1983). Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J. Geophys. Res. 88, 6109–6120. doi:10.1029/JA088iA08p06109

CrossRef Full Text | Google Scholar

Leroy, M. M., and Mangeney, A. (1984). A theory of energization of solar wind electrons by the Earth’s bow shock. Ann. Geophys. 2, 449–456.

Google Scholar

Li, G., and Zank, G. P. (2005). Mixed particle acceleration at CME-driven shocks and flares. Geophys. Res. Lett. 32, L02101. doi:10.1029/2004GL021250

CrossRef Full Text | Google Scholar

Li, G., and Zank, G. P. (2006). “Particle acceleration at a rippling termination shock,” in Physics of the Inner Heliosheath. Editors J. Heerikhuisen, V. Florinski, G. P. Zank, and N. V. Pogorelov (Oahu, HI: American Institute of Physics Conference Series), 858, 183–189.

Google Scholar

Li, X., Guo, F., Li, H., and Birn, J. (2018). The roles of fluid compression and shear in electron energization during magnetic reconnection. Astrophys. J. 855, 80. doi:10.3847/1538-4357/aaacd5

CrossRef Full Text | Google Scholar

Lowe, R. E., and Burgess, D. (2003). The properties and causes of rippling in quasi-perpendicular collisionless shock fronts. Ann. Geophys. 21, 671–679. doi:10.5194/angeo-21-671-2003

CrossRef Full Text | Google Scholar

Lu, Q., Hu, Q., and Zank, G. P. (2009). The interaction of alfvén waves with perpendicular shocks. Astrophys. J. 706, 687–692. doi:10.1088/0004-637X/706/1/687

CrossRef Full Text | Google Scholar

Masters, A., Stawarz, L., Fujimoto, M., Schwartz, S. J., Sergis, N., Thomsen, M. F., et al. (2013). Electron acceleration to relativistic energies at a strong quasi-parallel shock wave. Nat. Phys. 9, 164–167. doi:10.1038/nphys2541

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Goldstein, M. L. (1982). Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011–6028. doi:10.1029/JA087iA08p06011

CrossRef Full Text | Google Scholar

McComas, D. J., Christian, E. R., Schwadron, N. A., Fox, N., Westlake, J., Allegrini, F., et al. (2018). Interstellar mapping and acceleration Probe (IMAP): a new NASA mission. Space Sci. Rev. 214, 116. doi:10.1007/s11214-018-0550-1

CrossRef Full Text | Google Scholar

McComas, D. J., and Schwadron, N. A. (2006). An explanation of the Voyager paradox: particle acceleration at a blunt termination shock. Geophys. Res. Lett. 33, L04102. doi:10.1029/2005GL025437

CrossRef Full Text | Google Scholar

Mewaldt, R. A., Mason, G. M., and Cohen, C. M. S. (2012). “The dependence of solar energetic particle fluences on suprathermal seed-particle densities,” in Space Weather: the Space Radiation Environment: 11th Annual International AstroPhysics Conference, Palm Springs, CA. Editors Q. Hu, G. Li, G. P. Zank, X. Ao, O. Verkhoglyadova, and J. H. Adams (American Institute of Physics Conference Series), 128–133.

Google Scholar

Neergaard Parker, L., Zank, G. P., and Hu, Q. (2014). Particle acceleration at quasi-perpendicular shock waves: theory and observations at 1 AU. Astrophys. J. 782, 52. doi:10.1088/0004-637X/782/1/52

CrossRef Full Text | Google Scholar

Neergaard Parker, L., and Zank, G. P. (2012). Particle acceleration at quasi-parallel shock waves: theory and observations at 1 AU. Astrophys. J. 757, 97. doi:10.1088/0004-637X/757/1/97

CrossRef Full Text | Google Scholar

Neugebauer, M., Giacalone, J., Chollet, E., and Lario, D. (2006). Variability of low-energy ion flux profiles on interplanetary shock fronts. J. Geophys. Res. 111, A12107. doi:10.1029/2006JA011832

CrossRef Full Text | Google Scholar

Neugebauer, M., and Giacalone, J. (2005). Multispacecraft observations of interplanetary shocks: nonplanarity and energetic particles. J. Geophys. Res. 110, A12106. doi:10.1029/2005JA011380

CrossRef Full Text | Google Scholar

Neugebauer, M., and Giacalone, J. (2010). “Progress in the study of interplanetary discontinuities,” in Twelfth International Solar Wind Conference, Saint-Malo, France. Editors M. Maksimovic, K. Issautier, N. Meyer-Vernet, M. Moncuquet, and F. Pantellini (American Institute of Physics Conference Series), 194–197.

Google Scholar

Neugebauer, M. (2013). Propagating shocks. Space Sci. Rev. 176, 125–132. doi:10.1007/s11214-010-9707-2

CrossRef Full Text | Google Scholar

Oka, M., Otsuka, F., Matsukiyo, S., Wilson, L. B., Argall, M. R., et al. (2019). Electron scattering by low-frequency whistler waves at Earth’s bow shock. Astrophys. J. 886, 53. doi:10.3847/1538-4357/ab4a81

CrossRef Full Text | Google Scholar

Parker, E. N. (1979). “Cosmical magnetic fields,” in Their Origin and Their Activity (Oxford: The International Series of Monographs on Physics, Clarendon Press).

Google Scholar

Parker, E. N. (1965). The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 13, 9–49. doi:10.1016/0032-0633(65)90131-5

CrossRef Full Text | Google Scholar

Pulupa, M., and Bale, S. D. (2008). Structure on interplanetary shock fronts: type II radio burst source regions. Astrophys. J. 676, 1330–1337. doi:10.1086/526405

CrossRef Full Text | Google Scholar

Reames, D. V. (1999). Particle acceleration at the Sun and in the heliosphere. Space Sci. Rev. 90, 413–491. doi:10.1023/A:1005105831781

CrossRef Full Text | Google Scholar

Richardson, I. G., and Cane, H. V. (2010). Interplanetary circumstances of quasi-perpendicular interplanetary shocks in 1996–2005. J. Geophys. Res. 115, A07103. doi:10.1029/2009JA015039

CrossRef Full Text | Google Scholar

Scholer, M., Ipavich, F. M., Gloeckler, G., and Hovestadt, D. (1983). Acceleration of low-energy protons and alpha particles at interplanetary shock waves. J. Geophys. Res. 88, 1977–1988. doi:10.1029/JA088iA03p01977

CrossRef Full Text | Google Scholar

Senanayake, U. K., and Florinski, V. (2013). Is the acceleration of anomalous cosmic rays affected by the geometry of the termination shock? Astrophys. J. 778, 122. doi:10.1088/0004-637X/778/2/122

CrossRef Full Text | Google Scholar

Sheeley, J., N. R., Howard, R. A., Michels, D. J., Koomen, M. J., Schwenn, R., Muehlhaeuser, K. H., et al. (1985). Coronal mass ejections and interplanetary shocks. J. Geophys. Res. 90, 163–176. doi:10.1029/JA090iA01p00163

CrossRef Full Text | Google Scholar

Shimada, N., Terasawa, T., Hoshino, M., Naito, T., Matsui, H., Koi, T., et al. (1999). Diffusive shock acceleration of electrons at an interplanetary shock observed on 21 feb 1994. Astrophys. Space Sci. 264, 481–488. doi:10.1023/A:100249951377710.1007/978-94-011-4203-8_37

CrossRef Full Text | Google Scholar

Simnett, G. M., Sakai, J. I., and Forsyth, R. J. (2005). Proton and electron acceleration by quasi-perpendicular fast magnetosonic shocks in interplanetary space. Astrophys. Astron. 440, 759–766. doi:10.1051/0004-6361:20040229

CrossRef Full Text | Google Scholar

Stone, E. C., Cummings, A. C., McDonald, F. B., Heikkila, B. C., Lal, N., and Webber, W. R. (2005). Voyager 1 explores the termination shock region and the heliosheath beyond. Science 309, 2017–2020. doi:10.1126/science.1117684

PubMed Abstract | CrossRef Full Text | Google Scholar

Trotta, D., and Burgess, D. (2019). Electron acceleration at quasi-perpendicular shocks in sub- and supercritical regimes: 2D and 3D simulations. Mon. Notices Royal Astron. Soc. 482, 1154–1162. doi:10.1093/mnras/sty2756

CrossRef Full Text | Google Scholar

Trotta, D., Valentini, F., Burgess, D., and Servidio, S. (2020). The interaction between shocks and plasma turbulence: phase space transport. arXiv e-prints arXiv:2011.10417.

Google Scholar

Tsurutani, B. T., and Lin, R. P. (1985). Acceleration of >47 keV Ions and >2 keV electrons by interplanetary shocks at 1 AUkeV ions and keV electrons by interplanetary shocks at 1 AU. J. Geophys. Res. 90, 1–11. doi:10.1029/JA090iA01p00001

CrossRef Full Text | Google Scholar

Tu, C. Y., and Marsch, E. (1995). Magnetohydrodynamic structures waves and turbulence in the solar wind – observations and theories. Space Sci. Rev. 73, 1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

Wilson, L. B., Koval, A., Szabo, A., Breneman, A., and Cattell, C. A. (2012). Observations of electromagnetic whistler precursors at supercritical interplanetary shocks. Geophys. Res. Lett. 39, L08109. doi:10.1029/2012GL051581

CrossRef Full Text | Google Scholar

Wu, C. S. (1984). A fast Fermi process: energetic electrons accelerated by a nearly perpendicular bow shock. J. Geophys. Res. 89, 8857–8862. doi:10.1029/JA089iA10p08857

CrossRef Full Text | Google Scholar

Yang, L., Wang, L., Li, G., Wimmer-Schweingruber, R. F., He, J., Tu, C., et al. (2019). Electron acceleration by ICME-driven shocks at 1 au. Astrophys. J. 875, 104. doi:10.3847/1538-4357/ab1133

CrossRef Full Text | Google Scholar

Yang, L., Wang, L., Li, G., Wimmer-Schweingruber, R. F., He, J., Tu, C., et al. (2018). The strongest acceleration of > 40 keV electrons by ICME-driven shocks at 1 au. Astrophys. J. 853, 89. doi:10.3847/1538-4357/aaa245

CrossRef Full Text | Google Scholar

Yang, Z. W., Lembège, B., and Lu, Q. M. (2012). Impact of the rippling of a perpendicular shock front on ion dynamics. J. Geophys. Res. 117, A07222. doi:10.1029/2011JA017211

CrossRef Full Text | Google Scholar

Zank, G. P., Li, G., Florinski, V., Hu, Q., Lario, D., and Smith, C. W. (2006). Particle acceleration at perpendicular shock waves: model and observations. J. Geophys. Res. 111, A06108. doi:10.1029/2005JA011524

CrossRef Full Text | Google Scholar

Zank, G. P., Zhou, Y., Matthaeus, W. H., and Rice, W. K. M. (2003). “The interaction of turbulence with shock waves,” in Solar Wind Ten, Pisa, Italy. Editors M. Velli, R. Bruno, F. Malara, and B. Bucci (American Institute of Physics Conference Series), 417–420.

Google Scholar