- 1Department of Mechanical Engineering, University of Rochester, Rochester, NY, United States
- 2Department of Physics and Astronomy, University of Rochester, Rochester, NY, United States
The authors explore the possibility that near-earth, rubble pile asteroids might be used as habitats for human settlement by increasing their rotation to produce spin gravity. Using previously published scaling by Maindl et al. and studies of asteroid populations, it is shown that there is no class of hollowed body that would survive the spin-up process on its own without additional reinforcement. Large solid-rock asteroids (diameter D > 10 km) would not have the tensile strength to withstand the required rotation rates and would fracture and break apart. Smaller asteroids, being ‘rubble piles’, have little tensile strength and would quickly disperse. The possibility of containing the asteroid mass using higher-strength materials like carbon nanofiber is instead considered. It is found that a moderate tensile strength container can maintain the integrity of a large spinning cylinder composed of dispersed asteroid regolith. The research extends the range of possible asteroid habitat candidates, since it may become feasible to construct habitats from the more numerous smaller bodies, including NEAs (Near Earth Asteroids). The required tensile strength of the container material scales with habitat radius and thickness and is ∼ 200 MPa for a starting asteroid body of radius 300 m that is spun up to provide 0.3 g⊕ while increasing its radius to 3 km and maintaining a rubble and regolith shield thickness of 2 m to protect against cosmic rays. Ambient solar power can be harvested to aid in spin-up and material processing.
1 Introduction
The expansion of human civilization beyond the Earth’s surface has attracted new interest and investment via what is called the ‘New Space’ movement1. Represented by collaborations between government and private entities such as SpaceX, Blue Origin, and others, the goals of New Space extend beyond the exploratory goals of previous government-only space activities (Paikowsky, 2017). Proposed commercial development of Near Earth Orbit (NEO), cis-lunar (CL) and interplanetary spaces has taken many forms, including space tourism, asteroid mining, micro-g manufacturing, and power generation (Vedda, 2019).
If humanity is truly to become a space-faring species then it must have places in which to live and work. Much of the focus for the settlement of the Solar System, including discussions of terraforming, focuses on Mars (e.g., work by Teles (de Morais Teles, 2015).
Planets and large moons offer the advantage of larger in-situ gravitational fields and the possibility of building settlements underground to provide radiation shielding (Blamont, 2014).
Another possible site for human settlements that could provide radiation shielding and gravity is within asteroids that have been ‘spun-up’. Using Near Earth Asteroids (NEAs) in this fashion has the additional advantage of providing safe human transport through the Solar System, as these bodies are on elliptical orbits that cut across the inner Solar System. Hollowed and spinning asteroids have played an important role in a number of well-known science fiction accounts of the near-term settlement of the Solar System (for example, the ‘Asteroid terraria’ in the hard science fiction novel ‘2312’ by Kim Stanley Robinson).
While subsurface asteroid settlements can provide sufficient protective radiation shielding, the capability of these bodies to withstand the material stresses caused by rotating fast enough to support a significant fraction of Earth gravity is unclear. This consideration is critical given the detrimental effects low-g environments are known to have on human health (see Versari et al. (2013); Taibbi et al. (2013); Gasperi et al. (2014); Keyak et al. (2009)). Harris et al. (2014) showed that Martian gravity (∼ 0.38g⊕) is more than sufficient for people to stand upright without disorientation.
In a pioneering work, Maindl et al. (2019) calculated the material stresses produced at the midplane of an ellipsoidal asteroid that has been hollowed out and spun up to achieve artificial gravity. Ultimately, they concluded that a solid rocky asteroid with a few hundred meter radius would be capable of withstanding the internal stresses arising from spin-up to near Earth gravity.
In this paper the problem of habitat construction is reexamined in light of what is known about asteroid populations. This discussion is combined with calculations of forces, materials, and strategies for constructing rotating asteroid settlements. Design concepts are extended beyond hollowing out an existing body, exploring the expansion of an asteroid to fill an exterior containment structure by spinning it up beyond its yield point. The result is a hollow, shielded volume that may be spun up to a significant fraction of Earth’s gravity due to the additional strength provided by the supporting structure.
The layout of the paper is as follows: In Section 2 the stress estimates and conclusions of Maindl et al. (2019) are reviewed. In Section 3 asteroid compositions and population statistics are reviewed, revealing the likelihood of encountering asteroids composed primarily of rubble. This drives the assumptions and design concepts proposed in Section 4. The mechanism to spin up an asteroid in order to create a habitable cavity will be presented in Section 4.1. A proposed design for a strong, collapsible, external frame to support the expanded asteroid, backed by modeling work, will be evaluated in Section 4.2. Finally, Section 5 will conclude the work, summarizing findings and proposing next steps for future research.
2 Previous Results and Assumptions
Maindl et al. (2019) explored the possibility that a solid asteroid could be converted into a habitat if it were hollowed out and if its spin were increased so that centrifugal acceleration approached 0.38g⊕, thus matching the gravitational acceleration on the surface of Mars. In their study the asteroid was initially assumed to be an ellipsoidal, homogeneous solid. The asteroid was excavated so that it contains a cylindrical internal cavity that constitutes the habitable area. The spin of the hollow body is increased to produce a surface gravity of order gsurf = 0.3g⊕ on the interior of the cavity wall. Maindl et al. (2019) computed the maximum tensile stress within the spinning body in terms of the asteroid’s outer radius Ra:
Here ρa is the mean asteroid density and gc is the centripetal acceleration at the inner surface of the cavity. The factor
3 Asteroid Properties and Populations
3.1 Asteroid Composition
A problem with Maindl’s analysis is that small asteroids of the scale they studied are not expected to be solid bodies. Only the largest asteroids are essentially solid, due to internal deformation under pressure generated by self-gravity (Slyuta and Voropaev, 1997). Eq. (1) shows that the stress in the habitat shell depends linearly on the asteroid’s outer radius Ra. For larger asteroids with radii greater than a few hundred meters the required asteroid strength exceeds the yield strength of solid rocky material.
Rather than solid, asteroids with diameter D ≲ 10 km are ‘rubble piles’ (Walsh, 2018), loose conglomerations of material, with particles ranging in size from sand grains to boulders, that are held together by mutual gravitational attraction. Studies of brightness variations over time of asteroid populations, used to measure rotation rates, find few rapidly rotating bodies [e.g., (Burns, 1975; Pravec and Harris, 2000)]. These studies support the theory that asteroids are composed of a strengthless material bound only by self-gravity (Burns, 1975; Pravec and Harris, 2000; Walsh, 2018). Images obtained from recent missions to NEAs such as 25143 Itokawa, 101955 Bennu, and 162173 Ryugu further support the rubble pile interpretation, as they provided pictorial evidence of fractured and perched boulders, rubble fields, and regions of fine-grained particles called ‘regolith’ (Abe et al., 2006; Sugita et al., 2019; Walsh et al., 2019).
Inter-particle attractive forces in rubble asteroids are only able to sustain an internal strength on the order of 10 Pa (Scheeres et al., 2010; Rozitis et al., 2014; Sánchez and Scheeres, 2020). This value is far below Maindl’s requirement of 4 MPa (Maindl et al., 2019), suggesting the ‘hollowing-out’ technique for an asteroid habitat is not viable for rubble-pile type asteroids. An attempt to spin up an asteroid to achieve significant gravity would induce stress that would exceed its own comparatively small self-gravity (g ≪ g⊕), causing it to disassemble and fly apart.
In pursing the use of asteroids to create habitable environments providing both radiation shielding and gravity it is critical to recognize that most asteroids are rubble piles and to design habitats accordingly.
3.2 Asteroid Size Distribution
The choice by Maindl et al. (2019) to consider small asteroids has the advantage that smaller asteroids are more abundant than larger ones. Evolutionary models with collisional and dynamical processes show that the differential size distributions of the main-belt and NEA asteroids approximately follow power laws in the form.
with exponent p ∼ 3.5 and normalization constant B (O’Brien and Greenberg, 2005; Chodas, 2020). The total number of asteroids in a given size range [D1, D2] is
As the exponent significantly exceeds 1, smaller asteroids are much more numerous than large ones for both populations.
The population of NEAs is comprised mostly of smaller bodies originating from collisions of large bodies in the main-belt. There are over 104 NEAs with a diameter greater than 100 m but only about 900 with a diameter greater than 1 km (Chodas, 2020). This supports the design of habitats for 100 m scale rubble-type asteroids since they are bound to be far more prevalent throughout the Solar System than larger, solid asteroids. Additionally, NEAs provide sites that are in close proximity to the Earth, can be on interplanetary trajectories that could be utilized for transport and offer plentiful mass for building shields against harmful cosmic rays.
4 Manufacturing a Habitat From a Rubble Asteroid
In this study, it is assumed that an asteroid is initially comprised of rubble, with grains that are significantly smaller than the asteroid radius Ra.
Analysis will consider asteroids ranging from a radius of approximately 100 m to upwards of 500 m. A hypothetical asteroid with a 300 m radius, dimensionally similar to NEA 101955 Bennu that has a mean equatorial radius of 246 m (Daly et al., 2020) and bulk density
The process of converting an ellipsoidal rubble asteroid into a hollow cylindrical shell is proposed in two discrete stages.
In Stage I, the asteroid spin is gradually increased in a controlled fashion from some initial value to the desired rotation rate. The resultant centrifugal forces cause the rubble to separate and break apart into a free rubble field. The challenge in this stage is identifying the appropriate mechanism to use to induce spin-up.
In Stage II the free rubble field is captured in an external containment structure that begins in a compressed state enveloping the asteroid and is allowed to expand to the desired cylindrical geometry. An illustration of the final structure is provided in Figure 1.
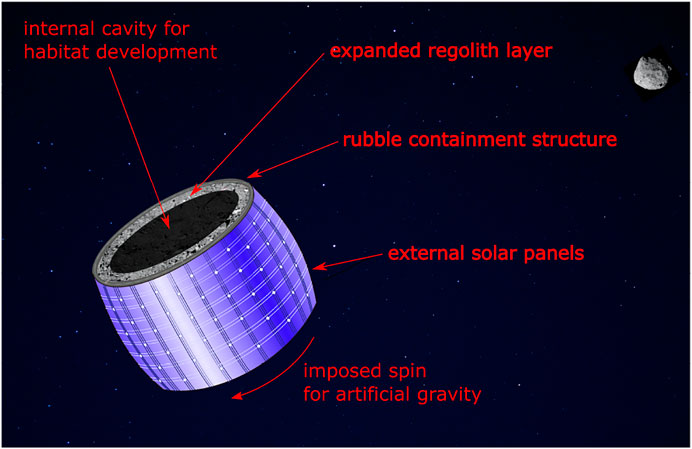
FIGURE 1. A cylindrical, spinning habitat that has been covered with solar panels. Inside is a thick layer of asteroid rubble and regolith that serves as a radiation shield. Just under the solar panels is a strong, stiff container that keeps the rubble from flying apart. The habitat is spun about its lengthwise axis to generate gravity on the inner surface.
In this section, proposals for handling Stage I and Stage II will be presented that consider the unique design requirements of this problem and the harsh environment in which the work must be completed.
4.1 Stage I: Facilitating Asteroid Break-Up
4.1.1 Spin-Up via Solar-Powered Cannons and Mass Ejection
In space, solar power is a dependable and renewable energy source. The total power that can be harvested depends on the total surface area in solar panels, the incident angle of the Sun upon them, and the efficiency of the panels themselves.
Assuming a constant spin axis during expansion and a cylindrical shell as the predominant geometry, the total energy required for spin-up is given by…
where
is the gravitational acceleration at the surface of the shell. A selected value for gsurf sets the spin rate ω in terms of the gravitational acceleration. The value used for the total asteroid mass M is selected to be similar to the mass of asteroid Bennu, and αI is a dimensionless parameter of order unity that specifies the moment of inertia about the spin axis (where αI = 1.0 for a hollow cylinder).
The requisite time for spin-up may be estimated from the radiative energy flux from the Sun. With the illuminated portion of the solar array having size
where the efficiency ϵ is the fraction of radiative solar energy that is harvested by the solar panels and not lost to heat or reflection. Here r is the distance of the asteroid from the Sun and L○ is the luminosity of the Sun, 3.8 × 1026 W.
Finally, by dividing the total rotation energy by the harvested solar power the requisite time for spin-up is found to be
For the specified parameters, the scaling laws from Eqs 4, 6 yield an estimated spin up time on the order of 10 days. This short time implies that solar power is sufficient to carry out phase I of the asteroid-to-habitat conversion.
The mechanism by which to exert torque on the asteroid to produce this spin-up must still be devised. It is proposed that the harvested solar energy can power ‘rubble cannons’ anchored around the outer face of the containment structure that would eject mass tangentially to the asteroid’s surface. Such cannons would be fed by conveyors or Archimedes’ screw-type equipment that supply rubble from the asteroid surface for ejection. By mounting these cannons to the structure, logistical challenges arising from directly anchoring to surface regolith are avoided.
Ejecting a total mass Δm at a velocity vej gives a change in the asteroid’s angular momentum of
Setting Δm = fmM, with fm the fraction of the asteroid mass ejected, and using Eq. 5 to set the spin rate, the required ejection velocity is
In contrast, the escape velocity would only be a few m/s:
The time required for spin-up is inversely proportional to shell radius and the ejection velocity is proportional to
In summary, a local solar array can provide sufficient power to eject rubble at these speeds with surface cannons. Furthermore, it is demonstrated that reasonable timelines for spin-up are attainable. But, since not all mass can be ejected at once, it is practical to note that the spin-up is an incremental process and thus could be achieved with rapid fire ejection of smaller payloads, infrequent ejection of larger payloads, or a mixture of the two. Habitat constructions with tight timelines and high budgets could afford to shorten spin-up time with aggressive mass ejection. Cost-saving undertakings with lower time pressures could follow a more gradual approach. It is these practical and eventually even economical considerations that truly determine spin-up time.
4.2 Stage II: Capturing Rubble Ejecta Into a Cylindrical Habitat
The radially expanding rubble field produced by Stage I must be captured and formed into the final cylindrical shell that will constitute the habitat. However, simply placing a rigid cylindrical scaffold concentrically around the disintegrating asteroid would not suffice. To do so risks unpredictable shock loading as rubble impacts the containment structure, drastically complicating its design requirements. So, the collapsible scaffold design is proposed. This structure will initially have a compressed radius equal to that of the asteroid, and energy from the expansion of the rubble will be used to push open the containment structure until it reaches its maximum, fully-expanded radius. In this design, energy-dissipating elements, e.g. viscous hinges, could be installed in the joints of the collapsible scaffold to gradually arrest the velocity of the expanding rubble and mitigate shock loading events.
Next, an assessment of the mechanical requirements for the external containment structure will be completed. The hoop stress sustained by the structure at steady state will be evaluated and a finite element model will be presented to visualize the expansion and loading of the external scaffold proposed in this work. Finally, a hypothetical case will be presented to add perspective to the theoretical discussion.
4.2.1 Structural Requirements for a Bennu-Based Habitat
The design of the cylindrical exterior structure/container/scaffold is key to the success of the habitat, as it provides material strength that the rubble cannot. In the habitat’s final configuration, the internal rubble layer of thickness tr is pressed radially outward against the external structure, with thickness td, which must sustain the pressure from the entire rubble layer. The cylindrical container has an outer radius of Rc > tr > td and it is assumed that the total mass of the rubble exceeds that of the container.
To analyze the strength required by the external structure the system is equivocated to a thin-walled cylindrical pressure vessel subject to a constant internal pressure. The parameter used to characterize the tensile stress in the container wall is often called a ‘hoop stress’, originally developed to improve the design of barrels holding fluids like molasses2.
Ignoring the strength of the top and bottom of the cylinder and using a thin wall approximation, the hoop stress can be estimated as
where P is the internal pressure.
The internal pressure P can be described in terms of the centrifugal acceleration of the cylindrical rubble layer. Neglecting mass on the top and bottom of the cylinder, the total mass of the rubble shell inside the container is M = 2πRchtrρa. The total centripetal force required at a particular angular rotation rate is given by F = Mω2Rc, and the area of the wall over which this rubble force is distributed is Ar = 2πRch. The pressure on the exterior shell is therefore given by
The total volume of the cylinder is
Assuming similar dimensions for cylinder radius and height such that h ≈ Rc, the expression for volume reduces to
When the asteroid is spun up and reaches its break up limit some material could escape the system as it is weakly bound. We assume the mass of the asteroid does not change as a result of spin up such that
where Va is the volume of the asteroid described roughly by
Finally, given that the centrifugal surface gravity can be expressed in terms of the spin rate (Eq. (5)), the hoop stress equation can be rewritten as
Shielding is required to protect passengers from solar and galactic radiation. A 7.4 cm thick aluminum hull would be capable of blocking most solar events (Townsend, 2020). A regolith layer with thickness of about tr = 2 m is sufficient for limiting radiation exposure to 100 mSv/yr equivalent dose on Mars (Röstel et al., 2020). For the case of an asteroid that has Ra = 300m, similar to Bennu, this rubble layer thickness gives a container radius
The corresponding hoop stress in the rubble cylinder is found to be approximately
The hoop stress on the container is independent of the length of the cylinder but does depends on the thicknesses of the rubble layer and the container.
To reiterate, this calculation assumes no structural integrity for the rubble layer that is contained by the external structure. Instead, the entire mass of the rubble layer presses outward, creating a distributed pressure on the inner surface of the container.
Figure 2 illustrates the variation of hoop stress for different values of spin gravity and habitat radius.
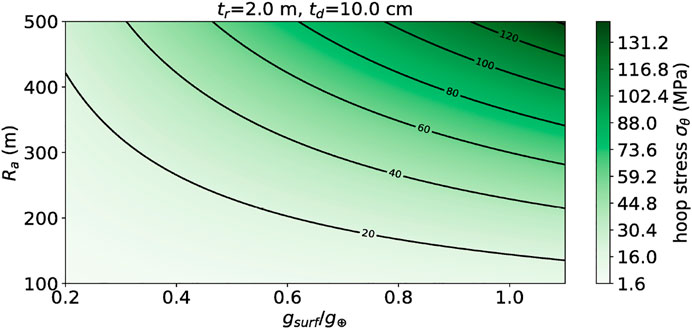
FIGURE 2. Plot of Eq. 17, the hoop stress for an asteroid spun up to form a cylindrical shell of thickness 2 m and contained in a scaffold of thickness 10 cm. The asteroid is assumed to have a uniform density of 1 g/cm3. The vertical axis is the radius of the asteroid Ra, in meters. The horizontal axis is the surface gravity of the asteroid in units of Earth surface gravity.
Were an external scaffold to be used in this application, it would be important to consider the materials used in its construction. This is because there will also be a hoop stress generated by the mass of the structure itself as it rotates with the rest of the habitat. This ‘self-weight’ hoop stress is superimposed upon hoop stresses already created by the rubble layer, and will scale rapidly with the weight of the external structure. Therefore, materials best suited to this application should be high-strength and low-density. In future work on this topic, the consideration of a self-weight hoop stress will be fundamental in considering the scalability of this type of asteroid-based habitat, since larger and larger examples will require the latest materials that meet such requirements.
For the above container, the pressure on the container wall
This is an order of magnitude lower than 1 atm (1 atm
4.3 Discrete Finite Element Models on Sustained Stresses
4.3.1 Model Overview
Finite element models have been designed to simulate the creation of the habitat shown in Figure 1. In keeping with earlier sections of this paper, the initial asteroid and compressed external structure have a radius of approximately 300 m while maximum radius of said structure expands to 3 km. The simulations are two dimensional, representing a quarter of a cross-section of the final cylindrical structure. Abaqus/Explicit finite elements software is used to carry out simulations, as it enables modeling of all desired components of the system.
The pieces of the fragmenting asteroid are modeled as monodisperse circular boulders with radii of 2.5 m. Each boulder is modeled discretely and meshed with 22 quadrilateral plane strain elements (CPE4R). The density of these boulders is set to 1
Interactions between objects are defined for the whole system with Abaqus’ Frictionless Hard Contact method. The normal component of contact is managed with Hertzian methods and the sliding component neglects friction, a decision made to simplify and expedite the settling of rubble against the boundary. It should also be noted that no inter-particular gravity is considered in this simulation.
At its fully expanded condition, rubble along the outer boundary should experience an effective gravity directed radially outward of approximately 0.3g⊕. This is accomplished by the centrifugal force generated from the spin-up of the asteroid and scaffold apparatus. For simulation purposes, the fragmentation and expansion of the rubble cluster is done by applying an acceleration field directed radially outward that is tuned to the desired effective gravity at maximum expansion. The components of the acceleration applied to the rubble pieces, calculated in terms of position, is given by ai = 0.000981 xi.
The simulation is run using Abaqus’ automatic incrementation feature. Since radial expansion is proscribed in simulation yet the realistic event would produce a ‘swirl’ effect of rubble outwards from the initial configuration, the perspective of the observer in simulation should be clarified. The perspective of simulation should be thought of as looking along the central axis of the cylindrical expanding structure. The observer is then set to spin about the long axis at the same rate as the structure/asteroid system, such that the expansion of rubble will appear purely radial to the observer. This simulation and perspective, though unconventional, produces the same final configuration of rubble pressed outward against the expanded structure as the more complex yet practical procedure presented earlier.
4.3.2 Simulation of Bennu-type Expansion
The simulations described in the prior section demonstrate an expansion of an asteroid, similar to Bennu in size, into an expandable structure to form a 3 km radius cylindrical shielded volume. The results of this expansion through various stages are shown in Table 1. Progress is described with percentage instead of a conventional time index. This was a deliberate choice to avoid confusion as the time that would be reported from simulation would not correspond nor be relevant to the timescales presented earlier in this paper, due to the simplified drivers for expansion applied in the model.
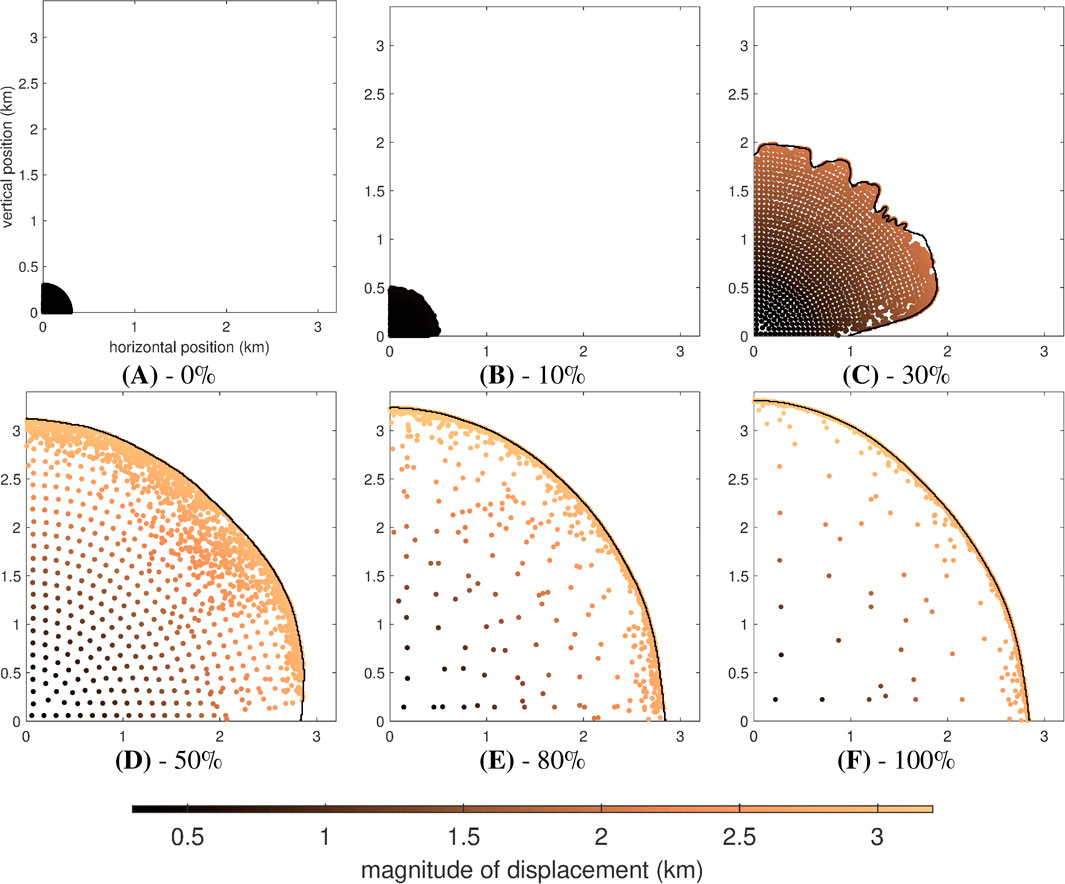
TABLE 1. Results from a quarter-symmetry discrete simulation of an approximately 300 m meter rubble pile asteroid spun to disintegration and contained by an expanding structure with a 3 km maximum radius. Granules are enlarged to improve visual quality in print. Percentages represent simulation progress. The spin of the system is about the zz axis.
Assessing the contents of Table 1, panel (A) shows the initial configuration with the expanding structure enclosed tightly around the not-yet-spun-up asteroid. Panel (B) shows the beginning of the expansion process and panel (C) realistically shows some unevenness that arises during the expansion, an artefact of not-perfect initial grain distribution and uneven distribution along the boundary. Despite this, panels (D) through (F) illustrate that a regular quarter section of the boundary is still achieved. To put the scale of these findings in context, for a cylindrical structure of radius 3 km and an equivalent length of 3km, the shielded region within spans 56km2—an area about the size of Manhattan.
4.3.3 Phenomena in the Expansion of Differently Sized Asteroids
An additional batch of simulations tests the expansion of asteroids of different sizes into an expandable structure with a maximum radius of 10km, with the same effective gravity requirement at maximum expansion. The smallest structure, denoted hab1, is simulated with 800 grains of rubble producing an asteroid of radius 1400 m and a total mass of 3.08 × 108 kg. Details for further asteroids simulated are presented in Table 2, extending up to hab5 which is composed of 6000 grains. By expanding each asteroid into a structure of the same size, rubble layers of differing thickness are produced against the expanded boundary.

TABLE 2. Setup and results for study of various-sized asteroids expanded into a 10 km radius structure.
For each case, the hoop stress is measured by dividing the reaction force at the anchor point of the boundary by the truss elements’ cross-sectional area. Also, based on the mass and size of the system, the pressure-vessel calculation method for hoop stress is used for an analytical estimate. The simulation measurement and analytical predictions for hoop stress for each system are shown in Table 2 in the Simulation and Analytical columns, respectively. Finally, by comparing the two values, an Accuracy measurement is presented as well, calculated by dividing the simulation measurement by the analytical prediction.
The results of Table 2 indicate a phenomenon within the granular rubble layer; self-sustainment of hoop stresses that offset the total stress sustained by the structure. For instance, the hab1 model shows the simulation measured hoop stress is approximately 91.2% of the value predicted using the total mass of the rubble. The hab1 model represents the smallest asteroid and, correspondingly, the thinnest final rubble layer with a thickness of around one grain. The hab5 model, however, only measured up to about 85.9% of the predicted value and produced a final rubble layer that is greater than ten grains thick. This trend is steady across all five variants of the model; the thicker the final rubble layer, the lower the hoop stress sustained by the external structure compared to analytical expectation.
This finding has implications in design optimization of this type of expanded-asteroid habitat, suggesting it may be possible to reduce the required strength of the external structure and instead have a fraction of the rubble layer’s own weight supported by its granular packing under centrifugal load. Given the vast amount of material required to create an external structure at this scale, such optimization could save large amounts of time, money, and resources.
5 Summary and Discussion
The exploration presented in this paper continues with the idea of using NEAs as a platform for humanity’s expansion into space. Due to their trajectories, a habitat built on an asteroid has implications for interplanetary transport. Manipulating an asteroid’s extensive mass could create shielding from the hazards of space, such as solar radiation. Finally, by carefully spinning such a habitat artificial gravity can be generated for the human occupants, thus solidifying the concept for long-term space travel.
The authors begin with an evaluation of Maindl et al. (2019) findings that a homogeneous, solid rock asteroid with a central cylindrical cavity could be spun about its axis to achieve artificial gravity similar to Earth’s. It is found that Maindl’s findings are flawed in that the majority of asteroids of radial size ∼ 100 m are actually of a rubble-pile composition that would be unable to withstand any substantial forced spin-up. Instead, it is proposed in this work to take advantage of the rubble composition and to intentionally disintegrate an asteroid with overwhelming spin so as to capture it into a larger cylindrical external containment structure. In doing so, a thick layer of regolith is created along the interior surface of this structure which forms a shielded interior volume that can be developed for human occupation. Furthermore, by using a stronger external frame the cylindrical habitat can be spun about it’s central axis to produce an artificial gravity field within.
The construction of such a habitat has been separated into two stages. Stage 1 employs solar-powered rubble cannons affixed to the external structure’s outer surface that eject mass tangentially to increase spin rate. Once enough mass has been ejected the asteroid will reach its break up limit and produce a radially expanding field of free rubble. By estimating collected solar power and the required mass ejection to produce spin-up, a prediction for the duration of Stage 1 is completed. It is found that spin-up for a 300 m asteroid would be feasible in just a few months.
Stage 2 of the habitat construction introduces the cylindrical external containment structure which features an accordion-like design that allows it to initially wrap around the asteroid in a close fashion. As the rubble field from Stage 1 is expanding, it forces the external structure to stretch and expand until the maximum design radius is reached. From this point the rubble against the external structure and forms the protective regolith layer. A finite element model has been created to visualize Stage 2 and the build-up of the rubble layer within the structure. Based on the total mass of the rubble and the desired artificial gravity, an assessment of the hoop stress sustained by the external rubble structure is completed. It is discovered that for a habitat constructed from a 500 m radius asteroid that is spun to mimic Earth’s gravity at 1g, the peak hoop stress in the structure is just over 130 MPa. This value and others calculated from analytics and simulation are well within the range of many currently existing construction materials.
In conclusion, we note that while our study clearly relies on engineering capacities that do not exist at present, our results indicate that the basic physics of transforming small asteroids into human habitats is feasible. In addition, our proposal is likely to be less costly and complex in terms of engineering than building a classic O’Neill habitat in which all structural materials must be fabricated and transported to the construction orbit (O’Neill, 1974). Given the current level of interest and investment in space, we believe looking across multi-decadal or even a century long timescales is appropriate for anticipating the engineering requirements needed for a vibrant human community in space. We hope our works represents a single fruitful step in that direction.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed on this document contributed equally to this work. PM conducted the FEM simulations, helped review hoop stress calculations, and carried out final editing of the document. JS carried out the multitude of theoretical calculations on the dynamics of solar-driven spin-up. Authors AD and EW completed the theoretical hoop stress calculations, and EW visualized the resulting equations. EW and AQ wrote much of the initial content and defined the core structure of the analysis sections. AQ provided much of the information about known asteroid properties and populations. HA provided initial FEM simulations models as well as crucial guidance in completion of the FEM work. HA’s procedures were key in discovering the interesting behaviors of thick versus thin granular layers in the habitat. AF initiated the study (based on ideas from James SA Corey and Kim Stanley Robinson) and his role was to steer the overall direction and narrative paper, helping all authors reconcile their findings into this document.
Funding
This material is based upon work supported in part by NASA grant 80NSSC17K0771, and National Science Foundation Grant No. PHY-1757062. We are also acknowledge support the Department of Energy grants DE-SC0001063, DE-SC0020432, and DE-SC0020434, the National Science Foundation grants AST-1515648 and AST-1813298 and NASA grant 19-EXO19-0078.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Miki Nakajima for helpful discussions. We miss Randal C. Nelson who would have given us a lucid (and possibly withering) critique of this manuscript.
Footnotes
1https://blog.satsearch.co/2019–02–26-lets-talk-about-newspace.html
2Faulty barrel design has caused disaster, e.g. https://en.wikipedia.org/wiki/Great_Molasses_Flood.
References
Abe, S., Mukai, T., Hirata, N., Barnouin-Jha, O. S., Cheng, A. F., Demura, H., et al. (2006). Mass and Local Topography Measurements of Itokawa by Hayabusa. Science 312, 1344–1347. doi:10.1126/science.1126272
Blamont, J. (2014). A Roadmap to Cave Dwelling on the Moon and Mars. Adv. Space Res. 54, 2140–2149. doi:10.1016/j.asr.2014.08.019
Burns, J. (1975). The Angular Momenta of Solar System Bodies: Implications for Asteroid Strengths. Icarus 25, 545–554. doi:10.1016/0019-1035(75)90035-4
Daly, M. G., Barnouin, O. S., Seabrook, J. A., Roberts, J., Dickinson, C., Walsh, K. J., et al. (2020). Hemispherical Differences in the Shape and Topography of Asteroid (101955) Bennu. Sci. Adv. 6, eabd3649. doi:10.1126/sciadv.abd3649
de MoraisTeles, M. A. (2015). “Mars Astrobiology: Recent Status and Progress,” in Planetary Exploration and Science: Recent Results and Advances. Editors S. Jin, N. Haghighipour, and W. Ip (Berlin and Heidelberg, Germany: Springer Geophysics), 147–245.
Gasperi, V., Rapino, C., Battista, N., Bari, M., Mastrangelo, N., Angeletti, S., et al. (20142014). A Functional Interplay between 5-lipoxygenase and μ-calpain Affects Survival and Cytokine Profile of Human Jurkat T Lymphocyte Exposed to Simulated Microgravity. Biomed. Res. Int. 2014, 782390. doi:10.1155/2014/782390
Harris, L. R., Herpers, R., Hofhammer, T., and Jenkin, M. (2014). How Much Gravity Is Needed to Establish the Perceptual Upright? PLOS ONE 9, e106207–7. doi:10.1371/journal.pone.0106207
Keyak, J. H., Koyama, A. K., LeBlanc, A., Lu, Y., and Lang, T. F. (2009). Reduction in Proximal Femoral Strength Due to Long-Duration Spaceflight. Bone 44, 449–453. doi:10.1016/j.bone.2008.11.014
Lauretta, D. S., DellaGiustina, D. N., DellaGiustina, D. N., Bennett, C. A., Golish, D. R., Becker, K. J., et al. (2019). The Unexpected Surface of Asteroid (101955) Bennu. Nature 568, 55–60. doi:10.1038/s41586-019-1033-6
Maindl, T. I., Miksch, R., and Loibnegger, B. (2019). Stability of a Rotating Asteroid Housing a Space Station. Front. Astron. Space Sci. 6, 37. doi:10.3389/fspas.2019.00037
O'Brien, D. P., and Greenberg, R. (2005). The Collisional and Dynamical Evolution of the Main-belt and NEA Size Distributions. Icarus 178, 179–212. doi:10.1016/j.icarus.2005.04.001
Paikowsky, D. (2017). What Is New Space? the Changing Ecosystem of Global Space Activity. New Space 5, 84–88. doi:10.1089/space.2016.0027
Pravec, P., and Harris, A. W. (2000). Fast and Slow Rotation of Asteroids. Icarus 148, 12–20. doi:10.1006/icar.2000.6482
Röstel, L., Guo, J., Banjac, S., Wimmer-Schweingruber, R. F., and Heber, B. (2020). Subsurface Radiation Environment of Mars and its Implication for Shielding Protection of Future Habitats. J. Geophys. Res. (Planets) 125, e06246. doi:10.1029/2019je006246
Rozitis, B., Maclennan, E., and Emery, J. P. (2014). Cohesive Forces Prevent the Rotational Breakup of Rubble-Pile Asteroid (29075) 1950 DA. Nature 512, 174–176. doi:10.1038/nature13632
Sánchez, P., and Scheeres, D. J. (2020). Cohesive Regolith on Fast Rotating Asteroids. Icarus 338, 113443. doi:10.1016/j.icarus.2019.113443
Scheeres, D. J., Hartzell, C. M., Sánchez, P., and Swift, M. (2010). Scaling Forces to Asteroid Surfaces: The Role of Cohesion. Icarus 210, 968–984. doi:10.1016/j.icarus.2010.07.009
Slyuta, E. N., and Voropaev, S. A. (1997). Gravitational Deformation in Shaping Asteroids and Small Satellites. Icarus 129, 401–414. doi:10.1006/icar.1997.5776
Sugita, S., Honda, R., Morota, T., Kameda, S., Sawada, H., Tatsumi, E., et al. (2019). The Geomorphology, Color, and thermal Properties of Ryugu: Implications for Parent-Body Processes. Science 364, 252. doi:10.1126/science.aaw0422
Taibbi, G., Kaplowitz, K., Cromwell, R. L., Godley, B. F., Zanello, S. B., and Vizzeri, G. (2013). Effects of 30-day Head-Down Bed Rest on Ocular Structures and Visual Function in a Healthy Subject. Aviat Space Environ. Med. 84, 148–154. doi:10.3357/asem.3520.2013
Vedda, J. (2019). Space Leadership in Transition. El Segundo, CA: Center for Space Policy and Strategy. Available at: https://csps.aerospace.org/papers/space-leadership-transition
Versari, S., Longinotti, G., Barenghi, L., Maier, J. A. M., and Bradamante, S. (2013). The Challenging Environment on Board the International Space Station Affects Endothelial Cell Function by Triggering Oxidative Stress through Thioredoxin Interacting Protein Overexpression: the ESA‐SPHINX experiment. FASEB j. 27, 4466–4475. doi:10.1096/fj.13-229195
Walsh, K. J., Jawin, E. R., Jawin, E. R., Ballouz, R.-L., Barnouin, O. S., Bierhaus, E. B., et al. (2019). Craters, Boulders and Regolith of (101955) Bennu Indicative of an Old and Dynamic Surface. Nat. Geosci. 12, 242–246. doi:10.1038/s41561-019-0326-6
Walsh, K. J. (2018). Rubble Pile Asteroids. Annu. Rev. Astron. Astrophys. 56, 593–624. doi:10.1146/annurev-astro-081817-052013
Nomenclature
Erot Asteroid rotational kinetic energy
fm = Δm/M Fraction of ejected mass
g⊕ Earth gravity
gsurf Surface gravity on interior shell wall
I Asteroid moment of Inertia
H Asteroid angular momentum
L○ Solar Luminosity
Lrad Total solar power
M Asteroid mass
Δm Ejected mass
P Internal Pressure
r Sun-asteroid distance
Ra Asteroid Radius
Rc Radius of cylindrical shell
tr Rubble layer thickness
td External container thickness
vej Ejection velocity
vesc Escape velocity
αI Dimensionless inertia parameter
ε Power efficiency
ρa Asteroid mean density
σθ Hoop stress
ω Asteroid spin rate
Keywords: habitat design, near earth asteroids, numerical simulations, rubble pile asteroids, hoop stress, finite element analysis
Citation: Miklavčič PM, Siu J, Wright E, Debrecht A, Askari H, Quillen AC and Frank A (2022) Habitat Bennu: Design Concepts for Spinning Habitats Constructed From Rubble Pile Near-Earth Asteroids. Front. Astron. Space Sci. 8:645363. doi: 10.3389/fspas.2021.645363
Received: 23 December 2020; Accepted: 10 November 2021;
Published: 03 January 2022.
Edited by:
George Livadiotis, Southwest Research Institute (SwRI), United StatesReviewed by:
Andrea Viale, University of Glasgow, United KingdomXenophon Moussas, National and Kapodistrian University of Athens, Greece
Copyright © 2022 Miklavčič, Siu, Wright, Debrecht, Askari, Quillen and Frank. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter M. Miklavčič, cG1pa2xhdmNAdXIucm9jaGVzdGVyLmVkdQ==
 Peter M. Miklavčič
Peter M. Miklavčič John Siu2
John Siu2 Alex Debrecht
Alex Debrecht