- 1Department of Physics, University of Illinois at Urbana-Champaign, Urbana, IL, United States
- 2Department of Astronomy, University of Illinois at Urbana-Champaign, Urbana, IL, United States
Neutron stars (NSs) are extraordinary not only because they are the densest form of matter in the visible Universe but also because they can generate magnetic fields ten orders of magnitude larger than those currently constructed on earth. The combination of extreme gravity with the enormous electromagnetic (EM) fields gives rise to spectacular phenomena like those observed on August 2017 with the merger of a binary neutron star system, an event that generated a gravitational wave (GW) signal, a short γ-ray burst (sGRB), and a kilonova. This event serves as the highlight so far of the era of multimessenger astronomy. In this review, we present the current state of our theoretical understanding of compact binary mergers containing NSs as gleaned from the latest general relativistic magnetohydrodynamic simulations. Such mergers can lead to events like the one on August 2017, GW170817, and its EM counterparts, GRB 170817 and AT 2017gfo. In addition to exploring the GW emission from binary black hole-neutron star and neutron star-neutron star mergers, we also focus on their counterpart EM signals. In particular, we are interested in identifying the conditions under which a relativistic jet can be launched following these mergers. Such a jet is an essential feature of most sGRB models and provides the main conduit of energy from the central object to the outer radiation regions. Jet properties, including their lifetimes and Poynting luminosities, the effects of the initial magnetic field geometries and spins of the coalescing NSs, as well as their governing equation of state, are discussed. Lastly, we present our current understanding of how the Blandford-Znajek mechanism arises from merger remnants as the trigger for launching jets, if, when and how a horizon is necessary for this mechanism, and the possibility that it can turn on in magnetized neutron ergostars, which contain ergoregions, but no horizons.
1. Introduction
Gravitational wave astronomy was launched in 2015 with the first-ever gravitational wave (GW) detection of the inspiral and merger of a binary black hole (BHBH) system as reported by the LIGO/Virgo (LV) scientific collaboration—event GW150914 (Abbott et al., 2016a,b). Two years later the simultaneous detection of GWs from an inspiraling binary neutron star (NSNS) system, event GW170817, and its post-merger emission of electromagnetic (EM) radiation spurred the era of multimessenger astronomy (Abbott et al., 2017a,b,c,d; Kozlova et al., 2017). Although at present the LV scientific collaboration almost weekly announces new GW signals whose progenitors may be BHBHs, NSNSs, or black hole-neutron star (BHNS) systems there has been no robust discovery of a BHNS system yet, while the subsequent NSNS candidates have been EM “orphans” i.e., no EM radiation has been associated with the GWs produced by them. Merging NSNSs and BHNSs are not only important sources of gravitational radiation, but also promising candidates for coincident EM counterparts, which could give new insight into their sources. Namely, GWs are sensitive to the density profile of NSs and their measurement enforces tight constraints on the equation of state (EOS) that governs matter at supranuclear densities (Lattimer and Prakash, 2016), while postmerger EM signatures can help to explain the phenomenology of short γ-ray bursts (sGRBs), and nucleosynthesis processes powering kilonovae (Li and Paczynski, 1998; Metzger, 2017). To understand these observations and, in particular, to understand the physics of matter under extreme conditions, it is crucial to compare them to predictions from theoretical modeling, which, due to the complexity of the underlying physical phenomena, is largely numerical in nature.
Although a spinning BH surrounded by an accretion disk is the remnant of a BHNS merger, this is not necessarily the case for an NSNS merger. Depending on the total mass of the system, as well as the EOS of the NS companions, the outcome of an NSNS merger can be a stable NS or a spinning BH, surrounded by an accretion disk in either case. Even when a BH is the remnant, the path toward such an outcome is extremely varied and can be decisive for a number of important issues, like the existence of a sGRB or the production of the heaviest elements in the Universe via a kilonova (Metzger and Fernández, 2014). The current consensus for the event GW170817 is the formation of a transient NS remnant sustaining itself for a brief period of time ≲1 s before collapsing to a BH (this was inferred from the existence of a sGRB, and the large amount of ejecta ≳ 0.02 M⊙ estimated from the kilonova AT 2017gfo). Assuming that this was the case, it is possible to place strong constraints on the maximum mass of a cold spherical NS and its EOS (Margalit and Metzger, 2017; Shibata et al., 2017, 2019; Rezzolla et al., 2018; Ruiz et al., 2018a). These constraints could also provide an explanation for the unidentified 2.6 M⊙ compact object in GW190814 as a rotating or even a non-rotating NS (Most et al., 2020; Tsokaros et al., 2020a). From a different point of view, the absence of a prompt collapse scenario and the large ejecta mass also puts constraints on NS radii or, equivalently, their tidal deformability (Bauswein et al., 2017; Radice et al., 2018). These constraints on the NS radius coming directly from the postmerger object were further refined by complementary analyses of the GW inspiral signal, which can be used to estimate the tidal deformability of the inspiraling NSs (Abbott et al., 2017c; De et al., 2018; Raithel et al., 2018).
Lattimer and Schramm (1974) and Symbalisty and Schramm (1982) suggested that unstable neutron-rich nuclei can be built in the mergers of BHNS or NSNS systems through rapid neutron bombardment, the r-process. Apart from the dynamical ejecta that emerge within milliseconds after merger, the ejecta that emerge much later are very important in the determination of whether or not heavier elements through the r-process are being produced. Li and Paczynski (1998) argued that the low mass and high velocity of these ejecta will make them transparent to their own radiation, resulting in emission whose peak will last around 1 day. Metzger et al. (2010) calculated the luminosity of the radioactively-powered transients in NS mergers and found these transients to be approximately 1,000 times brighter than typical novae, therefore calling them “kilonovae.” Metzger and Fernández (2014) argued that the lifetime of the merger remnant is directly imprinted in their early “blue” emission (from high electron fraction, lanthanide-poor ejecta) or late “red” emission (from low electron fraction, lanthanide-rich ejecta), both of which have been seen in event GW170817. The blue emission suggested ejecta composed of light r-process elements, while the red emission is consistent with heavier ones (lanthanide or actinides). The overall conclusion is the kilonova AT 2017gfo was a major source of r-process elements (Côté et al., 2017; Kasen et al., 2017).
Another important characteristic associated with event GW170817 was the observation of an sGRB—event GRB 170817A (Abbott et al., 2017b; Kozlova et al., 2017). This GRB was unusually weak, and various models have been proposed to explain this, including a choked-jet cocoon or a successful-jet cocoon (Hallinan et al., 2017; Kasliwal et al., 2017; Mooley et al., 2018). Recently, Mooley et al. (2018) using radio observations from very long-baseline interferometry were able to break the degeneracy between the choked and successful-jet cocoon models and concluded that the early-time radio emission was powered by a wide-angle outflow (a cocoon), while the late-time emission was most probably dominated by an energetic and narrowly collimated jet with an opening angle of <5°, and observed from a viewing angle of about 20°. This solidified theoretical predictions that NSNS, or at least a stellar binary where at least one of the companions is a NS, can be the progenitors of the central engine that power sGRBs (Paczynski, 1986; Eichler et al., 1989; Narayan et al., 1992).
Although GRB 170817A provided the long-sought observational evidence linking sGRBs with NSNS mergers, it did not reveal the nature of the central engine behind the launching of a relativistic jet. In particular, is a BH horizon necessary for the existence of a jet or is it just sufficient (Paschalidis et al., 2015; Ruiz et al., 2016, 2018b, 2019; Ruiz and Shapiro, 2017)? If necessary, then a stable NS remnant cannot be the generator of such jets. If not, is the jet from a stable NS qualitatively the same as the one launched from a spinning BH immersed in a gaseous disk? In particular, can one describe it as a Blandford and Znajek (1977) (BZ) jet? Notice that according to Komissarov (2002, 2004, 2005) and Ruiz et al. (2012), the driving mechanism behind a BZ jet is not the horizon but the ergoregion. Thus, while it may be that typical NSs cannot launch a BZ jet, NSs that contain ergoregions—ergostars—might be able to Ruiz et al. (2020c).
Since the pioneering general relativity (GR) simulations of NSNS mergers by Shibata and Uryu (2000) and BHNS mergers by Baumgarte et al. (2004), Shibata and Uryu (2006), and Faber et al. (2006a,b), a number of groups have produced a large body of work that captures the main characteristics of such events (see reviews by Shibata and Taniguchi, 2011; Baiotti and Rezzolla, 2017; Foucart, 2020). Below we will present a brief review of some of the important progress in the field, paying special attention to pure hydrodynamical vs. magnetohydrodynamical simulations. Details regarding the techniques used (either in evolution or in the initial data) will be omitted. We refer the reader to e.g., Alcubierre (2008), Baumgarte and Shapiro (2010), Shibata (2015) for such details. We also do not treat white dwarf-neutron star (WDNS) mergers, which, though important for GW detections by LISA, are not likely sources of sGRBs or kilonova. We refer readers interested to the GR simulations of Paschalidis et al. (2011) and references therein.
We adopt geometrized units with c = G = 1 unless otherwise indicated.
2. Black Hole-Neutron Star Mergers: Remnants and Incipient Jets
Motivated by the significance of BHNS binaries as copious sources of GW and EM radiation, many numerical studies have been performed over the past years. Before the pioneering BHBH simulations (Pretorius, 2005; Baker et al., 2006; Campanelli et al., 2006), most dynamical simulations of BHNS binaries were treated in Newtonian gravity, modeling the BH as a point mass (Lee, 2001; Kobayashi et al., 2004; Rosswog et al., 2004; Rosswog, 2005; Rantsiou et al., 2008). Although these studies gave first insights on the basic dynamics of BHNSs, full GR simulations are required to properly model the late inspiral, NS disruption, tidal tails, merger remnant, disk mass, fraction of unbound material ejected, sGRB engine, and most significantly the GWs emitted during merger. In the following section, we only review full GR studies of these binaries.
2.1. Nonmagnetized Evolutions
Most of the close BHNS binary orbits are likely quasi-circular, since gravitational radiation reduces the orbital eccentricity of the binary as it evolves toward smaller orbits (Peters, 1964). However, a small fraction may form in dense stellar regions, such as globular cluster or galactic nuclei, through dynamical capture, and they may merge with high eccentricities (Lee et al., 2010; Kocsis and Levin, 2012; Samsing et al., 2014).
Motivated by the above, different groups have generated quasi-equilibrium initial data for BHNSs on quasi-circular orbits (Baumgarte et al., 2004; Taniguchi et al., 2005, 2007; Grandclement, 2006; Shibata and Uryu, 2006, 2007; Foucart et al., 2008). Some of the earliest full GR simulations of these configurations were performed by Shibata and Uryu (2006, 2007), followed by Etienne et al. (2008) and Duez et al. (2008). In all of these studies the binary was formed by a nonspinning BH with a NS companion modeled as a Γ = 2 polytrope. These simulations showed that the fate of BHNS remnants can be classified in two basic categories: (1) the NS is tidally disrupted before reaching the innermost stable circular orbit (ISCO), inducing a long tidal tail of matter that eventually wraps around the BH and forms a significant accretion disk (typically with a mass ≳ 8% of the NS rest-mass); (2) the NS plunges into the BH, leaving a BH surrounded by a negligibly small accretion disk (typically with a mass ≲ 2% of the NS rest-mass).
Using a Smoothed Particle Hydrodynamics (SPH) code and an approximate “conformal” GR metric, Rantsiou et al. (2008) showed that the mass of the accretion disk remnant strongly depends on the magnitude and direction of the BH spin. In particular, it was found that only systems with a highly spinning BH, and slightly misaligned to the total angular of the system, yield significant accretion disk remnants. These results were later confirmed by full GR studies (Etienne et al., 2009; Foucart et al., 2011, 2012; Kyutoku et al., 2011) showing that for sufficiently high BH spins, mass ratios q = MBH/MNS ≲ 3, and/or lower NS compactions , a substantial disk can form following merger. Here MBH is the Christodoulou (1970) BH mass at infinite separation and MNS the NS rest mass, while and RNS are the gravitational [Arnowitt-Deser-Misner (ADM)] mass and the circumferential radius of the star in isolation, respectively.
Using the above numerical simulation results, Foucart (2012) constructed a simple fitting formula to predict the amount of matter remaining outside the BH horizon about 10ms following merger:
This expression is valid for mass ratios in the range q = 3−7, BH spins aBH/MBH = 0−0.9, and NSs with radii RNS = 11−16 km, thereby encompassing the most likely astrophysically relevant parameter space. Here, Mdisk and RISCO is the mass of the disk remnant and the radius of the ISCO, respectively. Note that Equation (1) explicitly shows that the mass of the disk remnant depends on the EOS and the BH spin, which determine the mass and radius of the NS and the position of the ISCO, respectively. It should be noticed that BHNSs with nearly-extremal BH spins have been considered by Lovelace et al. (2008); Lovelace et al. (2013). These studies found that upon NS disruption, less than half of the matter is promptly accreted by the BH, around 20% becomes unbound and escapes, and the remaining mass settles into a massive accretion disk.
Early population synthesis studies found that the distribution of mass ratios in BHNSs depends on the metallicity and peaks at q = 7 (Belczynski et al., 2008, 2010), but more recent works found that it is generally <10, peaking at q ≈ 5 (Giacobbo and Mapelli, 2018; Abbott et al., 2020a). Using Equation (1), one finds that, for a binary with mass ratio q = 5 in which the NS companion has radius 13.3 km and rest-mass MNS = 1.44M⊙ (compatible with NICER observations; Miller et al., 2019; Riley et al., 2019) a BH spin of aBH/MBH ≳ 0.65 is required to form an accretion disk with ≳ 10% of the NS rest mass. The power available for EM emission is usually taken to be proportional to the accretion rate. Under this assumption, it is expected that the luminosity of the disk remnant is LEM = ϵ Ṁdisk, where ϵ is the efficiency for converting accretion power to EM luminosity and Ṁdisk~ Mdisk/tacc is the rest-mass accretion rate, where tacc is the disk lifetime. Assuming a 1% efficiency and a disk lifetime of ~ 0.2 s, the luminosity is , consistent with typical EM luminosities of sGRBs. This value is also consistent with the “universal” merger scenario for generating EM emission from merger and collapse BH + disk remnants (Shapiro, 2017). These results allow us to conclude that the merger of NSs orbiting highly spinning BHs can be the progenitors of the engines that power sGRBs. However, the LV scientific collaboration has reported the observation of BHBHs having high mass and/or low spins (see e.g., Table VI in Abbott et al., 2020b). If this trend continues for LV-like BHNSs, then it is expected that LV-like BHNS remnants would have negligible accretion disks, which might disfavor their role as progenitors of sGRBs and/or observable kilonovae.
The previous numerical studies assumed that the NS companion is irrotational. Recently, East et al. (2015) and Ruiz et al. (2020a) showed that the NS spin has a strong impact on the disk remnant and the dynamical ejecta. As the prograde NS spin increases, the effective ISCO decreases (Barausse and Buonanno, 2010). In addition, as the magnitude of the NS spin increases, the star becomes less bound and the tidal separation radius rtid (separation at which tidal disruption begins) increases, also resulting in more pronounced disruption effects. This effect can be easily understood by estimating rtid by equating the inward gravitational force exerted by the NS on its fluid elements with the BH's outward tidal and the outgoing centrifugal forces to obtain
(Ruiz et al., 2020a) where Ω = aNSMNS/I. Here aNS is the NS spin parameter and I its moment of inertia. This simple Newtonian expression shows that the larger the mass ratio and/or the compaction of the NS, the closer the tidal separation to the ISCO. The NS then experiences tidal disruption effects only during a short time before the bulk of the NS plunges onto the BH. In contrast, the larger the magnitude of the NS spin, the farther away rtid is from the ISCO. In this case, the star can be tidally disrupted before being swallowed by the BH which increases the time for disruption and with it the amount of matter that spreads out to form the disk or escapes to infinity.
Recently, Barnes and Kasen (2013) showed that the opacities in r-process ejecta are likely dominated by lanthanides, which induce peak bolometric luminosities for kilonovae of
(East et al., 2015) and rise times of
(East et al., 2015) where veje and Meje are the mass-averaged velocity and rest-mass of the ejecta. The characteristic speed of the ejecta is veje/c≲ 0.2−0.3 with a rest-mass of (see e.g., East et al., 2015; Foucart et al., 2015; Hayashi et al., 2020; Ruiz et al., 2020a). Therefore, the bolometric luminosity of kilonova signals is with rise times of ≲ 7 h. These luminosities correspond to an R band magnitude of ~ 24 mag at 200 Mpc inside the aLIGO volume (Abbott et al., 2013), and above the LSST survey sensitivity of 24.5 mag (Barnes and Kasen, 2013; East et al., 2015). Hence some of these signals may be detectable by the LSST survey (Ruiz et al., 2020a).
It is worth noting that BHs and white dwarfs can also form binaries that undergo merger and eventually form a BH + disk remnant (see e.g., Nelemans et al., 2001; McKernan et al., 2020). These binaries are expected to be formed in dense star regions such as in galactic centers and globular clusters. Newtonian SPH calculations by Fryer et al. (1999) suggested that BH + massive WD binary mergers can release energies of 1048−1051 erg that may explain typical long duration GRBs, though population synthesis studies predict a (low) merger rate of 1.916 yr − 1 (see e.g., Nelemans et al., 2001).
2.2. Magnetized Evolutions
The previous numerical studies showed that BHNS mergers can create the right conditions to power sGRBs (i.e., a spinning BH + disk). However, they do not account for either magnetic fields or neutrino pair annihilation processes, the most popular components invoked in most sGRB models to drive jets (see e.g., Blandford and Znajek, 1977; Vlahakis and Konigl, 2003; Aloy et al., 2004; Piran, 2005). As the lifetime of the neutrino pair annihilation process might be too small to explain typical sGRBs (Kyutoku et al., 2018), we henceforth focus only on the magnetic process. However, it is worth noting that BH + disk remnants powering sGRBs may be dominated initially by neutrino pair annihilation processes followed by the BZ mechanism (Dirirsa, 2017), leading to a transition from a thermally-dominated fireball to a Poynting EM-dominated flow, as is inferred for some GRBs, such as GRB 160625B (Zhang et al., 2018).
Ideal GR magnetohydrodynamics (GRMHD) studies of magnetized BHNS mergers in which the NS is initially endowed with an interior-only poloidal magnetic field generated by the vector potential
were carried out by Chawla et al. (2010), Etienne et al. (2012a), and Kiuchi et al. (2015b), varying the mass ratio, the BH spin, and the strength of the magnetic field. Here the orbital plane is at z = 0, (xc, yc, 0) is the coordinate location of the center of mass of the NS, , and Ab, np, and Pcut are free parameters. The cutoff pressure parameter Pcut confines the magnetic field inside the NS within P > Pcut. The parameter nb determines the degree of central condensation of the magnetic field.
These numerical simulations showed that following merger, tidal tails of matter wrap around the BH, forming the accretion disk and dragging the frozen-in magnetic field into an almost purely toroidal configuration (see Figure 1). These simulations did not find any evidence of jet launching following the BH + disk formation. Nevertheless, Kiuchi et al. (2015b) reported that in their high-resolution simulations, in which the mass ratio is q = 4, the BH has a spin aBH/MBH = 0.75, and the NS is modeled by the APR EOS (Akmal et al., 1998), a thermally-driven wind (but no collimated) outflow emerges after ~ 50 ms following merger (see Figure 2).

Figure 1. The NS magnetic field lines (green) and rest-mass density ρ0 (reddish) normalized to the initial NS maximum value , at selected times for a BHNS with mass ratio q = 3. The initial BH spin is aBH/MBH = 0.75 and the NS is an irrotational Γ = 2 polytrope. Here the BH apparent horizon is shown as a black sphere. Following merger, the field lines are wound into an almost purely toroidal configuration (adapted from Etienne et al., 2012b).
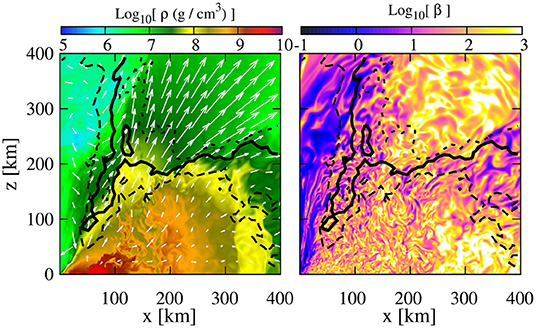
Figure 2. NS rest-mass density with fluid velocity arrows (left) and the gas-to-magnetic-pressure ratio (right) of a q = 4 BHNS remnant after ~ 50 ms following merger. A thermally-driven wind (but no collimated) outflow is observed (from Kiuchi et al., 2015b).
The lack of magnetically-driven jets in these simulations has been attributed to the fact that the magnetic field in the disk remnant is almost purely toroidal. Beckwith et al. (2008) showed that BH + disk systems can launch and support magnetically-driven jets only if a net poloidal magnetic flux is accreted onto the BH. Motivated by this conclusion, Etienne et al. (2012b) endowed the disk remnant from an unmagnetized BHNS simulation with a purely poloidal field and found that, indeed, under the right conditions, a jet can be launched from BHNS remnants. However, identifying the initial configuration of the seed magnetic field in the NS prior to tidal disruption that could lead to these conditions remained elusive for many years.
Paschalidis et al. (2015) then demonstrated that a more realistic initial magnetic configuration for the NS companion—a dipolar magnetic field extending from the NS interior into the exterior (as in pulsars)—could do the trick. Such a field can be generated by the vector potential
(Paschalidis et al., 2013) which approximately corresponds to a vector potential generated by an interior current loop. Here r0 is the current loop radius, I0 is the current, and r2 = ϖ2+z2, with . To reliably evolve the exterior magnetic field with an ideal GRMHD code and simultaneously mimic the magnetic-pressure dominant environment that characterizes a pulsar-like magnetosphere, a low and variable density atmosphere was installed initially in the exterior where magnetic field stresses dominate over the fluid pressure.
The above technique was used by Paschalidis et al. (2015) and Ruiz et al. (2018b, 2020a) to perform a series of BHNS simulations varying the density of the “artificial” atmosphere, the binary mass-ratio, the BH and NS spins, and the orientation of the seed magnetic field axis with respect to the orbital angular momentum. It was found that independent of the atmosphere or the NS spin, a magnetically driven, incipient jet is launched once the regions above the BH poles become nearly force-free () for small tilt-angle magnetic fields and binary mass ratios that yield a significant disk remnant. The jet is confined by a collimated, tightly wound, helical magnetic funnel above the BH poles. Following the onset of accretion, the magnetic field in the disk remains predominantly toroidal as in the previous simulations. However, the external magnetic field maintains a strong poloidal component that retains footpoints at the BH poles. Magnetic instabilities [mainly magnetic winding and magnetorotational (MRI)] amplify the magnetic field from to at the BH poles, and after Δt~ 90−150(MNS/1.4M⊙) ms following merger a bonafide jet finally emerges (see Figure 3). It is worth noting that the calculation of Ruiz et al. (2020a) showed that the larger the initial NS prograde spin, the larger the mass of the accretion disk remnant. Similar behavior was observed for the amount of unbound ejecta. These results suggest that moderately high-mass ratio BHNSs (q ≲ 5) that undergo merger, where the NS companion has a non-negligible spin, may give rise to detectable kilonovae even if magnetically-driven jets are not formed.
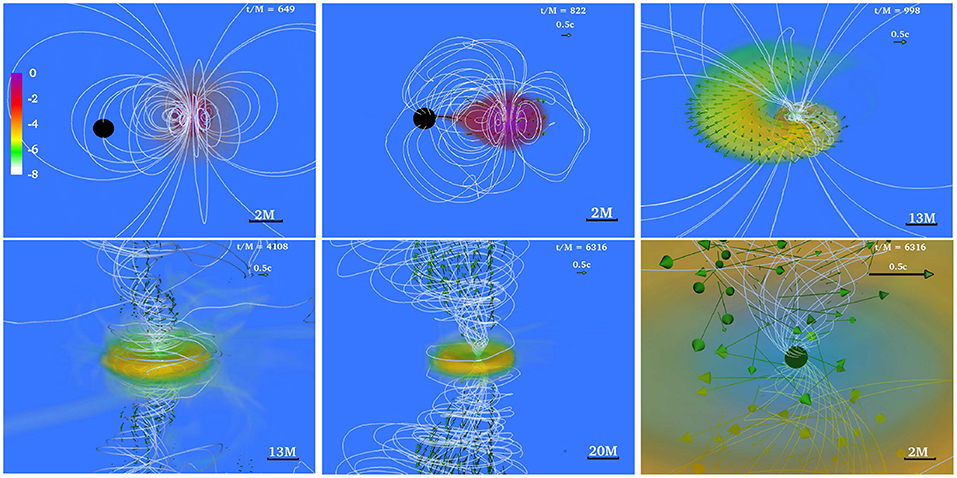
Figure 3. NS rest-mass density ρ0 normalized to its initial maximum value (log scale) at selected times for a BHNS with mass ratio q = 3. The initial BH spin is aBH/MBH = 0.75 and the NS is an irrotational Γ = 2 polytrope. Arrows indicate fluid velocities and white lines the magnetic field lines. Bottom panel shows the system after an incipient jet is launched. Here (from Paschalidis et al., 2015).
The Lorentz factor in the funnel is ΓL~ 1.2−1.3, and hence the jet just above the BH poles is only mildly relativistic. However, the maximum attainable Lorentz factor of a magnetically—powered, nearly axisymmetric jet is comparable to the force-free parameter inside the funnel (Vlahakis and Konigl, 2003). Near the end of the simulations the force-free parameter in the funnel reaches values ≳ 100. Thus, it is expected that the jet will be accelerated to ΓL≳ 100 as required by most sGRB models (Zou and Piran, 2010).
The lifetime of the disk is Δt ~ 500(MNS/1.4M⊙) − 700(MNS/1.4M⊙) ms and the outgoing EM Poynting luminosity is LEM ~ 1051±1 erg/s, and hence consistent with typical sGRBs (Bhat et al., 2016; Lien et al., 2016; Svinkin et al., 2016; Ajello et al., 2019). The luminosity is also consistent with that generated by the BZ mechanism
(Thorne et al., 1986) as well as with the simple analytic model that seems to apply universally for typically compact binaries mergers containing magnetized NSs that leave BH + disk remnants (Shapiro, 2017).
The above results were obtained with a high initial magnetic field. Paschalidis et al. (2015) argued that a smaller initial field will yield the same qualitative outcome because the magnetic field amplification following disruption is due largely to magnetic winding and the MRI. Amplification proceeds until appreciable differential rotational and internal energy of the plasma in the disk has been converted to magnetic energy. This amplification yields B ~ 1015 G at the BH poles nearly independent of the initial NS magnetic field. Winding occurs on an Alfvén timescale, so amplification may take longer the weaker the initial field.
2.3. GW190814: Spin and EOS for a NS Companion
One of the most intriguing GW detections to date was event GW190814 (Abbott et al., 2020a), a binary coalescence whose primary component had mass and therefore is a BH, while the secondary had mass , placing it at the boundary of the so-called “mass gap” and making its identification uncertain. Further ambiguity was added by the absence of an EM counterpart. While the nature of this compact object is not yet known, it was already suggested by Abbott et al. (2020a) that it can be a rapidly rotating NS, whose dimensionless spin was estimated to be 0.49 ≲ aNS/MNS ≲ 0.68 (Most et al., 2020). For this scenario to be viable the maximum mass of a spherical, non-rotating cold NS has to be ≳ 2.1 M⊙ (Most et al., 2020; Tsokaros et al., 2020a). Requiring rapid rotation for a NS companion in GW190814 is a direct consequence of the likely upper limits (2.2−2.3 M⊙) placed on a spherical, non-rotating NS mass by event GW170817 (Margalit and Metzger, 2017; Shibata et al., 2017, 2019; Rezzolla et al., 2018; Ruiz et al., 2018a). These upper limits were mostly based on the assumption that the companions in GW170817 were slowly rotating. Assuming rapid uniform NS rotation, instead, the upper limit allowed by event GW170817 increases (Abbott et al., 2017c; Ruiz et al., 2018a) and can explain the 2.6 M⊙ compact object in GW190814 as a slowly rotating NS. In fact, by allowing for the uncertainties and adopting a sufficiently stiff EOS, even a non-rotating NS can explain GW190814 (Tsokaros et al., 2020a). Note that although no robust discovery of a BHNS exists yet, the NSs in the 20 known NSNS systems (Tauris et al., 2017; Zhu et al., 2018) have low dimensionless spins. While one cannot draw definitive conclusions from these limited number of observations, one might safely argue that if spin-down due to EM emission is as efficient as in currently known binaries, then any scenario involving a highly spinning NS either in an NSNS (like GW170817) or in an BHNS system (like GW190814) is not probable. In summary, invoking rotation to explain the companion to the BH object in GW190814 depends on the stiffness of the EOS and the assumptions of the maximum mass of a spherical NS. For a soft EOS (low spherical maximum mass) such as SLy (Douchin and Haensel, 2001) rapid rotation is not sufficient, while for sufficiently stiff EOS such as DD2 (Hempel and Schaffner-Bielich, 2010) rapid rotation may not even be necessary. Such EOSs are neither rejected nor favored by GW170817, and they are in accordance with the results of NICER (see Figure 4).
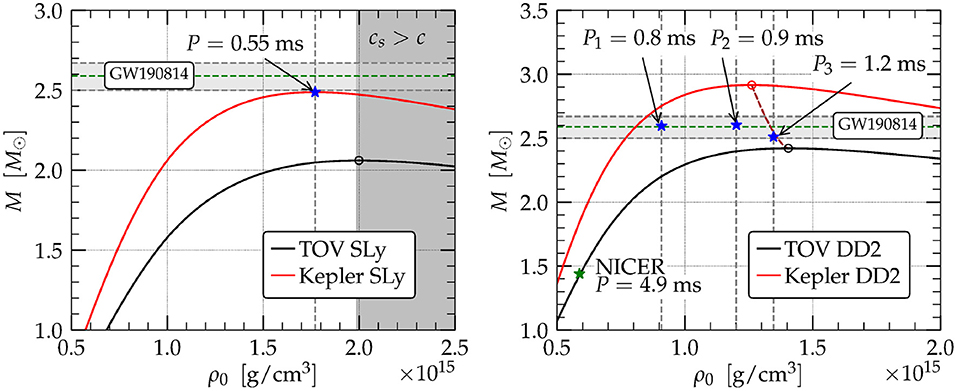
Figure 4. Two possibilities for the EOS of a NS companion in GW190814. The scenario on the left, which employs the SLy (soft) EOS, fails to provide a model for a uniformly rotating star, even at maximum uniform rotation. On the contrary, the scenario on the right that employs the DD2 (stiff) EOS succeeds and demonstrates the possibility of a slowly rotating NS. The lower (black) curves represent spherical, non-rotating models, while the upper (red) curves represent uniformly rotation models spinning at the Keplerian (mass-shedding) limit (from Tsokaros et al., 2020a).
3. NSNS Mergers: Remnants and Incipient Jets
Numerical simulations of NSNS binaries are somewhat simpler than BHNS binaries, since the latter must treat the BH singularity. Some of the first numerical studies of NSNSs employed Newtonian gravity, modeling the NS as a polytrope (Gilden and Shapiro, 1984; Oohara and Nakamura, 1989; Rasio and Shapiro, 1992, 1994; Shibata et al., 1992, 1993; Xing et al., 1994; New and Tohline, 1997). For circular orbit binaries it was found that following the binary merger, a highly differentially rotating remnant is formed. However, their simulations could not track its possible collapse to a BH with Newtonian gravity. Motivated by models of sGRBs and the ejection of r-process nuclei, Davies et al. (1994), Ruffert et al. (1996), and Ruffert and Janka (1998) extended the previous results by incorporating a simple treatment of the nuclear physics in their numerical calculations. One of the first approaches used to simulate NSNS coalescence in GR was the “conformal flatness approximation” (CFA) used by Wilson and Mathews (1995), which has been followed by several other treatments with increasing sophistication. Oechslin et al. (2002) evolved NSNS binaries using a Lagrangian SPH code with a multigrid elliptic solver to handle the gravitational field equations and corotating initial configurations. Faber et al. (2004) subsequently performed SPH simulations in the CFA using a spectral elliptic solver in spherical coordinates and employed the quasi-equilibrium, irrotational binary models of Taniguchi and Gourgoulhon (2002). These models are constructed using the conformal thin-sandwich formalism (York, 1999). Oechslin et al. (2007) extended their earlier studies by including the influence of a realistic nuclear EOS. These simulations showed that the dynamics and the final outcome of the merger depend sensitively on the EOS and the binary parameters, such as the gravitational mass of the system and its mass ratio. The first fully GR simulations of NSNS undergoing merger were performed by Shibata and Uryu (2000), Shibata and Uryū (2002), and Shibata et al. (2003) using a polytropic EOS to model the stars. Since then, great progress has been made to model NSNSs incorporating realistic microphysics and magnetic field effects in full GR and in alternative theories of gravity. In the following we only review full GR studies of these binaries. For earlier reviews and references, see, e.g., Baumgarte and Shapiro (2010) and Shibata (2015).
3.1. Nonmagnetized Evolutions
One of the first questions numerical studies of NSNS mergers in full GR were compelled to address was under what conditions the highly differentially rotating star remnant collapses to a BH. The uncertainties in the nuclear EOS, combined with theoretical arguments invoking GW170817 and its EM counterparts, allow non-rotating NSs with a maximum mass limit in the range ~ 2.1−2.4 M⊙ (Margalit and Metzger, 2017; Shibata et al., 2017, 2019; Rezzolla et al., 2018; Ruiz et al., 2018a). Uniform rotation allows NSs with up to ~ 20% more mass (“supramassive stars”; as coined by Cook et al., 1994a,b). Even larger masses can be supported against collapse with centrifugal support if the star is differentially rotating. Such stars were first constructed and explored by Baumgarte et al. (2000), who built dynamically stable Γ = 2 polytropic models with masses ≳ 3−4 M⊙. They coined the label “hypermassive neutron star” (HMNS) to describe such stars. It was demonstrated by Duez et al. (2004) that shear viscosity drives a HMNS to collapse to a BH on a (secular) viscous timescale and by Duez et al. (2006) that turbulent magnetic viscosity induced by MRI can also drive the secular collapse of the latter magnetic HMNSs. These viscous effects compete with neutrino and GW emission (when the HMNS remnant is non-axisymmetric) to drive collapse. In NSNS binaries, the fate of the remnant depends on the total mass of the NSNS binary, as we shall now discuss.
Shibata and Uryu (2000) and Shibata and Taniguchi (2006) found that there is a threshold mass Mth above which the remnant collapses immediately on a dynamical timescale to a BH, independently of the initial binary mass ratio. This threshold value depends strongly on the EOS. For Γ = 2 polytropes Mth ≈ 1.7 , while for stiffer EOSs, such as APR (Akmal et al., 1998) and SLy (Douchin and Haensel, 2001), it is ~ 1.3–1.35 . Shibata and Taniguchi (2006) also found that in the case of “prompt” collapse to a BH, the mass of the disk remnant increases sharply with increasing mass ratio for a fixed gravitational mass and EOS. In addition, if the mass of the binary is less than Mth the disk remnant turns out to be more massive than for those whose mass is larger than Mth. For binaries with M < Mth their remnants form a transient, highly deformed HMNS which, after ~ 8–50 ms, undergoes a “delayed” collapse to a BH surrounded by a significant accretion disk. The collapse occurs due to angular momentum losses from gravitational radiation in these simulations where neutrino cooling and magnetic fields are absent (Baiotti et al., 2008; Kiuchi et al., 2009; Rezzolla et al., 2010; Dietrich et al., 2015; Ruiz et al., 2019). These results have been extended by Hotokezaka et al. (2011) using a piecewise polytropic representation of nuclear EOSs (Özel and Psaltis, 2009; Read et al., 2009). It was found that the threshold value is in the range 1.3 ≲ Mth/ ≲ 1.7. These results were confirmed also for realistic finite-temperature EOSs (Bauswein et al., 2013). In addition, the ratio between the threshold mass and maximum mass is tightly correlated with the compactness of the . Finally, less massive binary mergers form a dynamically stable NS remnant that may collapse on longer time scales once dissipative processes, such as neutrino dissipation or gravitational radiation, take place (Cook et al., 1994a,b; Lasota et al., 1996; Breu and Rezzolla, 2016).
Most of the numerical calculations to date have focused on quasi-circular irrotational binaries, though it is expected that spin can modify the threshold value of prompt collapse, or at least change the lifetime of the remnant. Preliminary results reported by Kastaun and Galeazzi (2015), Dietrich et al. (2017), Ruiz et al. (2019), and Chaurasia et al. (2020) showed that depending on the NS spin, the lifetime of the remnant may change from ~ 8 to ≳ 40 ms. Effects of NS spin on the inspiral have been explored by Kiuchi et al. (2017), Bernuzzi et al. (2014), Dietrich et al. (2018), and Tsokaros et al. (2019a). On the other hand, the dynamically captured NSNS mergers that may arise in dense stellar regions, such as globular clusters, have been studied by East and Pretorius (2012). These results showed that Mth and the mass of the disk remnant depend not only on the EOS but also on the impact parameter. The calculations by Paschalidis et al. (2015) and East et al. (2016) demonstrated that the HMNS formed through dynamical capture may undergo the one-arm non-axisymmetric (mode m = 1) instability.
During merger, shock heating produces temperatures as high as ~ 100 MeV at the contact layer between the two stars. Subsequent compressions lead to average-temperatures of the order of 10 MeV in the central core of the NSNS remnant (Bauswein et al., 2010), and hence the binary remnant can be a strong emitter of neutrinos. The timescale of neutrino cooling radiation (typically ≲ 1 s) may also strongly affect the HMNS lifetime (Sekiguchi et al., 2011). Effects of neutrino cooling on the dynamical ejecta that can give rise to observable kilonova signatures have been studied in Radice et al. (2016), Lehner et al. (2016), and Sekiguchi et al. (2015) (see Radice et al., 2020 for a recently review). It is worth noting that the calculations of Bauswein et al. (2010) and Just et al. (2016) show that neutrino heating drives a wind from the surface of the remnant, creating very baryon-loaded environments in the polar regions that prevent the formation of incipient jets. Therefore, MHD processes are likely be a key ingredient to overcome this and to trigger the formation of relativistic jets.
Numerical simulations of NSs having a mass that falls inside the so-called “mass-gap” are scarce. The first such simulation was performed by Tsokaros et al. (2020c) with a binary NSNS in a quasi-equilibrium circular orbit. The gravitational mass of the binary was M = 7.90 M⊙, and each star is identical and has a compactness of . This value, which is even higher than the maximum possible compactness that can be achieved by solitonic boson stars (Palenzuela et al., 2017), is slightly smaller than the limiting compactness set by causality (Lattimer and Prakash, 2016). To build these binaries, Tsokaros et al. (2020c) employed the ALF2 EOS (Alford et al., 2005), but replaced the region where the rest-mass density satisfies by the maximally stiff EOS
with sound speed equal to the speed of light. Here ρ is the total energy density, and Ps the pressure at ρs, assumed known. The quasi-equilibrium initial data were built using the COCAL code (see e.g., Tsokaros et al., 2015, 2016). Due to the large compactions of the NSs the binary stars exhibit no tidal disruption up until merger, whereupon a prompt collapse is initiated even before a common core forms. Within the accuracy of the simulations the BH remnant from this NSNS binary exhibits ringdown radiation that is not easily distinguishable from a perturbed Kerr BH. Right panel of Figure 5 displays the dimensionless spin from the BH remnant from the NSNS and that from a BHBH binary having the same gravitational (ADM) mass. Also shown are the remnant spins as computed from the analytic Kerr formula whose input is the ratio Lp/Le of the polar to equatorial circumference. However, the inspiral leads to phase differences of the order of ~ 5 rad (left panel of Figure 5) over an ~ 81 km separation (~ 1.7 orbits). Although such a difference can be measured by current GW laser interferometers (e.g., LV scientific collaboration observatories), uncertainties in the individual masses and spins will likely prevent distinguishing such compact, massive NSNSs from BHBHs.
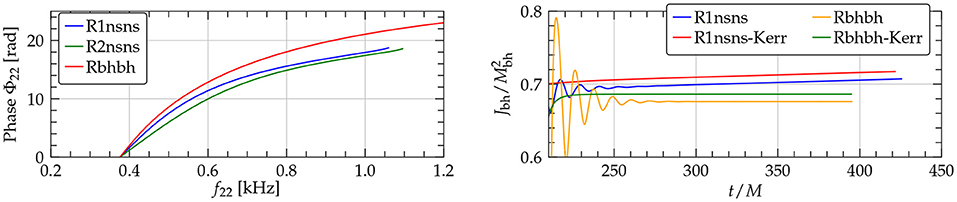
Figure 5. (Left) GW phase vs. frequency for the NSNS binary using two resolutions (R1nsns,R2nsnsn) and a BHBH binary having the same gravitational mass. (Right) Dimensionless spin of the remnant BH for the NSNS (R1nsnsn) and the BHBH (Rbhbh) binary. Also shown is the dimensionless spin as computed from the Kerr formula for the two systems (from Tsokaros et al., 2020c).
3.2. Magnetized Evolutions
Although NS may have very large magnetic fields (≳ 1014 G) at birth, it is expected that cooling processes significantly reduce their magnitudes (Pons et al., 2009). Pulsar observations indicate that the characteristic surface magnetic field strength of NSs is ~ 1010−1012 G (Lorimer, 2008; Lyne and Graham-Smith, 2012; Miller et al., 2019; Semena et al., 2019). Nevertheless, magnetic instabilities such as the Kelvin-Helmholtz instability (KHI; see e.g., Price and Rosswog, 2006; Anderson et al., 2008; Kiuchi et al., 2015a,b), MRI (see e.g., Duez et al., 2006; Shibata et al., 2006; Siegel et al., 2013; Kiuchi et al., 2015b), and magnetic winding (see e.g., Baumgarte et al., 2000; Kiuchi et al., 2015a; Sun et al., 2019) triggered during and after the NSNS merger can substantially boost the strength of these weak fields.
High-resolution simulations are required to properly capture the above instabilities because their fastest growing modes have short wavelengths. Kiuchi et al. (2015a,b) systematically studied the effects of numerical resolution on the magnetic field amplification in NSNS mergers and found that, at the unprecedented resolution of Δx = 17.5 m, an initial magnetic field of 1013 G is amplified to values ≳ 1015 G in the bulk of the remnant, with local values peaking at ~ 1017 G, after 5 ms following merger. Recently, the calculations by Aguilera-Miret et al. (2020) reported that at a resolution of Δx = 37 m an initial magnetic field of 5 × 1011 G is amplified to values of ~ 1017 G after about 10 ms following merger (see Figure 6). These extremely high-resolution simulations are computationally quite expensive and currently inaccessible for general studies. Typical NSNS simulations use a resolution ≳ 120 m (see e.g., Ciolfi et al., 2019; Ruiz et al., 2019; Bernuzzi et al., 2020; Vincent et al., 2020; Weih et al., 2020). To overcome the lack of resolution, some works have adopted subgrid models to mimic the effect of magnetic instabilities (see e.g., Giacomazzo et al., 2015; Palenzuela et al., 2015; Aguilera-Miret et al., 2020; Radice, 2020), while others have employed high, but dynamically weak initial magnetic fields to mimic the resulting magnetic field following the merger (see e.g., Ruiz et al., 2016; Ciolfi et al., 2019; Mösta et al., 2020). These two approaches allow the tracking of the secular evolution of the a quasi-stationary NSNS remnant consisting of a HMNS that ultimately undergoes delayed collapse to a highly spinning BH surrounded by an accretion disk with a strong magnetic field with finite computational resources.
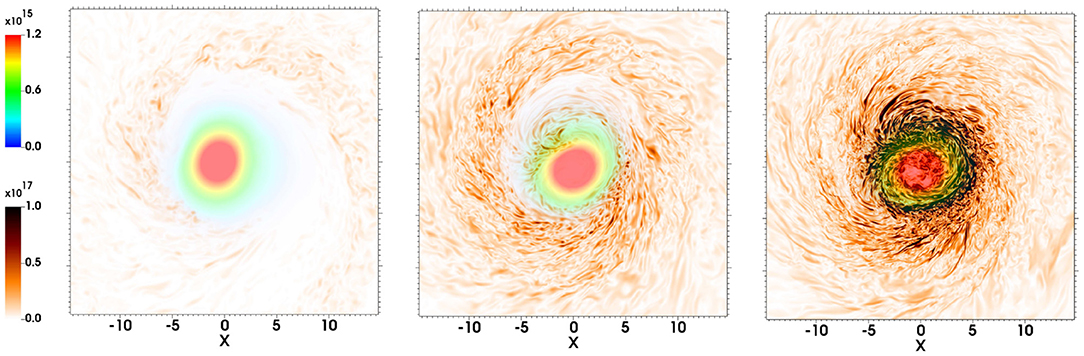
Figure 6. NS rest-mass density ρ0 (upper left rainbow colorbar) and magnetic field (lower left brownish colorbar) on the orbital plane at t = 10.0 ms following an NSNS merger at three different resolutions [Δx = 147 m (left), at Δx = 74 m (middle), and Δx = 37 m (right)]. The initial magnetic field strength is 5 × 1011 G (adapted from Aguilera-Miret et al., 2020).
Some of the first long-term ideal GRMHD studies of NSNS mergers were performed by Anderson et al. (2008) and Liu et al. (2008) using Γ = 2 polytropes endowed with a 1016 G polodial magnetic field confined to the NS interior (see Equation 5). The simulations of Anderson et al. (2008) reported the formation of a long-lived HMNS. During this phase, turbulent magnetic fields transport angular momentum away from the center, inducing the formation an axisymmetric central core that eventually collapses to a spinning BH. Liu et al. (2008) reported the evolution of equal and unequal binaries that promptly collapse to a BH following merger, surrounded by a disk with ≲ 2% of the total rest mass of the binary. Neither an outflow nor a magnetic field collimation were found.
The calculations of Rezzolla et al. (2011) reported that ~ 12 ms after the collapse of a HMNS remnant, MHD instabilities develop and form a central, low-density, poloidal-field funnel, though there were no evidences of an outflow. The initial data consist of a binary polytrope initially endowed with a 1012 G poloidal magnetic field confined to the stellar interior. The highest resolution used in these studies was Δx ≈ 221 m. A subsequent high-resolution study by Kiuchi et al. (2015b), employing an H4 EOS (Glendenning and Moszkowski, 1991) with seed poloidal magnetic fields confined to the stellar interior, found that during merger, the magnetic field is steeply amplified due to the KHI. In their high-resolution case (Δx = 70 m) the amplification is 40–50 times larger than that in the low-resolution case (Δx = 150 m). In contrast to the results of Rezzolla et al. (2011), the ram pressure of the fall-back debris prevents the formation of a coherent poloidal field. As the frozen-in magnetic field lines are anchored to the fluid elements, an outflow, which was not seen after 40 ms following merger (see Figure 7), is presumably necessary to generate a coherent poloidal magnetic field.
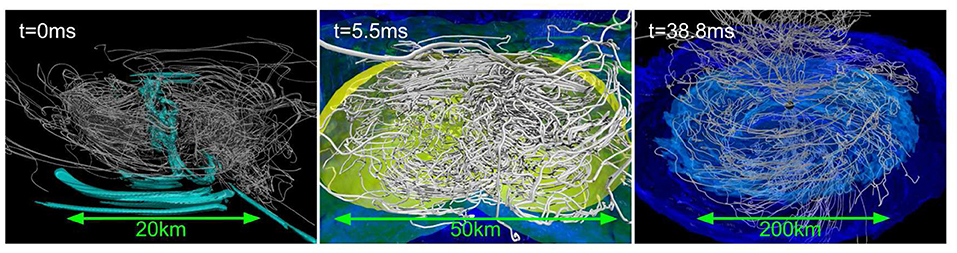
Figure 7. NS rest-mass density and magnetic field lines at t−tmrg ≈ 0.0 ms (left), t−tmrg ≈ 5.5 ms (middle), and t−tmrg ≈ 38.8 ms (right) following a NSNS merger. Here tmrg is the merger time. Cyan color on the left panel displays magnetic fields stronger than 1015.6 G. Yellow, green, and dark blue colors on the middle panel show rest-mass densities of 1014, 1012, and 1010 g/cm3, respectively. Light and dark blue colors on the right panel indicate rest-mass densities of 1010.5, and 1010 g/cm3, respectively (from Kiuchi et al., 2015b).
Ruiz et al. (2016) evolved the same NSNS configuration as in Rezzolla et al. (2011) but using higher resolution (Δx = 152 m). As this resolution is still not enough to properly capture the growth of the magnetic field due to the KHI, Ruiz et al. (2016) endowed the initial NSs with dynamically weak, purely poloidal magnetic fields with strengths Bpole≃1.75 × 1015(1.625M⊙/MNS) G at the poles of the stars, which matches the values of the field strength in the HMNS reached in Kiuchi et al. (2015b). It was found that by ~ 4, 000M ~ 60(MNS/1.625M⊙) ms following BH formation, the magnetic field above the BH poles has been wound into a tight, helical funnel inside of which fluid elements begin to flow outward: this is an incipient jet (see Figure 8). The lack of a jet in Kiuchi et al. (2015b) can be attributed to the persistent fall-back debris in the atmosphere, which increases the ram pressure above the BH poles. Therefore, a longer simulation like the one in Ruiz et al. (2016) is required for jet launching. Notice that jet launching may not be possible for all EOSs if the matter fall-back timescale is longer than the disk accretion timescale (Paschalidis, 2017).

Figure 8. NS rest-mass density ρ0 normalized to its initial maximum value (log scale) at selected times for an NSNS merger. Arrows display plasma velocities and white lines show magnetic field lines. Here = 4.43(MNS/1.625M⊙) km (Snapshots from case IH in Ruiz et al., 2016).
In addition, Ruiz et al. (2016) studied the impact of the magnetic configuration on the jet launching time. For this the NSs were endowed with the pulsar-like interior + exterior magnetic field generated by the vector field in Equation (6). To reliable evolve the exterior magnetic field, Ruiz et al. (2016) adopted the atmosphere treatment previously used by Paschalidis et al. (2015). As illustrated in Figure 8, a magnetically-driven jet is launched on the same time scale (see second column in Figure 9). Unlike in the BHNS case in Paschalidis et al. (2015), where the magnetic field grows following BH formation, the MRI and magnetic winding in the HMNS already amplifies the magnetic field to saturation levels before the onset of collapse to a BH. The incipient jet is then launched by the BH + disk remnant due to the emptying of the funnel as matter accretes onto the BH, thereby driving the magnetic field regions above the BH poles to nearly force-free values (). Notice that the initial magnetic field configuration affects the level of collimation of the incipient jet. The opening half-angle of the pulsar-like magnetic field case is ~ 25°, while for the magnetic field confined to the stellar interior it is ~ 30°. The Lorentz factor in the outflow is ΓL~ 1.2. Thus, the incipient jet is only mildly relativistic. However, the force-free parameter inside the funnel is 100 (see bottom panel of the second column in Figure 9), and therefore fluid elements can be accelerated to ΓL ~ 100 (Vlahakis and Konigl, 2003). The lifetime of the accretion disk (jet's fuel) is ~ 100(MNS/1.625M⊙) ms and hence consistent with sGRB lifetimes (Bhat et al., 2016; Lien et al., 2016; Svinkin et al., 2016; Ajello et al., 2019). The outgoing Poynting luminosity is , roughly consistent with the luminosity expected from the BZ effect (see Equation 7) and the universal merger model (Shapiro, 2017). As this equation is strictly valid for highly force-free magnetospheres, it is likely that any deviation from the expected Poynting luminosity is due to partial baryon-loaded surroundings.
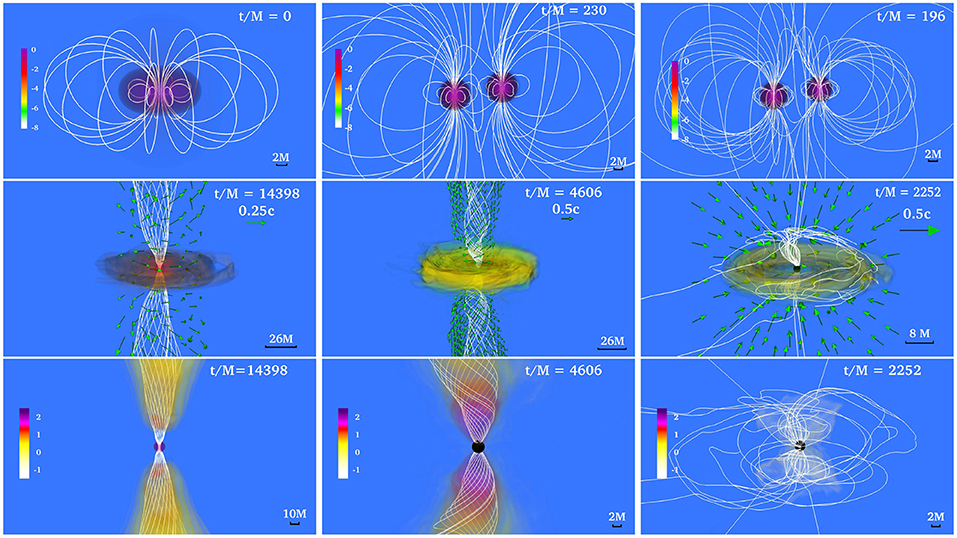
Figure 9. NS rest-mass density ρ0 normalized to its initial maximum value (log scale) for a NSNS binary that forms: a stable, supramassive remnant (left); a HMNS remnant that undergoes delayed collapse (middle); and a remnant that undergoes prompt collapse (right). Top row displays the NSs at the time of magnetic field insertion, while middle row displays the outcome once the remnant has reached quasi-equilibrium. Bottom row shows the force-free parameter (log scale). White lines represent magnetic field lines, while arrows represent fluid velocity flow vectors. The field lines form a tightly wound helical funnel and drive a jet following delayed collapse, but not in the other two cases. Here M = 0.0136(Mtot/2.74M⊙)ms = 4.07(Mtot/2.74M⊙) km; therefore quasi-equilibrium for the supramassive case (left column) is achieved at t ~ 200 ms (from Ruiz et al., 2018a).
To further assess the robustness of the emergence of the incipient jet in NSNS mergers, numerical studies by Ruiz et al. (2019, 2020b) probed the impact of the NS spin and the orientation of the seed poloidal magnetic field on the formation and lifetime of the HMNS, BH + disk remnant, and the jet launching time. Ruiz et al. (2019) found that the larger the co-rotating NS spin, the more massive the accretion disk, and hence the longer the jet's lifetime. In addition, the larger the NS spin, the shorter the time delay between the peak GW and the emergence of the incipient jet. On the other hand, the simulations of Ruiz et al. (2020b) suggest that there is a threshold value of the inclination of magnetic dipole moment with respect to the orbital angular momentum of the binary beyond which jet launching is suppressed. A jet is launched whenever a net poloidal magnetic flux with a consistent sign along is accreted onto the BH once above the BH poles. Tilted magnetic fields change the magnitude of this poloidal field component.
Kawamura et al. (2016) and Ciolfi et al. (2017) probed the effects of different EOSs, different mass ratios, and different orientations of poloidal magnetic field confined to the NS interior, with strengths ~ 1012−1015 G. The NSNS binaries were evolved with a resolution Δx≳ 177 m. These calculations found that after 22 ms following merger, an organized magnetic field structure above the BH emerges, though magnetically-driven outflow was not observed (see Figure 10). The lack of an incipient jet is likely due to insufficient resolution to properly capture the magnetic instabilities that boost the magnetic field strength to ≳ 1015.5 G, an essential ingredient for jet launching, and/or to too short evolutions times. Notice that the ram-pressure of the fall-back debris depends strongly on the EOS. More baryon-loaded surroundings require stronger magnetic fields to overcome the ram-pressure, delaying the launch of the jet while the fields amplify.
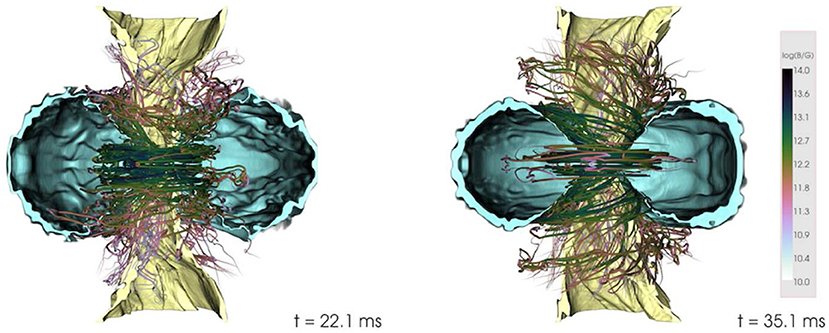
Figure 10. Magnetic field lines at ~ 22 ms (left) and ~ 32 ms (right) following an NSNS merger, along with two isosurfaces of rest-mass density 108 (yellow) and 1010 g/cm3 (cyan), cut off for y < 0 (from Kawamura et al., 2016).
The previous numerical studies involved NSNS mergers leading to the formation of a transient HMNS undergoing delayed collapse to a BH. The possibility of jet launching from a stable supramassive NS remnant has recently been investigated by Ruiz et al. (2018a), Ciolfi et al. (2019), and Ciolfi (2020). The calculation of Ruiz et al. (2018a) reported a long-term (~ 200 ms) simulation of a supramassive NS remnant initially threaded by a pulsar-like magnetic field. It was found that magnetic winding induces the formation of a tightly-wound-magnetic-field funnel within which some matter begins to flow outward (see first column in Figure 9). The maximum Lorentz factor in the outflow is ΓL ~ 1.03, and the force-free parameter inside the funnel is . The Poynting luminosity is ~ 1043 erg/s, and roughly matches the GR pulsar spindown luminosity (Ruiz et al., 2014). These calculations suggest that a supramassive NS remnant probably cannot be the progenitor of a sGRB. This has been confirmed by the simulations of Ciolfi et al. (2019) and Ciolfi (2020), which reported the emergence of an outflow with a maximum Lorentz factor of ΓL≲ 1.05 after ≳ 212 ms following the merger of a magnetized, low-mass NSNS. Recently, the calculation of Mösta et al. (2020) suggested that neutrino effects may help reduce the baryon-load in the region above the poles of the NS, inducing a growth of the force-free parameter in the funnel. They found a maximum Lorentz factor of ΓL≲ 5.0 inside the funnel. Thus, neutrinos processes may help to trigger the launching of an incipient jet. Finally, the numerical simulations of Ruiz and Shapiro (2017), who did not include neutrinos, probed whether or not prompt collapse NSNS remnants (BHs with small accretion disks) can launch incipient jets. No evidence of an outflow or magnetic field collimation was found (see third column on Figure 9). It was argued that the KHI and MRI do not have enough time to amplify the magnetic field prior to BH formation, and hence a jet can not be launched.
Although supramassive NS or prompt collapse remnants may not launch magnetically-driven jets, they may be the progenitors of fast radio bursts (FRBs)—a new class of radio transients lasting less than a few tens of milliseconds (Lorimer et al., 2007; Thornton et al., 2013). Falcke and Rezzolla (2014) have suggested that magnetic field reconfigurations during the collapse of a supramassive NS can induce a burst of EM radiation consistent with that of typical FRBs. Palenzuela et al. (2013) studied EM counterparts from the inspiral and merger of a NSNS binaries using full GR resistive MHD simulations. They found that the interaction between the stellar magnetospheres extracts kinetic energy from the binary and powers radiative Poynting fluxes as large as in a few milliseconds. Motivated by these results, Paschalidis and Ruiz (2018) performed numerical simulations of prompt collapse NSNS mergers in which the NSs are initially endowed with a pulsar-like magnetic field. Combining their numerical results with population studies, they concluded that FRBs may be the most likely EM counterpart of prompt collapse NSNSs, as previously claimed by Totani (2013).
3.3. GW170817 and the NS Maximum Mass
Event GW170817 (Abbott et al., 2017c) marked not only the first direct detection of a NSNS binary undergoing merger via GWs but also the simultaneous detection of the sGRB GRB 170817A, and kilonova AT 2017gfo, the latter with its afterglow radiation in the radio, optical/IR, and X-ray bands (Kozlova et al., 2017; von Kienlin et al., 2017). These observations have been used to impose constraints on the physical properties of a NS, and in particular, on the maximum mass of a non-rotating spherical NS, .
Margalit and Metzger (2017) argued that following the merger of the NSNS progenitor of GW170817, a transient HMNS is formed which collapses to a BH on a timescale of ~ 10–100 ms, producing the observed kilonova ejecta expanding at mildly relativistic velocities. This conclusion combined with the GW observation, led to their tight prediction that ≲ 2.17M⊙ with 90% confidence. On the other hand, Shibata et al. (2017) summarized a number of their relativistic hydrodynamic simulations favoring a long-lived, massive NS remnant surrounded by a torus to support their inferred requirement of a strong neutrino emitter that has a sufficiently high electron fraction (Ye ≳ 0.25) to avoid an enhancement of the ejecta opacity. This argument led then to the results that ~ 2.15–2.25M⊙. A recently review of these calculations by Shibata et al. (2019) using energy and angular momentum conservation laws again lead to ≲ 2.3M⊙. Rezzolla et al. (2018) assumed that the transient GW170817 remnant collapsed to a spinning BH once it had reached a mass close to but below the maximum mass of a supramassive star. This assumption combined with their quasi-universal rotating NS model relations led to ≲ . Ruiz et al. (2018a) used the existence of the sGRB GRB170817A, combined with their conclusion that only a NSNS merger that forms an HMNS that undergoes delayed collapse to a BH can be the progenitor of an engine that powers an sGRB (see Figure 9), to impose the bound ≲ 2.74/β (for low spin priors), where β is s the ratio of the maximum mass of an uniformly rotating NS (supramassive limit) to the maximum mass of a non-rotating star. Causality arguments allow β to be as high as 1.27, while most realistic candidate EOSs predict β ≃ 1.2, yielding in the range ~ 2.16–2.28M⊙. If instead one assumes high spin priors in interpreting the data for GW170817 their maximum mass limit becomes ~ 2.22–2.35M⊙. Thus, the different analyses seem to converge on a value for ~ 2.2–2.3M⊙.
4. Ergostars: Potential Multimessenger Engines
In the previous two sections, we summarized GRMHD simulations showing that the key requirement for the emergence of a magnetically-driven jet is the existence of a spinning BH remnant surrounded by an appreciable disk. In addition, these simulations also suggest that the BZ process is the driving mechanism to power them.
The BZ process can be explained using the membrane paradigm (Thorne et al., 1986), in which the BH horizon is treated as a spherical, rotating conductor of finite resistivity. The magnetic field lines threading the BH horizon transfer rotational kinetic energy from a spinning BH to an outgoing Poynting and matter flux. However, Komissarov (2002, 2004, 2005) has argued that the BH horizon is not the “driving force” behind the BZ mechanism, but rather it is the ergoregion. To disentangle the effects of the BH horizon and the ergoregion, Ruiz et al. (2012) performed force-free, numerical evolutions of magnetic fields on the fixed matter + metric background of an “ergostar” (a star with an internal ergoregion but no horizon) modeled by the EOS of incompressible, homogeneous matter with constant total mass-energy density. In addition, the same magnetic fields were evolved on the fixed background of a spinning BH. Ruiz et al. (2012) found that once the system reaches quasi-equilibrium, the configuration of the EM fields and currents on both backgrounds are the same, in agreement with Komissarov (2002, 2004, 2005). These preliminary results suggest that the BZ process is a mechanism driven by the ergoregion, and not by the BH horizon.
Recently, Tsokaros et al. (2019b, 2020b) constructed the first dynamically stable ergostars using compressible, causal EOSs based on the ALF2 and SLy EOSs, but with their inner core replaced by the maximally stiff EOS in Equation (8). The solutions are highly differentially rotating HMNSs with a corresponding spherical compaction of . In principle, such objects may form during NSNS mergers. Their stability was demonstrated by evolving them in full GR for over a hundred dynamical times (≳ 30 rotational periods) and observing their quasi-stationary behavior (see Figure 11). This stability was in contrast to earlier Γ = 3 polytropic models (Komatsu et al., 1989), which proved radially unstable to collapse (Tsokaros et al., 2019b).
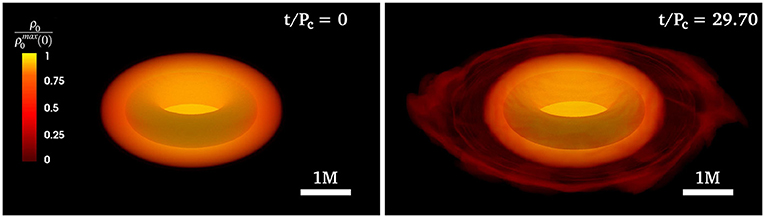
Figure 11. Initial and final profiles of a dynamically stable ergostar modeled with the ALF2cc EOS (see Equation 8). The rest-mass density ρ0 is normalized to its initial maximum value. The inner shaded torus indicates the position of the ergoregion. Here Pc is the initial rotation period measured at the point where the rest-mass density is maximum (from Tsokaros et al., 2019b).
Using the above models, Ruiz et al. (2020c) performed the first fully GRMHD simulations of dynamically stable ergostars to assess the impact of ergoregions on launching magnetically–driven outflows. In addition, and for comparison purposes, the evolution of a standard magnetic HMNS without an ergoregion and a highly spinning BH surrounded by a magnetized accretion disk were also considered. The ergostar and the standard HMNS were initially endowed with a pulsar-like magnetic field generated by the vector potential in Equation (6), while the accretion disk was endowed with a poloidal magnetic field confined to the interior (see Equation 5). In all cases, after a few Alfvén times, the seed magnetic field is wound into a helical structure from which matter begins to flow outward (see Figure 12). In the HMNS cases (ergostar and standard star), the maximum Lorentz factor in the outflow is ΓL ~ 2.5, while in the BH + disk case ΓL ~ 1.3. Therefore, a mildly relativistic jet is launched whether or not an ergoregion is present. However, only in the BH + disk case does the force-free parameter reach , whereby the outflow can be accelerated to ΓL ≳ 100 as required by sGRB models (Zou and Piran, 2010). These simulations suggest that the BZ process only operates when a BH is present, though the Poynting luminosity in all cases is comparable. Further studies are required to confirm this tentative conclusion.
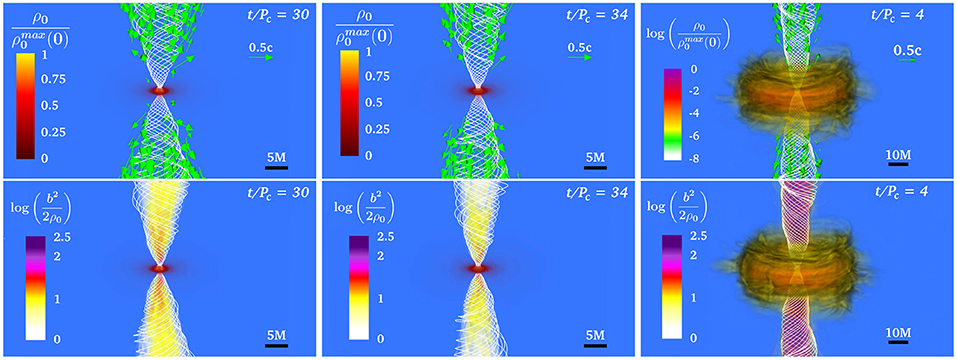
Figure 12. Final profiles of the rest-mass density ρ0 normalized to the initial maximum density (top), and the force-free parameter inside the helical magnetic funnel (bottom) for a standard HMNS (left), an ergostar (middle row), and BH + disk (right). White lines depict the magnetic field lines, while the arrows display fluid velocities. Pc is the rotation period measure at the point where the rest-mass density is maximum. Here M = 5.9 km and b2 = B2/4π. (from Ruiz et al., 2020c).
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work was supported by NSF Grants PHY-1662211 and PHY-2006066, and NASA Grant 80NSSC17K0070 to the University of Illinois at Urbana-Champaign. This work made use of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant No. TG-MCA99S008. This research is also part of the Frontera computing project at the Texas Advanced Computing Center. Frontera is made possible by National Science Foundation award OAC-1818253. Resources supporting this work were also provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank T. Baumgarte, C. Gammie, V. Paschalidis, and N. Yunes for useful discussions, and members of the Illinois Relativity group undergraduate research team (K. Nelli, M. N.T Nguyen, and S. Qunell) for assistance with some of the visualizations.
References
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016a). GW151226: observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys. Rev. Lett. 116:241103. doi: 10.1103/PhysRevLett.116.241103
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2016b). Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116:061102. doi: 10.1103/PhysRevLett.116.061102
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2017c). GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119:161101. doi: 10.1103/PhysRevLett.119.161101
Abbott, B. P., Abbott, R., Abbott, T. D., Abernathy, M. R., Acernese, F., Ackley, K., et al. (2017d). Multi-messenger observations of a binary neutron star merger. Astrophys. J. 848:L12. doi: 10.3847/2041-8213/aa91c9
Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2013). Prospects for observing and localizing gravitational-wave transients with advanced LIGO and advanced virgo. Living Rev. Rel. 19:1. doi: 10.1007/s41114-020-00026-9
Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2017a). Estimating the contribution of dynamical Ejecta in the Kilonova associated with GW170817. Astrophys. J. 850:L39. doi: 10.3847/2041-8213/aa9478
Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2017b). Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys. J. 848:L13.
Abbott, R., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2020a). GW190814: gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys. J. 896:L44. doi: 10.3847/2041-8213/ab960f
Abbott, R., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2020b). GWTC-2: compact binary coalescences observed by LIGO and Virgo during the first half of the third observing Run. arXiv:2010.14527
Aguilera-Miret, R., Viganó, D., Carrasco, F., Mi nano, B., and Palenzuela, C. (2020). Turbulent magnetic-field amplification in the first 10 milliseconds after a binary neutron star merger: comparing high-resolution and large-eddy simulations. Phys. Rev. D 102:103006. doi: 10.1103/PhysRevD.102.103006
Ajello, M., Bissaldi, E., Omodei, N., and Vianello, G. (2019). A decade of Gamma-ray bursts observed by fermi-LAT: the second GRB catalog. Astrophys. J. 878:52. doi: 10.3847/1538-4357/ab1d4e
Akmal, A., Pandharipande, V., and Ravenhall, D. (1998). The Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58, 1804–1828. doi: 10.1103/PhysRevC.58.1804
Alcubierre, M. (2008). Introduction to 3+1 Numerical Relativity. New York, NY: Oxford University Press. doi: 10.1093/acprof:oso/9780199205677.001.0001
Alford, M., Braby, M., Paris, M., and Reddy, S. (2005). Hybrid stars that masquerade as neutron stars. Astrophys. J. 629, 969–978. doi: 10.1086/430902
Aloy, M. A., Janka, H.-T., and Muller, E. (2004). Relativistic outflows from remnants of compact object mergers and their viability for short gamma-ray bursts. eConf C041213:0109. doi: 10.1051/0004-6361:20041865
Anderson, M., Hirschmann, E. W., Lehner, L., Liebling, S. L., Motl, P. M., Neilsen, D., et al. (2008). Magnetized neutron star mergers and gravitational wave signals. Phys. Rev. Lett. 100:191101. doi: 10.1103/PhysRevLett.100.191101
Baiotti, L., Giacomazzo, B., and Rezzolla, L. (2008). Accurate evolutions of inspiralling neutron-star binaries: prompt and delayed collapse to black hole. Phys. Rev. D 78:084033. doi: 10.1103/PhysRevD.78.084033
Baiotti, L., and Rezzolla, L. (2017). Binary neutron-star mergers: a review of Einstein's richest laboratory. Rept. Prog. Phys. 80:096901. doi: 10.1088/1361-6633/aa67bb
Baker, J. G., Centrella, J., Choi, D.-I., Koppitz, M., and van Meter, J. (2006). Gravitational-wave extraction from an inspiraling configuration of merging black holes. Phys. Rev. Lett. 96:111102. doi: 10.1103/PhysRevLett.96.111102
Barausse, E., and Buonanno, A. (2010). An Improved effective-one-body Hamiltonian for spinning black-hole binaries. Phys. Rev. D 81:084024. doi: 10.1103/PhysRevD.81.084024
Barnes, J., and Kasen, D. (2013). Effect of a high opacity on the light curves of radioactively powered transients from compact object mergers. Astrophys. J. 775:18. doi: 10.1088/0004-637X/775/1/18
Baumgarte, T. W., and Shapiro, S. L. (2010). Numerical Relativity: Solving Einstein's Equations on the Computer. Cambridge: Cambridge University Press. doi: 10.1017/CBO9781139193344
Baumgarte, T. W., Shapiro, S. L., and Shibata, M. (2000). On the maximum mass of differentially rotating neutron stars. Astrophys. J. Lett. 528:L29. doi: 10.1086/312425
Baumgarte, T. W., Skoge, M. L., and Shapiro, S. L. (2004). Black hole-neutron star binaries in general relativity: quasiequilibrium formulation. Phys. Rev. D 70:064040. doi: 10.1103/PhysRevD.70.064040
Bauswein, A., Baumgarte, T. W., and Janka, H. T. (2013). Prompt merger collapse and the maximum mass of neutron stars. Phys. Rev. Lett. 111:131101. doi: 10.1103/PhysRevLett.111.131101
Bauswein, A., Janka, H.-T., and Oechslin, R. (2010). Testing approximations of thermal effects in neutron star merger simulations. Phys. Rev. D 82:084043. doi: 10.1103/PhysRevD.82.084043
Bauswein, A., Just, O., Janka, H.-T., and Stergioulas, N. (2017). Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. 850:L34. doi: 10.3847/2041-8213/aa9994
Beckwith, K., Hawley, J. F., and Krolik, J. H. (2008). The influence of magnetic field geometry on the evolution of black hole accretion flows: similar disks, drastically different jets. Astrophys. J. 678, 1180–1199. doi: 10.1086/533492
Belczynski, K., Dominik, M., Bulik, T., O'Shaughnessy, R., Fryer, C., and Holz, D. (2010). The effect of metallicity on the detection prospects for gravitational waves. Astrophys. J. 715:L138. doi: 10.1088/2041-8205/715/2/L138
Belczynski, K., Taam, R. E., Rantsiou, E., and van der Sluys, M. (2008). Black hole spin evolution: implications for short-hard gamma ray bursts and gravitational wave detection. Astrophys. J. 682:474. doi: 10.1086/589609
Bernuzzi, S., Breschi, M., Daszuta, B., Endrizzi, A., Logoteta, D., Nedora, V., et al. (2020). Accretion-induced prompt black hole formation in asymmetric neutron star mergers, dynamical Ejecta and Kilonova signals. Mon. Not. Roy. Astron. Soc. 497, 1488–1507. doi: 10.1093/mnras/staa1860
Bernuzzi, S., Dietrich, T., Tichy, W., and Bruegmann, B. (2014). Mergers of binary neutron stars with realistic spin. Phys. Rev. D 89:104021. doi: 10.1103/PhysRevD.89.104021
Bhat, P. N. (2016). The third fermi GBM gamma-ray burst catalog: the first six years. Astrophys. J. Suppl. 223:28. doi: 10.3847/0067-0049/223/2/28
Blandford, R. D., and Znajek, R. L. (1977). Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 179, 433–456. doi: 10.1093/mnras/179.3.433
Breu, C., and Rezzolla, L. (2016). Maximum mass, moment of inertia and compactness of relativistic stars. Mon. Not. R. Astron. Soc. 459, 646–656. doi: 10.1093/mnras/stw575
Campanelli, M., Lousto, C. O., Marronetti, P., and Zlochower, Y. (2006). Accurate evolutions of orbiting black-hole binaries without excision. Phys. Rev. Lett. 96:111101. doi: 10.1103/PhysRevLett.96.111101
Chaurasia, S. V., Dietrich, T., Ujevic, M., Hendriks, K., Dudi, R., Fabbri, F. M., et al. (2020). Gravitational waves and mass Ejecta from binary neutron star mergers: effect of the spin orientation. Phys. Rev. D 102:024087. doi: 10.1103/PhysRevD.102.024087
Chawla, S., Anderson, M., Besselman, M., Lehner, L., Liebling, S. L., et al. (2010). Mergers of magnetized neutron stars with spinning black holes: disruption, accretion and fallback. Phys. Rev. Lett. 105:111101. doi: 10.1103/PhysRevLett.105.111101
Christodoulou, D. (1970). Reversible and irreversible transformations in black-hole physics. Phys. Rev. Lett. 25, 1596–1597. doi: 10.1103/PhysRevLett.25.1596
Ciolfi, R. (2020). Collimated outflows from long-lived binary neutron star merger remnants. Mon. Not. R. Astron. Soc. 495, L66–L70. doi: 10.1093/mnrasl/slaa062
Ciolfi, R., Kastaun, W., Giacomazzo, B., Endrizzi, A., Siegel, D. M., and Perna, R. (2017). General relativistic magnetohydrodynamic simulations of binary neutron star mergers forming a long-lived neutron star. Phys. Rev. D 95:063016. doi: 10.1103/PhysRevD.95.063016
Ciolfi, R., Kastaun, W., Kalinani, J. V., and Giacomazzo, B. (2019). First 100 ms of a long-lived magnetized neutron star formed in a binary neutron star merger. Phys. Rev. D 100:023005. doi: 10.1103/PhysRevD.100.023005
Cook, G. B., Shapiro, S. L., and Teukolsky, S. A. (1994a). Rapidly rotating neutron stars in general relativity: Realistic equations of state. Astrophys. J. 424:823. doi: 10.1086/173934
Cook, G. B., Shapiro, S. L., and Teukolsky, S. A. (1994b). Rapidly rotating polytropes in general relativity. Astrophys. J. 422, 227–242. doi: 10.1086/173721
Côté, B., Belczynski, K., Fryer, C. L., Ritter, C., Paul, A., Wehmeyer, B., et al. (2017). Advanced LIGO constraints on neutron star mergers and R-process sites. Astrophys. J. 836:230. doi: 10.3847/1538-4357/aa5c8d
Davies, M. B., Benz, W., Piran, T., and Thielemann, F. K. (1994). Merging neutron stars. I. Initial results for coalescence of noncorotating systems. Astrophys. J. 431:742. doi: 10.1086/174525
De, S., Finstad, D., Lattimer, J. M., Brown, D. A., Berger, E., and Biwer, C. M. (2018). Constraining the nuclear equation of state with GW170817. ArXiv e-prints. doi: 10.1103/PhysRevLett.121.091102
Dietrich, T., Bernuzzi, S., Brøgmann, B., Ujevic, M., and Tichy, W. (2018). Numerical relativity simulations of precessing binary neutron star mergers. Phys. Rev. D 97:064002. doi: 10.1103/PhysRevD.97.064002
Dietrich, T., Bernuzzi, S., Ujevic, M., and Bruegmann, B. (2015). Numerical relativity simulations of neutron star merger remnants using conservative mesh refinement. arXiv e-prints. doi: 10.1103/PhysRevD.91.124041
Dietrich, T., Bernuzzi, S., Ujevic, M., and Tichy, W. (2017). Gravitational waves and mass ejecta from binary neutron star mergers: effect of the stars' rotation. Phys. Rev. D 95:044045. doi: 10.1103/PhysRevD.95.044045
Dirirsa, F. F. (2017). Fermi observations of the bright LAT GRB 160625B. PoS HEASA2016:004. doi: 10.22323/1.275.0004
Douchin, F., and Haensel, P. (2001). A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 380, 151–167. doi: 10.1051/0004-6361:20011402
Duez, M. D., Foucart, F., Kidder, L. E., Pfeiffer, H. P., Scheel, M. A., and Teukolsky, S. A. (2008). Evolving black hole-neutron star binaries in general relativity using pseudospectral and finite difference methods. Phys. Rev. D 78:104015. doi: 10.1103/PhysRevD.78.104015
Duez, M. D., Liu, Y. T., Shapiro, S. L., Shibata, M., and Stephens, B. C. (2006). Collapse of magnetized hypermassive neutron stars in general relativity. Phys. Rev. Lett. 96:031101. doi: 10.1103/PhysRevLett.96.031101
Duez, M. D., Liu, Y. T., Shapiro, S. L., and Stephens, B. C. (2004). General relativistic hydrodynamics with viscosity: contraction, catastrophic collapse, and disk formation in hypermassive neutron stars. Phys. Rev. D 69:104030. doi: 10.1103/PhysRevD.69.104030
East, W. E., Paschalidis, V., and Pretorius, F. (2015). Eccentric mergers of black holes with spinning neutron stars. Astrophys. J. 807:L3. doi: 10.1088/2041-8205/807/1/L3
East, W. E., Paschalidis, V., Pretorius, F., and Shapiro, S. L. (2016). Relativistic simulations of eccentric binary neutron star mergers: one-arm spiral instability and effects of neutron star spin. Phys. Rev. D 93:024011. doi: 10.1103/PhysRevD.93.024011
East, W. E., and Pretorius, F. (2012). Dynamical capture binary neutron star mergers. Astrophys. J. Lett. 760:L4. doi: 10.1088/2041-8205/760/1/L4
Eichler, D., Livio, M., Piran, T., and Schramm, D. N. (1989). Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 340, 126–128. doi: 10.1038/340126a0
Etienne, Z. B., Faber, J. A., Liu, Y. T., Shapiro, S. L., Taniguchi, K., and Baumgarte, T. W. (2008). Fully general relativistic simulations of black hole-neutron star mergers. Phys. Rev. D 77:084002. doi: 10.1103/PhysRevD.77.084002
Etienne, Z. B., Liu, Y. T., Paschalidis, V., and Shapiro, S. L. (2012a). General relativistic simulations of black hole-neutron star mergers: effects of magnetic fields. Phys. Rev. D 85:064029. doi: 10.1103/PhysRevD.85.064029
Etienne, Z. B., Liu, Y. T., Shapiro, S. L., and Baumgarte, T. W. (2009). General relativistic simulations of black-hole-neutron-star mergers: effects of black-hole spin. Phys. Rev. D 79:044024. doi: 10.1103/PhysRevD.79.044024
Etienne, Z. B., Paschalidis, V., and Shapiro, S. L. (2012b). General relativistic simulations of black hole-neutron star mergers: effects of tilted magnetic fields. Phys. Rev. D 86:084026. doi: 10.1103/PhysRevD.86.084026
Faber, J. A., Baumgarte, T. W., Shapiro, S. L., and Taniguchi, K. (2006a). General relativistic binary merger simulations and short gamma-ray bursts. astrophys. J. Lett. 641, L93–L96. doi: 10.1086/504111
Faber, J. A., Baumgarte, T. W., Shapiro, S. L., Taniguchi, K., and Rasio, F. A. (2006b). Dynamical evolution of black hole-neutron star binaries in general relativity: simulations of tidal disruption. Phys. Rev. D 73:024012. doi: 10.1103/PhysRevD.73.024012
Faber, J. A., Grandclement, P., and Rasio, F. A. (2004). Mergers of irrotational neutron star binaries in conformally flat gravity. Phys. Rev. D 69:124036. doi: 10.1103/PhysRevD.69.124036
Falcke, H., and Rezzolla, L. (2014). Fast radio bursts: the last sign of supramassive neutron stars. Astron. Astrophys. 562:A137. doi: 10.1051/0004-6361/201321996
Foucart, F. (2012). Black hole-neutron star mergers: disk mass predictions. Phys. Rev. D 86:124007. doi: 10.1103/PhysRevD.86.124007
Foucart, F. (2020). A brief overview of black hole-neutron star mergers. Front. Astron. Space Sci. 7:46. doi: 10.3389/fspas.2020.00046
Foucart, F., Duez, M., Kidder, L., Nissanke, S., Pfeiffer, H., and Scheel, M. (2015). Numerical simulations of neutron star-black hole binaries in the near-equal-mass regime. Phys. Rev. Lett. 115:171101. doi: 10.1103/PhysRevLett.115.171101
Foucart, F., Duez, M. D., Kidder, L. E., Scheel, M. A., Szilagyi, B., and Teukolsky, S. A. (2012). Black hole-neutron star mergers for 10 solar mass black holes. Phys. Rev. D 85:044015. doi: 10.1103/PhysRevD.85.044015
Foucart, F., Duez, M. D., Kidder, L. E., and Teukolsky, S. A. (2011). Black hole-neutron star mergers: effects of the orientation of the black hole spin. Phys. Rev. D 83:024005. doi: 10.1103/PhysRevD.83.024005
Foucart, F., Kidder, L. E., Pfeiffer, H. P., and Teukolsky, S. A. (2008). Initial data for black hole-neutron star binaries: a Flexible, high-accuracy spectral method. Phys. Rev. D 77:124051. doi: 10.1103/PhysRevD.77.124051
Fryer, C. L., Woosley, S. E., Herant, M., and Davies, M. B. (1999). Merging white dwarf / black hole binaries and gamma-ray bursts. Astrophys. J. 520, 650–660. doi: 10.1086/307467
Giacobbo, N., and Mapelli, M. (2018). The progenitors of compact-object binaries: impact of metallicity, common envelope and natal kicks. Mon. Not. R. Astron. Soc. 480, 2011–2030. doi: 10.1093/mnras/sty1999
Giacomazzo, B., Zrake, J., Duffell, P., MacFadyen, A. I., and Perna, R. (2015). Producing magnetar magnetic fields in the merger of binary neutron stars. Astrophys. J. 809:39. doi: 10.1088/0004-637X/809/1/39
Gilden, D. L., and Shapiro, S. L. (1984). Gravitational radiation from colliding compact stars: hydrodynamical calculations in two-dimensions. Astrophys. J. 287:728. doi: 10.1086/162731
Glendenning, N. K., and Moszkowski, S. A. (1991). Reconciliation of neutron-star masses and binding of the Λ in hypernuclei. Phys. Rev. Lett. 67, 2414–2417. doi: 10.1103/PhysRevLett.67.2414
Grandclement, P. (2006). Accurate and realistic initial data for black hole-neutron star binaries. Phys. Rev. D 74:124002. doi: 10.1103/PhysRevD.74.124002
Hallinan, G., Corsi, A., Mooley, K. P., Hotokezaka, K., Nakar, E., Kasliwal, M. M., et al. (2017). A radio counterpart to a neutron star merger. Science 358, 1579–1583. doi: 10.1126/science.aap9855
Hayashi, K., Kawaguchi, K., Kiuchi, K., Kyutoku, K., and Shibata, M. (2020). Properties of the remnant disk and the dynamical ejecta produced in low-mass black hole-neutron star mergers. Phys. Rev. D 103:043007. doi: 10.1103/PhysRevD.103.043007
Hempel, M., and Schaffner-Bielich, J. (2010). A statistical model for a complete supernova equation of state. Nucl. Phys. A 837, 210–254. doi: 10.1016/j.nuclphysa.2010.02.010
Hotokezaka, K., Kyutoku, K., Okawa, H., Shibata, M., and Kiuchi, K. (2011). Binary neutron star mergers: dependence on the nuclear equation of state. Phys. Rev. D 83:124008. doi: 10.1103/PhysRevD.83.124008
Just, O., Obergaulinger, M., Janka, H. T., Bauswein, A., and Schwarz, N. (2016). Neutron-star merger ejecta as obstacles to neutrino-powered jets of gamma-ray bursts. Astrophys. J. 816:L30. doi: 10.3847/2041-8205/816/2/L30
Kasen, D., Metzger, B., Barnes, J., Quataert, E., and Ramirez-Ruiz, E. (2017). Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 551, 80–84. doi: 10.1038/nature24453
Kasliwal, M. M., Nakar, E., Singer, L. P., Kaplan, D. L., Cook, D. O., Van Sistine, A., et al. (2017). Illuminating gravitational waves: a concordant picture of photons from a neutron star merger. Science 358:1559. doi: 10.1126/science.aap9455
Kastaun, W., and Galeazzi, F. (2015). Properties of hypermassive neutron stars formed in mergers of spinning binaries. Phys. Rev. D 91:064027. doi: 10.1103/PhysRevD.91.064027
Kawamura, T., Giacomazzo, B., Kastaun, W., Ciolfi, R., Endrizzi, A., Baiotti, L., et al. (2016). Binary neutron star mergers and short gamma-ray bursts: effects of magnetic field orientation, equation of state, and mass ratio. Phys. Rev. D 94:064012. doi: 10.1103/PhysRevD.94.064012
Kiuchi, K., Cerdá-Durán, P., Kyutoku, K., Sekiguchi, Y., and Shibata, M. (2015a). Efficient magnetic-field amplification due to the Kelvin-Helmholtz instability in binary neutron star mergers. Phys. Rev. D 92:124034. doi: 10.1103/PhysRevD.92.124034
Kiuchi, K., Kawaguchi, K., Kyutoku, K., Sekiguchi, Y., Shibata, M., and Taniguchi, K. (2017). Sub-radian-accuracy gravitational waveforms of coalescing binary neutron stars in numerical relativity. Phys. Rev. D 96:084060. doi: 10.1103/PhysRevD.96.084060
Kiuchi, K., Sekiguchi, Y., Kyutoku, K., Shibata, M., Taniguchi, K., and Wada, T. (2015b). High resolution magnetohydrodynamic simulation of black hole-neutron star merger: mass ejection and short gamma ray bursts. Phys. Rev. D 92:064034. doi: 10.1103/PhysRevD.92.064034
Kiuchi, K., Sekiguchi, Y., Shibata, M., and Taniguchi, K. (2009). Long term general relativistic simulation of binary neutron stars collapsing to a black hole. Phys. Rev. D 80:064037. doi: 10.1103/PhysRevD.80.064037
Kobayashi, S., Laguna, P., Phinney, E. S., and Mészáros, P. (2004). Gravitational waves and X-ray signals from stellar disruption by a massive black hole. Astrophys. J. 615, 855–865. doi: 10.1086/424684
Kocsis, B., and Levin, J. (2012). Repeated bursts from relativistic scattering of compact objects in galactic nuclei. Phys. Rev. D 85:123005. doi: 10.1103/PhysRevD.85.123005
Komatsu, H., Eriguchi, Y., and Hachisu, I. (1989). Rapidly rotating general relativistic stars. II - Differentially rotating polytropes. Mon. Not. R. Astron. Soc. 239, 153–171. doi: 10.1093/mnras/239.1.153
Komissarov, S. (2002). “On the nature of the Blandford-Znajek mechanism,” in 3rd International Sakharov Conference on Physics (Moscow).
Komissarov, S. S. (2004). Electrodynamics of black hole magnetospheres. Mon. Not. R. Astron. Soc. 350:407. doi: 10.1111/j.1365-2966.2004.07598.x
Komissarov, S. S. (2005). Observations of the Blandford-Znajek process and the magnetohydrodynamic Penrose process in computer simulations of black hole magnetospheres. Mon. Not. R. Astron. Soc. 359, 801–808. doi: 10.1111/j.1365-2966.2005.08974.x
Kozlova, A., Golenetskii, S., Aptekar, R., Frederiks, D., Svinkin, D., Cline, T., et al. (2017). IPN Triangulation of GRB 170816A (Short/Hard). GRB Coordinates Network, Circular Service, No. 21517, #1 (2017), 1517.
Kyutoku, K., Kiuchi, K., Sekiguchi, Y., Shibata, M., and Taniguchi, K. (2018). Neutrino transport in black hole-neutron star binaries: neutrino emission and dynamical mass ejection. Phys. Rev. D 97:023009. doi: 10.1103/PhysRevD.97.023009
Kyutoku, K., Okawa, H., Shibata, M., and Taniguchi, K. (2011). Gravitational waves from spinning black hole-neutron star binaries: dependence on black hole spins and on neutron star equations of state. Phys. Rev. D 84:064018. doi: 10.1103/PhysRevD.84.064018
Lasota, J.-P., Haensel, P., and Abramowicz, M. A. (1996). Fast rotation of neutron stars. Astrophys. J. 456:300. doi: 10.1086/176650
Lattimer, J. M., and Prakash, M. (2016). The equation of state of hot, dense matter and neutron stars. Phys. Rept. 621, 127–164. doi: 10.1016/j.physrep.2015.12.005
Lattimer, J. M., and Schramm, D. N. (1974). Black-hole-neutron-star collisions. Astrophys. J. Lett. 192, L145–L147. doi: 10.1086/181612
Lee, W. H. (2001). Newtonian hydrodynamics of the coalescence of black holes with neutron stars - IV. Irrotational binaries with a soft equation of state. Mon. Not. R. Astron. Soc. 328, 583–600. doi: 10.1046/j.1365-8711.2001.04898.x
Lee, W. H., Ramirez-Ruiz, E., and van de Ven, G. (2010). Short gamma-ray bursts from dynamically assembled compact binaries in globular clusters: pathways, rates, hydrodynamics, and cosmological setting. Astrophys. J. 720, 953–975. doi: 10.1088/0004-637X/720/1/953
Lehner, L., Liebling, S. L., Palenzuela, C., Caballero, O., O'Connor, E., Anderson, M., et al. (2016). Unequal mass binary neutron star mergers and multimessenger signals. Class. Quant. Grav. 33:184002. doi: 10.1088/0264-9381/33/18/184002
Li, L.-X., and Paczynski, B. (1998). Transient events from neutron star mergers. Astrophys. J. 507:L59. doi: 10.1086/311680
Lien, A., Sakamoto, T, Barthelmy, S. D., Baumgartner, W. H., Cannizzo, J. K., Chen, K., et al. (2016). The third swift burst alert telescope gamma-ray burst catalog. Astrophys. J. 829:7. doi: 10.3847/0004-637X/829/1/7
Liu, Y. T., Shapiro, S. L., Etienne, Z. B., and Taniguchi, K. (2008). General relativistic simulations of magnetized binary neutron star mergers. Phys. Rev. D 78:024012. doi: 10.1103/PhysRevD.78.024012
Lorimer, D. R. (2008). Binary and millisecond pulsars. Living Rev. Relat. 11:1–90. doi: 10.12942/lrr-2008-8
Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., and Crawford, F. (2007). A bright millisecond radio burst of extragalactic origin. Science 318:777. doi: 10.1126/science.1147532
Lovelace, G., Duez, M. D., Foucart, F., Kidder, L. E., Pfeiffer, H. P., et al. (2013). Massive disc formation in the tidal disruption of a neutron star by a nearly extremal black hole. Class. Quant. Grav. 30:135004. doi: 10.1088/0264-9381/30/13/135004
Lovelace, G., Owen, R., Pfeiffer, H. P., and Chu, T. (2008). Binary-black-hole initial data with nearly-extremal spins. Phys. Rev. D 78:084017. doi: 10.1103/PhysRevD.78.084017
Lyne, A. G., and Graham-Smith, F. (2012). Pulsar Astronomy. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511844584
Margalit, B., and Metzger, B. D. (2017). Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophys. J. Lett. 850:L19. doi: 10.3847/2041-8213/aa991c
McKernan, B., Ford, K. E. S., and O'Shaughnessy, R. (2020). Black hole, neutron star, and white dwarf merger rates in AGN discs. Mon. Not. R. Astron. Soc. 498, 4088–4094. doi: 10.1093/mnras/staa2681
Metzger, B. D., and Fernández, R. (2014). Red or blue? A potential kilonova imprint of the delay until black hole formation following a neutron star merger. Mon. Not. R. Astron. Soc. 441, 3444–3453. doi: 10.1093/mnras/stu802
Metzger, B. D., Martínez-Pinedo, G., Darbha, S., Quataert, E., Arcones, A., Kasen, D., et al. (2010). Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 406, 2650–2662. doi: 10.1111/j.1365-2966.2010.16864.x
Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). PSR J0030+0451 mass and radius from NICER data and Implications for the properties of neutron star matter. Astrophys. J. Lett. 887:L24. doi: 10.3847/2041-8213/ab50c5
Mooley, K. P., Nakar, E., Hotokezaka, K., Hallinan, G., Corsi, A., Frail, D. A., et al. (2018). A mildly relativistic wide-angle outflow in the neutron-star merger event GW170817. Nature 554, 207–210. doi: 10.1038/nature25452
Most, E. R., Papenfort, L. J., Weih, L. R., and Rezzolla, L. (2020). A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. Mon. Not. R. Astron. Soc. 499, L82–L86. doi: 10.1093/mnrasl/slaa168
Mösta, P., Radice, D., Haas, R., Schnetter, E., and Bernuzzi, S. (2020). A magnetar engine for short GRBs and kilonovae. Astrophys. J. Lett. 901:L37. doi: 10.3847/2041-8213/abb6ef
Narayan, R., Paczynski, B., and Piran, T. (1992). Gamma-ray bursts as the death throes of massive binary stars. Astrophys. J. Lett. 395, L83–L86. doi: 10.1086/186493
Nelemans, G., Yungelson, L. R., and Portegies Zwart, S. F. (2001). The gravitational wave signal from the galactic disk population of binaries containing two compact objects. Astron. Astrophys. 375, 890–898. doi: 10.1051/0004-6361:20010683
New, K. C. B., and Tohline, J. E. (1997). The relative stability against merger of close, compact binaries. Astrophys. J. 490, 311–327. doi: 10.1086/304861
Oechslin, R., Janka, H. T., and Marek, A. (2007). Relativistic neutron star merger simulations with non-zero temperature equations of state. I. Variation of binary parameters and equation of state. Astron. Astrophys. 467, 395–409. doi: 10.1051/0004-6361:20066682
Oechslin, R., Rosswog, S., and Thielemann, F. K. (2002). Conformally flat smoothed particle hydrodynamics: application to neutron star mergers. Phys. Rev. D 65:103005. doi: 10.1103/PhysRevD.65.103005
Oohara, K., and Nakamura, T. (1989). Gravitational radiation from coalescing binary neutron stars. I. Prog. Theor. Phys. 82, 535–554. doi: 10.1143/PTP.82.535
Özel, F., and Psaltis, D. (2009). Reconstructing the neutron-star equation of state from astrophysical measurements. Phys. Rev. D 80:103003. doi: 10.1103/PhysRevD.80.103003
Paczynski, B. (1986). Gamma-ray bursters at cosmological distances. Astrophys. J. Lett. 308, L43–L46. doi: 10.1086/184740
Palenzuela, C., Lehner, L., Liebling, S. L., Ponce, M., Anderson, M., et al. (2013). Linking electromagnetic and gravitational radiation in coalescing binary neutron stars. Phys. Rev. D 88:043011. doi: 10.1103/PhysRevD.88.043011
Palenzuela, C., Liebling, S. L., Neilsen, D., Lehner, L., Caballero, O. L., O'Connor, E., et al. (2015). Effects of the microphysical equation of state in the mergers of magnetized neutron stars with neutrino cooling. Phys. Rev. D 92:044045. doi: 10.1103/PhysRevD.92.044045
Palenzuela, C., Pani, P., Bezares, M., Cardoso, V., Lehner, L., and Liebling, S. (2017). Gravitational wave signatures of highly compact boson star binaries. Phys. Rev. D 96:104058. doi: 10.1103/PhysRevD.96.104058
Paschalidis, V. (2017). General relativistic simulations of compact binary mergers as engines for short gamma-ray bursts. Class. Quant. Grav. 34:084002. doi: 10.1088/1361-6382/aa61ce
Paschalidis, V., East, W. E., Pretorius, F., and Shapiro, S. L. (2015). One-arm spiral instability in hypermassive neutron stars formed by dynamical-capture binary neutron star mergers. Phys. Rev. D 92:121502. doi: 10.1103/PhysRevD.92.121502
Paschalidis, V., Etienne, Z. B., and Shapiro, S. L. (2013). General relativistic simulations of binary black hole-neutron stars: precursor electromagnetic signals. Phys. Rev. D 88:021504. doi: 10.1103/PhysRevD.88.021504
Paschalidis, V., Liu, Y. T., Etienne, Z., and Shapiro, S. L. (2011). The merger of binary white dwarf-neutron stars: simulations in full general relativity. Phys. Rev. D 84:104032. doi: 10.1103/PhysRevD.84.104032
Paschalidis, V., and Ruiz, M. (2018). Are fast radio bursts the most likely electromagnetic counterpart of neutron star mergers resulting in prompt collapse? Phys. Rev. D 100:043001 doi: 10.1103/PhysRevD.100.043001
Paschalidis, V., Ruiz, M., and Shapiro, S. L. (2015). Relativistic simulations of black Hole-neutron star coalescence: the jet emerges. Astrophys. J. 806:L14. doi: 10.1088/2041-8205/806/1/L14
Peters, P. C. (1964). Gravitational radiation and the motion of two point masses. Phys. Rev. 136, B1224–B1232. doi: 10.1103/PhysRev.136.B1224
Piran, T. (2005). The physics of gamma-ray bursts. Rev. Modern Phys. 76, 1143–1210. doi: 10.1103/RevModPhys.76.1143
Pons, J., Miralles, J., and Geppert, U. (2009). Magneto-thermal evolution of neutron stars. Astron. Astrophys. 496, 207–216. doi: 10.1051/0004-6361:200811229
Pretorius, F. (2005). Evolution of binary black-hole spacetimes. Phys. Rev. Lett. 95:121101. doi: 10.1103/PhysRevLett.95.121101
Price, D., and Rosswog, S. (2006). Producing ultra-strong magnetic fields in neutron star mergers. Science 312:719. doi: 10.1126/science.1125201
Radice, D. (2020). Binary neutron star merger simulations with a calibrated turbulence model. Symmetry 12:1249. doi: 10.3390/sym12081249
Radice, D., Bernuzzi, S., and Perego, A. (2020). The dynamics of binary neutron star mergers and of GW170817. Ann. Rev. Nucl. Part Sci. 70, 95–119. doi: 10.26226/morressier.5fb692d74d4e91fe5c54c292
Radice, D., Galeazzi, F., Lippuner, J., Roberts, L. F., Ott, C. D., and Rezzolla, L. (2016). Dynamical mass ejection from binary neutron star mergers. Mon. Not. R. Astron. Soc. 460, 3255–3271. doi: 10.1093/mnras/stw1227
Radice, D., Perego, A., Zappa, F., and Bernuzzi, S. (2018). GW170817: joint constraint on the neutron star equation of state from multimessenger observations. Astrophys. J. 852:L29. doi: 10.3847/2041-8213/aaa402
Raithel, C., Özel, F., and Psaltis, D. (2018). Tidal deformability from GW170817 as a direct probe of the neutron star radius. Astrophys. J. Lett. 857:L23. doi: 10.3847/2041-8213/aabcbf
Rantsiou, E., Kobayashi, S., Laguna, P., and Rasio, F. A. (2008). Mergers of black hole-neutron star binaries. I. Methods and first results. Astrophys. J. 680, 1326–1349. doi: 10.1086/587858
Rasio, F. A., and Shapiro, S. L. (1992). Hydrodynamical evolution of coalescing binary neutron stars. Astrophys. J. 401:226. doi: 10.1086/172055
Rasio, F. A., and Shapiro, S. L. (1994). Hydrodynamics of binary coalescence. I. Polytropes with stiff equations of state. Astrophys. J. 432:242. doi: 10.1086/174566
Read, J. S., Lackey, B. D., Owen, B. J., and Friedman, J. L. (2009). Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 79:124032. doi: 10.1103/PhysRevD.79.124032
Rezzolla, L., Baiotti, L., Giacomazzo, B., Link, D., and Font, J. A. (2010). Accurate evolutions of unequal-mass neutron-star binaries: properties of the torus and short GRB engines. Class. Quant. Grav. 27:114105. doi: 10.1088/0264-9381/27/11/114105
Rezzolla, L., Giacomazzo, B., Baiotti, L., Granot, J., Kouveliotou, C., and Aloy, M. A. (2011). The missing link: merging neutron stars naturally produce jet-like structures and can power short gamma-ray bursts. Astrophys. J. Lett. 732:L6. doi: 10.1088/2041-8205/732/1/L6
Rezzolla, L., Most, E. R., and Weih, L. R. (2018). Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. 852:L25. doi: 10.3847/2041-8213/aaa401
Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A NICER view of PSR J0030+0451: millisecond pulsar parameter estimation. Astrophys. J. Lett. 887:L21. doi: 10.3847/2041-8213/ab481c
Rosswog, S. (2005). Mergers of neutron star-black hole binaries with small mass ratios: nucleosynthesis, gamma-ray bursts, and electromagnetic transients. Astrophys. J. 634, 1202–1213. doi: 10.1086/497062
Rosswog, S., Speith, R., and Wynn, G. A. (2004). Accretion dynamics in neutron star-black hole binaries. Mon. Not. R. Astron. Soc. 351, 1121–1133. doi: 10.1111/j.1365-2966.2004.07865.x
Ruffert, M., and Janka, H. T. (1998). Colliding neutron stars. Gravitational waves, neutrino emission, and gamma-ray bursts. Astron. Astrophys. 338, 535–555.
Ruffert, M., Janka, H. T., and Schaefer, G. (1996). Coalescing neutron stars - a step towards physical models. I. Hydrodynamic evolution and gravitational-wave emission. Astrophys. J. 311, 532–566.
Ruiz, M., Lang, R. N., Paschalidis, V., and Shapiro, S. L. (2016). Binary neutron star mergers: a jet engine for short gamma-ray bursts. Astrophys. J. 824:L6. doi: 10.3847/2041-8205/824/1/L6
Ruiz, M., Palenzuela, C., Galeazzi, F., and Bona, C. (2012). The role of the ergosphere in the Blandford-Znajek process. Mon. Not. R. Astron. Soc. 423, 1300–1308. doi: 10.1111/j.1365-2966.2012.20950.x
Ruiz, M., Paschalidis, V., and Shapiro, S. L. (2014). Pulsar spin-down luminosity: simulations in general relativity. Phys. Rev. D 89:084045. doi: 10.1103/PhysRevD.89.084045
Ruiz, M., Paschalidis, V., Tsokaros, A., and Shapiro, S. L. (2020a). Black hole-neutron star coalescence: effects of the neutron star spin on jet launching and dynamical ejecta mass. Phys. Rev. D 102:124077 doi: 10.1103/PhysRevD.102.124077
Ruiz, M., and Shapiro, S. L. (2017). GRMHD simulations of prompt-collapse neutron star mergers: the absence of jets. Phys. Rev. D 96:084063. doi: 10.1103/PhysRevD.96.084063
Ruiz, M., Shapiro, S. L., and Tsokaros, A. (2018a). GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass. Phys. Rev. D 97:021501. doi: 10.1103/PhysRevD.97.021501
Ruiz, M., Shapiro, S. L., and Tsokaros, A. (2018b). Jet launching from binary black hole-neutron star mergers: dependence on black hole spin, binary mass ratio and magnetic field orientation. Phys. Rev. D 98:123017. doi: 10.1103/PhysRevD.98.123017
Ruiz, M., Tsokaros, A., Paschalidis, V., and Shapiro, S. L. (2019). Effects of spin on magnetized binary neutron star mergers and jet launching. Phys. Rev. D 99:084032. doi: 10.1103/PhysRevD.99.084032
Ruiz, M., Tsokaros, A., and Shapiro, S. L. (2020b). Magnetohydrodynamic simulations of binary neutron star mergers in general relativity: effects of magnetic field orientation on jet launching. Phys. Rev. D 101:064042. doi: 10.1103/PhysRevD.101.064042
Ruiz, M., Tsokaros, A., Shapiro, S. L., Nelli, K. C., and Qunell, S. (2020c). Magnetic ergostars, jet formation and gamma-ray bursts: ergoregions versus horizons. Phys. Rev. D 102:104022. doi: 10.1103/PhysRevD.102.104022
Samsing, J., MacLeod, M., and Ramirez-Ruiz, E. (2014). The formation of eccentric compact binary inspirals and the role of gravitational wave emission in binary-single stellar encounters. Astrophys. J. 784:71. doi: 10.1088/0004-637X/784/1/71
Sekiguchi, Y., Kiuchi, K., Kyutoku, K., and Shibata, M. (2011). Gravitational waves and neutrino emission from the merger of binary neutron stars. Phys. Rev. Lett. 107:051102. doi: 10.1103/PhysRevLett.107.051102
Sekiguchi, Y., Kiuchi, K., Kyutoku, K., and Shibata, M. (2015). Dynamical mass ejection from binary neutron star mergers: radiation-hydrodynamics study in general relativity. Phys. Rev. D 91:064059. doi: 10.1103/PhysRevD.91.064059
Semena, A. N., Lutovinov, A. A., Mereminskiy, I. A., Tsygankov, S. S., Shtykovsky, A. E., Molkov, S. V., et al. (2019). Observational constraints on the magnetic field of the bright transient Be/X-ray pulsar SXP 4.78. Mon. Not. R. Astron. Soc. 490, 3355–3364. doi: 10.1093/mnras/stz2722
Shapiro, S. L. (2017). Black holes, disks, and jets following binary mergers and stellar collapse: the narrow range of electromagnetic luminosities and accretion rates. Phys. Rev. D 95:101303. doi: 10.1103/PhysRevD.95.101303
Shibata, M. (2015). 100 Years of General Relativity- Numerical Relativity. Singapore: World Scientific Publishing Company. doi: 10.1142/9692
Shibata, M., Duez, M. D., Liu, Y. T., Shapiro, S. L., and Stephens, B. C. (2006). Magnetized hypermassive neutron star collapse: a Central engine for short gamma-ray bursts. Phys. Rev. Lett. 96:031102. doi: 10.1103/PhysRevLett.96.031102
Shibata, M., Fujibayashi, S., Hotokezaka, K., Kiuchi, K., Kyutoku, K., Sekiguchi, Y., and Tanaka, M. (2017). Modeling gw170817 based on numerical relativity and its implications. Phys. Rev. D 96:123012. doi: 10.1103/PhysRevD.96.123012
Shibata, M., Nakamura, T., and Oohara, K.-I. (1992). Coalescence of spinning binary neutron stars of equal mass: 3D numerical simulations. Prog. Theor. Phys. 88, 1079–1095. doi: 10.1143/ptp/88.6.1079
Shibata, M., Nakamura, T., and Oohara, K.-I. (1993). Coalescence of spinning binary neutron stars with plunging orbit: newtonian 3D numerical simulation. Prog. Theor. Phys. 89, 809–819. doi: 10.1143/ptp/89.4.809
Shibata, M., and Taniguchi, K. (2006). Merger of binary neutron stars to a black hole: disk mass, short gamma-ray bursts, and quasinormal mode ringing. Phys. Rev. D 73:064027. doi: 10.1103/PhysRevD.73.064027
Shibata, M., and Taniguchi, K. (2011). Coalescence of black hole-neutron star binaries. Living Rev. Relat. 14:6. doi: 10.12942/lrr-2011-6
Shibata, M., Taniguchi, K., and Uryu, K. (2003). Merger of binary neutron stars of unequal mass in full general relativity. Phys. Rev. D 68:084020. doi: 10.1103/PhysRevD.68.084020
Shibata, M., and Uryu, K. (2000). Simulation of merging binary neutron stars in full general relativity: Γ=2 case. Phys. Rev. D 61:064001. doi: 10.1103/PhysRevD.61.064001
Shibata, M., and Uryū, K. (2002). Gravitational waves from the merger of binary neutron stars in a fully general relativistic simulation. Prog. Theor. Phys. 107:265. doi: 10.1143/PTP.107.265
Shibata, M., and Uryu, K. (2006). Merger of black hole-neutron star binaries: nonspinning black hole case. Phys. Rev. D 74:121503. doi: 10.1103/PhysRevD.74.121503
Shibata, M., and Uryu, K. (2007). Merger of black hole-neutron star binaries in full general relativity. Class. Quant. Grav. 24, S125–S138. doi: 10.1088/0264-9381/24/12/S09
Shibata, M., Zhou, E., Kiuchi, K., and Fujibayashi, S. (2019). Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. D 100:023015. doi: 10.1103/PhysRevD.100.023015
Siegel, D. M., Ciolfi, R., Harte, A. I., and Rezzolla, L. (2013). Magnetorotational instability in relativistic hypermassive neutron stars. Phys. Rev. D 87:121302. doi: 10.1103/PhysRevD.87.121302
Sun, L., Ruiz, M., and Shapiro, S. L. (2019). Magnetic braking and damping of differential rotation in massive stars. Phys. Rev. D 99:064057. doi: 10.1103/PhysRevD.99.064057
Svinkin, D. S., Frederiks, D. D., Aptekar, R. L., Golenetskii, S. V., Pal'shin, V. D., Oleynik, P. P., et al. (2016). The second Konus-Wind catalog of short gamma-ray bursts. Astrophys. J. Suppl. 224:10. doi: 10.3847/0067-0049/224/1/10
Taniguchi, K., Baumgarte, T. W., Faber, J. A., and Shapiro, S. L. (2005). Black hole-neutron star binaries in general relativity: effects of neutron star spin. Phys. Rev. D 72:044008. doi: 10.1103/PhysRevD.72.044008
Taniguchi, K., Baumgarte, T. W., Faber, J. A., and Shapiro, S. L. (2007). Quasiequilibrium black hole-neutron star binaries in general relativity. Phys. Rev. D 75:084005. doi: 10.1103/PhysRevD.75.084005
Taniguchi, K., and Gourgoulhon, E. (2002). Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. III. Identical and different mass stars with γ=2. Phys. Rev. D 66:104019. doi: 10.1103/PhysRevD.66.104019
Tauris, T. M., Kramer, M., Freire, P. C. C., Wex, N., Janka, H. T., Langer, N., et al. (2017). Formation of double neutron star systems. Astrophys. J. 846:170. doi: 10.3847/1538-4357/aa7e89
Thorne, K. S., Price, R. H., and Macdonald, D. A. (1986). The Membrane Paradigm. New Haven, CT: Yale University Press.
Thornton, D., Stappers, B., Bailes, M., Barsdell, B. R., Bates, S. D., Bhat, N. D. R., et al. (2013). A population of fast radio bursts at cosmological distances. Science 341, 53–56. doi: 10.1126/science.1236789
Totani, T. (2013). Cosmological fast radio bursts from binary neutron star mergers. Pub. Astron. Soc. Jpn. 65:L12. doi: 10.1093/pasj/65.5.L12
Tsokaros, A., Mundim, B. C., Galeazzi, F., Rezzolla, L., and Uryū, K. (2016). Initial-data contribution to the error budget of gravitational waves from neutron-star binaries. Phys. Rev. D 94:044049. doi: 10.1103/PhysRevD.94.044049
Tsokaros, A., Ruiz, M., Paschalidis, V., Shapiro, S. L., and Uryū, K. (2019a). Effect of spin on the inspiral of binary neutron stars. Phys. Rev. D 100:024061. doi: 10.1103/PhysRevD.100.024061
Tsokaros, A., Ruiz, M., and Shapiro, S. L. (2020a). GW190814: Spin and equation of state of a neutron star companion. Astrophys. J. 905:48. doi: 10.3847/1538-4357/abc421
Tsokaros, A., Ruiz, M., and Shapiro, S. L. (2020b). Locating ergostar models in parameter space. Phys. Rev. D 101:064069. doi: 10.1103/PhysRevD.101.064069
Tsokaros, A., Ruiz, M., Shapiro, S. L., Sun, L., and Uryū, K. (2020c). Great impostors: extremely compact, merging binary neutron stars in the mass gap posing as binary black holes. Phys. Rev. Lett. 124:071101. doi: 10.1103/PhysRevLett.124.071101
Tsokaros, A., Ruiz, M., Sun, L., Shapiro, S. L., and Uryū, K. (2019b). Dynamically stable ergostars exist: general relativistic models and simulations. Phys. Rev. Lett. 123:231103. doi: 10.1103/PhysRevLett.123.231103
Tsokaros, A., Uryū, K., and Rezzolla, L. (2015). New code for quasiequilibrium initial data of binary neutron stars: corotating, irrotational, and slowly spinning systems. Phys. Rev. D 91:104030. doi: 10.1103/PhysRevD.91.104030
Vincent, T., Foucart, F., Duez, M. D., Haas, R., Kidder, L. E., Pfeiffer, H. P., et al. (2020). Unequal mass binary neutron star simulations with neutrino transport: Ejecta and neutrino emission. Phys. Rev. D 101:044053. doi: 10.1103/PhysRevD.101.044053
Vlahakis, N., and Konigl, A. (2003). Relativistic magnetohydrodynamics with application to gamma-ray burst outflows: 2. Semianalytic super-Alfvenic solutions. doi: 10.1086/378227
von Kienlin, A., Meegan, C., and Goldstein, A. (2017). GRB 170817A: Fermi GBM Detection. GRB Coordinates Network, Circular Service, No. 21520, #1 (2017), 1520.
Weih, L. R., Hanauske, M., and Rezzolla, L. (2020). Postmerger gravitational-wave signatures of phase transitions in binary mergers. Phys. Rev. Lett. 124:171103. doi: 10.1103/PhysRevLett.124.171103
Wilson, J. R., and Mathews, G. J. (1995). Instabilities in close neutron star binaries. Phys. Rev. Lett. 75, 4161–4164. doi: 10.1103/PhysRevLett.75.4161
Xing, Z.-G., Centrella, J. M., and McMillan, S. L. (1994). Gravitational radiation from coalescing binary neutron stars. Phys. Rev. D 50, 6247–6261. doi: 10.1103/PhysRevD.50.6247
York James, W. J. (1999). Conformal “thin-sandwich” data for the initial-value problem of general relativity. Phys. Rev. Lett. 82, 1350–1353. doi: 10.1103/PhysRevLett.82.1350
Zhang, B.-B., Zhang, B., Castro-Tirado, A. J., Dai, Z. G., Tam, P.-H. T., Wang, X.-Y., et al. (2018). Transition from fireball to Poynting-flux-dominated outflow in the three-episode GRB 160625B. Nat. Astron. 2, 69–75. doi: 10.1038/s41550-017-0309-8
Zhu, X., Thrane, E., Oslowski, S., Levin, Y., and Lasky, P. D. (2018). Inferring the population properties of binary neutron stars with gravitational-wave measurements of spin. Phys. Rev. D 98:043002. doi: 10.1103/PhysRevD.98.043002
Keywords: black holes, neutron stars, gravitational waves, short gamma-ray bursts, numerical relativity, multimessenger astronomy
Citation: Ruiz M, Shapiro SL and Tsokaros A (2021) Multimessenger Binary Mergers Containing Neutron Stars: Gravitational Waves, Jets, and γ-Ray Bursts. Front. Astron. Space Sci. 8:656907. doi: 10.3389/fspas.2021.656907
Received: 21 January 2021; Accepted: 08 March 2021;
Published: 08 April 2021.
Edited by:
Ian Jones, University of Southamton, United KingdomReviewed by:
Vyacheslav Ivanovich Dokuchaev, Institute for Nuclear Research (RAS), RussiaHerman J. Mosquera Cuesta, Tecnologia e Innovacion, Colciencias, Colombia
Copyright © 2021 Ruiz, Shapiro and Tsokaros. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Milton Ruiz, cnVpem1AaWxsaW5vaXMuZWR1
 Milton Ruiz
Milton Ruiz Stuart L. Shapiro
Stuart L. Shapiro Antonios Tsokaros
Antonios Tsokaros