- Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge, United Kingdom
The study of stellar oscillations allows us to infer the properties of stellar interiors. Meanwhile, fundamental parameters such as mass and radius can be obtained by studying stars in binary systems. The synergy between binarity and asteroseismology can constrain the parameter space of stellar properties and facilitate the asteroseismic inference. On the other hand, binarity also introduces additional complexities such tides and mass transfer. From an observational perspective, we briefly review the recent advances in the study of tidal effects on stellar oscillations, focusing on upper main sequence stars (F-, A-, or OB- type). The effect can be roughly divided into two categories. The first one concerns the tidally excited oscillations (TEOs) in eccentric binaries where TEOs are mostly due to resonances between dynamical tides and gravity modes of the star. TEOs appear as orbital-harmonic oscillations on top of the eccentric ellipsoidal light curve variations (the “heartbeat” feature). The second category is regarding the self-excited oscillations perturbed by static tides in circularized and synchronized close binaries. It includes the tidal deformation of the propagation cavity and its effect on eigenfrequencies, eigenfunctions, and the pulsation alignment. We list binary systems that show these two types of tidal effect and summarize the orbital and pulsation observables. We also discuss the theoretical approaches used to model these tidal oscillations and relevant complications such as non-linear mode coupling and resonance locking. Further information can be extracted from the observations of these oscillations which will improve our understanding of tides. We also discuss the effect of mass transfer, the extreme result of tides, on stellar oscillations. We bring to the readers' attention: (1) oscillating stars undergoing mass accretion (A-, F-, and OB type pulsators and white dwarfs), for which the pulsation properties may be changed significantly by accretion; (2) post-mass transfer pulsators, which have undergone a stable or unstable Roche-Lobe overflow. These pulsators have great potential in probing detailed physical processes in stellar interiors and mass transfer, as well as in studying the binary star populations.
1. Introduction
Stars tend to reside in binary or multiple systems, especially for those of early-type (Raghavan et al., 2010; Moe and Di Stefano, 2017). The intermediate and massive stars also possess a stably stratified radiative envelope which facilitates the propagation of gravity waves. When forming global normal modes, these gravity (g) modes can be observed in photometry or spectroscopcy and be used to study the stellar interiors. Thanks to the recent space telescopes, significant advances have been made in asteroseismology (Aerts et al., 2010; Bowman, 2020) including, e.g., the self-excited g-mode pulsators such as the F or A type γ Dor stars (Van Reeth et al., 2016; Li et al., 2020b) and the Slowly Pulsating B-stars (SPB) (Pápics et al., 2017). In binary stars, tidal forcing from the companion star naturally falls into the low-frequency (inertial and gravity mode) regime1, with characteristic periods on the order of days. The tidally excited oscillations are crucial for the orbital evolution of binaries (Zahn, 1975, 1977; Ogilvie, 2014). It requires precise (generally <10−4 magnitude), long, and continuous observations to detect the direct effect of tides on stellar oscillations. We are witnessing a huge amount of evidence of tidal effects on stellar oscillations, including both the tidally excited modes and perturbed modes.
The effect of tides can be classified into two categories. First, the non-wavelike, equilibrium tide regime, where the tidal effect is a global static deformation (Remus et al., 2012). The shape can be approximated as a spheroid or, more generally, as the Roche model, which is frequently used in the modeling of binary star light curves (Wilson and Devinney, 1971; Prša and Zwitter, 2005; Sepinsky et al., 2007). Second, in the wave-like, dynamical tide regime, the harmonic tidal forcing induces gravity waves in the radiative envelope and inertial waves in the convective core. If the waves suffer from less damping and manifest themselves as temperature variations on the stellar surface, they can be observed and studied.
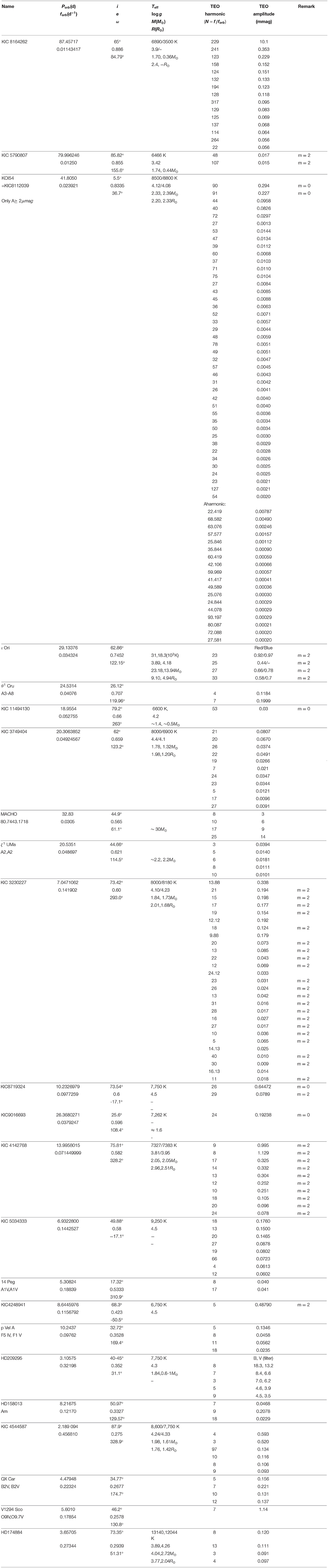
Observationally, we discuss two classes of pulsating binaries. The first is pulsating eccentric binaries, i.e., the heartbeat stars (HBs). HBs are eccentric binary systems showing the eccentric ellipsoidal variations (the “heartbeat,” sometimes similar to the electrocardiogram) near the periastron passage. Figure 1 shows the typical light curves of three HBs observed by Kepler from low to high inclinations. The heartbeat feature stems from the ellipsoidal variation (mainly from the temperature and geometric perturbations due to tidal deformation) and the reflection effect (mutual heating). Doppler boosting also contributes to the feature but to a much lesser degree (Loeb and Gaudi, 2003; van Kerkwijk et al., 2010; Hambleton et al., 2016). The prototype of HB is KOI-54, which consists of two A-type main-sequence stars in a face-on, very eccentric orbit (Welsh et al., 2011). Later compilations of HBs include Thompson et al. (2012) and Kirk et al. (2016). The spectroscopic follow-up studies include Smullen and Kobulnicky (2015), Shporer et al. (2016), Kjurkchieva et al. (2016), and Dimitrov et al. (2017). Detailed studies of individual systems have been performed (see below). Some HBs show tidally excited oscillations (TEOs) on top of the heartbeat feature, i.e., additional g-mode oscillations induced by the dynamical tide.
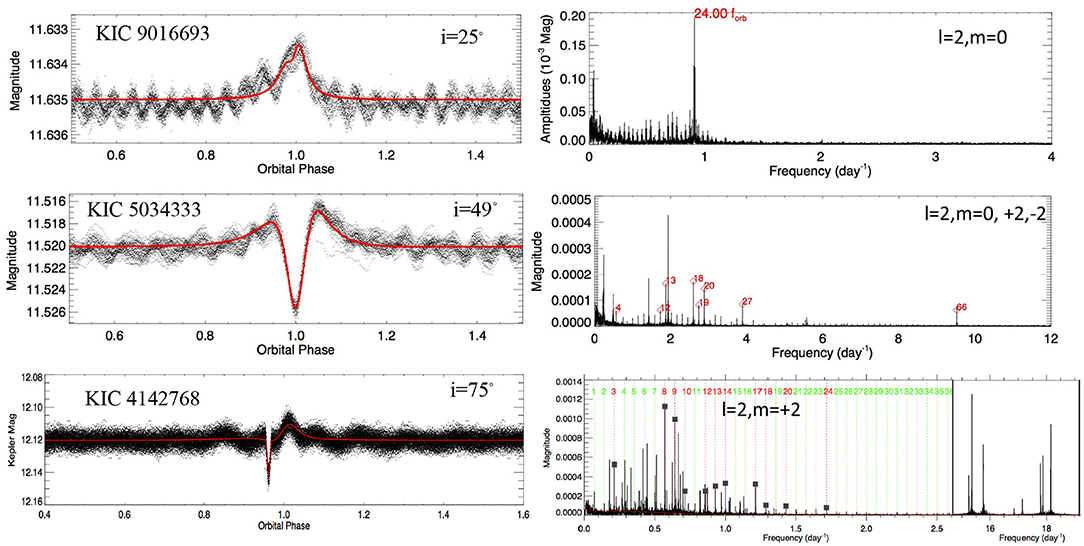
Figure 1. (Left) Kepler Light curves of three heartbeat binaries with TEOs, from low to high orbital inclinations (i). In particular, KIC 4142768 has an eclipse near the periastron (phase = 1.0). (Right) Fourier spectrum of the light curves after removing the equilibrium tide contribution (red lines in left panels). The TEOs (red symbols or gray squares) are labeled by their orbital harmonic number (N) in red, and their tentative mode identification (l and m) are also shown. In the lower panel, intrinsic self-excited oscillations (γ Dor g-modes in the frequency range f < 2 d−1 and δ Scuti p-modes in f > 15 d−1) are also present. Imperfect equilibrium-tide removal also generates a series of consecutive low-amplitude peaks, most notably in the upper and middle panels (see text). Adopted from Guo et al. (2019, 2020).
The other class is circularized and synchronized close binaries with self-excited oscillations. For example, the A or F-type, pressure(p)-mode pulsating stars of δ Scuti type (Breger, 1979; Rodŕıguez et al., 2000) have been frequently found in close binaries. Some systems show p-modes perturbed by static tides. The manifestation can be seen in the perturbed eigenfrequencies and pulsational alignment (tidal splittings) and the modified eigenfunctions (e.g., flux may be non-uniformly distributed on the stellar surface).
Lastly, in section 4, we also discuss the extreme case of tides: mass transfer, and its effect on stellar oscillations. Particular attention is paid to the mode excitation and the binary-channel formation of pulsating stars via mass transfer.
2. Eccentric Binaries With Tidally Excited Oscillations (TEOs)
The HBs depict the upper envelope of the classical orbital period-eccentricity diagram (Shporer et al., 2016). The relatively short period (mostly P ≲ 50 d) and high eccentricity (e ≳ 0.2) indicate an on-going strong tidal evolution (Dong et al., 2013). Zimmerman et al. (2017) showed that about 20 HBs have a surface rotation period ≈ 1.5 times longer than the pseudo-synchronous rotation period (Hut, 1981). Some heartbeat stars are actually in a hierarchical system. For example, high-resolution spectroscopy reveals a third spectral component in KIC 3230227 (Guo et al., 2017a; Lampens, 20172). The high eccentricity (e = 0.89) and spin-orbit misalignment of the heartbeat binary KIC 8164262 (Hambleton et al., 2018) suggest that it is probably formed via the Kozai-Lidov mechanism (Kozai, 1962; Lidov, 1962; Naoz, 2016), a possible formation channel for some HBs. It is quite possible that many HBs have a hidden tertiary companion (Anderson et al., 2017).
The heartbeat signature can be present in the light curve irrespective of the spectral type. We will not discuss HBs with red giant components (Nicholls and Wood, 2012; Gaulme et al., 2013, 2014; Beck et al., 2014; Kuszlewicz et al., 2019) but focus on HBs with A- F- and OB-type stars. These stars possess radiative envelopes which facilitate the observability of tidally excited oscillations.
Observationally, we subtract the contribution from the equilibrium tide (the heartbeat feature, red lines in Figure 1) before studying the oscillations in the Fourier domain (Figure 1, right panel). TEOs represent the dynamical tidal response of the star to the companion, mostly manifest as exact orbital-harmonic frequencies (except for non-linear TEOs, see section 2.2 below). In the right panels of Figure 1, the peaks labeled with red numbers or gray squares are orbital-harmonic TEOs. Very-low-inclination HBs usually show l = 2, m = 0 TEOs while near-edge-on HBs tend to show l = 2, m = 2 TEOs. Tentative mode identification (l and m) of TEOs are labeled in Figure 1. The amplitude and frequency range (orbital harmonic number N) of TEOs can be predicted from theory and these expectations can be used to distinguish from the aliases resulting from imperfect equilibrium-tide light curve removal and other artifacts generated in the data reduction (e.g., frequency peaks without labels in the Fourier spectra of the upper and middle panels of Figure 1). An estimate can be made to the largest possible amplitude of these aliases and thus they can usually be distinguished from real TEOs. Note that the Fourier spectrum can also contain self-excited oscillations (e.g., γ Dor type g-modes and δ Scuti p-modes in KIC 4142768, lower panel of Figure 1). Furthermore, modulations from the stellar spin also introduce frequency peaks at the rotation frequency and its harmonics.
We compile a list of 22 heartbeat binaries with TEOs:
OB- type: HD 177863 (Willems and Aerts, 2002); ι Ori (Pablo et al., 2017); MACHO80.7443.1718 (Jayasinghe et al., 2019); QX Car and V1294 Sco (Kołaczek-Szymański et al., 2020); two possible candidates: η Car (Richardson et al., 2018); R81 (Tubbesing et al., 2002).
A-F- type: HD209295 (Handler et al., 2002); KOI-54 (Welsh et al., 2011); KIC 3230227 (Guo et al., 2017a); KIC 4142768 (Guo et al., 2019); KIC 9016693, KIC 8719324 and KIC 4248941, KIC 5034333 (Guo et al., 2020); KIC 11494130 and KIC 5790807 (Cheng et al., 2020), KIC 4544587 (Hambleton et al., 2013); KIC 3749404 (Hambleton et al., 2016), KIC 8164262 (Fuller et al., 2017; Hambleton et al., 2018); p Vel, θ1 Cru, η1 UMa, HD158013 and 14 Peg (Kołaczek-Szymański et al., 2020).
This list is of course incomplete. Kirk et al. (2016) included 24 HBs with TEOs, which is about 15% of all heartbeat binaries in the Kepler eclipsing catalog. Only ten systems are included here since TEOs in the rest have not been studied in detail. Table 1 contains the stellar, orbital and oscillation parameters of 22 heartbeat binaries (A detailed online version can be found at: http://www.astro.gsu.edu/~guo/tides_review_table.pdf).
2.1. Tidally Excited Oscillations (TEOs) in Heartbeat Stars
We briefly describe the general physical picture of tidally excited waves in early-type stars. Early seminal studies used asymptotic approximations of gravity waves (Zahn, 1975, 1977; Goldreich and Nicholson, 1989), and it was extended to include the effect of rotation (Mathis, 2009). Later numerical calculations include the effect of non-adiabaticity and rotation (Savonije et al., 1995; Papaloizou and Savonije, 1997; Savonije and Papaloizou, 1997). Dedicated calculations (Witte and Savonije, 1999a,b) on massive stars studied the binary evolution and the intricate effects such as resonance locking. Other studies implemented the mode decomposition approach (Alexander, 1987; Lai et al., 1993; Lai, 1997; Schenk et al., 2002; Fuller, 2017).
Intermediate and massive stars possess a convective core and radiative envelope. In binaries containing these stars, internal gravity waves (IGW) are generated by the tidal potential (also by the convective motion in the core) at the radiative-convective boundary and propagate outward (Goldreich and Nicholson, 1989; Lecoanet and Quataert, 2013; Rogers et al., 2013; Edelmann et al., 2019; Lecoanet et al., 2019; Horst et al., 2020). They suffer from linear damping due to radiative diffusion (Press, 1981; Garcia Lopez and Spruit, 1991; Zahn et al., 1997). The low-frequency, short-wavelength waves are damped strongly and behave like traveling waves (Ratnasingam et al., 2019). Higher-frequency waves can be reflected at the outer turning points and interfere constructively to form global normal modes (Prat et al., 2016).
Most of the observed prominent TEOs in HBs are standing waves, suffering from less damping. When the TEO amplitudes surpass the parametric instability threshold, the TEOs begin to suffer from non-linear mode coupling and transfer energy to daughter modes or multiple pairs of daughter modes (Weinberg et al., 2012; Yu et al., 2020). The daughter modes may again become unstable and couple with grand-daughter modes. In general, a mode coupling network can be formed. Observationally, this can be seen as mode triplets or multiplets satisfying the resonance conditions. This weakly-nonlinear regime will be discussed in the next section.
The amplitudes of the tidally excited gravity waves, when propagating to the near-surface layers with smaller densities, increase significantly. If the waves become significantly non-linear (the multiplication of the radial wavenumber and radial displacement krξr ≳ 1), they overturn the stratification and break (Su et al., 2020). Thus, they deposit their energy (tidal heating) and angular momentum (tidal synchronization), and turn into small-scale turbulence. Thus, the surface layers are synchronized first and a differential rotation profile may be produced (Goldreich and Nicholson, 1989), although the hydromagnetic effects tend to smooth out differential rotation (Rüdiger et al., 2015; Townsend et al., 2018). Critical layers where the Doppler-shifted wave frequency approaches zero, may form and move inward (Alvan et al., 2013). The subsequent gravity waves cannot pass the critical layer and waves dissipate strongly. Observationally, single upper main-sequence stars tend to have a nearly uniform rotation profile in the radiative envelope, inferred from asteroseismology (Bowman, 2020; Aerts, 2021)3. The g-mode pulsating γ Dor stars (spectral type A-F-) in close binaries with Porb ≤ 10 d show a convective-core-boundary rotation period that is similar to the orbital period, suggesting that the tidal synchronization has already reached the deep interior (Guo et al., 2019; Li et al., 2020a; Saio, 2020). Nevertheless, Kallinger et al. (2017) found a Slowly Pulsating B-star in a triple system that appears to show a faster-rotating surface layer, which may fall into the Goldreich and Nicholson's outside-in synchronization scenario.
Since the TEOs are direct manifestation of dynamical tides, they are crucial for our understanding of the above physical processes. First, we show some general properties of the TEOs in heartbeat stars.
The overall strength of the tidal response of star 1 due to star 2 is determined by the tidal parameter ϵl:
where Dperi = a(1 − e). Since , it is usually sufficient to consider the dominant l = 2 component.
Thus, to have a larger tidal amplitude, one could (1) make the mass ratio M2/M14 larger (i.e., close to 1.0); (2) make the stellar radius R1 bigger; (3) have a smaller periastron distance Dperi. And indeed, observationally: (1) many heartbeat stars have a mass ratio close to unity5; (2) lots of heartbeat stars with tidally excited oscillations are slightly evolved main-sequence stars (e.g., KIC 4142768 has a primary star with M = 2.05M⊙, R = 2.96R⊙, Guo et al., 2019); (3) heartbeat binaries have a high eccentricity (≈ 0.2−0.9) and short periastron distance. The Dperi of 19 HBs in Shporer et al. (2016) ranges from 0.05 to 0.1AU, and the corresponding tidal parameter ϵ2 values are ≈ 10−3.
The observed TEOs correspond to the frequencies of stellar g-modes with radial orders from ≈ 10 to a few tens. For example, the primary star in KIC 3230227 (M = 1.84M⊙, R = 2.01R⊙, Guo et al., 2017a) shows orbital-harmonic oscillations corresponding to l = 2, m = 2 g modes, with radial order ng ~ 10−30; KOI 54 (M = 2.05M⊙, R = 2.33R⊙, O'Leary and Burkart, 2014) shows TEOs that mostly have l = 2, m = 0, corresponding to radial order ng ~ 10−50. The slightly evolved primary in KIC4142768 (Guo et al., 2017a) shows TEOs that are in agreement with ng ≈ 30 − 70 g modes.
In Figure 2, we stack the observed TEOs in 22 heartbeat binaries together, with decreasing orbital eccentricities from the top to the bottom. These Fourier spectra show that the TEOs generally have oscillation frequencies <~5 d−1. They mostly correspond to orbital harmonics N from 4 to 40, although in some special cases the N can reach much larger values (N ~ 300 in KIC 8164262). The TEO amplitudes can be as large as > 10 milli-mag although the majority are lower than 0.5 milli-mag (right panel in Figure 2).
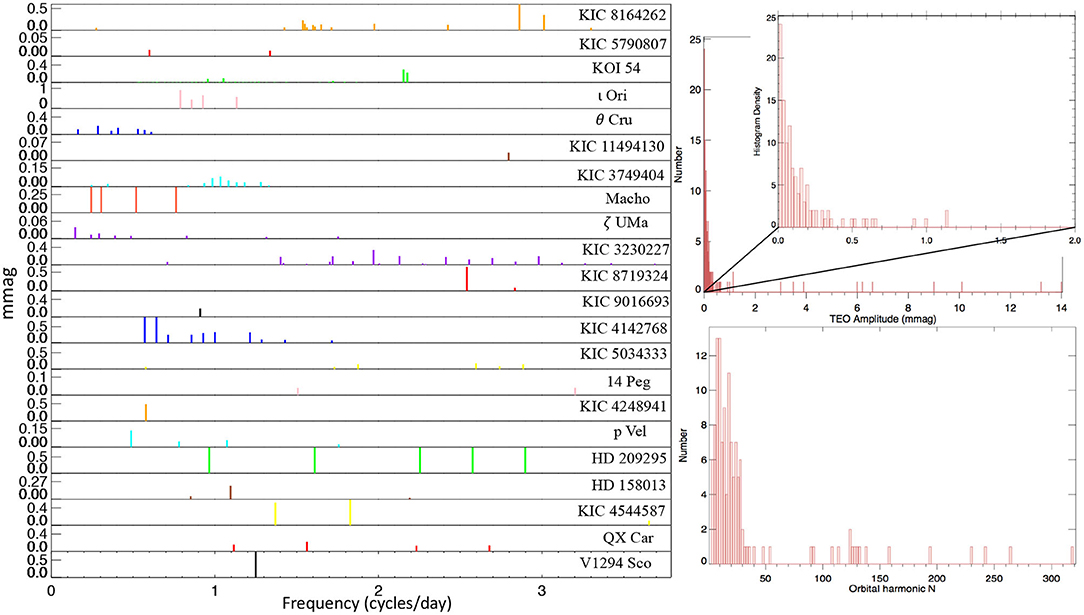
Figure 2. Fourier amplitude spectrum of all 22 heartbeat binaries with TEOs. The TEO amplitudes are shown in mmag. The inset plots show the TEO amplitude histogram (upper) and the orbital harmonic N histogram (lower).
In general, most of the observed TEOs are likely (linearly) excited by the dynamical tide (exact orbital-harmonic frequencies (Nforb, see next section for nonlinear non-harmonic TEOs), with the stellar response dominated by the closest frequency g-mode. But which orbital harmonics N are favorably excited? Following Burkart et al. (2012), the favorable range of orbital harmonics depends essentially on the multiplication of Qnl and Xlm (see immediately later in this paragraph for the definitions). First, not all g-modes couple with the tidal potential equally. The weights are described by the tidal overlap integral Qnl, which peaks around the dynamical frequency of the star. Qnl decreases toward lower frequencies since higher order g-modes have shorter wavelength and cannot couple well spatially with the tidal potential. Secondly, stars in eccentric orbits experience a series of forcing frequencies (Nforb, with |N| < ∞) which are weighted by the eccentricity-dependent Hansen coefficient Xlm. Xl = 2, m = 2 peaks at the periastron-passage frequency and decreases toward larger N; Xl = 2, m = 0 monotonically decreases as N increases (Willems, 2003, Figures 1, 2; Fuller, 2017, Figure 3). Thus, the favored range of orbital harmonics N is between the peaks of Qnl and Xlm (Burkart et al., 2012, Figures 2, 3).
In Figure 3, we show the observed TEO amplitudes (in magnitude variation Δmag or luminosity variation ΔL/L, related by ΔL/L ≈ 1.086Δmag) as a function of the orbital harmonic number (N) in four HBs KIC4142768, KIC3230227, ι Ori and KOI-54 (gray squares, circles, red squares, and red crosses, respectively). These observed TEOs should be compared with the theoretical amplitudes for m = 2, m = 2, m = 2, m = 0 modes (blue diamonds, open diamonds, blue circles, and open triangles, respectively, same ordering as above). It can be seen that the observed TEO range (between the two vertical lines) matches well with the theoretical expectations (the “bump” formed by background symbols. For ι Ori, the theoretical TEO amplitudes of m = 0 modes (cyan open circles) are below the detection limit and much lower than observed TEOs (m = 2). For KOI-54, the Δmag from the temperature effect (ΔmagT; upper) and geometrical effect (ΔmagG; lower) are distinguished. Note that the observed magnitude variations are primarily due to the temperature perturbations (slightly overestimated in Fuller and Lai, 2012).
Figure 3. The amplitude of TEOs in magnitude variation (Δmag) or relative luminosity variation (ΔL/L) as a function of orbital harmonic (N) for four heartbeat binaries. The observed TEOs are indicated by the gray squares (upper left, KIC 4142768), open circles (upper right, KIC 3230227), red squares (lower left, ι Ori), and red crosses (lower right, KOI-54). The theoretical TEO amplitudes are shown as blue diamonds (upper left, m = 2 modes), open diamonds (upper right, m = 2 modes), blue/cyan circles (lower left, m = 2/m = 0 modes), and open triangles/filled circles (lower right, m = 0/m = 2 modes, respectively). The two vertical lines in each panel show the lower and upper frequency limits of the observed TEOs.
However, to model the TEO amplitudes individually, one needs to consider the Lorentzian term ΔnlmN (a term describing the resonances, see Equation 13, Burkart et al., 2012), which depends sensitively on the frequency detuning, i.e., the closeness of a certain forcing frequency (Nforb) to the nearest eigenmode frequency. Unfortunately, even a change of 0.001M⊙ in stellar models can significantly change the detuning parameter, thus the Lorentzian term. A better way is to treat the detuning parameter as a random variable, which is uniformly distributed between its minimum value (= 0, perfect resonance) and maximum values (half of the adjacent g-mode spacing). In this way, a credible interval can be calculated for the Lorentzian term and thus the observed TEO amplitude (Fuller, 2017). For example, the 95% credible interval (±2σ) of theoretical TEO amplitude for KIC 4142768 is shown as the shaded region in the upper left panel of Figure 3.
TEO phases, measured with respect to the periastron, deserve a particular discussion. We expect most observed TEOs are standing waves and nearly adiabatic, and their phases are close to the adiabatic expectations which are essentially only a function of ω (argument of periastron) and m (Burkart et al., 2012; Guo et al., 2020). In Figure 4, we show the observed TEO phases (symbols) and the theoretical adiabatic phases (vertical lines) for five HBs. As expected, low inclination HBs tend to show m = 0 modes (top two systems), and intermediate/high inclination HBs usually present both m = 0 and m = 2 modes. The low-frequency TEOs experience more radiative damping, and they can be distinguished by their relatively large phase offset from adiabatic phases (O'Leary and Burkart, 2014, Figure 4; Guo et al., 2019, Figure 7). Weakly non-linear TEOs that experience non-linear mode coupling also show deviations from the adiabatic phases. It is possible that TEOs locked in resonance with the orbit still have relatively large frequency detuning compared with the mode damping rate, and thus they do not show arbitrary phases as in the perfect-resonance case.
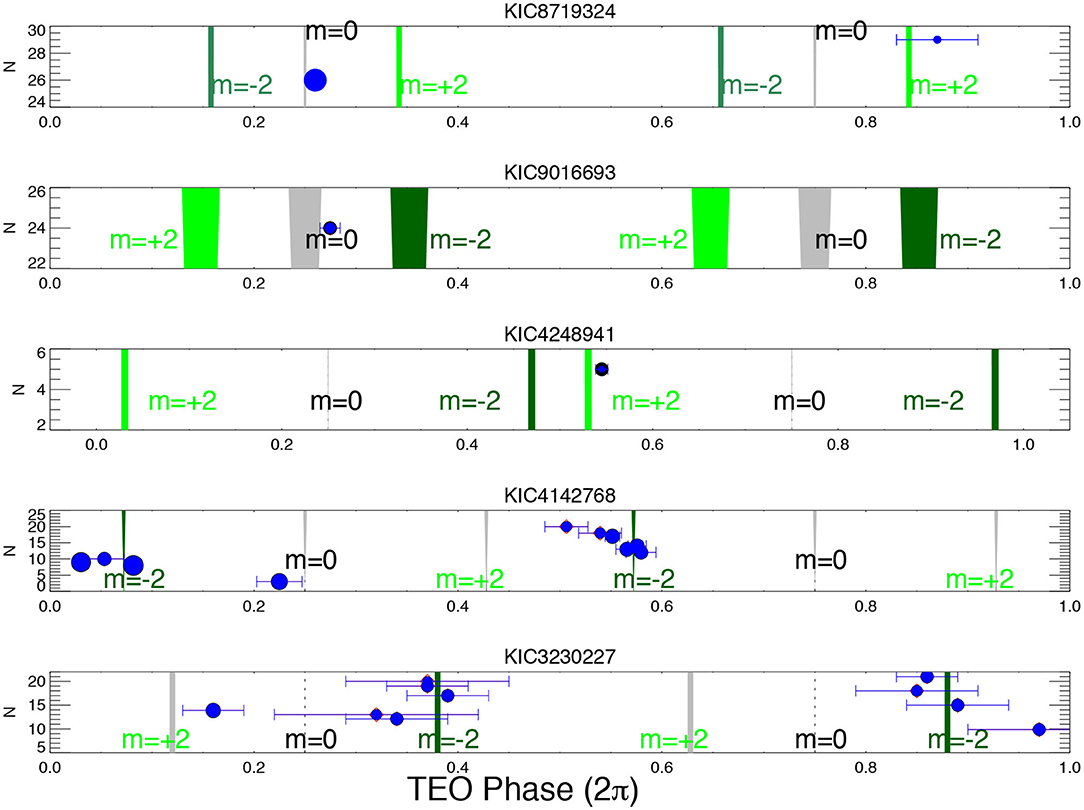
Figure 4. Observed TEO phases (symbols) as a function of orbital harmonics (N) for five heartbeat binary systems. The theoretical phases in the adiabatic approximation are indicated by vertical lines, with the azimuthal number m = 0, or ±2 labeled. Adopted from Guo et al. (2017a, 2020).
To summarize, the tidal response to a forcing frequency (Nforb) is a summation of the mode eigenfunctions weighted by the mode amplitude AnlmN ∝ ϵlQnlXlmΔnlmN (Burkart et al., 2012; Fuller, 2017). Roughly speaking, ϵl determines the overall strength, QnlXlm controls the range of excited orbital harmonics N, and ΔnlmN sets the detailed amplitude of each TEO. TEO phases are primarily determined by the orbital orientation. Most observed TEOs in HBs are chance resonances (i.e., random frequency detuning) with g-modes and can be modeled by the above theoretical framework. In fact, the aforementioned statistical approach is good for finding TEOs larger than expectation. These TEOs may be locked in resonance with the orbit and require a different modeling approach (see section 2.3).
2.2. Weakly Non-linear TEOs: Mode Coupling
Modes near resonances can non-linearly interact and observationally, this can generate combination frequencies in the form of mfa ± nfb, with m and n being integers. Resonance mode couplings have been observed and studied in free oscillations for B-type pulsators (Degroote et al., 2009), δ Scuti pulsators (Breger and Montgomery, 2014; Bowman et al., 2016) as well as compact pulsators (Zong et al., 2016a,b) and other types of variables. Theoretical studies include, e.g., Dziembowski and Krolikowska (1985), Van Hoolst (1994), and Buchler et al. (1997).
In the context of tidal oscillations, a striking feature in the observed TEOs is that some of them are not orbital harmonics. And the anharmonic frequencies can pair up and sum to an orbital harmonic (fa + fb ≈ Nforb). This can be explained by the non-linear resonance mode coupling.
When the tidally excited oscillations surpass the linear regime and become weakly non-linear, the oscillation mode can suffer from parametric instability (Schenk et al., 2002; Arras et al., 2003), which is the leading-order non-linear effect (Weinberg et al., 2012). In the dominant three-mode resonance coupling scenario (fA = fa + fb), the parent mode A is resonantly excited by a linear dynamical tide (an orbital harmonic Nforb); and when its amplitude exceeds the three-mode instability threshold, it can transfer energy to two daughter modes (a, b). In Figure 5, we show different mode coupling patterns. The upper left is the aforementioned basic three-mode coupling. The mode-coupling triplet (A, a, b) can also couple to other mode triplets, either by sharing the parent (lower left) or sharing a daughter mode (upper middle panel). Multiple mode-triplets can also couple together (lower middle panel). In KIC 3230227, we find that two mode-coupling triplets share one daughter mode. And the resonance conditions for the two mode triplets are labeled in Figure 5: fA(22) = fa(9.88) + fb(12.12) and fB(26) = fd(13.88) + fb(12.12), where all frequencies are in units of the orbital frequency. In KOI-54, it is found that the 91st orbital harmonic resonantly excites an eigenmode very close to it, and this parent mode has at least four pairs of daughter modes. Some of the pairs even share daughters (O'Leary and Burkart, 2014). Furthermore, third-order mode coupling is also evidenced (the rightmost panel in Figure 5).
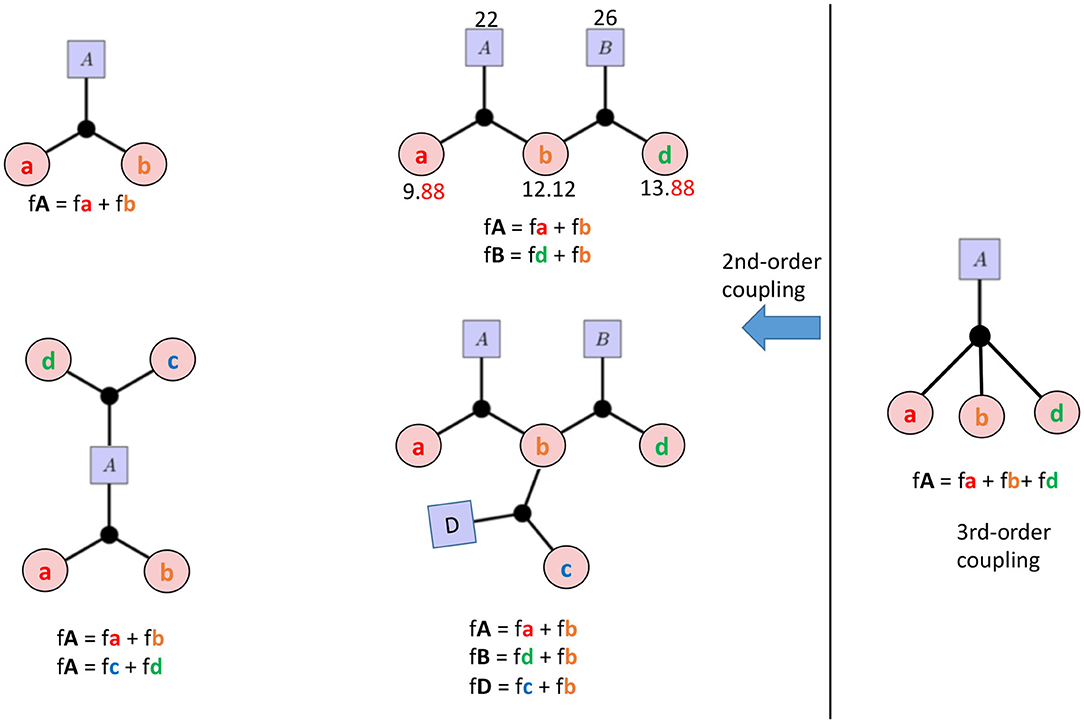
Figure 5. The patterns of multi-mode coupling observed in TEOs. Capital letters (A, B, D) represent parent modes and lowercase letters (a, b, c, d) correspond to daughter modes. The left four cases are second-order coupling and the right is a third-order coupling. For the upper middle pattern, we use the observed TEOs in KIC3230227 and label the TEO frequencies (fA, fB, fa, fb, fd) in units of the orbital frequency Ωorb.
Observationally, these non-linear coupled TEOs can offer us lots of information beyond the linear theory. Firstly, the selection rules (relating the modes' l and m, Dziembowski, 1982) in mode coupling can help to identify the daughter modes (O'Leary and Burkart, 2014; Guo, 2020). If we have a large number of these mode triplets, since the linearly driven parent modes can be identified from phases, we may be able to discern the g-mode period spacings among the daughter modes and possibly among the close-to-resonance parent modes. The asymptotic period spacing pattern has been routinely found in self-excited g-modes in γ Dor stars and SPB stars, but not in tidally excited modes. Secondly, parent modes that suffer from mode-coupling instability should be close to the eigenmode frequency (although they do not necessarily have a larger amplitude than the daughter modes). Together with the anharmonic daughter modes, these mode frequencies provide a list of eigenmodes that can be compared with stellar models. This kind of tidal asteroseismology can thus be performed. After the preliminary effort by Burkart et al. (2012), we are still waiting for its first concrete application in a real star. Thirdly, the observed parent mode amplitude can be compared to the mode-coupling threshold. This helps to determine the nature of coupling. For KOI-54, O'Leary and Burkart (2014) showed that five-mode coupling can decrease the threshold amplitude of parametric instability (i.e., smaller than three-mode coupling threshold). This explains the observed parent-mode amplitude being much smaller than the three-mode instability threshold. In fact, Weinberg et al. (2012) showed that, if the parent mode couples to N daughter-mode pairs, the threshold amplitude can decrease by a factor of N. Fourthly, the mode coupling systems can have different behavior (Wersinger et al., 1980; Wu and Goldreich, 2001), depending on the frequency detuning (the difference between the parent-mode frequency fA and the resonant linear tide at Nforb ≈ fA, and also between the parent-mode frequency and the daughter-mode frequency sum fa + fb) and the daughter-mode damping rates. Guo (2020) showed that the observed stable amplitudes/phases of the parent and daughter modes in KIC3230227 indicate the five-mode-coupling system has settled into an equilibrium state, and this agrees with the theoretical mode damping rates. The mode-coupling systems can show limit cycles (Moskalik, 1985) and observables such as cycle period can help to constrain mode parameters (e.g., damping rates). In ZZ Ceti (DAV) type pulsating white dwarfs, it is in fact limit cycles that explain the observed outbursts in the light curves (Luan and Goldreich, 2018). Non-linear mode coupling is believed to be the dominant amplitude limitation mechanism in many types of pulsators such as δ Scuti (Dziembowski and Krolikowska, 1985; Dziembowski et al., 1988) and SPB stars (Lee, 2012). The same limitation mechanism applies to the tidally excited g modes. Unfortunately, relevant studies in this direction are rare.
2.3. Resonance Locking
When the evolution of a mode frequency is in pace with that of the forcing frequency (i.e., their time derivatives are the same), the oscillation mode can be locked into resonance with the orbit. This resonance locking phenomenon can have significant consequences on the orbital evolution of not only stellar binaries, but also satellites of gaseous giant planets (Fuller et al., 2016; Lainey et al., 2020). In the context of heartbeat stars, it can have several observational implications. Firstly, the mode in resonance locking has a larger-than-expected amplitude (i.e., compared to the amplitude from the aforementioned statistical approach). This has been demonstrated for the dominant oscillation mode in the primary star of KIC 8164262 (Fuller et al., 2017; Hambleton et al., 2018). The mode in resonance locking has an orbital harmonic of N = 229 and is likely an m = 1 mode in this misaligned binary. Cheng et al. (2020) found that the oscillation at 53rd orbital harmonic is a possible candidate for resonance locking in KIC 11494130. Resonance locking can significantly enhance the tidal dissipation and orbital evolution (e.g., see Figure 3 in Witte and Savonije, 1999b for a 10M⊙ + 1.4M⊙ binary). For KIC 8164262, Fuller et al. (2017) estimated that the tidal quality factor Q′ is reduced from ≈ 2 × 107 to ≈ 5 × 104 due to the mode in resonance locking. Secondly, it remains to be seen observationally whether the TEOs in resonance locking suffer more from the (weakly) non-linear mode coupling and strong non-linear damping. In fact, the dominant TEO in KOI-54 at 91 times of orbital frequency has multiple daughter pairs, although the resonance-locking nature of this l = 2, m = 0 mode is still under debate. An examination of the resonantly-locked TEO amplitude and phase is desirable. Resonance locking depends on the evolutionary speed of the oscillation mode due to stellar evolution, and thus it is sensitive to the stellar age. A study of the resonance-locking condition spanning from ZAMS to TAMS, and for different orbital parameters would be very useful. The orbital harmonic N of a resonantly locked mode as a limited range and a predictable amplitude, allow for inference about whether resonance locking is occurring (Fuller and Lai, 2012; Burkart et al., 2014; Fuller, 2017).
3. Circular Binaries With Tidally Perturbed Modes
In the circularized and synchronized close binaries, tides do not dynamically excite oscillation modes but rather perturb the propagation cavity and pulsation alignment. The effects of equilibrium tides on stellar oscillations include:
(a) perturbed eigenfrequencies (tidal splitting):
The study of oscillations of tidally distorted polytropes can date back to early work by Chandrasekhar (1969). Other works using polytrope models include Saio (1981), Horedt (2004), Reyniers and Smeyers (2003), and also Roxburgh (unpublished). These works use the perturbative method and concentrate on the perturbing effect on eigenfrequencies. Preece et al. (2019) implemented a different method to calculate the oscillation frequencies of a tidally distorted sub-dwarf B star. It involves performing the surface-averaging of local oscillation frequencies calculated from the local density profile.
Observational work includes Balona (2018), in which he applied the above perturbative theory to KIC 41427686. Tidally perturbed oscillations have been found in U Gru (Bowman et al., 2019b), V453 Cyg (Southworth et al., 2020), VV Ori (Southworth et al., 2021), and RS Cha (Steindl et al., 2021). These are mostly close, nearly circular and synchronous, Algol-like binary systems with self-excited oscillations. In addition, tidally perturbed gravity modes (tidal splittings) have been found in the SPB star π5 Orionis (Jerzykiewicz et al., 2020), and this 3.7-day-binary also shows ellipsoidal variations7.
(b) perturbed eigenfunctions and pulsation alignment.
Recently, tidally tilted binaries have been found which show modulated oscillation amplitude and phase (similar to the oblique roAp pulsators, Kurtz, 1982). The pulsation axis is almost aligned with the tidal axis, and thus pulsation frequencies have side-lobes separated by the orbital frequencies. The first system HD74423, was found by Handler et al. (2020) and was termed a “single-sided pulsator.” Subsequent discoveries include CO Cam by Kurtz et al. (2020) and TIC 63328020 by Rappaport et al. (2021). Fuller et al. (2020) used the more general operator-perturbation method in Dahlen and Tromp (1998) and modeled the stellar response to the static tides by decomposing it into free-oscillation eigenfunctions. Thus, they obtained not only tidally perturbed eigenfrequencies, but also eigenfunctions. It is found that modes can be trapped at the pole, equator, or some intermediate latitude. The amplitude/phase modulation can be modeled and thus be used to as a mode identification method. Springer and Shaviv (2013) studied the propagation and damping of high-frequency acoustic waves in a Roche-lobe filling star.
The above tidal perturbation effect due to equilibrium tide should also work in the case of eccentric orbits, maybe in a different fashion since the tidal deformation is quite different at different orbital phases. In fact, in the eccentric binary KIC 4544587 (Hambleton et al., 2013), in addition to the orbital harmonic g-modes excited by the dynamical tide, p-modes separated by orbital frequency are also present. These modes are interpreted as tidally perturbed p modes. It would be interesting to re-examine this system and study the equilibrium tidal effect on the self-excited oscillations.
4. Oscillating Close Binaries With Mass transfer
4.1. Mass-Accreting Pulsators
In the strong-tide regime when a star fills its Roche lobe, tides induce mass transfer. Depending on the adjustment of the stellar radius and the Roche-lobe radius, the mass transfer can be in the form of stable or unstable Roche-lobe overflow (RLOF) (Vanbeveren and De Loore, 1994; Soberman et al., 1997). Mass transfer affects the evolution of the binary orbit (Dosopoulou and Kalogera, 2016a,b). But the asteroseismic consequences of accretion have not been studied. How does the mixing process modify the excitation of heat-driven pulsations? The κ-mechanism excitation occurs at the near-surface layer where the opacity due to the hydrogen/helium or iron-group elements ionization zones have a local maximum (Unno et al., 1989, chapter 5). In addition, another necessary condition for the driving is that the local thermal timescale has to be comparable to the oscillation period (Pamyatnykh, 1999). Even without material mixing, the accretion may drive the star out of thermal equilibrium, and this may also change the geometric depth of the ionization zone and thus the pulsation excitation and frequencies. If mixing (e.g., thermohaline mixing when a negative chemical composition gradient is present) does happen (Stancliffe and Glebbeek, 2008), the change of composition also needs to be taken into account.
Observationally, many mass-accreting stars do show pulsations. The Oscillating Algol (oEA) systems are a class of δ Scuti/γ Dor pulsators in Algol-type binaries with mass accretion (Mkrtichian et al., 2004, 2020). The companion is usually a low-mass star filling or nearly-filling its Roche lobe, depending on whether the mass transfer process is finished or not. To name a few, AS Eri (Mkrtichian et al., 2004), KIC 4739791 (Lee et al., 2016), KIC 8553788 (Liakos, 2018), V392 Orionis (Hong et al., 2019), KIC 10736223 (Cheng et al., 2020). Guo and Li (2019) found the period spacing pattern of dipole g modes in mass-accreting γ Dor star in KIC 9592855. A comparison with theoretical g-mode period spacings suggests that the mass of this primary star is lower than previously reported. Streamer et al. (2018) did detailed binary star evolution modeling and calculate the pulsation properties of the mass-accreting δ Scuti primary (≈ 2.2M⊙) in TT Hor. They managed to match the observed oscillation frequencies and found a likely evolutionary history for the δ Scuti pulsator. It was initially a 1.3M⊙ star and accreted about 0.9M⊙ from the companion. Accretion-driven variability in oEA binaries has been studied (Mkrtichian et al., 2018) and the Fourier spectrum of accreting δ Scuti pulsators can change during the outburst. Although some of these variabilities may be attributed to the variation of mass transfer rate, the pulsation changes also contribute to the variability. A significant number of Agol-type eclipsing binaries have δ Scuti pulsating components and it seems that many of them show very high-frequency p-modes (~60 d−1), which is a signature of youth and probably the result of rejuvenation from RLOF (Dray and Tout, 2007).
Previous works on how mass-transfer modifies stellar oscillations are scarce. Note that numerous oscillations of mass-accreting white dwarfs (WD) in Cataclysmic Variables (CVs) have been discovered (Mukadam et al., 2007, 2011). Arras et al. (2006) studied the g-mode pulsational instabilities of accreting WDs in CVs. He found that an envelope of solar-like composition (accreted material) on top of the pure-hydrogen layer of the WD can change the edge of the instability strip significantly. During the accretion, outbursts can heat the WD, bringing it out of the instability strip. Similar work to the pulsational instability of other types of opacity-driven pulsators would be interesting.
4.2. Post-mass Transfer Pulsating Binaries
Post-mass transfer binaries with a δ Scuti pulsating component have been discovered, including KIC 10661783 (Southworth et al., 2011; Lehmann et al., 2013), KIC 8262223 (Guo et al., 2017c), and the aforementioned TIC 63328020 (Rappaport et al., 2021). The previous-mass-gainer δ Scuti star in KIC 8262223 pulsates at about 60 d−1, suggesting that the system only just finished the mass transfer, i.e., the effect of rejuvenation is still present. In contrast, KIC 10661783 pulsates at much lower frequencies (15 d−1). This is likely due to the fact that it has finished the mass transfer long ago and the δ Scuti pulsator is already evolved. Similarly, post-mass transfer γ Dor and SPB-type pulsating binaries have also been identified (Matson et al., 2015; Guo et al., 2017b). It is quite clear that δ Scuti and γ Dor type pulsations are not suppressed in close binaries. This is in contrast with red giants in binaries, in which solar-like oscillations seem to be suppressed by binarity, probably due to the enhanced magnetic activity. The majority of the aforementioned binary can be formed in the formation channel of EL CVn binaries8 (Maxted et al., 2013, 2014). The formation involves the evolution of two low-mass stars with stable RLOF and mass reversal (Chen et al., 2017). In Figure 6, we show typical evolutionary tracks of an EL CVn type binary. Staring with two low-mass stars (M1 = 1.35, M2 = 1.15M⊙), the mass gainer can evolve to a δ Scuti/γ Dor pulsator (M = 1.72M⊙) or even an SPB star with slightly changed initial conditions. The mass donor can become a pre-ELM WD (extremely low-mass white dwarf precursor) pulsator (M ≲ 0.2M⊙) with p, or g-mode pulsations (Maxted et al., 2013; Gianninas et al., 2016; Istrate et al., 2016), and possibly later on the WD cooling track, become a g-mode pulsating helium WD. These five types of post-mass transfer pulsators have been marked in Figure 6 as ellipses.
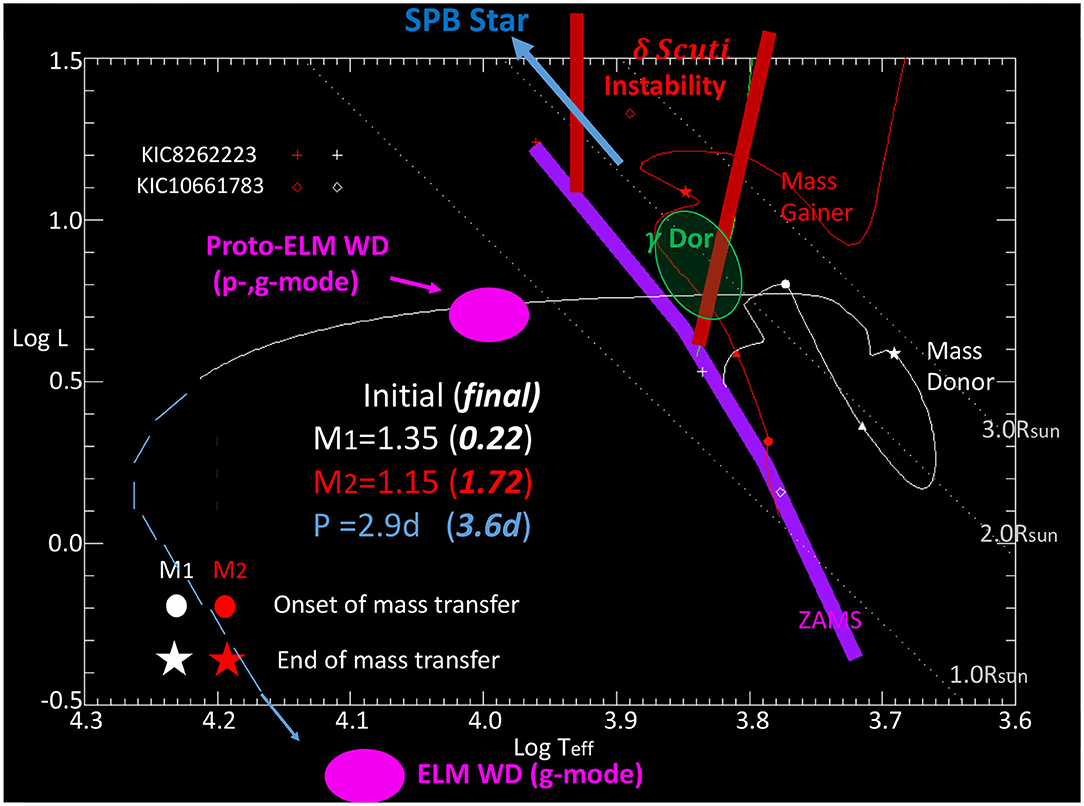
Figure 6. Typical evolutionary tracks for the formation an EL CVn type binary via stable RLOF mass transfer. This binary channel can generate 5 type of pulsating stars: Slowly Pulsating B-stars (SPB), δ Scuti stars (indicated by the red instability strip edges), γ Dor pulsators (green ellipses), Pre-ELM white dwarf, and He white dwarf pulsator (purple ellipses).
Post-mass transfer RR Lyrae and Cepheid pulsators have been found by Pietrzyński et al. (2012) and Pilecki et al. (2017), respectively. Gautschy and Saio (2017) studied the binary evolution channel to form anomalous Cepheids via RLOF and merger-like evolution. Similar work by Karczmarek et al. (2017) found stars crossing the classical instability strip of RR Lyrae and Cepheids via the binary channel. The formation of recently-discovered Blue Large-Amplitude Pulsators (BLAP) also involves binary evolution with mass transfer (Pietrukowicz et al., 2017). Recently, Byrne and Jeffery (2020) studied the non-adiabatic pulsational properties by using the post-mass-transfer stellar models. We also know sub-dwarf B-stars (sdB) and blue stragglers can be formed by mass-transfer or merger (Han et al., 2002, 2003). The list of post-mass transfer pulsators can go on and on. Binary channels can generate all kinds of exotic binary systems (de Loore and Doom, 1992; Hurley et al., 2002; Eggleton, 2006). It can also generate new types of pulsating stars and also contaminate the existing pulsators (Jeffery and Saio, 2016). Pulsational analysis of post-mass transfer systems is still the frontier of asteroseismology, and it holds great promise to improve our understanding on stellar structure and evolution.
5. Discussion and Future Prospects
Detailed analysis of existing Kepler HBs needs to be done on a one-by-one basis. There are also tidal oscillations in binaries that are not identified yet in Kepler data. Gaulme and Guzik (2019) identified KIC 11572363 as an HB with TEOs. They also find some other “tidal pulsators,” and most of them have circular orbits with self-excited modes, probably perturbed by tides. Sekaran et al. (2020) compiled 95 g-mode pulsators in eclipsing binaries. The sample may contain tidally perturbed modes or tidally excited modes. More tidally excited or perturbed oscillations can be obtained from the on-going surveys such as TESS (Ricker et al., 2015), KELT (Pepper et al., 2007), etc.
Willems and Aerts (2002) modeled the radial velocity (RV) variation from tides in an eccentric binary HD177863 with a B-type star component. Arras et al. (2012) predicted the tidally induced RV amplitude in exoplanet hosts. For heartbeat binaries, it was already noted by Welsh et al. (2011) that the radial velocity variations Δvr in KOI-54 show significant non-Gaussian RV residuals after removing the Keplerian orbit. The RV variations due to the equilibrium tide and dynamical tide can be calculated and compared with observations (Bunting and Terquem, 2021). Massive stars can show periastron activities, including non-Keplerian RV variations and line-profile variations (Koenigsberger et al., 2012; Richardson et al., 2017; Koenigsberger and Schmutz, 2020). It is worth a modeling effort although other effects (e.g., stellar wind and magnetic field) are also important in these hot stars. Other types of observation can also reveal the signature of tides, e.g., line profile variations from high-resolution spectroscopy, and spectro-polarimetric observations. In particular, multi-color observations of stellar oscillations are going to gain importance as more space surveys are underway.
The potential of tidal asteroseismology in constraining stellar parameters has not been exploited yet. Fuller et al. (2017) experimented with KIC 8164262 and found small amounts of convective core overshoot and diffusive mixing can yield better agreement with observed TEO amplitude. The convective boundary criterion adopted can also be important (Chernov, 2017). A detailed analysis would involve scanning the large multi-dimensional parameter space. Actually, Burkart et al. (2012) did preliminary asteroseismic modeling of the TEOs in KOI-54 by varying the stellar masses and radii, assuming fixed metallicity and the rotation period. They found that the TEO amplitude sensitively depends on the stellar models, and to match with observations requires a fined-tuned degree of resonance which is very difficult to capture in a grid of stellar models. Even a small difference in stellar models can significantly change the degree of resonance and thus the TEO amplitude. Their final adopted models have Fourier spectra semi-quantitatively consistent with the observations, although they also find that there are many local minima which can produce comparably good fits. Other factors also make tidal seismic modeling challenging, e.g., weak non-linearity of TEOs can set in and detailed mode-coupling calculations may involve many mode-coupling networks (Essick and Weinberg, 2016; Yu et al., 2020).
Convective motion in the core can excite internal gravity waves (Lecoanet and Quataert, 2013; Rogers et al., 2013; Edelmann et al., 2019; Lecoanet et al., 2019). This has have been observed as the low-frequency power excess of OB stars by Bowman et al. (2019a, 2020) (Other interpretation also exists, e.g., arising from the subsurface convection zone, Cantiello et al., 2021). Similarly, tidally excited internal gravity/gravito-inertial waves are also expected to be present in the observed Fourier spectra. It would be interesting to do a similar study of the low-frequency background of the Fourier spectrum and check if there is evidence of tidal origin.
The Rossby (r) modes and inertial modes constitute the very low-frequency part of the tidal response. Global r-modes have been discovered (Van Reeth et al., 2016; Saio et al., 2018; Saio, 2019) in many single γ Dor stars, B-type stars, eclipsing binaries including HBs, and white dwarfs in Cataclysmic Variables. Although r-modes can be heat-driven, the observations seem to favor a mechanical origin since most discoveries are related to fast-rotating systems. Theoretically, tidally excited r-modes can also be present in rotating early-type stars (e.g., see Witte and Savonije, 1999b, Figure 2 for a 10M⊙ example), although an observational confirmation is still awaiting. Recently, indirect evidence of pure inertial modes in the convective core has been discovered from their coupling effect with the dipole g-modes in the radiative envelope of γ Dor stars (Ouazzani et al., 2020; Saio et al., 2021). Observationally, this is inferred from the unexpected dips in the g-mode period spacing pattern which requires computations beyond the traditional approximation for rotation. Pure inertial waves can be induced by tides, similar to the inertial waves in the convective envelope of solar-type stars (Ogilvie and Lin, 2007). Again, the confirmation of theory awaits future observations.
In addition to the tidally excited oscillation, self-excited oscillations may also affect the orbital evolution. In the “inverse-tide” scenario (Fuller, 2021), angular momentum can be transferred from the self-excited modes to the orbit, and this may explain some of the very-slowly rotating convective cores discovered in γ Dor binaries (Guo and Li, 2019; Li et al., 2020a).
Studies on the tidal perturbative effect on the mode properties are still at an early stage, e.g., oscillations of tidally distorted stars are generally limited to simplified stellar models. Also some important factors have not been included. For example, detailed calculations in Fuller et al. (2020) only considered the effect of static tidal distortion on the mode eigenfrequencies and eigenfunctions and ignored the effect of Coriolis force. Close binaries with circular/synchronized orbits are easier to follow up observationally. Their oscillation properties are only studied on a one-by-one basis. Observationally, photometric and spectroscopic surveys are starting to offer a large sample of binary stars. The potential of these stars in constraining the tidal theory is still yet to be fully exploited (Justesen and Albrecht, 2021). With a large sample of various of binaries with pulsations and better theoretical understanding on mode properties, we may begin to perform the binary population synthesis with stellar oscillations included. The studies of stellar oscillations in binaries are, and will continue, revolutionizing the field of stellar astrophysics.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was supported by STFC (grant ST/T00049X/1).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the referees for the pertinent comments and suggestions. ZG is in debt to Gordon Ogilvie for the thorough reading of this article and his enlightening comments, to Phil Arras, Nevin Weinberg, Rich Townsend, and Meng Sun for illuminating discussions on tides. Jim Fuller kindly grants us permission to use his plots in Figure 2. We acknowledge the usage of Kepler data by NASA.
Footnotes
1. ^In some rare cases, pressure modes can also be tidally excited, e.g., in the central red giant star of the triple system HD181068 (Fuller et al., 2013).
2. ^Presented as a poster at the KASOC conference.
3. ^Asteroseismology of pre-Kepler β Cephei stars (since none were observed by Kepler) have a large range in their inferred interior rotation profiles.
4. ^Usually defined so that M2 ≤ M1.
5. ^(if the two components can be resolved in the spectra).
6. ^Although the method is valid, this system is found to be an eccentric binary with TEOs and the application is thus questionable.
7. ^Some of these systems may be slightly out of synchronization, and dynamical tides can also be viable in asynchronous rotating stars in circular orbits.
8. ^EL CVn binary is a type of binary consisting of an F-,A-type dwarf and a low-mass helium white dwarf precursor.
References
Aerts, C. (2021). Probing the interior physics of stars through asteroseismology. Rev. Modern Phys. 93:015001. doi: 10.1103/RevModPhys.93.015001
Aerts, C., Christensen-Dalsgaard, J., and Kurtz, D. W. (2010). Asteroseismology. Heidelberg: Springer. Available online at: https://ui.adsabs.harvard.edu/abs/2010aste.book.A/abstract
Alexander, M. E. (1987). Tidal resonances in binary star systems. Mon. Not. R. Astron. Soc. 227, 843–861. doi: 10.1093/mnras/227.4.843
Alvan, L., Mathis, S., and Decressin, T. (2013). Coupling between internal waves and shear-induced turbulence in stellar radiation zones: the critical layers. Astron. Astrophys. 553:A86. doi: 10.1051/0004-6361/201321210
Anderson, K. R., Lai, D., and Storch, N. I. (2017). Eccentricity and spin-orbit misalignment in short-period stellar binaries as a signpost of hidden tertiary companions. Mon. Not. R. Astron. Soc. 467, 3066–3082. doi: 10.1093/mnras/stx293
Arras, P., Burkart, J., Quataert, E., and Weinberg, N. N. (2012). The radial velocity signature of tides raised in stars hosting exoplanets. Mon. Not. R. Astron. Soc. 422, 1761–1766. doi: 10.1111/j.1365-2966.2012.20756.x
Arras, P., Flanagan, E. E., Morsink, S. M., Schenk, A. K., Teukolsky, S. A., and Wasserman, I. (2003). Saturation of the R-mode instability. Astrophys. J. 591, 1129–1151. doi: 10.1086/374657
Arras, P., Townsley, D. M., and Bildsten, L. (2006). Pulsational instabilities in accreting white dwarfs. Astrophys. J. Lett. 643, L119–L122. doi: 10.1086/505178
Balona, L. A. (2018). The effect of tides on self-driven stellar pulsations. Mon. Not. R. Astron. Soc. 476, 4840–4847. doi: 10.1093/mnras/sty544
Beck, P. G., Hambleton, K., Vos, J., Kallinger, T., Bloemen, S., Tkachenko, A., et al. (2014). Pulsating red giant stars in eccentric binary systems discovered from Kepler space-based photometry. A sample study and the analysis of KIC 5006817. Astron. Astrophys. 564:A36. doi: 10.1051/0004-6361/201322477
Bowman, D. M. (2020). Asteroseismology of high-mass stars: new insights of stellar interiors with space telescopes. Front. Astron. Space Sci. 7:70. doi: 10.3389/fspas.2020.578584
Bowman, D. M., Aerts, C., Johnston, C., Pedersen, M. G., Rogers, T. M., Edelmann, P. V. F., et al. (2019a). Photometric detection of internal gravity waves in upper main-sequence stars. I. Methodology and application to CoRoT targets. Astron. Astrophys. 621:A135. doi: 10.1051/0004-6361/201833662
Bowman, D. M., Burssens, S., Simón-Díaz, S., Edelmann, P. V. F., Rogers, T. M., Horst, L., et al. (2020). Photometric detection of internal gravity waves in upper main-sequence stars. II. Combined TESS photometry and high-resolution spectroscopy. Astron. Astrophys. 640:A36. doi: 10.1051/0004-6361/202038224
Bowman, D. M., Johnston, C., Tkachenko, A., Mkrtichian, D. E., Gunsriwiwat, K., and Aerts, C. (2019b). Discovery of tidally perturbed pulsations in the eclipsing binary U Gru: a crucial system for tidal asteroseismology. Astrophys. J. Lett. 883:L26. doi: 10.3847/2041-8213/ab3fb2
Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., and Holdsworth, D. L. (2016). Amplitude modulation in δSCT stars: statistics from an ensemble study of Kepler targets. Mon. Not. R. Astron. Soc. 460, 1970–1989. doi: 10.1093/mnras/stw1153
Breger, M. (1979). Delta Scuti and related stars. Publ. Astron. Soc. Pac. 91, 5–26. doi: 10.1086/130433
Breger, M., and Montgomery, M. H. (2014). Evidence of resonant mode coupling and the relationship between low and high frequencies in a rapidly rotating a star. Astrophys. J. 783:89. doi: 10.1088/0004-637X/783/2/89
Buchler, J. R., Goupil, M. J., and Hansen, C. J. (1997). On the role of resonances in nonradial pulsators. Astron. Astrophys. 321, 159–176.
Bunting, A., and Terquem, C. (2021). Tidally induced stellar oscillations: converting modelled oscillations excited by hot Jupiters into observables. Mon. Not. R. Astron. Soc. 500, 2711–2731. doi: 10.1093/mnras/staa3394
Burkart, J., Quataert, E., and Arras, P. (2014). Dynamical resonance locking in tidally interacting binary systems. Mon. Not. R. Astron. Soc. 443, 2957–2973. doi: 10.1093/mnras/stu1366
Burkart, J., Quataert, E., Arras, P., and Weinberg, N. N. (2012). Tidal asteroseismology: Kepler's KOI-54. Mon. Not. R. Astron. Soc. 421, 983–1006. doi: 10.1111/j.1365-2966.2011.20344.x
Byrne, C. M., and Jeffery, C. S. (2020). Pulsation in faint blue stars. Mon. Not. R. Astron. Soc. 492, 232–244. doi: 10.1093/mnras/stz3486
Cantiello, M., Lecoanet, D., Jermyn, A. S., and Grassitelli, L. (2021). On the origin of stochastic, low-frequency photometric variability in massive stars. arXiv [e-prints] arXiv:2102.05670
Chandrasekhar, S. (1969). The Silliman Foundation Lectures. New Haven, CT: Yale University Press. Available online at: https://ui.adsabs.harvard.edu/abs/1969efe.book.C/abstract
Chen, X., Maxted, P. F. L., Li, J., and Han, Z. (2017). The formation of EL CVn-type binaries. Mon. Not. R. Astron. Soc. 467, 1874–1889. doi: 10.1093/mnras/stx115
Cheng, S. J., Fuller, J., Guo, Z., Lehman, H., and Hambleton, K. (2020). Detailed characterization of heartbeat stars and their tidally excited oscillations. Astrophys. J. 903:122. doi: 10.3847/1538-4357/abb46d
Chernov, S. V. (2017). Zahn's theory of dynamical tides and its application to stars. Astron. Lett. 43, 429–437. doi: 10.1134/S1063773717060020
Dahlen, F., and Tromp, J. (1998). Theoretical Global Seismology. Princeton, New Jersey: Princeton University Press. doi: 10.1515/9780691216157
de Loore, C. W. H., and Doom, C. D. (1992). Structure and Evolution of Single and Binary Stars, Vol. 179. Boston, MA: Kluwer Academic Publisher. Available online at: https://ui.adsabs.harvard.edu/abs/1992ASSL.179.D/abstract
Degroote, P., Briquet, M., Catala, C., Uytterhoeven, K., Lefever, K., Morel, T., et al. (2009). Evidence for nonlinear resonant mode coupling in the βCephei star HD 180642 (V1449 Aquilae) from CoRoT photometry. Astron. Astrophys. 506, 111–123. doi: 10.1051/0004-6361/200911782
Dimitrov, D. P., Kjurkchieva, D. P., and Iliev, I. K. (2017). Simultaneous solutions of Kepler light curves and radial velocity curves of seven heartbeat variables. Mon. Not. R. Astron. Soc. 469, 2089–2101. doi: 10.1093/mnras/stx745
Dong, S., Katz, B., and Socrates, A. (2013). Exploring a “flow” of highly eccentric binaries with Kepler. Astrophys. J. Lett. 763:L2. doi: 10.1088/2041-8205/763/1/L2
Dosopoulou, F., and Kalogera, V. (2016a). Orbital evolution of mass-transferring eccentric binary systems. I. Phase-dependent evolution. Astrophys. J. 825:70. doi: 10.3847/0004-637X/825/1/70
Dosopoulou, F., and Kalogera, V. (2016b). Orbital evolution of mass-transferring eccentric binary systems. II. Secular evolution. Astrophys. J. 825:71. doi: 10.3847/0004-637X/825/1/71
Dray, L. M., and Tout, C. A. (2007). On rejuvenation in massive binary systems. Mon. Not. R. Astron. Soc. 376, 61–70. doi: 10.1111/j.1365-2966.2007.11431.x
Dziembowski, W. (1982). Nonlinear mode coupling in oscillating stars. I - Second order theory of the coherent mode coupling. Acta Astron. 32, 147–171.
Dziembowski, W., and Krolikowska, M. (1985). Nonlinear mode coupling in oscillating stars. II - Limiting amplitude effect of the parametric resonance in main sequence stars. Acta Astron. 35, 5–28.
Dziembowski, W., Krolikowska, M., and Kosovichev, A. (1988). Nonlinear mode coupling in oscillating stars. III. Amplitude limitingeffect of the rotation in the Delta Scuti stars. Acta Astron. 38, 61–75.
Edelmann, P. V. F., Ratnasingam, R. P., Pedersen, M. G., Bowman, D. M., Prat, V., and Rogers, T. M. (2019). Three-dimensional simulations of massive stars. I. Wave generation and propagation. Astrophys. J. 876:4. doi: 10.3847/1538-4357/ab12df
Eggleton, P. (2006). Evolutionary Processes in Binary and Multiple Stars. Cambridge: Cambridge University Press. Available online at: https://ui.adsabs.harvard.edu/abs/2006epbm.book.E/abstract
Essick, R., and Weinberg, N. N. (2016). Orbital decay of hot jupiters due to nonlinear tidal dissipation within solar-type hosts. Astrophys. J. 816:18. doi: 10.3847/0004-637X/816/1/18
Fuller, J. (2017). Heartbeat stars, tidally excited oscillations and resonance locking. Mon. Not. R. Astron. Soc. 472, 1538–1564. doi: 10.1093/mnras/stx2135
Fuller, J. (2021). Inverse tides in pulsating binary stars. Mon. Not. R. Astron. Soc. 501, 483–490. doi: 10.1093/mnras/staa3636
Fuller, J., Derekas, A., Borkovits, T., Huber, D., Bedding, T. R., and Kiss, L. L. (2013). Tidally induced oscillations and orbital decay in compact triple-star systems. Mon. Not. R. Astron. Soc. 429, 2425–2441. doi: 10.1093/mnras/sts511
Fuller, J., Hambleton, K., Shporer, A., Isaacson, H., and Thompson, S. (2017). Accelerated tidal circularization via resonance locking in KIC 8164262. Mon. Not. R. Astron. Soc. 472, L25–L29. doi: 10.1093/mnrasl/slx130
Fuller, J., Kurtz, D. W., Handler, G., and Rappaport, S. (2020). Tidally trapped pulsations in binary stars. Mon. Not. R. Astron. Soc. 498, 5730–5744. doi: 10.1093/mnras/staa2376
Fuller, J., and Lai, D. (2012). Dynamical tides in eccentric binaries and tidally excited stellar pulsations in Kepler KOI-54. Mon. Not. R. Astron. Soc. 420, 3126–3138. doi: 10.1111/j.1365-2966.2011.20237.x
Fuller, J., Luan, J., and Quataert, E. (2016). Resonance locking as the source of rapid tidal migration in the Jupiter and Saturn moon systems. Mon. Not. R. Astron. Soc. 458, 3867–3879. doi: 10.1093/mnras/stw609
Garcia Lopez, R. J., and Spruit, H. C. (1991). Li depletion in F stars by internal gravity waves. Astrophys. J. 377:268. doi: 10.1086/170356
Gaulme, P., and Guzik, J. A. (2019). Systematic search for stellar pulsators in the eclipsing binaries observed by Kepler. Astron. Astrophys. 630:A106. doi: 10.1051/0004-6361/201935821
Gaulme, P., Jackiewicz, J., Appourchaux, T., and Mosser, B. (2014). Surface activity and oscillation amplitudes of red giants in eclipsing binaries. Astrophys. J. 785:5. doi: 10.1088/0004-637X/785/1/5
Gaulme, P., McKeever, J., Rawls, M. L., Jackiewicz, J., Mosser, B., and Guzik, J. A. (2013). Red giants in eclipsing binary and multiple-star systems: modeling and asteroseismic analysis of 70 candidates from Kepler data. Astrophys. J. 767:82. doi: 10.1088/0004-637X/767/1/82
Gautschy, A., and Saio, H. (2017). On binary channels to anomalous Cepheids. Mon. Not. R. Astron. Soc. 468, 4419–4428. doi: 10.1093/mnras/stx811
Gianninas, A., Curd, B., Fontaine, G., Brown, W. R., and Kilic, M. (2016). Discovery of three pulsating, mixed-atmosphere, extremely low-mass white dwarf precursors. Astrophys. J. Lett. 822:L27. doi: 10.3847/2041-8205/822/2/L27
Goldreich, P., and Nicholson, P. D. (1989). Tidal friction in early-type stars. Astrophys. J. 342:1079. doi: 10.1086/167665
Guo, Z. (2020). Tidal asteroseismology: possible evidence of nonlinear mode coupling in an equilibrium state in Kepler eclipsing binary KIC 3230227. Astrophys. J. 896:161. doi: 10.3847/1538-4357/ab911f
Guo, Z., Fuller, J., Shporer, A., Li, G., Hambleton, K., Manuel, J., et al. (2019). KIC 4142768: an evolved gamma doradus/delta scuti hybrid pulsating eclipsing binary with tidally excited oscillations. Astrophys. J. 885:46. doi: 10.3847/1538-4357/ab41f6
Guo, Z., Gies, D. R., and Fuller, J. (2017a). Tidally induced pulsations in Kepler eclipsing binary KIC 3230227. Astrophys. J. 834:59. doi: 10.3847/1538-4357/834/1/59
Guo, Z., Gies, D. R., and Matson, R. A. (2017b). Gravity modes reveal the internal rotation of a post-mass-transfer gamma Doradus/Delta Scuti hybrid pulsator in Kepler eclipsing binary KIC 9592855. Astrophys. J. 851:39. doi: 10.3847/1538-4357/aa978c
Guo, Z., Gies, D. R., Matson, R. A., García Hernández, A., Han, Z., and Chen, X. (2017c). KIC 8262223: a post-mass transfer eclipsing binary consisting of a delta scuti pulsator and a helium white dwarf precursor. Astrophys. J. 837:114. doi: 10.3847/1538-4357/aa61a4
Guo, Z., and Li, G. (2019). A mass-accreting gamma doradus pulsator with a synchronized core in Kepler eclipsing binary KIC 7385478. Astrophys. J. Lett. 882:L5. doi: 10.3847/2041-8213/ab3a53
Guo, Z., Shporer, A., Hambleton, K., and Isaacson, H. (2020). Tidally excited oscillations in heartbeat binary stars: pulsation phases and mode identification. Astrophys. J. 888:95. doi: 10.3847/1538-4357/ab58c2
Hambleton, K., Fuller, J., Thompson, S., Prša, A., Kurtz, D. W., Shporer, A., et al. (2018). KIC 8164262: a heartbeat star showing tidally induced pulsations with resonant locking. Mon. Not. R. Astron. Soc. 473, 5165–5176. doi: 10.1093/mnras/stx2673
Hambleton, K., Kurtz, D. W., Prša, A., Quinn, S. N., Fuller, J., Murphy, S. J., et al. (2016). KIC 3749404: a heartbeat star with rapid apsidal advance indicative of a tertiary component. Mon. Not. R. Astron. Soc. 463, 1199–1212. doi: 10.1093/mnras/stw1970
Hambleton, K. M., Kurtz, D. W., Prša, A., Guzik, J. A., Pavlovski, K., Bloemen, S., et al. (2013). KIC 4544587: an eccentric, short-period binary system with δSct pulsations and tidally excited modes. Mon. Not. R. Astron. Soc. 434, 925–940. doi: 10.1093/mnras/stt886
Han, Z., Podsiadlowski, P., Maxted, P. F. L., and Marsh, T. R. (2003). The origin of subdwarf B stars - II. Mon. Not. R. Astron. Soc. 341, 669–691. doi: 10.1046/j.1365-8711.2003.06451.x
Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., and Ivanova, N. (2002). The origin of subdwarf B stars - I. The formation channels. Mon. Not. R. Astron. Soc. 336, 449–466. doi: 10.1046/j.1365-8711.2002.05752.x
Handler, G., Balona, L. A., Shobbrook, R. R., Koen, C., Bruch, A., Romero-Colmenero, E., et al. (2002). Discovery and analysis of p-mode and g-mode oscillations in the A-type primary of the eccentric binary HD 209295*. Mon. Not. R. Astron. Soc. 333, 262–279. doi: 10.1046/j.1365-8711.2002.05295.x
Handler, G., Kurtz, D. W., Rappaport, S. A., Saio, H., Fuller, J., Jones, D., et al. (2020). Tidally trapped pulsations in a close binary star system discovered by TESS. Nat. Astron. 4, 684–689. doi: 10.1038/s41550-020-1035-1
Hong, K., Lee, J. W., Koo, J.-R., Park, J.-H., Kim, S.-L., Rittipruk, P., et al. (2019). Time-series spectroscopy of the oscillating eclipsing algol system V392 orionis. Astron. J. 157:28. doi: 10.3847/1538-3881/aaf39f
Horedt, G. P. (2004). Polytropes - Applications in Astrophysics and Related Fields, Vol. 306. Dordrecht; Wessling: Deutsches Zentrum für Luft- und Raumfahrt DLR; Kluwer Academic Publishers. Available online at: https://ui.adsabs.harvard.edu/abs/2004ASSL.306.H/abstract
Horst, L., Edelmann, P. V. F., Andrássy, R., Röpke, F. K., Bowman, D. M., Aerts, C., et al. (2020). Fully compressible simulations of waves and core convection in main-sequence stars. Astron. Astrophys. 641:A18. doi: 10.1051/0004-6361/202037531
Hurley, J. R., Tout, C. A., and Pols, O. R. (2002). Evolution of binary stars and the effect of tides on binary populations. Mon. Not. R. Astron. Soc. 329, 897–928. doi: 10.1046/j.1365-8711.2002.05038.x
Istrate, A. G., Fontaine, G., Gianninas, A., Grassitelli, L., Marchant, P., Tauris, T. M., et al. (2016). Asteroseismic test of rotational mixing in low-mass white dwarfs. Astron. Astrophys. 595:L12. doi: 10.1051/0004-6361/201629876
Jayasinghe, T., Stanek, K. Z., Kochanek, C. S., Thompson, T. A., Shappee, B. J., and Fausnaugh, M. (2019). An extreme amplitude, massive heartbeat system in the LMC characterized using ASAS-SN and TESS. Mon. Not. R. Astron. Soc. 489, 4705–4711. doi: 10.1093/mnras/stz2460
Jeffery, C. S., and Saio, H. (2016). Radial pulsation as a function of hydrogen abundance. Mon. Not. R. Astron. Soc. 458, 1352–1373. doi: 10.1093/mnras/stw388
Jerzykiewicz, M., Pigulski, A., Handler, G., Moffat, A. F. J., Popowicz, A., Wade, G. A., et al. (2020). BRITE-Constellation photometry of π5 Orionis, an ellipsoidal SPB variable. Mon. Not. R. Astron. Soc. 496, 2391–2401. doi: 10.1093/mnras/staa1665
Justesen, A. B., and Albrecht, S. (2021). Temperature and distance dependence of tidal circularization in close binaries: a catalog of eclipsing binaries in the southern hemisphere observed by the TESS satellite. arXiv [e-prints] arXiv:2103.09216.
Kallinger, T., Weiss, W. W., Beck, P. G., Pigulski, A., Kuschnig, R., Tkachenko, A., et al. (2017). Triple system HD 201433 with a SPB star component seen by BRITE - Constellation: pulsation, differential rotation, and angular momentum transfer. Astron. Astrophys. 603:A13. doi: 10.1051/0004-6361/201730625
Karczmarek, P., Wiktorowicz, G., Iłkiewicz, K., Smolec, R., Stepień, K., Pietrzyński, G., et al. (2017). The occurrence of binary evolution pulsators in classical instability strip of RR Lyrae and Cepheid variables. Mon. Not. R. Astron. Soc. 466, 2842–2854. doi: 10.1093/mnras/stw3286
Kirk, B., Conroy, K., Prša, A., Abdul-Masih, M., Kochoska, A., Matijevič, G., et al. (2016). Kepler eclipsing binary stars. VII. The catalog of eclipsing binaries found in the entire Kepler data set. Astron. J. 151:68. doi: 10.3847/0004-6256/151/3/68
Kjurkchieva, D., Vasileva, D., and Dimitrov, D. (2016). Light curve solutions of 12 eccentric Kepler binaries and analysis of their out-of-eclipse variability. Astron. J. 152:189. doi: 10.3847/0004-6256/152/6/189
Koenigsberger, G., Moreno, E., and Harrington, D. M. (2012). Tidal effects on the radial velocity curve of HD 77581 (Vela X-1). Astron. Astrophys. 539:A84. doi: 10.1051/0004-6361/201118397
Koenigsberger, G., and Schmutz, W. (2020). The nature of the companion in the Wolf-Rayet system EZ Canis Majoris. Astron. Astrophys. 639:A18. doi: 10.1051/0004-6361/201937305
Kołaczek-Szymański, P. A., Pigulski, A., Michalska, G., Moździerski, D., and Różański, T. (2020). Massive heartbeat stars from TESS. I. TESS sectors 1-16. arXiv e-prints. arXiv:2012.11559. doi: 10.1051/0004-6361/202039553
Kozai, Y. (1962). Secular perturbations of asteroids with high inclination and eccentricity. Astron. J. 67, 591–598. doi: 10.1086/108790
Kurtz, D. W. (1982). Rapidly oscillating AP stars. Mon. Not. R. Astron. Soc. 200, 807–859. doi: 10.1093/mnras/200.3.807
Kurtz, D. W., Handler, G., Rappaport, S. A., Saio, H., Fuller, J., Jacobs, T., et al. (2020). The single-sided pulsator CO Camelopardalis. Mon. Not. R. Astron. Soc. 494, 5118–5133. doi: 10.1093/mnras/staa989
Kuszlewicz, J. S., North, T. S. H., Chaplin, W. J., Bieryla, A., Latham, D. W., Miglio, A., et al. (2019). KOI-3890: a high-mass-ratio asteroseismic red giant+M-dwarf eclipsing binary undergoing heartbeat tidal interactions. Mon. Not. R. Astron. Soc. 487, 14–23. doi: 10.1093/mnras/stz1185
Lai, D. (1997). Dynamical tides in rotating binary stars. Astrophys. J. 490, 847–862. doi: 10.1086/304899
Lai, D., Rasio, F. A., and Shapiro, S. L. (1993). Collisions and close encounters between massive main-sequence stars. Astrophys. J. 412:593. doi: 10.1086/172946
Lainey, V., Casajus, L. G., Fuller, J., Zannoni, M., Tortora, P., Cooper, N., et al. (2020). Resonance locking in giant planets indicated by the rapid orbital expansion of Titan. Nat. Astron. 4, 1053–1058. doi: 10.1038/s41550-020-1120-5
Lecoanet, D., Cantiello, M., Quataert, E., Couston, L.-A., Burns, K. J., Pope, B. J. S., et al. (2019). Low-frequency variability in massive stars: core generation or surface phenomenon? Astrophys. J. Lett. 886:L15. doi: 10.3847/2041-8213/ab5446
Lecoanet, D., and Quataert, E. (2013). Internal gravity wave excitation by turbulent convection. Mon. Not. R. Astron. Soc. 430, 2363–2376. doi: 10.1093/mnras/stt055
Lee, J. W., Kim, S.-L., Hong, K., Koo, J.-R., Lee, C.-U., and Youn, J.-H. (2016). KIC 4739791: a new R CMa-type eclipsing binary with a pulsating component. Astron. J. 151:25. doi: 10.3847/0004-6256/151/2/25
Lee, U. (2012). Amplitudes of low-frequency modes in rotating B-type stars. Mon. Not. R. Astron. Soc. 420, 2387–2398. doi: 10.1111/j.1365-2966.2011.20204.x
Lehmann, H., Southworth, J., Tkachenko, A., and Pavlovski, K. (2013). Physical properties of the eclipsing δScuti star KIC 10661783. Astron. Astrophys. 557:A79. doi: 10.1051/0004-6361/201321400
Li, G., Guo, Z., Fuller, J., Bedding, T. R., Murphy, S. J., Colman, I. L., et al. (2020a). The effect of tides on near-core rotation: analysis of 35 Kepler γDoradus stars in eclipsing and spectroscopic binaries. Mon. Not. R. Astron. Soc. 497, 4363–4375. doi: 10.1093/mnras/staa2266
Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., Antoci, V., Ouazzani, R.-M., et al. (2020b). Gravity-mode period spacings and near-core rotation rates of 611 γDoradus stars with Kepler. Mon. Not. R. Astron. Soc. 491, 3586–3605. doi: 10.1093/mnras/stz2906
Liakos, A. (2018). KIC 8553788: A pulsating Algol with an extreme mass ratio. Astron. Astrophys. 616:A130. doi: 10.1051/0004-6361/201832639
Lidov, M. L. (1962). The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 9, 719–759. doi: 10.1016/0032-0633(62)90129-0
Loeb, A., and Gaudi, B. S. (2003). Periodic flux variability of stars due to the reflex doppler effect induced by planetary companions. Astrophys. J. Lett. 588, L117–L120. doi: 10.1086/375551
Luan, J., and Goldreich, P. (2018). DAVs: red edge and outbursts. Astrophys. J. 863:82. doi: 10.3847/1538-4357/aad0f4
Mathis, S. (2009). Transport by gravito-inertial waves in differentially rotating stellar radiation zones. I - Theoretical formulation. Astron. Astrophys. 506, 811–828. doi: 10.1051/0004-6361/200810544
Matson, R. A., Gies, D. R., Guo, Z., Quinn, S. N., Buchhave, L. A., Latham, D. W., et al. (2015). HST/COS detection of the spectrum of the subdwarf companion of KOI-81. Astrophys. J. 806:155. doi: 10.1088/0004-637X/806/2/155
Maxted, P. F. L., Bloemen, S., Heber, U., Geier, S., Wheatley, P. J., Marsh, T. R., et al. (2014). EL CVn-type binaries - discovery of 17 helium white dwarf precursors in bright eclipsing binary star systems. Mon. Not. R. Astron. Soc. 437, 1681–1697. doi: 10.1093/mnras/stt2007
Maxted, P. F. L., Serenelli, A. M., Miglio, A., Marsh, T. R., Heber, U., Dhillon, V. S., et al. (2013). Multi-periodic pulsations of a stripped red-giant star in an eclipsing binary system. Nature 498, 463–465. doi: 10.1038/nature12192
Mkrtichian, D., Gunsriwiwat, K., Engelbrecht, C., A-thano, N., Lehmann, H., Lampens, P., et al. (2020). “The pulsation spectrum of a mass-accreting component of AS Eri,” in Stars and their Variability Observed from Space, eds C. Neiner, W. W. Weiss, D. Baade, R. E. Griffin, and C. C. Lovekin, and A. F. J. Moffat, 113–114. Available online at: https://ui.adsabs.harvard.edu/abs/2020svos.conf.113M/abstract
Mkrtichian, D. E., Kusakin, A. V., Rodriguez, E., Gamarova, A. Y., Kim, C., Kim, S. L., et al. (2004). Frequency spectrum of the rapidly-oscillating mass-accreting component of the Algol-type system AS Eri. Astron. Astrophys. 419, 1015–1024. doi: 10.1051/0004-6361:20040095
Mkrtichian, D. E., Lehmann, H., Rodríguez, E., Olson, E., Kim, S. L., Kusakin, A. V., et al. (2018). The eclipsing binary star RZ Cas: accretion-driven variability of the multimode oscillation spectrum. Mon. Not. R. Astron. Soc. 475, 4745–4767. doi: 10.1093/mnras/stx2841
Moe, M., and Di Stefano, R. (2017). Mind your Ps and Qs: the interrelation between period (P) and mass-ratio (Q) distributions of binary stars. Astrophys. J. Suppl. Ser. 230:15. doi: 10.3847/1538-4365/aa6fb6
Moskalik, P. (1985). Modulation of amplitudes in oscillating stars due to resonant mode coupling. Acta Astron. 35, 229–254.
Mukadam, A. S., Gänsicke, B. T., Szkody, P., Aungwerojwit, A., Howell, S. B., Fraser, O. J., et al. (2007). Discovery of two new accreting pulsating white dwarf stars. Astrophys. J. 667, 433–441. doi: 10.1086/520700
Mukadam, A. S., Townsley, D. M., Szkody, P., Gänsicke, B. T., Winget, D. E., Hermes, J. J., et al. (2011). First unambiguous detection of the return of pulsations in the accreting white dwarf SDSS J074531.92+453829.6 after an outburst. Astrophys. J. Lett. 728:L33. doi: 10.1088/2041-8205/728/2/L33
Naoz, S. (2016). The eccentric Kozai-Lidov effect and its applications. Annu. Rev. Astron. Astrophys. 54, 441–489. doi: 10.1146/annurev-astro-081915-023315
Nicholls, C. P., and Wood, P. R. (2012). Eccentric ellipsoidal red giant binaries in the LMC: complete orbital solutions and comments on interaction at periastron. Mon. Not. R. Astron. Soc. 421, 2616–2628. doi: 10.1111/j.1365-2966.2012.20492.x
Ogilvie, G. I. (2014). Tidal dissipation in stars and giant planets. Annu. Rev. Astron. Astrophys. 52, 171–210. doi: 10.1146/annurev-astro-081913-035941
Ogilvie, G. I., and Lin, D. N. C. (2007). Tidal dissipation in rotating solar-type stars. Astrophys. J. 661, 1180–1191. doi: 10.1086/515435
O'Leary, R. M., and Burkart, J. (2014). It takes a village to raise a tide: non-linear multiple-mode coupling and mode identification in KOI-54. Mon. Not. R. Astron. Soc. 440, 3036–3050. doi: 10.1093/mnras/stu335
Ouazzani, R. M., Ligniéres, F., Dupret, M. A., Salmon, S. J. A. J., Ballot, J., Christophe, S., et al. (2020). First evidence of inertial modes in γDoradus stars: the core rotation revealed. Astron. Astrophys. 640:A49. doi: 10.1051/0004-6361/201936653
Pablo, H., Richardson, N. D., Fuller, J., Rowe, J., Moffat, A. F. J., Kuschnig, R., et al. (2017). The most massive heartbeat: an in-depth analysis of ıOrionis. Mon. Not. R. Astron. Soc. 467, 2494–2503. doi: 10.1093/mnras/stx207
Pamyatnykh, A. A. (1999). Pulsational instability domains in the upper main sequence. Acta Astron. 49, 119–148.
Papaloizou, J. C. B., and Savonije, G. J. (1997). Non-adiabatic tidal forcing of a massive, uniformly rotating star - III. Asymptotic treatment for low frequencies in the inertial regime. Mon. Not. R. Astron. Soc. 291, 651–657. doi: 10.1093/mnras/291.4.651
Pápics, P. I., Tkachenko, A., Van Reeth, T., Aerts, C., Moravveji, E., Van de Sande, M., et al. (2017). Signatures of internal rotation discovered in the Kepler data of five slowly pulsating B stars. Astron. Astrophys. 598:A74. doi: 10.1051/0004-6361/201629814
Pepper, J., Pogge, R. W., DePoy, D. L., Marshall, J. L., Stanek, K. Z., Stutz, A. M., et al. (2007). The Kilodegree Extremely Little Telescope (KELT): a small robotic telescope for large-area synoptic surveys. Publ. Astron. Soc. Pac. 119, 923–935. doi: 10.1086/521836
Pietrukowicz, P., Dziembowski, W. A., Latour, M., Angeloni, R., Poleski, R., di Mille, F., et al. (2017). Blue large-amplitude pulsators as a new class of variable stars. Nat. Astron. 1:0166. doi: 10.1038/s41550-017-0166
Pietrzyński, G., Thompson, I. B., Gieren, W., Graczyk, D., Stepień, K., Bono, G., et al. (2012). RR-Lyrae-type pulsations from a 0.26-solar-mass star in a binary system. Nature 484, 75–77. doi: 10.1038/nature10966
Pilecki, B., Gieren, W., Smolec, R., Pietrzyński, G., Thompson, I. B., Anderson, R. I., et al. (2017). Mass and p-factor of the Type II Cepheid OGLE-LMC-T2CEP-098 in a binary system. Astrophys. J. 842:110. doi: 10.3847/1538-4357/aa6ff7
Prat, V., Ligniéres, F., and Ballot, J. (2016). Asymptotic theory of gravity modes in rotating stars. I. Ray dynamics. Astron. Astrophys. 587:A110. doi: 10.1051/0004-6361/201527737
Preece, H. P., Jeffery, C. S., and Tout, C. A. (2019). Asteroseismology of tidally distorted sdB stars. Mon. Not. R. Astron. Soc. 489, 3066–3072. doi: 10.1093/mnras/stz2292
Press W. H. (1981). Radiative and other effects from internal waves in solar and stellar interiors. Astrophys. J. 245, 286–303. doi: 10.1086/158809
Prša, A., and Zwitter, T. (2005). A computational guide to physics of eclipsing binaries. I. Demonstrations and perspectives. Astrophys. J. 628, 426–438. doi: 10.1086/430591
Raghavan, D., McAlister, H. A., Henry, T. J., Latham, D. W., Marcy, G. W., Mason, B. D., et al. (2010). A survey of stellar families: multiplicity of solar-type stars. Astrophys. J. Suppl. Ser. 190, 1–42. doi: 10.1088/0067-0049/190/1/1
Rappaport, S. A., Kurtz, D. W., Handler, G., Jones, D., Nelson, L. A., Saio, H., et al. (2021). A tidally tilted sectoral dipole pulsation mode in the eclipsing binary TIC 63328020. Mon. Not. R. Astron. Soc. 503, 254–269. doi: 10.1093/mnras/stab336
Ratnasingam, R. P., Edelmann, P. V. F., and Rogers, T. M. (2019). Onset of non-linear internal gravity waves in intermediate-mass stars. Mon. Not. R. Astron. Soc. 482, 5500–5512. doi: 10.1093/mnras/sty3086
Remus, F., Mathis, S., and Zahn, J. P. (2012). The equilibrium tide in stars and giant planets. I. The coplanar case. Astron. Astrophys. 544:A132. doi: 10.1051/0004-6361/201118160
Reyniers, K., and Smeyers, P. (2003). Tidal perturbations of linear, isentropic oscillations in components of circular-orbit close binaries. I. Synchronously rotating components. Astron. Astrophys. 404, 1051–1065. doi: 10.1051/0004-6361:20030501
Richardson, N. D., Pablo, H., Sterken, C., Pigulski, A., Koenigsberger, G., Moffat, A. F. J., et al. (2018). BRITE-Constellation reveals evidence for pulsations in the enigmatic binary ηCarinae. Mon. Not. R. Astron. Soc. 475, 5417–5423. doi: 10.1093/mnras/sty157
Richardson, N. D., Russell, C. M. P., St-Jean, L., Moffat, A. F. J., St-Louis, N., Shenar, T., et al. (2017). The variability of the BRITE-est Wolf-Rayet binary, γ2 Velorum-I. Photometric and spectroscopic evidence for colliding winds. Mon. Not. R. Astron. Soc. 471, 2715–2729. doi: 10.1093/mnras/stx1731
Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2015). Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 1:014003. doi: 10.1117/1.JATIS.1.1.014003
Rodríguez, E., López-González, M. J., and López de Coca, P. (2000). A revised catalogue of delta Sct stars. Astron. Astrophys. Suppl. Ser. 144, 469–474. doi: 10.1051/aas:2000221
Rogers, T. M., Lin, D. N. C., McElwaine, J. N., and Lau, H. H. B. (2013). Internal gravity waves in massive stars: angular momentum transport. Astrophys. J. 772:21. doi: 10.1088/0004-637X/772/1/21
Rüdiger, G., Gellert, M., Spada, F., and Tereshin, I. (2015). The angular momentum transport by unstable toroidal magnetic fields. Astron. Astrophys. 573:A80. doi: 10.1051/0004-6361/201424060
Saio, H. (1981). Rotational and tidal perturbations of nonradial oscillations in polytropic star. Astrophys. J. 244, 299–315. doi: 10.1086/158708
Saio, H. (2019). R-mode oscillations in accreting white dwarfs in cataclysmic variables. Mon. Not. R. Astron. Soc. 487, 2177–2190. doi: 10.1093/mnras/stz1407
Saio, H. (2020). “R-mode oscillations in eclipsing binaries,” in Proceedings of the Conference Stars and their Variability Observed from Space, eds C. Neiner, W. W. Weiss, D. Baade, R. E. Griffin, C. C. Lovekin, A. F. J. Moffat (Vienna: University of Vienna), 321–324. Available online at: https://ui.adsabs.harvard.edu/abs/2020svos.conf.321S/abstract
Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., and Lee, U. (2018). Theory and evidence of global Rossby waves in upper main-sequence stars: r-mode oscillations in many Kepler stars. Mon. Not. R. Astron. Soc. 474, 2774–2786. doi: 10.1093/mnras/stx2962
Saio, H., Takata, M., Lee, U., Li, G., and Van Reeth, T. (2021). Rotation of the convective core in γDor stars measured by dips in period spacings of g modes coupled with inertial modes. Mon. Not. R. Astron. Soc. 502, 5856–5874. doi: 10.1093/mnras/stab482
Savonije, G. J., and Papaloizou, J. C. B. (1997). Non-adiabatic tidal forcing of a massive, uniformly rotating star - II. The low-frequency, inertial regime. Mon. Not. R. Astron. Soc. 291, 633–650. doi: 10.1093/mnras/291.4.633
Savonije, G. J., Papaloizou, J. C. B., and Alberts, F. (1995). Nonadiabatic tidal forcing of a massive uniformly rotating star. Mon. Not. R. Astron. Soc. 277:471. doi: 10.1093/mnras/277.2.471
Schenk, A. K., Arras, P., Flanagan, É. É., Teukolsky, S. A., and Wasserman, I. (2002). Nonlinear mode coupling in rotating stars and the r-mode instability in neutron stars. Phys. Rev. D 65:024001. doi: 10.1103/PhysRevD.65.024001
Sekaran, S., Tkachenko, A., Abdul-Masih, M., Prša, A., Johnston, C., Huber, D., et al. (2020). Tango of celestial dancers: A sample of detached eclipsing binary systems containing g-mode pulsating components. A case study of KIC9850387. Astron. Astrophys. 643:A162. doi: 10.1051/0004-6361/202038989
Sepinsky, J. F., Willems, B., and Kalogera, V. (2007). Equipotential surfaces and lagrangian points in nonsynchronous, eccentric binary and planetary systems. Astrophys. J. 660, 1624–1635. doi: 10.1086/513736
Shporer, A., Fuller, J., Isaacson, H., Hambleton, K., Thompson, S. E., Prša, A., et al. (2016). Radial velocity monitoring of Kepler heartbeat stars. Astrophys. J. 829:34. doi: 10.3847/0004-637X/829/1/34
Smullen, R. A., and Kobulnicky, H. A. (2015). Heartbeat stars: spectroscopic orbital solutions for six eccentric binary systems. Astrophys. J. 808:166. doi: 10.1088/0004-637X/808/2/166
Soberman, G. E., Phinney, E. S., and van den Heuvel, E. P. J. (1997). Stability criteria for mass transfer in binary stellar evolution. Astron. Astrophys. 327, 620–635.
Southworth, J., Bowman, D. M., and Pavlovski, K. (2021). A βCephei pulsator and a changing orbital inclination in the high-mass eclipsing binary system VV Orionis. Mon. Not. R. Astron. Soc. 501, L65–L70. doi: 10.1093/mnrasl/slaa197
Southworth, J., Bowman, D. M., Tkachenko, A., and Pavlovski, K. (2020). Discovery of βCep pulsations in the eclipsing binary V453 Cygni. Mon. Not. R. Astron. Soc. 497, L19–L23. doi: 10.1093/mnrasl/slaa091
Southworth, J., Zima, W., Aerts, C., Bruntt, H., Lehmann, H., Kim, S. L., et al. (2011). Kepler photometry of KIC 10661783: a binary star with total eclipses and δScuti pulsations. Mon. Not. R. Astron. Soc. 414, 2413–2423. doi: 10.1111/j.1365-2966.2011.18559.x
Springer, O. M., and Shaviv, N. J. (2013). Asteroseismic effects in close binary stars. Mon. Not. R. Astron. Soc. 434, 1869–1882. doi: 10.1093/mnras/stt1041
Stancliffe, R. J., and Glebbeek, E. (2008). Thermohaline mixing and gravitational settling in carbon-enhanced metal-poor stars. Mon. Not. R. Astron. Soc. 389, 1828–1838. doi: 10.1111/j.1365-2966.2008.13700.x
Steindl, T., Zwintz, K., and Bowman, D. M. (2021). Tidally perturbed pulsations in the pre-main sequence δScuti binary RS Cha. Astron. Astrophys. 645:A119. doi: 10.1051/0004-6361/202039093
Streamer, M., Ireland, M. J., Murphy, S. J., and Bento, J. (2018). A window into δSct stellar interiors: understanding the eclipsing binary system TT Hor. Mon. Not. R. Astron. Soc. 480, 1372–1383. doi: 10.1093/mnras/sty1881
Su, Y., Lecoanet, D., and Lai, D. (2020). Physics of tidal dissipation in early-type stars and white dwarfs: hydrodynamical simulations of internal gravity wave breaking in stellar envelopes. Mon. Not. R. Astron. Soc. 495, 1239–1251. doi: 10.1093/mnras/staa1306
Thompson, S. E., Everett, M., Mullally, F., Barclay, T., Howell, S. B., Still, M., et al. (2012). A class of eccentric binaries with dynamic tidal distortions discovered with Kepler. Astrophys. J. 753:86. doi: 10.1088/0004-637X/753/1/86
Townsend, R. H. D., Goldstein, J., and Zweibel, E. G. (2018). Angular momentum transport by heat-driven g-modes in slowly pulsating B stars. Mon. Not. R. Astron. Soc. 475, 879–893. doi: 10.1093/mnras/stx3142
Tubbesing, S., Kaufer, A., Stahl, O., Wolf, B., Schmid, H. M., Korn, A. J., et al. (2002). The eclipsing hypergiant R 81 (B2.5Ia-O) in the Large Magellanic Cloud. System properties from spectroscopic and photometric monitoring. Astron. Astrophys. 389, 931–944. doi: 10.1051/0004-6361:20020682
Unno, W., Osaki, Y., Ando, H., Saio, H., and Shibahashi, H. (1989). Nonradial Oscillations of Stars, 2nd Edn. Tokyo: Tokyo Univ. Press). Available online at: https://ui.adsabs.harvard.edu/abs/1989nos.book.U/abstract
Van Hoolst, T. (1994). Coupled-mode equations and amplitude equations for nonadiabatic, nonradial oscillations of stars. Astron. Astrophys. 292, 471–480.
van Kerkwijk, M. H., Rappaport, S. A., Breton, R. P., Justham, S., Podsiadlowski, P., and Han, Z. (2010). Observations of doppler boosting in Kepler light curves. Astrophys. J. 715, 51–58. doi: 10.1088/0004-637X/715/1/51
Van Reeth, T., Tkachenko, A., and Aerts, C. (2016). Interior rotation of a sample of γDoradus stars from ensemble modelling of their gravity-mode period spacings. Astron. Astrophys. 593:A120. doi: 10.1051/0004-6361/201628616
Vanbeveren, D., and De Loore, C. (1994). The evolution of the mass gainer in massive close binaries. Astron. Astrophys. 290, 129–132. doi: 10.1007/978-94-011-1080-8
Weinberg, N. N., Arras, P., Quataert, E., and Burkart, J. (2012). Nonlinear tides in close binary systems. Astrophys. J. 751:136. doi: 10.1088/0004-637X/751/2/136
Welsh, W. F., Orosz, J. A., Aerts, C., Brown, T. M., Brugamyer, E., Cochran, W. D., et al. (2011). KOI-54: the Kepler discovery of tidally excited pulsations and brightenings in a highly eccentric binary. Astrophys. J. Suppl. Ser. 197:4. doi: 10.1088/0067-0049/197/1/4
Wersinger, J.-M., Finn, J., and Ott, E. (1980). Bifurcation and “strange” behavior in instability saturation by nonlinear three-wave mode coupling. Phys. Fluids 23, 1142–1154. doi: 10.1063/1.863116
Willems, B. (2003). Excitation of oscillation modes by tides in close binaries: constraints on stellar and orbital parameters. Mon. Not. R. Astron. Soc. 346, 968–976. doi: 10.1111/j.1365-2966.2003.07151.x
Willems, B., and Aerts, C. (2002). Tidally induced radial-velocity variations in close binaries. Astron. Astrophys. 384, 441–451. doi: 10.1051/0004-6361:20020021
Wilson, R. E., and Devinney, E. J. (1971). Realization of accurate close-binary light curves: application to MR Cygni. Astrophys. J. 166:605. doi: 10.1086/150986
Witte, M. G., and Savonije, G. J. (1999a). The dynamical tide in a rotating 10 Msun main sequence star. A study of G- and R-mode resonances. Astron. Astrophys. 341, 842–852.
Witte, M. G., and Savonije, G. J. (1999b). Tidal evolution of eccentric orbits in massive binary systems. A study of resonance locking. Astron. Astrophys. 350, 129–147.
Wu, Y., and Goldreich, P. (2001). Gravity modes in ZZ Ceti stars. IV. Amplitude saturation by parametric instability. Astrophys. J. 546, 469–483. doi: 10.1086/318234
Yu, H., Weinberg, N. N., and Fuller, J. (2020). Non-linear dynamical tides in white dwarf binaries. Mon. Not. R. Astron. Soc. 496, 5482–5502. doi: 10.1093/mnras/staa1858
Zahn, J. P. (1977). Reprint of 1977A&A.57.383Z. Tidal friction in close binary stars. Astron. Astrophys. 500, 121–132.
Zahn, J. P., Talon, S., and Matias, J. (1997). Angular momentum transport by internal waves in the solar interior. Astron. Astrophys. 322, 320–328.
Zimmerman, M. K., Thompson, S. E., Mullally, F., Fuller, J., Shporer, A., and Hambleton, K. (2017). The pseudosynchronization of binary stars undergoing strong tidal interactions. Astrophys. J. 846:147. doi: 10.3847/1538-4357/aa85e3
Zong, W., Charpinet, S., and Vauclair, G. (2016a). Signatures of nonlinear mode interactions in the pulsating hot B subdwarf star KIC 10139564. Astron. Astrophys. 594:A46. doi: 10.1051/0004-6361/201629132
Zong, W., Charpinet, S., Vauclair, G., Giammichele, N., and Van Grootel, V. (2016b). Amplitude and frequency variations of oscillation modes in the pulsating DB white dwarf star KIC 08626021. The likely signature of nonlinear resonant mode coupling. Astron. Astrophys. 585:A22. doi: 10.1051/0004-6361/201526300
Keywords: stars early-type, evolution, oscillations, stars: binaries, asteroseismology
Citation: Guo Z (2021) Asteroseismology of Close Binary Stars: Tides and Mass Transfer. Front. Astron. Space Sci. 8:663026. doi: 10.3389/fspas.2021.663026
Received: 02 February 2021; Accepted: 06 April 2021;
Published: 14 May 2021.
Edited by:
Andrzej S. Baran, Pedagogical University of Kraków, PolandReviewed by:
Jim Fuller, California Institute of Technology, United StatesDominic Bowman, KU Leuven, Belgium
Copyright © 2021 Guo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhao Guo, emcyODFAY2FtLmFjLnVr
 Zhao Guo
Zhao Guo