MagneToRE: Mapping the 3-D Magnetic Structure of the Solar Wind Using a Large Constellation of Nanosatellites

1 Introduction

1.1 Mission Motivation

The interplanetary magnetic field (IMF) emerges from the Sun and extends throughout the heliosphere (Parker, 1958). It plays a fundamental role in initially heating and accelerating the solar wind and continues to shape the dynamics of the expanding plasma. It propagates energy through linear and nonlinear dynamical couplings, participates in energy transfer and conversion across scales, and regulates the transport of solar energetic particles (SEPs).

The IMF’s structure is defined by the magnetic field’s strength and direction. These properties vary across many spatial and temporal scales (Owens and Forsyth, 2013; Verscharen et al., 2019) that are roughly grouped into three categories of descending size (Figure 1):

• Macroscales ($\sim {10}^6$ to ${10}^9\text{ km}$ at 1 au from the Sun) are dominated by the large-scale flux tubes that emerge from the Sun. Images of the solar corona and nascent solar wind reveal that the macroscale IMF is defined by the Parker spiral, interactions among solar wind streams, coronal mass ejections (CMEs), and other global structures and events (Balogh and Erdõs, 2013).

• Mesoscales ($\sim {10}^2$ to ${10}^6\text{ km}$) include the complex structures that arise from the interaction and “tearing” of flux tubes that occur as the plasma expands through the heliosphere.

• Microscales ($\sim {10}^{-2}$ to ${10}^2\text{ km}$) consist of the smallest-scale structures, whose dynamics are governed by the field-particle interactions of kinetic physics: heating, kinetic waves, microinstabilities, and magnetic reconnection (Marsch, 2006; Alexandrova et al., 2013; Osman et al., 2014).

FIGURE 1

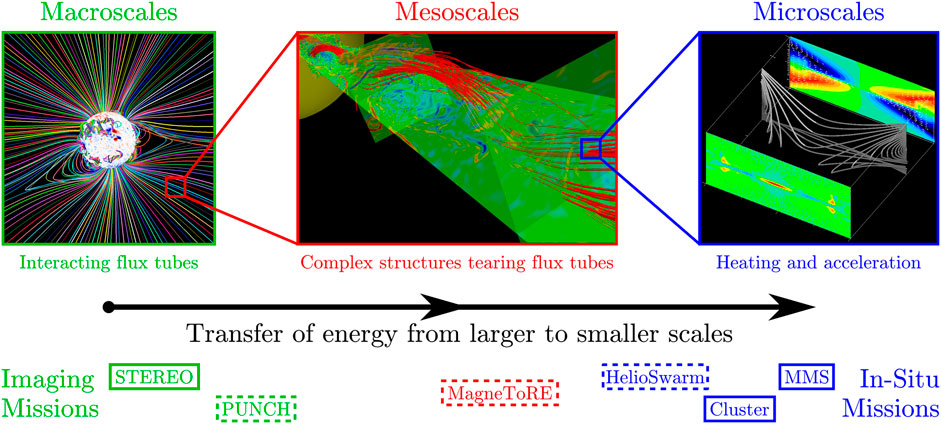
FIGURE 1. Representation of the three primary size scales in the interplanetary magnetic field (IMF). The approximate scales explored by select past/present (solid) and future (dashed) missions are also indicated. Left image: prediction of the solar corona’s magnetic field during the 21 August 2017 total solar eclipse performed by the team at Predictive Science, Inc., San Diego, CA, United States (Mikić et al., 2018). Center image: rendering of magnetic-field lines from simulations of reflection-driven Alfvén-wave turbulence inside a narrow magnetic flux tube (Jean C. Perez, Florida Institute of Technology). Right image: simulation of a magnetic reconnection region by Zenitani et al. (2011).

The mesoscale IMF plays a crucial but poorly understood role in solar-wind energy dynamics (Tu and Marsch, 1995). Energy is injected at macroscales by large-scale drivers (effectively “stirring” plasma streams) and passes through mesoscales via a combination of turbulent fluctuations and MHD waves that interact through shears and compressions. Ultimately, the energy in these complex mesoscale structures arrives at the microscales, where it dissipates as heating and particle acceleration (Alexandrova et al., 2009). The mesoscales, though, are not a mere conduit for the energy: rather, they process and transform the energy in ways that both impact the ultimate microscale dissipation and feed back on macroscale phenomena (Bruno and Carbone, 2005; 2013, 2016). To date, there have been no studies to comprehensively catalog individual mesoscale structures in 3-D: their morphology (shape), topology (relative placement), and interactions.

Mesoscale IMF structures constitute an important “missing link” in our understanding of solar-wind dynamics (Figure 1). Through remote imaging, we have traced the macroscale IMF, and, with in-situ measurements from single spacecraft and small constellations of spacecraft, we have observed microscale structures. To close this observational gap that limits our understanding of the mesoscale IMF, we describe herein a new mission concept, the Magnetic Topology Reconstruction Explorer (MagneToRE), which calls for a large constellation of nanosatellites to produce the first dynamic, 3-D maps of mesoscale structures in any space plasma. MagneToRE targets the smaller IMF structures of the mesoscale range: those a few orders-of-magnitude larger than the microscale range. Magnetic structures of this size have been nearly fully processed by mesocale dynamics and provide the 3-D context for microscale phenomena.

1.2 Overview and Outline

In this Article, we describe the MagneToRE mission concept and show how it would characterize the full, 3-D structure of the solar wind’s mesoscale magnetic field. Just as the mesoscales connect the energy dynamics of the IMF’s macro- and microscales, MagneToRE’s unique design would serve as a hybrid between in-situ and remote-imaging instrumentation (Figure 1). By utilizing a sufficiently large constellation of small, in-situ spacecraft, this mission would enable 3-D “images” of the magnetic structure to be reconstructed via advanced machine-learning techniques. These 3-D reconstructions of passing magnetic structures would be MagneToRE’s ultimate data product and would allow competing theories of solar-wind energy dynamics to be directly assessed. Our goal in this Article is to demonstrate the scientific importance and technological feasibility of MagneToRE. Though specific details of MagneToRE’s implementation require further study, the mission science and architecture presented here are targeted to fit within the scope of NASA’s Explorers Program (SMEX or MIDEX).

The outline of the remainder of this Article is as follows. Section 2 provides a brief overview of the theory and observations of IMF structure and its dynamics at mesoscales. We describe MagneToRE in Sections 3 and 4, which respectively contain the mission objectives and requirements and a high-level overview of possible mission implementation. We summarize the scientific impact of MagneToRE and possible augmentations to the mission in Section 5 and offer concluding remarks in Section 6.

2 Scientific Background

At mesoscales, turbulent fluctuations dominate solar-wind dynamics (Matthaeus, 2021). Energy injected by the Sun at macroscales cascades down through the mesoscales and dissipates at microscales (Coleman, 1968; Goldstein et al., 1994; Petrosyan et al., 2010; Kiyani et al., 2015; Bruno and Carbone, 2005, 2013, 2016). At $1\text{ au}$ from the Sun, mesoscales extend from the correlation length ($\approx {10}^6\text{ km}$) down to about $d_{\text{i}}$, the proton inertial length ($\approx 100\text{ km}$ for nominal solar wind conditions; see Figure 2):

$d_{\mathrm{i}}=\frac{c}{{\omega }_{\text{plas},\mathrm{p}}},(1)$

where ${\omega }_{\text{plas},\text{p}}$ is the proton plasma frequency.

FIGURE 2

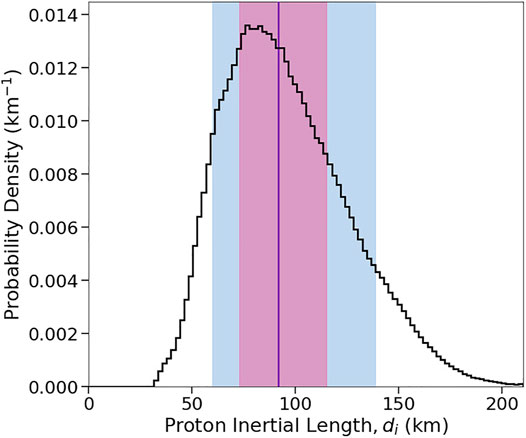
FIGURE 2. Probability distribution of proton inertial length, $d_{\text{i}}$, from the Wind spacecraft (Acuña et al., 1995; Ogilvie et al., 1995; Wilson et al., 2018). Shaded regions show the (magenta) ${25}^{\text{th}}$ to ${75}^{\text{th}}$ percentiles and (blue) ${10}^{\text{th}}$ to ${90}^{\text{th}}$ percentiles.

The solar wind’s high speed ($v\approx 300$ to $800\text{ km}/\text{s}$) means that temporal variations in IMF structures are minimal compared to their convection time. Taylor’s hypothesis (Taylor, 1938) links the frequency, f, of in-situ plasma measurements with the wavevector, k, of a passing structure:

$2\pi f\approx \mathbf{k}\cdot \mathbf{v},(2)$

where $\mathbf{v}$ is the solar-wind velocity.

Via Taylor’s hypothesis, time series of in-situ measurements from a single spacecraft provide essentially 1-D, straight-line cuts through the structure of the IMF (Wicks et al., 2010; Horbury et al., 2012). Such data are typically analyzed with statistical methods: e.g., Fourier power spectra, structure functions, and wavelet transforms (Matthaeus and Goldstein, 1982; Burlaga, 1991; Greco et al., 2012). Though useful, such methods fail to reveal the IMF’s 3-D structure, and thus single-point measurements cannot distinguish between spatial and temporal variations. Constellations of four or five spacecraft – the Cluster, Magnetospheric Mulsticale (MMS), and Time History of Events and Macroscale Interactions during Substorms (THEMIS) missions – addressed some of these shortcomings (Escoubet et al., 2001; Angelopoulos, 2008; Burch et al., 2016). These missions yielded important new information about IMF processes through the use of groundbreaking data-analysis techniques: e.g., wave telescope (Neubauer and Glassmeier, 1990; Motschmann et al., 2000; Pinçon and Motschmann, 2000) and discontinuity analysis (Russell et al., 1983; Mottez and Chanteur, 1994; Dunlop and Woodward, 2000). Nevertheless, because of the limited number of spacecraft in each of these missions, none could fully map out 3-D IMF structures. Even proposed missions with moderately larger numbers of spacecraft – e.g., Cross-Scale (Horbury et al., 2006), EIDOSCOPE (Vaivads et al., 2012), and HelioSwarm (Klein et al., 2019; Matthaeus et al., 2019; Spence, 2019; TenBarge et al., 2019) missions – would suffer this limitation.

In the following sections, we demonstrate that MagneToRE’s large nanosatellite constellation would transcend the capabilities of these other missions by simultaneously measuring the solar wind’s magnetic field at enough points in space to enable the first 3-D “images” of the IMF. These images would include the full, dynamic, 3-D information about the morphology and topology of the magnetic field. In the past, 3-D dynamic reconstructions of space plasmas have been pursued for understanding the Birkeland currents in Earth’s polar ionosphere (via the AMPERE missions; Anderson et al., 2000, Anderson et al., 2014), the magnetic reconnection X-line in the Earth’s magnetotail (Denton et al., 2020; Torbert et al., 2020), and the global magnetic field and large-scale current morphology throughout Earth’s magnetosphere (via a collection of decades of magnetic field measurements; Sitnov et al., 2019; Stephens et al., 2019). In contrast, we have optimized MagneToRE to enable the 3-D reconstruction of the solar wind’s magnetic field, which, unlike Earth’s magnetic field, is far weaker and subject to rapid convection.

In the absence of 3-D measurements from a mission such as MagneToRE, simulations have given rise to competing theories for the structure and evolution of the mesoscale IMF (Mininni et al., 2008; Eyink et al., 2013) and how it affects the solar wind’s overall dynamics at all scales. Table 1 summarizes the most prominent models. Though single-spacecraft observations have afforded plausibility to all these theories (Verscharen et al., 2019, and refs. therein), only a truly 3-D reconstruction of the IMF, such as the one MagneToRE would provide, can distinguish among them.

TABLE 1

TABLE 1. Comparison of prominent theories of solar-wind turbulence.

The difference among the turbulence theories in Table 1 is not merely an academic abstraction but rather one with profound, multifaceted consequences for our understanding of the heliosphere. As the simulations in Figure 3 show, different types of turbulent fluctuations produce vastly different magnetic structures, which, e.g., substantially affect the transport of energetic particles and plasma heating near intermittent structures (Bieber et al., 1996; Marsch and Tu, 1997). By creating 3-D images of the mesoscale IMF, MagneToRE would determine how wave-like IMF structures are (Belcher and Davis, 1971), what impact propagation effects have (Howes, 2015), the accuracy of force-free field approximations (Burlaga et al., 1998), and the presence of scale-dependent anisotropies and magnetic geometries potentially unstable to reconnection (Retinò et al., 2007; Priest and Pontin, 2009; Howes, 2016).

FIGURE 3

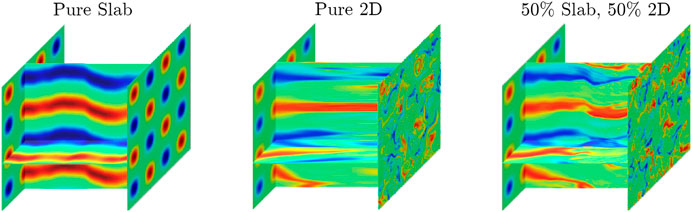
FIGURE 3. After Bieber et al. (1996), simulations of magnetic flux tubes perturbed by three types of fluctuations (injected at the left of each box), which evolve into vastly different structures.

3 Mission Overview

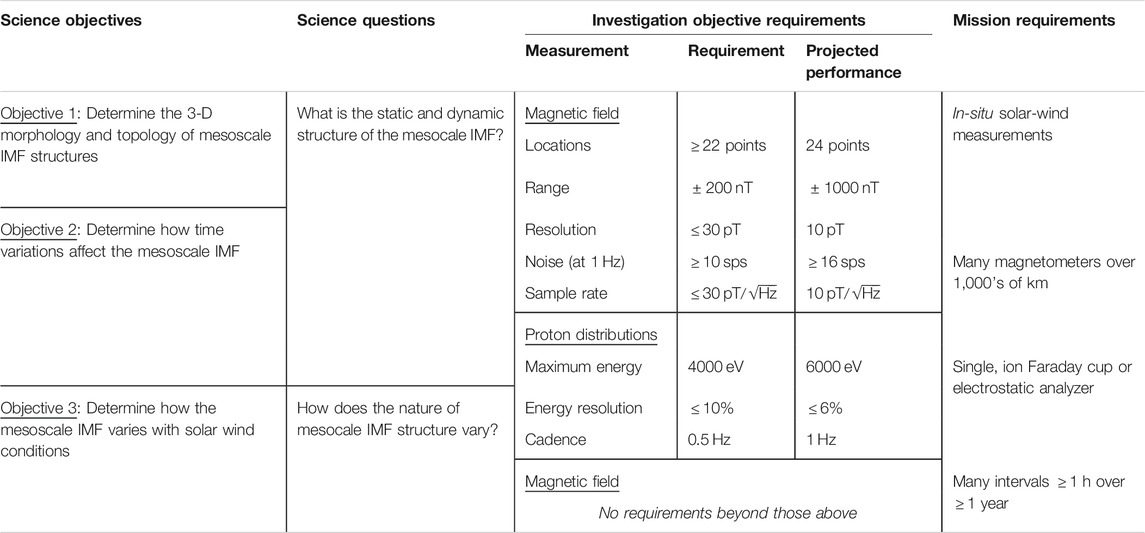
3.1 Mission Objectives

The MagneToRE mission’s large constellation of nanosatellites, would simultaneously fulfill three science objectives:

Objective 1: Determine the 3-D morphology and topology of mesoscale IMF structures. The turbulence theories listed in Table 1 predict different morphologies (shapes and “aspect ratios”) and topologies (orientations and placements) for magnetic structures. This information could be captured in 3-D “images” of the magnetic field, which would require measurements across at least one order-of-magnitude in scale. Since the mesoscale IMF provides the context for the kinetic processes at microscales, MagneToRE would target the lower end of the mesocale range: 10’s of $d_{\text{i}}$ (1,000’s of km) and above.

Objective 2: Determine how time variations affect the mesoscale IMF. This objective relates to distinguishing between spatial and temporal variations in the IMF. Different turbulence theories (Table 1) predict different types of temporal fluctuations, which define the IMF’s wave, dispersion, and propagation properties. MagneToRE would determine scale-dependent time decorrelation rates, which are crucial for interpreting the nature of IMF fluctuations. (Edwards, 1964; Zhou et al., 2004; Lugones et al., 2016).

Objective 3: Determine how the mesoscale IMF varies with solar-wind conditions. MagneToRE would need to sample many different streams of solar wind – fast and slow wind, co-rotating interaction region (CIR) interfaces, and coronal mass ejections (CMEs) – to fully characterize the breadth of turbulence behavior in the mesoscale IMF. These wind types and large-scale structures originate in different source regions of the solar corona and experience different expansion histories, so they may exhibit differences in magnetic structure and fluctuations (Bruno and Carbone, 2005, 2013, 2016; Chapman et al., 2009; Wicks et al., 2009).Scientific measurements in support of these three objectives need not necessarily be collected simultaneously. Indeed, some distributions of spacecraft within the constellation will be more conducive to one objective than another. For example, Objective 1 would be well served by a relatively planar constellation oriented perpendicular to the solar wind’s flow (Section 4.1.2). Conversely, Objective 2 favors a constellation that is more elongated along the flow – especially one in which multiple spacecraft are nearly aligned with the flow. Most of the trajectory options (Section 4. 2) for MagneToRE would allow the constellation to naturally evolve over the course of the mission.

3.2 Science Traceability

Table 2 shows the science traceability matrix (STM) for MagneToRE. In order to achieve science closure on the mission objectives (Section 3.1), two types of in-situ measurements are required: vector magnetic field observations at multiple points for 3-D image reconstruction (Section 4.1.2) and bulk proton moments (density, velocity, and temperature) at a single point to gauge overall plasma conditions and aid in the 3-D magnetic reconstructions.

TABLE 2

TABLE 2. Science traceability matrix (STM) for MagneToRE.

3.2.1 Vector Magnetic Field

Distributed measurements of the vector magnetic field are needed to fully characterize the IMF’s spatiotemporal variations. To explore mesoscale structures in particular, spatial separations $\mathrm{\gtrsim }10$’s of $d_{\text{i}}$ (Eq. 1) are required to avoid the transition into microscales. Furthermore, to “image” the 3-D magnetic structures, the range of spatial separations between measurements should span at least about one order of magnitude (Section 4.1.2).

Assuming the validity of Taylor’s hypothesis (Eq. 2), regular measurements at the same point in space correspond to spatial measurements along the plasma’s flow direction. We use Taylor’s hypothesis here only to make a rough estimate of the minimum sampling frequency. To keep that estimate conservative, we set the lower limit on the size of structures that we seek to resolve at one $d_{\text{i}}$ ($\approx 100\text{ km}$ at $1\text{ au}$; Figure 2). Applying the Nyquist criterion, this corresponds to a sampling frequency of the magnetic field of least $2v/d_{\text{i}}\approx 10\text{ Hz}$, where $v\approx 500\text{ km}/\text{s}$ is a typical solar wind speed.

The sensitivity of each magnetic-field measurement must be $\le 30\text{ pT}/\sqrt{\text{Hz}}$ at $1\text{ Hz}$, which is one order-of-magnitude below the typical turbulence power at the $d_{\text{i}}$-scale according to previous single-spacecraft measurements (Alexandrova et al., 2009; Woodham et al., 2018).

3.2.2 Proton Moments

Assuming an inter-spacecraft spacing of $\mathrm{\gtrsim }20d_{\text{i}}$, the Nyquist criterion gives a minimum sampling frequency for the proton moments of about $0.5\text{ Hz}$. For image reconstruction, the uncertainty in proton speed would need to be $\mathrm{\lesssim }5\text{\%}$ ($\mathrm{\lesssim }25\text{ km}/\text{s}$) and the uncertainty in flow direction $\mathrm{\lesssim }{5}^{\circ }$. To distinguish high- and low-${\beta }_{\text{p}}$ plasma, where

${\beta }_{\mathrm{p}}\equiv \left(\frac{2{\mu }_0{n}_{\mathrm{p}}{k}_{\mathrm{B}}{T}_{\mathrm{p}}}{B_0^2}\right),(3)$

proton density ($n_{\text{p}}$) and temperature ($T_{\text{p}}$) uncertainties need only be $\mathrm{\lesssim }10\text{\%}$ and $\mathrm{\lesssim }20\text{\%}$, respectively.

3.2.3 Sampling Duration and Mission Lifetime

Though MagneToRE need not continuously collect scientific measurements, the operations plan should ensure that it remains in its science mode for intervals of $\mathrm{\gtrsim }1\text{ hour}$. This roughly corresponds to the correlation time, which defines the boundary between the macro- and mesoscales. MagneToRE, over the course of its lifetime, should collect data over many such intervals. A mission lifetime of $\mathrm{\gtrsim }1\text{ year}$ would ensure that multiple Carrington rotations are sampled, which would provide a wide variety of plasma conditions for statistical studies.

3.2.4 Data Analysis and Science Closure

Science closure would require physics-based reconstructions that employ modern data science approaches (see Section 4.1.2) alongside the computation of field-line topologies (e.g., Priest and Pontin, 2009; Tooprakai et al., 2016) and the morphology and complexity of flux surfaces (e.g., Mininni et al., 2008; Servidio et al., 2014). Algorithms for identifying likely critical points (e.g., X- and O-points) would need to be developed based on those employed for MMS and other missions (Denton et al., 2010; Fu et al., 2015) and would be essential for assessing magnetic structure. Higher-order statistics of the magnetic field (e.g., scale-dependent kurtosis and multifractal analysis), which quantify the intermittency of structures (Kiyani et al., 2007; Chhiber et al., 2018), would also be employed.

4 Mission Implementation

Dynamic, 3-D maps of the mesoscale IMF could be effectively reconstructed (Section 4.1) from in-situ magnetic-field measurements from MagneToRE’s large constellation (Section 4.2) of spacecraft. Each of MagneToRE’s nanosatellite “probe” spacecraft (Section 4.3) would carry a compact fluxgate magnetometer. A larger “prime” spacecraft (Section 4.4) would be required to deploy the probe spacecraft, serve as their telemetry link to the ground, and host a Faraday cup or electrostatic analyzer (ESA) for measuring proton moments.

4.1 Magnetic Reconstruction

4.1.1 Select Existing Methods

Determining the structure of magnetic fields is a fundamental aspect of multi-spacecraft missions in heliophysics. The analysis of spatial gradients and volumetric tensors (Harvey, 1998) requires simultaneous, in-situ measurements from 4 or more spacecraft (Shen et al., 2003, Shen et al., 2007). Trilinear methods (Haynes and Parnell, 2007) and first-order Taylor expansion (Fu et al., 2016; Chen et al., 2019) are also useful in identifying and characterizing magnetic structures. These methods do not rely on Taylor’s hypothesis (Eq. 2), but they typically require that measurements be made at a minimum of 4 points (or 8 points in the case of trilinear methods) and perform best under specific spatial arrangements of the spacecraft. With more simultaneous measurement points, better estimates are possible of the volumetric tensor and gradients – even when the measurement points are randomly distributed (Watanabe and Nagata, 2017).

4.1.2 Case Study: A Novel Method

Though we are actively exploring extensions of the methods described in Section 4.1.1, we focus here on an alternative approach that utilizes modern machine-learning algorithms to reconstruct 3-D maps of the magnetic field from multi-point in-situ measurements. Development of this new method remains ongoing and will be the subject of a publication that is currently in preparation. Here, we present a case study to demonstrate the feasibility of the algorithm and to establish a baseline number of probe spacecraft for MagneToRE.

We began by using the output from a fully kinetic, 3-D plasma simulation (Roytershteyn et al., 2015) to generate synthetic, $\sim 13$ Hz time series of magnetic-field measurements for various constellations (number and arrangement) of probe spacecraft. For simplicity, we have initially focused on constellations in which the spacecraft are in a plane perpendicular to the plasma flow; under Taylor’s hypothesis (Eq. 2), applying a phase shift to any probe’s time series effectively shifts its location along the flow direction.

We carried out magnetic reconstruction in 3-D using the complete time-series from all spacecraft as a single dataset versus carrying out a series of 2-D, planar reconstructions. We interpolated the magnetic-field via the Gaussian Processes (GP) method (Rasmussen and Williams, 2006) as implemented in the scikit-learn package (Pedregosa et al., 2011; Buitinck et al., 2013) and with a Matern kernel, which is based on modified Bessel functions (Abramowitz et al., 1965).

Figure 4 shows one “slice” through our 3-D spatial reconstruction of the magnetic field. The constellation of spacecraft was distributed in the $xy$‐plane, and the plasma flowed along the z-axis (perpendicular to the page). For brevity, Figure 4 only shows the x-component ($B_x$); the Appendix shows renderings of the y and z-components ($B_y$ and $B_z$) and the magnitude $\left(B\equiv \right|\mathbf{B}\left|\right)$. Panel A shows a slice of the 3-D simulation (Roytershteyn et al., 2015), and Panels B–H show GP reconstructions based on synthetic time-series from various constellations (black dots). For constellations of 4 or 8 spacecraft (Panels B and C), the reconstruction poorly matches the original (Panel A). With 16 spacecraft (Panel D), some structure is captured, but the shape of the boundary between the red and blue regions (positive and negative $B_x$) is distorted. A constellation of 24 spacecraft (Panel E) provides a far better reconstruction, but 34 spacecraft (Panel F) provide little further improvement. Even when the 24 spacecraft have randomized positions (Panel G) and 2 spacecraft are removed (Panel H) to simulate unfavorable alignments or equipment failure, a reasonable reconstruction is still produced.

FIGURE 4

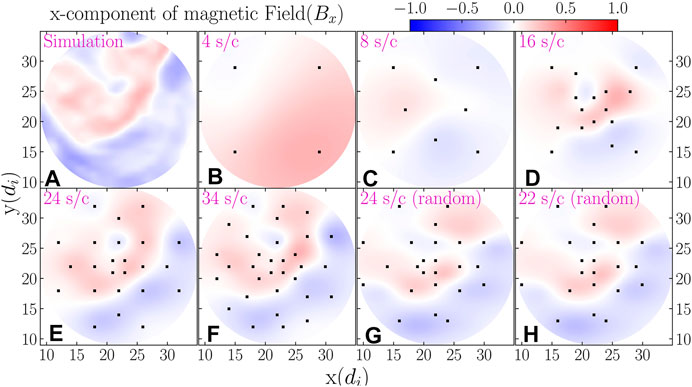
FIGURE 4. Plots of the normalized x-component of magnetic field ($B_x$) over the $xy$-plane (coordinates normalized by $d_{\text{i}}$): (A) slice from the 3-D simulation (Roytershteyn et al., 2015) and (B–H) GP reconstructions from synthetic time series from various constellations of spacecraft (black dots).

These results of our case study indicate that the baseline design for MagneToRE should be measuring the magnetic field at 24 points in space to enable a sufficiently detailed reconstruction of the 3-D magnetic field. These results also suggest that strict control over the trajectory of the individual spacecraft is not necessary since the algorithm performs well even when the spacecraft locations are randomly perturbed.

Nevertheless, our algorithm remains in active development, and we are focusing on several key areas of improvement. First, the current algorithm interpolates each component of the vector magnetic field independently of the other two. We are currently testing alternative implementations of the GP method that would simultaneously interpolate all three components and automatically enforce the requirement that the magnetic field be divergence-less, which could significantly improve the quality of the magnetic reconstructions. Second, we are developing methods for quantitatively comparing our algorithm’s magnetic reconstructions to each other and to the original simulation. These comparisons would be based on the automated identification and characterization of magnetic structures (see Section 3.2.4).

4.2 Constellation Orbits and Operations

The science requirements dictate that the MagneToRE constellation would need to spend $\mathrm{\gtrsim }1\text{ hour}$ at a time in the solar wind for multiple periods over $\mathrm{\gtrsim }1\text{ year}$, which could be achieved under various launch scenarios. The Earth-Sun L1 point affords continuous solar-wind observations, but insertion into lunar orbit may be more feasible for a rideshare (e.g., via the Artemis program). A rideshare with a deep-space (e.g., planetary) mission could also be suitable and offer the added benefits of easier constellation management and the opportunity to explore changes in IMF structure with distance from the Sun.

The launch, commission, and operation of 25 spacecraft poses significant logistical challenges that would require very careful consideration and planning. Nevertheless, in both the public and private sector, multi-spacecraft missions (including those utilizing CubeSats) are becoming increasingly common and often use some degree of semi-autonomous control. Operations for MagneToRE would be aided by having only a single science mode: e.g., no burst modes are anticipated. Likewise, while the relative positions of the spacecraft must be carefully measured, the controlling of those positions through precision formation flying is not required (Section 4.1.2).

4.3 Probe Spacecraft

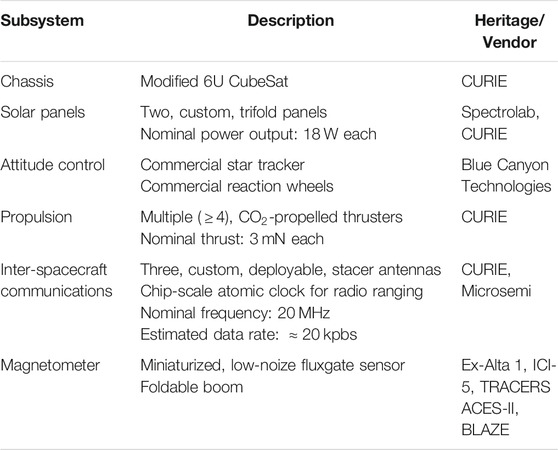
Until recently, a large constellation mission such as MagneToRE would have been cost-prohibitive under most funding programs due to the number of large and sophisticated spacecraft required. However, recent advancements in nanosatellites and instrument miniaturization now make such a constellation feasible (Liemohn et al., 2021). Each probe spacecraft could be built from a custom bus based on the well-established 6U CubeSat form factor (Figure 5) and designed to have a modest magnetic signature (Section 4.3.6).

FIGURE 5

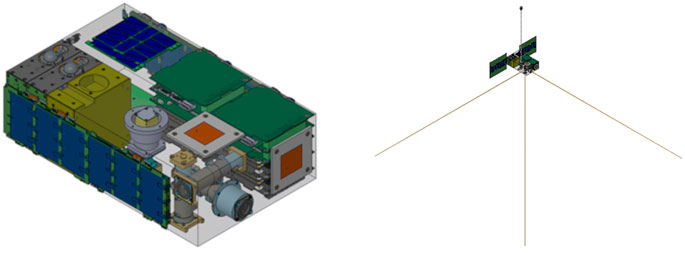
FIGURE 5. A “strawman” probe 6U Cubesat with stacer antennas, solar panels, and a placeholder magnetometer (left) stowed and (right) deployed. Note that the two images are shown at different scales.

Because all of the probe spacecraft would be identical, substantial resources could be used to formulate, implement, and validate their design. These development costs would be roughly independent of the number of spacecraft, so, for a large number, the incremental cost of each spacecraft would be modest. This would also make it practical for the probe spacecraft’s design to comply with all the requirements of NASA’s Explorers Program, which are far more rigorous than is typical for CubeSat missions.

In this Section, we describe one possible implementation of MagneToRE’s probe spacecraft that would satisfy the mission objectives described above (Section 3.1). In this scenario, which is summarized in Table 3, many of the spacecraft support systems would be based on components developed at the Space Sciences Laboratory at the University of California, Berkeley (UCB/SSL) for the Cubesat Radio Interferometry Experiment (CURIE) mission (Sundkvist et al., 2016), which is slated to launch and operate in late 2021. Likewise, the probe magnetometers would be based on instruments and technology (e.g., Miles et al., 2019) developed at the University of Iowa (UIowa).

TABLE 3

TABLE 3. Summary of design for probe spacecraft.

4.3.1 Power

Off-the-shelf electrical power systems (EPSs) and batteries from Clyde Space could be used to power each probe. Input power could be derived from trifold, deployable solar panels developed at UCB/SSL for CURIE (Figure 5). Each trifold panel provides up to $18\text{ W}$ of power (for a total of $36\text{ W}$) via Spectrolab space-rated photovoltaic cells.

4.3.2 Guidance and Navigation

Attitude control for each probe could be provided by a Blue Canyon XACT Attitude Control System (ACS), which has both a star tracker and reaction wheels. Deployment and control of the constellation could utilize a UCB/SSL propulsion unit based on that developed for the CURIE mission. Multiple thruster nozzles, each with a $3\text{ mN}$ nominal thrust and a $0.6\text{ mN}$ impulse burst bit, would allow on-axis thrusting and momentum dumping from the reaction wheels.

4.3.3 Radio Communications

The large separations (1,000’s of km) required for the probe spacecraft poses a challenge for probe-to-probe and probe-to-prime communications. Using high-frequency transceivers would require narrow antenna beam patterns and accurate pointing ability to function over such large distances. This would impose severe restrictions and complicate the design of the probe’s bus and ACS. Instead, given the moderate data-rates required, omnidirectional UCB/SSL stacer antennas (Figure 6) and a high-frequency (HF) transceiver system (about $20\text{ MHz}$ and $20\text{ kbps}$) based on CURIE heritage could comfortably close the link budget at these distances.

FIGURE 6

FIGURE 6. A deployed CURIE stacer antenna undergoing ground testing.

4.3.4 Radio Ranging and Position Reconstruction

The communication stacers would double as antennas for a radio ranging system that would deduce relative spacecraft positions and establish constellation geometry. Two-way transfer is a two-way radio-ranging method for accurately measuring the time-of-flight between two nodes. Each node is responsible for accurately measuring the local time delay between a receive and transmit pulse, which can be accomplished with nanosecond resolution using commercial, chip-scale atomic clocks (e.g., the Microsemi devices used on CURIE). The scalar distance between two nodes can be deduced by measuring the total time-of-flight from one node, to another, and back again. This method results in a distance measurement with an accuracy $\mathrm{\lesssim }10\text{ m}$ – more than sufficient for orbit station-keeping as well as baseline science. Together with a simultaneous goniopolarimetric measurement of the direction of radio propagation, position vectors can be established and the overall geometery of the spacecraft constellation determined.

4.3.5 Magnetometer

Each probe’s magnetometer system would consist of a vector fluxgate sensor, segmented boom, and radiation tolerant electronics package (Miles et al., 2013) such as has been developed at UIowa (Figures 7A–C, respectively). This system, based on the MGF instrument (Wallis et al., 2015) on Cassiope/e-POP, also draws heritage from the fluxgate magnetometer (Miles et al., 2016) for the Ex-Alta 1 CubeSat (Mann et al., 2020) in the QB50 constellation (Wicks and Miles, 2019). The next-generation, nanosatellite-scale “Tesseract” magnetometer sensor (Figure 7A) leverages low-noise custom fluxgate cores (Miles et al., 2019) to create a compact, rigid, symmetric, and magnetically stable probe. This sensor design also incorporates temperature compensation (Miles et al., 2017), which may be advantageous for some potential trajectories (e.g., lunar orbit; Section 4.2). Each magnetometer would deploy 60 cm from its probe via the BLAZE magnetometer boom (Figure 7B), which is composed of non-magnetic materials (titanium and carbon-fiber with phosphor bronze springs).

FIGURE 7

FIGURE 7. (A) Prototype magnetometer sensor for TRACERS. (B) BLAZE magnetometer boom. (C) Fluxgate electronics as-flown on the ICI-5 sounding rocket (November 2019).

4.3.6 Magnetic Cleanliness

Given the central role that magnetic-field measurements play in effecting science closure (Table 2), maintaining appropriate magnetic cleanliness in the probe spacecraft would be essential and would require careful management. A magnetometer boom (Figure 7B) would separate the fluxgate sensor from the spacecraft by $60\text{ cm}$. This approach proved highly effective for the 3U Ex-Alta 1 CubeSat (Miles et al., 2016). Active noise removal (e.g., Ness et al., 1971; Constantinescu et al., 2020) is also possible using an alternative gradiometer setup (e.g., two separated miniature sensors on the outer boom segment).

Since some prior CubeSat missions have encountered magnetic contamination from commercial components (e.g., Miles et al., 2016), the design and fabrication of the probe spacecraft would be largely kept “in house” and carefully managed to ensure compliance. At the prototype stage, potential parts and subsystems would be screened magnetically and, where appropriate, replaced with preferred materials such as titanium, aluminum, or engineering plastic. Custom solar panels (Section 4.3.1) would be wired to minimize their stray magnetic-field. Similarly, battery arrays would be selected and arranged to minimize stray field during charge/discharge. Though commercial reaction wheels would be required, these would have a custom control-system and be augmented by thrusters, which together would be used to keep the wheels from generating interference either at the base-band (DC) or at the second harmonic of the fluxgate drive frequency ($\sim 16\text{ kHz}$).

Particular attention would be paid to time-varying stray magnetic fields, which are the most challenging to remove in post-processing. Static offsets and long-duration trends can likely be mitigated using vector-vector calibration across the constellation of spacecraft. Over a sufficiently long interval, we can assume that all spacecraft will experience a common environment in the solar wind. Therefore, long-term deviations by an individual spacecraft from the ensemble average, particularly if the offset is constant in the frame of the spacecraft/instrument, likely result from local fields or instrumental offsets and can be trended and removed. Time varying fields, particularly those occurring on time-scales comparable to the measurement requirements, cannot be easily removed this way and must be mitigated by design pre-launch.

4.4 Prime Spacecraft

MagneToRE’s single prime spacecraft would have four main functions: transporting the probe spacecraft to their orbit insertion point, releasing the probes into a constellation, relaying data between the probes and the Earth, and obtaining solar-wind proton moments. The design and implementation of the prime spacecraft would follow the example of single-spacecraft missions from NASA’s Explorers Program and emphasize the use of components with extensive flight heritage.

4.4.1 Bus, Avionics, and Guidance

Various satellite designs could be used for the prime spacecraft. The EELV Secondary Payload Adapter (ESPA) is an existing design with low development-costs, high heritage, and compatibility with rideshares. An ESPA would accommodate commercial propulsion, avionics, and power systems. For a dedicated launch, a custom spacecraft could be designed with substantially lower mass.

4.4.2 Communications

The prime spacecraft would carry two radio systems. An HF transceiver, identical to that on each probe, would be used for communicating with the probes. An X-band system with a high-gain dish would communicate with the ground.

4.4.3 Ion Faraday Cup or Electrostatic Analyzer

The prime spacecraft’s only required scientific instrument would be an ion Faraday cup or electrostatic analyzer (ESA), which would measure bulk proton moments (density, velocity, and temperature), with nominal energies of $\sim$500–1,000 eV. The scientific requirements on the ion measurements (Section 3.2) are relatively modest, so various designs could be employed for this instrument. The important consideration for this measurement is that the instrument resolve the solar-wind proton population, which is supersonic and nearly unidirectional.

4.4.4 Magnetic Cleanliness

Since the prime spacecraft would not operate its own magnetometer, its requirements for magnetic cleanliness would be far less stringent than those on the probe spacecraft (Section 4.3.6). Only relatively modest efforts to control magnetic contamination would be needed to protect the unactivated probe spacecraft that it would carry and deploy.

Though, in principle, the prime spacecraft could include one or more magnetometers, doing so is not a requirement for mission success and would substantially increase the mission’s cost and complexity. Even if the prime spacecraft used the same magnetometer sensor and electronics (Section 4.3.5) as the probe spacecraft, it would require a different and larger boom to account for the prime spacecraft’s much larger size. Additionally, operating a magnetometer on the prime spacecraft would require much greater attention to magnetic cleanliness, which would almost certainly eliminate the possibility of using an existing commercial design for the spacecraft system (e.g., an ESPA; Section 4.4.1).

5 Discussion

5.1 Programmatic Context

The implementation of MagneToRE would enable substantial progress toward Key Science Goal 4 of the Heliophysics Decadal Survey (Committee on a Decadal Strategy for Solar and Space Physics, 2013), which seeks to “discover and characterize fundamental processes that occur within the heliosphere.” Analyses of MagneToRE’s observations would definitively characterize the mesoscale magnetic structure of the solar wind – including that upstream of Earth, which drives space weather. Moreover, different theories of IMF turbulent structure lead to drastically different predictions for the propagation of energetic particles (Section 2). Thus, MagneToRE would further our “understanding of the Sun and its effects on the Earth,” as sought by Objective 1 of NASA’s, 2018 Strategic Plan (NASA, 2018).

MagneToRE’s unique design and innovative data-processing algorithms would lay important groundwork for future multi-spacecraft missions such as the Magnetospheric Constellation (MagCon). The final report of the National Academies’ Committee on Achieving Science Goals with CubeSats (Committee on Achieving Science Goals with CubeSats, 2016) emphasizes that “constellations of 10–100 science spacecraft have the potential to enable critical measurements for space science.”

MagneToRE could also provide unique rideshare opportunities to other, smaller missions. In particular, if an ESPA bus was used as the mission’s prime spacecraft, it would have substantial capacity for additional payloads. This could enable missions-of-opportunity, which could include instruments fixed to the prime spacecraft and CubeSats deployed from it. Such small projects often have few options for accessing deep space, so they would greatly benefit from MagneToRE’s trajectory –whether that be to L1, lunar orbit, or beyond. Additionally, since the prime spacecraft would already be designed as a communications relay, it could potentially provide the smaller projects with data and power at very little additional cost.

5.2 Mission Augmentations

Though the MagneToRE mission concept as presented offers a compelling science case, it could be augmented in several ways to enhance its science return. A full trade study would be required to determine whether the additional science enabled by these augmentations would justify higher mission costs.

Given the importance of mesoscale IMF structure to the propagation of energetic particle populations – including solar energetic particles (SEPs), shock-accelerated particles associated with CMEs and CIRs, and galactic cosmic rays (GCRs) – adding instruments to detect and characterize such particles could be valuable for MagneToRE. While one or more large, sophisticated energetic-particle instruments could be added to the prime spacecraft, the probe spacecraft may be able to accommodate simpler, miniaturized detectors.

MagneToRE would be able to achieve all of its objectives (Section 3.1) with only a single thermal-particle instrument located on the prime spacecraft. Nevertheless, adding a thermal-particle instrument to some or all of the probe spacecraft would enable some additional science objectives – especially those related to field-particle correlation. An electrostatic analyzer or Faraday cup on each probe would provide the most detailed information but may require a larger chassis for the probes, which in turn could substantially increase the mission’s cost. Langmuir probes, Mach probes, or quasi-thermal noise instruments would return less information on the particles but would likely be less costly.

6 Conclusion

As Figure 1 shows, the MagneToRE mission concept described above would fill a critical gap in our understanding of the IMF’s dynamic structure. Energy in the solar wind is widely understood to be injected at large scales and then to shift to progressively smaller scales, but the process of this kind of turbulent cascade remains poorly understood and an active area of research. Indeed, two, multi-spacecraft missions – one upcoming and another under review – seek to begin exploring mesocale IMF turbulence with complementary techniques. First, PUNCH (DeForest et al., 2017) will use imaging instruments to explore the larger end of the mesoscale range. Second, HelioSwarm (Klein et al., 2019; Matthaeus et al., 2019; Spence, 2019; TenBarge et al., 2019) would be an in-situ mission that spans the transition from mesoscales to microscales. However, the number of spacecraft that would comprise the HelioSwarm mission would not fully allow for the “imaging” of the 3-D IMF structure and magnetic field reconstruction described here. MagneToRE would provide the “missing link” between these two missions by producing the first-ever, truly 3-D maps of the IMF at any scale.

Data Availability Statement

Publicly available datasets from the Wind spacecraft used for Figure 2 are available from NASA’s Coordinated Data Analysis Web (CDAWeb; https://cdaweb.gsfc.nasa.gov/index.html/).

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

BAM and RAQ are partially supported by NSF Award Number 1931435. JAAR is supported by the European Space Agency’s Networking/Partnership Initiative (NPI) programme and the Colombian programme Pasaporte a la Ciencia, Foco Sociedad - Reto 3 (Educación de calidad desde la ciencie, la tecnología y la innovación (CTel)), ICETEX. RB is partially supported by NASA award 80NSSC21K0739. RC and WHM are supported by NASA HSR grant 80NSSC18K1648. DMM is supported by NASA under grants and contracts 80NSSC19K0491, 80GSFC18C0008, 80NSSC18K1293, and 80NSSC20K1842. SS is supported by the European Union’s Horizon 2020 research and innovation program under Grant Agreement No. 776262 (AIDA, www.aida-space.eu). DS is supported by NASA award 80NSSC17K0032. SKV is supported by NASA contract NNG04EB99C and by NSF grants ATM-0739864 and ATM-1420184. DV is supported by STFC Ernest Rutherford Fellowship ST/P003826/1 and STFC Consolidated Grant ST/S000240/1. RTW is supported by STFC Consolidated Grant ST/V006320/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer FP declared a past co-authorship with the authors BAM, SS, DV, JHW and RTW to the handling editor.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Zoran Mikić, Jean C. Perez, and Seiji Zenitani for permission to reproduce their images in Figure 1. BAM and DV gratefully acknowledge the NSF’s SHINE program (https://shinecon.org/), whose 2019 annual meeting served as a venue for preliminary discussions about this mission concept. BAM and SKV extend further thanks to Erika Hamden and the 2019 NASA PI Launchpad workshop, which offered invaluable instruction and enabled refinement of the mission. The authors also thank George C. Ho, Clint T. Apland, and Michael V. Paul for fruitful discussions. This research made use of PlasmaPy, a community-developed open-source Python package for plasma science (PlasmaPy Community, 2020). The preparation of this manuscript made use of the SAO/NASA Astrophysics Data System (ADS): https://ui.adsabs.harvard.edu/.

Appendix

As described in Section 4.1.2, we used the 3-D kinetic plasma simulations of Roytershteyn et al. (2015) to generate synthetic in-situ magnetometer measurements, which we then used to reconstruct 3-D maps of the magnetic field. Though Section 4.1.2 focuses on the magnetic field’s x-component ($B_x$; Figure 4) as an example, we also considered the y- and z-components ($B_y$ and $B_z$; Figures A1, A2) and the magnitude of the magnetic field (Figure A3). Note that these figures show only a single slice (parallel to the $xy$-plane) from our 3-D reconstructions.

FIGURE A1

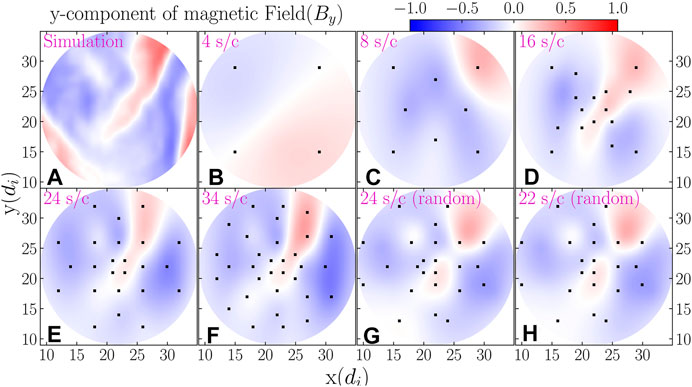
FIGURE A1. Same as Figure 4, but for $B_y$, the y-component of the magnetic field.

FIGURE A2

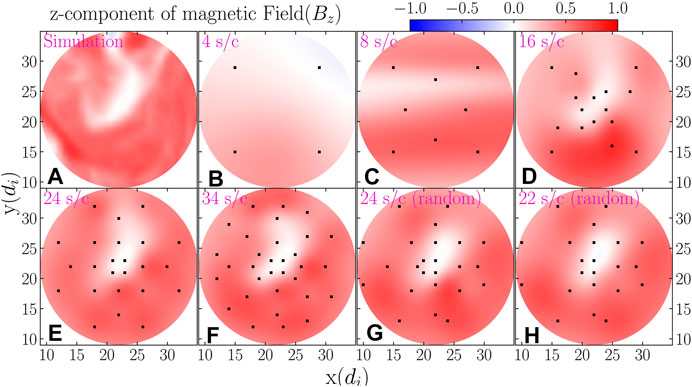
FIGURE A2. Same as Figure 4, but for $B_z$, the z-component of the magnetic field.

FIGURE A3

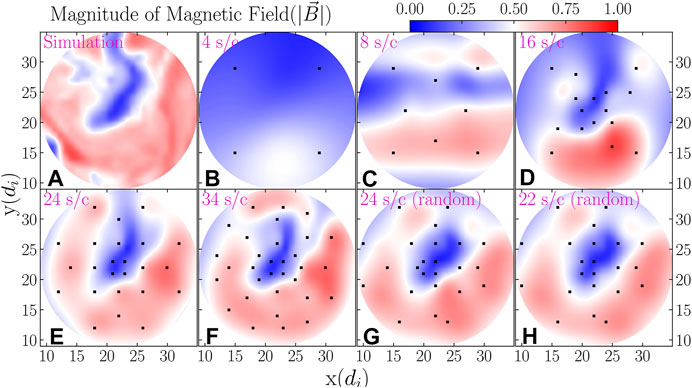
FIGURE A3. Same as Figure 4, but for $B\equiv \left|\mathbf{B}\right|$, the magnitude of the magnetic field.

The key results of Section 4.1.2 are supported by any one of these figures. A constellation of 4 or 8 spacecraft provides insufficient spacial coverage for this type of magnetic reconstruction. Though a 16-spacecraft constellation offers significant improvement, the reconstruction still contains major defects. Only with a constellation of $\mathrm{\gtrsim }24$ spacecraft is the reconstruction sufficiently robust for magnetic structure (i.e., morphology and topology) to be accurately discerned.

References

Abramowitz, M., Stegun, I. A., and Miller, D. (1965). Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables (National Bureau of Standards Applied Mathematics Series No. 55). J. Appl. Mech. 32, 239. doi:10.1115/1.3625776

CrossRef Full Text | Google Scholar

Acuña, M. H., Ogilvie, K. W., Baker, D., Curtis, S. A., Fairfield, D., and Mish, W. (1995). The Global Geospace Science Program and its investigations. Space Sci. Rev. 71, 5–21. doi:10.1007/BF00751323

Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar Wind Turbulence and the Role of Ion Instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8

CrossRef Full Text | Google Scholar

Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S. J., et al. (2009). Universality of Solar-Wind Turbulent Spectrum from Mhd to Electron Scales. Phys. Rev. Lett. 103, 165003. doi:10.1103/PhysRevLett.103.165003

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, B. J., Korth, H., Waters, C. L., Green, D. L., Merkin, V. G., Barnes, R. J., et al. (2014). Development of Large-Scale Birkeland Currents Determined from the Active Magnetosphere and Planetary Electrodynamics Response experiment. Geophys. Res. Lett. 41, 3017–3025. doi:10.1002/2014GL059941

CrossRef Full Text | Google Scholar

Anderson, B. J., Takahashi, K., and Toth, B. A. (2000). Sensing Global Birkeland Currents with Iridium Engineering Magnetometer Data. Geophys. Res. Lett. 27, 4045–4048. doi:10.1029/2000GL000094

CrossRef Full Text | Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Balogh, A., and Erdõs, G. (2013). The Heliospheric Magnetic Field. Space Sci. Rev. 176, 177–215. doi:10.1007/s11214-011-9835-3

CrossRef Full Text | Google Scholar

Belcher, J. W., and Davis, L. (1971). Large-amplitude Alfvén Waves in the Interplanetary Medium, 2. J. Geophys. Res. 76, 3534–3563. doi:10.1029/JA076i016p03534

CrossRef Full Text | Google Scholar

Bieber, J. W., Wanner, W., and Matthaeus, W. H. (1996). Dominant Two-Dimensional Solar Wind Turbulence with Implications for Cosmic ray Transport. J. Geophys. Res. 101, 2511–2522. doi:10.1029/95JA02588

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2005). The Solar Wind as a Turbulence Laboratory. Living Rev. Solar Phys. 2, 4. doi:10.12942/lrsp-2005-4

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2013). The Solar Wind as a Turbulence Laboratory. Living Rev. Solar Phys. 10, 2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2016). Turbulence in the Solar Wind. Switzerland: Springer. doi:10.1007/978-3-319-43440-7

CrossRef Full Text

Buitinck, L., Louppe, G., Blondel, M., Pedregosa, F., Mueller, A., Grisel, O., et al. (2013). API Design for Machine Learning Software: Experiences from the Scikit-Learn Project. ECML PKDD Workshop: Languages for Data Mining and Machine Learning, 108–122.

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-910.1007/978-94-024-0861-4_2

CrossRef Full Text | Google Scholar

Burlaga, L. F. (1991). Intermittent Turbulence in the Solar Wind. J. Geophys. Res. 96, 5847–5851. doi:10.1029/91JA00087

CrossRef Full Text | Google Scholar

Burlaga, L., Fitzenreiter, R., Lepping, R., Ogilvie, K., Szabo, A., Lazarus, A., et al. (1998). A Magnetic Cloud Containing Prominence Material: January 1997. J. Geophys. Res. 103, 277–285. doi:10.1029/97JA02768

CrossRef Full Text | Google Scholar

Chapman, S. C., Nicol, R. M., Leonardis, E., Kiyani, K., and Carbone, V. (2009). Observation of Universality in the Generalized Similarity of Evolving Solar Wind Turbulence as Seen by ulysses. ApJ 695, L185–L188. doi:10.1088/0004-637X/695/2/L185

CrossRef Full Text | Google Scholar

Chen, Z., Fu, H., Wang, T., Cao, D., Peng, F., Yang, J., et al. (2019). Reconstructing the Flux-Rope Topology Using the Fote Method. Sci. China Technol. Sci. 62, 144–150. doi:10.1007/s11431-017-9201-1

CrossRef Full Text | Google Scholar

Chhiber, R., Chasapis, A., Bandyopadhyay, R., Parashar, T. N., Matthaeus, W. H., Maruca, B., et al. (2018). Higher‐order Turbulence Statistics in the Earth's Magnetosheath and the Solar Wind Using Magnetospheric Multiscale Observations. J. Geophys. Res. Space Phys. 123, 9941–9954. doi:10.1029/2018JA025768

CrossRef Full Text | Google Scholar

Coleman, P. J. J. (1968). Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma. ApJ 153, 371. doi:10.1086/149674

CrossRef Full Text | Google Scholar

Committee on a Decadal Strategy for Solar and Space Physics (2013). Solar and Space Physics: A Science for a Technological Society. Washington, DC: Tech. rep. National Research Council. doi:10.17226/13060

CrossRef Full Text

Committee on Achieving Science Goals with CubeSats (2016). Achieving Science with Cubesats: Thinking inside the Box. Washington, DC: Tech. rep.National Academies of Sciences, Engineering, and Medicine. doi:10.17226/23503

CrossRef Full Text

Constantinescu, O. D., Auster, H.-U., Delva, M., Hillenmaier, O., Magnes, W., and Plaschke, F. (2020). Maximum-variance Gradiometer Technique for Removal of Spacecraft-Generated Disturbances from Magnetic Field Data. Geosci. Instrum. Method. Data Syst. 9, 451–469. doi:10.5194/gi-9-451-2020

CrossRef Full Text | Google Scholar

DeForest, C. E., de Koning, C. A., and Elliott, H. A. (2017). 3d Polarized Imaging of Coronal Mass Ejections: Chirality of a Cme. ApJ 850, 130. doi:10.3847/1538-4357/aa94ca

CrossRef Full Text | Google Scholar

Denton, R. E., Sonnerup, B. U. Ö., Birn, J., Teh, W.-L., Drake, J. F., Swisdak, M., et al. (2010). Test of Methods to Infer the Magnetic Reconnection Geometry from Spacecraft Data. J. Geophys. Res. 115, a–n. doi:10.1029/2010JA015420

CrossRef Full Text | Google Scholar

Denton, R. E., Torbert, R. B., Hasegawa, H., Dors, I., Genestreti, K. J., Argall, M. R., et al. (2020). Polynomial Reconstruction of the Reconnection Magnetic Field Observed by Multiple Spacecraft. J. Geophys. Res. Space Phys. 125, 027481. doi:10.1029/2019JA027481

CrossRef Full Text | Google Scholar

Dunlop, M. W., and Woodward, T. I. (2000). “Multi-spacecraft Discontinuity Analysis: Orientation and Motion,” in Analysis Methods For Multi-Spacecraft Data. Editors G. Paschmann, and P. W. Daly 1 edn (Bern, Switzerland: International Space Science Institute (ISSI)), 271–306. no. SR-001 in ISSI Scientific Reportchap. 11. 1.

Google Scholar

Edwards, S. F. (1964). The Statistical Dynamics of Homogeneous Turbulence. J. Fluid Mech. 18, 239–273. doi:10.1017/S0022112064000180

CrossRef Full Text | Google Scholar

Escoubet, C. P., Fehringer, M., and Goldstein, M. (2001). IntroductionThe Cluster mission. Ann. Geophys. 19, 1197–1200. doi:10.5194/angeo-19-1197-2001

CrossRef Full Text | Google Scholar

Eyink, G., Vishniac, E., Lalescu, C., Aluie, H., Kanov, K., Bürger, K., et al. (2013). Flux-freezing Breakdown in High-Conductivity Magnetohydrodynamic Turbulence. Nature 497, 466–469. doi:10.1038/nature12128

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, H. S., Cao, J. B., Vaivads, A., Khotyaintsev, Y. V., Andre, M., Dunlop, M., et al. (2016). Identifying Magnetic Reconnection Events Using the Fote Method. J. Geophys. Res. Space Phys. 121, 1263–1272. doi:10.1002/2015ja021701

CrossRef Full Text | Google Scholar

Fu, H. S., Vaivads, A., Khotyaintsev, Y. V., Olshevsky, V., André, M., Cao, J. B., et al. (2015). How to Find Magnetic Nulls and Reconstruct Field Topology with Mms Data? J. Geophys. Res. Space Phys. 120, 3758–3782. doi:10.1002/2015JA021082

CrossRef Full Text | Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a Theory of Interstellar Turbulence. 2: Strong Alfvenic Turbulence. ApJ 438, 763. doi:10.1086/175121

CrossRef Full Text | Google Scholar

Goldstein, M. L., Roberts, D. A., and Fitch, C. A. (1994). Properties of the Fluctuating Magnetic Helicity in the Inertial and Dissipation Ranges of Solar Wind Turbulence. J. Geophys. Res. 99, 11519–11538. doi:10.1029/94JA00789

CrossRef Full Text | Google Scholar

Greco, A., Matthaeus, W. H., D'Amicis, R., Servidio, S., and Dmitruk, P. (2012). Evidence for Nonlinear Development of Magnetohydrodynamic Scale Intermittency in the Inner Heliosphere. ApJ 749, 105. doi:10.1088/0004-637X/749/2/105

CrossRef Full Text | Google Scholar

Harvey, C. (1998). Use of sandy beach Habitat by Fundulus majalis, a Surf-Zone Fish. Mar. Ecol. Prog. Ser. 164, 307–310. doi:10.3354/meps164307

CrossRef Full Text | Google Scholar

Haynes, A. L., and Parnell, C. E. (2007). A Trilinear Method for Finding Null Points in a Three-Dimensional Vector Space. Phys. Plasmas 14, 082107. doi:10.1063/1.2756751

CrossRef Full Text | Google Scholar

Horbury, T., Louarn, P., Fujimoto, M., Baumjohann, W., Blomberg, L. G., Barabash, S., et al. (2006). “Cross-scale: a Multi-Spacecraft mission to Study Cross-Scale Coupling in Space Plasmas,” in Cluster and Double Star Symposium. Editor K Fletcher (ESA Special Publication), 598, 77.

Google Scholar

Horbury, T. S., Wicks, R. T., and Chen, C. H. K. (2012). Anisotropy in Space Plasma Turbulence: Solar Wind Observations. Space Sci. Rev. 172, 325–342. doi:10.1007/s11214-011-9821-9

CrossRef Full Text | Google Scholar

Howes, G. G. (2015). A Dynamical Model of Plasma Turbulence in the Solar Wind. Phil. Trans. R. Soc. A. 373, 20140145. doi:10.1098/rsta.2014.0145

PubMed Abstract | CrossRef Full Text | Google Scholar

Howes, G. G. (2016). The Dynamical Generation of Current Sheets in Astrophysical Plasma Turbulence. ApJ 827, L28. doi:10.3847/2041-8205/827/2/L28

CrossRef Full Text | Google Scholar

Kiyani, K., Chapman, S. C., Hnat, B., and Nicol, R. M. (2007). Self-similar Signature of the Active Solar corona within the Inertial Range of Solar-Wind Turbulence. Phys. Rev. Lett. 98, 211101. doi:10.1103/PhysRevLett.98.211101

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiyani, K. H., Osman, K. T., and Chapman, S. C. (2015). Dissipation and Heating in Solar Wind Turbulence: from the Macro to the Micro and Back Again. Phil. Trans. R. Soc. A. 373, 20140155. doi:10.1098/rsta.2014.0155

PubMed Abstract | CrossRef Full Text | Google Scholar

Klein, K. G., Alexandrova, O., Bookbinder, J., Caprioli, D., Case, A. W., Chandran, B. D. G., et al. (2019). Multipoint Measurements of the Solar Wind: A Proposed advance for Studying Magnetized Turbulence. arXiv:1903. 05740.

Kolmogorov, A. N. (1941). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Doklady Akademii Nauk SSSR 30, 301–305.

Google Scholar

Liemohn, M. W., Keesee, A. M., Kepko, L., and Moldwin, M. B. (2021). Instigators of Future Change in Magnetospheric Research. American Geophysical Union, 753–763. chap. 47. doi:10.1002/9781119815624.ch47

CrossRef Full Text

Lugones, R., Dmitruk, P., Mininni, P. D., Wan, M., and Matthaeus, W. H. (2016). On the Spatio-Temporal Behavior of Magnetohydrodynamic Turbulence in a Magnetized Plasma. Phys. Plasmas 23, 112304. doi:10.1063/1.4968236

CrossRef Full Text | Google Scholar

Mann, I. R., Nokes, C. D. A., Cupido, C., Miles, D. M., Bruner, B., Elliott, D. G., et al. (2020). The Experimental Albertan Satellite #1 (Ex-Alta 1) Cube-Satellite mission. Space Sci. Rev. 216, 96. doi:10.1007/s11214-020-00720-8

CrossRef Full Text | Google Scholar

Marsch, E. (2006). Kinetic Physics of the Solar corona and Solar Wind. Living Rev. Solar Phys. 3, 1. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

Marsch, E., and Tu, C.-Y. (1997). Intermittency, Non-gaussian Statistics and Fractal Scaling of Mhd Fluctuations in the Solar Wind. Nonlin. Process. Geophys. 4, 101–124. doi:10.5194/npg-4-101-1997

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Bandyopadhyay, R., Brown, M. R., Borovsky, J., Carbone, V., Caprioli, D., et al. (2019). The Essential Role of Multi-point Measurements in Turbulence Investigations: The Solar Wind beyond Single Scale and beyond the taylor Hypothesis. arXiv:1903.06890.

Matthaeus, W. H. (2021). Turbulence in Space Plasmas: Who Needs it? Phys. Plasmas 28, 032306. (in press). doi:10.1063/5.0041540

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Goldstein, M. L. (1982). Measurement of the Rugged Invariants of Magnetohydrodynamic Turbulence in the Solar Wind. J. Geophys. Res. 87, 6011–6028. doi:10.1029/JA087iA08p06011

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Goldstein, M. L., and Roberts, D. A. (1990). Evidence for the Presence of Quasi-Two-Dimensional Nearly Incompressible Fluctuations in the Solar Wind. J. Geophys. Res. 95, 20673–20683. doi:10.1029/JA095iA12p20673

CrossRef Full Text | Google Scholar

Mikić, Z., Downs, C., Linker, J. A., Caplan, R. M., Mackay, D. H., Upton, L. A., et al. (2018). Predicting the corona for the 21 August 2017 Total Solar Eclipse. Nat. Astron. 2, 913–921. doi:10.1038/s41550-018-0562-5

CrossRef Full Text | Google Scholar

Miles, D. M., Bennest, J. R., Mann, I. R., and Millling, D. K. (2013). A Radiation Hardened Digital Fluxgate Magnetometer for Space Applications. Geosci. Instrum. Method. Data Syst. 2, 213–224. doi:10.5194/gi-2-213-2013

CrossRef Full Text | Google Scholar

Miles, D. M., Ciurzynski, M., Barona, D., Narod, B. B., Bennest, J. R., Kale, A., et al. (2019). Low-noise Permalloy Ring Cores for Fluxgate Magnetometers. Geosci. Instrum. Method. Data Syst. 8, 227–240. doi:10.5194/gi-8-227-2019

CrossRef Full Text | Google Scholar

Miles, D. M., Mann, I. R., Ciurzynski, M., Barona, D., Narod, B. B., Bennest, J. R., et al. (2016). A Miniature, Low-Power Scientific Fluxgate Magnetometer: A Stepping-Stone to Cube-Satellite Constellation Missions. J. Geophys. Res. Space Phys. 121, 11839–11860. doi:10.1002/2016JA023147

CrossRef Full Text | Google Scholar

Miles, D. M., Mann, I. R., Kale, A., Milling, D. K., Narod, B. B., Bennest, J. R., et al. (2017). The Effect of Winding and Core Support Material on the thermal Gain Dependence of a Fluxgate Magnetometer Sensor. Geosci. Instrum. Method. Data Syst. 6, 377–396. doi:10.5194/gi-6-377-2017

CrossRef Full Text | Google Scholar

Mininni, P., Lee, E., Norton, A., and Clyne, J. (2008). Flow Visualization and Field Line Advection in Computational Fluid Dynamics: Application to Magnetic fields and Turbulent Flows. New J. Phys. 10, 125007. doi:10.1088/1367-2630/10/12/125007

CrossRef Full Text | Google Scholar

Montgomery, D. (1982). Major Disruptions, Inverse Cascades, and the Strauss Equations. Phys. Scr. T2A, 83–88. doi:10.1088/0031-8949/1982/T2A/009

CrossRef Full Text | Google Scholar

Motschmann, U., Glassmeier, K. H., and Pinçon, J. L. (2000). “Multi-spacecraft Filtering: Plasma Mode Recognition,” in Analysis Methods For Multi-Spacecraft Data. Editors G Paschmann, and PW Daly. 1 edn (Bern, Switzerland: International Space Science Institute (ISSI)), 79–90. no. SR-001 in ISSI Scientific Reportchap. 4. 1.

Google Scholar

Mottez, F., and Chanteur, G. (1994). Surface Crossing by a Group of Satellites: A Theoretical Study. J. Geophys. Res. 99, 13499–13507. doi:10.1029/93JA03326

CrossRef Full Text | Google Scholar

NASA (2018). Strategic Plan. Tech. rep.NASA.

Ness, N. F., Behannon, K. W., Lepping, R. P., and Schatten, K. H. (1971). Use of Two Magnetometers for Magnetic Field Measurements on a Spacecraft. J. Geophys. Res. 76, 3564–3573. doi:10.1029/JA076i016p03564

CrossRef Full Text | Google Scholar

Neubauer, F. M., and Glassmeier, K.-H. (1990). Use of an Array of Satellites as a Wave Telescope. J. Geophys. Res. 95, 19115–19122. doi:10.1029/JA095iA11p19115

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Chornay, D., Fritzenreiter, R., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, a comprehensive plasma instrument for the WIND spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/BF00751326

Osman, K. T., Matthaeus, W. H., Gosling, J. T., Greco, A., Servidio, S., Hnat, B., et al. (2014). Magnetic Reconnection and Intermittent Turbulence in the Solar Wind. Phys. Rev. Lett. 112, 215002. doi:10.1103/PhysRevLett.112.215002

CrossRef Full Text | Google Scholar

Oughton, S., Matthaeus, W. H., and Dmitruk, P. (2017). Reduced MHD in Astrophysical Applications: Two-Dimensional or Three-Dimensional? ApJ 839, 2. doi:10.3847/1538-4357/aa67e2

CrossRef Full Text | Google Scholar

Owens, M. J., and Forsyth, R. J. (2013). The Heliospheric Magnetic Field. Living Rev. Solar Phys. 10, 5. doi:10.12942/lrsp-2013-5

CrossRef Full Text | Google Scholar

Parker, E. N. (1958). Dynamics of the Interplanetary Gas and Magnetic fields. ApJ 128, 664–676. doi:10.1086/146579

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine Learning in Python. J. Machine Learn. Res. 12, 2825–2830.

Google Scholar

Petrosyan, A., Balogh, A., Goldstein, M. L., Léorat, J., Marsch, E., Petrovay, K., et al. (2010). Turbulence in the Solar Atmosphere and Solar Wind. Space Sci. Rev. 156, 135–238. doi:10.1007/s11214-010-9694-3

CrossRef Full Text | Google Scholar

Pinçon, J. L., and Motschmann, U. (2000). “Multi-spacecraft Filtering: General Framework,” in Analysis Methods For Multi-Spacecraft Data. Editors G Paschmann, and PW Daly. 1 edn (Bern, Switzerland: International Space Science Institute (ISSI)), 65–78. SR-001 in ISSI Scientific Reportchap. 3. 1.

Google Scholar

PlasmaPy Community (2020). Plasmapy Version 0.5.0. doi:10.5281/zenodo.4313063

CrossRef Full Text | Google Scholar

Priest, E. R., and Pontin, D. I. (2009). Three-dimensional Null point Reconnection Regimes. Phys. Plasmas 16, 122101. doi:10.1063/1.3257901

CrossRef Full Text | Google Scholar

Rasmussen, C. E., and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. MIT PressAvailable at: http://www.gaussianprocess.org/gpml/chapters/. (Accessed date February 9, 2021).

Retinò, A., Sundkvist, D., Vaivads, A., Mozer, F., André, M., and Owen, C. J. (2007). In Situ evidence of Magnetic Reconnection in Turbulent Plasma. Nat. Phys. 3, 235–238. doi:10.1038/nphys574

CrossRef Full Text | Google Scholar

Roytershteyn, V., Karimabadi, H., and Roberts, A. (2015). Generation of Magnetic Holes in Fully Kinetic Simulations of Collisionless Turbulence. Phil. Trans. R. Soc. A. 373, 20140151. doi:10.1098/rsta.2014.0151

PubMed Abstract | CrossRef Full Text | Google Scholar

Russell, C. T., Mellott, M. M., Smith, E. J., and King, J. H. (1983). Multiple Spacecraft Observations of Interplanetary Shocks: Four Spacecraft Determination of Shock Normals. J. Geophys. Res. 88, 4739–4748. doi:10.1029/JA088iA06p04739

CrossRef Full Text | Google Scholar

Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E., et al. (2009). Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas. ApJS 182, 310–377. doi:10.1088/0067-0049/182/1/310

CrossRef Full Text | Google Scholar

Servidio, S., Matthaeus, W. H., Wan, M., Ruffolo, D., Rappazzo, A. F., and Oughton, S. (2014). Complexity and Diffusion of Magnetic Flux Surfaces in Anisotropic Turbulence. ApJ 785, 56. doi:10.1088/0004-637X/785/1/56

CrossRef Full Text | Google Scholar

Shalchi, A., and Hussein, M. (2014). Perpendicular Diffusion of Energetic Particles in Noisy Reduced Magnetohydrodynamic Turbulence. ApJ 794, 56. doi:10.1088/0004-637X/794/1/56

CrossRef Full Text | Google Scholar

Shen, C., Li, X., Dunlop, M., Liu, Z., Balogh, A., Baker, D., et al. (2003). Analyses on the Geometrical Structure of Magnetic Field in the Current Sheet Based on Cluster Measurements. J. Geophys. Res. Space Phys. 108, 1168. doi:10.1029/2002ja009612

CrossRef Full Text | Google Scholar

Shen, C., Li, X., Dunlop, M., Shi, Q., Liu, Z., Lucek, E., et al. (2007). Magnetic Field Rotation Analysis and the Applications. J. Geophys. Res. Space Phys. 112, A06211. doi:10.1029/2005ja011584

CrossRef Full Text | Google Scholar

Sitnov, M. I., Stephens, G. K., Tsyganenko, N. A., Miyashita, Y., Merkin, V. G., Motoba, T., et al. (2019). Signatures of Nonideal Plasma Evolution during Substorms Obtained by Mining Multimission Magnetometer Data. J. Geophys. Res. Space Phys. 124, 8427–8456. doi:10.1029/2019JA027037

CrossRef Full Text | Google Scholar

Spence, H. E. (2019). Helioswarm: Unlocking the Multiscale Mysteries of Weakly-Collisional Magnetized Plasma Turbulence and Ion Heating. AGU Fall Meeting 9-13 December 2019 in San Francisco, CA, United States. Th. SH11B–04. Abstracts.

Google Scholar

Stephens, G. K., Sitnov, M. I., Korth, H., Tsyganenko, N. A., Ohtani, S., Gkioulidou, M., et al. (2019). Global Empirical Picture of Magnetospheric Substorms Inferred from Multimission Magnetometer Data. J. Geophys. Res. Space Phys. 124, 1085–1110. doi:10.1029/2018JA025843

CrossRef Full Text | Google Scholar

Sundkvist, D. J., Saint-Hilaire, P., Bain, H. M., Bale, S. D., Bonnell, J. W., Hurford, G. J., et al. (2016). “Curie: Cubesat Radio Interferometry experiment,” in AGU Fall Meeting 12-16 December 2016 in San Francisco, CA, United States., SH11C–2271. Abstracts.

Google Scholar

Taylor, G. I. (1938). The Spectrum of Turbulence. Proc. R. Soc. A. 164, 476–490. doi:10.1098/rspa.1938.0032

CrossRef Full Text | Google Scholar

TenBarge, J. M., Alexandrova, O., Boldyrev, S., Califano, F., Cerri, S. S., Chen, C. H. K., et al. (2019). Disentangling the Spatiotemporal Structure of Turbulence Using Multi-Spacecraft Data. arXiv:1903.05710.

Tooprakai, P., Seripienlert, A., Ruffolo, D., Chuychai, P., and Matthaeus, W. H. (2016). Simulations of Lateral Transport and Dropout Structure of Energetic Particles from Impulsive Solar Flares. ApJ 831, 195. doi:10.3847/0004-637X/831/2/195

CrossRef Full Text | Google Scholar

Torbert, R. B., Dors, I., Argall, M. R., Genestreti, K. J., Burch, J. L., Farrugia, C. J., et al. (2020). A New Method of 3‐D Magnetic Field Reconstruction. Geophys. Res. Lett. 47, 085542. doi:10.1029/2019GL085542

CrossRef Full Text | Google Scholar

Tu, C.-Y., and Marsch, E. (1995). MHD Structures, Waves and Turbulence in the Solar Wind: Observations and Theories. Space Sci. Rev. 73, 1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

Vaivads, A., Andersson, G., Bale, S. D., Cully, C. M., De Keyser, J., Fujimoto, M., et al. (2012). Eidoscope: Particle Acceleration at Plasma Boundaries. Exp. Astron. 33, 491–527. doi:10.1007/s10686-011-9233-6

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The Multi-Scale Nature of the Solar Wind. Living Rev. Sol. Phys. 16, 5. doi:10.1007/s41116-019-0021-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wallis, D. D., Miles, D. M., Narod, B. B., Bennest, J. R., Murphy, K. R., Mann, I. R., et al. (2015). The Cassiope/e-Pop Magnetic Field Instrument (Mgf). Space Sci. Rev. 189, 27–39. doi:10.1007/s11214-014-0105-z

CrossRef Full Text | Google Scholar

Watanabe, T., and Nagata, K. (2017). Gradients Estimation from Random Points with Volumetric Tensor in Turbulence. J. Comput. Phys. 350, 518–529. doi:10.1016/j.jcp.2017.08.057

CrossRef Full Text | Google Scholar

Wicks, R. T., Chapman, S. C., and Dendy, R. O. (2009). Spatial Correlation of Solar Wind Fluctuations and Their Solar Cycle Dependence. ApJ 690, 734–742. doi:10.1088/0004-637X/690/1/734

CrossRef Full Text | Google Scholar

Wicks, R. T., Horbury, T. S., Chen, C. H. K., and Schekochihin, A. A. (2010). Power and Spectral index Anisotropy of the Entire Inertial Range of Turbulence in the Fast Solar Wind. Monthly Notices R. Astronomical Soc. 407, L31–L35. doi:10.1111/j.1745-3933.2010.00898.x

CrossRef Full Text | Google Scholar

Wicks, R. T., and Miles, D. M. (2019). Editorial: Topical Collection on Multi-point Measurements of the Thermosphere with the Qb50 mission. Space Sci. Rev. 215, 15. doi:10.1007/s11214-019-0588-8

CrossRef Full Text | Google Scholar

Wilson, L. B., Stevens, M. L., Kasper, J. C., Klein, K., Maruca, B., Bale, S., et al. (2018). The Statistical Properties of Solar Wind Temperature Parameters Near 1 au. Astrophys. J. Suppl. 236, 41. doi:10.3847/1538-4365/aab71c

Woodham, L. D., Wicks, R. T., Verscharen, D., and Owen, C. J. (2018). The Role of Proton Cyclotron Resonance as a Dissipation Mechanism in Solar Wind Turbulence: A Statistical Study at Ion-Kinetic Scales. ApJ 856, 49. doi:10.3847/1538-4357/aab03d

CrossRef Full Text | Google Scholar

Zank, G. P., Adhikari, L., Hunana, P., Shiota, D., Bruno, R., and Telloni, D. (2017). Theory and Transport of Nearly Incompressible Magnetohydrodynamic Turbulence. ApJ 835, 147. doi:10.3847/1538-4357/835/2/147

CrossRef Full Text | Google Scholar

Zenitani, S., Hesse, M., Klimas, A., Black, C., and Kuznetsova, M. (2011). The Inner Structure of Collisionless Magnetic Reconnection: The Electron-Frame Dissipation Measure and Hall fields. Phys. Plasmas 18, 122108. doi:10.1063/1.3662430

CrossRef Full Text | Google Scholar

Zhou, Y., Matthaeus, W., and Dmitruk, P. (2004). Colloquium: Magnetohydrodynamic Turbulence and Time Scales in Astrophysical and Space Plasmas. Rev. Mod. Phys. 76, 1015–1035. doi:10.1103/RevModPhys.76.1015

CrossRef Full Text | Google Scholar