- 1Department of Astronomy/Steward Observatory, Tucson, AZ, United States
- 2The Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, United States
Accurate and stable spacecraft pointing is a requirement of many astronomical observations. Pointing particularly challenges nanosatellites because of an unfavorable surface area–to-mass ratio and a proportionally large volume required for even the smallest attitude control systems. This work explores the limitations on astrophysical attitude knowledge and control in a regime unrestricted by actuator precision or actuator-induced disturbances such as jitter. The external disturbances on an archetypal 6U CubeSat are modeled, and the limiting sensing knowledge is calculated from the available stellar flux and grasp of a telescope within the available volume. These inputs are integrated using a model-predictive control scheme. For a simple test case at 1 Hz, with an 85-mm telescope and a single 11th magnitude star, the achievable body pointing is predicted to be 0.39 arcseconds. For a more general limit, integrating available star light, the achievable attitude sensing is approximately 1 milliarcsecond, which leads to a predicted body pointing accuracy of 20 milliarcseconds after application of the control model. These results show significant room for attitude sensing and control systems to improve before astrophysical and environmental limits are reached.
1 Introduction
Astronomical observation with nanosatellites requires a level of precision that far exceeds what is possible with common attitude determination and control systems (ADCSs) present on Earth-imaging CubeSats. It should be noted that this work will refer to nanosatellites in an inclusive sense for any spacecraft weighing approximately 10 kg or below or those that are designed specifically to a CubeSat deployer standard (https://www.cubesat.org). Since astronomical light sources are dim and relatively static, these fine-pointing nanosatellites need to observe continuously, or “stare,” for minutes to hours [e.g., Weiss et al. (2014); Shkolnik (2018); Knapp et al. (2020a)]. An ideal astronomical ADCS would achieve this by slewing the nanosatellite to the target attitude and maintaining perfect inertial pointing indefinitely while rejecting transient disturbances that fall below the sampling accuracy of the instrument. Improving nanosatellite pointing enables a range of applications beyond the transformative photometry recently demonstrated by the ASTERIA mission (Knapp et al., 2020b). These applications span from direct exoplanet detection by interferometry (Dandumont et al., 2020) or starshades (Macintosh et al., 2019) to X-rays (Krizmanic et al., 2020) and the ultraviolet (Shkolnik, 2018).
Actuating the attitude of a spacecraft requires application of torque on the body of the spacecraft. In early nanosatellites, this was achieved by using onboard magnetorquers interacting with the Earth’s magnetic field, allowing for coarse aiming of solar panels and antenna. Miniaturization and implementation of reaction wheels, which are flywheels spun continuously using precision motors at tens to thousands of revolutions per minute, on these nanosatellites has enabled sub-1 arcminute nanosatellite pointing (Sinclair et al., 2007; Mason et al., 2016).
The attitude control performance of nanosatellites is limited by an unfavorable mass-to–surface area ratio of both the spacecraft and the small reaction wheels, increasing sensitivity to external disturbances and internal imbalances. While these actuators have been proven capable of fine pointing on larger spacecraft, they do not scale down well to smaller spacecraft, as demonstrated in Figure 1. State-of-the-art reaction wheels allow for precise pointing and rejection of slowly changing disturbances, for example, drag differentials, but imperfections in the reaction wheels can directly add uncontrolled jitter and excite spacecraft structural modes (Addari et al., 2017; Shields et al., 2017). Thermal drifts and misalignment between attitude sensor star-trackers and science payloads can be addressed when using a science telescope for attitude determination, but the higher-order jitter remains, for example, analysis in the studies by Smith et al. (2010) and Nguyen et al. (2018).
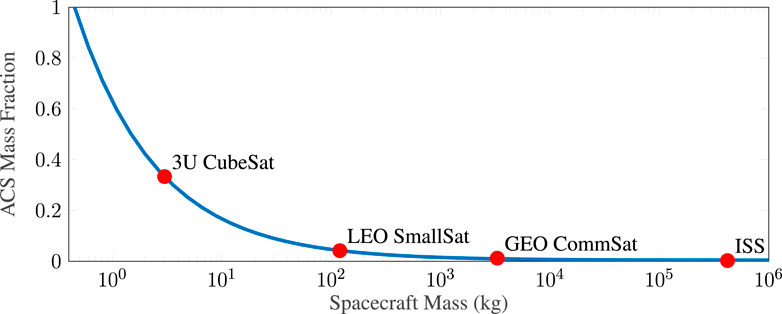
FIGURE 1. Approximate mass fraction consumed by momentum actuators as a function of spacecraft mass.
Large spacecraft often use control-moment gyros for attitude control, but their increased size, weight, and power (SWaP) and complexity make them impractical for most nanosatellites (Votel and Sinclair, 2012). Spacecraft like the largest NASA observatories are able to achieve the most exquisite pointing via passive damping of these actuators. This damping comes at the cost of significant mass and volume and becomes more difficult as the spacecraft mass decreases. Using great observatories as examples, HST uses viscous dampers (Davis, 1986), each Chandra reaction wheel is isolated using six damping springs arranged in a hexapodal configuration (Pendergast and Schauwecker, 1998), and JWST uses dual-stage passive isolation (Bronowicki, 2006). This simple, but fundamental, trade between pointing accuracy and SWaP is a major barrier in astrophysics with regard to nanosatellites.
Many proposed solutions to the attitude control limitations of CubeSats have been in the form of second-stage correction (Beierle et al., 2018; Pong, 2018; Cahoy et al., 2019). ASTERIA (Arcsecond Space Telescope Enabling Research in Astrophysics) is the first sub-arcsecond imaging CubeSat (Pong, 2018). The correction was accomplished by image–plane stabilization using a detector-shifting lead zirconate titanate (PZT) stage. The science telescope on ASTERIA operates at 20 Hz, reading out 50-ms exposures for science and pointing control, limiting the detectable stellar magnitude to mV < 7 since dimmer stars do not flip the detector’s first analog-to-digital bit (Knapp et al., 2020a) in an exposure. Similarly, the CLICK free-space laser communications CubeSats (Cahoy et al., 2019), due for launch in 2021, will use microelectromechanical systems (MEMS)-based steering mirrors to achieve fine pointing, while the DeMi mission launched in 2020 is designed to use a MEMS deformable mirror for fine wavefront steering (Morgan et al., 2019).
The combination of controller bandwidth and photon noise from stars presents a fundamental limit to attitude control with reaction wheels. Without a large aperture and a corresponding large number of photons per exposure, photoelectron shot noise limits the centroid accuracy of the star tracker or astronomical telescope. As a Poisson process, the error is proportional to the square root of the number of photoelectrons per exposure; thus, for a simple disturbance environment, the achievable pointing decreases linearly with the telescope diameter. Unfortunately, performance degrades faster than this in practice. Crossing a structural mode of the spacecraft can have devastating impacts on stability, and manufacturing tolerance limits mean that reaction wheel imbalances are an even larger fraction of the spacecraft inertia on nanosatellites, so higher bandwidths may be required when fewer photons are available.
This work seeks to define the sensing and control limits of satellite pointing, establishing the lower limit without considering the limitations imposed by actuators. Actuator disturbances are usually so dominant that environmental disturbances are entirely neglected in spacecraft design [e.g., Choueiri et al. (2018)].
The two-stage actuator approach is limited for several reasons: pointing correction stages add mass, power, complexity, and risk, not all astronomical optical layouts can accommodate a correction stage, and the bandwidth of the system must be sufficient to correct high-frequency reaction wheel disturbances. Single-stage approaches that minimize high-frequency noise have also been proposed, including electrospray thrusters (Mier-Hicks and Lozano, 2017), viscously damped reaction wheels (Underwood et al., 2015), and predictive magnetorquers (Gatherer and Manchester, 2018). While both approaches have various limitations in their actuation precision and dynamic range, they hold great promise. However, we find it imperative to assess the possible gains of these approaches by finding the fundamental limits placed by the input disturbances and sensing available on a nanosatellite platform. This provides a context and methodology for evaluating the limits on new controller technologies. Section 2 introduces our disturbance, sensing, and control models. Section 3 details the state-estimation framework used in the closed-loop simulations. Section 4 presents the resulting spacecraft body pointing as a function of sensor and control limitations. Section 5 discusses the impact of these results, comparing them to the limitations faced by current actuators, and the goals of future space astronomy missions.
2 Methods
2.1 Disturbances
Modern attitude control systems rely on flywheel-based momentum actuators like reaction wheels and control-moment gyroscopes. For a constant density, spacecraft inertia scales like the fifth power of spacecraft length, while disturbances like solar pressure, drag, and friction scale with the second power of spacecraft length (surface area). As shown in Figure 1, the mass and volume fraction consumed by momentum actuators increases dramatically as the size of the spacecraft shrinks.
This work neglects magnetic torques, which can be large (Inamori et al., 2013) but depend on the fine details of spacecraft design, since both the intrinsic magnetic moment and the dynamic magnetic moment due to onboard currents can be minimized with careful electrical design and spacecraft magnetic cleanliness [e.g., Mehlem (1978); Stern and DeLapp (2004); Junge and Marliani (2011); Belyayev et al. (2016); Lassakeur et al. (2020)].
Figure 2 depicts the frequency content of environmental disturbances acting on a 6U spacecraft in low-Earth orbit. This figure was generated by simulating 1,000 Monte-Carlo runs that included drag, solar radiation pressure, and gravity gradient torques (Wertz, 1978; Markley and Crassidis, 2014). The orbits were sampled uniformly from the range of all possible lower-Earth orbits with an eccentricity of less than 0.03 and altitudes between 400 and 600 km. The simulation epochs were sampled uniformly between 2014 and 2017 to avoid any bias in solar activity or third-body perturbations. The line in the figure is the result of the maximum RMS torque over all Monte-Carlo runs for each given frequency. It should be noted that the environmental disturbances that the control system must counteract are concentrated in the first few harmonics of the orbital frequency and lie almost entirely in the range of 0.1–10 mHz.
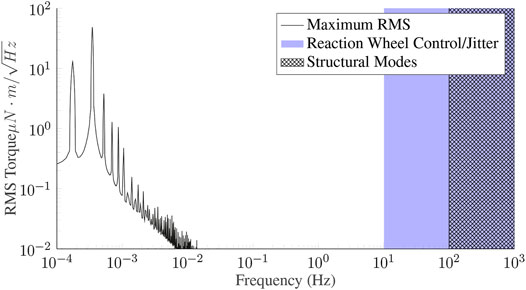
FIGURE 2. Frequency content of perturbation torques on a small satellite in low-Earth orbit. Disturbances are due to atmospheric drag, solar radiation pressure, and a gravity gradient. The disturbances manifest on the left as a solid curve representing the maximum value from an ensemble of orbits drawn from multiple years of credible low-Earth orbits. On the far right, solid shading illustrates typical actuator-induced error frequencies, and hatching represents typical nanosatellite structural modes.
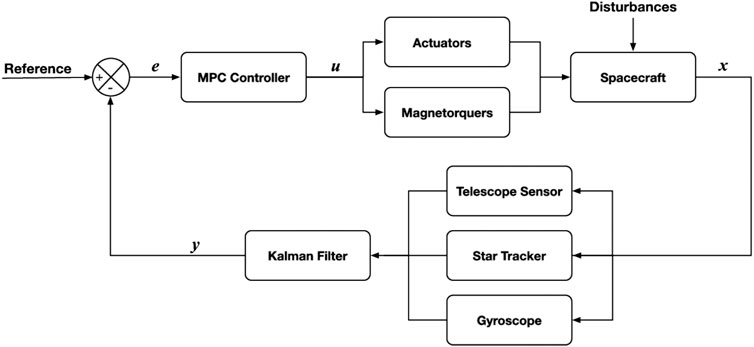
In addition to poor scaling for small spacecraft, reaction wheels also produce unwanted high-frequency jitter that is often the main source of pointing error on nanosatellites. This jitter is caused by small mass imbalances in the flywheels as they rotate at hundreds of Hertz. Notably, the frequency content of this jitter is several orders of magnitude higher than the environmental disturbances the wheels are supposed to counteract. The overall control loop for the system discussed here is depicted in Figure 3. Two notable features which will be detailed subsequently are the model-predictive controller and the addition of a telescope sensor to increase sensor precision.
2.2 Control Methodology
To effectively reason about actuator trade-offs and constraints, the control problem will be formulated as a constrained optimization problem and solved online in a model-predictive control (MPC) scheme. Recent advances in algorithm development and microprocessors have enabled state-of-the-art high-performance MPC solvers that can be run on embedded systems such as drones and CubeSats (Howell et al., 2019; Jackson et al., 2021; Tracy and Manchester, 2020). In typical MPC implementations, the problem in Eq. 1 is solved with a horizon of 10–100 time steps at rates between 10 Hz and 1 kHz. While MPC has been in use in industrial applications since the 1980s, its use has historically been limited by the ability to solve the necessary optimization problems at real-time rates on available computing hardware. Thanks to Moore’s law, it has become possible to do this on ever more complicated systems, and today, MPC is deployed in a wide range of aerospace and robotics applications, including SpaceX’s autonomous rocket landings (Blackmore, 2016), Boston Dynamics’ humanoid robots (Kuindersma et al., 2016), and autonomous cars (Beal and Gerdes, 2013).
Model-predictive control problems take the following general form:
where xk and uk are the state and control inputs of the system at time step k, ℓ(x, u) is a cost function that penalizes deviations from a desired reference, f (x, u) is a discrete-time dynamics model, and g (x, u) is a set of constraints on the system, including actuator limits and safety constraints. In our case, f (x, u) will encode the attitude dynamics of the spacecraft, the actuators, and the magnetic torque coils, ℓ(x, u) will penalize deviations from the desired pointing target and excessive control effort, and g (x, u) will enforce torque limits associated with candidate actuator systems.
2.3 Sensing
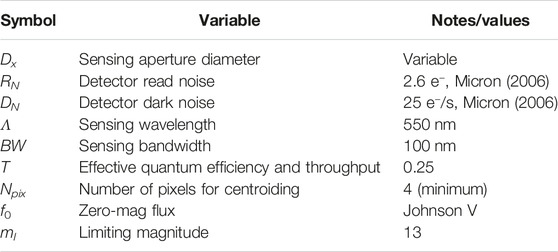
Attitude sensing using astronomical sources requires sufficient photon counts to determine direction by accurately measuring a star, or stars’, position(s) on a sensor. Here, we shall assume an astronomical telescope is included in the nanosatellite payload, either as the primary science instrument or as an adjuvant co-aligned with another sensor. Various means exist of pulling out attitude knowledge from a telescope and employing a separate science camera, for example, beamsplitters, dichroics, and field-slicing. We will neglect the details of the implementation except to limit our sensing to a single filter, BW = 100 nm, leaving most incoming light available for another specialized science sensor.
In the ideal case, the angular attitude knowledge Δϕ perpendicular to an axis 10) depends on the wavelength, (λ), and the dimension(s) of the photon-collecting aperture, (Δx). As shown by Lindegren et al. (2005), the fundamental pointing error depends on the uncertainty in the momentum of each incident photon. By Heisenberg’s uncertainty principle (ΔxΔp ≥ ℏ/2), the photon’s momentum uncertainty (Δp) decreases as uncertainty in the location of the photon increases. Thus, a larger telescope increases Δx and better constrains the angle of the incident photon.
For the case where there are N photons, Lindegren (2013, Eq. 16.1) gives us the following:
where N = σ2 is the variance in the photons from Poisson statistics. For a circular aperture diameter D, Δx = D/4 and then the following is the case:
The same relation can be derived by assuming a Poisson process and Fraunhofer diffraction (Lindegren, 1978, Eq. 32). The number of photons, N, received by the sensor depends on the exposure time and the light grasp or étendue of the system. The étendue is defined as the product of the collecting area, π(Dx/2)2, and the solid angle, Ω, subtended by the instrument. A complicating factor is that the number of stars visible within the collecting area varies with direction in the sky. To calculate the distribution of stars in the sky, we conservatively estimate the differential number of stars per square degree,
where f0 is the zero-point magnitude of the instrument band-pass, and τ is the effective throughput including losses due to optics and sensor quantum efficiency.
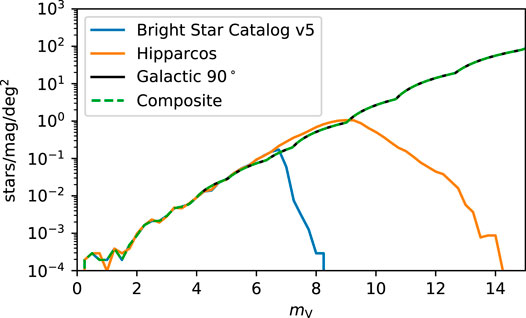
FIGURE 4. Star counts in units of stellar density per magnitude and per square degree. The dashed curve represents the density used in this work and represents a composite of the Bright Star catalog (Hoffleit D., 1991) for bright stars, and the galactic pole curve from the study by Bahcall and Soneira (1980) at dimmer magnitudes provides a lower limit on stellar density by assuming the observations are of the sparsest region of the sky. This composite represents a conservative estimate of the number of photons available to localize spacecraft attitude control.
For our analysis, we assume that the spacecraft is sufficiently stable that individual stars can be identified, and smearing in a given exposure is negligible. While not discussed here, the length of star smearing can be used to determine the angular rate of the spacecraft (Enright et al., 2010). Attitude sensing using astronomical sources requires sufficient photon counts to accurately determine direction by accurately measuring the star position(s). Figure 5 shows the sensing limits with (dashed curves) and without the addition of uncertainty due to a low-performance, high–technology readiness level (TRL) detector (dot-dashed curves) described in Section 4.
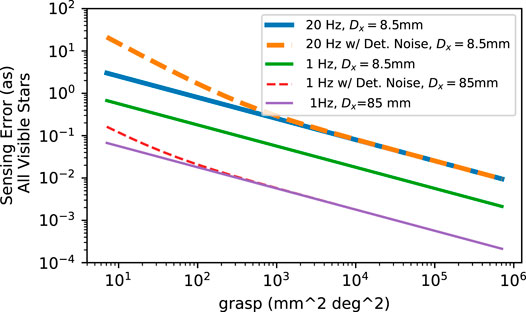
FIGURE 5. Attitude determination error versus system grasp or étendue. This photon noise limited case assumes the flux per square degree at the galactic poles for stars from zero to the 13th magnitude, (Figure 4). The upper bound on the x-axis corresponds to a telescope with a diameter of 85 mm with a ten-degree circular FOV. The 20-Hz curve is shown to emphasize the importance of short exposure times. At low grasps, the detector noise dominates, while at large grasps, the photon noise dominates. Small values of Dx show the importance of the sensor aperture to constraining body pointing; it should be noted that the largest grasps are likely to require an impractically large FOV for Dx = 8.5 mm.
3 State Estimation
In addition to the astronomical telescope, a compact star tracker and gyroscope are included in our model for coarse attitude determination. Typical COTS star trackers for CubeSats provide attitude determination with an accuracy of tens of arcseconds and are able to maintain tracking at slew rates of several degrees per second. Measurements from all sensors are fused in a multiplicative extended Kalman filter (MEKF) (Lefferts et al., 1982) to calculate a maximum-likelihood estimate of the spacecraft’s attitude.
In addition to estimating the attitude of the spacecraft body, parameterized by quaternion q, the filter also estimates a gyroscope bias vector b, an external bias torque τ, and the time derivative of this external torque
where νω, νb, and
where the function h(x) returns expected star locations in the sensor frames based on the current spacecraft state, and w is assumed to be drawn from a multivariate Gaussian distribution with a covariance matrix W calculated based on Figure 6.
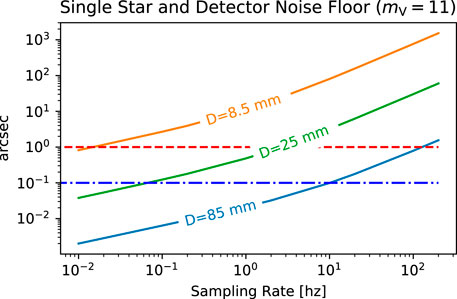
FIGURE 6. Attitude sensing limit curves assuming centroiding noise due to photon statistics and detector noise from the TRL-9 MT9P031 CMOS detectors widely used on nanosatellites. For an 85-mm space telescope, sub-arcsec sensing is readily achieved at 100 s sampling or slower rates, implying that ∼10-Hz bandwidth controllers are as fast as is feasible on dim stars.
4 Results
Figure 6 shows that, for example, a single mV = 11 guide star can provide sub-0.1′′ pointing knowledge to a 1-Hz sampling system, assuming typical detector noise levels in Table 1 for the calculation of σ. The assumed noise characteristics approximate the MT9P031 complementary metal–oxide–semiconductor (CMOS) sensor with 2.2 μm pixels, commonly used for precision nanosatellite applications (Becker et al., 2008; Enright et al., 2012; Allan et al., 2018). mV = 11 was chosen because they are common, ≫ 1/star sq. deg on average. Due to the extremely low frequency content of on-orbit environmental disturbances (Figure 2), the example sampling at 1 Hz is a far higher sample rate than would be needed for an idealized control loop.
Spacecraft body pointing while applying the control system (Figure 3) to input the disturbances, including photon and sensor noise for an 85-mm telescope observing a single mV star sampled at 1 Hz, is simulated in Figure 7. This figure shows the time evolution of body pointing for the proposed control system, with a one-arcsecond circle for reference. With the starting point outside the one-arcsecond circle, the body pointing of the reference 6U CubeSat orbit is quickly controlled to an RMS of 0.39 arcseconds.
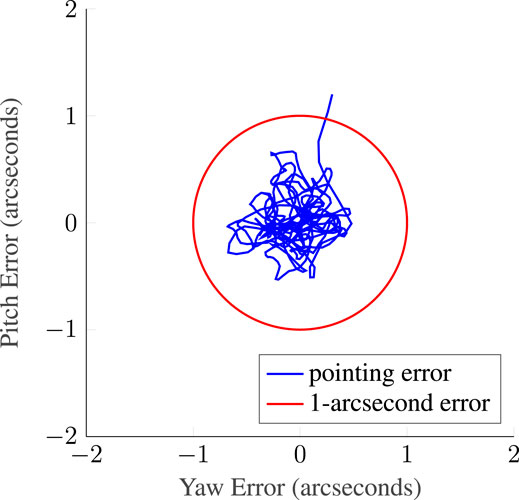
FIGURE 7. 1-Hz closed-loop control simulation with disturbances from Figure 2 and sensor noise corresponding to the largest practical telescope that might fit in a 6U CubeSat with a diameter of 85 mm, measuring the angle of a single mV = 11 star. The red circle indicates the one-arcsecond error. The initial state is outside the one-arcsecond circle, but the controller quickly recovers. The resulting RMS body-pointing error is 0.39′′.
Figure 8 extends this analysis to a range of sensing errors. The center line, bracketed by 3 − σ bounds, shows the RMS body pointing versus the absolute sensing error, demonstrating a relationship where the pointing error closely matches the sensing error over a broad range. This is noteworthy since it suggests that the limiting factor in pointing performance comes from the sensing errors instead of jitter induced by the actuators or bandwidth limits in the control system. The sensor grasp or aperture that would reach this level of performance can be found by observing the sensing errors in Figure 6 or Figure 5. For example, to reach 0.1′′ at 1 Hz using all available starlight, a grasp of ≳200 mm deg 2 is needed, while a single 11th magnitude star is insufficient to reach that level in a nanosatellite aperture.
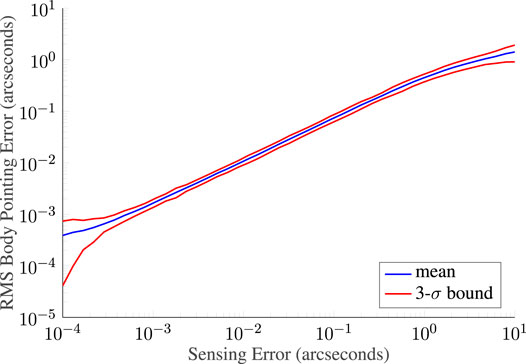
FIGURE 8. Body-pointing RMS error as it relates to the sensing error (whether photon or detector limited). Data are from 1,000 Monte-Carlo trials with full environmental disturbance torques. Each point on these curves corresponds to a full simulation analogous to that shown in Figure 7.
5 Conclusion
In 1980, Nancy Grace Roman said “pointing has been the pacing team that has really controlled what we’ve been able to do in space astronomy as the field has developed” (Roman and DeVorkin, 1980). This assertion, a “Roman’s Law” for spacecraft capabilities, continues to hold true, and pointing remains a particular challenge for nanosatellites.
Detector dynamic range constraints were neglected in this analysis: present-day sensors with limited bit depth will not be able to capture all the incident photons without saturating. This limits the useful input flux. Similarly, low-noise detectors allow sensing of dimmer stars, changing the brightness cutoff, ml. Since the brightest stars are also the rarest, this will generally have less impact than might be first assumed but suggests the importance of both improved actuators and high–dynamic range sensors and readout electronics for future ADCSs.
Detector pixel sampling was implicitly optimized across this analysis, and for physical designs, the FOV and grasp must be carefully weighed against pixel size and detector noise levels. Caution must be used when applying the sensing error–versus-grasp curve on Figure 5 to constrain physical designs. Physical designs must include detector noise, pixel sampling values, and centroiding precision. With sufficient flux rates, increasing detector noise by defocusing stars improves centroiding to millipixel levels (Buffington et al., 1991), but this must be balanced with per-pixel noise contributions and confusion limits.
The closed-loop simulation results presented here show that the low frequency of environmental disturbances allows for a very slow control loop for inertially pointing spacecraft. While further improvements in estimation and control algorithms are possible, this work demonstrates the practical limits of nanosatellite pointing far beyond the current state of the art and establishes the target for actuator improvements to enable precision astrophysics with nanosatellites.
Data Availability Statement
The original contributions presented in the study are publicly available. The study can be fully reproduced using publicly available data and archived Julia and Python code available here: Douglas et al. (2021), 10.5281/zenodo.4498807.
Author Contributions
ED led experiment design, simulation, and manuscript preparation. ZM led model design, optimization, and analysis and contributed to manuscript preparation. KT led disturbance simulations and contributed to literature review and manuscript preparation.
Funding
Portions of this work were supported by the Arizona Board of Regents Technology Research Initiative Fund (TRIF).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Laurent Pueyo for many helpful discussions and feedback. This research has made use of the VizieR catalog access tool, CDS, Strasbourg, France (DOI: 10.26093/cds/vizier). The original description of the VizieR service was published in 2000, A&AS 143, 23.
References
Addari, D., Aglietti, G. S., and Remedia, M. (2017). Experimental and Numerical Investigation of Coupled Microvibration Dynamics for Satellite Reaction Wheels. J. Sound Vibration 386, 225–241. doi:10.1016/j.jsv.2016.10.003
Allan, G., Douglas, E. S., Barnes, D., Egan, M., Furesz, G., Grunwald, W., et al. (2018). The Deformable Mirror Demonstration mission (DeMi) CubeSat: Optomechanical Design Validation and Laboratory Calibration. In Proc. SPIE. San Diego, CA: International Society for Optics and Photonics, 1069857.
Bahcall, J. N., and Soneira, R. M. (1980). The Universe at Faint Magnitudes. I-Models for the Galaxy and the Predicted star Counts. Astrophysical J. Suppl. Ser. 44, 73–110.
Beal, C. E., and Gerdes, J. C. (2013). Model Predictive Control for Vehicle Stabilization at the Limits of Handling. IEEE Trans. Control. Syst. Tech. 21, 1258–1269. doi:10.1109/TCST.2012.2200826
Becker, H. N., Dolphin, M. D., Thorbourn, D. O., Alexander, J. W., and Salomon, P. M. (2008). Commercial Sensory Survey Radiation Testing Progress Report. Pasadena, CA: Jet Propulsion Laboratory, National Aeronautics and Space Administration.
Beierle, C., D’Amico, S., Macintosh, B., and Norton, A. (2018). “Two-stage Attitude Control for Direct Imaging of Exoplanets with a CubeSat Telescope,” in Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave. Editors H. A. MacEwen, M. Lystrup, G. G. Fazio, N. Batalha, E. C. Tong, and N. Siegler (United States: SPIE), 69. doi:10.1117/12.2314233
Belyayev, S., Ivchenko, N., Dudkin, F., and Pronenko, V. (2016). PRACTICAL ANALYSIS AND IMPLEMENTATION OF A LOW MAGNETIC CONTAMINATION CUBESAT PLATFORM. The 4S Symp. 2016.
Bronowicki, A. J. (2006). Vibration Isolator for Large Space Telescopes. J. Spacecraft Rockets 43, 45–53. doi:10.2514/1.12036
Buffington, A., Booth, C. H., and Hudson, H. S. (1991). Using Image Area to Control CCD Systematic Errors in Spaceborne Photometric and Astrometric Time-Series Measurements. PASP 103, 685. doi:10.1086/132868
Cahoy, K., Grenfell, P., Crews, A., Long, M., Serra, P., Nguyen, A., et al. (2019). The CubeSat Laser Infrared CrosslinK Mission (CLICK). In International Conference on Space Optics — ICSO 2018. Chania, Greece: International Society for Optics and Photonics, 111800Y. doi:10.1117/12.2535953
Choueiri, M. N., Bell, M., and Peck, M. A. (2018). Cost-Effective and Readily Manufactured Attitude Determination and Control System for NanoSatellites. In 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference (American Institute of Aeronautics and Astronautics). AIAA SciTech Forum. doi:10.2514/6.2018-0802
Dandumont, C., Defrère, D., Kammerer, J., Absil, O., Quanz, S. P., and Loicq, J. (2020). Exoplanet Detection Yield of a Space-Based Bracewell Interferometer from Small to Medium Satellites. J. Astron. Telesc. Instrum. Syst. 6. doi:10.1117/1.JATIS.6.3.035004
Davis, L. P. (1986). “Hubble Space Telescope Reaction Wheel Assembly Vibration Isolation System,” in Damping Proceedings (Las Vegas, NV, USA: FLIGHT DYNAMICS LABORATORY AIR FORCE WRIGHT AERONAUTICAL LABORATORIES), 695.
Douglas, E., Manchester, Z., and Tracy, K. (2021). Douglase/FinePointing: CubeSat Star Sensor, Disturbance, and Control Sims – Initial Release. Zenodo. doi:10.5281/zenodo.4499318
Enright, J., Sinclair, D., and Dzamba, T. (2012). The Things You Can’t Ignore: Evolving a Sub-arcsecond Star Tracker. In AIAA/USU SmallSat Conference. vol. SSC12-X-7.
Enright, J., Sinclair, D., Grant, C., McVittie, G., and Dzamba, T. (2010). Towards Star Tracker Only Attitude Estimation. In Small Satellite Conference.
ESA (1997). The HIPPARCOS and TYCHO Catalogues. Astrometric and Photometric star Catalogues Derived from the ESA HIPPARCOS Space Astrometry Mission 1200.
Gatherer, A., and Manchester, Z. (2018). MAGNETORQUER-ONLY ATTITUDE CONTROL OF SMALL SATELLITES USING TRAJECTORY OPTIMIZATION. Adv. Astronautical Sci. AAS 19-927, 14.
Hoffleit, D., W. J. W. (1991). VizieR Online Data Catalog: Bright star Catalogue. 5th revised ed. V/50.
Howell, T. A., Jackson, B. E., and Manchester, Z. (2019). ALTRO: A Fast Solver for Constrained Trajectory Optimization. In IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Macau, China.
Inamori, T., Wang, J., Saisutjarit, P., and Nakasuka, S. (2013). Jitter Reduction of a Reaction Wheel by Management of Angular Momentum Using Magnetic Torquers in Nano- and Micro-satellites. Adv. Space Res. 52, 222–231. doi:10.1016/j.asr.2013.02.014
Jackson, B. E., Punnoose, T., Neamati, D., Tracy, K., and Jitosho, R. (2021). ALTRO-C: A Fast Solver for Conic Model-Predictive Control. In International Conference on Robotics and Automation (ICRA). Xi’an, China, 8.
J. R. Wertz (1978). Spacecraft Attitude Determination and Control. (Dordrecht: Astrophysics and Space Science LibrarySpringer Netherlands). doi:10.1007/978-94-009-9907-7
Junge, A., and Marliani, F. (2011). Prediction of DC Magnetic fields for Magnetic Cleanliness on Spacecraft. In 2011 IEEE International Symposium on Electromagnetic Compatibility. 834–839. doi:10.1109/ISEMC.2011.6038424
Knapp, M., Seager, S., Demory, B.-O., Krishnamurthy, A., Smith, M. W., Pong, C. M., et al. (2020a). Demonstrating high-precision photometry with a CubeSat: ASTERIA observations of 55 Cancri e. Astronomical J. 160, 23. doi:10.3847/1538-3881/ab8bcc
Knapp, M., Seager, S., Demory, B.-O., Krishnamurthy, A., Smith, M. W., Pong, C. M., et al. (2020b). Demonstrating High-precision Photometry with a CubeSat: ASTERIA Observations of 55 Cancri e. AJ 160, 23. doi:10.3847/1538-3881/ab8bcc
Krizmanic, J., Shah, N., Harding, A., Calhoun, P., Purves, L., Webster, C., et al. (2020). VTXO: the Virtual Telescope for X-ray Observations. arXiv:2006.12174 [astro-ph].
Kuindersma, S., Deits, R., Fallon, M., Valenzuela, A., Dai, H., Permenter, F., et al. (2016). Optimization-based Locomotion Planning, Estimation, and Control Design for Atlas. Autonomous Robots 40, 429–455. doi:10.1007/s10514-015-9479-3
Lassakeur, A., Underwood, C., Taylor, B., and Duke, R. (2020). Magnetic Cleanliness Program on CubeSats and Nanosatellites for Improved Attitude Stability. J. Aeronautics Space Tech. 13, 25–41.
Lefferts, E., Markley, F., and Shuster, M. (1982). Kalman Filtering for Spacecraft Attitude Estimation. J. Guidance, Control Dyn. 5, 417–429. doi:10.2514/3.56190
Lindegren, L. (2013). “High-accuracy Positioning: Astrometry,” in Observing Photons in Space: A Guide to Experimental Space Astronomy. Editors M. C. E. Huber, A. Pauluhn, J. L. Culhane, J. G. Timothy, K. Wilhelm, and A. Zehnder (New York, NY: Springer ISSI Scientific Report Series), 299–311. doi:10.1007/978-1-4614-7804-1\_16
Lindegren, L. (1978). Photoelectric Astrometry - A Comparison of Methods for Precise Image Location, 197–217.
Lindegren, L., Turon, C., O’Flaherty, K. S., and Perryman, M. A. C. (2005). “The Astrometric Instrument of Gaia: Principles,” in Proceedings of the Gaia Symposium ESA SP-576) (Meudon, France: Observatoire de Paris-Meudon), 29.
Macintosh, B., D’Amico, S., Koenig, A., and Madurowicz, A. (2019). Miniature Distributed Occulter Telescope (mDOT): A Concept for a Smallsat Mission to Observe Extrasolar Zodiacal Dust and Exoplanets. AGU Fall Meet. Abstr. 43.
Markley, F. L., and Crassidis, J. L. (2014). Fundamentals of Spacecraft Attitude Determination and Control. New York, NY: Springer New York. doi:10.1007/978-1-4939-0802-8
Mason, J., Baumgart, M., Woods, T., Hegel, D., Rogler, B., Stafford, G., et al. (2016). MinXSS CubeSat On-Orbit Performance and the First Flight of the Blue Canyon Technologies XACT 3- axis ADCS. In AIAA/USU Conference on Small Satellites.
Mehlem, K. (1978). Multiple Magnetic Dipole Modeling and Field Prediction of Satellites. IEEE Trans. Magnetics 14, 1064–1071. doi:10.1109/TMAG.1978.1059983
Mier-Hicks, F., and Lozano, P. C. (2017). Electrospray Thrusters as Precise Attitude Control Actuators for Small Satellites. J. Guidance, Control Dyn. 40, 642–649. doi:10.2514/1.G000736
Mora, A., Biermann, M., Bombrun, A., Boyadian, J., Chassat, F., Corberand, P., et al. (2016). Gaia: Focus, Straylight and Basic Angle. arXiv:1608.00045 [astro-ph], 99042D. doi:10.1117/12.2230763
Morgan, R. E., Douglas, E. S., Allan, G. W., Bierden, P., Chakrabarti, S., Cook, T., et al. (2019). MEMS Deformable Mirrors for Space-Based High-Contrast Imaging. Micromachines 10, 366. doi:10.3390/mi10060366
Nguyen, T., Morgan, E., Vanderspek, R., Levine, A., Kephart, M., Francis, J., et al. (2018). Fine-pointing Performance and Corresponding Photometric Precision of the Transiting Exoplanet Survey Satellite. JATIS 4, 047001. doi:10.1117/1.JATIS.4.4.047001
Pendergast, K. J., and Schauwecker, C. J. (1998). Use of a Passive Reaction Wheel Jitter Isolation System to Meet the Advanced X-Ray Astrophysics Facility Imaging Performance Requirements. In Space Telescopes and Instruments V. Kona, HI: International Society for Optics and Photonics, 1078–1094. doi:10.1117/12.324508
Pong, C. (2018). On-Orbit Performance & Operation of the Attitude & Pointing Control Subsystems on ASTERIA. In AIAA/USU Conference on Small Satellites.
Roman, N. G., and DeVorkin, D. H. (1980). Oral History Interview with Nancy Grace Roman AIP Oral Histories. College Park, MD: American Institute of Physics, Niels Bohr Library & Archives.
Shields, J., Pong, C., Lo, K., Jones, L., Mohan, S., Marom, C., et al. (2017). Characterization of CubeSat Reaction Wheel Assemblies. J. Small Satellites 6, 565–580.
Shkolnik, E. L. (2018). On the Verge of an Astronomy CubeSat Revolution. Nat. Astron. 2, 374–378. doi:10.1038/s41550-018-0438-8
Sinclair, D., Grant, C. C., and Zee, R. (2007). Enabling Reaction Wheel Technology for High Performance Nanosatellite Attitude Control. In AIAA/USU Conference on Small Satellites.
Smith, M. W., Seager, S., Pong, C. M., Villaseñor, J. S., Ricker, G. R., Miller, D. W., et al. (2010). “ExoplanetSat: Detecting Transiting Exoplanets Using a Low-Cost CubeSat Platform,” in Proc. SPIE. Editors J. M. OschmannJr., and M. C. Clampin (San Diego, CA: H. A. MacEwen), 773127. doi:10.1117/12.856559
Stern, T., and DeLapp, S. (2004). Techniques for Magnetic Cleanliness on Spacecraft Solar Arrays. In 2nd International Energy Conversion Engineering Conference. Providence, Rhode Island: American Institute of Aeronautics and Astronautics. doi:10.2514/6.2004-5581
Tracy, K., and Manchester, Z. (2020). Model-Predictive Attitude Control for Flexible Spacecraft during Thruster Firings. In AAS/AIAA Astrodynamics Specialist Conference. (Lake Tahoe, CA).
Underwood, C., Pellegrino, S., Lappas, V. J., Bridges, C. P., and Baker, J. (2015). Using CubeSat/micro-Satellite Technology to Demonstrate the Autonomous Assembly of a Reconfigurable Space Telescope (AAReST). Acta Astronautica 114, 112–122.
Votel, R., and Sinclair, D. (2012). Small Satellite Conference.Comparison of Control Moment Gyros and Reaction Wheels for Small Earth-Observing Satellites
Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., Schwarzenberg-Czerny, A., Koudelka, O. F., Grant, C. C., et al. (2014). BRITE-constellation: Nanosatellites for Precision Photometry of Bright Stars. San Francisco, CA: Publications of the Astronomical Society of the Pacific, 573–585. doi:10.1086/677236
Keywords: attitude sensing and control, environmental disturbances, CubeSats, astrophysics, satellite pointing, jitter, nanosatellites
Citation: Douglas ES, Tracy K and Manchester Z (2021) Practical Limits on Nanosatellite Telescope Pointing: The Impact of Disturbances and Photon Noise. Front. Astron. Space Sci. 8:676252. doi: 10.3389/fspas.2021.676252
Received: 04 March 2021; Accepted: 12 July 2021;
Published: 13 August 2021.
Edited by:
Jeff Kuhn, University of Hawaii, United StatesReviewed by:
Jonathan W. Arenberg, Northrop Grumman, United StatesM. Reza Emami, University of Toronto, Canada
Copyright © 2021 Douglas, Tracy and Manchester. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ewan S. Douglas, ZG91Z2xhc2VAYXJpem9uYS5lZHU=
 Ewan S. Douglas
Ewan S. Douglas Kevin Tracy
Kevin Tracy Zachary Manchester
Zachary Manchester