The Electron Structure of the Solar Wind

Time-series measurements of the number density n_core and temperature T_core of the core-electron population of the solar wind are examined at 1 AU and at 0.13 AU using measurements from the WIND and Parker Solar Probe spacecraft, respectively. A statistical analysis of the n_core and T_core measurements at 1 AU finds that the core-electron spatial structure of the solar wind is related to the magnetic-flux-tube structure of the solar wind; this electron structure is characterized by jumps in the values of n_core and T_core when passing from one magnetic flux tube into the next. The same types of flux-tube jumps are seen for T_core at 0.13 AU. Some models of the interplanetary electrical potential of the heliosphere predict that T_core is a direct measure of the local electrical potential in the heliosphere. If so, then jumps seen in T_core represent jumps in the electrical potential from flux tube to flux tube. This may imply that the interplanetary electrical potential (and its effect on the radial evolution away from the Sun of solar-wind ions and electrons) independently operates in each flux tube of the heliosphere.

Introduction

The magnetic structure of the solar wind at 1 AU is well observed, with ubiquitous strong current sheets (magnetic directional discontinuities) (Siscoe et al., 1968; Burlaga and Ness, 1969; Mariani et al., 1973; Vasquez et al., 2007) partitioning the magnetic field and plasma into numerous spatial domains. Over the years observations of the behavior of energetic-particles fluxes and anisotropies, the electron strahl, the proton plasma, the proton bulk flow, and the alpha-to-proton ion composition have led to a picture of the magnetic structure where the current sheets partition the field into filaments or a spaghetti of magnetic flux tubes (Bartley et al., 1966; McCracken and Ness, 1966; Michel, 1967; Bruno et al., 2001; Borovsky, 2008; Greco et al., 2008; Riazantseva et al., 2017; Pecora et al., 2019). There are, however, other depictions of the magnetic structure of the solar wind, for instance an admixture of flux tubes, plasmoids, magnetic islands, and localized magnetic structures (e.g., Khaborova et al., 2015; Khaborova et al., 2016; Adhikari et al., 2019; Malandraki et al., 2019; Khaborova et al., 2020), which is well depicted in Figure 24C of the review Khabarova et al. (2021). Certainly, it is well known that closed-field plasma blobs can be found in solar-wind plasma originating from coronal streamer stalks (Wang et al., 1999; Sheeley and Rouillard, 2010; Viall et al., 2010; Viall and Vourlidas, 2015; Kepko et al., 2016; Di Matteo et al., 2019). Relatedly, sector-reversal-region plasma (in which the heliospheric current sheet is found) tends to have magnetic fields that are less Parker-spiral oriented and tends to have a weaker electron strahl (Borovsky, 2021), both being indicative of impulsive emission of plasma from the Sun with poor magnetic connections back to the Sun. In the non-ejecta solar wind the magnetic flux tubes meander along the Parker-spiral direction (Borovsky, 2010). It is also known that there is a plasma structure to the solar wind at 1 AU that is related to the magnetic structure: changes (jumps) in plasma quantities are co-located with the strong current sheets that are the boundaries between magnetic flux tubes. This indicates that the plasma properties vary from magnetic-flux tube to magnetic flux tube.

The origins of the flux tube texture of the solar wind are uncertain: a major question is what portions of this structure are created locally in the solar wind far from the Sun and what portions are fossils from the solar corona (Neugebauer and Giacalone, 2010; Li and Qin, 2011; Owens et al., 2011; Neugebauer and Giacalone, 2015; Telloni et al., 2016; Tu et al., 2016; Viall and Borovsky, 2020). Ideas in the literature about the current-sheet origins include 1) current-sheet formation by nonlinear steepening of outward traveling Alfvén waves (Malara et al., 1996; Vasquez and Hollweg, 1999), 2) current-sheet formation and destruction in active MHD turbulence (Dmitruk et al., 2004; Greco et al., 2010, Greco et al., 2016), 3) fossil flux tubes from the corona advecting outward with the solar wind (Borovsky, 2008; Huang et al., 2014; Burkholder et al., 2019; Eselevich, 2019), and 4) the remnants of decayed near-Sun turbulence that are advected outward with the solar wind (e.g., Dobrowolny et al., 1980; Matthaeus et al., 2012; Servidio et al., 2014; Telloni et al., 2016). Mechanisms (1) and (2) have the structure created in situ in the solar wind; mechanism (4) has the structure created in the near-Sun solar wind; and mechanism (3) has the structure created in the corona.

For assessing the impact of the findings in this stud an item of consideration is the survivability of current sheets and flux tubes from the corona to 1 AU. In the upper solar corona, the plasma is partitioned into magnetic flux tubes by current sheets (Close et al., 2003; Close et al., 2005; DeForest et al., 2018; Burkholder et al., 2019). Three observations provide evidence for the survival of some current sheets. 1) Current sheets at 1 AU are seen that have strong jumps in the alpha-to-proton number-density ratio α/p across them (Borovsky, 2020a). Such α/p ion-composition boundaries in the ion composition can only be created in the corona, not in the solar wind away from the Sun: hence, those particular current sheets seen at 1 AU are fossils (relics) from the corona. 2) Similarly, current sheets at 1 AU are seen co-located with jumps in the intensity of the electron strahl (Borovsky, 2020a): for these current sheets the strahl jump is an indication that the current sheet is coherent back to the Sun (Gosling et al., 2004a,b; Borovsky, 2020a). The jumps in strahl intensity from tube to tube implies that different flux tubes in the magnetic spaghetti magnetically connect to different spots on the Sun (Gosling et al., 2004a,b; Borovsky, 2021). (Similarly, see Trenchi et al. (2013a,b) for coherence indicated by energetic-particle observations). 3) Examination of the compression and rarefaction of the magnetic structure in the solar wind at 1 AU (Borovsky and Denton, 2016; Borovsky, 2020d) indicates that the current sheets and flux tubes are long lived (many 10 s of hours to the age of the solar-wind plasma). If the flux tubes of the solar wind were to be destroyed, two possible mechanisms for their destruction are turbulence and reconnection. The notion that flux tubes from the Sun could be destroyed by the action of turbulence in the solar wind was tested by quantifying the amount of turbulent mixing (stretching and folding) that occurs in the solar wind between 0.3 and 1 AU (Borovsky, 2012b): no evidence for mixing was found. Similarly, periodic solar-wind structures with spatial scales in the “inertial subrange” survive to 1 AU and beyond without being destroyed by turbulence (Kepko and Spence, 2003; Viall et al., 2009; Di Matteo et al., 2019; Kepko and Viall, 2019; Birch and Hargreaves, 2020a,b). Reconnection also appears not to destroy the current sheets that are the walls of flux tubes. Solar-wind reconnection events are rare (Gosling et al., 2005; Phan et al., 2006; Gosling, 2012), unlike the ubiquitous current sheets. The strong current sheets of the solar wind are thick (several 100 s of km) (Siscoe et al., 1968; Vasquez et al., 2007; Miao et al., 2011; Borovsky and Steinberg, 2014) compared with the ion and electron kinetic scales (several 10 s of km) necessary to initiate reconnection in collisionless plasmas (Hesse et al., 2001; Pritchett, 2005). Further, the solar wind plasma is everywhere expanding with time (rather than driving structures together to initiate reconnection) and in the Alfvenic solar wind there are strong parallel-to-B velocity shears (Borovsky, 2020c) across the current sheets that tend to stabilize them to reconnection (Roth et al., 1996; Doss et al., 2015). The current-sheet evolution in the solar wind may be more consistent with Bohm and gyro-Bohm diffusion (Perkins et al., 1993; Hannum et al., 2001; Borovsky, 2006).

The electron distribution function in the solar wind generally exhibits three distinct components (e.g., Feldman et al., 1978; Maksimovic et al., 2005): lower-energy core electrons, higher-energy halo electrons, and a higher-energy magnetic-field-aligned strahl. It is generally accepted that the core electrons of the solar wind are a population that is “trapped” by (a) an interplanetary-electric-field potential barrier as the core electrons move away from the Sun and (b) the magnetic mirror force as the core electrons move toward the Sun (e.g., Lie-Svendsen and Leer, 2000; Marsch, 2006). This being the case, the temperature T_core of a measured distribution of core electrons is related to the electrical potential difference between the measurement location and the distant-from-the-Sun heliosphere (Feldman et al., 1975; Boldyrev et al., 2020; Moncuquet et al., 2020) [For a different interpretation of T_core, see Scudder (2019)]. On average, the core electron temperature of the solar wind decreases with distance from the Sun (Pilipp et al., 1990; McComas et al., 1992; Halekas et al., 2020; Moncuquet et al., 2020), in general agreement with exosphere models of the interplanetary electrical potential ϕ, with ϕ(r) decreasing in magnitude (with respect to infinity) with distance r from the Sun (Lemaire and Scherer, 1971; Meyer-Vernet and Issautier, 1998; Meyer-Vernet et al., 2003).

In the present study, we extend the analysis of the solar-wind plasma and magnetic structure to examine the core-electron structure of the solar wind and its relation to the magnetic structure. Jumps (boundaries) in the number density n_core and temperature T_core of the core electrons will be examined, statistically at 1 AU using the WIND spacecraft and briefly at 0.13 AU using the Parker Solar Probe spacecraft. Of interest is the relation of the core-electron structure of the solar wind to the magnetic structure of the solar wind: it will be seen that the values of T_core tend to vary from flux tube to flux tube.

If T_core is a measure of the local electrical potential ϕ in the solar wind, then spatial changes in T_core represent spatial changes in the electric potential. Changes in T_core from flux tube to flux tube represent changes in the electrical potential ϕ from tube to tube. This may indicate that the interplanetary potential ϕ (r) (Jockers, 1970; Lemons and Feldman, 1983; Lacombe et al., 2002; Salem et al., 2003; Lemaire, 2010) and its affect on solar-wind ion and electron evolution (e.g., Lie-Svendsen and Leer, 2000; Meyer-Vernet et al., 2003) acts on a tube-by-tube basis.

This study organized as follows. In Data the data sets that will be used are described, along with a numerical algorithm used at 1 AU to identify jumps in the n_core and T_core time series. The WIND Statistical Data Analysis at 1 AU describes the results of a statistical analysis of the WIND data set at 1 AU from the Sun and Examination of Parker Solar Probe Measurements Near the Sun describes a brief examination of Parker Solar Probe electron measurements at 0.13 AU. Summary and Discussion summarizes the findings and discusses implications of the observed core-electron structure of the solar wind.

Data

To examine the electron structure of the solar wind at 1 AU, 12-s time-resolution electron moments measurements from the SWE instrument (Ogilvie et al., 1995) on the WIND spacecraft are used in coordination with 3-s time-resolution magnetic-field measurements from the MFI instrument (Lepping et al., 1995) on WIND.

The first 120 days of the year 2005 were analyzed. This is the same time interval that was used for the analysis of the strahl structure and the alpha-to-proton number-density structure of the solar wind (Borovsky, 2020a). This is a time interval in the declining phase of the solar cycle that contains a good mix of the various types of plasma coming off the Sun with very few interplanetary shocks, which can confuse the categorization of the solar-wind plasma types. Using the Xu and Borovsky (2015) 1-AU solar-wind categorization scheme this 120-days interval was, by fraction of time, 40.2% coronal-hole-origin plasma, 30.0% streamer-belt-origin plasma, 14.5% sector-reversal-region plasma, and 15.4% ejecta. This is a variety that represents the solar-cycle-averaged variety of plasma types seen at 1 AU, with an emphasis on coronal-hole-origin plasma. It will be seen that this interval yields thousands of events for statistical analysis.

In the WIND time-series data, a numerical algorithm was used to locate jumps (shifts) in the magnitudes of the core-electron number density n_core and the core-electron temperature T_core that are greater than the noise level in the data. These jumps are taken to be spatial boundaries in the electron density and in the electron temperature. For every suspected temporal jump, the four data points prior to the jump and the four data points after the jump are examined. To be accepted as a valid jump, 1) the maximum value of the four data points on one side of the jump must be less than the minimum value of the four data points on the other side of the jump. Further, 2) a minimum value of the shift must be exceeded before the jump is accepted: the absolute value of the change in the average of the logariths of the four points before the jump from the logarithmic average of the four points after the jump must exceed a threshold value Q. With the notation that a data point “value” v before the jump is v_ibefore and a data point value after the jump is v_iafter, this second condition is written for the two sets of four points

${\text{|\hspace{0.17em}log}}_{10}\left({\text{v}}_{1\text{before}}{\text{v}}_{2\text{before}}{\text{v}}_{3\text{before}}{\text{v}}_{4\text{before}}\right){\hspace{0.17em}-\hspace{0.17em}\text{log}}_{10}({\text{v}}_{1\text{after}}{\text{v}}_{2\text{after}}{\text{v}}_{3\text{after}}{\text{v}}_{4\text{bafter}})\hspace{0.17em}\text{|}/4\text{>Q}(1)$

where log (A) + log (B) = log (AB) has been exploited in summing the four logarithms. For the density jumps Q = 0.0607 = log₁₀ (1.15) is taken (corresponding to a greater-than-15% change in the 4-point logarithmic average across the jump) and for the temperature jumps Q = 0.414 = log₁₀ (1.1) is taken (corresponding to a greater-than-10% change in the 4-point logarithmic average across the jump).

In the 120 days of WIND time-series measurements, 3,436 density jumps are identified (28.6 jumps per day on average) and 1,648 temperature jumps are identified (13.7 jumps per day). Five hundred-twenty six of the jumps are identified as both density jumps and temperature jumps.

Categorizing the solar-wind plasma type at the time of each n_core jump using the 1-AU Xu and Borovsky (2015) solar-wind categorization scheme, there are 1,382 n_core jumps in coronal-hole-origin plasma, 607 n_core jumps in streamer-belt-origin plasma, 256 n_core jumps in sector-reversal-region plasma, and 1,106 n_core jumps in ejecta plasma. Likewise, there are 903 T_core jumps in coronal-hole-origin plasma, 108 T_core jumps in streamer-belt-origin plasma, 29 T_core jumps in sector-reversal-region plasma, and 517 T_core jumps in ejecta plasma. Owing to absences of validated solar-wind-proton measurements, some of the n_core and T_core jumps could not be plasma categorized.

At 0.13 AU, 14-s cadence measurements of the core-electron temperature from the Parker Solar Probe SWEAP SPAN electron instrument (Kasper et al., 2016; Whittlesey et al., 2020) are used in conjunction with magnetic-field measurements from the PSP FIELDS fluxgate magnetometers (Bale et al., 2016). The core-electron temperatures are obtained from fits to the measured electron distribution functions with the fitting procedure described in the Appendix of Halekas et al. (2020).

To look for the occurrence of strong current sheets in the solar wind, directional changes in the magnetic-field-vector time series will be used. The angular change in the field direction Δθ over a fixed time difference (30 s is used here for the WIND measurements) will be examined. Based on a simple Ampere’s-law argument (Colburn and Sonett, 1966) and tested with 4-spacecraft data sets (Knetter et al., 2003; Knetter et al., 2004), examining Δθ is a standard method for identifying current sheets in the solar wind (e.g., Siscoe et al., 1968; Burlaga, 1969; Burlaga and Ness, 1969; Li, 2008; Miao et al., 2011).

The WIND Statistical Data Analysis at 1 AU

Figure 1A plots the occurrence distribution of the 24-s change in log₁₀ (n_core) in the first 120 days of 2005 (black points) and Figure 1B plots the occurrence distribution of the 24-s change in log₁₀ (T_core) in the first 120 days of 2005 (black points). Absolute values of the changes are used. Both occurrence distributions in Figure 1 exhibit two components: a population of small changes that is fit with a steep exponential (green dashed curves) and a second population of large changes that is fit with a shallower exponential (blue dashed curves). In both plots the sum of the two exponential fits is plotted as the red curve. Similar two-component distributions in the solar wind have been seen for changes in the magnetic-field strength B_mag, the proton specific entropy S_p, the intensity of the electron strahl, and the alpha-to-proton number-density ratio α/p [cf. Figure 3 of Borovsky (2008)], indicating spatial structure in those quantities: the larger-value components of those two-component distributions have been shown to be associated with crossings of current sheets. Below it will be shown that the large-change populations in Figures 1A,B are associated with the crossings of current sheets in the solar wind. Hence, the large-change population in Figure 1 is consistent with the crossings of boundaries of n_core in the solar wind and the population of large changes in Figure 1B is consistent with crossings of boundaries of T_core in the solar wind, with those boundaries being co-located with current sheets. The small-change populations in both panels are consistent with small fluctuations in n_core and T_core away from the boundaries, or with noise in the measurement values away from the boundaries.

FIGURE 1

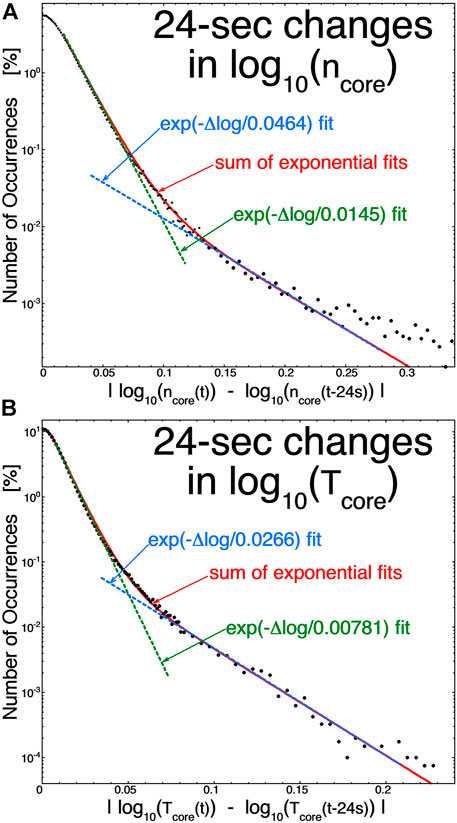
FIGURE 1. The occurrence distribution of the 24-s change in log₁₀(n_core) [panel (A)] and in log₁₀(T_core) [panel (B)] are binned for 120 days of WIND measurements at 1 AU.

A question that will be addressed is whether or not the boundaries of n_core and of T_core in the solar wind tend to be co-located with the current sheets of the solar-wind magnetic structure.

To determine whether or not there is a relationship between boundaries of the n_core and T_core structure and strong current sheets in the solar wind, the 30-s angular change in the magnetic-field direction Δθ is examined when the WIND spacecraft crosses the boundaries. Writing b(t) = B(t)/|B(t)|, the 30-s angular change in the magnetic-field direction at time t is calculated from the magnetic-field vector time series as

$\mathrm{\Delta \theta }=\text{arcos}\left(\mathbf{b}\left(\text{t}+15\text{s}\right)\cdot \mathbf{b}\left(\text{t}-15\text{s}\right)\right)(2)$

In Figure 2 some occurrence distributions of the 30-s change in the magnetic-field direction Δθ are plotted. The black points in Figure 2 plot the distribution of Δθ values for all times during the first 120 days of 2005, with the exclusion of times when the WIND spacecraft was in ejecta plasma. Note the two components to the black-point Δθ distribution, a small-angle component fit by exp(−Δθ/7.67^o) (green dashed curve) and a large-angle component fit by exp(−Δθ/25.5^o) (purple dashed curve). The solid-red curve is the sum of the two exponential fits [See also Figure 2 of Borovsky (2008) and Figure 6 of Miao et al. (2011) for similar two-component Δθ distributions]. The large-Δθ portion of the distribution has been interpreted as representing crossings of strong current sheets in the solar wind (Burlaga and Ness, 1969; Knetter et al., 2004; Borovsky, 2008) (flux-tube walls between one flux tube and its neighbor) and the small-Δθ portion of the distribution has been taken to represent small magnetic-field fluctuations in the interiors of the flux tubes. The large Δθ component of the black-point distribution is expected to extend down to smaller values of Δθ below the breakpoint in the curve: the red solid curve matching the black points is the sum of the two exponential fits. In the spaghetti of magnetic flux tubes, the angle of the magnetic-field direction in one tube with vs. the neighboring flux tube is a function of the distance along a tube so that sometimes the Δθ value crossing between tubes is large and sometimes the Δθ value is small, even zero. Hence, using the large-Δθ criterion to find flux-tube walls will fail to locate some of the walls (The walls sometimes can be located via other properties, such as jumps in the plasma properties). The mean value of Δθ for the exp (−Δθ/25.5^o) is <Δθ > = 25.5^o and the mean value of Δθ for the entire black-point distribution (the sum of the two exponential fits) is <Δθ> = 10.2^o. The blue points in Figure 2 plot the distribution of 30-s Δθ values during the times when jumps (boundaries) in n_core are seen. Those blue data points are fit with an exponential function exp(−Δθ/25.8^o) (dark-blue dashed curve), which is similar to the exp(−Δθ/25.5^o) large-Δθ fit of the current-sheet crossings for the black-point distribution in Figure 2. Note that this blue-point distribution extends down into small-Δθ values, which probably represents crossings between flux tubes that are locally nearly aligned at the crossing point. Hence, the Δθ values seen at the times of crossing n_core boundaries in the solar wind (blue points) are consistent with crossings of strong current sheets in the solar wind. The red points in Figure 2 plot the distribution of 30-s Δθ values during the times when jumps (boundaries) in T_core are seen. Those data points are fit with an exponential function exp(−Δθ/29.6^o) (dark-red dashed curve), which is also similar to the exp(−Δθ/25.5^o) fit of the current-sheet crossings for the black-point distribution in Figure 2. And note again that this red-point distribution extends down into small Δθ values. Hence, the Δθ values seen at the times of crossing T_core boundaries in the solar wind are consistent with crossings of strong current sheets in the solar wind (Note, in the collection of n_core and T_core boundaries, the two boundaries are often co-located).

FIGURE 2

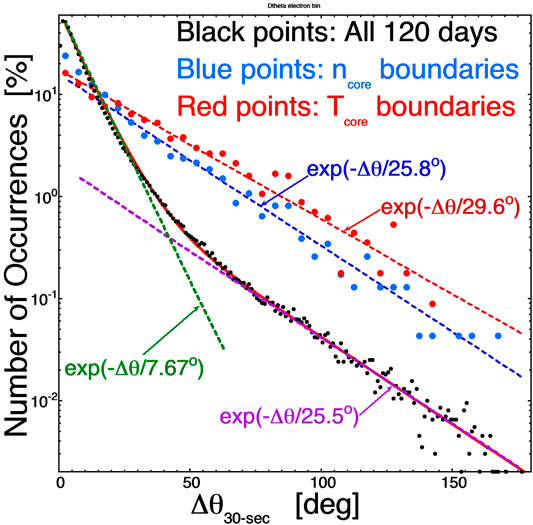
FIGURE 2. Distributions of the 30-s change in the magnetic field direction Δθ are plotted using WIND magnetic-field measurements. The black points are the distribution of all values in the first 120 days of 2005. The blue points are the Δθ values at the times that WIND was crossing boundaries in the core-electron number density and the red points are the Δθ values at the times that WIND was crossing boundaries in the core-electron temperature. The exponential fits are described in the text.

In Figure 3 the superposed epoch average value of the magnetic-field-direction change Δθ is plotted as a function of the time from the identified jumps in the values of n_core. A time shift τ_shift = 0 in the plot means the 30-s change Δθ in the magnetic-field direction is centered at the times of the n_core jumps, and time shifts away from 0 have the 30-s change Δθ centered at a time τ_shift away from the jumps in n_core. The individual curves in Figure 3 pertain to the sets of identified n_core boundaries in the different types of solar-wind plasma, as determined using the Xu and Borovsky (2015) plasma-categorization scheme. Excluded in Figure 3 are n_core boundaries found in ejecta plasma; ejecta plasma is often characterized by a smoothly varying magnetic-field direction (Klein and Burlaga, 1982; Cane and Richardson, 2003), a low level of field fluctuations (Lepping et al., 2005; Borovsky et al., 2019), and by a dearth of strong current sheets (Borovsky, 2008; Borovsky, 2012a). Note in Figure 3 that the average value of Δθ is much greater at the time of boundary crossings (τ_shift = 0) than it is away from the boundaries (τ_shift ≠ 0): this indicates that the n_core boundaries in the solar wind tend to be co-located with strong current sheets in the solar wind, as was also indicted in Figure 2. The values of Δθ at τ_shift = 0 in Figure 3 are consistent with the mean value <Δθ> = 25.5^o for the exp(−Δθ/25.5^o) portion of the black-point distribution in Figure 2. The values of Δθ away from τ_shift = 0 in Figure 3 are consistent with the <Δθ> = 10.2^o found for the total black-point (sheets and not sheets) distribution in Figure 2. Hence, changes in n_core tend to occur when crossing from one magnetic flux tube into another tube. Note in Figure 3 the systematically differing amplitude of Δθ in the different categories of solar-wind plasma (in the different colored curves); these systematic differences in the “wiggle angle” of the magnetic field in the differing plasma types have been explored in prior studies [cf. Figure 11 of Borovsky and Denton (2010) or Figure 8a of Borovsky et al. (2019)].

FIGURE 3

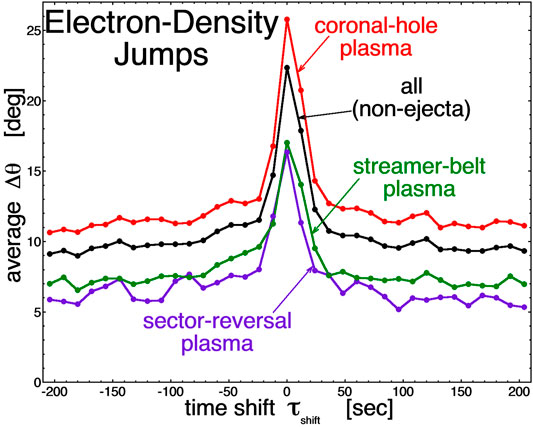
FIGURE 3. The superposed epoch average value of the 30-s change in the magnetic-field direction is plotted as a function of time from the identified core-electron density boundaries in the WIND data set at 1 AU.

Similarly, in Figure 4 the superposed epoch average of Δθ is plotted as a function of the time from the identified jumps in the values of T_core, with τ_shift = 0 meaning the 30-s change Δθ in the magnetic-field direction is centered at the times of the T_core jumps. The individual curves in Figure 4 pertain to the sets of identified T_core boundaries in the different types of solar-wind plasma. Again, excluded are T_core boundaries found in ejecta plasma. In Figure 4 the average value of Δθ is much greater at the time of T_core boundary crossings (τ_shift = 0) than it is away from the T_core boundaries (τ_shift ≠ 0). The values of Δθ at τ_shift = 0 in Figure 4 are again consistent with the mean value <Δθ> = 25.5^o for the exp(−Δθ/25.5^o) portion of the black-point distribution in Figure 2, and the values of Δθ away from τ_shift = 0 in Figure 4 are again consistent with the <Δθ> = 10.2^o found for the total black-point (sheets and not sheets) distribution in Figure 2. Figure 4 indicates that the T_core boundaries in the solar wind tend to be co-located with strong current sheets in the solar wind, as was also indicted in Figure 2. Hence, T_core changes tend to occur when crossing from one magnetic flux tube into another tube.

FIGURE 4

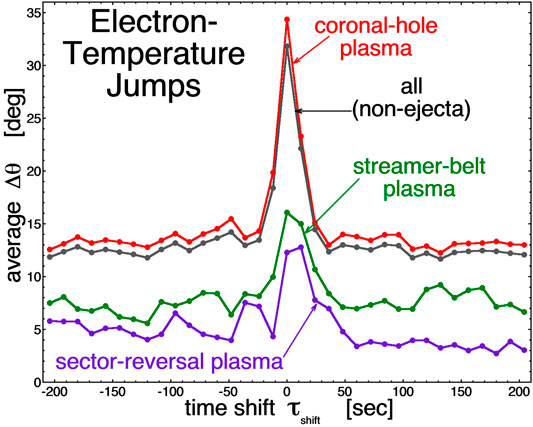
FIGURE 4. The superposed epoch average value of the 30-s change in the magnetic-field direction is plotted as a function of time from the identified core-electron temperature boundaries in the WIND data set at 1 AU. Note that the statistics of the purple sector-reversal-region-plasma curve are poor with only 29 identified temperature-boundary events.

Going back to the two component Δθ distribution of Figure 2, one can ask the question: What fraction of current-sheet crossings do not have Δθ values large enough to be detected out of the noise of the small-Δθ distribution. For the small-Δθ component of the black-point distribution of Figure 2 that is fit by exp (−Δθ/7.67^o), 95% of the points in that distribution have Δθ < 23.0^o. A Δθ value for an electron boundary that is greater than 23.0^o would probably stand out in a time series from the values of the background. Assuming that the exp(−Δθ/25.5^o) distribution of current-sheet crossings extends down to Δθ = 0^o (as do the red-point and blue-point distributions in Figure 2), then 41% of the points in the exp(−Δθ/25.5^o) distribution have Δθ > 23.0^o. Hence, about half (41%) of the cold-electron boundaries are expected to be individually identified as current-sheet crossings and about half (59%) are expected to have Δθ values too low to be clearly identified as current-sheet crossings, although they probably are.

In Figure 5 the amplitudes of the identified jumps in n_core (Figure 5A) and the identified jumps in T_core (Figure 5B) are examined. Here the occurrence distributions of the jump amplitudes are plotted, where the amplitudes are binned with linear bin sizes but plotted logarithmically. The jump amplitude here is measured by the absolute value of the difference between the average of the values of the four data points before the jump and the average of the values of the four data points after the jump. As seen in Figure 5A, typical jump values of n_core are ∼1 cm⁻³, with values as large as 5 cm⁻³ being not uncommon. Figure 5B displays the distribution of jump amplitudes for T_core: typical values are ∼1 eV and values of 5 eV or so are not uncommon.

FIGURE 5

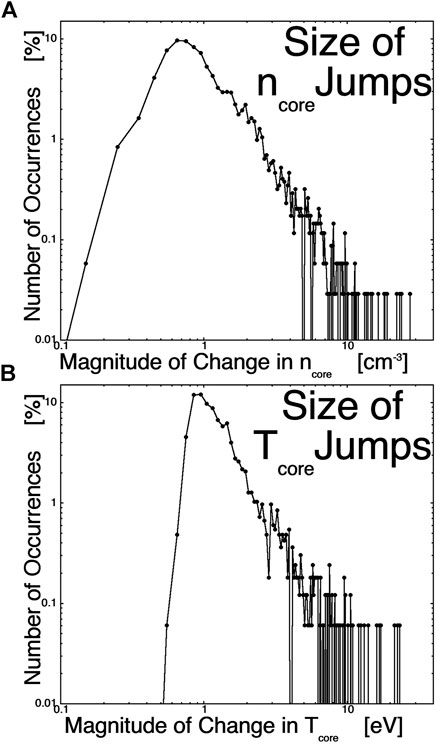
FIGURE 5. The distributions of jump sizes for the identified number-density boundaries [panel (A)] and for the identified temperature boundaries [panel (B)] are plotted. Note that the binning used linear bi sizes (horizontal axis), but the bin values are plotted logarithmically.

Examination of Parker Solar Probe Measurements Near the Sun

A brief, non-statistical examination is made of core electron measurements by the Parker Solar Probe spacecraft during the January-2020 close encounter with the Sun. Figures 6, 7 plot two time series of the temperature T_core of the core-electron population (blue) along with the 10-s change in the magnetic-field direction Δθ (green). Jumps in the value of T_core are indicated by vertical dashed line segments: these jumps are identified by visual inspection of the time series and they are not identified with the 8-point numerical algorithm [expression (1)] that was used to identify jumps in the WIND time series at 1 AU. Jumps in the value of T_core that are associated with strong changes Δθ in the field direction are denoted with red vertical dashed line segments and jumps in the value of T_core that are not associated with strong changes Δθ in the field direction are denoted with light-blue vertical dashed line segments. Figure 6 plots 48 min of measurements at 0.13 AU on January 29, 2020 and Figure 7 plots 15.6 min of measurements at 0.13 AU on January 30, 2020. In Figure 6 six jumps in T_core are marked with red vertical segments indicating that they are associated with localized large Δθ values, i.e., these shifts in the T_core value are associated with crossings of strong current sheets in the solar wind. In Figure 6 six jumps in T_core are marked with light-blue vertical segments indicating that they are not associated with crossings of current sheets in the solar wind that are strong enough to have Δθ values larger than the background values. (This is also the case for T_core jumps at 1 AU, as discussed in The WIND Statistical Data Analysis at 1 AU and as shown by the red-point distribution in Figure 2, where the distribution of Δθ values for T_core jumps extends down to low Δθ values.) Those low-Δθ Tcore jumps could be interpreted as jumps associated with flux tubes that are locally near parallel where the spacecraft crosses from one tube into the next. In Figure 7 all six observed shifts in T_core are associated with strong current-sheet crossings (red dashed line segments). Note in Figure 7 the magnitude of the Δθ values at the times of the T_core jumps, often showing a magnetic-field rotation of more than 90^o across the current sheets. The examination of the two time series in Figures 6, 7 indicates that, at 0.13 AU, the spatial structure of the core electron temperature T_core is related to the magnetic-flux-tube structure, as it is at 1 AU.

FIGURE 6

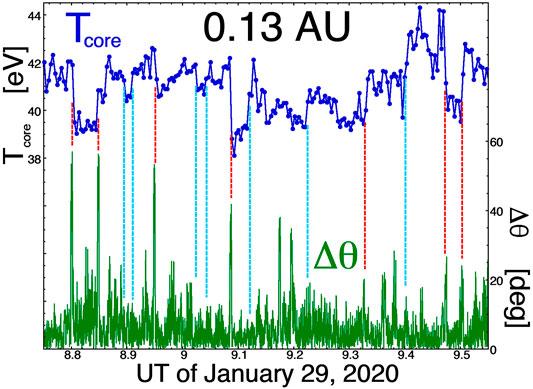
FIGURE 6. For 48 min of time-series measurements by Parker Solar Probe on January 29, 2020 the relationship between jumps in the core-electron temperature (blue curve) and current-sheet crossings as indicated by strong temporal changes in the magnetic-field direction (green curve) are examined.

FIGURE 7

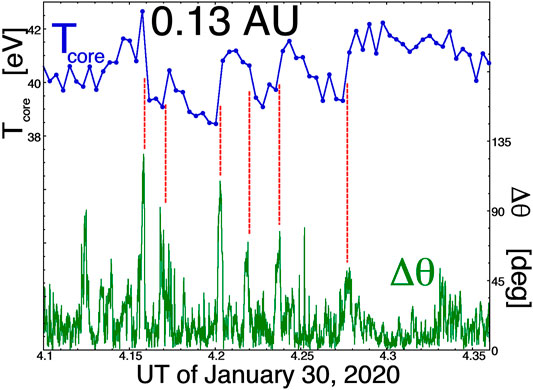
FIGURE 7. For 15.6 min of time-series measurements by Parker Solar Probe on January 30, 2020 the relationship between jumps in the core-electron temperature (blue curve) and current-sheet crossings as indicated by strong temporal changes in the magnetic-field direction (green curve) are examined.

Note that none of the T_core changes flagged in Figures 6, 7 are associated with magnetic switchbacks (field foldings or field inversions), which at times are prevalent in the Parker Solar Probe data set (Dudok de Wit et al., 2020; Macneil et al., 2020). The closest is the event at 4.203 UT in Figure 7, where the magnetic field makes a transition to a near-radial orientation from a transverse-to-radial orientation.

Typical changes in the value of T_core in the jumps marked in Figures 6, 7 are 2–3 eV.

Summary and Discussion

A statistical analysis of 120 days of solar-wind measurements at 1 AU show that the density structure and temperature structure of the core electrons of the solar wind are both related to the magnetic-flux-tube structure of the solar wind; in this structure the number density n_core and temperature T_core of the core-electron population tend to jump in value from flux tube to flux tube. An examination of T_core measurements at 0.13 AU shows the same features related to the magnetic structure, with T_core jumps associated with current-sheet crossings.

The relationship between the electron number density n_core and the magnetic flux tubes is no surprise in light of quasi-neutrality considerations, since it is known that the proton number density structure of the solar wind reflects the magnetic structure (Borovsky, 2012b; Borovsky, 2020b). The variations in T_core that are related to the magnetic-flux-tube structure are more interesting. If a local value of T_core represents a measurement of the local electrical potential ϕ, then T_core varying from tube to tube means ϕ varies from tube to tube. If ϕ(r) is (as in an exosphere model) determined by the evolution of the solar-wind ions and electrons away from the Sun, then variations of ϕ from tube to tube might mean that exosphere models apply tube by tube, i.e., that the solar-wind evolution is to some degree independent from tube to tube. There is no reason to argue that the differing flux tubes should not act independently. At 1 AU it is seen that the intensity of the electron stralh can vary from flux tube to flux tube (Borovsky, 2021): this strahl variation is an indication that different flux tubes at 1 AU are connected to different features in the corona (Gosling et al., 2004a,b; Borovsky, 2021). The differences in connection to the corona could result in independent exospheric scenarios in the different flux tubes.

If the solar-wind plasma is an admixture of open flux tubes plus other magnetic structures (e.g., Figure 24C of Khabarova et al., 2021) then the exosphere-model picture is more complicated. Further investigation of field and core-electron measurements at 1 AU, guided with measurements of the strahl intensity to judge magnetic connectivity to the Sun (Borovsky, 2021), is called for. In any closed-magnetic structure, the interpretation of T_core as an indication of the local electrical potential ϕ (e.g., Feldman et al., 1975; Boldyrev et al., 2020; Moncuquet et al., 2020) might no longer be possible.

At both 1 and 0.13 AU, the fractional variation of T_core in a typical jump is about 10% of the value of T_core, although occasional much-larger jumps (several tens of percent) can be found. This indicates a variation of the interplanetary potential of about 10% from tube to tube, although not every tube-wall crossing shows a jump in T_core.

At 1 AU typical T_core changes across flux-tube walls are ∼1 eV, although larger potentials can be found. This represents a change in electrical potential of ∼1 V across the boundary between adjacent flux tubes. If at 1 AU a current sheet (flux-tube wall) is 1,000-km thick (e.g., Siscoe et al., 1968; Vasquez et al., 2007) and the potential change is 1 V, then the electric field of this potential change is E = 1 × 10⁻⁶ V/m. For a magnetic field strength of 5 nT, this corresponds to an E × B drift speed of 0.2 km/s [Note that if the potential is a few times the core-electron temperature (cf. Maksimovic et al., 1997), then these electric-field values and drift speeds are a few times larger].

In future, a statistical analysis of the changes in T_core in the Parker Solar Probe data is needed accounting for the types of plasma being observed and the rapid longitudinal motion of the spacecraft. In particular this will be interesting when future closer passes to the Sun have occurred and the variations of the interplanetary electric potential can be examined where the potentials are anticipated to be greater in magnitude nearer to the Sun.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://cdaweb.gsfc.nasa.gov/index.html/.

Author Contributions

JB initiated this project, performed the data analysis, and wrote the initial draft of the manuscript. JH and PW prepared the Solar Probe Data and contributed to the final version of the manuscript.

Funding

This work was supported by the NSF SHINE program via grant no AGS-1723416, by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G, by the NSF GEM Program via grant no AGS-2027569, and by the NASA Heliophysics LWS program via award NNX16AB75G. JH and PW were supported by the PSP SWEAP contract NNN06AA01C.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Stas Boldyrev and Vadim Roytershteynure for helpful conversations.

References

Adhikari, L., Khabarova, O., Zank, G. P., and Zhao, L.-L. (2019). The Role of Magnetic Reconnection-Associated Processes in Local Particle Acceleration in the Solar Wind. ApJ 873, 72. doi:10.3847/1538-4357/ab05c6

CrossRef Full Text | Google Scholar

Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., de Wit, T. D., et al. (2016). The FIELDS Instrument Suite for Solar Probe Plus: Measuring the Coronal Plasma and Magnetic Field, Plasma Waves and Turbulence, and Radio Signatures of Solar Transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartley, W. C., Bukata, R. P., McCracken, K. G., and Rao, U. R. (1966). Anisotropic Cosmic Radiation Fluxes of Solar Origin. J. Geophys. Res. 71, 3297–3304. doi:10.1029/jz071i013p03297

CrossRef Full Text | Google Scholar

Birch, M. J., and Hargreaves, J. K. (2020a). Quasi-periodic Ripples in High-Latitude Electron Content, the Geomagnetic Field, and the Solar Wind. Nat. Scienific Rep 10, 1313. doi:10.1038/s41598-019-57201-4

CrossRef Full Text | Google Scholar

Birch, M. J., and Hargreaves, J. K. (2020b). Quasi-periodic Ripples in the Heliosphere from 1 to 40 AU. Adv. Space Res. 67, 678.

Google Scholar

Boldyrev, S., Forest, C., and Egedal, J. (2020). Electron Temperature of the Solar Wind. Proc. Natl. Acad. Sci. USA 117, 9232–9240. doi:10.1073/pnas.1917905117

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, J. E., and Denton, M. H. (2010). Solar Wind Turbulence and Shear: A Superposed-Epoch Analysis of Corotating Interaction Regions at 1 AU. J. Geophys. Res. 115, A10101. doi:10.1029/2009ja014966

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Denton, M. H. (2016). The Trailing Edges of High-Speed Streams at 1 AU. J. Geophys. Res. Space Phys. 121, 6107–6140. doi:10.1002/2016ja022863

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Steinberg, J. T. (2014). No Evidence for the Localized Heating of Solar Wind Protons at Intense Velocity Shear Zones. J. Geophys. Res. Space Phys. 119, 1455–1462. doi:10.1002/2013ja019746

CrossRef Full Text | Google Scholar

Borovsky, J. E., Denton, M. H., and Smith, C. W. (2019). Some Properties of the Solar-Wind Turbulence at 1 AU Statistically Examined in the Different Types of Solar-Wind Plasma. J. Geophys. Res. 124, 2406. doi:10.1029/2019JA026580

Google Scholar

Borovsky, J. E. (2006). The Eddy Viscosity and Flow Properties of the Solar Wind: CIRs, CME Sheaths, and Solar-Wind/magnetosphere Coupling. Phys. Plasmas 13, 056505. doi:10.1063/1.2200308

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2008). Flux Tube Texture of the Solar Wind: Strands of the Magnetic Carpet at 1 AU?. J. Geophys. Res. 113, A08110. doi:10.1029/2007ja012684

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2010). On the Variations of the Solar Wind Magnetic Field about the Parker Spiral Direction. J. Geophys. Res. 115, A09101. doi:10.1029/2009ja015040

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2012a). The Velocity and Magnetic Field Fluctuations of the Solar Wind at 1 AU: Statistical Analysis of Fourier Spectra and Correlations with Plasma Properties. J. Geophys. Res. 117, A05104. doi:10.1029/2011ja017499

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2012b). Looking for Evidence of Mixing in the Solar Wind from 0.31 to 0.98 AU. J. Geophys. Res. 117, A06107. doi:10.1029/2012ja017525

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020a). The Magnetic Structure of the Solar Wind: Ionic Composition and the Electron Strahl. Geophys. Res. Lett. 47, e2019GL084586. doi:10.1029/2019gl084586

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020b). Plasma and Magnetic-Field Structure of the Solar Wind at Inertial-Range Scale Sizes Discerned from Statistical Examinations of the Time-Series Measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020c). On the Motion of the Heliospheric Magnetic Structure through the Solar Wind Plasma. J. Geophys. Res. 125, e2019JA027377. doi:10.1029/2019ja027377

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020d). Compression of the Heliospheric Magnetic Structure by Interplanetary Shocks: Is the Structure at 1 AU a Manifestation of Solar-Wind Turbulence or Is it Fossil Structure from the Sun?. Front. Astron. Space Sci. 7, 582546. doi:10.3389/fspas.2020.582564

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2021). Exploring the Properties of the Electron Strahl at 1 AU as an Indicator of the Quality of the Magnetic Connection between the Earth and the Sun. Front. Astron. Space Sci. 8, 646443. doi:10.3389/fspas.2021.646443

CrossRef Full Text | Google Scholar

Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying Intermittency Events in the Solar Wind. Planet. Space Sci. 49, 1201–1210. doi:10.1016/s0032-0633(01)00061-7

CrossRef Full Text | Google Scholar

Burkholder, B. L., Otto, A., Delamere, P. A., and Borovsky, J. E. (2019). Magnetic Connectivity in the corona as a Source of Structure in the Solar Wind. J. Geophys. Res. Space Phys. 124, 32–49. doi:10.1029/2018ja026132

CrossRef Full Text | Google Scholar

Burlaga, L. F., and Ness, N. F. (1969). Tangential Discontinuities in the Solar Wind. Sol. Phys. 9, 467–477. doi:10.1007/bf02391672

CrossRef Full Text | Google Scholar

Burlaga, L. F. (1969). Directional Discontinuities in the Interplanetary Magnetic Field. Sol. Phys. 7, 54–71. doi:10.1007/bf00148406

CrossRef Full Text | Google Scholar

Cane, H. V., and Richardson, I. V. (2003). Interplanetary Coronal Mass Ejections in the Near-Earth Solar Wind during 1996-2002. J. Geophys. Res. 108, 1156. doi:10.1029/2002ja009817

CrossRef Full Text | Google Scholar

Close, R. M., Parnell, C. E., MacKay, D. H., and Priest, E. R. (2003). Statistical Flux Tube Properties of 3D Magnetic Carpet fields. Solar Phys. 212, 251–275. doi:10.1023/a:1022961913168

CrossRef Full Text | Google Scholar

Close, R. M., Parnell, C. E., and Priest, E. R. (2005). Separators in 3D Quiet-Sun Magnetic fields. Solar Phys. 225, 21. doi:10.1023/A:1022961913168

Google Scholar

Colburn, D. S., and Sonett, C. P. (1966). Discontinuities in the Solar Wind. Space Sci. Rev. 5, 439. doi:10.1007/bf00240575

CrossRef Full Text | Google Scholar

DeForest, C. E., Howard, R. A., Velli, M., Viall, N., and Vourlidas, A. (2018). The Highly Structured Outer Solar corona. ApJ 862, 18. doi:10.3847/1538-4357/aac8e3

CrossRef Full Text | Google Scholar

Di Matteo, S., Viall, N. M., Kepko, L., Wallace, S., Arge, C. N., and MacNeice, P. (2019). Helios Observations of Quasiperiodic Density Structures in the Slow Solar Wind at 0.3, 0.4, and 0.6 AU. J. Geophys. Res. Space Phys. 124, 837–860. doi:10.1029/2018ja026182

PubMed Abstract | CrossRef Full Text | Google Scholar

Dmitruk, P., Matthaeus, W. H., and Seenu, N. (2004). Test Particle Energization by Current Sheets and Nonuniform fields in Magnetohydrodynamic Turbulence. ApJ 617, 667–679. doi:10.1086/425301

CrossRef Full Text | Google Scholar

Dobrowolny, M., Mangeney, A., and Veltri, P. (1980). Fully Developed Anisotropic Hydromagnetic Turbulence in Interplanetary Space. Phys. Rev. Lett. 45, 144–147. doi:10.1103/physrevlett.45.144

CrossRef Full Text | Google Scholar

Doss, C. E., Komar, C. M., Cassak, P. A., Wilder, F. D., Eriksson, S., and Drake, J. F. (2015). Asymmetric Magnetic Reconnection with a Flow Shear and Applications to the Magnetopause. J. Geophys. Res. Space Phys. 120, 7748–7763. doi:10.1002/2015ja021489

CrossRef Full Text | Google Scholar

Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., Bonnell, J. W., Bowen, T. A., Chen, C. H. K., et al. (2020). Switchbacks in the Near-Sun Magnetic Field: Long Memory and Impact on the Turbulence cascade. ApJS 246, 39. doi:10.3847/1538-4365/ab5853

CrossRef Full Text | Google Scholar

Eselevich, V. G. (2019). Diamagnetic Structures as a Basis of Quasi-Stationary Slow Solar Wind. Solar-terr. Phys. 5 (3), 29.

Google Scholar

Feldman, W. C., Asbridge, J. R., Bame, S. J., Montgomery, M. D., and Gary, S. P. (1975). Solar Wind Electrons. J. Geophys. Res. 80, 4181–4196. doi:10.1029/ja080i031p04181

CrossRef Full Text | Google Scholar

Feldman, W. C., Asbridge, J. R., Bame, S. J., Gosling, J. T., and Lemons, D. S. (1978). Characteristic Electron Variations across Simple High-Speed Solar Wind Streams. J. Geophys. Res. 83, 5285. doi:10.1029/ja083ia11p05285

CrossRef Full Text | Google Scholar

Gosling, J. T., de Koning, C. A., Skoug, R. M., Steinberg, J. T., and McComas, D. J. (2004a). Dispersionless Modulations in Low-Energy Solar Electron Bursts and Discontinuous Changes in the Solar Wind Electron Strahl. J. Geophys. Res. 109, A05102. doi:10.1029/2003ja010338

CrossRef Full Text | Google Scholar

Gosling, J. T., Skoug, R. M., McComas, D. J., and Mazur, J. E. (2004b). Correlated Dispersionless Structure in Suprathermal Electrons and Solar Energetic Ions in the Solar Wind. ApJ 614, 412–419. doi:10.1086/423368

CrossRef Full Text | Google Scholar

Gosling, J. T., Skoug, R. M., McComas, D. J., and Smith, C. W. (2005). Direct Evidence for Magnetic Reconnection in the Solar Wind Near 1 AU. J. Geophys. Res. 110, A01107. doi:10.1029/2004ja010809

CrossRef Full Text | Google Scholar

Gosling, J. T. (2012). Magnetic Reconnection in the Solar Wind. Space Sci. Rev. 172, 187–200. doi:10.1007/s11214-011-9747-2

CrossRef Full Text | Google Scholar

Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent MHD Structures and Classical Discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008gl035454

CrossRef Full Text | Google Scholar

Greco, A., Matthaeus, W. H., Servidio, S., Dmitruk, P., Wan, M., Oughton, S., et al. (2010). Statistical Propertie of Solar Wind Discontinuities, Intermittent Turbulence, and Rapid Emergence of Non-gaussian Distribution. AIP Conf. Proc. 1216, 202. doi:10.1063/1.3395836

Google Scholar

Greco, A., Perri, S., Servidio, S., Yordanova, E., and Veltri, P. (2016). The Complex Structure of Magnetic Field Discontinuities in the Turbulent Solar Wind. ApJ 823, L39. doi:10.3847/2041-8205/823/2/l39

CrossRef Full Text | Google Scholar

Halekas, J. S., Whittlesey, P., Larson, D. E., McGinnis, D., Maksimovic, M., Berthomier, M., et al. (2020). Electrons in the Young Solar Wind: First Results from the Parker Solar Probe. ApJS 246, 22. doi:10.3847/1538-4365/ab4cec

CrossRef Full Text | Google Scholar

Hannum, D., Bateman, G., Kinsey, J., Kritz, A. H., Onjun, T., and Pankin, A. (2001). Comparison of High-Mode Predictive Simulations Using Mixed Bohm/gyro-Bohm and Multi-Mode (MMM95) Transport Models. Phys. Plasmas 8, 964–974. doi:10.1063/1.1338534

CrossRef Full Text | Google Scholar

Hesse, M., Birn, J., and Kuznetsova, M. (2001). Collisionless Magnetic Reconnection: Electron Processes and Transport Modeling. J. Geophys. Res. 106, 3721–3735. doi:10.1029/1999ja001002

CrossRef Full Text | Google Scholar

Huang, C., Yan, Y., Li, G., Deng, Y., and Tan, B. (2014). Tracking Back the Solar Wind to its Photospheric Footpoints from Wind Observations - A Statistical Study. Sol. Phys. 289, 3109–3119. doi:10.1007/s11207-014-0508-8

CrossRef Full Text | Google Scholar

Jockers, K. (1970). Solar Wind Models Based on Exospheric Theory. Astron. Astrophys. 6, 219.

Google Scholar

Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar Wind Electrons Alphas and Protons (SWEAP) Investigation: Design of the Solar Wind and Coronal Plasma Instrument Suite for Solar Probe Plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3

CrossRef Full Text | Google Scholar

Kepko, L., and Spence, H. E. (2003). Observations of Discrete, Global Magnetospheric Oscillations Directly Driven by Solar Wind Density Variations. J. Geophys. Res. 108, 1257. doi:10.1029/2002ja009676

CrossRef Full Text | Google Scholar

Kepko, L., and Viall, N. M. (2019). The Source, Significance, and Magnetospheric Impact of Periodic Density Structures within Stream Interaction Regions. J. Geophys. Res. 124, 2019JA026962. doi:10.1029/2019ja026962

CrossRef Full Text | Google Scholar

Kepko, L., Viall, N. M., Antiochos, S. K., Lepri, S. T., Kasper, J. C., and Weberg, M. (2016). Implications of L1 Observations for Slow Solar Wind Formation by Solar Reconnection. Geophys. Res. Lett. 43, 4089–4097. doi:10.1002/2016gl068607

CrossRef Full Text | Google Scholar

Khabarova, O., Zharkova, V., Xia, Q., and Malandraki, O. E. (2020). Counterstreaming Strahls and Heat Flux Dropouts as Possible Signatures of Local Particle Acceleration in the Solar Wind. ApJ 894, L12. doi:10.3847/2041-8213/ab8cb8

CrossRef Full Text | Google Scholar

Khabarova, O., Malandraki, O., malova, H., Kislov, R., Greco, A., Bruno, R., et al. (2021). Current Sheets, Plasmoids and Flux Ropes in the Heliosphere. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x

CrossRef Full Text | Google Scholar

Khaborova, O., Zank, G., Li, G., Le Roux, J. A., Webb, G. M., Dosch, A., et al. (2015). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. I. Dynamics of Magnetic Islands Near the Heliospheric Current Sheet. Astrophys. J. 808, 181. doi:10.1088/0004-637X/808/2/181

Google Scholar

Khaborova, O., Zank, G., Li, G., MalandrakiLe Roux, O. E. J. A., and Webb, G. M. (2016). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. II. Particle Energization inside Magnetically Confined Cavities. Astrophys. J. 827, 122. doi:10.3847/0004-637X/827/2/122

Google Scholar

Klein, L. W., and Burlaga, L. F. (1982). Interplanetary Magnetic Clouds at 1 AU. J. Geophys. Res. 87, 613. doi:10.1029/ja087ia02p00613

CrossRef Full Text | Google Scholar

Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2003). Discontinuity Observations with Cluster. Adv. Space Res. 32 (4), 543–548. doi:10.1016/s0273-1177(03)00335-1

CrossRef Full Text | Google Scholar

Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2004). Four-point Discontinuity Observations Using Cluster Magnetic Field Data: A Statistical Survey. J. Geophys. Res. 109, A06102. doi:10.1029/2003ja010099

CrossRef Full Text | Google Scholar

Lacombe, C., Salem, C., Mangeney, A., Hubert, D., Perche, C., Bougeret, J.-L., et al. (2002). Evidence for the Interplanetary Electric Potential? WIND Observations of Electrostatic Fluctuations. Ann. Geophys. 20, 609–618. doi:10.5194/angeo-20-609-2002

CrossRef Full Text | Google Scholar

Lemaire, J., and Scherer, M. (1971). Simple Model for an Ion-Exosphere in an Open Magnetic Field. Phys. Fluids 14, 1683. doi:10.1063/1.1693664

CrossRef Full Text | Google Scholar

Lemaire, J. (2010). Half a century of Kinetic Solar Wind Models. AIP Conf. Proc. 1216, 8. doi:10.1063/1.3395971

Google Scholar

Lemons, D. S., and Feldman, W. C. (1983). Collisional Modification to the Exospheric Theory of Solar Wind Halo Electron Pitch Angle Distributions. J. Geophys. Res. 88, 6881. doi:10.1029/ja088ia09p06881

CrossRef Full Text | Google Scholar

Lepping, R. P., Acũna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The WIND Magnetic Field Investigation. Space Sci. Rev. 71, 207–229. doi:10.1007/bf00751330

CrossRef Full Text | Google Scholar

Lepping, R. P., Wu, C.-C., and Berdichevsky, D. B. (2005). Automatic Identification of Magnetic Clouds and Cloud-like Regions at 1 AU: Occurrence Rate and Other Properties. Ann. Geophys. 23, 2687–2704. doi:10.5194/angeo-23-2687-2005

CrossRef Full Text | Google Scholar

Li, G., and Qin, G. (2011). A Solar Wind Model with Current Sheets. ASP Conf. Ser. 444, 117.

Google Scholar

Li, G. (2008). Identifying Current-sheet-like Structures in the Solar Wind. ApJ 672, L65–L68. doi:10.1086/525847

CrossRef Full Text | Google Scholar

Lie-Svendsen, Ø., and Leer, E. (2000). The Electron Velocity Distribution in the High-Speed Solar Wind: Modeling the Effects of Protons. J. Geophys. Res. 105, 35–46. doi:10.1029/1999ja900438

CrossRef Full Text | Google Scholar

Macneil, A. R., Owens, M. J., Wicks, R. T., Lockwood, M., Bentley, S. N., and Lang, M. (2020). The Evolution of Inverted Magnetic fields through the Inner Heliosphere. Mon. Not. R. Astron. Soc. 494, 3655. doi:10.1093/mnras/staa951

CrossRef Full Text | Google Scholar

Maksimovic, M., Pierrard, V., and Lemaire, J. F. (1997). A Kinetic Model of the Solar Wind with Kappa Distribution Functions in the corona. Astron. Astrophys. 324, 725.

Google Scholar

Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., Issautier, K., Scime, E. E., Littleton, J. E., et al. (2005). Radial Evolution of the Electron Distribution Functions in the Fast Solar Wind between 0.3 and 1.5 AU. J. Geophys. Res. 110, A09104. doi:10.1029/2005ja011119

CrossRef Full Text | Google Scholar

Malandraki, O., Khabarova, O., Bruno, R., Zank, G. P., Li, G., Jackson, B., et al. (2019). Current Sheets, Magnetic Islands, and Associated Particle Acceleration in the Solar Wind as Observed by Ulysses Near the Ecliptic Plane. ApJ 881, 116. doi:10.3847/1538-4357/ab289a

CrossRef Full Text | Google Scholar

Malara, F., Primavera, L., and Veltri, P. (1996). Gompressive Fluctuations Generated by Time Evolution of Alfvénic Perturbations in the Solar Wind Current Sheet. J. Geophys. Res. 101, 21597–21617. doi:10.1029/96ja01637

CrossRef Full Text | Google Scholar

Mariani, F., Bavassano, B., Villante, U., and Ness, N. F. (1973). Variations of the Occurrence Rate of Discontinuities in the Interplanetary Magnetic Field. J. Geophys. Res. 78, 8011–8022. doi:10.1029/ja078i034p08011

CrossRef Full Text | Google Scholar

Marsch, E. (2006). Kinetic Physics of the Solar corona and Solar Wind. Living Rev. Solar Phys. 3, 1. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Montgomery, D. C., Wan, M., and Servidio, S. (2012). A Review of Relaxation and Structure in Some Turbulent Plasmas: Magnetohydrodynamic and Related Models. J. Turb. 37, 1.

Google Scholar

McComas, D. J., Bame, S. J., Feldman, W. C., Gosling, J. T., and Phillips, J. L. (1992). Solar Wind Halo Electrons from 1-4 AU. Geophys. Res. Lett. 19, 1291–1294. doi:10.1029/92gl00631

CrossRef Full Text | Google Scholar

McCracken, K. G., and Ness, N. F. (1966). The Collimation of Cosmic Rays by the Interplanetary Magnetic Field. J. Geophys. Res. 71, 3315–3318. doi:10.1029/jz071i013p03315

CrossRef Full Text | Google Scholar

Meyer-Vernet, N., and Issautier, K. (1998). Electron Temperature in the Solar Wind: Generic Radial Variation from Kinetic Collisionless Models. J. Geophys. Res. 103, 29705–29717. doi:10.1029/98ja02853

CrossRef Full Text | Google Scholar

Meyer-Vernet, N., Mangeney, A., Maksimovic, M., Pantellini, F., and Issaurtier, K. (2003). Some Basic Aspects of Solar Wind Acceleration. AIP Conf. Proc. 679, 263. doi:10.1063/1.1618591

Google Scholar

Miao, B., Peng, B., and Li, G. (2011). Current Sheets from Ulysses Observation. Ann. Geophys. 29, 237–249. doi:10.5194/angeo-29-237-2011

CrossRef Full Text | Google Scholar

Michel, F. C. (1967). Model of Solar Wind Structure. J. Geophys. Res. 72, 1917–1932. doi:10.1029/jz072i007p01917

CrossRef Full Text | Google Scholar

Moncuquet, M., Meyer-Vernet, N., Issautier, K., Pulupa, M., Bonnell, J. W., Bale, S. D., et al. (2020). First In Situ Measurements of Electron Density and Temperature from Quasi-thermal Noise Spectroscopy with Parker Solar Probe/FIELDS. ApJS 246, 44. doi:10.3847/1538-4365/ab5a84

CrossRef Full Text | Google Scholar

Neugebauer, M., and Giacalone, J. (2010). Progress in the Study of Interplanetary Discontinuities. AIP Conf. Proc. 1216, 194. doi:10.1063/1.3395834

Google Scholar

Neugebauer, M., and Giacalone, J. (2015). Energetic Particles, Tangential Discontinuities, and Solar Flux Tubes. J. Geophys. Res. Space Phys. 120, 8281–8287. doi:10.1002/2015ja021632

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, a Comprehensive Plasma Instrument for the WIND Spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/bf00751326

CrossRef Full Text | Google Scholar

Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic Discontinuities in the Near-Earth Solar Wind: Evidence of In-Transit Turbulence or Remnants of Coronal Structure?. Sol. Phys. 269, 411–420. doi:10.1007/s11207-010-9695-0

CrossRef Full Text | Google Scholar

Pecora, F., Greco, A., Hu, Q., Servidio, S., Chasapis, A. G., and Matthaeus, W. H. (2019). Single-spacecraft Identification of Flux Tubes and Current Sheets in the Solar Wind. ApJ 881, L11. doi:10.3847/2041-8213/ab32d9

CrossRef Full Text | Google Scholar

Perkins, F. W., Barnes, C. W., Johnson, D. W., Scott, S. D., Zarnstorff, M. C., Bell, M. G., et al. (1993). Nondimensional Transport Scaling in the Tokamak Fusion Test Reactor: Is Tokamak Transport Bohm or gyro‐Bohm?. Phys. Fluids B: Plasma Phys. 5, 477–498. doi:10.1063/1.860534

CrossRef Full Text | Google Scholar

Phan, T. D., Gosling, J. T., Davis, M. S., Skoug, R. M., Øieroset, M., Lin, R. P., et al. (2006). A Magnetic Reconnection X-Line Extending More Than 390 Earth Radii in the Solar Wind. Nature 439, 175–178. doi:10.1038/nature04393

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilipp, W. G., Miggenrieder, H., Mühläuser, K.-H., Rosenbauer, H., and Schwenn, R. (1990). Large-scale Variations of thermal Electron Parameters in the Solar Wind between 0.3 and 1 AU. J. Geophys. Res. 95, 6305. doi:10.1029/ja095ia05p06305

CrossRef Full Text | Google Scholar

Pritchett, P. L. (2005). The “Newton Challenge”: Kinetic Aspects of Forced Magnetic Reconnection. J. Geophys. Res. 110, A10213. doi:10.1029/2005ja011228

CrossRef Full Text | Google Scholar

Riazantseva, M. O., Budaev, V., Rakhmanova, L., Zastenker, G., Yermolaev, Y., Lodkina, I., et al. (2017). Variety of Shapes of Solar Wind Ion Flux Spectra: Spektr-R Measurements. J. Plasma Phys. 83, 705830401. doi:10.1017/s0022377817000502

CrossRef Full Text | Google Scholar

Roth, M., De Keyser, J., and Kuznetsova, M. M. (1996). Vlasov Theory of the Equilibrium Structure of Tangential Discontinuities in Space Plasmas. Space Sci. Rev. 76, 251–317. doi:10.1007/bf00197842

CrossRef Full Text | Google Scholar

Salem, C., Lacombe, C., Mangeney, A., Kellogg, P. J., and Bougeret, J.-L. (2003). Weak Double Layers in the Solar Wind and Their Relation to the Interplanetary Electric Field. AIP Conf. Proc. 679, 513. doi:10.1063/1.1618647

Google Scholar

Scudder, J. D. (2019). Steady Electron Runaway Model SERM: Astrophysical Alternative for the Maxwellian assumption. ApJ 885, 138. doi:10.3847/1538-4357/ab4882

CrossRef Full Text | Google Scholar

Servidio, S., Gurgiolo, C., Carbone, V., and Goldstein, M. L. (2014). Relaxation Processes in Solar Wind Turbulence. ApJ 789, L44. doi:10.1088/2041-8205/789/2/l44

CrossRef Full Text | Google Scholar

Sheeley, N. R., and Rouillard, A. P. (2010). Tracking Streamer Blobs into the Heliosphere. ApJ 715, 300–309. doi:10.1088/0004-637x/715/1/300

CrossRef Full Text | Google Scholar

Siscoe, G. L., Davis, L., Coleman, P. J., Smith, E. J., and Jones, D. E. (1968). Power Spectra and Discontinuities of the Interplanetary Magnetic Field: Mariner 4. J. Geophys. Res. 73, 61–82. doi:10.1029/ja073i001p00061

CrossRef Full Text | Google Scholar

Telloni, D., Perri, S., Carbone, V., and Bruno, R. (2016). Selective Decay and Dynamic Alignment in the MHD Turbulence: the Role of the Rugged Invariants. AIP Conf. Proc. 1720, 040015. doi:10.1063/1.4943826

Google Scholar

Trenchi, L., Bruno, R., Telloni, D., D'amicis, R., Marcucci, M. F., Zurbuchen, T. H., et al. (2013a). Solar Energetic Particle Modulations Associated with Coherent Magnetic Structures. ApJ 770, 11. doi:10.1088/0004-637x/770/1/11

CrossRef Full Text | Google Scholar

Trenchi, L., Bruno, R., D'Amicis, R., Marcucci, M. F., and Telloni, D. (2013b). Observations of IMF Coherent Structures and Their Relationship to SEP Dropout Events. Ann. Geophys. 31, 1333–1341. doi:10.5194/angeo-31-1333-2013

CrossRef Full Text | Google Scholar

Tu, C. Y., Wang, X., He, J., Marsch, E., and Wang, L. (2016). Two Cases of Convecting Structure in the Slow Solar Wind Turbulence. AIP Conf. Proc. 1720, 040017. doi:10.1063/1.4943828

Google Scholar

Vasquez, B. J., and Hollweg, J. V. (1999). Formation of Pressure-Balanced Structures and Fast Waves from Nonlinear Alfvén Waves. J. Geophys. Res. 104, 4681–4696. doi:10.1029/1998ja900090

CrossRef Full Text | Google Scholar

Vasquez, B. J., Abramenko, V. I., Haggerty, D. K., and Smith, C. W. (2007). Numerous Small Magnetic Field Discontinuities of Bartels Rotation 2286 and the Potential Role of Alfvénic Turbulence. J. Geophys. Res. 112, A11102. doi:10.1029/2007ja012504

CrossRef Full Text | Google Scholar

Viall, N. M., and Borovsky, J. E. (2020). Nine Outstanding Questions of Solar Wind Physics. J. Geophys. Res. 125, e2018JA026005. doi:10.1029/2018ja026005

PubMed Abstract | CrossRef Full Text | Google Scholar

Viall, N. M., and Vourlidas, A. (2015). Periodic Density Structures and the Origin of the Slow Solar Wind. ApJ 807, 176. doi:10.1088/0004-637x/807/2/176

CrossRef Full Text | Google Scholar

Viall, N. M., Kepko, L., and Spence, H. E. (2009). Relative Occurrence Rates and Connection of Discrete Frequency Oscillations in the Solar Wind Density and Dayside Magnetosphere. J. Geophys. Res. 114, A01201. doi:10.1029/2008ja013334

CrossRef Full Text | Google Scholar

Viall, N. M., Spence, H. E., Vourlidas, A., and Howard, R. (2010). Examining Periodic Solar-Wind Density Structures Observed in the SECCHI Heliospheric Imagers. Sol. Phys. 267, 175–202. doi:10.1007/s11207-010-9633-1

CrossRef Full Text | Google Scholar

Wang, Y.-M., Sheeley, N. R., Howard, R. A., Rich, N. B., and Lamy, P. L. (1999). Streamer Disconnection Events Observed with the LASCO Coronagraph. Geophys. Res. Lett. 26, 1349–1352. doi:10.1029/1999gl900177

CrossRef Full Text | Google Scholar

Whittlesey, P. L., Larson, D. E., Kasper, J. C., Halekas, J., Abatcha, M., Abiad, R., et al. (2020). The Solar Probe ANalyzers-Electrons on the Parker Solar Probe. ApJS 246, 74. doi:10.3847/1538-4365/ab7370

CrossRef Full Text | Google Scholar

Xu, F., and Borovsky, J. E. (2015). A New Four-Plasma Categorization Scheme for the Solar Wind. J. Geophys. Res. Space Phys. 120, 70–100. doi:10.1002/2014ja020412

CrossRef Full Text | Google Scholar