Phenomenological Implications of Modified Loop Cosmologies: An Overview

In this paper, we first provide a brief review of the effective dynamics of two recently well-studied models of modified loop quantum cosmologies (mLQCs), which arise from different regularizations of the Hamiltonian constraint and show the robustness of a generic resolution of the big bang singularity, replaced by a quantum bounce due to non-perturbative Planck scale effects. As in loop quantum cosmology (LQC), in these modified models the slow-roll inflation happens generically. We consider the cosmological perturbations following the dressed and hybrid approaches and clarify some subtle issues regarding the ambiguity of the extension of the effective potential of the scalar perturbations across the quantum bounce, and the choice of initial conditions. Both of the modified regularizations yield primordial power spectra that are consistent with current observations for the Starobinsky potential within the framework of either the dressed or the hybrid approach. But differences in primordial power spectra are identified among the mLQCs and LQC. In addition, for mLQC-I, striking differences arise between the dressed and hybrid approaches in the infrared and oscillatory regimes. While the differences between the two modified models can be attributed to differences in the Planck scale physics, the permissible choices of the initial conditions and the differences between the two perturbation approaches have been reported for the first time. All these differences, due to either the different regularizations or the different perturbation approaches in principle can be observed in terms of non-Gaussianities.

1 Introduction

Despite offering a solution to several fundamental and conceptual problems of the standard big bang cosmology, including the flatness, horizon, and exotic-relic problems, the cosmic inflation in the early Universe also provides a mechanism to produce density perturbations and primordial gravitational waves (PGWs) (Starobinsky, 1980; Guth, 1981; Sato, 1981; Kodama and Sasaki, 1984; Mukhanov et al., 1992; Malik, 2001; Dodelson, 2003; Mukhanov, 2005; Weinberg, 2008; Malik and Wands, 2009; Senatore, 2017). The latter arise from quantum fluctuations of spacetimes and produce not only a temperature anisotropy, but also polarizations in the cosmic microwave background (CMB), a smoking gun of PGWs. However, the inflationary paradigm is incomplete without the knowledge of key elements from quantum gravity. First, it is well-known that the cosmic inflation is sensitive to the ultraviolet (UV) physics, and its successes are tightly contingent on the understanding of this UV physics (Brandenberger, 1999; Martin and Brandenberger, 2001; Niemeyer and Parentani, 2001; Bergstorm and Danielsson, 2002; Niemeyer and Parentani, 2002; Niemeyer and Parentani, 2003; Easther et al., 2005; McAllister and Silverstein, 2007; Joras and Marozzi, 2009; Ashoorioon et al., 2011; Jackson and Schalm, 2012; Kiefer and Krämer, 2012; Brandenberger and Martin, 2013; Burgess et al., 2013; Chernoff and Tye, 2014; Krauss and Wilczek, 2014; Woodard, 2014; Baumann and McAllister, 2015; Cicoli, 2016; Silverstein, 2016). In particular, if the inflationary phase lasts somewhat longer than the minimal period required to solve the above mentioned problems, the length scales we observe today will originate from modes that are smaller than the Planck length during inflation (Brandenberger, 1999; Martin and Brandenberger, 2001; Niemeyer and Parentani, 2001; Bergstorm and Danielsson, 2002; Niemeyer and Parentani, 2002; Niemeyer and Parentani, 2003; Easther et al., 2005; Joras and Marozzi, 2009; Ashoorioon et al., 2011; Jackson and Schalm, 2012; Brandenberger and Martin, 2013). Then, the treatment of the underlying quantum field theory on a classical spacetime becomes questionable, as now the quantum geometric effects are expected to be large, and the space and time cannot be treated classically any more. This is often referred to as the trans-Planckian problem of cosmological fluctuations¹.

The second problem of the inflationary paradigm is more severe. It is well known that inflationary spacetimes are past-incomplete because of the big bang singularity (Borde and Vilenkin, 1994; Borde et al., 2003), with which it is not clear how to impose the initial conditions. This problem gets aggravated for low energy inflation in spatially-closed models which are slightly favored by current observations where the Universe encounters a big crunch singularity and lasts only for a few Planck seconds (Linde, 2014; Linde, 2018).

Another problematic feature of inflation is that one often ignores the pre-inflationary dynamics and sets the Bunch-Davies (BD) vacuum in a very early time. But, it is not clear how such a vacuum state can be realized dynamically in the framework of quantum cosmology (McAllister and Silverstein, 2007; Burgess et al., 2013; Chernoff and Tye, 2014; Baumann and McAllister, 2015; Cicoli, 2016; Silverstein, 2016), considering the fact that a pre-inflationary phase always exists between the Plank and inflation scales, which are about ${10}^3\sim {10}^{12}$ orders of magnitude difference (Dodelson, 2003; Mukhanov, 2005; McAllister and Silverstein, 2007; Weinberg, 2008; Burgess et al., 2013; Chernoff and Tye, 2014; Baumann and McAllister, 2015; Cicoli, 2016; Silverstein, 2016). While these problems of inflationary paradigm demand a completion from quantum theory of spacetimes, they also open an avenue to overcome one of the main obstacles in the development of quantum gravity, which concerns with the lack of experimental evidences. Thus, understanding inflation in the framework of quantum gravity could offer valuable guidances to the construction of the underlying theory (Weinberg, 1980; Carlip, 2003; Kiefer, 2007; Green et al., 1999; Polchinski, 2001; Johson, 2003; Becker et al., 2007; Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Pullin, 2017).

In particular, when applying the techniques of loop quantum gravity (LQG) to homogeneous and isotropic Universe, namely loop quantum cosmology (LQC) (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017), it was shown that, purely due to quantum geometric effects, the big bang singularity is generically resolved and replaced by a quantum bounce at which the spacetime curvature becomes Planckian (Ashtekar et al., 2006; Ashtekar et al., 2006; Ashtekar et al., 2010). The robustness of the singularity resolution has been shown for a variety of isotropic and anisotropic spacetimes (Giesel et al., 2020). Interestingly, there exists a reliable effective spacetime description, which has been used to confirm a generic resolution of all strong curvature singularities (Singh, 2009; Singh, 2014). Various phenomenological implications have been studied using this effective spacetime description, whose validity has been verified for isotropic and anisotropic spacetimes (Diener et al., 2014; Diener et al., 2014; Agullo et al., 2017; Diener et al., 2017; Singh, 2018). For low energy inflation models with a positive spatial curvature, the singularity resolution and a successful onset of inflation for classically inadmissible initial conditions have been demonstrated (Dupuy and Singh, 2020; Gordon et al., 2021; Motaharfar and Singh, 2021).

In the last couple of years, several approaches have been proposed, in order to address the impacts of the quantum geometry on the primordial power spectra. These include the approaches of the deformed algebra (Bojowald et al., 2008; Cailleteau et al., 2012; Cailleteau et al., 2012), dressed metric (Agullo et al., 2012; Agullo et al., 2013; Agullo et al., 2013), and hybrid (Fernández-Méndez et al., 2012; Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015; Martínez and Olmedo, 2016) [For a recent discussion about similar ideas in anisotropic Bianchi I LQC spacetimes see Refs. (Gupt and Singh, 2012; Gupt and Singh, 2013; Agullo et al., 2020; Agullo et al., 2020) and references therein.]. In particular, the last two approaches have been widely studied and found that they are all consistent with current cosmological observations (Agullo and Morris, 2015; Bonga and Gupt, 2016; Bonga and Gupt, 2016; de Blas and Olmedo, 2016; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Castelló Gomar et al., 2017; Zhu et al., 2017; Zhu et al., 2017; Agullo et al., 2018; Elizaga Navascués et al., 2018; Navascues et al., 2018; Wu et al., 2018; Zhu et al., 2018). In addition, within the framework of the dressed metric approach recently it has been also shown that some anomalies from the CMB data (Akrami and Planck collaboration, 2020; Akrami and Planck collaboration, 2020; Schwarz et al., 2016) can be reconciled purely due to the quantum geometric effects (Ashtekar et al., 2020; Agullo et al., 2021; Agullo et al., 2021; Ashtekar et al., 2021).

In addition to the standard LQC, in which the Lorentzian term of the classical Hamiltonian constraint is first expressed in terms of the Euclidean term in the spatially flat Friedmann-Lemaître-Robertson-Walker (FLRW) Universe, and then only the quantization of the Euclidean term is considered, the robustness of the singularity resolution with respect to different quantizations of the classical Hamiltonian constraint in the symmetry reduced spacetimes have been extensively studied. Two notable examples are the so-called modified LQC-I (mLQC-I) and modified LQC-II (mLQC-II) models, which were first proposed by Yang, Ding and Ma more than a decade ago (Yang et al., 2009). In a recent study, Dapor and Liegener (DL) (Dapor and Liegener, 2018a; Dapor and Liegener, 2018b) obtained the expectation values of the Hamiltonian operator in LQG using complexifier coherent states (Thiemann, 2001a; Thiemann and Winkler, 2001b; Thiemann, 2006), adapted to the spatially flat FLRW Universe. Using the non-graph changing regularization of the Hamiltonian advocated by Thiemann (Thiemann, 1998a; Thiemann, 1998b; Giesel and Thiemann, 2007), DL obtained an effective Hamiltonian constraint, which, to the leading order, agrees with the mLQC-I model first obtained in (Yang et al., 2009). Sometimes, this model has also been referred to as the DL model or Thiemann regularized LQC. Strictly speaking, when constructing loops in (Dapor and Liegener, 2018a) DL treated the edge length μ as a free parameter, but in (Yang et al., 2009) it was considered as a specific triad dependent function, the so-called $\overline{\mu }$ scheme (Ashtekar et al., 2006), which is known to be the only possible choice in LQC, and results in physics that is independent from underlying fiducial structures used during quantization, and meanwhile yields a consistent infrared behavior for all matter obeying the weak energy condition (Corichi and Singh, 2008). Lately, the studies of (Dapor and Liegener, 2018a) have been extended to the $\overline{\mu }$ scheme (Assanioussi et al., 2018; Assanioussi et al., 2019a; Assanioussi et al., 2019b; Liegener and Singh, 2019).

In the two modified LQC models, mLQC-I and mLQC-II, since different regularizations of the Lorentzian term were used, the resulting equations become the fourth-order and non-singular quantum difference equations, instead of the second-order difference ones obtained in LQC. In these two models the big bang singularity is also generically resolved and replaced by a quantum bounce. In addition, the inflationary phase can naturally take place with a very high probability (Li et al., 2018a; Li et al., 2018b; Saini and Singh, 2019a; Saini and Singh, 2019b; Li et al., 2019). In addition, the dynamics in LQC and mLQC-II is qualitatively similar in the whole evolution of the Universe, while the one in mLQC-I becomes significantly different from LQC (as well as mLQC-II) in the contracting phase, in which an emergent quasi de Sitter space is present. This implies that the contracting phase in mLQC-I is purely a quantum regime without any classical limit².

An important question now is what are the effects of these models and approaches on the CMB observations. The answer to this question requires the knowledge of how the quantum fluctuations propagate on a quantum spacetime in LQC and modified loop cosmological models. In particular, in the framework of the dressed metric approach the power spectra of the cosmological perturbations for both mLQC-I and mLQC-II models were investigated (Li et al., 2020c). In the same framework but restricted only to the mLQC-I model, the power spectra of the cosmological perturbations were studied in (Agullo, 2018). More recently, the hybrid approach was applied to mLQC-I (García-Quismondo and Mena Marugán, 2019; Castelló Gomar et al., 2020; García-Quismondo and Mena Marugán, 2020), for which the time-dependent mass of the perturbations was studied in detail (García-Quismondo et al., 2020). The primordial scalar power spectra obtained in the three models, LQC, mLQC-I and mLQC-II, were also investigated in the hybrid approach (Li et al., 2020a), and found that the relative differences in the amplitudes of the power spectra among the three models could be as large as $2\text{\%}$ in the UV regime of the spectra, which is relevant to the current observations. Interestingly, in the above work, differences in primordial power spectra were found between the hybrid and dressed metric approaches in the infra-red and oscillatory regimes in mLQC-I.

In this brief review, we shall focus mainly on the states that are sharply peaked along the classical trajectories, so that the description of the “effective” dynamics of the Universe becomes available (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017), and the questions raised recently in (Kamiński et al., 2020) are avoided. This includes the studies of the “effective” dynamics of the homogeneous and isotropic mLQC-I and mLQC-II models, and their cosmological perturbations in the framework of the dressed metric and hybrid approaches. We shall first clarify the issue regarding the ambiguities in the extension of the effective potential for the scalar perturbations across the quantum bounce, and then pay particular attention to the differences among the three models, LQC, mLQC-I and mLQC-II, and possible observational signals. It is important to note that initial conditions are another subtle and important issue not only in LQC but also in mLQCs. This includes two parts: 1) when to impose the initial conditions, and 2) which kind of initial conditions one can impose consistently. To clarify this issue, we discuss it at length by showing the (generalized) comoving Hubble radius in each model and in each of the dressed and hybrid approaches. From this analysis, one can see clearly what initial conditions can and cannot be imposed at a chosen initial time.

The outline of this brief overview is as follows. In Sec. 2 we consider the effective dynamics of mLQC-I and mLQC-II, and discuss some universal features of their dynamics such as the resolution of big bang singularity. In addition, in this section we also show that for states such that the evolution of the homogeneous Universe was dominated initially at the bounce by the kinetic energy of the inflaton, that is, ${\dot{\varphi }}_B^2\gg V\left({\varphi }_B\right)$, the post-bounce evolution between the bounce and the reheating can be always divided universally into three different phases: the bouncing, transition, and slow-roll inflation [cf. Figure 1]. During each of these phases the expansion factor $a\left(t\right)$ and the scalar field $\varphi \left(t\right)$ can be given analytically. In particular, they are given by Eqs 2.54–2.55, 2.56–2.57 during the bouncing phase for mLQC-I and mLQC-II, respectively. In this same section, the probabilities of the slow-roll inflation is considered, and shown that it occurs generically. This particular consideration is restricted to the quadratic potential, but is expected to be also true for other cases.

FIGURE 1

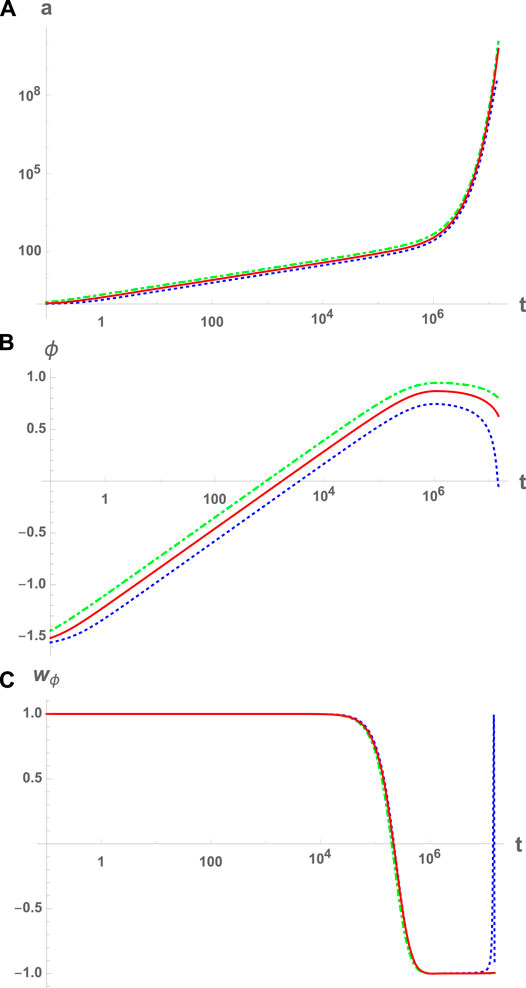
FIGURE 1. The evolution of the scale factor $a\left(t\right)$, the scalar field $\varphi \left(t\right)$, and the equation $w_{\varphi }$ of state of the scalar field (A–C) in the post-bounce phase are depicted and compared among the three modes, LQC (red solid curves), mLQC-I (blue dotted curves) and mLQC-II (green dot-dashed curves), with the Starobinsky potential. In the last panel, $w_{\varphi }$ is defined via $w_{\varphi }\equiv P\left(\varphi \right)/\rho \left(\varphi \right)=[{\dot{\varphi }}^2-2V\left(\varphi \right)]/[{\dot{\varphi }}^2+2V\left(\varphi \right)]$. The initial condition for the simulation is chosen at the bounce with ${\varphi }_B=-1.6m_{pl},{\dot{\varphi }}_B>0$(Li et al., 2019).

In Sec. 3, the cosmological perturbations of mLQC-I and mLQC-II are studied. We discuss initial conditions and the subtle issue of the ambiguity in the choice of the variables ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$ (present in the effective potential), which correspond to the quadratic and linear inverse of the momentum conjugate to the scale factor. In addition, to understand the issue of initial conditions properly, we first introduce the comoving Hubble radius ${\lambda }_H^2$ and then state clearly how this is resolved in GR [cf. Figure 2], and which are the relevant questions in mLQC-I [cf. Figure 5] and mLQC-II [cf. Figure 6]. From these figures it is clear that the BD vacuum cannot be consistently imposed at the bounce³, as now some modes are inside the (comoving) Hubble radius while others not. However, the fourth-order adiabatic vacuum may be imposed at this moment for both of these two modified LQC models, as that adopted in LQC (Agullo et al., 2013). In addition, in mLQC-I the de Sitter state given by Eq. 3.7⁴ can be imposed in the contracting phase as long as $t_0$ is sufficiently early, so the Universe is well inside the de Sitter phase. On the other hand, in mLQC-II and LQC, the BD vacuum can be imposed in the contracting phase as long as $t_0$ is sufficiently early, so the Universe becomes so large that the spacetime curvature is very small, and particle creation is negligible. With these in mind, the power spectra obtained in the three models, mLQC-I, mLQC-II and LQC, within the framework of the dressed metric approach were calculated and compared by imposing the initial conditions in the contracting phase. In particular, the spectra can be universally divided into three regimes, the infrared, intermediate and UV. In the infrared and intermediate regimes, the relative differences in the amplitudes of the spectra can be as large as $100\text{\%}$ between mLQC-I and mLQC-II (the same is also true between mLQC-I and LQC), but in the UV regime such differences get dramatically reduced, which is no larger than $0.1\text{\%}$. Since the modes in the UV regime are the relevant ones to the current observations and also their corresponding power spectra are scale-invariant, so these three models are all consistent with observations.

FIGURE 2

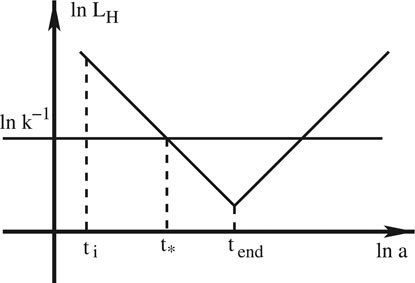
FIGURE 2. The evolution of the comoving Hubble radius $\text{ln}\left(L_H\right)$ vs. $\text{ln}\left(a\right)$ in GR, where $t_i$ denotes the moment of the onset of the slow-roll inflation, $t_{\text{∗}}$ the horizon crossing time of a mode with the wavenumber k, and $t_{\text{end}}$ the moment that the slow-roll inflation ends.

In Sec. 4, the cosmological perturbations of mLQC-I and mLQC-II are studied within the hybrid approach, and the subtleties of the initial conditions are shown in Figures 8–10, where Figures 8, 9 are respectively for the quadratic and Starobinsky potentials in mLQC-I, while Figure 10 is for the Starobinsky potential in mLQC-II. The case with the quadratic potential in mLQC-II is similar to that of mLQC-I, given by Figure 8. From these figures it is clear that imposing the initial conditions now becomes a more delicate issue, and sensitively depends on the potential $V\left(\varphi \right)$ of the inflaton field. First, in the cases described by Figures 8, 9, all the modes are oscillating during the time $t_i^p<t<t_i$, so one might intend to impose the BD vacuum at the bounce. However, for $t<t_i^p$ the quantity ${\text{Ω}}_{\text{tot}}$ defined in Eq. 3.9 experiences a period during which it is very large and negative. As a result, particle creation is expected not to be negligible during this period. Then, imposing the BD vacuum at the bounce will not account for these effects, and the resulting power spectra shall be quite different from the case, in which in the deep contracting phase ($t\ll t_B$) the BD vacuum is imposed for mLQC-II and LQC, and the de Sitter state for mLQC-I. On the other hand, in the case described by Figure 10, even if the BD vacuum is chosen at the bounce, it may not be quite different from the one imposed in the deep contracting phase, as now in the whole contracting phase all the modes are oscillating, and particle creation is not expected to be important up to the bounce. To compare the results from the three different models, in this section the second-order adiabatic vacuum conditions are chosen in the contracting phase, which is expected not to be much different from the de Sitter state for mLQC-I and the BD vacuum for mLQC-II and LQC, as long as $t_0\ll t_B$ in all the cases described by Figures 8–10. The ambiguities of the choice of ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$ also occur in this approach, but as far as the power spectra are concerned, different choices lead to similar conclusions (Castelló Gomar et al., 2020). So, in this section only the so-called prescription A is considered. Then, similar conclusions are obtained in this approach regarding the differences among the amplitudes of the power spectra in the three different models. In particular, the relative differences can be as large as $100\text{\%}$ between mLQC-I and mLQC-II/LQC, but in the UV regime such differences are reduced to about $2\text{\%}$. A remarkable feature between the two different approaches is also identified: in the infrared and oscillatory regimes, the power spectrum in mLQC-I is suppressed as compared with its counterpart in LQC in the hybrid approach. On the other hand, in the dressed metric approach, the power spectrum in mLQC-I is largely amplified in the infrared regime where its magnitude is as large as of the Planck scale (Agullo, 2018; Li et al., 2020c). The main reason for such differences is that the effective mass in the hybrid approach is strictly positive near the bounce, while it is strictly negative in the dressed metric approach for states that are initially dominated by the kinetic energy of the inflaton (Agullo, 2018; Castelló Gomar et al., 2020; Li et al., 2020c).

The review is concluded in Sec. 5, in which we summarize the main conclusions and point out some open questions for future studies.

2 Effective Quantum Dynamics in Modified LQCS

To facilitate our following discussions, let us first briefly review the standard process of quantization carried out in LQC, from which one can see clearly the similarities and differences among the three models, LQC, mLQC-I and mLQC-II.

2.1 Quantum Dynamics of LQC

The key idea of LQC is to use the fundamental variables and quantization techniques of LQG to cosmological spacetimes, by taking advantage of the simplifications that arise from the symmetries of these spacetimes. In the spatially-flat FLRW spacetime,

$\begin{array}{c}d{s}^2=-N^2\left(t\right)d{t}^2+q_{ab}\left(t\right)d{x}^{a}d{x}^b\\ \equiv -N^2\left(t\right)d{t}^2+a^2\left(t\right){\delta }_{ab}d{x}^{a}d{x}^b,\end{array}$(2.1)

there exists only one degree of freedom, the scale factor $a\left(t\right)$, where $N\left(t\right)$ is the lapse function and can be freely chosen, given the freedom in reparametrizing t, and $q_{ab}\left(t\right)$ denotes the 3-dimensional (3D) spatial metric of the hypersurface $t=$ Constant. In this paper, we shall use the indices $a,b,c,\dots$ to denote spatial coordinates and $i,j,k,\dots$ to denote the internal su (2) indices. Repeated indices will represent sum, unless otherwise specified.

In full GR, the gravitational phase space consists of the connection $A_a^i$ and density weighted triad $E_i^a$. In the present case, the 3D spatial space M has a ${\mathrm{ℝ}}^3$ topology, from which we can introduce a fiducial cell $\mathfrak{F}$ and restrict all integrations to this cell, in order to avoid some artificial divergences and have a well-defined symplectic structure. Within this cell, we introduce a fiducial flat metric ${\stackrel{\circ }{q}}_{ab}$ via the relation $q_{ab}\left(t\right)=a^2\left(t\right){\stackrel{\circ }{q}}_{ab}$, and then an associated constant orthogonal triad ${\stackrel{\circ }{e}}_i^a$ and a cotriad ${\stackrel{\circ }{\omega }}_a^i$. Then, after symmetry reduction $A_a^i$ and $E_i^a$ are given by,

$A_a^i=c{v}_o^{-1/3}{\stackrel{\circ }{\omega }}_a^i,E_i^a=\left|p\right|v_o^{-2/3}\sqrt{\stackrel{\circ }{q}}{\stackrel{\circ }{e}}_i^a,$(2.2)

where $\left|p\right|=v_o^{2/3}{a}^2,\kappa =8\pi G/c^4$, $v_o$ denotes the volume of the fiducial cell measured by ${\stackrel{\circ }{q}}_{ab}$, $\stackrel{\circ }{q}$ is the determinant of ${\stackrel{\circ }{q}}_{ab}$, and γ is the Barbero-Immirzi parameter whose value can be set to $\gamma \approx 0.2375$ using black hole thermodynamics in LQG (Meissner, 2004). For classical solutions, symmetry reduced connection c is related to time derivative of scale factor as $c=\gamma \dot{a}$, where an over dot denotes a derivative with respect to t for the choice $N=1$.

The physical triad and cotriad are given by $e_i^a=\left(\text{sgn p}\right)|p{|}^{-1/2}{v}_o^{1/3}{\stackrel{\circ }{e}}_i^a$ and ${\omega }_a^i=\left(\text{sgn p}\right)|p{|}^{1/2}{v}_o^{-1/3}{\stackrel{\circ }{\omega }}_a^i$, where (sgn p) arises because in connection dynamics the phase space contains triads with both orientations. In the following we choose this orientation to be positive and volume of the fiducial cell to be $v_o$ = 1. The variables c and p satisfy the communication relation,

$\left\{c,p\right\}=\frac{\kappa \gamma }{3}.$(2.3)

Then, the gravitational part of the Hamiltonian is a sum of the Euclidean and Lorentzian terms,

${\mathrm{\mathscr{H}}}_{\text{grav}}={\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(E\right)}-\left(1+{\gamma }^2\right){\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(L\right)},$(2.4)

where, with the choice $N=1$, these two terms are given, respectively, by

${\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(E\right)}=\frac{1}{2\kappa }{\displaystyle \int {\text{d}}^{3}x{\mathit{ϵ}}_{ijk}{F}_{ab}^i\frac{E^{aj}{E}^{bk}}{\sqrt{q}}},$(2.5)

${\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(L\right)}=\frac{1}{\kappa }{\displaystyle \int {\text{d}}^{3}x{K}_{[a}^j{K}_{b]}^k\frac{E^{aj}{E}^{bk}}{\sqrt{q}}},$(2.6)

where $q=\text{det}\left(q_{ab}\right)=a^6\stackrel{\circ }{q}$, $F_{ab}^k$ is the field strength of the connection $A_a^i$, and $K_a^i$ is the extrinsic curvature, given, respectively, by

$\begin{array}{l}{F}_{ab}^k\equiv 2{\partial }_{[a}{A}_{b]}^k+{\mathit{ϵ}}_{ij}^k{A}_a^i{A}_b^j=c^2{\mathit{ϵ}}_{ij}^k{\stackrel{\circ }{\omega }}_a^i{\stackrel{\circ }{\omega }}_b^j,\\ K_a^i\equiv K_{ab}{e}_i^b=\frac{e_i^b}{2N}({\dot{q}}_{ab}-2D_{(a}{N}_{b)})=\pm \dot{a}{\stackrel{\circ }{\omega }}_a^i.\end{array}$(2.7)

Upon quantization, ambiguities can arise due to different treatments of the Euclidean and Lorentzian terms in the Hamiltonian constraint. In particular, LQC takes the advantage that in the spatially-flat FLRW Universe the Lorentzian part is proportional to the Euclidean part,

${\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(L\right)}={\gamma }^{-2}{\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(E\right)},$(2.8)

so that, when coupled to a massless scalar field, the classical Hamiltonian can be rewritten as (Ashtekar et al., 2003; Ashtekar et al., 2006)

$\begin{array}{c}\mathrm{\mathscr{H}}\equiv {\mathrm{\mathscr{H}}}_{\text{grav}}+{\mathrm{\mathscr{H}}}_M\\ =-\frac{1}{2\kappa {\gamma }^2}{\displaystyle \int {\text{d}}^{3}x{\mathit{ϵ}}_{ijk}{F}_{ab}^i\frac{E^{aj}{E}^{bk}}{\sqrt{q}}+{\mathrm{\mathscr{H}}}_M},\end{array}$(2.9)

where ${\mathrm{\mathscr{H}}}_M=p_{\varphi }^2/\left(2\sqrt{q}\right)$, with $p_{\varphi }$ being the momentum conjugate of ϕ.

The elementary operators in the standard LQC are the triads⁵p and elements of the holonomies given by $\widehat{e^{i\overline{\mu }c/2}}$ of c, where $\overline{\mu }=\sqrt{\text{Δ}{l}_{pl}^2/\left|p\right|}$ with $\text{Δ}\equiv 4\sqrt{3}\pi \gamma$, and $\text{Δ}{l}_{pl}^2$ being the minimum non-zero eigenvalue of the area operator, and the Planck length $l_{pl}$ is defined as $l_{pl}\equiv \sqrt{\hslash G}$. However, it is found that, instead of using the eigenket $|p\rangle$ of the area operator p as the basis, it is more convenient to use the eigenket $|v\rangle$ of the volume operator $\widehat{v}\left(\equiv \text{sgn}\left(p\right)|p{|}^{3/2}\right)$, where

$\widehat{v}|v\rangle ={\left(\frac{8\pi \gamma }{6}\right)}^{3/2}\frac{\left|v\right|}{K}{l}_{pl}^3|v\rangle ,\widehat{e^{i\overline{\mu }c/2}}|v\rangle =|v+1\rangle ,$(2.10)

with $K\equiv 2\sqrt{2}{\left(3\sqrt{3\sqrt{3}}\right)}^{-1}$. Let $\text{Ψ}\left(v,\varphi \right)$ denote the wavefunction in the kinematical Hilbert space of the gravitational field coupled with the scalar field ϕ, we have

$\begin{array}{l}\widehat{\varphi }\text{Ψ}\left(v,\varphi \right)=\varphi \text{Ψ}\left(v,\varphi \right),\\ {\widehat{p}}_{\varphi }\text{Ψ}\left(v,\varphi \right)=-i\hslash \frac{\partial }{\partial \varphi }\text{Ψ}\left(v,\varphi \right),\\ \widehat{|p{|}^{-3/2}}\text{Ψ}\left(v,\varphi \right)=\mathrm{ℬ}\left(v\right)\text{Ψ}\left(v,\varphi \right),\end{array}$(2.11)

where

$\begin{array}{l}\mathrm{ℬ}\left(v\right)\equiv {\left(\frac{6}{8\pi \gamma l_{pl}^2}\right)}^{3/2}B\left(v\right),\\ B\left(v\right)\equiv {\left(\frac{3}{2}\right)}^{3}K\left|v\right|||v+1{|}^{1/3}-|v-1{|}^{1/3}{|}^3.\end{array}$(2.12)

Then, the equation satisfied by selecting the physical states $\widehat{\mathrm{\mathscr{H}}}\text{Ψ}\left(v,\varphi \right)=0$ can be cast in the form,

$\begin{array}{l}{\partial }_{\varphi }^2\text{Ψ}\left(v,\varphi \right)=\frac{1}{B\left(v\right)}[C^{+}\left(v\right)\text{Ψ}\left(v+4,\varphi \right)-C^o\left(v\right)\text{Ψ}\left(v,\varphi \right)\\ +C^{-}\left(v\right)\text{Ψ}\left(v-4,\varphi \right)],\end{array}$(2.13)

where

$\begin{array}{l}{C}^{+}\left(v\right)\equiv \frac{3\pi KG}{8}|v+2|\left|\right|v+1|-|v+3\left|\right|,\\ C^{-}\left(v\right)\equiv C^{+}\left(v-4\right),C^o\left(v\right)\equiv C^{+}\left(v\right)+C^{-}\left(v\right).\end{array}$(2.14)

This is the main result of LQC (Ashtekar et al., 2006), which shows that: 1) It is a second order quantum difference equation with uniform discreteness in volume, rather than a simple differential equation, a direct consequence of the discrete nature of loop quantum geometry. 2) It provides the evolution of the quantum cosmological wavefunction $\text{Ψ}\left(v,\varphi \right)$, in which the scalar field serves as a clock. Thus, once an initial state $\text{Ψ}\left(v,{\varphi }_0\right)$ is given at the initial moment ${\varphi }_0$, the study of the quantum dynamics of LQC can be carried out. It is found that, instead of a big bang singularity, a quantum bounce is generically produced, a result confirmed through extensive numerical simulations (Diener et al., 2014; Diener et al., 2014; Agullo et al., 2017; Diener et al., 2017; Singh, 2018) and an exactly solvable model (Ashtekar et al., 2010). Using this model, one can compute the probability for the quantum bounce which turns out to be unity for an arbitrary superposition of wavefunctions (Craig and Singh, 2013).

For the states sharply peaked around a classical solution, we can obtain “effective” Friedmann and Raychaudhuri (FR) equations, by using the geometric quantum mechanics in terms of the expectation values of the operators $\left(\widehat{b},\widehat{v},\widehat{\varphi },\widehat{p_{\varphi }}\right)$,

$\dot{b}=\left\{b,\mathrm{\mathscr{H}}\right\},\dot{v}=\left\{v,\mathrm{\mathscr{H}}\right\},$(2.15)

$\dot{\varphi }=\left\{\varphi ,\mathrm{\mathscr{H}}\right\},{\dot{p}}_{\varphi }=\left\{p_{\varphi },\mathrm{\mathscr{H}}\right\},$(2.16)

which take the same forms as their classical ones, but all the quantities now represent their expectation values, $A_I\equiv \langle \widehat{A_I}\rangle$. Then, it was found that the effective Hamiltonian is given by (Ashtekar et al., 2006),

${\mathrm{\mathscr{H}}}_{\text{eff}.}=-\frac{3}{8\pi {\gamma }^2{\overline{\mu }}^{2}G}|p{|}^{1/2}{\text{sin}}^2\left(\overline{\mu }c\right)+\frac{1}{2}|p{|}^{3/2}{p}_{\varphi }^2,$(2.17)

which can also be expressed in terms of v and b via the relations $v=|p{|}^{3/2}$ and $b=c/\sqrt{\left|p\right|}$. Then, from Eqs 2.15, 2.16 one can find that the “effective” FR equations are given by,

$H^2=\frac{8\pi G}{3}\rho \left(1-\frac{\rho }{{\rho }_c}\right),$(2.18)

$\dot{H}=-4\pi G\left(\rho +P\right)\left(1-\frac{\rho }{{\rho }_c}\right),$(2.19)

where

$\begin{array}{l}H\equiv \frac{\dot{v}}{3v}=\frac{\dot{a}}{a},{\rho }_c\equiv \frac{3}{8\pi \lambda a^2{\gamma }^{2}G},\\ \rho \equiv \frac{{\mathrm{\mathscr{H}}}_M}{v},P\equiv -\frac{\partial {\mathrm{\mathscr{H}}}_M}{\partial v},\end{array}$(2.20)

and $v=v_o{a}^3$. Since $H^2$ cannot be negative, from Eq. 2.18 we can see that we must have $\rho \le {\rho }_c$, and at $\rho ={\rho }_c$ we have $H^2=0$, that is, a quantum bounce occurs at this moment. When $\rho \ll {\rho }_c$, the quantum gravity effects are negligible, whereby the classical relativistic limit is obtained.

For a scalar field ϕ with its potential $V\left(\varphi \right)$, we have

${\mathrm{\mathscr{H}}}_M\equiv {\mathrm{\mathscr{H}}}_{\varphi }=v[\frac{p_{\varphi }^2}{2v^2}+V\left(\varphi \right)].$(2.21)

Then, from Eq. 2.16 we find that

$\dot{\varphi }=\frac{p_{\varphi }}{v},$(2.22)

${\dot{p}}_{\varphi }=-v{V}_{,\varphi }\left(\varphi \right).$(2.23)

In the rest of this review, we shall consider only the states that are sharply peaked around a classical solution, so the above “effective” descriptions are valid, and the questions raised recently in (Kamiński et al., 2020) are avoided.

2.2 Effective Dynamics of mLQC-I

As mentioned in the introduction, an important open issue in LQC is its connection with LQG (Brunnemann and Fleischhack, 2007; Engle, 2007; Brunnemann and Koslowski, 2011). In particular, in LQC the spacetime symmetry is first imposed (in the classical level), before the quantization process is carried out. However, it is well-known that this is different from the general process of LQG (Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Pullin, 2017), and as a result, different Hamiltonian constraints could be resulted, hence resulting in different Planck scale physics. Though the question of ambiguities in obtaining the Hamiltonian in LQG is still open, based on some rigorous proposals by Thiemann (Thiemann, 1998a; Thiemann, 1998b; Giesel and Thiemann, 2007), various attempts have been carried out, in order to obtain deeper insights into the question.

One of the first attempts to understand this issue was made in (Dapor and Liegener, 2018a), in which the Euclidean and Lorentzian terms given by Eqs 2.5, 2.6 are treated differently, by closely following the actual construction of LQG. To be more specific, in the full theory (Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Pullin, 2017), the extrinsic curvature in the Lorentzian term (2.6) can be expressed in terms of the connection and the volume as

$K_a^i=\frac{1}{\kappa {\gamma }^3}\left\{A_a^i,\left\{{\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(E\right)},V\right\}\right\},$(2.24)

which once substituted back into Eq. 2.6 lead to an expression of ${\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(L\right)}$ different from that of ${\mathrm{\mathscr{H}}}_{\text{grav}}^{\left(E\right)}$ in the standard LQC (see (Yang et al., 2009) for more details). Correspondingly, one is able to obtain the following “effective” Hamiltonian (Yang et al., 2009; Li et al., 2018a),

$\begin{array}{c}{\mathrm{\mathscr{H}}}_{\text{eff}.}^{\text{I}}=\frac{3v}{8\pi G{\lambda }^2}\left\{{\text{sin}}^2\left(\lambda b\right)-\frac{\left({\gamma }^2+1\right){\text{sin}}^2\left(2\lambda b\right)}{4{\gamma }^2}\right\}\\ +{\mathrm{\mathscr{H}}}_M.\end{array}$(2.25)

Hence, the Hamilton’s equations take the form,

$\dot{v}=\frac{3v\text{sin}\left(2\lambda b\right)}{2\gamma \lambda }\left\{\left({\gamma }^2+1\right)\text{cos}\left(2\lambda b\right)-{\gamma }^2\right\},$(2.26)

$\begin{array}{c}\dot{b}=\frac{3{\text{sin}}^2\left(\lambda b\right)}{2\gamma {\lambda }^2}\left\{{\gamma }^2{\text{sin}}^2\left(\lambda b\right)-{\text{cos}}^2\left(\lambda b\right)\right\}\\ -4\pi G\gamma P,\end{array}$(2.27)

where P represents the pressure defined in Eq. 2.20. Once the matter Hamiltonian ${\mathrm{\mathscr{H}}}_M$ is specified, together with the Hamiltonian constraint,

$\mathrm{\mathscr{H}}\approx 0,$(2.28)

Equations 2.26, 2.27 uniquely determine the evolution of the Universe. Using the non-graph changing regularization of the Hamiltonian (Thiemann, 1998a; Thiemann, 1998b; Giesel and Thiemann, 2007), the expectation values of the Hamiltonian operator yield the same “effective” Hamiltonian of Eq. 2.25 to the leading order (Dapor and Liegener, 2018a).

It has been shown in detail that the big bang singularity is generically replaced by a quantum bounce when the energy reaches its maximum ${\rho }_c^{\text{I}}$ (Yang et al., 2009; Dapor and Liegener, 2018a; Li et al., 2018a; Li et al., 2018b; Li et al., 2019), where

${\rho }_c^{\text{I}}\equiv \frac{{\rho }_c}{4\left(1+{\gamma }^2\right)},$(2.29)

and the Universe is asymmetric with respect to the bounce, in contrast to LQC.

To write Eqs 2.26–2.28 in terms of $H,\rho$ and P, it was found that one must distinguish the pre- and post- bounce phases (Li et al., 2018a). In particular, before the bounce, the modified FR equations take the form (Li et al., 2018a),

$H^2=\frac{8\pi G\alpha {\rho }_{\text{Λ}}}{3}\left(1-\frac{\rho }{{\rho }_c^{\text{I}}}\right)\left[1+\left(\frac{1-2{\gamma }^2+\sqrt{1-\rho /{\rho }_c^{\text{I}}}}{4{\gamma }^2\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)}\right)\frac{\rho }{{\rho }_c^{\text{I}}}\right],$(2.30)

$\begin{array}{c}\frac{\ddot{a}}{a}=-\frac{4\pi \alpha G}{3}\left(\rho +3P-2{\rho }_{\text{Λ}}\right)+4\pi G\alpha P\left(\frac{2-3{\gamma }^2+2\sqrt{1-\rho /{\rho }_c^{\text{I}}}}{\left(1-5{\gamma }^2\right)\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)}\right)\frac{\rho }{{\rho }_c^{\text{I}}}\\ -\frac{4\pi \alpha G\rho }{3}\left[\frac{2{\gamma }^2+5{\gamma }^2\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)-4{\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)}^2}{\left(1-5{\gamma }^2\right){\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)}^2}\right]\frac{\rho }{{\rho }_c^{\text{I}}},\end{array}$(2.31)

where

$\alpha \equiv \frac{1-5{\gamma }^2}{{\gamma }^2+1},{\rho }_{\text{Λ}}\equiv \frac{{\gamma }^2{\rho }_c}{\left(1+{\gamma }^2\right)\left(1-5{\gamma }^2\right)}.$(2.32)

As $\rho \ll {\rho }_c^{\text{I}}$, Eqs 2.30, 2.31 reduce, respectively, to

$H^2\approx \frac{8\pi \alpha G}{3}\left(\rho +{\rho }_{\text{Λ}}\right),$(2.33)

$\frac{\ddot{a}}{a}\approx -\frac{4\pi \alpha G}{3}\left(\rho +3P-2{\rho }_{\text{Λ}}\right).$(2.34)

These are exactly the FR equations in GR for an ordinary matter field coupled with a positive cosmological constant ${\rho }_{\text{Λ}}$, and a modified Newton’s constant, $G_{\alpha }\equiv \alpha G$. For $\gamma \approx 0.2375$, we have ${\rho }_{\text{Λ}}\approx 0.03{\rho }_{pl}$, which is of the same order as the one deduced conventionally in quantum field theory for the vacuum energy in our Universe. In addition, we also have

${\left|\frac{G_{\alpha }}{G}-1\right|}_{\gamma \approx 0.2375}\simeq 0.32>\frac{1}{8}.$(2.35)

Finally, we want to emphasize that the minimal energy density of this branch, for which the Hubble rate vanishes, turns out to be negative which can be shown as ${\rho }_{\text{min}}=-\frac{3}{8\pi G{\lambda }^2}\approx -0.023$. As a result, the necessary condition to generate a cyclic Universe in mLQC-I is the violation of the weak energy condition which is in contrast to the cyclic universes in LQC where the energy density is always non-negative (Li and Singh).

In the post-bounce phase ($t>t_B$), from Eqs 2.26–2.28 we find that (Li et al., 2018a),

$H^2=\frac{8\pi G\rho }{3}\left(1-\frac{\rho }{{\rho }_c^{\text{I}}}\right)\left[1+\frac{{\gamma }^2}{{\gamma }^2+1}{\left(\frac{\sqrt{\rho /{\rho }_c^{\text{I}}}}{1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}}\right)}^2\right],$(2.36)

$\begin{array}{c}\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\left(\rho +3P\right)+\frac{4\pi G\rho }{3}\left[\frac{\left(7{\gamma }^2+8\right)-4\rho /{\rho }_c^{\text{I}}+\left(5{\gamma }^{2}14+8\right)\sqrt{1-\rho /{\rho }_c^{\text{I}}}}{\left({\gamma }^2+1\right){\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)}^2}\right]\frac{\rho }{{\rho }_c^{\text{I}}}\\ +4\pi GP\left[\frac{3{\gamma }^2+2+2\sqrt{1-\rho /{\rho }_c^{\text{I}}}}{\left({\gamma }^2+1\right)\left(1+\sqrt{1-\rho /{\rho }_c^{\text{I}}}\right)}\right]\frac{\rho }{{\rho }_c^{\text{I}}},\end{array}$(2.37)

from which we obtain

$\dot{H}=\frac{4G\pi \left(P+\rho \right)}{\left(1+{\gamma }^2\right)}\left(2{\gamma }^2+2\frac{\rho }{{\rho }_c^{\text{I}}}-3{\gamma }^2\sqrt{1-\frac{\rho }{{\rho }_c^{\text{I}}}}-1\right).$(2.38)

Therefore, regardless of the matter content, the super-inflation (starting at the bounce) will always end at $\rho ={\rho }_s$, where

${\rho }_s=\frac{{\rho }_c^{\text{I}}}{8}\left(4-8{\gamma }^2-9{\gamma }^4+3{\gamma }^2\sqrt{8+16{\gamma }^2+9{\gamma }^4}\right),$(2.39)

for which we have $\dot{H}\left({\rho }_s\right)=0$.

In the classical limit $\rho /{\rho }_c^{\text{I}}\ll 1$, Eqs 2.36, 2.37 reduce, respectively, to

$H^2\approx \frac{8\pi G}{3}\rho ,$(2.40)

$\frac{\ddot{a}}{a}\approx -\frac{4\pi G}{3}\left(\rho +3P\right),$(2.41)

whereby the standard relativistic cosmology is recovered.

It is remarkable to note that in the pre-bounce phase the limit $\rho /{\rho }_c^{\text{I}}\ll 1$ leads to Eqs 2.33, 2.34 with a modified Newtonian constant $G_{\alpha }$, while in the post-bounce the same limits leads to Eqs 2.40, 2.41 but now with the precise Newtonian constant G.

2.3 Effective Dynamics of mLQC-II

In LQG, the fundamental variables for the gravitational sector are the su (2) Ashtekar-Barbero connection $A_a^i$ and the conjugate triad $E_i^a$. When the Gauss and spatial diffeomorphism constraints are fixed, in the homogeneous and isotropic Universe the only relevant constraint is the Hamiltonian constraint, from which we obtain the FR equations, as shown in the previous section. The Hamiltonian in mLQC-II arises from the substitution

$K_a^i=\frac{A_a^i}{\gamma },$(2.42)

in the Lorentzian term (2.6). Then, the following effective Hamiltonian is resulted (Yang et al., 2009),

$\begin{array}{c}{\mathrm{\mathscr{H}}}_{\text{eff}.}^{\text{II}}=-\frac{3v}{2\pi G{\lambda }^2{\gamma }^2}{\text{sin}}^2\left(\frac{\lambda b}{2}\right)\left\{1+{\gamma }^2{\text{sin}}^2\left(\frac{\lambda b}{2}\right)\right\}\\ +{\mathrm{\mathscr{H}}}_M,\end{array}$(2.43)

from which we find that the corresponding Hamilton’s equations are given by,

$\dot{v}=\frac{3v\text{sin}\left(\lambda b\right)}{\gamma \lambda }\left\{1+{\gamma }^2-{\gamma }^2\text{cos}\left(\lambda b\right)\right\},$(2.44)

$\begin{array}{c}\dot{b}=-\frac{6{\text{sin}}^2\left(\frac{\lambda b}{2}\right)}{\gamma {\lambda }^2}\left\{1+{\gamma }^2{\text{sin}}^2\left(\frac{\lambda b}{2}\right)\right\}-4\pi G\gamma P\\ =-4\pi G\gamma \left(\rho +P\right).\end{array}$(2.45)

It can be shown that the corresponding (modified) FR equations now read (Li et al., 2018b),

$H^2=\frac{8\pi G\rho }{3}\left(1+{\gamma }^2\frac{\rho }{{\rho }_c}\right)\left(1-\frac{\left({\gamma }^2+1\right)\rho }{{\text{Δ}}^2{\rho }_c}\right),$(2.46)

$\begin{array}{l}\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\left(\rho +3P\right)-\frac{4\pi GP\rho }{\text{Δ}{\rho }_c}\left[3\left({\gamma }^2+1\right)-2\text{Δ}\right]\\ -\frac{4\pi G{\rho }^2}{3{\text{Δ}}^2{\rho }_c}\left[7{\gamma }^2-1+\left(5{\gamma }^2-3\right)\left(\text{Δ}-1\right)-\frac{4{\gamma }^2\rho }{{\rho }_c}\right],\end{array}$(2.47)

where $\text{Δ}\equiv 1+\sqrt{1+{\gamma }^2\rho /{\rho }_c}$. From these equations we can see that now the quantum bounce occurs when $\rho ={\rho }_c^{\text{II}}$, at which we have $H=0$ and $\ddot{a}>0$, where

${\rho }_c^{\text{II}}=4\left({\gamma }^2+1\right){\rho }_c,$(2.48)

which is different from the critical density ${\rho }_c$ in LQC as well as the one ${\rho }_c^{\text{I}}$ in mLQC-I. Therefore, the big bang singularity is also resolved in this model, and replaced by a quantum bounce at $\rho ={\rho }_c^{\text{II}}$, similar to LQC and mLQC-I, despite the fact that the bounce in each of these models occurs at a different energy density. However, in contrast to mLQC-I, the evolution of the Universe is symmetric with respect to the bounce, which is quite similar to the standard LQC model.

In addition, similar to the other two cases, now the bounce is accompanied by a phase of super-inflation, i.e., $\dot{H}>0$, which ends at $\dot{H}\left({\rho }_s\right)=0$, but now ${\rho }_s$ is given by,

${\rho }_s=\frac{{\rho }_c}{8{\gamma }^2}\left(3\left({\gamma }^2+1\right)\sqrt{1+2{\gamma }^2+9{\gamma }^4}+9{\gamma }^4+10{\gamma }^2-3\right).$(2.49)

For $\gamma =0.2375$, we find ${\rho }_s=0.5132{\rho }_c^{\text{II}}$.

When $\rho \ll {\rho }_c^{\text{II}}$, the modified FR Eqs 2.46, 2.47 reduce to,

$H^2\approx \frac{8\pi G}{3}\rho ,$(2.50)

$\frac{\ddot{a}}{a}\approx -\frac{4\pi G}{3}\left(\rho +3P\right),$(2.51)

which are identical to those given in GR. Therefore, in this model, the classical limit is obtained in both pre- and post-bounce when the energy density ρ is much lower than the critical one ${\rho }_c^{\text{II}}$.

2.4 Universal Properties of mLQC-I/II Models

To study further the evolution of the Universe, it is necessary to specify the matter content ${\mathrm{\mathscr{H}}}_M$. For a single scalar field with its potential $V\left(\varphi \right)$, the corresponding Hamiltonian takes the form (2.21). As a result, the Hamilton’s equations of the matter sector are given by Eqs 2.22, 2.23.

The effective quantum dynamics of LQC, mLQC-I, and mLQC-II were studied in detail recently in (Li et al., 2018b) for a single scalar field with various potentials, including the chaotic inflation, Starobinsky inflation, fractional monodromy inflation, non-minimal Higgs inflation, and inflation with an exponential potential, by using dynamical system analysis. It was found that, while several features of LQC were shared by the mLQC-I and mLQC-II models, others belong to particular models. In particular, in the pre-bounce phase, the qualitative dynamics of LQC and mLQC-II are quite similar, but are strikingly different from that of mLQC-I. In all the three models, the non-perturbative quantum gravitational effects always result in a non-singular post-bounce phase, in which a short period of super-inflation always exists right after the bounce, and is succeeded by the conventional inflation. The latter is an attractor in the phase space for all the three models.

Moreover, similar to LQC (Zhu et al., 2017; Zhu et al., 2017)⁶, for the initially kinetic energy dominated conditions,

$\frac{1}{2}{\dot{\varphi }}_B^2\gg V\left({\varphi }_B\right),$(2.52)

it was found that the evolution of the Universe before the reheating is universal. In particular, in the post-bounce phase (between the quantum bounce and the reheating), the evolution can be uniquely divided into three phases: bouncing, transition and slow-roll inflation, as shown in Figure 1 for the Starobinsky potential,

$V\left(\varphi \right)=\frac{3m^2}{32\pi G}{\left(1-e^{-\sqrt{16\pi G/3}\varphi }\right)}^2.$(2.53)

For other potentials, similar results can be obtained, as long as at the bounce the evolution of the Universe is dominated by the kinetic energy of the inflaton $w\left({\varphi }_B\right)\simeq 1$ (Li et al., 2019; Xiao, 2020).

In each of these three phases, the evolutions of $a\left(t\right)$ and $\varphi \left(t\right)$ can be well approximated by analytical solutions. In particular, during the bouncing phase, they are given by

$\begin{array}{l}a\left(t\right)={\left[1+24\pi G{\rho }_c^{\text{I}}\left(1+\frac{A{\gamma }^2}{1+Bt}\right)t^2\right]}^{1/6},\\ \varphi \left(t\right)={\varphi }_{\text{B}}\pm \frac{m_{pl}\text{arcsinh}\left(\sqrt{24\pi G{\rho }_c^{\text{I}}\left(1+\frac{C{\gamma }^2}{1+Dt}\right)}t\right)}{\sqrt{12\pi G\left(1+\frac{C{\gamma }^2}{1+Dt}\right)}},\end{array}$(2.54)

for mLQC-I model, where the parameters A, B, C and D are fixed through numerical simulations. It was found that the best fitting is provided by (Li et al., 2019),

$A=C=1.2,B=6,D=2.$(2.55)

For the mLQC-II model, during the bouncing phase $a\left(t\right)$ and $\varphi \left(t\right)$ are given by

$\begin{array}{l}a\left(t\right)={\left[1+24\pi G{\rho }_c^{\text{II}}\left(1+\frac{A{\gamma }^2}{1+Bt}\right)t^2\right]}^{1/6},\\ \varphi \left(t\right)={\varphi }_{\text{B}}\pm \frac{m_{pl}\text{arcsinh}\left(\sqrt{24\pi G{\rho }_c^{\text{II}}\left(1+\frac{C{\gamma }^2}{1+Dt}\right)}t\right)}{\sqrt{12\pi G\left(1+\frac{C{\gamma }^2}{1+Dt}\right)}},\end{array}$(2.56)

but now with,

$A=2.5,B=7,C=D=2.$(2.57)

In the transition and slow-roll inflationary phases, the functions $a\left(t\right)$ and $\varphi \left(t\right)$ were given explicitly in (Li et al., 2019).

For the initially potential energy dominated cases,

$\frac{1}{2}{\dot{\varphi }}_B^2\ll V\left({\varphi }_B\right),$(2.58)

it was found that such universalities are lost. In particular, for the Starobinsky potential, the potential energy dominated bounce cannot give rise to any period of inflation for both mLQC-I and mLQC-II models, quite similar to what happens in LQC (Bonga and Gupt, 2016; Bonga and Gupt, 2016).

2.5 Probabilities of the Slow-Roll Inflation in mLQC-I/II Models

To consider the probability of the slow-roll inflation in the modified LQC models, let us start with the phase space $\mathbb{S}$ of the modified Friedmann and Klein-Gordon equations, which now is four-dimensional (4D), and consists of the four variables, $\left(v,b\right)$ and $\left(\varphi ,p_{\varphi }\right)$, from the gravitational and matter sectors, respectively. Using the canonical commutation relations, the symplectic form on the 4D phase space is given by (Singh et al., 2006; Zhang and Ling, 2007; Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b; Corichi and Karami, 2011; Linsefors and Barrau, 2013; Corichi and Sloan, 2014; Chen and Zhu, 2015; Bedic and Vereshchagin, 2019),

$\text{Ω}=d{p}_{\varphi }\wedge d\varphi +\frac{dv\wedge db}{4\pi G\gamma }.$(2.59)

However, after taking the effective Hamiltonian constraint into account,

$\mathcal{C}=16\pi G\left\{{\mathrm{\mathscr{H}}}_{grav}\left(v,b\right)+\frac{p_{\varphi }^2}{2v}+vV\left(\varphi \right)\right\}\simeq 0,$(2.60)

where $``\simeq "$ means that the equality holds only on $\overline{\text{Γ}}$, we can see that the 4D phase space $\mathbb{S}$ reduces to a three-dimensional (3D) hypersurface $\overline{\text{Γ}}$.

On the other hand, the phase space $\mathbb{S}$ is isomorphic to a 2-dimensional (2D) gauge-fixed surface $\widehat{\text{Γ}}$ of $\overline{\text{Γ}}$, which is intersected by each dynamical trajectory once and only once (Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b). From the FR equations, it can be shown that for both mLQC-I and mLQC-II the variable b satisfies the equation (Li et al., 2018a; Li et al., 2018b; Li et al., 2019),

$\dot{b}=-4\pi G\gamma \left(\rho +P\right).$(2.61)

For any given matter field that satisfies the weak energy condition (Hawking and Ellis, 1973), we have $\rho +P>0$, so the function b is monotonically decreasing. Then, a natural parameterization of this 2D surface is $b=$ constant, say, $b_0$. Hence, using the Hamiltonian constraint (2.60) we find

$p_{\varphi }^{\text{A}}=v{\left\{-2\left[{\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}+V\left(\varphi \right)\right]\right\}}^{1/2},$(2.62)

where $\text{A}=\text{I},\text{II}$, and

${\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\equiv v^{-1}{\mathrm{\mathscr{H}}}_{grav}^{\text{A}}\left(v,b_0\right).$(2.63)

On the other hand, from Eqs 2.25, 2.43 we find that ${\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}={\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\left(b_0\right)=$ constant on $\widehat{\text{Γ}}$. Thus, we find

$d{p}_{\varphi }^{\text{A}}{|}_{\widehat{\text{Γ}}}=\frac{p_{\varphi }^{\text{A}}}{v}dv-\frac{v^2{V}_{,\varphi }}{p_{\varphi }}d\varphi .$(2.64)

Inserting this expression into Eq. 2.59, we find that the pulled-back symplectic structure $\widehat{\text{Ω}}$ reads

${\widehat{\text{Ω}}}^{\text{A}}{|}_{\widehat{\text{Γ}}}={\left\{-2\left[{\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\left(b_0\right)+V\left(\varphi \right)\right]\right\}}^{1/2}d\varphi \wedge dv,$(2.65)

from which we find that the Liouville measure $d{\widehat{\mu }}_L$ on $\widehat{\text{Γ}}$ is given by

$d{\widehat{\mu }}_L^{\text{A}}={\left\{-2\left[{\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\left(b_0\right)+V\left(\varphi \right)\right]\right\}}^{1/2}d\varphi dv.$(2.66)

Note that $d{\widehat{\mu }}_L^{\text{A}}$ does not depend on v, so that the integral with respect to $dv$ is infinite. However, this divergency shall be canceled when calculating the probability, as it will appear in both denominator and numerator. Therefore, the measure for the space of physically distinct solutions can be finally taken as

$d{\omega }^{\text{A}}={\left\{-2\left[{\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\left(b_0\right)+V\left(\varphi \right)\right]\right\}}^{1/2}d\varphi ,$(2.67)

so that the 2D phase space $\widehat{\text{Γ}}$ is further reduced to an interval $\varphi \in \left({\varphi }_{\text{min}},{\varphi }_{\text{max}}\right)$. It should be noted that such a defined measure depends explicitly on $b_0$, and its choice in principle is arbitrary. However, in loop cosmology there exists a preferred choice, which is its value at the quantum bounce $b_0=b\left(t_B\right)$ (Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b). With such a choice, the probability of the occurrence of an event E becomes

$P\left(E\right)=\frac{1}{\mathcal{D}}\underset{\mathrm{ℐ}\left(E\right)}{{\displaystyle \int }}{\left\{-2\left[{\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\left(b_B\right)+V\left(\varphi \right)\right]\right\}}^{1/2}d\varphi ,$(2.68)

where $\mathrm{ℐ}\left(E\right)$ is the interval on the ${\varphi }_B$-axis, which corresponds to the physically distinct initial conditions in which the event E happens, and $\mathcal{D}$ is the total measure

$\mathcal{D}\equiv {\displaystyle {\int }_{{\varphi }_{\text{min}}}^{{\varphi }_{\text{max}}}{\left\{-2\left[{\widehat{\mathrm{\mathscr{H}}}}_{grav}^{\text{A}}\left(b_B\right)+V\left(\varphi \right)\right]\right\}}^{1/2}d\varphi }.$(2.69)

Once the probability is properly defined, we can calculate it in different models of the modified LQCs. In LQC (Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b), the calculations were carried out for the quadratic potential. In order to compare the results obtained in different models, let us consider the same potential. Then, for the mLQC-I model it was found that (Li et al., 2019)

$\text{sin}\left(\lambda b_B^{\text{I}}\right)=\sqrt{\frac{1}{2{\gamma }^2+2}},\text{sin}\left(2\lambda b_B^{\text{I}}\right)=\frac{\sqrt{2{\gamma }^2+1}}{{\gamma }^2+1},$

$p_{\varphi }^{\text{I}}=v{\left(2{\rho }_c^{\text{I}}-2V\right)}^{\frac{1}{2}},d{\omega }^{\text{I}}={\left(2{\rho }_c^{\text{I}}-2V\right)}^{\frac{1}{2}}d\varphi ,$(2.70)

so that the probability for the desired slow-roll not to happen is,

$P^{\text{I}}\left(\text{not}\text{realized}\right)\mathrm{\lesssim }\frac{{\displaystyle {\int }_{-5.158}^{0.917}d{\omega }^{\text{I}}}}{{{\displaystyle {\displaystyle {\int }_{-{\varphi }_{\text{max}}^{\text{I}}}^{{\varphi }_{\text{max}}^{\text{I}}}d{\omega }^{\text{I}}}}}^{\text{}}}\mathrm{\simeq }1.12\times {10}^{-5},$(2.71)

where ${\varphi }_{\text{max}}^{\text{I}}=3.49\times {10}^5{m}_{pl}$.

In mLQC-II, following a similar analysis, it can be shown that the probability for the desired slow-roll not to happen is (Li et al., 2019),

$P^{\text{II}}\left(\text{not realized}\right)\mathrm{\lesssim }2.62\times {10}^{-6}.$(2.72)

Note that in LQC the probability for the desired slow roll inflation not to occur is (Ashtekar and Sloan, 2011a; Ashtekar and Sloan, 2011b),

$P^{\text{LQC}}\left(\text{not realized}\right)\mathrm{\lesssim }2.74\times {10}^{-6},$(2.73)

which is smaller than that for mLQC-I and slightly larger than the one for mLQC-II. However, it is clear that the desired slow-roll inflation is very likely to occur in all the models, including the two modified LQC ones.

3 Primordial Power Spectra of Modified LQCS in Dressed Metric Approach

As mentioned above, in the literature there exist several approaches to investigate the inhomogeneities of the Universe. Such approaches can be generalized to the modified LQC models, including mLQC-I and mLQC-II. In this section we shall focus ourselves on cosmological perturbations in the framework of mLQCs following the dressed metric approach (Agullo et al., 2012; Agullo et al., 2013; Agullo et al., 2013), while in the next section we will be following the hybrid approach (Fernández-Méndez et al., 2012; Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015; Martínez and Olmedo, 2016). We shall restrict ourselves to the effective dynamics, as we did with the homogeneous background in the last section. Such investigations in general include two parts: 1) the initial conditions; and 2) the dynamical evolutions of perturbations. In the framework of effective dynamics, the latter is a second-order ordinary differential equation in the momentum space, so in principle once the initial conditions are given, it uniquely determines the cosmological (scalar and tensor) perturbations.

However, the initial conditions are a subtle issue, which is true not only in LQC but also in mLQCs. This is mainly because that in general there does not exist a preferred initial time and state for a quantum field in an arbitrarily curved space-time (Birrell and Davies, 1982; Wald, 1994; Mukhanov and Winitzki, 2007; Parker and Toms, 2009). If the Universe is sufficiently smooth and its evolution is sufficiently slow, so that the characteristic scale of perturbations is much larger than the wavelengths of all the relevant modes, a well justified initial state can be defined: the BD vacuum. This is precisely the initial state commonly adopted in GR at the beginning of the slow-roll inflation, in which all the relevant perturbation modes are well inside the comoving Hubble radius (Baumann, 2009) [cf. Figure 2].

However, in LQC/mLQCs, especially near the bounce, the evolution of the background is far from “slow,” and its geometry is also far from the de Sitter. In particular, for the perturbations during the bouncing phase, the wavelengths could be larger, equal, or smaller than the corresponding characteristic scale, as it can be seen, for example, from Figure 5. Thus, it is in general impossible to assume that the Universe is in the BD vacuum state at the bounce (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Zhu et al., 2017; Zhu et al., 2017). Therefore, in the following let us first elaborate in more details about the subtle issues regarding the initial conditions.

3.1 Initial Conditions for Cosmological Perturbations

The initial conditions for cosmological perturbations in fact consists of two parts: when and which? However, both questions are related to each other. In LQC literature, for cosmological perturbations, two different moments have been chosen so far in the dressed and hybrid approaches: 1) the remote past in the contracting phase (Li et al., 2020c) and 2) the bounce (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017). To see which conditions we need to impose at a given moment, let us first recall how to impose the initial conditions in GR, in which the scalar perturbations are governed by the equation,

$v_k\text{″}+\left(k^2-\frac{z\text{″}}{z}\right)v_k=0,$(3.1)

where k denotes the comoving wave number, and $z\equiv a\dot{\delta \varphi }/H$, with $\delta \varphi$ being the scalar field perturbations, $\varphi =\overline{\varphi }\left(t\right)+\delta \varphi \left(t,x\right)$. A prime denotes a derivative with respect to the conformal time η, while an over dot denotes a derivative with respect to the cosmic time t, where $d\eta =dt/a\left(t\right)$. The standard choice of the initial sate is the Minkowski vacuum of an incoming observer in the far past, $k\gg aH$ [cf. Figure 2]. In this limit, Eq. 3.1 becomes $v_k\text{″}+k^2{v}_k=0$, which has the solution,

$v_k\simeq \frac{{\alpha }_k}{\sqrt{2k}}{e}^{-ik\eta }+\frac{{\beta }_k}{\sqrt{2k}}{e}^{ik\eta },$(3.2)

where ${\alpha }_k$ and ${\beta }_k$ are two integration constants, and must satisfy the normalized condition,

$v_k^{\text{*}}{v}_k\text{′}-v_k^{\text{*}}\text{′}{v}_k=-i.$(3.3)

If we further require the vacuum to be the minimum energy state, a unique solution exists, which is given by ${\alpha }_k=1,{\beta }_k=0$, that is,

$\underset{k\gg aH}{\text{lim}}{v}_k\simeq \frac{1}{\sqrt{2k}}{e}^{-ik\eta },$(3.4)

which is often referred to as the BD vacuum (Baumann, 2009).

Consider the de Sitter space as the background, we have $a\left(\eta \right)=1/\left(-\eta H\right)$, and $z\text{″}/z=a\text{″}/a=2/L_H^2$, where $L_H\equiv 1/\left(aH\right)=-\eta$ is the corresponding comoving Hubble radius. Then, Eq. 3.1 reads,

$v_k\text{″}+\left(\frac{1}{{\lambda }^2}-\frac{2}{L_H^2}\right)v_k=0,$(3.5)

where $\lambda \left(\equiv 1/k\right)$ denotes the comoving wavelength. The above equation has the following exact solutions,

$v_k=\frac{{\alpha }_k}{\sqrt{2k}}{e}^{-ik\eta }\left(1-\frac{i}{k\eta }\right)+\frac{{\beta }_k}{\sqrt{2k}}{e}^{ik\eta }\left(1+\frac{i}{k\eta }\right).$(3.6)

It is clear that on scales much smaller than the comoving Hubble radius ($\lambda \ll L_H$), $v_k$ is oscillating with frequency k and constant amplitude, given by Eq. 3.2. Then, setting $\left({\alpha }_k,{\beta }_k\right)=\left(\mathrm{1,0}\right)$ we find that Eq. 3.6 reduces to

$v_k=\frac{1}{\sqrt{2k}}{e}^{-ik\eta }\left(1-\frac{i}{k\eta }\right).$(3.7)

Note that if the initial time $t_i$ is chosen sufficiently small, i.e., $t_i\ll t_{\text{end}}$ or $\left|k\eta \right|\gg 1$, all the modes are inside the comoving Hubble radius $L_H$ [cf. Figure 2], and the BD vacuum (3.4) becomes a natural choice.

However, on the scales much larger than the comoving Hubble radius ($\lambda \gg L_H$), the $k^2$ term is negligible compared to the squeezing term, $z\text{″}/z$, and as a result, the fluctuations will stop oscillating and the amplitude of $v_k$ starts to increase, yielding

$v_k\simeq z\left(\eta \right).$(3.8)

As shown in Figure 2, if the initial time $t_i$ is chosen to be sufficiently early, all the currently observed modes $k_{\text{ph}}\in \left(0.1,1000\right)\times k_0^{\text{*}}$ will be well inside the comoving Hubble radius at $t=t_i$, so the mode function $v_k$ can be well approximately given by Eq. 3.4, which is the well-known zeroth order adiabatic state, where $k_0^{\ast }=0.002$ Mpc⁻¹ and $k_{ph}\left(t\right)\equiv k/a\left(t\right)$ (Bennett et al., 1996; Banday et al., 1996; Komatsu et al., 2011; Larson et al., 2011; Ade and PLANCK Collaboration, 2016; Aghanim and PLANCK Collaboration, 2020).

In modified LQC models, the mode function $v_k$ satisfies the following modified equation,

$v_k\text{″}+{\text{Ω}}_{\text{tot}}^2\left(\eta ,k\right)v_k=0,$(3.9)

where ${\text{Ω}}_{\text{tot}}^2\left(\eta ,k\right)$ depends on the homogeneous background and the inflation potential $V\left(\varphi \right)$, so it is model-dependent. Therefore, the choice of the initial conditions will depend on not only the modified LQC models to be considered but also the moment at which the initial conditions are imposed.

One of the main reasons to choose the remote past in the contracting phase as the initial time for perturbations is that at such time either the background is well described by the de Sitter space (mLQC-I) or the expansion factor $a\left(t\right)$ becomes so large that the curvature of the background is negligible (mLQC-II and LQC), so imposing the BD vacuum for mLQC-II and LQC and the de Sitter state given by Eq. 3.7 for mLQC-I at this moment is well justified. It should be noted that the reason to refer to the state described by Eq. 3.7 as the de Sitter state is the following: In the slow-roll inflation, the homogeneous and isotropic Universe is almost de Sitter, as the Hubble parameter $H\equiv \dot{a}/a$ is almost a constant, so we have $a\left(\eta \right)\simeq 1/\left(-H\eta \right)$. For $t_i\ll t_{\text{end}}$ we have $a\left(\eta \right)\ll 1$, and $\left|\eta k\right|\simeq \left|H\eta \right|\gg 1$, so the choice $\left({\alpha }_k{\beta }_k\right)=\left(\mathrm{1,0}\right)$ will lead Eq. 3.7 directly to Eq. 3.4 at the onset of the slow-roll inflation [cf. Figure 2]. However, in the deep contracting phase of the same de Sitter space, now the Universe is very large, that is, $a\left(\eta \right)\gg 1$, so we must have $\left|H\eta \right|\ll 1$ and $\left|\eta k\right|\simeq |k/H_{\text{Λ}}|a^{-1}\left(\eta \right)$, which can be very small in sufficiently early times of the contracting phase, so the terms $i/\left(k\eta \right)$ in Eq. 3.6 now cannot be neglected. To distinguish this case from the one described by Eq.3.4, In this review we refer the state described by Eq. 3.7 with the term $i/\left(k\eta \right)$ not being negligible as the de Sitter state, while the state described by Eq. 3.4 is still called the BD vacuum state, or simply the BD vacuum.

On the other hand, if the initial time is chosen to be at the bounce, cautions must be taken on what initial conditions can be imposed consistently. In particular, if at this moment some modes are inside the comoving Hubble radius and others are not, it is clear that in this case imposing the BD vacuum at the bounce will lead to inconsistencies. In addition, there also exist the cases in which particle creation in the contracting phase is not negligible, then it is unclear how a BD vacuum can be imposed at the bounce, after the Universe is contracting for such a long time before the bounce. Thus, in these cases other initial conditions need to be considered, such as the fourth-order adiabatic vacuum (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Zhu et al., 2017; Zhu et al., 2017).

With the above in mind, in the following we turn to consider power spectra of the cosmological perturbations.

3.2 Power Spectra of Cosmological Perturbations

Since the evolutions of the effective dynamics of the homogeneous backgrounds for mLQC-I and mLQC-II are different, in this subsection let us first consider the case of mLQC-I and then mLQC-II. To compare the results with those obtained in LQC, at the end of this subsection, we also discuss the LQC case.

3.2.1 mLQC-I

For mLQC-I, the power spectrum of the cosmological scalar perturbations was first studied in (Agullo, 2018) for the quadratic ${\varphi }^2$ potential, and re-examined in (Li et al., 2020c). In the terminology used in (Agullo, 2018), it was found that the corresponding mode function $v_k\left(\equiv q_k/a\right)$ satisfies Eq. 3.9 with

$\begin{array}{l}{\text{Ω}}_{\text{tot}}^2=k^2-\frac{a\text{″}}{a}+{\mathfrak{A}}_{-},r\equiv \frac{24\pi G{\dot{\varphi }}^2}{\rho },\\ {\mathfrak{A}}_{-}\equiv a^2[V\left(\varphi \right)r-2V_{,\varphi }\left(\varphi \right)\sqrt{r}+V_{,\varphi \varphi }\left(\varphi \right)],\end{array}$(3.10)

where $r=24\pi G{\dot{\varphi }}^2/\rho$ and $V\left(\varphi \right)$ denotes the scalar field potential.

It should be noted that, when generalizing the classical expression of the function ${\mathfrak{A}}_{-}$ defined in Eq. 3.10 to its corresponding quantum mechanics operator, there exists ambiguities. In fact, classically ${\mathfrak{A}}_{-}$ only coincides with ${\text{Ω}}_Q^2$ in the expanding phase. The latter is a function of the phase space variables which is explicitly given by (Agullo et al., 2013; Agullo, 2018; Agullo et al., 2018; Li et al., 2020c),

${\text{Ω}}_Q^2=3\kappa \frac{p_{\varphi }^2}{a^4}-18\frac{p_{\varphi }^4}{a^6{\pi }_a^2}-12a\frac{p_{\varphi }}{{\pi }_a}{V}_{,\varphi }+a^2{V}_{,\varphi \varphi },$(3.11)

where ${\pi }_a$ is the moment conjugate to a, and given by one of Hamilton’s dynamical equations,

${\pi }_a=-\frac{3a^2}{4\pi G}H,$(3.12)

with the choice of the lapse function $N=1$. Therefore, ${\pi }_a<0({\pi }_a>0)$ corresponds to $H>0(H<0)$. At the quantum bounce we have $H\left(t_B\right)=0$, so that ${\pi }_a\left(t_B\right)=0$. Then, ${\text{Ω}}_Q^2$ defined by Eq. 3.11 diverges at the bounce. Hence, from the Friedmann equation, $H^2=\left(8\pi G/3\right)\rho$, we find that

$\frac{1}{{\pi }_a^2}=\frac{2\pi G}{3a^4\rho },\frac{1}{{\pi }_a}=\pm \sqrt{\frac{2\pi G}{3a^4\rho }},$(3.13)

where “-” corresponds to $H>0$, and “+” to $H<0$. Then, a direct generalization leads to (Li et al., 2020c),

${\text{Ω}}_Q^2=\{\begin{array}{cc}{\mathfrak{A}}_{-},& H\ge 0,\\ {\mathfrak{A}}_{+},& H\le 0,\end{array}$(3.14)

where

${\mathfrak{A}}_{\pm }\equiv a^2[V\left(\varphi \right)r\pm 2V_{,\varphi }\left(\varphi \right)\sqrt{r}+V_{,\varphi \varphi }\left(\varphi \right)].$(3.15)

It should be noted that in (Agullo, 2018) only the function ${\mathfrak{A}}_{-}$ was chosen over the whole process of the evolution of the Universe. The same choice was also adopted in (Agullo et al., 2018; Agullo et al., 2021; Agullo et al., 2021).

In addition, $\mathfrak{A}$ defined by Eq. 3.13 is not continuous across the bounce, as the coefficient $2V_{,\varphi }\left(\varphi \right)\sqrt{r}$ in general does not vanish at the bounce. In (Zhu et al., 2017; Zhu et al., 2017; Navascues et al., 2018) ${\mathfrak{A}}_{-}$ appearing in Eq. 3.10 was replaced by $U\left(\varphi \right)\left(\equiv {\text{Ω}}_{+}^2\right)$ over the whole process of the evolution of the homogeneous Universe, where

${\text{Ω}}_{\pm }^2\equiv a^2[{\mathfrak{F}}^{2}V\left(\varphi \right)\pm 2\mathfrak{F}{V}_{,\varphi }\left(\varphi \right)+V_{,\varphi \varphi }\left(\varphi \right)],$(3.16)

and $\mathfrak{F}\equiv {\left(24\pi G/\rho \right)}^{1/2}\dot{\varphi }$.

Another choice was introduced in (Li et al., 2020c), which was motivated from the following considerations. The functions ${\text{Ω}}_{\pm }^2$ defined above are not continuous across the bounce, quite similar to ${\mathfrak{A}}_{\pm }$. However, if we introduce the quantity ${\text{Ω}}^2$ as,

${\text{Ω}}^2=a^2[{\mathfrak{F}}^{2}V\left(\varphi \right)+2\text{Θ}\left(b\right)\mathfrak{F}{V}_{,\varphi }\left(\varphi \right)+V_{,\varphi \varphi }\left(\varphi \right)],$(3.17)

to replace ${\mathfrak{A}}_{-}$ in Eq. 3.10, it could be continuous across the bounce by properly choosing $\text{Θ}\left(b\right)$. In particular, the variable $b\left(t\right)$ satisfies Eq. 2.61 (Li et al., 2018a; Li et al., 2018b; Li et al., 2019)⁷, from which we can see that $b\left(t\right)$ is always a monotonically decreasing function for any matter that satisfies the weak energy condition (Hawking and Ellis, 1973). Moreover, one can construct a step-like function of b with the bounce as its symmetry axis (Li et al., 2018a; Li et al., 2018b; Li et al., 2019). Therefore, if we define $\text{Θ}\left(b\right)$ as

$\text{Θ}\left(b\right)=1-2\left(1+{\gamma }^2\right){\text{sin}}^2\left(\lambda b\right),$(3.18)

it behaves precisely as a step function, so that ${\text{Ω}}^2$ smoothly connects ${\text{Ω}}_{\pm }^2$ across the bounce, as shown in Figure 3.

FIGURE 3

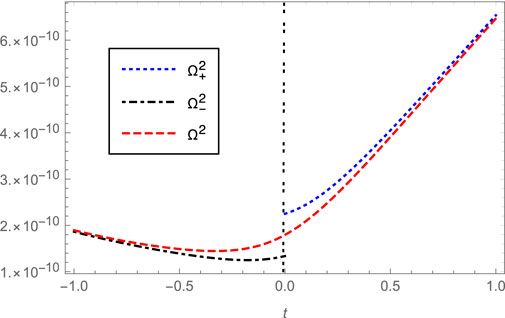
FIGURE 3. The potential terms ${\text{Ω}}_{+}^2$ and ${\text{Ω}}_{-}^2$ are compared with their smooth extension ${\text{Ω}}^2$ across the bounce in mLQC-I for the quadratic potential $V\left(\varphi \right)=\frac{1}{2}{m}^2{\varphi }^2$(Li et al., 2020c).

In addition to the above choices, motivated by the hybrid approach (Fernández-Méndez et al., 2012; Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015; Martínez and Olmedo, 2016), the following replacements for ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$ in Eq. 3.11 were also introduced in (Li et al., 2020c),

$\frac{1}{{\pi }_a^2}\to \frac{64{\pi }^2{G}^2{\lambda }^2{\gamma }^2}{9a^4\mathcal{D}},$(3.19)

$\frac{1}{{\pi }_a}\to -\frac{8\pi G\lambda \gamma \text{Θ}\left(b\right)}{3a^2{\mathcal{D}}^{1/2}},$(3.20)

where

$\mathcal{D}\equiv \left(1+{\gamma }^2\right){\text{sin}}^2\left(2\lambda b\right)-4{\gamma }^2{\text{sin}}^2\left(\lambda b\right).$(3.21)

Such obtained ${\text{Ω}}_Q^2$ was referred to as ${\text{Ω}}_{\text{eff}}^2$ in (Li et al., 2020c), and in Figure 4, we show the differences among ${\text{Ω}}^2$, ${\text{Ω}}_{\text{eff}}^2$ and the quantity $a\text{″}/a$, from which one can see that the term $a\text{″}/a$ dominates the other two terms over the whole range $t/t_{pl}\in \left(-8,{10}^4\right)$.

FIGURE 4

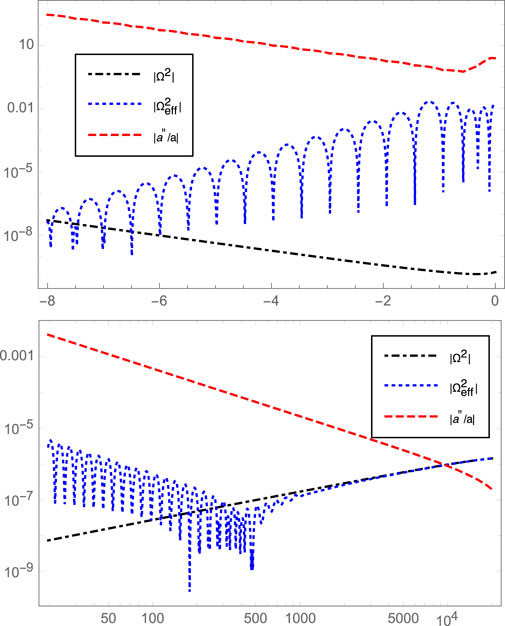
FIGURE 4. The potential terms ${\text{Ω}}^2$ and ${\text{Ω}}_{\text{eff}}^2$ are compared with the curvature term $a^{\text{''}}/a$ in mLQC-I near the bounce and the preinflationary regime for the quadratic potential $V\left(\varphi \right)=\frac{1}{2}{m}^2{\varphi }^2$(Li et al., 2020c).

To study the effects of the curvature term, let us first introduce the quantity,

$k_B^{\text{I}}={\left(\frac{a\text{″}}{a}\right)}^{1/2}{|}_{t=t_B}\approx 1.60,$(3.22)

which is much larger than other two terms ${\text{Ω}}^2$ and ${\text{Ω}}_{\text{eff}}^2$, where ${\text{Ω}}^2\left(t_B\right)=1.75\times {10}^{-10}$ and ${\text{Ω}}_{\text{eff}}^2\left(t_B\right)=0.006$. Therefore, the differences between ${\text{Ω}}^2$ and ${\text{Ω}}_{\text{eff}}^2$ near the bounce are highly diluted by the background. On the other hand, in the post-bounce phase, ${\text{Ω}}^2$ and ${\text{Ω}}_{\text{eff}}^2$ coincide after $t/t_{pl}\simeq {10}^4$, while near the onset of the inflation their amplitudes first become almost equal to that of the curvature term, and then quickly exceeds it during the slow-roll inflation, as we can see from Figure 4.

From Figure 4 we can also see that the difference between ${\text{Ω}}^2$ and ${\text{Ω}}_{\text{eff}}^2$ lies mainly in the region near the bounce. However, as the curvature term $a\text{″}/a$ overwhelmingly dominates in this region, it is usually expected that the impact of the different choices of ${\text{Ω}}^2$ on the power spectrum might not be very large (Agullo et al., 2013; Agullo, 2018; Agullo et al., 2018). However, in (Li et al., 2020c), it was found that the relative difference in the magnitude of the power spectrum in the IR and oscillating regimes could be as large as $10\text{\%}$, where the relative difference is defined as,

$\mathrm{ℰ}\equiv 2\left|\frac{{\mathcal{P}}_1-{\mathcal{P}}_2}{{\mathcal{P}}_1+{\mathcal{P}}_2}\right|.$(3.23)

However, the power spectra obtained from ${\text{Ω}}^2$ and ${\text{Ω}}_{\pm }^2$ are substantially different even in the UV regime due to the (tiny) difference between ${\text{Ω}}_{\pm }^2$ at the bounce, see Fig. 14 given in (Li et al., 202c). In fact, the difference is so large that the power spectrum calculated from ${\text{Ω}}_{\pm }^2$ is essentially already ruled out by current observations.

With the clarification of the ambiguities caused by the quantum mechanical generalization of the function ${\mathfrak{A}}_{-}$ defined in Eq. 3.10, now let us turn to the issue of the initial conditions, for which we consider only two representative potentials, the quadratic and Starobinsky, given explicitly by

$V=\{\begin{array}{cc}\frac{1}{2}{m}^2{\varphi }^2,& \text{quadratic},\\ \frac{3m^2}{32\pi G}{\left(1-e^{-\sqrt{16\pi G/3}\varphi }\right)}^2,& \text{Starobinsky}.\end{array}$(3.24)

In mLQC-I, the evolution of the effective (quantum) homogeneous Universe is asymmetric with respect to the bounce (Dapor and Liegener, 2018a; Li et al., 2018a; Li et al., 2018b; Li et al., 2019). In particular, before the bounce ($t<t_B$), the Universe is asymptotically de Sitter, and only very near the bounce (about several Planck seconds), the Hubble parameter H which is negative in the pre-bounce regime suddenly increases to zero at the bounce. Then, the Universe enters a very short super-acceleration phase $\dot{H}>0$ (super-inflation) right after the bounce, which lasts until $\rho \simeq {\rho }_c^{\text{I}}/2$, where $\dot{H}{\left(t\right)}_{\rho \simeq \frac{1}{2}{\rho }_c^{\text{I}}}=0$. Afterward, for a kinetic energy dominated bounce ${\dot{\varphi }}_B^2\gg V\left({\varphi }_B\right)$, it takes about ${10}^4\sim {10}^6$ Planck seconds before entering the slow-roll inflation (Li et al., 2018a; Li et al., 2018b; Li et al., 2019). Introducing the quantity,

${\lambda }_H^2\equiv \frac{a}{a\text{″}-a{\mathfrak{A}}_{-}}=-\frac{1}{m_{\text{eff}}},$(3.25)

where $m_{\text{eff}}$ is the effective mass of the modes, from Eq. 3.10 we find that

${\text{Ω}}_{\text{tot}}^2=\frac{1}{{\lambda }^2}-\frac{1}{{\lambda }_H^2}=\{\begin{array}{cc}>0,& {\lambda }_H^2>{\lambda }^2,\\ <0,& 0<{\lambda }_H^2<{\lambda }^2,\\ >0,& {\lambda }_H^2<0,\end{array}$(3.26)

where $\lambda \left(\equiv k^{-1}\right)$ denotes the comoving wavelength of the mode k, as mentioned above. Note that such a defined quantity ${\lambda }_H^2$ becomes negative when the effective mass is positive. In Figure 5, we plot ${\lambda }_H^2$ schematically for the quadratic and the Starobinsky potentials with the mass of the inflaton set to $1.21\times {10}^{-6}{m}_{\text{pl}}$ and $2.44\times {10}^{-6}{m}_{\text{pl}}$ respectively. The initial conditions for the background evolution are set as follows: for the quadratic potential, the inflaton starts with a positive velocity on the right wing of the potential and for the Starobinsky potential the inflaton is released from the left wing of the potential with a positive velocity. For both potentials, the initial conditions are set at the bounce which is dominated by the kinetic energy of the inflaton field. The same mass parameters and similar initial conditions are also used in the following figures where the comoving Hubble radius is plotted schematically. In Figure 5, the moments $t_H$ and $t_i$ are defined, respectively, by $a\text{″}\left(t_H\right)=a\text{″}\left(t_i\right)=0$, so $t_i$ represents the beginning of the inflationary phase, and during the slow-roll inflation (Region III), we have ${\lambda }_H^2\approx L_{\text{H}}^2/2\simeq 1/\left(2a^2{H}^2\right)$, which is exponentially decreasing, and all the modes observed today were inside the comoving Hubble radius at $t=t_i$. Between the times $t_H$ and $t_i$, ${\lambda }_H^2$ is negative, and ${\text{Ω}}_{\text{tot}}^2$ is strictly positive. Therefore, during this period the mode functions are oscillating, while during the epoch between $t_B$ and $t_H$, some modes ($k^{-2}>k_B^{-2}$) are inside the comoving Hubble radius, and others ($k^{-2}<k_B^{-2}$) are outside it right after the bounce, where $k_B\equiv {\lambda }_B^{-1}\left(t_B\right)$. In the contracting phase, when $t\ll t_B$, the Universe is quasi-de Sitter and ${\lambda }_H^2\simeq 1/\left(2a^2{H}^2\right)$ increases exponentially toward the bounce $t\to t_B$, as now $a\left(t\right)$ is decreasing exponentially. However, several Planck seconds before the bounce, the Universe enters a non-de Sitter state, during which ${\lambda }_H^2$ starts to decrease until the bounce, at which a characteristic Planck scale $k_B\left(\equiv 1/{\lambda }_H\right)$ can be well defined. Therefore, for $t\ll t_B$, all the modes are outside the comoving Hubble radius. Then, following our previous arguments, if the initial moment is chosen at $t_0\ll t_B$, the de Sitter state seems not to be viable. However, when $t_0\ll t_B$ we have $a\left(\eta \right)\simeq 1/\left(-\eta \left|H_{\text{Λ}}\right|\right)$, where $H_{\text{Λ}}=-{\left[\lambda \left(1+{\gamma }^2\right)\right]}^{-1}$ and

${\text{Ω}}_{\text{tot}}^2\simeq k^2-\frac{2}{{\eta }^2},$(3.27)

FIGURE 5

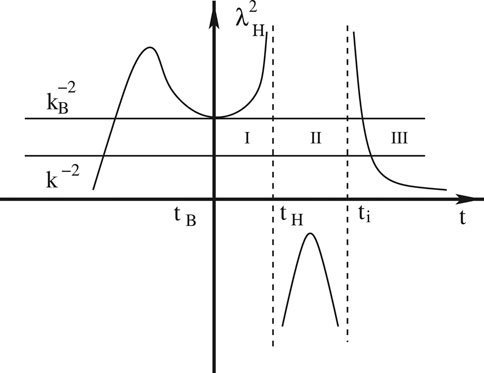
FIGURE 5. Schematic plot of ${\lambda }_H^2$ defined by Eq. 3.25 vs. t for mLQC-I in the dressed metric approach for the quadratic and the Starobinsky potentials, where $a\text{''}\left(t_H\right)=0$ and $a\text{''}\left(t_i\right)=0$ with $t_i$ being the starting time of the inflationary phase. During the slow-roll inflation, we have ${\lambda }_H^2\approx L_{\text{H}}^2/2$. In the contracting phase $t<t_B$, the universe is initially de Sitter and we still have ${\lambda }_H^2\approx L_{\text{H}}^2/2$, but now it increases exponentially toward bounce $t\to t_B$, as the universe in this phase is exponentially contracting. However, several Planck seconds before the bounce, the universe enters a non-de Sitter state, during which ${\lambda }_H^2$ starts to decrease until the bounce. The qualitative behavior of the comoving Hubble radius is the same for the quadratic and the Starobinsky potentials. Different potentials will change the values of $t_H$ and $t_i$ correspondingly.

for which Eq. 3.9 has the exact solutions given by Eq. 3.6. Therefore, at sufficient early times, choosing ${\alpha }_k=1,{\beta }_k=0$ leads us to the de Sitter state (3.7). From the above analysis it is clear that this is possible precisely because of the isometry of the de Sitter space, which is sufficient to single out a preferred state, the de Sitter state (Agullo, 2018).

With the exact solution (3.7) as the initial conditions imposed at the moment $t_0\left(\ll t_B\right)$ in the contracting phase, it was found that the power spectrum of the cosmological scalar perturbations can be divided into three different regimes: 1) the ultraviolet (UV) ($k>k_{\text{mLQC}-\text{I}}$); 2) intermediate ($k_i<k<k_{\text{mLQC}-\text{I}}$); and 3) infrared ($k<k_i$), where $k_{\text{mLQC}-\text{I}}\equiv a_B\sqrt{R_B/6}$ and $k_i=a_i\sqrt{R_i/6}$, and $R_B$ and $R_i$ are the curvatures given at the bounce and the beginning of the slow-roll inflation, respectively [cf. Figure 5]. During the infrared regime, the power spectrum increases as k increases, while in the intermediate regime it is oscillating very fast and the averaged amplitude of the power spectrum is decreasing as k increases. In the UV regime, the spectrum is almost scale-invariant, which is consistent with the current observations. There exists a narrow band, $0.1\times k_0^{\text{*}}<k<k_{\text{mLQC}-\text{I}}$, in which the quantum gravitational effects could be detectable by current or forthcoming cosmological observations (Agullo, 2018). Within the dressed metric approach, one of the most distinctive features of the power spectrum in mLQC-I is that its magnitude in the IR regime is of the Planck scale (Agullo, 2018; Li et al., 2020c). This is because those infrared modes are originally outside the Hubble horizon in the contracting phase and thus their magnitudes are frozen as they propagate across the bounce and then into the inflationary phase. Considering that the contracting phase is a quasi de Sitter phase with a Plank-scale Hubble rate, the magnitude of the IR modes is thus also Planckian (Li et al., 2020c).

It should be noted that if the initial conditions are imposed at the bounce, from Figure 5 we can see clearly that some modes are inside the comoving Hubble radius, and some are not. In addition, in the neighborhood of the bounce, the background is far from de Sitter. So, it is impossible to impose either the BD vacuum or the de Sitter state at the bounce. In this case, one of the choices of the initial conditions is the fourth-order adiabatic vacuum, similar to that in LQC (Agullo et al., 2013; Ashtekar and Gupt, 2017; Ashtekar and Gupt, 2017; Zhu et al., 2017; Zhu et al., 2017).

3.2.2 mLQC-II

In mLQC-II, the evolution of the effective homogeneous Universe is different from that of mLQC-I. In particular, it is symmetric with respect to the bounce and in the initially kinetic energy dominated case at the bounce the solutions can be well approximated by Eq. 2.56 in the bouncing phase (Li et al., 2018b; Li et al., 2019), similar to that of LQC (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017).

When considering the cosmological perturbations, similar ambiguities in the choices of ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$ in Eq. 3.11 exist. In particular, for the choice of Eq. 3.17 now the function $\text{Θ}\left(b\right)$ is replaced by

$\text{Θ}\left(b\right)=\text{cos}\left(\frac{\lambda b}{2}\right),$(3.28)

which behaves also like a step function across the bounce and picks up the right sign in both contracting and expanding phases, so it smoothly connects ${\text{Ω}}_{\pm }$ defined by Eq. 3.16.

On the other hand, ${\text{Ω}}_{\text{eff}}^2$ is obtained from Eq. 3.11 by the replacements,

$\frac{1}{{\pi }_a^2}\to \frac{4{\pi }^2{\gamma }^2{\lambda }^2}{9a^4{\text{sin}}^2\left(\lambda b/2\right)\mathcal{D}},$(3.29)

$\frac{1}{{\pi }_a}\to \frac{-2\pi \gamma \lambda \text{cos}\left(\lambda b/2\right)}{3a^2\text{sin}\left(\lambda b/2\right){\mathcal{D}}^{1/2}},$(3.30)

but now with

$\mathcal{D}\equiv 1+{\gamma }^2{\text{sin}}^2\left(\frac{\lambda b}{2}\right).$(3.31)

Such obtained ${\text{Ω}}^2$, ${\text{Ω}}_{\pm }^2$ and ${\text{Ω}}_{\text{eff}}^2$ are quite similar to those given by Figures 3, 4 in mLQC-I. In particular, at the bounce, we have

$\begin{array}{l}{\text{Ω}}^2\left(t_B\right)=1.59\times {10}^{-10},{\text{Ω}}_{\text{eff}}^2\left(t_B\right)=0.265,\\ k_B^{\text{II}}={\left(\frac{a\text{″}}{a}\right)}^{1/2}{|}_{t=t_B}\approx 6.84,\end{array}$(3.32)

that is, the curvature term $a\text{″}/a$ still dominates the evolution near the bounce.

To see how to impose the initial conditions, let us introduce the quantity ${\lambda }_H^2$ defined by Eq. 3.25 but now ${\mathfrak{A}}_{-}$ will be replaced either by ${\text{Ω}}^2$ or ${\text{Ω}}_{\text{eff}}^2$. The details here are not important, and ${\lambda }_H^2$ is schematically plotted in Figure 6, from which we can see that if the initial conditions are chosen to be imposed at the bounce, the BD vacuum (as well as the de Sitter state) is still not available, and the fourth-order adiabatic vacuum is one of the possible choices, similar to the LQC case. However, if the initial conditions are imposed in the contracting phase at $t_0\ll t_i^p$, the Universe becomes very large $a\left(t\right)\gg 1$ and can be practically considered as flat, then the BD vacuum can be chosen.

FIGURE 6

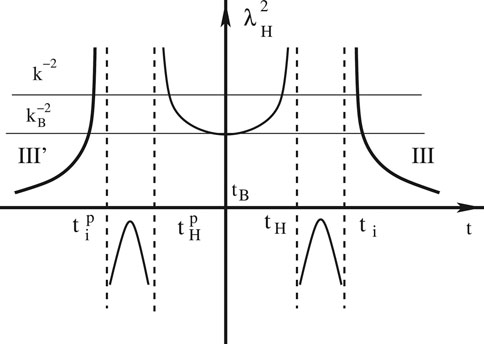
FIGURE 6. Schematic plot of ${\lambda }_H^2$ defined by Eq. 3.25 vs. t for mLQC-II in the dressed metric approach for the quadratic and the Starobinsky potentials, where $a\text{''}\left(t_H^p\right)=a\text{''}\left(t_H\right)=0$ and $a\text{''}\left(t_i^p\right)=a\text{''}\left(t_i\right)=0$, and $t=t_i$ denotes the starting time of the inflationary phase, while $t=t_i^p$ is the end time of the deflationary phase in the contracting branch. During the slow-roll inflation, we have ${\lambda }_H^2\approx L_{\text{H}}^2/2$. In particular, ${\lambda }_H^2$ is decreasing (increasing) exponentially in Region III (Region III′). The corresponding effective mass near the bounce is always negative. Similar behavior also happens in LQC in the dressed metric approach (Zhu et al., 2017). The bounce is dominated by the kinetic energy of the scalar field, which leads to $t_H^p\approx -t_H$. However, in general we find that $t_i^p\ne -t_i$ due to the effects of the potential energy of the scalar field far from the bouncing point. The comoving Hubble radius has the same qualitative behavior for the quadratic and the Starobinsky potentials, while the values of $t_i$ ($t_i^P$) and $t_H$ ($t_H^p$) depend on the type of the potentials and the initial conditions.

Certainly, one can choose different initial conditions. In particular, the fourth-order adiabatic vacuum was chosen even in the contracting phase in (Li et al., 2020c). With such a choice, the power spectra from ${\text{Ω}}^2$ and ${\text{Ω}}_{\text{eff}}^2$ in the region $k\in \left(5\times {10}^{-6},50\right)$ were studied and found that the relative difference in the magnitude of the power spectra is around $30\text{\%}$ in the IR regime and less than $10\text{\%}$ in the intermediate regime. In the UV regime, the relative difference can be as small as $0.1\text{\%}$ or even less.

3.2.3 LQC

To consider the effects of the ambiguities in the choice of ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$ in Eq. 3.11⁸, power spectra of the cosmological perturbations were also studied in the framework of LQC in (Li et al., 2020c). In this case, ${\text{Ω}}^2$ is obtained from Eq. 3.17 with

$\text{Θ}\left(b\right)=\text{cos}\left(\lambda b\right),$(3.33)

while ${\text{Ω}}_{\text{eff}}^2$ is obtained from Eq. 3.11 by the replacements,

$\frac{1}{{\pi }_a^2}\to \frac{16{\pi }^2{G}^2{\gamma }^2{\lambda }^2}{9a^4{\text{sin}}^2\left(\lambda b\right)},$(3.34)

$\frac{1}{{\pi }_a}\to \frac{-4\pi \gamma \lambda \text{cos}\left(\lambda b\right)}{3a^2\text{sin}\left(\lambda b\right)}.$(3.35)

As shown explicitly, the term ${\text{Ω}}_{+}^2$ is always negligible comparing with the curvature term $a\text{″}/a$ in the expression of ${\text{Ω}}_{\text{tot}}^2$ defined in Eq(B.1) by replacing ${\mathfrak{A}}_{-}$ with ${\text{Ω}}_{+}^2$. So, from Eq. 3.25 we find that

${\lambda }_H^2=\frac{1}{a\text{″}/a-{\text{Ω}}_{+}^2}\simeq \frac{a}{a\text{″}},$(3.36)

during the bouncing phase $t\in \left(t_B,t_i\right)$, and ${\lambda }_H^2\simeq a/a\text{″}$ was shown schematically by Fig. 18 in (Zhu et al., 2017), which is quite similar to Figure 6 given above for mLQC-II.

As a result, the initial states of the linear perturbations can be either imposed in the contracting phase at a moment $t_0\ll t_i^p$ as the BD vacuum, or at the bounce as the fourth-order adiabatic vacuum (Agullo et al., 2013). However, it was shown analytically that such two conditions lead to the same results (Zhu et al., 2017).

To compare the results obtained from the three different models, in (Li et al., 2020c) the fourth-order adiabatic vacuum was chosen even in the contracting phase for LQC. Here, we cite some of the results in Figure 7. In particular, it was found that the relative difference in the amplitudes of the power spectra of the scalar perturbations due to the choice of ${\text{Ω}}^2$ or ${\text{Ω}}_{\text{eff}}^2$ is about $10\text{\%}$ in the infrared regime, about $100\text{\%}$ in the intermediate regime, and about $0.1\text{\%}$ in the UV regime. Since only modes in the UV regime can be observed currently, clearly this difference is out of the sensitivities of the current and forhcoming observations (Abazajian, 2015; Abazajian, 2019).

FIGURE 7

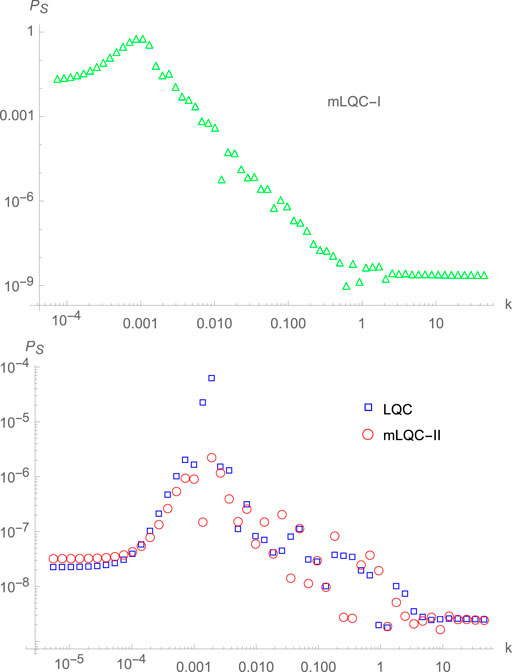
FIGURE 7. The figure shows the results of the scalar power spectra from three models presented in (Li et al., 2020c) when the potential term is given by ${\text{Ω}}_{\text{eff}}^2$. The inflationary potential is chosen to be the quadratic potential and the e-foldings of the inflationary phases in all three models are chosen to be 72.8. The first panel shows the scalar power spectrum in mLQC-I which is characterized by its unique infrared regime. In the second panel, we compare the scalar power spectra from LQC and mLQC-II.

However, comparing the power spectra obtained from the three different models, even with the same choice of ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$, it was found that the relative difference among LQC, mLQC-I and mQLC-II are significant only in the IR and oscillating regimes, while in the UV regime, all three models give quite similar results. In particular, with the same regularization of ${\pi }_a$ the difference can be as large as $100\text{\%}$ throughout the IR and oscillating regimes, while in the UV regime it is about $0.1\text{\%}$.

For the tensor perturbations, the potential term ${\text{Ω}}_Q$ vanishes identically, so no ambiguities related to the choice of ${\pi }_a$ exist. But, due to different models, the differences of the power spectra of the tensor perturbations can be still very large in the IR and oscillating regimes among the three models, although they are very small in the UV regime, see, for example, Fig. 12 given in (Li et al., 2020c).

4 Primordial Power Spectra of Modified LQCS in Hybrid Approach

As in the previous section, in this section we also consider the three different models, LQC, mLQC-I, and mLQC-II, but now in the hybrid approach, and pay particular attention to the differences of the power spectra among these models. Since the scalar perturbations are the most relevant ones in the current CMB observations, in the following we shall mainly focus on them, and such studies can be easily extended to the tensor perturbations.

4.1 mLQC-I

Power spectra of the cosmological scalar and tensor perturbations for the effective Hamilton in mLQC-I were recently studied in the hybrid approach (Fernández-Méndez et al., 2013; Castelló Gomar et al., 2014; Gomar et al., 2015). In particular, the mode function $v_k$ of the scalar perturbations satisfies the differential equation (Li et al., 2020b),

$v_k\text{″}+\left(k^2+s\right)v_k=0,$(4.1)

where

$\begin{array}{c}s=\frac{4\pi G{p}_{\varphi }^2}{3v^{4/3}}\left(19-24\pi G{\gamma }^2\frac{p_{\varphi }^2}{{\pi }_a^2}\right)\\ +v^{2/3}\left(V_{,\varphi \varphi }+\frac{16\pi G\gamma p_{\varphi }}{{\pi }_a}{V}_{,\varphi }-\frac{16\pi G}{3}V\right)\\ =-\frac{4\pi G}{3}{a}^2\left(\rho -3P\right)+\mathcal{U},\end{array}$(4.2)

which is the effective mass of the scalar mode, with

$\begin{array}{c}\mathcal{U}\equiv a^2[V_{,\varphi \varphi }-12\frac{V_{,\varphi }}{{\pi }_a}\\ +\frac{64a^{6}V\left(\varphi \right)}{\pi G}\left(\rho -\frac{3V\left(\varphi \right)}{4\pi G}\right)\frac{1}{{\pi }_a^2}].\end{array}$(4.3)

Note that in (Li et al. 2020a), instead of ${\pi }_a$, the symbol $\text{Ω}$ was used. In addition, the cosmological tensor perturbations are also given by Eqs 4.1, 4.2 but with the vanishing potential $\mathcal{U}=0$. Then, we immediately realize that in the hybrid approach quantum mechanically there are also ambiguities in the replacements ${\pi }_a^{-2}$ and ${\pi }_a^{-1}$, as mentioned in the last section. So far, two possibilities were considered (Castelló Gomar et al., 2020; García-Quismondo et al., 2020). One is given by the replacements,

$\frac{1}{{\pi }_a^2}\to \frac{1}{{\text{Ω}}_{\text{I}}^2},\frac{1}{{\pi }_a}\to \frac{{\text{Λ}}_{\text{I}}}{{\text{Ω}}_{\text{I}}^2},$(4.4)

in Eq. 4.2, where

$\begin{array}{l}{\text{Ω}}_{\text{I}}^2\equiv -\frac{v^2{\gamma }^2}{{\lambda }^2}\left\{{\text{sin}}^2\left(\lambda b\right)-\frac{{\gamma }^2+1}{4{\gamma }^2}{\text{sin}}^2\left(2\lambda b\right)\right\},\\ {\text{Λ}}_{\text{I}}\equiv v\frac{\text{sin}\left(2\lambda b\right)}{2\lambda }.\end{array}$(4.5)

This is the case referred to as prescription A in (García-Quismondo et al., 2020).

The other possibility is obtained by the replacement of Eqs 3.34, 3.35, which was referred to as Prescription B (García-Quismondo et al., 2020), and showed that the two prescriptions lead to almost the same results. So, in the rest of this section we restrict ourselves only to prescription A.

Then, for the case in which the evolution of the homogeneous Universe was dominated by kinetic energy at the bounce,

${\dot{\varphi }}_B^2\gg 2V\left({\varphi }_B\right),$(4.6)

it was shown that the effective mass is always positive at the bounce (García-Quismondo et al., 2020). In fact, near the bounce we have (Wu et al., 2018),

$\begin{array}{l}s=-\frac{4\pi G}{3}{a}^2\left(\rho -3P\right)+\mathcal{U}\left(\eta \right)\\ \simeq \frac{8\pi G}{3}{a}^2\rho >0.\end{array}$(4.7)

Note that in writing the above expression, we have used the fact that during the bouncing phase we have $w_{\varphi }\equiv P/\rho \simeq 1$, and $\left|\mathcal{U}\left(\eta \right)\right|\ll 1$. On the other hand, in the pre-bounce phase, when $t\ll t_B$ the background is a contracting de Sitter spacetime, so we have (García-Quismondo et al., 2020),

$\begin{array}{l}s=-\frac{4\pi G}{3}{a}^2\left(\rho -3P\right)+\mathcal{U}\left(\eta \right)\simeq \mathcal{U}\left(\eta \right)\simeq 5a^2{V}_{,\varphi \varphi },\\ a\simeq a_B{e}^{H_{\text{Λ}}\left(t-t_B\right)},\end{array}$(4.8)

where $H_{\text{Λ}}\equiv -\sqrt{8\pi \alpha G{\rho }_{\text{Λ}}/3}$. Thus, the effective mass remains positive in the pre-bounce phase, as long as $V_{,\varphi \varphi }(t\ll t_B)>0$. This is the case for both quadratic and Starobinsky potentials. In fact, from (3.24), we find that

$V_{,\varphi \varphi }=\{\begin{array}{cc}{m}^2,& \text{quadratic},\\ m^2\left(2-e^{4\sqrt{\pi G/3}\varphi }\right)e^{-8\sqrt{\pi G/3}\varphi },& \text{Starobinsky}.\end{array}$(4.9)

For the case that satisfies the condition (4.6) initially at the bounce, we find that $\varphi \left(t\right)$ becomes very negative at $t\ll t_B$ for the Starobinsky potential, so $V_{,\varphi \varphi }(t\ll t_B)$ is positive even in this case. Then, the quantity defined by

${\lambda }_H^2\equiv -\frac{1}{s},$(4.10)

has similar behavior in the post-bounce phases for the case in which the evolution of the homogeneous Universe was dominated by kinetic energy at the bounce, but has different behaviors in the pre-bounce phases, depending specifically on the potentials considered.

In Figures 8, 9 we show the comoving Hubble radius for the quadratic and Starobinsky potentials, respectively. From these figures it is clear that for $t_i^p<t<t_i$, ${\lambda }_H^2$ is strictly negative, which implies the effective mass s is positive in this regime. Hence, all the modes assume the oscillatory behavior as the modes inside the Hubble horizon, and we may impose the BD vacuum at the bounce. In addition, when $t\ll t_i^p$, the background is well described by the de Sitter space, so the de Sitter state can be imposed in the deep contracting phase. However, imposing the BD vacuum at the bounce will clearly lead to different power spectra at the end of the slow-roll inflation from that obtained by imposing the de Sitter state in the deep contracting phase. This is because, when the background is contracting to about the moments $t\simeq t_i^{p-}$, the effective mass becomes so large and negative that the mode function $v_k$ will be modified significantly, in comparison with that given at $t_0(\ll t_i^p$), or in other words, particle creation now becomes not negligible during the contracting phase. Then, other initial conditions at the bounce may need to be considered.

FIGURE 8

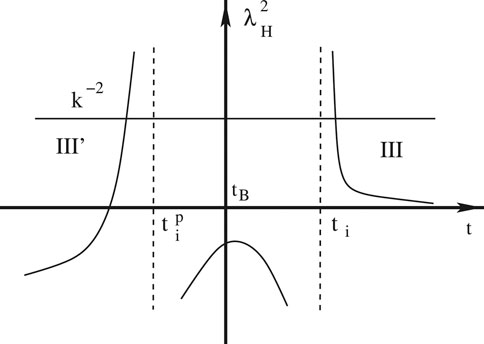
FIGURE 8. Schematic plot of ${\lambda }_H^2$ defined by Eq. 4.10 in mLQC-I for the quadratic potential in the hybrid approach, where $s\left(t_i\right)=s\left(t_i^p\right)=0$, and $t=t_i$ is the starting time of the inflationary phase. During the slow-roll inflation, we have ${\lambda }_H^2\approx L_{\text{H}}^2/2$ (Region III). In the contracting phase, the background is asymptotically de Sitter. The evolution of the universe is asymmetric with respect to the bounce. In particular, ${\lambda }_H^2$ is strictly negative for $t_i^p<t<t_i$, while for $t\simeq t_i^{p-}$ the “generalized” comoving Hubble radius ${\lambda }_H^2$ becomes positive and large. However, as t decreases, ${\lambda }_H^2$ becomes negative again. Although the values of $t_i$ and $t_H$ depend on the initial conditions for the background evolution, for example, when ${\varphi }_B=1.27m_{\text{pl}}$ at the bounce, $t_i\approx 7.55\times {10}^4{t}_{\text{pl}}$ and $t_H\approx -21.85t_{\text{pl}}$, the qualitative behavior of the comoving Hubble radius is robust with respect to the choice of the initial conditions as long as the bounce is dominated by the kinetic energy of the scalar field.

FIGURE 9

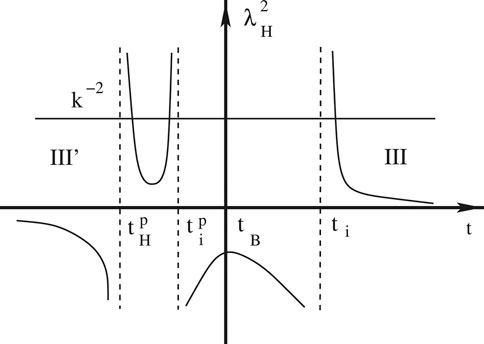
FIGURE 9. Schematic plot of ${\lambda }_H^2$ defined by Eq. 4.10 for the Starobinsky potential and mLQC-I in the hybrid approach, where $s\left(t_i\right)=s\left(t_i^p\right)=s\left(t_H^p\right)=0$, and $t=t_i$ is the starting time of the inflationary phase. During the slow-roll inflation, we have ${\lambda }_H^2\approx L_{\text{H}}^2/2$ (Region III). In the contracting phase, the background is asymptotically de Sitter. The evolution of the universe is asymmetric with respect to the bounce. In particular, ${\lambda }_H^2$ is strictly negative for $t_i^p<t<t_i$, while for $t\simeq t_i^{p-}$ it becomes positive and large. However, as t decreases, ${\lambda }_H^2$ becomes negative again. The qualitative behavior of ${\lambda }_H^2$ does not change with the choice of the initial conditions as long as the inflaton initially starts from the left wing of the potential at the kinetic-energy-dominated bounce. However, the exact values of $t_i$ and $t_H$ depend on the initial conditions. For example, when ${\varphi }_B=-1.32m_{\text{pl}}$, $t_H^p=-7.88t_{\text{pl}}$, $t_i^p=-4.11t_{\text{pl}}$ and $t_i=4.90\times {10}^5{t}_{\text{pl}}$.

4.2 mLQC-II

Similar to LQC, the homogeneous Universe of mLQC-II is symmetric with respect to the bounce, and is well described by the analytical solutions given by Eqs 2.56, 2.57 for the states that are dominated by kinetic energy at the bounce.

In this model, the cosmological perturbations are also given by Eqs 4.1–4.3 but now with the replacement (Li et al., 2020a),

$\frac{1}{{\pi }_a^2}\to \frac{1}{{\text{Ω}}_{\text{II}}^2},\frac{1}{{\pi }_a}\to \frac{{\text{Λ}}_{\text{II}}}{{\text{Ω}}_{\text{II}}^2},$(4.11)

where

$\begin{array}{l}{\text{Ω}}_{\text{II}}^2\equiv \frac{4v^2}{{\lambda }^2}{\text{sin}}^2\left(\frac{\lambda b}{2}\right)\left\{1+{\gamma }^2{\text{sin}}^2\left(\frac{\lambda b}{2}\right)\right\},\\ {\text{Λ}}_{\text{II}}\equiv v\frac{\text{sin}\left(\lambda b\right)}{\lambda }.\end{array}$(4.12)

In this case, it can be shown that the effective mass defined by Eq. 4.2 is always positive in the neighborhood of the bounce, but far from the bounce, the properties of ${\lambda }_H^2$ depend on the potential in the pre-bounce phase, similar to mLQC-I.

In Figure 10, we plot ${\lambda }_H^2$ for the Starobinsky potential, while for the quadratic one, it is quite similar to the corresponding one in mLQC-I, given by Figure 8. From Figure 10 we can see that ${\lambda }_H^2$ now is negative not only near the bounce but also in the whole contracting phase, so that all the modes are oscillating for $t<t_i$. Then, one can choose the BD vacuum at the bounce. It is remarkable that for the quadratic potential, this is impossible [cf. Figure 8].

FIGURE 10

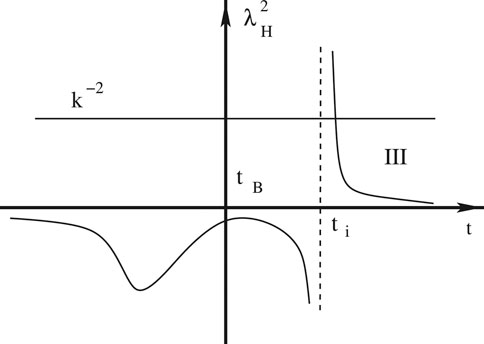
FIGURE 10. Schematic plot of ${\lambda }_H^2$ defined by Eq. 4.10 for the Starobinsky potential and mLQC-II in the hybrid approach, where $s\left(t_i\right)=0$, and $t=t_i$ is the starting time of the inflationary phase. During the slow-roll inflation, we have ${\lambda }_H^2\approx L_{\text{H}}^2/2$ (Region III) since the contribution from the potential is in general less than $a\text{''}/a$. Again the qualitative behavior of ${\lambda }_H^2$ remains the same as long as the inflaton starts from the left wing of the potential with a positive velocity and the bounce is initially dominated by the kinetic energy of the inflaton field.

Moreover, as $t\to -\infty$, the expansion factor becomes very large, and the corresponding curvature is quite low, so to a good approximation, the BD vacuum can also be chosen in the distant past, not only for the Starobinsky potential but also for other potentials. Due to the oscillating behavior of the mode function over the whole contracting phase, imposing the BD vacuum at the bounce is expected not to lead to significant difference in the power spectra from that in which the same condition is imposed in the deep contracting phase.

4.3 LQC

The evolution of the homogeneous Universe of standard LQC model is also symmetric with respect to the bounce, and is well described by the analytical solutions given in (Zhu et al., 2017; Zhu et al., 2017) for the states that are dominated by kinetic energy at the bounce.

In this model, the cosmological perturbations are also given by Eqs 4.1.3.–.Eqs 4.4.3 but now with the replacement (Li et al., 2020a),

$\frac{1}{{\pi }_a^2}\to \frac{1}{{\text{Ω}}_{\text{LQC}}^2},\frac{1}{{\pi }_a}\to \frac{{\text{Λ}}_{\text{LQC}}}{{\text{Ω}}_{LQC}^2},$(4.13)

where

${\text{Ω}}_{\text{LQC}}\equiv \frac{v\text{sin}\left(\lambda b\right)}{\lambda },{\text{Λ}}_{\text{LQC}}\equiv \frac{v\text{sin}\left(2\lambda b\right)}{2\lambda }.$(4.14)

In this case, it can be shown that the effective mass defined by Eq. 4.2 is always positive for the states that are dominated by kinetic energy at the bounce (Navascues et al., 2018; Wu et al., 2018), and the quantity ${\lambda }_H^2$ defined by Eq. 4.10 is negative near the bounce. Again, similar to the mLQC-II case, the modes are oscillating near the bounce. However, in the contracting phase the behavior of ${\lambda }_H^2$ sensitively depends on the inflation potentials. For the Starobinsky one, ${\lambda }_H^2$ behaves similar to that described by Figure 10, so the BD vacuum can be imposed either in the deep contracting phase or at the bounce, and such resulted power spectra are expected not to be significantly different from one another. But for the quadratic potential the situation is quite different, and a preferred choice is to impose the BD vacuum in the deep contracting phase ($t_0\ll t_B$).

4.4 Primordial Power Spectra

As it can be seen that one of the preferred moments to impose the initial conditions for the cosmological perturbations in all these three models is a moment in the contracting phase $t_0<t_B$. In this phase, we can impose the BD vacuum state as long as the moment is sufficiently earlier, $t_0\ll t_B$. Certainly, other initial conditions can also be chosen. In particular, in (Li et al., 2020a) the second-order adiabatic vacuum conditions were selected, but it was found that the same results can also be obtained even when the BD vacuum state or the fourth-order adiabatic vacuum is imposed initially.

The nth-order adiabatic vacuum conditions can be obtained as follows: Let us first consider the solution,

${\nu }_k=\frac{1}{\sqrt{2W_k}}{e}^{-i\stackrel{\eta }{{\displaystyle \int }}{W}_k\left(\overline{\eta }\right)d\overline{\eta }}.$(4.15)

Then, inserting it into (4.1), one can find an iterative equation for $W_k$. In particular, it can be shown that the zeroth-order solution is given by $W_k^{\left(0\right)}=k$, while the second and fourth order adiabatic solutions are given by,

$W_k^{\left(2\right)}=\sqrt{k^2+s},W_k^{\left(4\right)}=\frac{\sqrt{f\left(s,k\right)}}{4|k^2+s|}.$(4.16)

Here $f\left(s,k\right)=5s{\text{′}}^2+16k^4\left(k^2+3s\right)+16s^2\left(3k^2+s\right)-4s^{\text{″}}\left(s+k^2\right)$. It should be noted that, in order to compare directly with observations, it is found convenient to calculate the power spectrum of the comoving curvature perturbation ${\mathrm{ℛ}}_k$, which is related to the Mukhanov-Sasaki variable via the relation ${\mathrm{ℛ}}_k={\nu }_k/z$, with $z=a\dot{\varphi }/H$. Then, its power spectrum reads

${\mathcal{P}}_{{\mathrm{ℛ}}_k}=\frac{{\mathcal{P}}_{{\nu }_k}}{z^2}=\frac{k^3}{2{\pi }^2}\frac{{\left|{\nu }_k\right|}^2}{z^2}.$(4.17)

In addition, the power spectrum is normally evaluated at the end of inflation, at which all the relevant modes are well outside the Hubble horizon [cf. Figure 2].

It should be also noted that the above formula is only applicable to the case where $W_k^{\left(2\right)}$ and/or $W_k^{\left(4\right)}$ remains real at the initial time. This is equivalent to require $k^2+s\ge 0$ for $W_k^{\left(2\right)}$ and $f\left(s,k\right)\ge 0$ for $W_k^{\left(4\right)}$. Since the effective mass s in general depends on t, it is clear that the validity of (4.16) depends not only on the initial states but also on the initial times.

In addition, in the following only the Starobinsky potential given in Eq. 3.24 will be considered, as it represents one of the most favorable models by current observations (Bennett et al., 1996; Banday et al., 1996; Komatsu et al., 2011; Larson et al., 2011; Ade and PLANCK Collaboration, 2016; Aghanim and PLANCK Collaboration, 2020). Let us turn to consider the power spectrum of the scalar perturbations in each of the three models. Similar results can be also obtained for the tensor perturbations. In particular, it was found that the scalar power spectra in these three models can be still divided into three distinctive regimes: the infrared, oscillatory and UV, as shown in Figure 11.

FIGURE 11

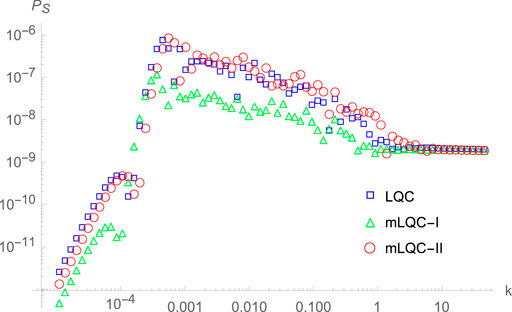
FIGURE 11. The primordial power spectra of the cosmological scalar perturbations in the hybrid approach with the Starobinsky potential, respectively, for LQC, mLQC-I, and mLQC-II. The mass of the inflaton field is set to $2.44\times {10}^{-6}{m}_{\text{pl}}$. The background evolution is chosen so that the pivot mode is $k_{\text{*}}=5.15$ in all three models. The initial states are the second-order adiabatic states imposed in the contracting phase at the moment $t_0$ with $t_0\ll t_B$(Li et al., 2020a).

In the infrared and oscillatory regimes, the relative difference between LQC and mLQC-I can be as large as $100\text{\%}$, while this difference reduces to less than $1\text{\%}$ in the UV regime. This is mainly because LQC and mLQC-I have the same classical limit in the post-bounce phase, and as shown in Figures 5, 8, the effective masses in both approaches tend to be the same during the inflationary phase.

However, it is interesting to note that in the infrared and oscillatory regimes, the power spectrum in mLQC-I is suppressed in comparison with that of LQC, which has been found only in the hybrid approach. As a matter of fact, in the dressed metric approach, the power spectrum in mLQC-I is largely amplified in the infrared regime, and its magnitude is of the Planck scale as depicted in Figure 7 (Agullo, 2018; Li et al., 2020c). The main reason might root in the distinctive behavior of the effective masses in the two approaches, as shown explicitly in Figures 5, 8.

On the other hand, the difference of the power spectra between LQC and mLQC-II is smaller than that between LQC and mLQC-I. In particular, in the infrared regime, it is about $50\text{\%}$. The large relative difference (more than $100\text{\%}$) of the power spectra between mLQC-I and mLQC-II also happens in the infrared and oscillatory regimes, while in the UV regime it reduces to about $2\text{\%}$.

To summarize, in the hybrid approach the maximum relative differences of the power spectra among these three different models always happen in the infrared and oscillatory regimes, while in the UV regime, the differences reduce to no larger than $2\text{\%}$, and all the three models predict a scale-invariant power spectrum, and is consistent with the current CMB observations. However, in the hybrid approach, the power spectrum in mLQC-I is suppressed in the infrared and oscillatory regimes. The latter is in a striking contrast to the results obtained from the dressed metric approach, which might be closely related to the fact that the effective masses in these two approaches are significantly different, especially near the bounce and in the prebounce stage.

5 Conclusion and Outlook

In the past 2 decades, LQC has been studied extensively, and several remarkable features have been found (Ashtekar and Singh, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017), including the generic resolution of the big bang singularity (replaced by a quantum bounce) in the Planckian scale, the slow-roll inflation as an attractor in the post-bounce evolution of the Universe, and the scale-invariant power spectra of the cosmological perturbations, which are consistent with the current CMB observations. Even more interestingly, it was shown recently that some anomalies from the CMB data (Akrami and Planck collaboration, 2020; Akrami and Planck collaboration, 2020; Schwarz et al., 2016) can be reconciled purely due to the quantum geometric effects in the framework of LQC (Ashtekar et al., 2020; Agullo et al., 2021; Agullo et al., 2021; Ashtekar et al., 2021).

Despite of all these achievements, LQC is still plagued with some ambiguities in the quantization procedure. In particular, its connection with LQG is still not established (Brunnemann and Fleischhack, 2007; Engle, 2007; Brunnemann and Koslowski, 2011), and the quantization procedure used in LQC owing to symmetry reduction before quantization can result in different Hamiltonian constraints than the one of LQG.

Motivated by the above considerations, recently various modified LQC models have been proposed, see, for example (Alesci and Cianfrani, 2013; Alesci and Cianfrani, 2015; Alesci et al., 2017; Oriti, 2017; Oriti et al., 2017; Wilson-Ewing, 2017; Engle and Vilensky, 2018; Gerhardt et al., 2018; Wilson-Ewing, 2018; Baytas et al., 2019; Engle and Vilensky, 2019; Neuser et al., 2019; Olmedo and Alesci, 2019; Schander and Thiemann, 2019; Schander and Thiemann, 2019; Han and Liu, 2020a; Han and Liu, 2020b; Giesel et al., 2020; Giesel et al., 2020; Han et al., 2020; Li et al., 2020b), and references therein. In this brief review, we have restricted ourselves only to mLQC-I and mLQC-II (Yang et al., 2009; Dapor and Liegener, 2018a; Dapor and Liegener, 2018b), as they are the ones that have been extensively studied in the literature not only the dynamics of the homogeneous Universe (Li et al., 2018a; Li et al., 2018b; Saini and Singh, 2019a; Saini and Singh, 2019b; García-Quismondo and Mena Marugán, 2019; Li et al., 2019; García-Quismondo and Mena Marugán, 2020), but also the cosmological perturbations (Agullo, 2018; Castelló Gomar et al., 2020; García-Quismondo et al., 2020; Li et al., 2020a; Li et al., 2020b).

In these two modified LQC models, it was found that the resolution of the big bang singularity is also generic (Li et al., 2018a; Li et al., 2018b; Saini and Singh, 2019a; Saini and Singh, 2019b; Li et al., 2019). This is closely related to the fact that the area operator in LQG has a minimal but nonzero eigenvalue (Ashtekar and Lewandowski, 2004; Thiemann, 2007; Rovelli, 2008; Ashtekar and Singh, 2011; Bojowald, 2011; Gambini and Pullin, 2011; Ashtekar and Barrau, 2015; Bojowald, 2015; Agullo and Singh, 2017; Ashtekar and Pullin, 2017), quite similar to the eigenvalue of the ground state of the energy operator of a simple harmonic oscillator in quantum mechanics. This deep connection also shows that the resolution of the big bang singularity is purely due to the quantum geometric effects. In addition, similar to LQC, the slow-roll inflation also occurs generically in both mLQC-I and mLQC-II (Li et al., 2019). In particular, when the inflaton has a quadratic potential, $V\left(\varphi \right)=m^2{\varphi }^2/2$, the probabilities for the desired slow-roll inflation not to occur are $\mathrm{\lesssim }1.12\times {10}^{-5}$, $\mathrm{\lesssim }2.62\times {10}^{-6}$, and $\mathrm{\lesssim }2.74\times {10}^{-6}$ for mLQC-I, mLQC-II and LQC, respectively.

When dealing with perturbations, another ambiguity rises in the replacement of the momentum conjugate ${\pi }_a$ of the expansion factor a in the effective potential of the scalar perturbations. This ambiguity occurs not only in the dressed metric approach [cf. Eq. 3.11] but also in the hybrid approach [cf. Eq. 4.2], as it is closely related to the quantization strategy used in LQG/LQC, because now only the holonomies (complex exponentials) of ${\pi }_a$ are defined as operators. Several choices have been proposed in the literature (Mena Marugán et al., 2011; Agullo et al., 2013; Agullo, 2018; Agullo et al., 2018; Castelló Gomar et al., 2020; García-Quismondo et al., 2020; Li et al., 2020a; Li et al., 2020b). In Secs. 3, 4, we have shown that for some choices the effects on the power spectra are non-trivial, while for others the effects are negligible. However, even with the same choice, the relative differences in the amplitudes of the power spectra among the three different models can be as large as $100\text{\%}$ in the infrared and intermediate regimes of the spectra, while in the UV regime the relative differences are no larger than $2\text{\%}$, and the corresponding power spectra are scale-invariant. Since only the modes in the UV regime are relevant to the current observations, the power spectra obtained in all the three models are consistent with current observations (Bennett et al., 1996; Banday et al., 1996; Komatsu et al., 2011; Larson et al., 2011; Ade and PLANCK Collaboration, 2016; Aghanim and PLANCK Collaboration, 2020).

However, the interactions between the infrared and UV modes appearing in non-Gaussianities might provide an excellent window to observe such effects. This was initially done in LQC (Agullo et al., 2018; Wu et al., 2018; Zhu et al., 2018), and lately generalized to bouncing cosmologies (Agullo et al., 2021; Agullo et al., 2021). It should be noted that in (Agullo et al., 2021; Agullo et al., 2021), the expansion factor $a\left(t\right)$ near the bounce was assumed to take the form,

$a\left(t\right)=a_B{\left(1+b{t}^2\right)}^n,$

where b and n are two free parameters. For example, for LQC we have $n=1/6$ and $b=R_B/2$, where $R_B$ is the Ricci scalar at the bounce (Zhu et al., 2017; Zhu et al., 2017). But, it is clear that near the bounce $a\left(t\right)$ takes forms different from the above expression for mLQC-I/II, as one can see from Eqs 2.54–2.57. Thus, it would be very interesting to study such effects in mLQC-I/II, and look for some observational signals.

Moreover, initial conditions are another subtle and important issue not only in LQC but also in mLQCs. As a matter of fact, the initial conditions consist of two parts: the initial time, and the initial conditions. Different choices of the initial times lead to different choices of the initial conditions, or vice versa. To clarify these issues, in Sections 3, 4 we have discussed it at length by showing the (generalized) comoving Hubble radius in each model as well as in each of the two approaches, dressed metric and hybrid. From these analyses, we have shown clearly which initial conditions can and cannot be imposed at a given initial time.

In addition, when the Universe changes from contraction to expansion at the bounce, particle and entropy creations are expected to be very large, and it is crucial to keep such creations under control, so that the basic assumptions of the models are valid, including the one that the cosmological perturbations are small and can be treated as test fields propagating on the quantum homogeneous background, as assumed in both the dressed metric and hybrid approaches.

Yet, different initial conditions also affect the amplitudes and shapes of the primordial power spectra, and it would be very interesting to investigate the consistency of such obtained spectra with current observations, in particular the possible explanations to the anomalies found in the CMB data (Akrami and Planck collaboration, 2020; Akrami and Planck collaboration, 2020; Schwarz et al., 2016), and the naturalness of such initial conditions.

On the other hand, bouncing cosmologies, as an alternative to the cosmic inflation paradigm, have been extensively studied in the literature, see, for example (Wand, 1999; Brandenberger and Peter, 2017), and references therein. However, in such classical bounces, exotic matter fields are required in order to keep the bounce open. This in turn raises the question of instabilities of the models. On the other hand, quantum bounces found in LQC/mLQCs are purely due to the quantum geometric effects, and the instability problem is automatically out of the question. So, it would be very interesting to study bouncing cosmologies in the framework of LQC/mLQCs. The first step in this direction has already been taken (Li et al., 2020b), and more detailed and extensive analyses are still needed.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

BL and PS are supported by NSF grant PHY-1454832. BL is also partially supported by the National Natural Science Foundation of China (NNSFC) with the Grants No. 12005186.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to Robert Brandenberger and David Wands for valuable comments on the manuscript and helpful discussions. We thank Javier Olmedo and Tao Zhu for various discussions related to works presented in this manuscript.

Footnotes

¹It has been conjectured using models in string theory that the trans-Planckian problem might never arise (Bedroya and Vafa, 2020), which results on severe constraints on various cosmological models [See (Bedroya et al., 2020; Brandenberger, 2021) for more details].

²A similar contracting branch is found in certain anisotropic models in the standard regularization of LQC [see for e.g., (Dadhich et al., 2015)].

³It should be noted that anisotropies rise during the contracting phase and generically dominate the earliest stages of the post-bounce of the homogeneous Universe (Gupt and Singh, 2012; Gupt and Singh, 2013; Agullo et al., 2020; Agullo et al., 2020). So, cautions must be taken, when imposing initial conditions at the bounce.

⁴To be distinguished from the BD vacuum described by Eq. 3.4 we refer to the state described by Eq. 3.7 as the de Sitter state. The difference between them is due to the term $i/\left(k\eta \right)$, which is not negligible in the deep contracting phase of the de Sitter background, as now $\left|k\eta \right|$ could be very small. For more details, see the discussions given in Sec. 3.A, especially the paragraph after Eq. 3.9.

⁵For a modification of LQC based on using gauge-covariant fluxes, see (Liegener and Singh, 2019; Liegener and Singh, 2020).

⁶In LQC, this universality was first found for the quadratic and Starobinsky potentials (Zhu et al., 2017; Zhu et al., 2017) [see also (Bhardwaj et al., 2019)], and later was shown that they are also true for other potentials, including the power-law potentials (Shahalam et al., 2017; Shahalam, 2018), α-attractor potentials (Shahalam et al., 2018; Shahalam et al., 2020), Monodromy potentials (Sharma et al., 2018), warm inflation (Xiao and Wang, 2020), Tachyonic inflation (Xiao, 2019) and even in Brans-Dicke LQC (Jin et al., 2019; Sharma et al., 2019).

⁷It is interesting to note that Eq. 2.61 holds not only in mLQC-I, but also in LQC and mLQC-II.

⁸In the framework of LQC, such effects were also studied in (Agullo et al., 2013; Zhu et al., 2017; Zhu et al., 2017; Navascues et al., 2018; Li et al., 2020). In particular, in (Agullo et al., 2018; Li et al., 2020; Agullo et al., 2021; Agullo et al., 2021) the function ${\mathfrak{A}}_{-}$ defined in Eq. 3.15 was chosen over the whole process of the evolution of the Universe.

References

Abazajian, K. (2019). CMB-S4 Decadal Survey APC White Paper. arXiv:1908.01062.

Abazajian, K. N. (2015). Inflation Physics from the Cosmic Microwave Background and Large Scale Structure. Astropart. Phys. 63, 55.

Google Scholar

Ade, P.PLANCK Collaboration (2016). Planck 2015 Results. XX. Constraints on Inflation. A&A 594, A20.

Google Scholar

Aghanim, N.PLANCK Collaboration (2020). Planck 2018 Results. X. Constraints on Inflation. A&A 641, A10.

Google Scholar

Agullo, I., Ashtekar, A., and Gupt, B. (2017). Phenomenology with Fluctuating Quantum Geometries in Loop Quantum Cosmology. Class. Quan. Grav. 34, 074003. doi:10.1088/1361-6382/aa60ec

CrossRef Full Text | Google Scholar

Agullo, I., Ashtekar, A., and Nelson, W. (2013). Extension of the Quantum Theory of Cosmological Perturbations to the Planck Era. Phys. Rev. D87, 043507.

Google Scholar

Agullo, I., Ashtekar, A., and Nelson, W. (2012). Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 109, 251301. doi:10.1103/physrevlett.109.251301

PubMed Abstract | CrossRef Full Text | Google Scholar

Agullo, I., Ashtekar, A., and Nelson, W. (2013). The Pre-inflationary Dynamics of Loop Quantum Cosmology: Confronting Quantum Gravity with Observations. Class. Quan. Grav. 30, 085014. doi:10.1088/0264-9381/30/8/085014

CrossRef Full Text | Google Scholar

Agullo, I., Bolliet, B., and Sreenath, V. (2018). Non-Gaussianity in Loop Quantum Cosmology. Phys. Rev. D97, 066021.

Google Scholar

Agullo, I., Kranas, D., and Sreenath, V. (2021). Anomalies in the CMB from a Cosmic Bounce. Gen. Relativ Gravit. 53, 17. doi:10.1007/s10714-020-02778-9

CrossRef Full Text | Google Scholar

Agullo, I., Kranas, D., and Sreenath, V. (2021). Large Scale Anomalies in the CMB and Non-gaussianity in Bouncing Cosmologies. Class. Quan. Grav. 38, 065010. doi:10.1088/1361-6382/abc521

CrossRef Full Text | Google Scholar

Agullo, I., and Morris, N. A. (2015). Detailed Analysis of the Predictions of Loop Quantum Cosmology for the Primordial Power Spectra. Phys. Rev. D 92, 124040. doi:10.1103/physrevd.92.124040

CrossRef Full Text | Google Scholar

Agullo, I., Olmedo, J., and Sreenath, V. (2020). Observational Consequences of Bianchi I Spacetimes in Loop Quantum Cosmology. Phys. Rev. D102, 043523.

Google Scholar

Agullo, I., Olmedo, J., and Sreenath, V. (2020). Predictions for the Cosmic Microwave Background from an Anisotropic Quantum Bounce. Phys. Rev. Lett. 124, 251301. doi:10.1103/physrevlett.124.251301

PubMed Abstract | CrossRef Full Text | Google Scholar

Agullo, I. (2018). Primordial Power Spectrum from the Dapor-Liegener Model of Loop Quantum Cosmology. Gen. Relativ Gravit. 50, 91. doi:10.1007/s10714-018-2413-1

CrossRef Full Text | Google Scholar

Agullo, I., and Singh, P. (2017). “Loop Quantum Cosmology,” in Loop Quantum Gravity: The First 30 Years. Editors A. Ashtekar, and J. Pullin (Singapore: Wald Scientific).

Google Scholar

Akrami, Y.Planck collaboration (2020). Planck 2018 Results. I. Overview and the Cosmological Legacy of Planck. A&A 641, A1.

Google Scholar

Akrami, Y.Planck collaboration (2020). Planck 2018 Results. VII. Isotropy and Statistics of the CMB. A&A 641, A7.

Google Scholar

Alesci, E., Botta, G., Cianfrani, F., and Liberati, S. (2017). Cosmological Singularity Resolution from Quantum Gravity: the Emergent-Bouncing Universe. Phys. Rev. D96, 046008.

Google Scholar

Alesci, E., and Cianfrani, F. (2015). Quantum Reduced Loop Gravity: a Realistic Universe. Phys. Rev. D92, 084065.

Google Scholar

Alesci, E., and Cianfrani, F. (2013). Quantum-Reduced Loop Gravity: Cosmology. Phys. Rev. D87, 083521.

Google Scholar

Ashoorioon, A., Chialva, D., and Danielsson, U. (2011). Effects of Nonlinear Dispersion Relations on Non-gaussianities. J. Cosmol. Astropart. Phys. 2011, 034. doi:10.1088/1475-7516/2011/06/034

CrossRef Full Text | Google Scholar

Ashtekar, A., Gupt, B., Jeong, D., and Sreenath, V. (2020). Alleviating the Tension in the Cosmic Microwave Background Using Planck-Scale Physics. Phys. Rev. Lett. 125, 051302. doi:10.1103/PhysRevLett.125.051302

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashtekar, A., Pawlowski, T., and Singh, P. (2006). Quantum Nature of the Big Bang. Phys. Rev. Lett. 96, 141301. doi:10.1103/PhysRevLett.96.141301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashtekar, A., and Barrau, A. (2015). Loop Quantum Cosmology: From Pre-inflationary Dynamics to Observations. Class. Quan. Grav. 32, 234001. doi:10.1088/0264-9381/32/23/234001

CrossRef Full Text | Google Scholar

Ashtekar, A., Bojowald, M., and Lewandowski, J. (2003). Mathematical Structure of Loop Quantum Cosmology. Adv. Theor. Math. Phys. 7, 233–268. doi:10.4310/atmp.2003.v7.n2.a2

CrossRef Full Text | Google Scholar

Ashtekar, A., Corichi, A., and Singh, P. (2010). Robustness of Key Features of Loop Quantum Cosmology. Phys. Rev. D77, 024046.

Google Scholar

Ashtekar, A., and Gupt, B. (2017). Initial Conditions for Cosmological Perturbations. Class. Quan. Grav. 34, 035004. doi:10.1088/1361-6382/aa52d4

CrossRef Full Text | Google Scholar

Ashtekar, A., Gupt, B., Jeong, D., and Sreenath, V. (2021). Cosmic Tango between the Very Small and the Very Large: Addressing CMB Anomalies through Loop Quantum Cosmology. arXiv:2103.14568.

Google Scholar

Ashtekar, A., and Gupt, B. (2017). Quantum Gravity in the Sky: Interplay between Fundamental Theory and Observations. Class. Quan. Grav. 34, 014002. doi:10.1088/1361-6382/34/1/014002

CrossRef Full Text | Google Scholar

Ashtekar, A., and Lewandowski, J. (2004). Background Independent Quantum Gravity: A Status Report. Class. Quan. Grav. 21, R53–R152. doi:10.1088/0264-9381/21/15/r01

CrossRef Full Text | Google Scholar

Ashtekar, A., Pawlowski, T., and Singh, P. (2006). Quantum Nature of the Big Bang: An Analytical and Numerical Investigation. Phys. Rev. D 73, 124038. doi:10.1103/physrevd.73.124038

CrossRef Full Text | Google Scholar

Ashtekar, A., and Pullin, J. (2017). Loop Quantum Gravity - the First 30 Years. Singapore: World Scientific.

Ashtekar, A., and Singh, P. (2011). Loop Quantum Cosmology: a Status Report. Class. Quan. Grav. 28, 213001. doi:10.1088/0264-9381/28/21/213001

CrossRef Full Text | Google Scholar

Ashtekar, A., and Sloan, D. (2011a). Probability of Inflation in Loop Quantum Cosmology. Gen. Relativ. Gravit. 43, 3619–3655. doi:10.1007/s10714-011-1246-y

CrossRef Full Text | Google Scholar

Ashtekar, A., and Sloan, D. (2011b). Loop Quantum Cosmology and Slow Roll Inflation. Phys. Lett. B 694, 108.

Google Scholar

Assanioussi, M., Dapor, A., Liegener, K., and Pawłowski, T. (2018). Emergent de Sitter epoch of the quantum Cosmos from Loop Quantum Cosmology. Phys. Rev. Lett. 121, 081303. doi:10.1103/PhysRevLett.121.081303

PubMed Abstract | CrossRef Full Text | Google Scholar

Assanioussi, M., Dapor, A., Liegener, K., and Pawlowski, T. (2019b). Challenges in Recovering a Consistent Cosmology from the Effective Dynamics of Loop Quantum Gravity. Phys. Rev. D100, 106016.

CrossRef Full Text | Google Scholar

Assanioussi, M., Dapor, A., Liegener, K., and Pawlowski, T. (2019a). Emergent de Sitter epoch of the loop quantum cosmos: A detailed analysis. Phys. Rev. D100, 084003.

Google Scholar

Banday, K. M. A. J., Bennett, C. L., Hinshaw, G., Kogut, A., Smoot, G. F., and Wright, E. L. (1996). Power Spectrum of Primordial Inhomogeneity Determined from the FOUR-Year [ITAL]COBE[/ITAL] DMR Sky Maps. ibid 464, L11–L15. doi:10.1086/310077

CrossRef Full Text | Google Scholar

Baumann, D., and McAllister, L. (2015). Inflation and String Theory. Cambridge: Cambridge Monographs on Mathematical Physics, Cambridge University Press.

Baumann, D. (2009). TASI Lectures on Inflation. arXiv:0907.5424.

Google Scholar

Baytas, B., Bojowald, M., and Crowe, S. (2019). Equivalence of Models in Loop Quantum Cosmology and Group Field Theory. Universe 5, 41.

CrossRef Full Text | Google Scholar

Becker, K., Becker, M., and Schwarz, J. H. (2007). String Theory and M-Theory. Cambridge: Cambridge University Press.

Bedic, S., and Vereshchagin, G. (2019). Probability of Inflation in Loop Quantum Cosmology. Phys. Rev. D99 (4), 043512.

Google Scholar

Bedroya, A., Brandenberger, R., Loverde, M., and Vafa, C. (2020). Trans-Planckian Censorship and Inflationary Cosmology. Phys. Rev. D 101, 103502. doi:10.1103/physrevd.101.103502

CrossRef Full Text | Google Scholar

Bedroya, A., and Vafa, C. (2020). Trans-Planckian Censorship and the Swampland. J. High Energ. Phys. 2020, 123. doi:10.1007/jhep09(2020)123

CrossRef Full Text | Google Scholar

Bennett, C. L., Banday, A. J., Górski, K. M., Hinshaw, G., Jackson, P., Keegstra, P., et al. (1996). Four-Year [ITAL]COBE[/ITAL] DMR Cosmic Microwave Background Observations: Maps and Basic Results. Astrophys. J. 464, L1–L4. doi:10.1086/310075

CrossRef Full Text | Google Scholar

Bergstorm, L., and Danielsson, U. H. (2002). Can MAP and Planck Map Planck Physics? J. High Energ. Phys. 12, 038.

Google Scholar

Bhardwaj, A., Copeland, E. J., and Louko, J. (2019). Inflation in Loop Quantum Cosmology. Phys. Rev. D99, 063520.

Google Scholar

Birrell, N. D., and Davies, P. C. W. (1982). Quantum fields in Curved Space. Cambridge: Cambridge University Press.

Bojowald, M. (2011). Canonical Gravity and Applications: Cosmology, Black Holes, and Quantum Gravity. Cambridge: Cambridge University Press.

Bojowald, M., Hossain, G. M., Kagan, M., and Shankaranarayanan, S. (2008). Anomaly freedom in Perturbative Loop Quantum Gravity. Phys. Rev. D78, 063547.

Google Scholar

Bojowald, M. (2015). Quantum Cosmology: a Review. Rep. Prog. Phys. 78, 023901. doi:10.1088/0034-4885/78/2/023901

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonga, B., and Gupt, B. (2016). Inflation with the Starobinsky Potential in Loop Quantum Cosmology. Gen. Relativ. Grav. 48, 1. doi:10.1007/s10714-016-2071-0

CrossRef Full Text | Google Scholar

Bonga, B., and Gupt, B. (2016). Phenomenological Investigation of a Quantum Gravity Extension of Inflation with the Starobinsky Potential. Phys. Rev. D93, 063513.

Google Scholar

Borde, A., Guth, A. H., and Vilenkin, A. (2003). Inflationary Spacetimes Are Incomplete in Past Directions. Phys. Rev. Lett. 90, 151301. doi:10.1103/physrevlett.90.151301

PubMed Abstract | CrossRef Full Text | Google Scholar

Borde, A., and Vilenkin, A. (1994). Eternal Inflation and the Initial Singularity. Phys. Rev. Lett. 72, 3305–3308. doi:10.1103/physrevlett.72.3305

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandenberger, R. H. (1999). Inflationary Cosmology: Progress and Problems. arXiv:hep-th/9910410.

Google Scholar

Brandenberger, R. H., and Martin, J. (2013). Trans-Planckian Issues for Inflationary Cosmology. Class. Quan. Grav. 30, 113001. doi:10.1088/0264-9381/30/11/113001

CrossRef Full Text | Google Scholar

Brandenberger, R., and Peter, P. (2017). Bouncing Cosmologies: Progress and Problems. Found. Phys. 47, 797–850. doi:10.1007/s10701-016-0057-0

CrossRef Full Text | Google Scholar

Brandenberger, R. (2021). Trans-Planckian Censorship Conjecture and Early Universe Cosmology. arXiv:2102.09641.

Google Scholar

Brunnemann, J., and Fleischhack, C. (2007). On the Configuration Spaces of Homogeneous Loop Quantum Cosmology and Loop Quantum Gravity. arXiv:0709.1621.

Google Scholar

Brunnemann, J., and Koslowski, T. A. (2011). Symmetry Reduction of Loop Quantum Gravity. Class. Quan. Grav. 28, 245014. doi:10.1088/0264-9381/28/24/245014

CrossRef Full Text | Google Scholar

Burgess, C. P., Cicoli, M., and Quevedo, F. (2013). String Inflation after Planck 2013. J. Cosmol. Astropart. Phys. 2013, 003. doi:10.1088/1475-7516/2013/11/003

CrossRef Full Text | Google Scholar

Cailleteau, T., Barrau, A., Grain, J., and Vidotto, F. (2012). Consistency of Holonomy-Corrected Scalar, Vector and Tensor Perturbations in Loop Quantum Cosmology. Phys. Rev. D86, 087301.

Google Scholar

Cailleteau, T., Mielczarek, J., Barrau, A., and Grain, J. (2012). Anomaly-free Scalar Perturbations with Holonomy Corrections in Loop Quantum Cosmology. Class. Quan. Grav. 29, 095010. doi:10.1088/0264-9381/29/9/095010

CrossRef Full Text | Google Scholar

Carlip, S. (2003). Quantum Gravity in 2+1 Dimensions. Cambridge: Cambridge Monographs on Mathematical Physics, Cambridge University Press.

Castelló Gomar, L., Fernández-Méndez, M., Mena Marugan, G. A., and Olmedo, J. (2014). Cosmological Perturbations in Hybrid Loop Quantum Cosmology: Mukhanov-Sasaki Variables. Phys. Rev. D90, 064015.

Google Scholar

Castelló Gomar, L., García-Quismondo, A., and Mena Marugán, G. A. (2020). Primordial Perturbations in the Dapor-Liegener Model of Hybrid Loop Quantum Cosmology. Phys. Rev. D102, 083524.

Google Scholar

Castelló Gomar, L., Mena Marugán, G. A., Martín de Blas, D., and Olmedo, J. (2017). Hybrid Loop Quantum Cosmology and Predictions for the Cosmic Microwave Background. Phys. Rev. D 96, 103528. doi:10.1103/physrevd.96.103528

CrossRef Full Text | Google Scholar

Chen, L., and Zhu, J.-Y. (2015). Loop Quantum Cosmology: The Horizon Problem and the Probability of Inflation. Phys. Rev. D92, 084063.

Google Scholar

Chernoff, D. F., and Tye, S.-H. H. (2014). Inflation, String Theory and Cosmology. arXiv:1412.0579.

Google Scholar

Cicoli, M. (2016). Recent Developments in String Model-Building and Cosmology. arXiv:1604.00904.

Google Scholar

Corichi, A., and Karami, A. (2011). Measure Problem in Slow Roll Inflation and Loop Quantum Cosmology. Phys. Rev. D 83, 104006. doi:10.1103/physrevd.83.104006

CrossRef Full Text | Google Scholar

Corichi, A., and Singh, P. (2008). Is Loop Quantization in Cosmology Unique? Phys. Rev. D78, 024034.

Google Scholar

Corichi, A., and Sloan, D. (2014). Inflationary Attractors and Their Measures. Class. Quan. Grav. 31, 062001. doi:10.1088/0264-9381/31/6/062001

CrossRef Full Text | Google Scholar

Craig, D. A., and Singh, P. (2013). Consistent Probabilities in Loop Quantum Cosmology. Class. Quan. Grav. 30, 205008. doi:10.1088/0264-9381/30/20/205008

CrossRef Full Text | Google Scholar

Dadhich, N., Joe, A., and Singh, P. (2015). Emergence of the Product of Constant Curvature Spaces in Loop Quantum Cosmology. Class. Quan. Grav. 32, 185006. doi:10.1088/0264-9381/32/18/185006

CrossRef Full Text | Google Scholar

Dapor, A., and Liegener, K. (2018b). Cosmological Coherent State Expectation Values in Loop Quantum Gravity I. Isotropic Kinematics. Class. Quan. Grav. 35, 135011. doi:10.1088/1361-6382/aac4ba

CrossRef Full Text | Google Scholar

Dapor, A., and Liegener, K. (2018a). Cosmological Effective Hamiltonian from Full Loop Quantum Gravity Dynamics. Phys. Lett. B 785, 506–510. doi:10.1016/j.physletb.2018.09.005

CrossRef Full Text | Google Scholar

de Blas, D. M., and Olmedo, J. (2016). Primordial Power Spectra for Scalar Perturbations in Loop Quantum Cosmology. J. Cosmol. Astropart. Phys. 2016, 029. doi:10.1088/1475-7516/2016/06/029

CrossRef Full Text | Google Scholar

Diener, P., Gupt, B., Megevand, M., and Singh, P. (2014). Numerical Evolution of Squeezed and Non-gaussian States in Loop Quantum Cosmology. Class. Quan. Grav. 31, 165006. doi:10.1088/0264-9381/31/16/165006

CrossRef Full Text | Google Scholar

Diener, P., Gupt, B., and Singh, P. (2014). Numerical Simulations of a Loop Quantum cosmos: Robustness of the Quantum Bounce and the Validity of Effective Dynamics. Class. Quan. Grav. 31, 105015. doi:10.1088/0264-9381/31/10/105015

CrossRef Full Text | Google Scholar

Diener, P., Joe, A., Megevand, M., and Singh, P. (2017). Numerical Simulations of Loop Quantum Bianchi-I Spacetimes. Class. Quan. Grav. 34, 094004. doi:10.1088/1361-6382/aa68b5

CrossRef Full Text | Google Scholar

Dodelson, S. (2003). Modern Cosmology. New York: Academic Press.

Dupuy, J. L., and Singh, P. (2020). Hysteresis and Beats in Loop Quantum Cosmology. Phys. Rev. D101, 086016.

Google Scholar

Easther, R., Kinney, W. H., and Peiris, H. (2005). Observing Trans-planckian Signatures in the Cosmic Microwave Background. J. Cosmol. Astropart. Phys. 2005, 009. doi:10.1088/1475-7516/2005/05/009

CrossRef Full Text | Google Scholar

Elizaga Navascués, B., Martín de Blas, D., and Mena Marugán, G. (2018). The Vacuum State of Primordial Fluctuations in Hybrid Loop Quantum Cosmology. Universe 4, 98. doi:10.3390/universe4100098

CrossRef Full Text | Google Scholar

Engle, J. (2007). Relating Loop Quantum Cosmology to Loop Quantum Gravity: Symmetric Sectors and Embeddings. Class. Quan. Grav. 24, 5777–5802. doi:10.1088/0264-9381/24/23/004

CrossRef Full Text | Google Scholar

Engle, J., and Vilensky, I. (2018). Deriving Loop Quantum Cosmology Dynamics from Diffeomorphism Invariance. Phys. Rev. D98, 023505.

Google Scholar

Engle, J., and Vilensky, I. (2019). Uniqueness of Minimal Loop Quantum Cosmology Dynamics. Phys. Rev. D 100, 121901. doi:10.1103/physrevd.100.121901

CrossRef Full Text | Google Scholar

Fernández-Méndez, M., Mena Marugán, G. A., and Olmedo, J. (2013). Hybrid Quantization of an Inflationary Model: The Flat Case. Phys. Rev. D88, 044013.

Google Scholar

Fernández-Méndez, M., Mena Marugán, G. A., and Olmedo, J. (2012). Hybrid Quantization of an Inflationary Universe. Phys. Rev. D86, 024003.

Google Scholar

Gambini, R., and Pullin, J. (2011). A First Course in Loop Quantum Gravity. Oxford: Oxford University Press.

García-Quismondo, A., and Mena Marugán, G. A. (2020). Dapor-Liegener Formalism of Loop Quantum Cosmology for Bianchi I Spacetimes. Phys. Rev. D101, 023520.

Google Scholar

García-Quismondo, A., and Mena Marugán, G. A. (2019). Martin-Benito-Mena Marugan-Olmedo Prescription for the Dapor-Liegener Model of Loop Quantum Cosmology. Phys. Rev. D99, 083505.

Google Scholar

García-Quismondo, A., Mena Marugán, G. A., and Pérez, G. S. (2020). The Time-dependent Mass of Cosmological Perturbations in Loop Quantum Cosmology: Dapor-Liegener Regularization. Class. Quan. Grav. 37, 195003. doi:10.1088/1361-6382/abac6d

CrossRef Full Text | Google Scholar

Gerhardt, F., Oriti, D., and Wilson-Ewing, E. (2018). The Separate Universe Framework in Group Field Theory Condensate Cosmology. Phys. Rev. D98, 066011.

Google Scholar

Giesel, K., Li, B.-F., and Singh, P. (2020). Revisiting the Bardeen and Mukhanov-Sasaki Equations in the Brown-Kuchar and Gaussian Dust Models. arXiv:2012.14443.

Google Scholar

Giesel, K., Li, B.-F., and Singh, P. (2020). Towards a Reduced Phase Space Quantization in Loop Quantum Cosmology with an Inflationary Potential. Phys. Rev. D 102, 126024. doi:10.1103/physrevd.102.126024

CrossRef Full Text | Google Scholar

Giesel, K., and Thiemann, T. (2007). Algebraic Quantum Gravity (AQG): I. Conceptual Setup. Class. Quan. Grav. 24, 2465–2497. doi:10.1088/0264-9381/24/10/003

CrossRef Full Text | Google Scholar

Gomar, L. C., Martín-Benito, M., and Marugán, G. A. M. (2015). Gauge-invariant Perturbations in Hybrid Quantum Cosmology. J. Cosmol. Astropart. Phys. 2015, 045. doi:10.1088/1475-7516/2015/06/045

CrossRef Full Text | Google Scholar

Gordon, L., Li, B.-F., and Singh, P. (2021). Quantum Gravitational Onset of Starobinsky Inflation in a Closed Universe. Phys. Rev. D103, 046016.

Google Scholar

Green, M. B., Schwarz, J. H., and Witten, E. (1999). Superstring Theory: Vol.1 & 2. Cambridge: Cambridge Monographs on Mathematical Physics, Cambridge University Press.

Gupt, B., and Singh, P. (2013). A Quantum Gravitational Inflationary Scenario in Bianchi-I Spacetime. Class. Quan. Grav. 30, 145013. doi:10.1088/0264-9381/30/14/145013

CrossRef Full Text | Google Scholar

Gupt, B., and Singh, P. (2012). Quantum Gravitational Kasner Transitions in Bianchi-I Spacetime. Phys. Rev. D86, 024034.

Google Scholar

Guth, A. H. (1981). Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 23, 347–356. doi:10.1103/physrevd.23.347

CrossRef Full Text | Google Scholar

Han, M., Li, H., and Liu, H. (2020). Manifestly Gauge-Invariant Cosmological Perturbation Theory from Full Loop Quantum Gravity. arXiv:2005.00883.

Google Scholar

Han, M., and Liu, H. (2020a). Effective Dynamics from Coherent State Path Integral of Full Loop Quantum Gravity. Phys. Rev. D101, 046003.

Google Scholar

Han, M., and Liu, H. (2020b). Semiclassical Limit of New Path Integral Formulation from Reduced Phase Space Loop Quantum Gravity. Phys. Rev. D102, 024083.

Google Scholar

Hawking, S. W., and Ellis, G. F. R. (1973). The Large Scale Structure of Spacetime. Cambridge: Cambridge University Press.

Jackson, M. G., and Schalm, K. (2012). Model Independent Signatures of New Physics in the Inflationary Power Spectrum. Phys. Rev. Lett. 108, 111301. doi:10.1103/physrevlett.108.111301

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, W.-J., Ma, Y.-G., and Zhu, T. (2019). Pre-inflationary Dynamics of Starobinsky Inflation and its Generalization in Loop Quantum Brans-Dicke Cosmology. JCAP 02, 010.

CrossRef Full Text | Google Scholar

Johson, C. V. (2003). D-Branes, Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press.

Joras, A. E., and Marozzi, G. (2009). Trans-Planckian Physics from a Nonlinear Dispersion Relation. Phys. Rev. D79, 023514.

Google Scholar

Kamiński, W., Kolanowski, M., and Lewandowski, J. (2020). Dressed Metric Predictions Revisited. Class. Quan. Grav 37, 095001. doi:10.1088/1361-6382/ab7ee0

CrossRef Full Text | Google Scholar

Kiefer, C., and Krämer, M. (2012). Quantum Gravitational Contributions to the Cosmic Microwave Background Anisotropy Spectrum. Phys. Rev. Lett. 108, 021301. doi:10.1103/PhysRevLett.108.021301

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiefer, C. (2007). Quantum Gravity. Oxford Science Publications, Oxford University Press.

Kodama, H., and Sasaki, M. (1984). Cosmological Perturbation Theory. Prog. Theor. Phys. Suppl. 78, 1–166. doi:10.1143/ptps.78.1

CrossRef Full Text | Google Scholar

Komatsu, E., Smith, K. M., Dunkley, J., Bennett, C. L., Gold, B., Hinshaw, G., et al. WMAP Collaboration (2011). Seven-year Wilkinson Microwave Anisotropy Probe ( Wmap ) Observations: Cosmological Interpretation. ApJS 192, 18. doi:10.1088/0067-0049/192/2/18

CrossRef Full Text | Google Scholar

Krauss, L. M., and Wilczek, F. (2014). Using Cosmology to Establish the Quantization of Gravity. Phys. Rev. D89, 047501.

Google Scholar

Larson, D., Dunkley, J., Hinshaw, G., Komatsu, E., Nolta, M. R., Bennett, C. L., et al. WMAP Collaboration (2011). Seven-year Wilkinson Microwave Anisotropy Probe ( Wmap ) Observations: Power Spectra and Wmap -Derived Parameters. ApJS 192, 16. doi:10.1088/0067-0049/192/2/16

CrossRef Full Text | Google Scholar

Li, B.-F., Olmedo, J., Singh, P., and Wang, A. (2020a). Primordial Scalar Power Spectrum from the Hybrid Approach in Loop Cosmologies. Phys. Rev. D 102, 126025. doi:10.1103/physrevd.102.126025

CrossRef Full Text | Google Scholar

Li, B.-F., Saini, S., and Singh, P. (2020b). Primordial Power Spectrum from a Matter-Ekpyrotic Bounce Scenario in Loop Quantum Cosmology. arXiv:2012.10462.

Google Scholar

Li, B.-F., and Singh, P. Singularity resolution may forbid a cyclic evolution (To Appear).

Li, B.-F., Singh, P., and Wang, A. (2019). Genericness of Pre-inflationary Dynamics and Probability of the Desired Slow-Roll Inflation in Modified Loop Quantum Cosmologies. Phys. Rev. D100, 063513.

Google Scholar

Li, B.-F., Singh, P., and Wang, A. (2020c). Primordial Power Spectrum from the Dressed Metric Approach in Loop Cosmologies. Phys. Rev. D100, 086004.

Google Scholar

Li, B.-F., Singh, P., and Wang, A. (2018b). Qualitative Dynamics and Inflationary Attractors in Loop Cosmology. Phys. Rev. D98, 066016.

Google Scholar

Li, B.-F., Singh, P., and Wang, A. (2018a). Towards Cosmological Dynamics from Loop Quantum Gravity. Phys. Rev. D97, 084029.

Google Scholar

Liegener, K., and Singh, P. (2020). Gauge-invariant Bounce from Loop Quantum Gravity. Class. Quan. Grav. 37, 085015. doi:10.1088/1361-6382/ab7962

CrossRef Full Text | Google Scholar

Liegener, K., and Singh, P. (2019). New Loop Quantum Cosmology Modifications from Gauge-Covariant Fluxes. Phys. Rev. D 100, 124048. doi:10.1103/physrevd.100.124048

CrossRef Full Text | Google Scholar

Liegener, K., and Singh, P. (2019). Some Physical Implications of Regularization Ambiguities in SU(2) Gauge-Invariant Loop Quantum Cosmology. Phys. Rev. D 100, 124049. doi:10.1103/physrevd.100.124049

CrossRef Full Text | Google Scholar

Linde, A. (2014). Inflationary Cosmology after Planck 2013. arXiv: 1402.0526.

Google Scholar

Linde, A. (2018). On the Problem of Initial Conditions for Inflation. Found. Phys. 48, 1246–1260. doi:10.1007/s10701-018-0177-9

CrossRef Full Text | Google Scholar

Linsefors, L., and Barrau, A. (2013). Duration of Inflation and Conditions at the Bounce as a Prediction of Effective Isotropic Loop Quantum Cosmology. Phys. Rev. D 87, 123509. doi:10.1103/physrevd.87.123509

CrossRef Full Text | Google Scholar

Malik, K. A. (2001). Cosmological Perturbations in an Inflationary Universe. arXiv:astro-ph/0101563.

Google Scholar

Malik, K. A., and Wands, D. (2009). Cosmological Perturbations. Phys. Rep. 475, 1–51. doi:10.1016/j.physrep.2009.03.001

CrossRef Full Text | Google Scholar

Martin, J., and Brandenberger, R. H. (2001). Trans-Planckian Problem of Inflationary Cosmology. Phys. Rev. D 63, 123501. doi:10.1103/physrevd.63.123501

CrossRef Full Text | Google Scholar

Martínez, F. B., and Olmedo, J. (2016). Primordial Tensor Modes of the Early Universe. Phys. Rev. D 93, 124008. doi:10.1103/physrevd.93.124008

CrossRef Full Text | Google Scholar

McAllister, L., and Silverstein, E. (2007). String Cosmology: A Review. Gen. Relativ. Grav. 40, 565.

Google Scholar

Meissner, K. A. (2004). Black-hole Entropy in Loop Quantum Gravity. Class. Quan. Grav. 21, 5245–5251. doi:10.1088/0264-9381/21/22/015

CrossRef Full Text | Google Scholar

Mena Marugán, G. A., Olmedo, J., and Pawlowski, T. (2011). Prescriptions in Loop Quantum Cosmology: A Comparative Analysis. Phys. Rev. D 84, 064012. doi:10.1103/physrevd.84.064012

CrossRef Full Text | Google Scholar

Motaharfar, M., and Singh, P. (2021). On the Role of Dissipative Effects in the Quantum Gravitational Onset of Warm Starobinsky Inflation in a Closed Universe. arXiv:gr-qc/2102.09578.

Mukhanov, V., Feldman, H. A., and Brandenberger, R. H. (1992). Theory of Cosmological Perturbations. Phys. Rep. 215, 203–333. doi:10.1016/0370-1573(92)90044-z

CrossRef Full Text | Google Scholar

Mukhanov, V. F., and Winitzki, S. (2007). Introduction to Quantum Effects in Gravity. Cambridge: Cambridge University Press.

Mukhanov, V. (2005). Physics Foundations of Cosmology. Cambridge: Cambridge University Press.

Navascues, B. E., de Blas, D. M., and Marugan, G. A. M. (2018). Time-dependent Mass of Cosmological Perturbations in the Hybrid and Dressed Metric Approaches to Loop Quantum Cosmology. Phys. Rev. D97, 043523.

Google Scholar

Neuser, J., Schander, S., and Thiemann, T. (2019). Quantum Cosmological Backreactions II: Purely Homogeneous Quantum Cosmology. arXiv:1906.08185.

Google Scholar

Niemeyer, J. C., and Parentani, R. (2002). Corley-Jacobson Dispersion Relation and Trans-planckian Inflation. Phys. Rev. D65, 103514.

Google Scholar

Niemeyer, J. C., and Parentani, R. (2003). Dependence of the Spectra of Fluctuations in Inflationary Cosmology on Trans-planckian Physics. Phys. Rev. D68, 063513.

Google Scholar

Niemeyer, J. C., and Parentani, R. (2001). Trans-Planckian Dispersion Relation and Scale Invariance of Inflationary Perturbations. Phys. Rev. D64, 101301(R).

Google Scholar

Olmedo, J., and Alesci, E. (2019). Power Spectrum of Primordial Perturbations for an Emergent Universe in Quantum Reduced Loop Gravity. J. Cosmol. Astropart. Phys. 2019, 030. doi:10.1088/1475-7516/2019/04/030

CrossRef Full Text | Google Scholar

Oriti, D., Sindoni, L., and Wilson-Ewing, E. (2017). Bouncing Cosmologies from Quantum Gravity Condensates. Class. Quan. Grav. 34, 04LT01. doi:10.1088/1361-6382/aa549a

CrossRef Full Text | Google Scholar

Oriti, D. (2017). The Universe as a Quantum Gravity Condensate. Comptes Rendus Physique 18, 235–245. doi:10.1016/j.crhy.2017.02.003

CrossRef Full Text | Google Scholar

Parker, L., and Toms, D. (2009). Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity. Cambridge: Cambridge University Press.

Polchinski, J. (2001). String Theory, Vol. 1 & 2. Cambridge: Cambridge University Press.

Rovelli, C. (2008). Quantum Gravity. Cambridge: Cambridge University Press.

Saini, S., and Singh, P. (2019a). Generic Absence of strong Singularities and Geodesic Completeness in Modified Loop Quantum Cosmologies. Class. Quan. Grav. 36, 105014. doi:10.1088/1361-6382/ab1274

CrossRef Full Text | Google Scholar

Saini, S., and Singh, P. (2019b). Von Neumann Stability of Modified Loop Quantum Cosmologies. Class. Quan. Grav. 36, 105010. doi:10.1088/1361-6382/ab1608

CrossRef Full Text | Google Scholar

Sato, K. (1981). First-order Phase Transition of a Vacuum and the Expansion of the Universe. Monthly Notices R. Astronomical Soc. 195, 467–479. doi:10.1093/mnras/195.3.467

CrossRef Full Text | Google Scholar

Schander, S., and Thiemann, T. (2019). Quantum Cosmological Backreactions I: Cosmological Space Adiabatic Perturbation Theory. arXiv:1906.08166.

Google Scholar

Schander, S., and Thiemann, T. (2019). Quantum Cosmological Backreactions III: Deparametrised Quantum Cosmological Perturbation Theory. arXiv:1906.08194.

Google Scholar

Schwarz, D. J., Copi, C. J., Huterer, D., and Starkman, G. D. (2016). CMB Anomalies after Planck. Class. Quan. Grav. 33, 184001. doi:10.1088/0264-9381/33/18/184001

CrossRef Full Text | Google Scholar

Senatore, L. (2017). “Lectures on Inflation,” in New Frontiers in Fields and Strings, Proceedings of the 2015 Theoretical Advanced Study Institute in Elementary Particle Physics, Boulder, Colorado, 1 - 26 June 2015. Editors J. Polchinski, P. Vieira, and O. DeWolfe (Singapore: World Scientific), 447–543.

Google Scholar

Shahalam, M., Al Ajmi, M., Myrzakulov, R., and Wang, A. (2020). Revisiting Pre-inflationary Universe of Family of α -attractor in Loop Quantum Cosmology. Class. Quan. Grav. 37, 195026. doi:10.1088/1361-6382/aba486

CrossRef Full Text | Google Scholar

Shahalam, M. (2018). Preinflationary Dynamics of Power-Law Potential in Loop Quantum Cosmology †. Universe 4, 87. doi:10.3390/universe4080087

CrossRef Full Text | Google Scholar

Shahalam, M., Sami, M., and Wang, A. (2018). Pre-inflationary Dynamics of α-attractor in Loop Quantum Cosmology. Phys. Rev. D98, 043524.

Google Scholar

Shahalam, M., Sharma, M., Wu, Q., and Wang, A. (2017). Preinflationary Dynamics in Loop Quantum Cosmology: Power-Law Potentials. Phys. Rev. D 96, 123533. doi:10.1103/physrevd.96.123533

CrossRef Full Text | Google Scholar

Sharma, M., Shahalam, M., Wu, Q., and Wang, A. (2018). Preinflationary Dynamics in Loop Quantum Cosmology: Monodromy Potential. J. Cosmol. Astropart. Phys. 2018, 003. doi:10.1088/1475-7516/2018/11/003

CrossRef Full Text | Google Scholar

Sharma, M., Zhu, T., and Wang, A. (2019). Background Dynamics of Pre-inflationary Scenario in Brans-Dicke Loop Quantum Cosmology. Commun. Theor. Phys. 71, 1205. doi:10.1088/0253-6102/71/10/1205

CrossRef Full Text | Google Scholar

Silverstein, E. (2016). TASI Lectures on Cosmological Observables and String Theory. arXiv:1606.03640.

Google Scholar

Singh, P. (2009). Are Loop Quantum cosmos Never Singular? Class. Quan. Grav. 26, 125005. doi:10.1088/0264-9381/26/12/125005

CrossRef Full Text | Google Scholar

Singh, P. (2018). Glimpses of Space-Time beyond the Singularities Using Supercomputers. Comput. Sci. Eng. 20, 26–38. doi:10.1109/mcse.2018.042781324

CrossRef Full Text | Google Scholar

Singh, P. (2014). Loop Quantum Cosmology and the Fate of Cosmological Singularities. Bull. Astron. Soc. India 42, 121.

Google Scholar

Singh, P., Vandersloot, K., and Vereshchagin, G. V. (2006). Non-singular Bouncing Universes in Loop Quantum Cosmology. Phys. Rev. D74, 043510.

Google Scholar

Starobinsky, A. A. (1980). A New Type of Isotropic Cosmological Models without Singularity. Phys. Lett. B 91, 99–102. doi:10.1016/0370-2693(80)90670-x

CrossRef Full Text | Google Scholar

Thiemann, T. (2006). Complexifier Coherent States for Quantum General Relativity. Class. Quan. Grav. 23, 2063–2117. doi:10.1088/0264-9381/23/6/013

CrossRef Full Text | Google Scholar

Thiemann, T. (2001a). Gauge Field Theory Coherent States (GCS): I. General Properties. Class. Quan. Grav. 18, 2025–2064. doi:10.1088/0264-9381/18/11/304

CrossRef Full Text | Google Scholar

Thiemann, T. (2007). Modern Canonical Quantum General Relativity. Cambridge: Cambridge University Press.

Thiemann, T. (1998a). Quantum Spin Dynamics (QSD). Class. Quan. Grav. 15, 839–873. doi:10.1088/0264-9381/15/4/011

CrossRef Full Text | Google Scholar

Thiemann, T. (1998b). Quantum Spin Dynamics (QSD): II. The Kernel of the Wheeler - DeWitt Constraint Operator. Class. Quan. Grav. 15, 875–905. doi:10.1088/0264-9381/15/4/012

CrossRef Full Text | Google Scholar

Thiemann, T., and Winkler, O. (2001b). Gauge Field Theory Coherent States (GCS): II. Peakedness Properties. Class. Quan. Grav. 18, 2561–2636. doi:10.1088/0264-9381/18/14/301

CrossRef Full Text | Google Scholar

Wald, R. M. (1994). Quantum Field Theory Om Curved Spacetime and Black Hole Thermodynamics. Chicago: The University of Chicago Press.

Wand, D. (1999). Duality Invariance of Cosmological Perturbation Spectra. Phys. Rev. D60, 023507.

Google Scholar

Weinberg, S. (1980). in General Relativity, an Einstein Centenary Survey. Editors S. W. Hawking, and W. Israel (Cambridge: Cambridge University Press).

Weinberg, S. (2008). Cosmology. Oxford: Oxford University Press.

Wilson-Ewing, E. (2017). Testing Loop Quantum Cosmology. Comptes Rendus Physique 18, 207–225. doi:10.1016/j.crhy.2017.02.004

CrossRef Full Text | Google Scholar

Wilson-Ewing, E. (2018). The Loop Quantum Cosmology Bounce as a Kasner Transition. Class. Quan. Grav. 35, 065005. doi:10.1088/1361-6382/aaab8b

CrossRef Full Text | Google Scholar

Woodard, R. P. (2014). Perturbative Quantum Gravity Comes of Age. arXiv:1407.4748.

Google Scholar

Wu, Q., Zhu, T., and Wang, A. (2018). Nonadiabatic Evolution of Primordial Perturbations and Non-gaussinity in Hybrid Approach of Loop Quantum Cosmology. Phys. Rev. D 98, 103528. doi:10.1103/physrevd.98.103528

CrossRef Full Text | Google Scholar

Xiao, K. (2020). Tachyon Field in Loop Cosmology. Phys. Lett. B 811, 135859. doi:10.1016/j.physletb.2020.135859

CrossRef Full Text | Google Scholar

Xiao, K. (2019). Tachyonic Inflation in Loop Quantum Cosmology. Eur. Phys. J. C 79, 1019. doi:10.1140/epjc/s10052-019-7538-1

CrossRef Full Text | Google Scholar

Xiao, K., and Wang, S.-Q. (2020). Pre-inflation Dynamical Behavior of Warm Inflation in Loop Quantum Cosmology. Mod. Phys. Lett. A. 35, 2050293. doi:10.1142/s0217732320502934

CrossRef Full Text | Google Scholar

Yang, J., Ding, Y., and Ma, Y. (2009). Alternative Quantization of the Hamiltonian in Loop Quantum Cosmology. Phys. Lett. B 682, 1–7. doi:10.1016/j.physletb.2009.10.072

CrossRef Full Text | Google Scholar

Zhang, X., and Ling, Y. (2007). Inflationary Universe in Loop Quantum Cosmology. JCAP 08, 012.

CrossRef Full Text | Google Scholar

Zhu, T., Wang, A., Kirsten, K., Cleaver, G., and Sheng, Q. (2017). Pre-inflationary Universe in Loop Quantum Cosmology. Phys. Rev. D96, 083520.

Google Scholar

Zhu, T., Wang, A., Kirsten, K., Cleaver, G., and Sheng, Q. (2018). Primoridial Non-gaussianity and Power Asymmetry with Quantum Gravitational Effects in Loop Quantum Cosmology. Phys. Rev. D97, 043501.

Google Scholar

Zhu, T., Wang, A., Kirsten, K., Cleaver, G., and Sheng, Q. (2017). Universal Features of Quantum Bounce in Loop Quantum Cosmology. Phys. Lett. B 773, 196–202. doi:10.1016/j.physletb.2017.08.025

CrossRef Full Text | Google Scholar