- Department of Chemistry & Biochemistry, University of Mississippi, University, Oxford, MS, United States
The atoms contributing to the strongest “single bonds” on the periodic table do not continue to produce the strongest “double bonds” or “triple bonds.” In fact, the opposite appears to be the case. This quantum chemical examination of nominal X = Y and X ≡ Y bonds in model molecules of atoms from the first three rows of the periodic table shows that the strongest “double bond” is in formaldehyde once the astrophysically-depleted Be and B atoms are removed from consideration. The strongest “triple bond” is a close match between acetylene and N2. However, these results indicate that astrophysical regions containing a high abundance of hydride species will likely be areas where inorganic oxide formation is favored. Those where H2 molecules have already been dissociated will favor organic/volatile astrochemistry.
1 Introduction
Recent work has shown that the strongest “single bonds” in neutral molecules for atoms on the first three rows of the periodic table are not between the atoms most commonly used in chemistry (Doerksen and Fortenberry, 2020). The strongest bonds are actually between Be/B atoms with F atoms in the HBeF and H2BF molecules. However, the Be, B, and F are the three least abundant elements on the periodic table until atoms beyond Fe are considered (Savage and Sembach, 1996). Hence, the strongest “single bonds” of any small molecules containing astrochemically-relevant atoms coincidentally also contain the elements that are most abundant in the earth’s lithosphere (specifically the mantle) and in rocky bodies in general: O, Mg, Si, and Al. To note, this previous work (Doerksen and Fortenberry, 2020) did not examine any molecules containing period 4 atoms or higher largely due to a combination of factors including the statistical increase in the sample set, the decrease in atomic abundance (save for Fe, of course), and the complexities of electronic structure computations on molecules involving the mid-row transition metal atoms, most notably iron (DeYonker, 2015).
In this previous study, the X−Y bond strengths are computed from model HmX − YHn molecules (Doerksen and Fortenberry, 2020). The X and Y are all atoms between Li and Cl. The m and n values are the number of hydrogen atoms necessary to fill the valency where a single bond is created between the heavy atoms. For instance, if X = Mg and Y = O, the molecule would be HMgOH with m, n = 1 since both atoms are divalent and one of the unpaired electrons is bonding with the other heavy atom. These strongest, common bonds are −126.32 kcal/mol, −118.00 kcal/mol, and −109.34 kcal/mol respective of AlH2OH, SiH3OH, and HMgOH (Doerksen and Fortenberry, 2020) computed with explicitly correlated coupled cluster theory at the singles, doubles, and perturbative triples level (CCSD(T)-F12) (Raghavachari et al., 1989; Knizia et al., 2009; Adler et al., 2007). The C−C bond in ethane, for instance, is computed at this same level to be 83.70 kcal/mol, in line with experimental values (Huber et al., 2018) but much less than the inorganic oxide bonds. Such a tantalizing coincidence between bond strengths and atomic abundances warrants further exploration.
Hence, the present work will explore bond strengths in a similar way but for what would naively be thought of as higher bond orders. A reduction of the hydrogen molar ratios in the model molecules and an increase in the interpretation of the bond order between the heavy atoms will be explored. Most of the materials in rocky bodies are largely hydrogen deficient (unless they are hydrates) (White, 2013), implying that the reactions leading to the creation of such inorganic networks involve hydrogen removal at some point in the formation process. The hydrogen most likely leaves in the form of H2 (Swinnen et al., 2009) which would be untraceable under most astrophysical conditions due to the overwhelming abundance yet difficulty in detecting non-polar molecular hydrogen. The present work will explore if small molecules can support the removal of the hydrogen atoms at the molecular stage before network-covalent nanocrystals begin to aggregate.
For example, while AlH2OH has not been observed in any astrophysical regions thus far and its spectra have only recently been provided quantum chemically (Watrous et al., 2021), the reduced but related AlOH molecule has been detected in astrophysical environments (Apponi et al., 1993; Tenenbaum and Ziurys, 2010). However, its higher energy isomer, HAlO, has not been observed (Trabelsi and Francisco, 2018). HAlO would be the direct dehydrogenation product of AlH2OH, but isomerization to the observed, lower energy AlOH products is certainly possible. Consequently, if the heavy atom bond strength in HAlO is higher than in AlH2OH, such a result would be one piece of supporting evidence for the hypothesis that hydrogen removal begins earlier in the nanocrystal aggregation stage. In any case, the stabilities of these small molecules may also offer clues as to whether or not such species may be present in astrophysical regions (Fortenberry, 2020; Fortenberry and DeYonker, 2021) regardless of their roles in any subsequent chemistry or materials formation.
2 Computational Details
Optimized geometry calculations are performed for all 55 molecules of the forms HmX = YHn and HmX ≡ YHn similar to but distinct from that employed previously (Doerksen and Fortenberry, 2020). The present set are equivalent to m–1 and n–1 of the previous. X and Y are period 2 and 3 atoms in groups 2 through 16 bonded to a defined number of hydrogen atoms: m, n = 0 for X and Y of groups 2,16; 1 for groups 13,15; and 2 for group 14. The number of hydrogen atoms bonded to atoms X and Y is chosen such that the X = Y bond would be a “double bond” if electrons are shared equally. The computed geometries are then used for harmonic vibrational frequency calculations to confirm a minimum energy structure is present and to provide the zero-point vibrational energies (ZPVEs) for each constituent. Both the optimized geometries and the harmonic vibrational frequencies are run using CCSD(T)-F12b with the cc-pVTZ-F12 basis set (Peterson et al., 2008; Hill and Peterson, 2010; Prascher et al., 2011) implemented in the MOLPRO 2020.1 program (Werner et al., 2019, 2012).
The above procedures are repeated for 21 molecules of the HmX ≡ YHn construction. X and Y are period 2 and 3 atoms in groups 13 through 15 bonded to a defined number of hydrogen atoms: m, n = 0 for groups 13,15 and m, n = 1 for group 14. In this set, the number of hydrogen atoms is chosen to simulate a “triple bond” between X and Y under conditions of nominal covalent bonding even though the molecules examined herein are likely to be classified across the scope of bond types.
X = Y and X ≡ Y bond dissociation energies (BDEs) are determined here by subtracting the total energy (including the ZPVE) of each molecule from the sum of the energies of the ground-state fragments formed by the homolytic cleavage of said bond. These fragment’s ground states are confirmed by comparing their singlet and triplet energies. Energies of all radical species are found using restricted open-shell Hartree-Fock references (Gauss et al., 1991; Lauderdale et al., 1991; Watts et al., 1993). Basis set superposition errors should not be present as no long-distance structures are considered, and the bond energy of weakly bound species will not be affected to an extent large enough to affect the overall discussion and conclusions.
3 Results and Discussion
3.1 “Double-Bonded” Molecules
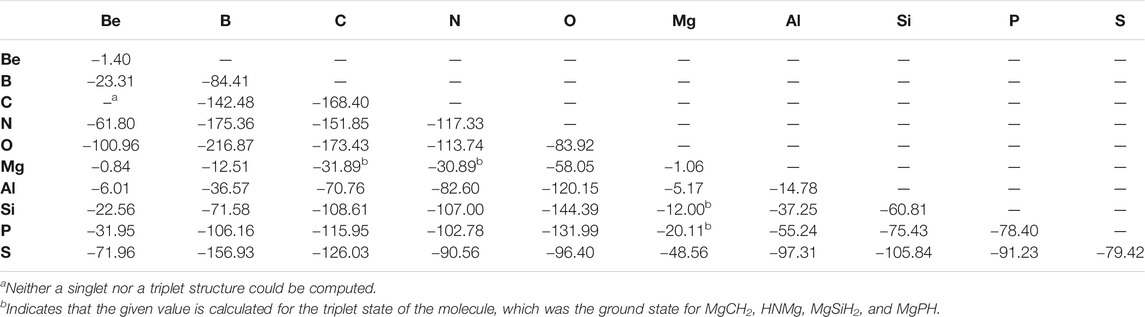
When considering the X = Y BDEs for the overall set of “double-bonded” molecules, a trend of increasing bond strength is usually followed when moving from left to right across a given period as listed in Table 1. For example, the Be = X bond strength increases continuously when shifting the identity of atom X left to right along both periods 2 and 3. The most significant exception to this trend occurs for nitrogen and oxygen bonded to period 2 atoms. Moving left to right, the N = X and O = X bond strengths both peak at boron (−175.36 kcal/mol and −216.87 kcal/mol, respectively) before decreasing afterwards. For benchmarking, the C = C bond in ethylne is computed to be −168.40 kcal/mol, nearly within the error bars of the 0 K experimental value of 171.0 ± 1.2 kcal/mol (Ervin et al., 1990). This mirrors the small error observed for the “single-bonded” species previously (Doerksen and Fortenberry, 2020). Additionally, Table 1 shows that bond strength is almost always lower for a given atom bonded to a period 3 atom compared to its period 2 congener or analogue as heavier atoms have a “reluctance to hybridize” (Kutzelnigg, 1984). For example, the C = S bond in CH2S is weaker than the C = O bond in CH2O. There are four exceptions to this trend in the data set, most notably the O = P bond in HPO at −131.99 kcal/mol, which is much stronger than the O = N bond in HNO (−113.74 kcal/mol).
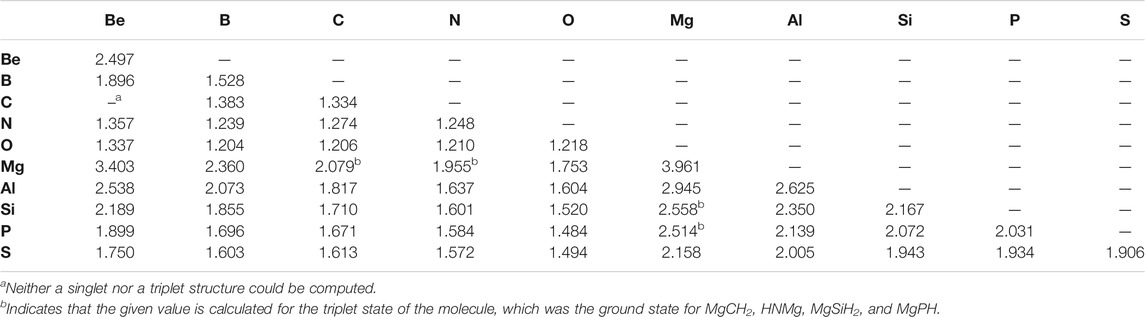
Similarly to the previous work, the bond lengths (Table 2) also correlate with the bond strengths. The longest bond shown is for the MgBe dimer at 3.403 Å. In turn, the weakest X = Y bond in the “double-bonded” set is for Be = Mg (−0.84 kcal/mol) followed by the familial group 2 homonuclear diatomics for the Mg =Mg bond (−1.06 kcal/mol) and Be = Be bond (−1.40 kcal/mol). The bond’s exceptional weakness (all less than 2 kcal/mol) can be explained principally by basic MO theory. The diatomic species that contain these bonds have an equal number of valence electrons occupying bonding and antibonding orbitals, which yields a bond order of 0, meaning that bond formation is not energetically favorable much like that present in noble gas dimers. Additionally, group 2 elements prefer 180° bond angles implying a strong preference for the valence electrons to be found on opposite sides of the atoms (Bassett and Fortenberry, 2018; Palmer and Fortenberry, 2018; Doerksen and Fortenberry, 2020; Watrous et al., 2021). In returning to the bond lengths, the Be = Be, Be = Mg, and Mg = Mg bonds are close to the sum of their constituent atom’s Van der Waals radii rather than their covalent radii. All of these points suggest that these molecules are not really bonds but rather weaker London interactions, thus accounting for the almost negligible bond energy. In order to address a possible 180° bond angle preference in these group 2 dimers, the triplet states have been computed. There are four Mg-bearing molecules in Table 1 where the triplet states are utilized since these are the ground-state configurations. All of the pure group 2 dimer triplets, however, are higher in energy than their singlet counterparts, nearly 25 kcal/mol higher in the case of triplet Be2, implying that group 2 dimers cannot employ low-lying excited states to alleviate their noble gas-like, non-bonding behavior.
The T1 diagnostics for these “double-bonded” species are all in the range 0.025 to 0.015 implying single-reference character (Lee and Taylor, 1989). The notable exceptions are those singlet states containing the Be and Mg Alkaline earth Metals. However, the triplet states of such molecules reduce this value to less than 0.020.
While the bonds to boron are strong here as they are for the “single-bonded” species, the bonds to Be are relatively weak across the board in Table 1, not just to other group 2 atoms. Additionally, the molecules with the strongest “single-bonds” from the previous work (those containing Al/Si/Mg bonded to O) (Doerksen and Fortenberry, 2020) are often not nearly as favorable in the “double bond” format. The best case for aluminum is for HAlO where the Al = O bond energy is computed here to be −120.15 kcal/mol. This is actually 6.22 kcal/mol weaker than the Al−O “single bond” in AlH2OH. Singlet, diatomic MgO has a bond strength of −58.05 kcal/mol, less than half of that for HMgOH. Interestingly, H2SiO is stronger than H3SiOH with a Si = O bond energy of −144.39 kcal/mol, nearly 30 kcal/mol stronger than the Si−O bond of −118.00 kcal/mol (Doerksen and Fortenberry, 2020). Hence, the p-block species retain strong bonding upon removal of two hydrogen atoms resulting in a presumably higher bond order. The s-block atoms lose this bond strength, and the group 13 elements are in between. As a result, the different types of chemistries utilized by Mg and Si, for instance, in reaction with oxides to form premineral species likely varies.
At this point, the strongest “double bonds,” besides those that contain the depleted boron atom, are the usual suspects for higher bond orders of carbon: ethylene, methylene imine, and formaldehyde. Again, this decrease of bond strength in the metal oxides and increase in bond strength of the organic species is not unexpected, but this is the opposite case for the “single-bonded” species (Doerksen and Fortenberry, 2020). As a result, organic chemistry appears to thrive in environments where hydrogen atoms are not present to stabilize small molecules.
3.2 “Triple-Bonded” Molecules
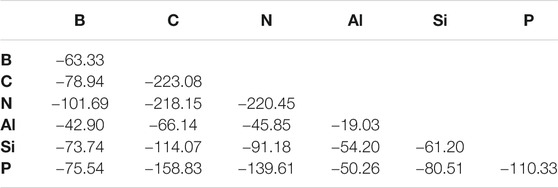
The second set of molecules in this work is similar to the first set, but with ostensibly X ≡ Y bonds. When considering the BDEs, there is a weak trend of increasing bond strength moving from left to right across a given period as shown in Table 3. For example, the B ≡ X bond strength increases continuously when shifting the identity of atom X left to right along both periods 2 and 3. Every exception to this trend involves the bond strength peaking at the middle atom of a given period. For example, the Al ≡ Si bond is stronger (−39.80 kcal/mol) than that of Al ≡ Al (−19.03 kcal/mol) or Al ≡ P (−35.99 kcal/mol). The BDE is lower for a given atom bonded to a period 3 atom than its period 2 congener with one exception of AlP (−50.26 kcal/mol) being stronger than AlN (−45.85 kcal/mol). The largest difference is between N ≡ C and N ≡ Si bonds at a whopping 126.97 kcal/mol.
The T1 diagnostics are, again, typically, in the range of 0.020 or less. The notable exceptions are some molecules containing the B and Al atoms, but these bonds are already weak and strained. Such will not change the interpretation of the results. This also points to a larger consideration that molecules containing B and Al atoms engaging in such bonding are clearly behaving differently from the other p-block species and are unlikely to be detected in astrophysical observations.
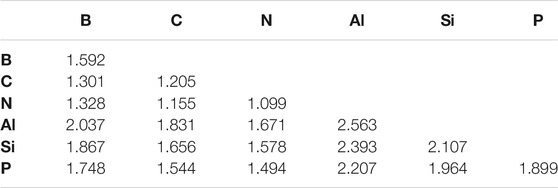
This regime of even fewer hydrogen atoms present in the molecules examined clearly favors the organic/volatile species. The strongest bonds overall are C ≡ C (−223.08 kcal/mol) in acetylene, N ≡ N (−220.45 kcal/mol) in N2, and C ≡ N (−218.15 kcal/mol) in HCN. The bond lengths in Table 4 also follow the bond strengths on the whole with the shortest bond that of the N ≡ N bond even though the C ≡ C BDE is 2.53 kcal/mol greater.
The five weakest bonds in the set are five of the six containing aluminum with Al ≡ Al (−19.03) topping the list. Consequently, p-block aluminum and even silicon weaken in their bond strengths implying that no refractory elements are considered highly stable in such bonding environments. On top of this, seemingly unexpected behavior also emerges. For instance, HCSiH is not of C∞v symmetry like its acetylene analogue. Instead, it assumes a bent, Cs geometry and actually prefers the H2CSi divalent structure as has been known for over 40 years (Murrell et al., 1977). Even so, this is still a surprising result to corroborate with more modern methods. The CCSD(T)-F12b/cc-pVTZ-F12 ZPVE-corrected barrier to linearity is computed here to be 7.40 kcal/mol in preference to the Cs HCSiH structure.
4 Conclusion
The results of the previous (Doerksen and Fortenberry, 2020) and present work imply that hydrogen-rich environments may very well favor gas phase formation of small molecules containing inorganic and refractory atoms as such molecules contain the strongest heavy atom bonds in molecules with highest molar percentage of hydrogen. As the available hydrogen decreases or is dissociated from the system, molecules containing p-block elements, whether volatile or refractory, have the highest BDEs. As the hydrogen percentage decreases further, organic molecular bond strengths (CC, CN, or NN bonds, specifically) increase greatly while inorganic BDEs, even for atoms in the p-block such as B and Si, weaken. This, of course, does not consider larger network covalent structures but highlights that the earliest stages of any small molecule gas phase chemistry will be influenced by different physical conditions of various astronomical environments. As a result, environments with a wealth of hydride species, such as those present in early stages of star formation or cold molecular clouds, likely promote inorganic astrochemistry involving the formation of species such as HMgOH or AlH2OH. Hydrogen-poor environments promote organic astrochemistry and some formation of silicates. Such could help to explain, in part, the astrophysical detection of diatomic SiO (Wilson et al., 1971) and lack of astrophysical lines and spectra linked to diatomic MgO, for instance. Molecular ions may have different bonding behaviors, and that is left for future work.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author Contributions
RCF conceived of the research idea; ESD performed the computations; RCF and ESD analyzed the data, wrote the manuscript, edited the manuscript; and RCF secured funding.
Funding
This work has been supported by NASA Grant NNX17AH15G, the University of Mississippi in the form of start-up funds, and the Mississippi Center for Supercomputing Research through NSF Grants CHE-1338056 and OIA-1757220.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adler, T. B., Knizia, G., and Werner, H.-J. (2007). A Simple and Efficient CCSD(T)-F12 Approximation. J. Chem. Phys. 127, 221106. doi:10.1063/1.2817618
Apponi, A. J., Barclay, W. L. J., and Ziurys, L. M. (1993). The Millimeter-Wave Spectrum of AlOH. ApJ 414, L129–L132. doi:10.1086/187013
Bassett, M. K., and Fortenberry, R. C. (2018). Magnesium Replacement in Formaldehyde: Theoretical Rovibrational Analysis of X∼3B1 MgCH2. J. Mol. Spectrosc. 344, 61–64. doi:10.1016/j.jms.2017.10.012
DeYonker, N. J. (2015). What a Difference a Decade Has Not Made: The Murky Electronic Structure of Iron Monocyanide (FeCN) and Iron Monoisocyanide (FeNC). J. Phys. Chem. A. 119, 215–223. doi:10.1021/jp5110906
Doerksen, E. S., and Fortenberry, R. C. (2020). Coincidence between Bond Strength, Atomic Abundance, and the Composition of Rocky Materials. ACS Earth Space Chem. 4, 812–817. doi:10.1021/acsearthspacechem.0c00029
Ervin, K. M., Gronert, S., Barlow, S. E., Gilles, M. K., Harrison, A. G., Bierbaum, V. M., et al. (1990). Bond Strengths of Ethylene and Acetylene. J. Am. Chem. Soc. 112, 5750–5759. doi:10.1021/ja00171a013
Fortenberry, R. C., and DeYonker, N. J. (2021). Rovibrational Quantum Chemical Treatment of Inorganic and Organometallic Astrochemicals. Acc. Chem. Res. 54, 271–279. doi:10.1021/acs.accounts.0c00631
Fortenberry, R. C. (2020). The Case for Gas-phase Astrochemistry without Carbon. Mol. Astrophysics 18, 100062. doi:10.1016/j.molap.2019.100062
Gauss, J., Lauderdale, W. J., Stanton, J. F., Watts, J. D., and Bartlett, R. J. (1991). Analytic Energy Gradients for Open-Shell Coupled-Cluster Singles and Doubles (Ccsd) Calculations Using Restricted Open-Shell Hartree-Fock (ROHF) Reference Functions. Chem. Phys. Lett. 182, 207–215. doi:10.1016/0009-2614(91)80203-a
Hill, J. G., and Peterson, K. A. (2010). Correlation Consistent Basis Sets for Explicitly Correlated Wavefunctions: Valence and Core-Valence Basis Sets for Li, Be, Na, and Mg. Phys. Chem. Chem. Phys. 12, 10460–10468. doi:10.1039/c0cp00020e
Huber, K. P., Herzberg, G., Gallagher, J. W., and Johnson, R. D. (2018). “Nist Chemistry Webbook,” in Constants of Diatomic Molecules. Editors P. J. Linstrom, and W. G. Mallard (Gaithersburg MD: National Institute of Standards and Technology), 69.
Knizia, G., Adler, T. B., and Werner, H.-J. (2009). Simplified CCSD(T)-F12 Methods: Theory and Benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300
Kutzelnigg, W. (1984). Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. Engl. 23, 272–295. doi:10.1002/anie.198402721
Lauderdale, W. J., Stanton, J. F., Gauss, J., Watts, J. D., and Bartlett, R. J. (1991). Many-body Perturbation Theory with a Restricted Open-Shell Hartree-Fock Reference. Chem. Phys. Lett. 187, 21–28. doi:10.1016/0009-2614(91)90478-r
Lee, T. J., and Taylor, P. R. (1989). A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods. Int. J. Quant. Chem. 36, 199–207.
Murrell, J. N., Kroto, H. W., and Guest, M. F. (1977). Double-bonded Divalent Silicon: Ab-Initio Calculations on the Species HSiN, HNSi, HCSiH, and H2CSi. J. Chem. Soc. Chem. Commun., 619–620. doi:10.1039/C39770000619
Palmer, C. Z., and Fortenberry, R. C. (2018). Rovibrational Considerations for the Monomers and Dimers of Magnesium Hydride and Magnesium Fluoride. J. Phys. Chem. A. 122, 7079–7088. doi:10.1021/acs.jpca.8b06611
Peterson, K. A., Adler, T. B., and Werner, H.-J. (2008). Systematically Convergent Basis Sets for Explicitly Correlated Wavefunctions: The Atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 128, 084102. doi:10.1063/1.2831537
Prascher, B. P., Woon, D. E., Peterson, K. A., Dunning, T. H., and Wilson, A. K. (2011). Gaussian Basis Sets for Use in Correlated Molecular Calculations. Vii. Valence, Core-Valence, and Scalar Relativistic Basis Sets for Li, Be, Na, and Mg. Theor. Chem. Acc. 128, 69–82. doi:10.1007/s00214-010-0764-0
Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A Fifth-Order Perturbation Comparison of Electron Correlation Theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6
Savage, B. D., and Sembach, K. R. (1996). Interstellar Abundances from Absorption-Line Observations with Thehubble Space Telescope. Annu. Rev. Astron. Astrophys. 34, 279–329. doi:10.1146/annurev.astro.34.1.279
Swinnen, S., Nguyen, V. S., Sakai, S., and Nguyen, M. T. (2009). Calculations Suggest Facile Hydrogen Release from Water Using Boranes and Alanes as Catalysts. Chem. Phys. Lett. 472, 175–180. doi:10.1016/j.cplett.2009.02.078
Tenenbaum, E. D., and Ziurys, L. M. (2010). Exotic Metal Molecules in Oxygen-Rich Envelopes: Detection of AlOH (X1Σ+) in VY Canis Majoris. ApJ 712, L93–L97. doi:10.1088/2041-8205/712/1/l93
Trabelsi, T., and Francisco, J. S. (2018). Is AlOH the Astrochemical Reservoir Molecule of AlO? Insights from Excited Electronic States. ApJ 863, 139. doi:10.3847/1538-4357/aad5e0
Watrous, A. G., Davis, M. C., and Fortenberry, R. C. (2021). Pathways to Detection of Strongly-Bound Inorganic Species: The Vibrational and Rotational Spectral Data of AlH2OH, HMgOH, AlH2NH2, and HMgNH2. Front. Astron. Space Sci. 8, 17. doi:10.3389/fspas.2021.643348
Watts, J. D., Gauss, J., and Bartlett, R. J. (1993). Coupled‐cluster Methods with Noniterative Triple Excitations for Restricted Open‐shell Hartree-Fock and Other General Single Determinant Reference Functions. Energies and Analytical Gradients. J. Chem. Phys. 98, 8718–8733. doi:10.1063/1.464480
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., Schütz, M., Celani, P., et al. (2019). Molpro, Version 2019.2, a Package of Ab Initio Programs. from http://www.molpro.net (Accessed 106, 2020).
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., and Schütz, M. (2012). Molpro: A General-Purpose Quantum Chemistry Program Package. Wires Comput. Mol. Sci. 2, 242–253. doi:10.1002/wcms.82
Keywords: bond dissociation energies, refractory astrochemistry, organic astrochemistry, quantum chemistry, astrochemical complexity
Citation: Doerksen ES and Fortenberry RC (2021) Further Astrochemical Insights From Bond Strengths of Small Molecules Containing Atoms From the First Three Rows of the Periodic Table. Front. Astron. Space Sci. 8:723530. doi: 10.3389/fspas.2021.723530
Received: 10 June 2021; Accepted: 29 July 2021;
Published: 13 August 2021.
Edited by:
Nicole Feautrier, Observatoire de Paris, Université de Sciences Lettres de Paris, FranceReviewed by:
Gilberte Chambaud, Université Paris Est Marne la Vallée, FranceMaria Luisa Senent, Consejo Superior de Investigaciones Científicas (CSIC), Spain
Copyright © 2021 Doerksen and Fortenberry. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan C. Fortenberry, cjQxMEBvbGVtaXNzLmVkdQ==
 Edmund S. Doerksen
Edmund S. Doerksen Ryan C. Fortenberry
Ryan C. Fortenberry