Assessment of the arrival signatures of the March 2012 CME–CME interaction event with respect to Mercury, Venus, Earth, STEREO-B, and Mars locations

In March 2012, favorable positions of Mercury, Venus, Earth, Mars, and STEREO-B in the inner Solar System provided an opportunity to understand the global structure and the propagation of two coronal mass ejections (CMEs) across the inner Solar System. On 7 March 2012, the Sun ejected two very fast CMEs from the solar active region NOAA AR11489, which were accompanied by two X-class flares. Initialization and subsequent fast expansion from lower coronal heights of flux rope structures were detected as their early eruption signatures in Solar Dynamics Observatory (SDO) observations. White-light observations have been imaged using SOHO/LASCO and STEREO/SECCHI/COR2 and followed from 00:24 UT on 7 March 2012. We examined the kinematics of the reported CMEs and found a significant exchange of momentum and kinetic energy during the interaction, indicating that the collision was almost inelastic. Furthermore, we observed the arrival of this merged CME event at different distances in the inner Solar System and compared the arrival time with other models. The reported event arrived on Mercury at 04:30 UT; Venus, at 13:28 UT on 7 March 2012; and it took roughly 36 h to reach STEREO-B on 08 March, 03:36 UT. The arrivals at Mercury and Venus are observed in the magnetometer measurements onboard MESSENGER and Venus Express (VEx), respectively. A powerful interplanetary shock was observed on 08 March, 10:19 UT at Earth around 30 h after the two X-class flares and CMEs’ eruption. Subsequently, a south-directed interplanetary magnetic field (IMF) was observed on Earth, indicating the arrival of an interplanetary coronal mass ejection (ICME). This event caused the sudden storm commencement and development of one of the major intense geomagnetic storms of SC 24, with a minimum Dst value of −148 nT. The observations by the Mars Express (MEX) mission indicated the arrival of a merged CME ∼2.5 days after its initial observation at Sun. We have analyzed the evolution of these CMEs and their propagation in the inner heliosphere and arrival signatures at four planetary locations. The propagation and arrival signatures are compared to simulations using the WSA-ENLIL + Cone model and the drag-based model at various vantage points. The study showcases the importance of multi-vantage point observations in understanding the propagation of CMEs and their interactions.

1 Introduction

Coronal mass ejections (CMEs) are massive eruptions of plasma and magnetic fields from the Sun that travel across the Solar System to propagate through the heliosphere and can affect Earth, other planets, and spacecraft. CMEs are considered to be the most significant drivers of severe space weather disruptions (Gosling et al., 1991; Gosling, 1993; Richardson and Cane, 2012). CMEs and their interplanetary consequences (such as CME-driven shocks, sheaths, and magnetic structures) have been observed to be the drivers of up to 87% of all intense geomagnetic storms (Dst = −100 nT) that occurred during 1996–2005 (Zhang et al., 2007). Several studies (Möstl et al., 2012; Lugaz et al., 2017; Scolini et al., 2020) established that CME–CME interactions are likely to increase the impact of individual CMEs on Earth (geo-effectiveness). The interplanetary plasma parameters (e.g., density and speed) change as a result of successive solar eruptions, and their complex magnetic structures can evolve during CME–CME interaction (Palmerio et al., 2021). The interaction of two CMEs can result in either significant deceleration or acceleration (Temmer et al., 2012) or a superelastic collision (Shen et al., 2012). Early kinematical deceleration has been observed for CMEs that collide with strong overlaying magnetic fields (Temmer et al., 2010). The form and orientation of the magnetic flux rope buried in CME is widely acknowledged as having a significant impact on its subsequent propagation and development in interplanetary space (Schmidt and Cargill, 2004; Lugaz et al., 2013). The interaction of multiple interplanetary coronal mass ejections (ICMEs) has gained considerable interest in this context.

Several studies have used multipoint in situ and remote measurements to show transient features and understand how CMEs propagate across the Solar System. For instance, Möstl et al. (2012) identified the arrival of many CMEs at different locations using data from a variety of instruments, such as MESSENGER (Mercury Surface, Space Environment, Geochemistry, and Ranging), VEx (Venus Express), STEREO (Solar Terrestrial Relations), and ACE (Advanced Composition Explorer). They showed that multi-location analysis might be the only way to get a clear picture of a complicated series of events. Multipoint observations were also used by Nieves-Chinchilla et al. (2013) to study the development of stealth CME that is deflected by high-speed streams from many adjacent coronal holes.

In this work, we analyze a space weather event triggered by two successive CME eruptions to understand its early evolution and arrival at different vantage points in the inner heliosphere. The geospace environment was subjected to strong space weather events from 7 March to 12 March 2012, including one of the largest geomagnetic storms of solar cycle 24. This event is basically two CMEs that erupted on 7 March within an interval of one hour; their first appearances on the LASCO/SOHO C2 coronagraph were at 00:24 UT and 01:30 UT, respectively. We analyzed the nature of their collision by estimating kinetic energy and momentum exchange after interaction. Data from a collection of spacecraft (MESSENGER: Mercury, VEX: Venus, ACE/WIND: Earth and STEREO, and MEX: Mars) have been used to obtain a comprehensive picture of CME propagation as it traveled throughout the inner Solar System and compare its arrival time with different models. The data on the eruption of the CMEs were observed and imaged on-disk by the EUV images obtained from different wavelength filters of the SDO/Atmospheric Imaging Assembly (AIA) (Lemen et al., 2012) and off the Sun with the Large Angle and Spectrometric Coronagraph (LASCO) (Brueckner et al., 1995) onboard SOHO (Domingo et al., 1995). This event was previously investigated using stereoscopic approaches by Davies et al. (2013), Patsourakos et al. (2016), and Liu et al. (2013). Davies et al. (2013) have used the generalized self-similar expansion (SSE) geometry to derive the propagation direction, radial distance, and speed profiles using STEREO-A and STEREO-B observations. Patsourakos et al. (2016) showed the evolution and propagation of the reported CMEs. They used the GCS model (Thernisien and Howard, 2006; Thernisien et al., 2009) to demonstrate the orientation of the reported CMEs and concluded that the geomagnetic storm on Earth was due to the CME that erupted at 01:30 UT on 7 March 2012. Liu et al. (2013) studied the CME’s Sun-to-Earth kinematics by combining wide-angle heliospheric imaging and interplanetary radio type II burst observations. They have mentioned that since Mars was almost radially aligned with Earth during the 7 March CME, the CME was likely to impact both Earth and Mars. Liu et al. (2014) analyzed the effect of this event up to 120 AU after 10 days of occurrences using Voyager-1 observations. In this paper, we have presented the kinematics and global structure of the reported CME events. During this period, MESSENGER (Solomon et al., 2001), VEx (Zhang et al., 2006), ACE (Lepping et al., 1995), and Mars Express (MEX) (Barabash et al., 2004) were separated only by 110˚ heliographic longitudes, and hence, the arrival of the interacting ICMEs could be detected at five separate points in interplanetary space at five different times. We used the drag-based model (DBM; Vrsnak et al., 2012) and the Wang–Sheeley–Arge (WSA)-ENLIL + Cone model (Odstrcil, 2003) to calculate the arrival time of ICMEs at different vantage points in the inner Solar System.

2 Data sources and methodology

We considered the classification of the active region’s magnetic configuration and area to explore its beginning and evolution. The Space Weather Prediction Center (ftp://ftp.swpc.noaa.gov/pub/warehouse/) has detailed information on the magnetic configuration and territory occupied by the active region. Images obtained from the 94 Å and 193 Å filters of the Atmospheric Imaging Assembly (AIA) onboard the Solar Dynamics Observatory (SDO; Pesnell et al., 2012) revealed flux rope orientation. The onset time and initial speeds of CMEs are determined from white-light observations taken by the Large Angle and Spectrometric Coronagraph (LASCO) onboard the Solar and Heliospheric Observatory (SOHO) spacecraft. Apart from this, images from the COR2 coronagraphs of the SECCHI instrument onboard STEREO (Howard et al., 2008) were also used. The magnetic field data taken by the magnetometer onboard MESSENGER are used in this investigation (MAG; Anderson et al., 2007). The data are obtained from NASA’s Planetary Data System (PDS) archive’s Planetary Plasma Interactions (PPIs) node (ppi.pds.nasa.gov/index.jsp). In this study, data with a 10-s time-averaged resolution were used. The data from the fluxgate magnetometer (Zhang et al., 2006) onboard VEx were used to detect the passage of ICME at the VEx orbit. The data from the magnetometer, which is a part of the In situ Measurements of Particles and CME Transients (IMPACT) (Luhmann et al., 2008), SUIT, and the data from the Plasma and Suprathermal Ion Composition (PLASTIC) instrument (Galvin et al., 2008), onboard STEREO-B were used to analyze the characteristics of the CME at 1 AU. The period between the occurrence of a CME (as visible in LASCO images) and the start of the interplanetary shock at 1 AU is used to estimate the arrival time of the CME. The data on solar wind plasma and magnetic field at Sun–Earth L1 and the Dst (SYM/H) observations were obtained from the Operating Missions as a Node on the Internet (OMNI) database originated from Advanced Composition Explorer (ACE)/WIND in situ observations (http://omniweb.gsfc.nasa.gov/). The observations near Venus were from the VEx mission. The magnetometer data from VEx (MAG; Zhang et al., 2006) with 4s resolution were used in this study. The observations near Mars were from the electron spectrometer (ELS) instrument, which is a part of the Analyzer of Space Plasma and Energetic Atoms (ASPERA-3) onboard on MEX spacecraft. For our study, we have taken the MESSENGER, VEx, and MEX data from http://amda.cdpp.eu/. The WSA + ENLIL Cone model is a global 3D MHD model simulated and provided by NASA’s Goddard Space Flight Center’s Community Coordinated Modeling Center (CCMC) (Mays et al., 2015) for space weather research and is available at

https://ccmc.gsfc.nasa.gov/results/viewrun.php?domain=SH&runnumber=Shirsh_Soni_110922_SH_1. The DBM (Vrsnak et al., 2012) is based on the concept that drag force controls the kinematical profile of a CME in interplanetary space (Vrsnak and Gopalswamy, 2002; Vrsnak and Gopalswamy 2002; Zic et al., 2015). The drag force is given in its simplest form by FD = (v - w)|v - w|, where w is the solar wind speed and v is the CME speed. The drag parameter γ is defined as γ = C_d A_CME ρ_sw m_CME, where C_d is the drag coefficient, A_CME is the cross-sectional area of the CME, ρ_sw is the density of the solar wind, and m_CME is the mass of the CME. C_d is a dimensionless number, typically of the order of unity. The DBM is accessible to the general public via a web interface at http://oh.geof.unizg.hr/CADBM/cadbm.php. The DBM has been tested with various input drag parameter values (mentioned in Section 4.6). The kinematical profile of CME eruption is calculated and compared to the kinematical profile determined from observations.

3 Results

3.1 Overview of the source region and evolution of CME events

Figure 1 shows the location of the trajectories of Mercury, Venus, Earth, Mars, and STEREO-B in the heliographic ecliptic plane on 7 March 2012. This provides the relative planetary and satellite positions during the period of our study. Compared to its previous cycles, solar cycle 24 appears to show low activity (Soni et al., 2020). However, throughout solar cycle 24, a few sunspot regions were highly active, resulting in a substantial number of flare occurrences and related CMEs. The active region AR11489 appeared on the east limb of the Sun on 03 March 2012 and remained active until 15 March 2012, when it moved to the rear of the Sun. It had an overall magnetic configuration of on 7 March 2012 (is a sunspot group with a magnetic configuration but contains one (or more) configurations), where a bipolar sunspot group complex is enough to allow a line to be drawn between spots of opposite polarity and is the umbrae of opposite polarity in a single penumbra (Ireland et al., 2008) and expanded to 1,270 millionths of a solar hemisphere (Msh) at the visible solar disc. During its journey from the Sun’s east to west limbs, AR11489 generated 58 X-ray flares (X-class: 03; M-class: 13; and C-class: 42). However, after crossing the Sun’s central meridian, the number of flares steadily decreased, as shown in Figure 2. Extreme flaring and ultra-fast CMEs resulted in space weather disturbances in geospace and beyond. The most significant erosive activity in this active region occurred on 7 March 2012, when a barrage of two X-class eruptive flares occurred in rapid sequence, each accompanied by two ultrafast CMEs (speed >1,800 km s⁻¹), both of which erupted within an hour (Figure 2). The AR11489 was near the east limb of the Sun on 7 March 2012, as shown in Figure 3A. The commencement of the X2.7-class flare was recorded at around 22:05 UT in the two wavelength bands of 1–8 Å and .5–4 Å by the X-ray sensor (XRS) onboard the GOES-15 satellite on 7 March 2012. Figure 3B depicts the flare event’s X-ray flux profiles in two wavelength bands. The fluxes in these channels began to climb around 22:07 UT, reaching a peak in approximately 4 minutes. In both the wavelength bands, the flare started at 21:30 UT, had its first peak at 22:07 UT, and then decreased for few minutes. Again, the flux started to rise, the second enhancement occurred at 23:30 UT, and then fell back to the background after almost 2 hours. The .5–4 Å component of the X-ray flux rose by more than three orders of magnitude when compared to the average background value. In comparison to the background, the magnitude of the soft X-ray (1–8 Å) spectrum increased by around two orders of magnitude. The hard X-ray was most likely produced by effective heating at the flare location. From the EUV images obtained from SDO/AIA 94 Å and 193 Å filters, we can estimate the direction of CMEs’ eruptions. The first CME (CME-1) erupted in a northeasterly direction, whereas the CME linked with the second flare (CME-2) erupted in a southwesterly direction (Figures 3C, D). We followed the propagation of these merged CMEs in the heliosphere by observing images obtained by three viewpoints, namely, STEREO-A, LASCO/SOHO, and STEREO-B, as represented in Figures 3E–H. We covered the large angle of field of view to observe their path and orientation by H1 and H2 observations of STEREO-A and STEREO-B (Figures 3I−L).

FIGURE 1

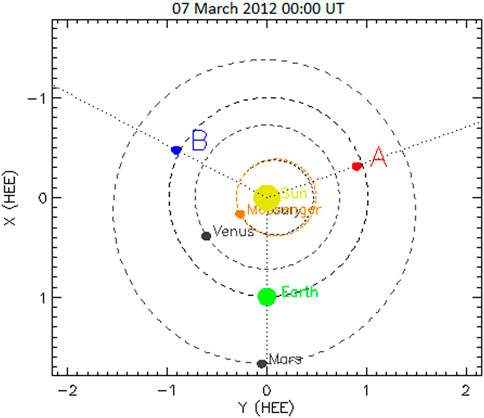
FIGURE 1. Position of STEREO-B is shown with the blue circle; STEREO-A, with red; Mercury (MESSENGER—orange); Venus; Earth (green circle); and Mars on 7 March 2012 00:00 UT.

FIGURE 2

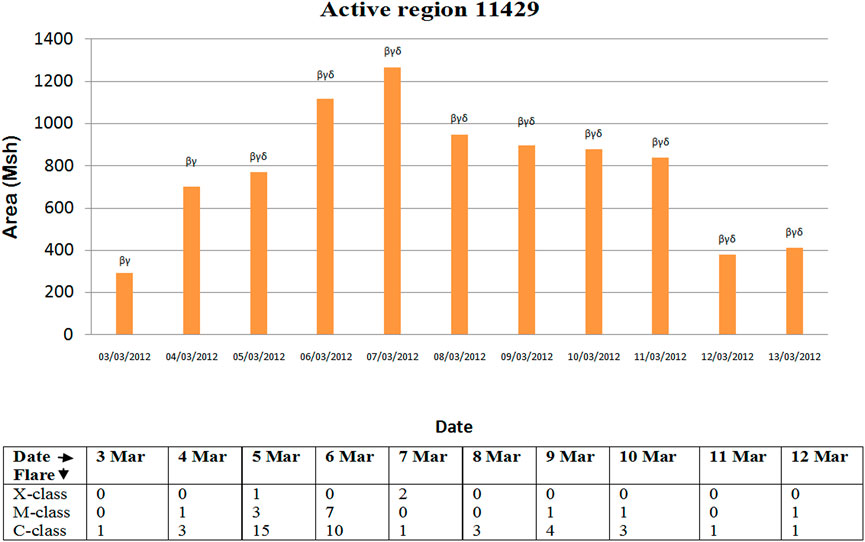
FIGURE 2. Bar chart showing the evolution of active regions in the area and magnetic complexity concerning the time.

FIGURE 3

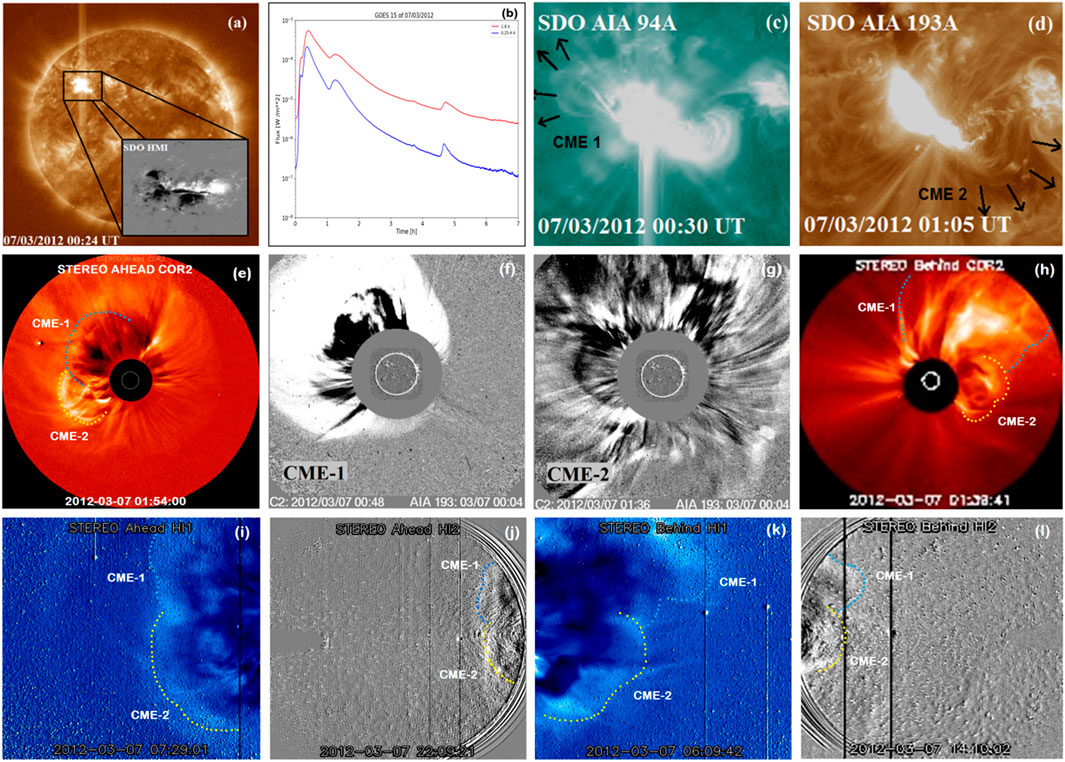
FIGURE 3. (A) SDO/AIA image of the solar disk on 7 March 2012 in the 94 Å and SDO/HMI filters (in highlighted square box). (B) Solar flares observed in 1–8 Å (red) and .25–4 Å (blue) wavelength bands by the X-ray sensor onboard the GOES satellite. (C)–(D) SDO/AIA EUV images in 94 Å and 193 Å filters showing the source location CME. The arrows represent the direction of CME’s fronts. Image (E) shows the reported CMEs in the field of view of STEREO-A COR2 CME-2. Image (F) and (G) present the eruption of CME-1 and CME-2 observed by C2 coronagraph of LASCO/SOHO, respectively. Image (H) shows the reported CMEs in the field of view of STEREO-B COR2. In the bottom panel, image (I–L) shows the propagation of merged CMEs in the heliosphere imaged in H1 and H2 field of view of STEREO-A and STEREO-B (blue and yellow dotted curved lines represent the position of CME-1 and CME-2, respectively).

3.2 Simulations of WSA-ENLIL + Cone model

The WSA model (Arge and Pizzo, 2000; Arge et al., 2004) has been widely used in space weather operations across the world, together with the global heliospheric ENLIL solar wind model (Odstril et al., 1996; Odstril et al., 2004). This model consists of three components: the WSA coronal model, which estimates the outflow of solar wind up to the solar wind critical point at 21.5 Rs; the ENLIL-3D magnetohydrodynamic numerical model, which provides a time-dependent characterization of the background magnetic field and solar wind plasma into which a CME can be introduced at the inner boundary (21.5 Rs); and the Cone model, which assumes isotropic growth, constant CME cone angular width, and radial propagation, is a typical technique for estimating the 3D CME kinematic and geometric characteristics (Zhao et al., 2002; Xie et al., 2004). A CME disturbance is often represented as slices of a spherical homogeneous plasma cloud with constant speed, temperature, and density as a time-dependent inner boundary condition with a stable magnetic field in the WSA-ENLIL model. Simulation data from DONKI (API) were used via a web service application program interface: https://kauai.ccmc.gsfc.nasa.gov/DONKI. The kinematical characteristics and source locations of both the reported CMEs were provided as input parameters to run the simulations. We have provided radial speed, 2,684 km/s; longitude, 31°; latitude, −323°; and full width, 27.1° for CME 1, and radial speed, 1,825 km/s; longitude, −12.8°; latitude, −320°; and full width, 23.4° for CME 2 as inputs in the model to simulate events from 7 March 2012 to 10 March 2012. Figures 4A–D show the snapshots from WSA-ENLIL + Cone simulations showing the arrivals of CME at Mercury, Venus, Earth, STEREO B, and Mars, respectively. The colors represent the density (as represented in the color bar). Whenever the simulated time series derivative of the dynamic pressure reaches a threshold at each site, the expected arrival times are automatically calculated and specified in DONKI for hits at all locations (Mercury, Venus, Earth, STEREO-B, and Mars). We have calculated the CME arrival time prediction error (Terr) by comparing the observed and modeled arrival time of CME. We have summarized the calculated arrival time and Terr for various locations in Table 1. The average Terr for all five locations is ∼4.6 h. It may be noted that Rollett et al. (2014) also presented the kinematics of these CME events into interplanetary space. They used STEREO/H1 observations to fit the self-similar expansion geometry (SSE; Davies et al., 2012). Based on the assumption of constant speed propagation, fixed direction, and the front of CME as a circle with fixed angular width, they described that the flank of CME merged with each other at near corona and that the merged CME front was propagating outward from the Sun into the interplanetary medium. They demonstrated that the southwest-directed segment approaches Earth and causes a major geomagnetic storm. Simulations using the WSA-ENLIL + Cone model show a similar scenario (Figure 4), where the northeast segment of the merged CME collided with Mercury, Venus, and STEREO-B and the southwest-directed segment hit Earth and Mars.

FIGURE 4

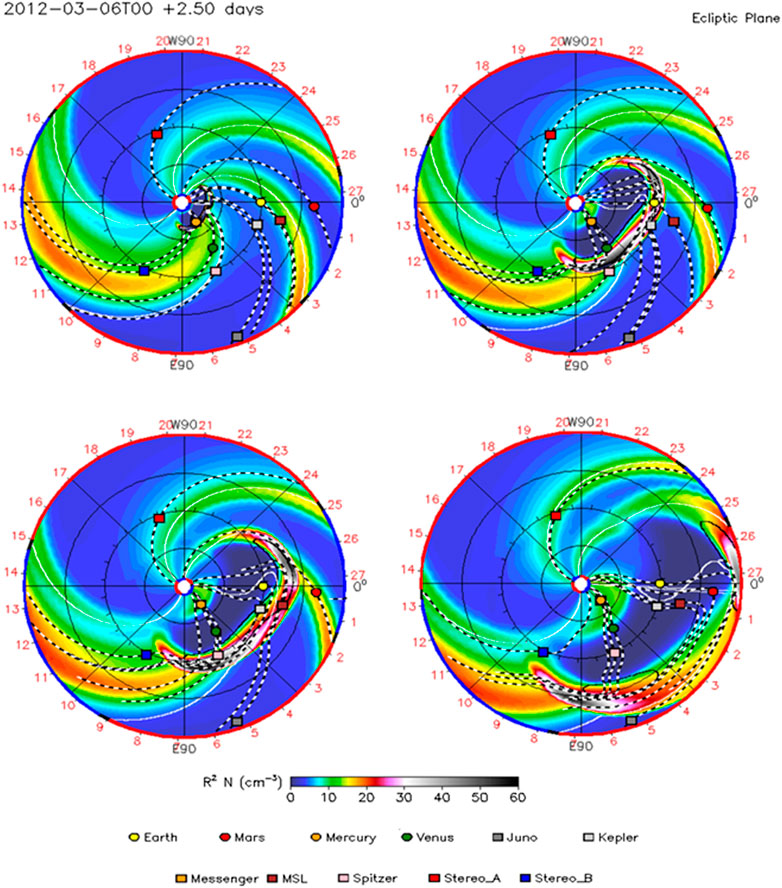
FIGURE 4. WSA-ENLIL + Cone model inner heliospheric simulation snapshots showing the solar wind density (color contour) and interplanetary magnetic field (IMF). The images show the CME arrival at Mercury, Venus, STEREO-B, Earth, and Mars. The scales for the density are given by the color bars at the right side. The relative positions of Mercury, Venus, Earth, Mars, and other spacecraft are indicated with the colored symbols.

TABLE 1

TABLE 1. Calculated hit time of shock by the WSA-ENLIL + Cone model at various locations in the inner Solar System along with the prediction error compared to the observed shock arrival time.

3.3 The nature of collision, energy, and momentum exchange

We can observe CMEs through white-light coronagraphs. These observations are based on the Thomson-scattered photospheric light from the electron within CME. The intensity of the scattered photos can be converted into the number of electrons, and then the mass of CME can be calculated. To calculate the true value of the mass of CME and the true direction of propagation, we use the method suggested by Calninno and Vourlidas (2009). Due to the effects of the Thomson-scattering geometry, the intensity of an observed CME is dependent on the angle it makes with the observed plane of the sky. From the intensity images observed from SECCHI-COR2 on STEREO-A and -B, they have calculated the integrated line-of-sight electron density and mass. Following this, we have estimated the masses of CME-1 and CME-2 to be 2.8 × 10¹⁵ kg and 5.4 × 10¹⁵ kg, respectively. Although CME is a three-dimensional structure, here we are estimating true masses, assuming that the mass of CME is concentrated on the plane of sky. So, there should be some uncertainty. But several studies (Shen et al., 2012; Mishra et al., 2016) show that the uncertainty of mass, in order to better understand the variation of the restitution coefficient, has been observed to be insignificant in determining the nature of interaction. To understand the nature of these highly magnetized CME collisions, we must calculate the coefficient of restitution (e) of CME-1 and CME-2 interaction. The coefficient of restitution evaluates the efficiency to rebounding (bounciness) and is defined as the ratio of their relative velocities of separation to relative velocity of approach. As a result, for e < 1, e = 1, and e > 1, collision is classified as inelastic, elastic, or super-elastic, and the kinetic energy after the interaction is found to be lower, equal, or higher than before the interaction. We calculated the velocities of CME-1 and CME-2 before collision using the COR2 field of view u₁ = 2,684 km s⁻¹ and u₂ = 1,825 km s⁻¹, respectively, and estimated velocities after interaction are v₁ = 2,100 km s⁻¹ and v₂ = 1,700 km s⁻¹ for CME-1 and CME-2, respectively. The estimated velocities from the observation have some inaccuracies and consequently do not show conservation of momentum, which is a compulsory condition of interaction. Therefore, we cautioned ourselves not to estimate the restitution coefficient by using before and after collision velocities directly, as this can lead to an erroneous calculation of the restitution coefficient. To prevent it, we used a method suggested by Mishra and Srivastava (2014) to estimate the theoretical values of velocity for CME-1 and CME-2 after collision, which follow the condition of conservation of total momentum for the interaction and to be closest to the observed velocities. We estimated the range of e and calculated the theoretical value of velocities (v_1th,v_2th) for CME-1 and CME-2 as v_1th = 1,852 km s⁻¹ and v_2th = 2,378 km s⁻¹, respectively, by using the aforementioned formula (for more details, see Mishra and Srivastava, 2014; Mishra et al., 2015). By using mass (m₁ and m₂) and estimated velocity values for CME-1 and CME-2 pre- and post-collision, we discovered that the restitution coefficient (e) was .46. As a result, our calculations show that the reported CME collisions are near-inelastic in nature. Before interaction, the kinetic energies of CME-1 and CME-2 were 3.7 × 10²⁰ J and 4.9 × 10²⁰ J, respectively, and we noticed that after interaction, the kinetic energy of CME-1 decreased by 32%, while the kinetic energy of CME-2 increased by 32% to their corresponding values before the collision. We also observed that after interaction, the momentum of CME-1 increased by 31% and deceased by 30% for CME-2 compared to their pre-collision momentum. The following analysis shows the proof of exchange of momentum and kinetic energy take place during the interaction of CMEs.

4 Arrival of CMEs at various locations in the inner Solar System: Observations

4.1 Observations at Mercury

In Figure 5, the distance of the orbit of the MESSENGER spacecraft from Mercury is plotted in panel (a). The panels (b) and (c) show the total magnetic field and component of the magnetic field in RTN coordinates, respectively. In this case, R points radially away from the Sun, T is the vector product of R and points to the solar rotation axis, and N completes the right-handed coordinate system. The panel (d) shows the projection angle Φ_RTN between the magnetic field and R-T plane and directed toward R. θ_RTN plotted in panel (e) represents the latitude angle of the magnetic field vector of the R-T plane and can be defined as sin⁻¹ (BN/B). As mentioned in the previous sections, the north-east segment of merged CME (front of CME-1) was toward the direction of Mercury. The MESSENGER was inside the Hermian magnetosphere at the time of the ICME’s arrival at Mercury, so we could not get the sudden increase in magnetic field strength as a signature of shock arrival, but we assume it arrives at 04:30 (15 min) UT and take it as possible shock arrival time. According to Good and Forsyth (2016), the parameters required for identifying any ICME recorded by MESSENGER are 1) reasonably monotonic, smooth rotations of the magnetic field direction, coinciding with 2) an elevated magnetic field intensity compared to the ambient solar wind, which 3) last for at least 4 h. We used these criteria to determine the imprints of CME that occurred on 7 March 2012. As depicted in Figure 5, the MESSENGER sensor detected perturbations in the magnetic field on 7 March 2012 at 04:30 UT (Figure 5). Mercury was toward the east of Earth at that time, with a radial distance of ∼68 Rs from the Sun. ICME had a very significant field magnitude increase spanning .43 days, with a very smooth rise and fall in the field magnitude that is common in magnetic clouds. The magnitude of the field is 3.5 times greater at its peak within the flux rope than that of the background solar wind, clearly confirming the second identification requirement. The shock caused by the flux rope was detected at 04:30 UT, and the duration of the flux rope interval was ∼10 h (ending at 12:50 UT), as presented in Figure 5. The magnetometer recorded the leading edge of the flux rope at ∼06:00 UT on 7 March 2012, and the trailing edge of the flux rope between 16:00 and 18:00 UT. It was observed that the overall magnetic field had reached its maximum magnitude of ∼ −130 nT.

FIGURE 5

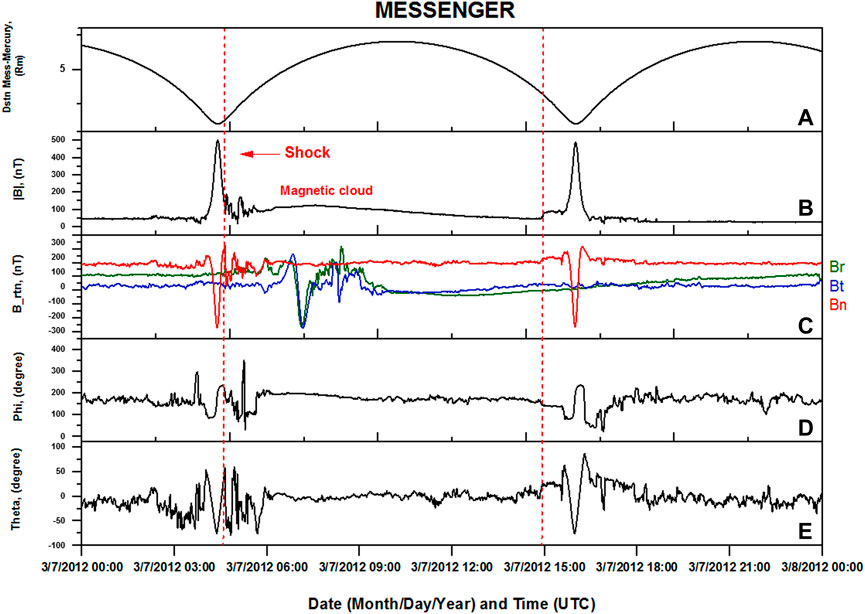
FIGURE 5. ICME signatures observed by MESSENGER during its orbit phase in March 2012. First vertical red dotted line depicts the arrival of shock. The distance of spacecraft from the Mercury surface is shown in (A). Panels (B) and (C) show the total magnetic field and its components (R, N, T coordinates), respectively. Panels (D) and (E) show the phi and theta components, respectively.

4.2 Arrival at Venus from Venus Express

The ICME signatures are seen in situ on Venus as ejecta. The magnetometer onboard the VEx offers a strong signal of the ICME arrival, as seen in Figure 6. Although Venus does not have an intrinsic magnetic field, it does have an induced magnetosphere caused by its interaction of ionosphere with the solar wind, which has many of the same characteristics as an actual magnetosphere, such as bow shock followed by a region of magnetosheath between the ionosphere and solar wind (Bertucci et al., 2011). As we observe from the WSA-ENLIL + Cone model, the north-east segment of merged CME impacted Venus. ICME arrived after 11 h, at a heliocentric distance of 154 Rs, east of Earth, on the same day (at 13:28 UT 07 March 2012). The shock rise in the magnetic field occurred around ∼13:28 UT on 07 March 2012, with a simultaneous increase in magnetic field variation in all magnetic field components. This shows that the magnetic field has been compressed. ESA reported that VEx has experienced high doses of radiation associated with the eruption of flare/CME on 7 March 2012, which causes the temporary deactivation of startracker cameras (ref: https://www.esa.int/Enabling_Support/Operations/Solar_flares_over_Venus_Express_restarts_science_investigations). Following this, when the shock arrived at Venus, VEX-MAG and plasma detectors got saturated, and due to this we were unable to identify the boundary of ICMEs.

FIGURE 6

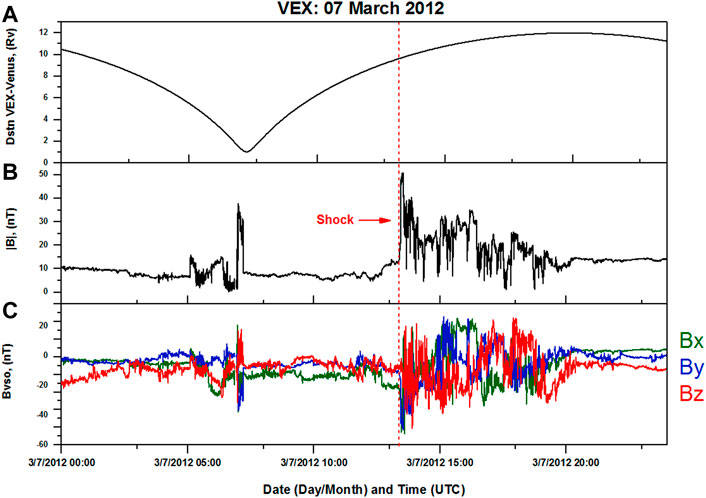
FIGURE 6. (A) Altitude of the VEx orbit in Venusian’s radii (Rv), (B) total magnetic field, and (C) components of magnetic field observations by VEx in VSO coordinates, where x is in the positive direction of the Sun along the Sun–Venus line, y is positive in the direction opposing orbital motion in the Venus orbital plane, and z is positive in the northward direction and parallel to the pole of the orbital plane. The vertical red dotted line marks the observed shock arrival (13:28 UT, 07 March 2012).

4.3 ICME arrival at STEREO-B

One day after the arrival of north-east segment of the merged CME at Venus, the ICME is detected by STEREO-B. As illustrated in Figure 7, the PLASTIC instrument provided in situ sampling of solar wind plasma, while the insights on magnetic field fluctuations were provided by a magnetometer onboard. During this time, the STEREO-B spacecraft was 110° behind Earth (Figure 1). So, we hypothesize that the enhancements detected in STEREO-B magnetometers at 13:40 UT on 8 March 2012 were caused by the flank (north-east segment) of merged CMEs. The magnetometer detected the magnetic field compression, which lasted around 15 h at STEREO-B (Figures 7A, B). The plasma parameters of the solar wind at STEREO-B show an increase in speed followed by a decrease and a slower increase in proton density (Figures 7E, F, respectively). The flanks of the CME structure interact with STEREO-B, as shown by the WSA model, resulting in the ejecta signatures. These variations detected at STEREO-B, beginning at 13:40 UT, indicated the arrival of an ICME. The isolated signature can also be observed around 11:00 UT as an increase in solar wind density and the phi parameter (Figures 7C, E), which do not correspond with solar wind velocity and total magnetic field. This variation in the ambient field may be due to some other transient features.

FIGURE 7

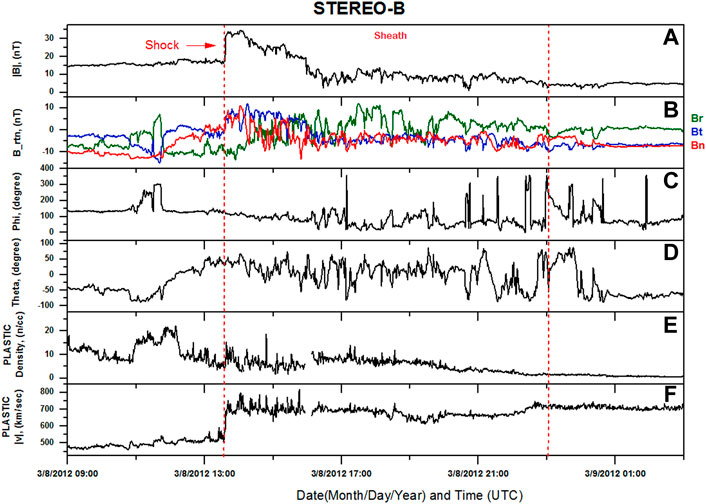
FIGURE 7. ICME sheath followed by shock detected by STEREO-B (within dotted red lines). From top to bottom (A–F), the panels show the total magnetic field; x, y, and z components of the magnetic field; phi; theta; density; and velocity, respectively. Theta and phi are the projection angles, as defined in Section 4.1.

4.4 ICME arrival at Earth

The WSA-ENLIL + Cone model simulations showed that the south-west segment of the merged CME was Earth directed. Figure 8 shows the interplanetary magnetic and plasma properties of disturbances related to the ambient solar wind and the CME recorded at 1 AU. Figures 8A–H from top to bottom show the variations in total magnetic field strength (nT), z-component of ambient solar wind magnetic field (nT), proton density (n/CC), proton temperature (K), flow pressure, plasma beta, flow velocity, and the symmetric horizontal (SYM/H) component of geomagnetic disturbance, which is the high-resolution Dst index (nT), respectively. When an IP shock comes into contact with the magnetopause of Earth, the magnetosphere is greatly compressed, resulting in a sudden increment of the geomagnetic H-component on the ground at mid and low latitudes, which can be traced as the sudden storm commencement in SYM/H at 10:15 UT on 8 March 2012. Figure 8 also shows that the signature of shocked plasma, denoted by a green line, demonstrates a sudden increase in the total magnetic field and plasma characteristics around 10:19 UT on 8 March 2012. After the shock, the sheath formed, and the magnetic cloud began at 01:00 UT on 9 March 2012 and lasted until 05:50 UT on 9 March 2012. The temporal evolution of the horizontal component of geomagnetic disturbance (i.e., SYM/H) shows a small change followed by the initial shock on 8 March 2012 at 10:19 UT, which was accompanied by a decrease in SYM/H, first to −105 nT on 9 March 2012, and then begins to recover.

FIGURE 8

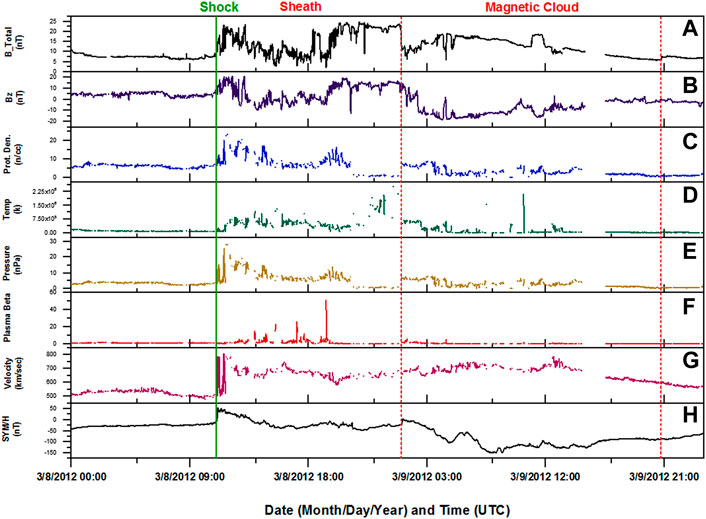
FIGURE 8. IP shock and ICME signatures at the Sun–Earth L1 point. The panels are (top to bottom) the total magnetic field (A), Bz component of the magnetic field (B), proton density (C), temperature (D), flow pressure (E), plasma beta (F), and solar wind velocity (G). Sym-H variation is shown in (H). The green and red dotted lines show the arrival of the shock and magnetic cloud of the ICME, respectively.

4.5 In situ measurements at Mars using MEX

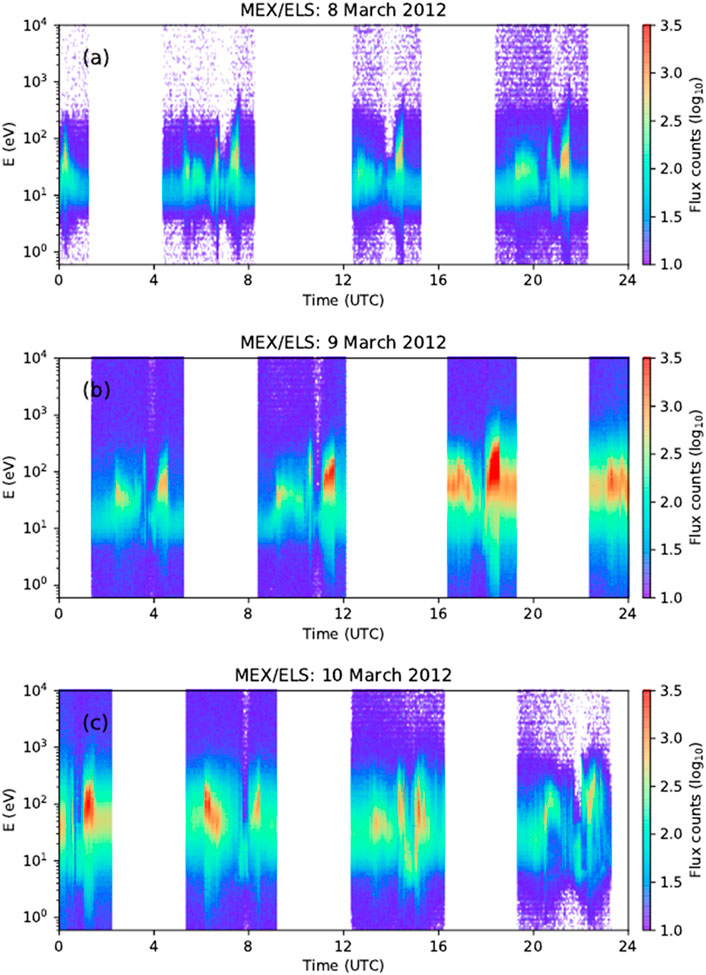
Due to the non-availability of magnetic field and solar wind plasma data from Mars Express during this period, detecting ICME and shock at Mars is a bit more difficult than those from other vantage points. There is evidence of solar wind disturbances arriving at Mars, albeit the dates and times could be less accurate than those reported at Mercury, Venus, Earth, and STEREO-B, as the identification is far less clear. Figure 9 shows the ELS spectrogram for 08–10 March 2012. Compared to 08 March 2012, there is an enhancement in electron flux on 09 March 2012, from the second orbit onward. In the second periapsis of 9 March 2012, enhanced electron fluxes from both the ionosphere and the solar wind can be seen. The ELS shows an enhancement in electron flux and that the electrons reach high energies. These observations indicate that CME has arrived on Mars on this day because the CME sheath contains denser and faster plasma than the typical slow solar wind, and the CME adds additional energy to Mars-induced magnetosphere. However, the ELS data could not be used for a more precise definition of the arrival time, but the observations indicate that the ICME arrived at Mars after ∼10 UTC on 9 March 2012. Furthermore, due to a lack of continuous observations, particularly magnetic field measurements, we are unable to separate the shock and ICME signatures at Mars. The ELS spectra can be seen to recover to quiet time values of fluxes on the following day.

FIGURE 9

FIGURE 9. ELS spectrogram for MEX from 8 March 2012 to 10 March 2012 (A–C).

4.6 Arrival time prediction by the drag-based model

The input parameters for the DBM are CME initial radial distance (r₀), asymptotic solar wind, CME speed at r₀ (v₀), ambient solar wind speed, and drag parameter. The DBM is accessible to the general public via a web interface at http://oh.geof.unizg.hr/CADBM/cadbm.php. The in situ observations at Sun–Earth L1 recorded an average plasma flow speed of ∼450 km s⁻¹, which we used as the asymptotic solar wind speed. We constructed the kinematical profile of CME-1 for Mercury, Venus, and STEREO-B (as the front of CME-1 was north-east direction) and CME-2 for Earth and Mars (as the front of CME-2 was south-west direction) based on this assumption and compared it to the kinematical profile inferred from observations. After providing all of the information for the CME-1 and CME-2 to the model, we have calculated the arrival time along with the estimated shock speed at different locations, which are listed in Table 2. The DBM calculates the arrival of ICMEs at different sites with an average time error of 6.2 h. However, it may be noted that the DBM is designed to calculate the arrival time of any individual CME, but in this case, we are trying to simulate two CME events that interacted at their flanks in the near corona and propagated into the interplanetary space as a wide front of merged CME. As both the CME events were extremely fast, they might get accelerated after the interaction. Therefore, we can conjecture that this delay in arrival time in the calculation by the DBM, compared to observations, could be due to the interaction of CME-1 and CME-2. The transit time predicted by the DBM is very close to the time estimated with the WSA-ENLIL model.

TABLE 2

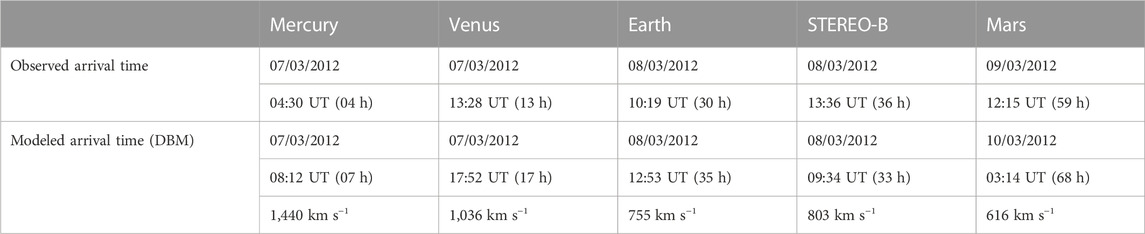
TABLE 2. Observed and calculated time of shock/CME arrival at various locations, compared with the arrival time and velocity estimated by the DBM.

5 Conclusion

ICMEs are in situ measurements of CMEs that can be observed by several spacecraft at various locations in the inner heliosphere. We refer to the CME as an ICME, with the signature of the shock coming first, followed by the sheath and magnetic structure (Rouillard et al., 2011). ICMEs are the primary causes of space weather disruptions, therefore studying their dynamics and kinematics has drawn a lot of interest in recent years. The development of a variety of methods to evaluate and forecast the direction, speed, and arrival time of a CME to Earth and other sites in the heliosphere has been spurred by EUV and white-light observations. The work presented here is related to a merged ICME as it propagates across the inner Solar System from the Sun to Mars. This is achieved by combining data from five distinct vantage points with WSA-ENLIL + Cone and drag-based prediction models. Early on 7 March 2012, two CMEs erupted from the Sun, at around the Sun–Earth line. Signatures of these merged CMEs were found at Mercury, Venus, STEREO-B, Earth, and Mars in plasma and/or magnetic data. Although not all of the in situ measurements produce the same parameters for simple comparison, the times of transient arrivals at several places have been successfully estimated, albeit with considerable uncertainty.

The source of these CMEs was NOAA AR11489, which had heliographic coordinates (N18E31) and a photospheric magnetic field configuration βγδ (Figure 2). The active region’s photospheric line-of-sight HMI magnetogram revealed a complicated polarity inversion line with significant gradients and fields (Figure 3A). Along the polarity inversion line, strong shearing movements were also seen (Chintzoglou et al., 2015). The two flares occurred on 7 March 2012 [Figure 3 panel (B)], and subsequently, two ultra-fast CMEs were launched from AR11489. In the 94 Å and 193 Å SDO/AIA channels, flux rope structures were found in the surrounding corona. CME-1, which was linked with the initial flare, was headed to the north-east (Figure 3C), while CME-2 (Figure 3D) was related with the second flare and was directed to the south-west. The large CME-driven mass eruption resulted in a post-eruption arcade bordered by coronal dimming. Linear fits of CMEs from SOHO LASCO C2/C3 height–time measurements available at the Coordinated Data Analysis Workshops (CDAWs) (Yashiro et al., 2004) yielded the speeds of 2,684 km s⁻¹ and 1,825 km s⁻¹, respectively. Remote white-light observations and in situ measurements at diverse places constrain the spatial structure and propagation of these CMEs. The arrival timings of the ICME on Mercury, Venus, STEREO-B, and Earth are interpreted from a rise in the interplanetary magnetic field, whereas on Mars, they are interpreted from a rise in electron counts and energy in the ELS spectrogram (MEX). In contrast to the reported CME event’s geo-effectiveness, previous research (Patsourakos et al., 2016) indicates that the south-west segment of the merged CME was the Earth-directed event, causing an intense geomagnetic storm at Earth.

The collision kinematics and post-interaction behavior are important for a better prediction of CME arrival at 1 AU. In the present case, the momentum increased by 31% and decreased by 30% for CME-1 and CME-2, respectively, compared to the values of the pre-interaction. Our study shows that the estimated restitution coefficient is .46, which proves that the nature of interaction is nearly inelastic. We analyzed the total kinetic energy of the system during the collision using the calculated mass and velocity pre- and post-interaction. We noticed that the kinetic energy of CME-1 decreased by 32%, while the kinetic energy of CME-2 increased by 30% compared to their values before collision, which proves the claim that there is a significant exchange in their dynamics after CME–CME collision. In this study, we evaluated the propagation of these CMEs to different locations using observations and model simulations. The WSA-ENLIL + Cone model simulations yield arrival predictions with an average error of ∼4.6 h in arrival time compared to observations. We also used the drag-based model (Vrsnak et al., 2012) to account for changing solar wind conditions (Temmer et al., 2012), compute and compare the drag parameters of two segments of the same CME, and link the results to the solar wind conditions observed along the propagation of the heliosphere. We were able to investigate the development of these CMEs in the inner heliosphere due to the in situ observations from different vantage points in the inner Solar System. We also used the DBM to calculate the arrival time of ICME for the observable parts of the merged CME, one (north-east segment) propagating toward Mercury and Venus and the other (south-west segment) toward Earth and Mars. This offers us a better understanding of the drag conditions that affect different parts of CME. At a heliocentric distance of .7 AU at Venus, the north-eastern section (primarily CME-1) of the merged CME, as seen by STEREO and LASCO, has a high speed (2,684 km s⁻¹), which gradually decreased to 1,700 km s⁻¹. The DBM has calculated 1,035 km s⁻¹. The western component (majorly CME-2) of merged CME reached the LASCO/SOHO field of view at a speed of 1,830 km s⁻¹ and abruptly decelerated to 1,000 km s⁻¹ at a heliocentric distance of 35 Rs. Beyond this range, this portion of the CME traveled at a nearly constant speed up to 1 AU, where WIND detected a shock arrival speed of 800 km s⁻¹. Corresponding to this, the speed calculated by the DBM is 755 km s⁻¹. This difference in observed and DBM-estimated speed of CMEs could be due to the acceleration in speed of CMEs after interaction. This study emphasizes that the CMEs can fragment into various sections with differing kinematics, deforming their morphologies and affecting the accuracy of estimating their arrival times, depending on the interaction with other CME and ambient solar wind structure. The study also shows the importance of multi-vantage point observations for future space weather research and for the validation of heliospheric models.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

SLS has done the acquisition, analysis, and interpretation of data for the article. ST has Have made a substantial contribution to the concept or design of the article and approved the final version version to be communicated. RS has participated in the identification of ICMEs boundaries in in-situ observations at different locations to justify the reviewer's suggestions. He also improved the manuscript text and revised it critically for important intellectual content as per reviewers comments.

Funding

Financial support: PDF/2021/002226: the research grant from the Science and Engineering Research Board, Department of Science and Technology, India. The work is supported by the Indian Space Research Organization (ISRO).

Acknowledgments

Authors are grateful to CME catalogue from SOHO/LASCO observation maintained and generated by CDAW data Centre by NASA, The WSA-ENLIL + Cone model simulations are used from CCMC (http://ccmc.gsfc.nasa.gov) and DBM team for providing online tool (http://oh.geof.unizg.hr/DBM/dbm.php). We thank the NASA OMNI Web team for providing the IMF and solar wind data at L1. We also acknowledge using solar observations from SDO/AIA. We would like to acknowledge the Venus Express, Mars Express and Messenger teams for providing the magnetic field data and plasma data. These are openly available the AMDA (http://amda.cdpp.eu/) science analysis system provided by IRAP supported by CNRS and CNES. I acknowledge to Dr. Smitha Thampi for her valuable suggestions to improve the manuscripts. Dr. SLS acknowledges the financial assistance provided by ISRO through a Research Associate fellowship.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, B. J., Acuna, M. H., Lohr, D. A., Scheifele, J., Raval, A., Korth, H., et al. (2007). The magnetometer instrument on MESSENGER. Space Sci. Rev. 131, 417. doi:10.1007/s11214-007-9246-7

CrossRef Full Text | Google Scholar

Arge, C. N., Luhmann, J. G., Odstrčil, D., Schrijver, C. J., and Li, Y. (2004). Stream structure and coronal sources of the solar wind during the May 12th, 1997 CME. J. Atmos. Sol-Terr Phys. 66, 1295–1309. doi:10.1016/j.jastp.2004.03.018

CrossRef Full Text | Google Scholar

Arge, C. N., and Pizzo, V. J. (2000). Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates. J. Geophys Res. 105, 10465–10479. doi:10.1029/1999JA000262

CrossRef Full Text | Google Scholar

Barabash, S., Lundin, R., Andersson, H., Gimholt, J., Holmström, V. J., Norberg, O., et al. (2004). ASPERA-3: Analyser of space plasmas and energetic ions for Mars Express. In Mars Express: The Scientific Payload 1240, 121–139.

Google Scholar

Bertucci, C., Duru, F., Edberg, N., Fraenz, M., Martinecz, C., Vaisberg, O., et al. (2011). The induced magnetospheres of Mars, Venus, and titan. Space Sci. Rev. 162, 113–171. doi:10.1007/s11214-011-9845-1

CrossRef Full Text | Google Scholar

Brueckner, G. E., Howard, R. A., Koomen, M. J., Korendyke, C. M., Michels, D. J., Moses, J. D., et al. (1995). The large angle spectroscopic coronagraph (LASCO). SoPh 162, 357–402. doi:10.1007/bf00733434

CrossRef Full Text | Google Scholar

Chintzoglou, G., Patsourakos, S., and Vourlidas, A. (2015). Formation Of Magnetic Flux Ropes During Confined Flaring Well Before The Onset Of A Pair Of Major Coronal Mass Ejections. ApJ 809, 34. doi:10.1088/0004-637x/809/1/34

CrossRef Full Text | Google Scholar

Colaninno, R. C., and Vourlidas, A. (2009). First determination of the true mass of coronal mass ejections: A novel approach to using the twostereoviewpoints. Astrophys. J. 698, 852–858. doi:10.1088/0004-637x/698/1/852

CrossRef Full Text | Google Scholar

Davies, J. A., Perry, C. H., Trines, R. M. G. M., Harrison, R. A., Lugaz, N., Mostl, C., et al. (2013). Establishing A stereoscopic technique for determining the kinematic properties of solar wind transients based on A generalized self-similarly expanding circular geometry. Astrophysical J. 777, 167. doi:10.1088/0004-637X/777/2/167

CrossRef Full Text | Google Scholar

Davies, J.∼A., Harrison, R.∼A., Perry, C.∼H., Lugaz, N., Rollett, T., Davis, C.∼J., et al. (2012). A self-similar expansion model for use in solar wind transient propagation studies. Astrophysical J. 750, 23. doi:10.1088/0004-637X/750/1/23

CrossRef Full Text | Google Scholar

Domingo, V., Fleck, B., and Poland, A. I. (1995). The SOHO mission: An overview. Sol. Phys. 162, 1–37. doi:10.1007/BF00733425

CrossRef Full Text | Google Scholar

Galvin, A. B., Kistler, L. M., Popecki, M. A., Farrugia, C. J., Simunac, K. D. C., Ellis, L., et al. (2008). The plasma and suprathermal Ion composition (PLASTIC) investigation on the STEREO observatories. Space Sci. Rev. 136, 437–486. doi:10.1007/s11214-007-9296-x

CrossRef Full Text | Google Scholar

Good, S. W., and Forsyth, R. J. (2016). Interplanetary coronal mass ejections observed by MESSENGER and Venus express. Sol. Phys. 291, 239–263. doi:10.1007/s11207-015-0828-3

CrossRef Full Text | Google Scholar

Gosling, J. T., McComas, D. J., Phillips, J. L., and Bame, S. (1991). Geomagnetic activity associated with Earth passage of interplanetary shock disturbances and coronal mass ejections. JGRA 96, 7831. doi:10.1029/91ja00316

CrossRef Full Text | Google Scholar

Gosling, J. T. (1993). The solar flare myth. JGRA 98, 18937–18949. doi:10.1029/93ja01896

CrossRef Full Text | Google Scholar

Howard, R.∼A., Moses, J.∼D., Vourlidas, A., Newmark, J.∼S., Socker, D.∼G., Plunkett, S.∼P., et al. (2008). Sun earth connection coronal and heliospheric investigation (SECCHI). SSRv 136, 67. doi:10.1007/s11214-008-9341-4

CrossRef Full Text | Google Scholar

Ireland, J., Young, C., Mcateer, J., Whelan, C., Hewett, R., and Gallagher, P. (2008). Multiresolution analysis of active region magnetic structure and its correlation with the mount wilson classification and flaring activity. Sol. Phys. 252, 121–137. doi:10.1007/s11207-008-9233-5

CrossRef Full Text | Google Scholar

Lemen, J. R., Title, A. M., Akin, D. J., Boerner, P. F., Chou, C., Drake, J. F., et al. (2012). The atmospheric imaging assembly (AIA) on the solar dynamics observatory (SDO). Sol. Phys. 275, 17–40. doi:10.1007/s11207-011-9776-8

CrossRef Full Text | Google Scholar

Lepping, R. P., Acũna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The WIND magnetic field investigation. Space Sci. Rev. 71 (1), 207–229. doi:10.1007/bf00751330

CrossRef Full Text | Google Scholar

Liu, Y. D., Luhmann, J. G., Lugaz, N., Mostl, C., Davies, J. A., Bale, S. D., et al. (2013). On sun-to-earth propagation of coronal mass ejections. Astrophysical J. 769, 45. doi:10.1088/0004-637X/769/1/45

CrossRef Full Text | Google Scholar

Lugaz, N., Farrugia, C. J., Manchester, W. B., and Schwadron, N. (2013). The interaction of two coronal mass ejections: Influence of relative orientation. Astrophysical J. 778, 20. doi:10.1088/0004-637x/778/1/20

CrossRef Full Text | Google Scholar

Lugaz, N., Temmer, M., Wang, Y., and Farrugia, C. (2017). The interaction of successive coronal mass ejections: A review. Sol. Phys. 292, 64. doi:10.1007/s11207-017-1091-6

CrossRef Full Text | Google Scholar

Luhmann, J., Mewaldt, R., Cummings, A., Stone, E., Davis, A., Cook, W., et al. (2008). STEREO IMPACT investigation goals, measurements, and data products overview. Space Sci. Rev. 136, 117–184. doi:10.1007/s11214-007-9170-x

CrossRef Full Text | Google Scholar

Mays, M. L., Taktakishvili, A., Pulkkinen, A., MacNeice, P. J., Rastätter, L., Odstrcil, D., et al. (2015). Ensemble modeling of CMEs using the WSA–ENLIL+Cone model. Sol. Phys. 290, 1775–1814. doi:10.1007/s11207-015-0692-1

CrossRef Full Text | Google Scholar

Mishra, W., Srivastava, N., and Chakrabarty, D. (2015). Evolution and consequences of interacting CMEs of 9 – 10 november 2012 using STEREO/SECCHI and in situ observations. Sol. Phys. 290, 527–552. doi:10.1007/s11207-014-0625-4

CrossRef Full Text | Google Scholar

Mishra, W., and Srivastava, N. (2014). Morphological and kinematic evolution of three interacting coronal mass ejections of 2011 february 13–15. Astrophysical J. 794, 64. doi:10.1088/0004-637x/794/1/64

CrossRef Full Text | Google Scholar

Mishra, W., Wang, Y., and Srivastava, N. (2016). On understanding the nature of collisions of coronal mass ejections observed bystereo. Astrophys. J. 831, 99. doi:10.3847/0004-637x/831/1/99

CrossRef Full Text | Google Scholar

Möstl, C., Farrugia, C. J., Kilpua, E. K. J., Jian, L. K., Liu, Y., Eastwood, J. P., et al. (2012). Multi-point shock and flux rope analysis of multiple interplanetary coronal mass ejections around 2010 august 1 in the inner heliosphere. Astrophys. J. 758, 10. doi:10.1088/0004-637X/758/1/10

CrossRef Full Text | Google Scholar

Nieves-Chinchilla, T., Vourlidas, A., Stenborg, G., Savani, N. P., Koval, A., Szabo, A., et al. (2013). Inner heliospheric evolution of A "stealth" cme derived from multi-view imaging and multipoint in situ observations. I. Propagation to 1 AU. Astrophys. J. 779, 55. doi:10.1088/0004-637X/779/1/55

CrossRef Full Text | Google Scholar

Odstrčil, D., Riley, P., and Zhao, X. P. (2004). Numerical simulation of the 12 May 1997 interplanetary CME event. J. Geophys Res. (Space Phys. 109, A02116. doi:10.1029/2003JA010135

CrossRef Full Text | Google Scholar

Odstrčil, D., Smith, Z., and Dryer, M. (1996). Distortion of the heliospheric plasma sheet by interplanetary shocks. Geophys Res. Lett. 23, 2521–2524. doi:10.1029/96GL00159

CrossRef Full Text | Google Scholar

Odstrčil, D. (2003). Modeling 3-D solar wind structure. Adv. Space Res. 32, 497–506. doi:10.1016/S0273-1177(03)00332-6

CrossRef Full Text | Google Scholar

Palmerio, E., Nieves-Chinchilla, T., Kilpua∼J., E.∼K., Barnes, D., Zhukov, A.∼N., Jian, L.∼K., et al. (2021). Magnetic structure and propagation of two interacting CMEs from the sun to saturn. JGRA 126, e2021JA029770. doi:10.1029/2021JA029770

CrossRef Full Text | Google Scholar

Patsourakos, S., Georgoulis, M. K., Vourlidas, A., Nindos, A., Sarris, T., Anagnostopoulos, G., et al. (2016). The major geoeffective solar eruptions of 2012 March 7: Comprehensive sun-to-earth analysis. Astrophys. J. 817:14. doi:10.3847/0004-637X/817/1/14

CrossRef Full Text | Google Scholar

Pesnell, W. D., Thompson, B. J., and Chamberlin, P. C. (2012). The solar dynamics observatory (SDO). Sol. Phys. 275, 3–15. doi:10.1007/s11207-011-9841-3

CrossRef Full Text | Google Scholar

Richardson, I. G., and Cane, H. V. (2012). Near-Earth solar wind flows and related geomagnetic activity during more than four solar cycles (1963–2011). JSWSC 2, A02. doi:10.1051/swsc/2012003

CrossRef Full Text | Google Scholar

Rollett, T., Mostl, C., Temmer, M., Frahm, R. A., Davies, J. A., Veronig, A. M., et al. (2014). Combined multipoint remote and in situ observations of the asymmetric evolution of A fast solar coronal mass ejection. Astrophysical J. Lett. 790 (7), L6. doi:10.1088/2041-8205/790/1/L6

CrossRef Full Text | Google Scholar

Rouillard, A. P., Sheeley, N. R., Cooper, T. J., Davies, J. A., Lavraud, B., Kilpua, E. K. J., et al. (2011). The solar origin of small interplanetary transients. Astrophysical J. 734, 7. doi:10.1088/0004-637X/734/1/7

CrossRef Full Text | Google Scholar

Schmidt, J., and Cargill, P. (2004). A numerical study of two interacting coronal mass ejections. AnGeo 22, 2245–2254. doi:10.5194/angeo-22-2245-2004

CrossRef Full Text | Google Scholar

Scolini, C., Chané, E., Pomoell, J., Rodriguez, L., and Poedts, S. (2020). Improving predictions of high-latitude coronal mass ejections throughout the heliosphere. Space weather. 18, e2019SW002246. doi:10.1029/2019SW002246

CrossRef Full Text | Google Scholar

Shen, C., Wang, Y., Wang, S., Liu, Y., Liu, R., Vourlidas, A., et al. (2012). Super-elastic collision of large-scale magnetized plasmoids in the heliosphere. Nature Physics 8 (12), 923–928. doi:10.1038/nphys2440

CrossRef Full Text | Google Scholar

Shen, C., Wang, Y., Wang, S., Liu, Y., Liu, R., Vourlidas, A., et al. (2012). Super-elastic collision of large-scale magnetized plasmoids in the heliosphere. Nature 8, 923–928. doi:10.1038/nphys2440

CrossRef Full Text | Google Scholar

Solomon, Sean C., McNutt, R. L., Gold, R. E., Acuna, M. H., Baker, D. N., Boynton, W. V., et al. (2001). The MESSENGER mission to Mercury: Scientific objectives and implementation. Planet. Space Sci. 49, 141445–151465. doi:10.1016/s0032-0633(01)00085-x

CrossRef Full Text | Google Scholar

Soni, L. S., Gupta, R. S., and Verma, P. L. (2020). Interplanetary consequences and geoeffectiveness of CME associated with major solar flare from NOAA AR 12673. Res. Astron. Astrophys. 20, 023. doi:10.1088/1674-4527/20/2/23

CrossRef Full Text | Google Scholar

Temmer, M., Veronig, A. M., Kontar, E. P., Krucker, S., and Vrsnak, B. (2010). Combinedstereo/rhessistudy of coronal mass ejection acceleration and particle acceleration in solar flares. Astrophysical J. 712, 1410–1420. doi:10.1088/0004-637x/712/2/1410

CrossRef Full Text | Google Scholar

Temmer, M., Vrsnak, B., Rollett, T., Bein, B., de Koning, C. A., Liu, Y., et al. (2012). Characteristics of kinematics of A coronal mass ejection during the 2010 august 1 cme–cme interaction event. Astrophysical J. 749, 57. doi:10.1088/0004-637x/749/1/57

CrossRef Full Text | Google Scholar

Thernisien, A., Vourlidas, A., and Howard, R.∼A. (2009). Forward modeling of coronal mass ejections using STEREO/SECCHI data. SoPh 256, 111–130. doi:10.1007/s11207-009-9346-5

CrossRef Full Text | Google Scholar

Thernisien, A.∼F.∼R., and Howard, R.∼A. (2006). Modeling of flux rope coronal mass ejections. Astrophysical J. 652, 763–773. doi:10.1086/508254

CrossRef Full Text | Google Scholar

Vrsnak, B., Žic, T., Vrbanec, D., Temmer, M., Amerstorfer, T., Mã¶stl, C., et al. (2012). Propagation of interplanetary coronal mass ejections: The drag-based model. Sol. Phys. 285, 295. doi:10.1007/s11207-012-0035-4

CrossRef Full Text | Google Scholar

Vrsnak, B., and Gopalswamy, N. (2002). Influence of the aerodynamic drag on the motion of interplanetary ejecta. J. Geophys. Res. 107, 2-1. doi:10.1029/2001ja000120

CrossRef Full Text | Google Scholar

Xie, H., Leon, O., and Gareth, L. (2004). Cone model for halo CMEs: Application to space weather forecasting. JGR-Space Phys. 209, A03109. doi:10.1029/2003JA010226

CrossRef Full Text | Google Scholar

Yashiro, S., Gopalswamy, N., St. Cyr, O., Plunkett, S., Rich, N., and Howard, R. (2004). A catalog of white light coronal mass ejections observed by the SOHO spacecraft. J. Geophys. Res. (Space Phys. 109, 7105. doi:10.1029/2003JA010282

CrossRef Full Text | Google Scholar

Zhang, J., Richardson, I. G., Webb, D. F., Gopalswamy, N., Huttunen, E., Kasper, J. C., et al. (2007). Solar and interplanetary sources of major geomagnetic storms (Dst <= −100 nT) during 1996-2005. Journal of Geophysical Research (Space Physics) 112, A10.

CrossRef Full Text | Google Scholar

Zhang, T. L., Baumjohann, W., Delva, M., Auster, H. U., Balogh, A., Russell, C., et al. (2006). Magnetic field investigation of the Venus plasma environment: Expected new results from Venus Express. Space Sci. 54, 1336–1343. doi:10.1016/j.pss.2006.04.018

CrossRef Full Text | Google Scholar

Zhao, X. P., Plunkett, S. P., and Liu, W. (2002). Determination of geometrical and kinematical properties of halo coronal mass ejections using the cone model. J. Geophys Res. (Space Phys. 107, 13-21. doi:10.1029/2001JA009143

CrossRef Full Text | Google Scholar

Žic, T., Vršnak, B., and Temmer, M. (2015). Heliospheric propagation of coronal mass ejections: Drag-based model fitting. Astrophysical J. Suppl. Ser. 218, 32. doi:10.1088/0067-0049/218/2/32

CrossRef Full Text | Google Scholar