Oblique propagation and temperature effects on the resonant right-hand ion beam instability

The resonant right-hand instability (RHI) is often the dominant mode driven by reflected ions upstream of Earth’s quasi-parallel bow shock. In the tradition of Peter Gary, this paper further explores the right-hand instability using numerical solutions of the plasma dispersion relation and non-linear kinetic simulations, with parameters inspired by observations from NASA’s Magnetospheric Multiscale (MMS) mission. Agreement is found between the ion distributions in the particle-in-cell simulations and Magnetospheric Multiscale spacecraft data, which show the gyrophase bunching characteristic of the instability. The non-linear structures created by right-hand instability tend to be stronger when the plasma beta is lower. These structures have sizes of around 100 to 200 ion inertial lengths perpendicular to the magnetic field, presenting planet-sized disturbances to the magnetosphere. 2d and 3D hybrid particle-in-cell simulations show that modes with a range of propagation angles oblique to the magnetic field are excited, providing a ground to understand previous statistical studies of observed foreshock waves.

1 Introduction

At Earth’s bow shock, like at other collisionless shocks, ions reflected back upstream may form a beam population in velocity space. The free energy of this backstreaming ion beam drives a range of kinetic instabilities in the foreshock. For relatively tenuous and fast (compared to the background Alfven speed) ion beams traveling parallel to the magnetic field, the fastest growing linear instability is the resonant right-hand instability (RHI) (Gary, 1991). For low beam densities, this mode is a low-frequency wave carried by the background and excited by a cyclotron resonance with the beam ions. As described in another article in this collection (Winske and Wilson, 2022), Peter Gary was a pioneer in the Vlasov theory of electromagnetic ion beam instabilities in space plasmas (Gary et al., 1984; Gary et al., 1985; Gary, 1991). Gary’s work is an important piece of a large body of research on the theory and observation of RHI waves in the foreshock. Here, we re-examine properties and dynamics of the RHI using a modern hybrid particle-in-cell (PIC) code and example data from NASA’s Magnetospheric Multiscale (MMS) mission. The hybrid PIC simulations show that a finite temperature of the background decreases the amplitude of non-linear structures that develop and that a relatively broadband spectrum of modes may be excited with a range of propagation angles oblique to the local magnetic field.

Many early studies of RHI were inspired by data from the International Sun-Earth Explorer (ISEE) spacecraft. The data showed abundant wave activity in the foreshock, and it was recognized that RHI and other low-freqency modes were associated with backstreaming ions (Hoppe et al., 1981). Some effects of these waves include modifying the transport and heating of ions in the upstream plasma (Lee, 1982). The RHI in particular may also drive ultra-low frequency (ULF) waves in the 30-s period range (Watanabe and Terasawa, 1984; Greenstadt et al., 1995), which couple to particles trapped in Earth’s radiation belts. The non-linear evolution of RHI was found to be a possible driver of large-amplitude magnetic pulsations observed in the forshock (Akimoto et al., 1993). More recent simulation studies of RHI have focused on the global context of (ULF) waves and their transport into the magnetosphere (Blanco-Cano et al., 2009; Palmroth et al., 2015; Kajdič et al., 2021; Turc et al., 2022). In addition, very high-resolution field and particle data are now available from NASA’s MMS mission (Burch et al., 2016). Meanwhile, laser-driven laboratory experiments have offered a means of taking detailed measurements of ion beam instabilities in a reproducible environment (Heuer et al., 2020).

Here, we revisit RHI with a hybrid PIC code to further explore the waves and non-linear structures associated with the instability. Because earlier work focused on moderately cool beams with v_thb ≲ v_A (Hoshino and Terasawa, 1985; Winske and Gary, 1986; Akimoto et al., 1993) we also consider the effects of warmer beam and background ion populations. The finite temperatures moderately reduce the RHI growth rate, and they tend to reduce the amplitude of non-linear structures. We also explore the spectrum of oblique waves excited by a parallel ion beam. A statistical analysis of Cluster spacecraft data uptream of the quasi-parallel bow shock showed that the beam-driven waves have a power spectrum peaked at oblique propagation angles (Eastwood et al., 2005). This is at first glance at odds with the fact that the fastest growing mode for the beam and plasma conditions is the purely parallel propagating RHI. We find a range of oblique modes are excited in 2D and 3D simulations, consistent with solutions of the hot plasma dispersion relation. The simulations predict a typical perpendicular scale length of the non-linear RHI structures to be $\sim 100$ to 200 d_i, indicating that the structures are planet-sized and may significantly impact the magnetosphere.

2 Review of the resonant ion beam instability

In this section, we include a brief review of the resonant right-hand instability (RHI) and define the conventions we use in our analysis. The RHI is a solution of the dispersion relation for magnetized plasmas with a beam ion population traveling along the magnetic field. For the cases of interest here, the fastest growing mode is purely parallel propagating. For purely parallel modes, the relevant dispersion relation for a plasma where each species j has an isotropic Maxwellian velocity distribution is (Gary et al., 1984):

$1-\frac{k^2{c}^2}{{\omega }^2}+\sum _j\frac{w_{pj}^2}{{\omega }^2}{\zeta }_{j}Z\left({\zeta }_j^{+}\right)=0(1)$

${\zeta }_j=\left(\omega -k{u}_j\right)/k{v}_{\mathit{thj}}(2)$

${\zeta }_j^{+}=\left(\omega -k{u}_j+{\omega }_{cj}\right)/k{v}_{\mathit{thj}}(3)$

where k is the parallel wavenumber, ${\omega }_{pj}^2=n_j{Z}_j^2{e}^2/{ϵ}_0{m}_j$, $v_{\mathit{thj}}=\sqrt{2T_j/m_j}$, u_j is the bulk fluid drift velocity, and Z(x) is the plasma dispersion function. In the quasi-neutral cold plasma limit, this results in a polynomial relation D(ω, k) = 0 that yields four distinct unstable modes (Weidl et al., 2019) including the RHI.

To study the linear growth rates of the RHI for oblique propagation including finite beam and background ion temperatures, we consider numerical solutions (Montgomery et al., 1975) of the full hot plasma dispersion relation assuming drifting Maxwellian ion distributions (see, for example the appendix of Gary, 1991). We use the open-source New Hampshire Dispersion Solver (NHDS) (Verscharen and Chandran, 2018). We work in the rest frame of the background plasma, where the background ions have no net drift. The background plasma is taken to be uniform and consisting of ions of mass m_i and unit charge. We denote the background density n₀ and the temperature T₀. The background magnetic field is also uniform, in the positive x direction, and of strength B₀. A drifting Maxwellian ion beam population is included with a density n_b, temperature T_b, and a drift speed u_b in the positive x direction. The Alfven Mach number of the beam is M_A = u_b/v_A, were we normalize the drift speed to the background Alfven speed $v_A=B_0/\sqrt{{\mu }_0{n}_0{m}_i}$. For simplicity, we take beam ions to be the same species as the background ions. The electron population is charge- and current-neutralizing.

At Earth’s bow shock, the reflected ion population is characteristically low-density (with relative beam fractions less than a few percent) and fast (with Alfven Mach numbers M_A > 2). Under these conditions, the low-frequency wave spectrum is dominated by the RHI. Figure 3 shows the maximum growth rate of the RHI over a range of propagation angles for a beam of density n_b/n₀ = .015 and an Alfven Mach number of M_A = 10, similar to typical parameters at Earth’s foreshock. The three curves show the growth rates for three different beam temperatures. The uppermost curve is a relatively cold beam, and the peak growth rate for parallel propagation agrees with the large M_A approximation for cold plasmas (Gary, 1978; Weidl et al., 2019), $\gamma /{\mathrm{\Omega }}_{ci}\sim {(n_b/2n_0)}^{1/3}$. When finite temperature effects are included, the growth rate decreases as the beam temperature increases. This is because a smaller fraction of the beam is gyroresonant with the mode. The background temperature has a very minor effect on the growth rates as long as the background thermal speed is relatively low (v_th0 ≪ u_b) as is typically observed at Earth’s foreshock. We note that while additional beam-driven modes, including oblique Alfven modes Daughton and Gary. (1998) and the non-resonant mode (e.g., Gary. (1991), Chen et al. (2022), exist over this range, the RHI is dominant for the relatively fast (M_A > 2) and tenuous beams that we consider here. In Section 3, we explore the non-linear development of the purely parallel-propagating RHI using a hybrid PIC code.

3 1D hybrid simulation and example event

We begin this section with an example of foreshock waves driven by reflected ions observed by NASA’s MMS mission (Burch et al., 2016). The MMS data are plotted in Figure 1, showing a fairly typical foreshock crossing in an interval upstream of the quasi-parallel bow shock on 30 January 2019. The magnetic field components in Figure 1A show a background field dominated by the radial B_x component along with large-amplitude wave fields (mainly B_y and B_z). The wave power is peaked near the local ion cyclotron frequency $(\sim 0.01Hz)$. In the spacecraft frame, the bulk solar wind velocity is u_x ∼ −300 km/s ∼ −10 v_A, and the reflected ions appear as a more diffuse population centered near v_x ∼ 0 (see Figure 1C). The approximate relative density of the reflected population is n_b/n₀ ≲ .05, and the relative parallel drift of the beam gives an Alven Mach number of M_A ∼ 10. These rough parameters, which are fairly typical of Earth’s foreshock, serve as the basis for the numerical simulations below.

FIGURE 1

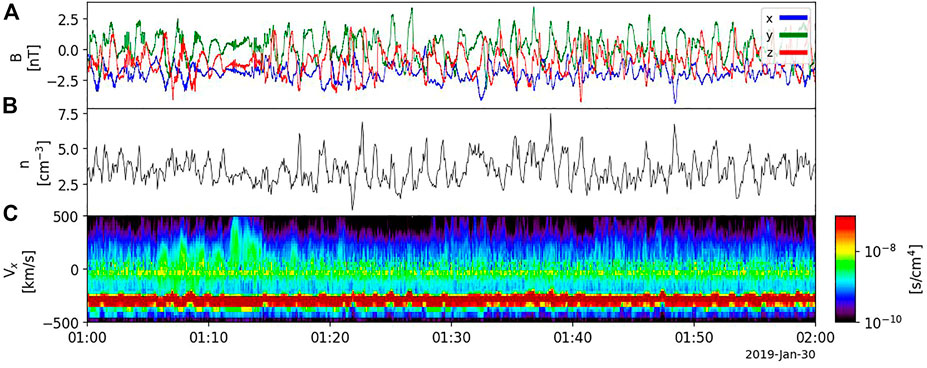
FIGURE 1. Example of RHI waves typical of the quasi-parallel foreshock as observed by the MMS2 spacecraft. The magnetic field in (A) is primarily in the x direction with large-amplitude waves in B_y and B_z. The total ion density it plotted in (B). The reduced ion velocity distribution in terms of v_x is plotted in (C). In the spacecraft frame, the background moves in the −v_x direction while the beam population is centered near v_x = 0. The reflected beam ions have a relatively broad velocity spread compared to the colder solar wind population.

Because the electrons are far from resonance with the RHI and the mode frequencies are well below the electron plasma and cyclotron frequencies, hybrid numerical codes (Lipatov, 2002; Winske et al., 2003) that treat the ions as a kinetic species and the electrons as a massless neutralizing background are suitable for studying the linear and non-linear evolution of the RHI. Here, we use a hybrid version of the particle-in-cell (PIC) code VPIC (Bowers et al., 2008; Le et al., 2021; Keenan et al., 2022) to model the RHI. Numerous earlier studies of ion streaming instabilities have used similar electromagnetic hybrid PIC codes (e.g.,Winske and Quest., 1986; Hada et al., 1987; Gary and Winske, 1990; Winske and Omidi, 1992; Akimoto et al., 1993; Dubouloz and Scholer, 1995; Hellinger and Mangeney, 1999; Wang and Lin, 2003; Heuer et al., 2018; Weidl et al., 2019; Holcomb and Spitkovsky, 2019). Because the simulations in this section are 1D in the x direction, they only allow the growth of the purely parallel propagating modes, which are the fastest growing modes for the parameters we use. Note that for 2D or 3D systems with oblique modes, damping on the electrons can become more important. While this effect is included in the linear dispersion solver, it is not captured by the fluid model of the hybrid code.

As in other hybrid PIC codes, the electron model in Hybrid-VPIC takes the form of an Ohm’s law for the electric field:

$\mathbf{E}=-{\mathbf{u}}_{\mathbf{i}}\times \mathbf{B}-\frac{1}{ne}\nabla p_e+\frac{1}{ne}\mathbf{J}\times \mathbf{B}+\eta \mathbf{J}-{\eta }_H{\nabla }^2\mathbf{J}(4)$

where quasi-neutrality imposes n = n_e = ∑_sZ_sn_s (including a sum over species s of ions), the velocity u_i is the charge-weighted ion flow u_i = ∑_sZ_sn_su_s/n_e, and the current density is taken in the low-frequency approximation as μ₀J = ∇ × B. We use a system of units based on the background magnetic field B₀ and ion density n₀, with times normalized by the cyclotron frequency ω_ci = eB₀/m_i and lengths given in terms of the ion inertial length $d_i={({ϵ}_0{m}_i{c}^2/e^2{n}_0)}^{1/2}$. Because we use particle shapes that are sums of quadratics in each direction, we choose grid resolutions with Δx ranging from .25 to 1 d_i to avoid an unphysical numerical dispersion that occurs when low spatial resolution and high-order particle shapes are used in hybrid PIC codes (Stanier et al., 2020). For these 1D simulations, we include 2000 particles per cell for each ion population. The normalized resistivity η/(B₀/n₀) and hyper-resistivity ${\eta }_H/(B_0/n_{0}e{d}_i^2)$ are set to small values in the range of 1 × 10^–4 to 5 × 10^–3. For the simulations here, the electron pressure follows a simple isothermal closure, such that the electron pressure is given by p_e = n_eT_e, with T_e a constant (Le et al., 2016). Test simulations with an adiabatic electron closure showed no discernible differences.

As described in Section 2, our 1D simulations contain a uniform background plasma of density n₀ and temperature T₀ (we set T_i = T_e = T₀) and magnetic field B₀ in the x direction. To this is added a streaming population of beam ions of density n_b (recall an equal number density of electrons is implicit in the quasi-neutral assumption of the hybrid code), drift velocity in the positive x direction u_b, and temperature T_b. Figure 2 shows typical results from an RHI simulation with relatively cold background and beam populations. The three sets of panels in Figure 2 are at three different times over the course of simulation.

FIGURE 2

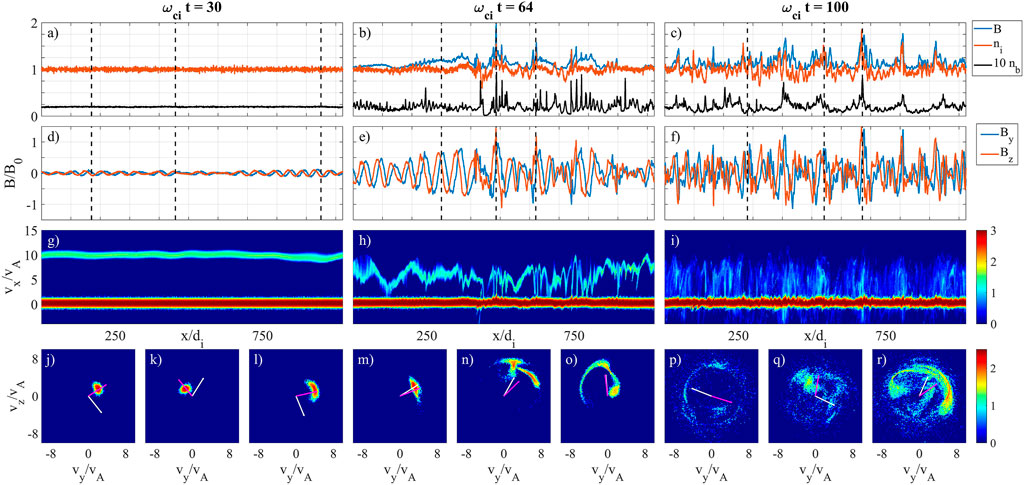
FIGURE 2. Results from 1D hybrid simulations of the resonant right-hand instability (RHI) with cold (v_thi = v_thb = 0.1v_A) ion populations. The left panels are at early time tω_ci = 30, middle panels are at tω_ci = 64, and right panels are at tω_ci = 100. (A–C) Background (red) and beam (black) ion density profiles and magnetic field strength (blue). (D–F) Wave magnetic field components B_y and B_z. (G–I) Parallel x−v_x phase space distribution of the ions, showing the dense background at v_x ∼ 0 and the beam with an Alfven Mach number of M_A = 10. (J–R) Beam ion distributions in the perpendicular v_y−v_z plane at the points marked by the vertical dashed lines in (A–C). The white lines show the direction of the perpendicular wave magnetic fields B_y and B_z, and the magenta lines show the direction of the bulk beam perpendicular velocity.

The leftmost panels are at time t*ω_ci = 30 when the RHI is nearing the end of a phase growth consistent with the linear instability. The background and beam density profiles as well as the total magnetic field magnitude in Figure 2A are relatively unperturbed. The ion phase space distribution in x−v_x space in Figure 2 shows a weak modulation of the beam ions (the population centered at v_x ∼ 10v_A). Nevertheless, the RHI is here already strong enough to modulate the beam ions in perpendicular velocity space. The three panels of Figures 2J–L show the perpendicular velocity distribution of the beam ions in v_y−v_z space at the three locations marked by vertical dashed lines in Figure 2A. These distributions exhibit gyrophase bunching, with the beam ions undergoing motion in the plane perpendicular to the magnetic field. As in previous simulations and observations (Hoshino and Terasawa, 1985; Thomsen et al., 1985; Fuselier et al., 1986; Gary et al., 1986), the gyrophase bunched ions are out of phase with the wave magnetic field. In Figures 2J–L, the white line gives the direction of the wave magnetic field (B_y and B_z), while the black line shows the direction of the local bulk beam velocity in the y−z plane. The field and beam velocity are roughly 90° out of phase.

At later time, the RHI waves steepen into non-linear features. Non-linear structures have been observed with beam populations upstream of the bow shock, and they have been identified as shocklets (Hoppe et al., 1981; Hada et al., 1987) or magnetic pulsations (Akimoto et al., 1993). As in the earlier simulations of Akimoto et al., 1993, the non-linear pulsations driven by the RHI are characterized by correlated magnetic field strength |B| perturbations (see the blue curve in Figure 2B) that are correlated with the density n perturbations (red curve).

Thermal velocity spreads of the background and beam ions that are not large compared to the relative drift speed do not qualitatively affect the linear properties of the RHI, though the finite temperatures moderately reduce the growth rates. The non-linear features that develop, however, are weaker in amplitude in our simulations with higher beam and background temperatures. We show example data from a simulation with a beam thermal spread v_thb = 3v_A and background thermal speed of v_th0 = v_A in Figure 3. For cold beams ions as in Figure 2, practically all of the beam ions can become bunched where the RHI waves steepen. In addition to bunching in gyrophase angle, these resonant beam ions can be dramatically slowed down in the parallel direction, even locally coming to a stop in the background frame (see Figure 2H). For hot beams that are more diffuse in velocity space, on the other hand, a relatively smaller fraction of the beams ions are near exact resonance with the RHI mode. As a result, a smaller fraction of the beam ions in Figure 3H are slowed by the wave fields. This results in a much less spiky beam ion density profile in Figure 3B than for the cold ions case. Furthermore, because the RHI couples to compressional modes, the higher background pressure weakens the amplitude of the non-linear features. For even higher background temperatures with v_th0 = 4v_A (not plotted), there are no discernible pulsations or spikes in the density or magnetic field profiles.

FIGURE 3

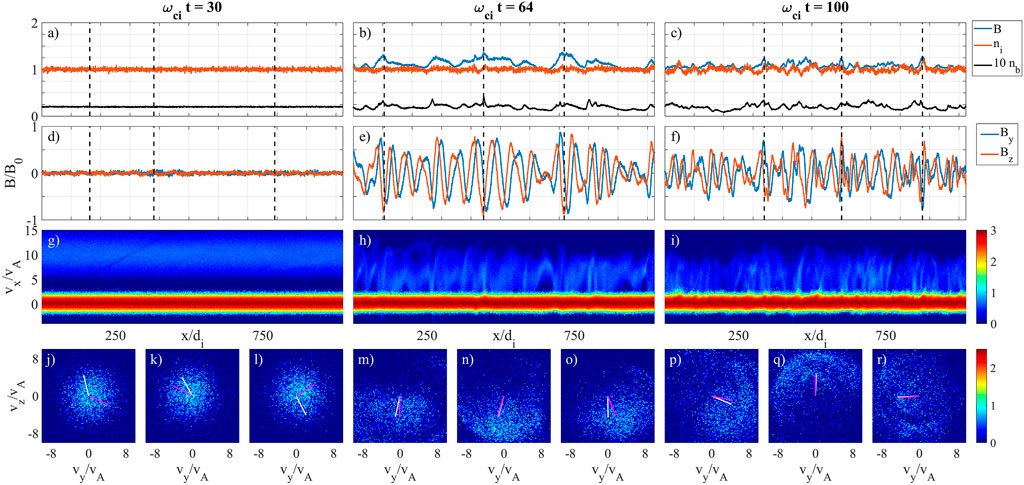
FIGURE 3. Similar plots as in Figure 2, but with warm background ($v_{\mathit{thi}}=\sqrt{2T_i/m_i}=v_A$ or β_i = 1) and beam (v_thb = 3v_A) ion populations. Again, the left panels are at early time tω_ci = 30, middle panels are at tω_ci = 64, and right panels are at tω_ci = 100. (A–C) Background (red) and beam (black) ion density profiles and magnetic field strength (blue). (D–F) Wave magnetic field components B_y and B_z. (G–I) Parallel x−v_x phase space distribution of the ions, showing the dense background at v_x ∼ 0 and the beam with an Alfven Mach number of M_A = 10. (J–R) Beam ion distributions in the perpendicular v_y−v_z plane at the points marked by the vertical dashed lines in (A–C). The white lines show the direction of the perpendicular wave magnetic fields B_y and B_z, and the magenta lines show the direction of the bulk beam perpendicular velocity.

The beam ions do display strong gyrophase bunching in perpendicular velocity space, although the non-linear structures that develop are relatively weak for the warmer beam and background temperatures (see Figure 3). We display side-by-side in Figure 4 ion v_y velocity distributions from the MMS event and from the Hybrid-VPIC simulation of Figure 3. The MMS data in Figure 4A show the v_y distribution of ions over time, which may be taken as a proxy for distance x because the waves rapidly cross the spacecraft. A distribution in x−v_y phase space from the hybrid PIC model is displayed in Figure 3B covering a range with a similar wave phase and amplitude as the MMS data. Note that $\sim 90°$ phase shift characteristic of the RHI between the wave fluctuations (carried by the background ions) and the gyro-bunched beam ions is visible in both the MMS data and the hybrid PIC simulation data.

FIGURE 4

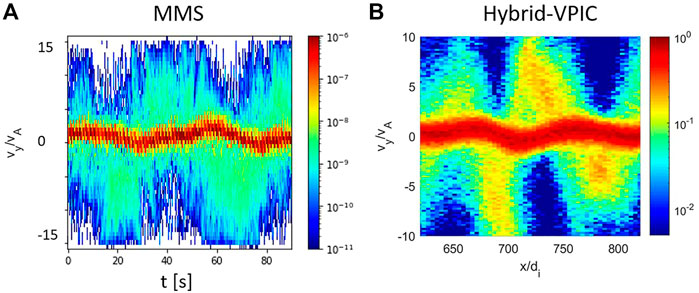
FIGURE 4. Ion velocity distributions in v_y from (A) the MMS event displayed in Figure 1 in an interval starting near time 01:05 and (B) from the hybrid PIC simulation with warm beam (v_thb = 3v_A) and background (v_th0 = v_A)) ions of Figure 3 at t = 40/ω_ci. In (A), the time t may be considered a proxy for the position x in (B) as the solar wind passes the spacecraft at the solar wind drift speed of 300 km/s ∼ 10v_A. The correspondence is 50 s ∼ 100 d_i.

4 2D and 3D hybrid simulations

In this section, we consider 2D and 3D hybrid simulations to study the evolution of the RHI in multiple spatial dimensions. The 2D or 3D geometry allows the development of a spectrum of modes with k vectors oblique to the magnetic field. As visible in Figure 5, the RHI growth rate is relatively insensitive to the propagation angle out to $\sim 35°$. Interestingly, a statistical survey of 30-s waves observed in the Earth’s foreshock found that the distribution of wave propagation angles was typically peaked at an oblique angle of $\sim 20°$ to the magnetic field (Eastwood et al., 2005). Previous hybrid simulations suggested that refraction of steepening waves driven by the fastest growing parallel propagating modes could explain the presence of oblique modes in observations (Dubouloz and Scholer, 1995). On the other hand, (Strumik et al. 2015) studied the development of ULF waves in the foreshock of a 2D hybrid global magnetosphere model with a quasi-radial IMF and quasi-parallel bow shock. They found that averaging over the spectrum of excited RHI modes at different propagation angles gave a spectrum similar to the observations. We consider this possibility in our simplified uniform beam simulations below.

FIGURE 5

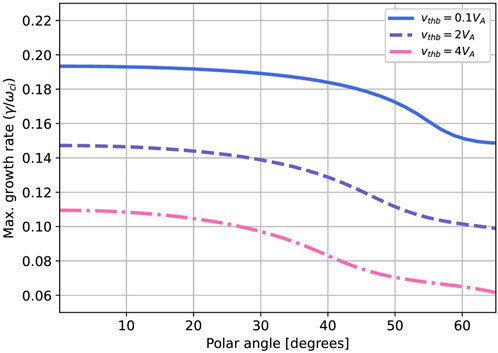
FIGURE 5. Growth rate of the RHI for oblique propagation as a function of the angle between the wave vector k and the background magnetic field for n_b/n₀ = .015 and M_A = 10. Note that the growth rate is very similar for angles ≲35°. The three curves show the growth rate for different beam temperatures with thermal speeds indicated in the legend.

To examine the spectrum of oblique modes, we consider a 2D simulation in the x−z plane of a uniform beam, building on early hybrid simulation work on 2D ion-ion beam instability growth (Winske and Quest, 1986). The simulation domain is of size L_x × L_z = 1024 d_i × 1024 d_i = 2048 × 2048 cells, the background (v_th0 = v_A) and beam (n_b/n₀ = .02, M_A = 10, v_thb = 4.3v_A) ion populations are each sampled by 400 particles per cell, and the time step is δt = .01/Ω_ci. In Figure 6, we compare the growth rates predicted by numerical solution of the hot plasma dispersion relation in (a) to the growth rates extracted directly from the hybrid PIC simulation in (b). The growth rate in each case is plotted in terms of the parallel (k_‖ and perpendicular k_⊥ wave numbers. The peak growth rate occurs for parallel propagation and corresponds to the usual RHI. Consistent with Figure 5, there is a relatively broad range of oblique wave vectors with growth rates very close to the maximum. Because of this, a wide spectrum of waves with varying propagation angles is excited. The modes plotted are all almost exactly right circularly polarized. The real frequency increases by a factor of few beyond propagation angles of 40°, and those more perpendicular modes may connect to a different wave branch.

FIGURE 6

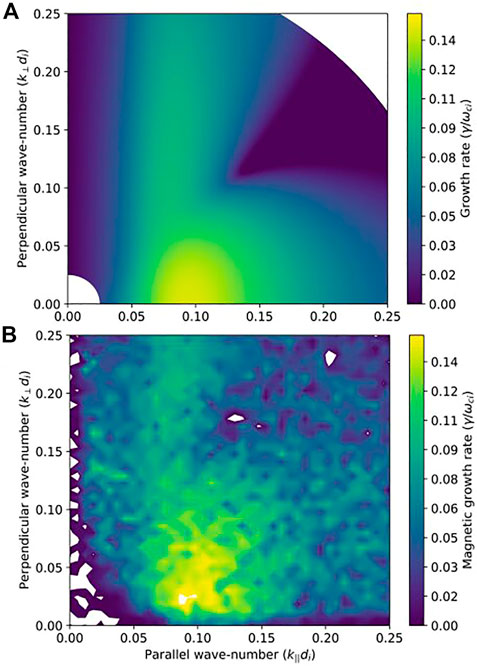
FIGURE 6. (A) Growth rate computed using the NHDS Verscharen and Chandran, (2018) as a function of parallel (k_‖d_i) and perpendicular ($k_{\perp }{d}_i$) normalized wave numbers for a beam of density n_b/n₀ = .02, Alfven Mach number M_A = 10, and beam thermal speed of v_thb = 3v_A. (B) Growth rate extracted from a 2D hybrid simulation with the same parameters as above measured by taking a time derivative of the magnetic field fluctuations.

The magnetic field and density structures that develop after the RHI saturates are very similar in 2D and 3D. Figure 7 shows comparisons of (a, c) the magnetic field component B_z and the (b, d) the plasma density between a 2D and a corresponding 3D hybrid simulation. These simulations are similar to the above simulation, but with a domain of size of L = 512d_i = 512 cells in each spatial dimension. The wide spectrum of unstable oblique modes produces magnetic fluctuations with oblique phase fronts. To quantify this effect, we show in Figure 8 a Fourier power spectrum of the wave magnetic field component B_z plotted in Figure 7A. The symmetry of the spectrum for k going to −k is simply a result of the Fourier transform of the real function B_z. The peak in the power spectrum is at k_xd_i ∼ .1, corresponding to a characteristic wavelength of $\sim 60d_i$. As noted by (Strumik et al., 2015), the fluctuation power density is spread over a range of different k vectors centered at k_z = 0. Averaging over this spectrum can explain the statistics of oblique ULF waves observed by (Eastwood et al., 2005) in Earth’s foreshock.

FIGURE 7

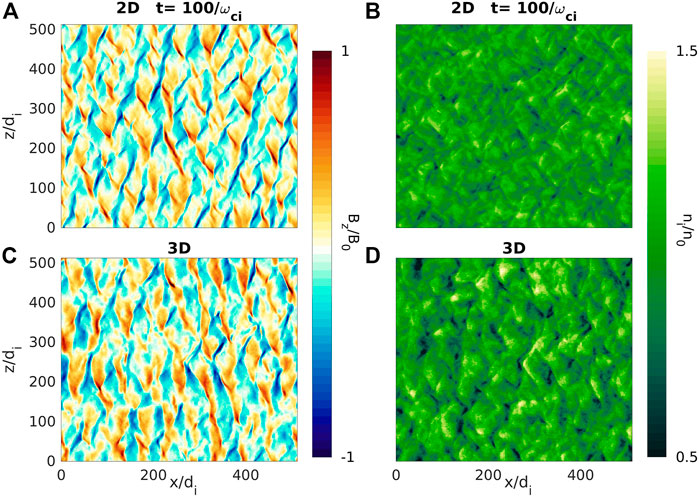
FIGURE 7. Comparison between (A, B) 2D and (C, D) 3D simulations. Left panels show B_z magnetic field component and right panels show density fluctuations in two runs with identical parameters (n_b/n₀ = .02, M_A = 10, β_i = 1, β_b = 4.5) at a late phase after the resonant mode has saturated.

FIGURE 8

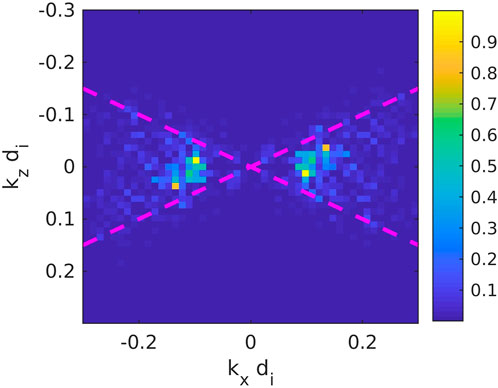
FIGURE 8. Power spectrum |B_z(k_x, k_z)|² of the magnetic field plotted in Figure 7A. The dashed magenta lines indicate where the propagation angle is 30° with respect to the background field B_x.

As another way of displaying the parallel and perpendicular structure of the saturated magnetic field fluctuations, we plot cuts of the magnetic field components in Figure 9 along the (a, c) parallel or x direction and the (b, d) perpendicular or z direction. Again, the characteristic parallel wavelengths here are $\sim 60d_i$. While the parallel mode (k_z = 0) is fastest growing, the cuts in z show large variations in the perpendicular direction. The typical perpendicular length scales are $\sim 100$ to 200 d_i and are associated with the excitation of a wide spectrum of oblique wave vectors in the original linear modes. Although not studied here, this spectrum of non-linear fluctuations in 3D can contribute to cross-field diffusion of ions (Kucharek et al., 2000).

FIGURE 9

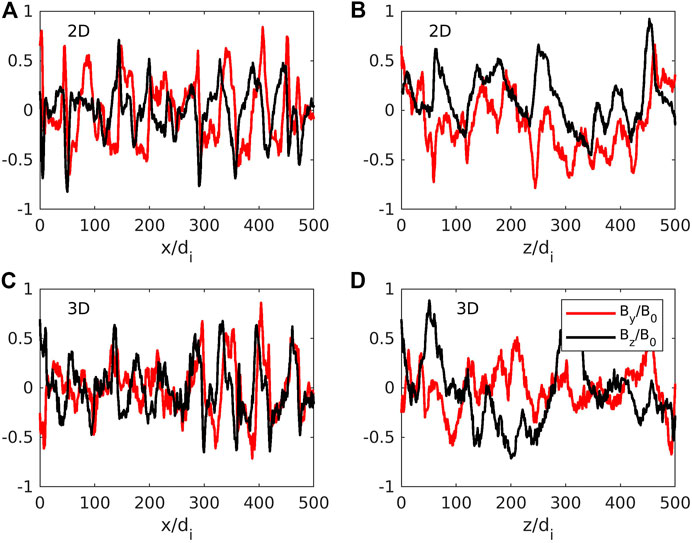
FIGURE 9. Comparison between (A, B) 2D and (C, D) 3D simulations. Left panels show B_z magnetic field component and right panels show density fluctuations in runs with identical parameters (n_b/n₀ = .02, M_A = 10, β_i = 1, β_b = 4.5) at a late phase after the resonant mode has saturated. The 2D and 3D simulations have similar characteristic parallel and perpendicular length scales.

5 Summary discussion

Using a modern hybrid PIC code, we revisited the resonant right-hand instability (RHI), which is the dominant electromagnetic ion beam instability for parallel-propagating ion beams that are relatively fast and tenuous. The parameters for the simulations were inspired by MMS observations of typical quasi-parallel foreshock fluctuations. RHI is prevalent upstream of the quasi-parallel region of Earth’s bow shock and has been the subject of a large number of previous observational and theoretical studies, including important early works by Peter Gary (Gary et al., 1984; Gary et al., 1985; Gary et al., 1986; Gary and Winske, 1990; Gary, 1991). Here, we focused on properties of the RHI related to finite temperature effects and oblique propagation. The hybrid simulations show that warm (β > 1) background and beam ion populations produce less steep non-linear features than the cold populations assumed in many previous studies. Note the RHI itself scatters reflected beam ions effectively, and it is possible that the RHI scatters an initially cooler beam into the more diffuse beam with a larger velocity spread observed by MMS. In any case, a high-beta background plasma requires additional energy to be compressed, which explains the weaker non-linear compressional features observed in simulations with high plasma beta (particularly β ≫ 1, which is not typical of the solar wind at Earth’s foreshock).

Multi-dimensional (2D and 3D) hybrid simulations demonstrated that a wide spectrum of oblique modes is excited, in agreement with growth rates predicted by numerical solution of the hot plasma dispersion relation. The RHI instability growth rate is a fairly flat function of propagation angle out to $\sim 35°$. The theoretical growth rates for the RHI agreed with the range of modes excited in the hybrid simulations, and the non-linear stage contained fluctuations with characteristic perpendicular length scales 2–3 times longer than the typical parallel wavelength. At Earth’s bow shock, typical parallel length scales would be 60d_i, which corresponds to .5 to 1.5 R_E (Earth radii) for typical solar wind densities. The corresponding perpendicular lengths scales are 2–3 R_E. These non-linear structures are therefore planet-sized, and they may impact the planetary magnetopshere.

Data availability statement

The simulation data for this study can be reproduced by running the open-source Hybrid-VPIC code branch found at https://github.com/lanl/vpic-kokkos/tree/hybridVPIC. MMS datasets are retained and available through https://lasp.colorado.edu/mms/sdc/public/.

Author contributions

AL conceived the paper idea and formulated the investigation with L-JC. AL ran simulations, analyzed data, and prepared the manuscript. L-JC prepared figures of MMS data. BW ran simulations and prepared figures. BK analyzed simulation data, ran the NHDS code, and prepared figures. All authors discussed the results and reviewed the manuscript.

Funding

This work was supported by the Los Alamos LDRD program and by NASA’s Magnetospheric Multiscale Mission. Simulations used LANL Institutional Computing resources.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akimoto, K., Winske, D., Gary, S., and Thomsen, M. (1993). Nonlinear evolution of electromagnetic ion beam instabilities. J. Geophys. Res. Space Phys. 98, 1419–1433. doi:10.1029/92ja02345

CrossRef Full Text | Google Scholar

Blanco-Cano, X., Omidi, N., and Russell, C. (2009). Global hybrid simulations: Foreshock waves and cavitons under radial interplanetary magnetic field geometry. J. Geophys. Res. Space Phys. 114, 13406. doi:10.1029/2008ja013406

CrossRef Full Text | Google Scholar

Bowers, K. J., Albright, B., Yin, L., Bergen, B., and Kwan, T. (2008). Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys. Plasmas 15, 055703. doi:10.1063/1.2840133

CrossRef Full Text | Google Scholar

Burch, J., Torbert, R., Phan, T., Chen, L. J., Moore, T., Ergun, R., et al. (2016). Electron-scale measurements of magnetic reconnection in space. Science 352, aaf2939. doi:10.1126/science.aaf2939

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L. J., Halekas, J., Wang, S., DiBraccio, G. A., Romanelli, N., Ng, J., et al. (2022). Solitary magnetic structures developed from gyro-resonance with solar wind ions at Mars and Earth. Geophys. Res. Lett. 49, e2021GL097600. doi:10.1029/2021gl097600

CrossRef Full Text | Google Scholar

Daughton, W., and Gary, S. P. (1998). Electromagnetic proton/proton instabilities in the solar wind. J. Geophys. Res. Space Phys. 103, 20613–20620. doi:10.1029/98ja01385

CrossRef Full Text | Google Scholar

Dubouloz, N., and Scholer, M. (1995). Two-dimensional simulations of magnetic pulsations upstream of the Earth’s bow shock. J. Geophys. Res. Space Phys. 100, 9461–9474. doi:10.1029/94ja03239

CrossRef Full Text | Google Scholar

Eastwood, J., Balogh, A., Lucek, E., Mazelle, C., and Dandouras, I. (2005). Quasi-monochromatic ulf foreshock waves as observed by the four-spacecraft cluster mission: 2. Oblique propagation. J. Geophys. Res. Space Phys. 110, A11220. doi:10.1029/2004ja010618

CrossRef Full Text | Google Scholar

Fuselier, S., Thomsen, M., Gary, S., Bame, S., Russell, C., and Parks, G. (1986). The phase relationship between gyrophase-bunched ions and mhd-like waves. Geophys. Res. Lett. 13, 60–63. doi:10.1029/gl013i001p00060

CrossRef Full Text | Google Scholar

Gary, S. P. (1991). Electromagnetic ion/ion instabilities and their consequences in space plasmas: A review. Space Sci. Rev. 56, 373–415. doi:10.1007/bf00196632

CrossRef Full Text | Google Scholar

Gary, S. P., Madland, C. D., and Tsurutani, B. T. (1985). Electromagnetic ion beam instabilities: Ii. Phys. fluids 28, 3691–3695. doi:10.1063/1.865101

CrossRef Full Text | Google Scholar

Gary, S. P., Smith, C. W., Lee, M. A., Goldstein, M. L., and Forslund, D. W. (1984). Electromagnetic ion beam instabilities. Phys. fluids 27, 1852–1862. doi:10.1063/1.864797

CrossRef Full Text | Google Scholar

Gary, S. P. (1978). The electromagnetic ion beam instability and energy loss of fast alpha particles. Nucl. fusion 18, 327–334. doi:10.1088/0029-5515/18/3/003

CrossRef Full Text | Google Scholar

Gary, S. P., Thomsen, M. F., and Fuselier, S. A. (1986). Electromagnetic instabilities and gyrophase-bunched particles. Phys. fluids 29, 531–535. doi:10.1063/1.865441

CrossRef Full Text | Google Scholar

Gary, S. P., and Winske, D. (1990). Computer simulations of electromagnetic instabilities in the plasma sheet boundary layer. J. Geophys. Res. Space Phys. 95, 8085–8094. doi:10.1029/ja095ia06p08085

CrossRef Full Text | Google Scholar

Greenstadt, E., Le, G., and Strangeway, R. (1995). Ulf waves in the foreshock. Adv. Space Res. 15, 71–84. doi:10.1016/0273-1177(94)00087-h

PubMed Abstract | CrossRef Full Text | Google Scholar

Hada, T., Kennel, C., and Terasawa, T. (1987). Excitation of compressional waves and the formation of shocklets in the Earth’s foreshock. J. Geophys. Res. Space Phys. 92, 4423–4435. doi:10.1029/ja092ia05p04423

CrossRef Full Text | Google Scholar

Hellinger, P., and Mangeney, A. (1999). Electromagnetic ion beam instabilities: Oblique pulsations. J. Geophys. Res. Space Phys. 104, 4669–4680. doi:10.1029/1998ja900157

CrossRef Full Text | Google Scholar

Heuer, P. V., Weidl, M. S., Dorst, R. S., Schaeffer, D. B., Tripathi, S. K., Vincena, S., et al. (2020). Laboratory observations of ultra-low-frequency analog waves driven by the right-hand resonant ion beam instability. Astrophysical J. Lett. 891, L11. doi:10.3847/2041-8213/ab75f4

PubMed Abstract | CrossRef Full Text | Google Scholar

Heuer, P., Weidl, M., Dorst, R., Schaeffer, D., Bondarenko, A., Tripathi, S., et al. (2018). Observations of a field-aligned ion/ion-beam instability in a magnetized laboratory plasma. Phys. Plasmas 25, 032104. doi:10.1063/1.5017637

CrossRef Full Text | Google Scholar

Holcomb, C., and Spitkovsky, A. (2019). On the growth and saturation of the gyroresonant streaming instabilities. Astrophysical J. 882, 3. doi:10.3847/1538-4357/ab328a

CrossRef Full Text | Google Scholar

Hoppe, M., Russell, C., Frank, L., Eastman, T., and Greenstadt, E. (1981). Upstream hydromagnetic waves and their association with backstreaming ion populations: Isee 1 and 2 observations. J. Geophys. Res. Space Phys. 86, 4471–4492. doi:10.1029/ja086ia06p04471

CrossRef Full Text | Google Scholar

Hoshino, M., and Terasawa, T. (1985). Numerical study of the upstream wave excitation mechanism: 1. Nonlinear phase bunching of beam ions. J. Geophys. Res. Space Phys. 90, 57–64. doi:10.1029/ja090ia01p00057

CrossRef Full Text | Google Scholar

Kajdič, P., Pfau-Kempf, Y., Turc, L., Dimmock, A. P., Palmroth, M., Takahashi, K., et al. (2021). Ulf wave transmission across collisionless shocks: 2.5 d local hybrid simulations. J. Geophys. Res. Space Phys. 126, e2021JA029283. doi:10.1029/2021ja029283

CrossRef Full Text | Google Scholar

Keenan, B. D., Le, A., Winske, D., Stanier, A., Wetherton, B., Cowee, M., et al. (2022). Hybrid particle-in-cell simulations of electromagnetic coupling and waves from streaming burst debris. Phys. Plasmas 29, 012107. doi:10.1063/5.0075482

CrossRef Full Text | Google Scholar

Kucharek, H., Scholder, M., and Matthews, A. (2000). Three-dimensional simulation of the electromagnetic ion/ion beam instability: Cross field diffusion. Nonlinear Process. Geophys. 7, 167–172. doi:10.5194/npg-7-167-2000

CrossRef Full Text | Google Scholar

Le, A., Daughton, W., Karimabadi, H., and Egedal, J. (2016). Hybrid simulations of magnetic reconnection with kinetic ions and fluid electron pressure anisotropy. Phys. Plasmas 23, 032114. doi:10.1063/1.4943893

CrossRef Full Text | Google Scholar

Le, A., Winske, D., Stanier, A., Daughton, W., Cowee, M., Wetherton, B., et al. (2021). Astrophysical explosions revisited: Collisionless coupling of debris to magnetized plasma. J. Geophys. Res. Space Phys. 126, e2021JA029125. doi:10.1029/2021ja029125

CrossRef Full Text | Google Scholar

Lee, M. A. (1982). Coupled hydromagnetic wave excitation and ion acceleration upstream of the Earth’s bow shock. J. Geophys. Res. Space Phys. 87, 5063–5080. doi:10.1029/ja087ia07p05063

CrossRef Full Text | Google Scholar

Lipatov, A. S. (2002). The hybrid multiscale simulation technology: An introduction with application to astrophysical and laboratory plasmas. Berlin, Germany: Springer Science & Business Media.

Google Scholar

Montgomery, M. D., Gary, S. P., Forslund, D., and Feldman, W. (1975). Electromagnetic ion-beam instabilities in the solar wind. Phys. Rev. Lett. 35, 890. doi:10.1103/physrevlett.35.890.3

CrossRef Full Text | Google Scholar

Palmroth, M., Archer, M., Vainio, R., Hietala, H., Pfau-Kempf, Y., Hoilijoki, S., et al. (2015). Ulf foreshock under radial imf: Themis observations and global kinetic simulation vlasiator results compared. J. Geophys. Res. Space Phys. 120, 8782–8798. doi:10.1002/2015ja021526

CrossRef Full Text | Google Scholar

Stanier, A., Chacon, L., and Le, A. (2020). A cancellation problem in hybrid particle-in-cell schemes due to finite particle size. J. Comput. Phys. 420, 109705. doi:10.1016/j.jcp.2020.109705

CrossRef Full Text | Google Scholar

Strumik, M., Roytershteyn, V., Karimabadi, H., Stasiewicz, K., Grzesiak, M., and Przepiórka, D. (2015). Identification of the dominant ulf wave mode and generation mechanism for obliquely propagating waves in the Earth’s foreshock. Geophys. Res. Lett. 42, 5109–5116. doi:10.1002/2015gl064915

CrossRef Full Text | Google Scholar

Thomsen, M., Gosling, J., Bame, S., and Russell, C. (1985). Gyrating ions and large-amplitude monochromatic mhd waves upstream of the Earth’s bow shock. J. Geophys. Res. Space Phys. 90, 267–273. doi:10.1029/ja090ia01p00267

CrossRef Full Text | Google Scholar

Turc, L., Zhou, H., Tarvus, V., Ala-Lahti, M., Battarbee, M., Pfau-Kempf, Y., et al. (2022). A global view of pc3 wave activity in near-Earth space: Results from hybrid-vlasov simulations. Front. Astronomy Space Sci. 9, 989369. doi:10.3389/fspas.2022.989369

CrossRef Full Text | Google Scholar

Verscharen, D., and Chandran, B. (2018). Nhds: The New Hampshire dispersion relation solver. Res. Notes AAS 2, 13. doi:10.3847/2515-5172/aabfe3

CrossRef Full Text | Google Scholar

Wang, X., and Lin, Y. (2003). Generation of nonlinear alfvén and magnetosonic waves by beam–plasma interaction. Phys. Plasmas 10, 3528–3538. doi:10.1063/1.1599359

CrossRef Full Text | Google Scholar

Watanabe, Y., and Terasawa, T. (1984). On the excitation mechanism of the low-frequency upstream waves. J. Geophys. Res. Space Phys. 89, 6623–6630. doi:10.1029/ja089ia08p06623

CrossRef Full Text | Google Scholar

Weidl, M. S., Winske, D., and Niemann, C. (2019). Three regimes and four modes for the resonant saturation of parallel ion-beam instabilities. Astrophysical J. 873, 57. doi:10.3847/1538-4357/ab0462

CrossRef Full Text | Google Scholar

Winske, D., and Gary, S. (1986). Electromagnetic instabilities driven by cool heavy ion beams. J. Geophys. Res. Space Phys. 91, 6825–6832. doi:10.1029/ja091ia06p06825

CrossRef Full Text | Google Scholar

Winske, D., and Omidi, N. (1992). Electromagnetic ion/ion cyclotron instability: Theory and simulations. J. Geophys. Res. Space Phys. 97, 14779–14799. doi:10.1029/92ja00902

CrossRef Full Text | Google Scholar

Winske, D., and Quest, K. (1986). Electromagnetic ion beam instabilities: Comparison of one-and two-dimensional simulations. J. Geophys. Res. Space Phys. 91, 8789–8797. doi:10.1029/ja091ia08p08789

CrossRef Full Text | Google Scholar

Winske, D., and Wilson, L. B. (2022). Linear theory of electromagnetic ion beam instabilities in the Earth’s forshock: Peter gary’s contributions (1981–1991). Front. Astronomy Space Sci. 9, 899642. doi:10.3389/fspas.2022.899642

CrossRef Full Text | Google Scholar

Winske, D., Yin, L., Omidi, N., Karimabadi, H., and Quest, K. (2003). “Hybrid simulation codes: Past, present and future—A tutorial,” in Space plasma simulation (Springer, Berlin, Heidelberg: Spinger), 136–165. doi:10.1007/3-540-36530-3_8

CrossRef Full Text | Google Scholar