A Self-Gravitating Exoring Around J1407b and Implications for In-Situ Exomoon Formation

We perform simulations of the $M_{\oplus }$ self-gravitating exoring thought to orbit the large exoplanet J1407b. We use a mass of $M_{J1407b}=20M_J$ (which is close to the revised upper limit) and a semi-major axis of $a=5AU$, equating to an orbital period of $\sim 11yrs$ about the primary. As J1407b is expected to have a high eccentricity, we test eight different models: where e = 0.2, 0.4, 0.6 and 0.8 in both the prograde and retrograde configurations. All prograde models show a strongly perturbed ring within the first orbit. As expected, the retrograde rings demonstrate a higher degree of stability, with the lower eccentricity models (e = 0.2 and 0.4) able to survive multiple orbits. However, even the higher eccentricity (e = 0.6 and 0.8) retrograde models quickly result in the loss of the ring after 200 years. Excitation of eccentricities in all retrograde rings are stable to gravitational collapse. When assuming the most recent mass estimate of $M_{J1407b}=20M_J$ the ring is unfavourable to the accretion of moons when J1407b is on an elliptical orbit. An interesting consequence of the strong perturbation for one model (retrograde and e = 0.6) during the first close passage is a transient gap located at 0.4AU. This is the same location as the inferred gap from the single transit in 2007 and does not require a nearby exomoon.

Introduction

In 2007 the active young solar mass star J1407, also known as V1400 Centauri, was observed to have an unusually long and complex transit of $\sim 56 days$ (Mamajek et al., 2012). No further transits have been detected despite dedicated surveys (Barmentloo et al., 2021). Subsequent work analysing the single transit suggests the cause was by a secondary companion with a mass $5-20 M_{Jup }$ (Mentel et al., 2018) and a ring system filling a significant fraction of its Hill sphere (Van Werkhoven et al., 2014; Kenworthy and Mamajek 2015; Rieder and Kenworthy 2016). Recent ALMA and NACO observations by Kenworthy et al. (2019) show an object located at an angular separation expected for a ring system that would have transited J1407 in 2007. However, the authors also note the source is unresolvable and could equally be a background object, like a galaxy.

Photometric studies after 2007 by the five ground-based telescopes All Sky Automated Survey (ASAN; Pojmanski (1997)) All Sky Automated Survey for Supernovae (ASAN-SN; Kochanek et al. (2017)), Kilodegree Extremely Little Telescope (KELT; Pepper et al. (2007); Pepper et al. (2012)), The Panchromatic Robotic Optical Monitoring and Polarimetry Telescopes (PROMPT; Reichart et al., 2005), Remote Observatory Atacama Desert (ROAD; Hambsch (2012)) and The Transiting Exoplanet Survey Satellite (TESS; Ricker et al. (2015)) revealed an activity cycle of 5.4 years for J1407, but no transiting companions or further deep transits associated with a ring system (Barmentloo et al., 2021).

A period of $\sim 11 yr$ and large eccentricities $\text{e}>0.7$ were required to account for radial velocity measurements and transit timing, but this resulted in the ring becoming unstable at periapsis. The outer region of the ring was found to become unbound from J1407b at large eccentricities due to the decrease in Hill radius $\left(R_{Hill}\right)$ at periapsis, falling well within the predicted outer ring edge (Rieder & Kenworthy 2016). Here, the Hill radius is the distance at which an object would remain bound to J1407b, despite the gravitational influence of the primary J1407 (V1400 Centauri), and is given below.

$R_{Hill}= a(1-e){\left(\frac{M_{J1047b}}{3M_{J1407}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}(1)$

The Hill radius is then a function of the semi-major axis ($a$), eccentricity ($e$) and a ratio of the primary $\left(M_{J1407}\right)$ and secondary $\left(M_{J1047b}\right)$ masses. Taking the semi-major axis as $a=5 AU$, the mass of J1407 as $1.0 M_{\odot }$ and J1407b as $20 M_{Jup }$ the Hill radius ranges from $0.93 AU$ for a circular orbit down to $0.185 AU (40-200 R_{\odot })$ for the more extreme case where $e=0.8$. Stability issues can be partially overcome by considering a ring orbiting in a retrograde manner instead of prograde (Rieder & Kenworthy 2016), which prevented a significant loss of material from the outer region of the ring during periapsis. However, this raises more questions on the origin of such a ring since retrograde orbits are generally the result of captured small objects, like many of the Solar System’s retrograde moons (Nesvorný et al., 2014; Higuchi and Ida 2016; Namouni and Morais 2018). Thus, a retrograde ring could represent the tidal disruption of a captured smaller planet in the system (Canup 2010; Hyodo et al., 2017), which then fills a significant portion of J1407b’s Hill sphere.

Like Saturn’s ring, J1407b’s ring is not radially uniform; instead, there are hints of an unseen exomoon in the form of gaps; or regions with relatively low surface densities. Three possible mechanisms can form a gap in a planetary ring: The first is due to Mean Motion Resonances (MMR) by moons external to the ring and is analogous to how Mimas causes the Cassini Division in Saturn’s rings (Goldreich and Tremaine 1978; Noyelles et al., 2016). However, models of moons placed at various MMR’s around J1407b’s ring showed this was not possible without causing significant disruption to the outer region of the ring edge (Sutton 2019). Secondly, moons embedded within the ring can carve out a gap proportional to their Hill radius. Saturn’s small moons Pan and Daphnis clear out gaps in the ring with a width related to their Hill radius $$ (Bromley and Kenyon 2013; Hedman et al., 2013; Weiss et al., 2009; Torrey et al., 2008; Lewis and Stewart 2006; Horn et al., 1996; Petit and Hénon 1988). For the case of Pan and Daphnis, the gap half-width was found to be $\Delta a\approx 3.8R_{hill}$ (Weiss et al., 2009), where $\Delta a$ is small in respect to the semi-major axis $a$ for the moon. This also assumes ring particles are on or close to circular orbits before they encounter the moon. Although more complicated, protoplanets in a circumstellar disk show a similar gap width relationship with their mass. It is also dependent on disk properties (Duffell and MacFadyen 2013; Fung and Chiang 2016; Kanagawa et al., 2016) but further strengthens the hypothesis of the mass being the key driver in gap width. Finally, inclined ring systems can also produce gaps without the need for moons (Speedie and Zanazzi 2020).

If moons are present around gas giants, typical timescales for in-situ formation in a gaseous circumplanetary disk ranges from ${10}^5-{10}^6$ years for gas starved-disk models (Canup and Ward 2002; Szulágyi et al., 2018) down to ${10}^2-{10}^4$ years for dense circumplanetary disks (Lunine and Stevenson 1982). With timescales for the formation of $1000km$ sized objects in gas depleted debris disks also falling within this range at $\sim {10}^3$ years (Hyodo and Charnoz 2017).

It is worth noting that the orbital architecture of Saturn, Uranus and Neptune’s regular moons suggest an alternative formation mechanism than those of the larger Galilean moons of Jupiter. Here, the masses of the satellites increase with increasing distance from the planets Roche limit. A viscously spreading ring will accrete moons once it exceeds the Roche limit, with moons being repelled outwards by angular momentum exchange with the disk (Crida and Charnoz, 2012). As the ring becomes depleted, the mass of the subsequent moons and migration rate decrease.Where J1407b is on a highly eccentric orbit about the primary, the potential presence of exomoons forming gaps is still unanswered. The location of the ring outside the Roche limit suggests a favourable environment for accretion of ring material into moons, but this does not consider the close passage at periapsis, which is likely to impact moon formation. While Saturn’s F ring is in a different tidal environment, it lies very close to the Roche Limit for water ice and is perturbed by the nearby moons Prometheus and Pandora. Yet, observations and models (Beurle et al., 2010; Sutton 2018) suggest moonlets can still form due to localised gravitational instabilities. Therefore, this does not rule out the formation of moons within a strongly perturbed ring.

Methods

We use the same ring model as used by Sutton (2019), which placed 10,000 particles around the exoplanet J1407b. Ring particles are distributed in the radial direction between $0.2AU<r<0.6AU$ to produce a surface density profile $\Sigma \propto 1/r$, which is a commonly used profile in models of astrophysical disks. Ring particles are then evenly distributed in the azimuthal position between $0<\theta <2\pi$. Assuming a constant velocity for ring particles on circular orbits their initial velocities were set according to $V=\sqrt{G{M}_{J1407b}/a}$ around J1407b. This time the total mass of the ring is set to current estimates of $\sim M_{\oplus }$ (Kenworthy and Mamajek 2015), with all ring particles given the same mass of $M_{ring}=\raisebox{1ex}{$M_{\oplus }$}\!\left/ \!\raisebox{-1ex}{$N_{ring}$}\right.$.

The primary star, J1407 (V1400 Centauri), is placed at the origin with a mass of $1.0 M_{\odot }.$ These fall within error of the inferred mass ($0.9\pm 0.1 M_{\odot })$ for J1407 determined by its position on the HR diagram (Van Werkhoven et al., 2014), and the same mass used by Rieder and Kenworthy (2016) in their N-body models. We use the revised upper mass limit of $20M_{Jup }$ (Mentel et al., 2018) for J1407b. This is lower than Rieder and Kenworthy (2016), who found a mass of $60-100M_{Jup }$ to be the most dynamically stable configuration. Due to the velocity of the origin transit, a highly eccentric orbit is required if J1407b is bound to star V1400 Centauri. Therefore, we use a semi-major axis of $a=5AU$ and increase eccentricity from $e=0.2$ to $e=0.8$ in $0.2$ increments to investigate the decreasing separation at periapsis. An orbital period of 11 year only permitted eccentricities up to $e=0.8$ (Von Werkhoven et al., 2014; Kenworthy and Mamajek 2015; Rieder and Kenworthy 2016), which we take as an upper limit for eccentricity in our models.

Numerical integration is carried out using Gadget-2 (Springel 2005), which uses a hierarchical multipole expansion to deal with gravitational interactions between particles in the form of a tree-walk to improve computational costs. Timesteps of particles are variable and scale with acceleration $a$ and is given as,

$\mathrm{\Delta }{t}_{grav}=\sqrt{\left(2\eta \mathit{ϵ}/\left|a\right|\right)}$

Here, $\mathit{ϵ}$ is the gravitational smoothing length and is given a value comparable to the physical size of the particle. $\eta$ is dimensionless and controls the accuracy of the timestep and is set as 0.05. Due to the single transit of the ring system it’s composition is not well constrained. For example, it is not known whether it is a thin layer of particles or is optically thick. There is also no evidence of gas located around J1407 and has led previous studies to infer the ring to be more reminiscent of a debris disk. Due to the uncertainty in the ring composition our models assume the ring to dusty with no gas component. Thus, ring particles evolve solely through gravitational interaction. Objects in our models do not undergo physical collisions with one another. Instead, gravitational forces during close encounters are reduced with a smoothing kernel within a set radius, known as the smoothing length. All objects have their smoothing lengths set to be comparable to their equivalent physical radii. For J1407b, the smoothing length used is appropriate for an internal density comparable to Jupiter $\rho =1.31 gc{m}^{-3}$. Currently, there is significant uncertainty on the mass, size, and density of J1407b. However, the smoothing length is not critical as ring particles do not encounter J1407b at such distances. J1407 is given a smoothing length of $R_{\odot }$ and ring particles adopt smoothing lengths that relate physical radii associated with densities of rocky asteroids $\left(2 gc{m}^{-3}\right)$.

Particles with radial distance $<0.001 AU$ from the J1407b particle are removed from the models as it is assumed particles are accreted by the planet. For reference, this is 1/3 of the Roche limit when assuming a comparable density of J1407b as Jupiter ($\rho =1.31 gc{m}^{-3}$) for rocky material $\left(2 gc{m}^{-3}\right).$

Previous work by Kenworthy and Rieder (2016) showed that both a prograde and retrograde ring system would lose the particles from outer region due to strong gravitational perturbations, which we also observed in our models. Consequently, ring particles with radial distances $>1 AU$ from J1047b were not considered in the analysis since they become unbound. The maximum Hill radius for J1407b is 0.93 AU in our configuration when it is assumed to be on a circular orbit. This is well within the 1 AU that we remove particles from and only decreases as eccentricity increases. “The stability of distant retrograde orbits is also demonstrated by many captured moons in the Solar System (Gladman et al., 2001; Nesvorný et al., 2014) and are beneficial for future space missions (Ming and Shijie 2009; Bezrouk and Parker 2017). Therefore, as a retrograde ring demonstrates longer-term stability compared with a prograde ring, we only consider a retrograde ring for the first 2000 years (corresponding to ∼182 orbits about the primary).

Prograde Ring

A prograde ring around J1407b is first considered, which is expected to be less stable during close passes at its pericenter, as reported by Rieder and Kenworthy (2016). Figure 1 shows the first orbit of the prograde ring, where it starts at the apocentre. As expected, increasing the eccentricity also increases the loss of ring particles, with the $e=0.6 \& 0.8$ models showing very little of the original ring remaining after just one close passage.

FIGURE 1

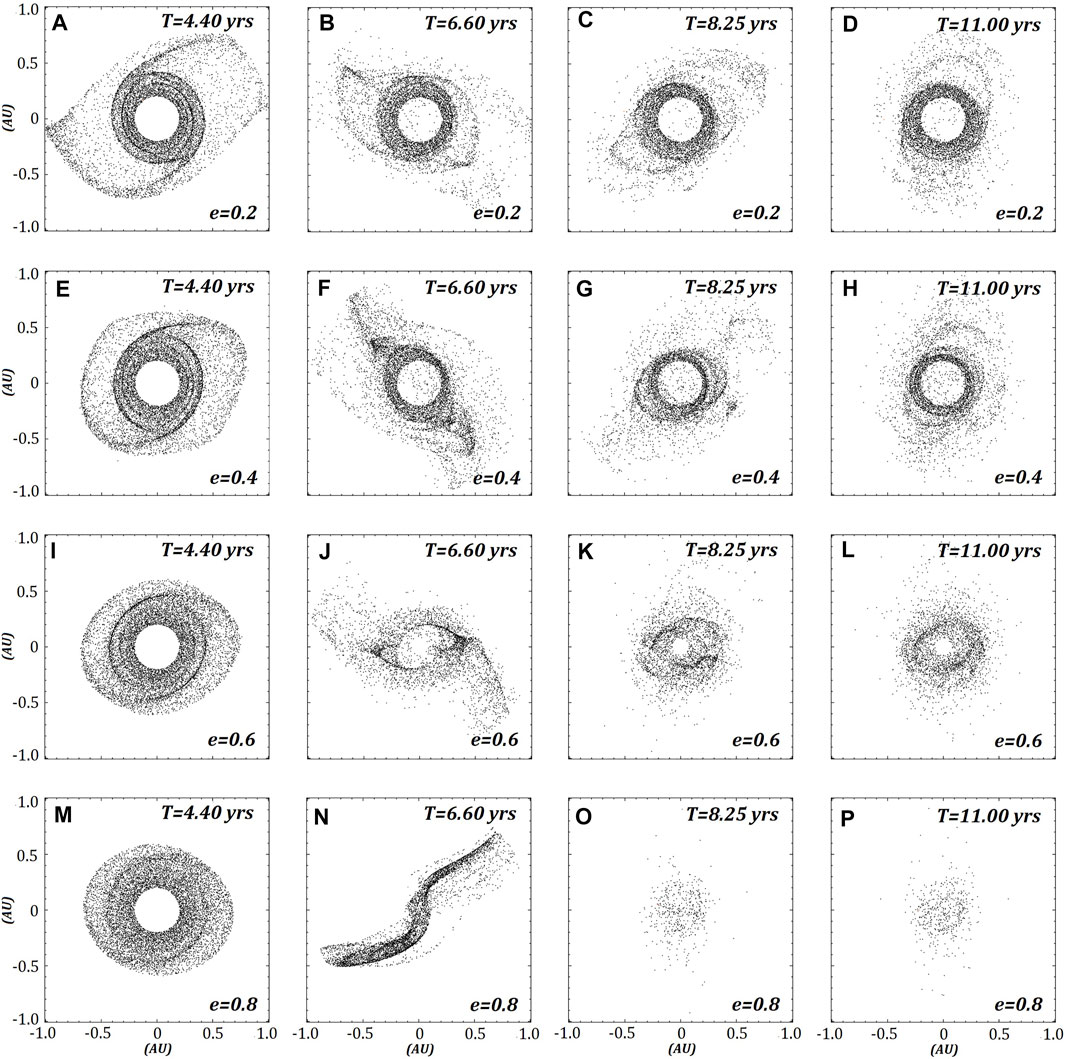
FIGURE 1. Four models of a ring around J1407b $\left(M=20M_J\right)$ for one complete orbit $\left(P=11 yrs\right)$ about the primary. The x and y axes represent the instanteous positions of ring particles around J1407b, which is at the origin. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H) $e=0.6$ (I–L) and $e=0.8$ (M–P), while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs (B, F, J \& N)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

Rendered plots of the surface density (Figure 2) show some models experience a short-term increase in local surface density. The lower eccentricity models ($e=0.2 \& e=0.4$) show a slight increase in surface density after the first close passage. However, these increases are confined to narrow rings located close to $<0.4AU$. The higher eccentricity models ($e=0.6 \& e=0.8$) see a larger initial increase in surface densities of up to $100 g c{m}^{-2}$. Although much of this material is quickly removed from the ring and goes on to orbit the primary. Most of the material from the outer region of the ring is lost in all the prograde models.

FIGURE 2

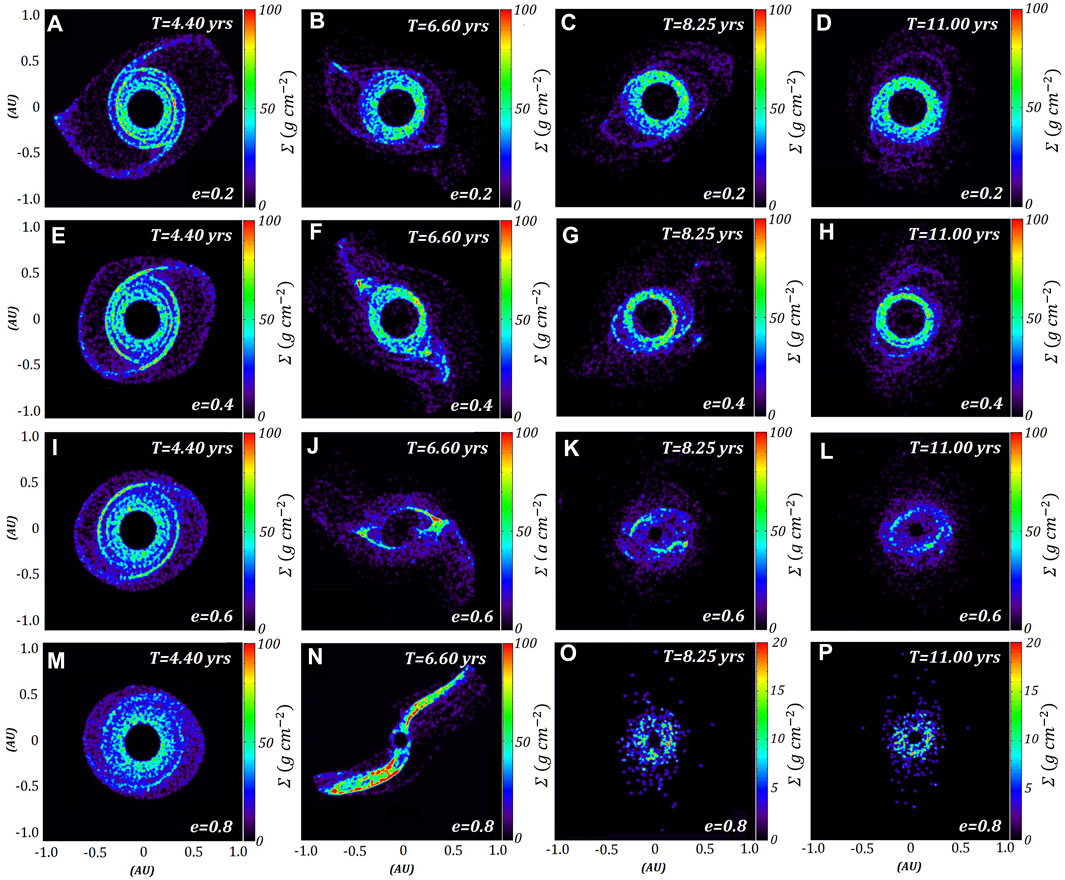
FIGURE 2. Surface densities of the same four models in Figure 1. The x and y axes represent the instanteous positions of ring particles around J1407b, which is at the origin. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ (I–L) and $e=0.8$ (M–P), while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs (B, F, J \& N)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

Retrograde Ring

Particles are placed in the same ring around J1407b but with retrograde velocities in respect to the orbit of J1407b. Rieder and Kenworthy (2016) identified that a retrograde ring would be more stable against strong perturbations caused by close passes to the primary due to a highly eccentric orbit. Therefore, a large proportion of the ring remains bound to J1407b for all eccentricities beyond one complete orbit (Figure 3) compared with a prograde ring (Figure 1). Evidence of spiral arm wave structures can be seen after the first orbital period, noted by their higher surface densities (Figure 4), which persist for multiple orbits of the low eccentricity models ($e=0.2 \& 0.4)$. Spiral arm formation due to the periodic forcing of the close passages was also reported by Reider and Kenworthy (2016) in their models and are described in more detail by Thebault et al. (2006). The ring only survives in three of the models after 2000 years or ∼182 orbits (Figure 5), with the highest eccentricity model ($e=0.8$) depleted within $\sim 200 years$. Despite local increases in surface density during the first few orbits, all models continue to lose mass during each successive periapsis. This naturally causes a global decrease in surface density and is counterproductive for the accretion of moons.

FIGURE 3

FIGURE 3. Four models of a retrograde ring around J1407b $\left(M=20M_J\right)$ for one complete orbit $\left(P=11 yrs\right)$ about the primary. The x and y axes represent the instanteous positions of ring particles around J1407b, which is at the origin. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ ($i-l)$ and $e=0.8$ ($m-p)$, while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs (B, F, J \& N)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

FIGURE 4

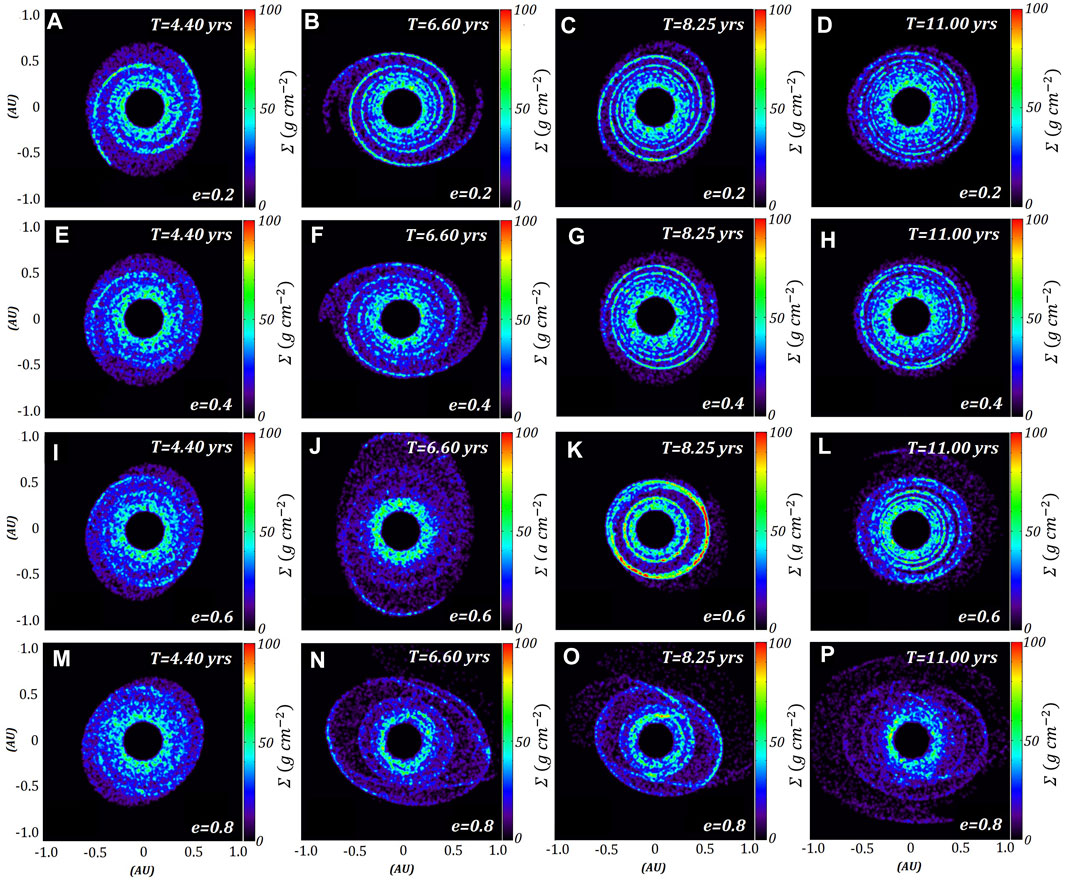
FIGURE 4. Surface densities of the same four models as Figure 3. The x and y axes represent the instanteous positions of ring particles around J1407b, which is at the origin. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ ($i-l)$ and $e=0.8$ ($m-p)$, while the column represents a snapshot in time at $T=4.40 yrs \left(A, E, I \& M\right)$, $T=6.60 yrs \left(B, F, J \& N\right)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

FIGURE 5

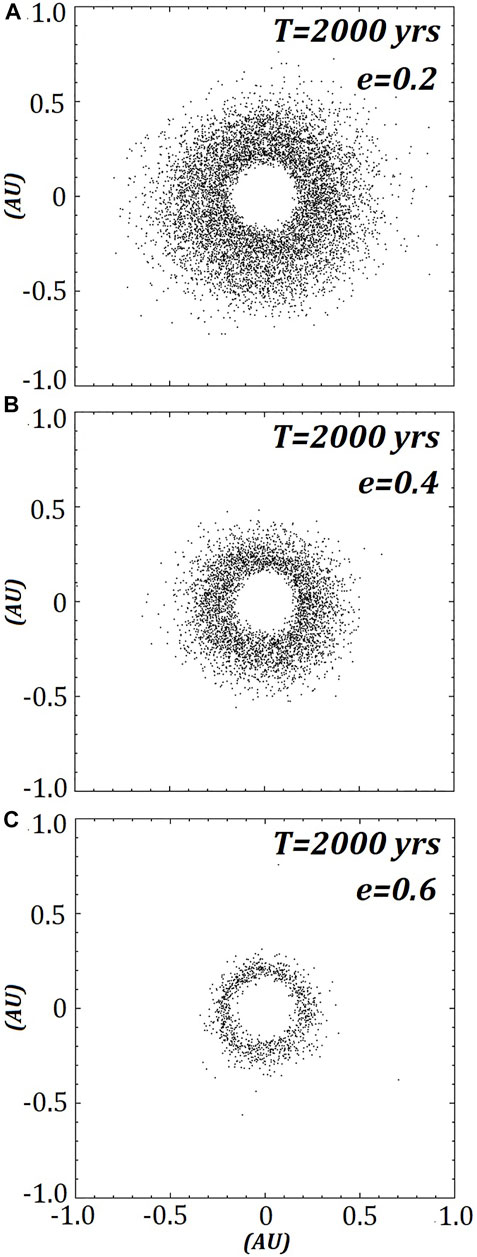
FIGURE 5. The three remaining models A) e = 0.2, B) e = 0.4 and C) e = 0.6 of a retrograde ring around J1407b (M = 20MJ) after 2000 years or ∼182 complete orbits about the primary.

Figure 6 shows total number of particles in each of the retrograde ring models over 2000yrs and is sampled at 100 years intervals. The remaining three models begin to plateau towards the 2000 year mark but still show a mass loss of $8.2\times {10}^{-7}{M}_{\oplus }y{r}^{-1}\left(e=0.2\right),7.5\times {10}^{-7}{M}_{\oplus }y{r}^{-1}$ (e = 0.4) and $8.6\times {10}^{-8}{M}_{\oplus }y{r}^{-1}$ (e = 0.6). The higher mass loss rates for the lower eccentricity models can be attributed to the rings being more massive despite being a smaller fraction of the total ring mass.

FIGURE 6

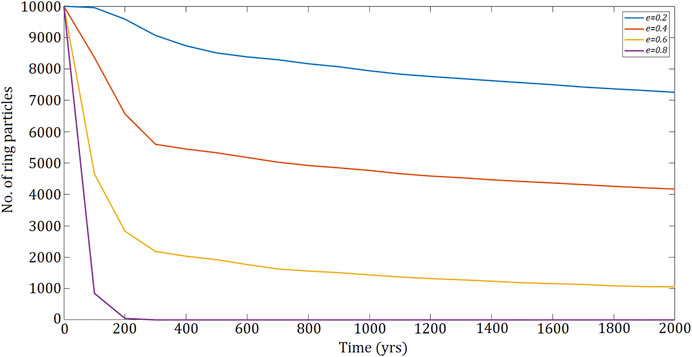
FIGURE 6. The number of particles in all 4 retrograde ring models is plotting against time and shows that the majority of particles lost occurs within ∼300 yrs.

Radial Profile

A key observation of the original transit suggested a gap in the ring could be indirect evidence of an exomoon. However, where J1407b is on an eccentric orbit, the radial profile of the ring can have regions of higher and lower density without the need for a moon. Here, we create radial profiles of the azimuthally averaged surface density to investigate features that could be interpreted as a gap.

Predictably, the surface density of the prograde ring (Figure 7) decreases significantly as eccentricity increases, with the lower eccentricity models having most of the mass shift inwards into a narrower ring. The spiral arms observed in the retrograde ring are evident in the radial profile (Figure 8), with alternating high and lower densities. An interesting feature in one of the retrograde models, $e=0.6$, shows a gap centred around 0.4AU, which is also the location identified as a gap from the transit (Kenworthy and Mamajek 2015). This feature is transitory and is no longer present $1/4$ of an orbit later. The minimum surface density measured in the gap at 0.4AU of the retrograde model with $e=0.6$ is $\Sigma =13g c{m}^{-2}$. If we assume that particle sizes are comparable to Saturn’s main rings $\left(\sim m\right)$, we come to an optical depth of $\tau \sim 0.05$. While the transmission through the ring significantly increases at the location of this gap it is not the same as reported by Kenworthy and Mamajek (2015), which had an optical depth of $\tau =0.00$ at the same radial location.

FIGURE 7

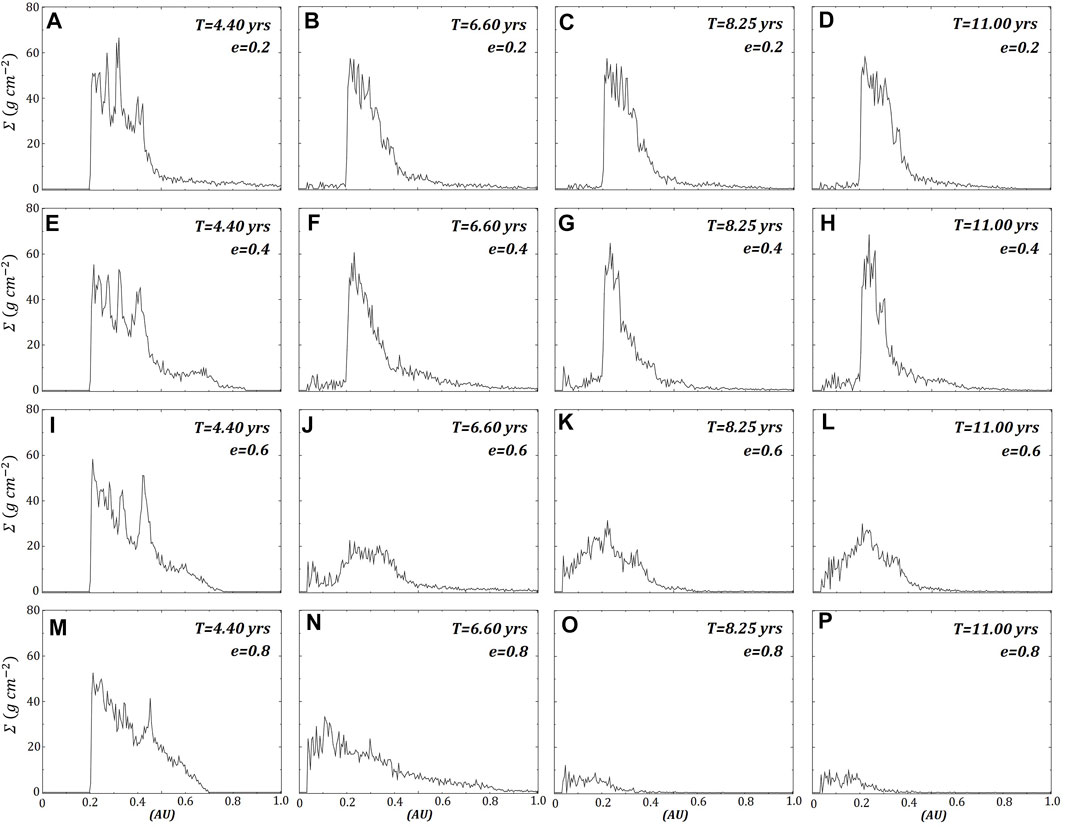
FIGURE 7. The same four prograde ring models shown in Figure 1 with their azimuthally averaged surface densities. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ (I–L) and $e=0.8$ (M–P), while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs \left(B, F, J \& N\right)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

FIGURE 8

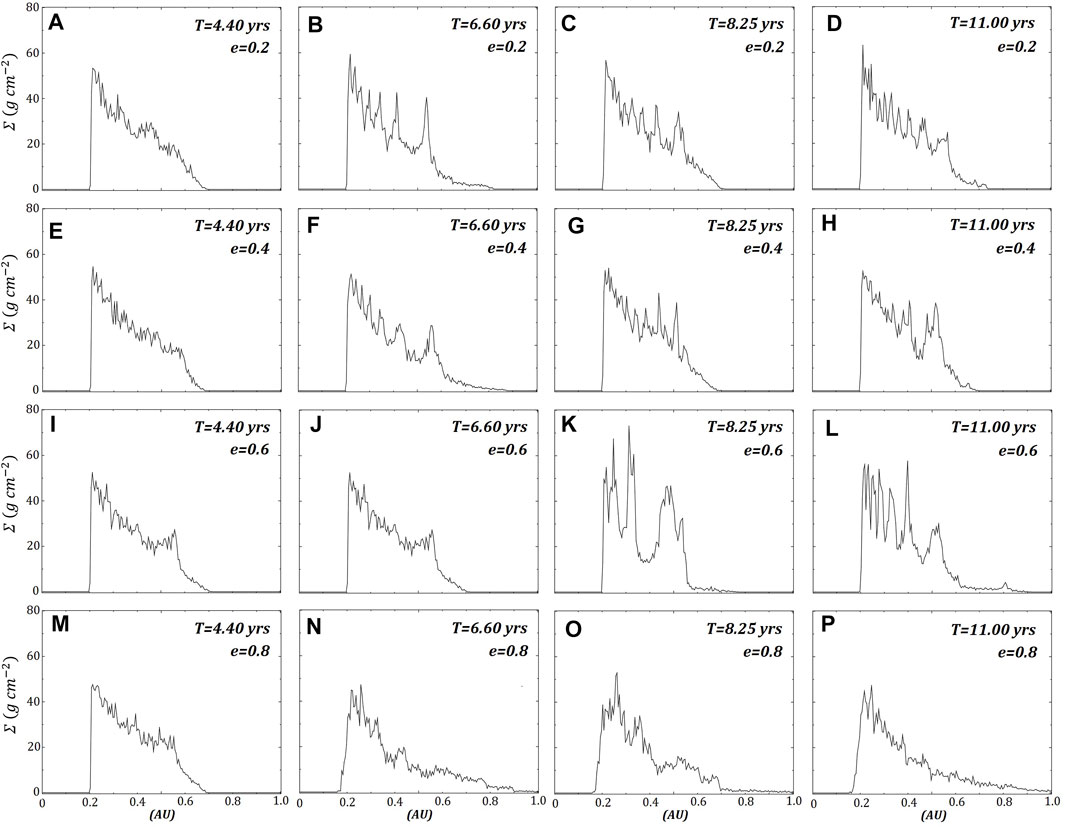
FIGURE 8. The same four retrograde ring models shown in Figure 3 with their azimuthally averaged surface densities. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ (I–L) and $e=0.8$ (M–P), while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs \left(B, F, J \& N\right)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

The surface density of the models that survive for 2000 years ($e=0.2,0.4 \& 0.6)$ continually decreases as material is stripped from the rings during each periapsis (Figure 9).

FIGURE 9

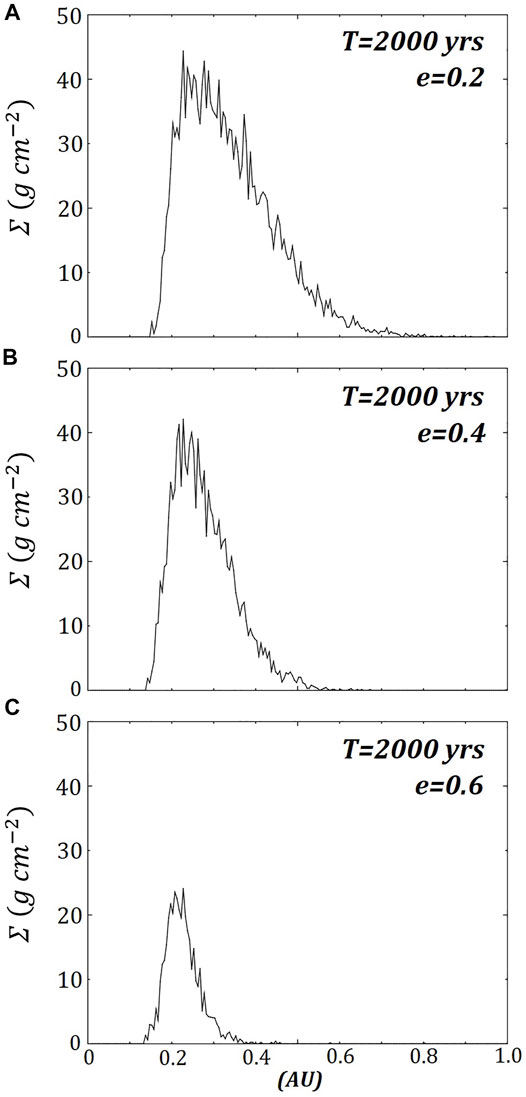
FIGURE 9. The same three retrograde ring models (A) e = 0.2, (B) e = 0.4 and (C) e = 0.6 are shown in Figure 5 with their azimuthally averaged surface densities after 2000 years or ∼182 complete orbits about the primary.

Eccentricity

We calculate the eccentricity by taking the eccentricity vector $\overrightarrow{e}$ shown below and plot it with respect to semi-major axis from J1407b for all models.

$\overrightarrow{e}=\left(\frac{{\left|\overrightarrow{v}\right|}^2}{\mu }-\frac{1}{\left|\overrightarrow{r}\right|}\right)\overrightarrow{r}-\frac{\overrightarrow{r}\cdot \overrightarrow{v}}{\mu }\overrightarrow{v}(2)$

All models show signs of excitation of eccentricity from the close passage at periapsis, with the prograde ring showing significant excitation of eccentricities (Figure 10) compared to the retrograde ring (Figure 11). The majority of excitation occurs during the first passage, with eccentricities only increasing each passage. After 2000 years, the three surviving retrograde rings all have significant eccentricities (Figure 12), including those particles located on the inner region of the ring.

FIGURE 10

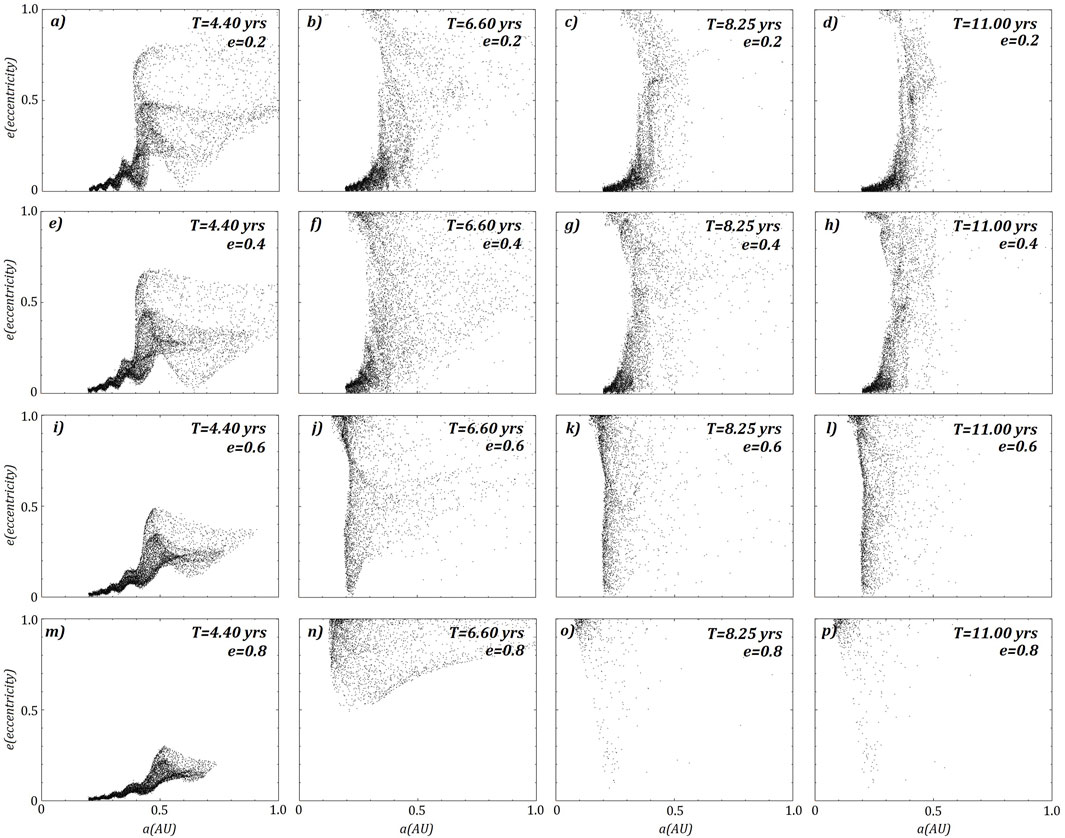
FIGURE 10. The same four prograde ring models shown in Figure 1. Here the calculated eccentricities and semi-major axis for all ring particles are plotted. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ (I–L) and $e=0.8$ (M–P), while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs \left(B, F, J \& N\right)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

FIGURE 11

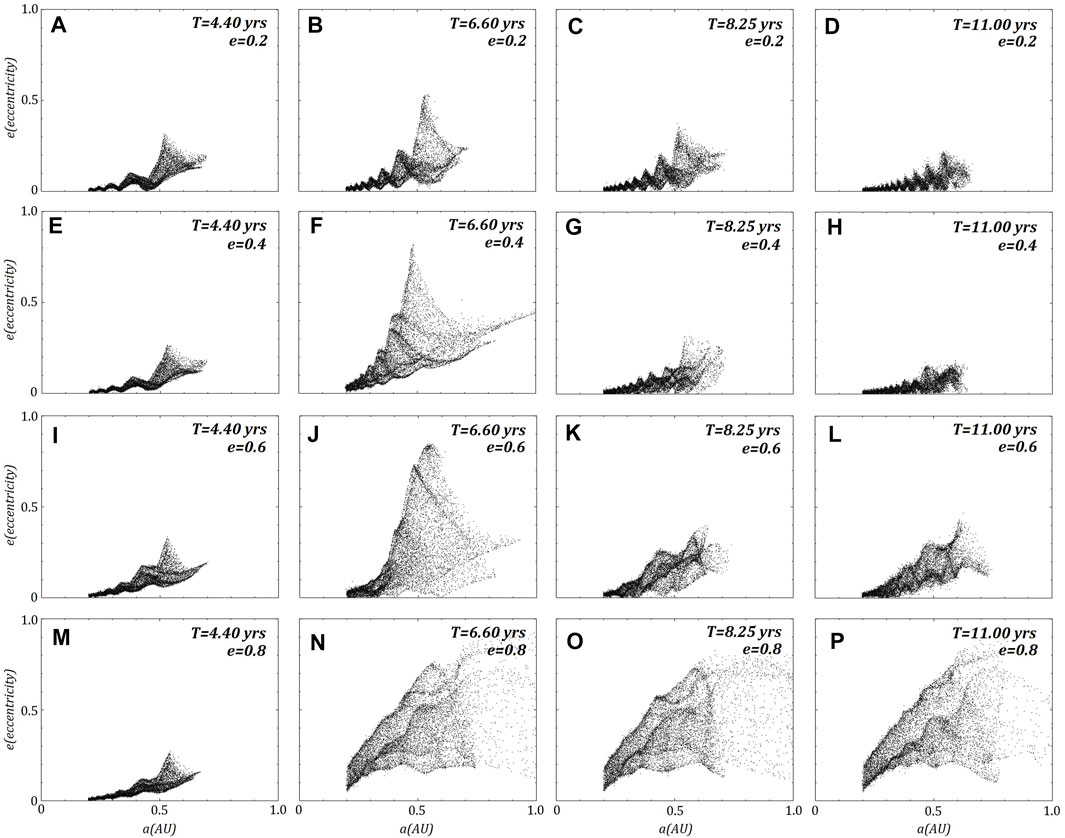
FIGURE 11. The same four retrograde ring models shown in Figure 2. Here the calculated eccentricities and semi-major axis for all ring particles are plotted. The rows represent each model, where $e=0.2$ (A–D), $e=0.4$ (E–H), $e=0.6$ (I–L) and $e=0.8$ (M–P), while the column represents a snapshot in time at $T=4.40 yrs (A, E, I \& M)$, $T=6.60 yrs \left(B, F, J \& N\right)$, $T=8.25 yrs (C, G, K \& O)$, $T=11.00 yrs (D, H, L \& P)$, where all models began at apocentre.

FIGURE 12

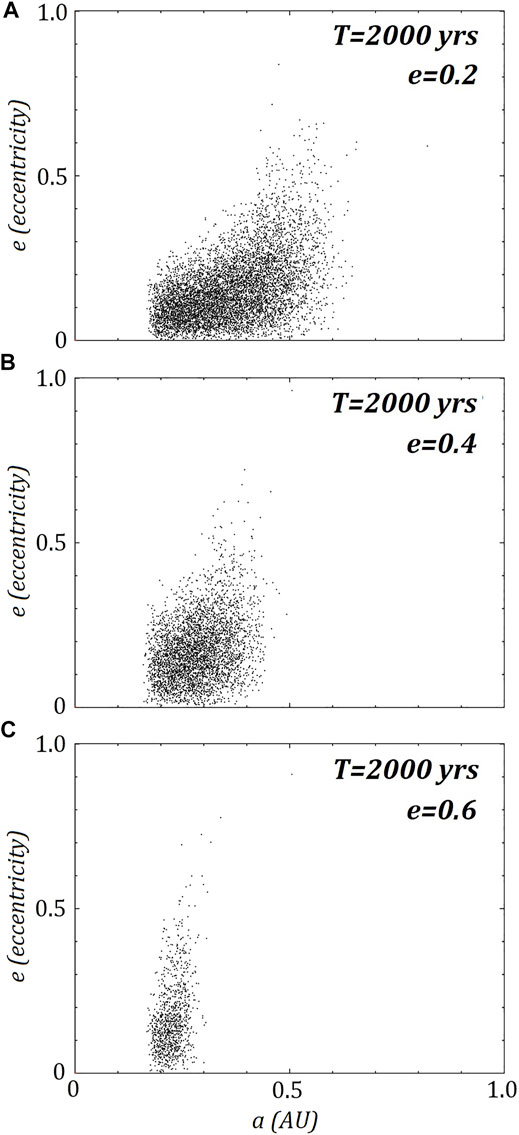
FIGURE 12. he same three retrograde ring models (A) e = 0.2, (B) e = 0.4 and (C) e = 0.6 are shown in Figure 5 with their calculated eccentricities and semi-major axis for all ring particles after 2000 years or ∼182 orbits about the primary.

It should be noted that eccentricities would be dampened where collisions between ring particles are considered, which are neglected in our models. In a non-perturbed planetary ring, particle collisions dampen individual particle’s eccentricities by introducing a viscosity (Daisaka et al., 2001). Collision frequency between particles in a ring can be given as $v_c\sim \mathit{\Omega }\tau$, where the optical depth $\tau$ is the collision rate per particle per orbit and $\mathit{\Omega }$ is the orbit frequency. Assuming particles are a similar size $\left(\sim m\right)$ to those in Saturn’s main rings and surface densities in our models range from ${\displaystyle \sum =10-100 g c{m}^{-2}}$ we find optical depths of $\tau \sim 0.04-0.38$. Therefore, collisions in our models occur less than the orbital period of a ring particle. One orbital period for a ring particle located at 0.4AU is 1.83 yrs and the orbital period of J1407b in our models is 11 year, which is the period of the strong perturbations on the ring. Collisions between particles in our models are then expected to occur up to approximately twice per orbit of J1407b for the highest optical depth regions. Collision frequencies are approximately the same as forcing frequency and are unlikely to offer significant dampening to excited eccentricities and inclinations during periapsis. Consequently, our models demonstrate that the frequency of the strong perturbations do not allow the ring to relax back to a more circular structure. In contrast, the optical depths in the observed ring are an order of magnitude greater at their peak ($\tau =4.65$). Therefore, collisions between ring particles would suppress the eccentricities to a greater extent than what we report in our models.

Discussion

Although our models agree with the retrograde scenario as the best solution for the long-term stability of a ring system, the lower mass of J1407b ($20M_J$), compared with Rieder and Kenworthy (2016), who used a mass of $60-80M_J$, still results in a short dynamic lifetime. High eccentricity retrograde models lose all ($e=0.8$) or the majority ($e=0.6$) of ring material within 20 orbits about the primary. While lower eccentricity models survive longer, they still undergo significant loss of ring material after 100 orbits, which continues for at least 181 orbits.

Research on the dynamic evolution of a debris disk around Saturn and the formation of moons can help give an indication on the timescales for the growth of a $1km$ ($R$) moon in an unperturbed ring (Hyodo and Charnoz 2017).

$T_{grow}\sim \frac{\rho R}{\mathit{\Omega }\Sigma \left(1+F_{grav)}\right)}(3)$

Where the surface density is $\Sigma =50 kg{m}^{-2},$ the density is taken as $\rho =1200 kg m^{-3}$, the orbital frequency is taken radially in the middle of the ring at $0.4 AU \mathit{\Omega }=1.089\times {10}^{-7}s$ and $F_{grav}$ is the gravitational focusing factor taken as $F_{grav}=1$, we get $T_{grow}\sim 3500 yrs$. This is orders of magnitude greater than the orbital period of J1407b $\left(\sim 11 yrs\right) w$hich causes significant perturbations to the ring during periapsis. After $2000 yrs$ all the models saw a significant decrease in surface densities from a loss of material, lengthening the growth time of potential moons without considering perturbations. However, if J1407b is detached from J1407 and is free-floating, the accretion of moons would be unimpeded and could likely grow to a size capable of carving out a gap.

While our simulations do not run for $>{10}^4$ orbits of the companion, like Rieder and Kenworthy (2016), the overall structure of the ring is defined within the first few passages to the primary. It is here that much of the outer region of the ring is lost with periodic forcing during periapsis, only increasing the eccentricity of individual ring particles during subsequent close passes. The excitation of eccentricities elevates radial velocity dispersions above critical values that would cause gravitational instabilities (Toomre 1964) and hinders the accretion of moons. The Toomre stability parameter ($Q$) for an astrophysical disk evaluates self-gravity against the Keplerian shear.

$Q=\frac{v_r\Omega }{\pi G\sum }(5)$

Where $\Omega \text{is the orbital angular frequency}{v}_r$ is the radial velocity dispersion and $G$ is the gravitational constant. The radial velocity dispersion was calculated by determining the deviation from the mean radial velocity of the ring. Here, the mean radial velocity is calculated from nearby particles (∼50) and the deviation from this by a ring particle gives rise to the radial velocity dispersion. All prograde and retrograde ring models had Toomre parameters $Q>2$ after the first close passage and remain elevated for the during of our simulations. $Q>1$ is typically taken to represent disks stable to gravitational collapse. Therefore, accretion in the ring appears to be difficult where J1407b is on an eccentric orbit. Furthermore, recent studies of exomoons around Hot Jupiter’s, which are also subjected to significant external perturbations, also highlight the difficulty of retaining exomoons due to the planet’s tidal migration (Hambsch, 2012). This is likely to have implications for the in-situ moon formation of Hot Jupiter’s in circumplanetary rings due to similar perturbations.

From our current understanding of the J1407b ring, we propose the following causes of the inferred gap initially observed in 2007:

1. A distortion of a ring during periapsis creating transient gaps that then transited J1407 (V1400 Centauri); transient features formed early on in one of the retrograde models ($e=0.6$) could account for the appearance of a gap observed at 0.4AU in the 2007 transit instead of an embedded moon.

2. J1407b is detached from the primary J1407 (V1400 Centauri) and is free-floating. With no strong perturbation from an elliptical orbit, moons would be able to accrete unimpeded within a few thousand years.

3. Pre-existing moon or captured moon that did not form in its current location. However, a moon clearing out a gap would not be able to maintain this due to the perturbations experienced at periapsis, which would fill in any gap in each orbit. The eccentricity of ring particles is excited by the periodic forcing during periapsis and causes significant radial movement of particles within the ring. A moon would only be able to clear a partial gap $\left(<2\pi \right)$ nearby, analogous to propeller structures regularly observed in Saturn’s rings caused by small moonlets (Michikoshi and Kokubo 2011).

4. An inclined circumplanetary disc is also capable of creating radial gaps through one of two dynamical resonances. Here, particles in the outer region of the disc have their eccentricities and inclinations excited by the Lidov-Kozai effect, while regions within the inner disc experience an ivection resonance (Speedie and Zanazzi 2020).

A final note is that in both the prograde and retrograde models, where the eccentricity of J1407b is $e>0.6$, a significant amount of material is removed from the ring and orbits the primary. In this scenario, it would be expected that some of this material would be observed to transit J1407 (V1400 Centauri), causing irregular variations in its light curve comparable to the star KIC 8462852 (Boyajian et al., 2016). Here, a large amount of material, in the form of comets or massive outgassing objects, is thought to be responsible for the unusual dips in brightness (Bodman and Quillen, 2016; Woods 2019). However, despite long-term monitoring of J1407 for a second transit, there is no evidence to suggest a significant amount of material is orbiting it, which only seeks to reaffirm that J1407b is not bound to J1407 and is most likely a free-floating object.

New telescopes, like the James Webb Space Telescope (JWST), not only offer significant advances in the study and characterisation of exoplanets but will be pivotal in future searches for exomoons and exorings. Spectrometers like the Near Infrared Spectrograph (NIRSpec) onboard JWST has the capabilities to study astrophysical disks, including J1407b’s, in greater detail and reveal particle sizes and compositions. Transmission spectroscopy of transiting gas giants could also identify smaller gaseous ring systems (Zuluaga et al., 2015; Gebek and Oza 2020) where moons, like the Galilean moons of Jupiter, form during the final stages of planet formation, which are still undergoing accretion of gas onto the planet.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

PS Created the models and wrote the manuscript. JM and BA contributed discussions that shaped the project and created tools used in the analysis of the models.

Funding

JM and BA were both funded by a University of Lincoln Undergraduate Research Opportunities Scheme (UROS).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barmentloo, S., Dik, C., Kenworthy, M. A., Mamajek, E. E., Hambsch, F. J., Reichart, D. E., et al. (2021). VizieR Online Data Catalog: Transit Search in the V1400 Cen System (Barmentloo+, 2021). VizieR Online Data Catalog, pp.J-A+.

Google Scholar

Beurle, K., Murray, C. D., Williams, G. A., Evans, M. W., Cooper, N. J., and Agnor, C. B. (2010). Direct Evidence for Gravitational Instability and Moonlet Formation in Saturn's Rings. ApJ 718 (2), L176–L180. doi:10.1088/2041-8205/718/2/l176

CrossRef Full Text | Google Scholar

Bezrouk, C., and Parker, J. S. (2017). Long Term Evolution of Distant Retrograde Orbits in the Earth-Moon System. Astrophys Space Sci. 362 (9), 176. doi:10.1007/s10509-017-3158-0

CrossRef Full Text | Google Scholar

Bodman, E. H., and Quillen, A. (2016). KIC 8462852: Transit of a Large Comet Family. Astrophysical J. Lett. 819 (2), L34.

CrossRef Full Text | Google Scholar

Boyajian, T. S., LaCourse, D. M., Rappaport, S. A., Fabrycky, D., Fischer, D. A., Gandolfi, D., et al. (2016). Planet Hunters IX. KIC 8462852 - Where's the Flux? Mon. Not. R. Astron. Soc. 457 (4), 3988–4004. doi:10.1093/mnras/stw218

CrossRef Full Text | Google Scholar

Bromley, B. C., and Kenyon, S. J. (2013). Migration of Small Moons in Saturn's Rings. ApJ 764 (2), 192. doi:10.1088/0004-637x/764/2/192

CrossRef Full Text | Google Scholar

Canup, R. M. (2010). Origin of Saturn's Rings and Inner Moons by Mass Removal from a Lost Titan-Sized Satellite. Nature 468 (7326), 943–946. doi:10.1038/nature09661

PubMed Abstract | CrossRef Full Text | Google Scholar

Canup, R. M., and Ward, W. R. (2002). Formation of the Galilean Satellites: Conditions of Accretion. Astronomical J. 124 (6), 3404–3423. doi:10.1086/344684

CrossRef Full Text | Google Scholar

Crida, A., and Charnoz, S. (2012). Formation of Regular Satellites from Ancient Massive Rings in the Solar System. Science 338 (6111), 1196–1199. doi:10.1126/science.1226477

PubMed Abstract | CrossRef Full Text | Google Scholar

Daisaka, H., Tanaka, H., and Ida, S. (2001). Viscosity in a Dense Planetary Ring with Self-Gravitating Particles. Icarus 154 (2), 296–312. doi:10.1006/icar.2001.6716

CrossRef Full Text | Google Scholar

Duffell, P. C., and MacFadyen, A. I. (2013). Gap Opening by Extremely Low-Mass Planets in a Viscous Disk. ApJ 769 (1), 41. doi:10.1088/0004-637x/769/1/41

CrossRef Full Text | Google Scholar

Fung, J., and Chiang, E. (2016). Gap Opening in 3D: Single-Planet Gaps. ApJ 832 (2), 105. doi:10.3847/0004-637x/832/2/105

CrossRef Full Text | Google Scholar

Gebek, A., and Oza, A. V. (2020). Alkaline Exospheres of Exoplanet Systems: Evaporative Transmission Spectra. Monthly Notices R. Astronomical Soc. 497 (4), 5271–5291. doi:10.1093/mnras/staa2193

CrossRef Full Text | Google Scholar

Gladman, B., Kavelaars, J. J., Holman, M., Nicholson, P. D., Burns, J. A., Hergenrother, C. W., et al. (2001). Discovery of 12 Satellites of Saturn Exhibiting Orbital Clustering. Nature 412 (6843), 163–166. doi:10.1038/35084032

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldreich, P., and Tremaine, S. (1978). The Formation of the Cassini Division in Saturn's Rings. Icarus 34 (2), 240–253. doi:10.1016/0019-1035(78)90165-3

CrossRef Full Text | Google Scholar

Hambsch, F. J. (2012). May. ROAD (Remote Observatory Atacama Desert): Intensive Observations of Variable Stars. Soc. Astronomical Sci. Annu. Symp. 31, 75–78.

Google Scholar

Hedman, M. M., Burns, J. A., Hamilton, D. P., and Showalter, M. R. (2013). Of Horseshoes and Heliotropes: Dynamics of Dust in the Encke Gap. Icarus 223 (1), 252–276. doi:10.1016/j.icarus.2012.11.036

CrossRef Full Text | Google Scholar

Higuchi, A., and Ida, S. (2016). Temporary Capture of Asteroids by a Planet: Dependence of Prograde/retrograde Capture on Asteroids' Semimajor Axes. Astronomical J. 151 (1), 16. doi:10.3847/0004-6256/151/1/16

CrossRef Full Text | Google Scholar

Horn, L. J., Showalter, M. R., and Russell, C. T. (1996). Detection and Behavior of Pan Wakes in Saturn's A Ring. Icarus 124 (2), 663–676. doi:10.1006/icar.1996.0240

CrossRef Full Text | Google Scholar

Hyodo, R., and Charnoz, S. (2017). Dynamical Evolution of the Debris Disk after a Satellite Catastrophic Disruption Around Saturn. Aj 154 (1), 34. doi:10.3847/1538-3881/aa74c9

CrossRef Full Text | Google Scholar

Hyodo, R., Charnoz, S., Ohtsuki, K., and Genda, H. (2017). Ring Formation Around Giant Planets by Tidal Disruption of a Single Passing Large Kuiper belt Object. Icarus 282, 195–213. doi:10.1016/j.icarus.2016.09.012

CrossRef Full Text | Google Scholar

Kanagawa, K. D., Muto, T., Tanaka, H., Tanigawa, T., Takeuchi, T., Tsukagoshi, T., et al. (2016). Mass Constraint for a Planet in a Protoplanetary Disk from the gap Width. Publ. Astron. Soc. Jpn. 68 (3), 43. doi:10.1093/pasj/psw037

CrossRef Full Text | Google Scholar

Kenworthy, M. (2019). ALMA and NACO Observations towards the Young Exoring Transit System J1407 (V1400 Cen). Astronomy & Astrophysics.

Google Scholar

Kenworthy, M. A., and Mamajek, E. E. (2015). Modeling Giant Extrasolar Ring Systems in Eclipse and the Case of J1407b: Sculpting by Exomoons? ApJ 800 (2), 126. doi:10.1088/0004-637x/800/2/126

CrossRef Full Text | Google Scholar

Kochanek, C. S., Shappee, B. J., Stanek, K. Z., Holoien, T. W.-S., Thompson, T. A., Prieto, J. L., et al. (2017). The All-Sky Automated Survey for Supernovae (ASAS-SN) Light Curve Server v1.0. Pasp 129 (980), 104502. doi:10.1088/1538-3873/aa80d9

CrossRef Full Text | Google Scholar

Lewis, M. C., and Stewart, G. R. (2006). September. Simulating the Keeler gap in Saturn's Rings: Wake and Edge Dynamics. Bull. Am. Astronomical Soc. 38, 560. doi:10.1112/s002460930601873x

CrossRef Full Text | Google Scholar

Lunine, J. I., and Stevenson, D. J. (1982). Formation of the Galilean Satellites in a Gaseous Nebula. Icarus 52 (1), 14–39. doi:10.1016/0019-1035(82)90166-x

CrossRef Full Text | Google Scholar

Mamajek, E. E., Quillen, A. C., Pecaut, M. J., Moolekamp, F., Scott, E. L., Kenworthy, M. A., et al. (2012). Planetary Construction Zones in Occultation: Discovery of an Extrasolar Ring System Transiting a Young Sun-like star and Future Prospects for Detecting Eclipses by Circumsecondary and Circumplanetary Disks. Astronomical J. 143 (3), 72. doi:10.1088/0004-6256/143/3/72

CrossRef Full Text | Google Scholar

Mentel, R. T., Kenworthy, M. A., Cameron, D. A., Scott, E. L., Mellon, S. N., Hudec, R., et al. (2018). Constraining the Period of the Ringed Secondary Companion to the Young star J1407 with Photographic Plates. A&A 619, A157. doi:10.1051/0004-6361/201834004

CrossRef Full Text | Google Scholar

Michikoshi, S., and Kokubo, E. (2011). Formation of a Propeller Structure by a Moonlet in a Dense Planetary Ring. ApJ 732 (2), L23. doi:10.1088/2041-8205/732/2/l23

CrossRef Full Text | Google Scholar

Ming, X., and Shijie, X. (2009). Exploration of Distant Retrograde Orbits Around Moon. Acta Astronautica 65 (5-6), 853–860. doi:10.1016/j.actaastro.2009.03.026

CrossRef Full Text | Google Scholar

Namouni, F., and Morais, M. H. M. (2018). An Interstellar Origin for Jupiter's Retrograde Co-orbital Asteroid. Monthly Notices R. Astronomical Soc. Lett. 477 (1), L117–L121. doi:10.1093/mnrasl/sly057

CrossRef Full Text | Google Scholar

Nesvorný, D., Vokrouhlický, D., and Deienno, R. (2014). Capture of Irregular Satellites at Jupiter. Astrophysical J. 784 (1), 22.

Google Scholar

Noyelles, B., Baillie, K., Lainey, V., and Charnoz, S. (2016). “October. How Mimas Cleared the Cassini Division,” in AAS/Division for Planetary Sciences Meeting Abstracts, 48.

Google Scholar

Pepper, J., Kuhn, R. B., Siverd, R., James, D., and Stassun, K. (2012). The KELT-South Telescope1. Publications Astronomical Soc. Pac. 124 (913), 230–241. doi:10.1086/665044

CrossRef Full Text | Google Scholar

Pepper, J., Pogge, R. W., DePoy, D. L., Marshall, J. L., Stanek, K. Z., Stutz, A. M., et al. (2007)., 119. Publications of the Astronomical Society of the Pacific, 923–935. doi:10.1086/521836The Kilodegree Extremely Little Telescope (KELT): A Small Robotic Telescope for Large‐Area Synoptic SurveysPubl. Astron. Soc. Pac.858

CrossRef Full Text | Google Scholar

Pojmanski, G. (1997). The All Sky Automated Survey. arXiv preprint astro-ph/9712146.

Google Scholar

Reichart, D., Nysewander, M., Moran, J., Bartelme, J., Bayliss, M., Foster, A., et al. (2005). PROMPT: Panchromatic Robotic Optical Monitoring and Polarimetry Telescopes. arXiv preprint astro-ph/0502429.

Google Scholar

Ricker, G. R., Winn, J. N., and Vanderspek, R. (2015). J. Astron. Teles. Inst. Syst. 1, 014003.

Rieder, S., and Kenworthy, M. A. (2016). Constraints on the Size and Dynamics of the J1407b Ring System, 596. A9: Astronomy & Astrophysics. doi:10.1051/0004-6361/201629567

CrossRef Full Text | Google Scholar

Speedie, J., and Zanazzi, J. J. (2020). The Structure and Stability of Extended, Inclined Circumplanetary Disc or Ring Systems. Monthly Notices R. Astronomical Soc. 497 (2), 1870–1883. doi:10.1093/mnras/staa2068

CrossRef Full Text | Google Scholar

Springel, V. (2005). The Cosmological Simulation Code GADGET-2. MNRAS 364 (4), 1105–1134. doi:10.1111/j.1365-2966.2005.09655.x

CrossRef Full Text | Google Scholar

Sutton, P. J. (2019). Mean Motion Resonances with Nearby Moons: an Unlikely Origin for the Gaps Observed in the Ring Around the Exoplanet J1407b. MNRAS 486 (2), 1681–1689. doi:10.1093/mnras/stz563

CrossRef Full Text | Google Scholar

Sutton, P. J. (2018). On the Tidal Environment of an Outwardly Migrating F Ring. MNRAS 478 (1), 416–424. doi:10.1093/mnras/sty995

CrossRef Full Text | Google Scholar

Szulágyi, J., Cilibrasi, M., and Mayer, L. (2018). In Situ formation of Icy Moons of Uranus and Neptune. Astrophysical J. Lett. 868 (1), L13.

Google Scholar

Thebault, P., Marzari, F., and Scholl, H. (2006). Relative Velocities Among Accreting Planetesimals in Binary Systems: The Circumprimary Case. Icarus 183 (1), 193–206. doi:10.1016/j.icarus.2006.01.022

CrossRef Full Text | Google Scholar

Toomre, A. (1964). On the Gravitational Stability of a Disk of Stars. ApJ 139, 1217. doi:10.1086/147861

CrossRef Full Text | Google Scholar

Torrey, P. A., Tiscareno, M. S., Burns, J. A., and Porco, C. C. (2008). “May. Mapping Complexity: the Wavy Edges of the Encke and Keeler Gaps in Saturn's Rings,” in AAS/Division of Dynamical Astronomy Meeting#, 3939.

Google Scholar

Trani, A. A., Hamers, A., and Geller, A. (2019). “August. Can a Hot Jupiter Host Exomoons?,” in AAS/Division for Extreme Solar Systems Abstracts, 4.

Google Scholar

Van Werkhoven, T. I. M., Kenworthy, M. A., and Mamajek, E. E. (2014). Analysis of 1SWASP J140747.93−394542.6 Eclipse fine-structure: Hints of Exomoons. Monthly Notices R. Astronomical Soc. 441 (4), 2845–2854. doi:10.1093/mnras/stu725

CrossRef Full Text | Google Scholar

Weiss, J. W., Porco, C. C., and Tiscareno, M. S. (2009). Ring Edge Waves and the Masses of Nearby Satellites. Astronomical J. 138 (1), 272–286. doi:10.1088/0004-6256/138/1/272

CrossRef Full Text | Google Scholar

Woods, P. (2019). Melting Moons Make Tabby’s Star Murky. Nat. Astron., 1.

Google Scholar

Zuluaga, J. I., Kipping, D. M., Sucerquia, M., and Alvarado, J. A. (2015). A Novel Method for Identifying Exoplanetary Rings. ApJ 803 (1), L14. doi:10.1088/2041-8205/803/1/l14

CrossRef Full Text | Google Scholar