The Planetary Nebula Luminosity Function in the Era of Precision Cosmology

One of the great surprises of the late 1980s was the discovery that the [O III] λ5007 planetary nebula luminosity function (PNLF) could be used as a precision extragalactic standard candle. Despite the lack of any robust theory for the phenomenon, the technique passed a myriad of internal and external tests, and became an extremely reliable tool for obtaining distances to large galaxies within $\sim 20$ Mpc. But in more recent years, the use of the technique has declined, due in part to the changing landscape of cosmology. Here we review the history of the PNLF, the experiments that confirmed its utility, and the reasons why interest in the method faded at the turn of the millennium. We also describe how and why the PNLF is making a comeback, and present some of the method’s recent results. Finally, we discuss how the PNLF must be analyzed in the era of precision cosmology, and detail the issues that must be overcome in order to address the current tension between local measures of the Hubble constant and values derived from the microwave background. If these issues can be understood, then the PNLF can provide a useful cross-check on distance measurements out to $\sim 40$ Mpc.

1 Introduction

The brightest stars of a galaxy have long been used as extragalactic standard candles (Hubble, 1936). However, it was not until the early 1960’s that it was appreciated that young planetary nebulae (PNe) also fall into the “brightest stars” category and might be useful for distance measurements (Henize and Westerlund, 1963; Hodge, 1966). At the time of their formation, PNe are just as luminous as their asymptotic giant branch (AGB) progenitors; the only difference is that instead of emitting most of their energy at optical or near infrared wavelengths, the bulk of a PN central star’s emission comes out in the far-UV, where it can ionize the gas of its former envelope. This trapped energy is then reprocessed into a series of emission lines, with the brightest feature typically being the forbidden line of doubly ionized oxygen at 5,007 Å. Thus, for all practical purposes, the nebula of a PN is a cosmic apparatus which transforms the continuum emission of an extremely bright star into monochromatic flux, with an efficiency that can be as high as $\sim 11\%$ (e.g., Dopita et al., 1992; Schönberner et al., 2010; Kwitter et al., 2012).

Figure 1 displays the spectrum of an [O III]-bright PNe in the inner bulge of M31. Despite being only 2.′2 from the galaxy’s nucleus, the high contrast of [O III] λ5007 over the continuum makes the object extremely easy to detect. Traditionally, one identifies extragalactic PNe by taking two images: one through a narrow-band (≲ 50 Å wide) filter centered on [O III] λ5007 at the redshift of the galaxy, and another located on a spectral region that is devoid of emission lines. When the images are subtracted, the continuum sources disappear, allowing the emission-line objects to stand out (see for example Ford et al., 1973; Jacoby et al., 1989). In an early-type galaxy, most, if not all, unresolved emission-line objects will be planetary nebulae.

FIGURE 1

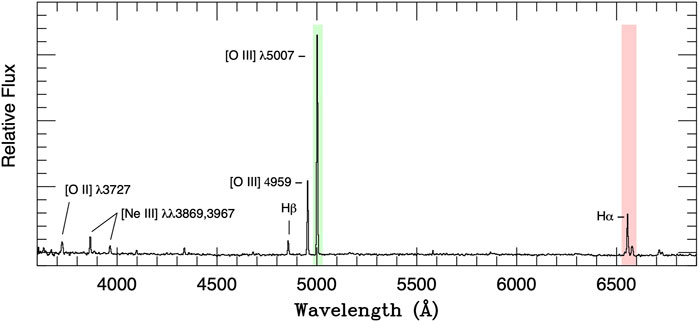
FIGURE 1. The spectrum of M31 bulge PN CJFN 29, a typical object in the top $\sim 1$ mag of the planetary nebula luminosity function. The PN is powered by a log  L/L_⊙ = 3.66 central star and almost 6% of the core’s total energy emerges in [O III] λ5007. The shaded areas represent the bandpasses of the interference filters used for the object’s detection. Note how much brighter [O III] λ5007 is compared to Hα and Hβ. From Jacoby and Ciardullo (1999).

Of course, just because an object is bright enough to be seen in a distant galaxy does not make it useful as a distance indicator. Indeed, based on the wide range of properties exhibited by Milky Way PNe (see, for example, Kwok, 2007; Kwitter and Henry, 2022), the utility of PNe as a standard candle would seem unlikely. Yet Ford and Jenner (1978) noticed that the brightest PNe in M31, M32, NGC 185, and NGC 205 all have roughly the same [O III] λ5007 luminosity, suggesting that further investigation was in order. This led to a series of papers in the late 1980s and 1990s that argued that the [O III] λ5007 planetary nebula luminosity function (PNLF) was not only viable as a standard candle, but was competitive with the very best techniques.

2 The Rise of the PNLF

One would expect the [O III] PNLF of a galaxy to be quite complex. A PN’s central star powers its nebula, so an ensemble of high-mass, rapidly evolving central stars, should produce a PNLF that reflects the stars’ luminosity evolution, modulated by changes in the ionization structure of the nebula. This line of reasoning argues for a non-monotonic PNLF, with a dip at intermediate magnitudes where the stars rapidly transition from their hydrogen-burning post-AGB tracks to the white dwarf cooling sequence. However, for lower-mass, slowly-evolving central stars, it is the timescale for nebular expansion that determines the evolution of the emission-lines. In this case, the line-emission from an optically thin, freely expanding nebula of radius R and number density N_H will evolve as

$\begin{array}{ll}\hfill & L\propto N_{\text{H}}{N}_e\cdot \left(\frac{4}{3}\pi R^3\right)\propto R^{-3}\propto t^{-3}\hfill \\ \hfill & \Rightarrow t\propto L^{-1/3}\propto 10^{M/7.5}\propto e^{0.307M}\hfill \end{array}(1)$

where M is the absolute magnitude of the object. As a result, if there are no changes to the nebula’s ionization structure, then

$N\left(M\right)\propto \frac{dt}{dM}\propto e^{0.307M}(2)$

(Henize and Westerlund, 1963). The observed PNLF of a galaxy should lie between these two regimes, and contain features driven by the distribution of PN core masses, the effects of stellar wind interactions, nebular geometry, the Lyman continuum optical depth of the material, and a host of other factors (e.g., Schönberner et al., 2010).

The first modern measurements of the PNLF were performed by Ciardullo et al. (1989b), who used a 0.9-m telescope, a narrow-band interference filter, and a CCD detector to measure the distribution of PN [O III] λ5007 magnitudes in the same four Local Group galaxies studied by Ford and Jenner (1978). These observations were quickly followed by similar measurements in M81 (Jacoby et al., 1989), the Leo I galaxy group (Ciardullo et al., 1989a), the Virgo Cluster (Jacoby et al., 1990a), the LMC (Jacoby et al., 1990b), NGC 5128 (Hui et al., 1993), and a several other systems. The data collected by these initial surveys and more modern observations, led to the following conclusions:

• The [O III] luminosity function of PNe is indeed complex. As illustrated in Figure 2 , different stellar populations have different PNLFs: in star-forming systems, such as the LMC and SMC, the PNLF exhibits at least two inflection points (e.g., Jacoby and De Marco, 2002; Reid and Parker, 2010; Ciardullo, 2010), while in older stellar populations, the luminosity function is monotonic, though not necessarily featureless (Bhattacharya et al., 2019; Bhattacharya et al., 2021). However, in all galaxies, the extreme bright-end of the PNLF undergoes a very rapid decline, which Ciardullo et al. (1989b) found could be modeled by imposing an exponential cutoff on Eq. 2. In other words,

$N\left(m\right)\propto e^{0.307m}\left\{1-e^{3\left(m^{\ast }-m\right)}\right\}(3)$

where the apparent magnitude of a PN, m, is related to its monochromatic [O III] λ5007 flux, F₅₀₀₇ (in ergs cm⁻² s⁻¹), by

$m=-2.5\log F_{\mathit{5007}}-13.74(4)$

and m^∗ is the apparent magnitude beyond which there are no planetary nebulae.

FIGURE 2

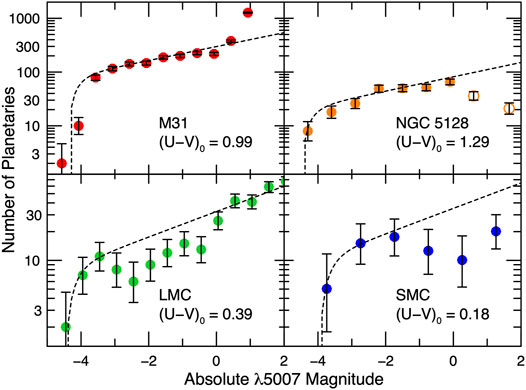
FIGURE 2. The [O III] planetary nebula luminosity functions of M31 (Bhattacharya et al., 2019), NGC 5128 (Ciardullo, 2010), the LMC (Reid and Parker, 2010), and the SMC (Jacoby and De Marco, 2002). The dashed curve shows the distribution predicted by Eq. 3. The PNLFs of the four galaxies vary substantially, but all have a very sharp bright-end cutoff at M₅₀₀₇ ∼ −4.5. (The cutoff is $\sim 0.5$ mag fainter in the SMC due to the galaxy’s low metallicity.) The survey of NGC 5128 is incomplete beyond M₅₀₀₇ ∼ 0 (open points).

Obviously, this expression is not meant to be applied universally. As Figure 2 demonstrates, star-forming populations have a non-monotonic PNLF that cannot readily be described via a one-parameter model. One way to address this behavior is to express the PNLF as the sum of two (or more) components, each of the form given by Eq. 3, but with its own normalization and value of m*. Rodríguez-González et al. (2015) have obtained reasonable fits using this formulation, though at the cost of an additional parameter which artificially truncates the faint end of one component. Alternatively, to mimic the variation of the PNLFs seen in Population II systems, Longobardi et al. (2013) generalized Eq. 3 so that

$N\left(m\right)\propto e^{c_{2}m}\left\{1-e^{3\left(m^{\ast }-m\right)}\right\},(5)$

with c₂ being the descriptor for the function’s faint-end slope. This expression has successfully been applied to deep PNLFs in the halos and intracluster regions of Leo I (Hartke et al., 2020) and Virgo (Longobardi et al., 2013; Hartke et al., 2017). More recently, Bhattacharya et al. (2019) combined the generalization of Longobardi et al. (2013) with the two-component formalism of Rodríguez-González et al. (2015) to reproduce the rapid upturn in the number counts of very faint (m > m* + 5) PN candidates in M31 (see Figure 2). Finally, numerical simulations which mate post-AGB stellar evolutionary tracks (e.g., Miller Bertolami, 2016) with assumptions about the distribution of post-AGB masses, nebular [O III]/Hβ line ratios, and Lyman continuum optical depths, predict a slightly shallower slope to the PNLF’s bright-end cutoff (e.g., Méndez et al., 2008; Valenzuela et al., 2019). However, given the number of assumptions imbedded in these models, their applicability to the general question of the PNLF is unclear.

Fortunately, for the study of extragalactic distances, it is the top $\sim 1$ mag of the PNLF that carries almost all of the information: variations in the PNLF’s faint-end slope and/or the presence of an inflection points far down the luminosity function do not affect the fit to the bright-end cutoff (Spriggs et al., 2021). Therefore for most applications of this type, the one-parameter expression given in Eq. 3 is all that is needed.

• The PNLF is capable of delivering a highly precise distance estimate for bright, massive galaxies. According to both models (Dopita et al., 1992) and observations (Ciardullo and Jacoby, 1992), the PNLF cutoff magnitude fades in systems with sub-LMC oxygen abundances. Since there is well-known correlation between the stellar mass of a galaxy and its gas-phase metallicity (e.g., Lequeux et al., 1979; Tremonti et al., 2004), this means that a correction factor is needed for PNLF measurements in low-mass, low-luminosity systems. Unfortunately, the precise amount of this correction is difficult to determine. Planetary nebulae are relatively rare objects: not only are they visible for only $\sim \mathrm{20,000}$ years (Jacob et al., 2013), but, from the fuel consumption theorem, an M_V ∼ −21.2 galaxy should create only one of these spectacular objects per year (Renzini and Buzzoni, 1986; Buzzoni et al., 2006). Since bright PNe – objects in the top $\sim 1$ mag of the luminosity function—represent less than $\sim 2\%$ of all planetaries, low-mass galaxies have very few objects in the magnitude range which defines the PNLF’s bright-end cutoff. As a result, one cannot reliably measure m∗ in low-mass, low-luminosity systems.

Conversely, in a massive L^∗ galaxy, the PNLF is very well defined, with as many as $\sim 100$ PNe within $\sim 1$ mag of m^∗. In these systems, the statistical error associated with fitting the PNLF is comparable to, or better than, those derived from measuring the Cepheid period-luminosity relation or determining the location of the tip of the red giant branch (TRGB). This is where the PNLF shines as an extragalactic standard candle.

• Remarkably, the value of M^∗ in large galaxies has almost no dependence on stellar population. The first true test of the behavior of M^∗ was performed by Ciardullo et al. (1989a), who showed that three galaxies in the core of the Leo I Group—NGC 3379 (M_V ≃ −20.8; Hubble type E0), NGC 3384 (M_V ≃ −20.2; SB0₁), and NGC 3377 (M_V ≃ −19.8; E6)—all had the same value of m^∗ to within the precision of the measurements. Subsequently, this consistency test was repeated in a number of environments, and in all cases the results were the same: to within the statistical uncertainty of the measurements, galaxies at (presumably) the same distance had the same value of m^∗. Figure 3 demonstrates this for the two most compelling test sites to date: the well-mixed Leo I Group (Ciardullo et al., 1989a; Feldmeier et al., 1997; Ciardullo et al., 2002a) and the Fornax Cluster (Spriggs et al., 2021). The former system has five galaxies with well-determined PNLF measurements, including NGC 3368 (M_V ≃ −21.0; Hubble type Sab) and NGC 3351 (M_V ≃ −20.5; type SBb); the latter cluster has data for 21 early-type galaxies. In both cases, the scatter in m^∗ is completely consistent with the internal errors of the measurements, and there is no discernible systematic associated with stellar mass, galaxy color, Hubble type, or star-formation rate.

FIGURE 3

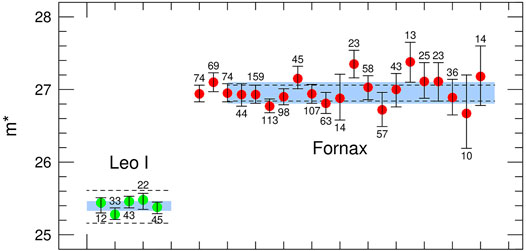
FIGURE 3. Measured values of m* in the galaxies of the Leo I group (Ciardullo et al., 1989a; Feldmeier et al., 1997; Ciardullo et al., 2002a) and the Fornax cluster (Spriggs et al., 2021). In Leo I, the galaxies are sorted by Hubble type, going from Sb on the left to E0 on the right. The Fornax cluster data are given in order of the galaxies’ Wise W1 magnitudes (brightest galaxies on the left) and span a range of over 4.5 mag. Immediately below or above each point are the number of PNe used in the PNLF fit; for Leo I galaxies, this number only includes objects above the 90% completeness limit; in Fornax, all the PN detected in a galaxy were used in the solution. The light blue shading shows the 1σ dispersion in the distribution of the best-fit values, and the dotted lines indicate a distance of ±1 Mpc from the mean value. The errors bars represent the uncertainties in the individual measurements, and are largely driven by the number of PNe in the top $\sim 0.5$ mag of the luminosity function. There is no indication that m* depends on any galaxy property.

• The PNLF can be applied to late-type galaxies through the use of emission-line diagnostics. Originally, the PNLF was envisioned as a Population II standard candle, due to the possible confusion with compact H II regions and supernova remnants (Jacoby et al., 1992). However, observations in the Magellanic Clouds (Jacoby et al., 1990b), M101 (Feldmeier et al., 1996), and then a host of other late-type galaxies (e.g., Feldmeier et al., 1997; Ciardullo et al., 2004) proved that unresolved H II regions could effectively be removed from a list of PN candidates using the [O III] λ5007 to Hα flux ratio as a discriminant. Briefly put: because the exciting stars of PNe in the top $\sim 1$ mag of the PNLF are so much hotter than the stars which ionize H II regions, and because the nebular densities of these PNe are much greater than the ISM density of a typical star-forming region, the λ5007 emission of a bright planetary nebula is generally more than twice that of Hα. In contrast, in the vast majority of H II regions, Hα dominates the luminosity of [O III]. This discriminant, which was first quantified by Herrmann et al. (2008), is displayed in Figure 4. Subsequent work then showed that this criterion would also exclude most supernova remnants (Davis et al., 2018a) and any SNR that was missed could be excluded via its Hα/[N II] and Hα/[S II] line ratios (Kreckel et al., 2017; Scheuermann et al., 2022).

FIGURE 4

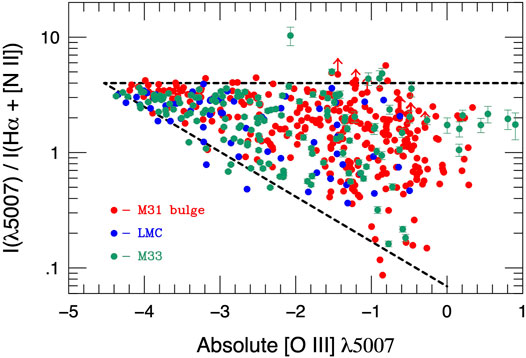
FIGURE 4. The ratio of [O III] λ5007 to Hα+[N II] observed for PNe in M31’s bulge, M33’s disk, and the Large Magellanic Cloud from Ciardullo (2005). The dashed lines outline the “cone of PNe” defined by Herrmann et al. (2008). In the top $\sim 1$ mag of the PNLF, [O III] λ5007 is always much brighter than Hα; in contrast, the vast majority of H II regions and supernova remnants have Hα brighter than [O III].

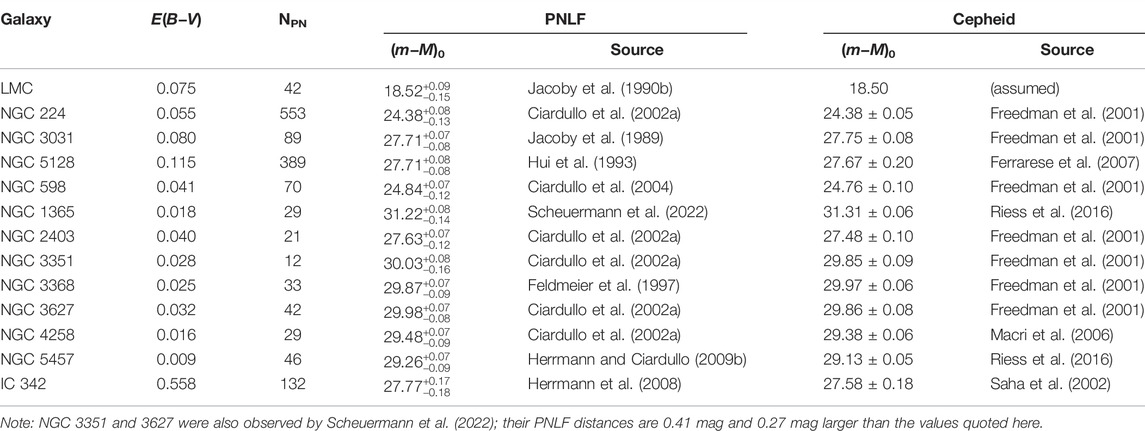
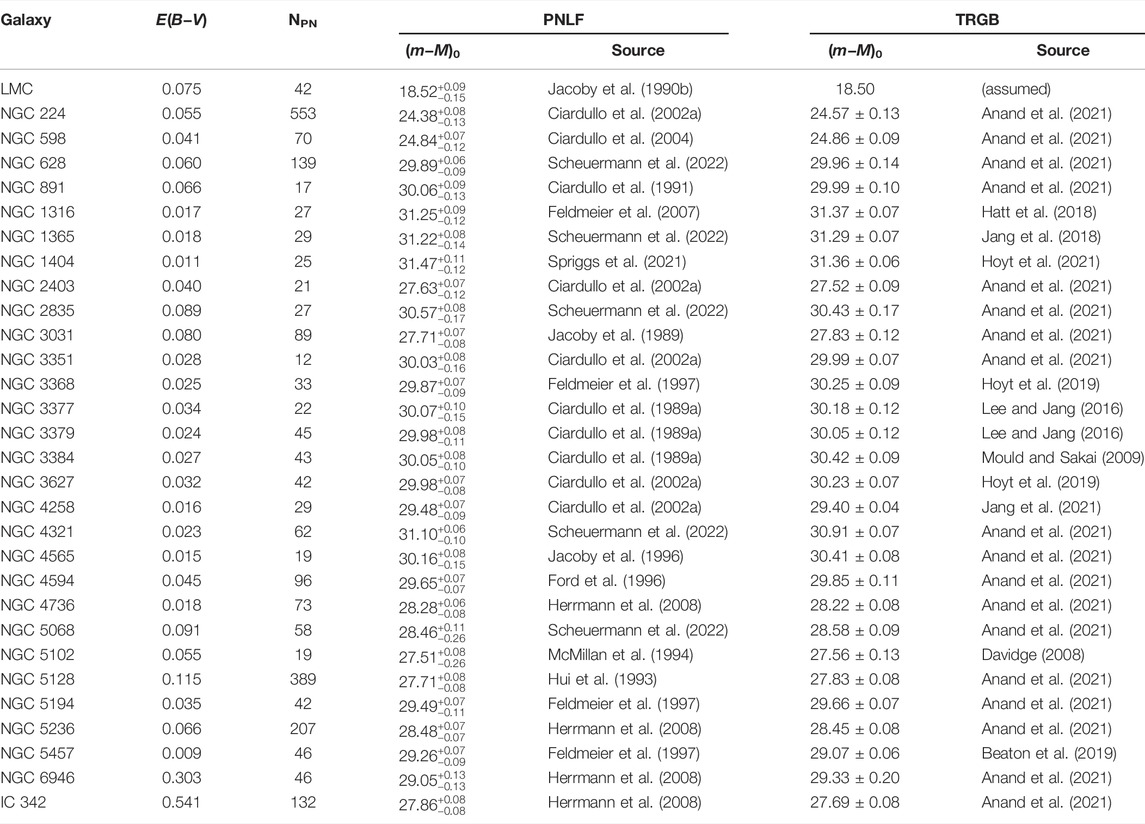
• There is excellent agreement between galaxy distances obtained from the Cepheid period-luminosity relation and the PNLF. Currently there are 13 luminous galaxies that have been surveyed by both techniques; the systems are listed in Table 1 and plotted in the left-hand panel of Figure 5, assuming M^∗ = −4.53 for all the galaxies in the sample. The correspondence between the two distance indicators is exactly what one would expect from two robust methods with similar precision. The scatter about the one-to-one line is consistent with the internal errors of the measurements, and there is little evidence for any systematic hidden in the data. Indeed, a diagram such as this suggests that the PNLF should be an integral part of the extragalactic distance ladder.

TABLE 1

TABLE 1. Galaxies with Cepheid distances.

FIGURE 5

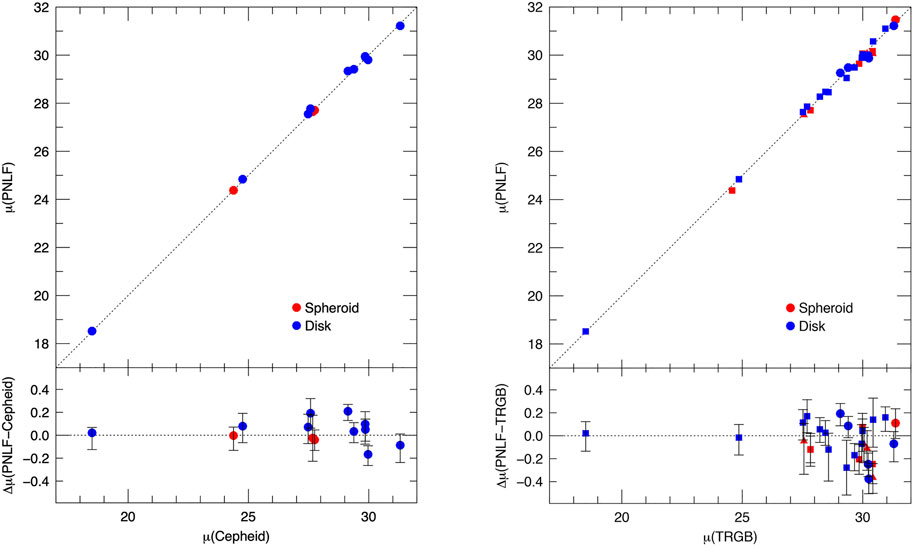
FIGURE 5. Left: Comparison of PNLF and Cepheid distances for 13 luminous galaxies, assuming M* = −4.53. The top panel shows the one-to-relation; the bottom panel displays the difference in the derived distance moduli. There is no evidence for any systematic behavior, and the scatter is consistent with the internal errors of the methods. Right: Comparison of the PNLF with TRGB distances. The circles are measurements from the Carnegie-Chicago Hubble program (Beaton et al., 2016), the squares represent values taken from Anand et al. (2021), and the triangles come from other sources. Here the scatter is larger than the internal errors, suggesting one or both methods have additional uncertainties.

On the other hand, the right-hand panel of Figure 5 displays the results of a PNLF-TRGB comparison. Unlike for the Cepheids, the amount of scatter in this diagram cannot be explained solely by the internal errors of the methods. While some component of the residuals may be due to the inhomogeneity of the measurements [most of the TRGB distances come either from the PHANGS survey (Anand et al., 2021) or the Carnegie Chicago Hubble Program (Beaton et al., 2016); see Table 2], the comparison does throw some doubt onto the overall robustness of PNLF technique, especially since the types of galaxies being studied have more variety that those in the Cepheid comparison.

TABLE 2

TABLE 2. Galaxies with TRGB distances.

3 The Fall of the PNLF

Between the years 1989 and 2010, there were almost a hundred refereed publications devoted to measuring and modeling the PNLFs of distant galaxies. But in the following decade, less than 30 papers were written on the subject, and most of those were concerned with the identification of faint PNe in Local Group galaxies. There were several reasons for this downturn.

The first is that, by 2012, the landscape of cosmology had changed. Measurements from the Cepheid-calibrated SN Ia distance ladder (Riess et al., 2011) and the microwave background (Hinshaw et al., 2013) had both claimed values of the Hubble constant that were good to $\sim 3\%$, and the goal was now to cut these uncertainties in half. To do this, one needed to reduce the errors associated with each method’s zero-point calibration, and, in practical terms, this meant avoiding the use of intermediate-distance standard candles. The path to the Hubble constant now started with the Milky Way distance scale and went directly to the parent galaxies of Type Ia supernovae.

This two-step approach skips the PNLF. In the Milky Way, PNe are resolved objects with (optically) faint central stars embedded within diffuse, often very high-surface brightness nebulae. This makes Gaia measurements to the brightest [O III] emitters difficult at best (Chornay and Walton, 2021; González-Santamaría et al., 2021). Moreover, observations of Milky Way PNe have to contend with Galactic extinction. The total reddening to a PN is easy to measure via the nebula’s Balmer decrement (e.g., Osterbrock and Ferland, 2006). But this reddening consists of two components: one produced by foreground material, and one associated with the PN itself, i.e., the object’s own circumnebular dust. The former is a contaminant whose effect needs to be removed, but the latter is an intrinsic property of the PN and must be left alone. Indeed, the circumnebular extinction measurements made by Davis et al. (2018b) suggest that the location and shape of the PNLF’s cutoff is largely defined by the behavior of this constituent. As a result, the PNLF cannot easily be calibrated via the observation of Milky Way planetaries.

The issue of the PNLF calibration is then exacerbated by the fact that there is no theoretical guidance as to the expected absolute magnitude of the PNLF cutoff. The emission lines of a planetary nebula are excited, either directly or indirectly, by the energy emitted by its central star, and this energy, in turn, depends on the star’s post-asymptotic giant branch mass (Vassiliadis and Wood, 1994; Miller Bertolami, 2016). Since PAGB core mass is tied to the star’s main-sequence mass via the initial-final mass relation (Cummings et al., 2018; El-Badry et al., 2018), this means that the maximum [O III] brightness a PN can attain is a strong function of the age of its progenitor star. The PNLF of a galaxy should therefore depend on the system’s star-formation rate history. For example, galaxies with on-going star formation should have PNLF cutoffs that are at least a magnitude brighter than the cutoffs found in the oldest stellar populations (Marigo et al., 2004; Gesicki et al., 2018). Yet this is certainly not the case, as the value of M^∗ observed in elliptical galaxies, (M₅₀₀₇ ≃ − 4.53 or L₅₀₀₇ ≃ 640L_⊙) is, within the uncertainties, identical to that measured in spirals.

The situation is made even more confusing when one considers that in the bulge and outer disk of M31, the median amount of circumnebular extinction affecting PNe within $\sim 1$ mag of M∗ is c_Hβ ∼ 0.20 dex (Jacoby et al., 1989; Kwitter et al., 2012; Davis et al., 2018b; Galera-Rosillo et al., 2022). This means that PNe with magnitudes near M^∗ are actually emitting ≳ 1000L_⊙ of power in their [O III] λ5007 line. Since both models (Dopita et al., 1992; Schönberner et al., 2010) and observations (Jacoby et al., 1989; Kwitter et al., 2012) suggest that no more than $\sim 11\%$ of a PN central star’s luminosity can be reprocessed into [O III] λ5007, the implication is that the central stars of M^∗ planetaries typically have luminosities close to 9000L_⊙. Even with the accelerated evolution models of Miller Bertolami (2016), this requires a population of $\sim 3$ Gyr old progenitors to be present in all stellar systems—even those in the old elliptical galaxies of Virgo and Fornax.

If M^∗ planetaries emit [O III] λ5007 with an efficiency greater than $\sim 11\%$, then this problem of post-asymptotic giant branch energy production can be avoided. But a more likely solution to this paradox may lie in binary evolution. There is good evidence to support the hypothesis that most PNe are produced by binary systems (e.g., De Marco, 2009; Boffin and Jones, 2019; Kwitter and Henry, 2022), and if this is the case, there may not be a simple relationship between population age and PN luminosity. Such scenarios would need to be modeled very carefully, since, as pointed out by Ciardullo et al. (2005), L ≳ 10, 000L_⊙ post-AGB stars are difficult for Pop II systems to create, even through binary evolution. Thus, the question of the origin of M^∗ PNe in old stellar systems is still open, leaving the PNLF without a robust theory and without a local calibration. M^∗ must therefore be calibrated in external galaxies with known distances, i.e., by minimizing the scatter in diagrams such as those shown in Figure 5. Present-day distance ladders try to avoid this additional uncertainty.

A second reason for the decline in PNLF usage was the discovery of a possible systematic error associated with its measurements. As shown in Figure 5, PNLF distances agree well with those derived from the Cepheid period-luminosity relation out to a distance of $\sim 10$ Mpc. But Ferrarese et al. (2000) noted that beyond this limit, there is a hint of an offset. More importantly, in both the Virgo and Fornax clusters, the PNLF distances to the systems’ elliptical galaxies were $\sim 0.2$ mag shorter than the Cepheid distances to the systems’ spirals. Since this offset was also present in a comparison with the results of the surface brightness fluctuation (SBF) method (Tonry et al., 2001), their conclusion was that the PNLF could not be pushed to the distances needed to calibrate rungs near the top of the distance ladder.

Ciardullo et al. (2002a) have argued that an apparent error between the PNLF and SBF distance scales can be caused by a systematic difference between the internal extinction within the late-type calibration galaxies of the local universe and that in the more distant elliptical and lenticular targets of the PNLF and SBF methods. (In brief, the two techniques react differently to errors in reddening—if the internal extinction is less than expected, then the PNLF distance will be underestimated, while the SBF distance will be overestimated.) Though this systematic does have the proper sign to explain the difference between the PNLF and SBF measurements, the hypothesis has been difficult to confirm, and, more importantly, it does not explain the offset with the Cepheid distances to Virgo and Fornax. The PNLF’s results in these two clusters call into question the entire premise of the method.

Possibly related to this distance offset is the issue of “overluminous” objects. During their deep [O III] surveys of the Virgo and Fornax clusters, Jacoby et al. (1990a) and McMillan et al. (1993) found a small population of unresolved [O III] sources with apparent magnitudes significantly brighter than m^∗. Initially, these objects were a puzzle, and challenged the basic assumption about the shape of the PNLF. However, within a few years, an accumulation of evidence suggested two possible explanations: the bright [O III] emitters could either be PNe foreground to their assumed parent galaxy, i.e., intracluster stars (Ferguson et al., 1998; Durrell et al., 2002; Mihos et al., 2005), or background galaxies with Lyα emission shifted into the bandpass of the narrow-band filter used for their discovery (Cowie and Hu, 1998; Hu et al., 1998; Hayashino et al., 2004). In fact, follow-up observations supported both these scenarios: while some objects had spectra consistent with that of a bright planetary nebula (Ciardullo et al., 2002b; Roth et al., 2021), others were clearly z ∼ 3.13 Lyα emitting galaxies (Kudritzki et al., 2000). However, despite these data, questions about the overluminous sources still persist today. For example, the apparent magnitudes of some of the spectroscopically-confirmed PNe found in Virgo and Fornax demand that the intracluster population extend at least $\sim 2$ Mpc in front of the targeted galaxy. This would require the distribution of intracluster stars to be quite elongated along our line-of-sight. Moreover, the intracluster hypothesis does not explain the observations of Sambhus et al. (2006), who found that the PNe of the Virgo elliptical galaxy NGC 4697 appear to be divided into two distinct kinematic populations, each with its own value of M^∗. This again undermines the basic assumptions behind the technique.

Finally, there was the issue of technology. The first wave of PNLF measurements were performed with 4-m class telescopes, using 30 to 50 Å wide interference filters centered on [O III] λ5007 at the redshift of the galaxy. Under good conditions, an all-night exposure with such a setup could detect PNe as far away as $\sim 20$ Mpc, placing the Virgo and Fornax clusters just within reach. In the initial burst of PNLF surveys, many of the largest, most important galaxies in the local universe were observed using the method.

The introduction of 8-m class telescopes in the late 1990’s extended the range of PNLF surveys. However, many of these next-generation facilities came equipped with imagers that were designed to work in fast beams and have large fields-of-view. Not only did this increase the full width at half-maximum of the filters’ bandpasses (Jacoby et al., 1989), but it also made the cost of a set of redshifted narrow-band [O III] and Hα interference filters prohibitively expensive. Thus, the larger collecting areas of the new telescopes were partially negated by the increased sky background associated with wider-bandpass filters. As a result, the improvements in PNLF distance measurements were more incremental, rather than transformative.

4 The Re-Birth of the PNLF

Prospects for the PNLF changed with the introduction of wide-field integral-field unit (IFU) spectrographs on 8-m class telescopes. IFU spectroscopy has a tremendous advantage over traditional narrow-band imaging for PNLF surveys: not only does it allow interloping contaminants to be immediately excluded from PN samples via spectral classification, but it can also deliver an effective bandpass for PN detections than is $\sim 5$ times narrower than that produced by conventional interference filters. Since extragalactic PN observations are always background limited, the higher contrast of the emission-line over the continuum immediately improves the signal-to-noise of all measurements by more than a factor of $\sim 2$. When coupled with larger telescope apertures, an IFU spectrograph can transform the PNLF from a niche method that resides on an intermediate rung on the distance ladder to a viable probe of cosmologically interesting distances.

Figure 6 shows one example of a PNLF survey conducted via wide-field IFU spectroscopy. This 20′ × 20′ [O III] λ5007 image is one slice of a data cube centered on M101, and was obtained as part of the Hobby Eberly Telescope Dark Energy Experiment (HETDEX; Gebhardt et al., 2021). The cube was created from a grid of 16 short (18 min) exposures with VIRUS, a set of 78 51′′ × 51″ IFU spectrographs that are distributed across the central 18′ diameter focal plane of the Hobby Eberly Telescope (Hill et al., 2021). Although the VIRUS units have relatively low spectral (R ∼ 800) and spatial (1.′′5) resolution, and have a limited wavelength range (3500 Å ≲ λ ≲ 5500 Å), they extend over an enormous area on the sky, enabling large galaxies, such as M101, to be surveyed with great efficiency. Moreover, while the lack of coverage in the red does exclude the use of [O III]/Hα+[N II] as an PN/H II region discriminant, the instrument’s high sensitivity at Hβ and access to [O II] λ3727 more than makes up for this limitation.

FIGURE 6

FIGURE 6. An [O III] λ5007 “image” of M101, as derived from VIRUS IFU observations during the HETDEX survey. The data represent 16 pointings at 18 min per pointing, and is 20′ on a side. The missing segments are due to IFUs that were malfunctioning or not installed at the time of the observations. The spectra of four PNe are highlighted.

An even better example of the power of IFUs to revolutionize PNLF studies comes from the Multi Unit Spectroscopic Explorer (MUSE) IFU spectrograph on the ESO Very Large Telescope (Bacon et al., 2010). Even in its wide-field mode, the MUSE IFU’s field-of-view is just 1 arcmin², but its superior image quality (as good as 0.′′4 with ground layer adaptive optics; Fusco et al., 2020), spectral resolution (R ∼ 2000), and wavelength coverage (4,800 Å ≲ λ ≲ 9,000 Å) enables a wide range of PNLF science not previously possible. Over the past few years, the MUSE+VLT system has been used to identify PNe in dozens of galaxies in the local universe, both spiral and elliptical, and has made PNLFs measurement out to $\sim 20$ Mpc routine (e.g., Spriggs et al., 2021; Scheuermann et al., 2022). More importantly, by using a differential emission-line filter (DELF) to mimic on-band/off-band image subtraction, Roth et al. (2021) was able to show that precision PNLF surveys are now feasible out to $\sim 40$ Mpc with a minimal amount of fixed-pattern noise associated with flatfield corrections.

The Roth et al. (2021) study was sub-optimal, as it was performed on archival images, and the most distant galaxy analyzed, the tidally-distorted elliptical NGC 474, only had two MUSE observations, both centered far in the galaxy’s halo. The precision of the m^∗ measurement was therefore limited, both by statistics (only 15 PN were found in NGC 474’s halo) and by systematics (from an uncertain aperture correction and flux calibration). Nevertheless, the analysis produced a distance with a total error of ≲ 10%. Dedicated, carefully chosen exposures with ground-layer adaptive optics would be capable of obtaining PNLF distances to galaxies as far away as $\sim 40$ Mpc with a statistical error of only $\sim 5\%$.

This is a cosmologically interesting distance. If the peculiar motion of a non-cluster galaxy is ≲ 300 km s⁻¹ (i.e., Giovanelli et al., 1998; Tonry et al., 2000), then at 40 Mpc, the error on H₀ caused by the galaxy’s motion in space will be of the order of $\sim 10\%$. If a typical PNLF measurement to a large galaxy carries a $\sim 5\%$ statistical uncertainty, then PNLF surveys in a dozen D ∼ 40 Mpc galaxies could generate a total (random) error on the Hubble constant of just $\sim 3\%$. PNLF measurements could then, in theory, help probe the current “tension” between the measurements of H₀ locally and that from the microwave background (Freedman, 2021).

5 The Future

The greatest criticism against the use of the PNLF as a standard candle comes from our lack of understanding about the precise behavior and systematics of its bright-end cutoff. Does Eq. 3 adequately represent the shape of the brightest $\sim 1$ mag of the luminosity function, and is M∗ really a constant across all (metal-rich) environments? Since we cannot calibrate the PNLF in the Milky Way, these questions must be addressed by careful analyses of extragalactic PN populations.

The first step towards addressing the issue of the PNLF cutoff is to learn more about the sources that seem not to obey the empirical law, i.e., the PN candidates that appear to have absolute [O III] magnitudes brighter than M^∗. As described in Section 3, these objects have generally been interpreted as either foreground PNe produced by intracluster stars (Ciardullo et al., 2002b), background Lyα emitting galaxies (Kudritzki et al., 2000), unresolved supernova remnants (Kreckel et al., 2017), or even compact extragalactic H II regions (Gerhard et al., 2003). However, recent MUSE analyses by Spriggs et al. (2021), Roth et al. (2021), and Scheuermann et al. (2022) have pointed to another possibility: the action of PN superpositions, i.e., the projection of two (or more) separate PNe onto a single spatial (and spectral) resolution element. Although a chance alignment of two rare objects would seem improbable, Roth et al. (2021) demonstrated that photometric blends happen more often than previously realized, and, if the superposed PNe have radial velocities that differ by less than $\sim 100$ km s⁻¹, even MUSE cannot disentangle their fluxes. An example of an [O III] source which is actually composed of three separate planetary nebulae is shown in Figure 7. In this case, the excellent (0.′′7) image quality of the observation allows two of the objects to be resolved spatially, but the third PNe can only be identified via a careful examination of the source’s emission-line profile. If the seeing were poorer, if the galaxy were further away, or if the resolution of MUSE were slightly less, the three sources would appear as a single overluminous PNe. Since the probability of a superposition goes as the square of the physical plate scale (i.e., pc arcsec⁻¹), this hypothesis provides a natural explanation for why the overluminous objects are only found in the most distant galaxies, and why the PNLF results for Virgo and Fornax appeared different from those of other distance indicators.

FIGURE 7

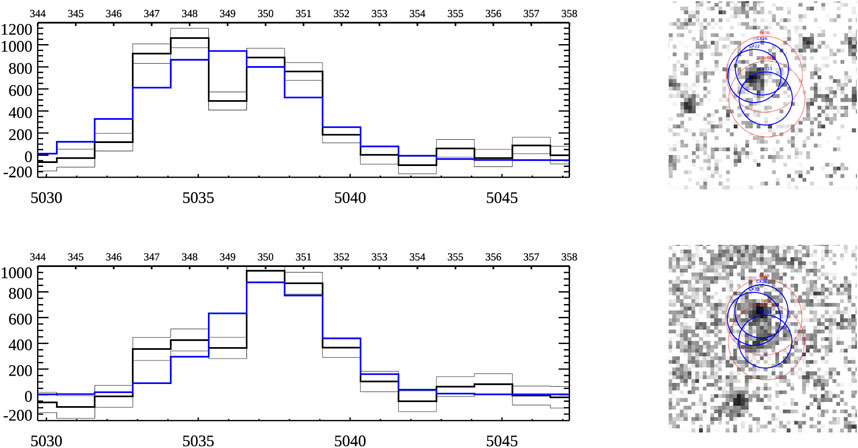
FIGURE 7. MUSE data of an [O III] source located 0.′3 from the nucleus of NGC 1380. The panels on the left display a segment of the source’s fitted spectrum (shown in blue) extracted in two 0.′′6 radius apertures separated by 0.′′55 on the sky; the right panels display two 1.25 Å wide “images” of the source, one centered at 5,034.72 Å (top) and the other at 5,037.22 Å (bottom). Careful inspection of the data demonstrates that the [O III] source actually consists of three separate PNe. The deblended spectra of the PNe are shown as the black and grey lines on the left, and the best-fit locations of the individual PNe are denoted by the blue circles on the right. If the galaxy were more distant, if the seeing were poorer, or the resolution of MUSE were less, the three objects would appear as one “overluminous” PNe. From Roth et al. (2021).

The formalism for including blends in a PNLF analysis is reasonably straightforward and is described in detail by Chase et al. (2022). If we let ϕ₁(F) represent the PNLF of single objects (i.e., Eq. 3, expressed in units of flux, rather than magnitude), then the flux distribution expected for sets of two superposed objects whose net emission-line flux is the sum of their component fluxes is simply ϕ₁(F) convolved with itself. If we then let ϕ₂(F) represent this convolved luminosity function, then the shape of a galaxy’s observed PNLF will be

${\varphi }_T\left(F\right)=a_1{\varphi }_1\left(F\right)+a_2{\varphi }_2\left(F\right)+a_3{\varphi }_3\left(F\right)+\dots (6)$

where the coefficients a_i represent the relative likelihood of an observed source being composed of i PNe, and each term, ϕ_i(F), is formed from a convolution with the previous term, i.e.,

${\varphi }_{i+1}\left(F\right)={\varphi }_1\left(F\right)\ast {\varphi }_i\left(F\right)(7)$

The only difficulties come from determining the appropriate expectation values for the analysis (a_i) and choosing an assumed shape for ϕ₁.

The former is made tractable by the fact that the ratio of PNe per unit light generally does not change much over the surface of a galaxy (e.g., Hui et al., 1993; Merrett et al., 2006; Longobardi et al., 2013; Hartke et al., 2017). If one knows the amount of galaxy light present in a single resolution element, and can estimate the number of PNe per unit galaxy luminosity (commonly called α), the expectation values can be computed quite easily. The latter issue is more problematic, since, as detailed in Section 2, it is only the most luminous $\sim 1$ mag of the PNLF that appears invariant. However, since the most important blends are those formed from the superposition of two bright objects, the errors introduced by not knowing the relative numbers of faint sources are small enough to be ignored.

Figure 8 demonstrates the effect of ignoring blends in the PNLF by showing the observed luminosity function of NGC 1380, the host galaxy of the Type Ia supernova SN 1992A. This galaxy has one clearly “overluminous” PNe, whose inclusion in a traditional PNLF fit would cause the distance to the galaxy to be underestimated. Both Spriggs et al. (2020, 2021) and Roth et al. (2021) excluded this object from their analysis, but as Figure 8 indicates, the arbitrary elimination of one bright object does not necessarily lead to an unbiased solution, as other, less luminous blends may still be present in the sample. In fact, in the case of NGC 1380, the inclusion of the higher order terms of Eq. 6 makes a significant difference in the end result, and moves the galaxy much closer to its SBF distance.

FIGURE 8

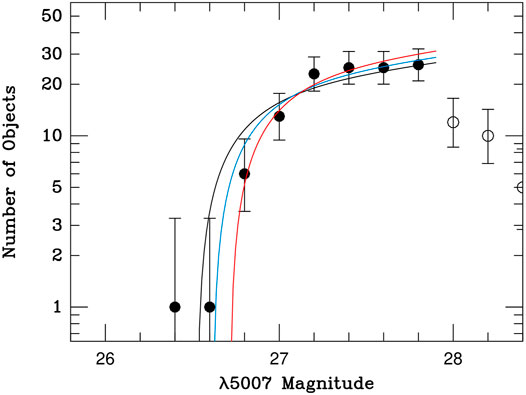
FIGURE 8. The observed PNLF of the Fornax Cluster lenticular galaxy NGC 1380 as measured by Roth et al. (2021). The open circles show measurements fainter than the 90% completeness limit. The black curve shows the best-fit of Eq. 3 to the data, while the blue curve displays the best fit if the brightest PNe is arbitrarily excluded from the analysis. The red curve represents the best fit when the possibility of PN superpositions is included in the analysis. The offsets between the curves illustrate how a fit using Eq. 3 can introduce a systematic error into PNLF distances, even when obvious overluminous objects are removed from the sample.

Finally, it is important to note that the red curve in Figure 8 does not “appear” to be a good fit to the data. This is because the a_i values depend on the galaxy’s underlying surface brightness, and this surface brightness changes from object to object. Consequently, when superpositions are included in the analysis, the expected luminosity function, ϕ_T, is different for every PN in the sample, and one curve cannot fit all the data. The red curve displayed in Figure 8 is only shown to allow a visual comparison of the best-fit distances.

The key question, of course, is whether the bright end of the PNLF is truly a standard candle. In the local universe, the only obvious systematic in the PNLF cutoff is a tendency for M^∗ to fade at low metallicity (Ciardullo and Jacoby, 1992; Ciardullo et al., 2002a). Such a dependence is unimportant, since, as described in Section 2, low-metallicity systems generally contain very few PNe. However, the absence of a known systematic does not mean that one does not exist. A ≲ 5% shift in M^∗ with galaxy color, metallicity, or star-formation rate could still be hidden in the noise.

Until now, it has been impossible to search for such minor systematics, as without spectral information, one could not guarantee that all the point-source objects found in an [O III] survey were actually PNe. One consequence of this limitation was the arbitrary exclusion of overluminous objects from the PNLF samples. At the sub-5% level, even one interloper or blended source with a magnitude near m^∗ may wash out the signal produced by a change in stellar population. The availability of IFU spectrographs are now removing much of this uncertainty and allowing a closer examination into the systematics of the technique.

The only way to discover subtle shifts in the PNLF cutoff is through careful comparisons with other standard candles. In the latter half of the 20th century, errors and biases in the distance ladder were identified by comparing the results of each measurement technique against those of all the others (e.g., van den Bergh, 1982; Rowan-Robinson, 1985; Jacoby et al., 1992). This cross-checking procedure culminated in the work of the Hubble Space Telescope Key Project, which carefully examined the distances produced by ten different methods (Ferrarese et al., 2000; Freedman et al., 2001).

Such cross-checks largely do not exist in the present era, since most extragalactic standard candles are not capable of $\sim 5\%$ precision. As stated in Section 3, modern estimates of the Hubble constant involve as few rungs on the distance ladder as possible. For example, the $\sim 1\%$ Hubble constant error quoted by Riess et al. (2019, 2021) is derived from a two-step approach, which goes from Milky Way and LMC photometry of Cepheid variables to Cepheids measurements in nearby SN Ia host galaxies, to the SN Ia maximum magnitude-rate of decline relation. The best cross-check on this is the 2% measurement by Freedman et al. (2019), which substitutes TRGB measurements for the Cepheids in the above ladder. Tantalizingly, the two results differ by almost 2σ. Megamasers (Pesce et al., 2020) and gravitationally lensed quasars (Wong et al., 2020) also give values consistent with the Cepheid numbers, but those methods are not part of the distance ladder and are difficult to confirm. Additional precision standard candles are needed, especially beyond $\sim 40$ Mpc, where the uncertainties associated with peculiar motions and bulk flows are less than $\sim 10\%$. The PNLF is now capable of reaching these distances; all that is needed is enough high-quality measurements to enable any small, systematic trends to be identified.

Finally, progress must be made in identifying the reason for the PNLF cutoff. This requires comparing PNLF observations to models which mate post-AGB stellar evolutionary tracks to the physics of an expanding nebula which is interacting with stellar winds. The resulting confrontation of theory with observations would provide added confidence to the assumptions underlying the PNLF, and help improve our knowledge of stellar evolution. Ironically, a major limitation on such a program is not in the modeling, as several studies (Dopita et al., 1992; Schönberner et al., 2010; Gesicki et al., 2018; Valenzuela et al., 2019) have simulated the properties of ensembles of extragalactic PNe. Instead, it is the PNLF observations themselves that are insufficient. The action of dust, which is formed during a star’s AGB phase, and is still close by when the star becomes hot enough to ionize its nebula, is critical to predicting the observed brightness of a luminous PN. A number of surveys (e.g., Herrmann and Ciardullo, 2009a; Kwitter et al., 2012; Fang et al., 2018; Galera-Rosillo et al., 2022) have demonstrated that PNe within $\sim 1$ mag of M^∗ have a significant amount of circumnebular extinction, and Davis et al. (2018b) showed that the shape of the de-reddened PNLF of M31’s bulge is likely quite different from that of the galaxy’s observed luminosity function. Yet currently, the LMC is the only galaxy for which a de-reddened PNLF has been measured (Reid and Parker, 2010). Obtaining de-reddened PNLFs is challenging, since it requires exposures that are deep enough to detect both Hα and Hβ, and the latter line is relatively faint (see Figure 1). In addition, neither VIRUS nor MUSE are designed for such a project: the former instrument does not cover Hα, while Hβ is at the extreme (low throughput) limit of MUSE’s wavelength range. Still, such observations are critical for a better understanding of the PNLF.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Institutional support, HETDEX is funded by the National Science Foundation (grant no. AST-0926815), the State of Texas, the US Air Force (AFRL FA9451-04-2-0355), and generous support from private individuals and foundations. The Institute for Gravitation and the Cosmos is supported by the Eberly College of Science, and the Office of the Senior Vice President for Research at the Pennsylvania State University.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The data cube for M101 was obtained via the Hobby–Eberly Telescope (HET), which is a joint project of the University of Texas at Austin, The Pennsylvania State University, the Ludwig-Maximilians-Universität München, and the Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby, and Robert E. Eberly. VIRUS is a joint project of the University of Texas at Austin (UTA), the Leibniz-Institut für Astrophysik Potsdam (AIP), Texas A&M University (TAMU), the Max-Planck-Institut für Extraterrestriche-Physik (MPE), the Ludwig-Maximilians-Universität München, The Pennsylvania State University, the Institut für Astrophysik Göttingen, the University of Oxford, the Max-Planck-Institut für Astrophysik (MPA), and The University of Tokyo. HETDEX is led by the University of Texas at Austin McDonald Observatory and Department of Astronomy, with participation from the Ludwig-Maximilians-Universität München, the Max-Planck-Institut für Extraterrestriche-Physik (MPE), the Leibniz-Institut für Astrophysik Potsdam (AIP), Texas A&M University, The Pennsylvania State University, the Institut für Astrophysik Göttingen, The University of Oxford, the Max-Planck-Institut für Astrophysik (MPA), The University of Tokyo, and Missouri University of Science and Technology.

References

Anand, G. S., Lee, J. C., Van Dyk, S. D., Leroy, A. K., Rosolowsky, E., Schinnerer, E., et al. (2021). Distances to PHANGS Galaxies: New Tip of the Red Giant Branch Measurements and Adopted Distances. Mon. Notices Royal Astron. Soc. 501, 3621–3639. doi:10.1093/mnras/staa3668

CrossRef Full Text | Google Scholar

Bacon, R., Accardo, M., Adjali, L., Anwand, H., Bauer, S., Biswas, I., et al. (2010). “The MUSE Second-Generation VLT Instrument,” in Ground-Based and Airborne Instrumentation for Astronomy III of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, San Diego, CA, June 27–July 2, 2010. Editors I. S. McLean, S. K. Ramsay, and H. Takami, 7735, 773508. doi:10.1117/12.856027

CrossRef Full Text | Google Scholar

Beaton, R. L., Freedman, W. L., Madore, B. F., Bono, G., Carlson, E. K., Clementini, G., et al. (2016). The Carnegie-Chicago Hubble Program. I. An Independent Approach to the Extragalactic Distance Scale Using Only Population II Distance Indicators. Astrophys. J. 832, 210. doi:10.3847/0004-637X/832/2/210

CrossRef Full Text | Google Scholar

Beaton, R. L., Seibert, M., Hatt, D., Freedman, W. L., Hoyt, T. J., Jang, I. S., et al. (2019). The Carnegie-Chicago Hubble Program. VII. The Distance to M101 via the Optical Tip of the Red Giant Branch Method. Astrophys. J. 885, 141. doi:10.3847/1538-4357/ab4263

CrossRef Full Text | Google Scholar

Bhattacharya, S., Arnaboldi, M., Gerhard, O., McConnachie, A., Caldwell, N., Hartke, J., et al. (2021). The Survey of Planetary Nebulae in Andromeda (M 31). III. Constraints from Deep Planetary Nebula Luminosity Functions on the Origin of the Inner Halo Substructures in M 31. Astron. Astrophys. 647, A130. doi:10.1051/0004-6361/202038366

CrossRef Full Text | Google Scholar

Bhattacharya, S., Arnaboldi, M., Hartke, J., Gerhard, O., Comte, V., McConnachie, A., et al. (2019). The Survey of Planetary Nebulae in Andromeda (M 31). I. Imaging the Disc and Halo with MegaCam at the CFHT. Astron. Astrophys. 624, A132. doi:10.1051/0004-6361/201834579

CrossRef Full Text | Google Scholar

Boffin, H. M. J., and Jones, D. (2019). The Importance of Binaries in the Formation and Evolution of Planetary Nebulae. Cambridge: Cambridge University Press. doi:10.1007/978-3-030-25059-1

CrossRef Full Text | Google Scholar

Buzzoni, A., Arnaboldi, M., and Corradi, R. L. M. (2006). Planetary Nebulae as Tracers of Galaxy Stellar Populations. Mon. Not. R. Astron. Soc. 368, 877–894. doi:10.1111/j.1365-2966.2006.10163.x

CrossRef Full Text | Google Scholar

Chase, O., Ciardullo, R., Roth, M. M., and Jacoby, G. H. (2022). The Effect of Superpositions on the Planetary Nebula Luminosity Function. Astrophys. J. (in press).

Google Scholar

Chornay, N., and Walton, N. A. (2021). One Star, Two Star, Red Star, Blue Star: an Updated Planetary Nebula Central Star Distance Catalogue from Gaia EDR3. Astron. Astrophys. 656, A110. doi:10.1051/0004-6361/202142008

CrossRef Full Text | Google Scholar

Ciardullo, R., Durrell, P. R., Laychak, M. B., Herrmann, K. A., Moody, K., Jacoby, G. H., et al. (2004). The Planetary Nebula System of M33. Astrophys. J. 614, 167–185. doi:10.1086/423414

CrossRef Full Text | Google Scholar

Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., Kuzio de Naray, R., Laychak, M. B., and Durrell, P. R. (2002a). Planetary Nebulae as Standard Candles. XII. Connecting the Population I and Population II Distance Scales. Astrophys. J. 577, 31–50. doi:10.1086/342180

CrossRef Full Text | Google Scholar

Ciardullo, R., Feldmeier, J. J., Krelove, K., Jacoby, G. H., and Gronwall, C. (2002b). A Measurement of the Contamination in [O III] λ5007 Surveys of Intracluster Stars and the Surface Density of z=3.13 Lyα Galaxies. Astrophys. J. 566, 784–793. doi:10.1086/338230

CrossRef Full Text | Google Scholar

Ciardullo, R., Jacoby, G. H., Ford, H. C., and Neill, J. D. (1989b). Planetary Nebulae as Standard Candles. II. The Calibration in M31 and its Companions. Astrophys. J. 339, 53. doi:10.1086/167275

CrossRef Full Text | Google Scholar

Ciardullo, R., Jacoby, G. H., and Ford, H. C. (1989a). Planetary Nebulae as Standard Candles. IV. A Test in the Leo I Group. Astrophys. J. 344, 715. doi:10.1086/167836

CrossRef Full Text | Google Scholar

Ciardullo, R., Jacoby, G. H., and Harris, W. E. (1991). Planetary Nebulae as Standard Candles. VII. A Test versus Hubble Type in the NGC 1023 Group. Astrophys. J. 383, 487. doi:10.1086/170807

CrossRef Full Text | Google Scholar

Ciardullo, R., and Jacoby, G. H. (1992). Planetary Nebulae as Standard Candles. VIII. Evidence for a Change in the Luminosity Function Cutoff at Low Metallicity. Astrophys. J. 388, 268. doi:10.1086/171150

CrossRef Full Text | Google Scholar

Ciardullo, R. (2005). “Planetary Nebulae and the Extragalactic Distance Scale,” in Planetary Nebulae as Astronomical Tools of American Institute of Physics Conference Series, Gdansk, Poland, June 29–July 2, 2005. Editors R. Szczerba, G. Stasińska, and S. K. Gorny, 804, 277–283. doi:10.1063/1.2146293

CrossRef Full Text | Google Scholar

Ciardullo, R., Sigurdsson, S., Feldmeier, J. J., and Jacoby, G. H. (2005). Close Binaries as the Progenitors of the Brightest Planetary Nebulae. Astrophys. J. 629, 499–506. doi:10.1086/431353

CrossRef Full Text | Google Scholar

Ciardullo, R. (2010). The Planetary Nebula Luminosity Function: Pieces of the Puzzle. Publ. Astron. Soc. Aus. 27, 149–155. doi:10.1071/AS09022

CrossRef Full Text | Google Scholar

Cowie, L. L., and Hu, E. M. (1998). High-z Lyalpha Emitters. I. A Blank-Field Search for Objects Near Redshift Z = 3.4 in and Around the Hubble Deep Field and the Hawaii Deep Field SSA 22. Astron. J. 115, 1319–1328. doi:10.1086/300309

CrossRef Full Text | Google Scholar

Cummings, J. D., Kalirai, J. S., Tremblay, P.-E., Ramirez-Ruiz, E., and Choi, J. (2018). The White Dwarf Initial-Final Mass Relation for Progenitor Stars from 0.85 to 7.5 M_⊙. Astrophys. J. 866, 21. doi:10.3847/1538-4357/aadfd6

CrossRef Full Text | Google Scholar

Davidge, T. J. (2008). The Stellar Content of the Post-Starburst S0 Galaxy Ngc 5102. Astronomical J. 5102135, 1636–1648. doi:10.1088/0004-6256/135/4/1636

CrossRef Full Text | Google Scholar

Davis, B. D., Ciardullo, R., Feldmeier, J. J., and Jacoby, G. H. (2018a). The Planetary Nebula Luminosity Function (PNLF): Contamination from Supernova Remnants. Res. Notes AAS 2, 32. doi:10.3847/2515-5172/aab045

CrossRef Full Text | Google Scholar

Davis, B. D., Ciardullo, R., Jacoby, G. H., Feldmeier, J. J., and Indahl, B. L. (2018b). The True Luminosities of Planetary Nebulae in M31's Bulge: Massive Central Stars from an Old Stellar Population. Astrophys. J. 863, 189. doi:10.3847/1538-4357/aad3c4

CrossRef Full Text | Google Scholar

De Marco, O. (2009). The Origin and Shaping of Planetary Nebulae: Putting the Binary Hypothesis to the Test. Publ. Astron. Soc. Pac. 121, 316–342. doi:10.1086/597765

CrossRef Full Text | Google Scholar

Dopita, M. A., Jacoby, G. H., and Vassiliadis, E. (1992). A Theoretical Calibration of the Planetary Nebular Cosmic Distance Scale. Astrophys. J. 389, 27. doi:10.1086/171186

CrossRef Full Text | Google Scholar

Durrell, P. R., Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., and Sigurdsson, S. (2002). Intracluster Red Giant Stars in the Virgo Cluster. Astrophys. J. 570, 119–131. doi:10.1086/339735

CrossRef Full Text | Google Scholar

El-Badry, K., Rix, H.-W., and Weisz, D. R. (2018). An Empirical Measurement of the Initial-Final Mass Relation with Gaia White Dwarfs. Astrophys. J. Lett. 860, L17. doi:10.3847/2041-8213/aaca9c

CrossRef Full Text | Google Scholar

Fang, X., García-Benito, R., Guerrero, M. A., Zhang, Y., Liu, X., Morisset, C., et al. (2018). Chemical Abundances of Planetary Nebulae in the Substructures of M31. II. The Extended Sample and a Comparison Study with the Outer-Disk Group. Astrophys. J. 853, 50. doi:10.3847/1538-4357/aaa1e5

CrossRef Full Text | Google Scholar

Feldmeier, J. J., Ciardullo, R., and Jacoby, G. H. (1997). Planetary Nebulae as Standard Candles. XI. Application to Spiral Galaxies. Astrophys. J. 479, 231–243. doi:10.1086/512787

CrossRef Full Text | Google Scholar

Feldmeier, J. J., Ciardullo, R., and Jacoby, G. H. (1996). The Planetary Nebula Distance to M101. Astrophys. J. Lett. 461, L25. doi:10.1086/309994

CrossRef Full Text | Google Scholar

Feldmeier, J. J., Jacoby, G. H., and Phillips, M. M. (2007). Calibrating Type Ia Supernovae Using the Planetary Nebula Luminosity Function. I. Initial Results. Astrophys. J. 657, 76–94. doi:10.1086/510897

CrossRef Full Text | Google Scholar

Ferguson, H. C., Tanvir, N. R., and von Hippel, T. (1998). Detection of Intergalactic Red-Giant-Branch Stars in the Virgo Cluster. Nature 391, 461–463. doi:10.1038/35087

CrossRef Full Text | Google Scholar

Ferrarese, L., Mould, J. R., Kennicutt, R. C., Ford, H. C., Freedman, W. L., Stetson, P. B., et al. (2000). The Hubble Space Telescope Key Project on the Extragalactic Distance Scale. XXVI. The Calibration of Population II Secondary Distance Indicators and the Value of the Hubble Constant. Astrophys. J. 529, 745–767. doi:10.1086/308309

CrossRef Full Text | Google Scholar

Ferrarese, L., Mould, J. R., Stetson, P. B., Tonry, J. L., Blakeslee, J. P., and Ajhar, E. A. (2007). The Discovery of Cepheids and a Distance to NGC 5128. Astrophys. J. 654, 186–218. doi:10.1086/506612

CrossRef Full Text | Google Scholar

Ford, H. C., Hui, X., Ciardullo, R., Jacoby, G. H., and Freeman, K. C. (1996). The Stellar Halo of M104. I. A Survey for Planetary Nebulae and the Planetary Nebula Luminosity Function Distance. Astrophys. J. 458, 455. doi:10.1086/176828

CrossRef Full Text | Google Scholar

Ford, H. C., Jenner, D. C., and Epps, H. W. (1973). Planetary Nebulae in Local-Group Galaxies. I. Identifications in NGC 185, NGC 205, and NGC 221. Astrophys. J. 221183, L73. doi:10.1086/181255

CrossRef Full Text | Google Scholar

Ford, H. C., and Jenner, D. C. (1978). Planetary Nebulae in the Nuclear Bulge of M81: A New Distance Determination. Bull. Am. Astronomical Soc. 10, 665.

Google Scholar

Freedman, W. L., Madore, B. F., Gibson, B. K., Ferrarese, L., Kelson, D. D., Sakai, S., et al. (2001). Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. Astrophys. J. 553, 47–72. doi:10.1086/320638

CrossRef Full Text | Google Scholar

Freedman, W. L., Madore, B. F., Hatt, D., Hoyt, T. J., Jang, I. S., Beaton, R. L., et al. (2019). The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 882, 34. doi:10.3847/1538-4357/ab2f73

CrossRef Full Text | Google Scholar

Freedman, W. L. (2021). Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 919, 16. doi:10.3847/1538-4357/ac0e95

CrossRef Full Text | Google Scholar

Fusco, T., Bacon, R., Kamann, S., Conseil, S., Neichel, B., Correia, C., et al. (2020). Reconstruction of the Ground-Layer Adaptive-Optics Point Spread Function for MUSE Wide Field Mode Observations. Astron. Astrophys. 635, A208. doi:10.1051/0004-6361/202037595

CrossRef Full Text | Google Scholar

Galera-Rosillo, R., Mampaso, A., Corradi, R. L. M., García-Rojas, J., Balick, B., Jones, D., et al. (2022). On the Most Luminous Planetary Nebulae of M 31. Astron. Astrophys. 657, 657A71. doi:10.1051/0004-6361/202141890

CrossRef Full Text | Google Scholar

Gebhardt, K., Mentuch Cooper, E., Ciardullo, R., Acquaviva, V., Bender, R., Bowman, W. P., et al. (2021). The Hobby-Eberly Telescope Dark Energy Experiment (HETDEX) Survey Design, Reductions, and Detections. Astrophys. J. 923, 217. doi:10.3847/1538-4357/ac2e03

CrossRef Full Text | Google Scholar

Gerhard, O., Arnaboldi, M., Freedman, K. C., and Okamura, S. (2003). “Isolated Star Formation in the Virgo Cluster,” in Star Formation at High Angular Resolution, IAU Symp. 221, Sydney, Australia, July 22–25, 2003. Editors M. Burton, R. Jayawardhana, and T. Bourke (San Francisco: Astronomical Society of the Pacific), 66.

Google Scholar

Gesicki, K., Zijlstra, A. A., and Miller Bertolami, M. M. (2018). The Mysterious Age Invariance of the Planetary Nebula Luminosity Function Bright Cut-Off. Nat. Astron 2, 580–584. doi:10.1038/s41550-018-0453-9

CrossRef Full Text | Google Scholar

Giovanelli, R., Haynes, M. P., Salzer, J. J., Wegner, G., da Costa, L. N., and Freudling, W. (1998). The Motions of Clusters of Galaxies and the Dipoles of the Peculiar Velocity Field. Astrophys. J. 116, 2632–2643. doi:10.1086/300652

CrossRef Full Text | Google Scholar

González-Santamaría, I., Manteiga, M., Manchado, A., Ulla, A., Dafonte, C., and López Varela, P. (2021). Planetary Nebulae in Gaia EDR3: Central Star Identification, Properties, and Binarity. Astron. Astrophys. 656, A51. doi:10.1051/0004-6361/202141916

CrossRef Full Text | Google Scholar

Hartke, J., Arnaboldi, M., Gerhard, O., Coccato, L., Pulsoni, C., Freeman, K. C., et al. (2020). The Halo of M 105 and its Group Environment as Traced by Planetary Nebula Populations. Astron. Astrophys. 642, A46. doi:10.1051/0004-6361/202038009

CrossRef Full Text | Google Scholar

Hartke, J., Arnaboldi, M., Longobardi, A., Gerhard, O., Freeman, K. C., Okamura, S., et al. (2017). The Halo of M 49 and its Environment as Traced by Planetary Nebulae Populations. Astron. Astrophys. 603, A104. doi:10.1051/0004-6361/201730463

CrossRef Full Text | Google Scholar

Hatt, D., Freedman, W. L., Madore, B. F., Jang, I. S., Beaton, R. L., Hoyt, T. J., et al. (2018). The Carnegie-Chicago Hubble Program. V. The Distances to NGC 1448 and NGC 1316 via the Tip of the Red Giant Branch. Astrophys. J. 866, 145. doi:10.3847/1538-4357/aadfe8

CrossRef Full Text | Google Scholar

Hayashino, T., Matsuda, Y., Tamura, H., Yamauchi, R., Yamada, T., Ajiki, M., et al. (2004). Large-Scale Structure of Emission-Line Galaxies Atz = 3.1. Astron J. 128, 2073–2079. doi:10.1086/424935

CrossRef Full Text | Google Scholar

Henize, K. G., and Westerlund, B. E. (1963). Dimensions of Diffuse and Planetary Nebulae in the Small Magellanic Cloud. Astrophys. J. 137, 747. doi:10.1086/147552

CrossRef Full Text | Google Scholar

Herrmann, K. A., Ciardullo, R., Feldmeier, J. J., and Vinciguerra, M. (2008). Planetary Nebulae in Face‐On Spiral Galaxies. I. Planetary Nebula Photometry and Distances. Astrophys. J. 683, 630–643. doi:10.1086/589920

CrossRef Full Text | Google Scholar

Herrmann, K. A., and Ciardullo, R. (2009b). Planetary Nebulae in Face-On Spiral Galaxies. Iii. Planetary Nebula Kinematics and Disk Mass. Astrophys. J. 705, 1686–1703. doi:10.1088/0004-637x/705/2/1686

CrossRef Full Text | Google Scholar

Herrmann, K. A., and Ciardullo, R. (2009a). Planetary Nebulae in Face-On Spiral Galaxies. II. Planetary Nebula Spectroscopy. Astrophys. J. 703, 894–904. doi:10.1088/0004-637x/703/1/894

CrossRef Full Text | Google Scholar

Hill, G. J., Lee, H., MacQueen, P. J., Kelz, A., Drory, N., Vattiat, B. L., et al. (2021). The HETDEX Instrumentation: Hobby-Eberly Telescope Wide-Field Upgrade and VIRUS. Astron. J. 162, 298. doi:10.3847/1538-3881/ac2c02

CrossRef Full Text | Google Scholar

Hinshaw, G., Larson, D., Komatsu, E., Spergel, D. N., Bennett, C. L., Dunkley, J., et al. (2013). Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 208, 19. doi:10.1088/0067-0049/208/2/19

CrossRef Full Text | Google Scholar

Hodge, P. W. (1966). The Physics and Astronomy of Galaxies and Cosmology. New York: McGraw-Hill.

Google Scholar

Hoyt, T. J., Beaton, R. L., Freedman, W. L., Jang, I. S., Lee, M. G., Madore, B. F., et al. (2021). The Carnegie Chicago Hubble Program X: Tip of the Red Giant Branch Distances to NGC 5643 and NGC 1404. Astrophys. J. 915, 34. doi:10.3847/1538-4357/abfe5a

CrossRef Full Text | Google Scholar

Hoyt, T. J., Freedman, W. L., Madore, B. F., Hatt, D., Beaton, R. L., Jang, I. S., et al. (2019). The Carnegie Chicago Hubble Program. VI. Tip of the Red Giant Branch Distances to M66 and M96 of the Leo I Group. Astrophys. J. 882, 150. doi:10.3847/1538-4357/ab1f81

CrossRef Full Text | Google Scholar

Hu, E. M., Cowie, L. L., and McMahon, R. G. (1998). The Density of Lyα Emitters at Very High Redshift. Astrophys. J. Lett. 502, L99–L103. doi:10.1086/311506

CrossRef Full Text | Google Scholar

Hubble, E. (1936). The Luminosity Function of Nebulae. II. The Luminosity Function as Indicated by Residuals in Velocity-Magnitude Relations. Astrophys. J. 84, 270. doi:10.1086/143764

CrossRef Full Text | Google Scholar

Hui, X., Ford, H. C., Ciardullo, R., and Jacoby, G. H. (1993). The Planetary Nebula System and Dynamics of NGC 5128. I. Planetary Nebulae as Standard Candles. Astrophys. J. 414, 463. doi:10.1086/173093

CrossRef Full Text | Google Scholar

Jacob, R., Schönberner, D., and Steffen, M. (2013). The Evolution of Planetary Nebulae. VIII. True Expansion Rates and Visibility Times. Astron. Astrophys. 558, A78. doi:10.1051/0004-6361/201321532

CrossRef Full Text | Google Scholar

Jacoby, G. H., Branch, D., Clardullo, R., Davies, R. L., Harris, W. E., Pierce, M. J., et al. (1992). A Critical Review of Selected Techniques for Measuring Extragalactic Distances. Publ. Astron. Soc. Pac. 104, 599. doi:10.1086/133035

CrossRef Full Text | Google Scholar

Jacoby, G. H., Ciardullo, R., Booth, J., and Ford, H. C. (1989). Planetary Nebulae as Standard Candles. III. The Distance to M81. Astrophys. J. 344, 704. doi:10.1086/167835

CrossRef Full Text | Google Scholar

Jacoby, G. H., and Ciardullo, R. (1999). Chemical Abundances of Planetary Nebulae in the Bulge and Disk of M31. Astrophys. J. 515, 169–190. doi:10.1086/307024

CrossRef Full Text | Google Scholar

Jacoby, G. H., Ciardullo, R., and Ford, H. C. (1990a). Planetary Nebulae as Standard Candles. V. The Distance to the Virgo Cluster. Astrophys. J. 356, 332. doi:10.1086/168843

CrossRef Full Text | Google Scholar

Jacoby, G. H., Ciardullo, R., and Harris, W. E. (1996). Planetary Nebulae as Standard Candles. X. Tests in the Coma I Region. Astrophys. J. 462, 1. doi:10.1086/177122

CrossRef Full Text | Google Scholar

Jacoby, G. H., Ciardullo, R., and Walker, A. R. (1990b). Planetary Nebulae as Standard Candles. VI. A Test in the Magellanic Clouds. Astrophys. J. 365, 471. doi:10.1086/169501

CrossRef Full Text | Google Scholar

Jacoby, G. H., and De Marco, O. (2002). A Survey for Very Faint Planetary Nebulae in the SMC. I. Identification, Confirmation, and Preliminary Analysis. Astron. J. 123, 269–278. doi:10.1086/324737

CrossRef Full Text | Google Scholar

Jang, I. S., Hatt, D., Beaton, R. L., Lee, M. G., Freedman, W. L., Madore, B. F., et al. (2018). The Carnegie-Chicago Hubble Program. III. The Distance to NGC 1365 via the Tip of the Red Giant Branch. Astrophys. J. 852, 60. doi:10.3847/1538-4357/aa9d92

CrossRef Full Text | Google Scholar

Jang, I. S., Hoyt, T. J., Beaton, R. L., Freedman, W. L., Madore, B. F., Lee, M. G., et al. (2021). The Carnegie-Chicago Hubble Program. IX. Calibration of the Tip of the Red Giant Branch Method in the Megamaser Host Galaxy, NGC 4258 (M106). Astrophys. J. 906, 125. doi:10.3847/1538-4357/abc8e9

CrossRef Full Text | Google Scholar

Kreckel, K., Groves, B., Bigiel, F., Blanc, G. A., Kruijssen, J. M. D., Hughes, A., et al. (2017). A Revised Planetary Nebula Luminosity Function Distance to NGC 628 Using MUSE. Astrophys. J. 834, 174. doi:10.3847/1538-4357/834/2/174

CrossRef Full Text | Google Scholar

Kudritzki, R. P., Mendez, R. H., Feldmeier, J. J., Ciardullo, R., Jacoby, G. H., Freeman, K. C., et al. (2000). Discovery of Nine Lyα Emitters at Redshift z˜3.1 Using Narrowband Imaging and VLT Spectroscopy. Astrophys. J. 536, 19–30. doi:10.1086/308925

CrossRef Full Text | Google Scholar

Kwitter, K. B., and Henry, R. B. C. (2022). Planetary Nebulae: Sources of Enlightenment. Publ. Astron. Soc. Pac. 134, 022001. doi:10.1088/1538-3873/ac32b1

CrossRef Full Text | Google Scholar

Kwitter, K. B., Lehman, E. M. M., Balick, B., and Henry, R. B. C. (2012). Abundances of Planetary Nebulae in the Outer Disk of M31. Astrophys. J. 753, 12. doi:10.1088/0004-637x/753/1/12

CrossRef Full Text | Google Scholar

Kwok, S. (2007). The Origin and Evolution of Planetary Nebulae. Cambridge: Cambridge University Press.

Google Scholar

Lee, M. G., and Jang, I. S. (2016). Dual Stellar Halos in the Standard Elliptical Galaxy M105 and Formation of Massive Early-type Galaxies. Astrophys. J. 822, 70. doi:10.3847/0004-637x/822/2/70

CrossRef Full Text | Google Scholar

Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., and Torres-Peimbert, S. (1979). Reprint of 1979A&A....80..155L. Chemical Composition and Evolution of Irregular and Blue Compact Galaxies. Astron. Astrophys. 500, 145–156.

Google Scholar

Longobardi, A., Arnaboldi, M., Gerhard, O., Coccato, L., Okamura, S., and Freeman, K. C. (2013). The Planetary Nebula Population in the Halo of M 87. Astron. Astrophys. 558, A42. doi:10.1051/0004-6361/201321652

CrossRef Full Text | Google Scholar

Macri, L. M., Stanek, K. Z., Bersier, D., Greenhill, L. J., and Reid, M. J. (2006). A New Cepheid Distance to the Maser‐Host Galaxy NGC 4258 and its Implications for the Hubble Constant. Astrophys. J. 652, 1133–1149. doi:10.1086/508530

CrossRef Full Text | Google Scholar

Marigo, P., Girardi, L., Weiss, A., Groenewegen, M. A. T., and Chiosi, C. (2004). Evolution of Planetary Nebulae. II. Population Effects on the Bright Cut-Off of the PNLF. Astron. Astrophys. 423, 995–1015. doi:10.1051/0004-6361:20040234

CrossRef Full Text | Google Scholar

McMillan, R., Ciardullo, R., and Jacoby, G. H. (1994). Ionized Gas and Planetary Nebulae in the Bulge of the Blue S0 Galaxy NGC 5102. Astrophys. J. 108, 1610. doi:10.1086/117181

CrossRef Full Text | Google Scholar

McMillan, R., Ciardullo, R., and Jacoby, G. H. (1993). Planetary Nebulae as Standard Candles. IX. The Distance to the Fornax Cluster. Astrophys. J. 416, 62. doi:10.1086/173215

CrossRef Full Text | Google Scholar

Méndez, R. H., Teodorescu, A. M., Schönberner, D., Jacob, R., and Steffen, M. (2008). Toward Better Simulations of Planetary Nebulae Luminosity Functions. Astrophys. J. 681, 325–332. doi:10.1086/588808

CrossRef Full Text | Google Scholar

Merrett, H. R., Merrifield, M. R., Douglas, N. G., Kuijken, K., Romanowsky, A. J., Napolitano, N. R., et al. (2006). A Deep Kinematic Survey of Planetary Nebulae in the Andromeda Galaxy Using the Planetary Nebula Spectrograph. Mon. Not. R. Astron. Soc. 369, 120–142. doi:10.1111/j.1365-2966.2006.10268.x

CrossRef Full Text | Google Scholar

Mihos, J. C., Harding, P., Feldmeier, J., and Morrison, H. (2005). Diffuse Light in the Virgo Cluster. Astrophys. J. Lett. 631, L41–L44. doi:10.1086/497030

CrossRef Full Text | Google Scholar

Miller Bertolami, M. M. (2016). New Models for the Evolution of Post-asymptotic Giant Branch Stars and Central Stars of Planetary Nebulae. Astron. Astrophys. 588, A25. doi:10.1051/0004-6361/201526577

CrossRef Full Text | Google Scholar

Mould, J., and Sakai, S. (2009). The Extragalactic Distance Scale without Cepheids. Ii. Surface Brightness Fluctuations. Astrophys. J. 694, 1331–1334. doi:10.1088/0004-637X/694/2/1331

CrossRef Full Text | Google Scholar

Osterbrock, D. E., and Ferland, G. J. (2006). Astrophysics of Gaseous Nebulae and Active Galactic Nuclei. Sausalito, CA: University Science Books.

Google Scholar

Pesce, D. W., Braatz, J. A., Reid, M. J., Riess, A. G., Scolnic, D., Condon, J. J., et al. (2020). The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. Astrophys. J. Lett. 891, L1. doi:10.3847/2041-8213/ab75f0

CrossRef Full Text | Google Scholar

Reid, W. A., and Parker, Q. A. (2010). A New Population of Planetary Nebulae Discovered in the Large Magellanic Cloud - III. The Luminosity Function. Mon. Not. R. Astron. Soc. 405, 1349–1374. doi:10.1111/j.1365-2966.2010.16635.x

CrossRef Full Text | Google Scholar

Renzini, A., and Buzzoni, A. (1986). “Global Properties of Stellar Populations and the Spectral Evolution of Galaxies,” in Spectral Evolution of Galaxies of Astrophysics and Space Science Library. Editors C. Chiosi, and A. Renzini (Dordrecht: Springer), 122, 195–235. doi:10.1007/978-94-009-4598-2_19

CrossRef Full Text | Google Scholar

Riess, A. G., Casertano, S., Yuan, W., Bowers, J. B., Macri, L., Zinn, J. C., et al. (2021). Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 908, L6. doi:10.3847/2041-8213/abdbaf

CrossRef Full Text | Google Scholar

Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., and Scolnic, D. (2019). Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 876, 85. doi:10.3847/1538-4357/ab1422

CrossRef Full Text | Google Scholar

Riess, A. G., Macri, L., Casertano, S., Lampeitl, H., Ferguson, H. C., Filippenko, A. V., et al. (2011). A 3% Solution: Determination of the Hubble Constant with the Hubble Space Telescope and Wide Field Camera 3. Astrophys. J. 730, 119. doi:10.1088/0004-637X/730/2/119

CrossRef Full Text | Google Scholar

Riess, A. G., Macri, L. M., Hoffmann, S. L., Scolnic, D., Casertano, S., Filippenko, A. V., et al. (2016). A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 826, 56. doi:10.3847/0004-637X/826/1/56

CrossRef Full Text | Google Scholar

Rodríguez-González, A., Hernández-Martínez, L., Esquivel, A., Raga, A. C., Stasińska, G., Peña, M., et al. (2015). A Two-Mode Planetary Nebula Luminosity Function. Astron. Astrophys. 575, A1. doi:10.1051/0004-6361/201423713

CrossRef Full Text | Google Scholar

Roth, M. M., Jacoby, G. H., Ciardullo, R., Davis, B. D., Chase, O., and Weilbacher, P. M. (2021). Toward Precision Cosmology with Improved PNLF Distances Using VLT-MUSEI. Methodology and Tests. Astrophys. J. 916, 21. doi:10.3847/1538-4357/ac02ca

CrossRef Full Text | Google Scholar

Rowan-Robinson, M. (1985). The Cosmological Distance Ladder : Distance and Time in the Universe. New York: W. H. Freeman.

Google Scholar

Saha, A., Claver, J., and Hoessel, J. G. (2002). Cepheids and Long-Period Variables in IC 342. Astron. J. 124, 839–861. doi:10.1086/341649

CrossRef Full Text | Google Scholar

Sambhus, N., Gerhard, O., and Méndez, R. H. (2006). Kinematic Evidence for Different Planetary Nebula Populations in the Elliptical Galaxy NGC 4697. Astron. J. 131, 837–848. doi:10.1086/499074

CrossRef Full Text | Google Scholar

Scheuermann, F., Kreckel, K., Anand, G. S., Blanc, G. A., Congiu, E., Santoro, F., et al. (2022). Planetary Nebula Luminosity Function Distances for 19 Galaxies Observed by PHANGS-MUSE. Mon. Not. R. Astron. Soc. 511 (4), 6087–6109. doi:10.1093/mnras/stac110

CrossRef Full Text | Google Scholar

Schönberner, D., Jacob, R., Sandin, C., and Steffen, M. (2010). The Evolution of Planetary Nebulae. VII. Modelling Planetary Nebulae of Distant Stellar Systems. Astron. Astrophys. 523, A86. doi:10.1051/0004-6361/200913427

CrossRef Full Text | Google Scholar

Spriggs, T. W., Sarzi, M., Galán-de Anta, P. M., Napiwotzki, R., Viaene, S., Nedelchev, B., et al. (2021). The Fornax3D Project: Planetary Nebulae Catalogue and Independent Distance Measurements to Fornax Cluster Galaxies. Astron. Astrophys. 653, A167. doi:10.1051/0004-6361/202141314

CrossRef Full Text | Google Scholar

Spriggs, T. W., Sarzi, M., Napiwotzki, R., Galán-de Anta, P. M., Viaene, S., Nedelchev, B., et al. (2020). Fornax 3D Project: Automated Detection of Planetary Nebulae in the Centres of Early-Type Galaxies and First Results. Astron. Astrophys. 637, A62. doi:10.1051/0004-6361/201936862

CrossRef Full Text | Google Scholar

Tonry, J. L., Blakeslee, J. P., Ajhar, E. A., and Dressler, A. (2000). The Surface Brightness Fluctuation Survey of Galaxy Distances. II. Local and Large‐Scale Flows. Astrophys. J. 530, 625–651. doi:10.1086/308409

CrossRef Full Text | Google Scholar

Tonry, J. L., Dressler, A., Blakeslee, J. P., Ajhar, E. A., Fletcher, A. B., Luppino, G. A., et al. (2001). The SBF Survey of Galaxy Distances. IV. SBF Magnitudes, Colors, and Distances. Astrophys. J. 546, 681–693. doi:10.1086/318301

CrossRef Full Text | Google Scholar

Tremonti, C. A., Heckman, T. M., Kauffmann, G., Brinchmann, J., Charlot, S., White, S. D. M., et al. (2004). The Origin of the Mass‐Metallicity Relation: Insights from 53,000 Star‐forming Galaxies in the Sloan Digital Sky Survey. Astrophys. J. 613, 898–913. doi:10.1086/423264

CrossRef Full Text | Google Scholar

Valenzuela, L. M., Méndez, R. H., and Miller Bertolami, M. M. (2019). Revised Simulations of the Planetary Nebulae Luminosity Function. Astrophys. J. 887, 65. doi:10.3847/1538-4357/ab4e96

CrossRef Full Text | Google Scholar

van den Bergh, S. (1982). In Search of the Hubble Parameter. Nature 299, 297–298. doi:10.1038/299297a0

CrossRef Full Text | Google Scholar

Vassiliadis, E., and Wood, P. R. (1994). Post-Asymptotic Giant Branch Evolution of Low- to Intermediate-Mass Stars. Astrophys. J. Suppl. Ser. 92, 125. doi:10.1086/191962

CrossRef Full Text | Google Scholar

Wong, K. C., Suyu, S. H., Chen, G. C.-F., Rusu, C. E., Millon, M., Sluse, D., et al. (2020). H0LiCOW - XIII. A 2.4 Per Cent Measurement of H0 from Lensed Quasars: 5.3σ Tension between Early- and Late-Universe Probes. Mon. Not. R. Astron. Soc. 498, 1420–1439. doi:10.1093/mnras/stz3094

CrossRef Full Text | Google Scholar