Revolutionizing Our Understanding of Particle Energization in Space Plasmas Using On-Board Wave-Particle Correlator Instrumentation

A leap forward in our understanding of particle energization in plasmas throughout the heliosphere is essential to answer longstanding questions in heliophysics, including the heating of the solar corona, acceleration of the solar wind, and energization of particles that lead to observable phenomena, such as the Earth’s aurora. The low densities and high temperatures of typical heliospheric environments lead to weakly collisional plasma conditions. Under these conditions, the energization of particles occurs primarily through collisionless interactions between the electromagnetic fields and the individual plasma particles with energies characteristic of a particular interaction. To understand how the plasma heating and particle acceleration impacts the macroscopic evolution of the heliosphere, impacting phenomena such as extreme space weather, it is critical to understand these collisionless wave-particle interactions on the characteristic ion and electron kinetic timescales. Such understanding requires high-cadence measurements of both the electromagnetic fields and the three-dimensional particle velocity distributions. Although existing instrument technology enables these measurements, a major challenge to maximize the scientific return from these measurements is the limited amount of data that can be transmitted to the ground due to telemetry constraints. A valuable, but underutilized, approach to overcome this limitation is to compute on-board correlations of the maximum-cadence field and particle measurements to improve the sampling time by several orders of magnitude. Here we review the fundamentals of the innovative field-particle correlation technique, present a formulation of the technique that can be implemented as an on-board wave-particle correlator, and estimate results that can be achieved with existing instrumental capabilities for particle velocity distribution measurements.

1 Introduction

One of the key goals in heliophysics and astrophysics is to discover and characterize the processes controlling the flow of energy and the impact of that energy on the evolution of the space plasma environment. For example, although the source of energy in the heliosphere is nuclear fusion occurring at the heart of the Sun, the mechanisms which mediate the flow of some fraction of that energy into the solar corona—where it ultimately heats the coronal plasma to temperatures in excess of one million Kelvin—remain poorly understood. In particular, the fundamental plasma physics mechanisms of turbulence, magnetic reconnection, shocks, and instabilities (e.g., see Howes, 2017; Hesse and Cassak, 2020; Verscharen et al., 2019; Wilson et al., 2021b,Wilson et al., 2021a, and references therein) play crucial roles in mediating the transport of energy in space and astrophysical plasmas, and have been identified as grand challenge problems in the 2013–2022 Decadal Survey in Solar and Space Physics by the National Research Council.

Under the typically low-density and high-temperature conditions of turbulent plasmas in the heliosphere and planetary magnetospheres, the energization of particles occurs primarily through the collisionless interaction between the electromagnetic fields and the individual plasma particles (Howes, 2017; Wilson et al., 2018). To understand how the consequent plasma heating and particle acceleration impacts the macroscopic evolution of the heliosphere, driving phenomena such as extreme space weather, it is critical to understand these collisionless wave-particle interactions on their characteristic ion and electron kinetic timescales. Such understanding requires high-cadence measurements of both the electromagnetic fields and the three-dimensional particle velocity distributions. Although existing instrument technology enables these measurements, a major challenge to maximize the scientific return from these measurements is the limited amount of data that can be transmitted to the ground due to telemetry constraints. A valuable, but not widely used, approach to overcome this limitation is to compute on-board correlations of the maximum-cadence field and particle measurements. Here we propose a novel spacecraft mission concept focused on the coordinated operation of field and particle instruments that has the potential to achieve an improvement in sampling time by orders of magnitude, opening the door for transformative progress in our understanding of particle energization in the heliosphere.

Nonlinear plasma kinetic theory dictates that the collisionless interactions between the electromagnetic fields and charged particles in weakly collisional heliospheric plasmas necessarily lead to correlations between the fields and fluctuations in the particle velocity distributions. This fundamental insight lead to the recent develoment of the field-particle correlation technique (Klein and Howes, 2016; Howes et al., 2017; Klein et al., 2017), which employs single-point measurements of the electromagnetic fields and particle velocity distributions to determine not only the net energy transfer between the fields and particles, but also how that transferred energy is distributed in particle velocity space. A variation of this technique, denoted the Particle Arrival Time Correlation for Heliophysics (PATCH) method (Verniero et al., 2021b), was devised specificially for implementation with on-board wave-particle correlator instrumentation. These developments provide a solid theoretical foundation for the pursuit of a new mission based on novel wave-particle correlator instrumentation.

1.1 History of Wave-Particle Correlator Instrumentation

Several previous rocket and spacecraft missions have indeed sought to perform on-board mathematical correlations between field measurements and particle measurements at the same point in space, thereby preserving the valuable phase information needed to establish definitively an interaction between the fields and particles. The earliest attempts to identify wave-particle interactions in space plasmas sought to measure the phase bunching of resonant electrons predicted to occur in the presence of sufficiently large-amplitude Langmuir wave fluctuations (Melrose, 1986). On-board particle auto-correlator instruments were developed to detect electron phase bunching at f ∼ 10⁶ Hz frequencies in the auroral ionosphere, even when electron count rates were ν ≲ 10⁵ Hz (Spiger et al., 1974; 1976; Gough, 1980; Gough et al., 1980), providing a critical foundation for the subsequent development of wave-particle correlators.

The first conclusive wave-particle correlator, that performed a direct correlation of the arrival times of electrons with the phase of the high-frequency wave field, flew on a sounding rocket in the auroral zone (Ergun et al., 1991a; b). This experiment indeed detected electron phase bunching during periods of intense Langmuir waves, driving subsequent theoretical work to develop refined theoretical predictions for finite-size Langmuir wavepackets (Muschietti et al., 1994). A wave-particle correlator was attempted on the Wind spacecraft (Wilson et al., 2021a between the WAVES and 3DP instruments but it did not correctly trigger. Another wave-particle correlator was flown on the NASA Combined Release and Radiation Effects Satellite (CRRES), computing correlations onboard between the Low Energy Plasma Analyzer and the electric field/Langmuir probe instrument (Watkins et al., 1996), and later a refined wave-particle correlator was implemented as a component of the Fields instrument on the FAST spacecraft (Ergun et al., 1998, 2001). Subsequent development lead to an improved wave-particle correlator design with higher phase resolution than previous instruments, flown on an auroral sounding rocket, which measured the reactive component of the electron phase bunching in a Langmuir wave (Kletzing et al., 2005; Kletzing and Muschietti, 2006). Further developments in wave-particle correlator instrumentation have continued (Fukuhara et al., 2009), with the latest implementation of a Software-type Wave-Particle Interaction Analyzer (S-WPIA) on-board the Japanese Arase spacecraft (Miyoshi et al., 2018) to study the energy transfer process between energetic electrons and whistler-mode chorus emissions in the Earth’s inner magnetosphere (Katoh et al., 2013; Katoh et al., 2018).

All of these previous wave-particle correlator instruments were specially designed to explore the energy transfer to particles from waves that have frequencies at or above the particle detector counting rate, f ≳ ν, for example studying the interaction of electrons with whistler waves or Langmuir waves in the Earth’s magnetosphere. But the Alfvénic turbulent fluctuations in the magnetosheath, solar wind, and solar corona have a much lower frequency than the whistler and Langmuir wave fluctuations of interest in the magnetosphere. Furthermore, current spacecraft missions—such as the Magnetospheric Multiscale (MMS) (Burch et al., 2016), Parker Solar Probe (Bale et al., 2016; Fox et al., 2016; Kasper et al., 2016; Whittlesey et al., 2020; Livi et al., 2021), and Solar Orbiter (Müller et al., 2013) missions—boast fast, three-dimensional particle velocity measurements at a sampling rate approaching or surpassing the frequency of the fluctuations involved in the collisionless transfer of energy between fields and particles, f ≲ ν. These unprecedented measurement capabilities, coupled with recent advances in plasma kinetic theory for determining particle energization from single-point measurements of electromagnetic field and particle velocity distribution measurements (Klein and Howes, 2016; Howes et al., 2017; Klein et al., 2017), make possible an entirely new approach to understanding particle energization using an on-board field-particle correlator, providing a strong motivation for the mission concept proposed here.

2 Materials and Equipment

In this section, we describe the heritage Electrostatic Analyzer (ESA) particle instrumentation, electromagnetic fields instrumentation, and electronics digital processing units (DPUs) that comprise the base elements upon which an onboard wave-particle correlator instrument would be designed. The specific details arise from two of the key instrument suites on the Parker Solar Probe (PSP) mission: 1) the Solar Wind Electron Alphas and Protons (SWEAP) investigation (Kasper et al., 2016) that measures the core (thermal) plasma populations; and 2) the FIELDS investigation (Bale et al., 2016) that measures the two-dimensional electric and three-dimensional magnetic fields.

2.1 Electrostatic Analyzer Instruments

Three of the four SWEAP sensors on PSP are electrostatic analyzers (2 electron and 1 ion) that detect single particles and return total accumulated counts within a short ( ∼1 ms) time interval that represents only one point in phase space (Kasper et al., 2016; Whittlesey et al., 2020; Livi et al., 2021). Even though this intrinsic time resolution may seem short, it is long compared to the time duration of some field-particle interactions. The goal is to use on-board electronics to correlate the particle counts from the electrostatic analyzer instruments with measurements of the electromagnetic fields simultaneous with the particle detections, yielding a new instrument denoted an Integrated Field-Particle Correlator (IFPC) instrument.

Current heritage instrument operational parameters are listed in Table 1 compared to the predicted requirements for an IFPC ion and electron instruments. Note that the requirements for ions and electrons are different. Although the process for modifying the SPAN-E heritage sensor to perform onboard field-particle correlation measurements is identical for ions and electrons (excepting the micro-channel plate supply modification), the science requirements for the electron IFPC and the ion IFPC are different, with electron IFPC requiring a substantially faster measurement cadence. Increasing the measurement cadence of the heritage electron instrument is achievable with an increase in consumed instrument power (currently ∼2 W depending on the area of phase space being scanned at the time) and additional modifications to the Field-Programmable Gate Array (FPGA) design.

TABLE 1

TABLE 1. Heritage electrostatic analyzer for electrons (SPAN-E) measurement performance and predicted performance requirements of proposed ion and electron Integrated Field-Particle Correlator (IFPC) instruments.

In the heritage wave-particle correlator instrument on Parker Solar Probe, SPAN-E, the correlator subsection is located on another board: in the case of PSP, the SPAN-E particle counts from either one or many anodes are summed together into a single channel, and are sent to the FIELDS suite, where they are correlated onboard the Time Domain Sampler (TDS) board (Bale et al., 2016). Modifications to implement an IFPC require upgrading the heritage instrument’s digital board and FPGA to preserve the angular resolution from the individual separate anodes in the correlation with electric and magnetic fields signals. The optimal method of doing this is to modify the FPGA firmware to perform correlations onboard the heritage instrument, where all 16 anodes’ channels are preserved separately, instead of running 16 output signals to an external instrument, which would then need 16 dedicated channels to process the correlations separately. Thus, instead of conducting correlations on a summation of 16 channels’ worth of signal with fields externally, we propose to introduce new input channels to the SPAN-E Engineering Test Unit’s (ETU) digital board to perform correlations internally.

2.2 Electromagnetic Fields Instruments

The detailed specifications of the electromagnetic fields instruments on Parker Solar Probe are presented in Bale et al. (2016), and so we only briefly describe the relevant fields instruments to be incorporated into a proposed IFPC here.

The electric fields essential to the computing field-particle correlations that probe the rate of energization of particles (see Section 3.1) are measured using four voltage sensors deployed in nearly orthogonal, co-linear pairs slightly behind the plane of the spacecraft heat shield. These voltage sensors are implemented as a current-biased resistively-coupled double probe instrument. Providing measurements at 2M samples/s, this instrument returns two-component electric field measurements over a bandwidth from DC up to 1 MHz. A calibration procedure to process these voltage measurements and return 2D electric field data is detailed in Mozer et al. (2020).

The magnetic fields are measured using both fluxgate and search-coil (induction) magnetometers mounted on a deployable boom. The fluxgate magnetometers measure the 3D magnetic field at 293 samples/s, covering a bandwidth from DC up to 140 Hz, with dynamic range of ±65,536 nT and a resolution of 16 bits. The search-coil magnetometer measures all three components of the AC magnetic signature of solar wind fluctuations, from 10 Hz up to 50 kHz and a single component from 1 kHz to 1 MHz.

The wide bandwidth and dynamic range of these electric and magnetic field instruments allows FIELDS to investigate transients caused by interplanetary shocks and reconnection, the turbulent cascade beyond the electron kinetic scale, and also numerous plasma wave modes. Within different plasma environments in the heliosphere, these processes are predicted to play a role in the energization of particles. These heritage instruments are sufficiently capable that, when integrated with the particle instrumentation described in Section 2.1, an IFPC can be developed to provide high-cadence and long-time statistical sampling of the heliospheric plasma dynamics to discover and characterize the dominant mechanisms of particle energization.

2.3 Electronic Digital Processing Units

The FIELDS instrument on Parker Solar Probe includes a waveform capture instrument which is intended to capture voltage time-series waveform bursts, V(t), from the FIELDS detectors. The FIELDS Time Domain Sampler (TDS) samples five analog voltage channels at a sampling speed of $\sim 2$M samples/s. This can include sampling any of the five FIELDS voltage probes (V1, V2, V3, V4 or V5) or the dipoles formed by sampling V1-V2 or V3-V4. In addition, the TDS can sample one mid-frequency winding of the magnetic search coil sensor.

TDS bursts are triggered to allow the capture of waveforms using a peak triggering mechanism. Triggered bursts are saved to catalog of bursts in instrument memory. Evaluation of waveforms using a combination of waveform RMS amplitude and waveform frequency provide selection criteria for sending “interesting” waveforms to the ground.

The TDS also incorporates a single-channel wave-particle correlator on Parker Solar Probe, as depicted in the diagram in Figure 1. The additional of a single connection (red) directly between the SWEAP Electronics Module (SWEM) and the FIELDS Time Domain Sampler (TDS) enables a simple implementation of a wave-particle correlator. In addition to the five analog channels of the TDS described above, each sampled at 2M samples/s, or 500 ns/sample, the TDS simultaneously counts incoming particles from the SWEAP instrument in an accumulator. As the analog samples are acquired during each 500ns sampling period, the number of accumulated particle pulses are also sampled and stored in TDS instrument memory. In this way, complete TDS bursts are returned to the ground with high-time resolution waveforms of electric and magnetic field values obtained simultaneously with the corresponding particle count time series.

FIGURE 1

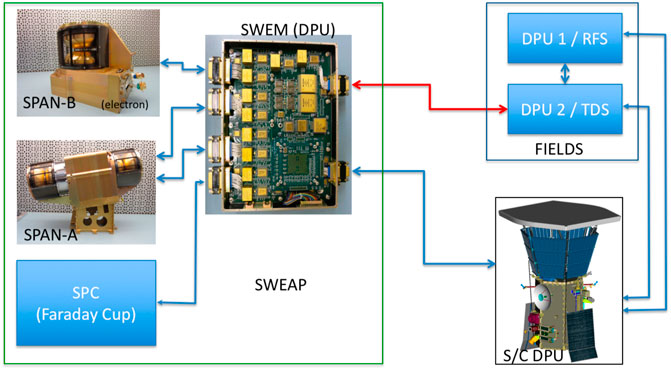
FIGURE 1. The SWEAP/FIELDS interface on PSP: the Wave-Particle Correlator (WPC). The additional hardware (mass resource) consists of a single cable (red) that allows the SWEAP and FIELDS instruments to communicate to each other without the need to pass through the spacecraft interface. Wires in this cable conduct a 200 ns long particle pulse signal every time a particle is detected in a SPAN. From Verniero et al. (2021b).

The wave-particle correlator implemented on Parker Solar Probe is rather limited in capability relative to the IFPC proposed here, and was included primarily as a proof-of-principle demonstration of a correlator instrument. Some of the shortcomings of this limited implementation are: 1) the duty cycle of selected events is extremely small; 2) correlations are not done on board, and thus there is no way to trigger on correlated events; 3) the on-board burst selection criteria is based only on wave amplitude, not on field-particle correlations; and 4) only a single point in phase space (1 of 16 anodes) can be correlated at a time.

3 Methods

In this section, we explain how the field-particle correlation technique is derived from the Boltzmann equation for the evolution of a weakly collisional plasma, detail refinements of the implementation of the technique for application to the discrete phase-space measurements of the particle velocity distributions provided by modern electrostatic analyzer instruments, describe modifcations of the technique for application to on-board wave-particle correlator instrumentation, and finally present the proposed design of a multi-channel, dedicated On-Board Wave-Particle Correlator instrument.

3.1 The Field-Particle Correlation Technique

The nonlinear evolution of a kinetic plasma is governed by the Maxwell-Boltzmann equations. Under the weakly collisional conditions typical of heliospheric plasmas, we can drop the collision term in the Boltzmann equation, which is unnecessary to describe the collisionless transfer of energy between fields and particles, to obtain the Vlasov equation.

To explore the energy transfer between fields and particles, we define the phase-space energy density for a particle species s by w_s (r, v, t) = m_sv²f_s (r, v, t)/2. Multiplying the Vlasov equation by m_sv²/2, we obtain an expression for the rate of change of the phase-space energy density,

$\frac{\partial w_s\left(\mathbf{r},\mathbf{v},t\right)}{\partial t}=-\mathbf{v}\cdot \nabla w_s-q_s\frac{v^2}{2}\mathbf{E}\cdot \frac{\partial f_s}{\partial \mathbf{v}}-\frac{q_s}{c}\frac{v^2}{2}\left(\mathbf{v}\times \mathbf{B}\right)\cdot \frac{\partial f_s}{\partial \mathbf{v}}.(1)$

Integrating over all velocity space and all physical space eliminates the first and third terms (Howes et al., 2017), yielding an equation for the rate of change of the energy W_s of a particle species s

$\begin{array}{ll}\hfill \frac{\partial W_s}{\partial t}& =-\int d^3\mathbf{r}\int d^3\mathbf{v}{q}_s\frac{v^2}{2}\frac{\partial f_s}{\partial \mathbf{v}}\cdot \mathbf{E}=\int d^3\mathbf{r}\left(\int d^3\mathbf{v}{q}_s\mathbf{v}{f}_s\right)\cdot \hfill \\ \hfill \mathbf{E}& =\int d^3\mathbf{r}{\mathbf{j}}_s\cdot \mathbf{E},\hfill \end{array}(2)$

where an integration by parts in velocity has been used between the second and third forms above. This expression shows that the change in species energy W_s is due to work done on that species by the electric field, j_s ⋅E. The two middle expressions also make clear the concept that measurements of the electric field E and particle velocity distribution f_s(v) contain sufficient information to determine the rate of energy transfer between the fields and particle species s.

Unfortunately spacecraft measurements provide information on the fields and particle velocity distributions at only one (or, for multi-spacecraft missions, a few) points in space as a function of time, a spatial sampling that is insufficient to perform the spatial integration in Eq. 2. To determine the energy transfer between fields and particles at a single point in space, we return to Eq. 2 which provides the rate of change of phase-space energy density ∂w_s (r₀, v)/∂t at a single point in space r₀.

From the previous analysis, we know that only the second term on the right-hand side of Eq. 1, − q_s (v²/2)E ⋅ ∂f_s/∂v, leads to a net change of particle energy when integrated over position and velocity. However, if the fields are oscillatory in time—for example, in the case of plasma turbulence—this term includes both contributions from the conservative oscillating energy transfer associated with undamped wave motion and from the secular energy transfer associated with the collisionless damping of the turbulent fluctuations (Klein and Howes, 2016; Howes et al., 2017). To eliminate the often larger amplitude oscillating energy transfer, we perform an unnormalized correlation (essentially a sliding time-average) between the particle and field measurements over a suitable correlation interval τ.

Note that the optimal choice of correlation interval τ depends on the physical mechanism under investigation. For turbulent fluctuations damped by collisionless wave-particle interactions (through resonant mechanisms such as Landau damping or ion cyclotron damping or other mechanisms such as stochastic ion heating, for example), it is generally necessary to choose an interval τ that is longer than several of the oscillation periods of the turbulent fluctuations at the scales suffering the collisionless damping (Klein and Howes, 2016; Howes et al., 2017; Klein et al., 2017).

To help diagnose the nature of the physical mechanism governing the energization of the particles, it is beneficial to separate out the contributions to the dot product in the second term on the right-hand side of Eq. 1 from the different components of E. For some cases, such as plasma turbulence, it can be beneficial to decompose E in a field-aligned coordinate (FAC) system, (E_⊥1, E_⊥2, E_∥). Thus, the field-particle correlations for each of the components¹ are given by

$C_{E_{\parallel }}\left(\mathbf{v},t,\tau \right)=C\left(-q_s\frac{v_{\parallel }^2}{2}\frac{\partial f_s\left({\mathbf{r}}_0,\mathbf{v},t\right)}{\partial v_{\parallel }},E_{\parallel }\left({\mathbf{r}}_0,t\right)\right)(3)$

$C_{E_{\perp 1}}\left(\mathbf{v},t,\tau \right)=C\left(-q_s\frac{v_{\perp 1}^2}{2}\frac{\partial f_s\left({\mathbf{r}}_0,\mathbf{v},t\right)}{\partial v_{\perp 1}},E_{\perp 1}\left({\mathbf{r}}_0,t\right)\right)(4)$

$C_{E_{\perp 2}}\left(\mathbf{v},t,\tau \right)=C\left(-q_s\frac{v_{\perp 2}^2}{2}\frac{\partial f_s\left({\mathbf{r}}_0,\mathbf{v},t\right)}{\partial v_{\perp 2}},E_{\perp 2}\left({\mathbf{r}}_0,t\right)\right).(5)$

Here, the unnormalized, time-centered correlation C (A, B) is essentially a sliding time average, and is defined at the discrete measurement time t_i by

$C\left(A,B\right)\equiv \frac{1}{n}\sum _{j=i-n/2}^{i+n/2}{A}_j{B}_j,(6)$

for quantities A and B, which together as a product represent a rate of change of energy density, measured at discrete times t_j = jΔt, with their product averaged over n measurements over a correlation interval of duration τ ≡ nΔt (Klein et al., 2017). Applying this correlation to a time series of electric field and particle velocity distribution measurements at a single point yields the velocity-space signature of the secular energy transfer.

In general, each component E_j of the electric field yields a signature in three-dimensional velocity space (3V). To aid in visualization of the rate of energy transfer in velocity space, it is useful to reduce these 3V determinations to a two-dimensional form for ease of visualization. The optimal choice for such a two-dimensional reduction depends on the physical process under investigation. In the case of plasma turbulence, the typically low-frequency dynamics (relative to the cyclotron frequencies of the particle species) can be usefully represented in the 2V gyrotropic phase space (v_∥, v_⊥), where one integrates over the gyroangle about the magnetic field to obtain variations as a function of the perpendicular velocity coordinate $v_{\perp }=\sqrt{v_{\perp 1}^2+v_{\perp 2}^2}$. For collisionless shocks, which generate decidedly agyrotropic distributions, one may integrate a general 3V velocity space (v_x, v_y, v_z) over each velocity dimension separately, obtaining three 2V representations (v_x, v_y), (v_y, v_z), and (v_z, v_x).

The application of the field-particle correlation technique yields a velocity-space signature of the rate of particle energization as a function of velocity. The qualitative and quantitative features of this velocity-space signature can typically be used to identify the physical mechanism responsible for the particle energization. In Figure 2, we show the velocity-space signatures of six different kinetic particle energization mechanisms, all of which are sufficiently unique to distinguish one mechanism from another. From a simulation of weakly collisional electromagnetic turbulence in a β_i = 1 and T_i/T_e = 1 plasma using the Astrophysical Gyrokinetics Code (AstroGK) (Numata et al., 2010), we plot in 1) the velocity-space signature of ion Landau damping using a visualization of the standard parallel field-particle correlation $C_{E_{\parallel }}(v_{\parallel },v_{\perp })$ on the gyrotropic velocity-space (Klein et al., 2017). The characteristic signature of Landau damping shows a loss of energy (blue) below the resonant velocity (vertical dashed line at v_∥/v_tp ≃ 1) and a gain of energy (red) above, corresponding to the familiar quasi-linear flattening of the distribution function (Howes et al., 2017). In panel 2) is the velocity-space signature of transit-time damping (Barnes, 1966) of a linear kinetic Alfvén wave in a β_i = 3 plasma due to the magnetic mirror force − μ∇_∥|B| acting on the magnetic moment of the particle’s gyromotion $\mu =m{v}_{\perp }^2/(2B)$, given by $C_{\delta B_{\parallel }}(v_{\parallel },v_{\perp })$, where ∇_∥ is the gradient along the magnetic field. In panel 3) is plotted the velocity-space signature of ion cyclotron damping $C_{E_{\perp }}(v_{\parallel },v_{\perp })$ from a Hybrid Vlasov-Maxwell (HVM) (Valentini et al., 2007) simulation of high-frequency plasma turbulence (Klein et al., 2020). In panel 4) is plotted the total field-particle correlation C_E (v_∥, v_⊥) for electron heating from a numerical model of magnetic pumping (Montag and Howes, 2022). In panel 5) is plotted the velocity-space signature of electron energization from a gyrokinetic simulation of magnetic reconnection in the strong-guide-field limit in a β_i = 0.01 plasma (McCubbin et al., 2022) using the parallel field-particle correlation $C_{E_{\parallel }}(v_{\parallel },v_{\perp })$. Finally, from a Gkeyll Vlasov simulation (Juno et al., 2018) of a perpendicular collisionless shock with Alfvén Mach number M_A ≃ 5, we show the velocity-space signature of shock-drift acceleration $C_{E_y}(v_x,v_y)$ (Juno et al., 2021). Together, these results show that the velocity-space signatures of these different kinetic energization mechanisms are qualitatively and quantitatively unique, providing a “Rosetta stone” for the identification of the physical mechanisms of particle energization. The results also strongly motivate the development on a dedicated instrument to provide velocity-space signatures from onboard computations of high-cadence field-particle correlations.

FIGURE 2

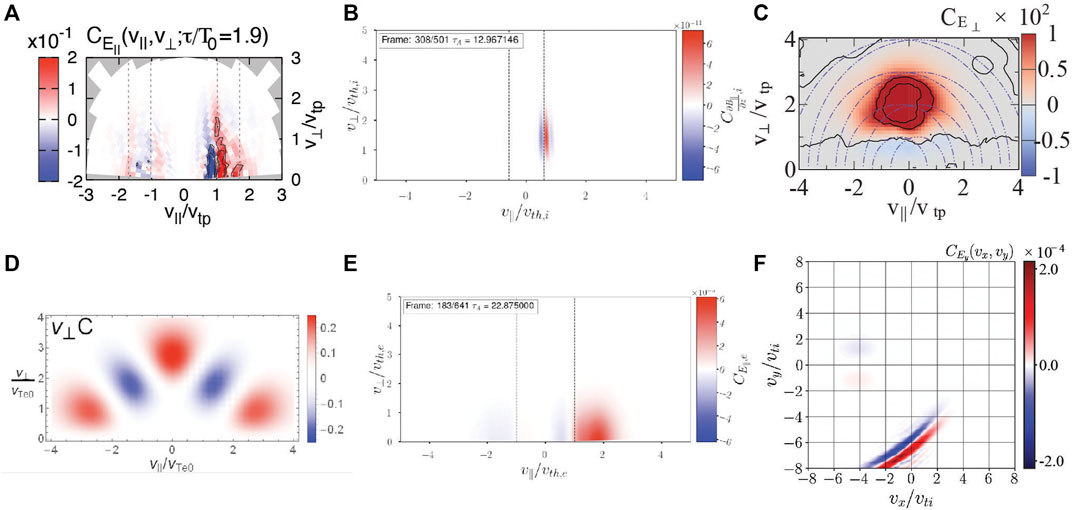
FIGURE 2. Velocity-space signatures from the application of the field-particle correlation technique to numerous kinetic particle energization mechanisms: (A) gyrotropic velocity-space signature from the standard parallel field-particle correlation $C_{E_{\parallel }}(v_{\parallel },v_{\perp })$ for ion Landau damping in a gyrokinetic simulation of plasma turbulence (Klein et al., 2017); (B) parallel field-particle correlation for transit-time damping by the magnetic mirror force $C_{\delta B_{\parallel }}(v_{\parallel },v_{\perp })$ for a linear kinetic Alfvén wave; (C) perpendicular field-particle correlation $C_{E_{\perp }}(v_{\parallel },v_{\perp })$ for ion cyclotron damping from a hybrid Vlasov-Maxwell simulation of high-frequency plasma turbulence (Klein et al., 2020); (D) total field-particle correlation C_E (v_∥, v_⊥) for electron heating from a numerical model of magnetic pumping (Montag and Howes, 2022); (E) parallel field-particle correlation $C_{E_{\parallel }}(v_{\parallel },v_{\perp })$ for electron energization from a strong-guide field reconnection simulation (McCubbin et al., 2022); and (F) velocity-space signature of shock-drift acceleration $C_{E_y}(v_x,v_y)$ from a Vlasov simulation of a perpendicular collisionless shock with Alfvén Mach number M_A ≃5 (Juno et al., 2021).

3.2 Refinements of the Implementation for Analysis of Spacecraft Measurements

The application of the field-particle correlation technique to data from kinetic simulations codes using a continuum representation of velocity space—where a complete grid of velocity space points is known at each point r in configuration space—is relatively straightforward. Specifically, one can simply implement a finite difference, or other discrete representation, of the derivative in velocity space needed in the field-particle correlations Eqs. 3–5. But for kinetic simulations codes that employ a Monte-Carlo sampling of velocity-space at a disordered set of velocity points (Juno et al., 2022), or for spacecraft instruments where the velocity phase-space measurements may not be uniformly distributed (Chen et al., 2019; Afshari et al., 2021), the computation of the velocty-space derivative ∂f_s/∂v represents a non-trivial exercise. Here we describe a specific implementation of the technique for these latter two cases that yields usable results.

First, we note that substituting for f_s = 2w_s/(m_sv²) in the Vlasov equation and solving for the evolution of the phase-space energy density w_s along trajectories in 3D-3V phase space yields

$\frac{\partial w_s}{\partial t}+\mathbf{v}\cdot \nabla w_s+\frac{q_s}{m_s}\left(\mathbf{E}+\frac{\mathbf{v}}{c}\times \mathbf{B}\right)\cdot \frac{\partial w_s}{\partial \mathbf{v}}=q_s\mathbf{v}\cdot \mathbf{E}{f}_s.(7)$

We define the right-hand side of Eq. 7 as the alternative field-particle correlation

$C_{E_j}^{\prime }\left(\mathbf{v},t,\tau \right)=C\left(q_s{v}_j{f}_s\left({\mathbf{r}}_0,\mathbf{v},t\right),E_j\left({\mathbf{r}}_0,t\right)\right),(8)$

for the electric field component E_j. Note that when integrated over all velocity space, this alternative form yields the same net rate of change of spatial energy density as the forms in Eqs. 3–5. The difference between the two forms of the field-particle correlation is that the standard correlation C(v) takes an Eulerian view of velocity space, showing which parts of velocity space are gaining or losing energy density, whereas the alternative correlation C′(v) takes a Lagrangian view of velocity space, showing how small volumes of phase space gain or lose energy along their Lagrangian particle trajectories in 3D-3V phase space. A key advantage of the alternative form Eq. 8 is that does not require velocity-space derivatives.

Here we describe specific choices for the implementation of the field-particle correlation technique to spacecraft measurements (Chen et al., 2019); the same choices can be used for an implementation with particle-based kinetic simulation codes, such as particle-in-cell (PIC) codes. First, the particle distribution measurements and electric field measurements are Lorentz transformed to the mean bulk flow velocity of species s over the interval to be analyzed. Second, it is also desirable to determine the mean velocity distribution f_s0(v) averaged over the same interval and substract it to obtain the perturbed velocity distribution δf_s(v, t) = f_s(v, t) − f_s0(v), computing the correlation with δf_s instead of f_s, although this is not strictly necessary. Third, the time-series of electric field measurements, which is usually sampled at a much higher cadence than the velocity distributions, is downsampled to the cadence of the velocity distribution measurements. With the δf_s(v, t) and E(t) measurements now at the same cadence, the alternative field-particle correlation $C_{E_j}^{\prime }({\mathbf{v}}_j,t_n)=q_s{v}_j{E}_j(t_n)\delta f_s({\mathbf{v}}_j,t_n)$ is computed at each point in 3V velocity space v_j for each timeslice t_n. Next, the alternative correlation $C_{E_j}^{\prime }({\mathbf{v}}_j,t_n)$ is binned in velocity space, with the choice of bins tailored for investigation of a particular particle energization process—for the application to turbulence, it is binned into 2V gyrotropic phase space (v_∥, v_⊥). The velocity derivatives needed to obtain the standard field-particle correlation $C_{E_j}({\mathbf{v}}_j,t_n)$ can be computed at this point; for the parallel correlation in the 2V gyrotropic velocity space, it would take the form

$C_{E_{\Vert ,\mathrm{e}}}\left(v_{\Vert },v_{\perp }\right)=-\frac{v_{\Vert }}{2}\frac{\partial C_{E_{\Vert ,\mathrm{e}}}^{\prime }\left(v_{\Vert },v_{\perp }\right)}{\partial v_{\Vert }}+\frac{C_{E_{\Vert ,\mathrm{e}}}^{\prime }\left(v_{\Vert },v_{\perp }\right)}{2},(9)$

For the analysis of particle energization by the dissipation of broadband plasma turbulence, it can be helpful to high-pass filter the electric field measurements to eliminate the large-amplitude contribution from the electric field fluctuations associated with large-scale, low-frequency waves—such waves typically have negligible net secular energy transfer associated with collisionless damping, so eliminating the often large-amplitude contribution to the rate of energy transfer due to undamped oscillations at large scales helps to expose the energy transfer due to smaller scale, higher frequency waves that dominate the collisionless damping of the turbulent fluctuations.

To demonstrate how these refinements of the implementation can yield a clear velocity-space signature, we present in Figure 3 the results from Chen et al. (2019) showing the 2D alternative field-particle correlation $C_{E_{\Vert },\mathrm{e}}^{\prime }(v_{\Vert },v_{\perp })$ and 1D standard field-particle correlation $C_{E_{\Vert },\mathrm{e}}(v_{\Vert })$ for electrons measured using 70 s of data from the MMS spacecraft in the Earth’s magnetosheath. The 2D correlation shows velocity-space structure primarily in v_‖ rather than v_⊥, and the 1D correlation directly represents the energy transfer at each parallel velocity. Since the energy transfer is from fields to particles $(C_{E_{\Vert },\mathrm{e}}>0)$ at |v_‖| > v_th,e and from particles to fields $(C_{E_{\Vert },\mathrm{e}}<0)$ at |v_‖| < v_th,e, and the expected resonant velocity for which the kinetic Alfvén wave damping becomes strong is ∼ v_th,e, this provides a clear signature that is consistent with the Landau damping of kinetic Alfvén turbulence in this region of space. Afshari et al. (2021) performed a follow-up study, applying this technique to 20 similar intervals, finding 95% displayed Landau-like signatures although most were more asymmetrical than in Figure 3, which is consistent with imbalanced turbulence, and is supported by kinetic numerical simulations (Horvath et al., 2020). Both Chen et al. (2019) and Afshari et al. (2021) noted that the total integrated transfer rate is comparable to the turbulent energy cascade rate, indicating that electron Landau damping plays a significant role in the dissipation of turbulence here. These results indicate that the field-particle correlation technique holds a lot of promise for answering important questions in space plasma physics.

FIGURE 3

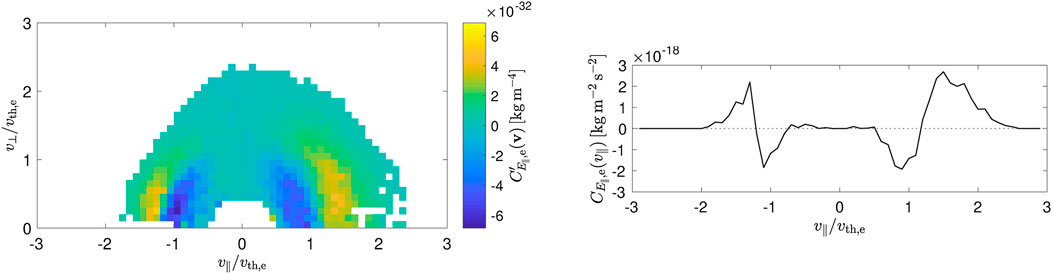
FIGURE 3. Parallel alternative field-particle correlation for electrons, $C_{E_{\Vert },\mathrm{e}}^{\prime }(v_{\parallel },v_{\perp })$, measured in the Earth’s magnetosheath from MMS data (left). Same data integrated over v_⊥ and converted to the standard field-particle correlation $C_{E_{\Vert },\mathrm{e}}(v_{\parallel })$. Both show a clear signature of electron Landau damping at v_‖ ∼±vth_{, e}. Figures from Chen et al. (2019).

3.3 The PATCH Algorithm

To take advantage of the high time resolution achievable with a Wave-Particle Correlator instrument that utilizes the particle arrival times, the field-particle correlation technique must be modified to exploit the arrival time information. Here we briefly describe the Particle Arrival Time Correlation for Heliophysics (PATCH) algorithm for determining the rate of energy transfer between electromagnetic fields and plasma particles using measurements at a single point in space; a detailed derivation of the PATCH algorithm from plasma kinetic theory is presented elsewhere (Verniero et al., 2021b).

An illustration of the concept of the PATCH algorithm for the correlation of field and particle measurements is shown in Figure 4, where we consider a single spatial dimension for simplicity, with a particle velocity distribution f (x, v, t) and an electric field E (x, t). Consider a single phase-space bin centered at velocity v_p with bin width Δv measured by the particle instrumentation at position x_p within a 1D spatial volume Δx. The distribution function at the 1D-1V phase-space position (x_p, v_p) is given by

$f\left(x_p,v_p,t\right)=\frac{N\left(t\right)}{\mathrm{\Delta }x\mathrm{\Delta }v},(10)$

where the number of particles within the 1D-1V phase-space volume ΔxΔv is given by N(t). In Figure 4, we plot electric field measured by the probe E (x_p, t) (red) and the time-varying number of particles in the phase-space volume ΔxΔv, given by N(t) (blue). Note that the probability that a particle in this phase-space bin is counted by the instrument is proportional to N(t).

FIGURE 4

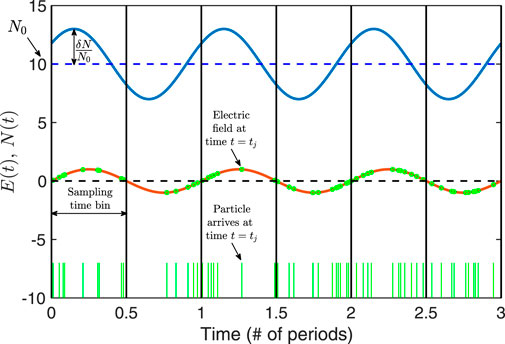
FIGURE 4. Demonstration of the concept underlying the PATCH algorithm: the variation of the particle number in a particular phase bin ΔxΔv is given by N(t) (blue) and the electric field E(t) (red). Individual particles, with a probability of detection proportional to N(t), arrive at discrete times t_j (vertical green lines). The PATCH correlation, $C_{\tau }^{*}$ gives the rate of work done by the electric field on the particles, and it is essentially the summed values of the electric field at the particle arrival times. From Verniero et al. (2021b).

The PATCH algorithm is based on the alternative correlation C′ given by Eq. 8, which essentially computes the rate of work done on a charged particle by the electric field. In Figure 4, we use Poisson statistics to determine whether a particle is counted by the detector based on the probabilities related to N(t), and each particle count is denoted as a green vertical line at the time of arrival at the bottom of figure. As detailed in Verniero et al. (2021b), the net rate of energy transfer to the particle distribution by the electric field E can be determined by the summing the rate of work done by the electric field on each particle that is counted, qEv_p. The resulting sum yields a discrete sampling of the in-phase component between N(t) and E(t), which determines the net energy transfer between the electric field and the particles over the correlation interval τ. Note that the weighting by the particle phase-space density f (x, v) is naturally included when summing the electric field at each particle arrival time, capturing the relative phases of the perturbations to f (x, v, t) and E (x, t).

For a particle instrument, such as the electrostatic analyzers on the MMS or PSP missions (Pollock et al., 2016; Whittlesey et al., 2020), the PATCH algorithm is relatively easy to implement in the 3D-3V phase space of an astrophysical plasma. The PATCH correlation $C_{\tau }^{*}$ over a correlation interval τ is defined by

$C_{\tau }^{\ast }=\frac{1}{\tau }\frac{1}{\mathrm{\Delta }{\mathbf{r}}_p\mathrm{\Delta }{\mathbf{v}}_p}\sum _{j=1}^{N_{\tau }}q{\mathbf{v}}_p\cdot \mathbf{E}\left(t_j\right)(11)$

where the measurement bin in 3D-3V phase space is given by Δr_pΔv_p, the 3V velocity of the phase bin is v_p, the number of particles counted in the phase bin over the correlation interval τ is N_τ, and the electric field at each particle arrival time is E (t_j). Note that the contributions to the dot product v_p ⋅E = v_pxE_x + v_pyE_y + v_pzE_z from each component of the electric field can be computed and saved separately, enabling a subsequent rotation of the coordinate system in post-processing, e.g., rotating to magnetic field aligned coordinates (FAC).

A demonstration of how the PATCH algorithm can be used to produce a velocity-space signature that can be used to identify a particular particle energization mechanism is shown in Figure 5. From a gyrokinetic simulation of strong plasma turbulence in a β_i = 1 and T_i/T_e = 1 plasma over the range 0.25 ≤ k_⊥ρ_i ≤ 5.5 (Klein et al., 2017), we can compute the alternative correlation with the parallel component of the electric field $C_{E_{\parallel }}^{\prime }(v_{\parallel },v_{\perp })$. The high velocity-space resolution simulation data has been downsampled to the PSP velocity-space resolution, and the pattern of $C_{E_{\parallel }}^{\prime }(v_{\parallel },v_{\perp })$ in Figure 5A shows a peak in the rate of change of the phase-space energy density at v_∥/v_ti ≃ 1.1, indicative of ion Landau damping. The PATCH algorithm, with only 25 ions counted in the phase-space bin at the peak of the distribution, is used to compute the correlation $C_{E_{\parallel }}^{*}(v_{\parallel },v_{\perp })$, recovering most of the qualitative and quantitative details of the velocity-space signature, as shown in Figure 5B (Verniero et al., 2021b). This result shows that an on-board implementation of the field-particle correlation technique, specifically the PATCH algorithm, indeed is able to recover the velocity-space signature of the ion energization, opening up many new opportunities in understanding energy transfer in space plasmas.

FIGURE 5

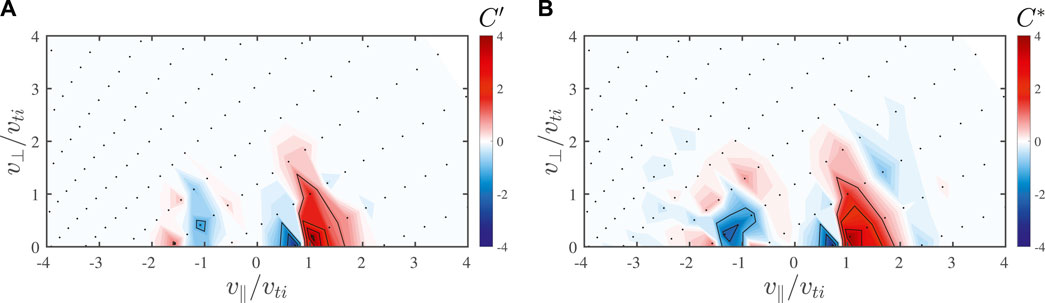
FIGURE 5. (A) Example of the alternative parallel electric field correlation $C_{E_{\parallel }}^{\prime }(v_{\parallel },v_{\perp })$ computed at a single spatial point in a gyrokinetic simulation of plasma turbulence and downsampled to the phase-space resolution of the SPAN-I instrument on Parker Solar Probe (Verniero et al., 2021a), compared to (B) the signature determined from applying the PATCH algorithm $C_{\tau }^{*}(v_{\parallel },v_{\perp })$, computed using N = 25 counts in the maximum density phase-space bin at the same phase-space resolution. From Verniero et al. (2021b).

3.4 A Multi-Channel, Integrated Field-Particle Correlator Instrument

Previous applications of the field-particle correlation technique to spacecraft measurements (Chen et al., 2019; Afshari et al., 2021) have relied on the downlink of burst-mode data for the electromagnetic field and particle velocity distribution measurements separately to implement later a ground-based computation of the field-particle correlations. Although this approach has indeed met with success—achieving the first definitive identification of electron Landau damping in a turbulent space plasma and assessing the importance of this particle energization channel to the total turbulent plasma heating—the limitations on telemetry of burst-mode data restricts such studies to a moderate sample size relative to the total sampling time in space. With the exception of the single-channel correlator connecting the FIELDS and SWEAP instrument suites on Parker Solar Probe, a dedicated, multi-channel Integrated Field-Particle Correlator (IFPC) instrument has never been developed. Here we describe a preliminary design concept for such an instrument.

Fortunately, the implementation of an IFPC can exploit the heritage instrumentation used on previous missions for the electromagnetic field and particle velocity distribution measurements, requiring only the development of the cables and firmware to interface these instruments with the digital processing unit (DPU) and the software to compute the correlations. In discussion below, let us consider the heritage instrumentation from the Parker Solar Probe mission, specifically the FIELDS (Bale et al., 2016) and SWEAP (Kasper et al., 2016) instrument suites as a specific example of modern instrumentation that could be incorporated into an IFPC.

The key principle of operation of the proposed IFPC follows. When the particle instrument detects a single particle (ion or electron) in a particular energy-angle bin (dictated by the energy sweep and deflector sweep voltages at that moment), it sends a δt_p = 200 ns pulse to the DPU with only a few ns delay. In addition, the FIELDS instrument provides two-component electric field measurements (strictly, differential voltage measurements from the dipole antennas) to the DPU at a 2 MHz sampling frequency and three-component magnetic field measurements at a 100 kHz sampling frequency (Bale et al., 2016). The PATCH algorithm for computing on-board correlations, described in Section 3.3, simply requires the electric field measurement at the time of the particle arrival and the 3V velocity representative of the energy-angle bin (dictated by the table for energy sweep and deflector sweep voltages). In addition, the local magnetic field direction at the particle arrival time can also be saved for subsequent projection of the PATCH correlation into magnetic field aligned coordinates (FAC), if desired.

The single-channel correlator implemented on Parker Solar Probe can only correlate the fields with a single phase-space bin. But the SWEAP electrostatic analyzer instruments actually count particles in the 16 azimuthal anodes simultaneously, so in principle 16 phase-bins can be correlated simultaneously. With minor modifications to the digital electronics board and some significant reprogramming of the FPGA firmware, it would be possible to convert the existing single-channel implementation into a 16-channel correlator. Fortuitously, the design of the heritage digital electronic board on Parker Solar Probe already has two 12-bit Analog to Digital Converter (ADC) chips which can be repurposed to process FIELDS measurements from an external source.

In the development of a dedicated IFPC instrument, there is one key difference from the implmentation of the single-channel correlator implemented on Parker Solar Probe. The existing correlator sends to the particle counts from SWEAP to the digital processing unit in the FIELDS suite, so to implement separate channels from multiple anodes would require multiple dedicated cables to transmit the signal from each anode. Instead, for a dedicated IFPC instrument, the measurements of the electric and magnetic fields would be transmitted to the electronic firmware for the particle instrument, enabling the correlation to be processed locally within the processing unit for the particle instrument.

The data products returned from the high-TRL, heritage electrostatic analyzer instruments are formatted by 16 discrete anodes and 256 energy times deflector bins. These three dimensions (anode, deflector, energy) can be summed in any direction to make smaller dimension products, but the primary data product from the heritage instrument is a 4,116 byte (16 Anodes x 8 Deflections x 32 Energies x 1 byte each +20 bytes of packet header) Low Voltage Differential Signal (LVDS) formatted packet that is produced every 0.218 s. After modification of the digital board and FPGA, we anticipate producing correlation plots such as those seen from previous work (see Figure 3) in addition to the same 4,116 byte science packets.

4 Anticipated Results

4.1 Laboratory Tests of a Wave-Particle Correlator

In order to test the PSP correlator system in the laboratory, our team devised a method to modulate the particle flux impinging on the PSP ion analyzer (SPAN-I) using an experimental setup with an ion source. An oscillating voltage applied to Vgate of the ion source resulted in a modulated ion flux while the ion beam energy remained constant in time. The same signal that controls the ion flux was also fed into the FIELDS instrument Time Domain Sampler (TDS), where it was digitized and recorded.

The top panel in Figure 6 (left) shows 2 cycles of a 200 Hz signal of the voltage that controlled the particle flux. The middle panel shows the number of particles detected within each 0.5μs time bin, where one 5 ms wave period contains 10,000 of these high-resolution time bins. Most bins have zero counts and the probability of obtaining more than 1 count is very low, indicating Poisson statistics are applicable for this implementation. The bottom panel of Figure 6 (left) shows the counts binned at the intrinsic time resolution of a single phase-space bin the PSP/SPAN instrument, δt = 0.85 ms. At this field modulation frequency, much faster than the fastest full SPAN energy-angle sweep of Δt = 0.218 s, the variation in the particle count rate can be resolved.

FIGURE 6

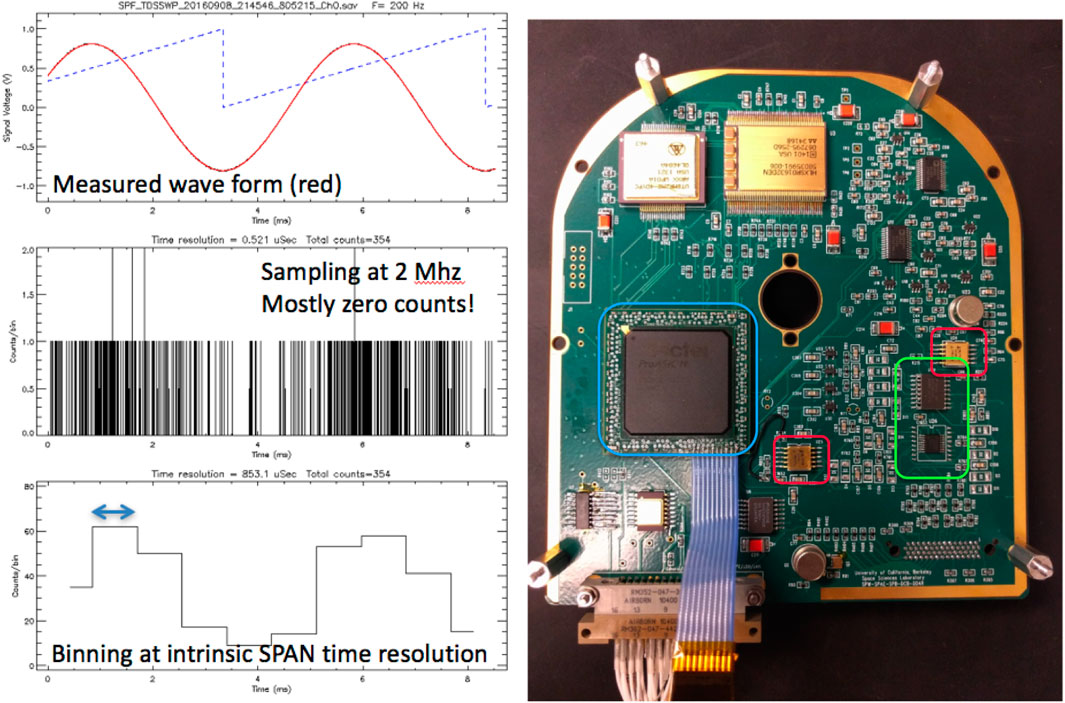
FIGURE 6. (Left top) Waveform of the oscillating voltage applied to modulate the ion source (red) at f = 200 Hz frequency. (Left middle) Particles counted within 0.5μs time bins, showing mostly 0 or 1 counts, indicating Poisson counting statistics. (Left bottom) At the SPAN phase-space bin time resolution of δt = 0.85 ms, the modulation in the number of detected ions at the f = 200 Hz frequency. (Right) Photograph of the SPAN-E digital electronics board.

Note that an implementation of a wave-particle correlator which bins all of the counts within each δt = 0.85 ms measurements for a particular energy-angle phase bin cannot access signals at frequencies f ≳ 588 Hz, but the implementation of the PATCH algorithm, because it uses the time of arrival of the particle, should in principle be able to probe physics at kHz frequencies and higher, such as Type III bursts. Note also that the current PSP flight software burst selection is based on the product of the root mean square wave amplitude and the frequency in one of the analog channels. This produces a nice sampling of, for example, Langmuir wave packets. It would be possible to include some aspects of the simultaneous particle count time series which could enhance the returned wave-particle correlator bursts. Finally, correlating with 16 channels of particle data would be possible with only minor modifications to the SPAN digital electronics board, shown in Figure 6 (right), along with some significant reprogramming of the Field-Programmable Gate Array (FPGA) firmware.

4.2 Predicted Capabilities of an Integrated Field-Particle Correlator

The energy transfer governed by the physics of particle energization in space plasmas—whether through the dissipation of plasma turbulence, through the release of magnetic energy via magnetic reconnection, or through the compression of the plasma and the acceleration of particles at plasma shocks—generally occurs on the characteristic kinetic timescales. Although a recent analysis has shown clearly that, with a sufficiently long correlation interval, the field-particle correlation technique can indeed recover the physics of particle occuring on frequencies above the Nyquist frequency of the sampling (Horvath et al., 2022), to resolve fully the details of the particle energization, one must generally sample the plasma at a faster cadence than the timescale of the process. For example, at a heliocentric distance of 1 AU in the solar wind, the frequency associated with fluctuations at ion length scales convected past a spacecraft at the solar wind velocity is typically f_i ∼ 1 Hz. For the frequency of the convected ion gyroradius, for example, this frequency scales as $f_i\propto V_{sw}B/T_i^{1/2}$. Estimates of the changes in solar wind flow velocity, magnetic field, and ion temperature enable predictions of these characteristic frequencies at different heliocentric distances (Bale et al., 2016). For example, at the heliocentric distance of the first perihelion of Parker Solar Probe at r ≃ 36R_⊙, this frequency rises to f_i ≳ 5 Hz; near the predicted Alfvén radius of the Sun at r ≃ 10R_⊙, the frequency may rise to f_i ≳ 30 Hz. Additional collisionless energy transfer with electrons occurs at yet higher frequencies.

The most significant obstacles to investigating the particle energization in space plasmas are 1) the limited cadence of particle instrumentation, such as electrostatic analyzers and 2) telemetry limitations that constrain the amount of measured data that can be transmitted back to the Earth for analysis. An on-board wave-particle correlator, such as the Integrated Field-Particle Correlator (IFPC) described in Section 3.4, is a potential approach to overcome both of these obstacles. Here we estimate the capabilities of an IFPC incorporating electromagnetic field and plasma instruments equivalent to those on the Parker Solar Probe mission.

The SPAN-E electrostatic analyzer instrument for electrons on PSP (Whittlesey et al., 2020) is capable of performing a full energy sweep of 32 steps in energy E and 8 steps in deflector angle θ over a sampling interval of Δt = 0.218 s. All 16 anodes covered the azimuthal angles ϕ are measured simultaneously, for a total of 4,096 (E, θ, ϕ) phase-space bins sampled in that interval. Each phase-bin is therefore measured in a time δt = Δt/(32 × 8) = 0.85 ms, equivalent to a sampling frequency greater than 1 kHz. The electric field components necessary to determine the rate of particle energization are measured by the FIELDS instrument at sampling frequency of 2 MHz (Bale et al., 2016). By combining the electric field and particle counts on-board using the PATCH algorithm, the effective sampling time is reduced from Δt = 0.218 s to δt = 0.85 ms, an improvement by a factor of 256, with a corresponding Nyquist frequency of the measurements of f ≃ 587 Hz.

The improvement in sampling cadence is actually even larger using the PATCH algorithm, since one of its key features is that the electric field used in the calculation is measured at the time of the arrival of the particle in the detector. For the δt_p = 200 ns pulse sent from the detector to the digital processing unit (DPU) when a particle arrives, the effective sampling frequency is 2.5 MHz, actually faster than the electric field measurement cadence. So within the δt = 0.85 ms measurement interval for a single phase-space bin, one obtains a Nyquist frequency of 1.25 MHz. Therefore, the improvement in time resolution from existing particle instrumentation could be up to a factor of Δt/δt_p ∼ 10⁶.

One significant caveat is that each individual phase-bin is only sampled once over an interval δt = 0.85 ms every Δt = 0.218 s. Therefore, one must interpret the correlated measurements carefully. For example, for the PATCH correlation of the parallel electric field $C_{E_{\parallel }}^{*}(v_{\parallel },v_{\perp })$ over the full velocity-space sweep interval of Δt = 0.218 s, which would appear similar to the right panel of Figure 5, each individual phase bin measurement over δt = 0.85 ms would be measured at a different time during the sweep. So, a plot of a single entire velocity-space sweep combines these measurements at different times, but the electric field and particle measurements in each of the phase bins would use a time accurate to approximately 200 ns. Significant modeling efforts would be needed to ensure that the results returned by the implementation of the PATCH algorithm can be interpreted accurately to reflect the underlying kinetic physics of particle energization.

Another potential capability of an IFPC is to enable alternative operating modes that are designed to sweep over a reduced region of 3V velocity-space on a much faster cadence. For example, one could select a single deflector angle θ and perform a sweep over all 32 energies with a sampling interval of Δt = 0.0273 s, improving time resolution by a factor of 8 by eliminating the deflector angle sweep; alternatively, one could select a single energy and sweep over only deflector angles with a sampling interval of Δt = 0.00068 s, improving time resolution by a factor of 32 by eliminating the energy sweep. This is not dissimilar from the existing alternating full and targeted sweeps that are already used by the SPAN-E electrostatic analyzer instrument. With scientific insight guiding the selection of a reduced sampling region in 3V velocity-space, one would potentially be able to tailor different operating modes to tackle different science questions.

5 Discussion

5.1 Improvements in Understanding Plasma Heating and Particle Acceleration in Space Plasmas

A spacecraft mission including an Integrated Field-Particle Correlator (IFPC) instrument, as described in Section 3.4, would enable significant advances in our understanding of particle energization in space plasmas, including plasma heating and particle acceleration. Note that, unlike previous applications of a wave-particle correlator that sorted the particle counts by wave phase (see Section 1.1), and therefore required a dominant single wave mode, because the IFPC correlates each particle count with the instantaneous field measurements, no single wave is necessary. The successful application of the ground-based FPC method on measurements of broadband turbulence in Earth’s magnetosheath to identify for the first time electron Landau damping in a space plasma is a proof of principle of the field-particle correlation technique (Chen et al., 2019; Afshari et al., 2021).

For key science questions, such as how the solar corona is heated and the solar wind accelerated—two of the primary science questions of both the Parker Solar Probe and Solar Orbiter missions—the vast improvement in the cadence of measurements using an IFPC would enable the kinetic physics of both ion and electron energization to be investigated in detail. Within the outer boundary of the solar corona, inside the Alfvén point, the frequencies of ion energization are likely tens of Hz, and the electron frequencies are up to $\sqrt{m_i/m_e}\simeq 43$ times higher, or approaching kHz frequencies. The much lower sampling frequency of existing particle velocity distribution instruments, with measurement cadences of Δt = 0.218 s, constitutes a significant obstacle in illuminating the kinetic physics involved. But with an IFPC, one can achieve sampling at or above the frequencies of these physical energy transfer mechanisms. In addition, kinetic instabilities may play an important role in the energetics of the solar wind (Bale et al., 2009), and since the energy transfer from the particle velocity distributions to unstable electromagnetic fluctuations can equally be explored with the field-particle correlation technique (Klein, 2017), an IFPC would be a valuable tool to explore this avenue of energy flow in the heliospheric plasma.

The higher effective cadence of an IFPC also enables new science investigations of collisionless field-particle interactions that simply cannot be considered using existing instrumentation. For example, Type III radio bursts with frequencies in the few MHz range can be scattered from density fluctuations in the solar wind turbulence (Krupar et al., 2020), so an IFPC could potentially explore the physics of this scattering using in situ measurements of the electrons and the electric field of these bursts. Furthermore, in the investigation of collisionless shocks, such as Earth’s bow shock or interplanetary shocks, a spacecraft passes through the ramp of the shock in a very short time interval. Being able to correlate the detection of particles with the electric fields at the time of detection will likely open up new avenues for the observational analysis of particle acceleration mechanisms, such as shock drift acceleration (Paschmann et al., 1982; Sckopke et al., 1983; Juno et al., 2021). For some of these new science targets, alternative operating modes may be utilized to focus on the regions of interest in phase-space for a given process, as described in Section 4.2, further increasing the time resolution of the observations.

In addition to new science targets enabled by the development and implementation of an IFPC instrument on an upcoming spacecraft mission, the on-board correlations can improve the statistics of sampling by orders of magnitude. For example, the MMS S-band downlink of 4 Gb/day allows only about 20 min of full-cadence, burst-mode data to be transmitted to the ground for analysis per day, even though the instruments are always sampling at burst-mode cadence. This leads to an effective duty cycle of 1.4%. In principle, on-board correlations could utilize the full 24 h of burst-mode measurements per day in computing correlations, leading to a factor of 72 improvement in total sampling time. For more distant spacecraft that are limited to lower downlink rates, such as Parker Solar Probe and Solar Orbiter, the improvement factor can be even larger. With the potential for the velocity-space signatures generated by the PATCH algorithm to be used to identify different physical mechanisms of particle energization and to quantify the rate of energization, this major improvement in sampling time would enable statistical studies of the fraction of turbulent energy dissipation via different mechanisms, a long term goal of the heliophysics community.

Additional opportunities are made possible by an IFPC, such as event-based triggering. Existing spacecraft can implement triggering based on the amplitude of field fluctuations or rapid changes in field direction, but these events do not necessarily correlate with significant energy transfer between particles and fields. By triggering on the amplitude of the PATCH correlation (possibly averaged over some suitably chosen time interval to eliminate large amplitude oscillatory energy transfer that yields little net particle energization), the operators can be alerted intervals of interest for deeper investigation, or the spacecraft can switch into an appropriate alternative operating mode. Overall, the development of an IFPC using heritage field and particle instrumentation opens up potentially transformative new avenues for investigating the physics of space plasmas.

5.2 Caveats and Challenges

The development of an IFPC instrument for the exploration of the kinetic physics of particle energization in space plasmas faces certain challenges that will need to be addressed before such an instrument can incorporated into a future spacecraft mission. Specific issues include performing the instrument calibration, transformation of electromagnetic fields and velocity coordinates to the frame of the plasma bulk flow, filtering in frequency, potential instrumental limitations of electric field measurements to only two of the three spatial dimensions, and developing the foundation of knowledge needed to interpret the velocity-space signatures of particle energization returned by the correlator measurements.

Data on-board spacecraft are stored in raw format, which does not include calibration factors that are typically determined on the ground. This impacts all of the measurements that PATCH, or any wave-particle correlation method, requires: magnetic field vector, electric field vector, velocity space values of particle measurements, and particle distribution functions. Magnetometers require an absolute calibration, often provided by rotating the spacecraft, to remove background fields caused by the spacecraft and remove drift of the sensor with time. Electric fields measurements by dipole antennas often require extensive calibration to convert the differential voltage measurements into electric field measurements, using cross-instrument calibration to determine DC offsets, effective antenna length, and an angular correction, all as a function of frequency (Mozer et al., 2020).

For ions, the common calibration issue is sensor efficiency (e.g., as set by micro-channel plate gain and threshold voltages) which will change in time as the sensor material ages and settings change to compensate (Lavraud and Larson, 2016). For electrons, the spacecraft charging environment strongly affects the low energy electrons. Most spacecraft charge up to approximately 10 V depending on size, orientation and surface material properties. The thermal energy of electrons in the solar wind is of order 10 eV and in the magnetosheath of order 100 eV and so the spacecraft potential magnitude and structure is frequently important for thermal electron calibration (Scime et al., 1994; Szita et al., 2001). The spacecraft potential accelerates the ambient electrons, both the space plasma populations, changing both energy and direction, and also photoelectrons generated from the spacecraft body, creating a high-density low energy contaminating population. This matters for the PATCH method because photoelectrons will contaminate the triggering events and the velocity of the particles being measured must be corrected for the spacecraft potential, and so the absolute value of correlation $C_{\tau }^{*}$ will have a systematic error based on the magnitude of the spacecraft potential (Lewis et al., 2010).

Typically, correction to the electron energy is performed on the ground, which removes photoelectrons at low energies and shifts the energy of the observed distribution to remove the spacecraft contribution. For most past and existing missions the spacecraft potential is estimated on the ground from the electron distribution and the DC electric field measurements, if they are available. One method to include the calibration factors in on-board data processing for field-particle correlators is to perform regular in flight calibrations on the ground and up-link calculated correction factors to the spacecraft to be included in calculations on board. This has the advantage that the calibration can be performed by a person on the ground, but the disadvantage that the calibration factors would be determined for a typical case and would not change with ambient conditions, as spacecraft potential does. A mission that includes electric potential measurements can provide an on-board estimate of spacecraft potential that can be included in the calibration of the energy of the electrons, but this requires accurate calibration of the spacecraft potential measurement on-board. The spacecraft potential environment can be modelled before launch (Guillemant et al., 2017), but the calibration of the electron distribution for this effect must be done in flight and so this leads to a necessary mission requirement of a time period for instrument calibration in space that is perhaps more extensive than usual in order to update on-board calibrations and not rely on the ground processing.

A significant challenge for the operation of an on-board field-particle correlator is how to implement the field-particle correlations in the appropriate frame of reference for the investigation of particle energization. The standard application to spacecraft measurements is to shift the measurements into the frame of the bulk flow of the plasma species (Chen et al., 2019; Afshari et al., 2021), taking care to perform the appropriate Lorentz transform of the electromagnetic fields. Consider transforming from the spacecraft rest frame ${\mathcal{K}}^{\prime }$ (primed) to the plasma species rest frame $\mathcal{K}$ (unprimed) moving at velocity U relative to the spacecraft frame. The particle velocity transforms as v = v′ − U, and for typical non-relativistic conditions in the heliosphere, the electromagnetic fields transform by E = E′ + U ×B′ and B = B′ (Howes et al., 2014). The PATCH correlation in the plasma frame can be expressed in terms of the spacecraft frame measurements by

$C_{\tau }^{\ast }\propto \sum _{j=1}^{N_{\tau }}q{\mathbf{v}}_p\cdot \mathbf{E}\left(t_j\right)=\sum _{j=1}^{N_{\tau }}\left\{q\left({\mathbf{v}}_p^{\prime }-\mathbf{U}\right)\cdot {\mathbf{E}}^{\prime }\left(t_j\right)-q{\mathbf{v}}_p^{\prime }\cdot \left[\mathbf{U}\times {\mathbf{B}}^{\prime }\left(t_j\right)\right]\right\}(12)$

To implement this transformation on-board requires saving at each particle arrival time t_j the instantaneous (spacecraft frame) electric and magnetic field measurements E′(t_j) and B′(t_j) over the correlation time τ. Note that ${\mathbf{v}}_p^{\prime }$ is the spacecraft frame velocity for each phase-bin, and is known from the applied operating voltages of the instrument at t_j. Over the correlation time, the average bulk fluid velocity of plasma species p is given by $\mathbf{U}={⟨{\mathbf{U}}_p(t)⟩}_{\tau }$, where the angle brackets indicate the time-average over the correlation interval τ. At the end of each correlation interval τ, the PATCH correlation $C_{\tau }^{*}$ can be computed on-board using the known U and measurements E′(t_j) and B′(t_j). Another complication of an on-board implementation of the field-particle correlation technique is how to high-pass filter the electric field measurements to eliminate large-amplitude, low frequency oscillations that yield zero net energy transfer (Chen et al., 2019; Afshari et al., 2021). One could, of course, design a high-pass electronic circuit to eliminate the low-frequency components, but since transformation to the plasma rest frame requires storage of data and on-board processing, a preferred approach is to perform on-board high-pass filtering of the high-cadence electric field measurements in flight software. To do so, one again uses a chosen correlation interval τ over which to save the highest cadence electric field time series E′(t), performs a Fourier transform in time E′(f), applies the appropriate filtering in frequency ${\tilde{\mathbf{E}}}^{\prime }(f)$, and then inverse transforms back to a time series ${\tilde{\mathbf{E}}}^{\prime }(t)$. One then simply replaces the E′(t_j) values in Eq. 12 with the filtered values ${\tilde{\mathbf{E}}}^{\prime }(t_j)$. Such a software-based filtering approach would enable high-pass, band-pass, or low-pass filtering, potentially enabling energy transfers at different frequencies to be isolated. Determining the appropriate correlation intervals τ (likely numerous operating modes with different τ will be designed to tackle different science targets) and the optimal algorithms for on-board frequency filtering will require substantial design work.

A final complication with the implementation of an IFPC instrument is that many spinning spacecraft obtain high-quality electric field measurements in the 2D spin-plane, but poor quality or no electric field measurements along the spin axis. Without full 3D electric field measurements, it is not possible to determine the rate of particle energization due to the unmeasured component of the electric field. But, one can still determine the energization by the two in-plane components of the electric field. Whether the missing component yields an important contribution to the total particle energization depends on the physical mechanism of energy transfer and the orientation of the magnetic field relative to the unmeasured direction, so the limitation must be assessed on a case-by-case basis. In general, selecting an electric field instrument that can provide reliable 3D electric field measurements should be prioritized highly for a proposed mission based on an IFPC instrument to ensure that all aspects of the particle energization can be probed.

In addition to these significant instrumental challenges with calibration, understanding and interpreting the velocity-space signatures generated by the correlated field and particle measurements represents a significant challenge for theory and computation. Significant progress has already been made using the field-particle correlation technique, from its initial conception in 2016 (Klein and Howes, 2016) to the first successful identification of electron Landau damping in a turbulent space plasma using MMS measurements in 2019 (Chen et al., 2019), to a moderate statistical sample demonstrating the relative contribution of electron Landau damping to the total dissipation in 2021 (Afshari et al., 2021). Nonetheless, theoretical and numerical investigations to identify new velocity-space signatures of different proposed particle energization mechanisms are ongoing, identifying electrostatic counterstreaming beam instabilities (Klein, 2017), ion Landau damping (Klein et al., 2017), ion cyclotron damping (Klein et al., 2020), magnetic pumping (Montag and Howes, 2022), electron energization in strong-guide-field collisionless magnetic reconnection (McCubbin et al., 2022), shock-drift acceleration of ions at a perpendicular collisionless shock (Juno et al., 2021), and adiabatic electron heating through the ramp of a perpendicular collisionless shock (Juno et al., 2021). But many more particle energization mechansisms are expected to play a role in space plasmas, and much more work to identify qualitatively their unique velocity-space signatures and to characterize quantitatively the energization rates of all of these mechanisms is necessary to exploit fully the promise of an IFPC instrument.

Furthermore, to take full advantage of the 100% duty cycle of correlated burst-mode measurements, it would be ideal to be able to automatically identify the signatures of different energization mechanisms to compile large statistical studies. Machine learning, and in particular the proven capabilities of Convolutional Neural Networks (CCNs) to learn geometric patterns in images (LeCun and Bengio, 1995, 2015), provide a potentially powerful avenue for classifying and identifying different mechanisms in the investigation of the physics of plasma heating and particle acceleration in space plasmas.

Finally, particle detector design can also be refined to employ more efficient representation of velocity distribution functions (VDFs), where the quest to optimize the scientific return of a mission based on the tragedy of insufficient downlink capabilities is universal among the astrophysical community. Ongoing efforts for tackling this hurdle show promise. For example, a wavelet-based compression for particle count data was explored on MMS data (Barrie et al., 2019). In addition, optimization of VDF basis functions using neural networks was performed to mitigate lossy compression artifacts (da Silva et al., 2020). Representation of the electron VDF using Legendre polynomials has shown to be useful in diagnosing anisotropies signifying net energy transfer (Carcaboso et al., 2020). In a similar vein, a spherical expansion of the ion VDF has been applied to Cluster data to show that only the coefficients of the expansion are needed to obtain the plasma moment information (Viñas and Gurgiolo, 2009). Based on these recent findings regarding optimal spacecraft data compression techniques, it is apparent the physical geometry of the detector is crucial for extracting the most optimal information. Further onboard methodologies considering optimal basis functions (such as polynomial expansion coefficients) for transmitting back both the particle and wave data will be developed in future work toward enhancement of scientific data return.

5.3 Future Mission Concepts

Due to the requirement for simultaneous and triggered measurements of multiple variables, the most effective way to perform the most accurate measurements of field-particle correlations is with a dedicated and specifically designed sensor payload. Future missions dedicated to plasma physics and the role of field-particle correlations are currently proposed, for example the Debye mission (Verscharen et al., 2021) with the European Space Agency, that could include such an Integrated Field-Particle Correlator (IFPC) instrument. As well as a coordinated payload, there are potentially changes to the design of the particle detectors themselves that can improve, or at least change, the performance of an IFPC.

Electrostatic analysers cycle through energy and look-direction by changing voltages in time. This means that different energies and different directions in elevation are not seen simultaneously, although different azimuths are. It is not clear that this kind of operation is optimized for a dedicated field-particle correlation mission. There are two different options that can change this set-up. First, there are novel designs of electrostatic sensors that use multiple entry apertures with distinct electrostatic deflection voltages to sample half of the sky simultaneously at one energy (Skoug et al., 2016; Morel et al., 2017). Thus field-particle correlations could be measured simultaneously in different directions but with different energies separated in time. The second option is to sample multiple energies simultaneously. This is possible using a magnetic field to deflect incoming particles and then separate energies using anodes on a micro-channel plate (MCP) at different distances from the entry aperture (Criton et al., 2020). Different look directions could then be sampled in time, but the energy distribution of the correlation could be measured very rapidly. Both of these ideas offer the opportunity to increase the speed of the particle observations by removing one dimension of the two-dimensional voltage sweeping in traditional ESAs. An alternative is that the time resolution can be kept as it is, but the count-rate will be increased due to the reduction in instrument dead time and increase in geometric factor for these designs, which will increase the accuracy and number of observations made by the instrument.

As highlighted above, the IFPC concept requires a dedicated data processing unit that links particle and field sensors. This has become more common in recent missions, for example the Solar Orbiter mission has shared DPU for the Solar Wind Analyser (SWA) (Owen et al., 2020) in-situ plasma detectors and a similar approach is proposed for Debye. However, these designs do not take into account the specialised needs of correlation measurements, such as the rapid pulse required for individual particle arrival time measurement.

The Debye mission has science goals to measure the energy transfer between fields and particles at electron scales. This requires high time-resolution measurements of fields and electron velocity distributions, so the application of the field-particle correlation techniques described here are of fundamental importance to this question. There is the potential to enhance the Debye mission with the integration of field-particle correlation measurements as a central feature of the mission. The payload includes all of the instruments required and a dedicated DPU—only the harnessing to provide the connections between the instruments and the firmware on the DPU is required to make the Debye proposal the first dedicated design for a field-particle correlation mission (Verscharen et al., 2021).

In conclusion, innovative wave-particle correlator instrumentation, in particular the proposal here for the design of a new Integrated Field-Particle Correlator (IFPC) instrument, show significant promise in overcoming the limits of telemetry to maximize the scientific return from upcoming spacecraft missions. Concerted efforts to develop such new instrumentation for onboard correlations are ongoing, with the potential for transformative progress in our understanding of particle energization mechanisms, leading to plasma heating and particle acceleration, operating in the heliosphere.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

GH organized the team and wrote much of the manuscript. Authors and contributors for sections of the manuscript follow: (Section 1) GH and LW; (Section 1.1) GH and JV; (Section 2.1) DL, JP, PW, RL and AR; (Section 2.2) SB; (Section 2.3) SB and KG; (Section 3.1) GH and KK; (Section 3.2) CC, KK and GH; (Section 3.3) JV and GH; (Section 3.4) GH, DL, PW, RL and JV; (Section 4.1) DL, KG, SB, PW and RL; (Section 4.2) GH, JV, SB, KG, DL, PW and RL; (Section 5.1) GH, SB and KG; (Section 5.2) RW, GH, JV and DL; (Section 5.3) RW and GH. All authors participated in discussions about the mission concept and contributed to comments, references, and interpretative feedback on the manuscript.

Funding

GGH was supported by NASA grants 80NSSC18K0643, 80NSSC18K1371, and 80NSSC20K1273, and by NSF grant AGS-1842561. CHKC was supported by STFC Consolidated Grant ST/T00018X/1. The PSP/FIELDS experiment was developed and is operated under NASA contract NNN06AA01C. RTW was supported by STFC Consolidated Grant ST/V006320/1. KK was supported by NASA ECIP Grant 80NSSC19K0912 and SWEAP contract NNN06AA01C. LW was supported by Wind MO&DA funds and two NASA grants.

Conflict of Interest

Author JK was employed by company BWX Technologies, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The mission concept proposed here was developed and refined as part of the Parker Solar Probe Wave-Particle Correlator Working Group, led by GGH. The work was supported by the International Space Science Institute’s (ISSI) International Teams programme (“Resolving the Microphysics of Collisionless Shock Waves” led by LW III) and the Geospace Environment Modeling (GEM) Focus Group “Particle Heating and Thermalization in Collisionless Shocks in the MMS Era” led by LW III.

Footnotes

¹Note that the physically essential boundary condition that f(v) → 0 as |v| → ∞ can be exploited to reduce the v² factor in the jth component of the dot product to $v_j^2$ (Klein et al., 2017).

References

Afshari, A. S., Howes, G. G., Kletzing, C. A., Hartley, D. P., and Boardsen, S. A. (2021). The Importance of Electron Landau Damping for the Dissipation of Turbulent Energy in Terrestrial Magnetosheath Plasma. JGR Space Phys. 126, e29578. doi:10.1029/2021JA029578

CrossRef Full Text | Google Scholar

Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., Dudok de Wit, T., et al. (2016). The FIELDS Instrument Suite for Solar Probe Plus. Measuring the Coronal Plasma and Magnetic Field, Plasma Waves and Turbulence, and Radio Signatures of Solar Transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bale, S. D., Kasper, J. C., Howes, G. G., Quataert, E., Salem, C., and Sundkvist, D. (2009). Magnetic Fluctuation Power Near Proton Temperature Anisotropy Instability Thresholds in the Solar Wind. Phys. Rev. Lett. 103, 211101. doi:10.1103/PhysRevLett.103.211101

PubMed Abstract | CrossRef Full Text | Google Scholar

Barnes, A. (1966). Collisionless Damping of Hydromagnetic Waves. Phys. Fluids 9, 1483–1495. doi:10.1063/1.1761882

CrossRef Full Text | Google Scholar

Barrie, A. C., Smith, D. L., Elkington, S. R., Sternovsky, Z., da Silva, D., Giles, B. L., et al. (2019). Wavelet Compression Performance of Mms/fpi Plasma Count Data with Plasma Environment. Earth Space Sci. 6, 116–135. doi:10.1029/2018EA000430

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Carcaboso, F., Gómez-Herrero, R., Espinosa Lara, F., Hidalgo, M. A., Cernuda, I., and Rodríguez-Pacheco, J. (2020). Characterisation of Suprathermal Electron Pitch-Angle Distributions - Bidirectional and Isotropic Periods in Solar Wind. A&A 635, A79. doi:10.1051/0004-6361/201936601

CrossRef Full Text | Google Scholar

Chen, C. H. K., Klein, K. G., and Howes, G. G. (2019). Evidence for Electron Landau Damping in Space Plasma Turbulence. Nat. Comm. 10, 740. doi:10.1038/s41467-019-08435-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Criton, B., Nicolaou, G., and Verscharen, D. (2020). Design and Optimization of a High-Time-Resolution Magnetic Plasma Analyzer (Mpa). Appl. Sci. 10. doi:10.3390/app10238483

CrossRef Full Text | Google Scholar

da Silva, D., Barrie, A., Gershman, D., Elkington, S., Dorelli, J., Giles, B., et al. (2020). Neural Network Repair of Lossy Compression Artifacts in the September 2015 to March 2016 Duration of the Mms/fpi Data Set. J. Geophys. Res. Space Phys. 125, e2019JA027181. doi:10.1029/2019JA027181

PubMed Abstract | CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Clemmons, J. H., and Boehm, M. H. (1991a). Langmuir Wave Growth and Electron Bunching - Results from a Wave-Particle Correlator. J. Geophys. Res. 96, 225–238. doi:10.1029/90JA01596

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Tonthat, D. M., and Clemmons, J. H. (1991b). Observation of Electron Bunching during Landau Growth and Damping. J. Geophys. Res. 96, 11. doi:10.1029/91JA00658

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., Mozer, F. S., Delory, G. T., Temerin, M., McFadden, J. P., et al. (2001). The FAST Satellite Fields Instrument. Space Sci. Rev. 98, 67–91. doi:10.1007/978-94-010-0332-2_3

CrossRef Full Text | Google Scholar

Ergun, R. E., McFadden, J. P., and Carlson, C. W. (1998). “Wave-Particle Correlator Instrument Design,” in Measurement Techniques in Space Plasmas:Particles (Washington DC: American Geophysical Union), 102, 325.

Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The Solar Probe Plus Mission: Humanity’s First Visit to Our Star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Fukuhara, H., Kojima, H., Ueda, Y., Omura, Y., Katoh, Y., and Yamakawa, H. (2009). A New Instrument for the Study of Wave-Particle Interactions in Space: One-Chip Wave-Particle Interaction Analyzer. Earth, Planets, Space 61, 765–778. doi:10.1186/bf03353183

CrossRef Full Text | Google Scholar

Gough, M. P. (1980). A Technique for Rocket-Borne Detection of Electron Bunching at Megahertz Frequencies. Nucl. Instrum. Methods 177, 581–587. doi:10.1016/0029-554X(80)90074-9

CrossRef Full Text | Google Scholar

Gough, M. P., Martelli, G., Smith, P. N., Maehlum, B. N., and Ventura, G. (1980). Bunching of 8-10 keV Auroral Electrons Near an Artificial Electron Beam. Nature 287, 15–17. doi:10.1038/287015a0

CrossRef Full Text | Google Scholar

Guillemant, S., Maksimovic, M., Hilgers, A., Pantellini, F., Lamy, L., Louarn, P., et al. (2017). A Study of Solar Orbiter Spacecraft–Plasma Interactions Effects on Electric Field and Particle Measurements. IEEE Trans. Plasma Sci. 45, 2578–2587. doi:10.1109/TPS.2017.2731054

CrossRef Full Text | Google Scholar

Hesse, M., and Cassak, P. A. (2020). Magnetic Reconnection in the Space Sciences: Past, Present, and Future. J. Geophys. Res. 125, e25935. doi:10.1029/2019JA02593510.1029/2018ja025935

CrossRef Full Text | Google Scholar

Horvath, S. A., Howes, G. G., and McCubbin, A. J. (2020). Electron Landau Damping of Kinetic Alfvà ⓒ N Waves in Simulated Magnetosheath Turbulence. Phys. Plasmas 27, 102901. doi:10.1063/5.0021727

CrossRef Full Text | Google Scholar

Horvath, S. A., Howes, G. G., and McCubbin, A. J. (2022). Observing Particle Energization above the Nyquist Frequency: An Application of the Field-Particle Correlation Technique. Phys. Plasmas. in press.

CrossRef Full Text | Google Scholar

Howes, G. G. (2017). A Prospectus on Kinetic Heliophysics. Phys. Plasmas 24, 055907. doi:10.1063/1.4983993

PubMed Abstract | CrossRef Full Text | Google Scholar

Howes, G. G., Klein, K. G., and Li, T. C. (2017). Diagnosing Collisionless Energy Transfer Using Field-Particle Correlations: Vlasov-Poisson Plasmas. J. Plasma Phys. 83, 705830102. doi:10.1017/S0022377816001197

CrossRef Full Text | Google Scholar

Howes, G. G., Klein, K. G., and TenBarge, J. M. (2014). Validity of the Taylor Hypothesis for Linear Kinetic Waves in the Weakly Collisional Solar Wind. Astrophys. J. 789, 106. doi:10.1088/0004-637X/789/2/106

CrossRef Full Text | Google Scholar

Juno, J., Brown, C., Howes, G. G., and Haggerty, C. (2022). A Field-Particle Correlation Analysis of a Quasiperpendicular Magnetized Collisionless Shock. J. Plasma Phys. In preparation.

Google Scholar

Juno, J., Hakim, A., TenBarge, J., Shi, E., and Dorland, W. (2018). Discontinuous Galerkin Algorithms for Fully Kinetic Plasmas. J. Comp. Phys. 353, 110–147. doi:10.1016/j.jcp.2017.10.009

CrossRef Full Text | Google Scholar

Juno, J., Howes, G. G., TenBarge, J. M., Wilson, L. B., Spitkovsky, A., Caprioli, D., et al. (2021). A Field-Particle Correlation Analysis of a Perpendicular Magnetized Collisionless Shock. J. Plasma Phys. 87, 905870316. doi:10.1017/S0022377821000623

CrossRef Full Text | Google Scholar

Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar Wind Electrons Alphas and Protons (SWEAP) Investigation: Design of the Solar Wind and Coronal Plasma Instrument Suite for Solar Probe Plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3

CrossRef Full Text | Google Scholar

Katoh, Y., Kitahara, M., Kojima, H., Omura, Y., Kasahara, S., Hirahara, M., et al. (2013). Significance of Wave-Particle Interaction Analyzer for Direct Measurements of Nonlinear Wave-Particle Interactions. Ann. Geophys. 31, 503–512. doi:10.5194/angeo-31-503-2013

CrossRef Full Text | Google Scholar

Katoh, Y., Kojima, H., Hikishima, M., Takashima, T., Asamura, K., Miyoshi, Y., et al. (2018). Software-type Wave-Particle Interaction Analyzer on Board the Arase Satellite. Earth, Planets, Space 70, 4. doi:10.1186/s40623-017-0771-7

CrossRef Full Text | Google Scholar

Klein, K. G. (2017). Characterizing Fluid and Kinetic Instabilities Using Field-Particle Correlations on Single-point Time Series. Phys. Plasmas 24, 055901. doi:10.1063/1.4977465

CrossRef Full Text | Google Scholar

Klein, K. G., and Howes, G. G. (2016). Measuring Collisionless Damping in Heliospheric Plasmas Using Field-Particle Correlations. Astrophys. J. Lett. 826, L30. doi:10.3847/2041-8205/826/2/L30

CrossRef Full Text | Google Scholar

Klein, K. G., Howes, G. G., and TenBarge, J. M. (2017). Diagnosing Collisionless Enegy Transfer Using Field-Particle Correlations: Gyrokinetic Turbulence. J. Plasma Phys. 83, 535830401. doi:10.1017/S0022377817000563

CrossRef Full Text | Google Scholar

Klein, K. G., Howes, G. G., TenBarge, J. M., and Valentini, F. (2020). Diagnosing Collisionless Energy Transfer Using Field-Particle Correlations: Alfvén-Ion Cyclotron Turbulence. J. Plasma Phys. 86, 905860402. doi:10.1017/S0022377820000689

CrossRef Full Text | Google Scholar

Kletzing, C. A., Bounds, S. R., LaBelle, J., and Samara, M. (2005). Observation of the Reactive Component of Langmuir Wave Phase-Bunched Electrons. Geophys. Res. Lett. 32, L05106. doi:10.1029/2004GL021175

CrossRef Full Text | Google Scholar

Kletzing, C. A., and Muschietti, L. (2006). “Phase Correlation of Electrons and Langmuir Waves,” in Geospace Electromagnetic Waves and RadiationBerlin Springer Verlag. Editors J. W. Labelle, and R. A. Treumann, 687, 313. Lect. Notes Phys.

Google Scholar

Krupar, V., Szabo, A., Maksimovic, M., Kruparova, O., Kontar, E. P., Balmaceda, L. A., et al. (2020). Density Fluctuations in the Solar Wind Based on Type III Radio Bursts Observed by Parker Solar Probe. Astrophys. J. Supp. 246, 57. doi:10.3847/1538-4365/ab65bd

CrossRef Full Text | Google Scholar

Lavraud, B., and Larson, D. E. (2016). Correcting Moments of In Situ Particle Distribution Functions for Spacecraft Electrostatic Charging. J. Geophys. Res. Space Phys. 121, 8462–8474. doi:10.1002/2016JA022591

CrossRef Full Text | Google Scholar

LeCun, Y., and Bengio, Y. (1995). “Convolutional Networks for Images, Speech, and Time Series,” in The Handbook of Brain Theory and Neural Networks (Cambridge, MA: MIT Press), 3361.

Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, G., Arridge, C., Linder, D., Gilbert, L., Kataria, D., Coates, A., et al. (2010). The Calibration of the Cassini–Huygens Caps Electron Spectrometer. Planet. Space Sci. 58, 427–436. doi:10.1016/j.pss.2009.11.008

CrossRef Full Text | Google Scholar

Livi, R., Larson, D. E., Kasper, J. C., Abiad, R., Case, A. W., Klein, K. G., et al. (2021). The Solar Probe Analyzer-Ions on Parker Solar Probe. Astrophys. J. Supp. in press

Google Scholar

McCubbin, A. J., Howes, G. G., and TenBarge, J. M. (2022). Characterizing Velocity-Space Signatures of Electron Energization in Large-Guide-Field Collisionless Magnetic Reconnection. Phys. Plasmas 29, 052105. doi:10.1063/5.0082213

CrossRef Full Text | Google Scholar

Melrose, D. B. (1986). Instabilities in Space and Laboratory Plasmas. Cambridge, UK: Cambridge University Press.

Google Scholar

Miyoshi, Y., Shinohara, I., Takashima, T., Asamura, K., Higashio, N., Mitani, T., et al. (2018). Geospace Exploration Project ERG. Earth, Planets, Space 70, 101. doi:10.1186/s40623-018-0862-0

CrossRef Full Text | Google Scholar

Montag, P., and Howes, G. G. (2022). A Field-Particle Correlation Analysis of Magnetic Pumping. Phys. Plasmas 29, 032901. doi:10.1063/5.0036825

CrossRef Full Text | Google Scholar

Morel, X., Berthomier, M., and Berthelier, J.-J. (2017). Electrostatic Analyzer with a 3-d Instantaneous Field of View for Fast Measurements of Plasma Distribution Functions in Space. J. Geophys. Res. Space Phys. 122, 3397–3410. doi:10.1002/2016JA023596

CrossRef Full Text | Google Scholar

Mozer, F. S., Agapitov, O. V., Bale, S. D., Bonnell, J. W., Bowen, T. A., and Vasko, I. (2020). DC and Low-Frequency Electric Field Measurements on the Parker Solar Probe. J. Geophys. Res. 125, e27980. doi:10.1029/2020JA027980

CrossRef Full Text | Google Scholar

Müller, D., Marsden, R. G., Cyr, St. O. C., and Gilbert, H. R. (2013). Solar Orbiter . Exploring the Sun-Heliosphere Connection. Sol. Phys. 285, 25–70. doi:10.1007/s11207-012-0085-7

CrossRef Full Text | Google Scholar

Muschietti, L., Roth, I., and Ergun, R. (1994). Interaction of Langmuir Wave Packets with Streaming Electrons: Phase-Correlation Aspects. Phys. Plasmas 1, 1008–1024. doi:10.1063/1.870781

CrossRef Full Text | Google Scholar

Numata, R., Howes, G. G., Tatsuno, T., Barnes, M., and Dorland, W. (2010). AstroGK: Astrophysical Gyrokinetics Code. J. Comp. Phys. 229, 9347. doi:10.1016/j.jcp.2010.09.006

CrossRef Full Text | Google Scholar

Owen, C. J., Bruno, R., Livi, S., Louarn, P., Al Janabi, K., Allegrini, F., et al. (2020). The Solar Orbiter Solar Wind Analyser (SWA) Suite. Astron. Astrophys. 642, A16. doi:10.1051/0004-6361/201937259

CrossRef Full Text | Google Scholar

Paschmann, G., Sckopke, N., Bame, S. J., and Gosling, J. T. (1982). Observations of Gyrating Ions in the Foot of the Nearly Perpendicular Bow Shock. Geophys. Res. Lett. 9, 881–884. doi:10.1029/GL009i008p00881

CrossRef Full Text | Google Scholar

Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

Scime, E. E., Phillips, J. L., and Bame, S. J. (1994). Effects of Spacecraft Potential on Three-Dimensional Electron Measurements in the Solar Wind. J. Geophys. Res. Space Phys. 99, 14769–14776. doi:10.1029/94JA00489

CrossRef Full Text | Google Scholar

Sckopke, N., Paschmann, G., Bame, S. J., Gosling, J. T., and Russell, C. T. (1983). Evolution of Ion Distributions across the Nearly Perpendicular Bow Shock - Specularly and Non-specularly Reflected-Gyrating Ions. J. Geophys. Res. 88, 6121–6136. doi:10.1029/JA088iA08p06121

CrossRef Full Text | Google Scholar

Skoug, R. M., Funsten, H. O., Mobius, E., Harper, R. W., Kihara, K. H., and Bower, J. S. (2016). A Wide Field of View Plasma Spectrometer. J. Geophys. Res. Space Phys. 121, 6590–6601. doi:10.1002/2016JA022581

CrossRef Full Text | Google Scholar

Spiger, R. J., Murphree, J. S., Anderson, H. R., and Loewenstein, R. F. (1976). Modulation of Auroral Electron Fluxes in the Frequency Range 50 kHz to 10 MHz. J. Geophys. Res. 81, 1269–1278. doi:10.1029/JA081i007p01269

CrossRef Full Text | Google Scholar

Spiger, R. J., Oehme, D., Loewenstein, R. F., Murphree, J., Anderson, H. R., and Anderson, R. (1974). A Detector for High Frequency Modulation in Auroral Particle Fluxes. Rev. Sci. Instrum. 45, 1214–1220. doi:10.1063/1.1686462

CrossRef Full Text | Google Scholar

Szita, S., Fazakerley, A. N., Carter, P. J., James, A. M., Trávnícek, P., Watson, G., et al. (2001). Cluster Peace Observations of Electrons of Spacecraft Origin. Ann. Geophys. 19, 1721–1730. doi:10.5194/angeo-19-1721-2001

CrossRef Full Text | Google Scholar

Valentini, F., Trávníček, P., Califano, F., Hellinger, P., and Mangeney, A. (2007). A Hybrid-Vlasov Model Based on the Current Advance Method for the Simulation of Collisionless Magnetized Plasma. J. Comp. Phys. 225, 753–770. doi:10.1016/j.jcp.2007.01.001

CrossRef Full Text | Google Scholar

Verniero, J. L., Howes, G. G., Stewart, D. E., and Klein, K. G. (2021a). Determining Threshold Instrumental Resolutions for Resolving the Velocity Space Signature of Ion Landau Damping. J. Geophys. Res. (Space Phys. 126, e28361. doi:10.1029/2020JA028361

CrossRef Full Text | Google Scholar

Verniero, J. L., Howes, G. G., Stewart, D. E., and Klein, K. G. (2021b). PATCH: Particle Arrival Time Correlation for Heliophysics. J. Geophys. Res. (Space Phys. 126, e28940. doi:10.1029/2020JA028940

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The Multi-Scale Nature of the Solar Wind. Living Rev. Sol. Phys. 16, 1. doi:10.1007/s41116-019-0021-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Verscharen, D., Wicks, R. T., Alexandrova, O., Bruno, R., Burgess, D., Chen, C. H., et al. (2021). A Case for Electron-Astrophysics. Exp. Astron. 57, 1. doi:10.1007/s10686-021-09761-5

CrossRef Full Text | Google Scholar

Viñas, A. F., and Gurgiolo, C. (2009). Spherical Harmonic Analysis of Particle Velocity Distribution Function: Comparison of Moments and Anisotropies Using Cluster Data. J. Geophys. Res. Space Phys. 114. doi:10.1029/2008JA013633

CrossRef Full Text | Google Scholar

Watkins, N. W., Bather, J. A., Chapman, S. C., Mouikis, C. G., Gough, M. P., Wygant, J. R., et al. (1996). Suspected Wave-Particle Interactions Coincident with a Pancake Distribution as Seen by the CRRES Spacecraft. Adv. Space Res. 17, 83–87. doi:10.1016/0273-1177(95)00698-E

PubMed Abstract | CrossRef Full Text | Google Scholar

Whittlesey, P. L., Larson, D. E., Kasper, J. C., Halekas, J., Abatcha, M., Abiad, R., et al. (2020). The Solar Probe ANalyzers—Electrons on the Parker Solar Probe. Astrophys. J. Supp. 246, 74. doi:10.3847/1538-4365/ab7370

CrossRef Full Text | Google Scholar

Wilson, L. B., Brosius, A. L., Gopalswamy, N., Nieves-Chinchilla, T., Szabo, A., Hurley, K., et al. (2021a). A Quarter Century of Wind Spacecraft Discoveries. Rev. Geophys. 59, e2020RG000714. doi:10.1029/2020RG000714

CrossRef Full Text | Google Scholar

Wilson, L. B., Chen, L.-J., and Roytershteyn, V. (2021b). The Discrepancy between Simulation and Observation of Electric Fields in Collisionless Shocks (Invited). Front. Astron. Space Sci. 7, 14. doi:10.3389/fspas.2020.592634

CrossRef Full Text | Google Scholar

Wilson, L. B., Stevens, M. L., Kasper, J. C., Klein, K. G., Maruca, B., Bale, S. D., et al. (2018). The Statistical Properties of Solar Wind Temperature Parameters Near 1 au. Astrophys. J. Suppl. 236, 41. doi:10.3847/1538-4365/aab71c

CrossRef Full Text | Google Scholar