Calculating periodic orbits of the Hénon–Heiles system

1 Introduction

The Hénon–Heiles system has been stated initially to describe the stars’ motion around a galactic center, and it remains a vital topic in both mathematical and physical sciences since it was first proposed in 1964 (Hénon and Heiles, 1964). The Hénon–Heiles system gives fertile dynamical behavior, and it is to be noted that the Wada property cannot be investigated in the Hamiltonian system, but it can be observed in the Hénon–Heiles system (Aguirre et al., 2001). In general, this system can be used to explore many dynamical concepts in particle motion passing by regular and periodic orbits to resonance behavior going to chaotic motion. It is considered one of the most important systems for characterizing how chaos appears.

In Churchill et al. (1979), some evaluated periodic orbits have been specified using geometric constructions, and the stability of these orbits is analyzed in terms of the variation of the energy levels of the system. Also, De Figueiredo et al. (1998) studied the dynamics of the two degrees of freedom within the Hénon–Heiles Hamiltonian system. They investigated many dynamical features such as existence of stochastic regions in specified parts of phase space, which are linked to two canonical invariants that can be explicitly evaluated. In Vallejo et al. (2003), different prototypical distributions of the finite-time Lyapunov exponent are calculated for a 2-dimensional Hénon–Heiles Hamiltonian system. Several forms are evaluated for each dynamical state, which characterize the local instability of the system.

In the framework of the general formula for the classical Hénon–Heiles potential, the non-linear stability features of the equilibrium points, which are like Lagrangian points, are studied. The conditions for the stability have been shown on the free parameters. Also, the stable character of the origin point has been proven for classical potential (Iñarrea et al., 2015). A considerable work is addressed in Antipov and Nagaitsev (2017), where the possibility of creating a Hénon–Heiles Hamiltonian system using sextupoles in a realistic accelerator lattice is studied. A special sextupole channel is proposed in order to generate the desired potential at the integrable optics test accelerator ring and study the 3-dimensional single-particle dynamics by frequency map analysis and Poincaré cross-section.

Dubeibe et al. (2018) constructed a series expansion up to the fifth degree, considering the axial and reflection symmetries of Hénon–Heiles potential. With some specified assumptions and mathematical transformations, the formula of the so-called generalized Hénon–Heiles potential is computed. Then, bounded and unbounded motions are analyzed, using the Poincaré section technique, while the corresponding Newton–Raphson basins of convergence to the equilibrium points, which are considered the attractors of the convergence process, are analyzed using a numerical approach. Hence, the locations and linear stability of these points are studied. Also, with the help of the multivariate version of the classical Newton–Raphson scheme, the regions of attraction are revealed and the basin entropy of the attracting domains is also investigated (Zotos et al., 2018).

Although the Hénon–Heiles system and its modified versions have been analytically and numerically extendedly studied, it remains a vivid subject in dynamical systems. In fact, we aim to study the possible periodic solutions of the generalized Hénon–Heiles system by using the averaging theory of dynamical systems. However, first, we will shed light on the importance of the periodic orbits and the used perturbation methods. Periodic orbits are special solutions corresponding to a dynamical system of differential equations, where these solutions repeat themselves after specified periods of time. In the case of the dynamical systems which display s periodic orbits, this phenomenon can be called an oscillator; otherwise, it can be called unstable.

The study of periodic solutions of non-linear ordinary differential systems is one of the main problems in qualitative theory, where periodic orbits are found in most of the dynamical systems that have an application in physics, quantum mechanics (Kottos and Smilansky, 1999), and celestial mechanics (Ershkov, 2017; Pathak et al., 2019a; Pathak et al., 2019b; Abozaid et al., 2020). These solutions can be used to describe the motion of planetary and stellar systems. In the framework of either the existence or non-existence of periodic orbits analytically, many and different techniques can be used to examine the existence (non-existence) of periodic orbits for autonomous dynamical systems, for example, index theory, Bendixson’s criterion, Poincare–Bendixson theorem (Guckenheimer et al., 1984), Liénard systems (Hannsgen, 1979), and Fast–Slow Planar Systems (Grasman et al., 1978; Mis’enko et al., 1994).

One of the main problems in celestial mechanics is Kepler motion, which is periodic under the mutual universal gravitational law when the energy takes a negative value. Furthermore, the solution of the restricted three-body problem, that comprises the basis of the Hill–Brown theory in celestial mechanics, is periodic. The major existence of oscillators’ phenomena is in the motion of celestial objects, which can be described by two- or three-body systems or N−body systems with periodic solutions. Many methods can be used to find periodic solutions, such as Lindstedt–Poincaré, multiple scales, and KB averaging methods (Kang, 2001; EAbouelmagd et al., 2015; Abouelmagd et al., 2016; Abouelmagd, 2018; Abouelmagd et al., 2020b). In the case of the extended first and second kind of periodic orbits, which are established by Poincaré, Barrar (1965) investigated the existence of these orbits by using Delaunay variables, while Abouelmagd et al. (2019) proved that these orbits for the unperturbed restricted three-body problem can be extended to the perturbed problem by solar sail and oblate effects.

We recall that periodic solutions can be calculated by using some numerical techniques when the solutions are stable by finding the basins of convergence via a numerical integration with proper selection for initial conditions. However, in the case of the instability of periodic solutions, we can use, for example, the Newton–Raphson scheme to calculate these solutions, rather than using it in the case of stable periodic solutions (Parker and Chua, 1989).

The averaging theory is a powerful perturbation method that can be used to find periodic orbits for some non-integrable systems and in galactic dynamics (Llibre and Jiménez-Lara, 2011; El-Sabaa et al., 2021). This method is used to show that there are two periodic orbits for the anisotropic Kepler system under the small anisotropy effect. Also, two approximate analytic solutions for these orbits are calculated (Abouelmagd et al., 2017). However, the global dynamics of the relativistic perturbed Kepler problem are studied in Abouelmagd et al. (2020a) using the same theory.

We remark that periodic orbits play a serious and substantial role for understanding the manner and modality of non-linear dynamical systems. In particular, the authors investigated the features of attractors in Celletti (2009). The periodic orbits have particular importance in the qualitative theory of differential equations, integral equations, functional differential equations, etc. Therefore, it is very important to obtain information on the qualitative behavior of periodic solutions of differential equations when there is no analytical expression for the solutions. Thus, the objective of this paper is using the averaging theory to prove the following theorem, which is considered the main result of the current work.

Theorem 1. At every positive energy level, the fifth-degree Hénon-Heiles Hamiltonian system (Ershkov, 2017) has at least seven periodic orbits.This work is organized as follows: a literature review on periodic orbits and the used methods are presented in Section 1. The feature analysis of Hénon–Heiles’s potential and the related critical points in different phase spaces are explored in Section 2. The generalized Hénon–Heiles systems are derived in Section 3. The fundamental results on the second-order averaging theory for a dynamical system are shown in Section 4. The standard form of generalized Hénon–Heiles systems is derived in Section 5 to apply the averaging theory. The main result, which is represented by Theorem 1, is established in Section 6. Finally, a conclusion is stated in the last section.

2 Hénon–Heiles potential properties

Through the work of Hénon and Heiles on the analysis of a star motion over the galactic center in the same plane, they found the third integral of motion in the framework of galactic dynamics (Hénon and Heiles, 1964). To study the existence of this integral, a non-linear potential with cylindrical symmetry was introduced to represent the galaxy gravitational potential in the following form:

$\begin{array}{c}\hfill V_0\left(x,y\right)=\frac{1}{2}\left(x^2+y^2\right)+x^{2}y-\frac{1}{3}{y}^3.\end{array}(1)$

We remark that the potential is formulated by adding two cube terms to the two-dimensional oscillator potential as in Eq. 1. Hénon and Heiles proved that the third integral can exist only for a limited range of initial conditions. The non-linear motions of stars in the framework of the classical Hénon–Heiles potential (we mean that the given potential in Eq. 1) are considerably studied, see, for example, Szücs-Csillik (2010); Llibre and Jiménez-Lara (2011), while a significant analysis on these motions within the frame of generalized Hénon–Heiles potential is conducted in Dubeibe et al. (2018); Zotos et al. (2018).

The generalized Hénon–Heiles or fifth-degree potential (V) is given by

$\begin{array}{c}\hfill V\left(x,y\right)=V_0+\delta \left[x^{4}y+x^2{y}^3-y^5-{\left(x^2+y^2\right)}^2\right],\end{array}(2)$

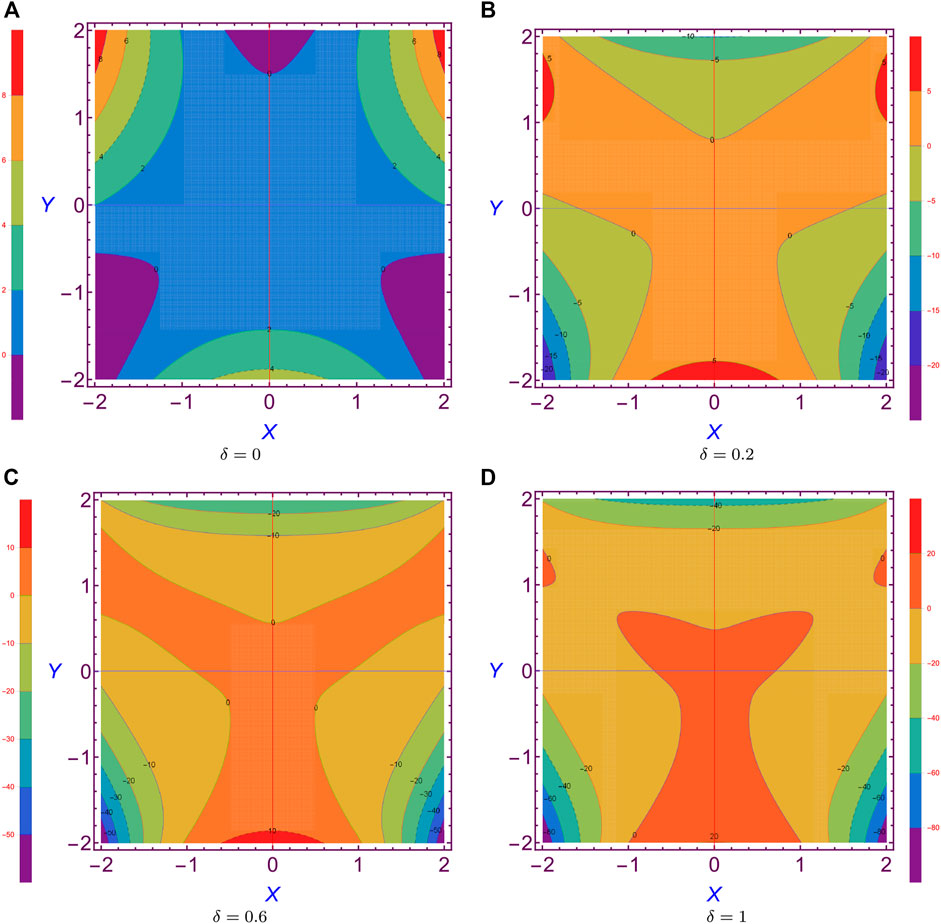
where δ is an arbitrary parameter, which embodies the transition from the classical Hénon–Heiles potential to the generalized one; details of constructions are given in Dubeibe et al. (2018). We can see the difference between the classical and generalized Hénon–Heiles potential through the isopleth of both potential in Figure 1 for different values of the transition parameter (δ).

FIGURE 1

FIGURE 1. Isopleth of the generalized Hénon–Heiles potential.

The contour lines or isopleth of Hénon–Heiles potential are shown in Figures 1A–D when δ = 0, .2, .6, 1. In brief, these figures show the plane sections of Hénon–Heiles potential for different values of the transition parameter or characterize the intensity map of the potential with some equipotential curves. After examining these figures, we remark that the plane sections of zero potential enlarge with the increase of the transition parameter value. In general, the contour lines form region boundaries of possible motions at different equipotential levels.

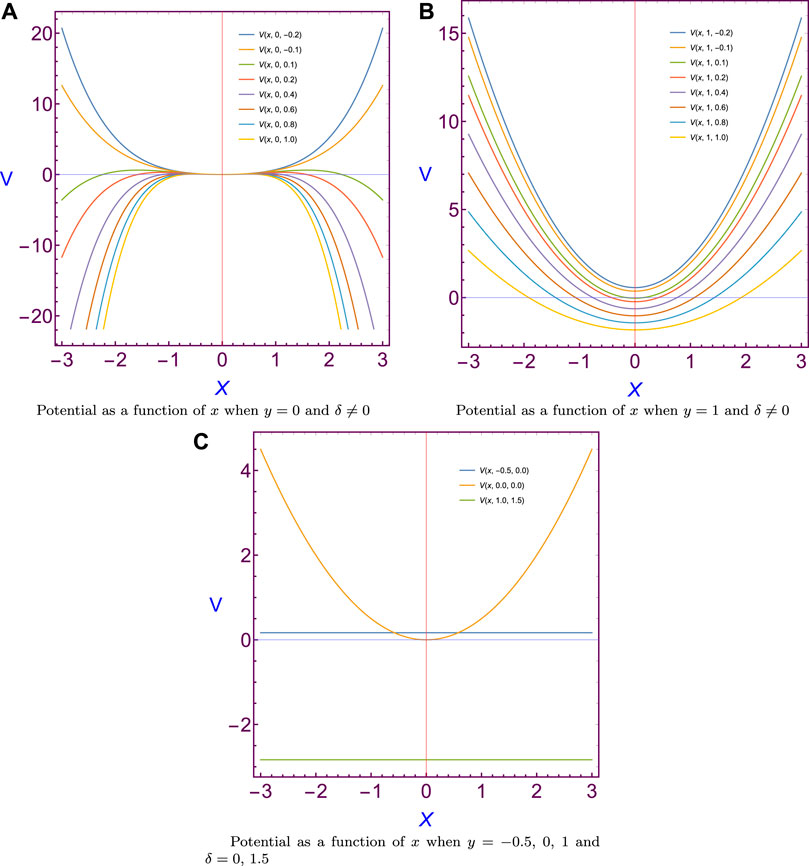
The sketched potential V (x, y) in Figure 1 has some interesting characteristics: when y is constant (say y = k), then the potential in Eq.2 can be rewritten as

$\begin{array}{ll}\hfill V\left(x,k,\delta \right)& =\frac{1}{6}{k}^2\left(3-2k\right)+\frac{1}{2}\left(2k+1\right)x^2\hfill \\ \hfill & -\delta \left[k^4\left(k+1\right)-k^2\left(k-2\right)x^2-\left(k-1\right)x^4\right].\hfill \end{array}(3)$

It is clear from Eq. 3 that the potential is represented by a biquadratic function when y is constant. Thereby, V (x, k, δ) = V (−x, k, δ) and the potential is symmetric about the V−axis; hence, the potential has the same infinite limit when x tends to positive or negative infinity. If the coefficient of x⁴ is positive, then the potential function will increase to positive infinity at both ends, and thus the potential function has a global minimum point. Likewise, if the coefficient of x⁴ is negative, the potential function will decrease to negative infinity and has a global maximum point. In both cases, it may or may not have another local maximum and another local minimum.

If y is constant, the curves of the Hénon–Heiles potential are shown in Figure 2 for some particular values of y. The classical potential (V₀) will be represented by a parabola formula. Also, the generalized Hénon–Heiles potential Eq. 3 will satisfy the same property when δ ≠ 0 and k = 1. The potential function Eq. 3 has different formulae depending on the value of the transition parameter; hence,

$V\left(x,y,\delta \right)=\left\{\begin{array}{cc}\frac{1}{2}\left(2k+1\right)x^2-\frac{1}{6}{k}^2\left(2k-3\right),\hfill & \text{when}y=k\ne -\frac{1}{2},\delta =0\hfill \\ \frac{1}{2}\left(x^2-2\delta x^4\right)\hfill & \text{when}y=k=0,\delta \ne 0\hfill \\ \frac{1}{2}\left(3-2\delta \right)x^2+\frac{1}{6}\left(1-12\delta \right),\hfill & \text{when}y=k=1,\delta \ne \frac{3}{2}\hfill \\ \frac{1}{6}{k}^2\left(3-2k\right)+\frac{1}{2}\left(2k+1\right)x^2\hfill \\ -\delta \left[k^4\left(k+1\right)-k^2\left(k-2\right)x^2-\left(k-1\right)x^4\right],\hfill & \text{when}y=k\ne 0,\delta \ne 0\hfill \end{array}\right..(4)$

FIGURE 2

FIGURE 2. Hénon–Heiles potential for different values of transition parameter δ when y is constant.

It is clear from the particular potential formulae in Eq.4 (when y is constant) that both of the classical and generalized Hénon–Heiles potential are represented by parabola formulae or straight lines as shown in Figure 2. In the case of y = 0 or y = 1 with some non-zero values for the parameter δ, the potential curves are shown in Figures 2A, B, while in the case of y = −.5, 0, 1.5 and δ = 0, 1.5, the potential curves are shown in Figure 2C.

We remark that the particular potential relation at y = k ≠ − 1/2 and δ = 0 has a critical point (0, k²(3 − 2k)/6), which will be minimum point when k ∈ (−1/2, ∞) and a maximum point when k ∈ (−∞, −1/2). It is also observed that V₀(x, −1/2, 0) and V(x, 1, 3/2) are constants, i.e., the classical and generalized potential relations represent two parallel lines, as shown in Figure 2C

In the case of y = 0 at δ ≠ 0, the potential has three critical points, one is a minimum point at (0,0) and two maximum points at $(-1/2\sqrt{\delta },1/16\delta )$ and $(1/2\sqrt{\delta },1/16\delta )$, where δ is a positive number. The minimum (maximum) point when y is constant will provide a stable (unstable) point on X−axes.

Now, we will investigate the properties of the potential when x is a constant (say x = q); then, the potential Eq. 2 can be rewritten as

$\begin{array}{ll}\hfill V\left(q,y,\delta \right)& =\frac{1}{2}\left(q^2+y^2\right)+q^{2}y-\frac{1}{3}{y}^3\hfill \\ \hfill & +\delta \left[q^4\left(y-1\right)+q^2\left(y-2\right)y^2-y^4\left(y+1\right)\right],\hfill \end{array}(5)$

Eq. 5 represents a quintic function in variable y; hence, the potential is represented by a polynomial of degree 5. In general, the graph of the quintic function is similar to that of the cubic function, unless it may possess extra local minimum and local maximum points. Furthermore, Eq. 5 can be rewritten as

$V\left(x,y,\delta \right)=\left\{\begin{array}{cc}\frac{1}{2}{y}^2-\frac{1}{3}{y}^3,\hfill & \text{when}x=q=0,\delta =0\hfill \\ \frac{1}{2}{q}^2+q^{2}y+\frac{1}{2}{y}^2-\frac{1}{3}{y}^3,\hfill & \text{when}x=q\ne 0,\delta =0\hfill \\ \frac{1}{6}\left(3-2y\right)y^2-\frac{1}{6}\delta \left(6y^3+6y^2\right)y^2,\hfill & \text{when}x=q=0,\delta \ne 0\hfill \\ \frac{1}{2}{q}^2+q^{2}y+\frac{1}{2}{y}^2-\frac{1}{3}{y}^3\hfill \\ +\delta \left[q^4\left(y-1\right)+q^2\left(y-2\right)y^2-y^4\left(y+1\right)\right].\hfill & \text{when}x=q\ne 0,\delta \ne 0\hfill \end{array}\right..(6)$

Equation 6 shows that the potential function may have one local minimum and one local maximum point when x is a constant and δ = 0. In the case of x = q = 0 and δ = 0, there are two critical points, where one of them is minimum (0, 0) and the other is maximum points (0, 1/6). In the case of x = q ≠ 0 and δ = 0, the potential function has two critical points (y₁, V₁) and (y₂, V₂), where the first is a minimum point and the second is maximum, which are given by

$\begin{array}{c}{y}_1=\frac{1}{2}\left(1-\sqrt{4q^2+1}\right),\\ V_1=-\frac{1}{3}{\left(4q^2+1\right)}^{3/2}+\frac{1}{2}\left(5q^2+1\right)+q^2\sqrt{4q^2+1},\\ y_2=\frac{1}{2}\left(1+\sqrt{4q^2+1}\right),\\ V_2=\frac{1}{3}{\left(4q^2+1\right)}^{3/2}+\frac{1}{2}\left(5q^2+1\right)-q^2\sqrt{4q^2+1}.\end{array}$

For the remaining two cases x = q = 0, δ ≠ 0 and x = q ≠ 0, δ ≠ 0, the potential is represented by a quintic function and there is at least one critical point.

If x is a constant, the curves of the Hénon–Heiles potential are shown in Figure 3 for some particular values of x at different values of the parameter δ, see Figures 3A, B when x = 0 while Figures 3C, D when x = 1. The classical potential relation (V₀) will be represented by a cubic curve. However, the generalized Hénon–Heiles potential will be represented by a quintic curve.

FIGURE 3

FIGURE 3. Hénon–Heiles potential for different values of transition parameter δ when x is constant.

2.1 Bounded and unbounded motion within the generalized Hénon–Heiles system

In order to investigate more properties of the Hénon–Heiles potential, we found first the critical points of the classical potential (we mean that δ = 0); hence, we found that there exist four points, which are (0,0,0) (0, 1, 1/6), $(-\sqrt{3}/2,-1/\mathrm{2,1}/6)$, and $(\sqrt{3}/2,-1/\mathrm{2,1}/6)$. After applying the derivative test, we found that the first point is a minimum point, but the last three are saddle points.

For graphical investigations, we zoomed the isopleth of plane sections in Figure 1 about the contour curve of V = 1/6 in Figure 4. In the zoomed diagram, the saddle points form the three vertices of the triangle for the equipotential curve of V = 1/6, which is shown in Figure 4A. The area of the triangle, which is determined by the potential curve V = 1/6, forms the region boundaries of bounded motions. This means that the motions are bounded inside the region of the triangle and will be bounded when the total system energy is lower than 1/6. It is also clear that from the contour lines the orbits of motion have a special appearance and form closed paths, which may vary from circular shape to a triangle, which can be seen at the equipotential curves V = 1/84, 1/24, and 1/12 in Sub–Figure 4A.

FIGURE 4

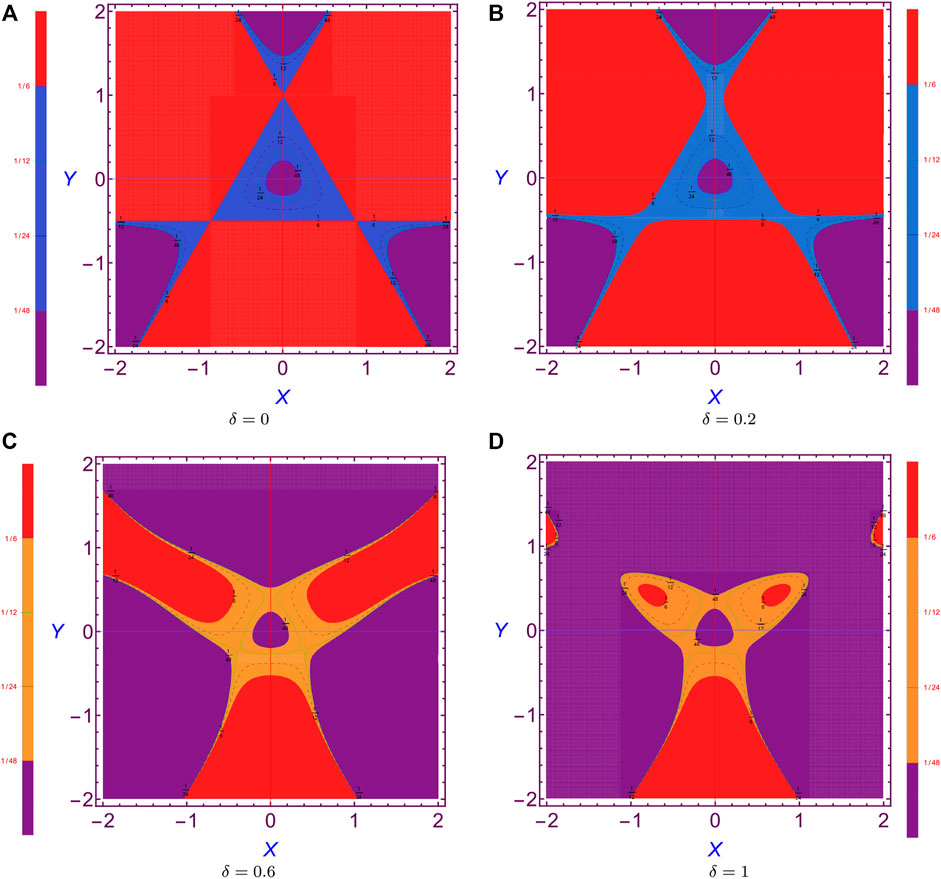
FIGURE 4. Zoomed view of Figure 1 near x, y ∈(1,1).

The Hamiltonian of the generalized system is defined by

$\begin{array}{ll}\hfill H\left(x,y,\dot{x},\dot{y}\right)& =\frac{1}{2}\left({\dot{x}}^2+{\dot{y}}^2+x^2+y^2\right)+x^{2}y-\frac{y^3}{3}\hfill \\ \hfill & +\delta \left[x^{4}y+x^2{y}^3-y^5-{\left(x^2+y^2\right)}^2\right],\hfill \end{array}(7)$

where $\dot{x}=\partial x/\partial t$ and $\dot{y}=\partial y/\partial t$ are the conjugate momenta per unit of mass of x and y, respectively. Since the total system energy is conserved when H is constant (i.e., H = E = constant), then the kind of motion is restricted to the defined region by

$\begin{array}{cc}\hfill E\left(x,y\right)& \ge \frac{1}{2}\left(x^2+y^2\right)+x^{2}y-\frac{y^3}{3}\hfill \\ \hfill & +\delta \left[x^{4}y+x^2{y}^3-y^5-{\left(x^2+y^2\right)}^2\right],\hfill \end{array}$

We found the critical minimum and maximum values of energy, E_min and E_max, respectively, at different values for transition parameter δ, as shown in Table 1 (in fact, we extended the evaluated values in Dubeibe et al. (2018) to include more critical minimum and maximum values of energy for transition parameter δ), in order to identify the kind of motions. We mean that the motion will be bounded when E < E_min and unbounded when E > E_max. If the total energy E is equal to or less than E_min, the equipotential curves are closed and the body cannot escape from the region where its motion is bounded, while if E > E_mim, the curves of the equipotential open, creating passageways, where the body may find its escaping gates to infinity way, which is shown in Figures 4B–D, when δ ≠ 0. Furthermore, the escape energy is identified by the value of E_mim, where the body can be escaped if its energy is larger than E_mim.

TABLE 1

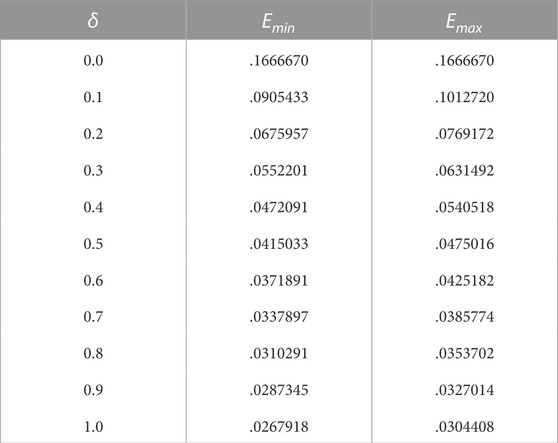
TABLE 1. Critical values of energy at different values of the transition parameter for bounded motion (E < E_min) and unbounded motion (E > E_max).

It is observed that the size of these gates enlarges with the increasing of the value of the transition parameter δ, which makes the escaping soft and rapid. The motion is stable with periodic orbits in the closed regions, while at every gate, the periodic orbits of motion are unstable, which are called Lyapunov orbits; these orbits have major significance for escaping from the system, where escaping is possible when the body orbit crosses one of these orbits. We demonstrated that the escape energy must be equal to or greater than the minimum value of critical energy (E_esc ≥ E_min). Thus, we conclude that the value of the parameter δ increases while the energy of escape decreases; this property is shown graphically in Figure 5; see also for details (Antipov and Nagaitsev, 2017; Dubeibe et al., 2018).

FIGURE 5

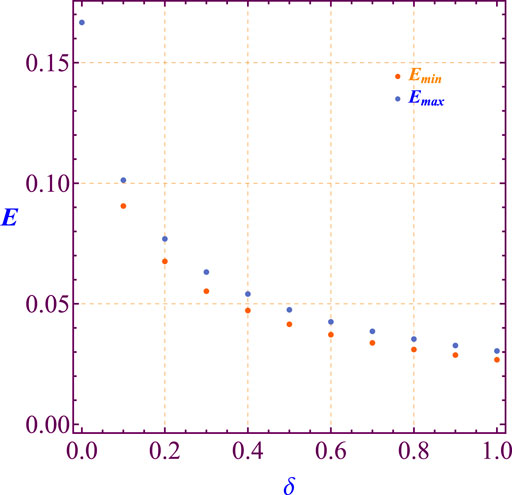
FIGURE 5. Critical values of energy versus transition parameter values for bounded motion (E < E_min) and unbounded motion (E > E_max).

3 Generalized Hénon–Heiles system

The Hamiltonian of the Hénon–Heiles system of fifth degree is given by

$\mathcal{H}={\mathcal{H}}_0+\delta {\mathcal{H}}_1,(8)$

where

$\begin{array}{cc}\hfill & {\mathcal{H}}_0=\frac{1}{2}\left(p_x^2+p_y^2\right)+\frac{1}{2}\left(x^2+y^2\right)+x^{2}y-\frac{y^3}{3},\hfill \\ \hfill & {\mathcal{H}}_1=x^{4}y+x^2{y}^3-y^5-{\left(x^2+y^2\right)}^2,\hfill \end{array}(9)$

Utilizing Eqs 8–9, the Hamiltonian equations of motion are given by

$\begin{array}{cc}\hfill \dot{x}=& p_x,\dot{y}=p_y,\hfill \\ \hfill {\dot{p}}_x=& -\frac{\partial {\mathcal{H}}_0}{\partial x}-\delta \frac{\partial {\mathcal{H}}_1}{\partial x},\hfill \\ \hfill {\dot{p}}_y=& -\frac{\partial {\mathcal{H}}_0}{\partial y}-\delta \frac{\partial {\mathcal{H}}_1}{\partial y}.\hfill \end{array}(10)$

The system (Eq. 10) is equivalent to the following differential equation system

$\begin{array}{cc}\hfill \dot{x}=& p_x,{\dot{p}}_x=-x+2xy-\delta \left[4x^{3}y+2x{y}^3-4x\left(x^2+y^2\right)\right]\hfill \\ \hfill \dot{y}=& p_y,{\dot{p}}_y=-y-x^2+y^2-\delta \left[x^4+3x^2{y}^2-5y^4-4y\left(x^2+y^2\right)\right].\hfill \end{array}(11)$

It is clear that the aforementioned system is not convenient for applying the averaging theory which needs the system to be a particular normal form. Indeed, a technical mathematical procedure is described in the following section for obtaining the adequate form of the previous system to apply the averaging theory.

4 On averaging theory

In this section, using the averaging theory of the second order of dynamical systems as a fundamental tool (Buică and Llibre, 2004), we are able to state the following result.

Theorem 2. Let us consider a system of ordinary differential equations in the normal form in the following way:

$\dot{\mathbf{x}}\left(t\right)=\nu {\mathcal{F}}_1\left(t,\mathbf{x}\right)+{\nu }^2{\mathcal{F}}_2\left(t,\mathbf{x}\right)+{\nu }^3\mathcal{G}\left(t,\mathbf{x},\nu \right),(12)$

with ${\mathcal{F}}_1,{\mathcal{F}}_2:\mathbb{R}\times D\to {\mathbb{R}}^n,\mathcal{G}:\mathbb{R}\times D\times \left(-{\nu }_f,{\nu }_f\right)\to {\mathbb{R}}^n$ being continuous real maps and periodic in the variable t with period $\mathcal{T}$. Here, D is a subset of ${\mathbb{R}}^n$ with open boundaries and ν is a small parameter as usual.Let us define the real maps $f_1,f_2:D\to {\mathbb{R}}^n$ as follows:

$\begin{array}{cc}\hfill & f_1\left(\mathbf{x}\right)={\int }_0^{\mathcal{T}}{\mathcal{F}}_1\left(t,\mathbf{x}\right)\mathrm{d}t,\hfill \\ \hfill & f_2\left(\mathbf{x}\right)={\int }_0^{\mathcal{T}}\left[D_x{\mathcal{F}}_1\left(t,\mathbf{x}\right){\int }_0^t{\mathcal{F}}_1\left(s,\mathbf{x}\right)\mathrm{d}s+{\mathcal{F}}_2\left(t,\mathbf{x}\right)\right]\mathrm{d}t.\hfill \end{array}$

Assume that the system holds the following two conditions.

1) ${\mathcal{F}}_1(t,\cdot )\in C^1(D)$ for each $t\in \mathbb{R},{\mathcal{F}}_1,{\mathcal{F}}_2,\mathcal{G}$, and $D_x{\mathcal{F}}_1$ are locally Lipschitz in the second variable, and $\mathcal{G}$ is twice differentiable with respect to ν.

2) There exists V ⊂ D, such that for each $\nu \in \left(-{\nu }_f,{\nu }_f\right)\backslash \{0\}$, there exists a ∈ V holding f₁(a) + νf₂(a) = 0 and $d_B\left(f_1+\nu f_2\right)\ne 0$ where $d_B\left(f_1+\nu f_2\right)$ denotes the degree Brouwer for the real map $f_1+\nu f_2:V\to {\mathbb{R}}^n$ at its fixed point a.

Then, there exists a periodic solution φ(⋅, ν) of period $\mathcal{T}$ for the system (Eq. 11), such that φ(0, ν) → a as ν → 0.For sufficient conditions for showing that the Brouwer index degree of a real map f at its fixed non-zero point a, which is the Jacobian of the real map f at a (when it is defined), is non-zero, see for more details (Lloyd, 1978).It is to be noted that if the averaging map of first-order f₁ is not identically 0, then the zeros of f₁+νf₂ are mainly the zeros of f₁ if ν is small enough. In this case, the previous theorem provides the so-called averaging theory of first order for differential systems. Also, if the map f₁ is identically zero and the averaging map of second-order f₂ is not identically 0, then the zeros of f₁+νf₂ are the zeros of f₂. In this case, the previous theorem provides the so-called averaging theory of second order for differential systems.

5 Standard form of the generalized Hénon–Heiles system

In order to apply the averaging theory, the following scales will be used:

$\begin{array}{cc}\hfill & x=\nu X,y=\nu Y,\hfill \\ \hfill & p_x=\nu p_X,p_y=\nu p_Y,\hfill \end{array}$

where ν is a very small parameter.

Now, we can rewrite the system (Eq. 11) with the new variables as

$\begin{array}{cc}\hfill \dot{X}=p_X,{\dot{p}}_X& =-X+2\nu XY-{\nu }^3\delta \left(4X^{3}Y+2X{Y}^3\right)\hfill \\ \hfill & +4{\nu }^2\delta X\left(X^2+Y^2\right),\hfill \\ \hfill \dot{Y}=p_Y,{\dot{p}}_Y& =-Y-\nu \left(X^2-Y^2\right)-{\nu }^3\delta \left(X^4+3X^2{Y}^2-5Y^4\right)\hfill \\ \hfill & +4{\nu }^2\delta Y\left(X^2+Y^2\right),\hfill \end{array}(13)$

This system again is a Hamiltonian system, and its Hamiltonian is given by

$\begin{array}{cc}\hfill \tilde{H}=& \frac{1}{2}\left(p_X^2+p_Y^2\right)+\frac{1}{2}\left(X^2+Y^2\right)+\nu \left(X^{2}Y-\frac{Y^3}{3}\right)\hfill \\ \hfill & -{\nu }^2\delta {\left(X^2+Y^2\right)}^2+{\nu }^3\delta \left(X^{4}Y+X^2{Y}^3-Y^5\right),\hfill \end{array}$

It is clear from Eq. (13) that the form of the new system is different from the standard form of Eq. (12); thus, we cannot apply the averaging theory. In order to use the averaging theory, two consequent transformations will be used to set the Hamiltonian of this system in the standard form in the following two subsections.

5.1 First transformation

In the context of setting the Hénon–Heiles system in the standard way, we use the following transformation:

$\begin{array}{cc}\hfill & X=r\mathcal{C}\left(\chi \right),p_X=r\mathcal{S}\left(\chi \right),\hfill \\ \hfill & Y=\varrho \mathcal{C}\left(\chi +\psi \right),p_Y=\varrho \mathcal{S}\left(\chi +\psi \right),\hfill \end{array}$

where $\mathcal{S}$ and $\mathcal{C}$ denote the trigonometric maps sin and cos, respectively, to avoid overlength in equations.

We remark that this is a transformation in variables when r > 0 and ϱ > 0. Furthermore, the angular variables χ and ψ will appear in the system with this transformation. Also, the χ−variable will be used to find the periodicity which is necessary for applying the averaging theory. Hence, the fixed value of energy in polar coordinates is

$\begin{array}{ll}\hfill h& =\frac{1}{2}\left[r^2+{\varrho }^2\right]+\nu \left(r^2\varrho {\left(\mathcal{C}\left(\chi \right)\right)}^2\mathcal{C}\left(\chi +\psi \right)-\frac{1}{3}{\varrho }^3{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3\right)\hfill \\ \hfill & -{\nu }^2\delta {\left[r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2+{\varrho }^2{\left(\mathcal{S}\left(\chi \right)\right)}^2\right]}^2+{\nu }^3\delta \left[r^4\varrho {\left(\mathcal{C}\left(\chi \right)\right)}^4\mathcal{C}\left(\chi +\psi \right)\right.\hfill \\ \hfill & \left.+r^2{\varrho }^3{\left(\mathcal{C}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3-{\varrho }^5{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^5\right],\hfill \end{array}(14)$

and the equations of motion are controlled by

$\begin{array}{cc}\hfill \dot{r}=& R_{11}\nu +R_{12}{\nu }^2+R_{13}{\nu }^3,\hfill \\ \hfill \dot{\chi }=& -1+R_{21}\nu +R_{22}{\nu }^2+R_{23}{\nu }^3,\hfill \\ \hfill \dot{\varrho }=& R_{31}\nu +R_{32}{\nu }^2+R_{33}{\nu }^3,\hfill \\ \hfill \dot{\psi }=& R_{41}\nu +R_{42}{\nu }^2+R_{43}{\nu }^3,\hfill \end{array}(15)$

where

$\begin{array}{cc}\hfill R_{11}=& -2r\mathcal{S}\left(\chi \right)\mathcal{C}\left(\chi \right)\varrho \mathcal{C}\left(\chi +\psi \right)\hfill \\ \hfill R_{12}=& -2r\mathcal{S}\left(\chi \right)\mathcal{C}\left(\chi \right)\left(-2\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2-2\delta {\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right)\hfill \\ \hfill R_{13}=& -2r\mathcal{S}\left(\chi \right)\mathcal{C}\left(\chi \right)\left(2\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\varrho \mathcal{C}\left(\chi +\psi \right)+\delta {\varrho }^3{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3\right),\hfill \\ \hfill R_{21}=& -2{\left(\mathcal{C}\left(\chi \right)\right)}^2\varrho \mathcal{C}\left(\chi +\psi \right)\hfill \\ \hfill R_{22}=& +4\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^4+4\delta {\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\hfill \\ \hfill R_{23}=& -2\delta {\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^3{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3-4\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^4\varrho \mathcal{C}\left(\chi +\psi \right),\hfill \end{array}$

$\begin{array}{cc}\hfill R_{31}& =-\mathcal{S}\left(\chi +\psi \right)\left(r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2-{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right)\hfill \\ \hfill R_{32}& =-\mathcal{S}\left(\chi +\psi \right)\left(-4\delta {\varrho }^3{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3-4\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\varrho \mathcal{C}\left(\chi +\psi \right)\right)\hfill \\ \hfill R_{33}& =-\mathcal{S}\left(\chi +\psi \right)\left(3\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2-5\delta {\varrho }^4{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^4\right.\hfill \\ \hfill & +\left.\delta r^4{\left(\mathcal{C}\left(\chi \right)\right)}^4\right),\hfill \\ \hfill R_{41}& =\frac{1}{\varrho }\left(-\mathcal{C}\left(\chi +\psi \right)r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2+{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3\right.\hfill \\ \hfill & \left.+2{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2\mathcal{C}\left(\chi +\psi \right)\right)\hfill \\ \hfill R_{42}& =\frac{1}{\varrho }\left(-4\delta r^2\varrho {\left(\mathcal{C}\left(\chi \right)\right)}^4-4\delta {\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^3{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right.\hfill \\ \hfill & +\left.4\delta {\varrho }^3{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^4+4\delta \varrho {\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2{r}^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right)\hfill \\ \hfill R_{43}& =+\frac{1}{\varrho }\left(2\delta {\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^4{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3+4\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^4{\varrho }^2\mathcal{C}\right.\hfill \\ \hfill & \times \left(\chi +\psi \right)+5\delta {\varrho }^4{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^5-\mathcal{C}\left(\chi +\psi \right)\delta r^4{\left(\mathcal{C}\left(\chi \right)\right)}^4\hfill \\ \hfill & \left.-3\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^3\right).\hfill \end{array}$

5.2 Second transformation

Now, we will change the old independent variable (t) by the new independent variable χ to make the left-hand side of the differential system (Eq. 15) be periodic to obtain the periodicity which is necessary for applying the averaging theory. Scaling system (Eq. 15) by $1/\dot{\chi }$ and eliminating the $\dot{\chi }$ equation, system (Eq. 15) can be read as

$\begin{array}{cc}\hfill r^{\prime }& =2r\mathcal{S}\left(\chi \right)\mathcal{C}\left(\chi \right)\varrho \mathcal{C}\left(\chi +\psi \right)\upsilon -4r\mathcal{S}\left(\chi \right)\mathcal{C}\left(\chi \right)\left(\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right.\hfill \\ \hfill & +\left.\delta {\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2+{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right){\upsilon }^2+O\left({\upsilon }^3\right),\hfill \\ \hfill {\varrho }^{\prime }& =\mathcal{S}\left(\chi +\psi \right)\left(r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2-{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right)\upsilon \hfill \\ \hfill & -2\mathcal{S}\left(\chi +\psi \right)\varrho \mathcal{C}\left(\chi +\psi \right)\left(2\delta {\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2+2\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right.\hfill \\ \hfill & +\left.{\left(\mathcal{C}\left(\chi \right)\right)}^4{r}^2-{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right){\upsilon }^2+O\left({\upsilon }^3\right),\hfill \\ \hfill {\psi }^{\prime }& =\frac{1}{\varrho }\left(\mathcal{C}\left(\chi +\psi \right)\left(r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2-{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2-2{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2\right)\right)\upsilon \hfill \\ \hfill & +\left(4\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^4+4\delta {\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right.\hfill \\ \hfill & -4\delta {\left(\mathcal{C}\left(\chi +\psi \right)\right)}^4{\varrho }^2-4\delta {\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2{r}^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\hfill \\ \hfill & -2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2{\left(\mathcal{C}\left(\chi \right)\right)}^4{r}^2+2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^4{\left(\mathcal{C}\left(\chi \right)\right)}^2{\varrho }^2\hfill \\ \hfill & +\left.4{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2{\left(\mathcal{C}\left(\chi \right)\right)}^4{\varrho }^2\right){\upsilon }^2+O\left({\upsilon }^3\right).\hfill \end{array}(16)$

By applying Theorem 2 to the Hamiltonian (Eq. 14) when H = h, where h > 0 and ϱ₁ ≠ 0 and then solving H = h for $\varrho ={\varrho }_0+\nu {\varrho }_1+O\left({\nu }^2\right)$, one obtains

$\begin{array}{ll}\hfill \varrho & =\sqrt{2h-r^2}+\frac{1}{6}\nu \left(-4{\left(\mathcal{S}\left(\chi \right)\right)}^3{\left(\mathcal{S}\left(\psi \right)\right)}^{3}h+2{\left(\mathcal{S}\left(\chi \right)\right)}^3{\left(\mathcal{S}\left(\psi \right)\right)}^3{r}^2\right.\hfill \\ \hfill & -6r^2{\left(\mathcal{C}\left(\chi \right)\right)}^3\mathcal{C}\left(\psi \right)+6r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\mathcal{S}\left(\chi \right)\mathcal{S}\left(\psi \right)\hfill \\ \hfill & +4{\left(\mathcal{C}\left(\chi \right)\right)}^3{\left(\mathcal{C}\left(\psi \right)\right)}^{3}h-2{\left(\mathcal{C}\left(\chi \right)\right)}^3{\left(\mathcal{C}\left(\psi \right)\right)}^3{r}^2\hfill \\ \hfill & +12\mathcal{C}\left(\chi \right)\mathcal{C}\left(\psi \right){\left(\mathcal{S}\left(\chi \right)\right)}^2{\left(\mathcal{S}\left(\psi \right)\right)}^{2}h-6\mathcal{C}\left(\chi \right)\mathcal{C}\left(\psi \right){\left(\mathcal{S}\left(\chi \right)\right)}^2\hfill \\ \hfill & \times {\left(\mathcal{S}\left(\psi \right)\right)}^2{r}^2-12{\left(\mathcal{C}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\psi \right)\right)}^2\mathcal{S}\left(\chi \right)\mathcal{S}\left(\psi \right)h\hfill \\ \hfill & \left.+6{\left(\mathcal{C}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\psi \right)\right)}^2\mathcal{S}\left(\chi \right)\mathcal{S}\left(\psi \right)r^2\right)+O\left({\nu }^2\right).\hfill \end{array}$

With some simple calculation, the aforementioned equation can be rewritten as

$\begin{array}{c}\hfill \varrho =\sqrt{2h-r^2}+\frac{1}{3}\nu \left(T_1+T_2+T_3\right)+O\left({\nu }^2\right)\end{array}(17)$

where

$\begin{array}{cc}\hfill & T_1=\left(2h-r^2\right)\left[{\left(\mathcal{C}\left(\chi \right)\right)}^3{\left(\mathcal{C}\left(\psi \right)\right)}^3-{\left(\mathcal{S}\left(\chi \right)\right)}^3{\left(\mathcal{S}\left(\psi \right)\right)}^3\right]\hfill \\ \hfill & T_2=-\frac{3}{4}\left(2h-r^2\right)\mathcal{S}\left(2\chi \right)\mathcal{S}\left(2\psi \right)\mathcal{C}\left(\chi +\psi \right)\hfill \\ \hfill & T_3=-3\left(2h-r^2\right)r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\mathcal{C}\left(\chi +\psi \right)\hfill \end{array}(18)$

Utilizing Eqs (17–18), we obtain

$\begin{array}{ll}\hfill \varrho & =\sqrt{2h-r^2}+\frac{1}{3}\nu \mathcal{C}\left(\chi +\psi \right)\left(\left(2h-r^2\right){\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right.\hfill \\ \hfill & \left.-3\left(2h-r^2\right)r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right)+O\left({\nu }^2\right)\hfill \end{array}(19)$

Substituting ϱ in system (Eq. 16) and developing it in power series of ν, we obtain the following two equations:

$\begin{array}{cc}\hfill r^{\prime }& =\left(2r\mathcal{S}\left(\chi \right){\left(\mathcal{C}\left(\chi \right)\right)}^2\sqrt{2h-r^2}\mathcal{C}\left(\chi \right)-2r{\left(\mathcal{S}\left(\chi \right)\right)}^2\mathcal{C}\left(\chi \right)\right.\hfill \\ \hfill & \left.\times \sqrt{2h-r^2}\mathcal{S}\left(\psi \right)\right)\upsilon +\left(-4r^3\mathcal{S}\left(\chi \right){\left(\mathcal{C}\left(\chi \right)\right)}^3\delta -8r\mathcal{S}\left(\chi \right)\right.\hfill \\ \hfill & \times {\left(\mathcal{C}\left(\chi \right)\right)}^3\delta h{\left(\mathcal{C}\left(\psi \right)\right)}^2+16r{\left(\mathcal{S}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\delta h\mathcal{C}\left(\psi \right)\mathcal{S}\left(\psi \right)\hfill \\ \hfill & -8r{\left(\mathcal{S}\left(\chi \right)\right)}^3\mathcal{C}\left(\chi \right)\delta h{\left(\mathcal{S}\left(\psi \right)\right)}^2+4r^3\mathcal{S}\left(\chi \right){\left(\mathcal{C}\left(\chi \right)\right)}^3\delta {\left(\mathcal{C}\left(\psi \right)\right)}^2\hfill \\ \hfill & -8r^3{\left(\mathcal{S}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\delta \mathcal{C}\left(\psi \right)\mathcal{S}\left(\psi \right)+4r^3{\left(\mathcal{S}\left(\chi \right)\right)}^3\mathcal{C}\left(\chi \right)\delta \hfill \\ \hfill & \times {\left(\mathcal{S}\left(\psi \right)\right)}^2-8r\mathcal{S}\left(\chi \right){\left(\mathcal{C}\left(\chi \right)\right)}^{5}h{\left(\mathcal{C}\left(\psi \right)\right)}^2+16r{\left(\mathcal{S}\left(\chi \right)\right)}^2\hfill \\ \hfill & \times {\left(\mathcal{C}\left(\chi \right)\right)}^{4}h\mathcal{C}\left(\psi \right)\mathcal{S}\left(\psi \right)-8r{\left(\mathcal{S}\left(\chi \right)\right)}^3{\left(\mathcal{C}\left(\chi \right)\right)}^{3}h{\left(\mathcal{S}\left(\psi \right)\right)}^2\hfill \\ \hfill & +4r^3\mathcal{S}\left(\chi \right){\left(\mathcal{C}\left(\chi \right)\right)}^5{\left(\mathcal{C}\left(\psi \right)\right)}^2-8r^3{\left(\mathcal{S}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\chi \right)\right)}^4\mathcal{C}\left(\psi \right)\hfill \\ \hfill & \times \mathcal{S}\left(\psi \right)\left.+4r^3{\left(\mathcal{S}\left(\chi \right)\right)}^3{\left(\mathcal{C}\left(\chi \right)\right)}^3{\left(\mathcal{S}\left(\psi \right)\right)}^2\right){\upsilon }^2+O\left({\upsilon }^3\right),\hfill \\ \hfill {\psi }^{\prime }& =-\mathcal{C}\left(\chi +\psi \right)\left(-r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2+\left(2h-r^2\right){\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right.\hfill \\ \hfill & \left.+2{\left(\mathcal{C}\left(\chi \right)\right)}^2\left(2h-r^2\right)\right)\frac{1}{\sqrt{2h-r^2}}\upsilon +\left(4\delta r^2{\left(\mathcal{C}\left(\chi \right)\right)}^4\right.\hfill \\ \hfill & +4\delta {\left(\mathcal{C}\left(\chi \right)\right)}^2\left(2h-r^2\right){\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2-4\delta {\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2{r}^2\hfill \\ \hfill & \times {\left(\mathcal{C}\left(\chi \right)\right)}^2-4\delta {\left(\mathcal{C}\left(\chi +\psi \right)\right)}^4\left(2h-r^2\right)-2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\hfill \\ \hfill & \times {\left(\mathcal{C}\left(\chi \right)\right)}^4{r}^2+2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^4{\left(\mathcal{C}\left(\chi \right)\right)}^2\left(2h-r^2\right)\hfill \\ \hfill & \left.+4{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2{\left(\mathcal{C}\left(\chi \right)\right)}^4\left(2h-r^2\right)\right){\upsilon }^2+O\left({\upsilon }^3\right).\hfill \end{array}(20)$

In the next section, we aim to prove Theorem 1.

6 Proof of theorem 1

It is observed that system (Eq. 20) satisfies the assumptions of Theorem 2, and it has the normal form for system (Eq. 12) with ${\mathcal{F}}_1=\left({\mathcal{F}}_{11},{\mathcal{F}}_{12}\right)$ and ${\mathcal{F}}_2=({\mathcal{F}}_{21},{\mathcal{F}}_{22})$, where

$\begin{array}{cc}\hfill {\mathcal{F}}_{11}& =r\sqrt{2h-r^2}\mathcal{S}\left(2\chi \right)\mathcal{C}\left(\chi +\psi \right),\hfill \\ \hfill {\mathcal{F}}_{12}& =\frac{\mathcal{C}\left(\chi +\psi \right)}{\sqrt{2h-r^2}}\left[r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2-\left(2h-r^2\right)\left({\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right.\right.\hfill \\ \hfill & \left.\left.+2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right)\right]\hfill \\ \hfill {\mathcal{F}}_{21}& =-2r^3\delta \mathcal{S}\left(2\chi \right){\left(\mathcal{C}\left(\chi \right)\right)}^2-r\left(2h-r^2\right)\left(\delta +{\left(\mathcal{C}\left(\chi \right)\right)}^2\right)\mathcal{S}\left(2\chi \right)\hfill \\ \hfill & \times \left[1+\mathcal{C}\left(2\chi \right)+\mathcal{C}\left(2\psi \right)-\mathcal{S}\left(2\psi \right)\right]\hfill \\ \hfill {\mathcal{F}}_{22}& =4\delta \mathcal{S}\left(\psi \right)\mathcal{S}\left(2\chi +\psi \right)\left[r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2+\left(2h-r^2\right){\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right]\hfill \\ \hfill & +2{\left(\mathcal{C}\left(\chi \right)\right)}^2{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\left[\left(2h-r^2\right)\left[2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right.\right.\hfill \\ \hfill & \left.\left.+{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right]-r^2{\left(\mathcal{C}\left(\chi \right)\right)}^2\right]\hfill \end{array}$

The maps ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$ are analytical when r ≠ 0. Moreover, these functions will be 2π−periodic in the variable χ, which is the independent variable of system (Eq. 20). The first-order averaging theory cannot be used because the average maps of ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$ over the period vanish.

$f_1\left(r,\psi \right)={\int }_0^{2\pi }\left({\mathcal{F}}_{11},{\mathcal{F}}_{12}\right)\mathrm{d}\chi =\left(\mathrm{0,0}\right).$

Since the map f₁ of Theorem 2 is 0, we will evaluate the map f₂ by applying the second-order averaging theory. Thus, f₂ is defined by

$f_2\left(r,\psi \right)={\int }_0^{2\pi }\left[D_{r\psi }{\mathcal{F}}_1\left(\chi ,r,\psi \right)\cdot y_1\left(\chi ,r,\psi \right)+{\mathcal{F}}_2\left(\chi ,r,\psi \right)\right]\mathrm{d}\chi ,(21)$

where

$y_1\left(\chi ,r,\psi \right)={\int }_0^{\chi }{\mathcal{F}}_1\left(s,r,\psi \right)\mathrm{d}s.$

The two components of y₁ are given by

$\begin{array}{cc}\hfill y_{11}=& {\int }_0^{\chi }{\mathcal{F}}_{11}\left(s,r,\psi \right)\mathrm{d}s,\hfill \\ \hfill y_{12}=& {\int }_0^{\chi }{\mathcal{F}}_{11}\left(s,r,\psi \right)\text{d}s,\hfill \end{array}$

Hence,

$\begin{array}{cc}\hfill y_{11}& =\frac{2}{3}r\sqrt{2h-r^2}\left[\mathcal{C}\left(\psi \right)-\mathcal{S}\left(\chi \right)\mathcal{S}\left(\psi \right)-{\left(\mathcal{C}\left(\chi \right)\right)}^2\mathcal{C}\left(\chi +\psi \right)\right],\hfill \\ \hfill y_{12}& =-\frac{1}{12\sqrt{2h-r^2}}\left[20r^2-32h-4\left(2h-r^2\right){\left(\mathcal{C}\left(\psi \right)\right)}^2\right.\hfill \\ \hfill & +\left(2h-r^2\right)\mathcal{S}\left[3\left(\chi +\psi \right)\right]+\left(4h-3r^2\right)\mathcal{S}\left(3\chi +\psi \right)\hfill \\ \hfill & \left.+\left(12h-9r^2\right)\mathcal{S}\left(\chi -\psi \right)+\left(42h-27r^2\right)\mathcal{S}\left(\chi +\psi \right)\right].\hfill \end{array}$

For the Jacobian matrix,

$D_{r,\psi }{\mathcal{F}}_1\left(\chi ,r,\psi \right)=\left(\begin{array}{cc}\hfill \frac{\partial {\mathcal{F}}_{11}}{\partial r}\hfill & \hfill \frac{\partial {\mathcal{F}}_{11}}{\partial \psi }\hfill \\ \hfill \frac{\partial {\mathcal{F}}_{12}}{\partial r}\hfill & \hfill \frac{\partial {\mathcal{F}}_{12}}{\partial \psi }\hfill \end{array}\right)$

we obtain

$D_{r\psi }{\mathcal{F}}_1\left(\chi ,r,\psi \right)=\left(\begin{array}{cc}\hfill T_{11}\hfill & \hfill T_{12}\hfill \\ \hfill T_{21}\hfill & \hfill T_{22}\hfill \end{array}\right),$

where

$\begin{array}{cc}\hfill T_{11}& =2\mathcal{S}\left(2\chi \right)\mathcal{C}\left(\chi +\psi \right)\left[\sqrt{2h-r^2}-\frac{r^2}{\sqrt{2h-r^2}}\right]\hfill \\ \hfill T_{12}& =-r\mathcal{S}\left(2\chi \right)\mathcal{S}\left(\chi +\psi \right)\sqrt{2h-r^2}\hfill \end{array}$

$\begin{array}{cc}\hfill T_{21}& =\frac{r\mathcal{C}\left(\chi +\psi \right)}{\sqrt{2h-r^2}}\left[6{\left(\mathcal{C}\left(\chi \right)\right)}^2-2{\left(\mathcal{C}\left(\psi \right)\right)}^2+{\left(\mathcal{C}\left(\chi +\psi \right)\right)}^2\right.\hfill \\ \hfill & \left.+\frac{r^2{\left(\mathcal{C}\left(\psi \right)\right)}^2}{\left(2h-r^2\right)}\right]\hfill \\ \hfill T_{22}& =\sqrt{2h-r^2}\left[2{\left(\mathcal{C}\left(\chi \right)\right)}^2+\frac{3}{2}\mathcal{C}\left(\chi +\psi \right)\mathcal{S}\left[2\left(\chi +\psi \right)\right]\right.\hfill \\ \hfill & \left.-\frac{r^2\mathcal{S}\left(\chi +\psi \right){\left(\mathcal{C}\left(\chi \right)\right)}^2}{\left(2h-r^2\right)}\right]\hfill \end{array}$

Now, we evaluate the map (Eq. 21) and obtain

$\begin{array}{cc}\hfill f_2\left(r,\psi \right)& =\left(\frac{\pi r\mathcal{S}\left(2\psi \right)}{12}\left(-19r^2+32h-12\delta r^2+24\delta h\right)\right.,\hfill \\ \hfill & \frac{\pi }{6\left(2h-r^2\right)}\left[-25r^4-49h^2-48\delta h^2-24\delta r^4\right.\hfill \\ \hfill & +72\delta h{r}^2+73r^{2}h+{\left(\mathcal{C}\left(\psi \right)\right)}^2\left[-108r^{2}h+35r^4\right.\hfill \\ \hfill & +\left.\left.\left.64h^2+48\delta h^2+24\delta r^4-72\delta h{r}^2\right]\right]\right).\hfill \end{array}$

We have to determine the zeros (r*, ψ*) of f₂ (r, ψ) and examine the Jacobian determinant

$\left|D_{r,\psi }{f}_2\left(r^{*},{\psi }^{*}\right)\right|\ne 0,$

Solving f₂(r, ψ) = 0, we obtain 8 − solutions (r*, ψ*) with r* >0, namely,

$\begin{array}{cc}\hfill & \left(\sqrt{3h},0\right),\left(\frac{\sqrt{2h}}{2},0\right),\\ \hfill & \left(\sqrt{\frac{8h\left(4+3\delta \right)}{\left(19+12\delta \right)}},\text{arccos}\left[\sqrt{\frac{\left(365+816\delta +432{\delta }^2\right)}{16\left(140+201\delta +72{\delta }^2\right)}}\right]\right),\\ \hfill & \left(\sqrt{\frac{8h\left(4+3\delta \right)}{\left(19+12\delta \right)}},\pi -\text{arccos}\left[\sqrt{\frac{\left(365+816\delta +432{\delta }^2\right)}{16\left(140+201\delta +72{\delta }^2\right)}}\right]\right),\\ \hfill & \left(\sqrt{\frac{h\left(73+72\delta +\sqrt{429+1008\delta +576{\delta }^2}\right)}{2\left(24\delta +25\right)}},\pm \frac{\pi }{2}\right),\\ \hfill & \left(\sqrt{\frac{h\left(73+72\delta -\sqrt{429+1008\delta +576{\delta }^2}\right)}{2\left(24\delta +25\right)}},\pm \frac{\pi }{2}\right).\end{array}$

The first solution is inconvenient for our assumptions because we obtain from system (Eq. 17) the value of $\varrho =\sqrt{-h}$ when ν = 0, which is not a real number (it is supposed that h > 0) and ϱ must be positive; thereby, the first solution is rejected. Finally, the generalized or fifth-degree Hénon–Heiles system (Eq. 11) has at least seven periodic orbits.

7 Conclusion

In this paper, a literature review on the Hénon–Heiles system, the significance of periodic orbits, the averaging theory of dynamical systems, and the main result are stated.

The generalized Hénon–Heiles potential and the critical values of energy for different values of the perturbed parameter are analyzed. The differences between the classical and generalized or fifth-degree Hénon–Heiles potential are also investigated. The equations of motion are derived in the framework of the fifth-degree Hamiltonian Hénon–Heiles system.

The fundamental results of the second order of the averaging theory for a dynamical system are stated. The standard or normal form of the generalized Hénon–Heiles system has been also deducted in order to apply the theory. We underline that this is a very technical work conducted ad hoc for this system. Two consequent transformations are used to set the Hamiltonian equations of this system in standard form. After that, the possible solutions of the generalized (fifth-degree) Hénon–Heiles system are analyzed by using the averaging theory. Consequently, eight solutions are found, but one of them is not consistent with the proposed assumptions, while the other seven solutions are proper and adequate to represent seven periodic orbits for the generalized Hénon–Heiles dynamical system.

We demonstrate that the Hénon–Heiles system has at least seven periodic orbits. However, we remark that the same model has been studied by Álvarez-Ramírez and García–Saldaña (2020). They applied the Lyapunov center and Weinstein–Moser theorems, as well as the averaging theory, and proved that the system has at least two families of stable periodic orbits for energy level h > 0. In fact, we aimed to use such potential in the paper (Álvarez-Ramírez and García–Saldaña, 2020), where such potential appears to be investigated further because we obtained five new periodic orbits unknown for this model in the literature complementing the previous work. Despite the fact that the Hénon–Heiles dynamical system has been derived initially to analyze the motion of stars around the center of the galaxy, it remains a vital topic in both mathematical and physical sciences since it was proposed first in 1964.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Formal analysis, EA, ZD, and SA; investigation, EA and ZD; SA and JG; methodology, EA and ZD; SA and JG; project administration, EA; software, EA; validation, EA, ZD, SA, and JG; visualization, EA; writing—original draft, EA; writing—review and editing, EA, ZD; SA and JG.

Funding

This work was funded by the National Research Institute of Astronomy and Geophysics (NRIAG), Helwan 11421, Cairo, Egypt. EA, therefore, acknowledges his gratitude for NRIAG’s technical and financial support. Moreover, this paper was partially supported by Ministerio de Ciencia, Innovación y Universidades, grant number PGC 2018-097198-BI00, and by Fundación Séneca of Región de Murcia, grant number 20783/PI/18.

Acknowledgments

Furthermore, the authors would also like to thank Prof. Sergey Ershkov for checking and improving the use of English in the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abouelmagd, E. I., Elshaboury, S., and Selim, H. (2016). Numerical integration of a relativistic two-body problem via a multiple scales method. Astrophysics Space Sci. 361 (1), 38. doi:10.1007/s10509-015-2625-8

CrossRef Full Text | Google Scholar

Abouelmagd, E. I., Guirao, J. L. G., and Llibre, J. (2019). Periodic orbits for the perturbed planar circular restricted 3–body problem. Discrete Continuous Dyn. Systems–B 24 (3), 1007–1020. doi:10.3934/dcdsb.2019003

CrossRef Full Text | Google Scholar

Abouelmagd, E. I., Guirao, J. L. G., and Llibre, J. (2020). The dynamics of the relativistic kepler problem. Results Phys. 19, 103406. doi:10.1016/j.rinp.2020.103406

CrossRef Full Text | Google Scholar

Abouelmagd, E. I., Guirao, J. L. G., and Pal, A. K. (2020). Periodic solution of the nonlinear sitnikov restricted three–body problem. New Astron. 75, 101319. doi:10.1016/j.newast.2019.101319

CrossRef Full Text | Google Scholar

Abouelmagd, E. I., Llibre, J., and Guirao, J. L. G. (2017). Periodic orbits of the planar anisotropic kepler problem. Int. J. Bifurcation Chaos 27 (3), 1750039. doi:10.1142/s0218127417500390

CrossRef Full Text | Google Scholar

Abouelmagd, E. I. (2018). Periodic solution of the two-body problem by kb averaging method within frame of the modified Newtonian potential. J. Astronautical Sci. 65 (3), 291–306. doi:10.1007/s40295-018-0128-x

CrossRef Full Text | Google Scholar

Abozaid, A. A., Selim, H. H., Gadallah, K. A., Hassan, I. A., and Abouelmagd, E. I. (2020). Periodic orbit in the frame work of restricted three bodies under the asteroids belt effect. Appl. Math. Nonlinear Sci. 5 (2), 157–176. doi:10.2478/amns.2020.2.00022

CrossRef Full Text | Google Scholar

Aguirre, J., Vallejo, J. C., and Sanjuán, M. A. (2001). Wada basins and chaotic invariant sets in the Hénon–Heiles system. Phys. Rev. E 64 (6), 066208. doi:10.1103/physreve.64.066208

PubMed Abstract | CrossRef Full Text | Google Scholar

Álvarez-Ramírez, M., and García–Saldaña, J. D. (2020). Periodic orbits of a generalized Hénon–Heiles system. J. Phys. A Math. Theor. 53 (6), 065204. doi:10.1088/1751-8121/ab661f

CrossRef Full Text | Google Scholar

Antipov, S. A., and Nagaitsev, S. (2017). “Hénon–heiles single particle dynamics at IOTA,” in 8th int. Particle accelerator conf.(IPAC’17) (Copenhagen, Denmark: JACOW), 2508–2511.

Google Scholar

Barrar, R. (1965). Existence of periodic orbits of the second kind in the restricted problems of three bodies. Astronomical J. 70, 3–4. doi:10.1086/109672

CrossRef Full Text | Google Scholar

Buică, A., and Llibre, J. (2004). Averaging methods for finding periodic orbits via brouwer degree. Bull. Des. Sci. Math. 128 (1), 7–22. doi:10.1016/j.bulsci.2003.09.002

CrossRef Full Text | Google Scholar

Celletti, A. (2009). Periodic and quasi–periodic attractors of weakly–dissipative nearly-integrable systems. Regul. Chaotic Dyn. 14 (1), 49–63. doi:10.1134/s1560354709010067

CrossRef Full Text | Google Scholar

Churchill, R. C., Pecelli, G., and Rod, D. L. (1979). A survey of the Hénon–Heiles Hamiltonian with applications to related examples. Stoch. Behav. Class. quantum Hamilt. Syst. 93, 76–136. doi:10.1007/bfb0021739

CrossRef Full Text | Google Scholar

De Figueiredo, J. B., Ragazzo, C. G., and Malta, C. P. (1998). Two important numbers in the Hénon–Heiles dynamics. Phys. Lett. A 241 (1-2), 35–40. doi:10.1016/s0375-9601(98)00101-7

CrossRef Full Text | Google Scholar

Dubeibe, F., Riaño-Doncel, A., and Zotos, E. E. (2018). Dynamical analysis of bounded and unbounded orbits in a generalized Hénon—Heiles system. Phys. Lett. A 382 (13), 904–910. doi:10.1016/j.physleta.2018.02.001

CrossRef Full Text | Google Scholar

Eabouelmagd, E. I., Guirao, J. L. G., and Vera, J. A. (2015). Dynamics of a dumbbell satellite under the zonal harmonic effect of an oblate body. Commun. Nonlinear Sci. Numer. Simul. 20 (3), 1057–1069. doi:10.1016/j.cnsns.2014.06.033

CrossRef Full Text | Google Scholar

El-Sabaa, F. M., Amer, T. S., Gad, H. M., and Bek, M. A. (2021). Existence of periodic solutions and their stability for a sextic galactic potential function. Astrophysics Space Sci. 366, 74. doi:10.1007/s10509-021-03981-z

CrossRef Full Text | Google Scholar

Ershkov, S. V. (2017). About tidal evolution of quasi-periodic orbits of satellites. Earth, Moon, Planets. 120 (1), 15–30. doi:10.1007/s11038-017-9505-x

CrossRef Full Text | Google Scholar

Grasman, J., Jansen, M. J. W., and Veling, E. J. M. (1978). Asymptotic methods for relaxation oscillations. Holl. Math. Stud. 31, 93–111. doi:10.1016/S0304-0208(08)70552-8

CrossRef Full Text | Google Scholar

Guckenheimer, J., Holmes, P., and Slemrod, M. (1984). Nonlinear oscillations, dynamical systems and bifurcations of vector fields. J. Appl. Mech. 51 (4), 947. doi:10.1115/1.3167759

CrossRef Full Text | Google Scholar

Hannsgen, K. B. (1979). Nonlinear ordinary differential equations (dw Jordan and p. smith). SIAM Rev. 21 (2), 264. doi:10.1137/1021042

CrossRef Full Text | Google Scholar

Hénon, M., and Heiles, C. (1964). The applicability of the third integral of motion: Some numerical experiments. Astronomical J. 69 (1), 73–79. doi:10.1086/109234

CrossRef Full Text | Google Scholar

Iñarrea, M., Lanchares, V., Palacián, J. F., Pascual, A. I., Salas, J. P., and Yanguas, P. (2015). Lyapunov stability for a generalized Hénon–Heiles system in a rotating reference frame. Appl. Math. Comput. 253, 159–171. doi:10.1016/j.amc.2014.12.072

CrossRef Full Text | Google Scholar

Kang, S. L. (2001). The method of multiple scales applied to the nonlinear stability problem of a truncated shallow spherical shell of variable thickness with the large geometrical parameter. Appl. Math. Mech. 22 (10), 1198–1209. doi:10.1007/bf02436456

CrossRef Full Text | Google Scholar

Kottos, T., and Smilansky, U. (1999). Periodic orbit theory and spectral statistics for quantum graphs. Ann. Phys. 274 (1), 76–124. doi:10.1006/aphy.1999.5904

CrossRef Full Text | Google Scholar

Llibre, J., and Jiménez-Lara, L. (2011). Periodic orbits and non integrability of Henon–Heiles systems. J. Phys. A Math. Theor. 44, 205103. doi:10.1088/1751-8113/44/20/205103

CrossRef Full Text | Google Scholar

Lloyd, N. G. (1978). Degree theory. Cambridge, New York, Melbourne: Cambridge University Press.

Google Scholar

Mishchenko, E. F., Kolesov, Y. S., Kolesov, A. Y., and Rozsov, N. K. (1994). Asymptotic methods in singularly perturbed systems. Monographs in Contemporary Mathematics (New York: Spinger).

CrossRef Full Text | Google Scholar

Parker, T. S., and Chua, L. O. (1989). Integration of trajectories. Practical numerical algorithms for chaotic systems (New York: Springer), 83–114.

CrossRef Full Text | Google Scholar

Pathak, N., Abouelmagd, E. I., and Thomas, V. (2019). On higher order resonant periodic orbits in the photo–gravitational planar restricted three-body problem with oblateness. J. Astronautical Sci. 66 (4), 475–505. doi:10.1007/s40295-019-00178-z

CrossRef Full Text | Google Scholar

Pathak, N., Thomas, V., Abouelmagd, E. I., and I. Abouelmagd, E. (2019). The perturbed photogravitational restricted three-body problem: Analysis of resonant periodic orbits. Discrete Continuous Dyn. Systems-S 12 (45), 849–875. doi:10.3934/dcdss.2019057

CrossRef Full Text | Google Scholar

Szücs-Csillik, I. H. (2010). The Lie–integrator and the Hénon–Heiles system. Romanian Astronomical J. 20 (1), 49–66.

Google Scholar

Vallejo, J. C., Aguirre, J., and Sanjuán, M. A. (2003). Characterization of the local instability in the Hénon–Heiles Hamiltonian. Phys. Lett. A 311 (1), 26–38. doi:10.1016/s0375-9601(03)00452-3

CrossRef Full Text | Google Scholar

Zotos, E. E., Riaño-Doncel, A., and Dubeibe, F. L. (2018). Basins of convergence of equilibrium points in the generalized Hénon–Heiles system. Int. J. Non-Linear Mech. 99, 218–228. doi:10.1016/j.ijnonlinmec.2017.12.004

CrossRef Full Text | Google Scholar